Формула индуктивности катушки. Индуктивность катушки: формула, единицы измерения и расчет

Что такое индуктивность катушки. Как рассчитать индуктивность. В каких единицах измеряется индуктивность. Какая формула для расчета индуктивности катушки. Чем отличается индуктивность от индуктивного сопротивления.

Что такое индуктивность катушки

Индуктивность — это способность проводника создавать магнитное поле при прохождении через него электрического тока. Катушка индуктивности представляет собой проводник, намотанный в виде спирали. При протекании тока через витки катушки возникает магнитное поле.

Индуктивность катушки зависит от следующих факторов:

• Количества витков
• Геометрических размеров катушки
• Наличия и материала сердечника
• Взаимного расположения витков

Чем больше витков и чем компактнее они расположены, тем выше индуктивность. Наличие ферромагнитного сердечника также значительно увеличивает индуктивность катушки.

Формула индуктивности катушки

Основная формула для расчета индуктивности катушки выглядит следующим образом:

L = Ф / I

где:

• L — индуктивность катушки
• Ф — магнитный поток, пронизывающий все витки катушки
• I — сила тока, протекающего через катушку

Для практических расчетов чаще используются более сложные формулы, учитывающие конкретную конструкцию катушки. Например, для цилиндрической многослойной катушки без сердечника:

L = μ₀ * N² * S / l

где:

• μ₀ — магнитная постоянная
• N — число витков
• S — площадь поперечного сечения катушки
• l — длина намотки

Единицы измерения индуктивности

Основной единицей измерения индуктивности в системе СИ является генри (Гн). Катушка имеет индуктивность 1 генри, если при изменении силы тока на 1 ампер за 1 секунду в ней возникает ЭДС самоиндукции 1 вольт.

На практике часто используются дольные единицы:

• Миллигенри (мГн) = 10⁻³ Гн
• Микрогенри (мкГн) = 10⁻⁶ Гн
• Наногенри (нГн) = 10⁻⁹ Гн

Для очень малых индуктивностей применяется внесистемная единица — сантиметр (см). 1 см индуктивности равен примерно 1 нГн.

Как рассчитать индуктивность катушки

Для расчета индуктивности катушки необходимо выполнить следующие шаги:

1. Определить тип катушки (цилиндрическая, тороидальная и т.д.)
2. Измерить геометрические размеры (диаметр, длина намотки, число витков)
3. Учесть наличие и материал сердечника
4. Подставить данные в соответствующую формулу расчета

Например, для цилиндрической однослойной катушки без сердечника можно воспользоваться формулой:

L = (μ₀ * N² * π * r² * K) / l

где r — радиус катушки, K — поправочный коэффициент.

Для более точных расчетов рекомендуется использовать специальные программы или онлайн-калькуляторы индуктивности.

Индуктивное сопротивление

Индуктивное сопротивление — это величина, характеризующая противодействие катушки переменному току. В отличие от индуктивности, индуктивное сопротивление зависит от частоты тока.

Формула для расчета индуктивного сопротивления:

X_L = ω * L = 2π * f * L

где:

• X_L — индуктивное сопротивление
• ω — угловая частота
• f — частота переменного тока
• L — индуктивность катушки

Индуктивное сопротивление измеряется в омах (Ом). При увеличении частоты тока индуктивное сопротивление возрастает.

Применение катушек индуктивности

Катушки индуктивности широко применяются в различных областях электротехники и электроники:

• Фильтры высоких и низких частот
• Колебательные контуры
• Трансформаторы и дроссели
• Электромагниты и реле
• Антенны и системы беспроводной передачи энергии

Благодаря способности накапливать энергию магнитного поля, катушки индуктивности используются для сглаживания пульсаций тока, разделения сигналов разных частот, создания управляемых магнитных полей.

Энергия магнитного поля катушки

При протекании тока через катушку индуктивности в ней запасается энергия магнитного поля. Эта энергия может быть рассчитана по формуле:

W = (L * I²) / 2

где:

• W — энергия магнитного поля
• L — индуктивность катушки
• I — сила тока

Энергия магнитного поля катушки пропорциональна квадрату силы тока. При отключении тока эта энергия может вызвать значительный скачок напряжения, что необходимо учитывать при проектировании электрических схем.

Факторы, влияющие на индуктивность катушки

На величину индуктивности катушки оказывают влияние следующие факторы:

• Количество витков — чем больше витков, тем выше индуктивность
• Диаметр катушки — увеличение диаметра повышает индуктивность
• Длина намотки — при увеличении длины индуктивность уменьшается
• Материал сердечника — ферромагнитный сердечник значительно увеличивает индуктивность
• Форма катушки — тороидальные катушки имеют более высокую индуктивность

Учет этих факторов позволяет оптимизировать конструкцию катушки для получения требуемого значения индуктивности.

Индуктивность катушки

Весьма важное практическое значение имеет один частный случай явления электромагнитной индукции, получивший название самоиндукции. Так, когда индукционная катушка образует ток, то одновременно с ним возникает и магнитный поток, который растет с увеличением тока. С изменением магнитного потока катушка индуктирует электродвижущую силу (ЭДС), величина которой пропорциональна изменению скорости магнитного потока.

Так как в данном случае проводник индуцирует электродвижущую силу в самом себе, то это явление называется самоиндукцией. Явление самоиндукции в электрических цепях иногда сравнивают с проявлением инертности в механике.

Электродвижущая сила, индуктированная в индукционной катушке под влиянием изменения её собственного магнитного потока, называется электродвижущей силой самоиндукции.

Согласно закону Ленца, во всё время роста магнитного потока, принизывающего витки катушки, ЭДС самоиндукции в катушке направлена против электродвижущей силы источника, включённого в данную цепь, и противодействует росту тока в цепи катушки.

Когда ток в катушке достигает постоянной величины, магнитный поток прекращает изменение, и ЭДС самоиндукции в катушке становится равной нулю.
При самоиндукции, как и при всяком процессе электромагнитной индукции, индуктированная электродвижущая сила пропорциональна скорости, с которой магнитный поток, сцепленный с контуром, по которому течёт ток, изменяется. Величина же магнитного потока при отсутствии в катушке железа пропорциональна скорости, с которой изменяется ток (∆I/∆t), создающий этот поток.

Таким образом, величина электродвижущей силы самоиндукции, возникающей в проводнике, пропорциональна скорости, с которой изменяется ток в нем.
Если брать проводники разной формы, то окажется, что имея одинаковую скорость изменения тока, электродвижущие силы самоиндукции, возникающие в них, будут различны.

Так, если взять катушку, а затем растянуть в один виток, то при одинаковой скорости, с которой происходит изменение тока, ЭДС самоиндукции катушки будет больше. Это связанно с тем, что каждая силовая линия, принизывая витки катушки, сцепляется с ней большее число раз, чем с одним витком.

Величина, характеризующая связь между скоростью, с которой ток изменяется в цепи, и возникающей при этом ЭДС самоиндукции — индуктивность цепи.

Обозначим индуктивность катушки буквой L; тогда зависимость величины электродвижущей силы самоиндукции от скорости, с которой происходит изменение тока, можно выразить следующей формулой:

E = — L (∆I/∆t)

Отсюда

ед. L = (ед.E ˖ ед. t)/(ед.I)

Полагая, что в этой формуле ∆t = 1 сек, ∆I = 1 амперу и Е = 1 вольту, получим:

ед. L = 1(в ˖ сек/а)

Такую единицу называют генри (Гн).

Следовательно,

1 Гн = 1 (в ˖ сек/а)

Итак, генри — это индуктивность катушки, в которой изменение тока на 1 ампер в секунду возбуждает электродвижущую силу самоиндукции, равную 1 вольту.
Для измерения малых индуктивностей применяются тысячные доли генри – миллигенри (мГн) и миллионные доли генри – микрогенри (мкГн).

Кроме того, часто применяется и другая единица – сантиметр индуктивности, причём 1 мкГн = 1000 см индуктивности.

Таким образом,

1 Гн = 1000 мГн = 1000000 мкГн = 1000000000 см

Индуктивность катушки находится в зависимости от её числа витков, формы и размеров. Чем больше число витков в катушке самоиндукции, тем больше ее индуктивность.

Также, самоиндукция, индуктивность катушки значительно увеличивается при внесении внутрь её сердечника из железа или какого-либо другого магнитного материала.
Большой индуктивностью обладают обмотки электромагнитов у генераторов и двигателей, в момент размыкания цепи, когда скорость изменения электрического тока (∆I/∆t) очень велика, в этих обмотках может возникнуть большая ЭДС самоиндукции, которая, если не принять соответствующих мер, приведёт к пробою изоляции обмоток.

Катушка индуктивности. Устройство и принцип работы.

Если существует замкнутый контур, в котором протекает ток, создающий магнитное поле (магнитный поток), то между током и потоком существует взаимосвязь. Коэффициент пропорциональностями между этими величинами является определением индуктивности.

Контур с током

Также эту пропорциональность можно назвать характеристикой инерционности электрической цепи, которая напрямую связана с понятием ЭДС самоиндукции, которая возникает в цепи, когда изменяется сила тока.

Самоиндукция и измерение индуктивности

Расчет катушки индуктивности

При изменении тока, который протекает в замкнутом электрическом контуре, меняется создаваемый им магнитный поток. Вследствие этого наводится ЭДС, которая называется ЭДС самоиндукции.

Напряжение ЭДС определяется формулой расчета индукции:

Ꜫ=-L∙di/dt.

То есть ЭДС прямо пропорциональна величине скорости изменения тока с некоторым коэффициентом L, который и называется «индуктивность».

Емкостное сопротивление

В цепи, содержащей емкость и источник переменного тока происходят изменения заряда. Такой емкостью обладают конденсаторы, обладающие максимальной энергией при полном заряде. Напряжение емкости создает сопротивление, противодействующее течению переменного тока, которое считается реактивным. В результате взаимодействия, конденсатор и источник тока постоянно обмениваются энергией.

В конструкцию конденсатора входят токопроводящие пластины в количестве двух и более штук, разделенных слоями диэлектрика. Такое разделение не позволяет постоянному току проходить через конденсатор. Переменный ток может проходить через емкостное устройство, отклоняясь при этом от своей первоначальной величины.

Изменения переменного тока происходят под влиянием емкостного сопротивления. Чтобы лучше понять схему работы, найдем и рассмотрим принцип действия данного явления. Переменное напряжение, приложенное к конденсатору, изменяется в форме синусоиды. Под его воздействием на обкладках наблюдается всплеск, одновременно здесь накапливаются заряды электроэнергии с противоположными знаками. Их общее количество ограничено емкостью устройства и его габаритами. Чем выше емкость устройства, тем больше времени требуется на зарядку.

В момент изменения полупериода колебания, напряжение на обкладках конденсатора меняет свою полярность на противоположное значение, потенциалы также изменяются, а заряды пластин перезаряжаются. За счет этого удается создать течение первичного тока и находить способ противодействовать его прохождению, при уменьшении величины и сдвиге угла. Зарядка обкладок позволяет току, проходящему через конденсатор, опережать напряжение на 90.

Обозначение и единицы измерения

Сопротивление тока: формула

В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.

Джозеф Генри

Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.

Как может обозначаться индуктивность в других системах:

• В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
• В системе СГСЭ – в статгенри.

Свойства

Имеет следующие свойства:

• Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
• Не может быть отрицательной;
• Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
• При увеличении частоты тока реактивное сопротивление катушки увеличивается;
• Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.

Расчет эквивалентного сопротивления элементов цепи

Определение общего цепного сопротивления будет зависеть от того, какого типа конфигурацию составляют компоненты цепи. Для параллельного и последовательного подключений правила расчета будут неодинаковыми. Опираться при вычислениях нужно на закон Ома.

Согласно ему, у всех последовательно соединенных деталей, подключенных в цепь переменного тока, будет одно и то же значение электротока:

I=U/Z, где Z – общий импеданс цепи.

Напряжения будут различаться и окажутся привязанными к сопротивлениям деталей: на концах резистора его значение будет равно UR = IR (здесь R – активная резистивность элемента), для дросселя – UL = IXL, для емкостного элемента – UC = IXC (XL и XC – реактивные показатели соответствующих устройств). Так как векторы напряженности катушки и конденсатора имеют противоположные направления, суммарный показатель на реактивных деталях будет равен: UX = UL – UC . Противодействие будет равно: X = XL – XC.

Напряжения (общее, реактивное и активное) могут быть представлены в виде прямоугольного треугольника. Из него получается, что U² = UR² + UX². Поскольку противодействия входящих в цепь компонентов пропорциональны напряжениям, имеем Z2=R2+X2=R2+(XL – XC)2.

Для параллельного соединения принято выводить значения импеданса из проводимостей элементов, которые обратны их сопротивлениям. Отсюда 1/z2 = 1/R2 + 1/X2. Таким образом, выходит следующая формула:

Z2=1/(1/R2+(1/ XL – 1/ XC)2).

Общее сопротивление определяется компонентным составом цепи и характером соединения ее элементов. При расчетах показателей используется закон Ома.

Советуем изучить Полярность аккумулятора

Схемы соединения катушек

Как радиотехнический элемент, катушки индуктивностей обладают свойствами соединений, полностью идентичными соединениям резисторов.

Параллельное соединение

Параллельное соединение:

L=1/(1/L1+1/L2+…+1/Ln).

Для двух элементов формула упрощается:

L=L1∙L2/(L1+L2).

Последовательное соединение

Общее значение последовательного соединения равняется сумме индуктивностей:

L=L1+L2+…+Ln.

Типы соединений

Добротность катушки

Одно из важнейших качеств катушек – это добротность. Данный параметр представляет собой отношение реактивного (индуктивного) сопротивления к активному. Активное сопротивление – это сопротивление проводника, из которого выполнен элемент, его можно считать постоянным, за исключением температурного коэффициента сопротивления материала, из которого выполнен провод.

Реактивное сопротивление прямо пропорционально частоте. Формула расчета добротности выглядит следующим образом:

Q=2∙π∙f∙L/R,

где:

• π – число пи, ≈3,14,
• f – частота,
• R – сопротивление.

Обратите внимание! С ростом частоты сигнала добротность катушки индуктивности возрастает.

От чего зависит индуктивное сопротивление

Данная величина связана напрямую с частотой приложенного напряжения (f) и значением индуктивности (L). Формула индуктивного сопротивления будет выглядеть следующим образом: XL = 2πfL. Прямая пропорциональная зависимость, в случае необходимости, позволяет путем преобразования основной формулы вычислить частоту или значение индуктивности.

Под действием переменного тока, проходящего по проводнику, вокруг этого проводника образуется переменное магнитное поле. Действие этого поля приводит к наведению в проводнике электродвижущей силы обратного направления, известной еще как ЭДС самоиндукции. Противодействие или сопротивление ЭДС переменному току получило название реактивного индуктивного сопротивления.

Существует такое понятие, как погонное индуктивное сопротивление, которое вычисляется по формуле: X0 = ω x (4,61g x (Dср/Rпр) + 0,5μ) x 10-4 = X0’ + X0’’, в которой ω является угловой частотой, μ – магнитной проницаемостью, Dср – среднегеометрическим расстоянием между фазами ЛЭП, а Rпр – радиусом провода.

Величины X0’ и X0’’ представляют собой две составные части погонного индуктивного сопротивления. Первая из них X0’ представляет собой внешнее индуктивное сопротивление, зависящее только от внешнего магнитного поля и размеров ЛЭП. Другая величина – X0’’ является внутренним сопротивлением, зависящим от внутреннего магнитного поля и магнитной проницаемости μ.

На линиях электропередачи высокого напряжения от 330 кВ и более, проходящие фазы расщепляются на несколько отдельных проводов. Например, при напряжении 330 кВ фаза разделяется на два провода, что позволяет снизить индуктивное сопротивление примерно на 19%. Три провода используются при напряжении 500 кВ – индуктивное сопротивление удается снизить на 28%. Напряжение 750 кВ допускает разделение фаз на 4-6 проводников, что способствует снижению сопротивления примерно на 33%.

Погонное индуктивное сопротивление имеет величину в зависимости от радиуса провода и совершенно не зависит от сечения. Если радиус проводника будет увеличиваться, то значение погонного индуктивного сопротивления будет соответственно уменьшаться. Существенное влияние оказывают проводники, расположенные рядом.

Одновитковой контур и катушка

Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:

L=Ф/I.

Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.

Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:

L=L1∙N2.

Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.

Какие отличия

Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.

Индуктивная величина и ее формулы

Важно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть. Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть

То есть, в окружающую среду полученная энергия не передается

Советуем изучить Переполюсовка

Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.

Комплексная сопротивляемость отдельного элетроэлемента сети R

В активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.

Активная сопротивляемость в цепи переменного синусоидального тока

Соленоид

Соленоид отличается от обычной катушки по двум признакам:

• Длина обмотки превышает диаметр в несколько раз;
• Толщина обмотки меньше диаметра катушки также в несколько раз.

Соленоидальный тип катушки

Параметры соленоида можно узнать из такого выражения:

L=µ0N2S/l,

где:

• µ0 – магнитная постоянная;
• N – количество витков;
• S – площадь поперечного сечения обмотки;
• l – длина обмотки.

Важно! Приведенное выражение справедливо для соленоида без сердечника. В противном случае необходимо дополнительно внести множитель µ, который равен магнитной проницаемости сердечника.

Обратите внимание! Используя подвижный сердечник, можно производить оперативное изменение параметров соленоида.

Чем большую магнитную проницаемость будет иметь сердечник, тем больше увеличится итоговое значение.

Расчет

Вычислить число витков, зная конструкцию, можно по формуле нахождения энергии и ее магнитного поля W = LI2/2, где L является индукцией, I — силой тока. Витки находятся из формулы L/d, где d является проводным диаметром. Стоит указать, что есть специальный калькулятор, в который нужно только подставить необходимые параметры. При этом можно определить, однослойный или многослойный проводник.

Схематическое расположение витков в катушке

С сердечником

Стоит отметить, что со стержнем, намоткой, обмоткой индукция вычисляется через замкнутый магнитный поток индуктивных элементов, в то время как без него учитывается поток, который пронизывает только проводник с токовой энергией. Расчитывая индуктивность подобных элементов, необходимо учесть размеры и материал центральной части. Обобщенно можно представить формулу схематично. При этом требуется взять в расчет источник с сопротивлением магнитной цепи, абсолютной магнитной проницаемостью вещества, площадью поперечного сердечникового сечения и длиной средней силовой линии. Зная это, можно посчитать индукцию. Стоит учитывать погрешность. Она будет равна 25%.

Вам это будет интересно Особенности конденсаторов

Расчет индуктивности катушки с сердечником

Без сердечника

Стоит указать, что без ферритового, геометрического и цилиндрического сердечника с мощным каркасом источник имеет небольшую индукцию, а с ним она повышается. Это связано с тем, что имеется материальная магнитная проницаемость. Форма бывает разная. Есть броневой, стержневой и тороидальный материал.

Обратите внимание! Рассчитать можно, используя метод эллиптических максвелловских интегралов и специальную онлайн программу.

Расчет индуктивности без сердечника

Катушка — незаменимый компонент любой электросети, который имеет вид скрученного или обвивающего элемента с проводником. Влияет на ее индукцию число проводных витков, площадь сечения, длина и материал сердечника. Отыскать количество витков и посчитать индуктивность с сердечником и без него несложно, главное — руководствоваться приведенными выше рекомендациями.

Тороидальная катушка (катушка с кольцевым сердечником)

Тороидальный тип обмотки рассчитывается по специальной формуле, которая предполагает, что используется соленоид с бесконечной длиной. Чтобы определять индуктивность формула для тора имеет следующий вид:

L=µ∙µ0N2S/(2π∙r),

где r – усредненный радиус тороидального сердечника.

Кольцевой сердечник прямоугольного сечения можно находить по следующей формуле:

L=µ∙µ0N2S∙h/(2π)∙ln(R/r),

где:

r – внутренний радиус сердечника;

R – внешний радиус;

h – высота.

Важно! Вторая формула позволяет узнавать результат с большей точностью.

Тороидальная намотка

Длинный прямой проводник

Как найти индуктивность прямого проводника? Существует формула, дающая точное значение при условии, что проводник имеет длину, значительно превышающую толщину:

L=µ0/(2π)∙l(µeln(l/r+1/4µi),

где:

• µe и µi – магнитная проницаемость среды и материала проводника, соответственно;
• l и r – длина и радиус проводника.

Какой магнитной проницаемостью обладает проводник, можно узнать из справочных материалов.

Колебательный контур

Емкость и индуктивный элемент, соединенные в цепь, образуют колебательный контур с резко выраженными частотными свойствами и будут являться резонансной системой. В качестве системы используется конденсатор, изменяя емкость которого, можно производить коррекцию частотных свойств.

Последовательный и параллельный колебательные контуры

Если измерить резонансную частоту, используя известный конденсатор, то можно определить индуктивность катушки.

Индуктивность – важнейший элемент в разных областях электротехники. Для правильного применения нужно знать все параметры используемых элементов.

Устройство, которое позволяет определить параметры катушек индуктивности, в том числе добротность, может называться L-метр или Q-метр.

Q-метр для измерения добротности

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.

Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Калькулятор накопления энергии в индукторе

Автор Wojciech Sas, PhD

Рассмотрение Богна Шик и Джек Боуотер

Последнее обновление: 21 декабря 2022 г. хранится в катушке формула

Как использовать калькулятор накопления энергии индуктора?

Применение накопителей магнитной энергии

Вам интересно, на что способен этот калькулятор накопления энергии с помощью индуктора? ну это оценивает энергию, запасенную в индукторе, когда через него проходит электрический ток . Мы также приводим уравнение для магнитной энергии в соленоиде и объясняем, откуда взялось это уравнение энергии. Далее в тексте вы также найдете полезную информацию о том, как мы можем использовать это явление на практике.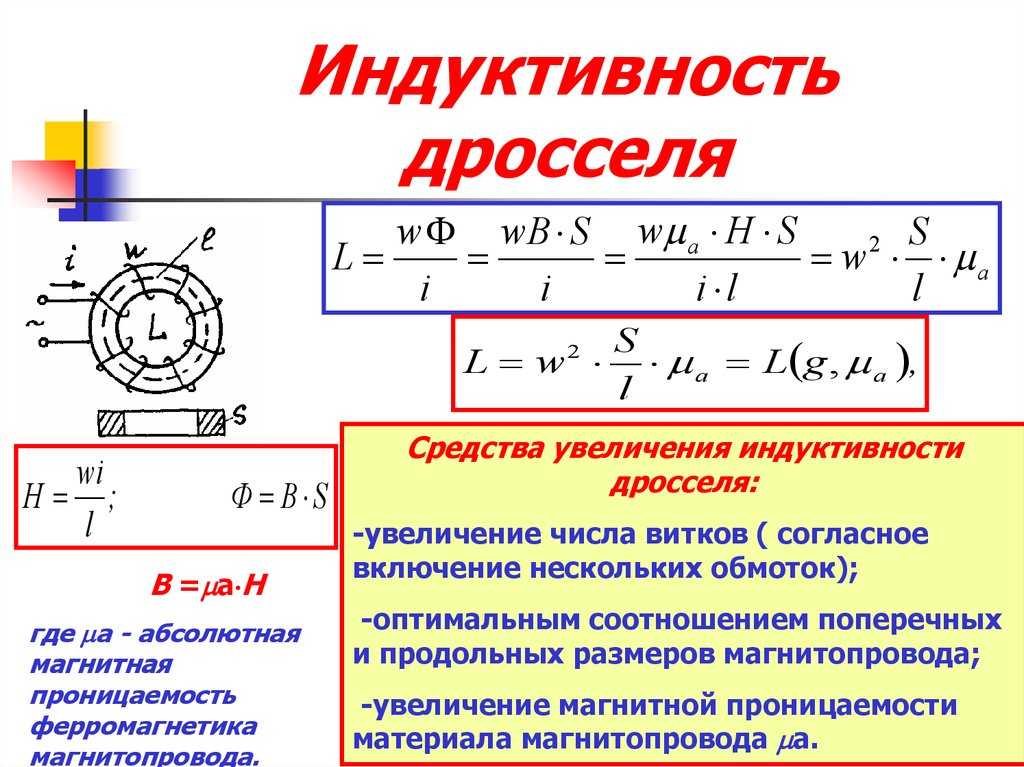

🙋 Вы всегда можете оценить индуктивность любой катушки с помощью нашего калькулятора индуктивности соленоида.

Какая энергия хранится в катушке индуктивности

Соленоид является одним из наиболее распространенных электронных компонентов. Соленоиды способны генерировать магнитные поля , и легкость, с которой соленоид может создавать это поле, известна как его индуктивность. Важно понимать, что это магнитное поле присутствует только в том случае, если через катушку протекает ток. Вы можете быстро оценить точное значение, используя магнитное поле проводного калькулятора Omni.

Интересно, что магнитное поле аккумулирует часть энергии, которая может высвобождаться (или поглощаться) при изменении величины тока. Вот почему индуктор является источником импеданса в цепях переменного тока.

Магнитная энергия, запасенная в катушке формула

Предполагая, что у нас есть электрическая цепь, содержащая источник питания и соленоид с индуктивностью L , мы можем написать уравнение магнитной энергии, E , хранящейся в катушке, как:

E = ½ × L × I² ,

, где I — ток, протекающий по проводу.

Другими словами, можно сказать, что эта энергия равна работе, совершаемой источником питания для создания такого магнитного поля.

Как видим, энергия, запасенная в катушке индуктивности, зависит от тока во второй степени. Это говорит нам о том, что соленоид предотвращает внезапный скачок тока в цепи, и по этой причине мы можем видеть искру при отключении некоторых электронных устройств.

Как использовать калькулятор накопления энергии индуктора?

Допустим, у нас есть цепь, содержащая источник питания и катушку индуктивности L = 20 мкГн . Мы ищем энергию, запасенную в индукторе, когда пропускаем постоянный ток I = 300 мА через систему.

1. Если вы не хотите путаться с единицами измерения, запишем все значения в экспоненциальном представлении: L = 2·10⁻⁵ H , I = 3·10⁻¹ A
2. Используйте формулу для магнитной энергии в соленоиде: E = ½ × 2·10⁻⁵ H × (3·10⁻¹ A)² = 9·10⁻⁷ Дж
3. Мы также можем записать энергию, запасенную в катушке индуктивности, как E = 0,9 мкДж или 900 нДж
4. Вы всегда можете использовать этот калькулятор накопления энергии индуктора, чтобы убедиться, что ваш результат правильный!

Иногда нам может понадобиться больше энергии для нашего приложения. Одна вещь, которую мы можем сделать, это увеличить индуктивность, добавив материал с высокой проницаемостью, такой как ферромагнитные сердечники.

🙋 Проверьте наш калькулятор проницаемости, чтобы узнать больше о том, как повысить производительность соленоида!

Применение накопления магнитной энергии

Одним из основных применений этой запасенной магнитной энергии являются LC-цепи (содержащие как индуктивность, так и емкость). В этих случаях энергия, запасенная в катушке индуктивности, преобразуется в электрическую энергию конденсатора и наоборот . Мы можем настроить систему на отправку и прием радиосигналов, когда текущие колебания достигнут резонансной частоты радиоволн.

Катушки индуктивности также широко используются в трансформаторах, которые изменяют амплитуду напряжения от одной цепи к другой. Магнитная энергия от одной катушки передается ко второй через мягкую ферромагнитную среду . Благодаря этому у нас есть удобный и безопасный доступ к электричеству в наших городах и домах.

Wojciech SAS, PhD

Индуктивность (L)

Current (I)

Хранитованная энергия (E)

Проверьте 48 аналогичные электроники и циклы Калькуляторы 💡

Размер размерного размера. — Индуктивность — Единицы индуктивности

Конденсатор хранит энергию в виде электрического поля, однако индуктор – катушка хранит энергию в виде магнитного поля благодаря явлению самоиндукции. Кабель, по которому циркулирует ток, окружен магнитным полем. Направление потока магнитного поля определяется законом правой руки.

Поскольку индуктор сделан из кабельных стержней, магнитное поле циркулирует по центру катушки и проходит по всему периметру, окружая стержни и возвращаясь к центру.

Одной из интересных особенностей является его противодействие резким изменениям протекающего через них электрического тока. Это означает, что когда мы пытаемся изменить ток, который циркулирует через них (например: подключаться и отключаться от источника питания постоянного тока), он будет пытаться сохранить свое прежнее состояние.

Это событие происходит на постоянной основе, когда индуктор подключен к источнику переменного тока и вызывает разность фаз между приложенным к нему напряжением и протекающим через него током.

Другими словами: Индуктор — это элемент, реагирующий на изменения электрического тока, протекающего через него, создавая на своих клеммах напряжение, противодействующее приложенному напряжению. Это пропорционально скорости изменения тока.

Катушка индуктивности – это пассивный электрический компонент, изготовленный из проводящего провода
, свернутого в виде пружины.

Что такое индуктивность? – Формула индуктивности

Индуктивность – это свойство электрического проводника, благодаря которому изменение тока через него индуцирует электродвижущую силу (ЭДС) как в самом проводнике, так и в любых близлежащих проводниках за счет взаимной индуктивности.

Катушка индуктивности имеет индуктивность (L) в один Генри (1H), когда ток, протекающий через катушку, изменяется со скоростью один ампер в секунду (A/s).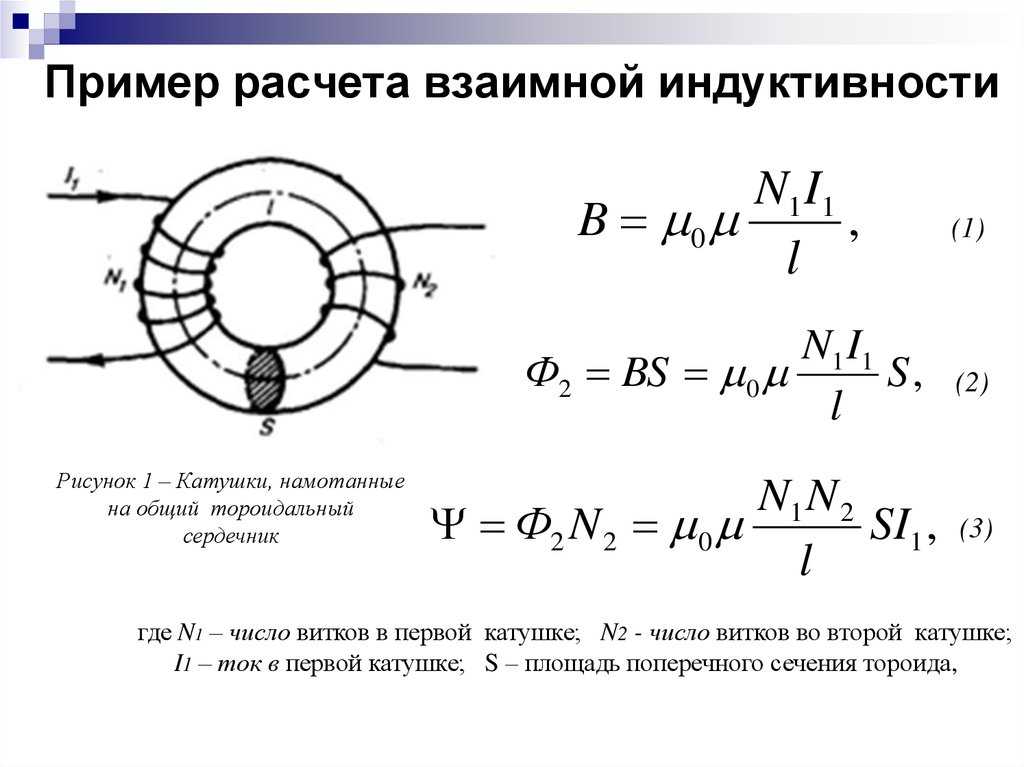 Это изменение индуцирует в нем напряжение в один вольт (1 В). (ВЛ).

VL = -L di/dt

Увеличивая количество витков в катушке, мы можем увеличить индуктивность катушки. Соотношение между индуктивностью (собственной индуктивностью) и числом витков:

Формула индуктивности: L = NΦ/I

где:

• L — индуктивность в генри
• N — число витков
• Φ магнитный поток в Веберсах (Вб)
• I ток в амперах

Единицы измерения индуктивности

Индуктивность измеряет величину сопротивления0019 индуктор  на поток электрического тока и измеряется в генри (Гн). Мы можем найти значения миллигенри (мГн), микрогенри (мГн). Это значение зависит от следующего:

• Количество витков катушки индуктивности (чем больше витков, тем больше индуктивность).
• Диаметр шпилей (поворот). Чем больше диаметр, тем больше индуктивность.
• Длина кабеля, из которого сделана катушка.
• Тип материала, из которого изготовлено ядро, если таковое имеется.

Силовые линии магнитного поля и противоэлектродвижущая сила (ВЭДС)

Силовые линии магнитного поля расширяются, начинаясь в центре электрического проводника и затем удаляясь.

Сначала силовые линии проходят через сам проводник, а затем через воздух. Пока эти силовые линии находятся в электрическом проводнике, в самом проводнике возникает электродвижущая сила (ЭДС). Генерируемое напряжение имеет противоположное направление электрического тока. Из-за этого сила называется: Противоэлектродвижущая сила (CEMF).

По индуктивной нагрузке – Собственный рисунок, выполненный в Inkscape 0.44, Public Domain, Ссылка

Этот эффект приводит к тому, что временно не достигается максимальное значение тока в проводнике. Когда, в конце концов, изменение тока исчезает (ток имеет постоянную величину), силовые линии перестают расширяться и противодействующая электродвижущая сила исчезает.

Когда по проводнику начинает течь ток, силовые линии магнитного поля начинают быстро расширяться и достигается большая противоэлектродвижущая сила. В это время противодействующая ЭДС почти равна приложенному источнику напряжения. Таким образом, источник напряжения и противодействующая электродвижущая сила почти компенсируют друг друга, а протекающий ток невелик.

Через некоторое время линии магнитного поля достигают своего максимального значения, Противоэлектродвижущая сила (ВЭДС) больше не генерируется, и единственной ЭДС является источник напряжения. В это время в цепи протекает максимальный ток, потому что нет противодействия индуктивности.

Опять же, это свойство противостоять изменениям тока, самоиндуцируя электродвижущую силу в противоположном направлении (противодействующая электродвижущая сила) называется индуктивностью . Единицей индуктивности является генри (Гн) и обозначается заглавной буквой «L».

Пример расчета индуктивности

Пример

Какова собственная индуктивность 200-витковой медной катушки, которая создает магнитный поток 2 мВб при пропускании постоянного тока силой 5 ампер?

• N = 200 витков
• Φ = 2 мВт = 0,002 Вебера
• I = 5 Ампер

Используя формулу для индуктивности: 80 мГн.