Формула мощности в физике
Содержание:
Определение и формулы мощности
Определение
Мощностью некоторой силы является скалярная физическая величина, которая характеризует скорость произведения работы данной силой. Мощность часто обозначают буквами: N, P.
$$P=\frac{\Delta A}{\Delta t}(1)$$В том случае, если за равные малые промежутки времени выполняется разная работа, то мощность является переменной во времени. Тогда вводят мгновенное значение мощности:
$$P=\lim _{\Delta t \rightarrow 0} \frac{\delta A}{\Delta t}=\frac{d A}{d t}$$где $\delta A$ – элементарная работа, которую выполняет сила, $\Delta t$ – отрезок времени в течение, которого данная работа была выполнена. Если мгновенная мощность не является постоянной величиной, то выражение (1) определяет среднюю мощностьза время $\Delta t$.
Мощность силы можно определить как скалярное произведение силы на скорость, с которой движется точка приложения рассматриваемой силы:
$$P=\bar{F} \bar{v}=F_{\tau} v$$ {k} \bar{F}_{i} \cdot \bar{v}_{i}(5)$$
{k} \bar{F}_{i} \cdot \bar{v}_{i}(5)$$
где $\bar{v}_{i}$ – скорость перемещения точки, к которой приложена сила $\bar{F}_{i}$.
В случае поступательного движения твердого тела со скоростью $\bar{v}$ мощность можно определить при помощи формулы:
$$P=\overline{F v}(6)$$где $\bar{F}$ – главный вектор внешних сил.
Если твердое тело совершает вращение вокруг точки О или вокруг неподвижной оси, которая проходит через точку О, то формулой для счет мощности можно считать выражение:
$$P=\bar{M} \bar{\omega}(7)$$где $\bar{M}$ – главный момент внешних сил по отношению к точке О, $\bar{omega}$ – мгновенная угловая скорость вращения тела.
Единицы измерения мощности
Основной единицей измерения мощности силы в системе СИ является: [P]=вт (ватт)
В СГС: [P]=эрг/с.
1 вт=107
эрг/( с).Примеры решения задач
Пример
Задание. Какова мощность (P(t)), развиваемая силой, если она действует на тело, которое имеет массу m и
под воздействием приложенной силы движется поступательно. {5}\right)$
{5}\right)$
Слишком сложно?
Формула мощности не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова мгновенная мощность силы тяжести на высоте h/2. если камень массы m падает с высоты h. Сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для мгновенной мощности вида:
$$P=\bar{F} \cdot \bar{v}(2.1)$$Сила, действующая на тело – сила тяжести. Она направлена по оси Y, выражение для ее проекции на ось Y запишем как:
$$F=m g(2.2)$$В начальный момент времени тело имело скорость равную нул
Формула мощности тока в физике
Содержание:
Электрический ток, на каком угодно участке цепи совершает некоторую работу (А). Допустим, что у нас есть произвольный участок цепи (рис.1) между концами которого имеется напряжение U.
Работа, которая выполняется при перемещении заряда равного 1 Кл между точками A и B (рис. {2}(6)$$
{2}(6)$$
где j – плотность тока, $\rho$ – удельное сопротивление.
Единицы измерения мощности тока
Основной единицей измерения мощности тока (как и мощности вообще) в системе СИ является: [P]=Вт=Дж/с.
В СГС: [P]=эрг/с.
1 Вт=107 эрг/( с).
Выражение (4) применяют в системе СИ для того, чтобы дать определение единицы напряжения. Так, единицей напряжения (U) является вольт (В), который равен: 1 В= (1 Вт)/(1 А).
Вольтом называют электрическое напряжение, которое порождает в электроцепи постоянный ток силы 1 А при мощности 1 Вт.
Примеры решения задач
ПримерЗадание. Какой должна быть сила тока, которая течет через обмотку электрического мотора для того, чтобы полезная мощность двигателя (PA) стала максимальной?Какова максимальная полезная мощность? Если двигатель постоянного тока подключен к напряжению U, сопротивление обмотки якоря – R.
Решение. Мощность, которую потребляет электроприбор, идет на нагревание (PQ) и совершение работы (PA):
$$P=P_{Q}+P_{A}(1. {2} R\right) ; U-2 I_{\max } R=0 \rightarrow I_{\max }=\frac{U}{2 R}(1.5)$$
{2} R\right) ; U-2 I_{\max } R=0 \rightarrow I_{\max }=\frac{U}{2 R}(1.5)$$
Репетитор-онлайн — подготовка к ЦТ
Пример 22. Два автомобиля одновременно трогаются с места и движутся равноускоренно. Массы автомобилей одинаковы. Во сколько раз средняя мощность первого автомобиля больше средней мощности второго, если за одно и то же время первый автомобиль развивает скорость вдвое большую, чем второй? Сопротивлением движению пренебречь.
Решение. Мощность двигателей автомобилей определяется формулой:
- для первого автомобиля
N1*=Fтяги1v1cosα,
- для второго автомобиля
N2*=Fтяги2v2cosα,
где Fтяги1 — величина силы тяги двигателя первого автомобиля; v1 — модуль скорости первого автомобиля; Fтяги2 — величина силы тяги двигателя второго автомобиля; v2 — модуль скорости второго автомобиля; α = 0° — угол между векторами силы тяги и скорости.
Силы, действующие на первый и второй автомобиль, направление движения и выбранная система координат показаны на рисунке.
Для определения величины силы тяги запишем второй закон Ньютона с учетом того, что автомобили движутся равноускоренно:
- для первого автомобиля
F→тяги1+m1g→+N→1=m1a→1,
или в проекциях на координатные оси —
Ox: Fтяги1=m1a1;Oy: N1−m1g=0,}
- для второго автомобиля
F→тяги2+m2g→+N→2=m2a→2,
или в проекциях на координатные оси —
Ox: Fтяги2=m2a2;Oy: N2−m2g=0,}
где m1 — масса первого автомобиля; m2 — масса второго автомобиля; g — модуль ускорения свободного падения; N1 — модуль силы нормальной реакции, действующей на первый автомобиль со стороны дороги; N2 — модуль силы нормальной реакции, действующей на второй автомобиль со стороны дороги; a1 — модуль ускорения первого автомобиля; a2 — модуль ускорения второго автомобиля.
Из записанных уравнений следует, что величины сил тяги первого и второго автомобиля определяются формулами:
- для первого автомобиля
Fтяги1 = m1a1,
- для второго автомобиля
Fтяги2 = m2a2.
Отношение модулей сил тяги (Fтяги1/Fтяги2) определяется отношением
Fтяги1Fтяги2=m1a1m2a2.
Движение автомобилей происходит равноускоренно без начальной скорости, поэтому их скорость с течением времени изменяется по законам:
- для первого автомобиля
v1 = a1t,
- для второго автомобиля
v2 = a2t,
где t — время.
Отношение модулей скоростей (v1/v2) определяется отношением величин ускорений (a1/a2):
v1v2=a1a2,
а отношение мощностей —
N1*N2*=Fтяги1v1cosαFтяги2v2cosα=Fтяги1Fтяги2v1v2.
Подставим в полученное отношение выражения для (Fтяги1/Fтяги2) и (v1/v2):
N1*N2*=m1a1m2a2a1a2=m1m2(a1a2)2.
Преобразование формулы с учетом равенства масс автомобилей (m1 = m2 = m) и замены (a1/a2 = v1/v2) дает искомое отношение мощностей:
N1*N2*=(v1v2)2=(2v2v2)2=22=4.
Таким образом, мощность первого автомобиля в 4 раза больше мощности второго автомобиля.
Мощность и коэффициент полезного действия — урок. Физика, 8 класс.
Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу времени.
Среднее значение мощности — это работа, выполненная за единицу времени.
Величина мощности прямо пропорциональна величине совершённой работы \(A\) и обратно пропорциональна времени \(t\), за которое работа была совершена.
Мощность \(N\) определяют по формуле:
N=At.
Единицей измерения мощности в системе \(СИ\) является \(Ватт\) (русское обозначение — \(Вт\), международное — \(W\)).
Для определения мощности двигателя автомобилей и других транспортных средств используют исторически более древнюю единицу измерения — лошадиная сила (л.с.), 1 л.с. = 736 Вт.
Пример:
Мощность двигателя автомобиля равна примерно \(90 л.с. = 66240 Вт\).
Мощность автомобиля или другого транспортного средства можно рассчитать, если известна сила тяги автомобиля \(F\) и скорость его движения (v).
N=F⋅v
Эту формулу получают, преобразуя основную формулу определения мощности.
Ни одно устройство не способно использовать \(100\) % от начально подведённой к нему энергии на совершение полезной работы. Поэтому важной характеристикой любого устройства является не только мощность, но и коэффициент полезного действия, который показывает, насколько эффективно используется энергия, подведённая к устройству.
Пример:
Для того чтобы автомобиль двигался, должны вращаться колёса. А для того чтобы вращались колёса, двигатель должен приводить в движение кривошипно-шатунный механизм (механизм, который возвратно-поступательное движение поршня двигателя преобразует во вращательное движение колёс). При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах \(40 — 45\) %. Таким образом, получается, что только около \(40\) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля.
Если мы заправим в бак автомобиля \(20\) литров бензина, тогда только \(8\) литров будут расходоваться на перемещение автомобиля, а \(12\) литров сгорят без совершения полезной работы.
Коэффициент полезного действия обозначается буквой греческого алфавита \(«эта»\) η, он является отношением полезной мощности \(N\) к полной или общей мощности Nполная.
Для его определения используют формулу: η=NNполная. Поскольку по определению коэффициент полезного действия является отношением мощностей, единицы измерения он не имеет.
Часто его выражают в процентах. Если коэффициент полезного действия выражают в процентах, тогда используют формулу: η=NNполная⋅100%.
Так как мощность является работой, проделанной за единицу времени, тогда коэффициент полезного действия можно выразить как отношение полезной проделанной работы \(A\) к общей или полной проделанной работе Aполная. В этом случае формула для определения коэффициента полезного действия будет выглядеть так:
η=AAполная⋅100%.
Коэффициент полезного действия всегда меньше \(1\), или \(100\) % (η < 1, или η < \(100\) %).
Источники:
E. Šilters, V. Regusts, A. Cābelis. «Fizika 10. klasei», Lielvārds, 2004, 256 lpp.
(Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр. )
)
Работа, мощность, КПД
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
\[ \large \boxed{ A = \left( \vec{F} , \vec{S} \right) }\]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
\[ \large \boxed{ A = \left| \vec{F} \right| \cdot \left| \vec{S} \right| \cdot cos(\alpha) }\]
\( F \left( H \right) \) – сила, перемещающая тело;
\( S \left( \text{м} \right) \) – перемещение тела под действием силы;
\( \alpha \) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом \(A\) и измеряют в Джоулях.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг.
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
\[ \large \boxed{ A = \Delta E_{k} }\]
\[ \large \Delta E_{k} = E_{k2} — E_{k1} \]
\[ \large \Delta E_{k} = 50000 – 500 = 49500 \left(\text{Дж} \right) \]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
\[ \large \boxed{ A = \Delta E }\]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.
\( h \left( \text{м}\right) \) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
\[ \large E_{p2} = 0,2 \cdot 10 \cdot 3 = 6 \left(\text{Дж} \right) \]
Потенциальная энергия яблока на столе
\[ \large E_{p1} = 0,2 \cdot 10 \cdot 1 = 2 \left(\text{Дж} \right) \]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
\[ \large \Delta E_{p} = E_{p2} — E_{p1} \]
\[ \large \Delta E_{p} = 2 – 6 = — 4 \left(\text{Дж} \right) \]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед \( \Delta E_{p}\) дополнительно допишем знак «минус».
\[ \large \boxed{ A = — \Delta E_{p} }\]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы \(\displaystyle F_{\text{тяж}}\) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы \(\displaystyle F_{\text{тяж}}\) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.
Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ \(\vec{N}\) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
\[ \large A = \Delta E_{k} \]
\[ \large A = \Delta E_{p} \]
\[ \large A = F \cdot S \cdot cos(\alpha) \]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
\[ \large \boxed{ P = \frac{A}{\Delta t} }\]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
\[ \large P = \left( \vec{F} , \vec{v} \right) \]
Формулу можно записать в скалярном виде:
\[ \large P = \left| \vec{F} \right| \cdot \left| \vec{v} \right| \cdot cos(\alpha) \]
\( F \left( H \right) \) – сила, перемещающая тело;
\( \displaystyle v \left( \frac{\text{м}}{c} \right) \) – скорость тела;
\( \alpha \) – угол между вектором силы и вектором скорости тела;
Когда векторы \(\vec{F}\) и \(\vec{v}\) параллельны, запись формулы упрощается:
\[ \large \boxed{ P = F \cdot v }\]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом \(\eta\) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент \(\eta\) для какого-либо устройства, механизма или процесса.
\[ \large \boxed{ \eta = \frac{ A_{\text{полезная}}}{ A_{\text{вся}}} }\]
\(\eta\) – КПД;
\( \large A_{\text{полезная}} \left(\text{Дж} \right)\) – полезная работа;
\(\large A_{\text{вся}} \left(\text{Дж} \right)\) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
\[ \large \boxed{ \eta \leq 1 }\]
Величина \(\eta\) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
\[ \large \boxed{ \eta = \frac{ P_{\text{полезная}}}{ P_{\text{вся затраченная}}} }\]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей.
 При этом наша работа положительная, а работа силы тяжести — отрицательная;
При этом наша работа положительная, а работа силы тяжести — отрицательная; - Сила тяжести — это консервативная сила. Поэтому, работа силы \(\displaystyle F_{\text{тяж}}\) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом \(\eta\) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности
формула, в чем измеряется, как определить работу
Что такое сила тяги
Сила тяги — сила, прикладываемая к телу для поддержания его в постоянном движении.
Действие силы тяги
Множество сил, действующих на движущийся объект, для упрощения вычислений делят на две группы: силу тяги и силы сопротивления.
Её прекращение
Когда действие силы тяги прекращается, движущееся тело замедляется и постепенно останавливается, так как на него воздействуют силы, мешающие продолжать двигаться, например, трение.
1 закон Ньютона о действии
Согласно этому закону в формулировке самого Ньютона, любое тело остается в покое или равномерно движется по прямой, пока на него не воздействуют силы, заставляющие его изменить это состояние.
В современной физике в формулировку внесены уточнения:
- закон применим только в системах отсчета, называемых инерциальными;
- тело может вращаться на месте, не находясь под воздействием внешних сил, поэтому вместо термина «тело» следует использовать термин «материальная точка».
Чтобы переместить неподвижный предмет, на него должна воздействовать некая сила. Чтобы изменить скорость движения предмета, также необходимо воздействие силы, замедляющей его или ускоряющей. Так как предметы обладают разной массой и соответственно разной инертностью, силы, достаточные для эффективного воздействия, тоже будут различаться.
Так как предметы обладают разной массой и соответственно разной инертностью, силы, достаточные для эффективного воздействия, тоже будут различаться.
Состояние ускорения после воздействия силы тяги
Когда движение равномерное, сила тяги и сила трения совершают одинаковую работу, уравновешивая друг друга. Воздействие силы на тело в направлении движения придает ему ускорение. Если направить ту же силу в противоположном направлении, она замедлит движение тела, что можно назвать отрицательным ускорением.
Формулы для определения силы тяги
Согласно второму закону Ньютона, сумма сил, воздействующих на движущееся тело, равна массе \(m\), умноженной на ускорение \(a\). Универсальной формулы, подходящей для любого сочетания сил, не существует. Чаще всего силу тяги находят с помощью общей формулы\( F_т-\;F_{с}=m\;\times\;a\), где \(F_т\) — сила тяги, \(F_{с}\) — силы сопротивления.
При решении конкретной задачи силы, воздействующие на тело, схематически изображают в виде векторов. На схеме:
На схеме:
- сила тяжести mg;
- сила реакции опоры \(N\);
- сила трения\( F_{тр}\);
- сила тяги \(F\).
При нахождении тела на горизонтальной поверхности сила тяжести и сила реакции опоры уравновесят друг друга. Но если транспортное средство движется в гору или под гору, придется учесть влияние уклона. Тогда формула может выглядеть так: \(F_т-\;F_с-\;mg\;\times\;\sin\alpha=m\;\times\;a.\)
Работа A, которую должна совершить сила тяги, сдвигая тело, связана с ней соотношением \(A\;=\;F\;\times\;s\). \(s\) здесь — расстояние, на которое тело переместилось.
Какое условие должно соблюдаться
Сила тяги всегда должна быть больше противодействующих ей сил.
Формула через мощность
Полезную механическую мощность \(N\) можно вычислить по формуле \(N=F_т\;\times\;v\), где \(v\) — скорость. Для определения силы тяги нужно разделить мощность на скорость: \(F_т\;=\;\frac N v. \)
\)
Измерение и обозначение силы тяги
Силу тяги обозначают \(F_т\) или \(F\). Единица измерения — ньютон (\(Н\)).
Для решения задач недостаточно измерить усилие, приложенное к объекту, и выразить его конкретным числом, так как сила обладает еще и направлением. Чтобы подчеркнуть, что сила — векторная величина, к буквенному обозначению добавляют стрелку.
Как определить силу тяги двигателя. Примеры решения задач
Задача 1
Автомобиль может разгоняться до 216 км/ч. Максимальная мощность двигателя равна 96 кВт. Определите максимальную силу тяги двигателя.
Решение
Переведем киловатты в ватты, а километры в час — в метры в секунду:
\(96\;\times\;1000=96000\;Вт\)
\(\frac{216\times1000}{3600}=60\frac мс\)
\(F_т\;=\;\frac N v = \frac{96000}{60} = 1600 Н\)
Задача 2
Троллейбус весом 12 тонн за 5 секунд проезжает по горизонтальной дороге 10 метров. {}=\frac{20}{25}\;=\;0,8\)
{}=\frac{20}{25}\;=\;0,8\)
\(F_т=\;12000\times0,8\;+\;2400\;=\;12000\;Н\;=\;12\;кН\)
Задача 3
Транспорт, весящий 4 тонны, едет в гору. Уклон — 1 метр на каждые 25 метров пути. \(\mu\) — 0,1 от силы тяжести, \(а = 0\). Определите силу тяги.
Решение
Начертим схему:
\(m\times g\;+\;N\;+\;F_{тр\;}+\;F_т\;=\;m\times a\)
Сделаем проекции на координатные оси:
\(OX: -\;mg\;\times\;\sin\alpha\;-\;F_{тр\;}+\;F_т\;=\;0\)
\(OY: N\;-\;mg\;\times\;\cos\alpha\;=\;0 => N\;=\;mg\;\times\;\cos\alpha\;\)
\(F_{тр}\;=\;\mu N\;=\;\mu mg\;\times\;\cos\alpha\)
Подставим значение \(F_{тр}\) в уравнение \(OX\) и определим \(F_т\):
\(-mg\;\times\;\sin\alpha\;-\;\mu\)
\(mg\;\times\;\cos\alpha\;+\;F_т\;=\;0\)
\(=> F\;=\;mg\;\left(\sin\alpha\;+\;\mu\;\times\;\cos\alpha\right)\)
Найдем синус и косинус \(\alpha\), подставим их в общую формулу:
\(\sin\alpha\;=\;\frac hl\;=\;\frac1{25}\)
\(\cos\alpha\;=\;\frac{\sqrt{l^{2\;}-\;h^2}}l\;\)
\(F\;=\;\frac{4\;\times\;10^{3\;}\;\times\;9,8\;\times\left(1\;+\;0,1\;\sqrt{l^{2\;}-\;h^2}\right)}{25}\;=\;5,5\;\times\;10^3\;Н\;=\;5,5\;кН\)
новейших вопросов ‘powerapps-formula’ — qaru
Переполнение стека
-
Около
-
Продукты
-
Для команд
-
Переполнение стека
Общественные вопросы и ответы
-
Переполнение стека для команд
Где разработчики и технологи делятся частными знаниями с коллегами
-
Вакансии
Программирование и связанные с ним технические возможности карьерного роста
-
Талант
Нанимайте технических специалистов и создавайте свой бренд работодателя
-
Реклама
Обратитесь к разработчикам и технологам со всего мира
-
Формулы и определения фрезерования
Определения фрезерных пластин
Геометрия пластины
Более пристальное изучение геометрии режущей кромки позволяет выявить два важных угла на пластине:
-
передний угол (γ)
-
угол режущей кромки (β)
Макро-геометрия разработана для работы в легких, средних и тяжелых условиях.
-
L (Light) геометрия имеет более положительный, но более слабый край (большой γ, маленький β)
-
H (тяжелая) геометрия имеет более прочную, но менее положительную кромку (малый γ, большой β).
Макро-геометрия влияет на многие параметры в процессе резки. Пластина с прочной режущей кромкой может работать при более высоких нагрузках, но также создает более высокие силы резания, потребляет больше энергии и выделяет больше тепла.Геометрия, оптимизированная для материалов, обозначается буквой классификации ISO. Например, геометрии для чугуна: -KL, -KM и -KH.
Пластина угловая конструкция
Самая важная часть режущей кромки для обработки поверхности — это параллельная фаска.
b s 1 или, если применимо, выпуклая поверхность стеклоочистителя
b s 2, или угловой радиус,
r ε .
Угловой радиус,
r Параллельная земля ( b s 1) Стеклоочиститель ( b s 2)
Определения фрез
Угол въезда, ( k r ) (градусы)
Главный угол режущей кромки ( k r ) фрезы является доминирующим фактором, поскольку он влияет на направление силы резания и толщину стружки.
Диаметр фрезы —
D c (мм)
Диаметр фрезы ( D c ) измеряется над точкой (PK), где основная режущая кромка встречается с параллельной фаской.
Наиболее важным диаметром, который следует учитывать, является ( D крышка ) — эффективный диаметр резания при фактической глубине резания ( a p ) — используемый для расчета истинной скорости резания.
D 3 — наибольший диаметр пластины, для некоторых фрез он равен
D c .
Глубина резания —
a p (мм)
Глубина резания ( a p ) — это разница между неотрезанной поверхностью и поверхностью резания в осевом направлении.Максимум
a p в первую очередь ограничивается размером пластины и мощностью станка.
Другим критическим фактором при черновой обработке является крутящий момент, а при чистовой обработке — вибрация.
Ширина реза,
a e (мм)
Радиальная ширина фрезы ( a e ), задействованной в резке. Особенно критично при перебеге врезания и вибрации при фрезеровании углов, где максимальная
a e особенно важны.
Радиальное погружение,
a e / D c
Радиальное погружение ( a e /
D c ) — ширина пропила по отношению к диаметру фрезы.
Количество эффективных режущих кромок на инструменте,
z c
Для определения подачи стола ( v f ) и производительности. Это часто имеет решающее влияние на удаление стружки и стабильность работы.
Общее количество режущих кромок на инструменте,
z n
Расстояние между рабочими режущими кромками, u
Для определенного диаметра фрезы вы можете выбирать между различными шагами: крупный (-L), близкий (-M), сверхмалый (-H). Знак X, добавленный к коду, обозначает версию фрезы, шаг которой немного ближе, чем ее базовая конструкция.
Дифференциальный шаг
Обозначает неравное расстояние между зубьями фрезы.п \]
Как видите, способ отображения уравнений зависит от разделителя, в данном случае \ [\] и \ (\) .
Открыть пример на обороте
LaTeX допускает два режима записи математических выражений: встроенный режим и режим отображения . Первый используется для написания формул, являющихся частью текста. Второй используется для записи выражений, которые не являются частью текста или абзаца и поэтому помещаются в отдельные строки.2 \]
открытый в 1905 году Альбертом Эйнштейном.
В натуральных единицах ($ c $ = 1) формула выражает тождество
\ begin {уравнение}
E = m
\ end {уравнение}
Первый используется для написания формул, являющихся частью текста. Второй используется для записи выражений, которые не являются частью текста или абзаца и поэтому помещаются в отдельные строки.2 \]
открытый в 1905 году Альбертом Эйнштейном.
В натуральных единицах ($ c $ = 1) формула выражает тождество
\ begin {уравнение}
E = m
\ end {уравнение}
Для печати уравнений в режиме отображения используйте один из следующих разделителей: \ [\] , \ begin {displaymath} \ end {displaymath} или \ begin {уравнение} \ end {уравнение}
Важное примечание: Equation * среда предоставляется внешним пакетом, обратитесь к статье amsmath .
Открыть пример на обороте
Ниже представлена таблица с некоторыми общими математическими символами. Для более полного списка см. Список греческих букв и математических символов:
Различные классы математических символов характеризуются разным форматированием (например, переменные выделены курсивом, а операторы — нет) и разным интервалом.
Открыть пример на обороте
Математический режим в LaTeX очень гибкий и мощный, с его помощью можно сделать гораздо больше:
Калькулятор процентов
Наш калькулятор процентов может помочь определить выплаты процентов и окончательный баланс не только по фиксированной основной сумме, но и по дополнительным периодическим взносам.Существуют также дополнительные факторы, доступные для рассмотрения, такие как налог на процентный доход и инфляция. Чтобы понять и сравнить различные способы начисления процентов, воспользуйтесь нашим калькулятором сложных процентов .
Результаты
Конечное сальдо 56 641,10 долл. США После корректировки на инфляцию 48 859,11 долл. США 458325325 Итого Основная сумма долга00 Итого проценты $ 11 641,10
Разбивка
График накопления остатка
Связанный калькулятор инвестиций | Калькулятор средней доходности | Калькулятор ROI Проценты — это компенсация, выплачиваемая заемщиком кредитору за использование денег в качестве процента или суммы. Концепция процента — это основа большинства финансовых инструментов в мире. Хотя проценты зарабатываются, они отличаются от прибыли тем, что они получают кредитор, а не владелец актива или инвестиции, хотя проценты могут быть частью прибыли от инвестиций.
Концепция процента — это основа большинства финансовых инструментов в мире. Хотя проценты зарабатываются, они отличаются от прибыли тем, что они получают кредитор, а не владелец актива или инвестиции, хотя проценты могут быть частью прибыли от инвестиций.
Существует два различных метода накопления процентов, которые подразделяются на простые проценты и сложные проценты.
Простой процент
Ниже приводится базовый пример того, как работают проценты. Дерек хотел бы занять у банка 100 долларов (обычно называемых основной суммой) на один год. Банк требует 10% годовых. Для расчета процентов:
100 $ × 10% = 10
$
Эти проценты добавляются к основной сумме, и сумма становится требуемой выплатой Дерека банку.
100 + 10 = 110
Дерек должен банку 110 долларов через год, 100 долларов в качестве основной суммы и 10 долларов в качестве процентов.
Предположим, Дерек хотел занять 100 долларов на два года вместо одного, и банк рассчитывает проценты ежегодно. С него просто взимали процентную ставку дважды, один раз в конце каждого года.
С него просто взимали процентную ставку дважды, один раз в конце каждого года.
100 долларов США + 10 долларов США (год 1) + 10 долларов США (год 2) = 120 долларов США
Два года спустя Дерек должен банку 120 долларов, 100 долларов в качестве основной суммы и 20 долларов в качестве процентов.
Формула для расчета простых процентов:
проценты = (основная сумма) × (процентная ставка) × (срок)
Если речь идет о более сложных частотах подачи процентов, например, ежемесячно или ежедневно, используйте формулу:
проценты = (основная сумма) × (процентная ставка) × (срок) / (частота)
Однако простые проценты очень редко используются в реальном мире.Даже когда люди используют повседневное слово «интерес», они обычно имеют в виду интерес, который составляет составной элемент.
Сложные проценты
Для начисления процентов требуется более одного периода, поэтому давайте вернемся к примеру, когда Дерек занял у банка 100 долларов на два года под 10% годовых. В первый год мы начисляем проценты как обычно.
В первый год мы начисляем проценты как обычно.
100 $ × 10% = 10
$
Эти проценты добавляются к основной сумме, и сумма становится требуемой выплатой Дерека банку на данный момент.
100 + 10 = 110
Однако год заканчивается, и наступает другой период. Для начисления сложных процентов вместо первоначальной суммы используется основная сумма + любые проценты, накопленные с тех пор. В случае Дерека:
110 $ × 10% = 11
$
Процентная ставка Дерека в конце второго года составляет 11 долларов. Это добавляется к сумме задолженности после 1 года:
110 + 11 = 121
По окончании ссуды банк получает от Дерека 121 доллар вместо 120, если бы вместо этого использовались простые проценты.Это потому, что проценты также начисляются на проценты.
Чем чаще начисляются проценты в течение периода времени, тем выше будут начисляться проценты по первоначальной основной сумме. Ниже приведен график из Википедии, показывающий только это: инвестиции в размере 1000 долларов США при различных частотах начисления сложных процентов, приносящие 20% -ный доход.
Вначале разница между всеми частотами небольшая, но со временем они постепенно начинают расходиться. Это сила сложных процентов, о которой все любят говорить, проиллюстрированная на краткой диаграмме.Непрерывное соединение всегда будет иметь самую высокую доходность из-за использования математического предела частоты начисления сложных процентов, которая может происходить в течение определенного периода времени.
Правило 72
Любой, кто хочет подсчитать сложный процент в уме, может найти правило 72 очень полезным. Не для точных расчетов, как это дают финансовые калькуляторы, а для того, чтобы получить представление о приблизительных цифрах. В нем говорится, что для определения количества лет (n), необходимого для удвоения определенной суммы денег при любой процентной ставке, просто разделите 72 на ту же ставку.
Пример: Сколько времени нужно, чтобы удвоить 1000 долларов при 8% ставке?
п = 72/8 = 9
Потребуется 9 лет, чтобы 1000 долларов превратились в 2000 долларов под 8% годовых. Эта формула лучше всего работает для процентных ставок от 6 до 10%, но она также должна работать достаточно хорошо для любых ставок ниже 20%.
Эта формула лучше всего работает для процентных ставок от 6 до 10%, но она также должна работать достаточно хорошо для любых ставок ниже 20%.
Фиксированная и плавающая процентная ставка
Процентная ставка по ссуде или сбережениям может быть «фиксированной» или «плавающей». Ссуды или сбережения с плавающей ставкой обычно основаны на некоторой справочной ставке, такой как U.S. Ставка по фондам Федеральной резервной системы (ФРС) или LIBOR (Лондонская межбанковская ставка предложения). Обычно ставка по ссуде немного выше, а норма сбережений немного ниже справочной ставки. Разница идет в прибыль банка. И ставка ФРС, и LIBOR представляют собой краткосрочные межбанковские процентные ставки, но ставка ФРС является основным инструментом, который Федеральная резервная система использует для воздействия на предложение денег в экономике США. LIBOR — это коммерческая ставка, рассчитываемая на основе преобладающих процентных ставок между учреждениями с высокой кредитоспособностью. Наш калькулятор процентов работает только с фиксированными процентными ставками.
Наш калькулятор процентов работает только с фиксированными процентными ставками.
Взносы
Важно различать взносы в том, происходят ли они в начале или в конце периодов начисления сложных процентов. Периодические выплаты, которые происходят в конце, имеют на одну сумму меньше процентного периода для каждого взноса.
Ставка налога
Некоторые формы процентного дохода облагаются налогами, включая облигации, сбережения и депозитные сертификаты (CD). В США корпоративные облигации почти всегда облагаются налогом.Некоторые виды облагаются налогом полностью, а другие — частично; например, хотя проценты, полученные по облигациям федерального казначейства США, могут облагаться налогом на федеральном уровне, они освобождаются от налогообложения на уровне штата и на местном уровне. Налоги могут иметь очень большое влияние на конечный баланс. Например, если Дерек откладывает 100 долларов под 6% в течение 20 лет, он получит:
100 $ × (1 + 6%) 20 = 320,71 $
Это не облагается налогом. Однако, если у Дерека предельная ставка налога 25%, он получит 239,78 доллара только потому, что ставка налога 25% применяется к каждому периоду начисления сложных процентов.
Однако, если у Дерека предельная ставка налога 25%, он получит 239,78 доллара только потому, что ставка налога 25% применяется к каждому периоду начисления сложных процентов.
Уровень инфляции
Инфляция определяется как повышение общего уровня цен, при котором фиксированная сумма денег позволяет относительно меньше. Средний уровень инфляции в США за последние 100 лет колебался около 3%. Для сравнения: средняя годовая доходность индекса S&P 500 (Standard & Poor’s) в США составляет около 10%. Пожалуйста, обратитесь к нашему калькулятору инфляции для получения более подробной информации об инфляции.
Оставьте уровень инфляции равным 0 для быстрых обобщенных результатов.Но для реальных и точных чисел можно ввести цифры, чтобы учесть инфляцию.
Сочетание налогов и инфляции затрудняет рост реальной стоимости денег. Например, в США для среднего класса предельная ставка налога составляет 25%, а средний уровень инфляции составляет 3%. Для поддержания стоимости денег необходимо получить стабильную процентную ставку или доходность инвестиций в размере 4% или выше, а этого нелегко достичь.
Формулы для быстрого расчета лошадиных сил и мощности
БЫСТРАЯ ОЦЕНКА
ФОРМУЛЫ
• лошадиные силы
Формулы
• Формулы крутящего момента
• Формулы электродвигателей переменного тока
• Формулы трехфазных электрических сетей
ПОДСТАВКА
ФОРМУЛЫ
Для
Вращающиеся объекты
л.с. =
Где
т
= Крутящий момент (фунт · фут)
N = скорость (об / мин)
Объекты
в линейном движении
л. с.
=
с.
=
Где
F
= Сила (фунты)
В = Скорость (фут / мин)
Для
Насосы
л.с.
=
л.с. =
Где
галлонов в минуту = галлонов на
Минуты
Напор = Высота воды (футы)
КПД насоса =% / 100
PSI = Фунтов на дюйм
Удельный вес
воды = 1. 0
0
1 куб.фут / сек. = 448 галлонов в минуту
1 фунт / кв. Дюйм = напор 2,309 фута (вес воды)
62,36 фунта на куб. Фут при 62 ° F
Для
Вентиляторы и нагнетатели
л.с. =
л.с. =
л.с. =
Где
куб. Футов в минуту =
Кубических футов в минуту
Футов в минуту =
Кубических футов в минуту
PSF = фунтов на квадратный фут
PIW = дюймов водяного столба
PSI = фунтов на квадратный дюйм
КПД вентилятора =% / 100
Для
Конвейеры
л.с. (по вертикали)
л.с. (горизонтальный)
Где
F = сила (фунты)
V = скорость (фут / мин)
Коэф.трения
• Шаровая или роликовая направляющая = 0,02
• Направляющая «ласточкин хвост» = 0,20
• Гидростатические способы = 0,01
• Прямоугольные направляющие с выступом = 0,01–0,25
МОМЕНТ
ФОРМУЛЫ
Т =
л. с.
х 5252
с.
х 5252
N
Где
T = крутящий момент
(Фунт-фут)
л.с. = мощность
л.с. = скорость (об / мин)
Т =
F x R
Где
T = крутящий момент
(Фунт-фут)
F = сила (фунт)
R = радиус (фут)
Ta (ускорение)
WK2
x Изменение об / мин
308 x t (сек)
Где
Ta = крутящий момент (фунт-фут)
WK2 = момент инерции на валу двигателя (фунт-фут) 2
t = время разгона (сек)
Примечание:
Чтобы изменить LbFt2 на InLbSec2, разделите на 2.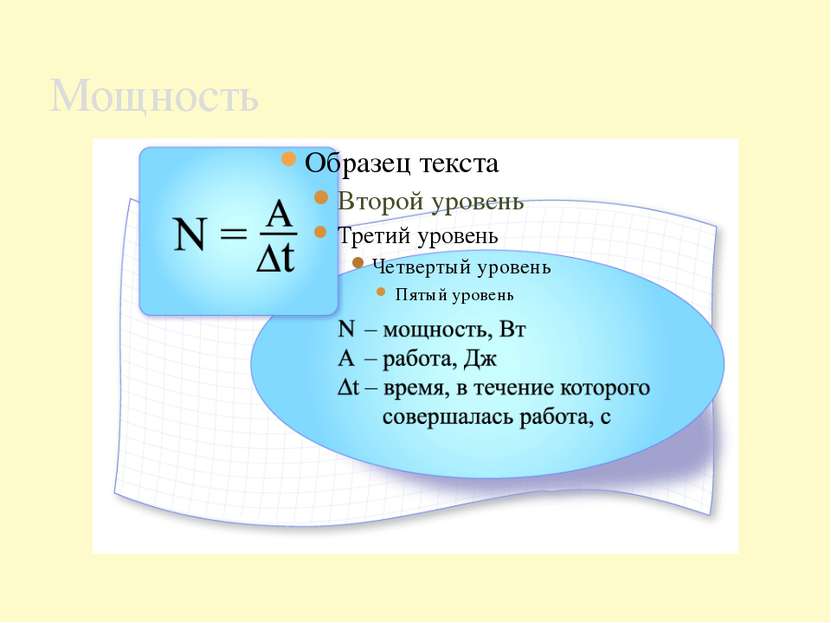 68
68
Чтобы изменить InLbSec2 на LbFt2, Mult. по 2.68
переменного тока
МОТОРНЫЕ ФОРМУЛЫ
Скорость синхронизации
=
Freq
х 120
Номер
поляков
Где
Скорость синхронизации
= Синхронная скорость (об / мин)
Частота = Частота (Гц)
% Скольжение
=
(синхронизация
Скорость — Скорость полета) x 100
Скорость синхронизации
Где
FL Скорость
= Скорость полной нагрузки (об / мин)
Синхронная скорость = Синхронная скорость (об / мин)
Отражено
WK2 =
WK2
загрузки
(уменьшение
Передаточное число) 2
Сколько мощности у двигателей F1?
Силовые агрегаты F1 очень близки к магическому числу 1000 л. с., но в настоящее время лучший двигатель в F1 2017 не соответствует этой цели — мы предлагаем обзор мощности двигателей в сегодняшней Формуле 1, основанный на данных GPS.
с., но в настоящее время лучший двигатель в F1 2017 не соответствует этой цели — мы предлагаем обзор мощности двигателей в сегодняшней Формуле 1, основанный на данных GPS.
Хотя точные данные о мощности двигателей в Формуле 1 всегда были засекречены, средства массовой информации часто получают неофициальную информацию от инженеров, а команды внимательно следят друг за другом с помощью данных GPS и, таким образом, могут установить некоторые общие значения.
Сирил Абитебул из Renault сказал перед сезоном Формулы-1 2017, что даже самые лучшие двигатели не будут иметь 1000 л.с., что оказалось правильным, а в конце 2017 года Mercedes также признал, что у них все еще нет волшебных 1000 л.с., несмотря на потрясающую КПД 50% на испытательном стенде, что является улучшением по сравнению с первоначальными 44% в 2014 году, когда началась эра гибридного турбонаддува.
Сегодняшние силовые агрегаты F1 состоят из 1,6-литрового турбодвигателя внутреннего сгорания V6, а система рекуперации энергии состоит из MGU-H, MGU-K и батарей. Вся система управляется управляющей электроникой.
Вся система управляется управляющей электроникой.
Поскольку мощность системы ERS ограничена максимумом 163 л.с. в течение 33,3 секунд на одном круге, это означает, что для общей мощности 1000 л.с. сам двигатель должен иметь не менее 837 л.с.
Auto Motor und Sport сообщает, что силовой агрегат Mercedes M08 EQ Power + развивает максимальную мощность 949 л.с., а у Ferrari на 15 л.с. меньше (934 л.с.).
Третий — Renault с отставанием в 42 л.с. от Mercedes (907 л.с.), в то время как Honda с их последней спецификацией силового агрегата RA617H имеет 881 л.с.
Mercedes — самый крепкий, надежный и экономичный
Это впечатляющие цифры из-за небольшого объема двигателя всего 1,6 литра, а также из-за ограничения расхода топлива 100 кг / ч и максимального расхода топлива в гонке 105 кг.
Старые двигатели V10 середины 2000-х годов развивали аналогичную мощность, но с тепловым КПД всего 30%.
Помимо максимальной мощности, Mercedes является единственным производителем, которому удалось завершить сезон F1 2017 года с использованием до четырех единиц каждого из шести элементов силового агрегата (за исключением преднамеренных изменений в автомобиле Hamilton. в Бразилии) со всеми шестью автомобилями, что будет чрезвычайно важно в следующем году, когда будет доступно только три двигателя.
в Бразилии) со всеми шестью автомобилями, что будет чрезвычайно важно в следующем году, когда будет доступно только три двигателя.
Еще одно преимущество Mercedes — расход топлива. В Мексике пилоты Mercedes начали с примерно на 10 кг топлива меньше, чем их соперники, что является огромным преимуществом (сокращение к концу гонки), что приводит к лучшему старту и снижению расхода топлива и шин.
Следует отметить, что низкому расходу топлива у Mercedes также способствует шасси, в котором используется очень низкий передний угол и очень узкая задняя часть из-за своей большой длины (самый длинный автомобиль в F1 2017).
Помимо того, что другие производители должны стремиться к мощности, они также должны добиться невероятной надежности и низкого расхода топлива, что заставляет их проявлять смелость при выборе технических решений.
ОБЗОР ДВИГАТЕЛЯ F1 2017 ГОДА
ПРОИЗВОДИТЕЛЬ
ОБЩАЯ МОЩНОСТЬ (V6 + ERS)
ТОЛЬКО V6
ЗАЗОР
Мерседес M08
949 л.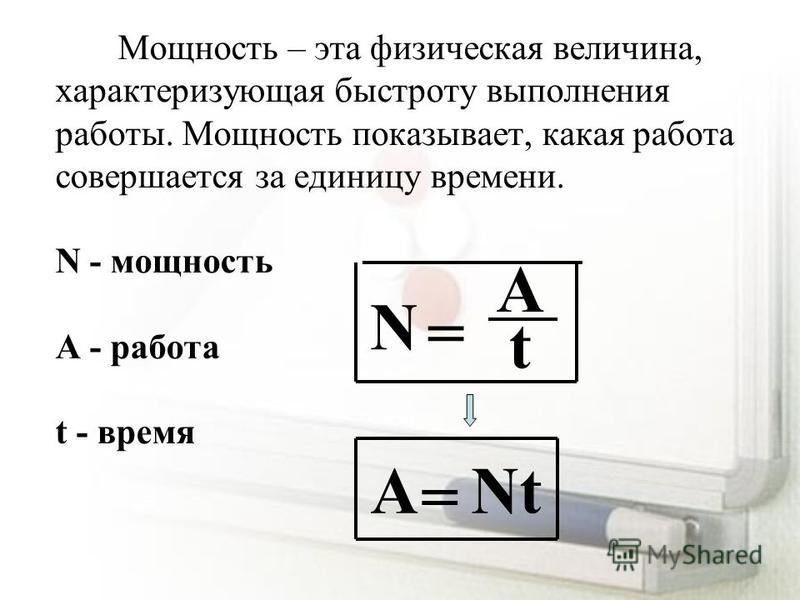 .
.
передний угол (γ)
угол режущей кромки (β)

L (Light) геометрия имеет более положительный, но более слабый край (большой γ, маленький β)
H (тяжелая) геометрия имеет более прочную, но менее положительную кромку (малый γ, большой β).



\ [\] и \ (\) .
 Первый используется для написания формул, являющихся частью текста. Второй используется для записи выражений, которые не являются частью текста или абзаца и поэтому помещаются в отдельные строки.2 \]
открытый в 1905 году Альбертом Эйнштейном.
В натуральных единицах ($ c $ = 1) формула выражает тождество
\ begin {уравнение}
E = m
\ end {уравнение}
Первый используется для написания формул, являющихся частью текста. Второй используется для записи выражений, которые не являются частью текста или абзаца и поэтому помещаются в отдельные строки.2 \]
открытый в 1905 году Альбертом Эйнштейном.
В натуральных единицах ($ c $ = 1) формула выражает тождество
\ begin {уравнение}
E = m
\ end {уравнение}
\ [\] , \ begin {displaymath} \ end {displaymath} или \ begin {уравнение} \ end {уравнение}
Equation * среда предоставляется внешним пакетом, обратитесь к статье amsmath .

Результаты
| Конечное сальдо | 56 641,10 долл. США |
| После корректировки на инфляцию | 48 859,11 долл. США |
| Итого проценты | $ 11 641,10 |
Разбивка
 Концепция процента — это основа большинства финансовых инструментов в мире. Хотя проценты зарабатываются, они отличаются от прибыли тем, что они получают кредитор, а не владелец актива или инвестиции, хотя проценты могут быть частью прибыли от инвестиций.
Концепция процента — это основа большинства финансовых инструментов в мире. Хотя проценты зарабатываются, они отличаются от прибыли тем, что они получают кредитор, а не владелец актива или инвестиции, хотя проценты могут быть частью прибыли от инвестиций. С него просто взимали процентную ставку дважды, один раз в конце каждого года.
С него просто взимали процентную ставку дважды, один раз в конце каждого года.  В первый год мы начисляем проценты как обычно.
В первый год мы начисляем проценты как обычно. 
 Эта формула лучше всего работает для процентных ставок от 6 до 10%, но она также должна работать достаточно хорошо для любых ставок ниже 20%.
Эта формула лучше всего работает для процентных ставок от 6 до 10%, но она также должна работать достаточно хорошо для любых ставок ниже 20%.  Наш калькулятор процентов работает только с фиксированными процентными ставками.
Наш калькулятор процентов работает только с фиксированными процентными ставками.  Однако, если у Дерека предельная ставка налога 25%, он получит 239,78 доллара только потому, что ставка налога 25% применяется к каждому периоду начисления сложных процентов.
Однако, если у Дерека предельная ставка налога 25%, он получит 239,78 доллара только потому, что ставка налога 25% применяется к каждому периоду начисления сложных процентов.
Формулы для быстрого расчета лошадиных сил и мощности
БЫСТРАЯ ОЦЕНКА ФОРМУЛЫ
• лошадиные силы
Формулы
• Формулы крутящего момента
• Формулы электродвигателей переменного тока
• Формулы трехфазных электрических сетей
л.с. =
N = скорость (об / мин)
 с.
=
с.
=
В = Скорость (фут / мин)
галлонов в минуту = галлонов на
Минуты
Напор = Высота воды (футы)
КПД насоса =% / 100
PSI = Фунтов на дюйм
Удельный вес
воды = 1. 0
0
1 куб.фут / сек. = 448 галлонов в минуту
1 фунт / кв. Дюйм = напор 2,309 фута (вес воды)
62,36 фунта на куб. Фут при 62 ° F
 Футов в минуту =
Кубических футов в минуту
Футов в минуту =
Кубических футов в минуту PSF = фунтов на квадратный фут
PIW = дюймов водяного столба
PSI = фунтов на квадратный дюйм
КПД вентилятора =% / 100
F = сила (фунты)
V = скорость (фут / мин)
Коэф.трения
• Шаровая или роликовая направляющая = 0,02
• Направляющая «ласточкин хвост» = 0,20
• Гидростатические способы = 0,01
• Прямоугольные направляющие с выступом = 0,01–0,25
 с.
х 5252
с.
х 5252 N
л.с. = мощность
л.с. = скорость (об / мин)
F = сила (фунт)
R = радиус (фут)
308 x t (сек)
Ta = крутящий момент (фунт-фут)
WK2 = момент инерции на валу двигателя (фунт-фут) 2
t = время разгона (сек)
Примечание:
Чтобы изменить LbFt2 на InLbSec2, разделите на 2. 68
68
Чтобы изменить InLbSec2 на LbFt2, Mult. по 2.68
Частота = Частота (Гц)
Скорость синхронизации
Синхронная скорость = Синхронная скорость (об / мин)
WK2 загрузки
 с., но в настоящее время лучший двигатель в F1 2017 не соответствует этой цели — мы предлагаем обзор мощности двигателей в сегодняшней Формуле 1, основанный на данных GPS.
с., но в настоящее время лучший двигатель в F1 2017 не соответствует этой цели — мы предлагаем обзор мощности двигателей в сегодняшней Формуле 1, основанный на данных GPS. Вся система управляется управляющей электроникой.
Вся система управляется управляющей электроникой.  в Бразилии) со всеми шестью автомобилями, что будет чрезвычайно важно в следующем году, когда будет доступно только три двигателя.
в Бразилии) со всеми шестью автомобилями, что будет чрезвычайно важно в следующем году, когда будет доступно только три двигателя. ОБЩАЯ МОЩНОСТЬ (V6 + ERS)


