Что такое параллельное соединение резисторов. Как рассчитать общее сопротивление при параллельном подключении. Когда применяется параллельное соединение резисторов. Какие существуют формулы для расчета параллельного соединения.
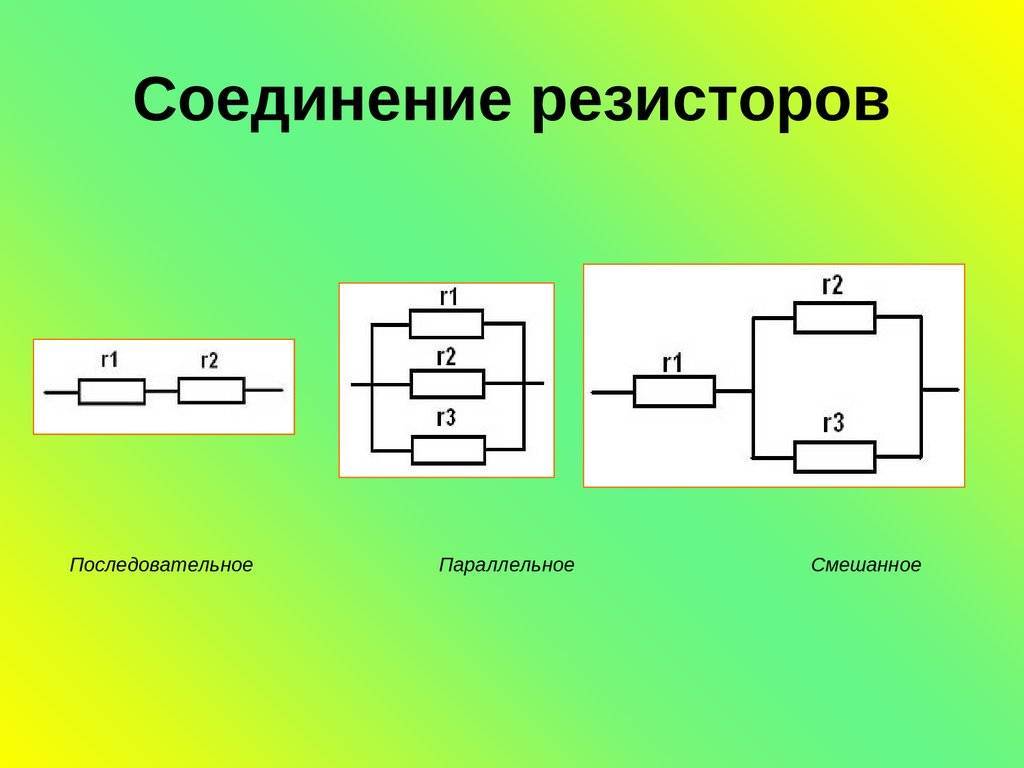
Что такое параллельное соединение резисторов
Параллельное соединение резисторов — это способ подключения, при котором все резисторы подсоединяются к одним и тем же двум точкам электрической цепи. При таком соединении:
- Напряжение на всех резисторах одинаково и равно напряжению источника
- Общий ток разветвляется между резисторами
- Общее сопротивление уменьшается
Схематично параллельное подключение резисторов выглядит следующим образом:
«` «`Формула расчета параллельного соединения резисторов
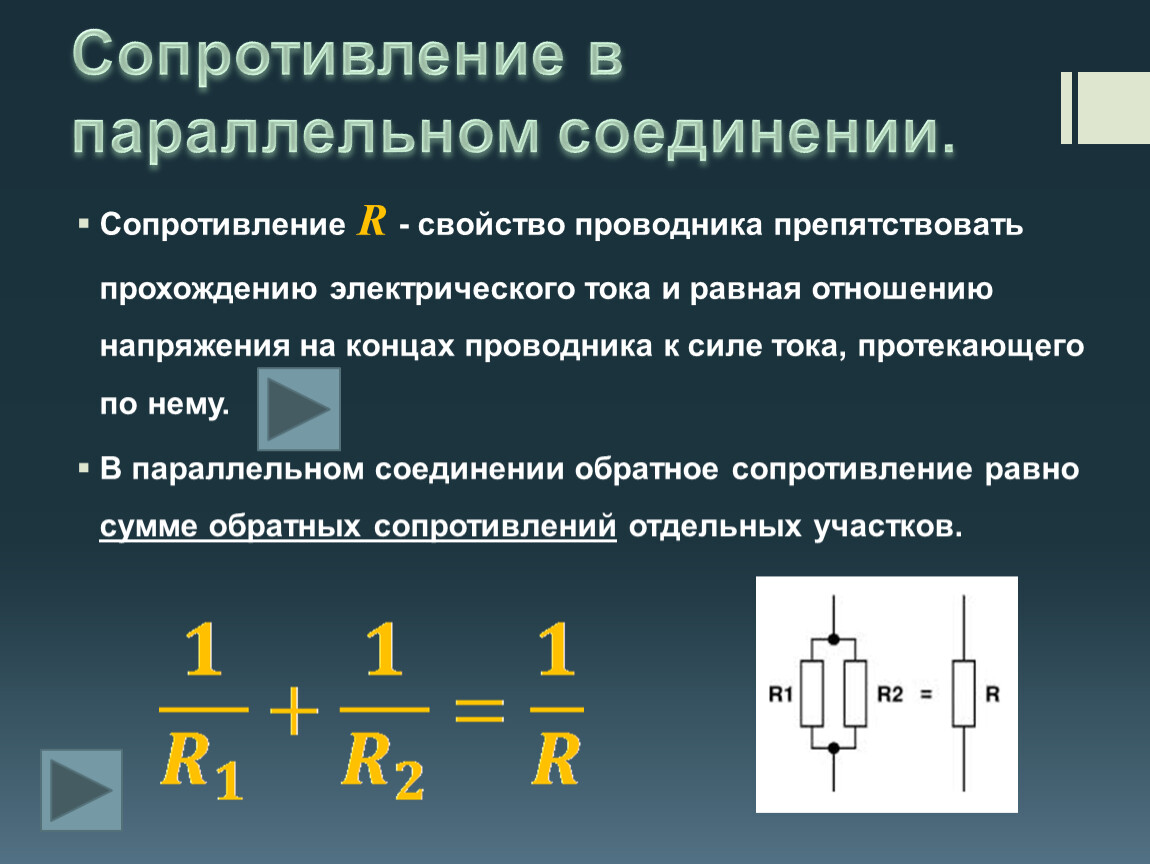
Для расчета общего сопротивления при параллельном соединении резисторов используется следующая формула:
1/R = 1/R1 + 1/R2 + 1/R3 + …
Где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Для двух параллельно соединенных резисторов формула упрощается:
R = (R1 * R2) / (R1 + R2)
Особенности параллельного соединения резисторов
При параллельном подключении резисторов наблюдаются следующие особенности:
- Общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи
- Чем больше резисторов подключено параллельно, тем меньше общее сопротивление
- При параллельном соединении одинаковых резисторов общее сопротивление уменьшается в число раз, равное количеству резисторов
Применение параллельного соединения резисторов
Параллельное соединение резисторов применяется в следующих случаях:
- Для уменьшения общего сопротивления цепи
- Для создания делителей тока
- Для получения нестандартных номиналов сопротивлений
- В измерительных приборах для расширения пределов измерения
- В силовой электронике для увеличения мощности рассеивания
Расчет параллельного соединения резисторов
Рассмотрим пример расчета параллельного соединения трех резисторов:
R1 = 100 Ом, R2 = 200 Ом, R3 = 300 Ом

Применяем формулу:
1/R = 1/100 + 1/200 + 1/300 = 0.01 + 0.005 + 0.0033 = 0.0183
R = 1/0.0183 = 54.6 Ом
Таким образом, общее сопротивление трех параллельно соединенных резисторов составит 54.6 Ом.
Преимущества параллельного соединения резисторов
Параллельное соединение резисторов имеет ряд преимуществ:
- Позволяет уменьшить общее сопротивление цепи
- Дает возможность получить нестандартные номиналы сопротивлений
- Увеличивает общую мощность рассеивания
- Обеспечивает резервирование в ответственных цепях
- Упрощает создание делителей тока
Сравнение параллельного и последовательного соединения резисторов
Параллельное и последовательное соединение резисторов имеют ряд отличий:
| Параметр | Параллельное соединение | Последовательное соединение |
|---|---|---|
| Общее сопротивление | Уменьшается | Увеличивается |
| Напряжение | Одинаковое на всех резисторах | Разное на каждом резисторе |
| Ток | Разный через каждый резистор | Одинаковый через все резисторы |
| Формула расчета | 1/R = 1/R1 + 1/R2 + … | R = R1 + R2 + … |
Практическое применение параллельного соединения резисторов
Рассмотрим несколько практических примеров применения параллельного соединения резисторов:

- Увеличение мощности рассеивания. Допустим, нужен резистор на 100 Ом мощностью 2 Вт, но есть только резисторы на 1 Вт. Можно параллельно соединить два резистора по 200 Ом.
- Получение нестандартного номинала. Например, нужен резистор 180 Ом, но есть только на 220 Ом и 1 кОм. Параллельное соединение этих резисторов даст примерно 180 Ом.
- Создание делителя тока. Параллельное подключение резисторов с разным сопротивлением позволяет разделить ток в нужной пропорции.
- Расширение пределов измерения амперметра. Параллельно прибору подключается шунт — резистор с малым сопротивлением.
Расчет мощности при параллельном соединении резисторов
При параллельном соединении резисторов важно правильно рассчитать мощность рассеивания. Общая мощность рассчитывается по формуле:
P = U^2 / R
Где U — напряжение, R — общее сопротивление параллельно соединенных резисторов.
Мощность, рассеиваемая на каждом резисторе, рассчитывается отдельно:
P1 = U^2 / R1
P2 = U^2 / R2
и т.д.
Важно, чтобы мощность, рассеиваемая на каждом резисторе, не превышала его номинальную мощность.
Заключение
Параллельное соединение резисторов — важный инструмент в электротехнике и электронике. Оно позволяет гибко управлять параметрами электрических цепей, создавать нужные конфигурации сопротивлений и токов. Понимание принципов параллельного соединения и умение производить расчеты необходимо для эффективного проектирования и анализа электронных схем.
Онлайн калькулятор расчета параллельного соединения резисторов
Последовательное и параллельное соединение. Применение и схемы
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединение
При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
Применение
Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Параллельное соединение
В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
Применение
Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.
Сила тока при параллельном подключении
Если было использовано последовательное подключение в цепи, то сила не изменится ни на одном участке ветви. Найти напряжение можно, применяя стандартное правило — нужно суммировать все показатели, которые присутствуют на концах каждого из резисторов, в итоге получится результат. Но при параллельном соединения намного сложней найти силу тока.
Даже при малой нагрузке в цепи будет формироваться определенное сопротивление. И тогда оно будет мешать продвижению электрического тока и будут потери. В общем, ток перемещается постепенно, от источника по подключенным заранее резисторам к нагруженным деталям.
Классическая формула Ома
Чтобы выполнить доступное прохождение тока по резисторам, нужно, чтобы он мог быстро и просто отдавать электроны, проще говоря иметь проводимость.
В современное время в основном применяются медные проводники, а важным элементом будут приемники электрической энергии. Такой элемент вызывает небольшую нагрузку и имеет свое сопротивление. Ниже описаны формулы для последовательного и параллельного соединения сопротивлений.
Вам это будет интересно Особенности управления освещением
Также при подключении необходимо использовать катушку индуктивности. Она способна подавлять помехи в электроцепи.
Параллельная схема соединения
В статье узнаете что такое параллельная схема соединения, как ее сделать, характеристики, сила тока в параллельной цепи, его сопротивление и мощность. А также преимущества и недостатки параллельной схемы.
Поведение схемы полностью зависит от конфигурации ее компонентов. В соответствии с конфигурацией их подключения эти цепи подразделяются на параллельные и последовательные. Этот пост раскрывает значение параллельной цепи, как создать параллельную схему, ее различные характеристики, области применения, преимущества и недостатки.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Вам это будет интересно Цифровой прибор мультиметр и измерение мультитестером
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
Вам это будет интересно Удельное электрическое сопротивление металлических проводников
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * [1 + a * (t — 20)] * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.
Что такое параллельная цепь
Схема называется параллельной, когда два или более компонентов подключены к одному узлу, а обе стороны компонентов подключены непосредственно к батарее или любому другому источнику. Ток в параллельной цепи имеет два или более пути прохождения через него.
Наиболее распространенным примером параллельной цепи является проводка автомобильных фар. Если бы фары были включены последовательно, то когда одна фара выходила из строя, другая также бы выключалась
Пример автомобильных фар, подключенных по параллельной цепи
Характеристики параллельной цепи
Основные характеристики параллельной цепи перечислены ниже:
Сила тока в параллельной цепи
Согласно закону Ома, I = U / R. Это подразумевает, что каждый резистор в этой цепи будет потреблять ток от источника. Следовательно, общий ток, потребляемый от источника, равен сумме токов ветвления, и ток, протекающий в каждом тракте, зависит от сопротивления ветви. Тем не менее, напряжение остается неизменным и создает разность потенциалов на его клеммах.
Общий ток (It) может быть рассчитан с использованием уравнения,
Давайте рассмотрим, что параллельная цепь построена с двумя резисторами (R1 и R2) с разными значениями (10 Ом и 5 Ом) соответственно. Напряжение 10V подается через резисторы , в результате тока 1А , проведенной от батареи через R1 и R2, который получен из уравнения I = U / R.
Следовательно, два тока ветвления в цепи составляют 1А и 2А, которые суммируют до 3А.
Сопротивления в параллельной цепи
Общее сопротивление любого количества резисторов рассчитывается по уравнению,
Взаимное значение R1 = 1/R1 = 1/10 = 0,1
Взаимное от R2 = 1/R2 = 1/5 = 0,2
Сумма обратных выше = 0,3
R t = 1 / 0,3 = 3,33 Ом
Мощность в параллельной цепи
Как только общий ток и приложенные значения напряжения известны, мощность может быть рассчитана с использованием уравнения P = UI . В приведенном выше примере, приложенное напряжение U = 10В и I = 3A, P = 10×3 = 30 Вт
Назначение и определение импеданса
Практически ни одно электронное устройство не обходится в своей схеме без резисторов. Являясь пассивными элементами, они имеют основное предназначение — ограничивать величину тока в электрической цепи. Кроме токоограничения, они служат делителями напряжения или шунтами в измерительных приборах.
Электрическое сопротивление — это величина, имеющая физическую природу и характеризующая возможность проводника пропускать электрический ток. Принцип работы резистора был описан выдающимся экспериментатором Омом. Позже в его честь и была названа единица измерения электрического сопротивления — Ом. Учёный, проводя ряд экспериментов, установил зависимость между силой тока, напряжением и сопротивлением в проводнике. В результате была выведена простая формула, известная как закон Ома: I = U/R, где:
- I — проходящая через проводник сила тока, измеряемая в Амперах;
- U — напряжение, приложенное к проводнику, единица измерения — Вольт;
- R — сопротивление проводника, измеряется в Омах.
Позже устройства, использующиеся только в качестве элементов сопротивления в электрических цепях, получили название — резисторы. Такие приборы, кроме величины сопротивления, характеризуются мощностью, рассчитывающейся по следующей формуле: P = I2 * R. Полученная величина измеряется в Ваттах.
В схемотехнике используется как параллельное, так и последовательное соединение проводников. В зависимости от этого изменяется и величина импеданса участка цепи. Вид соединения, если он не используется для подбора нужного значения, как раз и характеризует применение резисторов в первом случае как токоограничителей, а во втором — как делителей напряжения.
На схемах резисторы обозначаются в виде прямоугольника и подписываются латинской буквой R. Рядом указывается порядковый номер и значение сопротивления. Например, R23 1k обозначает, что резистор с номером 23 имеет сопротивление, равное одному килоОму. Полоски, изображённые внутри прямоугольника, характеризуют мощность, рассеиваемую на проводнике.
Фундаментальный закон сохранения энергии гласит: энергия никуда не исчезает и из ниоткуда не появляется, а только изменяет форму. Поэтому при ограничении тока часть энергии трансформируется в тепло. Именно эту часть и называют мощностью рассеивания резистора, т. е. такую её величину, которую может выдержать сопротивление без изменения своих параметров.
Сам по себе резистор может иметь различную конструкцию и вид. Например, быть проволочным, керамическим, слюдяным и т. п. Маркируется он тремя способами:
- Цветной полосочной системой. Каждая полоска отвечает за определённый множитель. Расшифровку полосок можно взять из справочников или онлайн-калькуляторов.
- Цифрами и буквами. Число указывает непосредственно значение сопротивления, а буква — множитель. Например,15M — пятнадцать мегаОм.
- Цифровая. Обычно используются три цифры, первая и вторая обозначают значение сопротивления, а последняя — множитель. Например, 103 — десять килоОм.
Поэтому видя, какие резисторы установлены в схеме, даже начинающему радиолюбителю не составит труда рассчитать общее сопротивление, особенно используя онлайн-калькулятор параллельного соединения резисторов или последовательного. В случае невозможности различить маркировку на корпусе его сопротивление возможно измерить мультиметром. Но опытные электротехники знают, что для точного измерения понадобится один вывод сопротивления отсоединить от схемы. Связано это как раз с видом подключения проводника.
Недостатки параллельной цепи
Недостатки параллельных цепей перечислены ниже:
- Дорого строить
- Короткое замыкание может произойти случайно в параллельной проводке и может начаться пожар
- Даже если один из компонентов неисправен, ток все равно может проходить через цепь.
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения “n” одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Свойства резисторов при параллельном подключении
При данном виде соединении скачки напряжения будут одинаковы на всех участках цепи. При этом показатель, обратный суммарному сопротивлению цепи, равен общей величине резисторов.
Обратите внимание! F тока в неразветвленной точке цепи равняется суммарной силе тока на отдельных участках проводника.
Вам это будет интересно Особенности переменного тока
Стандартная формула напряжения
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 – одним концом подключено к R5, а не к узлу. R5 – одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Определение параллельного соединения резисторов
Здравствуйте, уважаемые читатели сайта sesaga.ru. Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается резистор с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.
В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно, подбирают нужное сопротивление.
В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.
Последовательное соединение резисторов.
Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.
В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:
Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.
При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.
Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.
Параллельное соединение резисторов
При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.
При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:
Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:
При включении трех резисторов расчет общего сопротивления будет таким:
Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.
При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.
На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.
Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.
Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!
Это такое соединение, при котором все элементы идут один за одним без разветвлений.
Свойства последовательного соединения
3.Сопротивление по отношению к входным зажимам называется входным сопротивлением и равно сумме сопротивлений участков – Rвх= R1+ R2+ R3;
4. Чем больше сопротивление участка, тем больше на нём падает напряжение-.
Параллельное соединение резисторов
Это такое соединение, при котором все начала элементов соединяются в одну точку, а все концы в другую и к этим точкам подводится напряжение.
Свойства параллельного соединения резистора:
1. Общее напряжение цепи равно напряжению на каждом участке-
3. Чтобы найти входное сопротивление, рассчитывают вначале величину обратную входному сопротивлению
– проводимость (G)
Общая проводимость цепи равна сумме проводимостей на каждом участке.
4.Чем больше сопротивление участка, тем меньше ток, протекающий на нем.
При параллельном соединении двух резисторов формулу входного сопротивления можно преобразовать
1.
2. Если известен общий ток, то можно найти ток ветви, умножив общий ток на сопротивление противоположной ветви и разделить на сумму сопротивлений ;.
1.Являются ли при последовательном соединении резисторов напряжения участков пропорционально сопротивлениям этих участков.
2.Являются ли при параллельном соединении резисторов токи ветвей пропорциональны сопротивлениям этих ветвей.
3.Укажите по какому из приведенных математических выражений нельзя рассчитать входное сопротивление двух параллельно соединенных резисторов.
а) ; б);
в) ; г)
Смешанное соединение резисторов
Пример решения задач
РезисторыR2 и R3 параллельны между собой, и их общее сопротивление R2-3последовательно с R1.
А
; R4-6 = 10 Ом;
;
; R2-3 = 30 Ом
; ;
;
;
;
;
;
;
I=;
U3-6=I∙R3-6=1∙3=3В;
I3=;
I4=I5=I6=;
Cоставим подробное уравнение баланса мощностей для данной схемы. Оно является проверкой правильности решения задачи.
20Вт=20Вт- задача решена верно
Делитель напряжения- это четырёхполюсник, у которого коэффициент передачи меньше единицы.
Рассмотрим Г-образный делитель напряжения:
Чтобы рассчитать коэффициент передачи надо:
1) задать произвольное напряжение на входе;
2) любым способом рассчитать напряжение на выходе;
3) взять их отношения:
Для Г-образного делителя напряжения коэффициент передачи равен отношению выходного сопротивления ко входному.
б) Делитель напряжения с плавной регулировкой (потенциометр)
В нижнем положении движка К = 0. В верхнем положении движка К = 1
Так как в нижнем положении движка Uвых снимается с провода, а в верхнем положении
1) Если нагрузка не подключена делитель работает в режиме холостого хода и зависимость коэффициент передачи от положения движка потенциометра будет линейной.
2) Если подключить нагрузку, то характеристика будет другой: получается параллельное соединение Rн и r и при том же положении движка напряжение участка уменьшается. В крайних точках коэффициент передачи остаётся тем же, поэтому характеристика становиться нелинейной.
Вывод: чтобы при подключении нагрузки характеристика приближалась к линейной нагрузку нужно брать высокоомную.
1.Изменяется ли коэффициент передачи делителя напряжения в пределах 0 ÷ ∞?
2.Укажите среди приведенных математических выражений формулы коэффициента передачи по напряжению Г-образного делителя напряжения.
а) ; б); в); г); д).
3.Являются ли характеристики делителя напряжения с плавной регулировкой линейной, если подключить к делителю нагрузки?
Определение параллельного соединения
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) – это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 – одним концом подключено к R5, а не к узлу. R5 – одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
Параллельное и смешанное соединение резисторов: разные способы подключения сопротивления
Ни одна операция в электронике или электротехнике не обходится без вычисления сопротивления. В этом случае рассматривают только тот участок цепи, в котором находится смешанное соединение резисторов. Инженерам и физикам необходимо понимать то, как именно происходят расчёты в таких схемах. Всего разделяют несколько видов подключения, которые используются в цепях различной сложности.
Последовательное соединение
Выделяют такие способы соединения резисторов: последовательное, параллельное и комбинированное. При последовательном подключении конец первого резистора подключают к началу второго, его часть к третьему. Так действуют со всеми составляющими. То есть все компоненты цепи следуют друг за другом. Через них в таком подключении будет проходить один общий электрический ток. Для таких схем физики применяют формулу, в которой между точками А и В есть только один путь протекания заряженных электронов.
От количества подключённых резисторов зависит сопротивление протекающему электричеству. Чем больше составляющих, тем оно выше. Его рассчитывают по формуле: R общее = R1+R2+…+Rn, где:
- R общее — это сумма всех сопротивлений;
- R1 — первый резистор;
- R2 — второй компонент;
- Rn — последняя составляющая в цепи.
Параллельное подключение
Параллельное соединение подразумевает подключение начал резисторов к одной точке, а концов к другой. Сами компоненты при этом расположены на одинаковом расстоянии друг от друга, а их количество не ограничено. По каждой составляющей электричество протекает отдельно, выбирая один из нескольких путей.
Из-за того, что в цепи находится несколько компонентов и путей прохода тока, сопротивление значительно меньше, чем при последовательном соединении. То есть общая сумма противодействия уменьшается пропорционально увеличению количества составляющих. Формула для определения общей суммы противостояния электричеству: 1/R общее = 1/R1+1/R2+…+1/Rn.
В расчётах общее сопротивление всегда должно быть меньше любого из составляющих цепи. Способ вычисления суммы противостояния для схемы из двух резисторов немного отличается: 1/R общее = (R1 х R2)/(R1+R2). Если в системе у компонентов одинаковые показатели сопротивления, то общее число будет равно половине одного из составляющих.
Смешанный вариант
В смешанном соединении сопротивлений комбинируют последовательную и параллельную схему подключений. В этом случае несколько компонентов соединяют одним способом, а другие — вторым, но все они включены в одну цепь. В физике такой метод соединения называют последовательно-параллельным.
Для вычисления суммы противостояния электричеству схему нужно разбить на мелкие участки, в которых резисторы подключены одинаковым способом. Затем расчёты проводят по алгоритму:
- в цепи с параллельно соединёнными компонентами высчитывают эквивалентное сопротивление;
- после этого высчитывают противостояние на последовательно подключённых участках схемы;
- наглядную иллюстрацию нужно перерисовать, обычно получается цепь с последовательным соединением резисторов;
- рассчитывают сопротивление в новой схеме по одной из двух формул.
Лучше понять методы вычислений поможет пример. Если в схеме всего пять компонентов, они могут располагаться по-разному. Начало первого резистора подключено к точке А, конец — к В. От неё идёт отдельная схема с комбинированным соединением. Вторая и третья составляющие находятся на последовательной линии, четвёртый компонент параллелен им. От конечной точки этой цепи — Г — исходит последний резистор.
Сначала высчитывают сумму сопротивления последовательного участка внутренней схемы: R2+R3. После этого цепь перерисовывают так, чтобы второй и третий компоненты были соединены в один. В результате внутренняя цепь имеет параллельное подключение. Теперь высчитывают её противостояние: (R2,3xR4)/(R2,3+R4). Можно второй раз изобразить полученную цепь.
В схеме будет три резистора, соединённые последовательным методов. Причём средний включает параметры второго, третьего и четвёртого компонента.
Теперь можно узнать общую сумму сопротивлений. Для этого складывают показатели противостояний электричеству первого, пятого и остальных составляющих. Формула будет иметь вид: R1+(R2,3xR4)/(R2,3+R4)+R5. Можно сразу подставить в неё все параметры компонентов.
На практике последовательный и параллельный метод соединения используются редко, ведь в приборах схемы обычно сложные. Поэтому в цепях резисторы часто соединены комбинированным способом. Сопротивление в таких случаях высчитывают пошагово.
Если сразу выводить числа в общую формулу, то можно ошибиться и получить неверные результаты. А это может отрицательно сказаться на работе электрического прибора.
Последовательное соединение схема формула. Последовательное и параллельное соединение
Содержание:Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Напряжение при последовательном соединении
При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.
Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .
Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.
Напряжение при параллельном соединении
При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.
Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.
На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.
В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
2. Делитель токов.
Содержание:Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
В предыдущем конспекте был установлено, что сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R . Этот закон, установленный экспериментально, называется закон Ома (для участка цепи).
Закон Ома для участка цепи : сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника. Прежде всего закон всегда верен для твёрдых и жидких металлических проводников. А также для некоторых других веществ (как правило, твёрдых или жидких).
Потребители электрической энергии (лампочки, резисторы и пр.) могут по-разному соединяться друг с другом в электрической цепи. Д ва основных типа соединения проводников : последовательное и параллельное. А также есть еще два соединения, которые являются редкими: смешанное и мостовое.
Последовательное соединение проводниковПри последовательном соединении проводников конец одного проводника соединится с началом другого проводника, а его конец — с началом третьего и т.д. Например, соединение электрических лампочек в ёлочной гирлянде. При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.
Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: I 1 = I 2 = I .
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений : R 1 + R 2 = R . Потому что при последовательном соединении проводников их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: U 1 = I* R 1 , U 2 = I*R 2 . В таком случае общее напряжение равно U = I ( R 1 + R 2) . Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике : U = U 1 + U 2 .
Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
Для последовательного соединения проводников справедливы законы :1) сила тока во всех проводниках одинакова; 2) напряжение на всём соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Параллельное соединение проводниковПримером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи. А вторым концом к другой точке цепи. Вольтметр, подключенный к этим точкам, покажет напряжение и на проводнике 1, и на проводнике 2. В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U .
При параллельном соединении проводников электрическая цепь разветвляется. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: I = I 1 + I 2 .
В соответствии с законом Ома I = U/R, I 1 = U 1 /R 1 , I 2 = U 2 /R 2 . Отсюда следует: U/R = U 1 /R 1 + U 2 /R 2 , U = U 1 = U 2 , 1/R = 1/R 1 + 1/R 2 Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление г , то их общее сопротивление равно: R = г/2 . Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.
Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно. Они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие суммарной силы тока предельно допустимой силе тока.
Для параллельного соединения проводников справедливы законы:1) напряжение на всех проводниках одинаково; 2) сила тока в месте соединения проводников равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.
Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.
Определения
Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:
- Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
- Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.
На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.
Использование параллельного и последовательного соединения проводников
Термины, применяемые к электрическим цепям
Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.
Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.
Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:
- Внешняя часть цепи, где заряды движутся, увлекаемые полем.
- Внутренняя часть цепи, где заряды движутся против напряженности.
Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:
Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.
Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.
При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.
Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников
Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:
Посчитать сопротивления элементов при последовательном и параллельном соединении
Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:
- При последовательном включении суммируются сопротивления, при параллельном — проводимости:
- Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
- Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
- Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.
У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может. При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.
Пример решения уравнений Кирхгофа
Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:
- Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
- Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.
Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Формула параллельного соединения резисторов — Студопедия
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Рассчет сложных схем соединения резисторов.
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Электродвижущая сила ЭДС
Электродвижущая сила (ЭДС) — в устройстве, осуществляющем принудительное разделение положительных и отрицательных зарядов (генераторе), величина, численно равная разности потенциалов между зажимами генератора при отсутствии тока в его цепи, измеряется в Вольтах.
Источники электромагнитной энергии (генераторы) — устройства, преобразующие энергию любого неэлектрического вида в электрическую. Такими источниками, например, являются:
· генераторы на электростанциях (тепловых, ветровых, атомных, гидростанциях), преобразующие механическую энергию в электрическую;
· гальванические элементы (батареи) и аккумуляторы всех типов, преобразующие химическую энергию в электрическую и т. п.
ЭДС численно равна работе, которую совершают сторонние силы при перемещении единичного положительного заряда внутри источника или сам источник, проводя единичный положительный заряд по замкнутой цепи.
Электродвижущая сила ЭДС Е — скалярная величина, характеризующая способность стороннего поля и индуктированного электрического поля вызывать электрический ток. ЭДС Е численно равна работе (энергии) W в джоулях (Дж), затрачиваемой этим полем на перемещение единицы заряда (1 Кл) из одной точки поля в другую.
Единицей измерения ЭДС является вольт (В). Таким образом, ЭДС равна 1 В, если при перемещении заряда в 1 Кл по замкнутой цепи совершается работа в 1 Дж: [Е] = I Дж/1 Кл = 1 В.
Параллельное и последовательное соединение сопротивлений
Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил. Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой. Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.
Способы подключения и их особенности
Внешний вид резисторов и обозначения в схемахВиды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.
Последовательное соединение
Последовательное подключение — это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего. Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы. То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом. Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.
Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.
Схема последовательного соединения резисторовПараллельное соединение
Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы — во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.
Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом. В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.
Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.
Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.
Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь». А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.
Параллельное соединение резисторовПоследовательно-параллельное соединение
Последовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.
Подведем итог
Подводя итог всему вышеизложенному можно сделать следующие выводы:
- При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления. Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
- При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
- Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
- Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
- Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.
В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки. По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения. А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.
Похожие статьи:Последовательное и параллельное соединение резисторов
Последовательное и параллельное соединение резисторов
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
o Цепь разбивают на участки с только пареллельным или только последовательным соединением. o Вычисляют общее сопротивление для каждого отдельного участка.
o Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
o Если резисторы соединяются последоватеьно — складывать.
o Если резисторы соединяются параллельно — использовать условное обозначение «||». o Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
Рассчитайте сопротивление трех параллельных резисторов. Параллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушек
На практике часто встречается задача определения сопротивления проводников и резисторов при разных способах подключения. В статье обсуждается, как рассчитывается сопротивление, и некоторые другие технические вопросы.
Сопротивление проводника
Все проводники обладают способностью препятствовать прохождению электрического тока, это называется электрическим сопротивлением R, оно измеряется в омах.Это главное свойство проводниковых материалов.
Для проведения электрических расчетов применяется удельное сопротивление — ρ Ом · м / мм2. Все металлы являются хорошими проводниками, медь и алюминий используются чаще всего, а железо — гораздо реже. Лучший проводник — серебро, его используют в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.
При расчете сопротивления используется известная из школьного курса физики формула:
R = ρ · l / S, S — площадь сечения; l — длина.
Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.
и нагревательный провод
Для практических расчетов режимов работы проводников используется понятие плотности тока — δ А / мм 2, она рассчитывается по формуле:
δ = I / S, I — ток , S — поперечное сечение.
Ток, проходящий через проводник, нагревает его. Чем больше δ, тем сильнее нагревается проводник.Для проводов и кабелей разработаны нормы допустимой плотности, которые приведены в. Для жил нагревательных приборов существуют свои нормативы плотности тока.
Если плотность δ выше допустимой, проводник может разрушиться, например, если кабель перегреется, его изоляция разрушится.
Правила регулируют расчет кондукторов для отопления.
Способы подключения проводов
Любой проводник гораздо удобнее изобразить на схемах как электрическое сопротивление R, тогда их будет легче читать и анализировать.Подключить сопротивления можно всего тремя способами. Первый способ самый простой — последовательное подключение.
На фото видно, что импеданс: R = R 1 + R 2 + R 3.
Второй способ более сложный — параллельное подключение. Расчет сопротивления при параллельном включении выполняется поэтапно. Вычислите общую проводимость G = 1 / R, а затем импеданс R = 1 / G.
Вы можете сделать иначе, сначала рассчитать общее сопротивление с R1 и R2, затем повторить операцию и найти R.
Третий способ подключения самый сложный — смешанное подключение, то есть присутствуют все рассмотренные варианты. Схема представлена на фото.
Для расчета этой схемы ее следует упростить; для этого резисторы R2 и R3 заменяются на один R2.3. Получается простая схема.
R2,3,4 = R2,3 · R4 / (R2,3 + R4).
Схема становится еще проще, остаются резисторы с последовательным включением.В более сложных ситуациях используется тот же метод преобразования.
Типы проводов
В электронной технике на производстве проводники представляют собой тонкие полоски медной фольги. Из-за небольшой длины сопротивления у них мало, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном подключении уменьшается из-за увеличения поперечного сечения.
Большое сечение жил — это обмоточные провода. Доступны разного диаметра — от 0.02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей изготавливаются медные стержни прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельных меньшего размера.
К особому сечению проводников относятся провода и кабели, промышленность предоставляет самый широкий выбор марок для самых разных нужд. Часто приходится заменять один кабель несколькими меньшими отрезками. Причины тому самые разные, например, кабель сечением 240 мм 2 очень сложно прокладывать на трассе с крутыми изгибами.Его заменяют на 2 × 120 мм 2, и проблема решена.
Расчет проводов на обогрев
Проводник нагревается протекающим током, если его температура превышает допустимую, происходит разрушение изоляции. ПУЭ предусматривает расчет токопроводов на обогрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. Согласно этим данным, рекомендуемый проводник или кабель выбирается из таблиц в OLC).
На практике бывают ситуации, когда нагрузка на существующий кабель сильно увеличивается. Выхода два — заменить кабель на другой, может быть дорого, или проложить еще один параллельно ему, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном включении уменьшается, следовательно, уменьшается тепловыделение.
Чтобы правильно подобрать сечение второго кабеля, воспользуйтесь таблицами PES, важно не ошибиться с определением его рабочего тока.В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитывать сопротивление при параллельном подключении двух кабелей, чтобы более точно определить их теплоотдачу.
Расчет проводов на потерю напряжения
При расположении потребителя R n на большом расстоянии L от источника энергии U 1 на проводах линии остается достаточно большое количество. К потребителю R n поступает напряжение U 2 значительно ниже начального U 1.Практически в качестве нагрузки выступает различное электрооборудование, подключенное к линии параллельно.
Чтобы решить эту проблему, рассчитайте сопротивление, когда все оборудование подключено параллельно, и сопротивление нагрузки R n. Далее определяем сопротивление проводов линии.
R l = ρ · 2L / S,
Здесь S — сечение провода, мм 2.
В этой теме можно привести множество примеров из нашей повседневной жизни, касающихся параллельного соединения сопротивлений.Параллельное соединение одинаковых сопротивлений — яркий пример подключения люстры с n-м числом ламп и с одинаковым сопротивлением для каждой лампы \ рис.1 \.
Если предположить, что в люстре, состоящей из нескольких ламп \ с одинаковым сопротивлением \ одна лампа перегорела, а другую мощность заменили лампой другой мощности — в этом случае подключение люстры будет иметь вид параллельное соединение с разным сопротивлением.
Какие еще примеры можно привести из практики — с параллельным соединением сопротивлений? Допустим, вы подключили в своей квартире три бытовых электроприбора через удлинитель:
- плита электрическая; Стиральная машина
- ;
- телевидение.
Природа этого соединения будет , сопротивление параллельного соединения разное по величине. То есть для каждого прибора сопротивление имеет свое значение.
Расчет сопротивления при параллельном подключении
Как уже было сказано, при параллельном включении проводятся расчеты сопротивлений:
- с таким же сопротивлением;
- с разным сопротивлением
, а также выполнены расчеты сопротивлений для смешанного включения резисторов, при последовательном и параллельном включении \\ для одной цепи \\.Расчет сопротивления для смешанных подключений резисторов, больше подходит для различных блок-схем:
- аудиотехника;
- видеооборудование.
К этой теме расчеты для смешанных соединений отношения не имеют.
Параллельное соединение одинаковых сопротивлений
Представьте себе параллельное соединение, например, трех равных по величине сопротивлений \\ рис.2 \\, где R1 = R2 = R3 = 36 Ом \ сопротивление лампы накаливания мощностью 95 Вт. Напряжение 220 В подключается к двум узловым точкам \ A, B \.Необходимо рассчитать суммарное сопротивление всех трех ламп.
Для расчета общего сопротивления \ R total \ нам нужно 36 Ом разделить на количество сопротивлений. Решение простое, Rtotal = 12 Ом. То есть формула для расчета таких вычислений выглядит так:
R итого = R / n
Параллельное соединение разных сопротивлений
Допустим, мы берем выборочно три резистора, сопротивление:
- R1 = 20 Ом;
- R2 = 40 Ом;
- R3 = 10 Ом.
Необходимо определить полное сопротивление резисторов при параллельном включении. Для этого расчета мы используем формулу:
1 / R всего = 1 / R1 + 1 / R2 + 1 / R3.
Подставьте значения в формулу:
1 / R всего = 1/20 + 1/40 + 1/10 = 7/40 = 0,18
получаем: Rtotal = 1 / 0,18 = 5,5 Ом.
В каждой цепи есть резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: фиксированные и переменные.При разработке любой электрической схемы и ремонте электронных изделий часто приходится использовать резистор, имеющий необходимый номинал.
Несмотря на то, что для резисторов существуют различные значения , может случиться так, что не удастся найти нужный или даже один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать использование последовательного и параллельного подключения. Прочитав эту статью, вы узнаете об особенностях расчета и выбора различных значений сопротивления.
Часто при изготовлении любого устройства используют резисторы, которые подключаются по последовательной схеме. Эффект от использования такого варианта сборки сводится к увеличению общего сопротивления цепи. Для этого варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если сборка деталей выполняется по параллельной схеме, здесь нужно рассчитать сопротивление по формулам ниже.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача уменьшить общее сопротивление, и, кроме того, увеличить мощность для группы элементов, соединенных параллельно, которая должна быть больше, чем при их раздельном соединении.
Расчет сопротивления
В случае соединения частей между собой по параллельной схеме для расчета общего сопротивления будет использоваться следующая формула:
R (всего) = 1 / (1 / R1 + 1 / R2 + 1 / R3 + 1 / Rn).
- R1- R3 и Rn — резисторы, включенные параллельно.
Причем, если схема создана на основе всего двух элементов, то для определения общего номинального сопротивления используйте следующую формулу:
R (всего) = R1 * R2 / R1 + R2.
- R (total) — полное сопротивление;
- R1 и R2 — резисторы, включенные параллельно.
Универсальная схема расчета
Применительно к радиотехнике следует обратить внимание на одно важное правило: если элементы соединены между собой по параллельной схеме имеют одинаковый показатель , то для расчета общего номинала необходимо общее значение разделить на количество подключаемых узлов:
- R (total) — суммарное значение сопротивления;
- R — номинал резистора, включенного параллельно;
- n — количество подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно должен быть меньше по сравнению с номиналом любого элемента, подключенного к цепи.
Пример расчета
Для большей наглядности мы можем рассмотреть следующий пример: предположим, что у нас есть три резистора, номиналы которых составляют соответственно 100, 150 и 30 Ом. Если мы используем первую формулу для определения общей стоимости, мы получим следующее:
R (всего) = 1 / (1/100 + 1/150 + 1/30) = 1 / (0.01 + 0,007 + 0,03) = 1 / 0,047 = 21,28 Ом.
Если произвести несложные вычисления, можно получить следующее: для схемы, состоящей из трех частей, где наименьшее значение сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального номинала в цепочке почти на 30%.
Важные нюансы
Обычно для резисторов параллельное соединение применяется, когда стоит задача создать сопротивление большей мощности.Для ее решения потребуются резисторы, которые должны иметь одинаковое сопротивление и мощность. С помощью этой опции вы можете определить общую мощность следующим образом: : мощность одного элемента должна быть умножена на общее количество всех резисторов, которые составляют цепь, соединенную друг с другом в соответствии с параллельной цепью.
Допустим, если мы используем пять резисторов номиналом 100 Ом и мощностью каждого 1 Вт, которые соединены между собой по параллельной схеме, то общее сопротивление будет равно 20 Ом, а мощность будет 5 Вт.
Если взять те же резисторы, но подключить их по последовательной схеме, то конечная мощность будет 5 Вт, а общий номинал будет равен 500 Ом.
Заключение
Параллельная разводка резисторов очень востребована по той причине, что часто возникает задача создания такого номинала, которого нельзя достичь простым параллельным подключением. При этом процедура вычисления этого параметра довольно сложна, где необходимо учитывать разные параметры.
Здесь важную роль играет не только количество подключаемых элементов, но и рабочие параметры резисторов — в первую очередь сопротивление и мощность. Если один из подключаемых элементов будет иметь несоответствующий индикатор, то это не решит эффективно проблему создания необходимого номинала в цепи.
Параллельное соединение резисторов — один из двух типов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.Часто или параллельно с целью создания более сложных электронных схем.
Схема параллельного подключения показана на рисунке ниже. При параллельном соединении резисторов напряжение на всех резисторах будет одинаковым, а ток, протекающий через них, будет пропорционален их сопротивлению:
Формула для параллельного включения резисторов
Суммарное сопротивление нескольких параллельно включенных резисторов определяется по следующей формуле:
Ток, протекающий через одиночный резистор, согласно, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства возникла необходимость в установке резистора сопротивлением 8 Ом.Если просмотреть весь номинальный ряд стандартных номиналов резисторов, то мы увидим, что в нем нет резистора с сопротивлением 8 Ом.
Выход из этой ситуации — использование двух параллельно включенных резисторов. Эквивалентное значение сопротивления для двух параллельно включенных резисторов рассчитывается следующим образом:
Это уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. Следовательно, когда R = 8 Ом, R1 и R2 должны иметь значение 2 × 8 = 16 Ом.
Теперь проверим, рассчитав полное сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, подключив параллельно два резистора по 16 Ом.
Пример расчета № 2
Найдите полное сопротивление R трех параллельно соединенных резисторов:
Суммарное сопротивление R рассчитывается по формуле:
Этот метод расчета можно использовать для расчета любого количества отдельных сопротивлений, подключенных параллельно.
Один важный момент, который необходимо помнить при расчете параллельно соединенных резисторов, заключается в том, что полное сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать схемы подключения комплексных резисторов
Более сложные соединения резисторов можно рассчитать путем систематической группировки резисторов. На рисунке ниже нужно рассчитать полное сопротивление цепи, состоящей из трех резисторов:
Для упрощения расчетов сначала сгруппируем резисторы по параллельному и последовательному включению.
Резисторы R2 и R3 включены последовательно (группа 2). Они в свою очередь включены параллельно резистору R1 (группа 1).
Последовательное соединение резисторов группы 2 рассчитывается как сумма сопротивлений R2 и R3:
В результате упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей цепи можно рассчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить по законам Кирхгофа.
Ток, протекающий в цепи параллельно включенных резисторов
Полный ток I, протекающий в цепи параллельных резисторов, равен сумме отдельных токов, протекающих во всех параллельных ветвях, и ток в одной ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, на каждый резистор подается одинаковое напряжение. А поскольку значение сопротивления в параллельной цепи может быть разным, то величина тока, протекающего через каждый резистор, также будет отличаться (как определено законом Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, протекающий через каждый из резисторов (I1 и I2), будет отличаться друг от друга, поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который входит в цепь в точке «A», должен выходить из цепи в точке «B».
Первое правило Кирхгофа гласит: «Полный ток, исходящий из цепи, равен току, входящему в цепь.«
Таким образом, протекающий полный ток в цепи можно определить как:
Затем, используя закон Ома, мы можем вычислить ток, протекающий через каждый резистор:
Ток протекающий через R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток протекающий через R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить с помощью закона Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0.8 мА (то же)
, где 15 кОм — общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в заключение следует отметить, что большинство современных резисторов маркированы цветными полосами и их назначение можно встретить.
Параллельное соединение резисторов — онлайн калькулятор
Для быстрого расчета общего сопротивления двух или более резисторов, соединенных параллельно, вы можете использовать следующий онлайн-калькулятор:
Суммировать
Когда два или более резистора соединены так, что оба вывода одного резистора подключены к соответствующим выводам другого резистора или резисторов, они считаются подключенными параллельно друг другу.Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга в зависимости от сопротивления каждого резистора.
Эквивалент или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, включенного в параллельное соединение.
Проверьте правильность приведенных здесь формул в простом эксперименте.
Берем два резистора МЛТ-2 на 3 и 47 Ом и соедините их последовательно.Затем измеряем полное сопротивление получившейся цепи цифровым мультиметром. Как видим, он равен сумме сопротивлений резисторов, входящих в эту цепочку.
Измерение полного сопротивления при последовательном включении
Теперь мы подключаем наши резисторы параллельно и измеряем их полное сопротивление.
Параллельное измерение сопротивления
Как видите, результирующее сопротивление (2,9 Ом) меньше наименьшего (3 Ом) входящего в цепь.Это приводит к другому хорошо известному правилу, которое можно применить на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, включенного в эту цепь.
Что еще нужно учитывать при подключении резисторов?
В первую очередь обязательно учитывается их номинальная мощность . Например, нам нужно подобрать на замену резистор на 100 Ом и мощность на 1 Вт .Возьмите два резистора по 50 Ом и соедините их последовательно. Какова рассеиваемая мощность этих двух резисторов?
Так как через последовательно соединенные резисторы протекают одни и те же резисторы. Округ Колумбия. (допустим, 0,1 А ), а сопротивление каждого из них составляет 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В итоге каждый из них будет выделяться мощностью 0,5 Вт. По итогу это будет тот же 1 W .
Этот пример довольно грубый. Поэтому в случае сомнений стоит брать резисторы с запасом мощности.
Подробнее о рассеиваемой мощности резистора.
Во-вторых, для подключения следует использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это всего лишь рекомендация.
17,5 Параллельные резисторы | Электрические цепи
17,5 Параллельные резисторы (ЭСАФК)
Когда мы добавляем резисторы параллельно цепи:
-
Есть больше путей для прохождения тока, что обеспечивает разделение тока на разные Пути .
-
Напряжение на резисторах то же . Напряжение на АКБ в цепи равно напряжению на каждом из параллельных резисторов:
\ [{V} _ {\ text {battery}} = {V} _ {1} = {V} _ {2} = {V} _ {3} \ ldots \] -
Сопротивление току уменьшается . Полное сопротивление \ ({R} _ {P} \) дается по:
\ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]
При параллельном подключении резисторов начальная и конечная точки для всех резисторов одинаковы.Эти точки имеют одинаковую потенциальную энергию, поэтому разность потенциалов между ними одинакова, независимо от того, что вставьте между ними. У вас может быть один, два или несколько резисторов между двумя точками, разность потенциалов будет не изменить. Вы можете игнорировать любые компоненты, находящиеся между двумя точками в цепи, при вычислении разницы. между двумя точками.
Посмотрите на следующие принципиальные схемы. Аккумулятор во всех корпусах одинаковый, меняет только резисторы добавляются между точками, отмеченными черными точками.Если бы мы измерили разность потенциалов между две точки в этих схемах, мы получим одинаковый ответ для всех трех случаев.
Давайте посмотрим на два параллельно подключенных резистора более внимательно. Когда вы создаете схему, вы используете провода, и вы можете думаю, что измерение напряжения в разных местах на проводах будет иметь значение. Это неправда. В Измерение разности потенциалов или напряжения будет отличаться только в том случае, если вы измеряете другой набор компонентов.Все точки на проводах, между которыми нет компонентов цепи, дадут вам одинаковые измерения.
Все три измерения, показанные на рисунке ниже (т. Е. A – B, C – D и E – F), дадут вам такое же напряжение. Различные точки измерения слева не имеют компонентов между собой, поэтому нет изменение потенциальной энергии. То же самое относится и к разным точкам справа. Когда вы измеряете разность потенциалов между точками слева и справа вы получите одинаковый ответ.
Рабочий пример 7: Напряжения I
Рассмотрим принципиальную схему:
Какое напряжение на резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батареей и одним резистором. Нам известно напряжение на батарее. Мы хотим найти это напряжение на резисторе.
\ [{V} _ {\ text {battery}} = \ text {2} \ text {V} \]Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех остальных цепях. компоненты.
\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]Есть только один другой компонент схемы — резистор.
\ [{V} _ {\ text {total}} = {V} _ {1} \]Это означает, что напряжение на батарее такое же, как напряжение на резисторе.
\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} = {V} _ {1} \\ {V} _ {1} & = \ text {2} \ text {V} \ end {выровнять *}Рабочий пример 8: Напряжения II
Рассмотрим эту схему:
Какое напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батареей и двумя резисторами.Мы знаем напряжение на батарее и один из резисторы. Мы хотим найти это напряжение на резисторе.
\ begin {align *} {V} _ {\ text {battery}} & = \ text {2} \ text {V} \\ {V} _ {B} & = \ text {1} \ text {V} \ end {выровнять *}Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех остальных цепях. компоненты, которые находятся последовательно.
\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]Общее напряжение в цепи — это сумма напряжений на отдельных резисторах
\ [{V} _ {\ text {total}} = {V} _ {A} + {V} _ {B} \]Использование зависимости между напряжением на батарее и общим напряжением на резисторах
\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\\\ {V} _ {\ text {battery}} & = {V} _ {1} + {V} _ {\ text {resistor}} \\ \ text {2} \ text {V} & = {V} _ {1} + \ text {1} \ text {V} \\ {V} _ {1} & = \ text {1} \ text {V} \ end {выровнять *}Рабочий пример 9: Напряжения III
Рассмотрим принципиальную схему:
Какое напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батареей и тремя резисторами.Мы знаем напряжение на батарее и двух резисторы. Мы хотим найти это напряжение на неизвестном резисторе.
\ begin {align *} {V} _ {\ text {battery}} & = \ text {7} \ text {V} \\ {V} _ {\ text {известное}} & = {V} _ {A} + {V} _ {C} \\ & = \ текст {1} \ текст {V} + \ текст {4} \ текст {V} \ end {выровнять *}Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех остальных цепях. компоненты, которые находятся последовательно.
\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]Общее напряжение в цепи — это сумма напряжений на отдельных резисторах
\ [{V} _ {\ text {total}} = {V} _ {B} + {V} _ {\ text {known}} \]Использование зависимости между напряжением на батарее и общим напряжением на резисторах
\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\ {V} _ {\ text {battery}} & = {V} _ {B} + {V} _ {\ text {known}} \\ \ text {7} \ text {V} & = {V} _ {B} + \ text {5} \ text {V} \\ {V} _ {B} & = \ text {2} \ text {V} \ end {выровнять *}Рабочий пример 10: Напряжения IV
Рассмотрим принципиальную схему:
Какое напряжение на параллельной комбинации резисторов в показанной цепи? Подсказка: остальная часть Схема такая же, как и в предыдущей задаче.
Быстрый ответ
Схема такая же, как в предыдущем примере, и мы знаем, что разница напряжений между двумя точками в цепь не зависит от того, что находится между ними, поэтому ответ такой же, как указано выше \ ({V} _ {\ text {parallel}} = \ text {2} \ text {V} \).
Проверьте, что у вас есть и единицы — длинный ответ
У нас есть схема с батареей и пятью резисторами (два последовательно и три параллельно).Мы знаем напряжение на батарее и двух резисторах. Мы хотим найти это напряжение на параллельном резисторы, \ ({V} _ {\ text {parallel}} \).
\ begin {align *} {V} _ {\ text {battery}} = \ text {7} \ text {V} \\ {V} _ {\ text {известное}} = \ text {1} \ text {V} + \ text {4} \ text {V} \ end {выровнять *}Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех остальных цепях. компоненты.
\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]Напряжения складываются только алгебраически для последовательно соединенных компонентов. Параллельно подключенные резисторы можно рассматривать как один компонент, который включен последовательно с другими компонентами, а затем могут быть добавлены напряжения.
\ [{V} _ {\ text {total}} = {V} _ {\ text {parallel}} + {V} _ {\ text {известное}} \]Использование зависимости между напряжением на батарее и общим напряжением на резисторах
\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\ {V} _ {\ text {battery}} & = {V} _ {\ text {parallel}} + {V} _ {\ text {known}} \\ \ text {7} \ text {V} & = {V} _ {\ text {parallel}} + \ text {5} \ text {V} \\ {V} _ {\ text {parallel}} & = \ text {2} \ text {V} \ end {выровнять *} temp textВ отличие от последовательного случая, когда мы добавляем резисторы параллельно, мы создаем еще путей, вдоль какой ток может течь.Таким образом мы уменьшаем на общее сопротивление цепи на !
Взгляните на диаграмму ниже. Слева у нас та же схема, что и в предыдущем разделе с аккумулятором и резистор. Амперметр показывает ток \ (\ text {1} \) \ (\ text {A} \). Справа мы добавили второй резистор параллельно первому резистору. Это увеличило количество путей (ответвлений), по которым может пройти заряд. по цепи — общее сопротивление уменьшилось.Вы можете видеть, что ток в цепи имеет повысился. Также обратите внимание, что ток в разных ветвях может быть разным.
Общее сопротивление ряда параллельных резисторов НЕ является суммой отдельных сопротивлений, как общее сопротивление уменьшается с увеличением количества путей для тока. Дано полное сопротивление для параллельных резисторов. по:
\ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]Давайте рассмотрим случай, когда у нас есть два резистора, включенных параллельно, и выясним, каким будет конечное сопротивление.Эта ситуация показана на диаграмме ниже:
Применяя формулу для общего сопротивления, получаем:
\ begin {align *} \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \\ & \ text {Резисторов всего два} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} \\ & \ text {Добавить дроби} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} \ times \ frac {{R} _ {2}} {{R} _ {2 }} + \ frac {1} {{R} _ {2}} \ times \ frac {{R} _ {1}} {{R} _ {1}} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2}} {{R} _ {1} {R} _ {2}} + \ frac {{R} _ {1}} {{R} _ {1} {R} _ {2}} \\ & \ text {Переставить} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} + {R} _ {1}} {{R} _ {1} {R} _ {2} } \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2} } \\ {R} _ {P} & = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ end {выровнять *}Для любых двух параллельно включенных резисторов мы теперь знаем, что
\ [{R} _ {P} = \ frac {\ text {произведение сопротивлений}} {\ text {сумма сопротивлений}} = \ frac {{R} _ {1} {R} _ {2}} { {R} _ {1} + {R} _ {2}} \]Делители тока
Цель
Проверьте, что происходит с током и напряжением в последовательных цепях при добавлении дополнительных резисторов.
Аппарат
-
Аккумулятор
-
Вольтметр
-
Амперметр
-
Провода
-
Резисторы
Метод
-
Подключите каждую цепь, показанную ниже
-
Измерьте напряжение на каждом резисторе в цепи.
-
Измерьте ток до и после каждого резистора в цепи, а также до и после параллельного ветви.
Результаты и выводы
-
Сравните токи через отдельные резисторы между собой.
-
Сравните сумму токов через отдельные резисторы с током до параллельного ветви.
-
Сравните различные измерения напряжения на параллельных резисторах.
Рабочий пример 11: Параллельные резисторы I
Цепь содержит два параллельно включенных резистора. Резисторы имеют значения сопротивления \ (\ text {15} \) \ (\ text {Ω} \) и \ (\ text {7} \) \ (\ text {Ω} \).
Какое полное сопротивление в цепи?
Проанализировать вопрос
Нам говорят, что резисторы в цепи включены в параллельную цепь и что нам нужно рассчитать общую сопротивление.Значения двух резисторов указаны в правильных единицах, Ом.
Применять соответствующие принципы
Было показано, что полное сопротивление резисторов, включенных параллельно, является произведением сопротивлений, деленных на сумма. Мы можем использовать
\ [{R} _ {P} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \]У нас всего два резистора, и теперь мы резисторы. {2}} {\ text {22} \ text {Ω}} \\ & = \ текст {4,77} \ текст {Ω} \ end {выровнять *}
Цитировать окончательный результат
Полное сопротивление параллельно включенных резисторов \ (\ text {4,77} \) \ (\ text {Ω} \)
Рабочий пример 12: Параллельные резисторы II
Мы добавляем третий параллельный резистор в конфигурацию (настройку) в предыдущем примере.Дополнительные резистор имеет сопротивление \ (\ text {3} \) \ (\ text {Ω} \).
Какое полное сопротивление в цепи?
Проанализировать вопрос
Нам говорят, что резисторы в цепи включены в параллельную цепь и что нам нужно рассчитать общую сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Применять соответствующие принципы
Общее сопротивление резисторов, включенных параллельно, составляет
. \ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]У нас есть три резистора, и теперь мы резисторы.В данном случае это:
\ begin {align *} \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \\ & \ text {есть три резистора} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1 } {{R} _ {3}} \\ & \ text {добавить дроби} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} \ times \ frac {{R} _ {2} {R} _ {3}} {{R} _ {2} {R} _ {3}} + \ frac {1} {{R} _ {2}} \ times \ frac {{R} _ {1} {R} _ {3}} {{R} _ {1} {R} _ {3}} + \ frac {1} {{R} _ {3} } \ times \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} {R} _ {2}} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} {R} _ {3}} {{R} _ {1} {R} _ {2} { R} _ {3}} + \ frac {{R} _ {1} {R} _ {3}} {{R} _ {1} {R} _ {2} {R} _ {3}} + \ frac {{R} _ { 1} {R} _ {2}} {{R} _ {1} {R} _ {2} {R} _ {3}} \\ & \ text {переставить} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} {R} _ {3} + {R} _ {1} {R} _ {3} + { R} _ {2} {R} _ {3}} {{R} _ {1} {R} _ {2} {R} _ {3}} \\ {R} _ {P} & = \ frac {{R} _ {1} {R} _ {2} {R} _ {3}} {{R} _ {2} {R} _ {3} + {R} _ {1} {R} _ {3} + {R} _ {2} {R} _ {3}} \\ {R} _ {P} & = \ frac {\ left (\ text {15} \ text {Ω} \ right) \ left (\ text {7} \ text {Ω} \ right) \ left (\ text {3} \ text {Ω} \ right)} {\ left (\ text {7} \ text {Ω} \ right) \ left (\ text {3} \ text {Ω} \ right) + \ left (\ text {15} \ text {Ω} \ right) \ left (\ text {3} \ text {Ω} \ right) + \ left (\ text {7} \ text { Ω} \ right) \ left (\ text {15} \ text {Ω} \ right)} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {21 {\ Omega} ^ {2} + 45 {\ Omega} ^ {2} + 105 {\ Omega} ^ { 2}} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {171 {\ Omega} ^ {2}} \\ {R} _ {P} & = \ text {1,84} \ text {Ω} \ end {выровнять *}Цитировать окончательный результат
Полное сопротивление параллельно включенных резисторов \ (\ text {1,84} \) \ (\ text {Ω} \)
При расчете сопротивления для сложных конфигураций резисторов вы можете начать с любой комбинации двух резисторы (последовательно или параллельно) и рассчитайте их полное сопротивление.Затем вы можете заменить их одним резистор с рассчитанным вами полным сопротивлением. Теперь используйте этот новый резистор в сочетании с любым другим. резистор и повторяйте процесс, пока не останется только один резистор. В приведенном выше примере мы могли бы просто иметь использовали ответ из первого примера параллельно с новым резистором, и мы получили бы тот же ответ.
Рабочий пример 13: Параллельные резисторы III
Мы добавляем третий параллельный резистор к первой конфигурации (настройке), работающей параллельно.Дополнительные резистор имеет сопротивление \ (\ text {3} \) \ (\ text {Ω} \)
Какое полное сопротивление в цепи?
Проанализировать вопрос
Нам говорят, что резисторы в цепи включены в параллельную цепь и что нам нужно рассчитать общую сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Применять соответствующие принципы
Мы можем поменять местами резисторы, не меняя схему:
Мы уже рассчитали, что полное сопротивление двух резисторов в пунктирной рамке равно \ (\ text {4,77} \) \ (\ текст {Ω} \). {2}} {\ text {11,77} \ Omega} \\ & = \ текст {1,84} \ текст {Ω} \ end {выровнять *}
Цитировать окончательный результат
Полное сопротивление параллельно включенных резисторов равно \ (\ text {1,84} \) \ (\ text {Ω} \).Это тоже самое Результат как когда мы сложили сразу все три резистора.
Сопротивление
Учебное упражнение 17.1Как называется единица сопротивления и каков ее символ?
Решение пока недоступно
Объясните, что происходит с общим сопротивлением цепи, когда резисторы добавляются последовательно?
Решение пока недоступно
Объясните, что происходит с общим сопротивлением цепи, когда резисторы добавляются параллельно?
Решение пока недоступно
Почему батарейки разряжаются?
Решение пока недоступно
Серияи параллельные схемы — Обучение — ScienceFlip
Серия и параллельные схемы — Learn
Последовательная цепь имеет только один путь для прохождения электрического тока.Электрические компоненты подключаются друг за другом. Если один свет сломается или выключатель разомкнут в последовательной цепи, остальные огни выключатся, так как нет полной цепи. По мере того, как в последовательную цепь добавляется больше источников света, свет становится тусклее.
Параллельная цепь содержит более одного пути для прохождения электрического тока. Если одна лампочка гаснет или размыкается выключатель, ток может продолжать течь по другому пути. Параллельные схемы позволяют включать и выключать отдельные компоненты, не влияя на другие компоненты.Добавление или удаление световых глобусов не влияет на яркость каждого глобуса.
Когда схема содержит более одного резистора, одного закона Ома недостаточно для расчета протекающего тока и разности потенциалов на каждом резисторе. Цепи с более чем одним резистором необходимо анализировать по частям. Расчеты также будут зависеть от того, включена ли цепь последовательно или параллельно.
Анализ последовательных цепей
При последовательном соединении резисторов применяются следующие правила:
- Ток через каждый резистор одинаков.
- Сумма разностей потенциалов на каждом резисторе равна разности потенциалов (напряжению), подаваемой на всю цепь. Это также известно как закон напряжения Кирхгофа .
- Общее сопротивление цепи равно сумме отдельных сопротивлений. Это демонстрируется следующим уравнением и известно как эквивалентное эффективное сопротивление : .
Анализ параллельных цепей
При параллельном подключении резисторов применяются следующие правила:
- Напряжение на каждом резисторе одинаковое.
- Ток распределяется между резисторами. Это также известно как действующий закон Кирхгофа .
- Обратное полное сопротивление цепи равно сумме обратных сопротивлений отдельных сопротивлений. Эффективное сопротивление , эквивалентное параллельной цепи, определяется по формуле:
Сложные проблемы могут включать цепи, которые имеют как последовательные, так и параллельные участки. В этих случаях лучше всего сначала разобраться с параллельными участками, а затем с последовательными.
Пример 1: Последовательная цепь:
а) Рассчитайте эффективное эквивалентное сопротивление цепи:
б) Рассчитайте ток, протекающий по цепи:
c) Рассчитайте разность потенциалов на:
Ответы:
a) Использование:
б) Использование и полное сопротивление цепи:
c) Использование
(используя абсолютное значение из части b)
Пример 2: Параллельная цепь:
а) Рассчитайте эффективное эквивалентное сопротивление цепи:
б) Рассчитайте полный ток, протекающий по цепи:
c) Какова разность потенциалов:
г) Какой ток через
Ответы:
a) Использование:
б) Использование и полное сопротивление цепи:
c) Поскольку это простая параллельная цепь, разность потенциалов на и будет такой же и равна разности потенциалов, подаваемой в цепь:
Следовательно, разность потенциалов на
г) Использование
Пример 3: Сложные схемы (содержащие последовательные и параллельные секции)
а) Рассчитайте эффективное эквивалентное сопротивление цепи:
б) Рассчитайте полный ток, протекающий по цепи:
c) Какова разность потенциалов на каждом резисторе?
г) Какой ток через каждый резистор?
Ответы:
a) Сначала определяется эквивалентное эффективное сопротивление параллельной секции, а затем добавляется к другим последовательным компонентам:
б) Использование и полное сопротивление цепи:
c) Использование и сопротивление для каждого последовательного компонента или параллельной секции:
г) Используя закон Ома:
Если сложить и получим, что подтверждает действующий закон Кирхгофа.
Альтернативный текст Electrotech
Ниже приведены информация и вопросы по параллельным цепям.
Инструкции:
Для вопросов с несколькими вариантами ответов:
- выберите правильный ответ
- запишите свой ответ.
По вопросам расчета:
- вычислить неизвестное значение
- укажите соответствующий блок
- запишите свой ответ.
Примечание:
- Вы можете распечатать эту страницу и написать на ней свои ответы.
- Вы можете использовать калькулятор.
1. Какое напряжение приложено к каждому из резисторов в параллельной цепи?
- На резистор 1 (R1) подается наибольшее напряжение.
- На резистор 2 (R2) подается наибольшее напряжение.
- На резистор 1 и резистор 2 подается одинаковое напряжение.
В параллельной схеме каждый резистор подключен непосредственно к источнику напряжения, поэтому напряжение на каждом резисторе одинаковое, как показано на следующей диаграмме.
2. Какое из следующих утверждений отражает действующий закон Кирхгофа?
- Ток на выходе из источника питания больше, чем ток возврата.
- Ток на выходе из источника питания меньше обратного.
- Ток на выходе из источника равен обратному току.
Ток, протекающий от источника напряжения, всегда равен величине тока, возвращающегося к источнику напряжения, как показано на следующей диаграмме.
3. Как ток, протекающий от источника напряжения, будет проходить через каждый из резисторов?
- Наибольший ток будет протекать через резистор 1 (R1).
- Наибольший ток будет проходить через резистор 2 (R2).
- Такое же количество протекает через резистор 1 и резистор 2.
Ток от источника напряжения разделяется и проходит через каждый из резисторов.
Наибольший ток будет проходить через R1. Это связано с тем, что R1 имеет наименьшее значение сопротивления и, следовательно, наименьшее сопротивление протеканию тока, как показано на следующей диаграмме.
4.Рассчитайте ток, протекающий через R3 в этой цепи.
Общий ток, протекающий в параллельной цепи, равен сумме токов, протекающих через каждый резистор. Это можно представить формулой:
5. Что произойдет с общим сопротивлением параллельной цепи, если параллельно добавить дополнительный резистор?
- Общее сопротивление увеличивается.
- Общее сопротивление уменьшается.
- Общее сопротивление осталось прежним.
Добавляя еще один резистор параллельно, мы обеспечиваем дополнительный путь для прохождения тока. Следовательно, ток от источника напряжения увеличится. Увеличение тока от источника может произойти только потому, что общее сопротивление уменьшилось, как показано на следующей диаграмме.
6. По какой формуле определяется полное сопротивление параллельной цепи?
- RT = R1 + R2 + R3
- 1 / RT = 1 / R1 + 1 / R2 + 1 / R3
- RT = R1 x R2 x R3
- 1 / RT = 1 / R1x 1 / R2 x 1 / R3
Приведенная ниже формула является одной из нескольких формул, которые можно использовать для расчета общего сопротивления параллельной цепи.Эту формулу можно использовать для любого количества резисторов, и она действительна независимо от того, одинаковы или различаются каждое отдельное значение сопротивления.
7. Рассчитайте полное сопротивление этой цепи
На следующей схеме показан пример расчета полного сопротивления в цепи с двумя резисторами, подключенными параллельно.
Сводка параллельных цепей:
- Напряжение на каждом резисторе одинаковое.
- ток от источника напряжения равен току, возвращающемуся к источнику напряжения.
- величина тока, протекающего через каждый резистор, зависит от номинала резистора.
- сумма тока, протекающего через каждый резистор, равна току питания.
- Добавление резистора в параллельную ветвь снижает общее сопротивление.
- Общее сопротивление параллельной цепи можно рассчитать по следующей формуле:
Знание параллельных цепей и закона Ома позволит вам ответить на следующие вопросы.
8. Рассчитайте полное сопротивление этой цепи
9. Рассчитайте напряжение на R3 в этой цепи.
10. Рассчитайте ток, протекающий через R1 в этой цепи.
11. Рассчитайте ток, протекающий через R2 в этой цепи.
12.Рассчитайте ток, протекающий через R3 в этой цепи.
13. Рассчитайте общий ток, протекающий в этой цепи.
14. Вычислите значение сопротивления R2 в этой цепи.
Если у вас возникли проблемы с ответом на вопросы о параллельных цепях, дополнительную информацию можно получить по телефону:
Принципы электрооборудования раздел в Ресурсы
- учебники
- интернет-сайтов
- ваш тренер.
Повторите это действие «Укрепление» или перейдите к действию в условиях цепи.
Когда вы закончите:
- покажи свои ответы тренеру
- закройте это окно и выберите новое действие в меню.
Расчет и формула параллельной цепи | Как найти ток в параллельной цепи — стенограмма видео и урока
Ток в параллельной цепи
Чтобы понять ток в параллельной цепи, необходимо определить параллельную цепь.Параллельная цепь — это цепь, которая имеет два или более путей для прохождения электричества, которые считаются параллельными друг другу. На схеме показана схема, в которой три резистора подключены параллельно к источнику напряжения. Если один из этих резисторов выйдет из строя, ток все равно сможет протекать через другие.
Резистор — это электрический компонент, который препятствует прохождению тока в цепи.Сопротивление резистора показывает, насколько сильно он препятствует прохождению тока, и измеряется в омах ({eq} \ Omega {/ eq}). Падение напряжения описывает разницу в напряжении между двумя точками в электрической цепи из-за рассеяния энергии в цепи. Падение напряжения на резисторе зависит от тока в цепи и сопротивления.
Параллельные цепи отличаются от последовательных цепей, в которых все компоненты соединены одним путем. Если один из компонентов выходит из строя в последовательной цепи, цепь больше не будет работать.Рассмотрим цепочку лампочек. Если их соединить последовательно, то при перегорании одной лампочки вся гирлянда перестанет работать. Однако, если они соединены параллельно, лампочку можно снять, не повредив остальные лампочки.
В параллельной цепи напряжение на всех компонентах одинаково в соответствии с правилом петли Кирхгофа. Это связано с тем, что каждый компонент имеет набор общих точек, поэтому напряжение, измеренное на любом компоненте, измеряется в одних и тех же точках.Полный ток в цепи равен сумме ветвей. Это соответствует правилу пересечения Кирхгофа.
Используя комбинацию двух правил Кирхгофа и закона Ома, можно рассчитать токи, сопротивления или падения напряжения в параллельной цепи, если известно или дано достаточно информации. Это позволяет выполнять анализ схемы.
Правило соединения Кирхгофа
Правило соединения Кирхгофа гласит, что для любого узла или соединения сумма токов, текущих в узел, должна равняться сумме вытекающих.
На схеме показан узел, в котором три тока втекают, а один вытекает. Это означает, что согласно правилу соединения Кирхгофа
$$ I_1 + I_2 + I_4 = I_3 $$
Применяя это к узлу в параллельной цепи, становится ясно, что ток в каждом компоненте должен быть одинаковым. Затем общий ток в цепи можно найти, суммируя ток через каждый компонент
$$ I_ {total} = I_1 + I_2 +… + I_n $$
Правило петли Кирхгофа
Правило петли Кирхгофа гласит, что сумма падений напряжения вокруг любого замкнутого контура в цепи должна быть равна нулю. Цикл в цепи — это любой путь, который заканчивается в той же точке, в которой он начинается. На схеме показан пример параллельной цепи с обозначенными контурами.
Из диаграммы падение напряжения на первом резисторе можно найти с помощью:
$$ — V + V_1 = 0 $$
{eq} V_1 {/ eq} — это падение напряжения на {eq} R_1 {/ экв}.По соглашению источник напряжения отрицательный, а падение напряжения положительное. Для второго контура уравнение:
$$ V_2-V_1 = 0 $$
{eq} V_2 {/ eq} — это падение напряжения на втором резисторе. В этом контуре падение напряжения на первом резисторе отрицательное, потому что оно имеет противоположное направление. Следовательно, падение напряжения на двух компонентах одинаково и равно подаваемому напряжению, {eq} V {/ eq}. В более общем виде это можно записать как:
$$ V = V_1 = V_2 =… = V_n $$
Калькулятор параллельных резисторов• Электрические калькуляторы Org
Калькулятор параллельных резисторов — полезный инструмент для параллельного подключения двух или более чем двух резисторов. Он используется для расчета эквивалентного сопротивления параллельного резистора.
Что такое параллельные резисторы
Есть три основные конфигурации, в которых мы можем расположить электрические компоненты.
- Конфигурация серии
- Параллельная конфигурация
- Последовательно-параллельная конфигурация
Последовательно компоненты конфигурации просто соединяются друг с другом.С другой стороны, параллельная конфигурация сложна для понимания. Можно просто понять параллельную конфигурацию с помощью следующего определения.
Два или более компонента работают параллельно, если один конец всех компонентов соединен вместе с общим узлом, а хвосты соединены вместе с другим общим узлом, и между ними нет другого соединения.
На рисунке ниже показаны три резистора R 1 , R 2 и R 3 .
Верхний вывод всех резисторов имеет общий красный узел наверху. В то время как нижний вывод резисторов разделяет оранжевый узел. Поскольку это условие удовлетворяет условию параллельности резисторов, наша схема является параллельной.
Формула параллельного резистора| Как решить параллельные резисторы
Общая формула решения параллельных резисторов:
Где n — количество резисторов, а R eq — общее сопротивление, которое отображается на красном и оранжевом узлах.
В предыдущем случае трех параллельных резисторов мы можем применить формулу:
Рассмотрим случай двух параллельных резисторов.

