Как рассчитать общее сопротивление при параллельном и последовательном соединении резисторов. Какие формулы используются для вычислений. Чем отличаются эти виды соединений. На что еще нужно обращать внимание при расчетах.
Основные формулы для расчета соединений резисторов
При проектировании электрических цепей часто возникает необходимость рассчитать общее сопротивление нескольких резисторов, соединенных различными способами. Существует два основных вида соединения резисторов:
- Последовательное соединение
- Параллельное соединение
Каждый из этих видов соединения имеет свои особенности и формулы для расчета.
Формула для последовательного соединения резисторов
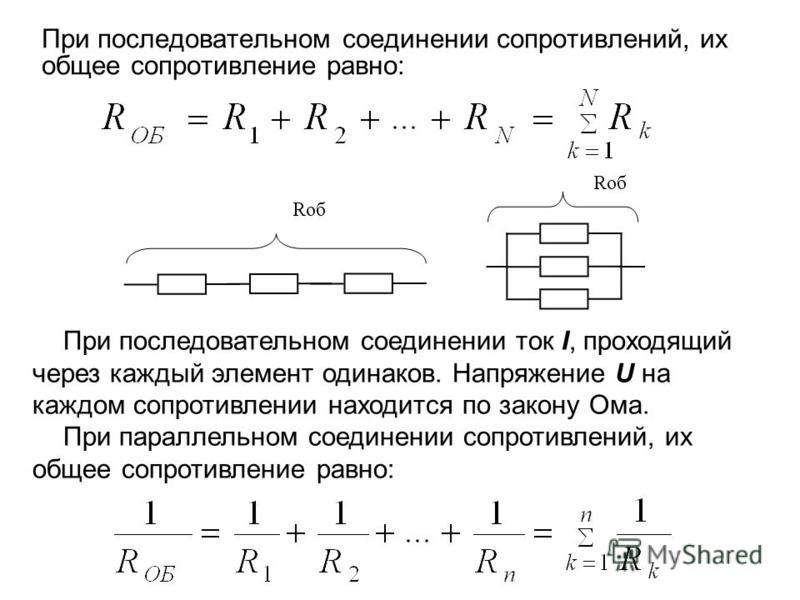
При последовательном соединении общее сопротивление цепи равно сумме сопротивлений всех резисторов:
R = R1 + R2 + R3 + … + Rn
Где R — общее сопротивление цепи, а R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Формула для параллельного соединения резисторов
При параллельном соединении используется следующая формула:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Где R — общее сопротивление цепи, а R1, R2, R3 и т.д. — сопротивления параллельно соединенных резисторов.
Особенности расчета параллельного соединения резисторов
Расчет общего сопротивления при параллельном соединении резисторов немного сложнее, чем при последовательном. Рассмотрим основные моменты, на которые стоит обратить внимание:
- Общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи
- Чем больше параллельно соединенных резисторов, тем меньше общее сопротивление
- Для двух параллельно соединенных резисторов можно использовать упрощенную формулу: R = (R1 * R2) / (R1 + R2)
Пример расчета параллельного соединения трех резисторов
Допустим, у нас есть три резистора со следующими сопротивлениями:
R1 = 10 Ом R2 = 20 Ом R3 = 30 Ом
Подставляем значения в формулу:
1/R = 1/10 + 1/20 + 1/30
1/R = 0.1 + 0.05 + 0.0333 = 0.1833
R = 1 / 0.1833 = 5.45 Ом
Таким образом, общее сопротивление трех параллельно соединенных резисторов составляет 5.45 Ом.

Сравнение последовательного и параллельного соединения резисторов
Последовательное и параллельное соединения резисторов имеют ряд отличий. Рассмотрим основные из них:
| Параметр | Последовательное соединение | Параллельное соединение |
|---|---|---|
| Общее сопротивление | Больше любого из резисторов | Меньше любого из резисторов |
| Ток | Одинаковый через все резисторы | Разный через каждый резистор |
| Напряжение | Разное на каждом резисторе | Одинаковое на всех резисторах |
Практическое применение формул расчета соединений резисторов
Знание формул расчета параллельного и последовательного соединения резисторов необходимо во многих областях электротехники и электроники. Рассмотрим несколько примеров практического применения:
- Проектирование делителей напряжения
- Расчет эквивалентного сопротивления сложных электрических цепей
- Подбор нужного сопротивления путем комбинирования стандартных номиналов резисторов
- Анализ распределения токов и напряжений в электрических схемах
Пример использования параллельного соединения для получения нужного сопротивления
Предположим, нам нужен резистор сопротивлением 40 Ом, но в наличии есть только резисторы номиналом 100 Ом. Как получить нужное сопротивление?
Можно соединить параллельно три резистора по 100 Ом. Рассчитаем общее сопротивление:
1/R = 1/100 + 1/100 + 1/100 = 3/100
R = 100/3 ≈ 33.33 Ом
Это значение близко к требуемым 40 Ом и во многих случаях может быть использовано.
Что еще нужно учитывать при расчете соединений резисторов
При проведении расчетов соединений резисторов важно помнить о следующих моментах:
- Мощность рассеивания — при параллельном соединении общая мощность увеличивается
- Допуски резисторов — реальное сопротивление может отличаться от номинального
- Температурные коэффициенты — сопротивление может меняться при изменении температуры
- Паразитные емкости и индуктивности — могут влиять на работу схемы на высоких частотах
Расчет мощности при параллельном соединении резисторов
При параллельном соединении резисторов общая рассеиваемая мощность увеличивается. Это нужно учитывать при проектировании схем. Рассмотрим пример:
Допустим, у нас есть два резистора по 100 Ом, рассчитанные на мощность 0.25 Вт каждый. При параллельном соединении общее сопротивление составит 50 Ом. Если приложить к этой цепи напряжение 10 В, то мощность рассеивания составит:
P = U^2 / R = 10^2 / 50 = 2 Вт
Это значительно превышает допустимую мощность каждого из резисторов. В такой ситуации необходимо использовать резисторы с большей допустимой мощностью рассеивания.
Инструменты для расчета соединений резисторов
Для упрощения расчетов соединений резисторов можно использовать различные инструменты:
- Онлайн-калькуляторы
- Мобильные приложения
- Специализированное программное обеспечение для электротехнических расчетов
- Электронные таблицы с предварительно настроенными формулами
Эти инструменты позволяют быстро и точно производить расчеты даже для сложных схем с большим количеством резисторов.
Заключение
Понимание принципов расчета параллельного и последовательного соединения резисторов является fundamental knowledge? важным для любого специалиста, работающего с электрическими цепями. Правильное применение формул позволяет точно рассчитывать параметры схем и избегать ошибок при проектировании. При этом важно учитывать не только теоретические аспекты, но и практические нюансы, такие как мощность рассеивания и допуски компонентов.
Расчет трубопровода с параллельными участками в Excel
Опубликовано 20 Дек 2014
Рубрика: Теплотехника | 22 комментария
Многие инженеры знают, что между процессом движения жидкости по трубам и процессом «движения» электрического тока по проводам можно провести некоторые аналогии.
Для пояснения законов Ома и Кирхгофа…
…в электрике часто используют наглядные примеры из гидравлики, заменяя проводники трубами, напряжение (U) – перепадом давления (dP), силу тока (I) – расходом жидкости (G), сопротивление участка цепи (R) – характеристикой сопротивления участка трубопровода (S).
Однако на деле оказывается, что электрика со своим законом Ома существенно проще и нагляднее гидравлики с её уравнением Бернулли и грудой эмпирических зависимостей Прандтля, Никурадзе, Блазиуса и целого ряда других ученых. В пору пытаться примерами из электрики пояснять процессы гидравлики, выполняя расчет трубопровода…
К тому же есть одно важное и существенное различие в главных зависимостях, описывающих процессы в вышеупомянутых разделах науки!
Электрика. Закон Ома:
Закон Ома:
U=I*R
Это уравнение прямой, причем сопротивление (R) – переменная независимая, как правило, в широком диапазоне практических значений ни от переменной – силы тока (I), ни от функции — напряжения (U).
Гидравлика. Формула для участка трубопровода при турбулентном движении жидкости:
dP=G2*S
Это уравнение параболы, к тому же характеристика сопротивления (S) – переменная, зависимая от расхода жидкости (G): S=f(G)!
Если мы воспользуемся программой из статьи «Гидравлический расчет трубопроводов» и, рассчитав ряд значений, построим график зависимости потерь давления (dP) от расхода воды (G), то убедимся, что функция имеет явно нелинейный – квадратичный — характер.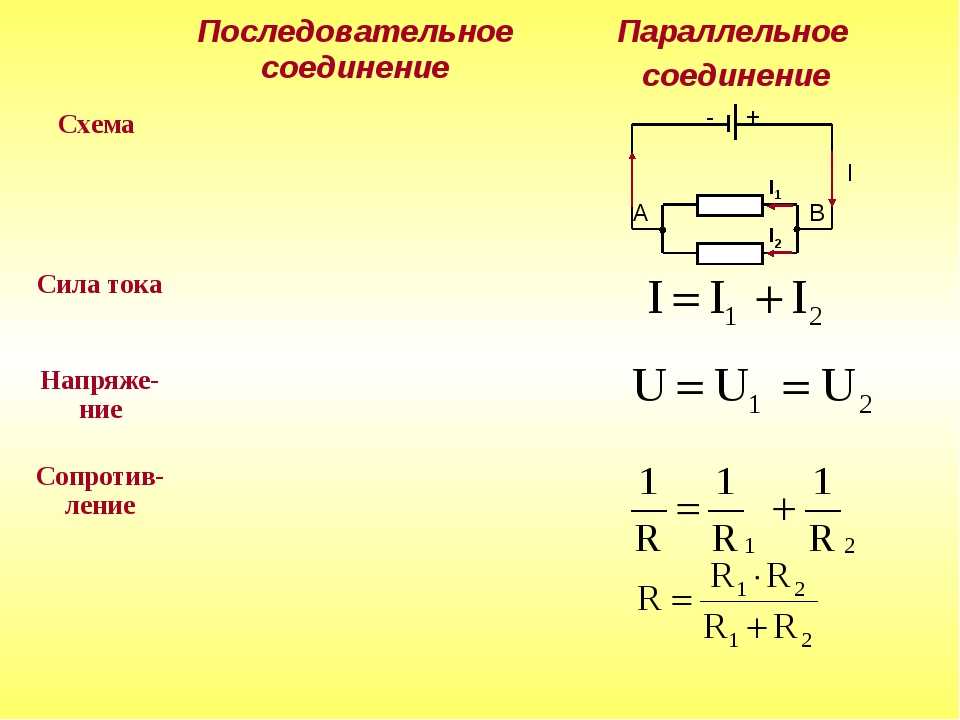
К чему все предыдущие умозаключения? К тому, что, не смотря на зависимый статус характеристики сопротивления (S), можно применить «гидравлический закон Ома» на практике, введя некоторые ограничения.
Скорость движения воды в трубах систем отопления (v) традиционно принимается в диапазоне от 0,25 до 1,0 м/с (реже — до 1,5 м/с). Минимальные значения обусловлены необходимостью гарантированного вытеснения воздушных пробок из системы, а максимальные лимитированы вероятностью возникновения недопустимого шума, а также неоправданным увеличением мощности насоса.
Если ограничить задачу скоростями движения жидкости (v) реально применяемыми на практике в теплотехнике, то в рассматриваемом диапазоне можно с погрешностью менее ± 10% принять удельную характеристику сопротивления (s) постоянной, то есть независимой от расхода (G)!
В примере на графике, приведенном выше, зеленым цветом выделены диапазон «реальных» скоростей (v) и среднее значение характеристики сопротивления S≈14 Па/(т/ч)2 для выбранной стальной трубы диаметром 100 мм и длиной 100 м.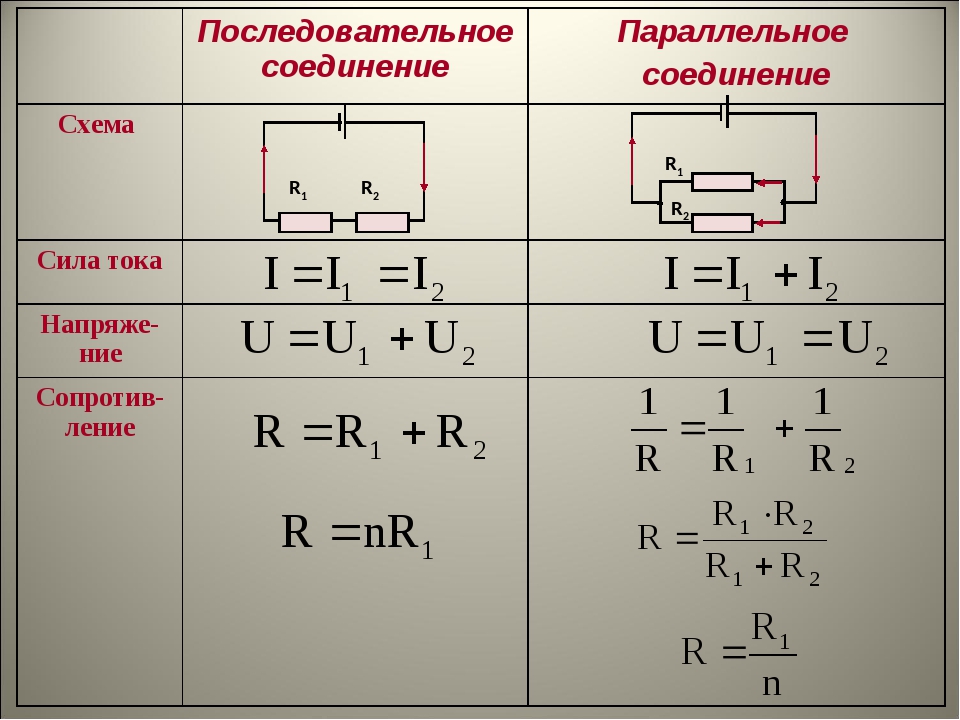
Итак, если ограничить гидравлический расчет трубопровода указанным диапазоном скоростей (v), то можно с большой долей уверенности считать, что движение воды будет турбулентным, а удельная характеристика сопротивления (s) будет близка к постоянной.
Основываясь на этих двух постулатах и определив практическими и/или теоретическими методами значения удельных характеристик сопротивления (s) для всех элементов гидравлической системы, можно по достаточно простым формулам выполнять расчеты сложных трубопроводов.
Расчетные формулы.
1. Перепад давления (гидравлическое сопротивление) на участке трубопровода
dPi=Gi2*Si
2. Суммарная характеристика сопротивления при последовательном соединении элементов трубопровода
Sij=Si+Sj
3. Суммарная характеристика сопротивления при параллельном соединении элементов трубопровода
Суммарная характеристика сопротивления при параллельном соединении элементов трубопровода
Sij=(Si-0,5+Sj-0,5)-2
4. Расход жидкости при последовательном соединении элементов трубопровода
Gij=Gi=Gj
5. Расход жидкости при параллельном соединении элементов трубопровода
Gij=Gi+Gj
6. Расход жидкости по одному из двух параллельных участков трубопровода
Gi=Gij*(Sij/Si)0,5
С изложенной методикой я познакомился в 2003 году, прочитав работу В. Ф. Гершковича «Расчеты систем отопления на Excel». В приложении к этой книге приведены таблицы со значениями удельных характеристик сопротивления (s) различных элементов систем отопления. Эти же таблицы можно найти в Приложении 2 к Пособию по проектированию систем водяного отопления к СНиП 2.04.05-91 «Отопление, вентиляция, кондиционирование».
Ф. Гершковича «Расчеты систем отопления на Excel». В приложении к этой книге приведены таблицы со значениями удельных характеристик сопротивления (s) различных элементов систем отопления. Эти же таблицы можно найти в Приложении 2 к Пособию по проектированию систем водяного отопления к СНиП 2.04.05-91 «Отопление, вентиляция, кондиционирование».
Рассмотрим использование предложенного подхода на простом примере — выполним расчет трубопровода с двумя параллельными участками.
Выполненный далее расчет в Excel, можно сделать также в программе Calc из свободно распространяемых пакетов Apache OpenOffice или LibreOffice.
Расчет в Excel «сложного» трубопровода.
Сколько воды потечет через трубу в два раза большего диаметра при параллельном присоединении к действующему замкнутому трубопроводу?
Какой перепад давления возникнет в точках присоединения насоса к трубопроводу при заданном расходе?
Ответим на поставленные вопросы, выполнив несложный расчет в Excel для замкнутого абстрактного трубопровода, схема которого представлена внизу на рисунке.
Исходные данные:
1. Суммарный расход воды через трубопровод GΣ в т/час вводим
в ячейку D3: 1,000
2. Среднюю плотность воды ρ в т/м3 записываем
в ячейку D4: 1,000
3. Внутренние диаметры труб в миллиметрах вписываем
d1 (dy20) — в ячейку D5: 21,25
d2 (dy40) — в ячейку D6: 41,00
4. Длины участков трубопроводов в метрах заносим
L1 — в ячейку D7: 2,500
L2 — в ячейку D8: 2,500
L3 — в ячейку D9: 1,000
5. Удельные характеристики гидравлического сопротивления элементов трубопровода записываем из справочных таблиц, которые можно найти в файле для скачивания внизу статьи
s20 (труба dy20) в (Па/(т/ч)2)/м — в ячейку D10: 587,0
s40 (труба dy40) в (Па/(т/ч)2)/м — в ячейку D11: 18,6
sо20 (отвод dy20) в (Па/(т/ч)2)/шт — в ячейку D12: 313,0
sтпр20 (тройник на проход dy20) в (Па/(т/ч)2)/шт — в ячейку D13: 313,0
sтпо20 (тройник на поворот dy20) в (Па/(т/ч)2)/шт — в ячейку D14: 470,0
Результаты расчетов:
6. Воспользуемся приведенными выше формулами для расчета характеристик сопротивления участков трубопровода.
Воспользуемся приведенными выше формулами для расчета характеристик сопротивления участков трубопровода.
6.1. Расчет характеристик сопротивления начинаем с крайнего правого по схеме участка 2-4-5. На этом участке последовательно соединены:
— 2 местных сопротивления «тройник на проход Dy20»
— 2 участка трубопровода с диаметром d1 и длиной L3
— 2 местных сопротивления «отвод Dy20»
— 1 участок трубопровода с диаметром d2 и длиной L1
Общую характеристику сопротивления участка S245 в Па/(т/ч)2 вычисляем
в ячейке D16: =2*D13+2*D9*D10+2*D12+D7*D11 =2472,5
S245=2*sтпр20+2*L3*s20+2*sтпо20+L1*s40
6. -2 =609,9
-2 =609,9
S25=(S245-0,5+S235-0,5)-2
6.4. и 6.5. На участках 1-2 и 5-6 соответственно последовательно присутствуют:
— 1 участок трубопровода с диаметром d1 и длиной L1/2
— 1 местное сопротивление «отвод Dy20»
— 1 участок трубопровода с диаметром d1 и длиной L2
Итоговые характеристики сопротивления последовательных участков S12 и S56 в Па/(т/ч)2 находим
в ячейке D19: =D7/2*D10+D12+D8*D10 =2514,3
S12=L1/2*s20+sо20+L2*s20
и в ячейке D20: =D8*D10+D12+D7/2*D10 =2514,3
S56=L2*s20+sо20+L1/2*s20
7. 2=5638,4
2=5638,4
dP16=dPΣ=SΣ*GΣ2
А в более привычные кг/см2 переводим
в ячейке D29: =D28/9,81/10000=0,057476
dP16’=dPΣ’= dPΣ/(10000*g)
Расчет трубопровода с параллельными участками выполнен. Расчет в Excel позволил достаточно быстро ответить на оба непростых вопроса, поставленных в начале задачи-примера.
Заключение.
К значениям удельных характеристик сопротивления, представленным в Пособии по проектированию систем водяного отопления к СНиП 2. 04.05-91 есть небольшое недоверие. Кое-где или числа переставлены местами, или просто допущены ошибки при наборе. Несмотря на это и некоторую неточность самого рассмотренного метода, применение его на практике дает замечательные и главное – понятные результаты, подтвержденные измерениями!
04.05-91 есть небольшое недоверие. Кое-где или числа переставлены местами, или просто допущены ошибки при наборе. Несмотря на это и некоторую неточность самого рассмотренного метода, применение его на практике дает замечательные и главное – понятные результаты, подтвержденные измерениями!
После составления программы расчета в Excel, изменяя диаметры труб, характеристики сопротивления запорно-регулирующей арматуры, удаляя или добавляя детали, можно быстро смоделировать различные ситуации и найти ответы на извечные вопросы гидравлики о давлении и расходе.
Программу расчета придется создавать индивидуально для каждой расчетной схемы трубопровода. После приобретения небольшого опыта делать это просто и недолго.
Можно существенно повысить точность метода, но это, возможно, тема другой статьи…
Ссылки на скачивание файлов:
gidravlicheskiy-raschet-truboprovoda-s-parallelnymi-uchastkami (xls 74KB)
posobiye-po-proyektirovaniyu-sistem-vodyanogo-otopleniya-k-snip-2. 04.05-91 (pdf 275KB)
04.05-91 (pdf 275KB)
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Формула сопротивления тока при параллельном соединении
Содержание
- Что ещё нужно учитывать при соединении резисторов?
- Формула параллельного соединения резисторов
- Параллельное соединение резисторов — расчет
- Пример №1
- Пример расчета №2
- Как рассчитать сложные схемы соединения резисторов
- Ток, протекающий в цепи параллельно соединенных резисторах
- Параллельное соединение резисторов — онлайн калькулятор
- Подведем итог
- Сопротивление проводника
- и нагрев проводника
- Способы соединения проводников
- Виды проводников
- Расчёт проводов на нагрев
- Расчёт проводников на потерю напряжения
- Виды соединений
- Последовательное соединение проводников
- Параллельное соединение резисторов
- Смешанное соединение проводников
- Последовательное соединение резисторов.

- Параллельное соединение резисторов.
- Смешанное соединение резисторов.
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
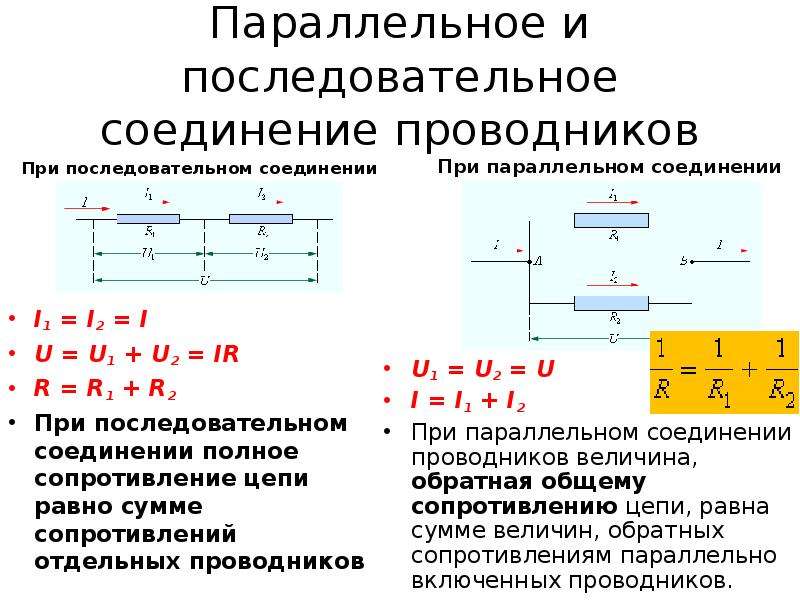
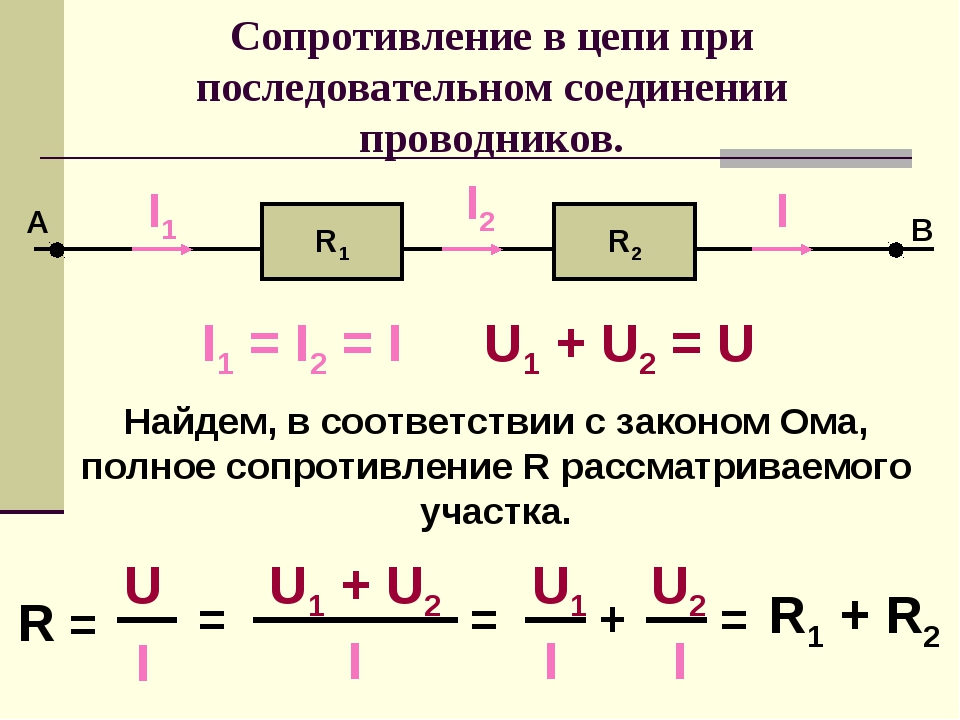
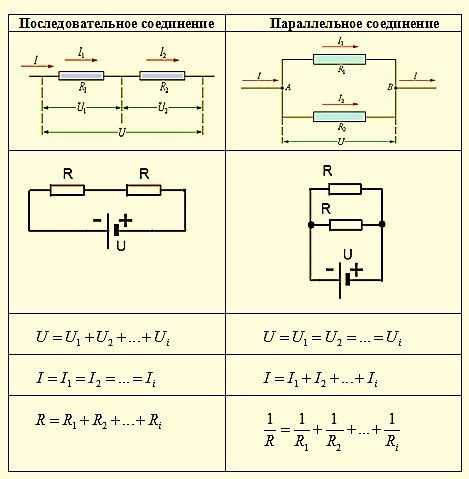
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
Последовательное соединение проводников
По закону Ома, напряжения U1 и U2 на проводниках равны
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
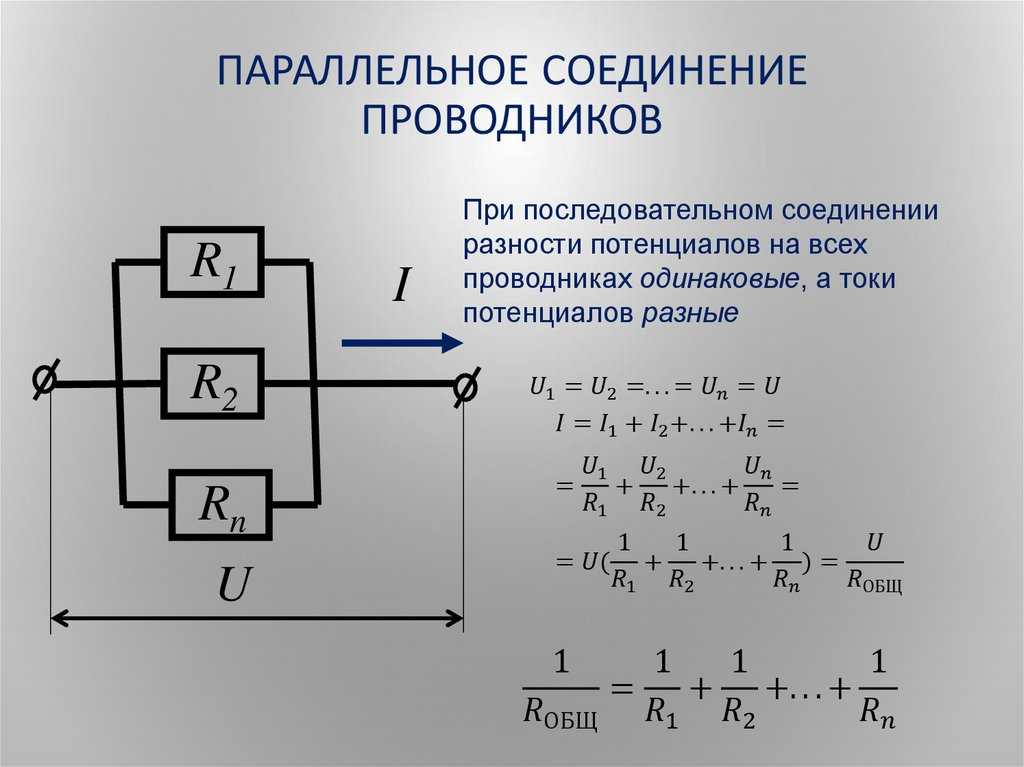
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды.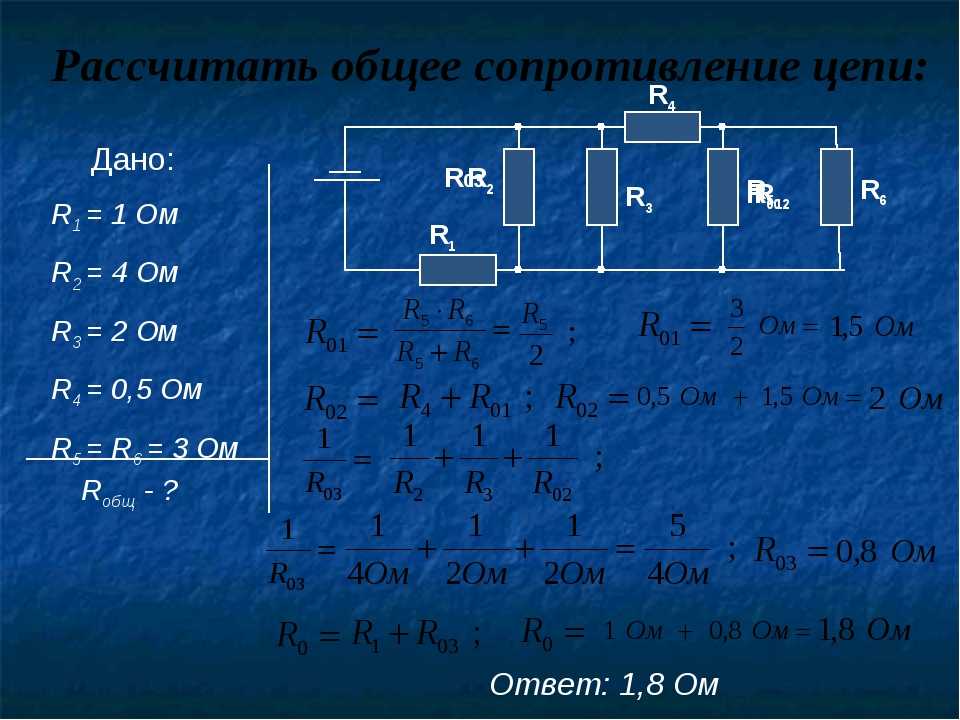 Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Параллельное соединение проводников
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)
Сопротивления всех проводников указаны вомах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.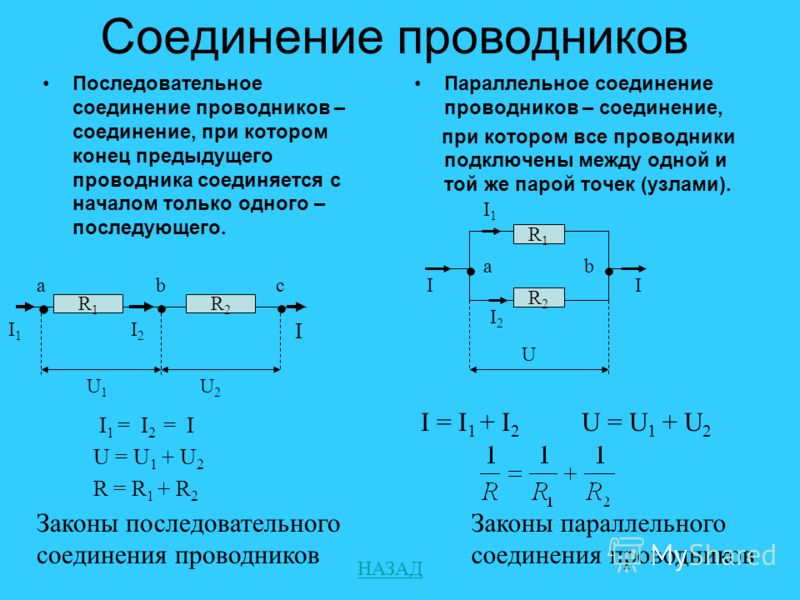
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .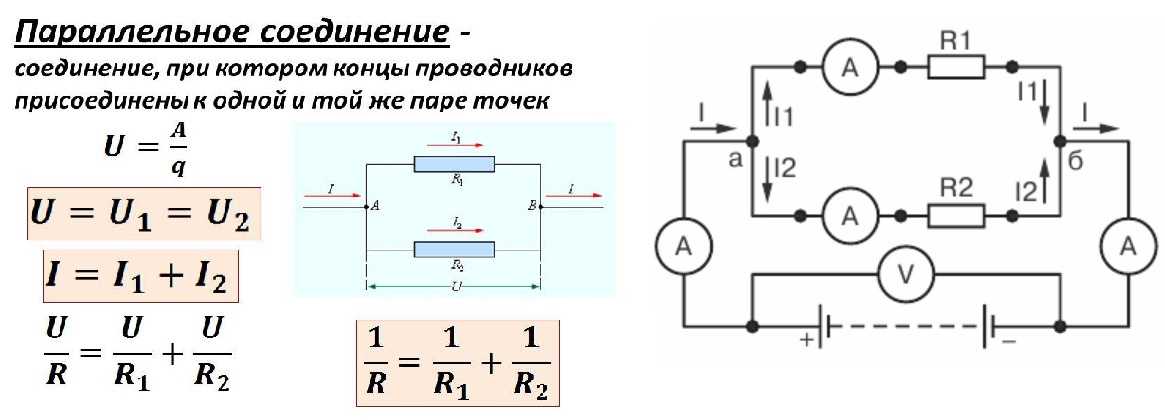
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.
Сопротивление проводника
Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.
Для ведения электротехнических расчётов применяется удельное сопротивление – ρ Ом·м/мм 2 . Все металлы – хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник – серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.
При расчёте сопротивления используется известная из школьного курса физики формула:
R = ρ · l/S, S – площадь сечения; l – длина.
Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.
и нагрев проводника
Для практических расчётов режимов работы проводников применяется понятие плотности тока – δ А/мм 2 , она вычисляется по формуле:
δ = I/S, I – ток, S – сечение.
Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.
Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.
Правилами регламентируется производить расчёт проводников на нагрев.
Способы соединения проводников
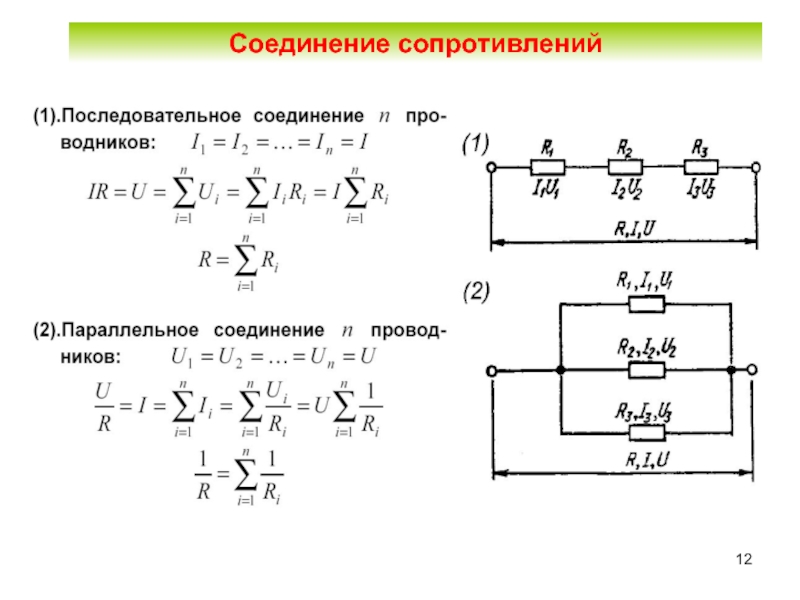
Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой – последовательное соединение.
На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .
Второй способ более сложный – параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.
Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.
Третий способ соединения наиболее сложный – смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.
Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.
R2,3,4 = R2,3 · R4/(R2,3 + R4).
Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.
Виды проводников
В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.
Большой раздел проводников представляют обмоточные провода.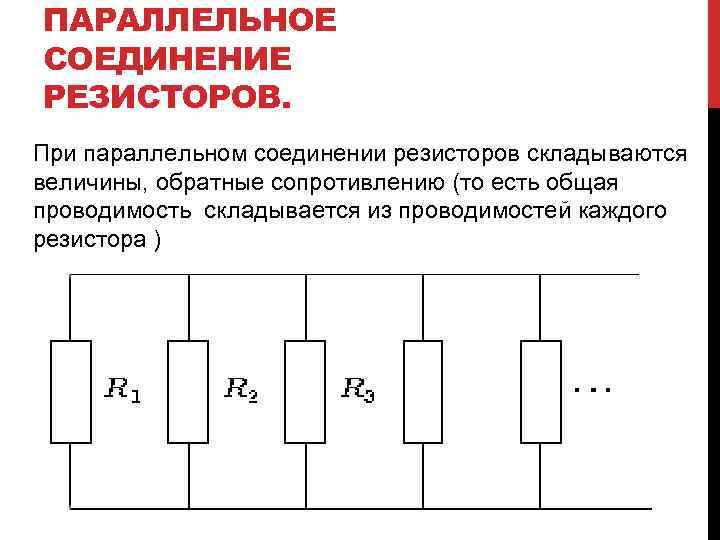 Они выпускаются разных диаметров – от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.
Они выпускаются разных диаметров – от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.
Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.
Расчёт проводов на нагрев
Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).
На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.
Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.
Расчёт проводников на потерю напряжения
При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.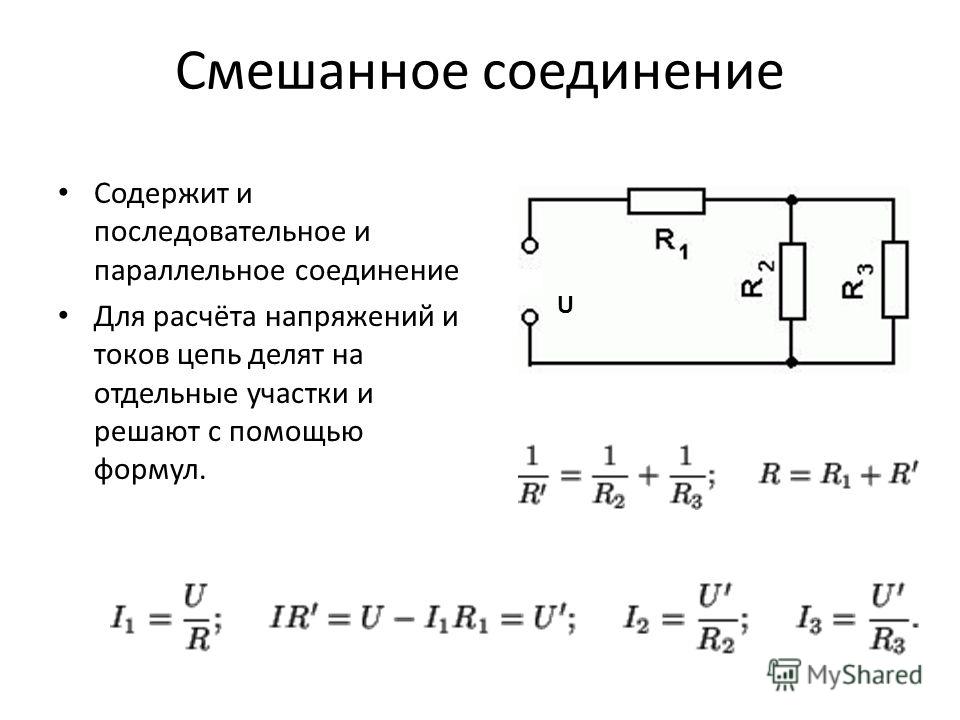
Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.
Здесь S – сечение провода линии, мм 2 .
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.
С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Виды соединений
Резистор – пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:
Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:
А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:
Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.
Последовательное соединение проводников
В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.
Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.
Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.
Примером последовательного соединения проводников в быту является ёлочная гирлянда.
Параллельное соединение резисторов
При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.
Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.
То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.
В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.
Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.
Примеры параллельного соединения проводников:
- Освещение.
- Розетки в квартире.
- Производственное оборудование.
Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.
Смешанное соединение проводников
Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.
Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.
Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.
В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения резисторов, в частности о последовательном соединении и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
Но для общего напряжение также справедлив закон Ома:
Здесь – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.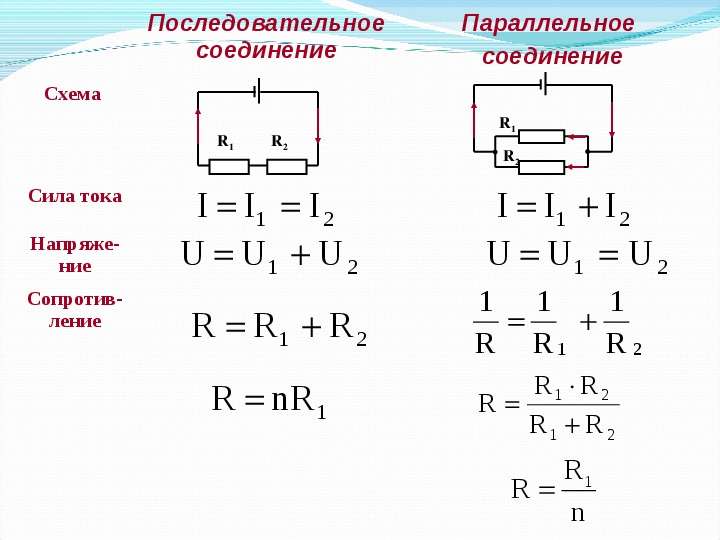
Например для следующей цепи:
Общее сопротивление будет равно:
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном соединении все сопротивления равны (), то общее сопротивление цепи составит:
в данной формуле равно количеству элементов цепи.
С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.
При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
Подставим эти выражения в формулу общего тока:
А по закону Ома ток:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
Данную формулу можно записать и несколько иначе:
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов и – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором :
Теперь у нас образовались две группы последовательно соединенных резисторов:
- и
- и
Заменим эти две группы двумя резисторами, сопротивление которых равно:
Как видите, схема стала уже совсем простой ) Заменим группу параллельно соединенных резисторов и одним резистором :
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
Общее сопротивление цепи получилось равным:
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов 😉
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях.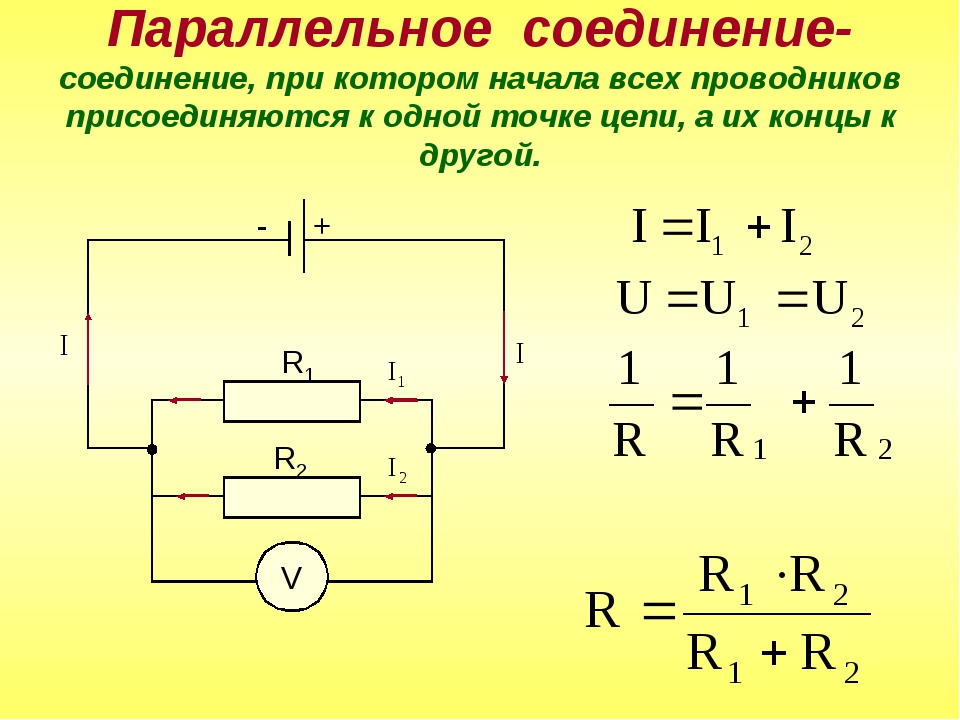 А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!
А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!
Калькулятор преобразования Параллельный и последовательный резистор
Параллельные резисторы
R1
Ом кОм МОм
R2
Ом кОм МОм
R3
Ом кОм МОм
R4
Ом кОм МОм
R5
Ом кОм МОм
R6
Ом кОм МОм
R7
Ом кОм МОм
R8
Ом кОм МОм
R9
Ом кОм МОм
R10
Ом кОм МОм
Добавить резистор
Формула параллельного резистора
Формат результата Ом кОм МОм
Общее сопротивление:
Резисторы серииR1
Ом кОм МОм
R2
Ом кОм МОм
R3
Ом кОм МОм
R4
Ом кОм МОм
R5
Ом кОм МОм
R6
Ом кОм МОм
R7
Ом кОм МОм
R8
Ом кОм МОм
R9
Ом кОм МОм
R10
Ом кОм МОм
Добавить резистор
Формула резистора серии
Формат результата Ом кОм МОм 9{-1} \tag*{}$
Код может показаться простым. Я пробовал:
Я пробовал:
Rp[list_] := 1/Sum[1/list[[k]], {k, Length[list]}];
Атрибуты[Rp] = {Список};
, где я использую Listable , потому что вход функции является списком/вектором. Чтобы проверить это, я создал список test = {1, 2, 3} , но когда я ввожу Rp[test] , я получаю сообщение об ошибке Power: Infinite expression 1/0 found . Почему это не работает?
- работа со списком
- функция-конструкция
$\endgroup$
2
$\begingroup$
Сумма действительно для символических сумм. Здесь некрасиво. Я предлагаю:
Rp[r_List] := 1/Всего[1/r]
$\endgroup$
2
$\begingroup$
Выйти[]
Rp[list_] := 1/Sum[1/list[[k]], {k, Length[list]}];
тест = {1, 2, 3}
9-1
прямым применением формулы.