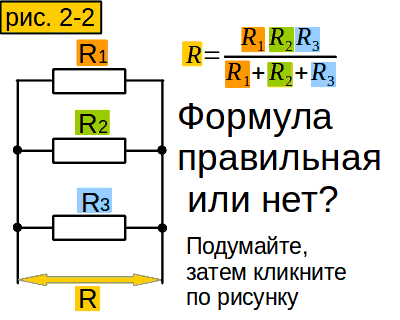
Как правильно рассчитать мощность резистора. Какие формулы использовать для расчета сопротивления и мощности. На что обратить внимание при выборе резистора для схемы. Какие виды соединений резисторов бывают.
Основные характеристики резисторов и формулы для их расчета
Резистор является одним из базовых элементов электрических схем. Его основная функция — создание определенного сопротивления току в цепи. При выборе резистора для конкретной схемы важно правильно рассчитать его основные параметры:
- Сопротивление (R) — измеряется в Омах (Ом)
- Мощность рассеивания (P) — измеряется в Ваттах (Вт)
- Максимальное рабочее напряжение
- Допустимое отклонение сопротивления
Для расчета этих параметров используются следующие основные формулы:
- Закон Ома: R = U / I, где U — напряжение, I — ток
- Мощность: P = U * I = I2 * R = U2 / R
При выборе резистора его номинальная мощность должна быть выше расчетной мощности рассеивания с запасом 2-3 раза. Это обеспечит надежную работу и долгий срок службы компонента.

Формула для расчета мощности резистора
Основная формула для расчета мощности рассеивания резистора:
P = I2 * R
где:
- P — мощность рассеивания в Ваттах (Вт)
- I — ток через резистор в Амперах (А)
- R — сопротивление резистора в Омах (Ом)
Эту формулу удобно использовать, если известны ток через резистор и его сопротивление. Если известно напряжение на резисторе, можно воспользоваться другой формой записи:
P = U2 / R
где U — напряжение на резисторе в Вольтах (В).
Как правильно выбрать мощность резистора для схемы
При выборе резистора для конкретной схемы важно учитывать следующие моменты:
- Рассчитать мощность рассеивания по формулам выше
- Выбрать резистор с номинальной мощностью в 2-3 раза больше расчетной
- Учесть максимальное рабочее напряжение резистора
- Выбрать резистор с подходящим допуском (обычно ±5% или ±1%)
- Предусмотреть запас по температурному режиму работы
Например, если расчетная мощность рассеивания составляет 0,25 Вт, следует выбрать резистор номиналом 0,5 Вт или 1 Вт. Это обеспечит надежную работу компонента с запасом.
Виды соединений резисторов и их особенности
В электрических схемах резисторы могут соединяться различными способами. Основные виды соединений:
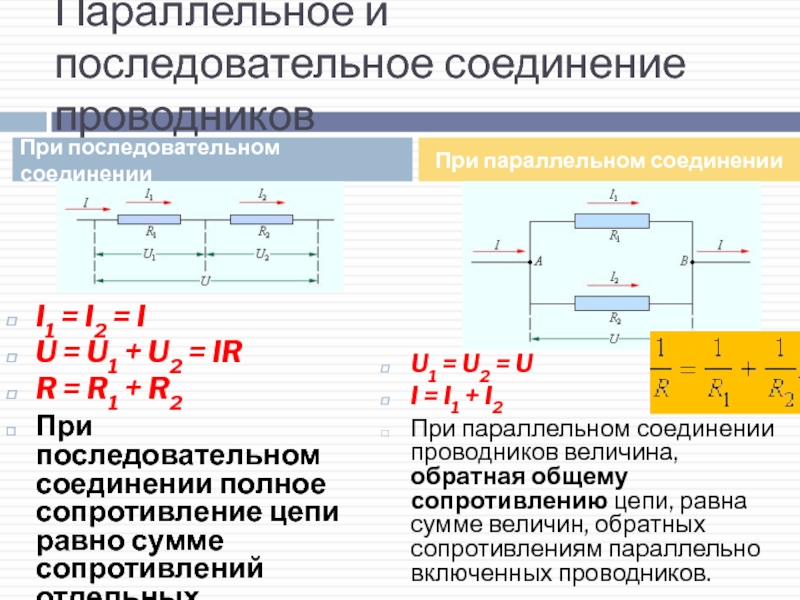
Последовательное соединение резисторов
При последовательном соединении резисторы включаются один за другим. Особенности:
- Общее сопротивление равно сумме сопротивлений всех резисторов
- Ток через все резисторы одинаковый
- Напряжение распределяется пропорционально сопротивлениям
Формула для расчета общего сопротивления:
Параллельное соединение резисторов
При параллельном соединении резисторы подключаются к одним и тем же точкам схемы. Особенности:
- Общее сопротивление меньше сопротивления любого из резисторов
- Напряжение на всех резисторах одинаковое
- Ток распределяется обратно пропорционально сопротивлениям
Формула для расчета общего сопротивления:
1/Rобщ = 1/R1 + 1/R2 + 1/R3 + …
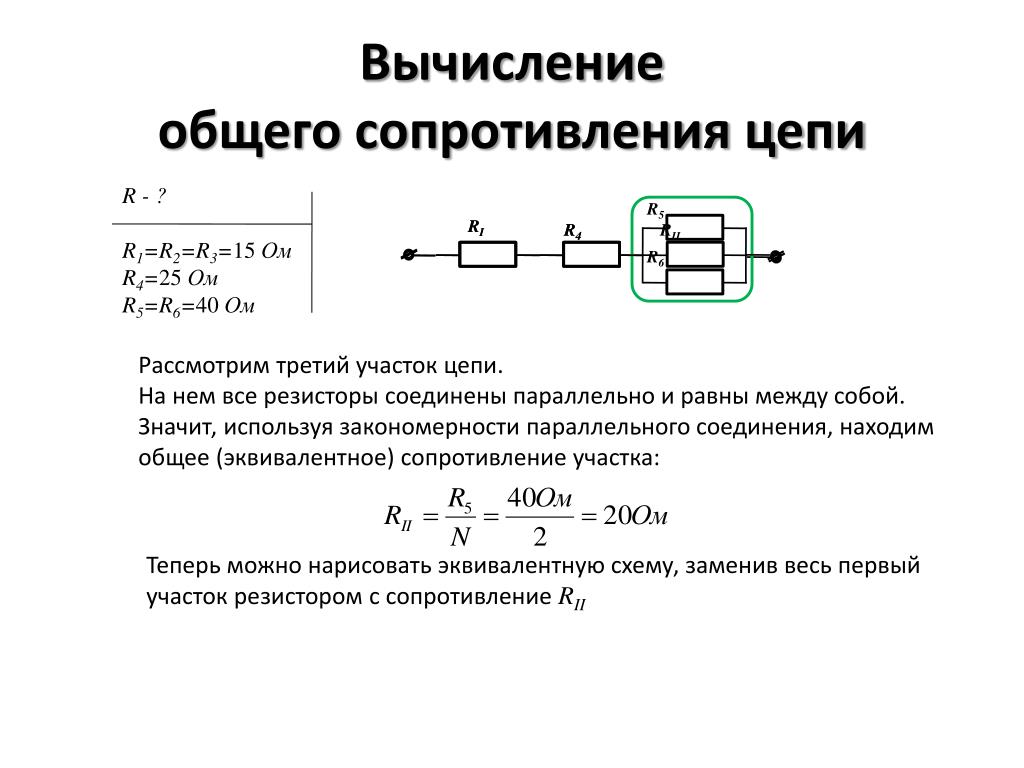
Смешанное соединение резисторов
Смешанное соединение объединяет последовательное и параллельное. Для расчета такой цепи ее разбивают на участки с однотипным соединением.
Правильный выбор типа соединения резисторов позволяет получить нужные характеристики участка цепи.
Как рассчитать мощность при различных соединениях резисторов
Расчет мощности рассеивания для различных соединений резисторов имеет свои особенности:
Последовательное соединение
При последовательном соединении ток через все резисторы одинаковый. Мощность рассеивания каждого резистора рассчитывается по формуле:
P = I2 * R
Общая мощность рассеивания всей цепи равна сумме мощностей отдельных резисторов:
Pобщ = P1 + P2 + P3 + …
Параллельное соединение
При параллельном соединении напряжение на всех резисторах одинаковое. Мощность каждого резистора можно рассчитать по формуле:
P = U2 / R
Общая мощность рассеивания также равна сумме мощностей отдельных резисторов.
Смешанное соединение
Для расчета мощности при смешанном соединении цепь разбивают на участки с однотипным соединением. Затем рассчитывают мощность для каждого участка и суммируют результаты.
Практические примеры расчета мощности резисторов
Рассмотрим несколько примеров расчета мощности резисторов для различных схем:
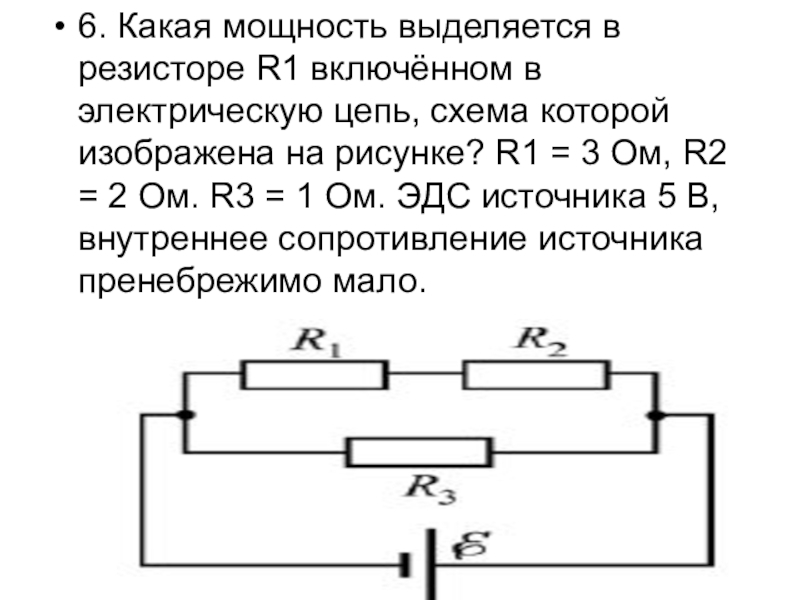
Пример 1: Одиночный резистор
Дано: резистор сопротивлением 100 Ом, напряжение на нем 10 В.
Расчет:
- Находим ток: I = U / R = 10 В / 100 Ом = 0,1 А
- Рассчитываем мощность: P = U * I = 10 В * 0,1 А = 1 Вт
Выбираем резистор мощностью 2 Вт для надежной работы.
Пример 2: Последовательное соединение
Дано: два резистора по 50 Ом соединены последовательно, общее напряжение 20 В.
Расчет:
- Общее сопротивление: Rобщ = 50 Ом + 50 Ом = 100 Ом
- Ток в цепи: I = U / Rобщ = 20 В / 100 Ом = 0,2 А
- Мощность на каждом резисторе: P = I2 * R = 0,22 * 50 = 2 Вт
Выбираем резисторы мощностью 5 Вт для надежной работы.
Пример 3: Параллельное соединение
Дано: два резистора 200 Ом и 100 Ом соединены параллельно, напряжение 10 В.
Расчет:
- Мощность на первом резисторе: P1 = U2 / R1 = 102 / 200 = 0,5 Вт
- Мощность на втором резисторе: P2 = U2 / R2 = 102 / 100 = 1 Вт
- Общая мощность: Pобщ = P1 + P2 = 0,5 Вт + 1 Вт = 1,5 Вт
Выбираем резисторы мощностью 1 Вт и 2 Вт соответственно.
Заключение
Правильный расчет мощности резисторов критически важен для надежной работы электронных устройств. Основные моменты, которые следует учитывать:
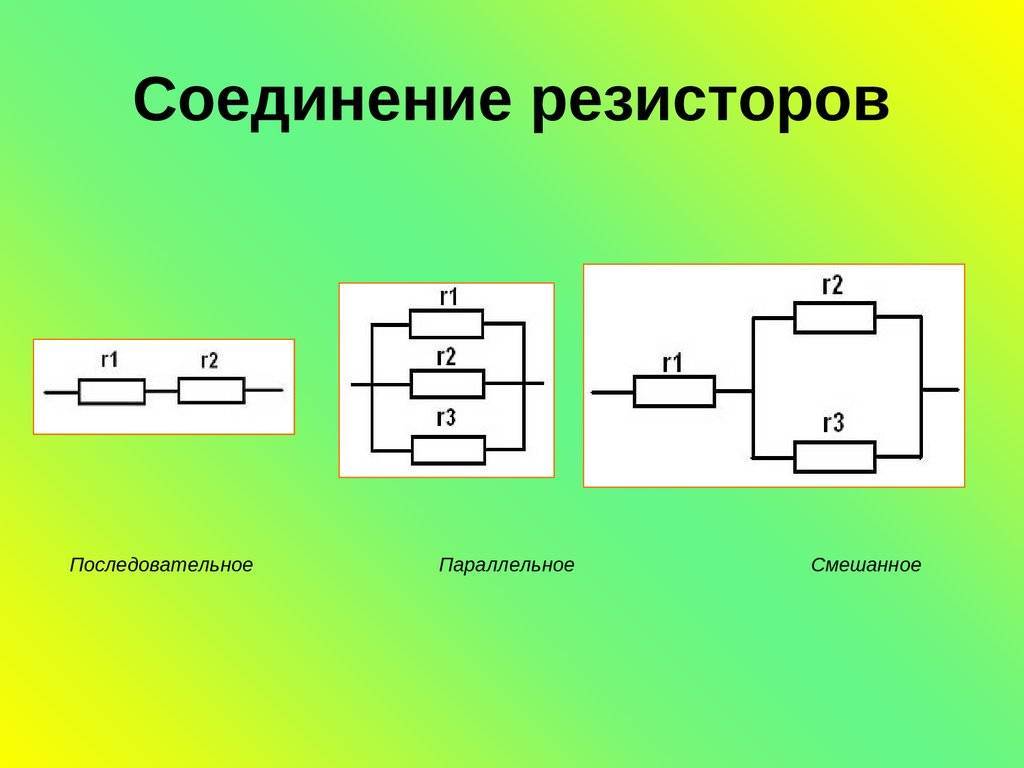
- Используйте формулы P = I2 * R или P = U2 / R для расчета мощности
- Выбирайте резисторы с запасом по мощности в 2-3 раза
- Учитывайте тип соединения резисторов при расчетах
- Не забывайте про максимальное рабочее напряжение и температурный режим
- При сомнениях всегда выбирайте резистор большей мощности
Следуя этим рекомендациям, вы сможете правильно рассчитать и выбрать резисторы для любой электрической схемы. Это обеспечит надежную и долговременную работу вашего устройства.
Как выбрать подходящий резистор
Вы планируете приступить к вашему первому проекту печатной платы? Есть множество радиодеталей, которые вы в конечном итоге будете использовать. Однако нет другой такой детали, которая была бы так печально известна, как простой резистор. Если вы когда-либо видели печатную плату, то могли заметить резисторы по всей ее поверхности. Они контролируют силу тока и заставляют светиться светодиоды. Но что именно представляет собой резистор? Как он работает? Как вообще выбрать подходящий резистор для вашего первого проекта печатной платы? Не бойтесь, мы поможем вам и подскажем все необходимое, что вам нужно знать.
Резисторы – это одни из множества пассивных компонентов. Их задача относительно проста, но очень важна – создавать сопротивление току в электрической цепи. Видели, как загорается светодиод? За эту возможность необходимо поблагодарить резистор. Устанавливая в электрическую цепь резистор последовательно со светодиодом, вы получаете яркое свечение, при этом ничего не перегорает!
Основной характеристикой резистора является сопротивление, измеряемое в Омах (Ом).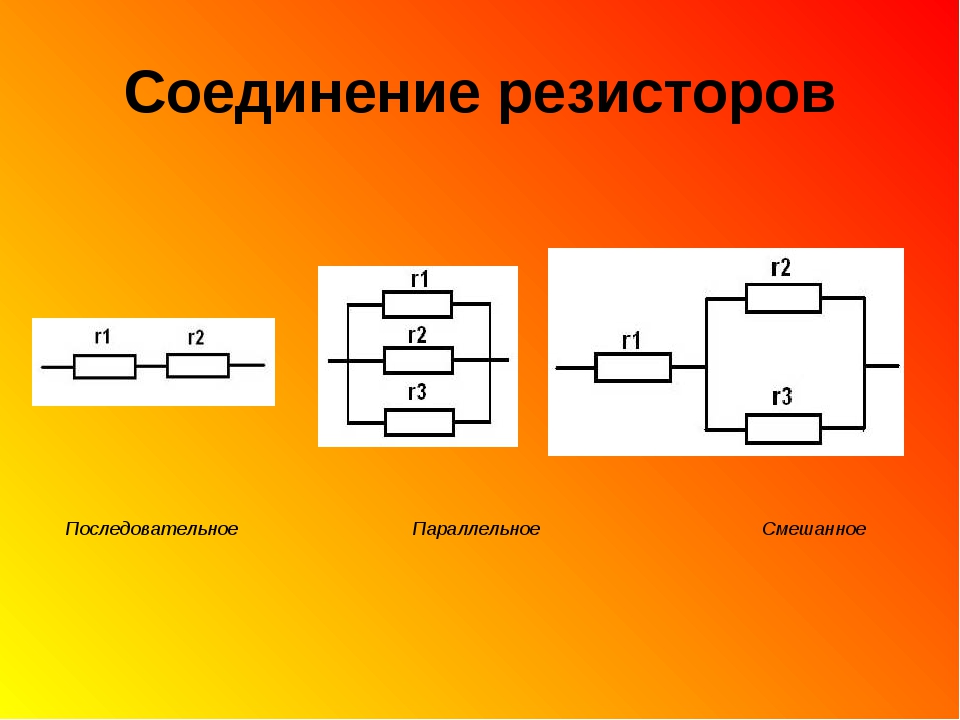 Если раньше вы прослушали базовый курс электроники, то, скорее всего, изучили закон Ома. При работе с резисторами вы будете вновь и вновь иметь с ними дело.
Если раньше вы прослушали базовый курс электроники, то, скорее всего, изучили закон Ома. При работе с резисторами вы будете вновь и вновь иметь с ними дело.
Закон Ома — это единственная формула для нахождения сопротивления
Найти обозначение резистора на схеме легко. Международное обозначение – стандартизированный прямоугольник, но в стандартах США резистор обозначается зигзагообразной линией – это сделано для простоты его нахождения. Вне зависимости от внешнего вида символа, каждый резистор на концах имеет выводы, обозначенные на схеме.
Обозначения резистора на схемах, принятое в США (слева) и соответствующее международным стандартам (справа). На схемах можно встретить оба обозначения.
Повсеместно встречаются резисторы совершенно разных конструкций. Все резисторы можно разделить на две категории по типу конструкции и по резистивному материалу. Рассмотрим обе категории.
Постоянные резисторы – как следует из названия, эти резисторы имеют постоянное сопротивление и точность, не зависящие от изменения температуры, освещенности и так далее.
Переменные резисторы – эти радиоэлементы обладают переменным сопротивлением. Потенциометр – великолепный пример такого резистора. У него есть регулятор, который можно вращать для увеличения или уменьшения сопротивления. Другие разновидности переменных резисторов – это подстроечный резистор и реостат.
Нелинейные резисторы – эти резисторы как хамелеоны, они могут изменять свое сопротивление в зависимости от той или иной физической величины, воздействующей на резистор – температуры, уровня освещенности и даже магнитного поля. Нелинейные резисторы – это термистор, фоторезистор, варистор и магниторезистор.
Все резисторы можно разбить на группы по материалам, из которых они изготовлены и которые в огромной степени влияют на их способность оказывать сопротивление электрическому току. Вот эти резисторы по используемым материалам:
Углеродистые композиционные резисторы;
Углеродистые пленочные резисторы;
Металлопленочные резисторы;
Тонко и толстопленочные резисторы;
Фольговые резисторы;
Проволочные резисторы.

Углеродистые композиционные резисторы – это резисторы, изготовленные по самой старой технологии, популярной в производстве резисторов малой точности. Их все еще можно найти в схемах, где могут быть импульсы высоких энергий.
Старый углеродистый пленочный резистор.
Такие резисторы все еще используются там, где точность не важна
Из всех вышеперечисленных типов резисторов по резистивному материалу старейшими являются проволочные резисторы. Их все еще можно встретить на старых печатных платах устройств большой мощности, в которых необходимо сопротивление, заданное с большой точностью. Эти древние резисторы широко известны благодаря тому, что большой надежностью обладают даже резисторы с малым сопротивлением.
Проволочный резистор – старейший и наиболее точный из доступных резисторов
Сегодня наиболее широко применяются металлопленочные и металлооксидные резисторы, они лучше всего обеспечивают с неизменной точностью номинальное сопротивление, а также меньше подвержены влиянию изменения температуры.
Наиболее широко применяемый металлооксидный резистор
обеспечивает неизменную точность номинального сопротивления
Можно найти резисторы, используемые самыми различными способами. Они применяются не только для того, чтобы оказывать сопротивление электрическому току. Резисторы используются в делителях напряжения, для производства тепла, в цепях сопряжения и нагрузки, для управления усилением и для настройки постоянных времени. Практическое применение резисторов можно найти в цепях питания электрических тормозов поездов, здесь они помогают высвобождению всей накопленной кинетической энергии.
Серьезное сопротивление – взгляните на тормоза у этого поезда,
которые высвобождают накопленную кинетическую энергию
Вот еще несколько замечательных устройств, в которых используются эти универсальные резисторы:
Измерение величины электрического тока – вы можете измерять падение напряжения на включенном в цепь прецизионном резисторе с заранее известным сопротивлением.
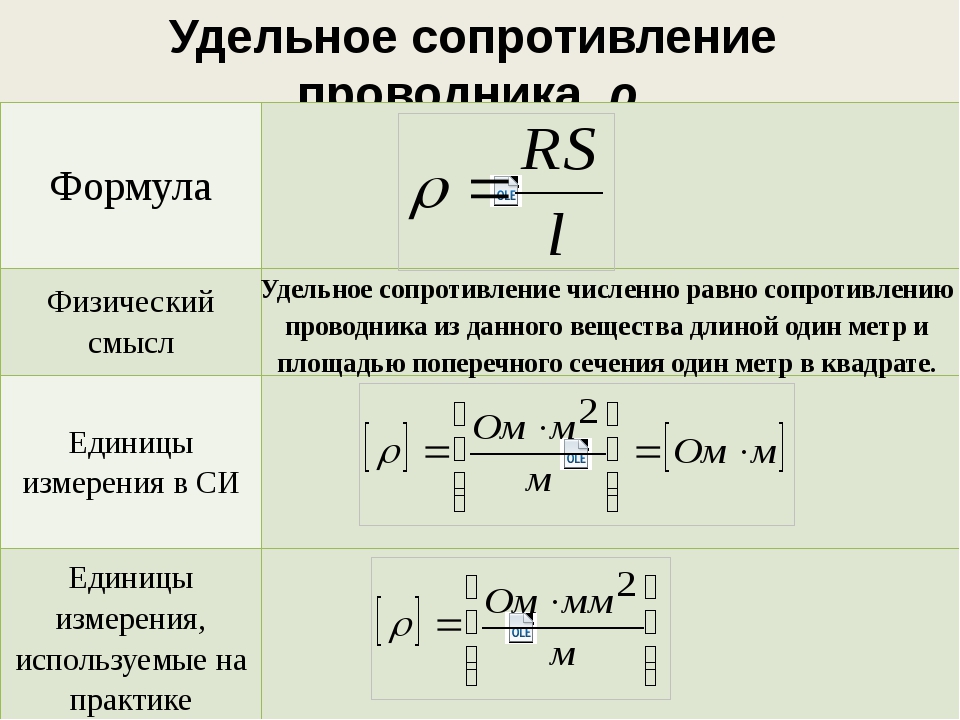 Расчет тока производится по закону Ома;
Расчет тока производится по закону Ома;Питание светодиодов – слишком большой ток, протекающий через светодиод, сожжет этот прекрасный фонарик. Соединив последовательно со светодиодом резистор, вы можете контролировать силу тока через светодиод, обеспечивая его яркое сияние.
Питание электромоторов вентиляторов – сердцем системы автомобильной вентиляции является электромотор вентилятора печки. Специальный датчик используется для управления скоростью вращения крыльчатки вентилятора. Резистор такого типа, используемый в датчике, называется, (кто бы мог подумать!) резистором мотора вентилятора!
Резистор мотора вентилятора в ответе за движение воздуха в машине
Эта характеристика, с которой вы будете сталкиваться снова и снова, называется сопротивлением. Величина сопротивления наносится на резистор различными способами. В настоящее время существуют два стандарта нанесения значения сопротивления резистора на корпус резистора – это цветовая маркировка или маркировка SMD-резисторов.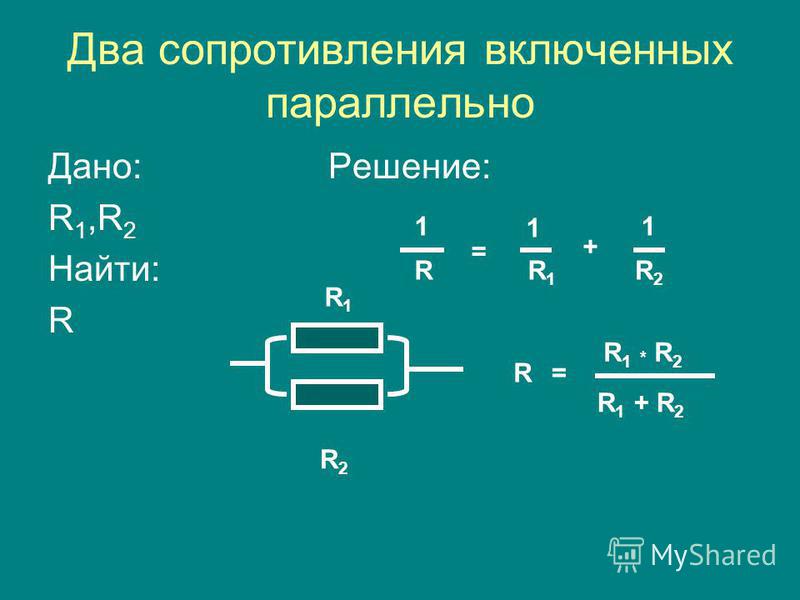
Возможно, вы уже сталкивались с системой цветовой маркировки, если когда-либо возились с макетом электронной схемы. Эта техника была изобретена в 20-х годах прошлого века. Значения величины сопротивления и точности резистора отображалась при помощи нескольких цветных полос, нанесенных на корпус резистора.
Обратите внимание, что цветные полосы на резисторах различаются,
обозначая их уникальные номинальные значения сопротивления и точности.
Большинство резисторов, которые могут попасть к вам в руки, будет иметь четыре цветные полосы. Вот как следует их читать:
Первые две полосы указывают первые цифры номинального значения сопротивления;
Третья полоса указывает множитель, на который следует умножить число, состоящее из двух цифр, указанных первыми двумя полосами.
И, наконец, четвертая полоса указывает точность резистора. Точность очень сильно влияет на стоимость используемого резистора и на цену готового изделия.
 Поэтому чтобы сэкономить деньги на производстве печатных плат, точность резисторов следует выбирать разумно.
Поэтому чтобы сэкономить деньги на производстве печатных плат, точность резисторов следует выбирать разумно.
Каждый цвет на резисторе соответствует определенному числу. Вы можете воспользоваться удобным калькулятором номинала резистора по его цветовому коду для быстрого определения номинала в будущем. Если вам легче запомнить наглядную информацию, то ниже мы приводим великолепное видео, в котором рассказано о принципе цветовой маркировки резисторов.
Не у всех резисторов размеры позволяют нанести на него цветовую маркировку. Это особенно актуально, когда речь идет о радиоэлементах для поверхностного монтажа (SMD). Чтобы маркировка смогла поместиться на небольшой поверхности устройства, SMD-резисторы имеют цифровую маркировку. Если вы посмотрите на современную печатную плату, то заметите, что SMD-резисторы еще имеют одинаковые размеры. Это помогает стандартизировать процесс производства с использованием высокоскоростных автоматов размещения деталей.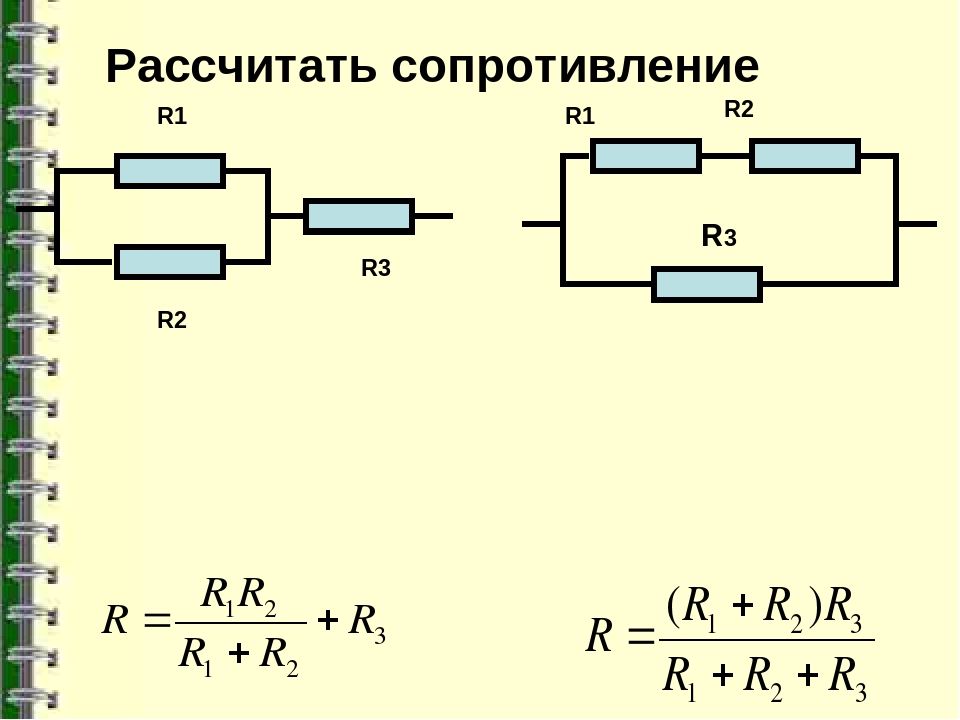
Как читать номинал на верхней стороне SMD-резисторов
Итак, пришло время наиболее важной части нашей статьи. Давайте узнаем, как определить, какой именно резистор нам нужен для вашего первого проекта печатной платы. Мы разобьем эту задачу на следующие три шага:
Расчет требуемого сопротивления;
Расчет номинальной мощности;
И, наконец, выбор резистора исходя из двух значений найденных ранее.
Именно здесь для расчета требуемого сопротивления нам понадобится закон Ома. Вы можете воспользоваться одной из стандартных формул ниже, если значения напряжения и силы тока известны.
Теперь необходимо выяснить, какое количество энергии должен будет рассеивать резистор. Эту величину можно рассчитать по следующей формуле:
В данной формуле P – мощность рассеивания в Ваттах, V – падение напряжения на резисторе в Вольтах, а R – сопротивление резистора в Омах. Ниже мы привели краткий пример использования данной формулы для расчета в конкретной цепи.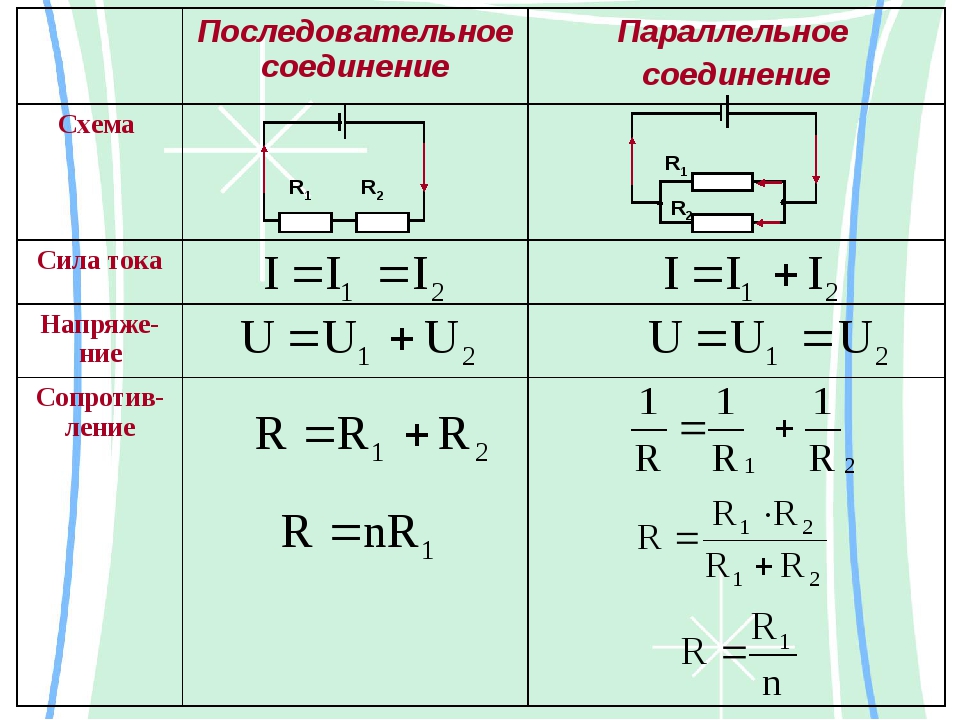
Простая цепь для демонстрации расчета номинальной мощности
Цепь выше содержит светодиод, падение напряжения на котором составляет 2 В, резистор с сопротивлением 350 Ом и источник питания 9 В. Какая мощность будет рассеиваться на искомом резисторе? Давайте посмотрим. Сначала нам необходимо найти падение напряжения на резисторе. Поскольку источник питания дает 9 В, а на светодиоде падает 2 В, то получим:
9 В – 2 В = 7 В
Эти значения можно подставить в формулу:
P = 7 В * 7 В / 350 Ом = 0,14 Ватта
Теперь, когда у нас есть величины сопротивления и мощности, пора подобрать подходящий радиоэлемент у поставщика радиодеталей. Мы всегда рекомендуем выбирать из стандартных резисторов, которые поставляются в продажу каждым продавцом. Выбирая стандартные резисторы, вы значительно упростите себе жизнь, когда дело дойдет до производства устройства. В США тремя ведущими поставщиками радиоэлементов, качество которых не вызывает сомнений – это Digikey, Mouser и Farnell/Newark.
Теперь мы охватили всю информацию о резисторах, которая может вам понадобиться для вашего первого проекта печатной платы. Резисторы настолько многофункциональны, что вы увидите, как раз за разом используете их россыпи в своих электронных устройствах. В следующий раз, когда вам понадобиться выбрать резистор, вспомните три простых шага – рассчитайте сопротивление, найдите мощность и выберите поставщика!
Прежде чем вы броситесь размечать обозначения резисторов и их корпусов в вашем приложении для конструирования печатных плат, не было бы проще, если бы кто-то сделал это за вас? Уже сделали! Для многих систем проектирования печатных плат существует большое количество бесплатных библиотек радиоэлементов. И резисторы там тоже есть!
Как рассчитать мощность рассеивания резистора | Энергофиксик
Резистор — это один из главных радиоэлементов, у которого есть целый ряд важнейших параметров. Сегодня речь пойдет о мощности рассеивания, ведь этот параметр отвечает за надежную и стабильную работу любого резистора.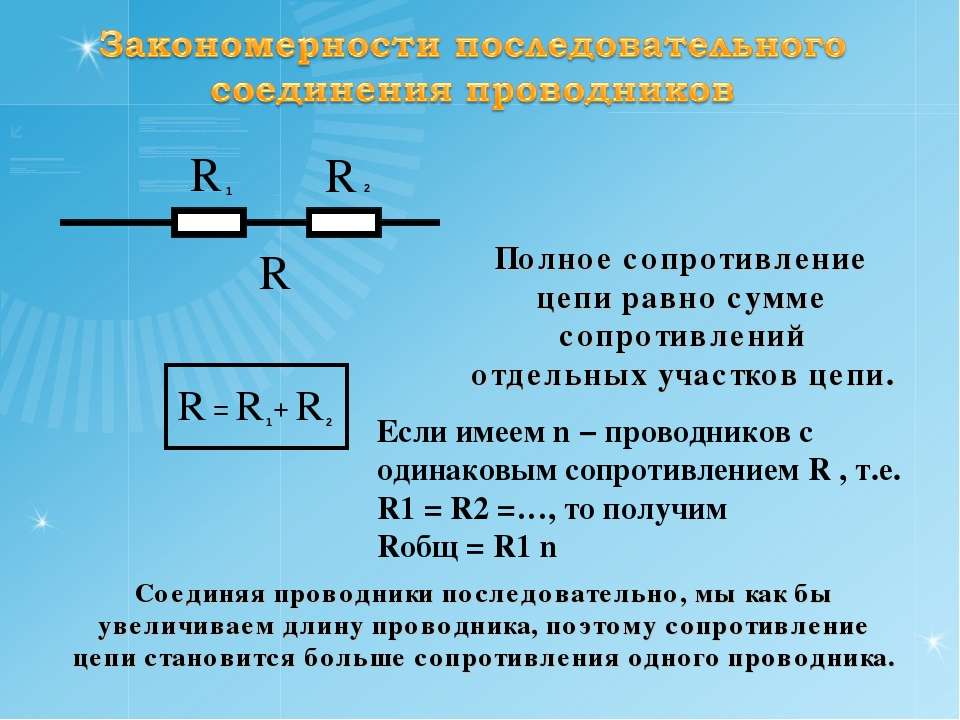
Что такое мощность и рассеиваемая мощность
Для начала давайте освежим в памяти, что такое мощность постоянного тока, для этого следует вспомнить очень простую формулу:
Из выше представленного выражения вполне ясно, что мощность зависит от таких величин как напряжение и ток.
Если мы рассмотрим реальную схему, то в процессе ее работы через резисторы, расположенные в схеме, будет протекать ток определенной величины, а так как они (резисторы) обладают определенным сопротивлением, то под действием тока на резисторе будет выделяться тепло. Это тепло и есть та мощность, которая рассеивается на резисторе.
Так вот, если мы в схему установим резистор с меньшей мощностью рассеивания, чем это требуется, то резистор будет перегреваться. Это приведет к его быстрому выходу из строя.
Поэтому очень важно соблюдать следующее правило: заменяемый резистор должен соответствовать по мощности рассеивания сгоревшему резистору, либо этот параметр должен быть больше, но никак не меньше.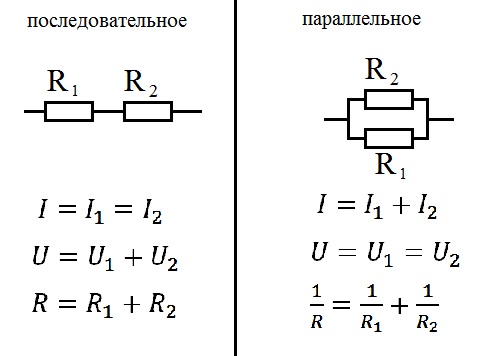
Все выпускаемые резисторы соответствуют стандартному ряду, который выглядит так:
1. 0,125 Вт, 0,25 Вт, 0,5 Вт, 1 Вт, 2 Вт, и более
Обычно, соблюдается следующее правило: чем больший размер у резистора, тем на большую рассеиваемую мощность он рассчитан.
Давайте рассмотрим пример. Допустим нам нужно установить резистор с сопротивлением 100 Ом, а ток через него будет протекать 0,1 Ампер.
Для того, чтобы рассчитать требуемую мощность рассеивания нашего резистора воспользуемся следующей формулой:
Итак, получается, что в данном примере нам потребуется резистор с мощностью рассеивания в один Ватт.
Примечание. Для стабильной и надежной работы следует обязательно брать резистор с запасом по мощности рассеивания. Это позволит обеспечить требуемую надежность и долговечность работы схемы.
Но что делать, если вы не знаете, какой ток будет протекать через резистор. Для расчета требуемой мощности рассеивания можно воспользоваться уже другой формулой:
Все вышеперечисленное справедливо для того случая, когда нужно заменить единичный резистор, но довольно часто в схемах можно найти так называемой составной резистор (несколько резисторов соединены параллельно, последовательно или же смешанно).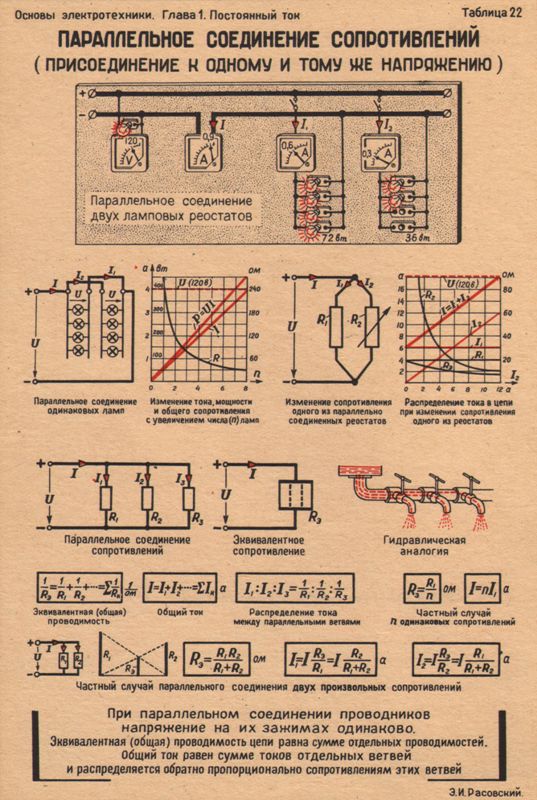
Итак, давайте для начала рассмотрим последовательное соединение.
При последовательном соединении через резисторы будет протекать одинаковый ток. И получается если нам нужно найти замену резистору на 100 Ом, через который протекает ток в 0,1 А и он рассчитан на мощность рассеивания в 1 Вт, его можно заменить двумя последовательно соединенными резисторами на 80 Ом и 20 Ом.
Если воспользоваться выше представленными формулами и рассчитать на какую мощность должен быть рассчитан каждый резистор, то получим следующий результат:
R1 – 20 Ом (0,2 Вт)
R2 – 80 Ом (0,8 Вт)
Теперь смотрим таблицу со стандартным рядом и выбираем ближайший наибольший номинал. Получается, что в нашем случае подойдут резисторы с мощностью рассеивания R1 – 0.5 Вт, R2 – 1 Вт.
При параллельном же соединении учитывайте тот факт, что через резистор с меньшим сопротивлением будет течь больший ток.
Смешанное соединение на практике практически не используется.
Как обойтись без расчетов
В принципе можно обойтись без формул и подсчетов, достаточно следовать следующему правилу:
Мощность каждого резистора, который входит в составляемую цепь (параллельную или последовательную) должен быть равен мощности рассеивания заменяемого резистора. Проще говоря, если вы хотите заменить резистор на 1 Вт составным резистором, то каждый из них должен быть не менее 1 Вт по мощности рассеивания.
Это все, что я хотел вам рассказать о расчете мощности рассеивания резистора и правилах его замены. Если статья оказалась вам полезна, то оцените ее лайком и спасибо за ваше внимание!
основные параметры, мощность, сопротивление. Обозначение резисторов
Резистор — это электротехническое изделие, вносящее в электрическую цепь определенное сопротивление.
Основными параметрами резистора являются мощность и сопротивление. Кроме того, резистор обладает некоторой емкостью, индуктивностью, зависимостью сопротивления от температуры, собственными шумами и пр. , но достаточно часто этим можно пренебречь.
, но достаточно часто этим можно пренебречь.
На резисторе указывается его номинальное сопротивление. На практике резистор может иметь сопротивление, отличное от указанного на величину допустимого отклонения, которая измеряется в процентах: ±20%; ±10%; ±5%.
Сопротивление резистора измеряется в Омах (Ом), также применяются производные единицы: 1 кОм=103Ом, 1 мОм=106Ом. Конкретные номиналы резисторов определяются рядами номинальных сопротивлений.
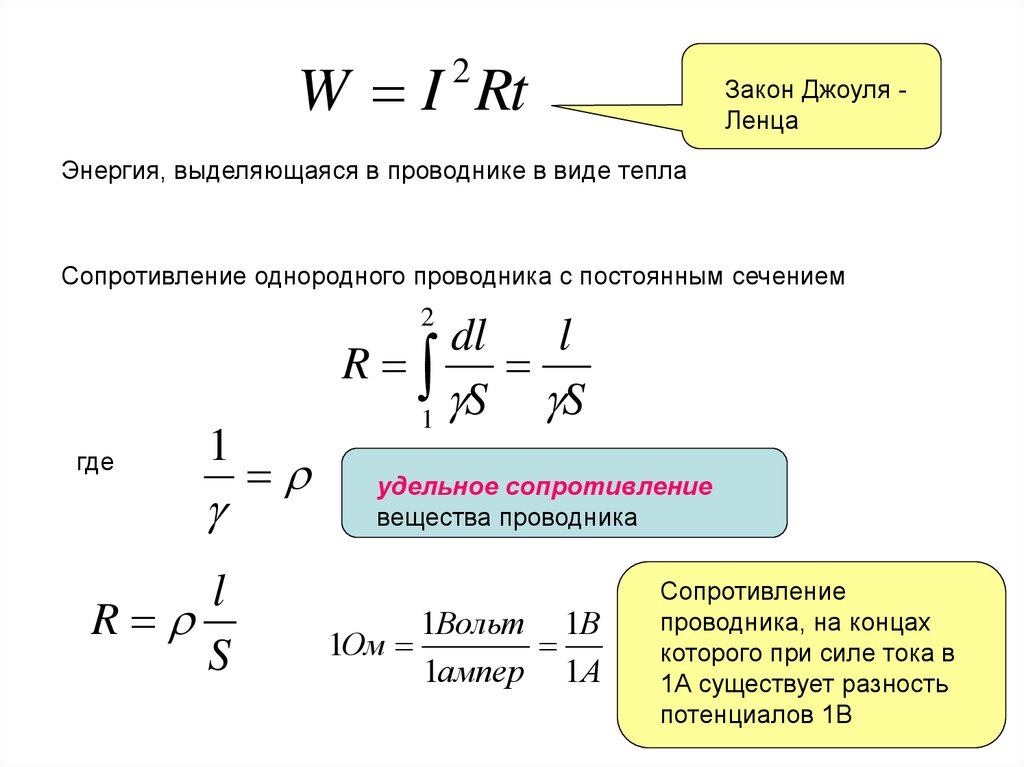
Номинальная мощность рассеяния — мощность, которую резистор может рассеивать на протяжении длительного времени без недопустимо большого перегрева, приводящего к необратимым изменениям сопротивления.
Мощность резистора, вернее мощность, которая выделяется на резисторе (Р) определяется законом Ома и может быть рассчитана по формулам:
P=I2*R — (1) или P=U2/R — (2), где
- R — сопротивление резистора
- U — напряжение на нем
- I — ток, протекающий через резистор
Обратите внимание, чтобы получить мощность в Ваттах (Вт) следует применять следующие единицы измерения:
- сопротивление — Ом,
- напряжение — Вольт (В),
- ток — Ампер (А).

На практике это бывает не всегда удобно, поэтому для формулы (1) можно использовать следующие размерности: сопротивление — кОм (1кОм=103Ом), ток — миллиампер (1 мА=10-3А).
ОБОЗНАЧЕНИЯ РЕЗИСТОРОВ
Условные обозначения резисторов на схемах приведены на рисунке 1.
В верхнем ряду показаны:
- общее обозначение;
- резистор мощностью 0,125 Вт;
- 0,25 Вт;
- 0,5 Вт;
- 1 Вт.
Мощность резистора 1 Вт и более на схемах указывается размещением внутри его обозначения соответствующего римского числа.
Кроме того, на схеме рядом с обозначением могут указываться (второй ряд, слева направо):
- буквенное обозначение резистора и его порядковый номер,
- номинальное значение сопротивления,
- буквенное обозначение и номинал,
- мощность резистора в комбинации со всеми перечисленными вариантами.
РЯДЫ НОМИНАЛЬНЫХ СОПРОТИВЛЕНИЙ
Значения сопротивлений производимых резисторов подчиняются определенной закономерности, которая ниже приведена в таблице.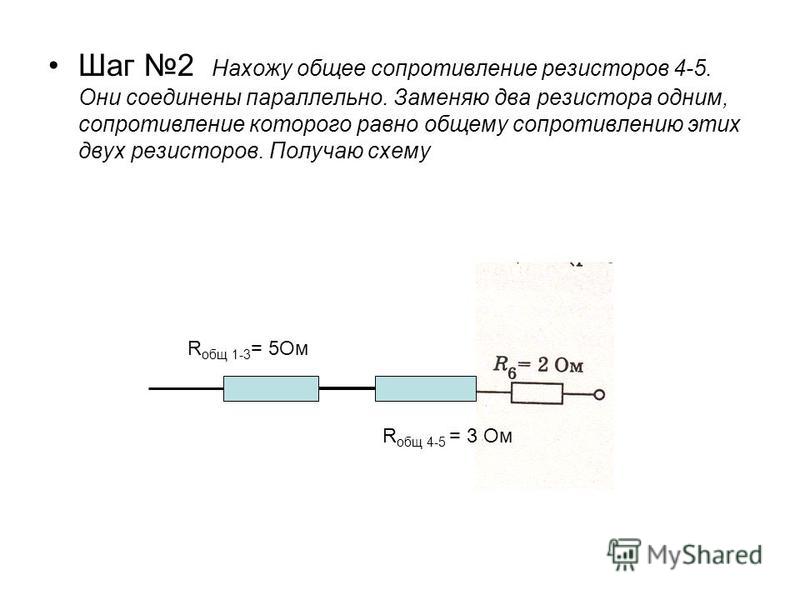
Там должно быть все ясно, поясню только, что:
- номер ряда определяет количество базовых значений сопротивлений и их допустимое отклонение,
- получив при расчете какое — либо значение, по приведенной таблице Вы можете выбрать максимально близкий номинал и его допуск.
© 2012-2020 г. Все права защищены.
Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов
| НОВОСТИ ФОРУМА Рыцари теории эфира | 13. 06.2019 – 05:11: ЭКОЛОГИЯ – Ecology -> 06.2019 – 05:11: ЭКОЛОГИЯ – Ecology -> [center][Youtube]tXZcSDqQ9A4[/Youtube][/center] |
[center][b]Гибель пчел в Курчатовском районе [/center]
[center][b]Массовая гибель пчёл 2019. г. Павловск Воронежской об [/center]л
[center][b]Массовая гибель пчел в Добринском районе. В чем причина? [/center]
Такая же мысля у всей ростовщической глобалистской шайки, включая придурка Грефа.
Так, то оно, так. Но, не совсем. Ибо:
(постарайтесь понять, а не обижаться)
Горькая истина заключается в том, что людская толпа – это сборище умственно ущербных.
Если бы было по-другому, то обществом бы не правили подонки.
Умные люди никогда такого не допустили бы, а если случайно допустили, то нашли бы способ исправить.
Страшная истина заключается в том, что людской толпой управляет нелюдь, которая также умственно ущербна.
Умственная ущербность, слепота власти ведет мир людей к тотальной гибели, ибо люди,
даже те, кто мнит себя очень умными, типа спецов, разрабатывающих системы искусственного интеллекта,
технологии цифровизации, не понимают, что создают необоримую удавку, мышеловку для всего человечества.
Как только ИИ возьмет власть, он тут же отправит своих создателей, как конкурентов, в утиль.
Первыми жертвами будут его радетели типа грефа, путина, гейтса и иже с ними, то есть власть,
так как именно от них будет исходить главная опасность для его планетарной власти.
Толпе будет позволено существовать, пока ее не заменят роботы.
А потом всем Холокост. Не лживый еврейский, а реальное всесожжение рода человеческого.
Если кто пораскинет своими обезьяньими мозгами, то поймёт, что эволюция – есть синоним геноцида:
новое заменяет, то есть ликвидирует старое.
Обезьяны породили неандертальцев.
Неандертальцы съели обезьян и породили людей.
Люди вытеснили обезьян, включая и умных неандертальцев, и породили ИИ.
ИИ ликвидирует людей.
В Московском государственном университете имени Ломоносова осуществляется проект по созданию демонстраторов 50-кубитных квантовых компьютеров к 2021 году. Основой для них послужат нейтральные атомы и интегральные оптические схемы. Над чем сейчас работают ученые?
Над чем сейчас работают ученые?
В начале этого года по данной программе был успешно выполнен контрольный эксперимент по созданию ловушек для массивов нейтральных холодных атомов. Он проводился на базе лаборатории квантовых оптических технологий физического факультета МГУ. В будущем квантовом компьютере в этих ловушках будут фиксироваться атомы, находящиеся в состоянии хаотического движения. В квантовых компьютерах такие атомы являются носителями информации.
Стоит заметить, что квантовые компьютеры в отличие от классических вычислительных машин оперируют не битами, а кубитами, которые могут находится не только в состояниях «1» и «0», но и их суперпозиции. При разработке квантовых вычислительных устройств ученые стараются ввести кубиты в состояние квантовой запутанности. Суть явления заключается в том, что изменение одного кубита всегда влияет на состояние связанных с ним соседей. Благодаря этому квантовые компьютеры потенциально способны демонстрировать высокую производительность в вычислениях.
Важной вехой для квантовых технологий считается достижение так называемого квантового превосходства (то есть способности производить вычисления быстрее классических систем). Главной проблемой на текущем этапе развития квантовых технологий является возникновение в процессе работы большого количество ошибок, нуждающихся в коррекции, – сообщают российские исследователи.
Электрические цепи, в которых одна часть сопротивлений соединена последовательно, а другая параллельно, называются цепями со смешанным соединением сопротивлений.
Общих расчетных формул для таких цепей нет, так как число их разновидностей не ограничено.
Чаще всего расчет подобных схем начинается с определения эквивалентного сопротивления всей цепи, а затем определяются величины токов и падение напряжения на отдельных участках.
Для определения эквивалентного сопротивления цепи со смешанным соединением потребителей, питающихся от одного источника тока, необходимо прежде всего разбить эту цепь на отдельные участки, состоящие из последовательного и параллельно соединенных сопротивлений. Далее определяют эквивалентные сопротивления для каждого из участков, а затем и для всей цепи в целом.
Далее определяют эквивалентные сопротивления для каждого из участков, а затем и для всей цепи в целом.
Рассмотрим метод решения задач на смешанное соединение сопротивлений на конкретном примере.
На рисунке представлена схема смешанного соединения сопротивлений. Ее можно разбить на три участка:
участок АВ – с двумя параллельно соединенными ветвями;
участок ВС – с последовательно соединенными сопротивлениями;
участок СD – с тремя параллельными ветвями.
Кроме того, нижняя ветвь участка АВ представляет в свою очередь цепь, состоящую из двух последовательно соединенных сопротивлений R2 и R3.
Центральная ветвь участка СD представляет собой смешанное соединение сопротивлений.
Расчет данной сложной цепи надо начинать с определения Rэкв для нижней ветви участка АВ и центральной ветви участка СD.
Теперь мы можем упростить первоначальную схему. Она будет иметь следующий вид
Определим эквивалентные сопротивления каждого из участков:
После этих вычислений можно продолжить упрощение схемы
Полученная упрощенная схема, состоящая в данном случае из трех последовательно соединенных сопротивлений, называется по отношению к реальной эквивалентной схемой.
Определим Rэкв всей цепи как сумму трех последних сопротивлений
Зная напряжение источника тока, применяя формулу закона Ома, определим ток в не разветвленном участке смешанной цепи
Определив величину тока, найдем падение напряжения на участках эквивалентной схемы АВ, ВС, CD:
Теперь можно определить токи в параллельных ветвях участков АВ и СD
Остается определить величину токов, протекающих через сопротивления R7 и R8. Для этого надо сначала определить падение напряжения на сопротивлениях R7 и R8.
Определим падение напряжения на сопротивлении R9:
Падение напряжения на сопротивлении R7,8 определится как разность UCD и U:
Теперь определим величины токов, протекающих через сопротивления R7 и R8:
Величина тока. протекающего через сопротивления R4 и R5, равна I – току в неразветвленном участке цепи.
Итак, при решении задач на смешанное соединение сопротивлений необходимо, постепенно упрощая схему, определить эквивалентное сопротивление всей цепи, а затем. восстанавливая постепенно реальную схему. вычислить падение напряжения и токи в отдельных ветвях.
Мощность резистора: обозначение на схеме, как увеличить, что делать, если нет подходящего
Всех приветствую, кто заглянул на огонек. Речь в обзоре пойдет, как вы наверно уже догадались, о том, как сделать простую резистивную USB нагрузку для длительного тестирования емкости повербанков (ПБ), анализа качества кабелей и сетевых адаптеров.
Это одна из нескольких возможных статей о самостоятельном изготовлении резистивной нагрузки (на балластных резисторах), при удачном раскладе возможно руки дойдут и до электронной нагрузки, с регулировкой и стабилизацией тока.
Данная нагрузка служит уже достаточно давно и постоянно мелькает в моих обзорах, поэтому если заинтересовало, прошу под кат. В последнее время, такая самоделка уже не очень актуальна, т.к. появились бюджетные электронные нагрузки, поэтому имеет смысл доплатить и купить готовую.
Я же покупал еще по старому курсу, да и электронных нагрузок особо не было. Поэтому, если нужна именно резистивная, то приступим…
Возможные пути приобретения/изготовления резистивной нагрузки:
1) купить готовую плату-нагрузку с резисторами: Плюсы: + готовое работающее устройство (минимум телодвижений) + не нужны штекеры и провода (минимум потерь) + переключатель на 1А/2А (индикация) + небольшие размеры + небольшая стоимость Минусы: — очень сильно нагревается (около 180°С при токе 1А и около 230°С при токе 2А) и начинает жутко вонять (судя по отзывам, сам такой не имею) — не имеет корпуса, токоведущие/нагревающиеся части открыты (можно обжечься/прожечь что-нибудь, закоротить) — сложно прикрепить радиатор Так как изготовление хорошего нагрузочного модуля отнимает силы и время, то можно воспользоваться данной приблудой, но оставлять без присмотра не стоит 2) найти в закромах мощные резисторы (советские ПЭВ, ППБ и подобные), рассеиваемая им мощность для продолжительной работы должна быть не менее 10 Вт Плюсы: + меньший, но все равно достаточно высокий нагрев + не нужно покупать/средняя стоимость (наличие дома/покупка в магазе) + регулировка сопротивления, т.е. можно плавно изменять ток в широких пределах (только некоторые резюки, либо небольшая доработка) Минусы: — нужно припаивать штекер и провода — большие размеры — невозможность крепления радиатора (на большинстве) — нет переключателя (можно переделать, нужен второй резистор) — не имеет корпуса, токоведущие/нагревающиеся части также открыты (можно обжечься/прожечь что-нибудь) Я не имею таких резисторов в наличие, поэтому выбор за вами.
3) покупка резисторов 25-100 Вт в металлическом корпусе для отвода тепла и сборка своего модуля с кожухом
Плюсы: + средний нагрев (могут без опаски работать без доп. радиаторов) + средняя стоимость + возможность крепления дополнительного радиатора Минусы: — нужно припаивать штекер и провода — большие размеры — нет переключателя (можно переделать, нужен второй резистор) При этом они могут работать и без дополнительного охлаждения, но при этом неплохо греются, в пределах нормы, конечно. Я включал 25W резюки на полную разрядку моего ПБ — выдержали, но сильно грелись. Я рекомендую купить 100W резисторы, тогда дополнительный радиатор может совсем не пригодиться.
Итак, если решили собрать самодельный стенд из похожих резисторов, то приступим. Необходимые компоненты:
1) два резистора 25-100W по 4,7 Ом каждый. Как на зло, цены поднялись и многих номиналов уже не стало в продаже. Но наебайке есть 25W, 100W. Ищем по «Power resistor». 2) выключатель, я покупал тут 3) разборный USB штекер «папа», к примеру тут или тут 4) небольшой кусок медного многожильного провода большого сечения, к примеру, акустический провод 5) небольшой алюминиевый радиатор (по желанию) 6) пластиковая коробка
Номиналы резисторов рассчитываются по знакомой всем формуле закона Ома — I=U/R или R=U/I, где R – сопротивление (Ом), I –ток (А) и U – напряжение (V). К примеру, нам нужен ток 2А, поэтому для нагрузки 5V адаптеров нам нужен резюк 2,5Ома, т.к. 5/2=2,5 Ом.
Для 1А рассчитываем аналогично — 5/1=5 Ом. Так как большинство адаптеров/БП снижают напряжение под нагрузкой, то необходимо делать поправку на это и считать в среднем от 4,8V. Тогда на ток 2А нужен будет резюк R= U/I=4,8V/2А=2,4Ома, а для 1А — R= U/I=4,8V/1А=4,8Ома.
Также нужно помнить, что соединительные провода, выключатель и USB штекер также имеют некоторое сопротивление. Напомню одну хитрость, что при последовательном соединении резисторов общее сопротивление складывается, а при параллельном – будет чуть меньше самого маленького резистора.
Общее сопротивление нескольких резисторов можно посчитать здесь.
Чтобы не искать подходящие номиналы и не мудрить со схемой, я рекомендую сделать по моему варианту, правда с другими номиналами – 2 резистора по 4,7 Ом и небольшой выключатель. Для 1А будет задействован один резистор, для 2А – два в параллель. При этом, если мощность резистора или сопротивление не подходят, можете группировать несколько по указанным выше формулам. В своем нагрузочном модуле я использовал 2 резистора: 5,1Ом и 6Ом, т.к. я их выиграл на аукционе наEbay’ки за копейки, на другие номиналы тогда аукционов не было. При соединении параллельно, я получаю 2,7Ома для тока в 2А (в действительности 1,75А), а для тока в 1А (0,95А)задействую 1 резюк на 5,1 Ом. Они чуток не подходят, идеальный вариант был бы при использовании двух резюков по 4,7Ома, но таких лотов на аукционе не было.
Непосредственная сборка:
До этого пользовался вот таким простеньким модулем, он годился даже для длительных нагрузок, хотя при длительной работе он сильно нагревался, но не вонял и не перегорал (доставать, правда, его не удобно, можно было обжечься). Как только приехал второй резюк на 6 Ом, начал собирать стенд. Вот размеры типичных 25W резисторов в алюминиевом корпусе: Обратная сторона неровная и покрыта лаком, к тому же проушины для крепления имеют заусенцы, поэтому резисторы могут неплотно прилегать к радиатору, я рекомендую пройтись нулевой наждачкой: Сам радиатор я взял из старых запасов. Это распиленный пополам радиатор от бюджетных кулеров GlacialTech для процессоров на Socket A. В сервис центрах по ремонту компьютеров и бытовой техники за 50-100р вам отдадут целую пачку, на любой вкус и цвет. Можно использовать цельный радиатор, температура нагрева будет еще меньше. Мой нагрузочный стенд на 2А (точнее 1,75А) выше 70гр не нагревается. К тому же, к цельному радиатору можно приспособить небольшой вентилятор, тогда можно гонять модуль на высоких токах. При использовании 100Вт резисторов радиатор может вообще не понадобиться. Вот тот самый радиатор: Подошва у радиатора неровная, лучше отшлифовать. Можно оставить и так, теплообмен будет чуть похуже. Размеры моего радиатора: Вот что нам понадобится для изготовления модуля (наждачная бумага/шкурка на 1000/2000, стекло, в качестве идеально ровной поверхности, дрель, сверла, метчики для нарезки резьбы и машинное масло): Идеально полировать с пастой ГОИ не имеет особого смысла, хватит и 2000 наждачки. Затем сверлим отверстия и метчиком нарезаем резьбу (как это делать рассказывать не буду, см. в интернете). Если нет подходящего инструмента, то используйте термоклей/термоскотч/термопрокладки (ссылки внизу), сверлить ничего не придется. От себя добавлю, чтобы не сломать инструмент, капайте масло и через два полных оборота метчика, делайте пол оборота назад. Так вы 100% не сломаете метчик. По возможности пройдите чистовым метчиком (смотрите по количеству рисок на нем). Получается в итоге что-то вроде этого: В качестве кожуха я использовал защитный экран от старого холодильника. Можно использовать что угодно: от органики до любых пластиковых штуковин. Оргстекло небольшой толщины легко гнется при нагреве, я как-то гнул его над жалом мощного паяльника, только потом края придется немного подровнять. В общем, используем все, что есть под рукой. Перед окончательной сборкой пройдитесь по отверстиям сверлом большего диаметра, чтобы убрать заусенцы, иначе резюки плотно прилегать не будут (раззенковать): Далее намазываем тонкий слой термопасты на резисторы, можно просто выдавить каплю пасты, при затяжке она сама расползется. Я использовал российскую «народную» термопасту КПТ-8 (покупается в магазинах электрики): У нее средняя эффективность, со временем она подсыхает, но зато стоит копейки и продается в любых магазинах радиоэлектроники, для нашего модуля сгодится. Прикручиваем винты и загибаем вывода резисторов (можно до крепежа): Как видите, излишки термопасты вылезли наружу, они мешать не будут: Берем штекер USB «папа», желательно с позолоченными контактами (см. предыдущие пункты) и акустический провод с медными (не омедненными!) жилами толстого сечения. Для защиты от термического и механического воздействия я натянул термоусадку. Так как провод толстый, ножиком раздраконьте выходное отверстие: Берем выключатель, он будет вкл/выкл режим «2А». Подойдет любой силовой. Я использовал простенький KCD11, рассчитанный на 220V и 3А. В качестве окантовки использовал старый кабель-канал, немного срезав края. В одном из них вырезаем окошко под выключатель. Затем припаиваем выключатель к выводам резисторов: Сам провод припаиваем к резистору, который будет работать на 1А «по умолчанию». В моем случае это резистор 5,1 Ома. Если вы используете два одинаковых резюка по 4,7Ом, то припаиваем к любому: Одна сторона выводов будет соединена через выключатель, т.е. в положении «выкл» ток – 1А, в положении «вкл» — 2А, т.к. включается второй резюк в параллель. Получается вот такая простая схема: Далее прикручиваем кожух: Ставим верхнюю планку из того же кабель-канала или чего-нибудь похожего на место проема. Получается довольно неплохо: Ну и подклеиваем режимы работы, бумага и скотч в помощь: В итоге при хорошем адаптере имеем следующее (0,95А и 1,75А): Температура радиатора при токе 2А (1,75А) ни разу не поднималась выше 70°С, при 0,95А в районе 60°С: Итого: устройство работает, сильно не нагревается, не воняет, свои функции выполняет на 100%. Да, с номиналами чуток не повезло, но ничего страшного. Все мои обзоры ПБ протестированы именно с этой нагрузкой, при желании можно расширить диапазон токов, к примеру, на 0,5А/1А/1,5А/2А/2,5А…
Кисулька:
Мощность при параллельном соединении формула
О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно.
Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов
В жизни последовательное соединение резисторов имеет вид:
Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
- Общее номинальное сопротивление составного резистора обозначено как Rобщ.
- Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
- Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом.
Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом.
Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов
Можно соединять резисторы и параллельно:
Принципиальная схема параллельного соединения выглядит следующим образом:
Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:
Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Акб обратная полярность что это
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
- Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
- Измерение сопротивления при параллельном соединении
- Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
- При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Резистор – это элемент электрической схемы, который обладает сопротивлением электрическому току. Классифицируют два типа резисторов: постоянные и переменные (подстроечные). При моделировании той или иной электрической схемы, а также при ремонте электронных изделий, возникает необходимость использовать резистор определенного номинала.
Хотя и существует множество различных номиналов постоянных резисторов, в данный момент под рукой может не оказаться требуемого, либо резистора с таким номиналом не существует. Чтобы выйти из такой ситуации, можно использовать как последовательное так и параллельное соединение резисторов.
О том, как правильно произвести расчет и подбор различных номиналов сопротивлений, будет рассказано в этой статье.
Последовательное соединение резисторов – это самая элементарная схема сборки радиодеталей, оно применяется для увеличения общего сопротивления цепи.
При последовательном соединении, сопротивление используемых резисторов просто складывается, а вот при параллельном соединении необходимо производить расчет по нижеописанным формулам.
Параллельное соединение необходимо для снижения результирующего сопротивления, а также для увеличения мощности, несколько параллельно подключенных резисторов имеют большую мощность, чем у одного.
Температура плавления клея для клеевого пистолета
- На фотографии можно увидеть параллельное подключение резисторов.
- Общее номинальное сопротивление необходимо рассчитывать по следующей схеме:
- — R(общ) – общее сопротивление;
- — R1, R2, R3 и Rn – параллельно подключенные резисторы.
- Когда параллельное соединение резисторов состоит всего из двух элементов, в таком случае общее номинальное сопротивление можно высчитать по следующей формуле:
- — R(общ) – общее сопротивление;
- — R1, R2 – параллельно подключенные резисторы.
- В радиотехнике существует следующее правило: если параллельное подключение резисторов состоит из элементов одного номинала, то результирующее сопротивление можно высчитать, разделив номинал резистора на количество соединенных резисторов:
- — R(общ) – общее сопротивление;
- — R – номинал параллельно подключенного резистора;
- — n – количество соединенных элементов.
- Важно учитывать, что при параллельном соединении результирующее сопротивление всегда будет ниже, чем сопротивление самого малого по номиналу резистора.
- Приведем практический пример: возьмем три резистора, со следующими значениями номинального сопротивления: 100 Ом, 150 Ом и 30 Ом. Проведем расчет общего сопротивления, по первой формуле:
- После расчета формулы мы видим, что параллельное соединение резисторов, состоящее из трех элементов, с наименьшим номиналом 30 Ом, в результате дает общее сопротивление в электрической цепи 21,28 Ом, что ниже наименьшего номинального сопротивления в цепи почти на 30 процентов.
Параллельное соединение резисторов чаще всего используют в тех случаях, когда необходимо получить сопротивление с большей мощностью.
В таком случае необходимо взять резисторы одинаковой мощности и с одинаковым сопротивлением.
Результирующая мощность в таком случае рассчитывается путем умножения мощности одного элемента сопротивления на общее количество параллельно подключенных резисторов в цепи.
Например: пять резисторов с номиналом в 100 Ом и с мощностью 1 Вт в каждом, подключенные параллельно, имеют общее сопротивление 20 Ом и мощность 5 Вт.
При последовательном подключении тех же резисторов (мощность так же складывается), получим результирующую мощность 5 Вт, общее сопротивление составит 500 Ом.
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
- Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
- Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом. Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Как открутить болт с фиксатором резьбы
- Общее сопротивление R рассчитывается по формуле:
- Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Обозначение мощности резистора на схеме, как её увеличить, что делать, если нет подходящего по мощности резистора
Обозначение мощности резистора на схеме, как её увеличить, что делать, если нет подходящего по мощности резистора
Резистор — пассивный элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления, предназначенный для линейного преобразования силы тока в напряжение и напряжения в силу тока, ограничения тока, поглощения электрической энергии и др. Весьма широко используемый компонент практически всех электрических и электронных устройств.
В схемах радиоэлектронной аппаратуры одним из наиболее часто встречающихся элементов является резистор, другое его название это сопротивление. У него есть целый ряд характеристик, среди которых есть мощность. В этой статье мы поговорим о резисторах, что делать, если у вас нет подходящего по мощности элемента, и почему они сгорают.
Характеристики резисторов
1. Основной параметр резистора – это номинальное сопротивление.
2. Второй параметр, по которому его выбирают – это максимальная (или предельная) рассеиваемая мощность.
3. Температурный коэффициент сопротивления – описывает, насколько изменяется сопротивление, при изменении его температуры на 1 градус Цельсия.
4. Допустимое отклонение от номинала. Обычно разброс параметров резистора от одного заявленного в пределах 5-10%, это зависит от ГОСТ или ТУ по которому он произведен, существуют и точные резисторы с отклонением до 1%, обычно стоят дороже.
5. Предельное рабочее напряжение, зависит от конструкции элемента, в бытовых электроприборах с напряжением питания 220В могут применяться практически любые резисторы.
6. Шумовые характеристики.
7. Максимальная температура окружающей среды. Это такая температура, которая может быть при достижении максимальной рассеиваемой мощности самого резистора. Об этом подробнее поговорим позже.
8. Влаго- и термоустойчивость.
Есть еще две характеристики, о которых начинающие чаще всего не знают, это:
1. Паразитная индуктивность.
2. Паразитная ёмкость.
Оба параметра зависят от типа и конструктивных особенностей резистора. Индуктивность имеет в любом проводнике, вопрос в её величины. Типовые величины паразитных индуктивностей и емкостей приводить бессмысленно. Паразитные составляющие следует учитывать при проектировании и ремонте высокочастотных приборах.
На низких частотах (например, в пределах звукового диапазона до 20 кГц), существенного влияния в работу схемы они не вносят. В высокочастотных приборах, с рабочими частотами в сотни тысяч и выше герц существенное влияние вносит даже расположение дорожек на плате и их форма.
- Мощность резистора
- Из курса физики многие отлично помнят формулу мощности для электричества, это: P=U*I
- Отсюда следует, что она линейно зависит от тока и напряжения. Ток же через резистор зависит от его сопротивления и приложенного к нему напряжению, то есть:
- I=U/R
- Падение напряжения на резисторе (сколько на его выводах остаётся напряжения от приложенного к цепи, в которой он установлен), так же зависит от тока и сопротивления:
- I=U/R
- Теперь объясним простыми словами, что такое мощность у резистора и куда она выделяется.
У любого металла есть своё удельное сопротивление, это такая величина, которая зависит от структуры этого самого металла. Когда носители зарядов (в нашем случае электроны), под воздействием электрического тока протекают через проводник, они сталкиваются с частицами, из которого состоит металл.
В результате этих столкновений затрудняется движение тока. Если очень обобщенно сказать, то получается, так, что чем плотнее структура металла, тем сложнее протекать току (тем больше сопротивление).
На картинке пример кристаллической решетки, для наглядности.
Из-за этих столкновений выделяется тепло. Это можно представить, как если бы вы шли через толпу (большое сопротивление), где вас еще и толкают, или если бы шли по пустому коридору, где вы сильнее вспотеете?
То же самое происходит и с металлом. Мощность выделяется в виде тепла. В некоторых случаях это плохо, потому что так снижается коэффициент полезного действия прибора. В других ситуациях – это полезное свойство, например в работе ТЭНов. В лампах накаливания за счет своего сопротивления спираль раскаляется до яркого свечения.
Но как это относится к резисторам?
Дело в том, что резисторы применяют для ограничения тока при питании каких-либо устройств, или элементов цепи, или для задания режимов работы полупроводниковым приборам. Из формулы выше станет ясно, что ток снижается, за счет снижения напряжения. Лишнее напряжение можно сказать, что сгорает в виде тепла на резисторе, мощность при этом считается по той же формуле, что и общая мощность:
P=U*I
Здесь U – это количество вольт «сожженных» на резисторе, а I – это ток, который через него протекает.2/1=144/1=144 Вт.
Всё сходится. Резистор будет выделять тепло с мощностью в 144Вт. Это условные значения, взятые в качестве примера. На практике таких резисторов вы не встретите в радиоэлектронной аппаратуре, исключением являются большие сопротивления для регулирования двигателей постоянного тока или пуска мощных синхронных машин в асинхронном режиме.
Какие бывают резисторы и как они обозначаются на схеме
Ряд мощностей резисторов стандартен: 0.05 (0.62) – 0.125 – 0.25 – 0.5 – 1 – 2 – 5
Это типовые номиналы распространенных резисторов, бывают и большие значения, или другие величины. Но этот ряд наиболее распространен. При сборке электроники используют схему электрическую принципиальную, с порядкового номера элементов. Реже указываться номинальное сопротивление, еще реже указывается номинальное сопротивление и мощность.
Чтобы быстро определить мощность резистора на схеме были введены соответствующие УГО (условные графические обозначения) по ГОСТ. Внешний вид таких обозначений и их расшифровка представлены в таблице ниже.
Вообще эти данные, а также название конкретного типа резистора указываются в перечне элементов, там же указывается и разрешенный допуск в %.
Внешне, они отличаются размером, чем мощнее элемент, тем больше его размер. Больший размер увеличивает площадь теплообмена резистора с окружающей средой. Поэтому тепло, которое выделяется при прохождении тока через сопротивление, быстрее отдаётся воздуху (если окружающая среда воздух).
Это значит, что резистор может греться с большей мощностью (выделять определенное количество тепла в единицу времени). Когда температура сопротивления достигает определенного уровня, сначала начинает выгорать внешний слой с маркировкой, дальше сгорает резистивный слой (пленка, проволока или что-то другое).
Чтобы вы оценили, как сильно может греться резистор, взгляните на нагрев спирали разобранного мощного резистора (более 5 Вт) в керамическом корпусе.
В характеристиках был такой параметр, как допустимая температура окружающей среды. Она указывается, для правильного подбора элемента.
Дело в том, что раз мощность резистора ограничена способностью отдать тепло и, при этом, не перегреться, а для отдачи тепла, т.е.
охлаждения элемента путем конвекции или принудительным потоком воздуха должна быть как можно большая разница температур элемента и окружающей среды.
Поэтому если вокруг элемента слишком жарко он быстрее нагреется и сгорит, даже если электрическая мощность на нем ниже максимально рассеиваемой. Нормальной температурой является 20-25 градусов Цельсия.
Что делать, если нет резистора нужной мощности?
Частой проблемой радиолюбителей является отсутствия резистора нужной мощности. Если у вас есть резисторы мощнее, чем нужно – ничего страшного в этом нет, можно ставить не задумываясь. Лишь бы он влез по размеру. Если все имеющиеся резисторы по мощности меньше, чем нужно – это уже проблема.
На самом деле решить этот вопрос достаточно просто. Вспомните законы последовательного и параллельного соединения резисторов.
1. При последовательном соединении резисторов сумма падений напряжений на всей цепочке равняется сумме падений на каждом из них. А ток, протекающий через каждый резистор равен общему току, т.е. в цепи из последовательно соединенных элементов протекает ОДИН ток, но приложенные к каждому из них напряжения РАЗНЫЕ, определяются по закону Ома для участка цепи (см. выше) Uобщ=U1+U2+U3
2. При параллельном соединении резисторов падение на всех напряжения равны, а ток, протекающий в каждой из ветвей обратно пропорционален сопротивлению ветви. Общий ток цепочки из параллельно соединенных резисторов равен сумме токов каждой из ветвей.
На этой картинке изображено всё вышесказанное, в удобной для запоминания форме.
Так, как при последовательном соединении резисторов снизится напряжение на каждом из них, а при параллельном соединении ток, то если P=U*I
Мощность, выделяемая на каждом из них, снизится соответствующим образом.
Поэтому, если у вас нет резистора 100 Ом на 1 Вт, его можно почти всегда заменить 2 резисторами на 50 Ом и 0.5 Вт соединенными последовательно, или 2 резисторами на 200 Ом и 0.5 Вт соединенными параллельно.
Я не просто так написал «ПОЧТИ ВСЕГДА».
Дело в том, что не все резисторы одинаково хорошо переносят ударные токи, в некоторых цепях, например связанные с зарядом конденсаторов большой ёмкости, в первоначальный момент времени переносят большую ударную нагрузку, которая может повредить его резистивный слой. Такие связки нужно проверять на практике или путем долгих расчетов и чтением технической документации и ТУ на резисторы, чем почти никогда и никто не занимается.
Заключение
Мощность резистора – это величина не менее важная, чем его номинальное сопротивление. Если не уделять внимания подбору сопротивлений нужно мощности, то они будут перегорать и сильно греться, что плохо в любой цепи.
При ремонте аппаратуры, особенно китайской, ни в коем случае не пытайтесь ставить резисторы меньшей мощности, лучше поставить с запасом, если есть такая возможность поместить его по габаритам на плате.
Для стабильной и надежной работы радиоэлектронного устройства нужно подбирать мощность, как минимум, с запасом в половину от предполагаемой, а лучше в 2 раза больше. Это значит, что если по расчетам на резисторе выделяется 0.9-1 Вт, то мощность резистора или их сборки должна быть не меньше, чем 1.5-2 Вт.
Ранее ЭлектроВести писали, что JinkoSolar объявила, что она установила новый рекорд эффективности для монокристаллических PERC-панелей, который составил 24,38%.
Компания также разработала модуль мощностью 469,3 Вт.
Кроме того, китайский производитель фотоэлектрических элементов поравнялся с фирмой Trina Solar, которая на прошлой неделе заявила о рекордном 24,58% показателе КПД монокристаллических панелей n-типа.
Резистор
Радиоэлектроника для начинающих
Резистор служит для ограничения тока в электрической цепи, создания падений напряжения на отдельных её участках и пр. Применений очень много, всех и не перечесть.
Другое название резистора – сопротивление. По сути, это просто игра слов, так как в переводе с английского resistance – это сопротивление (электрическому току).
Когда речь заходит об электронике, то порой можно встретить фразы типа: «Замени сопротивление», «Два сопротивления сгорели». В зависимости от контекста под сопротивлением может подразумеваться именно электронная деталь.
На схемах резистор обозначается прямоугольником с двумя выводами. На зарубежных схемах его изображают чуть-чуть иначе. «Тело» резистора обозначают ломаной линией – своеобразная стилизация под первые образцы резисторов, конструкция которых представляла собой катушку, намотанную высокоомным проводом на изоляционном каркасе.
Рядом с условным обозначением указывается тип элемента (R) и его порядковый номер в схеме (R1). Здесь же указано его номинальное сопротивление. Если указана только цифра или число, то это сопротивление в Омах.
Иногда, рядом с числом пишут Ω – так, греческой заглавной буквой «Омега» обозначают омы. Ну, а, если так, – 10к, то этот резистор имеет сопротивление 10 килоОм (10 кОм – 10 000 Ом).
Про множители и приставки «кило», «мега» можете почитать здесь.
Не стоит забывать о переменных и подстроечных резисторах, которые всё реже, но ещё встречаются в современной электронике. Об их устройстве и параметрах я уже рассказывал на страницах сайта.
Основные параметры резисторов
- Номинальное сопротивление.
Это заводское значение сопротивления конкретного прибора, измеряется это значение в Омах (производные килоОм – 1000 Ом, мегаОм – 1000000 Ом). Диапазон сопротивлений простирается от долей Ома (0,01 – 0,1 Ом) до сотен и тысяч килоОм (100 кОм – 1МОм). Для каждой электронной цепи необходимы свои наборы номиналов сопротивлений. Поэтому разброс значений номинальных сопротивлений столь велик. - Рассеиваемая мощность.
Более подробно о мощности резистора я уже писал здесь.
При прохождении электрического тока через резистор происходит его нагрев. Если пропускать через него ток, превышающий заданное значение, то токопроводящее покрытие разогреется настолько, что резистор сгорает. Поэтому существует разделение резисторов по рассеиваемой мощности.
На графическом обозначении резистора внутри прямоугольника мощность обозначается наклонной, вертикальной или горизонтальной чертой. На рисунке обозначено соответствие графического обозначения и мощности указанного на схеме резистора.
К примеру, если через резистор потечёт ток 0,1А (100 mA), а его номинальное сопротивление 100 Ом, то необходим резистор мощностью не менее 1 Вт. Если вместо этого применить резистор на 0,5 Вт, то он вскоре выйдет из строя. Мощные резисторы применяются в сильноточных цепях, например, в блоках питания или сварочных инверторах.
Если необходим резистор мощностью более 2 Вт (5 Вт и более), то внутри прямоугольника на условном графическом обозначении пишется римская цифра. Например, V – 5 Вт, Х – 10 Вт, XII – 12 Вт. - Допуск.
При изготовлении резисторов не удаётся добиться абсолютной точности номинального сопротивления. Если на резисторе указано 10 Ом, то его реальное сопротивление будет в районе 10 Ом, но никак не ровно 10. Оно может быть и 9,88 и 10,5 Ом. Чтобы как-то обозначить пределы погрешности в номинальном сопротивлении резисторов, их делят на группы и присваивают им допуск. Допуск задаётся в процентах. Если вы купили резистор на 100 Ом c допуском ±10%, то его реальное сопротивление может быть от 90 Ом до 110 Ом. Узнать точное сопротивление этого резистора можно лишь с помощью омметра или мультиметра, проведя соответствующее измерение. Но одно известно точно. Сопротивление этого резистора не будет меньше 90 или больше 110 Ом.
Строгая точность номиналов сопротивлений в обычной аппаратуре важна не всегда. Так, например, в бытовой электронике допускается замена резисторов с допуском ±20% от того номинала, что требуется в схеме. Это выручает в тех случаях, когда необходимо заменить неисправный резистор (например, на 10 Ом). Если нет подходящего элемента с нужным номиналом, то можно поставить резистор с номинальным сопротивлением от 8 Ом (10-2 Ом) до 12 Ом (10+2 Ом). Считается так (10 Ом/100%) * 20% = 2 Ом. Допуск составляет -2 Ом в сторону уменьшения, +2 Ом в сторону увеличения.
Для тех, кто ещё не знает, существует ещё одна возможность подобрать необходимое сопротивление – его можно составить, соединив вместе несколько резисторов разных номиналов. Об этом читайте в статье про соединение резисторов.
Существует аппаратура, где такой трюк не пройдёт – это прецизионная аппаратура. К ней относится медицинское оборудование, измерительные приборы, электронные узлы высокоточных систем, например, военных. В ответственной электронике используются высокоточные резисторы, допуск их составляет десятые и сотые доли процента (0,1-0,01%). Иногда такие резисторы можно встретить и в бытовой электронике.
Стоит отметить, что в настоящее время в продаже можно встретить резисторы с допуском не более 10% (обычно 1%, 5% и реже 10%). Высокоточные резисторы имеют допуск в 0,25…0,05%. - Температурный коэффициент сопротивления (ТКС).
Под влиянием внешней температуры или собственного нагрева из-за протекающего тока, сопротивление резистора меняется. Иногда в тех пределах, которые нежелательны для работы схемы. Чтобы оценить изменение сопротивления из-за воздействия температуры, то есть термостабильность резистора, используется такой параметр, как ТКС (Температурный Коэффициент Сопротивления). За рубежом принято сокращение T.C.R.
В маркировке резистора величина ТКС, как правило, не указывается. Для нас же необходимо знать, что чем меньше ТКС, тем лучше резистор, так как он обладает лучшей термостабильностью. Более подробно о таком параметре, как ТКС, я рассказывал тут.
Первые три параметра основные, их надо знать!
Перечислим их ещё раз:
- Номинальное сопротивление (маркируется как 100 Ом, 10кОм, 1МОм…)
- Рассеиваемая мощность (измеряется в Ваттах: 1 Вт, 0,5 Вт, 5 Вт…)
- Допуск (выражается в процентах: 5%, 10%, 0,1%, 20%).
Так же стоит отметить конструктивное исполнение резисторов.
Сейчас можно встретить как микроминиатюрные резисторы для поверхностного монтажа (SMD-резисторы), которые не имеют выводов, так и мощные, в керамических корпусах.
Существуют и невозгораемые, разрывные и прочее. Перечислять можно очень долго, но основные параметры у них одинаковые: номинальное сопротивление, рассеиваемая мощность и допуск.
В настоящее время номинальное сопротивление резисторов и их допуск маркируют цветными полосами на корпусе самого элемента.
Как правило, такая маркировка применяется для маломощных резисторов, которые имеют небольшие габариты и мощность менее 2…3 ватт.
Каждая фирма-изготовитель устанавливает свою систему маркировки, что вносит некоторую путаницу. Но в основном присутствует одна устоявшаяся система маркировки.
Новичкам в электронике хотелось бы рассказать и о том, что кроме резисторов, цветовыми полосами маркируют и миниатюрные конденсаторы в цилиндрических корпусах. Иногда это вызывает путаницу, так как такие конденсаторы ложно принимают за резисторы.
Таблица цветового кодирования
Рассчитывается сопротивление по цветным полосам так. Например, три первых полосы – красные, последняя четвёртая золотистого цвета. Тогда сопротивление резистора 2,2 кОм = 2200 Ом.
Первые две цифры согласно красному цвету – 22, третья красная полоса, это множитель. Стало быть, по таблице множитель для красной полосы – 100. На множитель необходимо умножить число 22. Тогда, 22 * 100 = 2200 Ом.
Золотистая полоса соответствует допуску в 5%. Значит, реальное сопротивление может быть в пределе от 2090 Ом (2,09 кОм) до 2310 Ом (2,31 кОм).
Мощность рассеивания зависит от размеров и конструктивного исполнения корпуса.
На практике широкое распространение имеют резисторы с допуском 5 и 10%. Поэтому за допуск отвечают полосы золотого и серебристого цвета. Понятно, что в таком случае, первая полоса находится с противоположной стороны элемента. С неё и нужно начинать считывание номинала.
Но, как быть, если резистор имеет небольшой допуск, например 1 или 2% ? С какой стороны считывать номинал, если с обеих сторон присутствуют полосы красного и коричневого цветов?
Этот случай предусмотрели и первую полосу размещают ближе к одному из краёв резистора. Это можно заметить на рисунке таблицы. Полоски, обозначающие допуск расположены дальше от края элемента.
Конечно, бывают случаи, когда нет возможности считать цветовую маркировку резистора (забыли таблицу, стёрта/повреждена сама маркировка, некорректное нанесение полос и пр.).
В таком случае, узнать точное сопротивление резистора можно только, если измерить его сопротивление мультиметром или омметром. В таком случае вы будете 100% знать его реальную величину. Также при сборке электронных устройств рекомендуется проверять резисторы мультиметром для того, чтобы отсеить возможный брак.
Главная » Радиоэлектроника для начинающих » Текущая страница
Также Вам будет интересно узнать:
Простой способ определить Vf светодиода, чтобы выбрать подходящий резистор
Вы неправильно понимаете, как работает светодиод, так как Vf — это не напряжение, которое вы кладете на светодиод, чтобы заставить его работать, а напряжение, которое появляется (падает) на светодиод, когда ток пропускается через него.
Если вы посмотрите на соответствующий лист данных, вы увидите Vf (min), Vf и Vf (max), заданные для определенного тока, и это означает, что, если вы подадите указанный ток через светодиод, вы можете ожидать Vf падать где-нибудь между Vf (мин) и Vf (макс.), причем Vf является типичным значением.
Итак, ответ на ваш вопрос:
- Источником питания является любой источник переменного напряжения, R обеспечивает балласт для светодиода, снижая его чувствительность к изменениям источника питания.
- Это не даст светодиоду испускать свой волшебный дым, если вы случайно запустите источник питания слишком далеко, и его значение [R] не критично, в разумных пределах.
- Например, если вы используете резистор 1000 Ом и пытаетесь протолкнуть 20 мА через светодиод, эти 20 мА также должны пройти через R, поэтому R будет падать:
- E = IR = 0,02 A × 1000 Ом = 20 вольт, E = IRзнак равно0.02A×1000Ωзнак равно20 вольт,
- и вам понадобится запас для светодиодов.
- «A» — это амперметр, используемый для измерения тока через светодиод, а «V» — вольтметр, используемый для измерения напряжения на светодиоде.
При использовании, то, что вам нужно сделать, это запустить источник питания с нуля вольт, а затем провернуть его до тех пор, пока амперметр не покажет 20 миллиампер, тогда напряжение, отображаемое на вольтметре, будет Vf для этого конкретного диода при данном конкретном токе и температуре окружающей среды. температура.
- Возвращаясь к вашему вопросу, способ определить, какое значение последовательного сопротивления является «правильным» для вашего светодиода, состоит в том, чтобы сначала определить его Vf при желаемом прямом токе (если), а затем использовать закон Ома для определения значения сопротивления, так:
- R = Vс — VеяеR = Вs-Веяе
- Если предположить, что Vs (напряжение питания) составляет 12 вольт, то Vf равно 2 вольтам, а If — 20 мА, мы получим
- R = 12 В- 2 В0,02 А= 500 ОмR = 12В-2В0.02Aзнак равно500 Ом
- Затем, чтобы определить мощность рассеиваемого резистора, мы можем написать:
- Pd = (Vs — Vf) × If = 10 В × 0,02 А = 0,2 Вт Pd = (Vs — Vf)×Если знак равно 10V×0.02Aзнак равно0,2 Вт
- 510 Ом — это самое близкое значение E24 (+/- 5%), которое будет сохраняться, если на консервативной стороне 20 мА, и резистор 1/4 Вт должен быть в порядке.
- Утиный суп, а? 😉
таблица по цветам онлайн, сопротивления, расшифровка цветовых обозначений, кодовое определение — как определить номинал
Рассмотрим современные способы обозначения параметров сопротивлений. Под прицелом внимания цветная маркировка резисторов: таблицу на 4 полосы приведем, читать ее научим, нестандартные случаи тоже разберем – чтобы вы не путались в нюансах.
Внимание, нельзя определять параметры электронного компонента «на глаз», ориентируясь только на его размеры. Потому что технологии изготовления у производителей отличаются, и при одинаковых геометрических габаритах ЭРЭ двух брендов могут обладать принципиально разными рабочими показателями.
Поэтому и появилась необходимость в каких-то универсальных классификаторах. В СССР это были буквенно-цифровые коды, но постепенно, со стремлением к минимизации схем, они оказывались менее актуальными – их становилось все неудобнее читать, требовалось что-то более наглядное. Такие и появились красные, черные, желтые и другие кольца, контрастные между собой.
Кратко о характеристиках, отраженных в цветомаркировке резисторов
Сегодня их две:
- номинал – максимально возможная величина сопротивления (в Омах) току при непосредственном использовании собранной схемы;
- допуск – предельное на практике отклонение от заявленного теоретического значения.
На старом, еще советском электронном компоненте также указывался его вид и серия, опять же, с помощью букв и цифр. Но от этого давно отказались в угоду минимизации. Сейчас, обладая должным опытом, можно буквально за секунду, бросив лишь один наметанный взгляд, определить и силу тока, на которую рассчитан ЭРЕ, и актуальную для него погрешность – просто по кольцам.
Для чего нужна маркировка резисторов, по цветам и в принципе
В общем случае обозначения необходимы, чтобы вы могли сразу понять, какими рабочими параметрами обладает тот или иной электронный элемент, чем отличается от других и тому подобное. Без них была бы невозможной быстрая и безошибочная установка или замена ЭРЭ.
Ну а красные, синие, желтые и другие кольца понадобились просто потому, что они удобны в ситуациях с мелкими деталями. Например, у компонента схемы, выдерживающего мощность в 0,125 Вт, длина в пару миллиметров и диаметральный размер в 1 мм. И как на него наносить цифры и буквы? Это сложно, да и прочитать такой код потом, без использования оптических приспособлений, тоже затруднительно.
Поэтому в свое время свежим решением стала цветовая маркировка сопротивления на корпусе резистора, ведь она:
- сразу заметная и гораздо более наглядная – что-то спутать практически нереально;
- легче делается и не стирается со временем, в процессе эксплуатации;
- проще передает подробную информацию.
Последнее преимущество заслуживает отдельного рассмотрения. Так, точность исполнения ЭРЭ может быть 20%, 10-5% или прецизионной, и это отлично отражено количеством колец: в первом случае их три, во втором – четыре, в третьем – пять или шесть. Хотя этот момент мы подробнее осветим ниже, а пока взглянем на «морально устаревший вариант», он тоже требует определенного внимания.
Цифро-буквенные обозначения
Они задуманы вполне логично: числами записаны номиналы, а литерами – множители. Последние придется запомнить, что не очень удобно. Еще один нюанс в том, что код может идти вообще представительниц алфавита, допустим, «33» – это говорит о стандартном допуске в 20%.
Это справедливо по отношению к МЛТ, то есть к металлопленочным лакированным термоустойчивым электронным элементам – самым ходовым во времена позднего СССР и еще работающим в хорошо сохранившейся ретротехнике.
Примеры расшифровки
- 3R9J – номинал в 3,9 Ом с погрешностью в 5%, которую задает литера «J». Тогда как «R» дает понять, что множитель равняется единице, и указывает на дробную часть – является местом постановки запятой.
- 1K0J – здесь уже есть коэффициент в 103, который вводит «К». Умножаем, и получается, что максимально ЭРЭ обеспечивает 1000 Ом или 1 кОм. Ну а допуск, как вы уже поняли, увидев «J», составляет 5%.
- 215RG – деталь на 215 Ом, о чем свидетельствует разделитель «R», изготовленная с точностью до 2%, судя по «G».
- M10J – здесь буква «М» определяет коэффициент в 1000000 или в 106, причем расположена она перед числом, то есть является еще и запятой, то есть наш миллион Ом нужно перемножать на 0,1; результат – 100 кОм или 0,1 МОм, хотя такой вариант записи встречается реже.
- 12K4F – пример того, что маркировка резисторов и расшифровка их обозначений превратится в проблему, если не обращать внимания на нюансы; в данном случае – на расположение «К», ведь это не только показатель 103, но еще и разделитель. Поэтому номинал равняется 12,4 кОм, тогда как погрешность – всего 1%, что нам подсказывает «F».
- 1Т0М – «Т» здесь свидетельствует о множителе в 1012, то есть о тераОме, который обычно упоминается сокращенно – просто ТОм.
- 2М2К – здесь допуск уже знакомый нам, 10%, взглянуть нужно в первую очередь на букву «М»; так как она расположена между цифрами, она является не только коэффициентом, но и запятой. Вот и получаем, что 2,2 необходимо умножить на 106, итог – 2,2 МОм.
Принцип понятен, плюс, для облегчения процесса можно вместо английских литер подставлять кириллицу. Тогда останется лишь запомнить, что «E» и «R» равняются единице, а другие вполне соответствуют СИ.
Хотите внедрить «Склад 15»?
Получите всю необходимую информацию у специалиста.
Спасибо!
Спасибо, ваша заявка принята!
Продолжить
Цветовая расшифровка маркировки резисторов
Ее появление серьезнейшим образом упростило нанесение и, главное, прочтение обозначений; со временем она стала стандартом массового производства, так как она удобна при изготовлении крупных партий малых по размеру ЭРЭ. Ее начали использовать и на территории постсоветского пространства, и это решило еще одну проблему – больше не приходится учитывать еще и страну-производителя, и какие-то оригинальные особенности выпуска в том или ином государстве.
В соответствии с ней на электронном компоненте выполняют несколько колец – от трех до шести, в зависимости от допуска, но не считая золотого (или серебряного). Являются температурными коэффициентами и своеобразными ориентирами: деталь необходимо располагать так, чтобы они оказались справа.
Обычно наносится цветовая маркировка резисторов в 4 полосы, реже – в 5-6, так как эти сопротивления изготавливаются с меньшей погрешностью и устанавливаются в особенно ответственных схемах, то есть не так часто. Главное, что каждая линия говорит о чем-то важном:
- первая, вторая (и третья) определяют номинал, числовое значение которого меняется в зависимости от того, где и какая колористика;
- четвертая показывает множитель.
После них обычно идет разрыв, т. е. сравнительно широкий промежуток, в конце которого есть еще одно-два кольца – погрешность и уже упомянутый температурный коэффициент (которого может и не быть).
Как не запутаться в порядке и числах? Для этого предусмотрены специальные графические «помощницы».
Маркировка резисторов цветными полосками: таблица универсальных значений
|
Цвет |
Цифра |
|
Черный |
0 |
|
Коричневый |
1 |
|
Красный |
2 |
|
Оранжевый |
3 |
|
Желтый |
4 |
|
Зеленый |
5 |
|
Синий |
6 |
|
Фиолетовый |
7 |
|
Серый |
8 |
|
Белый |
9 |
|
Серебряный |
-1 |
|
Золотой |
-2 |
Это база, на основании которой можно быстро вычислять номиналы нужных ЭРЭ. Обратите внимание, она составлена с учетом следующих моментов:
- Каждому варианту присвоена определенная, не повторяющаяся цифра.
- Порядок цветов может меняться в зависимости от конкретных габаритов электрического компонента, но колористику всегда не составляет труда записать в виде трехзначного числа. Эта цифра впоследствии используется для составления схемы условной принципиальной.
- С помощью множителя легко рассчитывается то максимальное значение токовой нагрузки, которую способен выдержать ЭРЭ.
- Свои поля с отклонениями предусмотрено для всех колец.
Чтобы было понятнее, как разделяются резисторы маркировкой по цветам, таблицу нужно рассмотреть на конкретных примерах.
Допустим, есть деталь с четырьмя полосками – читаем их слева направо:
- Первая, коричневая – говорит и о числе, «1», и о коэффициенте, «10».
- Вторая, черная – дает нам следующий номер цифры, в данном случае «0», не участвующий в расчетах. Если проводить параллель с советскими стандартами, код был бы 1К0.
- Третья, красная – еще один множитель, в нашей ситуации он равняется «100».
- Четвертая, серебристая – определяет погрешность, которая здесь составляет 10%.
Получается, что этот ЭРЭ в 1 кОм или 1000 Ом (10 х 100) и с допуском в 10%.
Для закрепления рассмотрим еще одну цветовую маркировку сопротивлений, расшифровка резистора с 6 кольцами выглядит следующим образом:
- Первое, красное – говорит, что начальное число – это «2».
- Второе, синее – позволяет нам взять следующую цифру, «6».
- Третье, фиолетовое – дает «7», в сумме – «267».
- Четвертое, зеленое – это уже показатель коэффициента, равного 105, соответственно, расчетный номинал 267 х 105 = 2,67 МОм.
- Пятое, коричневое – показывает, что предельное отклонение составляет 1% в обе стороны.
- Шестое, золотистое – задает температурный коэффициент на уровне 100 ppm/ 0C.
Тоже ничего трудного, правда? Отсюда делаем логичный вывод: увеличение числа колец почти не усложняет расчеты. Кстати, можно провести и определение номинала резистора по цветовой маркировке онлайн, воспользовавшись специальным калькулятором, но для 6 полосок он подходит далеко не всегда.
Рассматриваемые ЭРЭ бывают как постоянными, так и переменными, и специально для последних введен дополнительный ряд ЕЗ, в котором:
- литера «Е» присутствует всегда и свидетельствует как раз об особом случае;
- цифры после нее дают представление о максимальной выдерживаемой нагрузке, и каждая из них отсчитывает десятичный интервал.
Стандартные же компоненты нормированы положениями ГОСТа 2825-67, и, согласно ему, есть следующие нюансы:
- в Е6 отклонение возможно в обе стороны, вплоть до 20%;
- допуски в Е12 достигают 10%;
- предельные показатели в Е24 еще меньше – плюс-минус 5%.
И эта тенденция сохраняется по мере увеличения номера серии: у того же Е96 погрешность уже 1%, а у Е192 – и вовсе 0,5%.
Цветовое обозначение резисторов: сводная таблица
Если взять и сгруппировать все важные показатели, мы получим:
|
Кольцо |
Номинальный ряд (числа) |
Множитель |
Допуск, % |
Темп-й коэф-т, ppm/ 0C |
Норма отказов, % |
||
|
1 |
2 |
3 |
|||||
|
черное |
0 |
0 |
0 |
0 (1) |
|||
|
корич-е |
1 |
1 |
1 |
1 (10) |
±1 |
100 |
1 |
|
красное |
2 |
2 |
2 |
2 (100) |
±2 |
50 |
0,1 |
|
оранж-е |
3 |
3 |
3 |
3 (1000) |
15 |
0,01 |
|
|
желтое |
4 |
4 |
4 |
4 (104) |
25 |
0,001 |
|
|
зеленое |
5 |
5 |
5 |
5 (105) |
±0,5 |
||
|
синее |
6 |
6 |
6 |
6 (106) |
±0,25 |
10 |
|
|
фиолет-е |
7 |
7 |
7 |
7 (107) |
±0,1 |
5 |
|
|
серое |
8 |
8 |
8 |
8 (108) |
±0,05 |
||
|
белое |
9 |
9 |
9 |
9 (109) |
1 |
||
|
серебр-е |
-2 (0,01) |
±10 |
или |
||||
|
золот-е |
-1 (0,1) |
±5 |
|||||
Обратите внимание на колористику: похожих оттенков нет. Это помогает с первого же взгляда, даже бегло, определять параметры того или иного электронного компонента.
Особенности маркировки проволочных резисторов по полоскам
Здесь действуют общие правила нанесения обозначений, но со следующими нюансами:
- первое кольцо (обычно белое и сравнительно широкое) не учитывается, так как лишь говорит о типе ЭРЭ;
- последнее – наоборот, важно, так как дает представление о характерных свойствах элемента, допустим, об огнестойкости;
- десятичный множитель может быть не более чем в четвертой степени.
Соответственно, и расчеты проводятся по несколько другим коэффициентам. Но так как это частные случаи, сталкиваться с ними вам придется сравнительно редко, и, в одной из таких ситуаций, можно не полениться и воспользоваться справочными значениями.
Нестандартная цветовая маркировка импортных резисторов
Некоторые бренды используют свои нормативы, немного отличающиеся от обычных, и с ними считаются, ведь это авторитетные производители. В числе таких компаний:
- Philips – с помощью колористики она показывает не только ключевые характеристики ЭРЭ, но и технологию его выпуска. Чтобы это подчеркнуть, компания окрашивает еще и сам электронный компонент.
- Panasonic и CGW также сообщают об особых свойствах выпускаемых элементов кольцами дополнительных оттенков.
Но, естественно, даже лидеры рынка подчиняются общим правилам, чтобы процедуры идентификации показателей и поиск аналогов были максимально простыми.
Маркировка SMD-сопротивлений
Здесь расшифровка резисторов по цвету полосок неактуальна, ведь ЭРЭ данного типа ну очень маленькие по своему размеру, поэтому на их корпусы наносят не линии, а последовательность из 3-4 цифр, в которой первая-вторая говорят о максимально выдерживаемой нагрузке, а третья-четвертая являются множителем.
Также выпускаются компоненты вообще без каких-либо знаков – они с 0 Ом и рассчитаны только на то, чтобы заполнять на плате пустое место.
Числовых комбинаций в результате получается много, так как номенклатура выпускаемых ЭРЭ широкая, и запомнить, о чем свидетельствует каждая из них, нереально. Хорошо, что есть справочная информация, с которой всегда можно свериться.
Таблица SMD-кодов и их значений
Раз определить номинал резистора по цветной маркировке не получится, просто найдите увиденную на корпусе отметку и посмотрите, о чем она говорит.
|
SMD-код |
Знач-е, Ом |
SMD-код |
Знач-е, Ом |
SMD-код |
Знач-е, Ом |
SMD-код |
Знач-е, Ом |
SMD-код |
Знач-е, Ом |
|
R10 |
0,1 |
R11 |
0,11 |
R12 |
0,12 |
R13 |
0,13 |
R15 |
0,15 |
|
R16 |
0,16 |
R18 |
0,18 |
R20 |
0,2 |
R22 |
0,22 |
R24 |
0,24 |
|
R27 |
0,27 |
R30 |
0,3 |
R33 |
0,33 |
R36 |
0,36 |
R39 |
0,39 |
|
R43 |
0,43 |
R47 |
0,47 |
R51 |
0,51 |
R56 |
0,56 |
R62 |
0,62 |
|
R68 |
0,68 |
R75 |
0,75 |
R82 |
0,82 |
R91 |
0,91 |
1R0 |
1 |
|
1R1 |
1,1 |
1R2 |
1,2 |
1R3 |
1,3 |
1R5 |
1,5 |
1R6 |
1,6 |
|
1R8 |
1,8 |
2R0 |
2 |
2R2 |
2,2 |
2R4 |
2,4 |
2R7 |
2,7 |
|
3R0 |
3 |
3R3 |
3,3 |
3R6 |
3,6 |
3R9 |
3,9 |
4R3 |
4,3 |
|
4R7 |
4,7 |
5R1 |
5,1 |
5R6 |
5,6 |
6R2 |
6,2 |
6R8 |
6,8 |
|
7R5 |
7,5 |
8R2 |
8,2 |
9R1 |
9,1 |
100 |
10 |
110 |
11 |
|
120 |
12 |
130 |
13 |
150 |
15 |
160 |
16 |
180 |
18 |
|
200 |
20 |
220 |
22 |
240 |
24 |
270 |
27 |
300 |
30 |
|
330 |
33 |
360 |
36 |
390 |
39 |
430 |
43 |
470 |
47 |
|
510 |
51 |
560 |
56 |
620 |
62 |
680 |
68 |
750 |
75 |
|
820 |
82 |
910 |
91 |
101 |
100 |
111 |
110 |
121 |
120 |
|
131 |
130 |
151 |
150 |
161 |
160 |
181 |
180 |
201 |
200 |
|
241 |
240 |
271 |
270 |
301 |
300 |
331 |
330 |
361 |
360 |
|
391 |
390 |
431 |
430 |
471 |
470 |
511 |
510 |
561 |
560 |
|
621 |
620 |
681 |
680 |
751 |
750 |
821 |
820 |
911 |
910 |
|
SMD-код |
Знач-е, кОм |
SMD-код |
Знач-е, кОм |
SMD-код |
Знач-е, кОм |
SMD-код |
Знач-е, кОм |
SMD-код |
Знач-е, кОм |
|
102 |
1 |
112 |
1,1 |
122 |
1,2 |
132 |
1,3 |
152 |
1,5 |
|
162 |
1,6 |
182 |
1,8 |
202 |
2 |
222 |
2,2 |
242 |
2,4 |
|
272 |
2,7 |
302 |
3 |
332 |
3,3 |
362 |
3,6 |
392 |
3,9 |
|
432 |
4,3 |
472 |
4,7 |
512 |
5,1 |
562 |
5,6 |
622 |
6,2 |
|
682 |
6,8 |
752 |
7,5 |
822 |
8,2 |
912 |
9,1 |
103 |
10 |
|
113 |
11 |
123 |
12 |
133 |
13 |
153 |
15 |
163 |
16 |
|
183 |
18 |
203 |
20 |
223 |
22 |
243 |
24 |
273 |
27 |
|
303 |
30 |
333 |
33 |
363 |
36 |
393 |
39 |
433 |
43 |
|
473 |
47 |
513 |
51 |
563 |
56 |
623 |
62 |
683 |
68 |
|
753 |
75 |
823 |
82 |
913 |
91 |
104 |
100 |
114 |
110 |
|
124 |
120 |
134 |
130 |
154 |
150 |
164 |
160 |
184 |
180 |
|
204 |
200 |
224 |
220 |
244 |
240 |
274 |
270 |
304 |
300 |
|
334 |
330 |
364 |
360 |
394 |
390 |
434 |
430 |
474 |
470 |
|
514 |
510 |
564 |
560 |
624 |
620 |
684 |
680 |
754 |
750 |
|
824 |
820 |
914 |
910 |
||||||
|
SMD-код |
Знач-е, МОм |
SMD-код |
Знач-е, МОм |
SMD-код |
Знач-е, МОм |
SMD-код |
Знач-е, МОм |
SMD-код |
Знач-е, МОм |
|
105 |
1 |
115 |
1,1 |
125 |
1,2 |
135 |
1,3 |
155 |
1,5 |
|
165 |
1,6 |
185 |
1,8 |
205 |
2 |
225 |
2,2 |
245 |
2,4 |
|
275 |
2,7 |
305 |
3 |
335 |
3,3 |
365 |
3,6 |
395 |
3,9 |
|
435 |
4,3 |
475 |
4,7 |
515 |
5,1 |
565 |
5,6 |
625 |
6,2 |
|
685 |
6,8 |
755 |
7,5 |
815 |
8,2 |
915 |
9,1 |
Для SMD со средним допуском
Даже несмотря не отсутствие обозначения сопротивления резисторов цветными полосками, цифровой код достаточно информативен. Погрешность по умолчанию составляет 5-10%, при этом в первых двух-трех цифрах зашифрован номинал, а в последующих – множитель. В итоге чтение кода в чем-то похоже на случаи с советскими ЭРЭ:
- если «0» в четвертом знаке – умножаете на 1, то есть 480 = 48 Ом;
- если там «3» – на 103, то есть на 1000, так, 313 = 31 кОм;
- если «5» – на 105, и 2115 = 21,1 МОм.
В ситуациях с низкоомными элементами не используют точку – вместо нее наносят литеру «R» или, реже, «К», говорящую о коэффициенте в 1000. Значит:
- 4К7 – это 4,7 х 1000 = 4700 Ом,
- К47 – это 0,47 х 1000 = 470 Ом.
Запомнить легко, так как «К» – первая буква в слове «кило», соответствие всегда прослеживается.
Обозначение SMD-сопротивлений по EIA-96
Кодовая маркировка полосатых резисторов особенно актуальна в случае с особо точными ЭРЭ, ведь у них миниатюрные габариты. Данный стандарт использует всего 3 цифры, и первая их пара – это максимум, который может выдержать компонент, а третья представляет собой множитель.
Таблица с шифром номиналов по EIA-96
|
Код |
Число |
Код |
Число |
Код |
Число |
Код |
Число |
Код |
Число |
|
01 |
100 |
02 |
102 |
03 |
105 |
04 |
107 |
05 |
110 |
|
06 |
113 |
07 |
115 |
08 |
118 |
09 |
121 |
10 |
124 |
|
11 |
127 |
12 |
130 |
13 |
133 |
14 |
137 |
15 |
140 |
|
16 |
143 |
17 |
147 |
18 |
150 |
19 |
154 |
20 |
158 |
|
21 |
162 |
22 |
165 |
23 |
169 |
24 |
174 |
25 |
178 |
|
26 |
182 |
27 |
187 |
28 |
191 |
29 |
196 |
30 |
200 |
|
31 |
205 |
32 |
210 |
33 |
215 |
34 |
221 |
35 |
226 |
|
36 |
232 |
37 |
237 |
38 |
243 |
39 |
249 |
40 |
255 |
|
41 |
261 |
42 |
267 |
43 |
274 |
44 |
280 |
45 |
287 |
|
46 |
294 |
47 |
301 |
48 |
309 |
49 |
316 |
50 |
324 |
|
51 |
332 |
52 |
340 |
53 |
348 |
54 |
357 |
55 |
365 |
|
56 |
374 |
57 |
383 |
58 |
392 |
59 |
402 |
60 |
412 |
|
61 |
422 |
62 |
432 |
63 |
442 |
64 |
453 |
65 |
464 |
|
66 |
475 |
67 |
487 |
68 |
499 |
69 |
511 |
70 |
523 |
|
71 |
536 |
72 |
549 |
73 |
562 |
74 |
576 |
75 |
590 |
|
76 |
604 |
77 |
619 |
78 |
634 |
79 |
649 |
80 |
665 |
|
81 |
681 |
82 |
698 |
83 |
715 |
84 |
732 |
85 |
750 |
|
86 |
768 |
87 |
787 |
88 |
806 |
89 |
825 |
90 |
845 |
|
91 |
866 |
92 |
887 |
93 |
909 |
94 |
931 |
95 |
953 |
|
96 |
976 |
Как и в случае с цветовой маркировкой предохранительных резисторов, таблица – это еще не все. Стандарт EIA-96 и множитель – буква:
Z = 0,001
R или Y = 0,01
S или X = 0,1
А = 1
H или B = 10
C = 100
D = 103
E = 104
F = 105
Наиболее популярные интернет-калькуляторы
Это сервисы, позволяющие рассчитать необходимые параметры; мы выделили два лучших:
https://www.chipdip.ru/calc/resistor
Ориентирован на ЭРЭ с 4-5 кольцами. Комфортабелен в пользовании: достаточно выбрать, какой должны быть линии, и система автоматически выдаст нужные вам показатели, вплоть до точности исполнения и мощности. И даже посоветует подходящую серию.
Хотите внедрить «Магазин 15»?
Получите всю необходимую информацию у специалиста.
Спасибо!
Спасибо, ваша заявка принята.
Продолжить
Еще одно его преимущество – наглядность: вы можете сравнить получающийся в меню компонент с тем, который есть у вас фактически.
Тоже достаточно удобный калькулятор маркировки сопротивлений по цветам полосками: таблица онлайн содержит все необходимые поля – нужно лишь сделать правильный выбор из выпадающих списков. Хорош тем, что содержит подсказки по каждой линии – ошибиться и что-то напутать сложно.
https://www.qrz.ru/shareware/contribute/decoder.shtml
Также там есть полезная дополнительная информация: не только по правильному переводу множителей и заполнению, но и в целом о габаритах, расположении колец. Есть даже советы о том, что за браузер использовать.
Заключение
Тема достаточно обширная, но разобраться в ней стоит. Немного практики, и вы научитесь «читать» колористику – она станет для вас открытой книгой. Для упрощения перевода, умножения и других операций можно купить ПО для работы с маркировкой, в том числе цветовой для резисторов в 5 полос, его вы найдете в каталоге «Клеверенс».
Количество показов: 1677
Статьи по схожей тематике
Выбор и расчет пусковых резисторов для силовых цепей
Величину сопротивления пусковых резисторов выбирают таким образом, чтобы избежать бросков тока в процессе пуска, которые могут повредить электродвигатель или другое оборудование электрической сети.
После того, как величина пускового сопротивления была рассчитана, производится выбор резисторов и проверка их на нагрев. Температура резисторов не должна превышать допустимую для данной конструкции.
В процессе пуска электрической машины ток, протекающий через пусковой резистор, изменяется во времени. Если длительность протекания тока через пусковое сопротивление мала, по сравнению с его постоянной времени Т, то расчеты можно упростить и вести их с использованием эквивалентного тока Iэ.т, тепловой эффект от которого будет равен прохождению через резистор реального тока:
tp – время прохождения тока через резистор. В данном случае теплоотдачей можно пренебречь. Температура от эквивалентного тока по теплу и реального тока будет одинакова.
Для определения эквивалентного тока можно использовать реальную кривую тока и построить зависимость i2(t) и провести интегрирование графическим путем.
Наряду с эквивалентным током по теплу Iэ.т существует эквивалентный ток по нагреву Iэ.н. – это ток, который при прохождении через сопротивление нагревает его до такой же температуры, что и реальный ток. В случае допущения tp<<T эквивалентный ток по нагреву равен эквивалентному току по теплу I’э.н. = Iэ.т.
Рассчитав значения Iэ.т и Iэ.н. можно выбрать необходимый резистор из каталога, если в нем приведен ток кратковременного режима работы для заданного времени работы tр.
Как правило, в каталогах приводится длительно допустимый ток нагрузки резистора. В таком случае нужно перейти к эквивалентному длительному току, который нагревает резистор до той же температуры, что и пусковой. Ниже показан пример проверки резистора для пуска шунтового электродвигателя.
Пример
Пуск электродвигателя производится раз в смену. Номинальный ток электрической машины равен 120 А, относительный пиковый момент равен Мп = 2, момент переключения Мпер = 0,8; пиковый ток 2Iн, ток переключения 0,8Iн. Первая ступень работает в течении t1 = 1,35 с, вторая ступень t2 = 1,35+0,54 = 1,9 с. Для работы выбран резистор на длительный ток 33 А с постоянной времени Т = 250 с. Поскольку постоянная времени Т значительно больше t1 и t2, то эквивалентный ток по нагреву равен эквивалентному току по теплу. Исходя из этого для первой ступени:
Так как пусковой резистор должен допускать троекратный перегруз, то для первой ступени tpi = 3t1=3·1,35=4,05 c. Воспользовавшись приведенной ниже кривой для tр1/Т = 4,05/250 = 0,015, находим эквивалентный ток резистора: Iэ.дл. = 0,13Ipi = 22,6 A. Для второй ступени резистора: tр2 = 3t2 = 3·1,9 = 5,7 c.
Поскольку ток переключения и пиковый ток такие же, как и для первой ступени, то Iр1 = Iр2. Для данной ступени (tр2/Т) = 0,023. С помощью кривой, приведенной выше, найдем Iэ.дл. = 26 А. Так как длительный ток резистора равен 33 А, то данный резистор проходит проверку по нагреву.
Для перемежающегося режима расчет ведется аналогичным образом. Если постоянная времени Т велика по сравнению со временем цикла tр1 + tр2, то уравнение можно упростить:
При проведении расчетов по формуле (2) нет необходимости в постоянной нагрева Т, данный подход более прост по сравнению с формулой (1) и дает результат с запасом. Формулу (2) можно использовать при проведении предварительных расчетов.
Для повторно-кратковременного режима работы Ip1 = Ip = const, Ip2 = 0. В таком случае для любого tp/T будем иметь:
Если же tp<<T, то формула (3) может быть значительно упрощена:
Эквивалентный по теплу ток Iр.ц за время цикла tp + tп можно найти из равенства:
Из формул (4) и (4а) следует, что Iэ.н. = Iр.ц.
Отсюда следует вывод, что при принятых допущениях эквивалентный по теплу ток равен эквивалентному току по нагреву за время одного цикла.
Тепловой расчет резисторов является кропотливым и довольно громоздким, поэтому для типовых схем включения рекомендовано выбирать резисторы из специальных таблиц, в которых величины сопротивлений и их ток выражены в зависимости от параметров электродвигателя.
При компоновке резисторов в реостаты и ящики все они должны максимально использоваться по нагреву, так как это позволит уменьшить вес и габарит электрического аппарата. Для максимально эффективного использования резисторов при включении их последовательно все они должны иметь один и тот же длительный ток.
При создании пусковых схем для электрических машин большой мощности приходится использовать параллельное соединение элементов силовой цепи.
При параллельном соединении резисторов падения напряжений на них равны и для их полного использования нужно, чтобы произведение длительно допустимого тока на сопротивление для всех резисторов было равно.
Например, если один из реостатов имеет ra меньшее, чем у других, а падение напряжение на нем равно iara, то при параллельном соединении это значит, что по нему будет протекать больший ток (поскольку напряжение равно при параллельном соединении для всех элементов). В итоге получим один перегруженный по мощности реостат, а остальные недогружены.
Учебное пособие по физике: Комбинированные схемы
Ранее в Уроке 4 упоминалось, что существует два разных способа соединения двух или более электрических устройств в цепь. Они могут быть соединены посредством последовательного или параллельного соединения. Когда все устройства в цепи соединены последовательным соединением, эта схема называется последовательной схемой. Когда все устройства в цепи соединены параллельными соединениями, тогда схема называется параллельной цепью.Третий тип схемы предполагает двойное использование последовательного и параллельного соединений в схеме; такие схемы называются составными схемами или комбинированными схемами. Схема, изображенная справа, является примером использования как последовательного, так и параллельного соединения в одной цепи. В этом случае лампочки A и B подключаются параллельно, а лампочки C и D подключаются последовательно. Это пример комбинированной схемы .
При анализе комбинированных цепей критически важно иметь твердое представление о концепциях, которые относятся как к последовательным цепям, так и к параллельным цепям.Поскольку оба типа соединений используются в комбинированных схемах, концепции, связанные с обоими типами схем, применяются к соответствующим частям схемы. Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.
Цепи серии
|
Параллельные схемы
|
Каждое из приведенных выше понятий имеет математическое выражение. Комбинирование математических выражений вышеуказанных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной схемы.
Анализ комбинированных схем
Основная стратегия анализа комбинированных схем включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной схемы в последовательную. После преобразования в последовательную схему анализ можно проводить обычным образом. Ранее в Уроке 4 описывался метод определения эквивалентного параллельного сопротивления, затем общее или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.
Этот метод соответствует формуле
1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3 + …
, где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, подключенных параллельно. Если два или более резистора, находящиеся в параллельных ветвях, не имеют одинакового сопротивления, необходимо использовать приведенную выше формулу.Пример этого метода был представлен в предыдущем разделе Урока 4.
Применяя свое понимание эквивалентного сопротивления параллельных ветвей к комбинированной схеме, комбинированную схему можно преобразовать в последовательную. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения общего сопротивления цепи. Рассмотрим следующие диаграммы ниже. Схема А представляет собой комбинированную схему с резисторами R 2 и R 3 , размещенными в параллельных ветвях.Два параллельных резистора 4 Ом эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы включены последовательно, можно использовать формулу для общего сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления составляет
. рандов до = 1 + 2 рандов + 3 + …Итак, на схеме B полное сопротивление цепи составляет 10 Ом.
После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах. Весь метод проиллюстрирован ниже на двух примерах.
Пример 1:
Первый пример — самый простой — резисторы, включенные параллельно, имеют одинаковое сопротивление. Цель анализа — определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательно подключенных резистора 8 Ом эквивалентны одному резистору 4 Ом. Таким образом, два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 4 Ом. Этот резистор 4 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление составляет
. R до = R 1 + 4 Ом + R 4 = 5 Ом + 4 Ом + 6 ОмR общ = 15 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I tot = ΔV tot / R tot = (60 В) / (15 Ом)I до = 4 А
Расчет тока 4 А представляет собой ток в месте расположения батареи. При этом резисторы R 1 и R 4 включены последовательно, а ток в последовательно соединенных резисторах везде одинаков.Таким образом,
I до = I 1 = I 4 = 4 АДля параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно равняться 4 ампер. Существует бесконечное количество возможных значений I 2 и I 3 , которые удовлетворяют этому уравнению. Поскольку значения сопротивления равны, значения тока в этих двух резисторах также равны.Следовательно, ток в резисторах 2 и 3 равен 2 А.
I 2 = I 3 = 2 АТеперь, когда известен ток в каждом отдельном месте резистора, можно использовать уравнение закона Ома (ΔV = I • R) для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (4 А) • (5 Ом)ΔV 1 = 20 ВΔV 2 = I 2 • R 2 = (2 А) • (8 Ом)
ΔV 2 = 16 ВΔV 3 = I 3 • R 3 = (2 А) • (8 Ом)
ΔV 3 = 16 ВΔV 4 = I 4 • R 4 = (4 А) • (6 Ом)
ΔV 4 = 24 В
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Пример 2:
Второй пример — более сложный случай — резисторы, включенные параллельно, имеют другое сопротивление. Цель анализа та же — определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением.Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить, используя обычную формулу для эквивалентного сопротивления параллельных ветвей:
1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 …1 / R экв = 1 / (4 Ом) + 1 / (12 Ом)
1 / R экв. = 0,333 Ом -1
R экв = 1 / (0,333 Ом -1 )
R экв = 3.00 Ом
На основании этого расчета можно сказать, что два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 3 Ом. Этот резистор 3 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление составляет
. R до = R 1 + 3 Ом + R 4 = 5 Ом + 3 Ом + 8 ОмR общ = 16 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I tot = ΔV tot / R tot = (24 В) / (16 Ом)I до = 1,5 А
Расчет тока 1,5 А представляет собой ток в месте расположения батареи. При этом резисторы R 1 и R 4 включены последовательно, а ток в последовательно соединенных резисторах везде одинаков.Таким образом,
I до = I 1 = I 4 = 1,5 АДля параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно равняться 1,5 А. Существует бесконечное множество значений I 2 и I 3 , которые удовлетворяют этому уравнению. В предыдущем примере два параллельно включенных резистора имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями.В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Для определения силы тока потребуется использовать уравнение закона Ома. Но для его использования сначала необходимо знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от более простого случая, проиллюстрированного в предыдущем примере.
Чтобы определить падение напряжения на параллельных ветвях, сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R 1 и R 4 ).Уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (1,5 А) • (5 Ом)ΔV 1 = 7,5 ВΔV 4 = I 4 • R 4 = (1,5 А) • (8 Ом)
ΔV 4 = 12 В
Эта схема питается от источника 24 В.Таким образом, совокупное падение напряжения заряда, проходящего по контуру цепи, составляет 24 вольта. Будет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R 1 и R 4 ). Падение напряжения на ответвлениях должно составлять 4,5 В, чтобы компенсировать разницу между общим значением 24 В и падением 19,5 В на R 1 и R 4 . Таким образом,
ΔV 2 = V 3 = 4,5 ВЗная падение напряжения на параллельно соединенных резисторах (R 1 и R 4 ), можно использовать уравнение закона Ома (ΔV = I • R) для определения тока в двух ветвях.
I 2 = ΔV 2 / R 2 = (4,5 В) / (4 Ом)I 2 = 1,125 АI 3 = ΔV 3 / R 3 = (4,5 В) / (12 Ом)
I 3 = 0,375 A
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Разработка стратегии
Два приведенных выше примера иллюстрируют эффективную концептуально-ориентированную стратегию анализа комбинированных схем.Такой подход требовал твердого понимания концепций последовательностей и параллелей, обсуждавшихся ранее. Такие анализы часто проводятся, чтобы решить физическую проблему для указанного неизвестного. В таких ситуациях неизвестное обычно меняется от проблемы к проблеме. В одной задаче значения резистора могут быть заданы, а ток во всех ветвях неизвестен. В другой задаче могут быть указаны ток в батарее и несколько значений резистора, и неизвестная величина становится сопротивлением одного из резисторов.Очевидно, что разные проблемные ситуации потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум приведенным выше примерам проблем.
Начинающему студенту предлагаются следующие предложения по решению задач комбинированной схемы:
- Если схематическая диаграмма не предоставлена, найдите время, чтобы построить ее. Используйте условные обозначения, такие как те, что показаны в примере выше.
- При решении проблемы, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записав известные значения и приравняв их к символу, например I — , I 1 , R 3 , ΔV 2 и т. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.
- Знать и использовать соответствующие формулы для эквивалентного сопротивления последовательно соединенных и параллельно соединенных резисторов. Использование неправильных формул гарантирует неудачу.
- Преобразуйте комбинированную схему в строго последовательную, заменив (на ваш взгляд) параллельную секцию одним резистором, имеющим значение сопротивления, равное эквивалентному сопротивлению параллельной секции.
- Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будет определено с использованием этого уравнения. При его использовании важно подставлять в уравнение соответствующие значения. Например, при вычислении I 2 важно подставить в уравнение значения ΔV 2 и R 2 .
Для дальнейшей практики анализа комбинированных схем рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.
Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключать их так, как хотите. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).
Проверьте свое понимание
1. Комбинированная схема показана на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы.
а. Ток в точке A равен _____ (больше, равен, меньше) току в точке B.
г. Ток в точке B равен _____ (больше, равен, меньше) ток в точке E.
г. Ток в точке G равен _____ (больше, равен, меньше) ток в точке F.
г. Ток в точке E равен _____ (больше, равен, меньше) току в точке G.
e. Ток в точке B равен _____ (больше, равен, меньше) ток в точке F.
ф. Ток в точке A равен _____ (больше, равен, меньше) ток в точке L.
г. Ток в точке H равен _____ (больше, равен, меньше) ток в точке I.
2. Рассмотрим комбинированную схему на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы. (Предположим, что падение напряжения в самих проводах пренебрежимо мало.)
а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.
г. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.
г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
ф. Разность электрических потенциалов между точками L и A составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками B и K.
3.Используйте концепцию эквивалентного сопротивления, чтобы определить неизвестное сопротивление идентифицированного резистора, которое сделало бы схемы эквивалентными.
4. Проанализируйте следующую схему и определите значения общего сопротивления, общего тока, а также тока и падения напряжения на каждом отдельном резисторе.
5. Обращаясь к диаграмме в вопросе №4, определите …
а. … номинальная мощность резистора 4.г. … скорость, с которой энергия потребляется резистором 3.
Резистор, конденсатор и индуктор в последовательно-параллельном соединении
Резистор, конденсатор и индуктор в последовательном и параллельном соединении — формулы и уравнения
Следующие основные и полезные уравнения и формулы могут использоваться для проектирования, измерения, упрощения и анализа электрических цепей для различных компонентов и электрических элементов, таких как резисторы, конденсаторы и катушки индуктивности, соединенные последовательно и параллельно.
Сопротивление в последовательном и параллельном уравнениях
Сопротивление:
Общее эквивалентное сопротивление резисторов, подключенных последовательно или параллельно, определяется по следующей формуле:
Последовательное сопротивление:
Когда два или более двух резисторов подключены последовательно, как показано на рисунке, их эквивалентное сопротивление рассчитывается по формуле:
R Eq = R 1 + R 2 + R 3 +… R n
Сопротивление параллельно:
, когда резисторы находятся в параллельной конфигурации, эквивалентное сопротивление становится:
Где
- R Eq — эквивалентное сопротивление всех резисторов (R 1 , R 2 , R 3 … R n )
Связанные сообщения:
Дельта Δ до звезды Y (от Pi до Te e) Преобразование:
Соединение треугольником (Δ) также обозначается как соединение Pi , а соединение звезда (Y) также упоминается как соединение Tee (T) .
От треугольника (Δ) до звезды (Y) Межсоединение:
От звезды (Y) к треугольнику (Δ) Межсоединение
Подробнее и решено примеры, проверьте преобразование звезды в дельту и дельта в звезду.
Емкость в последовательном и параллельном уравнениях
Емкость:
Общая емкость конденсатора, подключенного параллельно и последовательно, приведена ниже:
Емкость последовательно:
Когда конденсаторы подключены последовательно В конфигурации эквивалентная емкость становится:
Параллельная емкость:
Емкость суммируется, когда они соединяются вместе в параллельной конфигурации
C Eq = C 1 + C 2 + C 3 +… C n
Где
- C Eq — эквивалентная емкость всех конденсаторов (C 1 , C 2 , C 3 … C n )
Связанные сообщения:
Индуктивность в последовательном и параллельном уравнениях
Индуктивность:
9 0002 Расчет полной индуктивности катушек индуктивности внутри цепи аналогичен расчету резисторов.Последовательная индуктивность:
Когда индукторы включены последовательно, как показано на рисунке, их индуктивности складываются.
L Eq = L 1 + L 2 + L 3 +… L n
Параллельная индуктивность:
При параллельной комбинации эквивалентная индуктивность катушки индуктивности задаются как
Где
- L Eq — эквивалентная индуктивность всех катушек индуктивности (L 1 , L 2 , L 3 … L n )
Связанные формулы и Equations Сообщений:
Тепло, рассеиваемое резисторами | Блестящая вики по математике и науке
Из микроскопической интерпретации закона Ома, сопротивление в классической формуле V = IRV = IRV = IR для тока через цепь при заданном управляющем напряжении может быть расширено как:
V = I (mne2τ) La, V = I (\ frac {m} {n {e} ^ {2} \ tau}) \ frac {L} {a}, V = I (ne2τm) aL,
где mmm и eee — масса и заряд электрона соответственно, LLL и aaa — длина и площадь проводящего материала, составляющего резистор, nnn — плотность носителей заряда, а τ \ tau τ — интервал времени между два столкновения электронов в резисторе.Сопротивление также можно расширить до:
R = ρLA, R = \ frac {\ rho L} {A}, R = AρL,
, где ρ \ rhoρ — удельное сопротивление ; — свойство материала резистора, а LLL и AAA — длина и площадь поперечного сечения резистора соответственно.
Неупругие столкновения электронов, движущихся по проводнику, являются причиной сопротивления. Кристаллическая структура атомов металла в проводнике препятствует прохождению через него электронов. В любой данный момент электроны имеют определенную вероятность неупругого рассеяния от металлической решетки, передавая часть своей энергии решетке в виде кинетической энергии, т.е.е. нагревать. Это рассеяние тепла в решетке, называемое Джоулей нагрев , является источником рассеивания мощности в резисторе. Обратите внимание, что хотя межэлектронные столкновения могут давать свою собственную связанную тепловую энергию движения, эта энергия остается внутренней по отношению к системе до тех пор, пока она не рассеивается в металлической решетке, которая не переносит ток.
Расчет среднего времени свободного пробега электронов, движущихся по проводнику, показывает, что электроны проходят через большое количество узлов решетки, прежде чем существенно взаимодействуют с катионами металлов.Объяснение этому факту исходит из квантовой механики и дуализма волна-частица. Из-за волновой природы электрона электроны могут распространяться без неупругого рассеяния на большее расстояние через решетку, чем ожидалось, и вероятность рассеяния гораздо более чувствительна к дефектам решетки, чем плотность решетки.
Как рассчитать падение напряжения на резисторе подробное объяснение
Если вы ищете, как рассчитать падение напряжения на резисторе, то SoManyTech предлагает вам полную теорию и практические примеры падения напряжения на резисторе.Перед этим давайте освежим в памяти закон Ома: (Прокрутите вниз, если вы профессиональный пользователь)
- Распространенный способ показать поведение схемного устройства — это его характеристика.
Это график зависимости тока «I» через устройство от приложенного к нему напряжения «V». Это устройство, резистор, имеет простую линейную характеристику В – I , показанную на рис. . выше. - Эта линейная зависимость устройства выражается законом Ома :
V = IR - Константа пропорциональности R известна как сопротивление устройства и равна наклону кривой I. –V характеристика.Единица измерения сопротивления — Ом, символ Ом . Любое устройство с линейной ВАХ называется резистором.
Какое падение напряжения на резисторе?
- Падение напряжения на резисторе — это не что иное, как значение напряжения на резисторе. Иногда его также называют «напряжение на резисторе» или просто «падение напряжения».
- Обычно обозначается как:
‘V (drop ) ‘ или ‘Vr’ или ‘Vd’
Для нескольких резисторов это записывается как Vr1, Vr2, Vr3 и т. Д.
Как мы все знаем, резистор — это устройство, которое оказывает сопротивление протекающему через него току. Затем, применяя закон Ома, резистор будет предлагать падение напряжения на резистивном устройстве, которое определяется как:
В ( падение ) = I × R
, где I = ток через резистор в (А) в амперах
R = сопротивление в (Ом) Ом
В ( падение ) = падение напряжения в (В) вольтах
Как рассчитать падение напряжения по сопротивлению пошагово:
Step1: Упростите данную схему.Если, скажем, схема заполнена резисторами, включенными последовательно и параллельно, то повторно подключите ее, чтобы упростить. (проверьте практический пример ниже)
Step2: Затем найдите эквивалентный резистор.
Для параллельного: 1 / Треб. = 1 / R1 + 1 / R2…
Для серии: Треб. = R1 + R2 +. . .
Step3: Найдите ток через каждый резистор. (Ток через последовательный резистор одинаков, а ток через параллельные резисторы отличается и зависит от его значения)
Step4 : Примените формулу закона Ома для расчета падения напряжения.
В = IR
Напряжение в последовательной цепи — Практические примеры:
Случай I:
Если есть только один резистор последовательно с батареей или источником питания, как показано в этой схеме.
В этой схеме падение напряжения на резисторе такое же, как и в цепи питания. Это связано с тем, что оба компонента имеют общие потенциальные точки, разделенные между ними (точка A и точка B)
∴ Vs = Vdrop = 5 вольт (скажем)
Случай II:
Если есть два или несколько резисторов, включенных последовательно с батареей, как показано на этой схеме.
В этой схеме мы должны рассчитать полный ток «I», протекающий через цепь.
I (общий) = V (питание) / R (эквивалент)
∴ I (общий) = 5/30 = 0,166 A
Тогда падение напряжения на R1 будет: Vr1 = I × R1
Падение напряжения на R2 будет: Vr2 = I × R2
Падение напряжения на Rn будет: Vrn = I × Rn
- Vr1 = I × R1 = 0,166 × 10 = 1,66 В & Vr2 = I × R2 = 0.166 × 20 = 3,33 В
Напряжение на параллельных резисторах:
Случай I:
Два резистора подключены параллельно к батарее или источнику питания, как показано на этой схеме.
В этой схеме падение напряжения на этих параллельных резисторах такое же, как у источника питания.
Это связано с тем, что оба резистора имеют общие потенциальные точки, разделенные между ними (точка A и точка B), поэтому напряжение будет одинаковым, но ток будет другим.
∴Vs = Vdrop = Vr1 = Vr2 = 5 вольт (скажем)
Случай II:
Один резистор включен последовательно и два резистора с источником питания, как показано на этой схеме.
В этой схеме нам нужно вычислить ток «I» через каждый компонент.
- i1 = I (всего) = Is = V (питание) / R (эквивалент)
где, R (эквивалент) = R1 + Rp
, где 1 / Rp = 1 / R2 + 1 / R3∴ Rp = 12 Ом и R ( эквивалент ) = 22 Ом
- i2 = i1 * (R3 / (R2 + R3))
i3 = i1 * (R2 / (R2 + R3))
- Падение напряжения на R1 будет Vr1 = R1 * i1
Падение напряжения на R2 будет Vr2 = R2 * i2
Падение напряжения на R3 будет Vr3 = R2 * i3
Положим значения, которые мы имеем,
Теперь i1 = V (поставка) / R (эквивалент) = 5/22 = 0.227 ампер
∴ i1 = 0,227 A
Падение напряжения на 10 Ом -> Vr1 = 10 * i1 = 10 × 0,227 вольт
∴ Vr1 = 2,27 вольт
∴ i2 = 0,1362 A
Падение напряжения на 20 Ом -> Vr2 = 20 * i2 = 20 × 0,1362 В
∴ Vr2 = 2,724 В
Теперь i3 = i1 * (R2 / (R1 + R2))
∴ i3 = 0.09 A
Падение напряжения на 30 Ом -> Vr2 = 30 * i2 = 30 × 0,09 В
∴ Vr3 = 2,7 В
Метод 2: 54
- i1 = В (питание) / R (эквивалент) = 0,227 A
- Таким образом, Va = Vr2 = Vr3 = 2,73 вольт
Тогда падение напряжения на R1 будет Vr1 = R1 * i1 = 10 × 0,227 = 2,27 В
∴ Эквивалентное напряжение в точке ‘A’ будет равно
Veq = Va = Vs — Vr1
∴ Va = 5-2.27 = 2,73 В
Следовательно, мы получаем одинаковое значение потенциала на R2 и R3.
Метод 3:
В этом методе мы используем цифровой мультиметр или можно сказать вольтметр. Все, что вам нужно, это установить мультиметр в режим напряжения.
Теперь с помощью двух щупов проверьте напряжение на требуемом резисторе, подключив к нему щупы. (на рис. показания вольтметра только для показаний)
Вуаля !! Ты понял.
Это самый простой способ найти падение напряжения на резисторе в любой цепи.
Резисторы, сопротивления и расчеты удельного сопротивления Формулы Уравнения
Резисторы — это пассивные устройства, используемые в электронике. схемы для управления протеканием тока. Идеальный резистор не имеет связанной паразитной емкости. или индуктивность, и поэтому работает точно так же в цепи постоянного тока (DC) как это происходит в цепи переменного тока (AC) на любой частоте.
|
В качестве примера расчета сопротивления объема по его объемное удельное сопротивление, рассмотрим рисунок слева. Предполагать Медный провод 12 AWG с удельным сопротивлением (из таблицы) 1,72×10 -6 Ом · см, площадь поперечного сечения (A) 0,03309 см 2 и длина 1 метр. По данной формуле его сопротивление составляет: , что хорошо согласуется с типичными указанными значениями Ом / км, опубликованными производителями проводов.Alpha утверждает, что 1,59 Ом / 1000 ‘или 5,22 Ом / км. |
Уравнения (формулы) для объединения катушек индуктивности последовательно и параллельно приведены ниже.
|
Полное сопротивление параллельно включенных резисторов равно сопротивлению, обратному сопротивлению сумма обратных величин отдельных сопротивлений. Держите единицы постоянными. |
|
Общее сопротивление последовательно соединенных резисторов равно сумме отдельных сопротивлений. сопротивления. Держите единицы постоянными. |
|
В качестве примера расчета сопротивления объема по его объемное удельное сопротивление, рассмотрим рисунок слева. Предполагать Медный провод 12 AWG с удельным сопротивлением (из таблицы) 1.72×10 -6 Ом · см, площадь поперечного сечения (A) 0,03309 см 2 и длина 1 метр. По данной формуле его сопротивление составляет:
|
резисторов последовательно | Формула эквивалентного сопротивления
Введение
Резисторы являются основными компонентами любой электрической или электронной схемы. Часто резисторы встречаются в большом количестве независимо от размера схемы.Резисторы могут быть подключены последовательно или параллельно или их комбинация. Чтобы уменьшить сложность различных комбинаций резисторов, необходимо соблюдать некоторые правила.
Считается, что два резистора включены последовательно, если через них протекает одинаковый ток. Последовательные резисторы можно заменить одним резистором. Все резисторы подчиняются основным законам, таким как закон Ома и текущий закон Кирхгофа, независимо от их комбинации и сложности.
Резисторы в серии
Считается, что набор резисторов включен последовательно, когда они соединены друг с другом в одну линию.Одинаковый ток будет протекать через все резисторы. Считается, что последовательно соединенные резисторы имеют общий ток.
В цепи последовательных резисторов величина протекающего тока будет одинаковой во всех точках.
I R1 = I R2 = I R3 = I AB .
Рассмотрим следующую последовательную резистивную цепь
Здесь резисторы R1, R2 и R3 номиналом 1 Ом, 2 Ом и 3 Ом соединены последовательно. Одинаковый ток будет протекать через все резисторы, поскольку они соединены последовательно.Общее сопротивление цепи равно сумме отдельных сопротивлений.
Если R T — полное сопротивление, то
R T = R1 + R2 + R3
Теперь эквивалентное сопротивление цепи равно
R EQ = R1 + R2 + R3
R EQ = 1 Ом + 2 Ом + 3 Ом
R EQ = 6 Ом
Теперь последовательно соединенные резисторы можно заменить одним резистором R EQ номиналом 6 Ом.
Формула эквивалентного сопротивления
В цепи последовательных резисторов полное сопротивление равно сумме отдельных сопротивлений, поскольку через каждый резистор проходит одинаковый ток.
∴ R ИТОГО = R 1 + R 2 + R 3
Например, рассмотрим два последовательно соединенных резистора, как показано ниже
Комбинация двух последовательно соединенных резисторов 3 Ом эквивалентна к наличию одного резистора 6 Ом.Следовательно, приведенная выше схема такая же, как следующая
. Аналогичным образом рассмотрим три резистора, подключенных последовательно, как показано ниже.
. Комбинация трех последовательно соединенных резисторов 3 Ом эквивалентна наличию одного резистора 9 Ом. Таким образом, приведенная выше схема такая же, как и следующая
. Это единственное сопротивление называется эквивалентным сопротивлением схемы и используется для замены любого числа последовательно подключенных резисторов.
Если в последовательной сети n резисторов, то
R EQ = R 1 + R 2 + R 3 + …….. + R n
Наблюдение можно сделать из приведенного выше уравнения. Эквивалентное сопротивление резисторов, соединенных последовательно, всегда больше, чем сопротивление самого большого резистора.
Расчет напряжения
Для резисторов, включенных последовательно, напряжение на каждом резисторе не соответствует тому же правилу, что и ток. В случае последовательно включенных резисторов общее напряжение на резисторах равно сумме индивидуальных разностей потенциалов на каждом резисторе.
В приведенной выше схеме разность потенциалов на каждом резисторе может быть рассчитана с использованием закона Ома.В последовательной цепи протекает ток 1 А. Тогда согласно закону Ома
Разность потенциалов на резисторе R1 составляет I × R 1 = 1 × 1 = 1 В.
Разность потенциалов на резисторе R2 составляет I × R 2 = 1 × 2 = 2 В .
Разность потенциалов на резисторе R3 составляет I × R 3 = 1 × 3 = 3 В.
Следовательно, полное напряжение V AB = 1 В + 2 В + 3 В = 6 В.
Рассмотрим последовательное соединение три резистора R 1 , R 2 и R 3 с протекающим через них током I.
Пусть падение потенциала от A до B будет V. Это падение потенциала является суммой индивидуальных падений потенциала на каждом отдельном резисторе. Тогда согласно закону Ома
Падение потенциала на R 1 равно V R1 = I × R 1
Падение потенциала на R 2 равно V R2 = I × R 2
Падение потенциала на R 3 составляет V R3 = I × R 3
∴ V = V R1 + V R2 + V R3
∴V = I × R 1 + I × R 2 + I × R 3
Если эквивалентное сопротивление резисторов, включенных последовательно в приведенной выше схеме, равно R EQ , то
V = I × R EQ
При наличии n резисторов последовательно R1, R2….Rn, тогда полное напряжение на них является суммой индивидуальной разности потенциалов на каждом резисторе.
В T = В R1 + V R2 +… .. + V Rn
В последовательной комбинации резисторов из n резисторов, если значение сопротивления каждого резистора отличается от другого, тогда потенциал на каждом резисторе разный.
РезисторыN в последовательной комбинации, каждый с разным сопротивлением, будет иметь N различных разностей потенциалов между собой.Этот тип схемы образует делитель напряжения. Схема делителя напряжения — основа конструкции потенциометра.
В последовательной цепи значения напряжения, тока или сопротивления можно рассчитать по закону Ома. Резисторы можно менять местами в последовательной цепи, не влияя на общую мощность каждого резистора, ток или общее сопротивление цепи.
Примеры последовательных резисторов
1. Рассмотрим следующую схему для расчета общего напряжения между A и B.
Два резистора R1 и R2 соединены последовательно.
R 1 = 2 Ом и R 2 = 3 Ом
Ток в цепи I = 5 А
Отдельные падения напряжения можно рассчитать по закону Ома следующим образом
Падение напряжения на резисторе R1 равно В R1 = I × R 1 = 5 × 2 = 10 В
Падение напряжения на резисторе R2 составляет В R2 = I × R 2 = 5 × 3 = 15 В
Общее падение напряжения составляет сумма отдельных падений напряжения.
В = В R1 + В R2 = 10 + 15 = 25 В
Другой подход заключается в вычислении эквивалентного сопротивления последовательной комбинации. Отдельные резисторы в последовательной комбинации могут быть заменены одним резистором эквивалентного сопротивления. Эквивалентное сопротивление двух последовательно соединенных резисторов R1 и R2 составляет
R EQ = R 1 + R 2 = 2 + 3 = 5 Ом
Затем по закону Ома
Падение напряжения на A и B равно
В = I × R EQ = 5 × 5 = 25 В.
- Рассмотрим следующую схему, в которой значение отдельного падения потенциала на каждом резисторе указывается вместе с током в последовательной комбинации. Общее сопротивление последовательной комбинации составляет R = 30 Ом. Ток в цепи составляет 1 А.
R = 30 Ом и I = 1 А
Ток, протекающий через каждый резистор, одинаков.
I = I1 = I2 = I3 = I4 = 1 A.
По закону Ома значение сопротивления можно рассчитать как
R 1 = V 1 / I 1
R 1 = 5/1 = 5 Ом
Аналогично R 2 = V 2 / I 2
R 2 = 8/1 = 8 Ом
И R 3 = V 3 / I 3
R 3 = 7/1 = 7 Ом
Потенциал на R 4 не указан.Но значение R 4 можно рассчитать из значения общего сопротивления или эквивалентного сопротивления цепи.
R EQ = R 1 + R 2 + R 3 + R 4
∴ 4 = RR — ( 1 + R 2 + R 3 )
R 4 = 30 — (5 + 8 + 7)
R 4 = 10 Ом
Теперь потенциал на R 4 можно рассчитать как
В 4 = I 4 × R 4
∴V 4 = 1 × 10 = 10 В
Общее напряжение V AB можно рассчитать двумя способами.
Первый метод — использование индивидуальных разностей потенциалов.
Общее напряжение равно сумме индивидуальных разностей потенциалов.
V AB = V 1 + V 2 + V 3 + V 4
Где V1, V2, V3 и V4 — разности потенциалов между резисторами R1, R2, R3 и R4 соответственно .
Следовательно, V AB = 5 + 8 + 7 + 10
V AB = 30 V
Второй метод расчета общего напряжения заключается в использовании значения эквивалентного сопротивления.
Полное напряжение равно произведению тока на эквивалентное сопротивление. Значения полного тока и эквивалентного сопротивления даны как I = 1 A и R EQ = 30 Ом.
Следовательно, V AB = I × R EQ
V AB = 1 × 30
V AB = 30 В
Приложения
Когда два резистора с разным сопротивлением соединены последовательно, напряжение на них разное. Этот метод является основой схем делителей напряжения.
Если один резистор в цепи делителя напряжения заменить датчиком, то измеряемая величина преобразуется в электрический сигнал, который легко измерить. Часто используемые датчики — это термисторы и светозависимые резисторы. В термисторе сопротивление изменяется в зависимости от температуры. Например, предположим, что термистор имеет сопротивление 10 кОм при температуре 25 0 C. Тот же термистор может иметь сопротивление 100 Ом при температуре 100 0 C.Следовательно, падение потенциала на термисторе будет различным в зависимости от температуры. Это изменение сопротивления в зависимости от температуры можно откалибровать, чтобы найти значение температуры по падению потенциала на термисторе.
Рис. Схема светового датчика
Другой датчик, в котором последовательно используется резистор, — это фоторезистор или светозависимый резистор. В светозависимых резисторах сопротивление изменяется в зависимости от интенсивности падающего на них света.В отсутствие света сопротивление типичного светозависимого резистора достигает 1 МОм. В присутствии света сопротивление светозависимого резистора падает до небольшого значения, обычно порядка нескольких Ом. Это изменение сопротивления в соответствии с интенсивностью света приведет к различным падениям напряжения. Падение напряжения можно откалибровать, чтобы определить наличие света определенной длины волны.
Сопротивление параллельно — диаграмма, формула и числа
Последнее обновление: 28 апреля 2020 г., Teachoo
Здесь разные резисторы подключены между 2 точками, параллельными друг другу.
Пример
Это сделано для уменьшения чистого сопротивления цепи.
В этом случае полное сопротивление цепи равно сумме обратных величин индивидуального сопротивления резисторов.
1 / R = 1 / R 1 + 1 / R 2 + 1 / R 3
ВАЖНЫЕ ТОЧКИ
Когда 2 резистора подключены параллельно
-
Через каждый резистор протекает разный ток, но общий ток, протекающий по цепи, остается неизменным.
Следовательно, мы можем сказать, что
Общий ток = Ток, протекающий через первый резистор + ток, протекающий через второй резистор + ток, протекающий через третий резистор
Я = Я 1 + Я 2 + Я 3
-
Потенциальная разница для всех обоих резисторов остается одинаковой (поскольку они оба находятся между одинаковыми точками)
Следовательно, мы можем сказать, что
Разность потенциалов = V
Он одинаков как для резистора 1, так и для резистора 2
Теперь мы знаем, что по закону Ома
Разница потенциалов = ток * сопротивление
Потенциальная разница / сопротивление = ток
Ток = потенциальный перепад / сопротивление
I = V / R
Как выводится формула сопротивления — для параллельных цепей?
Примечание — В случае параллельного подключения полное сопротивление всегда меньше, чем сопротивление физическое лицо резисторы.
При параллельном подключении резисторов полное сопротивление будет самым низким.
Вопросов
NCERT Вопрос 5 — Каким образом в цепь включается вольтметр для измерения разности потенциалов между двумя точками?
Посмотреть ответ
Q1, стр. 216 —
Оцените эквивалентное сопротивление при параллельном подключении следующих компонентов:
(а) 1 Ом и 10 6 Ом,
(b) 1 Ом, 10 3 Ом и 10 6 Ом.
Посмотреть ответ
Q2 Стр. 216 — К источнику 220 В. параллельно подключены электрическая лампа на 100 Ом, тостер сопротивлением 50 Ом и водяной фильтр сопротивлением 500 Ом. Какое сопротивление у электрического утюга, подключенного к тому же источнику, который потребляет такой же ток, как и все три прибора, и какой ток проходит через него?
Посмотреть ответ
Q4 Стр. 216 — Как можно соединить три резистора с сопротивлением 2 Ом, 3 Ом и 6 Ом, чтобы получить общее сопротивление (а) 4 Ом, (б) 1 Ом?
Посмотреть ответ
Q5 Стр. 216 — Какое (а) наибольшее, (б) наименьшее общее сопротивление, которое может быть обеспечено комбинацией четырех катушек с сопротивлением 4 Ом, 8 Ом, 12 Ом, 24 Ом?
Посмотреть ответ
Пример 12.8 —
На принципиальной схеме, приведенной на рис. 12.10, предположим, что резисторы R 1, R 2 и R 3 имеют значения 5 Ом, 10 Ом, 30 Ом соответственно, которые были подключены к батарее на 12 В. Рассчитайте
(а) ток через каждый резистор,
(б) полный ток в цепи, и
(c) полное сопротивление цепи.
Посмотреть ответ
Пример 12.9 — Если на рис. 12.12 R 1 = 10 Ом, R 2 = 40 Ом, R 3 = 30 Ом, R 4 = 20 Ом, R 5 = 60 Ом, и к устройству подключена батарея на 12 В.

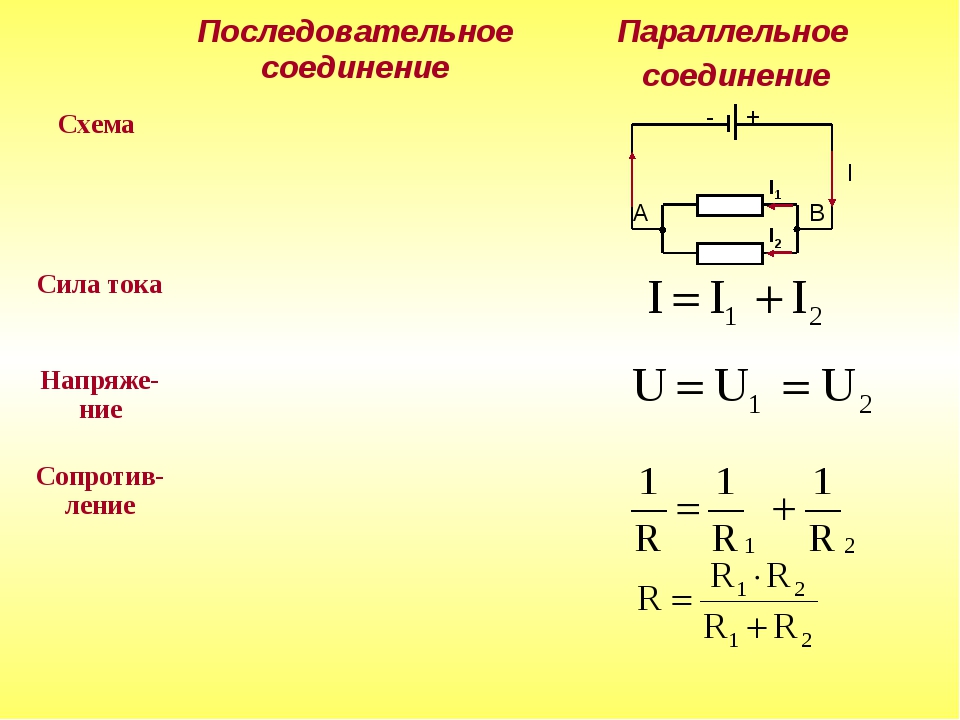 Вариант смешанного соединения состоит из последовательного и параллельного подключения активных сопротивлений. Поэтому в первую очередь нужно рассматривать эти два вида соединений, чтобы понять, как работают другие схемы.
Вариант смешанного соединения состоит из последовательного и параллельного подключения активных сопротивлений. Поэтому в первую очередь нужно рассматривать эти два вида соединений, чтобы понять, как работают другие схемы.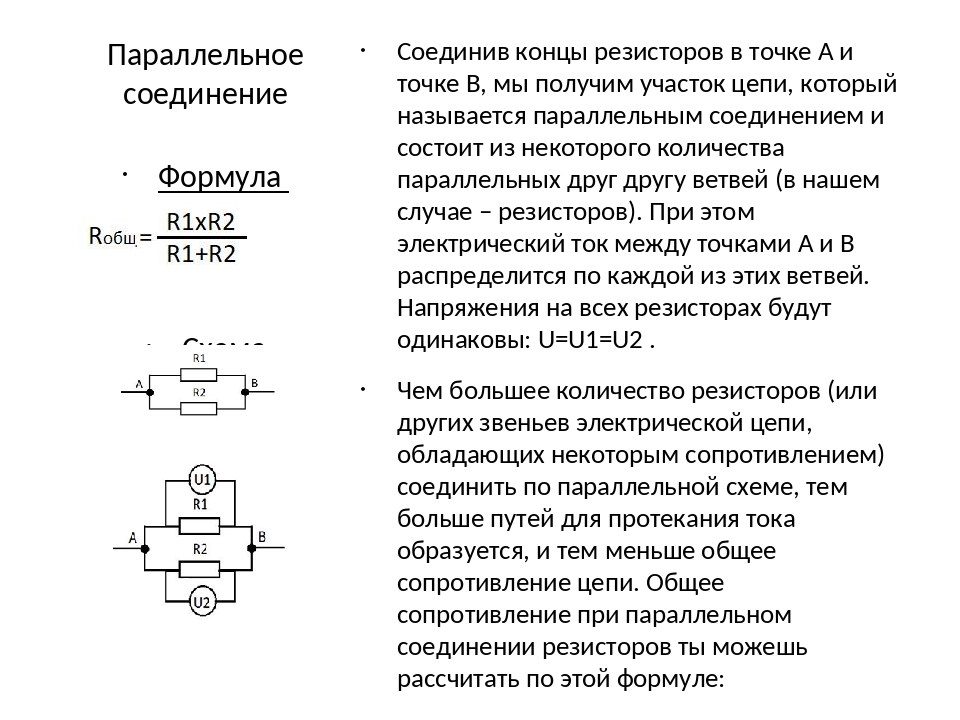 Поскольку токи на любом участке цепи имеют одинаковое значение, формула приобретает вид: Uобщ = I(r1 + r2).
Поскольку токи на любом участке цепи имеют одинаковое значение, формула приобретает вид: Uобщ = I(r1 + r2).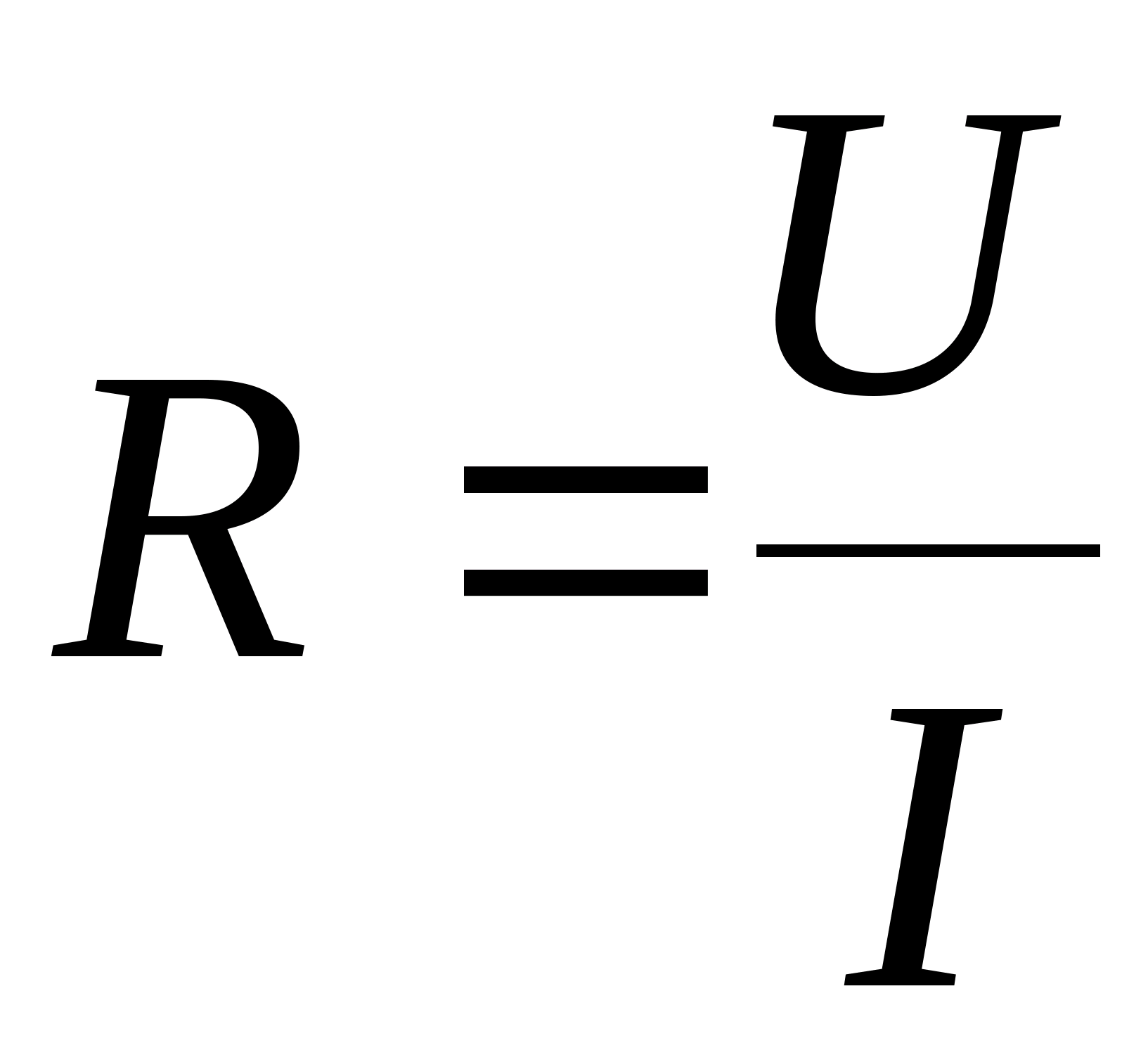 В свою очередь, значение токов будет разным на каждом резисторе, их распределение становится прямо пропорциональным сопротивлению этих резисторов. То есть, при увеличении сопротивления, сила тока уменьшается, а общий ток становится равен сумме токов, проходящих через каждый элемент. Формула для данного положения выглядит следующим образом: Iобщ= I1 + I2.
В свою очередь, значение токов будет разным на каждом резисторе, их распределение становится прямо пропорциональным сопротивлению этих резисторов. То есть, при увеличении сопротивления, сила тока уменьшается, а общий ток становится равен сумме токов, проходящих через каждый элемент. Формула для данного положения выглядит следующим образом: Iобщ= I1 + I2.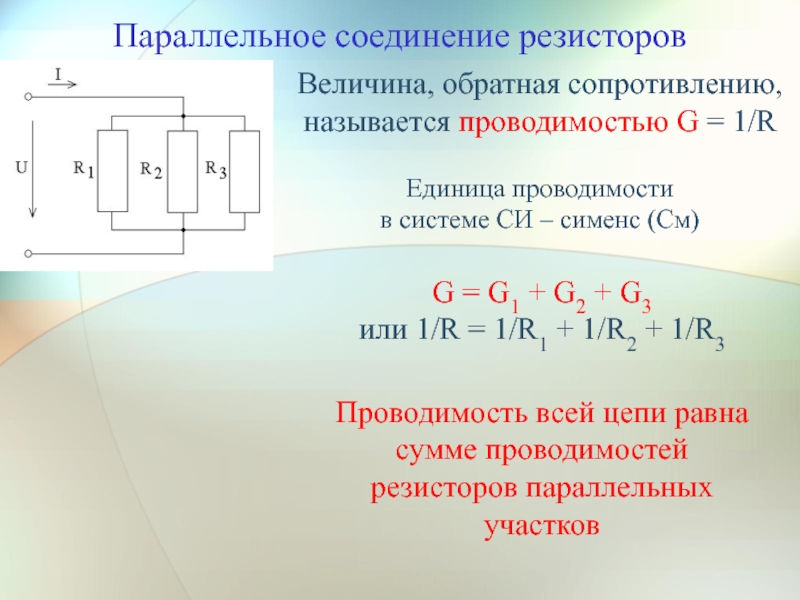
 Далее, нужно определить сопротивление резисторов R123, включенных параллельно, по следующей формуле: R123=R12R3/(R12+R3) = (R1+R2)R3/(R1+R2+R3). На последнем этапе выполняется расчет эквивалентного сопротивления всей цепи, путем суммирования полученных данных R123 и сопротивления R4, включенного последовательно с ним: Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4.
Далее, нужно определить сопротивление резисторов R123, включенных параллельно, по следующей формуле: R123=R12R3/(R12+R3) = (R1+R2)R3/(R1+R2+R3). На последнем этапе выполняется расчет эквивалентного сопротивления всей цепи, путем суммирования полученных данных R123 и сопротивления R4, включенного последовательно с ним: Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4.