Формула сопротивление тока. Электрическое сопротивление и закон Ома: формулы, единицы измерения и применение

Что такое электрическое сопротивление. Как формулируется закон Ома. В каких единицах измеряется сопротивление. Как сопротивление зависит от параметров проводника. Какие факторы влияют на электрическое сопротивление материалов.

Что такое электрическое сопротивление проводника

Электрическое сопротивление — это свойство проводника препятствовать прохождению электрического тока. Чем выше сопротивление, тем меньший ток протекает через проводник при заданном напряжении.

Сопротивление проводника зависит от следующих факторов:

• Материала проводника
• Длины проводника
• Площади поперечного сечения
• Температуры

Единица измерения электрического сопротивления в Международной системе единиц (СИ) — Ом. Один Ом — это сопротивление участка электрической цепи, на котором при силе тока 1 Ампер возникает напряжение 1 Вольт.

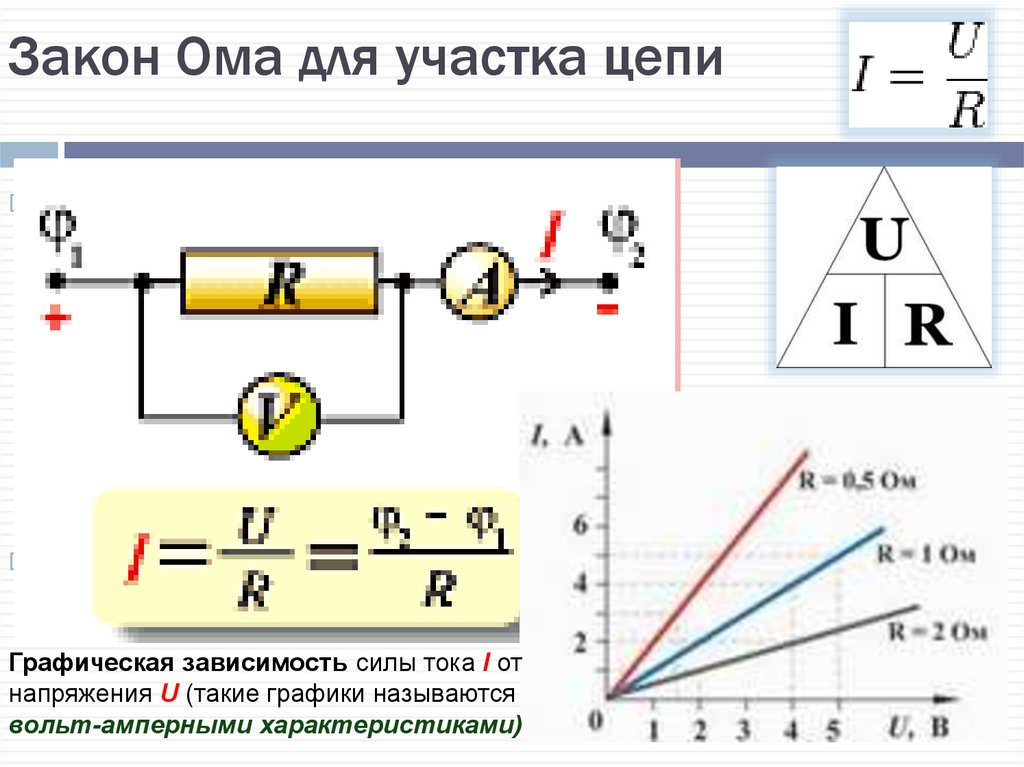
Закон Ома для участка цепи

Закон Ома устанавливает связь между силой тока, напряжением и сопротивлением участка цепи. Он формулируется следующим образом:

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

Математическая запись закона Ома:

I = U / R

где:

• I — сила тока (в Амперах)
• U — напряжение (в Вольтах)
• R — сопротивление (в Омах)

Из этой формулы можно выразить сопротивление:

R = U / I

Эта формула позволяет рассчитать сопротивление участка цепи, если известны протекающий по нему ток и напряжение на его концах.

Удельное электрическое сопротивление

Удельное электрическое сопротивление — это физическая величина, характеризующая способность материала проводника препятствовать прохождению электрического тока. Обозначается греческой буквой ρ (ро).

Формула для расчета сопротивления проводника через удельное сопротивление:

R = ρ * L / S

где:

• R — сопротивление проводника (Ом)
• ρ — удельное сопротивление материала (Ом·м)
• L — длина проводника (м)
• S — площадь поперечного сечения (м²)

Удельное сопротивление зависит от природы материала и его температуры. Для металлов оно увеличивается с ростом температуры.

Зависимость сопротивления от температуры

Электрическое сопротивление большинства проводников зависит от температуры. Для металлов эта зависимость описывается формулой:

R = R₀(1 + αΔT)

где:

• R — сопротивление при температуре T
• R₀ — сопротивление при начальной температуре T₀
• α — температурный коэффициент сопротивления
• ΔT — изменение температуры (T — T₀)

Для большинства металлов α > 0, то есть их сопротивление растет с увеличением температуры. Это объясняется усилением колебаний атомов кристаллической решетки, что затрудняет движение свободных электронов.

Последовательное и параллельное соединение резисторов

При последовательном соединении резисторов их общее сопротивление равно сумме сопротивлений отдельных резисторов:

R = R₁ + R₂ + R₃ + …

При параллельном соединении резисторов обратная величина общего сопротивления равна сумме обратных величин сопротивлений отдельных резисторов:

1/R = 1/R₁ + 1/R₂ + 1/R₃ + …

Эти формулы позволяют рассчитывать эквивалентное сопротивление сложных электрических цепей.

Применение закона Ома и понятия сопротивления

Закон Ома и понятие электрического сопротивления имеют широкое применение в электротехнике и электронике:

• Расчет параметров электрических цепей
• Подбор резисторов для ограничения тока в электронных схемах
• Проектирование систем электроснабжения
• Разработка электрических нагревательных приборов
• Создание измерительных приборов (амперметров, вольтметров)

Понимание закона Ома и свойств электрического сопротивления необходимо для безопасной и эффективной работы с электрическими устройствами и системами.

Ограничения закона Ома

Закон Ома выполняется не для всех проводников и электрических цепей. Существуют так называемые нелинейные элементы, для которых зависимость между током и напряжением не является линейной. К ним относятся:

• Полупроводниковые диоды
• Газоразрядные лампы
• Термисторы
• Варисторы

Для таких элементов вместо закона Ома используется понятие вольт-амперной характеристики — зависимости тока от напряжения, которая может иметь сложный нелинейный характер.

Измерение электрического сопротивления

Для измерения электрического сопротивления используются специальные приборы — омметры. Существует несколько методов измерения сопротивления:

Метод вольтметра-амперметра

Этот метод основан на законе Ома. Через измеряемое сопротивление пропускают ток и измеряют падение напряжения на нем. Сопротивление вычисляется по формуле R = U / I.

Мостовой метод

Использует схему моста Уитстона — электрическую цепь для измерения сопротивлений. Позволяет достичь высокой точности измерений.

Метод сравнения

Измеряемое сопротивление сравнивается с эталонным известным сопротивлением.

Выбор метода измерения зависит от требуемой точности, диапазона измеряемых сопротивлений и конкретных условий измерения.

Сверхпроводимость

Сверхпроводимость — это явление полного исчезновения электрического сопротивления в некоторых веществах при охлаждении их ниже определенной критической температуры. Сверхпроводимость была открыта голландским физиком Хейке Камерлинг-Оннесом в 1911 году.

Основные свойства сверхпроводников:

• Нулевое электрическое сопротивление
• Идеальный диамагнетизм (эффект Мейснера)
• Квантование магнитного потока

Сверхпроводимость находит применение в создании сильных электромагнитов, в магнитно-резонансной томографии, в системах передачи электроэнергии, в квантовых компьютерах.

Явление сверхпроводимости показывает, что при определенных условиях закон Ома может нарушаться, и электрическое сопротивление может полностью исчезать.

2.4. Закон Ома. Электрическое сопротивление. Закон Джоуля – Ленца — ЗФТШ, МФТИ

Как отмечалось выше, для поддержания постоянного тока в проводнике, т. е. движения электронов с постоянной скоростью, необходимо непрерывное действие сил электрического поля на носители заряда. Это означает, что электроны в проводниках движутся «с трением», иначе говоря, проводники обладают электрическим сопротивлением.

Если состояние проводника остаётся неизменным (не изменяется его температура и т. д.), то для каждого проводника существует однозначная зависимость между напряжением `U` на концах проводника и силой `I` тока в нём `I=f(U)`. Она называется вольтамперной характеристикой данного проводника.

Для многих проводников эта зависимость особенно проста – линейная: сила тока прямо пропорциональна приложенному напряжению, т. е.

где `R` – электрическое сопротивление проводника (постоянная при неизменных условиях величина).

Этот закон носит название закона Ома. Немецкий физик Г. Ом в 1827 г. в результате серии экспериментов установил, что для широкого класса проводников сила `I` электрического тока в проводнике пропорциональна напряжению `U` на концах проводника.

Сопротивление `R` проводника зависит от рода вещества проводника, от его размеров и формы, а также от состояния проводника.

Единицей сопротивления в СИ является один Ом (Ом). За один Ом принимается сопротивление такого проводника, в котором при напряжении между его концами один вольт течёт постоянный ток силой один ампер: `1`Ом`=1`В`//1`A.

Вытекающее из закона Ома (8) соотношение

можно рассматривать и как определение сопротивления по приведённой формуле.

Г. Ом установил, что для проводников  $$ R$$ не зависит от $$ U.$$ 

В технических приложениях для описания процессов в электрических цепях часто используется понятие  вольтамперной характеристики. Для проводников, подчиняющихся закону Ома (8), графиком зависимости силы `I` тока в проводнике от напряжения `U` на нём будет прямая линия, проходящая через начало координат (см. рис. 1). При этом говорят, что проводник имеет линейную вольтамперную характеристику.

В то же время для полупроводников, электронных ламп, диодов, транзисторов зависимость `I=f(U)` носит сложный характер, и такие элементы называют нелинейными (или неомическими). Для таких элементов величина `R`, вычисленная по формуле `R=U/I`, зависит от `U`. В частности, при измерении вольтамперной характеристики лампочки накаливания с вольфрамовой нитью мы обнаружим, что она имеет вид, схематически показанный на рис. 2. Искривление вольтамперной характеристики связано с нагревом нити и увеличением сопротивления нити накала с ростом температуры. В некоторых устройствах, таких как диод, сопротивление зависит от направления тока.

Обсудим вопрос о тепловыделении в проводнике. С учётом закона Ома (8) формула (7) для мощности тепловыделения принимает вид:

Другими словами, если через резистор `R` протекает постоянный ток силой `I`, то за `t` секунд в резисторе выделяется количество теплоты, равное

Соотношения (10), (11) являются математическим выражением закона, открытого в XIX веке практически одновременно и независимо английским физиком Д. Джоулем и русским физиком Э.Х. Ленцем.

Обратим внимание, что полученный закон является прямым следствием закона сохранения энергии в применении к движению электрических зарядов под действием сил электрического поля.

Влияние температуры проводника на его сопротивление

Промышленность

Образование

Наука

Типовые примеры

Отзывы

Пользователи

Главная >> Применение >> Типовые примеры >>

тепловая зависимость сопротивления кабеля, зависимость сопротивления от температуры

К алюминиевому проводнику приложено напряжение и течет ток. В результате теплового действия тока происходит нагрев проводника и изменение его линейных размеров и электропроводности. Определить сопротивление проводника с учетом его нагрева.

Тип задачи:
Осесимметричная мультифизичная задача электрического поля постоянных токов, стационарной теплопередачи и механики.

Геометрия:

Дано
Площадь поверхности проводника S_бок= 35 мм²;
Коэффициент конвекции α= 30 Вт/К·м.

Решение
К проводнику приложено напряжение. Сопротивление проводника, исходя из полученной силы тока может быть найдено из закона Ома:

R = ΔU·I ,
где ΔU — потеря напряжения в проводнике,
I — сила тока.

При протекании тока в проводнике в нём выделяется тепло, пропорциональное его сопротивлению. В результате этого проводник греется. Изменяется омическое сопротивление проводника.

ρ = ρ₀ · (1 + α·ΔT),

где ρ₀ — удельное сопротивление проводника при 20 °С,
α — температурный коэффициент сопротивления,
ΔT — перегрев проводника.

Также изменяются линейные размеры проводника в следствии тепловой деформации. Оба этих фактора приводят к изменению сопротивления проводника и к изменению величины протекающего тока. Таким образом, решение задачи носит итерационный характер:

1. Задать номинальные размеры и проводимость проводника.
2. Приложить напряжение и посчитать ток, тепловыделение (решить задачу эл. поля постоянных токов).
3. Определить температуру проводника (решить задачу теплопередачи).
4. Определить изменение электропроводности (по формуле).
5. Определить изменение линейных размеров (решить задачу упругих деформаций).
6. Скорректировать размеры проводника и его проводимость, вернуться к п.2.

Результаты расчета:

Итерация	I, A	R, мОм	Температура проводника T, °C	ΔR, %
0	163.4	6.73	48.6	-
1	135.2	8.14	43.5	17%
2	137.7	7.99	44.1	1.8%
3	137. 4	8.00	44.2	0.2%

Распределение электрического потенциала в проводнике

Температура проводника

Тепловые деформации

• Скачать файлы задачи

Закон

Ома (сопротивление) — Mypdh.engineer

Два фундаментальных свойства тока и напряжения связаны третьим свойством, известным как сопротивление. В любой электрической цепи при приложении к ней напряжения возникает ток. Сопротивление проводника будет определять величину тока, протекающего при заданном напряжении. В большинстве случаев чем больше сопротивление цепи, тем меньше ток. Если сопротивление уменьшить, то ток возрастет. Эта зависимость имеет линейный характер и известна как закон Ома.

Рис. 38. Зависимость напряжения от тока в цепи постоянного сопротивления.

Под линейно-пропорциональной характеристикой подразумевается, что если одна единица отношения увеличивается или уменьшается на определенный процент, другие переменные отношения увеличиваются или уменьшаются на тот же процент.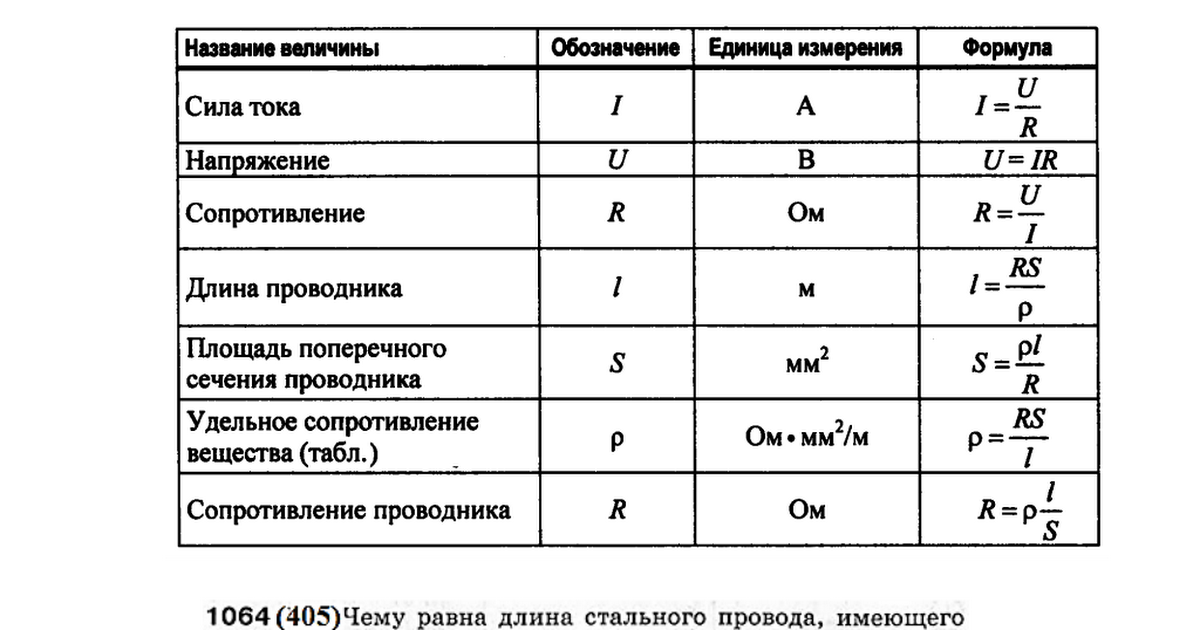 Например, если напряжение на резисторе удвоится, то ток через резистор удвоится. Следует добавить, что это соотношение справедливо только в том случае, если сопротивление в цепи остается постоянным. Ведь видно, что при изменении сопротивления меняется и ток. График этой зависимости показан на рис. 38, где используется постоянное сопротивление 20 Ом. Зависимость между напряжением и током в этом примере показывает напряжение, отложенное горизонтально по оси X в значениях от 0 до 120 вольт, а соответствующие значения тока отложены вертикально в значениях от 0 до 6,0 ампер по оси Y. Прямая линия, проведенная через все точки пересечения линий напряжения и тока, представляет собой уравнение 9.0011 I = E⁄20 и называется линейной зависимостью.

Закон Ома может быть выражен в виде следующего уравнения:

Уравнение 1

Где I — ток в амперах, E — разность потенциалов, измеренная в вольтах, а R — сопротивление, измеренное в омах. Если известны любые две из этих схемных величин, третью можно найти простым алгебраическим преобразованием. С помощью этого уравнения мы можем рассчитать ток в цепи, если известны напряжение и сопротивление. Эту же формулу можно использовать для расчета напряжения. Умножая обе части уравнения 1 на R, мы получаем эквивалентную форму закона Ома, а именно:

Уравнение 2 Уравнение 3 Рисунок 39. Диаграмма закона Ома.

Все три формулы, представленные в этом разделе, эквивалентны друг другу и представляют собой просто разные способы выражения закона Ома.

Различные уравнения, которые можно вывести путем перестановки основного закона, можно легко получить, используя треугольники на рис. 39.

Треугольники, содержащие E, R и I, разделены на две части, причем E над линией и I × R под ним. Чтобы определить неизвестную величину цепи, когда известны две другие, закройте неизвестную величину большим пальцем. Расположение оставшихся непокрытых букв в треугольнике укажет на выполняемую математическую операцию. Например, чтобы найти I, обратитесь к рисунку 39.А и прикрыть I большим пальцем. Незакрашенные буквы означают, что E нужно разделить на R, или I = E/R. Чтобы найти R, обратитесь к Рисунку 39B и закройте R большим пальцем. Результат показывает, что E нужно разделить на I, или R = E/I. Чтобы найти E, обратитесь к рисунку 39C и закройте E большим пальцем. Результат показывает, что I следует умножить на R, или E = I × R.

Эта таблица полезна при изучении закона Ома. Его следует использовать для дополнения знаний новичка об алгебраическом методе.

Резистивный электрический поток — закон Ома

Движущийся заряд испытывает сопротивление

Когда электрический заряд движется через материал, он обычно испытывает сопротивление, которое имеет тенденцию противодействовать движению, возникающее из-за их взаимодействия с другими зарядами в материале, движущемся термически. *

Исходя из нашего опыта с силами сопротивления, мы не можем быть уверены, зависит ли сопротивление, ощущаемое движущимся зарядом, от скорости (например, трение), пропорционально скорости (например, вязкость) или пропорционально квадрату скорости ( как драг).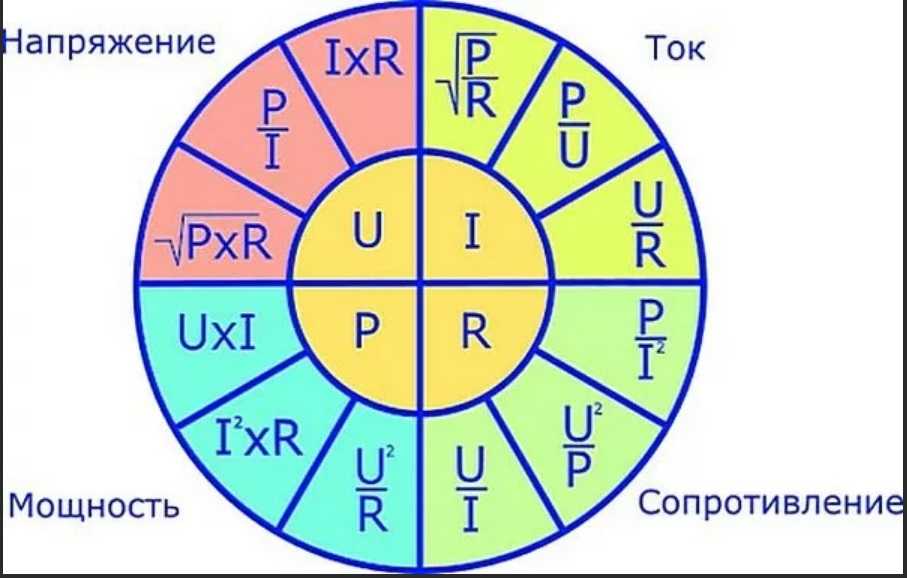 Во многих ситуациях кажется, что сила сопротивления, которую ощущает движущийся заряд, больше похожа на вязкость — пропорциональна скорости. Мы увидим, что предположение о том, что это именно то сопротивление, эквивалентно 9{resistive} = -bv$$

Знак минус говорит о том, что сила направлена ​​против скорости.

Что держит его на плаву?

Чтобы заряд продолжал двигаться через резистивную среду, нам нужна сила, уравновешивающая сопротивление. Поскольку мы хотим перемещать заряды, наиболее естественно думать об электрической силе как о силе, толкающей их через резистивную среду.

Чтобы заряд $q$ двигался с постоянной скоростью через сопротивляющуюся среду, нам нужна электрическая сила $qE$. Если наш заряд движется со скоростью $v$, чтобы поддерживать его движение с постоянной скоростью, нам необходимо уравновесить две силы (согласно второму закону Ньютона): 9{net} = qE — bv = 0$$

или

$$qE = bv.$$

Закон Ома

Теперь рассмотрим цилиндр, состоящий, скажем, из ионов и электронов, на который мы поместим электрическую поле. Ионы будут реагировать, возможно, в 120 000 раз меньше, чем электроны (отношение массы иона меди к массе электрона), поэтому мы можем игнорировать движение ионов.

Рассмотрим цилиндр заряда площадью поперечного сечения A и длиной $L$ с носителями заряда $q$ плотностью $n$. Чтобы получить поле E по всему объему, мы наложим разность потенциалов $ΔV$. Это даст среднее поле E

$$E = ΔV/L.$$

Баланс наших сил дает

$$qE = bv$$

$$qΔV/L = bv$$

Теперь мы хотим избавиться от $v $ в пользу текущего, $I$ . Напомним, что ток определяется (см. страницу, количественное определение электрического тока) количеством заряда, пересекающего площадь в секунду, или ;площадь\;в\;а\;время} Δt}{Δt}$$

Так как $I$ = (заряд на один носитель)(количество носителей в единице объема) x 92nA}.$$

Результатом является сильное уравнение, Закон Ома ,

$$ΔV = IR.$$

Что это значит?

В принципе, мы можем видеть из вывода, откуда берется закон Ома. Все начинается с утверждения, что толчок (исходящий из поля E) уравновешивается сопротивлением (пропорционально v), поэтому мы поддерживаем постоянную скорость (согласно второму закону Ньютона).

Поскольку мы не можем легко создавать поля E количественно, но можем легко манипулировать потенциалом, мы выражаем это через разность потенциалов на цилиндре (сопротивлении). Поскольку мы не можем легко измерить скорость наших носителей тока, но у нас есть устройства (амперметры) для непосредственного измерения тока, удобно выразить скорость через ток.

Результат интуитивно понятен: чем больше толчок, тем больше поток; большее сопротивление для того же толчка приводит к меньшему потоку.   Это стандартное уравнение потока, управляемое градиентом, в котором изменение некоторого скалярного поля в пространстве приводит к движению чего-либо. Другие примеры включают уравнение HP, тепловой поток за счет теплопроводности и закон диффузии Фика.

Чтобы понять, каковы последствия этого, нам придется рассмотреть множество моделей и установить некоторые принципы использования этого закона, чтобы помочь понять, что и куда течет.

Биолог против Закона Ома инженера-электрика

Поскольку электрические резисторы в основном пассивны, инженерам-электрикам очень нравится идея сопротивления — материя сопротивляется протеканию тока. Но в биологических системах система часто регулирует свое сопротивление, чтобы активно манипулировать потоком тока. В этих ситуациях иногда удобнее считать ток результатом не просто падения напряжения, $\Delta V$, а обратного 92nA}{bL}$$

$$I = G∆V$$

Это равноправные формы закона Ома. (Это ничем не отличается от описания движения в терминах скорости — мили в час или обратного шага — минут на милю. Что проще использовать, зависит от того, что вы вычисляете, и формально они полностью эквивалентны.)  

Удельное сопротивление: плотность сопротивления

Когда мы получили свойства материи, которые зависят как от того, что это за материя, так и от ее формы, мы сочли полезным создать плотность . Очевидным примером является масса, где масса объекта равна его (массовой) плотности, умноженной на его объем: $m = \rho V$ (здесь объем, а не потенциал).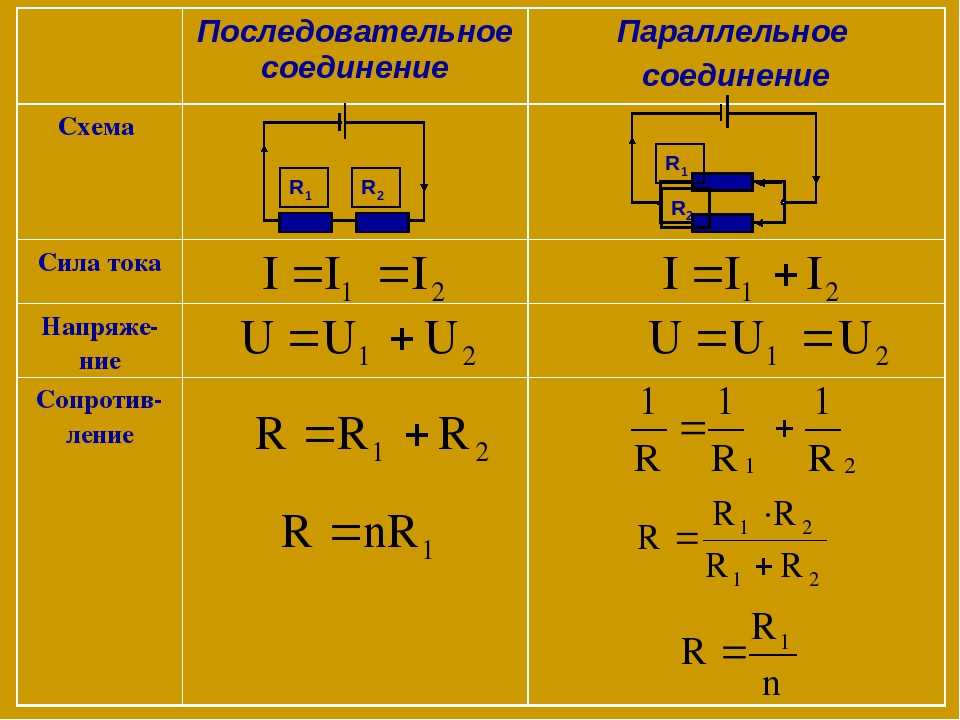 Еще одно место, где мы это использовали, было в создании постоянной пружины для блока материи: $k = YA/L$, где $Y$ — модуль Юнга. Вы можете найти ряд других.

Здесь электрическое сопротивление также можно разделить на плотностьподобную величину, которая зависит только от материала и свойств материала:   

92n$ зависит только от вещества, а не от конкретной формы сопротивления. Комбинация называется удельным электрическим сопротивлением   и часто пишется как $\rho$. (Извините за это.) 

Обратите внимание, что уравнение HP для потока жидкости в трубе имеет форму, очень похожую на закон Ома: разница давлений создает поток через сопротивление:

$$\Delta p = R Q$$

, где $p$ — перепад давления, $Q$ — объемный расход, а сопротивление жидкости, $R$, равно 92$, а не по $1/A$. Видите ли вы из выводов, в чем источник этого различия?

Откуда берется разница в напряжении?

Поскольку мы знали, что у нас есть постоянный ток, и поскольку мы знали, что у нас есть некоторое сопротивление, Ньютон 2 сказал нам, что нам нужна толкающая сила, чтобы уравновесить силу сопротивления. Мы предположили, что это вызвано полем Е, связанным с разностью потенциалов. Но откуда берется эта разность потенциалов?

Давайте рассмотрим идеализированную модель, в которой у нас есть батарея (которая создает разность потенциалов и, следовательно, электрическое поле), передающая заряды по проводу. Если провод практически не имеет сопротивления (а большинство проводов имеют очень низкое сопротивление), любые заряды, которые начинают двигаться, не замедляются. Они продолжают двигаться с постоянной скоростью. Но предположим, что теперь произошло попадание в резистивную область, как показано на рисунке ниже.

Когда движущиеся заряды (синие или + на этой диаграмме) сталкиваются с резистором, они чувствуют сопротивление и начинают замедляться, накапливая избыточный + заряд на переднем конце резистора. Эти избыточные заряды создают поле E в резисторе, которое вытесняет положительные заряды, оставляя дефицит +, который является избытком — зарядов.

Как только это стабилизируется (примерно за наносекунду в типичной макроскопической схеме), у нас есть слой + на одной стороне резистора и слой — на другой стороне. Это похоже на конденсатор, создающий поле E между ними, которого как раз достаточно, чтобы поддерживать движение зарядов с постоянной скоростью. (В этом нет никакой магии. Если бы не было достаточно зарядов, чтобы не дать им замедлиться, то накопилось бы больше зарядов, увеличивая поле E до тех пор, пока его не стало бы достаточно. Тогда оно больше не увеличивалось бы, и устойчивое состояние было бы установлено.)

Мы можем измерить разность напряжений на концах резистора. Если бы поле E было постоянным внутри, то его величина была бы равна

$$E = \frac{\Delta V}{\Delta x} = \frac{\Delta V}{L}$$

Хотя $ E$, вероятно, не является постоянным, это все равно будет среднее поле E, $\langle E \rangle$.

Единицы

 

Из закона Ома ясно, что подходящей единицей измерения сопротивления является «вольт/ампер». Эту комбинацию можно распаковать —

• вольт = Джоуль/Кулон,
• Ампер = Кулон/сек,

, поэтому единицей сопротивления является

• вольт/ампер = джоуль*сек/кулон ² = кг-м ² /C ² -с.