Что такое закон Ома и как он применяется в электротехнике. Какие формулы используются для расчета тока, напряжения и сопротивления. Как закон Ома работает в цепях постоянного и переменного тока. Какие ограничения имеет закон Ома.
Закон Ома: основные формулы и определения
Закон Ома является одним из фундаментальных законов электротехники, описывающим взаимосвязь между током, напряжением и сопротивлением в электрической цепи. Он был открыт немецким физиком Георгом Омом в 1827 году и с тех пор широко используется для расчетов электрических цепей.
Основная формула закона Ома для участка цепи выглядит следующим образом:
I = U / R
где:
- I — сила тока в амперах (А)
- U — напряжение в вольтах (В)
- R — сопротивление в омах (Ом)
Эта формула показывает, что сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Зная любые две величины, можно рассчитать третью.
Применение закона Ома в цепях постоянного тока
В цепях постоянного тока закон Ома применяется наиболее просто. Рассмотрим несколько примеров расчетов:

Расчет силы тока
Если известно напряжение и сопротивление участка цепи, силу тока можно рассчитать по формуле:
I = U / R
Например, при напряжении 12 В и сопротивлении 4 Ом сила тока составит:
I = 12 В / 4 Ом = 3 А
Расчет напряжения
Напряжение на участке цепи можно рассчитать, зная силу тока и сопротивление:
U = I * R
Если через резистор 100 Ом протекает ток 0,5 А, напряжение на нем составит:
U = 0,5 А * 100 Ом = 50 В
Расчет сопротивления
Сопротивление участка цепи определяется по формуле:
R = U / I
При напряжении 220 В и токе 2 А сопротивление составит:
R = 220 В / 2 А = 110 Ом
Закон Ома для полной цепи
Для полной электрической цепи, содержащей источник ЭДС, закон Ома записывается в виде:
I = E / (R + r)
где:
- E — электродвижущая сила источника
- R — сопротивление внешней цепи
- r — внутреннее сопротивление источника
Эта формула учитывает влияние внутреннего сопротивления источника тока на общий ток в цепи.
Применение закона Ома в цепях переменного тока
В цепях переменного тока закон Ома применяется с учетом реактивных сопротивлений. Основная формула принимает вид:

I = U / Z
где Z — полное сопротивление цепи (импеданс).
Импеданс учитывает активное сопротивление, индуктивное и емкостное сопротивления:
Z = sqrt(R^2 + (X_L — X_C)^2)
где X_L — индуктивное сопротивление, X_C — емкостное сопротивление.
Ограничения закона Ома
Закон Ома имеет ряд ограничений и не применим в следующих случаях:
- Для нелинейных элементов (диоды, транзисторы)
- При очень высоких напряжениях и токах
- В сверхпроводниках
- При быстропеременных процессах
В этих случаях используются более сложные модели и уравнения для описания поведения электрических цепей.
Практическое применение закона Ома
Закон Ома широко применяется в электротехнике и электронике для:
- Расчета параметров электрических цепей
- Выбора номиналов резисторов
- Расчета мощности электроприборов
- Определения потерь в проводах
- Проектирования источников питания
Понимание и умение применять закон Ома необходимо для всех специалистов, работающих с электрическими системами.
Экспериментальная проверка закона Ома
Закон Ома можно легко проверить экспериментально, измеряя ток и напряжение на резисторе при различных значениях сопротивления. Для этого собирается простая электрическая схема:

- Источник постоянного напряжения
- Резистор с переменным сопротивлением (реостат)
- Амперметр для измерения тока
- Вольтметр для измерения напряжения
Изменяя сопротивление реостата, можно убедиться, что отношение напряжения к току остается постоянным и равным сопротивлению.
Закон Ома в дифференциальной форме
Для неоднородных проводников закон Ома записывается в дифференциальной форме:
j = σE
где:
- j — плотность тока
- σ — удельная электропроводность
- E — напряженность электрического поля
Эта форма закона Ома позволяет анализировать распределение тока в объемных проводниках.
Применение закона Ома в сложных цепях
В сложных электрических цепях с несколькими источниками ЭДС и разветвлениями закон Ома применяется совместно с правилами Кирхгофа. Это позволяет составить систему уравнений и рассчитать токи во всех ветвях цепи.
Для расчета сложных цепей часто используются методы:
- Контурных токов
- Узловых потенциалов
- Наложения
- Эквивалентного генератора
Все эти методы основаны на применении закона Ома к отдельным участкам цепи.

Заключение
Закон Ома является одним из основополагающих законов электротехники, позволяющим анализировать и рассчитывать электрические цепи. Несмотря на простоту формулировки, он имеет широчайшее практическое применение во всех областях, связанных с электричеством. Понимание закона Ома необходимо для проектирования и эксплуатации любых электрических устройств и систем.
Закон Ома. Калькулятор. Полезные формулы
Закон Ома. Калькулятор. Полезные формулы
Для расчета введите любые два значения:
| Вольты | Амперы | Омы | Ватты |
Полезные формулы
| Постоянный ток |
| Ток (А) = | Ватты / Вольты | I = P / V | A = W / V |
| Мощность (Вт) = | Вольты * Амперы | P = V * I | W = V * A |
| Напряжение (В) = | Ватты / Амперы | V = P / I | V = W / A |
Мощность в лошад. силах= силах= |
(V * A * EFF) / 746 | ||
| Efficiency= | (746 * HP) / (V * A) | ||
Прим.: EFF = Efficiency HP = Мощность в лошадиных силах (Horsepower) |
|||
| Ток (А) = | Ватты /(Вольты * PF) | I=P/(V * PF) | A=W/(V * PF) |
| Мощность (Вт) = | Вольты * Амперы * PF | P=V * I * PF | W=V * A * PF |
| Напряжение (В) = | Ватты / Амперы | V=P / I | V=W / A |
| Вольт-ампер (В·А)= | Вольты * Амперы | VA=V * I | VA=V * A |
Мощность в лошад. силах=
силах= |
(V * A * EFF * PF) / 746 | ||
| Коэффициент мощности= | INPUT WATTS / (V * A) | ||
| Efficiency= | (746 * HP) / (V * A * PF) | ||
Прим.: EFF = Efficiency PF = Коэффициент мощности (Powerfactor) HP = Мощность в лошадиных силах (Horsepower) |
|||
| Переменные ток — три фазы |
| Ток (А) = | WATTS / (1.732 * VOLTS * PF) | I = P / (1.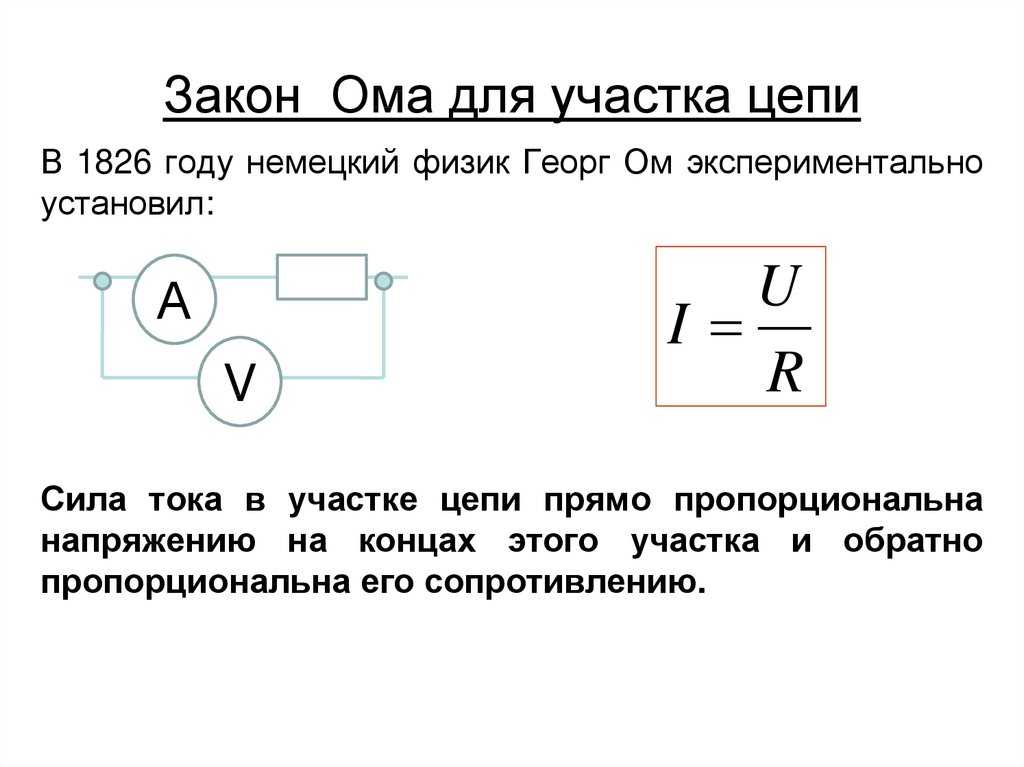 732 * E * PF) 732 * E * PF) |
| Мощность (Вт) = | 1.732 * VOLTS * AMPS * PF | P = 1.732 * V * I * PF |
| Напряжение (В) = | WATTS / AMPS | V=P / I |
| Вольт-ампер (В·А)= | 1.732 * VOLTS * AMPS | VA=1.732 * V * I |
| Мощность в лошад. силах= | (1.732 * V * A * EFF * PF) / 746 | |
| Коэффициент мощности= | INPUT WATTS / (1.732 * V * A) | |
| Efficiency= | (746 * HP) / (1.732 * V * A * PF) | |
Прим.: EFF = Efficiency PF = Коэффициент мощности (Powerfactor) HP = Мощность в лошадиных силах (Horsepower) |
||
Вольт — единица электрического напряжения.
Ампер — диница измерения силы электрического тока.
Ватт — единица мощности.
Efficiency — выходная мощность, поделенная на входную мощность (отношение произведенной работы к использованной энергии).
варианты записи формулы, описание и объяснение © Геостарт
Рубрика: Электроприборы и освещение
Закон Ома для полной цепи и для участка цепи: варианты записи формулы, описание и объяснение
Профессиональному электрику, специалисту электронщику никак не обойти в собственной деятельности закон Ома, решая любые задачи, связанные с наладкой, настройкой, ремонтом электронных и электрических схем.
Собственно, понимание этого закона необходимо каждому. Потому что каждому в быту приходится иметь дело с электричеством.
И хотя учебным курсом средней школы закон немецкого физика Ома и предусмотрен, но на практике не всегда своевременно изучается. Поэтому рассмотрим в нашем материале такую актуальную для жизни тему и разберемся с вариантами записи формулы.
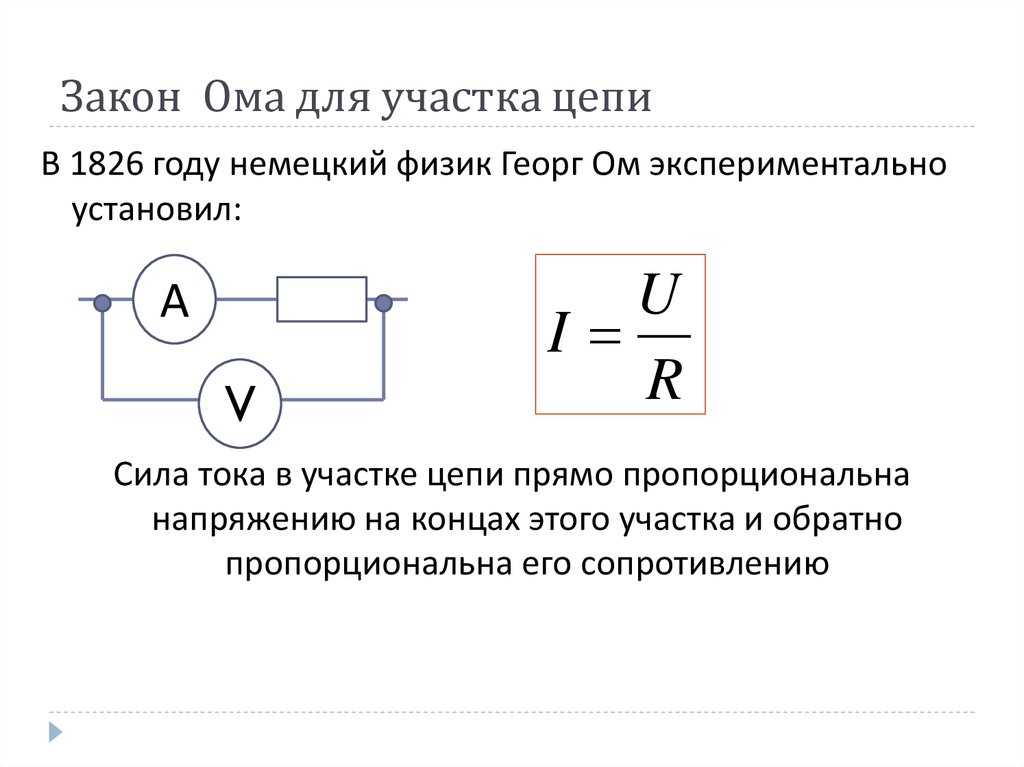
Отдельный участок и полная электрическая цепь
Рассматривая электрическую цепь с точки зрения применения к схеме закона Ома, следует отметить два возможных варианта расчета: для отдельно взятого участка и для полноценной схемы.
Расчет тока участка электрической схемы
Участком электрической цепи, как правило, рассматривается часть схемы, исключающая источник ЭДС, как обладающий дополнительным внутренним сопротивлением.
Поэтому расчетная формула, в данном случае, выглядит просто:
I = U/ R ,
Где, соответственно:
- I – сила тока;
- U – приложенное напряжение;
- R – сопротивление.
Трактовка формулы простая – ток, протекающий по некоему участок цепи, пропорционален приложенному к нему напряжению, а сопротивлению – обратно пропорционален.
Так называемая графическая «ромашка», посредством которой представлен весь набор вариаций формулировок, основанных на законе Ома. Удобный инструмент для карманного хранения: сектор «P» — формулы мощности; сектор «U» — формулы напряжения; сектор «I» — формулы тока; сектор «R» — формулы сопротивления
Таким образом, формулой чётко описывается зависимость протекания тока по отдельному участку электрической цепи относительно определенных значений напряжения и сопротивления.
Формулой удобно пользоваться, например, рассчитывая параметры сопротивления, которое требуется впаять в схему, если заданы напряжение с током.
Закон Ома и два следствия, которыми необходимо владеть каждому профессиональному электромеханику, инженеру-электрику, электронщику и всем, кто связан с работой электрических цепей. Слева направо: 1 — определение тока; 2 — определение сопротивления; 3 — определение напряжения, где I — сила тока, U — напряжение, R — сопротивление
Вышеприведенный рисунок поможет определить, например ток, протекающий через 10-омное сопротивление, к которому приложено напряжение 12 вольт. Подставив значения, найдем – I = 12 / 10 = 1.2 ампера.
Подставив значения, найдем – I = 12 / 10 = 1.2 ампера.
Аналогично решаются задачи поиска сопротивления (когда известны ток с напряжением) или напряжения (когда известны напряжение с током).
Тем самым всегда можно подобрать требуемое рабочее напряжение, нужную силу тока и оптимальный резистивный элемент.
Формула, которой предложено пользоваться, не требует учитывать параметры источника напряжения. Однако, схема, содержащая, например, аккумулятор, будет рассчитываться по другой формуле. На схеме: А – включение амперметра; V – включение вольтметра.
Кстати, соединительные провода любой схемы – это сопротивления. Величина нагрузки, которую им предстоит нести, определяется напряжением.
Соответственно, опять же пользуясь законом Ома, становится допустимым точный подбор необходимого сечения проводника, в зависимости от материала жилы.
У нас на сайте есть подробная инструкция по расчету сечения кабеля по мощности и току.
Вариант расчета для полной цепи
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС.
Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС.
Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Для расчетов в условиях полноценной электрической цепи всегда берется к учету резистивное значение источника ЭДС. Это значение суммируется с резистивным сопротивлением непосредственно электрической цепи. На схеме: I — прохождение тока; R — резистивный элемент внешний; r — резистивный фактор ЭДС (источника энергии)
На схеме: I — прохождение тока; R — резистивный элемент внешний; r — резистивный фактор ЭДС (источника энергии)
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины.
Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Рассмотрение действия закона к переменной величине
Понятие «сопротивление» к условиям прохождения переменного тока следует рассматривать уже больше как понятие «импеданса». Здесь имеется в виду сочетание активной резистивной нагрузки (Ra) и нагрузки, образованной реактивным резистором (Rr).
Обусловлены подобные явления параметрами индуктивных элементов и законами коммутации применительно к переменной величине напряжения — синусоидальной величине тока.
Такой видится эквивалентная схема электрической цепи переменного тока под расчет с применением формулировок, исходящих из принципов закона Ома: R — резистивная составляющая; С — емкостная составляющая; L — индуктивная составляющая; ЭДС -источник энергии; I -прохождение тока
Другими словами, имеет место эффект опережения (отставания) токовых значений от значений напряжения, что сопровождается появлением активной (резистивной) и реактивной (индуктивной или емкостной) мощностей.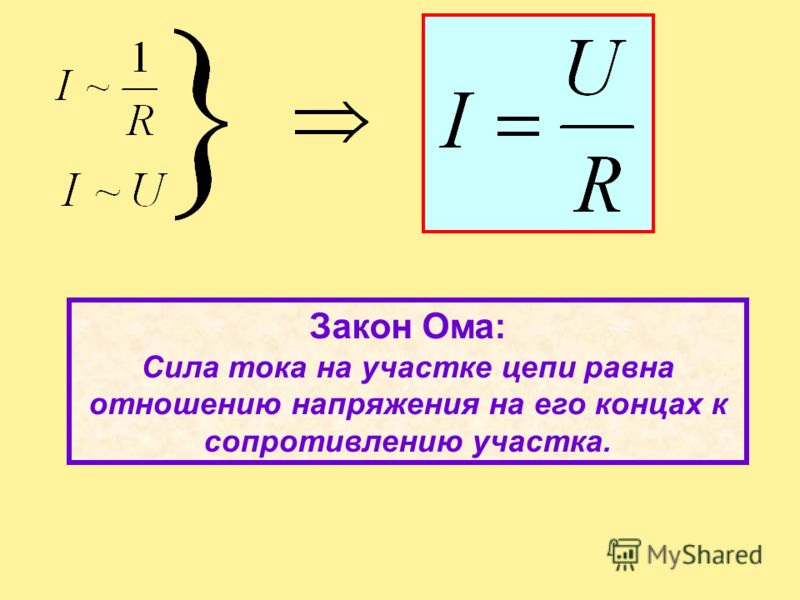
Расчёт подобных явлений ведётся при помощи формулы:
Z = U / I или Z = R + J * (X L — X C )
где: Z – импеданс; R – активная нагрузка; X L , X C – индуктивная и емкостная нагрузка; J – коэффициент.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.
Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I 1 = I 2 ;
- U = U 1 + U 2 ;
- R = R 1 + R 2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.
Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U, U1, U2 — приложенное напряжение
Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx .
Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I 1 + I 2 … ;
- U = U 1 = U 2 … ;
- 1 / R = 1 / R 1 + 1 / R 2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.
Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U — подведённое напряжение; А, В — точки входа/выхода
Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.
Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E
Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ
Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Работа электрика или деятельность электронщика неотъемлемо связана с моментами, когда реально приходится наблюдать закон Георга Ома в действии. Это своего рода прописные истины, которые следует знать каждому профессионалу.
Объёмных знаний по данному вопросу не требуется — достаточно выучить три основных вариации формулировки, чтобы успешно применять на практике.
|
автор Измайлов Илья |
Формулы и уравнения для законов Ома, Кирхгофа и Кулона
Содержание
Формулы закона Ома
Закон Ома показывает взаимосвязь между током «I» и напряжением «V», где сопротивление «R» является постоянной величиной в электрической цепи.
Закон Ома в цепях постоянного тока
- I = V/R Для расчета тока
- В = IR Для расчета напряжения
- R = V/I Для расчета сопротивления
Закон Ома в цепях переменного тока
- I = V/Z Для расчета тока
- В = IZ Для расчета напряжения
- Z = V/I Для расчета импеданса
Где
- I = ток в амперах (А)
- В = напряжение в вольтах (В)
- R = сопротивление в омах (Ом)
- Z = Полное сопротивление в Омах (Ом)
Текущий закон Кирхгофа – KCL
Сумма всех токов, поступающих в узел или соединение, равна 0 . Или сумма входящих и выходящих токов в точке равна нулю. Другими словами, ток, входящий в точку, равен току, выходящему из этой точки.
∑I Вход = ∑I Выход
∑I = 0
- Текущий вход в узел обозначен положительным знаком (+).
- Ток, выходящий из узла, записывается со знаком минус (-).
Закон Кирхгофа о напряжении – KVL
Сумма всех разностей потенциалов в контуре равна 0 . Произведение I «Ток» и R «Сопротивление» в замкнутом пути (также известном как сетка), расположенном в сети, равно приложенной ЭДС.
∑ IR = ∑ E
- Подробнее о KVL и KCL можно узнать здесь.
Закон Кулона
Законы электростатики Кулона определяют силу притяжения или отталкивания между двумя зарядами или заряженными телами.
или
- F = сила отталкивания или притяжения между зарядами
- ε 0 = диэлектрическая проницаемость в пространстве
- ε r = относительная диэлектрическая проницаемость материала
- q 1 , q 2 = 1 st & 2 nd количество заряда соответственно в кулонах
- r = Расстояние между зарядами в метрах
- k = константа
Связанные формулы и уравнения Посты:
- Основные формулы и уравнения электротехники
- Сопротивление, емкость и индуктивность в последовательно-параллельном соединении – уравнения и формулы
- Уравнения и формулы для цепей RLC (последовательные и параллельные)
- Формулы сопротивления, проводимости, импеданса и проводимости
- Основные формулы электрических величин
- Формулы мощности в однофазных и трехфазных цепях постоянного и переменного тока
- Правила делителя напряжения и тока (VDR и CDR) Уравнения
- Формула и уравнения для индуктора и индуктивности
- Формула и уравнения для конденсатора и емкости
- Формулы электрического и магнитного потока, плотности и напряженности поля
- Потери в электрических машинах – формулы и уравнения
- Формулы и уравнения генератора постоянного тока
- Уравнение мощности, напряжения и ЭДС двигателя постоянного тока – формулы
- Формулы и уравнения синхронного генератора и генератора переменного тока
- Формулы и уравнения для синхронных, шаговых и двигателей переменного тока
- Асинхронный двигатель и линейные асинхронные двигатели Формулы и уравнения
- Трансформаторные формулы и уравнения
- Формулы и уравнения в области электротехники и электроники
- Электрические и электронные элементы и символы
Показать полную статью
Похожие статьи
Кнопка «Вернуться к началу»
Закон Ома — веб-формулы
Закон Ома гласит, что ток, протекающий через устройство, прямо пропорционален разности потенциалов, приложенной к устройству. Постоянная пропорции называется сопротивлением устройства, если она математически сформулирована как:
Постоянная пропорции называется сопротивлением устройства, если она математически сформулирована как:
В = I R
Где В — напряжение на элементе цепи в вольтах, I — ток, проходящий через элемент в амперах, а R — сопротивление элемента в омах. Учитывая любые две из этих величин, закон Ома можно использовать для решения третьей.
Соответствующие единицы СИ:
вольт (В) = ом (Ом) ∙ ампер (А)
Закон Ома можно переписать как:
Я = В/Р
R = V/I
Электрическая схема для проверки закона Ома:
Для проверки закона Ома используется следующая схема.
На приведенной выше схеме показана схема, используемая в лаборатории для проверки закона Ома.
В цепи: B — батарея для подачи тока в цепь, Rh — реостат для контроля тока в цепи, K — ключ для соединения или размыкания цепи, A — амперметр для измерения тока в цепи, V — вольтметр для измерения разности потенциалов на проводе сопротивления, а R — провод сопротивления для обеспечения сопротивления.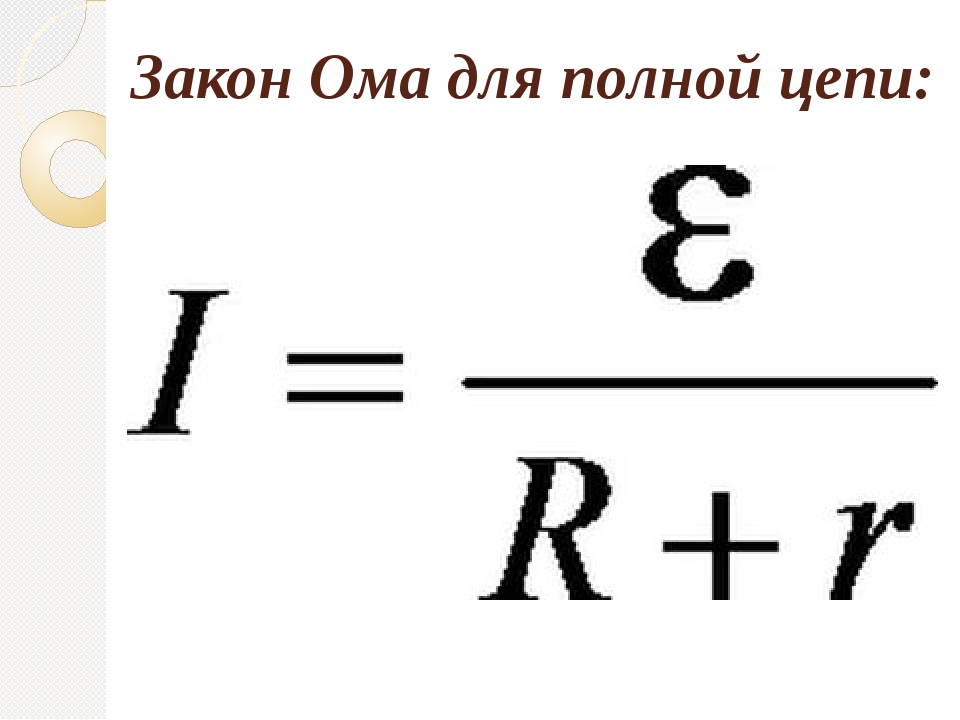
Обратите внимание:
1. Реостат Rh, ключ K, амперметр A и резистивный провод R соединены последовательно с батареей B.
2. Положительная сторона амперметра должна быть направлена к положительной клемме аккумулятора.
3. Вольтметр V подключен параллельно проводу сопротивления.
4. Положительная сторона вольтметра должна быть направлена к положительной стороне батареи.
Процедура проверки закона Ома:
1. Закрывают ключ К и реостат регулируют так, чтобы получить минимальные показания амперметра и вольтметра.
- Затем реостат постепенно перемещают так, чтобы ток в цепи увеличивался.
- При каждом перемещении реостата измеряют показания тока (I), протекающего в цепи, и разности потенциалов на сопротивлении, записывая показания амперметра и вольтметра.
- Таким образом, в таблице получаются различные наборы значений, и для каждого набора значений рассчитывается отношение тока (I) и разности потенциалов (V).


