Формулы последовательного и параллельного соединения в проводниках. Последовательное и параллельное соединение проводников и конденсаторов: формулы, свойства, применение

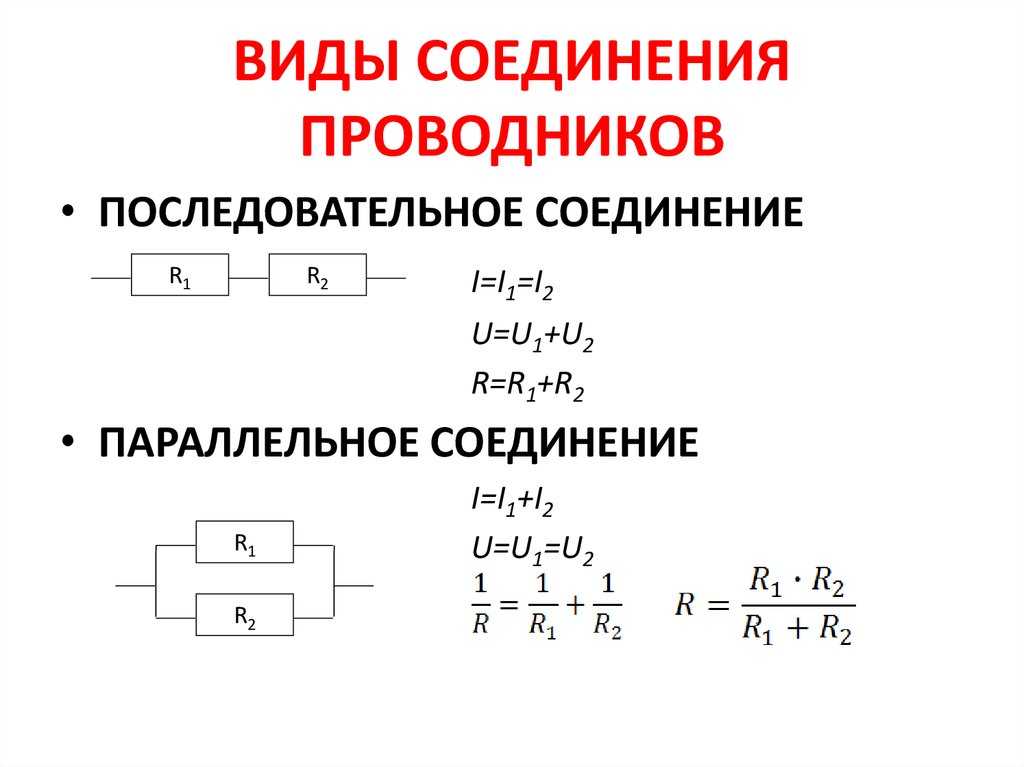
Как работает последовательное и параллельное соединение проводников и конденсаторов. Какие формулы используются для расчета общего сопротивления и емкости. Где применяются различные типы соединений в электрических цепях. Каковы основные свойства и особенности последовательного и параллельного подключения.

Основные типы соединений проводников в электрических цепях

В электротехнике используются два основных способа соединения проводников:

• Последовательное соединение
• Параллельное соединение

Также встречается смешанное соединение, сочетающее оба типа. Каждый вид соединения имеет свои особенности и области применения.

Последовательное соединение проводников: особенности и свойства

При последовательном соединении проводники подключаются один за другим, образуя единую неразветвленную цепь. Основные свойства:

• Сила тока одинакова во всех участках цепи
• Общее напряжение равно сумме напряжений на отдельных участках
• Общее сопротивление равно сумме сопротивлений отдельных проводников

Формула для расчета общего сопротивления при последовательном соединении:

R = R1 + R2 + R3 + …

где R — общее сопротивление, R1, R2, R3 — сопротивления отдельных проводников.

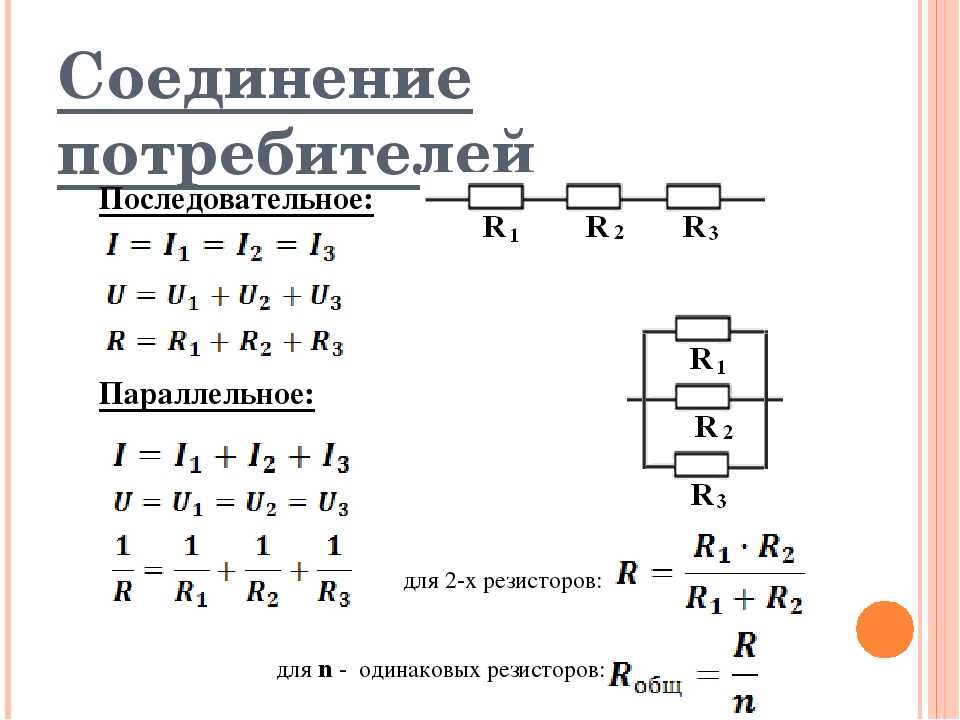
Параллельное соединение проводников: характеристики и формулы

При параллельном соединении все проводники подключаются к одним и тем же точкам цепи. Ключевые особенности:

• Напряжение одинаково на всех параллельных участках
• Общий ток равен сумме токов в отдельных ветвях
• Обратная величина общего сопротивления равна сумме обратных величин сопротивлений отдельных проводников

Формула для расчета общего сопротивления при параллельном соединении:

1/R = 1/R1 + 1/R2 + 1/R3 + …

Общее сопротивление при параллельном соединении всегда меньше наименьшего из сопротивлений отдельных проводников.

Применение последовательного и параллельного соединения проводников

Последовательное соединение используется:

• В елочных гирляндах
• Для подключения выключателей и предохранителей
• В измерительных приборах (амперметрах)

Параллельное соединение применяется:

• Для подключения бытовых электроприборов к сети
• В системах освещения
• В измерительных приборах (вольтметрах)

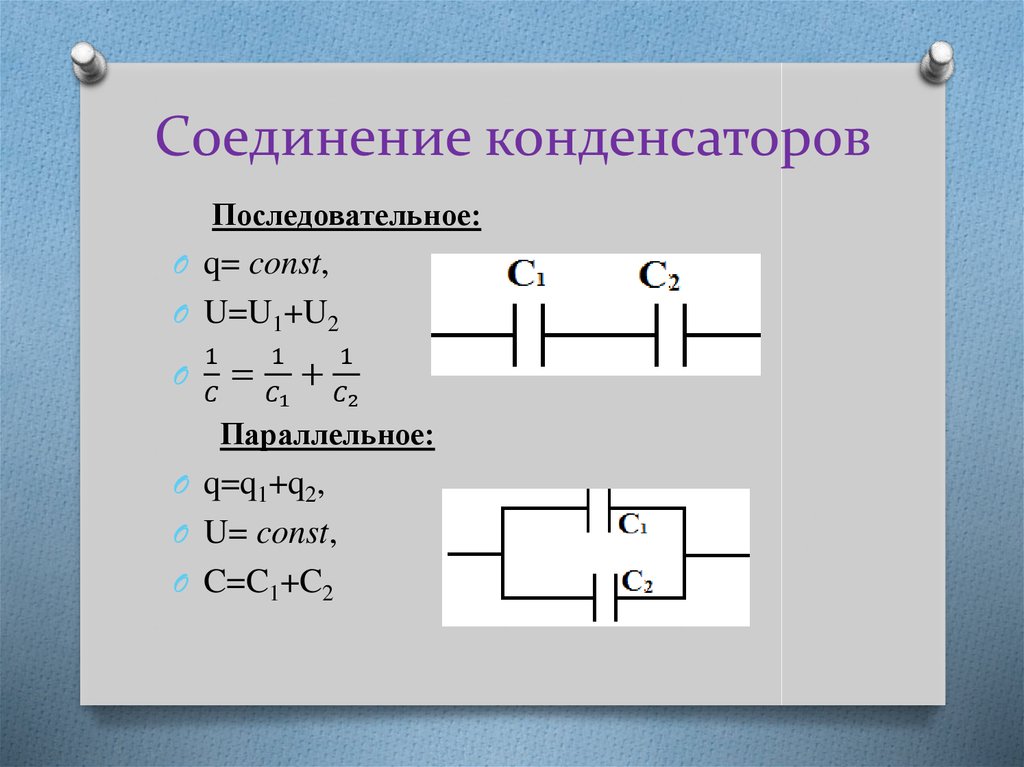
Последовательное соединение конденсаторов: формулы и свойства

При последовательном соединении конденсаторов:

• Заряд на всех конденсаторах одинаковый
• Общее напряжение равно сумме напряжений на отдельных конденсаторах
• Обратная величина общей емкости равна сумме обратных величин емкостей отдельных конденсаторов

Формула для расчета общей емкости при последовательном соединении конденсаторов:

1/C = 1/C1 + 1/C2 + 1/C3 + …

где C — общая емкость, C1, C2, C3 — емкости отдельных конденсаторов.

Параллельное соединение конденсаторов: характеристики и расчеты

При параллельном соединении конденсаторов:

• Напряжение на всех конденсаторах одинаковое
• Общий заряд равен сумме зарядов на отдельных конденсаторах
• Общая емкость равна сумме емкостей отдельных конденсаторов

Формула для расчета общей емкости при параллельном соединении конденсаторов:

C = C1 + C2 + C3 + …

Сравнение последовательного и параллельного соединения конденсаторов

Основные различия между двумя типами соединений конденсаторов:

• При последовательном соединении общая емкость всегда меньше наименьшей из емкостей отдельных конденсаторов
• При параллельном соединении общая емкость всегда больше наибольшей из емкостей отдельных конденсаторов
• Последовательное соединение используется для увеличения рабочего напряжения батареи конденсаторов
• Параллельное соединение применяется для увеличения общей емкости

Практическое применение различных соединений конденсаторов

Последовательное соединение конденсаторов используется:

• В высоковольтных цепях для увеличения пробивного напряжения
• В фильтрах высоких частот
• В резонансных контурах

Параллельное соединение конденсаторов применяется:

• Для увеличения емкости в низковольтных цепях
• В сглаживающих фильтрах источников питания
• В цепях развязки и шунтирования

Смешанное соединение проводников и конденсаторов

В реальных электрических схемах часто встречаются комбинации последовательного и параллельного соединения. Для расчета таких цепей:

• Выделяют участки с однотипным соединением
• Рассчитывают эквивалентное сопротивление или емкость для каждого участка
• Объединяют полученные значения, используя соответствующие формулы

Правильный анализ сложных схем позволяет свести их к более простым эквивалентным цепям.

Проводники: последовательное и параллельное соединение

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие разным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно заранее учитывать при проектировании цепей.

Содержание

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

• Сила тока на всех участках цепи будет одинаковой.
• Общее напряжение цепи составляет сумму напряжений на каждом участке.
• Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R – общее сопротивление, R1 – сопротивление одного элемента, а n – количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является елочная гирлянда, когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный амперметр. Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.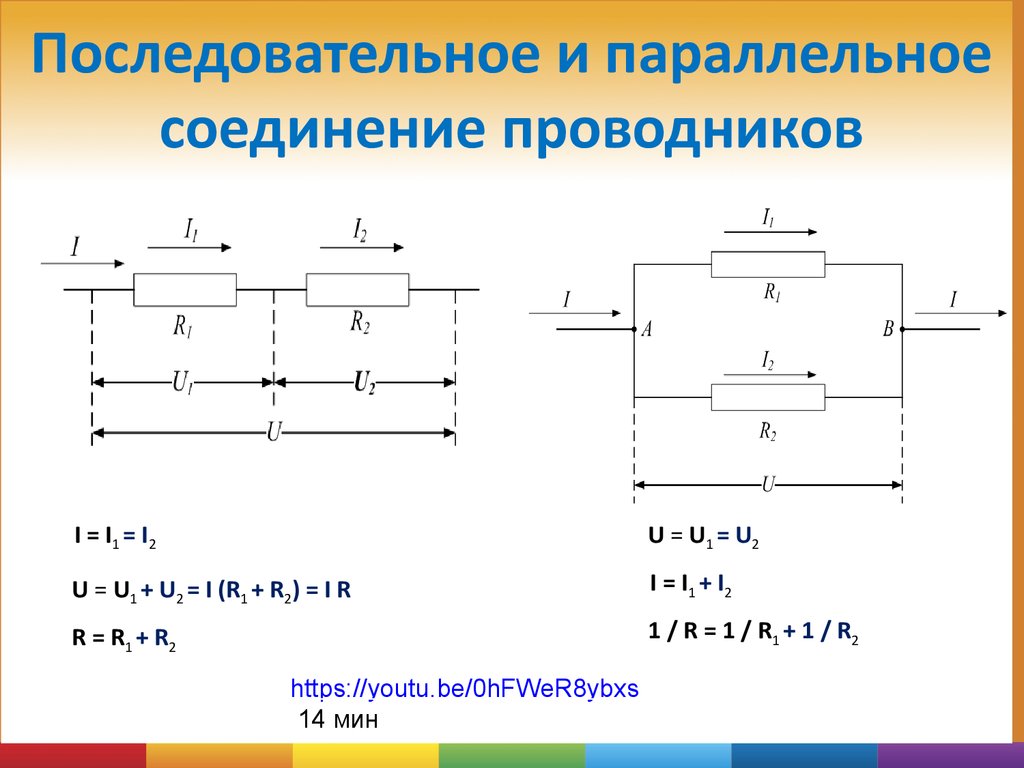

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 – силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 – сопротивления обеих лампочек, U = U1 = U2 – значение напряжения, показываемое вольтметром.

Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях – увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.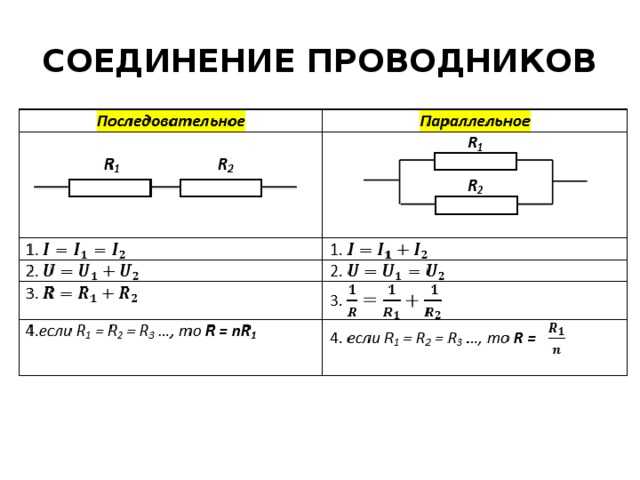

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

• Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
• Закон ома параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
• Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
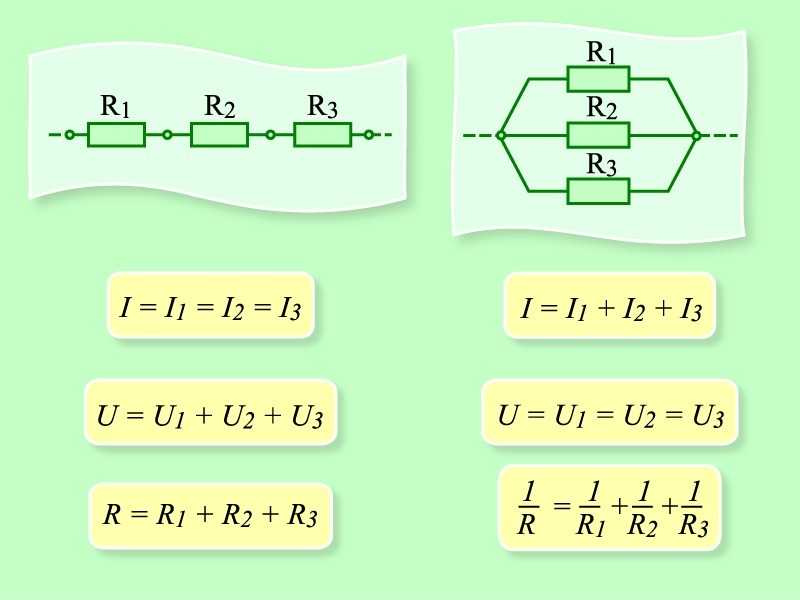
• При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
• Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.

Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей.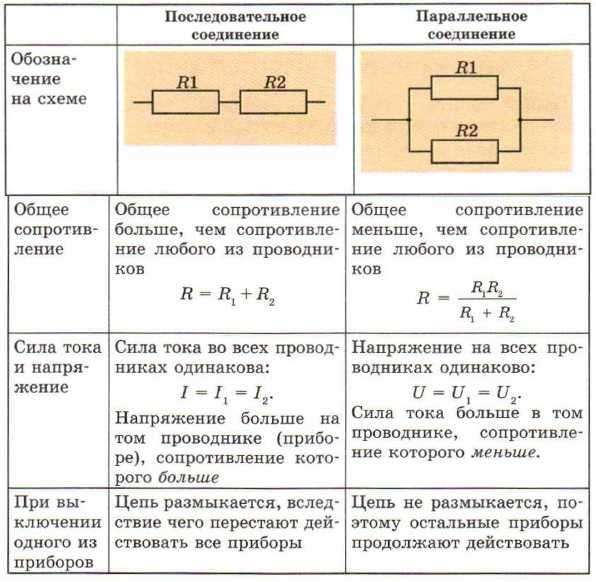 Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Последовательное и параллельное соединение проводников

Известно, что ток в электрической сети перемещается при помощи проводников и следует от источника питания к любому предмету бытовой техники и электрооборудованию.

Схемы состоят из выполненной из меди проводки и определенного количества приемников, сопротивление в которых разное. Наиболее распространенные типы – путем последовательного подсоединения и параллельного. Может встретиться и смешанный, когда прибегают к обоим видам.

Проектируя цепи, нужно обязательно исходить из того, что схемы отнюдь не одинаковы и имеют свои, присущие им качества.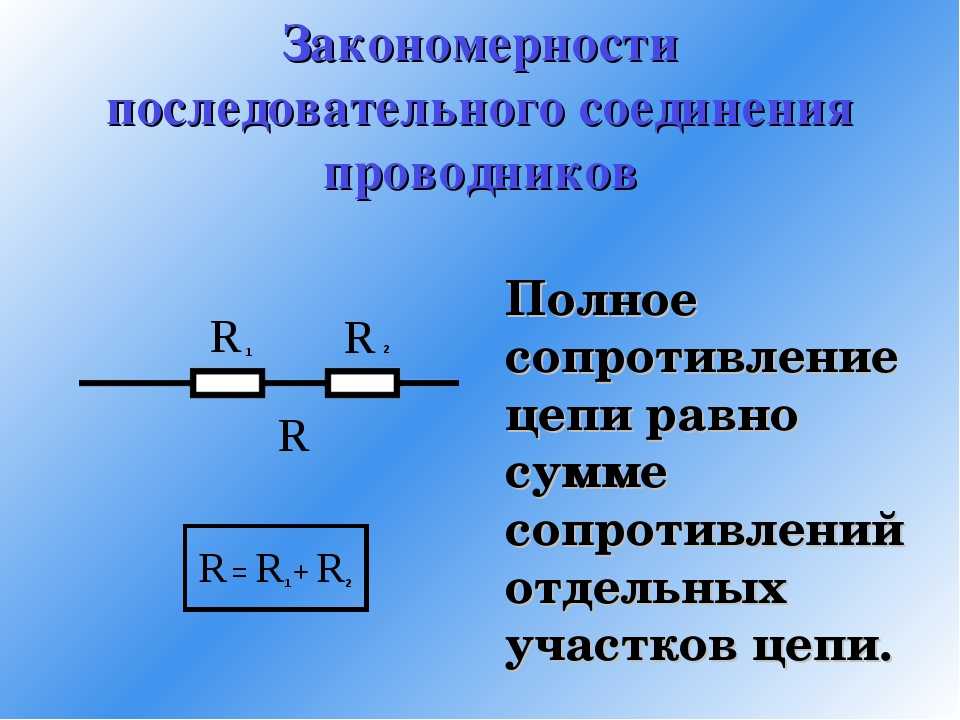 Люди в повседневной жизни постоянно убеждаются в том, что от соединения проводников зависят многие происходящие явления.

На елочной гирлянде могут внезапно погаснуть лампочки одного цвета, поскольку все они соединены последовательно друг за другом. Также именно этот фактор влияет на то, почему все розетки в доме имеют 220 В.

Содержание

Последовательное

В промышленности и в быту проводники обычно соединяются обоими перечисленными выше способами. Последовательное подключение можно охарактеризовать так, что ток поступает как бы по очереди.

В действительности это выглядит, когда конечная часть одного проводника подсоединяется к начальной другого. А конец этого соответственно с началом 3-его. Таким образом можно достичь нужной протяженности цепи.

Подобное расположение очень удобно при включении и выключении разных электрических устройств и техники. Наглядный пример – звонок в школе, оповещающий учеников о том, что пришло время немного отдохнуть. Он последовательно подведен к источнику напряжения и ключу.

Такая схема также повсеместно встречается:

• Для подачи света в пассажирские поезда и трамваи.
• В праздничных гирляндах.
• В карманных фонариках.
• В амперметре для измерения тока.

Таким образом, провода соединяют оба конца цепи, без каких-либо ответвлений.

Отличительные особенности

Чтобы их рассмотреть, можно взять разные участки и использовать следующие обозначения:

• I1 и I2 – ток;
• U1 и U2 – напряжение;
• R1 и R2 – сопротивление.

Зависимость определяется:

• I = I1 = I2
• U = U1 + U2
• R = R1 + R2.

Чтобы удостовериться в правильности данных значений, можно использовать специальные приборы. Проведя ряд экспериментов, легко убедиться, что при последовательном подсоединении наблюдается тенденция:

• Постоянная и неизменная сила тока.
• Напряжение складывается из его показателя на отрезках.
• Сопротивление включает в себя то, которое имеется на проводниках.

Такое соотношение действительно, независимо от того, какое их количество участвовало в эксперименте. Сопротивление будет превосходить то, которое имеется на любом конкретном проводнике. Это объясняется увеличением их протяженности, повлечет за собой и повышение.

При определенном числе одинаковых элементов можно вывести формулу:

R = n х R1, где

R1 – сопротивление единичного элемента, а n – их количество.

Несколько иначе производится расчет напряжения U, где его нужно разделить на части. Они будут обладать значениями, в n раз меньшими, чем общее. Для наглядного образца можно взять случай с лампами. При включении в сеть 10 штук равной мощности, не составит труда узнать показатель: U1 = U/10 = 22 вольта.

Имеется один очень важный нюанс, который нельзя проигнорировать. При поломке хотя бы одной составляющей цепи, ток перестает поступать во все другие части.

Эта особенность демонстрирует отказ работы всей елочной гирлянды при перегорании лишь одной лампочки. Чтобы заставить систему вновь функционировать, необходимо найти ту, которая вышла из строя.

Параллельное

Это еще одна разновидность соединения проводников в электрической сети. Для данного типа характерно размещение начал всех проводников в одной точке цепочки электричества, а окончаний — в другой.

К данному методу прибегают при необходимости подключения электроприборов обособленно, отдельно от других. Такой порядок наиболее удобен в квартирах и частных жилых строениях.

Если произошел сбой в работе какой-то бытовой техники, то это не повлечет за собой отказа в функционировании другого электрического устройства. Отключив чайник, холодильник продолжит морозить, а перегоревшая лампочка в люстре не оставит помещение без света из-за того, что другие не погаснут.

Примеры параллельного соединения:

• Освещение в просторных супермаркетах, магазинах и других местах торговли.
• Электрооборудование в жилище.
• Компьютеры в кабинете информатики.
• Прибор вольтметр.

На отрезках напряжение является неизменной величиной:

U = U1 = U2 = … = Un.

Отсюда ясно видно, что начала и концы соединены, а сами они находятся параллельно. Цепь нередко содержит пару, тройку, а то и большее количество параллельно расположенных проводников.

Свойства

Чтобы убедиться, что это соответствует действительности, можно провести исследование. Для измерения тока подойдут 2 подключенные параллельно лампы накаливания с одинаковым сопротивлением. Для проверки к ним подсоединен свой амперметр. Дополнительный прибор используется для контроля всей цепи.

Схема также включает источник питания и ключ, нужно будет определить значения:

• Лампа 1 — I1
• Лампа 2 – I2.

Амперметр установит суммарную величину силы тока при параллельном соединении:

I = I1 + I2.

В отличие от предыдущего случая последовательного подключения, при прекращении подачи света одной из лампочек, другая продолжит освещать жилое пространство или цех на производстве. Путем вычислений аналогично выясняют сопротивление, которое заменит все составляющие электрической сети. Согласно правилу Ома, при параллельном подключении I = U/R, тогда выводят:

U/R = U1/R1 + U2/R2, где

R – показатель сопротивления, R1 и R2 – значение в лампочках, а U = U1 = U2 – указанный прибором результат. Также нужно учесть, что токи на участках цепи будут равны общему показателю. Исходя из этого, получается следующая величина:

1/R = 1/R1 + 1/R2.

Если в подобной цепи будут добавлены другие элементы, то соответственно вырастет их число в формуле. Поскольку эквивалентное сопротивление не столь велико, сила тока будет значительной. Это обстоятельство следует иметь ввиду, включая в розетки слишком много электроприборов. Из-за увеличения силы тока кабельные линии могут перегреться, что приведет к их возгоранию.

Чтобы не возникло проблем с электропроводкой и обеспечением домов электроэнергией, нужно хорошо представлять себе, что означают последовательное и параллельное соединения проводников. Для выполнения сложных строительных и монтажных работ лучше всего обращаться за помощью к специалисту.

Фото параллельного и последовательного соединения

????????????????????????????????????

Автор статьи:

19.6 Конденсаторы, включенные последовательно и параллельно – College Physics

Глава 19 Электрический потенциал и электрическое поле

Резюме

• Выведите выражения для полной емкости при последовательном и параллельном подключении.
• Определите последовательное и параллельное соединение конденсаторов.
• Рассчитайте эффективную емкость при последовательном и параллельном подключении по отдельным емкостям.

Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Существует два простых и распространенных типа соединений, называемых 9.0017 серии и параллельно , для которых мы можем легко рассчитать общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного соединения.

На рис. 1(а) показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением [latex]{C = \frac{Q}{V}}[/latex].

Обратите внимание на рис. 1, что противоположные заряды величиной [латекс]{Q}[/латекс] текут по обеим сторонам первоначально незаряженной комбинации конденсаторов при приложении напряжения [латекс]{В}[/латекс]. Сохранение заряда требует, чтобы на пластинах отдельных конденсаторов создавались заряды равной величины, поскольку в этих изначально нейтральных устройствах заряд только разделяется. Конечным результатом является то, что комбинация напоминает один конденсатор с эффективным расстоянием между пластинами больше, чем у отдельных конденсаторов по отдельности. (См. рис. 1(b).) Большее расстояние между пластинами означает меньшую емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.

Рисунок 1. (а) Конденсаторы, соединенные последовательно. Величина заряда на каждой пластине равна Å . (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d .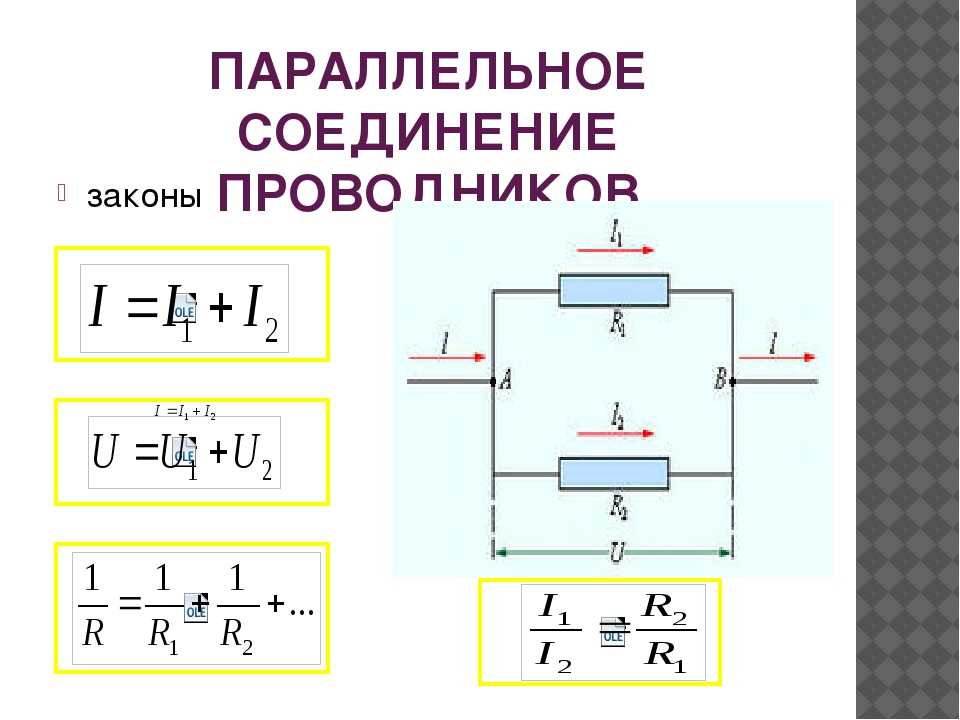 Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.

Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение [латекс]{С = \frac{Q}{V}}[/латекс] для [латекс]{В} [/latex] дает [latex]{V = \frac{Q}{C}}[/latex]. Таким образом, напряжения на отдельных конденсаторах равны [латекс]{V_1 = \frac{Q}{C_1}}[/latex], [латекс]{V_2 = \frac{Q}{C_2}}[/latex] и [ латекс]{V_3 = \frac{Q}{C_3}}[/латекс]. Общее напряжение представляет собой сумму отдельных напряжений:

[латекс] {V = V_1 + V_2 + V_3}.[/латекс]

Теперь, называя общую емкость [латекс]{C_S}[/латекс] последовательной емкостью, считайте, что

[латекс] {V =} [/латекс] [латекс] {\ гидроразрыва {Q} {C_S}} [/ латекс] [латекс] { = V_1 + V_2 + V_3}. [/латекс]

Введя выражения для [латекс]{V_1}[/латекс], [латекс]{V_2}[/латекс] и [латекс]{V_3}[/латекс], мы получим

[латекс] {\ гидроразрыва {Q} {C_S} = \ гидроразрыва {Q} {C_1} + \ гидроразрыва {Q} {C_2} + \ гидроразрыва {Q} {C_3}}. [/латекс]

Отменяя [латекс]{Q}[/латекс], мы получаем уравнение для полной емкости последовательно [латекс]{C_S}[/латекс] равной

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {C_1}} [/ латекс] [латекс] {+ } [/латекс] [латекс] {\ гидроразрыва {1} {C_2}} [/ латекс] [латекс] {+} [/латекс] [латекс] {\ гидроразрыва {1} {C_3}} [/латекс] [ латекс]{+ \cdots},[/латекс]

, где «…» указывает, что выражение справедливо для любого количества последовательно соединенных конденсаторов. Выражение этой формы всегда приводит к тому, что общая емкость [латекс]{C_S}[/латекс] меньше любой из отдельных емкостей [латекс]{С_1}[/латекс], [латекс]{С_2}[/латекс]. ], …, как показано в следующем примере.

Полная последовательная емкость,

C _с

Полная последовательная емкость: [латекс] {\ frac {1} {C_S} = \ frac {1} {C_1} + \ frac {1} {C_2} + \frac{1}{C_3} + \cdots}[/latex]

Пример 1: Что такое последовательная емкость?

Найдите общую емкость трех последовательно соединенных конденсаторов, если их отдельные емкости равны 1000, 5000 и 8000 [латекс]\мк\текст{F}[/латекс].

Стратегия

Имея данную информацию, общую емкость можно найти, используя уравнение для последовательной емкости.

Решение

Ввод данных емкостей в выражение для [латекс]{\ гидроразрыва {1} {C_S}} [/латекс] дает [латекс] {\ гидроразрыва {1} {C_S} = \ гидроразрыва {1 {C_1} + \frac{1}{C_2} + \frac{1}{C_3}}[/latex].

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {1,000 \; \ мю \ текст {F}} }[/латекс] [латекс]{+}[/латекс] [латекс]{\гидроразрыва{1}{5.000 \;\текст{F}}}[/латекс] [латекс]{+}[/латекс] [ латекс] {\ гидроразрыва {1} {8.000 \; \ му \ текст {F}}} [/ латекс]  [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1,325} {\ му \ текст { F}}}[/латекс]

Инвертирование для нахождения [латекс]{C_S}[/латекс] дает [латекс]{C_S = \frac{\mu \text{F}}{1,325} = 0,755 \;\mu \text{F}}[/ латекс].

Обсуждение

Суммарная последовательная емкость [латекс]{C_s}[/латекс] меньше наименьшей индивидуальной емкости, как и было обещано. При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {40} {40 \; \ мю \ текст {F}} }[/латекс] [латекс]{+}[/латекс] [латекс]{\гидроразрыва{8}{40 \;\му \текст{F}}}[/латекс] [латекс]{+}[/латекс ] [латекс] {\ гидроразрыва {5} {40 \; \ му \ текст {F}}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {53} {40 \; \mu \text{F}}},[/latex]

, так что

[латекс]{C_S =}[/латекс] [латекс]{\frac{40 \;\mu \text{F}}{ 53}}[/латекс] [латекс]{= 0,755 \; \mu \text{F}}.[/latex]

На рис. 2(а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти проще, чем в последовательном случае.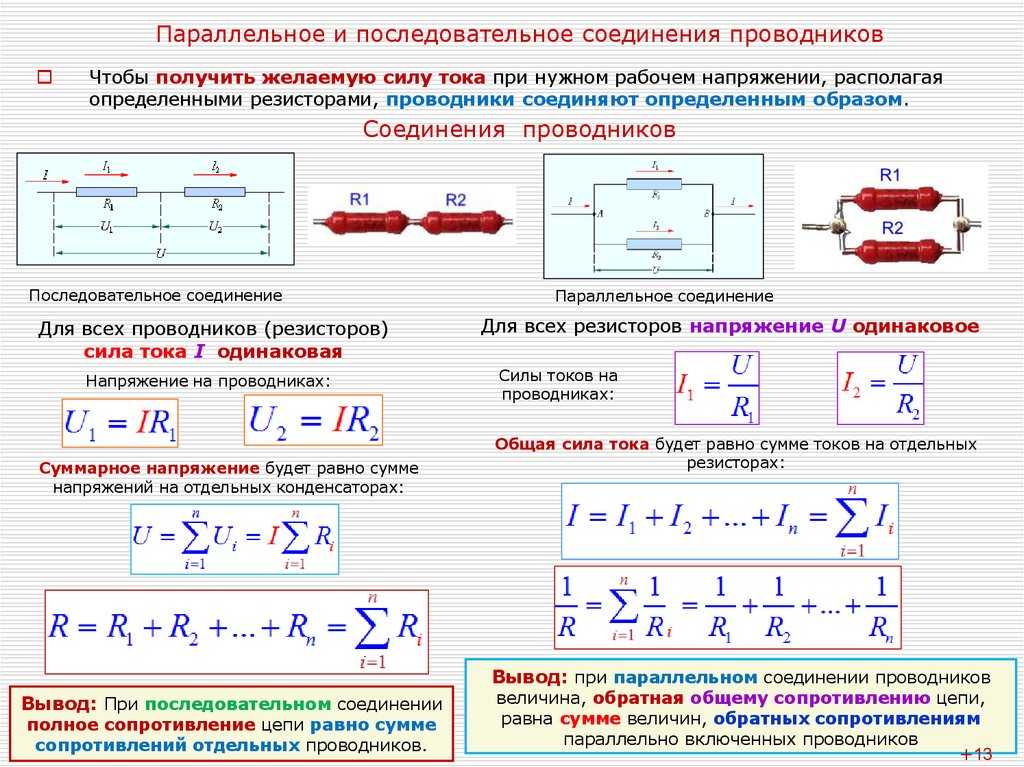 Чтобы найти эквивалентную общую емкость [латекс]{\текст{С}_{\текст{р}}}[/латекс], сначала отметим, что напряжение на каждом конденсаторе равно [латекс]{В}[/латекс], такие же, как и у источника, так как они подключены непосредственно к нему через проводник. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют на себе такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий заряд [латекс]{Q}[/латекс] представляет собой сумму отдельных сборов:

[латекс] {Q = Q_1 + Q_2 + Q_3}.[/латекс]

Рис. 2. (a) Параллельное подключение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, и поэтому общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы.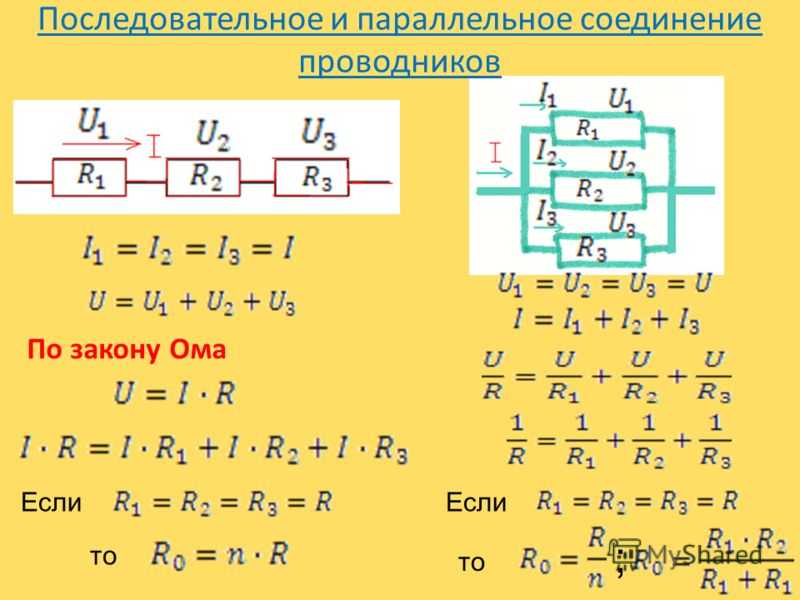

Используя соотношение [латекс]{Q = CV}[/латекс], мы видим, что общий заряд равен [латекс]{Q = C_{\text{p}}V}[/латекс], а отдельные заряды равны [латекс]{Q_1 = C_1 V}[/латекс] ,  [латекс]{Q_2 = C_2 V}[/латекс] , и [латекс]{Q_3 = C_3 V}[/латекс]. Ввод их в предыдущее уравнение дает

[латекс] {C_{\text{p}} V = C_1 V + C_2 V + C_3 V} .[/latex]

Исключая [латекс]{V}[/латекс] из уравнения, мы получаем уравнение для полной емкости параллельно [латекс]{С_{\текст{р}}}[/латекс]:

[латекс] {C_{\text{p}} = C_1 + C_2 + C_3 \cdots}[/латекс].

Общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (Опять «…” указывает, что выражение справедливо для любого количества конденсаторов, соединенных параллельно.) Так, например, если бы конденсаторы в приведенном выше примере были соединены параллельно, их емкость была бы

[латекс]{C_{\text{p}} = 1,000 \;\mu \text{F} + 5,000 \;\mu \text{F} + 8,000 \;\mu \text{F} = 14,000 \; \mu \text{F}}.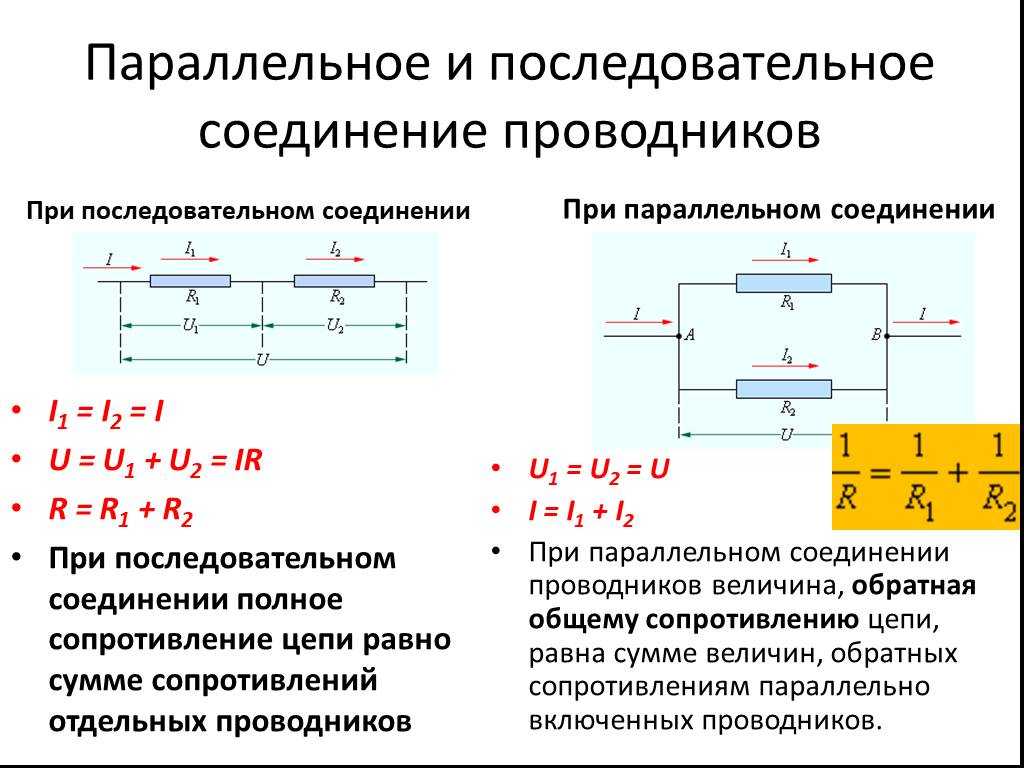 [/latex]

Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на рис. 2(b).

Суммарная емкость при параллельном подключении,

C _p [латекс] {C_{\text{p}}}[/latex]

Суммарная емкость при параллельном подключении [латекс]{C_{\text{p}} = C_1 + C_2 + C_3 + \cdots}[/латекс]

Более сложные соединения конденсаторов иногда могут представлять собой комбинации последовательного и параллельного соединения. (См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.

Рис. 3. (а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C ₁ и C ₂ расположены последовательно; их эквивалентная емкость C _S меньше любого из них. (c) Обратите внимание, что C _S находится параллельно с C ₃ . Полная емкость равна, таким образом, сумме C _S и С ₃ .

Смесь последовательных и параллельных емкостей

Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех знаков после запятой ([latex]{C_1 = 1,000 \;\mu\text {F}}[/латекс], [латекс]{C_2 = 5.000 \;\mu \text{F}}[/латекс] и [латекс]{C_3 = 8.000 \;\mu \text{F}}[ /latex]) и округлить ответ до трех знаков после запятой.

Стратегия

Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы подключены последовательно, а какие параллельно. Конденсаторы [латекс]{C_1}[/латекс] и [латекс]{С_2}[/латекс] включены последовательно. Их комбинация, обозначенная на рисунке [латекс]{C_S}[/латекс], параллельна [латекс]{С_3}[/латекс].

Решение

Поскольку [латекс]{C_1}[/латекс] и [латекс]{С_2}[/латекс] соединены последовательно, их общая емкость определяется как [латекс]{\ гидроразрыва {1} {C_S } = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}}[/latex].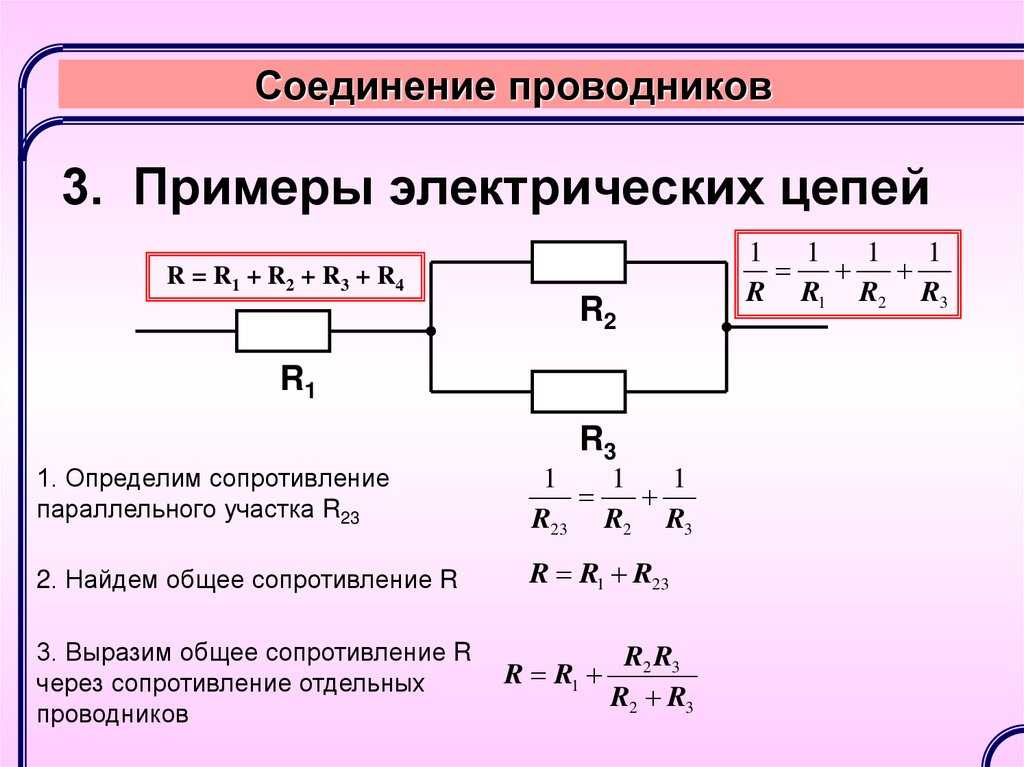 Ввод их значений в уравнение дает

[латекс] {\ гидроразрыва {1} {C_1}} [/латекс] [латекс] {+} [/латекс] [латекс] {\ гидроразрыва {1} {C_2}} [ / латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {1,000 \; \ mu \ текст {F}}} [/ латекс] [латекс] {+} [/ латекс] [ латекс] {\ гидроразрыва {1} {5,000 \; \ му \ текст {F}}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1,200} \ му \ текст { F}}}.[/латекс]

Инвертирование дает

[латекс] {C_{\text{S}} = 0,833 \;\mu \text{F}} .[/latex]

Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; таким образом, общее количество равно сумме

[латекс]\begin{array}{r @{{}={}} l} {C_{\text{tot}}}\;= & {C_S + C_S} \\ [1em]= & {0,833 \;\mu \text{F} + 8,000 \;\mu \text{F}} \\[1em]= & {8,833 \;\mu \text{F}}. \end{array}[/latex]

Обсуждение

Этот метод анализа комбинаций конденсаторов по частям до тех пор, пока не будет получена сумма, может быть применен к большим комбинациям конденсаторов.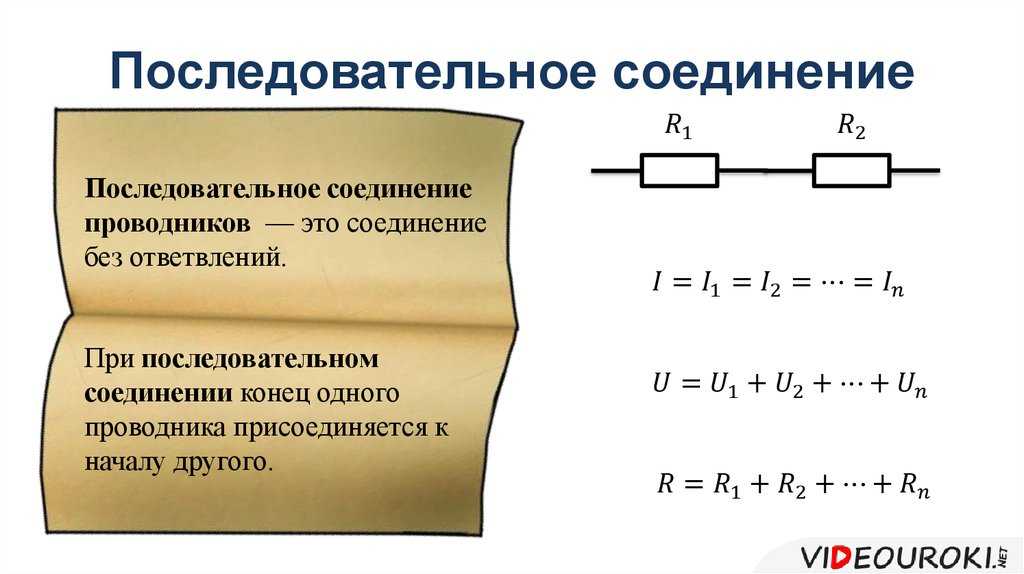

 

• Суммарная емкость последовательно [латекс] {\ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} C_3} + \cdots}[/латекс]
• Общая емкость при параллельном соединении [латекс] {C_{\text{p}} = C_1 + C_2 + C_3 + \cdots}[/latex]
• Если цепь содержит комбинацию конденсаторов, соединенных последовательно и параллельно, определите последовательные и параллельные части, вычислите их емкости, а затем найдите общую сумму.

 

 

Как рассчитать силу тока в последовательной цепи

Последовательные цепи соединяют резисторы таким образом, что ток, измеряемый по амплитуде или силе тока, следует по одному пути в цепи и остается постоянным на всем протяжении. Ток течет в противоположном направлении электронов через каждый резистор, которые препятствуют потоку электронов, один за другим в одном направлении от положительного конца батареи к отрицательному. Нет никаких внешних ветвей или путей, по которым может проходить ток, как это было бы в параллельной цепи.

Примеры серийных цепей

Серийные схемы широко распространены в повседневной жизни. Примеры включают некоторые типы рождественских или праздничных огней. Другим распространенным примером является выключатель света. Кроме того, компьютеры, телевизоры и другие бытовые электронные устройства работают по принципу последовательной схемы.

• ​ В последовательной цепи сила тока или амплитуда тока остается постоянной и может быть рассчитана по закону Ома получить общее сопротивление. Напротив, в параллельной цепи амплитуда тока через разветвляющие резисторы изменяется, а напряжение остается постоянным. ​

Сила тока (или амперы) в последовательной цепи

Вы можете рассчитать амплитуду последовательной цепи в амперах или амперах, заданную переменной A, путем суммирования сопротивлений на каждом резисторе в цепи. как R и суммирование падений напряжения как В , затем решение для I в уравнении В = I/R , в котором В напряжение батареи в вольтах , I текущая, а R — общее сопротивление резисторов в омах (Ом). Падение напряжения должно быть равно напряжению батареи в последовательной цепи.

Уравнение ​ V = I/R ​, известное как закон Ома, также верно для каждого резистора в цепи. Ток, протекающий через последовательную цепь, постоянен, что означает, что он одинаков на каждом резисторе. Вы можете рассчитать падение напряжения на каждом резисторе, используя закон Ома. При последовательном соединении напряжение батарей увеличивается, а это означает, что они служат меньше времени, чем если бы они были соединены параллельно.

Схема цепи и формула серии

••• Сайед Хуссейн Атер

В приведенной выше схеме каждый резистор (обозначен зигзагообразными линиями) подключен к источнику напряжения, аккумулятору (обозначен + и — окружающие разъединенные линии), последовательно.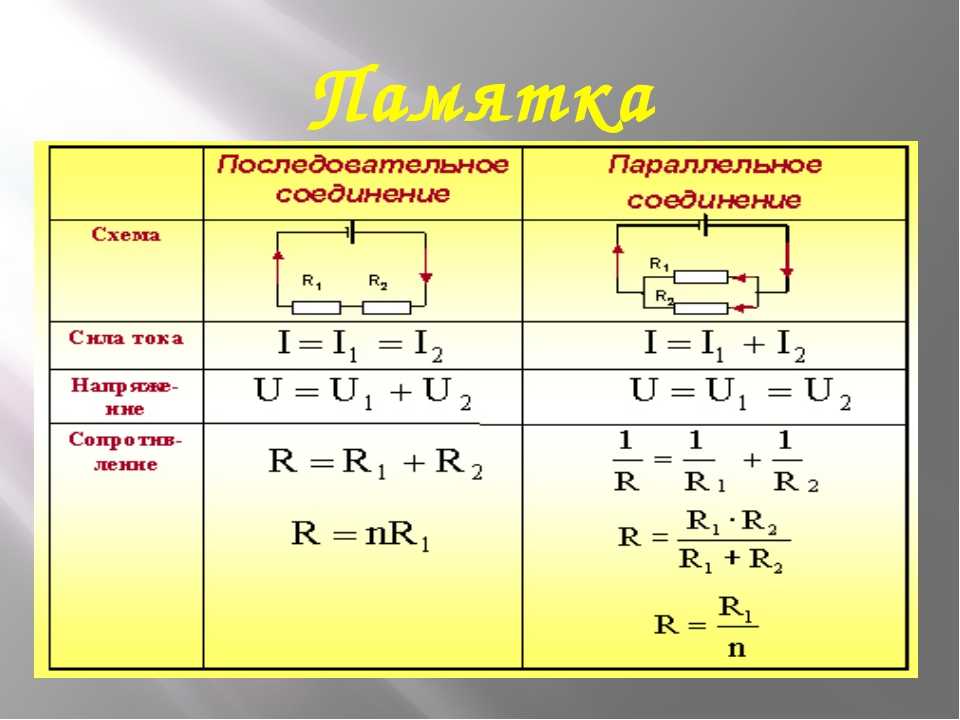 Ток течет в одном направлении и остается постоянным в каждой части цепи.

Если вы просуммируете все резисторы, вы получите общее сопротивление 18 Ом (Ом, где Ом — мера сопротивления). Это означает, что вы можете рассчитать ток, используя 9{-t/(RC)}

, где V – вольты, R – омы, C – фарады, t – время в секундах и​ I ​ в амперах. Здесь e относится к постоянной Эйлера e .

Общая емкость последовательной цепи определяется выражением

\frac{1}{C_{total}}=\frac{1}{C_1}+\frac{1}{C_2}+…

in где каждая обратная величина каждого отдельного конденсатора суммируется в правой части (​ 1/C 9{-tR/L}

, где общая индуктивность L представляет собой сумму значений индуктивности отдельных катушек индуктивности, измеренных в Генри. Когда последовательная цепь создает заряд по мере протекания тока, катушка индуктивности, представляющая собой проволочную катушку, которая обычно окружает магнитный сердечник, создает магнитное поле в ответ на протекание тока. Их можно использовать в фильтрах и осцилляторах, сериях

и параллельных цепях

При работе с параллельными цепями, в которых ток разветвляется по разным частям цепей, расчеты «переворачиваются». Вместо того, чтобы определять общее сопротивление как сумму отдельных сопротивлений, общее сопротивление определяется как

\frac{1}{R_{total}}=\frac{1}{R_1}+\frac{1}{R_2}+…

(тот же способ вычисления полной емкости последовательной цепи) .

Напряжение, а не ток, постоянно во всей цепи. Общий ток параллельной цепи равен сумме токов в каждой ветви. Вы можете рассчитать как ток, так и напряжение, используя закон Ома ( В = I/R ).

••• Syed Hussain Ather

В приведенной выше параллельной цепи общее сопротивление будет определяться следующими четырьмя шагами:

1. ​ 1/R _всего ​ = 1/R1 + 1/R2 + 1/R3
2. ​ 1/R _всего /
3. Ом = + +
4. Ом 1/5 Ом
5. ​ 1/R _всего ​ = 20/20 Ом + 5/20 Ом + 4/20 Ом
6. ​ 1/R _всего
   9 ​ 1/R _всего
   9 1 5 Ω 29/2030
7. R _всего = 20/29 Ом или около 0,69 Ом левая сторона ( 1/R _всего ​) и только один член с правой стороны (29/20 Ом).

   Аналогично, общая емкость в параллельной цепи представляет собой просто сумму каждого отдельного конденсатора, а общая индуктивность также определяется обратной зависимостью (​ 1/л всего ​ ​ ​ = 1/л 1 ​ + 1/л 2 ​ ​ + … ​ ).

   Постоянный ток в сравнении с переменным током 

   В цепях ток может либо течь постоянно, как в случае постоянного тока (DC), либо волнообразно колебаться в цепях переменного тока (AC). В цепи переменного тока ток изменяется между положительным и отрицательным направлением в цепи.

   Британский физик Майкл Фарадей продемонстрировал мощность постоянного тока с помощью динамо-электрогенератора в 1832 году, но он не мог передавать его мощность на большие расстояния, а для постоянного напряжения требовались сложные схемы.

   Когда сербско-американский физик Никола Тесла в 1887 году создал асинхронный двигатель, использующий переменный ток, он продемонстрировал, как легко он передается на большие расстояния и может преобразовываться между высокими и низкими значениями с помощью трансформаторов, устройств, используемых для изменения напряжения.