Гистерезис ферромагнетиков. Изучение магнитного гистерезиса ферромагнетиков: характеристики и применение

Что такое магнитный гистерезис. Как происходит намагничивание ферромагнетиков. Какие основные характеристики петли гистерезиса. Как применяются явления гистерезиса на практике.

Физическая природа магнитного гистерезиса

Магнитный гистерезис — это явление отставания изменения намагниченности ферромагнитного материала от изменения внешнего магнитного поля. Оно обусловлено необратимыми процессами перемагничивания доменной структуры ферромагнетика.

Основные причины возникновения магнитного гистерезиса:

• Наличие доменной структуры ферромагнетиков
• Необратимые смещения доменных границ при намагничивании
• Задержка вращения векторов намагниченности доменов
• Магнитная анизотропия кристаллической решетки
• Наличие дефектов структуры, препятствующих движению доменных стенок

При циклическом изменении внешнего магнитного поля намагниченность ферромагнетика изменяется по замкнутой кривой, называемой петлей гистерезиса. Форма и параметры этой петли определяют магнитные свойства материала.

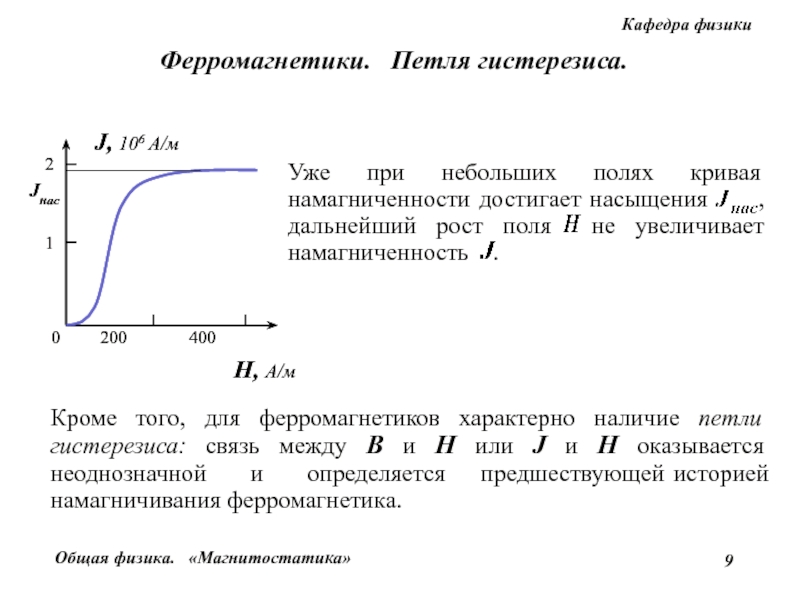
Основные характеристики петли магнитного гистерезиса

Петля гистерезиса имеет ряд важных характеристик, определяющих магнитные свойства ферромагнетика:

• Коэрцитивная сила (Hc) — напряженность магнитного поля, необходимая для полного размагничивания образца
• Остаточная индукция (Br) — магнитная индукция, сохраняющаяся после снятия внешнего поля
• Индукция насыщения (Bs) — максимальное значение индукции при сильном внешнем поле
• Площадь петли гистерезиса — характеризует потери энергии на перемагничивание

Чем больше площадь петли гистерезиса, тем выше потери энергии при циклическом перемагничивании материала. Это важно учитывать при использовании ферромагнетиков в электротехнических устройствах.

Процесс намагничивания ферромагнетиков

Процесс намагничивания ферромагнитного образца из размагниченного состояния происходит в несколько стадий:

1. Обратимое смещение доменных границ при слабых полях
2. Необратимое смещение доменных границ в средних полях
3. Вращение векторов спонтанной намагниченности доменов в сильных полях
4. Парапроцесс — увеличение спонтанной намагниченности в очень сильных полях

На каждой стадии действуют различные механизмы намагничивания, что приводит к нелинейной зависимости намагниченности от поля. При снятии поля часть доменов сохраняет новую ориентацию, что обуславливает остаточную намагниченность.

Классификация ферромагнитных материалов по магнитным свойствам

По форме петли гистерезиса и величине коэрцитивной силы ферромагнетики делятся на:

• Магнитомягкие материалы (Hc < 4 кА/м) - узкая петля гистерезиса, малые потери на перемагничивание
• Магнитотвердые материалы (Hc > 4 кА/м) — широкая петля гистерезиса, высокая остаточная индукция

Магнитомягкие материалы (электротехнические стали, пермаллои) применяются в трансформаторах, электродвигателях. Магнитотвердые (альнико, ферриты) используются для изготовления постоянных магнитов.

Факторы, влияющие на магнитный гистерезис

На параметры петли гистерезиса ферромагнетиков оказывают влияние следующие факторы:

• Химический состав и структура материала
• Наличие примесей и дефектов кристаллической решетки
• Размер зерен в поликристаллических образцах
• Механические напряжения и деформации
• Термическая и магнитная предыстория образца
• Температура (при приближении к точке Кюри гистерезис исчезает)

Управляя этими факторами в процессе получения и обработки материалов, можно целенаправленно изменять их магнитные характеристики для конкретных применений.

Практическое применение явлений магнитного гистерезиса

Явление магнитного гистерезиса находит широкое практическое применение в различных областях техники:

• Создание постоянных магнитов с высокой остаточной индукцией
• Магнитная запись информации на жестких дисках и магнитных лентах
• Изготовление сердечников трансформаторов и электрических машин
• Создание магнитных экранов и магнитопроводов
• Разработка датчиков магнитного поля на основе эффекта Баркгаузена
• Неразрушающий контроль ферромагнитных изделий

В то же время необходимо учитывать негативные эффекты гистерезиса, такие как потери энергии на перемагничивание в электрических машинах и трансформаторах.

Методы исследования магнитного гистерезиса

Для экспериментального исследования магнитного гистерезиса ферромагнетиков применяются различные методы:

• Индукционный метод с использованием катушек индуктивности
• Вибрационный магнитометр
• Метод вращающегося магнитного поля
• Магнитооптические методы (эффект Керра, Фарадея)
• Метод осциллографирования петли гистерезиса

Выбор конкретного метода зависит от формы и размеров образца, требуемой точности измерений, диапазона полей и других факторов. Наиболее распространен метод осциллографирования, позволяющий непосредственно наблюдать петлю гистерезиса на экране.

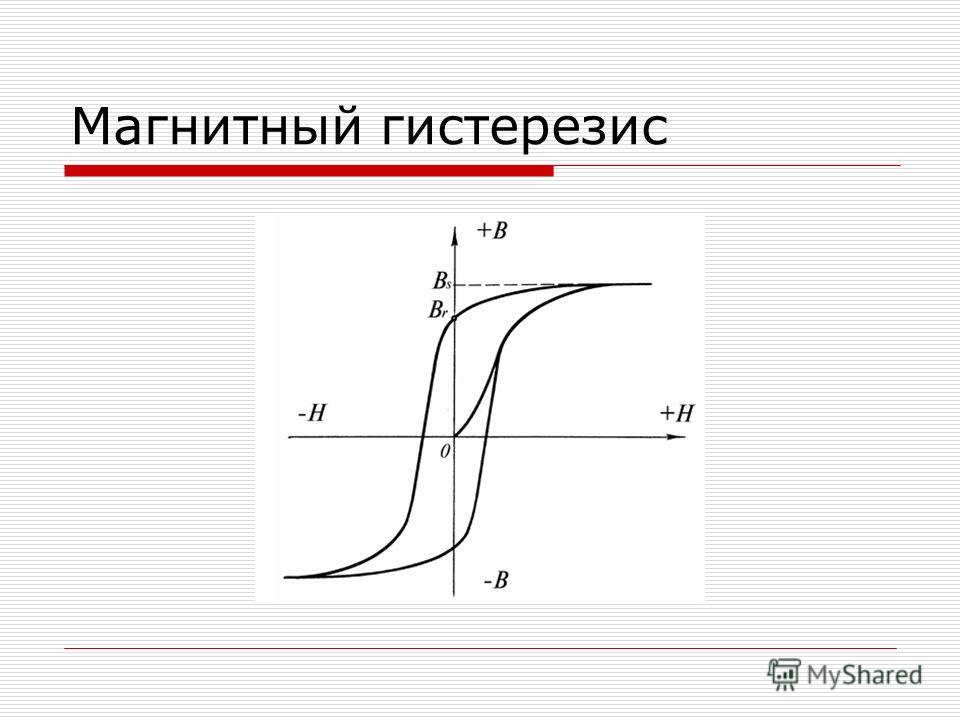
Теоретические модели магнитного гистерезиса

Для описания процессов намагничивания ферромагнетиков и объяснения явлений гистерезиса разработан ряд теоретических моделей:

• Модель Прейзаха — основана на суперпозиции элементарных прямоугольных петель
• Модель Джилса-Атертона — учитывает процессы смещения доменных границ
• Модель Стонера-Вольфарта — для однодоменных частиц
• Феноменологическая модель Релея — для слабых полей

Эти модели позволяют рассчитывать параметры петли гистерезиса и прогнозировать поведение ферромагнитных материалов в различных условиях. Однако полного теоретического описания всех аспектов гистерезиса пока не существует из-за сложности процессов перемагничивания.

Таким образом, магнитный гистерезис является фундаментальным свойством ферромагнетиков, определяющим их поведение во внешнем магнитном поле. Изучение этого явления имеет большое значение как для понимания физики магнетизма, так и для практических применений магнитных материалов в современных технологиях.

Изучение магнитного гистерезиса ферромагнетиков

Цель работы: изучить магнитный гистерезис ферромагнетика, определить остаточную индукцию и коэрцитивную силу ферромагнетика.

Приборы и оборудование: трансформатор с сердечником из пермаллоя, три резистора, амперметр переменного тока, конденсатор, потенциометр, осцилло­граф, ключ.

Теоретические сведения

Всякое вещество является магнетиком, т.е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Намагниченное вещество создает магнитное поле, характеризующееся вектором магнитной индукции

‘, которое накладывается на обусловленное токами поле с индукцией . В итоге вектор магнитной индукции результирующего поля определяется суммой ‘. Истинное (микроскопическое) поле в магнетике сильно изменяется в пределах межмолекулярных расстояний, поэтому описывает усредненное (макроскопическое) поле.

Для объяснения намагничивания тел Ампер предположил, что в молекулах вещества циркулируют круговые (молекулярные) токи, каждый из которых обладает магнитным моментом и создает в окружающем пространстве магнитное поле.

Так орбитальный магнитный момент электрона на круговой орбите равен вектору модуль которого определяется частотой ν вращения электрона на орбите площадью S, т.к. соответствующая сила тока , а направление – положительной нормалью к плоскости орбиты

Кроме орбитального магнитного момента электрон обладает собственным (спиновым) магнитным моментом Проекция спинового магнитного момента на направление вектора может принимать только одно из двух значений: где магнетон Бора, являющийся единицей магнитного момента электрона, h – постоянная Планка. Таким образом, магнитный момент электрона складывается из орбитального и спинового магнитных моментов.

Магнитный момент атома (молекулы) определяется магнитными моментами составляющих его электронов и спиновым магнитным моментом ядра. Тяжелые атомные ядра движутся значительно медленнее легких электронов, поэтому их магнитные моменты в тысячи раз меньше магнитных моментов электронов. Ядерный магнетизм становится существенным только вблизи абсолютного нуля температур, да и то при условии, что магнитные моменты электронов скомпенсированы.

В отсутствие внешнего магнитного поля магнитные моменты отдельных молекул ориентированы беспорядочным образом, и суммарный магнитный момент тела равен нулю. Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается. Магнитные поля отдельных молекулярных токов уже не компенсируют друг друга, и возникает поле ‘.

Намагничивание магнетика характеризуют намагниченностью, под которой понимают магнитный момент единицы объема.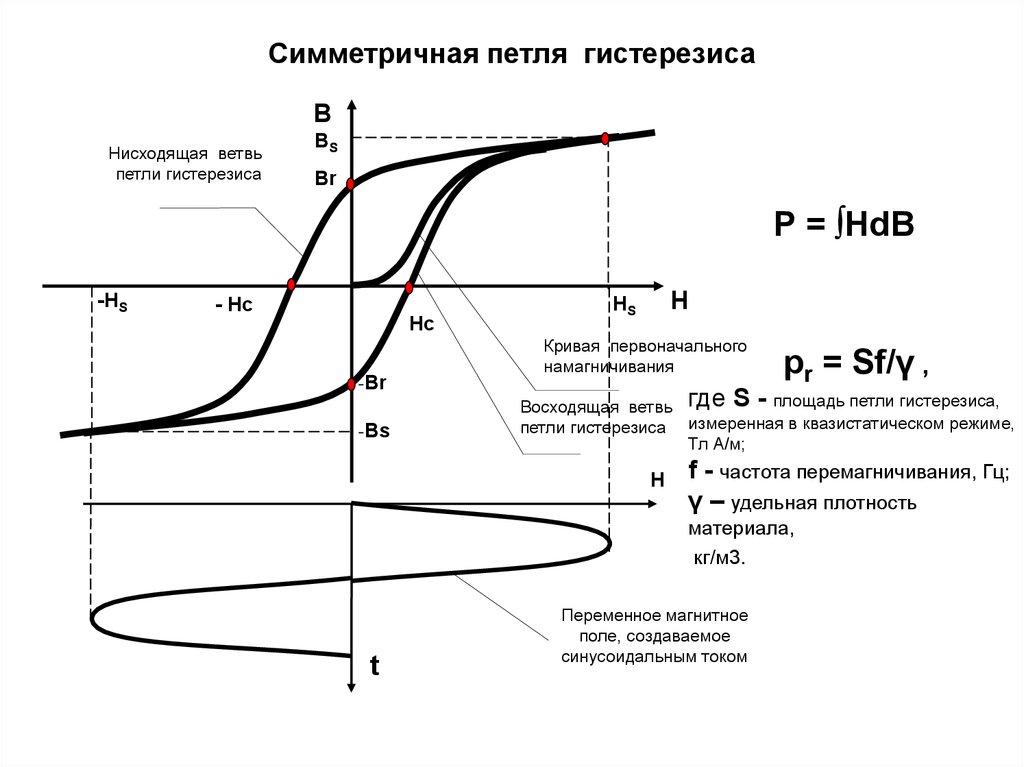 Ее принято связывать не с магнитной индукцией , а с напряженностью магнитного поля, порожденного макротоками: — . Полагают, что в каждой точке магнетика , где — характерная для данного магнетика безразмерная величина, называемая магнитной восприимчивостью. Опыт показывает, что для слабомагнитных веществ при не слишком сильных полях

не зависит от Тогда для напряженности магнитного поля получаем . Безразмерная величина называется магнитной проницаемостью вещества.

В зависимости от знака и величины магнитной восприимчивости все магнетики делятся на слабомагнитные и сильно­магнитные. К первым относятся диамагнетики ( отрицательна и мала по величине) и парамагнетики ( тоже невелика, но положительна), ко вторым – ферромагнетики ( положительна, является функцией напряженности магнитного поля и достигает очень больших значений, до раз превосходящей восприимчивость диа- и парамагнетиков) и антиферромагнетики, которые можно представить как две вставленные друг в друга ферромагнитные подрешетки, намагниченные в противоположных направлениях.

К диамагнетикам относятся, например, висмут, серебро, золото, медь, цинк, кремний, свинец, германий, а также вода, каменная соль, кварц, большинство органических соединений. Молекулы таких веществ не имеют результирующего магнитного момента (магнитные моменты электронов скомпенсированы) в отсутствие внешнего магнитного поля. При внесении их в магнитное поле в молекулах возникают индукционные токи, магнитное поле которых направлено навстречу внешнем полю (по правилу Ленца), поэтому поле внутри вещества ослабляется.

У парамагнетиков (олово, марганец, платина, эбонит, вольфрам, алюминий, воздух, газообразный азот, кислород) в отсутствие внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, т.е. магнитные моменты молекул не равны нулю. Однако, вследствие теплового движения, они ориентированы беспорядочно, и, следовательно, такие вещества не намагничены. При внесении парамагнетика в магнитное поле устанавливается преимущественная ориентация магнитных моментов молекул по направлению поля (т.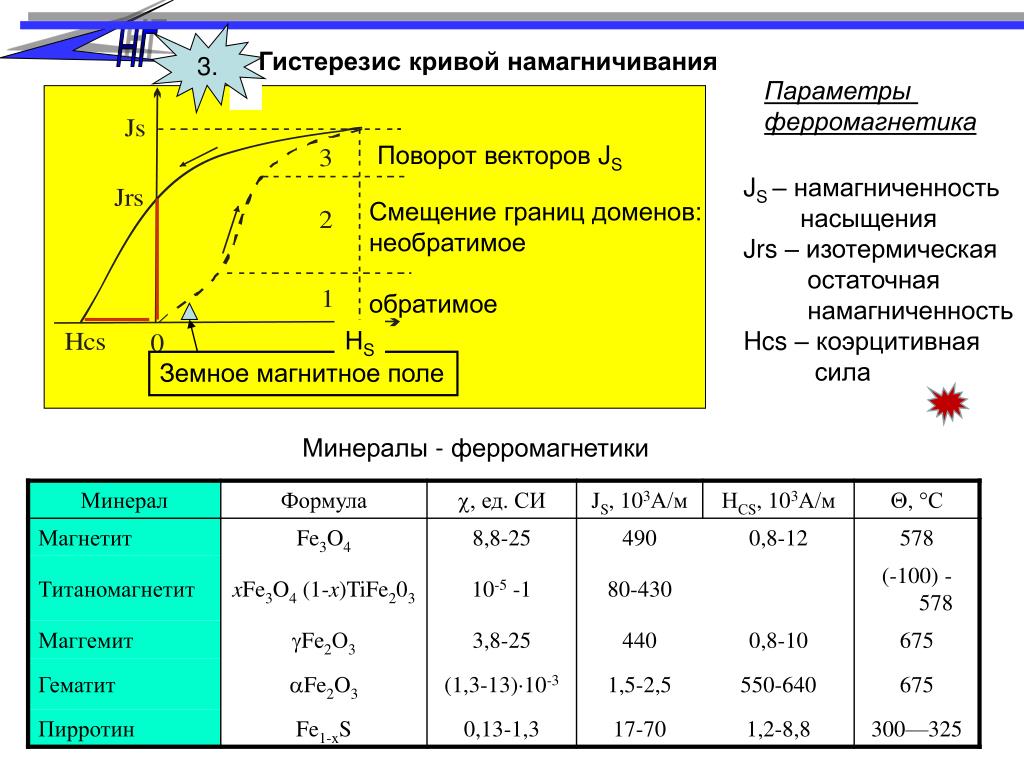 е. возникает намагниченность в направлении поля), и магнитное поле внутри парамагнетика усиливается.

Так как диамагнитный эффект обусловлен явлением электромагнитной индукции, возникающим в ответ на включение внешнего магнитного поля, то он присущ всем веществам. Однако, если молекулы вещества имеют собственный магнитный момент, то диамагнитный эффект становится малым по сравнению с парамагнитным.

Ферромагнетики — твердые тела, обладающие спонтанной намагниченно­стью, т.е. ферромагнетики могут быть намагничены уже в отсутствие магнитного поля. К этому классу магнитных веществ относятся кристаллы переходных металлов (железа, кобальта, никеля, гадолиния) и ряд их сплавов. Изучение характеристик ферромагнетиков представляет большой интерес, т.к. подобные вещества часто применяются в трансформаторах, дросселях, машинах переменного тока, т.е. в устройствах, в которых они подвергаются периодическому перемагничиванию.

Рассмотрим магнитный гистерезис в ферромагнетиках.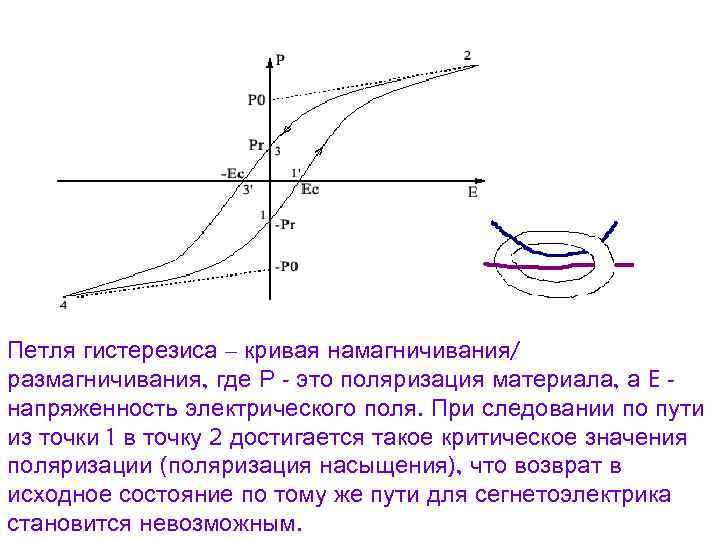 Магнитный гистерезис — явление, состоящее в том, что физическая величина, характеризующая состояние тел (например, намагниченность), неоднозначно зависит от физической величины, характеризующей внешние условия (например, магнитного поля). Обычно ферромагнетик разбит на домены – области однородной самопроизвольной (спонтанной) максимальной намагниченности, размеры которых порядка 1-10 мкм. Направления векторов магнитных моментов соседних доменов обычно различаются, так что в отсутствие внешнего поля суммарный магнитный момент всего тела равен нулю. Под действием внешнего магнитного поля число и размеры доменов, намагниченных по полю, увеличиваются за счет других доменов. Вначале, при слабых полях, наблюдается смещение границ доменов, в результате чего происходит увеличение тех доменов, направление намагниченности которых составляет меньший угол с направлением поля. Процесс происходит до тех пор, пока энергетически менее выгодные домены полностью не будут поглощены. На следующей стадии магнитные моменты разросшихся доменов поворачиваются в направлении поля.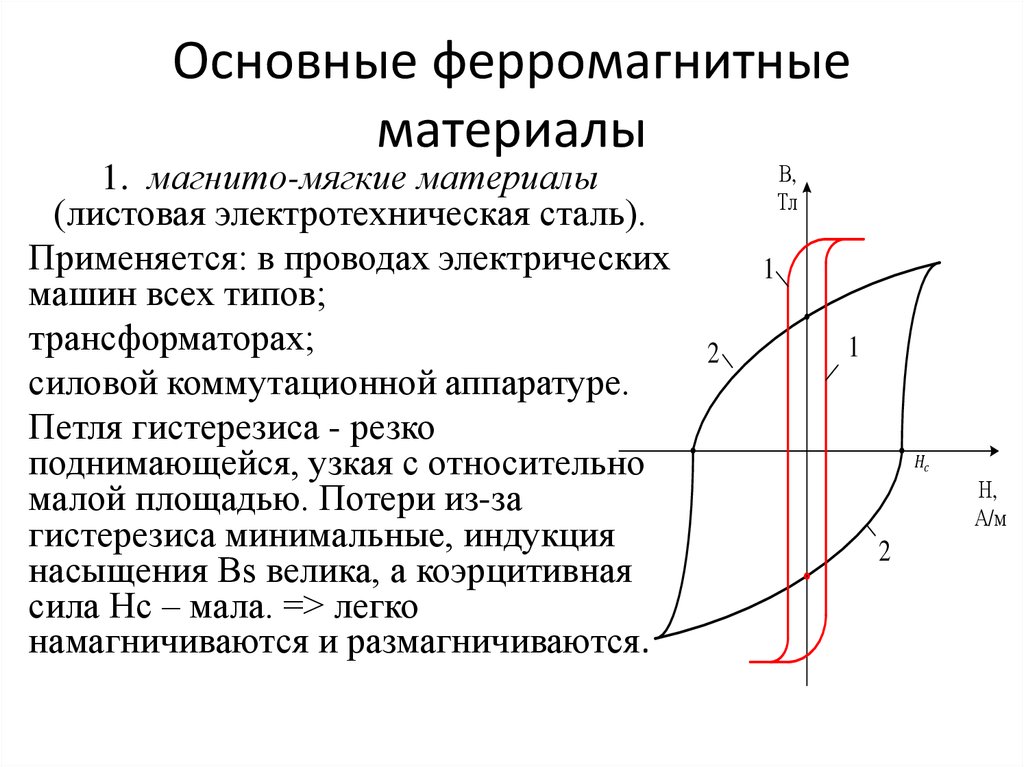 При этом магнитные моменты электронов в пределах домена поворачиваются одновременно, без нарушения их строгой параллельности друг другу (ответственными за это являются обменные силы, объяснение которых дает только квантовая механика).

Для каждого ферромагнетика имеется определенная температура при которой области спонтанного намагничивания распадаются и вещество становится парамагнетиком. Эта температура называется точкой Кюри (для железа она равна для никеля .

На рис. 1 изображены (в диаграмме B-H) кривые намагничивания и размагничивания ферромагнитного образца, магнитный момент которого первоначально был равен нулю, при наличии гистерезиса. В достаточно сильном магнитном поле образец намагничивается до насыщения (точка 1). Намагниченность насыщения направлена по полю. Затем при уменьшении напряженности внешнего магнитного поля Н значение индукции (и намагниченности) будет уменьшаться не по первоначальной кривой 0-1, а по кривой 1-2 (преимущественно за счет возникновения и роста доменов с магнитным моментом, направленным против поля).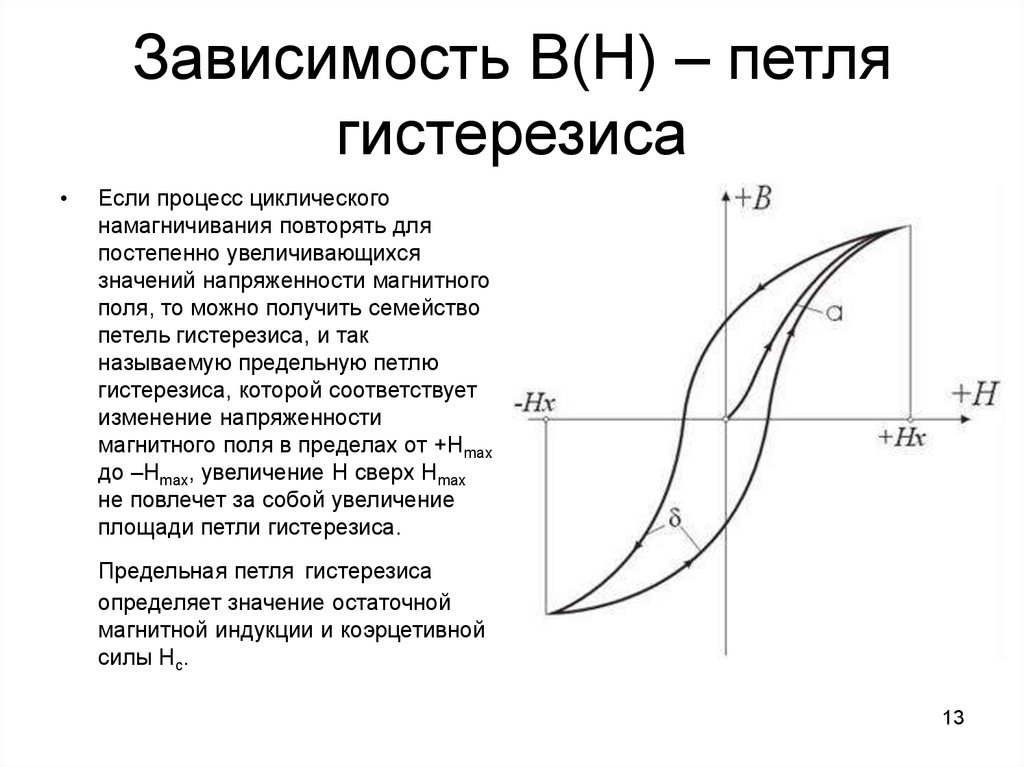 При уменьшении Н до нуля (точка 2) у образца сохраняется так называемая остаточная индукция (или остаточная намагниченность ). Образец полностью размагничивается лишь в достаточно сильном поле противоположного направления, которое называется коэрцитивным полем (коэрцитивной силой) Н_с (точка 3). При дальнейшем увеличении магнитного поля обратного направления образец вновь намагничивается вдоль поля до насыщения (точка 4). Перемагничивание образца происходит по кривой 4-1. Таким образом, при циклическом изменении поля кривая, характеризующая изменение намагниченности образца, образует петлю магнитного гистерезиса. Если поле Н циклически изменять в таких пределах, что насыщение не достигается, то получается непредельная петля магнитного гистерезиса (пунктирная кривая). Уменьшая амплитуду изменения поля Н до нуля, можно полностью размагнитить образец (прийти в точку 0).

Существование остаточной намагниченности делает возможным изготовление постоянных магнитов (тел, которые обладают магнитным моментом и создают в окружающем пространстве магнитное поле). Постоянный магнит тем лучше сохраняет свои свойства, чем больше коэрцитивная сила материала, из которого он изготовлен. Площадь петли гистерезиса пропорциональна энергии, затраченной на перемагничивание ферромагнетика переменным магнитным полем. Ферромагнетики с большой коэрцитивной силой (больше 200А/м) называются жесткими (например, углеродистые и вольфрамовые стали). Для них характерна широкая петля гистерезиса. Так для сплава алнико (Al:Ni:Co:Fe=10:19:18:53) Н_с =52000А/м. Мягкие ферромагнетики (например, железо, сплав железа с никелем) имеют малую Н_с (до 100-200А/м). Они применяются для изготовления сердечников трансформаторов.

Рис.1

В данной работе петли гистерезиса ферромагнетика получают на экране электронного осциллографа. Известно, что электронный пучок отклоняется под действием электрического поля. Поэтому петли гистерезиса можно исследо­вать, используя метод электрических смещающих полей.

Собирается установка, схематически изображенная на рис. 2. Основными ее элементами являются трансформатор Т с первичной и вторичной обмотками (с числом витков соответственно N₁ и N₂) и осциллограф. В первичную цепь трансформатора включают два сопротивления R и R₁, а также амперметр.

Рис.2

Назначение реостата R — изменение силы тока в первичной цепи транс­форматора (сердечник приводится в состояние магнитного насыщения). На концах сопротивления R₁ возникает переменная ЭДС, величина которой прямо пропорциональна напряженности магнитного поля Н, намагничивающего сер­дечник. ЭДС подают на пластины осциллографа, которые вызывают горизон­тальное отклонение электронного пучка. Вторичную обмотку трансформатора замыкают через сопротивление R₂ и емкость С. Переменное напряжение кон­денсатора С подают на вертикальные пластины осциллографа. Если реактивное сопротивление конденсатора намного меньше сопротивления R₂, то значение переменного напряжения будет прямо пропорционально изменению индукции В в сердечнике трансформатора. В результате суммарного воздействия на элек­тронный пучок двух взаимно перпендикулярных переменных электрических полей светлое пятно на экране осциллографа примет форму, воспроизводящую петлю гисте­резиса. За один период синусоидального тока электронный луч на экране опи­шет полную петлю гистерезиса, а в каждый следующий период в точности ее повторит. Поэтому на экране петля будет выглядеть неподвижной.

Напряженность магнитного поля трансформатора (с числом витков обмотки N₁ и длиной осевой линии сердечника ), по которому течет ток , определяется по формуле . Напряжение на горизонтально отклоняющих пластинах U_x=I₁R₁. Так как , то U_x прямо пропорционально Н:

. (1)

Во вторичной обмотке ток I₂ возникает под действием ЭДС магнитной ин­дукции ε. Если Ф — потокосцепление вторичной обмотки, S — площадь, охватываемая одним витком, a N₂ — число витков во вторичной цепи, то Ф=BSN₂ и

. (3)

Пренебрегая самоиндукцией во вторичной цепи, получим по закону Ома

ε = U₂+I₂R₂, (4)

, (5)

где U_c = U_y— напряжение на конденсаторе, подаваемое на вертикально отклоняющие пластины осциллографа, q — заряд конденсатора, С — ем­кость.

Так как значение R₂ берется достаточно большим, то первым членом в формуле (4) можно пренебречь.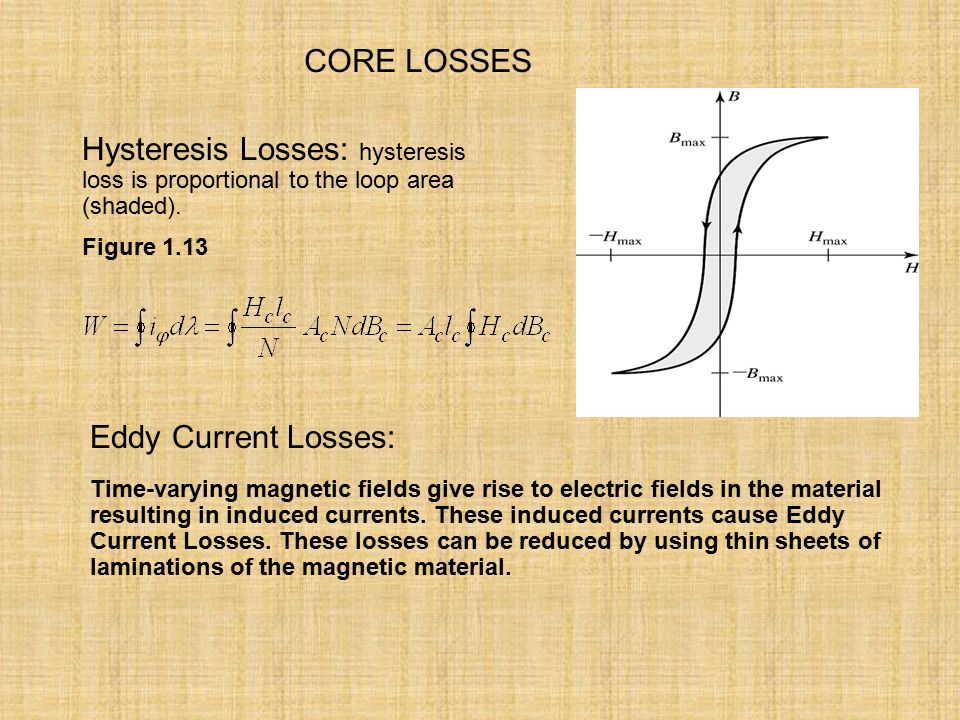 Тогда

.

Откуда

. (6)

Подставляя полученное выражение для I₂ в формулу (5), получим

, (7)

т.е. напряжение, пода­ваемое на вертикально отклоняющие пласти­ны осциллографа, прямо пропорцио­нально величине магнитной индукции В.

Осциллограф становится измерительным прибором, если его проградуировать. Для градуировки необходимо отсоединить осциллограф от стенда и на верти­кально отклоняющие пластины (вход У) подать контрольное напряжение (оно указано на стенде и, обычно, на наших установках U_к=1,5В). На экране будет наблюдаться вертикальная линия. Ее длина соответствует удвоенному числу делений, т.е. 2n₀. Напряжение U_0y, которое нужно подать на вертикально отклоняющие пластины, чтобы электронный луч сме­стился вдоль оси ОУ на одно деление можно узнать по формуле:

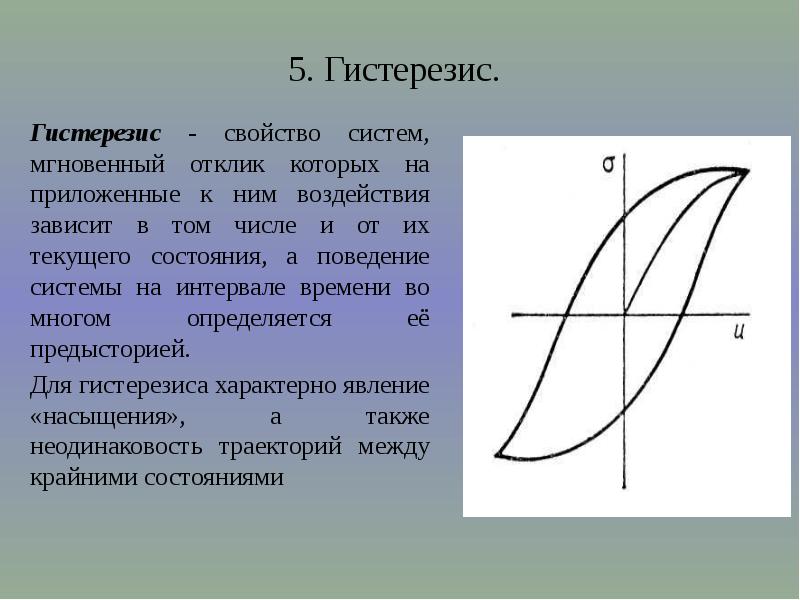. (8)

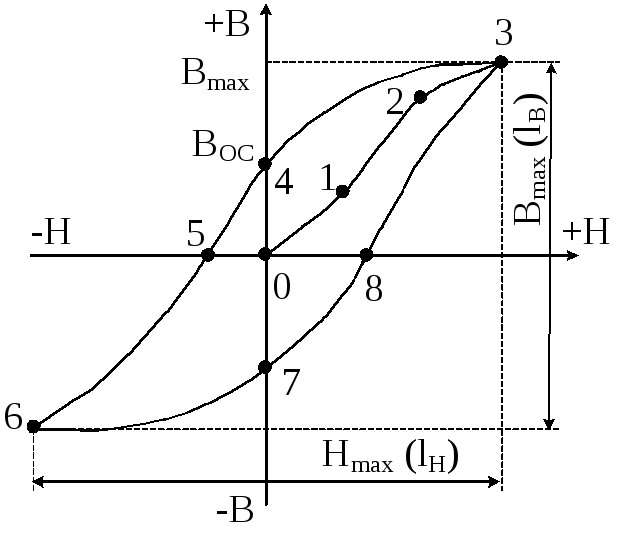
Для произвольной точки петли гистерезиса с ординатой n_i, соответствующей индукции В в образце (рис. 3):

U_у=U_0уn_i. (9)

Pис. 3

Из формул (7) и (9) получаем, что величина магнитной индукции равна

. (10)

Остаточная индукция B_r (точка С петли гистерезиса с ординатой n_с)находится по формуле

. (11)

Аналогично, для определения величины индукции насыщения (точка А петли гистерезиса с ординатой ) получаем

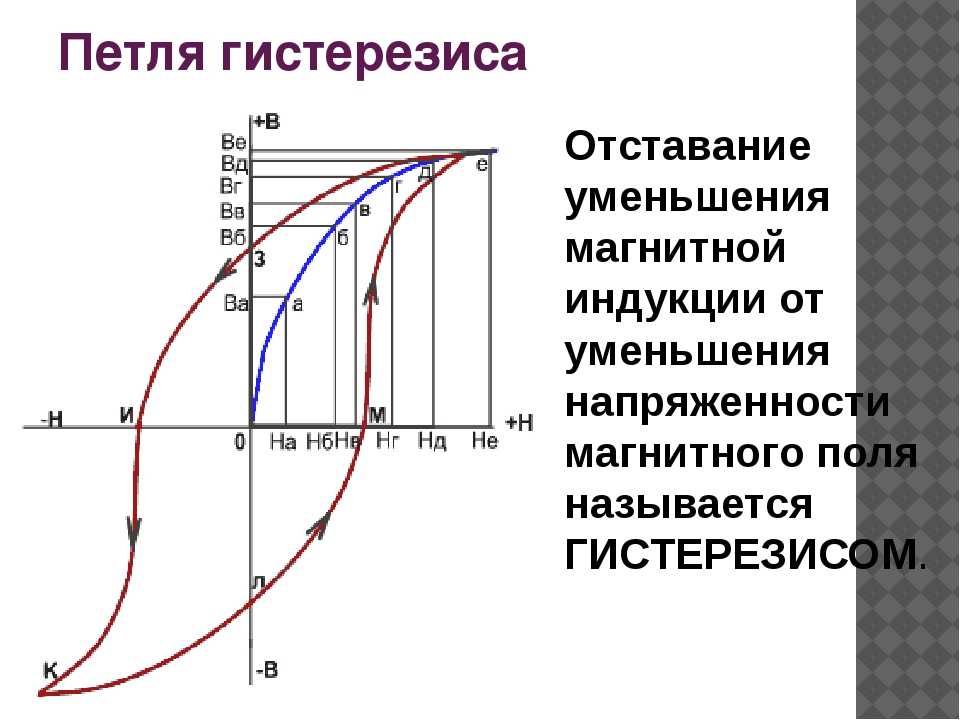. (12)

При градуировке горизонтальной оси осциллографа получают значение напряженности поля Н₀, которому соответствует отклонение электронного пучка по оси ОX на одно деление. Из рис. 1 и рис. 3 видно, что полю Н_А, при котором наблюдается насыщение, соответ­ствует смещение луча на m_А делений. Следовательно,

. (13)

Так как , то коэрцитивная сила ( точки К и К’ петли гистерезиса) равна

. (14)

При подсчетах нужно учесть, что в работе амперметром измеряется эффективное значение силы тока I_эфф. В формуле (14) используется амплитудное значение силы тока I_А, определяющее отклонение луча в осциллографе:

I_А .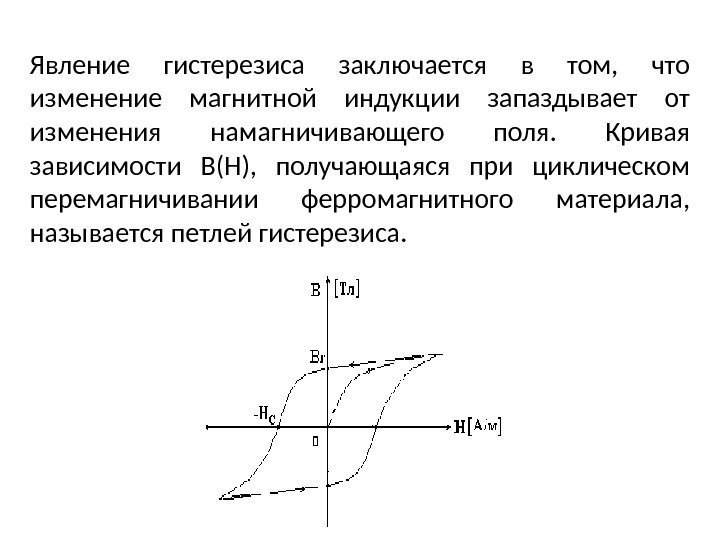 (15)

Порядок выполнения работы

1. Включить осциллограф и прогреть его в течение 1-2 мин.

2. Замкнуть цепь ключом К. Тумблер «Петля гистерезиса» перевести в верхнее положение. Потенциометром установить такую величину силы тока I_эфф, чтобы петля гистерезиса имела участок насыщения. Снять координаты 10-12 точек петли в делениях сетки осциллографа. Перенести рисунок в тетрадь.

3. Провести градуировку вертикальной оси осциллографа. Контрольное напряжение U_к=1,5 В.

4. Определить значения остаточной индукции В_r и индукции насыщения В_s по формулам (11) и (12), и коэрцитив­ной силы Н_K по формуле (14). Величины R₂, С, N₁, N₂, S, указаны на лабо­раторном стенде.

Контрольные вопросы

1. Как классифицируются магнетики? Какие тела являются ферромагнетиками, какими свойствами они обладают?

2. Что такое магнитный момент атома и чем он определяется? Как классифицируются магнетики на дио-, пара, и ферромагнетики?

3. Что такое намагниченность?

4. Что такое вектор магнитной индукции, напряженность магнитного поля? Какова связь между ними? Единицы измерения.

5. Каков физический смысл площади фигуры, ограниченной петлей гистерезиса?

6. В чем заключается явление электромагнитной индукции и каким образом оно используется в данной работе?

ЛАБОРАТОРНАЯ РАБОТА №7

ГИСТЕРЕЗИС • Большая российская энциклопедия

Авторы: Б. Н. Филиппов, Б. А. Струков, В. Н. Кузнецов

ГИСТЕРЕ́ЗИС (от греч. ὑστέρησις – от­ста­ва­ние, за­паз­ды­ва­ние), за­паз­ды­ва­ние из­ме­не­ния фи­зич. ве­ли­чи­ны, ха­рак­те­ри­зую­щей со­стоя­ние ве­ще­ст­ва, от из­ме­не­ния др. фи­зич. ве­ли­чи­ны, оп­ре­де­ляю­щей внеш­ние ус­ло­вия. Г. име­ет ме­сто в тех слу­ча­ях, ко­гда со­стоя­ние те­ла в дан­ный мо­мент вре­ме­ни оп­ре­де­ля­ет­ся внеш­ни­ми ус­ло­вия­ми не толь­ко в тот же, но и в пред­ше­ст­вую­щие мо­мен­ты вре­ме­ни. В ре­зуль­та­те для цик­лич. про­цес­са (рост и умень­ше­ние внеш­не­го воз­дей­ст­вия) по­лу­ча­ет­ся пет­ле­об­раз­ная (не­од­но­знач­ная) диа­грам­ма, ко­то­рая на­зы­ва­ет­ся пет­лёй ги­стере­зи­са. Воз­ни­ка­ет Г. в разл. ве­ще­ст­вах и при раз­ных фи­зич. про­цес­сах. Наи­боль­ший ин­те­рес пред­став­ля­ют маг­нит­ный, сег­не­то­элек­три­че­ский и уп­ру­гий гис­те­ре­зис.

Маг­нит­ный Г. – не­од­но­знач­ная за­ви­си­мость на­маг­ни­чен­но­сти $\boldsymbol M$ маг­ни­то­упо­ря­до­чен­но­го ве­ще­ст­ва (маг­не­ти­ка, напр., фер­ро- или фер­ри­маг­не­ти­ка) от внеш­не­го маг­нит­но­го по­ля $\boldsymbol H$ при его цик­лич. из­ме­не­нии (уве­ли­че­нии и умень­ше­нии). При­чи­ной су­ще­ст­во­ва­ния маг­нит­но­го Г. яв­ля­ет­ся на­ли­чие в оп­ре­де­лён­ном ин­тер­ва­ле из­ме­не­ния $\boldsymbol H$ сре­ди со­стоя­ний маг­не­ти­ка, от­ве­чаю­щих ми­ни­му­му тер­мо­ди­на­мич. по­тен­циа­ла, ме­та­ста­биль­ных со­стоя­ний (на­ря­ду со ста­биль­ны­ми) и не­об­ра­ти­мых пе­ре­хо­дов ме­ж­ду ни­ми. Маг­нит­ный Г. мож­но так­же рас­смат­ри­вать как про­яв­ле­ние маг­нит­ных ори­ен­та­ци­он­ных фа­зо­вых пе­ре­хо­дов 1-го ро­да, для ко­то­рых пря­мой и об­рат­ный пе­ре­хо­ды ме­ж­ду фа­за­ми в за­ви­си­мо­сти от $\boldsymbol H$ про­ис­хо­дят, в си­лу ука­зан­ной ме­та­ста­биль­но­сти со­стоя­ний, при разл.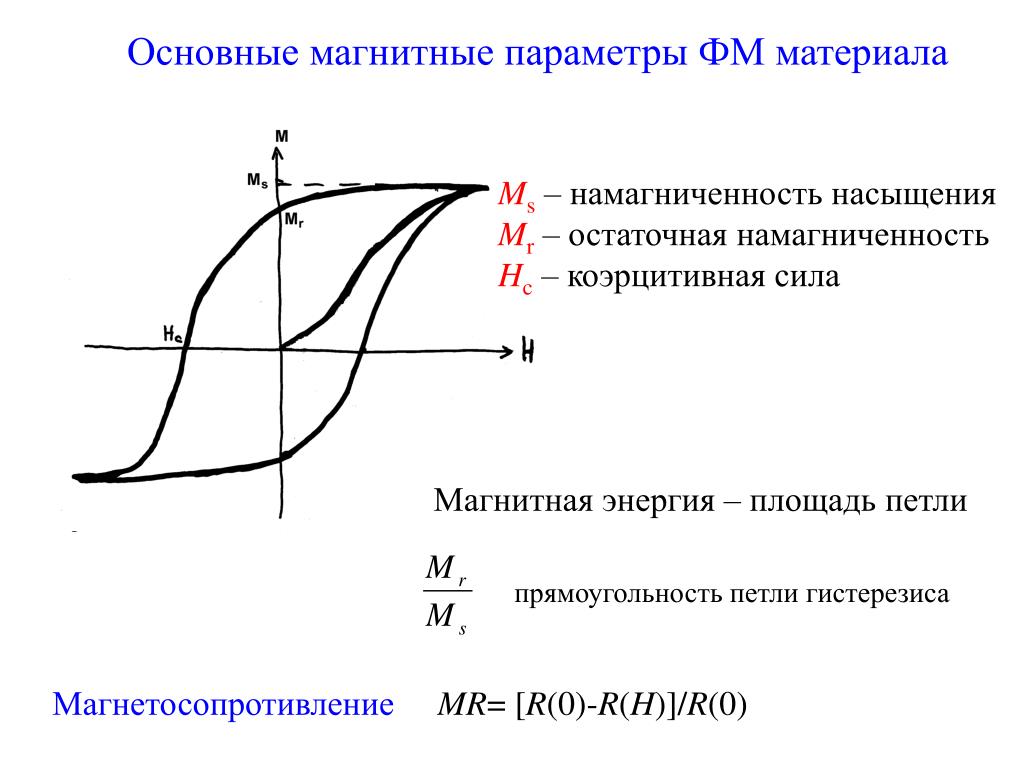 зна­че­ни­ях $\boldsymbol H$.

Рис. 1. Петли магнитного гистерезиса:1 – максимальная, 2 – частная; а – кривая намагничивания, б и в – кривые перемагничивания; МR – остаточная намагниченность, Нс – коэрцитивная сила, Ms – намагничен…

На рис. 1 схе­ма­ти­че­ски по­ка­за­на ти­пич­ная за­ви­си­мость $M$ от $H$ в фер­ро­маг­не­ти­ке; из со­стоя­ния $M=0$ при $H=0$ с уве­ли­че­ни­ем $H$ зна­че­ние $M$ рас­тёт (осн. кри­вая на­маг­ни­чи­ва­ния, $\it а$) и в дос­та­точ­но силь­ном по­ле $H⩾H_{\text m}$ $M$ ста­но­вит­ся прак­ти­че­ски по­сто­ян­ной и рав­ной на­маг­ни­чен­но­сти на­сы­ще­ния $M_{\text s}$. При умень­ше­нии $H$ от зна­че­ния $H_{\text m}$ на­маг­ни­чен­ность из­ме­ня­ет­ся вдоль вет­ви $\it б$ и при $H=0$ при­ни­ма­ет зна­че­ние $M=M_{\text R}$ (ос­та­точ­ная на­маг­ни­чен­ность). Для раз­маг­ни­чи­ва­ния ве­ще­ст­ва ($M=0$) не­об­хо­ди­мо при­ло­жить об­рат­ное по­ле $H= –H_{\text c}$, на­зы­вае­мое ко­эр­ци­тив­ной си­лой. Да­лее при $H=–H_{\text m}$ об­ра­зец на­маг­ни­чи­ва­ет­ся до на­сы­ще­ния ($M=–M_{\text s}$) в об­рат­ном на­прав­ле­нии. При из­ме­не­нии $H$ от $–H_{\text m}$ до $+H_{\text m}$ на­маг­ни­чен­ность из­ме­ня­ет­ся вдоль кри­вой $\it в$. Вет­ви $\it б$ и $\it в$, по­лу­чаю­щие­ся при из­ме­не­нии $H$ от $+H_{\text m}$ до $–H_{\text m}$ и об­рат­но, об­ра­зу­ют замк­ну­тую кри­вую, на­зы­вае­мую мак­си­маль­ной (или пре­дель­ной) пет­лёй Г. Вет­ви $\it б$ и $\it в$ на­зы­ва­ют­ся, со­от­вет­ст­вен­но, нис­хо­дя­щей и вос­хо­дя­щей вет­вя­ми пет­ли Г. При из­ме­не­нии $H$ на от­рез­ке $[–H_1, H_1]$ с $H_1$ за­ви­си­мость $M(H)$ опи­сы­ва­ет­ся замк­ну­той кри­вой (ча­ст­ной пет­лёй Г.), це­ли­ком ле­жа­щей внут­ри макс. пет­ли ги­сте­ре­зи­са.

Опи­сан­ные пет­ли Г. ха­рак­тер­ны для дос­та­точ­но мед­лен­ных (ква­зи­ста­ти­че­ских) про­цес­сов пе­ре­маг­ни­чи­ва­ния. От­ста­ва­ние $M$ от $H$ при на­маг­ни­чи­ва­нии и раз­маг­ни­чи­ва­нии при­во­дит к то­му, что энер­гия, при­об­ре­тае­мая маг­не­ти­ком при на­маг­ни­чи­ва­нии, не пол­но­стью от­да­ёт­ся при paзмагничивании. Те­ряе­мая за один цикл энер­гия оп­ре­де­ля­ет­ся пло­ща­дью пет­ли Г. Эти по­те­ри энер­гии на­зы­ва­ют­ся гис­те­ре­зис­ны­ми. При ди­на­мич. пе­ре­маг­ни­чи­ва­нии об­раз­ца пе­ре­мен­ным маг­нит­ным по­лем $\boldsymbol H_{\sim}$ пет­ля Г. ока­зы­ва­ет­ся ши­ре ста­ти­че­ской вслед­ст­вие то­го, что к ква­зи­рав­но­вес­ным гис­те­ре­зис­ным по­те­рям до­бав­ля­ют­ся ди­на­ми­че­ские, ко­то­рые мо­гут быть свя­за­ны с вих­ре­вы­ми то­ка­ми (в про­вод­ни­ках) и ре­лак­са­ци­он­ны­ми яв­ле­ния­ми.

Фор­ма пет­ли Г. и наи­бо­лее важ­ные ха­рак­те­ри­сти­ки маг­нит­но­го Г. (гис­те­ре­зис­ные по­те­ри, $H_с$, $M_{\text R}$ и др.) за­ви­сят от хи­мич. со­ста­ва ве­ще­ст­ва, его струк­тур­но­го со­стоя­ния и темп-ры, от ха­рак­те­ра и рас­пре­де­ле­ния де­фек­тов в об­раз­це, а сле­до­ва­тель­но, от тех­но­ло­гии его пригoтовления и по­сле­дую­щих фи­зич. об­ра­бо­ток (те­п­ло­вой, ме­ха­нич., тер­мо­маг­нит­ной и др.). С маг­нит­ным Г. свя­за­но гис­те­ре­зис­ное по­ве­де­ние це­ло­го ря­да др. фи­зич. свойств, напр. Г. маг­ни­то­стрик­ции, Г. галь­ва­но­маг­нит­ных и маг­ни­то­оп­тич. яв­ле­ний и т. д.

Сег­не­то­элек­три­че­ский Г. – не­од­но­знач­ная за­ви­си­мость ве­ли­чи­ны век­то­ра элек­трич. по­ля­ри­за­ции $\boldsymbol P$ сег­не­то­элек­три­ков от на­пря­жён­но­сти $\boldsymbol E$ внеш­не­го элек­трич. по­ля при цик­лич. из­ме­не­нии по­след­не­го. Сег­не­то­элек­три­ки об­ла­да­ют в оп­ре­де­лён­ном тем­пе­ра­тур­ном ин­тер­ва­ле спон­тан­ной (т. е. са­мо­про­из­воль­ной, воз­ни­каю­щей в от­сут­ст­вие внеш­не­го по­ля) по­ля­ри­за­ци­ей $\boldsymbol P_{сп}$. На­прав­ле­ние по­ля­ри­за­ции мо­жет быть из­ме­не­но элек­трич. по­лем, при этом зна­че­ние $\boldsymbol P$ при дан­ном $\boldsymbol E$ за­ви­сит от пре­дыс­то­рии, т. е. от то­го, ка­ким бы­ло элек­трич. по­ле в пред­ше­ст­вую­щие мо­мен­ты вре­ме­ни. Сег­не­то­элек­трич. Г. име­ет вид ха­рак­тер­ной пет­ли (пет­ля Г.), осн. па­ра­мет­ра­ми ко­то­рой яв­ля­ют­ся ос­та­точ­ная по­ля­ри­за­ция $\boldsymbol P_{ост}$ при $\boldsymbol E=0$ и ко­эр­ци­тив­ное по­ле $\boldsymbol E_к$, при ко­то­ром про­ис­хо­дит из­ме­не­ние на­прав­ле­ния (пере­клю­че­ние) век­то­ра $\boldsymbol P_{сп}$. Для со­вер­шен­ных мо­но­кри­стал­лов пет­ля Г. име­ет фор­му, близ­кую к пря­мо­уголь­ной, и $\boldsymbol P_{ост}=\boldsymbol P_{сп}$. В ре­аль­ных кри­стал­лах ос­та­точ­ная по­ля­ри­за­ция мень­ше спон­тан­ной из-за раз­биения кри­стал­ла на до­ме­ны.

Су­ще­ст­во­ва­ние сег­не­то­элек­трич. Г. сле­ду­ет из фе­но­ме­но­ло­гич. тео­рии сег­не­то­элек­трич. яв­ле­ний, в со­от­вет­ст­вии с ко­то­рой рав­но­вес­ным зна­че­ни­ям $\boldsymbol P_{сп}$ при лю­бой темп-ре ни­же темп-ры сег­не­то­элек­трич. фа­зо­во­го пе­ре­хо­да от­ве­ча­ют два сим­мет­рич­ных ми­ни­му­ма тер­мо­ди­на­мич. по­тен­циа­ла, раз­де­лён­ные по­тен­ци­аль­ным барь­е­ром. При $E=±E_к$ один из ми­ни­му­мов ис­че­за­ет, и кри­сталл ока­зы­ва­ет­ся в со­стоя­нии с оп­ре­де­лён­ным на­прав­ле­ни­ем век­то­ра $\boldsymbol P_{сп}$. При цик­лич. пе­ре­клю­че­нии спон­тан­ной по­ля­ри­за­ции пло­щадь пет­ли Г. оп­ре­де­ля­ет гис­те­ре­зис­ные по­те­ри – ко­ли­че­ст­во энер­гии элек­трич. по­ля, пе­ре­хо­дя­щей в те­п­ло­ту. Ве­ли­чи­на ко­эр­ци­тив­но­го по­ля свя­за­на так­же с про­цес­са­ми за­ро­ж­де­ния и эво­лю­ции в элек­трич. по­ле сег­не­то­элек­трич. до­ме­нов – об­лас­тей кри­стал­ла с вы­де­лен­ным элек­трич. по­лем на­прав­ле­ни­ем век­то­ра спон­тан­ной по­ля­ри­за­ции.

Рис. 2. Петля упругого гистерезиса.

Уп­ру­гий Г. – не­од­но­знач­ная за­ви­си­мость ме­ха­нического на­пря­же­ния от де­фор­ма­ции уп­ру­го­го те­ла при цик­лич. при­ло­же­нии и сня­тии на­груз­ки. Гра­фик за­ви­си­мо­сти на­пря­же­ния $σ$ от де­фор­мации $ε$ от­ли­ча­ет­ся от от­рез­ка пря­мой ли­нии, со­от­вет­ст­вую­щей за­ко­ну Гу­ка, и пред­став­ля­ет со­бой пет­лю Г. (рис. 2). Пло­щадь этой пет­ли про­пор­цио­наль­на ме­ха­нической энер­гии, ко­то­рая рас­сея­лась (пре­вра­ти­лась в те­п­ло­ту) во вре­мя цик­ла.

По­яв­ле­ние уп­ру­го­го Г. в ме­тал­лах свя­за­но с тем, что в не­ко­то­рых зёр­нах по­ли­кри­стал­ла мик­ро­на­пря­же­ния су­ще­ст­вен­но пре­вы­ша­ют ср. на­пря­же­ния в об­раз­це, что при­во­дит к по­яв­ле­нию пла­стич. де­фор­ма­ций и тем са­мым к рас­сея­нию ме­ха­нич. энер­гии. В не­ко­то­рых слу­ча­ях вклад в уп­ру­гий Г. да­ют элек­тро­маг­нит­ные яв­ле­ния.

Уп­ру­гий Г. как про­яв­ле­ние от­ли­чия ре­аль­но­го уп­ру­го­го те­ла от иде­аль­но уп­ру­го­го на­блю­да­ет­ся у всех твёр­дых тел, да­же при весь­ма низ­ких темп-рах. Уп­ру­гий Г. яв­ля­ет­ся при­чи­ной за­ту­ха­ния сво­бод­ных ко­ле­ба­ний уп­ру­гих тел, за­ту­ха­ния в них зву­ка, умень­ше­ния ко­эф. вос­ста­нов­ле­ния при не­уп­ру­гом уда­ре и др. В об­щем слу­чае от­кло­не­ние уп­ру­го­сти от иде­аль­ной вклю­ча­ет­ся в по­ня­тие внут­рен­не­го тре­ния.

Ферромагнетизм — определение, причины, свойства, гистерезис

Существует несколько типов магнетизма, из которых ферромагнетизм является самым сильным. Ферромагнитные материалы имеют спонтанную результирующую намагниченность на атомном уровне даже при отсутствии внешнего магнитного поля. Когда ферромагнитные материалы подвергаются воздействию внешнего магнитного поля, они сильно намагничиваются в направлении поля.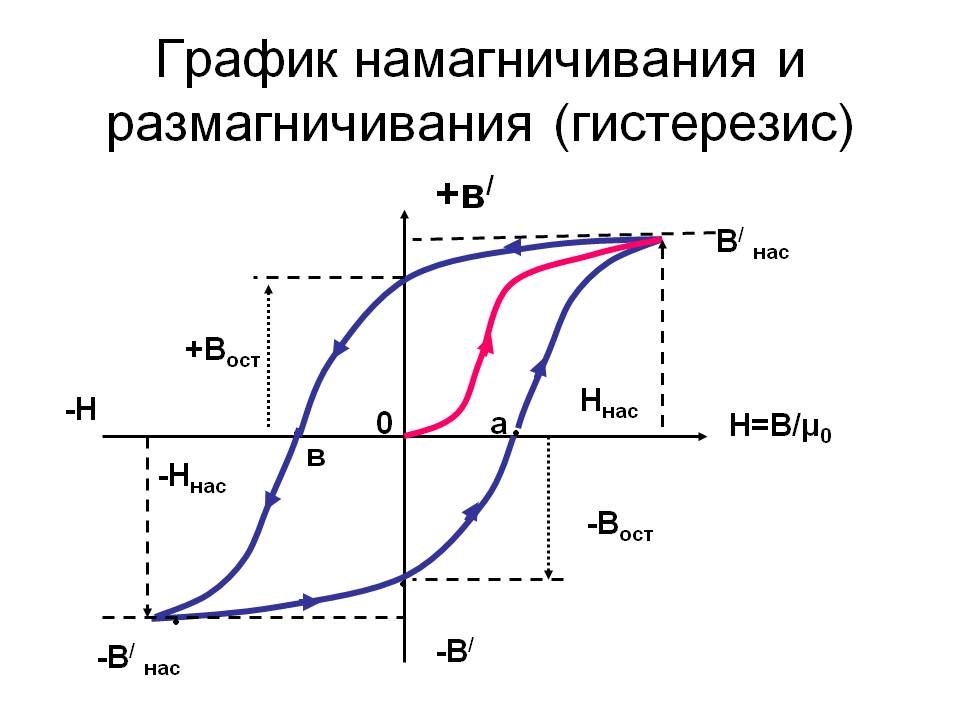 Магнит агрессивно притягивает ферромагнитные материалы. Даже когда внешнее намагничивающее поле снимается, эти материалы сохраняют свою намагниченность в течение определенного периода времени. Гистерезис — это название этой характеристики.

Что такое ферромагнетизм?

Ферромагнетизм получил свое название от термина «железо», которое относится к железу, которое было первым обнаруженным металлом с характеристиками притяжения магнитного поля.

Ферромагнетизм — это магнитное свойство, которым обладают некоторые материалы, такие как железо, кобальт, сплавы и другие. Это явление, при котором некоторые материалы приобретают стойкие магнитные или притягивающие свойства. Он также известен как процесс, при котором электрически незаряженные элементы агрессивно притягиваются друг к другу. Ферромагнетизм — это характеристика, учитывающая не только химический состав материала, но также его микроструктуру и кристаллическую структуру.

Причины ферромагнетизма

Атомные диполи в крошечных областях, называемых доменами в ненамагниченном ферромагнитном материале, ориентированы в одном направлении. Даже в отсутствие внешнего намагничивающего поля домены обладают суммарным магнитным моментом. Магнитные моменты соседних доменов, напротив, направлены в противоположные стороны. Они компенсируют друг друга, в результате чего чистый магнитный момент материала равен нулю. Когда приложено внешнее магнитное поле, все эти домены выравниваются в направлении приложенного поля. В результате этого процесса материал сильно намагничивается в направлении, параллельном намагничивающему полю.

Ферромагнитные материалы

Ферромагнитные материалы представляют собой класс материалов, которые при воздействии магнитного поля склонны проявлять или проявлять значительный магнетизм в направлении поля. Образцы выравнивания атомов компонентов этих материалов в первую очередь ответственны за их магнитные свойства. Эти атомы имеют тенденцию действовать как основные электромагниты.

Примеры ферромагнитных материалов

Большинство ферромагнитных материалов составляют металлы. Распространенными примерами являются железо, кобальт, никель и другие ферромагнитные материалы. Кроме того, ферромагнитные материалы включают металлические сплавы и редкоземельные магниты. Окисление железа в оксид дает магнетит, ферромагнитное вещество. Он имеет температуру Кюри 580°C. Ранее он был известен как магнитное вещество. Магнетит — самый магнитный из природных минералов на планете.

Свойства ферромагнитных материалов

• В доменах атомы ферромагнитных веществ обладают постоянным дипольным моментом.
• В ферромагнитных материалах атомные диполи ориентированы в том же направлении, что и внешнее магнитное поле.
• Магнитный дипольный момент большой и ориентирован в направлении намагничивающего поля.
• Интенсивность намагничивания (M) чрезвычайно высока и положительна, и она изменяется линейно с намагничивающим полем (H). В результате насыщенность определяется составом материала.
• Магнитная восприимчивость достаточно высокая и положительная. 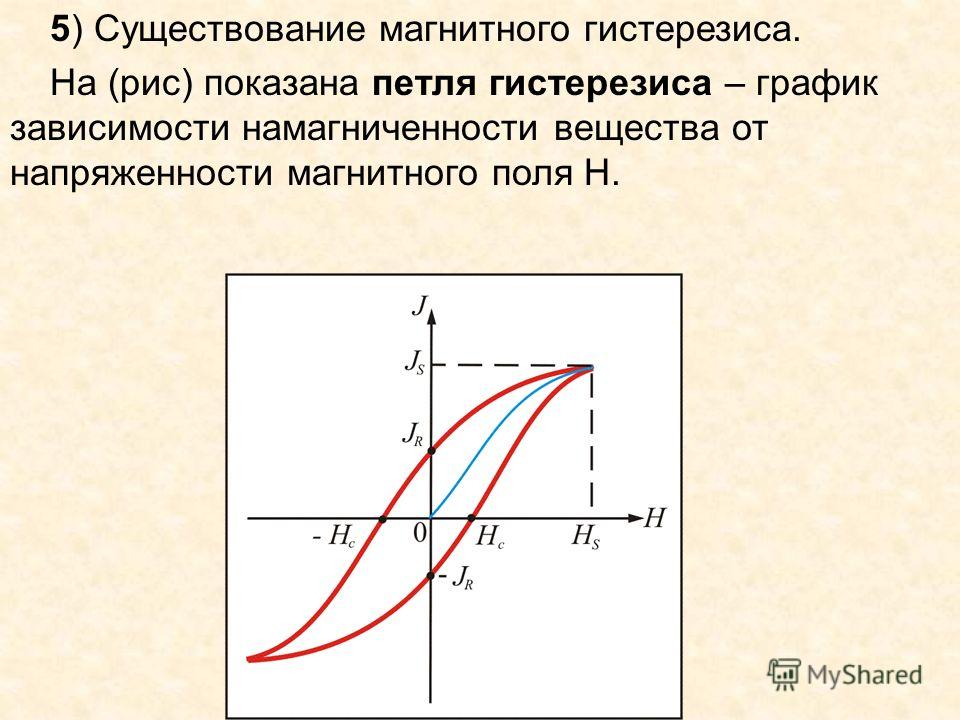Магнитная восприимчивость определяется как X _м = M ⁄ H , где M — интенсивность намагниченности, а H — напряженность приложенного магнитного поля.
• Плотность магнитного потока материала будет очень высокой и положительной. Внутри ферромагнитных материалов линии магнитного поля становятся чрезвычайно толстыми. B = ε ₀ (H + M) плотность магнитного потока, где ε ₀ — магнитная проницаемость свободного пространства, H — напряженность приложенного магнитного поля, а M — интенсивность намагниченности.
• Относительная магнитная проницаемость также довольно высока и изменяется линейно с магнитным полем. Магнитное поле внутри материала значительно больше, чем магнитное поле снаружи материала. Они имеют тенденцию вытягивать из материала большое количество силовых линий.
• Поле агрессивно притягивает ферромагнитные материалы. Они предпочитают цепляться за полюса, где поле сильнее в неоднородном поле.
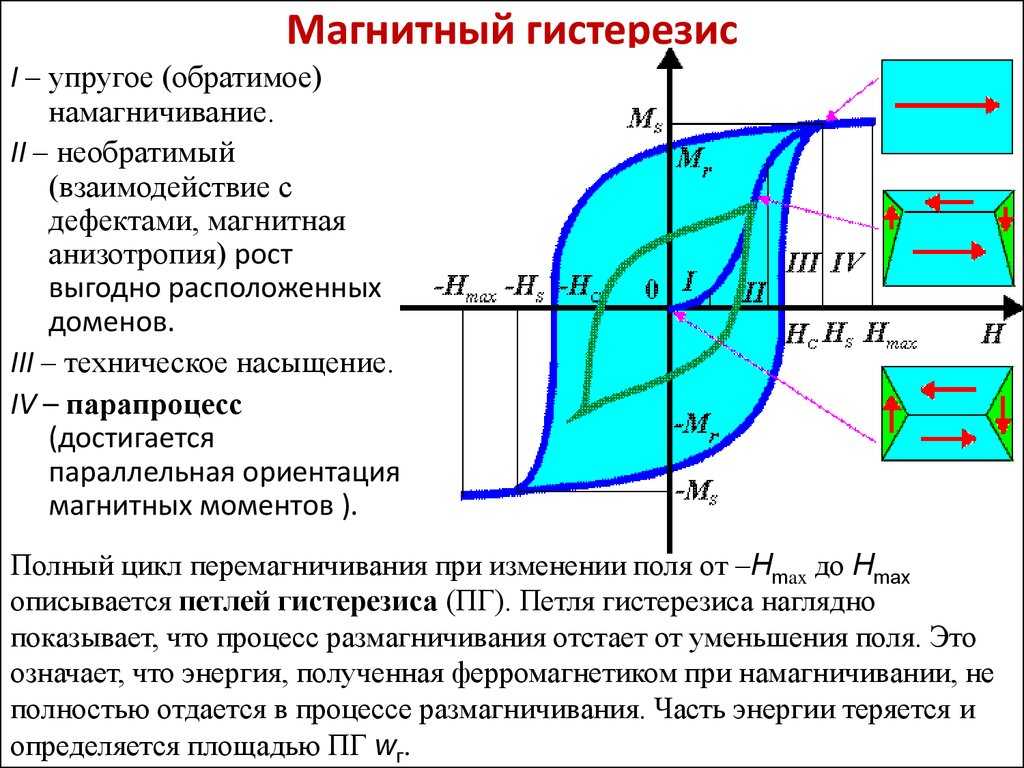
• Если ферромагнитный порошок поместить в часовое стекло, установленное на двух полюсах, которые находятся на достаточном расстоянии друг от друга, порошок скапливается по бокам и образует углубление в центре, потому что поле сильнее всего на полюсах.
• Ферромагнитный материал теряет свои ферромагнитные характеристики при сжижении из-за более высокой температуры.

Гистерезис

Ферромагнитное вещество не полностью размагничивается при снятии внешнего магнитного поля. Магнитное поле в противоположном направлении должно быть приложено, чтобы вернуть материал к нулевой намагниченности. Гистерезис — это характеристика ферромагнитных материалов, которая позволяет им сохранять свою намагниченность при снятии внешнего поля.

Когда намагниченность материала измеряется с точки зрения плотности магнитного потока (B) и напряженности внешнего магнитного поля (H), образуется петля. Это известно как петля гистерезиса.

Петля гистерезиса

Когда сила намагничивания уменьшается до нуля, сохраняющая способность представляет собой сохраняющуюся плотность магнитного потока. Сила обратного намагничивающего поля, которое необходимо приложить для полного размагничивания материала, называется коэрцитивной силой.

Температура Кюри

Температура влияет на ферромагнитные свойства. Ферромагнитные вещества становятся парамагнитными при нагревании до достаточно высокой температуры. Температура Кюри – это температура, при которой происходит этот переход. T _c — это аббревиатура.

Использование ферромагнитных материалов

Ферромагнитные материалы находят широкое применение в промышленности. Электродвигатели, телефоны, генераторы, громкоговорители, трансформаторы и магнитная полоса на обратной стороне кредитных карт — все это примеры оборудования, в котором они используются.

Примеры задач

Задача 1. Что такое ферромагнетизм?

Решение:

Ферромагнетизм — это физическое явление (дальний порядок), при котором некоторые материалы, такие как железо, сильно притягиваются друг к другу. Редкоземельные минералы, включая гадолиний, содержат ферромагнетики. Магнетизм в магнитах вызван одним из наиболее распространенных явлений, наблюдаемых в повседневной жизни.

Задача 2. Домен ферромагнитного железа имеет форму куба со стороной 1 мкм. Найдите количество атомов железа в домене. (Молекулярная масса железа = 55 г моль ⁻¹ и плотностью = 7,92 г ⁄ см ³ )

Решение:

Дано:

Длина стороны, l = 1 мкм, V = 1 куб. ) ³

= (1 × 10 ⁻⁶ M) ³

= 1 × 10 ⁻¹² CM ³

, M = V × D

= 1 × ³

, M = V × D

= 1 × ³

. −12 см ³ × 7,92 г ⁄ см ³  

= 7,92 × 10 ⁻¹² г

Теперь число Авогадро (6,023 × 10 ²³ ) атомов железа имеет массу 55 г, поэтому количество атомов в домене:

N = 7,92 × 10 ⁻¹² г × 6,023 × 10 ²³ ÷ 55

= 0,867 × 10 ¹¹

Отсюда число атомов в домене равно 0,867 × 10 ¹¹ атомов.

Задача 3. Как повлияет на магнитные домены помещение ферромагнитного материала во внешнее магнитное поле?

Решение:

В случае ферромагнитного материала магнитные домены выстраиваются в направлении внешнего магнитного поля. Домены по существу представляют собой направленные крошечные области атомов. Когда домены, ориентированные по полю, сохраняются во внешнем магнитном поле, домены, ориентированные по полю, растут и захватывают области, ранее заселенные доменами, ориентированными против поля. Следовательно, домены увеличиваются в размерах.

Задача 4: Что такое температура Кюри?

Решение:

Температура Кюри, также известная как точка Кюри, представляет собой температуру, при которой некоторые материалы теряют свои постоянные магнитные характеристики, позволяя наведенному магнетизму занять их место.

Задача 5. Какие приложения имеет ферромагнетизм?

Решение:

Ферромагнитный материал имеет широкий спектр применения. Актуальность кривой гистерезиса невозможно переоценить. В трансформаторах, электромагнитах и ​​записи на магнитную ленту используется ферромагнетизм.

Асимметричные петли гистерезиса в структурированных ферромагнитных наночастицах с жесткими/мягкими областями

• Список журналов
• Наноматериалы (Базель)
• PMC8003930

Наноматериалы (Базель). 2021 март; 11(3): 800.

Опубликовано онлайн 2021 март 21. doi: 10.3390/nano11030800

, ¹ , ¹ , ² и ^{1, *}

Ana María Díez-Pascal, Academecme

Ana María Díez-Pascual, Academecme

Ana María Díez-Pascual, Academeman

. Информация об авторских правах и лицензиях Отказ от ответственности

Заявление о доступности данных

Горизонтально смещенные и асимметричные петли гистерезиса часто связаны с образцами с обменным смещением, состоящим из обмена ферромагнетиком в сочетании с антиферромагнетиком. В чисто ферромагнитных образцах такие эффекты могут возникать из-за необнаруженных малых петель или тепловых эффектов. Моделирование ферромагнитных наноструктур при нулевой температуре с достаточно большими полями насыщения не должно приводить к таким асимметриям. Здесь мы сообщаем о микромагнитном моделировании при нулевой температуре, выполненном на напыленных наночастицах с различной структурой. Небольшие отклонения систем из-за случайной ориентации анизотропии в разных зернах могут не только приводить к сильным отклонениям процессов перемагничивания и петель гистерезиса, но и приводить к резко асимметричным, сдвинутым по горизонтали петлям гистерезиса в чисто ферромагнитных наночастицах.

Ключевые слова: псевдообменное смещение, малая петля, микромагнитное моделирование, OOMMF, спинтроника сдвиг петли гистерезиса, часто в сочетании с асимметрией петли [1]. Обменное смещение, впервые обнаруженное в наночастицах ядро/оболочка Co/CoO [2], в настоящее время в основном исследуется в тонкопленочных системах [3,4,5,6]. Технологически этот эффект особенно актуален для головок чтения жестких дисков, спиновых клапанов и других устройств спинтроники [7,8,9].,10].

Хотя происхождение ЭП еще не полностью изучено количественно, существует общее мнение, что интерфейс между ферромагнетиком и антиферромагнетиком — или ферримагнетиком — играет решающую роль в этом эффекте [11,12,13]. Недавно было показано дополнительное влияние дальнодействующих взаимодействий в антиферромагнетике [14,15]. С другой стороны, это означает, что в чисто ферромагнитных системах, независимо от размера или формы, не следует ожидать ни смещения петли гистерезиса, ни асимметрии петли гистерезиса.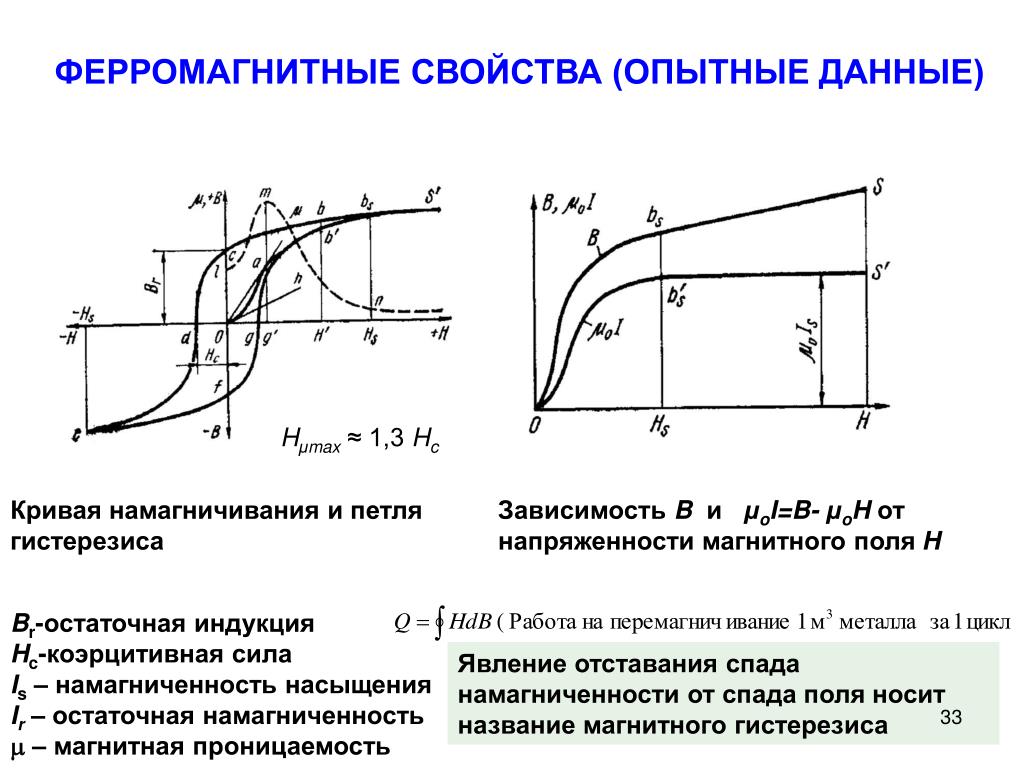

Тем не менее, только несколько исследований сообщают о таких эффектах. В частности, измерения намагниченности с использованием магнитооптического эффекта Керра (МОКЭ), где обнаруживаются только различия в намагниченности, в то время как абсолютная намагниченность не может быть измерена, не показывают возможного вертикального смещения петли гистерезиса, так что этот метод подвержен ошибочным ошибкам. измерение малых петель, которые кажутся полностью закрытыми, хотя насыщение еще не достигнуто [16]. С другой стороны, в чистых антиферромагнетиках сообщалось о сдвигах петель, подобных обменному смещению, где они объяснялись нескомпенсированными спинами внутри антиферромагнетика, что приводило к устойчивой к полю намагниченности [17].

Здесь мы показываем микромагнитное моделирование с использованием Object Oriented MicroMagnetic Framework (OOMMF) при нулевой температуре, выполненное на симметричных распыленных наночастицах с различными формами и отверстиями или прорезями внутри. Такие структуры интересны тем, что их часто можно использовать для изготовления четверичных устройств памяти, в которых два (или даже больше) бита могут храниться в одной позиции хранения [18]. Наши результаты показывают, что не только малые отклонения исследуемых систем из-за случайной ориентации анизотропии в разных зернах могут приводить к сильным отклонениям процессов перемагничивания и петель гистерезиса, но и отчетливо асимметричные, сдвинутые по горизонтали петли гистерезиса могут возникать в чисто чистом виде. ферромагнитная наночастица.

Были смоделированы различные наноструктуры, как показано на рис. Боковые размеры кадров всегда 100 нм × 100 нм, а высота определена как 10 нм.

Открыть в отдельном окне

Разные маски М1-М4 с исследуемыми слотами. Черные области изображают Fe, а белые области пусты — заполнены воздухом.

По результатам моделирования и дополнительных предварительных испытаний были разработаны дополнительные структуры с поперечными размерами 500 нм × 500 нм (465 нм/600 нм) для квадратных (гексагональных/неправильных) рисунков и толщиной 50 нм.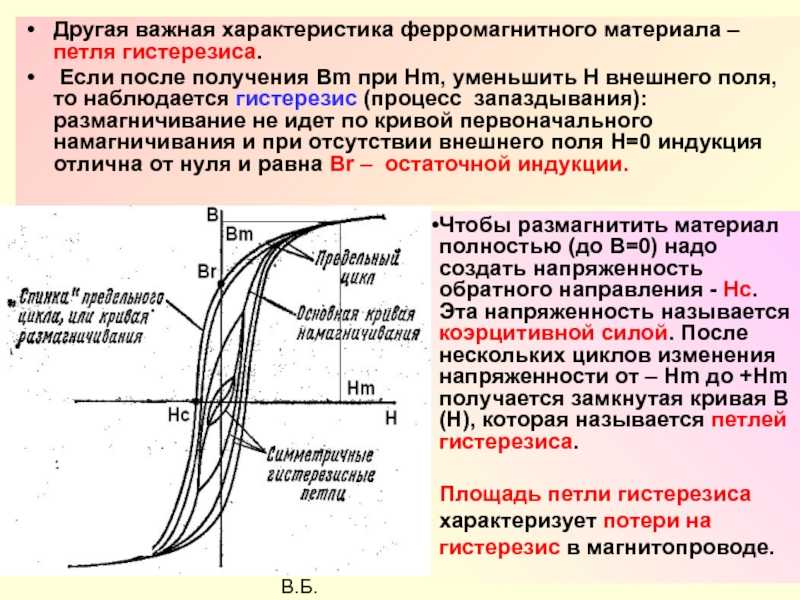 . Части образцов имеют уменьшенную толщину 25 нм (видны серыми областями на соответствующих снимках процессов перемагничивания), а черным и белым показаны железо в полный рост и снова воздух соответственно.

Для моделирования использовалась OOMMF [19], которая основана на конечных разностях для построения сетки и динамического решения уравнения движения Ландау-Лифшица-Гилберта (LLG) [20]. Параметры материала были выбраны как типичные литературные значения для железа (Fe): намагниченность при насыщении M _S = 1700·10 ³ А/м, константа обмена A = 21·10 ⁻¹² Дж/м, магнито- константа кристаллической анизотропии K ₁ = 48·10 ³ Дж/м ³ .

Поскольку такие наноструктуры обычно изготавливаются методом электронно-лучевой литографии [21], оси анизотропии в соседних кубических ячейках с 5 нм ³ были выбраны случайным образом, так что конфигурационная анизотропия в основном определяет перемагничивание [22]. Установка константы демпфирования Гилберта на уровне α = 0,5 приводит к моделированию реалистичного квазистатического случая. Внешние магнитные поля прикладывались в плоскости образца и менялись между различными максимальными полями под разными углами. Следует отметить, что температура была установлена ​​равной 0 К, чтобы избежать тепловых флуктуаций, которые могли бы помешать процессу перемагничивания.

Часть результатов опубликована в [23].

Первоначальная цель этого исследования состояла в том, чтобы исследовать возможные структуры для четырехкомпонентных приложений хранения. показывает этот эффект на примере маски M1 под углом 0° (горизонтальная ориентация в ). а изображает продольную составляющую намагниченности M _L , параллельную внешнему магнитному полю. Здесь развертку поля останавливали только для самых широких ступеней, уменьшая внешнее магнитное поле до 0, чтобы исследовать устойчивость различных состояний, достигаемых таким образом при остаточной намагниченности (состояния 1 и 3 на рисунке). Таким образом, в дополнение к обычным двум состояниям можно было проверить еще два устойчивых состояния при остаточной намагниченности. Моментальные снимки, соответствующие номерам промежуточных состояний в a, изображены в b.

Открыть в отдельном окне

( a ) Петля гистерезиса и ( b ) снимки устойчивых промежуточных состояний #0–3, смоделированные для маски M1 при угле поля 0°.

Здесь становится ясно, почему эта структура наночастиц хорошо подходит для обеспечения более чем одного стабильного состояния при остаточной намагниченности: разные участки структуры не переключают намагниченность одновременно, и эти частично переключаемые состояния соответствуют ступеням по наклону петля гистерезиса (а).

Однако следует отметить, что остальные ступени либо не коррелируют с устойчивыми промежуточными состояниями (здесь не показаны), либо слишком узки (в смысле ширины ступени), чтобы быть технологически важными, и поэтому дополнительно не исследовались.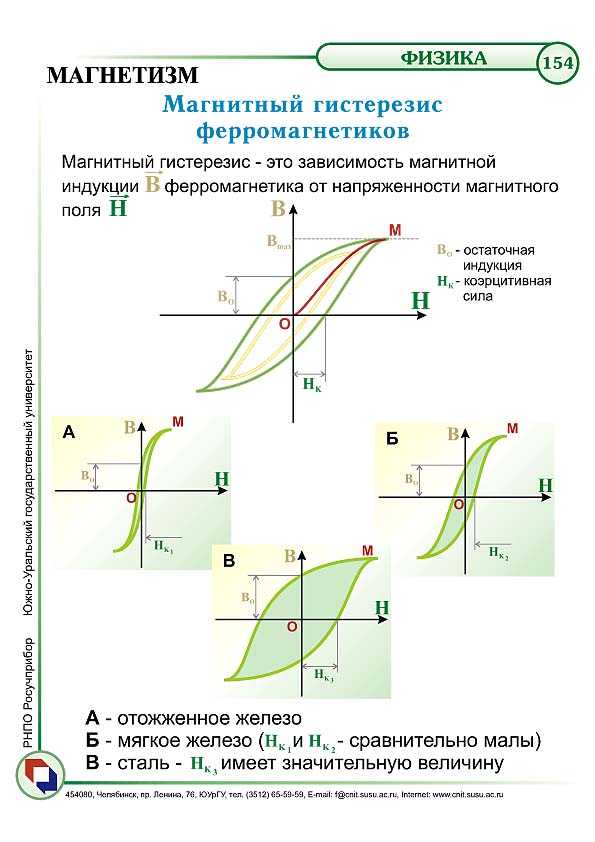 здесь. Тем не менее, различные положения щели в образце допускают интересные магнитные состояния и поэтому должны быть исследованы более подробно в ближайшем будущем путем изменения всех размеров этого нанообъекта.

Очень похожий эффект обнаруживается в маске M4, как показано на . Здесь каждая полоса переключается последовательно, что теоретически допускает даже восемь различных состояний при остаточной намагниченности. Однако более узкие ступени снова не тестировались, поскольку они практически менее актуальны из-за их ограниченной ширины.

Открыть в отдельном окне

( a ) Петля гистерезиса и ( b ) снимки устойчивых промежуточных состояний #0–3, смоделированные для маски M4 при угле поля 0°.

Аналогичные эффекты были обнаружены для образца М2 при угле 0°. Однако поворот внешнего магнитного поля на 90° привел к неожиданной находке. Как видно, в этом случае возникает горизонтально смещенная асимметричная кривая гистерезиса, которая показывает типичную форму, например, Fe/MnF ₂ тонкопленочные системы с обменным смещением [24]. Как обсуждалось выше, в случае чистого ферромагнетика такой вывод следует отнести к измерению малой петли.

Открыть в отдельном окне

Открыть в отдельном окне

( a – f ) Продольные и поперечные петли гистерезиса ML и MT, смоделированные для маски M2 при угле поля ~90° с применением различных максимальных полей , вкл. различные прогоны с максимальным внешним магнитным полем 10 Тл.

Хотя применяемые здесь максимальные поля ± 1 Тл уже достаточно велики, известно, что поля насыщения могут быть намного больше коэрцитивных полей; поэтому в следующих симуляциях применялось максимальное поле 10 Тл (диапазон поля не полностью показан на рисунке). Этот порядок величин доступен с обычными магнитами в криостатах. Два результата показаны на b, c. Следует отметить, что все параметры испытаний были сохранены идентичными, единственной переменной был угол магнитокристаллической анизотропии на зерно, который произвольно выбирался при каждом новом прогоне моделирования, соответствующем реальной ситуации с напыленными образцами. Оба эксперимента дали симметричные кривые. Тем не менее, несмотря на моделирование одной и той же ситуации, были обнаружены разные коэрцитивные поля, а также разные процессы перемагничивания, так как сильно отличающиеся петли поперечного гистерезиса M _T показать. Сравнивая a с этими 10 T-насыщенными измерениями, становится очевидным, что асимметричная петля в a содержит результаты обеих петель гистерезиса, показанных в b, c, подчеркивая идею о том, что a показывает псевдо-EB из-за моделирования второстепенной петли.

Затем было проверено, повысит ли незначительное нарушение симметрии дальнейшим поворотом образца на 1° воспроизводимость результатов. Этот подход хорошо работает в масках M1 и M4, где по вращению внешнего магнитного поля можно определить, начинается ли перемагничивание в «верхней» или «нижней» горизонтальной полосе. Однако, как показано на c – f, этот подход не увенчался успехом. Все продольные и поперечные компоненты намагниченности четко различаются. Также видно, что поперечные компоненты намагниченности насыщаются только при абсолютных полях больше 900 мТл, тогда как продольные петли кажутся насыщенными менее чем в половине этих полей. Это подчеркивает сделанный ранее вывод о том, что малые петли могут оставаться не обнаруженными в экспериментах, где поперечные компоненты намагниченности часто не измеряются отдельно [16], и еще раз показывает отсутствие воспроизводимости процессов перемагничивания в наночастицах с малыми областями, которые могут оставаться неизменными. Очень похожие результаты были получены в образце M3 под углом 0° (здесь не показан), где в последующих моделированиях также наблюдались три различных процесса перемагничивания.

В то время как отсутствие надежности в некоторых образцах проблематично для возможного технологического применения, смещение псевдообмена даже технологически важно для приложений спинтроники. Следует подчеркнуть, что, хотя этот эффект демонстрирует сходное поведение с обменным смещением, он не связан с обменной связью между различными магнитными материалами или между различными частицами в одном магнитном материале [3] и, следовательно, не может рассматриваться как обменное смещение, но является на основе малых петель.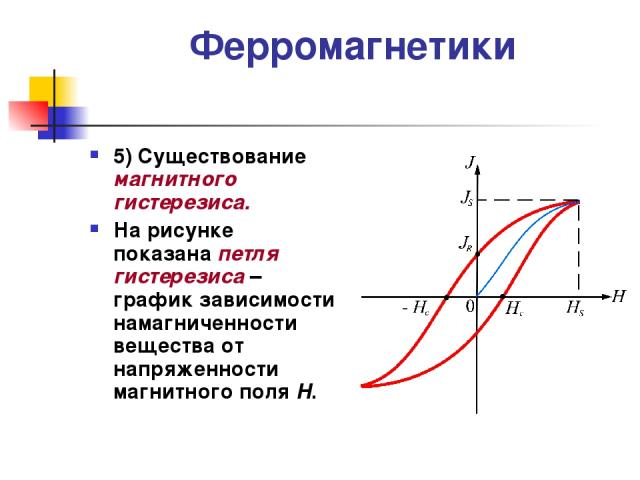 Таких незначительных петель обычно избегают в большинстве измерений, поскольку они могут привести к неправильной интерпретации. Однако возможность изготовления чисто ферромагнитной системы с псевдо-ЭП может открыть новые возможности для создания более простых спиновых вентилей и других элементов спинтроники, для которых обычно требуется много слоев, в том числе ферромагнитный слой, закрепленный антиферромагнетиком для увеличения поля переключения. Если возможно подготовить слои с собственным псевдо-ЭП из-за сложной геометрии слоев, что приводит к соседним областям с магнитомягким и магнитотвердым поведением, антиферромагнетик можно исключить, и, таким образом, устройства спинтроники можно производить из более простых пакетов слоев.

Вот почему в следующей части этого исследования моделировались более крупные образцы с повторяющимися элементарными ячейками. Путем непрерывного повторения этих симуляций мы обнаружили, что более высокая толщина (теперь 50 нм вместо 10 нм в первой части исследования) и мозаичный узор вместо одной структурированной наночастицы приводят к более воспроизводимым результатам по сравнению с показанными. до. Следует отметить, что исходная конфигурация тем не менее влияет на результаты, как видно из сравнения с a,b. Для систем с очень большими полями насыщения, т. е. с возможностью имитации обменного смещения малой петлей, можно предположить, что это начальное насыщение работает так же, как охлаждающее поле в классических ЭП-системах.

Открыть в отдельном окне

( a ) Петли продольного и поперечного гистерезиса M _L и M _T , смоделированные для шестиугольной мозаики (см. вставки), ( a ) после установки большого магнита поле 5 Тл; ( b ) начиная с нулевого поля. Таким образом,

показывает продольные и поперечные петли гистерезиса, смоделированные после установки большого внешнего магнитного поля + 5 Тл для достижения положительного насыщения для различных мозаичных изображений, как показано на вставках.

Открыть в отдельном окне

( a – d ) Продольные и поперечные петли гистерезиса ML и MT, смоделированные для различных тесселяций (см.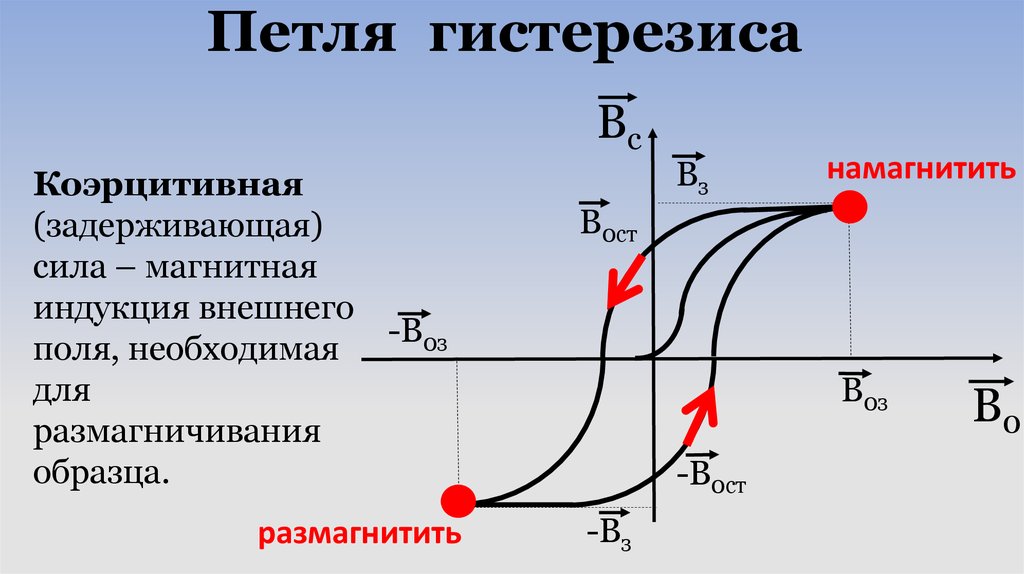 вставки) после задания большого магнитного поля 5 Тл.

В большинстве случаев В случаях (a–c) возможно создание асимметричных петель гистерезиса с помощью начальной настройки поля. Однако это не работает в случае d, где большая часть наночастицы имеет максимальную высоту, разделенную тонкими линиями воздуха. Эти первые результаты предполагают, что для достижения этого эффекта необходима более высокая «сетка», связанная с более тонкими заполненными магнитными областями.

Следует также отметить, что эта асимметрия обычно наблюдается в поперечной, а не в продольной петле гистерезиса. Кроме того, при повторном моделировании всегда обнаруживались вертикальные сдвиги поперечной намагниченности в сторону отрицательных значений, а форма продольного гистерезиса незначительно менялась из-за произвольной ориентации осей магнитокристаллической анизотропии в одиночных зернах. Это означает, что для потенциального применения поперечная составляющая намагниченности — или намагниченность в другом направлении — может быть более подходящей, чем продольная.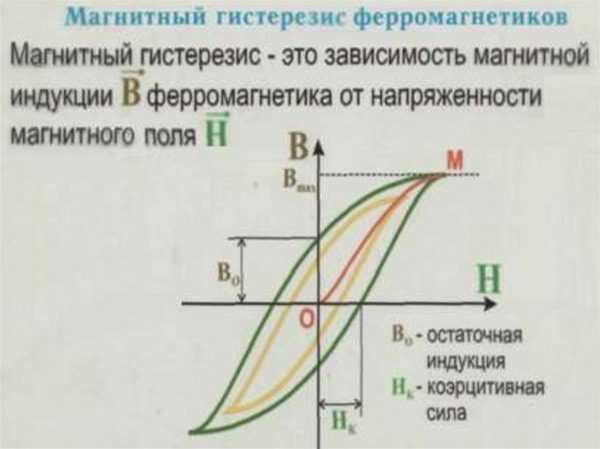

Сравнивая эти структуры с первым набором М1–М4, необходимо также отметить, что надежность перемагничивания по коэрцитивным полям и форма продольной петли гистерезиса задаются в мозаичных структурах, если образцы исследуются из с макроскопической точки зрения, т. е. по их общей намагниченности. Однако с микроскопической точки зрения процессы перемагничивания на малых масштабах все же могут различаться из-за вариаций угла магнитокристаллической анизотропии в каждой отдельной ячейке. Таким образом, порядок или обращение отдельных плиток этих мозаик будет отличаться от одного прогона симуляции к другому.

В общем, следует подчеркнуть, что эффект, изображенный здесь для некоторых примеров, не является эквивалентом системы обменного смещения, которая обычно состоит из обменно-связанного ферромагнетика с антиферромагнетиком, а является комбинацией более твердого и более мягкого ферромагнетика. . В отличие от спиновых клапанов и подобных устройств спинтроники, система не содержит слоев жесткого и мягкого ферромагнетиков, а оба свойства перемешаны внутри единой ферромагнитной наноструктуры.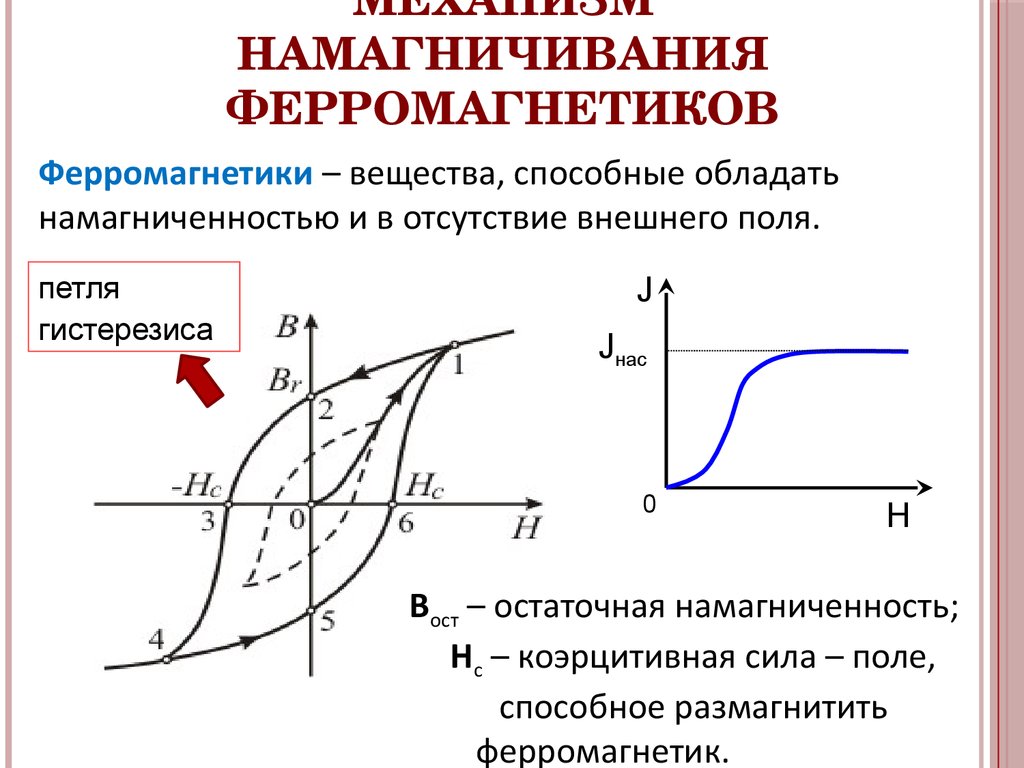 Как правило, твердые ферромагнитные части представляют собой тонкие, более высокие линии с их сильной анизотропией формы, в то время как более крупные и плоские части между ними ответственны за мягкое ферромагнитное поведение.

Чтобы надежно использовать этот эффект, необходимо проверить его устойчивость к малым отклонениям конструкции и угла приложения внешнего магнитного поля, что будет сделано в следующем исследовании.

Чистые ферромагнитные наночастицы с внутренними прорезями или линиями увеличенной высоты были исследованы с помощью микромагнитного моделирования. В нескольких случаях были обнаружены явно асимметричные петли гистерезиса, которые обычно коррелируют с системами обменного смещения, но здесь могут быть отнесены к моделированию второстепенных петель. Особенно хорошо асимметрия была видна в поперечных петлях гистерезиса.

В то время как асимметрия в системе с обменным смещением возникает из-за обменной связи между ферро- и антиферромагнетиком, здесь ее можно отнести к взаимодействию между жестким и легким ферромагнетиком, которые, в отличие от спиновых вентилей и других обычных тонкопленочных системы, не разделенные в пространстве, а смешанные.

Будущие исследования покажут, можно ли надежно использовать такие структуры вместо систем обменного смещения в различных устройствах спинтроники.

Концептуализация, Д.Д., К.К., Т.Б. и А.Е.; расследование, Д.Д., К.К., Т.Б. и А.Е.; написание — подготовка первоначального проекта, А.Э.; написание — обзор и редактирование, J.D., K.K. и Т.Б. Все авторы прочитали и согласились с опубликованной версией рукописи.

APC финансируется Фондом публикаций открытого доступа Билефельдского университета прикладных наук.

Неприменимо.

Все данные, полученные в ходе исследования, представлены в этой статье.

Авторы заявляют об отсутствии конфликта интересов. Спонсоры не участвовали в разработке исследования; при сборе, анализе или интерпретации данных; в написании рукописи или в решении опубликовать результаты.

Примечание издателя: MDPI сохраняет нейтралитет в отношении юрисдикционных претензий в опубликованных картах и ​​институциональной принадлежности.

1. Моралес Т., Басаран А.С., Вильегас Х.Е., Навас Д., Сориано Н., Мора Б., Редондо С., Батле Х., Шуллер И.К. Феномен обменного смещения: роль ферромагнитной спиновой структуры. физ. Преподобный Летт. 2015;114:097202. doi: 10.1103/PhysRevLett.114.097202. [PubMed] [CrossRef] [Google Scholar]

2. Meiklejohn W.P., Bean C.P. Новая магнитная анизотропия. физ. 1956; 102:1413. doi: 10.1103/PhysRev.102.1413. [CrossRef] [Google Scholar]

3. Блахович Т., Эрманн А. Обменное смещение в тонких пленках — обновление. Покрытия. 2021;11:122. дои: 10.3390/покрытия11020122. [CrossRef] [Google Scholar]

4. Блахович Т., Тилльманнс А., Фраун М., Гадими Р., Бесхотен Б., Гюнтеродт Г. Обменное смещение в эпитаксиальных бислоях CoO/Co с различной кристаллографической симметрией. физ. Ред. Б. 2007; 75:054425. doi: 10.1103/PhysRevB.75.054425. [CrossRef] [Google Scholar]

5. О’Грэйди К., Фернансез-Оутон Л.Е., Вальехо-Фернандес Г. Новая парадигма обменного смещения в поликристаллических тонких пленках. Дж. Магн. Магн. Матер. 2010; 322: 883–899. doi: 10.1016/j.jmmm.2009.12.011. [CrossRef] [Google Scholar]

6. Эрманн А., Блахович Б. Сдвиг горизонтальной петли, зависящий от угла и направления вращения, в эпитаксиальных бислоях Co/CoO на MgO(100) AIP Adv. 2017;7:115223. doi: 10.1063/1.4985032. [CrossRef] [Google Scholar]

7. Паркин С., Цзян С., Кайзер С., Панчула А., Рош К., Самант М. Магнито-инженерные датчики спинтроники и память. проц. IEEE. 2003; 91: 661–680. doi: 10.1109/JPROC.2003.811807. [CrossRef] [Google Scholar]

8. Anh Nguyen T.N., Fang Y., Fallahi V., Benatmane N., Mohseni S.M., Dumas R.K., Akerman J. Обменные пружины [Co/Pd]–NiFe с регулируемым углом наклона намагниченности . заявл. физ. лат. 2011;98:172502. doi: 10.1063/1.3580612. [CrossRef] [Google Scholar]

9. Bonfirm M., Ghiringhelli G., Montaigne F., Pizzini S., Brookes N.B., Petroff F., Vogel J., Camarero J., Fontaine A. Наносекундная намагниченность по элементам динамика в магнитных гетероструктурах. физ. Преподобный Летт. 2001;86:3646. doi: 10.1103/PhysRevLett.86.3646. [PubMed] [CrossRef] [Google Scholar]

10. Гаси Т., Наяк А.К., Винтерлик Дж., Ксенофонтов В., Адлер П., Никлас М., Фельсер К. Обменно-пружинное магнитное поведение тетрагонального Гейслера соединение Mn ₂ FeGa как кандидат на передачу крутящего момента. заявл. физ. лат. 2013;102:202402. doi: 10.1063/1.4807427. [CrossRef] [Google Scholar]

11. Meiklejohn W.H. Обменная анизотропия — обзор. Дж. Заявл. физ. 1962; 33:1328. doi: 10.1063/1.1728716. [CrossRef] [Google Scholar]

12. Nogués J., Schuller I.K. Предвзятость обмена. Дж. Магн. Магн. Матер. 1999;192:203–232. doi: 10.1016/S0304-8853(98)00266-2. [CrossRef] [Google Scholar]

13. Beschoten B., Keller J., Tillmanns A., Güntherodt G. Модель состояния предметной области для смещения обмена: обучающий эффект разбавленного Co _1-й O на обменном смещении в Co-CoO. IEEE транс. Магн. 2002; 38: 2744–2746. doi: 10.1109/TMAG. 2002.802866. [CrossRef] [Google Scholar]

14. Моралес Р., Ли З.-П., Оламит Дж., Лю К., Аламеда Дж.М., Шуллер И.К. Роль антиферромагнитной спиновой структуры Балка в обменном смещении. физ. Преподобный Летт. 2009;102:097201. doi: 10.1103/PhysRevLett.102.097201. [PubMed] [CrossRef] [Google Scholar]

15. Хан М.Ю., Ву С.-Б., Куч В. Закрепленные магнитные моменты в обменном смещении: роль антиферромагнитной объемной спиновой структуры. физ. Ред. Б. 2014; 89:094427. doi: 10.1103/PhysRevB.89.094427. [CrossRef] [Google Scholar]

16. Эрманн А., Комраус С., Блахович Т., Домино К., Нис М.К., Якобс П.Дж., Лейсте Х., Матес М., Шаршмидт М. Псевдообменное смещение из-за вращения анизотропия. Дж. Магн. Магн. Матер. 2016; 412:7–10. doi: 10.1016/j.jmmm.2016.03.071. [CrossRef] [Google Scholar]

17. Хенне Б., Ней В., де Соуза М., Ней А. Эффект обменного смещения нескомпенсированного антиферромагнетика. физ. Ред. Б. 2016; 93:144406. doi: 10.1103/PhysRevB.93.144406. [CrossRef] [Google Scholar]

18. Yoo T.H., Khym S., Yea S.-y., Lee S.H., Liu X., Furdyna J.K. Четыре дискретных состояния сопротивления Холла в однослойной пленке Fe для четырехкомпонентных устройств памяти. заявл. физ. лат. 2009;95:202505. doi: 10.1063/1.3266826. [CrossRef] [Google Scholar]

19. Донахью М.Дж., Портер Д.Г. Руководство пользователя OOMMF, версия 1.0, Межведомственный отчет NISTIR 6376. Национальный институт стандартов и технологий; Gaithersburg, MD, USA: 1999. [Google Scholar]

20. Гилберт Т.Л. Феноменологическая теория затухания в ферромагнитных материалах. IEEE транс. Магн. 2004;40:3443. doi: 10.1109/TMAG.2004.836740. [CrossRef] [Google Scholar]

21. Sudsom D., Juhász Junger I., Döpke C., Blachowicz T., Hahn L., Ehrmann A. Микромагнитное моделирование развития вихрей в магнитных двухматериальных структурах-бабочках. конд. Иметь значение. 2020;5:5. doi: 10.3390/condmat5010005. [CrossRef] [Google Scholar]

22. Коуберн Р.П., Адейе А.О., Велланд М.Е. Конфигурационная анизотропия в наномагнетиках.