Что такое логические элементы и как они работают. Как выглядят таблицы истинности для основных логических операций. Какие законы алгебры логики существуют. Как применяются логические элементы в вычислительной технике.
Что такое алгебра логики и логические элементы
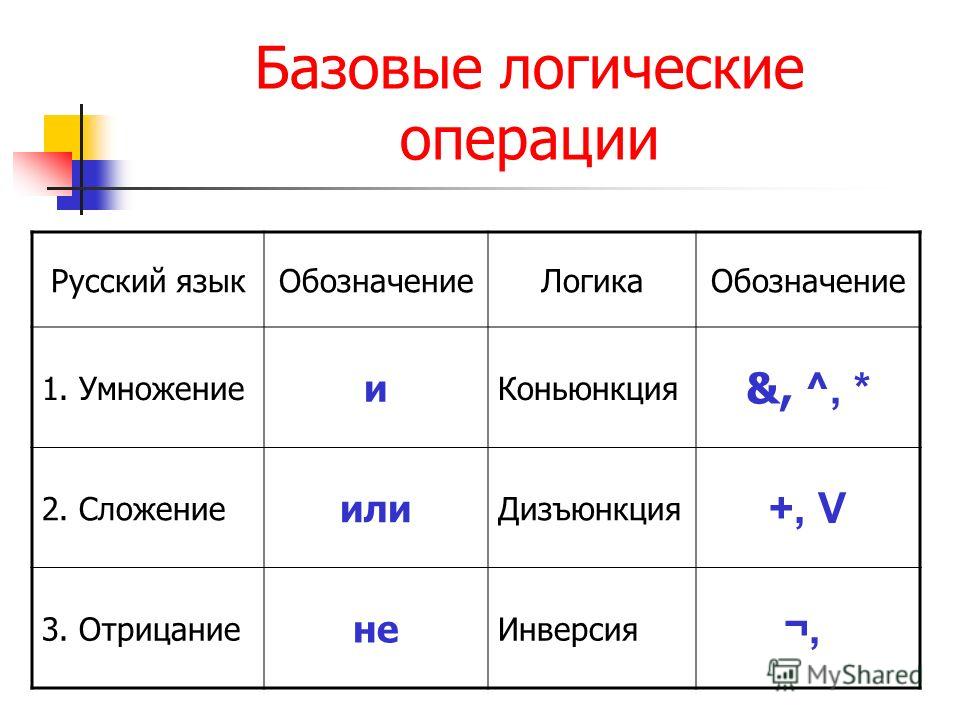
Алгебра логики — это раздел математики, изучающий логические операции и выражения. Основными объектами алгебры логики являются логические переменные, которые могут принимать только два значения — истина (1) или ложь (0).
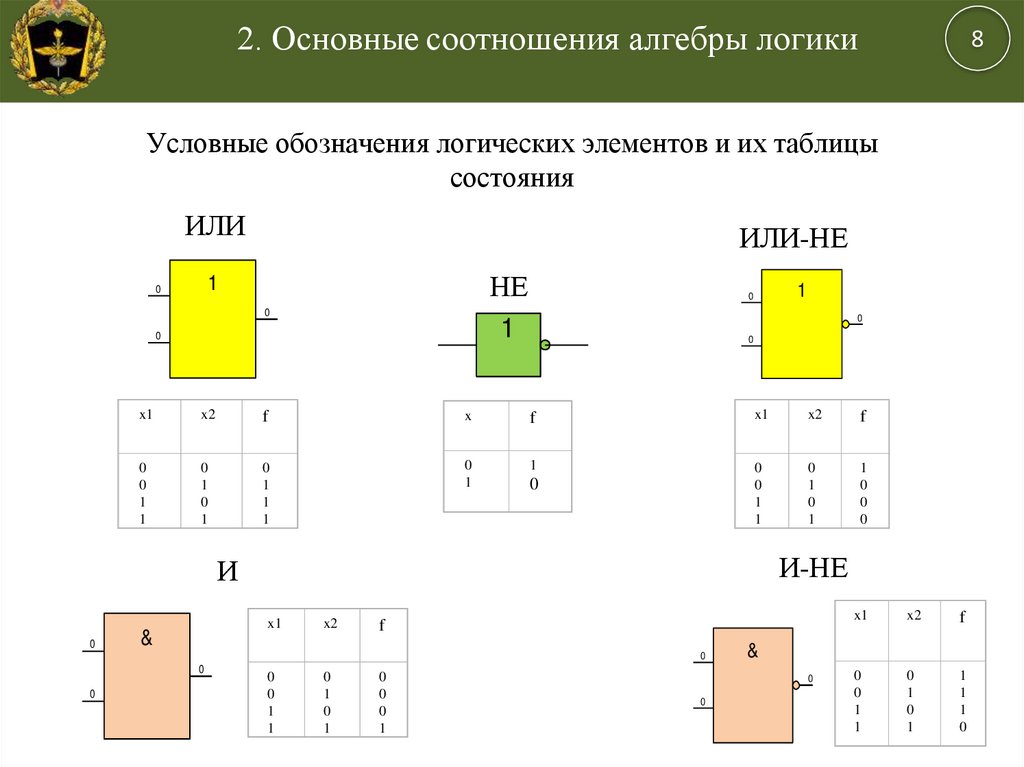
Логические элементы — это устройства, реализующие базовые логические операции. Основными логическими элементами являются:
- Элемент И (конъюнкция)
- Элемент ИЛИ (дизъюнкция)
- Элемент НЕ (инверсия)
Эти элементы позволяют строить более сложные логические схемы и выражения. Работа логических элементов описывается с помощью таблиц истинности.
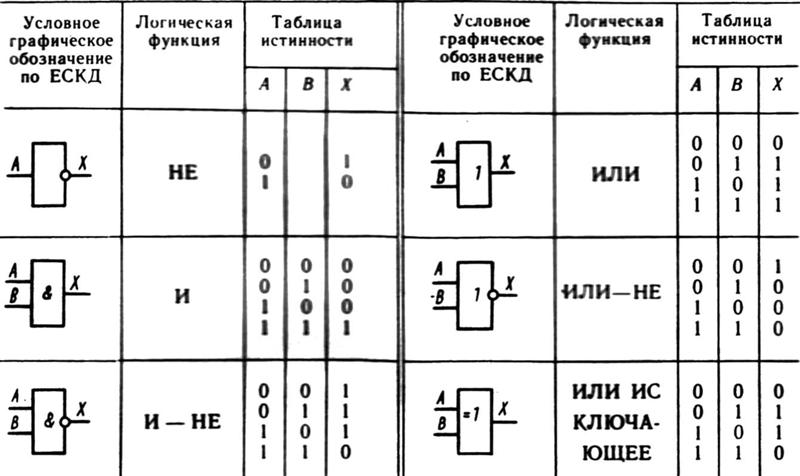
Таблицы истинности основных логических операций
Таблица истинности — это таблица, описывающая поведение логического элемента или выражения для всех возможных комбинаций входных значений.
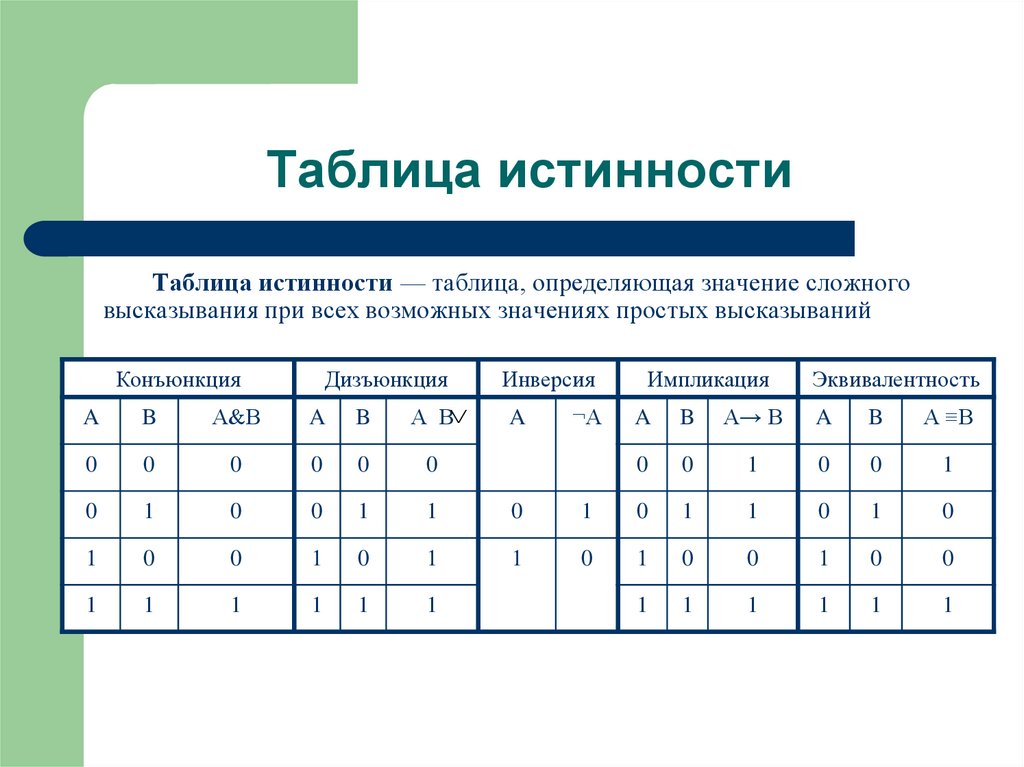
Таблица истинности операции И (конъюнкция)
| A | B | A И B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Операция И возвращает истину только если все входные значения истинны.
Таблица истинности операции ИЛИ (дизъюнкция)
| A | B | A ИЛИ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Операция ИЛИ возвращает истину, если хотя бы одно из входных значений истинно.
Таблица истинности операции НЕ (инверсия)
| A | НЕ A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Операция НЕ инвертирует входное значение.
Основные законы алгебры логики
Алгебра логики подчиняется ряду законов, позволяющих упрощать и преобразовывать логические выражения:
- Закон коммутативности: A И B = B И A, A ИЛИ B = B ИЛИ A
- Закон ассоциативности: (A И B) И C = A И (B И C), (A ИЛИ B) ИЛИ C = A ИЛИ (B ИЛИ C)
- Закон дистрибутивности: A И (B ИЛИ C) = (A И B) ИЛИ (A И C)
- Законы де Моргана: НЕ(A И B) = (НЕ A) ИЛИ (НЕ B), НЕ(A ИЛИ B) = (НЕ A) И (НЕ B)
Эти законы позволяют упрощать сложные логические выражения и строить оптимальные логические схемы.
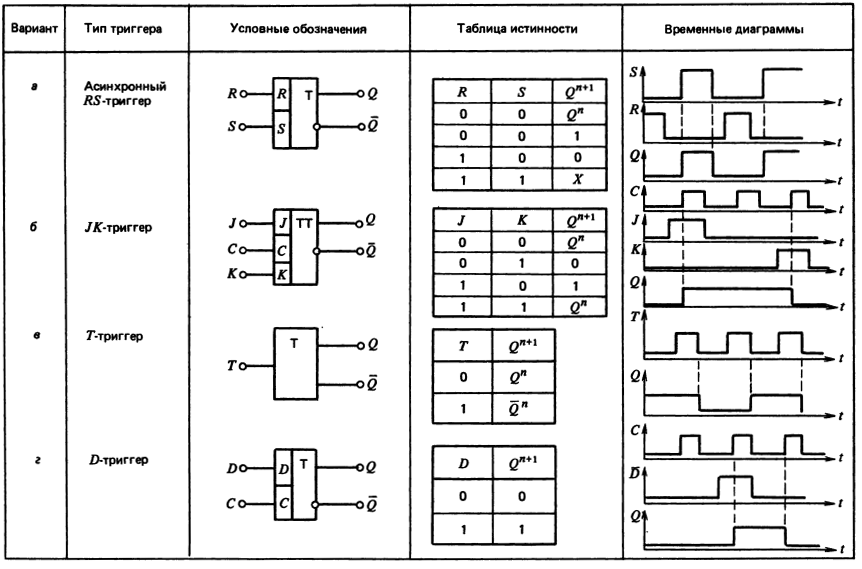
Как применяются логические элементы в вычислительной технике
Логические элементы являются основой работы цифровых устройств и компьютеров. Они используются для построения:
- Арифметико-логических устройств
- Устройств управления
- Триггеров и регистров памяти
- Шифраторов и дешифраторов
- Мультиплексоров и демультиплексоров
С помощью логических элементов реализуются все вычислительные и управляющие операции в цифровых системах. Поэтому понимание принципов работы логических элементов крайне важно для разработки цифровой электроники и программного обеспечения.
Виды логических элементов
Помимо базовых логических элементов И, ИЛИ и НЕ существуют также другие виды логических элементов:
- Исключающее ИЛИ (XOR)
- И-НЕ (NAND)
- ИЛИ-НЕ (NOR)
- Импликация
- Эквивалентность
Эти элементы позволяют более компактно реализовывать сложные логические функции. Например, элемент И-НЕ (NAND) является функционально полным, то есть с его помощью можно реализовать любую логическую функцию.
Логические выражения и их минимизация
Логические выражения — это формулы, описывающие логические функции с помощью логических операций и переменных. Например:
F = (A И B) ИЛИ (НЕ A И C)
Минимизация логических выражений позволяет упростить их и сократить количество используемых логических элементов. Для минимизации применяются:
- Законы алгебры логики
- Карты Карно
- Метод Квайна-Мак-Класки
Минимизация особенно важна при разработке цифровых устройств, так как позволяет сократить их сложность и энергопотребление.
Применение логических элементов в программировании
Логические элементы и операции широко используются в программировании:
- Для построения условных выражений и ветвлений
- В битовых операциях
- При работе с булевыми переменными
- Для оптимизации алгоритмов
Понимание принципов работы логических элементов помогает писать более эффективный и оптимизированный код. Например, использование битовых операций вместо арифметических может значительно ускорить работу программы.
Синтез логических схем
Синтез логических схем — это процесс построения логической схемы по заданной логической функции. Он включает следующие этапы:
- Составление таблицы истинности функции
- Запись логического выражения
- Минимизация выражения
- Построение логической схемы
При синтезе стремятся получить схему с минимальным количеством логических элементов, удовлетворяющую заданным требованиям по быстродействию и надежности.
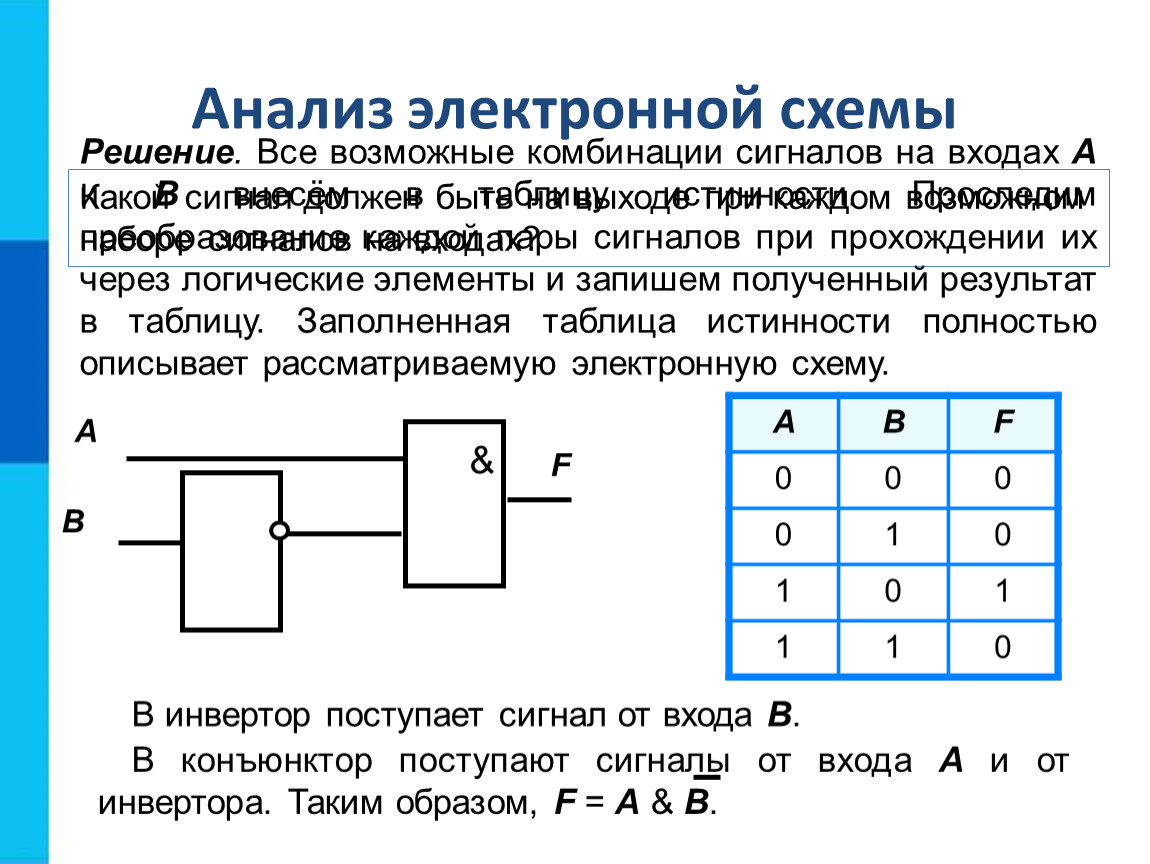
|
Логика очень древняя наука. Ещё в античные времена была известна формальная логика, позволяющая делать заключения о правильности какого-либо суждения не по его фактическому содержанию, а только по форме его построения. Например, уже в древности был известен закон исключения третьего. Его содержательная трактовка была такова: «Во время своих странствований Платон был в Египте ИЛИ не был Платон в Египте». Ещё один закон, известный в древности — закон отрицания: «Если НЕ верно, что Платон НЕ был в Египте, то значит, Платон был в Египте». Формальная логика основана на “высказываниях”. “Высказывание” — это основной элемент логики, определяемый как повествовательное предложение, относительно которого можно однозначно сказать, истинное или ложное утверждение оно содержит. 
Например: Листва на деревьях опадает осенью. Земля прямоугольная. Первое высказывание содержит истинную информацию, а второе — ложную. Вопросительное, побудительное и восклицательное предложения не являются высказываниями, так как в них ничего не утверждается и не отрицается. Пример предложений, не являющихся высказываниями: Не пейте сырую воду! Кто не хочет быть счастливым? Высказывания могут быть и такими: 2>1, Н2О+SO3=h3SO4. Здесь используются языки математических символов и химических формул. Приведённые выше примеры высказываний являются простыми. Но из простых высказываний можно получить сложные, объединив их с помощью логических связок. Логические связки — это слова, которые подразумевают определённые логические связи между высказываниями. Основные логические связки издавна употребляются не только в научном языке, но и в обыденном, — это “и”, “или”, “не”, “если … то”, “либо . 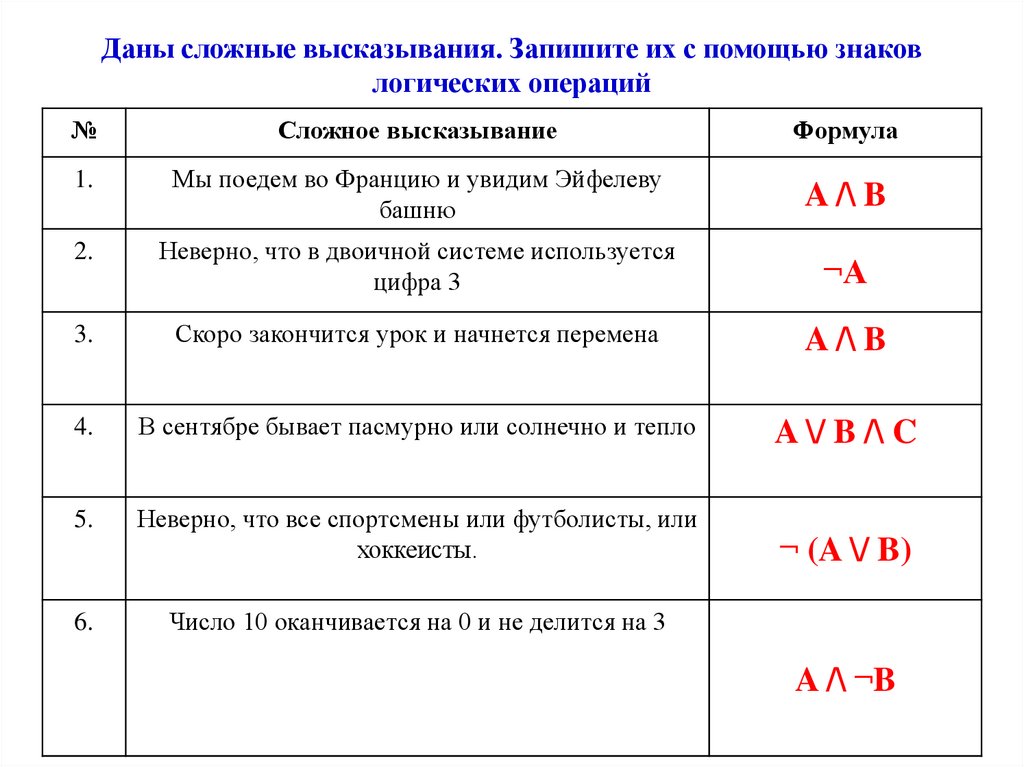 .. либо” и другие известные нам из русского языка связки. В рассмотренных нами трёх законах формальной логики использовались связки “и”, “или”, “не”, “если … то” для связи простых высказываний в сложные. .. либо” и другие известные нам из русского языка связки. В рассмотренных нами трёх законах формальной логики использовались связки “и”, “или”, “не”, “если … то” для связи простых высказываний в сложные.
Формальная логика была известна в средневековой Европе, она развивалась и обогащалась новыми законами и правилами, но при этом вплоть до 19 века она оставалась обобщением конкретных содержательных данных и её законы сохраняли форму высказываний на разговорном языке. В 1847 году английский математик Джордж Буль, преподаватель провинциального университета в маленьком городке Корке на юге Англии разработал алгебру логики. Алгебра логики очень проста, так как каждая переменная может принимать только два значения: истинно или ложно. Трудность изучения алгебры логики возникает из-за того, что для обозначения переменных принимают символы 0 и 1, которые по написанию совпадают с обычными арифметическими единицей и нулём. Но совпадение это только внешнее, так как смысл они имеют совсем иной. Логическая 1 означает, что какое-то событие истинно, в противоположность этому логический 0 означает, что высказывание не соответствует истине, т.е. ложно. Высказывание заменилось на логическое выражение, которое строится из логических переменных (А, В, Х, …) и логических операций (связок). В алгебре логики знаки операций обозначают лишь три логические связки ИЛИ, И, НЕ. 1.Логическая операция ИЛИ. Логическую функцию принято задавать в виде таблицы. В левой части этой таблицы перечисляются все возможные значения 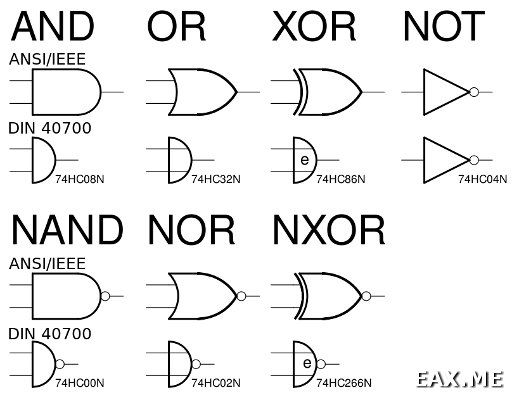 Для элементарных функций получается таблица истинности данной логической операции. Для операции ИЛИ таблица истинности имеет вид: Для элементарных функций получается таблица истинности данной логической операции. Для операции ИЛИ таблица истинности имеет вид:
Операцию ИЛИ называют также логическим сложением, и потому её можно обозначать знаком «+».
Из таблицы истинности следует, что операция И — это логическое умножение, которое ничем не отличается от традиционно известного умножения в обычной алгебре. В формальной логике операции логического умножения соответствуют связки и, а, но, хотя.
Читается в обоих случаях одинаково «Не А». Таблица истинности для этой функции имеет вид: В вычислительной технике операцию НЕ называют отрицанием или инверсией, операцию ИЛИ — дизъюнкцией, операцию И — конъюнкцией. Набор логических функций “И”, “ИЛИ”, “НЕ” является функционально полным набором или базисом алгебры логики. С помощью него можно выразить любые другие логические функции, например операции “строгой дизъюнкции”, “импликации” и “эквивалентности” и др. Операция “строгая дизъюнкция” выражается через логические функции “И”, “ИЛИ”, “НЕ” любой из двух логических формул: и иначе называется операцией неравнозначности или “сложения по модулю 2”, так как при сложении чётного количества единиц, результатом будет “0”, а при сложении нечётного числа единиц, результат станет равен “1”.
Операцию “импликация” можно обозначить по-разному: Эти выражения эквивалентны и читаются одинаково: «Игрек равен импликации от А и В». Логическая операция “эквивалентность” (равнозначность). Этой логической операции соответствуют логические связки “если и только если”, «тогда и только тогда, когда». Таблица истинности для этой функции имеет вид: Операция “эквивалентность” обозначается по-разному. Выражения обозначают одно и тоже, и можно сказать, что А эквивалентна В, если и только если они равнозначны. Логическая операция “эквивалентность” выражается через логические функции “И”, “ИЛИ”, “НЕ” в виде логической формулы С помощью алгебры логики можно очень кратко записать законы формальной логики и дать им математически строгое доказательство. В алгебре логики, как в элементарной, справедливы переместительный (закон коммутативности), сочетательный (закон ассоциативности) и распределительный (закон дистрибутивности) законы, а также аксиома идемпотентности (отсутствие степеней и коэффициэнтов) и др., в записях которых используются логические переменные, принимающие только два значения — логический ноль и логическая единица. Применение этих законов позволяет производить упрощение логических функций, т.е. находить для них выражения, имеющие наиболее простую форму. Основные аксиомы и законы алгебры логики приведены в таблице: |
|
||
Логические выражения и операторы. Урок 6 курса «Python. Введение в программирование»
Логические выражения и логический тип данных
Часто в реальной жизни мы соглашаемся с каким-либо утверждением или отрицаем его. Например, если вам скажут, что сумма чисел 3 и 5 больше 7, вы согласитесь, скажете: «Да, это правда». Если же кто-то будет утверждать, что сумма трех и пяти меньше семи, то вы расцените такое утверждение как ложное.
Подобные фразы предполагают только два возможных ответа – либо «да», когда выражение оценивается как правда/истина, либо «нет», когда утверждение оценивается как ошибочное/ложное. В программировании и математике если результатом вычисления выражения может быть лишь истина или ложь, то такое выражение называется логическим.
Например, выражение 4 > 5 является логическим, так как его результатом является либо правда, либо ложь.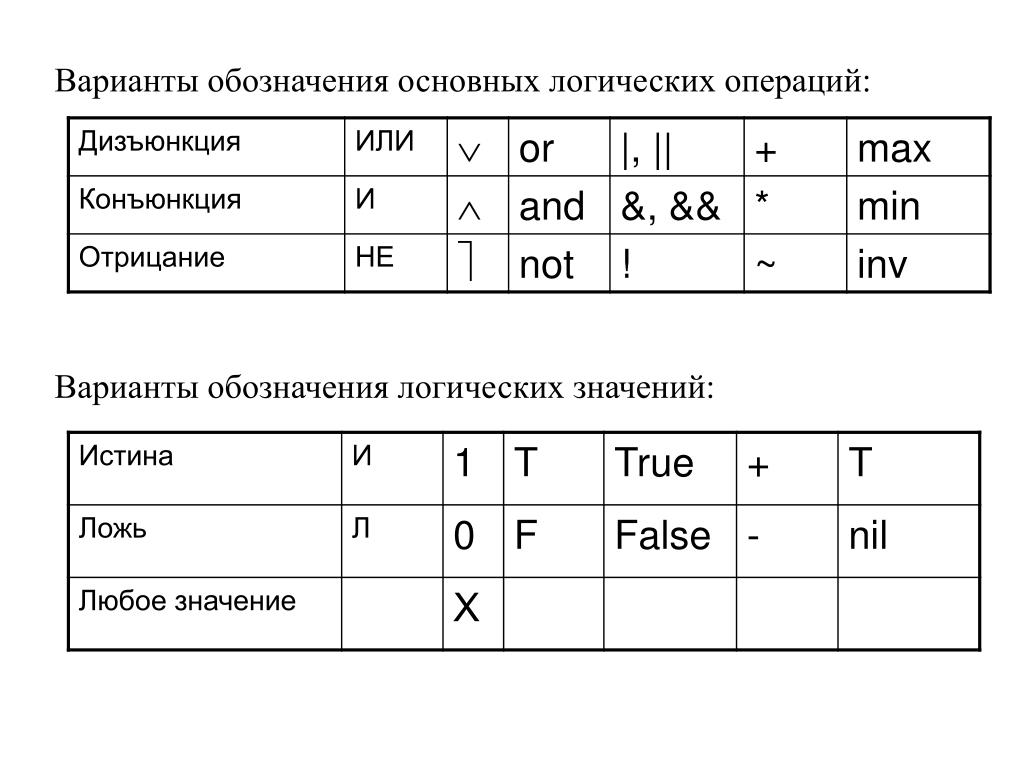 Выражение 4 + 5 не является логическим, так как результатом его выполнения является число.
Выражение 4 + 5 не является логическим, так как результатом его выполнения является число.
На позапрошлом уроке мы познакомились с тремя типами данных – целыми и вещественными числами, а также строками. Сегодня введем четвертый – логический тип данных (тип bool). Его также называют булевым. У этого типа всего два возможных значения: True (правда) и False (ложь).
>>> a = True >>> type(a) <class 'bool'> >>> b = False >>> type(b) <class 'bool'>
Здесь переменной a было присвоено значение True, после чего с помощью встроенной в Python функции type() проверен ее тип. Интерпретатор сообщил, что это переменная класса bool. Понятия «класс» и «тип данных» в данном случае одно и то же. Переменная b также связана с булевым значением.
В программировании False обычно приравнивают к нулю, а True – к единице.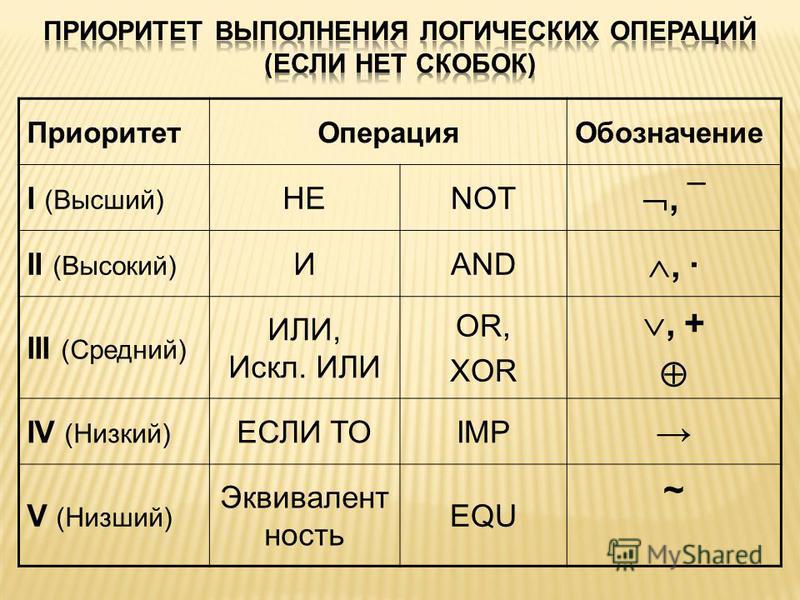 Чтобы в этом убедиться, можно преобразовать булево значение к целочисленному типу:
Чтобы в этом убедиться, можно преобразовать булево значение к целочисленному типу:
>>> int(True) 1 >>> int(False) 0
Возможно и обратное. Можно преобразовать какое-либо значение к булевому типу:
>>> bool(3.4)
True
>>> bool(-150)
True
>>> bool(0)
False
>>> bool(' ')
True
>>> bool('')
False
И здесь работает правило: всё, что не 0 и не пустота, является правдой.
Логические операторы
Говоря на естественном языке (например, русском) мы обозначаем сравнения словами «равно», «больше», «меньше». В языках программирования используются специальные знаки, подобные тем, которые используются в математике: > (больше), < (меньше), >= (больше или равно), <= (меньше или равно), == (равно), != (не равно).
Не путайте операцию присваивания значения переменной, обозначаемую в языке Python одиночным знаком «равно», и операцию сравнения (два знака «равно»). Присваивание и сравнение – разные операции.
Присваивание и сравнение – разные операции.
>>> a = 10 >>> b = 5 >>> a + b > 14 True >>> a < 14 - b False >>> a <= b + 5 True >>> a != b True >>> a == b False >>> c = a == b >>> a, b, c (10, 5, False)
В данном примере выражение c = a == b состоит из двух подвыражений. Сначала происходит сравнение (==) переменных a и b. После этого результат логической операции присваивается переменной c. Выражение a, b, c просто выводит значения переменных на экран.
Сложные логические выражения
Логические выражения типа kbyte >= 1023 являются простыми, так как в них выполняется только одна логическая операция. Однако, на практике нередко возникает необходимость в более сложных выражениях. Может понадобиться получить ответа «Да» или «Нет» в зависимости от результата выполнения двух простых выражений. Например, «на улице идет снег или дождь», «переменная news больше 12 и меньше 20″.
Например, «на улице идет снег или дождь», «переменная news больше 12 и меньше 20″.
В таких случаях используются специальные операторы, объединяющие два и более простых логических выражения. Широко используются два оператора – так называемые логические И (and) и ИЛИ (or).
Чтобы получить True при использовании оператора and, необходимо, чтобы результаты обоих простых выражений, которые связывает данный оператор, были истинными. Если хотя бы в одном случае результатом будет False, то и все сложное выражение будет ложным.
Чтобы получить True при использовании оператора or, необходимо, чтобы результат хотя бы одного простого выражения, входящего в состав сложного, был истинным. В случае оператора or сложное выражение становится ложным лишь тогда, когда ложны оба составляющие его простые выражения.
Допустим, переменной x было присвоено значение 8 (x = 8), переменной y присвоили 13 (y = 13). Логическое выражение
Логическое выражение y < 15 and x > 8 будет выполняться следующим образом. Сначала выполнится выражение y < 15. Его результатом будет True. Затем выполнится выражение x > 8. Его результатом будет False. Далее выражение сведется к True and False, что вернет False.
>>> x = 8 >>> y = 13 >>> y < 15 and x > 8 False
Если бы мы записали выражение так: x > 8 and y < 15, то оно также вернуло бы False. Однако сравнение y < 15 не выполнялось бы интерпретатором, так как его незачем выполнять. Ведь первое простое логическое выражение (x > 8) уже вернуло ложь, которая, в случае оператора and, превращает все выражение в ложь.
В случае с оператором or второе простое выражение проверяется, если первое вернуло ложь, и не проверяется, если уже первое вернуло истину. Так как для истинности всего выражения достаточно единственного
Так как для истинности всего выражения достаточно единственного True, неважно по какую сторону от or оно стоит.
>>> y < 15 or x > 8 True
В языке Python есть еще унарный логический оператор not, то есть отрицание. Он превращает правду в ложь, а ложь в правду. Унарный он потому, что применяется к одному выражению, стоящему после него, а не справа и слева от него как в случае бинарных and и or.
>>> not y < 15 False
Здесь у < 15 возвращает True. Отрицая это, мы получаем False.
>>> a = 5 >>> b = 0 >>> not a False >>> not b True
Число 5 трактуется как истина, отрицание истины дает ложь. Ноль приравнивается к False. Отрицание False дает True.
Практическая работа
-
Присвойте двум переменным любые числовые значения.
-
Используя переменные из п. 1, с помощью оператора
andсоставьте два сложных логических выражения, одно из которых дает истину, другое – ложь. -
Аналогично выполните п. 2, но уже с оператором
or. -
Попробуйте использовать в логических выражениях переменные строкового типа. Объясните результат.
-
Напишите программу, которая запрашивала бы у пользователя два числа и выводила бы
TrueилиFalseв зависимости от того, больше первое число второго или нет.
Примеры решения и дополнительные уроки в pdf-версии курса
Полный список логических символов
В философии и математике логика играет ключевую роль в формализации действительных дедуктивных выводов и других форм рассуждений. Ниже приводится полный список наиболее известных символов в логике, включающий символы из логики высказываний, логики предикатов, булевой логики и модальной логики.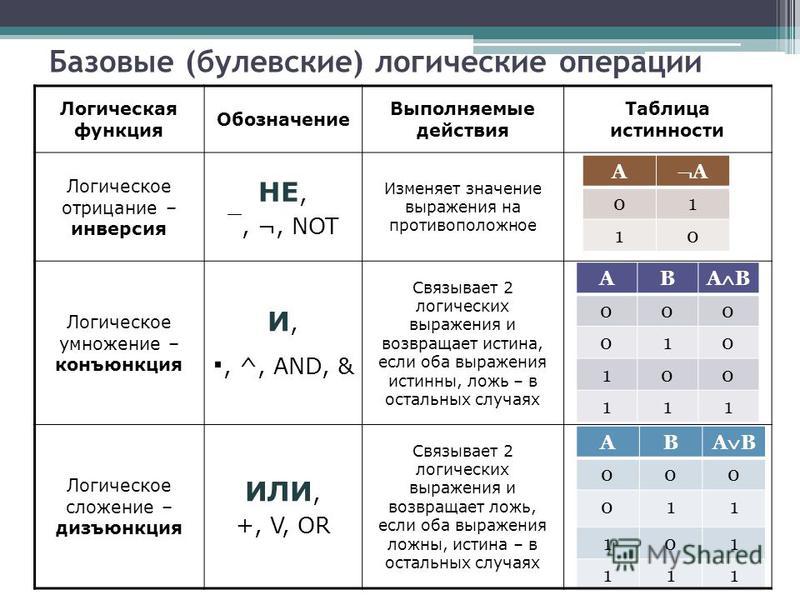
Для удобства чтения эти символы разделены по функциям на таблицы . Другие полные списки символов — с разбивкой по темам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации).
Содержание
Предпочитаете версию в формате PDF?
Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.
Да. Это было бы полезно.
Константы
В логике константы часто используются для обозначения определенных объектов в логической системе. В следующей таблице представлены наиболее примечательные из них, а также их соответствующий пример и значение.
| Symbol Name | Explanation | Example |
|---|---|---|
| $a, b, c$ | General constants (within a logical system) | $b \ge a_1 + a_2$ |
| $\mathbb{B}$ | Логическая область | В булевой логике $\mathbb{B} = \{ 0 ,1\}$. |
| $\top$ (или $1$ в булевой логике) | Тавтология , Значение истинности «истина» | $P \lor \lnot P \equiv \top$ |
| $\bot$ (или $0$ в булевой логике) | Противоречие , $Q30 Значение истинности’ | ‘ложь \land \lnot Q \equiv \bot$
Переменные
Как и в других областях математики, переменных используются в качестве символов-заполнителей для различных объектов в логике. В следующей таблице представлены наиболее примечательные из них, а также их соответствующий пример и значение.
| Название символа | Объяснение | Пример | |
|---|---|---|---|
| $ x, y, w, z $ | . {x}, \mathbf{y}, \mathbf{w}, \mathbf{z}$ | Метапеременные для количественных переменных | Для всех переменных $\mathbf{x}_1$ и $\mathbf{x} _2$, ‘$\mathbf{x}_1 = \mathbf{x}_2$’ — это формула. |
| $f, g, h$ | Функциональные символы | $h\left( f_1(x), g(x, y) \right)$ | |
| $\mathbf{s}, \mathbf{ t}$ | Метапеременные для термов | Для всех термов $\mathbf{t}_1$ и $\mathbf{t}_2$, ‘$f(\mathbf{t}_1, \mathbf{t}_2 )$’ является термином. | |
| $P, Q, R$ | Пропозициональные / Предикатные символы | $P(x, a) \land Q_1(z)$ | Метапеременные для формул | Для всех формул $\alpha$ и $\beta$, $\alpha \land \beta \equiv \beta \land \alpha$. |
| $\Sigma, \Phi, \Psi$ | Метапеременные для наборов предложений | Если $\Sigma$ несовместима, то $\Sigma \cup \Phi$ несовместима. | |
| $\mathcal{L}$ | Метапеременная для формальных языков | формула в $\mathcal{L}$. |
Операторы
Операторы — это символы, используемые для обозначения математических операций, которые служат для преобразования одного или нескольких входных данных в аналогичный выходной. В логике к этим операторам относятся логические связки из пропозициональной/модальной логики, кванторы из логики предикатов, а также другие операторы, связанные с синтаксической подстановкой и семантическим оцениванием.
Унарные логические связки
| Имя символа | Пояснение | Пример |
|---|---|---|
| $\lnot P$, $\sim\!\!P$, $\overline{P}$ | Отрицание $P$ (не $P$) | $\lnot \lnot P \equiv P$ |
| $\Diamond P$ | Возможно $P$ | Если $\Diamond P$, то $\Diamond \Diamond P$. |
| $\Box P$ | Обязательно $P$ | Если $\Box P$, то $\neg \Diamond \neg P$.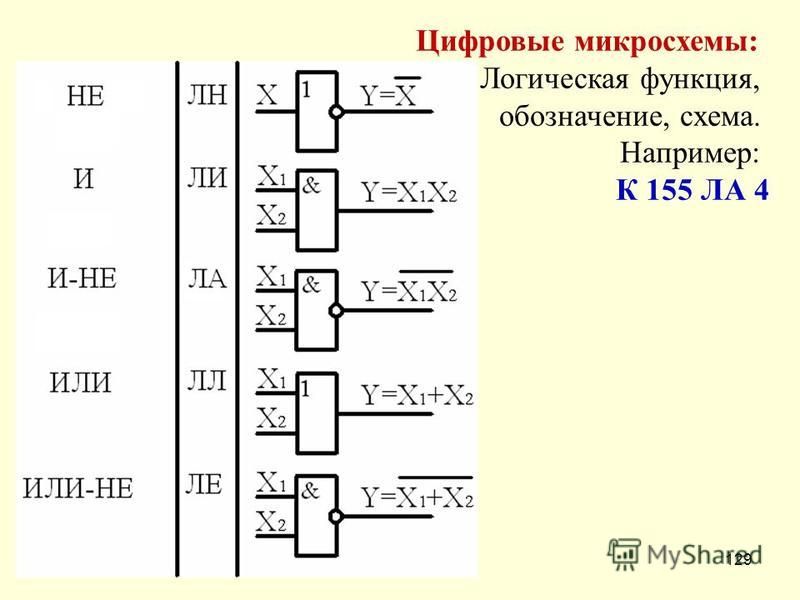 |
двоичных логических соединений
| Название символа | Объяснение | Пример |
|---|---|---|
| $ P \ Land Q $ | CONCUNCTION ($ P $ Q QU QU QU QU QU QU QU QU QU QU QU QU QU QU QU QU QU QU QU QU QU QU QU Q QU QU QU QU QU QU QU QU QU QU QU QU QU QU QUST QU QU QUST | |
| $. P \equiv P$ | ||
| $P \lor Q$ | Дизъюнкция ($P$ или $Q$) | $\neg (P \lor Q) \equiv$ $\neg P \ земля \neg Q$ |
| $P \veebar Q$, $P \oplus Q$ | Эксклюзивная дизъюнкция ($P$ xor $Q$) | $P \oplus Q \equiv$ $(P \lor Q) \land \neg(P \land Q)$ |
| $P \uparrow Q$ | Отрицание конъюнкции ($P$ nand $Q$) | $P \uparrow Q \equiv \neg (P \land Q)$ |
| $P \downarrow Q$ | Отрицание дизъюнкция ($P$ или $Q$) | $P \downarrow Q \equiv \\ (\neg P \land \neg Q)$ |
| $P \to Q$ | Условное (Если $P$, то $Q$) | Для всех $P$, $P\to P$ является тавтологией. |
| $P \not\to Q$ | Безусловный (Не ‘если $P$, то $Q$’) | $P \not\to Q \equiv P \land \neg Q$ |
| $P \leftarrow Q$ | Обратное условное (Если $Q$, то $P$) | $Q \leftarrow (P \land Q)$ |
| not\leftarrow Q$ | Обратное безусловное (Не ‘если $Q$, то $P$’) | $(P \to Q) \land \\ (P \not\leftarrow Q)$ |
| $P \leftrightarrow Q$ | Бикондиционал ($P$ тогда и только тогда, когда $Q$) | $P \leftrightarrow Q \equiv$ $(P \to Q) \land (P \leftarrow Q)$ |
| $P \not \leftrightarrow Q$ | Безусловный (Не ‘$P$ тогда и только тогда, когда $Q$’) | Если $P \not\to Q$, то $P \not\leftrightarrow Q$. |
| $\существует ! \mathbf{x}$ | Квантификация уникальности (Существует единственный $\mathbf{x}$) | $\exists !\, q, r \in \mathbb{Z}\,$ $( n=dq+r \, \land$ $0 \le|r| |
| $\mathrm{N} \mathbf{x}$, $\nexists \mathbf{x}$ | Квантификация несуществования ($\mathbf{x}$ не существует) | $\mathrm{N}x P(x) \equiv \\ \forall x \, \neg P(x)$ |
| $\exists_n\mathbf{x}$ | Численная квантификация (имеется ровно $n$ $\mathbf{x}$) | $\exists_3 x \in \mathbb{Z}\, (5 < x < 9)$ |
| $ \exists_{\ge n} \mathbf{x}$ | Числовая квантификация (Существует не менее $n$ $\mathbf{x}$) | $\exists_{\ge 2} x \, Q (x) \equiv$ $\exists x \exists y \, (Q(x) \land$ $Q(y) \land x \ne y)$ |
| $\exists_{\le n} \mathbf{x}$ | Численный количественный анализ 92 + 5$ | |
| $\mathbf{\alpha}[\mathbf{x}/\mathbf{t_0}]$ | Формула подстановки (формула $\mathbf{\alpha}$ со свободными вхождениями $\mathbf{x}$ заменяется термином $\mathbf{t_0}$) | $(\forall x (x = y)) [x/a] =$ $\forall x (x = y)$ |
Операторы на основе оценки
| Символ Название | Объяснение | Пример |
|---|---|---|
{\ сигма (х / и)} = \ топ $. |
Реляционные символы
В логике реляционные символы играют ключевую роль в превращении одной или нескольких математических единиц в формулы и предложения и могут встречаться как внутри логической системы, так и вне ее (как металогические символы). В следующей таблице представлены наиболее примечательные из этих символов, а также их соответствующее значение и пример.
| Символ Название | Пояснение | Пример |
|---|---|---|
| $\mathbf{t}_1 = \mathbf{t}_2$ | Идентификационный символ в логической системе с равенством | ‘1($\neg \left ) \right)$’ — формула языка арифметики первого порядка. |
| $\альфа\! \ подразумевает \! \beta$ | Предложение $\alpha$ подразумевает предложение $\beta$ | $\forall x \, (x \ge 1) \! \подразумевает 1 \ge 1$ |
| $\альфа \! \подразумевается\! \бета$ | Предложение $\alpha$ следует из предложения $\beta$ | $5 \mid x \! \подразумевается\! 5 \mid 7x$ |
| $\alpha \equiv \beta$, $\alpha \Leftrightarrow \beta$, $\alpha \! \ифф\! \beta$ | Предложения $\alpha$ и $\beta$ логически эквивалентны | $\neg (P \to Q) \equiv \\ P \land \neg Q$ |
| $\sigma \ модели \alpha$ | Оценка $\sigma$ удовлетворяет формуле $\alpha$ | 9{\sigma} = \top$, затем $\sigma\models\phi$.|
| $\Phi \models \phi$ | Множество предложений $\Phi$ влечет за собой предложения $\phi$ ($\phi$ является логическим следствием $\Phi$) | Если $\ Phi\models\phi$, затем $\Phi\cup\Psi\models\phi$. |
| $\Phi \nvDash \phi$ | Набор предложений $\Phi$ не влечет за собой предложение $\phi$ | $\{P \to Q, Q \to R \} \nvDash R $ |
| $\модели\фи$ | Предложение $\phi$ является тавтологией | $\models \forall x \, (x = x)$ |
| $\Phi \vdash \phi$ | Набор предложений $\Phi$ доказывает предложения $\phi$ | $\forall x \, P(x,a) \vdash \\ P(a,a)$ |
| $\Phi \nvdash \phi$ | Набор предложений $ \Phi$ не доказывает предложения $\phi$ | $\exists x \, R(x) \nvdash R(a)$ |
| $\vdash \phi$ | {\circ}$ | |
| $\Phi \следовательно \phi$ | $\Phi$, следовательно $\phi$ | $P \lor Q, \neg P \\ \следовательно Q$ |
Основной список символов см. в разделе математические символы. Списки символов, классифицированных по типу и предмету , см. на соответствующих страницах ниже.
в разделе математические символы. Списки символов, классифицированных по типу и предмету , см. на соответствующих страницах ниже.
Предпочитаете версию в формате PDF?
Получите основную сводку математических символов в электронной книге , форма — вместе с использованием каждого символа и кодом LaTeX.
Да. Это было бы полезно.
Дополнительные ресурсы. процесс более упорядоченный, более эффективный и менее болезненный
404: страница не найдена
Страница, которую вы пытались открыть по этому адресу, похоже, не существует. Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства.
Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства.
Что я могу сделать сейчас?
Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся. Вот куда вы можете пойти отсюда:
Поиск- Пожалуйста, свяжитесь с нами, чтобы сообщить, что эта страница отсутствует, или используйте поле выше, чтобы продолжить поиск
- Наша страница «О нас» содержит дополнительную информацию о сайте, на котором вы находитесь, WhatIs.com.
- Посетите нашу домашнюю страницу и просмотрите наши технические темы
Поиск по категории
Сеть
-
ACK (подтверждение)
В некоторых протоколах цифровой связи ACK — сокращение от «подтверждение» — относится к сигналу, который устройство посылает, чтобы указать…
-
поставщик сетевых услуг (NSP)
Поставщик сетевых услуг (NSP) — это компания, которая владеет, управляет и продает доступ к магистральной инфраструктуре Интернета и .
 ..
.. -
неэкранированная витая пара (UTP)
Неэкранированная витая пара (UTP) — это повсеместно распространенный тип медных кабелей, используемых в телефонной проводке и локальных сетях (LAN).
Безопасность
-
Требования PCI DSS 12
Требования PCI DSS 12 представляют собой набор мер безопасности, которые предприятия должны внедрить для защиты данных кредитных карт и соблюдения …
-
данные держателя карты (CD)
Данные держателя карты (CD) — это любая личная информация (PII), связанная с лицом, у которого есть кредитная или дебетовая карта.
-
Уровни продавца PCI DSS
Стандарт безопасности данных индустрии платежных карт (PCI DSS)
ранжирует продавцов по количеству транзакций за …
ИТ-директор
-
системное мышление
Системное мышление — это целостный подход к анализу, который фокусируется на том, как взаимодействуют составные части системы и как.
 ..
.. -
краудсорсинг
Краудсорсинг — это практика обращения к группе людей для получения необходимых знаний, товаров или услуг.
-
синтетические данные
Синтетические данные — это информация, созданная искусственно, а не в результате событий реального мира.
HRSoftware
-
вовлечения сотрудников
Вовлеченность сотрудников — это эмоциональная и профессиональная связь, которую сотрудник испытывает к своей организации, коллегам и работе.
-
кадровый резерв
Кадровый резерв — это база данных кандидатов на работу, которые могут удовлетворить немедленные и долгосрочные потребности организации.
-
разнообразие, равенство и инклюзивность (DEI)
Разнообразие, равенство и инклюзивность — термин, используемый для описания политики и программ, которые способствуют представительству и .


 В такой форме это или любое другое выражение будут правильны (тогда говорили: истинно). Ничего другого быть не может: Платон либо был, либо не был в Египте — третьего не дано.
В такой форме это или любое другое выражение будут правильны (тогда говорили: истинно). Ничего другого быть не может: Платон либо был, либо не был в Египте — третьего не дано.

 Операцию И можно обозначить знаком по-разному:
Операцию И можно обозначить знаком по-разному: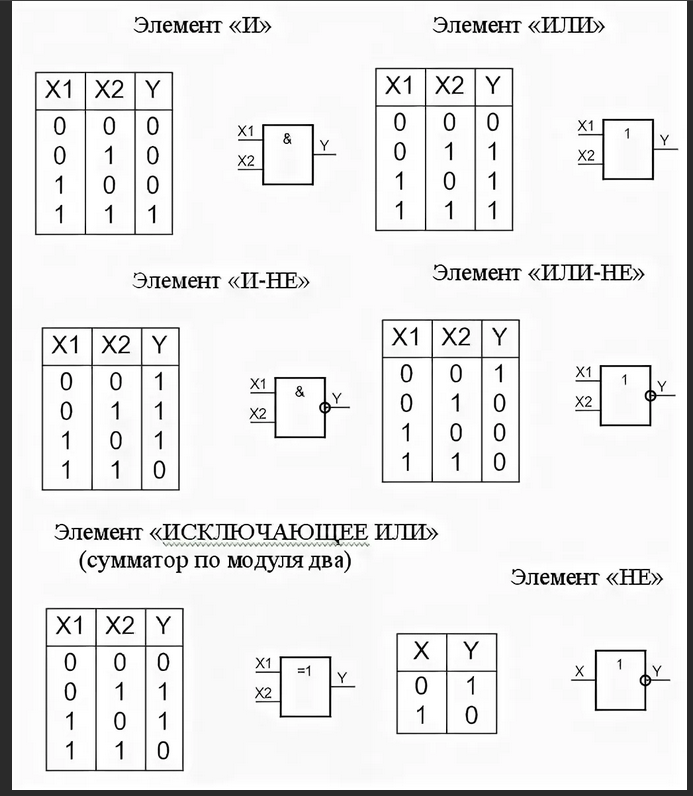 Рассмотрим некоторые из них.
Рассмотрим некоторые из них.
 Операция “импликация” выражается через логические функции “ИЛИ”, “НЕ” в виде логической формулы
Операция “импликация” выражается через логические функции “ИЛИ”, “НЕ” в виде логической формулы

 технологии
технологии