Индукция катушки формула. Индуктивность катушки: формула, расчет, применение и особенности

Что такое индуктивность катушки. Как рассчитать индуктивность. От чего зависит индуктивность катушки. Какие бывают виды катушек индуктивности. Где применяются катушки индуктивности.

Что такое индуктивность катушки и как она определяется

Индуктивность катушки — это способность катушки накапливать энергию магнитного поля при прохождении через нее электрического тока. Индуктивность определяется отношением магнитного потока, пронизывающего катушку, к силе тока, протекающего через нее:

L = Ф / I

где L — индуктивность, Ф — магнитный поток, I — сила тока.

Единицей измерения индуктивности в СИ является генри (Гн). 1 генри — это индуктивность катушки, в которой при изменении силы тока на 1 ампер за 1 секунду возникает ЭДС самоиндукции 1 вольт.

Формула для расчета индуктивности катушки

Индуктивность катушки можно рассчитать по следующей формуле:

L = μ0 * μ * N^2 * S / l

где:

• L — индуктивность катушки (Гн)
• μ0 — магнитная постоянная (4π * 10^-7 Гн/м)
• μ — относительная магнитная проницаемость сердечника
• N — число витков катушки
• S — площадь поперечного сечения катушки (м^2)
• l — длина катушки (м)

От чего зависит индуктивность катушки

Основные факторы, влияющие на индуктивность катушки:

• Количество витков — чем больше витков, тем выше индуктивность
• Размеры катушки — индуктивность пропорциональна площади сечения и обратно пропорциональна длине
• Материал сердечника — ферромагнитный сердечник значительно увеличивает индуктивность
• Форма катушки — тороидальные катушки имеют бóльшую индуктивность, чем соленоидные
• Частота тока — на высоких частотах индуктивность уменьшается из-за скин-эффекта

Виды катушек индуктивности

Существует несколько основных видов катушек индуктивности:

Катушки с воздушным сердечником

Это простейший вид катушек без магнитного сердечника. Они имеют небольшую индуктивность (до 1 мГн), но могут работать на высоких частотах и пропускать большие токи. Применяются в высокочастотных цепях.

Катушки с ферромагнитным сердечником

Использование железного или ферритового сердечника позволяет значительно увеличить индуктивность. Однако такие катушки имеют ограничения по максимальному току и частоте из-за насыщения сердечника.

Тороидальные катушки

Имеют кольцевой сердечник, на который намотан провод. Обладают высокой индуктивностью при меньших размерах. Магнитный поток замкнут внутри сердечника, что уменьшает паразитные связи.

Катушки на чашечных сердечниках

Обмотка размещается внутри сердечника из двух половинок в форме чашек. Имеют высокую индуктивность при малых габаритах. Магнитный поток также замкнут внутри сердечника.

Применение катушек индуктивности

Катушки индуктивности широко используются в различных областях электроники и электротехники:

• Фильтры в цепях питания и сигнальных цепях
• Колебательные контуры в радиоаппаратуре
• Дроссели для подавления помех
• Трансформаторы и дроссели импульсных источников питания
• Катушки зажигания в автомобилях
• Электромагниты и соленоиды
• Датчики в измерительных приборах

Особенности поведения катушки индуктивности в электрических цепях

Катушка индуктивности обладает рядом важных свойств в электрических цепях:

• Противодействует изменению тока, создавая ЭДС самоиндукции
• В цепи постоянного тока ведет себя как простой проводник
• В цепи переменного тока создает индуктивное сопротивление, пропорциональное частоте
• Сдвигает фазу тока относительно напряжения на 90°
• Может накапливать и отдавать энергию магнитного поля

Знание этих особенностей позволяет эффективно использовать катушки индуктивности в различных электронных устройствах.

Расчет индуктивного сопротивления

В цепях переменного тока катушка индуктивности создает индуктивное сопротивление, которое рассчитывается по формуле:

XL = 2πfL

где:

• XL — индуктивное сопротивление (Ом)
• f — частота переменного тока (Гц)
• L — индуктивность катушки (Гн)

Чем выше частота и индуктивность, тем больше индуктивное сопротивление. Это свойство используется для создания частотно-зависимых цепей и фильтров.

Явление самоиндукции в катушке

Самоиндукция — это явление возникновения ЭДС в проводнике при изменении протекающего через него тока. В катушке индуктивности самоиндукция проявляется особенно сильно из-за большого количества витков.

При увеличении тока в катушке возникает ЭДС самоиндукции, направленная против изменения тока. При уменьшении тока ЭДС самоиндукции стремится поддержать ток.

ЭДС самоиндукции определяется формулой:

E = -L * dI/dt

где L — индуктивность, dI/dt — скорость изменения тока.

Явление самоиндукции объясняет, почему ток в катушке не может измениться мгновенно.

От чего зависит индуктивность. Индуктивность катушки, её назначение, характеристики, формулы

Содержание

Что такое индуктивность

Этим термином обозначают зависимость, которая устанавливается между силой тока в проводнике (I) и созданным магнитным потоком (Ф):

L = Ф/ I.

С учетом базового определения несложно понять зависимость индуктивности от свойств окружающей среды, оказывающей влияние на распределение силовых линий. Определенное значение имеют размеры и конфигурация проводящего элемента.

Индуктивность подобна механической инерции. Только в данном случае речь идет о действиях с электрическими величинами. Этим коэффициентом характеризуют способность рассматриваемого компонента противодействовать изменению проходящего через него тока.

Самоиндукция

Индуктивность: формула

Если через замкнутый контур пропускать переменный ток, можно зарегистрировать с помощью простых экспериментов магнитное поле в окружающей среде. Изменение силовых параметров сопровождается появлением в цепи наведенной электродвижущей силы. Данное явление называют самоиндукцией.

Величину ЭДС можно вычислить по формуле:

Е = -L * (Δi/Δt).

Это выражение показывает зависимость напряжения от изменения тока за единицу времени. Поправочный коэффициент (L) обозначает особенности проводника (индукционной катушки). Знак «-» характеризует инерционные свойства явления.

При пропускании синусоидального сигнала следует учитывать отставание напряжения (векторное выражение) от тока на 90 градусов. Амплитуда будет прямо пропорциональна частоте (w):

E = L * I * w.

Расчёт поправки на собственную индуктивность витков

Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности LP и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆1L и поправки на взаимную индуктивность витков ∆2L

Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки

Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.

В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению

где μ – магнитная постоянная, μ = 4π•10-7 Гн/м;

ω – число витков соленоида;

DСР – средний диаметр катушки, м;

I – коэффициент, зависящий от расположения витков катушки.

Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.

Для варианта а), провод намотан с небольшим коэффициентом заполнения

где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).

Для варианта б), провод намотан с большим коэффициентом заполнения

где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).

Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки

где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).

Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности LP

— если при вычислении расчётной индуктивности LP толщина намотки t принята равной диаметру голого провода sP, то коэффициент I будет равен

— если при вычислении расчётной индуктивности LP толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен

где p – шаг намотки по длине катушки, sp – диаметр голого провода (без изоляции).

Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая

— если при вычислении расчётной индуктивности LP длина намотки l принята равной диаметру голого провода sP, то коэффициент I будет равен

— если при вычислении расчётной индуктивности LP длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен

где q – шаг намотки по толщине катушки, sp – диаметр голого провода (без изоляции).

Индуктивность в электрических цепях

В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:

Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:

где ω является угловой частотой резонансной частоты F:

Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов.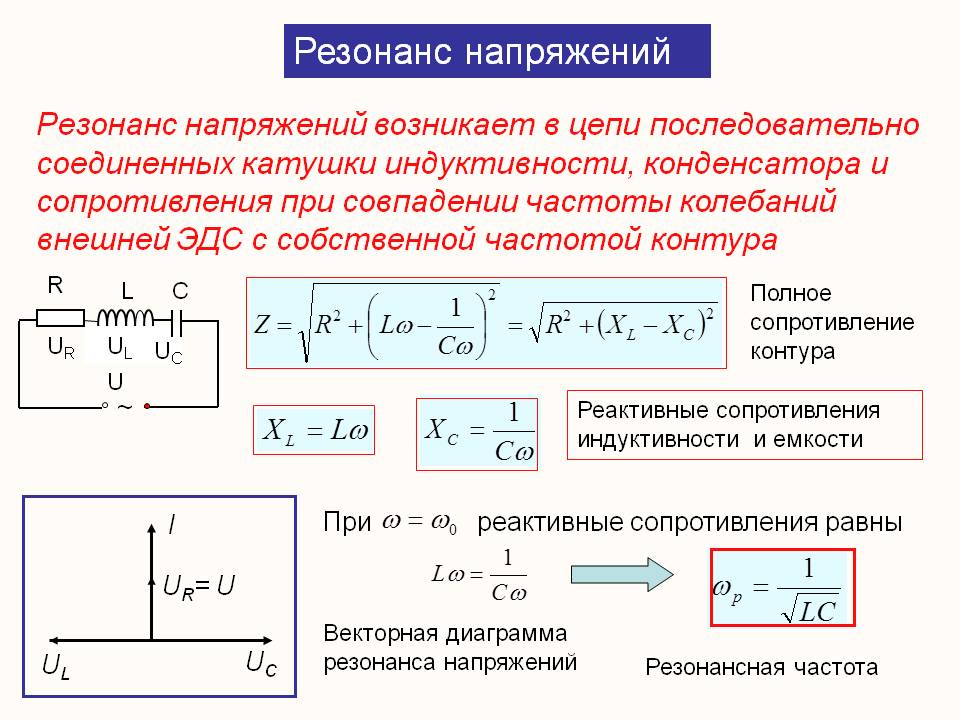 Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.

 Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.

Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:

Индуктивность и емкость в цепи переменного тока

Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения ϕ и ψ. При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:

i = Iм sin ωt

u = Uм sin (ϕ + ωt),

e = Ɛm sin (ψ + ωt).

Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току и находить по формуле:

R=(pl/S)(1 + at).

В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.

График и схема подключения

Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление XL, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением.  Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:

ХL = ωL.

Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.

Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.

Катушки индуктивности

Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток.  Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока. Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте ω;

Хс = 1/ωС

Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Ха отстает по фазе от тока. Индуктивное XL и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:

Будет интересно➡  Фантомное питание для микрофона: схема подключения

X = XL—XC

и имеет индуктивный характер при XL > Хс и емкостный характер при XL < Xc.

В заключение заметим, что средняя активная мощность переменного тока, показывающая, сколько энергии за единицу времени передается электрическим током данному участку цепи, определяется формулой:

P = IU cos ϕ.

Мощность, затрачиваемая только на тепловое действие тока, выражается формулой:

Р = I2R

Для увеличения активной мощности переменного тока нужно повышать cos ϕ. (Объясните, почему наибольшее значение cos ϕ имеет при XL=XC.)

Индуктивность

Показатель добротности

Добротность – это отношение между реактивным и индуктивным (активным) сопротивлением.

Активное – это показатель естественного сопротивления материала. Реактивное возникает, если изменения действующего значения напряжения, тока или емкости.

Для измерения используется следующее уравнение:

Q=2∙π∙f∙L/R,

Где:

• π– число Пи, равное 3,14;
• F – частотность;
• R – сопротивление.

Проблема может возникать с понятием «частота», т. к. многие не знают, что представляет собой колебательный контур. Это некоторая цепь, в которой присутствует катушка.

Как правило, колебательный контур состоит из источника питания, индукционного элемента и конденсатора. Определяется частота по формуле Томсона (она же формула резонансной частоты).

Чем выше показатель частотности, тем «добротнее» считается катушка.

Дроссель

Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.

Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:

Практическое руководство по катушкам индуктивности

Большинство проводящих материалов (металлов) является парамагнитными или ферромагнитными, в то время как большинство непроводящих материалов (неметаллов) является диамагнитными. Любой проводник обладает некоторой индуктивностью в ответ на изменение величины или направления протекания тока. Даже обычный прямой провод имеет индуктивность, хотя она достаточно мала, чтобы пренебрегать ею. Если провод свернуть в петлю — его индуктивность увеличится. Чем больше сделать таких одинаковых витков, тем большая индуктивность будет присуща проводу. Индуктивность одиночной петли или катушки из провода может быть многократно увеличена с помощью подходящего ферромагнитного сердечника.

Простейшими катушками индуктивности являются катушки с воздушным сердечником (рисунок 1).

Они сделаны путем намотки провода вокруг пластмассового, деревянного или любого не ферромагнитного сердечника. Индуктивность катушки зависит от числа витков, радиуса и общей формы, также она пропорциональна числу витков и диаметру катушки. Индуктивность обратно пропорциональна длине провода для заданного диаметра катушки и числу витков. Итак, чем ближе будут витки, тем больше будет индуктивность. Электропроводность катушек индуктивности зависит от материала и толщины провода. Потери (в виде тепла) в значительной степени зависят от материала, используемого в качестве сердечника.

 

Рис. 1. Пример катушки индуктивности с воздушным сердечником 

Катушки с воздушным сердечником имеют небольшую индуктивность, которая может составлять максимум 1 мГн. Катушки с воздушным сердечником могут быть рассчитаны так, что будут пропускать через себя ток практически неограниченной величины при условии использования проводника большой длины, смотанного в катушку большого радиуса.

Такие катушки индуктивности практически не вносят потерь, так как воздух не рассеивает много энергии в виде тепла. Чем выше частота переменного тока, тем меньше индуктивность, необходимая для получения значительных эффектов. Таким образом, катушки индуктивности с воздушным сердечником вполне подходят для применения в высокочастотных цепях переменного тока благодаря отсутствию потерь, способности пропускать через себя большие токи и достаточным значениям индуктивности.

При использовании железных или ферритовых сердечников индуктивность может быть значительно увеличена. Однако порошкообразный, железный или ферритовый сердечник вносит значительные потери электрической энергии в виде тепла. Использование ферромагнитных сердечников также ограничивает максимальную величину рабочего тока катушек индуктивности. В ферромагнитных сердечниках насыщение происходит при протекании максимального рабочего тока. При увеличении тока сверх этого критического значения индуктивность может начать уменьшаться.

При больших токах ферромагнитные сердечники могут достаточно сильно нагреваться, что может привести к их разрушению и необратимому существенному изменению номинальной индуктивности катушки.

Соленоид против катушек индуктивности

 

Соленоиды часто путают с катушками индуктивности. Соленоиды — это катушки проводов, которые предназначены для использования в качестве электромагнитов. Многие индукторы также являются катушками проводов, но они предназначены для обеспечения индуктивности в электрической цепи. Катушки индуктивности цилиндрической формы также называют соленоидными катушками, но только из-за их конструкции, схожей с конструкцией соленоида. Тем не менее, они не предназначены для использования в качестве электромагнита. Соленоиды специально используются в качестве электромагнитов и обычно имеют подвижный или статический сердечник. Обычно соленоиды используются в качестве электромагнитов в электрических звонках, электродвигателях, работающих на постоянном токе, и в реле.

Соленоидные катушки как индуктивности

 

Простейшими и наиболее распространенными индуктивностями являются соленоидные катушки. Эти индуктивности представляют собой цилиндрические катушки, намотанные вокруг диамагнитного или ферромагнитного сердечника. Они являются самыми простыми с точки зрения проектирования и изготовления.

Соленоидная, или цилиндрическая катушка может быть легко использована для подстройки величины индуктивности, если в конструкцию интегрировать механизм перемещения ферромагнитного сердечника катушки внутрь и наружу. Путем перемещения сердечника внутрь катушки и обратно можно изменять ее эффективную магнитную проницаемость и, следовательно, величину индуктивности. Это называется настройкой магнитной проницаемости и используется для подстройки частот в радиочастотных схемах.

Сердечник можно сделать подвижным, прикрепив его к винтовому валу и закрепив гайкой на другом конце катушки. Когда вал винта вращается по часовой стрелке — сердечник перемещается внутрь катушки, увеличивая эффективную магнитную проницаемость и, следовательно, величину индуктивности. Когда вал винта вращается против часовой стрелки — сердечник выдвигается, уменьшая эффективную магнитную проницаемость и, следовательно, величину индуктивности.

Тороиды как катушки индуктивности

Сегодня еще одной наиболее распространенной формой катушек индуктивности является тороид. Тороиды имеют кольцевой ферромагнитный сердечник, на который намотан провод. Тороиды нуждаются в меньшем числе витков и физически меньше при той же величине индуктивности и рабочей величине тока, по сравнению с соленоидными катушками (рисунок 2). Другим важным преимуществом тороидов является то, что магнитный поток находится внутри сердечника, что позволяет избежать нежелательной взаимной индуктивности.

Рис. 2. Сильноточные тороидальные катушки индуктивности 

Однако намотать провод на тороид сложно. Регулировать магнитную проницаемость тороида еще сложнее. Проектирование катушек с тороидальным сердечником и переменной величиной индуктивности требует реализации громоздкой и сложной конструкции. В цепях, где требуется взаимная индуктивность, катушки должны быть намотаны на один и тот же сердечник в случае, если тороид используется в качестве катушки индуктивности.

Индуктивности на основе чашеобразных Р-сердечников*

 

В типичных катушках индуктивности — соленоидных и тороидных — провод намотан вокруг ферромагнитного сердечника. Катушки индуктивности на основе чашеобразных сердечников – это другой тип индуктивностей, в котором обмотка катушки находится внутри ферромагнитного сердечника. Чашеобразный ферромагнитный сердечник имеет форму двух половин в виде чаш со специальным цилиндрическим выступом (керном) на дне одной из половин, на котором размещается обмотка. Обе половины имеют отверстия, из которых извлекается провод катушки. Вся сборка скрепляется болтом и гайкой.

Катушки данного типа, как и тороиды, обладают большой индуктивностью и электропроводностью при небольших габаритах и меньшем числе витков. Магнитный поток, как и в случае с тороидами, остается внутри. Таким образом, нет нежелательной взаимной индуктивности с сердечниками. Опять же, как и в случае с тороидами, очень трудно варьировать величину индуктивности катушек данного типа. Изменять величину индуктивности в катушках индуктивности на основе Р-сердечников возможно только путем изменения числа витков и при использовании отводов в разных точках катушки.

*- В литературе также встречается термин “Р-сердечник закрытого типа”. В ГОСТ 19197-73 данному типу сердечников присвоено название – “броневой”.

Линия передачи как индуктивность

В цепях постоянного тока катушки индуктивности ведут себя почти так же, как и обычный провод, обладая незначительным сопротивлением, но не более того. Таким образом, они находят применение преимущественно в электрических цепях переменного тока. В аудиосхемах в качестве индуктивностей обычно используются тороиды, катушки на основе круглых чашеобразных сердечников или аудиотрансформаторы. Номинал индуктивности, применяемый в таких электрических цепях, варьируется от нескольких мГн до 1 Гн. Катушки индуктивности вместе с конденсаторами используются в аудиосхемах для подстройки. В настоящее время микросхемы практически полностью вытеснили катушки индуктивности и конденсаторы в аудиосистемах и других подобных областях применения.

При увеличении частоты должны использоваться индуктивности с сердечниками меньшей проницаемости. На нижнем конце радиочастотного спектра используются те же катушки индуктивности, что и в аудиоприложениях. На частотах до нескольких МГц весьма распространены катушки индуктивности с тороидальным сердечником. Для частот 30…100 МГц предпочтительны катушки с воздушным сердечником. Для частот более 100 МГц в линии передачи используются высокочастотные индуктивности и специальные трансформаторы. Линии передачи малой длины (четверть длины волны сигнала или меньше) сами могут быть использованы в качестве индуктивности для подстройки частоты радиосигналов. Линия передачи, используемая в качестве подобной индуктивности, обычно представляет собой коаксиальный кабель.

Индуктивности в цепях постоянного тока

Катушки индуктивности практически бесполезны в цепях постоянного тока. Однако можно предположить, что катушка индуктивности, подключенная к цепи постоянного тока, может быть полезна для понимания принципов ее работы и особенностей поведения пульсирующих напряжений постоянного тока. Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:

V_L = – L*(di/dt),   (1)

где:

• V_L – напряжение (обратная ЭДС), индуцированная на катушке;
• L – индуктивность катушки;
• di/dt – скорость изменения тока во времени.

Согласно приведенной формуле 1, внезапное изменение тока через катушку индуктивности дает бесконечное напряжение, что физически невозможно. Таким образом, ток через катушку индуктивности не может измениться мгновенно. Ток сталкивается с влиянием индуктивности при каждом небольшом изменении его величины и медленно возрастает до своего пикового постоянного значения. Итак, в начальный момент времени катушка индуктивности представляет собой разрыв цепи, когда переключатель замкнут. Обратная ЭДС наводится на катушку индуктивности до тех пор, пока изменяется значение протекающего через нее тока. Индуцированная обратная ЭДС всегда остается равной и противоположной возрастающему приложенному напряжению. Когда напряжение и ток от источника приближаются к постоянному значению, обратная ЭДС падает до нуля, а катушка индуктивности начинает вести себя как обычный провод. При подаче напряжения на катушку индуктивности мощность, запасенная ею, определяется по формуле 2:

P = V * I = L*i*di/dt,   (2)

где:

• P – электрическая мощность, запасенная в катушке;
• V – величина пикового напряжения на катушке индуктивности;
• I – величина пикового тока, протекающего через катушку индуктивности.

Энергия, запасенная индуктивностью при подаче напряжения, определяется по формуле 3:

W = ?P.dt = ?L*i*(di/dt)dt = (1/2)LI²,   (3)

где:

• W – электрическая энергия, запасенная в катушке индуктивности в виде магнитного поля;
• I – максимальное значение тока, протекающего через катушку.

Когда происходит отключение источника напряжения (путем размыкания ключа), напряжение на индуктивности падает с постоянного пикового значения до нуля. В отличие от конденсаторов, при отключении источника напряжения напряжение на индуктивности не поддерживается. Фактически оно уже упало до нуля, тогда как ток, проходящий через него стал постоянным. Теперь, когда приложенное напряжение падает от пикового постоянного значения до нуля, ток, протекающий через катушку индуктивности, также падает с постоянного пикового значения до нуля. Катушка противодействует падению тока, вызывая прямую ЭДС в направлении приложенного напряжения. Из-за индуцированной прямой ЭДС ток, проходящий через катушку индуктивности, падает до нуля с более медленной скоростью. Как только ток уменьшается до нуля, прямая ЭДС также падает до нуля.

Таким образом, при подаче напряжения питания электрическая энергия преобразовывалась в магнитное поле в катушке индуктивности, что было очевидно по обратной ЭДС, индуцированной на ней. При отключении напряжения питания та же самая электрическая энергия возвращается индуктором в цепь в форме прямой ЭДС. Всякий раз, когда напряжение на катушке индуктивности увеличивается, возникает обратная ЭДС, а всякий раз, когда напряжение на катушке уменьшается, возникает прямая ЭДС.

На практике обратная или прямая ЭДС, которая наводится на катушке индуктивности, во много раз больше приложенного напряжения. Если источник индуктивности подключен к источнику напряжения или катушка индуктивности подключена к цепи постоянного тока без какой-либо защиты, электрическая энергия, возвращаемая при размыкании переключателя, выделяется в виде скачка напряжения или искры на контактах переключателя. Если индуктивность или ток в цепи достигают достаточно больших значений, то энергия выделяется в форме дуги или искры на контакте переключателя и может даже сжечь или расплавить его. Этого можно избежать, используя резистор и конденсатор, соединенные в RC-цепь и включенные последовательно с контактом переключателя. Такая RC-цепь называется снабберной и позволяет электрической энергии, выделяемой катушкой индуктивности, заряжать и разряжать конденсатор, поэтому она не повреждает другие компоненты. Во многих электрических цепях для сохранения компонентов схемы от обратной или прямой ЭДС катушек индуктивности или соленоидов используются защитные диоды.

Катушка индуктивности в цепи переменного тока

Катушка индуктивности противодействует любому изменению тока, который протекает через нее, а переменный ток, в свою очередь, отстает на 90° от напряжения. В начальный момент времени, когда напряжение источника подается на катушку, ток через нее протекает максимальный, но в противоположном направлении. При подаче напряжения ток протекает через катушку индуктивности из-за индуцированной обратной ЭДС, которая противоположна приложенному напряжению. Индуцированное на катушке напряжение всегда равно и противоположно по знаку приложенному напряжению в любой момент времени. Когда приложенное напряжение возрастает от нуля до пикового значения, ток через катушку падает от максимума до нуля.

Когда прикладываемое напряжение падает от максимального значения до нуля, то на катушке индуцируется прямая ЭДС, заставляя ток противоположного направления расти от нуля до пикового значения. Когда приложенное напряжение меняет полярность и возрастает до пикового значения, ЭДС снова индуцируется на катушке, вызывая падение обратного тока от пикового значения до нуля. Когда приложенное напряжение снова падает до нуля в обратном направлении, в катушке индуцируется прямая ЭДС, заставляющая ток снова расти от нуля до максимального значения в противоположном направлении. Это продолжается для каждого цикла протекания переменного тока.

Индуктивное сопротивление

Противодействие протекающему току из-за наличия индуктивности называется индуктивным сопротивлением. Амплитуда тока через катушку индуктивности обратно пропорциональна частоте приложенного напряжения. Поскольку напряжение на катушке (обратная или прямая ЭДС) пропорционально индуктивности, то амплитуда тока также обратно пропорциональна величине индуктивности. Итак, противодействие току из-за наличия индуктивности в виде индуктивного сопротивления определяется по формуле 4:

X_L = 2?fL= ?L   (4)

Соответственно, пиковая амплитуда тока, проходящего через катушку индуктивности, определяется по формуле 5:

I_peak = V_peak/X_L= V_peak/ ?L,   (5)

где:

• I_peak – пиковое значение переменного тока, протекающего через катушку индуктивности;
• V_peak – пиковое значение переменного напряжения, приложенного к катушке;
• X_L – индуктивное сопротивление.

Как резистивное и емкостное сопротивление, так и единица индуктивного сопротивления измеряется в омах. Следует отметить, что в электрических цепях нет потерь энергии из-за наличия емкостного или индуктивного сопротивления, что нельзя сказать об обычном резистивном сопротивлении. Тем не менее, реактивное сопротивление может ограничивать уровни тока через конденсатор или катушку индуктивности.

Применение катушек индуктивности

Катушки индуктивности используются в электрических цепях переменного тока. Они обычно применяются в аналоговых схемах, схемах обработки сигналов и в системах телекоммуникаций, а также используются вместе с конденсаторами для создания фильтров различных топологий. В телекоммуникационных системах индуктивности применяются в составе специальных фильтров, которые нужны для подавления возможных бросков напряжения и предотвращения утечки информации через линии системы электропитания.

Трансформаторы, которые используются для повышения или понижения напряжения переменного тока, состоят из двух катушек индуктивности, объединенных в единую конструкцию определенным образом. Индуктивности также используются для временного хранения электрической энергии в цепях выборки-хранения и источниках бесперебойного питания. В цепях электропитания катушки индуктивности (где они называются фильтрующими дросселями) используются для сглаживания пульсирующих токов.

Поведение индуктивности при прохождении через нее сигнала можно определить следующим образом:

• Всякий раз, когда приложенное к катушке индуктивности напряжение увеличивается, катушка генерирует обратную ЭДС, в результате чего ток через нее падает с максимального значения до нуля или даже ниже этого уровня. Всякий раз, когда прикладываемое напряжение уменьшается, катушка создает прямую ЭДС, в результате чего ток через нее повышается с нуля или текущего уровня до максимального значения или даже до более высокого.
• Обратная или прямая ЭДС сохраняется на катушке индуктивности до тех пор, пока приложенное напряжение, а следовательно и ток через нее изменяются. Когда приложенное напряжение достигает определенного постоянного значения, обратная или прямая ЭДС падает до нуля, и постоянный ток протекает через катушку индуктивности без какого-либо противодействия, как в обычном соединительном проводе.
• Из-за наличия индуктивности скорость изменения тока в цепи замедляется. Если сигнал переменный, то ток всегда будет отставать от напряжения на 90° из-за наличия индуктивности.
• Благодаря индуктивному или емкостному сопротивлению потери энергии отсутствуют. Энергия, запасенная катушкой индуктивности в форме магнитного поля или конденсатором в форме электростатического поля, возвращается обратно в цепь, как только приложенное напряжение падает до нуля или меняет полярность. Однако из-за реактивного сопротивления пиковый уровень тока (амплитуда сигнала) ограничен.

Источник: https://www.engineersgarage.com

Автор: Нихил Агнихотри Переводчик: Алексей Катков (г. Санкт-Петербург)

Разделы: Дроссели

Опубликовано: 30.01.2020

14.2 Самоиндукция и катушки индуктивности – University Physics Volume 2

Глава 14. Индуктивность

Цели обучения

К концу этого раздела вы сможете:

• Соотносить скорость изменения тока с ЭДС индукции, создаваемой этим током в той же цепи
• Рассчитать собственную индуктивность цилиндрического соленоида
• Расчет собственной индуктивности прямоугольного тороида

Взаимная индуктивность возникает, когда ток в одной цепи создает изменяющееся магнитное поле, которое индуцирует ЭДС в другой цепи. Но может ли магнитное поле повлиять на ток в исходной цепи, создавшей поле? Ответ положительный, и это явление называется самоиндукцией .

Катушки индуктивности

На рис. 14.5 показаны некоторые силовые линии магнитного поля, обусловленные током в круглой проволочной петле. Если ток постоянен, магнитный поток через контур также постоянен. Однако, если текущие 9Если бы 0019 I изменялись со временем, скажем, сразу после замыкания переключателя S, то магнитный поток [латекс]{\текст{Ф}}_{\текст{м}}[/латекс] соответственно изменился бы. Тогда закон Фарадея говорит нам, что в цепи будет индуцироваться ЭДС [латекс]\эпсилон[/латекс], где

[латекс]\эпсилон =-\frac{d{\text{Φ}}_{\text{ m}}}{dt}.[/latex]

Поскольку магнитное поле, создаваемое проводом с током, прямо пропорционально току, поток, создаваемый этим полем, также пропорционален току; то есть

[латекс]{\текст{Ф}}_{\текст{м}}\пропто I.[/латекс]

Рис. 14.5  Магнитное поле создается током I в контуре. Если бы я менялся со временем, магнитный поток через петлю также менялся бы, и в петле индуцировалась бы ЭДС.

Это также можно записать как

[латекс] {\ текст {Φ}} _ {\ текст {м}} = LI [/латекс]

, где константа пропорциональности L известна как само- индуктивность проволочного контура. Если в цикле N витков, это уравнение принимает вид связана с током по правилу правой руки, поэтому на рис. 14.5 нормаль направлена ​​вниз. Согласно этому соглашению, [latex]{\text{Φ}}_{\text{m}}[/latex] положительно в уравнении 14.9, поэтому L всегда имеет положительное значение .

Для петли с N витков [латекс]\epsilon =\text{−}Nd{\text{Φ}}_{\text{m}}\text{/}dt,[/latex] поэтому ЭДС индукции может быть записана через самоиндукцию как

[латекс]\epsilon =\text{−}L\frac{dI}{dt}.[/latex]

При использовании этого уравнения для определения L проще всего игнорировать знаки [латекс] \epsilon \phantom{\rule{0. 2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}dI\text{/}dt,[/latex] и вычислить L как

[латекс]L=\frac{|\epsilon |}{|dI\text{/}dt|}.[/latex]

Поскольку самоиндукция связана с магнитным полем, создаваемым током, любой конфигурация проводников обладает самоиндукцией. Например, помимо проволочной петли длинный прямой провод обладает собственной индуктивностью, как и коаксиальный кабель. Коаксиальный кабель чаще всего используется в индустрии кабельного телевидения, и его также можно обнаружить при подключении к кабельному модему. Коаксиальные кабели используются из-за их способности передавать электрические сигналы с минимальными искажениями. Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и собственной индуктивностью, что может иметь нежелательные последствия.

Элемент схемы, используемый для обеспечения собственной индуктивности, известен как катушка индуктивности . Он представлен символом, показанным на рис. 14.6, который напоминает катушку проволоки, основную форму катушки индуктивности. На рис. 14.7 показано несколько типов катушек индуктивности, обычно используемых в цепях.

Рисунок 14.6 Символ, используемый для обозначения катушки индуктивности в цепи. Рисунок 14.7  Различные катушки индуктивности. Независимо от того, заключены ли они в капсулу, как показаны три верхние, или намотаны на катушку, как самая нижняя, каждая из них представляет собой просто относительно длинную катушку провода. (кредит: Уинделл Оскей)

В соответствии с законом Ленца отрицательный знак в уравнении 14.10 указывает на то, что ЭДС индукции на катушке индуктивности всегда имеет полярность, которая противодействует изменению тока. Например, если ток, протекающий от А к В на рис. 14.8(а), увеличивается, ЭДС индукции (представленная воображаемой батареей) будет иметь указанную полярность, чтобы противодействовать увеличению. Если бы ток от А до В уменьшался, то ЭДС индукции имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока (рис. 14.8 (б)). Наконец, если бы ток через индуктор был постоянным, в катушке не индуцировалась бы ЭДС.

Рисунок 14.8  ЭДС индукции на катушке индуктивности всегда препятствует изменению тока. Это можно представить как воображаемую батарею, заставляющую течь ток, противодействующий изменению в (а) и усиливающий изменение в (б).

Одним из распространенных применений индуктивности является определение сигналов светофора, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом, где остановится ожидающий автомобиль. Кузов автомобиля увеличивает индуктивность, и цепь меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал от катушки передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути (рис. 14.9).). Металлодетекторы можно настроить на чувствительность, а также они могут обнаруживать наличие металла на человеке.

Рисунок 14.9  Знакомые ворота безопасности в аэропорту не только обнаруживают металлы, но и могут указывать их приблизительную высоту над полом. (кредит: «Alexbuirds»/Wikimedia Commons)

Во вспышках фотокамер обнаружены большие индуцированные напряжения. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор , чтобы индуцировать большие напряжения. Напомним из книги «Колебания о колебаниях», что «колебание» определяется как колебание величины или повторяющиеся регулярные колебания величины между двумя крайними значениями вокруг среднего значения. Также вспомните (из электромагнитной индукции об электромагнитной индукции), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке. Система генератора делает это много раз, когда напряжение батареи повышается до более чем 1000 вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки.

Пример

Собственная индуктивность катушки

ЭДС индукции 2,0 В измеряется в катушке из 50 тесно намотанных витков, при этом ток через нее равномерно увеличивается от 0,0 до 5,0 А за 0,10 с. а) Чему равна собственная индуктивность катушки? б) Чему равен поток через каждый виток катушки при силе тока 5,0 А?

Стратегия

Обе части этой задачи дают всю информацию, необходимую для решения собственной индуктивности в части (a) или потока через каждый виток катушки в части (b). Необходимые уравнения: уравнение 14.10 для части (а) и уравнение 14.9.{-3}\phantom{\rule{0.2em}{0ex}}\text{Wb}.[/latex]

Значение

Собственная индуктивность и поток, рассчитанные в частях (a) и (b), являются типичными значениями для катушек, используемых в современных устройствах. Если ток не меняется во времени, поток не меняется во времени, поэтому ЭДС не индуцируется.

Проверьте правильность понимания

Ток протекает через катушку индуктивности на рис. 14.8 от B к A вместо A к B , как показано на рисунке. Ток увеличивается или уменьшается, чтобы создать ЭДС, указанную на диаграмме (а)? На схеме (б)?

Показать решение

а. уменьшение; б. увеличение; Так как ток течет в противоположном направлении диаграммы, то для получения положительной ЭДС в левой части диаграммы (а) нужно уменьшить ток влево, что создает усиленную ЭДС там, где положительный конец находится с левой стороны. Чтобы получить положительную ЭДС в правой части диаграммы (b), нам нужно увеличить ток влево, что создает усиленную ЭДС, где положительный конец находится на правой стороне.

Проверьте свои знания

Изменяющийся ток индуцирует ЭДС 10 В на катушке индуктивности 0,25 Гн. С какой скоростью меняется ток?

Show Solution

40 A/s

Хороший подход к расчету собственной индуктивности катушки индуктивности состоит из следующих шагов:

Стратегия решения проблем: собственная индуктивность

1. Предположим, что ток I протекает через катушку индуктивности.
2. Определите магнитное поле [латекс]\stackrel{\to }{\textbf{B}}[/латекс], создаваемое током. Если есть соответствующая симметрия, вы можете сделать это с помощью закона Ампера.
3. Получите магнитный поток, [латекс] {\ текст {Φ}} _ {\ текст {м}}. [/латекс]
4. При известном потоке собственная индуктивность может быть найдена из уравнения 14.9, [латекс]L=N{\text{Φ}}_{\text{m}}\text{/}I[/latex].

Чтобы продемонстрировать эту процедуру, мы теперь рассчитаем собственные индуктивности двух катушек индуктивности.

Цилиндрический соленоид

Рассмотрим длинный цилиндрический соленоид длиной l , площадью поперечного сечения A и N витков провода. Мы предполагаем, что длина соленоида настолько больше его диаметра, что мы можем принять магнитное поле равным [латекс] B = {\ mu }_{0} nI [/латекс] во всей внутренней части соленоида, что то есть мы игнорируем концевые эффекты в соленоиде. С током 9{2}\left(V\right),[/latex]

, где [latex]V=Al[/latex] — объем соленоида. Обратите внимание, что собственная индуктивность длинного соленоида зависит только от его физических свойств (таких как число витков провода на единицу длины и объем), а не от магнитного поля или тока. Это справедливо для катушек индуктивности в целом.

Прямоугольный тороид

Тороид прямоугольного сечения показан на рис. 14.10. Внутренний и внешний радиусы тороида равны [латекс]{R}_{1}\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}} {R}_{2},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}h[/latex] — высота тороида . Применяя закон Ампера так же, как мы это делали в примере 13.8 для тороида с круглым поперечным сечением, мы находим, что магнитное поле внутри прямоугольного тороида также определяется выражением 9{2}[/латекс]

Сводка

• Текущие изменения в устройстве индуцируют ЭДС в самом устройстве, называемую собственной индуктивностью,

  [латекс]\epsilon =\text{−}L\frac{dI}{dt},[/latex]

  
  , где L  – собственная индуктивность катушки индуктивности, а [latex]dI\text{/}dt[/latex] – скорость изменения тока через нее. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца. Единицей самоиндукции и индуктивности является генри (Гн), где 0ex}}\text{Ω}·\text{s}[/latex]. 9{-7}\phantom{\rule{0.2em}{0ex}}\text{T}·\text{m/A}[/latex] — проницаемость свободного пространства.

Концептуальные вопросы

Зависит ли собственная индуктивность от величины магнитного потока? Зависит ли это от силы тока в проводе? Соотнесите ваши ответы с уравнением к текущему. Однако, поскольку магнитный поток зависит от тока I , эти эффекты компенсируются. Это означает, что собственная индуктивность не зависит от тока. Если ЭДС индуцируется в элементе, она зависит от того, как ток изменяется со временем.

Будет ли собственная индуктивность туго намотанного соленоида длиной 1,0 м отличаться от собственной индуктивности на метр бесконечного, но в остальном идентичного соленоида?

Обсудите, как можно определить собственную индуктивность на единицу длины длинного прямого провода.

Показать решение

Считайте концы провода частью цепи RL и определите самоиндукцию по этой цепи.

Собственная индуктивность катушки равна нулю, если по обмоткам не течет ток. Правда или ложь?

Как соотносится собственная индуктивность на единицу длины вблизи центра соленоида (вдали от концов) с ее значением вблизи конца соленоида?

Показать решение

Магнитное поле будет расширяться в конце соленоида, поэтому поток через последний виток меньше, чем через середину соленоида.

Задачи

ЭДС 0,40 В индуцируется в катушке, когда ток через нее изменяется равномерно от 0,10 до 0,60 А за 0,30 с. Чему равна собственная индуктивность катушки?

Показать решение

0,24 H

Ток, показанный в части (a) ниже, увеличивается, а ток, показанный в части (b), уменьшается. В каждом случае определите, какой конец индуктора находится под более высоким потенциалом.

С какой скоростью изменяется ток через катушку 0,30 Гн, если на катушке индуцируется ЭДС 0,12 В?

Показать решение

0,4 A/s

Когда в камере используется вспышка, полностью заряженный конденсатор разряжается через катушку индуктивности. За какое время необходимо включить или выключить ток 0,100 А через дроссель 2,00 мГн, чтобы навести ЭДС 500 В?

По катушке с собственной индуктивностью 2,0 Гн протекает ток, который изменяется со временем по закону [латекс]I\left(t\right)=\left(2.0\phantom{\rule{0.2em}{0ex}} \text{A}\right)\text{sin}\phantom{\rule{0.2em}{0ex}}120\pi t.[/latex] Найдите выражение для ЭДС, индуцируемой в катушке. 9{2}[/latex] Какова собственная индуктивность соленоида?

По катушке с собственной индуктивностью 3,0 Гн течет ток, уменьшающийся с постоянной скоростью [latex]dI\text{/}dt=-0,050\phantom{\rule{0.2em}{0ex}}\text{ А/с}[/латекс]. Чему равна ЭДС индукции в катушке? Опишите полярность ЭДС индукции.

Показать решение

0,15 В. Это та же полярность, что и ЭДС, управляющая током.

Ток I(t) через катушку индуктивности 5,0 мГн изменяется со временем, как показано ниже. Сопротивление индуктора равно [латекс]5,0\фантом{\правило{0,2em}{0ex}}\текст{Ом}.[/латекс] Рассчитайте напряжение на индукторе при [латекс]t=2,0\фантом{\ правило {0. 2em} {0ex}} \ text {мс}, t = 4.0 \ фантом {\ правило {0.2em} {0ex}} \ текст {мс}, \ фантом {\ правило {0.2em} {0ex}} \text{and}\phantom{\rule{0.2em}{0ex}}t=8.0\phantom{\rule{0.2em}{0ex}}\text{ms}[/latex].

Длинный цилиндрический соленоид с числом оборотов 100 на сантиметр имеет радиус 1,5 см. (a) Пренебрегая концевыми эффектами, какова собственная индуктивность на единицу длины соленоида? б) Если ток через соленоид изменяется со скоростью 5,0 А/с, какая ЭДС индуцируется на единицу длины?

Показать решение

а. 0,089 Гн/м; б. 0,44 В/м

Предположим, что прямоугольный тор имеет 2000 витков и собственную индуктивность 0,040 Гн. отношение его внешнего радиуса к внутреннему радиусу? 9{-7}\phantom{\rule{0.2em}{0ex}}\text{H/m}[/latex]

Глоссарий

Катушка индуктивности

часть электрической цепи для обеспечения собственной индуктивности, которая обозначена катушкой провода

самоиндукция

действие устройства, индуцирующего ЭДС само по себе

Лицензии и атрибуты

Самоиндукция и катушки индуктивности. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/14-2-self-inductance-and-inductors. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction

Индукционная катушка и ее применение в практике инженера-электронщика

Несмотря на широкое использование цифровых схем, таких как процессоры, программируемые логические устройства и однокристальные схемы, представляющих собой комбинацию этих двух, иногда разработчику электроники приходится «аналоговые» элементы, такие как: резисторы, конденсаторы или индукционные катушки. Что интересно, если относительно легко включить резистор или конденсатор (с емкостью, исчисляемой в пикофарадах) в структуру интегральной схемы, то очень сложно сделать это с помощью индукционной катушки. Вот почему в примечаниях по применению многих элементов до сих пор упоминается индукционная катушка в качестве внешнего компонента, добавляемого в набор. В данной статье представлены некоторые основные сведения об индукционных катушках и описание элементов их конструкции, влияющих на их параметры.

• Структура индукционной катушки
• Что такое индукционная катушка?
• Индукционная катушка – основные параметры
• Несовершенная катушка
• Заключительные замечания

Структура индукционной катушки

Индукционная катушка не является сложной. Он состоит из сердечника и намотанных на него изолированных проводов. Сердечник может быть как воздушным, так и магнитным. Важно, чтобы провода, намотанные на сердечник, были изолированы, поэтому для изготовления катушек используют изолированный провод, либо наматывают неизолированным проводом (например, так называемой серебряной сталью), но с воздушным зазором, обеспечивающим необходимое расстояние между отдельными витками провода. Если неизолированный провод наматывать виток за витком, то произойдет короткое замыкание и, хотя некоторая индуктивность будет присутствовать, она обязательно будет отличаться от нужной.

На практике часто встречается повреждение индукционной катушки , т.е. короткое замыкание между витками провода в результате пробоя изоляции, из-за превышения максимально допустимой температуры или напряжения. Поврежденную таким образом катушку необходимо перемотать или заменить на новую. Сетевые трансформаторы также повреждаются таким образом. Дальнейшее использование такого поврежденного трансформатора может привести к его перегреву, короткому замыканию в сети или даже возгоранию трансформатора или питаемого от него устройства.

Что такое индукционная катушка?

Индукционная катушка представляет собой элемент, который накапливает энергию в виде магнитного поля в сердечнике, поэтому он преобразует энергию электрического тока в энергию магнитного поля или наоборот. Изменение тока, протекающего по обмоткам, приводит к возникновению электродвижущей силы в направлении, противодействующем этому изменению. Точно так же переменное магнитное поле, проникающее в сердечник, вызывает индукцию напряжения. Это можно показать с помощью следующей формулы:

В этой формуле:

• e — обозначает электродвижущую силу (напряжение в вольтах), создаваемую катушкой,
• dϕ/dt — изменение магнитного потока во времени,
• di/dt — текущее изменение времени,
• L — обозначает параметр катушки, называемый индуктивностью; его единица измерения — генри.

Легко заметить упомянутую ранее особенность – ЭДС e имеет противоположное направление, чем напряжение, вызывающее протекание тока. Он противодействует резким изменениям тока, протекающего через катушку, и позволяет катушке выполнять одну из своих основных функций – использоваться в качестве так называемого импедера .

Индукционная катушка – основные параметры

Основными параметрами катушки являются ее индуктивность и резонансная частота. Другими словами, индуктивность — это способность катушки накапливать энергию в виде магнитного поля, вызванного протеканием тока.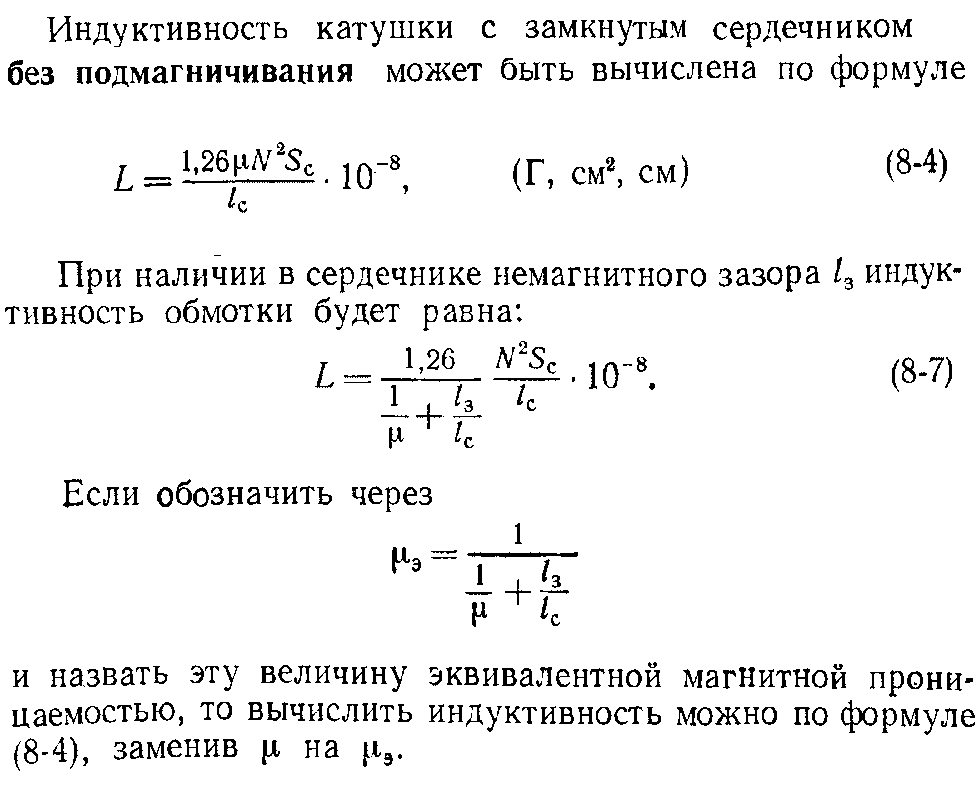 Индуктивность измеряется в генри и определяется как отношение временного изменения напряжения к изменению тока во времени.

Диаграммы, показывающие падение тока и напряжения на выводе индукционной катушки. Падение максимально в момент включения питания и уменьшается со временем. Падение противодействует увеличению тока, следовательно, сила тока минимальна в момент включения источника питания и увеличивается со временем. Часто говорят, что напряжение опережает ток на катушке

На рисунке выше показано, что происходит с напряжением на катушке и с током, протекающим через нее после подачи питания на ее клеммы. Сплошная красная линия иллюстрирует течение тока. Как мы можем наблюдать, ток увеличивается после подачи питания до своего пикового значения, определяемого законом Ома, т. е. отношения напряжения на клеммах к катушка сопротивление, достигается. Синяя пунктирная линия показывает падение напряжения на катушке. Как мы видим, это падение максимально в момент подачи питания и минимально после того, как ток достигает своего пикового значения. Это связано с упомянутым ранее фактом, что индукционное напряжение имеет противоположное направление, чем напряжение, приложенное к клеммам.

При описании параметров неидеальной катушки обсуждается резонансная частота катушки, так как она связана с паразитной емкостью.

Материал сердечника и относительная магнитная проницаемость

Очень важным элементом индукционной катушки является ее сердечник. Сердечник характеризуется типом используемого материала и связанной с ним относительной магнитной проницаемостью. Он называется относительным, потому что определяется по отношению к проницаемости вакуума. Это безразмерное число, определяемое как отношение магнитной проницаемости (абсолютное значение мк ) данной среды к магнитной проницаемости вакуума мк ₀ .

Согласно определению, магнитная проницаемость – это способность данного материала или среды изменять магнитную индукцию вместе с изменением напряженности магнитного поля. Другими словами, магнитная проницаемость — это свойство материала или среды, характеризующее его способность концентрировать линии магнитного поля.

Магнитная проницаемость, согласно данным, опубликованным в 2002 г. Комитетом по данным для науки и технологий (CODATA), представляет собой скаляр, который обозначается цифрой 9.0019 μ ₀ символ и значение которого в Международной системе единиц (СИ) равно μ ₀ = 4·Π·10 ^-7 = ок. 12,566370614·10 ^-7 [Гн/м = В·с/А·м] .

Индуктивность катушки выражается по следующей формуле:

Символы, используемые в формуле, означают:

• L — индуктивность в генри,
• μ ₀ — магнитная проницаемость вакуума,
• μ — относительная проницаемость материала сердцевины,
• Z — количество витков провода в катушке,
• S — площадь поперечного сечения катушки,
• l — длина змеевика.

Относительная проницаемость незагрязненного воздуха мало чем отличается от проницаемости вакуума, поэтому для упрощения в инженерной практике принято, что мк = 1 и формула индуктивности воздушной катушки:

Синими линиями показаны линии силы магнитного поля, направленные в соответствии с правилом Ленца (так называемое правило правой руки).

По магнитным свойствам материалы делятся на парамагнитные материалы (материалы, которые превращаются в магниты после помещения их в магнитное поле), ферромагнитные материалы (намагничиваются в присутствии магнитного поля) и диамагнитные материалы ( ослабление магнитного поля). Тип материала сердечника сильно влияет на параметры катушки. В идеальном вакууме нет частиц, которые могли бы повлиять на корреляцию между индуктивностью и напряженностью магнитного поля. При этом в каждой материальной среде формула индуктивности будет изменяться в зависимости от проницаемости этой конкретной среды. В случае вакуума значение проницаемости равно 1. Для парамагнетиков относительная проницаемость чуть выше 1, для диамагнетиков чуть меньше 1 — различия в обоих случаях настолько малы, что в технических приложениях ими пренебрегают. а значение принимается равным 1,

Подытожим этот абзац, перечислив параметры катушки, оказывающие наиболее существенное влияние на ее индуктивность:

Для чего используются сердечники? Во-первых, благодаря этому можно хранить больше энергии при меньшем количестве витков, чем в случае эквивалента с воздушным сердечником. Во-вторых, это связано с механической конструкцией катушки – сердечник является опорой для витков проволоки и обеспечивает правильную установку в целевом устройстве. Третьей важной причиной является концентрация и проводимость магнитного поля. В некоторых приложениях также будет важна возможность регулировать индуктивность катушки, изменяя положение сердечника относительно витков провода, например, вставляя или выталкивая его.

Неидеальная катушка

До этого момента мы обсуждали параметры идеальной катушки. Между тем, в реальных условиях провод обмотки будет иметь некоторое сопротивление и емкость, что повлияет на фактические параметры катушки, которые мы еще не рассматривали.

На рисунке показана эквивалентная схема постоянного тока реальной катушки. Резистор, представляющий сопротивление провода обмотки, был подключен последовательно к виткам катушки. При протекании тока через катушку это вызовет не только падение напряжения, но и потерю мощности в виде тепла, что может привести к перегреву катушки и изменению параметров сердечника. Как следствие, снижается и электрический КПД всего устройства.

Альтернативная принципиальная схема постоянного тока реальной катушки

В случае анализа переменного тока следует также учитывать паразитную емкость, создаваемую неизолированными слоями проводника, и поэтому эквивалентная схема, кроме резистора , включает также конденсатор, подключенный параллельно клеммам катушки. Так создается RLC-контур, а сама катушка до достижения резонансной частоты является индуктивной, а после ее достижения становится емкостной. Вот почему импеданс катушки увеличивается с резонансной частотой, достигая своего максимального значения в резонансе, и уменьшается после превышения частоты.

Изменение реальной катушки с индуктивной на емкостную после достижения резонансной частоты. Обозначения на эквивалентной принципиальной схеме: L – индуктивность, EPC – паразитная емкость, EPR – параллельное сопротивление, обозначающее потери мощности, ESR – последовательное сопротивление, обозначающее сопротивление сердечника обмотки)

Три вида потерь мощности в индукционных катушках

При применении катушек рассматриваются три основных типа потерь мощности. Первый из них уже упоминался ранее, а именно потери, происходящие в последовательном сопротивлении, т. е. в проводе обмотки. Эту потерю мощности следует особенно учитывать, когда ток, протекающий через катушку, имеет большую силу тока. Это наиболее распространенная потеря мощности в источниках питания и силовых цепях. Это вызывает перегрев катушки и, как следствие, всего устройства. Это также наиболее распространенная причина повреждения, так как высокая температура может повредить изоляцию и вызвать короткое замыкание на катушках.

Второй тип потери мощности происходит в активной зоне. Это результат несовершенства изготовления, возникновения вихревых токов и изменения положения магнитных доменов. Такие потери являются доминирующими, когда ток, протекающий через катушку, имеет малую силу тока. Они возникают в цепях с высокой частотой, цифровых разделителях сигналов и других. Это может привести не столько к повреждению катушки, сколько к потере уровня сигнала в чувствительных цепях.

Третий вид потерь мощности возникает в результате потери магнитного потока, который может быть рассеян механическими монтажными элементами, воздушными зазорами в сердечнике или небрежным качеством изготовления самой катушки.

Ознакомьтесь с нашим предложением

Заключительные замечания

Индукционная катушка является простым компонентом, и поэтому ею часто пренебрегают. Между тем, при монтаже электронной схемы, оснащенной дросселями или преобразователями, особое внимание следует уделить выбору индуктивных компонентов, в том числе их резонансным частотам или параметрам материала сердечника. Используются разные ядра с текущей частотой десятки и сотни герц и разные с частотой сотни мегагерц и более. Иногда для высокочастотных сигналов достаточно ферритовой шайбы.

Индукционные катушки могут изготавливаться различными способами. Обычно на сердечник наматывают от нескольких до нескольких сотен витков провода. В некоторых приложениях витки наматываются в виде дорожек на печатной плате, а иногда и замыкаются в ферритовом сердечнике.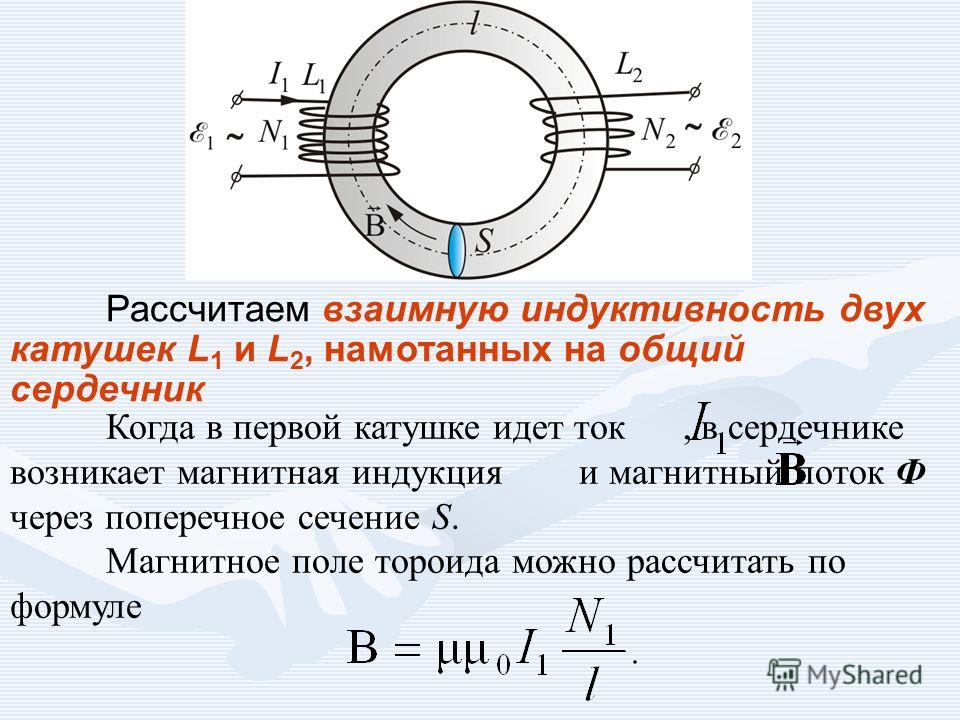 В настоящее время большинство катушек, в частности дросселей, используемых в силовых цепях, изготавливаются с целью монтажа SMT. Тем не менее, технологическая гонка идет жестко, и разрабатываются все новые магнитные материалы, способные сохранять свои характеристики и ограничивать потери, несмотря на повышение температуры и т. д.

Катушка, предназначенная для работы на низкой частоте, обычно имеет железный сердечник и большое количество витков, что делает ее относительно тяжелой. Вот почему во многих приложениях, особенно уязвимых к ударам и перенапряжениям, важную роль играет способ монтажа. Обычно припаять катушку недостаточно — ее сердечник нужно правильно зафиксировать с помощью зажима, держателя или винта. При выборе катушки или преобразователя для устройства стоит учитывать этот аспект.

Применение индукционных катушек в электронике

Катушки используются для:

• блокировки протекания переменного тока в цепи,
• КЗ постоянного тока (напряжения),
• измерение времени на основе снижения текущего расхода,
• построить колебательный контур,
• построить фильтры для определенных частот,
• пара каскадов усилителя,
• уменьшить или увеличить напряжение.