Индукция обозначение. Магнитная индукция: определение, формулы и применение в физике

Что такое магнитная индукция. Как обозначается и измеряется магнитная индукция. Какова формула для расчета магнитной индукции. Где применяется магнитная индукция в науке и технике.

Что такое магнитная индукция и как она обозначается

Магнитная индукция — это важнейшая характеристика магнитного поля, показывающая его силовое воздействие на движущиеся электрические заряды и проводники с током. В физике магнитная индукция обозначается латинской буквой B и является векторной величиной.

Магнитная индукция характеризует интенсивность магнитного поля и определяет силу, действующую на проводник с током или движущуюся заряженную частицу. Чем больше магнитная индукция, тем сильнее магнитное поле и его воздействие.

Единицы измерения и формула магнитной индукции

В Международной системе единиц (СИ) магнитная индукция измеряется в теслах (Тл). Эта единица названа в честь выдающегося сербского физика и изобретателя Николы Теслы.

Магнитную индукцию можно рассчитать по следующей формуле:

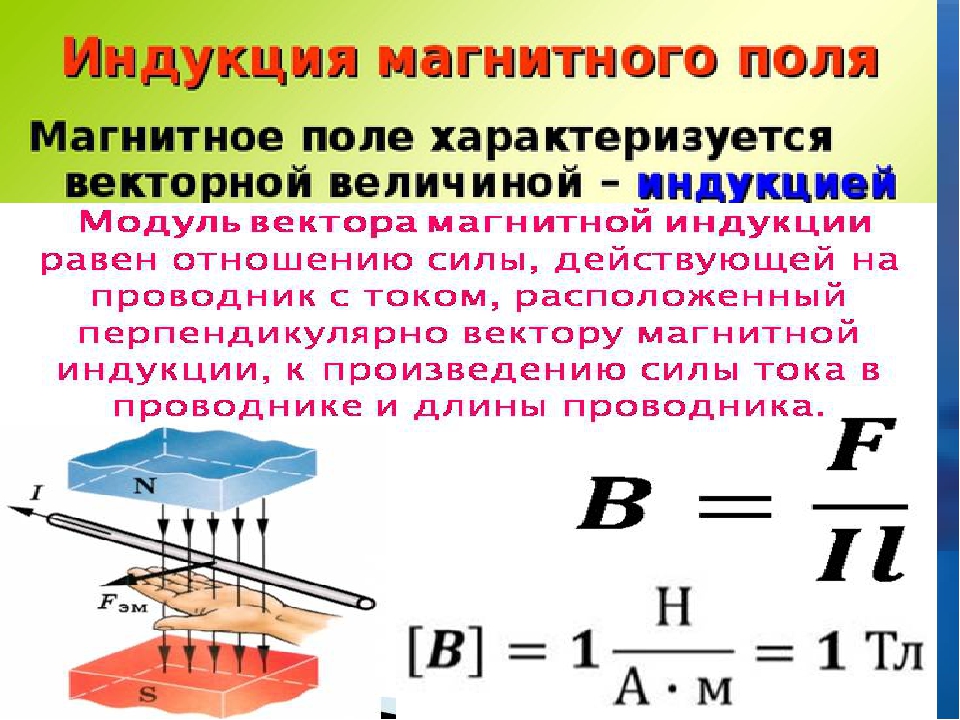
B = F / (I * l)

где:

• B — магнитная индукция (Тл)
• F — сила Ампера, действующая на проводник (Н)
• I — сила тока в проводнике (А)
• l — активная длина проводника (м)

Таким образом, магнитная индукция численно равна силе, действующей на единицу длины проводника при единичном токе, расположенном перпендикулярно линиям магнитной индукции.

Физический смысл и свойства магнитной индукции

Какой физический смысл имеет магнитная индукция. Магнитная индукция характеризует способность магнитного поля оказывать силовое действие на движущиеся электрические заряды и проводники с током. Чем больше величина магнитной индукции, тем сильнее это воздействие.

Основные свойства магнитной индукции:

• Является векторной величиной — имеет не только числовое значение, но и направление в пространстве
• В каждой точке магнитного поля вектор магнитной индукции направлен по касательной к силовой линии поля
• Силовые линии магнитного поля всегда замкнуты, не имеют начала и конца
• Магнитная индукция подчиняется принципу суперпозиции — индукция результирующего поля равна векторной сумме индукций складываемых полей

Способы создания и измерения магнитной индукции

Как можно создать магнитное поле с определенной индукцией. Существует несколько основных способов:

1. С помощью постоянных магнитов
2. Электромагнитами — катушками с током
3. Движущимися электрическими зарядами
4. Проводниками с током

Для измерения магнитной индукции применяются специальные приборы — тесламетры. Принцип их действия основан на эффекте Холла — возникновении поперечной разности потенциалов в проводнике с током, помещенном в магнитное поле.

Применение магнитной индукции в науке и технике

Где используется магнитная индукция на практике. Знание магнитной индукции и умение ее рассчитывать важно во многих областях:

• Электротехника — расчет и проектирование электрических машин, трансформаторов
• Физика элементарных частиц — управление пучками заряженных частиц
• Медицина — магнитно-резонансная томография
• Геология — исследование магнитного поля Земли
• Космонавтика — защита от космической радиации
• Магнитная левитация в транспорте

Таким образом, магнитная индукция находит широкое практическое применение в современной науке и технологиях.

Связь магнитной индукции с другими характеристиками поля

Как магнитная индукция связана с другими параметрами магнитного поля. Существуют важные соотношения:

1. Магнитный поток Ф = B * S, где S — площадь поверхности
2. Напряженность магнитного поля H = B / μ, где μ — магнитная проницаемость среды
3. Сила Лоренца F = q * v * B * sinα, где q — заряд частицы, v — ее скорость, α — угол между v и B

Эти соотношения позволяют связать магнитную индукцию с другими характеристиками поля и рассчитывать различные эффекты.

Магнитная индукция в разных средах

Как меняется магнитная индукция в различных веществах. В зависимости от магнитных свойств среды, индукция может усиливаться или ослабляться:

• Диамагнетики слегка ослабляют внешнее магнитное поле
• Парамагнетики немного усиливают поле
• Ферромагнетики значительно усиливают магнитное поле

Это связано с различным поведением атомов вещества во внешнем магнитном поле. Например, в ферромагнетиках происходит выстраивание магнитных моментов атомов, что многократно усиливает поле.

Магнитная индукция Земли

Магнитное поле Земли имеет сложную структуру. У поверхности планеты индукция составляет от 25 до 65 мкТл, увеличиваясь от экватора к полюсам. Магнитное поле Земли защищает биосферу от космической радиации и играет важную роль в ориентации многих живых организмов.

Историческое развитие представлений о магнитной индукции

Как развивались знания о магнитной индукции. Основные этапы:

1. Древние греки и китайцы обнаружили явление магнетизма
2. В 1600 г. Уильям Гильберт опубликовал первый научный трактат о магнетизме
3. В 1820 г. Эрстед открыл связь электричества и магнетизма
4. Фарадей и Максвелл в XIX веке создали теорию электромагнитного поля
5. В XX веке развитие квантовой механики позволило объяснить природу магнетизма на атомном уровне

Эти открытия заложили фундамент современных представлений о магнитной индукции и ее роли в природе.

Вклад Николы Теслы

Никола Тесла внес огромный вклад в изучение электромагнетизма. Он изобрел вращающееся магнитное поле, асинхронный электродвигатель, систему передачи электроэнергии на большие расстояния. Именно в честь Теслы названа единица измерения магнитной индукции.

Перспективные направления исследований магнитной индукции

Какие новые области применения магнитной индукции развиваются сегодня. Среди перспективных направлений:

• Сверхпроводящие магнитные системы для термоядерных реакторов
• Магнитные наноматериалы для хранения информации
• Магнитные методы очистки воды и воздуха
• Магнитная гипертермия для лечения рака
• Магнитные системы для защиты от космической радиации

Эти исследования открывают новые возможности применения знаний о магнитной индукции для решения глобальных проблем человечества.

Как обозначается индукция магнитного поля в физике? Формула и теория / Справочник :: Бингоскул

Как обозначается индукция магнитного поля в физике? Формула и теория

добавить в закладки удалить из закладок

Содержание:

Магнитное поле относится к силовым физическим величинам – воздействует на проводник, пропускающий электрический ток. Зависит от активной длины проводника, силы Ампера и протекающего тока. Ознакомимся подробнее с понятием магнитная индукция, формулой для её вычисления, причинами появления, практическим использованием.

Теория

Магнитное поле относится к силовым, значит, его характеризуют индукцией. Последняя обнаруживается двумя путями:

•  по наличию силы Ампера, оказывающей воздействие на прямой проводник, пропускающий электрический ток;
•  пиковым вращающим моментом, действующим на закрытый контур с магнитным моментом.

Исследуя магнитные поля посредством проводящего электричество проводника, модуль их индукции вычисляется как отношение пикового значения силы Ампера FA, оказывающей воздействие на проводник к произведению силы проходящего по нему тока, умноженную на активную длину проводящего ток провода. Магнитное поле относится к однородным, если в его точках вектор B одинаков по модулю и направлению.

Направление индукции определяется по следующему алгоритму:

1. Прямолинейный проводник ориентируется в поле так, чтобы действовала как можно большая сила FA.
2. Левая рука с раскрытой ладонью помещается у проводника.
3. Четыре пальца указывают на направление протекания тока.
4. Большой палец отгибается на 90°, указывает направление F_A.
5. Вектор индукции направлен в раскрытую ладонь под углом 90°.

Алгоритм называется правилом левой руки.

Вектор индукции для соленоида входит в катушку со стороны, где ток двигается по ходу часовой стрелки. 

Силовые линии обнаруживаются и при помощи металлических опилок.

Изменяя параметры поля и соленоида, формируют интересные узоры.

Магнитная индукция: формула, единица измерения

В физике индукция магнитного поля обозначается буквой B. Вычисляется по формуле:

B= F / Il, здесь:

•  F – максимальная сила Ампера;
•  I – значение тока;
•  l – длина проводника.

Единица измерения B: Н / (А*м) = 1 Тл – Тесла. Названа в честь югославского физика и изобретателя Никола Тесла.

Исследуя магнитную составляющую проводника при помощи замкнутого контура, направление вектора B принимают за направление, расположенное под 90° к плоскости, где установлен вращающийся контур.

По модулю B также равняется отношению пикового момента сил M, оказывающего воздействие на контур с током, к величине тока, протекающего по рамке, и её площади:

B = M / IS.

Единица измерения совпадает с описанной ранее: Н*м /А*м² = Н / А* м = 1 Тл.

Задача

Вычислить индукцию куска провода длиной 10 см, расположенного в магнитном поле 50 мН, если по нему протекает ток 5 А.

B = F / Il. Всё известно, подставляем значения в формулу.

B = 0,05 / (5*0,1) = 0,2 Тл.

Ответ: индукция равняется 0,02 Тл.

Поделитесь в социальных сетях:

24 октября 2021, 21:03

Физика

Could not load xLike class!

Магнитная индукция, магнитный поток: определение, формулы, смысл

Пример HTML-страницы

Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.

Магнитная индукция определяется способностью влиять на объект с помощью магнитного поля. Эта способность проявляется при перемещении постоянного магнита в катушке, в результате чего в катушке индуцируется (возникает) ток, при этом магнитный поток в катушке также увеличивается.

Содержание

1. Физический смысл магнитной индукции
2. Формула магнитной индукции
3. Магнитный поток

Физический смысл магнитной индукции

Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.

Васильев Дмитрий Петрович

Профессор электротехники СПбГПУ

Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки — именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.

В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.

При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.

Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.

Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.

Формула магнитной индукции

где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.

Магнитный поток

Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур.

Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла.

Магнитометры, используемые для ее измерения, называют теслометрами.

Абрамян Евгений Павлович

Доцент кафедры электротехники СПбГПУ

Единицей измерения магнитной индукции в системе СИ является Тесла (Тл). 2\frac1k$. 9{2n}\frac1k \end{align}$$

как и должно было быть показано!

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

индукция — Обозначение переменной в индуктивном шаге?

$\begingroup$

Индукция обычно используется для таких утверждений:

$\forall n \in \mathbb{N}:~P(n)$

фиксированный» $n$ или $k$. Существует ли хорошая и, надеюсь, короткая математическая запись для «Пусть $n$ или $k$ — произвольное, но фиксированное целое число»? Я думал написать

$\forall n \in \mathbb{N}:~P(n)$ или

$\forall k \in \mathbb{N}:~P(k)$

в предположении индукции означает «произвольное, но фиксированное», но это то же самое утверждение, которое мы пытаемся доказать. Итак, нам сказали в классе, что это неправильно.

Может быть, мое понимание слов «forall» и «произвольный, но фиксированный» неверно, но если они одинаковы, то почему мы не можем написать $\forall n \in \mathbb{N}:~P(n)$? И если «все» и «произвольное, но фиксированное» не одно и то же, почему мы можем просто переопределить n (я читал, что переключение переменной просто для ясности, но вы можете использовать n дважды. Почему мы используем другую переменную на индуктивном шаге математической индукция?)

Спасибо.

• обозначение
• индукция

$\endgroup$

1

$\begingroup$

Принцип индукции состоит в том, что вы можете доказать утверждение вида $\forall n \in \mathbb N : P(n)$, доказав $$P(0) \wedge \forall k \in \mathbb N: (P(k) \ подразумевает P(k+1))$$ вместо этого (или сдвинутые версии этого, чтобы ваши натуральные числа начинались с $1$ и так далее). Таким образом, у вас все еще есть утверждение, которое универсально квантифицируется для натуральных чисел, но это другое утверждение (а именно, $P(k) \ подразумевает P(k+1)$ вместо $P(n)$). Это новое доказательство часто значительно проще.

Теперь, чтобы доказать что-то вида $\forall x \in X : (P(x) \implis Q(x))$ (где $Q(x) :\equiv P(x + 1)$ в этом случай), мы предполагаем, что у нас есть элемент $x$, который удовлетворяет $P(x)$, и мы показываем, что в этом контексте $Q(x)$ также выполняется.

Этот контекст предположений не имеет формальной записи в традиционной математике, но вместо этого написан на естественном языке. (Исключением могут быть области, которые изучают доказательства и системы рассуждений, но даже там естественный язык обычно используется для метатеории.) Преимущество этого заключается в лучшем потоке текста и большей гибкости в количестве деталей, которые вы даете.

В частности, для индукции правильно указать свою гипотезу индукции (т. е. что $k \in \mathbb N$ и $P(k)$), часто просто написав перед ней «гипотеза индукции». . Добавлено позже : Также обратите внимание, что вам нужно показать $\forall k \in \mathbb N: (P(k) \подразумевает P(k+1))$ при использовании индукции, которая не имеет $\forall k \in \mathbb N : P(k)$ как подвыражение (круглые скобки расставлены по-другому), поэтому $\forall k \in \mathbb N : P(k)$ не имеет смысла как гипотеза индукции.

$\endgroup$

$\begingroup$

Когда вы пишете $\forall n P(n),$, тогда $n$ является произвольным, но переменным натуральным числом: вы буквально делаете утверждение для всех натуральных чисел одновременно.