Индуктивное сопротивление это. Индуктивное сопротивление: особенности, формулы расчета и применение

Что такое индуктивное сопротивление. Как рассчитывается индуктивное сопротивление. От чего зависит величина индуктивного сопротивления. Какое влияние оказывает индуктивное сопротивление на цепи переменного тока. Как связаны индуктивное сопротивление и частота.

Что такое индуктивное сопротивление

Индуктивное сопротивление (XL) — это величина, характеризующая противодействие катушки индуктивности изменению тока в цепи переменного тока. Оно обусловлено явлением самоиндукции в катушке. Индуктивное сопротивление измеряется в омах и зависит от индуктивности катушки и частоты переменного тока.

Основные характеристики индуктивного сопротивления:

• Возникает только в цепях переменного тока
• Пропорционально частоте переменного тока и индуктивности катушки
• Вызывает отставание тока от напряжения по фазе на 90°
• Измеряется в омах (Ом)
• Не вызывает потерь энергии в виде тепла

Формула расчета индуктивного сопротивления

Индуктивное сопротивление XL рассчитывается по формуле:

XL = 2πfL

где:

• XL — индуктивное сопротивление (Ом)
• f — частота переменного тока (Гц)
• L — индуктивность катушки (Гн)
• π ≈ 3,14159

Как видно из формулы, индуктивное сопротивление прямо пропорционально частоте и индуктивности. При увеличении частоты или индуктивности индуктивное сопротивление возрастает.

Влияние индуктивного сопротивления на цепь переменного тока

Индуктивное сопротивление оказывает следующее влияние на цепь переменного тока:

• Ограничивает силу тока в цепи
• Вызывает сдвиг фаз между током и напряжением
• Создает реактивную мощность в цепи
• Влияет на полное сопротивление цепи

Какая взаимосвязь между током и напряжением в цепи с индуктивностью? В такой цепи ток отстает от напряжения по фазе на 90°. Это происходит из-за того, что катушка индуктивности препятствует изменению тока, создавая ЭДС самоиндукции.

Зависимость индуктивного сопротивления от частоты

Индуктивное сопротивление прямо пропорционально частоте переменного тока. При увеличении частоты индуктивное сопротивление возрастает. Это объясняется тем, что при более высокой частоте скорость изменения тока больше, а значит сильнее проявляется эффект самоиндукции в катушке.

Как частота влияет на индуктивное сопротивление:

• При f = 0 (постоянный ток) XL = 0
• При увеличении f индуктивное сопротивление XL растет линейно
• При f → ∞ индуктивное сопротивление XL → ∞

Индуктивное сопротивление в различных электрических устройствах

Индуктивное сопротивление играет важную роль в работе многих электрических устройств и систем:

• Трансформаторы — влияет на передачу энергии между обмотками
• Электродвигатели — создает вращающееся магнитное поле статора
• Дроссели — ограничивает пульсации тока
• ЛЭП — вызывает потери при передаче электроэнергии
• Фильтры — используется для частотной селекции сигналов

Где еще проявляется индуктивное сопротивление? Оно играет важную роль в работе импульсных источников питания, сварочных аппаратов, систем зажигания автомобилей и многих других устройств.

Сравнение индуктивного и активного сопротивления

Индуктивное и активное сопротивление имеют ряд ключевых отличий:

Параметр	Индуктивное сопротивление	Активное сопротивление
Обозначение	XL	R
Зависимость от частоты	Зависит	Не зависит
Сдвиг фаз	Вызывает сдвиг на 90°	Не вызывает сдвига фаз
Рассеивание энергии	Не рассеивает	Рассеивает в виде тепла

Какое главное отличие индуктивного сопротивления от активного? Индуктивное сопротивление не приводит к потерям энергии в виде тепла, а лишь вызывает сдвиг фаз между током и напряжением.

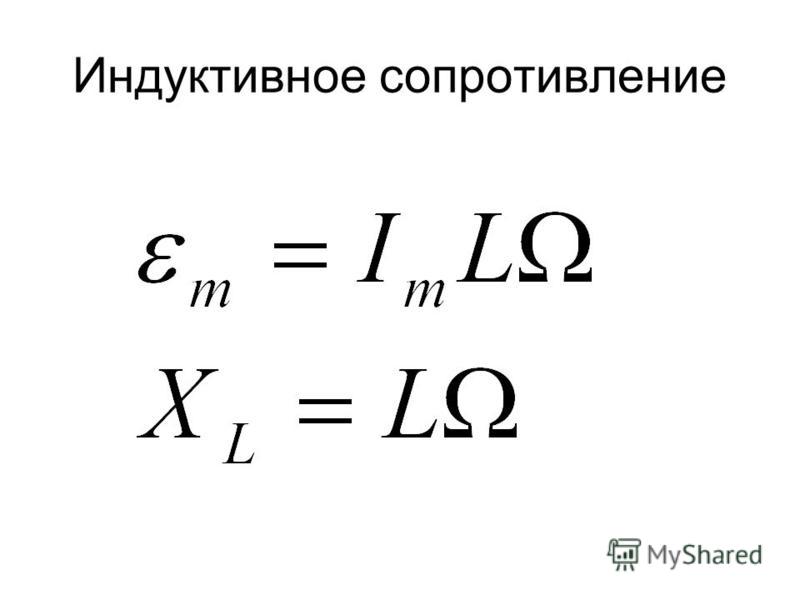
Расчет тока в цепи с индуктивным сопротивлением

Для расчета действующего значения тока в цепи с индуктивным сопротивлением используется закон Ома:

I = U / XL

где:

• I — действующее значение тока (А)
• U — действующее значение напряжения (В)
• XL — индуктивное сопротивление (Ом)

Пример расчета: При напряжении 220 В, частоте 50 Гц и индуктивности 0,1 Гн ток в цепи составит:

XL = 2π * 50 * 0,1 = 31,4 Ом

I = 220 / 31,4 = 7 А

Применение индуктивного сопротивления в электротехнике

Знание свойств индуктивного сопротивления широко используется в электротехнике для решения различных задач:

• Создание фазосдвигающих цепей
• Частотная фильтрация сигналов
• Ограничение пусковых токов двигателей
• Компенсация реактивной мощности
• Настройка колебательных контуров

Как используется индуктивное сопротивление в электрических фильтрах? В фильтрах нижних частот индуктивное сопротивление катушки растет с увеличением частоты, что позволяет подавлять высокочастотные составляющие сигнала.

Что такое индуктивное сопротивление: 29 важных фактов

Катушка индуктивности:

Индуктор — это пассивный компонент электрической цепи, противодействующий току. Это моток проволоки, обернутый вокруг магнитного материала. Приложенное напряжение индуцирует ток через катушку индуктивности. Когда ток течет через индуктор, он создает магнитное поле. Магнитные поля не меняются. Следовательно, индуктор пытается предотвратить изменение тока, протекающего через него.

Реактивность:

Реактивное сопротивление определяется как сопротивление току, протекающему в электрическая цепь, Обозначается ?. 

Индуктивное реактивное сопротивление X_L:

Индуктивное реактивное сопротивление — это реактивное сопротивление, обеспечиваемое катушкой индуктивности: чем больше реактивное сопротивление, тем меньше ток. 

В цепи постоянного тока индуктивное реактивное сопротивление будет равно нулю (короткое замыкание), на высоких частотах индуктор имеет бесконечное реактивное сопротивление (разомкнутая цепь).

Единицы индуктивного реактивного сопротивления | Единица СИ индуктивного реактивного сопротивления

Индуктивное реактивное сопротивление противодействует протеканию тока в цепи. Таким образом, единица измерения индуктивного сопротивления в системе СИ такая же, как и у сопротивления, то есть Ом. 

Символ индуктивного сопротивления

Индуктивное сопротивление обозначается ?_L or X_L. 

Вывод индуктивного сопротивления 

Предположим, у нас есть следующая электрическая цепь с индуктивностью L, подключенная к источнику переменного напряжения. Этот источник создает переменный ток, который течет внутри индуктора, если переключатель замкнут. Таким образом, электрический ток в цепи в любой момент определяется выражением

я=я_OCosωt

Где я₀= пиковое значение тока

           ω = угловая частота

Теперь, если мы применим второй закон Кирхгофа или закон петли Кирхгофа в этой схеме, мы получим,

Таким образом, напряжение на катушке индуктивности V равно индуктивности, умноженной на производную электрического тока I по времени.  

Если cos (ωt + 90 °) = 1, то V = V₀= LI₀ω (пиковое напряжение)

Мы знаем по закону Ома, 

Внутри резистора 

V₀=I₀R 

где R = сопротивление

V₀=I₀\X_L   

Поскольку индуктивное реактивное сопротивление аналогично сопротивлению, мы можем получить аналогичное уравнение:

где?_L= индуктивное реактивное сопротивление

Сравнивая V₀ найденное в предыдущем уравнении, можно сделать вывод, что,

X_L = ωL = 2πfL

где f = частота

Формула индуктивного сопротивления

Индуктивное сопротивление катушки составляет,

?_L= ωL или ?_L= 2? FL

Где ω — угловая частота, f — частота приложенного напряжения, а L — индуктивность катушки.

Вывод индуктивного сопротивления

Индуктивное реактивное сопротивление последовательно

В приведенной выше схеме три индуктивности L₁, L₂ и я₃ соединены последовательно. Следовательно, если мы применим закон Кирхгофа,

Взяв пиковое значение, мы можем сказать, что,

V_o = Я_oω(L₁ + L₂+ L₃)

Итак, общая индуктивность L = L₁+L₂+L₃

Следовательно, индуктивное реактивное сопротивление при последовательном включении, ?_L= ω(L₁+L₂+L₃+… ..L_n)

Индуктивное реактивное сопротивление параллельно

В приведенной выше схеме три индуктивности, L₁, L₂ и я₃, соединены параллельно. Если полная индуктивность равна L, по закону Кирхгофа мы можем сказать:

Итак,

Следовательно, индуктивное реактивное сопротивление при параллельном включении,

Индуктивность и индуктивное сопротивление

Магнетизм и электричество сосуществуют в электрических цепях. Если проводник помещен в постоянно изменяющееся магнитное поле, в проводнике создается сила. Это называется электродвижущей силой или ЭДС. Способность создавать напряжение для изменения протекания тока называется индуктивность. 

ЭДС помогает току течь в цепи. Пока ток проходит через катушку индуктивности, она пытается противодействовать току. Эта реакция известна как индуктивное сопротивление.

В чем разница между индуктивностью и индуктивным сопротивлением?

Индуктивность

• Индуктивность:

• Единица индуктивности — Генри или Х.
• Размер индуктивности [ML₂T_-2A_-2]
• Это не зависит от частоты.
• Чем больше индуктивность, тем больше будут наведенные ЭДС и ток.

Индуктивное сопротивление

• Индуктивное сопротивление XL=ωL.
• Единицей индуктивного сопротивления является ом или Ом.
• Размер индуктивного реактивного сопротивления составляет [ML₂T_-3I_-2].
• Это зависит от частоты.
• Чем больше индуктивное сопротивление, тем меньше будет ток.

Индуктивное реактивное сопротивление в цепи постоянного тока

В цепи постоянного тока частота сети равна нулю. Следовательно ?_L также равен нулю. Катушка индуктивности в установившемся режиме ведет себя как короткое замыкание.

Связь между индуктивностью и реактивным сопротивлением

реактанс ? состоит из двух компонентов —

• Индуктивное реактивное сопротивление или ?_L
• Емкостное реактивное сопротивление или ?_C

Поэтому

Формула полного индуктивного реактивного сопротивления

Разница между индуктивностью и реактивным сопротивлением

Индуктивность:

• Единица индуктивности — Генри или Х.
• Размер индуктивности [ML²T^-2A^-2]
• Это не зависит от частоты.
• Индуктивность прямо пропорциональна току.

Индуктивное сопротивление

• реактанс

• Единица реактивного сопротивления — Ом или Ом.
• Размер индуктивного реактивного сопротивления составляет [ML²T^-3I^-2]
• Это зависит от частоты. 
• Реактивное сопротивление обратно пропорционально току.

Инверсия индуктивного реактивного сопротивления — это восприимчивость.

Величина, обратная индуктивному реактивному сопротивлению, известна как индуктивная восприимчивость. Обозначается B_L. 

Индуктивная проводимость аналогична проводимости G, которая является обратной величине сопротивления.

Итак, единица B_L также siemen или S.

Физически индуктивная восприимчивость представляет собой способность чисто индуктивной электрической цепи пропускать через нее ток.

Реактивность и восприимчивость 

Реактивное сопротивление измеряет реакцию цепи на изменение тока во времени, в то время как восприимчивость измеряет, насколько восприимчива цепь к проведению изменяющегося тока.

Сопротивление, реактивное сопротивление, емкость, сопротивление индуктивности, сопротивление. 

параметры	Сопротивление	реактанс	емкость	Индуктивность	полное сопротивление
Определение	Мера препятствия, создаваемого проводником по направлению тока, известна как сопротивление.	Характеристика катушки индуктивности и конденсатора противодействовать любому изменению тока называется реактивным сопротивлением.	Способность проводника накапливать электрический заряд называется емкостью.	Свойство проводника генерировать ЭДС из-за изменения тока известно как индуктивность.	Импеданс — это полное противодействие в электрической цепи, вызванное катушкой индуктивности, конденсатором и резистором.
Символ	Сопротивление обозначается R	Реактивное сопротивление представлено ?	Емкость обозначается C	Индуктивность обозначена L	Импеданс представлен Z
Ед. изм	ом	ом	фарада	Henry	ом
Общее выражение	Сопротивление в цепи с напряжением v и током i равно, R = V/I	Реактивное сопротивление в цепи с угловой частотой источника напряжения ω равно, X= ωL + 1/ωC	Емкость плоского конденсатора со средней диэлектрической проницаемостью ϵ, площадью пластин A и расстоянием между пластинами d составляет C=ϵA/d.	Индуктивность катушки с наведенным напряжением V равна, L=V/ dI/dT	Полный импеданс цепи можно записать как Z = ZR+ZC+ZL

Емкостное сопротивление

Как и индуктивное реактивное сопротивление, емкостное реактивное сопротивление — это импеданс, вызванный конденсатором. Обозначается Xc. Когда в RC-цепи подается постоянное напряжение, конденсатор начинает заряжаться. Впоследствии ток течет, и внутреннее сопротивление конденсатора препятствует ему.  

Емкостное сопротивление

В чем разница между индуктивным и емкостным сопротивлением?

Емкостное реактивное сопротивление против индуктивного реактивного сопротивления

Емкостное сопротивление	Индуктивное сопротивление
Реактивное сопротивление конденсатора	Реактивное сопротивление катушки индуктивности
Обозначается XC	Обозначается XL
XC =1/ωС	XL =ωL
Когда на конденсатор подается синусоидальное переменное напряжение, ток опережает напряжение на фазовый угол 90 °.	Когда синусоидальное переменное напряжение подается на катушку индуктивности, ток отстает от напряжения на фазовый угол 90 °.
Она обратно пропорциональна частоте.	Она прямо пропорциональна частоте
При питании постоянным током конденсатор ведет себя как разомкнутая цепь.	При питании постоянным током катушка индуктивности ведет себя как короткое замыкание.
На высокой частоте конденсатор действует как короткое замыкание.	На высокой частоте индуктор действует как разомкнутая цепь.

Цепь переменного тока в комбинации серии LR

В приведенной выше цепи есть два компонента — резистор R и катушка индуктивности L. Пусть напряжение на резисторе Vr, а напряжение на катушке индуктивности VL.

На векторной диаграмме видно, что полное напряжение V, напряжение резистора V_r и напряжение индуктора V_L образует прямоугольный треугольник.

Применяя теорему Пифагора, получаем,

V²=V_r²+V_L²

где φ = фазовый угол

Как найти индуктивное сопротивление? | Важные формулы

X_L = 2πfL

Мощность Р=В_RMSI_RMSпокупкаφ

Рассчитайте индуктивное реактивное сопротивление | Пример расчета индуктивного реактивного сопротивления

Найдите напряжение переменного тока, необходимое для протекания тока 20 мА через катушку индуктивности 100 мГн.

Частота питания 500 Гц.

Дано: i = 20 мА f = 400 Гц L = 100 мГн

Поскольку серия является чисто индуктивной, полное сопротивление в цепи Z = X_L

Мы знаем, X_L= ωL = 2? fL = 2 x 3.14 x 400 x 0.1 = 251.2 Ом

Следовательно, напряжение питания V = iX_L= 02 x 251.2 = 5.024 вольт

Рассчитать X

_L индуктивности 5 мГн при подаче переменного напряжения 50 Гц. Также нахожу я_RMS на каждой частоте, когда V_RMS составляет 125 вольт.

X_L= 2? FL = 2 x 3.14 x 50 x 5 x 001 = 1.57 Ом

Рассчитайте индуктивное реактивное сопротивление, используя напряжение и ток

Сопротивление 20 Ом, индуктивность 200 мГн и емкость 100 мкФ подключены последовательно к сети 220 В, 50 Гц. Определить X

_L, ИКС_C и ток, протекающий по цепи.

Мы знаем, V = 220 вольт R = 20 Ом L = 0.2 H f = 50 Гц

X_L= 2? FL = 2 x 3.14 x 50 x 0.2 = 62.8 Ом

= 1 / (2 x 3. 14 x 50 x 0.0001) = 31.8 Ом

Следовательно, полное сопротивление,

= (20)2+(62.8-31.8)2=36.8 ohm

Итак, текущий

Сопротивление-реактивное сопротивление-импеданс: сравнительное исследование

Сопротивление	реактанс	полное сопротивление
Противодействует потоку электронов	Противостоит изменениям в текущем	Сочетание реактивного сопротивления и сопротивления
R = V / I	Х = ХL + XC	Z=(R2 + XL2)1/2
Измеряется в Ом	Измеряется в Ом	Измеряется в Ом
Не зависит от частоты	Зависит от частоты	Зависит от частоты

Реактивное сопротивление утечки в асинхронном двигателе

Реактивное сопротивление утечки — это полное сопротивление, вызванное индуктором рассеяния в асинхронном двигателе. Вращающееся магнитное поле возникает в асинхронном двигателе из-за приложенного трехфазного питания. Большинство линий магнитного потока, генерируемых обмоткой статора, проходят через ротор. Хотя очень немногие силовые линии закрываются в воздушном зазоре и не вносят вклад в напряженность магнитного поля. Это поток утечки.

Из-за этого потока рассеяния в обмотке индуцируется самоиндукция. Это известно как реактивное сопротивление утечки.

Субпереходное реактивное сопротивление асинхронного двигателя

При коротком замыкании магнитный поток, генерируемый в демпферной обмотке, снижает установившееся реактивное сопротивление. Он известен как субпереходное реактивное сопротивление. Термин «субпереходный» предполагает, что величина работает даже быстрее, чем «переходный». 

Часто задаваемые вопросы

Чему пропорционально индуктивное сопротивление? 

Индуктивное реактивное сопротивление прямо пропорционально частоте.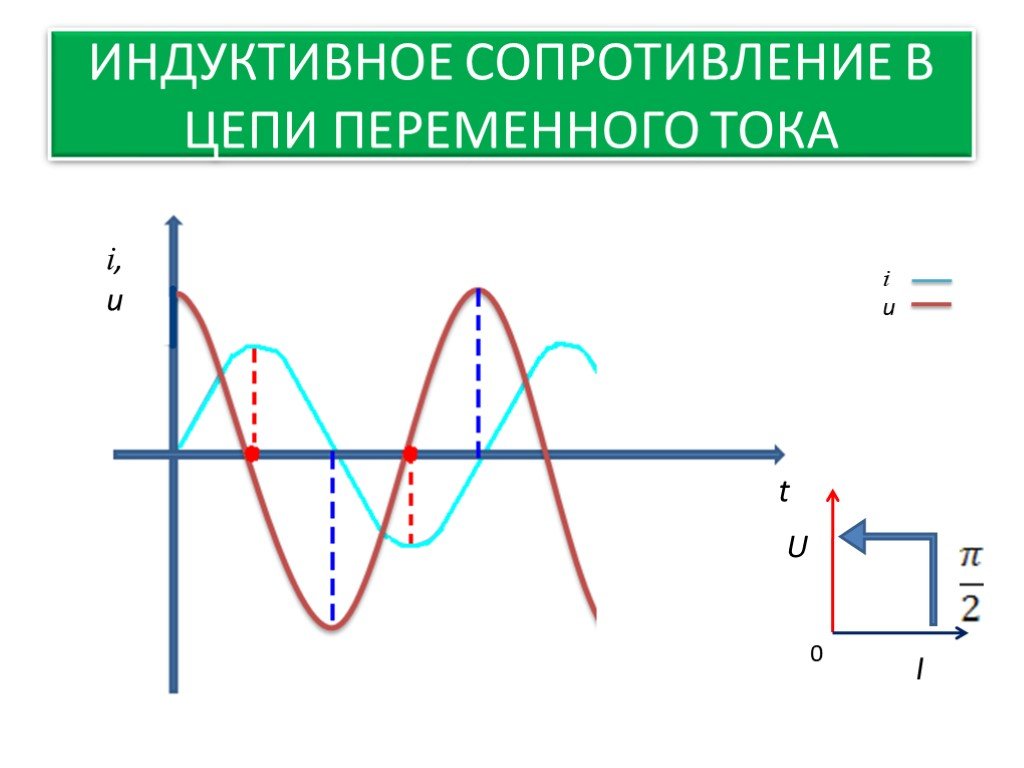

Что такое индуктивное реактивное сопротивление и как оно влияет на цепь переменного тока?

В отличие от ДК, в Цепь переменного тока, ток меняется во времени. 

Что происходит, когда емкостное реактивное сопротивление больше индуктивного?

Если X_C больше чем X_L, тогда общее реактивное сопротивление будет емкостным. 

Что такое индукция?

Изменение магнитного поля вызывает в цепи напряжение и ток. Это явление известно как индукционный. 

Что делает индуктивность в цепи?

Индуктивность препятствует изменению тока, протекающего по цепи.

Что такое индуктивность катушки?

Компания индуктивность катушки возникает из-за магнитного поля из-за переменного тока.

Почему L используется для индуктивности?

Судя по инициалам, я должен был использоваться для обозначения индуктивности. Но поскольку I уже используется для тока, L используется для индуктивности в честь ученого. Генрих Ленц за его выдающийся вклад в области электромагнетизма. 

Может ли самоиндукция быть отрицательной?

Самоиндукция — это чисто геометрическая величина, и она зависит от внешней схемы. Следовательно, это не может быть отрицательным. Знак минус в законе Ленца указывает на противоположный характер ЭДС по отношению к магнитному полю.

Есть ли у двигателей индуктивность?

Обратная ЭДС — решающий фактор в двигателях. В двигателях переменного и постоянного тока для измерения индуктивности используется источник низкого переменного напряжения.

Что такое единица индуктивности?

В системе СИ единица индуктивности — вольт-секунда на ампер или Генри.

Почему индуктор блокирует переменный ток и допускает постоянный ток?

Катушка индуктивности создает ЭДС, когда через нее протекает ток. В переменном токе ЭДС очень высока при увеличении частоты. Следовательно, противодействие также значимо. Но в питании постоянного тока нет ЭДС, и, следовательно, нет противодействия. Говорят, что индуктор блокирует переменный ток и допускает постоянный ток.

Допускает ли индуктор постоянный ток?

Индуктор пропускает постоянный ток, поскольку в цепи нет противоположной силы.

Подробнее о теории цепей нажмите здесь.

Активное и индуктивное сопротивление | У электрика.ру

by Электрик со стажем  15/03/2018 | 9:25 0 Posted in Основы электротехники 

Различные факторы играют важную роль для вычисления потерь в линиях транспортировки электрической энергии. Для постоянного тока вполне хватает стандартных данных об омическом сопротивлении. А вот для цепей переменной разновидности необходимо учитывать активное и индуктивное сопротивление в сочетании с емкостной проводимостью токопроводников.

Можно воспользоваться для вычислений специальными таблицами.

В них представлены с большой точностью различные варианты для выполнения расчетов в сетях переменного тока. Но, чтобы быстро разобраться в специфике представленных характеристик, желательно знать природу подобного явления и его основные характеристики.

Особенности активного сопротивления

В общем виде данный параметр выглядит, как противодействие определенного участка цепи проходящему по нему току. Полученная в результате такого процесса величина участвует в преобразовании энергии и ее переходе в какое-то другое состояние.

Важно! Это явление наблюдается исключительно в ситуациях с переменным током. Только он способен образовывать в кабелях оба вида противодействия.

Величина активного сопротивления обусловлена эффектом поверхностного типа. Наблюдается процесс своеобразного перемещения тока от центра к поверхности проводника. Сечение кабеля используется не полностью, а возникающее противодействие будет значительно превышать аналогичный омический показатель.

Обратим внимание на такой момент:

1. Поверхностный эффект имеет незначительную величину в линиях из металлов, относящихся к категории цветных. Активное сопротивление приравнивают к омическому и считают его при условной температуре в +20°С, без учета фактических показателей окружающей среды. В справочниках имеются данные определения для использования в основном выражении R=r0l, с учетом того, что r0 – это номинальное значение искомой величины для 1 км провода, а l – его фактическая протяженность.
2. А вот в стальных изделиях данный показатель намного выше. Обязательно потребуется брать во внимание, зависящее от сечения явление перемагничивания и влияние таких компонентов, как вихревые токи. На практике обычно при больших нагрузках пользуются справочными данными. При этом, само явление ослабевает в проводниках многопроволочного типа.

Индуктивное сопротивление

Созданное в ходе передачи энергии переменное магнитное поле становится источником реактивного сопротивления подобного вида. Индуктивный вариант в основном зависит от характеристик проходящего тока, диаметра и расстояния между проводами.

Само сопротивление обычно классифицируют следующим образом:

• зависящее от параметров тока и материала — внутреннее;
• обусловленное геометрическими особенностями линии — внешнее. В этом случае данный показатель будет постоянной величиной, не зависящей от каких-либо других факторов.

Заводы по производству кабельной продукции всегда указывают в своих каталогах информацию об индуктивном сопротивлении.

Данный параметр обычно определяется следующим выражением:

в котором индуктивный показатель для 1 км провода – , а L – протяженность.

Х километрового участка рассчитывается по следующей формуле:

Где: Dср – расстояние среднее по центральной оси имеющихся проводов, мм; d – диаметр рабочего токопроводника, мм; μт –относительная магнитная проницаемость.

Принцип действия индуктивного сопротивления линий

Именно индуктивность признана главной характеристикой для катушек наряду с аналогичным показателем для их обмоток. R реактивного вида, проявляющееся под действием самоиндукционной ЭДС, растет в прямой пропорции с частотой тока.

Реактивная и активная составляющие обуславливают полное сопротивление, которое можно представить в виде суммы квадратов каждого показателя.

Оперативно справиться с поставленной задачей по расчету номинальных показателей помогут специальные таблицы. В них для самых распространенных проводников приведены все главные характеристики. Но на практике часто требуется узнать Х для участка с конкретной протяженностью. В этом случае главным инструментом является уже приводившееся выражение 

Емкостная проводимость

Одним из эксплуатационных показателей остается данный параметр, обозначающий емкость между проводниками и землей, а также аналогичный показатель между самими токопроводниками.

Для его определения в трехфазной линии воздушных передач применяется выражение:

Можно увидеть прямую зависимость рабочей емкости от уменьшения расстояния между кабелями и их сечения. Следовательно, для линий низкого напряжения данная величина всегда будет больше, чем для высокого.

Проводимость подобного вида в воздушных линиях одноцепной конструкции рассчитывается так:Токи емкостного происхождения существенно влияют на работу линий с рабочими характеристиками напряжения лот 110 кВ и более, а также в магистралях уложенными кабелями с идентичными параметрами выше 10 кВ.

Попытка применить именно подобный способ для самостоятельного выполнения будет весьма непростой задачей, ведь в нем применяются и различные конструктивные нюансы типа геометрических характеристик, и диэлектрическая проницаемость изоляционного слоя, и многие другие вводные. Следовательно, оптимальным решением будет информация из таблиц, составленных производителями для конкретной марки кабеля. В каталогах все данные приведены с учетом номинального напряжения для каждой модификации.

Для начала линии, когда мы имеем дело с холостым ходом, емкостный ток определяется так:

Данный показатель будет объективным только при полностью обесточенных приемниках электричества.

Большое значение обозначенная емкость в любой рассматриваемой конструкции имеет для точного выполнения предварительных расчетов для устройств компонентов защиты и элементов заземления.

Для воздушной линии действительна такая формула:

Для кабельных магистралей:

Электрик со стажем

23.11 Реактивное, индуктивное и емкостное сопротивление – College Physics: OpenStax

Глава 23 Электромагнитная индукция, цепи переменного тока и электрические технологии

Сводка

• Зарисовка зависимости напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
• Рассчитать индуктивное и емкостное сопротивление.
• Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.

Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения.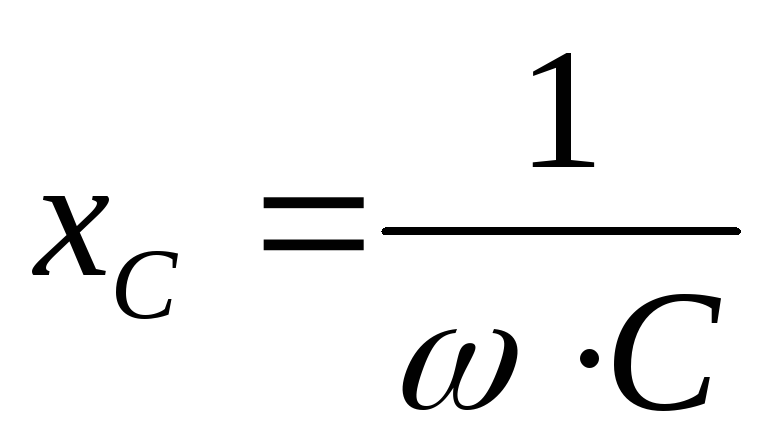 Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рисунке 1. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.

Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.

График на рис. 2(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика после управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение.

Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом: 9{\circ}}[/latex] фазовый угол.

Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует обратную ЭДС [латекс]\boldsymbol{V= -L(\Delta I/ \Delta t)}[/latex]. Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока [латекс]\boldsymbol{I}[/латекс] через катушку индуктивности [латекс]\жирный символ{L}[/латекс] определяется версией закона Ома:

[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_L}},[/латекс]

, где [latex]\boldsymbol{V}[/latex] — среднеквадратичное напряжение на катушке индуктивности, а [latex]\boldsymbol{X_L}[/latex] определяется как

.

[латекс]\boldsymbol{X_L = 2 \pi fL},[/латекс]

с [latex]\boldsymbol{f}[/latex] частотой источника переменного напряжения в герцах (анализ цепи с использованием правила цикла Кирхгофа и исчисления фактически дает это выражение). [latex]\boldsymbol{X_L}[/latex] называется индуктивным реактивным сопротивлением, потому что индуктор препятствует протеканию тока. [latex]\boldsymbol{X_L}[/latex] имеет единицы измерения в омах ([latex]\boldsymbol{1 \;\textbf{H}=1 \;\Omega \cdot \;\textbf{s}}[/latex ], так что частота, умноженная на индуктивность, имеет единицы измерения (циклы/с)([латекс]\boldsymbol{\Omega \cdot \;\textbf{s}}[/латекс])= [латекс]\boldsymbol{\Omega}[ /латекс]), в соответствии с его ролью эффективного сопротивления. Имеет смысл, что [латекс]\жирныйсимвол{X_L}[/латекс] пропорционален [латекс]\жирныйсимвол{L}[/латекс], поскольку чем больше индукция, тем больше его сопротивление изменению. Также разумно, что [латекс]\boldsymbol{X_L}[/латекс] пропорционален частоте [латекс]\жирныйсимвол{f}[/латекс], поскольку большая частота означает большее изменение тока. То есть [latex]\boldsymbol{\Delta I/ \Delta t}[/latex] велико для больших частот (большой [latex]\boldsymbol{f}[/latex] , маленький [латекс]\boldsymbol{\Delta t}[/латекс]). Чем больше изменение, тем больше сопротивление индуктора.

Пример 1. Расчет индуктивного реактивного сопротивления, а затем тока

(a) Рассчитайте индуктивное реактивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Индуктивное сопротивление находится непосредственно из выражения [латекс]\boldsymbol{X_L = 2 \pi fL}[/латекс]. Как только [latex]\boldsymbol{X_L}[/latex] найден на каждой частоте, можно использовать закон Ома, указанный в уравнении [latex]\boldsymbol{I=V/X_L}[/latex], чтобы найти ток на каждой частоте. 94 \;\textbf{/s})(3,00 \;\textbf{мГн}) = 188 \;\Omega \;\textbf{at} 10 \;\textbf{кГц}}[/latex]

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении [латекс]\boldsymbol{I = V/X_L}[/латекс], при условии, что приложенное среднеквадратичное напряжение составляет 120 В. Для первого частота, это дает

[латекс]\жирныйсимвол{I=}[/латекс][латекс]\жирныйсимвол{\гидроразрыва{V}{X_L}}[/латекс][латекс]\жирныйсимвол{=}[/латекс] [латекс]\boldsymbol{\frac{120 \;\textbf{V}}{1,13 \;\Omega}}[/latex][латекс]\boldsymbol{= 106 \;\textbf{A at} \; 60 \;\textbf{Гц}}.[/latex]

Аналогично, на частоте 10 кГц

[латекс]\boldsymbol{I=}[/латекс][латекс]\boldsymbol{\frac{V}{X_L}}[/латекс][латекс]\boldsymbol{=} [/латекс][латекс]\boldsymbol{\frac{120 \;\textbf{V}}{188 \;\Omega}}[/latex][латекс]\boldsymbol{= 0,637 \;\textbf{A at} \; 10 \;\textbf{кГц}}.[/latex]

Обсуждение

Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.

Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.

Рис. 2. (a) Источник переменного напряжения, включенный последовательно с конденсатором C , имеющим незначительное сопротивление. (б) График тока и напряжения на конденсаторе в зависимости от времени.

График на рис. 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке a конденсатор полностью разряжен ([латекс]\boldsymbol{Q = 0}[/латекс] на нем), и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла: 9{\circ}}[/latex] фазовый угол.

Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока [латекс]\boldsymbol{I}[/латекс] в цепи, содержащей только конденсатор [латекс]\boldsymbol{C}[/латекс] по другой версии закона Ома дается как

[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_C}},[/латекс]

, где [latex]\boldsymbol{V}[/latex] — среднеквадратичное значение напряжения, а [latex]\boldsymbol{X_C}[/latex] определяется (как и в случае [latex]\boldsymbol{X_L}[/latex], это выражение для [latex]\boldsymbol{X_C}[/latex] в результате анализа схемы с использованием правил Кирхгофа и исчисления) равно

[латекс]\boldsymbol{X_C =}[/латекс][латекс]\boldsymbol{\frac{1}{2 \pi fC}},[/латекс]

, где [latex]\boldsymbol{X_C}[/latex] называется емкостным реактивным сопротивлением, потому что конденсатор реагирует на сопротивление току. [latex]\boldsymbol{X_C}[/latex] измеряется в омах (проверка оставлена ​​читателю в качестве упражнения). [латекс]\boldsymbol{X_C}[/латекс] обратно пропорциональна емкости [латекс]\жирныйсимвол{С}[/латекс]; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Это также обратно пропорционально частоте [латекс]\boldsymbol{f}[/латекс]; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример 2. Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения в [latex]\boldsymbol{X_C = \frac{1}{2 \pi fC}}[/latex]. Как только [латекс]\boldsymbol{X_C}[/latex] найден для каждой частоты, можно использовать закон Ома, сформулированный как [латекс]\boldsymbol{I = V/X_C}[/latex], чтобы найти ток на каждой частоте.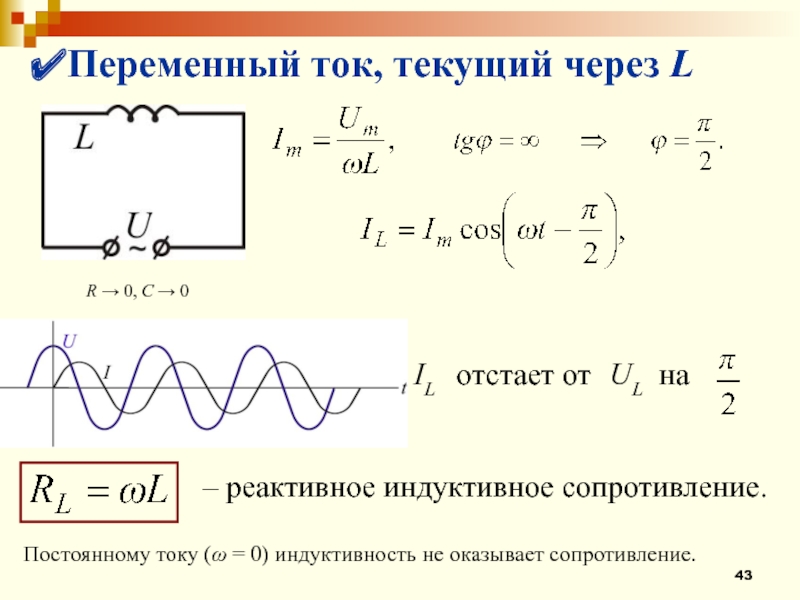 4 \;\textbf{/s})(5,00 \;\mu \ textbf{F})}} \\[1em] & \boldsymbol{3.18 \;\Omega \;\textbf{at} \; 10 \;\textbf{Гц}}. \end{массив}[/латекс]

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в [latex]\boldsymbol{I = V/X_C}[/latex], при условии, что приложенное среднеквадратичное напряжение составляет 120 В. Для первой частоты это дает

[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_C}}[/латекс][латекс]\boldsymbol{=}[ /латекс][латекс]\boldsymbol{\frac{120 \;\textbf{V}}{531 \;\Omega}}[/latex][латекс]\boldsymbol{= 0,226 \;\textbf{A at} \ ; 60 \;\textbf{Гц}}.[/latex]

Аналогично, при 10 кГц,

[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_C}}[/латекс][латекс]\boldsymbol{=}[/латекс][латекс]\ boldsymbol{\frac{120 \;\textbf{V}}{3,18 \;\Omega}}[/latex][latex]\boldsymbol{= 37,7 \;\textbf{A at} \; 10 \;\textbf{кГц}}.[/latex]

Обсуждение

Конденсатор очень по-разному реагирует на двух разных частотах, и совершенно противоположным образом реагирует катушка индуктивности. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), [latex]\boldsymbol{X_C}[/latex] стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы оказывают на цепи переменного тока противоположное действие катушек индуктивности .

В качестве напоминания рассмотрите рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:

Рис. 3. (a) Источник переменного напряжения последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе. 9{\circ}}[/latex] фазовый угол.

Противодействие катушки индуктивности изменению тока выражается как тип сопротивления переменному току.

Закон Ома для катушки индуктивности

[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_L}},[/латекс]

, где [latex]\boldsymbol{V}[/latex] — среднеквадратичное напряжение на катушке индуктивности.

[латекс]\boldsymbol{X_L}[/латекс] определяется как индуктивное реактивное сопротивление, определяемое формулой

[латекс]\boldsymbol{X_L = 2 \pi fL},[/латекс] 9{\circ}}[/latex] фазовый угол.

Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора

[латекс]\boldsymbol{I =}[/латекс][латекс]\boldsymbol{\frac{V}{X_C}},[/латекс]

, где [latex]\boldsymbol{V}[/latex] — среднеквадратичное напряжение на конденсаторе.

[латекс]\boldsymbol{X_C}[/латекс] определяется как емкостное реактивное сопротивление, определяемое выражением

[латекс]\boldsymbol{X_C =}[/latex][латекс]\boldsymbol{\frac{1}{2 \pi fC}}.[/latex]

[латекс]\boldsymbol{X_C}[/латекс] измеряется в омах и максимален на низких частотах.

Задачи и упражнения

1: На какой частоте дроссель 30,0 мГн будет иметь реактивное сопротивление [латекс]\boldsymbol{100 \;\Омега}[/латекс]

2: Какое значение индуктивности должно быть используется, если требуется [латекс]\boldsymbol{20,0 \;\textbf{k} \Omega}[/latex] реактивное сопротивление на частоте 500 Гц?

3: Какую емкость следует использовать для получения реактивного сопротивления [латекс]\boldsymbol{2,00 \;\textbf{M} \Omega}[/latex] на частоте 60,0 Гц?

4: При какой частоте конденсатор емкостью 80,0 мФ будет иметь реактивное сопротивление [латекс]\boldsymbol{0,250 \;\Омега}[/латекс]?

5: (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока с частотой 60,0 Гц и напряжением 480 В. б) Какой будет сила тока на частоте 100 кГц?

6: (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к конденсатору [латекс]\boldsymbol{0,250 \;\мкФ}[/латекс]? б) Какой будет сила тока на частоте 25,0 кГц?

7: Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, производит ток силой 2,00 А. Индуктивность какая?

8: Источник 20,0 Гц, 16,0 В производит ток 2,00 мА при подключении к конденсатору. Какова емкость?

9: (a) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, устанавливается последовательно с компьютером. Какой минимальной индуктивностью он должен обладать, чтобы создавать реактивное сопротивление [латекс]\жирныйсимвол{2,00\;\текстбф{к}\Омега}[/латекс] для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?

10: Конденсатор на рис. 4(а) предназначен для фильтрации низкочастотных сигналов, препятствующих их передаче между цепями. а) Какая емкость необходима для получения реактивного сопротивления [латекс]\жирныйсимвол{100\;\textbf{k}\Омега}[/латекс] на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

11: Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. (a) Какая емкость необходима для создания реактивного сопротивления [латекс]\boldsymbol{10,0 \;\textbf{м} \Омега}[/латекс] для сигнала 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

12: необоснованные результаты

При записи напряжений, вызванных активностью головного мозга (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, производящий ток 100 мА. Сопротивление незначительно. а) Чему равна емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?

13: Создайте свою собственную задачу

Рассмотрим использование катушки индуктивности последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — приемлемое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.

индуктивное сопротивление

сопротивление катушки индуктивности изменению тока; рассчитано по [латекс]\boldsymbol{X_L = 2 \pi fL}[/латекс]

емкостное реактивное сопротивление

противодействие конденсатора изменению тока; рассчитано по формуле [латекс]\boldsymbol{X_C = \frac{1}{2 \pi fC}}[/latex]

 

Inductive Reactance — ElectronicsHub

Если к одной и той же цепи, в которой катушка индуктивности подключена последовательно с нагрузкой, приложены равные значения постоянного и переменного напряжения, в цепи постоянного тока будет протекать больший ток, чем в цепи переменного тока.

Это связано с тем, что только наведенное напряжение препятствует протеканию тока в цепи постоянного тока, когда ток приближается к своему максимальному значению, и как только он достигает установившегося значения, индуктивного эффекта больше не будет.

В цепях переменного тока ток постоянно меняется, поэтому индуктивный эффект присутствует постоянно. Рассмотрим следующие цепи постоянного и переменного тока, чтобы понять эту концепцию.

Схема

Индуктивная цепь постоянного тока

На приведенном выше рисунке, если переключатель работает от узла A к узлу B и сразу от узла B к узлу A, изменение тока протекает через цепь.

Это изменение тока индуцирует ЭДС в катушке индуктивности, пропорциональную скорости изменения тока, и эта ЭДС противодействует приложенному напряжению (что является причиной возникновения тока). Это называется самоиндукцией.

Как только ток достигает установившегося значения, в катушке индуктивности не будет самоиндукции и, следовательно, не будет противодействия току.

Индуктивная цепь переменного тока

Мы знаем, что, когда в цепь подается переменный ток, ток непрерывно изменяется с частотой питающей сети, и, следовательно, противо-ЭДС будет соответственно изменяться.

Эта противо-ЭДС противодействует напряжению питания, поэтому ток ограничен. Следовательно, фактическое противодействие току, создаваемому катушкой индуктивности в цепи переменного тока, называется индуктивным реактивным сопротивлением.

Индуктивное сопротивление в индукторе

В индуктивной цепи, наблюдая за собственной индуктивностью и ее влиянием в цепи, мы можем определить индуктивное сопротивление. Магнитное поле индуцирует в индукторе напряжение, всегда противоположное по полярности напряжению, которое его создает, т. е. приложенному напряжению.

Это противоположное напряжение ограничивает ток, протекающий через катушку индуктивности, и называется реактивным сопротивлением (X). Поскольку это реактивное сопротивление обусловлено индуктивностью, оно называется индуктивным реактивным сопротивлением (X _L ). Измеряется в Омах.

Величина индуктивного сопротивления катушки индуктивности пропорциональна индуктивности и частоте приложенного напряжения. Это реактивное сопротивление можно определить по следующей формуле.

X _L = 2 π fL

Где X _L = индуктивное сопротивление в омах

π = 3,14

f = частота в герцах (Гц)

L = индуктивность в Генри (Гн)

Согласно закону Ома, индуктивное сопротивление прямо пропорционально приложенному напряжению и обратно пропорциональна току. Его можно выразить как

I = V/X _L

Из приведенного выше уравнения видно, что увеличение напряжения или уменьшение индуктивного сопротивления вызывает увеличение тока. Точно так же ток уменьшается с увеличением индуктивного сопротивления и уменьшением напряжения.

Любая практическая катушка индуктивности должна быть изготовлена ​​из намотанной проволоки, состоящей из некоторого сопротивления, поэтому невозможно получить чисто индуктивную катушку.

Таким образом, есть два фактора, которые препятствуют протеканию тока в индукторе, а именно сопротивление, связанное с катушкой (которая рассматривается как отдельный резистор R, включенный последовательно с индуктором), и индуктивное реактивное сопротивление, обеспечиваемое свойством индуктивности.

Таким образом, свойство ограничения полного тока катушки индуктивности в цепи переменного тока представляет собой комбинацию сопротивления и реактивного сопротивления, которая называется импедансом, Z.

Это значение импеданса рассчитывается по закону Ома и имеет вид через цепь

Треугольник импеданса

Другим методом определения импеданса является использование метода треугольника импеданса, когда известны значения индуктивного реактивного сопротивления и сопротивления. На приведенной ниже диаграмме показан треугольник импеданса, который состоит из векторов сопротивления и реактивного сопротивления.

На приведенном выше рисунке вектор сопротивления расположен вдоль горизонтальной линии (поскольку сопротивление не дает фазового сдвига), а вектор индуктивного сопротивления — вдоль вертикальной линии (поскольку чистая индуктивность дает 90 ⁰ фазового сдвига).

Соединив концы этих двух векторов, получим импеданс Z. Следовательно, полное сопротивление току или импедансу можно рассчитать как

Z = √[(R) ² + (X _L ) ²  ]

Где

Z = импеданс в омах

R = сопротивление в омах

X _L = индуктивное сопротивление в омах ∅= X _L /R

sin ∅= X _L /R

cos∅= R/Z

Влияние частоты или индуктивности на индуктивное сопротивление

Как обсуждалось выше, индуктивное сопротивление определяется по формуле

X _{L 9030 6 = 2 π f L}

В данном уравнении значение индуктивного сопротивления пропорционально индуктивности и частоте.

Индуктивное сопротивление увеличивается либо с увеличением индуктивности, либо с увеличением частоты. Следовательно, индуктивное сопротивление линейно зависит от индуктивности и частоты.

Таким образом, сопротивление току увеличивается с увеличением индуктивности или частоты. Рассмотрим приведенные ниже графики для четкого понимания этой взаимосвязи.

Рассмотрим приведенный выше рисунок, на котором показана зависимость индуктивного сопротивления от частоты при фиксированной индуктивности. При нулевой частоте индуктивное сопротивление равно нулю, а по мере увеличения частоты индуктивное сопротивление увеличивается соответствующим образом.

Рассмотрим приведенный выше рисунок, на котором показана зависимость индуктивного сопротивления от индуктивности при фиксированной частоте. Можно предположить, что по мере увеличения индуктивности индуктора увеличивается и индуктивное реактивное сопротивление.

Пример индуктивного реактивного сопротивления

Рассмотрим дроссель с индуктивностью (L) 100 мкГн при рабочей частоте (f) 1 МГц. Затем индуктивная индуктивность рассчитывается следующим образом:

X _L = 2πfL=2π×1MHz×100µH

X _L = 628 Ом

RL Цепи и индуктивное сопротивление

На рисунке ниже показано соотношение между приложенным напряжением и током через индуктивную цепь. В чисто индуктивной цепи ток отстает от напряжения источника на 900. Можно также утверждать, что напряжение источника опережает ток на 90 ⁰ в индуктивной цепи.

Когда катушка индуктивности соединена последовательно с резистором RL, получается последовательная цепь, как показано ниже. Это также можно рассматривать как индуктивность, состоящую из некоторого сопротивления (которое считается последовательным сопротивлением), поскольку оно сделано из провода.

Таким образом, ток и напряжение не точно поддерживают фазовый сдвиг 90 ⁰ , но меньше, чем в чисто индуктивном случае, как показано ниже.

На рисунке ниже показана векторная диаграмма последовательной цепи RL, состоящая из векторов падения напряжения на резисторе и катушке индуктивности. AE представляет текущую опорную линию. AB представляет собой падение напряжения на сопротивлении, которое находится в фазе с линией тока.

AD представляет индуктивное падение напряжения, которое опережает ток на 90 ⁰ .