Как рассчитать индуктивность катушки без сердечника. От чего зависит индуктивность катушки. Какие параметры влияют на индуктивность. Формулы для расчета индуктивности однослойной и многослойной катушки. Онлайн-калькулятор для быстрого расчета.
Что такое индуктивность катушки и от чего она зависит
Индуктивность катушки — это способность катушки накапливать энергию магнитного поля при протекании через нее электрического тока. Чем больше индуктивность, тем сильнее катушка препятствует изменениям тока в цепи.
Основные факторы, влияющие на индуктивность катушки без сердечника:
- Количество витков — чем больше витков, тем выше индуктивность
- Диаметр катушки — индуктивность растет с увеличением диаметра
- Длина намотки — при увеличении длины индуктивность уменьшается
- Форма сечения катушки — круглое сечение дает большую индуктивность, чем прямоугольное
- Шаг намотки — чем плотнее намотка, тем выше индуктивность
Формулы для расчета индуктивности катушки без сердечника
Для расчета индуктивности однослойной цилиндрической катушки без сердечника используется формула:
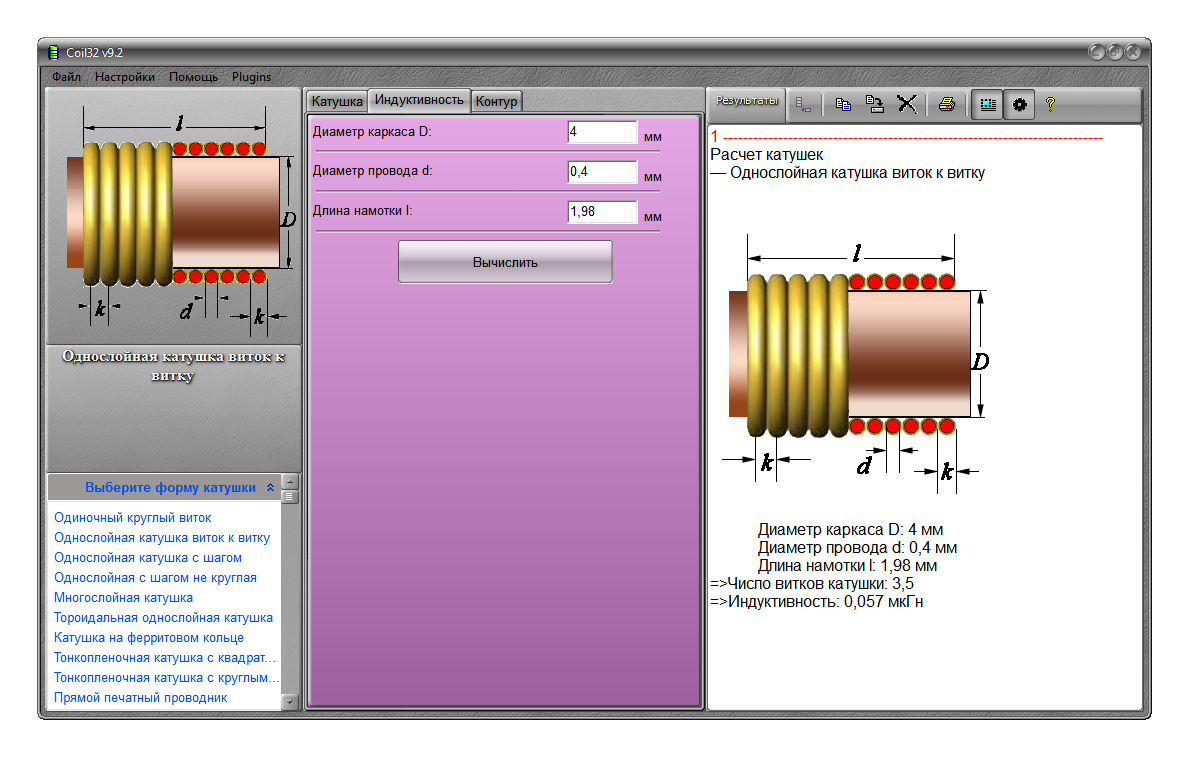
L = (μ0 * N^2 * S) / l
где:
- L — индуктивность катушки, Гн
- μ0 — магнитная постоянная, 4π * 10^(-7) Гн/м
- N — число витков
- S — площадь поперечного сечения катушки, м^2
- l — длина намотки, м
Для многослойных катушек применяется более сложная формула:
L = (0.001 * N^2 * d^2) / (l + 0.45 * d)
где d — средний диаметр катушки, мм.
Как рассчитать количество витков катушки
Если известна требуемая индуктивность, то количество витков можно рассчитать по формуле:
N = √(L * l / (μ0 * S))
Здесь L — заданная индуктивность, l — длина намотки, S — площадь сечения катушки.
Онлайн-калькулятор для расчета индуктивности катушки
Для быстрого и точного расчета индуктивности катушки без сердечника можно воспользоваться онлайн-калькулятором. Он позволяет рассчитать как индуктивность по заданным параметрам, так и необходимое число витков для получения нужной индуктивности.
Калькулятор учитывает следующие параметры катушки:
- Диаметр намотки
- Длина намотки
- Число витков
- Число слоев (для многослойных катушек)
- Диаметр провода
Результаты расчета выводятся в микрогенри (мкГн).
Практические советы по намотке катушек индуктивности
При самостоятельном изготовлении катушек индуктивности без сердечника следует учитывать несколько практических моментов:
- Для получения максимальной индуктивности при минимальных габаритах оптимальное соотношение диаметра к длине катушки составляет примерно 1:1.
- Витки следует наматывать максимально плотно друг к другу, без зазоров. Это повышает индуктивность.
- Для уменьшения паразитной емкости катушки лучше использовать однослойную намотку. Многослойная намотка дает большую индуктивность, но и большую емкость.
- Намотку лучше вести проводом с эмалевой изоляцией. Это позволяет получить более плотную намотку.
- После намотки катушку желательно пропитать лаком или эпоксидной смолой для фиксации витков.
Проверка расчетной индуктивности катушки
После изготовления катушки необходимо проверить ее фактическую индуктивность. Для этого можно использовать:
- Измеритель RLC — самый точный способ измерения индуктивности
- Мультиметр с функцией измерения индуктивности — подходит для грубой оценки
- LC-метр на основе микроконтроллера — можно собрать самостоятельно
- Косвенный метод через измерение резонансной частоты LC-контура
Обычно реальная индуктивность катушки отличается от расчетной на 5-10% в меньшую сторону. Это связано с неидеальностью намотки и другими факторами.

Применение катушек индуктивности без сердечника
Катушки индуктивности без магнитного сердечника широко применяются в различных областях радиоэлектроники:
- В колебательных LC-контурах радиоприемников и передатчиков
- В фильтрах высоких и низких частот
- В согласующих цепях антенн
- В измерительных приборах
- В импульсных источниках питания
- В радиолюбительских конструкциях
Основные преимущества катушек без сердечника — линейность характеристик, широкий частотный диапазон, отсутствие насыщения. Недостатки — большие габариты и низкая добротность по сравнению с катушками на сердечниках.
Заключение
Расчет и изготовление катушек индуктивности без сердечника — важный навык для радиолюбителей и инженеров. Зная основные формулы и используя онлайн-калькуляторы, можно быстро рассчитать параметры катушки для конкретной задачи. При этом важно учитывать практические нюансы намотки и проверять результат измерениями.
|
Создадим 2D-модель катушки. При создании геометрии учтём тот факт, что в плоскопараллельной модели сечения катушек — это бесконечные проводники. Подразумевается, что на торцах они виртуально соединены друг с другом (см. рисунок П.1.1). Рисунок П.1.1 – Плоскопараллельная модель катушки в 2D В нашем же случае необходимо строить тело вращения. Для этих целей необходимо изменить тип геометрии в окне Solution Type, установить параметр Geometry Mode в значение: Cylindrical about Z (осевая симметрия). После чего создадим геометрию с учётом того, что модель строится вращением тела вокруг оси Z. Получим геометрию, изображённую на рисунке П.1.2 Рисунок П.1.2 – Цилиндрическая модель геометрии 2D (a) и её представление в 3D(б) Зададим параметры катушки. Выделяем объект-катушку, указываем значение тока равным 1 амперу (Assign Excitation > Current…) Т.к. мы считаем индуктивность катушки на постоянном токе, не важно, какова будет величина тока, т.к. поток будет расти пропорционально току. Не забываем указать, что катушка распределённая (Stranded). Создадим матрицу для расчета индуктивности катушки (ПКМ на пункт Parameters > Assign > Matrix…) Далее выбираем созданную катушку (Current1). На вкладке Post Processing задаём число витков катушки (Рисунок П.1.3). Внешней границе полукруга задаём граничное условие (ПКМ на внешней линии окружности > Далее создаём сетку конечных элементов, предварительно выделив все объекты модели (Assign Mesh Operation > Inside Selection > Length Based… ) Создаём новое задание на расчёт с параметрами по умолчанию (ПКМ на Analysis > Add Solution Setup) Запускаем задачу на расчёт. Результат расчёта можно посмотреть в окне Solution Data на вкладке Matrix, предварительно установив галочку PostProcessing (Рисунок П.1.4). Рисунок П.1.3 — Задание элемента Matrix. Рисунок П.1.4 — Результаты расчёта модели Итого, индуктивность, рассчитанная МКЭ, составила Lм = 1,053 мкГн. Сравнивая с результатами, полученными по формуле Виллера (L = 1,152 мкГн), можно сделать вывод, что задача посчитана правильно, и расхождение двух методов расчета составляет менее 10%. Автор материалов: Drakon (С) 2014. Редактор: Админ |
Катушки индуктивности без сердечников — Энциклопедия по машиностроению XXL
КАТУШКИ ИНДУКТИВНОСТИ БЕЗ СЕРДЕЧНИКОВ [c.374]Зарядный индуктивный элемент может быть выполнен в виде зарядного дросселя со стальным сердечником либо как катушка индуктивности без стального сердечника. [c.51]
Для отыскания места короткого замыкания в рельсовой цепи переменного тока применяют катушку индуктивности (с сердечником или без него) с телефоном. При поднесении катушки к рельсу, по которому идёт переменный ток, в телефоне прослушивается индуктированный ток. Проходя с катушкой вдоль рельсовой цепи, легко обнаружить место короткого замыкания или большой сосредоточенной утечки. За точкой замыкания звук в телефоне более или менее резко снижается, и, поднеся катушку к предполагаемому пути замыкания (как, например, гарнитура стрелки, изолирующий стык), в телефоне будет слышен звук. Для удобства прослушивания целесообразно периодически прерывать цепь питания, создавая импульсы тока в рельсе.
Здесь первый пример описывает связанные индуктивности без сердечника К1, второй — ферромагнитный сердечник К2, на котором находятся две катушки индуктивностей L1, L2. [c.21]
Катушки индуктивности дроссель без сердечника [c.271]
Индуктивность катушки без сердечника [c.146]
Добротность (Q ) катушки определяется по отношению индуктивного сопротивления к эквивалентному сопротивлению всех потерь плюс омическое сопротивление провода обмотки. В контурах применяют катушки с сердечником, имеющие добротность Q =30- 500. Катушки связи и дроссели высокой частоты имеют меньшую добротность. Зависимость добротности катушек с сердечником и без сердечника от частоты показана на рис. 10.3, [c.371]
В табл. 84 приведены сравнительные данные катушки без сердечника и катушки той же индуктивности с сердечником из магнитодиэлектрика. [c.334]
Добротность катушки с магнитным сердечником зависит от потерь в материале, величины и очень сильно от частоты. Приближенно можно считать, что на относительно невысоких частотах добротность катушки с сердечником в раз больше добротности катушки с той же индуктивностью, но без сердечника. С увеличением частоты добротность падает, так как потери в сердечнике растут, а Не уменьшается. Частоту, на которой введение сердечника не увеличивает добротность катушки, можно считать верхней границей рабочего диапазона. На частотах выше граничной сердечники применяют только для подстройки индуктивности [c.378]
Катушка индуктивности L берется без сердечника для получения малых потерь. Величины Ri == 10.. . 100 ом, R 50 ком магазин сопротивлений R% == 0… 5000 ом. Погрешность при [c.60]
КАТУШКА ИНДУКТИВНОСТИ — электрический проводник в форме спирали с ферромагнитным сердечником или без него, обладающий свойством накапливать магнитную энергию при прохождении по нему электрического тока. [c.59]
Кроме рабочих обмоток, имеются следующие обмотки управления, задающая, регулировочная, стабилизирующая, которые обхватывают оба сердечника, причем управляющая обмотка включена встречно другим. Катушки выполнены без каркаса и залиты эпоксидным компаундом. При изменении тока в обмотках подмагничивания меняется индуктивное сопротивление, а значит, и ток рабочих обмоток. Основные данные обмоток амплистата приведены в табл. 18. [c.151]
Катушка индуктивности представляет собой высокочастотный дроссель без сердечника. Он включен в цепь первичной обмотки силового трансформатора, находится под напряжением контактной сети и вместе с конденсатором смонтирован на крыше вагона. [c.29]
Емкость контура может быть легко изменена специальным переключающим устройством. Катушка индуктивности является основной индуктивностью контура и выполнена без ферромагнитного сердечника. Вариометр, управляемый с пульта ультразвуковой установки, обеспечивает плавную оперативную подстройку частоты. Некоторое изменение частоты осуществляется также регулировкой (в небольших пределах) тока подмагничивания преобразователя. Значение частоты контролируется по стрелочному измерителю частоты, расположенному на том же пульте. Величина постоянного тока подмагничивания осуществляется амперметром, расположенным на пульте, на котором расположены также органы регулировки режимом колебаний и сигнализации. [c.509]
Для защиты от помех радиоприему, которые вызываются искрением на токоприемнике, коммутацией тяговых двигателей и аппаратов силовой цепи, применяют индуктивный фильтр ФС-ЗБ-3 дроссельного типа. Последний включен в силовую цепь между токоприемником и воздушным выключателем. Благодаря наличию индуктивного фильтра радиопомехи снижаются примерно в 10 раз и гасится переменная составляющая. Индуктивный фильтр представляет собой высокочастотный дроссель без сердечника в виде изолированной катушки 4 (рис. 203). С
Независимо от используемого метода регулирования, существенным фактором является самоиндукция роторной обмотки. Индукция — это свойство обмотки, состоящее в том, что ток в ней не может измениться мгновенно, а скорость его уменьшения или возрастания определяется параметрами электрической цепи. Катушка с железным сердечником обладает во много раз большей индуктивностью, чем катушка без сердечнике. Чем больше индуктивность, тем ниже скорость изменения тока в катушке. [c.48]
Укажем на способ конструктивной реализации цементов фильтра. Для получения заданной емкости подбирают набор неполярных (бумажных, тонкопленочных и др.) конденсаторов на рабочее напряжение не менее 55 В. Что касается индуктивности, то ее получают путем намотки обмоточного провода на катушки. Привести рекомендации по расчету числа витков катушек, изготовленных с применением ферритовых сердечников, невозможно ввиду значительного разброса магнитных свойств феррита, а потому приведем рекомендации по изготовлению катушек без ферромагнитных сердечников. Оптимальная конструкция катушки в смысле максимума отношения ее индуктивности к активному сопротивлению получается, когда внутренний диаметр цилиндрической обмотки катушки вдвое больше ее высоты /i, а внешний диаметр в 4 раза больше высоты и и в 2 раза больше внутреннего диаметра. При [c.157]
Трансформаторы с последовательно включенной в первичную цепь индуктивной катушкой (рис. 29, а). Индуктивность катушки должна быть постоянной, поэтому катушка может быть либо вообще без стального сердечника, либо иметь ненасыщенный сердечник. Насыщающийся трансформатор 1 может быть либо 110 [c.110]
Последнее слагаемое часто превышает первое, поэтому температурная стабильность катушки с сердечником всегда хуже, чем без него, и в основном определяется его температурными свойствами. Для малогабаритных и миниатюрных катушек, в которых используются ферритовые сердечники, стабильность индуктивности, как правило, низкая при этом, чем больше д сердечника, тем стабильность ниже. Это существенный недостаток ферритовых сердечников. [c.191]
В приборах с накладными датчиками применяются катушки индуктивности без сердечников и с сердечниками из магнитодиэлектрических материалов, например 12 [c.12]
Расчет показывает [65], что объем и, следовательно, масса сердечника зарядного дросселя прямо пропорциональны энергии, запасаемой в емкостном накопителе, и не зависят от мощности зарядного устройства. Умень-ищть массу зарядного индуктивного элемента можно Применением катушки индуктивности без стального сер- [c.51]
Лучшее совмещение магнитных и электрических свойств получается у ферритов, которые имеют р = 10 —10 ом-см и = 15+-2000. Основным параметром является Цдфф—эффективная магнитная проницаемость, определяемая на эталонных высокочастотных катушках индуктивности с сердечником и без сердечника из соотношения [c.378]
Альсиферовые и карбонильные сердечники изготавливаются из высокодисперсных ферромагнитных частиц, которые изолируются полистироловой или бакелитовой смолой эта масса затем прессуется в сердечники нужной формы. Расчет индуктивности катушек с ферритовыми и другими магнитодиэлектрическими сердечниками весьма сложен. Уменьшение магнитного сопротивления может быть учтено с помощью так называемой катушечной эффективной магнитной проницаемости, представляющей собой отношение индуктивности катушки с сердечником к индуктивности той же катушки без сердечника. [c.15]
Примем, что кольцевой зазор, через который замыкаются силовые линии, идущие вне катушки, настолько мал, что им можно пренебречь. Если обозначить через абсолютную магнитную проницаемость сердечника / — среднюю длину силовой линии в сердечнике L — индуктивность катушги без сердечника, то индуктивность изображенной на рис. 11 катушки L= i L, где Ид — эффективная магнитная проницаемость с учетом зазора [c.201]
При работе электрических машин и аппаратуры электровоза, а также при искрении на токоприемнике создаются радиопомехи, для подавления которых на электровозах ВЛЮ, ВЛ8 и ВЛ23 применяются дроссель и высоковольтный конденсатор. Дроссели представляют собой две индуктивные катушки без сердечников, устанавливаемые на четырех изоляторах на крыше электровоза. Индуктивные катушки включаются в силовую цепь между крышевыми разъединителями и электрическим оборудованием электровоза и служат для подавления переменных составляющих тока помех. Конденсатор с бумажной изоляцией, герметизированный, рассчитанный на напряжение Ю /се и емкость [c.198]
Приведем перечень аналоговых элементов конденсаторы, резисторы, катушки индуктивности, длинные линии с потерями и без потерь, биполярные п-р-п- и р-п ii-r t — диоды, Mai ни 1ные сердечники с во адушным а ю- [c.8]
Катушка индуктивности представляет собой высокочастотный дроссель без сердечника. Он включен в силовую схему между токоприемником и главным разъединителем, находится под напряжением контактной сети и вместе с конденсатором смонтирован на крыше вагона. На электропоезде ЭТ2М применяется дроссель типа ДП-32, на остальных — 1ДР.050 (рис. 2.34). [c.47]
Магаитные бесконтактные аппараты. Основным элементом бесконтактных магнитных аппаратов является магнитный усилитель. Он позволяет плавно изменять переменный ток за счет изменения индуктивного сопротивления катушки с ферромагнитным сердечником. Магнитные усршители подразделяются на простые (без обратной связи), с обратной связью и др. [c.308]
Катушки лндуктивности колебательных контуров радиолюбители наматывают самостоятельно, нередко используя каркасы заводского изготовления. Наиболее распространены однослойные цилиндрические катушки без сердечников нли с сердечниками из карбонильного железа или феррита. Широко применяют также катушки на ферритовых кольцах. Индуктивность однослойной цилиндрической катушки без сердечника [c.10]
Катушки без сердечника рассчитывают по импирическим формула с погрешностью 10%, причем для каждого вида обмотки существую свои формулы. При необходимости обеспечения требуемого значени индуктивности с меньшей погрешностью количество витков катушк [c.134]
Вторичная обмотка трансформаторов предназначена для включения непосредственно в сильноточный разрядный контур. В момевт разрядки накопителя к обмотке прикладывается полное напряжение и ферритовый магнитопровод быстро насыщается. В данных трансформаторах индуктивность вторичной о бмотки после асыщения сердечников имеет относительно большие значения (порядка 100 мкГ). Это позволяет для однозвенных ЬС-формирующих линий обойтись без включения дополнительных разрядных катушек индуктивности. В рассматриваемой конструкции функции импульсного трансформатора и разрядной катушки оказываются совмещенными в одном элементе, что вдвое сокращает массу и объем такого устройства по сравнению со случаем использования импульсных трансформаторов, у которых после насыщения магнитопровода индуктивность, как правило, имеет величину 10—15 мкГ. [c.56]
Наиболее существенным дестабилизирующим фактором при работе частотных преобразователей является изменение температуры окружающей среды. При этом в наибольшей степени изменяется индуктивность катушки. Для оценки этой температурной погрешности были проведены экспериментальные исследования, состоящие в измерении девиации частоты измерительного автогенератора при нагревании и охлаждении катушек индуктивности, выполненных на основе ферритовых сердечников, как это было сказано выше. Катушки были намотаны проводом типа ПЭВ-0,08 на фторопластовые каркасы и имели оптимальное значение Ким- При нагревании температура фиксировалась через каждые 10°С. При охлаждении фиксировалась лишь конечная температура. На рис. 2 графически представлены результаты экспериментов. Кривые 1—3 соответствуют катушке с ферри-товым сердечником типа 41 без стержня, а кривые 1С—ЗС соответствуют тем же условиям, но со стержнем, внесенным на половину длины катушки. [c.119]
Калькулятор расчета индуктивности катушки без сердечника — MOREREMONTA
Онлайн расчет многослойной катушки. Калькулятор считает по алгоритму с применением эллиптических интегралов Максвелла.
Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность.
Сайт для радиолюбителей
Как известно индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки. Чем больше диаметр, длина намотки и число витков тем больше индуктивность.
Для определения индуктивности уже готовой катушки заполните предложенную форму для расчета, в ней необходимо указать диаметр катушки, длину намотки и число витков.
Если необходимо намотать катушку определенной индуктивности, то можно рассчитать кол-во витков катушки исходя из диаметра катушки и длины намотки.
Если по результатам расчета окажется, что у Вас нет провода нужного диаметра, то можно взять ближайший по диаметру в большую или меньшую сторону (не более чем на 25%) и сделать перерасчет.
Катушка индуктивности представляет собой электрическую сборную конструкцию, которая может изготавливаться в следующих исполнениях:
- В виде намотанной на каркас обмотки из провода определенного диаметра.
- Как витая бескаркасная спираль, предварительно сформированная на твердой основе, а затем снятая с нее.
- Катушка, намотанная многослойным проводом в специальной матерчатой изоляции.
Особенностью этого электротехнического компонента является наличие у него значительной по величине индуктивности при относительно малой емкостной составляющей и низком активном сопротивлении. Это приводит к тому, что при протекании переменного тока она проявляет себя как элемент, обладающий большой инерционностью.
Обратите внимание: Благодаря этой особенности катушки текущий по ней ток отстает от приложенного напряжения на определенный угол (90 градусов). У профессионалов это явление получило название «отставание по фазе».
Для того, чтобы получить точные значения индуктивности катушки заданной формы, следует ввести ее основные параметры в онлайн-калькулятор. В нем автоматически рассчитывается такой важный показатель, как число витков в данном изделии. После ввода данных в специальную форму вы мгновенно получите искомое значение.
Наш онлайн-калькулятор производит автоматизированный расчет значений катушки индуктивности без сердечника с использованием метода эллиптических интегралов Максвелла. Калькулятор предусматривает расчет значений как однослойных обмоток, так и многослойных.
А вот формула индуктивности:
- L – индуктивность;
- D – диаметр витка;
- N – число витков;
- h – длина намотки;
- g – количество слоев
Преимущества расчета значений параметров катушки с помощью онлайн-калькулятора очевиден.
Расчёт катушки индуктивности под динамик
Данный расчет является примером для определения данных катушки индуктивности на воздушном сердечнике, нагруженной динамиком. В этом примере выбрана катушка без сердечника во избежание искажений, обусловленных перемагничиванием сердечника.
На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению. Конструкция получается, когда внутренний диаметр цилиндрического слоя обмотки вдвое больше его высоты, а внешний диаметр в четыре раза больше высоты и в два раза больше внутреннего диаметра.
высота 1 см; внутренний диаметр 2 см; внешний диаметр 4 см.
Пример расчета
Современные программы по расчету пассивных фильтров для акустики, дают значение катушек индуктивности в мГн, здесь нужно перевести в мкГн, т.е. умножить на 1000.
Определим данные катушки с индуктивностью 1,25 мГн (или 1250 мкГн) разделительного фильтра, нагруженного динамиком сопротивлением 4 Ом. Активное сопротивление рассчитываемой катушки должно составлять 5% сопротивления динамика. Это соотношение можно считать вполне приемлемым. Активное сопротивление катушки: R = 0,05 х 4 = 0,2 Ом.
- откуда: L/R = 1250 / 0,2 = 6250 мкГн/Ом;
- далее имеем: h = √ ((L/R) / 8,6) = √ (6250 / 8,6) = 26,96 мм;
- длинна жилы: l = 187,3 х √ (L х h) = 187,3 х √ (1250 х 26,96) = 34383 мм = 34,3 м;
- количество витков: ω = 19,88 √(L / h) = 19,88 х √ (1250 / 26,96) = 135,36 витков;
- диаметр жилы: d =0,84h / √ω = 0,84 х 26,96 / √ 135,36 = 1,95 мм;
- масса намотки: m = (h3 х 10-3) / 21,4 = (26,963 х 10-3) / 21,4 = (19595,65 х 0,001) / 21,4= 0,9 кг.
Полученные значения должны быть округлены (в первую очередь диаметр жилы) до ближайшего стандартизированного. Окончательные значения индуктивности подгоняют путем отматывания нескольких витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным.
Итак имеем данные, которые понадобятся для расчета будущей катушки:
- высота намотки h = 26,96 мм;
- значит внутренний диаметр a = 53,92 мм;
- соответственно внешний: b = 107,84 мм;
- длинна жилы: 34,3 м;
- количество витков: 135;
- диаметр жилы, соответствует стандартизированному: 1,95 мм (по меди).
Статья специально подготовлена для сайта ldsound.ru
Как рассчитать индуктивность катушек с замкнутыми сердечниками?
Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Особенности расчёта индуктивных элементов с сердечниками
В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.
Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения
где ω – количество витков катушки,
RM – сопротивление магнитной цепи,
μа – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,
SM – площадь поперечного сечения сердечника,
lM – длина средней магнитной силовой линии,
Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.
Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии le и эффективная площадь поперечного сечения Se сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективный путь магнитной линии сердечника.
Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм-1;
С2 – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3;
где N – количество разнородных участков сердечника,
lN – длина N – го участка сердечника,
SN – площадь N – го участка сердечника.
Тогда величины Se и le определятся из следующих выражений
Кроме индуктивности с помощью постоянных С1 и С2 определяют эффективный объём Ve, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С1 по следующему выражению
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.
Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.
Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.
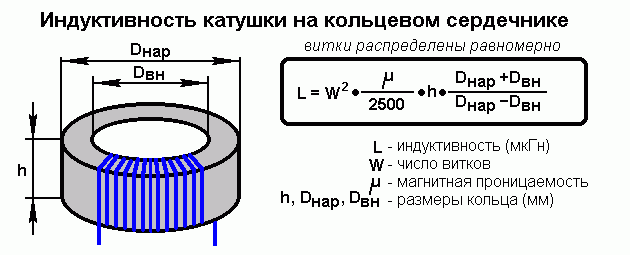
Расчёт катушки с тороидальным сердечником
Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.
Тороидальный сердечник.
Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D1 – внешний диаметр, D2 – внутренний диаметр, h – высота сердечника.
Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С1 и С2, которые составляют
где he – эффективная высота сердечника,
D1 – внешний диаметр сердечника,
D2 – внутренний диаметр сердечника.
Расчёт эффективной высоты he сердечника зависит от конструктивных особенностей.
Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).
Рассмотрим несколько случаев:
а) прямоугольное поперечное сечение с острыми кромками
б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления rs
в) трапецеидальное поперечное сечение с острыми кромками
г) трапецеидальное поперечное сечение со скруглёнными кромками
Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D1 = 20 мм, D2 = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления rs = 0,5 мм, относительная магнитная проницаемость материала сердечника μr = 1000.
Так как рассчитываем только индуктивность, то в расчёте коэффициента С2 нет необходимости
Расчёт катушки с П–образным сердечником прямоугольного сечения
В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.
Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.
П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).
Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника
Сечение П-образного прямоугольного сердечника.
Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят
Неизвестные величины можно найти следующим образом
Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μr = 1950, количество витков ω = 150.
Сердечник Epcos U93/76/16.
Таким образом, расчётные параметры сердечника составят
Таким образом коэффициент С1 и индуктивность L составят
Расчёт катушки с П-образным сердечником круглого сечения
Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей
П-образный сердечник с круговым сечением.
Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.
Сечение П-образного сердечника с круговым сечением.
Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь
Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μr = 2500), количество витков ω = 60.
Сердечник типа SDMR 40 UY20.
Параметры сердечника для расчёта составят
Таким образом коэффициент С1 и индуктивность L составят
На сегодня всё. Продолжение смотри в следующей статье.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Inductance Calculator
Inductance Calculator
Расчет катушки индуктивности
Расчет однослойной воздушной катушки индуктивности
Расчет дросселя без сердечника
Расчетная формула:
Индуктивность в мкГн = R2 * N2 / ( 25.4*R + 22.9*L )
|
R = радиус катушки по центру провода (см) N = количество витков в катушке (может быть не целым числом) L = длина катушки (см) — возможна намотка не виток к витку, а с зазором. |
результат конечно приблизителен!
|
Реклама недорогих радиодеталей почтой:
|
А вот
результаты измерения реальных катушек
с помощью Вы можете проверить по этим таблицам результат расчета. Все катушки мотались медным эмалевым обмоточным проводом 0.6 мм. Максимальная добротность достигается при намотке с зазором между витками равными диаметру провода!
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. Факторы, влияющие на индуктивность катушки | 14. Катушки индуктивности | Часть1
3. Факторы, влияющие на индуктивность катушки
Факторы, влияющие на индуктивность катушки
На индуктивность катушки оказывают влияние следующие основные факторы:
Число витков провода в катушке: При прочих равных условиях, увеличение числа витков приводит к увеличению индуктивности; уменьшение числа витков приводит к уменьшению индуктивности.
Пояснение: чем больше количество витков, тем больше будет магнитодвижущая сила для заданной величины тока.
Площадь поперечного сечения катушки: При прочих равных условиях, катушка с большей площадью поперечного сечения будет иметь большую индуктивность; а катушка с меньшей площадью поперечного сечения — меньшую индуктивность.
Пояснение: Катушка с большей площадью поперечного сечения оказывает меньшее сопротивление формированию магнитного потока для заданной величины магнитодвижущей силы.
Длина катушки: При прочих равных условиях, чем больше длина катушки, тем меньше ее индуктивность; чем меньше длина катушки, тем больше ее индуктивность.
Пояснение: Чем больше длина катушки, тем большее сопротивление она оказывает формированию магнитного потока для заданной величины магнитодвижущей силы.
Материал сердечника: При прочих равных условиях, чем больше магнитная проницаемость сердечника, вокруг которого намотана катушка, тем больше индуктивность; чем меньше магнитная проницаемость сердечника — тем меньше индуктивность.
Пояснение: Материал сердечника с большей магнитной проницаемостью способствует формированию большего магнитного потока для заданной величины магнитодвижущей силы.
Приблизительное значение индуктивности любой катушки можно найти по следующей формуле:
Следует понимать, что данная формула дает только приблизительные цифры. Одной из причин такого положения дел является изменение величины магнитной проницаемости при изменении напряженности магнитного поля (вспомните нелинейность кривой В/Н для разных материалов). Очевидно, если проницаемость (µ) в уравнении будет непостоянна, то и индуктивность (L) также будет в некоторой степени непостоянна. Если гистерезис материала сердечника будет существенным, то это непременно отразится на индуктивности катушки. Разработчики катушек индуктивности пытаются минимизировать эти эффекты, проектируя сердечник таким образом, чтобы его намагниченность никогда не приближалась к уровням насыщения, и катушка работала в более линейной части кривой B/H.
Если катушку сделать таким образом, что любой из вышеперечисленных факторов у нее можно механически изменить, то получится катушка с регулируемой величиной индуктивности или вариометр. Наиболее часто встречаются вариометры, индуктивность которых регулируется количеством витков или положением сердечника (который перемещается внутри катушки). Пример вариометра с изменяемым количеством витков можно увидеть на следующей фотографии:
Это устройство использует подвижные медные контакты, которые подключаются к катушке в различных точках ее длины. Подобные катушки, имеющие воздушный сердечник, применялись в разработке самых первых радиоприемных устройств.
Катушка с фиксированными значениями индуктивности, показанная на следующей фотографии, представляет собой еще одно раритетное устройство, использовавшееся в первых радиостанциях. Здесь вы можете увидеть несколько витков относительно толстого провода, а так же соединительные выводы:
А это еще одна катушка индуктивности, так же предназначенная для радиостанций. Для большей жесткости ее провод намотан на керамический каркас:
Многие катушки индуктивности обладают небольшими размерами, что позволяет монтировать их непосредственно на печатные платы. Посмотрев внимательно на следующую фотографию, можно увидеть две расположенные рядом катушки:
Две катушки индуктивности расположены справа в центре этой платы и имеют обозначения L1 и L2. В непосредственной близости от них находятся резистор R3 и конденсатор С16. Показанные на плате катушки называются «торроидальными», так как их провод намотан вокруг сердечника, имеющего форму тора.
Как резисторы и конденсаторы, катушки индуктивности могут выполняться в корпусе для поверхностного монтажа (SMD). На следующей фотографии представлено несколько таких катушек:
Две индуктивности здесь расположены справа в центре платы. Они представляют собой маленькие черные чипы с номером «100», а над одной из них можно увидеть обозначение L5.
— Инструменты для электротехники и электроники
Этот калькулятор помогает вычислить индуктивность катушки.
Обзор
Катушка — это самая узнаваемая форма индуктора. Этот инструмент предназначен для расчета индуктивности катушки с проволокой с учетом количества витков, диаметра петли, диаметра проволоки и проницаемости среды. Обратите внимание, что вы можете выбрать единицу измерения для диаметра петли и диаметра проволоки.{2} $$ = количество витков
$$ \ mu_ {0} $$ = проницаемость свободного пространства = 4π × 10 −7
$$ \ mu_ {r} $$ = относительная проницаемость
$$ D $$ = диаметр петли
$$ d $$ = диаметр проволоки
Приложения
Лампа для вспышки камеры
Индуктор (или катушка) играет важную роль в схеме лампы вспышки камеры. Для камеры это важный компонент, который привел к высокому всплеску напряжения на катушке запуска, которое затем усиливалось действием автотрансформатора вторичной обмотки, чтобы генерировать 4000 В, необходимые для зажигания лампы-вспышки.Конденсатор, включенный параллельно катушке триггера, заряжается до 300 В по низкоомной цепи, обеспечиваемой тринистором. Однако, как только конденсатор был полностью заряжен, путь короткого замыкания на землю, обеспечиваемый SCR, был удален, и конденсатор немедленно начал разряжаться через катушку запуска. Поскольку единственным сопротивлением постоянной времени индуктивной сети является относительно низкое сопротивление самой катушки, ток через катушку нарастал очень быстро. Затем на катушке возникло значительное напряжение.Это напряжение, в свою очередь, увеличивалось за счет воздействия трансформатора на вторичную обмотку автотрансформатора, и лампа-вспышка зажигалась. Это высокое напряжение, генерируемое на триггерной катушке, также будет появляться непосредственно на конденсаторе триггерной сети. В результате он снова начнет заряжаться, пока генерируемое напряжение на катушке не упадет до нуля вольт. Однако, когда он упадет, конденсатор снова разрядится через катушку, установит другой зарядный ток через катушку и снова создаст напряжение на катушке.Высокочастотный обмен энергией между катушкой и конденсатором называется обратным ходом из-за «обратного потока» энергии от одного накопительного элемента к другому.
Диммер бытовой
Катушки индуктивностиможно найти в самых разных электронных схемах дома. В типичном бытовом диммере используется индуктор для защиты других компонентов и приложенной нагрузки от «бросковых» токов — токов, которые нарастают с очень высокой скоростью и часто до чрезмерно высоких уровней.Эта функция особенно важна для диммеров, поскольку они чаще всего используются для управления интенсивностью света лампы накаливания. При «включении» сопротивление ламп накаливания обычно очень низкое, и относительно высокие токи могут протекать в течение коротких периодов времени, пока нить накаливания лампы не нагреется. Катушка индуктивности также эффективно блокирует высокочастотный шум (RFI), создаваемый переключающим действием симистора в диммере. Конденсатор также обычно включается от линии к нейтрали, чтобы любые скачки напряжения не влияли на работу диммера и приложенной нагрузки (лампы и т. Д.) и помочь в подавлении помех от радиопомех.
Дополнительная литература
Расчет и расчет многослойного змеевика
Подробнее о индукторах с воздушным сердечником
Что такое индуктор с воздушным сердечником?
«Индуктор с воздушным сердечником» — это индуктор, который
не зависит от ферромагнитного материала для достижения
его указанная индуктивность. Некоторые индукторы намотаны без
шпулька и просто воздух в качестве сердечника.Некоторые другие ранены
на катушке из бакелита, пластика, керамики и т. д.
Преимущества катушки с воздушным сердечником:
На ее индуктивность не влияет ток, который она несет.
Это контрастирует с ситуацией с катушками, использующими ферромагнитные
сердечники, индуктивность которых имеет тенденцию достигать пика при умеренных
напряженности поля перед падением к нулю как насыщение
подходы.Иногда нелинейность намагниченности
кривой можно терпеть; например в коммутационной мощности
источников питания и в некоторых топологиях коммутации это
преимущество.
В схемах, таких как фильтры кроссовера аудио в Hi-Fi
акустические системы необходимо избегать искажений; затем воздух
катушка — хороший выбор. Большинство радиопередатчиков полагаются
на воздушных змеевиках для предотвращения образования гармоник.
Воздушные змеевики также не имеют «потерь в стали».
что проблема с ферромагнитными сердечниками. Как частота
увеличивается, это преимущество становится все больше
важный. Вы получаете лучшую добротность, большую эффективность,
большая мощность и меньше искажений.
Наконец, воздушные змеевики могут быть спроектированы для работы на частотах
до 1 ГГц.Большинство ферромагнитных сердечников имеют тенденцию быть
довольно с потерями на частотах выше 100 МГц.
И «обратная сторона»:
Без сердечника с высокой проницаемостью нужно иметь больше
и / или большее количество витков для достижения заданного значения индуктивности.
Больше витков означает большие катушки, меньший резонанс
из-за более высокой межобмоточной емкости и более высокой меди
потеря. На более высоких частотах обычно не требуется
высокая индуктивность, поэтому это не проблема.
Излучение и захват большего поля рассеяния:
С замкнутыми магнитными путями, используемыми в индукторах с сердечником
радиация гораздо менее серьезна. По мере увеличения диаметра
к длине волны (лямбда = c / f), потери из-за электромагнитных
радиация станет значительной. Вы можете
уменьшить эту проблему, заключив катушку в экран,
или установив его под прямым углом к другим катушкам,
может быть связан с.
Возможно, вы используете змеевик с воздушным сердечником не потому, что вам нужен
элемент схемы с определенной индуктивностью как таковой
но поскольку ваша катушка используется как датчик приближения,
рамочная антенна, индукционный нагреватель, катушка Тесла, электромагнит,
головка магнитометра или отклоняющая балка и т. д. Затем внешний
излучаемое поле может быть каким угодно.
Катушка Брукса:
Интересная задача — найти максимальную индуктивность
с заданной длиной провода.Брукс, написавший статью
в 1931 г. вычислил, что идеальное значение для среднего
радиус очень близок к 3A / 2. Как видно из
на рисунке ниже катушка имеет квадратное поперечное сечение (A = B)
а внутренний диаметр равен удвоенной высоте
(или ширину) обмотки катушки.
Мы называем катушку с такими размерами катушкой Брукса.
Соотношение ручьев не критично.2
где r — средний радиус индуктора (в см).
N — количество витков.
(r = средняя длина радиуса катушки, измеренная от
центр катушки к центру высоты катушки,
как показано на рисунке выше.)
Дроссели, дроссели и катушки по индивидуальному заказу
Катушки индуктивности и катушки
Катушки индуктивности — один из важнейших компонентов электроники.Обычно они используются для хранения энергии, но также могут использоваться в качестве ВЧ-дросселей (см. Ниже). Когда ток проходит через катушку индуктивности, он создает магнитное поле вокруг катушки. Сила этого магнитного поля представляет собой накопленную энергию. Мера способности катушки индуктивности накапливать энергию называется индуктивностью, измеряется в единицах Генри (H) и обозначается буквой L.
Применения индуктора включают:
- Накопитель энергии
- Преобразователи солнечной / ветровой энергии
- Обработка сигналов
- Импульсные источники питания
Мы можем разработать индивидуальный высокочастотный индуктор в соответствии с вашими требованиями, включая:
- Индуктивность
- Текущая емкость
- Частота (до 1 МГц)
- Крепление
- Специальное место для установки
- SMD или TH
Катушки индуктивности с воздушным сердечником — это индукторы без сердечника, которые не намотаны на ферромагнетик (т.е.е. ферритовый сердечник. Традиционно индукторы с воздушным сердечником наматываются исключительно на пластиковую бобину, но нередко можно увидеть индукторы с воздушным сердечником в виде жесткой проволоки, намотанной в форме катушки.
Преимущество индуктора с воздушным сердечником заключается в том, что он не насыщается, как индуктор с ферритовым / железным сердечником, на более высоких частотах. Недостатком использования индуктора с воздушным сердечником является то, что требуется гораздо больше витков для удовлетворения требований к индуктивности.
Дроссели
«Дроссель» — относительно старый термин, который больше не используется, и сегодня люди используют слова «индуктор» и «дроссель» как синонимы.Несмотря на то, что дроссели и катушки индуктивности используются для той же цели, дроссели традиционно использовались в ВЧ приложениях для блокировки высокочастотных сигналов переменного тока.
Синфазные дроссели
Синфазный дроссель (CMM) служит эффективным способом фильтрации синфазных линий питания, позволяя оборудованию соответствовать строгим требованиям к электрическому излучению. Он помогает фильтровать и блокировать высокочастотные синфазные токовые шумы в линиях питания. Этот шум может потенциально повредить другие электрические компоненты или устройства в вашей системе, если его не фильтровать.
Синфазные дроссели используются в следующих приложениях:
- Сети связи
- Линии электропередач и кабели (обычно находятся в основании в виде борта)
- Приложения для передачи и приема (телевизоры и мониторы)
Мы можем разработать индивидуальный высокочастотный синфазный дроссель в соответствии с вашими конкретными требованиями, в том числе:
- Индуктивность
- Текущая емкость
- Частота (до 1 МГц)
- Количество фаз
- Крепление
- Специальное место для установки
- SMD или TH
Анализ, проектирование и оптимизация компактных сверхвысокочувствительных датчиков с индукционной катушкой без сердечника
Для бесконтактной индукционной томографии потока нам требуется компактная система измерения магнитного поля с динамическим диапазоном 5 порядков величины, чтобы определять амплитуду и фазу переменного магнитного поля силой 1 мТл с точностью лучше 5 нТл и фазовая погрешность не более 10 −2 град.В некоторых приложениях также присутствует статическое магнитное поле около 300 мТл, что приводит к общему динамическому диапазону 7 порядков величины.
Мы представляем теоретические и экспериментальные анализы градиентометрических датчиков с индукционной катушкой абсолютного и первого порядка с чувствительностью более 500 В / Тл (Гц) и диаметром 28 мм. Из их эквивалентных схем мы выводим соответствующие комплексные передаточные функции и подгоняем их к калибровочным измерениям, тем самым определяя значения компонентов эквивалентной схемы.Это позволяет нам компенсировать их нелинейные частотно-зависимые амплитудно-фазовые характеристики. Кроме того, мы демонстрируем оптимизацию катушек на основе конструкции равных квадратов Брукса в адаптации Мургатройда, которая максимизирует индуктивность (и тем самым, скорее всего, чувствительность) катушек. Наконец, мы проектируем новую катушку диаметром 74 мм и чувствительностью 577 В / (ТГц) с аналитически предсказанным эквивалентным шумом магнитного поля примерно в диапазоне частот 1 Гц, что затем подтверждается измерениями на изготовленных опытный образец.
Для бесконтактной индукционной томографии потока (CIFT), которая может измерять трехмерное поле потока жидких металлов [1, 2], необходима система измерения магнитного поля с динамическим диапазоном 5 порядков величины для измерения потока. -индуцированные изменения магнитного поля приложенного магнитного поля вне расплава. Для этого метода переменное первичное магнитное поле силой около 1 мТл проникает в текучий расплав. Взаимодействие между первичным полем и расплавом создает переменное вторичное магнитное поле силой 100 нТл.Вторичное магнитное поле должно быть извлечено из суперпозиции первичного и вторичного полей с точностью лучше 5 нТл. В некоторых случаях может присутствовать и дополнительное постоянное магнитное поле с амплитудой 300 мТл [3, 4]. В результате общий динамический диапазон в 7 порядков величины создает огромную проблему даже для современных датчиков магнитного поля.
Кроме того, мы обнаружили, что в этих экспериментах присутствуют источники магнитного поля с частотами, подобными частоте нашего возбуждения, и переменными фазами [4].Следовательно, требуемое выделение индуцированного потоком магнитного поля должно выполняться с фазовой ошибкой не более 10 −2 град.
1.1. Почему индукционные катушки?
Датчики Fluxgate, несмотря на то, что они демонстрируют необходимую точность, здесь не годятся, поскольку их магнитный сердечник насыщается примерно при 1 мТл. СКВИДы обычно способны охватывать весь требуемый здесь диапазон магнитных полей, но поскольку их принцип работы основан на сверхпроводимости, их необходимо охлаждать до очень низких температур; соответствующая сложность в нашем случае нежелательна.GMR также исключены, поскольку их характеристика R — H проявляет гистерезисные эффекты и нелинейности до нескольких процентов от их максимального диапазона [5]. В настоящее время эти эффекты не могут быть скомпенсированы с точностью, необходимой для нашего приложения [6, 7].
В то время как все больше новых датчиков, таких как магнитные резонаторы MEMS, становятся все популярнее, они не могут быть использованы здесь, поскольку их принцип действия основан на силах Лоренца, которые возникают в результате взаимодействия источника внутреннего поля с внешним полем [8, 9].Это заставляет их обнаруживать как постоянное, так и переменное магнитные поля. Следовательно, им потребуется разрешить полные 7 порядков величины динамического диапазона. Насколько нам известно, не существует датчика MEMS, который мог бы надежно распознавать сигналы с таким широким динамическим диапазоном. Для получения дополнительной информации о других методах магнитного зондирования обратитесь к [10, 11].
Поскольку датчики с индукционной катушкой не улавливают постоянные магнитные поля и тем самым уменьшают динамический диапазон входного магнитного сигнала с 7 до всего лишь 5 порядков величины, они хорошо подходят для этой задачи.
1.2. Соображения по конструкции
В своей основной форме индукционные катушки состоят из нескольких витков электрического проводника, помещенного в магнитное поле, с поперечным сечением катушки, ориентированным перпендикулярно силовым линиям (см. Рисунок 1). На выводах катушки можно измерить напряжение U , которое пропорционально производной по времени приложенного магнитного потока. Эта простая конструкция обладает преимуществом идеальной линейности в отношении амплитуды магнитного поля и отсутствия верхнего предела диапазона; нижний предел разрешения определяется шумом в катушке.
Увеличить Уменьшить Сбросить размер изображения
Рис. 1. Простая цилиндрическая индукционная катушка, пронизанная ортогональным магнитным полем.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияЗа последние десятилетия стали доступны многочисленные улучшения основного принципа, в результате чего экспериментатор получил четыре варианта дизайна. Первый касается порядка датчика.Базовая конструкция катушки на рисунке 1 представляет собой датчик абсолютной индукционной катушки, поскольку измеряется абсолютное значение производной по времени магнитного потока. Кроме того, возможно дифференциальное измерение выходного напряжения между двумя или более катушками (обычно подключенными с противоположной полярностью), что позволяет определять пространственный градиент магнитного поля. Следовательно, такие датчики называют градиентометрическими индукционными катушками [12]. Градиометрический датчик, состоящий из двух катушек, будет называться градиентометрическим датчиком 1-го порядка, три катушки составляют градиентометрический датчик 2-го порядка и так далее.
Другой возможностью оптимизации является использование ферромагнитных сердечников внутри обмоток [13] или концентраторов потока перед или за обмотками [14]. Ферромагнитные материалы концентрируют окружающий магнитный поток в пределах эффективной площади сенсора, тем самым резко увеличивая его чувствительность и снижая эквивалентный магнитный шум, что также позволяет создавать сенсоры меньшего размера. Обычно для этого используются материалы с высокой проницаемостью, такие как Metglas или пермаллой [15], которые имеют значения µ r > 90 000.Следовательно, такие катушки показывают рабочие параметры, аналогичные параметрам феррозондовых датчиков, которые обычно демонстрируют разрешение 100 пТл и погрешность линейности лучше 10 ppm [16]. Хотя индукционные катушки с ферромагнитными компонентами также наследуют недостаток магнитных вентилей, заключающийся в довольно небольшом верхнем пределе диапазона около 1 мТл, вызванном появлением эффектов насыщения в ферромагнитном материале.
Третий выбор конструкции — это режим работы катушки, который может быть режимом напряжения или током.В режиме напряжения входное сопротивление подключенного измерительного оборудования должно быть достаточно большим, что приводит к линейной и пропорциональной f амплитудной характеристике ниже резонансной частоты катушки. Для сравнения, в токовом режиме катушка работает с закороченным выходом, что позволяет избежать паразитной емкости катушки. В конечном итоге это приводит к плоской амплитудной характеристике для частот f > R (2 π L ) −1 [15, 17].
Наконец, конструкция датчика нуждается в какой-то схеме считывания. Это могут быть простые мультиметры и аналого-цифровые преобразователи (АЦП), усилители, интеграторы [18], преобразователи тока в напряжение и схемы обратной связи по потоку [19, 20].
1.3. Оценка конструкции
В этой статье мы оценим различные конструкции датчиков, используя три основных числа электрических характеристик. Первый из них — это чувствительность катушки, которая представляет собой отношение выходного напряжения к напряженности входного магнитного поля и может составлять от 1 мВ / Тл до 1 ГВ / Тл [13, 21], особенно когда размер катушки не ограничивается внешними факторами [22], используются концентраторы потока и усилители с высоким коэффициентом усиления.
Во-вторых, передаточная функция конструкции играет важную роль, поскольку она определяет амплитуду и фазовый отклик, оба из которых демонстрируют нелинейные частотно-зависимые характеристики. Преимущественно можно использовать передаточную функцию, например, если измеряемое поле имеет постоянную известную частоту, резонансная частота может быть спроектирована так, чтобы соответствовать частоте возбуждения, тем самым увеличивая эффективную чувствительность датчика. Фазовая характеристика датчиков с индукционной катушкой часто упускается из виду в литературе, за некоторыми исключениями [23].
Наконец, хорошая конструкция датчика должна минимизировать шум. Общий шум напряжения или тока катушки и присоединенной схемы обычно преобразуется в эквивалентный шум входного магнитного поля, что упрощает сравнение различных конструкций. Помимо использования малошумящей считывающей электроники, большое значение имеет конструкция катушки с минимальным собственным шумом. Использование систем охлаждения, например с жидким азотом, также может значительно снизить шум [15], хотя для наших целей это нецелесообразно.
На основании этих размышлений мы решили решить задачу измерения, упомянутую в начале введения, с помощью абсолютных и градиентометрических датчиков с индукционной катушкой 1-го порядка без сердечника, работающих в режиме напряжения с прямым считыванием высокоточного АЦП. Чтобы измерить описанные крохотные магнитные поля в компактных экспериментах, катушкам требуется очень большое количество витков, около 100 000 проволоки малого диаметра порядка 20–100 мкм, с общими размерами в диапазоне нескольких сантиметров.
Такие индукционные катушки обладают некоторыми недостатками. Их частотно-пропорциональная чувствительность вызывает повышенную \ hbox {восприимчивость} к высокочастотному магнитному шуму, который можно найти в большинстве сред. Если необходимо удовлетворить дополнительные требования, такие как повышенная термостойкость, эти змеевики могут быть довольно дорогими и стоить от 200 до 500 евро за штуку. Кроме того, масса обмотки и малый диаметр проволоки делают катушки восприимчивыми к повреждению из-за рывков.Обрыв провода внутри обмотки не подлежит ремонту, поэтому с катушками необходимо обращаться с особой осторожностью.
1,4. Цели и структура
Эта статья организована следующим образом: для достижения цели минимизации неопределенности амплитуды и фазы в разделе 2 вводится теория индукционных катушек, используемых для CIFT, и разрабатывается их комплексная передаточная функция. В разделе 3 уравнения модели будут затем адаптированы к калибровочным измерениям для нескольких частот. Затем модель можно использовать для расчета и корректировки фазовой и амплитудной характеристики для любой частоты.
Вторая цель — разработать новую абсолютную индукционную катушку с оптимальным отношением чувствительности к шуму, которая будет рассмотрена в разделе 4. Наконец, мы сосредоточимся на аналитическом прогнозе шума датчика и подтверждении измерений в разделе 5. Исходя из этого В результате анализа мы получим эквивалентный нормированный на ширину полосы шум входного магнитного поля, который можно использовать для оценки погрешности измерения датчиков, что является третьей целью данной статьи.
Обратите внимание, что измерительная задача, для которой были разработаны все катушки в этой статье, довольно особенная.Нам неизвестна литература других исследователей, в которой описаны катушки с аналогичным размером, числом витков, чувствительностью и используемым частотным диапазоном. Поэтому сравнение с аналогичными работами в данной статье проводиться не будет.
Датчики с индукционной катушкой без сердечника основаны на принципе индукции Фарадея, согласно которому изменяющееся во времени магнитное поле создает электрическое поле в электрических проводниках. Пусть будет индуцированное напряжение в катушке с числом витков n и поперечным сечением области A , которое пронизано магнитным полем с плотностью потока B , изменяющейся во времени t .Пусть, кроме того, магнитное поле и поперечное сечение ортогональны друг другу (рисунок 1). Основное соотношение между этими величинами составляет
. В этой статье мы сосредоточимся на цилиндрических змеевиках с толстыми слоями, что приведет к значительным различиям между внешним диаметром d o и внутренним диаметром d i обмоток. В этом случае средняя эффективная площадь равна
. Если мы дополнительно предположим, что B является временной гармоникой
с амплитудой, частотой f и нулевой фазой 0 , мы находим
Продукт S будет Чувствительность катушки обозначена единицами измерения [ S ] = В / (ТГц) и полностью определяется геометрическими свойствами катушки.
Эквивалентная схема датчика абсолютной индукционной катушки с присоединенным АЦП показана на рисунке 2 (а). Сама катушка содержит эквивалентное напряжение источника, последовательное сопротивление R s , последовательную индуктивность L s и паразитную емкость C p . Катушка подключена к АЦП с оконечным резистором R t и оконечной емкостью C t .Напряжение U t ( t ) измеряется в параллельной цепи C p , R t и C t . Вместо гармонического анализа этой схемы по времени мы анализируем ее в комплексной области. Поэтому напряжения, зависящие от времени, теперь обозначаются как комплексные и.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 2. Эквивалентная электрическая схема обоих типов катушек.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияСвязь между измеренным и индуцированным значениями определяется выражением
, где — комплексная передаточная функция делителя напряжения:
В этих уравнениях ω = 2 π f — угловая частота и мнимая единица. . Оператор обозначает параллельную схему
Для градиентометрической катушки 1-го порядка эквивалентная схема показана на рисунке 2 (b).Он состоит из двух абсолютных катушек с индивидуальным сопротивлением, индуктивностью и емкостью. Считывание осуществляется в виде дифференциального входа АЦП, правая ветвь которого подключена к положительному входу, а левая ветвь — к отрицательному входу. И левый, и правый концы схемы также связаны друг с другом дополнительной паразитной емкостью, которая здесь не показана, поскольку она не оказывает существенного влияния на передаточную функцию в нашем случае, что можно увидеть после подбора данных в следующем раздел.Отсутствие емкости значительно облегчает расчеты для этой сети.
Поскольку обе отдельные катушки магнитно связаны, они представляют собой трансформатор. В этой схеме M — это взаимная индуктивность между обеими катушками с
Фактор k c — это коэффициент связи, который был бы близок к 1 для трансформатора, но в нашем случае имеет меньшее значение. из-за конструкции без сердечника и расстояния между двумя обмотками.Кроме того, он отрицательный, так как обе катушки соединены противоположными знаками. Эффективная индуктивность каждой отдельной катушки — это так называемая «паразитная индуктивность»:
Результирующая электрическая сеть оценивается с использованием принципа суперпозиции и расчета эквивалентных двухпортовых сетей. Сначала мы предполагаем, что две ветви сети симметричны:
После этого схема может быть упрощена до следующих импедансов:
Исходя из этого, передаточные функции обеих ветвей могут быть записаны как
Наконец, напряжения на обоих клеммах можно рассчитать по наведенному напряжению в каждой отдельной катушке.Это позволяет рассчитать дифференциальное напряжение с использованием
Калибровка сенсорных катушек служит для эмпирического определения их чувствительности, амплитудной характеристики и фазовой характеристики. Мы использовали калибровку специально, чтобы подогнать наши модели к измеренным амплитудным и фазовым характеристикам для определенных частот. Величины L s и C p были выбраны в качестве параметров для подгонки. Используя подобранную модель, мы можем скорректировать коэффициент амплитуды и фазовый сдвиг катушек для любой частоты.
Для первых калибровочных измерений мы использовали имеющиеся цилиндрические датчики с индукционной катушкой как абсолютного, так и градиентометрического типа 1-го порядка, как показано на рисунке 3. Тип абсолютного датчика с 340 000 витков провода 25 мкм обозначен как ‘340k катушка », а тип градиентометрического датчика с 2х 160 000 витков одного и того же провода обозначается как« катушка 2x160k ». Поскольку анализ сигналов для CIFT осуществляется исключительно в цифровой области, мы минимизируем количество аналоговых схем и подаем выходное напряжение катушек непосредственно в высокоточный аналого-цифровой преобразователь, в частности модель LTT24 от Labortechnik Tasler. .
Увеличить Уменьшить Сбросить размер изображения
Рис. 3. Эскиз конструкции датчика с индукционной катушкой (a) 340k (абсолютное) и (b) градиентометрической индукционной катушки (2x160k), используемого для CIFT (все размеры в мм, диаметр провода без масштабирования)
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияДля калибровки мы расположили одну из имеющихся абсолютных катушек в центре достаточно большой пары катушек Гельмгольца с радиусом R = 142 мм.Затем мы измерили амплитуду и фазовый отклик катушки в зависимости от тока возбуждения, возбуждающего магнитное поле Гельмгольца. Когда это выполняется для достаточного количества частот (в нашем случае 40), модели из раздела 2 могут быть адаптированы к измеренным данным, тем самым получая индуктивность и емкость катушки. Сопротивление легко измерить любым мультиметром.
Поскольку градиентометрические катушки не генерируют выходного напряжения для однородных магнитных полей, для них вместо них используются катушки Гельмгольца в качестве катушек Максвелла, которые создают магнитное поле с почти постоянным градиентом в центре обеих катушек.Для градиентометрических катушек при калибровке также необходимо учитывать коэффициент связи k c . Перед калибровкой мы вычислили k c = −0,549 с помощью численного моделирования в Opera2D, который был установлен в качестве фиксированного параметра в нашей модели.
Для катушек любого типа амплитуда и фазовая характеристика были рассчитаны на основе временного ряда измеренного выходного напряжения с использованием метода квадратурной демодуляции [24].Что касается частот измерения, мы выбрали распределение со многими частотами в диапазоне ниже f <50 Гц и около резонансной частоты для каждой катушки. На рисунке 4 показаны результаты калибровки абсолютной катушки, а на рисунке 5 показаны соответствующие данные для градиентометрической катушки. Видно поразительное общее согласие между нашими моделями и данными измерений. Из наших измерений мы получили значения, показанные в таблице 1. Стандартная ошибка подобранной модели для C p и L s равна 0.2%.
Увеличить Уменьшить Сбросить размер изображения
Рис. 4. Измерение и подогнанная модель для датчика абсолютного давления 340k. Для наглядности показаны не все точки измерения ниже 100 Гц.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияУвеличить Уменьшить Сбросить размер изображения
Рисунок 5. Измерение и подогнанная модель для градиентометрического датчика 2 × 160k.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияТаблица 1. Результаты калибровки обеих катушек.
| Диаметр проволоки | 25 мкм | 25 мкм |
| Оборотов | 340 000 | 2 × 160 000 |
| S / В / (Т Гц) | 531.3 | 260,3 |
| R с / кОм | 592,0 | 274,9 |
| Д с / В | 463,4 | 71,69 |
| C p / pF | 412,4 | 505,5 |
| к к | н / д | -0,549 |
| 5.70 × 10 −5 | 1,62 × 10 −5 | |
| −2,70 × 10 −1 | -1,50 × 10 -1 |
Для новой, гораздо более крупной экспериментальной установки с CIFT нам потребовалось разработать более крупные датчики с индукционной катушкой. Естественно, мы хотели, чтобы у нашего сенсора было максимально возможное отношение чувствительности к шуму. В обзоре литературы мы не смогли найти аналитического решения для этой оптимизации.Тем не менее, поскольку индуктивность и чувствительность катушки связаны, мы можем вместо этого максимизировать индуктивность нашей конструкции датчика. В то время как индуктивность представляет собой меру количества энергии, которое катушка с возбуждающим электрическим током может накапливать в своем магнитном поле, чувствительность связывает ортогональное магнитное поле с выходным напряжением катушки. Обе величины имеют общее то, что они зависят только от геометрических параметров, таких как диаметр и количество витков.
Популярным эмпирическим приближением для катушки с оптимальной индуктивностью является «конструкция из четырех квадратов» Брукса и Тернера [25], которая показана на рисунке 6 (а).Эта конструкция делит поперечное сечение (A-A) катушки на четыре соединенных квадрата с длиной ребра c . Два внутренних квадрата представляют собой цилиндрический сердечник, а два внешних содержат витки проволоки. Таким образом, размеры датчика определяются длиной края c одного из квадратов. Нам не удалось найти конструкции, которые обеспечивали бы значительно лучшую индуктивность для таких же компактных и простых в изготовлении форм катушек.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 6. Конструкция датчиков с индукционной катушкой с использованием метода квадратов Брукса для постоянного внешнего диаметра.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияИз этого дизайна Мургатройд [26, 27] вывел две альтернативы: дизайн трех квадратов и дизайн пяти квадратов, см. Рисунки 6 (b) и (c). Обе альтернативы достигают индуктивности примерно на 2% меньше, чем у конструкции Брукса, при той же длине провода, что приемлемо для нашего приложения.
Катушки дополнительно должны удовлетворять трем следующим ограничениям. (A) Максимально допустимый диаметр катушки составляет 74 мм. Это следует из геометрии упомянутого нового эксперимента, в котором измеряемая структура потока простирается более чем на 700 мм. В этом доступном пространстве мы хотели бы разместить до девяти катушек, уложенных друг рядом с другом в направлении диаметра катушек. Если необходимо соблюдать минимальное расстояние 3 мм между двумя соседними катушками, следует заявленный диаметр катушки 74 мм.(B) Катушка должна быть довольно плоской, что приводит к выбору дизайна с пятью квадратами с c = 14,8 мм. Требуемая плоскостность следует из топологии магнитного поля в экспериментах CIFT. В очень грубом приближении вторичное магнитное поле CIFT можно представить как исходящее от одного магнитного диполя в рамках эксперимента, а затем уменьшающееся вне эксперимента с r −2 . Тогда становится ясно, что любое измерение магнитного поля должно проводиться как можно ближе к эксперименту, и что толстая катушка (с длинным цилиндром) имеет тот недостаток, что витки, наиболее удаленные от эксперимента, вносят небольшой вклад в общее выходное напряжение. при этом в равной степени способствуя шуму датчика.(C) Чувствительность должна быть больше, чем S ≥ 530 В / (Т Гц), что является такой же чувствительностью, как у катушки 340 кОм. Поскольку предыдущие измерения CIFT с катушкой 340 кОм были успешными, мы решили, что новая конструкция должна иметь такую же или немного большую чувствительность.
Чтобы рассчитать значения производительности для конструкции катушки с пятью квадратами с c = 14,8 мм, сначала нам понадобятся уравнения (2) для эффективной площади и (4) для чувствительности, где d i = 3 c и d o = 5 c .Для расчетов шума, представленных в следующих разделах, мы, кроме того, должны рассчитать сопротивление R , что можно сделать следующим образом. Сначала определим количество витков
, где — коэффициент заполнения провода, который описывает соотношение между проводящей площадью и общей площадью в квадрате c 2 при заполнении проволокой с диаметром сердечника г в . Тогда мы можем определить
, где ρ = ρ ( d c ), являющееся сопротивлением провода на единицу длины.У поставщика Elektrisola мы выбрали провод с d w = 71 мкм, k f = 0,575 и ρ = 4,318 Ом / м, что дало расчетные параметры n = 31812, R = 25,81 кОм и S = 561 В / (Т Гц). Затем новый датчик был изготовлен компанией Michael Müller Spulenwickeltechnik.
Новый датчик с индукционной катушкой, обозначенный как «катушка 30 кОм», показан на рисунке 7. Он был откалиброван таким же образом, как и меньшая абсолютная катушка; результаты можно увидеть на рисунке 8 и в таблице 2.Расчетные параметры незначительно отличаются от реальных значений изготовленного датчика.
Таблица 2. Свойства новой катушки 30k.
| Диаметр проволоки | 71 мкм |
| Оборотов | 32800 |
| S / В / (Т Гц) | 577,2 |
| R с / кОм | 25.03 |
| Д с / В | 38,52 |
| C p / pF | 377,6 |
| 5,81 × 10 −6 | |
| −4,68 × 10 −2 |
Хотя общее совпадение измеренной фазы и рассчитанной фазы поразительно, модель не полностью согласуется с измерениями для очень низких частот.Мы стремились к фазовой ошибке не более 1 × 10 −2 градуса, но в среднем наше отклонение составляет 4,4 × 10 −2 градуса. Наиболее вероятная причина этого кроется в небольших механических неточностях нашей калибровочной установки. Кроме того, датчик тока, который мы использовали для измерения тока возбуждения во время калибровки, мог сам показывать небольшой фазовый сдвиг. Это необходимо будет изучить в будущей работе.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 7. Новый датчик с индукционной катушкой 30 кОм. Нижний конец катушки должен быть направлен к эксперименту. Каркас изготовлен из PEEK, а обмотка защищена резиновым покрытием красного цвета.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияУвеличить Уменьшить Сбросить размер изображения
Рис. 8. Размеры и подогнанная модель для катушки 30k.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияНа последнем этапе наша цель состоит в том, чтобы количественно оценить шум магнитного поля нашей измерительной системы для всех трех представленных датчиков с помощью аналитического подхода, который подтверждается измерениями.Знание спектра шума наших датчиков позволяет нам констатировать максимальную погрешность измерения и, кроме того, позволяет нам убедиться, что наша оптимизация была правильной.
Для системы датчиков с индукционной катушкой обычно можно выделить три соответствующих источника шума [28]. Первый — это напряжение теплового шума u r в резисторе R :
Здесь k b — постоянная Больцмана, а T — абсолютная температура резистора.Переменная описывает аналоговую полосу пропускания измерения. Поскольку этот источник шума не зависит от f , он называется белым шумом.
Кроме того, нам необходимо рассмотреть два источника шума тока, которые обычно создают шумовые напряжения, протекая через резисторы. Первый токовый шум — это фликкер-шум i f , который вызван несовершенным контактом между двумя проводниками, когда через оба из них протекает постоянный ток, что приводит к колебаниям проводимости:
K n — коэффициент фликкер-шума, I — постоянный ток, m — показатель степени фликкер-шума и n 1.Этот термин превращает i f в розовый шум.
Наконец, дробовой шум создается «случайным испусканием электронов и случайным прохождением носителей заряда через потенциальные барьеры» [28].
Величина q относится к элементарному электрическому заряду.
Для всех практических вопросов мы учитываем только тепловой шум самого датчика и шум АЦП, поскольку только эти два фактора вносят значительный вклад в общий шум, как это видно из результатов измерений в конце этого раздела.Шум АЦП указан из его таблицы данных, как при использовании входа U = 5 В. Это создает напряжение шума
Шум от АЦП и катушки необходимо складывать квадратично, чтобы получить общий шум u n , поскольку они оба относятся к мощности шума:
Обычно рекомендуется нормализовать измеренное напряжение шума до ширины полосы измерения. Кроме того, часто желательно указать эквивалентный шум магнитного поля b n , а не измеренное напряжение шума u n , чтобы облегчить сравнение различных конструкций датчиков.Исходя из этих соображений, мы можем определить нормализованный по ширине полосы эквивалентный входной шум для наших датчиков:
Используя эти уравнения и определенные значения компонентов эквивалентной схемы катушек, мы можем аналитически рассчитать для самих катушек, а также для катушек. с подключенным АЦП, см. рисунок 9.
Увеличить Уменьшить Сбросить размер изображения
Рис. 9. Аналитический нормированный по ширине полосы эквивалентный шум магнитного поля всех трех индукционных катушек, с АЦП и без него.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияФорма графиков в основном определяется передаточной функцией амплитуды соответствующих катушек согласно уравнению (26). Следовательно, входной шум становится минимальным на резонансной частоте. Поскольку неявно предполагалось, что шум АЦП не зависит от частоты, добавление его к шуму катушки смещает графики равномерно в сторону большего шума магнитного поля.
Как ясно видно, вклад АЦП в общий шум намного больше, чем вклад датчиков, особенно для новой конструкции датчика 30k.Ни при каких обстоятельствах шум сенсора не превышает, а общий уровень шума всегда ниже. Новый датчик 30k превосходит два меньших более чем в 5 раз по аналогичной чувствительности и демонстрирует общий шум не более чем.
Общий шум никогда не превышает. Если предполагается измерение на центральной частоте 1 Гц и полосе пропускания 1 Гц, мы обнаружим, что с вероятностью 99,7% (соответствует 3 σ ) общая точность лучше 5 нТл, как было указано во введении. .
Данные также показывают, что новый оптимизированный датчик 30k действительно работает примерно так же хорошо, как датчик 340k, если шум АЦП включен в расчеты. Хотя оптимизация датчика привела к значительному снижению собственного шума, общее улучшение незначительно в диапазоне 5 В. АЦП также имеет входной диапазон 250 мВ с отношением сигнал / шум всего 105 дБ, что снижает общий шум. Соответствующие графики не показаны, потому что это выходит за рамки данной статьи.
Чтобы подтвердить наш теоретический анализ шума, мы измерили шум напряжения u n нашей системы датчиков магнитного поля для каждого типа катушки следующим образом. Датчик помещался в коробку из пермаллоя с внутренними размерами (90 × 90 × 40) мм 3 и толщиной стенок 1,5 мм. Коробка из пермаллоя экранирует внешнее магнитное поле, так что в основном измеряется шум датчика. При такой настройке мы записали 100 с данных с частотой дискретизации 5 кГц, используя диапазон входного напряжения АЦП по умолчанию 5 В, см. Рисунок 10.Записанный временной ряд затем был преобразован в частотную область с помощью БПФ и масштабирован с помощью (26) для сравнения с аналитическим решением. Рисунок 11 иллюстрирует процедуру.
Увеличить Уменьшить Сбросить размер изображения
Рис. 10. Экспериментальная установка для измерения шума со снятой крышкой с металлической коробки
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияУвеличить Уменьшить Сбросить размер изображения
Рисунок 11. Схема установки для измерения шума.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияРисунок 12 показывает отличное согласие между расчетами и измерениями. Это подтверждает наш теоретический подход и подчеркивает, что основные рабочие характеристики индукционных катушек могут быть определены на этапе проектирования с достаточной точностью. Пики в измеренных спектрах указывают на то, что экранирующая коробка из пермаллоя слишком тонкая для полного подавления внешнего поля или что магнитное поле окружающей среды может проникать в коробку через зазоры или отверстие для кабеля датчика.
Увеличить Уменьшить Сбросить размер изображения
Рис. 12. Измеренный эквивалентный шум магнитного поля всех трех датчиков.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияДля частот, близких к частоте Найквиста 2,5 кГц, пики появляются чаще из-за логарифмической оси f . Тем не менее, нижняя часть графика измерений соответствует аналитическому расчету с хорошим согласием.Резкое снижение данных измерений выше 2 кГц, а также несоответствие измерения и модели вокруг резонансной частоты в настоящий момент не могут быть объяснены.
В этой статье мы продемонстрировали, как абсолютные датчики с индукционной катушкой и градиентометрические датчики 1-го порядка могут быть проанализированы аналитически и с помощью практических экспериментов. Используя их комплексные передаточные функции, нелинейные амплитудные и фазовые характеристики этих типов датчиков могут быть скомпенсированы, если известны значения их эквивалентных элементов схемы.Один из способов добиться этого — провести калибровочное измерение внутри пары катушек Гельмгольца или Максвелла.
Кроме того, мы разработали новую катушку абсолютной индукции с использованием конструкции из пяти равных квадратов. Этот датчик, который будет применяться для измерений CIFT, имеет общий шум менее чем. Кроме того, мы указали, как наиболее важные рабочие характеристики индукционных катушек, такие как чувствительность и уровень шума, могут быть определены на этапе проектирования с помощью набора довольно простых уравнений и надежных таблиц данных.
Дальнейшие усилия могут касаться, например, градиентометрических датчиков катушек более высокого порядка и различного расположения отдельных обмоток. Также большой интерес представляет компенсация теплового дрейфа катушек.
Двигатели с низкой индуктивностью— достижение оптимальной производительности системы движения
Пример:
Основные характеристики двигателя
Ke = 14,8 В / об / мин
Kt = 0,14 Нм / А
R = 13,6 Ом
L = 0.6 мч
Ir = 1,0 ампер (номинальный непрерывный ток)
24 вольт / 0,000600 Генри = рост тока 40,000 ампер / сек
При частоте ШИМ 20 кГц пульсации тока могут достигать +/- 1,0 ампер. При частоте ШИМ 100 кГц пульсации тока уменьшаются до +/- 0,2 ампер. Хорошая цель для пульсаций тока — 10% номинального тока двигателя.
В то время как выходной крутящий момент в зависимости от угла очень синусоидален, а движение очень плавное для двигателей с нулевым зазором, такая низкая индуктивность приведет к большим колебаниям тока по сравнению с номинальным продолжительным током двигателя.Это означает, что у вас в среднем 1 ампер с +/- 1 ампер пульсации в худших условиях. При напряжении шины 24 В этому двигателю требуется частота ШИМ 100 кГц, чтобы пульсации тока были близки к 10%.
Низковольтные и высокоскоростные двигатели
Все бесщеточные двигатели с постоянными магнитами вырабатывают напряжение, пропорциональное скорости. Максимальная скорость, с которой будет работать данный двигатель, напрямую зависит от напряжения на шине и постоянной напряжения Ke. Следовательно, низковольтные приложения будут работать только с низкими значениями Ke.Понижение Ke осуществляется за счет уменьшения числа витков фазы, что, как описано ранее, уменьшает индуктивность на квадрат разницы.
Следующий пример демонстрирует это явление.
Начальная конфигурация двигателя:
Ke = 10 В / krpm
Kt = 0,1 нм / ампер
R = 1 Ом
L = 1 мч
При питании 24 В максимальная скорость для этой системы составляет 2400 об. / Мин.
Новая конфигурация двигателя:
Для нового проекта требуется скорость 5000 об / мин при напряжении 24 В.В той же раме двигателя обмотку можно масштабировать для снижения постоянной напряжения путем регулировки витков катушки. Настроенный двигатель будет иметь следующие параметры.
Ke = 4,8 вольт / оборот в минуту
Kt = 0,045 нм / ампер
R = 0,23 Ом
L = 0,23 мч
Максимальная скорость этого двигателя теперь составляет 5000 об / мин. Сопротивление и индуктивность масштабируются квадратичной функцией из-за свойств фазного магнита двигателя. Объем мотора и объем меди одинаковы. Kt и Ke масштабируются напрямую с количеством витков.
Пример:
24 В / 0,000230 Генри = 104 000 ампер / сек нарастание тока.
При частоте ШИМ 20 кГц пульсации тока могут достигать +/- 2,6 ампер. При частоте ШИМ 100 кГц пульсации тока уменьшаются до +/- 0,5 ампер. Как указывалось ранее, хорошей целью для пульсаций тока является 10% номинального тока двигателя.
Заключение
По мере того, как конструкция двигателя становится меньше, плавнее, эффективнее и отзывчивее, низкая индуктивность может стать новой проблемой для разработчиков систем управления движением.Индуктивность может быть очень низкой в двигателях без пауз или в приложениях с низким напряжением, требующих высокой скорости.
Решение проблемы состоит в том, чтобы согласовать частоту ШИМ контроллера двигателя с двигателем, чтобы минимизировать пульсации тока. Другие варианты включают добавление последовательной индуктивности к фазам двигателя или использование линейного контроллера двигателя вместо контроллера ШИМ.
Низкая индуктивность дает множество преимуществ, включая более быструю реакцию двигателя за счет более низких постоянных времени, более плавный крутящий момент, более низкую пульсацию скорости и более высокую скорость при работе от источников питания с низким напряжением.
Катушка индуктивности: краткое введение
Мы постоянно сталкиваемся с этими объектами, но вряд ли добавим им какой-либо конкретный смысл. Для нас это обычное дело. Фактически, индукторы сегодня используются почти в каждом устройстве, но трансформаторы являются наиболее ярким примером их использования. Если вы думаете, что трансформаторы можно использовать только на силовых подстанциях, то вы действительно ошибаетесь: ваш ноутбук или мобильный преобразователь — это своего рода трансформатор, только меньшего размера, чем те, которые используются на электростанциях и распределительных подстанциях.
Любой индуктор состоит из обмотки и сердечника. Центр — стержень из ферромагнитного или диэлектрического материала, на который намотана обмотка. Чаще всего это делается из медной проволоки.
Количество витков обмотки напрямую связано с величиной результирующей магнитной индукции катушки. Теперь мы собираемся подумать о том, какие параметры и свойства мы собираемся определить, прежде чем мы начнем вычислять индуктивность катушек и формулы, необходимые для этого.
Какие параметры у катушки индуктивности?
Катушка имеет множество физических характеристик, отражающих ее стабильность и пригодность для конкретной работы. Один из них — индуктивность. Отношение потока магнитного поля, создаваемого катушкой, к величине этого тока численно равно. Индуктивность выражается в единицах Генри (GN), которые в большинстве случаев принимают значения от микрогенри до сотен Генри.
Индуктивность, вероятно, самый важный параметр катушки.И не удивительно, что большинство людей даже не думают, что существуют другие величины, которые могут характеризовать действия катушки и представлять ее пригодность для конкретного применения.
Профессионалы также обращают внимание на сопротивление потерь при выборе индуктора. Как вы можете понять из этого выражения, оно представляет серьезность потери электричества, вызванной ложными эффектами, такими как нагревательные провода, которые возникают в соответствии с законом Джоуля-Ленца. Легко понять, что чем лучше катушка, тем меньше значение.Еще один параметр, который необходимо учитывать, — добротность схемы. Он тесно связан с предыдущим параметром, который представляет коэффициент активной реакции (сопротивления потерь).
Соответственно, чем добротность выше, тем лучше. Увеличение достигается за счет выбора оптимального диаметра проволоки, материала и диаметра сердечника, а также количества витков.
Зачем нужен расчет индуктивности?
В мире существует множество различных типов катушек.Они различаются по свойствам, а значит, и по применению. Многие из них используются в высокопрочных трансформаторах, другие — в соленоидах, служат в качестве высокопрочных электромагнитов. В дополнение к этому, есть несколько приложений индуктивности. И для всего этого требуются разные типы катушек. Их активы различаются. Но большинство этих свойств можно объединить, используя принцип индуктивности.
Мы вплотную подошли к описанию того, что требуется по формуле для измерения индуктивности катушки. Но стоит отметить, что мы говорим не о «формуле», а о «формулах», потому что все катушки можно разделить на множество широких классов, каждый из которых имеет свою собственную отдельную формулу.
Типы катушек
Функциональные возможности различаются между петлевыми катушками, используемыми в радиофизике, катушками связи, используемыми в трансформаторах, и вариометрами, то есть катушками, выход которых можно изменять, регулируя относительное расположение катушек. Есть даже катушки вроде дросселей.
В этом классе также есть разделение на обычные и двойные. Они имеют высокое сопротивление переменному току и очень низкое сопротивление постоянному току, благодаря чему они могут действовать как хороший фильтр, пропускающий постоянный ток и задержку переменного тока.Двойные дроссели более эффективны по сравнению с традиционными при высоких токах и частотах.
Формулы расчета
Пора перейти к основной теме статьи. Начнем с того, что поговорим о том, как измерить индуктивность сердечника катушки. Это простейшая форма расчета. Но и здесь есть свои тонкости. Для простоты возьмем катушку с однослойной обмоткой.
Для нее действителен расчет однослойной катушки индуктивности:
L = D 2 * n 2 / (45D + 100l)
Здесь L — индуктивность, D — диаметр катушки в сантиметрах, n — количество витков, l — длина намотки в сантиметрах.Однослойная катушка предполагает, что толщина обмотки не превышает одного слоя, что означает, что для нее справедливы измерения с плоской катушкой индуктивности. Большинство формул для расчета индуктивностей обычно очень похожи: основные различия в числителе и знаменателе только в коэффициентах переменных. Самым простым здесь является измерение индуктивности провода без сердечника.
Также представляет интерес формула для расчета индуктивности катушки с большим числом витков:
L = 0.08 * Д 2 * п 2 / (3 * Д + 9 * б + 10 * в)
Здесь b — ширина провода, c — высота провода. Такой состав эффективен для измерения многослойного индуктора. На практике он применяется немного реже, чем тот, о котором пойдет речь ниже.
Возможно, наиболее важным было бы измерение индуктивности катушки с сердечником. Существует специальная формула, которая показывает, что эту индуктивность определяет материал, из которого изготовлен сердечник, или, скорее, его магнитная проницаемость. Дизайн выглядит так:
L = m * m 0 * n 2 * S / l
Где m — магнитная проницаемость материала сердечника, m 0 — магнитная постоянная (это 12.56 · 10-7 Гн / м), S — поперечное сечение поля катушки, длительность l-витка.
Вычислить количество витков индуктора очень просто: это количество слоев намотки проводника в центре.
Мы разобрались с формулами, а теперь немного о том, где именно эти формулы и вычисления могут быть полезны.
Практическое использование
Из-за широкого распространения индукторов эти формулы используются очень часто. Как мы уже выяснили, существуют разные типы катушек, каждая из которых соответствует своему применению.В связи с этим становится в некотором роде необходимым разделение их по характеристикам, потому что в каждой отрасли нужны свои определенные индуктивность и добротность.
Катушка индуктивности в электронной промышленности
В основном на производстве и в электротехнике используется измерение индуктивности катушек. Каждый любитель должен уметь рассчитать индуктивность, в противном случае он должен уметь определить, какая катушка из огромного массива подходит для их целей, а какая нет.
Вам интересно?
Большинство современных ученых интересуются магнетизмом и магнитными явлениями. Исследователи изучали как магнитную, так и электрическую стороны объектов, пытаясь найти закономерности и синтезировать сильные магниты с определенными желаемыми свойствами: например, с высокой температурой плавления или сверхпроводимостью. Многие из этих компонентов можно найти во многих отраслях промышленности.
Приведем пример аэрокосмической отрасли: перспективными являются ракеты с ионными двигателями для дальних межзвездных полетов, которые создают тягу за счет выброса ионизированного газа из сопла.Интенсивность удара в таком двигателе зависит от температуры газа и его скорости. Соответственно, чтобы придать газу полную мощность ускорения, нам нужен очень мощный магнит, который ускоряет заряженные частицы, а также имеет очень высокую температуру плавления, чтобы при выходе газов из сопла они не плавились. {- 1/4} a \).{13/4} / 8 = 3,22 \). Такое отношение среднего радиуса к полувысоте заметно отличается от 3,7 или 3, предложенных соответственно Максвеллом и Бруксом, см. Рис. 2а, что свидетельствует о том, что этот метод слишком груб, чтобы выявить истинную оптимальную геометрию катушки.
Рисунок 2Сечения оптимальных катушек. ( a ) Конструкции, предложенные Gauss 3 , Maxwell 4 и Brooks 6 . ( b ) Результаты, полученные в данной работе. Поперечное сечение изменяется от почти круглого до эллиптического и серповидного по мере увеличения \ (\ omega \).2}, \ quad k = \ frac {| {\ mathbf {r}} — {\ mathbf {r}} ‘|} {\ sqrt {4 \ rho \ rho’}} \ end {выровнен} \ end {выровнен } $$
(9)
— взаимная индуктивность коаксиальных линейных токов 5 , пронизывающих поперечное сечение в \ ({\ mathbf {r}} \) и \ ({\ mathbf {r}} ‘\); K ( м ) и E ( м ) — полные эллиптические интегралы. 2} {4} \ right], \ end {align} $$
(13)
действительно для \ (k \ ll 1 \) [Ур.{2}} \ frac {\ xi _1} {\ xi _1 + \ xi _2}, \ end {align} $$
(15)
, которая является обобщением формулы Рэлея 12 для случая \ (b = a \) и является ключевым улучшением по сравнению с (5). Используя эту формулу для L и другую, \ (W = \ pi ab \ bar {\ rho} n_2 \), для ограничения длины, мы смогли легко найти оптимальное значение \ (\ xi _1 \), \ (\ xi _2 \) численно, воспроизводя (10).
Возвращаясь к коэффициенту Q , мы перепишем (1) в терминах наших характерных масштабов \ (L_c \), \ (Q_c \), \ (\ omega _c \):
$$ \ begin {выровнено } Q = \ frac {\ pi} {2} \ frac {\ omega} {\ omega _c} \ frac {L / L_c} {1 + F (\ omega)} Q_c, \ end {align} $$
(16)
, где мы ввели коэффициент увеличения потерь
$$ \ begin {align} F (\ omega) \ Equiv \ frac {R (\ omega)} {R (0)} — 1.

