Как измерить импульсное магнитное поле вне соленоида конечной длины. Какие методы калибровки датчиков магнитного поля используются. Как сравнить экспериментальные результаты с теоретическими расчетами. Какие факторы влияют на точность измерений импульсных магнитных полей.
Введение в измерение импульсных магнитных полей
Измерение импульсных магнитных полей представляет собой важную задачу в различных областях науки и техники. Импульсные магнитные поля широко используются в ускорителях частиц, термоядерных установках, системах магнитно-импульсной обработки материалов и других приложениях. Точное измерение параметров таких полей необходимо для оптимизации работы устройств и проведения научных исследований.
Основные сложности при измерении импульсных магнитных полей связаны с их быстрым изменением во времени и пространстве, а также высокой напряженностью. Традиционные методы на основе эффекта Холла или магниторезистивного эффекта часто оказываются неприменимы из-за ограниченного быстродействия датчиков. Поэтому для регистрации импульсных полей чаще всего используются индукционные датчики — поисковые катушки.
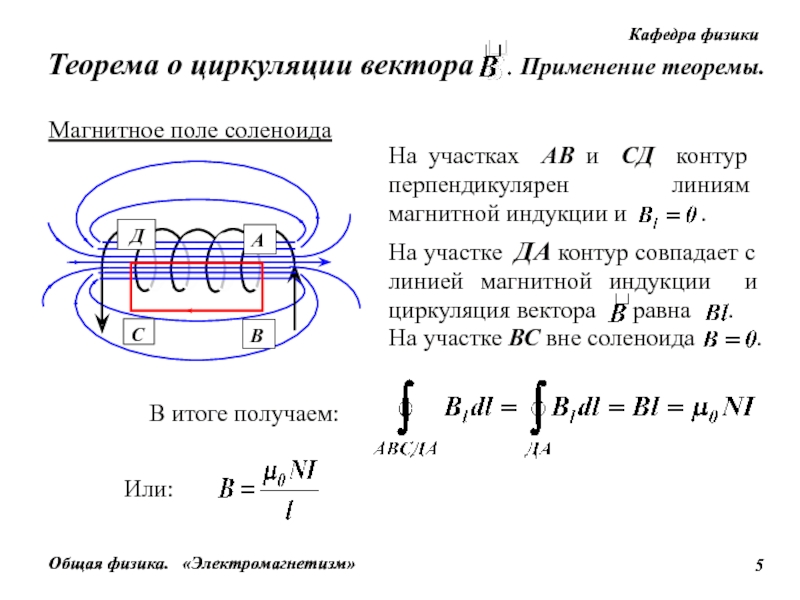
В данной работе исследуется распределение магнитного поля вне соленоида конечной длины при протекании через него импульсного тока. Такая конфигурация часто встречается на практике, например, в импульсных электромагнитах. Измерение поля проводилось с помощью специально разработанного индукционного датчика. Полученные экспериментальные результаты сравнивались с теоретическими расчетами.
Методика измерения импульсного магнитного поля
Для измерения импульсного магнитного поля использовался индукционный датчик — поисковая катушка собственной разработки. Основные характеристики датчика:
- Диаметр катушки: 5 мм
- Число витков: 20
- Сопротивление: 1.2 Ом
- Индуктивность: 0.8 мкГн
Поисковая катушка располагалась на различных расстояниях от оси соленоида и регистрировала ЭДС индукции, возникающую при изменении магнитного потока через витки катушки. Для калибровки датчика использовался оригинальный метод, основанный на измерении азимутальной компоненты магнитного поля прямого провода с током. Такой подход позволил избежать необходимости интегрирования сигнала с катушки.

Сигнал с поисковой катушки подавался на цифровой осциллограф через экранированный кабель. Для подавления электростатических наводок использовался дифференциальный усилитель. Временное разрешение системы регистрации составляло около 10 нс.
Конструкция соленоида и система генерации импульсного тока
Исследуемый соленоид имел следующие параметры:
- Длина: 100 мм
- Внутренний диаметр: 50 мм
- Число витков: 100
- Индуктивность: 25 мкГн
Для создания импульсного тока через соленоид использовался емкостной накопитель энергии на основе конденсаторной батареи емкостью 100 мкФ, заряжаемой до напряжения 5 кВ. Коммутация разряда осуществлялась с помощью управляемого искрового разрядника. Форма импульса тока была близка к синусоидальной полуволне с амплитудой около 10 кА и длительностью 10 мкс.
Экспериментальные результаты измерения магнитного поля
Измерения проводились в различных точках пространства вокруг соленоида. Регистрировались следующие компоненты магнитного поля:
- Аксиальная компонента Bz вдоль оси соленоида
- Радиальная компонента Br перпендикулярно оси
Основные результаты измерений:
- Максимальная индукция поля на оси в центре соленоида составила 2.5 Тл
- На расстоянии 1 см от торца соленоида индукция снижалась до 1.2 Тл
- На расстоянии, равном радиусу соленоида, индукция падала примерно в 5 раз
- Радиальная компонента поля была максимальна вблизи торцов соленоида
Погрешность измерений оценивается на уровне 5-7%. Основные источники погрешностей:
- Неточность позиционирования датчика
- Конечные размеры поисковой катушки
- Влияние электростатических наводок
Теоретический расчет магнитного поля соленоида
Для сравнения с экспериментом был выполнен теоретический расчет магнитного поля соленоида. Использовались два подхода:
- Аналитический расчет на основе закона Био-Савара-Лапласа
- Численное моделирование методом конечных элементов
При аналитическом расчете соленоид аппроксимировался набором круговых витков с током. Индукция поля находилась интегрированием вкладов от отдельных витков:
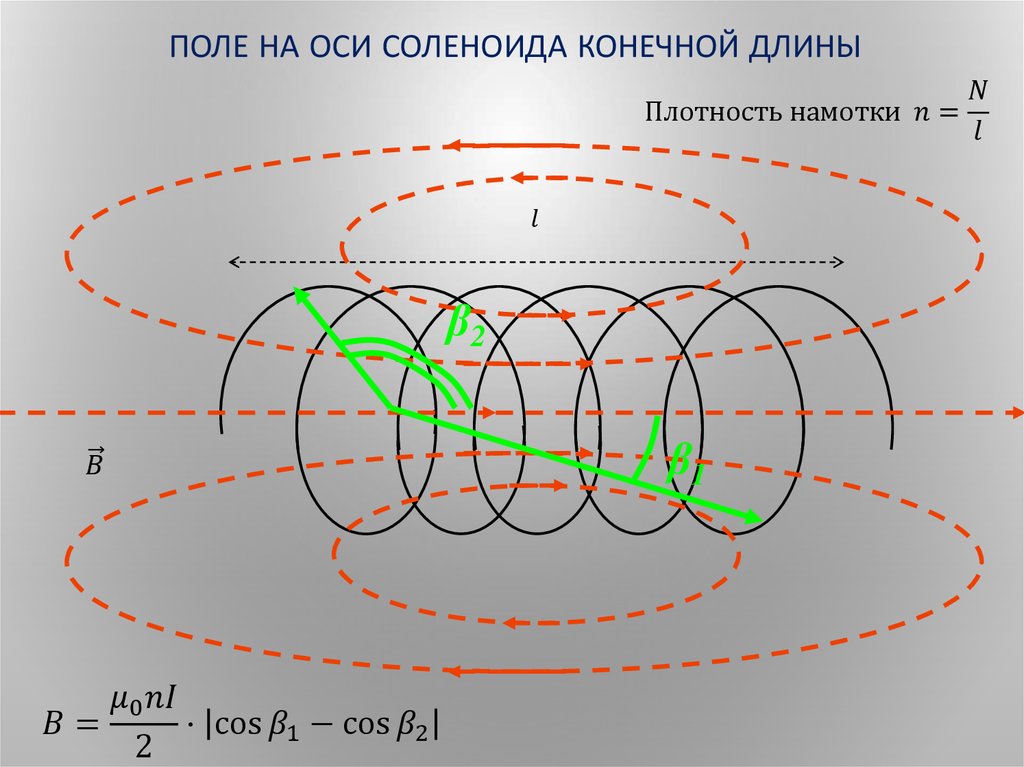
B = (μ0NI/2L) * [cos(α1) — cos(α2)]
где N — число витков, I — ток, L — длина соленоида, α1 и α2 — углы между осью и направлениями на концы соленоида из точки наблюдения.
Численное моделирование проводилось в пакете COMSOL Multiphysics. Решалось уравнение Максвелла для векторного потенциала магнитного поля с учетом реальной геометрии системы.
Сравнение экспериментальных и расчетных результатов
Сравнение измеренных значений магнитного поля с результатами теоретических расчетов показало хорошее согласие. Отклонение экспериментальных данных от расчетных не превышало 10% во всем исследованном диапазоне.
Основные выводы:
- Аналитический расчет дает несколько завышенные значения поля вблизи оси соленоида
- Численное моделирование точнее описывает распределение поля у торцов соленоида
- Экспериментальные данные лежат между результатами аналитического и численного расчетов
Наблюдаемые различия объясняются следующими факторами:
- Неидеальность реальной геометрии соленоида
- Влияние вихревых токов в элементах конструкции
- Неоднородность распределения тока по сечению проводника
Особенности измерения импульсных магнитных полей
При измерении быстро меняющихся магнитных полей необходимо учитывать ряд специфических факторов:

- Конечное время нарастания сигнала в датчике
- Искажение формы импульса из-за паразитных емкостей и индуктивностей
- Наводки от изменяющихся электрических полей
- Скин-эффект в проводящих элементах конструкции
Для минимизации влияния этих эффектов в работе были предприняты следующие меры:
- Использование малоиндуктивных датчиков
- Применение экранированных кабелей и дифференциальных усилителей
- Оптимизация конструкции соленоида для уменьшения паразитных параметров
- Учет влияния скин-эффекта при обработке результатов
Применение результатов исследования
Полученные результаты по измерению и расчету импульсных магнитных полей могут найти применение в следующих областях:
- Разработка импульсных электромагнитов для ускорителей частиц
- Проектирование систем магнитно-импульсной обработки материалов
- Исследование процессов диффузии магнитного поля в проводящие среды
- Калибровка и тестирование датчиков импульсных магнитных полей
Разработанная методика измерений может быть адаптирована для исследования полей сложной конфигурации, создаваемых многовитковыми и многосекционными системами катушек.
Перспективы дальнейших исследований
Для развития данного направления исследований представляют интерес следующие задачи:
- Измерение полей предельно коротких (наносекундных) импульсов
- Исследование полей в проводящих средах с учетом скин-эффекта
- Разработка методов томографии импульсных магнитных полей
- Создание высокочувствительных широкополосных датчиков
- Развитие методов абсолютной калибровки импульсных датчиков
Решение этих задач позволит существенно расширить возможности диагностики импульсных электромагнитных полей в различных научных и технических приложениях.
Заключение
В работе проведено комплексное исследование импульсного магнитного поля, создаваемого соленоидом конечной длины. Разработана и апробирована методика измерений на основе калиброванного индукционного датчика. Получены экспериментальные данные о пространственном распределении поля вне соленоида. Проведено сравнение результатов измерений с аналитическими и численными расчетами.
Основные результаты работы:

- Предложен оригинальный метод калибровки датчиков импульсного магнитного поля
- Разработана методика измерений, позволяющая минимизировать влияние паразитных эффектов
- Получены экспериментальные данные о распределении поля с погрешностью не более 7%
- Показано хорошее согласие измерений с результатами теоретических расчетов
- Выявлены основные факторы, влияющие на точность измерений и расчетов
Полученные результаты могут быть использованы при разработке и оптимизации различных импульсных электромагнитных систем. Предложенная методика измерений применима для исследования полей сложной пространственной конфигурации.
Курс физики (Геворкян Р. Г.)
Курс физики (Геворкян Р. Г.)
ОглавлениеПРЕДИСЛОВИЕЧасть I. МЕХАНИКА § 1. СИСТЕМЫ ОТСЧЕТА; ЛИНЕЙНЫЕ И УГЛОВЫЕ СКОРОСТИ И УСКОРЕНИЯ ДВИЖЕНИЕ ПО КРИВОЛИНЕЙНОЙ ТРАЕКТОРИИ § 2.  ЗАКОНЫ МЕХАНИКИ НЬЮТОНА. СИСТЕМЫ ЕДИНИЦ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА. СИСТЕМЫ ЕДИНИЦСИЛА. ДЕФОРМАЦИЯ. МАССА ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ ИМПУЛЬС. РАБОТА. МОЩНОСТЬ ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН § 3. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ ГРАВИТАЦИОННОЕ ПОЛЕ. ВЕС ТЕЛА ДВИЖЕНИЕ КОСМИЧЕСКИХ ОБЪЕКТОВ § 4. ДВИЖЕНИЕ ТЕЛ С ПЕРЕМЕННОЙ МАССОЙ § 5. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ ПРЕОБРАЗОВАНИЯ КООРДИНАТ, СКОРОСТЕЙ И УСКОРЕНИЙ § 6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА; МОМЕНТ ИНЕРЦИИ ТЕЛ § 7. ЗАКОНЫ МЕХАНИКИ ДЛЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ § 8. СВОБОДНЫЕ ОСИ. БАЛАНСИРОВКА РОТОРОВ. ГИРОСКОПЫ Глава 3. ЗАКОНЫ СОХРАНЕНИЯ В СИСТЕМЕ ВЗАИМОДЕЙСТВУЮЩИХ ТЕЛ § 9. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА (КОЛИЧЕСТВА ДВИЖЕНИЯ) § 10. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА (МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ) § 11. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ § 12. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ НЕКОТОРЫХ СИСТЕМ § 13. СТОЛКНОВЕНИЕ ШАРОВ § 14. О ЦЕНТРЕ МАСС СИСТЕМЫ Глава 4. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ § 15.  ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ; ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ; ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ§ 16. СКОРОСТЬ И УСКОРЕНИЕ КОЛЕБЛЮЩЕГОСЯ ТЕЛА. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ § 17. СИЛА И ЭНЕРГИЯ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ. ПРОСТЕЙШИЕ МЕХАНИЧЕСКИЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ § 18. СОБСТВЕННЫЕ, СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИЙ § 19. ПОНЯТИЕ О НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ § 20. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ КОЛЕБАНИЙ § 21. АВТОКОЛЕБАНИЯ Глава 5. ВОЛНОВЫЕ ПРОЦЕССЫ; ОСНОВЫ АКУСТИКИ § 22. ОБРАЗОВАНИЕ И РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕ § 23. ФОРМУЛА ГАРМОНИЧЕСКОЙ ВОЛНЫ ВОЛНА В УПРУГОЙ СРЕДЕ § 24. ПОТОК ЭНЕРГИИ В ВОЛНОВЫХ ПРОЦЕССАХ § 25. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ВОЛН. РАСПРОСТРАНЕНИЕ ВОЛН В СРЕДАХ С ДИСПЕРСИЕЙ § 26. СТОЯЧИЕ ВОЛНЫ § 27. ЗВУКОВЫЕ КОЛЕБАНИЯ И ВОЛНЫ ЭФФЕКТ ДОПЛЕРА ХАРАКТЕРИСТИКИ ЗВУКОВОГО ОЩУЩЕНИЯ § 28. УЛЬТРАЗВУКИ И ИХ ПРИМЕНЕНИЯ Глава 6. МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ § 29. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА § 30.  ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ. ФОРМУЛА БЕРНУЛЛИ ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ. ФОРМУЛА БЕРНУЛЛИСЖИМАЕМОСТЬ И ВЯЗКОСТЬ В ПОТОКЕ РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ЛАМИНАРНОМ ПОТОКЕ Часть II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА § 1. ТЕПЛОВОЕ ДВИЖЕНИЕ § 2. ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ; ЭНЕРГИЯ СВЯЗИ МОЛЕКУЛ § 3. АГРЕГАТНЫЕ СОСТОЯНИЯ И ФАЗОВЫЕ ПЕРЕХОДЫ. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ И ПРОЦЕССЫ СВОЙСТВА ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ ВИДЫ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ § 4. ВНУТРЕННЯЯ ЭНЕРГИЯ ТЕРМОДИНАМИЧЕСКОЙ СИСТЕМЫ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ § 5. ВНЕШНЯЯ РАБОТА СИСТЕМЫ И ТЕПЛООБМЕН С ОКРУЖАЮЩЕЙ СРЕДОЙ. ТЕПЛОЕМКОСТЬ ТЕЛ § 6. ИЗОПРОЦЕССЫ; АДИАБАТИЧЕСКИЙ ПРОЦЕСС. ЭНТРОПИЯ СИСТЕМЫ. ЗАМКНУТЫЕ (КРУГОВЫЕ) ПРОЦЕССЫ ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ИЗОПРОЦЕССОВ КРУГОВЫЕ ПРОЦЕССЫ § 7. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ. ЗАКОН ВОЗРАСТАНИЯ ЭНТРОПИИ ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ ЭНТРОПИЯ И ВЕРОЯТНОСТЬ Глава 2. ИДЕАЛЬНЫЙ ГАЗ § 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. СРЕДНИЕ СКОРОСТИ МОЛЕКУЛ § 9.  УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА§ 10. ИЗОПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ; ТЕПЛОЕМКОСТИ ГАЗОВ § 11. КРУГОВЫЕ ПРОЦЕССЫ, СОВЕРШАЕМЫЕ ИДЕАЛЬНЫМ ГАЗОМ; ЦИКЛ КАРНО. ЭНТРОПИЯ ИДЕАЛЬНОГО ГАЗА ЦИКЛ КАРНО ПРОЦЕССЫ, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЕ ЭНТРОПИИ ПАРАДОКС ГИББСА § 12. ДИФФУЗИЯ, ТЕПЛОПРОВОДНОСТЬ И ВНУТРЕННЕЕ ТРЕНИЕ В ГАЗАХ; ЧИСЛО СТОЛКНОВЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ Глава 3. РЕАЛЬНЫЕ ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ТЕЛА § 13. ОТСТУПЛЕНИЯ ОТ ЗАКОНОВ ИДЕАЛЬНЫХ ГАЗОВ. НАСЫЩЕННЫЕ ПАРЫ. КРИТИЧЕСКОЕ СОСТОЯНИЕ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ГАЗОВ ПАР ПЕРЕХОДЫ в СИСТЕМЕ ЖИДКОСТЬ — ПАР — ГАЗ § 14. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА ПАРАМЕТРЫ КРИТИЧЕСКОГО СОСТОЯНИЯ ПРИМЕНЕНИЯ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА § 15. ЖИДКОСТИ; ИХ ОСНОВНЫЕ СВОЙСТВА. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ И ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ СВОЙСТВА ЖИДКОСТЕЙ МОЛЕКУЛЯРНЫЕ СИЛЫ В ПОВЕРХНОСТНОМ СЛОЕ § 16. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ § 17. ИСПАРЕНИЕ И КИПЕНИЕ ЖИДКОСТЕЙ; КОНДЕНСАЦИЯ ПАРОВ ИСПАРЕНИЕ И КОНДЕНСАЦИЯ КИПЕНИЕ УДЕЛЬНАЯ ТЕПЛОТА ПАРООБРАЗОВАНИЯ § 18. 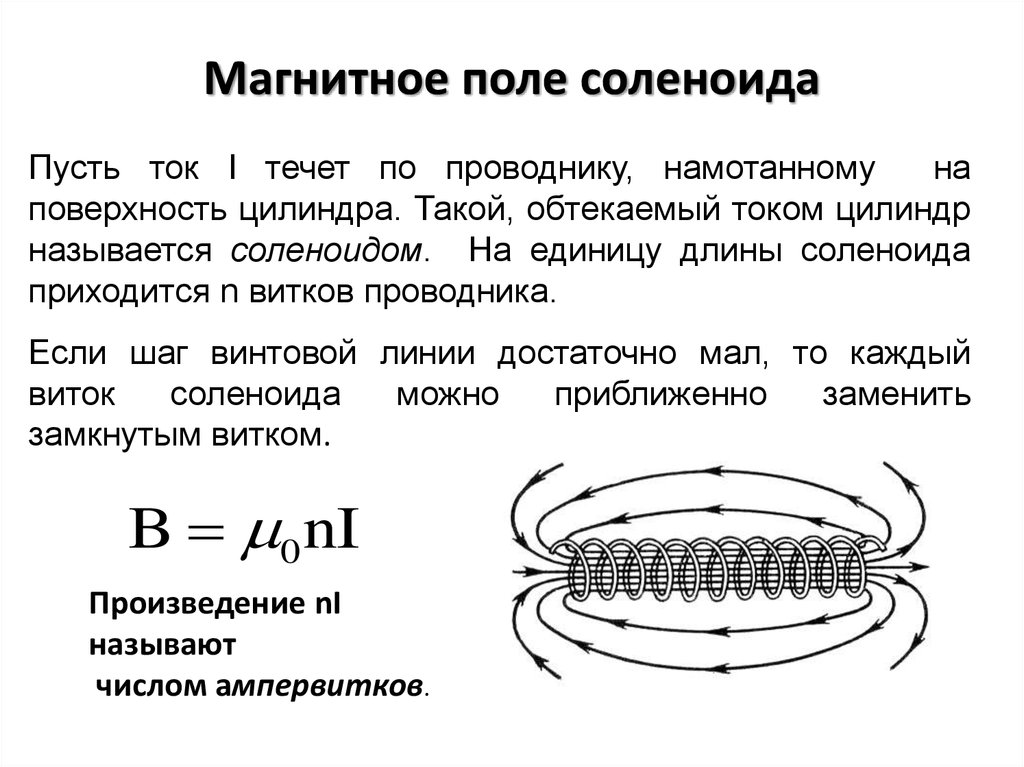 КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА. КРИСТАЛЛИЗАЦИЯ, ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛ КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА. КРИСТАЛЛИЗАЦИЯ, ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛКРИСТАЛЛИЗАЦИЯ ТЕМПЕРАТУРА ПЛАВЛЕНИЯ ТРОЙНАЯ ТОЧКА § 19. ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК. ТЕПЛОВЫЕ И УПРУГИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ ТЕПЛОЕМКОСТЬ КРИСТАЛЛА ТЕПЛОВОЕ РАСШИРЕНИЕ КРИСТАЛЛОВ УПРУГОСТЬ И ПЛАСТИЧНОСТЬ ЖИДКИЕ КРИСТАЛЛЫ Часть III. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ § 1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ПРОВОДНИКИ И ДИЭЛЕКТРИКИ § 2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ; ИНДУКЦИЯ И НАПРЯЖЕННОСТЬ ПОЛЯ. ЗАКОН КУЛОНА § 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ СИСТЕМЫ ЗАРЯДОВ; ТЕОРЕМА ОСТРОГРАДСКОГО—ГАУССА ПРИМЕНЕНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО—ГАУССА ФОРМУЛЫ ДЛЯ НАПРЯЖЕННОСТИ ПОЛЯ § 4. РАБОТА ПЕРЕМЕЩЕНИЯ ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ; РАЗНОСТЬ ПОТЕНЦИАЛОВ. ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ ЗАРЯДОВ § 5. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 6. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ ЭЛЕКТРОСТРИКЦИЯ ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ СЕГНЕТОЭЛЕКТРИКИ ЭЛЕКТРЕТЫ § 7. ЭЛЕКТРОЕМКОСТЬ. ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА.  ПЛОТНОСТЬ ЭНЕРГИИ ПОЛЯ ПЛОТНОСТЬ ЭНЕРГИИ ПОЛЯГлава 2. ЭЛЕКТРИЧЕСКИЙ ТОК § 8. ЭЛЕКТРИЧЕСКИЙ ТОК ПРОВОДИМОСТИ; ПЛОТНОСТЬ ТОКА § 9. ЭЛЕКТРОННАЯ ТЕОРИЯ ПРОВОДИМОСТИ МЕТАЛЛОВ. ЗАКОНЫ ОМА И ДЖОУЛЯ—ЛЕНЦА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ. СВЯЗЬ МЕЖДУ ЭЛЕКТРОПРОВОДНОСТЬЮ И ТЕПЛОПРОВОДНОСТЬЮ § 10. РАБОТА ЭЛЕКТРИЧЕСКОГО ТОКА. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ. СВЕРХПРОВОДИМОСТЬ § 11. ЭЛЕКТРОДВИЖУЩАЯ СИЛА; ЗАКОН ОМА И ПРАВИЛА КИРХГОФА ЗАКОН ОМА ДЛЯ ЗАМКНУТОГО КОНТУРА ПРАВИЛА КИРХГОФА ЭЛЕКТРОСТАТИЧЕСКИЙ ГЕНЕРАТОР ТОКА § 12. РАБОТА ВЫХОДА ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА. КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ ЭМИССИЯ ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ ЗАКОН ВОЛЬТА. ТЕРМОЭЛЕМЕНТЫ ЭФФЕКТ ПЕЛЬТЬЕ § 13. ТЕРМОЭЛЕКТРОННАЯ ЭМИССИЯ. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ. ЭЛЕКТРОННАЯ ЛАМПА § 14. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ. ПОНЯТИЕ О ПЛАЗМЕ ДВИЖЕНИЕ ИОНОВ В ГАЗЕ ВИДЫ РАЗРЯДОВ В ГАЗАХ ПЛАЗМА § 15. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ. ЗАКОНЫ ФАРАДЕЯ § 16. ПОЛУПРОВОДНИКИ И ИХ ПРИМЕНЕНИЯ ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ ЯВЛЕНИЯ НА ГРАНИЦЕ ДВУХ ПОЛУПРОВОДНИКОВ ПРИМЕНЕНИЯ ПОЛУПРОВОДНИКОВ Глава 3. 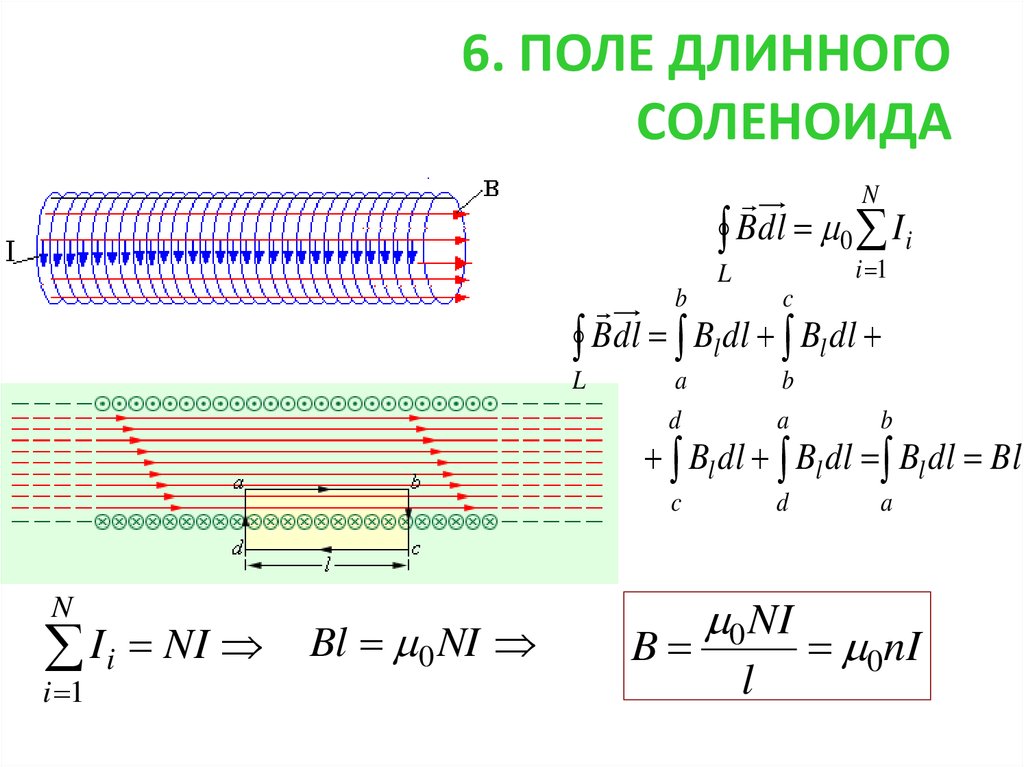 ЭЛЕКТРОМАГНЕТИЗМ ЭЛЕКТРОМАГНЕТИЗМ§ 17. МАГНИТНОЕ ПОЛЕ § 18. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ ВОКРУГ ДВИЖУЩЕГОСЯ ЗАРЯДА И ПРОВОДНИКОВ С ТОКАМИ § 19. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ПРОВОДНИКИ С ТОКОМ; СИЛА ЛОРЕНЦА И ЗАКОН АМПЕРА. ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ § 20. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА КОНТУР С ТОКОМ. ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ МАГНИТНЫЙ МОМЕНТ ЭЛЕКТРОНА ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ ЭФФЕКТ ХОЛЛА § 21. РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ § 22. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ; ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА. ВРАЩАЮЩИИСЯ ВИТОК В МАГНИТНОМ ПОЛЕ РАМКА В МАГНИТНОМ ПОЛЕ ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА § 23. ЯВЛЕНИЯ САМОИНДУКЦИИ И ВЗАИМОИНДУКЦИИ. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ВИХРЕВЫЕ ТОКИ ИНДУКТИВНОСТЬ СОЛЕНОИДА РАСЧЕТ ИНДУКЦИОННЫХ ТОКОВ ВЗАИМНАЯ ИНДУКЦИЯ ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКИ ФУКО § 24. ТОК СМЕЩЕНИЯ И ЕГО МАГНИТНОЕ ПОЛЕ; ТЕОРИЯ МАКСВЕЛЛА § 25. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ. ДИАМАГНЕТИЗМ; ПАРАМАГНИТНЫЕ И ФЕРРОМАГНИТНЫЕ ВЕЩЕСТВА НАМАГНИЧЕННОСТЬ МАГНИТНЫЕ СВОЙСТВА АТОМОВ И МОЛЕКУЛ ДИАМАГНЕТИЗМ И ПАРАМАГНЕТИЗМ ФЕРРОМАГНЕТИКИ ПАРАМАГНИТНЫЙ РЕЗОНАНС § 26.  МАГНИТНОЕ ПОЛЕ В ФЕРРОМАГНИТНЫХ ТЕЛАХ РАЗЛИЧНОЙ ФОРМЫ; МАГНИТОДВИЖУЩАЯ СИЛА И МАГНИТНОЕ СОПРОТИВЛЕНИЕ МАГНИТНОЕ ПОЛЕ В ФЕРРОМАГНИТНЫХ ТЕЛАХ РАЗЛИЧНОЙ ФОРМЫ; МАГНИТОДВИЖУЩАЯ СИЛА И МАГНИТНОЕ СОПРОТИВЛЕНИЕГлава 4. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ § 27. КОЛЕБАТЕЛЬНЫЙ КОНТУР. НЕЗАТУХАЮЩИЕ И ЗАТУХАЮЩИЕ КОЛЕБАНИЯ § 28. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ; ЭЛЕКТРИЧЕСКИЙ РЕЗОНАНС § 29. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ УРАВНЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ ИЗЛУЧЕНИЕ ВОЛНЫ ЭЛЕКТРОНОМ ЧЕРЕНКОВСКОЕ ИЗЛУЧЕНИЕ Часть IV. ОПТИКА И ФИЗИКА АТОМА § 1. ВОЛНОВАЯ (ЭЛЕКТРОМАГНИТНАЯ) И КОРПУСКУЛЯРНАЯ (ФОТОННАЯ) ТЕОРИИ СВЕТА СПЕКТРАЛЬНЫЙ СОСТАВ ИЗЛУЧЕНИЯ ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ИДЕАЛИЗАЦИЯ СВЕТОВОЙ ВОЛНЫ § 2. ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ВЕЛИЧИНЫ. ДАВЛЕНИЕ СВЕТА § 3. РАСПРОСТРАНЕНИЕ, ОТРАЖЕНИЕ, ПРЕЛОМЛЕНИЕ И ПОГЛОЩЕНИЕ СВЕТА. ДИСПЕРСИЯ. РАССЕЯНИЕ СВЕТА СБЕТ НА ГРАНИЦЕ ДВУХ СРЕД СВЕТ И ЦВЕТ ДИСПЕРСИЯ СВЕТА РАССЕЯНИЕ СВЕТА § 4. ИНТЕРФЕРЕНЦИЯ СВЕТА; КОГЕРЕНТНОСТЬ СВЕТОВЫХ ЛУЧЕЙ. ИНТЕРФЕРОМЕТРЫ § 5. ДИФРАКЦИЯ СВЕТА; ДИФРАКЦИОННЫЙ СПЕКТР ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ ПРЯМОЛИНЕЙНОЙ ТОНКОЙ ЩЕЛИ ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ НЕСКОЛЬКИХ ЩЕЛЕЙ ДИФРАКЦИОННАЯ РЕШЕТКА § 6.  РАСПРОСТРАНЕНИЕ СВЕТА В АНИЗОТРОПНОЙ СРЕДЕ, ПОЛУЧЕНИЕ И ПРИМЕНЕНИЕ ПОЛЯРИЗОВАННОГО СВЕТА РАСПРОСТРАНЕНИЕ СВЕТА В АНИЗОТРОПНОЙ СРЕДЕ, ПОЛУЧЕНИЕ И ПРИМЕНЕНИЕ ПОЛЯРИЗОВАННОГО СВЕТАПОЛЯРИЗОВАННЫЙ СВЕТ СПОСОБЫ ПОЛУЧЕНИЯ ПОЛЯРИЗОВАННОГО СВЕТА ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННОГО СВЕТА ОПТИЧЕСКАЯ АНИЗОТРОПИЯ § 7. ЛИНЗЫ; ИХ ОПТИЧЕСКАЯ СИЛА. АБЕРРАЦИИ. ДИАФРАГМЫ В ОПТИЧЕСКИХ ПРИБОРАХ ТОЛСТЫЕ ЛИНЗЫ. АБЕРРАЦИИ § 8. ПОНЯТИЕ О ГОЛОГРАФИИ Глава 2. ФИЗИКА АТОМОВ И МОЛЕКУЛ. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ § 9. СТРОЕНИЕ АТОМА. ОПЫТЫ РЕЗЕРФОРДА, ФРАНКА И ГЕРЦА. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ АТОМА ВОДОРОДА ОПЫТ ФРАНКА И ГЕРЦА СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ ТЕОРИЯ АТОМА ВОДОРОДА § 10. КОРПУСКУЛЯРНО-ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ. ФОРМУЛА ДЕ БРОЙЛЯ. ДИФРАКЦИЯ ЭЛЕКТРОНОВ ЭФФЕКТ КОМПТОНА ФОТОН И ЭЛЕКТРОМАГНИТНАЯ ВОЛНА ФОРМУЛА ДЕ БРОЙЛЯ ДИФРАКЦИЯ ЭЛЕКТРОНОВ § 11. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ТЕОРИИ. УРАВНЕНИЕ ШРЕДИНГЕРА. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА УРАВНЕНИЕ ШРЕДИНГЕРА РЕШЕНИЯ УРАВНЕНИЯ ШРЕДИНГЕРА СВОБОДНЫЙ ЭЛЕКТРОН ПОТЕНЦИАЛЬНЫЙ БАРЬЕР ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ АТОМ ВОДОРОДА.  КВАНТОВЫЕ ЧИСЛА КВАНТОВЫЕ ЧИСЛАСООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ § 12. ЧАСТИЦЫ И ФИЗИЧЕСКИЕ СИСТЕМЫ. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ЧАСТИЦ ПО СОСТОЯНИЯМ. ПОНЯТИЕ ТЕМПЕРАТУРЫ РОЛЬ ТЕПЛОВОГО ДВИЖЕНИЯ ЧАСТИЦ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ПО СОСТОЯНИЯМ ТЕМПЕРАТУРА ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИСТЕМЫ РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ § 13. ВЗАИМОДЕЙСТВИЕ АТОМОВ И МОЛЕКУЛ. ЭНЕРГИЯ СВЯЗИ АТОМОВ ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ ИОННАЯ СВЯЗЬ РОЛЬ ЭЛЕКТРОННОГО ГАЗА В МЕТАЛЛАХ Глава 3. ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ ЭНЕРГИИ АТОМАМИ И МОЛЕКУЛАМИ § 14. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ ИЗЛУЧЕНИЯ; СПОСОБЫ ВОЗБУЖДЕНИЯ СТРУКТУРА ЭЛЕКТРОННОЙ ОБОЛОЧКИ СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ СПЕКТРЫ ИЗЛУЧЕНИЯ МОЛЕКУЛ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА § 15. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ФОРМУЛА ПЛАНКА ЗАКОНЫ ИЗЛУЧЕНИЯ ЧЕРНОГО ТЕЛА ПРИМЕНЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ § 16. РЕНТГЕНОВСКИЕ ЛУЧИ. ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР ЭЛЕМЕНТОВ ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР ДИФРАКЦИЯ И ИНТЕРФЕРЕНЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ ДОЗИМЕТРИЯ § 17. 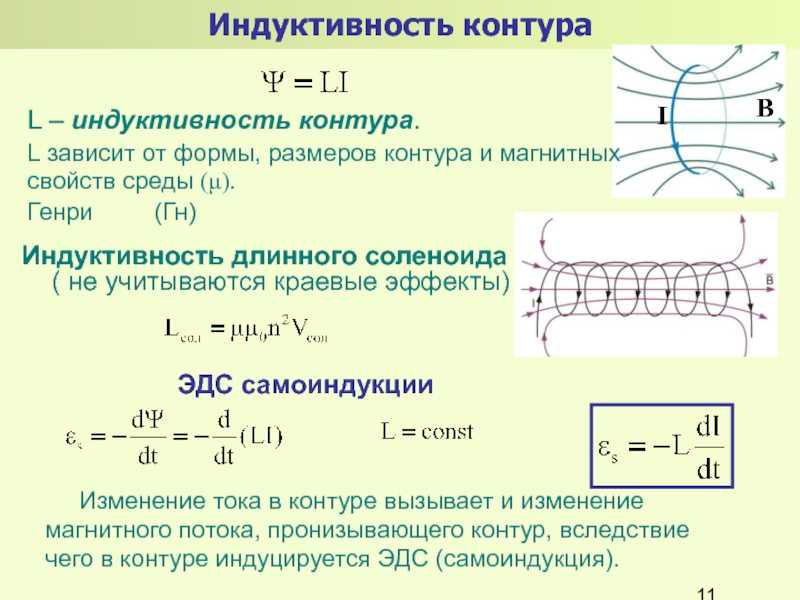 ЛЮМИНЕСЦЕНТНОЕ ИЗЛУЧЕНИЕ ЛЮМИНЕСЦЕНТНОЕ ИЗЛУЧЕНИЕПРИРОДА ЛЮМИНЕСЦЕНЦИИ ХАРАКТЕРИСТИКИ ЛЮМИНЕСЦИРУЮЩИХ ВЕЩЕСТВ ГАШЕНИЕ ЛЮМИНЕСЦЕНЦИИ ПРИМЕНЕНИЯ ЛЮМИНЕСЦЕНЦИИ § 18. ИНДУЦИРОВАННОЕ ИЗЛУЧЕНИЕ. ЛАЗЕРЫ ЛАЗЕРЫ ПРЕИМУЩЕСТВА ЛАЗЕРОВ ПРИМЕНЕНИЕ ЛАЗЕРОВ Глава 4. АТОМНЫЕ ЯДРА И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ § 19. ОСНОВНЫЕ СВОЙСТВА АТОМНЫХ ЯДЕР РАДИОАКТИВНОСТЬ ВНУТРИЯДЕРНЫЕ СИЛЫ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕР МЕХАНИЧЕСКИЙ МОМЕНТ ЯДРА МАГНИТНЫЕ МОМЕНТЫ ЯДЕР ЭЛЕКТРИЧЕСКИЕ МОМЕНТЫ ЯДЕР СПЕКТР ВОЗБУЖДЕННЫХ СОСТОЯНИЙ § 20. МОДЕЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О СТРУКТУРЕ ЯДЕР КАПЕЛЬНАЯ МОДЕЛЬ ЯДРА ОБОЛОЧЕЧНАЯ МОДЕЛЬ ОБОБЩЕННАЯ МОДЕЛЬ ОПТИЧЕСКАЯ МОДЕЛЬ УСЛОВИЕ СТАБИЛЬНОСТИ § 21. РАДИОАКТИВНЫЕ ЯДРА И ИХ ИЗЛУЧЕНИЯ СЕМЕЙСТВА РАДИОАКТИВНЫХ ЭЛЕМЕНТОВ ВЗАИМОДЕЙСТВИЯ ЯДЕРНЫХ ИЗЛУЧЕНИЙ С ВЕЩЕСТВОМ БЕТА-РАСПАД ЯДЕР ЭНЕРГИЯ СВЯЗИ ЯДЕР ИЗОМЕРЫ § 22. ЯДЕРНЫЕ РЕАКЦИИ ДЕЛЕНИЯ И СИНТЕЗА. ТЕРМОЯДЕРНЫЕ РЕАКЦИИ БОМБАРДИРОВКА ЯДЕР ЧАСТИЦАМИ ЭФФЕКТИВНЫЕ СЕЧЕНИЯ РЕАКЦИЙ ЯДЕРНЫЕ РЕАКТОРЫ ЯДЕРНЫЙ СИНТЕЗ § 23.  ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫРАСПАДЫ ЧАСТИЦ ВИДЫ ВЗАИМОДЕЙСТВИЯ ЗАКЛЮЧЕНИЕ § 1. ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ. СВЯЗЬ МЕЖДУ СПОСОБАМИ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН И ФОРМУЛИРОВКАМИ ЗАКОНОВ ФИЗИКИ § 2. О ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА § 3. ЗАКОНЫ СОХРАНЕНИЯ, ПРЕВРАЩЕНИЯ И ПЕРЕРАСПРЕДЕЛЕНИЯ ЭНЕРГИИ В ФИЗИЧЕСКИХ СИСТЕМАХ § 4. О ВАРИАЦИОННЫХ ПРИНЦИПАХ ФИЗИКИ § 5. СТАТИСТИЧЕСКИЕ ЗАКОНЫ И ФЛУКТУАЦИИ § 6. О ДУАЛИЗМЕ В ФИЗИКЕ |
|
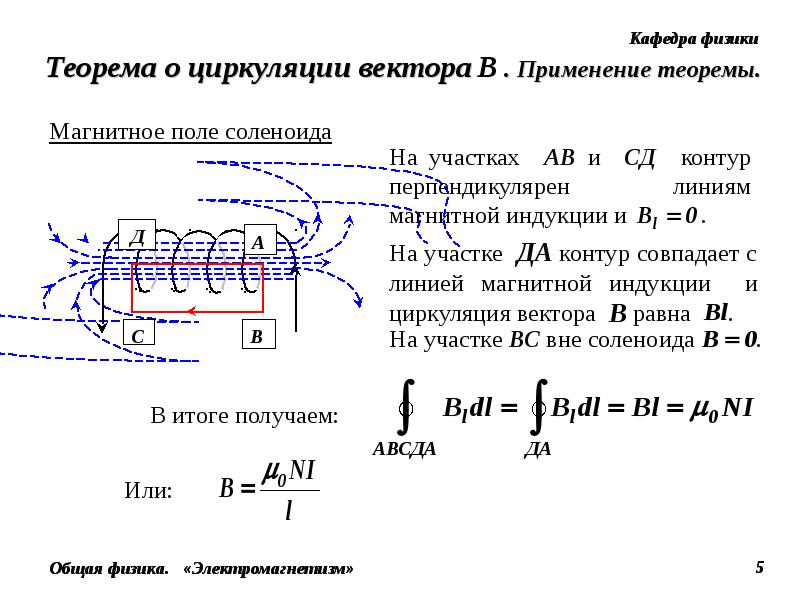
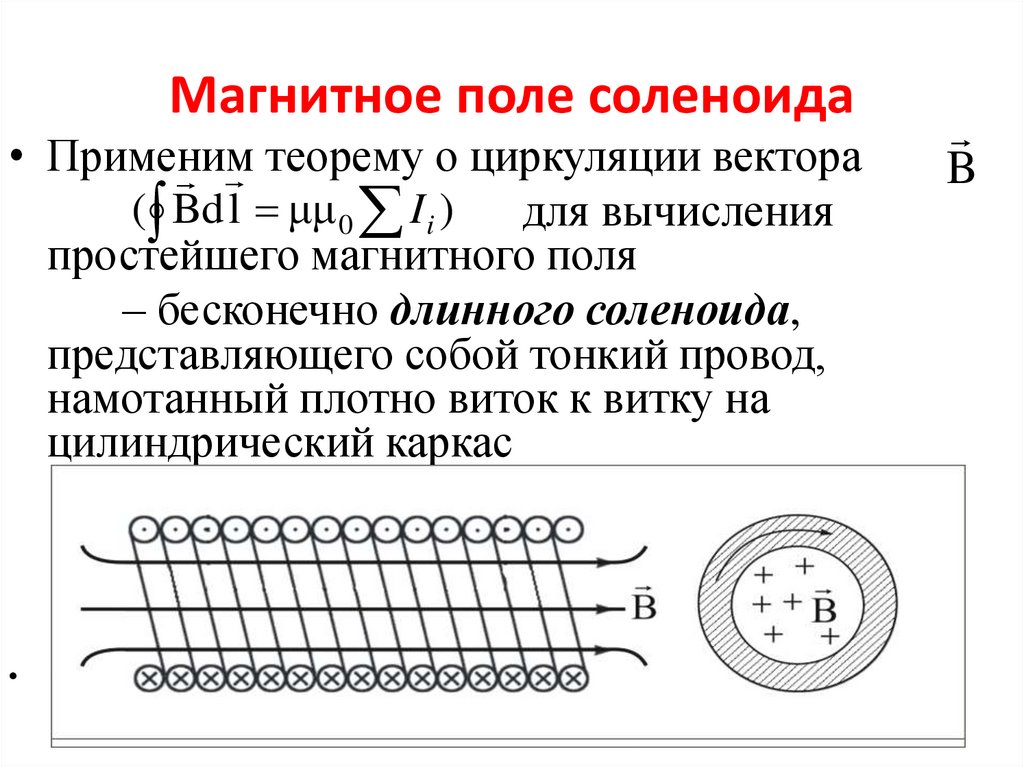
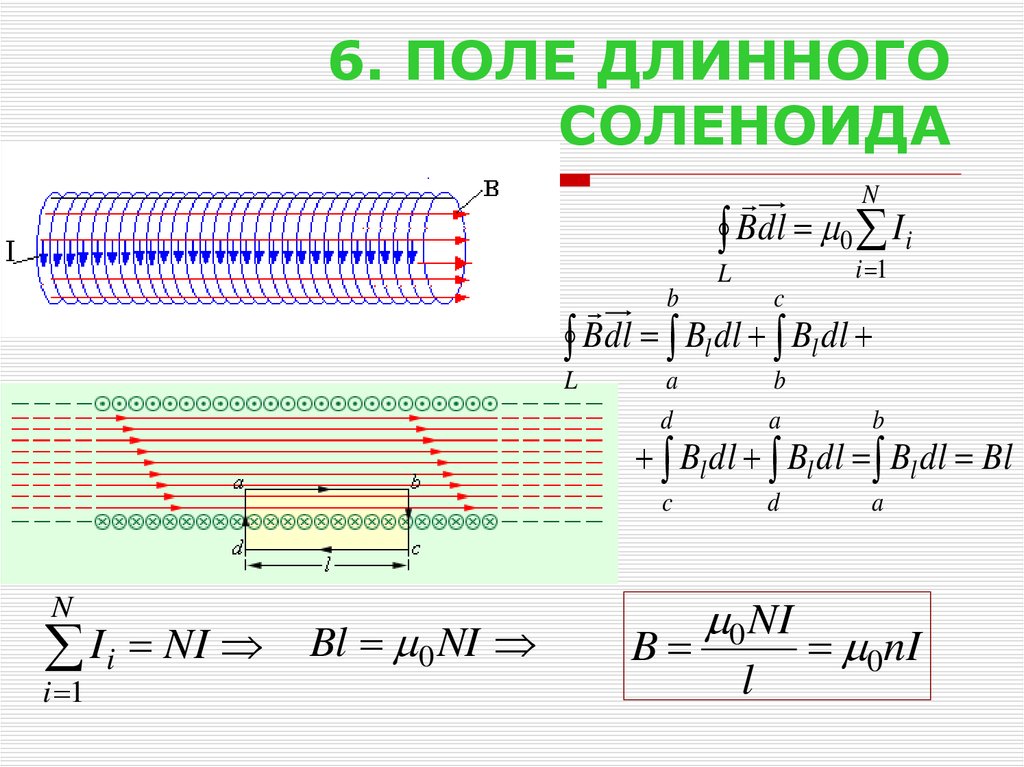
⇐ Предыдущая28293031323334353637Следующая ⇒ Соленоид характеризуется числом витков , длиной или числом витков на единицу длины . Соленоид можно считать бесконечным, если его длина много больше его диаметра. В этом случае магнитное поле практически все находится внутри соленоида и направлено вдоль его оси. . Интеграл по замкнутому контуру можно разбить на четыре интеграла по отдельным частям:
. Так как, интегралы 2,3 и 4 равны нулю, то . Отсюда магнитная индукция внутри бесконечно длинного соленоида: , где – ампер – витки на единицу длины соленоида, – магнитная постоянная. При наличии магнитного сердечника: , где – магнитная проницаемость магнетика.
На практике используются соленоиды конечной длины, для которых условие не выполняется. Расчеты показывают, что в этом случае индукция магнитного поля в соленоиде: , где и – углы, под которыми из точки наблюдения виды радиусы ближнего и дальнего концов соленоида (рис.
, . Максимальное значение индукции наблюдается при ; ; Из приведенных уравнений следует, что В монотонно убывает от центра соленоида к краям. Поток вектора через сечение соленоида равен: = Коэффициент называется индуктивностью бесконечного соленоида и измеряется в генри (Гн). Индуктивность соленоида конечной длины и радиуса определятся с учетом коэффициентов размагничивания .
Соленоиды с железным сердечником имеют большую индуктивность и находят применение в цепях переменного тока.
Распределение магнитного поля в данной работе исследуется с помощью подвижной измерительной катушки, связанной с баллистическим гальванометром (рис. 13) При замыкании кнопки магнитный поток нарастает от 0 до . Согласно закону электромагнитной индукции в цепи измерительной катушки возникает электродвижущая сила и обусловленный ею индукционный ток: , где – суммарное сопротивление измерительной цепи. За время нарастания магнитного потока от 0 до по цепи измерительной катушки пройдет заряд: , где – магнитный поток через один виток, – число витков в измерительной катушке. Отсюда искомая величина магнитной индукции: . Знак «–», в данном случае, означает, что «зайчик» гальванометра отклонится в сторону, противоположную, принятой за положительное отклонение. Можно считать: , где — емкость баллистического гальванометра и = , где обозначим: (2) Размыкание ключа приводит к изменению магнитного потока до нуля. В этом случае гальванометр дает отброс по величине близкой к , но противоположного знака. Таким образом, определяя значения отклонений даваемых баллистическим гальванометром при замыкании и размыкании цепи соленоида, можно определить значение магнитной индукции на оси соленоида. ⇐ Предыдущая28293031323334353637Следующая ⇒
|
Собственная индуктивность
Собственная индуктивностьСледующий: Взаимная индуктивность Вверх: Магнитная индукция Предыдущий: Индуктивность Рассмотрим длинный соленоид длины и радиуса , число витков на единицу длины, и несет ток.
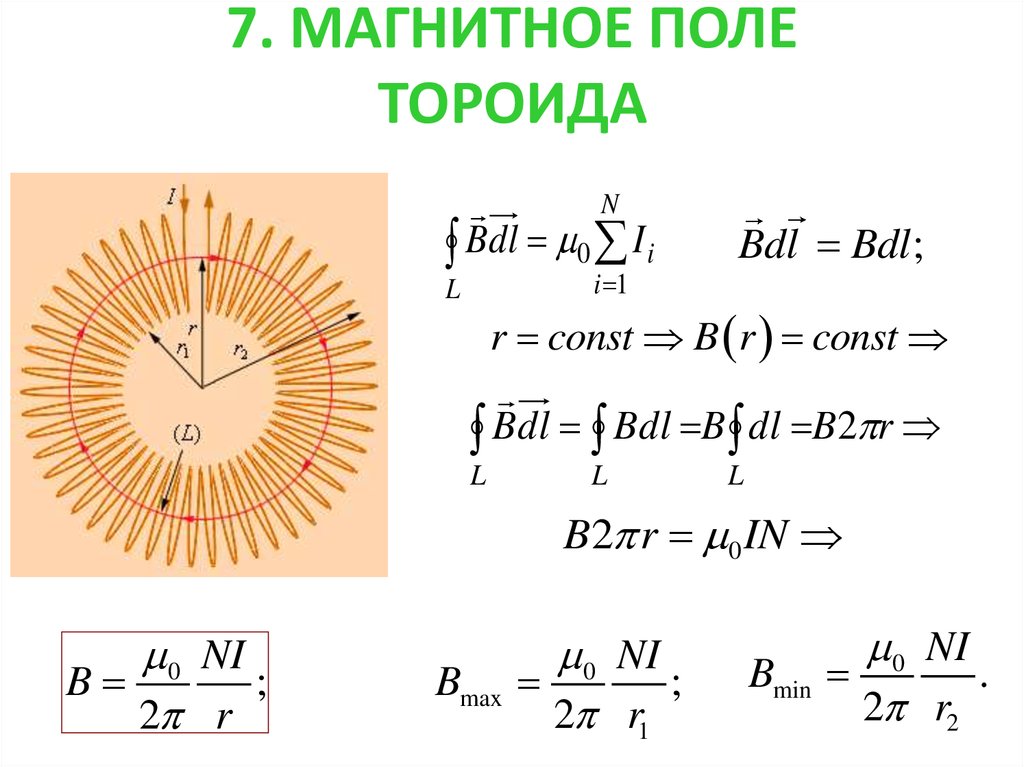 Продольный ( т.е. , направленный вдоль
оси соленоида) магнитное поле внутри соленоида приблизительно однородно,
и дается
Продольный ( т.е. , направленный вдоль
оси соленоида) магнитное поле внутри соленоида приблизительно однородно,
и дается
| (907) |
Этот результат легко получить, интегрируя закон Ампера по прямоугольному петля, длинные стороны которой идут параллельно оси соленоида, одна внутри соленоида, а другой снаружи, короткие стороны которого проходят перпендикулярно ось. Магнитный поток через каждый виток петли равен . Общий поток через провод соленоида, который имеет витки,
| (908) |
Таким образом, собственная индуктивность соленоида равна
| (909) |
Обратите внимание, что самоиндукция зависит только от геометрических величин, таких как число витков на единицу длины соленоида и площади поперечного сечения витков.

Предположим, что ток, протекающий через соленоид, изменяется. Мы должны предположим, что изменение происходит достаточно медленно, чтобы можно было пренебречь смещением эффекты тока и запаздывания в наших расчетах. Это означает, что типичный временной масштаб изменения должен быть намного больше, чем время прохождения световым лучом схема. Если это так, то приведенные выше формулы остаются в силе.
Изменение тока подразумевает изменение магнитного потока, связывающего соленоид
провод, так как
. По Фарадею
Закон, это изменение
генерирует э.д.с. в проводе. По закону Ленца Э.Д.С. это так
а против изменения тока — т.е. , это противо-Э.Д.С. Мы можем написать
| (910) |
где – генерируемая Э.Д.С.
 Давайте
соедините концы соленоида с клеммами батареи
ЭДС . Что сейчас произойдет? Эквивалентная схема показана на рис. 51.
Индуктивность и сопротивление соленоида представлены идеальным
катушка индуктивности , и идеальный резистор , соединенные последовательно. Падение напряжения
между катушкой индуктивности и резистором равна э.д.с. батареи,
. Падение напряжения на резисторе просто , тогда как
падение напряжения на катушке индуктивности ( т. е. , противоэдс) равно
. Здесь — ток, протекающий через соленоид.
Следует, что
Давайте
соедините концы соленоида с клеммами батареи
ЭДС . Что сейчас произойдет? Эквивалентная схема показана на рис. 51.
Индуктивность и сопротивление соленоида представлены идеальным
катушка индуктивности , и идеальный резистор , соединенные последовательно. Падение напряжения
между катушкой индуктивности и резистором равна э.д.с. батареи,
. Падение напряжения на резисторе просто , тогда как
падение напряжения на катушке индуктивности ( т. е. , противоэдс) равно
. Здесь — ток, протекающий через соленоид.
Следует, что
| (911) |
Это дифференциальное уравнение для тока. Мы можем переставить его на давать
| (912) |
Общее решение
| (913) |
Константа фиксируется граничными условиями.
 Предположим, что
аккумулятор подключен во время , если . Отсюда следует, что
что
Предположим, что
аккумулятор подключен во время , если . Отсюда следует, что
что
| (914) |
Эта кривая представлена на рис. 52. Видно, что после подключения батареи ток нарастает и достигает стационарного значения (которое исходит из уравнения Ома). закон), на характерном временном масштабе
| (915) |
Эта временная шкала иногда называется постоянной времени схемы или, несколько невообразимо, L за время R цепи.
Теперь мы можем оценить значение самоиндукции. Задняя э.д.с.
генерируемый в катушке индуктивности, поскольку ток пытается измениться, эффективно предотвращает
ток от роста (или падения) намного быстрее, чем время.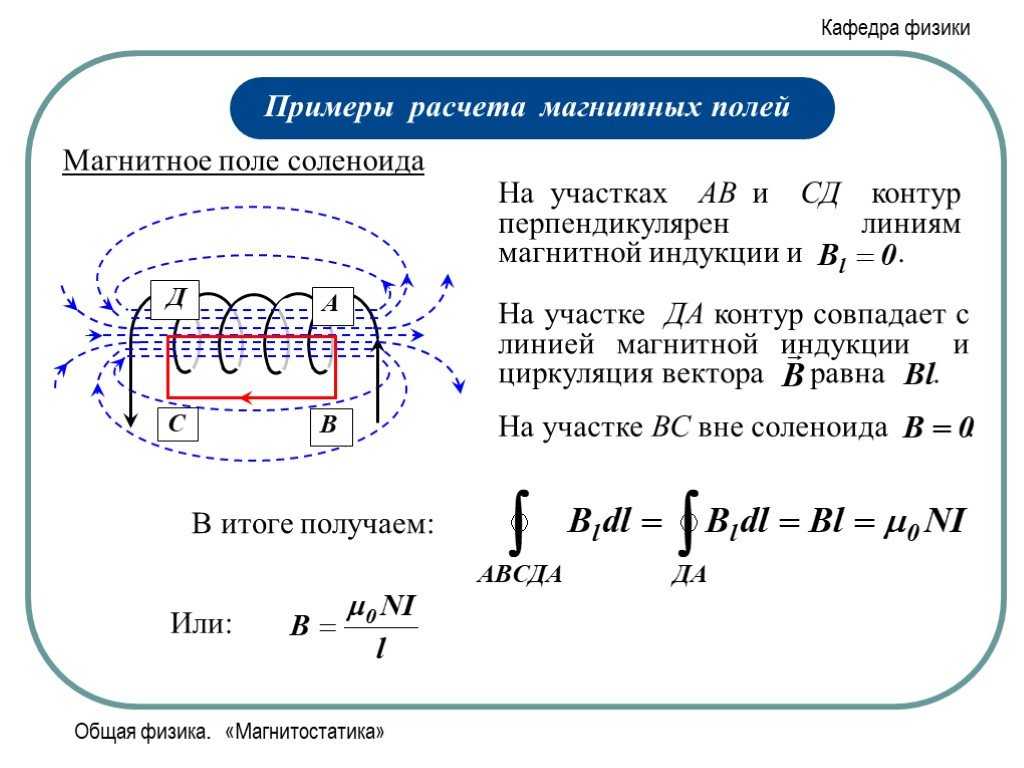 Этот эффект
иногда выгодно, но часто это большая неприятность.
Все элементы схемы обладают некоторой собственной индуктивностью, а также некоторым сопротивлением и, следовательно, имеют конечное время. Это означает, что когда мы включаем цепь, ток
мгновенно не достигает стационарного значения. Вместо этого
подъем распределяется по времени L/R цепи. Это хорошая вещь.
Если бы ток возрастал мгновенно, то чрезвычайно большие электрические
поля будут генерироваться внезапным скачком индуцированного магнитного поля, ведущим,
неизбежно к пробою и возникновению электрической дуги. Так что, если бы не было такого
как самоиндукция, то каждый раз, когда вы включали или выключали электрическую цепь
будет синяя вспышка из-за искрения между проводниками. Самоиндукция
тоже может быть плохо. Предположим, что у нас есть навороченный источник питания, и мы хотим
использовать его для отправки электрического сигнала по проводу (или линии передачи).
Конечно, провод или линия передачи будут обладать как сопротивлением, так и индуктивностью.
Этот эффект
иногда выгодно, но часто это большая неприятность.
Все элементы схемы обладают некоторой собственной индуктивностью, а также некоторым сопротивлением и, следовательно, имеют конечное время. Это означает, что когда мы включаем цепь, ток
мгновенно не достигает стационарного значения. Вместо этого
подъем распределяется по времени L/R цепи. Это хорошая вещь.
Если бы ток возрастал мгновенно, то чрезвычайно большие электрические
поля будут генерироваться внезапным скачком индуцированного магнитного поля, ведущим,
неизбежно к пробою и возникновению электрической дуги. Так что, если бы не было такого
как самоиндукция, то каждый раз, когда вы включали или выключали электрическую цепь
будет синяя вспышка из-за искрения между проводниками. Самоиндукция
тоже может быть плохо. Предположим, что у нас есть навороченный источник питания, и мы хотим
использовать его для отправки электрического сигнала по проводу (или линии передачи).
Конечно, провод или линия передачи будут обладать как сопротивлением, так и индуктивностью. и поэтому будет иметь некоторое характерное время. Предположим, что мы
попробуйте послать прямоугольный сигнал по проводу. Так как ток в проводе
не может расти или опускаться быстрее, чем время, передний и задний фронты
сигнал со временем сглаживается. Типичная разница между
сигнал, подаваемый в провод (верхняя дорожка), и тот, который выходит из
другой конец (нижняя дорожка) показан на рис. 53. Очевидно, что мало
точка с причудливым источником питания, если вы также не обладаете низкой индуктивностью
провода или линии передачи, так что сигнал от источника питания может быть
передается на какое-либо нагрузочное устройство без серьезных искажений.
и поэтому будет иметь некоторое характерное время. Предположим, что мы
попробуйте послать прямоугольный сигнал по проводу. Так как ток в проводе
не может расти или опускаться быстрее, чем время, передний и задний фронты
сигнал со временем сглаживается. Типичная разница между
сигнал, подаваемый в провод (верхняя дорожка), и тот, который выходит из
другой конец (нижняя дорожка) показан на рис. 53. Очевидно, что мало
точка с причудливым источником питания, если вы также не обладаете низкой индуктивностью
провода или линии передачи, так что сигнал от источника питания может быть
передается на какое-либо нагрузочное устройство без серьезных искажений.
Следующий: Взаимная индуктивность Вверх: Магнитная индукция Предыдущий: Индуктивность Ричард Фицпатрик 2006-02-02
Экспериментальные результаты и математическая проверка
Журнал электромагнитного анализа и приложений
Том 5 № 10 (2013 г. ), идентификатор статьи: 38528, 8 страниц DOI: 10.4236/jemaa.2013.510059
), идентификатор статьи: 38528, 8 страниц DOI: 10.4236/jemaa.2013.510059
Pulsed Magnetic Field Measurement Outside Finite Length Solenoid: Experimental Results & Mathematical Verification
Shibaji Basu 1 , Siddhartha Shankar Pany 2 , Partha Bannerjee 3 , Sabyasachi Mitra 4
1 Accelerator & Pulse Power Division, Центр атомных исследований Бхабха, Вишакапатнам, Индия; 2 Отдел обслуживания электроники и приборостроения, Центр атомных исследований Бхабха, Мумбаи, Индия; 3 Отдел энергетики и электромагнетизма, Центр атомных исследований Бхабха, Вишакапатнам, Индия; 4 Accelerator & Pulse Power Division, Центр атомных исследований Бхабха, Мумбаи, Индия.
Электронная почта: [email protected]
Copyright © 2013 Shibaji Basu et al. Эта статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Поступила в редакцию 24.03.-го -го, 2013 г.; пересмотрено 27 апреля th , 2013; принята 28 мая th , 2013
Ключевые слова: Импульсное магнитное поле; Закон Био-Савара; Поисковая катушка
АННОТАЦИЯ
В статье рассматривается картирование магнитного поля вне соленоидного электромагнита конечной длины с помощью разработанного и откалиброванного индуктивного датчика или поисковой катушки собственной разработки. Поисковая катушка калибруется по уникальной методике, основанной на азимутальной составляющей магнитного поля, создаваемой прямым проводом. Этот уникальный метод калибровки помогает нам избежать дополнительных схем для интеграции сигнала, полученного от поисковой катушки. Методика оказывается полезной при исследованиях диффузии, имплозии, где частота сигнала изменяется в зависимости от размеров и материала экспериментальной заготовки (полая металлическая трубка). Были предприняты корректирующие меры, чтобы избежать электростатического емкостного навода (который в конечном итоге усугубляется интеграцией), сохраняя простоту и точность измерений.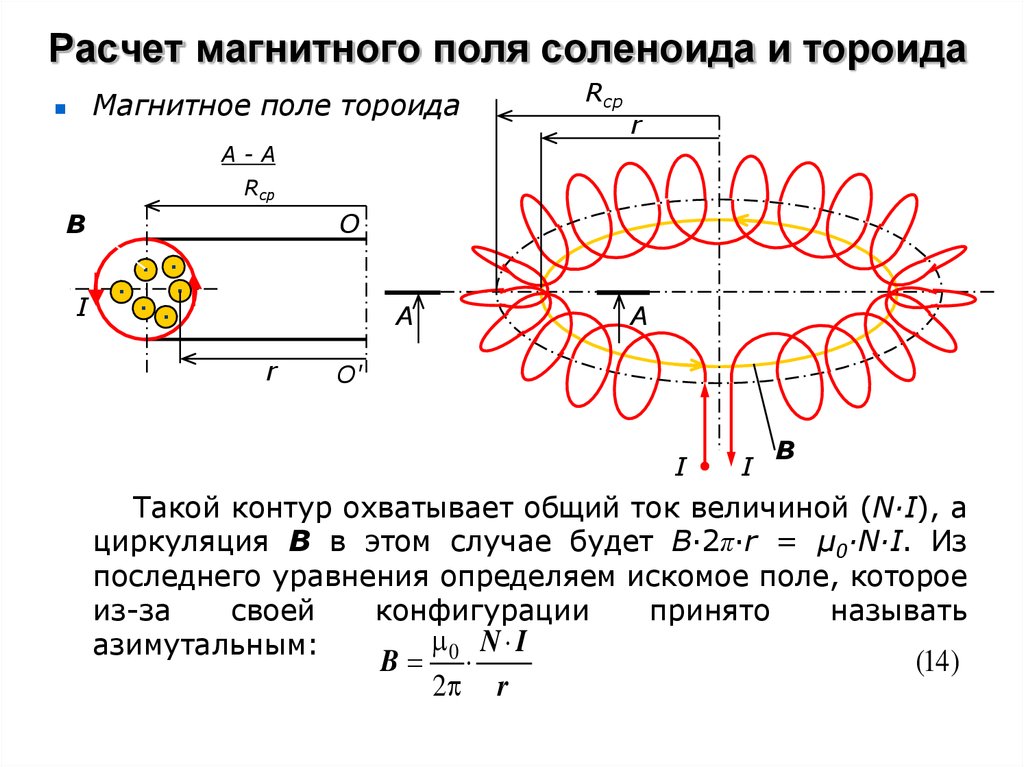 Экспериментально измеренные значения поля также сравнивались с результатами электромагнитного поля, полученными в результате математических расчетов и моделирования на основе конечных элементов. Были продемонстрированы два различных математических подхода к расчету поля на основе закона Био-Савара. Оба метода учитывали точную геометрию соленоида, включая межвитковые зазоры. Методы используют соответствующую комбинацию математического выражения в закрытой форме и методов численного интегрирования и способны определять все векторные компоненты магнитного поля в любом месте вокруг соленоида конечной длины. Математические расчеты являются не менее важным вкладом в статью, особенно потому, что точное определение магнитных полей вне соленоидов конечной длины не обсуждалось в достаточной степени в уже существующей литературе. Математические расчеты, моделирование методом конечных элементов и экспериментальная проверка вместе обеспечивают целостное решение проблем определения магнитного поля в приложениях импульсной мощности, которые не обсуждались в доступной литературе или книгах в конкретных деталях.
Экспериментально измеренные значения поля также сравнивались с результатами электромагнитного поля, полученными в результате математических расчетов и моделирования на основе конечных элементов. Были продемонстрированы два различных математических подхода к расчету поля на основе закона Био-Савара. Оба метода учитывали точную геометрию соленоида, включая межвитковые зазоры. Методы используют соответствующую комбинацию математического выражения в закрытой форме и методов численного интегрирования и способны определять все векторные компоненты магнитного поля в любом месте вокруг соленоида конечной длины. Математические расчеты являются не менее важным вкладом в статью, особенно потому, что точное определение магнитных полей вне соленоидов конечной длины не обсуждалось в достаточной степени в уже существующей литературе. Математические расчеты, моделирование методом конечных элементов и экспериментальная проверка вместе обеспечивают целостное решение проблем определения магнитного поля в приложениях импульсной мощности, которые не обсуждались в доступной литературе или книгах в конкретных деталях.
1. Введение
Исследования магнитного поля соленоида конечной длины вне соленоида, несмотря на его важность во многих областях исследований и разработок, очень мало изучены. В литературе [1-4] основное внимание уделяется определению магнитного поля вне бесконечно длинного соленоида и в некоторых частных случаях вдоль оси. Вычисление магнитного поля вокруг конечного соленоида, как обсуждалось в [5-8], включает его определение путем оценки магнитного векторного потенциала. В настоящей работе разъясняются две отдельные вычислительные методики, включающие прямое определение магнитного поля по закону Био-Савара. Физически проводились измерения импульсного магнитного поля, и полученные результаты сравнивались с расчетными значениями.
Измерение импульсного магнитного поля, как правило, осуществляется по индуктивному принципу (т.е. с помощью поисковой катушки [4,9-12]). Однако доступная литература не описывает метод калибровки поисковой катушки. Новицкий [11] сравнил результаты поисковой катушки с датчиком La 0,67 Ca 0,33 MnO 3 (принцип колоссального магнитосопротивления). В настоящей работе делается попытка решить эту проблему, выполняя калибровку в самой экспериментальной установке, без необходимости использования дополнительных интегрирующих схем. Электростатический сигнал срабатывания, который при последующем интегрировании ухудшает измерение, не должен вызывать беспокойства.
В настоящей работе делается попытка решить эту проблему, выполняя калибровку в самой экспериментальной установке, без необходимости использования дополнительных интегрирующих схем. Электростатический сигнал срабатывания, который при последующем интегрировании ухудшает измерение, не должен вызывать беспокойства.
Импульсное магнитное поле создается соленоидом конечной длины с индуктивностью 14 мкГн, а измерение проводится сразу за соленоидом; данные важны для магнитоформирующих приложений, исследований диффузии (взаимодействия импульсного магнитного поля с металлическими телами), приложений, использующих силы, создаваемые катушками (например, удаленные перемещения металлических объектов, где доступ человека невозможен). Представлена стандартная методика проектирования магнитных поисковых катушек и новый метод ее калибровки. Результаты, представленные в [13], уточняются и дополнительно подтверждаются сравнением экспериментальных и смоделированных результатов с использованием двух методологий математических вычислений.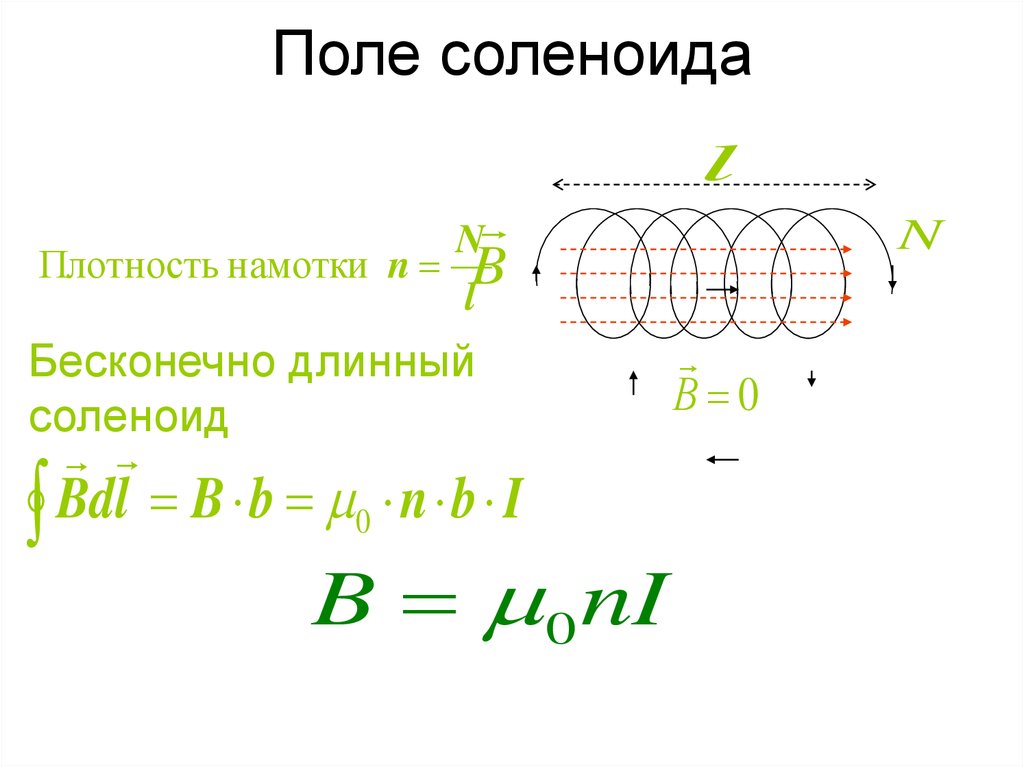
2. Вычислительные методологии для оценки магнитного поля
В следующих разделах представлен целостный подход к вычислительным методологиям, используемым для определения поля. Размеры нагрузочной катушки приведены в следующем разделе, который является необходимым вводом данных для определения магнитного поля катушки соленоида при питании импульсным током. Поскольку эксперименты проводились в низкочастотном режиме (несколько кГц), пространственное распределение плотности тока по поперечному сечению провода соленоида принималось равномерным.
2.1. Магнитное поле снаружи соленоида конечной длины — метод 1
Магнитное поле в любой точке проводника с током можно рассчитать по закону Био-Савара, который определяется следующим уравнением. Вычислительный подход этого метода заключается в разделении витков спиральной катушки на несколько небольших секций и нахождении магнитного поля в любой точке как векторной суммы всех магнитных полей, создаваемых отдельными секциями.
(1)
Здесь dl — текущий элемент; r — расстояние между текущим элементом и контрольной точкой, в которой должно быть измерено магнитное поле. Элемент dl направлен в направлении тока I. Проводник с током можно разделить на ряд элементов по его длине одинаковой величины, но разных направлений в зависимости от геометрии. Результирующее магнитное поле в точке будет векторной суммой всех магнитных полей, вызванных каждым элементом тока. Здесь предполагается, что по проводу течет равномерный ток по всей его длине. Этот принцип расчета магнитного поля можно использовать для расчета того же для геометрии соленоида.
Мы рассматриваем спиральную катушку со следующими характеристиками.
Number of turns : n (21)
Coil inside diameter : D i (55 mm)
Coil length (end-to-end) : l c (87 mm)
Pitch : p ( 38,5 мм)
(Межцентровое расстояние проволоки)
Диаметр проволоки : D w (10 мм)
Теперь разделим один виток катушки на N отрезков вдоль провода.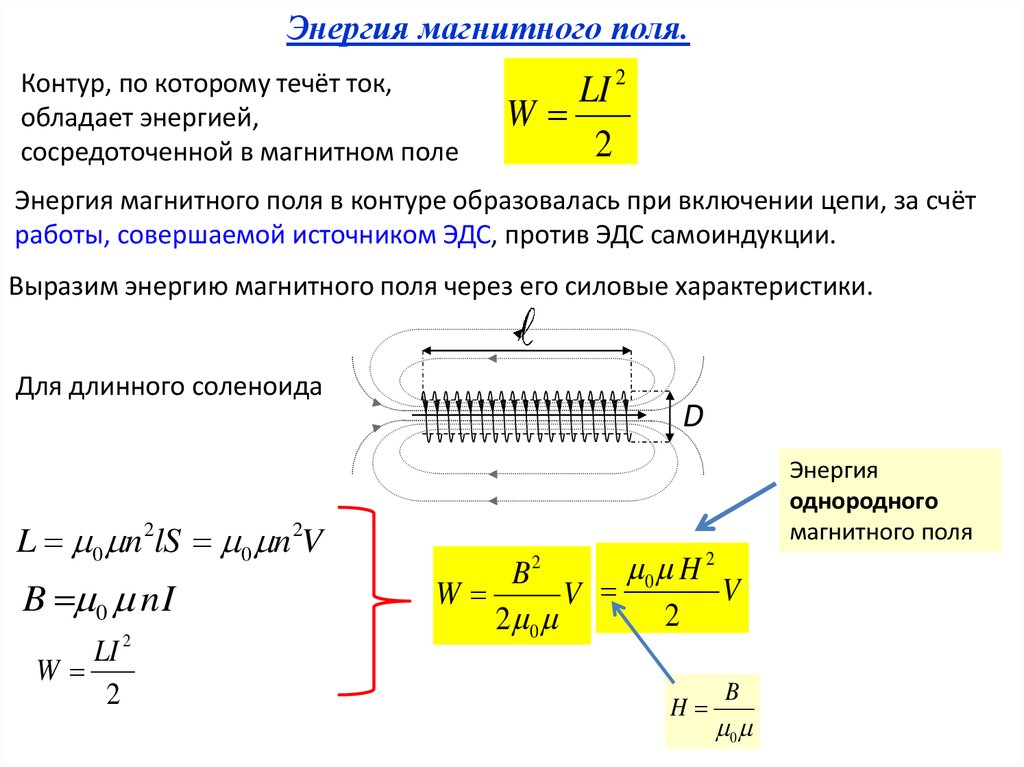 Таким образом, каждый сегмент охватывает азимутальный угол.
Таким образом, каждый сегмент охватывает азимутальный угол.
(2)
Определим декартову систему координат как ось z вдоль центральной оси спирального витка. Оси x и y проходят в радиальном направлении, но перпендикулярны друг другу. Каждый текущий элемент имеет три компонента dx, dy, dz. Соответствующие направления текущего элемента задаются следующими уравнениями.
(3а)
(3b)
(3c)
Элементарный азимутальный угол определяется следующим уравнением:
(4)
текущий элемент. Таким образом, для каждого текущего элемента
(5)
Местоположение каждого текущего элемента или сегмента определяется как: — координата z местоположения предыдущего сегмента. Местоположение точки, в которой должно быть измерено магнитное поле, также задается тремя координатами:
(7a)
(7b)
(7c)
Таким образом,
(8)
Используя уравнения (5) и (8) в (1), мы можем найти магнитное поле в любой заданной точке по формуле текущий элемент.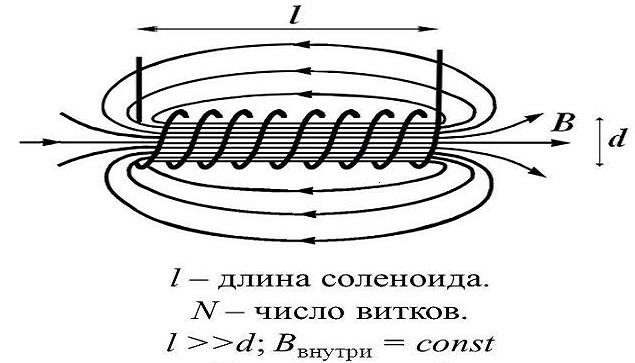
Чтобы найти магнитное поле в любой точке с помощью геометрии спиральной катушки, мы должны сначала инициализировать точки z и θ. Здесь z l начинается с (D w /2 + dz/2), а θ 1 начинается с dθ/2. Наконец, интегрируя магнитное поле в желаемой точке каждым элементом по всем виткам (всего n × N элементов), мы можем найти чистое магнитное поле в желаемой точке спиральной катушки. Результаты вычислительной методологии для настоящего случая приведены в последующих разделах.
2.2. Магнитное поле вне соленоида конечной длины — метод 2
Метод расчета магнитного поля вокруг соленоида конечных размеров уже обсуждался в предыдущем разделе. Настоящий метод (метод 2) также определяет поле вокруг того же соленоидного электромагнита с использованием закона Био-Савара с некоторыми допущениями. Считалось, что соленоидный электромагнит (который по существу имеет спиральную форму) состоит из нескольких круглых токовых колец очень небольшой площади поперечного сечения, идущих по азимуту проводника. Предположение обосновано тем, что шаг витков в соленоиде очень мал по сравнению с общей длиной соленоида и поэтому при обходе соленоида пространственное отклонение токоведущего проводника от плоскости, перпендикулярной оси соленоида не имеет значения. Теперь, когда спиральный соленоидный электромагнит представлен как пучок отдельных круговых токовых колец, окружающих его, магнитное поле соленоида будет по существу суммой полей, создаваемых каждым отдельным токовым кольцом. Этот метод специально учитывает толщину или глубину и ширину каждого витка катушки, тем самым учитывая вклад, обусловленный ее физическими размерами.
Предположение обосновано тем, что шаг витков в соленоиде очень мал по сравнению с общей длиной соленоида и поэтому при обходе соленоида пространственное отклонение токоведущего проводника от плоскости, перпендикулярной оси соленоида не имеет значения. Теперь, когда спиральный соленоидный электромагнит представлен как пучок отдельных круговых токовых колец, окружающих его, магнитное поле соленоида будет по существу суммой полей, создаваемых каждым отдельным токовым кольцом. Этот метод специально учитывает толщину или глубину и ширину каждого витка катушки, тем самым учитывая вклад, обусловленный ее физическими размерами.
Магнитное поле, создаваемое в любой точке пространства кольцевым током, можно определить с помощью закона Био-Савара, выражение для которого показано в уравнении (1). Рассмотрим точку P(x 90 251 1 90 252 , y 90 251 1 90 252 , z 90 251 1 90 252 ), где магнитное поле должно быть определено за счет токового кольца с центром в точке O(0, 0, z) и радиусом как R. Поскольку кольцо круглое, положение текущего элемента длины dl на кольце можно представить как (Rcosφ, Rsinφ, z), где φ — любой угол между 0 и 2π.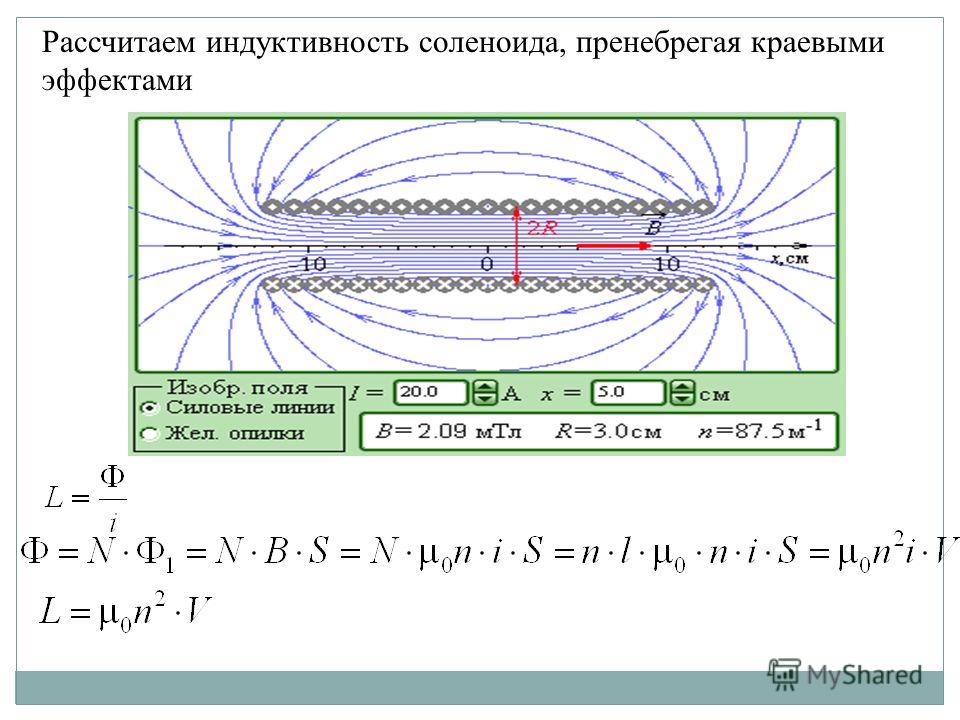
Для текущего элемента:
(9a)
и,
(9b)
снова,
(9c)
Используя уравнения (9a), (9b), (9c) в уравнении (1) , магнитное поле из-за одиночного токового кольца можно определить в точке P как:
(9d)
(9e)
(9f)
однотоковое кольцо, по которому течет ток I. Для определения магнитного поля соленоидного электромагнита необходимо было суммировать магнитные поля, создаваемые каждым витком проводника. Поскольку проводник имел конечные размеры, каждый виток далее делился на ряд круговых токовых колец, поля определялись для каждого кольца и, наконец, суммировались вклады всех колец, чтобы получить полное поле, создаваемое соленоидом.
Катушка соленоида состоит из 21 витка провода Если предположить, что плотность тока J через каждый виток проводника в соленоиде одинаковая, выражение для магнитного поля, создаваемого одним витком провода прямоугольного сечения, глубиной от R I до R O и ширина от Z L до Z H , приведен в качестве:
(10A)
(10B)
(10C)
(10B)
(10A) . ), (10б) и (10в) решались численно. Каждый отдельный виток проводника делился на 625 токовых колец, поле рассчитывалось для каждого кольца и суммировалось, чтобы получить магнитное поле для соответствующего витка соленоида. Интеграл по φ вычислялся от 0 до 2π за 500 шагов. Наконец, поля, создаваемые всеми 21 витком, складывались, чтобы получить поле, обусловленное полным магнитным полем в точке, обусловленной соленоидом.
), (10б) и (10в) решались численно. Каждый отдельный виток проводника делился на 625 токовых колец, поле рассчитывалось для каждого кольца и суммировалось, чтобы получить магнитное поле для соответствующего витка соленоида. Интеграл по φ вычислялся от 0 до 2π за 500 шагов. Наконец, поля, создаваемые всеми 21 витком, складывались, чтобы получить поле, обусловленное полным магнитным полем в точке, обусловленной соленоидом. 2.3. FEM Simulation
Моделирование магнитного поля, создаваемого соленоидом, было выполнено в FEMM, вычислительном электромагнитном решателе с открытым исходным кодом, который использует метод конечных элементов (FEM) для моделирования электромагнитного поля [14]. Входными данными для программного обеспечения являются размеры катушки, число витков, частота работы, пиковая величина тока, граничные условия. Распределение магнитного поля представлено на рисунках 1 и 2.
Вывод программы позволяет определить значение магнитного поля в любой точке пространства в пределах внешней границы для заданных тока и частоты. На внешней границе используется асимптотическое граничное условие; сетка была создана с 12106 узлами. Центр катушки соленоида принимается равным z = 0. Указанное в дальнейшем положение относится к центру (z > 0 выше центра, z
На внешней границе используется асимптотическое граничное условие; сетка была создана с 12106 узлами. Центр катушки соленоида принимается равным z = 0. Указанное в дальнейшем положение относится к центру (z > 0 выше центра, z
3. Экспериментальная установка
В следующих разделах обсуждаются экспериментальная установка, необходимое оборудование и процедуры, принятые для экспериментального измерения импульсного магнитного поля.
В экспериментах использовались следующие компоненты:
1) Конденсаторная батарея емкостью 750 мкФ (15 шт. по 50 мкФ делают конденсаторы соединенными параллельно).
2) Устройства для зарядки батареи конденсаторов.
3) Катушка нагрузки соленоидного типа 14 мкГн (21 виток).
4) Искровой разрядник в сборе (ручной переключатель).
5) Токовый шунт 5 мОм, 30 Вт T & M Research Products, INC.
6) Поисковая катушка или индукционная приемная катушка.
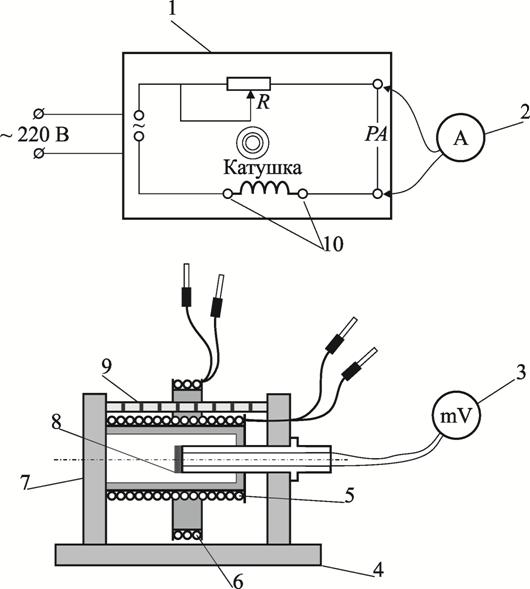
Экспериментальные схемы показаны на рисунках 3-6.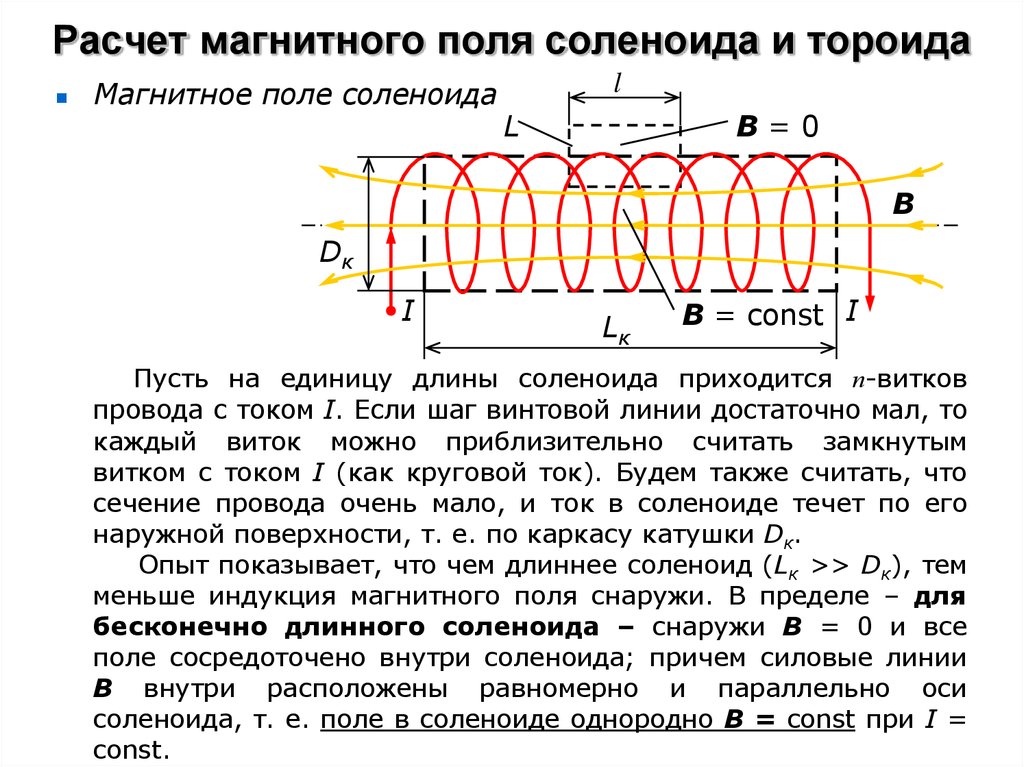
Рис. 1. Распределение магнитного поля.
Рис. 2. Увеличенная часть катушки.
Рис. 3. Экспериментальная установка.
Рис. 4. Схема экспериментальной установки.
Рис. 5. Измерение радиального магнитного поля.
Рис. 6. Измерение осевого магнитного поля.
3.1. Конструкция и калибровка поисковой катушки
Измерение импульсного поля основано на принципе индукции [4], а оценка магнитного поля осуществляется на основе индуцированного напряжения в поисковой катушке [4,13]. В настоящей работе поисковая катушка имеет нейлоновый каркас диаметром 6 мм и длиной 5 мм. Он был намотан проводом SWG 44, концы которого были подключены к коаксиальному разъему (поддерживаемому листом FRP). Поисковая катушка, использованная в экспериментах, и ее схема показаны на рисунках 7 и 8.
Размеры являются эмпирическими с учетом небольшого размера, но опять же обеспечивают достаточно места для применения достаточного количества витков к наведенному измеряемому напряжению в осциллографе.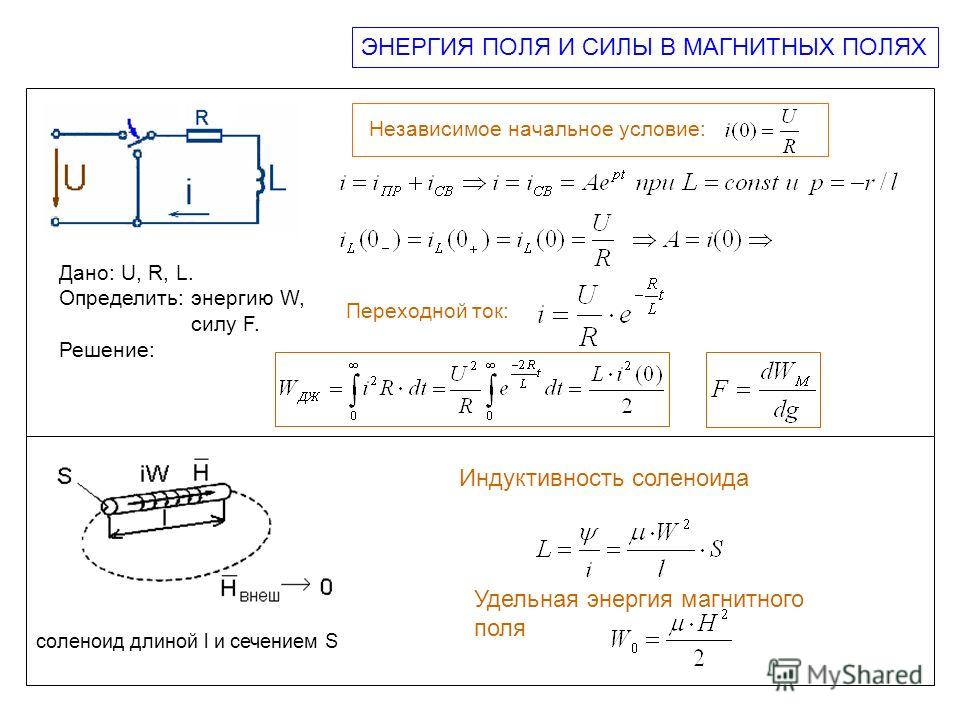 Из представленной информации можно сделать вывод, что наведенное напряжение в поисковой катушке из N витков потокосцепления, скажем, «В» Т задается следующим образом (без учета отрицательного знака).
Из представленной информации можно сделать вывод, что наведенное напряжение в поисковой катушке из N витков потокосцепления, скажем, «В» Т задается следующим образом (без учета отрицательного знака).
(11)
В приведенном выше случае частота 1,389 кГц (текущая частота сигнала), площадь поперечного сечения поисковой катушки 28,2 кв.мм.
Следовательно, для потокосцепления из-за 9 мТл (возможные значения поля были определены по результатам моделирования, обсуждаемым в разделе 3) и, скажем, 60 витков, наведенное напряжение составляет заметное значение 135 мВ, хорошо различимое в разрешении осциллографа. Конструкция была чисто математической, согласованность (оценка поля
Рис. 7. Поисковая катушка.
Рис. 8. Схема поисковой катушки.
по наведенному напряжению) которого можно было определить только из калибровки, как в [14]. ]. Эксперимент был проведен путем изменения количества витков, прежде чем заморозить конструкцию до числа витков, равного 60.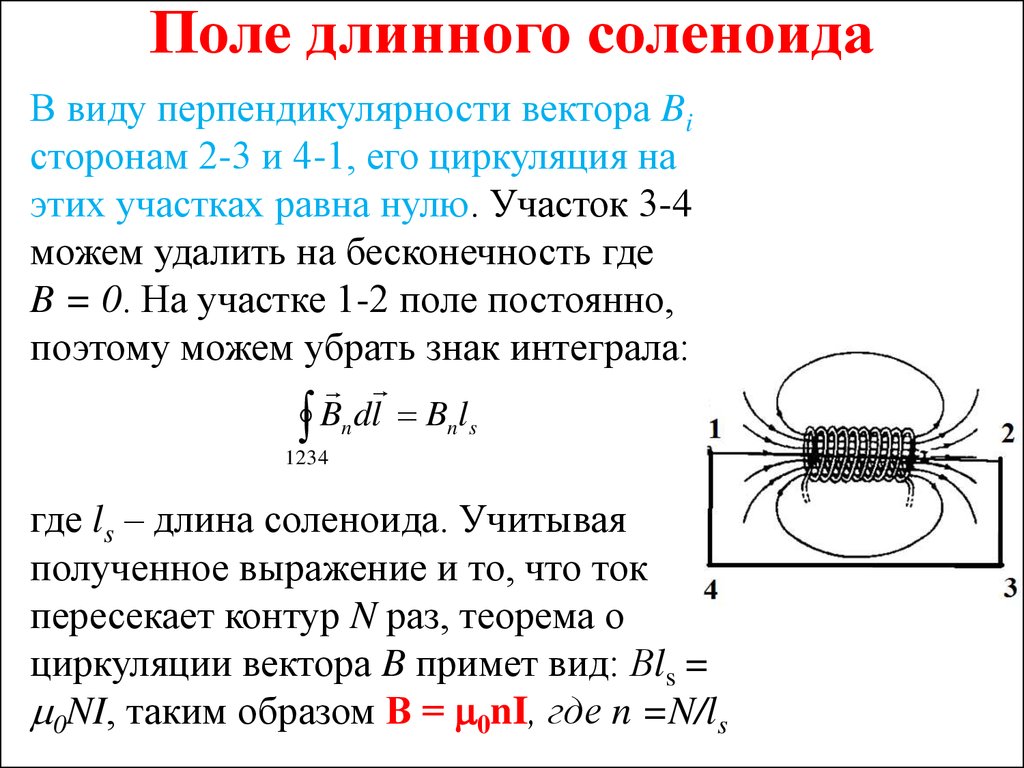 Все результаты соответствовали теории. Поисковая катушка должна быть значительно меньше по размеру, чтобы точно соответствовать точечным измерениям, а ее постоянная времени L/R должна быть достаточно малой по сравнению со временем нарастания генерируемого сигнала, чтобы соответствующим образом реагировать на него. Оба условия выполняются в данном случае.
Все результаты соответствовали теории. Поисковая катушка должна быть значительно меньше по размеру, чтобы точно соответствовать точечным измерениям, а ее постоянная времени L/R должна быть достаточно малой по сравнению со временем нарастания генерируемого сигнала, чтобы соответствующим образом реагировать на него. Оба условия выполняются в данном случае.
Экспериментальная установка для определения калибровочного коэффициента (КФ) [14] показана ниже на рис. 9. Относительно длинный провод подключается между батареей конденсаторов и ручным переключателем. Экспериментальный снимок делается путем натягивания длинного провода, удерживая поисковую катушку прямо над проводом. Таким образом, поисковая катушка касается θ-поля генерируемого магнитного поля.
Генерируемое поле можно оценить [14: Руководство MIT], а соответствующее наведенное напряжение записать на осциллографе.
Таким образом, два параметра, наведенное напряжение и оценочное магнитное поле, нанесены на график, наклон графика дает значение коэффициента калибровки. График показан на рис. 10.
График показан на рис. 10.
Осциллограммы, полученные при определении коэффициента калибровки, такие же, как и при измерении поля катушки соленоида, с учетом более поздних разделов. Расстояние между проводом и поисковой катушкой составляло 1,2 — 1,3 см, параметры, зависящие от положения, и составляли 0,99 и 0,98 соответственно.
3.2. Экспериментальная методика оценки магнитного поля
Расстояние между центром поисковой катушки и нагрузочной катушки
Рис. 9. Экспериментальная установка для определения CF.
Рис. 10. Наведенное напряжение в зависимости от магнитного поля: CF составляет 0,041 Тл/В.
4,83 см. При сохранении этого радиального расстояния фиксированным осевая и радиальная составляющие магнитного поля определяются путем изменения осевого расстояния. Ось поисковой катушки должна быть ориентирована один раз параллельно нагрузочной катушке, а другой раз перпендикулярно ей для определения z-поля и r-поля соответственно (рис.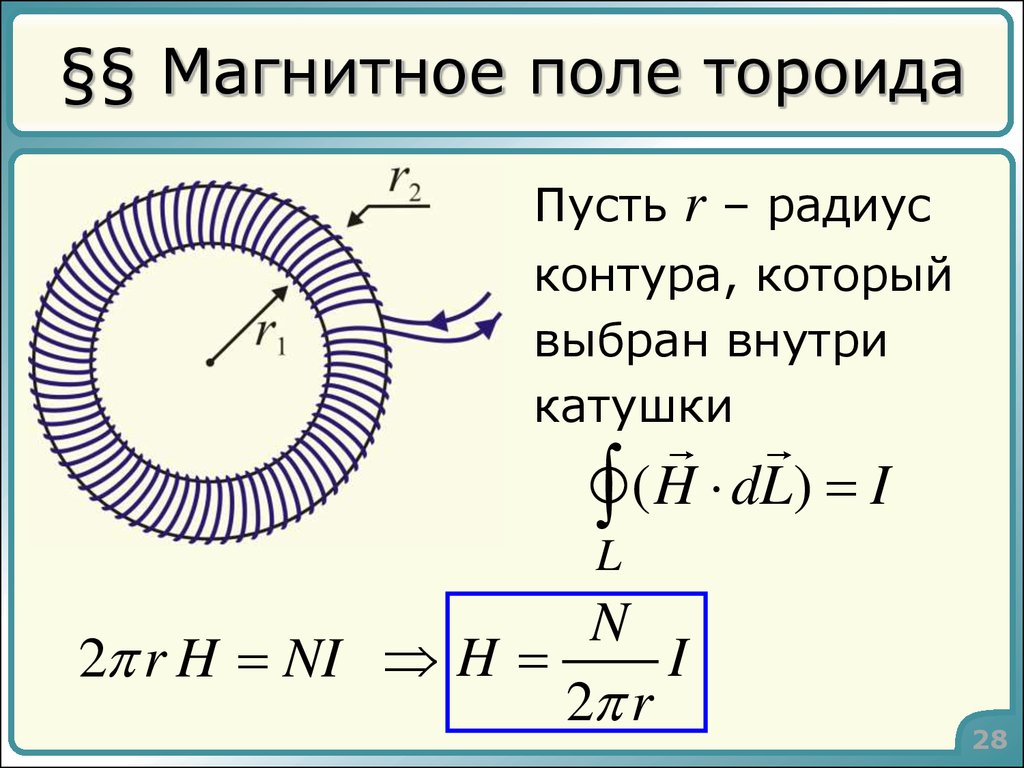 2 и 3 для r и z-поля соответственно). Предварительно заряженная батарея конденсаторов разряжается в соленоидной нагрузочной катушке через ручной переключатель для создания импульсного затухающего тока синусоидальной природы; ток, в свою очередь, генерирует поле. Следует помнить, что точность измерения зависит от положения и ориентации. Ошибка в оценке будет возникать из-за пространственного изменения поисковой катушки, что неизбежно. Следует иметь в виду, что измерение зависит от ориентации.
2 и 3 для r и z-поля соответственно). Предварительно заряженная батарея конденсаторов разряжается в соленоидной нагрузочной катушке через ручной переключатель для создания импульсного затухающего тока синусоидальной природы; ток, в свою очередь, генерирует поле. Следует помнить, что точность измерения зависит от положения и ориентации. Ошибка в оценке будет возникать из-за пространственного изменения поисковой катушки, что неизбежно. Следует иметь в виду, что измерение зависит от ориентации.
Подставка для реторты и зажим для бюретки использовались для прочного удержания поисковой катушки в заданном положении и правильной ориентации. Эти тонкие факторы были учтены при максимальных усилиях во время измерения.
Форма кривой тока (синяя) и соответствующее наведенное напряжение в поисковой катушке (розовая или желтая) показаны на кривых в следующем разделе. Величина магнитного поля (радиальная или осевая составляющая) в данной точке из-за данной величины тока на заданной рабочей частоте определяется произведением пиковой величины косинусоидальной волны (наведенного напряжения) и CF (0,041 Тл/ V) определено ранее. Экспериментальные результаты и проверка каждого из упомянутых выше вычислительных методов представлены в разделах ниже.
Экспериментальные результаты и проверка каждого из упомянутых выше вычислительных методов представлены в разделах ниже.
4. Результаты и обсуждение
В этом разделе мы представляем сравнение значений магнитного поля, полученных посредством моделирования и физических измерений. Осевые и радиальные значения поля обсуждались отдельно.
4.1. Экспериментальные результаты: аксиальное магнитное поле
Настоящий раздел посвящен измерению аксиального магнитного поля. Некоторые типичные экспериментальные результаты показаны в таблице ниже. Измерение поля проводится на фиксированном радиальном расстоянии 4,83 см от центра нагрузочной катушки и в различных осевых положениях. Типичные результаты изображают осевое положение вблизи центра (z = 0,3) и в пределах диапазона намотки катушки (z = −2,55) на рисунке 11.9.0052
График значений осевого магнитного поля для импульсного пикового тока 520 А по длине катушки соленоида приведен на рисунке 12.
4.2. Экспериментальные результаты: радиальное магнитное поле
Настоящий раздел посвящен измерению радиального магнитного поля.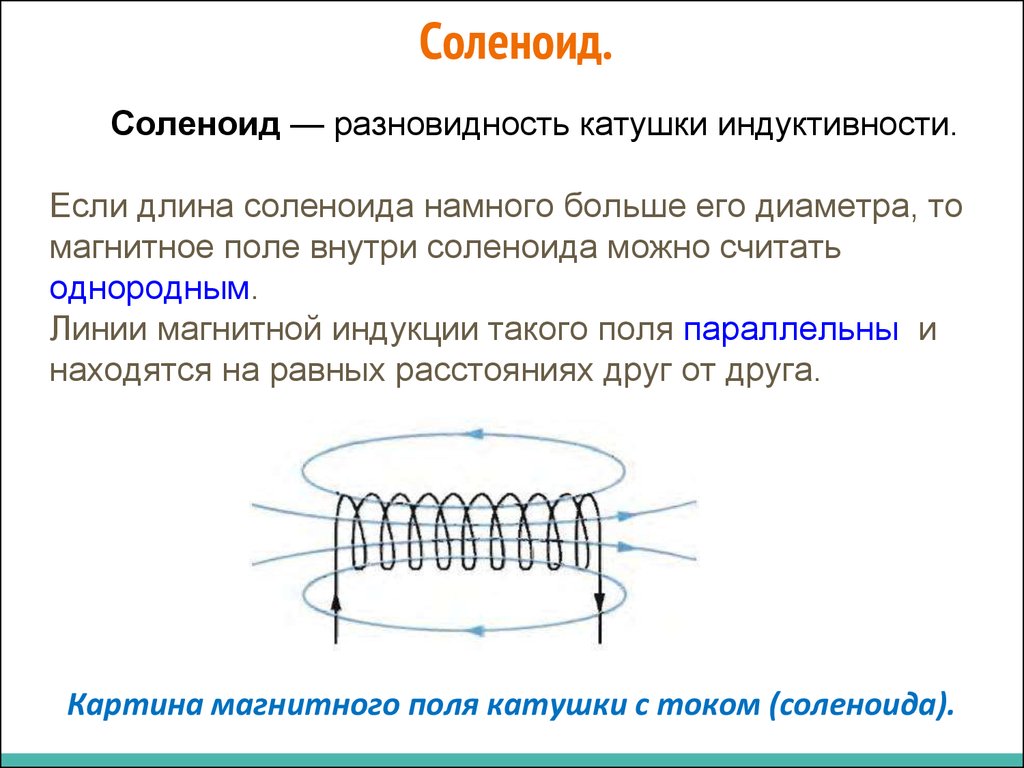 Некоторые типичные экспериментальные результаты показаны в таблице ниже. Измерение поля было получено на фиксированном радиальном расстоянии 4,83 см от центра нагрузочной катушки и в различных осевых положениях. Типичные результаты соответствуют осевому положению вблизи центра (z = 0,45) и точки максимального радиального поля, т. е. (z = −4,55) на рисунке 13.
Некоторые типичные экспериментальные результаты показаны в таблице ниже. Измерение поля было получено на фиксированном радиальном расстоянии 4,83 см от центра нагрузочной катушки и в различных осевых положениях. Типичные результаты соответствуют осевому положению вблизи центра (z = 0,45) и точки максимального радиального поля, т. е. (z = −4,55) на рисунке 13.
График значений осевого магнитного поля для импульсного пикового тока 520 А по длине катушки соленоида приведен на рисунке 14.
4.3. Обсуждение результатов
Вышеупомянутые формулировки использовались для непосредственного определения плотности магнитного потока и не включали промежуточный этап определения магнитного векторного потенциала. Хотя метод Био-Савара уже включает вычисление магнитного векторного потенциала, поэтому в рецептурах можно избежать дополнительных этапов определения векторного потенциала за счет прямого применения метода Био-Савара.
Формулировка метода 1 учитывает потоки тока.
Рис.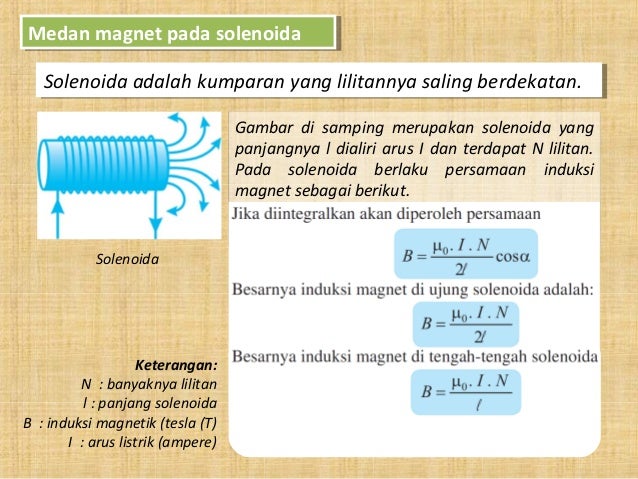 13,4, Bz (экспериментальный в мТл): -11,52, Bz (метод 1 в мТл): -11,57, Bz (метод 2 в мТл): -13,3, канал 2: 200 А/дел, канал 3: 100 мВ/дел.
13,4, Bz (экспериментальный в мТл): -11,52, Bz (метод 1 в мТл): -11,57, Bz (метод 2 в мТл): -13,3, канал 2: 200 А/дел, канал 3: 100 мВ/дел.
Рис. 12. Осевое изменение магнитного поля по длине катушки.
. Метод 1 в мТл): 3,36, Br (Метод 2 в мТл): 1,8, Ch2: 197 А/дел, канал 3: 19,5 мВ/дел.
Рис. 14. Изменение радиального магнитного поля по длине катушки.
прокат через одну репрезентативную точку на внутреннем диаметре нагрузочной катушки, а не по всему сечению провода. Кроме того, состав не учитывает влияние глубины скин-слоя и эффекта близости. Следовательно, результаты на краях катушки показывают несоответствие с соответствующими результатами моделирования FEM. В формулировке метода 2 учитываются именно размеры провода, используемого для намотки катушки. Следовательно, он показывает лучшее совпадение с результатами моделирования, чем метод 1.
Формулировка, упомянутая как метод 2, может также использоваться для учета вращательной асимметрии в проволочной петле и, таким образом, потенциально может определять магнитное поле для любой общей геометрии токонесущей петли за пределами большинства идеализаций. Концепция токовых петель основана на предположении, что каждый виток в основном круговой. Поэтому он не рассматривает идеальную винтовую геометрию соленоида, хотя изменение результата в рассматриваемом сценарии не будет значительным, так как межвитковое расстояние довольно мало. Тем не менее, в программу всегда можно внести соответствующие изменения, чтобы включить точную спиральную геометрию соленоида. Это планируется в следующей версии того же самого. Программа предполагает равномерную плотность тока по сечению проводника соленоида. При работе в квазистатическом режиме, хотя и с тем порядком частот, с которым мы имели дело в текущем эксперименте, погрешности, вносимые из предположения, не были значительными, но чтобы быть полностью уверенным в точности получаемых результатов , следующая версия кода будет включать эффекты кожи.
Концепция токовых петель основана на предположении, что каждый виток в основном круговой. Поэтому он не рассматривает идеальную винтовую геометрию соленоида, хотя изменение результата в рассматриваемом сценарии не будет значительным, так как межвитковое расстояние довольно мало. Тем не менее, в программу всегда можно внести соответствующие изменения, чтобы включить точную спиральную геометрию соленоида. Это планируется в следующей версии того же самого. Программа предполагает равномерную плотность тока по сечению проводника соленоида. При работе в квазистатическом режиме, хотя и с тем порядком частот, с которым мы имели дело в текущем эксперименте, погрешности, вносимые из предположения, не были значительными, но чтобы быть полностью уверенным в точности получаемых результатов , следующая версия кода будет включать эффекты кожи.
Магнитное поле (в направлении тета), создаваемое прямым проводником с током, имеет решение в замкнутой форме, зависящее только от положения датчика поля относительно проводника. Принимая меры предосторожности для позиционирования, корреляция поля, генерируемого с наведенным напряжением, является прямой на заданной частоте. Следовательно, не требуется другого стандартного устройства измерения поля, такого как датчик Холла, что обеспечивает его уникальность. Для заданной частоты можно получить непосредственный коэффициент калибровки в V/T. Методика измерений уникальна тем, что использует дифференцированный сигнал для оценки магнитного поля. Таким образом, можно безопасно избежать использования дополнительного оборудования с точки зрения интегратора RC, усилителя. Однако проблема заключается в повторной калибровке поисковой катушки при каждом изменении рабочей частоты.
Принимая меры предосторожности для позиционирования, корреляция поля, генерируемого с наведенным напряжением, является прямой на заданной частоте. Следовательно, не требуется другого стандартного устройства измерения поля, такого как датчик Холла, что обеспечивает его уникальность. Для заданной частоты можно получить непосредственный коэффициент калибровки в V/T. Методика измерений уникальна тем, что использует дифференцированный сигнал для оценки магнитного поля. Таким образом, можно безопасно избежать использования дополнительного оборудования с точки зрения интегратора RC, усилителя. Однако проблема заключается в повторной калибровке поисковой катушки при каждом изменении рабочей частоты.
5. Заключение
Магнитное поле, генерируемое вне катушки соленоида, возбуждаемой импульсным током, подробно исследовано и представлено в этой статье. Это тема, имеющая большое значение в области импульсной мощности, которая используется в области электромагнитного формования. Тонкие нюансы математических, симуляционных и экспериментальных результатов скудны в доступной литературе, и на них подробно подчеркнуто в статье.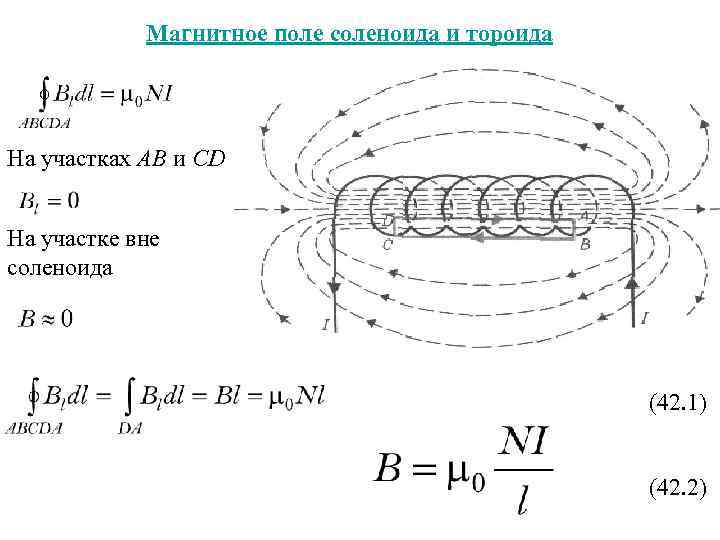 Численные формулировки закона Био-Савара использовались для определения магнитного поля вокруг соленоида конечной длины. Результаты, полученные теоретически, сравнивались с результатами, полученными при моделировании МКЭ, и с экспериментальными результатами. Замечено, что результаты, полученные с помощью различных методик, находятся в близком совпадении друг с другом. Также было продемонстрировано, что расчетные допущения, сделанные в ходе процесса, могут быть разумно учтены без внесения существенных ошибок в результаты. Дальнейшие усовершенствования вычислительных и экспериментальных методов направлены на то, чтобы снизить незначительное количество присутствующих ошибок до еще более незначительного уровня. Обсуждаемая здесь методология определения поля может оказаться очень полезной в электромагнитных экспериментах, проводимых в промышленных масштабах.
Численные формулировки закона Био-Савара использовались для определения магнитного поля вокруг соленоида конечной длины. Результаты, полученные теоретически, сравнивались с результатами, полученными при моделировании МКЭ, и с экспериментальными результатами. Замечено, что результаты, полученные с помощью различных методик, находятся в близком совпадении друг с другом. Также было продемонстрировано, что расчетные допущения, сделанные в ходе процесса, могут быть разумно учтены без внесения существенных ошибок в результаты. Дальнейшие усовершенствования вычислительных и экспериментальных методов направлены на то, чтобы снизить незначительное количество присутствующих ошибок до еще более незначительного уровня. Обсуждаемая здесь методология определения поля может оказаться очень полезной в электромагнитных экспериментах, проводимых в промышленных масштабах.
СПИСОК ЛИТЕРАТУРЫ
- Эспиноса О., Слюсаренко В. Магнитное поле бесконечного соленоида // Американский журнал физики.
 71, № 9, 2003, стр. 953-954. http://dx.doi.org/10.1119/1.1571841
71, № 9, 2003, стр. 953-954. http://dx.doi.org/10.1119/1.1571841 - Дж. Фарли и Р. Х. Прайс, «Поле сразу за длинным соленоидом», Американский журнал физики, том. 69, № 7, 2001, с. 751. http://dx.doi.org/10.1119/1.1362694
- Б. Б. Дасгупта, «Магнитное поле, создаваемое соленоидом», Американский журнал физики, Vol. 53, № 8, 1985, стр. 782-783. http://dx.doi.org/10.1119/1.14318
- H. E. Knoepfel, «Импульсные сильные магнитные поля», издательство NorthHolland Publishing Company, Амстердам, Лондон.
- В. Лабинак, Н. Эрцег и Д. Котник-Каруза, «Магнитное поле цилиндрической катушки», Американский журнал физики, Vol. 74, № 7, 2006, с. 621.
- А. И. Русинов, «Высокоточный расчет магнитных полей соленоида методами Гарретта», IEEE Transactions on Magnetics, Vol. 30, № 4, 1994, стр. 2685-2688. http://dx.doi.org/10.1109/20.305833
- Данилов В.И., Янович М. Магнитные поля толстых конечных соленоидов постоянного тока // Ядерные приборы и методы. 94, № 3, 1971, стр.
 541-550. http://dx.doi.org/10.1016/0029-554X(71)
541-550. http://dx.doi.org/10.1016/0029-554X(71)

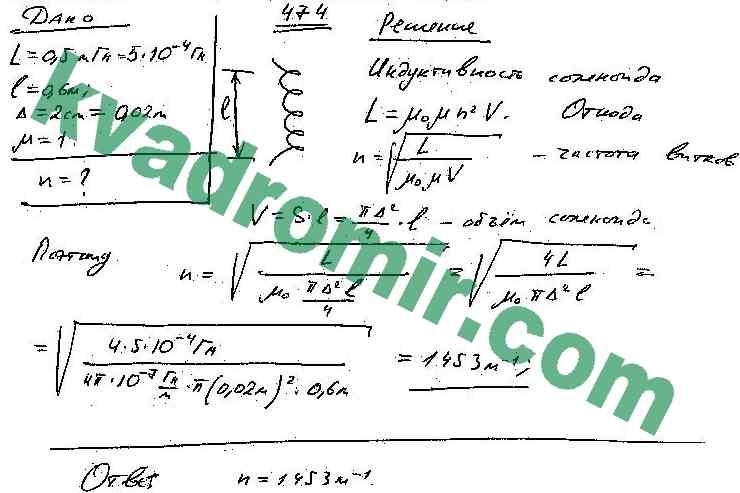
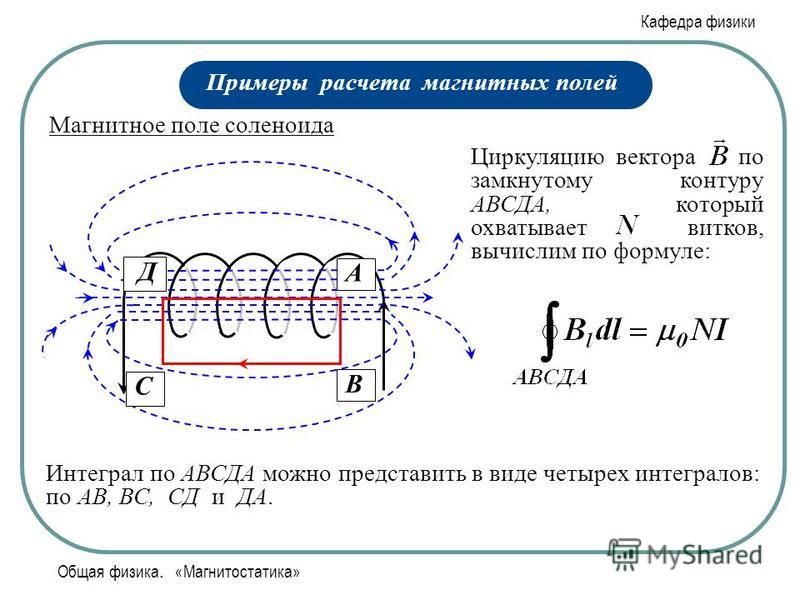 Найдём выражение для индукции магнитного поля соленоида, используя выражение для циркуляции вектора (рис.11):
Найдём выражение для индукции магнитного поля соленоида, используя выражение для циркуляции вектора (рис.11): 12) и
12) и
 Для этого все десять пальцев разбиваются на пять пар…
Для этого все десять пальцев разбиваются на пять пар… , 20 лет, с детства отмечается повышенное АД, уровень которого в настоящее время составляет 180-200/110-120 мм рт. ст. Влияние психоэмоциональных факторов отсутствует. Колебаний АД практически нет. Головной боли нет. Нормализовать…
, 20 лет, с детства отмечается повышенное АД, уровень которого в настоящее время составляет 180-200/110-120 мм рт. ст. Влияние психоэмоциональных факторов отсутствует. Колебаний АД практически нет. Головной боли нет. Нормализовать…
