Индуктивность тока. Индуктивность в электротехнике: принцип работы, виды и применение — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое индуктивность в электротехнике. Как работает катушка индуктивности. Какие бывают виды индуктивностей. Где применяются индуктивности в электронике. Как выбрать индуктивность для схемы.

Содержание

Что такое индуктивность и как она работает

Индуктивность — это способность проводника создавать магнитное поле при протекании через него электрического тока. Основным элементом, обладающим индуктивностью, является катушка индуктивности.

Катушка индуктивности состоит из провода, намотанного в виде спирали. При протекании тока через такую катушку вокруг нее возникает магнитное поле. Основные свойства индуктивности:

Препятствует изменению тока в цепи
Накапливает энергию в магнитном поле
При изменении тока в катушке возникает ЭДС самоиндукции

Единица измерения индуктивности — Генри (Гн). Индуктивность 1 Генри создает ЭДС самоиндукции 1 Вольт при изменении тока на 1 Ампер за 1 секунду.

Виды и конструкции индуктивностей

В зависимости от конструкции и технологии изготовления различают следующие основные виды индуктивностей:

1. Моточные индуктивности

Представляют собой провод, намотанный на каркас или сердечник. Бывают с воздушным сердечником или с магнитным (ферритовым, железным и др.). Моточные индуктивности обеспечивают большие значения индуктивности.

2. Многослойные индуктивности

Изготавливаются путем послойного нанесения проводящих дорожек и изолирующих слоев. Имеют компактные размеры, но меньшие значения индуктивности по сравнению с моточными.

3. Тонкопленочные индуктивности

Формируются напылением тонких магнитных и проводящих слоев на подложку. Обладают наименьшими размерами, но и небольшими значениями индуктивности.

По типу используемого магнитного материала различают индуктивности:

С ферритовым сердечником — высокая индуктивность, но низкая индукция насыщения
С сердечником из порошковых сплавов — высокая индукция насыщения, работа при больших токах

Основные параметры индуктивностей

При выборе индуктивности для схемы необходимо учитывать следующие ключевые параметры:

1. Номинальная индуктивность

Измеряется в Генри (Гн) и его дольных единицах (мГн, мкГн). Определяет основное свойство компонента.

2. Допустимый ток

Различают два вида допустимого тока:

Ток насыщения — максимальный ток, при котором индуктивность уменьшается не более чем на 40% от номинального значения.
Ток нагрева — максимальный ток, при котором температура компонента повышается не более чем на 40°C.

В качестве номинального выбирается меньшее из этих двух значений.

3. Сопротивление постоянному току

Активное сопротивление обмотки, влияет на потери в меди при прохождении тока.

4. Добротность

Характеризует качество индуктивности, отношение реактивного сопротивления к активному на рабочей частоте.

Применение индуктивностей в электронике

Индуктивности широко используются в различных областях электроники:

1. Источники питания

В импульсных источниках питания индуктивности применяются в качестве накопителей энергии. Они позволяют сглаживать пульсации тока и напряжения.

2. Фильтры

Индуктивности входят в состав LC-фильтров для подавления высокочастотных помех и выделения полезного сигнала.

3. Резонансные контуры

В сочетании с конденсатором индуктивность образует колебательный контур, используемый в радиотехнике.

4. Трансформаторы

Индуктивно связанные катушки используются для преобразования напряжений и гальванической развязки цепей.

Особенности выбора индуктивности для схемы

При выборе индуктивности для конкретного применения необходимо учитывать следующие факторы:

1. Требуемое значение индуктивности

Определяется исходя из расчета схемы. Для импульсных преобразователей обычно выбирают индуктивность так, чтобы пульсации тока составляли 20-30% от номинального значения.

2. Рабочий ток

Максимальный ток через индуктивность не должен превышать допустимых значений по насыщению и нагреву.

3. Частотный диапазон

На высоких частотах возрастают потери в сердечнике, что необходимо учитывать при выборе материала.

4. Габаритные размеры

В условиях миниатюризации важно выбирать компактные индуктивности с оптимальными параметрами.

5. Стоимость

Необходимо находить баланс между ценой и качеством компонента.

Потери в индуктивностях

При работе индуктивности возникают различные виды потерь, которые приводят к нагреву компонента:

1. Потери в меди

Связаны с активным сопротивлением обмотки. Возрастают пропорционально квадрату тока. На высоких частотах увеличиваются из-за скин-эффекта.

2. Потери в сердечнике

Включают потери на вихревые токи и на перемагничивание (гистерезис). Зависят от свойств магнитного материала и растут с увеличением частоты.

При малых нагрузках преобладают потери в сердечнике, при больших — потери в меди. Для повышения эффективности важно выбирать материалы с низкими потерями.

Режимы работы индуктивности в импульсных преобразователях

В импульсных преобразователях индуктивность может работать в двух основных режимах:

1. Режим непрерывного тока

Ток через индуктивность никогда не спадает до нуля. Обеспечивает стабильную работу преобразователя.

2. Режим прерывистого тока

Возникает при малых нагрузках, когда ток через индуктивность периодически спадает до нуля. Может вызывать нестабильность и акустический шум.

Для обеспечения стабильной работы обычно стремятся работать в режиме непрерывного тока, выбирая соответствующее значение индуктивности.

Индуктивность / Хабр

Выше мы рассматривали два основных понятия в электротехнике — идеальный генератор напряжения и идеальный генератор тока.

Идеальный генератор напряжения выдает заданное напряжения U (давление в водопроводной аналогии) на любой нагрузке (сопротивлении внешней цепи).

При этом в соответствии с законом Ома I=U/R, даже если R стремится к нулю, а ток возрастает до бесконечности.

Внутренне сопротивление идеального генератора напряжения равно 0.

Идеальный генератор тока выдает заданный ток I (поток в водопроводной аналогии), даже если сопротивление внешней цепи стремится к бесконечности. Напряжение на нагрузке при этом также стремится к бесконечности U=I*R.

Внутреннее сопротивление идеального генератора тока равно ∞.

Тут можно увидеть определенную симметрию, дуализм.

Мы рассматривали конденсатор С который может накапливать заряд (потому и называется — емкость) С=Q/U. Чем больше емкость, тем медленнее растет напряжение (давление) при закачке в конденсатор заряда U=Q/C.

Если емкость заряда очень большая (стремится к бесконечности), то такой

конденсатор бесконечной емкости будет являться идеальным генератором напряжения. Он никогда не разрядится и при этом может выдать ток любой величины, и напряжение на нем будет оставаться постоянным.

Симметричным (дуальным) к конденсатору элементом будет являться индуктивность. Индуктивность обозначается буквой L (см схему ниже).

Обычно сам электронный компонент называется катушка индуктивности, а его параметр — индуктивность L.

рис 13. Подключение катушки индуктивности к генератору напряжения.

Если конденсатор является генератором напряжения, то индуктивность является генератором тока. Индуктивность стремиться поддерживать ток в цепи постоянным, то есть препятствует изменению тока в цепи.

Индуктивность бесконечной величины является идеальным генератором тока, то есть будет бесконечно гнать заданный ток I независимо от сопротивления нагрузки.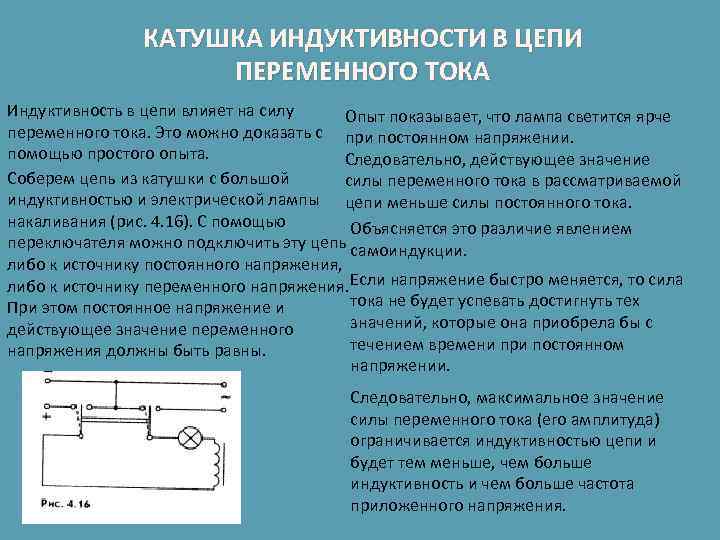

Как хорошо сказано в wiki — “При сопоставлении силы электрического тока со скоростью в механике и электрической индуктивности с массой в механике ЭДС самоиндукции сходна с силой инерции.”

Это похоже как если вы подойдете к стоящей на рельсах вагонетке и станете ее толкать (приложите к ней силу). Вагонетка начнет медленно разгоняться и «ток все быстрее и быстрее побежит по проводам». А потом попробуйте вагонетку тормозить и она будет медленно останавливаться.

Так и в индуктивности, после подачи напряжения ток будет постепенно расти (вагонетка разгоняется), а при подаче напряжения другой полярности — постепенно уменьшаться (вагонетка тормозится).

Отсюда следует вывод «~~Поезд мгновенно остановить нельзя!»~~

«Ток в индуктивности мгновенно остановить нельзя!»

То есть даже если щелкнуть выключателем S4 на схеме и разомкнуть цепь, ток в первый момент после этого будет продолжать идти! На практике это приводит к тому, что в момент размыкания контактов в выключателе между ними будет проскакивать искра.

Сопротивление при размыкании контактов увеличивается до бесконечности (в реальности до очень больших величин) и протекающий ток создаст на этом сопротивлении напряжение очень большой величины, так что воздушный промежуток между контактами будет пробит.

В водопроводной аналогии этому явлению можно сопоставить гидравлический удар, когда масса воды в водопроводе набирает скорость, и при резком закрытии крана вода, продолжая двигаться по инерции, создает высокое давление, что может привести к разрыву трубы.

Причины по которой индуктивность имеет такие свойства (поддержание тока в цепи) хорошо описаны в wiki — https://ru.wikipedia.org/wiki/Самоиндукция

“При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока.”

По отношению к конденсатору , основным отличием индуктивности, если говорить простыми словами, является то, что конденсатор пропускает переменный ток и не пропускает постоянный, а индуктивность наоборот — пропускает постоянный ток и не пропускает переменный.

Тут есть некий момент — постоянный ток это ток, который не меняется со временем, то, что называется «постоянная составляющая» частотой равной 0 Гц. Ее конденсатор не пропускает. Совсем.

А вот индуктивность совсем не пропускает переменный ток бесконечной частоты. А просто переменный ток любой конечной частоты немножко пропускает.

Но к понятию напряжения переменного тока мы вернемся позже.

Рассмотрим цепь на рис. 13 — подключение катушки индуктивности к генератору напряжения.
Ниже представлен график тока в индуктивности при подаче на нее постоянного напряжения от генератора напряжения.

рис. 14 График тока в индуктивности при подаче на нее постоянного напряжения.

При подаче на индуктивность постоянного напряжения ток в ней линейно возрастает со временем.

Мы помним аналогичную картину для конденсатора.

Напряжение на конденсаторе линейно возрастает при его заряде постоянным током.

А что будет, если запитать индуктивность от генератора тока?

рис 15. Подключение индуктивности к генератору тока.

Ну тут из серии «кто кого заборет — слон или кит».

Попробуйте проанализировать работу схемы (hint — вообще схема изображена с ошибкой. В чем она заключается? Как нарисовать схему правильно?)

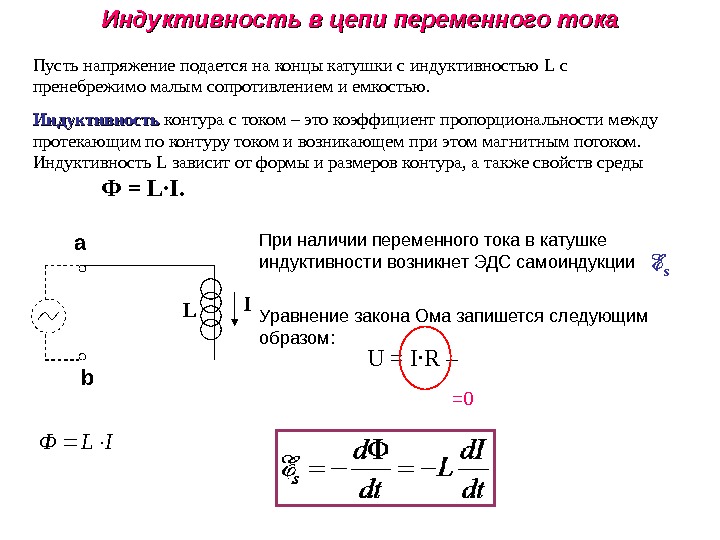
Цепи, содержащие конденсатор и индуктивность

Как было отмечено выше, индуктивность в электротехнике играет ту же роль, что масса в механике. А что является аналогом конденсатора в механике? Конденсатор является генератором напряжения, то есть создает силу, которая двигает поток заряда по проводам. Выше мы приводили аналог конденсатора в виде водонапорной башни, которая заполняется водой (зарядом) и давление (напряжение) в ней увеличивается.

Но можно также представить конденсатор в виде пружины — при заряде пружина сжимается и сила сжатия (напряжение) увеличивается. Емкость в этом случае величина обратная жесткости пружины. Чем пружина жестче, тем быстрее возрастает сила при сжатии. То есть соединение конденсатора и индуктивности эквивалентно вагонетке закрепленной на пружине. )

Что же будет происходить, если конденсатор соединить с индуктивностью, например как в схеме на рис. 16

рис 16. Параллельное включение конденсатора и катушки индуктивности.

Пусть конденсатор С заряжен до напряжения U. Ключ S2 замыкается и в цепи начинает течь ток. Это эквивалентно тому, как если бы мы сжали пружину и затем в какой-то момент отпустили (замкнули ключ S2).

В первый момент после замыкания ключа ток в цепи будет равен 0, так как индуктивность препятствует изменению тока. К вагонетке приложили силу, но в первый момент времени ее скорость равна 0. Затем ток начинает возрастать (вагонетка разгоняется). Пружина разжимается все больше и больше, скорость вагонетки (ток) растет и в какой-то момент времени пружина оказывается не сжата. Конденсатор разрядился до 0. Но. Мы помним что «ток в индуктивности мгновенно остановить нельзя!» Вагонетка разогналась и даже если мы не будем ее толкать, она будет двигаться по инерции. То есть индуктивность будет поддерживать ток и при этом заряжать конденсатор, но уже в другой полярности — заряды теперь будут скапливаться на другой обкладке конденсатора. Растущее напряжение противоположного знака на конденсаторе будет препятствовать движению зарядов, и в конце концов ток в цепи станет равным нулю. Но при этом конденсатор уже зарядился напряжением U другой полярности!

То есть цепь пришла в состояние когда конденсатор заряжен, ток в ней равен нулю.
Хм.. но это то же состояние, с которого мы начали, только полярность напряжения противоположная. Следовательно процесс повторится, только ток потечет уже в другую сторону и система вернется в исходное состояние. Вагонетка поедет обратно, проедет положение равновесия и по инерции снова сожмет пружину.

Возникнет колебательный процесс. То есть вагонетка на пружине так и будет кататься туда-сюда и в отсутствие потерь энергии (трения) этот процесс будет длиться бесконечно.

Таким образом соединение конденсатора с индуктивностью образует колебательное звено. Такие звенья широко используются в электротехнике для создания генераторов и фильтров напряжения переменного тока.

Понятие переменного тока рассмотрим в следующей статье.

UPD.
Поскольку возник диспут экспоненциально ли растет ток при подключении катушки индуктивности к генератору напряжения или линейно, скажу еще пару слов по этому вопросу.

Откуда же берется экспонента роста тока в схеме на рис.13?
Ответ- ниоткуда. Ее там нет. Ток растет линейно и зависимость тока от напряжения описывается формулой

ЭДС самоиндукции в цепи прямо пропорциональна скорости изменения силы тока в этой цепи.
Чтобы обеспечить U=const (а U – это производная от тока в катушке), ток должен линейно расти.

А откуда тогда вообще зашел разговор об экспоненте? А зашел он потому, что ток линейно растет только в идеальном случае — в схеме с идеальным генератором напряжения (бесконечной мощности и с нулевым внутренним сопротивлением) и идеальной индуктивностью (с нулевым внутренним сопротивлением).
В реальном случае с учетом внутреннего сопротивления схема будет выглядеть так.

рис 17. Подключение катушки индуктивности к генератору напряжения с учетом внутреннего сопротивления.

На схеме рис.17 R символизирует собой внутреннее сопротивление генератора и катушки индуктивности. (они все равно включены последовательно, поэтому можно обойтись одним R, как суммой этих сопротивлений)

В этом случае процесс разворачивается следующим образом. При замыкании ключа S4 цепь замкнется и должен был бы пойти ток. Однако, катушка индуктивности препятствует изменению тока, и в первый момент времени после замыкания ключа ток останется равным 0! По сути дела катушка в этот момент представляет собой разрыв цепи с бесконечным сопротивлением. Поэтому напряжение U будет приложено к катушке целиком. Можно и по другому подойти — Ur=I*R. Падение напряжения на резисторе равно I*R, I у нас равен 0, поэтому напряжение на резисторе тоже равно 0, и к катушке будет приложено полное напряжение U. Дальше ток в катушке будет расти. В области 0 линейно кстати (см рис 19 ~~«Переход Суворова через Альпы»~~ «Экспонента проходит через 0 под углом 45 градусов»). Ток будет расти и падение напряжения на резисторе тоже будет расти. А на катушке соответственно падать, потому что часть напряжения будет забирать на себя резистор. Поэтому со временем линейность роста тока в цепи будет нарушаться. Когда падение напряжения на резисторе I*R сравняется с напряжением генератора U рост тока прекратится совсем, потому что напряжение на катушке будет равно 0 (все напряжение будет падать на резисторе).

Вот в этом случае и получится такой экспоненциальный график роста тока в индуктивности.

Рис. 18 Экспоненциальный график роста тока в индуктивности.ис 19 «Экспонента проходит через 0 под углом 45 градусов»

зы. В интернете столько разнообразной ереси на тему катушек индуктивности. Просто диву даешься.
«Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение. Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения.»
Ну.. поскольку про резистор в цепи ничего не сказано, то не на короткий промежуток, а пока входное напряжение не будет снято. Вторая часть звучит бредово, но направление верное — ток с цепи растет от нуля до.. без резистора до бесконечности, с резистором до I=Uвх/R.

Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:

VL = – L*(di/dt), (1)
где:
VL – напряжение (обратная ЭДС), индуцированная на катушке;
L – индуктивность катушки;
di/dt – скорость изменения тока во времени.

Видимо здесь попытались описать начальный момент возникновения ЭДС самоиндукции, но получилась ерунда. Говорить, что «индуцированное напряжение противоположно по полярности приложенному напряжению» это то же самое, что «падение напряжения на резисторе противоположно по полярности приложенному напряжению.» Ага, точно, приложенное напряжение сложили с падением напряжения и после резистора получили 0. Так и есть, лол.
«ЭДС самоиндукции» в катушке это аналог «падения напряжения» на резисторе. Только в резисторе электрическая энергия рассеивается, переходит в тепло, а в индуктивности — накапливается, переходит в энергию магнитного поля. В водопроводной аналогии индуктивность это такая турбинка, вставленная в водопроводную трубу, и которая имеет момент инерции. Турбинка пропускает воду только когда вращается. И вот крантель открыли, давление к турбинке приложили, она начала вращаться и пошел ток дальше по трубе. И чем быстрее турбинка вращается, тем больше ее пропускная способность. Турбинка раскручивается, ток возрастает и так до бесконечности. Это если нет потерь энергии — резистора. А если есть резистор (трение), то часть давления расходуется на преодоление трения. И когда вся входная энергия будет расходоваться на трение, турбинка перестанет ускоряться и ток достигнет максимальной величины.

Рис.20 Переходной процесс в цепи с индуктивностью

Картинка неправильная. В правильном варианте при отключении источника, подключался резистор и цепь оставалась замкнутой.

Рассмотрим следующую цепь

Рис.21 Цепь с индуктивностью и переключателем

Вопрос на засыпку: Чему будет равно напряжение на индуктивности в первый момент после переключения ключа S из верхнего положения в нижнее?

Hint: Не надо выносить себе мозг, пытаясь сообразить с каким там знаком возникнет ЭДС самоиндукции и что с ней будет дальше. Надо применять простое правило:
Ток в индуктивности в первый момент времени после переключения сохраняется неизменным.
Дальше применять закон Ома.

Особенности применения силовых индуктивностей

Поскольку технические параметры современных электронных устройств постоянно совершенствуются, для БИС, используемых в таких изделиях, характерно снижение напряжения питания. В этой связи, энергопотребление может уменьшаться, а скорость работы увеличиваться. Однако снижение напряжения источника питания также предполагает более жесткие требования, учитывающие колебания напряжения, что приводит к необходимости использования высокопроизводительных DC-DC преобразователей. Силовые индуктивности при этом являются важными компонентами, существенно влияющими на эффективность преобразователей.

Компания TDK выпускает широкую линейку силовых индуктивностей. В данной статье рассмотрены эффективные способы применения данных компонентов, а также ключевые особенности при выборе катушек индуктивности в соответствии с требуемыми характеристиками преобразователей постоянного тока.

Силовые индуктивности являются важными компонентами, влияющими на производительность DC-DC- преобразователей.

Несмотря на то, что катушка индуктивности может плавно пропускать постоянный ток, при любом изменении его величины она будет генерировать ЭДС, препятствующую этим колебаниям. Такое явление известно как самоиндукция. При подключении к источнику переменного тока катушка индуктивности оказывает сопротивление проходящему по ней переменному току. Таким образом, если ток прошел через индуктивность, он будет накапливаться в виде энергии, а если процесс передачи тока нарушен, эта энергия будет разряжаться. Данная отличительная особенность эффективно используется в цепях источников питания, в преобразователях постоянного тока. На рисунке 1 представлена основная схема понижающего преобразователя постоянного тока (диодный выпрямитель). Силовые индуктивности являются ключевыми компонентами, оказывающие существенное влияние на его производительность.

Параметры, связанные с характеристиками индуктивности, имеют сложную компромиссную связь друг с другом

Сложности в процессе разработки силовых индуктивностей обусловлены изменчивостью характеристик в зависимости от степени воздействия таких факторов как температура и величина тока. Так, например, индуктивность (L) имеет тенденцию к снижению, поскольку величина тока становится больше (характеристика наложения тока DC), а рост температуры, вызванный повышением силы тока, может вызвать изменение как магнитной проницаемости (μ) сердечника, так и индукции насыщения (B_s). Даже при одинаковых значениях индуктивности сопротивление постоянному току (R_dc) будет меняться в зависимости от толщины обмотки и количества витков, вызывающих изменения в степени тепловыделения. Различия в структуре магнитного экрана также могут влиять на шумовые характеристики. Эти параметры имеют сложную компромиссную взаимосвязь, поэтому крайне важно выбрать наиболее подходящую индуктивность для требуемой области применения с учетом эффективности, размеров и стоимости преобразователей постоянного тока.

Ключевой момент: Силовые индуктивности могут быть классифицированы на моточные, многослойные и тонкопленочные в зависимости от различий в методах изготовления, с сердечниками на основе феррита или порошкового сплава. Ферриты характеризуются высокими значениями проницаемости (μ) и индуктивности, в то время как сердечники на основе порошковых материалов имеют высокие значения индукции насыщения, что делает их подходящими для использования при больших величинах тока.

Ключевой момент: Выделяется два определения номинального тока для силовых индуктивностей: допустимый ток при суперпозиции DC и допустимый ток при возрастании температуры. Если сердечник войдет в насыщение, величина его индуктивности будет снижена. Рекомендуемая величина максимального тока, который может быть передан без достижения магнитного насыщения, соответствует допустимому току при наложении постоянного тока (пример: падение на 40% от начального значения индуктивности). Ток, определяемый тепловыделением в соответствии с электрическим сопротивлением обмоток, является допустимым током при повышении температуры (например, повышение температуры на 40 °С в результате тепловыделения). В качестве номинального обычно принимают значение тока, меньшее из рассмотренных выше двух типов допустимых токов.

Условия, при которых возникают потери, будут меняться в зависимости от размеров и частотного диапазона нагрузок

Ключевой момент: К основным типам потерь, которые могут вызвать скачок температуры можно отнести: потери в меди, появляющиеся из-за обмотки проводом, а также потери в магнитопроводе.

Потери в меди возникают из-за сопротивления DC (R_DC) обмотки и увеличиваются пропорционально величине тока в квадрате. Кроме того, когда частота переменного тока становится выше, существует тенденция концентрации тока в области недалеко от поверхности проводника и увеличения эффективного значения сопротивления (скин-эффект). В высокочастотном диапазоне также добавляются потери в меди, возникающие в результате протекания переменного тока.

Потери в магнитопроводе соответствуют сумме потерь на вихревые токи и на гистерезис. Потери на вихревые токи пропорциональны квадрату частоты, поэтому в высокочастотных областях потери в сердечнике, вызванные потерями на вихревые токи, становятся больше. Одним из ключевых моментов для повышения эффективности является выбор материалов сердечника, характеризующихся низкими потерями даже в высокочастотном диапазоне.

Ключевой момент: Потери в меди становятся доминирующими в случае подключения умеренной или интенсивной нагрузки, в то время как вклад потерь в магнитопроводе становится существенным уже при включении небольшой нагрузки. Для тока, протекающего через индуктивность при включении умеренной и большой нагрузки, вклад смещения (DC bias current) достаточно велик, в этой связи потери в меди, появляющиеся в результате сопротивления постоянному току (R_DC), становятся доминирующими. С другой стороны, при подключении неполной нагрузки тока смещения (DC bias) практически нет. В этой связи, уровень потерь в меди снижается, но поскольку операция переключения с постоянной частотой выполняется даже в режиме ожидания, потери в сердечнике из-за особенностей материала феррита становятся существенными , а эффективность значительно уменьшается (рисунок 3).

Важно установить соответствующие требованиям значения индуктивности с учетом таких факторов, как пульсирующий ток

Ключевой момент: использование компонентов в режиме прерывистого тока влияет на стабильность источников питания.

В силовых индуктивностях, применяемых в понижающих DC-DC преобразователях, будет протекать пульсирующий ток (ΔI_L) с формой непрерывных треугольных волн в сочетании с операцией ВКЛ/ВЫКЛ для переключающих элементов (рисунок 4).

В ходе подключения нагрузки от умеренной до интенсивной ΔI_L будет накладываться на смещение по постоянному току, поэтому ток индуктивности будет протекать непрерывно (режим непрерывного тока (I_вых ＞ 1 / 2ΔI_L)). Однако в преобразователях постоянного тока с диодным выпрямлением при подключении легкой нагрузки, где I_вых ＜ 1/2ΔI_L, будут периоды, когда ток индуктивности станет нулевым. В этом состоянии (режим прерывистого тока) ток индуктивности будет периодически прерываться, что, в свою очередь, будет влиять на стабильность источника питания. Кроме того, если катушка индуктивности работает в режиме прерывистого тока, также будет возникать акустический шум. В результате переключения будет генерироваться импульсный сигнал напряжения, что будет способствовать появлению шума.

Ключевой момент: Необходимо задавать такую величину индуктивности, чтобы вклад пульсирующего тока составлял 20-30% от номинального тока.

Величина пульсирующего тока связана с индуктивностью. В этой связи, преобразователи постоянного тока с диодным выпрямлением должны быть спроектированы таким образом, чтобы избежать проблем, связанных с работой в режиме прерывистого тока путем ограничения вклада пульсирующего тока. Если предпочтительно применение компонента с небольшим значением индуктивности из-за размеров или стоимости, величина пульсирующего тока станет больше. И наоборот, если требуется уменьшить пульсирующий ток, необходима большая индуктивность, что может привести к недостаткам, связанным с размером или стоимостью, а также вызвать ухудшение характеристик переходного процесса при внезапных изменениях нагрузки. Таким образом, обычно принято указывать такое значение индуктивности, при которой величина пульсирующего тока будет составлять 20-30% от номинального (прерывистый ток будет фиксироваться в области, когда пульсирующий ток будет составлять примерно 10% от номинального).

Ключевой момент: выбор правильного подхода при снижении значения индуктивности может улучшить характеристики отклика нагрузки.

В случае, когда, например, отмечается внезапный рост нагрузки, будет происходить падение выходного напряжения. В ходе последующего восстановления через индуктивность в течение короткого времени может протекать аномально большой пиковый ток для зарядки выходного конденсатора совместно с током нагрузки. Однако, если будет установлено небольшое значение пульсирующего тока, достичь требуемых характеристик переходного процесса для быстрого восстановления после внезапного падения выходного напряжения будет невозможно. Одним из способов решения этой ситуации могло бы стать уменьшение значения индуктивности и, таким образом, увеличение величины пульсирующего тока. Как показано на рисунке 6, выходное напряжение существенно падает, если характеристики отклика нагрузки плохие. В то же время, если значение индуктивности соответствующим образом снижается, и пульсирующий ток увеличивается, изменение величины тока индуктивности становится более существенным, что вызывает снижение вклада падения напряжения и способствует более быстрому восстановлению. Однако при понижении значения индуктивности важно использовать настройку, которая учитывает общий баланс системы.

Катушка индуктивности i-v уравнение в действии

Катушка индуктивности является одним из идеальных элементов цепи. Мы узнаем больше о том, как ведет себя индуктор, внимательно изучив его уравнение $i$-$v$.

Автор Вилли Макаллистер.

Содержание

Уравнения индуктора $i$-$v$
Напряжение дросселя пропорционально скорости изменения тока
Катушка индуктивности и источник тока
- Имитационная модель
- Иногда индуктор «выглядит» как короткое замыкание 9{\,T} v\,\text dt + i_0$
  Это производная и интегральная формы уравнений индуктора.
  $\text L$ индуктивность , физическое свойство катушки индуктивности.
  $\text L$ — коэффициент масштабирования между $v$ и $di/dt$.
  $\text L$ показывает, сколько $v$ генерируется для заданного количества $di/dt$.
  $i_0$ — начальный ток, протекающий в катушке индуктивности при $t=0$.
  обозначение исчисления: $di/dt$
  $v = \text L\,\dfrac{di}{dt}$
  9{\,T} v\,\text dt + i_0$
  Зацикленный символ $\int$ тоже из исчисления. Это интегральный признак. Его значение аналогично символу суммирования $\Sigma$. В уравнении индуктора знак интеграла представляет собой бегущую сумму произведения $v\,\times \,dt$, начиная с момента времени $t=0$ и заканчивая моментом времени $t=T$. Интегрирование противоположно взятию производной.
  Напряжение на дросселе пропорционально
  скорости изменения тока
  Когда мы узнали о резисторах, закон Ома сказал нам, что напряжение на резисторе пропорционально току через резистор: $v = \text R\,i$ .
  Теперь у нас есть индуктор с уравнением $i$-$v$: $v = \text L\,\dfrac{di}{dt}$.
  Это говорит нам, что напряжение на катушке индуктивности пропорционально не току, а скорости изменения тока через катушку индуктивности. Вот что означает $di/dt$.
  Для реальных резисторов мы должны позаботиться о том, чтобы напряжение и ток не становились слишком большими для резистора. Для реальных катушек индуктивности мы должны быть осторожны со скоростью изменения тока .0014 не слишком велик для катушки индуктивности. Это может быть непросто. Очень легко создать большое изменение тока при размыкании или замыкании переключателя. В статье об отдаче индуктора мы разрабатываем для этой ситуации.
  Катушка индуктивности и источник тока
  Теперь мы рассмотрим несколько различных простых схем, чтобы понять, что означают уравнения $i$-$v$ для катушки индуктивности. По пути мы увидим, как уравнения учат нас некоторым простым практическим правилам относительно катушки индуктивности.
  Первый пример — катушка индуктивности, подключенная к идеальному источнику тока.
  Источник тока подает постоянный ток на катушку индуктивности, $i = \text I$.
  Например, пусть $i = 2 \,\text{mA}$.
  Какое напряжение на дросселе?
  Уравнение индуктора говорит нам:
  $v = \text L\,\dfrac{di}{dt}$
  Источник тока обеспечивает постоянный ток $2\,\text{мА}$. Это интересно, но что нам действительно нужно знать, так это скорость изменения тока?
  $\dfrac{di}{dt} = \dfrac{d2}{dt} = 0\qquad$ (все знают, что $2$ не меняется со временем)
  Следовательно, напряжение на индукторе равно:
  $v = \text L\cdot 0 = 0$
  Если ток в индукторе постоянный, то $v = \text L\,di/dt = 0$ . На катушке индуктивности появляется ноль вольт. Это верно для любого значения тока и любого значения индуктора.
  Имитационная модель
  Вот имитационная модель катушки индуктивности $5\,\mu\text H$ с постоянным источником тока $2\,\text{мА}$. Откройте ссылку и нажмите TRANS в верхней строке меню, чтобы запустить переходную симуляцию. Результат довольно скучный. Напряжение на катушке индуктивности равно $0$. Измените катушку индуктивности или ток на что угодно, ответ всегда будет $0$.
  Иногда индуктор «выглядит как» короткий
  Очень популярно рисовать мысленные образы индуктора, говоря, что он «похож» на что-то. Вот наш первый пример.
  При постоянном токе разность потенциалов между концами катушки индуктивности составляет $0\,\text V$. В этом состоянии индуктор ведет себя как идеальный провод. (Идеальный провод имеет $0\,\text V$ между концами, несмотря ни на что.)
  Катушка индуктивности «выглядит» как короткое замыкание, когда ток в ней постоянный.
  Катушка индуктивности и источник напряжения
  Теперь давайте сравним источник тока с идеальным источником постоянного напряжения и посмотрим, что предсказывает уравнение $i$-$v$. Давайте конкретизируем и скажем, что $\text V = 3\,\text V$ и $\text L = 10\,\text{mH}$. {-3}} = 300 \,\text{ампер}/\text{сек}$
  Это означает, что ток через индуктор будет иметь крутизну нарастания $300\,\text{ампер}/\text{секунда}$.
  Удивительно, но именно это и предсказывает уравнение. Излишне говорить, что это не практическая схема. Мы просто хотим посмотреть, что происходит с постоянным напряжением. Если мы построим эту схему, ток будет увеличиваться до тех пор, пока наш реальный источник напряжения не сможет удовлетворить потребность в большем токе. Но в течение короткого промежутка времени именно так работают настоящие катушки индуктивности.
  Имитационная модель
  Вот имитационная модель катушки индуктивности со схемой источника напряжения. Откройте ссылку и нажмите TRANS в верхнем меню, чтобы запустить переходную симуляцию.
  Пример
  На самом деле мы можем придумать что-то более полезное, чем линейно возрастающее линейное изменение тока. Если мы изменим источник напряжения так, чтобы время от времени он менял направление, мы получим более интересную и потенциально полезную схему.
  Вот вам задание: предположим, что амплитуда прямоугольного сигнала равна $\pm1\,\text V$, а частота равна $1\,\text{MHz}$ $($имеет период $1\,\mu \текст{сек})$.
  Нарисуйте форму текущего сигнала и найдите пиковые значения.
  Посмотрите, сможете ли вы это сделать, прежде чем смотреть ответ или имитационную модель.
  Подсказка: Рассчитайте $di/dt$ для двух различных состояний входного напряжения.
  показать ответ
  Форма волны тока представляет собой треугольную волну, нарастающую при положительном напряжении и убывающую при отрицательном напряжении.
  Мы решим это по частям. Сначала определите ток при напряжении $+1\,\text V$, 9{+6} \,\text{ампер}/\text{сек}$
  Нарастание тока составляет $200{,}000\,\text{ампер}/\text{секунда}$.
  То же, что и $200\,\text{мА}/\мю\текст{сек}$.
  Напряжение меняется с $+1\,\text V$ на $-1\,\text V$ каждые $0,5\,\mu\text{сек}$.
  Насколько сильно возрастает ток на участке $v = +1\,\text V$ прямоугольной волны?
  $i_{\text{+peak}} = 200\,\text{мА}/\mu\text{сек} \times 0,5\,\mu\text{сек} = 100\,\text{мА}$
  Максимальное значение тока достигает $100\,\text{мА}$.
  Когда напряжение падает, весь процесс меняется на противоположный. Для части $v = -1\,\text V$ вы можете снова выполнить математику с $-1\,\text V$ в уравнении наклона. Текущий наклон вниз с отрицательным наклоном той же величины. В конце отрицательного напряжения ток вернется к $0$.
  $i_{\text{-пик}} = 0\,\text{мА}$.
  Ток будет зигзагами между двумя пиками с прямыми линиями между ними. Откройте ссылку на симуляцию ниже и запустите симуляцию переходного процесса, чтобы посмотреть, что произойдет.
  Имитационная модель
  Имитационная модель схемы источника импульсного напряжения. Откройте ссылку и нажмите TRANS, чтобы запустить переходную симуляцию.
  Катушка индуктивности «интегрирует» напряжение по времени, на что указывает значение тока в любой момент. Это точный «двойник» конденсатора, интегрирующий ток.
  Исследовать
  Что произойдет с током, если вы…?
  Изменить значение индуктора на немного $(2\times)$ и на много $(100\times)$.
  Изменить амплитуду или частоту источника напряжения.
  Измените уровни напряжения, чтобы они не были симметричными.
  Измените рабочий цикл напряжения с $50\%$ на другое значение, например $40\%$.
  что означает «рабочий цикл»?
  Рабочий цикл описывает импульсный сигнал. Это относится к проценту времени, в течение которого напряжение находится в высоком состоянии. Если рабочий цикл равен $25\%$, напряжение равно $+1\,\text V$ в течение четверти времени цикла. Если рабочий цикл составляет $50\%$, напряжение симметрично, проводя половину времени высоким и половину времени низким. Рабочий цикл может варьироваться от $0\%$ до $100\%$.
  Аналогия с массой
  Это самый полезный мысленный образ, который возникает при взгляде на индуктор.
  Индуктивность, $\text L$, аналогична массе или инерции в механической системе. Энергия магнитного поля катушки индуктивности не позволяет току изменяться мгновенно, точно так же, как тяжелая масса автомобиля имеет тенденцию сопротивляться изменению скорости. Автомобиль не может завестись или остановиться мгновенно. Требуется время, чтобы разогнаться или затормозить. Катушка индуктивности представляет собой электрическую версию первого закона движения Ньютона (также называемого законом инерции): движущееся тело имеет тенденцию оставаться в движении. Для катушки индуктивности это выглядит так: движущийся ток имеет тенденцию оставаться в движении.
  Ток в катушке индуктивности не изменяется (не будет) мгновенно.
  Резюме
  Ток в катушке индуктивности не изменяется мгновенно.
  При постоянном токе индуктор выглядит как короткое замыкание.
  Будьте осторожны при включении катушек индуктивности. Внезапное изменение тока, например размыкание выключателя, прерывающее путь тока, означает, что производная тока, $di/dt$, может стать очень большой. Уравнение индуктора говорит нам, что на индукторе может быть большое напряжение.
  Один из способов справиться с потенциально разрушительным напряжением катушки индуктивности — спроектировать путь для тока, чтобы не было больших $di/dt$. Мы показали, как добавить диод, чтобы обеспечить путь тока и зафиксировать напряжение катушки индуктивности до приемлемого значения, когда переключатель был разомкнут.
  Формула индуктивности — GeeksforGeeks
  Индуктивность — это термин, с которым должен быть знаком каждый студент-физик. Он имеет собственную формулу и часто комбинируется с сопротивлением и емкостью. Оливер Хевисайд впервые придумал эту фразу в 1886 году. Кроме того, мы используем букву L для обозначения катушек индуктивности на принципиальных схемах и индуктивности в уравнениях в честь выдающегося физика Генриха. Давайте узнаем о формуле индуктивности и о том, как ее использовать для определения индуктивности. любой предмет.
  Индуктивность
  Индуктивность — это свойство электрического проводника, которое заставляет его сопротивляться изменениям проходящего через него электрического тока. Поток электрического тока создает вокруг проводника магнитное поле. Напряженность поля пропорциональна величине тока и не зависит от колебаний тока. Согласно закону индукции Фарадея, любое изменение магнитного поля в цепи создает электродвижущую силу (ЭДС) (напряжение) в проводниках. Этот процесс известен как электромагнитная индукция.
  Индуктивность присутствует во многих электрических и электронных системах, а также в цепях. Шестерни доступны в различных формах и размерах, а также различных названиях. Примеры включают катушки, дроссели, трансформаторы, катушки индуктивности и другие детали. Единицей индуктивности в СИ является генри (Гн) , что может быть представлено в скорости изменения тока и напряжения.
  Формула индуктивности
  Ниже приведена формула индуктивности
  L = мкН ² А/л
  Где,
  L = индуктивность (Гн),
  мк = проницаемость (Вб/ампер),
  Н = катушка число витков,
  А = площадь поперечного сечения змеевика,
  l = длина змеевика (м).
  Вывод
  Дано:
  E = N(dϕ/dt)
  Количество витков в катушке равно N, а ЭДС индукции в катушке равно E. 900 03
  Используя закон Ленца, перепишите приведенное выше уравнение,
  E = -N(dϕ/dt)
  Предыдущее уравнение изменено для вычисления значения индуктивности.
  E = -N(dϕ/dt)
  ∴ E = -L(di/dt)
  N = dΦ = L di
  NΦ = Li
  Следовательно,
  Плотность потока обозначается Б, и площадь катушки обозначена A.
  li = nφ = NBA
  HL = Ni
  Сила намагничивания магнитного потока обозначается H.
  B = μH
  LI = NBA
  L = NBA / я = N ² BA/Ni
  N ² BA/Hl = N ² мкГа/Hl
  ∴ L = мкН ² A/л 9010 7
  При индуктивности L индуцированное напряжение в катушке (В) равно,
  В = L × (di/dt)
  Где,
  В = напряжение (вольт),
  L = значение индуктивности (Гн),
  i = Ток (А),
  t = Затраченное время (с).
  Реактивное сопротивление индуктивности рассчитывается следующим образом,
  X = 2πfL
  Где,
  X = реактивное сопротивление (Ом),
  f = частота (Гц),
  L = индуктивность (Гн).
  Если индуктивность последовательно
  L = L ₁ + L ₂ + L ₃ . . . . + L _n
  Если индуктивность параллельна
  1/л = 1/л ₁ + 1/л _{2 90 390 + 1/л ₃ . . . . + 1/L _n}
  Примеры вопросов по формуле индуктивности
  Вопрос 1: Дайте определение индуктивности.
  Ответ :
  Индуктивность — это свойство электрического проводника, которое заставляет его сопротивляться изменениям проходящего через него электрического тока. Поскольку индуктивность имеет N в формуле, это означает, что количество витков в проводнике прямо пропорционально присутствующей индуктивности. Однако интересным фактом является то, что даже прямые проводники несут индуктивность очень мало, чтобы быть значительной.
  Вопрос 2: Что такое единица индуктивности в системе СИ?
  Ответ:
  Единицей индуктивности в системе СИ является генри (Гн). Открытие индуктивности приписывают Фарадею, однако введение собственной индуктивности для одиночной цепи было впервые введено Генри. Поэтому единица индуктивности посвящена имени ученого.
  Вопрос 3: Определите самоиндукцию 210-виткового соленоида с площадью поперечного сечения 17 см ² и длиной 66,2 см.
  Решение:
  Дано: μ = 4π × 10 ^-7 Н/Д ² , N = 210 витков, A = 17 × 10 ^{-4 9 0266 м ² , l = 66,2 × 10 ^-2 м}
  Т.к. 2 × (17 × 10 ^-4 ))/(66,2 × 10 ^-2 )
  ∴ L = 0,0001422
  ∴ L = 14,22 × 10 ^-5 H
  Вопрос 4: Каково соответствующее сопротивление при последовательном соединении катушек индуктивности 16H, 10H и 21H?
  Раствор :
  Дано: L ₁ = 16 H, L ₂ = 10 H, L ₃ = 21 H
  Так как,
  L = L ₁ + L ₂ + L ₃
  ∴ L = 16 + 10 + 21
  ∴ L = 47 61 Гн, а частота 240 Гц предоставил.