Из двоичной системы в десятичную. Как преобразовать двоичное число в десятичное: пошаговое руководство — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как перевести двоичное число в десятичное. Какие существуют методы конвертации двоичной системы в десятичную. Почему важно уметь переводить числа между системами счисления. Какие формулы используются при переводе двоичных чисел в десятичные.

Содержание

Основы двоичной и десятичной систем счисления

Двоичная и десятичная системы счисления являются фундаментальными в информатике и вычислительной технике. Понимание этих систем и умение переводить числа между ними крайне важно для работы с компьютерными технологиями.

Что такое двоичная система счисления?

Двоичная система использует только две цифры — 0 и 1. Каждый разряд в двоичном числе представляет степень двойки. Например, число 1010 в двоичной системе равно:

1 * 2^3 = 8
0 * 2^2 = 0
1 * 2^1 = 2
0 * 2^0 = 0

Сумма этих значений дает десятичное число 10.

Что представляет собой десятичная система?

Десятичная система использует 10 цифр от 0 до 9. Это привычная нам система счисления, в которой каждый разряд представляет степень 10. Например, число 2748 в десятичной системе означает:

2 * 10^3 = 2000
7 * 10^2 = 700
4 * 10^1 = 40
8 * 10^0 = 8

Методы перевода двоичных чисел в десятичные

Существует несколько способов перевода двоичных чисел в десятичные. Рассмотрим основные из них.

Метод разложения по степеням двойки

Этот метод основан на представлении двоичного числа в виде суммы степеней двойки:

Записываем двоичное число
Нумеруем разряды справа налево, начиная с 0
Умножаем каждую цифру на 2 в степени ее номера разряда
Суммируем полученные значения

Пример: переведем число 10110 из двоичной системы в десятичную.

1 * 2^4 = 16
0 * 2^3 = 0
1 * 2^2 = 4
1 * 2^1 = 2
0 * 2^0 = 0

Сумма: 16 + 0 + 4 + 2 + 0 = 22

Метод последовательного удвоения

Этот метод удобен для устного счета:

Берем первую (левую) цифру двоичного числа
Умножаем ее на 2 и прибавляем следующую цифру
Повторяем шаг 2 для всех оставшихся цифр

Пример: переведем число 1011 из двоичной системы в десятичную.

1
1 * 2 + 0 = 2
2 * 2 + 1 = 5
5 * 2 + 1 = 11

Результат: 11

Важность перевода между системами счисления

Умение переводить числа между двоичной и десятичной системами счисления важно по нескольким причинам:

Компьютеры работают с двоичными данными, а люди привыкли к десятичной системе
Перевод необходим при работе с низкоуровневым программированием и аппаратным обеспечением
Понимание систем счисления помогает в изучении компьютерных наук и информатики

Навыки перевода полезны при работе с сетевыми технологиями и IP-адресацией

Формула перевода двоичного числа в десятичное

Общая формула для перевода двоичного числа в десятичное выглядит следующим образом:

(a_na_n-1…a₁a₀)₂ = a_n*2ⁿ + a_n-1*2^n-1 + … + a₁*2¹ + a₀*2⁰

Где a_i — это цифры двоичного числа (0 или 1), а n — количество разрядов минус один.

Практические примеры перевода

Рассмотрим несколько примеров перевода двоичных чисел в десятичные:

Пример 1: Перевод целого двоичного числа

Переведем число 1101 из двоичной системы в десятичную:

1 * 2^3 = 8
1 * 2^2 = 4
0 * 2^1 = 0
1 * 2^0 = 1

Сумма: 8 + 4 + 0 + 1 = 13

Таким образом, (1101)₂ = (13)₁₀

Пример 2: Перевод дробного двоичного числа

Переведем число 101.11 из двоичной системы в десятичную:

Целая часть: 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 4 + 0 + 1 = 5
Дробная часть: 1 * 2^-1 + 1 * 2^-2 = 0.5 + 0.25 = 0.75

Сумма: 5 + 0.75 = 5.75

Таким образом, (101.11)₂ = (5.75)₁₀

Применение навыков перевода в реальной жизни

Умение переводить числа между двоичной и десятичной системами счисления находит применение во многих областях:

Программирование: работа с битовыми операциями и низкоуровневым кодом
Сетевые технологии: понимание IP-адресов и подсетевых масок
Криптография: работа с ключами и алгоритмами шифрования
Компьютерная графика: работа с цветовыми моделями и сжатием изображений
Системное администрирование: настройка прав доступа и работа с журналами

Инструменты для автоматизации перевода

Хотя важно уметь выполнять перевод вручную, существуют инструменты, которые могут автоматизировать этот процесс:

Онлайн-калькуляторы систем счисления
Программируемые калькуляторы с функциями перевода
Встроенные функции в языках программирования (например, int() в Python)
Специализированные приложения для инженеров и программистов

Однако важно помнить, что понимание процесса перевода остается критически важным для эффективной работы с различными системами счисления.

Заключение и рекомендации по практике

Перевод чисел между двоичной и десятичной системами счисления — важный навык для всех, кто работает с компьютерными технологиями. Чтобы улучшить свои навыки, рекомендуется:

Регулярно практиковаться в ручном переводе чисел
Решать задачи, связанные с системами счисления
Изучать применение двоичной системы в реальных компьютерных системах
Экспериментировать с различными методами перевода и находить наиболее удобный для себя

Помните, что уверенное владение этим навыком поможет вам лучше понимать работу компьютеров и эффективнее решать задачи в области информационных технологий.

Перевод из двоичной в десятичную систему счисления, калькулятор

Исходное число

Направление перевода

2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

Сообщить об ошибке

В избранное

Виджет

Вы можете сохранять ваши расчеты и они будут отображаться здесь.

Для сохранения расчета воспользуйтесь кнопкой под формой калькулятора.

Преобразовать число из двоичной системы счисления в десятичную можно следующим образом: каждый разряд числа необходимо умножить на 2ⁿ, где n — номер разряда, начиная с 0. Затем суммировать полученные значения.

abc₂ = (a×2² + b×2¹ + c×2⁰)₁₀

110

2 = (1*2² + 1*2¹ + 0*2⁰)₁₀ = 6₁₀

10010010₂ = (1*2⁷ + 0*2⁶ + 0*2⁵ + 1*2⁴ + 0*2³ + 0*2² + 1*2¹ + 0*2⁰)₁₀ = 146₁₀

Смотрите также

Перевод из двоичной в восьмеричную
Перевод из двоичной в шестнадцатеричную
Перевод из десятичной в двоичную
Перевод из десятичной в восьмеричную
Перевод из десятичной в шестнадцатеричную
Перевод из восьмеричной в двоичную
Перевод из восьмеричной в десятичную
Перевод из шестнадцатеричной в двоичную
Перевод из шестнадцатеричной в десятичную

Перевод чисел в различные системы счисления с решением | Онлайн калькулятор

Калькулятор позволяет переводить целые и дробные числа из одной системы счисления в другую.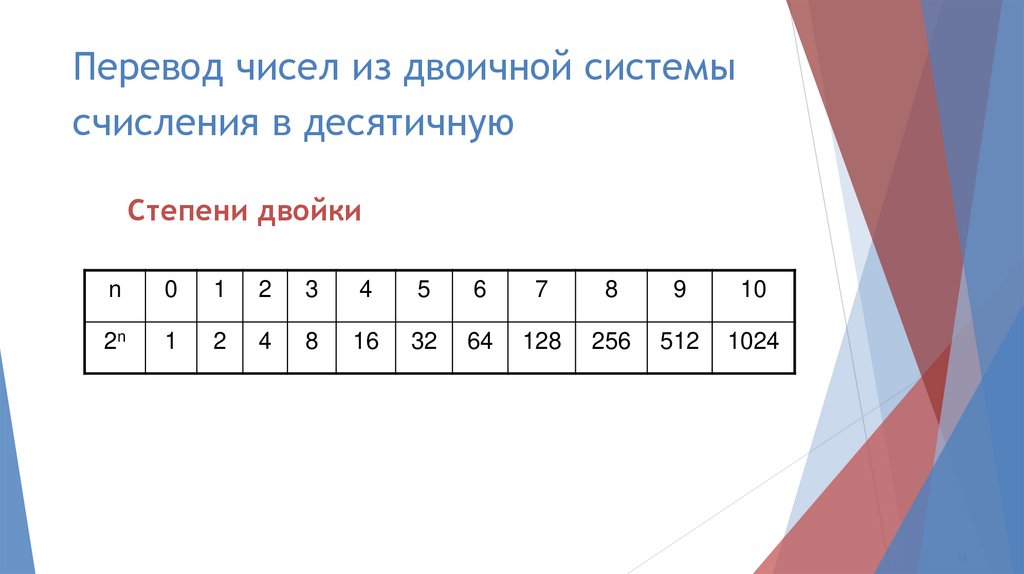

Основание системы счисления не может быть меньше 2 и больше 36 (10 цифр и 26 латинских букв всё-таки). Длина чисел не должна превышать 30 символов. Для ввода дробных чисел используйте символ . или ,. Чтобы перевести число из одной системы в другую, введите исходное число в первое поле, основание исходной системы счисления во второе и основание системы счисления, в которую нужно перевести число, в третье поле, после чего нажмите кнопку «Получить запись».

Исходное число записано в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.

Хочу получить запись числа в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.

Получить запись

_{= _{Выполнено переводов:
Также может быть интересно:
Калькулятор таблицы истинности. СДНФ. СКНФ. Полином Жегалкина
Калькулятор комплексных чисел
Системы счисления
Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.
Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:
Число: 5 9 2 1
Позиция: 3 2 1 0
Число 5921 можно записать в следующем виде: 5921 = 5000+900+20+1 = 5·10³+9·10²+2·10¹+1·10⁰
. Число 10 является характеристикой, определяющей систему счисления. В качестве степеней взяты значения позиции данного числа.
Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:
Число: 1 2 3 4 5 6 7
Позиция: 3 2 1 0 -1 -2 -3
Число 1234. 567 можно записать в следующем виде: 1234.567 = 1000+200+30+4+0.5+0.06+0.007 = 1·10³+2·10²+3·10¹+4·10⁰+5·10^-1+6·10^-2+7·10^-3.
Перевод чисел из одной системы счисления в другую
Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:
1. Перевести число 1001101.1101₂ в десятичную систему счисления.
Решение: 1001101. 1101₂ = 1·2⁶+0·2⁵+0·2⁴+1·2³+1·2²+0·2¹+1·2⁰+1·2^-1+1·2^-2+0·2^-3+1·2^-4 = 64+8++4+1+0.5+0.25+0.0625 = 77.8125₁₀
Ответ: 1001101.1101₂ = 77.8125₁₀
2. Перевести число E8F.2D₁₆ в десятичную систему счисления.
Решение: E8F.2D₁₆ = 14·16²+8·16¹+15·16⁰+2·16^-1+13·16^-2 = 3584+128+15+0.125+0.05078125 = 3727.17578125₁₀
Ответ: E8F.2D₁₆ = 3727.17578125₁₀
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.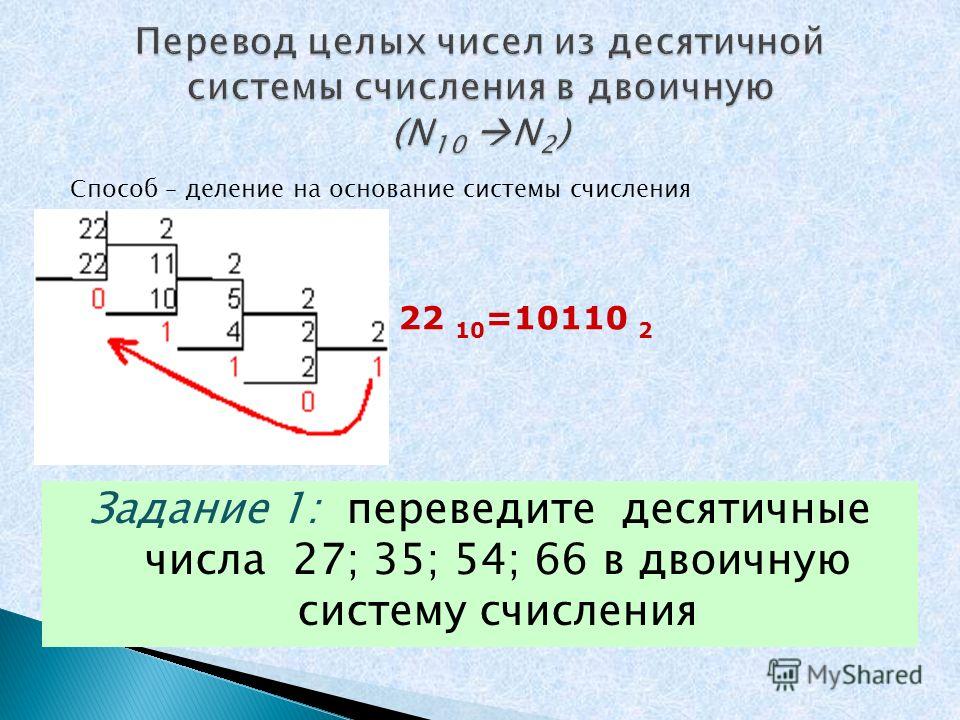
Перевод целой части числа из десятичной системы счисления в другую систему счисления
Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.
3. Перевести число 273₁₀ в восьмиричную систему счисления.
Решение: 273 / 8 = 34 и остаток 1, 34 / 8 = 4 и остаток 2, 4 меньше 8, поэтому вычисления завершены. Запись из остатков будет иметь следующий вид: 421
Проверка: 4·8²+2·8¹+1·8⁰ = 256+16+1 = 273 = 273, результат совпал. Значит перевод выполнен правильно.
Ответ: 273₁₀ = 421₈
Рассмотрим перевод правильных десятичных дробей в различные системы счисления.
Перевод дробной части числа из десятичной системы счисления в другую систему счисления
Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.
4. Перевести число 0.125₁₀ в двоичную систему счисления.
Решение: 0.125·2 = 0.25 (0 — целая часть, которая станет первой цифрой результата), 0.25·2 = 0.5 (0 — вторая цифра результата), 0.5·2 = 1.0 (1 — третья цифра результата, а так как дробная часть равна нулю, то перевод завершён).
Ответ: 0.125₁₀ = 0.001₂
Как преобразовать двоичное число в десятичное
Как преобразовать двоичное число в десятичное | преобразование чисел Главная›Конвертация›Преобразование чисел› Как преобразовать двоичное число в десятичное
Десятичное число равно сумме двоичных цифр (d _n ), умноженных на их степень 2 (2 ⁿ ):
десятичное = d ₀ × 2 ⁰ + d ₁ × 2 ¹ + d ₂ × 2 0 ^{3 # 1 9000 80031}
Найти десятичное значение 111001 ₂ :
двоичное число: 1 1 1 0 0 1
степень двойки: 2 ⁵ 2 ⁴ 2 ³ 2 ² 2 ¹ 2 ⁰
111001 ₂ = 1⋅2 ⁵ +1⋅2 ⁴ +1=2 ³ +0 % ² +0 % ¹ +1ac2 ⁰ = 57 ₁₀
Пример #2
Найти десятичное значение 100011 ₂ :
двоичное число: 1 0 0 0 1 1
степень двойки: 2 ⁵ 2 ⁴ 2 ³ 2 ² 2 ¹ 2 ⁰
100011 ₂ = 1t2 ⁵ +0 % ⁴ +0 % ³ +0 % ² +1 % 2 ¹ +1t2 ⁰ = 35 ₁₀
Преобразователь двоичного кода в десятичный ►
Таблица преобразования двоичного кода в десятичный
Двоичный Десятичный
0 0
1 1
10 2
11 3
100 4
101 5
110 6
111 7
1000 8
1001 9
1010 10
1011 11
1100 12
1101 13
1110 14
1111 15
10000 16
10001 17
10010 18
10011 19
10100 20
10101 21
10110 22
10111 23
11000 24
11001 25
11010 26
11011 27
11100 28
11101 29
11110 30
11111 31
100000 32
1000000 64
10000000 128
100000000 256

Преобразование десятичного числа в двоичное ►

См.
также Преобразователь двоичного кода в десятичный
Преобразователь двоичного кода в шестнадцатеричный
Преобразователь десятичного кода в двоичный
Напишите, как улучшить эту страницу
ПРЕОБРАЗОВАНИЕ ЧИСЛА
Двоичное число в десятичное
Двоичный код в шестнадцатеричный
Преобразование десятичного числа в двоичное
Десятичная дробь
Десятичный в шестнадцатеричный
Градусов в Радиан
Дробь до десятичной дроби
Шестнадцатеричный в десятичный
Шестнадцатеричный код в двоичный
Номер в латинице
Проценты к ppm
ppm в
процентов радиан в
градусов Роман на номер
БЫСТРЫЕ СТОЛЫ
Рекомендовать сайт
Отправить отзыв
О
Как преобразовать двоичное число в десятичное
Содержание
В этом блоге мы узнаем о четырех типах систем счисления, узнаем, как преобразовать двоичное число в десятичное и какие существуют различные методы преобразования. Итак, не теряя времени, приступим!
Введение
Что такое двоичная система счисления?
Что такое десятичная система счисления?
Что такое преобразование двоичного кода в десятичный?
Binary to Decimal Conversion Methods
Binary to Decimal Formula
How to Convert Binary to Decimal
Conclusion
Introduction In Mathematics, a number system is a way представления чисел. Существует четыре типа систем счисления, а именно:
Двоичная система счисления (основание 2)
Восьмеричная система счисления (основание 8)
Десятичная система счисления (основание 10)
Шестнадцатеричная система счисления (основание 16)
Система счисления играет важную роль в основном во всех компьютерных гаджетах и особенно в компьютерной архитектуре. Он используется компьютерными инженерами, специалистами по связи, сетями и другими специалистами. Прежде чем перейти к преобразованию двоичной системы в десятичную, давайте разберемся в обеих системах счисления.
Что такое двоичная система счисления? Двоичная система счисления — это простейшая форма системы счисления, в которой используются только две цифры: 0 (ноль) и 1 (единица). Ее также называют системой счисления с основанием 2. Этот номер в основном используется в компьютерной архитектуре и электронных устройствах.
Примеры двоичной системы счисления: 01, 101, 1110, 10011, 1011101 и т. д.
Что такое десятичная система счисления? Десятичная система счисления представляет собой представление чисел от 0 до 9. Десятичная система счисления является наиболее распространенной системой счисления, используемой широкой публикой. Эти системы счисления также известны как система счисления с основанием 10.
Пример десятичной системы счисления: 10, 121, 485, 8483, 82940 и т. д.
Что такое преобразование двоичного кода в десятичный? Преобразование двоичной системы счисления в десятичную выполняется для преобразования двоичной системы счисления в десятичную систему счисления, что означает преобразование системы счисления с основанием 2 в систему счисления с основанием 10. Важно знать двоичное преобразование в десятичное из-за приложений для компьютерного программирования. Таким образом, машина может понимать только двоичную систему счисления в форме 0 и 1, тогда как люди могут легко понять десятичную систему счисления, включающую все 10 цифр. Итак, важно понимать, как преобразовать двоичные системы счисления в десятичные системы счисления.
Методы преобразования двоичных чисел в десятичные Существует два основных метода преобразования двоичных систем счисления в десятичные. Это следующие методы:
Позиционная запись
Удвоение
Преобразование с использованием позиционной записи Запишите двоичное число и посчитайте степень 2 справа налево, начиная с 0 и далее.
Теперь каждое двоичное число имеет соответствующую степень двойки, начиная справа налево. Таким образом, самый старший бит будет иметь наивысшую степень 2.
Добавьте произведение второго шага
Окончательный ответ будет преобразован в десятичное число с основанием 10.
Пример позиционной записи Двоичное число: (101)2
1 0 1
1 х 22 + 0 х 21 + 1 х 20
4 + 0 + 1
(5)10
Итак, десятичное число (101)2 равно (5)10.
Аналогично мы можем представить дробное двоичное число в десятичные дроби
Двоичный номер: (0,101)2
1 0 1 . 1 0 1
1 х 22 + 0 х 21 + 1 х 20. 1 х 2-1 + 0 х 2-2 + 1 х 2-3
(4 + 0 + 1) . (0,5 + 0 + 0,125)
(5,625)10
Итак, десятичное число (0,101)2 равно (5,625)10.

Преобразование с использованием удвоения Преобразование с использованием удвоения — один из самых простых способов преобразования двоичных чисел в десятичные числа. Нам нужно взять самый старший разряд или крайнюю левую цифру числа. Затем умножьте цифру на 2, добавьте второй крайний левый бит и сохраните результат. Точно так же нам нужно взять результат и умножить его на 2, взять третий крайний левый бит и обновить результат. Этот процесс будет продолжаться до тех пор, пока мы не достигнем самого младшего бита, который является самым правым битом. Поскольку мы умножаем на 2, этот процесс известен как удвоение.
Пример удвоения Двоичное число: (101) ₂
= 1
= 1 x 2 + 0 = 2
= 2 x 2
= 2 x 2 9 00 3 десятичное число 5 (101) ₂ is (5) ₁₀
Формула преобразования двоичной системы счисления в десятичную Формула преобразования двоичной системы счисления в десятичную может быть представлена следующим образом: + х _н-1 * б ^н-1 + ….. + х ₁ * B ¹ + x ₀ * B ⁰
Где,
A представляет собой целое число
x представляет значение цифры
B представляет базовое значение
Например:
. (1000) ₂ = 1 x 2 ³ + 0 x 2 ² + 0 x 2 ¹ + 0 x 2 ⁰
Tabular. Номер Binary1 Decimal1 Binary2 Decimal2
0000 0 1000 8
0001 1 1001 9
0010 2 1010 10
0011 3 1011 11
0100 4 1100 12
0101 5 1101 13
0110 6 1110 14
0111 7 1111 15
Как преобразовать двоичное число в десятичное
Использование позиционной записи0408 (10001) ₂ 1 0 0 0 1
= 1 х 24 + 0 х 23 + 0 х 22 + 0 х 21 + 1 х 20
= 16 + 0 + 0 + 0 + 1
= (17)10

(1000.}}