Из треугольника в звезду. Преобразование треугольника в звезду: подробное руководство по эквивалентному преобразованию электрических схем

Как выполнить преобразование треугольника в звезду в электрических цепях. Какие формулы используются для расчета сопротивлений. Почему это преобразование полезно при анализе сложных схем. Как применить преобразование на практике.

Содержание

Что такое преобразование треугольника в звезду

Преобразование треугольника в звезду (также известное как преобразование дельта-игрек) — это метод, используемый в теории электрических цепей для упрощения анализа схем. Он позволяет заменить три резистора, соединенных треугольником, на три эквивалентных резистора, соединенных звездой.

Основная идея этого преобразования заключается в том, что сопротивление между любыми двумя точками треугольника должно быть равно сопротивлению между теми же точками в эквивалентной звезде. Это позволяет преобразовать сложную схему в более простую для анализа конфигурацию.

Формулы для преобразования треугольника в звезду

Для выполнения преобразования треугольника в звезду используются следующие формулы:

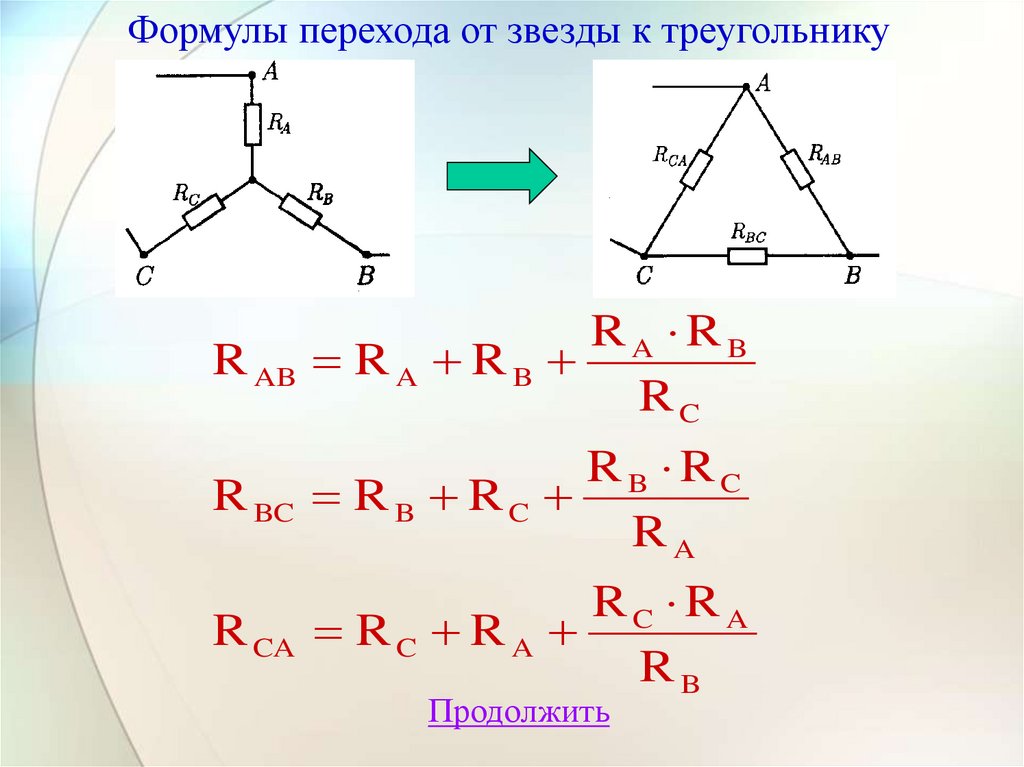
R1 = (Ra * Rb) / (Ra + Rb + Rc)
R2 = (Rb * Rc) / (Ra + Rb + Rc)
R3 = (Ra * Rc) / (Ra + Rb + Rc)

Где R1, R2, R3 — сопротивления ветвей звезды, а Ra, Rb, Rc — сопротивления сторон треугольника.

Для обратного преобразования звезды в треугольник используются формулы:

Ra = (R1 * R2 + R2 * R3 + R3 * R1) / R3
Rb = (R1 * R2 + R2 * R3 + R3 * R1) / R2
Rc = (R1 * R2 + R2 * R3 + R3 * R1) / R1

Зачем нужно преобразование треугольника в звезду

Преобразование треугольника в звезду позволяет упростить анализ сложных электрических схем. Оно особенно полезно в следующих случаях:

Когда в схеме есть участки, соединенные треугольником, которые нельзя упростить обычными методами последовательного и параллельного соединения.
Для расчета эквивалентного сопротивления сложных цепей.
При анализе трехфазных систем электроснабжения.
Для упрощения топологии схемы и уменьшения количества узлов.

Применяя это преобразование, можно свести сложную схему к более простой конфигурации, которую легче анализировать традиционными методами.

Пошаговая инструкция по выполнению преобразования

Чтобы выполнить преобразование треугольника в звезду, следуйте этим шагам:

Определите участок схемы, соединенный треугольником, который нужно преобразовать.
Обозначьте сопротивления сторон треугольника как Ra, Rb и Rc.
Рассчитайте сопротивления ветвей звезды R1, R2 и R3 по формулам, приведенным выше.
Замените треугольник эквивалентной звездой в схеме.
Продолжите анализ упрощенной схемы обычными методами.

Важно помнить, что после преобразования токи и напряжения в остальной части схемы останутся неизменными.

Пример применения преобразования треугольника в звезду

Рассмотрим пример использования преобразования для упрощения схемы:

Дана схема с резисторами, соединенными треугольником:

Ra = 10 Ом
Rb = 20 Ом
Rc = 30 Ом

Выполним преобразование в звезду:

R1 = (10 * 20) / (10 + 20 + 30) = 3.33 Ом
R2 = (20 * 30) / (10 + 20 + 30) = 10 Ом
R3 = (10 * 30) / (10 + 20 + 30) = 5 Ом

Теперь треугольник можно заменить звездой с сопротивлениями 3.33 Ом, 10 Ом и 5 Ом. Это позволит упростить дальнейший анализ схемы.

Ограничения и особенности применения преобразования

При использовании преобразования треугольника в звезду следует учитывать следующие моменты:

Преобразование применимо только к линейным резистивным цепям.
Оно не меняет токи и напряжения в остальной части схемы.
Преобразование может быть применено к любой части схемы, соединенной треугольником.
В некоторых случаях может потребоваться обратное преобразование звезды в треугольник.

При наличии источников тока или напряжения внутри треугольника преобразование усложняется.

Понимание этих особенностей позволит корректно применять метод в различных ситуациях.

Альтернативные методы анализа сложных схем

Хотя преобразование треугольника в звезду очень полезно, существуют и другие методы анализа сложных электрических цепей:

Метод контурных токов
Метод узловых потенциалов
Метод наложения
Теорема Тевенена
Теорема Нортона

Каждый из этих методов имеет свои преимущества и может быть более эффективным в определенных ситуациях. Выбор конкретного метода зависит от типа схемы и поставленной задачи.

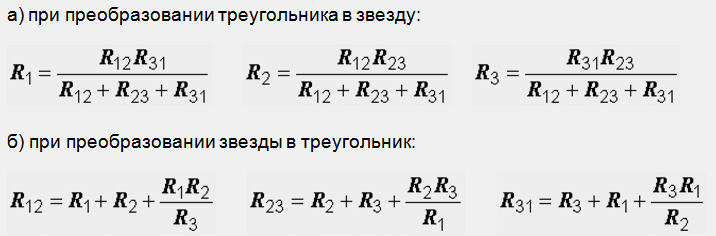
Заключение

Преобразование треугольника в звезду — это мощный инструмент для упрощения и анализа сложных электрических схем. Оно позволяет преобразовать труднорешаемые конфигурации в более простые эквивалентные схемы. Понимание принципов и правильное применение этого метода значительно облегчает расчеты в электротехнике и электронике.

Освоив технику преобразования треугольника в звезду, инженеры и студенты получают возможность эффективно решать широкий спектр задач, связанных с анализом электрических цепей. Это умение является важной составляющей профессионального инструментария в области электротехники.

Преобразование треугольник/звезда: что за сценой?

Добавлено 17 июня 2019 в 12:15

Преобразования треугольник/звезда позволяют нам заменить часть схемы другой схемой, которая, хотя и эквивалентна в поведении, но может значительно упростить анализ общей схемы. Здесь мы узнаем, откуда берутся эти преобразования.

Зачем?

Когда мы начали изучать электронику, резисторы были соединены либо последовательно, либо параллельно, и мы научились заменять такие комбинации их эквивалентными сопротивлениями, часто с целью уменьшения всей сети сопротивлений до единственного эквивалентного сопротивления, видимого из источника питания. После этого появились схемы (рисунок 1), которые содержали резисторы, которые не были ни последовательными, ни параллельными, но их всё же можно было убрать, тщательно определяя и сокращая фрагменты схемы в правильном порядке. Обратите внимание, что R₁ не параллелен и не последователен ни с R₂, ни с R₃, но путем объединения R₂ последовательно с R₄, и объединяя R₃ последовательно с R₅, мы можем затем объединить эти два эквивалентных сопротивления параллельно и, наконец, объединив результат последовательно с R₁, получить полное сопротивление, видимое источнику питания, которое, используя закон Ома, поможет получить общий ток источника питания.

Рисунок 1

Но теперь мы подошли к схемам (рисунок 2), где нет никаких пар резисторов, которые включены последовательно или параллельно, – похоже, мы зашли в тупик. Одним из способов анализа этой схемы является использование закона напряжений Кирхгофа (второй закон) и закона токов Кирхгофа (первый закон) для получения алгебраических уравнений, которые мы можем решить для напряжений и токов. Хотя этот подход будет работать всегда (для этой и большинства других типов схем), он может быть довольно громоздким. Мы могли бы смириться с этим как с ценой возможности анализа этих более сложных схем, но иногда мы можем избежать оплаты этого счета, изменяя или «преобразовывая» фрагменты схемы, чтобы превратить ее в нечто, что мы можем уменьшить, используя только правила последовательного/параллельного объединения.

Рисунок 2

Для простоты мы будем рассматривать только цепи постоянного тока с резисторами, но эти принципы применимы к любой линейной системе переменного или постоянного тока. Кроме того, чтобы сфокусировать обсуждение на преобразованиях, мы найдем только общий ток, поставляемый источником напряжения, что означает, что мы стремимся свести всю сеть резисторов в единое эквивалентное сопротивление.

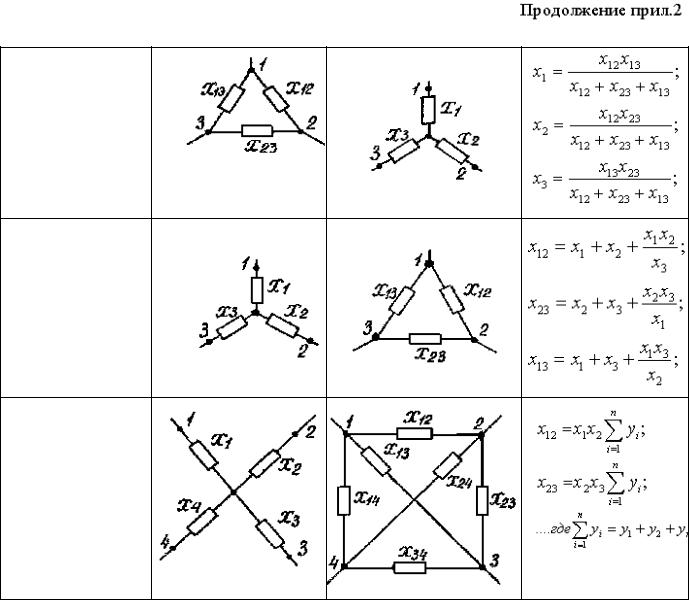
Давайте рассмотрим эти две схемы немного подробнее (рисунок 3). Мы видим, что единственная разница между ними заключается в том, что находится внутри пунктирных окружностей. В каждом случае цепь в окружности имеет три контакта, которые пересекают окружность для взаимодействия с остальной частью схемы. В левой цепи (рисунок 3(a)) резисторы подключены к контактам в конфигурации «треугольник» (в англоязычной литературе, конфигурация «delta», «дельта», названная в честь заглавной греческой буквы Δ). А в правой цепи резисторы подключены в конфигурации «звезда» (в англоязычной литературе, конфигурация «wye», «уай», названная в честь заглавной английской буквы Y, хотя в схеме она перевернута).

Рисунок 3

Теперь представьте, что резисторы внутри пунктирной окружности в левой цепи помещены в черный ящик, этот ящик удален из схемы и заменен другим черным ящиком, который заставляет схему вести себя точно так же. Далее представьте, что, когда вы открываете, этот новый ящик он содержит три резистора, расположенных как в правой цепи. Кто бы ни придумал второй черный ящик, он очень тщательно выбрал значения резисторов так, чтобы эти два блока были неразличимы для остальной части схемы: мы знаем, как анализировать правую схему, и теперь мы знаем, что когда мы это делаем, результаты можно применить к левой схеме, потому что они эквивалентны. Вот зачем выполнять преобразования «треугольник→звезда» и «звезда→треугольник».

Основные соотношения

Чтобы определить уравнения, связывающие резисторы в цепи, соединенной треугольником, с резисторами в цепи, соединенной звездой, нам ничего не нужно, кроме наших надежных формул для последовательных/параллельных соединений (и немного алгебры). Идея заключается в выравнивании эквивалентных сопротивлений между соответствующими парами контактов при отключенном оставшемся контакте (рисунок 4)

Рисунок 4

Выполнив это для эквивалентного сопротивления между контактами B-C, мы получим:

\[R_B + R_C = \frac{R_{BC} \left( R_{AB} + R_{AC} \right) }{R_{AB} + R_{BC} + R_{AC}}\]

Если мы повторим этот процесс для каждой другой пары контактов по очереди, мы получим еще два аналогичных уравнения, и любое из них даст нам необходимую нам информацию (при условии, что мы распознаем задействованную симметрию).

Частный случай: симметричные схемы

Если сопротивления в каждом плече цепи, соединенной треугольником или звездой, равны, такая цепь считается «симметричной». Это означает, что

\[R_∆ = R_{AB} = R_{BC} = R_{AC}\]

\[R_Y = R_A = R_B = R_C\]

Комбинация этого условия с соотношением из предыдущего раздела сразу приводит к уравнению преобразования для случая симметрии.

\[2R_Y = \frac{R_∆(2R_∆)}{3R_∆}\]

\[R_Y = \frac{R_∆}{3}\]

\[R_∆ = 3R_Y\]

Это гораздо более значительный результат, чем может показаться на первый взгляд, и причина довольно проста – когда инженеры проектируют схемы с соединениями треугольник или звезда, они часто стараются сделать эти схемы симметричными. Хотя, конечно, это не всегда возможно, и поэтому мы должны иметь возможность разобраться с общим случаем, когда схема не симметрична.

Общий случай преобразования треугольник→звезда

Для преобразования треугольник/звезда нам дана известная схема, соединенная треугольником, и мы хотим найти значения для эквивалентной схемы, соединенной звездой, – поэтому мы пытаемся найти {R_A, R_B, R_C} для заданных {R_AB, R_BC, R_AC}.

Мы начнем с того, что запишем наши основные соотношения из первоначального вида в несколько более компактной форме, определив новую величину, R_ΔS, которая равна сумме сопротивлений всех резисторов в цепи, соединенной треугольником.

\[R_{ΔS}=R_{AB}+R_{BC}+R_{AC}\]

Затем мы делаем перестановку нашего соотношения для получения вида линейного алгебраического уравнения с неизвестными {R_A, R_B, R_C}.

\[(0)R_A+(R_{ΔS})R_B+(R_{ΔS})R_C=R_{AB}R_{BC}+R_{BC}R_{AC}\]

Поскольку у нас есть три неизвестных, нам нужно еще два уравнения. Они получаются из эквивалентных сопротивлений, видимых при рассмотрении двух других пар контактов. Выполнив это (или используя симметрию) мы получаем

\[(R_{ΔS})R_A+(0)R_B+(R_{ΔS})R_C=R_{AB}R_{AC}+R_{BC}R_{AC}\]

\[(R_{ΔS})R_A+(R_{ΔS})R_B+(0)R_C=R_{AB}R_{AC}+R_{AB}R_{BC}\]

Сложив эти два уравнения вместе и вычтя наше первое уравнение, мы получим

\[2(R_{ΔS})R_A=2R_{AB}R_{AC}\]

\[R_A= {R_{AB}R_{AC} \over R_{ΔS}}\]

Мы можем решить систему уравнению для двух других неизвестных сопротивлений (или использовать симметрию), чтобы получить

\[R_B= {R_{AB}R_{BC} \over R_{ΔS}}\]

\[R_C= {R_{AC}R_{BC} \over R_{ΔS}}\]

Эти отношения могут быть обобщены очень компактно. Сопротивление, подключенное к каждому узлу в эквивалентной цепи, соединенной звездой, равно произведению сопротивлений, подключенных к соответствующему узлу в цепи, соединенной треугольником, деленному на сумму сопротивлений всех резисторов в треугольнике. Обычно это выражается формулой, такой как

\[R_N= {R_{N1}R_{N2} \over R_{ΔS}}\]

где

R_N – резистор, подключенный к контакту N в схеме «звезда»;
R_N1 и R_N2 – резисторы, подключенные к контакту N в схеме «треугольник»

Общий случай преобразования звезда→треугольник

Для преобразования звезда→треугольник нам дана известная схема, соединенная звездой, и мы хотим найти значения для эквивалентной схемы, соединенной треугольником. Следовательно, мы пытаемся найти {R_AB, R_BC, R_AC} для заданных {R_A, R_B, R_C}.

Это не так просто, как в случае преобразования треугольник→звезда потому, что неизвестные сопротивления перемножаются вместе, делая результирующие уравнения нелинейными. К счастью, мы можем обойти это неудобство, рассмотрев отношения сопротивлений резисторов в каждой цепи. Например, взяв отношение R_A к R_B, мы получаем

\[{R_A \over R_B} = { R_{AB}R_{AC} \over R_{AB}R_{BC} } = {R_{AC} \over R_{BC} }\]

Другими словами, отношение сопротивлений резисторов, подключенных к любым двум контактам в схеме звезда, равно отношению сопротивлений резисторов, соединяющих те же самые два контакта с третьим контактом в схеме треугольник. Следовательно, два других соотношения будут следующими

\[{R_B \over R_C} = {R_{AB} \over R_{AC} }\]

\[{R_A \over R_C} = {R_{AB} \over R_{BC} }\]

Вооружившись этим, мы могли бы вернуться к нашим основным соотношениям и продолжить работу с ними, но в качестве отправной точки проще использовать одно из отношений из общего случая преобразования треугольник→звезда.

\[R_A= {R_{AB}R_{AC} \over R_{AB} + R_{BC}+R_{AC} }\]

\[R_{AB}R_{AC} = R_A (R_{AB} + R_{BC}+R_{AC})\]

\[R_{AB} = R_A \left( {R_{AB} + R_{BC}+R_{AC} \over R_{AC} } \right)\]

\[R_{AB} = R_A \left( {R_{AB} \over R_{AC}} + {R_{BC} \over R_{AC} } + 1 \right)\]

\[R_{AB} = R_A \left( {R_{B} \over R_{C}} + {R_{B} \over R_{A} } + 1 \right)\]

\[R_{AB} = R_A + R_B + {R_AR_B \over R_C } \]

Два других выражения получаются аналогично (или согласно симметрии):

\[R_{BC} = R_B + R_C + {R_B R_C \over R_A } \]

\[R_{AC} = R_A + R_C + {R_A R_C \over R_B } \]

Эти выражения могут быть обобщены очень компактно. Сопротивление, подключенное между каждой парой узлов в эквивалентной схеме, соединенной треугольником, равно сумме сопротивлений двух резисторов, подключенных к соответствующим узлам в схеме, соединенной звездой, плюс произведение сопротивлений этих двух резисторов, деленное на сопротивление третьего резистора.

Общий способ выразить это состоит в том, чтобы поместить правую часть под общим знаменателем, а затем отметить, что числитель в каждом выражении является суммой произведений каждой пары сопротивлений в цепи, соединенной звездой, а знаменатель – это сопротивление, подключенное к третьему контакту.

\[R_{AB}={R_P \over R_C}\]

\[R_P = R_A R_B + R_B R_C + R_A R_C\]

Пример

Рисунок 5

Давайте поработаем с задачей, показанной на рисунке 5. Прежде чем мы начнем, давайте определим ожидаемый ответ, чтобы у нас была хорошая проверка того, является ли наш окончательный ответ правильным. Для этого рассмотрим роль мостового резистора 150 Ом. Этот резистор служит для уменьшения общего сопротивления, обеспечивая путь между левой и правой сторонами цепи. Следовательно, самое высокое эффективное сопротивление будет иметь место, если этот резистор будет удален полностью, и в этом случае полное сопротивление будет равно параллельной комбинации левой и правой сторон, что приведет к

\[R_{экв.max}=(100 +220)||(470+330)=228,6 \; Ом\]

С другой стороны, наименьшее общее сопротивление было бы получено путем уменьшения мостового резистора до прямого короткого замыкания, и в этом случае общее сопротивление было бы равно параллельной комбинации двух верхних резисторов, включенной последовательно с параллельной комбинацией двух нижних резисторов, что приведет к

\[R_{экв. min}=(100||470)+(220||330)=214,5 \; Ом\]

Теперь мы ЗНАЕМ, что наш ответ ДОЛЖЕН быть между этими двумя предельными значениями. Во многих случаях простой анализ границ, такой как этот, приводит к ответу, который «достаточно хорошо» подходит для данной цели, но давайте предположим, что это не так. Используя приведенные выше уравнения преобразования треугольник→звезда, мы сначала определяем сумму сопротивлений резисторов треугольника.

\[R_{ΔS}=100+150+470=720 \; Ом\]

А затем находим значение R₁, перемножив сопротивления двух резисторов, которые подключены к верхнему контакту, и разделив это произведение на сумму всех трех сопротивлений.

\[R_1={100⋅470 \over 720}=65,28 \; Ом\]

Повторим это же для R₂.

\[R_2={100⋅150 \over 720}=20,83 \; Ом\]

Мы могли бы повторить это еще раз для R₃, но давайте, вместо этого, определим R₃, используя свойства отношений.

\[{R_3 \over R_1}={150 \over 100}⇒R_3=1,5R_1=97,92 \; Ом\]

Теперь, когда у нас есть все сопротивления для эквивалентной схемы звезда, мы можем очень легко определить общее сопротивление.

\[R_{экв.}=R_1+[(R_2+220)||(R_3+330)]=219,4 \; Ом\]

Поскольку это значение находится между нашими минимальной и максимальной границами, мы полностью уверены, что это правильный ответ, или, даже если мы допустили ошибку, наш ответ довольно близок к правильному. Поэтому суммарный ток равен

\[I={12\; В \over 219,4 \; Ом}=54,7 \; мА\]

Заключение

Теперь мы увидели, что преобразования треугольник/звезда полезны, и, что более важно, увидели, как их можно легко выполнить, используя не более чем концепцию эквивалентных сопротивлений с использованием последовательных/параллельных комбинаций резисторов. Это может хорошо вам помочь, поскольку дает вам возможность вывести эти формулы на лету, если когда-нибудь возникнет в них необходимость, и у вас не будет подходящего справочного материала. Но что еще более важно, это должно служить для более прочного закрепления фундаментальных понятий в наборе инструментов, который хранится у вас в голове, позволяя вам использовать в своей работе еще более эффективные навыки анализа цепей.

В конце мы должны принять к сведению распространенное заблуждение, заключающееся в том, что преобразования треугольник↔звезда являются ЕДИНСТВЕННЫМ способом анализа цепей, которые нельзя уменьшить другими способами. В действительности, хотя эти преобразования могут сделать нашу жизнь проще, они не обязательны, поскольку ЛЮБОЙ контур, который можно проанализировать с их помощью, также можно проанализировать с помощью правил Кирхгофа, либо напрямую, либо с помощью одного из более формализованных методов их применения, включая метод контурных токов или метод узловых напряжений, а также с методиками, такими как эквивалентная схема Тевенина.

Оригинал статьи:

William Bahn. Delta/Wye Transforms: Behind the Scenes

Эквивалентное преобразование треугольника и звезды сопротивлений

Пусть требуется рассчитать цепь, показанную на рис. 1.12, (а).

Расчет можно осуществить одним из описанных выше методов. Но так как в цепи имеется только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.

Треугольник и звезда сопротивлений имеют вид, показанный на рис. 1.13.

Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.

Можно показать, что условием эквивалентности являются следующие уравнения:

а) при преобразовании треугольника в звезду:

б) при преобразовании звезды в треугольник:

Структура приведенных формул проста и легко запоминается.

Например, сопротивление звезды R₁, присоединенное к узлу 1, получается перемножением сопротивлений R₁₂ и R₃₁ треугольника, присоединенных к этому же узлу, и делением полученного произведения на сумму всех сопротивлений треугольника.

При обратном преобразовании сопротивление треугольника R₁₂, лежащее между узлами 1 и 2, равно сумме сопротивлений звезды R₁ и R₂, присоединенных к этим узлам, плюс их произведение, деленное на сопротивление третьего луча звезды R₃.

Пример 1.3. Рассчитать токи в цепи, изображенной на рис. 1.12, а, при следующих числовых значениях ее параметров: Е = 660 В,
R₁= 20 Ом, R₂= 30 Ом, R₃= 5 Ом, R₄= 20 Ом, R₅= 50 Ом.

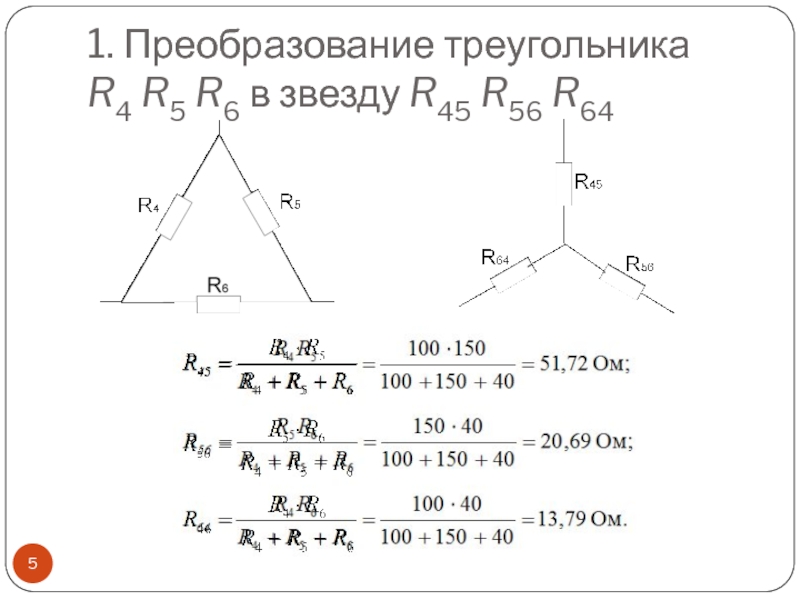
а) Решение преобразования треугольника в звезду:

после преобразования треугольника, образованного сопротивлениями R₁, R₂ и R₅, в звезду, получаем схему, показанную на рис. 1.12, б. Обращаем внимание на то, что токи в непреобразованной части схемы (I, I₃ и I₄) остались теми же.

Сопротивления звезды определяем по сформулированному выше правилу:

Где,общее сопротивление цепи легко находится по последней формуле R_общ= 16,5 Ом.

Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен:

Токи в параллельных ветвях:

где, I₃ = 28 A и I₄ = 12 A соответственно.

Возвращаемся к исходной схеме (рис. 1.12, а):

где, I₁ = 26 A и I₂ = 14 A соответственно.

Ток в пятой ветви находим из первого закона Кирхгофа: I₅= I₁–I₃= 26–28 = –2 A. Знак (—) минус говорит о том, что действительное направление тока I₅противоположно указанному на схеме.

б) Решение преобразованием звезды в треугольник.

Преобразуем звезду, образуемую в схеме на рис. 1.12, а сопротивлениями R₁, R₅ и R₃, в эквивалентный треугольник (рис. 1.12, в).

Определяем сопротивления треугольника:

Теперь рассчитываем преобразованную цепь.

Сначала находим эквивалентные сопротивления участков ac и cd:

Затем определяем общее сопротивление и токи:

Возвращаемся к исходной схеме:

Для решения в приведенных формулах, вставьте числовые значения параметров цепи и сравните результаты вычислений с полученными выше решения в примере 1. 3а.

Волчки деревянные треугольные звезды

Похоже, в вашем браузере отключен JavaScript.
Для использования функций этого веб-сайта в вашем браузере должен быть включен JavaScript.

Изделия для рукоделия
- Изделия для рукоделия в зависимости от материала
  - Изделия из керамики и гипса
  - Изделия из ткани
  - Изделия из пенопласта
  - Изделия из кожи
  - Поделки из шаров и воздушных шаров
    - Поделки из шаров
    - Поделки из воздушных шаров
  - Поделки из сумок
  - Поделки из банков0015
  - Beadging Crafts
  - Сделано для спальни
    - Clock Crafts
    - Дверные костюмы
    - Ночные световые ремесла
    - Picture Frame Crafts
  - BINOCLESTER FIRESTER, CARFOPPOPPOPE & PERISCTS
  - .
  - Поделки для книг
    - Поделки для журналов
    - Поделки для закладок
    - Поделки для книжных полок
  - Поделки из бутылок и чашек
  - коробка, контейнер и баночные ремесла
  - Свеча ремесло
  - Car & Articopter. Поделки-клоуны
  - Поделки-подставки и подставки
  - Книжки-раскраски
  - Поделки-раскраски
  - Поделки-декупажи
  - Поделки-куклы
  - Поделки-веера
  - Fine Motor Skills Crafts
  - Гибкие деревянные ремесла
  - Flower & Garden Crafts
    - Цветовые и деревья
    - Crafts Crafts
    - Поделки из еды
      - Поделки из чашек, кружек и бутылок с водой
      - Поделки под салфетки
      - Поделки из угощений
    - Поделки из фрисби
    - Fuse Bead Crafts
      - Super Beads
      - Magic Beads
    - Hanging Crafts
      - Dream Catcher Crafts
      - Ornament Crafts
      - Suncatcher Crafts
      - Wind Chime Crafts
    - Heart Crafts
    - Inflatable Crafts
    - Поделки-цепочки для ключей
    - Поделки из воздушных змеев
    - Поделки-ночники и лампы
    - Поделки-магниты
    - Поделки из глины для лепки
    - Monster Crafts
  - Расходные материалы
  - Игрушки и игры
  - S. T.E.A.M.
  - Праздники и события
  - Распродажи
  - Рекламные товары
  - Блог
  Дважды щелкните изображение выше, чтобы просмотреть его в полном размере. Сложите деревянные треугольники так, чтобы получилась звезда.
  Часто покупают вместе…
  Обзоры продуктов
  Напишите свой собственный обзор
  
  Зимний треугольник – Путеводитель по созвездиям и Сириус. Три яркие звезды образуют равносторонний треугольник, который доминирует на вечернем небе зимой в северном полушарии. Астеризм появляется вблизи небесного экватора и виден из большинства мест на Земле, по крайней мере, часть года.
  Зимний треугольник, изображение предоставлено Европейским космическим агентством Хаббла, Akira Fujii.
  Бетельгейзе, вторая по яркости звезда Ориона, является частью узнаваемой фигуры небесного Охотника в виде песочных часов. Красный сверхгигант отмечает правое плечо Ориона (левое с нашей точки зрения) и появляется прямо над Поясом Ориона, одним из наиболее узнаваемых астеризмов на ночном небе.
  Сириус, самая яркая звезда в созвездии Большого Пса, отмечает морду Большого Пса. Это самая южная звезда в воображаемом равностороннем треугольнике, который она образует с Бетельгейзе и Проционом, и единственная из трех звезд, которая находится в южном небесном полушарии.
  Созвездия Зимнего Треугольника, изображение: Stellarium
  Процион — самая яркая звезда в слабом созвездии Малого Пса. Представляя собой меньшую из двух собак, следующих за Орионом, Малый Пес появляется прямо к югу от Кастора и Поллукса, самых ярких звезд в Близнецах.
  Большой и Малый Пес не граничат друг с другом. Их разделяет Единорог (Единорог), слабое созвездие, лежащее к востоку от Ориона. Большая часть Единорога находится в пределах Зимнего Треугольника, и три яркие звезды Зимнего Треугольника могут быть использованы для поиска нескольких хорошо известных объектов глубокого космоса в созвездии, включая туманность Розетка и туманность Конус.
  Звезды
  Звезды Зимнего треугольника — одни из самых ярких звезд на небе. Сириус, светило Большого Пса (Большого Пса), является самой яркой звездой на земном небе. С визуальной величиной -1,46 она почти вдвое ярче Канопуса, второй по яркости звезды, расположенной в созвездии Киля.
  Процион, ярчайшая звезда Малого Пса, является восьмой по яркости звездой на небе, а Бетельгейзе — 10-й по яркости звездой. Бетельгейзе немного тусклее, чем ее соседка с Ориона Ригель, светлая звезда созвездия. Человеческому глазу красный сверхгигант кажется таким же ярким, как Ахернар, девятая по яркости звезда.
  Звезды Зимнего Треугольника: Сириус, Процион и Бетельгейзе, изображение: Stellarium
  Три звезды лежат вблизи небесного экватора и видны из обоих полушарий. Несмотря на то, что они находятся в области, полной других ярких звезд, звезды Зимнего Треугольника легко выделяются на небе.
  Сириус и Процион являются первичными звездами в звездных системах, которые также включают компаньонов белых карликов, в то время как Бетельгейзе является одиночной звездой. Бетельгейзе — сверхгигантская звезда с естественной яркостью, расположенная в сотнях световых лет от нас, в то время как Сириус и Процион кажутся такими яркими, потому что находятся по соседству с Солнцем.
  Сириус
  Сириус, Альфа Большого Пса (α CMa), является второй ближайшей видимой звездой к Солнцу и седьмой индивидуальной ближайшей звездой к Земле. Это белая звезда главной последовательности спектрального класса A0mA1 Va, расположенная всего в 8,60 световых годах от нас.
  Широко известный как Звезда Пса, Сириус имеет массу, примерно вдвое превышающую массу Солнца, и радиус 1,711 солнечного радиуса. При температуре поверхности 9 940 К он светит с яркостью 25,4 солнечной. Предполагаемый возраст звезды составляет около 242 миллионов лет.
  Имя Сириус происходит от древнегреческого Σείριος ( Seirios ), что означает «светящийся» или «палящий». Возможно, он был связан с богом Осирисом в Древнем Египте.
  У Сириуса есть двойной компаньон, слабый белый карлик спектрального класса DA2, ласково называемый Щенок.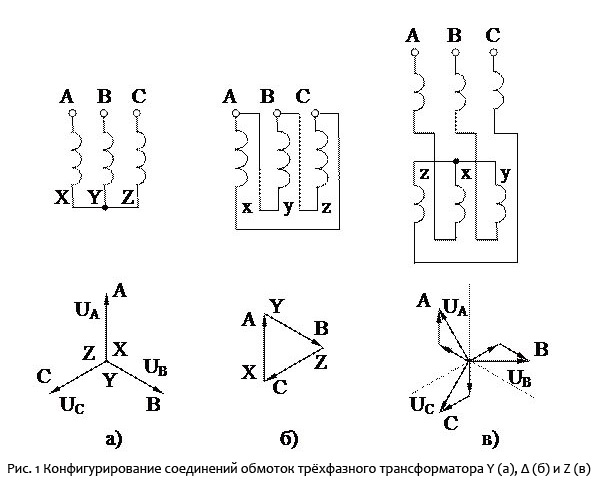 Сириус B сияет с величиной 8,44, и его невозможно увидеть без бинокля. Лежит 8.709световых лет от нас.
  Звездный остаток упаковывает массу Солнца в радиус всего 0,0084 солнечного радиуса. Это один из самых массивных известных белых карликов. Он имеет эффективную температуру 25 000 К и сияет с яркостью 0,056 солнечной.
  Сириус и Сириус B имеют период обращения 50,1284 года. На небе их разделяют 7,4957 угловых секунды. Физическое расстояние между ними колеблется от 8,2 до 31,5 астрономических единиц.
  Процион
  Процион, Альфа Малого Пса (α CMi), является 18-й ближайшей индивидуальной звездой к Солнцу и четвертой ближайшей видимой звездой. Она имеет видимую величину 0,34 и находится на расстоянии 11,46 световых лет от нас.
  Процион — более развитая звезда, чем Сириус. Она имеет звездную классификацию F5 IV – V, указывающую на звезду, которая подходит к концу своей жизни на главной последовательности и превращается в субгиганта. Процион превратится в гигантскую звезду в течение следующих 10–100 миллионов лет, после чего он вырастет в 80–150 раз по сравнению с нынешним размером.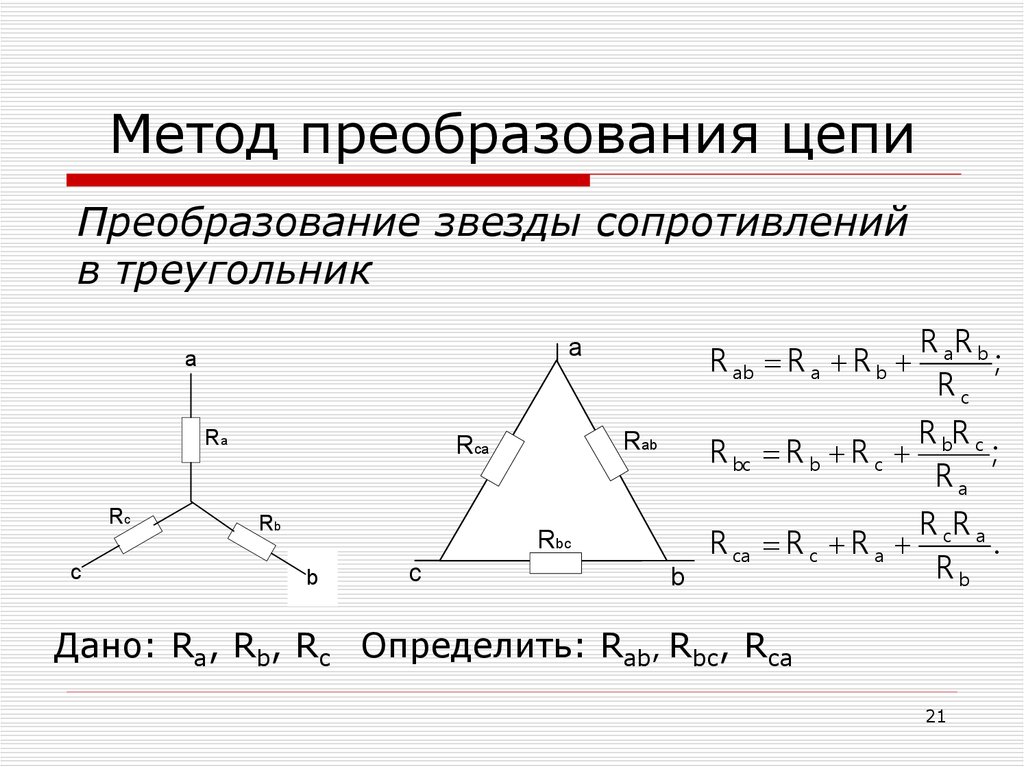
  Звезда имеет массу 1,499 массы Солнца и радиус примерно в два раза больше, чем у Солнца. Он в 6,93 раза ярче Солнца и имеет температуру поверхности около 6530 К. Предполагаемый возраст Проциона составляет около 1,87 миллиарда лет.
  Имя Процион происходит от древнегреческого Προκύων ( Prokyon ), что означает «перед собакой». Название является отсылкой к тому факту, что Процион восходит перед более яркой Собачьей звездой (Сириусом), если смотреть из средних северных широт.
  Как и Сириус, Процион является частью звездной системы. У него есть компаньон — белый карлик, Процион B. Два компонента вращаются вокруг друг друга с периодом 40 840 лет при среднем расстоянии 15 астрономических единиц.
  Процион B имеет звездную классификацию DQZ. Его масса составляет 60,2% массы Солнца, а радиус всего 1,234% солнечного. При эффективной температуре 7740 К он светит с 0,00049солнечные светимости. Он имеет видимую величину 10,7 и невидим невооруженным глазом.
  Зимний треугольник, фото: Европейское космическое агентство Хаббла, Akira Fujii
  Бетельгейзе
  Бетельгейзе, Альфа Ориона (α Ориона), красный сверхгигант с видимой величиной 0,50. Это самая удаленная из трех звезд Зимнего треугольника, находящаяся на расстоянии около 548 световых лет.
  Бетельгейзе имеет звездную классификацию M1-M2 Ia-ab. Классифицируется как полуправильная переменная звезда. Его яркость варьируется от 0,0 до 1,6 звездной величины. Это означает, что сверхгигант иногда затмевает обычно более яркий Ригель и становится самой яркой звездой Ориона. Иногда она может даже затмить Вегу, пятую по яркости звезду на небе.
  Самая тусклая звезда Бетельгейзе достигает второй величины и сияет так же ярко, как Кастор в созвездии Близнецов и Шаула в Скорпионе.
  Бетельгейзе — кандидат в сверхновые. Он уже потерял значительную часть своей первоначальной массы из-за сильного звездного ветра и, как ожидается, достигнет конца своего эволюционного цикла в течение следующих 100 000 лет.
  Сейчас масса звезды составляет от 16,5 до 19 масс Солнца, а предполагаемый радиус примерно в 764 раза больше, чем у Солнца. При температуре поверхности 3600 К он примерно в 126 000 раз ярче Солнца. Предполагаемый возраст звезды составляет от 8 до 8,5 миллионов лет.
  Происхождение имени Бетельгейзе неизвестно, но оно может происходить от арабского Yad al-Jauzā’ , что означает «Рука al-Jauzā’ ». В арабской астрономии аль-Джауза (Орион) был женской фигурой в старой арабской легенде.
  Расположение
  Три звезды Зимнего треугольника легко найти, поскольку они находятся вблизи Пояса Ориона, одного из самых известных астеризмов на небе. Бетельгейзе — яркая красная звезда над Альнитак, самой восточной звездой Пояса. Сириус можно найти, следуя линии, образованной звездами Пояса, на юго-восток, а Процион лежит в верхнем левом углу Сириуса.
  Зимний треугольник виден в ночном небе в северном полушарии в зимние месяцы, с декабря по март. В первые летние месяцы Орион остается за горизонтом, и астеризм невидим.
  Расположение Зимнего Треугольника, изображение: Stellarium
  Северные наблюдатели могут видеть Зимний Треугольник в другое время года, но звездный узор не так заметен на небе, как зимой. В конце лета и начале осени он поднимается над восточным горизонтом ранним утром. В весенние месяцы он заходит на западе ранним вечером.
  В южном полушарии астеризм выглядит перевернутым. В июне и июле его не видно.
  Зимний треугольник, вид из южного полушария, изображение: Stellarium
  Зимний треугольник и Зимний круг
  Зимний шестиугольник (или Зимний круг) имеет две общие вершины — Сириус и Процион — с Зимним треугольником. Образованный шестью звездами первой величины, этот астеризм доминирует на зимнем небе. Другие четыре звезды, образующие его, — это Поллукс в созвездии Близнецов, Капелла в Возничем, Альдебаран в Тельце и Ригель в Орионе. Бетельгейзе появляется в центре, но не является частью астеризма.
  Капелла, Ригель, Альдебаран и Поллукс — самые яркие звезды в своих созвездиях. Это шестая, седьмая, 14-я и 17-я самые яркие звезды на небе.
  
  Winter Hexagon, изображение: Wikisky
  В отличие от Сириуса и Проциона, которые кажутся яркими, потому что находятся в окрестностях Солнца, эти четыре звезды являются эволюционировавшими, светящимися по своей природе звездами, которые находятся намного дальше. Все четыре эволюционировали от основной последовательности и превратились в гигантов.
  Капелла — желтый гигант в двойной системе с оранжевым гигантом, расположенный на расстоянии 42,919 световых лет. Он в 78,7 раз ярче Солнца.
  Ригель — самая далекая из звезд Зимнего Гексагона. Это голубой сверхгигант, расположенный примерно в 863 световых годах от нас. Он в 21 раз массивнее Солнца и в 120 000 раз ярче.
  Альдебаран — оранжевый гигант на ветви красных гигантов, расположенный на расстоянии 65,3 световых года от нас. Он имеет массу 1,16 массы Солнца и светимость 439Солнца.
  Поллукс тоже оранжевый гигант. Его масса в 1,91 раза больше массы Солнца, а светимость составляет 32,7 солнечных. Звезда находится на расстоянии 33,78 световых года от нас.
  Зимний треугольник и египетский X
  Звезды Зимнего треугольника образуют большой астеризм, известный как египетский X, с Наосом (Дзета Корма) и Фактом (Альфа Колумба). Светила Корма и Колумбы образуют с Сириусом равносторонний треугольник, который соединяет его с Зимним треугольником.
  Факт находится вдоль воображаемой линии, проходящей от Проциона через Сириус, а Наос лежит на линии, проведенной от Бетельгейзе через Сириус.
  И Наос, и Факт — исключительно горячие и яркие звезды. Phact — звезда главной последовательности B-типа, примерно в 1000 раз более яркая, чем Солнце, а Naos — сверхгигант O-типа с массой в 56,1 раза больше солнечной и светимостью в 813000 раз больше, чем у нашей звезды. Это одна из самых ярких звезд, видимых невооруженным глазом. Он находится на расстоянии 1080 световых лет от нас.
  Египетский X, изображение: Stellarium
  Объекты глубокого космоса
  Астеризм «Зимний треугольник» можно использовать для поиска множества ярких объектов глубокого космоса, которые появляются в той же области неба. Некоторые из них лежат в районе между Бетельгейзе и Проционом. Туманность Розетка появляется ниже воображаемой линии, соединяющей две звезды, а туманность Конус, Переменная туманность Хаббла и туманность Дрейера появляются к северу от той же линии.
  
  Туманность Розетка и скопление спутников являются одними из самых популярных объектов для астрофотографии в небе. Туманность звездообразования имеет диаметр 1,3 градуса. Она находится на расстоянии 5200 световых лет от нас и имеет видимую величину 9,0. Ассоциированное скопление спутников (NGC 2244) состоит из молодых звезд, образовавшихся внутри туманности. Туманность и скопление имеют физический диаметр около 130 световых лет.
  Процион, Бетельгейзе, туманность Конус, туманность Розетка, IC 2169 и Мессье 78, изображение: Wikisky
  Туманность Конус — еще одна область H II.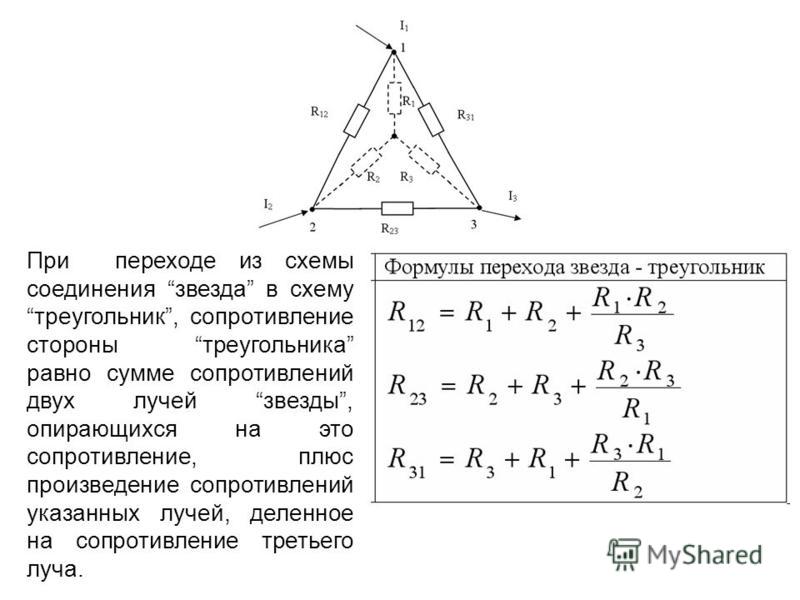 Он связан с молодой группой «Рождественская елка», названной в честь ее праздничной формы. Туманность находится на расстоянии 2700 световых лет от нас и имеет диаметр 3 угловых минуты.
  Туманность Дрейера (IC 2169, IC 447), отражательная туманность диаметром около 25 угловых минут, появляется к западу от туманности Конус.
  
  Переменная туманность Хаббла (NGC 2261) появляется между туманностью Дрейера и туманностью Розетка. Это переменная туманность, освещенная молодой двойной звездой R Единорога. R Единорога — звезда до главной последовательности, которая еще не вышла из своего родительского облака. Туманность выглядит как комета, но ее форма и яркость медленно меняются в течение недель и месяцев.
  Бетельгейзе и Сириус можно использовать для поиска яркой отражательной туманности Мессье 78. Туманность находится на пересечении воображаемых линий, соединяющих Бетельгейзе и Альнитак (крайняя левая звезда Пояса Ориона) и Сириус и Беллатрикс (звезда, отмечающая другое плечо Ориона).
  Сириус находится в области, полной относительно ярких объектов глубокого космоса. Яркое рассеянное скопление Мессье 41 находится в 4 градусах к югу от звезды. С видимой величиной 4,5 и видимым размером 38 угловых минут скопление легко наблюдать в бинокль и небольшие телескопы.
  
  Скопление Каролины (NGC 2360) находится всего в 3,5 градусах к востоку от Гаммы Большого Пса. Это яркое рассеянное скопление (величина 7,2), расположенное примерно в 3700 световых годах от нас. Он был назван в честь Кэролайн Гершель, британского астронома немецкого происхождения, открывшего его в 1783 году. изображение: Wikisky
  Рассеянные скопления Мессье 46 и Мессье 47 лежат в созвездии Корма. Мессье 47 находится примерно в 12 градусах к востоку и в 2 градусах к северу от Сириуса, а Мессье 46 — примерно в градусе к востоку от M47. Несмотря на то, что скопления кажутся на небе всего лишь в градусе друг от друга, они не связаны физически. М46 лежит 4,940 световых лет от нас, а более яркая M47 — 1624 световых года.
  Эмиссионная туманность NGC 2359 более известна под своим популярным прозвищем «Туманность Шлем Тора». Она появляется рядом с Сириусом, примерно на полпути между Проционом и Адхарой, самой яркой из трех звезд Большого Пса, образующих треугольник под Сириусом.
  Рассеянное скопление Мессье 50 (скопление в форме сердца) появляется примерно в 8 градусах к северу от Сириуса в направлении Проциона. С видимой величиной 5,9 она видна в небольшие телескопы.
  Область звездообразования IC 2177 и рассеянные скопления NGC 2335 и NGC 2343 видны прямо под Мессье 50. Область H II широко известна как туманность Чайка. Она находится на расстоянии 3650 световых лет от нас.
  Рыхлое рассеянное скопление NGC 2353 находится на том же расстоянии и видно в небольшие телескопы. Он имеет видимую величину 7,1 и видимый размер 20 угловых минут.
  Другие объекты глубокого космоса, которые могут быть обнаружены с помощью звезд Зимнего треугольника, включают Мессье 9.3 в созвездии Кормы, Мессье 48 в Гидре и скопление Тау Большого Пса (NGC 2362) в Большом Псе.