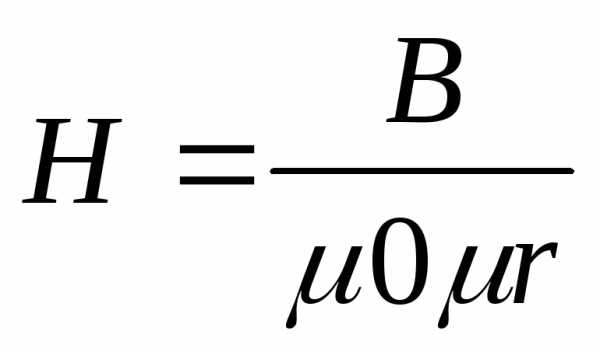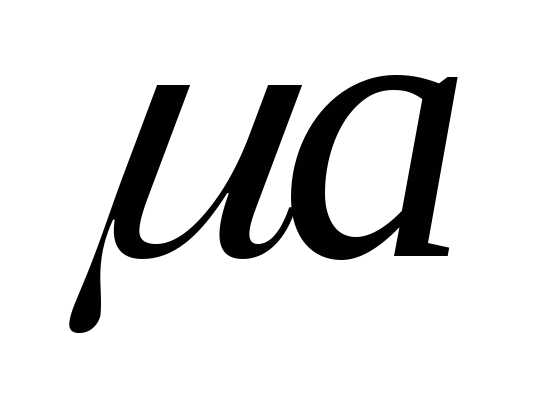Измерение магнитной индукции – Закон электромагнитной индукции

Закон электромагнитной индукции

Закон электромагнитной индукции Фарадея-Ленца гласит, что при всяком измении магнитного потока сквозь площадку, ограниченную контуром, в последнем возникает эдс индукции, численно равная и противоположная по знаку скорости изменения магнитного потока:

_i= — dФ/dt , (16)

где _i — величина эдс электромагнитной индукции, dФ/dt — скорость изменения магнитного потока сквозь площадку, ограниченную контуром проводника. Если сопротивление контура R, то сила индукционного тока в нем:

(17)

Количество электричества q, которое протекает в контуре вследствие электромагнитной индукции, можно найти по формуле:

(18)

Таким образом, по величине индукционного заряда, протекавшего по контуру, можно судить о величине изменения магнитного потока.

Измерение магнитной индукции

Простой и удобный способ измерения магнитной индукции основан на явлении электромагнитной индукции. Поместим в рассматриваемую точку магнитного поля (рис.5) перпендикулярно линиям 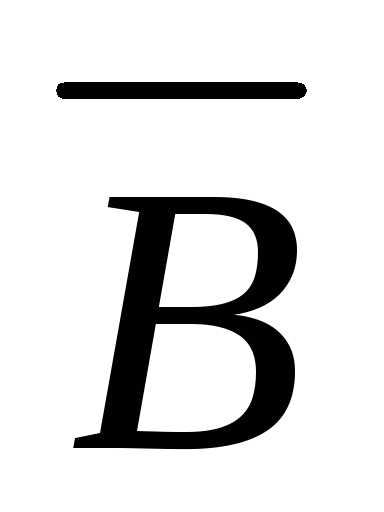небольшую плоскую катушку, имеющую N витков и площадь одного витка S. Катушку соединим с баллистическим гальванометром Г. Магнитный поток через катушку на основании (13) равен:

Ф = B ·N

·S (19)

При изменении магнитного потока в цепи гальванометра будет наводиться эдс индукции. Если магнитный поток через катушку менять от Ф до –Ф, изменяя направление тока на противоположное, то полный заряд, протекший через гальванометр, учитывая (18), равен:

q=2Ф/R=2BNS/R=(2NS/R)B=aB, (20)

где: а — постоянная цепи, содержащей гальванометр.

Измеряя заряд, протекший через гальванометр, и постоянную а, можно определить В в данной точке магнитного поля.

Баллистический гальванометр обладает таким свойством, что величина заряда q, прошедшего по цепи, содержащей гальванометр, прямо пропорциональна максимальному отбросу m светового «зайчика» (указателя) по шкале гальванометра, т.е.

q=b

‘·m (21)

где b‘ — баллистическая постоянная цепи гальванометра. Приравнивая (20) и (21), определяют величину магнитной индукции в том месте, где располагается небольшая плоская катушка, в которой изменяется магнитный поток.

Обоснование метода измерений

Индукционный метод определения величины магнитной индукции В на оси кругового тока заключается в следующем. На оси кругового тока, создаваемого катушкой L_K (рис.6), располагают небольшую плоскую катушку L, имеющую N₁витков и площадь одного витка S₁,которая замкнута на баллистический гальванометр. При изменении направления тока в круговом витке L_Kна противоположное , магнитный поток через Lизменяется от –Ф до +Ф. В катушке L возникает ЭДС индукции, и в цепи гальванометра – индукционный ток. При этом заряд

q , протекший по

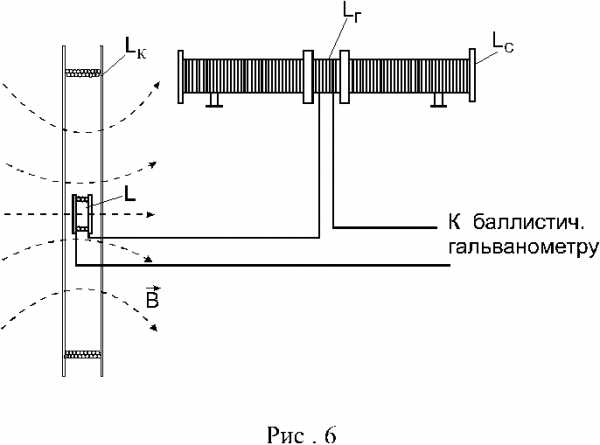
баллистическому гальванометру, оказывается пропорциональным значению В в том месте поля, где располагается измерительная катушка L. На основании (20) и (21) можно записать:

(2N₁S₁/R₂)B = b‘ m , (22)

где R₂ – сопротивление цепи баллистического гальванометра.

Из (22) следует:

B = (R₂/2N₁S₁) b‘ m = A₂b‘ m (23)

Величины R₂, N₁, S

₁входящие в А₂, остаются неизменными параметрами цепи гальванометра, которые могут быть измерены при изготовлении установки.

Равенство (23) позволяет определить В, измерив отброс « m » зайчика гальванометра при коммутации тока, создающего исследуемое магнитное поле, и определив заранее b‘.

Баллистическую постоянную b‘ установки определяют, используя известное магнитное поле, или поле, магнитная индукция которого сравнительно легко и достаточно точно может быть рассчитана. Таким полем может быть поле внутри «бесконечного соленоида» L_C, представляющего собой катушку, длина которой (намотанной части катушки) в несколько раз больше диаметра ее витка. Для проведения измерений на бесконечный соленоид L_Cнадевают катушку L_Г, включенную в цепь гальванометра

Г последовательно с подвижной катушкой L. При изменении направления тока в соленоиде L_Cна противоположное , в катушке L_Гсоздается эдс индукции и гальванометр фиксирует отброс m_с. На основании (22) можно записать:

(2NS/R₂ ) В_C = b‘m_с , (24)

где N -число витков катушки L_Г,, S — площадь ее витка, R₂ — сопротивление цепи гальванометра, В_с— магнитная индукция на оси соленоида L_c.

Величина В_с определяется:

B

_c=m m₀ i_C n , (25)

где i_C — ток по соленоиду L_C, n — количество витков приходящихся на единицу длины намотки соденоида .

На основании (24) и (25) имеем: (2NSmm₀i_Cn)/R₂ =b’m_C

откуда

b ‘=(2mm_CnNS i_C )/R₂ m_C=A₁ i_C m_C (26)

Величины, входящие в А₁, являются неизменными параметрами используемой установки. Значения А₁ и А₂ указаны около рабочей панели.

Используя бесконечный соленоид, измерив его ток

i_C и отброс m_C зайчика гальванометра при коммутации тока i_C , можно определить значение баллистической постоянной b‘.

Величину магнитного потока Фчерез измерительную подвижную катушкуLможно определить, воспользовавшись (22):

Ф = N₁S₁B = (R₂/2) b‘ m (27)

studfiles.net

Принципиальные методы измерения напряженности и индукции магнитного поля в магнетиках

Прямое измерение индукции магнитного поля

Прямое измерение индукции магнитного поля при помощи витка с током основано на явлении электромагнитной индукции Фарадея.

Напомним один из основных законов электромагнетизма.

Закон электромагнитной индукции Фарадея

При изменении магнитного потока, проходящего через замкнутый контур, в контуре возникает ЭДС индукции.

Скорость изменения магнитного потока через замкнутый контур по модулю равна ЭДС индукции, возникающей в контуре.

Как измерить индукцию магнитного поля прямым методом? Сначала проводник в виде небольшой плоской петли замыкают на гальванометр и ориентируют так, чтобы линии магнитной индукции магнитного поля были перпендикулярны плоскости проводника. Затем проводник поворачивают вокруг своей оси на 90°. По закону электромагнитной индукции через гальванометр при этом должен пройти импульс тока. Измерив этот импульс, определяют среднее значение магнитной индукции B в области петли. 

Косвенные методы измерение напряженности и индукции магнитного поля

Прямое (непосредственное) измерение величины B описанным выше способом возможно не всегда. Например, так невозможно измерить индукцию магнитного поля в веществе. 

Необходимо принимать во внимание, что при переходе границы магнетика нормальные составляющие вектора магнитной индукции и тангенциальные составляющие вектора напряженности непрерывны. 

Как измеряют вектор магнитной индукции в веществе? Для этого в исследуемом материале делают полость и проводят измерение. Также при обработке результатов учитывают форму полости.

Способ 1. В магнетике делают параллельный магнитному полю и бесконечно узкий канал. Так как канал бесконечно узкий, можно принять, что напряженность поля в нем и в окружающем магнетике одинаковы. В канал помещается пробный виток, измеряется величина магнитной индукции. Так как в канале отсутствует вещество магнетика и μ=1, получаем:

B→=μ0H→.

Способ 2. В магнетике создают бесконечно узкую щель. Удаление вещества, учитывая бескон

zaochnik.com

Магнитная индукция, магнитный поток: определение, формулы, смысл

Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.

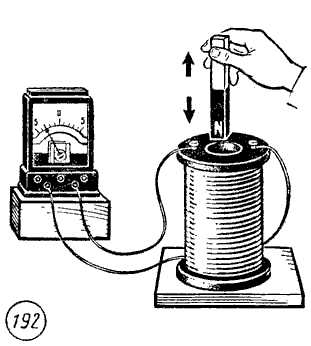
Магнитная индукция определяется способностью влиять на объект с помощью магнитного поля. Эта способность проявляется при перемещении постоянного магнита в катушке, в результате чего в катушке индуцируется (возникает) ток, при этом магнитный поток в катушке также увеличивается.

Физический смысл магнитной индукции

Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.

Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки — именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.

 В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.

При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.

Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.

Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.

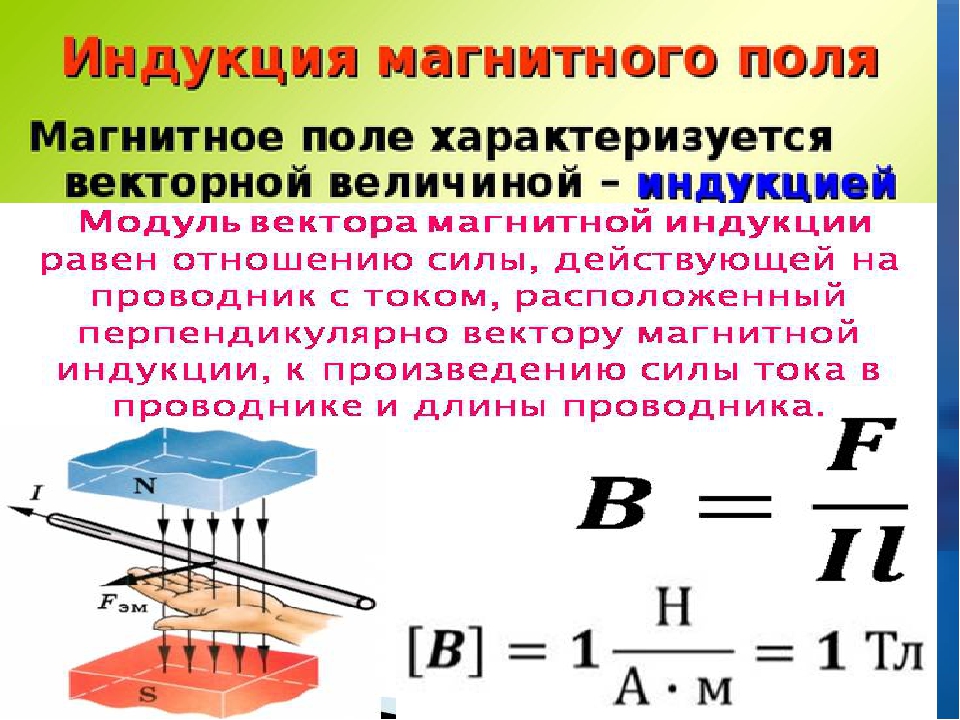
Формула магнитной индукции

где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.

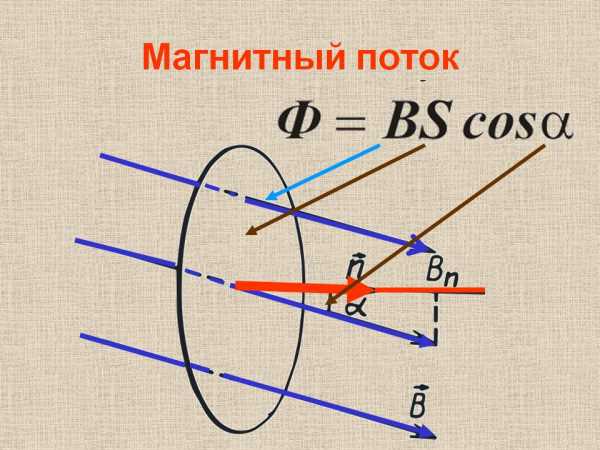
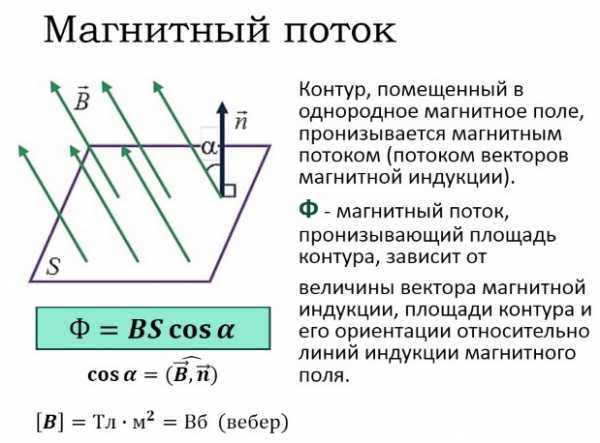
Магнитный поток

Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур. 

Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла. 

Магнитометры, используемые для ее измерения, называют теслометрами.

Единицей измерения магнитной индукции в системе СИ является Тесла (Тл).

После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства.

pue8.ru

Принципиальные методы измерения напряженности и индукции магнитного поля в магнетиках

Непосредственное измерение магнитной индукции с помощью витка с током

Изменение индукции магнитного поля наиболее просто можно провести, используя закон электромагнитной индукции Фарадея. Проводник в виде небольшой плоской петли, замыкают на гальванометр, ориентируют в плоскости, которая перпендикулярна $\overrightarrow{B}$, потом проводник поворачивают на 900 вокруг оси, которая лежит в этой плоскости. Через гальванометр пойдет импульс тока. По этому импульсу определяют среднюю магнитную индукцию в поля в области петли. Можно не поворачивать рамку, а выключить магнитное поле.

Принципиальные методы измерения напряженности и индукции

Непосредственное измерение магнитного поля в веществе с помощью рамки с током (пробного витка) возможно не всегда. Так как, например, в твердое вещество пробный виток не поместишь. Но даже, если бы это было возможно не совсем ясно, как по силе, действующей на виток и ее моменту найти векторы $\overrightarrow{B\ }и\ \overrightarrow{H}$.

Существование граничных условий:

нормальные составляющие вектора индукции непрерывны при переходе границы магнетика и в отсутствии токов проводимости непрерывны тангенциальные составляющие вектора напряженности на границе раздела магнетика:

указывает принципиальный метод измерения магнитного поля в веществе.

Для измерения $\overrightarrow{B\ }и\ \overrightarrow{H}$ в веществе следует сделать полость и измерить вектор магнитной индукции в ней. Однако надо понимать, что результат будет зависеть от формы полости.

Рассмотрим два наиболее часто используемые метода.

1. В магнетике делают бесконечно узкий канал, который параллелен магнитному полю. Считают, что удаление вещества в таком случае чрезвычайно мало изменят магнитное поле в окружающем магнетике. Так как мы имеем граничное условие (2), то напряженность магнитного поля в канале и окружающем магнетике одинаковы. Пробный виток помещается в канал, там измеряется величина магнитной индукции. Так как в канале магнетика нет, $\mu =1$, следовательно,
\[\overrightarrow{B}={\mu }_0\overrightarrow{H}\left(3\right).\]
2. В магнетике делают щель, которая ограничена двумя бесконечно близкими плоскостями, которые перпендикулярны магнитному полю. Опять-таки, удаление вещества из такой щели не существенно скажется на магнитном поле в окружающем магнетике. В силу граничного условия (1) векторы магнитной индукции в щели и в окружающем магнетике одинаковы. Измеряется величина $\overrightarrow{B}\ $в щели, следовательно, мы узнаем магнитную индукцию в веществе.

Пример 1

Задание: Лабораторный магнит состоит их железного сердечника, на котором находятся катушки с током (I). Сердечник имеет узкий воздушный зазор (длина его равна $l_v$). Линии магнитной индукции сосредоточены в основном внутри сердечника. Вектор магнитной индукции пересекает границу воздушный зазор — сердечник по нормали к поверхности раздела. Чему равна магнитная индукция в зазоре электромагнита? Число витков с током равно N.

Рис. 1

Решение:

Согласно граничному условию:

\[B_{1n}=B_{2n}\left(1.1\right)\]

магнитная индукция в зазоре и железном сердечнике одинакова по модулю. Используем теорему о циркуляции вектора напряженности ($\overrightarrow{H}$). В качестве контура возьмем контур, который проходит по оси сердечника. Будем считать, что напряженность в железе везде одна и равна:

\[H_{Fe}=\frac{B}{{\mu }_0{\mu }_{Fe}}\ \left(1.2\right).\]

В воздухе напряженность равна:

\[H_v=\frac{B}{{\mu }_0{\mu }_v}\ \left(1.3\right).\]

Циркуляция вектора напряженности может быть записана как:

\[H_{Fe}l_{Fe}+H_vl_v=NI\ \left(1.4\right),\]

где $l_{Fe}$ — длина контура в железном сердечнике, $l_v$ — длина контура в воздухе, $N$ — суммарное число витков в катушке, I — сила тока в катушке. Подставим (1.2) и (1.3) в (1.4), получим:

\[\frac{B}{{\mu }_0{\mu }_{Fe}}l_{Fe}+\frac{B}{{\mu }_0{\mu }_v}l_v=NI\ \left(1.5\right).\]

Выразим из (1.5) магнитную индукцию, имеем:

\[B={\mu }_0I\frac{N}{\frac{l_v}{{\mu }_v}+\frac{l_{Fe}}{{\mu }_{Fe}}}\approx {\mu }_0I\frac{N}{l_v+\frac{l_{Fe}}{{\mu }_{Fe}}}(1.6).\]

${\mu }_v\approx 1$. Магнитная проницаемость железа (${\mu }_{Fe}$) весьма велика, порядка, несколько тысяч, поэтому часто отношением $\frac{l_{Fe}}{{\mu }_{Fe}}\ll 1$ пренебрегают, тогда формула (1.6) приобретет вид:

\[B={\mu }_0I\frac{N}{l_v}.\]

Ответ: $B={\mu }_0I\frac{N}{l_v}.$

Определение

Постоянные магниты — магнетики, вектор намагниченности ($\overrightarrow{J}$) которых почти не изменяется при внесении магнита во внешнее не очень сильное магнитное поле.

На этом основывается метод Гаусса для измерения напряженности магнитного поля. Берется магнит, который имеет форму прямого стержня, намагничен он параллельно оси. В однородном магнитном поле с индукцией $\overrightarrow{B}$ на стержень действует вращающий момент ($\overrightarrow{M}$), равный:

\[\overrightarrow{M}=\left[\overrightarrow{P_m}\overrightarrow{B}\right]\ \left(2.1\right),\]

где $P_m$ — магнитный момент стержня. Если магнитный стержень может вращаться вокруг своего центра масс, то под действием вращающего момента он установится вдоль вектора поля ($\overrightarrow{B}$). Если вывести слегка стержень из положения равновесия, то возникнут колебания и их период (T) равен:

\[T=2\pi \sqrt{\frac{\theta }{\overrightarrow{P_m}\overrightarrow{B}}}\left(2.2\right),\]

где $\theta $ — момент инерции стержня.

Закрепим магнит-стержень перпендикулярно к магнитному полю $\overrightarrow{B}$, поместим вдали от стержня маленькую магнитную стрелку. Стержень-магнит можно считать магнитным диполем, для магнитного поля $B_1$ стержня в месте нахождения стрелки можно записать:

\[B_1=\frac{2P_m}{r^3}\ \left(2.3\right),\]

где r — расстояние между центрами стрелки и стержня. Поле направлено вдоль оси магнита — стержня, то есть перпендикулярно к измеряемому полю. Под воздействием $\overrightarrow{B_1}$ и $\overrightarrow{B}$ стрелка установится под некоторым углом $\alpha $ к полю $\overrightarrow{B}$, который определен как:

\[tg\alpha =\frac{B_1}{B}=\frac{2P_m}{Br^3}\left(2.4\right).\]

Измеряя угол $\alpha $ и время T, вычисляют индукцию поля и магнитный момент стрежня.

Данный метод применяется для измерения магнитного поля Земли.

spravochnick.ru

Магнитная индукция

2

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ — существует вокруг электрического заряда, материально. Основное свойство электрического поля: действие с силой на эл.заряд, внесенный в него. Электростатическое поле— поле неподвижного эл.заряда, не меняется со временем. Напряженность электрического поля. — количественная характеристика эл. поля. — это отношение силы, с которой поле действует на внесенный точечный заряд к величине этого заряда. — не зависит от величины внесенного заряда, а характеризует электрическое поле!

Направление вектора напряженности  совпадает с направлением вектора силы, действующей на положительный заряд, и противоположно направлению силы, действующий на отрицательный заряд.

Напряженность поля точечного заряда:

где q0 — заряд, создающий электрическое поле. В любой точке поля напряженность направлена всегда вдоль прямой, соединяющей эту точку и q0.

3

ПРИНЦИП СУПЕРПОЗИЦИИ ( НАЛОЖЕНИЯ ) ПОЛЕЙ

Если в данной точке пространства различные электрически заряженные частицы 1, 2, 3… и т.д. создают электрические поля с напряженностью Е1, Е2, Е3 … и т.д., то результирующая напряженность в данной точке поля равна геометрической сумме напряженностей.

Силовые линии эл. поля — непрерывные линии, касательными к которым являются векторы напряженности эл.поля в этих точках. Однородное эл.поле — напряженность поля одинакова во всех точках этого поля. Свойства силовых линий: не замкнуты (идут от + заряда к _ ), непрерывны, не пересекаются, их густота говорит о напряженности поля (чем гуще линии, тем больше напряженность).

Графически надо уметь показать эл.поля: точечного заряда, двух точечных зарядов, обкладок конденсатора ( в учебнике есть).

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ заряженного шара.

Есть заряженный проводящий шар радиусом R.

— заряд равномерно рапределен лишь по поверхности шара!  Напряженность эл. поля снаружи:

Напряженность внутри шара:  Е = 0

12

ЭЛЕКТРОЕМКОСТЬ — характеризует способность двух проводников накапливать электрический заряд.  — не зависит от q и U. — зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.

Единицы измерения в СИ: ( Ф — фарад )

КОНДЕНСАТОРЫ

— электротехническое устройство, накапливающее заряд ( два проводника, разделенных слоем диэлектрика ).

где d много меньше размеров проводника. Обозначение на электрических схемах:

Все электрическое поле сосредоточено внутри конденсатора. Заряд конденсатора — это абсолютное значение заряда одной из обкладок конденсатора.

Виды конденсаторов: 1. по виду диэлектрика: воздушные, слюдяные, керамические, электролитические 2. по форме обкладок: плоские, сферические. 3. по величине емкости: постоянные, переменные (подстроечные).

Электроемкость плоского конденсатора

где S — площадь пластины (обкладки) конденсатора d — расстояние между пластинами eо — электрическая постоянная e — диэлектрическая проницаемость диэлектрика

Включение конденсаторов в электрическую цепь

параллельное

последовательное

Тогда общая электроемкость (С):

при параллельном включении

.при последовательном включении

ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА

Конденсатор — это система заряженных тел и обладает энергией. Энергия любого конденсатора:

где С — емкость конденсатора q — заряд конденсатора U — напряжение на обкладках конденсатора Энергия конденсатора равна работе, которую совершит электрическое поле при сближении пластин конденсатора вплотную, или равна работе по разделению положительных и отрицательных зарядов , необходимой при зарядке конденсатора.

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА

Энергия конденсатора приблизительно равна квадрату напряженности эл. поля внутри конденсатора. Плотность энергии эл. поля конденсатора:

14

Электри́ческий ток — направленное (упорядоченное) движение заряженных частиц^[1][2][3]. Такими частицами могут являться: в металлах —электроны, в электролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определенных условиях — электроны, вполупроводниках — электроны и дырки (электронно-дырочная проводимость). Иногда электрическим током называют также ток смещения, возникающий в результате изменения во времени электрического поля^].

Сила тока — физическая величина , равная отношению количества заряда , прошедшего через некоторую поверхность за время , к величине этого промежутка времени^[1]:

В качестве рассматриваемой поверхности часто используется поперечное сечение проводника.

Сила тока в Международной системе единиц (СИ) измеряется в амперах (русское обозначение: А; международное: A), ампер является одной из семиосновных единиц СИ. 1 А = 1 Кл/с.

По закону Ома сила тока для участка цепи прямо пропорциональна приложенному напряжению к участку цепи и обратно пропорциональнасопротивлению проводника этого участка цепи:

Носителями заряда, движение которых, приводит к возникновению тока, являются заряженные частицы, в роли которых обычно выступаютэлектроны, ионы или дырки. Сила тока зависит от заряда этих частиц, их концентрации , средней скорости упорядоченного движения частиц , а также площади и формы поверхности, через которую течёт ток.

Если и постоянны по объёму проводника, а интересующая поверхность плоская, то выражение для силы тока можно представить в виде

где  — угол между скоростью частиц и вектором нормали к поверхности.

В более общем случае, когда сформулированные выше ограничения не выполняются, аналогичное выражение можно записать только для силы тока , протекающего через малый элемент поверхности площадью :

Тогда выражение для силы тока, протекающего через всю поверхность, записывается в виде интеграла по поверхности

В металлах заряд переносят электроны, соответственно в этом случае выражение для силы тока имеет вид

где e — элементарный электрический заряд.

Вектор называют плотностью электрического тока. Как следует из сказанного выше, его величина равна силе тока, протекающей через малый элемент поверхности единичной площади, расположенный перпендикулярно скорости , а направление совпадает с направлением упорядоченного движения заряженных частиц^[2].

Для измерения силы тока используют специальный прибор — амперметр (для приборов, предназначенных для измерения малых токов, также используются названия миллиамперметр, микроамперметр, гальванометр). Его включают в разрыв цепи в том месте, где нужно измерить силу тока. Основные методы измерения силы тока: магнитоэлектрический, электромагнитный и косвенный (путём измерения вольтметром напряжения на известном сопротивлении).

В случае переменного тока различают мгновенную силу тока, амплитудную (пиковую) силу тока и эффективную силу тока (равную силе постоянного тока, который выделяет такую же мощность).

Пло́тность то́ка — векторная физическая величина, имеющая смысл силы тока, протекающего через элемент поверхности единичной площади^[1]. Например, при равномерном распределении плотности тока и всюду ортогональности её плоскости сечения, через которое вычисляется или измеряется ток, величина вектора плотности тока:

где I — сила тока через поперечное сечение проводника площадью S (также см.рисунок).

Иногда речь может идти о скалярной^[2] плотности тока, в таких случаях под ней подразумевается именно та величина j, которая приведена в формуле.

В общем случае:

,

где  — нормальная (ортогональная) составляющая вектора плотности тока по отношению к элементу поверхности площадью ; вектор — специально вводимый вектор элемента поверхности, ортогональный элементарной площадке и имеющий абсолютную величину, равную её площади, позволяющий записать подынтегральное выражение как обычное скалярное произведение.

Как видим из этого определения, сила тока есть поток вектора плотности тока через некую заданную фиксированную поверхность.

В простейшем предположении, что все носители тока (заряженные частицы) двигаются с одинаковым вектором скорости и имеют одинаковые заряды (такое предположение может иногда быть приближенно верным; оно позволяет лучше всего понять физический смысл плотности тока), а концентрация их ,

или

где — плотность заряда этих носителей.

Направление вектора соответствует направлению вектора скорости , с которой движутся заряды, создающие ток, если q положительно.

В реальности даже носители одного типа движутся вообще говоря и как правило с различными скоростями. Тогда под следует понимать среднюю скорость.

В сложных системах (с различными типами носителей заряда, например, в плазме или электролитах)

то есть вектор плотности тока есть сумма плотностей тока по всем типам подвижных носителей; где — концентрация частиц каждого типа, — заряд частицы данного типа, — вектор средней скорости частиц этого типа.

Выражение для общего случая может быть записано также через сумму по всем индивидуальным частицам:

15

Зако́н О́ма — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде : ,

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r^[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

, (2)

где:

•  — ЭДС источника напряжения,

•  — сила тока в цепи,

•  — сопротивление всех внешних элементов цепи,

•  — внутреннее сопротивление источника напряжения.

Из закона Ома для полной цепи вытекают следствия:

• При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения

• При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто^[2] выражение:

 (3)

(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

 (4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

 (5)

применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

 (6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо^[3], в Международной системе единиц (СИ) единицей измерения проводимости является си́менс (русское обозначение: См; международное: S), величина которого равна обратному ому.

ЗАКОН ДЖОУЛЯ -ЛЕНЦА

При прохождениии тока по проводнику проводник нагревается, и происходит теплообмен с окружающей средой, т.е. проводник отдает теплоту окружающим его телам.

Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.

По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время.

В системе СИ:

[Q] = 1 Дж

19

МАГНИТНОЕ ПОЛЕ

— это особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами.

СВОЙСТВА ( стационарного) МАГНИТНОГО ПОЛЯ

Постоянное (или стационарное) магнитное поле — это магнитное поле, неизменяющееся во времени .

1. Магнитное поле создается движущимися заряженными частицами и телами, проводниками с током, постоянными магнитами.

2. Магнитное поле действует на движущиеся заряженные частицы и тела, на проводники с током, на постоянные магниты, на рамку с током.

3. Магнитное поле вихревое, т.е. не имеет источника.

— это силовая характеристика магнитного поля.

Вектор магнитной индукции направлен всегда так, как сориентирована свободно вращающаяся магнитная стрелка в магнитном поле.

Единица измерения магнитной индукции в системе СИ:

Направление линий магнитной индукции

— определяется по правилу буравчика или по правилу правой руки.

Правило буравчика ( в основном для прямого проводника с током):

Если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.

Правило правой руки ( в основном для определения направления магнитных линий  внутри соленоида):

Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.

Существуют другие возможные варианты применения правил буравчика и правой руки.

Сила ампера

— это сила, с которой магнитное поле действует на проводник с током.

Модуль силы Ампера равен произведению силы тока в проводнике на модуль вектора магнитной индуции, длину проводника и синус угла между вектором магнитной индукции и направлением тока в проводнике.

Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.

Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.

Направление силы Ампера определяется по правилу левой руки:

Если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а 4 вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующий на проводник с током.

Примеры:

или 

Действие магнитного поля на рамку с током

Однородное магнитное поле ориентирует рамку (т.е. создается вращающий момент и рамка поворачивается в положение, когда вектор магнитной индукции перпендикулярен плоскости рамки).

Неоднородное магнитное поле ориентирует + притягивает или отталкивает рамку с током. Так, в магнитном поле прямого проводника с током (оно неоднородно) рамка с током ориентируется вдоль радиуса магнитной линии и притягивается или отталкивается от прямого проводника с током в зависимости от направления токов.

22

Магнитный момент витка с током это физическая величина, как и любой  другой магнитный момент, характеризует магнитные свойства данной системы. В нашем случае систему представляет круговой виток с током. Этот ток создает магнитное поле, которое взаимодействует с внешним магнитным полем. Это может быть как поле земли, так и поле постоянного или электромагнита.

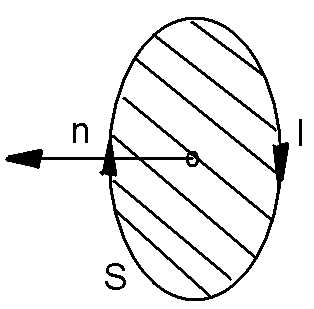
Рисунок — 1 круговой виток с током

 Круговой виток с током можно представить в виде короткого магнита. Причем этот магнит будет направлен перпендикулярно плоскости витка. Расположение полюсов такого магнита определяется с помощью правила буравчика. Согласно которому северный плюс будет находиться за плоскостью витка, если ток в нем будет двигаться по часовой стрелке.

Рисунок—  2 Воображаемый полосовой магнит на оси витка

 На этот магнит, то есть на наш круговой виток с током, как и на любой другой магнит, будет воздействовать внешнее магнитное поле. Если это поле будет однородным, то возникнет вращающий момент, который будет стремиться развернуть виток. Поле буде поворачивать виток так чтобы его ось расположилась вдоль поля. При этом силовые линии самого витка, как маленького магнита, должны совпасть по направлению с внешним полем.

 Если же внешнее поле будет не однородным, то к вращающему моменту добавится и поступательное движение. Это движение возникнет вследствие того что участки поля с большей индукцией будут притягивать наш магнит в виде витка больше чем участки с меньшей индукцией. И виток начнет двигаться в сторону поля с большей индукцией.

 Величину магнитного момента кругового витка с током можно определить по формуле.

studfiles.net

Измерение — магнитная индукция — Большая Энциклопедия Нефти и Газа, статья, страница 1

Измерение — магнитная индукция

Cтраница 1

Измерение магнитной индукции в межполюсном пространстве постоянных магнитов основано на принципе взаимодействия двух магнитных полей: поля, образованного протекаемым током через подвижную катушку пробника-зонда, помещенного в межполюсное пространство, и измеряемого поля постоянного магнита. В результате взаимодействия двух указанных магнитных полей катушка пробника зонда повернется на определенный угол, а вместе с ней повернется насаженная на ось катушки указательная стрелка.  [1]

Измерение магнитной индукции в неравномерном магнитном поле сводится по существу к определению этой величины в определенной точке магнитного поля. Для этого измерительная катушка выполняется небольших размеров и помещается в различные точки исследуемого магнитного поля. Чем меньше габариты измерительной катушки, тем, очевидно, точнее можно определить индукцию в данной точке поля.  [2]

Измерение магнитной индукции в различных частях магнитопровода сводится к определению магнитного потока через выбранные сечения, которые должны быть определены с достаточной степенью точности. В случае, если магнитопровод шихтованный, нужно учитывать, что сечение детали не соответствует сечению стали из-за прослоек лака ( толщиной 0 02 мм), бумаги ( толщина 0 032 мм) или другой изоляции, разделяющей отдельные пластины.  [3]

Измерение магнитной индукции осуществляется на основе явления ядерного магнитного резонанса ( ЯМР -) или эффекта Холла.  [4]

Измерение магнитной индукции в зазорах магнитов ИМ производят теслоамперметром Ф4354 / 1 завода Электроизмеритель. Прибор предназначен для измерения индукции постоянных магнитных полей и величины постоянного тока. При измерении магнитной индукции используют германиевый датчик ЭДС Холла, который помещают в исследуемом поле. Размеры щупа датчика позволяют производить измерение в зазорах от 1 мм и выше магнитных систем приборов и счетчиков. Прибор позволяет также измерять индукцию в точках неравномерного поля.  [5]

Измерения магнитной индукции в разных точках поля вокруг проводника, по которому идет ток, показывают, что магнитная индукция в каждой точке всегда пропорциональна силе тока в проводнике. Но при данной силе тока магнитная индукция в различных точках поля различна и чрезвычайно сложно зависит от размеров и формы проводника, по которому проходит ток. Мы ограничимся одним важным случаем, когда эти зависимости сравнительно просты.  [6]

Для измерения магнитной индукции в кольце на него наложена еще вторичная обмотка, имеющая w витков.  [7]

Для измерения магнитной индукции в данной точке поля применяется маленькая круглая катушка, устанавливаемая так, чтобы ее центр совпал с исследуемой точкой поля, а ось — с направлением магнитной индукции.  [8]

Для измерения магнитной индукции в зазорах электромагнитных устройств постоянного тока применяется, в частности, измеритель магнитной индукции ИМИ-3 ( Е11 — 3), снабженный измерительными зондами, внутри которых вмонтированы неподвижно полупроводниковые датчики Холла. Так как ЭДС Холла пропорциональна измеряемой напряженности поля, отсчетный делитель напряжения ИМИ-3 градуируется в единицах индукции, что дает возможность при размещении измерительного зонда в исследуемом зазоре электромагнитного устройства располагать его таким образом, чтобы направление измеряемого магнитного потока было строго перпендикулярно плоскости датчика, положение которой в зонде указано на его корпусе.  [9]

Для измерения магнитной индукции в зазоре электромагнита может быть применен прибор Ф4354 / 1, использующий датчики Холла со следующими характеристиками: пределы измерений — от 150 до 1500 мТл, основная погрешность-не более 2 5 %; размеры полупроводниковой пластины датчика 1 5X2X0 3 мм; размеры щупа 80X4 5×0 75 мм.  [10]

Для измерения магнитной индукции в подавляющем большинстве случаев предпочтение отдается преобразователям Холла, которые при питании их постоянным током управления обладают линейной функцией преобразования в очень широком диапазоне магнитных индукций. Преобразователи Холла позволяют осуществлять непрерывное измерение индукции магнитных полей с точностью до 1 % в пределах от 10 — 4 до 10 Тл. Миниатюрные размеры преобразователей позволяют производить замеры в труднодоступных местах, где использование других методов оказывается невозможным. Применяя магнитные концентраторы, с помощью преобразователей Холла можно измерять магнитную индукцию — до 10-в Тл. Использование преобразователей, обладающих более высокой магнитной чувствительностью ( например, ГМР преобразователей), позволяет производить измерения интенсивности магнитных полей без магнитных концентраторов, однако при этом падают динамический диапазон измерения и точность.  [11]

Для измерения магнитной индукции и напряженности магнитного поля используют различные виды тесламетров и приборов для измерений напряженности магнитного поля ( см. § 10 — 2 и табл. 15 — 8 и 15 — 9), которые упрощают процесс измерений по сравнению с описанным выше способом, а иногда позволяют расширить диапазон измеряемых величин и повысить точность измерений.  [12]

Помимо измерения магнитной индукции, ядерные преобразователи применяются для измерения постоянных электрических токов и других величин с предварительным преобразованием в магнитном поле.  [13]

Для измерения магнитной индукции по методу ЯМР широко применяются измерительные цепи савтодиннымиЯС — генераторами.  [14]

Для измерения магнитной индукции и напряженности магнитного поля в настоящее время используют эффект Холла и эффект Гаусса.  [15]

Страницы:      1    2    3    4

www.ngpedia.ru

Магнитная индукция и магнитные поток

Напряженность магнитного поля не является основной величиной, характеризующей магнитное поле, хотя определение напряжённости действительно для расчёта катушек без магнитопровода.

Для катушки с магнитопроводом основной величиной характеризующей магнитное поле, является магнитная индукция В. Это векторная величина, т.е. она (как и напряженность) задаётся численным значением и направлением в пространстве. Магнитная индукция определяется по силе, действующей на движущуюся заряженную частицу. При изображении картины магнитного поля при помощи магнитных линий, их рисуют гуще в той части поля, где больше индукция.

Единицей измерения магнитной индукции является тесла (Тл). Ранее применялась другая единица измерения магнитной индукции – гаусс (Гс).

Эти единицы связаны соотношением: 1Тл = 10000Гс.

Произведение магнитной индукции В на площадь S, перпендикулярную вектору магнитной индукции (магнитным линиям), называется магнитным потоком Ф. Таким образом магнитный поток:

Ф = B*S

Единицей измерения магнитного потока является вебер (Вб). При одной и той же напряжённости магнитного поля Н, в разных материалах получаются различные магнитные индукции В. Отношение В/Н называется абсолютной магнитной проницаемостью материала μ_а, т.е.

Абсолютная магнитная проницаемость материала μ_а равна произведению магнитной постоянной (магнитной проницаемости вакуума) μ₀ и относительной магнитной проницаемости μ_r:

раоорропор

Магнитная постоянная

Гн/м (генри на метр, генри единица измерения индуктивности).

Величина μ_rпоказывает, во сколько раз μ_а материала больше, чем магнитная постоянная μ₀.

В материале, магнитная проницаемость которого равна μ_r,

а в вакууме (практически и в воздухе)

где В выражается в теслах, а Н в А/м.

При измерении магнитной индукции в гауссах, а напряжённости магнитного поля в А/см, для магнитной индукции в воздухе получим:

У ферромагнитных материалов относительная магнитная проницаемость μ_r во много раз больше 1, она изменяется с изменением индукции В. Зависимость между В и Н для ферромагнитных материалов чаще изображается графиком в виде кривых намагничивания.

В практических задачах (магнитные цепи электрических машин и аппаратов) для расчёта силы тяги, ЭДС, силы притяжения и т.д. требуется определить магнитный поток Ф или индукцию В. Значение этих величин определяют по кривым намагничивания, если известна напряженность магнитного поля Н, которая, в свою очередь, задаётся магнитным напряжением или МДС.

Величина	Обозначение	Единица величины	Обозначение единицы	Расчётная формула
Напряженность магнитного поля а. в магнитном материале	Н	Ампер на метр	А/м	Н=Iw/l
б. в вакууме (воздухе)
Магнитная сила	F	Ампер		F=wI
Магнитная индукция	В	Тесла (Вебер на 1 м2)	Тл (Вб/м2)
Магнитный поток	Ф	Вебер	Вб	Ф = ВS
Абсолютная магнитная проницаемость		Генри на метр	Гн/м

Задача 1.

Н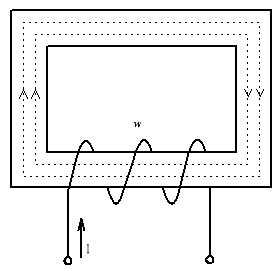апряжённость магнитного поля катушки

H = 500 А/м. Какова будет магнитная индукция, если в катушку вставить магнитопровод из трансформаторной стали (на рис.), относительная магнитная проницаемость которой μ_r= 2400.

Решение

B = μ_а*Н = μ_о*μ_r*Н = 4*π*10^-7*2400*500 = 1.5 Тл

Задача 2.

Для трансформаторной стали, содержащей 4% Si, магнитная индукция В при напряжённости магнитного поля катушки 500 А/м равна 1.19 Тл (см. кривые намагничивания на рис.). Определить абсолютную магнитную проницаемость трансформаторной стали в рабочей точке μ_а и относительную магнитную проницаемость μ_r. Напомним, что величина μ_r показывает во сколько раз μ_а материала больше, чем магнитная проницаемость

μ_о = 4*π*10^-7.

Решение

Абсолютная магнитная проницаемость

μ_а = В/Н = 1.19/500

μ_а = μ_r*μ_о = 4*π*10^-7*μ_r.

Отсюда

μ_r = μ_а/μ_о = В/Н =1.19/(500*4*π*10^-7) = 1893.9

Задача 3.

По заданным экспериментальным зависимостям В и Н для различных материалов определить коэффициенты полиномов второго порядка, наилучшим способом (по минимуму суммы квадратов ошибок) обеспечивающих аналитическое их описание (математическую модель).

Листовая сталь

Н (А/м)	100	150	200	250	300	350	400	450	500	550
В (Тл)	0.60	0.75	0.86	0.96	1.05	1.12	1.19	1.23	1.30	1.36

Трансформаторная сталь (4% Si)

Н (А/м)	100	200	300	400	500	600
В (Тл)	0.48	0.78	0.96	1.08	1.19	1.27

Литая сталь

Н (А/м)	100	200	300	400	500	600
В (Тл)	0.35	0.60	0.85	1.00	1.10	1.16

Решение

Для оценки коэффициентов полинома

В = a*Н² + b*Н + С

Запишем вектор

Н = [100 150 200 250 300 350 400 450 500 550]’. size A = 10,1

Затем составим матрицу А:

А = [Н^2 Н ones(V(1),1)]

И образуем вектор В:

B = [0.6 0.75 0.86 0.96 1.05 1.12 1.19 1.23 1.3 1.36]’.

Выполним оценку коэффициентов

а х = А\В

С помощью файла sah575.m. В нём выполнены оценки коэффициентов квадратного полинома для листовой стали

а1 = [-0.0206 0.2952 0.3429],

для трансформаторной стали

а2 = [-0.0246 0.3239 0.2000]

и для листовой стали

а3 = [-0.0277 0.2566 0.0150].

Необходимо выполнить расчёты для каждого вида материала в режиме прямых вычислений.

/здесь приводится файл sah 375.m/

Задача 4.

Каков будет магнитный поток Ф в магнитопроводе (см. задачу 1.), если сечение магнитопровода S = 4 см²?

Решение

Магнитный поток, измеряемый в веберах (Вб), равен

Ф = В*S = 1.5*4*10^-4 = 0.0006 Вб

(Тл = Вб/м²)

Задача 5.

Число витков катушки w=500. В магнитопроводе из трансформаторной стали длиной l=25 см необходимо обеспечить магнитную индукцию В=1.19 Тл. Какая м.д.с. и ток необходим для этого?

Решение

По кривой намагничивания трансформаторной стали (см. рис.) находим, что для создания В = 1.19 Тл требуется создать напряжённость магнитного поля Н = 500 А/м. При длине магнитопровода (с катушкой) l = 25 см = 0.25 м необходимая м.д.с. вычисляется по формуле

I*w = H*l = 500 А/м * 0.25 м = 125 А,

Отсюда I = I*w/w = 125/500 = 0.25 А

Задача 6.

Каковы напряжённость, индукция и магнитный поток внутри цилиндрической катушки (рис.) которая имеет длину 20 см, диаметр 3см, число витков 1600 и ток 3 А?

Решение

Напряжённость магнитного поля

Н = I*w/l = 3*1600/0.2 = 24000 А/м

Поскольку катушка без сердечника, то магнитную индукцию следует вычислять по формуле:

В = μ_о*Н = 4*π*10^-7*2.4*10⁴ = 3.02*10^-2 Тл

Сечение катушки

S = π*d²/4 = 3.14*0.03²/4 = 7.06*10^-4 м².

Следовательно, магнитный поток

Ф = В*S = 3.02*10^-2*7.06*10^-4 = 21.3*10^-6 Вб

Дополнение

Задача 1

Какое количество электричества пройдёт через лампу за 3 часа при токе 0,18А?

Решение:

Задача 2

Свинцовый аккумулятор ёмкостью 14А*ч заряжается током I зар = 1.4А. Как долго он должен заряжаться и через сколько времени он разрядится через лампы током Iраз = 0.3А?

Решение:

Зарядка: t = Q/Iзар = 14А*ч/1.4А = 10ч,

т.е. аккумулятор должен заряжаться 10ч

Разрядка: t = Q/Iраз = 14А*ч/0.3А = 47ч,

т.е. лампы горели 47ч. Через лампы прошёл ток 14А*ч, пока аккумулятор не разрядился.

Задача 3

Заряженный аккумулятор имеет ёмкость 28А*ч. 1) Какое количество электричества в кулонах содержит аккумулятор? 2) Какой ток необходим для зарядки аккумулятора за 10ч. Каким током разрядится он за 140ч.?

Решение.

1. 1А*ч = 360 А*с = 3600Кл

28А*ч = 28*3600Кл = 100800 Кл.

2. Iзар = Q/t = 28А*ч/10ч = 2.8А, т.е. аккумулятор зарядится за 10часов током 2.8А

3. Iраз = Q/t = 28А*ч/140ч = 0.2А.

Задача 4

Сколько ампер-часов содержтся в 96480 кулонах (заряд Фарадея)?

1А*ч = 3600А*с = 3600Кл;

96480/3600 = 26.8 А*ч, т.е. 96489 Кл. эквивалентен 26,8 А*ч

Задачи для самостоятельного решения:

1. Какой электрический заряд нужен от гальванического элемента, если он разряжается током 0,05А в течении 12ч.? (0,6 А*ч)

2. Через электродвигатель при токе I проходит количество электричества Q = 7500А*с за время t = 5мин/ Чему равен ток? (30мА)

3. Какой ток протекал по проводнику, если через его поперечное сечение за 30мин прошел заряд 54А*с? (30мА)

4. Через аппарат проходит ток I = 20мА в течение 9мин. Определить количество электричества, которое прошло через аппарат?

5. Аккумулятор ёмкостью 10А*ч заряжается током 4А. Как долго должен заряжаться? (10ч)

Задача 1.

Через медный проводник с площадью поперечного сечения S = 4 мм²

протекает ток I=10А. Какова плотность тока?

Решение:

Плотность тока

J = I/S = 10A/4мм² = 2.5 A/мм²

По площади 1 мм² поперечного сечения протекает ток I = 2.5A;

По всему поперечному сечению S проходит общий ток I = 10А.

По таблице проверить, допустима ли плотность тока 2.5 А/мм²?

Задача 2.

По шине разделительного устройства площадью прямоугольного поперечного сечения (20х80)мм проходит ток I = 1000A. Какова плотность тока в шине?

Решение

Площадь поперечного сечения шины S = 20х80 = 1600 мм². Плотность тока

J = I/S = 1000A/1600 мм² = 0.625A/мм²

Задача 3.

У катушки провод имеет круглое сечение диаметром 0,8мм и допускает плотность тока 2,5А/мм². Какой допустимый ток может проходить по проводу (нагрев не должен превышать допустимый)?

Решение:

Площадь поперечного сечения провода:

Допустимый ток:

Задача 4.

Допустимая плотность тока для обмотки трансформатора J = 2.5 А/мм²

Через обмотку проходит ток I = 4A. Каким должно быть поперечное сечение круглого проводника, чтобы обмотка не перегревалась?

Решение:

Площадь поперечного сечения

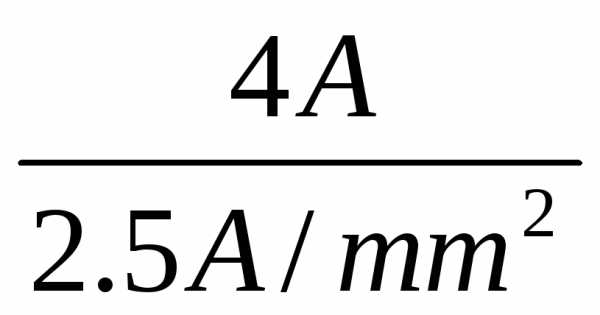
S=I/J=

Этому сечению соответствует диаметр провода 1.42мм.

Задача 5.

По изолированному медному проводу сечением 4 мм² проходит максимально допустимый ток 38А (см таблицу). Какая допустимая плотность тока? Чему равны допустимые плотности токов для медных проводов с площадями поперечного сечения 1, 10, 16 мм²?

Решение.

1. Допустимая плотность тока

2. Для сечения 1 мм² допустимая плотность тока (см табл)

3. Для сечения 10 мм² допустимая плотность тока

4. Для сечения 16 мм² допустимая плотность тока

Допустимая плотность тока с увеличением сечения кабеля тоже действительна для проводов с изоляцией класса В.

Задачи для самостоятельного решения.

1. Через обмотку трансформатора должен протекать ток I = 4A. Каким должно быть сечение обмоточного провода при допустимой плотности тока J = 2.5 А/мм² (S = 1.6 мм²)

2. По проводу диаметром 0,3 мм проходит ток 100А. Какова плотность тока (J = 1.415 А/мм²)

3. По обмотке электромагнита из медного изолированного провода диаметром d = 2.26мм (без учёта изоляции) проходит ток 10А. Какова плотность тока? (J= 2.5 А/мм²)

studfiles.net