Как из двоичной в десятичную. Как преобразовать двоичное число в десятичное: пошаговое руководство

Как правильно перевести двоичное число в десятичное. Какие методы используются для конвертации. Какие формулы применяются при переводе двоичных чисел в десятичные. Как быстро научиться переводить числа из двоичной системы в десятичную.

Основы двоичной и десятичной систем счисления

Двоичная и десятичная системы счисления являются фундаментальными в компьютерных науках и математике. Рассмотрим их особенности:

Двоичная система счисления

Двоичная система использует только две цифры — 0 и 1. Каждый разряд в двоичном числе представляет степень двойки. Например, число 1010 в двоичной системе можно представить как:

• 1 * 2^3 = 8
• 0 * 2^2 = 0
• 1 * 2^1 = 2
• 0 * 2^0 = 0

Суммируя эти значения, получаем 10 в десятичной системе.

Десятичная система счисления

Десятичная система использует 10 цифр от 0 до 9. Это наиболее привычная для нас система. В ней каждый разряд представляет степень 10. Например, число 2023 можно представить как:

• 2 * 10^3 = 2000
• 0 * 10^2 = 0
• 2 * 10^1 = 20
• 3 * 10^0 = 3

Методы перевода двоичных чисел в десятичные

Существует несколько методов перевода двоичных чисел в десятичные. Рассмотрим наиболее популярные из них:

Метод разложения по степеням двойки

Этот метод основан на представлении двоичного числа в виде суммы степеней двойки. Каждый разряд умножается на соответствующую степень двойки, затем результаты складываются.

Пример: переведем число 1101 из двоичной системы в десятичную

• 1 * 2^3 = 8
• 1 * 2^2 = 4
• 0 * 2^1 = 0
• 1 * 2^0 = 1

Сумма: 8 + 4 + 0 + 1 = 13

Метод последовательного удвоения

Этот метод предполагает последовательное удвоение результата и добавление текущей цифры двоичного числа. Процесс начинается с крайней левой цифры.

Пример: переведем число 1101 из двоичной системы в десятичную

1. Начинаем с 0
2. 0 * 2 + 1 = 1
3. 1 * 2 + 1 = 3
4. 3 * 2 + 0 = 6
5. 6 * 2 + 1 = 13

Результат: 13

Практические приемы быстрого перевода

Существуют некоторые практические приемы, которые могут ускорить процесс перевода двоичных чисел в десятичные:

Использование степеней двойки

Запомните степени двойки: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024. Это поможет быстро определять значение каждого разряда двоичного числа.

Группировка по три бита

Группируя биты по три, можно быстро переводить двоичные числа в восьмеричные, а затем в десятичные. Каждая группа из трех битов соответствует одной восьмеричной цифре.

Применение перевода двоичных чисел в десятичные

Перевод двоичных чисел в десятичные имеет широкое применение в различных областях:

Компьютерные науки

В компьютерных науках двоичная система используется для представления и обработки данных. Умение переводить двоичные числа в десятичные необходимо для понимания работы компьютерных систем.

Цифровая электроника

В цифровой электронике двоичная система используется для представления логических состояний. Перевод в десятичную систему помогает интерпретировать эти состояния в более понятной форме.

Распространенные ошибки при переводе двоичных чисел в десятичные

При переводе двоичных чисел в десятичные часто допускаются следующие ошибки:

Неправильное определение разрядов

Важно помнить, что в двоичной системе каждый разряд представляет степень двойки. Ошибка в определении разряда приведет к неверному результату.

Пропуск нулей

Нули в двоичном числе также важны. Пропуск нуля изменит значение числа и приведет к неправильному переводу.

Инструменты для автоматизации перевода

Существуют различные инструменты, которые могут автоматизировать процесс перевода двоичных чисел в десятичные:

Онлайн-калькуляторы

Множество онлайн-калькуляторов позволяют быстро переводить числа из одной системы счисления в другую. Они удобны для проверки результатов ручных вычислений.

Программируемые калькуляторы

Многие научные калькуляторы имеют функцию перевода между различными системами счисления, включая двоичную и десятичную.

Обратный процесс: перевод десятичных чисел в двоичные

Понимание обратного процесса — перевода десятичных чисел в двоичные — также важно. Это помогает лучше понять связь между двумя системами счисления.

Метод последовательного деления

Десятичное число последовательно делится на 2, остатки от деления формируют двоичное число (читается снизу вверх).

Пример: переведем число 13 из десятичной системы в двоичную

• 13 / 2 = 6 остаток 1
• 6 / 2 = 3 остаток 0
• 3 / 2 = 1 остаток 1
• 1 / 2 = 0 остаток 1

Результат: 1101

Заключение

Умение переводить числа из двоичной системы в десятичную и обратно является важным навыком в современном цифровом мире. Это основа для понимания работы компьютерных систем и цифровой электроники. Практика и использование различных методов помогут быстро и точно выполнять такие преобразования.

Перевод из двоичной в десятичную систему счисления, калькулятор

Сохраненные расчеты (0)

Исходное число

Направление перевода

2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

Сообщить об ошибке

В избранное

Виджет

Преобразовать число из двоичной системы счисления в десятичную можно следующим образом: каждый разряд числа необходимо умножить на 2ⁿ, где n — номер разряда, начиная с 0. Затем суммировать полученные значения.

abc₂ = (a×2² + b×2¹ + c×2⁰)₁₀

110₂ = (1*2² + 1*2¹ + 0*2⁰)₁₀ = 6₁₀

10010010₂ = (1*2⁷ + 0*2⁶ + 0*2⁵ + 1*2⁴ + 0*2³ + 0*2² + 1*2¹ + 0*2⁰)₁₀ = 146₁₀

Смотрите также

• Перевод из десятичной в восьмеричную
• Перевод из двоичной в восьмеричную
• Перевод из двоичной в шестнадцатеричную
• Перевод из десятичной в двоичную
• Перевод из десятичной в шестнадцатеричную
• Перевод из восьмеричной в двоичную
• Перевод из восьмеричной в десятичную
• Перевод из шестнадцатеричной в двоичную
• Перевод из шестнадцатеричной в десятичную

Системы счисления.

Перевод из одной системы в другую.

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100.

И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):

0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):

0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

 

 
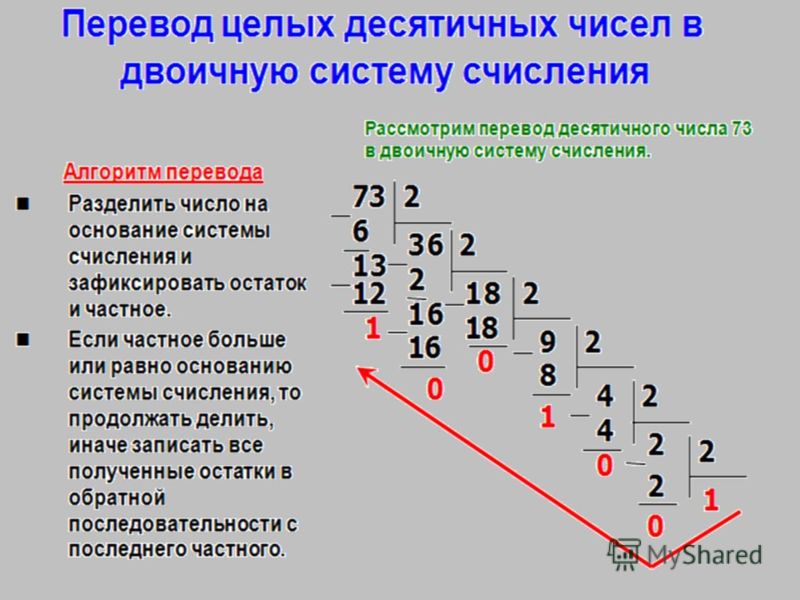
2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания.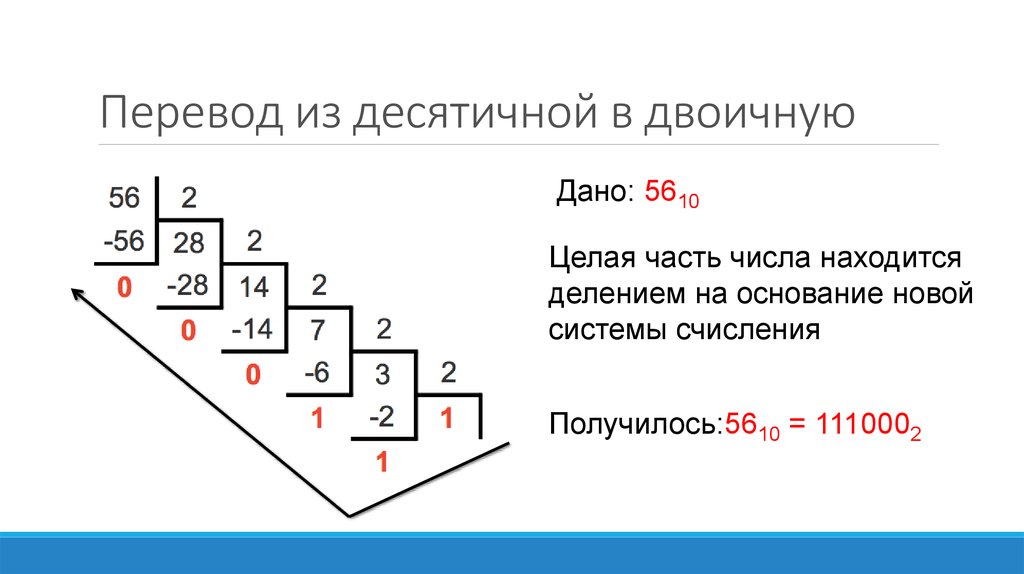 В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т. е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т. е.

Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Системы счисления. Перевод из одной системы в другую.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 08.04.2023

Как преобразовать двоичное число в десятичное

Содержание

В этом блоге мы узнаем о четырех типах систем счисления, узнаем, как преобразовать двоичное число в десятичное и какие существуют различные методы преобразования. Итак, не теряя времени, приступим!

• Введение
• Что такое двоичная система счисления?
• Что такое десятичная система счисления?
• Что такое преобразование двоичного кода в десятичный?
• Методы преобразования двоичных чисел в десятичные
• Формула двоичных чисел в десятичные
• Как преобразовать двоичные числа в десятичные
• Заключение 040 Введение

  В математике система счисления — это способ представления чисел. Существует четыре типа систем счисления:

  1. Двоичная система счисления (Основание – 2)
  2. Восьмеричная система счисления (Основание – 8)
  3. Десятичная система счисления (основание – 10)
  4. Шестнадцатеричная система счисления (основание – 16)

  Система счисления играет важную роль в основном во всех компьютерных устройствах и особенно в компьютерной архитектуре. Он используется компьютерными инженерами, специалистами по связи, сетями и другими специалистами. Прежде чем перейти к преобразованию двоичной системы в десятичную, давайте разберемся в обеих системах счисления.

  Что такое двоичная система счисления?

  Двоичная система счисления — это простейшая форма системы счисления, в которой используются только две цифры: 0 (ноль) и 1 (единица). Ее также называют системой счисления с основанием 2. Этот номер в основном используется в компьютерной архитектуре и электронных устройствах.

  Примеры двоичной системы счисления: 01, 101, 1110, 10011, 1011101 и т. д.

  Что такое десятичная система счисления?

  Десятичная система счисления представляет собой представление чисел от 0 до 9. Десятичная система счисления является наиболее распространенной системой счисления, используемой широкой публикой. Эти системы счисления также известны как система счисления с основанием 10.

  Пример десятичной системы счисления: 10, 121, 485, 8483, 82940 и т. д.

  Что такое преобразование двоичного кода в десятичный?

  Преобразование двоичной системы счисления в десятичную выполняется для преобразования двоичной системы счисления в десятичную систему счисления, что означает преобразование системы счисления с основанием 2 в систему счисления с основанием 10. Важно знать двоичное преобразование в десятичное из-за приложений для компьютерного программирования. Таким образом, машина может понимать только двоичную систему счисления в форме 0 и 1, тогда как люди могут легко понять десятичную систему счисления, включающую все 10 цифр. Итак, важно понимать, как преобразовать двоичные системы счисления в десятичные системы счисления.

  Методы преобразования двоичной системы счисления в десятичную

  Существует два основных метода преобразования двоичной системы счисления в десятичную. Вот эти методы:

  1. Позиционная запись
  2. Удвоение
  Преобразование с использованием позиционной записи
  • Запишите двоичное число и посчитайте степень 2 справа налево, начиная с 0 и далее.
  • Теперь каждое двоичное число имеет соответствующую степень двойки, начиная справа налево. Таким образом, самый старший бит будет иметь наивысшую степень 2. 
  • Добавьте произведение второго шага
  • Окончательный ответ будет преобразован в десятичное число с основанием 10.
  Пример позиционной записи

   Двоичное число: (101)2
  1 0 1
  1 х 22 + 0 х 21 + 1 х 20
  4 + 0 + 1
  (5)10
  Итак, десятичное число (101)2 равно (5)10.
  Аналогично мы можем представить дробное двоичное число в десятичные дроби
  Двоичный номер: (0,101)2
  1 0 1 . 1 0 1
  1 х 22 + 0 х 21 + 1 х 20. 1 х 2-1 + 0 х 2-2 + 1 х 2-3
  (4 + 0 + 1) . (0,5 + 0 + 0,125)
  (5,625)10
  Итак, десятичное число (0,101)2 равно (5,625)10.
   

  Преобразование с помощью удвоения

  Преобразование с помощью удвоения — один из самых простых способов преобразования двоичных чисел в десятичные. Нам нужно взять самый старший разряд или крайнюю левую цифру числа. Затем умножьте цифру на 2, добавьте второй крайний левый бит и сохраните результат. Точно так же нам нужно взять результат и умножить его на 2, взять третий крайний левый бит и обновить результат. Этот процесс будет продолжаться до тех пор, пока мы не достигнем самого младшего бита, который является самым правым битом. Поскольку мы умножаем на 2, этот процесс известен как удвоение.

  Пример удвоения

  Двоичный номер: (101) ₂ 

  = 1

  = 1 x 2 + 0 = 2

  = 2 x 2 9002, 9002, 000 5 маленькое количество (101) ₂ равно (5) ₁₀

  Формула преобразования двоичной системы счисления в десятичную

  Формула преобразования двоичной системы счисления в десятичную может быть представлена ​​следующим образом: + х _н-1 * б ^н-1 + ….. + х ₁ * b ¹ + x ₀ * b ⁰

  Где

  A представляет целое число

  x представляет числовое значение

  b0 представляет базовое значение 03 Например:

  (1000) ₂ = 1 х 2 ³ + 0 х 2 ² + 0 х 2 0003

  Табличное представление двоичного кода в десятичный Номер 1 30 20219 2119

  Двоичный1	Десятичный1	Двоичный2	8 Десятичный2 2 6
  0000	0	1000	8
  0001	1	1	9
  0010	2	1010	10
  00211 0 90 1011	11
  0100	4	1100	12
  0101	5
  0110	6	1110	14
  0111	7	1111	15

  Как преобразовать двоичное число в десятичное
  Использование позиционной записи 6
• (10001) ₂

 1 0 0 0 1
= 1 х 24 + 0 х 23 + 0 х 22 + 0 х 21 + 1 х 20
= 16 + 0 + 0 + 0 + 1
= (17)10
 

• (1000. 101) ₂

 1 0 0 0 . 1 0 1
= (1 х 23 + 0 х 22 + 0 х 21 + 0 х 20) . (1 х 2-1 + 0 х 2-2 + 1 х 2-3)
= (8 + 0 + 0) . (0,5 + 0 + 0,125)
= (8,625)10 

Использование удвоения

Примеры :

• (10011) ₂

 1 0 0 1 1
= 1
= 1 х 2 + 0 = 2
= 2 х 2 + 0 = 4
= 4 х 2 + 1 = 9
= 9 х 2 + 1 = 19
= (19)10 

• (10000101) ₂

 1 0 0 0 0 1 0 1
= 1
= 1 х 2 + 0 = 2
= 2 х 2 + 0 = 4
= 4 х 2 + 0 = 8
= 8 х 2 + 0 = 16
= 16 х 2 + 1 = 33
= 33 х 2 + 0 = 66
= 66 х 2 + 1 = 133
= (133)10
 

В заключение

Итак, мы увидели, как легко можно преобразовать двоичные числа в десятичную систему счисления, и это облегчает понимание и чтение. Кроме того, важно знать, что двоичное число также может быть десятичным числом, например, 10 может быть двоичным числом, поскольку оно состоит из 0 и 1, но, с другой стороны, 10 также может быть десятичным числом, поскольку оно создается из цифры 0-9. Поэтому, чтобы избежать этой путаницы, всегда ориентируйтесь на базовое значение этого числа, например (10) ₂ — двоичное число, потому что основание равно 2, а (10) ₁₀ — десятичное число, потому что основание равно 10.  

Как преобразовать двоичное число в десятичное

Как преобразовать двоичное число в десятичное | преобразование чисел

Главная›Конвертация›Преобразование чисел› Как преобразовать двоичное число в десятичное

Десятичное число равно сумме двоичных цифр (d _n ), умноженных на их степень 2 (2 ⁿ ):

десятичное = d ₀ × 2 ⁰ + d ₁ × 2 ¹ + 3 d 2 ×2 ² + …

Пример #1

Найдите десятичное значение 111001 ₂ :

двоичное число:	1	1	1	0	0	1
степень 2:	2 5	2 4	2 3	2 2	2 1	2 0

111001 ₂ = 1⋅2 ⁵ +1⋅2 ⁴ +1⋅2 ³ +0⋅2 ² +01⋅72 ⋅2 ⁰ = 57 ₁₀

Пример №2

Найдите десятичное значение 100011 ₂ :

	1	0	0	0	1	1
степень 2:	2 5	2 4	2 3	2 2	2 1	2 0

100011 ₂ = 1⋅2 ⁵ +0⋅2 ⁴ +0⋅2 ³ +0⋅2 ² +1 91⋅72 91⋅72 ⋅2 ⁰ = 35 ₁₀

Преобразователь двоичного кода в десятичный ►

Таблица преобразования двоичного кода в десятичный

Двоичный	Десятичный
0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	10
1011	11
1100	12
1101	13
1110	14
1111	15
10000	16
10001	17
10010	18
10011	19
10100	20
10101	21
10110	22
10111	23
11000	24
11001	25
11010	26
11011	27
11100	28
11101	29
11110	30
11111	31
100000	32
1000000	64
10000000	128
100000000	256

 

Как преобразовать десятичную систему в двоичную ►

 

---

См.