Как измерить волновое сопротивление коаксиального кабеля: методы и особенности

Как определить волновое сопротивление коаксиального кабеля. Какие существуют способы измерения Z0. Почему нельзя измерить Z0 обычным омметром. Какие приборы и методы позволяют точно измерить характеристический импеданс.

Что такое волновое сопротивление коаксиального кабеля

Волновое сопротивление (характеристический импеданс, Z0) — это важный параметр коаксиального кабеля, который определяет его свойства при передаче высокочастотных сигналов. Z0 выражается в омах и обычно составляет 50 или 75 Ом для большинства коаксиальных кабелей.

Волновое сопротивление зависит от геометрических размеров кабеля и свойств диэлектрика между проводниками. Оно определяет, как кабель будет согласовываться с источником сигнала и нагрузкой.

Почему нельзя измерить Z0 обычным омметром

Распространено заблуждение, что волновое сопротивление коаксиального кабеля можно измерить простым омметром. Однако это невозможно по следующим причинам:

• Z0 — это не активное сопротивление постоянному току
• Омметр измеряет сопротивление между проводниками, которое стремится к бесконечности для разомкнутого кабеля
• Z0 проявляется только при передаче высокочастотных сигналов

Попытка измерить Z0 омметром приведет к неверным результатам и ошибочным выводам о параметрах кабеля.

Корректные методы измерения волнового сопротивления

Для точного определения Z0 коаксиального кабеля используются следующие методы:

Измерение с помощью анализатора цепей

Векторный анализатор цепей позволяет измерить S-параметры кабеля в широком диапазоне частот. По измеренным S-параметрам можно рассчитать Z0.

Метод рефлектометрии во временной области (TDR)

TDR-измеритель посылает в кабель короткий импульс и анализирует отраженный сигнал. По форме отражения определяется Z0 кабеля.

Измерение погонной емкости и индуктивности

Измерив погонную емкость C и индуктивность L кабеля, можно рассчитать Z0 по формуле:

Z0 = √(L/C)

Особенности измерения Z0 на высоких частотах

При измерении волнового сопротивления на высоких частотах необходимо учитывать следующие факторы:

• Дисперсию параметров кабеля
• Влияние скин-эффекта
• Потери в диэлектрике
• Неоднородности кабеля

Это приводит к частотной зависимости Z0. Поэтому важно проводить измерения в требуемом диапазоне рабочих частот кабеля.

Влияние волнового сопротивления на характеристики линии передачи

Волновое сопротивление кабеля влияет на следующие важные параметры:

• Коэффициент отражения сигнала
• Коэффициент стоячей волны (КСВ)
• Вносимые потери
• Согласование с источником и нагрузкой

Поэтому точное знание Z0 необходимо для правильного применения коаксиальных кабелей в высокочастотных системах.

Согласование волнового сопротивления в линиях передачи

Для минимизации отражений и потерь важно согласовывать волновые сопротивления источника сигнала, кабеля и нагрузки. Основные методы согласования:

• Подбор кабеля с нужным Z0
• Использование согласующих трансформаторов
• Применение четвертьволновых отрезков линии
• Согласование с помощью шлейфов

Правильное согласование позволяет максимально эффективно передавать сигнал по коаксиальному кабелю.

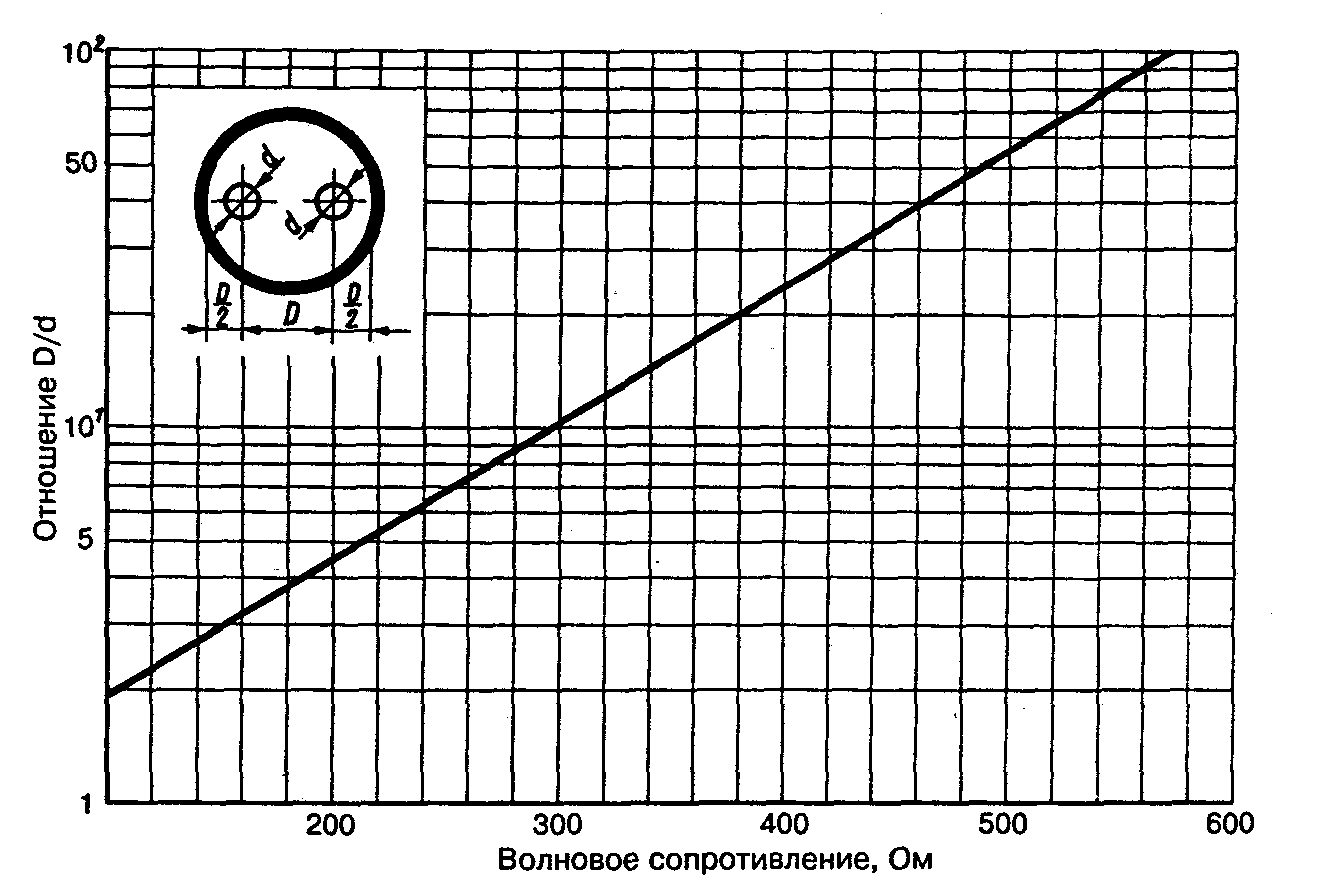
Зависимость волнового сопротивления от геометрии кабеля

Волновое сопротивление коаксиального кабеля зависит от соотношения диаметров внешнего и внутреннего проводников, а также от диэлектрической проницаемости изоляции. Эта зависимость описывается формулой:

Z0 = (138 / √ε_r) * log(D/d)

где:

• ε_r — относительная диэлектрическая проницаемость изоляции
• D — внутренний диаметр внешнего проводника
• d — внешний диаметр центрального проводника

Изменяя эти параметры, производители могут создавать кабели с различным волновым сопротивлением.

Практические рекомендации по измерению Z0 коаксиальных кабелей

При измерении волнового сопротивления кабелей следует соблюдать следующие правила:

• Использовать качественные измерительные приборы с калибровкой
• Учитывать влияние разъемов и переходников
• Проводить измерения на нескольких образцах кабеля
• Контролировать температуру окружающей среды
• Сравнивать результаты, полученные разными методами

Соблюдение этих рекомендаций позволит получить достоверные данные о волновом сопротивлении исследуемых кабелей.

Как измерить длину коаксиального кабеля и его волновое сопротивление с помощью осциллографа. » Хабстаб

Для того чтобы передавать информацию через линию передачи данных необходимо, что бы сопротивление нагрузки было равно, волновому сопротивлению линии. Если это условие не выполнено и сопротивление нагрузки на конце линии велико, то энергия сигнала, дойдя до конца линии, не сможет выйти из неё и отразится обратно. Отражённый сигнал спустя некоторое время вернётся ко входу линии и сложится с сигналом, направленным в линию в итоге форма, передаваемого сигнала будет искажена, а информация потеряна.

Зная время, которое сигнал был в пути и его скорость можно вычислить расстояние, которое он прошёл. Скорость распространения сигнала по коаксиальному кабелю равна 2/3 скорости света, в среднем считается, что за 1 nS сигнал проходит 20 cm, на самом деле чуть меньше.
Для этого эксперимента нам потребуется собрать генератор меандра, с крутым фронтом.

Время нарастания сигнала в такой схеме составляет несколько nS, у меня получилось 3,4 , а частота в зависимости от партии микросхемы колеблется от 2 до 6 KHz.

Схема изготавливается из двух кусков текстолита, на одном распаивается микросхема, в другом закрепляется BNC разъём.

С помощью Т-образного BNC коннектора подключим генератор и исследуемый кабель к осциллографу, длина кабеля 157 cm.

На осциллограмме видна некоторая задержка при нарастании фронта. Она возникает в месте где амплитуда сигнала, направленного в линию максимальна, а амплитуда отражённого сигнала равна нулю. Пока отражённый сигнал достиг начала линии, он прошёл путь равный 314 cm. Таким образом, время задержки должно быть равно 15,7 nS, измеренное время задержки равно 15,2 nS, разница обусловлена погрешностью метода.

Давайте к другому концу кабеля подключим подстроечный резистор и посмотрим как будет изменяться осциллограмма в зависимости от сопротивления.
При совпадении сопротивления резистора с волновым сопротивлением кабеля, вся энергия сигнала будет беспрепятственно переходить из линии в резистор и «ступенька», которая возникала за счёт отражённого сигнала, должна исчезнуть.
Сопротивление резистора 0 Ohm.

Сопротивление резистора 50 Ohm.

Сопротивление резистора 75 Ohm.

Сопротивление резистора 100 Ohm.

Из этих осциллограмм нельзя сделать однозначный вывод, какое волновое сопротивление этого кабеля.

Если увеличить длину кабеля, увеличится время задержки и изменение сопротивления на конце линии будет более наглядно. Длинного куска кабеля под рукой нет, но есть кабель, проложенный по плинтусу из одного помещения в другое. Подключил этот кабель к осциллографу с генератором.

Длина «ступеньки» увеличилась, подпаиваем с другого конца сопротивление и начинаем крутить.
Сопротивление резистора 0 Ohm.

Сопротивление резистора 50 Ohm.

Сопротивление резистора 75 Ohm.

Сопротивление резистора 100 Ohm.

Из осциллограмм видно, что волновое сопротивление кабеля равно 75 Ohm, при других значениях сопротивления «ступенька» снова появлялась.
Опираясь на полученные знания можно вычислить скорость распространения сигнала, в любой другой линии передачи данных, измерив задержку в двухметровом куске. А зная скорость можно описанным способом вычислить длину более длинного кабеля.
Теперь мы знаем как измерить длину кабеля и его волновое сопротивление с помощью осциллографа.

 Измерительные кабели | Измерения на высоком напряжении

Подробности

Категория: Разное-архив

• эксплуатация
• испытание
• диагностика и измерения

Содержание материала

• Измерения на высоком напряжении
• Общие вопросы осциллографирования
•  Измерительные кабели
• Помехи
• Применение дифференциальных усилителей в схемах измерения
• Фотографическая запись
• Измерение импульсов высокого напряжения при помощи делителя напряжения и осциллографа
• Генераторы импульсов для измерения переходной функции
• Время нарастания импульса и время ответа
• Влияние делителя напряжения на процессы в высоковольтном контуре
• Компенсированные делители напряжения без учета индуктивностей и емкостей
• Омические делители напряжения с учетом паразитных емкостей на землю
• Низкоомные делители напряжения
• Влияние подводящих проводов на переходную функцию емкостных делителей
• Чисто емкостные делители напряжения
• Демпфированные емкостные делители напряжения
• Согласованное подключение низковольтной части емкостного делителя
• Схема замещения в виде цепной линии
• Измерение импульсов при помощи ячейки Керра и светопровода
• Высокоомные сопротивления и делители напряжения  — измерение высокого напряжения
• Электростатические вольтметры
• Измерение действующих значений переменных напряжений — добавочные сопротивления и делители напряжения
• Измерение действующих значений переменных напряжений — индуктивные трансформаторы напряжения
• Измерение амплитуд импульсных, переменных и постоянных высоких напряжений шаровым разрядником
• Измерение амплитуд высоких переменных и импульсных напряжений
• Измерение амплитуд напряжения по Хубу и Фортескье
• Измерение амплитуд — пик-вольтметры для переменного напряжения
• Измерение амплитуд — импульсные пик-вольтметры
• Измерения роторными и генерирующими вольтметрами
• Измерение электростатических зарядов
• Измерение больших быстропеременных токов электроннолучевым осциллографом
• Чувствительность, образцовый конденсатор
• Паразитные емкости и экранирование
• Нуль-индикаторы
• Измерение емкости и tg дельта у заземленных объектов
•  Измерение частичных разрядов
• Испытуемый объект с распределенными параметрами
• Приборы для измерения величин частичных разрядов с помощью четырехполюсника связи
• Другие способы измерения частичных разрядов

Страница 3 из 39

Из соображений безопасности, для уменьшения полей рассеяния, а также для удобства обслуживания электроннолучевой осциллограф чаще всего устанавливают в удалении от делителя импульсного напряжения или измерительного шунта для импульсных токов.

Рис. 4. Возникновение напряжений помех от соседнего провода, обтекаемого током.
а — соединение, выполненное обычными проводами; б —то же коаксиальным кабелем.

Поэтому измеряемый сигнал u(t) нужно передать к входу осциллографа по коаксиальному кабелю. Для сравнительно медленно изменяющихся напряжений достаточно коаксиального расположения подводящих проводов; необходимо лишь экранирование измерительных цепей от помех. На рис. 4 вблизи двух подводящих проводов измерительной цепи показан третий провод, обтекаемый током i(t). Этот ток создает изменяющееся по времени магнитное поле, которое пронизывает измерительные цепи. Индуктированное в этих цепях напряжение накладывается в виде помех на измеряемый сигнал. Одновременно через паразитную емкость

С в измерительную цепь проникает электрическая составляющая напряжения помехи. Чтобы подавить обе составляющие, подводящие провода измерительной цепи выполняют коаксиальными (рис. 4,б). Тогда помеха, проникающая через емкость, может быть исключена, так как силовые линии электрического поля между проводом, обтекаемым током, и измерительной цепью заканчиваются на заземленной оболочке кабеля.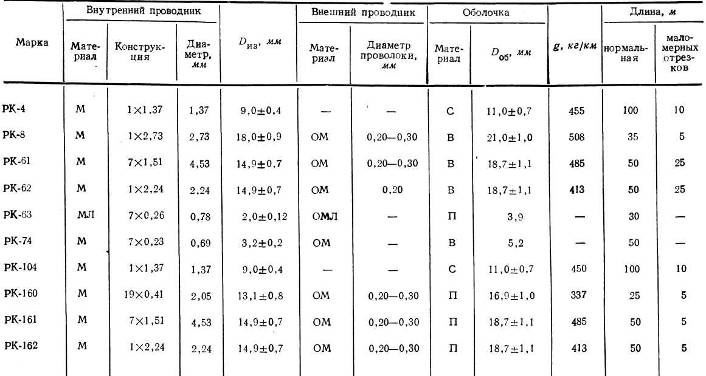 Однако экранирование от электрических полей здесь не идеально, поскольку оболочка коаксиального кабеля состоит из проволочной плетенки и сквозь нее возможно проникновение силовых линий во внутреннее пространство. Специальный гибкий гофрированный кабель, экран которого состоит из гофрированной металлической трубки, полностью экранирует внутреннюю жилу от электрического поля.
Экранирование магнитной составляющей поля обеспечивается встречным полем, создаваемым вихревыми токами, индуктированными в экране кабеля внешним магнитным полем помехи. Обычные немагнитные экраны коаксиальных кабелей не. экранируют постоянные магнитные поля и плохо экранируют переменные магнитные поля низкой частоты, так как в таких экранах вихревые токи совсем не индуцируются или очень малы. Это, однако, не имеет значения, так как индуктированное напряжение помехи пропорционально частоте тока помехи; соответственно при малых частотах это напряжение невелико и не требует экранирования. С увеличением частоты экранирующее действие для магнитных полей, определяемое, главным образом, толщиной проволочной ткани, возрастает. У гибкого гофрированного кабеля экранирующее действие для магнитных полей возрастает с увеличением частоты вследствие вытеснения тока.
Несмотря на применение коаксиальных кабелей, при измерении быстропеременных процессов возникают другие напряжения помех. Причины возникновения этих помех и способы экранирования от них рассматриваются позднее.
Для процессов, спектры которых не содержат высоких частот, кабели и подводящие провода, в зависимости от их соединения на конце, представляют собой емкости или индуктивности. При очень быстрых изменениях напряжения в кабеле с волновым сопротивлением Zn появляется волна напряжения независимо от того, разомкнут ли кабель на конце, закорочен или нагружен любым сопротивлением. Нагрузка, подключенная к концу кабеля, скажется у начала кабеля после времени двойного пробега по нему волны напряжения. Кабель должен рассматриваться как проводник с распределенными параметрами, если время пробега по нему волны напряжения приблизительно равно времени нарастания импульса, подлежащего передаче. Например, для импульса с временем возрастания t=1 на кабели длиной менее 10 см уже являются проводниками с распределенными параметрами.
Скорость распространения сигнала по проводнику равна:
где с=3-1010 см/с — скорость распространения света в вакууме; ε и μ — относительная диэлектрическая и магнитная проницаемости изоляции кабеля.
Так как для измерительного кабеля μ=1, то равенство упрощается
У диэлектриков, применяемых для коаксиальных измерительных кабелей, v=0,5:0,7 с. Время пробега волны по единице длины кабеля (мкс/м)

Абсолютное время распространения волны по кабелю вычисляется по уравнению

Из этого уравнения можно определить длину кабеля, необходимую для получения заданной задержки измеряемого сигнала.
При сопротивлении внешней цепи, не равном ZВ, часть сигнала отражается от конца кабеля и возвращается к началу. Если внутреннее сопротивление источника Zi также не равно ZB, то возвращающаяся волна напряжения вновь отражается и на экране электроннолучевого осциллографа воспроизводится напряжение, совершенно не соответствующее измеряемому сигналу  u(t). Для точной передачи измеряемого сигнала измерительный кабель нужно нагрузить сопротивлением величиной Zв (рис. 5). К сожалению, осуществить это с достаточной точностью практически невозможно, так как параллельно нагрузочному сопротивлению всегда оказывается подключенным входное полное сопротивление электроннолучевого осциллографа (чаще всего это активное сопротивление Rn.o≈1 МОм и емкость Сэ.о=10:50 пФ). При низких частотах это параллельно подключенное сопротивление практически не сказывается; однако на высоких частотах значение 1/<оС30 становится величиной того же порядка, что и ΖΒ, так что о получении требуемого нагрузочного сопротивления на конце кабеля не может быть и речи (например, при Сэ.о=20 пФ и f=100 МГц значение 1/wСэ.о=80 Ом). Чтобы отраженный от конца кабеля сигнал повторно не отражался у начала кабеля, целесообразно, если это только возможно, иметь у источника внутреннее сопротивление Zi = Zn. При этом следует иметь в виду, что при согласованном рабочем режиме, т. е. когда внутреннее сопротивление источника, волновое сопротивление измерительного кабеля и нагрузочное сопротивление имеют одинаковые значения, наблюдаемое на экране электроннолучевого осциллографа напряжение нужно увеличить вдвое, чтобы получить действительное значение напряжения на зажимах источника при холостом ходе. Например если омический делитель напряжения R1—R2 имеет передаточное отношение при холостом ходе

и снятое с его низковольтной части R2 напряжение подается на электроннолучевой осциллограф по согласованному кабелю, то практически передаточное отношение всей измерительной схемы равно
2 000, так как сопротивление низковольтной части схемы, вследствие параллельного подключения волнового сопротивления кабеля ΖΒ=R2 уменьшается вдвое.
Рис. 5. Соединение генератора регистрируемых импульсов с электроннолучевым осциллографом коаксиальным кабелем.
1 — генератор импульсов с внутренним сопротивлением Z;

1. — коаксиальный кабель с волновым сопротивлением ZB;
2. — нагрузочное сопротивление ZB; 4 —входное полное сопротивление электроннолучевого осциллографа.

Затухание в кабеле и связанная с ним зависящая от частоты погрешность передачи для данного типа кабеля тем меньше, чем короче кабель. В технике измерения импульсов высокого напряжения могут применяться кабели длиной менее 10 м. Эти кабели можно считать проводниками без потерь и затухания, так как создаваемая ими погрешность значительно меньше, чем в остальных частях измерительного устройства. С этой точки зрения предпочтителен упомянутый выше третий способ управляемого запуска генератора импульсов, при котором кабель от делителя напряжения к отклоняющим пластинам электроннолучевого осциллографа может быть коротким.
Длинный коаксиальный кабель нельзя рассматривать как проводник без потерь. При передаче импульсов с большой длиной волны у последовательно соединенных сопротивления кабеля Rtl и активного нагрузочного сопротивления R возникает деление напряжения, которое приводит к так называемым погрешностям постоянного напряжения:
Если нужно передать крутые фронты, например, косоугольной формы, то при большой крутизне следует считаться с сильным снижением амплитуды u2(t) вследствие увеличения активного сопротивления из-за поверхностного эффекта.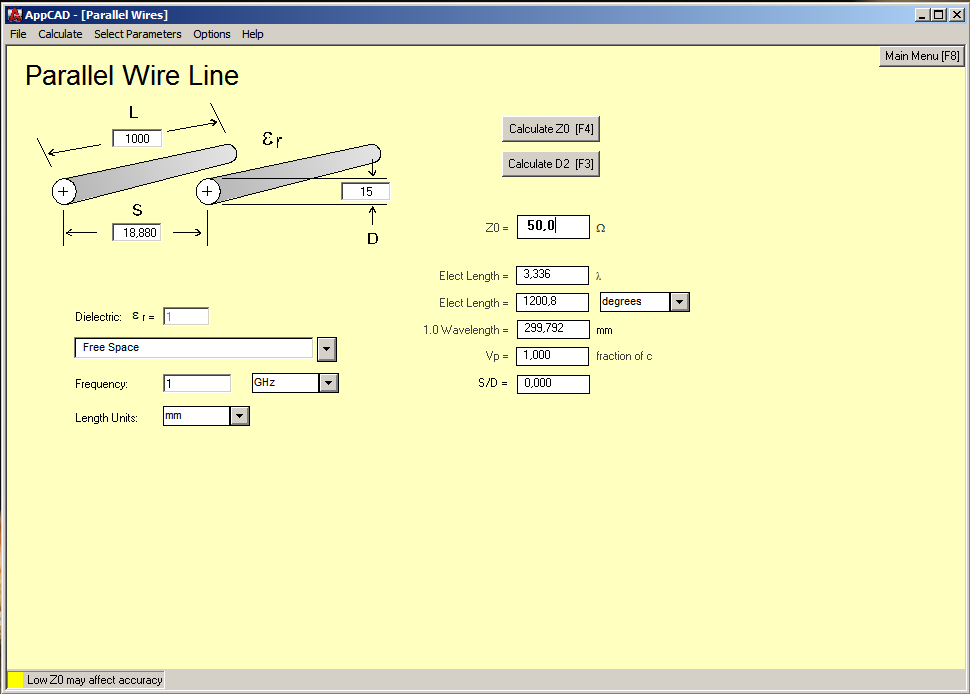 Обе погрешности при длинах кабеля менее 10 м несущественны. При больших длинах рекомендуется применять кабель с малым волновым сопротивлением, так как при большом диаметре внутренней жилы он обладает малым сопротивлением на единицу длины Ri. Подробные сведения по расчету погрешностей передачи у длинных коаксиальных кабелей можно найти в [Л. 3—5, 19—22].
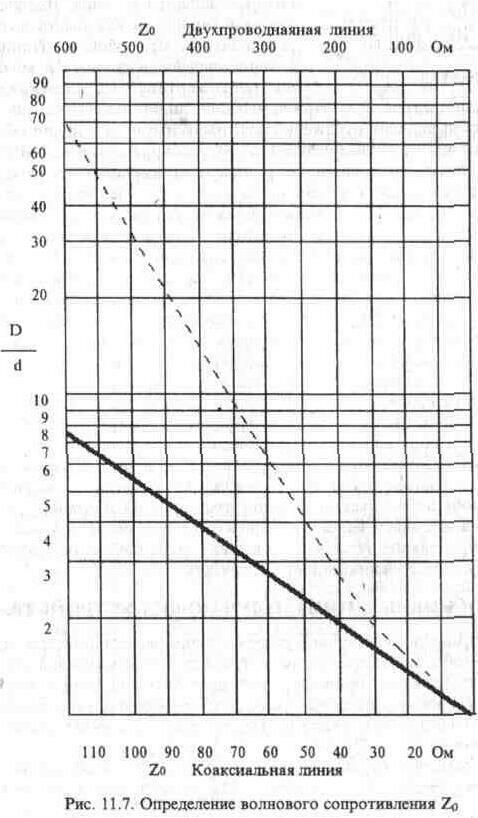
Часто ставится задача определения волнового сопротивления имеющегося в наличии кабеля. Изготовители кабелей применяют для этой цели специальные измерительные стенды, которые позволяют производить измерения параметров кабеля в широком диапазоне частот. Однако волновое сопротивление можно определить и более простыми приборами с достаточной для рассматриваемого случая точностью. Как известно, волновое сопротивление коаксиального кабеля с малыми потерями равно:
Если известны индуктивность и емкость на единицу длины кабеля, то по приведенной выше формуле можно вычислить волновое сопротивление. Оба упомянутых выше параметра на единицу длины могут быть очень просто определены экспериментально. Мостом для измерения индуктивности (либо резонансным способом) измеряют индуктивность у закороченного на оболочку отрезка кабеля. Затем у того же отрезка измеряют емкость при разомкнутых его концах. Корень квадратный из отношения обоих измерений дает волновое сопротивление.
Емкость кабеля с полиэфирной изоляцией в первом приближении не зависит от частоты, а индуктивность в диапазоне частот 105—107 Гц в зависимости от типа кабеля уменьшается примерно на 20% (вследствие вытеснения тока индуктивность внутренней жилы стремится к нулю). Так как волновое сопротивление изменяется пропорционально L, уменьшение волнового сопротивления в том же диапазоне частот составит примерно 10%. Поэтому измеренное значение ZB зависит от частоты, на которой производится измерение индуктивности. Чаще всего приборы для измерения индуктивности работают на частотах не более 1 МГц, что приводит к завышению значения индуктивности. При передаче сигнала с крутым фронтом следует произвести округление вычисленного значения до ближайшего меньшего нормированного волнового сопротивления, которое определяется изготовителем кабеля при частоте несколько сотен МГц.

• Назад
• Вперёд

• Назад
• Вперёд

• Вы здесь:  
• Главная
• Архив
• Разное архив
• Судовые станции и сети

Еще по теме:

• Контроль качества и испытания высоковольтных выключателей АББ
• Высоковольтное испытательное оборудование и измерения
• Испытания и измерения при ремонте электродвигателей
• Электрические испытания и измерения при ремонте электродвигателей
• Средства измерений для испытаний трансформаторов

Микроволны101 | Измерение характеристического импеданса

Нажмите здесь, чтобы перейти на нашу главную страницу измерений

Нажмите здесь, чтобы перейти на нашу страницу, посвященную характеристическому импедансу

Нажмите здесь, чтобы перейти на нашу страницу диаграммы Смита

Нажмите здесь, чтобы перейти на нашу страницу рефлектометрии во временной области

Щелкните здесь, чтобы перейти на нашу страницу о четвертьволновых трансформаторах

На этой странице будут объединены несколько различных попыток измерения волнового сопротивления (Z0).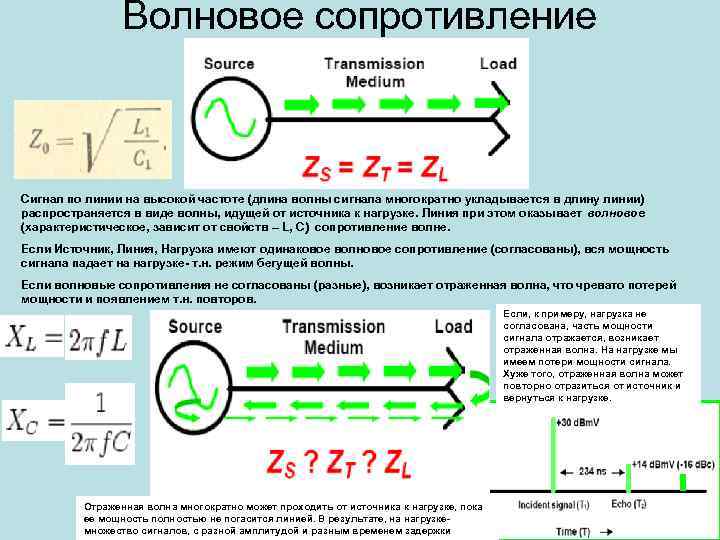 Единственное, что у них общего, это то, что все они используют электрические измерения линий передачи, в отличие от электромагнитных или закрытых моделей. Только одно решение (пока) способно измерять Z0 по частоте так, чтобы можно было наблюдать дисперсию.

Можно ли измерить Z0 омметром?

Измерение Z0 с использованием коэффициента отражения

Измерение Z0 на диаграмме Смита

Microwaves101 способ измерения Z0

Измерение Z0 с помощью рефлектометрии во временной области (отдельная страница)

Можно ли измерить Z0 омметром?

Ниже приведен текст, который мы нашли на веб-сайте «E-how» в 2012 году, в котором показано, как тестировать кабель на 50 или 75 Ом. С тех пор этот контент был удален. Во всемирной паутине много дезинформации, нужно быть осторожным. У них наверняка есть много рекламных ссылок!

1. Установите мультиметр на шкалу сопротивления около 100 Ом. Более высокая шкала работает, но избегайте перехода к шкале, близкой к 1 кОм или выше. Коаксиальный кабель обычно рассчитан на работу при сопротивлении 50 или 75 Ом, поэтому шкала должна быть на уровне или выше этих значений.

2. Отсоедините оба конца кабеля от разъемов.

3. Проверьте длину кабеля, поместив щуп мультиметра на каждый конец кабеля, касаясь центрального провода, выходящего из коаксиального разъема.

4. Прочтите показания мультиметра. Значение сопротивления кабеля около 50 Ом или 75 Ом указывает на то, что кабель работает правильно по всей длине. Показание бесконечного сопротивления указывает на разрыв где-то внутри кабеля. Нулевое значение указывает на короткое замыкание между внутренним кабелем и его экраном.

Нет лучшего способа сказать это, чем «какой идиот!» Плохие советы постоянны, больше давать не будем.

Что это за характеристика импеданса, также известная как «Z-ноль»? Начнем с распространенного заблуждения. Если у вас есть коаксиальный кабель на 50 Ом (или микрополосковая линия, или любая другая линия передачи на 50 Ом), который ни к чему не подключен на обоих концах, и подключите к нему омметр, вы можете рассчитывать на 50 Ом, если вы новичок. к СВЧ-технике. Но вы измерите разомкнутую цепь (если что-то не нагружает противоположный конец, что означает, что вы не следовали нашим простым инструкциям …) далеко не пятьдесят Ом. В чем дело?

Но подождите, Йенс из Дании хочет, чтобы вы знали, что приведенное выше утверждение не на 100% технически верно:

На новой странице характеристического импеданса вы начинаете с утверждения, что вы не можете ничего измерить, если подсоедините обычный омметр к 50-омному кабелю или микрополосковой полосе. Это просто потому, что линия слишком коротка, чтобы счетчик мог получить показания. Измерителю может потребоваться около 1 секунды, чтобы получить стабильные показания. Если вы возьмете передачу без потерь, скажем, c x 1,5 (около 4,5 x exp(8) метров!), вы получите показание, которое длится около 3 секунд. Однако у вас могут возникнуть некоторые практические проблемы с этим экспериментом. Линия будет обматывать экватор около 11,25 раз. И получить его без потерь тоже будет непросто.

Спасибо, и сообщите нам, когда у вас будет этот кабель, чтобы мы могли выполнить измерение!

А теперь противоположная точка зрения от Рафаэля…

Я полагаю, Йенс как-то неправильно делает выводы из явлений распространения волн. Насколько я понимаю, если вы можете провести эксперимент, вы никогда не увидите (скажем) 50 Ом на своем измерителе, потому что традиционные мультиметры получают сопротивление из измеренного напряжения и тока для отображения результата V / I, и у вас никогда не будет тока. течет между двумя проводниками.

Определение сопротивления — это «противодействие потоку электрического тока», тогда как определение импеданса — это «противодействие переменному току». Это означает, что «сопротивление» 50 Ом ведет себя одинаково (предлагает одинаковое сопротивление току) как при постоянном, так и при переменном токе. С другой стороны, «импеданс» 50 Ом не обязательно ведет себя одинаково при постоянном или переменном токе.

Это не потому, что импеданс имеет только действительную часть, это обязательно «сопротивление» … это может быть просто «импеданс».
Z = R + jX
Z = R

Мы склонны согласиться с Рафаэлем, но с нетерпением ждем дальнейшего обсуждения! А вот и еще обсуждение от Марка, который согласен с Йенсом…

Хотя измерение постоянного тока действительно не покажет никакого тока, проходящего через ненагруженный коаксиальный кабель, в краткосрочной перспективе (думаю, в наносекундах) это неверно. Когда вы прикасаетесь проводами измерителя к кабелю, эти выводы имеют разный электрический потенциал по сравнению с электрическим потенциалом между центральным проводником и экраном. Для выравнивания потенциалов между измерительными проводами и кабелем ДОЛЖЕН протекать ток. В конце концов, вам нужен заряд, чтобы иметь электрический потенциал, и вам нужен ток, чтобы создать этот заряд. В течение того времени, когда начальная энергия, приложенная к кабелю, все еще распространяется от счетчика, счетчик действительно показывает 50 Ом. Проблема в том, как указал Йенс, что вам понадобится либо очень быстрый мультиметр, либо очень длинный кабель, чтобы на самом деле увидеть 50 Ом на дисплее.

Если посмотреть на это с другой стороны, кабель без потерь может быть аппроксимирован как бесконечный ряд L-образных последовательных индукторов и пар шунтирующих конденсаторов. Когда вы думаете о последовательных катушках индуктивности и шунтирующих конденсаторах, вы можете легко представить себе получение различных показаний, пока все L и C не стабилизируются на своих установившихся значениях.

Чтобы заявить, что счетчик всегда будет показывать открытие, требуется, чтобы информация перемещалась со скоростью, превышающей скорость света. В конце концов, как счетчик может узнать, заделка ли кабеля, пока он не «запросит» его электронами? В течение первых 100 мкс кабель длиной 100 мкс будет выглядеть одинаково с точностью до метра, независимо от наличия обрыва, короткого замыкания или нагрузки на другом конце. В противном случае потребовалось бы, чтобы информация распространялась быстрее, чем волна, распространяющаяся по кабелю.

У меня возникли проблемы с сообщением о том, что прибор «посмотрит» на импеданс в первую наносекунду и выдаст значимый результат. Оператор ждал несколько секунд для измерения, и он видел открытие, а затем съедал еще один кусочек своего пончика. Но вы все дали нам пищу для размышлений! — Неизвестный редактор

Измерение Z0 по коэффициенту отражения

Это пришло от Дуга. Спасибо! Мы также видели это в учебнике Microwave Office. Между прочим, существует много путаницы с обозначениями Z0, которое является характеристическим сопротивлением линии передачи, и ZT, которое представляет собой полное сопротивление завершения. Поскольку Z0 часто сопоставляется с ZT, люди склонны использовать эти термины взаимозаменяемо. Благодаря Parit мы попытались очистить следующий текст, чтобы он следовал правилам.

Если вы измеряете неизвестный кабель с неизвестным значением Z0, просто возьмите измеренные S-параметры и перенормируйте их до значения, обеспечивающего наибольшие обратные потери (например, S11< -20 дБ или около того). Это не будет зависеть от длины (однако она должна иметь некоторую измеримую длину, скажем, большую, чем лямбда/8). Нормализованный импеданс, дающий наименьшее значение, представляет собой Z0 неизвестной линии передачи. Например, в идеале линия передачи на 75 Ом, нормализованная до 75 Ом, даст бесконечные обратные потери.

Если вы отобразите это на диаграмме Смита, правильным Z0 будет тот, который даст вам самый плотный шар в центре. На днях добавим фото. Но имейте в виду, что при использовании этого метода невозможно увидеть небольшие эффекты дисперсии (которые могут немного изменить импеданс линии передачи в зависимости от частоты).

Измерение Z0 на диаграмме Смита

Если вы нанесете S11 на диаграмму Смита, для длины линии с неизвестным импедансом она очертит окружность с одной точкой на окружности в центре диаграммы. Диаметр круга математически связан с импедансом линии. Если бы линия была четвертьволновой, если бы вы начертили ее по частоте до точки четверти волны, она транскрибировала бы полукруг. В этом случае легко определить зависимость импеданса линии.

Ниже показана линия Z0 на 25 Ом, «измеренная» между двумя выводами ZT на пятьдесят Ом:

Когда мы наносим коэффициент отражения на диаграмму Смита, вы можете видеть круг, который появляется слева от ZT = 50 Ом. точка. Когда линия достигает половины длины волны, круг завершается, затем она просто повторяет саму себя по мере того, как вы поднимаетесь по частоте. Маркер показывает импеданс 0,25, нормализованный к ZT, или 12,5 Ом (0,25 x 50 Ом).

На отметке m1 линия образует классический четвертьволновый трансформатор, на этой частоте сеть выглядит как 92/50=12,5

, где Z0 — это импеданс линии (действующей как четвертьволновой трансформатор), Zin — это импеданс, смотрящий на нее, а Z0 — это импеданс системы, которая ограничивает оба конца линии.

Решение для Z0, когда оно неизвестно, просто:

Z0=SWRT(Zin*ZT)

Таким образом, импеданс линии связан с диаметром окружности, где коэффициент отражения зависит от частоты. Только не делайте ошибку, что центр круга представляет импеданс трансформатора, это НЕ так. Вы должны использовать уравнение, показанное выше, чтобы найти ZT.

Кстати, модуль коэффициента отражения, когда вы находитесь на реальной оси слева от Z0:

ро=(Z0-Zin)/(Z0+Zin)

Что в данном случае равно 0,6 (или -4,43 дБ, если вы предпочитаете децибелы).

Если бы ваш коэффициент отражения был справа от Z0 (и на реальной оси), коэффициент отражения был бы:

ро=(Zin-Z0)/(Zin+Z0).

Если вы их перепутаете, единственная ошибка будет заключаться в том, что количество будет отрицательным числом.

Микроволны101

способ измерения Z0

Ниже мы обсудим идею, которая возникла у нас для измерения волнового сопротивления линии передачи, основанную на вопросе, который возник у нас. Вероятно, это не более чем математическое упражнение, но никогда не знаешь, когда оно может оказаться полезным. Если кто-то дал вам коаксиальный кабель и не знал, 75 или 50 Ом, этот трюк может сработать. Это действительно расчет Z0 на основе прямого измерения коэффициента отражения. И он вполне способен измерять дисперсию или то свойство микрополосковых и других не совсем TEM-линий передачи, когда Z0 изменяется с частотой (по крайней мере, теоретически!) Вот предпосылка:

Вам не нужна полная линия полуволны, чтобы обвести круг, чтобы найти его диаметр… чтобы определить диаметр круга, вам нужно всего лишь три точки. Описанную окружность треугольника, который они образуют, легко вычислить, вы можете посмотреть формулу в Википедии. Теперь вы можете измерить волновое сопротивление линии по трем частотным точкам с величиной и углом S11!

Мы сделали лист Excel, который делает расчет «диаметра» для каждого набора из трех последовательных частотных точек. Затем он преобразуется в зависимость импеданса от частоты. Файл Excel называется Калькулятор импеданса 101. xls, ищите его здесь.

Существуют возможные ошибки, которые необходимо свести к минимуму, чтобы этот метод дал точную оценку Z0. Если в измерении есть паразитные помехи (например, разъемы на концах кабеля с неизвестным импедансом), то расчет может быть отключен. S-параметры должны быть полностью исключены для достижения наилучших результатов. Вы увидите на графике, что рассчитанный импеданс зависит от частоты. Возможно, самая низкая ошибка возникает на самой низкой частоте, если кто-то еще хочет порассуждать об этом, мы хотели бы услышать от вас!

У математики есть два решения. Мы не придумали, как сделать электронную таблицу достаточно умной, чтобы выбрать правильную, но выбрать правильную легко. Если круг находится слева от центра, Z0ZT.

Пример 1

Мы получили коэффициент отражения из электромагнитного моделирования линии передачи. Ниже он нанесен (по электронной таблице) от нуля до 10 ГГц. Круг находится справа от начала координат, поэтому сопротивление линии передачи должно быть больше 50 Ом. Извините, нам было лень отображать данные на настоящей диаграмме Смита!

Теперь вот что показывает электронная таблица для Z0: волновое сопротивление линии находится где-то между 69 и 75 Ом. Трансформатор на 69 Ом сделал бы нагрузку похожей на нагрузку на 95,2 Ом, или коэффициент отражения 0,311, что примерно соответствует тому месту, где этот круг пересекает ось X.

 

Почему импеданс зависит от частоты? Вероятно, нет … это «ошибка измерения» из-за паразитных явлений в электромагнитном моделировании.

 

Есть информация об измерении волнового сопротивления? Отправьте это нам. пожалуйста!

 

 

Измерение волнового сопротивления

Copyright 2020, лицензия Creative Commons BY-NC-SA

0. Домашняя страница
1. • Инженерные калькуляторы RF
   • Компоненты антенны
2. Измерительный Z _c

Во многих случаях требуется проектирование и строительство собственной линии электропередачи. На ум приходят фидеры для логопериодических дипольных решеток (LPDA), все виды открытых линий передачи, полосковые фильтры, микрополосковые схемы, линии с витой парой, дроссели и балуны Guanella и даже дорожки шины памяти компьютера. .

На этом сайте фактически размещены калькуляторы линий передачи для:

• параллельной линии передачи с круглым проводом,
• линия передачи с параллельным квадратным проводником и
• звездная четверная линия передачи.

При самостоятельном строительстве ЛЭП, конечно, важно проверить, соответствует ли волновое сопротивление расчетному значению. В этой статье объясняется, как можно легко определить характеристический импеданс линии передачи на основе измерений двух векторных анализаторов цепей (ВАЦ).

Характеристическое сопротивление \(Z_\text{c}\) длины \(\ell\) линии передачи может быть получено путем измерения ее входного сопротивления \(Z_\text{in}\) один раз с линией передачи прекращено на короткое время и второй раз оставлено открытым. Очевидно, что перед подключением линии передачи анализатор ВАЦ калибруется на порте тестируемого устройства (DUT) с короткозамкнутой, разомкнутой нагрузкой и сопротивлением 50 Ом (SOL).

Можно показать (см. ниже), что волновое сопротивление \(Z_\text{c}\) — комплексное число при наличии потерь — соответствует:

\[Z_\text{c} = \sqrt{\rule{0em}{2ex} Z_\text{in,$\,$short} \cdot Z_\text{in,$\,$open}}\ ]

Частота измерения заданной длины \(\ell\) линии передачи не может быть выбрана произвольно. Чтобы свести погрешности измерения к минимуму, частота измерения должна быть такой, чтобы электрическая длина \(\ell\), учитывающая коэффициент скорости, более или менее соответствовала нечетному кратному восьмеркам длина волны. ^1,2 Это объясняется далее.

ВАЦ должен быть способен измерять симметричные импедансы, если линейные проводники симметричны (например, параллельная проводная линия или экранированная пара). ² Для этого может потребоваться установка балуна перед калибровочной плоскостью. Однако балун не требуется, когда асимметричный (коаксиальный) векторный анализатор цепей работает от батарей без заземления. Это также относится к случаям, когда безголовый асимметричный векторный анализатор цепей подключен по беспроводной сети к компьютеру рулевого управления. Mini Radio Solutions miniVNA PRO — отличный пример беспроводного устройства VNA с батарейным питанием.

Входной импеданс \(Z_\text{in,$\,$short}\) ответвления линии передачи, заканчивающегося коротким замыканием, определяется по формуле:

\[Z_\text{in,$\,$short } = Z_\text{c} \tanh{(\gamma\ell)} \ приблизительно \text{j}\tan{(\beta\ell)}\,Z_\text{c}\]

где:
\(\gamma = \alpha + \text{j}\beta\) – постоянная распространения \(\gamma\),
\(\alpha\) – постоянная затухания, а
\(\beta\) – фазовая постоянная.

Принимая во внимание, что входной импеданс \(Z_\text{in,$\,$open}\) ответвления линии передачи с разомкнутой цепью определяется по формуле: 92} = Z_\text{c}\]

Однако, если длина линии передачи составляет почти нечетное число четвертей длины волны, угол \((\beta\ell)\) будет почти нечетное целое число, умноженное на \ (\pi/2\) радиан.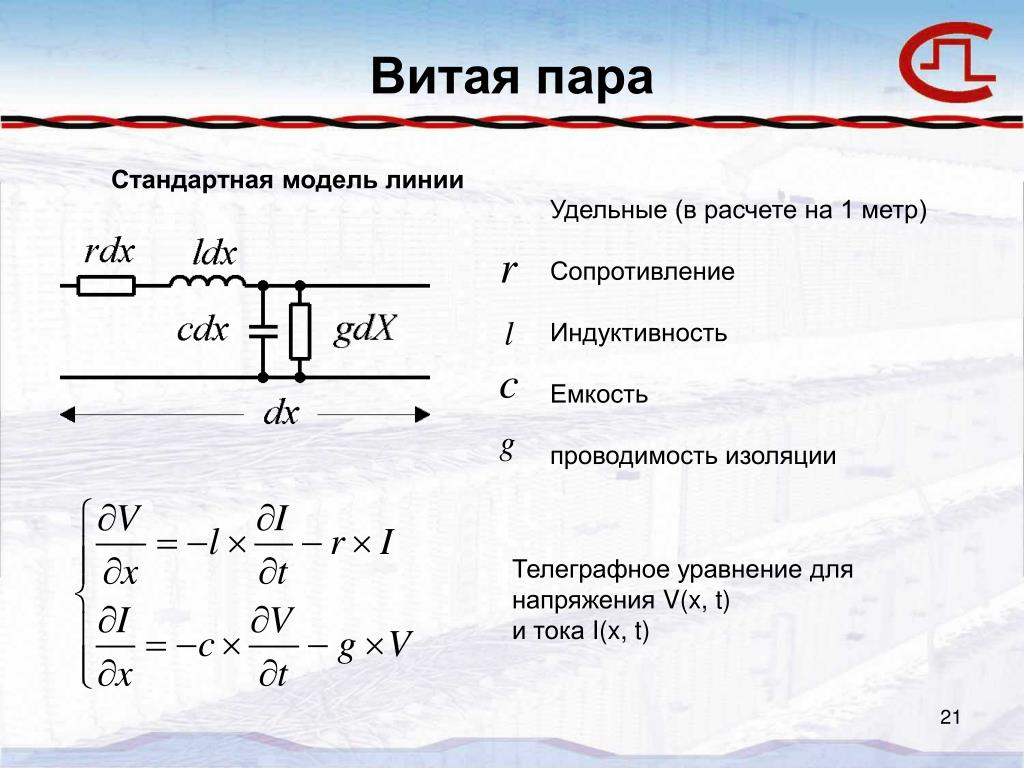 Затем \(Z_\text{in,$\,$short}\) приблизится к разомкнутой цепи, а \(Z_\text{in,$\,$open}\) приблизится к короткому замыканию. Это сделало бы выполнение точных измерений чрезвычайно трудным. ^1,3

И наоборот, если длина линии передачи составляет почти четное число четвертей длины волны, то \(Z_\text{in,$\,$short}\) будет очень низким и \(Z_\ text{in,$\,$open}\) будет чрезвычайно высоким.

Ошибки измерения импеданса можно значительно уменьшить, если величины \(Z_\text{in,$\,$short}\) и \(Z_\text{in,$\,$open}\) примерно одинаковы и соответствует VNA. Это происходит, когда:

\[\tan{(\beta\ell)} \приблизительно \cot{(\beta\ell)} \приблизительно 1\]

Следовательно,

\[\beta\ell \приблизительно ( 2n + 1) \ frac {\ pi} {4} \ quad \ Rightarrow \ quad \ ell \ приблизительно (2n + 1) \ frac {\ pi} {4} \ frac {\ lambda} {2 \ pi} = ( 2n+1)\frac{\lambda}{8}\]

, где:
\(n\) – целое число, а
\(\beta \equiv \frac{2\pi}{\lambda}\) – фазовая постоянная в \(\frac{rad}{m}\).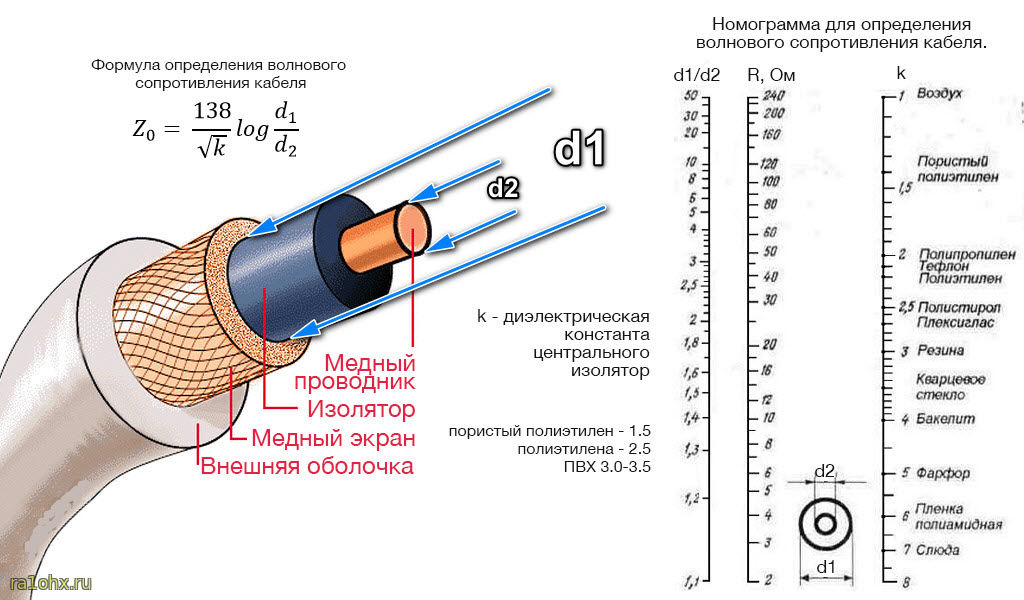

Другими словами, электрическая длина тестируемой линии передачи должна составлять более или менее нечетное число восьмых длин волны.

Однако, если общее затухание высокое, изменение импеданса в зависимости от длины не такое сильное, и нет необходимости выбирать длину линии передачи с такой тщательностью. ^1,3

1.

Уолтер С. Джонсон. Линии и сети передачи . Книжная компания McGraw-Hill; 1963.

2.

Роберт А. Чипман. Теория и проблемы линий электропередач . Книжная компания McGraw-Hill; 1968.

3.

Чеманды Электроника. Измерение волнового сопротивления дорожек печатной платы с помощью векторного анализатора цепей. Опубликовано в 2019 г. https://chemandy.com/technical-articles/measuring-track-characteristic-impedance/measuring-track-characteristic-impedance-article1.htm

5

Держите этот сайт в сети

Эта работа находится под лицензией Международная лицензия Creative Commons Attribution-NonCommercial-ShareAlike 4. 0.
Другие лицензии доступны по запросу.

Если не указано иное, все исходное программное обеспечение на этом сайте лицензировано в соответствии с условиями GNU GPL версии 3.

На этом статическом веб-сайте нет базы данных .
Таким образом, нет персональных данных не собирается и соответствие GDPR соблюдается.
Кроме того, этот домен , а не , устанавливает какие-либо собственные файлы cookie.

Все объявления Google, показанные на этом веб-сайте, независимо от вашего местоположения,
ограничен в обработке данных для соответствия требованиям CCPA и GDPR.
Однако Google AdSense может устанавливать сторонние файлы cookie для анализа трафика и
использовать JavaScript для получения уникального набора данных браузера.
Ваш браузер может быть настроен на блокировку сторонних файлов cookie.
Кроме того, установка блокировщика рекламы, такого как Privacy Badger от EFF
заблокирует JavaScript рекламы.
С политикой Google в отношении рекламы можно ознакомиться здесь.

На этой странице используется серверный скрипт.

Эта страница включает клиентский сценарий с открытым исходным кодом, написанный на
перекодирован, чтобы заставить его работать как безопасный JavaScript в браузере.

Статический XHTML, сгенерированный из Markdown с помощью и
команды make, sed и gpp.

математическая разметка, отображаемая с помощью .
ссылок лучше читать с расширением .

Автоматический набор CSS с помощью .

Эта работа опубликована по адресу https://hamwaves.