Как найти мощность при параллельном соединении. Параллельное соединение резисторов: расчет мощности и особенности применения

Как рассчитать мощность при параллельном соединении резисторов. Какие формулы использовать для расчета общего сопротивления. Где применяется параллельное соединение на практике. Как подобрать резисторы для параллельного соединения.

Что такое параллельное соединение резисторов

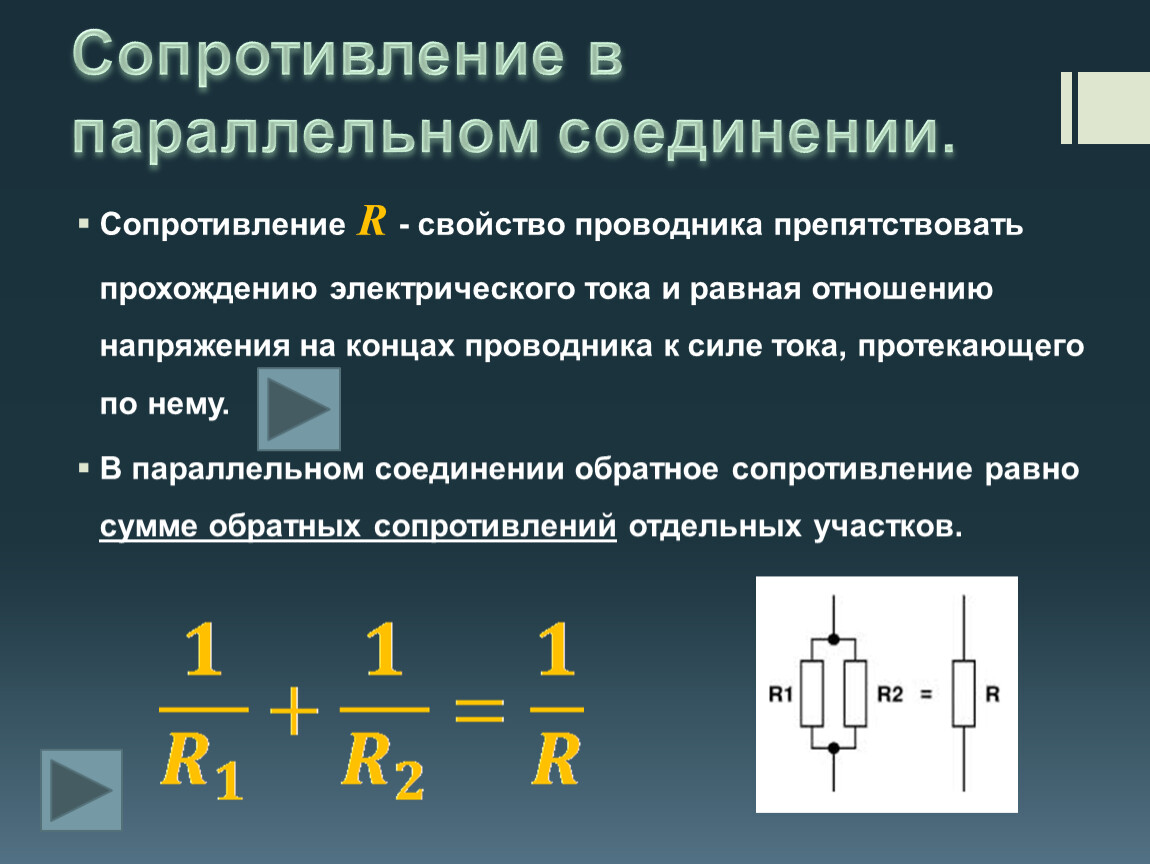
Параллельное соединение резисторов — это такой способ подключения, при котором все резисторы присоединяются своими выводами к двум общим точкам (узлам) электрической цепи. При этом напряжение на всех резисторах одинаково и равно общему приложенному напряжению, а токи через резисторы различны.

Основные свойства параллельного соединения:

• Напряжение на всех резисторах одинаково
• Общий ток равен сумме токов через отдельные резисторы
• Общее сопротивление всегда меньше сопротивления любого из параллельно соединенных резисторов

Формулы для расчета параллельного соединения

Для расчета параметров параллельного соединения резисторов используются следующие основные формулы:

1. Общее сопротивление: 1/R = 1/R1 + 1/R2 + 1/R3 + …
2. Общий ток: I = I1 + I2 + I3 + …
3. Напряжение: U = U1 = U2 = U3 = …
4. Мощность: P = P1 + P2 + P3 + …

Где R — общее сопротивление, R1, R2, R3 — сопротивления отдельных резисторов, I — общий ток, I1, I2, I3 — токи через отдельные резисторы, U — напряжение, P — общая мощность, P1, P2, P3 — мощности на отдельных резисторах.

Как рассчитать мощность при параллельном соединении

Для расчета мощности при параллельном соединении резисторов можно использовать следующий алгоритм:

1. Рассчитать общее сопротивление по формуле 1/R = 1/R1 + 1/R2 + 1/R3 + …
2. Определить общий ток I = U / R, где U — приложенное напряжение
3. Рассчитать токи через каждый резистор I1 = U / R1, I2 = U / R2 и т.д.
4. Вычислить мощность на каждом резисторе P1 = I1^2 * R1, P2 = I2^2 * R2 и т.д.
5. Суммировать мощности P = P1 + P2 + P3 + …

Также можно использовать формулу P = U^2 / R, где R — общее сопротивление параллельного соединения.

Особенности параллельного соединения резисторов

При параллельном соединении резисторов следует учитывать некоторые важные особенности:

• Общее сопротивление всегда меньше сопротивления резистора с наименьшим номиналом
• Через резистор с меньшим сопротивлением протекает больший ток
• Мощность, рассеиваемая на резисторе с меньшим сопротивлением, больше
• При выходе из строя одного резистора цепь продолжает работать
• Параллельное соединение позволяет увеличить общую мощность и уменьшить общее сопротивление

Применение параллельного соединения на практике

Параллельное соединение резисторов широко применяется в электротехнике и электронике для решения различных задач:

• Получение требуемого значения сопротивления
• Увеличение допустимой мощности рассеяния
• Создание делителей тока
• Шунтирование измерительных приборов
• Подключение нескольких потребителей к одному источнику питания

Как подобрать резисторы для параллельного соединения

При подборе резисторов для параллельного соединения следует учитывать несколько факторов:

1. Требуемое общее сопротивление
2. Допустимая мощность рассеяния
3. Точность номиналов резисторов
4. Доступность резисторов нужных номиналов

Для получения нужного сопротивления можно использовать онлайн-калькуляторы или специальные таблицы. При этом лучше выбирать резисторы близких номиналов для более равномерного распределения мощности.

Преимущества и недостатки параллельного соединения

Параллельное соединение резисторов имеет свои плюсы и минусы:

Преимущества:

• Уменьшение общего сопротивления
• Увеличение общей мощности рассеяния
• Возможность получения нестандартных номиналов
• Повышение надежности цепи

Недостатки:

• Увеличение общего тока
• Неравномерное распределение мощности
• Сложность точного расчета при большом количестве резисторов

Сравнение параллельного и последовательного соединения

Параллельное и последовательное соединения резисторов имеют принципиальные отличия:

Параметр	Параллельное	Последовательное
Напряжение	Одинаковое на всех	Сумма напряжений
Ток	Сумма токов	Одинаковый через все
Сопротивление	Уменьшается	Увеличивается
Мощность	Увеличивается	Распределяется

Примеры расчета параллельного соединения

Рассмотрим несколько примеров расчета параллельного соединения резисторов:

Пример 1

Даны резисторы 100 Ом, 200 Ом и 300 Ом. Найти общее сопротивление при параллельном соединении.

Решение:

1. 1/R = 1/100 + 1/200 + 1/300
2. 1/R = 0.01 + 0.005 + 0.00333 = 0.01833
3. R = 1 / 0.01833 = 54.54 Ом

Пример 2

К источнику 12 В подключены параллельно резисторы 30 Ом и 60 Ом. Определить общий ток и мощность.

Решение:

1. Общее сопротивление: 1/R = 1/30 + 1/60 = 0.05, R = 20 Ом
2. Общий ток: I = U/R = 12/20 = 0.6 A
3. Мощность: P = U * I = 12 * 0.6 = 7.2 Вт

Заключение

Параллельное соединение резисторов — важный способ подключения, широко используемый в электротехнике. Оно позволяет уменьшать общее сопротивление, увеличивать мощность и создавать сложные электрические цепи. Правильный расчет параметров параллельного соединения необходим для корректной работы электрических схем и устройств.

Как найти мощность при параллельном соединении

По­сле­до­ва­тель­ным называется со­еди­не­ние, при котором потребители соединены друг за другом, без разветвлений.

По­сле­до­ва­тель­ное вклю­че­ние двух ламп в элек­три­че­скую цепь

Для последовательного соединения выполняются правила:

1. Сила тока во всех элементах цепи одинакова и равна об­ще­му току, про­те­ка­ю­ще­му в элек­три­че­ской цепи. То есть

Это можно срав­нить с те­че­ни­ем реки: ко­ли­че­ство воды, про­те­ка­ю­щее за одно и то же время в раз­ных ме­стах этой реки, будет оди­на­ко­во.

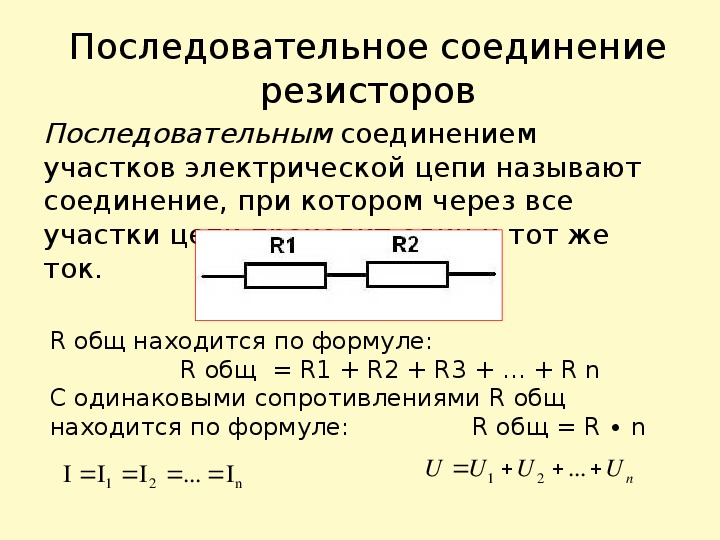
2. Общее на­пря­же­ние на элементах U равно сумме на­пря­же­ний на каж­дом элементе U₁ и U₂, то есть

3. Общее сопротивление при последовательном соединении определяется как сумма сопротивлений всех элементов, то есть

Па­рал­лель­ным со­еди­не­ни­ем про­вод­ни­ков на­зы­ва­ет­ся такое со­еди­не­ние, при ко­то­ром на­ча­ла и концы про­вод­ни­ков со­еди­ня­ют­ся вме­сте, то есть разветвления у потребителей.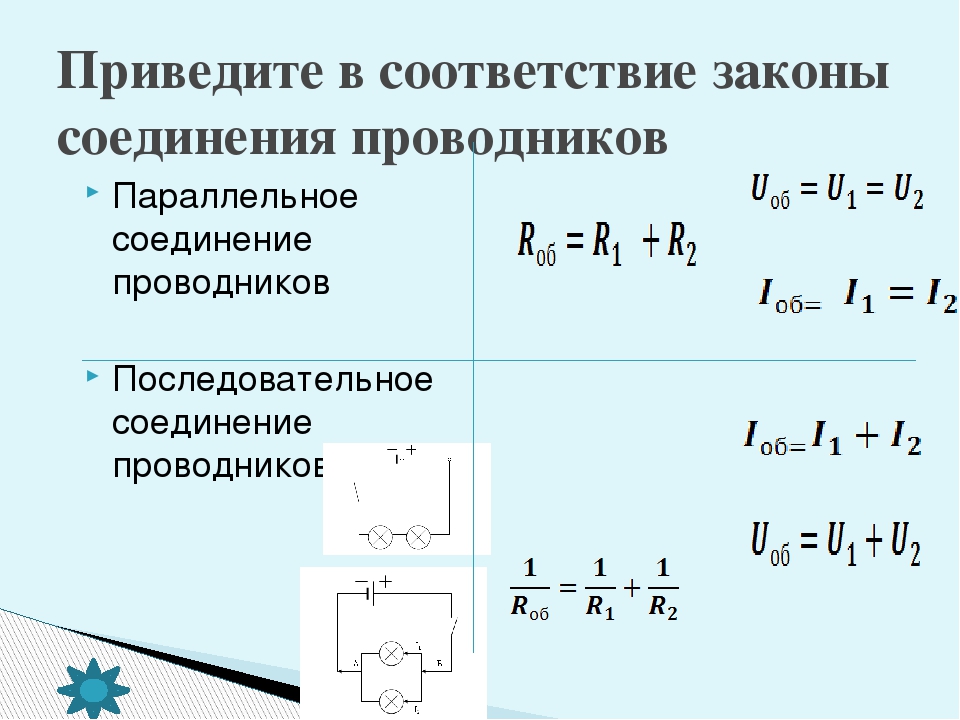 На схеме такое со­еди­не­ние может выглядеть сле­ду­ю­щим об­ра­зом:

Па­рал­лель­ное со­еди­не­ние двух ламп

Для параллельного соединения выполняются правила:

1. Сила тока во всех элементах цепи складывается и сумма равна об­ще­му току, про­те­ка­ю­ще­му в элек­три­че­ской цепи. То есть

Это можно срав­нить с те­че­ни­ем реки: ко­ли­че­ство воды, про­те­ка­ю­щее во всех рукавах реки, будет равно общему количеству воды.

2. На­пря­же­ние на всех элементах U одинаково, то есть

3. Общее сопротивление при параллельном соединении определяется формуле

но можно использовать формулы для частных случаев:

для любого количества одинаковых сопротивлений, для двух разных сопротивлений.

Ра­бо­та элек­три­че­ско­го тока – это про­из­ве­де­ние элек­три­че­ско­го на­пря­же­ния на заряд, про­те­ка­ю­щий по про­вод­ни­ку.

Если подставить в эту формулу q = I * t , получим, что

Ра­бо­та элек­три­че­ско­го тока равна про­из­ве­де­нию силы тока на участ­ке цепи, на­пря­же­нию на кон­цах этого участ­ка и вре­ме­ни, в те­че­ние ко­то­ро­го про­те­ка­ет ток по про­вод­ни­ку.

Если применить закон Ома для участка цепи, можно получить еще две формулы:

Ра­бо­та тока измеряется в джо­улях – Дж;

Мощ­ность – ра­бо­та, вы­пол­нен­ная в еди­ни­цу вре­ме­ни.

Чтобы опре­де­лить элек­три­че­скую мощ­ность, нужно ра­бо­ту тока раз­де­лить на время про­те­ка­ния этого тока по элек­три­че­ской цепи.

N или Р – элек­три­че­ская мощ­ность. Мощ­ность измеряется в ват­тах – Вт.

Тогда для мощности можно использовать формулы:

Резистор – это элемент электрической схемы, который обладает сопротивлением электрическому току. Классифицируют два типа резисторов: постоянные и переменные (подстроечные). При моделировании той или иной электрической схемы, а также при ремонте электронных изделий, возникает необходимость использовать резистор определенного номинала. Хотя и существует множество различных номиналов постоянных резисторов, в данный момент под рукой может не оказаться требуемого, либо резистора с таким номиналом не существует.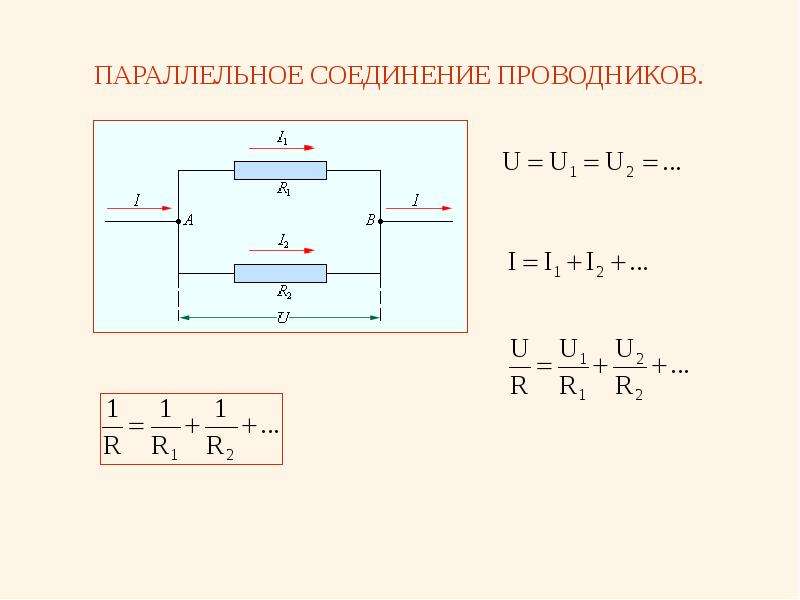 Чтобы выйти из такой ситуации, можно использовать как последовательное так и параллельное соединение резисторов. О том, как правильно произвести расчет и подбор различных номиналов сопротивлений, будет рассказано в этой статье.

Последовательное соединение резисторов – это самая элементарная схема сборки радиодеталей, оно применяется для увеличения общего сопротивления цепи. При последовательном соединении, сопротивление используемых резисторов просто складывается, а вот при параллельном соединении необходимо производить расчет по нижеописанным формулам. Параллельное соединение необходимо для снижения результирующего сопротивления, а также для увеличения мощности, несколько параллельно подключенных резисторов имеют большую мощность, чем у одного.

На фотографии можно увидеть параллельное подключение резисторов.

Общее номинальное сопротивление необходимо рассчитывать по следующей схеме:

– R(общ) – общее сопротивление;

– R1, R2, R3 и Rn – параллельно подключенные резисторы.

Когда параллельное соединение резисторов состоит всего из двух элементов, в таком случае общее номинальное сопротивление можно высчитать по следующей формуле:

– R(общ) – общее сопротивление;

– R1, R2 – параллельно подключенные резисторы.

В радиотехнике существует следующее правило: если параллельное подключение резисторов состоит из элементов одного номинала, то результирующее сопротивление можно высчитать, разделив номинал резистора на количество соединенных резисторов:

– R(общ) – общее сопротивление;

– R – номинал параллельно подключенного резистора;

– n – количество соединенных элементов.

Важно учитывать, что при параллельном соединении результирующее сопротивление всегда будет ниже, чем сопротивление самого малого по номиналу резистора.

Приведем практический пример: возьмем три резистора, со следующими значениями номинального сопротивления: 100 Ом, 150 Ом и 30 Ом. Проведем расчет общего сопротивления, по первой формуле:

После расчета формулы мы видим, что параллельное соединение резисторов, состоящее из трех элементов, с наименьшим номиналом 30 Ом, в результате дает общее сопротивление в электрической цепи 21,28 Ом, что ниже наименьшего номинального сопротивления в цепи почти на 30 процентов.

Параллельное соединение резисторов чаще всего используют в тех случаях, когда необходимо получить сопротивление с большей мощностью. В таком случае необходимо взять резисторы одинаковой мощности и с одинаковым сопротивлением. Результирующая мощность в таком случае рассчитывается путем умножения мощности одного элемента сопротивления на общее количество параллельно подключенных резисторов в цепи.

Например: пять резисторов с номиналом в 100 Ом и с мощностью 1 Вт в каждом, подключенные параллельно, имеют общее сопротивление 20 Ом и мощность 5 Вт.

При последовательном подключении тех же резисторов (мощность так же складывается), получим результирующую мощность 5 Вт, общее сопротивление составит 500 Ом.

Параллельным соединением резисторов (или приемников энергии, ветвей,сопротивлений) называется такое, при котором к одним и тем же двум узлам электрической цепи (рисунок 1) присоединены несколько резисторов (ветвей).

Рис. 1 Изображение параллельного соединения трех резисторов

Проводимость при параллельном соединении

Сопротивление при параллельном соединении:

Для трёх параллельно соединенных сопротивлений

Для двух параллельно соединенных сопротивлений

Для ветвей с одинаковым сопротивлением где n количество ветвей

Ток при параллельном соединении

Мощность при параллельном соединении

Доказательство

Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U. Согласно закону Ома токи в сопртивлениях определяются по формулам

Из этих формул следует, что токи в параллельных ветвях с сопротивлениями распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям. Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:

т. е. эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Следовательно, эквивалентное сопротивление будет меньше самого малого из параллельно соединенных резисторов.
Формула (1) дает возможность определить и эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость

и эквивалентное сопротивление

Для двух резисторов

Если сопротивление ветвей одинаково R1 = R2 = R3, то можно воспользоваться формулой

в общем случае при соединении n резисторов с одинаковым сопротивлением R1 эквивалентное сопротивление равно

Мощности параллельно соединенных резисторов равна сумме мощностей всех резисторов

Формулы параллельного, последовательного и смешанного соединения резисторов

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Что такое резистор и для чего он нужен

Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.

Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.

Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).

Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.

Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:

1. С правого края – правый.
2. С левого края – левый.

Постоянный ток

Господа, в прошлый раз мы с вами говорили про последовательное сопротивление резисторов. Сегодня я бы хотел вам рассказать про другой возможный вид соединения – параллельное.

Чем различается последовательное и параллельное соединение я уже писал в предыдущей статье. Но все-таки вытащу сюда картинку из той прошлой статьи, я ж знаю, что вам будет лень ходить по ссылкам .

А) – Последовательное соединение

В) – Параллельное соединение

Рисунок 1 – Последовательное и параллельное соединение

Как мы видим из рисунка 1, параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.

Сейчас наша задача будет разобраться, как ведут себя токи, напряжения, сопротивления и мощности при таком подключении. Для этого прошу вас взглянуть на рисунок 2, где подробно разрисован расклад дел для параллельного соединения. Будем полагать, что мы знаем величины R1, R2 и R3, а также величину приложенного к схеме напряжения U. Про токи же мы ничего не знаем.

Рисунок 2 – Параллельное соединения

Что мы видим на рисунке 2? Ну, в первую очередь – два узла А и B. В узел А сходятся одни концы всех резисторов, а в узел В – другие концы. Пусть узел А имеет потенциал φ1, а узел В – потенциал φ2. Из рисунка 2 видно, что для всех резисторов R1, R2 и R3 у нас одна и та же разность потенциалов U.

Как следует из статьи про потенциалы, это означает, что напряжение на всех резисторах у нас одинаково и равно приложенному напряжению U. Это важный вывод, его следует хорошо запомнить.

С токами дело обстоит по-другому. Проанализируем рисунок 2 слева направо. Пусть у нас в цепи течет ток I. Течет он себе, течет, никого не трогает и тут вдруг натыкается на узел А. Что в этом случае говорит полюбившаяся вам статья про первый закон Кирхгофа? А то, что ток I в узле А разделится на три тока I1, I2, I3. При этом будет выполняться равенство

То есть через резистор R1 будет протекать ток I1, через резистор R2 – ток I2, а через резистор R3 – ток I3.

Итак, у нас в системе уже тихо-мирно текут себе три тока. И все хорошо, пока они не наткнуться на узел В. Тут снова вступает в силу первый закон Кирхгофа. Эти три тока I1, I2, I3 вновь соединятся в один ток I. Причем после узла В ток будет иметь такую же величину I, какой он был до узла А.

То есть если все вышесказанное воплотить в лаконичный язык наскальной живописи, положение дел можно представить себе вот так

Как же найти эти самые токи I1, I2, I3? Господа, полагаю, вы уже догадались, что на помощь нам придет горячо нами всеми любимый закон Ома.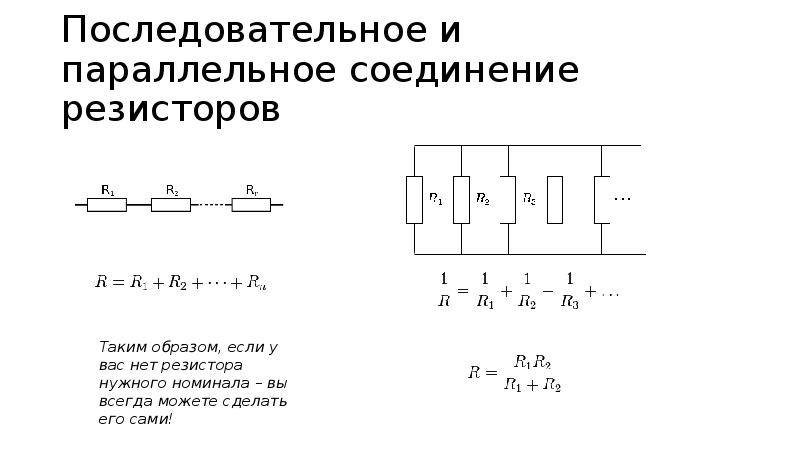 Действительно, мы знаем сопротивления резисторов и, кроме того, нам известно, что на всех них падает одно и тоже напряжение U. Поэтому легко находим токи

Отлично, мы разобрались с напряжениями и с токами в такой схеме. А помните в статье про последовательное сопротивление мы ловко преобразовали три резистора в один с эквивалентным им сопротивлением? Нельзя ли и здесь сделать что-то подобное? Оказывается, вполне себе можно. Как мы помним, токи в схеме распределены таким вот образом

Обзовем эквивалентное сопротивление буковкой R. И подставим в это выражение только что найденные нами токи I1, I2, I3

Видим, что здесь без проблем можно сократить левую и правую части на U. Получаем

Господа, важный вывод: при параллельном соединении резисторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных резисторов.

То есть для упрощения различных расчетов электрических схем такую вот цепочку параллельно соединенных резисторов можно заменить одним резистором с соответствующим сопротивлением, как показано на рисунке 3.

Рисунок 3 – Преобразование параллельного соединение

Весьма частый случай на практике, когда соединены параллельно не много резисторов, а всего два. Поэтому полезно знать наизусть итоговое сопротивление такой схемы. Давайте посмотрим, чему оно равно:

То есть, если у вас два сопротивления соединены параллельно, то по этой формуле вы легко высчитаете общее сопротивление. Рассмотрим пример. Пусть у нас параллельно соединены два резистора 10 кОм и 15 кОм. Чему равно их общее сопротивление?

Заметьте, господа, итоговое сопротивление у нас получилось 6 кОм, что меньше 10 кОм и 15 кОм. То есть при параллельном соединении общее сопротивление меньше любого из составляющих. Это всегда верно для любого количества резисторов, а не только для двух. Итоговое сопротивление всегда уменьшается (в отличии от последовательного сопротивления, где итоговое сопротивление всегда растет). Этот факт полезно запомнить.

Еще один часто встречающийся на практике случай – когда параллельно соединены несколько резисторов с одинаковым сопротивлением. Допустим, каждый из них обладает сопротивлением R1 и всего их N штук. Тогда по нашей общей формуле для эквивалентного сопротивления

То есть при параллельном соединении N одинаковых резисторов с сопротивлением R1 итоговое сопротивление будет в N раз меньше этого самого сопротивления R1.

Так-с, с током разобрались, с напряжением разобрались, с эквивалентным сопротивлением вроде тоже…осталась мощность. Для этого воспользуемся вот этим выражением, которое мы писали чуть выше в статье

Умножим левую и правую части на напряжение U.

Как мы помним из статьи про мощность произведение тока на напряжение есть мощность. То есть мы можем записать

где Р – мощность, выдаваемая источником;

P1 – мощность, рассеиваемая на резисторе R1;

P2 – мощность, рассеиваемая на резисторе R2;

P3 – мощность, рассеиваемая на резисторе R3.

Заметьте, господа, формула в точности такая же, как и для случая последовательного соединения резисторов. И там и там мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на резисторах цепи.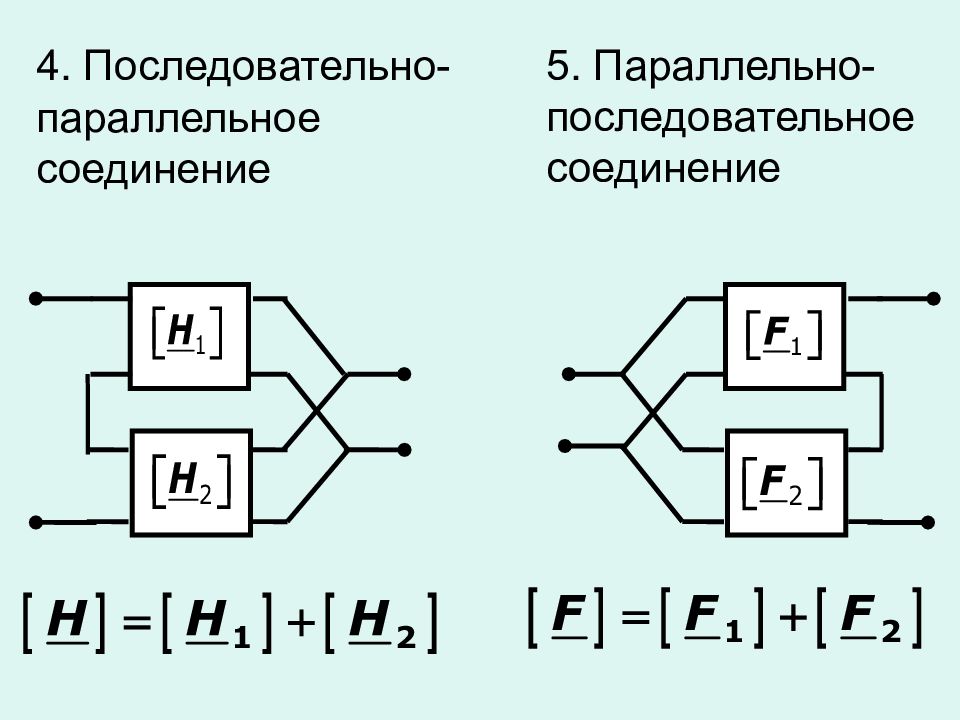

Итак, господа, мы рассмотрели основные соотношения при параллельном соединении резисторов. Теперь осталось поговорить, где это параллельное соединение можно использовать и для чего.

1) Ну, во-первых, параллельное соединение применяют во всех случаях, когда хотят запитать несколько нагрузок от одного источника напряжения. При этом пользуются тем свойством, что при параллельном соединении напряжения на всех нагрузках одинаково. То есть, допустим, вы берете источник напряжения, выставляете на нем напряжение 5 В и цепляете к этому источнику сразу несколько своих устройств. Узлами А и В в этом случае будут клеммы источника. На каждое из устройств в этом случае придет напряжение 5 В. Да и все устройства в вашей квартире (лампочки, компьютеры, телевизоры и все прочее) соединены между собой параллельно.

2) Второе возможное применение встречается не так часто, но, думаю, о нем тоже следует рассказать. Допустим, вы делаете какую-то схему, где необходим очень точный подгон сопротивления. Скажем, надо получить сопротивление 6 кОм. Такое сопротивление найти нелегко, их просто не продают. Зато у вас есть два сопротивления 10 кОм и 15 кОм. Вы их соединяете параллельно и получаете требуемые 6 кОм. Как показывает практика, 3 параллельных резисторов достаточно для получения итогового результирующего сопротивления требуемого номинала с весьма хорошей точностью. Конечно, таких вещей лучше избегать и, если есть возможность, всегда стараться применять стандартные сопротивления. Но бывают случаи, когда это невозможно, и тогда приходит на помощь этот метод.

3) Третий пункт будет немного похож на первый. Его суть заключается в следующим. Допустим, нам надо снять с источника питания 10 Вт мощности. А у нас в наличии только резисторы, которые позволяют рассеивать на себе 1 Вт. Что делать? Можно соединить 10 резисторов параллельно и с каждого снимать по 1 Вт. Мы же помним нашу формулу

Конечно, лучше брать не 10 резисторов, а хотя бы 15 и рассеивать на них меньше, чем 1 Вт. Работать на пределе никогда не следует.

Кстати, тут очень вовремя к моменту написания статьи пришли платы с производства! Господа, прошу вас взглянуть на рисунок 4.

Рисунок 4 – Плата нагревателя

На нем изображена плата нагревателя (флешка для масштаба). В чем суть? Имеется весьма сложное устройство, предназначенное для работы в арктических условиях. Найти же компоненты, которые надежно функционировать при температурах минус 55 градусов и при этом стоят адекватных денег и обладают адекватными размерами бывает непросто. Обычно элементная база в лучшем случае рассчитана на минус 40 градусов. И было принято решение разработать вот такой вот нагреватель для прогрева чувствительных к холоду аналоговых узлов устройства. Он управляется с микроконтроллера и автоматически включается при температурах меньше минус 40 градусов. Как вы можете видеть из рисунка 4, этот нагреватель представляет собой 30 параллельно соединенных резисторов с сопротивлениями 150 Ом. Каждый резистор, согласно документации, способен рассеивать до 1 Вт мощности. Используя изученные формулки, мы можем посчитать, что в сумме такая система обладает сопротивлением

и теоретически может рассеивать мощность

Ну, с сопротивлением вопросов нет, оно действительно равно 5 Ом. Ну, плюс-минус 5 % на допуск резисторов, что в данном случае вообще не критично. А вот с мощностью тут не так все однозначно. Помните про закон Джоуля-Ленца, который мы рассматривали? Резисторы будут греться, причем не слабо. Как показывает практика, если нагружать резисторы по полной, то есть рассеивать на каждом по 1 Вт, то в течении нескольких секунд их температура улетит за 150 градусов. Такая высокая температура критична для резистора и может привести к его разрушению. Я был готов к такому развитию событий, поэтому заложил для платы нагревателя максимальное напряжение 9 вольт. Это значит, что на каждом резисторе будет выделяться

что почти в два раза меньше максимально допустимой мощности в 1 Вт. В сумме на всей плате выделялось, соответственно

Эксперимент показал, что резисторы достигли температуры с комнатных 25 градусов до критичных 120 градусов приблизительно за 10 секунд работы и температура продолжала уверенно расти.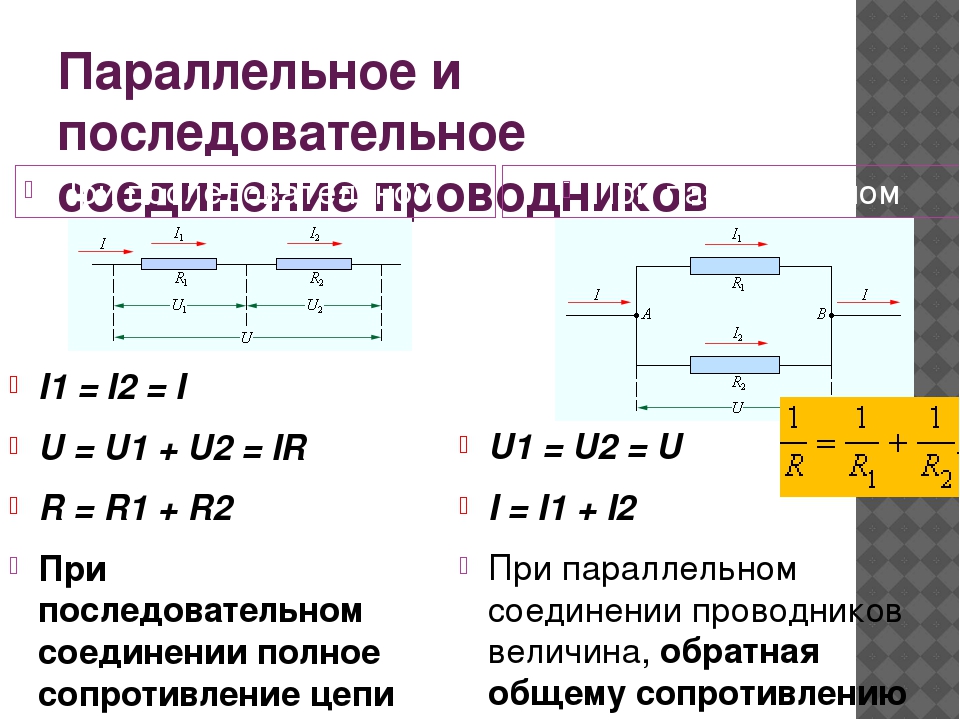 Очевидно, если оставить на длительное время включенным такой нагреватель при комнатной температуре, он неминуемо выйдет из строя. Возможно, при работе на минус 55 градусах перегрев бы не был столь критичным, однако хотелось исключить вариант спалить плату на столе, поэтому я понизил напряжение, подаваемое на плату на 3 вольта: стал подавать 6 вольт. Теперь на каждом резисторе рассеивалось

а на всей плате

Теперь температура поднималась до 100-110 градусов примерно за 30-40 секунд работы и оставалась на этом уровне (выходила в точку термодинамического равновесия). Эта температура вполне подходит для нагревателя. Однако пока это были лишь эксперименты на столе при комнатной температуре, главный эксперимент – в термокамере на минус 55 градусах – впереди. Возможно, по его результатам потребуется чуть увеличить рассеиваемую мощность. А может все останется как есть и этой мощности будет достаточно для вывода девайса на режим за адекватное время, время покажет .

На сегодня все, господа.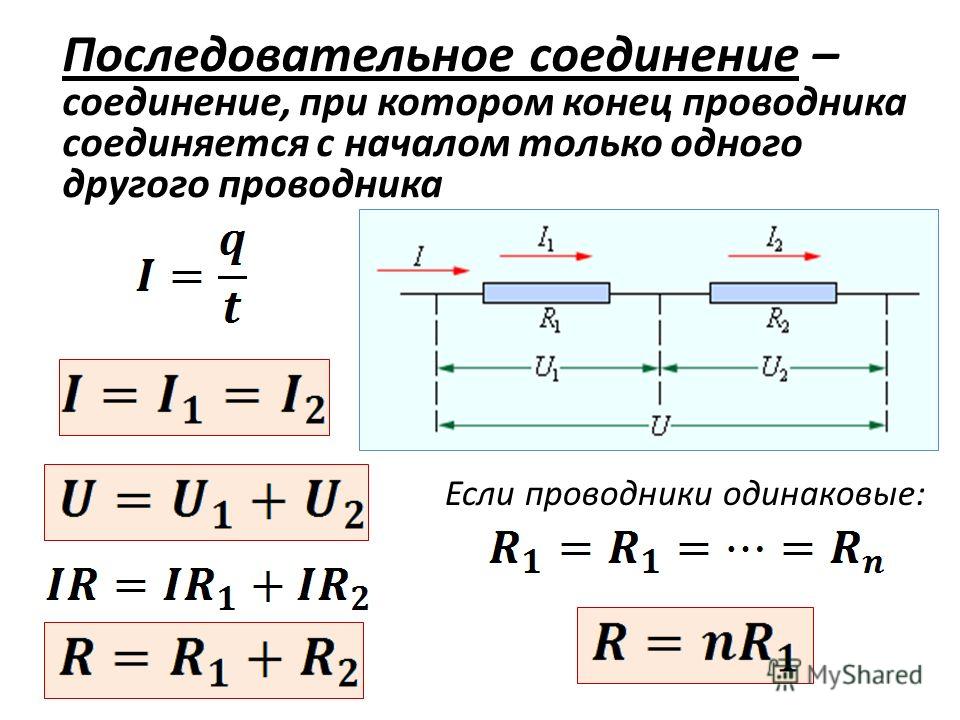 Удачи вам и до новых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Social button for Joomla

Понятие параллельного подключения резисторов

При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Последовательное подключение

При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.

При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Какая мощность тока при последовательном и параллельном соединении

Определение мощности отдельного резистивного элемента производится по формуле

P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.

Мощность при параллельном соединении

Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где

• R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
• I – сила тока в цепи.

При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.

Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.

Мощность при последовательном соединении

Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где

• R – рассчитанное нами сопротивление для определенной схемы;
• U – падение напряжения на данном резистивном элементе.

Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как правильно рассчитать сопротивление

Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где

• U – падение напряжение на конкретном резистивном элементе;
• I – ток, протекающий через него.

При последовательном соединении

Для двух элементов считаем Rобщ = R1+R2.

Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.

При параллельном соединении

Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).

Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле

Rобщ = 1/(1/R1+1/R2+1/R3+…+1/Rn).

Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.

Как рассчитать сложные схемы соединения резисторов

Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.

Перед нами сложная схема – задача рассчитать общее сопротивление:

1. R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
2. R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
3. R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом. Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Работа и мощность тока. Закон Джоуля — Ленца

6 Дуговая печь потребляет ток I=200 А от сети с напряжением V=120B через ограничивающее сопротивление R = 0,2 Ом. Найти мощность, потребляемую печью.

Решение:
N=I(V-IR)=16 кВт.

7 Нагревательная спираль электроаппарата для испарения воды имеет при температуре t=100°С сопротивление R= 10 Ом. Какой ток I надо пропускать через эту спираль, чтобы аппарат испарял массу воды m=100г за время τ=1 мин? Удельная теплота парообразования воды λ = 2,3 МДж/кг.

Решение:
Считая, что вся электрическая энергия затрачивается на испарение воды, получим

8 Электропечь должна давать количество теплоты Q = 0,1 МДж за время τ = 10 мин. Какова должна быть длина нихромовой проволоки сечения S=0,5 мм², если печь предназначается для сети с напряжением V=36 В? Удельное сопротивление нихрома ρ=1,2мкОм⋅м.
Решение:
По закону Джоуля — Ленца
-сопротивление проволоки, l-ее длина; отсюда

9 Комната теряет в сутки количество теплоты Q = 87 МДж. Какой длины l надо взять нихромовую проволоку диаметра D = 1 мм для намотки электропечи, поддерживающей температуру комнаты неизменной? Печь включается в сеть с напряжением V=120В, удельное сопротивление нихрома ρ=1,2мкОм⋅м.

Решение:

10 В сосуд, содержащий массу воды m = 480 г, помещен электронагреватель мощности N=40 Вт. Насколько изменилась температура воды в сосуде, если ток через нагреватель проходил в течение времени τ = 21 мин? Удельная теплоемкость воды с=4,2 кДж/(кг·К), теплоемкость сосуда вместе с нагревателем С_с=100Дж/К.

Решение:
Полученное количество теплоты идет на нагревание воды и сосуда с нагревателем, поэтому

где t1 и t2-начальная и конечная температуры воды. Изменение температуры воды

11 Найти мощность N электронагревателя кастрюли, если в ней за время τ = 20 мин можно вскипятить объем воды V=2 л. К.п.д. электронагревателя η = 70%. Удельная теплоемкость воды с = 4,2 кДж/(кг·К), начальная температура воды t₁ = 20° С.

Решение:
Электрическая энергия, идущая на нагревание воды,

где

— масса воды, t2 = 100° С- конечная температура воды; отсюда

12 Сколько времени надо нагревать на электроплитке мощности N=600 Вт при к.п.д. η = 75% массу льда m_л = 2кг, взятого при температуре t₁ = —16° С, чтобы обратить его в воду, а воду нагреть до температуры t₂ = 100°C? Удельная теплоемкость льда с_л = 2,1 кДж/(кг·К), удельная теплота плавления льда r=0,33 МДж/кг, удельная теплоемкость воды с = 4,2 кДж/(кг·К).

Решение:
Время нагревания определяется из уравнения теплового баланса (tо=0°С):

13 Какова должна быть длина нихромовой проволоки диаметра D = 0,3 мм, чтобы при включении последовательно с 40-ваттной лампочкой, рассчитанной на 127 В, проволока давала нормальный накал при напряжении в сети V=220 В? Удельное сопротивление нихрома ρ = 1,2 мкОм⋅м.

Решение:


14 Реостат с полным сопротивлением R подключен к сети с напряжением V (рис. 134). Во сколько раз изменится потребляемая от сети мощность, если движок реостата переместить на 1/4 длины от его конца?

Решение:
Отношение выделяемых на реостате мощностей N₀/N=4/3.

15 Найти к.п.д. насосной установки, которая подает в единицу времени объем воды V_τ = 75 л/с на высоту h = 4,7 м через трубу, имеющую сечение S=0,01 м², если мотор потребляет мощность N=10 кВт.

Решение:
Для подачи воды на высоту А необходима мощность

К. п. д. установки


16 Моторы электропоезда при движении со скоростью υ = 54 км/ч потребляют мощность N=900 кВт. К.п.д. моторов и передающих механизмов h = 80%. Найти силу тяги F, развиваемую моторами.
Решение:
Мощность, необходимая для движения поезда, равна

отсюда

17 Железная и медная проволоки одинаковых длин и сечений соединены последовательно и включены в сеть. Найти отношение количеств теплоты, выделившихся в каждой проволоке. Удельные сопротивления железа и меди равны ρ₁ =0,12 мкОм⋅м и ρ₂ = 0,017 мкОм⋅м. Решить эту же задачу для случая параллельного соединения проволок.

Решение:
Токи, идущие через обе проволоки, соединенные последовательно, одинаковы и равны I. При этом в проволоках за время t выделяются количества теплоты

-сопротивления железной и медной проволок, l и S-их длина и площадь сечения. Отношение количеств теплоты при последовательном соединении

При параллельном соединении токи в железной и медной проволоках

где V-напряжение в сети. В этом случае за время τ в проволоках выделяются количества теплоты
Их отношение


18 Железная и медная проволоки одинаковых длин и сечений включены в сеть на равные промежутки времени сначала последовательно, затем параллельно. Найти отношение количеств теплоты, выделившихся в проволоках в обоих случаях, если по железной проволоке тек один и тот же ток. Удельные сопротивления железа и меди ρ₁ =0,12 мкОм·м и ρ₂ = 0,017 мкОм·м.

Решение:


19 За время τ₁=40c в цепи из трех одинаковых проводников, соединенных параллельно и включенных в сеть, выделилось некоторое количество теплоты. За какое время τ₂ выделится такое же количество теплоты, если проводники соединить последовательно?

Решение:


20 Два одинаковых электронагревателя, потребляющих каждый мощность N = 200 Вт при напряжении V= 120 В, длинными и тонкими проводами подключены к источнику тока. Найти сопротивление проводов R, если при последовательном и при параллельном соединениях нагревателей они выделяют в единицу времени одно и то же количество теплоты.

Решение:


21 В электрочайнике с двумя нагревателями необходимо нагреть объем воды V=2 л от комнатной температуры (t₀ = 20° С) до температуры кипения. Каждый нагреватель, включенный в сеть отдельно, выделяет мощность N₁ = 250 Вт. Через какое время закипит вода, если ее подогревать одним нагревателем или двумя, включенными в ту же сеть последовательно или параллельно друг другу? К.п.д. нагревателя η = 80%. Удельная теплоемкость воды с = 4,2 кДж/(кг·К).

Решение:
Для нагревания воды до температуры кипения t=100° С необходимо количество теплоты
—
масса воды в чайнике. При включении одного нагревателя его мощность N₁=IV, где I-ток, текущий через него, и V-напряжение сети. В этом случае на нагревание воды идет часть теплоты, выделяемой нагревателем,

отсюда время нагревания воды одним нагревателем

При параллельном включении двух нагревателей, как и при включении одного из них, на каждом нагревателе будет напряжение сети V. Следовательно, в каждом из них будет выделяться та же мощность N₁ и общая мощность будет N₂ = 2N₁; отсюда время нагревания воды двумя нагревателями

При последовательном включении нагревателей общий ток через них будет равен 1/2. Поэтому общая мощность, выделяемая в них,

Следовательно, время нагревания воды в этом случае

22 Электрочайник имеет в нагревателе две секции. При включении первой секции вода в чайнике закипает за время τ₁ = 10 мин, а при включении второй секции — за время τ₂ = 40мин. Через какое время закипит вода, если включить обе секции параллельно или последовательно?

Решение:
При последовательном соединении секций

при параллельном соединении секций

23 Две лампы имеют одинаковые мощности. Одна из них рассчитана на напряжение V₁ = 120 В, другая—на напряжение V₂ = 220 В. Во сколько раз отличаются сопротивления ламп?

Решение:
Используя закон Джоуля-Ленца

находим

24 Какое сопротивление имеют 40- и 75-ваттные лампы, рассчитанные на включение в сеть с напряжением V=120 В? Какой ток течет через каждую лампу?

Решение:
Мощность лампы

где I-ток, текущий через лампу, R-ее сопротивление; отсюда для первой и второй ламп имеем

25 Какую мощность будет потреблять 25-ваттная лампочка, рассчитанная на напряжение V₁ = 120 В, если ее включить в сеть с напряжением V₂ = 220 В?

Решение:


26 100-ваттная лампа включена в сеть с напряжением V=120В. Сопротивление лампы в накаленном состоянии больше, чем в холодном (при температуре t₀ = 0° С), в 10 раз. Найти температурный коэффициент сопротивления материала нити и сопротивление лампы в холодном состоянии, если во время горения лампы температура нити t = 2000° С.

Решение:
Когда лампа включена,

-сопротивление нити горящей лампы и Ro=R/10-сопротивление нити лампы при температуре t0; отсюда

27 Найти сопротивление 100-ваттной лампы при комнатной температуре t₀ = 20° С, если при напряжении сети V=220 В температура нити t = 2800° С. Температурный коэффициент сопротивления материала нити .

Решение:


28 К источнику тока с э.д.с. ε = 140 В на расстоянии l=400 м от него подключена лампа, рассчитанная на напряжение V=120B и мощность N=100 Вт. Как изменится падение напряжения на лампе, если параллельно ей подключить вторую такую же лампу? Удельное сопротивление провода ρ = 0,028 мкОм⋅м, его сечение S=1 мм².

Решение:
Сопротивления лампы и проводов

Ток, текущий по линии, и падение напряжения на лампе равны

При подключении второй лампы сопротивление двух ламп равно R₁/2. Поэтому ток, текущий по линии, и падение напряжения на лампах равны

Изменение напряжения на лампе

Знак минус показывает, что при включении второй лампы падение напряжения на первой уменьшается.

29 На какое расстояние l можно передавать электроэнергию от источника тока с э.д.с. ε = 5 кВ так, чтобы на нагрузке с сопротивлением R=1,6 кОм выделялась мощность N=10 кВт? Удельное сопротивление провода ρ = 0,017 мкОм⋅м, его сечение S=1 мм².

Решение:


30 Под каким напряжением V нужно передавать электроэнергию на расстояние l=10 км, чтобы при плотности тока j = 0,5 А/мм² в стальных проводах двухпроводной линии электропередачи потери в линии составляли 1% передаваемой мощности? Удельное сопротивление стали ρ = 0,12 мкОм⋅м.

Решение:

31 Цепь состоит из двух параллельно включенных ламп мощности N=30 Вт каждая. Потери мощности в подводящих проводах составляют 10% полезной мощности. Найти напряжение на зажимах источника тока, если он обеспечивает в цепи ток I=2 A.

Решение:
Напряжение на зажимах источника тока

где V₁ и V₂ — падения напряжения на нагрузке и на проводах линии.
Мощность, выделяемая на нагрузке,

Потери мощности в линии

отсюда


32 От источника тока с напряжением V=750 В необходимо передать мощность N=5 кВт на некоторое расстояние. Какое наибольшее сопротивление R может иметь линия передачи, чтобы потери энергии в ней не превышали 10% передаваемой мощности?

Решение:

33 Какой наибольшей мощности электропечь можно установить в конце двухпроводной линии, имеющей сопротивление R=10 Ом, если источник тока развивает мощность N=6 кВт при напряжении V= 1 кВ?

Решение:
Ток в линии I=N/V. Потери мощности в линии

Мощность электропечи

34 Два параллельно соединенных резистора с сопротивлениями R₁=6 Ом и R₂ = 12 Ом подключены последовательно с резистором, имеющим сопротивление R= 15 Ом, к зажимам генератора с э.д.с. ε = 200 В и внутренним сопротивлением r=1 Ом. Найти мощность, выделяющуюся на резисторе R.

Решение:

35 Элемент с э.д.с. ε = 12 В и внутренним сопротивлением r = 4 Ом замкнут на сопротивление R = 8 Ом. Какое количество теплоты будет выделяться во внешней цепи в единицу времени?

Решение:
Ток в цепи I=ε/(R+r). Количество теплоты, выделяемое во внешней цепи в единицу времени,

36 Найти полную мощность элемента при сопротивлении внешней цепи R = 4 Ом, если внутреннее сопротивление элемента r = 2 Ом, а напряжение на его зажимах V=6 В.

Решение:
Полная мощность элемента

где I-ток в цепи. Так как

37 Батарея элементов, замкнутая на сопротивление R₁ = 2 Ом, дает ток I₁ = 1,6 А. Та же батарея, замкнутая на сопротивление R₂ = 1 Ом, дает ток I₂ = 2 А. Найти мощность, теряемую внутри батареи во втором случае.

Решение:
Внутри батареи теряется мощность

где r-внутреннее сопротивление батареи. Если ε — э. д. с. батареи, то по закону Ома для полной цепи в первом и втором случаях

отсюда


38 Найти э.д.с. ε и внутреннее сопротивление r аккумулятора, если при токе I₁ = 15 А он отдает во внешнюю цепь мощность N₁=135 Вт, а при токе I₂ = 6 А — мощность N₂ = 64,8 Вт.

Решение:


39 К источнику тока с э.д.с. ε = 8 В подключена нагрузка. Напряжение на зажимах источника V=6,4 В. Найти к.п.д. схемы.

Решение:
К. п. д.- это отношение полезной работы (мощности) ко всей затраченной работе (полной мощности). Полезной мощностью в данном случае является мощность, выделяемая на нагрузке, N₁=IV, где I-ток в цепи. Так как э. д. с. ε по определению представляет собой полную работу, совершаемую источником тока при перемещении по цепи единичного заряда, а в единицу времени через сечение проводника проходит заряд, численно равный I, то полная мощность источника тока равна

Таким образом, к.п.д. схемы

40 Найти к.п.д. схемы, изображенной на рис. 135. Сопротивления резисторов R₁ = 2 Ом и R₂ = 5 Ом, внутреннее сопротивление источника тока r = 0,5 Ом.

Суммарное сопротивление при последовательном соединении. Последовательное и параллельное соединение сопротивлений

Содержание:

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.

Свойства и технические характеристики резисторов

Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для — последовательное.

На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав , нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: + 20, + 10, + 5, + 2, + 1% и так далее до величины + 0,001%.

Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.

Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

Мощность при последовательном соединение

При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, сила тока будет составлять I = U/R = 100/390 = 0,256 A.На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.

• P 1 = I 2 x R 1 = 0,256 2 x 200 = 13,11 Вт;
• P 2 = I 2 x R 2 = 0,256 2 x 100 = 6,55 Вт;
• P 3 = I 2 x R 3 = 0,256 2 x 51 = 3,34 Вт;
• P 4 = I 2 x R 4 = 0,256 2 x 39 = 2,55 Вт.

Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.

Мощность при паралл ельном соединение

При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы — с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:

• 1/R = 1/R 1 +1/R 2 +1/R 3 +1/R 4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
• Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
• Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
• Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
• Расчет силы тока для каждого резистора выполняется по формулам: I 1 = U/R 1 = 100/200 = 0,5A; I 2 = U/R 2 = 100/100 = 1A; I 3 = U/R 3 = 100/51 = 1,96A; I 4 = U/R 4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.

Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P 1 = U 2 /R 1 = 100 2 /200 = 50 Вт; P 2 = U 2 /R 2 = 100 2 /100 = 100 Вт; P 3 = U 2 /R 3 = 100 2 /51 = 195,9 Вт; P 4 = U 2 /R 4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р 1 +Р 2 +Р 3 +Р 4 = 50+100+195,9+256,4 = 602,3 Вт.

Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.

Содержание:

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

• Сила тока на всех участках цепи будет одинаковой.
• Общее напряжение цепи составляет сумму напряжений на каждом участке.
• Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.

Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

• Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
• параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
• Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
• При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
• Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.

Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.

Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или

I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)

Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :

G эк = G 1 + G 2 +G 3 (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R эк =R 1 R 2 /(R 1 +R 2)

при трех параллельно включенных резисторах

R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

1. Постоянные.
2. Переменные.

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:

1. Последовательное.
2. Параллельное.
3. Смешанное.

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

1. Освещение.
2. Розетки в квартире.
3. Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.

Шаги

Последовательное соединение

Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.

Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь. Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.

• Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.

Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.

Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.

• Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: R O = 12 В / 8 А = 1,5 Ом.

Параллельное соединение

1. Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.

   Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления: , где R 1 – сопротивление первой ветви, R 2 – сопротивление второй ветви и так далее до последней ветви R n .

   Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.

   Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.

   • Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: R O = 9 В / 3 А = 3 Ом.

2. Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.

Комбинированное соединение

Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.

• Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.

Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи: 1 R O = 1 R 1 + 1 R 2 + 1 R 3 + . . . 1 R n {\displaystyle {\frac {1}{R_{O}}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+{\frac {1}{R_{3}}}+…{\frac {1}{R_{n}}}} .

Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.

• В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.

Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.

Как выбрать правильное подключение ТЭНов?

Поэтому мощность 1-го ТЭНа, может не соответствовать по параметрам, для нагрева сосуда и быть больше или меньше. В таких случаях, для получения необходимой мощности нагрева,  можно использовать несколько ТЭНов, соединенных последовательно или последовательно-параллельно. Коммутируя различные комбинации соединения ТЭНов, переключателем от бытовой  эл. плиты, можно получать различную мощность. Например имея восемь врезанных ТЭНов, по 1.25 кВт каждый, в зависимости от комбинации включения, можно получить следующую мощность.

1. 625 Вт
2. 933 Вт
3. 1,25 кВт
4. 1,6 кВт
5. 1,8 кВт
6. 2,5 кВт

Такого диапазона вполне хватит для регулировки и поддержания нужной температуры. Но можно получить и иную мощность, добавив количество режимов переключения и используя различные комбинации включения.

Последовательное соединение  2-х ТЭНов по 1.25 кВт и подключение их к сети 220В, в сумме дает 625 Вт. Параллельное соединение, в сумме дает 2.5 кВт.

 

Рассчитать можно по следующей формуле.

Мы знаем напряжение, действующее в сети, это 220В. Далее мы так же знаем мощность ТЭН, выбитую на его поверхности допустим это 1,25 кВт, значит, нам нужно узнать силу тока, протекающую в этой цепи. Силу тока, зная напряжение и мощность, узнаем из следующей формулы.

Сила тока = мощность, деленная на напряжение в сети.

Записывается она так: I = P / U.

Где I — сила тока в амперах.

P — мощность в ваттах.

U — напряжение в вольтах.

При подсчете нужно мощность, указанную на корпусе ТЭН в кВт, перевести в  ватты.

1,25 кВт = 1250Вт.  Подставляем известные значения в эту формулу и получаем силу тока.

I = 1250Вт / 220 = 5,681 А

Далее зная силу тока подсчитываем сопротивление ТЭНа, по следующей формуле.

R = U / I, где

R — сопротивление в Омах

U — напряжение в вольтах

I — сила тока в амперах

Подставляем известные значения в формулу и узнаем сопротивление 1 ТЭНа.

R = 220 / 5.681 = 38,725 Ом.

Далее подсчитываем общее сопротивление всех последовательно соединенных ТЭНов. Общее сопротивление равно сумме всех сопротивлений, соединенных последовательно ТЭНов

Rобщ = R1+ R2 + R3 и т.д.

Таким образом, два последовательно соединенных ТЭНа, имеют сопротивление равное 77,45 Ом. Теперь нетрудно подсчитать мощность выделяемую этими двумя ТЭНами.

P = U2 / R где,

P — мощность в ваттах

U2 — напряжение в квадрате, в вольтах

R — общее сопротивление всех посл. соед. ТЭНов

P = 624,919 Вт, округляем до значения 625 Вт.

Далее при необходимости можно подсчитать мощность любого количества последовательно соединенных ТЭНов, или ориентироваться на таблицу.

В таблице 1.1 приведены значения для последовательного соединения ТЭНов.

Таблица 1.1

Кол-во ТЭН	Мощность (Вт)	Сопротивление (Ом)	Напряжение (В)	Сила тока (А)
1	1250,000	38,725	220	5,68
Последовательное соединение
2	625	2 ТЭН = 77,45	220	2,84
3	416	3 ТЭН =1 16,175	220	1,89
4	312	4 ТЭН=154,9	220	1,42
5	250	5 ТЭН=193,625	220	1,13
6	208	6 ТЭН=232,35	220	0,94
7	178	7 ТЭН=271,075	220	0,81
8	156	8 ТЭН=309,8	220	0,71

В таблице 1.2 приведены значения для параллельного соединения ТЭНов.

Таблица 1.2

Кол-во ТЭН	Мощность (Вт)	Сопротивление (Ом)	Напряжение (В)	Сила тока (А)
Параллельное соединение
2	2500	2 ТЭН=19,3625	220	11,36
3	3750	3 ТЭН=12,9083	220	17,04
4	5000	4 ТЭН=9,68125	220	22,72
5	6250	5 ТЭН=7,7450	220	28,40
6	7500	6 ТЭН=6,45415	220	34,08
7	8750	7 ТЭН=5,5321	220	39,76
8	10000	8 ТЭН=4,840	220	45,45

Чему равна сила тока в параллельном соединении. Параллельное и последовательное соединение проводников

Содержание:

Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил. Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой. Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.

Способы подключения и их особенности

Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.

Последовательное соединение

Последовательное подключение — это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего. Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы. То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом. Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.

Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.

Параллельное соединение

Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы — во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.

Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом. В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.

Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.

Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.

Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь». А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.

Последовательно-параллельное соединение

Последовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.

Подведем итог

Подводя итог всему вышеизложенному можно сделать следующие выводы:

1. При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления. Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
2. При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
3. Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
4. Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
5. Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.

В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки. По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения. А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.

Знаете ли Вы, что такое мысленный эксперимент, gedanken experiment?
Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, «мысленный эксперимент» фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей «мысленных экспериментов» является обман слушателя или читателя путем замены настоящего физического эксперимента его «куклой» — фиктивными рассуждениями под честное слово без самой физической проверки.
Заполнение физики воображаемыми, «мысленными экспериментами» привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие «фантики» от настоящих ценностей.

Релятивисты и позитивисты утверждают, что «мысленный эксперимент» весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.

Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: «Если факт не соответствует теории — измените факт» (В другом варианте » — Факт не соответствует теории? — Тем хуже для факта»).

Максимально, на что может претендовать «мысленный эксперимент» — это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.

Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.

Последовательное и параллельное соединение проводников это основные виды соединения проводников, встречающиеся на практике. Так как электрические цепи, как правило, не состоят из однородных проводников одинакового сечения. Как же найти сопротивление цепи, если известны сопротивления ее отдельных частей.

Рассмотрим два типичных случая. Первый из них это когда два или боле проводников обладающих сопротивлением включены последовательно. Последовательно значит, что конец первого проводника подключен к началу второго и так далее. При таком включении проводников сила тока в каждом из них будет одинакова. А вот напряжение на каждом из них будет различным.

Рисунок 1 — последовательное соединение проводников

Падение напряжения на сопротивлениях можно определить исходя из закона Ома.

Формула 1 — Падение напряжения на сопротивлении

Сумма этих напряжений будет равна полному напряжению, приложенному к цепи. Напряжение на проводниках будет распределяться пропорционально их сопротивлению. То есть можно записать.

Формула 2 — соотношение между сопротивлением и напряжением

Суммарное же сопротивление цепи будет равно сумме всех сопротивлений включенных последовательно.

Формула 3 — вычисление суммарного сопротивления при параллельном включении

Второй случай, когда сопротивления в цепи включены параллельно друг другу. То есть в цепи есть два узла и все проводники обладающие сопротивлением подключаются к этим узлам. В такой цепи токи во всех ветвях в общем случае не равны друг другу. Но сумма всех токов в цепи после разветвления будет равна току до разветвления.

Рисунок 2 — Параллельное соединение проводников

Формула 4 — соотношение между токами в параллельных ветвях

Сила тока в каждой из разветвлённой цепи также подчиняется закону Ома. Напряжение на всех проводниках будет одинаково. Но сила тока будет разлучаться. В цепи, состоящей из параллельно соединенных проводников, токи распределяются пропорционально сопротивлениям.

Формула 5 — Распределение токов в параллельных ветвях

Чтобы найти полное сопротивление цепи в этом случае необходимо сложить величины обратные сопротивлениям то есть проводимости.

Формула 6 — Сопротивление параллельно включённых проводников

Также существует упрощённая формула для частного случая когда параллельно включены два одинаковых сопротивления.

Содержание:

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.

Свойства и технические характеристики резисторов

Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для — последовательное.

На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав , нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: + 20, + 10, + 5, + 2, + 1% и так далее до величины + 0,001%.

Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.

Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

Мощность при последовательном соединение

При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, сила тока будет составлять I = U/R = 100/390 = 0,256 A.На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.

• P 1 = I 2 x R 1 = 0,256 2 x 200 = 13,11 Вт;
• P 2 = I 2 x R 2 = 0,256 2 x 100 = 6,55 Вт;
• P 3 = I 2 x R 3 = 0,256 2 x 51 = 3,34 Вт;
• P 4 = I 2 x R 4 = 0,256 2 x 39 = 2,55 Вт.

Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.

Мощность при паралл ельном соединение

При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы — с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:

• 1/R = 1/R 1 +1/R 2 +1/R 3 +1/R 4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
• Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
• Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
• Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
• Расчет силы тока для каждого резистора выполняется по формулам: I 1 = U/R 1 = 100/200 = 0,5A; I 2 = U/R 2 = 100/100 = 1A; I 3 = U/R 3 = 100/51 = 1,96A; I 4 = U/R 4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.

Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P 1 = U 2 /R 1 = 100 2 /200 = 50 Вт; P 2 = U 2 /R 2 = 100 2 /100 = 100 Вт; P 3 = U 2 /R 3 = 100 2 /51 = 195,9 Вт; P 4 = U 2 /R 4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р 1 +Р 2 +Р 3 +Р 4 = 50+100+195,9+256,4 = 602,3 Вт.

Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.

Содержание:

В электрических цепях используются различные типы соединений. Основными являются последовательные, параллельные и смешанные схемы подключений. В первом случае используется несколько сопротивлений, соединенных в единую цепочку друг за другом. То есть, начало одного резистора соединяется с концом второго, а начало второго — с концом третьего и так далее, до любого количества сопротивлений. Сила тока при последовательном соединении будет одинаковой во всех точках и на всех участках. Для определения и сравнения других параметров электрической цепи, следует рассматривать и остальные виды соединений, обладающие собственными свойствами и характеристиками.

Последовательное и параллельное соединение сопротивлений

Любая нагрузка обладает сопротивлением, препятствующим свободному течению электрического тока. Его путь проходит от источника тока, через проводники к нагрузке. Для нормального прохождения тока, проводник должен обладать хорошей проводимостью и легко отдавать электроны. Это положение пригодится далее при рассмотрении вопроса, что такое последовательное соединение.

В большинстве электрических цепей применяются медные проводники. Каждая цепь содержит приемники энергии — нагрузки, обладающие различными сопротивлениями. Параметры соединения лучше всего рассматривать на примере внешней цепи источника тока, состоящей из трех резисторов R1, R2, R3. Последовательное соединение предполагает поочередное включение этих элементов в замкнутую цепь. То есть начало R1 соединяется с концом R2, а начало R2 — с концом R3 и так далее. В такой цепочке может быть любое количество резисторов. Эти символы используют в расчетах .

На всех участках будет одинаковой: I = I1 = I2 = I3, а общее сопротивление цепи составит сумму сопротивлений всех нагрузок: R = R1 + R2 + R3. Остается лишь определить, каким будет при последовательном соединении. В соответствии с законом Ома, напряжение представляет собой силу тока и сопротивления: U = IR. Отсюда следует, что напряжение на источнике тока будет равно сумме напряжений на каждой нагрузке, поскольку ток везде одинаковый: U = U1 + U2 + U3.

При постоянном значении напряжения, ток при последовательном соединении будет находиться в зависимости от сопротивления цепи. Поэтому при изменении сопротивления хотя-бы на одной из нагрузок, произойдет изменение сопротивления во всей цепи. Кроме того, изменятся ток и напряжение на каждой нагрузке. Основным недостатком последовательного соединения считается прекращение работы всех элементов цепи, при выходе из строя даже одного из них.

Совершенно другие характеристики тока, напряжения и сопротивления получаются при использовании параллельного соединения. В этом случае начала и концы нагрузок соединяются в двух общих точках. Происходит своеобразное разветвление тока, что приводит к снижению общего сопротивления и росту общей проводимости электрической цепи.

Для того чтобы отобразить эти свойства, вновь понадобится закон Ома. В данном случае сила тока при параллельном соединении и его формула будет выглядеть так: I = U/R. Таким образом, при параллельном соединении n-го количества одинаковых резисторов, общее сопротивление цепи будет в n раз меньше любого из них: Rобщ = R/n. Это указывает на обратно пропорциональное распределение токов в нагрузках по отношению к сопротивлениям этих нагрузок. То есть, при увеличении параллельно включенных сопротивлений, сила тока в них будет пропорционально уменьшаться. В виде формул все характеристики отображаются следующим образом: сила тока — I = I1 + I2 + I3, напряжение — U = U1 = U2 = U3, сопротивление — 1/R = 1/R1 + 1/R2 + 1/R3.

При неизменном значении напряжения между элементами, токи в этих резисторах не имеют зависимости друг от друга. Если один или несколько резисторов будут выключены из цепи, это никак не повлияет на работу других устройств, остающихся включенными. Данный фактор является основным преимуществом параллельного соединения электроприборов.

В схемах обычно не используется только последовательное соединение и параллельное соединение сопротивлений, они применяются в комбинированном виде, известном как . Для вычисления характеристик таких цепей применяются формулы обоих вариантов. Все расчеты разбиваются на несколько этапов, когда вначале определяются параметры отдельных участков, после чего они складываются и получается общий результат.

Законы последовательного и параллельного соединения проводников

Основным законом, применяемым при расчетах различных видов соединений, является закон Ома. Его основным положением является наличие на участке цепи силы тока, прямо пропорциональной напряжению и обратно пропорциональной сопротивлению на данном участке. В виде формулы этот закон выглядит так: I = U/R. Он служит основой для проведения расчетов электрических цепей, соединяемых последовательно или параллельно. Порядок вычислений и зависимость всех параметров от закона Ома наглядно показаны на рисунке. Отсюда выводится и формула последовательного соединения.

Более сложные вычисления с участием других величин требуют применения . Его основное положение заключается в том, что несколько последовательно соединенных источников тока, будут обладать электродвижущей силой (ЭДС), составляющей алгебраическую сумму ЭДС каждого из них. Общее сопротивление этих батарей будет состоять из суммы сопротивлений каждой батареи. Если выполняется параллельное подключение n-го количества источников с равными ЭДС и внутренними сопротивлениями, то общая сумма ЭДС будет равно ЭДС на любом из источников. Значение внутреннего сопротивления составит rв = r/n. Эти положения актуальны не только для источников тока, но и для проводников, в том числе и формулы параллельное соединение проводников.

В том случае, когда ЭДС источников будет иметь разное значение, для расчетов силы тока на различных участках цепи применяются дополнительные правила Кирхгофа.

Основы электроники и электротехники — Лабораторная работа №3

Исследование сопротивлений резисторов при последовательном и параллельном соединениях.

Цель работы: Опытом проверить закономерности электрической цепи при последовательном и паралельном соединениях резисторов. 

 

1.Пояснение к работе 

Краткие теоретические сведения

    Последовательным соединением сопротивлений называется такое соединение, при котором конец первого сопротивления соединяется с началом второго, конец второго — с началом третьего и т. д. 

Общее сопротивление последовательно соединенных резисторов равно сумме их сопротивлений. 
R_общ.=R₁+R₂+R₃ 
R_общ=5ом+10ом+25ом=40ом 

        Величина тока в последовательной цепи 

         Так как в данной цепи отсутствует ответвление тока, то очевидно, что количество электричества, протекающее через поперечное сечение проводника за единицу времени. в любой точке цепи будет одинаковым. 
         Следовательно во всех точках последовательной цепи величина тока одинакова. 
     Эти четыре амперметра покажут одинаковые величины тока. Поэтому при последовательном соединении  для измерения тока достаточно включать один амперметр на любом участке цепи. 

 

Распределение напряжения в последовательной цепи 

Напряжение источника тока приложенное к внешнему участку цепи распределяется по участкам цепи прямо пропорционально сопротивлениям этих участков. Напряжение приложенное к каждому из этих резисторов определяется по формуле: 

Так как ток в последовательной цепи везде одинаков значит действительно напряжение на ее участках зависит от сопротивления чем больше сопротивление тем большее напряжение приложено к данному участку. 

 

Сумма напряжений на участках последовательной цепи равна напряжению источника тока 

Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму — концы.

Общее сопротивление параллельно включенных сопротивлений определяется по формуле:

 

 Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение. 

 На вышеуказанном рисунке мы можем сразу сказать что общее сопротивление будет меньше 10 ом.

Первый частный случай 

 Если параллельно включено только два резистора  то их общее сопротивление можно определить по формуле:

Второй частный случай

 Если параллельно включено любое количество резисторов одинаковых сопротивлений то их общее сопротивление можно определить  если сопротивление одного резистора разделить на количество резисторов. 

 

Распределение токов и напряжения в параллельных ветвях

 

Так как начала всех сопротивлений сведены в одну общую точку, а концы — в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками. 

 Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.

 Если разветвление подключено непосредственно к зажимам источника тока, то напряжение на каждом из сопротивлений равно напряжению на зажимах источника.

 Второе свойство цепи с параллельным соединением  заключается в том, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям. 

 Это значит что, чем больше сопротивление, тем меньше по нему пойдет ток. 

Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I1, I2, I3 утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду утекающему от нее: 

  Следовательно, третье свойство параллельного соединения может сформулирована так: 

Величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях.    

 

2.Техническое задание 
2.1.Собрать электрическую цепь последовательного соединения резисторов (рисунок 1) 

Рисунок 1. Схема электрическая принципиальная.

2.2.Собрать электрическую цепь паралельного соединения резисторов (рисунок 2) 

Рисунок 2. Схема электрическая принципиальная.

2.3.Снять показания приборов и записать их в таблицу 
2.4.Произвести расчеты 
2.5. Построить графики 
2.6.Ответить на контрольные вопросы 
2.7. Сделать вывод 

3.Работа в лаборатории 

 

3.1. Исследование последовательного соединения резисторов

3.1.1 Собрать схему (Рисунок 3).

 

Рисунок 3. Схема исследования.

 

3.1.2 Установить на схеме величины R1=100 Ом + N, R2=100 Ом + 2N и R3=130 Ом + 4N,
где N — номер студента по журналу (мощность резисторов 1 Вт).
3.1.3. Включить источник и установить напряжение U=15 В, 24 В.
3.1.4. Измерить величину тока, протекающего в цепи и занести значение в таблицу 1.                                                                  
3.1.5. Измерить напряжение на каждом резисторе и записать в таблицу 1.
3.1.6. Измерить сопротивление каждого резистора и записать в таблицу 1.
3.1.7. Отключить схему.
3.1.8. Рассчитать сопротивление резисторов по формулам:

Таблица 1 — Измеренные параметры

№измерения

Измерением

Расчетом

U

I

U1

U2

U3

R1

R2

R3

RЭ

R1

R2

R3

RЭ

В

А

В

В

В

Ом

Ом

Ом

Ом

Ом

Ом

Ом

Ом

1

15

2

24

 

3.2. Исследование параллельного соединения реисторов

3.2.1. Собрать схему (Рисунок 4).

 

Рисунок 4. Схема исследования.

3.2.2. Установить на схеме величины R1=70 Ом + N, R2=100 Ом + N и R3=150 Ом + N,
где N — номер студента по журналу (мощность резисторов более 1 Вт). 
3.2.3. Включить источник и установить напряжение U=15 В, 24 В.
3.2.4. Измерить величину тока, протекающего во всей цепи и занести значение в таблицу 2.                                                                  
3.2.5. Измерить величину тока, протекающего в каждом резисторе и записать в таблицу 2.
3.2.6. Расчитать проводимость каждого резистора и записать в таблицу 2 (установкой):

3.2.7. Рассчитать проводимость каждого резистора через ток и напряжение и записать в таблицу 2 (расчетом):

3.2.8. Отключить схему.

 

Таблица 2 — Измеренные параметры

№ измер.

Измерением

Установкой

Расчетом

U

I

I1

I2

I3

g1

g2

g3

gэ

Rэ

g1

g2

g3

gэ

Rэ

А

А

А

А

А

См

См

См

См

Ом

См

См

См

См

Ом

1

15

2

24

 

4. Содержание отчета
4.1. Название и цель работы
4.2. Схемы
4.3. Таблицы
4.4. Расчеты по формулам
4.5. Ответы на контрольные вопросы
4.6. Вывод

 

5.Контрольные вопросы

5.1. Какое соединение резисторов называют последовательным?
5.2. Как определить общее сопротивление резисторов при последовательном соединении?
5.3. Что называется проводимостью и в каких единицах она измеряется?
5.4. Чему равен общий ток цепи и напряжение на участках при последовательном соединении?
5.5.  Как определяется мощность на участках цепи и всей цепи при последовательном соединении?
5.6. Какое соединение резисторов называют паралельным?
5.7. Как определить общее сопротивление резисторов при паралельным соединении?
5.8. Чему равен общий ток цепи и напряжение на участках при паралельным соединении?
5.9.  Как определяется мощность на участках цепи и всей цепи при паралельным соединении?

Параллельные цепи — преимущества, мощность, ток, напряжение и эффективное сопротивление

Введение

В этом уроке мы рассмотрим параллельные схемы. Посмотрим, почему они так распространены. Мы также рассмотрим напряжение, мощность, ток и эффективное сопротивление.

Активность, показывающая, что параллельные лампы одинаково ярки, потому что они всегда подключены к одному и тому же напряжению.

Преимущество параллельных цепей перед последовательными цепями

Если мы хотим подключить две лампочки к одной батарее, очевидный способ их подключения — последовательно.Это означает, что обе лампы находятся на одном и том же проводящем пути от одного вывода батареи к другому.

Проблема с последовательным соединением двух лампочек заключается в том, что обе лампы тусклые, и если вы выключите одну лампочку, они обе погаснут.

Анимация показывает, что ток, потребляемый от батареи, увеличивается по мере того, как все больше компонентов подключаются параллельно.

Параллельное подключение ламп дает два преимущества.

1. Все они получают полное напряжение батареи, поэтому все они яркие
2. Все они в собственном проводящем контуре, поэтому вы можете выключить одну лампочку, не затрагивая другие.

Параллельные схемы в доме

Дома все ваши приборы подключены параллельно друг другу. Это означает, что все они получают полное сетевое напряжение, и вы можете включить телевизор, не включая микроволновую печь.

Анимация, показывающая, как все наши бытовые приборы подключаются параллельно друг другу.

Как это работает?

Электрические кабели в вашем доме состоят из трех проводов. Мы пока проигнорируем Землю и сконцентрируемся на двух из них: живом и нейтральном.В Европе живая коричневая, а нейтральная голубая. В США жить может быть черным, красным или желтым; а нейтральный обычно бывает белым или белым с желтыми полосами.

Есть напряжение между фазой и нейтралью, потому что они косвенно подключены к электростанции. Каждая электрическая розетка в вашем доме подключена к фазе и нейтрали. Металлические штыри вилки обеспечивают электрическое соединение с розеткой. Штепсель, опять же с проводом под напряжением и нулевым проводом, соединяет вилку с устройством.

Каждый прибор имеет собственное соединение между фазой и нейтралью, поэтому каждый прибор можно переключать отдельно, и на него подается полное напряжение под напряжением.

Параллельное добавление всегда увеличивает общий ток

Даже если все приборы в вашем доме подключены к одному напряжению, все они потребляют разные токи. Электрическая духовка быстро передает энергию, поэтому потребляемый ею ток будет большим. Телевизор передает энергию довольно медленно, поэтому потребляемый им ток будет довольно небольшим.

Действие для визуализации увеличения тока, потребляемого от батареи, при параллельном добавлении дополнительного компонента.

Все эти токи должны добавляться к источнику питания, поскольку он должен обеспечивать их все одновременно. Чем больше подключено устройств, тем больше потребляемый ток.

Почему ток не «расщепляется» на переходах в параллельных цепях

Часто говорят, что ток разделяется на переходах в параллельных цепях, но с этой идеей нужно быть очень осторожным.Это часто может привести к постоянному заблуждению.

Анимация, объясняющая, почему о разделении тока на стыках лучше не думать.

Первое, что нужно запомнить, это то, что заряды не начинаются с батареи, а затем проходят через пустые провода, пока не дойдут до места соединения, а затем нужно решить, что делать. Заряды уже есть повсюду в цепи, и все они начинают очень медленно течь повсюду одновременно.

Другая проблема в том, что нет «течения», которое могло бы течь.Чем больше устройств вы подключаете параллельно, тем больше ток, потребляемый от источника питания. Один и тот же ток не разделяется по-разному.

Иногда проще представить компоненты как активные объекты, требующие тока от источника питания. Если схема настроена так, что иногда эти токи должны протекать по одному проводу, вам необходимо их сложить.

Расчет токов в параллельных цепях

При параллельном подключении лампочек на них должно быть одинаковое напряжение.Вы можете относиться к ним так, как будто каждый из них находится в своей собственной цепи (что, если рассматривать схему как цикл смысла, так оно и есть).

Анимация, демонстрирующая, как рассчитать токи в параллельных цепях.

Если лампы разные, то лампа с меньшим сопротивлением потребляет больший ток и будет ярче. Это просто закон Ома: маленькое сопротивление означает большой ток.

Это стратегия:

• рассчитать ток через каждую лампочку по закону Ома
• сложите токи, чтобы найти ток, потребляемый от батареи

Вы можете рассчитать ток, используя уравнение закона Ома V = IR.Сначала вам нужно переставить его так, чтобы I = V / R, и помните, что V — это просто напряжение батареи.

Добавление элементов параллельно всегда снижает эффективное сопротивление

Батарея параллельной цепи не «знает», что к ней подключено. Все, что он ощущает, — это общее сопротивление (или, если вам нравится общий спрос на ток). Сопротивление, которое испытывает аккумулятор, называется эффективным сопротивлением цепи.

Анимация, объясняющая параллельные сопротивления как дыры в ванне.

По мере того, как вы добавляете все больше и больше компонентов параллельно, ток, потребляемый от источника питания, становится все больше и больше. Если ток становится больше, сопротивление должно уменьшаться. Таким образом, добавляя сопротивления, вы фактически уменьшаете эффективное сопротивление, что кажется странным.

Неважно, насколько велико сопротивление, добавление его параллельно всегда снижает эффективное сопротивление. Для объяснения этого есть пара аналогий.

Если у вас есть ванна с отверстием на дне, она опустеет.Если вы добавите еще одно отверстие, независимо от того, насколько оно маленькое, ванна всегда опорожняется быстрее.

Или представьте себе огромную толпу, покидающую стадион через главные ворота. Если даже крохотные боковые ворота открываются, то количество людей, покидающих стадион каждую минуту, возрастает.

Эмпирические правила расчета эффективного сопротивления параллельных цепей

График, иллюстрирующий некоторые практические правила для эффективного сопротивления параллельных цепей.

1. Общее сопротивление всегда меньше наименьшего сопротивления (потому что вы всегда можете представить, как сначала строите схему с наименьшим сопротивлением, а затем эффективное сопротивление продолжает уменьшаться по мере добавления большего сопротивления).
2. Два идентичных резистора имеют эффективное сопротивление, равное половине их значения (поскольку добавление второго сопротивления удваивает ток, поэтому сопротивление уменьшается вдвое).
3. Три одинаковых резистора имеют эффективное сопротивление, равное трети их номинала, и так далее.
4. Очень большое сопротивление и очень маленькое сопротивление, включенные параллельно, имеют эффективное сопротивление немного меньше, чем небольшое сопротивление (маленькое сопротивление похоже на большое отверстие в ванне, добавление еще одного крошечного отверстия все равно увеличивает общую скорость потока на крошечную величину. )

Игра Попрактикуйтесь в эффективном сопротивлении параллельно включенных резисторов.Направляйте космический вездеход над черной дырой, используя только квадраты с эффективным сопротивлением менее 10 Ом.

Расчет эффективного сопротивления параллельных цепей

Анимация показывает, как использовать формулу для расчета эффективного сопротивления.

Формула для вычисления эффективного сопротивления параллельных цепей выглядит довольно сложной, возможно, поэтому параллельные цепи часто преподаются после последовательных цепей, хотя параллельные цепи гораздо более распространены и полезны.

Эту формулу довольно легко вывести, если вы не против иметь дело с дробями.

Использовать формулу не так уж и сложно. Просто подставьте свои значения для сопротивлений, а затем сложите дроби.

Остерегайтесь, после того, как вы сложите дроби, вы получите не _{рэндов с эффективностью} , а 1/ _{с эффективностью} , поэтому вам нужно перевернуть результат, чтобы найти эффективное сопротивление.

В качестве проверки убедитесь, что результат меньше наименьшего сопротивления.

Расчет эффективного сопротивления путем расчета полного потребляемого тока

График, объясняющий, как рассчитать эффективное сопротивление, вычислив полный ток, потребляемый от батареи.

Вместо того, чтобы использовать формулу, мы можем рассчитать общий ток, потребляемый от источника питания, а затем использовать R _{эффективное} = V _{аккумулятор} / I _всего для расчета эффективного сопротивления.

Фактически, это то, что делает формула, но иногда вопрос дает вам токи через компоненты, а не их сопротивления, поэтому быстрее использовать этот метод, чем сначала рассчитывать сопротивления, а затем использовать формулу.

Вернуться к объяснению электроснабжения

Серия

и параллельные схемы в источниках питания

Фотоэлектрические модули и батареи являются строительными блоками системы. Хотя каждый модуль или батарея имеют номинальное напряжение или силу тока, их также можно соединить вместе, чтобы получить желаемое напряжение в системе.

1. Последовательные схемы

Последовательные подключения проводов выполняются между положительным (+) концом одного модуля и отрицательным (-) концом другого модуля. Когда нагрузки или источники питания подключаются последовательно, напряжение увеличивается.Последовательная проводка не увеличивает вырабатываемый ток. На изображении справа показаны два модуля, подключенных последовательно, что дает 24 В и 3 А. Цепи серии

можно также проиллюстрировать с помощью батарей для фонарей. Батареи фонарей часто подключаются последовательно для увеличения напряжения и питания лампы с более высоким напряжением, чем одна батарея могла бы питать в одиночку.

Вопрос: Каково результирующее напряжение при последовательном подключении четырех батарей 1,5 В постоянного тока?

Ответ: 6 вольт

2.Параллельные цепи

Параллельные проводные соединения выполняются от положительных (+) к положительным (+) клеммам и от отрицательных (-) к отрицательным (-) клеммам между модулями. Когда нагрузки или источники подключаются параллельно, токи складываются, а напряжение одинаково во всех частях цепи. Чтобы увеличить силу тока в системе, источники напряжения должны быть подключены параллельно. На изображении справа показаны фотоэлектрические модули, подключенные параллельно, чтобы получить систему на 12 В, 6 А. Обратите внимание, что параллельная проводка увеличивает производимый ток и не увеличивает напряжение.

Батареи также часто подключаются параллельно для увеличения общего ампер-часа, что увеличивает емкость накопителя и продлевает время работы. S

3. Последовательные и параллельные схемы

Системы могут использовать сочетание последовательной и параллельной проводки для получить требуемые напряжения и силы тока. На изображении справа показаны четыре модуля на 3 А, 12 В постоянного тока, подключенных последовательно и параллельно. Гирлянды из двух модулей соединены последовательно, увеличивая напряжение до 24 В. Каждая из этих струн подключается параллельно цепи, увеличивая силу тока до 6 ампер.В результате получилась система на 6 ампер и 24 В постоянного тока.

4. Батареи, включенные последовательно и параллельно

Преимущества параллельной схемы можно проиллюстрировать, наблюдая, сколько времени проработает фонарик, прежде чем батареи полностью разрядятся. Чтобы фонарик прослужил вдвое дольше, необходимо вдвое увеличить емкость аккумулятора.

На картинке слева последовательно добавлена ​​цепочка из четырех батарей параллельно другой цепочке из четырех батарей для увеличения емкости (ампер-часов).Новая цепочка батарей подключается параллельно, что увеличивает доступные ампер-часы, тем самым добавляя дополнительную емкость и увеличивая время использования. Вторую цепочку нельзя было добавить последовательно, потому что общее напряжение будет 12 вольт, что несовместимо с 6-вольтовой лампой.

5. Высоковольтные фотоэлектрические массивы

До сих пор в этой главе мы обсуждали только входное напряжение до номинального 24 В. Сегодня для большинства инверторов с подключением к сети без батарей требуется вход постоянного тока высокого напряжения.Это входное окно обычно находится в диапазоне от 350 до 550 В постоянного тока. Из-за требований инвертора к входу высокого напряжения фотоэлектрические модули должны быть подключены последовательно, чтобы в достаточной степени увеличить напряжение.

6. Примеры последовательного и параллельного подключения и инструкции

1. Подключите фотоэлектрические модули (массив) последовательно или параллельно, чтобы получить желаемое напряжение в системе.

2. Рассчитайте общую мощность модуля для вольт и ампер.

3. Подключите массив к контроллеру заряда.

4. Подключите батареи последовательно или параллельно, чтобы получить желаемое напряжение в системе.

5. Рассчитайте общее напряжение аккумуляторной батареи и емкость ампер-часов.

6. Подключите аккумуляторную батарею к контроллеру заряда.

Источник : «ФОТОЭЛЕКТРОЭНЕРГИЯ — Руководство по проектированию и установке» компании Solar Energy International.

Тренинг по сертификации солнечной энергии от профессиональных установщиков солнечных батарей

С 18 сертифицированными IREC-ISPQ инструкторами по солнечной фотоэлектрической системе и 24 сертифицированными специалистами по установке солнечных фотоэлектрических систем, сертифицированными NABCEP — больше, чем в любой другой учебной организации по солнечной энергии, — опытная команда Solar Energy International находится в авангарде образования в области возобновляемых источников энергии.Если вы ищете онлайн-обучение по солнечной энергии или личное лабораторное обучение для сдачи экзамена начального уровня NABCEP или сертификации установщика NABCEP, почему бы не получить свое образование от команды самых опытных специалистов по установке солнечных батарей в отрасли? Многие инструкторы SEI участвовали в самых известных солнечных установках в своих общинах в США и в развивающихся странах.

Чтобы начать свой путь солнечной тренировки сегодня с Solar Energy International, щелкните здесь.

Подключение источников питания параллельно или последовательно для увеличения выходной мощности

В некоторых приложениях использования одного источника питания может быть недостаточно для обеспечения мощности, необходимой для нагрузки.Причины использования нескольких источников питания могут включать избыточную работу для повышения надежности или увеличения выходной мощности. При обеспечении комбинированного питания необходимо следить за тем, чтобы все источники питания передавали его сбалансированным образом.

Источники питания, подключенные для резервирования

Резервные источники питания — это топология, в которой выходы нескольких источников питания соединены для повышения надежности системы, но не для увеличения выходной мощности. Резервные конфигурации обычно предназначены для получения выходного тока только от основных источников питания и для получения тока от резервных источников питания при отказе одного из основных источников питания.Поскольку потребление тока нагрузки создает нагрузку на компоненты в источнике питания, высокая надежность в системе достигается, когда ток не потребляется от резервных источников до тех пор, пока не возникнет проблема с одним из основных источников питания.

• Источники питания A и B — аналогичные блоки; Vout и максимальный Iout одинаковые
• Напряжение нагрузки равно напряжению питания
• Максимальный ток нагрузки равен максимальному выходному току одного источника
• Электронный переключатель подключает один из выходов питания к нагрузке

Источники питания с параллельно подключенными выходами

Обычная топология, используемая для увеличения выходной мощности, заключается в параллельном подключении выходов двух или более источников питания.В этой конфигурации каждый источник питания обеспечивает необходимое напряжение нагрузки, а параллельное подключение источников увеличивает доступный ток нагрузки и, следовательно, доступную мощность нагрузки.

Эту топологию можно успешно реализовать, но есть много соображений для обеспечения эффективности конфигурации. Для параллельных конфигураций предпочтительны источники питания с внутренними цепями, поскольку внутренние цепи улучшают эффективность распределения тока. Если источники питания, используемые в приложении для разделения тока, не имеют внутренних цепей разделения, необходимо использовать внешние методы, которые могут быть менее эффективными.

Основная проблема заключается в том, насколько равномерно ток нагрузки распределяется между источниками питания. Распределение тока нагрузки зависит как от конструкции источников питания, так и от конструкции внешней цепи и проводников, используемых для параллельного соединения выходов источников питания. Практически всегда при параллельном подключении используются одинаковые блоки питания из-за проблем, связанных с эффективной настройкой блоков питания. Однако можно настроить источники питания параллельно с согласованными выходными напряжениями и несовпадающими максимальными выходными токами.

Более подробное обсуждение параллельного подключения источников питания можно найти в нашем техническом документе Current Sharing with Power Supplies.

• Источники питания A и B должны иметь одинаковый Vout; Максимум Iout может быть разным
• Напряжение нагрузки равно напряжению питания
• Максимальный ток нагрузки равен сумме максимального выходного тока обоих источников
• Цепи контроля тока уравновешивают ток нагрузки между источниками питания

Источники питания с выходами, подключенными последовательно

Другой вариант увеличения мощности, подаваемой на нагрузку, — это соединение выходов нескольких источников питания последовательно, а не параллельно.Некоторые из преимуществ использования последовательной топологии включают в себя: почти идеальное использование подачи питания между источниками, отсутствие необходимости в конфигурации или совместном использовании цепей, а также устойчивость к большому разнообразию конструкций приложений. Как упоминалось ранее, при параллельном подключении выходов источников питания каждый источник обеспечивает необходимое напряжение, а ток нагрузки распределяется между источниками. Для сравнения, когда выходы источников питания соединены последовательно, каждый источник обеспечивает требуемый ток нагрузки, а выходное напряжение, подаваемое на нагрузку, будет представлять собой комбинацию последовательно включенных источников.

Следует отметить, что когда блоки питания сконфигурированы с последовательным соединением выходов, источники питания не обязательно должны иметь аналогичные выходные характеристики. Ток нагрузки будет ограничен наименьшим допустимым током нагрузки любого из источников в конфигурации, а напряжение нагрузки будет суммой выходных напряжений всех источников в цепочке.

Есть несколько ограничений, налагаемых на источники питания, когда они используются в конфигурации с последовательным выходом.Одно из ограничений заключается в том, что выход источников питания должен быть спроектирован так, чтобы выдерживать смещение напряжения из-за последовательной конфигурации. Это напряжение смещения обычно не является проблемой, но выходные напряжения источников питания с заземлением не могут быть суммированы на выходах других источников. Второе ограничение заключается в том, что выход источника питания может подвергаться обратному напряжению, если выход неактивен, когда активны остальные выходы в цепочке. Проблема обратного напряжения может быть легко решена путем размещения диода с обратным смещением на выходе каждого источника питания.Номинальное напряжение пробоя диода должно быть больше, чем выходное напряжение отдельного источника питания, а номинальный ток диода должен быть больше, чем максимальный номинальный выходной ток любого источника питания в последовательной цепочке.

• Источники питания A и B могут иметь разные максимальные значения Vout и Iout
• Напряжение нагрузки равно сумме выходных напряжений питания
• Максимальный ток нагрузки равен наименьшему из максимального выходного тока любого источника
• Диоды обратного смещения защищают выходы источников питания

Сводка

Источники питания, подключенные параллельно:

• Плохое использование мощности из-за допуска управления разделением тока между источниками
• Требуется специальная цепь для управления разделением тока между источниками
• Чувствительность к конструкции и конструкции проводов, соединяющих источники питания параллельно
• Наиболее простая конструкция с аналогичными блоками питания

Источники питания, подключенные последовательно:

• Эффективное использование мощности ограничено только точностью выходного напряжения каждого источника
• Нет необходимости в цепях для управления распределением напряжения или тока между источниками
• Отсутствие чувствительности к конструкции или конструкции проводников, соединяющих источники питания в серии
• Простая конструкция с любой комбинацией источников питания

Хотя общий метод, используемый для увеличения мощности нагрузки, подаваемой от источников питания, заключается в параллельном подключении выходов, другое решение может заключаться в последовательном соединении выходов нескольких источников питания.У поставщиков блоков питания, таких как CUI, есть технический персонал, который может помочь настроить приемлемое решение для этих и других проблем, связанных с применением блоков питания.

Категории: Основы , Выбор продукта

Дополнительные ресурсы

---

У вас есть комментарии к этому сообщению или темам, которые вы хотели бы, чтобы мы освещали в будущем?
Отправьте нам письмо по адресу powerblog @ cui.ком

Энергия при последовательном и параллельном подключении

Электрическая цепь

Электричество и магнетизм

Энергия при последовательном и параллельном подключении

Повествование о физике для 14-16

Как энергия сдвигается в цепях с разными соединениями

Две лампы, соединенные параллельно, светятся так же ярко, как и одна, соединенная сама по себе.К настоящему времени вы могли ожидать этого, потому что лампы часто используются в качестве неофициальных амперметров в классных комнатах, а разность потенциалов одинакова для обеих ламп. Таким образом, в схеме с параллельным подключением передается в два раза больше энергии по сравнению с простой схемой с одной лампой. Следствием этого является то, что химический запас энергии, связанный с батареей, истощается вдвое больше после того, как цепи проработали идентичные промежутки времени.

Две последовательно соединенные лампы разряжают батарею намного меньше, потому что ток в цепи меньше, чем в цепи с одной лампой и батареей, а разность потенциалов одинакова для обеих цепей.Две лампы передают меньше энергии по сравнению с одной лампой.

Мощность в пути и время определяют сдвиг энергии для накопления

Те же модели рассеяния энергии применимы к резисторам, только они не светятся (по крайней мере, визуально, но они могут излучать на частотах ниже тех, которые мы видим, возможно, в инфракрасном диапазоне). Резисторы передают часть энергии в накопитель тепла, используя нагрев за счет пути излучения, и, как правило, гораздо больше энергии за счет нагрева за счет пути частиц.

Чтобы точно рассчитать, сколько энергии смещается в течение 1 секунды в каждой лампе во всех ситуациях, вам необходимо определить, сколько электричества происходит: мощность в электрическом тракте. Этому и посвящен эпизод 02.

Как подключить батареи последовательно и параллельно

Если вы когда-либо работали с батареями, вы, вероятно, встречали термины серия , параллельный и последовательно-параллельный , но что именно означают эти термины?

Series, Series-Parallel и Parallel — это соединение двух батарей вместе, но зачем вам вообще нужно соединять две или более батарей вместе?

Подключив две или более батарей последовательно, последовательно, параллельно или параллельно, вы можете увеличить напряжение или емкость в ампер-часах, или даже и то, и другое; что позволяет использовать приложения с более высоким напряжением или энергоемкие приложения.

ПОДКЛЮЧЕНИЕ АККУМУЛЯТОРОВ СЕРИИ

Последовательное подключение батареи — это когда вы соединяете две или более батареи вместе для увеличения общего напряжения системы батарей, последовательное соединение батарей не увеличивает емкость, а только напряжение.
Например, если вы подключите четыре батареи 12 Вольт 26 Ач, у вас будет напряжение батареи 48 В и емкость батареи 26 Ач.

Для настройки батарей с последовательным подключением каждая батарея должна иметь одинаковое напряжение и номинальную емкость, иначе вы можете повредить батареи.Например, вы можете подключить две батареи 6 В 10 Ач вместе последовательно, но вы не можете подключить одну батарею 6 В 10 Ач с одной батареей 12 В 10 Ач.

Для последовательного соединения группы батарей вы подключаете отрицательную клемму одной батареи к положительной клемме другой и так до тех пор, пока не будут подключены все батареи, затем вы должны подключить перемычку / кабель к отрицательной клемме первой батареи в вашем цепочку батарей к вашему приложению, затем еще один кабель к положительной клемме последней батареи в вашей цепочке к вашему приложению.

При последовательной зарядке аккумуляторов необходимо использовать зарядное устройство, соответствующее напряжению аккумуляторной системы. Мы рекомендуем заряжать каждую батарею индивидуально, чтобы избежать дисбаланса батареи.

Герметичные свинцово-кислотные батареи

уже много лет являются предпочтительным выбором для систем с длинными линиями высоковольтных аккумуляторных батарей, хотя литиевые батареи могут быть сконфигурированы последовательно, это требует внимания к BMS или PCM.

ПОДКЛЮЧЕНИЕ АККУМУЛЯТОРОВ ПАРАЛЛЕЛЬНО

Параллельное подключение батареи — это когда вы соединяете две или более батареи вместе для увеличения емкости в ампер-часах, при параллельном подключении батареи емкость увеличивается, однако напряжение батареи остается прежним.

Например, если вы подключите четыре аккумулятора 12 В 100 Ач, вы получите систему аккумуляторов 12 В 400 Ач.

При параллельном подключении батарей отрицательная клемма одной батареи подключается к отрицательной клемме следующей и т. Д. Через цепочку аккумуляторов, то же самое происходит с положительными клеммами, то есть положительный полюс одной батареи к положительной клемме батареи. следующий. Например, если вам нужна аккумуляторная система 12 В 300 Ач, вам нужно будет подключить три батареи 12 В 100 Ач вместе параллельно.

Параллельная конфигурация батарей помогает увеличить время, в течение которого батареи могут питать оборудование, но из-за увеличенной емкости в ампер-часах они могут заряжаться дольше, чем батареи, соединенные последовательно.

СЕРИЯ

— АККУМУЛЯТОРЫ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ

И последнее, но не менее важное! Батареи соединены последовательно-параллельно. Последовательно-параллельное соединение — это когда вы подключаете цепочку батарей для увеличения как напряжения, так и емкости системы батарей.

Например, вы можете соединить шесть батарей 6 В 100 Ач вместе, чтобы получить батарею 24 В 200 Ач, это достигается путем настройки двух цепочек по четыре батареи.

В связи с этим у вас будет два или более комплектов батарей, которые будут настроены как последовательно, так и параллельно для увеличения емкости системы.

Если вам нужна помощь в настройке батарей в последовательном, параллельном или последовательном параллельном соединении, пожалуйста, свяжитесь с одним из наших экспертов по батареям.

Пример 2: Три резистора подключены параллельно, как показано. Разность потенциалов 18,0 В …

Четыре резистора подключены к батарее с напряжением на клеммах 12 В, как показано…

Четыре резистора подключаются к аккумулятору с выводом напряжение 12 В, как показано на рисунке ниже. (Предполагать R1 = 31,0 Ом и R2 = 70,0 Ω.) (а) Как бы вы уменьшили схему до эквивалентной одиночной резистор подключен к аккумулятору? Используйте эту процедуру, чтобы найти эквивалентное сопротивление цепи. Ω (b) Найдите ток, подаваемый батареей на этот эквивалент. сопротивление. А (c) Определите мощность, отдаваемую аккумулятором. W …

Пример 1: Четыре резистора подключены, как показано (A) Найдите эквивалентное сопротивление между точками a…

Пример 1: Четыре резистора подключены, как показано (A). Найдите эквивалентное сопротивление между точками a и c / 80 Ом 4,0 (). IIT, I C 9 3,0 Ом (B) Каков ток в каждом резисторе, если между a и c поддерживается разность потенциалов 42 В?

Если можно ответить на оба вопроса Благодарность! Найдите эквивалентное сопротивление Четыре резистора подключены как …

Если можно ответить на оба вопроса Благодарность! Найдите эквивалентное сопротивление. Четыре резистора подключены, как показано на рисунке (a) ниже.(Пусть R = 3.000.) Исходная сеть резисторов сокращается до одного эквивалентного сопротивления. 4,00 Вт 3,0 22 2,0.2 Рег. ad btw b Reg, ac i (a) Найдите эквивалентное сопротивление между точками a и C. РЕШЕНИЕ Представьте себе заряды, текущие в эту комбинацию и через нее слева. Все обвинения должны переходить с а на б …

Сопротивление 16,8 Ом и резистор 22 Ом подключены параллельно. Разница в потенциале …

Сопротивление 16,8 Ом и резистор 22 Ом подключены параллельно.К комбинации приложена разность потенциалов 41,5 В. Какое эквивалентное сопротивление параллельной цепи? Ответ в единицах Ом 020 (часть 2 из 3) 10,0 балла Какой ток в цепи? Ответ в единицах A 021 (часть 3 из 3) 10,0 балла Сколько тока проходит через резистор 16,8 Ом? Ответ в единицах А.

5. Пять резисторов подключены к идеальной батарее 8-24 В по схеме, как показано …

5. Пять резисторов подключены к идеальной батарее 8-24 В по схеме, как показано на рисунке; (b) рассеиваемая мощность и (C) напряжение на 2.4 резистор 2? . Что такое (а) ток 6,00 Ом 240 Ом 8 6,00 Ом 6,00 Ом 9,00 Ом

Рассмотрим схему ниже с тремя резисторами Два резистора, R2 (10 Ом) и R3 (10 Ом) …

Рассмотрим схему ниже с тремя резисторами. Два резистора R2 (10 Ом) и R3 (10 Ом) подключены параллельно другому резистору R1 (5 Ом). Схема подключена к источнику питания 20 В. 9. Найдите эквивалентное сопротивление (R) схемы, показанной выше. (3 балла) Ответ 10. Найдите ток, который проходит через R1.(4 балла) Ответ 11. Найдите разность потенциалов через резисторы, включенные параллельно (R2 и R3). (4 балла) Ответ

Подключены три резистора, как показано на рисунке. Разница потенциалов между точками А и …

Подключены три резистора, как показано на рисунке. Разность потенциалов между точками A и B составляет 26 В. 2,0 Ом 4,0 Ом 13. Какое эквивалентное сопротивление между точками A и B? A) 3,8 Ом B) 4,3 Ом C) 5,1 Ом D) 6,8 Ом E) 9,0 Ом

Четыре резистора подключены к батарее с напряжением на клеммах 12 В, как показано на рис…

Четыре резистора подключены к батарее с напряжением на клеммах 12 В, как показано на рисунке ниже. При необходимости используйте следующие переменные: R1 = 34,0 Ом и R2 = 85,0 Ом. (A) Как бы вы уменьшили схему до эквивалентного одиночного резистора, подключенного к батарее? Используйте эту процедуру, чтобы найти эквивалентное сопротивление цепи .________ Ом (b) Найдите ток, отдаваемый батареей этому эквивалентному сопротивлению .________ A (c) Определите мощность, отдаваемую батареей .______ W (d) Определите…

Три резистора 4,3 Ом подключены последовательно с напряжением 16,0 В. аккумулятор. Найдите следующее ….

Три резистора 4,3 Ом подключены последовательно с напряжением 16,0 В. аккумулятор. Найдите следующее. (а) эквивалентное сопротивление цепи (б) ток в каждом резисторе (c) Повторите то же самое для случая, когда все три резистора подключены. параллельно через батарею. эквивалентное сопротивление ______ ток в каждом резисторе _______

Три 4.Резисторы 3 Ом подключены последовательно с напряжением 16,0 В. аккумулятор. Найдите следующее ….

Три резистора 4,3 Ом подключены последовательно с напряжением 16,0 В. аккумулятор. Найдите следующее. (а) эквивалентное сопротивление цепи (б) ток в каждом резисторе (c) Повторите то же самое для случая, когда все три резистора подключены. параллельно через батарею. эквивалентное сопротивление ______ ток в каждом резисторе _______

параллельная цепь RL | Диаграмма фазора | Треугольник импеданса и мощности

В этом руководстве рассматриваются анализ параллельных цепей RL, фазорная диаграмма, треугольник импеданса и мощности, а также несколько решенных примеров с ответами на вопросы для обзора.

Комбинация резистора и катушки индуктивности, подключенных параллельно к источнику переменного тока, как показано на фиг. , ​​рис. 1, называется цепью , ​​параллельной RL . В параллельной цепи постоянного тока напряжение на каждой из параллельных ветвей одинаковое. Это также верно для параллельной цепи переменного тока .

Напряжения на каждой параллельной ветви:

• То же значение.
• Равно общему приложенному напряжению E _T .
• Все синхронно друг с другом.

Рисунок 1 Параллельная цепь RL .

Следовательно, для параллельной цепи RL

n параллельных цепей постоянного тока простая арифметическая сумма отдельных токов ветви равна общему току. То же самое верно и в параллельной цепи переменного тока, если параллельно подключены только чистые резисторы или только чистые катушки индуктивности.

Однако, когда резистор и катушка индуктивности соединены параллельно, два тока будут на сдвинуты по фазе на друг с другом.В этом случае полный ток равен векторной сумме , а не арифметической сумме токов.

Напомним, что напряжение и ток через резистор синфазны, но через чистый индуктор ток отстает от напряжения ровно на 90 градусов. Это все еще имеет место, когда два соединены параллельно.

Параллельная схема RL

Взаимосвязь между напряжением и токами в параллельной цепи RL проиллюстрирована на векторной диаграмме Рисунок 2 и резюмирована следующим образом:

• опорный вектор обозначен E и представляет собой напряжение в цепи, общее для всех элементов.
• Поскольку ток через резистор находится в фазе с напряжением на нем, I _R (2 A) показано наложенным на вектор напряжения.
• Ток в катушке индуктивности I _L (4 А) отстает от напряжения на 90 градусов и расположен в направлении вниз, отставая от вектора напряжения на 90 градусов.
• Сложение векторов I _R и I _L дает результат, который представляет собой общий (IT) или линейный ток (4.5 А).
• Угол тета (θ) представляет собой фазу между приложенным линейным напряжением и током.

Рисунок 2 Параллельная RL векторная диаграмма (вектор) .

Как и во всех параллельных цепях, ток в каждой ветви параллельной цепи RL действует независимо от токов в других ветвях. Ток в каждой ветви определяется напряжением на этой ветви и противодействием току в форме сопротивления или индуктивного реактивного сопротивления, содержащегося в ветви.

Закон Ома может быть использован для нахождения отдельных токов ответвления следующим образом:

Резистивный ток ответвления имеет ту же фазу, что и приложенное напряжение, но индуктивный ток ответвления отстает от приложенного напряжения на 90 градусов. . В результате общий линейный ток (IT) состоит из I _R и I _L , сдвинутых по фазе на 90 градусов.

Ток, протекающий через резистор и катушку индуктивности, образует катеты прямоугольного треугольника, а полный ток — это гипотенуза.Следовательно, можно применить теорему Пифагора, чтобы сложить эти токи вместе, используя уравнение:

Во всех параллельных цепях RL фазовый угол тета (θ), на который общий ток отстает от напряжения, находится где-то между 0 и 90 градусов. Величина угла определяется тем, есть ли на больше индуктивного тока или резистивного тока.

Если индуктивный ток больше, фазовый угол будет ближе к 90 градусам.Он будет ближе к 0 градусам, если будет более резистивный ток. Из векторной диаграммы схемы вы можете видеть, что значение фазового угла можно рассчитать по уравнению:

Ток в параллельной цепи RL, пример 1

Для параллельной цепи RL , показанной на Рисунок 3 , определите:

1. Ток, протекающий через резистор.
2. Ток через индуктор.
3. Полный линейный ток.
4. Фазовый угол между напряжением и полным током.
5. Выразите все токи в полярных обозначениях.
6. Используйте калькулятор, чтобы преобразовать все токи в прямоугольную форму.

Рисунок 3 Схема для примера 1.

Решение:

\ [\ text {a} \ text {. } {{\ text {I}} _ {\ text {R}}} \ text {=} \ frac {\ text {E}} {\ text {R}} \ text {=} \ frac {\ text { 120 В}} {\ text {30} \! \! \ Omega \! \! \ Text {}} \ text {= 4A} \]

\ [\ text {b} \ text {.{\ text {o}}} \\\ end {matrix} \]

\ [\ text {f} \ text {.} \ begin {matrix} \ text {} {{\ text {I}} _ { \ text {T}}} \ text {= 4-j3} & {{\ text {I}} _ {\ text {R}}} \ text {= 4 + j0} & {{\ text {I}} _ {\ text {L}}} \ text {= 0-j3} \\\ end {matrix} \]

Сопротивление параллельной цепи RL

Полное сопротивление ( Z ) параллельной цепи RL Цепь представляет собой полное противодействие протеканию тока. Он включает противодействие ( R ), обеспечиваемое резистивной ветвью, и индуктивное реактивное сопротивление (XL), обеспечиваемое индуктивной ветвью.

Полное сопротивление параллельной цепи RL вычисляется аналогично параллельной резистивной цепи. Однако, поскольку X _L и R являются векторными величинами, они должны быть добавлены векторно. В результате уравнение для полного сопротивления параллельной цепи RL , состоящей из одного резистора и катушки индуктивности, имеет следующий вид:

Где величина в знаменателе — это векторная сумма сопротивления и индуктивного реактивного сопротивления.Если имеется более одной резистивной или индуктивной ветви, R и X _L должны равняться общему сопротивлению или реактивному сопротивлению этих параллельных ветвей.

Когда известны полный ток (IT) и приложенное напряжение, импеданс равен , что проще вычислить , используя закон Ома следующим образом:

Импеданс параллельной цепи RL всегда равен на меньше, чем сопротивление или индуктивное реактивное сопротивление любой ветви.Это связано с тем, что каждая ветвь создает отдельный путь для прохождения тока, тем самым уменьшая общее или общее сопротивление цепи протеканию тока.

Ветвь, которая имеет большее количество тока (или меньшее сопротивление), оказывает наибольшее влияние на фазовый угол. Это напротив цепи серии RL . В параллельной цепи RL , если X _L больше, чем R, резистивный ток ветви больше, чем индуктивный ток ветви, поэтому фазовый угол между приложенным напряжением и полным током ближе к 0 градусов ( более резистивный по своей природе ).

Импеданс в параллельной цепи RL, Пример 2

Для параллельной цепи RL , показанной на рисунке 4, определите:

1. Импеданс ( Z ) на основе данных R и X _L значения.
2. Ток, протекающий через резистор и катушку индуктивности.
3. Полный линейный ток.
4. Импеданс ( Z ), основанный на полном токе (IT) и значениях приложенного напряжения.

Рисунок 4 Схема для примера 2.{2}}} = 2.36A \]

\ [Z = \ frac {E} {{{I} _ {T}}} = \ frac {100V} {2.36A} = 42.4 \ Omega \]

Мощность в параллельной цепи RL

В параллельной цепи RL ВА (полная мощность) включает как Вт, (истинная мощность), так и переменные (реактивная мощность), как показано на рисунке Рисунок 5. Значение Истинная мощность (Вт) — это мощность, рассеиваемая резистивной ветвью, а реактивная мощность (VAR) — это мощность, возвращаемая источнику индуктивной ветвью.

Взаимосвязь VA, W и VAR: такой же для параллельной цепи RL , как и для последовательной цепи RL . Ниже приводится краткое изложение этих формул:

• Истинная мощность в ваттах равна падению напряжения на резисторе , умноженному на тока, протекающего через него:

• Реактивная мощность в ВАР равна падению напряжения на катушке индуктивности , умноженному на тока, протекающего через нее:

• Полная мощность в ВА равна приложенному напряжению умножить на общий ток:

Рисунок 5 Силовые компоненты параллельной цепи RL .

На рисунке 6 показан треугольник мощности для параллельной цепи RL . Примените теорему Пифагора, и различные компоненты мощности можно определить с помощью следующих уравнений:

Рисунок 6 Треугольник мощности для параллельной цепи RL .

Коэффициент мощности в параллельной цепи RL

Коэффициент мощности (PF) в параллельной цепи RL — это отношение истинной мощности к полной мощности, как в цепи последовательного RL .Однако есть некоторые различия в других формулах, используемых для расчета коэффициента мощности в последовательной и параллельной цепях RL .

В цепи RL серии коэффициент мощности можно определить путем деления падения напряжения на резисторе на общее приложенное напряжение. В параллельной цепи напряжение одинаково, но токи разные, и коэффициент мощности можно рассчитать по формуле

Другая формула коэффициента мощности, которая отличается, включает сопротивление и импеданс.В параллельной цепи RL полное сопротивление будет на меньше, чем на , чем сопротивление. Следовательно, когда коэффициент мощности вычисляется с использованием сопротивления и импеданса, используется формула:

Пример расчета параллельной цепи RL 3

Для параллельной цепи RL , показанной на рисунке Рисунок 7, определите:

1. Текущий поток через резистор.
2. Истинная мощность в ваттах.
3. Ток через индуктор.
4. Реактивная мощность в вар.
5. Индуктивность индуктора.
6. Общий текущий расход.
7. Сопротивление цепи.
8. Полная мощность в ВА.
9. Коэффициент мощности.
10. Фазовый угол цепи θ.

Рисунок 7 Схема для примера 3.

Решение:

• Шаг 1 . Составьте таблицу и запишите все известные значения.

• Шаг 2 . Рассчитайте ток через резистор и введите значение в таблицу.

• Шаг 3 . Рассчитайте истинную мощность и введите значение в таблицу.

• Шаг 4 . Рассчитайте ток через катушку индуктивности и введите значение в таблицу.

• Шаг 5 . Рассчитайте реактивную мощность и введите значение в таблицу.

• Шаг 6. Рассчитайте индуктивность индуктора и введите значение в таблицу.

• Шаг 7 . Рассчитайте общий ток и введите значение в таблицу.

• Шаг 8 . Рассчитайте полное сопротивление и введите значение в таблицу.

• Шаг 9 . Рассчитайте полную мощность и введите значение в таблицу.

• Шаг 10 . Рассчитайте коэффициент мощности и введите значение в таблицу.

• Шаг 11 . Рассчитайте фазовый угол цепи θ и введите значение в таблицу.

Контрольные вопросы

1. Перечислите три характеристики напряжения на каждой ветви параллельной цепи RL .
2. В параллельной цепи RL полный ток равен векторной сумме, а не арифметической сумме. Почему?
3. Что используется в качестве опорного вектора в векторной диаграмме параллельной цепи RL ?
4. Предположим, что резистивный элемент параллельной цепи RL увеличен.Приведет ли это к увеличению или уменьшению фазового угла схемы? Почему?
5. В параллельной цепи RL полное сопротивление или полное противодействие всегда меньше, чем у отдельного сопротивления или индуктивного реактивного сопротивления. Почему?
6. Определите термины полная мощность , реактивная мощность, и истинная мощность применительно к параллельной цепи RL .
7. Измерения тока в параллельной цепи RL показывают, что ток 2 ампера через резистивную ветвь и 4 ампера через индуктивную.Определите:
   1. Значение полного текущего расхода.
   2. Фазовый угол между напряжением и полным током.
8. Для параллельной цепи RL , показанной на рис. 8, определите:
   1. Полная мощность.
   2. Истинная мощность.
   3. Реактивная мощность.
   4. Коэффициент мощности цепи.

Рисунок 8 Цепь для контрольного вопроса 8.

9. Заполните таблицу для всех заданных и неизвестных величин для параллельной цепи RL , показанной на Рисунок 9.

Рисунок 9 Цепь для контрольного вопроса 9.

Контрольные вопросы — ответы

1. Напряжение на каждой ветви параллельной цепи RL имеет одинаковое значение, равное общему приложенному напряжению, E. _T и синхронизированы друг с другом.
2. Полный ток в параллельной цепи RL равен векторной сумме токов ответвления, потому что токи ответвления не совпадают по фазе друг с другом.
3. Опорным вектором в параллельной цепи RL является приложенное напряжение E.
4. Если резистивный элемент параллельной цепи RL увеличивается, резистивный ток будет уменьшаться, а фазовый угол увеличится, потому что теперь цепь более индуктивна.
5. Каждая ветвь создает отдельный путь для прохождения тока, уменьшая общее или общее сопротивление цепи.
6. В параллельной цепи RL VA (полная мощность) включает в себя как ватты (истинную мощность), так и VAR (реактивную мощность), истинная мощность (ватты) — это мощность, рассеиваемая резистивной ветвью, и реактивная мощность ( VARs) — это мощность, возвращаемая источнику индуктивной ветвью.
7. (а) 4,47 А, (б) 63,4 °
8. (а) 3120 ВА, (б) 2880 Вт, (в) 1200 ВАр, (г) отставание 92,3%

	E	I	R / X L / Z	Вт / VA / VARs		PF
R			Ом	1000 Вт	0
L	100 В	5 A	20 Ом	500 ВАР	90
100 1134
100 1137 911 930 Всего2 A	8,93 Ом	1120 VA	26,8	89,3%

.