Как найти напряжение если известно сопротивление. Закон Ома: формулы, расчеты и применение в электротехнике

Что такое закон Ома и как он применяется в электротехнике. Какие формулы используются для расчета силы тока, напряжения и сопротивления. Как рассчитать мощность в электрической цепи. На какие практические задачи отвечает закон Ома.

Что такое закон Ома и его основная формула

Закон Ома — это фундаментальный закон электротехники, который устанавливает связь между силой тока, напряжением и сопротивлением в электрической цепи. Он был открыт немецким физиком Георгом Омом в 1826 году.

Основная формула закона Ома выглядит следующим образом:

I = U / R

Где:

• I — сила тока (измеряется в амперах, А)
• U — напряжение (измеряется в вольтах, В)
• R — сопротивление (измеряется в омах, Ом)

Эта формула показывает, что сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи.

Как рассчитать силу тока по закону Ома

Чтобы рассчитать силу тока, зная напряжение и сопротивление, используется следующая формула:

I = U / R

Например, если напряжение в цепи 12 В, а сопротивление 4 Ом, то сила тока будет равна:

I = 12 В / 4 Ом = 3 А

Таким образом, в данной цепи будет протекать ток силой 3 ампера.

Расчет напряжения по закону Ома

Для расчета напряжения при известных значениях силы тока и сопротивления используется формула:

U = I * R

Пример: Если через резистор с сопротивлением 100 Ом протекает ток 0,5 А, то напряжение на резисторе составит:

U = 0,5 А * 100 Ом = 50 В

Как найти сопротивление по закону Ома

Сопротивление участка цепи можно рассчитать, зная напряжение и силу тока:

R = U / I

Например, если напряжение на участке цепи 220 В, а сила тока 2 А, то сопротивление равно:

R = 220 В / 2 А = 110 Ом

Расчет мощности в электрической цепи

Для расчета мощности, выделяемой на участке электрической цепи, используется формула:

P = U * I

Где P — мощность, измеряемая в ваттах (Вт).

Эту формулу можно преобразовать, используя закон Ома:

P = U * I = U * (U / R) = U^2 / R = I^2 * R

Таким образом, мощность можно рассчитать тремя способами, зная разные параметры цепи.

Применение закона Ома на практике

Закон Ома широко применяется в электротехнике для решения различных практических задач:

• Расчет параметров электрических цепей
• Проектирование электрооборудования
• Выбор проводов нужного сечения
• Настройка систем электроснабжения
• Диагностика неисправностей в электрических схемах

Ограничения закона Ома

Важно понимать, что закон Ома применим не во всех случаях. Он имеет ряд ограничений:

• Действует только для линейных элементов цепи
• Не применим к полупроводниковым приборам
• Не работает для сверхпроводников
• Нарушается при высоких напряжениях и токах

В этих случаях используются более сложные модели и уравнения для описания электрических процессов.

Закон Ома для участка цепи

Закон Ома для участка цепи формулируется следующим образом: сила тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

Математически это выражается формулой:

I = (φ1 — φ2) / R

Где φ1 и φ2 — потенциалы начала и конца участка цепи.

Закон Ома в дифференциальной форме

Для неоднородных проводников закон Ома записывается в дифференциальной форме:

j = σE

Где:

• j — плотность тока
• σ — удельная проводимость среды
• E — напряженность электрического поля

Эта форма закона Ома позволяет анализировать распределение тока в объемных проводниках.

Как решать задачи с применением закона Ома

При решении задач на закон Ома рекомендуется придерживаться следующего алгоритма:

1. Внимательно прочитать условие задачи
2. Выписать все известные величины
3. Определить, что требуется найти
4. Выбрать подходящую формулу закона Ома
5. Подставить известные значения в формулу
6. Произвести вычисления
7. Проверить размерность полученного результата

Такой подход позволит избежать ошибок и получить верное решение.

Последовательное и параллельное соединение проводников

При последовательном соединении проводников:

• Общее сопротивление равно сумме сопротивлений: R = R1 + R2 + R3 + …
• Сила тока одинакова на всех участках
• Общее напряжение равно сумме напряжений на участках

При параллельном соединении:

• Обратная величина общего сопротивления равна сумме обратных величин сопротивлений участков: 1/R = 1/R1 + 1/R2 + 1/R3 + …
• Напряжение одинаково на всех участках
• Общий ток равен сумме токов через параллельные участки

Заключение

Закон Ома является фундаментальным законом электротехники, позволяющим рассчитывать основные параметры электрических цепей. Понимание и умение применять этот закон необходимо для решения широкого спектра задач в области электротехники и электроники. Несмотря на свою простоту, закон Ома остается одним из самых важных инструментов в арсенале инженеров-электриков и радиотехников.

Закон Ома онлайн — формулы и калькулятор

На этой странице вы можете рассчитать силу тока, напряжение и сопротивление по закону Ома для участка цепи с помощью удобного калькулятора онлайн

Закон Ома — один из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Он был открыт эмпирическим путем Георгом Омом в 1826 году.

Содержание:

1. калькулятор закона Ома
2. закон Ома для участка цепи
3. формула силы тока
4. формула напряжения
5. формула сопротивления
6. примеры задач

Закон Ома для участка цепи

Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи I= \dfrac{U}{R}

Формула силы тока

Формула позволяет найти силу тока I через напряжение U и сопротивление R по закону Ома для участка цепи.

{I = \dfrac{U}{R}}

I — сила тока

U — напряжение

R — сопротивление

Сила тока (I) в проводнике прямо пропорциональна напряжению (U) на его концах и обратно пропорциональна его сопротивлению (R).

Формула напряжения

Формула позволяет найти напряжение U через силу тока I и сопротивление R по закону Ома для участка цепи.

{U = I \cdot R}

U — напряжение

I — сила тока

R — сопротивление

Падение напряжение на проводнике равно произведению сопротивления проводника на силу тока в нем.

Формула сопротивления

Формула позволяет найти сопротивление R через силу тока I и напряжение U по закону Ома для участка цепи.

{R = \dfrac{U}{I}}

R — сопротивление

U — напряжение

I — сила тока

Сопротивление проводника прямо пропорционально напряжению на его концах и обратно пропорционально величине силы тока, протекающего через него.

Примеры задач на нахождение силы тока, напряжения и сопротивления по закону Ома

Задача 1

Найдите силу тока в участке цепи, если его сопротивление 40 Ом, а напряжение на его концах 4 В.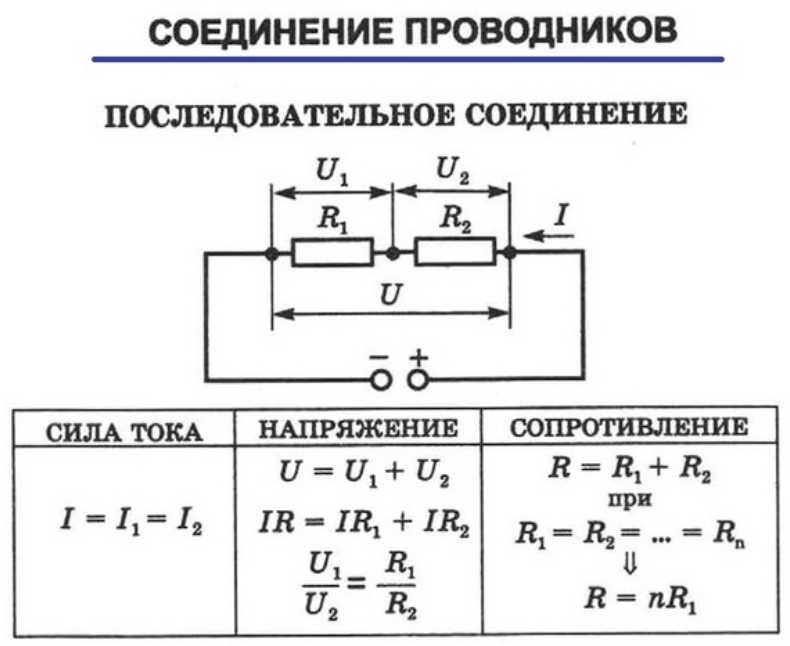

Решение

Воспользуемся формулой силы тока. Подставим в нее значения напряжения и сопротивления, после чего останется произвести простейший математический расчет.

I = \dfrac{U}{R} = \dfrac{4}{40} = 0.1 А

Ответ: 0.1 А

На этой странице есть калькулятор, который поможет проверить полученный ответ.

Задача 2

Найдите напряжение на концах нагревательного элемента, если его сопротивление 40 Ом, а сила тока 2А.

Решение

Для решения этой задачи нам пригодится формула напряжения.

U = I \cdot R = 2 \cdot 40 = 80 В

Ответ: 80 В

Проверим получившийся результат с помощью калькулятора .

Задача 3

Найдите сопротивление спирали, сила тока в которой 0.5 А, а напряжение на ее концах 120 В.

Решение

Чтобы найти сопротивление спирали нам потребуется формула сопротивления.

R = \dfrac{U}{I} = \dfrac{120}{0. 5} = 240 Ом

Ответ: 240 Ом

Проверка .

10 формул по физике

Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“

Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.

Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.

В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.

Соотношения закона Ома

Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:

Искомая величина	Формула
Напряжение, В	U=I*R
Ток, А	I=U/R
Сопротивление, Ом	R=U/I
Мощность, Вт	P=U*I

В этой таблице используются следующие общепринятые обозначения физических величин:

U — напряжение (В),

I — ток (А),

Р — мощность (Вт),

R — сопротивление (Ом),

Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.

А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:

I = U / R

Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.

Что же в этой формуле есть что? Рассмотрим переменные подробнее.

> U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.

>  I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.

> R: искомое сопротивление токоограничивающего резистора, в омах.

В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:

R = U/I = 8,5 В / 0,050 А= 170 Ом

Расчёты сопротивления

Рассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.

Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.

> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.

> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.

Расчет сопротивления последовательных резисторов

Формула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления:

Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)

В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.

Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.

Расчет сопротивления параллельных резисторов

Все немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид:

R общ = R1 * R2 / (R1 ­­+ R2)

где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим

776,47 = 2640000 / 3400

Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:

Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина.

Расчёты ёмкости

Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.

Расчет емкости параллельных конденсаторов

Если нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:

Собщ = CI + С2 + СЗ + …

В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.

Расчет емкости последовательных конденсаторов

Для вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:

Собщ  = С1 * С2 /( С1+С2)

где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи

Расчет емкости трех и более последовательно соединенных конденсаторов

В схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:

И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ. — суммарная величина.

Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.

Расчёт энергетических уравнений

Наиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:

ватт-часы = Р х Т

В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.

Расчёт постоянной ёмкости RC-цепочки

В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).

Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.

Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.

T = RC

В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.

Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.

Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:

Значение емкости конденсатора, мкФ	Емкость конденсатора для расчета
10	0,000 01
1	0,000 001
0,1	0,000 000 1
0,01	0,000 000 01

Расчёты частоты и длины волны

Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.

Расчет частоты сигнала

Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны:

Частота = 300000 / длина волны

Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.

Расчет длины волны сигнала

Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:

Длина волны = 300000 / Частота

Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.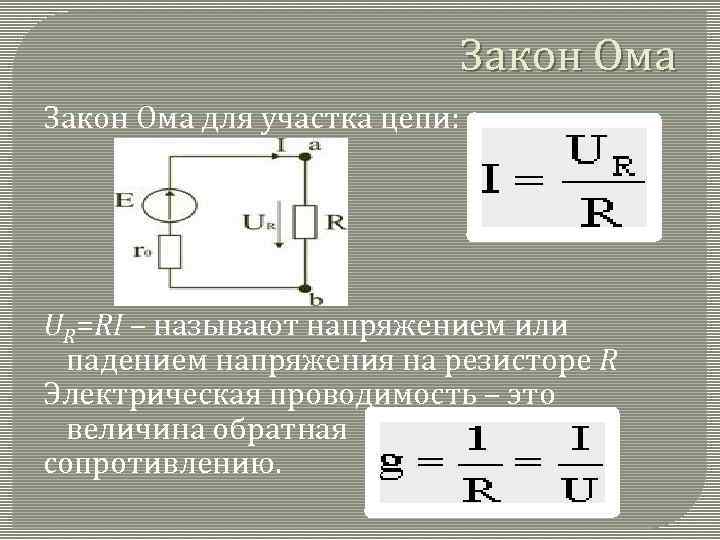

Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:

6000 миллиметров = 300000 / 50 МГц

Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!

---

---

САМАЯ ПРОСТАЯ ЦЕПЬ:

САМАЯ ПРОСТАЯ ЦЕПЬ:

ЗАКОН ОМА

САМАЯ ПРОСТАЯ ЦЕПЬ:

Мы можем заставить ток течь по кругу (контуру) путем соединения клемм аккумулятора вместе. Это растопит проволока, пусть летят искры и, возможно, начинается пожар, так что не делайте этого. Вместо этого подключите что-нибудь для управления током. Способность к управляющий ток называется сопротивлением, и все материалы имеют его некоторой степени — на самом деле мы классифицируем материалы в соответствии с их сопротивление: те, у которых очень низкое сопротивление, являются проводниками, те, у которых большим сопротивлением являются изоляторы. Есть устройства, называемые резисторами. которые используются в электронных гаджетах — они имеют сопротивление, которое нечто среднее между проводимостью и изоляцией, и предсказуемое. Так вот безопасная схема:

Аккумулятор имеет определенное количество толчков, называется электродвижущей силой или ЭДС. Измеряется в единицах, называемых вольт . ЭДС (часто называемую напряжением) в формулах обозначаем буквой Е . Напряжение должно измеряться между двумя точками цепи в так же, как высота должна быть измерена между двумя точками на сторона горы. Нет такой вещи, как «0 вольт», за исключением того, что напряжение между двумя точками равно 0, если они соединены вместе.

Резистор имеет определенную величину сопротивление, измеряемое в единицах, называемых Ом . Мы указываем сопротивление в формулах с буквой R .

Когда протекает ток, мы измеряем его в единицы называют ампер , и обозначают его буквой I .

Три связаны простой формулой называется законом Ома:

И=Э/Р

Также написано Э = IR или R=E/I.

Это говорит нам о токе, если мы знаем напряжение и сопротивление, или напряжение, если мы знаем ток и сопротивление, или сопротивление, если мы знаем ток и напряжение. Если это кажется вам немного круговым, вы правы. Мы можем измерить ток силой магнитного поля, который он будет генерировать, но там не является критерием для напряжения, кроме как посмотреть, сколько тока течет через известное сопротивление. А как узнать сопротивление? Мы применяем известное напряжение и посмотреть, сколько тока течет.

Определение единиц также круговое: 1 Ампер — это сила тока, протекающая через резистор сопротивлением 1 Ом. если подать 1 вольт.

---

Два резистора последовательно:

Немного сложнее, если есть два резистора:

Каким бы ни был ток, он один и тот же в точке А, B и C. (Току больше некуда течь. )

Напряжение между A и C равно между A и B, добавленным к тому, что между B и C.

Е АС = Е АВ + Е БК

Напряжения складываются, как и высота дом есть сумма высот его этажей.

Напряжение на каждом резисторе пропорционально сопротивлению каждого резистора.

Е АВ / Р 1 = Е ВС / Р 2

 

Видите ли, закон Ома верен для каждой части цепи, так и цепи в целом. Какой бы ток ни протекал, это то же самое в каждом резисторе, поэтому напряжения будут регулироваться сами себя.

Общее сопротивление R 1 + Р 2

---

Два резистора параллельно

Ток через А равен току через B плюс ток через C. Ток разделяется и приходит вместе, как вода, обтекающая остров.

Напряжение на R 1 такое же, как на напряжение на R 2.

Е АВ = Е АС, так я б Р 1 = I C R 2 и I Б / Р 2 = I C / R 1

Другими словами, ток через каждый сопротивление обратно пропорционально номиналам резисторов.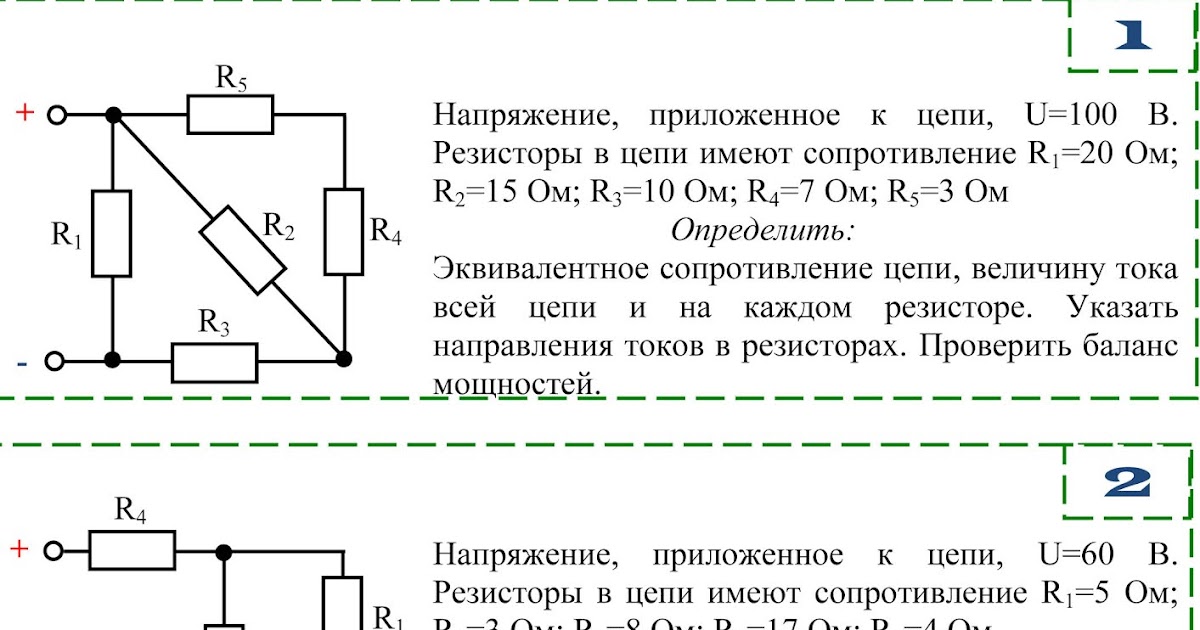 Также важно помнить резистор высокого номинала пропускает небольшой текущий.

Мы можем решить приведенное выше для полного тока ( I Б + I C) и получить эквивалент сопротивление для двух резисторов:

В особом случае, когда резисторы То же, эквивалентное сопротивление Р 1 /2. Это встречается чаще, чем вы может ожидать.

В другом особом случае, когда R2 больше 100-кратное значение R1, R2 составляет такую ​​небольшую часть тока, что мы не удосужились включить его в расчеты. Тогда мы говорим, что R2 не загрузить цепь.

---

Вот более сложный пример:

R1 — специальный тип резистора. с регулируемым краном посередине. Это действительно заставляет R1 вести себя как два резистора последовательно. Если мы скажем, что R2 в 100 раз больше R1, мы можем исключить его из расчетов и найти, что напряжение Е2 будет напрямую зависит от положения крана.

Если бы R2 был сопоставим по стоимости с R1, мы бы должны понять это, сначала решив R2 и нижнюю часть R1 как два резистора параллельно, и используя результат этого последовательно расчетом найти напряжение Е2 и полный ток. результирующая кривая напряжения (то, что вы получите, если начертите E2 для различных положения крана) довольно беспорядочно, поэтому мы действительно предпочитаем иметь R2, который не нагружает цепь.

Вернуться к темам Mu126

ОМ’SLAW

 

ЗАКОН ОМА ЗАКОН ОМА

Наиболее важным законом, применимым к изучению электричества, является закон Ома. закон. Этот закон, описывающий зависимость между напряжением, током, и сопротивление в электрической цепи впервые было установлено немецким физик Джордж Саймон Ом (1787 — 1854). Этот закон распространяется на все прямые токовые цепи. В модифицированном виде он может применяться к чередующимся цепи, которые будут изучены позже в этом тексте. Опыты Ома показали, что ток в электрической цепи прямо пропорционален величине напряжения, приложенного к цепи. Другими словами, этот закон говорит, что при увеличении напряжения увеличивается ток; и когда напряжение уменьшается, ток уменьшается. Следует добавить, что это соотношение верно только в том случае, если сопротивление в цепи остается постоянный. Ведь легко видеть, что при изменении сопротивления ток также меняется.

Закон Ома может быть выражен следующим уравнением:

Где I ток в амперах, E потенциал разность измеряется в вольтах, а R – сопротивление, измеряемое в ом (обозначается греческой буквой омега, символ которой ). Если известны любые две из этих величин цепи, можно найти третью. простой алгебраической транспозицией. Схема, показанная на рис. 8-47, содержит источник напряжения 24 вольта и сопротивление 3 Ом.

Если в цепь включен амперметр, как показано на рис. 8-47, сила тока, протекающего в цепи, может быть считана напрямую. Предполагая что нет амперметра, можно определить силу тока используя закон Ома следующим образом:

Некоторые особенности рисунка 8-47, характерные для всех электрических цепей нарисованные в схематическом виде, должны быть пересмотрены. Электрическое давление или разность потенциалов, приложенная к цепи, представлена ​​на схеме символом батареи. Знак минус расположен рядом с единицей стороне, чтобы указать отрицательную клемму источника или батареи. Противоположный сторона отмечена положительной с символом +. Стрелки иногда используются для обозначения направление тока от отрицательной клеммы через проводящую провода и другие цепные устройства, к положительному выводу источника.

На рис. 8-48 показано, что значения напряжения и тока известны. Чтобы найти величину сопротивления в цепи, воспользуйтесь законом Ома. можно транспонировать, чтобы решить для R. Преобразование основной формулы I = E/R в R = E/I и замена известные значения цепи в уравнении, R = 24 вольт/8 ампер = 3 Ом, или 3.

Закон Ома также можно транспонировать для определения напряжения, приложенного к цепь, когда ток и сопротивление известны, как показано на рисунке 8-49.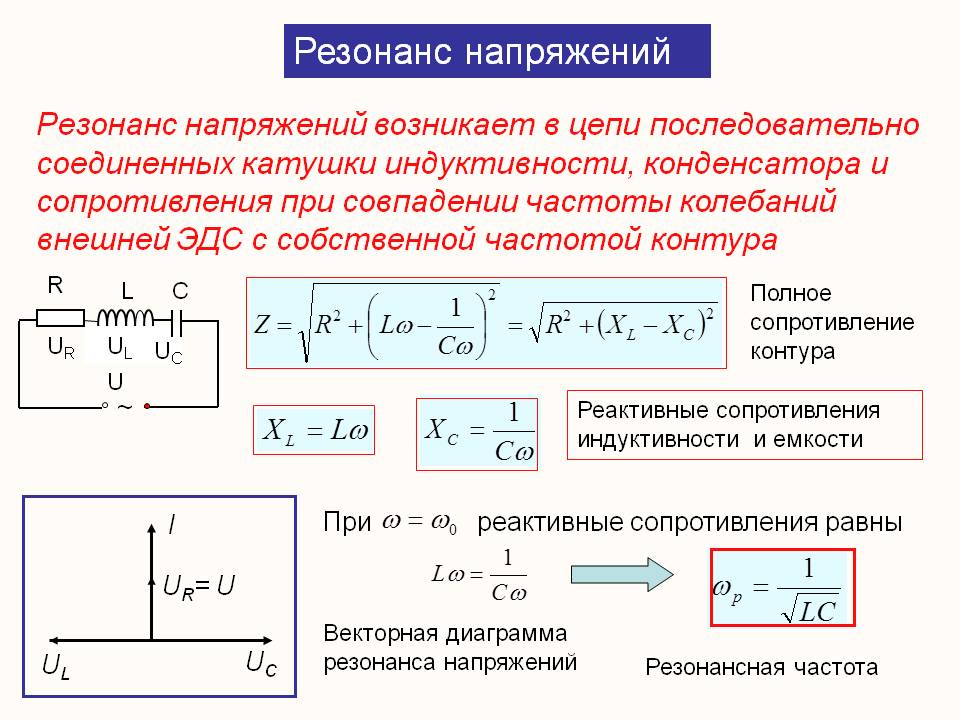 В этой цепи представлена ​​неизвестная величина цепи, напряжение. символом Е. Величина сопротивления 3 Ом, а протекающий ток составляет 8 ампер. (Слово амперы часто сокращают до «ампер».) Преобразование закона Ома из его основной формулы, уравнение для решения для E становится E = I x R.

Подставляя известные значения в уравнение,

Е = 8 х 3
E = 24 В или 24 В

Взаимосвязь между различными параметрами контура может быть дополнительно проявляется, если сопротивление в цепи поддерживается постоянным. В таком В этом случае ток будет увеличиваться или уменьшаться прямо пропорционально увеличение или уменьшение напряжения, подаваемого на цепь. Например, если напряжение, приложенное к цепи, составляет 120 вольт, а сопротивление цепи 20 Ом, ток будет 120/20, или 6 ампер. Если это сопротивление остается постоянным на уровне 20 Ом, график зависимости напряжения от тока, как показано на рис. 8-50, можно построить.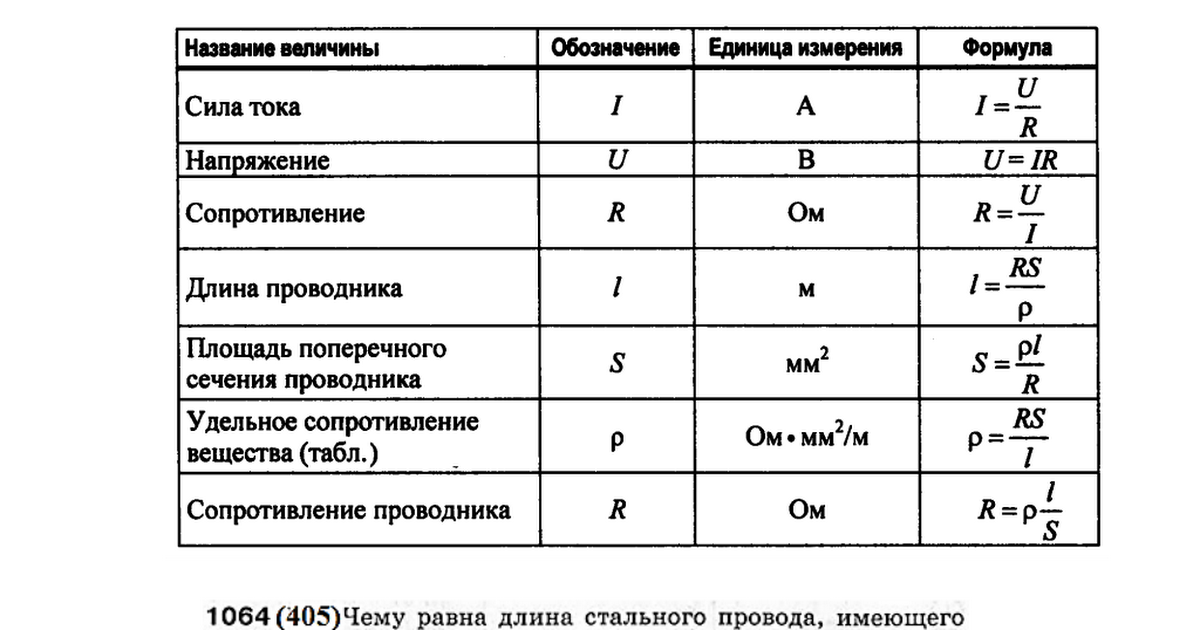

Зависимость между напряжением и током в этом примере показывает напряжение, отложенное горизонтально по оси X в значениях от 0 до 120 вольт, а соответствующие значения тока нанесены вертикально в значениях от 0 до 6,0 ампер по оси Y. Нарисована прямая линия через все точки, где встречаются линии напряжения и тока, представляет собой уравнение I = E/20 и называется линейной зависимостью. Постоянная, 20, представляет собой сопротивление, которое, как предполагается, не изменение в этом примере. Этот график представляет важную характеристику основного закона, что сила тока прямо зависит от приложенного напряжения если сопротивление остается постоянным. Основные уравнения, полученные из закона Ома, суммированы вместе с единицами измерения схемных величин, на рис. 8-51.

Различные уравнения, которые могут быть получены путем перестановки основных закон можно легко получить, используя треугольники на рис. 8-52.

Треугольники, содержащие E, I и R, разделены на две части с E над линией и I x R под ней. Чтобы определить неизвестную величину контура когда известны два других, закройте неизвестное количество большим пальцем. Расположение оставшихся непокрытых букв в треугольнике укажет выполняемая математическая операция. Например, чтобы найти I, обратитесь к (а) рисунка 8-52, и закройте I большим пальцем. Незакрытые буквы указывают, что E должно быть разделено на R, или I = E/R. Чтобы найти R, см. (b) на рис. 8-52, и закройте R большим пальцем. Результат указывает на то, что E должно быть разделено на I, или R = E/I. Чтобы найти E, обратитесь к (c) рисунка. 8-52 и закройте E большим пальцем. Результат указывает на то, что я должен быть умножен на R, или E = I x R.

Эта таблица полезна при изучении закона Ома. Его следует использовать чтобы дополнить знания новичка об алгебраическом методе.

Мощность

Помимо вольта, ампера и ома часто используется еще одна единица измерения используется при расчетах электрических цепей. Это единица мощности. единицей измерения мощности в электрических цепях постоянного тока является ватт. Власть определяется как скорость выполнения работы и равна произведению напряжение и ток в цепи постоянного тока. Когда ток в амперах (I) умножить на ЭДС в вольтах (E), в результате получится мощность, измеренная в ваттах. (П). Это указывает на то, что электрическая мощность, подаваемая в цепь, изменяется непосредственно с приложенным напряжением и током, протекающим в цепи. Выраженный как уравнение, это становится

Р = ИЭ

Это уравнение можно транспонировать для определения любой из трех цепей величин, пока известны два других. Таким образом, если мощность читается прямо с ваттметра и напряжение измеряется вольтметром, можно определить силу тока (I), протекающего в цепи путем преобразования основного уравнения в I = P/E. Точно так же напряжение (E) можно найти, переставив основную формулу мощности в E = P/I.

Поскольку некоторые значения, используемые для определения мощности, подаваемой на схемы такие же, как и в законе Ома, можно заменить Значения закона Ома для эквивалентов в формуле мощности.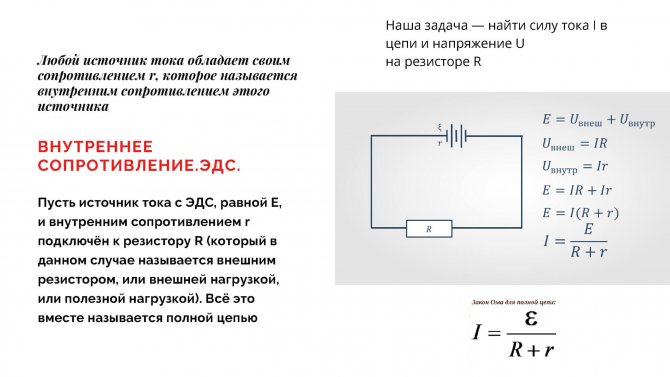

По закону Ома I = E/R. Если это значение E/R заменить на I в формула мощности, становится

Это уравнение P = E2/R показывает, что мощность в ваттах, подаваемая цепи зависит прямо от квадрата приложенного напряжения и обратно пропорционально сопротивлению цепи.

Ватт назван в честь Джеймса Уатта, изобретателя паровой машины. Уатт провел эксперимент по измерению силы лошади, чтобы найти средство измерения механической мощности его паровой машины. Один лошадиных сил требуется, чтобы переместить 33 000 фунтов на 1 фут за 1 минуту. С мощность – это скорость выполнения работы, она равна работе, деленной на время. В виде формулы это

Электрическая мощность может быть оценена аналогичным образом. Например, электрический двигатель мощностью 1 лошадиная сила требует 746 Вт электроэнергии. Но ватт – это относительно небольшая единица мощности. Гораздо чаще встречается киловатт или 1000 ватт.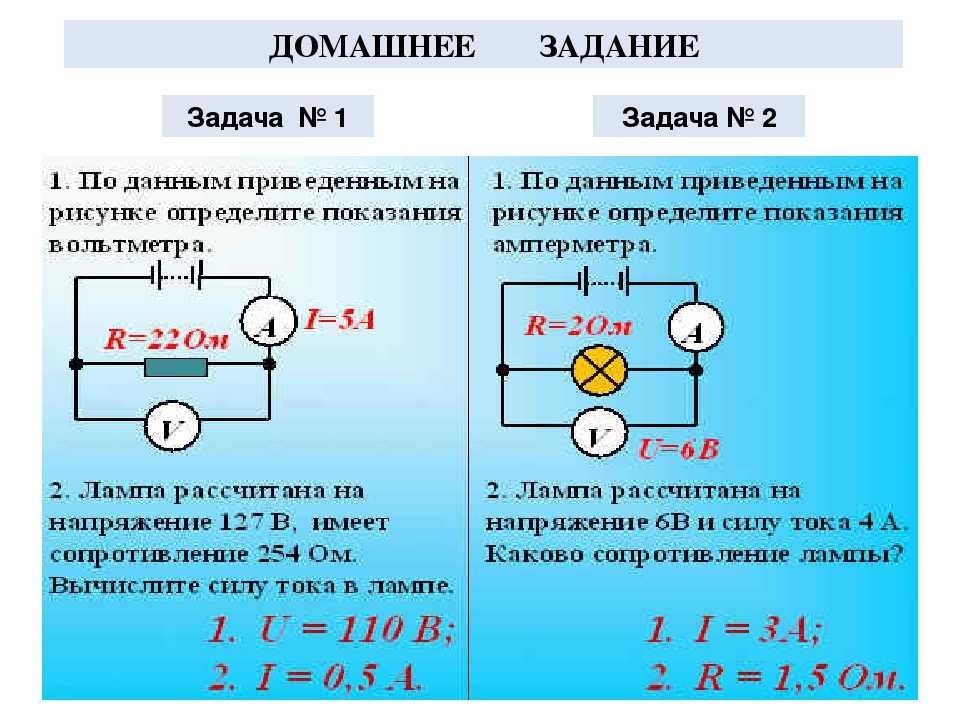 (Приставка килограмм означает 1000.) В измерении количества потребляемой электроэнергии используется киловатт-час. Например, если 100-ваттная лампочка потребляет электроэнергию в течение 20 часов, она израсходовала 2000 ватт-часов или 2 киловатт-часа электроэнергии.

Электроэнергия, которая теряется в виде тепла при протекании тока через электрическое устройство часто называют потерей мощности. Это тепло обычно рассеивается в окружающем воздухе и не служит никакой полезной цели, за исключением случаев, когда они используются для обогрева. Поскольку все проводники обладают некоторым сопротивлением, схемы предназначены для уменьшения этих потерь. Еще раз обратимся к основному формула мощности, P = I x E, можно подставить значения закона Ома для E в формуле мощности, чтобы получить формулу мощности, которая непосредственно отражает потери мощности в сопротивлении.

Р = I х Е; Е = I х Р.

Подставляя значение закона Ома вместо E (I x R) в формуле мощности,

P = I x I x R.

Сбор терминов, это дает,

Из этого уравнения видно, что мощность в ваттах в цепи изменяется пропорционально квадрату тока цепи в амперах и изменяется прямо с сопротивлением цепи в омах.

Наконец, мощность, подаваемая в цепь, может быть выражена как функция тока и сопротивления путем преобразования уравнения мощности

Транспонирование для решения текущего дает

и извлекая квадратный корень из обеих частей уравнения,

I = квадратный корень из P/R

Таким образом, ток через нагрузку 500 Вт, 100 Ом (сопротивление) равен следует:

I = квадратный корень из P/R = 500/100 = 2,24 ампера.

Электрические уравнения, полученные из закона Ома и основной мощности формула не раскрывает всего о поведении цепей. Они указывают числовое соотношение между вольтом, ампером, омом и ваттом. Фигура 8-53 дает сводку всех возможных транспозиций этих формулы в круге из 12 сегментов.