Какие виды мощности существуют в цепях переменного тока. Как рассчитать активную, реактивную и полную мощность. Для чего нужен коэффициент мощности. Как компенсировать реактивную мощность.
Виды мощности в цепях переменного тока
В цепях переменного тока выделяют три основных вида мощности:
- Активная мощность (P) — измеряется в ваттах (Вт)
- Реактивная мощность (Q) — измеряется в вольт-амперах реактивных (вар)
- Полная мощность (S) — измеряется в вольт-амперах (ВА)
Каждый вид мощности имеет свое назначение и особенности. Рассмотрим их подробнее.
Активная мощность: полезная работа тока
Активная мощность — это та часть полной мощности, которая преобразуется в полезную работу или тепло. Она характеризует скорость преобразования электрической энергии в другие виды энергии.
Формула для расчета активной мощности:
P = U * I * cos φ
где:
- P — активная мощность (Вт)
- U — действующее значение напряжения (В)
- I — действующее значение тока (А)
- cos φ — коэффициент мощности
Почему активная мощность важна?
Активная мощность имеет ключевое значение, так как именно она выполняет полезную работу в электрических цепях. Например:

- Нагревает проводники (лампы накаливания, электрические плиты)
- Создает механическое движение в двигателях
- Обеспечивает работу электронных устройств
Реактивная мощность: циркуляция энергии
Реактивная мощность связана с обменом энергией между источником и реактивными элементами цепи (индуктивностями и емкостями). Она не преобразуется в полезную работу, но необходима для работы некоторых устройств.
Формула для расчета реактивной мощности:
Q = U * I * sin φ
где:
- Q — реактивная мощность (вар)
- U — действующее значение напряжения (В)
- I — действующее значение тока (А)
- sin φ — синус угла сдвига фаз между током и напряжением
В чем особенность реактивной мощности?
Реактивная мощность имеет ряд важных особенностей:
- Не выполняет полезной работы, но нагружает сеть
- Циркулирует между источником и потребителем
- Необходима для работы некоторых устройств (например, электродвигателей)
- Может быть как индуктивной, так и емкостной
Полная мощность: общая нагрузка на сеть
Полная мощность — это геометрическая сумма активной и реактивной мощностей. Она характеризует общую нагрузку на электрическую сеть.

Формула для расчета полной мощности:
S = √(P² + Q²) = U * I
где:
- S — полная мощность (ВА)
- P — активная мощность (Вт)
- Q — реактивная мощность (вар)
- U — действующее значение напряжения (В)
- I — действующее значение тока (А)
Зачем нужно знать полную мощность?
Полная мощность важна по нескольким причинам:
- Определяет общую нагрузку на электрическую сеть
- Используется для выбора сечения проводов и кабелей
- Необходима для расчета мощности трансформаторов и генераторов
- Помогает оценить эффективность использования электроэнергии
Коэффициент мощности: показатель эффективности
Коэффициент мощности (cos φ) — это отношение активной мощности к полной. Он показывает, какая часть полной мощности преобразуется в полезную работу.
Формула для расчета коэффициента мощности:
cos φ = P / S
где:
- cos φ — коэффициент мощности
- P — активная мощность (Вт)
- S — полная мощность (ВА)
Почему важен высокий коэффициент мощности?
Высокий коэффициент мощности (близкий к 1) имеет ряд преимуществ:
- Снижает потери в электрических сетях
- Уменьшает нагрузку на трансформаторы и генераторы
- Позволяет более эффективно использовать электроэнергию
- Снижает затраты на электроэнергию для предприятий
Треугольник мощностей: визуальное представление
Треугольник мощностей — это графическое изображение соотношения между активной, реактивной и полной мощностью в виде прямоугольного треугольника.
Как построить треугольник мощностей?
Для построения треугольника мощностей:
- Активную мощность (P) откладывают по горизонтали
- Реактивную мощность (Q) откладывают по вертикали
- Полная мощность (S) образует гипотенузу треугольника
- Угол между P и S — это угол φ, косинус которого равен коэффициенту мощности
Компенсация реактивной мощности: повышение эффективности
Компенсация реактивной мощности — это мероприятия по снижению потребления реактивной мощности из сети. Цель — повысить коэффициент мощности и уменьшить нагрузку на электрическую сеть.
Как осуществляется компенсация реактивной мощности?
Основные методы компенсации реактивной мощности:
- Установка конденсаторных батарей
- Использование синхронных компенсаторов
- Применение активных фильтров гармоник
- Оптимизация режимов работы оборудования
Расчет мощности в цепях переменного тока
Для расчета мощности в цепях переменного тока используются различные формулы и методы. Рассмотрим основные из них.
Как рассчитать активную мощность?
Активную мощность можно рассчитать несколькими способами:

- По формуле: P = U * I * cos φ
- Через полную мощность: P = S * cos φ
- Через реактивную мощность: P = √(S² — Q²)
Как определить реактивную мощность?
Реактивную мощность можно найти следующими методами:
- По формуле: Q = U * I * sin φ
- Через полную и активную мощность: Q = √(S² — P²)
- Используя тангенс угла φ: Q = P * tg φ
Практическое применение знаний о мощности
Понимание различных видов мощности и их взаимосвязи имеет важное практическое значение в электротехнике и энергетике.
Где применяются расчеты мощности?
Расчеты мощности используются в различных областях:
- Проектирование электрических сетей и систем
- Выбор электрооборудования (трансформаторов, двигателей)
- Оценка эффективности работы электроустановок
- Разработка мероприятий по энергосбережению
- Расчет тарифов на электроэнергию
Измерение мощности в электрических цепях
Для измерения различных видов мощности в электрических цепях используются специальные приборы и методы.
Какие приборы используются для измерения мощности?
Основные приборы для измерения мощности:
- Ваттметры — для измерения активной мощности
- Варметры — для измерения реактивной мощности
- Фазометры — для определения коэффициента мощности
- Анализаторы мощности — для комплексного анализа параметров сети
Как проводятся измерения мощности?
Процесс измерения мощности включает следующие этапы:
- Выбор подходящего измерительного прибора
- Правильное подключение прибора к электрической цепи
- Проведение измерений согласно инструкции прибора
- Анализ полученных результатов
- Учет погрешностей измерений
Активная, реактивная и полная мощность
В отличии от сетей постоянного тока, где мощность имеет выражение и не изменяется во времени, в сетях переменного тока это не так.
Мощность в цепи переменного тока также есть переменной величиной. На любом участке цепи в любой момент времени t она определяется как произведение мгновенных значений напряжения и тока.
Рассмотрим, что представляет активная мощность
В цепи с чисто активным сопротивлением она равна:
Если принять и тогда выйдет:
Где
Исходя из выражений выше — активная энергия состоит из двух частей — постоянной и переменной , которая меняется с двойной частотой. Среднее ее значение
График Р(ωt)Отличие реактивной мощности от активной
В цепи, где есть реактивное сопротивление (возьмем для примера индуктивное) значение мгновенной мощности равно:
Соответственно и в итоге получим:
Данное выражение показывает, что реактивная энергия содержит только переменную часть, которая изменяется с двойной частотой, а ее среднее значение равно нулю
График q(ωt)Если ток и напряжение имеют синусоидальную форму и сеть содержит элементы типа R-L или R-C, то в таких сетях кроме преобразования энергии в активном элементе R вдобавок еще и изменяется энергия электрического и магнитного полей в реактивных элементах L и C.
В таком случае полная мощность сети будет равна сумме:
Что такое полная мощность на примере простой R-L цепи
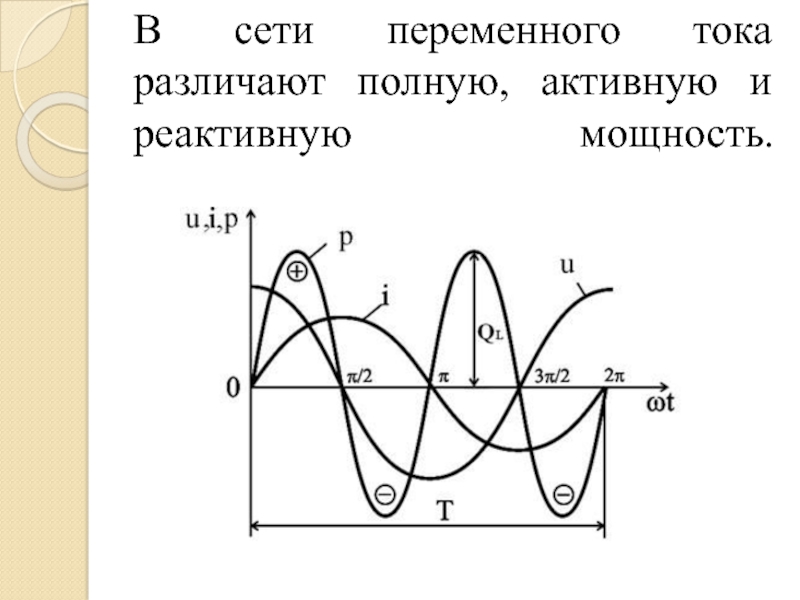
Графики изменения мгновенных значений u,i:
Графики изменения мгновенных значений u,i:φ — фазовый сдвиг между током и напряжением
Уравнение для S примет следующий вид
Подставим вместо и заменим амплитудные значения на действующие:
Значение S рассматривается как сумма двух величин , где
и — мгновенные активные и реактивные мощности на участках R-L.
Графики p,q,s:Как видим из графика, наличие индуктивной составляющей повлекло за собой появление отрицательной части в полной мощности (заштрихованная часть графика), что снижает ее среднее значение. Это происходит из-за фазового сдвига, в какой-то момент времени ток и напряжение находятся в противофазе, поэтому появляется отрицательное значение S.
Итоговые выражения для действующих значений:
Активная составляющая сети выражается в ваттах (Вт), а реактивная в вольт-амперах реактивных (вар).
Полная мощность сети S, обусловлена номинальными данными генератора. Для генератора она обусловлена выражением:
Для нормальной работы генератора ток в обмотках и напряжение на зажимах не должны превышать номинальные значения Iн, Uн. Для генератора значения P и S одинаковы, однако все-таки на практике условились S выражать в вольт-амперах (ВА).
Также энергию сети можно выразить через каждую составляющую отдельно:
Где S, P, Q – соответственно активное, реактивное и полное сопротивление сети. Они образуют треугольник мощностей:
Треугольник мощностей с преобладающей индуктивной нагрузкойЕсли вспомнить теорему Пифагора, то из прямоугольного треугольника можно получить такое выражение:
Реактивная составляющая в треугольнике является положительной (QL), когда ток отстает от напряжения, и отрицательной (QC), когда опережает:
Треугольник мощностей с преобладающей емкостной нагрузкойДля реактивной составляющей сети справедливо алгебраическое выражение:
Из чего следует что индуктивная и емкостная энергия взаимозаменяемы. То есть если вы хотите уменьшить влияние индуктивной части цепи, вам необходимо добавить емкость, и наоборот. Ниже пример данной схемы :
Схема компенсации реактивной составляющейВекторная диаграмма показывает влияние конденсатора на cosφ. Как видно, что при включении конденсатора cosφ2> cosφ1 и Iл<I.
Векторная диаграммаСвязь между полной и реактивной энергии выражается:
Отсюда:
сosφ – это коэффициент мощности. он показывает какую долю от полной энергии составляет активная энергия. Чем ближе он к 1, тем больше полезной энергии потребляется из сети.
Выводы о трех составляющих цепи переменного тока
В отличии от цепей постоянного тока, цепи переменного напряжения имеют три вида мощности – активная, реактивная, полная. Активная энергия, как и в цепях постоянного тока, выполняет полезную работу. Реактивная – не выполняет ничего полезного, а только снижает КПД сети, греет провода, грузит генератор. Полная – сумма активной и реактивной, она равна мощности сети. Индуктивная составляющая реактивной энергии может быть скомпенсирована емкостной. На практике в промышленности это реализовано в виде конденсаторных установок.
Мгновенная мощность
В отличие от цепей постоянного тока, где мощность в течение определенного промежутка времени остается неизменной, в цепях переменного тока дело обстоит иначе. Так как ток и напряжение постоянно меняют своё значение, то и мощность соответственно будет меняться в каждый момент времени. Такая мощность называется мгновенной.
Мгновенной мощностью p(t) называют произведение приложенного к цепи мгновенного напряжения u(t) на мгновенное значение тока i(t) в этой цепи.
График мгновенной мощности представлен на рисунке ниже
Мощность обозначена заштрихованной областью. Знак мощности зависит от сдвига фаз между током и напряжением. В данном случае в цепи присутствуют только активные сопротивления, которые не создают сдвига фаз, поэтому мощность имеет только положительные значения.
Рассмотрим другой график
На данном графике имеются области отрицательных значений мгновенной мощности. Такой график может соответствовать цепи, в которой присутствуют конденсатор или катушка, причем положительные участки — это мощность, которая пошла в цепь и рассеялась на сопротивлении, либо запаслась в качестве энергии полей конденсаторов или катушек, а отрицательные участки это мощность, которая была возвращена обратно источнику.
Активная мощность
Чтобы понять какое количество энергии потребляет источник, целесообразнее взять среднюю мощность за период. Для этого вернемся к первому графику.
На графике мгновенной мощности выделяют прямоугольник со сторонами T и Pm/2. Часть графика, которая находится выше линии Pm/2 точно укладывается в незаштрихованную часть прямоугольника. Таким образом, с помощью линии
В нашем случае сдвиг фаз равен нулю, поэтому коэффициент мощности равен единице, но в случаях с реактивными элементами нужно этот момент учитывать.
Активная мощность измеряется в ваттах – Вт.
cosφ – коэффициент мощности, который показывает отношение активной мощности к полной мощности.
Реактивная мощность
Реактивная мощность – это энергия, которая периодически циркулирует между источником и приемником. Реактивная мощность возникает потому, что конденсатор и катушка способны накапливать энергию, а затем снова отдавать её в сеть. На практике от реактивной мощности зачастую стараются избавиться.
Реактивная мощность измеряется в вольт амперах реактивных – ВАр.
Полная мощность
Полная мощность — это максимальное значение активной мощности.
Полная мощность измеряется в вольт-амперах — ВА.
Для наглядного представления существует треугольник мощностей, в котором гипотенузой является полная мощность, а катетами – активная и реактивная составляющие.
Читайте также — Последовательная RL-цепь
Расчет реактивной мощности КРМ
Спасибо за интерес, проявленный к нашей Компании
Расчет реактивной мощности КРМ
Отправить другу
НЕОБХОДИМА КОНСУЛЬТАЦИЯ?
Теория расчета реактивной мощности КРМ
Q = Pa· ( tgφ1-tgφ2)- реактивная мощность установки КРМ (кВАр)
Q = Pa · K
Pa -активная мощность (кВт)
K- коэффициент из таблицы
Pa= S· cosφ
S -полная мощность(кВА)
cos φ — коэффициент мощности
tg(φ1+φ2) согласуются со значениями cos φ в таблице.
Таблица определения реактивной мощности конденсаторной установки — КРМ (кВАр), необходимой для достижения заданного cos(φ).
| Текущий (действующий) | Требуемый (достижимый) cos (φ) | ||||||||||
| tan (φ) | cos (φ) | 0.80 | 0.82 | 0.85 | 0.88 | 0.90 | 0.92 | 0.94 | 0.96 | 0.98 | 1.00 |
| Коэффициент K | |||||||||||
| 3.18 | 0.30 | 2.43 | 2.48 | 2.56 | 2.64 | 2.70 | 2.75 | 2.82 | 2.89 | 2.98 | 3.18 |
| 2.96 | 0.32 | 2.21 | 2.26 | 2.34 | 2.42 | 2.48 | 2.53 | 2.60 | 2.67 | 2.76 | 2.96 |
| 2.77 | 0.34 | 2.02 | 2.07 | 2.15 | 2.23 | 2.28 | 2.34 | 2.41 | 2.48 | 2.56 | 2.77 |
| 2.59 | 0.36 | 1.84 | 1.89 | 1.97 | 2.05 | 2.10 | 2.17 | 2.23 | 2.30 | 2.39 | 2.59 |
| 2.43 | 0.38 | 1.68 | 1.73 | 1.81 | 1.89 | 1.95 | 2.01 | 2.07 | 2.14 | 2.23 | 2.43 |
| 2.29 | 0.40 | 1.54 | 1.59 | 1.67 | 1.75 | 1.81 | 1.87 | 1.93 | 2.00 | 2.09 | 2.29 |
| 2.16 | 0.42 | 1.41 | 1.46 | 1.54 | 1.62 | 1.68 | 1.73 | 1.80 | 1.87 | 1.96 | 2.16 |
| 2.04 | 0.44 | 1.29 | 1.34 | 1.42 | 1.50 | 1.56 | 1.61 | 1.68 | 1.75 | 1.84 | 2.04 |
| 1.93 | 0.46 | 1.18 | 1.23 | 1.31 | 1.39 | 1.45 | 1.50 | 1.57 | 1.64 | 1.73 | 1.93 |
| 1.83 | 0.48 | 1.08 | 1.13 | 1.21 | 1.29 | 1.34 | 1.40 | 1.47 | 1.54 | 1.62 | 1.83 |
| 1.73 | 0.50 | 0.98 | 1.03 | 1.11 | 1.19 | 1.25 | 1.31 | 1.37 | 1.45 | 1.63 | 1.73 |
| 1.64 | 0.52 | 0.89 | 0.94 | 1.02 | 1.10 | 1.16 | 1.22 | 1.28 | 1.35 | 1.44 | 1.64 |
| 1.56 | 0.54 | 0.81 | 0.86 | 0.94 | 1.02 | 1.07 | 1.13 | 1.20 | 1.27 | 1.36 | 1.56 |
| 1.48 | 0.56 | 0.73 | 0.78 | 0.86 | 0.94 | 1.00 | 1.05 | 1.12 | 1.19 | 1.28 | 1.48 |
| 1.40 | 0.58 | 0.65 | 0.70 | 0.78 | 0.86 | 0.92 | 0.98 | 1.04 | 1.11 | 1.20 | 1.40 |
| 1.33 | 0.60 | 0.58 | 0.63 | 0.71 | 0.79 | 0.85 | 0.91 | 0.97 | 1.04 | 1.13 | 1.33 |
| 1.30 | 0.61 | 0.55 | 0.60 | 0.68 | 0.76 | 0.81 | 0.87 | 0.94 | 1.01 | 1.10 | 1.30 |
| 1.27 | 0.62 | 0.52 | 0.57 | 0.65 | 0.73 | 0.78 | 0.84 | 0.91 | 0.99 | 1.06 | 1.27 |
| 1.23 | 0.63 | 0.48 | 0.53 | 0.61 | 0.69 | 0.75 | 0.81 | 0.87 | 0.94 | 1.03 | 1.23 |
| 1.20 | 0.64 | 0.45 | 0.50 | 0.58 | 0.66 | 0.72 | 0.77 | 0.84 | 0.91 | 1.00 | 1.20 |
| 1.17 | 0.65 | 0.42 | 0.47 | 0.55 | 0.63 | 0.68 | 0.74 | 0.81 | 0.88 | 0.97 | 1.17 |
| 1.14 | 0.66 | 0.39 | 0.44 | 0.52 | 0.60 | 0.65 | 0.71 | 0.78 | 0.85 | 0.94 | 1.14 |
| 1.11 | 0.67 | 0.36 | 0.41 | 0.49 | 0.57 | 0.63 | 0.68 | 0.75 | 0.82 | 0.90 | 1.11 |
| 1.08 | 0.68 | 0.33 | 0.38 | 0.46 | 0.54 | 0.59 | 0.65 | 0.72 | 0.79 | 0.88 | 1.08 |
| 1.05 | 0.69 | 0.30 | 0.35 | 0.43 | 0.51 | 0.56 | 0.62 | 0.69 | 0.76 | 0.85 | 1.05 |
| 1.02 | 0.70 | 0.27 | 0.32 | 0.40 | 0.48 | 0.54 | 0.59 | 0.66 | 0.73 | 0.82 | 1.02 |
| 0.99 | 0.71 | 0.24 | 0.29 | 0.37 | 0.45 | 0.51 | 0.57 | 0.63 | 0.70 | 0.79 | 0.99 |
| 0.96 | 0.72 | 0.21 | 0.26 | 0.34 | 0.42 | 0.48 | 0.54 | 0.60 | 0.67 | 0.76 | 0.96 |
| 0.94 | 0.73 | 0.19 | 0.24 | 0.32 | 0.40 | 0.45 | 0.51 | 0.58 | 0.65 | 0.73 | 0.94 |
| 0.91 | 0.74 | 0.16 | 0.21 | 0.29 | 0.37 | 0.42 | 0.48 | 0.55 | 0.62 | 0.71 | 0.91 |
| 0.88 | 0.75 | 0.13 | 0.18 | 0.26 | 0.34 | 0.40 | 0.46 | 0.52 | 0.59 | 0.68 | 0.88 |
| 0.86 | 0.76 | 0.11 | 0.16 | 0.24 | 0.32 | 0.37 | 0.43 | 0.50 | 0.57 | 0.65 | 0.86 |
| 0.83 | 0.77 | 0.08 | 0.13 | 0.21 | 0.29 | 0.34 | 0.40 | 0.47 | 0.54 | 0.63 | 0.83 |
| 0.80 | 0.78 | 0.05 | 0.10 | 0.18 | 0.26 | 0.32 | 0.38 | 0.44 | 0.51 | 0.60 | 0.80 |
| 0.78 | 0.79 | 0.03 | 0.08 | 0.16 | 0.24 | 0.29 | 0.35 | 0.42 | 0.49 | 0.57 | 0.78 |
| 0.75 | 0.80 | 0.05 | 0.13 | 0.21 | 0.27 | 0.32 | 0.39 | 0.46 | 0.55 | 0.75 | |
| 0.72 | 0.81 | 0.10 | 0.18 | 0.24 | 0.30 | 0.36 | 0.43 | 0.52 | 0.72 | ||
| 0.70 | 0.82 | 0.08 | 0.16 | 0.21 | 0.27 | 0.34 | 0.41 | 0.49 | 0.70 | ||
| 0.67 | 0.83 | 0.05 | 0.13 | 0.19 | 0.25 | 0.31 | 0.38 | 0.47 | 0.67 | ||
| 0.65 | 0.84 | 0.03 | 0.11 | 0.16 | 0.22 | 0.29 | 0.36 | 0.44 | 0.65 | ||
| 0.62 | 0.85 | 0.08 | 0.14 | 0.19 | 0.26 | 0.33 | 0.42 | 0.62 | |||
| 0.59 | 0.86 | 0.05 | 0.11 | 0.17 | 0.23 | 0.30 | 0.39 | 0.59 | |||
| 0.57 | 0.87 | 0.08 | 0.14 | 0.21 | 0.28 | 0.36 | 0.57 | ||||
| 0.54 | 0.88 | 0.06 | 0.11 | 0.18 | 0.25 | 0.34 | 0.54 | ||||
| 0.51 | 0.89 | 0.03 | 0.09 | 0.15 | 0.22 | 0.31 | 0.51 | ||||
| 0.48 | 0.90 | 0.06 | 0.12 | 0.19 | 0.28 | 0.48 | |||||
| 0.46 | 0.91 | 0.03 | 0.10 | 0.17 | 0.25 | 0.46 | |||||
| 0.43 | 0.92 | 0.07 | 0.14 | 0.22 | 0.43 | ||||||
| 0.40 | 0.93 | 0.04 | 0.11 | 0.19 | 0.40 | ||||||
| 0.36 | 0.94 | 0.07 | 0.16 | 0.36 | |||||||
| 0.33 | 0.95 | 0.13 | 0.33 | ||||||||
Пример:
Активная мощность двигателя : P=100 кВт
Действующий cos φ = 0.61
Требуемый cos φ = 0.96
Коэффициент K из таблицы = 1.01
Необходимая реактивная мощности КРМ (кВАр):
Q = 100 · 1.01=101 кВАр
НЕОБХОДИМА КОНСУЛЬТАЦИЯ?
Возврат к списку
Расчёт мощности генератора
Для начала вспомним школу.
Что такое электрическая мощность?
Электрическая мощность обозначается при написании формул латинской буквой Р и измеряется в ваттах Вт или на латинице W, киловаттах (кВт или kW), мегаваттах (МВт или MW) и так далее.
Электрическая мощность равна произведению напряжения и тока:
P (Вт) = U (В) * I (А)
Различают следующие виды электрической мощности, которые, соответственно, по-разному обозначаются:
Активная мощность:
Обозначение: P
Единица измерения: Вт (W)
Это мощность, отдаваемая при подключении к источнику тока (генератору) нагрузки, имеющей активное (омическое) сопротивление. Если нагрузка, имеет только активное сопротивление и не содержит реактивных сопротивлений, то активная мощность будет равна полной мощности.
Расчёт производится по формуле: P = U * I * cos φ
Примеры: лампы накаливания, нагревательные приборы и т. п.
Реактивная мощность:
Обозначение: Q
Единица измерения: вар или VAr (вольт-ампер реактивный)
Это мощность, отдаваемая при подключении к источнику тока компонента сети или нагрузки, имеющей индуктивные (электродвигатель) или ёмкостные (конденсатор) элементы.
Расчёт производится по формуле: Q = U * I * sin φ
Примеры:
Потребители, придающие нагрузке индуктивный характер: электродвигатели, сварочные трансформаторы и т.п.
Потребители, придающие нагрузке ёмкостной характер: конденсаторы в компенсаторных устройствах, конденсаторы, создающие реактивную мощность в цепи возбуждения генераторов и т.п.
Полная мощность:
Обозначение: S
Единица измерения: В·A или VA (вольт-ампер)
Полная электрическая мощность равна произведению сдвинутых по фазе напряжения и тока. Полная мощность непосредственно связана с активной и реактивной мощностями. Её расчёт производится по формуле, выражающей закон Пифагора. Полная электрическая мощность представляет собой максимальную мощность электрического тока, которая может быть выработана генератором или использована.
Расчёт производится по формуле: S = U * I или S = P + Q
Изображенный на рисунке треугольник отображает взаимосвязь между электрическими мощностями или соответствующими им напряжениями.
Теперь о расчёте мощности генератора.
Для точного определения области применения и пригодности любого электроагрегата для выполнения поставленных задач необходимо прежде всего определить суммарную мощность потребителей тока. Только таким образом можно определить, какой электроагрегат может быть использован для данных целей. При выборе необходимой мощности электроагрегата можно использовать приведённые ниже эмпирические формулы.
1. Потребители, являющиеся только активной нагрузкой (например, электронагреватели, лампы накаливания и подобные им приборы с чисто омическим сопротивлением).
Суммарную мощность можно расчитать путём простого сложения мощностей отдельных потребителей, которые могут быть подключены к генератору. В данном случае полная электрическая мощность, измеряемая в ВА или VA (Вольт-ампер) равна активной мощности, измеряемой в Вт или W (Ватт). Необходимая мощность электроагрегата определяется путём увеличения суммарной мощности подключаемых потребителей на 10% (т.е. с учётом определённых технических факторов).
Пример: Суммарная мощность потребителей * 110% = Мощность, требуемая от электроагрегата.
Если суммарная мощность всех потребителей 2000 Вт (в данном случае 2000 Вт = 2000 ВА ), то требуемая мощность электроагрегата будет: 2000 ВА * 110% = 2200ВА
2. Потребители, имеющие индуктивную составляющую мощности (компрессоры, насосы и прочие электродвигатели). Эти нагрузки потребляют очень большой ток при пуске и выходе на рабочий режим. В данном случае, сначала необходимо определить точное значение мощности одновременно подключаемых потребителей. Далее следует выбрать мощность электроагрегата.
Полная мощность такого электроагрегата должна быть не менее, чем в 3,5 раза больше суммарной мощности потребителей. В исключительных случаях она должна превышать мощность потребителей в 4—5 раз.
Пример: Суммарная мощность потребителей * 3,5 = Мощность, требуемая от электроагрегата.
Если суммарная мощность всех потребителей 2000 ВА, то требуемая мощность электроагрегата будет: 2000 ВА * 3,5 = 7000 ВА
Как посчитать реактивную энергию зная активную. Разбираемся с понятиями активной и реактивной нагрузки
Реактивная мощность
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Если элемент цепи — резистор c электрическим сопротивлением R , то
Мощность переменного тока
Активная мощность
Среднее за период Т значение мгновенной мощности называется активной мощностью: . В цепях однофазного синусоидального тока , где U и I — действующие значения напряжения и тока , φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением . Единица активной мощности — ватт (W , Вт ). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
Реактивная мощность
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока, равна произведению действующих значений напряжения U и тока I , умноженному на синус угла сдвига фаз φ между ними: Q = UI sin φ . Единица реактивной мощности — вольт-ампер реактивный (var , вар ). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: . Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.
Необходимо отметить, что величина sinφ для значений φ от 0 до плюс 90 ° является положительной величиной. Величина sinφ для значений φ от 0 до минус 90 ° является отрицательной величиной. В соответствии с формулой Q = UI sinφ реактивная мощность может быть отрицательной величиной. Но отрицательное значение мощности нагрузки характеризует нагрузку как генератор энергии. Активное, индуктивное, емкостное сопротивление не могут быть источниками постоянной энергии. Модуль величины Q = UI sinφ приблизительно описывает реальные процессы преобразования энергии в магнитных полях индуктивностей и в электрических полях емкостей. Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения. Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ , более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.
Полная мощность
Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи I и напряжения U на её зажимах: S = U×I ; связана с активной и реактивной мощностями соотношением: , где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0 , а при ёмкостной Q ). Единица полной электрической мощности — вольт-ампер (VA , ВА ).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Измерения
- Для измерения электрической мощности применяются ваттметры и варметры , можно также использовать косвенный метод, с помощью вольтметра и амперметра .
- Для измерения коэффициента реактивной мощности применяют фазометры
Литература
- Бессонов Л. А. — Теоретические основы электротехники: Электрические цепи — М.: Высш. школа,
Ссылки
См. также
- Список параметров напряжения и силы электрического тока
Wikimedia Foundation . 2010 .
Смотреть что такое «Реактивная мощность» в других словарях:
реактивная мощность — Величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током двухполюсника. [ГОСТ Р 52002 2003]… … Справочник технического переводчика
Электр. мощность в цепи переменного тока, расходуемая на поддержание вызываемых переменным током периодических изменений: 1) магнитного поля при наличии в цепи индуктивности; 2) заряда конденсаторов при наличии конденсаторов и проводов (напр.… … Технический железнодорожный словарь
Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля. Для синусоидального тока равна произведению действующих тока I и напряжения U на синус угла сдвига фаз между ними: Q =… … Большой Энциклопедический словарь
РЕАКТИВНАЯ МОЩНОСТЬ — величина, характеризующая скорость обмена энергией между генератором переменного тока и магнитным (млн. электрическим) полем цепи, создаваемым электротехническими устройствами (индуктивностью и ёмкостью). Р. м. возникает в цепи при наличии сдвига … Большая политехническая энциклопедия
реактивная мощность — 3.1.5 реактивная мощность (вар): Реактивная мощность сигналов синусоидальной формы какой либо отдельной частоты в однофазной цепи, определяемая как произведение среднеквадратических значений тока и напряжения и синуса фазового угла между ними.… … Словарь-справочник терминов нормативно-технической документации
реактивная мощность — reaktyvioji galia statusas T sritis Standartizacija ir metrologija apibrėžtis Menamoji kompleksinės galios dalis, skaičiuojama pagal formulę Q² = S² – P²; čia Q – reaktyvioji galia, S – pilnutinė galia, P – aktyvioji galia. Matavimo vienetas –… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
реактивная мощность — reaktyvioji galia statusas T sritis fizika atitikmenys: angl. reactive power; wattless power vok. Blindleistung, f; wattlose Leistung, f rus. безваттная мощность, f; реактивная мощность, f pranc. puissance déwatée, f; puissance réactive, f … Fizikos terminų žodynas
Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля. Для синусоидального тока равна произведению действующих тока I и напряжения U на синус угла сдвига фаз между ними:… … Энциклопедический словарь
реактивная мощность — reaktyvioji galia statusas T sritis automatika atitikmenys: angl. reactive power vok. Blindleistung, f; wattlose Leistung, f rus. реактивная мощность, f pranc. puissance réactive, f … Automatikos terminų žodynas
Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока (См. Переменный ток). Р. м. Q равна произведению действующих значений напряжения U и тока… … Большая советская энциклопедия
Книги
- Электротехника и электроника на судах рыбопромыслового флота , Белов О.А., Парфенкин А.И.. Рассмотрены общие вопросы электротехники и электроники, физические явления, лежащие в основе производства и использования электричества, работы электронных устройств. Приведены примеры…
Активная и реактивная мощность — потребители электрической энергии на то и потребители, чтобы эту энергию потреблять. Потребителя интересует та энергия, потребление которой идет ему на пользу, эту энергию можно назвать полезной, но в электротехнике ее принято называть активной. Это энергия, которая идет на нагрев помещений, готовку пищи, выработку холода, и превращаемая в механическую энергию (работа электродрелей, перфораторов, электронасосов и пр.).
Кроме активной электроэнергии существует еще и реактивная. Это та часть полной энергии, которая не расходуется на полезную работу. Как понятно из вышесказанного, полная мощность – это активная и реактивная мощность в целом.
В понятиях активная и реактивная мощность сталкиваются противоречивые интересы потребителей электрической энергии и ее поставщиков. Потребителю выгодно платить только за потребленную им полезную электроэнергию, поставщику выгодно получать оплату за сумму активной и реактивной электроэнергии. Можно ли совместить эти кажущиеся противоречивыми требования? Да, если свести количество реактивной электроэнергии к нулю. Рассмотрим, возможно ли подобное, и насколько можно приблизиться к идеалу.
Активная и реактивная мощность Активная мощностьСуществуют потребители электроэнергии, у которых полная и активная мощности совпадают. Это потребители, у которых нагрузка представлена активными сопротивлениями (резисторами). Среди бытовых электроприборов примерами подобной нагрузки являются лампы накаливания, электроплиты, жарочные шкафы и духовки, обогреватели, утюги, паяльники и пр.
Указанная у этих приборов в паспорте, одновременно является активная и реактивная мощность. Это тот случай, когда мощность нагрузки можно определить по известной из школьного курса физики формуле, перемножив ток нагрузки на напряжение в сети. Ток измеряется в амперах (А), напряжение в вольтах (В), мощность в ваттах (Вт). Конфорка электрической плиты в сети с напряжением 220 В при токе в 4,5 А потребляет мощность 4,5 х 220 = 990 (Вт).
Реактивная мощностьИногда, проходя по улице, можно увидеть, что стекла балконов покрыты изнутри блестящей тонкой пленкой. Эта пленка изъята из бракованных электрических конденсаторов, устанавливаемых с определенными целями на питающих мощных потребителей электрической энергии распределительных подстанциях. Конденсатор – типичный потребитель реактивной мощности. В отличие от потребителей активной мощности, где главным элементом конструкции является некий проводящий электричество материал (вольфрамовый проводник в лампах накаливания, нихромовая спираль в электроплитке и т.п.). В конденсаторе главный элемент – не проводящий электрический ток (тонкая полимерная пленка или пропитанная маслом бумага).
Реактивная емкостная мощностьКрасивые блестящие пленки, что вы видели на балконе – это обкладки конденсатора из токопроводящего тонкого материала. Конденсатор замечателен тем, что он может накапливать электрическую энергию, а затем отдавать ее – своеобразный такой аккумулятор. Если включить конденсатор в сеть постоянного тока, он зарядится кратковременным импульсом тока, а затем ток через него протекать не будет. Вернуть конденсатор в исходное состояние можно, отключив его от источника напряжения и подключив к его обкладкам нагрузку. Некоторое время через нагрузку будет течь электрический ток, и идеальный конденсатор отдает в нагрузку ровно столько электрической энергии, сколько он получил при зарядке. Подключенная к выводам конденсатора лампочка может на короткое время вспыхнуть, электрический резистор нагреется, а неосторожного человека может «тряхнуть» или даже убить при достаточном напряжении на выводах и запасенном количестве электричества.
Интересная картина получается при подключении конденсатора к источнику переменного электрического напряжения. Поскольку у источника переменного напряжения постоянно меняются полярность и мгновенное значение напряжения (в домашней электросети по закону, близкому к синусоидальному). Конденсатор будет непрерывно заряжаться и разряжаться, через него будет непрерывно протекать переменный ток. Но этот ток не будет совпадать по фазе с напряжением источника переменного напряжения, а будет опережать его на 90°, т.е. на четверть периода.
Это приведет к тому, что суммарно половину периода переменного напряжения конденсатор потребляет энергию из сети, а половину периода отдает, при этом суммарная потребляемая активная электрическая мощность равна нулю. Но, поскольку через конденсатор течет значительный ток, который может быть измерен амперметром, принято говорить, что конденсатор – потребитель реактивной электрической мощности.
Вычисляется реактивная мощность как произведение тока на напряжение, но единица измерения уже не ватт, а вольт-ампер реактивный (ВАр). Так, через подключенный к сети 220 В частотой 50 Гц электрический конденсатор емкостью 4 мкФ течет ток порядка 0,3 А. Это означает, что конденсатор потребляет 0,3 х 220 = 66 (ВАр) реактивной мощности – сравнимо с мощностью средней лампы накаливания, но конденсатор, в отличие от лампы, при этом не светится и не нагревается.
Реактивная индуктивная мощностьЕсли в конденсаторе ток опережает напряжение, то существуют ли потребители, где ток отстает от напряжения? Да, и такие потребители, в отличие от емкостных потребителей, называются индуктивными, оставаясь при этом потребителями реактивной энергии. Типичная индуктивная электрическая нагрузка – катушка с определенным количеством витков хорошо проводящего провода, намотанного на замкнутый сердечник из специального магнитного материала.
На практике хорошим приближением чисто индуктивной нагрузки является работающий без нагрузки трансформатор (или стабилизатор напряжения с автотрансформатором). Хорошо сконструированный трансформатор на холостом ходу потребляет очень мало активной мощности, потребляя мощность в основном реактивную.
Реальные потребители электрической энергии и полная электрическая мощностьИз рассмотрения особенностей емкостной и индуктивной нагрузки возникает интересный вопрос – что произойдет, если емкостную и индуктивную нагрузку включить одновременно и параллельно. Ввиду их противоположной реакции на приложенное напряжение, эти две реакции начнут компенсировать друг друга. Суммарная нагрузка окажется только емкостной или индуктивной, и в некотором идеальном случае удастся добиться полной компенсации. Выглядеть это будет парадоксально – подключенные амперметры зафиксируют значительные (и равные!) токи через конденсатор и катушку индуктивности, и полное отсутствие тока в объединяющих их общей цепи. Описанная картина несколько нарушается лишь тем, что не существует идеальных конденсаторов и катушек индуктивности, но подобная идеализация помогает понять суть происходящих процессов.
Вернемся к реальным потребителям электрической энергии. В быту мы пользуемся в основном потребителями чисто активной мощности (примеры приведены выше), и смешанной активно-индуктивной. Это электродрели, перфораторы, электродвигатели холодильников, стиральных машин и прочей бытовой техники. Также к ним относятся электрические трансформаторы источников питания бытовой радиоэлектронной аппаратуры и стабилизаторов напряжения. В случае подобной смешанной нагрузки, помимо активной (полезной) мощности, нагрузка потребляет еще и реактивную мощность, в итоге полная мощность отказывается больше активной мощности. Полная мощность измеряется в вольт-амперах (ВА), и всегда представляет собой произведение тока в нагрузке на напряжение на нагрузке.
Таинственный «косинус фи»Отношение активной мощности к полной называется в электротехнике «косинусом фи». Обозначается cos φ. Это отношение называется также и коэффициентом мощности. Нетрудно видеть, что для случая чисто активной нагрузки, где полная мощность совпадает с активной, cos φ = 1. Для случаев чисто емкостной или индуктивной нагрузок, где нулю равна активная мощность, cos φ = 0.
В случае смешанной нагрузки значение коэффициента мощности заключается в пределах от 0 до 1. Для бытовой техники обычно в диапазоне 0,5-0,9. В среднем можно считать его равным 0,7, более точное значение указывается в паспорте электроприбора.
За что платим?И, наконец, самый интересный вопрос – за какой вид энергии платит потребитель. Исходя из того, что реактивная составляющая суммарной энергии не приносит потребителю никакой пользы, при этом долю периода реактивная энергия потребляется, а долю отдается, платить за реактивную мощность незачем. Но бес, как известно, кроется в деталях. Поскольку смешанная нагрузка увеличивает ток в сети, возникают проблемы на электростанциях, где электроэнергия вырабатывается синхронными генераторами, а именно: индуктивная нагрузка «развозбуждает» генератор, и приведение его в прежнее состояние обходится в затраты уже реальной активной мощности на его «довозбуждение».
Таким образом, заставить потребителя платить за потребляемую реактивную индуктивную мощность вполне справедливо. Это побуждает потребителя компенсировать реактивную составляющую своей нагрузки, а, поскольку эта составляющая в основном индуктивная, компенсация заключается в подключении конденсаторов наперед рассчитанной емкости.
Потребитель находит возможность платить меньшеЕсли потребителем оплачивается отдельно потребляемая активная и реактивная мощность. Он готов идти на дополнительные затраты и устанавливать на своем предприятии батареи конденсаторов, включаемые строго по графику в зависимости от средней статистики потребления электроэнергии по часам суток.
Существует также возможность установки на предприятии специальных устройств (компенсаторов реактивной мощности), подключающих конденсаторы автоматически в зависимости от величины и характера потребляемой в данный момент мощности. Эти компенсаторы позволяют поднять значение коэффициента мощности с 0,6 до 0,97, т.е. практически до единицы.
Принято также, что если соотношение потребленной реактивной энергии и общей не превышает 0,15, то корпоративный потребитель от оплаты за реактивную энергию освобождается.
Что же касается индивидуальных потребителей, то, ввиду сравнительно невысокой потребляемой ими мощности, разделять счета на оплату потребляемой электроэнергии на активную и реактивную не принято. Бытовые электрической энергии учитывают лишь активную мощность электрической нагрузки, за нее и выставляется счет на оплату. Т.е. в настоящее время даже не существует технической возможности выставить индивидуальному потребителю счет за потребленную реактивную мощность.
Особых стимулов компенсировать индуктивную составляющую нагрузки у потребителя нет, да это и сложно осуществить технически. Постоянно подключенные конденсаторы при отключении индуктивной нагрузки будут бесполезно нагружать подводящую электропроводку. За электросчетчиком (перед счетчиком тоже, но за то потребитель не платит), что вызовет потребление активной мощности с соответствующим увеличением счета на оплату, а автоматические компенсаторы дороги и вряд ли оправдают затраты на их приобретение.
Другое дело, что производитель иногда устанавливает компенсационные конденсаторы на входе потребителей с индуктивной составляющей нагрузки. Эти конденсаторы, при правильном их подборе, несколько снизят потери энергии в подводящих проводах, при этом несколько повысив напряжение на подключенном электроприборе за счет уменьшения падения напряжения на подводящих проводах.
Но, что самое главное, компенсация реактивной энергии у каждого потребителя, от квартиры до огромного предприятия, снизит токи во всех линиях электропитания, от электростанции до квартирного щитка. За счет реактивной составляющей полного тока, что уменьшит потери энергии в линиях и повысит коэффициент полезного действия электросистем.
Содержание:В электротехнике среди множества определений довольно часто используются такие понятия, как активная, реактивная и полная мощность. Эти параметры напрямую связаны с током и напряжением , когда включены какие-либо потребители. Для проведения вычислений применяются различные формулы, среди которых основной является произведение напряжения и силы тока. Прежде всего это касается постоянного напряжения. Однако в цепях переменного разделяется на несколько составляющих, отмеченных выше. Вычисление каждой из них также осуществляется с помощью формул, благодаря которым можно получить точные результаты.
Формулы активной, реактивной и полной мощности
Основной составляющей считается активная мощность. Она представляет собой величину, характеризующую процесс преобразования электрической энергии в другие виды энергии. То есть по-другому является скоростью, с какой . Именно это значение отображается на электросчетчике и оплачивается потребителями. Вычисление активной мощности выполняется по формуле : P = U x I x cosф.
В отличие от активной, которая относится к той энергии, которая непосредственно потребляется электроприборами и преобразуется в другие виды энергии — тепловую, световую, механическую и т.д., реактивная мощность является своеобразным невидимым помощником. С ее участием создаются электромагнитные поля, потребляемые электродвигателями. Прежде всего она определяет характер нагрузки, и может не только генерироваться, но и потребляться. Расчеты реактивной мощности производятся по формуле : Q = U x I x sinф.
Полной мощностью является величина, состоящая из активной и реактивной составляющих. Именно она обеспечивает потребителям необходимое количество электроэнергии и поддерживает их в рабочем состоянии. Для ее расчетов применяется формула: S = .
Как найти активную, реактивную и полную мощность
Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.
В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени. Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления. Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.
При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.
Существует определенная зависимость реактивной мощности от знака угла ф, отображенного на рисунке. В связи с этим, она будет иметь положительное или отрицательное значение. В отличие от активной мощности, измеряемой в , реактивная мощность измеряется в вар — вольт-амперах реактивных. Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.
Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).
Специфика сети переменного тока приводит к тому, что в фиксированный момент времени синусоиды напряжения и тока на приемнике совпадают только в случае так называемой активной нагрузки, полностью переводящей ток в тепло или механическую работу. Практически это всевозможные электронагревательные приборы, лампы накаливания, в каком-то приближении электродвигатели и электромагниты под нагрузкой и звуковоспроизводящая аппаратура. Ситуация полностью меняется, если нагрузка, не создающая механической работы, обладает большой индуктивностью при малом сопротивлении. Это характерный случай электродвигателя или трансформатора на холостом ходу.
Подключение подобного потребителя к источнику постоянного тока привело бы к , здесь же ничего особенного с сетью не случится, но мгновенный ток будет отставать от мгновенного напряжения примерно на четверть периода. В случае же чисто емкостной нагрузки (если в розетку вставить конденсатор), ток на нем будет, наоборот, на ту же четверть периода опережать напряжение.
Реактивные токи
Практически такое несовпадение тока и напряжения, не производя на приемнике полезной работы, создает в проводах дополнительные, или, как принято их называть, реактивные токи, которые в особо неблагоприятных случаях могут привести к разрушительным последствиям. При меньшей величине это явление все равно требует расходовать излишний металл на более толстую проводку, повышать мощность питающих генераторов и трансформаторов электроэнергии. Поэтому экономически оправдано устранять в сети реактивную мощность всеми возможными способами. При этом следует учитывать суммарную реактивную мощность всей сети, при том, что отдельные элементы могут обладать значительными значениями реактивной мощности.
Реактивная электроэнергия
С количественной стороны влияние реактивной электроэнергии на работу сети оценивается косинусом угла потерь, который равен отношению активной мощности к полной. Полная мощность считается как векторная величина, которая зависит от сдвига фаз между током и напряжением на всех элементах сети. В отличие от активной мощности, которую, как и механическую измеряют в ваттах, полную мощность измеряют в вольт-амперах, так как эта величина присутствует только в электрической цепи. Таким образом, чем ближе косинус угла потерь к единице, тем полнее используется и мощность, вырабатываемая генератором.
Основные пути снижения реактивной мощности — взаимная компенсация сдвигов фаз, создаваемых индуктивными и емкостными приемниками и использование приемников с малым углом потерь.
Для энергетиков предприятий и крупных торговых центров сомнений в существовании реактивной энергии нет. Ежемесячные счета и вполне реальные деньги, которые уходят на оплату реактивной электроэнергии , убеждают в реальности ее существования. Но некоторые электротехники всерьез, с математическими выкладками, доказывают, что данный тип электроэнергии фикция, что разделение электрической энергии на активную и реактивную составляющие искусственно.
Давайте попробуем и мы разобраться в этом вопросе, тем более, что на незнании отличий разных видов электроэнергии спекулируют создатели . Обещая огромные проценты , они сознательно или по незнанию подменяют один вид электрической энергии другим.
Начнем с понятий активной и реактивной электроэнергии. Не вдаваясь в дебри формул электротехники, можно определить активную энергию как ту, которая совершает работу: нагревает пищу на электроплитах, освещает ваше помещение, охлаждает воздух с помощью кондиционера. А реактивная электроэнергия создает необходимые условия для совершения подобной работы. Не будет реактивной энергии, и двигатели не смогут вращаться, холодильник не будет работать. В ваше помещение не поступит напряжение величиной 220 Вольт, так как ни один силовой трансформатор не работает без потребления реактивной электроэнергии.
Если на осциллографе одновременно наблюдать сигналы тока и напряжения, то две эти синусоиды всегда имеют сдвиг относительно друг друга на величину, называемую фазовым углом . Вот этот сдвиг и характеризует вклад реактивной энергии в полную энергию, потребляемую нагрузкой. Измеряя только ток в нагрузке, выделить реактивную часть энергии невозможно.
Учитывая, что реактивная энергия не совершает работы, ее можно вырабатывать на месте потребления. Для этого служат конденсаторы. Дело в том, что катушки и конденсаторы потребляют различные виды реактивной энергии: индуктивную и емкостную соответственно. Они сдвигают кривую тока по отношению к напряжению в противоположные стороны.
В силу этих обстоятельств конденсатор можно считать потребителем емкостной энергии или генератором индуктивной. Для двигателя, потребляющего индуктивную энергию, конденсатор, расположенный рядом, может стать ее источником. Такая обратимость возможна только для реактивных элементов схемы, не совершающих работу. Для активной энергии подобная обратимость не существует: ее генерация связана с затратами топлива. Ведь прежде чем совершить работу, нужно затратить энергию.
В бытовых условиях за реактивную энергию электропередающие организации плату не изымают, и бытовой счетчик считает только активную составляющую электрической энергии. Совершенно другая ситуация на крупных предприятиях: большое количество электродвигателей, сварочных аппаратов и трансформаторов, для работы которых требуется реактивная энергия, создают дополнительную нагрузку на линии электропередач. При этом растет ток и тепловые потери уже активной энергии.
В этих случаях потребление реактивной энергии учитывается счетчиком и отдельно оплачивается. Стоимость реактивной электроэнергии меньше стоимости активной, но при больших объемах ее потребления платежи могут быть очень значительными. Кроме этого, за потребление реактивной энергии сверх оговоренных значений, накладываются штрафы. Поэтому экономически выгодно для подобных предприятий становится выработка подобной энергии на месте ее потребления.
Для этого применяются или отдельные конденсаторы, или автоматические установки компенсации, которые отслеживают объемы потребления и подключают или отключают конденсаторные батареи. Современные системы компенсации позволяют значительно уменьшить потребление реактивной энергии из внешней сети.
Возвращаясь к вопросу в заголовке статьи, можно ответить на него утвердительно. Реактивная энергия существует. Без нее невозможна работа электроустановок, в которых создается магнитное поле. Не совершая видимой работы, она, тем не менее, является необходимым условием для выполнения работ, совершаемой активной электрической энергией.
Коэффициент мощности (cos φ, косинус фи ), Полная (кажущаяся), активная и реактивная мощность электродвигателя=электромотора и не только его. Коэффициент мощности для трехфазного электродвигателя.
Коэффициент мощности (cos φ, косинус фи ), Полная (кажущаяся), активная и реактивная мощность электродвигателя=электромотора и не только его. Коэффициент мощности для трехфазного электродвигателя.
На шильдиках многих электромоторов (электродвигателей и др. устройств) указывают активную мощность в Вт и cosφ / или λ /или PF. Что тут к чему см. ниже.
Подразумеваем,что переменное напряжение в сети синусоидальное — обычное, хотя все рассуждения ниже верны и для всех гармоник по отдельности других периодических напряжений.
Полная, или кажущаяся мощность S (apparent power) измеряется в вольт-амперах (ВА или VA) и определяется произведением переменных напряжения и тока системы. Удобно считать, что полная мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой.
|
Активная мощность P (active power = real power =true power) измеряется в ваттах (Вт, W) и это та мощность, которая потребляется электрическим сопротивлением системы на тепло и полезную работу. Для сетей переменного тока:
- P=U*I*cosφ, где U и I — действующие=эффективные=среднеквадратичные значения напряжения и тока, а φ- сдвиг фаз между ними
Реактивная мощность Q (reactive power) измеряется в вольт-амперах реактивных (вар, var) и это электромагнитная мощность, которая запасается и отдается обратно в сеть колебательным контуром системы. Реактивная мощность в идеале не выполняет работы, т.е. название вводит в заблуждение. Легко догадаться глядя на рисунок, что:
- P=U*I*sinφ, где U и I — действующие=эффективные=среднеквадратичные значения напряжения и тока, а φ- сдвиг фаз между ними
Сама концепция активной и реактивной мощности актуальна для устройств (приемников) переменного тока. Она малоактуальна=никогда не упоминатеся для приемников постоянного тока в силу малости (мизерности) соответствующих эффектов, связанных только с переходными процессами при включении/выключении.
Любая система, как известно, имеет емкость и индуктивность = является неким колебательным контуром. Переменный ток в одной фазе накачивает электромагнитное поле этого контура энергией а в противоположной фазе эта энергия уходит обратно в генератор ( в сеть). Это вызывает в РФ 3 проблемы (для поставщика энергии!)
- Хотя теоретически, при нулевых сопротивлениях передачи, на выработку реактивной мощности не тратится мощность генератора, но практически для передачи реактивной мощности по сети требуется дополнительная, активная мощность генератора (потери передачи).
- Сеть должна пропускать и активные и реактивные токи, т.е иметь запас по пропускным характеристикам.
- Генератор мог бы, выдавая те же ток и напряжение, поставлять потребителю электроэнергии больше активной мощности.
попробуем догадаться, что делает поставщик электроэнергии? Правильно, пытается навязать Вам различные тарифы для разлиных значений cos φ. Что можно сделать: можно заказать компенсацию реактивной мощности ( т.е. установку неких блоков конденсаторов или катушек), которые заставят реактивную нагрузку колебаться внутри Вашего предприятия/устройства. Стоит ли это делать? Зависит от стоимости установки, наценок за коэффициент мощности и очень даже часто не имеет экономического смысла. В некоторых странах качество питающего напряжения тоже может пострадать от избытка реактивной мощности, но в РФ проблема неактуальна в силу изначально очень низкго качества в питающей сети.
Естественно, хотелось бы ввести величину, которая характеризовала бы степень линейности нагрузки. И такая величина вводится под названием коэффициент мощности («косинус фи», power factor, PF), как отношение активной мощности к полной, естественно сразу в 2-х видах, в РФ это:
- λ=P/S*100% — то есть, если в %, то это лямбда, P в (Вт), S в (ВА)
- cosφ=P/S — более распространенная величина , P в (Вт), S в (ВА)
Коэффициент мощности для трехфазного асинхронного (обычного) электродвигателя.
cosφ = P / (√3*U*I)
где
cosφ = косинус фи
√3 = квадратный корень из трех
P = активная мощность (Вт)
U = Напряжение (В)
I = Ток (А)
Реактивная мощность. Расчёт
Реактивная мощность обусловлена способностью реактивных элементов накапливать и отдавать электрическую или магнитную энергию.
Eмкостная нагрузка в цепи переменного тока за время половины периода накапливает заряд в обкладках конденсаторов и отдаёт его обратно в источник.
Индуктивная нагрузка накапливает магнитную энергию в катушках и возвращает её в источник питания в виде электрической энергии.
Напряжение на выводах реактивного элемента будет достигать максимального значения во время смены направления тока, следовательно, расхождение во времени между напряжением и током в пределах элемента составит четверть периода (сдвиг фаз 90°).
Угол сдвига фаз φ в цепи нагрузки определяется соотношением активного и реактивного сопротивлений нагрузки.
Реактивная мощность характеризует потери, созданные реактивными элементами в цепи переменного тока, и выражается формулой Q = UIsinφ.
Природу потерь в цепи с реактивными элементами можно рассмотреть с помощью графиков на рисунках.
φ = 90° sin90° = 1 cos90° = 0
При отсутствии активной составляющей в нагрузке, сдвиг фаз между напряжением и током составит 90°.
В начале периода, когда напряжение максимально – ток будет равен нулю, следовательно, мгновенное значение мощности UI в это время будет равно нулю.
В течении первой четверти периода, мощность можно видеть на графике, как произведение UI,
которое станет равным нулю при максимуме тока и нулевом значении напряжения.
В следующую четверть периода на графике UI принимает отрицательное значение, следовательно, мощность возвращается обратно в источник питания. То же самое произойдёт и в отрицательном полупериоде тока. В результате средняя (активная) потребляемая мощность P avg за период будет равна нулю.
В таком случае:
Реактивная мощность Q = UIsin90° = UI
Потребляемая мощность P = UIcos90° = 0
Полная мощность S = UI = √(P² + Q²) будет равна реактивной мощности
Коэффициент мощности P/S = 0
При отсутствии реактивных элементов и сдвига фаз в нагрузках, мгновенная мощность в полупериоде Umax*Imax будет максимальной, и в следующем полупериоде произведение отрицательного напряжения с отрицательным током дадут положительный результат – полезную мощность в нагрузке.
φ = 0° sin90° = 0 cos90° = 1
В этом случае:
Реактивная мощность Q = UIsin0 = 0
Потребляемая мощность P = UIcos0 = UI
Полная мощность S = UI = √(P² + Q²) будет равна потребляемой мощности
Коэффициент мощности P/S = 1
Ниже представлен рисунок графиков со сдвигом фаз 45°, для случая равенства активного и реактивного сопротивлений в нагрузке.
φ = 45° sin45° = cos45° = √2/2 ≈ 0.71
Здесь:
Реактивная мощность Q = UIsin45° = 0.71UI
Потребляемая мощность P = UIcos45° = 0.71UI
Полная мощность S = √(P² + Q²) = UI
Коэффициент мощности P/S = 0.71
В примерах рассмотрены случаи с индуктивной нагрузкой, когда ток отстаёт от напряжения (положительный сдвиг фаз).
В случаях с ёмкостной нагрузкой, процессы и расчёты аналогичны,
только напряжение будет отставать от тока (отрицательный сдвиг фаз).
Угол сдвига фаз в сети определится соотношением активного и реактивного сопротивлений нагрузок в
параллельном соединении следующим образом:
XL и XС соответственно индуктивное и ёмкостное сопротивление нагрузок.
Преобладание индуктивных нагрузок будет уменьшать общее индуктивное сопротивление.
Из выражения видно, что угол в этом случае будет принимать положительный знак,
а преобладание ёмкостных нагрузок будет уменьшать ёмкостное сопротивление и вызывать отрицательный сдвиг.
При равенстве индуктивного и ёмкостного сопротивлений, угол сдвига будет равен нулю.
В бытовых и производственных потребителях индуктивное сопротивление обычно существенно преобладает над ёмкостным.
Подробнее о вычислениях общего угла сдвига φ для вариантов соединений активного и реактивного сопротивлений в нагрузках можно ознакомиться на страничке электрический импеданс.
Компенсация реактивной мощности
Огромное количество индуктивных нагрузок в сети суммарно обладает колоссальной реактивной мощностью, которая возвращается в генераторы и не совершает никакой полезной работы, расходуя энергию на нагрев кабелей и проводов ЛЭП, перегружает трансформаторы, снижая их КПД, тем самым уменьшая пропускную способность активных токов.
Если параллельно индуктивной нагрузке подключить конденсатор,
фаза тока в цепи источника будет смещаться в противоположную сторону, компенсируя угол, созданный индуктивностью нагрузки.
При определённом соотношении номиналов,
можно добиться отсутствия сдвига фаз, следовательно, и отсутствия реактивных токов в цепи источника питания.
Ёмкость конденсатора определяется реактивным (индуктивным) сопротивлением нагрузки, которое необходимо компенсировать:
C = 1/(2πƒX),
X = U²/Q — реактивное сопротивление нагрузки,
Q — реактивная мощность нагрузки.
Компенсация реактивных токов в сети позволяет значительно уменьшить потери на активном сопротивлении проводов ЛЭП, кабелей и обмоток трансформаторов питающей сети.
В целях компенсации реактивной мощности на производственных предприятиях, где основными потребителями энергии являются асинхронные электродвигатели,
индукционные печи, люминесцентное освещение, которые обладают индуктивным сопротивлением, часто применяют специальные конденсаторные
установки, способные в ручном или автоматическом режиме поддерживать нулевой сдвиг фаз, тем самым минимизировать реактивные потери.
В масштабах энергосистемы компенсация происходит непосредственно на электростанциях путём контроля сдвига фаз и обеспечения соответствующего тока подмагничивания роторных обмоток синхронных генераторов станций.
Компенсация реактивной мощности — одна из составляющих комплекса мер по Коррекции Коэффициента Мощности (ККМ) в электросети (Power Factor Correction — PFC в англоязычной литературе). Применяется в целях уменьшения потерь электроэнергии, как на паразитную реактивную, так и нелинейную составляющую искажений тока в энергосистеме. Более подробно с материалом о ККМ (PFC) можно ознакомиться на странице — коэффициент мощности.
Онлайн-калькулятор расчёта реактивной мощности и её компенсации.
Достаточно вписать значения и кликнуть мышкой в таблице.
|
Реактивная мощность Q = √((UI)²-P²) |
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать частоту резонанса колебательного контура LC.
Рассчитать реактивное сопротивление катушки индуктивности L и конденсатора C.
Альтернативные статьи:
Дизель-генератор.
кВАр (реактивная мощность): Расчет кВАр, формула и единица коэффициента мощности кВАр Работа
Если вы хотите сэкономить на расходах на энергопотребление, то вы, вероятно, слышали об агрегате кВАр или энергосберегающих устройствах кВАр. Это устройства, которые помогают жилым домам и коммерческим предприятиям экономить на счетах за электроэнергию, особенно при использовании систем переменного тока.
Есть три термина, которые можно использовать для обозначения переменного тока переменного тока. Первый — это киловатт, который представляет реальную мощность.Это измерение, используемое для регистрации мощности в счетчиках электроэнергии рядом с вашим домом. Вторая — это реактивная мощность, которая измеряется в кВАр или реактивных киловольт-амперах. В контексте передачи и распределения электроэнергии термин «киловольт-ампер реактивная» используется для обозначения единицы измерения реактивной мощности. Однако вы не платите за это, поэтому KVAR не отображается на ваших счетчиках коммунальных услуг. Третий член — полная мощность, обозначаемая как кВА. Чтобы лучше понять эти концепции, вам нужно упомянуть коэффициент мощности, который представляет собой соотношение между полной и активной мощностью.Полная мощность, в свою очередь, состоит из двух типов мощности: активной и реактивной. Чем ниже составляющая реактивной мощности, тем выше коэффициент мощности, что приводит к большей экономии для вас.
Как производится расчет KVAR?
Есть несколько способов выполнить расчет KVAR, если вам нужно рассчитать реактивную мощность данной нагрузки. Если вы хотите применить практический подход, используйте вольтметр вместе с амперметром или амперметром. Произведение показаний даст вам полную мощность нагрузки в вольт-амперах.Полученное значение также поможет вам определить истинную мощность в ваттах для данной нагрузки. Учитывая эти числа, поиск векторной разницы не вызовет никаких проблем. Определив реактивную мощность, вы сможете найти подходящие конденсаторы, необходимые для снижения полной мощности компонентов в ваших системах. Таким образом можно снизить коэффициент мощности, если вы хотите сэкономить на расходах. Например, если вы установите конденсаторы мощностью 30 кВАр, они снизят реактивную мощность, обеспечиваемую энергокомпанией, до 30 кВАр.С другой стороны, полная мощность, поставляемая коммунальным предприятием, упадет примерно до 85,4 кВА.
Что такое формула реактивной мощности / кВАр?
Реактивная мощность — это неиспользованная мощность, генерируемая реактивными компонентами в цепи или системе переменного тока, и измеряется в кВАр. Что касается коэффициента мощности, то чем больше реактивная мощность, тем выше полная мощность или кВА. В жилых домах количество потребляемой электроэнергии довольно мало. Вот почему компании не взимают плату за жилую недвижимость.Низкое энергопотребление не вызывает опасений у электроэнергетических компаний. Однако коммерческие и промышленные электрические компании потребляют это в огромных количествах, поэтому электроэнергетические компании взимают с них надбавку. Для формулы KVAR это выглядит следующим образом: Q = X * I * I. В формуле реактивной мощности X означает реактивное сопротивление цепи, а I — ток, протекающий по цепи. Вам нужно понять формулу, чтобы узнать больше об использовании реактивной мощности.
Как работает блок коэффициента мощности KVAR?
Прежде чем вы поймете, как работает коэффициент мощности KVAR, вам необходимо четко определить, что такое коэффициент мощности.По сути, это мера того, насколько эффективно использование входящей мощности в вашей электрической системе. Отношение рабочей мощности к полной или полной мощности. Это формула коэффициента мощности. Чтобы понять, что такое KVAR для коррекции коэффициента мощности, помните, что коэффициент мощности — это соотношение между реальной и полной мощностью. Это означает, что чем выше процент KVAR в вашей нагрузке, тем ниже отношение кВт к кВА. Результат дает плохой коэффициент мощности. Используйте это наблюдение при выполнении формулы расчета коэффициента мощности KVAR.
Как установить регулятор энергии KVAR?
Если вы хотите сэкономить и планируете установить регулятор энергии KVAR в своей системе, придерживайтесь основ. Внимательно следуйте инструкциям. Убедитесь, что вы выключили питание, прежде чем приступить к установке энергосберегающего устройства KVAR. Если у вас нет инструментов, опыта и знаний — не говоря уже о времени и навыках — для выполнения этой задачи, тогда вам повезет — и вы добьетесь большего успеха, когда наймете профессионала.Найдите кого-нибудь с опытом и знаниями, чтобы добавить энергосберегающий блок к вашей существующей системе. После этого вам нужно только подождать, пока экономия средств не начнет влиять на ваши счета.
Что такое кВА и как его рассчитать?
В то время как KVAR означает реактивный киловольт-ампер, kVA означает киловольт-ампер. По большей части его обычно называют киловаттом или киловаттом, что является общим термином. Это единица измерения, используемая для оценки большинства (если не всех) электрических предметов, имеющихся у вас дома.
Термин относится к количеству энергии, которая используется для работы и преобразуется в выходную мощность, поэтому, когда вы говорите о кВт, вы говорите о фактической мощности. Чтобы рассчитать фактическую мощность или потребляемую мощность устройства, вам необходимо определить полную мощность. Это можно рассчитать по следующей формуле: Ампер x Вольт = Вольт-Ампер. Определив кажущуюся мощность, вы сможете определить реальную мощность. Например, это будет означать, что амперы x вольт x коэффициент мощности = ватты. Это расчет KVA.
Чтобы формула кВА дала желаемые результаты, вам также необходимо определить коэффициент мощности. Коэффициент мощности важен, если вы хотите узнать реальную потребляемую мощность устройства в вашем доме, например, вашего переменного тока. Когда вы закончите, вы получите точный расчет энергопотребления вашей системы. Эта информация поможет вам управлять счетами за коммунальные услуги в вашем доме или учреждении.
В чем разница между кВА и кВАр?
Электроэнергия, которую нам поставляют электроэнергетические компании, называется полной мощностью.Это фактическая мощность, измеренная в кВА и выраженная в виде напряжения и тока, которая затем разбивается на два типа мощности: активная мощность (кВт) и реактивная мощность (кВАр). Если вы хотите уточнить разницу между кВА и кВАр, кВА обозначает активную или фактическую мощность, а кВАр обозначает реактивную или индуктивную мощность.
Когда вы видите энергию, которая создает движение, свет, тепло и звук, все они питаются активной мощностью. Реактивная мощность — это мощность, которая создает магнитные поля, приводящие в движение вращающееся оборудование, и зависит от коэффициента мощности.Формула коэффициента мощности следующая: активная мощность x 100 / полная мощность.
Если вы ищете способ сэкономить на расходах на потребление энергии, подумайте об установке конденсаторов. Использование правильных конденсаторов снизит составляющую реактивной мощности энергосистемы, что приведет к падению составляющей полной мощности. Результат? В результате вы получите более высокий коэффициент мощности.
Получение помощи
Понимание этих концепций может помочь вам повысить энергоэффективность вашего предприятия.Если вы устали платить больше, чем нужно, по счетам за электроэнергию, поищите специалистов, которые могут предоставить вам оценку энергопотребления дома. Узнайте, что вы можете сделать, чтобы снизить уровень потребления энергии. С помощью команды опытных и проверенных электриков, которые выполнят эту работу за вас, вы сможете найти способ сэкономить на расходах и обеспечить лучшие финансовые показатели вашего предприятия.
Чтобы выбрать подходящего поставщика услуг, убедитесь, что вы делаете свою домашнюю работу. Ознакомьтесь с отзывами о фирме.Много жалоб или положительных отзывов? Что в большинстве отзывов говорится о качестве услуг фирмы? Учитывайте это при поиске поставщика электрических услуг. Также изучите предысторию компании. Как давно это было в бизнесе? Достаточно ли опыта, чтобы заработать прочную репутацию в отрасли? Предоставляет ли фирма качественные результаты?
Эти соображения имеют значение. Чем больше вы будете знать, тем легче вам будет выбрать фирму, которая будет удовлетворять ваши потребности в энергии.Если вы хотите сэкономить на расходах, начните искать подходящую фирму, которая поможет вам снизить потребление энергии и счета за коммунальные услуги.
Что такое комплексная мощность и как она фигурирует в анализе мощности
Мощность, потребляемая данной нагрузкой
За годы были затрачены значительные усилия на то, чтобы выразить соотношение мощности как можно проще. Энергетики придумали термин комплексная мощность, который они используют, чтобы найти общий эффект от параллельных нагрузок.
Что такое комплексная мощность и ее функция в анализе мощности (на фото: Регистратор качества электроэнергии Amprobe DM-III Multitest F 3000A)Комплексная мощность важна при анализе мощности, поскольку она содержит всю информацию, относящуюся к мощности , потребляемой данным нагрузка .
Рисунок 1 — Векторы напряжения и тока, связанные с нагрузкойРассмотрим нагрузку переменного тока на Рисунке 1 выше. Учитывая векторную форму V = V m ∠θ v и I = I m ∠θ i напряжения v (t) и тока i (t), комплексная мощность S потребляемая нагрузкой переменного тока является произведением напряжения и комплексно-сопряженного тока, или:
(1.10)
при условии использования пассивных знаков (см. Рисунок 1). В терминах среднеквадратичных значений:
(1.11)
, где
(1.12)
и
(1.13)
Таким образом, мы можем написать уравнение. (1.11) как:
(1.14)
Мы замечаем из уравнения. (1.14) что величина комплексной мощности — это кажущаяся мощность . Следовательно, комплексная мощность измеряется в вольт-амперах (ВА). Также мы замечаем, что угол комплексной мощности — это угол коэффициента мощности.
Комплексная мощность может быть выражена через импеданс нагрузки Z . Сопротивление нагрузки Z можно записать как:
(1,15)
Таким образом, В среднеквадратичное значение = Z × I среднеквадратичное значение . Подставляя это в формулу. (1.11) дает
(1.16)
Поскольку Z = R + jX , уравнение. (1.16) становится
(1.17)
, где P и Q — действительная и мнимая части комплексной степени ; то есть
(1.18, 1.19)
P — средняя или активная мощность , и она зависит от сопротивления нагрузки R. Q зависит от реактивного сопротивления нагрузки X и называется реактивной (или квадратурной) мощностью .
Сравнение ур. (1.14) с формулой. (1.17), мы замечаем, что:
(1.20)
Реальная мощность P — это средняя мощность в ваттах, подаваемая на нагрузку. Это единственная полезная мощность. Это фактическая мощность, рассеиваемая нагрузкой. Реактивная мощность Q является мерой обмена энергией между источником и реактивной частью нагрузки.
Единица измерения Q представляет собой реактивную вольт-амперную (ВАР) , чтобы отличить ее от реальной мощности, единицей измерения которой является ватт.
Мы знаем, что элементы аккумулирования энергии не рассеивают и не подают энергию, а обмениваются энергией туда и обратно с остальной частью сети. Таким же образом реактивная мощность передается между нагрузкой и источником. Он представляет собой обмен без потерь между нагрузкой и источником .Обратите внимание, что:
- Q = 0 для резистивных нагрузок (единица pf)
- Q <0 для емкостных нагрузок (опережающая pf)
- Q> 0 для индуктивных нагрузок (запаздывающая pf)
Таким образом,
Комплексная мощность (в ВА) является произведением вектора среднеквадратичного напряжения и комплексно-сопряженной вектора среднеквадратичного значения тока. Как комплексная величина, ее действительная часть — это активная мощность P, а ее мнимая часть — это реактивная мощность Q.
Введение комплексной мощности позволяет нам получить реальную и реактивную мощности непосредственно из векторов напряжения и тока.
(1.21)
Это показывает, как комплексная мощность содержит всю соответствующую информацию о мощности в данной нагрузке.
Стандартной практикой является представление S, P и Q в форме треугольника, известного как треугольник мощности , показанного на рис.2 (а). Это похоже на треугольник импеданса, показывающий взаимосвязь между Z, R и X, показанный на рис. 2 (b).
Рисунок 2 — (a) Треугольник мощности, (b) треугольник импедансаS содержит всю информацию о мощности нагрузки. Действительная часть S — это активная мощность P. Мнимая часть — это реактивная мощность Q . Его величина составляет кажущаяся мощность S . А косинус его фазового угла равен коэффициенту мощности PF .
Треугольник мощности состоит из четырех элементов:
- Полная / полная мощность,
- Реальная мощность,
- Реактивная мощность и
- Угол коэффициента мощности.
Учитывая два из этих элементов, два других можно легко получить из треугольника.
Рисунок 3 — Треугольник мощностиКак показано на рисунке 3, когда S лежит в первом квадранте, , мы имеем индуктивную нагрузку и отстающий коэффициент мощности . Когда S находится в четвертом квадранте, нагрузка является емкостной, а коэффициент мощности опережает. Также возможно, что комплексная мощность находится во втором или третьем квадранте.
Для этого требуется, чтобы полное сопротивление нагрузки имело отрицательное сопротивление, что возможно в активных цепях.
Пример с комплексным расчетом мощности
Примеры комплексной мощности, коэффициента мощности, средней мощности и полной мощности
Ссылка // Основы электрических схем Чарльза К. Александер и Мэтью NO Sadiku (покупка бумажной копии у Amazon)
Как преобразовать трехфазную мощность в амперы
Обновлено 14 декабря 2020 г.
Автор: J.Р. Камбак
В промышленных и бытовых аварийных генераторах используются трехфазные электродвигатели. Все три выхода пропускают одинаковый ток, а передача мощности остается постоянной, поступая на линейную и сбалансированную нагрузку. Чтобы преобразовать мощность в амперы, вам необходимо знать коэффициенты напряжения и мощности электродвигателя. Коэффициент мощности определяет задержку между напряжением и фактическим протеканием электрического тока. Этот номер указан на паспортной табличке большинства крупных электродвигателей, использующих трехфазное питание.
Эта формула вычисляет мощность генератора для определенного тока или ампер при заданном напряжении:
P = VI
Только в этом случае умножьте результат на 1,732.
Важно выделить три типа мощности:
Активная (действительная или истинная) мощность измеряется в ваттах (Вт) и представляет собой мощность, потребляемую электрическим сопротивлением системы, выполняющей полезную работу.
Реактивная мощность вольт-ампер (ВАР) для измерения реактивной мощности. Индуктивные двигатели, трансформаторы и соленоиды накапливают и разряжают реактивную мощность.
Вольт-амперы (ВА) для измерения полной мощности. Это напряжение в системе переменного тока, умноженное на весь ток, протекающий в ней, и сумму активной и реактивной мощности.
Соотношение между активной и полной мощностью:
1 \ text {kVA} = \ frac {1 \ text {kW}} {\ text {power factor}}
Убедитесь, что ваши измерения соответствуют стандарту единицы. Для двигателя или генератора, выраженного в киловаттах, переведите его в ватты: 1 кВт = 1000 Вт.
Получите измерение напряжения, если оно еще не предоставлено.Используйте качественный цифровой вольтметр для измерения линейного напряжения между любыми двумя из трех выходов.
Найдите коэффициент мощности (p.f.) на паспортной табличке. Для чисто резистивной схемы коэффициент мощности равен 1,0 (идеально).
Используйте формулу закона Ома:
P = VI
Составьте уравнение для трехфазной мощности, чтобы определить ток (амперы):
I = \ frac {P} {1,732V \ times \ text {коэффициент мощности }}
Подставьте значение мощности, которую необходимо преобразовать (в ваттах), значение напряжения (в вольтах) и коэффициент мощности, чтобы найти ток (в амперах).
Например, используйте следующую формулу для расчета тока трехфазного электрического генератора мощностью 114 кВт, заданным напряжением 440 В и номинальным коэффициентом мощности 0,8:
I = \ frac {P } {1,732V \ times \ text {power factor}} = \ frac {1141000} {4401.732 \ times 0.8} = 187 \ text {amps}
Как измерить выходную мощность от батареи
Выходная мощность батарей при они подключены к цепи. Батарея, которая не подключена к цепи, не дает тока и, следовательно, не выводит энергию.Однако после того, как вы подключили батарею к цепи, вы можете определить выходную мощность, измерив падение напряжения на нагрузке цепи. Если вы знакомы с уравнениями, связывающими мощность с напряжением, током и сопротивлением, вы сможете легко перемещаться между этими понятиями.
Расчет мощности
Мощность — это произведение тока и напряжения. Следовательно, чтобы рассчитать выходную мощность батареи, вы должны измерить эти два аспекта цепи.Ток — это поток заряда в единицу времени, а напряжение — это электрическая потенциальная энергия. Единицами измерения тока и напряжения являются амперы и вольт соответственно. Кроме того, напряжение — это произведение тока и сопротивления. Сопротивление — это величина сопротивления току. Предметы, подверженные электрическому потенциалу или напряжению, обладают характеристическим сопротивлением. Сопротивление измеряется в Ом. Из-за взаимосвязанного характера мощности, напряжения, тока и сопротивления вы можете определить мощность, даже если вам известны только две другие величины.Например, мощность равна квадрату тока, умноженному на сопротивление, или квадрату напряжения, деленному на сопротивление.
Проведение измерений
Чтобы измерить выходную мощность батареи, вы должны измерить ее, когда она подключена к внешнему сопротивлению, также называемому сопротивлением нагрузки. В противном случае аккумулятор не будет работать и, следовательно, не будет обеспечивать выходную мощность. Сопротивление нагрузки создает измеримое падение напряжения. Если вы знаете сопротивление нагрузки, вы можете определить ток.Используйте мультиметр, чтобы проверить падение напряжения на нагрузке. Поверните шкалу мультиметра, чтобы контролировать напряжение постоянного тока. Затем поместите два провода измерителя по обе стороны от нагрузки. Полярность значения не имеет. Разделите это напряжение на сопротивление нагрузки, чтобы получить ток. Как только у вас есть ток и напряжение, умножьте их, чтобы получить выходную мощность. Вы заметите, что выходная мощность батареи зависит от схемы, в которой она запитана. Это связано с тем, что ток изменяется в зависимости от сопротивления нагрузки.
Напряжение замкнутой и разомкнутой цепи
Напряжение батареи меняется в зависимости от того, приложено ли оно к цепи. Подробное описание батареи часто будет включать цифры напряжения как в замкнутой, так и в разомкнутой схемах. Напряжение замкнутой цепи аккумулятора также называется напряжением на его клеммах. Кроме того, эти напряжения могут варьироваться в зависимости от состояния заряда аккумулятора и зарядного тока, где это применимо. Это еще одна причина, по которой вы должны измерять напряжение батареи, когда она подключена к цепи.
Внутреннее сопротивление
Батарея показывает внутреннее сопротивление в дополнение к любому сопротивлению в цепи. По мере увеличения этого внутреннего сопротивления выходная мощность батареи уменьшается, поскольку некоторая мощность рассеивается внутри. Когда это происходит, напряжение на клеммах аккумулятора уменьшается. Если внутреннее сопротивление батареи становится слишком высоким, батарея больше не будет обеспечивать достаточный потенциал для пропускания тока через нагрузку.
Номинальные характеристики аккумуляторов
На аккумуляторах есть несколько напечатанных номинальных значений их емкости и мощности.Общий электростатический потенциал батареи указывается в вольтах. Это одна из самых выдающихся характеристик батареи, и она имеет большое значение для выходной мощности батареи: как правило, чем выше номинальное напряжение, тем больше выходная мощность. Также емкость аккумулятора указана в ампер-часах. Это выражение количества ампер, которое батарея будет выдавать в течение заданного количества часов. Например, батарея на 140 ампер-час может выдавать ток 7 ампер в течение 20 часов, прежде чем потребуется зарядка.
Определение мощности и размера выборки
Определение мощности и размера выборки Определение мощности и размера выборки
Автор:
Лиза Салливан, доктор философии
Профессор биосатистики
Школа общественного здравоохранения Бостонского университета
Критически важным аспектом любого исследования является определение подходящего размера выборки для ответа на исследовательский вопрос.В этом модуле основное внимание уделяется формулам, которые можно использовать для оценки размера выборки, необходимого для получения оценки доверительного интервала с заданным пределом погрешности (точности) или для гарантии того, что проверка гипотезы имеет высокую вероятность обнаружения значимой разницы в параметр.
Исследования должны быть разработаны таким образом, чтобы включать достаточное количество участников для адекватного ответа на вопрос исследования. Исследования, в которых участвует либо недостаточное количество участников, либо чрезмерно большое количество участников, расточительны с точки зрения времени участников и исследователей, ресурсов для проведения оценок, аналитических усилий и т. Д.Эти ситуации также можно рассматривать как неэтичные, поскольку участники могли подвергнуться риску в рамках исследования, которое не смогло ответить на важный вопрос. Исследования, которые намного больше, чем они должны быть, чтобы ответить на вопросы исследования, также расточительны.
Представленные здесь формулы позволяют получить оценки необходимого размера выборки на основе статистических критериев. Однако во многих исследованиях размер выборки определяется финансовыми или логистическими ограничениями. Например, предположим, что предлагается исследование для оценки нового скринингового теста на синдром Дауна.Предположим, что скрининговый тест основан на анализе пробы крови, взятой у женщины на ранних сроках беременности. Чтобы оценить свойства скринингового теста (например, чувствительность и специфичность), каждой беременной женщине будет предложено сдать образец крови и, в дополнение, пройти амниоцентез. Амниоцентез включен в качестве золотого стандарта, и его план состоит в том, чтобы сравнить результаты скринингового теста с результатами амниоцентеза. Предположим, что сбор и обработка образца крови стоит 250 долларов на участника, а амниоцентез — 900 долларов на участника.Одни только эти финансовые ограничения могут существенно ограничить число женщин, которые могут быть зачислены. Точно так же, как важно учитывать статистическую и клиническую значимость при интерпретации результатов статистического анализа, важно также взвесить как статистические, так и логистические вопросы при определении размера выборки для исследования.
После завершения этого модуля студент сможет:
- Приведите примеры, демонстрирующие, как предел погрешности, размер эффекта и изменчивость результата влияют на вычисления размера выборки.
- Вычислите размер выборки, необходимый для точной оценки параметров генеральной совокупности.
- Интерпретируйте статистическую силу при проверке гипотез.
- Вычислите размер выборки, необходимый для обеспечения высокой мощности при проверке гипотез.
Модуль доверительных интервалов предоставляет методы оценки доверительных интервалов для различных параметров (например, μ, p, (μ 1 — μ 2 ), μ d , (p 1 -p 2 ) )).Доверительные интервалы для каждого параметра имеют следующий общий вид:
Оценка вбалла + Погрешность
В модуле доверительных интервалов мы вывели формулу доверительного интервала для μ как
На практике мы используем стандартное отклонение выборки для оценки стандартного отклонения генеральной совокупности. Обратите внимание, что существует альтернативная формула для оценки среднего значения непрерывного результата в одной генеральной совокупности, и она используется, когда размер выборки невелик (n <30).Он включает значение из распределения t, в отличие от значения из стандартного нормального распределения, чтобы отразить желаемый уровень достоверности. При вычислении размера выборки мы используем формулу для большой выборки, показанную здесь. [Примечание: размер результирующей выборки может быть небольшим, и на этапе анализа необходимо использовать соответствующую формулу доверительного интервала.]
Точечная оценка среднего для генеральной совокупности является выборочным средним, а предел погрешности составляет
.
При планировании исследований мы хотим определить размер выборки, необходимый для обеспечения того, чтобы предел погрешности был достаточно малым, чтобы быть информативным.Например, предположим, что мы хотим оценить средний вес студенток колледжа. Мы проводим исследование и получаем 95% доверительный интервал следующим образом: 125 + 40 фунтов, или от 85 до 165 фунтов. Предел погрешности настолько велик, что доверительный интервал неинформативен. Чтобы быть информативным, исследователь может захотеть, чтобы предел погрешности составлял не более 5 или 10 фунтов (это означает, что 95% доверительный интервал будет иметь ширину (от нижнего предела до верхнего предела) 10 или 20 фунтов). Чтобы определить необходимый размер выборки , исследователь должен указать желаемую погрешность .Важно отметить, что это не статистический вопрос, а клинический или практический. Например, предположим, что мы хотим оценить средний вес при рождении младенцев, рожденных матерями, которые курят сигареты во время беременности. Вес при рождении у младенцев явно имеет гораздо более ограниченный диапазон, чем у студенток колледжа. Следовательно, мы, вероятно, захотим создать доверительный интервал для среднего веса при рождении, который имеет погрешность, не превышающую 1–2 фунта.
Предел погрешности в доверительном интервале одной выборки для μ можно записать следующим образом:
.
Наша цель — определить размер выборки n, который гарантирует, что предел погрешности « E » не превышает указанного значения. Мы можем взять приведенную выше формулу и с помощью некоторой алгебры решить относительно n :
Сначала умножьте обе части уравнения на квадратный корень из n . Затем вычтите квадратный корень из n из числителя и знаменателя в правой части уравнения (поскольку любое число, деленное само на себя, равно 1). Остается:
Теперь разделите обе части на «E» и вычеркните «E» из числителя и знаменателя в левой части.Остается:
Наконец, возведите обе части уравнения в квадрат, чтобы получить:
Эта формула генерирует размер выборки n , необходимый для обеспечения того, чтобы предел погрешности E не превышал заданного значения. Чтобы найти n , мы должны ввести « Z », « σ», « и« E ».
- Z — значение из таблицы вероятностей стандартного нормального распределения для желаемого уровня достоверности (например,g., Z = 1,96 для 95% достоверности)
- E — это предел погрешности, который исследователь определяет как важный с клинической или практической точки зрения.
- σ — стандартное отклонение интересующего результата.
Иногда бывает сложно оценить σ . Когда мы используем приведенную выше формулу размера выборки (или одну из других формул, которые мы представим в следующих разделах), мы планируем исследование для оценки неизвестного среднего значения конкретной переменной результата в популяции.Маловероятно, что мы узнаем стандартное отклонение этой переменной. При вычислении размера выборки исследователи часто используют значение стандартного отклонения от предыдущего исследования или исследования, проведенного в другой, но сопоставимой совокупности. Расчет размера выборки не является применением статистических выводов, и поэтому разумно использовать соответствующую оценку стандартного отклонения. Оценка может быть получена из другого исследования, о котором сообщалось в литературе; некоторые исследователи проводят небольшое пилотное исследование для оценки стандартного отклонения.Пилотное исследование обычно включает небольшое количество участников (например, n = 10), которые выбираются по удобству, а не методом случайной выборки. Данные участников пилотного исследования можно использовать для вычисления стандартного отклонения выборки, которое служит хорошей оценкой для σ в формуле размера выборки. Независимо от того, как получается оценка изменчивости результата, она всегда должна быть консервативной (т.е. настолько большой, насколько это разумно), чтобы размер результирующей выборки не был слишком маленьким.
Формула дает минимальный размер выборки, чтобы гарантировать, что предел ошибки в доверительном интервале не будет превышать E . Планируя исследования, исследователи также должны учитывать выбытие или отказ от последующего наблюдения. Приведенная выше формула дает количество участников, необходимое с полными данными, чтобы гарантировать, что предел ошибки в доверительном интервале не превышает E . Мы проиллюстрируем, как устраняется истощение при планировании исследований, на примерах в следующих разделах.
В исследованиях, в которых планируется оценить среднее значение переменной непрерывного результата в одной популяции, ниже приводится формула для определения размера выборки:
, где Z — значение из стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (например, Z = 1,96 для 95%), σ — стандартное отклонение выходной переменной, а E — желаемое. погрешность.Приведенная выше формула генерирует минимальное количество субъектов, необходимое для обеспечения того, чтобы предел погрешности доверительного интервала для μ не превышал E .
Пример 1:
Исследователь хочет оценить среднее систолическое артериальное давление у детей с врожденным пороком сердца в возрасте от 3 до 5 лет. Сколько детей должно быть включено в исследование? Исследователь планирует использовать 95% доверительный интервал (так Z = 1,96) и хочет погрешность в 5 единиц.Стандартное отклонение систолического артериального давления неизвестно, но исследователи провели поиск литературы и обнаружили, что стандартное отклонение систолического артериального давления у детей с другими пороками сердца составляет от 15 до 20. Чтобы оценить размер выборки, мы рассматриваем больший стандарт отклонение, чтобы получить наиболее консервативный (самый большой) размер выборки.
Чтобы гарантировать, что 95% -ный доверительный интервал оценки среднего систолического артериального давления у детей в возрасте от 3 до 5 лет с врожденным пороком сердца находится в пределах 5 единиц от истинного среднего значения, необходима выборка размером 62.[ Примечание : Мы всегда округляем в большую сторону; формулы размера выборки всегда генерируют минимальное количество субъектов, необходимое для обеспечения указанной точности.] Если бы мы приняли стандартное отклонение, равное 15, размер выборки был бы n = 35. Поскольку оценки стандартного отклонения были получены из исследований детей с другими пороками сердца, было бы целесообразно использовать большее стандартное отклонение и запланировать исследование с 62 детьми. Выбор меньшего размера выборки потенциально может дать оценку доверительного интервала с большей погрешностью.
Исследователь хочет оценить средний вес при рождении доношенных детей (примерно 40 недель беременности) от матерей в возрасте 19 лет и младше. Средний вес новорожденных, рожденных доношенными от матерей в возрасте 20 лет и старше, составляет 3 510 граммов со стандартным отклонением 385 граммов. Сколько женщин в возрасте 19 лет и младше должны быть включены в исследование, чтобы гарантировать, что 95% -ный доверительный интервал оценки средней массы тела при рождении их младенцев имеет погрешность, не превышающую 100 граммов? Прежде чем смотреть на ответ, попробуйте выполнить расчет.
Ответ
В исследованиях, в которых план состоит в оценке доли успехов по дихотомической переменной результата (да / нет) в одной популяции, формула для определения размера выборки:
, где Z — значение из стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (например, Z = 1,96 для 95%), а E — желаемый предел погрешности. p — доля успехов в популяции.Здесь мы планируем исследование для получения 95% доверительного интервала для неизвестной доли населения, p . Уравнение для определения размера выборки для определения p, кажется, требует знания p, но, очевидно, это круговой аргумент, потому что, если бы мы знали долю успехов в популяции, то в исследовании не было бы необходимости! Что нам действительно нужно, так это приблизительное значение p или ожидаемое значение. Диапазон p составляет от 0 до 1, и, следовательно, диапазон p (1-p) составляет от 0 до 1.Значение p, которое максимизирует p (1-p), равно p = 0,5. Следовательно, если нет информации для приближения p, то p = 0,5 можно использовать для получения наиболее консервативного или наибольшего размера выборки.
Пример 2:
Исследователь хочет оценить долю первокурсников в его университете, которые в настоящее время курят сигареты (т. Е. Распространенность курения). Сколько первокурсников должно быть вовлечено в исследование, чтобы гарантировать, что оценка доли курящих первокурсников с доверительным интервалом 95% находится в пределах 5% от истинной доли?
Поскольку у нас нет информации о доле курящих первокурсников, мы используем 0.5 для оценки размера выборки следующим образом:
Чтобы гарантировать, что оценка 95% доверительного интервала доли курящих первокурсников находится в пределах 5% от истинной доли, необходима выборка размером 385.
Предположим, что подобное исследование было проведено 2 года назад и обнаружило, что распространенность курения среди первокурсников составляет 27%. Если исследователь считает, что это разумная оценка распространенности через 2 года, ее можно использовать для планирования следующего исследования.Используя эту оценку p, какой размер выборки необходим (при условии, что снова будет использоваться 95% доверительный интервал и нам нужен такой же уровень точности)?
Ответ
Пример 3:
Исследователь хочет оценить распространенность рака груди среди женщин в возрасте от 40 до 45 лет, проживающих в Бостоне. Сколько женщин должно быть вовлечено в исследование, чтобы оценка была точной? Национальные данные показывают, что к 40 годам у 1 из 235 женщин диагностируется рак груди.Это соответствует доле 0,0043 (0,43%) или 43 на 10 000 женщин. Предположим, исследователь хочет, чтобы оценка была в пределах 10 на 10 000 женщин с достоверностью 95%. Размер выборки рассчитывается следующим образом:
Выборка размером n = 16 448 гарантирует, что оценка распространенности рака груди с доверительным интервалом 95% находится в пределах 0,10 (или в пределах 10 женщин на 10 000) от его истинного значения. Это ситуация, когда исследователи могут решить, что выборка такого размера невозможна.Предположим, что исследователи думали, что выборка размером 5 000 будет разумной с практической точки зрения. Насколько точно мы можем оценить распространенность на выборке размером n = 5000? Напомним, что формула доверительного интервала для оценки распространенности:
.
Предполагая, что распространенность рака груди в выборке будет близка к той, которая основана на национальных данных, мы ожидаем, что предел погрешности будет примерно равен следующему:
Таким образом, при n = 5000 женщин можно ожидать, что 95% доверительный интервал будет иметь погрешность, равную 0.0018 (или 18 на 10 000). Исследователи должны решить, будет ли это достаточно точным, чтобы ответить на исследовательский вопрос. Обратите внимание, что вышеизложенное основано на предположении, что распространенность рака груди в Бостоне аналогична общенациональной. Это может быть, а может и не быть разумным предположением. Фактически, цель настоящего исследования — оценить распространенность в Бостоне. Исследовательская группа при участии клинических исследователей и биостатистов должна тщательно оценить последствия выбора выборки размером n = 5000, n = 16 448 или любого промежуточного размера.
В исследованиях, в которых планируется оценить разницу средних значений между двумя независимыми популяциями, ниже приводится формула для определения размеров выборки в каждой группе сравнения:
, где n i — размер выборки, необходимый в каждой группе (i = 1,2), Z — значение стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться, а E — желаемый предел погрешности. σ снова отражает стандартное отклонение переменной результата.Вспомните из модуля по доверительным интервалам, что, когда мы генерировали оценку доверительного интервала для разницы в средних, мы использовали Sp, объединенную оценку общего стандартного отклонения, как меру изменчивости в результате (на основе объединения данных). , где Sp вычисляется следующим образом:
Если доступны данные о вариабельности результата в каждой группе сравнения, то Sp можно вычислить и использовать в формуле размера выборки. Однако чаще всего данные о вариабельности исходов доступны только по одной группе, часто не получавшей лечения (например,g., плацебо-контроль) или группу, не подвергавшуюся воздействию. При планировании клинического испытания нового препарата или процедуры часто доступны данные из других испытаний, в которых принимали участие плацебо или активная контрольная группа (т. Е. Стандартное лекарство или лечение, назначенное для исследуемого состояния). Стандартное отклонение переменной результата, измеренное у пациентов, отнесенных к группе плацебо, контрольной или неэкспонированной группе, можно использовать для планирования будущего исследования, как показано ниже.
Обратите внимание, что формула размера выборки генерирует оценки размера выборки для выборок равного размера.Если планируется исследование, в котором будет назначено разное количество пациентов или разное количество пациентов будет составлять группы сравнения, тогда можно использовать альтернативные формулы.
Пример 4:
Исследователь хочет запланировать клиническое испытание для оценки эффективности нового препарата, предназначенного для повышения уровня холестерина ЛПВП («хорошего» холестерина). План состоит в том, чтобы зарегистрировать участников и случайным образом распределить их для приема нового препарата или плацебо. Холестерин ЛПВП будет измеряться у каждого участника через 12 недель назначенного лечения.Основываясь на предыдущем опыте проведения подобных исследований, исследователь ожидает, что 10% всех участников будут потеряны для последующего наблюдения или выбыли из исследования в течение 12 недель. Будет рассчитан 95% доверительный интервал для количественной оценки разницы в средних уровнях ЛПВП между пациентами, принимающими новый препарат, по сравнению с плацебо. Исследователь хотел бы, чтобы погрешность была не более 3 единиц. Сколько пациентов следует включить в исследование?
Размеры выборки рассчитываются следующим образом:
Основной проблемой является определение вариабельности интересующего результата (σ), в данном случае стандартного отклонения холестерина ЛПВП.Чтобы спланировать это исследование, мы можем использовать данные Фрамингемского исследования сердца. У участников, которые присутствовали на седьмом обследовании исследования потомства и не лечились от высокого холестерина, стандартное отклонение холестерина ЛПВП составляет 17,1. Мы будем использовать это значение и другие входные данные для вычисления размеров выборки следующим образом:
Образцы размера n 1 = 250 и n 2 = 250 гарантируют, что 95% доверительный интервал для разницы средних уровней ЛПВП будет иметь погрешность не более 3 единиц.Опять же, эти размеры выборки относятся к количеству участников с полными данными. Исследователи предположили, что процент отсева (или отсева) составляет 10% (в обеих группах). Чтобы гарантировать, что общий размер выборки 500 доступен через 12 недель, исследователь должен набрать больше участников, чтобы учесть их выбывание.
N (число для включения) * (% оставшихся) = желаемый размер выборки
Следовательно, N (число для включения) = желаемый размер выборки / (оставшийся%)
N = 500/0.90 = 556
Если они ожидают 10% отсева, исследователи должны зарегистрировать 556 участников. Это обеспечит N = 500 с полными данными в конце испытания.
Пример 5:
Исследователь хочет сравнить две диеты для детей, страдающих ожирением. Одна диета — это диета с низким содержанием жиров, а другая — с низким содержанием углеводов. План состоит в том, чтобы набрать детей и взвесить их в начале исследования. Затем каждому ребенку будет случайным образом назначена диета с низким содержанием жиров или углеводов.Каждый ребенок будет соблюдать назначенную диету в течение 8 недель, после чего они снова будут взвешиваться. Количество потерянных фунтов будет подсчитано для каждого ребенка. Основываясь на данных, полученных в результате испытаний диеты у взрослых, исследователь ожидает, что 20% всех детей не завершат исследование. Для количественной оценки разницы в потерянном весе между двумя диетами будет рассчитан 95% доверительный интервал, и исследователь хотел бы, чтобы погрешность составляла не более 3 фунтов. Сколько детей следует включить в исследование?
Размеры выборки рассчитываются следующим образом:
Опять же, проблема заключается в определении изменчивости интересующего результата (σ), здесь стандартное отклонение в фунтах, потерянных за 8 недель.Чтобы спланировать это исследование, исследователи используют данные опубликованного исследования взрослых. Предположим, что в одном из таких исследований сравнивали одни и те же диеты у взрослых и участвовали по 100 участников в каждой диетической группе. В исследовании сообщалось о стандартном отклонении веса, потерянном за 8 недель на диете с низким содержанием жиров на 8,4 фунта, и о стандартном отклонении веса, потерянном за 8 недель на диете с низким содержанием углеводов, в размере 7,7 фунтов. Эти данные можно использовать для оценки общего стандартного отклонения потери веса следующим образом:
Теперь мы используем это значение и другие входные данные для вычисления размеров выборки:
Образцы размера n 1 = 56 и n 2 = 56 гарантируют, что 95% доверительный интервал для разницы в потерянном весе между диетами будет иметь погрешность не более 3 фунтов.Опять же, эти размеры выборки относятся к количеству детей с полными данными. Исследователи ожидают 20% отсева. Чтобы гарантировать, что общий размер выборки 112 будет доступен через 8 недель, исследователь должен набрать больше участников, чтобы учесть их выбытие.
N (число для включения) * (% оставшихся) = желаемый размер выборки
Следовательно, N (число для включения) = желаемый размер выборки / (оставшийся%)
N = 112 / 0,80 = 140
В исследованиях, в которых планируется оценить среднюю разницу непрерывного результата на основе сопоставленных данных, ниже приводится формула для определения размера выборки:
, где Z — значение стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (например,g., Z = 1,96 для 95%), E — желаемый предел погрешности, а σ d — стандартное отклонение разницы оценок. Чрезвычайно важно, чтобы стандартное отклонение разницы баллов (например, разница, основанная на измерениях с течением времени или разница между согласованными парами) использовалось здесь для надлежащей оценки размера выборки.
В исследованиях, в которых планируется оценить разницу в пропорциях между двумя независимыми популяциями (т.д., для оценки разницы рисков) формула для определения размеров выборки, требуемой в каждой группе сравнения:
, где n i — размер выборки, необходимый в каждой группе (i = 1,2), Z — значение из стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (например, Z = 1,96 для 95%), и E — желаемая погрешность. p 1 и p 2 — это доли успехов в каждой группе сравнения. Опять же, здесь мы планируем исследование для получения 95% доверительного интервала для разницы в неизвестных пропорциях, а формула для оценки необходимых размеров выборки требует p 1 и p 2 .Чтобы оценить размер выборки, нам нужны приблизительные значения p 1 и p 2 . Значения p 1 и p 2 , которые максимизируют размер выборки, равны p 1 = p 2 = 0,5. Таким образом, если нет доступной информации для приближения p 1 и p 2 , то можно использовать 0,5 для создания наиболее консервативных или наибольших размеров выборки.
Подобно ситуации для двух независимых выборок и непрерывного результата в верхней части этой страницы, возможно, имеются данные о доле успешных результатов в одной группе, обычно необработанной (например.g., плацебо-контроль) или группу, не подвергавшуюся воздействию. В таком случае известная пропорция может использоваться как для p 1 , так и для p 2 в приведенной выше формуле. Приведенная выше формула генерирует оценки размера выборки для выборок равного размера. Если планируется исследование, в котором будет назначено разное количество пациентов или разное количество пациентов будет составлять группы сравнения, тогда можно использовать альтернативные формулы. Заинтересованные читатели могут увидеть Флейсс для более подробной информации. 4
Пример 6:
Исследователь хочет оценить влияние курения во время беременности на преждевременные роды.Нормальная беременность длится примерно 40 недель, а преждевременные роды — это те, которые происходят до 37 недель. В отчете Национальной статистики естественного движения населения за 2005 год указывается, что примерно 12% младенцев рождаются преждевременно в Соединенных Штатах. 5 Исследователь планирует собрать данные посредством обзора медицинских карт и создать 95% доверительный интервал для разницы в долях детей, рожденных недоношенными женщинами, которые курили во время беременности, по сравнению с теми, кто этого не сделал. Сколько женщин должно быть включено в исследование, чтобы гарантировать, что 95% доверительный интервал для разницы в пропорциях имеет погрешность не более 4%?
Размеры выборки (т.е., количество женщин, которые курили и не курили во время беременности), можно вычислить по формуле, показанной выше. Национальные данные показывают, что 12% младенцев рождаются преждевременно. Мы будем использовать эту оценку для обеих групп при вычислении размера выборки.
Образцы размера n 1 = 508 женщин, которые курили во время беременности, и n 2 = 508 женщин, которые не курили во время беременности, обеспечат 95% -ный доверительный интервал для разницы в пропорциях преждевременных родов. погрешность не более 4%.
Здесь проблема истощения?
Ответ
В модуле проверки гипотез для средних и пропорций мы представили методы для средних, пропорций, различий в средних и различий в пропорциях. Хотя каждый тест включал детали, которые были специфичны для интересующего результата (например, непрерывный или дихотомический) и для количества групп сравнения (одна, две, более двух), для каждого теста были общие элементы.Например, в каждой проверке гипотезы можно совершить две ошибки. Первая называется ошибкой типа I и относится к ситуации, когда мы неправильно отклоняем H 0 , хотя на самом деле это правда. На первом этапе любой проверки гипотезы мы выбираем уровень значимости, α, и α = P (ошибка типа I) = P (отклонить H 0 | H 0 верно). Поскольку мы намеренно выбираем небольшое значение для α, мы контролируем вероятность совершения ошибки типа I. Второй тип ошибок называется ошибкой типа II и определяется как вероятность того, что мы не отклоним H 0 , если оно ложно.Вероятность ошибки типа II обозначается β, а β = P (ошибка типа II) = P (Не отклонять H 0 | H 0 ложно). При проверке гипотез мы обычно сосредотачиваемся на мощности, которая определяется как вероятность того, что мы отклоним H 0 , когда оно ложно, то есть мощность = 1- β = P (Отклонить H 0 | H 0 ложно ). Мощность — это вероятность того, что тест правильно отклонит ложную нулевую гипотезу. Хороший тест — это тест с низкой вероятностью совершения ошибки типа I (т.е., малое α) и высокое увеличение (то есть малое β, высокое увеличение).
Здесь мы представляем формулы для определения размера выборки, необходимого для обеспечения высокой мощности теста. Вычисления размера выборки зависят от уровня значимости, aα, желаемой мощности теста (эквивалентной 1-β), вариабельности результата и величины эффекта. Величина эффекта — это разница в интересующем параметре, которая представляет собой клинически значимое различие. Подобно пределу погрешности в приложениях с доверительным интервалом, величина эффекта определяется на основе клинических или практических критериев, а не статистических критериев.
Понятие статистической мощности может быть трудным для понимания. Прежде чем представить формулы для определения размеров выборки, необходимых для обеспечения высокой мощности в тесте, мы сначала обсудим мощность с концептуальной точки зрения.
Предположим, мы хотим проверить следующие гипотезы при aα = 0,05: H 0 : μ = 90 по сравнению с H 1 : μ ≠ 90. Чтобы проверить гипотезы, предположим, что мы выбрали выборку размером n = 100. В этом примере предположим, что стандартное отклонение результата составляет σ = 20.Мы вычисляем выборочное среднее, а затем должны решить, предоставляет ли выборочное среднее доказательства в поддержку альтернативной гипотезы или нет. Это делается путем вычисления статистики теста и сравнения статистики теста с соответствующим критическим значением. Если нулевая гипотеза верна (μ = 90), то мы, вероятно, выберем образец, среднее значение которого близко к значению 90. Однако также можно выбрать образец, среднее значение которого намного больше или намного меньше 90. Напомним из Центральной предельной теоремы (см. Стр. 11 в модуле Вероятность), что для больших n (здесь n = 100 достаточно велико) распределение выборочных средних приблизительно нормально со средним значением
и
Если нулевая гипотеза верна, можно наблюдать любое среднее значение выборки, показанное на рисунке ниже; все возможно в рамках H 0 : μ = 90.
Когда мы устанавливаем решающее правило для нашей проверки гипотезы, мы определяем критические значения на основе α = 0,05 и двустороннего теста. Когда мы запускаем проверку гипотез, мы обычно стандартизируем данные (например, конвертируем в Z или t), а критические значения — это соответствующие значения из распределения вероятностей, используемого в тесте. Чтобы облегчить интерпретацию, мы продолжим это обсуждение вместо Z. Критические значения для двустороннего теста с α = 0,05 равны 86.06 и 93,92 (эти значения соответствуют -1,96 и 1,96 соответственно по шкале Z), поэтому правило принятия решения следующее: Отклонить H 0 , если < 86,06 или если > 93,92. Область отклонения показана в хвостах рисунка ниже.
Область отклонения для теста H 0 : μ = 90 по сравнению с H 1 : μ ≠ 90 при α = 0,05
.
Области в двух хвостах кривой представляют вероятность ошибки типа I, α = 0.05. Эта концепция обсуждалась в модуле по проверке гипотез.
Теперь предположим, что альтернативная гипотеза H 1 верна (т. Е. Μ ≠ 90) и что истинное среднее на самом деле составляет 94. На рисунке ниже показаны распределения выборочного среднего при нулевой и альтернативной гипотезах. значения выборочного среднего показаны по горизонтальной оси.
Распределение ниже H 0 : μ = 90 и ниже H 1 : μ = 94
Если истинное среднее значение равно 94, то альтернативная гипотеза верна.В нашем тесте мы выбрали α = 0,05 и отклонили H 0 , если наблюдаемое среднее значение выборки превышает 93,92 (на данный момент фокусируясь на верхнем хвосте области отклонения). Критическое значение (93,92) указано вертикальной линией. Вероятность ошибки типа II обозначается β, а β = P (Не отклонять H 0 | H 0 ложно), то есть вероятность не отклонить нулевую гипотезу, если нулевая гипотеза верна. β показано на рисунке выше как область под крайней правой кривой (H 1 ) слева от вертикальной линии (где мы не отклоняем H 0 ).Мощность определяется как 1- β = P (отклонение H 0 | H 0 неверно) и показано на рисунке как область под крайней правой кривой (H 1 ) справа от вертикальной линии ( где мы отклоняем H 0 ).
Обратите внимание, что β и мощность связаны с α, изменчивостью результата и величиной эффекта. Из рисунка выше мы можем видеть, что произойдет с β и мощностью, если мы увеличим α. Предположим, например, что мы увеличиваем α до α = 0,10. Верхнее критическое значение будет 92.56 вместо 93.92. Вертикальная линия сместится влево, увеличивая α, уменьшая β и увеличивая мощность. Хотя лучший тест — это тест с более высокой мощностью, не рекомендуется увеличивать α как средство увеличения мощности. Тем не менее, существует прямая зависимость между α и мощностью (с увеличением α увеличивается и мощность).
β и мощность также связаны с изменчивостью результата и величиной эффекта. Величина эффекта — это разница в интересующем параметре (например, μ), которая представляет собой клинически значимое различие.На приведенном выше рисунке графически отображаются α, β и степень, когда разница в среднем под нулевым значением по сравнению с альтернативной гипотезой составляет 4 единицы (то есть 90 против 94). На рисунке ниже показаны те же компоненты для ситуации, когда среднее значение согласно альтернативной гипотезе равно 98.
Рисунок — Распределение ниже H 0 : μ = 90 и ниже H 1 : μ = 98.
Обратите внимание на то, что мощность намного выше, когда разница между средним значением H 0 больше по сравнению с H 1 (т.е.э., 90 против 98). Статистический тест с гораздо большей вероятностью отклонит нулевую гипотезу в пользу альтернативы, если истинное среднее значение равно 98, чем если истинное среднее значение равно 94. Также обратите внимание на то, что в этом случае существует небольшое перекрытие в распределениях при нулевой и альтернативной гипотезах. . Если наблюдается выборочное среднее значение 97 или выше, очень маловероятно, что оно получено из распределения, среднее значение которого равно 90. На предыдущем рисунке для H 0 : μ = 90 и H 1 : μ = 94, если мы Наблюдая, например, выборочное среднее значение 93, было бы не так ясно, было ли оно получено из распределения, среднее значение которого равно 90, или того, которое имеет среднее значение 94.
При разработке исследований большинство людей рассматривают степень вероятности 80% или 90% (так же, как мы обычно используем 95% в качестве уровня достоверности для оценок доверительного интервала). Входные данные для формул размера выборки включают желаемую мощность, уровень значимости и размер эффекта. Величина эффекта выбрана так, чтобы представить клинически значимую или практически важную разницу в интересующем параметре, как мы проиллюстрируем.
Формулы, которые мы представляем ниже, определяют минимальный размер выборки, чтобы гарантировать, что проверка гипотезы будет иметь заданную вероятность отклонения нулевой гипотезы, если она ложна (т.е., указанная мощность). Планируя исследования, исследователи снова должны учитывать выбывание или потерю для последующего наблюдения. Формулы, показанные ниже, позволяют определить необходимое количество участников с полными данными, и мы проиллюстрируем, как отсев участников учитывается при планировании исследований.
В исследованиях, в которых планируется провести проверку гипотезы, сравнивая среднее значение переменной непрерывного результата в одной популяции с известным средним значением, представляют интерес гипотезы:
H 0 : μ = μ 0 и H 1 : μ ≠ μ 0 , где μ 0 — известное среднее значение (например,г., исторический контроль). Формула для определения размера выборки, чтобы гарантировать, что тест имеет заданную мощность, приведена ниже:
, где α — выбранный уровень значимости, а Z 1-α / 2 — значение из стандартного нормального распределения, удерживающего 1- α / 2 ниже него. Например, если α = 0,05, то 1- α / 2 = 0,975 и Z = 1,960. 1- β — это выбранная мощность, а Z 1-β — значение из стандартного нормального распределения, при котором 1- β ниже. Оценка размера выборки для проверки гипотез часто основана на достижении 80% или 90% мощности.Значения Z 1-β для этих популярных сценариев приведены ниже:
- Для 80% мощности Z 0,80 = 0,84
- Для мощности 90% Z 0,90 = 1,282
ES — размер эффекта , определяемый следующим образом:
, где μ 0 — среднее значение для H 0 , μ 1 — среднее значение для H 1 , а σ — стандартное отклонение интересующего результата.Числитель величины эффекта, абсолютное значение разницы средних | μ 1 — μ 0 |, представляет собой то, что считается клинически значимым или практически важным различием в средствах. Подобно проблеме, с которой мы столкнулись при планировании исследований для оценки доверительных интервалов, иногда бывает трудно оценить стандартное отклонение. При вычислении размера выборки исследователи часто используют значение стандартного отклонения от предыдущего исследования или исследования, выполненного в другой, но сопоставимой совокупности.Независимо от того, как получается оценка изменчивости результата, она всегда должна быть консервативной (т.е. настолько большой, насколько это разумно), чтобы размер результирующей выборки не был слишком маленьким.
Пример 7:
Исследователь предполагает, что у людей, не страдающих диабетом, уровень глюкозы в крови натощак, фактор риска ишемической болезни сердца, выше у тех, кто пьет не менее 2 чашек кофе в день. Планируется перекрестное исследование для оценки среднего уровня глюкозы в крови натощак у людей, которые пьют не менее двух чашек кофе в день.Средний уровень глюкозы в крови натощак у людей, не страдающих диабетом, составляет 95,0 мг / дл со стандартным отклонением 9,8 мг / дл. 7 Если средний уровень глюкозы в крови у людей, выпивающих не менее 2 чашек кофе в день, составляет 100 мг / дл, это будет иметь клиническое значение. Сколько пациентов следует включить в исследование, чтобы убедиться, что мощность теста составляет 80% для выявления этой разницы? Будет использоваться двусторонний тест с уровнем значимости 5%.
Размер эффекта рассчитывается как:
.
Размер эффекта представляет собой значимую разницу в среднем генеральной совокупности — здесь 95 против 100 или 0,51 единицы стандартного отклонения. Теперь мы заменим размер эффекта и соответствующие значения Z на выбранные α и мощность, чтобы вычислить размер выборки.
Таким образом, выборка размером n = 31 гарантирует, что двусторонний тест с α = 0,05 будет иметь 80% -ную мощность для обнаружения разницы в 5 мг / дл в средних уровнях глюкозы в крови натощак.
В запланированном исследовании участников попросят голодать в течение ночи и сдать образец крови для анализа уровня глюкозы.Основываясь на предыдущем опыте, исследователи предполагают, что 10% участников не будут голодать или откажутся соблюдать протокол исследования. Таким образом, в исследование будут включены в общей сложности 35 участников, чтобы обеспечить доступность 31 для анализа (см. Ниже).
N (число для включения) * (%, соблюдающие протокол) = желаемый размер выборки
Следовательно, N (число для включения) = желаемый размер выборки / (оставшийся%)
N = 31 / 0,90 = 35.
В исследованиях, в которых планируется провести проверку гипотезы, сравнивая долю успехов в переменной дихотомического результата в одной популяции с известной долей, представляют интерес гипотезы:
против
, где p 0 — известная пропорция (т.е.г., исторический контроль). Формула для определения размера выборки для обеспечения заданной мощности теста приведена ниже:
, где α — выбранный уровень значимости, а Z 1-α / 2 — значение из стандартного нормального распределения, удерживающего 1- α / 2 ниже него. 1- β — выбранная мощность, а Z 1-β — значение из стандартного нормального распределения, удерживающее 1- β ниже него, а ES — величина эффекта, определяемая следующим образом:
, где p 0 — пропорция согласно H 0 , а p 1 — пропорция согласно H 1 .Числитель величины эффекта, абсолютное значение разницы в пропорциях | p 1 -p 0 |, снова представляет то, что считается клинически значимой или практически важной разницей в пропорциях.
Пример 8:
Недавний отчет Фрамингемского исследования сердца показал, что 26% людей, не страдающих сердечно-сосудистыми заболеваниями, имели повышенный уровень холестерина ЛПНП, определяемый как ЛПНП> 159 мг / дл. 9 Исследователь предполагает, что более высокая доля пациентов с сердечно-сосудистыми заболеваниями в анамнезе будет иметь повышенный холестерин ЛПНП.Сколько пациентов следует обследовать, чтобы убедиться, что мощность теста составляет 90%, чтобы обнаружить разницу в 5% в пропорции с повышенным холестерином ЛПНП? Будет использоваться двусторонний тест с уровнем значимости 5%.
Сначала вычисляем размер эффекта:
Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранного α и мощности, чтобы вычислить размер выборки.
Выборка размером n = 869 обеспечит двусторонний тест с α = 0.05 имеет 90% -ную мощность для обнаружения 5% -ной разницы в доле пациентов с сердечно-сосудистыми заболеваниями в анамнезе, у которых повышен уровень холестерина ЛПНП.
Производитель медицинского оборудования производит имплантируемые стенты. В процессе производства приблизительно 10% стентов считаются дефектными. Производитель хочет проверить, не превышает ли доля дефектных стентов 10%. Если в результате процесса образуется более 15% дефектных стентов, необходимо предпринять корректирующие действия.Поэтому производитель хочет, чтобы тест имел мощность 90%, чтобы обнаруживать разницу в пропорциях такой величины. Сколько стентов необходимо оценить? Для расчетов используйте двусторонний тест с уровнем значимости 5%. (Проведите вычисления самостоятельно, прежде чем смотреть ответ.)
Ответ
В исследованиях, в которых планируется провести проверку гипотезы, сравнивая средние значения непрерывной переменной результата в двух независимых популяциях, представляют интерес гипотезы:
против
, где μ 1 и μ 2 — средние значения в двух сравниваемых популяциях.Формула для определения размеров выборки для обеспечения заданной мощности теста:
, где n i — размер выборки, необходимый в каждой группе (i = 1,2), α — выбранный уровень значимости, а Z 1-α / 2 — значение из стандартного нормального распределения, содержащего 1- α. / 2 ниже, а 1- β — выбранная степень, а Z 1-β — значение из стандартного нормального распределения, удерживающего 1- β ниже него. ES — размер эффекта, определяемый как:
где | μ 1 — μ 2 | — абсолютное значение разницы в средних между двумя группами, ожидаемая согласно альтернативной гипотезе, H 1 .σ — стандартное отклонение интересующего результата. Напомним из модуля по проверке гипотез, когда мы выполняли тесты гипотез, сравнивая средние значения двух независимых групп, мы использовали Sp, объединенную оценку общего стандартного отклонения, как меру изменчивости результата.
Sp рассчитывается следующим образом:
Если доступны данные о вариабельности результата в каждой группе сравнения, то Sp можно вычислить и использовать для генерации размеров выборки.Однако чаще всего данные о вариабельности исходов доступны только по одной группе, обычно необработанной (например, контрольная группа плацебо) или группе, не подвергавшейся воздействию. При планировании клинического испытания нового препарата или процедуры часто доступны данные из других испытаний, которые могли включать плацебо или активную контрольную группу (т. Е. Стандартное лекарство или лечение, назначенное для исследуемого состояния). Стандартное отклонение переменной результата, измеренной у пациентов, отнесенных к группе плацебо, контрольной или неэкспонированной группе, можно использовать для планирования будущего исследования, как показано.
Также обратите внимание, что приведенная выше формула генерирует оценки размера выборки для выборок равного размера. Если планируется исследование, в котором будет назначено разное количество пациентов или разное количество пациентов будет составлять группы сравнения, тогда можно использовать альтернативные формулы (более подробную информацию см. В Howell 3 ).
Пример 9:
Исследователь планирует клиническое испытание для оценки эффективности нового препарата, предназначенного для снижения систолического артериального давления.План состоит в том, чтобы зарегистрировать участников и случайным образом распределить их для приема нового препарата или плацебо. Систолическое артериальное давление будет измеряться у каждого участника через 12 недель назначенного лечения. Основываясь на предыдущем опыте проведения подобных исследований, исследователь ожидает, что 10% всех участников будут потеряны для последующего наблюдения или выбыли из исследования. Если новый препарат показывает снижение среднего систолического артериального давления на 5 единиц, это будет представлять собой клинически значимое снижение. Сколько пациентов следует включить в исследование, чтобы убедиться, что мощность теста составляет 80% для выявления этой разницы? Будет использоваться двусторонний тест с уровнем значимости 5%.
Чтобы вычислить величину эффекта, необходима оценка вариабельности систолического артериального давления. Анализ данных Framingham Heart Study показал, что стандартное отклонение систолического артериального давления составило 19,0. Это значение можно использовать для планирования испытания.
Размер эффекта:
Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранного α и мощности, чтобы вычислить размер выборки.
Образцы размером n 1 = 232 и n 2 = 232 гарантируют, что проверка гипотезы будет иметь мощность 80% для обнаружения разницы в 5 единиц среднего систолического артериального давления у пациентов, принимающих новый препарат, по сравнению с пациентами. получение плацебо.Тем не менее, исследователи предположили, что показатель отсева составляет 10% (в обеих группах), и чтобы обеспечить общий размер выборки 232, они должны учитывать отсев.
N (число для включения) * (% оставшихся) = желаемый размер выборки
Следовательно, N (число для включения) = желаемый размер выборки / (оставшийся%)
N = 232 / 0,90 = 258.
Исследователь должен набрать 258 участников, которые будут случайным образом распределены для приема нового препарата или плацебо.
Исследователь планирует исследование для оценки связи между потреблением алкоголя и средним баллом среди выпускников колледжа.План состоит в том, чтобы классифицировать студентов как сильно пьющих или не употребляющих 5 или более напитков в обычный день выпивки в качестве критерия алкоголя. Средние средние баллы будут сравниваться между учащимися, отнесенными к категории сильно пьющих, по сравнению с не использующими две независимые выборки проверки средних значений. Предполагается, что стандартное отклонение средних баллов составляет 0,42, а значимая разница в средних баллах (относительно статуса потребления алкоголя) составляет 0,25 единицы. Сколько выпускников колледжа должны быть включены в исследование, чтобы убедиться, что мощность теста составляет 80% для определения 0.25 единиц разницы в среднем среднем балле? Используйте двусторонний тест с уровнем значимости 5%.
Ответ
В исследованиях, в которых планируется провести проверку гипотезы о средней разнице в непрерывной переменной результата на основе сопоставленных данных, представляют интерес гипотезы:
против
, где μ d — средняя разница в генеральной совокупности. Формула для определения размера выборки для обеспечения заданной мощности теста приведена ниже:
, где α — выбранный уровень значимости, а Z 1-α / 2 — значение из стандартного нормального распределения, удерживающего 1- α / 2 ниже него, 1- β — выбранная степень, а Z 1-β — значение из стандартного нормального распределения, удерживающее 1- β ниже него, а ES — величина эффекта, определяемая следующим образом:
, где μ d — средняя разница, ожидаемая согласно альтернативной гипотезе, H 1 , а σ d — стандартное отклонение разницы в результате (например,g., разница, основанная на измерениях с течением времени или разница между согласованными парами).
Пример 10:
Исследователь хочет оценить эффективность лечения иглоукалыванием для уменьшения боли у пациентов с хронической мигренью. Планируется набор пациентов, страдающих мигренью. Каждого перед тем, как назначить какое-либо лечение, попросят оценить серьезность боли, которую он испытывает при следующей мигрени.Боль будет регистрироваться по шкале от 1 до 100, причем более высокие баллы указывают на более сильную боль. Затем каждый пациент будет проходить курс лечения иглоукалыванием. При следующей мигрени (после лечения) каждого пациента снова попросят оценить тяжесть боли. Разница в боли будет рассчитана для каждого пациента. Будет проведена двусторонняя проверка гипотезы при α = 0,05, чтобы оценить, существует ли статистически значимая разница в оценке боли до и после лечения. Сколько пациентов должно быть вовлечено в исследование, чтобы убедиться, что тест имеет мощность 80% для определения разницы в 10 единиц по шкале боли? Предположим, что стандартное отклонение разницы оценок составляет примерно 20 единиц.
Сначала вычислите размер эффекта:
Затем подставьте размер эффекта и соответствующие значения Z для выбранного α и мощности, чтобы вычислить размер выборки.
Выборка размером n = 32 пациента с мигренью гарантирует, что двусторонний тест с α = 0,05 будет иметь 80% мощность для определения средней разницы в 10 баллов боли до и после лечения, при условии, что все 32 пациента завершили лечение. .
В исследованиях, в которых планируется провести проверку гипотезы, сравнивая пропорции успехов в двух независимых популяциях, представляют интерес гипотезы:
H 0 : p 1 = p 2 по сравнению с H 1 : p 1 ≠ p 2
, где p 1 и p 2 — пропорции в двух сравниваемых популяциях.Формула для определения размеров выборки для обеспечения заданной мощности теста приведена ниже:
, где n i — размер выборки, необходимый в каждой группе (i = 1,2), α — выбранный уровень значимости, а Z 1-α / 2 — значение из стандартного нормального распределения, содержащего 1- α. / 2 под ним, а 1- β — выбранная степень, а Z 1-β — значение из стандартного нормального распределения, удерживающего 1- β под ним. ES — величина эффекта, определяемая следующим образом:
,
, где | p 1 — p 2 | — абсолютное значение разницы в пропорциях между двумя группами, ожидаемых согласно альтернативной гипотезе, H 1 , а p — общая пропорция, основанная на объединении данных из двух групп сравнения (p можно вычислить, взяв среднее значение пропорций в двух группах сравнения, предполагая, что группы будут примерно одинакового размера).
Пример 11:
Исследователь выдвинул гипотезу о более высокой заболеваемости гриппом среди студентов, регулярно пользующихся спортивными сооружениями, чем среди их сверстников, которые этого не делают. Исследование будет проведено весной. Каждого ученика спросят, пользовались ли они спортивным сооружением регулярно в течение последних 6 месяцев и не болели ли они гриппом. Будет проведена проверка гипотезы для сравнения доли студентов, которые регулярно использовали спортивные сооружения и заболели гриппом, с долей студентов, которые этого не сделали и заболели гриппом.В течение обычного года примерно 35% студентов болеют гриппом. Исследователи считают, что увеличение заболеваемости гриппом на 30% среди тех, кто регулярно пользовался спортивным сооружением, было бы клинически значимым. Сколько студентов должно быть привлечено к исследованию, чтобы убедиться, что мощность теста составляет 80%, чтобы обнаружить эту разницу в пропорциях? Будет использоваться двусторонний тест с уровнем значимости 5%.
Сначала мы вычисляем размер эффекта, подставляя доли учащихся в каждой группе, у которых ожидается развитие гриппа, p 1 = 0.46 (т.е. 0,35 * 1,30 = 0,46) и p 2 = 0,35, а общая пропорция, p = 0,41 (т.е. (0,46 + 0,35) / 2):
Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранного α и мощности, чтобы вычислить размер выборки.
Выборки размера n 1 = 324 и n 2 = 324 гарантируют, что проверка гипотезы будет иметь 80% -ную мощность для выявления 30% -ной разницы в доле учащихся, заболевших гриппом, между теми, кто болеет, и не болеет. регулярно пользоваться спортивными сооружениями.
Донорские фекалии? Действительно? Clostridium difficile (также называемая «C. difficile» или «C. diff.») Представляет собой бактериальный вид, который можно найти в толстой кишке человека, хотя его численность контролируется другой нормальной флорой толстой кишки. Антибактериальная терапия иногда снижает нормальную флору в толстой кишке до такой степени, что процветает C. difficile и вызывает инфекцию с симптомами, варьирующимися от диареи до опасного для жизни воспаления толстой кишки. Болезнь от C.difficile чаще всего поражает пожилых людей в больницах или учреждениях длительного ухода и обычно возникает после приема антибиотиков. В последние годы инфекции, вызванные C. difficile, стали более частыми, тяжелыми и трудно поддающимися лечению. По иронии судьбы, C. difficile сначала лечится путем прекращения приема антибиотиков, если они все еще назначаются. Если это не помогло, инфекцию вылечили путем перехода на другой антибиотик. Однако лечение другим антибиотиком часто не излечивает C.difficile. Были спорадические сообщения об успешном лечении путем вливания фекалий здоровых доноров в двенадцатиперстную кишку пациентов, страдающих C. difficile. (Юк!) Это восстанавливает нормальную микробиоту в толстой кишке и противодействует чрезмерному росту C. diff. Эффективность этого подхода была проверена в рандомизированном клиническом исследовании, опубликованном в Медицинском журнале Новой Англии (январь 2013 г.). Исследователи планировали случайным образом распределить пациентов с рецидивирующей инфекцией C. difficile либо на антибактериальную терапию, либо на дуоденальную инфузию донорских фекалий.Чтобы оценить размер необходимой пробы, исследователи предположили, что инфузия кала будет успешной в 90% случаев, а терапия антибиотиками будет успешной в 60% случаев. Сколько субъектов потребуется в каждой группе, чтобы гарантировать, что мощность исследования составляет 80% с уровнем значимости α = 0,05?
Ответ
Определение подходящего дизайна исследования более важно, чем статистический анализ; плохо спланированное исследование никогда нельзя спасти, тогда как плохо проанализированное исследование можно повторно проанализировать.Важнейшим компонентом дизайна исследования является определение подходящего размера выборки. Размер выборки должен быть достаточно большим, чтобы адекватно ответить на вопрос исследования, но не слишком большим, чтобы охватить слишком много пациентов, когда было бы достаточно меньшего. Определение подходящего размера выборки включает статистические критерии, а также клинические или практические соображения. Определение размера выборки требует совместной работы; Биостатисты должны работать в тесном сотрудничестве с клиническими исследователями, чтобы определить размер выборки, которая позволит решить интересующий вопрос исследования с достаточной точностью или мощностью для получения клинически значимых результатов.
В следующей таблице приведены формулы размера выборки для каждого описанного здесь сценария. Формулы организованы по предлагаемому анализу, оценке доверительного интервала или проверке гипотез.
|
Ситуация |
Размер выборки до Оценка доверительного интервала |
Размер выборки для проверки гипотезы |
|---|---|---|
|
Непрерывный результат, Один образец: CI для μ, H 0 : μ = μ 0 |
|
|
|
Непрерывный результат, Два независимых образца: CI для (μ 1 -μ 2 ), H 0 : μ 1 = μ 2 |
|
|
|
Непрерывный результат, Два совпадающих образца: CI для μ d , H 0 : μ d = 0 |
|
|
|
Дихотомический результат, Один образец: CI для p, H 0 : p = p 0 |
|
|
|
Дихотомический результат, Два независимых образца: CI для (p 1 -p 2 ), H 0 : p 1 = p 2 |
|
|
- Бушман Н.А., Фостер Дж., Викерс П.Девочки-подростки и их дети: достижение оптимальной массы тела при рождении. Гестационная прибавка в весе и исход беременности с точки зрения гестации при родах и веса новорожденного: сравнение между подростками до 16 лет и взрослыми женщинами. Ребенок: уход, здоровье и развитие. 2001; 27 (2): 163-171.
- Feuer EJ, Wun LM. ДЕВКАН: Вероятность развития или смерти от рака. Версия 4.0 .Bethesda, MD: Национальный институт рака, 1999.
- Хауэлл, округ Колумбия. Статистические методы психологии.Бостон, Массачусетс: Duxbury Press, 1982.
- Fleiss JL. Статистические методы расчета ставок и пропорций. Нью-Йорк, штат Нью-Йорк: John Wiley and Sons, Inc., 1981.
- Национальный центр статистики здравоохранения. Здоровье, США, 2005 г., с диаграммой тенденций в области здоровья американцев. Хяттсвилл, Мэриленд: Типография правительства США; 2005.
- Пласкон Л.А., Пенсон Д.Ф., Воган Т.Л., Стэнфордский университет. Курение сигарет и риск рака простаты у мужчин среднего возраста. Биомаркеры и профилактика эпидемиологии рака.2003; 12: 604-609.
- Rutter MK, Meigs JB, Sullivan LM, D’Agostino RB, Wilson PW. C-реактивный белок, метаболический синдром и прогноз сердечно-сосудистых событий в исследовании Framingham Offspring Study. Тираж. 2004; 110: 380-385.
- Рамачандран В., Салливан Л.М., Уилсон П.В., Семпос, Т.Т., Сандстрем Дж., Каннел В.Б., Леви Д., Д’Агостино, РБ. Относительное значение пограничных и повышенных уровней факторов риска ишемической болезни сердца. Анналы внутренней медицины. 2005; 142: 393-402.
- Векслер Х., Ли Дж. Э., Куо М., Ли Х. Выпивка в колледже в 1990-е годы: постоянная проблема Результаты Гарвардской школы общественного здравоохранения, 1999 г., Здоровье колледжей, 2000 г .; 48: 199-210.
Ответ на вопрос о массе тела при рождении — стр. 3
Исследователь хочет оценить средний вес при рождении доношенных детей (примерно 40 недель беременности) от матерей в возрасте 19 лет и младше. Средний вес новорожденных, рожденных доношенными от матерей в возрасте 20 лет и старше, составляет 3 510 граммов со стандартным отклонением 385 граммов.Сколько женщин в возрасте 19 лет и младше должны быть включены в исследование, чтобы гарантировать, что 95% -ный доверительный интервал оценки средней массы тела при рождении их младенцев имеет погрешность, не превышающую 100 граммов?
Чтобы гарантировать, что оценка среднего веса при рождении с доверительным интервалом 95% находится в пределах 100 граммов от истинного среднего, необходима выборка размером 57. При планировании исследования исследователь должен учитывать тот факт, что у некоторых женщин могут возникать преждевременные роды.Если женщины будут включены в исследование во время беременности, то необходимо будет включить в исследование более 57 женщин, чтобы после исключения преждевременных родов 57 женщин с информацией о результатах были доступны для анализа. Например, если ожидается, что 5% женщин родят преждевременные роды (т. Е. 95% родят доношенными), то необходимо включить 60 женщин, чтобы гарантировать, что 57 роды будут доношенными. Количество женщин, которые должны быть зачислены, N, рассчитывается следующим образом:
N (число для включения) * (% оставшихся) = желаемый размер выборки
N (0.95) = 57
N = 57 / 0,95 = 60,
Ответ первокурсников о курении — стр. 4
Предположим, что подобное исследование было проведено 2 года назад и обнаружило, что распространенность курения среди первокурсников составляет 27%. Если исследователь считает, что это разумная оценка распространенности через 2 года, ее можно использовать для планирования следующего исследования. Используя эту оценку p, какой размер выборки необходим (при условии, что снова будет использоваться 95% доверительный интервал и нам нужен такой же уровень точности)?
Чтобы гарантировать, что 95% доверительный интервал оценки доли курящих первокурсников находится в пределах 5% от истинной доли, необходима выборка размером 303.Обратите внимание, что этот размер выборки существенно меньше, чем рассчитанный выше. Наличие некоторой информации о величине доли в генеральной совокупности всегда дает размер выборки, который меньше или равен тому, который основан на доле генеральной совокупности 0,5. Однако оценка должна быть реалистичной.
Ответ на проблему с медицинским устройством — страница 7
Производитель медицинского оборудования производит имплантируемые стенты. В процессе производства приблизительно 10% стентов считаются дефектными.Производитель хочет проверить, не превышает ли доля дефектных стентов 10%. Если в результате процесса образуется более 15% дефектных стентов, необходимо предпринять корректирующие действия. Поэтому производитель хочет, чтобы тест имел мощность 90%, чтобы обнаруживать разницу в пропорциях такой величины. Сколько стентов необходимо оценить? Для расчетов используйте двусторонний тест с уровнем значимости 5%.
Затем подставьте размер эффекта и соответствующие значения z для выбранных альфа и мощности, чтобы вычислить размер выборки.
Размер выборки из 364 стентов гарантирует, что двусторонний тест с α = 0,05 будет иметь мощность 90% для обнаружения 0,05 или 5% разницы в пропорции произведенных дефектных стентов.
Ответ на алкоголь и средний балл — страница 8
Исследователь планирует исследование для оценки связи между потреблением алкоголя и средним баллом среди выпускников колледжа. План состоит в том, чтобы классифицировать студентов как сильно пьющих или не употребляющих 5 или более напитков в обычный день выпивки в качестве критерия алкоголя.Средние средние баллы будут сравниваться между учащимися, отнесенными к категории сильно пьющих, по сравнению с не использующими две независимые выборки проверки средних значений. Предполагается, что стандартное отклонение средних баллов составляет 0,42, а значимая разница в средних баллах (относительно статуса потребления алкоголя) составляет 0,25 единицы. Сколько выпускников колледжа должны быть включены в исследование, чтобы убедиться, что мощность теста составляет 80%, чтобы обнаружить разницу в 0,25 единицы в средних средних баллах? Используйте двусторонний тест с уровнем значимости 5%.
Сначала вычислите размер эффекта.
Теперь замените размер эффекта и соответствующие значения z на альфа и мощность, чтобы вычислить размер выборки.
Размер выборки n i = 44 сильно пьющих и 44, которые выпивают менее пяти напитков за обычный день, гарантирует, что проверка гипотезы будет иметь 80% -ную мощность для выявления разницы в 0,25 единицы средних средних баллов.
Ответ на донорские фекалии — страница 8
Сначала мы вычисляем величину эффекта, подставляя доли пациентов, которые, как ожидается, будут излечены при каждом лечении, p 1 = 0.6 и p 2 = 0,9, а общая пропорция p = 0,75:
Теперь мы заменяем размер эффекта и соответствующие значения Z на выбранные a и мощность, чтобы вычислить размер выборки.
Образцы размера n 1 = 33 и n 2 = 33 гарантируют, что проверка гипотезы будет иметь 80% -ную мощность для обнаружения этой разницы в долях пациентов, излечившихся от C. diff. инфузией кала по сравнению с терапией антибиотиками.
Фактически, исследователи включили по 38 в каждую группу, чтобы учесть отсев. Тем не менее, после промежуточного анализа исследование было остановлено. Из 16 пациентов в группе инфузии у 13 (81%) отмечалось исчезновение диареи, связанной с C. difficile, после первой инфузии. Остальным 3 пациентам была проведена вторая инфузия с фекалиями от другого донора с разрешением у 2 пациентов. Излечение C. difficile произошло только у 4 из 13 пациентов (31%), получавших антибиотик ванкомицин.
Введение в оценку мощности и размера выборки
ЦЕЛИ
-
Понимание оценки мощности и размера выборки.
-
Поймите, почему мощность является важной частью как дизайна исследования, так и анализа.
-
Поймите разницу между расчетами размера выборки в сравнительных и диагностических исследованиях.
-
Узнайте, как выполнить расчет размера выборки.
-
— (a) Для непрерывных данных
-
— (b) Для прерывистых данных
-
— (c) Для диагностических тестов
-
МОЩНОСТЬ И ОЦЕНКА РАЗМЕРА ОБРАЗЦА
Оценка мощности и размера выборки является мерой того, сколько пациентов необходимо для исследования.Практически все клинические исследования предполагают изучение выборки пациентов с определенной характеристикой, а не всей популяции. Затем мы используем эту выборку, чтобы сделать выводы обо всей совокупности.
В предыдущих статьях серии по статистике, опубликованной в этом журнале, статистический вывод использовался, чтобы определить, верны ли найденные результаты или, возможно, только случайно. Ясно, что мы можем уменьшить вероятность того, что наши результаты будут получены случайно, устранив предвзятость в дизайне исследования, используя такие методы, как рандомизация, ослепление и т. Д.Однако на возможность того, что наши результаты могут быть неверными, влияет другой фактор — количество обследованных пациентов. Интуитивно мы предполагаем, что чем больше доля исследуемой популяции, тем ближе мы подойдем к истинному ответу для этой популяции. Но скольких нам нужно изучить, чтобы как можно ближе подойти к правильному ответу?
ЧТО ТАКОЕ МОЩНОСТЬ И ПОЧЕМУ ЭТО ВАЖНО?
Оценка мощности и размера выборки используется исследователями для определения количества субъектов, необходимых для ответа на исследовательский вопрос (или нулевую гипотезу).
Примером может служить тромболизис при остром инфаркте миокарда (ОИМ). В течение многих лет врачи считали, что это лечение принесет пользу, учитывая предполагаемую этиологию ОИМ, однако последовательные исследования не подтвердили этот факт. Только после завершения «мега-испытаний» с достаточной мощностью было доказано небольшое, но важное преимущество тромболизиса.
Как правило, в этих испытаниях сравнивали тромболизис с плацебо, и часто в качестве основного критерия оценки исхода использовалась смертность через определенное количество дней.Основная гипотеза исследований могла заключаться в сравнении, например, смертности от тромболизиса на 21 день по сравнению с плацебо. Тогда есть две гипотезы, которые нам нужно рассмотреть:
-
Нулевая гипотеза состоит в том, что нет разницы между видами лечения с точки зрения смертности.
-
Альтернативная гипотеза состоит в том, что существует разница между методами лечения с точки зрения смертности.
Пытаясь определить, являются ли две группы одинаковыми (принимая нулевую гипотезу) или они разные (принимая альтернативную гипотезу), мы потенциально можем допустить два вида ошибок.Они называются ошибкой типа I и ошибкой типа II.
Считается, что ошибка типа I возникла, когда мы неверно отклонили нулевую гипотезу (то есть она верна и между двумя группами нет разницы) и сообщаем о различии между двумя изучаемыми группами.
Считается, что ошибка типа II возникает, когда мы принимаем нулевую гипотезу неправильно (то есть она ложна и существует разница между двумя группами, которая является альтернативной гипотезой) и сообщаем, что между двумя группами нет никакой разницы.
Их можно представить в виде таблицы два на два (таблица 1).
Расчеты мощности говорят нам, сколько пациентов необходимо, чтобы избежать ошибок типа I или типа II.
Термин «мощность» обычно используется в отношении всех оценок размера выборки в исследованиях. Строго говоря, «мощность» означает количество пациентов, необходимое для того, чтобы избежать ошибки типа II в сравнительном исследовании. Оценка размера выборки — это более всеобъемлющий термин, который рассматривает больше, чем просто ошибку типа II, и применим ко всем типам исследований.В просторечии эти термины используются как синонимы.
ЧТО ВЛИЯЕТ НА МОЩНОСТЬ ИССЛЕДОВАНИЯ?
Есть несколько факторов, которые могут повлиять на силу исследования. Это следует учитывать на ранней стадии разработки исследования. Некоторые факторы мы контролируем, другие — нет.
Точность и дисперсия измерений в пределах любого образца
Почему исследование может не найти разницы, если она действительно есть? Для любого данного результата от выборки пациентов мы можем определить только распределение вероятностей вокруг этого значения, которое подскажет, где находится истинное значение для популяции.Самый известный пример этого — 95% доверительный интервал. Размер доверительного интервала обратно пропорционален количеству изучаемых предметов. Таким образом, чем больше людей мы изучаем, тем точнее мы можем определить истинную ценность населения.
Рисунок 1 показывает, что для одного измерения, чем больше предметов изучается, тем уже становится распределение вероятностей. В группе 1 среднее значение равно 5 с широкими доверительными интервалами (3–7). Удвоив количество обследованных пациентов (но в нашем примере сохранив те же значения), доверительные интервалы сузились (3.5–6.5), что дает более точную оценку истинного среднего значения по совокупности.
Рисунок 1Изменение ширины доверительного интервала с увеличением числа испытуемых.
Распределение вероятности того, где находится истинное значение, является неотъемлемой частью большинства статистических тестов для сравнения между группами (например, t тестов). Исследование с небольшим размером выборки будет иметь большие доверительные интервалы и будет отображаться как статистически ненормальное, только если между двумя группами существует большая разница.На рисунке 2 показано, как увеличение числа испытуемых может дать более точную оценку различий.
Рисунок 2Эффект уменьшения доверительного интервала для демонстрации истинной разницы в средних. Этот пример показывает, что первоначальное сравнение между группами 1 и 3 не показало статистической разницы, поскольку доверительные интервалы перекрывались. В 3-й и 4-й группах количество пациентов увеличилось вдвое (хотя среднее значение осталось прежним). Мы видим, что доверительные интервалы больше не перекрываются, указывая на то, что разница в средних вряд ли произошла случайно.
Величина клинически значимой разницы
Если мы пытаемся обнаружить очень небольшие различия между видами лечения, требуются очень точные оценки истинной численности населения. Это связано с тем, что нам необходимо очень точно определить истинное значение населения для каждой группы лечения. И наоборот, если мы обнаруживаем или ищем большую разницу, может быть приемлемо довольно широкое распределение вероятностей.
Другими словами, если мы ищем большую разницу между методами лечения, мы можем принять широкое распределение вероятностей, если мы хотим обнаружить небольшую разницу, нам потребуются большая точность и малые распределения вероятностей.Поскольку ширина вероятностных распределений в значительной степени определяется тем, сколько предметов мы изучаем, очевидно, что искомая разница влияет на расчеты размера выборки.
Факторы, влияющие на расчет мощности
-
Точность и дисперсия измерений в пределах любого образца
-
Величина клинически значимой разницы
-
Насколько мы уверены, чтобы избежать ошибки типа 1
-
Тип статистического теста, который мы проводим
При сравнении двух или более образцов мы обычно мало контролируем размер эффекта.Однако нам нужно убедиться, что разницу стоит обнаружить. Например, можно разработать исследование, которое продемонстрирует сокращение времени начала местной анестезии с 60 до 59 секунд, но такая небольшая разница не будет иметь клинического значения. И наоборот, исследование, демонстрирующее разницу от 60 секунд до 10 минут, однозначно будет. Определение «клинически важного различия» является ключевым компонентом расчета размера выборки.
Насколько важна ошибка типа I или типа II для рассматриваемого исследования?
Мы можем указать, насколько мы должны быть обеспокоены, чтобы избежать ошибок типа I или типа II.Считается, что ошибка типа I возникла, когда мы неверно отклонили нулевую гипотезу. Обычно мы выбираем вероятность ошибки I типа <0,05. Это означает, что если мы найдем положительный результат, шансы найти это (или большую разницу) будут менее чем в 5% случаев. Этот показатель, или уровень значимости, обозначается как pα и обычно устанавливается нами заранее на ранних этапах планирования исследования при выполнении расчета размера выборки. По соглашению, а не по замыслу, мы чаще выбираем 0.05. Чем ниже уровень значимости, тем ниже мощность, поэтому использование 0,01 соответственно уменьшит нашу мощность.
(Чтобы избежать ошибки типа I — то есть, если мы найдем положительный результат, шансы обнаружить это или большую разницу будут иметь место менее чем в α% случаев)
Считается, что ошибка типа II возникает, когда мы неправильно принимаем нулевую гипотезу и сообщаем об отсутствии разницы между двумя группами. Если действительно существует разница между вмешательствами, мы выражаем вероятность получения ошибки типа II и то, насколько вероятно, что мы ее обнаружим.Этот рисунок обозначается как pβ. Существует меньше договоренностей относительно принятого уровня pβ, но цифры 0,8–0,9 являются общими (то есть, если разница действительно существует между вмешательствами, то мы обнаружим ее в 80–90% случаев).
Предотвращение ошибки типа II — суть расчетов мощности. Мощность исследования pβ — это вероятность того, что исследование обнаружит заранее определенную разницу в измерениях между двумя группами, если она действительно существует, при заданном значении pα и размере выборки N.
Тип статистического теста, который мы проводим
Расчеты размера выборки показывают, как вероятнее всего будут работать статистические тесты, использованные в исследовании. Поэтому неудивительно, что тип используемого теста влияет на то, как рассчитывается размер выборки. Например, параметрические тесты лучше при обнаружении различий между группами, чем непараметрические тесты (именно поэтому мы часто пытаемся преобразовать базовые данные в нормальные распределения). Следовательно, для анализа, основанного на непараметрическом тесте (например, Mann-Whitney U), потребуется больше пациентов, чем один на основе параметрического теста (например, тест Стьюдента t ).
СЛЕДУЕТ ВЫПОЛНЯТЬ РАСЧЕТ РАЗМЕРА ОБРАЗЦА ДО ИЛИ ПОСЛЕ ИССЛЕДОВАНИЯ?
Ответ определенно до, иногда во время, а иногда и после.
При разработке исследования мы хотим удостовериться, что проделанная нами работа стоит того, чтобы получить правильный ответ и получить его наиболее эффективным способом. Это делается для того, чтобы мы могли набрать достаточно пациентов, чтобы наши результаты были адекватными, но не слишком много, чтобы мы тратили время на получение большего количества данных, чем нам нужно.К сожалению, при разработке исследования нам, возможно, придется сделать предположения о желаемой величине эффекта и дисперсии данных.
Промежуточные расчеты мощности используются иногда, когда известно, что данные, использованные в исходных расчетах, сомнительны. Их следует использовать с осторожностью, поскольку повторный анализ может привести к тому, что исследователь остановит исследование, как только будет получена статистическая значимость (что может произойти случайно несколько раз во время набора субъектов). Как только исследование начнется, можно будет использовать анализ промежуточных результатов для выполнения дальнейших расчетов мощности и внесения соответствующих корректировок в размер выборки.Это может быть сделано, чтобы избежать преждевременного завершения исследования, или в случае спасения жизни или опасных методов лечения, чтобы избежать продления исследования. Расчет промежуточного размера выборки следует использовать только в том случае, если это указано в методе априорного исследования.
Когда мы оцениваем результаты испытаний с отрицательными результатами, особенно важно поставить под сомнение размер выборки исследования. Вполне возможно, что исследование было недостаточно мощным и что мы неверно приняли нулевую гипотезу, что является ошибкой типа II.Если бы в исследовании было больше испытуемых, то разница вполне могла бы быть обнаружена. В идеальном мире этого никогда не должно происходить, потому что расчет размера выборки должен появляться в разделе методов всех документов, реальность показывает нам, что это не так. Как потребитель исследований мы должны иметь возможность оценивать эффективность исследования по предоставленным результатам.
Ретроспективный расчет размера выборки в этой статье не рассматривается. Несколько калькуляторов ретроспективного размера выборки доступны в Интернете (калькуляторы мощности UCLA (http: // калькуляторы.stat.ucla.edu/powercalc/), Интерактивные статистические страницы (http://www.statistics.com/content/javastat.html).
КАКОЙ ТИП ИССЛЕДОВАНИЯ ДОЛЖЕН ВЫПОЛНИТЬ РАСЧЕТ МОЩНОСТИ?
Почти все количественные исследования могут быть подвергнуты расчету размера выборки. Однако они могут иметь небольшую ценность в ранних поисковых исследованиях, где доступны скудные данные, на которых можно основывать расчеты (хотя это можно решить, предварительно выполнив пилотное исследование и используя полученные данные).
Очевидно, что расчет размера выборки является ключевым компонентом клинических испытаний, поскольку в большинстве этих исследований упор делается на выявление величины различий между терапиями. Все клинические испытания должны иметь оценку размера выборки.
В других типах исследований оценка размера выборки должна выполняться для повышения точности наших окончательных результатов. Например, основными показателями результатов для многих диагностических исследований будут чувствительность и специфичность для конкретного теста, обычно указываемые с доверительными интервалами для этих значений.Как и в случае сравнительных исследований, чем больше изучается число пациентов, тем больше вероятность того, что результаты выборки будут отражать истинную ценность населения. Выполняя расчет размера выборки для диагностического исследования, мы можем указать точность, с которой мы хотели бы сообщить доверительные интервалы для чувствительности и специфичности.
Поскольку клинические испытания и диагностические исследования, вероятно, составят основу исследовательской работы в области экстренной медицины, в данной статье мы сосредоточились на них.
МОЩНОСТЬ В СРАВНИТЕЛЬНЫХ ИССЛЕДОВАНИЯХ
Исследования, содержащие непрерывные нормально распределенные данные
Предположим, что Эгберт Эверард участвовал в клинических испытаниях с участием пациентов с гипертонией. Новый антигипертензивный препарат, сок Джабба, сравнивался с бендрофлуазидом в качестве нового препарата первой линии для лечения гипертонии (таблица 2).
Стол 2Эгберт записывает некоторые вещи, которые, по его мнению, важны для расчетов
Как видите, цифры для pα и pβ несколько типичны.Обычно они устанавливаются по соглашению, а не меняются от одного исследования к другому, хотя, как мы увидим ниже, они могут меняться.
Ключевым требованием является «клинически важное различие», которое мы хотим выявить между группами лечения. Как обсуждалось выше, это должна быть разница, которая имеет клиническое значение, поскольку, если она очень мала, о ней, возможно, не стоит знать.
Еще одна цифра, которую нам необходимо знать, — это стандартное отклонение переменной в исследуемой популяции.Измерения артериального давления представляют собой форму нормально распределенных непрерывных данных и, как таковые, будут иметь стандартное отклонение, которое Эгберт обнаружил в других исследованиях, посвященных аналогичным группам людей.
Когда мы узнаем эти последние две цифры, мы сможем вычислить стандартизированную разницу, а затем использовать таблицу, чтобы дать нам представление о необходимом количестве пациентов.
Разница между средними значениями является клинически важной разницей, то есть она представляет собой разницу между средним артериальным давлением в группе бендрофлуазида и средним артериальным давлением в новой группе лечения.
Из каракулей Эгберта:
Используя таблицу 3, мы можем видеть, что при стандартизованной разнице 0,5 и уровне мощности (pβ) 0,8 необходимое количество пациентов составляет 64. Эта таблица предназначена для односторонней гипотезы (?) Нулевая гипотеза требует, чтобы исследование быть достаточно мощным, чтобы определить, какое лечение лучше или хуже другого, поэтому нам потребуется минимум 64 × 2 = 128 пациентов. Это сделано для того, чтобы мы были уверены, что у нас есть пациенты, которые попадают в обе стороны от установленной нами средней разницы.
Стол 3Как мощность изменяется со стандартизованной разницей
Другой метод установки размера выборки — использование номограммы, разработанной Гором и Альтманом 2 , как показано на рисунке 3.
Рисунок 3Номограмма для расчета объема выборки.
Из этого мы можем использовать линейку, чтобы присоединить стандартизованную разницу к мощности, необходимой для исследования.Если край пересекает среднюю переменную, это указывает на требуемое число N.
Номограмму также можно использовать для расчета мощности для двустороннего сравнения гипотез непрерывного измерения с одинаковым количеством пациентов в каждой группе.
Если данные не распределяются нормально, номограмма ненадежна, и следует искать официальную статистическую помощь.
Исследования с категориальными данными
Предположим, что Эгберт Эверард в своем постоянном стремлении улучшить уход за своими пациентами, страдающими инфарктом миокарда, был убежден фармацевтическим представителем помочь в проведении исследования нового препарата для посттромболизиса, Jedi Flow.Из предыдущих исследований он знал, что потребуются большие числа, поэтому выполнил расчет размера выборки, чтобы определить, насколько сложной будет задача (таблица 4).
Стол 4Расчет размера выборки
И снова значения pα и pβ стандартные, и мы установили уровень для клинически важной разницы.
В отличие от непрерывных данных, расчет размера выборки для категориальных данных основан на пропорциях.Однако, как и в случае с непрерывными данными, нам все равно необходимо рассчитать стандартизированную разницу. Это позволяет нам использовать номограмму, чтобы определить, сколько пациентов необходимо.
p 1 = пропорциональная смертность в группе тромболизиса = 12% или 0,12
p 2 = пропорциональная смертность в группе Jedi Flow = 9% или 0,09 (это 3% клинически важная разница в смертности, которую мы хотим показать).
P = (p 1+ p 2 ) / 2 =
Стандартизированная разница составляет 0,1. Если мы воспользуемся номограммой и проведем линию от 0,1 до оси мощности на 0,8, мы увидим, что от точки пересечения с центральной осью на уровне 0,05 pα нам нужно 3000 пациентов для исследования. Это означает, что нам нужно 1500 пациентов в группе Jedi Flow и 1500 в группе тромболизиса.
МОЩНОСТЬ В ДИАГНОСТИЧЕСКИХ ИСПЫТАНИЯХ
Расчеты мощности редко используются в диагностических исследованиях, и, по нашему опыту, мало кто о них знает. Они имеют особое значение для практики неотложной медицины в связи с характером нашей работы. Описанные здесь методы взяты из работы Buderer. 3
Доктор Эгберт Эверард решает, что диагностику переломов голеностопного сустава можно улучшить с помощью нового портативного ультразвукового устройства в отделении неотложной помощи «Звезды Смерти».Устройство DefRay используется для исследования голеностопного сустава и позволяет определить, сломана ли лодыжка. Доктор Эверард считает, что это новое устройство может снизить потребность пациентов в часах ожидания в радиологическом отделении, тем самым избавляя пациентов от боли в ушах, когда они возвращаются. Он считает, что DefRay можно использовать в качестве инструмента скрининга, только пациенты с положительным результатом теста DefRay будут отправлены в отделение радиологии, чтобы продемонстрировать точный характер травмы.
Он разрабатывает диагностическое исследование, в котором все пациенты с подозрением на перелом лодыжки обследуются в отделении неотложной помощи с помощью DefRay.Этот результат записывается, а затем пациенты отправляются на рентгенограмму независимо от результата теста DefRay. Затем доктор Эверард и его коллеги сравнят результаты DefRay со стандартной рентгенограммой.
Пропущенные переломы лодыжки стоили отделению доктора Эверарда больших денег в прошлом году, поэтому очень важно, чтобы DefRay работал хорошо, если он будет принят в качестве скринингового теста. Эгберту интересно, сколько пациентов ему понадобится. Он записывает несколько заметок (таблица 5).
Стол 5Расчеты Эверарда
Для диагностического исследования мы рассчитываем мощность, необходимую для достижения либо адекватной чувствительности, либо адекватной специфичности. При расчетах используется стандартный способ представления диагностических данных «два на два», как показано в таблице 6.
Стол 6Таблица отчетов два на два для диагностических тестов
Для расчета потребности в адекватной чувствительности
Для расчета потребности в адекватной специфичности
Если бы Эгберт был в равной степени заинтересован в тесте со специфичностью и чувствительностью, мы бы выбрали большее из двух, но это не так.Он больше всего заинтересован в том, чтобы тест имел высокую чувствительность, чтобы исключить переломы лодыжки. Поэтому он принимает цифру за чувствительность — 243 пациента.
ЗАКЛЮЧЕНИЕ
Оценка размера выборки является ключом к проведению эффективных сравнительных исследований. Понимание концепций мощности, размера выборки и ошибок типа I и II поможет исследователю и критическому читателю медицинской литературы.
ВИКТОРИНА
-
Какие факторы влияют на расчет мощности для пробной терапии?
-
Доктор Эгберт Эверард хочет сделать новый анализ крови (ситтастический) для диагностики гена темной стороны. Он хочет, чтобы тест имел чувствительность не менее 70% и специфичность 90% с уровнем достоверности 5%. Распространенность заболевания в этой популяции составляет 10%.
-
Если д-р Эверард должен был испытать новое средство от ожогов легкой саблей, надеялись, что это снизит смертность с 55% до 45%.Он устанавливает pα на 0,05 и pβ на 0,99, но обнаруживает, что ему нужно много пациентов, поэтому, чтобы облегчить себе жизнь, он меняет мощность на 0,80.
-
Сколько пациентов в каждой группе ему понадобилось с pα равным 0,05 и pβ до 0,80?
-
Сколько пациентов ему нужно с большей (исходной) мощностью?
-
Ответы на викторину
-
См. Рамку.
-
(i) 2881 пациент; (ii) 81 пациент
-
(i) около 400 пациентов в каждой группе; (ii) около 900 пациентов в каждой группе
Благодарности
Мы хотели бы поблагодарить Фиону Леки, почетного старшего преподавателя по неотложной медицине, Госпиталь Хоуп, Салфорд, за ее помощь в подготовке этой статьи.
ССЫЛКИ
-
Driscoll P , Wardrope J.Введение в статистику. Дж. Accid Emerg Med2000; 17: 205.
- ↵
Гор СМ , Альтман Д.Г. Насколько велика выборка. В: Статистика на практике . Лондон: Издательство BMJ, 2001: 6–8.
- ↵
Будерер Н.М. . Статистическая методология: I. Включение распространенности заболевания в расчет размера выборки для определения чувствительности и специфичности. Acad Emerg Med 1996; 3: 895–900.
Введение в электронные компоненты: активные и пассивные компоненты
ОСНОВНЫЕ ЗНАНИЯ — ЭЛЕКТРОННЫЕ КОМПОНЕНТЫ Введение в электронные компоненты: активные и пассивные компоненты
Одним из ключевых факторов, который отличает типы электронных компонентов друг от друга, является то, являются ли они пассивными или активный. Однако многие люди не уверены, что именно влечет за собой эта разница. Эта статья здесь, чтобы помочь.
Связанные компании
Активные и пассивные компоненты систем силовой электроники.Ключевое различие между активными и пассивными компонентами
Электронные компоненты делятся на активные и пассивные в зависимости от функций, которые они могут выполнять. Короче говоря, активные компоненты могут, вообще говоря, вводить мощность в цепь и способны электрически контролировать и усиливать поток электрического тока, в то время как пассивные компоненты не могут.
В отличие от активных компонентов, пассивные компоненты либо потребляют, либо накапливают энергию. Простой способ проверить, активен ли компонент, — это измерить разницу между его входными и выходными сигналами.Если есть спад мощности, компонент пассивный. Если сигнал усилен, он активен.
Все электронные схемы должны содержать хотя бы один активный компонент, а большинство электронных устройств содержат как активные, так и пассивные компоненты.
Активные компоненты и их функции
Активным компонентам требуется источник энергии, обычно в виде постоянного тока, для выполнения своей конкретной функции. Они могут каким-то образом управлять потоком электричества.Большинство активных компонентов состоят из полупроводниковых устройств, таких как диоды, транзисторы и интегральные схемы.
- Транзистор: В основном используется для усиления электрических сигналов или в качестве переключающих устройств
- Диод: Позволяет электричеству течь только в одном направлении
- Интегральная схема (микросхемы или микрочипы): несколько сложных схем на печатной плате; используется для выполнения всевозможных задач; все еще считается компонентом, несмотря на то, что он состоит из многих других компонентов
- Устройства отображения , такие как ЖК-дисплеи, светодиоды и ЭЛТ-дисплеи
- Источники питания , такие как батареи и другие источники переменного или постоянного тока ( DC)
Пассивные компоненты и их функции
Пассивные компоненты могут влиять на электрический ток, проходящий через них.Например, они могут сопротивляться его потоку, накапливать энергию для дальнейшего использования или создавать индуктивность. Однако сами они не могут контролировать или усиливать электричество.
Наиболее распространенные компоненты и их функции:
- Резистор: Сопротивляет прохождению электрического тока в цепи; используется для понижения напряжения
- Конденсатор: Накапливает электрическую энергию электростатически в электрическом поле (так называемая «зарядка») и может высвобождать ее позже, когда это необходимо.
- Индуктор: Сохраняет электрическую энергию в магнитном поле ; позволяет протекать через него постоянному току (DC), но не переменному (AC)
- Преобразователь: Преобразует входной сигнал из одного типа энергии в другой; датчики — это тип преобразователя, который преобразует физическое воздействие / входной сигнал в электрический сигнал
Типичные области применения активных и пассивных компонентов
Эти крошечные электронные элементы окружают нас в повседневной жизни.Они спрятаны внутри фонарей, звуковых систем, компьютеров, телефонов, автомобилей и многого другого. По определению, активные компоненты можно найти в каждом электронном устройстве, поэтому у них есть бесчисленное множество вариантов использования. Классические примеры включают любые устройства с вычислительной мощностью (интегральные схемы), устройства со встроенным аккумулятором или дисплеем и светодиодные фонари (светоизлучающие диоды).
Когда дело доходит до пассивных компонентов, лампы накаливания являются прекрасным примером преобразователей в действии — они преобразуют электрическую энергию в световую и тепловую.Громкоговорители используют преобразователи для преобразования электрического входного сигнала в механический выходной сигнал, заставляя конусы внутри динамиков вибрировать, тем самым генерируя звуковые волны, которые мы можем слышать. Датчики — это еще один тип преобразователей, которые давно используются в научных исследованиях и становятся все более и более повсеместными благодаря «умелости» бесчисленных устройств и машин.
Другие варианты использования пассивных компонентов включают микроволновые и радиочастотные приложения, такие как системы удаленного доступа без ключа, в которых используются индукторы.Антенны также являются пассивными и используются в радиоприемниках, устройствах GPS, спутниках, беспроводных модемах и маршрутизаторах, общественном транспорте и т. Д.
Следуйте за нами в LinkedIn
Вам понравилось читать эту статью? Тогда подпишитесь на нас в LinkedIn и будьте в курсе последних событий в отрасли, продуктов и приложений, инструментов и программного обеспечения, а также исследований и разработок.
Следуйте за нами здесь!(ID: 46300364)
.
