Как рассчитать силу тока, зная мощность и напряжение. Как определить напряжение через силу тока и сопротивление. Формулы для вычисления мощности в электрической цепи. Примеры расчетов основных электрических величин.
Основные формулы для расчета электрических величин
При расчетах электрических цепей и параметров электрооборудования часто возникает необходимость определить одну из основных электрических величин, зная другие. Ключевыми параметрами являются:
- Сила тока (I) — измеряется в амперах (А)
- Напряжение (U) — измеряется в вольтах (В)
- Мощность (P) — измеряется в ваттах (Вт)
- Сопротивление (R) — измеряется в омах (Ом)
Все эти величины взаимосвязаны между собой. Рассмотрим основные формулы для их расчета.
Как рассчитать силу тока
Силу тока можно определить несколькими способами в зависимости от известных параметров:
Расчет силы тока через мощность и напряжение
Если известны мощность потребителя и напряжение в сети, силу тока можно найти по формуле:
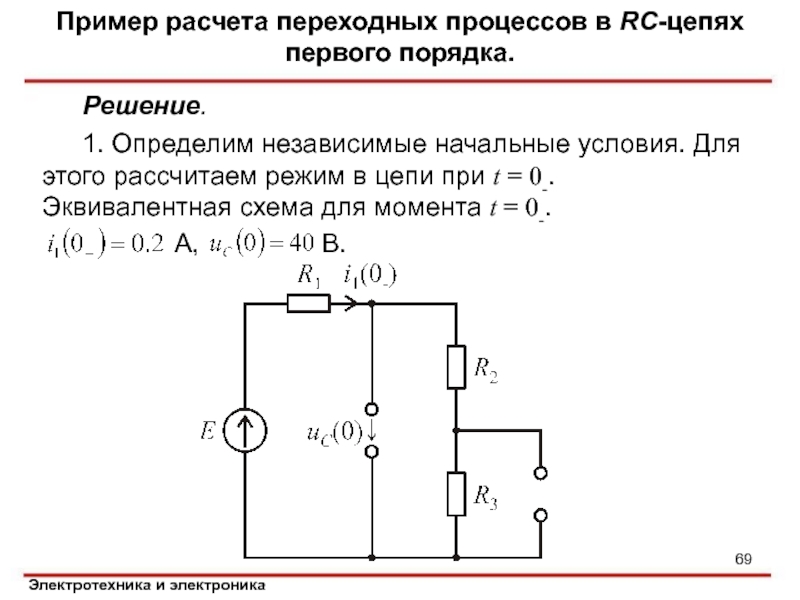
I = P / U
Где:
- I — сила тока (А)
- P — мощность (Вт)
- U — напряжение (В)
Расчет силы тока через напряжение и сопротивление
При известных значениях напряжения и сопротивления участка цепи, силу тока рассчитывают по закону Ома:
I = U / R
Где:
- I — сила тока (А)
- U — напряжение (В)
- R — сопротивление (Ом)
Как определить напряжение
Напряжение в электрической цепи можно найти, зная другие параметры:
Расчет напряжения через силу тока и сопротивление
По закону Ома напряжение определяется как:
U = I * R
Где:
- U — напряжение (В)
- I — сила тока (А)
- R — сопротивление (Ом)
Расчет напряжения через мощность и силу тока
Если известны мощность и сила тока, напряжение находят по формуле:
U = P / I
Где:
- U — напряжение (В)
- P — мощность (Вт)
- I — сила тока (А)
Формулы для вычисления мощности
Мощность электрической цепи или устройства можно рассчитать несколькими способами:Расчет мощности через напряжение и силу тока
Базовая формула для определения мощности:
P = U * I
Где:
- P — мощность (Вт)
- U — напряжение (В)
- I — сила тока (А)
Расчет мощности через напряжение и сопротивление
Если известно сопротивление, мощность находят по формуле:

P = U2 / R
Где:
- P — мощность (Вт)
- U — напряжение (В)
- R — сопротивление (Ом)
Примеры расчетов электрических величин
Рассмотрим несколько примеров для закрепления материала:
Пример 1. Расчет силы тока
Задача: Определить силу тока в электрочайнике мощностью 2000 Вт при напряжении сети 220 В.
Решение:
- Используем формулу I = P / U
- Подставляем значения: I = 2000 Вт / 220 В
- Вычисляем: I = 9,09 А
Ответ: Сила тока в электрочайнике составляет 9,09 А.
Пример 2. Определение напряжения
Задача: Найти напряжение на участке цепи с сопротивлением 100 Ом при силе тока 0,5 А.
Решение:
- Используем формулу U = I * R
- Подставляем значения: U = 0,5 А * 100 Ом
- Вычисляем: U = 50 В
Ответ: Напряжение на участке цепи равно 50 В.
Пример 3. Вычисление мощности
Задача: Рассчитать мощность электроплиты, если она потребляет ток 10 А при напряжении 220 В.
Решение:
- Используем формулу P = U * I
- Подставляем значения: P = 220 В * 10 А
- Вычисляем: P = 2200 Вт
Ответ: Мощность электроплиты составляет 2200 Вт или 2,2 кВт.

Выбор сечения проводов по мощности нагрузки
При проектировании электропроводки важно правильно подобрать сечение проводов. Это обеспечит безопасность и долговечность электрической сети. Основные факторы, влияющие на выбор сечения:
- Мощность подключаемой нагрузки
- Длина кабельной линии
- Материал проводника (медь или алюминий)
- Способ прокладки кабеля
- Температура окружающей среды
Чтобы выбрать подходящее сечение провода, нужно:
- Рассчитать силу тока в линии по формуле I = P / U
- Определить допустимый ток для разных сечений по справочным таблицам
- Выбрать сечение с ближайшим большим допустимым током
Например, для нагрузки мощностью 5 кВт при напряжении 220 В:
- I = 5000 Вт / 220 В = 22,7 А
- По таблице для медного провода находим, что току 22,7 А соответствует сечение 2,5 мм²
- Выбираем провод сечением 2,5 мм²
При выборе сечения всегда следует учитывать запас по нагрузке и возможность увеличения мощности потребителей в будущем.
Заключение
Понимание взаимосвязи между основными электрическими величинами — силой тока, напряжением, мощностью и сопротивлением — необходимо для грамотного проектирования и эксплуатации электрических сетей и оборудования. Представленные формулы и примеры расчетов помогут в решении практических задач, связанных с электричеством.
Важно помнить, что при работе с электроустановками следует строго соблюдать правила электробезопасности. Сложные расчеты и монтаж электропроводки лучше доверить квалифицированным специалистам.
Закон Ома и Джоуля-Ленца – формулы, калькуляторы для расчета
В природе существует два основных вида материалов, проводящие ток и непроводящие (диэлектрики). Отличаются эти материалы наличием условий для перемещения в них электрического тока (электронов).
Из токопроводящих материалов (медь, алюминий, графит, и многие другие), делают электрические проводники, в них электроны не связаны и могут свободно перемещаться.
В диэлектриках электроны привязаны к атомам намертво, поэтому ток в них течь не может. Из них делают изоляцию для проводов, детали электроприборов.
Для того чтобы электроны начали перемещаться в проводнике (по участку цепи пошел ток), им нужно создать условия. Для этого в начале участка цепи должен быть избыток электронов, а в конце – недостаток. Для создания таких условий используют источники напряжения – аккумуляторы, батарейки, электростанции.
Формула Закона Ома
В 1827 году Георг Симон Ом открыл закон силы электрического тока. Его именем назвали Закон и единицу измерения величины сопротивления. Смысл закона в следующем.

Чем толще труба и больше давление воды в водопроводе (с увеличением диаметра трубы уменьшается сопротивление воде) – тем больше потечет воды. Если представить, что вода это электроны (электрический ток), то, чем толще провод и больше напряжение (с увеличением сечения провода уменьшается сопротивление току) – тем больший ток будет протекать по участку цепи.
Сила тока, протекающая по электрической цепи, прямо пропорциональна приложенному напряжению и обратно пропорциональна величине сопротивления цепи.

- где
- I – сила тока, измеряется в амперах и обозначается буквой А;
- U – напряжение, измеряется в вольтах и обозначается буквой В;
- R – сопротивление, измеряется в омах и обозначается Oм.
Если известны напряжение питания U и сопротивление электроприбора R, то с помощью вышеприведенной формулы, воспользовавшись онлайн калькулятором, легко определить силу протекающего по цепи тока I.
Как рассчитать мощность электрического тока?
Большинство бытовых приборов, подключаемых к сети, характеризуются таким параметром, как электрическая мощность устройства. С физической точки зрения мощность представляет собой количественное выражение совершаемой работы. Поэтому для оценки эффективности того или иного устройства вам необходимо знать нагрузку, которую он будет создавать в цепи. Далее мы рассмотрим особенности самого понятия и как найти мощность тока, обладая различными характеристиками самого устройства и электрической сети.
Понятие электрической мощности и способы ее расчета
С электротехнической точки зрения она представляет собой количественное выражение взаимодействия энергии с материалом проводников и элементами при протекании тока в электрической цепи. Из-за наличия электрического сопротивления во всех деталях, задействованных в проведения электротока, направленное движение заряженных частиц встречает препятствие на пути следования. Это и обуславливает столкновение носителей заряда, электроэнергия переходит в другие виды и выделяется в виде излучения, тепла или механической энергии в окружающее пространство. Преобразование одного вида в другой и есть потребляемая мощность прибора или участка электрической цепи.
В зависимости от параметров источника тока и напряжения мощность также имеет отличительные характеристики. В электротехнике обозначается S, P и Q, единица измерения согласно международной системы СИ – ватты. Вычислить мощность можно через различные параметры приборов и электрических приборов. Рассмотрим каждый из них более детально.
Через напряжение и ток
Наиболее актуальный способ, чтобы рассчитать мощность в цепях постоянного тока – это использование данных о силе тока и приложенного напряжения. Для этого вам необходимо использовать формулу расчета: P = U*I
Где:
Этот вариант подходит только для активной нагрузки, где постоянный ток не обеспечивает взаимодействия с реактивной составляющей цепи. Чтобы найти мощность вам нужно выполнить произведение силы тока на напряжение. Обе величины должны находиться в одних единицах измерения – Вольты и Амперы, тогда результат также получится в Ваттах. Можно использовать и другие способы кВ, кА, мВ, мА, мкВ, мкА и т.д., но и параметр мощности пропорционально изменит свой десятичный показатель.
Через напряжение и сопротивление
Для большинства электрических устройств известен такой параметр, как внутреннее сопротивление, которое принимается за константу на весь период их эксплуатации. Так как бытовые или промышленные единицы подключаются к источнику с известным номиналом напряжения, определять мощность достаточно просто. Активная мощность находится из предыдущего соотношения и закона Ома, согласно которого ток на участке прямо пропорционален величине приложенного напряжения и имеет обратную пропорциональность к сопротивлению:
I = U/R
Если выражение для вычисления токовой нагрузки подставить в предыдущую формулу, то получится такое выражение для определения мощности:
P = U*(U/R)=U2/R
Где,
- P – величина нагрузки;
- U – приложенная разность потенциалов;
- R – сопротивление нагрузки.
Через ток и сопротивление
Бывает ситуация, когда разность потенциалов, приложенная к электрическому прибору, неизвестна или требует трудоемких вычислений, что не всегда удобно. Особенно актуален данный вопрос, если несколько устройств подключены последовательно и вам неизвестно, каким образом потребляемая электроэнергия распределяется между ними. Подход в определении здесь ничем не отличается от предыдущего способа, за основу берется базовое утверждение, что электрическая нагрузка рассчитывается как P = U×I, с той разницей, что напряжение нам не известно.
Поэтому ее мы также выведем из закона Ома, согласно которого нам известно, что падение напряжения на каком-либо отрезке линии или электроустановки прямо пропорционально току, протекающему по этому участку и сопротивлению отрезка цепи:
U=I*R
после того как выражение подставить в формулу мощности, получим:
P = (I*R)*I =I2*R
Как видите, мощность будет равна квадрату силы тока умноженной на сопротивление.
Полная мощность в цепи переменного тока
Сети переменного тока кардинально отличаются от постоянного тем, что изменение электрических величин, приводит к появлению не только активной, но и реактивной составляющей. В итоге суммарная мощность будет также состоять активной и реактивной энергии:

Где,
- S – полная мощность
- P – активная составляющая – возникает при взаимодействии электротока с активным сопротивлением;
- Q – реактивная составляющая – возникает при взаимодействии электротока с реактивным сопротивлением.
Также составляющие вычисляются через тригонометрические функции, так:
P = U*I*cosφ
Q = U*I*sinφ
что активно используется в расчете электрических машин.
 Рис. 1. Треугольник мощностей
Рис. 1. Треугольник мощностей Пример расчета полной мощности для электродвигателя
Отдельный интерес представляет собой нагрузка, подключенная к трехфазной сети, так как электрические величины, протекающие в ней, напрямую зависят от номинальной нагрузки каждой из фаз. Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.
Особенность питания и асинхронной и синхронной электрической машины заключается в том, что на обмотки может подаваться и фазное и линейное напряжение. Тот или иной вариант, как правило, обуславливается способом соединения обмоток электродвигателя. Тогда мощность будет вычисляться по формуле:
S = 3*Uф*Iф
В случае выполнения расчетов с линейным напряжением, чтобы найти мощность формула примет вид:

Активная и реактивная мощности будут вычисляться по аналогии с сетями переменного тока, как было рассмотрено ранее.
Теперь рассмотрим вычисления на примере конкретной электрической машины асинхронного типа. Следует отметить, что официальная производительность, указываемая в паспортных данных электродвигателя – это полезная мощность, которую двигатель может выдать при совершении оборотов вала. Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.
 Рис. 2. Шильд электродвигателя
Рис. 2. Шильд электродвигателяКак видите, для вычислений с шильда мы возьмем следующую информацию об электродвигателе:
- полезная производительность – 3 кВт, а в переводе на систему измерения – 3000 Вт;
- коэффициент полезного действия – 80%, а в пересчете для вычислений будем пользоваться показателем 0,8;
- тригонометрическая функция соотношения активных и реактивных составляющих – 0,74%;
- напряжение, при соединении обмоток треугольником составит 220 В;
- сила тока при том же способе соединения – 13,3 А.
С таким перечнем характеристик можно воспользоваться несколькими способами:
S = 1,732*220*13,3 = 5067 Вт
Чтобы найти искомую величину, сначала определяем активную составляющую:
P = Pполезная / КПД = 3000/0.8 = 3750 Вт
Далее полную по способу деления активной на коэффициент cos φ:
S = P/cos φ = 3750/0.74 = 5067 Вт
Как видите, и в первом, и во втором случае искомая величина получилась одинакового значения.
Примеры задач
Для примера рассмотрим вычисление на участках электрической цепи с последовательным и параллельным соединением элементов. Первый вариант предусматривает ситуацию, когда все детали соединяются друг за другом от одного полюса источника питания до другого.
 Рис. 3. Последовательная расчетная цепь
Рис. 3. Последовательная расчетная цепьКак видите на рисунке, в качестве источника мы используем батарейку с номинальным напряжением 9 В и три резистора по 10, 20 и 30 Ом соответственно. Так как номинальный ток нам не известен, расчет произведем через напряжение и сопротивление:
P = U2/R = 81 / (10+20+30) = 1.35 Вт
Для параллельной схемы подключения возьмем в качестве примера участок цепи с двумя резисторами и одним источником тока:
 Рис. 4. Параллельная схема подключения
Рис. 4. Параллельная схема подключенияКак видите, для удобства расчетов нам нужно привести параллельно подключенные резисторы к схеме замещения, из чего получится:
Rобщ = (R1*R2) / (R1+R2) = (10*15) / (10+15) = 6 Ом
Тогда искомый номинал нагрузки мы можем узнать через значение тока и сопротивления:
P = I2*R = 25*6 = 150 Вт
Видео по теме
Как найти силу тока через мощность, сопротивление и напряжение
Одной из основных характеристик электрической цепи является сила тока. Она измеряется в амперах и определяет нагрузку на токопроводящие провода, шины или дорожки плат. Эта величина отражает количество электричества, которое протекло в проводнике за единицу времени. Определить её можно несколькими способами в зависимости от известных вам данных. Соответственно студенты и начинающие электрики из-за этого часто сталкиваются с проблемами при решении учебных заданий или практических ситуаций. В этой статье мы и расскажем, как найти силу тока через мощность и напряжение или сопротивление.
Если известна мощность и напряжение
Допустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой:
P=UI
После несложных мы получаем формулу для вычислений
I=P/U
Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:
Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:
Р1 = Р2/η
Здесь P2 – активная полезная мощность на валу, η – КПД, оба этих параметра обычно указывают на шильдике.

Находим полную мощность с учетом cosФ (он также указывается на шильдике):
S = P1/cosφ
Определяем потребляемый ток по формуле:
Iном = S/(1,73·U)
Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В.
Если известно напряжение или мощность и сопротивление
Но встречаются задачи, когда вам известно напряжение на участке цепи и величина нагрузки, тогда чтобы найти силу тока без мощности воспользуйтесь законом Ома, с его помощью проводим расчёт силы тока через сопротивление и напряжение.
I=U/R
Но иногда случается так, что нужно определить силу тока без напряжения, то есть когда вам известна только мощность цепи и её сопротивление. В этом случае:
P=UI
При этом согласно тому же закону Ома:
U=IR
То:
P=I2*R
Значит расчёт проводим по формуле:
I2=P/R
Или возьмем выражение в правой части выражения под корень:
I=(P/R)1/2
Если известно ЭДС, внутреннее сопротивление и нагрузка
Ко студенческим задачам с подвохом можно отнести случаи, когда вам дают величину ЭДС и внутреннее сопротивление источника питания. В этом случае вы можете определить силу тока в схеме по закону Ома для полной цепи:
I=E/(R+r)
Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.
Закон Джоуля-Ленца
Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником. Для этого вспомним закон Джоуля-Ленца.
Его формула выглядит так:
Q=I2Rt
Тогда расчет проводите так:
I2=QRt
Или внесите правую часть уравнения под корень:
I=(Q/Rt)1/2
Несколько примеров
В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.
1 задача: Рассчитать I в цепи из двух резисторов при последовательном соединении и при параллельном соединении. R резисторов 1 и 2 Ома, источник питания на 12 Вольт.
Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.
R1+R2=1+2=3 Ома
Тогда рассчитать силу тока можно по закону Ома:
I=U/R=12/3=4 Ампера
При параллельном соединении двух элементов Rобщее можно рассчитать так:
Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67
Тогда дальнейшие вычисления можно проводить так:
I=12*0,67=18А
2 задача: рассчитать ток при смешанном соединении элементов. На выходе источника питания 24В, а резисторы на: R1=1 Ом, R2=3 Ома, R3=3 Ома.

В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.
Rприв=(R2*R3)/(R2+R3)=(3*3)|(3+3)=9/6=3/2=1,5 Ома
Теперь схема примет вид:

Далее находим ток по тому же закону Ома:
I=U/(R1+Rприв)=24/(1+1,5)=24/2,5=9,6 Ампер
Теперь вы знаете, как найти силу тока, зная мощность, сопротивление и напряжение. Надеемся, предоставленные формулы и примеры расчетов помогли вам усвоить материал!
Наверняка вы не знаете:
РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ОНЛАЙН — ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ, ТОКА, МОЩНОСТИ И СЕЧЕНИЯ ПРОВОДНИКА
Наверное, каждый кто делал или делает ремонт электрики сталкивался с проблемой определения той или иной электрической величины. Для кого-то это становится настоящим камнем преткновения, а для кого-то все предельно ясно и каких-либо сложностей при определении той или иной величины нет. Данная статья посвящена именно первой категории – то есть для тех, кто не очень силен в теории электрических цепей и тех показателей, которые для них характерны.
Итак, для начала вернемся немного в прошлое и постараемся вспомнить школьный курс физики, касательно электрики. Как мы помним, основные электрические величины определяются на основании всего одного закона – закона Ома. Именно этот закон является базой проведения абсолютно для любых расчетов и имеет вид:
Отметим, что в данном случае речь идет о расчете самой простейшей электрической цепи, которая выглядит следующим образом:
Подчеркнем, что абсолютно любой расчет ведется именно посредством этой формулы. То есть путем не сложных математических вычислений можно определить ту или иную величину зная при этом два иных электрических параметра. Как бы там ни было, наш ресурс призван упростить жизнь тому кто делает ремонт, а поэтому мы упростим решение задачи определения электрических параметров, вывив основные формулы и предоставив возможность произвести расчет электрических цепей онлайн.
Как узнать ток зная мощность и напряжение?
В данном случае формула вычисления выглядит следующим образом:
Расчет силы тока онлайн:
(Не целые числа вводим через точку. Например: 0.5)
Как узнать напряжение зная силу тока?
Для того, чтобы узнать напряжение, зная при этом сопротивление потребителя тока можно воспользоваться формулой:
Расчет напряжения онлайн:
Если же сопротивление неизвестно, но зато известна мощность потребителя, то напряжение вычисляется по формуле:
Определение величины онлайн:
Как рассчитать мощность зная силу тока и напряжения?
Здесь необходимо знать величины действующего напряжения и действующей силы тока в электрической цепи. Согласно формуле предоставленной выше, мощность определяется путем умножения силы тока на действующее напряжение.
Расчет цепи онлайн:
Как определить потребляемую мощность цепи имея тестер, который меряет сопротивление?
Этот вопрос был задан в комментарие в одном из материалов нашего сайта. Поспешим дать ответ на этот вопрос. Итак, для начала измеряем тестером сопротивление электроприбора (для этого достаточно подсоединить щупы тестера к вилке шнура питания). Узнав сопротивление мы можем определить и мощность, для чего необходимо напряжение в квадрате разделить на сопротивление.
Онлайн расчет:
Формула расчета сечения провода и как определяется сечение провода
Довольно много вопросов связано с определением сечения провода при построении электропроводки. Если углубиться в электротехническую теорию, то формула расчета сечения имеет такой вид:
Конечно же, на практике, такой формулой пользуются довольно редко, прибегая к более простой схеме вычислений. Эта схема довольно проста: определяют силу тока, которая будет действовать в цепи, после чего согласно специальной таблице определяют сечение. Более детально по этому поводу можно почитать в материале – «Сечение провода для электропроводки»
Приведем пример. Есть бойлер мощностью 2000 Вт, какое сечение провода должно быть, чтобы подключить его к бытовой электропрводке? Для начала определим силу тока, которая будет действовать в цепи:
I=P/U=2000/220В = 9А
Как видим, сила тока получается довольно приличной. Округляем значение до 10 А и обращаемся к таблице:
Таким образом, для нашего бойлера потребуется провод сечением 1,7 мм. Для большей надежности используем провод сечением 2 или 2,5 мм.
Рекомендуем ознакомиться:
— БЛОК ПИТАНИЯ ДЛЯ СВЕТОДИОДНЫХ ЛЕНТ
— ЗАЩИТНОЕ ЗАНУЛЕНИЕ
— СВЕТОДИОДНЫЕ СВЕТИЛЬНИКИ — ЛУЧШЕ НЕ ПРИДУМАЕШЬ!
— АЛМАЗНАЯ РЕЗКА БЕТОНА И ЖБ КОНСТРУКЦИЙ
Автор — Антон Писарев
Как найти силу тока в цепи

Формулы, с помощью которых вы можете рассчитать силу тока в цепи. Примеры решения популярных задач.
Одной из основных характеристик электрической цепи является сила тока. Она измеряется в амперах и определяет нагрузку на токопроводящие провода, шины или дорожки плат. Эта величина отражает количество электричества, которое протекло в проводнике за единицу времени. Определить её можно несколькими способами в зависимости от известных вам данных. Соответственно студенты и начинающие электрики из-за этого часто сталкиваются с проблемами при решении учебных заданий или практических ситуаций. В этой статье мы и расскажем, как найти силу тока через мощность и напряжение или сопротивление. Содержание:
Если известна мощность и напряжение
Допустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой:
P=UI
После несложных мы получаем формулу для вычислений
I=P/U
Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:
Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:
Р1 = Р2/η
Здесь P2 – активная полезная мощность на валу, η – КПД, оба этих параметра обычно указывают на шильдике.

Находим полную мощность с учетом cosФ (он также указывается на шильдике):
S = P1/cosφ
Определяем потребляемый ток по формуле:
Iном = S/(1,73·U)
Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В.
Если известно напряжение или мощность и сопротивление
Но встречаются задачи, когда вам известно напряжение на участке цепи и величина нагрузки, тогда чтобы найти силу тока без мощности воспользуйтесь законом Ома, с его помощью проводим расчёт силы тока через сопротивление и напряжение.
I=U/R
Но иногда случается так, что нужно определить силу тока без напряжения, то есть когда вам известна только мощность цепи и её сопротивление. В этом случае:
P=UI
При этом согласно тому же закону Ома:
U=IR
То:
P=I2*R
Значит расчёт проводим по формуле:
I2=P/R
Или возьмем выражение в правой части выражения под корень:
I=(P/R)1/2
Если известно ЭДС, внутреннее сопротивление и нагрузка
Ко студенческим задачам с подвохом можно отнести случаи, когда вам дают величину ЭДС и внутреннее сопротивление источника питания. В этом случае вы можете определить силу тока в схеме по закону Ома для полной цепи:
I=E/(R+r)
Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.
Закон Джоуля-Ленца
Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником. Для этого вспомним закон Джоуля-Ленца.
Его формула выглядит так:
Q=I2Rt
Тогда расчет проводите так:
I2=QRt
Или внесите правую часть уравнения под корень:
I=(Q/Rt)1/2
Несколько примеров
В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.
1 задача: Рассчитать I в цепи из двух резисторов при последовательном соединении и при параллельном соединении. R резисторов 1 и 2 Ома, источник питания на 12 Вольт.
Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.
R1+R2=1+2=3 Ома
Тогда рассчитать силу тока можно по закону Ома:
I=U/R=12/3=4 Ампера
При параллельном соединении двух элементов Rобщее можно рассчитать так:
Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67
Тогда дальнейшие вычисления можно проводить так:
I=12*0,67=18А
2 задача: рассчитать ток при смешанном соединении элементов. На выходе источника питания 24В, а резисторы на: R1=1 Ом, R2=3 Ома, R3=3 Ома.

В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.
Rприв=(R2*R3)/(R2+R3)=(3*3)|(3+3)=9/6=3/2=1,5 Ома
Теперь схема примет вид:

Далее находим ток по тому же закону Ома:
I=U/(R1+Rприв)=24/(1+1,5)=24/2,5=9,6 Ампер
Теперь вы знаете, как найти силу тока, зная мощность, сопротивление и напряжение. Надеемся, предоставленные формулы и примеры расчетов помогли вам усвоить материал!
Наверняка вы не знаете:
- Как рассчитать сечение кабеля
- Как перевести амперы в киловатты
- Как найти провод в стене
 0)Не нравится
0)Не нравится 0)
0)
Мощность ток напряжение. Расчёт нагрузки и выбор питающих кабелей
Электроэнергия давно используется человеком для удовлетворения своих потребностей, но она невидима, не воспринимается органами чувств, потому сложна для понимания. Мощность ток напряжение, все эти характеристики электроэнергии исследованы известными учеными, которые дали им определения и описали математическими методами взаимные связи между ними.
Мощность ток напряжение сопротивление
Так же следует помнить, на величину электрического сопротивления влияет несколько факторов:
- строение вещества, определяющее наличие свободных электронов в проводнике и влияющее на удельное сопротивление
- площадь поперечного сечения и длина токовода
- температура
В приведенной таблице показаны общие соотношения для цепей постоянного и переменного тока, которые можно применять для анализа работы схем электроснабжения.
Расчёт сечения питающего кабеля и проводки
Для обеспечения безопасности при эксплуатации бытовых электроприборов необходимо верно вычислить сечение питающего кабеля и проводки. Поскольку ошибочно выбранное сечение жил кабеля способно привести к перегреву провода, плавление его изоляции и в итоге, возгоранию, из-за короткого замыкания.
Мощность ток напряжение, удобная шпаргалка
Основным параметром, по которому производят расчет сечения провода, является его продолжительная допустимая токовая нагрузка. Т.е, это такая номинальная величина тока, которую проводник способен через себя пропускать на протяжении длительного времени. Для определения величины номинального тока, необходимо знать приблизительную мощность всех подключаемых электроприборов и оборудования в квартире.
И так, что мы имеем:
- От значения величины тока зависит выбор питающего кабеля (провода), по которому могут быть подключены приборы энергопотребления к сети
- Зная напряжение электрической сети и полную нагрузку электроприборов, можно по формуле вычислить силу тока, который потребуется пропускать по проводнику(проводу, кабелю). По его величине выбирают площадь сечения жил.
Расчет тока, выполняем самостоятельно
Если известны электро-потребители в квартире или доме, необходимо выполнить несложные расчёты, чтобы правильно смонтировать схему электроснабжения.
Аналогичные расчёты выполняются для производственных целей: определения необходимой площади сечения жил кабеля при осуществлении подключения промышленного оборудования (различных промышленных электрических двигателей и механизмов).
Мощность ток напряжение, расчёты для однофазной сети 220 В
Сила тока I (в амперах, А) подсчитывается по формуле:
I = P / U,
где
P – электрическая полная нагрузка (обязательно указывается в техническом паспорте устройства), Вт (ватт)
U – напряжение электрической сети, В (вольт)
Ниже в таблице представлены величины нагрузки типичных бытовых электроприборов и потребляемый ими ток (для напряжения 220 В).
| Электроприбор | Потребляемая мощность, Вт | Сила тока, А |
| Стиральная машина | 2000 – 2500 | 9,0 – 11,4 |
| Джакузи | 2000 – 2500 | 9,0 – 11,4 |
| Электроподогрев пола | 800 – 1400 | 3,6 – 6,4 |
| Стационарная электрическая плита | 4500 – 8500 | 20,5 – 38,6 |
| СВЧ печь | 900 – 1300 | 4,1 – 5,9 |
| Посудомоечная машина | 2000 — 2500 | 9,0 – 11,4 |
| Морозильники, холодильники | 140 — 300 | 0,6 – 1,4 |
| Мясорубка с электроприводом | 1100 — 1200 | 5,0 — 5,5 |
| Электрочайник | 1850 – 2000 | 8,4 – 9,0 |
| Электрическая кофеварка | 6з0 — 1200 | 3,0 – 5,5 |
| Соковыжималка | 240 — 360 | 1,1 – 1,6 |
| Тостер | 640 — 1100 | 2,9 — 5,0 |
| Миксер | 250 — 400 | 1,1 – 1,8 |
| Фен | 400 — 1600 | 1,8 – 7,3 |
| Утюг | 900 — 1700 | 4,1 – 7,7 |
| Пылесос | 680 — 1400 | 3,1 – 6,4 |
| Вентилятор | 250 — 400 | 1,0 – 1,8 |
| Телевизор | 125 — 180 | 0,6 – 0,8 |
| Радиоаппаратура | 70 — 100 | 0,3 – 0,5 |
| Приборы освещения | 20 — 100 | 0,1 – 0,4 |
Различные потребители электроэнергии подключаются через соответствующие автоматы к электросчётчику и далее общему автомату, который должен быть рассчитан на нагрузку приборов, которыми будет оборудована квартира. Провод, который подводит питание также должен удовлетворять нагрузке энергопотребителей.
Как рассчитать ток защитного автомата
Для группы розеток, предназначенных для питания бытовых электроприборов на кухне, необходимо подобрать защитный автоматический выключатель. Мощности приборов по паспортным данным составляют 2,0, 1,5 и 0,6 кВт.
Решение. В квартире используется однофазная переменная сеть 220 вольт. Общая мощность всех приборов, подключенных в работу одновременно, составит 2,0+1,5+0,6=4,1 кВт=4100 Вт.
По формуле I = P / U определим общий ток группы потребителей: 4100/220=18,64 А.
Ближайший по номиналу автоматический выключатель имеет величину срабатывания 20 ампер. Его и выбираем. Автомат меньшего значения на 16 А будет постоянно отключаться от перегрузки.
Ниже приводится таблица для скрытой проводки при однофазной схеме подключения квартиры для подбора провода при напряжении 220 В
| Сечение жилы провода, мм2 | Диаметр жилы проводника, мм | Медные жилы | Алюминиевые жилы | ||
| Ток, А | Мощность, Вт | Ток, А | Мощность, кВт | ||
| 0,50 | 0,80 | 6 | 1300 | ||
| 0,75 | 0,98 | 10 | 2200 | ||
| 1,00 | 1,13 | 14 | 3100 | ||
| 1,50 | 1,38 | 15 | 3300 | 10 | 2200 |
| 2,00 | 1,60 | 19 | 4200 | 14 | 3100 |
| 2,50 | 1,78 | 21 | 4600 | 16 | 3500 |
| 4,00 | 2,26 | 27 | 5900 | 21 | 4600 |
| 6,00 | 2,76 | 34 | 7500 | 26 | 5700 |
| 10,00 | 3,57 | 50 | 11000 | 38 | 8400 |
| 16,00 | 4,51 | 80 | 17600 | 55 | 12100 |
| 25,00 | 5,64 | 100 | 22000 | 65 | 14300 |
Как видно из таблицы сечение жил зависит кроме нагрузки и от материала, из которого изготовлен провод.
Мощность ток напряжение, расчёты для трёхфазной сети 380 В
При трёхфазном электроснабжении сила тока I (в амперах, А) вычисляется по формуле:
I = P /1,73 U,
где P -потребляемая мощность, Вт;
U — напряжение в сети, В,
так как напряжение при трёхфазной схеме электроснабжения 380 В, формула примет вид:
I = P /657, 4.
Сечение жил в питающем кабеле при различной нагрузке при трёхфазной схеме напряжением 380 В для скрытой проводки представлена в таблице.
| Сечение жилы провода, мм2 | Диаметр жилы проводника, мм | Медные жилы | Алюминиевые жилы | ||
| Ток, А | Мощность, Вт | Ток, А | Мощность, кВт | ||
| 0,50 | 0,80 | 6 | 2250 | ||
| 0,75 | 0,98 | 10 | 3800 | ||
| 1,00 | 1,13 | 14 | 5300 | ||
| 1,50 | 1,38 | 15 | 5700 | 10 | 3800 |
| 2,00 | 1,60 | 19 | 7200 | 14 | 5300 |
| 2,50 | 1,78 | 21 | 7900 | 16 | 6000 |
| 4,00 | 2,26 | 27 | 10000 | 21 | 7900 |
| 6,00 | 2,76 | 34 | 12000 | 26 | 9800 |
| 10,00 | 3,57 | 50 | 19000 | 38 | 14000 |
| 16,00 | 4,51 | 80 | 30000 | 55 | 20000 |
| 25,00 | 5,64 | 100 | 38000 | 65 | 24000 |
Для расчёта тока в цепях питания нагрузки, характеризующейся большой реактивной полной мощностью, что характерно применению электроснабжения в промышленности:
- электрические двигатели
- дроссели приборов освещения
- сварочные трансформаторы
- индукционные печи
В мощных приборах и оборудовании, доля реактивной нагрузки выше и поэтому для таких приборов в расчетах коэффициент мощности принимают равным 0,8.
На практике принято считать, что при подсчёте электрических нагрузок для бытовых целей запас мощности принимают 5%. В случае расчёта электрических сетей для промышленного производства запас мощности принимают 20%.
Будем рады, если подпишетесь на наш Блог!
[wysija_form id=»1″]
Как найти мощность тока — формулы с примерами расчетов

Формулы, позволяющие выполнить расчет мощности, зная силу тока и напряжение либо сопротивление и напряжение. Пример расчетных работ.
В физике достаточно много внимания уделено энергии и мощности устройств, веществ или тел. В электротехнике эти понятия играют не менее важную роль чем в других разделах физики, ведь от них зависит насколько быстро установка выполнит свою работу и какую нагрузку понесут линии электропередач. Исходя из этих сведений подбираются трансформаторы для подстанций, генераторы для электростанций и сечение проводников передающих линий. В этой статье мы расскажем, как найти мощность электрического прибора или установки, зная силу тока, напряжение и сопротивление. Содержание:
Определение
Мощность – это скалярная величина. В общем случае она равна отношению выполненной работы ко времени:
P=dA/dt
Простыми словами эта величина определяет, как быстро выполняется работа. Она может обозначаться не только буквой P, но и W или N, измеряется в Ваттах или киловаттах, что сокращенно пишется как Вт и кВт соответственно.
Электрическая мощность равна произведению тока на напряжение или:
P=UI
Как это связано с работой? U – это отношение работы по переносу единичного заряда, а I определяет, какой заряд прошёл через провод за единицу времени. В результате преобразований и получилась такая формула, с помощью которой можно найти мощность, зная силу тока и напряжение.
Формулы для расчётов цепи постоянного тока
Проще всего посчитать мощность для цепи постоянного тока. Если есть сила тока и напряжение, тогда нужно просто по формуле, приведенной выше, выполнить расчет:
P=UI
Но не всегда есть возможность найти мощность по току и напряжению. Если вам они не известны – вы можете определить P, зная сопротивление и напряжение:
P=U2/R
Также можно выполнить расчет, зная ток и сопротивление:
P=I2*R
Последними двумя формулами удобен расчёт мощности участка цепи, если вы знаете R элемента I или U, которое на нём падает.
Для переменного тока
Однако для электрической цепи переменного тока нужно учитывать полную, активную и реактивную, а также коэффициент мощности (соsФ). Подробнее все эти понятия мы рассматривали в этой статье: https://samelectrik.ru/chto-takoe-aktivnaya-reaktivnaya-i-polnaya-moshhnost.html.
Отметим лишь, что чтобы найти полную мощность в однофазной сети по току и напряжению нужно их перемножить:
S=UI
Результат получится в вольт-амперах, чтобы определить активную мощность (ватты), нужно S умножить на коэффициент cosФ. Его можно найти в технической документации на устройство.
P=UIcosФ
Для определения реактивной мощности (вольт-амперы реактивные) вместо cosФ используют sinФ.
Q=UIsinФ
Или выразить из этого выражения:

И отсюда вычислить искомую величину.
Найти мощность в трёхфазной сети также несложно, для определения S (полной) воспользуйтесь формулой расчета по току и фазному напряжению:
S=3Uф/ф
А зная Uлинейное:
S=1,73*UлIл
1,73 или корень из 3 – эта величина используется для расчётов трёхфазных цепей.
Тогда по аналогии чтобы найти P активную:
P=3Uф/ф*cosФ=1,73*UлIл*cosФ
Определить реактивную мощность можно:
Q=3Uф/ф*sinФ=1,73*UлIл*sinФ
На этом теоретические сведения заканчиваются и мы перейдём к практике.
Пример расчёта полной мощности для электродвигателя
Мощность у электродвигателей бывает полезная или механическая на валу и электрическая. Они отличаются на величину коэффициента полезного действия (КПД), эта информация обычно указана на шильдике электродвигателя.

Отсюда берём данные для расчета подключения в треугольник на Uлинейное 380 Вольт:
- Pна валу=160 кВт = 160000 Вт
- n=0,94
- cosФ=0,9
- U=380
Тогда найти активную электрическую мощность можно по формуле:
P=Pна валу/n=160000/0,94=170213 Вт
Теперь можно найти S:
S=P/cosφ=170213/0,9=189126 Вт
Именно её нужно найти и учитывать, подбирая кабель или трансформатор для электродвигателя. На этом расчёты окончены.
Расчет для параллельного и последовательного подключения
При расчете схемы электронного устройства часто нужно найти мощность, которая выделяется на отдельном элементе. Тогда нужно определить, какое напряжение падает на нём, если речь идёт о последовательном подключении, или какая сила тока протекает при параллельном включении, рассмотрим конкретные случаи.

Здесь Iобщий равен:
I=U/(R1+R2)=12/(10+10)=12/20=0,6
Общая мощность:
P=UI=12*0,6=7,2 Ватт
На каждом резисторе R1 и R2, так как их сопротивление одинаково, напряжение падает по:
U=IR=0,6*10=6 Вольт
И выделяется по:
Pна резисторе=UI=6*0,6=3,6 Ватта
Тогда при параллельном подключении в такой схеме:

Сначала ищем I в каждой ветви:
I1=U/R1=12/1=12 Ампер
I2=U/R2=12/2=6 Ампер
И выделяется на каждом по:
PR1=12*6=72 Ватта
PR2=12*12=144 Ватта
Выделяется всего:
P=UI=12*(6+12)=216 Ватт
Или через общее сопротивление, тогда:
Rобщее=(R1*R2)/( R1+R2)=(1*2)/(1+2)=2/3=0,66 Ом
I=12/0,66=18 Ампер
P=12*18=216 Ватт
Все расчёты совпали, значит найденные значения верны.
Заключение
Как вы могли убедиться найти мощность цепи или её участка совсем несложно, неважно речь идёт о постоянке или переменке. Важнее правильно определить общее сопротивление, ток и напряжение. Кстати этих знаний уже достаточно для правильного определения параметров схемы и подбора элементов – на сколько ватт подбирать резисторы, сечения кабелей и трансформаторов. Также будьте внимательны при расчёте S полной при вычислении подкоренного выражения. Стоит добавить лишь то, что при оплате счетов за коммунальные услуги мы оплачиваем за киловатт-часы или кВт/ч, они равняются количеству мощности, потребленной за промежуток времени. Например, если вы подключили 2 киловаттный обогреватель на пол часа, то счётчик намотает 1 кВт/ч, а за час – 2 кВт/ч и так далее по аналогии.
Напоследок рекомендуем просмотреть полезное видео по теме статьи:
Также читают:
- Как определить потребляемую мощность приборов
- Как рассчитать сечения кабеля
- Маркировка резисторов по мощности и сопротивлению
Нравится
 0)Не нравится
0)Не нравится 0)
Закон
0)
Закон Ома | Электрические цепи
Закон 11,2 Ома (ESBQ6)
Три основные величины для электрических цепей: ток, напряжение (разность потенциалов) и сопротивление . Резюме:
-
Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.
-
Разность потенциалов или напряжение \ (В \) — это количество энергии на единицу заряда, необходимое для перемещения этого заряда между двумя точками в цепи.
-
Сопротивление, \ (R \), является мерой того, насколько «трудно» протолкнуть ток через элемент схемы.
Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.
Важная взаимосвязь между током, напряжением и сопротивлением в цепи была обнаружена Георгом Симоном Омом и называется законом Ома .
- Закон Ома
-
Величина электрического тока через металлический проводник при постоянной температуре в цепи пропорциональна напряжению на проводнике и может быть описана как
. \ (I = \ frac {V} {R} \)где \ (I \) — ток через проводник, \ (V \) — напряжение на проводнике, а \ (R \) — сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводника постоянно, независимо от приложенного к нему напряжения или проходящего через него тока.
Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, текущий по проводнику, прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на ось x графика, а ток на ось y графика, мы получим прямую линию.
Наклон прямолинейного графика связан с сопротивлением проводника как \ [\ frac {I} {V} = \ frac {1} {R}.\] С точки зрения постоянного сопротивления это можно изменить как: \ [R = \ frac {V} {I}. \]
Закон Ома
Цель
Для определения взаимосвязи между током, протекающим через резистор, и разностью потенциалов (напряжением) на том же резисторе.
Аппарат
4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода
Метод
Этот эксперимент состоит из двух частей. В первой части мы будем варьировать приложенное к резистору напряжение и измерять результирующий ток в цепи.Во второй части мы будем изменять ток в цепи и измерять результирующее напряжение на резисторе. После получения обоих наборов измерений мы исследуем взаимосвязь между током и напряжением на резисторе.
-
Изменение напряжения:
-
Настройте схему в соответствии со схемой 1), начиная с одной ячейки.
-
Нарисуйте следующую таблицу в своем лабораторном журнале.
Количество ячеек
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)
-
Попросите учителя проверить электрическую цепь перед включением питания.
-
Измерьте напряжение на резисторе с помощью вольтметра и ток в цепи с помощью амперметра.
-
Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.
-
Повторяйте, пока не получите четыре ячейки и не заполните таблицу.
-
-
Изменение тока:
-
Настройте схему в соответствии со схемой 2), начиная с одного резистора в цепи.
-
Нарисуйте следующую таблицу в своем лабораторном журнале.
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
-
Попросите учителя проверить вашу электрическую схему перед включением питания.
-
Измерьте ток и напряжение на единственном резисторе.
-
Теперь добавьте еще один резистор в цепь и снова измерьте ток и напряжение только на исходном резисторе. Продолжайте добавлять резисторы, пока у вас не будет четырех последовательно, но не забывайте каждый раз измерять напряжение только на исходном резисторе. Введите измеренные вами значения в таблицу.
-
Анализ и результаты
-
Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения.Поскольку напряжение — это переменная, которую мы изменяем напрямую, это независимая переменная, которая будет отложена по оси \ (x \). Ток является зависимой переменной и должен быть нанесен на ось \ (y \).
-
Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом случае независимой переменной является ток, который должен быть нанесен на ось \ (x \), а напряжение является зависимой переменной и должно быть нанесено на ось \ (y \).
Выводы
-
Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?
-
Изучите график, который вы построили на основе второй таблицы. Что происходит с напряжением на резисторе, когда ток через резистор увеличивается? т.е. увеличивается или уменьшается?
-
Подтверждают ли результаты ваших экспериментов закон Ома? Объясни.
Вопросы и обсуждение
- Для каждого из ваших графиков рассчитайте градиент и по нему определите сопротивление исходного резистора. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?
-
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_0 \)?
Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.
Зарегистрируйтесь здесьЗакон Ома
Упражнение 11.1Постройте график напряжения (по оси X) и тока (по оси Y).
Какой тип графика вы получите (прямолинейный, парабола, другая кривая)
прямая линия
Рассчитайте градиент графика.
Градиент графика (\ (m \)) — это изменение тока, деленное на изменение напряжения:
\ begin {align *} m & = \ frac {\ Delta I} {\ Delta V} \\ & = \ frac {(\ text {1,6}) — (\ text {0,4})} {(\ text {12}) — (\ text {3})} \\ & = \ текст {0,13} \ end {выровнять *}Подтверждают ли результаты ваших экспериментов закон Ома? Объясни.
Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_ {0} \)?
Вы начинаете с подключения известного резистора в цепь с источником питания. Теперь вы читаете напряжение источника питания и записываете его.
Затем вы последовательно подключаете два резистора.Теперь вы можете измерить напряжение на каждом из резисторов.
Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:
\ [V = IR \]Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток везде одинаковый в цепи, мы можем найти неизвестное сопротивление.
\ begin {align *} V_ {0} & = IR_ {0} \\ I & = \ frac {V_ {0}} {R_ {0}} \\ V_ {U} & = IR_ {U} \\ I & = \ frac {V_ {U}} {R_ {U}} \\ \ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\ \ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}} \ end {выровнять *}Омические и неомические проводники (ESBQ7)
Проводники, которые подчиняются закону Ома, имеют постоянное сопротивление, когда на них изменяется напряжение или увеличивается ток через них.Эти проводники называются омическими проводниками, проводниками. График зависимости тока от напряжения на этих проводниках будет прямолинейным. Некоторые примеры омических проводников — резисторы цепи и нихромовая проволока.
Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Это связано с тем, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводников называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка — типичный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.
В лампочке сопротивление нити накала резко возрастает, когда она нагревается от комнатной до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, то увеличение тока приведет к увеличению температуры нити накала, что приведет к увеличению ее сопротивления. Это эффективно ограничивает увеличение тока.В этом случае напряжение и ток не подчиняются закону Ома.
Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорировать. При применении металлических нитей накала ламп, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \) и начиная с комнатной температуры), изменение довольно велико.
В общем, для неомических проводов график зависимости напряжения от тока не будет прямолинейным, что означает, что сопротивление не является постоянным для всех значений напряжения и тока.
Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определят, какой из них подчиняется закону Ома. Вам потребуются лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр. Учащиеся должны обнаружить, что резистор подчиняется закону Ома, а лампочка — нет.
Омические и неомические проводники
Aim
Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома
Аппарат
4 ячейки, резистор, лампочка, соединительные провода, вольтметр, амперметр
Метод
Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой есть резистор, а во второй — лампочка.Настройте обе схемы выше, начиная с 1 ячейки. Для каждой цепи:
-
Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметра.
-
Измерьте ток в цепи с помощью амперметра.
-
Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.
Результаты
Нарисуйте в своей книге две таблицы, которые выглядят следующим образом.У вас должна быть одна таблица для измерений первой цепи с резистором и другая таблица для измерений второй цепи с лампочкой.
| Количество ячеек | Напряжение, В (\ (\ text {V} \)) | Ток, I (\ (\ text {A} \)) |
| \ (\ text {1} \) | ||
| \ (\ text {2} \) | ||
| \ (\ text {3} \) | ||
| \ (\ text {4} \) |
Анализ
Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) — ось) vs.\ (V \) (\ (x \) — ось), один для резистора и один для лампочки.
Вопросы и обсуждение
Внимательно изучите свои графики и ответьте на следующие вопросы:
-
Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?
-
Один или оба ваших графика выглядят так?
-
Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка закону Ома?
-
Имеет ли лампочка омический или неомический провод?
Использование закона Ома (ESBQ8)
Теперь мы готовы увидеть, как закон Ома используется для анализа схем.
Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \), а напряжение на резисторе равно \ (\ text { 5} \) \ (\ text {V} \), то мы можем использовать закон Ома для расчета тока, протекающего через резистор. Наша первая задача — нарисовать принципиальную схему. Решая любую проблему с электрическими цепями, очень важно составить схему схемы перед тем, как производить какие-либо расчеты. Принципиальная схема этой проблемы выглядит следующим образом:
Уравнение закона Ома: \ [R = \ frac {V} {I} \]
, который можно преобразовать в: \ [I = \ frac {V} {R} \]
Ток, протекающий через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\ & = \ текст {1} \ текст {А} \ end {align *}
Рабочий пример 1: Закон Ома
Изучите принципиальную схему ниже:
Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор, равен \ (\ text {4} \) \ (\ text {A} \ ).Какова разность потенциалов (напряжение) на резисторе?
Определите, как подойти к проблеме
Нам задают сопротивление резистора и ток, проходящий через него, и просят вычислить напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \ [R = \ frac {V} {I}. \]
Решить проблему
Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \). \ begin {align *} R & = \ frac {V} {I} \\ R \ times I & = \ frac {V} {I} \ times I \\ V & = I \ раз R \\ & = \ текст {10} \ times \ text {4} \\ & = \ текст {40} \ текст {V} \ end {align *}
Напишите окончательный ответ
Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).
Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.
Зарегистрируйтесь здесьЗакон Ома
Упражнение 11.2Рассчитайте сопротивление резистора, разность потенциалов которого равна \ (\ text {8} \) \ (\ text {V} \), когда ток равен \ (\ text {2} \) \ (\ text {A} \) протекает через него. Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {8} {2} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}Какой ток будет протекать через резистор \ (\ text {6} \) \ (\ text {Ω} \) при разности потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {18} {6} \\ & = \ текст {3} \ текст {А} \ end {выровнять *}Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \) при токе \ (\ text {1,5} \) \ (\ text {A} \) течет хоть это? Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} V & = I \ cdot R \\ & = (\ текст {1,5}) (10) \\ & = \ текст {15} \ текст {V} \ end {выровнять *}Резисторы последовательно и параллельно (ESBQ9)
В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы соединены последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. В параллельной цепи есть несколько путей, по которым течет ток.
Когда в цепи более одного резистора, мы обычно можем рассчитать общее суммарное сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .
Эквивалентное последовательное сопротивление
В цепи, в которой резисторы соединены последовательно, эквивалентное сопротивление — это просто сумма сопротивлений всех резисторов.
- Эквивалентное сопротивление в последовательной цепи,
-
Для последовательно подключенных n резисторов эквивалентное сопротивление составляет:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]
Применим это к следующей схеме.
Резисторы включены последовательно, следовательно:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\ & = \ текст {18} \ текст {Ω} \ end {align *}Эквивалентное параллельное сопротивление
В цепи, в которой резисторы включены параллельно, эквивалентное сопротивление определяется следующим определением.
- Эквивалентное сопротивление в параллельной цепи
-
Для резисторов \ (n \), включенных параллельно, эквивалентное сопротивление составляет:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]
Применим эту формулу к следующей схеме.
Какое полное (эквивалентное) сопротивление в цепи?
\ begin {align *} \ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \право) \\ & = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text { 1} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text {Ω}} {\ text {10} \ text { Ω}} \ right) \\ & = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\ R_ {p} & = \ text {0,625} \ text {Ω} \ end {align *}.Согласно закону Ома, I ∝ V, но I 1 / V в уравнении мощности. Как?
In I = V / R, ток прямо пропорционален напряжению, но ток обратно пропорционален напряжению в P = VI?
Это еще один запутанный вопрос, который чаще всего задают на собеседованиях по электротехнике и электронике.
Согласно закону Ома, Ток увеличивается при увеличении напряжения (I = V / R), но Ток уменьшается при увеличении напряжения согласно формуле (P = VI).Как объяснить?
, т.е.
- По закону Ома: I ∝ V (ток прямо пропорционален напряжению. I = V / R)
- Согласно формуле мощности: I ∝ 1 / V (ток обратно пропорционален напряжению. I = P / V)
Короче говоря, согласно закону Ома (V = IR или I = V / R), который показывает, что ток прямо пропорционален напряжению, но согласно P = VI или I = P / V , это показывает, что ток обратно пропорционален напряжению.
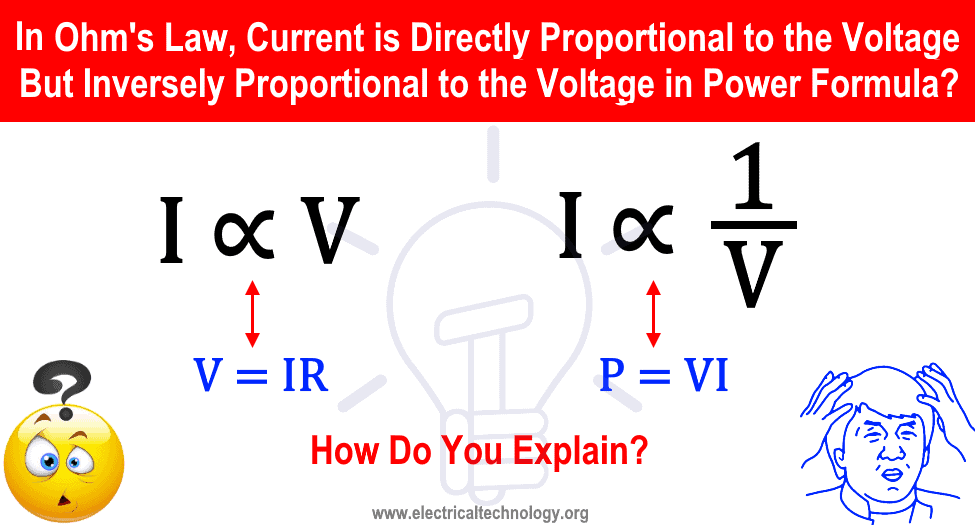

Давайте устраним путаницу, связанную с утверждением.
P = V x I
На самом деле, это зависит от того, как вы увеличиваете параметры, то есть увеличиваете ли вы напряжение, сохраняя мощность источника постоянной, или она меняется.
- Если мощность источника постоянна, ток будет уменьшаться при увеличении напряжения.
- Если вы не заботитесь о мощности и просто замените батарею на новую с более высокой номинальной мощностью, это может увеличить ток при повышении напряжения, поскольку мощность больше не постоянна i.е. мощность также была увеличена.
В случае трансформатора, когда напряжение увеличивается, ток уменьшается, потому что мощность остается постоянной, т.е. мощность на обеих сторонах равна P = VI (без учета коэффициента мощности: Cos θ).
В = I x R
По закону Ома ток (I) прямо пропорционален напряжению (В), если сопротивление (R) и температура остаются постоянными.
Согласно формуле мощности, в ней говорится, что ток обратно пропорционален напряжению, если мощность остается прежней.
Как мы уже знаем, в повышающем трансформаторе, если напряжение увеличивается, ток уменьшается там, где мощность такая же (поскольку трансформатор только повышает или понижает значение тока и напряжения и не меняет значение мощность). Точно так же напряжение уменьшается при увеличении тока в понижающем трансформаторе.
То же самое и с электростанцией, где выработка электроэнергии постоянна. Если мощность на стороне генерации улучшится, увеличатся как ток, так и напряжение.
Вкратце:
- Если мощность постоянна = Напряжение обратно пропорционально току , т.е. В 1 / I в P = VxI .
- Если сопротивление и температура постоянны: Напряжение прямо пропорционально току , т.е. В ∝ I в В = IxR .
Это точная причина , почему по закону Ома ток прямо пропорционален напряжению, но обратно пропорционален формуле напряжения в мощности.
Связанные вопросы / ответы:
.Как использовать теорему Тевенина | ОРЕЛ
Существует множество доступных методов анализа сложных электрических цепей, таких как анализ сетки, узловой анализ или законы Кирхгофа для цепей. Проблема в том, что при проектировании сети постоянного тока у вас будет нагрузка, значение которой будет меняться по мере развития процесса проектирования. Вместо того, чтобы пересчитывать ток и напряжение всей вашей цепи при каждом изменении нагрузки, вы можете упростить этот процесс с помощью теоремы Тевенина.В этом блоге мы рассмотрим, как упростить любую сложную линейную схему до единого источника напряжения и последовательного сопротивления. Оттуда мы можем использовать нашу эквивалентную схему Тевенина, чтобы быстро рассчитать ток и напряжение. Давай начнем.
Что такое теорема Тевенина?
Как и все другие математические и научные теории / законы, теорема Тевенина была изобретена самим человеком, Леоном Шарлем Тевенином, французским телеграфным инженером, родившимся в Мо, Франция. После службы в корпусе инженеров-телеграфистов Тевенин был назначен инспектором по обучению в Высшей школе телеграфии в 1882 году.Именно здесь он заинтересовался измерением электрических цепей с использованием двух доступных в то время методов — законов Кирхгофа и закона Ома.

Леон Шарль Тевенин (Источник изображения)
В попытке упростить анализ сложных схем для каждого инженера, Тевенин разработал свою теперь известную теорему Тевенина, которая сводит сложные схемы к упрощенным эквивалентным схемам Тевенина.
Эта теорема утверждает, что вы можете взять любую линейную цепь, которая может содержать несколько ЭДС и резистивные компоненты, и упростить схему до одного источника напряжения и последовательного сопротивления, подключенного к нагрузке.

Упрощенная эквивалентная схема Тевенина с одним источником напряжения и сопротивлением. (Источник изображения)
В данном случае линейная цепь — это цепь, которая включает в себя пассивные компоненты, такие как резисторы, катушки индуктивности и конденсаторы. Однако, если вы работаете со схемой, которая включает газоразрядные или полупроводниковые компоненты, то у вас нелинейная схема. Теорема Тевенина не для этого годилась. Так зачем использовать эту теорему для анализа линейных цепей?
- Эффективность .Теорема Тевенина обеспечивает простой метод анализа силовых цепей, которые обычно имеют нагрузку, которая меняет значение в процессе анализа. Эта теорема обеспечивает эффективный способ вычисления напряжения и тока, протекающих через нагрузку, без необходимости заново рассчитывать всю схему.
- Фокус . Теорема Тевенина также предоставляет эффективный способ сосредоточить анализ на определенной части схемы. Это позволяет рассчитать напряжение и ток на конкретном терминале, упростив остальную часть схемы с помощью эквивалента Тевенина.
Посмотрите на пример схемы ниже. Здесь в качестве нагрузки используется резистор R2. Мы хотим рассчитать напряжение и ток, протекающие через этот резистор, без необходимости использовать трудоемкий метод анализа, такой как Branch Current, Mesh Current и т. Д., Каждый раз, когда значение резистора нагрузки изменяется.

(Источник изображения)
Чтобы упростить задачу, мы можем использовать теорему Тевенина, чтобы удалить сопротивление нагрузки и напряжения. Затем мы упрощаем остальную часть схемы как единый источник напряжения и последовательное сопротивление.В этой упрощенной схеме Тевенина два резистора R1 и R3 вместе с вторичным напряжением B2 упрощены до единого источника напряжения и последовательного сопротивления. Что касается нагрузочного резистора, то упрощенные напряжение и сопротивление будут работать так же, как и наша исходная схема. Теперь у нас есть только две простые переменные, с которыми мы будем работать в наших расчетах.

(Источник изображения)
Теорема Тевенина в действии
Давайте посмотрим на пример схемы и вычислим ток, протекающий через нагрузочный резистор между двумя выводами.Процесс анализа цепи постоянного тока с использованием теоремы Тевенина требует следующих шагов:
- Найдите сопротивление Тевенину, отключив все источники напряжения и нагрузочный резистор.
- Найдите напряжение Thevenin, подключив напряжение.
- Используйте сопротивление и напряжение Тевенина, чтобы найти ток, протекающий через нагрузку.
Вот пример схемы, с которой мы будем работать:

(Источник изображения)
Шаг 1 — Сопротивление Тевенину
Сначала нам нужно снять нагрузочный резистор 40 Ом, соединяющий клеммы A и B, вместе со всеми источниками напряжения.Это даст нам обрыв цепи при нулевом напряжении, в результате чего останется только два резистора, подключенных последовательно.

(Источник изображения)
Чтобы вычислить общее сопротивление тевенину, мы можем использовать следующий процесс:

Шаг 2 — Напряжение Thevenin

Затем мы можем использовать закон Ома для вычисления полного тока, протекающего по цепи, следующим образом:

Поскольку эти резисторы соединены последовательно, они будут иметь одинаковый 0.33 ампера. Мы можем использовать эти значения резисторов и наш ток для расчета падения напряжения, которое составляет:

Шаг 3 — Ток нагрузки
Теперь, когда у нас есть сопротивление и напряжение Тевенина, мы можем соединить нашу эквивалентную схему Тевенина с нашим исходным нагрузочным резистором, как показано ниже.

Отсюда мы можем использовать закон Ома для расчета полного тока, протекающего через нагрузочный резистор, следующим образом:


Готовы проверить свои навыки? Используйте теорему Тевенина, чтобы найти iload и vload для схемы ниже!

Запомните трехэтапный процесс:
- Найдите сопротивление Тевенину, отключив все источники напряжения и нагрузку.
- Найдите напряжение Thevenin, повторно подключив источники напряжения.
- Используйте сопротивление и напряжение Тевенина, чтобы найти полный ток, протекающий через нагрузку.
Сохраняйте простоту
Планируете разработать схему питания постоянного тока? Скорее всего, вы включите нагрузку, значение которой изменится во время анализа схемы. Вместо того, чтобы пересчитывать всю схему каждый раз, когда вы меняете значение этой нагрузки, теперь у вас есть теорема Тевенина, которая упростит вашу работу.
Эта теорема позволяет вам взять любую сложную линейную схему с множеством резистивных компонентов и ЭДС и упростить ее до эквивалентной схемы Тевенина. С помощью этой упрощенной схемы вы можете легко рассчитать полный ток и напряжение, протекающие через нагрузку. Это огромная экономия времени для любого инженера, которому необходимо эффективно анализировать схемы для силовых схем и других сложных приложений.
Тем из вас, кто изучает визуальное / кинестетическое мышление, обязательно посмотрите видео ниже, в котором показано, как использовать теорему Тевенина шаг за шагом.
Готовы спроектировать свою первую силовую цепь? Попробуйте Autodesk EAGLE бесплатно сегодня!
.Растущее внутреннее сопротивление — Battery University
Понимание важности низкой проводимости
Емкость сама по себе имеет ограниченное использование, если батарея не может эффективно передавать накопленную энергию; аккумулятор также нуждается в низком внутреннем сопротивлении. Измеренное в миллиомах (мОм) сопротивление является привратником батареи; чем ниже сопротивление, тем меньше ограничений для пакета. Это особенно важно при тяжелых нагрузках, таких как электроинструменты и электрические трансмиссии.Высокое сопротивление вызывает нагрев батареи и падение напряжения под нагрузкой, вызывая преждевременное отключение. На рис. 1 показана батарея с низким внутренним сопротивлением в виде свободно протекающего отвода по сравнению с батареей с повышенным сопротивлением, в которой отвод ограничен.
|
Низкое сопротивление, подает высокий ток по запросу; батарея остается прохладной. |
Высокое сопротивление, ток ограничен, напряжение падает под нагрузкой; аккумулятор нагревается. |
Рис. 1: Влияние внутреннего сопротивления батареи. Батарея с низким внутренним сопротивлением обеспечивает высокий ток по запросу. Высокое сопротивление вызывает нагрев батареи и падение напряжения. Оборудование отключается, оставляя энергию позади. Предоставлено Cadex
|
Свинцово-кислотный имеет очень низкое внутреннее сопротивление, и батарея хорошо реагирует на сильные всплески тока, которые длятся несколько секунд.Однако из-за присущей медлительности свинцово-кислотная кислота неэффективна при длительном сильноточном разряде; аккумулятор быстро утомляется и ему требуется отдых для восстановления. Некоторая медлительность проявляется во всех батареях в разной степени, но особенно ярко она проявляется у свинцово-кислотных. Это намекает на то, что подача энергии основана не только на внутреннем сопротивлении, но и на чувствительности химического состава, а также на температуре. В этом отношении технологии на основе никеля и лития более чувствительны, чем свинцово-кислотные.
Сульфатирование и коррозия решетки являются основными факторами повышения внутреннего сопротивления свинцово-кислотной кислоты. Температура также влияет на сопротивление; тепло понижает его, а холод повышает. Нагрев батареи на мгновение снизит внутреннее сопротивление, чтобы обеспечить дополнительное время работы. Однако это не восстанавливает батарею и добавляет кратковременное напряжение.
Кристаллическое образование, также известное как «память», способствует внутреннему сопротивлению в никелевых батареях. Это часто можно исправить с помощью глубокого цикла.Внутреннее сопротивление литий-ионных аккумуляторов также увеличивается по мере использования и старения, но были внесены улучшения с добавлением электролитных добавок, чтобы держать под контролем образование пленок на электродах. (
.
