Что такое индуктивность и какую роль она играет в электрических цепях. Как рассчитывается индуктивность. Какие факторы влияют на величину индуктивности. Где применяется индуктивность на практике.

Что такое индуктивность и как она определяется

Индуктивность — это физическая величина, характеризующая магнитные свойства электрической цепи. Она показывает способность проводника создавать магнитное поле при протекании через него электрического тока.

Индуктивность определяется как коэффициент пропорциональности между магнитным потоком Ф, пронизывающим контур, и силой тока I в этом контуре:

Ф = L * I

где L — индуктивность контура.

Единицей измерения индуктивности в системе СИ является генри (Гн). 1 генри — это индуктивность контура, в котором при изменении силы тока на 1 ампер за 1 секунду возникает ЭДС самоиндукции в 1 вольт.

Факторы, влияющие на величину индуктивности

Индуктивность контура зависит от следующих основных факторов:

• Геометрические размеры и форма контура
• Число витков (для катушек индуктивности)
• Магнитная проницаемость среды
• Наличие ферромагнитного сердечника

Чем больше размеры контура и число витков катушки, тем выше индуктивность. Наличие ферромагнитного сердечника значительно увеличивает индуктивность катушки за счет усиления магнитного поля.

Расчет индуктивности для различных конфигураций

Для расчета индуктивности используются различные формулы в зависимости от конфигурации проводника или катушки:

Индуктивность длинного соленоида

L = μ * μ0 * N^2 * S / l

где:

• μ — относительная магнитная проницаемость среды
• μ0 — магнитная постоянная
• N — число витков
• S — площадь поперечного сечения
• l — длина соленоида

Индуктивность тороидальной катушки

L = μ * μ0 * N^2 * S / (2 * π * R)

где R — средний радиус тороида

Индуктивность прямого провода

L = (μ0 / 2π) * l * ln(2l / d)

где l — длина провода, d — его диаметр

Практическое применение индуктивности

Индуктивность широко применяется в различных областях электротехники и электроники:

• Фильтры в электрических цепях
• Колебательные контуры
• Трансформаторы
• Дроссели
• Электродвигатели
• Генераторы
• Антенны

Катушки индуктивности используются для создания магнитных полей, накопления энергии, сглаживания пульсаций тока и напряжения.

Индуктивность в колебательном контуре

Одно из важнейших применений индуктивности — колебательный контур. Он состоит из катушки индуктивности L и конденсатора емкостью C. В таком контуре возникают электромагнитные колебания с частотой:

f = 1 / (2π * √(LC))

Колебательные контуры широко используются в радиотехнике для генерации и фильтрации сигналов определенной частоты.

Взаимная индуктивность

Помимо собственной индуктивности существует также понятие взаимной индуктивности M между двумя контурами. Она характеризует магнитную связь между контурами и определяется как:

M = k * √(L1 * L2)

где k — коэффициент связи (0 ≤ k ≤ 1), L1 и L2 — индуктивности контуров.

Взаимная индуктивность лежит в основе работы трансформаторов.

Индуктивность и энергия магнитного поля

Индуктивность определяет энергию W магнитного поля, создаваемого током I в контуре:

W = L * I^2 / 2

Эта формула показывает, что индуктивность характеризует способность контура накапливать энергию в магнитном поле.

Влияние индуктивности на переходные процессы

Индуктивность играет важную роль в переходных процессах в электрических цепях. При изменении тока в индуктивном элементе возникает ЭДС самоиндукции, препятствующая этому изменению:

ε = -L * dI/dt

Это приводит к тому, что ток в индуктивности не может измениться мгновенно. Время установления тока зависит от величины индуктивности.

Измерение индуктивности

Для измерения индуктивности применяются специальные приборы — измерители индуктивности (LC-метры). Основные методы измерения:

• Резонансный метод
• Мостовой метод
• Метод вольтметра-амперметра

Выбор метода зависит от требуемой точности и диапазона измеряемых величин.

Индуктивность в электронных схемах

В электронных схемах индуктивность используется для:

• Фильтрации высокочастотных помех
• Создания задержки сигналов
• Формирования частотных характеристик цепей
• Согласования импедансов

Правильный выбор индуктивности важен для обеспечения стабильной работы электронных устройств.

Заключение

Индуктивность — фундаментальная характеристика электрических цепей, играющая важную роль во многих областях электротехники и электроники. Понимание свойств и особенностей применения индуктивности необходимо для проектирования и анализа различных электротехнических устройств.

формула. Измерение индуктивности. Индуктивность контура

Кто в школе не изучал физику? Для кого-то она была интересна и понятна, а кто-то корпел над учебниками, пытаясь выучить наизусть сложные понятия. Но каждый из нас запомнил, что мир основан на физических знаниях. Сегодня мы поговорим о таких понятиях, как индуктивность тока, индуктивность контура, и узнаем, какие бывают конденсаторы и что такое соленоид.

Электрическая цепь и индуктивность

Индуктивность служит для характеристики магнитных свойств электрической цепи. Ее определяют как коэффициент пропорциональности между текущим электрическим током и магнитным потоком в замкнутом контуре. Поток создается этим током через поверхность контура. Еще одно определение гласит, что индуктивность является параметром электрической цепи и определяет ЭДС самоиндукции. Термин применяется для указания элемента цепи и приходится характеристикой эффекта самоиндукции, который был открыт Д. Генри и М. Фарадеем независимо друг от друга. Индуктивность связана с формой, размером контура и значением магнитной проницаемости окружающей среды. В единице измерения СИ эта величина измеряется в генри и обозначается как L.

Самоиндукция и измерение индуктивности

Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:

Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.

Как найти индуктивность

Формула, которая является простейшей для нахождения величины, следующая:

где F – магнитный поток, I – ток в контуре.

Через индуктивность можно выразить ЭДС самоиндукции:

Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.

Переменная индуктивность дает возможность найти и энергию магнитного поля:

«Катушка ниток»

Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.

Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:

где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.

Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.

Катушку можно разделить на два вида:

1. С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
2. С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.

Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:

• L = 10µ0ΠN²R² : 9R + 10l.

А вот уже для многослойной другая формула:

• L= µ0N²R² :^{2Π(6R + 9l + 10w).}

Основные выводы, связанные с работой катушек:

1. На цилиндрическом феррите самая большая индуктивность возникает в середине.
2. Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
3. Индуктивность тем меньше, чем меньше количество витков.
4. В тороидальном сердечнике расстояние между витками не играет роли катушки.
5. Значение индуктивности зависит от «витков в квадрате».
6. Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
7. При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.

Соленоид

Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:

Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом – ярмом.

В наше время устройство может соединять в себе гидравлику и электронику. На этой основе созданы четыре модели:

• Первая способна контролировать линейное давление.
• Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
• Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
• Четвертая управляется гидравлическим способом или клапанами.

Необходимые формулы для расчетов

Чтобы найти индуктивность соленоида, формула применяется следующая:

где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.

Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:

где S – это площадь поперечного сечения, а l – длина соленоида.

Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.

Работа на постоянном и переменном токе

Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:

где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.

Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:

где L показывает значение индуктивности, а E – запасающую энергию.

ЭДС самоиндукции возникает при изменении тока в соленоиде.

В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.

Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.

Колебательные контуры

Простейшей резонансной цепью является последовательный колебательный контур, состоящий из включенных катушек индуктивности и конденсатора, через которые протекает переменный ток. Чтобы определить индуктивность катушки, формула используется следующая:

где XL показывает реактивное сопротивление катушки, а W — круговая частота.

Если используется реактивное сопротивление конденсатора, то формула будет выглядеть следующим образом:

Xc = 1 : W х C.

Важными характеристиками колебательного контура являются резонансная частота, волновое сопротивление и добротность контура. Первая характеризует частоту, где сопротивление контура имеет активный характер. Вторая показывает, как проходит реактивное сопротивление на резонансной частоте между такими величинами, как емкость и индуктивность колебательного контура. Третья характеристика определяет амплитуду и ширину амплитудно-частотных характеристик (АЧХ) резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.

При параллельном колебательном контуре включены два реактивных элемента с разной силой реактивности. Использование такого вида контура подразумевает знание, что при параллельном включении элементов нужно складывать только их проводимости, но не сопротивления. На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:

При работе параллельного контура за один период колебаний дважды происходит энергетический обмен между конденсатором и катушкой. В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.

Работа конденсатора

Устройство представляет собой двухполюсник малой проводимости и с переменным или постоянным значением емкости. Когда конденсатор не заряжен, сопротивление его близко к нулю, в противном случае оно равно бесконечности. Если источник тока отсоединить от данного элемента, то он становится этим источником до своей разрядки. Использование конденсатора в электронике заключается в роли фильтров, которые удаляют помехи. Данное устройство в блоках питания на силовых цепях применяются для подпитки системы при больших нагрузках. Это основано на способности элемента пропускать переменную составляющую, но непостоянный ток. Чем выше частота составляющей, тем меньше у конденсатора сопротивление. В результате через конденсатор глушатся все помехи, которые идут поверх постоянного напряжения.

Сопротивление элемента зависит от емкости. Исходя из этого, правильнее будет ставить конденсаторы с различным объемом, чтобы улавливать разного рода помехи. Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.

Конденсаторы бывают многих типов. В основном используется классификация по типу диэлектрика, так как этот параметр определяет стабильность емкости, сопротивление изоляции и так далее. Систематизация по данной величине следующая:

1. Конденсаторы с газообразным диэлектриком.
2. Вакуумные.
3. С жидким диэлектриком.
4. С твердым неорганическим диэлектриком.
5. С твердым органическим диэлектриком.
6. Твердотельные.
7. Электролитические.

Существует классификация конденсаторов по назначению (общий или специальный), по характеру защиты от внешних факторов (защищенные и незащищенные, изолированные и неизолированные, уплотненные и герметизированные), по технике монтажа (для навесного, печатного, поверхностного, с выводами под винт, с защелкивающимися выводами). Также устройства можно различить по способности к изменению емкости:

1. Постоянные конденсаторы, то есть у которых емкость остается всегда постоянной.
2. Подстроечные. У них емкость не меняется при работе аппаратуры, но можно ее регулировать разово или периодически.
3. Переменные. Это конденсаторы, которые допускают в процессе функционирования аппаратуры изменение ее емкости.

Индуктивность и конденсатор

Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:

где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.

Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.

Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:

где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.

Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:

• Lk = Lc : n + µ0 l х d : (3b) + Lb,

где l – длина шин, b – ее ширина, а d – расстояние между шинами.

Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.

fb.ru

Магнитная индукция — Википедия

Материал из Википедии — свободной энциклопедии

Магни́тная инду́кция B→{\displaystyle {\vec {B}}} — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой F→{\displaystyle {\vec {F}}} магнитное поле действует на заряд q{\displaystyle q}, движущийся со скоростью v→{\displaystyle {\vec {v}}}.

Более конкретно, B→{\displaystyle {\vec {B}}} — это такой вектор, что сила Лоренца F→{\displaystyle {\vec {F}}}, действующая со стороны магнитного поля^[1] на заряд q{\displaystyle q}, движущийся со скоростью v→{\displaystyle {\vec {v}}}, равна

F→=q[v→×B→]{\displaystyle {\vec {F}}=q\left[{\vec {v}}\times {\vec {B}}\right]}

F=qvBsin⁡α{\displaystyle F=qvB\sin \alpha }

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора F→{\displaystyle {\vec {F}}} перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещённую в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС единицей магнитной индукции является гаусс (Гс), в СИ — тесла (Тл)

1 Тл = 10⁴ Гс

Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

• (Здесь формулы приведем в СИ, в виде для вакуума^[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике[править | править код]

В магнитостатическом пределе^[4] наиболее важными являются:

• Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:

  B→(r→)=μ04π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right){\vec {dL_{1}}}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

  B→(r→)=μ04π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

• Теорема Ампера о циркуляции магнитного поля^[5]:

  ∮∂S⁡B→⋅dl→=μ0IS≡μ0∫Sj→⋅dS→,{\displaystyle \oint \limits _{\partial S}{\vec {B}}\cdot {\vec {dl}}=\mu _{0}I_{S}\equiv \mu _{0}\int \limits _{S}{\vec {j}}\cdot {\vec {dS}},}

  rotB→≡∇→×B→=μ0j→.{\displaystyle \mathrm {rot} \,{\vec {B}}\equiv {\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}.}

В общем случае[править | править код]

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{\displaystyle {\vec {B}}}:

divE→=ρε0,   rotE→=−∂B→∂t{\displaystyle \mathrm {div} \,{\vec {E}}={\frac {\rho }{\varepsilon _{0}}},\ \ \ \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}

divB→=0,    rotB→=μ0j→+1c2∂E→∂t{\displaystyle \mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}}

а именно:

divB→=0,{\displaystyle \mathrm {div} \,{\vec {B}}=0,}

rotE→=−∂B→∂t,{\displaystyle \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}

rotB→=μ0j→+1c2∂E→∂t.{\displaystyle \mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}.}

F→=qE→+q[v→×B→],{\displaystyle {\vec {F}}=q{\vec {E}}+q\left[{\vec {v}}\times {\vec {B}}\right],}

Следствия из неё, такие как

• Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)

dF→=[Idl→×B→],{\displaystyle d{\vec {F}}=\left[I{\vec {dl}}\times {\vec {B}}\right],}

dF→=[j→dV×B→],{\displaystyle d{\vec {F}}=\left[{\vec {j}}dV\times {\vec {B}}\right],}

M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}

• выражение для потенциальной энергии магнитного диполя в магнитном поле:

U=−m→⋅B→,{\displaystyle U=-{\vec {m}}\cdot {\vec {B}},}

• а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
• Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:

F→=Kqmr→r3.{\displaystyle {\vec {F}}=K{\frac {q_{m}{\vec {r}}}{r^{3}}}.}

• (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля

w=B22μ0{\displaystyle w={\frac {B^{2}}{2\mu _{0}}}}

• Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

1. ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид:

   F→=qE→+q[v→×B→].{\displaystyle {\vec {F}}=q{\vec {E}}+q[{\vec {v}}\times {\vec {B}}].}

   При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведённую в основном тексте.
2. ↑ Это определение с современной точки зрения менее фундаментально, чем приведённое выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
3. ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
4. ↑ То есть в частном случае

ru.wikipedia.org

Индуктивность — Большая советская энциклопедия

Индукти́вность

(от лат. inductio — наведение, побуждение)

физическая величина, характеризующая магнитные свойства электрической цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пространстве магнитное поле, причём Магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо пропорционален силе тока I :

Коэффициент пропорциональности L называется И. или коэффициентом самоиндукции контура. И. зависит от размеров и формы контура, а также от магнитной проницаемости (См. Магнитная проницаемость) окружающей среды. В Международной системе единиц (См. Международная система единиц) (СИ) И. измеряется в Генри, в СГС системе единиц (См. СГС система единиц) (Гаусса) И. имеет размерность длины и поэтому единица И. называется сантиметром (1 гн = 10⁹см).

Через И. выражается эдс самоиндукции (См. Самоиндукция) в контуре, возникающая при изменении в нём тока:

(ΔI — изменение тока за время Δt). При заданной силе тока И. определяет энергию W магнитного поля тока:

Чем больше И., тем больше магнитная энергия, накапливаемая в пространстве вокруг контура с током. Если провести аналогию между электрическими и механическими явлениями, то магнитную энергию следует сопоставить с кинетической энергией тела Т = mv²/2 (где m — масса тела, v — скорость его движения), при этом И. будет играть роль массы, а ток — роль скорости. Таким образом, И. определяет инерционные свойства тока.

Практически участки цепи со значительной И. выполняют в виде индуктивности катушек (См. Индуктивности катушка). Для увеличения L применяют катушки с железными сердечниками, но в этом случае, в силу зависимости магнитной проницаемости μ ферромагнетиков (См. Ферромагнетики) от напряжённости поля, а следовательно, и от силы тока, И. становится зависящей от I. И. длинного соленоида из N витков, имеющего площадь поперечного сечения S и длину l, в среде с магнитной проницаемостью μ равна (в единицах СИ): L = μμ₀N ²S/l, где μ₀ — Магнитная постоянная, или магнитная проницаемость вакуума.

Лит.: Калашников С. Г., Электричество, М., 1970 (Общий курс физики, т. 2), гл. 9.

Г. Я. Мякишев.

Источник: Большая советская энциклопедия на Gufo.me

---

Значения в других словарях

1. ИНДУКТИВНОСТЬ — (от лат. inductio — наведение, побуждение), величина, характеризующая магн. св-ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр-ве магн. Физический энциклопедический словарь
2. индуктивность — ИНДУКТ’ИВНОСТЬ, индуктивности, мн. нет, ·жен. (·книж. спец.). ·отвлеч. сущ. к индуктивный. Ииндуктивность доказательств. Толковый словарь Ушакова
3. индуктивность — Индукт/и́вн/ость/. Морфемно-орфографический словарь
4. индуктивность — индуктивность I ж. Отвлеч. сущ. по прил. индуктивный I 2. II ж. Физическая величина, характеризующая магнитные свойства электрических цепей. Толковый словарь Ефремовой
5. индуктивность — орф. индуктивность, -и Орфографический словарь Лопатина
6. индуктивность — -и, ж. лог., физ. Свойство по знач. прил. индуктивный. Индуктивность доказательств. Индуктивность проводника. Малый академический словарь
7. индуктивность — Индуктивность, индуктивности, индуктивности, индуктивностей, индуктивности, индуктивностям, индуктивность, индуктивности, индуктивностью, индуктивностями, индуктивности, индуктивностях Грамматический словарь Зализняка
8. ИНДУКТИВНОСТЬ — ИНДУКТИВНОСТЬ — физическая величина, характеризующая магнитные свойства электрических цепей и равная отношению потока Ф магнитной индукции, пересекающего поверхность, ограниченную проводящим контуром, к силе тока в этом контуре, создающем Ф; в СИ измеряется в генри. Большой энциклопедический словарь
9. ИНДУКТИВНОСТЬ — ИНДУКТИВНОСТЬ, свойство электрической цепи или элемента цепи, создающий ЭЛЕКТРОДВИЖУЩУЮ СИЛУ (ЭДС) при изменении электрического тока. В системе СИ единицей измерения служит ГЕНРИ. Научно-технический словарь
10. индуктивность — сущ., кол-во синонимов: 1 индуктанц 1 Словарь синонимов русского языка

gufo.me

Индуктивность

Индуктивность — это физическая (электрическая) величина, которая характеризует магнитные свойства электрической цепи. Как известно электрический ток, протекающий через проводящий контур, создает вокруг него магнитное поле. Это происходит потому, что ток изначально несет в себе энергию. Проходя через проводник, он частично отдает ее, и она превращается в энергию магнитного поля. Индуктивность, по сути, является коэффициентом пропорциональности между протекающим током и возникающим при этом магнитным полем.

Чем выше индуктивность проводника, тем больше будет магнитное поле при одном и том же значении электрического тока. Физически индуктивность в электрической цепи – это катушка, состоящая из пассивного (диэлектрик) или активного (ферромагнитный материал, железо) сердечника и намотанного на него электрического провода. Это один из самых обсуждаемых электрических компонентов на форумах любителей электроники.

Если протекающий ток изменяет свою величину во времени, то есть является не постоянным, а переменным, то в индуктивном контуре меняется магнитное поле, вследствие чего возникает ЭДС (электродвижущая сила) самоиндукции. Эта ЭДС также как и электрическое напряжение измеряется в вольтах (В).

Единицей измерения индуктивности является Гн (генри). Она названа в честь Джозефа Генри – американского ученого, открывшего явление самоиндукции. Считается, что контур (катушка индуктивности) имеет величину 1 Гн, если при изменении тока в 1 А (ампер) за одну секунду в нем возникает ЭДС величиною в 1 В (вольт). Обозначается индуктивность буквой L, в честь Эмиля Христиановича Ленца – знаменитого российского физика. Термин «индуктивность» был предложен Оливером Хевисайдом – английским ученым-самоучкой в 1886 году.

< Предыдущая		Следующая >

scsiexplorer.com.ua

Индуктивность | Страница 3 из 3 | Electronov.net

Основные параметры индуктивностей:

• Номинальная индуктивность:

Заводское значение индуктивности конкретного прибора, измеряется это значение в Генри (производные наноГенри (нГн), микроГенри (мкГн) и т.д). Номинальные значения индуктивностей выбираются из специальных номинальных рядов Е6, Е12, Е24 и т.д.

• Допуск (точность):

Допустимое отклонение величины реальной индуктивности от номинальной. Указывается в процентах от номинального значения индуктивности. Допуск может достигать 20%.

• Ток насыщения:

Величина тока, при достижении которой, происходит интенсивное рассеяние магнитного потока вне сердечника, что вызывает наведение токов индукции в близко расположенных проводниках. При периодическом насыщении возникают всплески помех, частоты которых распространяются и на звуковых частотах, и в радиочастотном диапазоне. Также насыщение сердечника приводит к его перегреву, вплоть до физического разрушения.

• Температурный коэффициент индуктивности:

Параметр, характеризующий зависимость индуктивности катушки от температуры. Температурная нестабильность индуктивности обусловлена целым рядом факторов: при нагреве увеличивается длина и диаметр провода обмотки, увеличивается длина и диаметр каркаса, в результате чего изменяются шаг и диаметр витков; кроме того при изменении температуры изменяются диэлектрическая проницаемость материала каркаса, что ведёт к изменению собственной ёмкости катушки. Очень существенно влияние температуры на магнитную проницаемость ферромагнетика сердечника.

Маркировка индуктивностей:

Кодовая маркировка:

Применяется 2 варианта кодовой маркировки:

1 Вариант: XYZ обозначает XY•10^Z мкГн, причем для индуктивностей менее 10 мкГн десятичным разделителем является буква «R», менее 1 мкГн – буква «N», и в этом случае значение индуктивности в нГн.

Иначе говоря, первые 2 цифры определяют число (мантиссу), а последняя цифра определяет количество нулей (десятичная степень).

2 Вариант: значение номинальной индуктивности непосредственно указано числом в мкГн.

После цифрового кода указывается буквенный код допуска, в случае его отсутствия – допуск 20%.

Например: 102 — это 10•10² мкГн = 1000 мкГн = 1 мГн, допуск — 20%; 6R8J – 6.8 мкГн, допуск — 5%; R68K – 0.68 мкГн, допуск — 10%; 22N – 22 нГн, допуск — 20%; 2N2D – 2.2 нГн, допуск — ±0,3 нГн.

Таблица 1 — Кодирование допуска индуктивности.

Цветовая маркировка:

Наиболее часто применяется кодировка 4 или 3 цветными кольцами или точками.

Первые две метки указывают на значение номинальной индуктивности (мантисса) в микрогенри (мкГн, uН), третья метка — множитель (десятичная степень), четвертая — допуск. В случае кодирования 3 метками подразумевается допуск 20%. Цветное кольцо, обозначающее первую цифру номинала, может быть шире, чем все остальные.

Рисунок 2 — Цветовое кодирование индуктивности.

Условное обозначение индуктивностей на схемах:

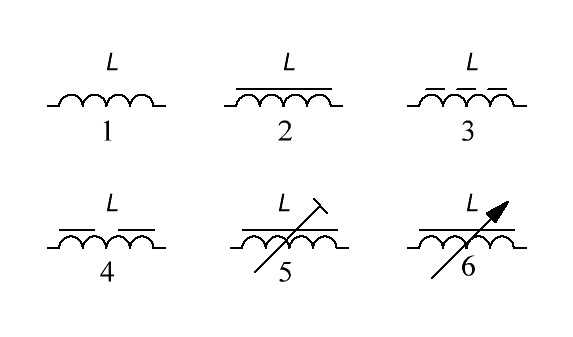Рисунок 3 — УГО индуктивности.

1. – бескаркасная индуктивность;
2. – индуктивность с ферритовым сердечником;
3. – индуктивность с сердечником из магнитодиэлектрика, т.е. диэлектрического магнитного материала;
4. – индуктивность с ферритовым сердечником с зазором;
5. – индуктивность с возможностью регулировки положения ферритового сердечника;
6. – переменная индуктивность (вариометр).

Рядом с условным обозначением указывается тип элемента (L) и порядковый номер, также рядом с условным обозначением может указываться (не является обязательным требованием) номинал элемента.

На электрических принципиальных схемах номинальная индуктивность обычно указывается в микрогенри (1 мкГн = 1·10³ нГн = 1·10⁻⁶ Гн).

Внешний вид катушек индуктивности:

Рисунок 4 — Внешний вид индуктивностей.

electronov.net