Как определить цену деления нониуса штангенциркуля и рассчитать результат измерения — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как устроен штангенциркуль с нониусом. Как найти цену деления нониуса. Как правильно снять показания со шкал штангенциркуля. Как рассчитать результат измерения с учетом нулевой погрешности. Какие бывают типы штангенциркулей и их точность.

Содержание

Устройство и принцип работы штангенциркуля с нониусом

Штангенциркуль с нониусом — это высокоточный измерительный инструмент, позволяющий измерять линейные размеры с точностью до десятых и сотых долей миллиметра. Его основными частями являются:

Штанга с основной миллиметровой шкалой
Рамка с нониусом, перемещающаяся вдоль штанги
Измерительные губки для наружных и внутренних измерений
Глубиномер для измерения глубины отверстий

Принцип работы штангенциркуля основан на использовании дополнительной шкалы — нониуса, позволяющей повысить точность отсчета. Как это работает?

Что такое цена деления нониуса и как ее определить

Цена деления нониуса (точность нониуса) — это величина, на которую повышается точность измерения по сравнению с основной шкалой. Она рассчитывается по формуле:

i = a/n

где:

i — цена деления нониуса
a — цена деления основной шкалы (обычно 1 мм)
n — число делений нониуса

Например, если на нониусе 10 делений, соответствующих 9 мм основной шкалы, то цена деления нониуса составит:

i = 1 мм / 10 = 0,1 мм

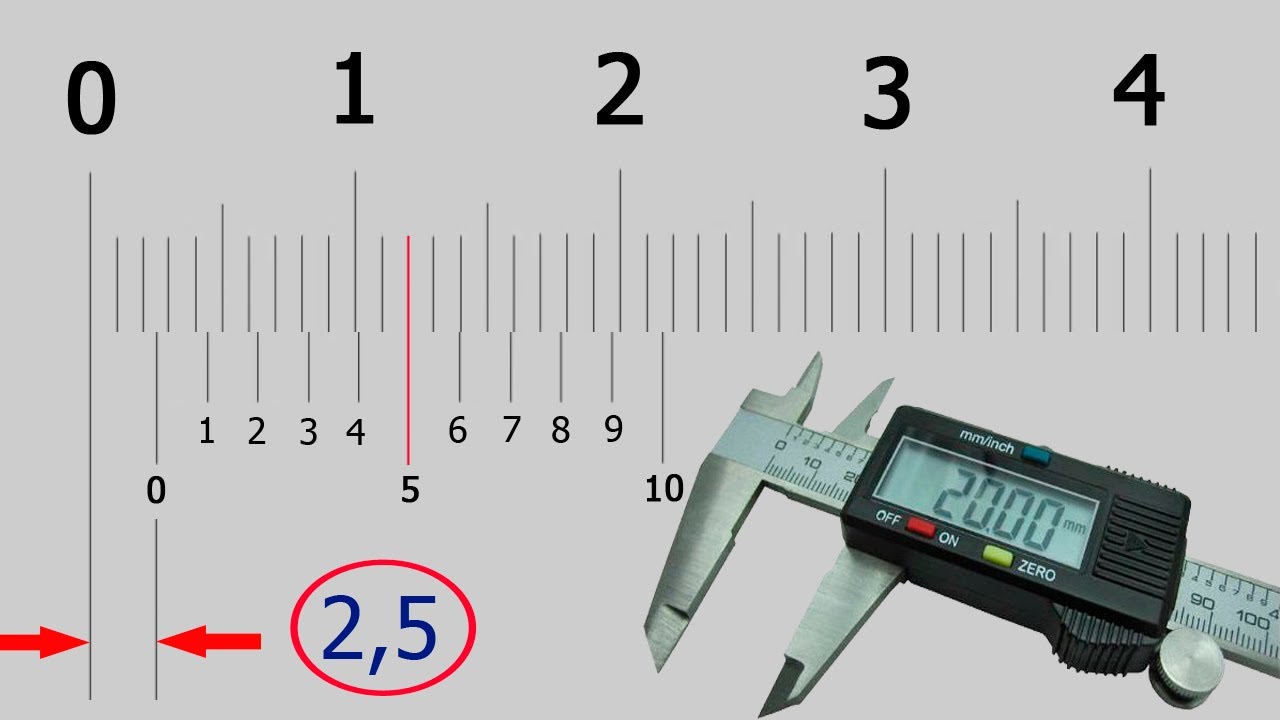
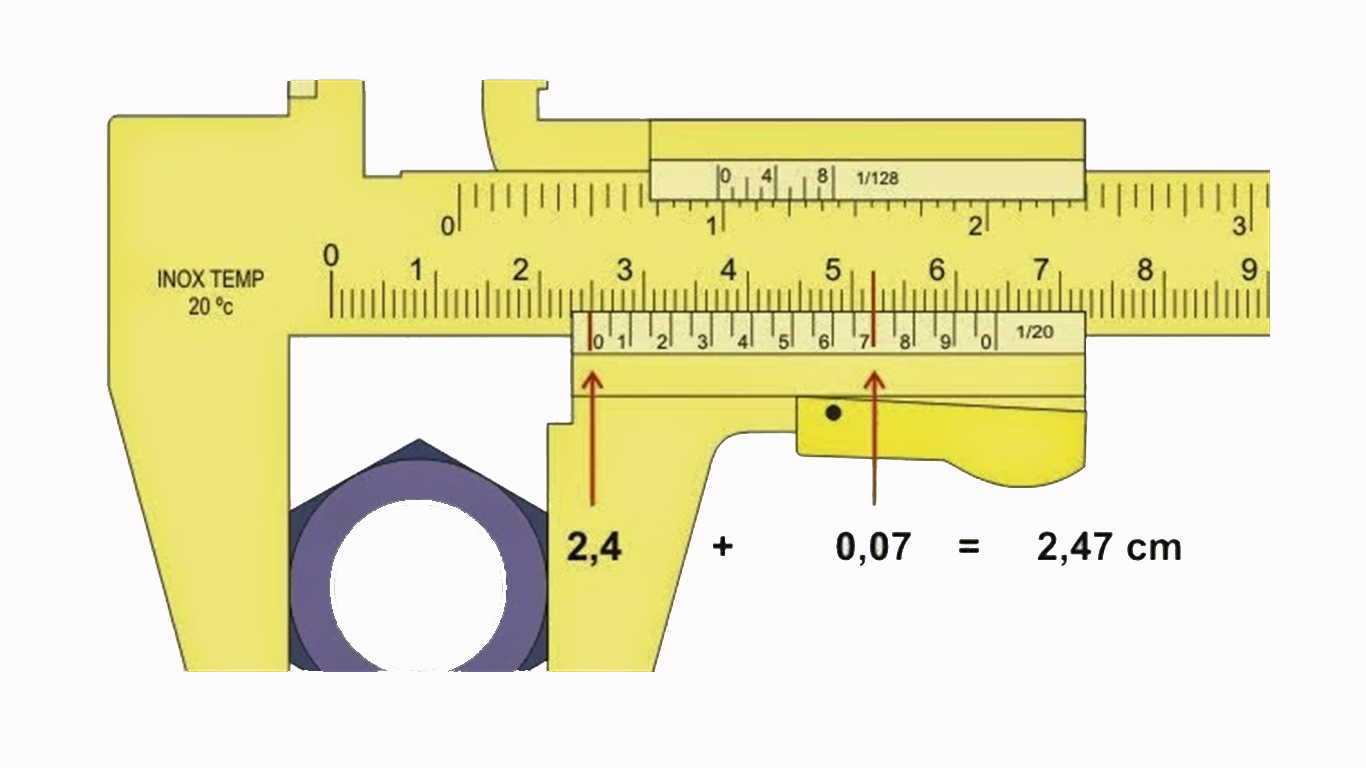
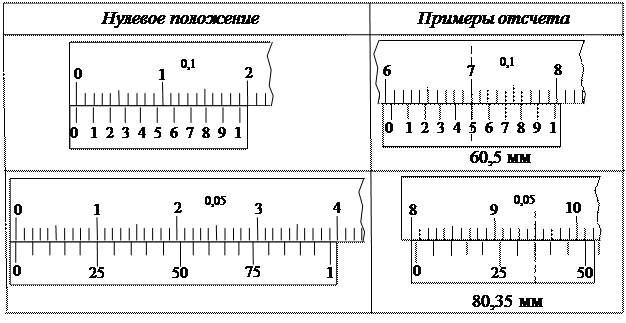
Как правильно снимать показания со штангенциркуля

Чтобы правильно определить размер измеряемой детали, нужно:

По основной шкале определить целое число миллиметров до нулевого штриха нониуса
На нониусе найти штрих, точно совпадающий с любым штрихом основной шкалы
Умножить номер совпавшего штриха нониуса на его цену деления
Сложить целое число миллиметров и дробную часть

Учет нулевой погрешности при измерении штангенциркулем

Нулевая погрешность возникает, когда при сомкнутых губках штангенциркуля нулевые штрихи основной шкалы и нониуса не совпадают. Ее нужно учитывать при расчете результата измерения:

Если нулевой штрих нониуса смещен вправо — погрешность положительная, ее нужно вычесть из результата
Если нулевой штрих нониуса смещен влево — погрешность отрицательная, ее нужно прибавить к результату

Формула для расчета результата измерения штангенциркулем

Итоговый результат измерения штангенциркулем рассчитывается по формуле:

L = A + Bn — C

где:

L — искомый размер детали
A — показание основной шкалы
B — цена деления нониуса
n — номер совпавшего штриха нониуса
C — нулевая погрешность (с учетом знака)

Типы штангенциркулей и их точность

Существует несколько типов штангенциркулей, различающихся ценой деления нониуса:

ШЦ-I — цена деления 0,1 мм, общая погрешность ±0,1 мм
ШЦ-II — цена деления 0,05 мм, общая погрешность ±0,05 мм

ШЦ-III — цена деления 0,05 мм или 0,1 мм, общая погрешность ±0,04 мм

Чем меньше цена деления нониуса, тем выше точность измерения, но и сложнее считывать показания.

Практические советы по работе со штангенциркулем

Чтобы обеспечить высокую точность измерений штангенциркулем:

Перед измерением проверьте нулевую установку и при необходимости учтите погрешность
Не прикладывайте чрезмерных усилий при измерении, чтобы не деформировать деталь
Старайтесь располагать измеряемую поверхность перпендикулярно губкам штангенциркуля
Периодически протирайте измерительные поверхности от загрязнений
Храните штангенциркуль в футляре, оберегая от ударов и падений

Распространенные ошибки при измерении штангенциркулем

При работе со штангенциркулем следует избегать типичных ошибок:

Неправильное считывание показаний основной шкалы и нониуса

Игнорирование нулевой погрешности инструмента
Приложение чрезмерного усилия, приводящее к деформации детали
Неперпендикулярное расположение губок относительно измеряемой поверхности
Измерение загрязненных или влажных поверхностей

Сравнение штангенциркуля с другими измерительными приборами

По сравнению с другими инструментами штангенциркуль имеет ряд преимуществ:

Более высокая точность, чем у линейки или рулетки
Возможность измерения внутренних и наружных размеров, а также глубины
Простота конструкции и невысокая стоимость по сравнению с микрометром
Универсальность применения для различных измерительных задач

Однако для измерений с точностью менее 0,05 мм лучше использовать микрометр или другие более точные приборы.

Расчет шкалы нониуса штангенциркуля. Пример решения задачи.

Примеры решения задач по метрологии

Решение:

1. Размеры деталей на рисунках, измеренные штангенциркулем:

а) – 38,8 мм;

б) – 58,6 мм.

2. Метод измерений.
В данном случае измерение проводилось штангенциркулем, размер измерялся непосредственно с детали (или изделия), поэтому метод измерений является абсолютным.

Абсолютное измерение основано на прямых измерениях величины и/или использовании значения физической постоянной, например измерение размеров детали штангенциркулем или микрометром.

Относительное измерение основано на сравнении измеряемой величины с известным значением меры, например измерение отношения величины к одноименной величине, играющей роль единицы. Размер в этом случае определяется алгебраической суммой размера установленной меры и показаний прибора.

3. Выполнить расчет нониуса штангенциркуля при точности i = 0,1 мм и модуле φ = 2.

Основной характеристикой при расчете нониуса является величины отсчета или точность нониуса i.

Сначала определяем число делений нониуса:

n = c/i = 1/0,1 = 10,

где c — интервал деления основной шкалы; с = 1 мм.

Интервал деления шкалы нониуса:

b = φc – i = 2×1 – 0,1 = 1,9,

где φ — модуль, натуральное число 1,2,3…, служащее для увеличения интервала деления нониусной шкалы.

Определяем длину шкалы нониуса:

l = bn = (φc – i)n = 1,9×10 = 19 мм.

4. Указать пределы измерений штангенциркулей.

Штангенинструменты предназначены для определения абсолютных значений линейных размеров, а также для воспроизведения размеров деталей при разметке.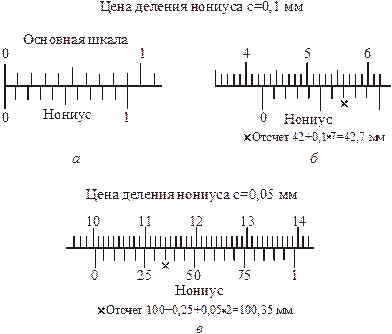

К штангенинструментам относятся:

штангенциркули;
штангенглубинометры;

штангенрейсмусы.

ГОСТ 166-73 предусматривается выпуск трех типов штангенциркулей: ШЦ-I с ценой деления 0,1мм; ШЦ-II с ценой деления 0,05мм и ШЦ-III с ценой деления 0,1мм и 0,05мм.
Кроме того, на заводах используются ранее изготовленные штангенциркули с ценой деления 0,02 мм.

***

Общее устройство штангенинструментов

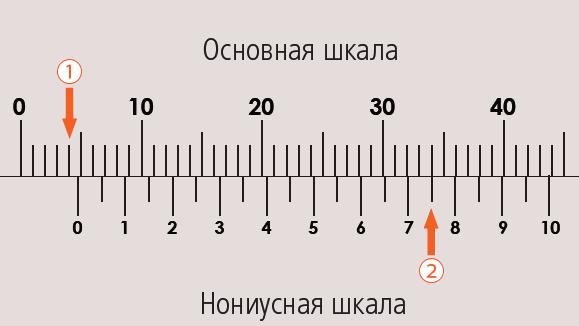
Основными частями штангенциркуля являются: шкала-линейка (штанга) с ценой деления 1 мм и перемещающаяся по линейке вспомогательная шкала-нониус. По нониусу отсчитывают десятые и сотые доли миллиметра.
Наибольшее распространение получили нониусы с ценой деления 0,1, 0,05 и 0,02 мм.

Для отсчета с помощью нониуса сначала определяется по основной шкале целое число миллиметров перед нулевым значением нониуса.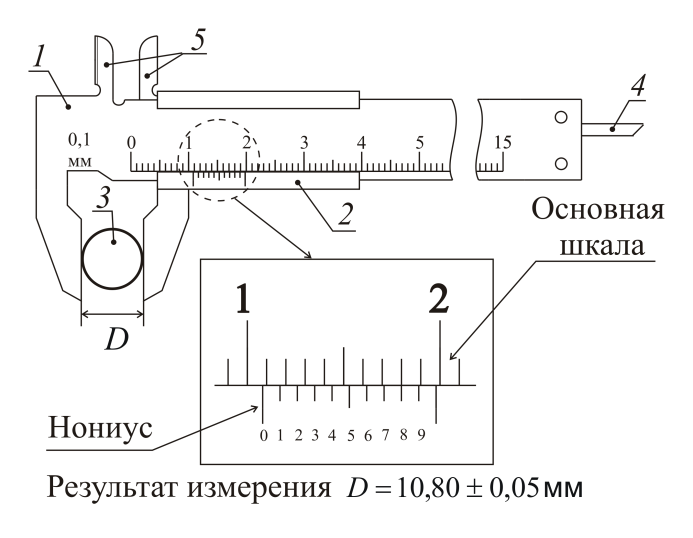 Затем добавляют к нему целое значение долей по нониусу в соответствии с тем, какой штрих шкалы нониуса ближе к штриху основной шкалы (

см. рисунок 1).
Так, например, на рис. 1, а – измеряемый размер равен 38,8 мм; а на рис. 1, б – 58,6 мм.

Для плавного перемещения рамки по шкале-линейке предусмотрено микрометрическое устройство, состоящее из хомутика, зажима и гайки микрометрической подачи.
На подвижной рамке установлен стопорный винт.
Наружные размеры можно измерять верхними и нижними губками. Для измерения внутренних размеров предназначены нижние губки, для разметки – верхние.

С более подробной информацией о штангенинструментах можно ознакомиться здесь.

***

Допуски и посадки подшипников качения

Главная страница

Страничка абитуриента

Дистанционное образование

Группа ТО-81
Группа М-81
Группа ТО-71

Специальности

Ветеринария
Механизация сельского хозяйства
Коммерция
Техническое обслуживание и ремонт автотранспорта

Учебные дисциплины

Инженерная графика
МДК. 01.01. «Устройство автомобилей»
Карта раздела
Общее устройство автомобиля
Автомобильный двигатель
Трансмиссия автомобиля
Рулевое управление
Тормозная система
Подвеска
Колеса
Кузов
Электрооборудование автомобиля
Основы теории автомобиля
Основы технической диагностики

Основы гидравлики и теплотехники
Метрология и стандартизация
Сельскохозяйственные машины
Основы агрономии
Перевозка опасных грузов
Материаловедение
Менеджмент
Техническая механика
Советы дипломнику

Олимпиады и тесты

«Инженерная графика»
«Техническая механика»
«Двигатель и его системы»
«Шасси автомобиля»
«Электрооборудование автомобиля»

6)Как рассчитывается Точность нониуса

В науке и технике для определения длин и расстояний используется много приборов, обеспечивающих измерение их с различной точностью.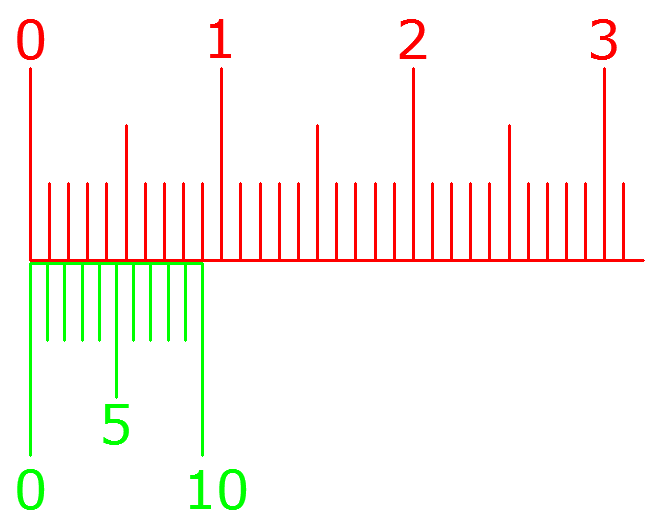 Широко применяется для измерения длин масштабная линейка с нониусом.Нониусом наз-ся дополнение к масштабу,позволяющее повысить точность измерения в 10,20 раз. Разница между ценой делений масштаба и нониуса называется точностью нониуса. a-x = a – (a – x/m)=a/m. Принцип работы нониуса основан на следующем. Точность визу-

альной интерполяции положения указателя между делениями шкалы низка (около

1/3 деления), однако глаз может с гораздо большей точностью фиксировать точ-

ное совпадение двух рисок. Ошибка в регистрации такого совпадения составляет

доли толщины риски, что при тонких рисках значительно меньше, чем вышеупо-

мянутая 1/3 расстояния между самими рисками. Нониус и позволяет перевести

информацию о положении указателя между делениями шкалы в регистрацию точ-

ного совпадения двух рисок – риски самой шкалы с риской вспомогательной шка-

лы – нониуса. Нониус представляет собой связанную с указателем подвижную

шкалу, скользящую вдоль основной шкалы.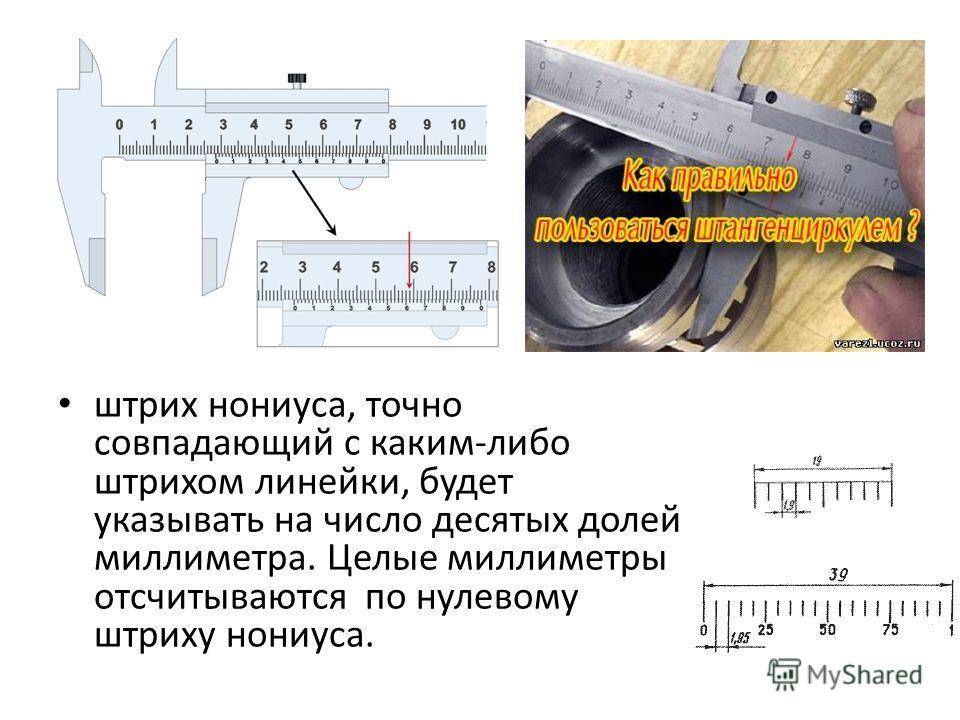 Указатель является одновременно

“нулем” шкалы нониуса.

Деления на шкале нониуса наносятся следующим образом. Выбирается точность

нониуса δ = D/N, где D – цена деления основной шкалы, N – натуральное число,

обычно 10 или 20. Если совместить нуль нониуса с одним из делений основной

шкалы, то первая риска нониуса наносится так, чтобы она отставала относительно

следующей риски шкалы на δ, вторая – на 2δ, n-я – на nδ (см. рис.1, случай N=10).

Последняя N-ая риска нониуса снова совпадает с одной из рисок шкалы.

Если в процессе измерений указатель шкалы (который является и нулем нониуса)

сместить вправо на δ, мы увидим совпадение для первой риски нониуса n = 1, на

2δ – для риски n = 2 и т.д. Таким образом, если при измерении n-ая риска нониуса

дала совпадение, значит, указатель шкалы смещен вправо на nδ от последнего

пройденного деления основной шкалы. Полный результат измерения длины L

находится суммированием значения, соответствующего этому последнему деле-

нию основной шкалы, и смещению nδ: L = KD + nδ, где K – номер деления основ-

ной шкалы

В данной работе используется один из наиболее распространенных приборов с

нониусом – штангенциркуль, служащий для измерения линейных размеров. Цена

деления основной шкалы штангенциркуля составляет 1 мм, цена деления нониуса

δ указана на самом нониусе и обычно равна 0.1 – 0.05 мм.

7)Чему равна приборная погрешность микрометра,штангерциркуля Приборная погрешность штангенциркуля и микрометра равна половине цены деления нониуса каждого прибора. .Микрометр

Для более точных измерений применяют микрометрические инструменты. Они бывают нескольких типов: микрометр для наружных измерений, микрометрический глубинометр и микрометрический нутромер.

Микрометр для наружных измерений (рис. 2.4.) состоит из полого стержня, жестко соединенного скобой. В полость стержня ввинчен микрометрический винт (А). При измерении предмет зажимается между неподвижным стержнем и подвижным торцом микрометрического винта А. Микровинт вращают, держась за трещетку В. Вместе с микровинтом вращается барабан С, перемещаясь при этом поступательно относительно стержня. Отсчетное устройство микрометра состоит из двух шкал. Горизонтальная шкала стержня представляет собой двойную шкалу с ценой деления 0,5 мм, нанесенную по обе стороны продольной черты, таким образом, что верхняя сдвинута относительно нижней на половину деления.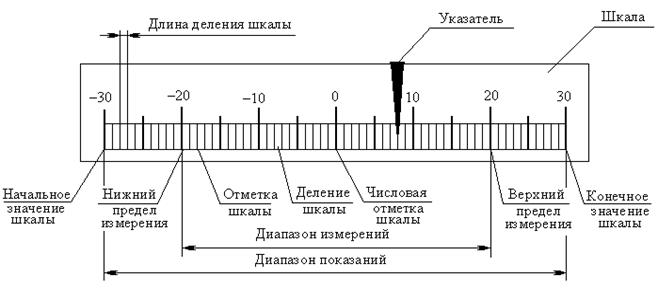 Цена деления шкалы барабана может быть установлена следующим образом. Пусть число делений круговой шкалы барабана n=50. Шаг микровинта h=0,5 мм, т.е. одному полному обороту микровинта (и барабана) соответвует линейное перемещение края барабана на 0,5 мм.

Цена деления круговой шкалы:

. Штангенциркуль

Штангенциркуль (рис.2.3.) состоит из миллиметрового масштаба М (шкалы прибора), жестко связанного с ножкой LA. Вдоль масштаба может перемещаться нониус N, с которым жестко связана вторая ножка LB и рейка F прибора. Подвижная часть штангенциркуля снабжена зажимным винтом С. Когда между ножками А и В отсутствует зазор, нулевые деления нониуса и шкалы совпадают.

Для промера наружных размеров предмет вводят между ножками А и В, которые сдвигают до соприкосновения с предметом. Затем закрепляют подвижную ножку зажимом С и производят отсчет. Число целых миллиметров отсчитывается непосредственно по шкале прибора до нулевой метки нониуса, число долей миллиметра – по нониусу. При внутренних промерах употребляют ножки LL, для измерения глубины – рейку F. Штангенциркули изготовляют с нониусом n=10, 20, 50 делений.

Штангенциркули Made Easy

Содержимое

Что мы знаем о штангенциркуле Вернье?
Проработанные примеры 1 | 2 | 3 | 4 | 5
Решенные проблемы IIT JEE 2003 | 2005 | 2010 | 2013 | 2015 | 2016
Проблемы с упражнениями
Более…

Что мы знаем о штангенциркуле?

Измерение является фундаментальной частью всех научных экспериментов, в том числе Физика. С одной стороны, наша необъятная Вселенная расширяет это упражнение по измерению до световых лет, а расстояния настолько огромны, что мы не можем видеть их невооруженным глазом. На другая крайность мельчайших расстояний, новые открытия толкают ее вплоть до фемтометров (10 ^-15 м) или даже меньше. Эти расстояния так малы что мы не можем видеть их своими глазами. На каждые 1-2 порядка изменение расстояния, наши инструменты для точного измерения расстояний может отличаться. Когда расстояния, которые мы хотим измерить, находятся в диапазоне 10 ^-2 мм до 1 мм, мы используем штангенциркуль и винтовой калибр для точной измерение. В этой статье мы сосредоточимся на этих измерительных приборах. только.

В классе 11 ^th Physics lab нас учили отвечать на следующие вопросы:

Как найти наименьший счет (LC) или постоянную нониуса?
Как читать показания основной шкалы (MSR) и показания шкалы нониуса (ВСР)?
Как найти ошибку нуля?
Как использовать приведенные выше данные для получения окончательного измерения?

Ответы на эти вопросы «как на вопросы» держали нас довольными в течение 22 лет. Но это не было достаточно для решения проблемы IIT JEE 2016. Нам нужно было выяснить еще кое-что интересно почему такие вопросы:

Почему наименьший счет — это отношение «значения 1 деления основной шкалы» к «общему количеству делений на нониусной шкале».
Почему измеренное значение определяется как: Наблюдаемое значение = MSR + LC×VSR.
Почему ошибка нуля вычитается из наблюдаемого значения, т. е. истинное значение = измеренное значение — ошибка нуля.

Начнем наше путешествие с штангенциркуля без нулевой погрешности. Когда двое челюсти закрыты, отметка 0 ^th на шкале нониуса совмещена с отметкой 0 ^th отметка на основной шкале, как показано на рисунке 1. Также обратите внимание, что 10 ^th отметка на нониусной шкале совпадает с отметкой 9 ^th на основной шкале.

Одно главное деление шкалы (МСД) – это расстояние между двумя последовательными отметки на основной шкале. На рисунке 1 указано, что 1 СКО равен до 1 мм. Одно деление шкалы Вернье (VSD) — это расстояние между двумя последовательные отметки по шкале нониуса. Принято, что 10 ВСД = 9 МСД. Таким образом, 1 ВСД = (9/10) СКО = 0,9мм, т. е. расстояние между двумя последовательными отметок по шкале нониуса составляет 0,9 мм.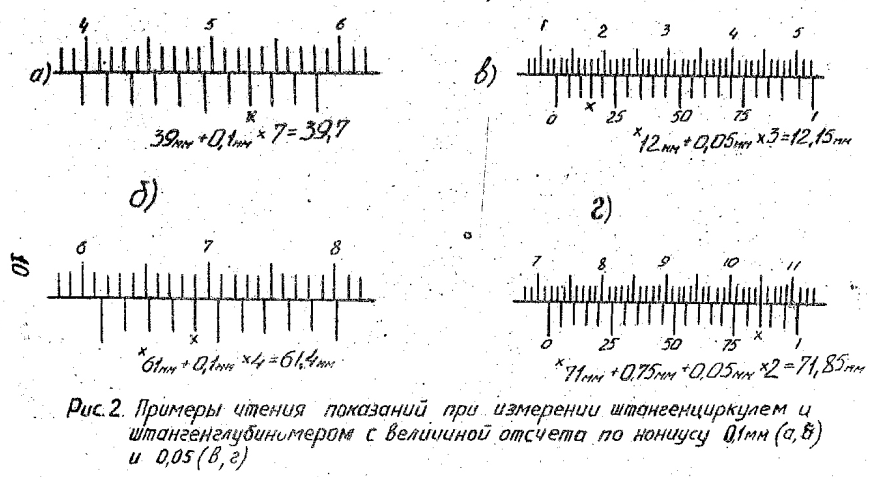

Рисунок 1: Штангенциркули без ошибки нуля

Теперь давайте воспользуемся этим штангенциркулем для измерения диаметра D мраморного шара. (мраморные шары обычно имеют D = 1/2 дюйма). Измерение показано на рисунке 2. Здесь x _m0 — расстояние между губкой, прикрепленной к основной шкале (левая челюсть), и отметкой 0 ^th на основной шкале, а x _v0 — расстояние между челюсть прикреплена к шкале Вернье (правая челюсть) и 0,^th отметка по нониусной шкале. Обратите внимание, что диаметр определяется выражением \начать{выравнивать} Д=х_{м0}+х \end{выравнивание} где x — расстояние между отметкой 0 ^th на основной шкале и правой челюстью.

Теперь обратите внимание, что отметка 7 ^th на нониусной шкале совпадает с 1,9 см на основной шкале. Эта точка называется точкой совпадения . Расстояние между отметкой 0 ^th на главной шкале и точкой совпадения составляет x _м, а расстояние между отметкой 0 ^th отметка по шкале нониуса и точка совпадения x _v . Таким образом, \начать{выравнивать} х+х_{v0}+х_в=х_м \end{выравнивание} Подставьте x из приведенного выше уравнения в первое уравнение, чтобы получить \начать{выравнивать} D=(x_m-x_v)-(x_{m0}-x_{v0}) \end{выравнивание}

Величина ($x_{m0}-x_{v0}$) называется ошибкой нуля штангенциркуля. Отрицательная нулевая ошибка называется коррекция нуля . Обратите внимание, что $x_{m0}=x_{v0}$ в штангенциркуле без нулевой ошибки (что верно в данном случае). Также, $x_m=19\mathrm{MSD}=19$ мм и $x_v=7\mathrm{VSD}=7(9/10)=6,3$ мм. Подставьте эти значения в приведенное выше уравнение, чтобы получить D = 12,7 мм = 1,27 см (полдюйма мрамора).

Рисунок 2: Измерение диаметра мраморного шара

Есть еще один более простой способ получить измеренное значение. Показание основной шкалы (MSR) – это первое показание на основной шкале непосредственно слева от нуля Шкала нониуса (в данном примере MSR = 12 мм). Показание нониуса (VSR) – это отметка на нониусной шкале, точно совпадающая с отметкой на основной масштаб (VSR = 7 в этом примере). Обратите внимание, что на основной шкале между отметкой MSR (т.е. отметка на основной шкале сразу слева от нуля шкалы нониуса) и точка совпадения. Таким образом, \начать{выравнивать} x_v&=\mathrm{VSR}\times\mathrm{VSD},\\ x_m&=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{MSD} \end{выравнивание} Соответствующие значения параметров для ошибок нуля равны \начать{выравнивать} x_{v0}&=\mathrm{VSR_0}\times\mathrm{VSD},\\ x_{m0}&=\mathrm{MSR_0}+\mathrm{VSR_0}\times\mathrm{MSD} \end{выравнивание} Подставьте в выражение вместо D, чтобы получить \начать{выравнивать} D=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{LC}-\mathrm{Ноль\,Ошибка} \end{выравнивание} где LC = MSD — VSD называется наименьший счет или постоянная Вернье . Это наименьшая длина, которую можно точно измерить штангенциркулем.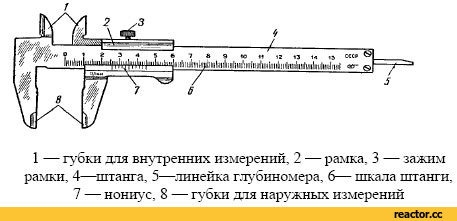 Для данных штангенциркулей \начать{выравнивать} \mathrm{LC}&=\mathrm{MSD}-\mathrm{VSD} \без номера\\ &=1-9/10=0,1\,\mathrm{мм}, \\ D&=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{LC}\nonumber\\ &=12+7(0,1)=1,27\,\mathrm{мм} \end{выравнивание}

Обратите внимание, что штангенциркуль можно использовать для измерения (1) внешних размеров, таких как диаметр сферы или грани куба (2) внутренние размеры, такие как внутренний диаметр полого цилиндра и (3) глубина полого цилиндра.

Разработанные примеры

Пример 1

Губки штангенциркуля, показанного на рисунке, соприкасаются друг с другом. Найдите погрешность нуля этого штангенциркуля.

Рисунок 3: (Пример 1) Штангенциркули с положительной погрешностью нуля

Решение: Наименьшее количество заданных штангенциркулей равно \начать{выравнивать} \mathrm{LC}&=\mathrm{MSD}-\mathrm{VSD} \\ &=1-9/10=0,1\,\mathrm{мм} \end{выравнивание}

Показание основной шкалы MSR ₀ = 0 мм, а показания шкалы нониуса ВСР ₀ = 3.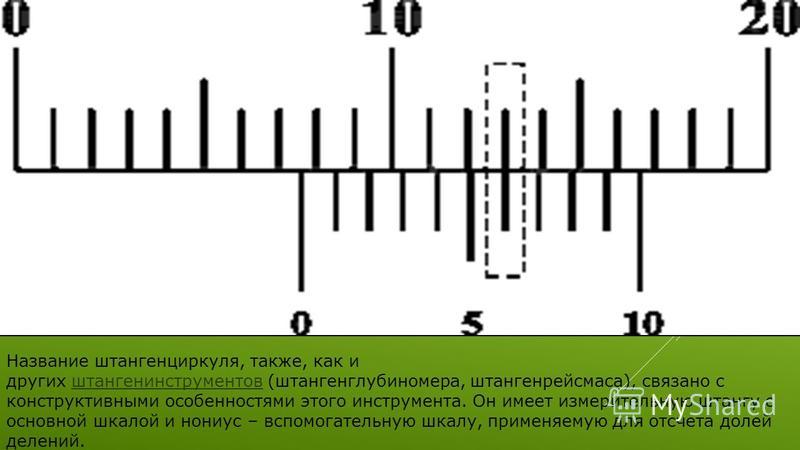 Таким образом, \начать{выравнивать} \mathrm{Ноль\, Ошибка}&=\mathrm{MSR_0}+\mathrm{VSR_0}\times\mathrm{LC} \\ &=0+3\умножить на 0,1=0,3\,\mathrm{мм} \end{выравнивание}

Пример 2

Штангенциркуль из примера 1 используется для измерения ребра куба. Показания показаны на рисунке 4. Найдите длину ребра куб.

Рисунок 4: (Пример 2) Измерение ребра куба

Решение: Показания MSR = 25 мм и VSR = 7. Таким образом, \начать{выравнивать} a&=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{LC}- \mathrm{Ноль\, Ошибка} \\ &=25+7\times 0,1-0,3=25,4,\mathrm{мм}. \end{выравнивание}

Пример 3

Губки штангенциркуля, показанного на рис. 5, соприкасаются с друг друга. Найдите погрешность нуля этого штангенциркуля.

Рисунок 5: (Пример 3) Штангенциркули с отрицательной погрешностью нуля

Решение: Это интересная проблема. Что такое MSR ₀? Это первое показание на основной шкале сразу слева от нуля шкалы нониуса. Но на основной шкале нет отметок перед нулем шкалы нониуса. Мы утверждаем, что MSR ₀ = -1 мм (внимательно наблюдайте, почему MSR ₀ не равно -2 мм? Показания нониуса равны VSR ₀ = 4, а наименьшее значение LC = 0,1 мм. Подставьте эти значения получить, \начать{выравнивать} \mathrm{Ноль\, Ошибка}&=\mathrm{MSR_0}+\mathrm{VSR_0}\times\mathrm{LC}\\ &=-1+4\умножить на 0,1=-0,6\,\mathrm{мм}. \end{выравнивание}

Пример 4

Штангенциркуль из примера 3 используется для измерения ребра куба. Показания показаны на рисунке 6. Найдите длину ребра куба.

Рисунок 6: (Пример 4) Измерение длины ребра куба

Решение: Показания MSR = 24 мм и VSR = 8. Таким образом, \начать{выравнивать} a&=\mathrm{MSR+VSR\times LC-Zero\,Error} \\ &=24+8(0,1)-(-0,6)=25,4\,\mathrm{мм}. \end{выравнивание}

Пример 5

Чему равен LC штангенциркуля, изображенного на рисунке 7?

Рисунок 7: (Пример 5) Наименьшее количество штангенциркулей

Решение: Одно деление основной шкалы равно 1 СКО = 1 мм. Поскольку 5 VSD = 4 MSD, мы получаем 1 ВСД = (4/5) СКО = 0,8. Таким образом, наименьшее количество этих суппортов LC = MSD — VSD = 1 — 0,8 = 0,2 мм.

Решенные проблемы IIT JEE

Проблема IIT JEE 2003

N делений на основной шкале штангенциркуля совпадают с (N + 1) делениями на его шкале. Если каждое деление на основной шкале соответствует единице, определите наименьшее количество инструментов.

Решение: Учитывая, что главное деление шкалы (МСД) штангенциркуля равно $N=a$. Так как (N + 1) делений нониуса (VSD) равны N делениям основной шкалы, получаем \начать{выравнивать} 1\,\mathrm{VSD}=\frac{N}{N+1}\mathrm{MSD}=\frac{Na}{N+1} \end{выравнивание} Наименьшее количество дается \начать{выравнивать} \mathrm{LC}=1\mathrm{MSD}-1\mathrm{VSD}=a/(N+1). \end{выравнивание}

Проблема от IIT JEE 2005

Ребро куба измеряется штангенциркулем (9 делений основная шкала равна 10 делениям шкалы Вернье и 1 основной шкале деление 1 мм). Показания основного деления шкалы – 10, а первое деление Шкала нониуса оказалась совпадающей с основной шкалой.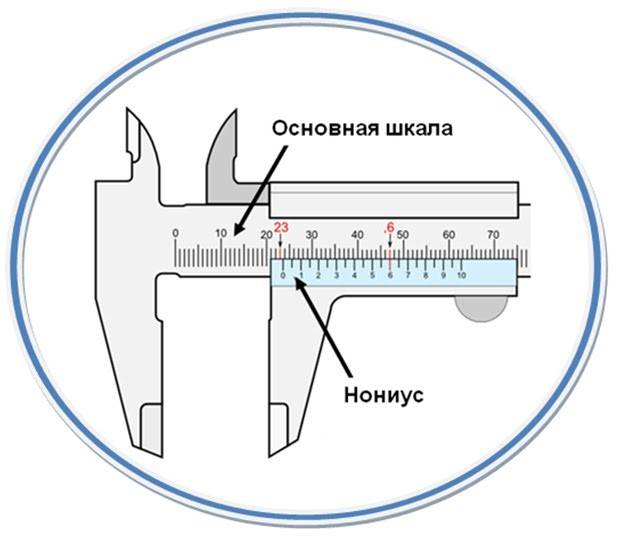 Масса куб 2,736 г. Рассчитайте плотность в г/см ³ с точностью до значащих цифр.

Решение> Из приведенных данных одно главное деление шкалы (СКО) равно 1 СКО = 1 мм. Поскольку 10 делений шкалы Вернье (VSD) равны 9СКО, получаем 1 СКО = 9/10 ССО = 0,9 мм. Наименьшее количество (LC) определяется как LC = 1 MSD — 1 VSD = 1,0 — 0,9 = 0,1 мм.

Учитывая, что показание основной шкалы (MSR) равно 10, а показание шкалы Vernier (VSR) равно 1. Измеренное значение края определяется выражением \начать{выравнивать} a&=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{LC}\\ &=10+1\умножить на 0,1=10,1\,\mathrm{мм}. \end{выравнивание}

Измерение a имеет три значащих цифры. Объем куба V = a ³ = 1,03 см ^{3}
\end{выравнивание}
(после округления до трех значащих цифр).}

Проблема из IIT JEE 2010

Штангенциркули имеют отметки 1 мм на основной шкале. имеет 20 равных деления шкалы нониуса, соответствующие 16 делениям основной шкалы. Для этого Штангенциркули, наименьшее количество

0,02 мм
0,05 мм
0,1 мм
0,2 мм

Решение: Для данных штангенциркулей одно главное деление шкалы (MSD) 1 СКО = 1 мм. Так как 20 делений шкалы нониуса (ЧД) равны 16 СКО, то получаем 1 ДСП = 16/20 СКО = 0,8 мм. Количество лизингов определяется как LC = 1 MSD — 1 VSD = 1 — 0,8 = 0,2 мм.

Проблема от IIT JEE 2013

Диаметр цилиндра измеряют штангенциркулем без нулевая ошибка. Установлено, что ноль шкалы нониуса лежит между 5,10 см и 5,15 см основной шкалы. Шкала нониуса имеет 50 делений, соответствующих 2,45 см. 24 деление шкалы нониуса в точности совпадает с одним из основных делений шкалы. Диаметр цилиндра

5,112 см
5,124 см
5,136 см
5,148 см

Решение: Из приведенных данных одно деление основной шкалы (СКО) и одно деление шкалы нониуса (ЧС) составляют 1 СКО = 5,15 — 5,10 = 0,05 см и 1 СКО = 2,45/50 = 0,049 мм. Наименьшее количество данных штангенциркулей составляет LC = 1 MSD — 1 VSD = 0,001 см.

Для данного измерения показание основной шкалы (MSR) составляет 5,10 см, а Отсчет нониуса (VSR) равен 24.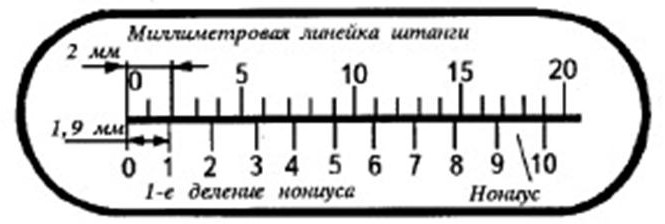 Следовательно, диаметр D цилиндра равен \начать{выравнивать} D&=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{LC} \\ &=5,10+24\умножить на 0,001=5,124\,\mathrm{см}. \end{выравнивание}

Проблема от IIT JEE 2015

Рассмотрим штангенциркуль, у которого каждый 1 см на основной шкале равен разделенный на 8 равных делений и винтовой датчик со 100 делениями на его круглая шкала. В штангенциркуле совпадают 5 делений шкалы нониуса с 4 делениями на основной шкале и на винтовом манометре, один полный вращение круговой шкалы перемещает ее на два деления по линейной шкале. Затем,

Если шаг калибра в два раза больше наименьшего значения штангенциркуля, наименьшее значение калибра составляет 0,01 мм.
Если шаг калибра винта в два раза меньше наименьшего значения нониуса штангенциркуль, наименьший отсчет калибра 0,005 мм.
Если наименьший отсчет линейной шкалы винтового калибра в два раза больше наименьшего количество штангенциркулей, наименьшее количество винтовых калибров составляет 0,01 мм.
Если наименьшее значение линейной шкалы калибра-винта в два раза превышает наименьшее значение шкалы штангенциркуля, наименьшее значение калибра-винта составляет 0,005 мм.

Решение: В данных штангенциркулях каждый 1 см делится поровну на 8 основных делений шкалы (СКО). Таким образом, 1 СКО = 1/8 = 0,125 см. Далее 4 основных деления шкалы совпадают с 5 делениями шкалы нониуса (VSD), т. е. 4 MSD = 5 VSD. Таким образом, 1 ВСД = 4/5 СКО = 0,1 см. Наименьшее количество штангенциркулей нониус определяется как LC = 1 MSD — 1 VSD = 0,125 — 0,1 = 0,025 см.

В винтовом калибре пусть l будет расстоянием между двумя соседними делениями на линейной шкала. Шаг p винтового калибра — это пройденное расстояние по линейной шкале. когда он делает один полный оборот. Так как круговая шкала смещается на два деления по линейный масштаб, когда он делает один полный оборот, мы получаем p = 2l. Наименьшее количество калибра винта определяется как отношение шага к числу делений на круговая шкала (n), т. е. \начать{выравнивать} \mathrm{lc}=p/n=2l/100=l/50. \end{выравнивание}

Если $p=2\mathrm{LC}=2(0,025)=0,05$ см, то $l=p/2=0,025$ см. Подставьте в приведенное выше уравнение, чтобы получить наименьшее значение калибра винта lc = 0,005 мм.

Если $l=2\mathrm{LC}=2(0,025)=0,05$ см, то приведенное выше уравнение дает lc = 0,01 мм.

Проблема из IIT JEE 2016

Есть два штангенциркуля, каждый из которых имеет 1 см, разделенный на 10. равные деления на основной шкале. Шкала нониуса одного из штангенциркулей (C ₁) имеет 10 равных делений, соответствующих 9деления основной шкалы. Вернье шкала другого штангенциркуля (C ₂ ) имеет 10 равных делений, соответствующих 11 основных делений шкалы. Показания двух штангенциркулей показаны на фигура. Измеренные значения (в см) штангенциркулем C ₁ и C ₂ соответственно равны

2,85 и 2,82
2,87 и 2,83
2,87 и 2,86
2,87 и 2,87

Решение: В обоих суппортах C ₁ и C ₂ , 1 см делится на 10 равных деления на основной шкале.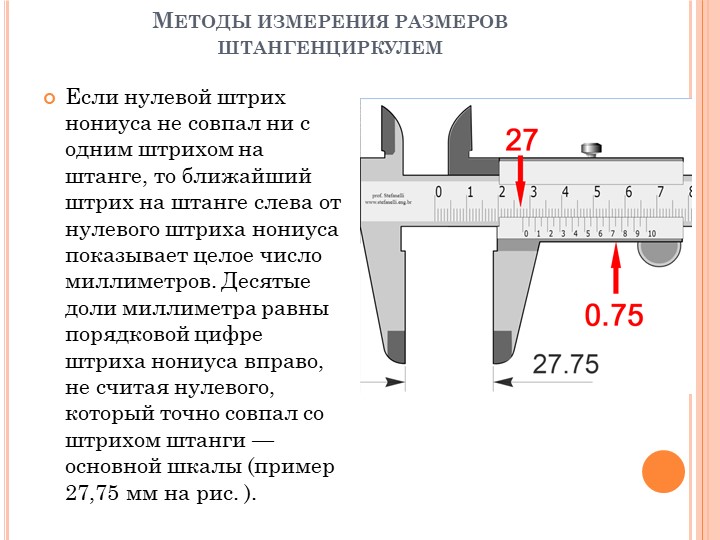 Таким образом, 1 деление по основной шкале равно $x_{m1}=x_{m2}=1/10=0,1$ см. В штангенциркуле С ₁ 10 равных делений шкалы нониуса равны 9 делениям основной шкалы. Таким образом, 1 деление по шкале нониуса C ₁ равно $x_{v1}=9x_{m1}/10=0,09$ см. В штангенциркуле С ₂ 10 равных делений шкалы нониуса равны 11 делениям основной шкалы. Таким образом, 1 деление по шкале нониуса С ₂ равно $x_{v2}=11x_{м2}/10=0,11$ см.

Пусть отсчет основной шкалы равен MSR и v ^-е-е деление шкалы нониуса совпадает с m ^-м-м делением основной шкалы (m отсчитывается за MSR). Значение, измеренное этим штангенциркулем, равно \начать{выравнивать} X&=\mathrm{MSR}+x &=\mathrm{MSR}+mx_m-vx_v \end{выравнивание}

В суппортах C ₁, MSR ₁ = 2,8 см, m ₁ = 7 и v ₁ = 7, а в суппортах C ₂ , MSR ₂ = 2,8 см, м ₂ = 8 и v ₂ = 7. Подставьте эти значения в приведенное выше уравнение, чтобы получить \начать{выравнивать} X_1&=\mathrm{MSR}_1+m_1 x_{m1} -v_1 x_{v1}=2,87\,\mathrm{см}\\ X_2&=\mathrm{MSR}_2+m_2 x_{m2} -v_2 x_{v2}=2,83. \end{выравнивание}

Упражнения

Губки штангенциркуля, показанного на рис. 8, соприкасаются с друг друга. Найдите погрешность нуля этого штангенциркуля. Рисунок 8: Нулевая погрешность штангенциркуля
Ответ: 1,9 мм
Губки штангенциркуля, показанного на рисунке 9, соприкасаются друг с другом. Найдите погрешность нуля этого штангенциркуля. Рисунок 9: Нулевая погрешность штангенциркуля
Ответ: -1,2 мм
Погрешность нуля штангенциркуля, показанного на рис. 10, составляет 0,9 мм. Какой диаметр сферы измеряется на рисунке 10. Рисунок 10: Измерение диаметра сферы ошибочным штангенциркулем
Ответ: 3,14 см.
Погрешность нуля штангенциркуля, показанного на рис. 11, составляет -0,5 мм. Какой диаметр измеряемого шара на рисунке? Рисунок 11: Измерение диаметра сферы ошибочным штангенциркулем
Ответ: 3,14 см.
Выберите неверное утверждение для нулевой ошибки и нулевой коррекции
1. Если ноль шкалы нониуса не совпадает с нулем основной шкале, то говорят, что прибор имеет нулевую ошибку.
2. Ошибка нуля положительна, если ноль шкалы нониуса лежит слева от ноль основной шкалы.
3. Коррекция нуля имеет величину, равную ошибке нуля, но противоположный знак к нулевой ошибке.
4. Все вышеперечисленное неверно.
Ответ: (В)
Что такое постоянная Вернье?
1. Это значение одного основного деления шкалы, деленное на общее количество деления на основной шкале.
2. Это значение одного деления шкалы Вернье, деленное на общее количество деления по шкале Вернье.
3. Это разница между значением одного деления основной шкалы и одного деления шкалы нониуса.
4. Это также наименьшее значение шкалы Вернье.
Ответ: (С), (Г)
Наименьшее деление на основной шкале штангенциркуля – 1 мм. 10 делений шкалы нониуса совпадают с 9деления основной шкалы. При измерении длины линии нулевая отметка шкалы нониуса находится между 10,2 см и 10,3 см. и третье деление шкалы нониуса совпадают с делением основной шкалы. (а) Определите наименьшее количество штангенциркулей и (б) длину линии.
Ответ: 0,01 см, 10,23 см.
Основная шкала штангенциркуля откалибрована в миллиметрах. 19 делений основной шкалы по длине равны 20 делениям нониуса. В при измерении этим прибором диаметра цилиндра основная шкала показывает 35 деления и 4-е деление нониуса совпадает с делением основной шкалы. Найдите (а) наименьшее количество штангенциркулей и (б) радиус цилиндра.
Ответ: 0,005 см, 1,76 см.
Наименьший отсчет штангенциркуля — 0,01 см. Когда две челюсти инструмента касаются друг друга 5 деление шкалы нониуса совпадают с делением основной шкалы, а ноль шкалы нониуса лежит левее нуля основной шкалы. Кроме того, при измерении диаметра сферы нулевая отметка шкалы нониуса лежит между 2,4 см и 2,5 см, а деление 6 ^th нониуса совпадает с делением основной шкалы. Вычислите диаметр шара.
Ответ: 2,51 см.
В эксперименте углы должны быть измерены с помощью инструмент. 29 делений основной шкалы точно совпадают с 30 делениями шкале Вернье. Если наименьшее деление основной шкалы составляет полградуса (= 0,5 градуса), то наименьшее значение инструмента равно (AIEEE 2009).
1. одна минута
2. полминуты
3. один градус
4. полградуса
Ответ: (А)
Ученик измерил длину стержня и написал, что она равна 3,50 см. Какой прибор он использовал для измерения?
1. Измерительная шкала
2. Штангенциркуль, у которого 10 делений шкалы нониуса совпадают с 9 делений в основной шкале и основная шкала имеет 10 делений в 1 см
3. Винтовой калибр, имеющий 100 делений по круговой шкале и шаг, как 1 мм
4. Винтовой калибр с 50 делениями по круговой шкале и шагом 1 мм
Ответ: (В)
19 делений на основной шкале штангенциркуля совпадают с 20 делений по шкале Вернье. Если каждое деление на основной шкале равно 1 см, определяют наименьший счет прибора.
Ответ: 0,05 см
Угол призмы измеряется спектрометром. Основная шкала показание составляет 58,5 градусов, а по шкале Вернье – 9подразделения. Учитывая, что 1 дивизия по основной шкале соответствует 0,5 градуса, а 30 делений по шкале Вернье соответствуют с 29 делениями на основной шкале. Угол призмы из приведенных выше данных есть (AIEEE 2012)
1. 58,59 градуса
2. 58,77 градуса
3. 58,65 градусов
4. 59 градусов
Ответ: (С)
1 см по основной шкале штангенциркуля делится на 10 равных части. Если 10 делений нониуса совпадают с 8 малыми делениями основной шкалы, то наименьшее количество штангенциркулей равно
1. 0,01 см
2. 0,05 см
3. 0,005 см
4. 0,02 см
Ответ: (Г)
Губки штангенциркуля нониуса касаются внутренней стенки калориметра. без излишнего давления. Положение нуля шкалы нониуса на основной шкале читает 3,48 см. 6-е деление шкалы нониуса совпадает с делением основной шкалы. Нониусная постоянная штангенциркуля равна 0,01 см. Найдите фактический внутренний диаметр калориметра, если видно, что погрешность нуля шкалы нониуса составляет -0,03 см.
1. 3,37 см
2. 3,57 см
3. 3,42 см
4. 3,54 см
Ответ: (В)
В передвижном микроскопе 1 см по основной шкале делится на 20 равных делений, а на шкале нониуса 50 делений. Каков наименьший счет микроскопа?
Ответ: 0,001 см
Постоянная Вернье передвижного микроскопа равна 0,001 см. Если 49 делений основной шкалы совпадают с 50 делениями шкалы Вернье, то значение 1 основное деление шкалы
1. 0,1 мм
2. 0,4 мм
3. 0,5 мм
4. 1 мм
Ответ: (С)
Тонкая металлическая полоска штангенциркуля нониуса движется сверху вниз до дна таким образом, чтобы он едва касался поверхности стакана. Основной отсчет шкалы штангенциркуля составляет 6,4 см, тогда как его постоянная нониуса составляет 0,1 мм. Четвертое деление шкалы нониуса совпадает с делением основной шкалы. фактическая глубина стакана (при совпадении нуля нониуса с нулем основного шкала)
1. 6,64 см
2. 6,42 см
3. 6,44 см
4. 6,13 см
Ответ: (С)
В инструменте есть 25 делений по шкале нониуса, которые совпадает с 24 делениями основного масштаба. 1 см по основной шкале делится на 20 равных частей. Наименьшее количество инструментов
1. 0,002 см
2. 0,05 см
3. 0,001 см
4. 0,02 см
Ответ: (А)
1 см основной шкалы штангенциркуля разделен на 10 делений. Если наименьшее количество штангенциркулей составляет 0,005 см, то шкала нониуса должна иметь
1. 10 отделов
2. 20 дивизий
3. 25 дивизий
4. 50 делений
Ответ: (В)
В штангенциркуле есть 10 делений на шкале нониуса и 1 см по основной шкале делится на 10 частей. При измерении длины, ноль шкалы Вернье находится сразу перед отметкой 1,8 см и 4-м делением шкалы Вернье совпадает с основным делением шкалы. Значение длины является
1. 1,804 см
2. 1840 см
3. 1800 см
4. Ни один из этих
Ответ: (D)
Диаметр стального шарика измеряют штангенциркулем, который имеет деление 0,1 см на основной шкале (MS), а 10 делений его шкалы нониуса (VS) соответствуют 9 делениям на основной шкале. Три таких измерения для мяча: (1) MSR = 0,5 см, VSD = 8 (2) MSR = 0,5 см, VSD = 4 (3) MSR = 0,5 см, VSD = 6. Если погрешность нуля составляет -0,03 см, то средний скорректированный диаметр равен
1. 0,53 см
2. 0,56 см
3. 0,59 см
4. 0,52 см
Ответ: (С)
Каждое деление на основной шкале равно 1 мм. Какие из следующих Весы нониуса дают константу нониуса, равную 0,01 мм?
1. 9 мм разделен на 10 делений
2. 90 мм, разделенный на 100 делений
3. 99 мм, разделенный на 100 делений
4. 9 мм, разделенный на 100 делений
Ответ: (К)
В штангенциркуле 1 см основной шкалы делится на 20 равных части. 19 делений основной шкалы совпадают с 20 делениями нониусной шкалы. Найдите наименьшее количество инструментов.
Ответ: 0,025 см
В штангенциркуле одно основное деление шкалы — это х см и n делений. нониуса совпадают с (n-1) делениями основной шкалы. Наименьшее количество (в см) суппортов составляет (АМУ ПМТ 2009 г.)
1. $(n-1)x/n$
2. $nx/(n-1)$
3. $x/n$
4. $x/(n-1)$
Ответ: (С)

Подробнее…

Вы можете сделать недорогие штангенциркули, нарисовав основную шкалу и шкалу нониуса на полоски бумаги и т. д. Линии на основной шкале могут быть разделены на 1 см. Чтобы получить линии на шкале нониуса, вы можете разделить 9 делений основной шкалы на 10 равных делений (это проверка ваших знаний по геометрии).

Возьмите чешую длиной 30 см и другую чешуйку длиной 15 см. Более крупный масштаб — это основная шкала ваших штангенциркулей, а меньшая шкала — шкала нониуса. Ничья 30 параллельные линии на основной шкале на расстоянии 1 см каждая. Нарисуйте 10 параллельных линий на Шкала нониуса по 0,9 см каждая. Ваш штангенциркуль готов (см. рис. 12). Возьмите другую шкалу (или любую другую прямоугольную деталь) в качестве опоры. Объект, длина которого измеряется, помещается между опорой и нониусной шкалой.

Рисунок 12: Ваши штангенциркули

Вернье-двигатель — это ракетный двигатель, используемый на космическом корабле для точной регулировки скорость космического корабля. Название происходит от штангенциркуля нониуса (названного в честь Pierre Vernier), которые имеют первичную шкалу для валовых измерений и вторичную шкала для точных измерений.

Каталожные номера

Как пользоваться штангенциркулем. https://www.miniphysics.com/how-to-read-a-vernier-caliper.html. Доступ: 2017-07-15.
С помощью штангенциркуля и микрометрического винта измерять. http://www.phy.uct.ac.za/courses/phylab1/vernier. Доступ: 2017-07-15.
Проблемы с штангенциркулем и решениями. https://examinationsecrets.wordpress.com/2017/04/28/vernier-callipers-problems/. Доступ: 2017-07-15.
Штангенциркули в онлайн-лабораториях университета Амрита. http://amrita.olabs.edu.in/?sub=1&brch=5&sim=16&cnt=1. Доступ: 2017-07-15.
Видео на Youtube о штангенциркуле Edunovus. https://youtu.be/ySRN3yuZUT0. YouTube.

Ваши конструктивные комментарии

Линейные измерения

Пожалуй, самое распространенное устройство для измерения длины является линейка или измерительная линейка. Это трудно, однако, чтобы оценить доли каждого деления, поэтому, если большая точность требуется, необходимо внести некоторые уточнения.

Штангенциркуль представляет собой устройство, использует вспомогательную (нониусную) шкалу, которая позволяет более точно измерения мелких долей основного деления шкалы. Шкала нониуса состоит из N равноотстоящих делений, которые имеют такая же общая длина, как ( N — 1) деления основной шкалы. На штангенциркуль, основная (неподвижная) шкала разделена на миллиметры. Вернье (подвижная) шкала 9мм в длину и состоит из 10 отделов. Каждое деление по шкале Вернье, то имеет длину 0,9 мм, или на 0,1 мм меньше основной шкалы подразделения. Следовательно, номер линии нониуса, которая лучше всего совмещенная с линией на основной шкале равна числу десятых миллиметра от последнего показания основной шкалы на нулевая отметка по шкале Вернера.

Рис. 1 — штангенциркуль

Изучите рисунок выше. Губки суппорта выдвинуты на 11,7 мм. Прежде всего, вы можете сказать что нулевая отметка шкалы нониуса (обозначена крайним левым стрелка вверх) прошел отметку 11,0 мм (обозначенную стрелкой вниз). стрелка) на основной шкале. Номер линии Вернье, которая лучше всего совместить с линией на основной шкале 7 (обозначается самая правая стрелка вверх). Следовательно, нулевая отметка нониуса шкала прошла 7 десятых миллиметра за отметку 11,0 мм, давая общее чтение 11,7 мм. Наименьшее количество штангенциркуля составляет 0,1 мм. То есть 0,1 мм — это наименьшее значение шкалы, которое можно производиться без оценки.

Практика чтения Штангенциркуль ниже! Когда Java-апплет загрузится, щелкните и перетащите на картинке с помощью мыши установить штангенциркуль для нового измерение.