Как определить сопротивление коаксиального кабеля. Определение сопротивления и параметров коаксиального кабеля: подробный анализ

Как рассчитать сопротивление коаксиального кабеля. Какие основные параметры влияют на характеристики коаксиального кабеля. Каковы методы проверки и измерения параметров коаксиального кабеля.

Основные параметры коаксиального кабеля

Коаксиальный кабель состоит из нескольких ключевых элементов, каждый из которых влияет на его характеристики:

• Центральный проводник — обычно медная жила
• Диэлектрик — изоляционный слой вокруг центрального проводника
• Экранирующая оплетка — внешний проводящий слой
• Внешняя изоляция — защитная оболочка кабеля

Основными электрическими параметрами коаксиального кабеля являются:

• Волновое сопротивление (импеданс) — обычно 50 или 75 Ом
• Погонное сопротивление проводников
• Погонная емкость
• Погонная индуктивность
• Коэффициент затухания сигнала

Расчет сопротивления коаксиального кабеля

Для расчета сопротивления коаксиального кабеля используется формула:

R = (ρ / 2πL) * ln(b/a)

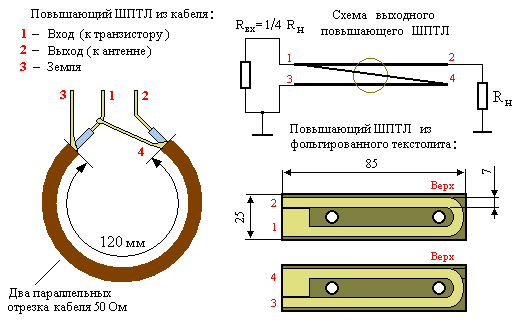
Где:

• R — сопротивление кабеля
• ρ — удельное сопротивление материала проводника
• L — длина кабеля
• b — внутренний радиус внешнего проводника (экрана)
• a — радиус центрального проводника

Почему используется такая формула для расчета сопротивления?

Данная формула учитывает особенности конструкции коаксиального кабеля:

• Ток протекает радиально от центрального проводника к экрану
• Площадь сечения, через которое протекает ток, увеличивается с увеличением радиуса
• Сопротивление каждого элементарного слоя обратно пропорционально его радиусу

Интегрирование элементарных сопротивлений по всей толщине диэлектрика приводит к логарифмической зависимости.

Как вывести формулу сопротивления коаксиального кабеля?

Рассмотрим вывод формулы пошагово:

1. Запишем формулу для элементарного сопротивления тонкого цилиндрического слоя: dR = (ρ * dr) / (2πrL)
2. Проинтегрируем это выражение от a до b: R = ∫(ρ / 2πL) * (dr / r)
3. После интегрирования получаем: R = (ρ / 2πL) * ln(b/a)

Таким образом, мы учитываем изменение площади сечения по мере увеличения радиуса.

Методы измерения параметров коаксиального кабеля

Для проверки характеристик коаксиального кабеля используются различные методы:

Измерение сопротивления

Проводится с помощью мультиметра между центральным проводником и экраном. Однако этот метод не всегда эффективен для обнаружения повреждений.

Измерение емкости

Выполняется специальным измерителем емкости. Позволяет оценить целостность диэлектрика.

Измерение индуктивности

Требует специального оборудования. Помогает выявить нарушения геометрии кабеля.

Рефлектометрия

Наиболее эффективный метод для локализации повреждений. Основан на анализе отраженного сигнала.

Особенности тестирования коаксиальных кабелей

При проверке коаксиальных кабелей следует учитывать:

• Простое измерение сопротивления не всегда выявляет повреждения
• Необходимо проводить комплекс измерений разных параметров
• Для точной диагностики требуется специализированное оборудование
• Важно учитывать частотные характеристики кабеля

Влияние параметров на характеристики коаксиального кабеля

Различные параметры по-разному влияют на свойства кабеля:

Волновое сопротивление

Определяется соотношением радиусов проводников и свойствами диэлектрика. Влияет на согласование линии передачи.

Погонное сопротивление

Зависит от материала и сечения проводников. Определяет потери в кабеле на постоянном токе и низких частотах.

Погонная емкость

Связана с диэлектрической проницаемостью изоляции. Влияет на скорость распространения сигнала.

Коэффициент затухания

Характеризует потери сигнала в кабеле. Зависит от частоты, конструкции и материалов кабеля.

Применение коаксиальных кабелей

Коаксиальные кабели широко используются в различных областях:

• Телевизионные и радиосистемы
• Компьютерные сети
• Измерительное оборудование
• Системы безопасности
• Авиационная и космическая техника

Выбор типа кабеля зависит от конкретного применения и требуемых характеристик.

Заключение

Понимание параметров коаксиальных кабелей и методов их измерения критически важно для эффективного проектирования и обслуживания систем передачи сигналов. Правильный расчет и измерение сопротивления, а также других характеристик, позволяет обеспечить надежную работу оборудования в различных областях применения.

Основные параметры коаксиального кабеля

Основные параметры коаксиального кабеля

Расскажем только о самых главных понятиях в коаксиальных кабелях. Импеданс — это главный показатель, который определяет возможность передачи энергии сигнала по кабелю между источником и приемником. У всех элементов на пути сигнала, это разъемы и кабель должен быть один импеданс. Если это правило не соблюдать, это может привести к внутренним отражениям в кабеле, вследствие чего на изображении появляются двойные контуры. Одна из главных причин появления отражений, это некачественные разъемы или их неправильная установка, или же применение разъемов и кабелей разного импеданса. Стандартный импеданс видеокабелей составляет 75 Ом. Затухание — это показатель потерь энергии сигнала внутри кабеля. У каждого кабеля свои частотные свойства, поэтому ослабление на разных частотах будет разное. Чем частота выше, тем ослабление больше. Сопротивление — это показатель качества проводника, который буквально показывает, какая часть энергии сигнала превратится в тепло. Результат таких потерь — это показания снижение уровня сигнала и динамической яркости изображения. Сопротивление измеряется в омах (Om), Для кабелей сопротивление указывается как Ом на 100 метров (Om/100m) или Ом на 1000 футов (Om/1,000 feet. Такой показатель, как сопротивление зависит от материала проводника, его размеров и температуры. Самые хорошие кабели имеют сигнальные проводники из химически чистой меди или покрываются тонким слоем серебра. Следующий показатель, это емкость По конструкции любой коаксиальный кабель — вытянутый конденсатор. Емкость измеряется в фарадах (F), а емкость кабеля в пикофарадах на метр (pF/m) или в пикофарадах на фут (pF/ft). Емкость кабеля влияет на высокочастотные составляющие видеосигнала, то есть на четкость и детализацию изображения. 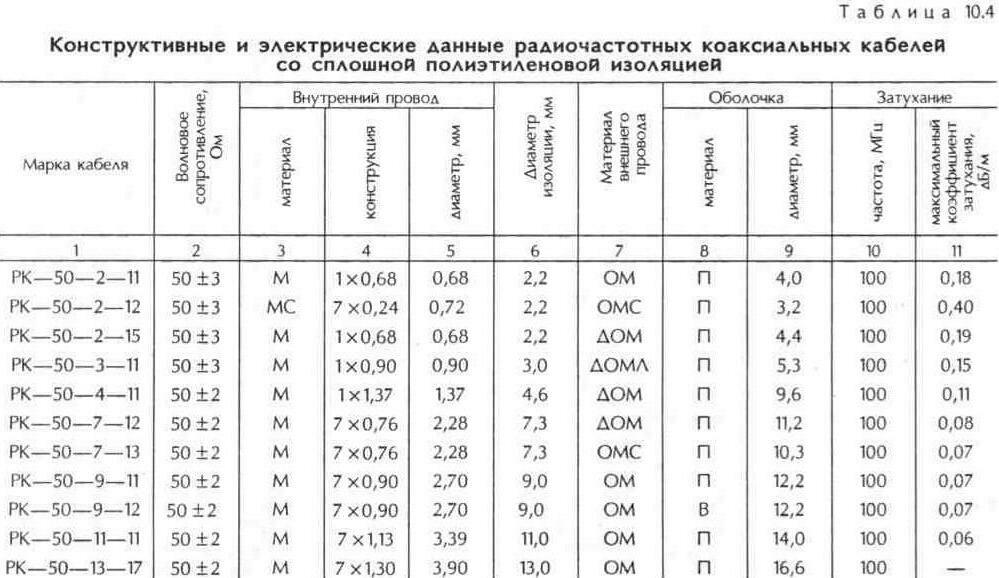Емкость определяется качеством диэлектрика и конструкцией кабеля. Этот параметр особенно важен при передаче цифровых сигналов. Применяемые для систем видеонаблюдения коаксильные кабели всех видов (кабели снижения, магистральный кабель, распределительный кабель, абонентский кабель) должны иметь волновое сопротивление 75 Ом. Условные обозначения отечественных коаксиальных кабелей согласно ГОСТу 11326.0.78 имеет следующий вид:РК.W-d-mn-q. Первые две буквы (РК) указывают тип кабеля-радиочастотный, коаксиальный. Первое число W означает величину номинального волнового сопротивления (50, 75, 100, 150, 200 Ом). Второе число d соответствует номинальному диаметру изоляции округленному до меньшего ближайшего целого числа для диаметров более 2 мм (за исключением диаметра 2,95 мм, который округляется до 3 мм и диаметра 3,7 мм, который не округляется). В зависимости от диаметра по изоляции кабеля подразделяются на субминиатюрные (до 1 мм), миниатюрные (1,5-2,95 мм), среднегабаритные (3,7-11,5 мм) и крупногабаритные (более 11,5 мм). 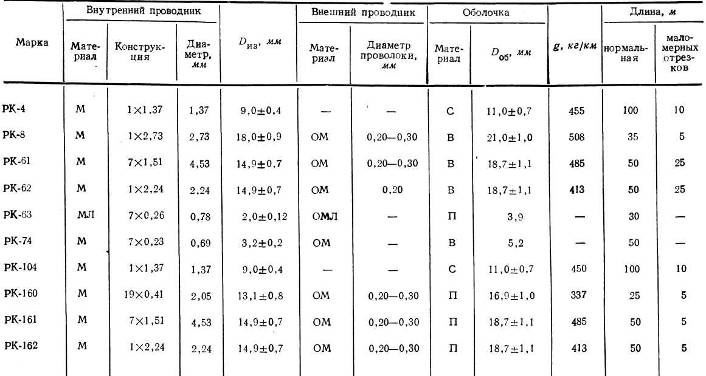Номинальный диаметр по изоляции коаксиального кабеля должен быть равен одной из величин следующего ряда: 0,15; 0,3; 0,6; 0,87; 1; 1,5; 2,2; 2,95; 3,7; 4,6; 4,8; 5,6; 7,25; 9; 11,5; 13; 17,3; 24; 33; 44; 60; 75 мм. Для соединений между аппаратурой применяются в основном кабели от 5,6 до 7,5мм, для магистральных соединений применяются кабели 9-13 мм. Обычно самый лучший 11,5 мм. Число «m» обозначает группу изоляции и категорию теплостойкости кабеля: 1-кабели со сплошной изоляцией обычной теплостойкости; 2-кабели со сплошной изоляцией повышенной теплостойкости; 3-кабели с полувоздушной изоляцией обычной теплостойкости; 4-кабели с полувоздушной изоляцией повышенной теплостойкости; 5-кабели с воздушной изоляцией обычной теплостойкости; 6-кабели с воздушной изоляцией повышенной теплостойкости; 7-кабели высокой теплостойкости. Число « n» указывает на порядковый номер разработки. В отдельных случаях в условное обозначение вводится дополнительная буква ( q) : С — кабель повышенной однородности и фазовой стабильности; Г — герметичный; Б — имеет бронепокров; ОП — имеет поверх оболочки вылетку стальных оцинкованных проволок. 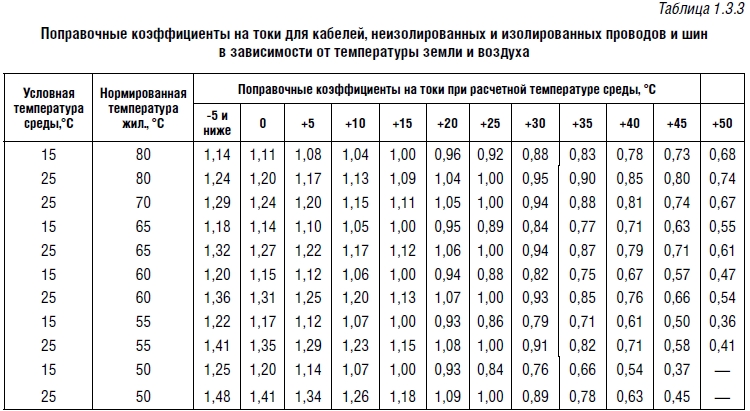Например: РК-75-4-11-С-это означает радиочастотный, коаксиальный с номинальным волновым сопротивлением 75 Ом, номинальным диаметром изоляции 4,6 мм, со сплошной изоляцией обычной теплостойкости, порядковый номер разработки 1, кабель повышенной однородности. Маркировка и обозначения импортных кабелей устанавливается международными, национальными стандартами, а также собственными стандартами предприятий-изготовителей (наиболее распространённые серии марок RG, DG и др.) При монтаже коаксиальных кабелей необходимо соблюдать минимальные радиусы изгиба (оговариваются в стандарте или ТУ на кабели разных марок). Так, для кабеля РК-75-4-11 минимальный радиус изгиба при t> +5°C — 40 мм, а при t< +5°C — 70 мм. Сгибать кабель под меньшим радиусом не рекомендуется. Следует также учитывать, что под действием собственного веса кабель вытягивается. 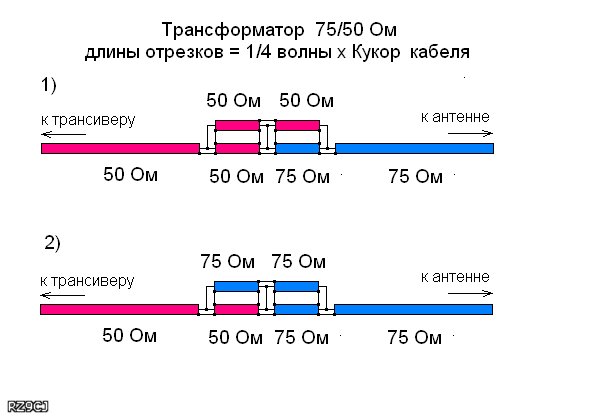Это необходимо учитывать при прокладке кабеля (по вертикали) и между строениями. Его следует закреплять к стене (мачте) или вспомогательному тросу через каждые 1-2 м. При хранении кабелей с воздушной и полувоздушной изоляцией их концы должны быть защищены от проникновения влаги внутрь кабеля, а при эксплуатации необходимо применять герметичные соединители. Срастить два отрезка коаксиального кабеля можно разными способами включая пайку. Наиболее простой способ соединения пайкой с помощью проволочного бандажа показан на рис. 3-1. При этом часть изоляции кабеля не восстанавливается, что приводит к нарушению волнового сопротивления в месте пайки, кроме того, возрастают потери сигнала. Поэтому такой способ сращивания кабелей пригоден только на радиочастотах метровых волн (до 200…300 МГц). Однако его иногда приходится использовать при соединении синфазных антенн, сборке фильтров сложения и других устройств. .

Расчет параметров коаксиального кабеля — Студопедия

Поделись  

Рассмотрим коаксиальную кабельную линию длиной (рис.3.10) и определим ее параметры — активное сопротивление прямого и обратного провода, индуктивность , емкость , а также проводимость утечки изоляции кабеля .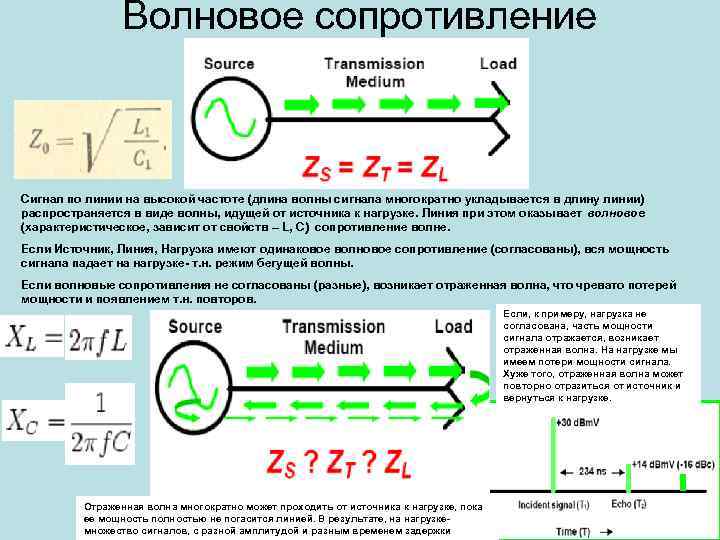

Пусть известны радиус жилы , внутренний и внешний радиусы оболочки , . Удельная электрическая проводимость материала жилы и оболочки , магнитная проницаемость . Диэлектрическая проницаемость изоляции, расположенной между жилой и оболочкой равна , удельная проводимость изоляции .

Сопротивление коаксиальной линии постоянному току складывается из сопротивлений внутреннего сплошного цилиндрического провода и внешнего трубчатого провода оболочки и равно

Индуктивность коаксиального кабеля равна , где полное потокосцепление определится в виде

Первое слагаемое в этом выражении представляет собой потокосцепление, обусловленное внутренним магнитным потоком цилиндрического провода, и равно (см. раздел «Магнитное поле»).

Поскольку магнитный поток в диэлектрике охватывает весь ток внутреннего провода, можем записать

Это потокосцепление определяет так называемую внешнюю индуктивность кабеля на постоянном токе.

Замыкающийся в оболочке магнитный поток сцеплен не только с током прямого провода, но и с частью тока, протекающего по оболочке поэтому

Из закона полного тока напряженность магнитного поля в оболочке определится из соотношения

Следовательно,

Подставив полученные аналитические выражения для интегралов в соотношение для потокосцепления коаксиального кабеля, получим формулу для расчета его индуктивности в виде

На практике обычно пренебрегают магнитным потоком в оболочке кабеля вследствие малости ее толщины, что значительно упрощает выражение для определения индуктивности:

В пространстве между жилой и оболочкой кроме магнитного поля существует и электрическое поле. Поэтому кабель обладает емкостью , где — заряд отрезка жилы кабеля длиной , — разность потенциалов между внутренним и внешним проводниками.

Разность потенциалов определим как линейный интеграл от напряженности электрического поля, взятый по радиальному направлению в пространстве между проводниками

Выражение для функции получим, используя постулат Максвелла Следовательно,

и для емкости коаксиального кабеля имеем:

При несовершенстве изоляции между проводниками под действием электрического поля возникает ток утечки. Этот ток зависит от проводимости изоляции кабеля . Величина ее может быть найдена как отношение тока утечки в изоляции к разности потенциалов между проводниками :

Ток утечки определится выражением , где — плотность тока утечки в изоляции. Этот ток протекает через цилиндрическую поверхность площадью . Выразив разность потенциалов между проводниками через ток утечки

получим следующее выражение для расчета проводимости изоляции



Проверка коаксиального кабеля на наличие повреждений с помощью мультиметра

Ключевые выводы

• Мультиметры не подходят для определения повреждений коаксиального кабеля.
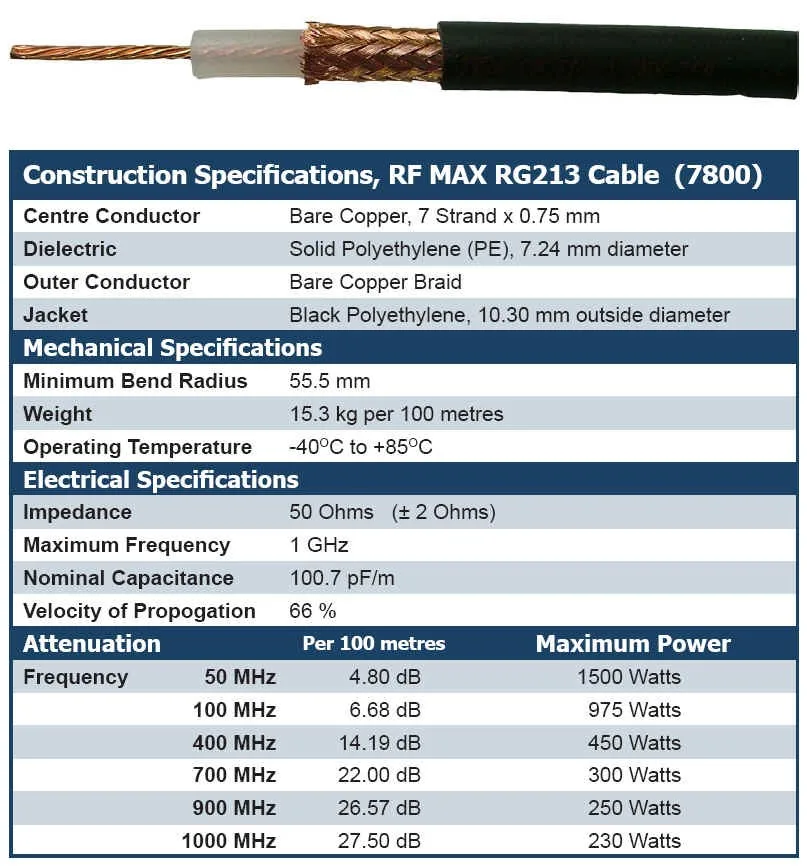
• Даже при значительном повреждении оболочки и экрана мультиметры не смогут обнаружить каких-либо заметных изменений.
• Для обнаружения повреждений коаксиального кабеля необходимы не мультиметровые методы.
• Часть 2 этой статьи можно найти здесь.

Электронный мультиметр — отличный инструмент; изобрел в 1920-х годов миллионы техников и инженеров использовали мультиметр для измерения электрических цепей и устранения неполадок с электричеством. Эти инструменты сейчас настолько распространены, что практически невозможно считать набор инструментов полным без них.

Хотя это отличные инструменты, которые можно использовать в миллионе ситуаций, они не являются волшебным инструментом, который может диагностировать каждую цепь. Если только одно запомнить из этой статьи: мультиметры не тот инструмент, который можно использовать для коаксиальных кабелей.

Чтобы помочь тем, кто не знаком с тестами коаксиальных кабелей, мы рассмотрим, что такое коаксиальные кабели, некоторые теории их использования и способы устранения неполадок в их работе.

Основы

Итак, что такое коаксиальный кабель? Базовая конструкция коаксиального кабеля представляет собой одножильный проводник посередине изолирующего слоя материала (обычно обозначаемого в коаксиальных кабелях как «диэлектрик»), проводящего слоя (идентифицируемого как экран), все защищены внешней оболочкой. . Описание коаксиальных кабелей очень общее, потому что они используются для самых разных приложений, от «кабельного» телевидения до передачи сигналов в самолетах, и существует множество вариаций для удовлетворения требований каждого приложения.

Для каждого элемента кабеля (проводника, диэлектрика, экрана и оболочки) существуют уникальные требования к конструкции и характеристикам. Многие из них обсуждались в предыдущей статье Lectromec.

Для чего они используются

Основным преимуществом коаксиальных кабелей является то, что экран действует как двусторонний барьер для электромагнитных помех (ЭМП). Высокочастотные сигналы, передаваемые по этим кабелям, ограничиваются электрическим и магнитным полем между проводником и экраном кабеля. Внешние помехи снова ограничиваются в основном взаимодействием с экраном, не затрагивая внутренний передаваемый сигнал.

Конечно, тип защиты имеет большое значение. Плетеный экран обеспечивает хорошие характеристики, но обычно обеспечивает 85–95% оптического покрытия (промежутки между плетеными жилами). Спиральный экран обеспечивает более высокое оптическое покрытие, но также снижает гибкость кабеля.

Тестирование коаксиальных кабелей

Как оценить характеристики коаксиальных кабелей? Для этого мы будем использовать примеры кабелей, показанные на прилагаемой фотографии. Два кабеля длиной 12 дюймов с разъемами TNC на обоих концах. В середине первого кабеля (далее именуемого «Поврежденный кабель») внесена неисправность. Эта ошибка была создана с помощью лезвия бритвы, удаляющего 270 ^или оболочки и экрана в центре кабеля. Длина повреждения 5 мм.

С 5-миллиметровым экраном и оболочкой, поврежденными в центре коаксиального кабеля, должно быть довольно легко обнаружить повреждение? Тестирование говорит об обратном.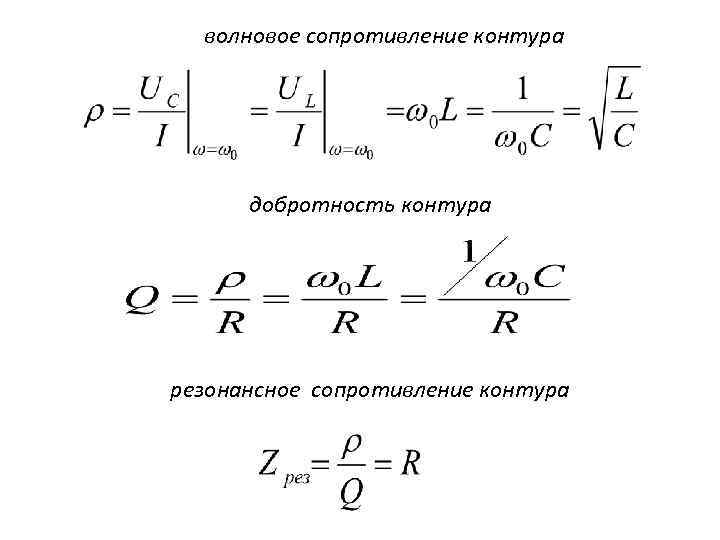

Что можно ожидать от результата в приложении? Подключенная система испытывает потерю/повреждение пакетов данных, но функциональные проверки на месте не выявили проблем. Производительность системы может ухудшиться, когда активируются другие системы самолета.

Итак, давайте проверим эти кабели и посмотрим, можно ли обнаружить это повреждение с помощью мультиметра.

Проверка сопротивления

Сопротивление кабеля и экрана измеряется стандартным мультиметром. Вычитая сопротивление измерительных проводов, мы получаем, что сопротивление проводника составляет около 0,0 Ом (ограниченная точность мультиметра) и 0,0 Ом для экрана. Тестирование «Нового кабеля» показало те же результаты.

Почему это так? Несмотря на то, что экранирующий проводник поврежден, его более чем достаточно, чтобы выдержать испытательное напряжение мультиметра. Если на экран не подается сильный ток, заметного изменения измеренного сопротивления не произойдет.

Проверка емкости

Следующей диагностической проверкой двух кабелей является проверка емкости. При этом кабель отсоединяется с обоих концов, а щупы мультиметра присоединяются к оболочке и проводнику. Измерения, проведенные на этих двух кабелях, показали следующее:

• Поврежденная емкость кабеля: 33,6 пФ
• Новый Емкость кабеля: 34,4 пФ

Нет заметной разницы между ними и находится в пределах ожидаемых различий в характеристиках кабелей. Повторное выполнение этого измерения не означает, что поврежденный кабель поврежден.

Проверка индуктивности

Затем выполняется проверка индуктивности двух кабелей. Здесь кабель разъединен с обоих концов, на дальнем конце экран соединен коротким проводом с центральным проводником, а на ближнем конце кабель подключен к датчику индуктивности. Измерения, проведенные на этих двух кабелях, показали следующее:

• Индуктивность поврежденного кабеля: 94 нГн
• Новая индуктивность кабеля: 95 нГн

Опять же, никакой заметной разницы. Используя информацию для испытаний как емкости, так и индуктивности, мы можем рассчитать волновое сопротивление обоих кабелей.

• Поврежден Характеристическое сопротивление кабеля: 53 Ом
• Новое волновое сопротивление кабеля: 53 Ом

При трех разностных измерениях поврежденного кабеля (сопротивление, емкость и индуктивность) признаков, указывающих на повреждение кабеля, нет. С положительной стороны, это показывает надежность аэрокосмических кабелей. Иметь так много физических повреждений кабеля и при этом сохранять большую часть его электрических свойств, безусловно, впечатляет.

Однако техник на этой должности, оснащенный только мультиметром и измерителем LCR, посмотрит на данные и скажет, что с кабелем все в порядке, и проблема, вероятно, связана с LRU. Это было бы началом очень дорогостоящего цикла без обнаружения неисправностей (NFF), который в конечном итоге привел бы к физическому осмотру кабеля.

Что делать?

К счастью, существуют другие инструменты и методы для определения повреждения сигнального кабеля. В следующей статье Lectromec мы обсудим эти технологии и то, что они обнаруживают при применении к тестовым кабелям.

Майкл Траскос

Президент, Lectromec

[email protected]

Майкл уже более десяти лет занимается оценкой износа и отказов проводов. Он работал над десятками проектов по оценке надежности и квалификации компонентов EWIS. Майкл является представителем FAA DER с делегированными полномочиями по сертификации EWIS и председателем комитета по установке SAE AE-8A EWIS.

Расчет сопротивления коаксиального кабеля

спросил 1 год, 10 месяцев назад

Изменено 6 месяцев назад

Просмотрено 2к раз

\$\начало группы\$

Как указано здесь, вывод сопротивления для коаксиальных кабелей

Рассмотрим коаксиальный кабель длиной \$L\$, состоящий из цилиндрического проводника радиуса a, окруженного цилиндрической проводящей оболочкой радиуса \$b\$. Пространство между проводниками заполнено изоляционным материалом. 9б\frac1rdr$$ Следовательно $$R = \frac{ρ}{2\pi L} \ln\bigg(\frac ba\bigg)$$ Обычно это сопротивление составляет несколько сотен 90 131 Ом/м 90 132, чтобы свести к минимуму «ток утечки», который проходит через изоляционный материал между проводниками.

Дело в том, что я не могу этого понять, но я знаю, что это полностью объясняет. Может быть, кто-то другой, читающий, поймет это. Я просто хочу спросить, может ли кто-нибудь объяснить это более подробно? Например, вы можете полностью использовать те же переменные и вывод, как показано на рисунке, просто объясните это по-другому. Таким образом, я могу оглянуться на источник и понять, что происходит, из более подробных объяснений.

Я знаком с основной формулой сопротивления
$$ R = \frac {ρL}{A} $$ Основываясь на информации, мое номинальное значение представления переменных составляет

• Сопротивление: \$R \rightarrow dR\$
• Удельное сопротивление : \$\rho \rightarrow \rho\$
• Длина: \$L \rightarrow dr\$
• Площадь поперечного сечения: \$A \rightarrow 2\pi rL\$

Ну, я думаю, что где-то не так. Я думаю, что \$dr\$ должен быть связан с площадью поперечного сечения. Поэтому я был бы признателен, если бы можно было объяснить аналоги оригинальной формулы. Я могу взять на себя решение оттуда, так как я знаком с интегральными формулами, и \$dr/r\$ определенно приводит к ответу, имеющему натуральный логарифм. \$a\$ — нижний предел, радиус кабеля, а \$b\$ — верхний предел, который представляет собой радиус кабеля, включая изоляцию.

• сопротивление
• кабели
• проводники
• удельное сопротивление
• коаксиальный

\$\конечная группа\$

2

\$\начало группы\$

Исходя из основной формулы для сопротивления :

R = \$\rho L/A\$ рассмотрим концентрические цилиндрические оболочки и длину кабеля G

Мы хотим рассчитать сопротивление от одной стороны до другой тонкая цилиндрическая оболочка длиной G и толщиной dr (ток проходит радиально через оболочку).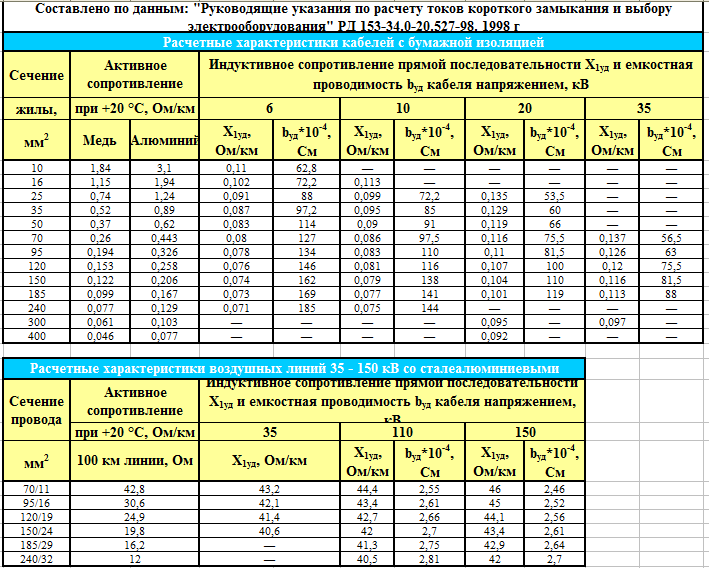

Таким образом, L в этом случае представляет собой бесконечно малое изменение радиуса dr

Мы будем использовать тонкий срез в радиальном направлении, потому что радиус изменяется при движении изнутри наружу, и, таким образом, сопротивление среза той же толщины dr уменьшается когда мы идем наружу, и мы хотим интегрироваться по этому пути, чтобы найти полное сопротивление. Мы интегрируем по пути, по которому ток следует от внутреннего проводника к внешнему проводнику. Предполагается пренебрежимо малое сопротивление вдоль центрального и внешнего проводников. 9b\frac{1}{r}dr\$

Определенный интеграл, который мы знаем, равен ln(b)-ln(a) = ln(b/a), и мы получаем решение с сайта.

\$\конечная группа\$

9

\$\начало группы\$

Утверждение «Как правило, это сопротивление составляет несколько сотен Ом/м для минимизации [утечки]» вводит в заблуждение как минимум по двум причинам.

Во-первых, это проблема единиц измерения. Единица «Ом/м» означает, что существует сопротивление, которое увеличивается с расстоянием. Однако сопротивление утечки 9{-15}\$См/м будет ближе к сопротивлению утечки типичного коаксиального кабеля.

Как указывалось в комментариях, расчет проводимости/длины по удельному сопротивлению изоляционного материала требует интегрирования по площади, но формула приведена в задаче.

\$\конечная группа\$

2

\$\начало группы\$

Итак, обычная формула для сопротивления, или способ, которым вы ее найдете, состоит в том, чтобы интегрировать путь, по которому идет ток. Если ток течет в направлении +x, вы интегрируете по x. Каждая секция, которую вы интегрируете, имеет сопротивление rho / A * dx. А — площадь поперечного сечения проводника. ОБЫЧНО в этих задачах A равномерна. Константа. Это можно вытащить вперед, прежде чем делать интеграл. Так что это вряд ли интеграл, и вы просто умножаете ро на экстент в x и делите на площадь. Так что обычно Rtotal — это просто ро*длина/площадь.

Но в нашем случае сечение неоднородное, поэтому интеграл сложнее. Кроме того, поскольку ток не течет по длине L, мы используем L в другом месте, что также сбивает с толку.

Итак, какие есть аналоги? Вместо dx у нас есть dr, потому что ток течет наружу радиально. Вместо А у нас длина окружности * длина. Итак, A = (2 * pi * r * L).

Итак, наше выражение обретает форму. Это просто:

Rshell = (rho / (2 * pi * r * L)) dr

Вы собираетесь интегрировать от r = a до r = b. Все постоянно, кроме dr/r, поэтому rho/(2 * pi * r * L) выдвигается вперед. Если мы предположим, что L равно 1 метру, то он исчезает.

Не уверен, что это имеет для вас смысл. Суть в том, что вы интегрируете по пути тока и делите на площадь поперечного сечения этого пути.

До сих пор я не выучил mathjax.