Как перевести децибелы в разы. Децибелы и разы: как перевести и что означают эти величины — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое децибел и как его перевести в разы. Почему используют логарифмическую шкалу децибел. Как рассчитать и интерпретировать значения в децибелах. Таблица соответствия децибел и разов.

Содержание

Что такое децибел и почему его используют

Децибел (дБ) — это логарифмическая единица, используемая для выражения отношения двух величин. Основные особенности децибела:

Это не абсолютная, а относительная единица измерения
Показывает, во сколько раз одна величина больше или меньше другой
Использует логарифмическую шкалу
1 децибел равен 0,1 бела

Децибелы широко применяются в акустике, радиотехнике, связи и других областях. Почему используют именно децибелы, а не обычные разы?

Преимущества использования децибел:

Позволяют работать с величинами, меняющимися в очень широких пределах
Упрощают расчеты — вместо умножения/деления можно складывать/вычитать
Хорошо отражают восприятие человеком звука, света и других воздействий
Удобны для построения графиков и диаграмм

Например, диапазон слышимых человеком звуков составляет примерно 120 дБ. В линейной шкале это соответствовало бы отношению 1 000 000 000 000 : 1, что крайне неудобно.

Как рассчитать значение в децибелах

Для расчета значения в децибелах используются следующие формулы:

Для энергетических величин (мощность, энергия):
N (дБ) = 10 * log10(P1 / P0)
Для амплитудных величин (напряжение, сила тока, давление):
N (дБ) = 20 * log10(A1 / A0)

Где P1 и A1 — измеряемые значения, P0 и A0 — опорные значения.

Например, если мощность сигнала увеличилась в 2 раза, то:

N = 10 * log10(2) = 3 дБ

То есть увеличение в 2 раза соответствует изменению на 3 дБ.

Как интерпретировать значения в децибелах

Основные соотношения, которые полезно запомнить:

+3 дБ = увеличение мощности в 2 раза
+6 дБ = увеличение напряжения в 2 раза

+10 дБ = увеличение мощности в 10 раз
+20 дБ = увеличение напряжения в 10 раз
-3 дБ = уменьшение мощности в 2 раза

Изменение на 1 дБ соответствует едва различимой человеком разнице в громкости звука. Увеличение на 10 дБ воспринимается как примерно двукратное увеличение громкости.

Таблица соответствия децибел и разов

Для удобства перевода децибел в разы и обратно можно использовать следующую таблицу:

дБ	Разы (мощность)	Разы (напряжение)
0	1	1
3	2	1.4
6	4	2
10	10	3.2
20	100	10
30	1000	31.6

Применение децибел в различных областях

Децибелы широко используются в следующих сферах:

1. Акустика и шумометрия

В акустике децибелы применяются для измерения уровня звукового давления. За точку отсчета (0 дБ) принят порог слышимости — 20 мкПа. Некоторые типичные уровни шума:

0 дБ — порог слышимости
20-30 дБ — шепот
50-60 дБ — обычный разговор
80-90 дБ — шумная улица
120 дБ — болевой порог

2. Радиотехника и связь

В радиотехнике децибелы используются для оценки усиления сигналов, потерь в линиях связи и т.д. Часто применяются следующие величины:

дБм (dBm) — уровень мощности относительно 1 мВт
дБВ (dBV) — уровень напряжения относительно 1 В
дБи (dBi) — коэффициент усиления антенны относительно изотропного излучателя

3. Оптика

В оптике и фотометрии децибелы применяются для измерения:

Коэффициента пропускания оптических элементов
Потерь в оптоволоконных линиях связи
Контрастности изображений

Преимущества и недостатки использования децибел

Рассмотрим основные плюсы и минусы применения децибельной шкалы:

Преимущества:

Возможность работы с величинами, меняющимися в очень широких пределах
Упрощение расчетов — сложение вместо умножения
Хорошее соответствие субъективному восприятию человека
Удобство построения графиков
Универсальность — можно применять к любым величинам

Недостатки:

Сложность интуитивного понимания для неподготовленных людей
Необходимость дополнительных расчетов при переводе в линейные величины
Возможность ошибок при работе с отрицательными значениями

Несмотря на некоторые сложности, преимущества децибельной шкалы обуславливают ее широкое применение в науке и технике.

Как правильно использовать децибелы в расчетах

При работе с децибелами важно помнить несколько правил:

Всегда указывайте опорный уровень (например, дБм, дБВ)
Не складывайте/вычитайте децибелы для разных величин (например, дБм и дБВ)
Помните о разнице формул для энергетических и амплитудных величин
При сложении/вычитании в децибелах соблюдайте правила:
- Сложение: L = 10*log10(10^(L1/10) + 10^(L2/10))
- Вычитание: L = 10*log10(10^(L1/10) — 10^(L2/10))

Соблюдение этих правил поможет избежать ошибок в расчетах и корректно интерпретировать результаты.

Заключение: почему важно понимать децибелы

Понимание концепции децибел и умение работать с этой единицей измерения крайне важно для специалистов во многих областях науки и техники. Децибелы позволяют:

Эффективно работать с величинами, меняющимися в широких пределах
Упростить многие расчеты и измерения
Лучше понимать процессы в акустике, радиотехнике, оптике и других областях
Корректно интерпретировать технические характеристики оборудования

Освоив принципы работы с децибелами, вы сможете более эффективно решать профессиональные задачи и лучше понимать многие явления окружающего мира.

Что такое децибел (дБ)? Перевод из децибел в разы.

Перевод из децибел в разы и обратно

Довольно часто в популярной радиотехнической литературе, в описании электронных схем употребляется единица измерения – децибел (дБ или dB).

При изучении электроники начинающий радиолюбитель привык к таким абсолютным единицам измерения как Ампер (сила тока), Вольт (напряжение и ЭДС), Ом (электрическое сопротивление) и многим другим, с помощью которых обозначают количественно тот или иной электрический параметр (ёмкость, индуктивность, частоту).

Начинающему радиолюбителю, как правило, не составляет особого труда разобраться, что такое ампер или вольт. Тут всё понятно, есть электрический параметр или величина, которую нужно измерить. Есть начальный уровень отсчёта, который принимается по умолчанию в формулировке данной единицы измерения. Есть условное обозначение этого параметра или величины (A, V). И вправду, как только мы читаем надпись 12 V, то мы понимаем, что речь идёт о напряжении, аналогичном, например, напряжению автомобильной аккумуляторной батареи.

Но как только встречается надпись, к примеру: напряжение повысилось на 3 дБ или мощность сигнала составляет 10 дБм (10 dBm), то у многих возникает недоумение. Как это? Почему упоминается напряжение или мощность, а значение указывается в каких-то децибелах?

Практика показывает, что не многие начинающие радиолюбители понимают, что же такое децибел. Попытаемся развеять непроглядный туман над такой таинственной единицей измерения как децибел.

Что такое децибел?

Единицу измерения под названием Бел стали впервые применять инженеры телефонной лаборатории Белла. Децибел является десятой частью Бела (1 децибел = 0,1 Бел). На практике широко используется как раз децибел.

Как уже говорилось, децибел, это особенная единица измерения. Стоит отметить, что децибел не является частью официальной системы единиц СИ. Но, несмотря на это, децибел получил признание и занял прочное место наряду с другими единицами измерения.

Вспомните, когда мы хотим объяснить какое-либо изменение, мы говорим, что, например, стало ярче в 2 раза. Или, например, напряжение упало в 10 раз. При этом мы устанавливаем определённый порог отсчёта, относительно которого и произошло изменение в 10 или 2 раза. С помощью децибел также измеряют эти “разы”, только в логарифмическом масштабе.

График логарифмической зависимости

Например, изменение на 1 дБ, соответствует изменению энергетической величины в 1,26 раза. Изменение на 3 дБ соответствует изменению энергетической величины в 2 раза.

Но зачем так заморачиваться с децибелами, если отношения можно измерять в разах? На этот вопрос нет однозначного ответа. Но уж, поскольку, децибелы активно применяются, то наверняка это оправдано.

Причины для использования децибел всё-таки есть. Перечислим их.

Частично ответ на этот вопрос кроется в так называемом законе Вебера-Фехнера. Это эмпирический психофизиологический закон, т.е основан он на результатах реальных, а не теоретических экспериментов. Суть его заключается в том, что любые изменения каких-либо величин (яркости, громкости, веса) ощущаются нами при условии, если эти изменения носят логарифмический характер.

График зависимости ощущения громкости от силы (мощности) звука. Закон Вебера-Фехнера

Так, например, чувствительность человеческого уха уменьшается с ростом уровня громкости звукового сигнала. Именно поэтому, при выборе переменного резистора, который планируется применить в регуляторе громкости звукового усилителя стоит брать с показательной зависимостью сопротивления от угла поворота ручки регулятора. В этом случае, при повороте движка регулятора громкости звук в динамике будет нарастать плавно. Регулировка громкости будет линейной, так как показательная зависимость регулятора громкости компенсирует логарифмическую зависимость нашего слуха и в сумме станет линейной. При взгляде на рисунок это станет более понятно.

Зависимость сопротивления переменного резистора от угла поворота движка (А-линейная, Б-логарифмическая, В-показательная)

Здесь показаны графики зависимости сопротивления переменных резисторов разных типов: А – линейная, Б – логарифмическая, В – показательная. Как правило, на переменных резисторах отечественного производства указывается, какой зависимостью обладает переменный резистор. На тех же принципах основаны цифровые и электронные регуляторы громкости.

Также стоит отметить, что человеческое ухо воспринимает звуки, мощность которых различается на колоссальную величину в 10 000 000 000 000 раз! Таким образом, самый громкий звук отличается от самого тихого, который может уловить наш слух, на 130 дБ (10 000 000 000 000 раз).

Вторая причина широкого использования децибел является простота вычислений.

Согласитесь, что куда проще при вычислениях использовать небольшие числа вроде 10, 20, 60,80,100,130 (наиболее часто используемые числа при расчёте в децибелах) по сравнению с числами 100 (20 дБ), 1000 (30 дБ), 1000 000 (60 дБ),100 000 000 (80 дБ),10 000 000 000 (100 дБ), 10 000 000 000 000 (130 дБ). Ещё одним достоинством децибел является то, что их просто суммируют. Если проводить вычисления в разах, то числа необходимо умножать.

Например, 30 дБ + 30 дБ = 60 дБ (в разах: 1000 * 1000 = 1000 000). Думаю, с этим всё ясно.

Также децибелы очень удобны при графическом построении различных зависимостей. Все графики вроде диаграмм направленности антенн, амплитудно-частотных характеристик усилителей выполняют с применением децибел.

Децибел является безразмерной единицей измерения. Мы уже выяснили, что децибел на самом деле показывает, во сколько раз возросла, либо уменьшилась какая-либо величина (ток, напряжение, мощность). Отличие децибел от разов заключается лишь в том, что происходит измерение по логарифмическому масштабу. Чтобы это как-то обозначить и приписывают обозначение дБ. Так или иначе, при оценке приходится переходить от децибел к разам. Сравнивать с помощью децибел можно любые единицы измерения (не только ток, напряжение и проч.), так как децибел является относительной, безразмерной величиной.

Если указывается знак “-”, например, –1 дБ, то значение измеряемой величины, например, мощности, уменьшилось в 1,26 раз. Если перед децибелами не ставят никакого знака, то речь идёт об увеличении, росте величины. Это стоит учитывать. Иногда вместо знака “-” говорят о затуханиях, снижении коэффициента усиления.

Переход от децибел к разам.

На практике чаще всего приходится переходить от децибел к разам. Для этого есть простая формула:

Внимание! Данные формулы применяются для так называемых “энергетических” величин. Таких как энергия и мощность.

m = 10^{(n / 10)} ,где m – отношение в разах, n – отношение в децибелах.

Например, 1дБ равен 10^{(1дБ / 10)} = 1,258925…= 1,26 раза.

Аналогично,

Но, не всё так просто. Есть и подводные камни. Например, затухание сигнала составляет -10 дБ. Тогда:

при -10 дБ: 10^{(-10дБ / 10)} = 0,1
Если мощность с 5 Вт уменьшилась до 0,5 Вт, то снижение мощности равно -10 дБ (уменьшению в 10 раз).
при -20 дБ: 10^{(-20дБ / 10)} = 0,01
Здесь аналогично. При снижении мощности с 5 Вт до 0,05 Вт, в децибелах падение мощности составит -20 дБ (уменьшению в 100 раз).

Таким образом, при -10 дБ мощность сигнала уменьшилась в 10 раз! При этом если мы перемножим начальную величину сигнала на 0,1 ,то и получим значение мощности сигнала при затухании в -10 дБ. Именно поэтому значение 0,1 и указано без «разов», как в предыдущих примерах. Учитывайте эту особенность при подстановке в данные формулы значений децибел со знаком «-«.

Переход от разов к децибелам можно осуществить по следующей формуле:

n = 10 * log₁₀(m) ,где n – значение в децибелах, m – отношение в разах.
Например, рост мощности в 4 раза будет соответствовать значению в 6,021 дБ.
10 * log₁₀(4) = 6,021 дБ.

Внимание! Для пересчёта отношений таких величин как напряжение и сила тока существуют немного иные формулы:

(Сила тока и напряжение, это так называемые “силовые” величины. Поэтому и формулы отличаются.)

n – значение в децибелах, m – отношение в разах.

Если Вы успешно дошли до этих строк, то считайте, что сделали ещё один весомый шаг в освоении электроники!

Главная &raquo Радиоэлектроника для начинающих &raquo Текущая страница

Также Вам будет интересно узнать:

Онлайн калькулятор децибелы в разы, напряжения в мощность

Децибел… Что за странный пассажир? Ладно бы дебил, или, на худой конец, имбецил, так ведь нет — децибел, мать его.
Выпили по децелу, закусили, понимания не прибавило, ещё по сто, уже лучше — начали генерить мыслю.
И на кой хрен нам в батарее разводить мудрёные величины, да ещё (не при бабах будет сказано), численно равные десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять?

Всё равно — как отмеряли потери сигнала в линиях километрами стандартного кабеля, так и будем отмерять.

Ответ не сложен — для удобства мировосприятия.
Природа наша такова, что воздействие на органы чувств многих физических и биологических процессов пропорционально не амплитуде входного воздействия, а логарифму входного воздействия. Поэтому и созерцать отображения больших диапазонов изменяющихся величин удобнее всего в логарифмическом масштабе.

Если в лесах Чухломы у нас затерялось какое-либо электронное устройство, то в качестве отношения напряжений (либо токов, либо мощностей) принимается отношение выходной величины к входной, и это отношение называется коэффициентом передачи, или коэффициентом преобразования данного устройства.

Пока хватит, нарисуем таблицу.

ТАБЛИЦА ПЕРЕВОДА ОТНОШЕНИЙ ВЕЛИЧИН В ДЕЦИБЕЛЛЫ

Коэффициент передачи, выраженный в децибелах, может иметь знак плюс или минус в зависимости от соотношения величин на выходе и входе (если выходная величина больше входной — плюс, если меньше — минус).

А ТЕПЕРЬ НАОБОРОТ, ДЕЦИБЕЛЛЫ В ОТНОШЕНИЯ

В случае включения по каскадной схеме (последовательно, друг за другом) нескольких устройств — общий коэффициент передачи в децибельном выражении вычисляется простым сложением значений Кпер.(дБ) каждого из устройств.

А теперь переведём логарифмическую меру мощности, измеряемую в дБм (dBm — децибел на милливатт) в мощность устройства, измеряемую в привычных нашему организму ваттах.
Формула выглядит так: . Для чего нам сдался этот дБм?
На всякий пожарный — некоторые производители указывают именно этот параметр, характеризуя богатырскую мощь своих изделий.

ТАБЛИЦА ПЕРЕВОДА ДБМ В ВАТТЫ

Так ведь мало того, что мощность усилителей надумали измерять в дБм, посягнули и на святое — на чувствительность приёмной аппаратуры. Чувствительность стали определять как отношение мощности на входе приёмника к уровню мощности 1 мВт и также выражать в логарифмическом масштабе в дБм.
Куда деваться бедному крестьянину? Придётся привести таблицу и для этого бесчинства.

ТАБЛИЦА ПЕРЕВОДА ДБМ В МИКРОВОЛЬТЫ

А ещё, иногда бывает полезно знать, каким должен быть размах выходного напряжения на нагрузке, для получения заданного параметра мощности. Некоторые при расчёте выходной мощности пользуются простой формулой , подставляя вместо Uд — пиковое значение (амплитудное значение, равное максимальной амплитуде полуволны выходного сигнала). Это не правильно, вернее правильно только для сигналов прямоугольной формы. Для синусоидальных, для получения точного результата надо подставлять действующее значение напряжения — .
Лучше понять, что такое амплитудное значение, и как найти действующее для различных форм сигналов можно на странице ссылка на страницу.

ЗАВИСИМОСТЬ АМПЛИТУДЫ НАПРЯЖЕНИЯ ОТ МОЩНОСТИ

ЗАВИСИМОСТЬ МОЩНОСТИ ОТ ВЫХОДНОГО НАПРЯЖЕНИЯ

Что такое децибел, что обозначает, как переводить в разы и обратно

Мы часто встречаем уровни звука, указанные в децибелах — дБ или dBu и привыкли считать что это единица измерения шума, звука. А вот и нет. Это совсем не так. Децибел — это не единица измерения вообще. Это относительная характеристика, которая может отражать напряжение, мощность, силу тока и т.д. Что-то типа процентов, долей, но в логарифмической зависимости. Сначала понять, что такое децибел, непросто, но затем оказывается, что это очень удобно.

Содержание статьи

Понятие децибела

Мы хорошо воспринимаем измерение каких-либо параметров в прямых величинах. Например, напряжение измеряется в вольтах, сила тока — в амперах, сопротивление — в омах и т.д. Когда говорим об этом, все ясно и понятно. Когда говорим об увеличении или снижении в этих прямых единицах измерения тоже все понятно. Например, напряжение с 220 вольт снизилось до 150 вольт. Все понятно. Выражение «мощность возросла на 50 ватт» тоже вопросов не вызывает.

Как понять что такое децибел и что он означает

Но иногда говорят об увеличении или уменьшении того же напряжения или мощности на 2 децибела. Как это понять? Что измеряется в децибелах? Ведь мощность меряем в ваттах? Как соотнести децибелы с ваттами или вольтами, амперами и другими величинами. Ведь так описывают многие параметры. Тут надо разбираться. Не очень просто сначала понять, но потом все становится очевидным.

Что значит бел и децибел

Сразу стоит уяснить, что бел и децибел — это не единицы измерения чего-либо. Это не результат измерений. Децибел — это величина, которая показывает насколько/во сколько раз изменился тот или иной параметр. То есть бел или децибел — это относительная величина, которая высчитывается при сравнении двух измерений одного и того же параметра.

Например, на рисунке дан график, который построили по результатам измерения напряжение на выходе прибора при изменении подаваемой на вход частоты (АЧХ). Сняты были характеристики при уровне сигнала 1 V (график 1) и 100 мV (график 2). Если смотреть на графики прямых измерений, понять что-то сложно. На втором рисунке график построен в децибелах. На этом графике очевидно, что реакция прибора одинаковая, изменился только уровень сигнала на выходе, что и понятно.

Два графика измерений. Левый — прямая зависимость (напряжения от частоты), правый — изменение напряжения в дБ при изменении частоты

Первоначально стали использовать единицу Бел. Международное обозначение бела — B, российское — Б (например, 10Б или 10B). Но более удобным оказалось применение одной ее десятой доли — децибела или дБ в российском обозначении и dBu в международном. То есть один децибел — это 0,1 Бела.

Дальше, к сожалению, без математики не обойтись. Придется вспомнить что такое десятичный логарифм. Десятичный логарифм показывает, в какую степень надо возвести число 10 чтобы получить требуемую цифру. На рисунке вы видите соотношение, возможно будет понятнее в таком виде.

Несколько значений десятичных логарифмов

Теперь, собственно о Белах и децибелах. Если говорить об определениях, то Бел — это десятичный логарифм отношения двух величин. Любых двух величин. Мощностей, напряжения, силы звука, частоты и т.д. Давайте на примере. Надо понять, что выдает прибор на выходе при изменении параметров на входе. Выбирают какую-то точку отсчета — базу. Затем изменяют параметр, проводят измерение результата, делят его на «базу» и берут десятичный логарифм. Получают результат измерения в децибелах. Так измеряют параметры, пересчитывают в децибелы и строят зависимости.

Формула, которая поясняет что такое дБ (децибел) и как их считают

На рисунке даны две формулы — для вычисления энергетических величин (по мощности) и амплитудных (по напряжению). Как видите, они отличаются только коэффициентом. U1 тут — это результат измерений, а Uo — базовая величина, с который сравнивают измерений.

Почему используют децибелы, а не прямые величины

Использование логарифмических зависимостей часто более понятно и несет больше информации, чем прямые измерения. Это видно на примере построения графиков амплитудно-частотной характеристики. И такой случай не единичный, многие зависимости более информативны в логарифмической зависимости.

Кроме того, децибелы используют в тех областях, где параметры изменяются в очень широком диапазоне. Более понятна нам ситуация со звуками. Человек в состоянии воспринимать частоты от 20 Гц до 20 000 Гц. Ничего себе разброс! В тысячу раз.

Интенсивность звука и его соответствие в дБА

С уровнем звука еще круче. Нижний предел восприятия — 10^-12 Вт/м, а уровень, при котором возникает боль — 10 Вт/м. То есть, диапазон измерения значений — 13 порядков. Это 10 000 000 000 000 раз. Оперировать такими цифрами, как минимум неудобно. С использованием относительных величин — децибел — цифры получаются значительно меньше, работать, воспринимать и запоминать их легче. Несколько примеров:

Если показатель увеличился в 10 раз, говорят, что он увеличился на 1 Бел.
Если тот же показатель увеличился в 100 раз, то говорят об увеличении на 2 Бела.
Увеличение в 100 000 тысяч раз — всего на 5 Бел.

Заметили разницу? Показатель увеличился в 100 раз, а в белах увеличился на 2 Б. Это удобнее. Согласитесь, проще оперировать единицами, чем сотнями тысяч. Важно просто понимать смысл сказанного. При возрастании прямых величин их надо умножать на то число, на которое параметр увеличился. При оперировании децибелами их складывают. Согласитесь, это проще.

Что такое dBm, dBv, dBA (дБм, дБв, дБА)

Как вы уже поняли, децибел — это относительная величина и отражать она может что угодно. Надо только выбрать точку отсчета, базу, эталон, с которым сравнивают все последующие изменения. База для сравнения может быть взята произвольно. Но тогда непонятно как соотносить разные измерения. В таком случае, обычно, указывают относительно чего считался логарифм. То есть, что подставляли в знаменатель (в формуле выше это Uo).

Для электротехники и мощностей были выбраны базовые точки отсчета — две величины напряжения, с которыми сравнивают большую часть измерений электрических величин.

Основная база — это мощность в один милливатт (1 мВт) при нагрузке 600 Ом. Если пересчитать, то напряжение получаем 0,775 Вольта. Именно эти значения и являются той базой, относительно которой высчитывают логарифмы. Это принято и в международных измерениях, и в отечественных. Именно при использовании такой базы ставят обозначение dBu или дБ в русском варианте. Реже встречается обозначение dBm. Это тоже, что dBu.
Иногда выходное напряжение сравнивают с 1 В. В этом случае результат подписывают как dBv или дБв.

На что влияет точка отсчета? Просто на уровень, на котором строится зависимость. Если же по данным построить график, он будет иметь ту же форму.

При описании звуков и шумов употребляют дБА (dBA) или акустические децибелы. При таком исчислении за точку отсчета берут нижний порог слышимости или частоты, которую различает человеческое ухо. Это 2·10^-5Па и относительно нее вычисляют отношение.

Как считают децибелы

Больше в ходу не Белы, а их десятая часть — децибелы (обозначение dB или дБ). Ведь чаще увеличение не в сотни и тысячи раз, а чуть поскромнее. Так что обычно говорят об увеличении того или иного показания или характеристики на 5 дБ или на 10 дБ.

Пример соответствия децибел и «раз»

Но важно помнить, что описанная выше прямая зависимость характерна только для энергетических величин (это если мощность возросла в 10 раз, то она увеличилась на 10 дБ). Для других зависимость тоже логарифмическая, но вычисляется по другой формуле. И это надо помнить.

Децибелы	Соотношение мощностей	Соотношение амплитуд
-3	0,5	0,7
-6	0,25	0,5
-10	0,1	0,3
-20	1,01	0,1
-25	0,03	0,05
-40	0,01	0,0001
-60	0,001	0,000001

Возможно, поможет понять что такое децибел следующие сравнение. Представим, что мощность изменяется литрами. Соотношение между 0,5 литра и 1 литром такое же как и между 1 литром и 2 литрами. Это 0,5 и равно оно 6 дБ. Но если сравнивать 0,5 и 0,75 литра, то они относятся как 0,66(6) что в децибелах около 3,6 дБ. Примерно так.

Децибелы в акустике

Вы, возможно, удивитесь, но для акустики децибелы подходят просто идеально. Собственно, Александр Белл ввел понятие Бел при исследовании порога слышимости. Он определил, что «громкость» мы воспринимаем не по реальной мощности сигнала, а по десятичному логарифму от этой мощности. Как так? Давайте рассмотрим пример.

Имеется усилитель, который выдает сигнал мощностью 1 Вт. Чтобы увеличить его в 1,1 раза, добавить надо только 0,1 Вт. А если на выходе у нас 100 Вт, то чтобы увеличить мощность в 1,1 раза надо поднять мощность на 10 Вт. Увеличение громкости в обоих случаях будет «для уха» одинаковым, а увеличение мощности имеет явно нелинейный характер.

Мы воспринимаем не реальный уровень сигнала, а логарифмическую зависимость

На основании вот этого явления Белл и вывел то самое логарифмическое отношение. В его честь и названа эта относительная единица измерений. Что еще это нам дает? А вот такие факты:

1 дБ — это минимальный уровень слышимости сигнала. Звуки с более низкой мощностью (о дБ и ниже) большинство людей не замечают и определяют как «абсолютную тишину».
Если говорят о том, что мощность сигнала/звука возросла на 3 дБ, то значит она возросла в два раза. Не путайте с громкостью.
При увеличении мощности звука на 10 дБ, громкость увеличивается в 2 раза.
Увеличение напряжения в два раза — это 6 дБ.

Принять децибелы не так легко. Но наверное, вы уже поняли, что в децибелах громкость звука/шума не измеряется. Эта цифра показывает насколько изменился сигнал относительно «нулевой» точки восприятия. Примерно так можно это сформулировать.

Таблица уровней шумов

Ну, а чтобы было понятнее, приведем таблицу сравнений привычных, знакомых звуков и их среднего уровня.

дБ	С чем можно сравнить	дБ	С чем можно сравнить
0 дБ	Полная тишина	90 дБ	Звук работающего фена, мотоцикла, поезда
1 дБ	Самый нижний порог слышимости	100-105 дБ	Ремонт и рок-концерт
10-24 дБ	Шелест листвы	110 дБ	Музыка в ночном клубе
20 дБ	Шепот	120 дБ	Автомобильный гудок
40 дБ	Так звучит дождь	130-135 дБ	Звук работающей дрели
45 дБ	Тихий разговор	140 дБ	Шум турбин самолета
60 дБ	Громкий разговор	160 дБ	Звук выстрела возле уха
80-90 дБ	Шоссе с интенсивным движением	200 дБ	Смертельный уровень шума

Каждый шум или звук имеет определенный уровень мощности, но проще его описывать в децибелах

Факты, которые позволят оценить важность акустики и децибелов:

Комфортным уровнем шума считается 50-55 дБ. Как видите, эту величину можно сравнить с разговором обычной «громкости». Именно этот уровень по СНиПу определен как приемлемый для дневного времени.
Уровень 70-90 дБ относится к «терпимым», но длительное воздействие может привести к заболеваниям нервной системы.
Длительное воздействие шума в 100 дБ приводит к снижению слуха и глухоте.
Звуки мощностью 130 дБ вызывают болевые ощущения.
Мощность звука в 200 дБ может быть смертельной.

Вообще, постоянное нахождение в шумном помещении сильно снижает способность воспринимать звуки. Мало того, оно приводит к расстройствам психики, сна, что негативно сказывается и на общем самочувствии. Поэтому шумные производства — зона риска. Чтобы хорошо себя чувствовать, просто необходимо время от времени находится если не при полной тишине, то при низком уровне шума.

Перевод децибелов в разы

Давайте попробуем сформулировать что такое децибел по-другому. Децибел — это логарифм соотношения двух величин. Эта относительная величина, которая показывает во сколько одно значение больше или меньше другого (базового). «Во сколько раз» это нам понятно. Поэтому часто приходится переводить децибелы в разы и наоборот. Можно, конечно, посчитать, но проще пользоваться таблицей.

дБ	Увеличение напряжения (силы тока) в разы	Увеличение мощности (энергетической составляющей) в разы	дБ	Увеличение напряжения (силы тока) в разы	Увеличение мощности (энергетической составляющей) в разы
0	1	1	28	25,12	631
1	1,12	1,26	29	28,17	794
2	1,26	1,59	30	31,64	1000
3	1,41	2	31	35,46	1257
4	1,59	2,51	32	39,84	1587
5	1,78	3,16	33	44,64	1993
6	2	2,98	34	48,08	2312
7	2,24	5,01	35	56,82	3165
8	2,51	6,31	36	63,29	4006
9	2,82	7,94	37	70,92	5030
10	3,16	10	38	79,36	6298
11	3,55	12,59	39	89,29	7973
12	3,98	15,85	40	100	10000
13	4,47	19,96	41	112,23	12596
14	5,01	25,12	42	125,94	15861
15	5,62	31,65	43	141,24	19949
16	6,31	39,84	44	158,48	25116
17	7,08	48,08	45	177,94	31663
18	7,94	63,59	46	199,60	39840
19	8,91	79,36	47	223,71	50046
20	10	100	48	251,26	63132
21	11,22	125,94	49	281,69	79349
22	12,59	158,48	50	316,5	100 000
23	14,12	199,60	60	1 000	1 000 000
24	15,85	251,26	70	3165	10 000 000
25	17,79	316,50	80	10 000	100 000 000
26	19,96	398,4	90	31650	1 000 000 000
27	22,37	500,42	100	100 000	10 000 000 000

Как видите, чтобы напряжение увеличилось в три раза, мощность необходимо поднять в 10 раз. Впечатляющая разница. Эта таблица позволяет точно понять связь между этими величинами.

Но сигналы и величины не только увеличиваются, они могут и снижаться. Следующая таблица дана для падения значений относительно эталона.

дБ	Снижение напряжения (силы тока) в разы	Снижение мощности (энергетической составляющей) в разы	дБ	Снижение напряжения (силы тока) в разы	Снижение мощности (энергетической составляющей) в разы
0	1	1	-8,0	0,398	0,159
-0,1	0,989	0,977	-9,0	0,355	0,126
-0,2	0,977	0,955	-10	0,316	0,1
-0,3	0,966	0,933	-11	0,282	0,0794
-0,4	0,955	0,912	-12	0,251	0,0631
-0,5	0,944	0,891	-13	0,224	0,0501
-0,6	0,933	0,871	-14	0,2	0,0398
-0,8	0,912	0,832	-15	0,178	0,0316
-1,0	0,891	0,794	-16	0,159	0,0251
-1,5	0,841	0,708	-18	0,126	0,0159
-2,0	0,794	0,631	-20	0,1	0,01
-2,5	0,750	0,562	-30	0,0316	0,001
-3,0	0,668	0,501	-40	0,01	0,0001
-3,5	0,631	0,447	-50	0,00316	0,00001
-4,0	0,596	0,398	-60	0,001	0,000001
-4,5	0,562	0,355	-70	0,000316	0,0000001
-5,0	0,501	0,316	-80	0,0001	0,00000001
-6,0	0,501	0,251	-90	0,0000316	0,000000001
-7,0	0,447	0,2	-100	0,00001	0,0000000001

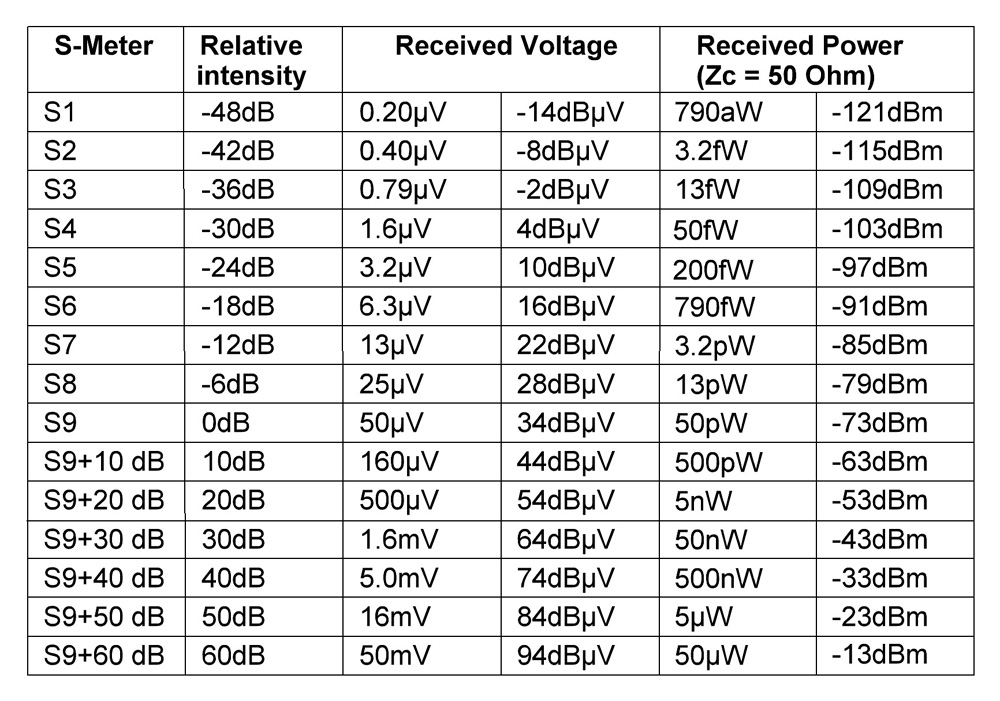
Ослабление того или иного сигнала проще описывать в децибелах. Простые цифры легче запоминаются. Но иногда надо знать и реальный уровень мощности. Для этого используют таблицы (перевод дБ в мкВ)

Перевод ослабления сигнала в дБ в микровольты мкВ

Перевод из дб в разы формула | 2019

Перевод величин из децибелов в абсолютные значения и мощность

При проведении измерений параметров радиоаппаратуры довольно часто приходится иметь дело с относительными величинами выраженными в децибелах [дБ]. В децибелах выражают интенсивность звука, усиление каскада по напряжению, току или мощности, потери передачи или ослабление сигнала, и т.д.

Децибел — это универсальная логарифмическая единица. Широкое использование представления величин в дБ связано с удобством логарифмического масштаба, а при расчетах децибелы подчиняются законам арифметики — их можно складывать и вычитать, если сигналы имеют одинаковую форму.

Существует формула для пересчета отношения двух напряжений в число децибелов (аналогичная формула справедлива и для токов):

Например, если выходной сигнал U2 имеет уровень вдвое больше, чем U1, то это отношение составит +6 дБ (Ig2=0,301). Если U2>U1 в 10 раз, то отношение сигналов составляет 20 дБ (Ig10=1). Если U1>U2, то знак у отношения меняется на минус 20 дБ.

Так, например, у измерительного генератора аттенюатор для ослабления выходного сигнала может иметь градуировку в дБ. В этом случае для перевода величины из децибелов в абсолютное значение быстрей будет получен результат, если воспользоваться уже посчитанной табл. 6; 1. Она имеет дискретность 1 дБ (что вполне достаточно в большинстве случаев) и диапазон значений 0. -119 дБ.

Табл. 6.1 можно использовать для перевода децибелов ослабления аттенюатора в уровень выходного напряжения. Для удобства использования таблицы потребуется на выходе генератора установить при отсутствии ослабления (0 дБ на аттенюаторе) уровень напряжения 1 В (действующего или амплитудного). В этом случае соответствующее нужное значение выходного напряжения после установки ослабления находится на пересечении горизонтальной и вертикальной граф (значения в децибелах складываются арифметически).

Величина выходного напряжения в таблице указана в микровольтах (1 мкВ=10-6 В). I

Воспользовавшись данной таблицей, не трудно решить и обратную задачу — по необходимому напряжению определить, какое нужно установить ослабление сигнала на аттенюаторе в децибелах. Например, чтобы получить на выходе генератора напряжения 5 мкВ, как видно из таблицы, на аттенюаторе потребуется установить ослабление 100+6=106 дБ. Отношение мощностей двух сигналов в децибелах вычисляется по формуле:

Формула для мощности справедлива при условии, что входное и выходное сопротивления устройства одинаковые, что часто выполняется в высокочастотных устройствах для облегчения их согласования между собой.

Для определения мощности можно воспользоваться посчитанной табл. 6.2

Нередко при практическом использовании дБ важно знать и абсолютное значение соотношения двух величин, т.е. во сколько раз напряжение или мощность на выходе больше, чем на входе (или наоборот). Если отношение двух величин обозначить: K=U2/U1 или К=Р2/Р1, то можно воспользоваться табл. 6.3 для перевода величины из дБ в разы (К) и наоборот.

Так, например, антенный усилитель обеспечивает усиление сигнала по мощности на 28 дБ. Из табл. 6.3 видно, что усиление сигнала выполняется в 631 раз.

Литература: И.П. Шелестов — Радиолюбителям полезные схемы, книга 3.

Онлайн калькулятор перевода децибел в разы, напряжений в мощность.

Децибел. Что за странный пассажир? Ладно бы дебил, или, на худой конец, имбецил, так ведь нет — децибел, мать его.
Выпили по децелу, закусили, понимания не прибавило, ещё по сто, уже лучше — начали генерить мыслю.
И на кой хрен нам в батарее разводить мудрёные величины, да ещё (не при бабах будет сказано), численно равные десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять?
Всё равно — как отмеряли потери сигнала в линиях километрами стандартного кабеля, так и будем отмерять.

Итак, децибелы — это соотношение двух величин, выраженное в логарифмическом масштабе. При этом отношение токов и напряжений имеет коэффициент 20, а отношение мощностей — коэффициент 10.
Для напряжений формула приобретает вид , а для мощностей — .
Если в лесах Чухломы у нас затерялось какое-либо электронное устройство, то в качестве отношения напряжений (либо токов, либо мощностей) принимается отношение выходной величины к входной, и это отношение называется коэффициентом передачи, или коэффициентом преобразования данного устройства.

Пока хватит, нарисуем таблицу.

ТАБЛИЦА ПЕРЕВОДА ОТНОШЕНИЙ ВЕЛИЧИН В ДЕЦИБЕЛЛЫ

А ТЕПЕРЬ НАОБОРОТ, ДЕЦИБЕЛЛЫ В ОТНОШЕНИЯ

ТАБЛИЦА ПЕРЕВОДА ДБМ В ВАТТЫ

ТАБЛИЦА ПЕРЕВОДА ДБМ В МИКРОВОЛЬТЫ

ЗАВИСИМОСТЬ АМПЛИТУДЫ НАПРЯЖЕНИЯ ОТ МОЩНОСТИ

ЗАВИСИМОСТЬ МОЩНОСТИ ОТ ВЫХОДНОГО НАПРЯЖЕНИЯ

Децибелы «по мощности», «по напряжению» и «по току»

Из правила (см. выше) следует, что дБ бывают только «по мощности». Тем не менее, в случае равенства R₁ = R_{(в частности, если R₁ и R_{— одно и то же сопротивление, или в случае, если соотношение сопротивлений R₁ и R_{по той или иной причине не важно) говорят о дБ «по напряжению» и «по току», подразумевая при этом выражения:}}}

дБ по напряжению = ;

дБ по току = .

Для перехода от «дБ по напряжению» («дБ по току») к «дБ по мощности» следует чётко определить, на каких именно сопротивлениях (равных или не равных друг другу) регистрировались напряжение (ток). Если R₁ не равно R_{, следует пользоваться выражением для общего случая (см. выше).}

Нетрудно подсчитать, что, в частности:

при регистрации мощности изменению на +1 дБ (+1 дБ «по мощности») соответствует приращение мощности в ≈1,259 раза, изменению на −3,01 дБ — снижение мощности в два раза, в то время как

при регистрации напряжения (силы тока) изменению на +1 дБ (+1 дБ «по напряжению», «по току») будет соответствовать приращение напряжения (силы тока) в ≈1,122 раза, при изменении на −3,01 дБ напряжение (сила тока) снизятся и составят ≈ 0,707 от своего исходного значения.

Примеры вычислений Переход к дБ

Пусть значение мощности P₁ стало в 2 раза больше исходного значения мощности P_{, тогда}

10 lg(P₁/P_{) = 10 lg(2) ≈3,0103 дБ ≈ 3 дБ,}

то есть рост мощности на 3 дБ означает её увеличение в 2 раза.

Пусть значение мощности P₁ стало в 2 раза меньше исходного значения мощности P_{, то есть P₁ = 0,5 P_{. Тогда}}

то есть снижение мощности на 3 дБ означает её снижение в 2 раза. По аналогии:

рост мощности в 10 раз: 10 lg(P₁/P_{) = 10 lg(10) = 10 дБ, снижение в 10 раз: 10 lg(P₁/P_{) = 10 lg(0,1)= −10 дБ;}}

рост в 1 млн раз: 10 lg(P₁/P_{) = 10 lg(1 000 000) = 60 дБ, снижение в 1 млн раз: 10 lg(P₁/P_{) = 10 lg(0,000001) = −60 дБ.}}

Переход от дБ к «разам»

Изменение «в разах» по известному изменению в дБ (условное обозначение «dB» в формулах ниже) вычисляется следующим образом:

для мощности: ; таким образом, например, если изменение мощности составило +20 децибел, это значит, что «P₁ больше P_{на два порядка» или «P₁ больше P_{в 100 раз»;}}

для напряжения (силы тока): ; таким образом, например, если изменение напряжения составило +20 децибел, это значит, что «U₁больше U_{на порядок» или «в 10 раз».}

Что такое децибел?

Перевод из децибел в разы и обратно

Что такое децибел?

График логарифмической зависимости

Причины для использования децибел всё-таки есть. Перечислим их.

График зависимости ощущения громкости от силы (мощности) звука. Закон Вебера-Фехнера

Вторая причина широкого использования децибел является простота вычислений.

Например, 30 дБ + 30 дБ = 60 дБ (в разах: 1000 * 1000 = 1000 000). Думаю, с этим всё ясно.

Переход от децибел к разам.

На практике чаще всего приходится переходить от децибел к разам. Для этого есть простая формула:

m = 10 (n / 10) ,где m – отношение в разах, n – отношение в децибелах.

Например, 1дБ равен 10 (1дБ / 10) = 1,258925…= 1,26 раза.

при 20 дБ: 10 (20дБ / 10) = 100 (увеличение величины в 100 раз)

при 10 дБ: 10 (10дБ / 10) = 10 (увеличение в 10 раз)

Но, не всё так просто. Есть и подводные камни. Например, затухание сигнала составляет -10 дБ. Тогда:

при -10 дБ: 10 (-10дБ / 10) = 0,1

Если мощность с 5 Вт уменьшилась до 0,5 Вт, то снижение мощности равно -10 дБ (уменьшению в 10 раз).

при -20 дБ: 10 (-20дБ / 10) = 0,01

Здесь аналогично. При снижении мощности с 5 Вт до 0,05 Вт, в децибелах падение мощности составит -20 дБ (уменьшению в 100 раз).

Переход от разов к децибелам можно осуществить по следующей формуле:

n = 10 * log₁₀(m) ,где n – значение в децибелах, m – отношение в разах.

Например, рост мощности в 4 раза будет соответствовать значению в 6,021 дБ.

10 * log₁₀(4) = 6,021 дБ.

Внимание! Для пересчёта отношений таких величин как напряжение и сила тока существуют немного иные формулы:

(Сила тока и напряжение, это так называемые “силовые” величины. Поэтому и формулы отличаются.)

Для перехода к децибелам: n = 20 * log₁₀(m)

Для перехода от децибел к разам: m = 10 (n / 20)

n – значение в децибелах, m – отношение в разах.

Если Вы успешно дошли до этих строк, то считайте, что сделали ещё один весомый шаг в освоении электроники!

Перевод величин из децибелов в абсолютные значения и мощность

Величина выходного напряжения в таблице указана в микровольтах (1 мкВ=10-6 В). I

Для определения мощности можно воспользоваться посчитанной табл. 6.2

Литература: И.П. Шелестов — Радиолюбителям полезные схемы, книга 3.

Online калькулятор разы и проценты в децибелы

Урок третий+. Учимся разбирать электрические схемы.

Так как тема довольно таки обширная и теоретического материала много, его сокращение будет лежать на плечах учителя, проводящего занятия. Нужно учитывать так же усвояемость материала и затягивать данную тему сильно не стоит. Может даже имеет смысль этот материал разбирать с перерывами на другие темы ну или например по определнным дням недели.

В подборе материала я решил не «изобретать велосипед» и воспользоваться готовыми материалами от сайта «Практическая электроника».
Подробнее…

Как создавать материалы в JCE редакторе

В Джумле материалы не как в блоге, по хронологии, а пишутся в базу данных, что даёт возможность группировать их по особому, выводить в нужное время в нужное место и т.д. То есть надо помимо самого текста и картинок указать другие, служебные параметры. Главных два — это категория и опубликовать или придержать в редактор на самом деле в БД). Итак заходим на hammania.net, в меню выбираем Статьи — создать материал. Попадаем на этот экран. Если не попадаем то или не прошли авторизацию, или не дали прав.

Подробнее…

Урок второй. Электричество — подробнее

В наше повседневной жизни мы часто сталкиваемся с таким понятием как «электрический ток». Что же это такое и всегда ли люди знали о его существовании?

Сейчас без электричества представить нашу жизнь невозможно. Электричество настолько глубоко проникло в нашу обыденную жизнь, что мы порой и не задумываемся, что это явление помогает нам во всех аспектах нашей жизни.

Подробное изучение электрического тока можно отнести к периоду конца девятнадцатого века, но первые электрические явления люди наблюдали ещё в пятом веке до нашей эры. Они замечали, что потёртый мехом или шерстью кусок янтаря притягивает к себе лёгкие тела, например, пылинки. Древние греки даже научились использовать это явление – для удаления пыли с дорогих одежд. Ещё они заметили, что, если сухие волосы расчесать янтарным гребнем, они поднимаются, отталкиваясь друг от друга.
Подробнее…

Перечень знаний и умений на ECC Report 089 CEPT (ENTRY LEVEL)

Тематический перечень для экзаменационных вопросов для присвоения категории

согласно положениям рекомендации ECC Report 089 CEPT (ENTRY LEVEL)

1. Практические рабочие аспекты

1.1. Знакомство с управлением передатчика или трансивера

1.1.1. Включение/выключение питания, переключатель диапазонов, настройка и индикация частоты, громкость, уровень мощности и дисплей, усиление звукового сигнала с микрофона.

1.2. Работа на коротких волнах

1.2.1. Настройка в режиме SSB с верхней и нижней боковой полосой,

1.2.2. Вызов корреспондента, общий вызов,

1.2.3. Способность проведения радиосвязи в приемлемом формате, рапорта, обмен информации об имени оператора, информации о станции. Демонстрация использования аппаратуры
Подробнее…

Как мы будем учить

Увважаемые читатели. Мы открывает нашу виртуальную школу при виртуальной коллективной радиостанции для того чтобы дать вам возможность приобщиться к очень интересному занятию — радиолюбительству. Наши уроки будут очными, заочными и контрольными. Материалы будут излагаться короткими тезисами, не более 50-100 строк за раз, очень простым языком. По вечерам наши преподы (сенсей Гена, сенсей Саша и сенсей Гоша) часто будут доступны в онлайн, где попытаются ответить на ваши вопросы. Еще удобнее форма общения в форуме, потому что снимает вопрос времени : когда вам удобно.

Урок первый. Электричество.

Начнём с простого. Батарейка. Это «законсервированное» электричество. Оно находится внутри и по команде (замыканию выключателя) может делать какую-то работу: светить, вращать моторчик ручного вентилятора, когда жарко, обеспечивать вас звуком от работающего радиоприёмника на пляже…. Пока контакты не замкнуты, электричество есть, но работу не делает. Спит. Это называется напряжение. Или потенциал. Типа может делать, но пока не делает. Напряжение всегда подают по ДВУМ проводам: плюс и минус. Вообще-то бывает еще и переменное напряжение, но о нём позже.
Подробнее…

Что такое децибел | Что измеряют в децибелах, формулы.

Очень часто новички сталкивается с таким понятием, как децибел. Многие из них интуитивно догадываются, что это такое, но у большинства до сих пор возникают вопросы.

Что такое децибел?

Относительные логарифмические единицы Белы (децибелы) широко используются при количественных оценках параметров различных аудио, видео, измерительных устройств. Физическая природа сравниваемых мощностей может быть любой — электрической, электромагнитной, акустической, механической, — важно лишь, чтобы обе величины были выражены в одинаковых единицах — ваттах, милливаттах и т. п. Бел выражает отношение двух значений энергетической величины десятичным логарифмом этого отношения, причем под энергетическими величинами понимаются: мощность, энергия.

Кстати, эта единица получила свое название в честь Александра Белл (1847 – 1922) – американского ученого шотландского происхождения, основоположника телефонии, основателя всемирно известных компаний AT&T и “Bell Laboratories”. Еще интересно напомнить, что во многих современных мобильных телефонах (смартфонах) обязательно есть выбираемый звук звонка (оповещения), так и называемый “bell”. Впрочем, Бел относится к единицам, не входящим в Международную систему единиц (СИ), но в соответствии с решением Международного комитета мер и весов допускается к применению без ограничений совместно с единицами СИ. В основном применяется в электросвязи, акустике, радиотехнике.

Формулы для вычисления децибелов

Бел (Б) = lg (P2/P1)

где

P₁– мощность до усиления, Вт

P₂– мощность после усиления или ослабления, Вт

На практике, оказалось, что удобнее пользоваться уменьшенным в 10 раз значением Бел, т.е. децибел, поэтому:

дециБел (дБ) = 10 * lg(P2/P1)

Усиление или ослабление мощности в децибелах выражается формулой:

где

N_дБ – усиление, либо ослабление мощности в децибелах

P₁– мощность до усиления, Вт

P₂– мощность после усиления или ослабления, Вт

Значения Бел, децибел могут быть со знаком “плюс”, если P2 > P1 (усиление сигнала) и со знаком “минус”, если P2 < P1 (ослабление сигнала)

Во многих случаях, сравнение сигналов путем измерения мощностей может быть неудобным или невозможным – проще измерить напряжение или ток.
В этом случае, если мы сравниваем напряжения или токи, формула примет уже другой вид:

где

N_дБ – усиление, либо ослабление мощности в децибелах

U₁ – это напряжение до усиления, В

U₂ – напряжение после усиления, В

I₁ – сила тока до усиления, А

I₂– сила тока после усиления, А

Вот небольшая табличка, в которой приведены основные отношения напряжений и соответствующее число децибел:

Дело в том, что операции умножения и деления над числами в обычном базисе, заменяются операциями сложения и вычитания в логарифмическом базисе. Например, у нас есть два каскадно-включенных усилителя с коэффициентами усиления K1 = 963 и K2 = 48. Какой общий коэффициент усиления? Правильно – он равен произведению K = K1 * K2. Вы можете в уме быстро вычислить 963*48? Я – нет. Я могу прикинуть K = 1000*50 = 50 тыс., не более. А, если нам известно, что K1 = 59 дБ и K2 = 33 дБ, то К = 59+33 = 92 дБ – сложить было не трудно, надеюсь.

Впрочем, актуальность таких вычислений было велика в эпоху, когда ввели понятие Бел и когда не было не то, что айфонов, но и электронных калькуляторов. Сейчас же достаточно открыть калькулятор на ваших гаджетах и быстренько посчитать , что есть что. Ну и чтобы не париться каждый раз при переводе дБ в разы, удобнее всего найти в интернете онлайн-калькулятор. Да хотя бы вот.

Закон Вебера-Фехнера

Почему именно децибелы? Все исходит от закона Вебера-Фехнера, который говорит нам, что интенсивность ощущения человеческих чувств прямо-пропорциональна логарифму интенсивности какого-либо раздражителя.

Так светильник, в котором восемь лампочек, кажется нам настолько же ярче светильника из четырёх лампочек, насколько светильник из четырёх лампочек ярче светильника из двух лампочек. То есть количество лампочек должно увеличиваться каждый раз вдвое, чтобы нам казалось, что прирост яркости постоянен. То есть если добавить к нашим 32 лампочкам на графике еще одну лампочку, то мы даже и не заметим разницы. Для того, чтобы для нашего глаза была заметна разница, мы должны к 32 лампочкам добавить еще 32 лампочки, и т.д. Или иными словами, для того, чтобы нам казалось, что наш светильник плавно набирает яркость, нам надо зажигать вдвое больше лампочек каждый раз, чем было предыдущее значение.

Поэтому децибел действительно удобнее в некоторых случаях, так как сравнивать две величины намного проще в маленьких цифрах, чем в миллионах и миллиардах. А так как электроника – это чисто физическое явление, то и децибелы не обошли ее стороной.

[quads id=1]

Децибелы и АЧХ усилителя

Как вы помните в прошлом примере с ОУ, у нас неинвертирующий усилитель усиливал сигнал в 10 раз. Если посмотреть в нашу табличку, то это получается 20 дБ относительно входного сигнала. Ну да, так оно и есть:

Также в дБ на некоторых графиках АЧХ обозначают наклон характеристики АЧХ. Это может выглядеть примерно вот так:

На графике мы видим АЧХ полосового фильтра. Изменение сигнала +20 дБ на декаду (дБ/дек, dB/dec) говорит нам о том, что при каждом увеличении частоты в 10 раз, амплитуда сигнала возрастает на 20 дБ. То же самое можно сказать и про спад сигнала -20 дБ на декаду. При каждом увеличении частоты в 10 раз, у нас амплитуда сигнала будет уменьшаться на -20 дБ. Есть также похожая характеристика дБ на октаву (дБ/окт, dB/oct). Здесь почти все то же самое, только изменение сигнала происходит при каждом увеличении частоты в 2 раза.

Давайте рассмотрим пример. Имеем фильтр высоких частот (ФВЧ) первого порядка, собранного на RC-цепи.

Его АЧХ будет выглядеть следующим образом (кликните для полного открытия)

Нас сейчас интересует наклонная прямая линия АЧХ. Так как у нее наклон примерно одинаковый до частоты среза в -3дБ, то можно найти ее крутизну, то есть узнать, во сколько раз увеличивается сигнал при каждом увеличении частоты в 10 раз.

Итак возьмем первую точку на частоте в 10 Герц. На частоте в 10 Герц амплитуда сигнала уменьшилась на 44 дБ, это видно в правом нижнем углу (out:-44)

Умножаем частоту на 10 (декада) и получаем вторую точку в 100 Герц. На частоте в 100 Герц наш сигнал уменьшился приблизительно на 24 дБ

То есть получается за одну декаду у нас сигнал увеличился с -44 до -24 дБ на декаду. То есть наклон характеристики составил +20 дБ/декаду. Если +20 дБ/декаду перевести в дБ на октаву, то получится 6 дБ/октаву.

Достаточно часто, дискретные аттенюаторы (делители) выходного сигнала на измерительных приборах (особенно на генераторах) проградуированы в децибелах:
0, -3, -6, -10, -20, -30, -40 дБ. Это позволяет быстро ориентироваться в относительном уровне выходного сигнала.

Что еще измеряют в децибелах?

Также очень часто в дБ выражают отношение сигнал-шум (signal-to-noise ratio, сокр. SNR)

где

U_c – это эффективное значение напряжения сигнала, В

U_ш – эффективное значение напряжения шума, В

Чем выше значение сигнал/шум, тем более чистый звук обеспечивается аудиосистемой. Для музыкальной аппаратуры желательно, чтобы это отношение было не менее 75 дБ, а для Hi-Fi аппаратуры не менее 90 дБ. Не имеет значение физическая природа сигнала, важно, чтобы единицы были в одинаковых измерениях.

В качестве единицы логарифмического отношения двух одноимённых физических величин применяется также непер (Нп) — 1 Нп ~ 0,8686 Б. В основе лежит не десятичный (lg), а натуральный (ln) логарифм отношений. В настоящее время используется редко.

Во многих случаях, удобно сравнивать между собой не произвольные величины, а одну величину относительно другой, названной условно опорной (нулевой, базовой).
В электротехнике, в качестве такой опорной или нулевой величины выбрано значение мощности равное 1 мВт выделяемое на резисторе сопротивлением 600 Ом.
В этом случае, базовыми значениями при сравнении напряжений или токов станут величины 0.775 В или 1.29 мА.

Для звуковой мощности такой базовой величиной является 20 микроПаскаль (0 дБ), а порог +130 дБ считается болевым для человека:

Более подробно об этом написано в Википедии по этой ссылке.

Для случаев когда в качестве базовых значений используются те или иные конкретные величины, придуманы даже специальные обозначения единиц измерений:

dbW (дБВт) – здесь отсчет идет относительно 1 Ватта (Вт). Например, пусть уровень мощности составил +20 дБВт. Это значит что мощность увеличилась в 100 раз, то есть на 100 Вт.

dBm (дБм) – здесь у нас отсчет уже идет относительно 1 милливатта (мВт). Например, уровень мощности в +30дБм будет соответственно равен 1 Вт. Не забываем, что это у нас энергетические децибелы, поэтому для них будет справедлива формула

Следующие характеристики – это уже амплитудные децибелы. Для них будет справедлива формула

dBV (дБВ) – как вы догадались, опорное напряжение 1 Вольт. Например, +20дБВ даст – это 10 Вольт

От дБВ также вытекают другие виды децибелов с разными приставками:

dBmV (дБмВ) – опорный уровень 1 милливольт.

dBuV (дБмкВ) – опорное напряжение 1 микровольт.

Здесь я привел наиболее употребимые специальные виды децибелов в электронике.

Децибелы используются и в других отраслях, где они также показывают отношение каких-либо двух измеряемых величин в логарифмическом масштабе.

Также на YouTube есть интересное видео о децибелах.

При участии Jeer

Калькулятор
дБ для расчета коэффициента усиления и коэффициента затухания (потерь) аудиоусилителя, децибел, дБ.

● Расчет : Усиление ( усиление ) и демпфирование ( убыток )
как коэффициент ( отношение ) до уровень децибел ( дБ ) ●

отношение между величинами
выходные и входные сигналы.
Регуляторы усиления на усилителе в основном представляют собой небольшие потенциометры (переменная
резисторы) или регуляторы громкости, которые позволяют регулировать входящий сигнал на
усилитель звука.

Коэффициент усиления, также называемый усилением, — это степень, в которой устройство увеличивает мощность сигнала.
Коэффициент демпфирования, также называемый потерями, — это степень, в которой устройство снижает мощность сигнала.

Введите два значения и нажмите правую полосу вычисления в строке отсутствующего ответа.
Используемый браузер не поддерживает Javascript.
Программа указана, но фактическая функция отсутствует.

В аналоговой аудиотехнике мы имеем дело только с усилением (усилением) и демпфированием (потерями) «напряжения».
В ₁ = В _в и В ₂ = В _вне
В ₂> В ₁ или В _вне> В _в означает усиление . Значение дБ положительное (+).
В ₂ < В ₁ или В _{на выходе} < В _в означает демпфирования. Значение дБ отрицательное (-).
В ₂ / В ₁ или В _вне / В _дюйм означает соотношение . Усиление или затухание в дБ составляет:
L = 20 × log (отношение напряжений В ₂/ В ₁) в дБ. В ₁ = В _в является справочным.
В физике затухание считается положительным значением.
Это, естественно, приводит к знаковым ошибкам при вводе чисел.
3 дБ ≡ В 1,414 раза больше напряжения (-) 3 дБ ≡ демпфирование до значения 0,707
6 дБ ≡ Напряжение в 2 раза больше (-) 6 дБ ≡ демпфирование до значения 0.5
10 дБ ≡ В 3,162 раза больше напряжения (-) 10 дБ ≡ демпфирование до значения 0,316
12 дБ ≡ в 4 раза больше напряжения (-) 12 дБ ≡ демпфирование до значения 0,25
20 дБ ≡ В 10 раз больше напряжения (-) 20 дБ ≡ демпфирование до значения 0,1

Используя напряжение, получаем: Уровень в дБ: L = 20 × log (отношение напряжений)

6 дБ = удвоенное напряжение
12 дБ = в четыре раза больше напряжения
20 дБ = в десять раз больше напряжения
40 дБ = в сто раз больше напряжения
Если говорить о звуковой инженерии, нас обычно не интересует мощность.
Не спрашивайте, что означает усиление мощности.
Оставьте это телефонным компаниям или передающим антеннам (антенны).
В аудиотехнике усиление мощности действительно не используется.
Действительно ли нам нужно усиление мощности (энергии)?
Прочтите текст внизу.
3 дБ ≡ мощность в 2 раза больше (−3) дБ ≡ демпфирование до значения 0,5
6 дБ ≡ в 4 раза больше (−6) дБ ≡ демпфирование до значения 0.25
10 дБ ≡ в 10 раз больше (−10) дБ ≡ демпфирование до значения 0,1
12 дБ ≡ в 16 раз больше (−12) дБ ≡ демпфирование до значения 0,0625
20 дБ ≡ в 100 раз больше мощности (−20) дБ ≡ демпфирование на значение 0,01
Используя мощность, мы получаем: Уровень в дБ: L = 10 × log (коэффициент мощности)
3 дБ = удвоенная мощность
6 дБ = в четыре раза больше мощности
10 дБ = в десять раз больше мощности
20 дБ = в сто раз больше мощности
Если вы ищете коэффициент усиления, учитывая значение в дБ,
затем заходим в программу расчета дБ
Усиление (усиление) и демпфирование (потеря)
Чтобы использовать калькулятор, просто введите значение.
Калькулятор работает в обоих направлениях знака ↔ .

В звуковой технике следующее «усиление мощности или энергии» довольно необычно.
Напряжение / давление
коэффициент усиления 1
1,414
= √2 2
3,16
= √10 4
10
20
40
100
1000
Увеличение x дБ 0 3 6 10 12 20 26 32 40 60

Мощность / интенсивность
коэффициент усиления 1
1.414
= √2 2
3,16
= √10 4
10
20
40
100
1000
Увеличение y дБ 0 1,5 3 5 6 10 13 16 20 30

На частоте отсечки f _c падение напряжения всегда падает до значения
1 / √2 = 0.7071 (70,7%), а уровень напряжения L демпфируется до 20 × log ₁₀ (1 / √2) = (-) 3,0103 дБ.

На частоте среза f _c упавшая мощность всегда падает до значения
1/2 = 0,5 (50%), а уровень мощности L демпфируется до 10 × log ₁₀ (½) = (-) 3,0103 дБ.

Выраженное усиление напряжения в дБ (усиление напряжения) на частоте среза f _c равно
20 × log ₁₀ (1 / √2) = (-) 3.0103 дБ меньше максимального усиления по напряжению.

Выраженное усиление мощности в дБ (усиление мощности) на частоте среза f _c равно
10 × log ₁₀ (½) = (-) на 3,0103 дБ меньше максимального усиления мощности.

Чтобы использовать калькулятор, просто введите значение.
Калькулятор работает в обоих направлениях знака ↔ .

Напряжение всегда указывается как среднеквадратичное значение, но это не относится к электроэнергии.
Имеется также эталонная мощность P ₀ = 1 милливатт или 0,001 Вт ≡ 0 дБ _м
Уровень в психоакустике как субъективно воспринимаемая громкость (громкость)
Указано смутное человеческое ощущение двойной громкости (громкости)
примерно от 6 до 10 дБ. Это личное чувство не является точно измеримой величиной.

Преобразование : Усиление G , Коэффициент напряжения A _В и Коэффициент мощности 0 A
1 0 A
1

Коэффициент усиления по напряжению в дБ

Коэффициент усиления по мощности в дБ

Коэффициент усиления = коэффициент усиления (напряжение)
Коэффициент мощности = коэффициент усиления (мощность)
В ₁ = В _в и В ₂ = В _из.
В ₂> В ₁ или В _вне> В _в означает усиление . Значение дБ положительное. (+)
V ₂ < V ₁ или V _out < V _in означает демпфирования. Значение дБ отрицательное. (-)
V ₂ / V ₁ или V _out / V _in означает соотношение .Усиление или затухание в дБ составляет:
L = 20 × log (отношение напряжений В ₂/ В ₁) в дБ. В ₁ = В _в является справочным.

Слово «усилитель мощности» используется неправильно, особенно в аудиотехнике.
Напряжение и ток можно усилить. Странный термин «усилитель мощности» имеет
стали пониматься как усилитель, предназначенный для управления нагрузкой, такой как
как громкоговоритель.
Мы называем произведение усиления по току и усилению по напряжению «усилением мощности».

Усиление мощности в децибелах
При проектировании или работе со схемами усилителя и фильтра некоторые числа, используемые в расчетах, могут быть очень большими или очень маленькими.Например, если мы каскадируем два каскада усилителя вместе с коэффициентом усиления мощности или напряжения, скажем, 20 и 36 соответственно, то общее усиление будет 720 (20 * 36).
Точно так же, если мы подключим каскад к цепям RC-фильтров первого порядка с затуханиями 0,7071 каждая, общее затухание будет 0,5 (0,7071 * 0,7071). Помня, конечно, что если выход схемы положительный, то он производит усиление или усиление, а если его выход отрицательный, то он производит затухание или потери.
При анализе схем в частотной области удобнее сравнивать отношение амплитуд выходных и входных значений в логарифмическом масштабе, а не в линейном масштабе.Таким образом, если мы используем логарифмическое отношение двух величин, P ₁ и P ₂, мы получим новую величину или уровень, который может быть представлен с использованием децибел .
В отличие от напряжения или тока, которые измеряются в вольтах и амперах соответственно, децибел , или просто дБ для краткости, представляет собой просто отношение двух значений, на самом деле отношение одного значения к другому известному или фиксированному значению, поэтому следовательно, децибел является безразмерной величиной, но имеет в качестве единиц измерения «Бел» в честь изобретателя телефона Александра Грэхема Белла.
Отношение любых двух значений, где одно фиксированное или известное и одного и того же количества или единиц, будь то мощность, напряжение или ток, может быть представлено в децибелах (дБ), где «деци» означает одну десятую (1/10) от Бел. Очевидно, что в расчете на один бел приходится 10 децибел (10 дБ), или 1 бел = 10 децибел.
Децибел обычно используется для отображения коэффициента изменения мощности (увеличения или уменьшения) и обычно определяется как значение, которое в десять раз превышает логарифм по основанию 10 двух уровней мощности.Так, например, 1 Вт к 10 Вт — это то же соотношение мощности, что и 10 Вт к 100 Вт, то есть 10: 1, поэтому, хотя есть большая разница в количестве ватт, 9 по сравнению с 90, соотношение децибел будет точно так же.
Надеюсь, тогда мы сможем увидеть, что значение в децибелах (дБ) — это отношение, используемое для сравнения и расчета уровней изменения мощности, а не сама мощность. Итак, если у нас есть две величины мощности, например: P ₁ и P ₂, соотношение этих двух величин будет представлено уравнением:
дБ = 10log ₁₀ [P ₂ / P ₁]
Где P ₁ представляет входную мощность, а P ₂ представляет выходную мощность (P _OUT / P _IN).
Поскольку децибел представляет собой логарифмическое изменение по основанию 10 для двух уровней мощности, мы можем расширить это уравнение, используя антилогарифмы, чтобы показать, насколько на самом деле изменение одного децибела (1 дБ).
дБ = 10log ₁₀ [P ₂ / P ₁]
Если P ₂ / P ₁ равно 1, то есть P ₁ = P ₂, тогда:
дБ = 10 log ₁₀ [1] = log ₁₀ [1/10] = log ₁₀ [0.1] = антилог [0,1]
Таким образом, изменение значения в дБ равно: 10 ^0,1 = 1,259
Очевидно, что логарифмическое изменение двух степеней имеет отношение 1,259, что означает, что изменение на 1 дБ представляет собой увеличение (или уменьшение) мощности на 25,9% (или округленное значение на 26%).
Итак, если схема или система имеет коэффициент усиления, скажем, 5 (7 дБ), и он увеличивается на 26%, то новое отношение мощности схемы будет: 5 * 1,26 = 6,3, поэтому 10log ₁₀ (6,3) = 8 дБ. Увеличение усиления на + 1 дБ, что еще раз доказывает, что изменение на + 1 дБ представляет собой логарифмическое увеличение мощности на 26%, а не линейное изменение.
Децибел Пример No1
Аудиоусилитель выдает 100 Вт на нагрузку динамика 8 Ом при подаче входного сигнала 100 мВт. Рассчитайте коэффициент усиления усилителя в децибелах.
Мы можем выразить усиление мощности усилителя в децибелах независимо от его входных или выходных значений, поскольку усилитель, обеспечивающий выходную мощность 40 Вт для входной 40 мВт, также будет иметь мощность усиление 30 дБ и так далее.
Мы также могли бы, если бы захотели, преобразовать это значение децибел усилителя обратно в линейное значение, сначала преобразовав децибелы (дБ) в бел, помня, что децибел составляет 1/10 бела.Например:
Усилитель звука мощностью 100 Вт имеет коэффициент усиления 30 дБ. Какое будет его максимальное входное значение.
Таким образом, результат составляет 100 мВт, как заявлено в примере №1.
Одним из преимуществ использования логарифмического отношения двух мощностей по основанию 10 является то, что при работе с каскадом нескольких каскадов усилителя, фильтра или аттенюатора, мы можем просто сложить или вычесть их значения в децибелах вместо умножения или деления их линейных значений. Другими словами, общее усиление схемы (+ дБ) или затухание (-дБ) представляет собой сумму отдельных усилений и ослаблений для всех каскадов, подключенных между входом и выходом.
Например, если одноступенчатый усилитель имеет коэффициент усиления по мощности 20 дБ и питает пассивную резистивную сеть с ослаблением 2, прежде чем сигнал будет снова усилен с использованием второго каскада усилителя с коэффициентом усиления 200. Тогда общая мощность коэффициент усиления цепи между входом и выходом в децибелах будет:
Для пассивной схемы затухание, равное 2, означает, что схема имеет положительный коэффициент усиления 1/2 = 0,5, таким образом, коэффициент усиления по мощности пассивной секции составляет:
дБ Усиление = 10log ₁₀ [0.5] = -3 дБ (обратите внимание на отрицательное значение)
Усилитель второго каскада имеет коэффициент усиления 200, таким образом, коэффициент усиления по мощности в этой секции составляет:
дБ Усиление = 10log ₁₀ [200] = + 23 дБ
Тогда общий коэффициент усиления схемы будет:
20-3 + 23 = + 40 дБ
Мы можем дважды проверить наш ответ 40 дБ, умножив индивидуальные коэффициенты усиления каждой ступени обычным способом следующим образом:
Прирост мощности 20 дБ в децибелах равен усилению 100, так как 10 ^(20/10) = 100.Итак:
100 x 0,5 x 200 = 10 000 (или в 10 000 раз больше)
Преобразование этого обратно в значение в децибелах дает:
дБ Усиление = 10log ₁₀ [10,000] = 40 дБ
Тогда ясно видно, что коэффициент усиления 10000 равен коэффициенту усиления мощности +40 дБ, как показано выше, и что мы можем использовать значение в децибелах для выражения больших отношений мощностей с гораздо меньшими числами, поскольку 40 дБ — это коэффициент мощности 10000. , тогда как -40 дБ — это коэффициент мощности 0,0001. Таким образом, использование децибел упрощает вычисления.
Децибел напряжения и тока
Любой уровень мощности можно выразить как напряжение или ток, если нам известно сопротивление. Согласно закону Ома, P = V ² / R и P = I ² R. Поскольку V и I относятся к проходящему через него току и напряжению на одном и том же сопротивлении, если (и только если) мы сделаем R = R = 1, то значения в дБ для отношений напряжения (V ₁ и V ₂), а также для тока (I ₁ и I ₂) будут представлены как:
, что составляет 20log (усиление по напряжению), а для усиления по току будет:
Таким образом, единственная разница между расчетами мощности, напряжения и тока в децибелах (дБ) — это постоянные 10 и 20, и что для того, чтобы отношение дБ было правильным во всех случаях, две величины должны иметь одинаковые единицы измерения, либо ватты, милливатты, вольты, милливольты, амперы или миллиамперы или любые другие единицы измерения.
Децибел Пример No2
Пассивная резистивная сеть используется для обеспечения ослабления (потерь) 10 дБ при входном напряжении 12 В. Каким будет значение выходного напряжения сети.
Поскольку децибел представляет собой логарифмическое изменение мощности, напряжения или тока, мы можем построить таблицу, чтобы показать конкретные коэффициенты усиления и их эквивалентные значения в децибелах ниже.
Децибел Таблица прироста
31,62 900
дБ Значение Коэффициент мощности
10log (A) Отношение напряжение / ток
20log (A)
-20dB 0.01 0,1
-10 дБ 0,1 0,3162
-6 дБ 0,25 1/2 = 0,5
-3 дБ 1/2 = 0,5 1 / √ 2 = 0,707
-1 дБ 0,79 0,89
0 дБ 1 1
1 дБ 1,26 1,1
3dB 2 √2 = 1.414
6 дБ 4 2
10 дБ 10 √10 = 3,162
20 дБ 100 10
30 дБ 1000
Из приведенной выше таблицы в децибелах видно, что при 0 дБ коэффициент усиления по мощности, напряжению и току равен «1» (единица). Это означает, что схема (или система) не производит усиления или потерь между входными и выходными сигналами.Таким образом, нулевой дБ соответствует единичному усилению, то есть A = 1, а не нулевому усилению.
Мы также можем видеть, что при + 3 дБ выход схемы (или системы) удвоил свое входное значение, что означает положительное усиление (усиление) в дБ, поэтому A> 1. Аналогично, при -3 дБ выходной сигнал схемы равен половине его. входное значение, означающее отрицательное усиление (затухание) в дБ, поэтому A <1. Это значение -3 дБ обычно называется точкой «половинной мощности» и определяет граничную частоту в сетях фильтров.
Все хорошо и хорошо табулировать прирост мощности по отношению к децибелам в справочной таблице, но при работе с усилителями и фильтрами инженеры-электрики предпочитают использовать графики Боде, диаграммы или графики в качестве визуального отображения частотной характеристики цепей (или систем). характеристики.Затем, используя значения данных в таблице выше, мы можем создать следующий график Боде «децибел», показывающий различные положения точек мощности.
График мощности Боде в децибелах
Тогда мы можем ясно видеть, что кривая мощности не является линейной, а следует логарифмическому коэффициенту 1,259.
Децибел Краткое изложение руководства
Мы видели в этом руководстве о децибелах (дБ), что это логарифмическая единица изменения мощности Base-10 и что децибел представляет собой безразмерное значение 1/10 от бел (1 бел = 10 децибел или 1 дБ = 0.1Б). Децибел позволяет нам представить большие отношения мощностей с использованием небольших чисел, и мы видели выше, что 30 дБ эквивалентно соотношению мощностей 1000 с наиболее часто используемыми значениями в децибелах: 3 дБ, 6 дБ, 10 дБ и 20 дБ (и их отрицательные эквиваленты). . Однако 20 дБ не вдвое больше мощности 10 дБ.
Децибел также показывает нам, что любое изменение мощности на то же отношение будет иметь такое же отношение децибел. Например, удвоение мощности с 1 до 2 Вт — это то же соотношение, что и с 10 Вт до 20 Вт, то есть изменение на + 3 дБ, в то время как изменение на -3 дБ означает, что коэффициент мощности будет уменьшен вдвое.
Если отношение дБ положительное по значению, это означает, что усиление или усиление присутствует, так как выходная мощность превышает входную мощность (P _OUT> P _IN). Однако, если коэффициент мощности в дБ имеет отрицательное значение, это означает, что на схему влияет затухание или потери, поскольку выходная мощность будет меньше, чем входная мощность схемы (P _OUT
IN ). Очевидно, что 0 дБ означает, что коэффициент мощности равен без уменьшения или усиления сигнала.
Преобразование
децибел: коэффициент 10 или коэффициент 20?
Децибел используется в широком диапазоне приложений. Децибелы особенно используются, когда речь идет о мощности или производной мере, значения которых могут варьироваться в широком диапазоне. Наиболее часто децибелы используются для измерения громкости звука. Так, например, звук 0 дБ едва слышен, тогда как у пылесоса в среднем 75 дБ, а на рок-концерте — около 110 дБ.
В классе вы часто найдете следующие определения чего-либо в децибелах
$$ X_ {dB} = 10 \ log_ {10} \ left (\ frac {X_ {lin}} {X_ {ref}} \ right). $$
Это уравнение преобразует величину $ X_ {lin} $ из линейного масштаба к величине в шкале дБ $ X_ {дБ} $. Для этого сначала линейная величина связана с эталонной величиной $ X_ {ref} $, и их соотношение преобразуется в лог-область. По-видимому, в $ X_ {dB} $ на самом деле нет единицы измерения, и мы искусственно добавляем дБ , чтобы было ясно, что мы находимся в логарифмической шкале.Когда $ X_ {lin} $ равняется опорному уровню, шкала дБ становится равной нулю:
$$ X_ {дБ} = 10 \ log_ {10} \ left. \ Left (\ frac {X_ {lin}} {X_ {ref}} \ right) \ right | _ {X_ {lin} = X_ {ref} } = 0 дБ. $$
Кроме того, когда $ X_ {lin}> X_ {ref} $, $ X_ {dB} $ положительно, а если $ X_ {lin}
Пока все хорошо. Но, с другой стороны, чаще всего вы также видите следующее определение:
$$ Y_ {dB} = 20 \ log_ {10} \ left (\ frac {Y} {Y_ {ref}} \ right), $$
т.е. множитель перед логарифмом равен 20 вместо 10. Какая версия верна ? Обе формулы верны, но при выборе формулы необходимо соблюдать осторожность. Итак, вот правило:
Если вы преобразуете величину, которая относится к мощности, или энергии, коэффициент составит 10 .
Если преобразовать величину, относящуюся к амплитуде , коэффициент составит 20 .
Как узнать, относится ли величина к мощности или амплитуде? Проверьте, имеет ли смысл возведение количества в квадрат! Если возведение в квадрат имеет смысл, ваша величина, скорее всего, будет амплитудой. Если это не имеет смысла, вы, вероятно, столкнетесь с мощным количеством.Например, нет смысла возводить мощность сигнала в квадрат. Но имеет смысл возводить в квадрат амплитуду сигнала, поскольку это дает мощность сигнала.
Другой индикатор, когда использовать 10 или 20, следующий:
Если ваше количество $ X_ {lin} $ следует из некоторого вычисления, которое включает возведение в квадрат некоторого другого количества, используйте множитель 10.
Некоторые примеры¶
Далее мы вычисляем некоторые примеры преобразования линейной шкалы в шкалу дБ:
Преобразуйте 100 Вт в шкалу дБ.Ссылка $ X_ {ref} = 1 мВт $.
{ref} $,>
Что такое децибел (дБ)?
Определение децибел (дБ), как преобразовать, калькулятор и таблица соотношения дБ.
Определение децибел (дБ)
Децибел (символ: дБ) — логарифмическая единица, указывающая коэффициент или коэффициент усиления.
Децибел используется для обозначения уровня акустических волн и электронных сигналов.
Логарифмическая шкала может описывать очень большие или очень маленькие числа в более коротких обозначениях.
Уровень дБ можно рассматривать как относительное усиление одного уровня по сравнению с другим уровнем или как уровень абсолютной логарифмической шкалы для хорошо известных опорных уровней.
Децибел — безразмерная единица.
Отношение в белах — это десятичный логарифм отношения P ₁ и P ₀:
Соотношение _B = бревно ₁₀ ( P ₁/ P ₀)
Децибел составляет одну десятую бела, поэтому 1 бел равен 10 децибелам:
1B = 10 дБ
Передаточное число
Коэффициент мощности в децибелах (дБ) равен десятикратному логарифму по основанию 10 отношения P ₁ и P ₀:
Коэффициент _дБ = 10⋅log ₁₀ ( P ₁/ P ₀)
Соотношение амплитуд
Соотношение таких величин, как напряжение, сила тока и уровень звукового давления, рассчитывается как отношение квадратов.
Отношение амплитуд в децибелах (дБ) составляет 20 логарифмов по основанию 10 отношения V ₁ и V ₀:
Коэффициент _дБ = 10⋅log ₁₀ ( V ₁ ²/ V ₀ ²) = 20⋅log ₁₀ ( V ₁ / В ₀)
Децибел в ватты, вольты, герцы, калькулятор преобразования паскалей
Преобразование дБ, дБм, дБВт, дБВ, дБмВ, дБмкВ, дБу, дБмкА, дБГц, дБУЗД, дБА в ватты, вольты, амперы, герцы, звуковое давление.
Установите тип количества и единицу децибел.
Введите значения в одно или два текстовых поля и нажмите соответствующую кнопку Преобразовать :
Отношение мощности к преобразованию в дБ
Коэффициент усиления G _дБ равен десятикратному логарифму по основанию 10 отношения мощности P ₂ и опорной мощности _{P ₁.}
G _дБ = 10 log ₁₀ ( P ₂/ P ₁)
P ₂ — уровень мощности.
P ₁ — эталонный уровень мощности.
G _дБ — коэффициент мощности или усиление в дБ.
Пример
Найдите коэффициент усиления в дБ для системы с входной мощностью 5 Вт и выходной мощностью 10 Вт.
G _дБ = 10 log ₁₀ ( P _{на выходе} / P _на ) = 10 log ₁₀ (10 Вт / 5 Вт) = 3,01 дБ
дБ для преобразования отношения мощности
Мощность P ₂ равна опорной мощности P ₁, умноженной на 10, увеличенной на усиление в G _дБ, деленное на 10.
P ₂ = P ₁ ⋅ 10 ^{( G} дБ ^{/ 10)}
P ₂ — уровень мощности.
P ₁ — эталонный уровень мощности.
G _дБ — коэффициент мощности или усиление в дБ.
Отношение амплитуды к преобразованию в дБ
Для амплитуды волн, таких как напряжение, ток и уровень звукового давления:
G _дБ = 20 log ₁₀ ( A ₂/ A ₁)
A ₂ — уровень амплитуды.
A ₁ — эталонный уровень амплитуды.
G _дБ — отношение амплитуд или усиление в дБ.
дБ для преобразования отношения амплитуды
A ₂ = A ₁ ⋅ 10 ^{( G} дБ ^{/ 20)}
A ₂ — уровень амплитуды.
A ₁ — эталонный уровень амплитуды.
G _дБ — отношение амплитуд или усиление в дБ.
Пример
Найдите выходное напряжение для системы с входным напряжением 5 В и усилением по напряжению 6 дБ.
В _выход = В _дюйм 10 ^{( G} дБ ^/20) = 5 В ⋅ 10 ^{(6 дБ / 20)} = 9,976 В ≈ 10 В
Коэффициент усиления по напряжению
Коэффициент усиления по напряжению ( G, , _дБ,) в 20 раз превышает логарифм по основанию 10 отношения выходного напряжения ( В, , _{, выход}) и входного напряжения ( В, , _{, дюйм}):
G _дБ = 20⋅log ₁₀ ( В _{на выходе}/ В _дюйм)
Текущая прибыль
Коэффициент усиления по току ( G _дБ) в 20 раз больше логарифма по основанию 10 отношения выходного тока ( I _из) и входного тока ( I _в):
G _дБ = 20⋅log ₁₀ ( I _out/ I _дюйм)
Акустическое усиление
Акустическое усиление слухового аппарата ( G _дБ) в 20 раз больше логарифма по основанию 10 отношения выходного уровня звука ( L _из) и входной уровень звука ( L, , _,).
G _дБ = 20⋅log ₁₀ ( L _{на выходе}/ L _дюйм)
Отношение сигнал / шум (SNR)
Отношение сигнал / шум ( SNR _дБ) в 10 раз больше логарифма по основанию 10 амплитуды сигнала ( A _сигнал) и амплитуда шума ( A _noise):
SNR _дБ = 10⋅log ₁₀ ( A _сигнал/ A _шум)
Абсолютные единицы в децибелах
Абсолютные единицы децибел относятся к определенной величине единицы измерения:
Блок Имя Номер ссылки Кол. Акций Коэффициент
дБм децибел милливатт 1 мВт электрическая мощность передаточное число
дБВт децибел ватт 1 Вт электрическая мощность передаточное число
дБrn опорный шум в децибелах 1пВт электрическая мощность передаточное число
дБмкВ децибел микровольт 1 мкВ _СКЗ напряжение отношение амплитуд
дБмВ децибел милливольт 1 мВ _RMS напряжение отношение амплитуд
дБВ децибел вольт 1 В _RMS напряжение отношение амплитуд
дБн децибел без нагрузки 0.775 В _RMS напряжение отношение амплитуд
дБZ децибел Z 1 мкм ³ отражательная способность отношение амплитуд
дБмкА децибел микроампер 1 мкА текущий отношение амплитуд
дБОм децибел Ом 1 Ом сопротивление отношение амплитуд
дБГц децибел герц 1 Гц частота передаточное число
дБSPL децибел уровень звукового давления 20 мкПа звуковое давление отношение амплитуд
дБА децибел по шкале А 20 мкПа звуковое давление отношение амплитуд
Относительные децибелы
децибел
Блок Имя Номер ссылки Кол. Акций Коэффициент
дБ децибел – – мощность / поле
дБн несущая несущая мощность электрическая мощность передаточное число
дБи децибел изотропный изотропная плотность мощности антенны удельная мощность передаточное число
дБFS децибел полная шкала полная цифровая шкала напряжение отношение амплитуд
дБrn опорный шум в децибелах
Шумомер
Измеритель уровня звука или Измеритель SPL — это устройство, которое измеряет уровень звукового давления (SPL) звуковых волн в децибелах. (дБ-УЗД) единиц.
Измеритель
SPL используется для тестирования и измерения громкости звуковых волн, а также для мониторинга шумового загрязнения.
Единица измерения уровня звукового давления — паскаль (Па), а в логарифмической шкале используется дБ-УЗД.
дБ-SPL таблица
Таблица общих уровней звукового давления в дБSPL:
Тип звука Уровень шума (дБ-УЗД)
Порог слышимости 0 дБSPL
Шепот 30 дБ SPL
Кондиционер 50-70 дБ SPL
Разговор 50-70 дБ SPL
Трафик 60-85 дБ SPL
Громкая музыка 90-110 дБ SPL
Самолет 120-140 дБ SPL
дБ в таблице преобразования
дБ Соотношение амплитуд Передаточное число
-100 дБ 10 ^-5 10 ^-10
-50 дБ 0.00316 0,00001
-40 дБ 0,010 0,0001
-30 дБ 0,032 0,001
-20 дБ 0,1 0,01
-10 дБ 0,316 0,1
-6 дБ 0,501 0,251
-3 дБ 0,708 0,501
-2 дБ 0.794 0,631
-1 дБ 0,891 0,794
0 дБ 1 1
1 дБ 1,122 1,259
2 дБ 1,259 1,585
3 дБ 1,413 2 ≈ 1,995
6 дБ 2 ≈ 1,995 3,981
10 дБ 3.162 10
20 дБ 10 100
30 дБ 31,623 1000
40 дБ 100 10000
50 дБ 316,228 100000
100 дБ 10 ⁵ 10 ¹⁰
дБм ►
См. Также
Усиление
и децибелы
Изучив этот раздел, вы сможете:
Опишите усиление напряжения как коэффициент.
Сравните линейную и логарифмическую шкалы.
Опишите отношения в децибелах.
• Положительные и отрицательные значения децибел.
• Преобразование усиления мощности в децибелы.
• Преобразуйте усиление напряжения в децибелы.
• Распознавать обычно используемые значения в дБ.
Усиление напряжения
Коэффициент усиления напряжения (Av) или усиления усилителя напряжения определяется по формуле:
При обоих напряжениях, измеренных одинаково (т.е. оба RMS, оба Peak или оба Peak to Peak), Av — это отношение того, насколько вывод больше, чем ввод, и поэтому не имеет единиц измерения. Это основная мера усиления или эффективности усилителя.
Поскольку выходной сигнал усилителя изменяется при разных частотах сигнала, измерения выходной мощности или часто напряжения, которое легче измерить, чем мощность, наносятся на график в зависимости от частоты на графике (кривая отклика), чтобы показать сравнительный выходной сигнал в рабочем диапазоне частот. усилителя.
Логарифмические весы
Кривые отклика
обычно используют логарифмическую шкалу частоты, нанесенную на горизонтальную ось абсцисс. Это позволяет использовать более широкий диапазон частот, чем при использовании линейной шкалы.
Рис. 1.3.1 Логарифмическая и линейная шкалы в сравнении
Вертикальная ось Y размечена в виде линейных делений, но с использованием логарифмических единиц в децибелах, что обеспечивает гораздо больший диапазон на том же расстоянии. Используемая логарифмическая единица — децибел, который составляет одну десятую бела, единица измерения, изначально предназначенная для измерения потерь в телефонных кабелях, но поскольку Бел обычно слишком велик для большинства электронных применений, децибел (дБ) является единицей выбора. .Помимо обеспечения более удобной шкалы, децибел имеет еще одно преимущество при отображении звуковой информации, человеческое ухо также реагирует на громкость звука аналогично логарифмической шкале, поэтому использование шкалы децибел дает более значимое представление уровней звука.
Рис. 1.3.2 Кривая отклика мощности звука
Прирост мощности в дБс
Чтобы описать изменение выходной мощности во всем частотном диапазоне усилителя, кривая отклика в децибелах используется для отображения изменений выходной мощности.Мощность на различных частотах во всем диапазоне сравнивается с определенной опорной частотой (средней частотой полосы). Разница в мощности на средней частоте полосы и мощности на любой другой измеряемой частоте выражается в количестве децибел больше (+ дБ) или меньше (-дБ), чем частота средней полосы, которой присвоено значение 0 дБ. Обратите внимание, что на логарифмической шкале частот на рис. 1.3.1 середина диапазона от 10 Гц до 100 кГц составляет 1 кГц, и частоты около этого числа (где выходной сигнал обычно максимален) обычно выбираются в качестве опорной частоты.
Преобразование коэффициента усиления мощности в дБ вычисляется путем умножения логарифма отношения на 10:
Где P ₁ — мощность в средней полосе, а P ₂ — измеряемая мощность.
Примечание:
При использовании этой формулы в калькуляторе важно использовать скобки, так что используется 10-кратный логарифм (P ₁ / P ₂), а не 10-кратный логарифм P ₁, деленный на П ₂.
например если P ₁ = 6 и P ₂ = 3
10 x log (6/3) = 3 дБ (правильный ответ), но 10 x log 6/3 = 2.6 дБ (неправильный ответ).
Коэффициент усиления напряжения в дБс
Хотя обычно коэффициент усиления усилителя по напряжению описывается как очень много децибел, это не совсем точное использование устройства. Можно использовать децибелы для сравнения выхода усилителя на разных частотах, поскольку все измерения выходной мощности или напряжения проводятся на одном и том же импедансе (нагрузка усилителя), но при описании усиления напряжения (между входом и выходом) В усилителе входное и выходное напряжения имеют совершенно разные импедансы.Однако довольно широко принято также описывать усиление напряжения в децибелах.
Рис. 1.3.3 Кривая отклика звукового напряжения
Когда коэффициент усиления по напряжению (A _v) или коэффициент усиления по току (A _i) отображается в зависимости от частоты, в точках –3 дБ коэффициент усиления падает до 0,707 от максимального (средняя полоса) усиления.
Обратите внимание, что для преобразования отношений напряжений в дБ используется логарифм 20 (В _{на выходе} / В _на)
Описание коэффициента усиления по напряжению усилителя с выходным напряжением 3.и также обычно Shift + log. Используйте ту же формулу для коэффициента усиления в дБ, а для преобразования дБ в коэффициент мощности просто замените 20 в формуле на 10.
Преимущество использования дБ для индикации усиления усилителей состоит в том, что в многокаскадных усилителях общий коэффициент усиления серии усилителей, выраженный в простых соотношениях, будет произведением отдельных коэффициентов усиления:
Av1 x Av2 x Av3 x Av4 … и т. Д.
Это может привести к очень большим числам, но общее индивидуальное усиление, выраженное в децибелах, будет суммой индивидуальных усилений:
Av1 + Av2 + Av3 + Av4…так далее.
Аналогичным образом вычитаются потери из-за таких цепей, как фильтры, аттенюаторы и т. Д., Чтобы получить общие потери.
Часто встречающиеся значения в дБ
0 дБ Опорный уровень, к которому относятся все значения + дБ и –дБ.
± 1 дБ Наименее заметное изменение уровней звука, также используемое для ограничения полосы пропускания на высококачественных усилителях звука.
−3 дБ Обычно используется для ограничения полосы пропускания в усилителях с указанием точек, где:
а.Выходное напряжение упало до 0,707 максимального (среднего диапазона) выходного сигнала.
г. Выходная мощность упала до половины максимальной или средней мощности.
(половина амплитуды НАПРЯЖЕНИЯ составляет −6 дБ )
Часто приводятся цифры аттенюаторов, предназначенных для уменьшения выходной мощности генераторов сигналов на измеряемые величины.
−20 дБ Амплитуда напряжения сигнала, деленная на 10
−40 дБ Амплитуда напряжения сигнала, деленная на 100
Преобразование между дБ и усилением мощности или напряжения
Таблица 1.3.1 Коэффициент мощности / дБ
Коэффициент мощности дБ
P _выход / P _дюйм 10 лог (P _из / P _в)
10 000 000 000 100
1 000 000 000 90
100 000 000 80
10 000 000 70
1 000 000 60
100 000 50
10 000 40
1 000 30
100 20
10 10
4 6
2 3
1.26 1
1 0
0,79 -1
0,5 −3
0,25 −6
0,1 −10
0,01 −20
0,001 −30
0,000 1 −40
0.000 01 −50
0,000 001 −60
0,000 000 1 −70
0,000 000 01 −80
0,000 000 001 −90
0,000 000 000 1 −100
Таблица 1.3.2 Соотношение напряжения или тока / дБ
Коэффициент напряжения или тока дБ
В _{на выходе} / В _{на выходе} или на _{на выходе} / на _{на выходе} 20log (V _из / V _из) 20log (I _из / I _из)
100 000 100
31 623 90
10 000 80
3 162 70
1 000 60
316.23 50
100 40
31,623 30
10 20
3,162 10
2 6
1,414 3
1,122 1
1 0
0,891 -1
0.707 −3
0,5 −6
0,316 2 −10
0,1 −20
0,031 62 −30
0,01 −40
0,003 162 −50
0,001 −60
0,000 316 2 −70
0.000 1 −80
0,000 0316 2 −90
0,000 01 −100
децибел (дБ) — IPS
Человеческое ухо не реагирует на изменения звука простым, линейным образом. Чтобы удвоить громкость звука, например, увеличив громкость на аудиоусилителе, большинство людей обнаруживают, что им необходимо увеличить мощность, производимую громкоговорителем, примерно в десять раз.Если бы мы увеличили мощность еще в десять раз, то есть в 100 раз больше мощности, с которой мы начали, звук снова бы только удвоился по громкости — так субъективно он был бы примерно в четыре раза громче, чем исходный звук. .
Десятикратное соотношение мощности определяется как 1 бел (от Александра Грэхема Белла (1847-1922)). Таким образом, шкала бел является логарифмической по отношению к основанию 10. Таким образом, отношение мощности, выраженное в белах (называемое «разницей уровней»), находится путем взятия логарифма (основание 10) отношения уровней мощности.Эта единица измерения слишком велика для практических целей, поэтому мы используем одну десятую бел — децибел:
.
Разность уровней = 10log (10) (P2 / P1) дБ.
Обратите внимание на правильную нотацию: маленькая b означает бел, когда написано полностью (так как это обычное слово), большая B — сокращение (в честь мистера Белла) и маленькая d — деци.
При хороших условиях прослушивания минимальное изменение уровня звука, которое может уловить человеческое ухо, составляет один децибел (1 дБ).
С этого момента все логарифмы принимаются по основанию 10.
дБ, мощность и напряжение
Чтобы использовать систему децибел для уровней напряжения, мы должны использовать закон Ома для преобразования мощности в напряжение. Мощность W (в ваттах) — это напряжение V (в вольтах), умноженное на ток I (в амперах): W = VI, а закон Ома дает I = V / R, где R — сопротивление (в Ом). Простая замена показывает, что мощность изменяется как квадрат напряжения. Возведение числа в квадрат соответствует удвоению его логарифма, поэтому:
Разность уровней = 20log (V1 / V2) дБ
Утверждение, что мощность изменяется пропорционально квадрату напряжения, верно только в том случае, если сравниваемые напряжения имеют одинаковый импеданс.В аудио нас в основном интересует напряжение, а не мощность (не говоря уже об усилителях громкоговорителей), поэтому очень удобно вообще забыть об импедансах и независимо сравнивать напряжения, используя приведенную выше формулу; и это то, что мы делаем.
Это означает, что мы не можем преобразовать обратно в отношение мощностей разность уровней, полученную из отношения напряжений, если только мы не знаем, что напряжения имеют одинаковый импеданс.
Вычисление в децибелах
Когда вы складываете логарифмы двух чисел вместе, результатом является логарифм произведения двух чисел: logA + logB = log (AB)
Таким образом, эффект умножения напряжения на ряд соотношений можно рассчитать, сложив соответствующие децибелы.Например, соотношение мощностей 2: 1 — это разность уровней 3 дБ, а соотношение мощностей 3: 1 — разность уровней 4,8 дБ, поэтому соотношение мощностей 6: 1 (2 x 3) является уровнем разница (3 + 4,8) = 7,8 дБ.
Точно так же деление на коэффициент соответствует вычитанию соответствующей разницы уровней в децибелах.
Чтобы преобразовать разницу уровней обратно в соотношение мощности или напряжения: разделите на 10, чтобы преобразовать ее в бел; (только если преобразовать в коэффициент напряжения, разделите на два;) возьмите 10 в степень полученного числа (также называемого антилогарифмом или антилогарифмом).
Использование
Любая форма коэффициента мощности может быть выражена в децибелах; например, отношение акустической мощности, производимой громкоговорителем, к его потребляемой электрической мощности. На практике децибелы находят наибольшее применение со звуком и сигналами в телекоммуникациях и радиовещании.
Помимо мощности, они обычно используются со многими величинами, которые напрямую связаны с мощностью, такими как напряжение, звуковое давление и напряженность радиочастотного поля. Поскольку децибелы описывают отношения, их также можно использовать для определения таких факторов, как усиление электронных усилителей и потери в аттенюаторах, электронных или акустических.
Похожие записи
1.2: Децибел — Engineering LibreTexts
Большинство людей знакомы с термином «децибел» в отношении звукового давления. Нередко можно услышать, как кто-то говорит что-то вроде «Вчера вечером на концерте было 110 децибел, а в ушах все еще звенит». Это популярное использование несколько неточно, но показывает, что децибелы указывают на какую-то величину — в данном случае уровень звукового давления.
1.2.1: Представление мощности и напряжения в децибелах
В простейшей форме децибел используется для измерения некоторого коэффициента усиления, например усиления мощности или напряжения.В отличие от обычных измерений усиления, с которыми вы, возможно, знакомы, форма децибел является логарифмической. Из-за этого он может быть очень полезен для отображения соотношений изменений, а также абсолютных изменений. Базовая единица — Бел. Чтобы преобразовать обычное усиление в его аналог Bel, просто возьмите общий логарифм (основание 10) усиления. В форме уравнения:
\ [\ text {усиление Бел} = \ log_ {10} (обычное \ усиление) \ nonumber \]
Обратите внимание, что в большинстве калькуляторов общий журнал обозначается как «\ (\ log \)», а натуральный журнал — как «\ (\ ln \)».К сожалению, некоторые языки программирования используют «\ (\ log \)» для обозначения натурального журнала и «\ (\ log 10 \)» для общего журнала. Этот баг укусил не один ученик, будьте осторожны! В качестве примера, если схема выдает выходную мощность 200 милливатт для входной 10 милливатт, мы обычно говорим, что она имеет коэффициент усиления по мощности:
\ [G = \ frac {P_ {out}} {P_ {in}} \\ G = \ frac {200 \ mW} {10 \ mW} \\ G = 20 \ nonumber \]
Для версии Bel просто возьмите журнал этого результата.{‘} = 1,301 \ nonumber \]
Коэффициент усиления по белу составляет 1,3 бел. Термин «бел» не является единицей в строгом смысле слова (как в «ваттах»), а просто используется для обозначения того, что это не обычное усиление. Напротив, обычные коэффициенты усиления мощности и напряжения иногда указываются в единицах Вт / Вт и В / В, чтобы отличить их от коэффициентов усиления Bel. Также обратите внимание, что символ усиления мощности Bel — это \ (G ‘\), а не \ (G \). Во избежание путаницы все коэффициенты усиления по белу обозначаются следующим штрихом (’). Поскольку белки, как правило, довольно большие, мы обычно используем одну десятую бела как норму.{‘} = 10 \ log_ {10} G \ label {1.1} \]
Где результат в дБ.
На этом этапе вам может быть интересно узнать, в чем большое преимущество децибельной системы. Чтобы ответить на этот вопрос, вспомните несколько идентификаторов журналов. Нормальное умножение становится сложением в системе журналов, а деление становится вычитанием. Точно так же силы и корни становятся умножением и делением. Из-за этого обнаруживаются две важные вещи. Во-первых, коэффициенты изменения становятся постоянными смещениями в системе децибел, а во-вторых, весь диапазон значений уменьшается в размере.{‘} = 10 \ log_ {10} G \) 1 0 дБ 2 3,01 дБ 4 6,02 дБ 8 9,03 дБ 10 10 дБ
Мы также можем рассмотреть дробные коэффициенты (т.е. потери вместо прибыли).
Фактор дБ Значение
0.5 −3,01 дБ
0,25 −6,02 дБ
0,125 −9,03 дБ
0,1 −10 дБ
Если вы посмотрите внимательно, вы заметите, что удвоение представлено увеличением примерно на 3 дБ. Фактор 4 — это, по сути, два удвоения. Следовательно, это эквивалентно 3 дБ + 3 дБ или 6 дБ.Помните, поскольку мы используем журналы, умножение превращается в простое сложение. Аналогичным образом уменьшение вдвое представлено примерно на -3 дБ. Знак минус указывает на уменьшение. Чтобы немного упростить ситуацию, представьте множители 2 как \ (\ pm \) 3 дБ, знак, указывающий, увеличиваете ли вы (умножаете) или уменьшаете (деление). Как видите, коэффициент 10 дает очень удобные 10 дБ. {‘} = 10 \ times 2.{-1} \ frac {23} {10} \\ G = 199,5 \ nonumber \]
Следовательно, \ (P_ {out} = 199,5 \ cdot 1 \) мВт, или 199,5 мВт
Вы также можете использовать технику аппроксимации в обратном порядке. Для этого разделите усиление дБ на блоки по 10 и 3 дБ:
\ [23 \ дБ = 3 \ дБ + 10 \ дБ + 10 \ дБ \ nonumber \]
Теперь замените каждый фрагмент соответствующим множителем и умножьте их вместе (помните, что при переходе от журнала к обычной форме сложение превращается в умножение).
\ [3 дБ = 2X \ 10 \ дБ = 10X, \ text {so,} \\ G = 2 \ times 10 \ times 10 \\ G = 200 \ nonumber \]
Хотя метод аппроксимации кажется медленнее, чем калькулятор, практика покажет обратное.{‘} _ {total} = 40 \ дБ \ nonumber \]
Как вы могли заметить, во всех примерах до этого момента использовалось усиление по мощности, а не по напряжению. У вас может возникнуть соблазн использовать те же уравнения для усиления напряжения. Одним словом, НЕ. Если вы на мгновение вспомните, вы вспомните, что мощность изменяется как квадрат напряжения. Другими словами, удвоение напряжения приведет к четырехкратному увеличению мощности. Если бы вы использовали те же преобразования дБ, удвоение напряжения составило бы 3 дБ, но, поскольку мощность увеличилась в четыре раза, это указывало бы на повышение на 6 дБ.{‘} _v = 20 \ \ log_ {10} \ A_v \ label {1.2} \]
Однако будьте осторожны, усиление напряжения Bel равняется усилению мощности Bel только в том случае, если входное и выходное сопротивление системы согласованы (вы, возможно, помните из своей предыдущей работы, что вполне возможно спроектировать схему с сильно различающимся коэффициентом усиления напряжения и мощности. . Повторитель по напряжению, например, демонстрирует умеренный прирост мощности с коэффициентом усиления по напряжению, равным единице. Вполне вероятно, что повторитель не будет демонстрировать согласованные импедансы.) Если бы мы пересчитали нашу предыдущую таблицу общих коэффициентов, мы бы обнаружили, что удвоение усиления по напряжению эквивалентно увеличению на 6 дБ, а десятикратное увеличение эквивалентно увеличению на 20 дБ, что вдвое превышает размер их аналогов по усилению мощности.{-1} \ frac {26} {20} \\ A_v = 19.95 \\ V_ {out} = A_v \ V_ {in} \\ V_ {out} = 19.95 \ times 10 \ mV \ nonumber \]
Последний момент, который следует отметить в этом разделе, заключается в том, что, как и в случае усиления мощности, отрицательное значение в дБ указывает на потерю. Следовательно, делитель напряжения 2: 1 будет иметь коэффициент усиления -6 дБ.
1.2.2: Представление сигнала в дБВт и дБВ
Как видно из предыдущего раздела, можно потратить значительное время на преобразование между усилением децибел и обычными напряжениями и мощностями.Поскольку форма в децибелах действительно дает преимущества при измерении усиления, было бы разумно использовать форму в децибелах также для уровней мощности и напряжения. Это относительно простой процесс. Нет причин, по которым мы не можем выразить мощность или напряжение в логарифмической форме. Поскольку значение в дБ просто указывает на соотношение, все, что нам нужно сделать, это выбрать эталон (то есть сравнительную базу для отношения). Для измерения мощности вероятным выбором будет 1 ватт. Другими словами, мы можем описать мощность как определенное количество дБ выше или ниже 1 ватта.{‘} = 20,8 \ дБВт \ nonumber \]
Нет ничего святого в 1-ваттном эталоне, если не считать его удобства. Мы могли бы так же легко выбрать другую ссылку. Другие общие контрольные точки — 1 милливатт (дБм) и 1 фемтоватт (дБф). Очевидно, что dBf используется для очень низких уровней сигнала, например, исходящих от антенны. дБм очень широко используется в индустрии связи. Чтобы использовать эти другие ссылки, просто разделите данную степень на новую ссылку.
Пример \ (\ PageIndex {8} \)
Небольшой персональный аудиоплеер выдает на наушники мощность 200 мВт.{‘} _ {out} = -7 \ dBV \ nonumber \]
Обратите внимание, что конечными единицами измерения являются дБВ, а не дБ, что указывает на напряжение, а не только на усиление.
Пример \ (\ PageIndex {12} \)
Гитарному усилителю мощности требуется входная мощность 20 дБмВт для достижения выходной мощности 25 дБВт. Какой коэффициент усиления усилителя в дБ?
Во-первых, необходимо преобразовать показания мощности так, чтобы они использовали одну и ту же эталонную единицу. Поскольку дБм представляет собой эталон на 30 дБ меньше эталонного дБВт, просто вычтите 30 дБ для компенсации.{‘} = 35 \ дБ \ nonumber \]
Обратите внимание, что единицы измерения — дБ, а не дБВт. Это очень важно! Сказать, что усиление составляет «столько» дБВт, то же самое, что сказать, что усиление «столько» ватт. Очевидно, что прирост — это «чистые» числа и не содержат таких единиц, как ватты или вольты.
Использование системы на основе дБ графически показано на рисунке \ (\ PageIndex {1} \). Обратите внимание, как усиление каскада добавляется к входному сигналу для формирования выходного сигнала. В этой форме можно быстро проанализировать даже большие схемы.Чтобы сделать жизнь в лаборатории еще проще, можно проводить измерения непосредственно в форме дБ. Поступая таким образом, вам никогда не придется выполнять конвертацию при поиске и устранении неисправностей в дизайне.