Как посчитать индуктивность катушки. Расчет индуктивности катушки: формулы, примеры и онлайн калькулятор

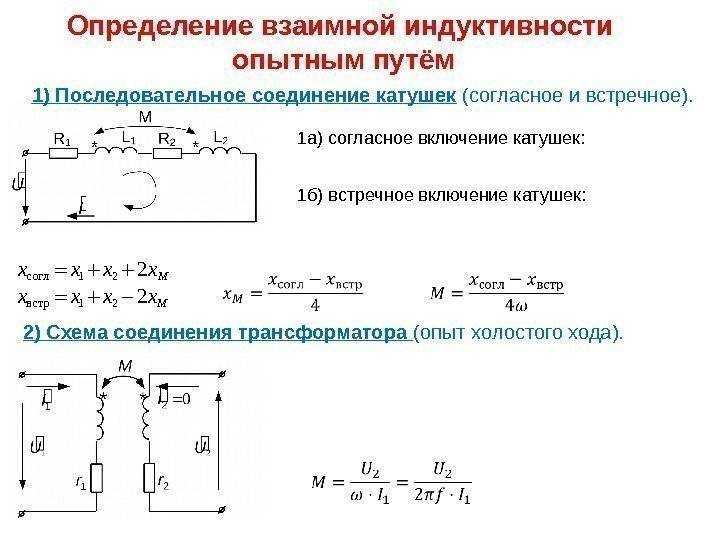
Как рассчитать индуктивность катушки. Какие формулы используются для вычисления индуктивности. Какие факторы влияют на индуктивность катушки. Как работает онлайн калькулятор для расчета индуктивности. Какие виды катушек индуктивности существуют.

Что такое индуктивность катушки и как она измеряется

Индуктивность — это способность катушки накапливать энергию магнитного поля при протекании через нее электрического тока. Индуктивность измеряется в генри (Гн). Один генри — это индуктивность, при которой ток силой в 1 ампер создает магнитный поток в 1 вебер.

Основные факторы, влияющие на индуктивность катушки:

• Количество витков провода
• Диаметр катушки
• Длина намотки
• Материал сердечника
• Форма сечения катушки

Чем больше витков и диаметр катушки, тем выше ее индуктивность. Применение ферромагнитного сердечника также значительно увеличивает индуктивность.

Основные формулы для расчета индуктивности катушки

Рассмотрим основные формулы, используемые для вычисления индуктивности катушек различных типов:

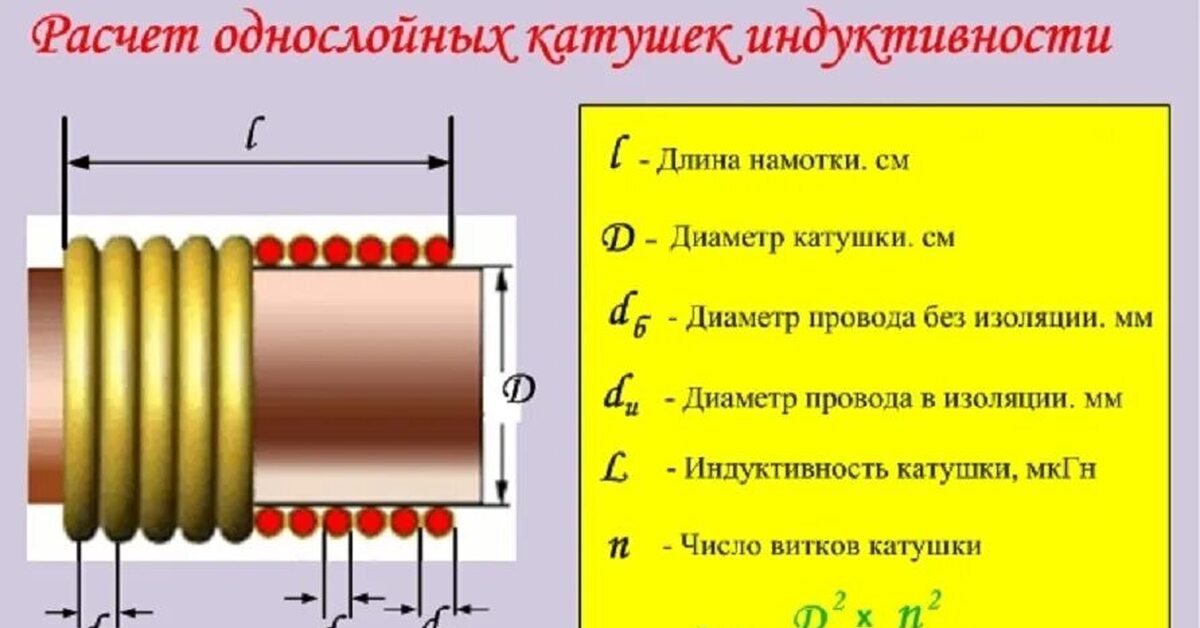
1. Формула для однослойной цилиндрической катушки без сердечника:

L = (μ0 * N^2 * S) / l

где:

• L — индуктивность в генри (Гн)
• μ0 — магнитная проницаемость вакуума (4π * 10^-7 Гн/м)
• N — число витков
• S — площадь поперечного сечения катушки (м^2)
• l — длина намотки (м)

2. Формула для многослойной цилиндрической катушки:

L = (0.31 * (d * N)^2) / (6d + 9l + 10h)

где:

• d — средний диаметр катушки (см)
• N — число витков
• l — длина намотки (см)
• h — толщина обмотки (см)

3. Формула для катушки с ферромагнитным сердечником:

L = (μ0 * μr * N^2 * S) / l

где μr — относительная магнитная проницаемость материала сердечника.

Пример расчета индуктивности катушки

Рассчитаем индуктивность однослойной цилиндрической катушки со следующими параметрами:

• Число витков N = 100
• Диаметр катушки d = 5 см = 0.05 м
• Длина намотки l = 10 см = 0.1 м

Площадь поперечного сечения S = π * (d/2)^2 = 3.14 * (0.05/2)^2 = 0.00196 м^2

Подставляем значения в формулу:

L = (4π * 10^-7 * 100^2 * 0.00196) / 0.1 = 246 мкГн

Таким образом, индуктивность данной катушки составляет 246 микрогенри.

Онлайн калькулятор для расчета индуктивности катушки

Для удобства расчетов можно воспользоваться онлайн калькулятором индуктивности. Принцип его работы:

1. Вводятся исходные параметры катушки (число витков, размеры, материал сердечника)
2. Выбирается тип катушки и соответствующая формула расчета
3. Калькулятор автоматически вычисляет индуктивность по заданной формуле
4. Результат выводится в нужных единицах измерения (мкГн, мГн или Гн)

Такие калькуляторы значительно упрощают и ускоряют процесс расчета индуктивности, особенно для сложных многослойных катушек.

Основные виды катушек индуктивности

В электронике применяются различные типы катушек индуктивности:

1. Воздушные катушки

Простейший тип без сердечника. Используются в высокочастотных цепях.

2. Катушки с ферромагнитным сердечником

Обладают повышенной индуктивностью за счет сердечника. Применяются в низкочастотных цепях.

3. Тороидальные катушки

Имеют форму тора. Отличаются малыми габаритами и высокой добротностью.

4. Спиральные катушки

Плоские катушки, намотанные по спирали. Используются в печатных платах.

5. Вариометры

Катушки с изменяемой индуктивностью за счет перемещения частей.

Выбор типа катушки зависит от конкретного применения, требуемой индуктивности, рабочей частоты и других факторов.

Практическое применение катушек индуктивности

Катушки индуктивности широко используются в различных областях электроники и электротехники:

• Фильтры в радиотехнических устройствах
• Колебательные контуры
• Трансформаторы и дроссели
• Электромагниты и реле
• Антенны
• Датчики

Правильный расчет индуктивности катушек критически важен для корректной работы этих устройств. Поэтому инженерам необходимо хорошо владеть методами расчета и измерения индуктивности.

Измерение индуктивности катушек

Для точного определения индуктивности катушек используются специальные приборы — измерители индуктивности (LCR-метры). Основные методы измерения:

1. Метод вольтметра-амперметра

Измеряется напряжение и ток на катушке при подключении переменного напряжения известной частоты. Индуктивность вычисляется по формуле:

L = U / (2πfI)

где U — напряжение, I — ток, f — частота.

2. Резонансный метод

Катушка включается в колебательный контур с конденсатором известной емкости. По резонансной частоте контура определяется индуктивность катушки.

3. Мостовой метод

Используется мост переменного тока, в одно плечо которого включается измеряемая катушка. При балансировке моста определяется индуктивность.

Современные цифровые LCR-метры позволяют быстро и точно измерять индуктивность в широком диапазоне значений.

Заключение

Расчет индуктивности катушек — важная инженерная задача при проектировании электронных устройств. Знание основных формул и методов расчета позволяет правильно подбирать параметры катушек для конкретных применений. Использование онлайн калькуляторов значительно упрощает процесс вычислений. При необходимости высокой точности рекомендуется проводить практические измерения индуктивности специальными приборами.

Помогите решить / разобраться (Ф)

EUgeneUS в [url=/post1354947.html#p1354947]сообщении #1354947[/url] писал(а): Kiev в сообщении #1354850 писал(а): Подскажите, как получают квадратичную зависимость? Примерно, как Вы и написали. Важно понимать вот что: квадратичная зависимость получается при некоторой идеализации — 100% магнитосцеплении. То есть 100% магнитного потока от одного любого витка проходят через каждый другой виток. Да конечно, коэффициент связи идеальных контуров, у меня равен 1. Просто я пытался понять логику получения квадратичной зависимости от числа витков . — 18.11.2018, 15:13 — realeugene в [url=/post1354964.html#p1354964]сообщении #1354964[/url] писал(а): Kiev в сообщении #1354959 писал(а): Это взаимоиндукция идеальных витков? Нет, если вы рассматриваете индуктивность одной катушки целиком. У вас один общий контур, а не два контура. В котором ни один виток сам по себе не является замкнутым контуром. Поэтому, на мой взгляд, про взаимоиндукцию витков тут лучше не рассуждать. Можно ли аналог катушки, составить из идеальных несвязных (общим током) контуров расположенных на близком расстоянии друг от друга? Если да, то получаем взаимоиндукцию и эффект квадратичной зависимости общей индуктивности от числа контуров (витков). — 18.11.2018, 15:33 — EUgeneUS в [url=/post1354957.html#p1354957]сообщении #1354957[/url] писал(а): Kiev Если Вы проследите ход Ваших рассуждений\вычислений, то увидите, что используется (явно или не явно) условие: магнитный поток от одного витка полностью проходит через каждый другой виток. В реальном мире а) это может выполняться приближенно, и с хорошей точностью — тогда зависимость индуктивности от количества витков можно считать квадратичной. б) для некоторых геометрий катушек это может выполняться приближенно, но характер зависимости остается квадратичным, например, для «толстой катушки». в) для некоторых геометрий катушек может приводить к неточной формуле для индуктивности. Например, если мы смотаем провод в соленоид, то его индуктивность будет пропорциональная количеству витков в квадрате, а значит квадрату длины провода. Далее начинаем вытягивать соленоид в прямой провод, а у прямого провода зависимость индуктивности от длины уже не квадратичная. Да я взял 100%-й коэффициент связи витков по полю, то есть бесконечно близко их сблизил (наложил), при этом сказал что токи не суммируются (ток последовательный, как и в катушке). Мне главное было понять, логику происхождения ~ в идеальном случае. — 18.11.2018, 15:55 — Простое объяснение зависимости ~ У изолированных витков с током есть только — самоиндукция. У связных (в катушку) витков появляется и взаимоиндукция. И сумма Самоиндукций и Взаимоиндукций даёт . В отличии от суммы Самоиндукций которые дают только .

Колебательный контур — что это такое? Формулы и схемы

Покажем, как применять знание физики в жизни

Начать учиться

Сегодня нас ждёт увлекательный эксперимент: мы перейдём от этапа «вообще не понимаю, что это» к «надо же, как всё просто и логично» всего за одну статью. Не верите? Мы вам обещаем! Мы поговорим о колебательных контурах, электромагнитных волнах и том, как мы встречаемся с этими понятиями в обычной жизни.

Колебания

Начнём обсуждение этой темы с колебаний. В обычной жизни мы часто слышим это слово: «цветок колеблется на ветру», «я не могу принять решение, колеблюсь», «температура воздуха колеблется в диапазоне…». Но что такое колебания в физике?

Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

Попробуйте привести несколько примеров такого движения. Верно, к колебаниям можно отнести движение стрелки, вращение качели, качание маятника часов.

Колебания бывают вынужденными и свободными.

• Вынужденные колебания — это колебания, происходящие под действием внешней периодически меняющейся силы.

  Посадите свою маленькую сестрёнку или братишку на качели: раскачивая их, вы станете той самой внешней силой, под действием которой качели движутся, совершая при этом вынужденные колебания.

• Свободные колебания — это колебания, происходящие под действием внутренних сил в колебательной системе.

  Груз колеблется на нити или пружине — вот самый распространённый пример свободных колебаний. Такие колебания всегда затухающие, потому что ни у одной системы нет бесконечного запаса энергии для такого движения: рано или поздно колебание прекратится.

Что может совершать свободные колебания? Математический (груз + нить) и пружинный (груз + пружина) маятники, а также электромагнитные волны.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Электромагнитные волны

В курсе школьной физики 8-го класса вы изучали отдельно главы про электричество и магнетизм, и только в 9–10-х классах узнали, что такое разделение не совсем верно. Дело в том, что электричество и магнетизм — две стороны одной монеты, они не могут существовать друг без друга. Движущееся электрическое поле порождает магнитное, а движущееся магнитное поле порождает электрическое. Эти поля распространяются в пространстве одновременно и, что удивительно, в разных плоскостях. Взгляните на рисунок!

Электромагнитные волны — это распространение в пространстве с течением времени переменных (вихревых) электрических и магнитных полей.

Вихревым электрическим полем называется поле, силовые линии которого представляют собой замкнутые линии.

В разрезе этой темы стоит запомнить две фамилии: Максвелл и Герц. Вот увидите, как сойдёт с ума от счастья учитель физики, когда вы их назовёте. 😅 Джеймс Максвелл описал основные положения электромагнитной теории, а Генрих Герц доказал существование электромагнитных волн опытным путём.

К электромагнитным волнам относятся радио, Wi-Fi и даже свет. Более подробно об этом можно прочесть в нашей статье.

Что такое колебательный контур?

Колебательный контур — это устройство, в котором могут происходить свободные электромагнитные колебания.

Также можно сказать, что колебательный контур — это электрическая цепь, работа которой порождает электромагнитное поле.

Но зачем кому-то создавать такие колебания?

Колебательные контуры — неотъемлемая часть многих производственных процессов. С их помощью изготавливают радиоприёмники, генераторы сигналов, блоки измерения частоты, контроллеры частоты напряжения на двигателях.

Возможно, вам может показаться, что это устройство давно устарело и используется в каких-то непонятных вещах, но стоит понимать, что без них не было бы возможно создание домофона, электромагнитов, различных датчиков, с которыми мы встречаемся ежедневно.

Колебательный контур состоит из двух компонентов: катушки и конденсатора, и выглядит вот так:

Катушка индуктивности (или соленоид) — это стержень с несколькими слоями обмотки медной проволокой. Именно он создаёт колебания в колебательном контуре. Стержень, находящийся в середине катушки, называется дроссель, или сердечник.

Катушка способна создавать колебания, только если есть электрический заряд. Она обладает низким сопротивлением.

Конденсатор — это элемент, способный накопить в себе большое количество электрического заряда. Он состоит из двух обкладок, между которыми находится диэлектрик (вещество, не проводящее электрический ток).

В чём его отличие от обычного аккумулятора? В аккумуляторе происходит превращение механической, химической, световой и других энергий в электрическую, в конденсаторе же накапливается заряд, который он может отдать весь сразу.

Часто в электрическую цепь колебательного контура подключают ещё один элемент — резистор, который обладает сопротивлением и контролирует силу тока и напряжение в цепи.

Виды колебательных контуров

По типу соединения колебательные контуры можно разделить на последовательный и параллельный.

Колебательный контур, схема последовательного соединенияКолебательный контур, схема параллельного соединения

Также физики выделяют особый тип контура — идеальный.

Идеальный колебательный контур — контур, сопротивление которого отсутствует, порождая при этом незатухающие свободные электромагнитные колебания.

Как вы думаете, можно ли создать такой контур и работать с ним на практике? К сожалению, такое маловероятно. Идеальный колебательный контур — всего лишь математическая модель, допущение, с помощью которого можно вывести формулы, ускорить расчёты и оценить характеристики контура в производстве.

Характеристики колебательного контура

Главные характеристики как параллельного, так и последовательного колебательного контура:

• L — индуктивность катушки;

• С — электроёмкость конденсатора.

Индуктивность катушки — это показатель, который численно равен электродвижущей силе (в вольтах), возникающей в цепи при изменении силы тока на 1 А за 1 секунду. Измеряется в генри (Гн).

Когда катушка подключена к цепи постоянного тока, то её индуктивность описывает энергию магнитного поля, которое создается этим током по формуле:

, где W — энергия магнитного поля, L — индуктивность, I — сила тока в цепи.

Индуктивность зависит от геометрических размеров контура и магнитных свойств среды (сердечника).

Электроёмкость — характеристика конденсатора, равная отношению заряда конденсатора к напряжению, под которым он находится. Измеряется в фарадах (Ф).

Электроёмкость можно вычислить по следующим формулам:

• , где e₀ — диэлектрическая проницаемость материала диэлектрика (табличная величина), S — площадь обкладок конденсатора, d — расстояние между пластинами.
• , где q — заряд, U — напряжение в цепи.

Кстати, 1 фарад — весьма большая величина, поэтому электроёмкость конденсатора чаще всего выражается в пико- или нанофарадах.

Принцип действия колебательного контура

Итак, каким же образом работает колебательный контур? Разделим процесс на два этапа.

Первый этап

Второй этап (обратный)

Заряженная положительно пластина конденсатора начинает разряжаться. Ток поступает в электрическую цепь, протекая от положительного заряда к отрицательному через соленоид. В контуре возникают электромагнитные колебания. Ток разряда конденсатора, проходя по виткам катушки, порождает магнитное поле. В катушке возникает ЭДС самоиндукции, препятствующая мгновенной разрядке конденсатора, ток нарастает постепенно. С ростом тока разряда убывает электрическое поле в конденсаторе, но возрастает магнитное поле катушки. В момент, когда поле конденсатора исчезнет (конденсатор разрядится), магнитное поле катушки будет максимальным. Ток, пройдя через соленоид, переходит на вторую пластину и заряжает её положительно (в то время как первая обкладка, с которой шёл ток, получает отрицательный заряд).

Процесс происходит в обратном порядке: Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнёт заряжаться вновь. По мере заряда ток ослабевает, а вместе с ним и магнитное поле. Ток проходит через катушку с положительно заряженной пластины (той, которая в начале первого этапа была заряжена отрицательно) на отрицательно заряженную. Все заряды встают на свои первоначальные места.

Цикл повторяется до тех пор, пока на конденсаторе будет заряд. В идеальном колебательном контуре этот процесс происходил бы бесконечно, а в реальном неизбежны потери энергии, и колебания затухают.

Формула Томпсона

Характеристики L и С колебательного контура связаны между собой с помощью формулы Томпсона, которая описывает период свободных колебаний в LC-контуре:

, где T — период электромагнитных колебаний, L — индуктивность катушки колебательного контура, C — ёмкость конденсатора, π — число пи.

Эта формула для колебательного контура является одной из основных, обратите на неё особенное внимание!

Закон сохранения энергии в колебательном контуре

В колебаниях, как и в любом другом движении, работают законы сохранения энергии. Как именно это выражается?

Принцип работы контура основан на трансформации энергии, превращении электрической энергии в магнитную и наоборот. Тогда энергию колебательного контура можно описать так:

W = WC(t) + WL(t) = const

Когда энергия электрического поля становится максимальной, энергия магнитного поля равна нулю, что работает и в обратном направлении.

Этап	Энергия электрического поля	Энергия магнитного поля
1	Максимальна при q max:	0
2	0	Максимальна при I max::

Так как энергии достигают своего максимума с равным числовым значением, сделаем вывод:

Резонанс в LC-контуре

Обещаем, последнее на сегодня!

Помимо вышеперечисленных характеристик, есть ещё одна величина, которая описывает колебания в контуре, и это резонансная частота.

Ну, здесь всё просто. Помним, что частота колебаний и период — взаимно обратные величины, а значит:

«Ну хорошо», — скажете вы, «и в чём вообще суть?».

А вот в чём: в электрическом колебательном контуре резонанс (резкое увеличение амплитуды колебаний) происходит на определённой частоте, когда индуктивность L и ёмкость C уравновешены. Благодаря этому энергии могут свободно циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Наше сегодняшнее путешествие в мир физики было весьма увлекательным, хоть и непростым, согласны? На онлайн-курсе физики в школе Skysmart вы сможете ещё больше утвердиться в мысли, что физика — наука для жизни, а ещё подготовитесь к экзаменам и научитесь уверенно и без затруднений делать лабораторные работы.

Дарья Вишнякова

К предыдущей статье

Оптическая сила линзы

К следующей статье

Явление резонанса

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Индуктивность | Физика II |

Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется индуктивностью . Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. См. рис. 1, где простые катушки наводят друг в друге ЭДС.

Рисунок 1. Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Заметим, что « E ₂ индуцируется» представляет ЭДС индукции в катушке 2. )

Во многих случаях, когда геометрия устройств фиксирована, поток изменяется за счет изменения тока. Поэтому мы сосредоточимся на скорости изменения тока, ∆ I / ∆ t , как на причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в виде уравнения как −MΔtΔI1​​

, где M определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на Рисунке 1 имеют маленькое значение M  по сравнению с катушками трансформатора на Рисунке 3 от компании Transformers. Единицами для M являются (В ⋅ с) / A = Ω ⋅ с, который назван Генри (H) в честь Джозефа Генри. То есть 1 Гн = 1 Ом⋅с. Природа здесь симметрична. Если мы изменим текущий I ₂ в катушке 2 индуцируем ЭДС ₁ в катушке 1, которая определяется как

э.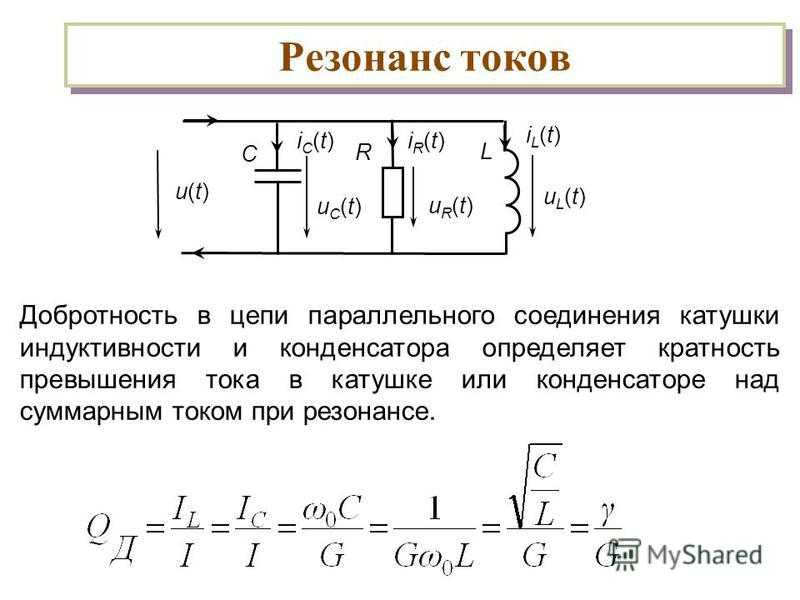 д.с. {I}_{2}}{\Delta t}\\emf1​=−MΔtΔI2​​

, где M — то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью, или взаимная индуктивность M . Большая взаимная индуктивность М может быть или не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M предназначен для противодействия катушкам, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 2.)

Рис. 2. Нагревательные спирали электрической сушилки для белья можно намотать встречно, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.

Самоиндукция , также существует действие закона Фарадея об индукции устройства на себя. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока Δ I через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Она определяется как

ЭДС=-LΔIΔt\text{ЭДС}=-L\frac{\Delta I}{\Delta t}ЭДС=-LΔtΔI​

, где L — собственная индуктивность прибора. Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначено символом на рисунке 3.

Рисунок 3.

Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность L устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большую L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо получить небольшую катушку L , например, путем встречной обмотки катушек, как показано на рис. 2. Катушка индуктивности 1 Гн является большой катушкой индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с л = 1,0 Гн, через которое протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, определяемая как ЭДС = − L (Δ I /Δ t ), будет противодействовать изменению. Таким образом, будет индуцироваться ЭДС, определяемая как ЭДС = — л (Δ I / Δ t ) = (1,0 Гн)[(10 А)/(1,0 мс)] = 10000 В. Положительный знак означает, что это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока. Есть применение такому большому наведенному напряжению. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 4.)

Рис. 4. Благодаря быстрому переключению катушки индуктивности батареи напряжением 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.

Можно рассчитать L для индуктора, зная его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность L обычно заданное количество. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется законом индукции Фарадея как ЭДС = — Н (Δ Φ / t ) и, по определению самоиндукции, как ЭДС = — л (Δ I / Δ t ). Приравнивание этих выходов

ЭДС = -NΔΦΔt = -LΔIΔt \ текст {ЭДС} = -N \ гидроразрыва {\ Delta \ Phi {\ Delta t} = -L \ гидроразрыва {\ Delta I} {\ Delta t} \\ ЭДС = -NΔtΔΦ ​=−LΔtΔI​

Решение для L дает

L=NΔΦΔIL=N\frac{\Delta \Phi }{\Delta I}\\L=NΔIΔΦ​

Это уравнение для собственной индуктивности L устройства всегда верно . Это означает, что собственная индуктивность L зависит от того, насколько эффективен ток в создании потока; тем эффективнее, чем больше Δ Φ / Δ I . Воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Так как район A соленоида фиксирован, изменение потока Δ Φ = Δ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется формулой NI}{\ell}\\B=µ0​nI=µ0​ℓNI​

. (Здесь n  =  N / ℓ , где N — количество витков, а ℓ — длина соленоида.) Изменяется только ток, так что 9{2}A}{\ell}\text{(соленоид)}\\L=ℓμ0​N2A​(соленоид)

. Это собственная индуктивность соленоида с площадью поперечного сечения А и длиной ℓ . Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению. {2}\right)}{0,100 \text{ m}}\\ & =& 0,632 \text{ mH}\end{array} \\L​==​0,100 м (4π × 10–7 T⋅ м/А) (200)2 (1,26 × 10–3 м2)​0,632 мГн​

.

Обсуждение

Этот соленоид имеет средние размеры. Его индуктивность около миллигенри также считается умеренной.

Одно распространенное применение индуктивности используется в светофорах, которые могут определить, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была обнаружена на «подрывнике в нижнем белье».) См. рис. 5.

Рисунок 5. Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (кредит: Alexbuirds, Wikimedia Commons)

Концептуальные вопросы

1. Как бы вы поместили две одинаковые плоские катушки в контакт, чтобы они имели наибольшую взаимную индуктивность? В мере?
2. Как бы вы сформировали провод заданной длины, чтобы придать ему наибольшую самоиндукцию? В мере?
3. Проверить, как было сделано без доказательства в примере 1 (выше), что единицы T ⋅ m ² / А  = Ом ⋅ с = Г.

Задачи и упражнения

1. Две катушки расположены близко друг к другу в физической лаборатории, чтобы продемонстрировать закон индукции Фарадея. Ток 5,00 А в одном отключается за 1,00 мс, индуцируя ЭДС 9,00 В в другом. Чему равна их взаимная индуктивность?

2. Если две катушки, расположенные рядом друг с другом, имеют взаимную индуктивность 5,00 мГн, какое напряжение индуцируется в одной, когда ток силой 2,00 А в другой отключается через 30,0 мс?

3. Ток 4,00 А через катушку индуктивности 7,50 мГн отключается за 8,33 мс. Какая ЭДС индуцирует противодействие этому?

4. Устройство включено, и через него через 0,100 мс проходит ток 3,00 А. Чему равна собственная индуктивность прибора, если ей противодействует ЭДС наведенного напряжения 150 В?

5. Начиная с

emf2=-MΔI1Δt{\text{emf}}_{2}=-M\frac{\Delta {I}_{1}}{\Delta t}\\emf2​=-MΔtΔI1​​

, покажите, что единицами измерения индуктивности являются (В ⋅ с)/A = Ом ⋅ с.

6. Вспышки камеры заряжают конденсатор до высокого напряжения, быстро включая и выключая ток через катушку индуктивности. За какое время необходимо включить или выключить ток 0,100 А через катушку индуктивности 2,00 мГн, чтобы индуцировать ЭДС 500 В?

7. Большой исследовательский соленоид имеет собственную индуктивность 25,0 Гн. а) Какая ЭДС наведения препятствует его отключению, если протекающий через него ток 100 А отключается за 80,0 мс? б) Сколько энергии запасается в катушке индуктивности при полном токе? в) С какой скоростью в ваттах должна рассеиваться энергия, чтобы ток выключился за 80,0 мс? (d) Принимая во внимание ответ на последнюю часть, удивительно ли, что так быстро закрыть его сложно?

8. (a) Рассчитайте собственную индуктивность соленоида длиной 50,0 см и диаметром 10,0 см, имеющего 1000 витков. б) Сколько энергии запасается в этом индукторе при протекании через него тока силой 20,0 А? в) Как быстро его можно выключить, если ЭДС индукции не может превышать 3,00 В?

9. Прецизионный лабораторный резистор изготовлен из витка проволоки диаметром 1,50 см и длиной 4,00 см и имеет 500 витков. а) Чему равна его собственная индуктивность? б) Какая средняя ЭДС индуцируется, если ток 12,0 А через него включается за 5,00 мс (одна четвертая периода для переменного тока частотой 50 Гц)? в) Какова его индуктивность, если его укоротить наполовину и намотать встречно (два слоя по 250 витков в противоположных направлениях)?

10. Нагревательные спирали в фене имеют диаметр 0,800 см, общую длину 1,00 м и 400 витков. а) Какова их полная собственная индуктивность, если предположить, что они действуют как одиночный соленоид? б) Сколько энергии запасается в них при токе 6,00 А? (c) Какая средняя ЭДС препятствует их отключению, если это делается за 5,00 мс (одна четвертая часть цикла для переменного тока с частотой 50 Гц)?

11. Когда ток 20,0 А через индуктор отключается за 1,50 мс, индуцируется ЭДС 800 В, противодействующая изменению. Каково значение собственной индуктивности?

12. Как быстро может быть отключен ток 150 А через дроссель 0,250 Гн, если ЭДС индукции не может превышать 75,0 В?

13. Integrated Concepts  Очень большой сверхпроводящий соленоид, такой как тот, который используется в МРТ-сканировании, сохраняет 1,00 МДж энергии в своем магнитном поле при токе 100 А. а) Найдите его индуктивность. (б) Если катушки «идут нормально», они приобретают сопротивление и начинают рассеивать тепловую энергию. Какой прирост температуры произойдёт, если вся накопленная энергия пойдет на нагрев магнита массой 1000 кг при средней удельной теплоемкости 200 Дж/кг · ºC?

14. Необоснованные результаты  В катушке индуктивности 25,0 Гн ток 100 А отключается за 1,00 мс. а) Какое напряжение индуцируется, чтобы противостоять этому? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?

Взаимная индуктивность и собственная индуктивность | Формула и пример

Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.

Электромагнитная индукция возникает, когда магнитный поток, движущийся относительно отдельного проводника или катушки, индуцирует ЭДС в проводнике или катушке. Поскольку увеличение или уменьшение тока через катушку создает изменяющийся поток, ЭДС индуцируется в катушке за счет собственного изменения тока. Тот же эффект может вызвать ЭДС в соседней катушке. Уровень индуцированной ЭДС в каждом случае зависит от собственной индуктивности катушки или от взаимной индуктивности между двумя катушками. Во всех случаях полярность ЭДС индукции такова, что она противодействует первоначальному изменению, вызвавшему ЭДС.

Компоненты, называемые катушками индуктивности или дросселями, имеют заданные значения индуктивности. Индукторы могут работать последовательно или параллельно. Даже самый короткий проводник имеет индуктивность. Обычно это нежелательная величина, которую называют паразитной индуктивностью.

Собственная индуктивность

Индуктивность катушки и проводника

Было показано, что ЭДС индуцируется в проводнике, движущемся в магнитном поле, и что рост тока в катушке может индуцировать ЭДС в другом магнитном поле. спаренная катушка. Катушка также может индуцировать напряжение сама по себе при изменении уровня тока. Это явление известно как самоиндукция, и его принцип показан на рис. 1.9.0007

Рис.1: Токопроводящая катушка и ее площадь поперечного сечения

Магнитный поток, нарастающий наружу вокруг витков катушки, пересекает (или задевает) витки другой катушки и индуцирует ЭДС в катушке

Катушка и площадь ее поперечного сечения показаны на рис. 1 с хвостами стрелок и точками, указывающими направления тока в каждом витке. Вокруг каждого витка катушки возникает поток, создаваемый током, протекающим через катушку. Однако для удобства на рисунке показан рост потока только вокруг одного витка катушки. Видно, что по мере роста тока поток расширяется наружу и перерезает (или задевает) остальные витки. Это вызывает индукцию токов в других витках, и направление индуцированных токов таково, что они создают поток, противодействующий потоку, индуцирующему их.

Вспоминая, что ток через катушку вызывает рост потока вокруг всех витков сразу, видно, что поток от каждого витка индуцирует ток, который противодействует ему в каждом другом витке.

Для создания противоположных потоков индуцированный ток в катушке должен быть противоположен току, протекающему через катушку от внешнего источника питания. Индуцированный ток, конечно, является результатом индуцированной ЭДС. Таким образом, видно, что собственная индуктивность катушки создает ЭДС индукции, которая противодействует внешней ЭДС, которая пропускает ток через катушку. Поскольку эта ЭДС индукции противоположна напряжению питания, ее обычно называют противо-ЭДС или противо-ЭДС . Противоэдс возникает только при увеличении или уменьшении тока катушки. Когда ток достигает постоянного уровня, поток больше не изменяется и не генерируется противо-ЭДС.

Самоиндукция есть даже у одного проводника. На рис. 2 показано, что при увеличении тока в проводнике поток может увеличиваться наружу от центра проводника. Этот поток пересекает другие части проводника и индуцирует противо-ЭДС.

Рис. 2: поперечное сечение проводника

Рост тока внутри проводника индуцирует ЭДС в других частях проводника.

На рис. 3 показана полярность противоЭДС, индуцируемой в катушке, для заданной полярности напряжения питания. На рисунке 3(а) ключ замкнут, и ток I начинает расти от нуля. Полярность противоЭДС (e _L ) такова, что она противостоит росту I, поэтому она последовательно противодействует напряжению питания. Когда переключатель разомкнут (рис. 3(b)), ток стремится упасть до нуля. Но теперь полярность е _L таков, что препятствует падению I. Он последовательно поддерживает напряжение питания. Фактически, e _L может вызвать искрение на клеммах выключателя, так как это зависит от индуктивности катушки.

Рис.3: Полярность ЭДС индукции

ПротивоЭДС, индуцированная в катушке, всегда противостоит нарастанию или спаду тока.

Единицей индуктивности в системе СИ является Генри (Гн).

Индуктивность цепи равна одному Генри, когда ЭДС 1 В индуцируется током, изменяющимся со скоростью 1 А/с.

Таким образом, соотношение между индуктивностью, наведенным напряжением и скоростью изменения тока:

\[\begin{matrix}   L=\frac{{{e}_{L}}}{{\Delta i}/ {\Delta t}\;} & {} & \left( 1 \right)  \\\end{matrix}\]

Где L — индуктивность в Генри, e _L — противоЭДС индукции в вольтах скорость изменения тока в А/с. перед e _L иногда ставится отрицательный знак, чтобы показать, что ЭДС индуцирования противоположна приложенной ЭДС. Когда е _L =1В и =1А/с, L=1H. Если скорость изменения тока равна 2 А/с, а e _L = 1 В, индуктивность равна 0,5 Гн.

Катушку, имеющую определенную индуктивность, обычно называют катушкой индуктивности или дросселем. Обратите внимание на графические символы катушки индуктивности, показанные на рис. 3.

Формула собственной индуктивности

Выражение для индуктивности может быть получено с учетом размеров катушки и количества витков [см. рис. 4].

Рис.4: Количество витков в катушке

Индуктивность катушки зависит от количества витков и от изменений потока и тока.

Из уравнения (2):

\[\begin{matrix}   {{e}_{L}}=N\frac{\Delta \phi}}{\Delta t} & {} & \left( 2 \right)  \\\end{matrix}\]

Подстановка e _L в уравнение (1) дает

\[L=N\frac{{\Delta \phi}/{\Delta t}\ ;}{{\Delta i}/{\Delta t}\;}\]

Или

\[\begin{matrix}   L=N\frac{\Delta \phi }{\Delta i} & {} & \left( 3 \right)  \\\end{matrix}\]

Кроме того,

\[\phi =B\times A\]

And

$B={{\mu }_{o}}\times {{\mu }_{r}}\times H ={{\mu }_{o}}\times {{\mu }_{r}}\times \frac{IN}{l}$

Следовательно,

$\phi = {{\mu }_ {o}}\times {{\mu }_{r}}\times IN\times \frac{A}{l}$

Так как I является максимальным уровнем тока, он также представляет собой изменение тока (∆i ) от нуля до максимального уровня. Следовательно, изменение потока равно

$\Delta \phi = {{\mu }_{o}}\times {{\mu }_{r}}\times \Delta i\times N\times \frac{A {л}$ 9{A}/{}_{l} & {} & \left( 4 \right)  \\\end{matrix}\]

Обратите внимание, что, как показано на рисунке 5, индуктивность пропорциональна поперечному сечению площади катушки и квадрату числа витков. Он также обратно пропорционален длине катушки. Поэтому максимальная индуктивность получается при короткой катушке, имеющей большую площадь поперечного сечения и большое количество витков.

Рис.5: Размеры катушки

Индуктивность катушки можно рассчитать исходя из ее размеров и проницаемости сердечника.

Уравнение (4) теперь позволяет вычислить индуктивность катушки известных размеров. В качестве альтернативы его можно использовать для определения необходимых размеров катушки, чтобы она имела заданную индуктивность. Однако его не так легко применить к катушкам с железным сердечником, поскольку магнитная проницаемость ферромагнитного материала изменяется при изменении плотности потока. Следовательно, индуктивность катушки с железным сердечником постоянно изменяется по мере увеличения и уменьшения тока катушки.

Неиндуктивная катушка

Во многих случаях желательно иметь неиндуктивную катушку; например, прецизионные резисторы обычно неиндуктивны. Чтобы построить такую ​​катушку, обмотка состоит из двух проводников, расположенных бок о бок, как показано на рисунке 6. Каждый виток катушки имеет соседний виток, по которому течет ток в противоположном направлении. Магнитные поля, создаваемые соседними витками, компенсируют друг друга. Следовательно, противоЭДС не генерируется, и катушка не индуктивная.

Рис. 6: Безиндуктивная катушка

Пример с собственной индуктивностью

Соленоид с 900 витками имеет общий поток 1,33 X 10 ^-7 Вб через воздушный сердечник при токе катушки 100 мА. Если потоку требуется 75 мс, чтобы вырасти от нуля до максимального уровня, рассчитайте индуктивность катушки. {-7}}Wb \\ & \Delta i=100 мА \\ & \Delta t=75 мс \ \\конец{выравнивание}$ 9{-3}}}=1,6 мВ\]

Взаимная индуктивность

Когда поток от одной катушки пересекает другую соседнюю (или магнитно связанную) катушку, во второй катушке индуцируется ЭДС. По закону Ленца ЭДС, индуцируемая во второй катушке, создает поток, противоположный первоначальному потоку от первой катушки. Таким образом, ЭДС индукции снова является противоЭДС, и в этом случае индуктивный эффект называется взаимной индуктивностью. На рис. 7 показаны графические символы, используемые для катушек с взаимной индуктивностью, также называемых связанными катушками.

Рис. 7: Графические обозначения катушек с воздушным и железным сердечником

Подобно самоиндукции, взаимная индуктивность измеряется в Генри (Гн) .

Формула взаимной индуктивности

Две катушки имеют взаимную индуктивность 1Гн, когда ЭДС 1В индуцируется в одной катушке за счет тока, изменяющегося со скоростью 1 А/с в другой катушке.

Это определение приводит к уравнению, связывающему взаимную индуктивность с наведенным напряжением и скоростью изменения тока:

\[\begin{matrix}   M=\frac{{{e}_{L}}}{{\Delta i}/{\Delta t}\;} & {} & \left( 5 \right) \\\end{matrix}\]

Где M — взаимная индуктивность в Генри, e _L — ЭДС в вольтах, индуцированных во вторичной катушке, и — скорость изменения тока в первичной катушке в А/с .

Катушка, через которую проходит ток от внешнего источника, называется первичной, а катушка, в которой индуцируется ЭДС, называется вторичной.

Уравнение для ЭДС, индуцированной во вторичной обмотке, можно записать в виде:

\[\begin{matrix}   {{e}_{L}}={{N}_{s}}\frac{\Delta \phi}}{\Delta t} & {} & \left( 6 \ справа)  \\\end{matrix}\]

Здесь ∆ϕ — полное изменение потока, связанного со вторичной обмоткой, N _с — число витков вторичной обмотки, ∆t — время, необходимое для изменение потока.

Замена e _L из уравнения (6) в уравнение (5) дает

\[M={{N}_{s}}\frac{{\Delta \phi}/{\Delta t}\ ;}{{\Delta i}/{\Delta t}\;}\]

Следовательно,

\[\begin{matrix}   M={{N}_{s}}\frac{\Delta \phi }{\Delta i} & {} & \left( 7 \right)  \\ \end{matrix}\]

Рисунок 8(a) иллюстрирует тот факт, что когда две катушки намотаны на один ферромагнитный сердечник, фактически весь поток, создаваемый первичной катушкой, связывается со вторичной катушкой. Однако, когда катушки с воздушным сердечником, только часть потока от первичной обмотки может быть связана со вторичной обмоткой [см. рис. 8 (b)]. В зависимости от того, какая часть первичного потока пересекает вторичный, катушки можно разделить на слабосвязанные или сильносвязанные. Один из способов обеспечения жесткой связи показан на рис. 8(с), где каждый виток вторичной обмотки расположен рядом с одним витком первичной обмотки. Катушки, намотанные таким образом, называются бифилярными.

Рис.8: Потокосцепление в первичной и вторичной обмотках

Величина потока от первичной обмотки, которая связана со вторичной обмоткой, зависит от того, насколько тесно связаны катушки. Коэффициент сцепления определяет сцепление.

Величина потоковой связи от первичной обмотки к вторичной также определяется коэффициентом связи k. Если весь первичный поток связан со вторичным, коэффициент связи равен 1. Когда только 50% первичного потока связаны со вторичной катушкой, коэффициент связи равен 0,5. Таким образом,

\[k=\frac{flux\text{ }связи\текст{ }между\text{ }первичным\текстом{ }и\текстом{ }\второстепенным}{всего\текст{ }поток, произведенный\текст{ }по \text{ }primary}\]

Возвращаемся к уравнению (7). Когда ∆ϕ представляет собой полное изменение потока в первичной обмотке, поток, связанный со вторичной обмоткой, равен k∆ϕ. Следовательно, уравнение для M 

\[\begin{matrix}   M=k{{N}_{s}}\frac{\Delta \phi }{\Delta i} & {} & \left( 8 \right )  \\\end{matrix}\]

Кроме того, заменив $\Delta \phi = {{\mu }_{o}}\times {{\mu }_{r}}\times \Delta i\ раз N\times \frac{A}{l}$ в уравнение (8) дает 9{2}}$

Или

\[\begin{matrix}   \sqrt{{{L}_{1}}\times {{L}_{2}}}={{N}_{p} } \ times {{N} _ {s}} \ times {{\ mu } _ {o}} \ times {{\ mu } _ {r}} \ times \ frac {A} {l} & {} & \left( 10 \right)  \\\end{matrix}\]

Сравнивая уравнения 9 и 10, видно, что

\[\begin{matrix}   M=k\sqrt{{{L}_{ 1}}\times {{L}_{2}}} & {} & \left( 11 \right)  \\\end{matrix}\]

Пример взаимной индуктивности

Намотаны две одинаковые катушки кольцеобразный железный сердечник с относительной магнитной проницаемостью 500.