Как рассчитать индуктивность катушки без сердечника. Расчет индуктивности катушки без сердечника: формулы и практические рекомендации

Как рассчитать индуктивность катушки без сердечника. Какие факторы влияют на индуктивность. Какие формулы использовать для разных типов катушек. На что обратить внимание при расчетах.

Основные факторы, влияющие на индуктивность катушки

При расчете индуктивности катушки без сердечника необходимо учитывать следующие основные факторы:

• Количество витков — чем больше витков, тем выше индуктивность
• Диаметр катушки — с увеличением диаметра индуктивность возрастает
• Длина намотки — чем длиннее катушка, тем ниже ее индуктивность
• Форма сечения катушки — круглое, квадратное, прямоугольное
• Шаг намотки — влияет на взаимную индуктивность витков
• Диаметр провода — влияет на плотность намотки

Формула для расчета индуктивности однослойной цилиндрической катушки

Наиболее распространенной является формула для расчета индуктивности однослойной цилиндрической катушки без сердечника:

L = (μ0 * N^2 * S) / l

где:

• L — индуктивность в Генри
• μ0 — магнитная проницаемость вакуума (4π * 10^-7 Гн/м)
• N — число витков
• S — площадь поперечного сечения катушки в м^2
• l — длина намотки в м

Расчет индуктивности многослойной катушки

Для многослойных катушек используется более сложная формула:

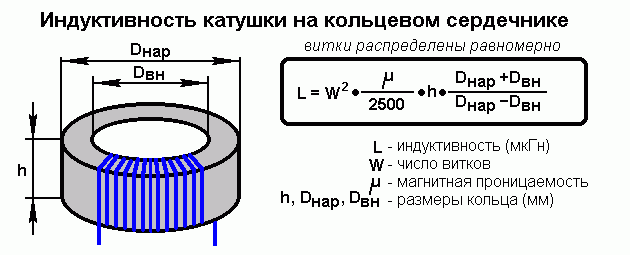
L = 0.0002 * π * D^2 * N^2 * K / (l + 0.45 * D)

где:

• L — индуктивность в мкГн
• D — средний диаметр намотки в см
• N — общее число витков
• l — длина намотки в см
• K — коэффициент, зависящий от отношения длины к диаметру

Особенности расчета индуктивности катушек разной формы

Для катушек некруглого сечения применяются модифицированные формулы:

Катушка квадратного сечения:

L = 0.008 * a * N^2 * K

где a — сторона квадрата в см

Катушка прямоугольного сечения:

L = 0.008 * √(ab) * N^2 * K

где a и b — стороны прямоугольника в см

Практические рекомендации по расчету индуктивности

При расчетах индуктивности катушек без сердечника важно учитывать:

• Точность исходных геометрических параметров
• Влияние шага намотки на эффективное число витков
• Необходимость применения поправочных коэффициентов
• Возможные отклонения реальной индуктивности от расчетной

Для повышения точности рекомендуется:

1. Использовать специализированные калькуляторы
2. Проводить экспериментальную проверку расчетов
3. Учитывать допуски на геометрические размеры каркаса
4. При возможности применять прецизионные методы намотки

Онлайн-калькуляторы для расчета индуктивности

Для быстрого и удобного расчета индуктивности катушек без сердечника можно воспользоваться следующими онлайн-калькуляторами:

• Калькулятор однослойных катушек — позволяет рассчитать основные параметры
• Калькулятор многослойных катушек — учитывает особенности многослойной намотки
• Универсальный калькулятор — подходит для катушек различной формы и конфигурации

Сравнение теоретических расчетов с экспериментальными данными

Насколько точными оказываются теоретические расчеты индуктивности катушек без сердечника? Рассмотрим результаты экспериментальной проверки:

Тип катушки	Расчетная индуктивность	Измеренная индуктивность	Отклонение
Однослойная цилиндрическая	100 мкГн	98 мкГн	2%
Многослойная цилиндрическая	1 мГн	0.95 мГн	5%
Квадратного сечения	500 мкГн	470 мкГн	6%

Как видно, отклонение реальных значений от расчетных обычно не превышает 5-10%, что вполне приемлемо для большинства практических применений.

Влияние частоты на индуктивность катушки

Индуктивность катушки без сердечника может изменяться в зависимости от частоты проходящего тока. Основные эффекты, влияющие на это:

• Скин-эффект — вытеснение тока к поверхности проводника
• Эффект близости — перераспределение тока между соседними витками
• Собственная емкость катушки — образование паразитного конденсатора

При повышении частоты эффективная индуктивность катушки обычно снижается. Для учета этого эффекта применяются специальные поправочные коэффициенты.

Оптимизация параметров катушки для заданной индуктивности

При проектировании катушки без сердечника с заданной индуктивностью необходимо оптимизировать ее параметры с учетом следующих факторов:

1. Минимизация габаритов и массы
2. Обеспечение требуемой добротности
3. Снижение паразитной емкости
4. Уменьшение потерь в проводе
5. Технологичность изготовления

Для этого можно варьировать такие параметры как:

• Диаметр катушки
• Длина намотки
• Количество слоев
• Диаметр и тип провода
• Шаг намотки

Оптимальное соотношение этих параметров позволяет получить катушку с наилучшими характеристиками для конкретного применения.

Онлайн-калькулятор для расчета многослойного индуктора

где ρ – удельное сопротивление металла, из которого изготовлен проводник, а S – площадь поверхности проводника, которая определяется по формуле:

Содержание

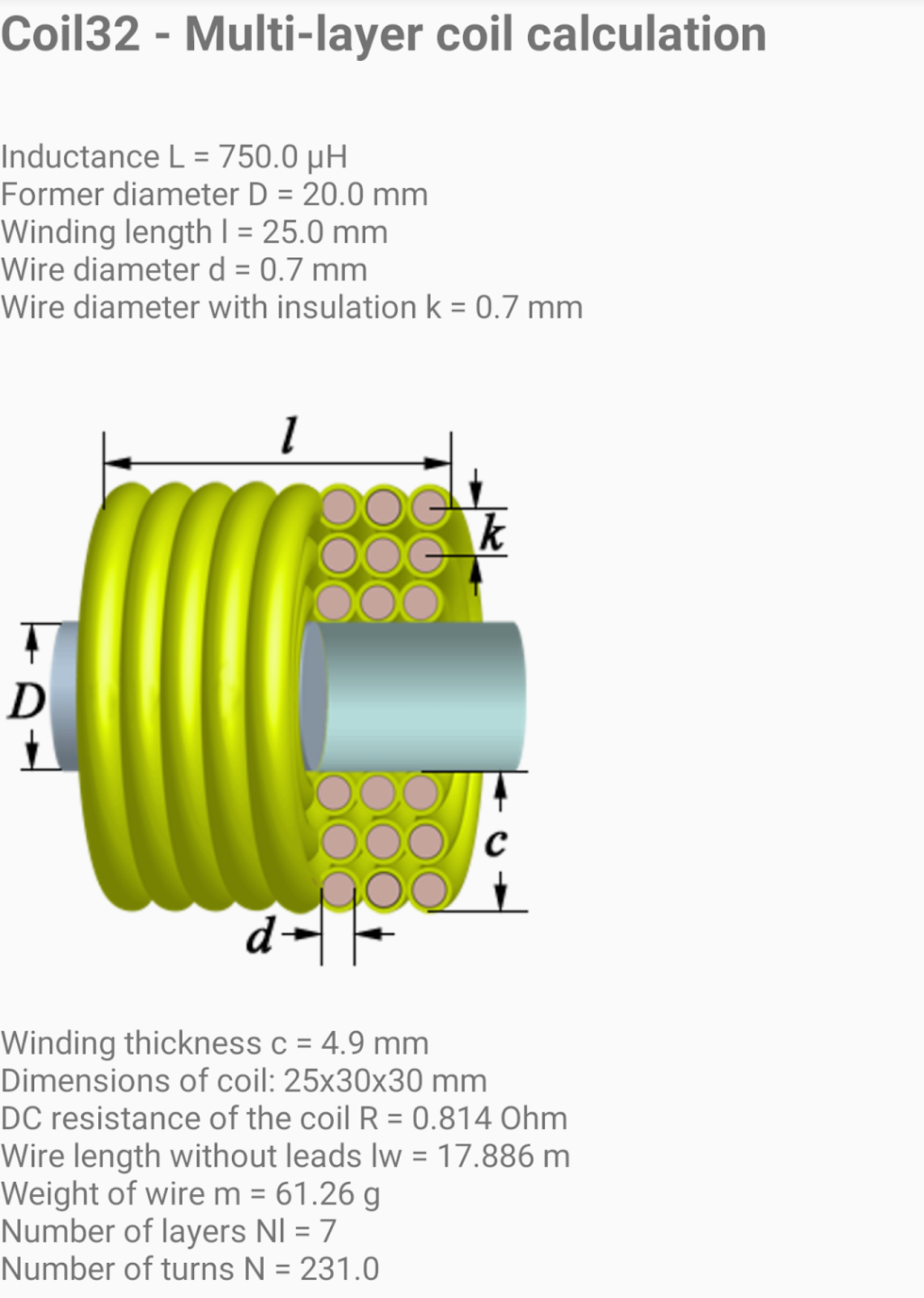
Калькулятор многослойных катушек

На практике часто случается, что когда индуктор ломается, его необходимо отремонтировать – намотать новый провод на место старого. В этом случае вы уже знаете геометрические параметры катушки, но вам нужно знать, сколько витков, слоев, их толщину и необходимую длину проволоки. Стоит отметить, что при намотке витки должны лежать вплотную друг к другу без зазора.

Для расчета индуктивности многослойной катушки используется следующая формула:

• d – сумма диаметра каркаса и толщины обмотки только с одной стороны;
• n – количество обмоток;
• g – толщина намотанного провода
• h – высота намотанного провода;

Из этой формулы, зная значение индуктивности, можно вывести толщину обмотки:

Чтобы определить количество оборотов, используйте формулу:

• d_апрель – диаметр проволоки
• h – высота катушки
• g – толщина обмотки.

Длина одной катушки может быть определена следующим образом:

Где π – константа, а d_{катушка_}– диаметр катушки.

Затем, зная общее количество витков и предполагая, что d – средний диаметр для всех витков, длина всего провода будет определена по формуле:

По сопротивлению проволоки можно определить диаметр, выразив сопротивление через геометрические параметры устройства.

где ρ – удельное сопротивление металла, из которого изготовлен проводник, а S – площадь поверхности проводника, которая определяется по формуле:

Подставив значение площади поверхности и длины проводника, мы получим выражение для сопротивления:

Из значения сопротивления можно вывести формулу для определения диаметра проволоки, предварительно подставив в формулу для расчета числа витков:

Получив диаметр провода, можно определить число витков, которое вместе с другими данными подставляется в первую формулу для расчета индуктивности.

Количество слоев можно определить, разделив толщину обмотки на диаметр проволоки:

Используя приведенные выше расчеты, можно определить все параметры многослойного индуктора, что позволит вам создать устройство с требуемыми параметрами. Вы также можете воспользоваться нашим онлайн-калькулятором ниже, чтобы облегчить расчеты.

Поделиться в социальных сетях

При расчете катушки вы можете столкнуться с двумя случаями:

Как рассчитать индуктивность катушки

Индуктивность катушки зависит от ее геометрических размеров, количества витков и способа намотки. Чем больше диаметр, длина намотки и количество витков катушки, тем выше индуктивность.

Если катушка намотана плотно, индуктивность будет больше, чем если она намотана свободно, с зазорами между витками. Если катушка должна быть намотана до определенного размера, а подходящего диаметра провода нет, то для достижения необходимой индуктивности число витков должно быть немного увеличено при использовании более толстого провода и уменьшено при использовании более тонкого провода.

Все вышеизложенные соображения справедливы при намотке катушек без ферритовых сердечников.

Расчет для однослойных цилиндрических катушек производится по формуле

где L – индуктивность катушки, мкГн; D – диаметр катушки, см; l – длина витка катушки, см; n – число витков катушки.

При расчете катушки могут возникнуть два случая:

(a) Используя заданные геометрические размеры, определите индуктивность катушки;

(b) если индуктивность известна, определите число витков и диаметр провода катушки.

В первом случае все исходные данные в формуле известны, и расчет прост.

Пример. Определим индуктивность катушки, изображенной на рис. 97; для этого подставим все необходимые значения в формулу:

Во втором случае известны диаметр катушки и длина намотки, которые, в свою очередь, зависят от числа витков и диаметра провода. Поэтому рекомендуется проводить расчеты в следующем порядке. Исходя из проектных предпосылок, размеры катушки, диаметр и

длину обмотки, а затем рассчитать количество витков по формуле

Определив число витков, определяют диаметр изолированного провода по формуле

где d – диаметр провода, мм, l – длина катушки, мм, n – количество витков.

Пример. Необходимо изготовить катушку диаметром 1 см и длиной намотки 2 см с индуктивностью 0,8 мкГн.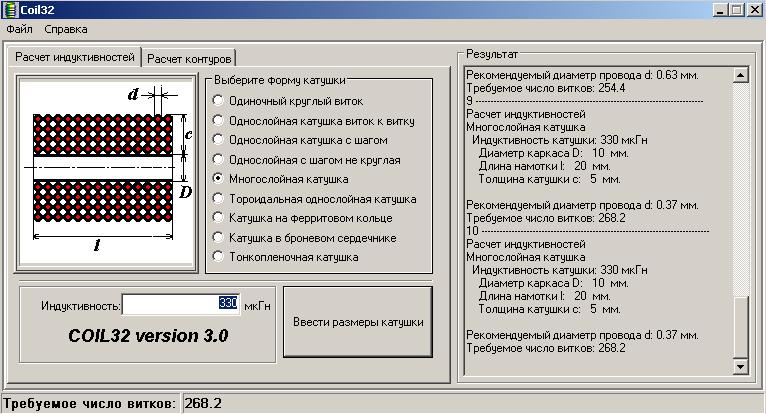 Катушка наматывается последовательно с витками на катушке.

Возьмите за основу значения, приведенные в последней формуле,

Если эта катушка намотана проводом меньшего диаметра, то рассчитанные 14 витков должны быть распределены по всей длине катушки (20 мм) с равным расстоянием между витками, т.е. с шагом намотки. Индуктивность такой катушки будет на 1-2% ниже номинальной, что следует учитывать при изготовлении таких катушек. В случае намотки проволокой толщиной более 1,43 мм следует произвести новые расчеты, при необходимости увеличив диаметр или длину намотки катушки. Также может потребоваться одновременное увеличение обоих параметров, пока размеры катушки не станут подходящими для данной индуктивности.

Следует отметить, что, используя приведенные выше формулы, рекомендуется рассчитывать катушки с длиной намотки l, равной или большей половины диаметра. Если длина обмотки меньше половины диаметра D/2 , то более точные результаты можно получить по формулам

Вы можете рассчитать индуктивность самостоятельно или сделать расчет онлайн с помощью специального калькулятора.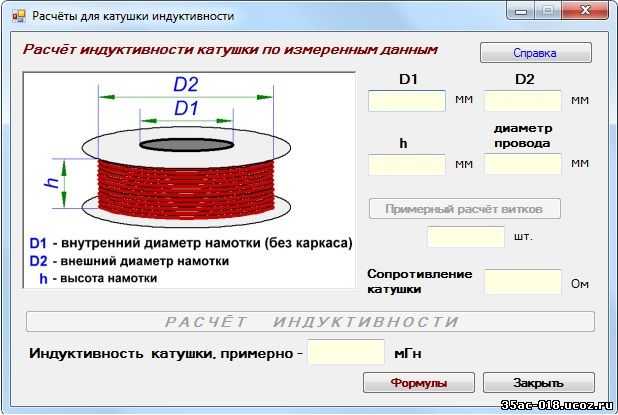 Наиболее часто используемой программой для автоматических расчетов является Coil32. Вы можете бесплатно скачать его с сайта Coil32 или воспользоваться онлайн-калькулятором. Калькулятор прост в использовании.

Калькулятор расчета катушки

Значение индуктивности можно рассчитать автоматически или рассчитать онлайн с помощью калькулятора. Наиболее часто используемой программой для автоматических расчетов является Coil32. Его можно бесплатно загрузить с сайта Coil32 или использовать в качестве онлайн-калькулятора. Пользоваться этой программой довольно просто.

Сначала выберите тип продукта (однослойный или многослойный, с ферритовым сердечником или без него, возможны и другие варианты). Введя в калькулятор рассчитанные геометрические параметры, диаметр провода, количество витков и свойства сердечника, программа может получить ожидаемую индуктивность изделия. Количество витков и диаметр проволоки могут быть изменены в расчете для получения требуемого значения.

Собранное изделие можно проверить на соответствие требуемым параметрам с помощью тестера. Такое устройство называется LC-тестером. Он измеряет индуктивность индукторов и емкость конденсаторов. Если результаты измерения отклоняются от заданного значения, можно увеличить или уменьшить количество витков проволоки на изделии.

При желании вы можете самостоятельно рассчитать индуктивность катушки без сердечника или с сердечником. Единой формулы не существует, она строго индивидуальна для каждого случая. В общем, они прямо пропорциональны количеству витков и диаметру катушки. Например, расчет для однослойной цилиндрической обмотки производится по формуле:

L = (D/10)2*n2/(4.5*D+10*l)

Где L – индуктивность в микро Генри, D – диаметр в мм, L – длина в мм и n – число витков. Эта эмпирическая формула очень проста и не учитывает диаметр проволоки или рабочую частоту, на которой будет использоваться изделие.

Расчет индуктивности катушки с сердечником более сложен. Когда добавляется сердечник, индуктивность значительно увеличивается. При расчете в формулу добавляются параметры магнитных свойств сердечника.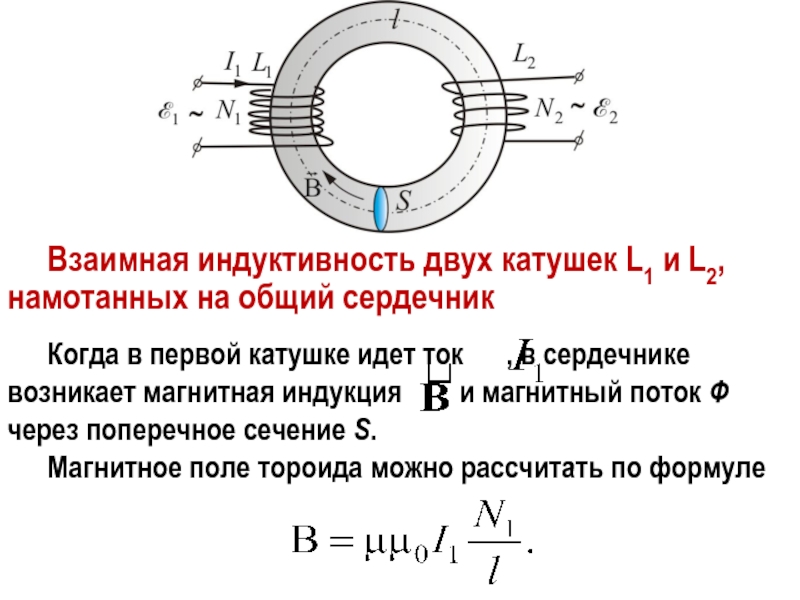 Еще более сложными являются формулы для многослойных или тороидальных катушек. Для редкого или первого использования лучше всего использовать специальный калькулятор. Полученные расчеты можно проверить вручную с помощью формул. В любом случае, параметры собранного изделия можно проверить после изготовления и при необходимости изменить.

Пример: Рассчитайте число витков и длину намотки катушки 10 мкГн, намотанной эмалированным проводом диаметром 0,65 мм (0,7 мм с изоляцией) на оправке длиной 2 см.

Факторы, влияющие на индуктивность катушки

Существует несколько факторов, влияющих на индуктивность катушки.

Количество поворотов. Катушка с большим количеством витков имеет большую индуктивность, чем катушка с меньшим количеством витков.

Для расчета индуктивности необходимо знать форму самой катушки и магнитную проницаемость среды внутри нее (относительная магнитная проницаемость среды – это отношение магнитной проницаемости вакуума к магнитной проницаемости среды). Это очевидно для разных материалов).

Как рассчитать индуктивность

Подобно тому, как тело, обладающее массой в механике, противостоит ускорению в пространстве, проявляя инерцию, индуктивность противостоит изменению тока в проводнике, проявляя самоиндуцированную ЭДС. Это самоиндукционный ЭМП, который сопротивляется как уменьшению тока, стремясь сохранить его, так и увеличению тока, стремясь уменьшить его.

Дело в том, что в процессе изменения (увеличения или уменьшения) тока в контуре, изменяется и создаваемый этим током магнитный поток, расположенный в основном в области, ограниченной этим контуром. А поскольку магнитный поток увеличивается или уменьшается, он наводит в той же цепи ЭДС самоиндукции (согласно принципу Ленца – против вызвавшей ее причины, т.е. против упомянутого тока). Индуктивность L – это коэффициент пропорциональности между током I и общим магнитным потоком Ф, создаваемым этим током:

Таким образом, чем больше индуктивность цепи, тем больше она мешает изменению тока под действием создаваемого ею магнитного поля (того же поля), а это значит, что изменение тока под действием большей индуктивности при том же приложенном напряжении занимает больше времени. Верно и следующее утверждение: чем больше индуктивность, тем больше напряжение, которое будет создаваться на концах цепи при изменении магнитного потока через нее.

Предположим, что мы изменяем магнитный поток в определенной области с постоянной скоростью, тогда, покрывая эту область различными контурами, большее напряжение будет на том контуре, индуктивность которого больше (этот принцип работает в трансформаторе, катушке Румкорфа и т.д.).

Но как рассчитать индуктивность цепи? Как найти коэффициент пропорциональности между током и магнитным потоком? Первое, что нужно запомнить, это то, что индуктивность изменяется по Генри (Gn). На выходах цепи с индуктивностью 1 генри будет создано напряжение 1 В, если ток в цепи изменяется на один ампер в секунду.

Величина индуктивности зависит от двух параметров: геометрических размеров цепи (длина, ширина, количество витков и т.д.) и магнитных свойств среды (если, например, внутри катушки находится ферритовый сердечник, то ее индуктивность будет больше, чем при отсутствии сердечника).

Чтобы рассчитать полезную индуктивность, необходимо знать форму самой катушки и магнитную проницаемость среды внутри нее (относительная магнитная проницаемость среды – это отношение магнитной проницаемости вакуума к магнитной проницаемости среды). Это очевидно для разных материалов).

Рассмотрим формулы для расчета индуктивности наиболее распространенных форм катушек (цилиндрический соленоид, тороид и длинный проводник).

Вот формула для расчета индуктивности соленоида – катушки, длина которой намного больше ее диаметра:

Как видно, зная число витков N, длину обмотки l и площадь поперечного сечения катушки S, можно найти приблизительную индуктивность катушки без сердечника или с сердечником, при постоянной магнитной проницаемости вакуума:

Индуктивность тороидальной катушки, где h – высота тороида, r – внутренний диаметр тороида, R – внешний диаметр тороида:

Индуктивность тонкого проводника (радиус поперечного сечения намного меньше его длины), где l – длина проводника, а r – радиус его поперечного сечения. Mu с индексами i и e – относительные магнитные проницаемости внутренней (внутренней, материал проводника) и внешней (внешней, материал вне проводника) среды:

Таблица относительных магнитных проницаемостей поможет вам оценить, какую индуктивность можно ожидать от цепи (проводника, катушки), если в качестве сердечника использовать данный магнитный материал:

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это очень поможет в развитии нашего сайта!

Сопротивление катушки R может быть выражено как

Рассчитать индуктивность многослойной катушки без сердечника, используя линейку и омметр

Если размеры катушки выражены в миллиметрах, то ее индуктивность в микрогеннах можно рассчитать по формуле:

• D – средний диаметр катушки,
• h – высота катушки
• g – глубина (толщина намотки) катушки,
• N – количество витков (рис. 1).

Если число витков неизвестно, индуктивность может быть рассчитана по значению постоянного сопротивления катушки. Предполагается, что катушка намотана аккуратно, от витка к витку, цилиндрическим эмалированным проводом (рис. 2). В этом случае приблизительное выражение для числа витков будет следующим:

Где d – диаметр проволоки.

Однако мы будем считать, что диаметр нам неизвестен.

Рисунок 2.

Индуктивность тщательно намотанной катушки можно оценить по ее размеру и сопротивлению обмотки.

Поскольку средняя длина катушки равна π×D, общая длина провода составит N×π×D. Площадь поперечного сечения провода равна

Сопротивление катушки R может быть выражено как

где ρ – удельное сопротивление, выраженное в [Ом-м], а сопротивление – в [Ом-м]. Это дает выражение для квадрата диаметра проволоки:

Теперь подставьте d2 в выражение для числа оборотов:

После возведения в квадрат обеих частей уравнения и сокращения дроби получаем

Подставляя N2 в первое уравнение, получаем

Заменив ρ на медь, мы получим выражение для L, зависящее только от сопротивления и физического размера катушки:

Кстати, отметим интересный вывод, вытекающий из того, что R и L пропорциональны друг другу: коэффициент добротности Q катушки заданных размеров D, g и h при постоянной угловой частоте w =2πF постоянен:

Читайте далее:

• Намотка индукторов.
• Катушка – это катушка. Что такое катушка?.
• Расчет электрической печи: важные моменты проектирования. Методика расчета печи с формулами и допусками.
• Самоиндукция. Энергия самоиндукции, индуктивность – материал по физике PSE.
• 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
• Шаговые двигатели: свойства и практические схемы управления. Часть 2.
• Определите число витков катушки индуктивностью 2,5 Гн, если ток.

Тест катушек индуктивности с сердечником | HiFiCompass

 

  Проблематика

Очень часто в сети поднимаются споры о том какие катушки индуктивности, с сердечником или без, лучше использовать в НЧ секции кроссовера АС. Безусловно, воздушные катушки имеют гораздо лучшие электрические характеристики, за исключением омического сопротивления, и одновременно просто неприличные массо-габаритные параметры. Омическое сопротивление можно значительно уменьшить, используя провод или ленту большего сечения, но, в итоге, получаем катушку громадных размеров и такой же стоимости, которая к тому же является приличной излучающей антенной и не всегда может поместиться внутри АС.

Вообще говоря, если басовый динамик имеет низкую полную добротность, Qts менее 0.3, то дополнительное сопртивление катушки в НЧ фильтре никогда не повредит и можно смело использовать воздушную катушку с вменяемым сечением провода и габаритными размерами. Получаем бескомпромиссный вариант, только необходимо на этапе проектирования корпуса АС учесть эффект влияния дополнительного сопротивления. Такой путь позволит вытянуть немного более низкую граничную частоту АС ценой небольшой уступки в чувствительности и габаритах корпуса.

Но, что делать, если добротность динамика достаточно высока и впритык стыкуется с объемом уже имеющегося корпуса? Как раз с таким случаем мне пришлось столкнуться при разработке АС. Динамик Lambda Acoustics TD15X с мотором повышенной линейности «Apollo» в закрытом ящике объемом 165 литров уже имеет добротность Qts=0.73 — на грани допустимого. Дизайн кроссовера требует две катушки с индуктивностью 5.6 мГн и 3.3 мГн. Естественно, хочется применить воздушные катушки, чтобы не вносить дополнительную нелинейность и не свести на нет труды разработчиков динамика.

Расчеты показали, что катушки с воздушным сердечником будут иметь следующие параметры:

5.6 мГн — R=0.43 Ома, диаметр провода 2 мм, диаметр катушки 130 мм, высота 30 мм, масса 2,23 кг.
3.3 мГн — R=0.31 Ома, диаметр провода 2 мм, диаметр катушки 110 мм, высота 30мм, масса 1,62 кг.

Шутка ли, общий вес катушек 7.7 кг? А габариты и размещение их в корпусе АС?

Суммарное сопротивление двух последовательно включенных катушек дает R=0.74 Ома, что приводит к добротности динамика в корпусе Qts=0.81 и потере чувствительности 0.91 дБ.

Имеется альтернативный вариант — применить катушки с сердечником  «Sledgehammer» Steel Laminate 3.3 mH 15 AWG (сопротивление 0.185 Ома) и «Sledgehammer» Steel Laminate 5.0 mH 15 AWG (сопротивление 0.24 Ома). Катушку 5 мГн можно домотать до 5.6 мГн проводом 2 мм, и выйти на сопротивление 0.25 Ома. В итоге, получаем суммарное сопротивление двух катушек 0.435 Ома и полную добротность динамика 0.78 и потерю в чувствительности 0.5 дБ. Близким аналогом этих катушек являются катушки MCoil FERON (Mundorf) серии BS140.

Сердечники обеих типов катушек набраны из пластин электротехнического железа толщиной 0.35 мм.

С точки зрения итоговой добротности, потери чувствительности, габаритов, массы и цены однозначное преимущество у катушек с сердечником. А как насчет качества? Не будут ли они насыщаться при больших токах? Насколько нелинейность сердечника скажется на общей линейности системы динамик + катушки? 

К сожалению, никто из производителей катушек с сердечниками не приводит никаких внятных данных о поведении их изделий при больших токах. С этой проблемой приходится сталкиваться разработчикам АС и принимать на веру заявления производителя типа «High current design», даже не предполагая, что скрывается за этими словами. Ну, что ж, остается самим провести лабораторную работу и закрыть для себя этот вопрос раз и навсегда. 

С этой целью была собрана простая схема для проведения измерений. Синусоидальное напряжение подавалось от усилителя мощности с максимальным выходным током, ограниченным внутренней защитой, на последовательную цепочку из испытуемой катушки и измерительного добавочного резистора сопротивлением 0. 1 Ом, в виде трех параллельно соединенных резисторов 0.3 Ома мощностью 5 Вт. Сигнал с добавочного резистора подавался на анализатор спектра. Измерения проводились на частотах 20, 50, 100, 200 и 500 Гц при токах от 1 до 8 Ампер. В качестве эталона для сравнения результатов использовались измерения ленточной катушки с воздушным сердечником Mundorf CFC14 6.8 мГн.

Ниже приводятся диаграммы результатов измерений. Анализируя диаграммы, имейте в виду, что при сопротивлении нагрузки-динамика 4 Ома (8 Ом), токи от 1 до 8 Ампер соответствуют следующим мощностям нагрузки:

1 А — 4 Вт (8 Вт для 8 Ом)
2 А — 16 Вт (32 Вт для 8 Ом)
3 А — 36 Вт (72 Вт для 8 Ом)
4 А — 64 Вт (128 Вт для 8 Ом)
5 А — 125 Вт (250 Вт для 8 Ом)
6 А — 144 Вт (288 Вт для 8 Ом)
7 А — 196 Вт (392 Вт для 8 Ом)
8 А — 256 Вт (512 Вт для 8 Ом)

  Измерения катушки Sledgehammer Steel Laminate 3.3 mH на частоте 50 Гц

  Измерения катушки Sledgehammer Steel Laminate 3. 3 mH на частоте 100 Гц

  Измерения катушки Sledgehammer Steel Laminate 3.3 mH на частоте 200 Гц

  Измерения катушки Sledgehammer Steel Laminate 3.3 mH на частоте 500 Гц

 

  Измерения катушки Sledgehammer Steel Laminate 5 mH на частоте 20 Гц

  Измерения катушки Sledgehammer Steel Laminate 5 mH на частоте 50 Гц

  Измерения катушки Sledgehammer Steel Laminate 5 mH на частоте 100 Гц

  Измерения катушки Sledgehammer Steel Laminate 5 mH на частоте 200 Гц

  Измерения катушки Sledgehammer Steel Laminate 5 mH на частоте 500 Гц

  Измерения катушки Mundorf CFC14 6.8 5 mH на частотах 50 Гц/8 Ампер и 200 Гц/4 Ампера

  Измерения АЧХ цепей с катушками Sledgehammer 3.3 mH, 5 mH и Mundorf CFC14 6.8 mH

  Итоги

Итак, какие же выводы можно сделать из анализа этого массива диаграмм?

1. Для катушек с сердечником стабильно обнаруживается зависимость между уровнем нелинейных искажений и величиной проходящего тока
2. Искажения катушек с воздушным сердечником не зависят от тока. В принципе, так и должно быть.
3. Амплитудно-частотные характеристики катушек с сердечником и без в диапазоне частот до 5 кГц практически не отличаются друг от друга.
4. С повышением частоты от 20 Гц до 500 Гц нелинейные искажения катушек с сердечником незначительно растут. К примеру, для катушки 5 мГн увеличение составляет в 2 раза.
5. Минимальный уровень нелинейных искажений для одного из самых лучших с этой точки зрения динамиков Lambda Acoustics TD15X при напряжении 11.2 Вольта, что соответствует току примерно 1.5 Ампера (порядка 18 Вт), составляет -50 ÷ -53 dB, в то время как собственный уровень искажений катушки 3.3 мГн составляет -80 дБ, а катушки 5 мГн -76 дБ. Даже при величине тока 8 А, что соответствует мощности приблизительно 512 Вт, искажения катушки 5 мГн не превышают -59 дБ.

Все это говорит о том, что катушки с сердечниками типа Sledgehammer Steel Laminate AWG15 и Mundorf MCoil FERON могут смело использоваться в цепях НЧ фильтров высококачественных акустических систем с самыми линейными НЧ динамиками без риска заметного снижения качества звучания.

Формула для индуктивности с прямоугольной катушкой без воздушного сердечника?

спросил 1 год, 9 месяцев назад

Изменено 1 год, 9 месяцев назад

Просмотрено 146 раз

\$\начало группы\$

У кого-нибудь есть формула для расчета индуктивности катушки, намотанной на прямоугольный невоздушный сердечник? Кажется тривиальным, но это самое близкое, что я искал, и это только для воздушного сердечника: http://electronbunker. ca/eb/InductanceCalcRc.html

Я пытаюсь определить величину индуктивности, которую я буду иметь с сердечником 25,4 мм x 6,36 мм, который в настоящее время состоит из смеси микрометаллов 40 (60 мкм) (https://www.micrometals.com/products/materials/ -40/) и N витков провода. Хотя я могу просто умножить значение с вышеуказанного сайта на 60 для низких частот, которые я использую (< 5 кГц, если они будут работать непрерывно), не зная используемой формулы, я не уверен в этом.

пока не знаю ни количество витков катушки (буду использовать сколько потребуется), ни импульсную силу тока (т.к. зависит от суммарной индуктивности и сопротивления, которые я пытаюсь минимизировать, чтобы уменьшить общий ток необходимый). Мой лучший WAG для тока составляет около 100 ампер при 6 В в течение <0,1 мс. Минимизация ширины катушек важна для того, чтобы линии магнитного потока были как можно короче до держателя.

Физически сердечник расположен по образцу, как показано ниже, подобно U для трансформатора. Между вертикальными сердечниками вставлен постоянный магнит (ширина 6,36 мм, как показано, глубина 25,4 мм). Одна «пара катушек» находится на каждой стороне U. Эти катушки будут быстро пульсировать (возможно, 3T) один раз, чтобы создать большую магнитную силу, чтобы изменить путь потока постоянного магнита от прохождения через держатель к прохождению через зазор в дно (с куском стали на месте, как показано на дне). Затем полярность катушки можно изменить на противоположную и быстро запустить импульс, чтобы запустить путь потока через кипер, чтобы высвободить сталь. 92 на N витков.

\$A_L\$ зависит от геометрии, размера и проницаемости. Обычно используются сердечники E или торроиды, а не кубические прямоугольники.

Неверно определять сердечник как неметаллический, поскольку он представляет собой ферритовую смесь магнитных, диэлектрических и металлических частиц. Это специальная смесь, которая представляет собой NP0/C0G на 25 футах и ​​NTC за пределами этого диапазона на параболической кривой.

Iмакс. обычно оценивается при 90 % L ном.

NP0 означает 0 отрицательных температурных коэффициентов (NTC) и 0 PTC, но с допуском +/- xx ppm, часто произносится как NP-Oh.

Для расчета L с определенными допусками необходимо указать каталог или техническое описание, а также фактическую трехмерную геометрию, диаметр провода и частоту. Не следует делать никаких предположений, кроме как следовать рекомендациям производителя оригинального оборудования в соответствии с приведенной выше формулой.

\$\конечная группа\$

10

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.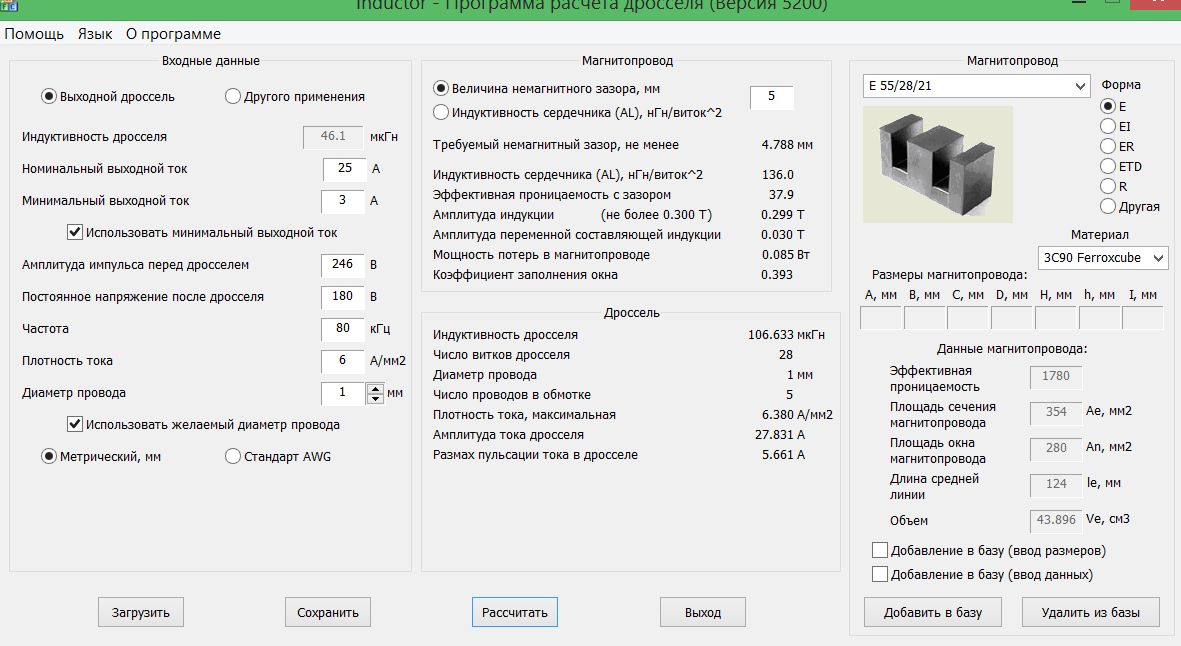

индуктор — Путаница в расчете индуктивности катушки

спросил 5 лет, 3 месяца назад

Изменено 5 лет, 3 месяца назад

Просмотрено 4к раз

\$\начало группы\$

Я немного не понимаю, как рассчитать индуктивность проволочной катушки. Хотя я думал, что это будет действительно ясно, меня смущает то, что, похоже, существуют разные способы его расчета. В этом вопросе результат формулы индуктивности зависит от площади поперечного сечения, количества витков, проницаемости и длины катушки. Для калькулятора на EEWeb входными данными являются диаметр (и, следовательно, площадь поперечного сечения), количество витков, магнитная проницаемость и диаметр провода, а не длина катушки. Я не понимаю, как связаны формулы или какую из них использовать. Я предполагаю, что второй расчет определяет индуктивность катушки длиной один метр, и мне нужно разделить на длину катушки, индуктивность которой я хочу найти, но я не уверен.

• катушка индуктивности
• индуктивность

\$\конечная группа\$

2

\$\начало группы\$

Я предполагаю, что 2-й расчет определяет индуктивность для катушка длиной один метр, и я должен разделить на длину катушки, которую я бы хочу найти индуктивность, но я не уверен.

Нет, это не имеет отношения к соленоиду длиной 1 метр.

Калькулятор EEweb определенно проблематичен, потому что он предполагает, что все «витки» расположены друг над другом, а не расположены как соленоид. Это можно легко доказать. Например, если я задаю диаметр петли 279 мм и диаметр провода 1 мм, я получаю индуктивность 1 мкГн.

Если я удвою витки, то получу 4 мкГн. Если я сделаю 100 витков, я получу 10 мГн — именно так изменится индуктивность, если намотать на сердечник без потока рассеяния, т.е. индуктивность пропорциональна квадрату витков.

Однако 100 витков не могут занимать сплоченный объем пространства и вообще возможно надеяться на 100% сцепление каждого витка друг с другом.

По сути, это куча ду-ду.

\$\конечная группа\$

\$\начало группы\$

Расчеты индуктивности очень чувствительны к геометрии обмотки, и существуют академические поправочные коэффициенты. Это потому, что есть много других переменных от простых конструкций до сложных.

Базовый расчет должен включать диаметр провода, длину и средний диаметр обмотки, так как коэффициент заполнения, изоляция и перекрытие имеют некоторые вариации.

Полученный отсюда эффективный диаметр Deff используется для расчета индуктивности однослойной спиральной катушки:

где:

мк: магнитная проницаемость сердечника катушки
Н: количество витков
l: длина катушки, измерено от центра к центру соединительных проводов
kL: поправочный коэффициент неравномерности поля по Lundin
ks: поправочный коэффициент на самоиндукцию круглого провода по Розе
km: поправочный коэффициент на взаимную индуктивность круглого провода по Гроверу и Найту

\$\конечная группа\$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.