Какое соединение элементов называется параллельным. Параллельное соединение элементов электрической цепи: особенности и применение

Что такое параллельное соединение элементов цепи. Как рассчитать параметры параллельного участка. Какие преимущества дает параллельное подключение. Где применяется параллельное соединение в электротехнике.

Что представляет собой параллельное соединение элементов цепи

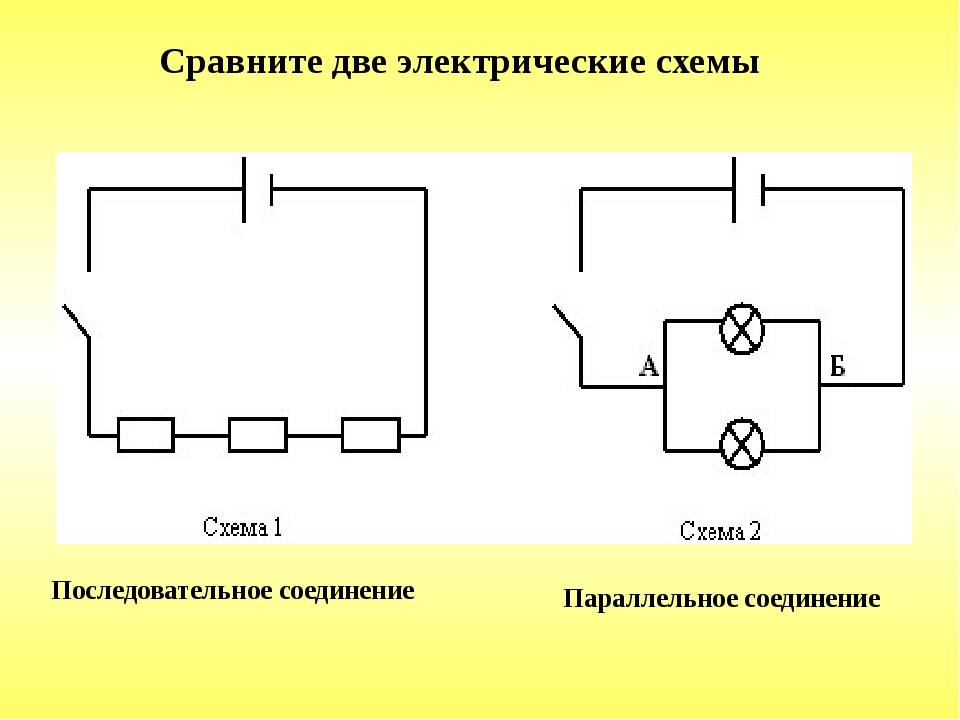
Параллельное соединение элементов электрической цепи — это такое соединение, при котором все элементы подключаются к одним и тем же двум узлам цепи. При этом:

• Напряжение на всех параллельно соединенных элементах одинаково и равно напряжению источника питания.
• Общий ток цепи равен сумме токов, протекающих через отдельные параллельные ветви.
• Общее сопротивление цепи при параллельном соединении всегда меньше сопротивления любого из параллельно включенных элементов.

Схема параллельного соединения элементов выглядит следующим образом:

[Здесь было бы изображение схемы параллельного соединения]

Как рассчитать параметры параллельного участка цепи

При расчете параллельного соединения элементов используются следующие формулы:

1. Общий ток цепи: I = I1 + I2 + … + In, где I1, I2, …, In — токи в отдельных параллельных ветвях.
2. Общее сопротивление: 1/R = 1/R1 + 1/R2 + … + 1/Rn, где R1, R2, …, Rn — сопротивления отдельных параллельных ветвей.
3. Общая проводимость: G = G1 + G2 + … + Gn, где G1, G2, …, Gn — проводимости отдельных параллельных ветвей.

Для двух параллельно соединенных резисторов можно использовать упрощенную формулу:

R = (R1 * R2) / (R1 + R2)

Преимущества параллельного соединения элементов

Параллельное соединение имеет ряд важных преимуществ:

• Позволяет уменьшить общее сопротивление цепи.
• Обеспечивает независимую работу параллельно включенных элементов.
• Дает возможность подключать и отключать отдельные элементы без нарушения работы всей цепи.
• Повышает надежность цепи за счет резервирования.

Где применяется параллельное соединение в электротехнике

Параллельное соединение широко используется в различных областях электротехники:

• В бытовых электрических сетях для подключения розеток и электроприборов.
• В системах освещения для соединения нескольких светильников.
• В электронных схемах для создания делителей тока.
• В системах электроснабжения для параллельного подключения генераторов или трансформаторов.
• В автомобильной электрике для подключения фар, стоп-сигналов и других потребителей.

Расчет параллельного соединения на практике

Рассмотрим пример расчета параллельного участка цепи с тремя резисторами:

Дано: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 12 В

Необходимо рассчитать общее сопротивление, общий ток и токи в каждой ветви.

1. Рассчитаем общее сопротивление: 1/R = 1/10 + 1/20 + 1/30 = 0.1 + 0.05 + 0.033 = 0.183 R = 1/0.183 = 5.46 Ом
2. Рассчитаем общий ток: I = U/R = 12/5.46 = 2.2 А
3. Рассчитаем токи в каждой ветви: I1 = U/R1 = 12/10 = 1.2 А I2 = U/R2 = 12/20 = 0.6 А I3 = U/R3 = 12/30 = 0.4 А

Проверим: I = I1 + I2 + I3 = 1.2 + 0.6 + 0.4 = 2.2 А

Особенности параллельного соединения источников тока

При параллельном соединении источников тока:

• Напряжение на зажимах всех источников одинаково.
• Общий ток равен сумме токов отдельных источников.
• Внутренние сопротивления источников соединяются параллельно.

Параллельное соединение используется для увеличения тока нагрузки. При этом источники должны иметь одинаковое напряжение.

Сравнение параллельного и последовательного соединения

Основные различия между параллельным и последовательным соединением:

Параметр	Параллельное соединение	Последовательное соединение
Напряжение	Одинаковое на всех элементах	Сумма напряжений на элементах
Ток	Сумма токов через элементы	Одинаковый через все элементы
Сопротивление	Меньше наименьшего	Сумма сопротивлений элементов

Правила безопасности при работе с параллельными цепями

При работе с параллельными электрическими цепями важно соблюдать следующие правила безопасности:

• Не превышать допустимую нагрузку на общий участок цепи.
• Использовать провода и элементы с соответствующим сечением и мощностью.
• Применять защитные устройства от перегрузки и короткого замыкания.
• Соблюдать полярность при подключении источников питания.
• Не допускать контакта оголенных проводов параллельных ветвей.

Заключение

Параллельное соединение элементов электрической цепи — важный способ построения электрических схем, имеющий широкое практическое применение. Понимание принципов работы и расчета параллельных цепей необходимо для грамотного проектирования и эксплуатации электротехнических устройств. При правильном использовании параллельное соединение позволяет эффективно решать многие задачи в электротехнике и электронике.

Электротехника часть 4. Соединение элементов цепи

Всем доброго времени суток. В прошлой статье я рассмотрел закон Ома, применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса токов, называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и сопротивлениями.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Последовательное соединение приемников энергии

Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии

Пример последовательного подключения приемников энергии.

В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с напряжением U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления

Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.

Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями

где R – эквивалентное последовательное сопротивление.

Применение последовательного соединения

Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр

Делитель напряжения (слева) и потенциометр (справа).

В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.

Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.

Параллельное соединение приемников энергии

Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже

Пример параллельного соединения приемников энергии.

Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви

Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений

Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.

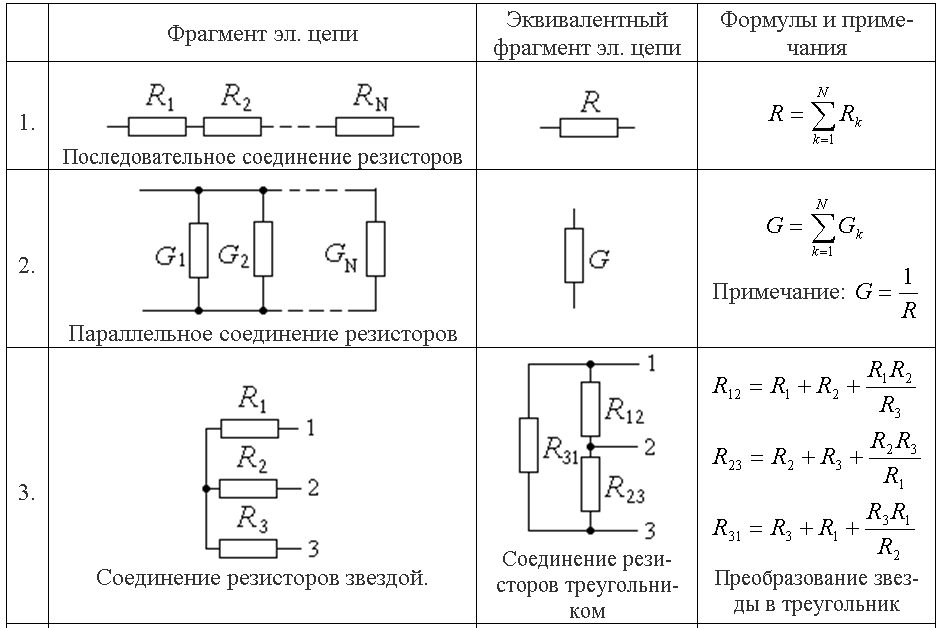
Смешанное соединение приемников энергии

Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии

Пример смешанного соединения приемников энергии.

В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид

В результате получили цепь из двух последовательных приемников энергии R₁₂R₃₄₅ эквивалентное сопротивление и ток, протекающий через них, составит

Тогда падение напряжения по участкам составит

Тогда токи, протекающие через каждый приемник энергии, составят

Первый закон Кирхгофа

Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.

Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением

где ∑ — обозначает алгебраическую сумму.

Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа

Изображение первого закона Кирхгофа.

На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид

Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.

Второй закон Кирхгофа

Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением

В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур

Схема, иллюстрирующая второй закон Кирхгофа.

Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид

Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.

Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

Последовательное соединение элементов электрической цепи

Последовательным называется соединение, когда конец одного элемента соединяется с условным началом второго, конец второго – с началом третьего и т.д.

Рис. 1.1. Схема последовательного соединения элементов

Свойства последовательного соединения элементов.

1. Последовательное соединение характеризуется общим для всех элементов током:

2. Эквивалентное сопротивление последовательного участка схемы:

3. Падения напряжения на отдельных элементах распределяются пропорционально величинам их сопротивлений и в совокупности равны напряжению, подаваемому на схему (следует из второго закона Кирхгофа):

4.  Суммарная мощность приёмников, равная мощности источника (следует из уравнения баланса мощности):

Мощность, потребляемая отдельным элементом:

Параллельное соединение элементов электрической цепи

Параллельным называется соединение, при котором объединяются в узел начала приёмников и соответственно их концы. Напряжение подаётся на узлы.

Рис. 1.2. Схема параллельного соединения элементов

Свойства параллельного соединения элементов.

1. Параллельное соединение характеризуется общим для всех элементов напряжением, равным напряжению питающей сети:

2. Эквивалентное сопротивление параллельного участка схемы:

Эквивалентная проводимость параллельного участка схемы:

Проводимость отдельного элемента:

3.

 Токи в ветвях схемы распределяются обратно пропорционально сопротивлениям элементов и в совокупности равны току в неразветвленной части схемы (следует из первого закона Кирхгофа):

4. Суммарная мощность приёмников, равная мощности источника (следует из уравнения баланса мощности):

Мощность, потребляемая отдельным элементом:

Смешанное соединение элементов электрической цепи

Смешанным называется соединение, при котором имеют место и последовательное, и параллельное соединения элементов.

Рис. 1.3. Схема смешанного соединения элементов

Один из способов расчёта цепей смешанного соединения элементов – метод эквивалентных преобразований, основанный на последовательном преобразовании участков цепи, имеющих параллельное или последовательное соединение элементов

На рис. 1.

3 резисторы R₂иR₃соединены параллельно, следовательно, их эквивалентное сопротивлениеR₂₃равно:

Полученный элемент R₂₃последовательно соединён с сопротивлениемR₁, следовательно, эквивалентное сопротивление всей цепи равно:

Остальные параметры схемы на рис. 1.3 определяются исходя из аналогичных рассуждений.

ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ №1

Перед началом работы со стендом проверьте, что автомат под столешницей отключён (находится в нижнем положении).

Опыт №1. Последовательное соединение элементов электрической цепи

Соберите цепь по схеме на рис. 1.4 (рекомендации по сборке даны во введении).

Рис.1.4. Схема проведения опыта №1

Убедитесь, что рукоятка ЛАТРа вывернута против часовой стрелки до упора.

Подайте питание на стенд, включив автомат под столешницей. Нажмите кнопку включения сети «ВКЛ». Включите источник питания «ПОСТОЯННОЕ». ЛАТРом плавно увеличивайте напряжение, подаваемое на собранную цепь, до значения, указанное преподавателем. Проведите на стенде необходимые измерения, результаты занесите в табл. 1.1. По окончании опыта выверните рукоятку ЛАТРа против часовой стрелки до упора и отключите источник питания.

Ветви, узлы и циклы с последовательностью и параллельностью

Опубликовано 7 июля 2020 г.

Каждый шаг в процессе обучения необходим для создания основы для следующего шага. В некоторых случаях это более верно, чем в других случаях. В данном случае это вдвойне верно, так как многие вещи, которые мы обсуждаем сегодня, не будут напрямую применимы к решению схем, но будут абсолютно фундаментальными для понимания структуры схем, что, возможно, является первым шагом в решении схемы. Так что, возможно, я противоречу себе. Но со временем это станет настолько естественным, что даже не будет осознанным шагом.

Первая часть схемы, которую мы собираемся обсудить, — это ответвления. Ответвление — это общий термин, обозначающий один элемент в цепи. Это может быть источник напряжения, резистор, конденсатор, катушка индуктивности или что-то еще. Он охватывает любой двухполюсник. Более сложные устройства, такие как операционные усилители или микроконтроллеры, не подходят под термин «ветвь», но ничего страшного, мы пока не будем иметь дело с чем-то настолько сложным.

Второй частью цепи является узел. Это точка соединения между двумя или более ветвями. Хороший способ думать об этом может быть соединением, где токи втекают и вытекают в зависимости от разных ветвей. Узлы являются важной частью анализа и проектирования схем, поэтому давайте рассмотрим пару примеров того, что такое узлы:

Наконец, последняя часть цепи, которая важна для нас в данный момент, — это петля. Петля – это замкнутый путь в цепи. Замкнутый путь означает, что он начинается в узле, проходит через другие узлы и заканчивается в том же узле, не проходя через какой-либо другой узел дважды. Обратите внимание, что определение является гибким в том смысле, что вы можете включать больше узлов или исключать узлы, если вы не проходите через один и тот же узел дважды, кроме начального/конечного узла. Давайте рассмотрим пример одной и той же цепи и двух разных петель, которые перекрываются.

Это важно, потому что при анализе цепей у вас есть преимущество в том, что вы можете выбирать циклы, которые наилучшим образом соответствуют ситуации, но есть недостаток, заключающийся в том, что они немного сложнее, поскольку вам нужно убедиться, что ваши циклы имеют математический смысл. и в сочетании друг с другом. С большой гибкостью приходит большая ответственность.

Теперь, когда мы рассмотрели эти термины и, в частности, узнали, что такое узлы, мы можем поговорить о последовательных и параллельных ответвлениях и в чем их отличия.

Последовательное и параллельное

Ветвь или элемент с двумя клеммами соединены последовательно с одной или несколькими другими ветвями, когда они используют только один узел и пропускают одинаковую величину тока. Обычно они выглядят так, как будто они соединены последовательно, один за другим, как цепочка. Лучший способ описать это, вероятно, с помощью нескольких изображений. В качестве примера мы будем использовать резисторы, которыми славится наш друг CircuitBread, компания Ohmite.

Как вы можете видеть на первом изображении, есть две ветви, обе резисторы, и между ними есть узел, который является исключительным для этих двух ветвей. Таким образом, любой ток, протекающий через один резистор, будет протекать через другой.

На втором изображении есть три ответвления, два резистора сверху и один резистор снизу. Это более сложный пример, поскольку есть один узел, к которому подключены все три ветви. Если посмотреть на это с одной стороны, сгруппировав два верхних резистора, то два верхних резистора включены последовательно с нижним резистором. Любой ток, протекающий через эти верхние резисторы, будет протекать через нижний резистор, поэтому оба этих верхних резистора включены последовательно с нижним резистором. Важно отметить, что только один из этих резисторов наверху имеет номинал 9.0029, а не последовательно с нижним резистором, это то, что оба из этих резисторов наверху последовательно соединены с одним резистором внизу.

Ветки параллельны, когда два или более двухполюсных элемента подключены к одним и тем же двум узлам. В этом случае не имеет значения, подключены ли другие вещи к любому из этих узлов — пока оба элемента двухполюсника подключены к одним и тем же узлам, они параллельны. В то время как последовательные устройства имеют одинаковый ток через них, параллельные устройства имеют одинаковое напряжение на них. Еще раз, некоторые изображения, надеюсь, помогут.

Как вы можете легко видеть на первом и втором изображениях, эти ветви, снова представленные резисторами, имеют обе стороны своих узлов.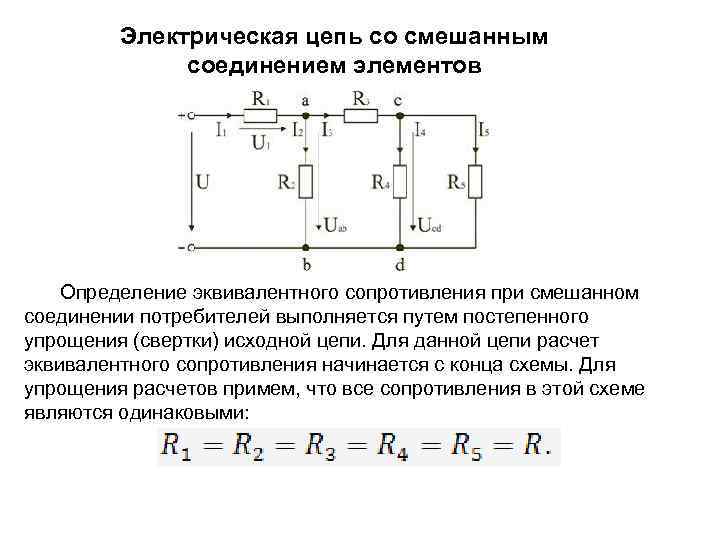 На втором изображении, несмотря на то, что ветвей больше, все они имеют одни и те же два узла, поэтому все они параллельны. Однако третье изображение немного усложняет ситуацию. Есть два последовательно соединенных резистора, и эти два последовательно соединенных резистора параллельны одному резистору. Иногда сложные массивы резисторов или любые другие ответвления можно легко упростить, если вы можете распознавать такие вещи.

Прежде чем мы будем слишком взволнованы, мы должны помнить, что не все происходит последовательно или параллельно, но это происходит достаточно часто, так что вы не только должны, но и почти наверняка станете естественным в идентификации и получении информации из последовательностей и параллельных схемы.

Помимо знания того, что последовательные ветви имеют общий ток, а параллельные ветви имеют одинаковое напряжение на них, одна из важных причин важности параллельных и последовательных компонентов заключается в том, что их обычно можно упростить. Давайте рассмотрим, как это сделать, и я хотел бы отметить, что это применимо только к резисторам, хотя позже принципы будут довольно хорошо перенесены на другие компоненты.

Чтобы упростить последовательные резисторы, просто сложите их вместе. Это очень просто и безболезненно. Это также имеет смысл — если электричество должно сначала пройти через один резистор, а затем через другой, оно должно пробиться через сопротивление обоих из них. Давайте посмотрим на несколько очень быстрых примеров.

Мы всегда рекомендуем проводить практические эксперименты во время обучения, так как это помогает усвоить ситуацию. Компания Ohmite известна своими мощными резисторами, которые определенно являются излишними для этих примеров (хотя их интересно проверить!), но вы можете получить некоторые из них. Маленькие резисторы Rebel, которые являются отличными резисторами, но намного, намного дешевле, чем резисторы большой мощности. Если вы можете, я рекомендую выбрать несколько разных значений и попробовать эти схемы с помощью недорогого мультиметра или омметра.

Упрощение параллельных резисторов немного сложнее, но все же просто, и есть даже случаи, когда шаги можно упростить еще больше. В общем, для расчета эквивалентного сопротивления параллельных резисторов вы просто используете это уравнение:

Little Rebel Resistors

Высококачественные, но недорогие резисторы от Ohmite, которые можно использовать для проверки этих концепций на макетной плате.

Купить онлайн

ОТ Ohmite

Это очень просто, если у вас есть калькулятор, а у нас есть инструмент, который делает это еще проще. уравнение. Убедитесь, что вы не пропустите этот шаг! Тем не менее, самое главное — получить интуитивное представление об этом. Одна вещь, которую вы должны понимать, заключается в том, что параллельные резисторы создают эквивалентное сопротивление, меньшее, чем сопротивление самого маленького резистора. И чем больше резисторов вы соедините параллельно, тем меньше будет общее сопротивление.

Есть два случая, когда вы можете упростить это уравнение. Дело в том, что у вас всего два резистора. Тогда уравнение упрощается до:

В последнем случае, если два резистора имеют одинаковое сопротивление, то эквивалентное сопротивление составляет половину двух резисторов. Вы можете подставить любое число в любое уравнение и доказать это себе, если вы недоверчивый тип.

Краткое описание ветвей, узлов и контуров с последовательными и параллельными компонентами

Теперь мы на шаг ближе к тому, чтобы анализировать существующие схемы и разрабатывать собственные! Мы узнали несколько важных терминов об электронных схемах и теперь можем идентифицировать ветви, узлы и петли. Мы использовали наши знания о ветвях и узлах, чтобы узнать о последовательных и параллельных цепях, как их идентифицировать и как их упростить. Мы скоро воспользуемся нашими знаниями о петлях, когда узнаем о законах тока и напряжения Кирхгофа (KCL и KVL соответственно), двух больших частях анализа цепей, которые откроют огромный сундук с инструментами для вашего электронного арсенала. Однако, прежде чем мы узнаем о KCL и KVL, осталось узнать о различных источниках питания в нашем следующем руководстве.

Автор:

Джош Бишоп

Интересуясь встраиваемыми системами, туризмом, кулинарией и чтением, Джош получил степень бакалавра электротехники в Университете штата Бойсе.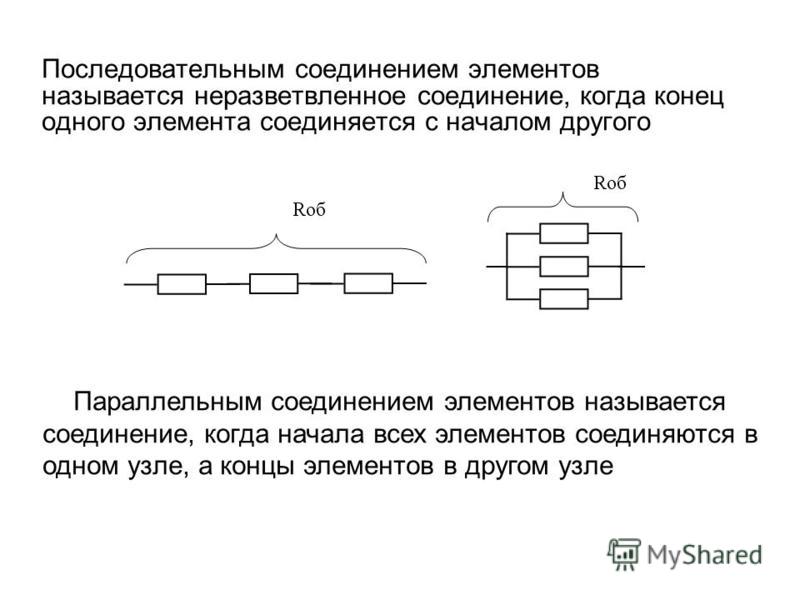 Проработав несколько лет офицером CEC (Seabee) в ВМС США, Джош уволился и в конце концов начал работать над CircuitBread с кучей замечательных людей. В настоящее время Джош живет на юге Айдахо с женой и четырьмя детьми.

---

Создано с нашим другом:

Компания Ohmite является ведущим поставщиком резистивных изделий для сильноточных, высоковольтных и высокоэнергетических приложений …

Узнать больше

Бонусы от этого друга:

• Калькулятор закона Ома

Социальная сеть друзей

• YouTube
• Линкедин

Получите новейшие инструменты и учебные пособия, только что из тостера.

Является ли двухэлементная цепь последовательной или параллельной?

спросил 8 лет, 8 месяцев назад

Изменено 6 лет, 7 месяцев назад

Просмотрено 3к раз

\$\начало группы\$

Источник напряжения подключен к резистору последовательно или параллельно? Если источник напряжения подключен параллельно резистору, то почему они разделяют один и тот же ток? Если источник напряжения включен последовательно с резистором, то почему они имеют одинаковое напряжение?

Они и последовательно и параллельно, верно?

• параллельный
• последовательный

\$\конечная группа\$

4

\$\начало группы\$

A Источник и его нагрузки всегда имеют одни и те же ток и напряжение, что и источник и нагрузки. Мы говорим о параллельном/последовательном соединении их по отдельности, а не вместе. Это означает, что мы говорим либо о двух (или более) нагрузках последовательно/параллельно друг с другом, либо о двух (или более) последовательно/параллельно источниках.

\$\конечная группа\$

\$\начало группы\$

Да. Ваше рассуждение верно. Они имеют один и тот же ток, поэтому они включены последовательно. Однако они также параллельны, поскольку имеют одинаковое напряжение.

\$\конечная группа\$

\$\начало группы\$

Два элемента в основном вырожденный случай. Ток через оба элемента одинаков, поэтому они включены последовательно. Напряжения на обоих элементах одинаковы, поэтому они параллельны. Однако большинство схем состоят из более чем двух элементов, поэтому в большинстве практических случаев различие более очевидно.

\$\конечная группа\$

\$\начало группы\$

На мой взгляд, вы создаете путаницу, включая источник питания в качестве «элемента». И думать, что «элемент» — это то же самое, что и груз. Термины конфигурации «последовательный» или «параллельный» применяются к двум или более нагрузкам . Поскольку ваша схема имеет только одну нагрузку , ни один термин не применяется.

\$\конечная группа\$

\$\начало группы\$

Это не последовательная или параллельная цепь, поскольку определение основано на нагрузке, а не на проводах. У вас есть два провода, подключенных только к одному элементу. Кроме того, источник питания не считается «элементом», как вы имели в виду.

Подумайте об этом так:

У вас есть одна линия, как показано ниже:

_________________________-

Эта линия параллельна или перпендикулярна?
Ответ: Ни то, ни другое. Вам нужны две линии, чтобы определить, параллельна она или перпендикулярна.

Теперь у вас есть две линии:
__________________-
__________________-

Они параллельны.