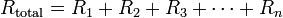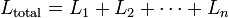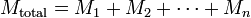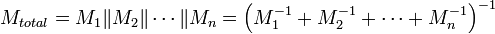Чем отличается последовательное соединение проводников от параллельного. Как рассчитать силу тока, напряжение и сопротивление при разных типах соединений. Какие формулы применяются для расчета параметров электрической цепи при последовательном и параллельном подключении. Примеры решения задач на расчет цепей с различными соединениями проводников.
Ключевые отличия последовательного и параллельного соединения проводников
Последовательное и параллельное соединение проводников имеют принципиальные различия в характере протекания тока и распределении напряжения:
- При последовательном соединении ток во всех элементах цепи одинаков, а напряжение распределяется между ними.
- При параллельном соединении напряжение на всех элементах одинаково, а ток делится между параллельными ветвями.
Рассмотрим подробнее особенности каждого типа соединения.
Особенности последовательного соединения проводников
При последовательном соединении проводники располагаются друг за другом, образуя единую неразветвленную цепь. Основные характеристики:

- Сила тока одинакова во всех элементах цепи: I = I1 = I2 = … = In
- Общее напряжение равно сумме напряжений на отдельных участках: U = U1 + U2 + … + Un
- Общее сопротивление равно сумме сопротивлений участков: R = R1 + R2 + … + Rn
Особенности параллельного соединения проводников
При параллельном соединении все элементы подключены к общим точкам начала и конца. Ключевые свойства:
- Напряжение одинаково на всех параллельных ветвях: U = U1 = U2 = … = Un
- Общий ток равен сумме токов в отдельных ветвях: I = I1 + I2 + … + In
- Обратная величина общего сопротивления равна сумме обратных величин сопротивлений ветвей: 1/R = 1/R1 + 1/R2 + … + 1/Rn
Формулы для расчета параметров электрической цепи при последовательном соединении
При последовательном соединении проводников применяются следующие формулы:
- Общее сопротивление: R = R1 + R2 + … + Rn
- Сила тока: I = U / R, где U — общее напряжение, R — общее сопротивление
- Напряжение на участке: Ui = I * Ri
- Общее напряжение: U = U1 + U2 + … + Un = I * (R1 + R2 + … + Rn)
Формулы для расчета параметров электрической цепи при параллельном соединении
Для параллельного соединения проводников используются формулы:

- Общее сопротивление: 1/R = 1/R1 + 1/R2 + … + 1/Rn
- Сила тока в ветви: Ii = U / Ri, где U — общее напряжение
- Общий ток: I = I1 + I2 + … + In = U * (1/R1 + 1/R2 + … + 1/Rn)
- Напряжение: U = U1 = U2 = … = Un
Примеры решения задач на последовательное соединение проводников
Рассмотрим пример расчета цепи с последовательным соединением резисторов:
Задача: Три резистора с сопротивлениями R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом соединены последовательно. Напряжение источника U = 120 В. Определить силу тока в цепи и напряжение на каждом резисторе.
Решение:
- Находим общее сопротивление цепи: R = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом
- Рассчитываем силу тока: I = U / R = 120 В / 60 Ом = 2 А
- Определяем напряжение на каждом резисторе: U1 = I * R1 = 2 А * 10 Ом = 20 В U2 = I * R2 = 2 А * 20 Ом = 40 В U3 = I * R3 = 2 А * 30 Ом = 60 В
Проверка: U1 + U2 + U3 = 20 В + 40 В + 60 В = 120 В, что соответствует напряжению источника.
Примеры решения задач на параллельное соединение проводников
Разберем задачу на расчет параллельного соединения резисторов:

Задача: Два резистора с сопротивлениями R1 = 30 Ом и R2 = 60 Ом соединены параллельно. Напряжение на участке U = 120 В. Определить силу тока в каждой ветви и общий ток.
Решение:
- Рассчитываем токи в каждой ветви: I1 = U / R1 = 120 В / 30 Ом = 4 А I2 = U / R2 = 120 В / 60 Ом = 2 А
- Находим общий ток: I = I1 + I2 = 4 А + 2 А = 6 А
- Проверяем, используя формулу общего сопротивления: 1/R = 1/R1 + 1/R2 = 1/30 + 1/60 = 3/60 = 1/20 R = 20 Ом I = U / R = 120 В / 20 Ом = 6 А
Результат совпадает с суммой токов в ветвях.
Применение последовательного и параллельного соединения в электротехнике
Последовательное и параллельное соединение проводников широко используется в различных электротехнических устройствах:
- Последовательное соединение применяется в электрических цепях, где требуется одинаковый ток во всех элементах, например, в елочных гирляндах.
- Параллельное соединение используется для подключения бытовых электроприборов к электросети, что обеспечивает одинаковое напряжение на всех устройствах.
- Комбинация последовательного и параллельного соединения позволяет создавать сложные электрические схемы с нужными характеристиками.
Как выбрать оптимальный тип соединения проводников для конкретной задачи
При выборе типа соединения проводников следует учитывать несколько факторов:

- Цель: последовательное соединение подходит для создания делителей напряжения, параллельное — для равномерного распределения тока.
- Требования к надежности: при параллельном соединении выход из строя одного элемента не нарушает работу остальных.
- Ограничения по напряжению и току: последовательное соединение увеличивает общее сопротивление, параллельное — уменьшает.
- Необходимость регулировки: последовательное соединение позволяет легко изменять общее сопротивление цепи.
Правильный выбор типа соединения проводников позволяет оптимизировать работу электрической цепи и обеспечить ее эффективное функционирование.
- Последовательное соединение
-

Последовательное соединение проводников.
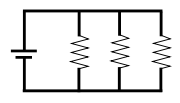
Параллельное соединение проводников.
Последовательное и параллельное соединение в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все, входящие в цепь, элементы объединены двумя узлами и не имеют связей с другими узлами. При последовательном соединении проводников сила тока во всех проводниках одинакова.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Последовательное соединение
При последовательном соединении проводников сила тока в любых частях цепи одна и та же:
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: U = U1 + U2
Резисторы
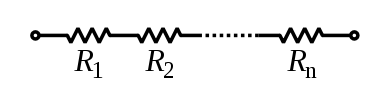
Катушка индуктивности
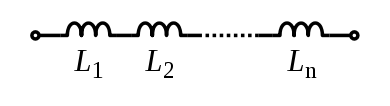
Электрический конденсатор
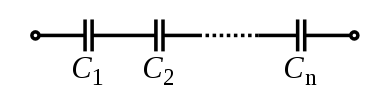
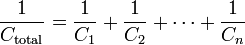 .
.
Мемристоры
Параллельное соединение
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках: I = I1 + I2
Напряжение на участках цепи АВ и на концах всех параллельно соединенных проводников одно и то же: U = U1 = U2
Резисторы
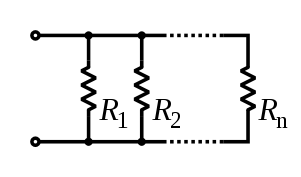
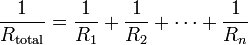 .
.
Катушка индуктивности
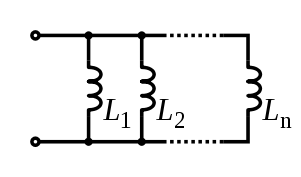
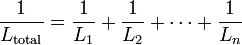 .
.
Электрический конденсатор
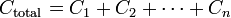 .
.
Мемристоры
См. также
Wikimedia Foundation. 2010.
- Последняя фантазия
- Последовательности баркера
Смотреть что такое «Последовательное соединение» в других словарях:
последовательное соединение — Электрическое соединение, при котором через рассматриваемые участки электрической цепи возможен только один и тот же электрический ток. [ГОСТ Р 52002 2003] Тематики электротехника, основные понятия Синонимы последовательное соединение участков… … Справочник технического переводчика
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ — в электротехнике 1) соединение двухполюсников, при котором через них проходит один и тот же ток.2) Соединение четырехполюсников, при котором напряжение и ток на выходе предыдущего четырехполюсника равны напряжению и току на входе последующего … Большой Энциклопедический словарь
последовательное соединение — в электротехнике, 1) соединение двухполюсников, при котором через них проходит один и тот же ток. 2) Соединение четырёхполюсников, при котором напряжение и ток на выходе предыдущего четырёхполюсника равны напряжению и току на входе последующего.… … Энциклопедический словарь
последовательное соединение — nuoseklusis jungimas statusas T sritis automatika atitikmenys: angl. connection in series; series connection vok. Reihenschaltung, f; Serienschaltung, f rus. последовательное соединение, n pranc. couplage en série, m; couplage série, m … Automatikos terminų žodynas
последовательное соединение — nuoseklusis jungimas statusas T sritis chemija apibrėžtis Elektrinės grandinės elementų jungimas vienas paskui kitą (kiekviename jų teka tokio pat stiprio srovė). atitikmenys: angl. series connection rus. последовательное соединение … Chemijos terminų aiškinamasis žodynas
последовательное соединение — nuoseklusis jungimas statusas T sritis fizika atitikmenys: angl. connection in series; series connection vok. Reihenschaltung, f; Reihenschluß, m; Serienschaltung, f rus. последовательное соединение, n pranc. connexion en série, f; montage en… … Fizikos terminų žodynas
Последовательное соединение — в электротехнике, 1) соединение Двухполюсников, при котором через них проходит один и тот же ток, т.к. для него имеется один единственный путь. П. с. источников электроэнергии применяется для получения напряжения, превышающего эдс одного… … Большая советская энциклопедия
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ — в электротехнике 1) соединение двухполюсников, при к ром через них проходит один и тот же ток, т. к. для него имеется единств. путь. П. с. источников электроэнергии применяется для получения напряжения, превышающего эдс одного источника. При П. с … Большой энциклопедический политехнический словарь
последовательное соединение — см. в ст. Электрическая цепь. Энциклопедия «Техника». М.: Росмэн. 2006 … Энциклопедия техники
Последовательное соединение элементов системы — [serial linkage] такое соединение элементов в единую систему, при котором выход предыдущего является входом следующего. Таким образом, вход системы совпадает со входом первого звена, а выходом системы служит выход последнего звена. (Рис. П.4).… … Экономико-математический словарь

В реальной жизни сложно себе представить существование в электрической цепи одного единственного потребителя. Такие цепи существуют, но всегда очень примитивны. Например, если мы с вами включим в розетку одну единственную лампочку, то в цепи лампочка-розетка, мы будем иметь одно единственное устройство-потребитель. Но на практике таких устройств всегда гораздо больше и если рассмотреть ту же самую цепь в разрезе электростанция-лампочка, то схема подключения будет содержать уже множество дополнительных потребителей.

Внутри электрических устройств также используются целые схемы, которые содержат в своем составе множество элементов. Например, управляющая схема телевизора состоит из множества резисторов, транзисторов, диодов и других элементов. Достаточно взглянуть на любую печатную плату и обратить внимание на количество вспомогательных «дорожек». Все они соединены последовательно или параллельно. Кроме того, типы соединений могут смешиваться.
Каждый тип соединения подразумевает определенное соотношение между основными параметрами, такими как напряжение, сила тока и сопротивление.
Типов соединения бывает всего два, а третий – это комбинированный вариант подключения.
Первый вариант соединения – это последовательное подключение. Второй вариант – параллельное подключение. Эти подключения могут комбинироваться в реальной практике.
Чем отличаются параллельное и последовательное подключения
Последовательное подключение представляет собой последовательное соединение проводников в одной общей электрической цепи.

Почему оно последовательное?
Всё очень просто – проводники располагаются в электрической цепи аналогично птицам, которые сидят на проводе – один за другим. В данном случае представим, что птицы держатся за лапы – каждая птица держит своей левой лапой правую лапу ближайшей птицы. Получаем ёлочную гирлянду. Все сидят последовательно.
Кстати говоря, если свободные лапы крайних птиц прислонить к источнику питания, то выйдет фейерверк :)…

Представим, например, светодиод, который имеет + и -. Для того, чтобы объединить такие светодиоды в единую последовательную цепь, мы должны соединить ножку + первого светодиода с плюсом источника постоянного тока, а ножку – соединить с ножкой + следующего светодиода. Ножку – следующего светодиода мы подключаем также к ножке + следующего светодиода, а – подключаем к – источника постоянного тока. Вот мы и собрали простейшую последовательную цепь из трех элементов.
Параллельное подключение выглядит немного иначе.

Если вернуться к примеру с птицами, то птицы уже не сидят на проводе одна за другой, а держат друг друга лапами.
Причем, птицы так извернулись, что одна птица держит своей правой лапой, правую лапу соседней птицы, а левой лапой левую лапу этой же птицы.
Для того, чтобы зажарить таких птиц, остаётся только прислонить букет из этих соответствующих друг другу лап к полюсам источника тока.

Здесь мы берем, скажем, два светодиода, которые имеют ножки + и – соответственно, и соединяем сначала ножки светодиодов по принципу + к + и – к -.
Собранную цепь мы подключаем к источнику тока соответственно полюсам, т.е. общий плюс от двух светодиодов присоединяем к + источника тока, а общий – к минусу источника тока. В результате получили параллельную цепь.
Смешанное соединение сочетает в себе как параллельное, так и последовательные соединения. В зависимости от цели, эти комбинации могут быть различными.

На практике чаще всего используются именно смешанные схемы. Часто анализ такого соединения вызывает затруднения у студентов и школьников.
На самом же деле, тут нет ничего сложного.
Для того, чтобы разобраться во всех параметрах, нужно попросту разложить цепь на удобные фрагменты.

Так, если мы имеем ряд последовательно подключенных резисторов, которые скомпонованы вместе с параллельно соединенными резисторами, то цепь можно разбить на два обобщенных условных участка, где и определить значимый параметр.
Часто испуг вызывает появление в схеме поворотов, углов и изгибов. Человек теряется и не понимает, что от смены направления линии соединительных проводов, логика не меняется.
Основные параметры последовательного и параллельного подключений
Типы подключений следует различать из-за особенностей основных параметров электрической цепи при таких подключениях.
При параллельном подключении, напряжение на элементах цепи всегда будет постоянным, а сила тока суммируется из токов на каждом элементе. Есть еще такой параметр, как сопротивление. Мы не рекомендуем заучивать наизусть все формулы, а руководствоваться законом Ома, предположив, что один из параметров будет постоянным. Но для ускорения решения задач заучить выкладку может быть полезно. Собственно, там отношение единицы к сопротивлению цепи, равно сумме отношений 1 к каждому из сопротивлений.

При последовательном подключении, напряжение на каждом элементе будет суммироваться, а сила тока будет постоянной. Сопротивление мы также можем узнать из закона Ома. Или же запомнить, что сопротивление равно сумме сопротивлений элементов цепи.

Особенности параметров при последовательном и параллельном подключениях можно легко запомнить, если представить, что соединительные провода – это трубы, а электрический ток вода. Сравнить с водой тут можно именно силу тока. Почему же силу тока? Потому что ток характеризуется количеством заряженных частиц (читай, как наличие воды в трубе).
Представим, что в случае последовательного подключения мы соединяем две трубы одинакового сечения (представим именно одинаковое сечение, т.к. дальше уже начинают влиять такие параметры, как сопротивление) и в каждой трубе есть вода при её наличии в водопроводе. Если же мы соединим две трубы параллельно, то поток распределится равномерно (а на деле в соответствии с геометрическими параметрами труб) между двумя трубами, т.е сила тока будет суммироваться из всех участков.
Почему всё происходит именно так и почему при параллельном подключении ток распределяется именно по двум проводникам и суммируется? Это сложный фундаментальный вопрос, обсуждение которого займет ни одну статью. На данный момент предлагаю считать, что это просто свойство, которое нужно знать. Как и то, что лёд ощущается холодным, а огонь горячим.
При смешанном подключении мы предварительно должны разбить цепь на простые для понимания участки, а затем проанализировать, как они в итоге будут соединены. Соответственно, на выходе мы получим простой вариант несложного подключения, которое однозначно будет или последовательное, или параллельное.
Зная все эти параметры, мы легко можем проанализировать любую электрическую цепь и собрать новую с нужными параметрами.
Как пользоваться знаниями про особенности параллельного и последовательного подключений
Наверное, самый главный вопрос, который встаёт перед учеником – это зачем вообще всё это знать?
Тут всё довольно просто. Зная эти параметры, можно легко собрать нужную цепь. Например, представим, что мы хотим соединить два аккумулятора, напряжение каждого из которых 6 В для подключения автомобильного светодиода, рассчитанного на 12 В. Как соединить аккумуляторы? Если параллельно, то получим повышенную емкость и напряжение 6 В. Диод не «раскурится». Если же использовать последовательное подключение, то на выходе будем иметь сумму 6 В + 6 В = 12 В. Задача решена. Таких примеров можно привести очень и очень много.

Ещё один вопрос, как рассчитывать другие параметры (емкость, мощность, индуктивность) при последовательном и параллельном соединении проводников.
Например, если мы подключим последовательно 5 конденсаторов, как узнать общую емкость этой цепи? Конечно же, можно, опять-таки, заучить формулы. На практике вы их забудете сразу, как перестанете решать подобные задачи. Поэтому, гораздо важнее держать в уме физическое определение ёмкости, а уже из него выводить конкретный частный случай, помня, что при последовательном подключении сила тока всегда одинакова, а напряжение суммируется.
Вас также может заинтересовать
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединение
При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
Применение
Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Параллельное соединение
В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
Применение
Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.
Работа тока
Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:
А = I х U х t, где А – работа тока, t – время течения по проводнику.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:
А=I х (U1 + U2) х t
Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:
А = А1+А2
Мощность тока
При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:
Р=U х I
После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:
Р=Р1 + Р2
Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
Влияние схемы соединения на новогоднюю гирлянду
После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.
При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.
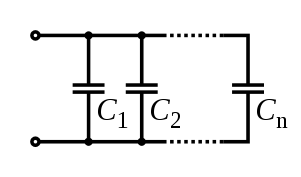
Последовательное и параллельное соединение для конденсаторов
При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
qобщ= q1 = q2 = q3
Для определения напряжения на любом конденсаторе, необходима формула:
U= q/С
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
С= q/(U1 + U2 + U3)
Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:
1/С= 1/С1 + 1/С2 + 1/C3
Немного иначе рассчитывается параллельное соединение конденсаторов.
Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
С= (q1 + q2 + q3)/U
Это значение рассчитывается как сумма каждого прибора в схеме:
С=С1 + С2 + С3
Смешанное соединение проводников
В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.
Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.
Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Теперь используем формулу расчета сопротивления:
- Первая формула для последовательного вида соединения.
- Далее, для параллельной схемы.
- И окончательно для последовательной схемы.
Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.
Похожие темы:
Последовательное и параллельное соединение
В данной статье речь пойдет о последовательном и параллельном соединении проводников. На примерах будут рассмотрены данные соединения и как при таких соединениях будут изменяться такие величины как:
- ток;
- напряжение;
- сопротивление.
В таблице 1.8 [Л2, с.24] приведены схемы и формулы по определению сопротивлений, токов и напряжений при параллельном и последовательном соединении.
Последовательное соединение
Последовательным соединением называются те участки цепи, по которым всегда проходят одинаковые токи.
При последовательном соединении:
- сила тока во всех проводниках одинакова;
- напряжение на всём соединении равно сумме напряжений на отдельных проводниках;
- сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Пример 1
Последовательно подключены две лампы накаливания одинаковой мощности Рл1=Рл2=100 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляет Rл1=Rл2=122 Ом. Номинальное напряжение для ламп равно 220 B. На рис.1 показано последовательное включение ламп.
Решение
Составляем схему замещения, выражая каждую из входящих элементов цепи (в данном случае лампы накаливания) в виде сопротивлений.
1. Определяем ток протекающей по участкам цепи:
Iн = Uн/Rл1+ Rл2 = 220/122+122 = 0,9 A
2. Определяем напряжение на каждой из ламп накаливания, так как мощность ламп у нас одинаковая, то и напряжение для каждой из ламп будет одинаково:
Uл1=Uл2 = Iн*R = 0,9*122 = 110 B
Как мы видим напряжение источника (в данном примере 220 В) разделиться поровну, между обоими последовательно включенными лампами. При этом лампы будут ели светит, их накал будет неполным.
Для того чтобы лампы горели с полным накалом, нужно увеличить напряжение источника с 220В до 440В, при этом на каждой из ламп установиться номинальное (рабочее) напряжение равное 220В.
Пример 2
Последовательно подключены две лампы накаливания мощность Рл1 = 100 Вт и Рл2 = 75 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляют Rл1= 122 Ом для стоваттной лампы и Rл2= 153 Ом для семидесяти пяти ватной лампы.
Решение
1. Определяем ток протекающей по участкам цепи:
Iн = Uн/Rл1+ Rл2 = 220/100+75 = 0,8 A
2. Определяем напряжение на каждой из ламп накаливания:
Uл1= Iн*Rл1 = 0,8*122 = 98 B
Uл2= Iн*Rл2 = 0,8*153 = 122 B
Исходя из результатов расчетов, более мощная лампа 100 Вт получает при этом меньшее напряжение. Но ток в двух последовательно включенных даже разных лампах остается одинаковым. Например, если одна из ламп перегорит (порвется ее нить накаливания), погаснут обе лампы.
Данное соединение лампочек, например, используется в трамвайном вагоне для освещения салона.
Параллельное соединение
Параллельное соединение – это соединение, при котором начала всех проводников присоединяются к одной точке цепи, а их концы к другой.
Точки цепи, к которым сходится несколько проводов, называют узлами. Участки цепи, соединяющие между собой узлы, называют ветвями.
При параллельном соединении:
- напряжение на всех проводниках одинаково;
- сила тока в месте соединения проводников равна сумме токов в отдельных проводниках;
- величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.
Пример 3
Определить токи и напряжения всех участков цепи (рис.5), если известно:
- Номинальное напряжение сети Uн = 220В;
- Сопротивление нити в лампах HL1 и HL2 составляют Rл1 = Rл2 = 122 Ом.
- Сопротивление нити в лампе HL3 составляют Rл3 = 153 Ом.
Решение
Составляем схему замещения для схемы, представленной на рис.5.
1. Определяем проводимость всей цепи [Л1, с.47] и согласно таблицы 1.8:
2. Определяем сопротивление всей цепи [Л1, с.47]:
3. Определяем силу тока цепи по закону Ома:
4. Определяем токи для каждой цепи [Л1, с.47]:
5. Выполним проверку, согласно которой, сила тока в месте соединения проводников равна сумме токов в отдельных проводниках:
Iл1+ Iл2+ Iл3=Iобщ.=1,8+1,8+1,44=5,04=5,04 (условие выполняется)
Смешанное соединение
Смешанным соединением – называется последовательно-параллельное соединение сопротивлений или участков цепи.
Пример 4
Определить токи и напряжения всех участков цепи (рис.7), если известно:
- Номинальное напряжение сети Uн = 220В;
- Сопротивление нити в лампах HL1, HL2, HL3 составляют Rл1 = Rл2 = Rл3 = 122 Ом.
- Сопротивление нити в лампе HL4 составляют Rл4 = 153 Ом.
- Результаты расчетов для участка цепи ВС (параллельное соединение проводников) применим из примера 3:
Сопротивление цепи ВС составляет Rвс = 43,668 Ом.
Решение
Составляем схему замещения для схемы, представленной на рис.7.
1. Определяем сопротивление всей цепи:
Rобщ = Rав+Rвс = Rл1+Rвс = 122+43,688 = 165,688 Ом
2. Определяем силу тока цепи, согласно закона Ома:
3. Определяем напряжение на первом сопротивлении:
Uав=Uл1= Iобщ*Rл1 = 1,33*122 = 162 B
4. Определяем напряжение на участке ВС:
Uвс= Iобщ*Rвс = 1,33*43,688 = 58,1 B
5. Определяем токи для каждой цепи участка ВС:
6. Выполним проверку для участка цепи ВС:
Iл2+ Iл3+ Iл4= Iобщ.=0,48+0,48+0,38=1,33=1,33 (условие выполняется)
Литература:
- Общая электротехника с основами электроники, В.С. Попов, 1972 г.
- Справочная книга электрика. В.И. Григорьева. 2004 г.
В статье вы узнаете что такое последовательная схема соединения, принцип работы, её характеристики, преимущества и недостатки, а также где последовательная цепь используется.
Два типа цепей, которые обычно используются для подачи электроэнергии, это последовательные и параллельные цепи. Основным задачей любой электрической цепи является подача электроэнергии для электрического устройства. Эта статья дает вам представление о последовательных цепях, принципах работы, характеристиках последовательных цепей, приложениях, преимуществах и недостатках.
Посмотрите также: Параллельная схема соединения.
Что такое последовательная цепь
Последовательная цепь — это цепь, в которой электричество должно проходить через все компоненты в цепи и не имеет альтернативного пути, называется последовательной цепью.
В этой схеме все компоненты соединены в одном контуре. Наиболее распространенный пример последовательной цепи — гирлянда.


Рис. 1 — Пример последовательной схемы
Как строится последовательная цепь (принцип работы)
Путь для потока электронов (электричества) называется цепью. Назначение любой электрической цепи состоит в том, чтобы поставлять электричество для прибора или любого электрического устройства. Эти устройства называются нагрузками. До того, как нагрузка заработает, электричество должно иметь определенный путь от источника к нагрузке и обратно к источнику.
На рисунке ниже показана типичная последовательная схема, в которой резисторы (R1, R2, R3) впоследствии соединяются с концом одного резистора, соединенным с другим концом следующего резистора, чтобы образовать петлю. Ток течет от отрицательной клеммы батареи через резисторы и, следовательно, ток одинаков для всех компонентов последовательной цепи.
Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений. Напряжение на разных резисторах различно, а сумма напряжения на каждом компоненте (резисторе) равна приложенному напряжению. Разрыв в последовательной цепи остановит ток, протекающий через цепь.


Рис. 2 — Схематическое изображение последовательной цепи
Рис. 2 — Схематическое изображение последовательной цепи
Характеристики последовательной цепи
Ниже приведены важные характеристики последовательных цепей:
Сопротивление в последовательной цепи
Rn = R1 + R2 + R3 +…Rn
Где Rn = общее сопротивление
Если R1 = 10 Ом, R2 = 20 Ом, R3 = 40 Ом
Rn = 10 + 20 + 40
Rn = 70 Ом
Сила тока в последовательной схеме
Предположим, что приложенное напряжение (U) = 10 В, тогда ток (I) можно рассчитать по формуле:
I = U / R = 10/70 = 1/7 Ампер = 0,1428 Ампер = 142,8 миллиампер
I = 142,8 миллиампер
Напряжение в последовательной схеме
Поскольку значения сопротивления и тока известны, напряжение можно рассчитать по формуле:
U = IR
Назовем напряжение на резисторе 1, 2, 3 как UR1,
UR2 и UR3 соответственно.
UR1 = IR1 = 0,142 x 10 = 1,42 В
UR2 = IR2 = 0,142 x 20 = 2,84 В
UR3 = IR3 = 0,142 x 40 = 5,68 В
Общее напряжение в последовательной цепи
Поскольку мы знаем, что общее напряжения на каждом резисторе равна сумме напряжений,
UR = UR1 + UR2 + UR3 = 1,42 + 2,84 + 5,68
= 9,94 вольт (с ошибкой округления) ≈ 10 В (Общее напряжение)
Применения последовательной цепи
Последовательная цепь применяется в:
- Последовательные резистивные цепи используются в цепях малой мощности.
- Последовательные цепи используются в цепях делителя напряжения.
Преимущества
Преимущества последовательной цепи включают в себя:
- Легко спроектировать и построить схему.
- Если компонент ломается, текущий поток останавливается.
- Он действует как регулятор тока.
- Стоимость построения последовательной цепи меньше по сравнению с параллельной схемой.
Недостатки
К недостаткам последовательных цепей относятся:
- Если сгорела одна лампочка в цепи, ток не будет течь в цепи.
- Если нагрузка увеличивается, т.е. если подключено больше лампочек, то свет тускнеет
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: параллельное и последовательное соединение проводников, смешанное соединение проводников.
Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.
Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.
Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1):

Рис. 1. Резистор
Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2):

Рис. 2.
Стационарное поле совершает при этом положительную работу .
Так как и , то и , т. е. .
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3):

Рис. 3.
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным. В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.

Рис. 4. Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.
1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике.
Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:
Можно и более формально, без всяких словесных объяснений:
3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.
Пусть — сопротивление участка . По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .
Сопротивления проводников равны:
Эти два проводника образуют единый проводник длиной и сопротивлением
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).

Рис. 5. Параллельное соединение
Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от к (по направлению тока) называется неразветвлённой частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.
1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .
Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:
что и требовалось.
3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:
Сокращая на , получим:
(1)
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти :
(2)
К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
(3)
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:

откуда
Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.
Смешанное соединение
Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
Рассмотрим пример смешанного соединения проводников (рис. 6).

Рис. 6. Смешанное соединение
Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :
Ом.
Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:
Ом.
Сопротивление цепи:
Ом.
Теперь находим силу тока в цепи:
A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
B;
B.
(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора и находятся под напряжением , поэтому:
A;
A.
(В сумме имеем А, как и должно быть при параллельном соединении.)
Сила тока в резисторах и одинакова, так как они соединены последовательно:
А.
Стало быть, через резистор течёт ток A.
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Рис. 25. Схемы последовательного соединения приемников
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк (19)
где Rэк = R1 + R2 + R3.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U1=IR1; U2 = IR2, U3 = IRз и в данном случае E = U, то длярассматриваемой цепи
U = U1 + U2 +U3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U1 : U2 : U3 = R1 : R2 : R3 (21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
U1 = U/n. (22)
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
Рис. 26. Схемы параллельного соединения приемников
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или
I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/Rэк = 1/R1 + 1/R2 + 1/R3 (24)
Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Gэк = G1+ G2 +G3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
Rэк=R1R2/(R1+R2)
при трех параллельно включенных резисторах
Rэк=R1R2R3/(R1R2+R2R3+R1R3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
Rэк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
Рис. 27. Схемы смешанного соединения приемников
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R123=R12R3/(R12+R3)=(R1+R2)R3/(R1+R2+R3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
Последовательный класс
Последовательный класс
tf.keras.Sequential (слоев = нет, имя = нет)
Последовательный группирует линейный стек слоев в tf.keras.Model .
Последовательный обеспечивает функции обучения и вывода на этой модели.
Примеры
>>>
>>> модель = tf.keras.Sequential ()
>>> модель.адд (тф.keras.layers.Dense (8, input_shape = (16,)))
>>>
>>> model.add (tf.keras.layers.Dense (4))
>>>
>>> модель = tf.keras.Sequential ()
>>> model.add (tf.keras.Input (shape = (16,)))
>>> model.add (tf.keras.layers.Dense (8))
>>>
>>>
>>>
>>> модель = tf.keras.Sequential ()
>>> model.add (tf.keras.layers.Dense (8))
>>> model.add (tf.keras.layers.Dense (4))
>>>
>>>
>>>
>>> модель = тф.keras.Sequential ()
>>> model.add (tf.keras.layers.Dense (8, input_shape = (16,)))
>>> model.add (tf.keras.layers.Dense (4))
>>> лен (модель.веса)
4
>>>
>>>
>>>
>>> модель = tf.keras.Sequential ()
>>> model.add (tf.keras.layers.Dense (8))
>>> model.add (tf.keras.layers.Dense (4))
>>> model.build ((Нет, 16))
>>> лен (модель.весы)
4
# Обратите внимание, что при использовании шаблона отложенного построения (не указана форма ввода),
# модель строится в первый раз, когда вы вызываете `fit`,` eval` или `Forect`,
# или в первый раз, когда вы вызываете модель для некоторых входных данных.model = tf.keras.Sequential ()
model.add (tf.keras.layers.Dense (8))
model.add (tf.keras.layers.Dense (1))
model.compile (оптимизатор = 'sgd', потеря = 'mse')
# Это строит модель в первый раз:
model.fit (x, y, batch_size = 32, epochs = 10)
добавить метод
Добавляет экземпляр слоя поверх стека слоев.
Аргументы
Повышает
- TypeError : Если
, уровеньне является экземпляром уровня. - ValueError : если аргумент
layerне соответствует знать его входную форму. - ValueError : в случае, если аргумент
layerимеет несколько выходных тензоров или уже подключены где-то еще (запрещено впоследовательныхмоделей).
поп метод
Удаляет последний слой в модели.
Повышает
- TypeError : если в модели нет слоев.
,
Последовательная модель
Автор: fchollet
Дата создания: 2020/04/12
Последнее изменение: 2020/04/12
Описание: Полное руководство по последовательной модели.
Просмотреть в Colab •
GitHub source
Настройка
импорт тензор потока как тф
из тензор потока импортных керас
из tenensflow.keras импортировать слои
Когда использовать последовательную модель
Модель с последовательным номером подходит для простого набора слоев
где каждый слой имеет ровно один входной тензор и один выходной тензор .
Схематично следующая модель Последовательная модель :
# Определить последовательную модель с 3 слоями
model = keras.Sequential (
[
layer.Dense (2, активация = "relu", name = "layer1"),
layer.Dense (3, активация = "relu", name = "layer2"),
layer.Dense (4, name = "layer3"),
]
)
# Вызвать модель на тестовом входе
x = tf.ones ((3, 3))
у = модель (х)
соответствует этой функции:
# Создать 3 слоя
layer1 = слои.Плотный (2, активация = "relu", name = "layer1")
layer2 = layer.Dense (3, активация = "relu", name = "layer2")
layer3 = layer.Dense (4, name = "layer3")
# Вызов слоев на тестовом входе
x = tf.ones ((3, 3))
y = layer3 (layer2 (layer1 (x)))
Последовательная модель не подходит , когда:
- Ваша модель имеет несколько входов или несколько выходов
- Любой из ваших слоев имеет несколько входов или несколько выходов
- Вам нужно сделать совместное использование слоя
- Требуется нелинейная топология (например,грамм. остаточное соединение, многоотраслевой модель)
Создание последовательной модели
Вы можете создать последовательную модель, передав список слоев в последовательный конструктор:
модель = керас. Последовательный (
[
layer.Dense (2, активация = "relu"),
layer.Dense (3, активация = "relu"),
layers.Dense (4),
]
)
Его слои доступны через слоев. Атрибут :
[<тензор потока.python.keras.layers.core.Dense at 0x148873e90>,
,
]
Вы также можете постепенно создать последовательную модель с помощью метода add () :
модель = keras.Sequential ()
model.add (Layers.Dense (2, Activation = "Relu"))
model.add (Layers.Dense (3, Activation = "Relu"))
model.add (layers.Dense (4))
Обратите внимание, что существует также соответствующий метод pop () для удаления слоев:
Последовательная модель ведет себя очень похоже на список слоев.
model.pop ()
print (len (model.layers)) # 2
Также обратите внимание, что конструктор Sequential принимает аргумент name , как
любой слой или модель в керасе. Это полезно для аннотирования графиков TensorBoard
с семантически значимыми именами.
модель = keras.Sequential (name = "my_sequential")
model.add (layer.Dense (2, активация = "relu", name = "layer1"))
model.add (layer.Dense (3, активация = "relu", name = "layer2"))
model.add (layer.Dense (4, name = "layer3"))
Задание формы ввода заранее
Как правило, все слои в Keras должны знать форму своих входов чтобы иметь возможность создавать свои веса.Поэтому, когда вы создаете слой как это, изначально, он не имеет веса:
слой = слои. Густой (3)
layer.weights # Пусто
Создает свои веса при первом вызове на входе, поскольку форма вес зависит от формы входов:
# Уровень вызова на тестовом входе
x = tf.ones ((1, 4))
у = слой (х)
layer.weights # Теперь у него есть веса, формы (4, 3) и (3,)
[,
]
Естественно, это также относится к последовательным моделям. Когда вы создаете
Последовательная модель без входной формы, она не «построена»: она не имеет весов
(и звонит
Модель .вес приводит к ошибке, утверждающей только это). Весы созданы
когда модель впервые видит некоторые входные данные:
модель = керас. Последовательный (
[
layer.Dense (2, активация = "relu"),
layer.Dense (3, активация = "relu"),
layers.Dense (4),
]
) # Нет весов на этом этапе!
# На данный момент вы не можете сделать это:
# model.weights
# Вы также не можете сделать это:
# model.summary ()
# Вызвать модель на тестовом входе
x = tf.ones ((1, 4))
у = модель (х)
print («Количество весов после вызова модели:», len (model.весов)) # 6
Количество весов после вызова модели: 6
После того, как модель «построена», вы можете вызвать ее метод summary () , чтобы отобразить ее
содержание:
Модель: "sequential_3"
_________________________________________________________________
Слой (тип) Выходная форма Параметр #
================================================== ===============
плотность_7 (плотная) (1, 2) 10
_________________________________________________________________
density_8 (Плотный) (1, 3) 9
_________________________________________________________________
density_9 (Плотный) (1, 4) 16
================================================== ===============
Всего параметров: 35
Обучаемые параметры: 35
Не обучаемые параметры: 0
_________________________________________________________________
Однако, это может быть очень полезно при построении последовательной модели постепенно
чтобы иметь возможность отображать краткую информацию о модели, включая текущую
Форма выхода.В этом случае вы должны начать свою модель, передав Input
Объект вашей модели, чтобы он знал свою входную форму с самого начала:
модель = keras.Sequential ()
model.add (keras.Input (форма = (4,)))
model.add (Layers.Dense (2, Activation = "Relu"))
model.summary ()
Модель: "sequential_4"
_________________________________________________________________
Слой (тип) Выходная форма Параметр #
================================================== ===============
density_10 (Плотный) (Нет, 2) 10
================================================== ===============
Всего параметров: 10
Обучаемые параметры: 10
Не обучаемые параметры: 0
_________________________________________________________________
Обратите внимание, что объект Input не отображается как часть модели .слои , так как
это не слой:
[]
Простая альтернатива — просто передать аргумент input_shape вашему первому
слой:
модель = keras.Sequential ()
model.add (Layers.Dense (2, активация = "relu", input_shape = (4,)))
model.summary ()
Модель: "sequential_5"
_________________________________________________________________
Слой (тип) Выходная форма Параметр #
================================================== ===============
density_11 (Плотный) (Нет, 2) 10
================================================== ===============
Всего параметров: 10
Обучаемые параметры: 10
Не обучаемые параметры: 0
_________________________________________________________________
Модели, построенные с предопределенной формой ввода, как это, всегда имеют вес (даже прежде чем увидеть какие-либо данные) и всегда иметь определенную форму вывода.
В общем, рекомендуется всегда указывать форму ввода последовательной модели заранее, если вы знаете, что это такое.
Общий рабочий процесс отладки: add () + Summary ()
При построении новой последовательной архитектуры полезно наращивать в стеке
слои с добавить () и часто печатать сводки моделей. Например, это
позволяет отслеживать, как работает стек из слоев Conv2D и MaxPooling2D
карты изображения с понижающей дискретизацией:
модель = керас.Последовательное ()
model.add (keras.Input (shape = (250, 250, 3))) # 250x250 RGB-изображений
model.add (слои. Conv2D (32, 5, шаг = 2, активация = "relu"))
model.add (layer.Conv2D (32, 3, активация = "relu"))
model.add (layers.MaxPooling2D (3))
# Можете ли вы угадать, какова текущая форма вывода на данный момент? Возможно нет.
# Давайте просто напечатать это:
model.summary ()
# Ответ был: (40, 40, 32), так что мы можем продолжать понижать выборку ...
model.add (layer.Conv2D (32, 3, активация = "relu"))
model.add (layer.Conv2D (32, 3, активация = "relu"))
модель.Добавить (layers.MaxPooling2D (3))
model.add (layer.Conv2D (32, 3, активация = "relu"))
model.add (layer.Conv2D (32, 3, активация = "relu"))
model.add (layers.MaxPooling2D (2))
# И сейчас?
model.summary ()
# Теперь, когда у нас есть карты объектов 4x4, пришло время применить глобальный максимальный пул.
model.add (layers.GlobalMaxPooling2D ())
# Наконец, мы добавляем слой классификации.
model.add (layers.Dense (10))
Модель: "sequential_6"
_________________________________________________________________
Слой (тип) Выходная форма Параметр #
================================================== ===============
conv2d (Conv2D) (Нет, 123, 123, 32) 2432
_________________________________________________________________
conv2d_1 (Conv2D) (нет, 121, 121, 32) 9248
_________________________________________________________________
max_pooling2d (MaxPooling2D) (нет, 40, 40, 32) 0
================================================== ===============
Всего параметров: 11 680
Обучаемые параметры: 11680
Не обучаемые параметры: 0
_________________________________________________________________
Модель: "sequential_6"
_________________________________________________________________
Слой (тип) Выходная форма Параметр #
================================================== ===============
conv2d (Conv2D) (Нет, 123, 123, 32) 2432
_________________________________________________________________
conv2d_1 (Conv2D) (нет, 121, 121, 32) 9248
_________________________________________________________________
max_pooling2d (MaxPooling2D) (нет, 40, 40, 32) 0
_________________________________________________________________
conv2d_2 (Conv2D) (нет, 38, 38, 32) 9248
_________________________________________________________________
conv2d_3 (Conv2D) (Нет, 36, 36, 32) 9248
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (Нет, 12, 12, 32) 0
_________________________________________________________________
conv2d_4 (Conv2D) (нет, 10, 10, 32) 9248
_________________________________________________________________
conv2d_5 (Conv2D) (нет, 8, 8, 32) 9248
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (Нет, 4, 4, 32) 0
================================================== ===============
Всего параметров: 48 672
Обучаемые параметры: 48,672
Не обучаемые параметры: 0
_________________________________________________________________
Очень практично, правда?
Что делать, если у вас есть модель
?Как только ваша модель архитектуры будет готова, вы захотите:
После создания последовательной модели она ведет себя как функциональный API
модель.Это означает, что каждый слой имеет вход
и выводят атрибутов. Эти атрибуты могут использоваться, чтобы делать аккуратные вещи, такие как
быстро
создание модели, которая извлекает выходные данные всех промежуточных слоев в
Последовательная модель:
initial_model = keras.Sequential (
[
keras.Input (форма = (250, 250, 3)),
слои.Conv2D (32, 5, шаг = 2, активация = "relu"),
слои.Conv2D (32, 3, активация = "relu"),
слои.Conv2D (32, 3, активация = "relu"),
]
)
feature_extractor = керас.Модель(
входов = initial_model.inputs,
output = [layer.output для слоя в initial_model.layers],
)
# Вызов функции извлечения на тестовом вводе.
x = tf.ones ((1, 250, 250, 3))
features = feature_extractor (x)
Вот аналогичный пример, который извлекает объекты только из одного слоя:
initial_model = keras.Sequential (
[
keras.Input (форма = (250, 250, 3)),
слои.Conv2D (32, 5, шаг = 2, активация = "relu"),
слои.Conv2D (32, 3, активация = "relu", имя = "my_intermediate_layer"),
слои.Conv2D (32, 3, активация = "relu"),
]
)
feature_extractor = keras.Model (
входов = initial_model.inputs,
Выходы = initial_model.get_layer (имя = "my_intermediate_layer"). Выход,
)
# Вызов функции извлечения на тестовом вводе.
x = tf.ones ((1, 250, 250, 3))
features = feature_extractor (x)
Передача обучения с последовательной моделью
Трансферное обучение состоит из замораживания нижних слоев в модели и только обучения верхние слои. Если вы не знакомы с ним, обязательно прочитайте наше руководство передать обучение.
Вот два распространенных проекта обучения передаче с использованием последовательных моделей.
Во-первых, предположим, что у вас есть последовательная модель, и вы хотите заморозить все
слои, кроме последнего. В этом случае вы просто перебрали бы
model.layers и set layer.trainable = False на каждом слое, кроме
последний. Как это:
модель = керас. Последовательный ([
keras.Input (форма = (784))
layer.Dense (32, активация = 'relu'),
слои.Плотный (32, активация = 'relu'),
layer.Dense (32, активация = 'relu'),
layers.Dense (10),
])
# Предположительно, вы хотели бы сначала загрузить предварительно обученные веса.
model.load_weights (...)
# Заморозить все слои, кроме последнего.
для слоя в model.layers [: - 1]:
layer.trainable = False
# Перекомпилируйте и обучите (это только обновит веса последнего слоя).
model.compile (...)
model.fit (...)
Еще одним распространенным планом является использование последовательной модели для укладки предварительно обученных модель и некоторые недавно инициализированные слои классификации.Как это:
# Загрузите сверточную базу предварительно подготовленными гирьками
base_model = keras.applications.Xception (
вес = 'imagenet',
include_top = False,
Пулы = «ср»)
# Заморозить базовую модель
base_model.trainable = False
# Используйте последовательную модель, чтобы добавить обучаемый классификатор сверху
model = keras.Sequential ([
base_model,
layers.Dense (1000),
])
# Компилировать и обучать
model.compile (...)
model.fit (...)
Если вы все же перенесете обучение, вы, вероятно, будете часто использовать эти две модели.
Это все, что вам нужно знать о последовательных моделях!
Чтобы узнать больше о создании моделей в Керасе, см .:
,Комбинационная схема может быть определена как схема, выход которой зависит только от входов в тот же момент времени, а последовательная цепь может быть определена как схема, выход которой зависит не только от текущих входов, но и от прошлой истории. входов.
Для последовательной цепи значения переменной обычно указываются в определенные моменты дискретного времени, а не в течение всего непрерывного времени.Половина сумматора, Полное сумматор, Половина вычитателя, Полное вычитание — примеры комбинационных схем, в то время как триггеры, счетчики образуют последовательную схему.
Последовательная схема состоит из комбинационной схемы, к которой подключены элементы памяти, чтобы сформировать путь обратной связи, как показано на блок-схеме ниже:
Дальнейшие различия между комбинационных и последовательных цепей могут быть перечислены следующим образом:
| с.№ |
комбинационная схема |
Последовательная цепь |
| 1. | не содержит элементов памяти | содержит элементы памяти |
| 2. | Текущая стоимость его выходов определяется исключительно приведенными значениями его входов | Текущая стоимость его результатов определяется текущей стоимостью его входов и прошлым состоянием | .
| 3. | Его поведение описывается набором функций вывода | Его поведение описывается набором функций следующего состояния (памяти) и набором функций вывода |
Последовательный канал может быть далее разделен на Синхронный и Асинхронный.
Надеюсь, вы найдете информацию, представленную здесь, полезной. Пожалуйста, оставляйте свои следы в разделе комментариев ниже для любых вопросов, отзывов или предложений … !!
[amazon_carousel widget_type = «SearchAndAdd» title = «Книги, которые вам могут понравиться:» market_place = «» shuffle_products = «True» show_border = «False» ключевые слова = «цифровая электроника» browse_node = «» search_index = «Books» /]
,