Какой из непрерывных сигналов – INFOблог. Непрерывные и дискретные сигналы: сравнительный анализ и особенности преобразования

Чем отличаются непрерывные сигналы от дискретных. Как происходит преобразование непрерывных сигналов в дискретные. Какие существуют виды дискретизации сигналов. В чем заключаются преимущества и недостатки разных типов сигналов.

Непрерывные и дискретные сигналы: основные определения

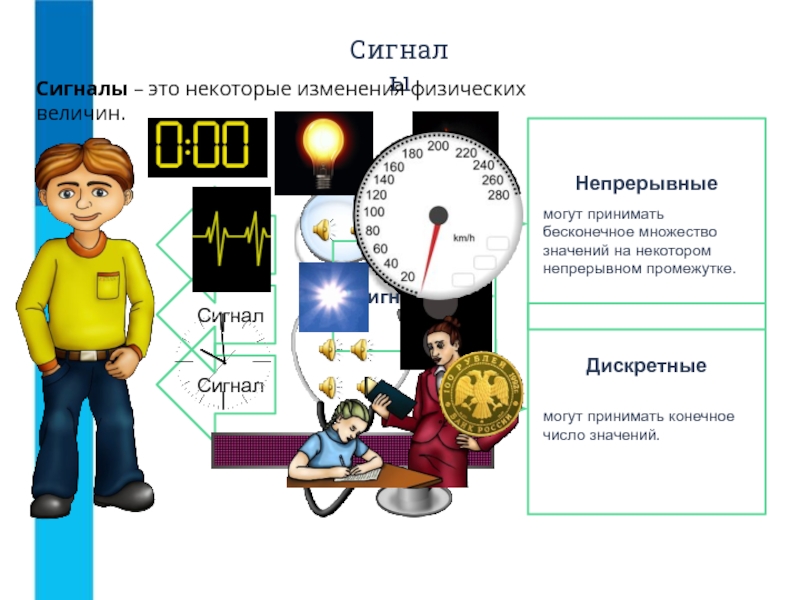
Сигналы, используемые для передачи информации, можно разделить на два основных типа:

• Непрерывные сигналы — сигналы, которые могут принимать любые значения в заданном диапазоне. Они описываются непрерывной функцией времени.
• Дискретные сигналы — сигналы, принимающие конечное число значений. Они представляются в виде последовательности отдельных значений.

В чем заключаются ключевые различия между этими типами сигналов? Непрерывный сигнал может иметь бесконечное множество значений, в то время как дискретный ограничен конечным набором. Это фундаментальное отличие определяет особенности обработки и передачи каждого типа сигналов.

Характеристики непрерывных сигналов

Основные свойства непрерывных сигналов:

• Описываются непрерывной функцией времени X(t)
• Могут принимать любые значения в заданном диапазоне (Xmin, Xmax)
• Аргумент t может принимать любые значения на интервале (0, T)
• Множество значений бесконечно

Примерами непрерывных сигналов являются:

• Звуковые колебания, улавливаемые микрофоном
• Изменение температуры, регистрируемое термопарой
• Электрический сигнал, измеряемый осциллографом

Особенности дискретных сигналов

Ключевые характеристики дискретных сигналов:

• Состоят из конечного набора значений
• Описываются последовательностью чисел
• Значения определены только в дискретные моменты времени
• Образуют алфавит источника дискретной информации

Примеры дискретных сигналов:

• Показания цифровых измерительных приборов
• Текст в книге
• Двоичный код в компьютерных системах

Преобразование непрерывных сигналов в дискретные

Для обработки непрерывных сигналов на компьютерах и передачи по цифровым каналам связи их необходимо преобразовывать в дискретную форму. Это преобразование осуществляется с помощью двух основных операций:

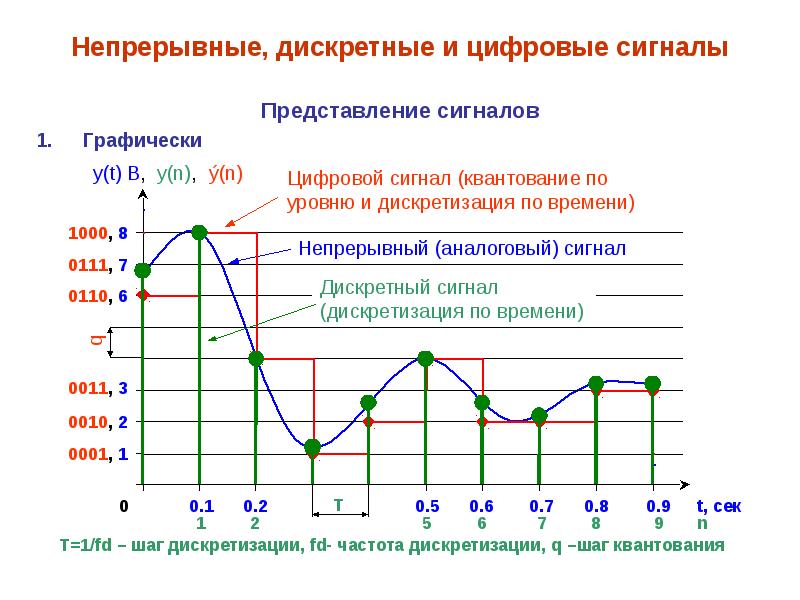
1. Дискретизация по времени — взятие отсчетов сигнала через равные промежутки времени
2. Квантование по уровню — округление значений сигнала до ближайшего разрешенного уровня

При совместном применении этих операций непрерывный сигнал X(t) преобразуется в дискретный сигнал X(ti), где ti — дискретные моменты времени.

Виды дискретизации сигналов

Существует несколько способов дискретизации непрерывных сигналов:

• Равномерная дискретизация — отсчеты берутся через равные интервалы времени Δt
• Неравномерная дискретизация — интервал между отсчетами может меняться
• Адаптивная дискретизация — шаг изменяется в зависимости от характера сигнала
• Программируемая дискретизация — интервал задается по определенному алгоритму

Какой из этих методов лучше? Равномерная дискретизация проще в реализации, но может приводить к избыточности данных. Адаптивные методы позволяют более эффективно представлять сигнал, но сложнее в реализации.

Теорема Котельникова и выбор частоты дискретизации

Важнейший вопрос при дискретизации — как часто нужно брать отсчеты сигнала? Ответ на него дает теорема Котельникова:

Непрерывный сигнал с ограниченным спектром может быть полностью восстановлен по своим дискретным отсчетам, взятым с частотой не менее удвоенной максимальной частоты в спектре сигнала.

Из теоремы следует, что частота дискретизации должна быть:

f_д ≥ 2f_max

где f_max — максимальная частота в спектре сигнала.

Это позволяет определить минимально необходимую частоту дискретизации, чтобы не потерять информацию о сигнале. На практике частоту дискретизации выбирают с некоторым запасом.

Квантование сигналов по уровню

При квантовании непрерывные значения сигнала заменяются ближайшими разрешенными уровнями. Основные характеристики квантования:

• Шаг квантования ΔX — расстояние между соседними уровнями
• Число уровней квантования N — определяет точность представления сигнала
• Погрешность квантования — максимальная ошибка округления (до 0.5ΔX)

Квантование может быть равномерным (с постоянным шагом) или неравномерным. Выбор параметров квантования влияет на точность представления сигнала и объем данных.

Преимущества и недостатки разных типов сигналов

Сравним основные достоинства и недостатки непрерывных и дискретных сигналов:

Преимущества непрерывных сигналов:

• Высокая точность представления
• Простота получения от физических датчиков
• Отсутствие эффектов дискретизации

Недостатки непрерывных сигналов:

• Чувствительность к помехам
• Сложность обработки на компьютерах
• Трудности при передаче на большие расстояния

Преимущества дискретных сигналов:

• Высокая помехоустойчивость
• Простота цифровой обработки
• Возможность сжатия данных

Недостатки дискретных сигналов:

• Потеря информации при дискретизации
• Эффекты квантования (ступенчатость)
• Необходимость высокой частоты дискретизации

Выбор типа сигнала зависит от конкретной задачи и требований к системе обработки информации.

Применение разных типов сигналов

Области применения непрерывных и дискретных сигналов:

Непрерывные сигналы:

• Аналоговое телевидение и радиовещание
• Телефония
• Аналоговые измерительные приборы

Дискретные сигналы:

• Цифровое телевидение и радио
• Компьютерные сети и интернет
• Цифровая звукозапись
• Системы сотовой связи

Современные тенденции показывают все большее распространение цифровых методов обработки сигналов во всех областях.

Заключение

Непрерывные и дискретные сигналы имеют свои особенности и области применения. Понимание их свойств и методов преобразования необходимо для эффективной работы с информационными системами. Развитие цифровых технологий привело к широкому распространению дискретных сигналов, однако непрерывные сигналы по-прежнему играют важную роль во многих приложениях.

INFOблог: Непрерывные и дискретные сигналы

В предыдущем посте мы рассматривали различные определения понятия «информация» и пришли к выводу, что информация может быть определена множеством разных способов в зависимости от выбранного подхода. Но об одном мы можем говорить однозначно: информация — знания, данные, сведения, характеристики, отражения и т.д. — категория

нематериальная. Но мы живем в мире материальном. Следовательно, для существования и распространения в нашем мире информация должна быть связана с какой-либо материальной основой. Без нее информация не может передаваться и сохраняться.

Тогда материальный объект (или среда), с помощью которого представляется та или иная информация будет являться носителем информации, а изменение какой-либо характеристики носителя мы будем называть сигналом.
Например, представим равномерно горящую лампочку, она не передает никакой информации. Но, если мы будем включать и выключать лампочку (т.е. изменять ее яркость), тогда с помощью чередований вспышек и пауз мы сможем передать какое-нибудь сообщение (например, посредством азбуки Морзе). Аналогично, равномерный гул не дает возможности передать какую-либо информацию, однако, если мы будем изменять высоту и громкость звука, то сможем сформировать некоторое сообщение (что мы и делаем с помощью устной речи).

При этом сигналы могут быть двух видов: непрерывный (или аналоговый) и дискретный.
В учебнике даны следующие определения.

Непрерывный сигнал принимает множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.
Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами.

Немного уточним эти определения.
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала.

Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.

Графики этих сигналов выглядят следующим образом

Примерами непрерывных сигналов могут быть музыка, речь, изображения, показания термометра (высота столба ртути может быть любой и представляет собой ряд непрерывных значений).

Примерами дискретных сигналов могут быть показания механических или электронных часов, тексты в книгах, показания цифровых измерительных приборов и т.д.

Вернемся к примерам, рассмотренным в начале сообщения — мигающая лампочка и человеческая речь. Какой из этих сигналов является непрерывным, а какой дискретным? Ответьте в комментариях и аргументируйте свой ответ. Можно ли непрерывную информацию преобразовать в дискретную? Если да — приведите примеры.

infodp84.blogspot.com

26 вопросов и ответов. Теория электрических цепей. Курс лекций

Комплексная спектральная плотность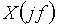

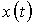непрерывного сигнала (в дальнейшем для краткости будем говорить: спектр сигнала) вычисляется по формуле прямого преобразования Фурье

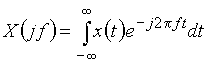. (3)

Сигнал 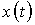может быть восстановлен по спектру 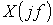с помощью обратного преобразования Фурье, или интеграла Фурье

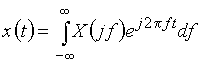. (4)

В соответствии с принципом неопределенности сигнал, имеющий ограниченную протяженность во времени, обладает неограниченным по полосе спектром (рис. 9, а). И наоборот, сигнал с ограниченным спектром имеет бесконечную протяженность во времени (рис. 10, а). Как следует из этих рисунков, непрерывный сигнал, и ограниченной и бесконечной протяженности во времени, имеет сплошной спектр.

Если сигнал 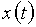является периодическим, то спектр его – дискретный, т.е. теперь вместо 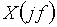используют отсчеты 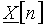. Эта ситуация показана на рис. 9, б. Период сигнала равен длительности сигнала 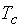. Интервал дискретизации спектра по частоте F определяется, как известно, периодом сигнала, в данном случае 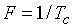. Формулы для прямого и обратного преобразований Фурье получаются из (3) и (4) путем замены непрерывной частоты f на дискретные значения nF. При этом следует учесть известную связь между амплитудами гармоник 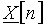периодического сигнала и отсчетами 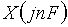спектральной плотности 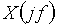непрерывного сигнала:

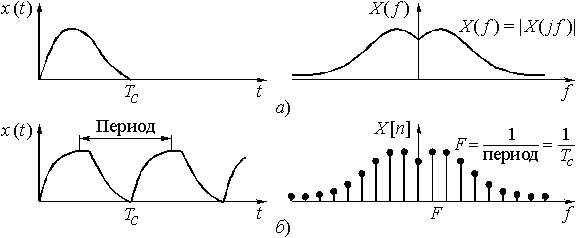
Рис. 9

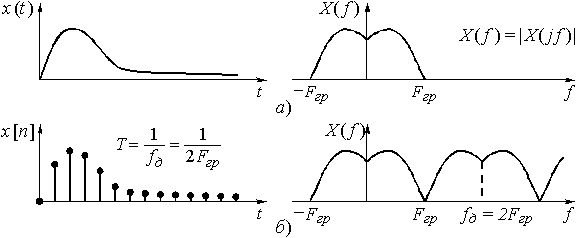
Рис. 10

.

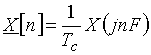Спектр 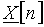периодического сигнала вычисляется по формуле

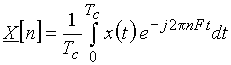. (5)

Сигнал 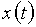можно восстановить по его дискретному спектру, воспользовавшись формулой

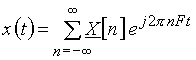. (6)

В соответствии с принципом дуальности можно сказать: если периодическим является спектр, то дискретным будет сигнал (рис. 10, б). Обозначая период повторения спектра 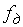, получим интервал дискретизации сигнала .

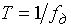Формулы прямого и обратного преобразований Фурье для дискретных сигналов имеют вид

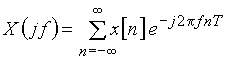; (7)

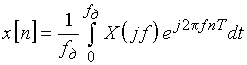. (8)

В формулах (7) и (8) использовано обозначение .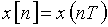

Пример 4.1. Рассчитаем спектр дискретного сигнала, состоящего из одного отсчета .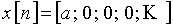

Воспользуемся формулой (7), в которую подставим значения 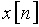заданного сигнала

.

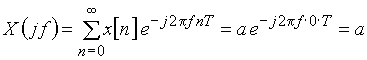Пример 4.2. Рассчитаем спектр экспоненциальной дискретной функции 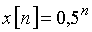, n³ 0.

График дискретной функции 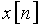приведен на рис. 11, а ее отсчеты можно записать в виде последовательности 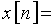{1; 0,5; 0,25; 0,125; 0,0625; …}.

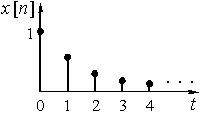
Рис. 11

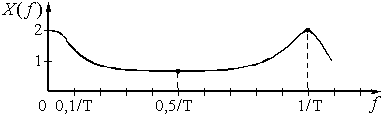
Рис. 12

Спектр дискретной экспоненты рассчитаем по формуле (7)

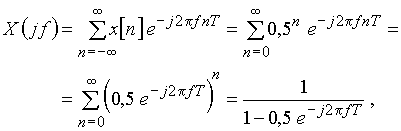
где для суммирования ряда использована формула

.

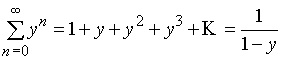Получим выражение для расчета спектра амплитуд 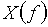, используя формулу Эйлера .

.

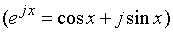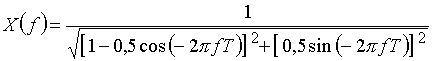Для построения графика будем задавать значения f от 0 до 1/Т с шагом 0,1/T и рассчитывать .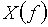

График спектра амплитуд 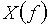экспоненциальной дискретной функции 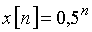приведен на рисунке 12.

Как видно из графика, спектр дискретного сигнала сплошной и периодический с периодом .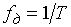

Самоконтроль

1. Как рассчитывается спектр непериодического (и периодического) непрерывного сигнала?

2. Как восстановить непрерывный сигнал по его спектру (сплош­ному и дискретному)?

3. Сформулируйте принцип неопределенности.

4. Как рассчитывается спектр дискретного сигнала?

5. Какой спектр у дискретного сигнала: сплошной или дискретный, периодический или непериодический?

6. Как рассчитывается дискретный сигнал, если известен его спектр?

7. Найдите спектр дискретного сигнала, состоящего из одного отсчета .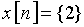

8. Найдите значения спектра дискретного сигнала, заданного двумя отсчетами 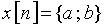, на частотах 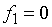и .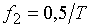

siblec.ru

Чем отличается непрерывный сигнал от дискретного

Для связи и передачи сообщений используют сигналы, которые отличаются друг от друга. Существуют непрерывные (НС) и дискретные сигналы (ДС).

Особенности непрерывного сигнала

Если дискретный сигнал квантуется как по времени, так и по уровню, то его называют цифровым сигналом

Сигнал считается непрерывным, если в заданных пределах он может иметь любое значение. С математической точки зрения это означает, что НС можно представить в виде непрерывной функции. Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре.

Аналоговые системы для передачи информации, использующие НС, имеют следующие недостатки:

• пониженную помехозащищённость — это свойство связано с тем, что из-за непрерывности системы помеху, попавшую в сигнал, невозможно отличить от самого сигнала;
• затруднения при передаче сигналов управления;
• трудности при сопряжении с компьютером и другими цифровыми устройствами;
• трудности шифрования.

Что такое дискретный

Дискретность применяется в вычислительной технике для пакетной передачи данных

Дискретный сигнал — тот, который в некотором интервале может принимать определённое число значений. К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.

Благодаря достижениям в цифровой технике большинство электронных устройств в настоящее время являются цифровыми и работают с ДС. В то же время физические сигналы в природе имеют аналоговый вид. Преобразование НС в дискретный вид производится путём дискретизации его с помощью специальных устройств (АЦП). Обратное преобразование сигнала производится с помощью ЦАП.

Достоинствами цифровых систем, работающих на ДС, являются:

• высокая помехозащищённость и возможность работы каналов связи при больших шумах;
• простота передачи команд управления каналами;
• возможность цифровой обработки сигналов;
• лёгкость засекречивания.

Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер — цифровая машина, то есть внутреннее представление информации в нём дискретно. Дискретизация входных сигналов (если она непрерывна) позволяет сделать их пригодными для дискретной обработки.

Отличия двух видов сигналов

Все значения дискретного сигнала можно пронумеровать целыми числами

Основным отличием непрерывного сигнала от ДС является то, что он может иметь в заданном диапазоне любое значение, тогда как ДС может принимать только определённые значения.

К недостаткам систем, использующих ДС, можно отнести:

• увеличение полосы частот, требуемой для передачи сообщений;
• для обеспечения точного воспроизведения непрерывного сигнала при дискретизации требуется значительное количество уровней квантования и высокая частота;
• требование синхронизации;
• плохая совместимость с уже имеющимися аналоговыми системами.

Различные процессы могут быть описаны с помощью непрерывных или дискретных сигналов. Непрерывный сигнал может иметь любое значение из некоторого диапазона величин, тогда как для дискретного сигнала возможные его значения определены заранее. Во многих случаях при использовании цифровых методов обработки информации полезно преобразовать непрерывные сигналы в дискретные.

elektro.guru

непрерывный сигнал — это… Что такое непрерывный сигнал?



непрерывный сигнал

Сигнал, описываемый непрерывной функцией времени.

Политехнический терминологический толковый словарь. Составление: В. Бутаков, И. Фаградянц. 2014.

• непрерывный режим
• неприводимые диаграммы фейнмана

Смотреть что такое «непрерывный сигнал» в других словарях:

• непрерывный сигнал — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN continuous signal …   Справочник технического переводчика

• непрерывный сигнал — 06.01.20 непрерывный сигнал [ continuous wave]: Непрерывный гармонический сигнал заданной частоты, поступающий от устройства считывания/опроса и обеспечивающий электропитание пассивной радиочастотной метки, не подвергнутый амплитудной и/или… …   Словарь-справочник терминов нормативно-технической документации

• непрерывный сигнал — analoginis signalas statusas T sritis Standartizacija ir metrologija apibrėžtis Signalas, išreiškiamas laiko funkcija, kartojančia atitinkamo dydžio kitimo dėsnį. atitikmenys: angl. analog signal; analogue signal vok. analoges Signal, n;… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• непрерывный сигнал — analoginis signalas statusas T sritis fizika atitikmenys: angl. analog signal; analogue signal vok. analoges Signal, n; Analogsignal, n rus. аналоговый сигнал, m; непрерывный сигнал, m pranc. signal analogique, m; signal analogue, m …   Fizikos terminų žodynas

• непрерывный сигнал — tolydusis signalas statusas T sritis fizika atitikmenys: angl. analog signal; analogue signal; continuous signal vok. analoges Signal, n; kontinuierliches Signal, n; stetiges Signal, n rus. аналоговый сигнал, m; непрерывный сигнал, m pranc.… …   Fizikos terminų žodynas

• непрерывный сигнал — аналоговый сигнал …   Словарь русских синонимов по технологиям автоматического контроля

• Сигнал бедствия — У этого термина существуют и другие значения, см. Сигнал (значения). Часы радиста. Цветными секторами на циферблате обозначены трехминутные периоды радиомолчания, когда все служебные станции должны прослушивать частоты сигналов бедствия:… …   Википедия

• аналоговый сигнал — непрерывный сигнал …   Словарь русских синонимов по технологиям автоматического контроля

• аналоговый сигнал — analoginis signalas statusas T sritis Standartizacija ir metrologija apibrėžtis Signalas, išreiškiamas laiko funkcija, kartojančia atitinkamo dydžio kitimo dėsnį. atitikmenys: angl. analog signal; analogue signal vok. analoges Signal, n;… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• аналоговый сигнал — analoginis signalas statusas T sritis fizika atitikmenys: angl. analog signal; analogue signal vok. analoges Signal, n; Analogsignal, n rus. аналоговый сигнал, m; непрерывный сигнал, m pranc. signal analogique, m; signal analogue, m …   Fizikos terminų žodynas

technical_terminology.academic.ru

1.3 Сигналы непрерывные и дискретные. Преобразование сигналов.

Информация (сообщения и сигналы) может существовать в двух формах: непрерывной и дискретной.

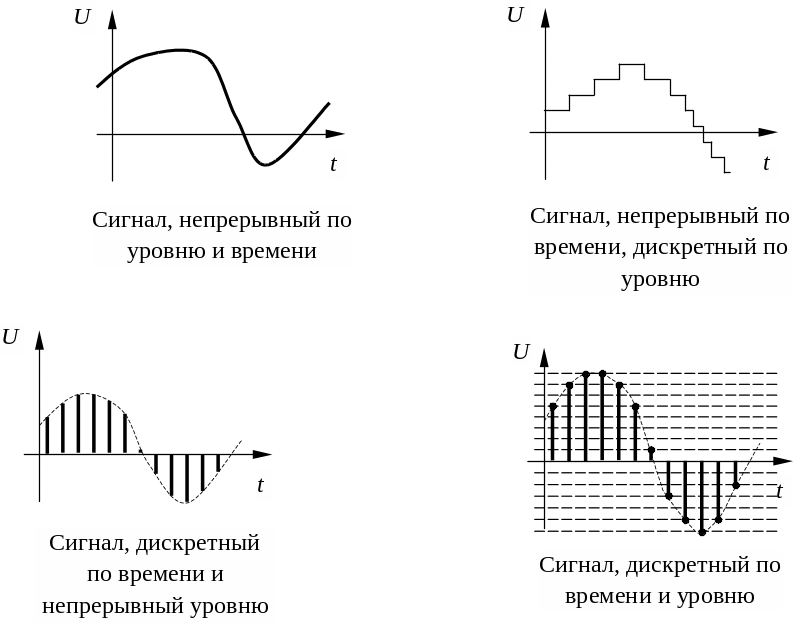
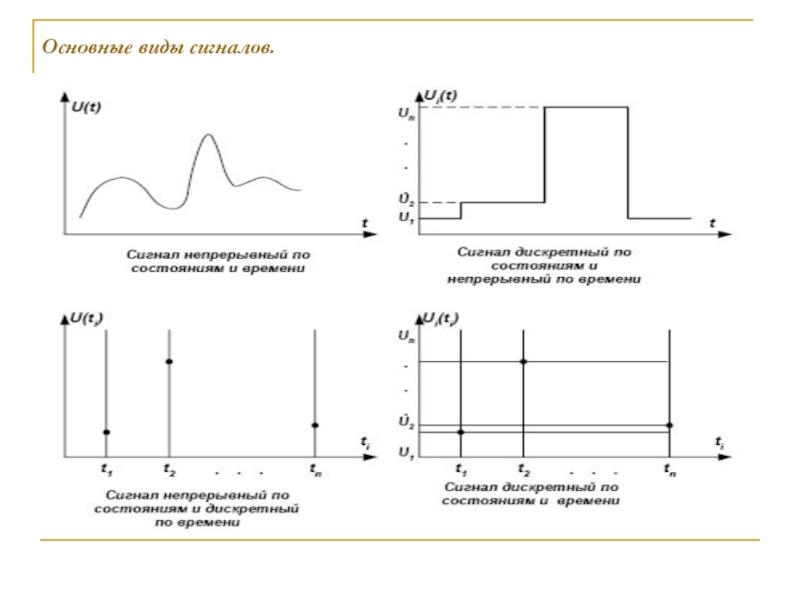
В большинстве случаев информация о протекании того или иного физического процесса вырабатывается соответствующими датчиками в виде сигналов, непрерывно изменяющихся во времени. Такой сигнал можно представить в виде непрерывной функции Х(t) непрерывного аргументаt– функции, которая может принимать любые вещественные значения в интервале (X_min,X_max) для любых значений аргументаtв интервале (0, Т) (рис. 1.10а). Множество значений непрерывной функции бесконечно.

Дискретные сообщения и сигналы состоят из конечного множества элементов, поступающих последовательно во времени. Набор элементов (символов) составляет алфавит источника дискретной информации. Обычно элементами дискретных сигналов являются последовательности чисел.

Для передачи информации по каналу связи и ее дальнейшей обработки средствами вычислительной техники непрерывный сигнал преобразуют в дискретный. Это преобразование осуществляется с помощью специальных устройств – преобразователей непрерывных сигналов и может быть выполнено дискретизацией во времени, квантованием по уровню или одновременно дискретизацией во времени и квантованием по уровню. При этом соответственно возможны три разновидности сигналов.

Дискретизация во временисостоит в преобразовании непрерывного сигнала Х(t) непрерывного аргументаt(рис. 1.10а) в непрерывный сигнал Х(t_i) дискретного аргументаt_iс шагом дискретизации ∆t(рис. 1.10б). Сигнала Х(t_i) может принимать любые значения в интервале (X_min,X_max), но лишь на дискретном множестве значений аргументаt_i(t₁,t₂, …,t_к) в интервале (0, Т). Какой бы малый шаг дискретизации не выбирался, множество значений дискретной функции будет конечно (ограничено). Примером такого сигнала может быть последовательность импульсов, модулированных по амплитуде. Рассмотренная дискретизации является равномерной, т.к. длительность шага дискретизации ∆t_i=constна всем интервале (0, Т). Дискретизация может быть и неравномерной, если длительность шага ∆t_iразлична (∆t_i=var). Методы изменения шага ∆t_iмогут быть адаптивными, когда он изменяется в зависимости от текущего изменения параметров сигнала, и программируемыми, когда он изменяется в соответствии с заранее установленной программой или оператором, на основе анализа поступающей информации. Очевидно, что каждый вид дискретизации имеет свои преимущества и недостатки. Все же в основном, применяется равномерная дискретизация, так как алгоритмы и аппаратура для ее реализации существенно проще. Однако очевидно, что при этом в случае медленно изменяющихся сигналов возможны «лишние» отсчеты, т.е. избыточность информации.

К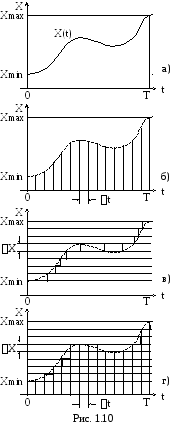вантование по уровнюсостоит в преобразовании непрерывных значений сигнала Х(t_i) в дискретные значения. При этом образуется дискретный сигнал непрерывного аргумента; соседние значения сигнала различаются на элементарную величину ∆Х – квант (рис. 1.10в). Значения, которые может принимать сигнал Х(t), образуют дискретный ряд заранее заданных чисел Х₁, Х₂,…Х_кили уровней 1, 2, 3, 4 и т.д.; значение аргументаtможет быть любым в интервале (0,Т). Примером такого сигнала может быть сигнал на выходе проволочного потенциометра, выходное напряжение которого квантуется за счет скачков сопротивления при перемещении движка с витка на виток. Можно отметить, что квантование по уровню может быть и неравномерным, если ∆Х=var. В основном, используется равномерное квантование — ∆Х=const.

С

Преобразование непрерывного сигнала в дискретный

овместное применение операции дискретизации во времени и квантования по уровнюпозволяет преобразовать непрерывный сигнал Х(t) в дискретный по координатам Х иt(рис. 1.10г). При этом образуется дискретный сигнал дискретного аргумента. Значения сигнала Х(t) и аргументаtобразуют дискретные ряды чисел Х₁, Х₂, …Х_киt₁,t₂, …t_к, заполняющие интервалы (Х_min,Х_max) и (0,Т) соответственно.

Первые две из рассмотренных разновидностей принадлежат дискретно-непрерывным сигналам, а третья – дискретному сигналу. Последний называется также цифровым, так как дискретные значения сигнала обычно представляются в цифровой форме.

Рассмотрим некоторые вопросы, связанные с точностью представления непрерывных сигналов Х(t) в результате дискретизации во времени и квантования по уровню.

В результате дискретизации во времени исходный непрерывный сигнал Х(t) представляется конечной последовательностью отдельных значений Х(t_i), измеренных с шагом дискретизации ∆t=t_i-t_i-1. По значениям Х(t_i) можно восстановить исходный сигнал Х(t) с некоторой погрешностью. Функцию Х(t), полученную в результате восстановления (интерполяции) по значениям Х(t_i), называют воспроизводящей. При дискретизации возникает вопрос о точности преобразования, которая очевидно зависит от частоты отсчетов функцииf_k=1/∆t_i, т.е. от выбранного шага дискретизации ∆t_i. С одной стороны, очевидно, что с уменьшением (увеличением) ∆t_iточность преобразования будет расти (уменьшаться) за счет увеличения (уменьшения) количества отсчетов. С другой стороны, очевидно, что нет смысла стремиться всегда брать отсчеты как можно чаще, независимо от вида сигнала Х(t), так как в случае медленно изменяющегося сигнала Х(t) два соседних значения Х(t_i) и Х(t_i+1) могут быть настолько связаны (коррелированны) между собой, что по одному из них Х(t_i) можно прогнозировать другое Х(t_i+1), т.е. никакой новой информации о сигнале при его последующем восстановлении по отсчетам это не дает. Проблема обеспечении точности дискретизации может быть сформулирована следующим образом: с каким максимальным интервалом необходимо брать отсчеты значений сигнала Х(t_i), чтобы не пропустить существенных его изменений или, другими словами, какое минимальное количество отсчетов необходимо брать для обеспечения заданной точности воспроизведения сигнала Х(t). От этого, в конечном счете, зависит количество информации, которую надо хранить и преобразовывать в вычислительном устройстве.

Возможны различные пути решения указанной проблемы.

В общем виде задача о представлении некоторого сигнала, являющегося непрерывной функцией времени, в виде конечного числа значений, взятых для дискретных значений времени, решена В.А. Котельниковым. В двух теоремах В.А. Котельников применительно к системе передачи сообщений по линии связи определил, как следует выбрать частоту дискретизации, обеспечивающую по полученным дискретным данным последующее воспроизведение исходного сигнала с заданной точностью.

Теорема 1. Любую функцию Х(t), имеющую спектр частот от 0 доf_m, можно представить суммой функцииsinx/x, т.е. рядом:

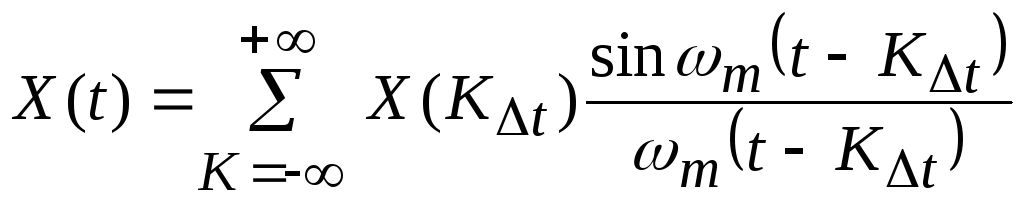, (1.51)

где K– целое число,

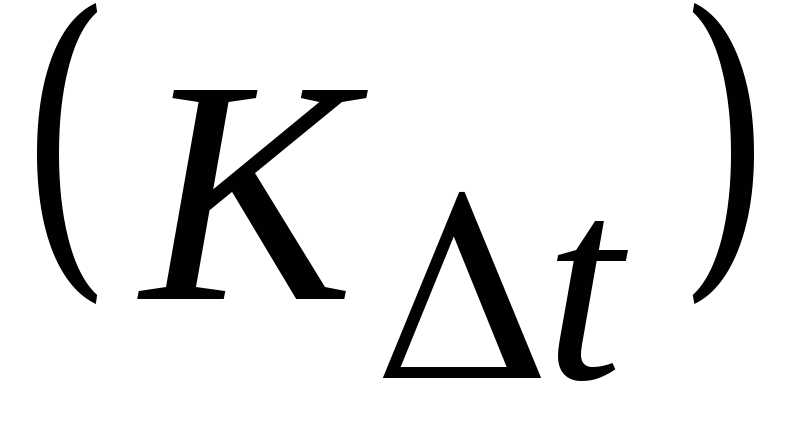– отсчеты мгновенных значений функции Х(t) с шагом дискретизации ∆t,

ω_m= 2πf_m,f_m– максимальная частота в спектре частот сигнала Х(t), Гц

ω_m– круговая частота.

Из этой теоремы может быть сделан и обратный вывод: любая функция, представленная рядом Котельникова (1.51), имеет спектр, состоящий из частот от 0 до f_m.

Теорема 2. Любая функция Х(t), содержащая частоты от 0 доf_m, полностью определяется дискретными значениями этой функции, следующими друг за другом с частотой 2f_m, т.е. через интервал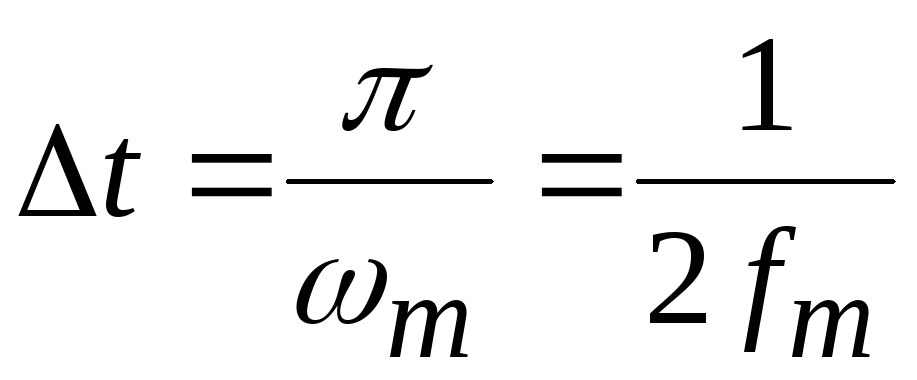сек. Таким образом, передачу непрерывного сигнала Х(t) с ограниченным спектром частот, поступающего от какого-либо датчика, можно свести к передаче последовательности дискретных чисел – значений этого сигнала, взятых через интервал времени 1/2f_m; число этих значений равно 2f_m. Через полученные значения ординат, при обработке результатов измерений, можно провести единственным способом воспроизводящую непрерывную функцию. Поэтому, проще говоря, нет смысла брать отсчеты чаще, чем интервал 1/2f_m, так как никакой новой информации о функции при ее последующем восстановлении по отсчетам это не дает. Следует подчеркнуть, что сказанное справедливо только в том случае, если в получаемой информации действительно отсутствует частоты вышеf_m.

Теоремы В.А. Котельникова, являющиеся основой современной теории передачи сообщений, очень удобны для исследования всевозможных линий связи, вследствие того, что для этих линий известны частотные характеристики, а спектр передаваемых сигналов ограничен. Другое дело – реальные сигналы, имеющие конечную длительность Т. Для их точного представления, в отличие от моделей сигналов с ограниченным спектром (1.51), необходим спектр, который простирался бы от нуля до бесконечности. Теоретически, чтобы избежать погрешности дискретизации, для такого спектра требуется бесконечно большая частота взятия отсчетов. Практически выбирают такую частоту дискретизации, при которой погрешность не превышает заданной величины В этой связи теорему 2 В.А. Котельникова можно рассматривать как приближенную для функций с неограниченным спектром. На практике частоту отсчетов часто определяют как 2f_mk, т.е. интервал между отсчетами

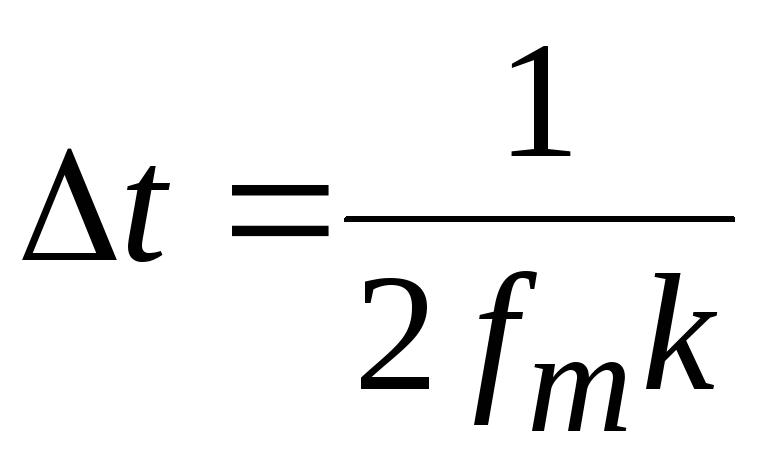(1.52)

где f_m– максимальная допустимая частота в спектре сигнала Х(t)

k– коэффициент запаса (обычно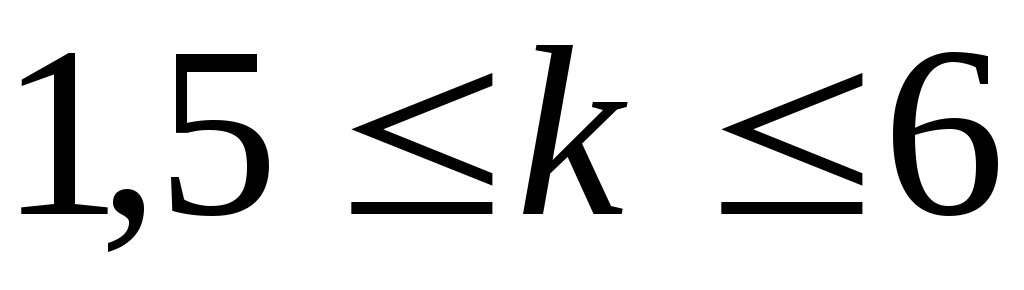). Так как безграничный частотный спектр заменяется ограниченным, вне которого спектральная плотность принимается равной нулю, то погрешность дискретизации будет определяться соотношением составляющих, лежащих внутри спектра и вне его.

Другой, практически легко реализуемый путь определения оптимального интервала дискретизации ∆tнепрерывного сигнала Х(t) заключается в построении автокорреляционной функции сигнала и нахождении интервала корреляции τ_к .Дискретные отсчеты, взятые через интервал ∆t=τ_к, будут независимыми и информативными; для их обработки могут быть использованы методы математической статистики.

В случае, когда непрерывный сигнал Х(t) представлен своими дискретными значениями, полученными при равномерной или неравномерной дискретизации, он может быть заменен некоторой приближающей (аппроксимирующей) зависимостью. В общем случае исходный сигнал может быть аппроксимирован специальной функцией или полиномом, график которого проходит через известные дискретные значения. Наиболее часто используются степенные алгебраические полиномы, но так как обычно исходный сигнал задается в графическом или табличном, а не в аналитическом виде, то проведение аппроксимации полиномами с порядком выше первого затруднительно. При аппроксимации полиномом первого порядка все точки кривой, соответствующие дискретным моментам времени, соединяются отрезками прямых (кусочно-линейная аппроксимация). Алгебраические полиномы удобны для программирования и обработки с помощью вычислительной техники

При квантовании исходного сигнала по уровню возникает погрешность квантования. Так как в процессе преобразования значение сигнала Х(t) обычно отображается ближайшим уровнем квантования Х_m, то все значения, кроме кратныхХ, представляются с некоторой погрешностью, максимальное значение которой равно 0,5.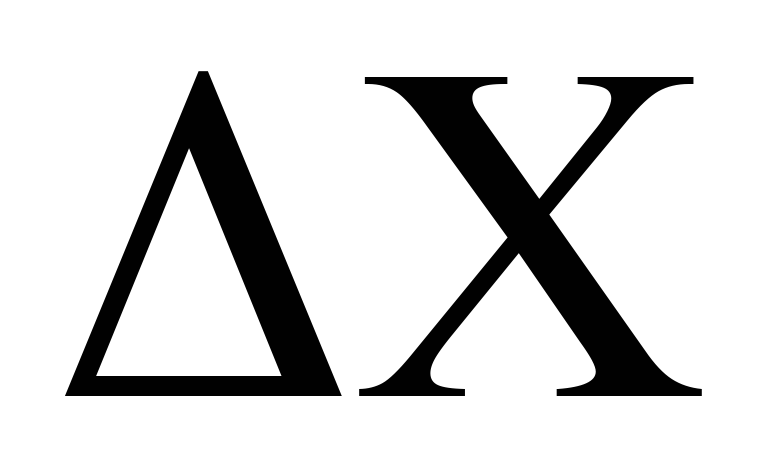

В заключение этого параграфа отметим, что дискретизация и квантование находят широкое применение в преобразователях информации, используемых для связи вычислительных устройств с реальными объектами.

studfile.net

3. Сигналы. Виды сигналов и их параметры. Введение в специальность

Характеристики различных сигналов

Все сигналы могут быть подразделены на периодические и непериодические.

Периодическим называется сигнал, значения которого повторяются через определенные равные промежутки времени, называемые периодом повторения сигнала, или просто периодом. Для непериодического сигнала это условие не выполняется.

Простейшим периодическим сигналом является гармоническое колебание.

,

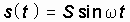где S, w – амплитуда и угловая частота колебания.

Другим примером периодического сигнала является последовательность прямоугольных импульсов (рис. 3.2, а). Как вы думаете, из чего состоит эта последовательность импульсов? Оказывается, из синусоид. Взгляните на рис. 3.2. В качестве исходной синусоиды выберем такую, у которой период колебаний совпадает с периодом T прямоугольных импульсов (рис. 3.2, б)

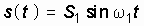, (3.1)

где 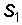– амплитуда синусоиды, а .

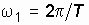Колебание (3.2.) заданной частоты и амплитуды 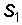можно представить в виде графика: на оси частот отметить значение и изобразить вертикальную линию высотой, равной амплитуде сигнала 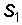(см. рис. 3.2, б).

Следующая синусоида имеет частоту колебаний в 3 раза большую, а амплитуду – в 3 раза меньшую.

Сумма этих двух синусоид пока еще мало похожа на прямоугольные импульсы (рис. 3.2, в). Но если мы добавим к ним синусоиды с частотами колебаний в 5, 7, 9, 11, и т.д. раз большими, а с амплитудами в 5, 7, 9, 11, и т.д. раз меньшими, то сумма всех этих колебаний:

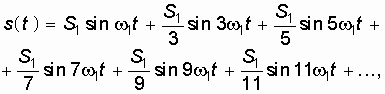
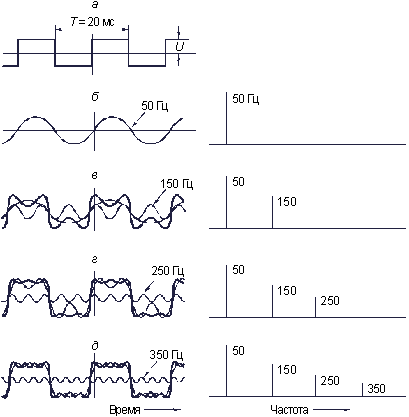
Рис. 3.2. Периодическая последовательность прямоугольных импульсов (а) и формирование ее сигнала (б–д)

где 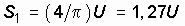, будет не так уже сильно отличатся от прямоугольных импульсов (рис. 3.2, г и д). Таким образом, степень “прямоугольности” импульсов определяется тем, сколько синусоид со все более высокими частотами колебаний мы будем суммировать.

Может показаться, что представление прямоугольных импульсов в виде совокупности синусоид есть не более чем математический прием и не имеет никакого отношения к реальности. Однако это не так. Радиоинженерам хорошо знакомы приборы (они называются анализаторами спектров), которые позволяют выделить каждую входящую в сложный сигнал синусоиду.

Тот факт, что сигнал произвольной формы (а не только прямоугольные импульсы) можно “разложить” на сумму обыкновенных синусоид, впервые доказал в 20-х годах прошлого века французский математик Ж. Фурье. Такой набор синусоид получил название спектра сигнала. Каждый сигнал (отличающийся от других по форме) имеет свой сугубо индивидуальный спектр, т.е. может быть получен только из синусоид со строго определенными частотами и амплитудами.

Непериодический сигнал легко получить из периодического, увеличивая период вплоть до 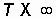(рис. 3.3, а–г). Спектр амплитуд для сигналов с разными периодами показаны на рис. 3.4, а–в.

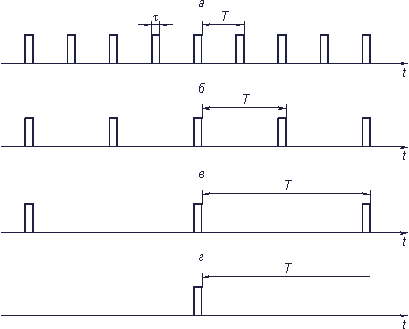
Рис. 3.3. Увеличение периода последовательности прямоугольных импульсов

При увеличении периода сигнала частота первой гармоники 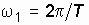понижается. Спектральные линии становятся гуще. Амплитуды гармоник уменьшаются. Последнее становится понятным, если учесть, что энергия сигнала, оставаясь неизменной, перераспределяется теперь между возросшим числом гармоник. Естественно, доля каждой гармоники в общем сигнале падает.

Следовательно, при переходе к непериодическому сигналу (например, к одиночному импульсу) мы получаем в спектре такого сигнала вместо отдельных гармоник бесконечно большое число синусоидальных колебаний с бесконечно близкими частотами, заполняющими всю шкалу частот. Причем амплитуда каждого такого колебания становится исчезающе малой, потому что на его долю приходится бесконечно малая часть энергии сигнала. Другими словами, в любой бесконечно узкой полосе частот мы всегда обнаружим синусоидальное колебание, правда, бесконечно малой амплитуды.

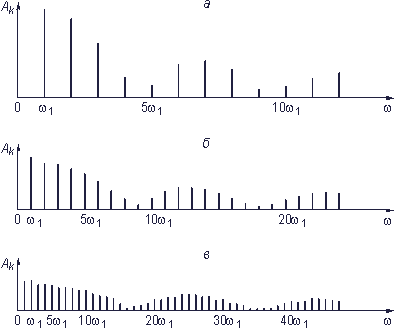
Рис. 3.4. Спектры амплитуд периодических последовательностей импульсов с разными периодами а–в см. в тексте

Поскольку сравнивать между собой бесконечно малые величины неудобно, то вместо амплитуд 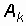по оси ординат откладывают произведение 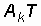, которое с увеличением периода Т остается постоянным. В новых координатах спектры, показанные на рис. 3.4, а–в, будут выглядеть так, как показано на рис. 3.5, а–г. Понятие спектра амплитуд здесь лишено смысла и заменяется понятием спектральной плотности амплитуд, которая указывает, по сути, на удельный вес бесконечно малой амплитуды синусоидального колебания в любой бесконечно узкой полосе частот. Понятие спектра фаз заменяется понятием спектральной плотности фаз. Таким образом, спектр непериодического сигнала является в общем случае не дискретным, а непрерывным.

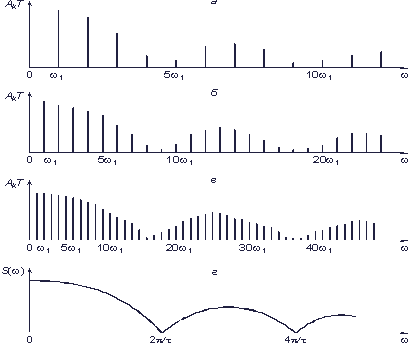
Рис. 3.5. Переход к спектральной плотности (г) одиночного прямоугольного импульса а–в см. в тексте

Уровни сигналов

Для сравнения мощностей сигналов, передаваемых по системе электросвязи, часто пользуются логарифмическими единицами – децибелами. Децибел (русское обознач. ДБ, международное – dB), как показывает приставка “деци”, составляет десятую часть другой, более крупной единицы, названной белом в честь А.Г. Белла – изобретателя телефона. Бел – это десятичный логарифм отношения двух мощностей. Если известны две мощности: Р₁ и Р₂, то их отношение, выраженное в белах, определяется формулой p=lg(P₂/P₁).

Для практики бел – слишком крупная величина. Обычно отношение мощностей выражают в децибелах, для чего при расчетах пользуются формулой p=10lg(p₂/p₁).

Динамический диапазон и пик-фактор сигналов. Мгновенная мощность сигналов связи может принимать различные значения в самых широких пределах. Чтобы охарактеризовать эти пределы, вводят понятия динамического диапазона и пик-фактора сигналов.

Динамический диапазон сигнала, дБ, определяется выражением:

D_c=10lg(P_max/P_min),

где P_max, P_min – максимальное и минимальное значения мгновенной мощности.

Пик-фактором сигнала называют отношение его максимальной мощности к средней, выраженное в логарифмических единицах:

Q=10lg(P_max/P_ср).

Пример. Пусть имеется периодический прямоугольный сигнал

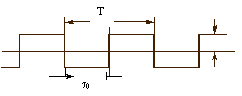
Он может быть разложен на составляющие с частотами f₁=1/T, f₃=3/T, f₅=5/T и т.д. Число составляющих бесконечно, но чем выше частота, тем меньше амплитуда. Следовательно, теоретически полоса частот, которую занимает данный сигнал, стремится к Ґ .

Для передачи такого сигнала требуется канал, имеющий бесконечную полосу пропускания. Во-первых, таких каналов нет, во-вторых, чем шире полоса пропускания канала, тем он дороже. Но т.к. чем выше частота составляющей, тем ниже амплитуда, то составляющими с частотой і f_n можно пренебречь.

Возьмём только составляющие f₁, f₃, f₅. Полоса частот, которую занимают эти составляющие, f₅ – f₁=D f_c.

Пусть f₁=1000 Гц, f₃=3000 Гц, f₅=5000 Гц.

Занимаемая этими составляющими, полоса частот:

5000-1000 = 4000 Гц.

Уменьшим длительность единичного элемента в 3 раза, тогда f₁=3000 Гц, f₃=9000 Гц, f₅=15000 Гц и занимаемая полоса 12000 Гц.

Вывод. Чем меньше длительность единичного элемента (t ₀), тем шире полоса частот, занимаемая сигналом!

Отсюда следствие: чем больше скорость телеграфирования В, тем шире полоса частот, занимаемая сигналом, и тем шире требуется канал и, следовательно, тем дороже доставка информации.

Сигналы электросвязи и их спектры. Рассмотрим наиболее часто встречающиеся сигналы электросвязи и обсудим их спектры.

Телефонные (речевые) сигналы. Человек набрал в легкие воздух и издал звук. Что же произошло? Воздух, выходя из легких, заставляет вибрировать голосовые связки. От них колебания воздуха передаются через гортань голосовому аппарату, заканчивающемуся ротовой и носовой полостями (рис. 3.6).

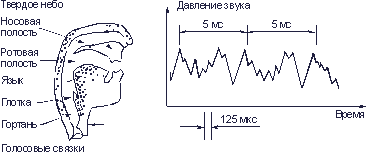
Рис. 3.6. Кривая звукового давления при произнесении звука «а» мужским голосом

Последние выполняют роль резонаторов – они усиливают колебания воздуха, подобно тому, как полый корпус гитары или скрипки, также являясь резонатором, усиливает звуки струн. Колебания воздуха из голосового аппарата человека передаются окружающему воздуху. Возникает звуковая волна. Характер издаваемого звука определяется натяжением голосовых связок, формой ротовой полости, положением языка, губ и т.д.Из описания голосового аппарата человека нетрудно понять, что голосовые связки играют роль своеобразных струн, они создают основной тон и обильное количество обертонов. Частота основного тона речи лежит в пределах от 50…80 Гц (очень низкий голос – бас) до 200…250 Гц (женский и детский голоса). При разговоре частота основного тона меняется в значительных пределах, особенно при переходе от гласных звуков к согласным и наоборот.

В совместном звучании основной тон и обертоны создают соответствующую окраску звука или тембр. Один тембр отличается от другого числом и силой обертонов. При преобладании в человеческом голосе высоких обертонов над низкими мы слышим в нем “звучание металла”. Люди, у которых в голосе преобладают низкие обертоны, говорят мягким, бархатным голосом.

Для получения формы кривой звукового давления, создаваемого речью человека, нужно сложить синусоидальные кривые основного тона и обертонов. Из-за наличия большого числа обертонов форма результирующей кривой будет сложной. На рис. 3.6 показано, какое давление создает звук “а”, произнесенный мужским голосом с частотой основного тона 200 Гц (период основного тона 5 мс). Для передачи звука на расстояние он в телефонном аппарате превращается в сигнал. Для этой цели служит микрофон.

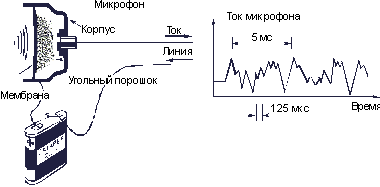
Рис. 3.7. Превращение звука в электрический сигнал с помощью микрофона

Телефон был изобретен А.Г. Беллом, учителем в школе глухонемых в американском городе Бостоне в 1876 г. С тех пор в его конструкцию было внесено много усовершенствований. В частности, в современном телефоне используется чувствительный угольный микрофон (рис. 3.7). В нем мембрана соприкасается с угольным порошком. Пока в микрофон не говорят, сопротивление порошка остается неизменным и через него от батареи в линию (провода) протекает постоянный ток. Стоит произнести в микрофон какое-нибудь слово, порошок под действием колеблющейся мембраны будет то спрессовываться, то разрыхляться. Изменение плотности порошка приводит к изменению его электрического сопротивления, а значит, и к изменению тока, текущего через порошок. В проводах, идущих от микрофона, рождается электрический ток, повторяющий форму звукового давления.

Изучение речи показывает, что речь – это процесс, частотный спектр которого находится в пределах от 50…100 до 8000…10000 Гц. Установлено однако, что качество речи остается вполне удовлетворительным, если ограничить спектр снизу и сверху частотами 300 и 3400 Гц. Эти частоты приняты Международным союзом электросвязи (МСЭ) в качестве границ эффективного спектра речи. При указанной полосе частот сохраняется хорошая разборчивость речи и удовлетворительная натуральность ее звучания.

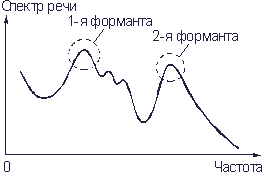
Рис. 3.8. Спектр человеческой речи

На рис. 3.8 показан спектр речи. Как видно из рисунка, некоторые частотные составляющие речи усилены, а другие ослаблены. Усиленные области спектра частот называются формантами. Звуки речи различных людей отличаются числом формант и их расположением в частотном спектре. Отдельные звуки могут иметь до шести формант, из которых только одна или две являются определяющими. Они обязательно находятся в диапазоне частот 300…3400 Гц. Между формантами лежат менее мощные составляющие звуковых частот. Однако именно они придают голосу каждого человека индивидуальность, позволяющую узнавать говорящего.

Сигналы звукового вещания. Источниками звука при передаче программ вещания обычно являются музыкальные инструменты или голос человека. Формирование сигналов звукового вещания и их прием осуществляется так же, как и телефонных сигналов. Используются лишь другие типы микрофонов.

Спектр звукового сигнала занимает полосу частот 20…20000 Гц. Однако в зависимости от требований к качеству воспроизведения ширина спектра сигнала вещания может быть ограничена. Для достаточно высокого качества (каналы вещания первого класса) полоса частот должна составлять 50…10000 Гц, для безукоризненного воспроизведения программ вещания (каналы высшего класса) – 30…15000 Гц.

Факсимильные сигналы. Обратите внимание на то, как вы читаете книгу. Ваши глаза скользят по строке слева направо, затем вы переходите к началу другой строки и т.д. до конца страницы. Словом вы “просматриваете” все элементы строки последовательно. Можно сказать, что при чтении книги происходит построчная развертка текстового изображения.

Именно по такому принципу “просматривается” изображение в современных факсимильных аппаратах, предназначенных для передачи на расстоянии различного рода неподвижных изображений (документов, чертежей, рисунков, фотографий). Для этого с помощью источника света и системы оптических линз формируют световое пятно так, чтобы освещать на передаваемом изображении площадку размером, скажем, 0,2ґ 0,2 мм. Это световое пятно перемещается сначала вдоль одной строки, затем переходит на другую и движется по ней – и так до конца последней строки. Свет, отражаясь от каждой элементарной площадки, попадает на фотоэлемент и вызывает в его цепи ток (рис. 3.9). Значение этого тока зависит от яркости отраженного света, а последняя – от яркости освещенной площадки. Таким образом, при переходе светового пятна на изображении от одной элементарной площадки к другой ток в цепи фотоэлемента меняется пропорционально яркости площадок: мы получаем точную электрическую копию изображения.

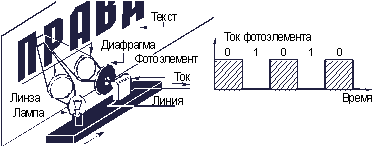
Рис. 3.9. Преобразование изображения в электрический сигнал в факсимильном аппарате

Рассмотрим изображение, состоящее только из двух цветов: черного и белого, например, страницу книги, какой-либо чертеж и т.п. Очевидно, каждый элемент изображения (напомним, что размером он всего 0,2ґ 0,2 мм) будет представлять собой либо черную, либо белую площадку, напоминая чередованием шахматную доску. Черные площадки практически полностью поглощают падающий на них свет. Яркость отраженного ими света при этом настолько ничтожна, что при просмотре черных площадок ток в цепи фотоэлемента не возникает. Наоборот, площадки белого цвета почти полностью отражают падающий на них свет, и при попадании на них светового луча ток в цепи фотоэлемента скачком принимает максимальное значение. Таким образом, перемещая световое пятно, а вслед за ним и фотоэлемент вдоль каждой строки изображения, получаем на выходе фотоэлемента последовательность импульсов (рис. 3.9).

При таком “шахматном” чередовании элементов изображения спектр факсимильного сигнала будет шире, чем для любого другого изображения, поскольку круче фронтов импульсов, чем у прямоугольных, не бывает.

Ширина спектра факсимильного сигнала зависит от скорости развертки изображения и размеров светового пятна.

На стандартном листе бумаги формата А4 в строке помещается примерно 1000 черно-белых элементов изображения при ширине пятна 0,2 мм. Если в факсимильном аппарате скорость развертки составляет 60 строк/мин, т.е. каждая строка считывается за 1 с, то за эту секунду 500 раз будет осуществлен переход с черного на белое, или наоборот. Это означает, что максимальная частота чередования импульсов равна 500 Гц. При ширине светового пятна 0,1 мм в строке будет в 2 раза больше элементов изображения, и максимальная частота чередования импульсов повысится до 1000 Гц. Так как для сохранения хорошей степени “прямоугольности” импульсов нужно передавать кроме основной гармоники еще и несколько высших, то ширина спектра факсимильного сигнала может простираться до 1,5…3,0 кГц.

При увеличении скорости развертки изображения черные и белые площадки будут считываться чаще и, следовательно, спектр факсимильного сигнала будет шире. При передаче изображений с полутонами получается сигнал сложной формы, спектр которого является непрерывным и соединяет все частоты от нуля до максимальной.

Факсимильная связь широко используется для передачи газетных полос (т.е. их изображений) в пункты централизованного печатания. Для передачи газет используют специальные высокоскоростные факсимильные аппараты с шириной светового пятна 0,05 мм. Повышенная скорость развертки позволяет передавать одну газетную полосу за 2–3 минуты. Это приводит к расширению спектра факсимильного сигнала до 180 кГц.

Телевизионные сигналы. Любое подвижное изображение – это, как правило, смена через каждые 40 мс одного неподвижного изображения другим (25 кадров в 1 с). За время между сменой кадров нужно успеть просмотреть все неподвижное изображение, которое содержит полмиллиона элементарных площадок или элементов изображения (625 строк по 833 элемента в строке). Значит, каждый элемент изображения придется рассматривать в течение одной полумиллионной доли от отведенных на весь кадр 40 мс. Это непостижимо короткий отрезок времени – всего две десятимиллиардных доли секунды! Ясно, что ни одно механическое устройство не способно перемещать световое пятно и фотоэлемент по строкам изображения с такой скоростью.

Вы никогда не задумывались над тем, что вы видите на экране телевизора, когда усаживаетесь перед ним в свободный вечер? Изображение? Нет, в действительности на экране никакого изображения нет, абсолютно никакого! Если бы мы сумели открыть глаза на какую-то ничтожную долю секунды (а речь идет о миллионных и даже миллиардных долях), то увидели бы на экране всего одну светящуюся точку. Это она бежит с невероятной скоростью по экрану, оставляя в нашем глазу след (мы видим то, чего уже нет, еще в течение 0,1 с), изменяющийся по яркости.

Что же заставляет светящуюся точку перемещаться с такой головокружительной быстротой? Электронный луч. Это он способен почти мгновенно отклоняться под действием изменяющегося магнитного поля и развертывать “картинки”. Это его можно очень точно сфокусировать с помощью специальных электрических “линз”. Первые опыты с электронным лучом начались в самом начале XX в. Еще в 1907 г. профессор Петербургского технологического института Б.Л. Розинг сконструировал первую электронно-лучевую трубку и получил на ней изображение, правда, невысокого качества. Изобретение в начале 30-х годов этого столетия первых качественных передающих трубок связано с именами советских ученых, пионеров отечественного телевидения С.И. Катаева и П.И. Шмакова.

Как бы не отличались конструкции передающих телевизионных трубок разных лет, все они в чем-то имитируют глаз. Роль хрусталика выполняет объектив, роль зрачка – диафрагма. Имеется в трубке и своя “сетчатка” – пластинка, напоминающая пчелиные соты, в ячейках которых располагаются микроскопические фотоэлементы. Конечно, их намного меньше, чем фоторецепторов в глазу: всего около 0,5 млн. Изображение, которое нужно превратить в серию электрических импульсов, проектируется с помощью объектива на эту искусственную “сетчатку”. Каждый микроскопический фотоэлемент (представляющий собой капельку светочувствительного серебряно-цезиевого сплава) получает свою порцию света и, если его подключить к внешней цепи, создаст ток, пропорциональный освещенности. Что касается электронного луча, то он как раз и подключает поочередно каждый из 500000 фотоэлементов к внешней цепи трубки, причем отводится ему на это всего 40 мс, пока не сменится кадр. Таким образом, на одном элементе изображения луч “задерживается” не более 80 миллиардных долей секунды (т.е. 80 нс). Величина тока во внешней цепи трубки отражает в каждый момент времени яркость соответствующего элемента изображения, спроектированного объективом на “сетчатку” передающей трубки, и является точной электронной копией передаваемого изображения.

Подсчитаем ширину спектра телевизионного сигнала. Пусть и на этот раз чередуются черные и белые площадки (элементы). Всего таких элементов будет 625 строк ґ 833 элемента = 520 625. В секунду меняется 25 кадров, т.е. 25 ґ 520 625 = 133 015 625 элементов. Значит переход с черного на белое, или наоборот, происходит примерно 6500000 раз в 1 с. Максимальная частота повторения импульсов равна 6,5 мГц, что и принято за верхнюю границу ширины спектра телевизионного сигнала. Нижней границей считают 50 Гц (нижняя граница сигнала звукового сопровождения).

Во время смены строк и кадров развертывающий луч приемной трубки должен быть погашен. Кроме того, необходимо синхронизировать лучи приемной и передающей трубок. Таким образом, кроме сигнала изображения необходимо передавать вспомогательные управляющие импульсы (гасящие и синхронизирующие). Электрический сигнал, включающий в себя сигнал изображения и управляющие импульсы, называется полным телевизионным сигналом.

В системах цветного телевидения передаваемое изображение расчленяется с помощью светофильтров на три одноцветных изображения – красное, зеленое и синее. Красные, зеленые и синие лучи попадают каждый на свою телевизионную трубку. В приемном устройстве путем сложения трех одноцветных изображений воспроизводится передаваемое цветное изображение.

Таким образом, спектр телевизионного сигнала простирается от 50 Гц до 6,5 мГц.

Телеграфные сигналы и сигналы передачи данных. Все рассматриваемые до сих пор сообщения и сигналы являются непрерывными. Сообщения и сигналы телеграфии и передачи данных относятся к дискретным.

Устройства преобразования телеграфных сообщений и данных в электрический сигнал представляют каждый знак сообщения (букву, цифру) в виде определенной комбинации импульсов и пауз одинаковой длительности. Импульс соответствует наличию тока на выходе устройства преобразования (например, телеграфного аппарата), пауза – отсутствию тока.

В телеграфии таблица, которая ставит в соответствие буквам, цифрам и другим знакам комбинации импульсов и пауз, называется телеграфным кодом. Если обозначить импульс через 1, а паузу через 0 и воспользоваться международным телеграфным кодом МТК-2, то можно, например, знак А записать в виде 11000, знак В – в виде 10011 и т.д.

Для передачи данных используют более сложные коды, которые позволяют обнаруживать и исправлять ошибки в принятой комбинации импульсов, возникающие от действия помех.

Устройства преобразования сигналов телеграфии и передачи данных в сообщения по принятым комбинациям импульсов и пауз восстанавливают в соответствии с таблицей кода знаки сообщения (буквы, цифры и др.) и выдают их на печатающее устройство либо на экран дисплея.

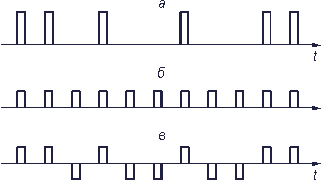
Рис. 3.10. Представление потока импульсов (а) в виде регулярной (б) и случайной (в) составляющих

Заметим, что чем меньше длительность импульсов, отображающих сообщения, тем больше их будет передано в единицу времени. Величина, обратная длительности импульса, называется скоростью телеграфирования: 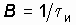, где 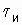– длительность импульса, с.

В честь французского инженера Ж. Бодо единицу скорости телеграфирования назвали бодом. При длительности импульса 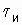= 1 с скорость В = 1 Бод. В телеграфии используются импульсы длительностью 0,02 с, что соответствует стандартной скорости телеграфирования 50 Бод. Применяются и другие скорости телеграфирования (например, 75 Бод). Скорости передачи данных существенно выше. Существует аппаратура передачи данных со скоростями 200, 600, 1200 Бод и более.

Сигналы телеграфии и передачи данных обычно имеют вид последовательностей прямоугольных импульсов.

Посмотрите внимательно на рис. 3.10. Можно представить (разумеется, чисто условно) поток импульсов в виде суммы двух последовательностей: регулярной и случайной. Спектр регулярной последовательности дискретный и создает нечетные гармоники тактовой частоты (т.е. частоты следования), а случайная последовательность имеет непрерывный заштрихованный спектр. Эти спектры показаны на рис. 3.11.

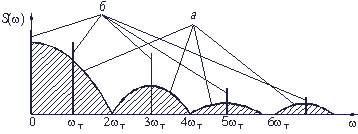
Рис. 3.11. Спектры случайной (а) и регулярной (б) составляющей потока импульсов

При передаче двоичных сигналов (т.е. 0 и 1) нет необходимости восстанавливать в приемнике импульсы без искажений, т.е. сохранять их форму; для восстановления информации достаточно зафиксировать только знак импульса при двуполярном сигнале либо наличие или отсутствие при однополярном сигнале. Расчеты показывают, что импульсы можно уверенно зафиксировать, если для их передачи используется ширина полосы частот, численно равная скорости передачи в бодах. Так, для стандартной скорости телеграфирования 50 Бод ширина спектра телеграфного сигнала составит 50 Гц. При скорости 2400 Бод (среднескоростная система передачи данных) ширина спектра сигнала равна примерно 2400 Гц.

Для удобства спектры основных сигналов электросвязи сведены в табл. 3.1. Даже беглый взгляд на табл. 3.1 позволяет понять, что для передачи разных видов сигналов требуется различная ширина полосы пропускания системы электросвязи.

Таблица 3.1. Ширина спектров сигналов электросвязи

Вид сигнала	Ширина спектра, Гц
Телеграфный	0…100
Передачи данных со скоростью 2 400 Бод	0…2 400
Телефонный	300…3 400
Звукового вещания	50…10 000
Факсимильный – при скорости 120 мин-1 – при передаче газет	0…1 465 0…180 000
Телевизионный	50…6 000 000

Контрольные вопросы

1. На какие простейшие составляющие “раскладывается” периодически повторяющийся прямоугольный импульс?
2. Чем отличается спектр периодического сигнала от спектра непериодического сигнала?
3. У какого импульса амплитуда спектральных составляющих убывает быстрее: а) более короткого или более длинного? б) с более крутым фронтом или с более пологим? в) повторяющегося чаще или реже?
4. Какие частотные диапазоны занимают спектры основных сигналов электросвязи

Список литературы

1. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей: Учебник для вузов; Под ред. В.П.Бакалова. – М.: Радио и связь, 2000. – 592 с.
2. Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей. Учебник для вузов: под ред. В.П. Бакалова – М.: Радио и связь. 1998. – 444 с.
3. Бакалов В.П., Журавлева О.Б., Крук Б.И. Анализ линейных электрических цепей: Учебное пособие для дистанционного обучения. – Новосибирск: СибГУТИ. 2001г.

siblec.ru

Чем отличается непрерывный сигнал от дискретного?

Непрерывный сигнал определен в каждый момент времени и принимает все значения в своей области значений. Дискретный сигнал определен либо только в определенные моменты времени (квантование по времени, решетчатая функция), либо его значение может принимать только определенные значения (квантование по уровню, ступенчатая функция). Если дискретный сигнал квантуется как по времени, так и по уровню, то его называют цифровым сигналом.

один прерываеться во времени другой нет

Различить довольно легко. Все что происходит периодически или ступенями, является дискретым. Все что постоянно и неизменно то непрерывно.

неверное сопоставление. это напоминает абракадабру . летели два гуся . один зеленый .другой на юг. непрерывный — он и есть дискретный. символизирующий или 1 или 0.

touch.otvet.mail.ru