Что такое непрерывный сигнал. Чем он отличается от дискретного сигнала. Каковы основные характеристики и области применения непрерывных и дискретных сигналов. Как выбрать подходящий тип сигнала для различных задач.
Что такое непрерывный сигнал и чем он отличается от дискретного
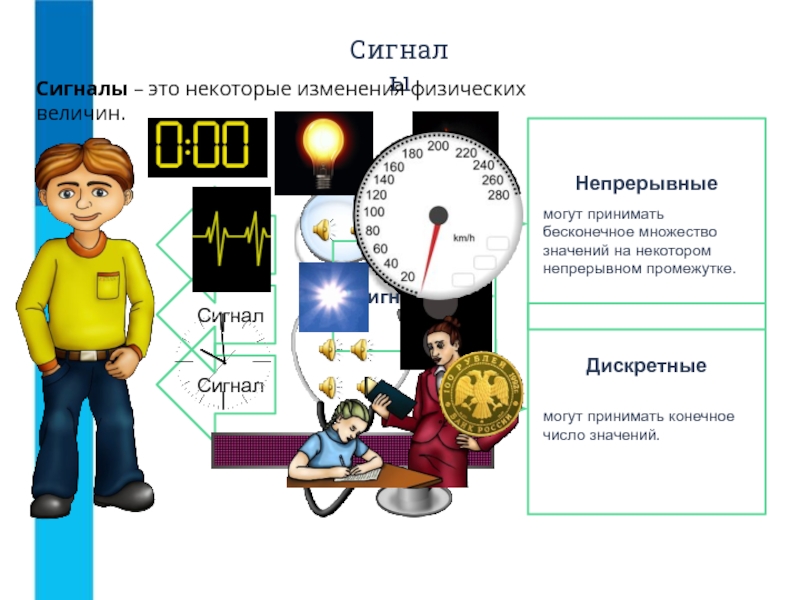
Непрерывный сигнал — это сигнал, который может принимать любые значения в любой момент времени в пределах заданного диапазона. Дискретный сигнал, напротив, определен только в отдельные моменты времени и принимает конечное число значений.
Ключевые отличия непрерывных и дискретных сигналов:
- Непрерывный сигнал определен для всех моментов времени, дискретный — только для отдельных точек
- Непрерывный сигнал может принимать бесконечное число значений, дискретный — конечное
- Непрерывный сигнал описывается непрерывной функцией, дискретный — последовательностью чисел
- Непрерывный сигнал имеет бесконечную полосу частот, дискретный — ограниченную
Основные характеристики непрерывных сигналов
Непрерывные сигналы обладают следующими ключевыми характеристиками:

- Могут принимать любые значения в заданном диапазоне
- Описываются непрерывными математическими функциями
- Имеют непрерывный частотный спектр
- Требуют аналого-цифрового преобразования для цифровой обработки
- Более чувствительны к шумам и помехам
- Анализируются методами непрерывного времени (преобразование Лапласа, Фурье и др.)
Ключевые особенности дискретных сигналов
Дискретные сигналы характеризуются следующими свойствами:
- Определены только в отдельные моменты времени
- Представляются последовательностью чисел
- Имеют ограниченный частотный спектр
- Легко обрабатываются цифровыми методами
- Менее подвержены шумам при цифровой передаче
- Анализируются методами дискретного времени (Z-преобразование, ДПФ и др.)
Области применения непрерывных и дискретных сигналов
Непрерывные сигналы широко используются в следующих областях:
- Аналоговые системы связи
- Аналоговое радио и телевидение
- Аналоговые измерительные приборы
- Аналоговые системы управления
Дискретные сигналы применяются в таких сферах как:
- Цифровые системы связи
- Цифровое радио и телевидение
- Компьютерные системы
- Цифровая обработка сигналов и изображений
Преимущества и недостатки непрерывных сигналов
Преимущества непрерывных сигналов:
- Высокая точность представления исходного физического процесса
- Отсутствие эффекта наложения спектров
- Простота генерации и обработки аналоговыми методами
Недостатки непрерывных сигналов:
- Сложность математического анализа
- Чувствительность к шумам и помехам
- Сложность хранения и передачи в цифровом виде
Достоинства и ограничения дискретных сигналов
Достоинства дискретных сигналов:
- Простота цифровой обработки и анализа
- Высокая помехоустойчивость при цифровой передаче
- Легкость хранения и передачи в цифровом виде
Ограничения дискретных сигналов:
- Ограниченная полоса частот
- Эффект наложения спектров при недостаточной частоте дискретизации
- Необходимость аналого-цифрового преобразования для работы с непрерывными сигналами
Как выбрать между непрерывным и дискретным сигналом
При выборе между непрерывным и дискретным представлением сигнала следует учитывать следующие факторы:
- Требуемая точность представления сигнала
- Необходимая полоса частот
- Методы последующей обработки и анализа
- Требования к помехоустойчивости
- Способ хранения и передачи сигнала
Для высокоточного представления быстроменяющихся процессов часто используют непрерывные сигналы. Для цифровой обработки и передачи по цифровым каналам применяют дискретные сигналы.
Преобразование непрерывных сигналов в дискретные
Для преобразования непрерывного сигнала в дискретный выполняют следующие операции:
- Дискретизация по времени — измерение значений сигнала через равные промежутки времени
- Квантование по уровню — округление измеренных значений до ближайших дискретных уровней
- Кодирование — представление квантованных значений в цифровом виде
Важно выбрать достаточную частоту дискретизации и количество уровней квантования, чтобы избежать потери информации.
Математическое описание непрерывных и дискретных сигналов
Непрерывный сигнал x(t) описывается непрерывной функцией времени t. Например:
x(t) = A*sin(2πft)
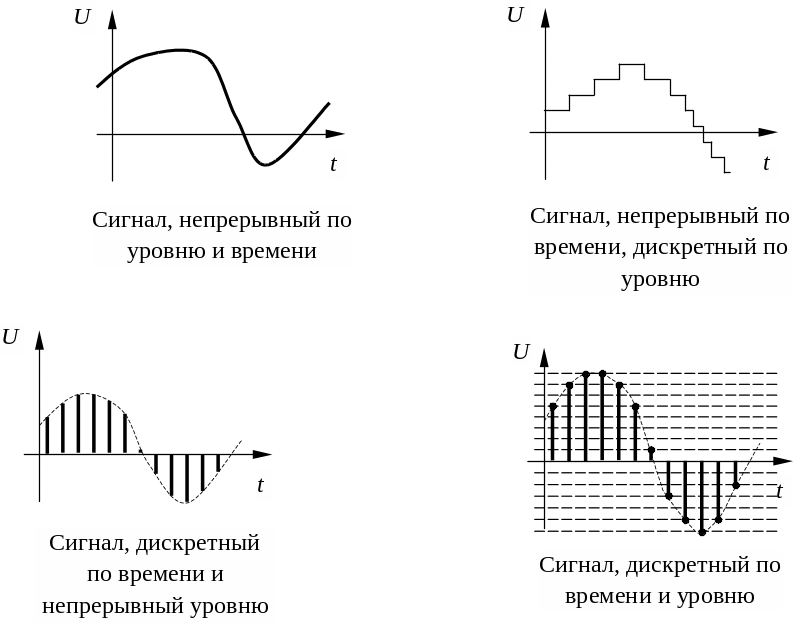
Дискретный сигнал x[n] задается последовательностью отсчетов в дискретные моменты времени n. Например:
x[n] = A*sin(2πfnT)
где T — период дискретизации.
Спектральный анализ непрерывных и дискретных сигналов
Для спектрального анализа непрерывных сигналов применяют преобразование Фурье:
X(f) = ∫ x(t)e^(-j2πft)dt
Для дискретных сигналов используют дискретное преобразование Фурье:
X[k] = Σ x[n]e^(-j2πkn/N)
Спектр непрерывного сигнала бесконечен, а дискретного — ограничен частотой Найквиста.
Заключение
Непрерывные и дискретные сигналы имеют свои особенности и области применения. Понимание их ключевых характеристик позволяет выбрать оптимальный тип сигнала для конкретной задачи. В современных системах часто используют комбинацию непрерывных и дискретных методов обработки сигналов.
Чем отличается непрерывный сигнал от дискретного • Мир электрики
На чтение: 3 минОбновлено: Рубрика: Основы электротехникиАвтор: admin
Содержание
- Особенности непрерывного сигнала
- Что такое дискретный
- Отличия двух видов сигналов
Для связи и передачи сообщений используют сигналы, которые отличаются друг от друга. Существуют непрерывные (НС) и дискретные сигналы (ДС).
Если дискретный сигнал квантуется как по времени, так и по уровню, то его называют цифровым сигналом
Сигнал считается непрерывным, если в заданных пределах он может иметь любое значение. С математической точки зрения это означает, что НС можно представить в виде непрерывной функции. Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре.
Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре.
Аналоговые системы для передачи информации, использующие НС, имеют следующие недостатки:
- пониженную помехозащищённость — это свойство связано с тем, что из-за непрерывности системы помеху, попавшую в сигнал, невозможно отличить от самого сигнала;
- затруднения при передаче сигналов управления;
- трудности при сопряжении с компьютером и другими цифровыми устройствами;
- трудности шифрования.
Что такое дискретный
Дискретность применяется в вычислительной технике для пакетной передачи данных
Дискретный сигнал — тот, который в некотором интервале может принимать определённое число значений. К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.
Благодаря достижениям в цифровой технике большинство электронных устройств в настоящее время являются цифровыми и работают с ДС. В то же время физические сигналы в природе имеют аналоговый вид. Преобразование НС в дискретный вид производится путём дискретизации его с помощью специальных устройств (АЦП). Обратное преобразование сигнала производится с помощью ЦАП.
В то же время физические сигналы в природе имеют аналоговый вид. Преобразование НС в дискретный вид производится путём дискретизации его с помощью специальных устройств (АЦП). Обратное преобразование сигнала производится с помощью ЦАП.
Достоинствами цифровых систем, работающих на ДС, являются:
- высокая помехозащищённость и возможность работы каналов связи при больших шумах;
- простота передачи команд управления каналами;
- возможность цифровой обработки сигналов;
- лёгкость засекречивания.
Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер — цифровая машина, то есть внутреннее представление информации в нём дискретно. Дискретизация входных сигналов (если она непрерывна) позволяет сделать их пригодными для дискретной обработки.
Все значения дискретного сигнала можно пронумеровать целыми числами
Основным отличием непрерывного сигнала от ДС является то, что он может иметь в заданном диапазоне любое значение, тогда как ДС может принимать только определённые значения.
К недостаткам систем, использующих ДС, можно отнести:
- увеличение полосы частот, требуемой для передачи сообщений;
- для обеспечения точного воспроизведения непрерывного сигнала при дискретизации требуется значительное количество уровней квантования и высокая частота;
- требование синхронизации;
- плохая совместимость с уже имеющимися аналоговыми системами.
Различные процессы могут быть описаны с помощью непрерывных или дискретных сигналов. Непрерывный сигнал может иметь любое значение из некоторого диапазона величин, тогда как для дискретного сигнала возможные его значения определены заранее. Во многих случаях при использовании цифровых методов обработки информации полезно преобразовать непрерывные сигналы в дискретные.
Рейтинг
( 2 оценки, среднее 2 из 5 )
0
admin/ автор статьи
Понравилась статья? Поделиться с друзьями:
Что такое непрерывный сигнал в информатике?
Что такое непрерывный сигнал в информатике?
Сигнал называется непрерывным, если его параметр может принимать любое значение в пределах некоторого интервала (рис. 1). Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала (рис. 2).
1). Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала (рис. 2).
Что значит непрерывный сигнал?
Непрерывная волна или непрерывный сигнал (англ. Continuous wave, CW) — электромагнитная волна с постоянными амплитудой, частотой и, в математическом анализе, с бесконечной продолжительностью.
Что такое дискретные сигналы?
discretus — «прерывистый», «разделённый») — сигнал, который является прерывистым (в отличие от аналогового) и который изменяется во времени и принимает любое значение из списка возможных значений. … Сэмплирования, который производит непрерывный сигнал дискретного времени
Как называется процесс преобразования аналогового непрерывного звука в цифровую форму?
Реальный аудио сигнал – это сложное по форме колебание, некая сложная зависимость амплитуды звуковой волны от времени. Преобразование аналогового звукового сигнала в цифровой вид называется аналогово-цифровым преобразованием или оцифровкой.
Как передать цифровой сигнал?
Чтобы передать цифровой сигнал по аналоговому каналу (радио или электрическому), его преобразуют, то есть модулируют. А при приеме — обратно демодулируют. Цифровой сигнал обладает важным свойством, которое заключается в возможности полностью его регенерировать в ретрансляторе.
Чем цифровой сигнал лучше аналогового?
Цифровая связь и вещания считаются более защищенными от помех и от внешних воздействий. Все дело в том, что при использовании «цифры» аналоговый сигнал с микрофона на передающей станции зашифровывается в цифровой код.
Что представляет собой цифровой сигнал?
Цифровой сигнал — сигнал, который можно представить в виде последовательности дискретных (цифровых) значений. В наше время наиболее распространены двоичные цифровые сигналы (битовый поток) в связи с простотой кодирования и используемостью в двоичной электронике.
Что такое цифровые и аналоговые приборы?
В аналоговых приборах — это схема считывания показаний датчика и передачи информации в аналоговом виде. В цифровых — каждый прибор является миниатюрным компьютером, содержит 8-разрядный микропроцессор с энергонезависимой флэш-памятью, в которой содержатся все настройки прибора и различные типы счетчиков.
В цифровых — каждый прибор является миниатюрным компьютером, содержит 8-разрядный микропроцессор с энергонезависимой флэш-памятью, в которой содержатся все настройки прибора и различные типы счетчиков.
Почему при использовании аналоговой техники передача информации всегда происходит с искажениями?
Дело в том, что при передаче сигнала всегда есть помехи, которые искажают его значения. В большинстве случаев эти искажения — случайные ошибки, не поддающиеся учёту. Фактически приёмник получает не исходный сигнал, посланный источником (сплошная линия на рис. 2.
Каковы преимущества цифровых устройств по сравнению с аналоговыми?
Аналоговые устройства могут работать с более быстро меняющимися сигналами, чем цифровые. Скорость обработки и передачи информации аналоговым устройством всегда может быть выше, чем скорость обработки и передачи цифровым устройством./span>
Что такое аналоговая связь?
Аналоговая связь — это передача непрерывного сигнала. Цифровая связь — это передача информации в дискретной форме (цифровом виде). Цифровой сигнал по своей физической природе является аналоговым, однако передаваемая с его помощью информация определяется конечным набором уровней сигнала.
Цифровая связь — это передача информации в дискретной форме (цифровом виде). Цифровой сигнал по своей физической природе является аналоговым, однако передаваемая с его помощью информация определяется конечным набором уровней сигнала.
Как происходит передача данных по сети?
Она используется для электронной связи и обмена информацией. Передача данных в сети Интернет происходит посредством коммуникационных протоколов TCP / IP UDP / IP, определяют правила, по которым происходит общение между компьютерами разных типов. … Практически все услуги сети построены на принципе клиент-сервер./span>
Что такое передача данных в мобильном телефоне?
Передача данных в телефоне или смартфоне означает мобильный интернет. Если нажать на указанную выше кнопку, включится мобильная передача данных, то есть мобильный интернет. Разумеется, интернет включится, если он поддерживается вашим тарифным планом. … То же самое можно увидеть и в меню смартфона.
Каким образом происходит передача информации?
Передача информации — физический процесс, посредством которого осуществляется перемещение информации в пространстве. … Информация представляется и передается в форме последовательности сигналов, символов. От источника к приёмнику сообщение передается через некоторую материальную среду.
Как происходит передача информации в компьютере?
История компьютера — Передача информации Информация передается в виде сообщений от некоторого источника информации к ее приемнику посредством канала связи между ними. Источник посылает передаваемое сообщение, которое кодируется в передаваемый сигнал. Этот сигнал посылается по каналу связи.
1.1: Классификация и свойства сигналов
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 22837
- Richard Baraniuk et al.

- Университет Райса
Введение
В этом модуле мы начнем изучение сигналов и систем с изложения некоторых основ классификации сигналов. По сути, это введение в важные определения и свойства, лежащие в основе обсуждения сигналов и систем, с кратким обсуждением каждого из них.
Классификации сигналов
Сравнение непрерывного времени и дискретного времени
Как следует из названий, эта классификация определяется тем, является ли ось времени 9 или нет.0040 дискретный (исчисляемый) или непрерывный (рисунок \(\PageIndex{1}\)). Сигнал непрерывного времени будет содержать значение для всех действительных чисел по оси времени. В отличие от этого, сигнал с дискретным временем, часто создаваемый путем дискретизации непрерывного сигнала, будет иметь значения только через равные промежутки времени по оси времени.
Рисунок \(\PageIndex{1}\)
Аналоговый и цифровой
Разница между аналоговым и цифровым аналогична разнице между непрерывным и дискретным временем. Однако в этом случае разница касается значений функции. Аналоговый соответствует непрерывному набору возможных значений функции, а цифровой соответствует дискретному набору возможных значений функции. Типичным примером цифрового сигнала является двоичная последовательность, где значения функции могут быть только единицей или нулем.
Однако в этом случае разница касается значений функции. Аналоговый соответствует непрерывному набору возможных значений функции, а цифровой соответствует дискретному набору возможных значений функции. Типичным примером цифрового сигнала является двоичная последовательность, где значения функции могут быть только единицей или нулем.
Рисунок \(\PageIndex{2}\)
Периодические и апериодические
Периодические сигналы повторяются примерно с периодом
\[f(t)=f(t+T) \label {1.1} \]
фундаментальный период нашей функции, \(f(t)\), является наименьшим значением \(T\), которое все еще позволяет уравнению \ref{1.1} быть верным.
(а) (б) Рисунок \(\PageIndex{3}\): (a) Периодический сигнал с периодом \(T_0\) (b) Апериодический сигналКонечная и бесконечная длина
Другой способ классификации сигнала — его длина вдоль временной оси. Определен ли сигнал для всех возможных значений времени или только для определенных значений времени? Математически говоря, \(f(t)\) является сигналом конечной длины , если он определен только на конечном интервале
Определен ли сигнал для всех возможных значений времени или только для определенных значений времени? Математически говоря, \(f(t)\) является сигналом конечной длины , если он определен только на конечном интервале
\[ t_{1} где \(t_1 < t_2\). Точно так же сигнал бесконечной длины , \(f(t)\), определен для всех значений: Каузальные сигналы — это сигналы, равные нулю в течение всего отрицательного времени, тогда как антикаузальные — это сигналы, равные нулю в течение всего положительного времени. Некаузальные сигналы — это сигналы, которые имеют ненулевые значения как в положительном, так и в отрицательном времени (рисунок \(\PageIndex{4}\)). Четный сигнал — это любой сигнал \(f\), такой что \(f(t) = f(-t)\). Используя определения четных и нечетных сигналов, мы можем показать, что любой сигнал можно записать как комбинацию четного и нечетного сигналов. То есть каждый сигнал имеет нечетно-четное разложение. Чтобы продемонстрировать это, мы не должны смотреть дальше одного уравнения. Четный против нечетного
 Даже сигналы можно легко заметить, поскольку они симметричны относительно вертикальной оси. С другой стороны, нечетный сигнал является сигналом \(f\), таким что \(f(t)=-f(-t)\) (рис. \(\PageIndex{5}\)).
Даже сигналы можно легко заметить, поскольку они симметричны относительно вертикальной оси. С другой стороны, нечетный сигнал является сигналом \(f\), таким что \(f(t)=-f(-t)\) (рис. \(\PageIndex{5}\)).
Умножая и складывая это выражение, можно показать, что оно истинно. Кроме того, можно показать, что \(f(t)+f(-t)\) удовлетворяет требованию четной функции, а \(f(t)-f(-t)\) удовлетворяет требованию нечетной функции. (рис. \(\PageIndex{6}\)).
(а)(б)(в)(г) Рисунок \(\PageIndex{6}\): (a) Сигнал, который мы разложим, используя разложение на чет-нечет (b) Четная часть: \(e(t)=\frac{1}{2}(f(t) +f(−t))\) (c) Нечетная часть: \(o(t)=\frac{1}{2}(f(t)−f(−t))\) (d) Проверка: \ (е (т) + о (т) = f (т) \)Детерминистический и случайный
Детерминированный сигнал — это сигнал, в котором каждое значение сигнала является фиксированным и определяется математическим выражением, правилом или таблицей. С другой стороны, значения случайного сигнала строго не определены, а подвержены некоторой изменчивости.
С другой стороны, значения случайного сигнала строго не определены, а подвержены некоторой изменчивости.
Рассмотрим сигнал, определенный для всех действительных \(t\), описанных как
\[f(t)=\left\{\begin{array}{cc}
\sin (2 \pi t) / t & t \ geq 1 \\
0 & t<1
\end{массив}\right. \nonumber \]
Этот сигнал является непрерывным во времени, аналоговым, апериодическим, бесконечной длины, причинным, ни четным, ни нечетным, и, по определению, детерминированным.
Краткий обзор классификаций сигналов
В этом модуле описываются лишь некоторые из многих способов классификации сигналов. Они могут быть непрерывными или дискретными, аналоговыми или цифровыми, периодическими или апериодическими, конечными или бесконечными, детерминированными или случайными. Мы также можем разделить их на основе их свойств причинности и симметрии.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Ричард Баранюк и др.

- Лицензия
- СС BY
- Программа OER или Publisher
- OpenStax CNX
- Показать оглавление
- нет
- Теги
- аналог
- антикаузальный
- причинный
- непрерывный сигнал времени
- детерминированный сигнал
- цифровой
- дискретный временной сигнал
- сигнал конечной длины
- основной период
- сигнал бесконечной длины
- непричинный
- случайный сигнал
Сигнал непрерывного времени и сигнал дискретного времени | Разница, схема и информация
Сигнал непрерывного времени и сигнал дискретного времени | Отличия, схема и информация
Просмотров сообщений: 537
В сигналах с непрерывным временем сигнал определяется в непрерывном диапазоне времени. Это означает, что сигнал может принимать любое значение в любой момент времени. Примером непрерывного сигнала времени является аналоговый аудиосигнал, который может принимать бесконечное число значений в пределах определенного диапазона амплитуд с течением времени.
Это означает, что сигнал может принимать любое значение в любой момент времени. Примером непрерывного сигнала времени является аналоговый аудиосигнал, который может принимать бесконечное число значений в пределах определенного диапазона амплитуд с течением времени.
Сигналы дискретного времени определяются только в определенные изолированные моменты времени. Сигнал может принимать значение только в этих дискретных точках. Примером дискретного сигнала времени является последовательность цифровых аудиосэмплов, которые определяются в определенные моменты времени и обычно представлены серией двоичных цифр.
Чтобы лучше понять, вот дополнительная информация о сигналах с непрерывным и дискретным временем: Одно из ключевых различий между сигналами с непрерывным временем и сигналами с дискретным временем заключается в том, что сигналами с непрерывным временем, как правило, труднее манипулировать и математически анализировать из-за бесконечности. количество возможных значений, которые они могут принимать. С дискретными временными сигналами, с другой стороны, намного проще работать, поскольку они определяются в определенные моменты времени и могут быть представлены конечным рядом дискретных значений.
С дискретными временными сигналами, с другой стороны, намного проще работать, поскольку они определяются в определенные моменты времени и могут быть представлены конечным рядом дискретных значений.
Как непрерывные, так и дискретные сигналы времени можно обрабатывать и анализировать с использованием математических методов, таких как анализ Фурье, который позволяет нам представлять сигнал с точки зрения его частотных составляющих. Однако методы, используемые для анализа, могут различаться в зависимости от того, является ли сигнал непрерывным или дискретным.
Скачать изображение выше в HD | Размер: 170 КБ | Изображение JPG
Текстовая версия:
| СР. НЕТ. | ПАРАМЕТР | НЕПРЕРЫВНЫЙ СИГНАЛ ВРЕМЕНИ | ДИСКРЕТНЫЙ СИГНАЛ ВРЕМЕНИ |
|---|---|---|---|
| 1 | Определение | Непрерывный сигналы времени являются функциями непрерывной переменной, такой как время. | Сигналы дискретного времени представляют собой последовательности значений, которые определяются через дискретные, равномерно распределенные интервалы времени. |
| 2 | Представление | Непрерывные сигналы времени обычно представляются с использованием математических функций, таких как синусоидальные или косинусоидальные волны. | Сигналы дискретного времени обычно представляются последовательностями чисел. |
| 3 | Анализ | Непрерывные сигналы во времени можно анализировать с использованием методов непрерывной временной области, таких как преобразования Лапласа и преобразования Фурье. | Сигналы дискретного времени можно анализировать с использованием методов дискретной области времени, таких как z-преобразование и дискретное преобразование Фурье. |
| 4 | Частота | Непрерывные сигналы времени имеют непрерывный частотный спектр. | Сигналы дискретного времени имеют дискретный частотный спектр. |
| 5 | Цифровая обработка сигналов | С другой стороны, сигналы непрерывного времени требуют аналого-цифрового преобразования, прежде чем их можно будет обрабатывать в цифровом виде. | Сигналы дискретного времени широко используются в цифровой обработке сигналов, поскольку они легко обрабатываются компьютерами. |
| 6 | Хранение | Непрерывные сигналы времени, с другой стороны, требуют больше места для хранения и не могут быть переданы в цифровом виде без предварительной выборки и квантования. | Сигналы дискретного времени можно легко хранить и передавать в цифровом виде, поскольку они представлены рядом чисел. |
| 7 | Полоса пропускания | Непрерывные сигналы времени имеют бесконечную полосу пропускания. | Сигналы дискретного времени имеют конечную полосу пропускания. |
| 8 | Модуляция | Непрерывные сигналы времени можно модулировать с помощью аналоговых методов, таких как амплитудная, частотная и фазовая модуляция. | Сигналы дискретного времени обычно модулируются с использованием цифровых методов, таких как импульсно-кодовая модуляция (ИКМ) и квадратурная амплитудная модуляция (КАМ). |
| 9 | Шум | Непрерывные временные сигналы более чувствительны к шуму и помехам, поскольку они передаются по аналоговым каналам. | Сигналы дискретного времени менее подвержены шуму, так как передаются в цифровом виде. |
| 10 | Фильтрация | Фильтрация сигналов непрерывного времени обычно выполняется с использованием аналоговых фильтров. | Фильтрация сигналов дискретного времени обычно выполняется с помощью цифровых фильтров. |
| 11 | Устойчивость | Системы с непрерывным временем можно анализировать с использованием таких критериев устойчивости, как критерий устойчивости Рауса-Гурвица и критерий устойчивости Найквиста. | Системы с дискретным временем можно анализировать с использованием таких критериев устойчивости, как критерий устойчивости Жюри и критерий устойчивости Гурвица. |
| 12 | Причинность | Системы с непрерывным временем могут быть либо причинными, либо некаузальными. | Дискретные системы времени всегда причинны. |
| 13 | Задержка по времени | Системы с непрерывным временем могут иметь произвольную задержку по времени. | Системы с дискретным временем имеют фиксированную временную задержку, равную одному периоду выборки. |
| 14 | Математические операции | Непрерывными сигналами времени можно манипулировать, используя непрерывные математические операции во временной области, такие как интегрирование и дифференцирование. | Сигналами дискретного времени можно манипулировать с помощью математических операций в области дискретного времени, таких как дискретное интегрирование и дискретное дифференцирование.
. |

