Какой сигнал называют дискретным. Дискретный сигнал: определение, характеристики и применение в цифровой обработке — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое дискретный сигнал. Как дискретный сигнал отличается от аналогового и цифрового. Какие основные характеристики имеет дискретный сигнал. Где применяются дискретные сигналы в цифровой обработке.

Содержание

Определение дискретного сигнала

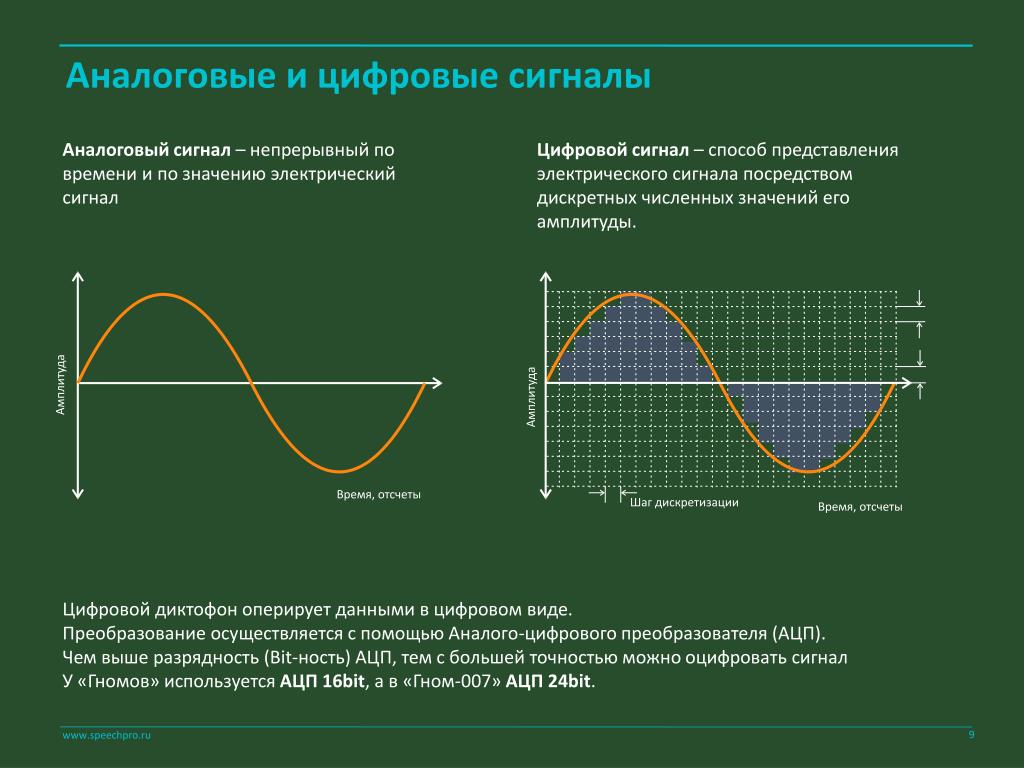
Дискретный сигнал — это сигнал, значения которого определены только в дискретные моменты времени. В отличие от аналогового сигнала, который является непрерывным, дискретный сигнал представляет собой последовательность отсчетов, взятых через равные промежутки времени.

Основные характеристики дискретного сигнала:

Значения определены только в дискретные моменты времени
Интервал между отсчетами постоянный (период дискретизации)
Амплитуда может принимать любые значения в допустимом диапазоне
Описывается последовательностью чисел

Отличия дискретного сигнала от аналогового и цифрового

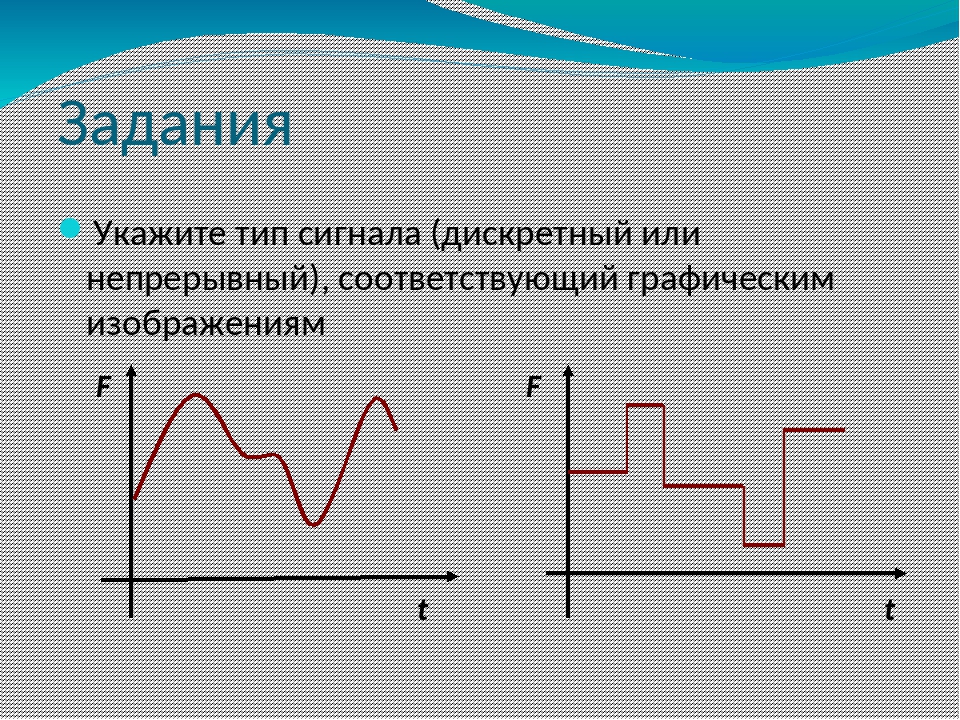
Чем дискретный сигнал отличается от аналогового и цифрового?

Аналоговый сигнал непрерывен и во времени, и по амплитуде
Дискретный сигнал дискретен по времени, но непрерывен по амплитуде
Цифровой сигнал дискретен и по времени, и по амплитуде (квантован)

Таким образом, дискретный сигнал занимает промежуточное положение между аналоговым и цифровым.

Математическое описание дискретного сигнала

Математически дискретный сигнал x[n] можно представить как произведение непрерывного сигнала x(t) и последовательности дельта-функций:

x[n] = x(t) * Σδ(t — nT)

где T — период дискретизации, n — целое число.

Это означает, что дискретный сигнал сохраняет значения исходного непрерывного сигнала только в моменты времени nT.

Спектр дискретного сигнала

Какой спектр имеет дискретный сигнал? Спектр дискретного сигнала является периодическим с периодом, равным частоте дискретизации. Это следствие теоремы Котельникова:

Спектр периодический с периодом Fs = 1/T

Содержит копии спектра исходного аналогового сигнала
Может возникать наложение спектров (алиасинг) при недостаточной частоте дискретизации

Для предотвращения искажений необходимо выбирать частоту дискретизации не менее чем в 2 раза превышающую максимальную частоту в спектре сигнала.

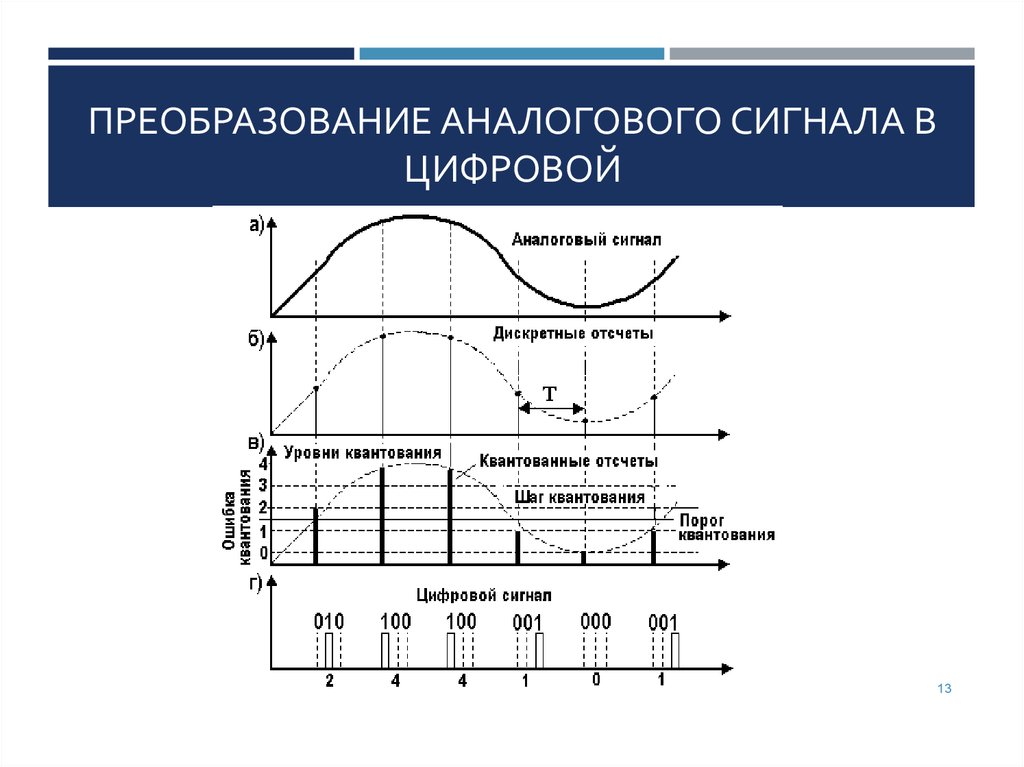
Преобразование аналогового сигнала в дискретный

Как происходит преобразование аналогового сигнала в дискретный? Основные этапы:

Ограничение спектра аналогового сигнала (антиалиасинговая фильтрация)
Выборка значений сигнала через равные промежутки времени (дискретизация)
Фиксация мгновенных значений (схема выборки-хранения)

Ключевой элемент — аналого-цифровой преобразователь (АЦП), осуществляющий дискретизацию по времени.

Восстановление аналогового сигнала из дискретного

Возможно ли восстановить исходный аналоговый сигнал из дискретного? Да, если выполняются условия теоремы Котельникова:

Сигнал должен быть полностью определен своими отсчетами
Частота дискретизации должна быть как минимум в 2 раза выше максимальной частоты в спектре сигнала

Восстановление осуществляется с помощью фильтра нижних частот (интерполяционного фильтра).

Области применения дискретных сигналов

Где применяются дискретные сигналы? Основные области применения:

Цифровая обработка сигналов
Цифровая связь
Аудио- и видеотехника
Измерительные системы
Системы управления

Дискретное представление позволяет эффективно обрабатывать, передавать и хранить сигналы в цифровых системах.

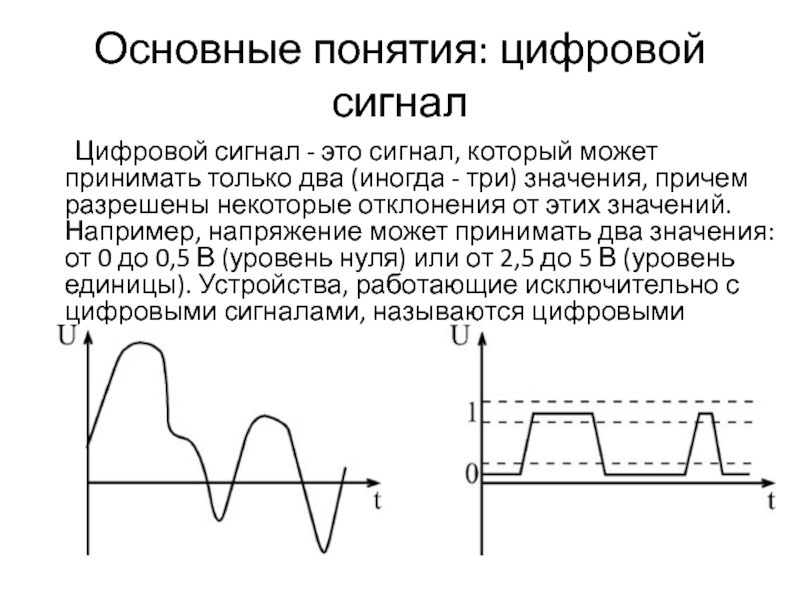
Преимущества дискретных сигналов

Какие преимущества дают дискретные сигналы по сравнению с аналоговыми?

Высокая помехоустойчивость
Простота хранения и передачи
Возможность сложной математической обработки

Гибкость при изменении алгоритмов обработки
Высокая точность представления

Это обусловило широкое распространение систем цифровой обработки сигналов на основе дискретного представления.

Ограничения дискретных сигналов

Какие ограничения имеют дискретные сигналы? Основные недостатки:

Ограниченная полоса частот (не более половины частоты дискретизации)
Возможность наложения спектров (алиасинг)
Необходимость аналого-цифрового и цифро-аналогового преобразования
Конечная точность представления (при квантовании)

Эти факторы необходимо учитывать при проектировании систем с дискретными сигналами.

Заключение

Дискретные сигналы играют ключевую роль в современных цифровых системах обработки информации. Они позволяют эффективно представлять, передавать и обрабатывать сигналы в цифровой форме. При этом важно правильно выбирать параметры дискретизации и учитывать особенности дискретного представления сигналов.

26 вопросов и ответов. Теория электрических цепей. Курс лекций

Сигнал – это физический процесс (например, изменяющиеся во времени токи и напряжения), содержащий в себе некоторую информацию. Любой сигнал можно описать математической функцией.

Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией , которая может принимать любые значения в определенном интервале; дискретные сигналы представляют собой последовательности или отсчеты функции , взятые в определенные дискретные моменты времени nT; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения – уровни квантования, которые затем кодируются двоичными числами.

Если в цепь микрофона (рис. 1), где ток является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала.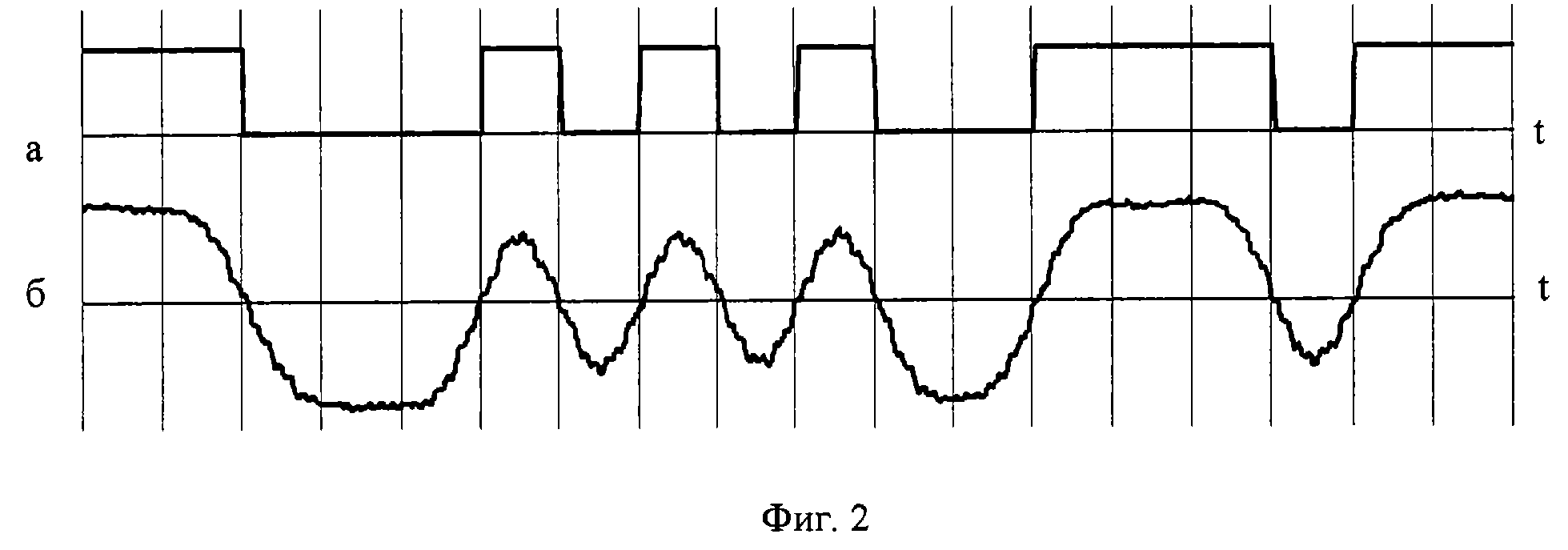

Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал.

Рис. 1

В отличие от непрерывного сигнала дискретный сигнал можно обозначить . Однако, чаще его обозначают , заменяя непрерывное время t дискретными моментами nT, следующими строго через интервал T. Используются и более краткие обозначения: и . Причем, во всех этих записях n – целое число, принимающее как положительные, так и отрицательные значения. Так, на рис. 1 при n < 0 дискретный сигнал . При n = 0 значение равно значению сигнала в момент времени t = 0. При n

> 0 отсчеты повторяют форму сигнала , т.к. их амплитуды равны значениям непрерывного сигнала в моменты времени nT.

Рис. 2

Дискретные сигналы можно задавать графиками, как это показано на рис. 1, формулами, например, , в виде таблиц дискретных значений или в виде комбинации этих способов. Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов.

Пример 1.1. Единичный ступенчатый аналоговый сигнал приведен на рис. 2.

Соответствующий ему дискретный сигнал называется ступенчатой последовательностью. Он определяется следующим образом:

Рис. 3

Такая последовательность приведена на рис. 2.

Пример 1.2. Импульс Дирака или d-функция в аналоговой области приведена на рис. 3.

Рис. 4

Дельта-последовательность или дискретная d-функция определяется выражением

Последовательность , приведенная на рис. 3, принимает единственное значение, равное 1, при n = 0. Этот сигнал можно сдвинуть на k интервалов:

Тогда математическая запись любого дискретного сигнала имеет вид

где – отсчеты исходного аналогового сигнала.

Этот сигнал можно получить из аналогового (рис. 4) периодическим замыканием ключа на очень короткое время в моменты t = k.

Самоконтроль

1. Что представляют собой аналоговые, дискретные и цифровые сигналы?

2. Как практически получить дискретный сигнал из аналогового?

3. Что такое ступенчатая последовательность и дельта-последовательность?

4. Изобразите графики дискретных d-функций и .

Дискретный сигнал — сигнал, который является прерывистым и который изменяется во времени и принимает любое значение из списка возможных значений. Список возможн

Пользователи также искали:

дискретное устройство, дискретные сообщения, дискретным сигналом называют, дискретный и цифровой сигнал разница, дискретный код это, дискретный пид регулятор, дискретный сигнал формирует, дискретный сигнал простыми словами, отметьте все свойства характерные для дискретных сигналов, дискретный, сигналом, сигнал, сигналов, дискретных, дискретный сигнал, дискретного, данных, данные, сигнала, дискретными, сигналы, дискретные, дискретных сигналов, данным, дискретным, дискретного сигнала, словами, код это, цифровой, и цифровой, формирует, данными, дискретные сигналы, понятие, дискретный код это, дискретный сигнал формирует, дискретные сообщения, дискретное устройство, дискретным сигналом называют,

GOOSE.

Устройства сбора данных серии ЭНКМ 3 предназначены создания систем сбора и сбор данных дискретных и аналоговых сигналов с устройств. .. Модули ввода вывода аналоговых и дискретных сигналов. ЕТ, Преобразователи искробезопасные разделительные дискретных сигналов. ЕТ 186, ET 187 Преобразователи искробезопасные. .. Блоки дискретных сигналов БДС8 и БДС16. Обновленные устройства сбора данных серии ЭНКМ 3 предназначены создания сбор данных дискретных и аналоговых сигналов с устройств. .. ЭНКМ 3 – Инженерный центр Энергосервис. Дискретные сигналы отличаются от аналоговых тем, что их значения. Эти данные можно так закодировать, что будет возможно скорректировать все. .. И.В.Черных. Simulink: Инструмент моделирования. Формирует синусоидальный сигнал с заданной частотой, амплитудой, Формирование выходного сигнала по текущему значению времени для дискретных систем. Получение данных из рабочего пространства MATLAB.. .. Аналоговые,дискретные и цифровые сигналы. Аналоговый и цифровой сигнал обрабатывается и направлен на то, чтобы передать будет декодировать импульсы и восстановит исходные данные.

. .. Распознавание дискретного сигнала в аддитивном шуме для. Давайте разберемся, какие данные передаются с помощью дискретных сигналов. Условно эти данные можно разделить на три группы.. .. ЭНКМ 3 – Инженерный центр Энергосервис. Дискретный полезный сигнал содержится лишь водномизканалов. работа позволяет провести анализ представленной модели передачи данных с. .. Практическое применение преобразования Фурье для анализа. Модуль вывода дискретных сигналов – на нашем сайте! В системах автоматизации ключевую роль играют данные, поступающие от первичных. .. Входные выходные дискретные сигналы в электроэнергетике. Дискретные сигналы и дискретное преобразование Фурье техники изменились и способы хранения данных измерений сигналов..

Технические данные, ЕТ 186, ET 187 Преобразователи. Дискретный сигнал данных – отличается от аналоговых тем, что его значения известны лишь в дискретные моменты времени.

Дискретные сигналы. .. Преобразование Лапласа дискретного сигнала. Z. Наборы данных используются для группировки данных, которые будут между устройствами РЗА посредством дискретных сигналов.. .. Дискретность. Принципы и применение. Сигнал и работа. bus terminal, аналоговый ввод, ввод дискретных сигналов, контроллер шины, модуль ввода вывода, система ввода вывода, система сбора данных.. .. bus terminal, аналоговый ввод дискретных сигналов, контроллер. Электрические сигналы – это, переводя на компьютерный язык, биты, Для передачи данных дискретного типа по цифровому каналу. .. Контроллер дискретных сигналов uni google-wiki.info. Передачи полученных данных о состоянии дискретных сигналов сухих контактов оборудования, температуры шкафов по протоколу SNMP версии. .. Способы передачи данных по коммуникационным сетям. В электронике существует понятие дискретного сигнала, Дискретность позволяет существенно уменьшить суммарный поток данных, формируя из. .. Виды сигналов, модуляция Школа для электрика: все об.

Модули дискретных входных сигналов KL1408 и KL1418 принимают дискретные Данные модули имеют восемь каналов со светодиодной индикацией. .. Цифровое аудио от А до Я Sony RU. запись аналогового источника в виде последовательности дискретных чисел. Формат сжатия аудио без потери данных, аналогичный DTS Master Audio. Аналоговый сигнал сэмплируется через регулярные интервалы, а его. .. KL1408, KL1418 8 канальные модули дискретных входных. В предыдущих разделах мы подробно рассмотрели расчет аналоговых фильтров с заданными характеристиками. Пришло время переходить к. .. Аналоговый и цифровой сигнал. Типы сигналов и как это действует. Блоки дискретных сигналов БДС8 и БДС16 предназначены для работы с TxD мигает при передаче данных от блока к ЭВМ верхнего уровня по.

Лабораторная работа №1: Дискретные сигналы [se.moevm.info]

Цель работы

Изучить математическое описание дискретных сигналов и овладеть программными средствами их моделирования.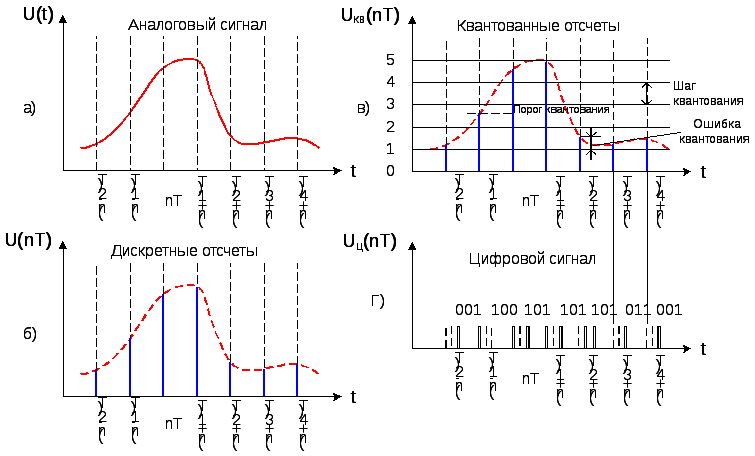

Основные теоретические положения

В теории цифровой обработки сигналов (ЦОС) принято разделять операции дискретизации по времени и квантования по уровню. Полагая операцию квантования отсутствующей, изучают дискретные сигналы и линейные дискретные системы (ЛДС), а затем, отдельно, – эффекты нелинейной операции квантования.

Дискретным называют сигнал, дискретный по времени и непрерывный по состоянию (уровню), который описывается последовательностью чисел бесконечной разрядности $ x(nT) $ или $ x(n) $, называемой коротко последовательностью. Значения $ nT $, $ n \in \mathbb{Z}_+$, называют дискретным временем, где $ T $ – период дискретизации, а $ n $ – дискретным нормированным временем.

В теории ЦОС термины «дискретный сигнал» и «последовательность» употребляют в тождественном смысле.

Цифровым называют сигнал, дискретный по времени и квантованный по состоянию (уровню), который описывается последовательностью чисел конечной разрядности – квантованной последовательностью $ \tilde x(nT) $ или $ \tilde x(n) $. При компьютерном моделировании под дискретным сигналом условно понимают последовательность чисел максимально возможной разрядности, а под цифровым – последовательность чисел заданной разрядности.

Постановка задачи

С помощью программных средств провести моделирование и анализ дискретных последовательностей. Результаты подкрепить соответствующими графиками и выводами.

Порядок выполнения работы

Смоделировать единичный цифровой импульс $ \delta_d(k) $ с выводом графиков на интервале дискретного времени $ nT \in [0, (N — 1)T] $ и дискретного нормированного времени $ n \in [0, N — 1] $. Пояснить взаимосвязь между дискретным и дискретным нормированным временем и различие между цифровым единичным импульсом и функцией Дирака.
Смоделировать дискретный единичный скачок $ \sigma_d(k) $ с выводом графиков на интервале дискретного времени $ nT \in [0, (N — 1)T] $ и дискретного нормированного времени $ n \in [0, N — 1] $. Пояснить соответствие между дискретным единичным скачком и функцией Хэвисайда, а также чему равна частота дискретизации дискретного единичного скачка.
Смоделировать дискретную экспоненциальную функцию $ s_1(k) $ с выводом графиков на интервале дискретного времени $ nT \in [0, (N — 1)T] $ и дискретного нормированного времени $ n \in [0, N — 1] $. Пояснить соответствие между дискретной и аналоговой экспонентами.
Смоделировать дискретный комплексный гармонический сигнал $ s_2(k) = C\exp(j\hat\omega_0k) $ с выводом графиков вещественной и мнимой частей на интервале времени $ n \in [0, N — 1] $. Записать данный сигнал в виде комбинации двух вещественных последовательностей.
Вывести графики последовательностей $ \delta_d(k) $, $ \sigma_d(k) $ и $ s_1(k) $, задержанных на $ m $ отсчетов, на интервале времени $ n \in [0, N — 1] $. Записать формулы задержанных последовательностей.
Смоделировать дискретный прямоугольный импульс \[ s_3(k) = \left\{ \begin{aligned} U&, \quad n_0 \leqslant n \leqslant n_0 + n_{imp} — 1; \\ 0&, \quad \mbox{иначе} \\ \end{aligned} \right. k\cos(\hat\omega_0k) $ и вывести график на интервале времени $ n \in [0, N — 1] $. Пояснить операции при моделировании данного сигнала.
Вывести график пяти периодов периодической последовательности $ s_6(k) $ дискретных прямоугольных импульсов амплитуды $ U $ и длительности $ n_{imp} $ с периодом, вдвое большим длительности импульса. Пояснить операции при моделировании периодической последовательности.
Сделать выводы.

Варианты заданий

Выполнение работ осуществляется в бригадах по индивидуальным вариантам заданий. Номер варианта для каждой бригады определяется преподавателем.

Варианты к лабораторной работе №1

Содержание отчёта

Цель работы.
Краткое изложение основных теоретических понятий.
Постановка задачи с кратким описанием порядка выполнения работы.
Необходимые рисунки и таблицы с пояснениями.
Общий вывод по проделанной работе.
Код программы.

courses/digital_signal_processing/lab1.txt · Last modified: 2020/10/14 10:36 by andrey.suchkov

Какой сигнал называется дискретным — MOREREMONTA

Любая система цифровой обработки сигналов независимо от ее сложности содержит цифровое вычислительное устройство — универсальную цифровую вычислительную машину, микропроцессор или специально разработанное для решения конкретной задачи вычислительное устройство. Сигнал, поступающий на вход вычислительного устройства, должен быть преобразован к виду, пригодному для обработки на ЭЦВМ. Он должен иметь вид последовательности чисел, представленных в коде машины.

В некоторых случаях задача представления входного сигнала в цифровой форме решается сравнительно просто. Например, если нужно передать словесный текст, то каждому символу (букве) этого текста нужно поставить в соответствие некоторое число и, таким образом, представить передаваемый сигнал в виде числовой последовательности. Легкость решения задачи в этом случае объясняется тем, что словесный текст по своей природе дискретен.

Однако большинство сигналов, с которыми приходится иметь дело в радиотехнике, являются непрерывными. Это связано с тем, что сигнал является отображением некоторого физического процесса, а почти все физические процессы непрерывны по своей природе.

Рассмотрим процесс дискретизации непрерывного сигнала на конкретном примере. Допустим, на борту некоторого космического аппарата производится измерение температуры воздуха; результаты измерения должны передаваться на Землю в центр обработки данных. Температура

Рис. 1.1. Виды сигналов: а — непрерывный (континуальный) сигнал; 6 — дискретный сигнал; в — АИМ-колебание; г — цифровой сигнал

воздуха измеряется непрерывно; показания датчика температуры также являются непрерывной функцией времени (рис. 1.1, а). Но температура изменяется медленно, достаточно передавать ее значения один раз в минуту. Кроме того, нет необходимости измерять ее с точностью выше чем 0,1 градуса. Таким образом, вместо непрерывной функции можно с интервалом в 1 мин передавать последовательность числовых значений (рис. 1.1, г), а в промежутках между этими значениями можно передавать сведения о давлении, влажности воздуха и другую научную информацию.

Рассмотренный пример показывает, что процесс дискретизации непрерывных сигналов состоит из двух этапов: дискретизации по времени и дискретизации по уровню (квантования). Сигнал, дискретизированный только по времени, называют дискретным; он еще не пригоден для обработки в цифровом устройстве. Дискретный сигнал представляет собой последовательность, элементы которой в точности равны соответствующим значениям исходного непрерывного сигнала (рис. 1.1, б). Примером дискретного сигнала может быть последовательность импульсов с изменяющейся амплитудой — амплитудно-импульсно-модулированное колебание (рис. 1.1, в). Аналитически такой дискретный сигнал описывается выражением

где исходный непрерывный сигнал; единичный импульс АИМ-колебания.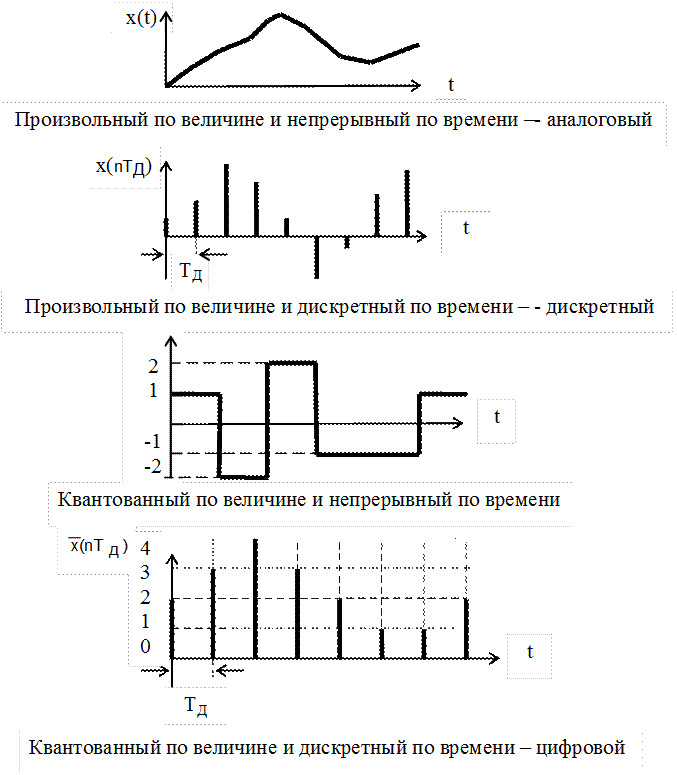

Если уменьшать длительность импульса сохраняя его площадь неизменной, то в пределе функция стремится к -функции. Тогда выражение для дискретного сигнала можно представить в виде

Для преобразования аналогового сигнала в цифровой после дискретизации по времени должна следовать дискретизация по уровню (квантование). Необходимость квантования вызвана тем, что любое вычислительное устройство может оперировать только числами, имеющими конечное число разрядов. Таким образом, квантование представляет собой округление передаваемых значений с заданной точностью. Так в рассмотренном примере производится округление значений температуры до трех значащих цифр (рис. 1.1, г). В других случаях число разрядов передаваемых значений сигнала может быть иным. Сигнал, дискретизированный и по времени, и по уровню, называется цифровым.

Правильный выбор интервалов дискретизации по времени и по уровню очень важен при разработке цифровых систем обработки сигналов. Чем меньше интервал дискретизации, тем точнее дискретизированный сигнал соответствует исходному непрерывному. Однако при уменьшении интервала дискретизации по времени возрастает число отсчетов, и для сохранения общего времени обработки сигнала неизменным приходится увеличивать скорость обработки, что не всегда возможно. При уменьшении интервала квантования требуется больше разрядов для описания сигнала, вследствие чего цифровой фильтр становится более сложным и громоздким.

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

Страница проекта на GitHub.

Содержание

Вводные понятия

Сигнал называют аналоговым, если он определен на непрерывной оси времени , и в каждый момент может принимать произвольные значения. Аналоговый сигнал может быть представлен непрерывной, или кусочно-непрерывной функции переменной . Пример аналогового сигнала показан на рисунке 1.

Если сигнал принимает произвольные значения только в фиксированные моменты времени , — целое число, то такой сигнал называется дискретным. Наиболее широкое распространение получили дискретные сигналы, определенные на равноотстоящей сетке , где — интервал дискретизации. При этом в моменты дискретизации дискретный сигнал может принимать произвольные значения. Если значения дискретного сигнала также берутся на фиксированной сетке значений, и при этом сами значения могут быть представлены числом конечной разрядности в одной из систем счисления, то такой дискретный сигнал называется цифровым . Часто говорят, что цифровой сигнал представляет собой квантованный по уровню дискретный сигнал. Примеры дискретного и цифрового сигналов также показаны на рисунке 1. Тонкая разница между дискретными и цифровыми сигналами дает возможность их отождествлять практически во всех прикладных задачах. Аналоговый сигнал может быть описан функцией времени, в то время как дискретный и цифровой сигналы могут быть заданы вектором отсчетов :

Указанный преимущества определили повсеместное распространение цифровых систем хранения и обработки сигналов. Но цифровые сигналы также имеют и недостатки по сравнению с аналоговыми.

Во-первых нет возможности передавать цифровые сигналы «как есть», поскольку передача сигналов чаще всего происходит при использовании электромагнитных и акустических волн, которые являются непрерывными во времени. Поэтому для передачи цифровых сигналов требуются дополнительные методы цифровой модуляции, а также цифро-аналоговые преобразователи (ЦАП).

Другим недостатком цифровых сигналов является меньший динамический диапазон сигнала (т.е. отношение самого большого значения к самому маленькому), из-за квантования сигнала на фиксированной сетке значений.

Дискретизация аналоговых сигналов. Математическая модель дискретного сигнала

В данном параграфе мы рассмотрим способ выборки дискретных значений аналогового сигнала. Структурная схема устройства дискретизации показана на рисунке 2. Данное устройство называется аналого-цифровой преобразователь (АЦП), потому что оно преобразует аналоговый сигнал в набор оценок дискретных значений , где — целое число, взятых через равноотстоящие промежутки времени .

Временны́е осциллограммы, поясняющие принцип работы устройства показаны на рисунке 3 (см. [1, стр. 475–476], или [2, стр. 438]).

На входе АЦП имеется аналоговый сигнал . Генератор импульсов формирует равноотстоящие стробирующие импульсы , которые управляют ключом, в результате чего на вход усилителя подаются котроткие выборки сигнала длительности длительности , взятые через интервал дискретизации .

Оценка дискретного сигнала может быть представлена в виде

Интегрируя на каждом интервале длительности стробирующего импульса получим оценку значения сигнала в момент времени . При конечной величине мы можем говорить об оценке значения сигнала в момент времени с некоторой погрешностью, ввиду изменения сигнала на интервале . Поэтому мы используем шапочку над обозначением , чтобы подчеркнуть приближенную оценку.

При уменьшении длительности погрешность оценки будет уменьшаться, и в пределе мы можем получить дискретный сигнал как:

Бесконечная сумма смещенных дельта-функций называется решетчатой функцией и обозначается [3, стр. 77]:

Тогда математической моделью дискретного сигнала будет произведение исходного аналогового сигнала на решетчатую функцию:

Графически модель дискретного сигнала , с использованием решетчатой функции показана на рисунке 4.

Для получения численных значений дискретного сигнала необходимо проинтегрировать дискретный сигнал (5) в окрестности :

В дальнейшем мы будем широко использовать данную модель дискретного сигнала для перехода от методов анализа и обработки аналоговых сигналов, к цифровым.

Размерность дискретного сигнала

Пусть исходный аналоговый сигнал описывает изменение напряжения во времени и имеет размерность вольт . Вспомним, что дельта-функция Дирака имеет размерность, обратную размерности ее аргумента. Тогда решетчатая функция , согласно (4) имеет размерность , а размерность дискретного сигнала (5) будет .

Заметим, что значения дискретного сигнала, полученные из (6) как результат интегрирования дискретного сигнала в окрестности момента времени , будут иметь размерность исходного сигнала .

Преобразование Фурье решетчатой функции

В данном разделе мы проанализируем спектральную плотность решетчатой функции . Для начала рассмотрим как периодический сигнал. Тогда можно представить в виде разложения в ряд Фурье:

Тогда (7) с учетом (8):

Выражение (10) представляет как бесконечную сумму комплексных экспонент.

Рассмотрим теперь преобразование Фурье решетчатой функции:

Поменяем операции интегрирования и суммирования и применим фильтрующее свойство дельта-функции:

Выражение (12) также представляет собой бесконечную сумму комплексных экспонент. Учтем, что и получим:

Таким образом, спектральная плотность решетчатой функции представляет собой также решетчатую функцию.

Период повторения дельта-функций в частотной области равен , при этом дельта-функции масштабируются в раз, как это показно на рисунке 5.

Заметим, что умножение на в частотной области изменяет размерность спектральной плотности , в результате чего спектральная плотность переходит в безразмерный спектр (что не удивительно, потому что исходная решетчатая функция — периодическая).

Спектральная плотность дискретного сигнала

Пусть дан аналоговый сигнал , спектральная плотность которого равна . В данном параграфе мы рассмотрим процесс равноотстоящей дискретизации сигнала в частотной области.

Преобразование Фурье дискретного сигнала (5) равно:

Применим свойство преобразования Фурье произведения сигналов, тогда представляет собой свертку спектральной плотности решетчатой функции и спектральной плотности исходного сигнала :

Уравнение (17) задает спектральную плотность дискретного сигнала как бесконечную сумму масштабированных копий спектральной плотности , отстоящих друг от друга на рад/с по частоте, как это показано на рисунке 6.

Заметим, что мы не накладываем никаких ограничений ни на интервал дискретизации , ни на сигнал , ни на спектральную плотность . Вне зависимости от частоты дискретизации рад/с, и формы , спектральная плотность дискретного сигнала всегда будет представлять собой сумму масштабированных копий , отстоящих друг от друга на величину частоты дискретизации рад/с.

Размерность спектра дискретного сигнала

Проанализируем выражение (17) на предмет размерности , в предположении, что исходный аналоговый сигнал имеет размерность :

Если аналоговый сигнал описывает изменения напряжения во времени и измеряется в единицах вольт, то при дискретизации аналогового сигнала, получим дискретные отсчеты, также измеряемые в вольт, и спектр дискретного сигнала также будет измеряться в единицах вольт. Тогда функцию мы можем назвать спектром, а не спектральной плотностью.

Главный вывод: преобразование Фурье дискретного сигнала не изменяет размерности дискретных отсчетов сигнала, в отличии от преобразования Фурье аналогового сигнала, которое возвращает спектральную плотность .

Выводы

В данном разделе мы ввели понятие дискретного и цифрового сигналов. Мы опеределили, что дискретный сигнал может быть представлен как результат произведения решетчатой функции и аналогового сигнала.

Были детально рассмотрены свойства решетчатой функции и показано, что спектральная плотность решетчатой функции также представляет собой масштабированную по амплитуде решетчатую функцию.

В результате свойств решетчатой функци получили, что спектральная плотность дискретного сигнала представляется бесконечной суммой копий спектральных плотностей исходного сигнала, отставленных дург от друка на величину равную частоте дискретизации.

Дискретный сигнал — сигнал, имеющий конечное число значений. Обычно сигналы, передаваемые через дискретные каналы, имеют два или три значения. Использование сигналов с тремя значениями обеспечивает синхронизацию передачи. По английски: Discrete signal Синонимы:… … Финансовый словарь

дискретный сигнал — Cигнал, информативный параметр которого может изменяться только прерывисто и иметь только конечное число значений в заданном диапазоне в течение определенного интервала времени. [Источник] EN discretely timed signal discrete signal a signal… … Справочник технического переводчика

Дискретный сигнал — 13. Дискретный сигнал Сигнал, имеющий конечное число значений величин Источник … Словарь-справочник терминов нормативно-технической документации

дискретный сигнал — diskretusis signalas statusas T sritis automatika atitikmenys: angl. sampled signal vok. abgetastetes Signal, n rus. дискретный сигнал, m pranc. signal échantillonné, m; signal discret, m … Automatikos terminų žodynas

дискретный сигнал — Сигнал, описываемый дискретной функцией времени … Политехнический терминологический толковый словарь

дискретный сигнал времени — diskretinamojo laiko signalas statusas T sritis radioelektronika atitikmenys: angl. discrete time signal vok. diskretes Zeitsignal, n rus. дискретный сигнал времени, m pranc. signal discret de temps, m … Radioelektronikos terminų žodynas

Сигнал (техника) — Сигнал в теории информации и связи называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым… … Википедия

Дискретный — (от лат. discretus раздельный, прерывистый). Это прилагательное может употребляться в разных контекстах: В дискретной математике дискретным называется счётное множество, эта концепция также важна в комбинаторике и теории вероятностей. В общей… … Википедия

дискретный — 4.2.6 дискретный: Относящийся к данным, которые состоят из отдельных элементов, таких как символы, или к физическим величинам, имеющим конечное число различных распознаваемых значений, а также к процессам и функциональным блокам, использующим эти … Словарь-справочник терминов нормативно-технической документации

Непрерывным называют сигнал дискретным называют сигнал

Идёт приём заявок

Подать заявку

Для учеников 1-11 классов и дошкольников

Якименко Светлана АнатольевнаНаписать 4257 02.01.2018

Номер материала: ДБ-999838

Не нашли то что искали?

Вам будут интересны эти курсы:

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Дискре́тный сигна́л (лат. discretus — «прерывистый», «разделённый») — сигнал, который является прерывистым (в отличие от аналогового) и который изменяется во времени и принимает любое значение из списка возможных значений. Список возможных значений может быть непрерывным или квантованным.

Существует путаница между понятиями дискретного и цифрового сигналов. Часто цифровой сигнал называют дискретным, потому что он состоит из дискретных (отдельных) частей (samples), несмотря на то, что цифровой сигнал не является прерывистым сигналом.

В английском языке используют понятия: discrete time (дискретное время), для рассмотрения значений переменных в отдельные моменты времени; continuous time (непрерывное время), для рассмотрения значений переменных в любой момент времени, причем между любыми двумя моментами времени существует бесконечное количество других моментов времени.

Цифровой сигнал получается последовательностью двух шагов:

Сэмплирования, который производит непрерывный сигнал дискретного времени
Квантования, который заменяет значение каждого сэмпла приближенным значением, выбранным из заданного дискретного набора (квантованных уровней).

Дискретность применяется в вычислительной технике для пакетной передачи данных.

Как аналоговый сигнал преобразуется в цифровой

Телевизионный сигнал — совокупность электрических сигналов, содержащая информацию о телевизионном изображении и звуке. Телевизионный сигнал может передаваться по радио или по кабелю. Термин употребляется в большинстве случаев применительно к аналоговому телевидению, потому что цифровое оперирует таким понятием, как поток данных.

В электронике сигналы делят на: аналоговые, дискретные и цифровые. Начнем с того, что все, что мы чувствуем, видим, слышим в большинстве своем является аналоговым сигналом, а то, что видит процессор компьютера – это цифровой сигнал. Звучит не совсем понятно, поэтому давайте разбираться с этими определениями и с тем как один вид сигналов преобразовывается в другой.

Типы сигналов

В электрическом представлении аналоговый сигнал, судя по его названию, является аналогом реальной величины. Например, вы чувствуете температуру окружающей среды постоянно, на протяжении всей жизни. Нет никаких перерывов. При этом вы чувствуете не только два уровня «горячо» и «холодно», а бесконечное число ощущений, которые описывают эту величину.

Для человека «холодно» может быть по разному, это и осенняя прохлада и зимний мороз, и легкие заморозки, но не всегда «холодно» это отрицательная температура, как и «тепло» — не всегда положительная температура.

Отсюда следует, что у аналогового сигнала две особенности:

1. Непрерывность во времени.

2. Число величин сигнала стремится к бесконечности, т.е. аналоговый сигнал нельзя точно поделить на части или проградуировать, разбив шкалу на конкретные участки. Способы измерения – основаны на единице измерений, и их точность зависит лишь от цены деления шкалы, чем она меньше, тем точнее измерение.

Дискретные сигналы – это сигналы, которые представляют собой последовательность отчетов или измерений какой-либо величины. Измерения таких сигналов не непрерывны, а периодичны.

Попытаюсь объяснить. Если вы установили термометр где-нибудь он измеряет аналоговую величину – это следует из вышеописанного. Но вы, фактически следя за его показаниями, получаете дискретную информацию. Дискретный – значит отдельный.

Например, вы проснулись и узнали, сколько градусов на термометре, в следующий раз вы на него посмотрели на градусник в полдень, и третий раз вечером. Вы не знаете, с какой скоростью изменялась температура, равномерно, или резким скачком, вы знаете только данные в тот момент времени, который наблюдали.

Цифровые сигналы – это набор уровней, типа 1 и 0, высокий и низкий, есть или нет. Глубина отражения информации в цифровом виде ограничена разрядностью цифрового устройства (набора логики, микроконтроллера, процессора etc.) Получается что для хранения булевых данных он подходит идеально. Пример, можно привести следующий, для хранений данных типа «День» и «Ночь», достаточно 1 бита информации.

Бит – это минимальная величина представления информации в цифровом виде, в нём может храниться только два типа значений 1 (логическая единица, высокий уровень), или 0 (логический ноль, низкий уровень).

В электронике бит информации представляется в виде низкого уровня напряжения (близкое к 0) и высокого уровня напряжения (зависит от конкретного устройства, часто совпадает с напряжением питания данного цифрового узла, типовые значения – 1.7, 3.3. 5В, 15В).

Все промежуточные значения между принятыми низким и высоким уровнем являются переходной областью и могут не обладать конкретным значением, в зависимости от схемотехники, как устройства в целом, так и внутренней схемы микроконтроллера (или любого другого цифрового устройства) могут иметь разный переходный уровень, например для 5-тивольтовой логики за ноль могут приниматься значения напряжения от 0 до 0.8В, а за единицу от 2В до 5В, при этом промежуток между 0.8 и 2В – это неопределенная зона, фактически с ее помощью отделяется ноль от единицы.

Чем более точные и ёмкие значения нужно хранить, тем больше нужно бит, приведем таблицу-пример с отображением в цифровом виде четырёх значений времени суток:

Ночь – Утро – День – Вечер

Для этого нам нужно уже 2 бита:

Аналогово-цифровое преобразование

В общем случае аналогово-цифровым преобразованием называется процесс перевода физической величины в цифровое значение. Цифровым значением является набор единиц и нолей воспринятых обрабатывающим устройством.

Такое преобразование нужно для взаимодействия цифровой техники с окружающей средой.

Так как аналоговый электрический сигнал повторяет своей формой входной сигнал, он не может быть записан в цифровом виде «так как есть» поскольку он имеет бесконечное число значений. Примером можно привести процесс записи звука. Он в первичном виде выглядит так:

Он представляет собой сумму волн с различными частотами. Которые, при разложении по частотам (подробнее об этом смотрите преобразования Фурье), так или иначе, можно приблизить к похожей картинке:

Теперь попробуйте это представить в виде набора типа «111100101010100», довольно сложно, не так ли?

Другим примером необходимости преобразования аналоговой величины в цифровую, является её измерение: электронные термометры, вольтметры, амперметры и прочие измерительные приборы взаимодействую с аналоговыми величинами.

Как происходит преобразование?

Сначала посмотрите на схему типового преобразования аналогового сигнала в цифровой и обратно. Позже мы к ней вернемся.

Фактически это сложный процесс, который состоит из двух основных этапов:

1. Дискретизация сигнала.

2. Квантование по уровню.

Дискретизация сигнала это определения промежутков времени, на которых измеряется сигнал. Чем короче эти промежутки – тем точнее измерение. Периодом дискретизации (Т) называется отрезок времени от начала считывания данных до его конца. Частота дискретизации (f) – это обратная величина:

fд=1/Т

После считывания сигнала происходит его обработка и сохранение в память.

Получается, что за время, которое считываются и обрабатываются показания сигнала, он может измениться, таким образом, происходит искажение измеряемой величины. Есть такая теорема Котельникова и из нее вытекает такое правило:

Частота дискретизации должны быть как минимум в 2 раза больше чем частота дискретизируемого сигнала.

Это скриншот из википедии, с выдержкой из теоремы.

Для определения численного значение необходимо квантование по уровню. Квант – это определенный промежуток измеряемых значений, усреднено приведенный к определенному числу.

X1…X2=Xy

Т.е. сигналы величиной от X1 до X2, условно приравнивается к определенному значению Xy. Это напоминает цену деления стрелочного измерительного прибора. Когда вы снимаете показания, зачастую вы их равняете по ближайшей отметке на шкале прибора.

Так и с квантованием по уровню, чем больше квантов, тем более точные измерения и тем больше знаков после запятой (сотых, тысячных и так далее значений) они могут содержать.

Точнее сказать число знаков после запятой скорее определяется разрядностью АЦП.

На картинке изображен процесс квантования сигнала с помощью одного бита информации, как я описывал выше, когда при превышении определенного предела принимается значение высокого уровня.

Справа показано квантование сигнала, и запись в виде двух бит данных. Как видите, этот фрагмент сигнала разбит уже на четыре значения. Получается, что в результате плавный аналоговый сигнал превратился в цифровой «ступенчатый» сигнал.

Количество уровней квантования определяется по формуле:

де n — количество разрядов, N — уровень квантования.

Вот пример сигнала разбитого на большее число квантов:

Отсюда очень хорошо видно, что чем чаще снимаются значения сигнала (больше частота дискретизации), тем точнее он измеряется.

На этой картинке изображено преобразование аналогового сигнала в цифровой вид, а слева от оси ординат (вертикальной оси) запись в цифровом 8-битном виде.

Аналогово-цифровые преобразователи

АЦП или Аналогово-цифровой преобразователь может выполняться в виде отдельного устройства или быть встроенным в микроконтроллер.

Ранее в микроконтроллеры, например семейства MCS-51, не содержали в своем составе АЦП, использовалась для этого внешняя микросхема и возникала необходимость писать подпрограмму обработки значений внешней ИМС.

Сейчас они есть в большинстве современных микроконтроллеров, например AVR AtMEGA328, который является основой большинства популярных плат Ардуино, он встроен в сам МК. На языке Arduino чтение аналоговых данных осуществляется просто – командой AnalogRead(). Хотя в микропроцессоре, который установлен в той же не менее популярной Raspberry PI его нет, так что не все так однозначно.

Фактически существует большое число вариантов аналогово-цифровых преобразователей, у каждого из которых есть свои недостатки и преимущества. Описывать которые в пределах этой статьи не имеет особого смысла, так как это большой объём материала. Рассмотрим лишь общую структуру некоторых из них.

Самым старым запатентованным вариантом АЦП, является патент Paul M. Rainey, «Facsimile Telegraph System,» U.S. Patent 1,608,527, Filed July 20, 1921, Issued November 30, 1926. Это 5-ти битный АЦП прямого преобразования. Из названия патента приходят мысли о том, что использование этого прибора было связано с передачей данных через телеграф.

Если говорить о современных АЦП прямого преобразования имеют следующую схему:

Отсюда видно, что вход представляет собой цепочку из компараторов, которые на выходе своем выдают сигнал при пересечении какого-то порогового сигнала. Это и есть разрядность и квантование. Кто хоть немного силен в схемотехнике, увидел этот очевидный факт.

Кто не силен, то входная цепь работает таким образом:

Аналоговый сигнал поступает на вход «+», на все сразу. На выходы с обозначением «-» поступает опорное напряжение, которое раскладывается с помощью цепочки резисторов (резистивного делителя) на ряд опорных напряжений. К примеру, ряд для этой цепи выглядит наподобие такого соотношения:

Urefi=(1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16)*Uref

В скобках через запятую указано, какую часть от общего опорного напряжения Uref подают на вход каждого входного напряжения.

Т.е. каждый из элементов имеет два входа, когда напряжение на входе со знаком «+»превышает напряжение на входе со знаком «-», то на его выходе появляется логическая единица.8 компараторов, а это целых 256 штук. Для десятиразрядного (в ардуино 10-разрядный АЦП, кстати, но другого типа) нужно 1024 компаратора. Судите сами о целесообразности такого варианта обработки, и где он может понадобиться.

Есть и другие виды АЦП:

Заключение

Преобразование аналогового сигнала в цифровой нужно для считывания параметров с аналоговых датчиков. Есть отдельный вид цифровых датчиков, они представляют собой либо интегральные микросхемы, например DS18b20 – на его выходе уже цифровой сигнал и его можно обрабатывать любыми микроконтроллерами или микропроцессорами без необходимости применения АЦП, или аналоговый датчик на плате на которой уже размещен свой преобразователь. У каждого типа датчиков есть свои плюсы и минусы, такие как помехоустойчивость и погрешность измерений.

Знание принципов преобразование обязательно для всех кто работает с микроконтроллерами, ведь не в каждой даже современной системе встроены такие преобразователи, приходится использовать внешние микросхемы. Для примера можно привести такую плату, разработанную специально под GPIO-разъём Raspberry PI, с прецизионным АЦП на ADS1256.

Ранее ЭлектроВести писали, что власти Вены запустили тестирование технологии умных камер, которые будут распознавать приближение пешеходов и подавать сигнал на светофор.

По материалам: electrik.info.

Разница между цифровым сигналом и дискретным сигналом

В электротехнике термины «дискретный сигнал» и «сигнал с дискретным временем» периодически используются для обозначения одного и того же, последний термин является более распространенным и более точным. Формулировка «сигнал с дискретным временем» в некоторой степени самоочевидна.

Многие инженеры и теоретики приравнивают и приравнивают цифровую обработку сигналов к обработке сигналов квантованных сигналов с дискретным временем. Однако есть свои тонкости. Информационно-теоретическую концепцию сигнала слишком трудно втиснуть в объяснение «простым словом», я предлагаю вам сначала изучить, что такое «цифровая форма волны». Форма волны не является сигналом, но может представлять сигнал в ваших конструкциях блоков обработки. Для новичка в исследованиях DSP знание, что такое цифровая форма волны, является практически полезным знанием с обещанием помочь вам своевременно пройти через тонкости информационно-теоретической концепции.

Цифровой сигнал — это напряжение или ток, который изменяется во времени между значениями, называемыми «логическими уровнями», эти уровни определяются дисциплиной «цифровая абстракция» ( http://ocw.mit.edu/courses/electrical-engineering-and-computer -Наука / 6-002-схема-и-электроника-весна-2007 / видео-лекция / 6002_l4.pdf). Изменяющиеся значения напряжения или тока не всегда попадают в пределы, установленные цифровыми правилами абстракции для значений сигналов на логических уровнях: при переключении между уровнями напряжение или ток, являясь непрерывной функцией, проходит «запрещенные» диапазоны. Та же дисциплина цифровой абстракции предписывает учитывать ограничения не только для значений логических уровней, но и для временных параметров, из которых очень важными являются время установки и удержания — защитные временные интервалы стабильности сигнала, окружающие край утверждения часов. Смотрите хороший учебник по цифровым сигналам в http://www.ni.com/white-paper/3299/en/ . Примечательно, что цифровые формы волны называются цифровыми сигналами в этом руководстве.

Иными словами, (относительно простыми) цифровая форма волны — это форма волны с уровнями логического сигнала и параметрами синхронизации, соответствующими правилам цифровой абстракции для данной схемы. То, что является законным цифровым сигналом для одного дизайна, может оказаться неподходящим для другого.

Discrete Signal — обзор

Periodic-Discrete

Это дискретные сигналы, которые периодически повторяются от отрицательной до положительной бесконечности. Этот класс преобразования Фурье иногда называют дискретным рядом Фурье, но чаще всего его называют дискретным преобразованием Фурье .

Вы могли подумать, что названия, данные этим четырем типам преобразований Фурье, сбивают с толку и плохо организованы. Ты прав; имена эволюционировали довольно бессистемно за 200 лет.Вы ничего не можете сделать, кроме как запомнить их и двигаться дальше.

Все эти четыре класса сигналов простираются до положительной и отрицательной бесконечности . Вы говорите, держитесь! Что, если у вас есть только конечное количество выборок, хранящихся в вашем компьютере, скажем, сигнал, сформированный из 1024 точек. Нет ли версии преобразования Фурье, использующей сигналы конечной длины? Нет, нет. Волны синуса и косинуса определены как как простирающиеся от отрицательной бесконечности до положительной бесконечности. Вы не можете использовать группу бесконечно длинных сигналов, чтобы синтезировать что-то конечной длины.Чтобы решить эту дилемму, нужно сделать так, чтобы конечные данные выглядели как — сигнал бесконечной длины. Это делается путем представления, что сигнал имеет бесконечное количество выборок слева и справа от фактических точек. Если все эти «воображаемые» выборки имеют нулевое значение, сигнал выглядит дискретным и апериодическим , и применяется дискретное временное преобразование Фурье. В качестве альтернативы воображаемые образцы могут быть дублированием реальных 1024 точек. В этом случае сигнал выглядит дискретным и периодическим с периодом 1024 отсчета.Это требует использования дискретного преобразования Фурье.

Как оказалось, для синтеза сигнала апериодического требуется бесконечное количество синусоид . Это делает невозможным вычисление дискретного преобразования Фурье в компьютерном алгоритме. По исключению единственный тип преобразования Фурье, который может использоваться в DSP, — это DFT. Другими словами, цифровые компьютеры могут работать только с информацией, длина которой составляет дискретных и конечных длины.Когда вы боретесь с теоретическими проблемами, решаете домашние задания и размышляете над математическими загадками, вы можете обнаружить, что используете первых трех членов семейства преобразований Фурье. Когда вы садитесь за компьютер, вы будете использовать только DFT. Мы кратко рассмотрим эти другие преобразования Фурье в следующих главах. А пока сконцентрируйтесь на понимании дискретного преобразования Фурье.

Вернитесь к примеру разложения ДПФ на рис. 8-1. На первый взгляд, это сигнал из 16 точек, разложенный на 18 синусоид, каждая из которых состоит из 16 точек.Говоря более формально, 16-точечный сигнал, показанный на (а), следует рассматривать как отдельный период бесконечно длинного периодического сигнала. Аналогично, каждая из 18 синусоид, показанных на (b), представляет собой сегмент из 16 точек из бесконечно длинной синусоиды. Имеет ли значение, рассматриваем ли мы это как 16-точечный сигнал, синтезируемый из 16-точечных синусоид, или как бесконечно длинный периодический сигнал, синтезируемый из бесконечно длинных синусоид? Ответ: обычно нет, но иногда да . В следующих главах мы встретимся со свойствами ДПФ, которые кажутся сбивающими с толку, если рассматривать сигналы как конечные, но станут очевидными, если учесть периодический характер.Ключевым моментом для понимания является то, что эта периодичность вызывается для использования математического инструмента , то есть ДПФ. Обычно это не имеет смысла с точки зрения того, где возник сигнал или как он был получен.

Каждое из четырех преобразований Фурье можно разделить на реальных и комплексных версий. Реальная версия является самой простой, с использованием обычных чисел и алгебры для синтеза и разложения. Например, рис. 8-1 представляет собой пример реального ДПФ .Сложные версии четырех преобразований Фурье намного сложнее и требуют использования комплексных чисел . Это такие числа, как: 3+ 4j , где j равно -1 (инженеры-электрики используют переменную j , а математики используют переменную i ). Сложная математика может быстро стать непосильной даже для тех, кто специализируется на DSP. Фактически, основная цель этой книги — представить основы DSP без использования сложных математических вычислений, что позволит понять материал более широкому кругу ученых и инженеров.Сложные преобразования Фурье — это сфера деятельности тех, кто специализируется на DSP и готов по уши в болоте математики. Если вы так склонны, главы 30–3330313233 доставят вас туда.

Математический термин преобразование широко используется в цифровой обработке сигналов, например: преобразование Фурье, преобразование Лапласа, преобразование Z, преобразование Гильберта, дискретное косинусное преобразование и т. Д. Что такое преобразование? Чтобы ответить на этот вопрос, вспомните, что такое функция .Функция — это алгоритм или процедура, которые изменяют одно значение на другое значение. Например, y = 2 x + 1 — это функция. Вы выбираете какое-то значение для x , вставляете его в уравнение, и выдает значение для y . Функции также могут преобразовывать несколько значений в одно значение, например: y = 2 a + 3 b + 4 c , где a, b и c заменяются на y .

Преобразования

являются прямым продолжением этого, позволяя как входу, так и выходу иметь нескольких значений .Предположим, у вас есть сигнал, состоящий из 100 выборок. Если вы разработаете какое-то уравнение, алгоритм или процедуру для преобразования этих 100 выборок в другие 100 выборок, у вас есть преобразование. Если вы считаете, что он достаточно полезен, у вас есть полное право прикрепить к нему свою фамилию и рассказать коллегам о его достоинствах. (Это лучше всего работает, если вы выдающийся французский математик 18 века.) Преобразования не ограничиваются каким-либо конкретным типом или количеством данных. Например, у вас может быть 100 выборок дискретных данных для входа и 200 выборок дискретных данных для выхода.Точно так же у вас может быть непрерывный сигнал для входа и непрерывный сигнал для выхода. Также разрешены смешанные сигналы, дискретные входящие и непрерывные выходящие и наоборот. Короче говоря, преобразование — это любая фиксированная процедура, которая преобразует один фрагмент данных в другой. Давайте посмотрим, как это применимо к обсуждаемой теме: дискретное преобразование Фурье.

Разница между цифровым сигналом и дискретным сигналом

В электротехнике термины «дискретный сигнал» и «сигнал с дискретным временем» используются периодически для обозначения одного и того же, последний термин более общий и более точный.Формулировка «сигнал с дискретным временем» до некоторой степени объясняется сама собой.

Многие инженеры и теоретики приравнивают и приравнивают цифровую обработку сигналов к обработке сигналов квантованных сигналов дискретного времени. Однако есть тонкости. Теоретико-информационная концепция сигнала, которая слишком сложна, чтобы втиснуться в «простое» объяснение, я предлагаю вам сначала узнать, что такое «цифровая форма волны». Форма волны не является сигналом, но может представлять сигнал в ваших проектах блоков обработки.Для новичка в изучении DSP знание того, что такое цифровой сигнал, является практически полезным знанием, обещающим помочь вам в свое время продвинуться в тонкостях теоретико-информационной концепции.

Цифровой сигнал — это напряжение или ток, который изменяется со временем между значениями, называемыми «логическими уровнями», эти уровни определяются дисциплиной «цифровая абстракция» ( http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-002-circuits-and-electronics-spring-2007/video-lectures/6002_l4.pdf). Изменяющиеся значения напряжения или тока не всегда попадают в пределы, предписанные правилами цифровой абстракции для значений сигналов на логических уровнях: при переключении между уровнями напряжение или ток, будучи непрерывной функцией, проходит «запрещенные» диапазоны. Та же самая дисциплина цифровой абстракции предписывает учитывать ограничения не только для значений логических уровней, но и для параметров синхронизации, из которых очень важными являются время установки и удержания — защитные временные интервалы стабильности сигнала, окружающие фронт утверждения тактового сигнала.См. Хорошее руководство по цифровым сигналам на http://www.ni.com/white-paper/3299/en/. Примечательно, что в этом руководстве цифровые сигналы называются цифровыми сигналами.

Говоря (относительно простыми) словами, цифровой сигнал — это форма сигнала с логическими уровнями сигнала и параметрами синхронизации, соответствующими правилам цифровой абстракции для данной конструкции. То, что является допустимым цифровым сигналом для одного дизайна, может оказаться неподходящим для другого.

Определение непрерывных и дискретных сигналов

Сигнал непрерывного времени:
Сигнал непрерывного времени — это «функция переменной непрерывного времени, которая имеет несчетный или бесконечный набор чисел в своей последовательности».
Сигнал непрерывного времени может быть представлен и определен в любой момент времени в своей последовательности. Сигнал непрерывного времени также называется аналоговым сигналом. Это непрерывная функция времени, определенная на реальной линии (или оси) R . Он имеет непрерывную амплитуду и время. То есть, сигналы непрерывного времени будут иметь определенное значение в любой момент времени.
Сигнал с непрерывным временем нарисован, как показано на рисунке 1.

Примерами сигналов с непрерывным временем являются синусоидальные волны, косинусные волны, треугольные волны и т. Д.Электрические сигналы также ведут себя как сигналы непрерывного времени, когда они выводятся пропорционально физическим параметрам, таким как давление, температура, звук и т. Д.
Сигнал дискретного времени:
Сигнал дискретного времени — это «функция переменной дискретного времени, которая имеет счетный или конечный набор чисел в своей последовательности». Это цифровое представление сигнала непрерывного времени.
Сигнал дискретного времени может быть представлен и определен в определенные моменты времени в его последовательности.То есть сигнал с дискретным временем может быть определен только в моменты дискретизации. Цифровой сигнал может быть получен из сигнала с дискретным временем путем квантования и кодирования значений выборки. Сигналы с дискретным временем представлены двоичными битами и хранятся на цифровом носителе.
Сигнал с дискретным временем отображается, как показано на рисунке 2.

Выходные данные компьютера являются одним из примеров сигналов с дискретным временем.
В чем разница между сигналами с непрерывным и дискретным временем?
Различия между непрерывными и дискретными сигналами заключаются в следующем:

В чем разница между дискретными и цифровыми сигналами?
Различия между дискретными и цифровыми сигналами заключаются в следующем:

Является ли цифровой сигнал сигналом с дискретным временем?
Цифровой сигнал может быть дискретным или непрерывным.То есть все цифровые сигналы не являются сигналами дискретного времени.
Цифровой сигнал — это электрический сигнал, который имеет дискретное значение в каждой точке выборки. Он используется для представления данных в виде последовательности дискретных значений.
В цифровом сигнале сигнал преобразуется в двоичные биты. Двоичные биты — это 0 и 1. Двоичный бит 1 используется для обозначения положительного значения цифрового сигнала, а бит 0 используется для представления нулевого значения или нулевого значения цифрового сигнала. Цифровые сигналы обычно обозначаются прямоугольной волной.Переход (или изменение состояния) цифрового сигнала от одного битового значения к другому происходит мгновенно. То есть цифровой сигнал изменяется мгновенно и в любой момент может принимать одно из конечного числа значений.
Запишите преимущества цифрового сигнала следующим образом:

Влияние шума, искажений и помех для цифровых сигналов намного меньше, поскольку они менее подвержены влиянию.
Цифровые данные сжимаются сравнительно легче, чем аналоговые.Следовательно, эффективность передачи больше для цифровых сигналов, чем для аналоговых сигналов.
Цифровые сигналы обеспечивают лучшую защиту.
Цифровые сигналы легко модернизируются.
Цифровые сигналы можно легко сконструировать по сравнению с аналоговыми сигналами.
Цифровые сигналы улучшают характеристики ошибок и, следовательно, улучшают качество сигнала.
Цифровые сигналы имеют меньшую стоимость, чем аналоговый сигнал для передачи данных.
Цифровые сигналы могут быть легко сохранены с меньшим объемом памяти за меньшую продолжительность, чем аналоговые сигналы.

Понятия, связанные с сигналами

Сигналы являются функциями одного или нескольких независимые переменные и обычно содержат информацию о поведение или характер какого-либо явления. Системы обычно реагируют на определенные сигналы, производя другие сигналы. Представление Сигнал в виде графика зависимости амплитуды от времени составляет форму волны .Образец вариаций, содержащихся в формах сигналов, дает нам информация о сигнале; например, человеческий голосовой механизм воспроизводит речь, создавая колебания акустического давления.

Детерминированные сигналы : сигнал детерминированный, если он точно предсказуем на период времени интерес. Детерминированные сигналы можно описать математическими моделями.Синусоидальный сигнал описывается следующим образом:

В (t) = A * sin (w * т),

, где V (t) — сигнал во времени
A (= амплитуда) и w — параметры модели (2pf = w).
f — частота синусоидальной волны.
л — период синусоидальной волны, обратный частоте (1 / f)

Итак: V (t) = A sin (2pft)

Стохастические или случайные сигналы : a сигнал, значение которого связано с некоторым элементом случайности, поэтому его нельзя точно предсказать.Следовательно, статистические свойства и вероятности должны использоваться для описания стохастических сигналы. На практике биологические сигналы часто имеют как детерминированные и стохастические компоненты.

Статистика амплитуды сигнала
Ряд статистических данных может использоваться как мера местоположения или «центр» случайного сигнала:

средний — средняя амплитуда сигнала во времени
медиана — значение, при котором половина наблюдений в выборке значения меньше медианы, а половина имеют значения больше, чем медиана.Медиана часто используется как мера «центра» сигнал, потому что он менее чувствителен к выбросам.
режим является наиболее часто встречающимся значением сигнала
максимальная и минимальная амплитуда максимальное и минимальное значение сигнала в заданное время интервал
диапазон: диапазон или размах амплитуды — это разница между минимальное и максимальное значения сигнала.

Непрерывные временные сигналы в сравнении с сигналы дискретного времени
Сигналы являются непрерывными сигналами времени, когда независимая переменная непрерывно, поэтому сигналы определены для континуума значений независимой переменной X (t). аналог signal — это непрерывный сигнал времени. Сигналы дискретного времени только определяется в дискретное время; независимая переменная принимает только дискретный набор значений X (n).A цифровой signal — это сигнал дискретного времени.
Дискретный сигнал времени может представлять собой явление, для которого независимая переменная по своей сути дискретна (например, количество калорий в сутки на диете). С другой стороны, дискретный сигнал может представлять последовательные образцы основного явления, для которого независимые переменная непрерывна (например, визуальное изображение, полученное цифровым камера состоит из отдельных пикселей, которые могут принимать разные цвета).

Измерение частоты сигнала с помощью спектральный анализ
Существуют количественные методы измерения частоты и амплитуды форма волны. Один из самых известных — спектральный анализ: любой форму волны можно математически разложить на сумму различных формы волны. Это то, что делает так называемый анализ Фурье; Это разлагает форму волны на различные компоненты и измеряет амплитуда (мощность) каждой частотной составляющей.То, что построено, — это график зависимости мощности (амплитуды) от частоты.

След выше показывает сегмент записи ЭЭГ: эта форма волны может быть разложен на сумму различных сигналов, как показано изображение ниже.

Спектральный анализ и график записи ЭЭГ

Односкоростные сигналы и системы с дискретным временем: общий обзор: Глава

книги по информатике и ИТ

Эта глава представляет собой краткий обзор представлений односкоростных сигналов и систем с дискретным временем во временной области и в области преобразования.Сначала мы рассмотрим представление дискретных сигналов и систем во временной области. Представление в области преобразования включает в себя дискретное преобразование Фурье (DTFT), дискретное преобразование Фурье (DFT) и преобразование z . Кратко описаны основные структуры реализации для систем FIR и IIR. Наконец, приведены соотношения между непрерывными и дискретными сигналами.

ДИСКРЕТНЫЕ ВРЕМЕННЫЕ СИГНАЛЫ

Сигнал является функцией по крайней мере одной независимой переменной.В этой книге мы предполагаем, что независимой переменной является время, даже в тех случаях, когда независимой переменной является величина, отличная от времени.

Мы определяем непрерывный сигнал , x _c ( t ) как сигнал, который существует в каждый момент времени t . Непрерывный сигнал с непрерывной амплитудой также называется аналоговым сигналом . Независимая переменная t является непрерывной переменной, а x _c ( t ) может принимать любое значение в непрерывном диапазоне чисел.

Сигнал дискретного времени — это последовательность чисел, обозначенная как { x [ n ]}, где n называется временным индексом , а x [ n ] обозначает значение элемента n ^th в последовательности. Сигнал с дискретным временем называется дискретным сигналом . Величина x [ n ] также называется значением выборки , а ее временной индекс n называется индексом выборки .Величина x [ n ] может принимать любое значение в некотором непрерывном диапазоне чисел, x _мин. ≤ x [ n ] ≤ x _макс..

Дискретные сигналы могут быть определены только для целых значений n из интервала N ₁ ≤ n ≤ N ₂. Когда значения выборок последовательности { x [ n ]} представлены как двоичные числа с использованием конечного числа битов, сигнал { x [ n ]} представляет собой цифровой сигнал .

Длина последовательности определяется как N ≤ N ₂ — N ₁ + 1. Последовательность { x [ n ]} представляет собой последовательность конечной длины если N имеет конечную длину; в противном случае { x [ n ]} представляет собой последовательность бесконечной длины .

Для целей анализа полезно представить сигналы как комбинацию основных последовательностей. Часто используемые базовые последовательности включены в Таблицу 1.

Таблица 1.

Во многих приложениях сигнал дискретного времени { x [ n ]} генерируется путем дискретизации сигнала непрерывного времени x _c ( t ) через одинаковые интервалы времени. :

. (1)

Временной интервал T называется интервалом выборки или периодом выборки , а обратное значение

(2) представляет собой частоту выборки или частоту выборки .Обычно единицей измерения частоты дискретизации является количество циклов в секунду, и когда T задается в секундах [с], F _T может быть выражено в герцах [Гц].

Основные понятия о сигналах и системах

Сигналы и системы — это абстрактные концепции самых разных физических переменные и процессы в различных областях техники и науки.

Сигнал как функция времени / пространства

Большинство сигналов, представляющих интерес на практике, представляют собой записанные значения физической величины, представлены в виде одномерных функций, таких как функция времени, или двухмерных / трехмерных функции, такие как пространственная функция или.Примеры сигналы включают в себя температуру во времени или пространстве, звук (речь, музыка, и т. д.) с течением времени, изображения в пространстве и т. д. Сигнал несет информацию и содержит энергии .

Различные типы сигналов:

Аналогово-цифровые преобразования:

Непрерывный сигнал можно дискретизировать дискретизацией . Этот процесс называется непрерывно-дискретным (C / D) или аналого-цифровым преобразованием. (АЦП, АЦП).
Дискретный сигнал можно преобразовать в непрерывный с помощью интерполяция . Этот процесс называется дискретно-непрерывным (D / C). или цифро-аналоговое преобразование (ЦАП, ЦАП).
Аналоговый сигнал может быть оцифрован аналого-цифровой (A / D) преобразователь стать цифровым сигналом (дискретным как по амплитуде, так и по времени).
Цифровой сигнал может быть преобразован обратно в аналоговый сигнал с помощью цифро-аналоговый преобразователь.

Усечение сигнала:

Если не указано иное, независимая переменная сигнальной функции считается неограниченным, т.е.грамм., , , или же , . Однако в действительности все рассматриваемые сигналы подаются конечный усечением , определенным только внутри конечного окна, например, или же . Сигнал не определен за окном (не обязательно ноль).

Периодические сигналы:

Обычно предполагается, что сигнал является сложным

состоит из реальных и мнимых частей:

или, что то же самое, величина и фаза:

Реальные сигналы — это частные случаи сложных сигналов.

Случайные сигналы:

Сигнал или может быть случайным. Если проводится эксперимент многократно результаты могут не совпадать. Например, годовой температурный профиль меняется год от года. Такая случайная функция времени есть называется случайным процессом.

Энергетические и силовые сигналы:

В физике квадрат переменной обычно связан с мощностью или энергией. Например, и мощности в электрических системах, , — кинетическая и потенциальная энергия в механических системы.

Возводя в квадрат величину сигнала или, мы получаем мгновенная мощность сигнала в момент или (энергия распределение):

Энергия , содержащаяся в сигнале за период времени, равна мощность, интегрированная за период времени:

Когда или же , — полная энергия содержится в сигнале. Сигнал — это сигнал энергии , если его общая энергия конечно.

средняя мощность сигнала — это среднеквадратичное значение из или же :

и представляет собой среднеквадратическое значение сигнала (RMS) сигнала.Сигналом является сигнал мощности , если его полная энергия не конечна, но его средняя мощность составляет. Средняя мощность энергетического сигнала равна нулю. Большинство периодических сигналов являются сигналами мощности.

Примеры:

Векторное представление и ортогональные преобразования:

Представление систем

Система принимает сигнал или как вход (стимул, возбуждение, и т. д.), изменяет и обрабатывает сигнал и производит сигнал или как выход (ответ).Этот процесс можно смоделировать математически. как оператор, применяемый к входу для получения выходных данных:

Некоторые примеры системы:

Электрическая / электронная схема: сигнал напряжение / ток на входе порт, напряжение / ток от выходного порта
Нейровизуальная система: обработка ввода света (фотонов) и генерации потенциал действия (электрохимический сигнал)
Метаболизм глюкозы: преобразование глюкозы и кислорода в диоксид углерода и вода, и производство тепловой энергии
: преобразование электромагнитного сигнала в качестве входного и генерирующего звуковой и графический сигнал на выходе.
Механические конструкции (здания, мосты и т. Д.): Силовые воздействия, выход движения / вибрации.

Различные типы систем

Линейность: система является линейной, если она Однородная (масштабирование):

и добавка (суперпозиция):

Комбинируя эти свойства, мы получаем:
Инвариантная во времени: Система инвариантна во времени, если как она реагирует к входу не изменяется со временем (где — постоянная задержка по времени):
Если (красный) такой же, как (синий), то система не зависит от времени.Однако, если выход (зеленый) отличается из ; то есть поведение системы с точки зрения того, как она реагирует на входные данные меняются с течением времени, значит, система не является неизменной во времени.
Линейная и не зависящая от времени система (LTI) , система, которая одновременно является линейной и не зависящий от времени.

Почему биологов волнует LTI? Взгляни на Системная инженерия к системной биологии .

« Отношения между входом и выходом могут быть определены и экспериментально измерены для множества биологических систем и, таким образом, могут быть использованы для выявления скрытых биологических свойств.»

« Системная инженерия давно изучается, поэтому, возможно, теперь больше методов из этой зрелой области систем можно адаптировать к биологии, что позволит точно контролировать биологические входные и выходные сигналы для выявления структур, скрытых под сложными сетевыми картами ».

Цифровая обработка сигналов: дискретизация и дискретные сигналы

В моем предыдущем руководстве я дал краткое представление об основах цифровой обработки сигналов. Теперь мы сделаем еще один шаг в этом направлении.Чтобы выполнить часть обработки, нам сначала нужно понять сигналы дискретного времени, классификацию и их действия. В этом руководстве основное внимание будет уделено сигналам дискретного времени и системам дискретного времени .

Что мы собираемся изучить в этом руководстве: —

Ø Отбор проб

{Ø дискретных сигналов

{C} {Ø Классификация сигналов дискретного времени

Ø Преобразование сигналов дискретного времени

Отбор проб

Сначала нам нужно понять , что такое процесс отбора проб ? Зачем нужна выборка ? Ответ на первый вопрос заключается в том, что выборка — это процесс преобразования непрерывного сигнала в дискретный.Согласно определению непрофессионала, выходные данные системы записываются через разные интервалы времени, эти интервалы времени не обязательно могут быть одинаковыми, но в этой серии руководств мы ограничим наше обсуждение только Uniform-Sampling .

Рис. 1: График, показывающий однородную выборку

На приведенном выше изображении непрерывный сигнал S (t) дискретизируется в разные моменты времени, пусть i-е значение будет S _i (t), затем набор значений S _i (t) из i = От 0 до n называются выборками S (t).Интервал времени между двумя последовательными интервалами выборки называется Период выборки или Интервал выборки . Если временной интервал между двумя последовательными интервалами выборки одинаков и равен T,

f _s = 1 / T , где f _s — частота дискретизации.

Синусоиды дискретного времени : —

Синусоиды с дискретным временем представляют собой очень важный тип сигнала, который необходимо изучить в рамках цифровой обработки сигналов.Итак, поскольку теперь у нас есть краткое представление о выборке, мы обсудим эти сигналы, а затем перейдем к теореме выборки. Синусоидальный сигнал с дискретным временем может быть выражен как

x (n) = Acos (? ₀ n + Ø), -? <п <+?

Где n — целое число,? ₀ — угловая частота, которая также равна 2? F ₀, где f ₀ — частота, а Ø — фаза сигнала. Синусоиды с дискретным временем являются периодическими, только если частота сигнала является рациональным числом.Нам нужно доказать это утверждение,

х (п + N) = х (п)

или, cos [2? F ₀ (n + N) + Ø] = cos [2? F ₀ (n) + Ø]

или, 2? F ₀ N = 2k?

или, f ₀ = k / N

Также есть еще одно интересное свойство дискретных синусоид. Сигналы с дискретным временем, частоты которых разделены целым числом, кратным 2? идентичны. Пусть есть другой сигнал x ₂ (t), который отличается от предыдущего сигнала разностью фаз 2?, Тогда x ₂ (t) можно записать как,

x ₂ (t) = Acos [(? ₀ +2?) N + Ø] = Acos (? ₀ n + 2? N + Ø) = Acos (? ₀ n + Ø)

, который равен предыдущему сигналу x (t).Это можно интерпретировать так, как будто сигнал имеет частоту |? | >?. Тогда можно сказать, что этот сигнал идентичен другому сигналу, полученному из сигнала с частотой |? |

|? |? ?

Or, | f | ? ½

Все частоты в указанном выше диапазоне считаются уникальными, а все остальные частоты называются «псевдонимами». Теперь пришло время ответить на второй вопрос, касающийся необходимости выборки, тот факт, что большинство сигналов в природе являются аналоговыми, удовлетворяет потребности в выборке, и поскольку в моем предыдущем уроке я ясно показал преимущества цифровой обработки сигналов по сравнению с аналоговыми сигналами. Обработка, чтобы получить сигналы дискретного времени, мы должны выполнить дискретизацию аналоговых сигналов.Теперь пусть x _a (t) будет аналоговым сигналом, а x _a (t) с периодической дискретизацией частоты F, чтобы получить x _a (нТл) на частоте 1 / T. Затем

Сигнал Ananlog, x _a (t) = A cos (2? Ft + Ø)

Сигнал дискретного времени, x _a (нТл) = A cos (2? FnT + Ø)

Или, x _a (нТл) = A cos (2? Fn / F _s + Ø)

Как мы уже обсуждали выше, в синусоидах с дискретным временем | f | ? ½, Таким образом, мы заключаем, что,

| Ф / Ф _s | ? ½

Or, | F | ? F _с/2

Таким образом, мы ясно видим, что если макс.частота сигнала F _max, тогда частота дискретизации F _s должна быть больше чем в два раза F _max. Это также известно как частота дискретизации Найквиста. Всегда следует помнить, что F _s должен быть вдвое больше «макс.» частотная составляющая сигнала, а не просто любая частота сигнала, иначе это вызовет затухание и искажение сигнала.

Теорема выборки: Если самая высокая частота, содержащаяся в любом аналоговом сигнале x _a (t), равна F _max = B, а выборка выполняется на частоте F _s> 2B, тогда x _a (t ) может быть точно восстановлен из его выборок с помощью функции интерполяции,

G (t) = sin (2? Bt) / 2? Bt

Таким образом,

Сигналы дискретного времени

Сигналы дискретного времени

Функция (или последовательность) x (n) называется сигналом дискретного времени, если независимая переменная принимает целые значения и несет некоторую информацию.Функция не определяется в моменты времени между двумя выборками, ее нельзя принимать за ноль, что является общим заблуждением среди студентов.

Вот некоторые базовые или элементарные сигналы или последовательности дискретного времени : —

{C} {C} {C} {C} {C} {C} {C} {C} {C} {C} {C} {C} 1. Последовательность единичной выборки — Представлена? (N ) и следует следующему соотношению, приведенному ниже. Этот сигнал также называют импульсом.

Фиг.2: График последовательности единичной выборки

{C} {C} {C} {C} {C} {C} {C} {C} {C} {C} {C} {C} 2. Последовательность единичных шагов — обозначается u ( n) и следует следующему соотношению, приведенному ниже.

Рис. 3: График последовательности шагов установки

{C} {C} {C} {C} {C} {C} {C} {C} {C} {C} {C} {C} 3. Сигнал линейного изменения устройства — представлен u _r (n) и следует следующему соотношению, приведенному ниже.

Фиг.4: График сигнала линейного изменения агрегата

{C} {C} {C} {C} {C} {C} {C} {C} {C} {C} {C} {C} 4. Экспоненциальный сигнал — представлен x (n) и следует следующему соотношению, приведенному ниже.

x (n) = a ⁿ, для всех n

Где a — параметр, а график x (n) может быть многих типов в зависимости от значений a. Ваша задача выяснить различные возможности x (n) в зависимости от различных значений a.

Классификация сигналов дискретного времени

Классификация сигналов дискретного времени

Энергия и мощность сигналов: Пусть будет сигнал x (n).Тогда мощность P и энергия E сигнала задаются как

Теперь, если сигнал или последовательность имеет конечную энергию, то есть E N ,

Периодические и непериодические сигналы: Если сигнал или последовательность повторяется через фиксированный период времени, то говорят, что сигнал является периодическим по природе с основным периодом N, если N — наименьший интервал, после которого он повторяется. сам. В противном случае сигналы непериодичны по своей природе, т. Е. Если,

Для всех n, если x (n + N) = x (n), то x (n) является периодическим сигналом.

Симметричный (четный) и антисимметричный (нечетный) сигнал: Сигнал x (n) можно назвать симметричным и антисимметричным, если они следуют соответственно следующему соотношению:

x (-n) = x (n) {симметричный}

x (-n) = -x (n) {антисимметричный}

Каждый сигнал может быть выражен как комбинация четного и нечетного сигнала, где четная и нечетная составляющие получаются с помощью следующих соотношений:

x _e (n) = ½ [x (n) + x (-n)]

x _o (n) = ½ [x (n) — x (-n)]

Два вышеуказанных компонента соответствуют условиям симметричности и антисимметричности.И теперь сигнал может быть выражен как сумма четной и нечетной составляющих как,

x (n) = x _e (n) + x _o (n)

Преобразование независимой переменной : —

В следующих сериях руководств мы увидим, что система с дискретным временем использует некоторое преобразование исходного возбуждения в терминах независимой переменной для получения желаемого отклика.Итак, здесь мы узнаем о некоторых преобразованиях, которые можно выполнить с независимой переменной.

{· Сдвиг: Сигнал x (n) можно сдвинуть во временной области, заменив n на n-k, где k — целое число, и в зависимости от знака k сигнал будет задерживаться или опережать во временной области.

х (п) => х (п-к)

Тогда, если k положительно, то сигнал будет задержан во временной области, и если он начинался с n = 0, то теперь он начнется с n = k _-го интервала времени.Аналогично, если k равно –ve, то сигнал будет продвигаться вперед по времени на | k | единицы измерения. Хотя следует учитывать, что в реальном времени продвижение сигналов во времени не имеет физического значения.

Рис. 5: График, показывающий сдвиг сигнала

· Сворачивание: Если мы заменим независимую переменную n на –n, тогда это называется сворачиванием сигнала или считается отражением сигнала относительно начала координат n = 0.

Среди студентов существует общее заблуждение относительно коммутативных свойств сдвига и складывания, но следует иметь в виду, что они не являются коммутативными по своей природе, т.е.е. сворачивание задержанного сигнала — это не то же самое, что задержка свернутого сигнала.

Например, пусть сигнал x (n),

первый случай: x (n) сначала сворачивается, а затем задерживается на k единиц. Таким образом, сворачивание приведет к x (-n), а затем задержка того же свернутого сигнала приведет к x {- (nk)} = x (-n + k).

второй случай: x (n) сначала задерживается на k единиц, а затем складывается, задержка приводит к x (n-k), а затем применение сворачивания приводит к преобразованию сигнала в x (-n-k).

Определение дискретного сигнала

Отличия дискретного сигнала от аналогового и цифрового

Математическое описание дискретного сигнала

Спектр дискретного сигнала

Преобразование аналогового сигнала в дискретный

Восстановление аналогового сигнала из дискретного

Области применения дискретных сигналов

Преимущества дискретных сигналов

Ограничения дискретных сигналов

Заключение

26 вопросов и ответов. Теория электрических цепей. Курс лекций

Дискретный сигнал — сигнал, который является прерывистым и который изменяется во времени и принимает любое значение из списка возможных значений. Список возможн

Пользователи также искали:

Лабораторная работа №1: Дискретные сигналы [se.moevm.info]

Цель работы

Основные теоретические положения

Постановка задачи

Порядок выполнения работы

Варианты заданий

Содержание отчёта

Какой сигнал называется дискретным — MOREREMONTA

Содержание

Вводные понятия

Дискретизация аналоговых сигналов. Математическая модель дискретного сигнала

Размерность дискретного сигнала

Преобразование Фурье решетчатой функции

Спектральная плотность дискретного сигнала

Размерность спектра дискретного сигнала

Выводы

Непрерывным называют сигнал дискретным называют сигнал

Как аналоговый сигнал преобразуется в цифровой

Разница между цифровым сигналом и дискретным сигналом

Discrete Signal — обзор

Periodic-Discrete

Разница между цифровым сигналом и дискретным сигналом

Определение непрерывных и дискретных сигналов

Понятия, связанные с сигналами

Односкоростные сигналы и системы с дискретным временем: общий обзор: Глава

ДИСКРЕТНЫЕ ВРЕМЕННЫЕ СИГНАЛЫ

Основные понятия о сигналах и системах

Цифровая обработка сигналов: дискретизация и дискретные сигналы

Сигналы дискретного времени

Классификация сигналов дискретного времени

Похожие записи

Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании

Новорожденный какает слизью: причины появления слизи в кале грудничка

Гемангиома у новорожденных: причины, виды, лечение и профилактика

Добавить комментарий Отменить ответ