Что такое дискретный сигнал в информатике. Как дискретные сигналы отличаются от непрерывных. Для чего используются дискретные сигналы в цифровых системах. Как происходит обработка дискретных сигналов.
Что такое дискретный сигнал в информатике
Дискретный сигнал — это сигнал, значения которого определены только в отдельные моменты времени, следующие с некоторым интервалом. В отличие от непрерывного сигнала, который имеет значение в любой момент времени, дискретный сигнал представляет собой последовательность отдельных значений или отсчетов.
Основные характеристики дискретного сигнала:
- Значения определены только в дискретные моменты времени
- Между отсчетами значение сигнала не определено
- Интервал между отсчетами называется периодом дискретизации
- Обратная величина периода дискретизации — частота дискретизации
Дискретные сигналы широко используются в цифровых системах обработки информации, так как они легко представляются в виде последовательности чисел и могут обрабатываться цифровыми устройствами.
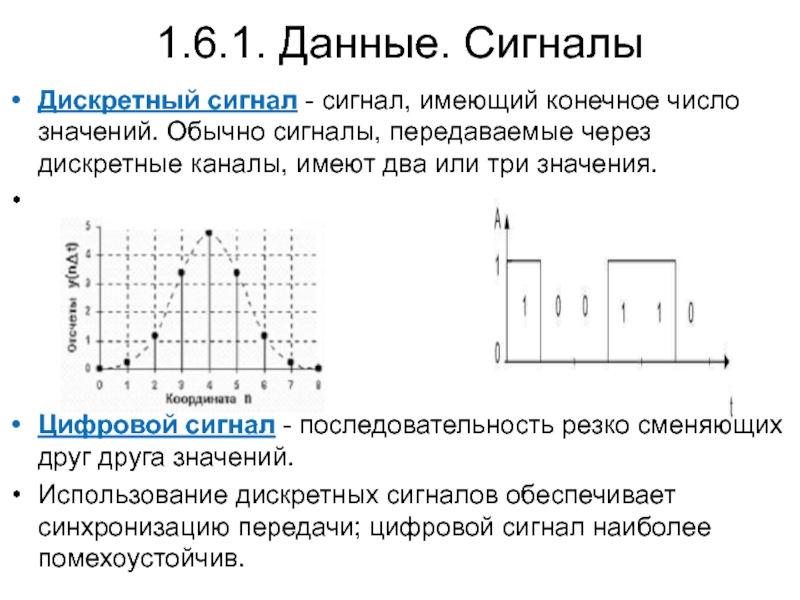
Отличия дискретных и непрерывных сигналов
Дискретные и непрерывные сигналы имеют ряд существенных отличий:
- Непрерывность во времени:
- Непрерывный сигнал определен в любой момент времени
- Дискретный сигнал определен только в отдельные моменты времени
- Форма представления:
- Непрерывный сигнал — непрерывная функция времени
- Дискретный сигнал — последовательность отсчетов
- Спектральный состав:
- Спектр непрерывного сигнала теоретически бесконечен
- Спектр дискретного сигнала ограничен частотой Найквиста
- Обработка:
- Непрерывные сигналы обрабатываются аналоговыми системами
- Дискретные сигналы обрабатываются цифровыми системами
Понимание этих отличий важно для правильного выбора методов обработки сигналов в разных системах.
Применение дискретных сигналов в цифровых системах
Дискретные сигналы нашли широкое применение в современных цифровых системах обработки информации. Основные области применения включают:
- Цифровая обработка сигналов (ЦОС)
- Системы связи
- Цифровое аудио и видео
- Измерительные системы
- Системы управления
Рассмотрим некоторые конкретные примеры использования дискретных сигналов:
Цифровая обработка звука
При цифровой обработке звука непрерывный аудиосигнал преобразуется в дискретный путем периодической выборки значений амплитуды. Это позволяет применять к звуку различные цифровые эффекты и преобразования.
Цифровая связь
В системах цифровой связи информация передается в виде дискретных сигналов — последовательностей битов или символов. Это обеспечивает помехоустойчивость и возможность восстановления сигнала.
Цифровые измерения
Измерительные системы преобразуют непрерывные физические величины в дискретные сигналы для дальнейшей цифровой обработки и анализа данных.
Таким образом, дискретные сигналы являются основой для работы большинства современных цифровых систем.
Преобразование непрерывных сигналов в дискретные
Для преобразования непрерывного сигнала в дискретный используется процесс дискретизации. Он включает следующие этапы:
- Выборка значений сигнала через равные промежутки времени
- Квантование полученных значений по уровню
- Кодирование квантованных значений двоичным кодом
Частота дискретизации должна выбираться в соответствии с теоремой Котельникова: она должна быть как минимум в два раза выше максимальной частоты в спектре исходного сигнала. Это позволяет избежать наложения спектров (эффекта элайзинга) и обеспечить возможность точного восстановления сигнала.
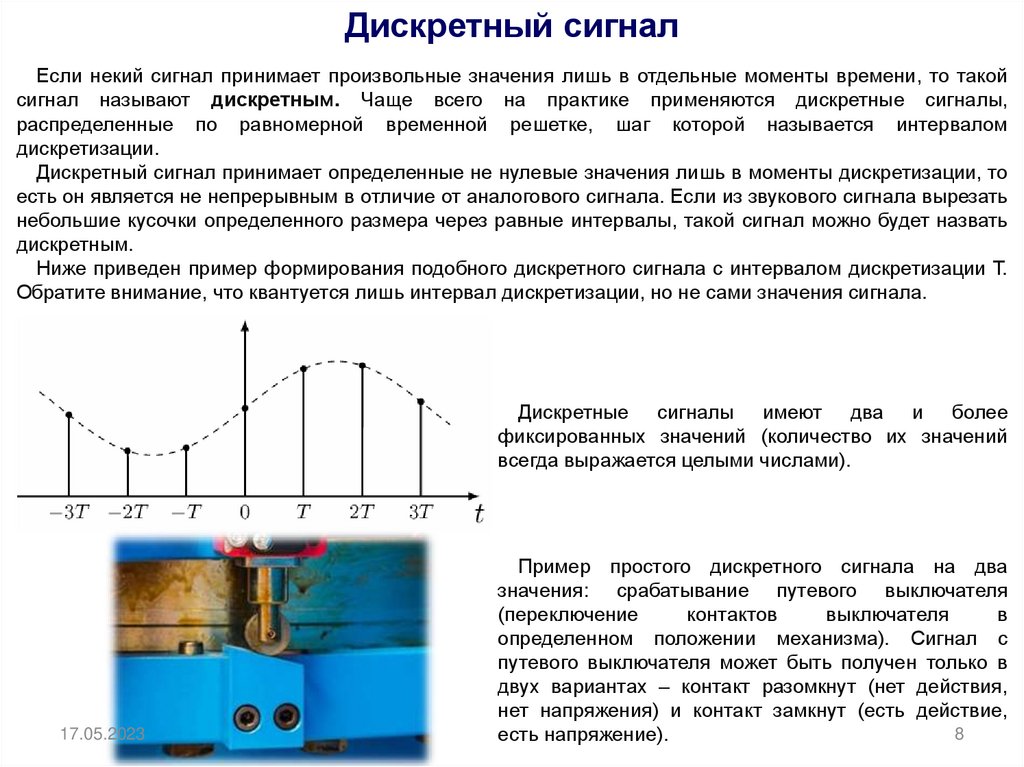
При квантовании непрерывный диапазон значений сигнала разбивается на конечное число уровней. Каждому уровню присваивается цифровой код. Количество уровней квантования определяет разрядность цифрового представления сигнала.
В результате этого процесса непрерывный сигнал преобразуется в последовательность цифровых отсчетов — дискретный сигнал.
Обработка дискретных сигналов
Обработка дискретных сигналов выполняется с помощью цифровых систем обработки сигналов. Основные методы обработки включают:
- Цифровую фильтрацию
- Дискретное преобразование Фурье
- Корреляционный анализ
- Интерполяцию и децимацию
Рассмотрим подробнее цифровую фильтрацию как один из базовых методов обработки дискретных сигналов.
Цифровая фильтрация
Цифровая фильтрация позволяет изменять спектральный состав сигнала. Различают фильтры с конечной (КИХ) и бесконечной (БИХ) импульсной характеристикой.
КИХ-фильтры реализуются как взвешенная сумма текущего и предыдущих отсчетов входного сигнала:
y[n] = b[0]*x[n] + b[1]*x[n-1] + ... + b[M]*x[n-M]
БИХ-фильтры дополнительно используют предыдущие значения выходного сигнала:
y[n] = (b[0]*x[n] + ... + b[M]*x[n-M]) - (a[1]*y[n-1] + ... + a[N]*y[n-N])
Выбор типа и параметров фильтра зависит от решаемой задачи обработки сигнала.
Преимущества использования дискретных сигналов
Использование дискретных сигналов в цифровых системах имеет ряд важных преимуществ:
- Помехоустойчивость — цифровой сигнал может быть восстановлен даже при наличии шумов
- Точность представления — разрядность кодирования определяет точность
- Гибкость обработки — возможность реализации сложных алгоритмов
- Простота хранения и передачи — дискретные сигналы легко записываются и передаются в цифровом виде
- Возможность сжатия данных
Эти преимущества обусловили широкое распространение систем цифровой обработки сигналов во многих областях техники.
Заключение
Дискретные сигналы играют ключевую роль в современных цифровых системах обработки информации. Понимание их свойств и методов обработки необходимо для разработки эффективных алгоритмов и устройств цифровой обработки сигналов. Развитие теории и практики работы с дискретными сигналами остается актуальным направлением в области информационных технологий.
Дискретные и непрерывные сигналы Носители информации
Тема урока:
Тема урока:
Можете ли вы полностью ответить на следующие вопросы:
- Знаете ли вы, что такое система ?
- Что такое информационная система
- Знаете ли вы, что такое сигнал ?
- Знаете ли вы, что такое дискретный и непрерывный сигналы?
- Что такое носители информации и какими они бывают?
Цели урока:
- Рассмотреть, что такое дискретный и непрерывный сигналы.
- Узнать, что такое носители информации и виды носителей информации существуют.
КРОССВОРД – ПОВТОРЕНИЕ
Заполните кроссворд, и отгадайте зашифрованное слово, обозначающее сложный объект, состоящий из взаимосвязанных частей и существующий как единое целое :
4
1
6
7
2
5
3
- Физический процесс (явление), несущий сообщение (информацию).
- На схеме:
- Канал связи или __________ ( впишите в кроссворд пропущенное слово ).
- Это предмет, явление, процесс, отношение, на которое обращено наше внимание с целью его изучения.
- Интегративность, или системный _________ ( впишите в кроссворд пропущенное слово ).
- Наука, изучающая методы представления, накопления, передачи и обработки информации с помощью компьютера.
- Знания, сведения, полученные из окружающего мира, которыми обладает человек.
ПОЛУЧАТЕЛЬ
канал связи
Эталон ответа к КРОССВОРДУ
4
О
Б
7
6
1
И
С
Ъ
И
2
5
Е
Э
3
Н
И
Н
И
Ф
С
Ф
С
Ф
К
Г
О
Ф
О
Т
Р
Т
Н
Е
Р
Р
О
Е
А
М
К
М
Д
Л
Ч
А
А
Н
Т
А
Ц
Т
И
И
К
И
К
Я
А
Носители информации
Чтобы сообщение было передано от источника к получателю, необходим носитель информации.
Носитель информации – это материальный объект, предназначенный для хранения и передачи данных.
ИСТОЧНИК
ПОЛУЧАТЕЛЬ
канал связи
помехи
Для передачи и хранения информации используют два вида носителей – знак и сигнал , в зависимости от природы системы, в которой протекает информационный процесс.
Сигнал – это физический процесс, содержащий в себе некоторую информацию.
Последовательность сигналов называется сообщением .
Параметр сигнала — та из его характеристик, которая используется для представления сообщений.
Дискретные и непрерывные сигналы
Информация может поступать непрерывно или дискретно, т. е. в виде последовательности отдельных сигналов.
Соответственно различают непрерывную и дискретную информацию .
Сигналы
Непрерывный
1. Определение
Дискретный
2. Примеры
3. Пример графика
4. Возможность обработки на компьютере.
нет
да
Непрерывный (аналоговый) сигнал – это сигнал, параметр которого
Информация представленная таким способом называется непрерывной .
Примером непрерывного сообщения служит человеческая речь, живая музыка, передаваемая модулированной звуковой волной; параметром сигнала в этом случае является давление, создаваемое этой волной в точке нахождения приемника — человеческого уха.
Аналоговый способ представления информации имеет недостатки : точность представления информации определяется точностью измерительного прибора, наличие помех может сильно исказить представляемую информацию.
Дискретный сигнал – это сигнал, параметр которого принимает конечное число значений, меняющееся через определенные промежутки времени (скачками).
Информация, передаваемая источником, в этом случае называется дискретной .
Дискретными являются показания цифровых измерительных приборов. Дискретной является распечатка матричного принтера.
Дискретна таблица значений функции, но когда мы наносим точки из нее на миллиметровую бумагу и соединяем плавной линией, получается непрерывный график.
Механический переключатель диапазонов в современных радиоприемниках сконструирован так, чтобы он принимал только фиксированные положения.
Рассмотрим 2 графика функций:
График отображает непрерывный сигнал
График отображает дискретный сигнал
Любое непрерывное сообщение можно преобразовать в дискретное, и такая процедура называется дискретизацией (оцифровыванием).
Компьютер — цифровая машина, т.е. внутреннее представление информации в нем дискретно.
Дискретизация входной информации (если она непрерывна) позволяет сделать ее пригодной для компьютерной обработки.
Что такое знак?
Знаками можно считать алфавит любого языка, цифры и числа, знаки языка жестов, любые коды или шифры, ноты, символы и т.д. Знак может быть составным, то есть состоять из нескольких других знаков.
При обработке текста на компьютере знаки представляются в форме последовательностей электрических импульсов (компьютерных кодов).
Таким образом, данные – это зарегистрированные (зафиксированные) сигналы.
Чтобы зарегистрировать сигналы используют знаки.
Знак – это материальный объект, замещающий или представляющий другой объект и несущий информацию о нем.
Практическое тестовое задание:
В текстовом редакторе с помощью знаков (алфавита и дополнительных символов), создавая компьютерный текстовый документ, напишите вопросы теста, добавив пропущенные слова и выбрав правильный вариант ответа из предложенных.
Итоги урока:
- Мы рассмотрели что такое дискретный и непрерывный сигналы.
- Узнали, что такое носители информации, установили связь между ними .
- Продолжили совершенствовать навыки работы с тестом на компьютере.
ДОМАШНЕЕ ЗАДАНИЕ
Приведите примеры продуктов, имеющих дискретную и непрерывную структуру.
Какие сигналы помогают определить нам качество продукта?
26 вопросов и ответов. Теория электрических цепей. Курс лекций
Сигнал – это физический процесс (например, изменяющиеся во времени токи и напряжения), содержащий в себе некоторую информацию. Любой сигнал можно описать математической функцией.
Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией , которая может принимать любые значения в определенном интервале; дискретные сигналы представляют собой последовательности или отсчеты функции , взятые в определенные дискретные моменты времени nT; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения – уровни квантования, которые затем кодируются двоичными числами.
Если в цепь микрофона (рис. 1), где ток является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал.
Рис. 1
В отличие от непрерывного сигнала дискретный сигнал можно обозначить . Однако, чаще его обозначают , заменяя непрерывное время t дискретными моментами nT, следующими строго через интервал T. Используются и более краткие обозначения: и . Причем, во всех этих записях n – целое число, принимающее как положительные, так и отрицательные значения. Так, на рис. 1 при n < 0 дискретный сигнал . При n = 0 значение равно значению сигнала в момент времени t = 0.
При n > 0 отсчеты повторяют форму сигнала , т.к. их амплитуды равны значениям непрерывного сигнала в моменты времени nT.
Рис. 2
Дискретные сигналы можно задавать графиками, как это показано на рис. 1, формулами, например, , в виде таблиц дискретных значений или в виде комбинации этих способов. Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов.
Пример 1.1. Единичный ступенчатый аналоговый сигнал приведен на рис. 2.
Соответствующий ему дискретный сигнал называется ступенчатой последовательностью. Он определяется следующим образом:
Рис. 3
Такая последовательность приведена на рис. 2.
Пример 1.2. Импульс Дирака или d-функция в аналоговой области приведена на рис. 3.
Рис.
4
Дельта-последовательность или дискретная d-функция определяется выражением
Последовательность , приведенная на рис. 3, принимает единственное значение, равное 1, при n = 0. Этот сигнал можно сдвинуть на k интервалов:
Тогда математическая запись любого дискретного сигнала имеет вид
где – отсчеты исходного аналогового сигнала.
Этот сигнал можно получить из аналогового (рис. 4) периодическим замыканием ключа на очень короткое время в моменты t = k.
Самоконтроль
1. Что представляют собой аналоговые, дискретные и цифровые сигналы?
2. Как практически получить дискретный сигнал из аналогового?
3. Что такое ступенчатая последовательность и дельта-последовательность?
4.
Изобразите графики дискретных d-функций и .
Сигналы и системы с дискретным временем — манекены
Сигналы и системы с дискретным временем маршируют в такт часам. Математическое моделирование сигналов и систем с дискретным временем показывает, что активность происходит с целым (целочисленным) интервалом, но сигналы в реальном мире работают в соответствии с периодами времени или частотой обновления, также известной как частота дискретизации .
Сигналы с дискретным временем, которые также можно рассматривать как последовательности, существуют только в тиках, и системы, обрабатывающие эти сигналы, математически говоря, отдыхают в периодах между сигнальной активностью.
Системы принимают входные данные и производят выходные данные с одним и тем же тактом, вообще говоря. В зависимости от характера цифрового оборудования и сложности системы вычисления, выполняемые системой, продолжаются между тактами, чтобы гарантировать, что следующий выход системы будет доступен на следующем такте, когда на вход поступает новая выборка сигнала.
Сигналы дискретного времени
Сигналы дискретного времени являются функцией индекса времени n. Дискретно-временной сигнал x [ n ], в отличие от непрерывного сигнала x ( t ), принимает значения только при целочисленных значениях независимой переменной n. Это означает, что сигнал активен только в определенные периоды времени. Сигналы с дискретным временем могут храниться в памяти компьютера, потому что количество значений сигналов, которые необходимо сохранить для представления конечного интервала времени, конечно.
Следующий простой сигнал, последовательность импульсов, показан как шток plot — график, на котором вы размещаете вертикальные линии, начиная с 0 до значения выборки, вместе с маркером, например, закрашенным кругом. Сюжет стебля также известен как сюжет леденцов на палочке — серьезно.
Стержневой график показывает только дискретные значения последовательности.
Системы дискретного времени
Система с дискретным временем, как и ее аналог с непрерывным временем, представляет собой функцию T {}, которая отображает вход x [ n ] на выход y [ n ] = Y { x [ n ]}. Примером системы с дискретным временем является фильтр с двумя ответвлениями :
Термин отвод означает, что выход в момент времени n формируется из двух моментов времени входа, n и n – 1. Посмотрите блок-схему двухотводной системы фильтрации.
Другими словами, эта система масштабирует текущие входные данные на 3/4 и добавляет их к прошлому значению входных данных, масштабированному на 1/4. Понятие прошлого входа возникает потому, что x [ n – 1] отстает на одну выборку от x [ n ]. Термин фильтр описывает выходные данные как ave r старение текущего ввода и предыдущего ввода.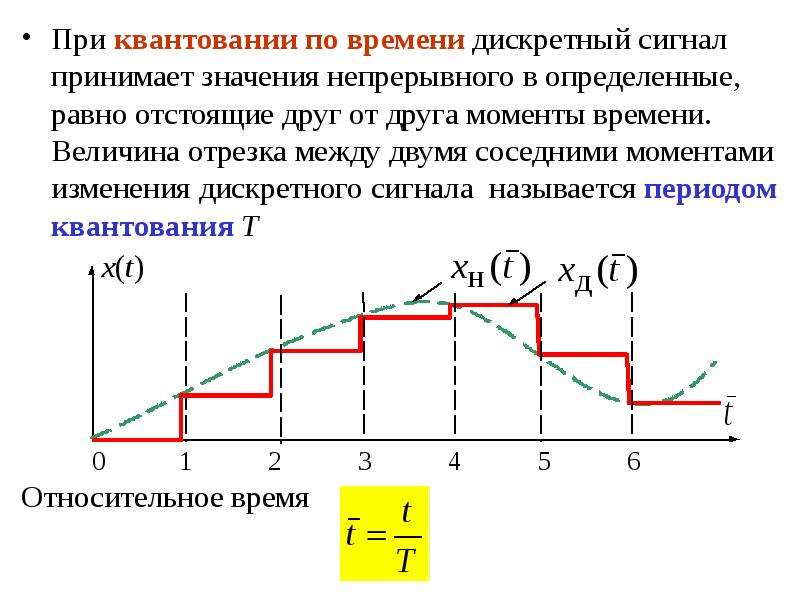
Усреднение — это форма фильтрации.
Об этой статье
Эта статья взята из книги:
- Сигналы и системы для чайников,
Об авторе книги:
Марк Викерт, доктор наук, профессор электротехники и вычислительной техники в Университете Колорадо, Колорадо-Спрингс. Он является членом IEEE и занимается решением реальных проблем с сигналами и системами в качестве консультанта местной промышленности.
Эту статью можно найти в категории:
- Профессиональная, техническая и инженерная карьера,
10.7: Дискретная обработка сигналов непрерывного времени
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 23163
- Richard Baraniuk et al.
- Университет Райса
Введение
Цифровые компьютеры могут обрабатывать дискретные сигналы времени, используя чрезвычайно гибкие и мощные алгоритмы. Однако большинство представляющих интерес сигналов представляют собой непрерывные сигналы во времени, именно так данные почти всегда появляются в природе. Теперь, когда была обсуждена теория, поддерживающая методы генерации дискретного сигнала времени из непрерывного сигнала времени путем дискретизации и последующего точного восстановления исходного сигнала из его выборок без ошибок, будет показано, как это можно применить для реализации непрерывного времени, линейного инвариантные во времени системы, использующие дискретное время, линейные инвариантные во времени системы. Это имеет ключевое значение для многих современных технологий, поскольку позволяет использовать возможности цифровых вычислений для обработки аналоговых сигналов.
Дискретная обработка сигналов непрерывного времени
Структура процесса
С целью обработки сигналов непрерывного времени с использованием системы дискретного времени мы рассмотрим одну из наиболее распространенных структур технологий цифровой обработки сигналов.
В качестве обзора принятого подхода исходный сигнал непрерывного времени \(x\) преобразуется в сигнал дискретного времени \(x_s\) таким образом, что периоды спектра выборок \(X_s\) максимально близки возможно по форме к спектру \(X\). Затем применяется дискретный, линейный во времени инвариантный фильтр \(H_2\), который изменяет форму спектра отсчетов \(X_s\), но не может увеличить предел полосы пропускания \(X_s\), чтобы создать другой сигнал \(y_s\ ). Это восстанавливается с помощью подходящего фильтра реконструкции для получения выходного сигнала непрерывного времени \(y\), тем самым эффективно реализуя некоторую систему непрерывного времени \(H_1\). Этот процесс показан на рисунке \(\PageIndex{1}\), а спектры показаны для конкретного случая на рисунке \(\PageIndex{2}\).
Необходимо дальнейшее обсуждение каждого из этих шагов, и мы начнем с обсуждения аналого-цифрового преобразователя, часто обозначаемого АЦП или АЦП.
Понятно, что для обработки сигнала непрерывного времени с использованием методов дискретного времени мы должны произвести выборку сигнала в качестве начального шага. По сути, это и есть цель АЦП, хотя есть и практические вопросы, которые будут обсуждаться позже. АЦП принимает аналоговый сигнал с непрерывным временем в качестве входного сигнала и формирует цифровой сигнал с дискретным временем в качестве выходного с идеальным случаем бесконечной точности, соответствующим выборке. Как утверждает теорема Найквиста-Шеннона о дискретизации, для того, чтобы сохранить всю информацию об исходном сигнале, нам обычно требуется выборка выше частоты Найквиста \(\omega_s≥2B\), где полоса исходного сигнала ограничена до \((−B, Б)\). Когда невозможно гарантировать это условие, следует использовать фильтр сглаживания.
В фильтре дискретного времени происходят преднамеренные изменения информации о сигнале. Это обычно делается в программном обеспечении для цифровых компьютеров после того, как сигнал был оцифрован аппаратным АЦП и до того, как он будет использован аппаратным ЦАП для создания выходного сигнала.
Это позволяет описанной выше настройке быть достаточно гибкой в фильтре, который она реализует. Если выборка выше частоты Найквиста. Любые изменения, которые дискретный фильтр вносит в эту форму, могут быть переданы в непрерывный временной сигнал, предполагающий идеальную реконструкцию. Следовательно, описанный процесс будет реализовывать непрерывный во времени линейный инвариантный во времени фильтр. Это будет объяснено более математически подробно в следующем разделе. Как обычно, есть, конечно, практические ограничения, которые будут обсуждаться позже.
Наконец, мы обсудим цифро-аналоговый преобразователь, часто обозначаемый DAC или D/A. Поскольку фильтры непрерывного времени имеют входы непрерывного времени и выходы непрерывного времени, мы должны создать сигнал непрерывного времени из нашего отфильтрованного сигнала дискретного времени. Предполагая, что мы произвели выборку с ограниченной полосой пропускания с достаточно высокой скоростью, в идеальном случае это было бы сделано с использованием идеальной реконструкции с помощью интерполяционной формулы Уиттакера-Шеннона.
Однако, опять же, есть практические проблемы, препятствующие этому, которые будут обсуждаться позже.
Фильтр дискретного времени
После некоторого начального обсуждения процесса, показанного на рисунке \(\PageIndex{1}\), связь между инвариантным линейным фильтром непрерывного времени \(H_1\) и дискретным временем, линейным временем инвариантный фильтр \(H_2\) можно изучить. Мы будем предполагать использование идеальных АЦП и ЦАП с бесконечной точностью, которые выполняют дискретизацию и идеальную реконструкцию соответственно, используя частоту дискретизации \(\omega_s=2 \pi /T_s≥2B\), где входной сигнал \(x\) равен полоса ограничена до \((−B,B)\).
Обратите внимание, что эти аргументы терпят неудачу, если это условие не выполняется и происходит псевдоним. В этом случае для сохранения этих аргументов необходимо предварительное применение фильтра сглаживания. 9{\infty} H_{1}\left(\frac{\omega-2 \pi k}{T_{s}}\right)(u(\omega-(2k-1) \pi) -u(\ омега-(2k+1) \pi)). \nonumber \]
Проще говоря, \(H_2\) является \(2 \pi\) периодическим и \(H_2(\omega)=H_1( \omega /T_s)\) для \(\omega \in[ -\пи, \пи)\).
При заданном постоянном линейном инвариантном во времени фильтре \(H_1\) приведенное выше уравнение решает задачу проектирования системы при условии, что мы знаем, как реализовать \(H_2\). Фильтр \(H_2\) должен быть выбран таким, чтобы он имел частотную характеристику, где каждый период имел ту же форму, что и частотная характеристика \(H_1\) на \(\left(-\pi / T_{s}, \ pi / T_{s}\right)\). Это показано на частотных характеристиках, показанных на рисунке \(\PageIndex{2}\).
Мы могли бы также рассмотреть задачу системного анализа, в которой задан конкретный дискретный, линейный во времени инвариантный фильтр \(H_2\), и мы хотим описать фильтр \(H_1\).
Таких фильтров много, но мы можем описать их частотные характеристики на \(\left(-\pi / T_{s}, \pi / T_{s}\right)\), используя приведенное выше уравнение. Выделение одного периода \(H_2(\omega)\) приводит к выводу, что \(H_{1}(\omega)=H_{2}\left(\omega T_{s}\right)\) для \(\ омега \in\left(-\pi / T_{s}, \pi / T_{s}\right)\). Поскольку предполагалось, что \(x\) ограничен полосой до \(\left(-\pi / T_{s}, \pi / T_{s}\right)\), значение частотной характеристики в другом месте не имеет значения.
Практические соображения
Как упоминалось ранее, существует несколько практических соображений, которые необходимо учитывать на каждом этапе процесса, показанного на рисунке \(\PageIndex{1}\). Некоторые из них будут кратко рассмотрены здесь, а более полная модель дискретной обработки сигналов непрерывного времени представлена на рисунке \(\PageIndex{3}\).
Рисунок \(\PageIndex{3}\): Более полная модель того, как дискретная обработка сигналов непрерывного времени реализуется на практике.
Обратите внимание на добавление фильтров сглаживания и защиты от изображения, чтобы способствовать ограничению входной и выходной полосы пропускания. Показано, что АЦП выполняет выборку с квантованием. Далее указывается, что цифровой фильтр является причинным. Показано, что ЦАП выполняет несовершенную реконструкцию, в этом случае сохраняется нулевой порядок.Anti-Aliasing Filter
В действительности мы обычно не можем гарантировать, что входной сигнал будет иметь определенное ограничение полосы пропускания, и не всегда может быть достигнута достаточно высокая частота дискретизации. Поскольку крайне важно, чтобы высокочастотные компоненты не маскировались под более низкочастотные компоненты посредством наложения спектров, необходимо использовать сглаживающие фильтры с частотой среза, меньшей или равной \(\omega_s/2\) АЦП. Блок-схема на рисунке \(\PageIndex{3}\) отражает это дополнение.
Как описано в предыдущем разделе, идеальный фильтр нижних частот, удаляющий всю энергию на частотах выше \(\omega_s/2\), был бы оптимальным.
Конечно, это недостижимо, поэтому необходимо принять аппроксимацию идеального фильтра нижних частот с низким коэффициентом усиления выше \(\omega_s/2\). Это означает, что некоторый алиасинг неизбежен, но его можно уменьшить до незначительного уровня.
Квантование сигнала
В нашем предыдущем обсуждении дискретной обработки сигналов с непрерывным временем мы предположили идеальный случай, в котором АЦП точно выполняет выборку. Однако, хотя АЦП преобразует непрерывный сигнал времени в сигнал дискретного времени, он также должен преобразовывать аналоговые значения в цифровые значения для использования в цифровом логическом устройстве, что называется квантованием. Подсистема ADC на блок-схеме на рисунке \(\PageIndex{3}\) отражает это дополнение.
Данные, полученные АЦП, должны храниться в виде конечного числа бит внутри цифрового логического устройства. Таким образом, существует только конечное число значений, которые может принимать цифровая выборка, а именно \(2N\), где \(N\) — количество битов, в то время как аналоговая выборка может принимать неисчислимое множество значений.
Следовательно, что-то должно быть потеряно в процессе квантования. В результате квантование ограничивает как диапазон, так и точность выходного сигнала АЦП. Оба являются конечными, и улучшение одного при постоянном числе битов требует жертвовать качеством другого.
Реализуемость фильтра
В реальных условиях, если входной сигнал является функцией времени, будущие значения сигнала не могут быть использованы для вычисления выходного сигнала. Таким образом, цифровой фильтр \(H_2\) и система в целом \(H_1\) должны быть причинно-следственными. Аннотация фильтра на рисунке \(\PageIndex{3}\) отражает это добавление. Если искомая система не является причинной, но имеет импульсную характеристику, равную нулю до некоторого времени \(t_0\), можно ввести задержку, чтобы сделать ее причинной. Однако, если эта задержка чрезмерна или импульсная характеристика имеет бесконечную длину, для практического решения проблемы становится необходимой оконная схема. Умножение на окно для уменьшения длины импульсной характеристики может уменьшить необходимую задержку и уменьшить требования к вычислениям.
Возьмем, к примеру, идеальный фильтр нижних частот. Она акаузальна и бесконечна по протяженности в обоих направлениях. Таким образом, мы должны довольствоваться приближением. Можно предположить, что эти аппроксимации могут быть достигнуты путем усечения синхроимпульсной характеристики фильтра нижних частот на одном из его нулей, эффективно обрабатывая его прямоугольным импульсом. Однако это приведет к плохим результатам в частотной области, так как результирующая свертка значительно расширит энергию сигнала. Другие оконные функции, которых существует множество, меньше распространяют сигнал в частотной области и, таким образом, гораздо полезнее для получения этих приближений.
Anti-Image Filter
В нашем предыдущем обсуждении дискретной обработки сигналов непрерывного времени мы предположили идеальный случай, в котором ЦАП выполняет идеальную реконструкцию. Однако при рассмотрении практических вопросов важно помнить, что функция sinc, используемая для интерполяции Уиттакера-Шеннона, бесконечна по длине и акаузальна.
Следовательно, для ЦАП было бы невозможно реализовать идеальную реконструкцию.
Вместо этого ЦАП реализует причинно-следственную фиксацию нулевого порядка или другую простую схему реконструкции относительно частоты дискретизации \(\omega_s\), используемой АЦП. Однако это приведет к тому, что функция не будет ограничена пропускной способностью \((−\omega_s/2,\omega_s/2)\). Следовательно, к выходу необходимо применить дополнительный фильтр нижних частот, называемый фильтром подавления изображений. Процесс, показанный на рисунке \(\PageIndex{3}\), отражает эти добавления. Фильтр подавления изображений пытается ограничить полосу пропускания сигнала до \((−\omega_s/2,\omega_s/2)\), поэтому оптимальным будет идеальный фильтр нижних частот. Однако, как уже было сказано, это невозможно. Следовательно, должны быть приняты приближения идеального фильтра нижних частот с низким коэффициентом усиления выше \(\omega_s/2\). Фильтр подавления изображений обычно имеет те же характеристики, что и фильтр сглаживания.
Дискретная обработка сигналов непрерывного времени Сводка
Как было показано, выборка и реконструкция могут использоваться для реализации систем непрерывного времени с использованием систем дискретного времени, которые очень эффективны благодаря универсальности, гибкости и скорости цифровых компьютеров. . Однако существует большое количество практических соображений, которые необходимо учитывать при попытке выполнить это, включая шум квантования и сглаживание в аналого-цифровом преобразователе, реализуемость фильтра в дискретном временном фильтре, оконную реконструкцию и связанные с этим проблемы. в цифро-аналоговом преобразователе. Многие современные технологии решают эти проблемы и используют этот процесс.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Ричард Баранюк и др.
