Какому логическому элементу соответствует таблица истинности. Логические элементы и таблицы истинности: все, что нужно знать

alexxlabРазное
Что такое логические элементы и как они работают. Какие бывают основные типы логических элементов. Как выглядят таблицы истинности для разных логических операций. Где применяются логические элементы в цифровой технике.

Содержание

Основные понятия логических элементов

Логические элементы — это базовые «кирпичики», из которых строятся все цифровые схемы. Они выполняют простейшие логические операции над входными сигналами и формируют выходной сигнал в соответствии с заданной логической функцией.

Ключевые особенности логических элементов:

  • Имеют один или несколько входов и один выход
  • Оперируют только двумя логическими уровнями сигналов — 0 и 1
  • Выполняют элементарные логические функции — И, ИЛИ, НЕ и т.д.
  • Являются основой для построения более сложных цифровых устройств

Работа логического элемента полностью описывается его таблицей истинности, которая задает зависимость выходного сигнала от комбинации входных сигналов.

Основные типы логических элементов

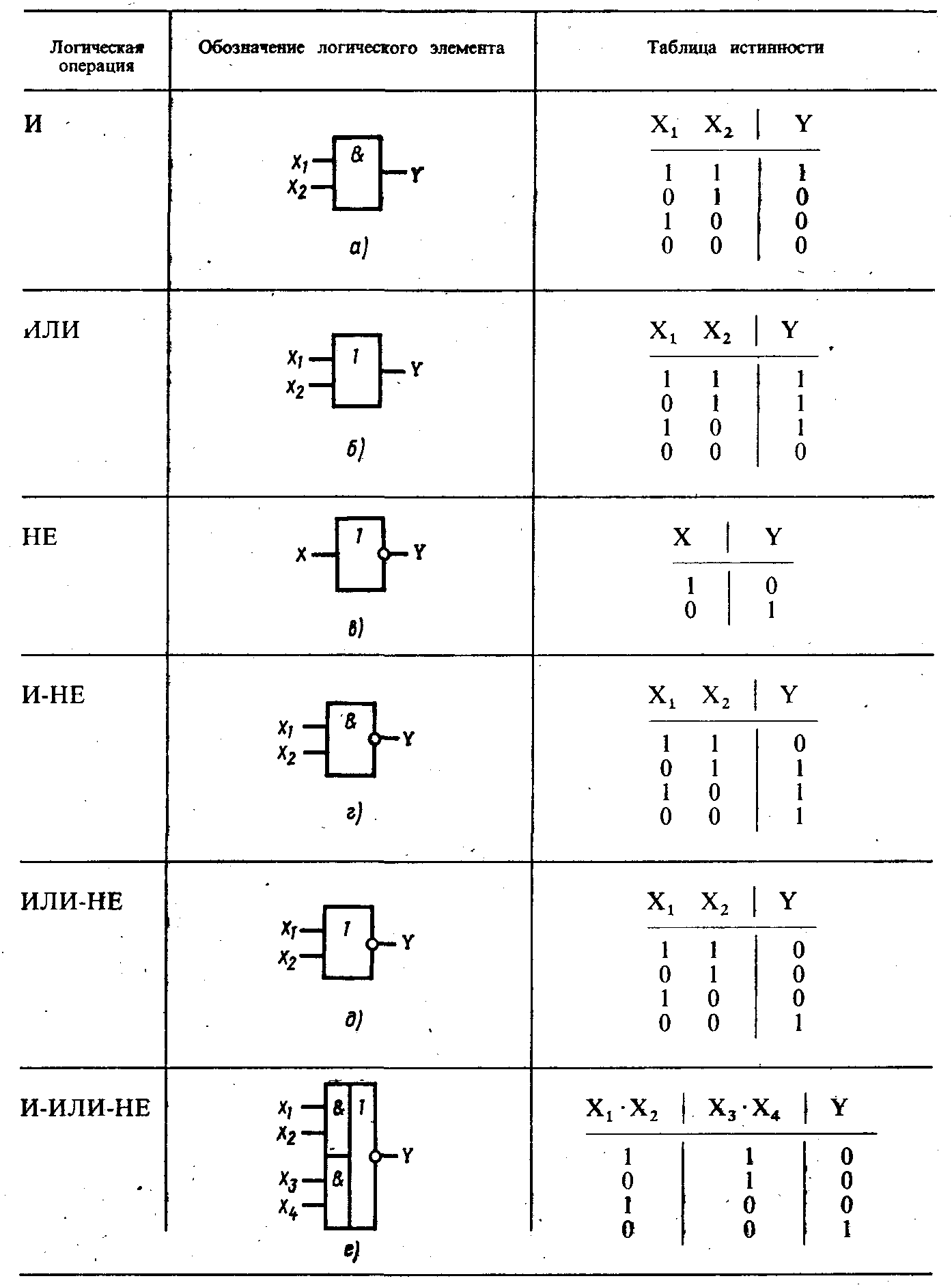
Рассмотрим наиболее распространенные логические элементы и их функции:


Элемент И (AND)

Выполняет операцию логического умножения. Выход равен 1 только если все входы равны 1.

Элемент ИЛИ (OR)

Реализует операцию логического сложения. Выход равен 1, если хотя бы один из входов равен 1.

Элемент НЕ (NOT)

Выполняет операцию логического отрицания (инверсии). Инвертирует входной сигнал.

Элемент И-НЕ (NAND)

Комбинация элементов И и НЕ. Выход равен 0 только если все входы равны 1.

Элемент ИЛИ-НЕ (NOR)

Комбинация элементов ИЛИ и НЕ. Выход равен 0, если хотя бы один из входов равен 1.

Элемент Исключающее ИЛИ (XOR)

Выход равен 1, если входные сигналы не совпадают (различны).

Таблицы истинности логических элементов

Таблица истинности — это способ описания поведения логического элемента, показывающий зависимость выходного сигнала от всех возможных комбинаций входных сигналов.

Рассмотрим таблицы истинности для основных логических элементов:

Таблица истинности элемента И

A | B | Y 0 | 0 | 0 0 | 1 | 0 1 | 0 | 0 1 | 1 | 1

Как видим, выход Y равен 1 только когда оба входа A и B равны 1.


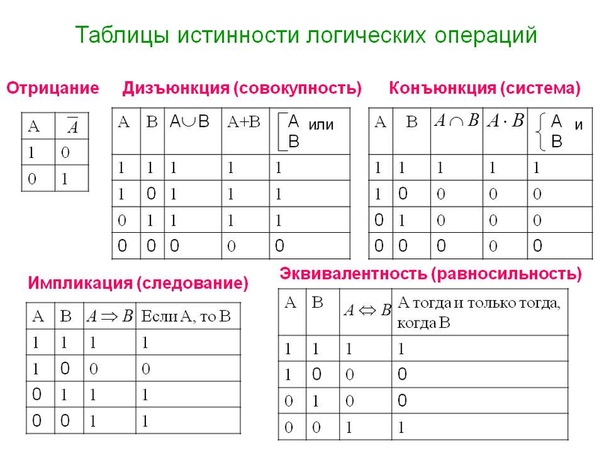
Таблица истинности элемента ИЛИ

A | B | Y 0 | 0 | 0 0 | 1 | 1 1 | 0 | 1 1 | 1 | 1

Выход Y равен 1, если хотя бы один из входов A или B равен 1.

Таблица истинности элемента НЕ

A | Y 0 | 1 1 | 0

Выход Y инвертирует входной сигнал A.

Применение логических элементов

Логические элементы являются базовыми компонентами при построении цифровых устройств. Области их применения включают:

  • Процессоры и микроконтроллеры
  • Оперативная и постоянная память
  • Шифраторы и дешифраторы
  • Мультиплексоры и демультиплексоры
  • Цифровые компараторы
  • Сумматоры и вычитатели
  • Триггеры и регистры
  • Счетчики импульсов

По сути, любое цифровое устройство в своей основе состоит из комбинации логических элементов, выполняющих требуемые функции обработки данных.

Синтез логических схем

На основе базовых логических элементов можно синтезировать более сложные логические функции и схемы. Для этого используются методы:

  • Алгебраические преобразования логических выражений
  • Построение карт Карно
  • Метод неопределенных коэффициентов
  • Декомпозиция сложных функций

С помощью этих методов любую логическую функцию можно представить в виде комбинации простейших логических элементов.


Реализация логических элементов

На практике логические элементы реализуются в виде интегральных микросхем. Существует несколько технологий изготовления логических элементов:

  • Транзисторно-транзисторная логика (ТТЛ)
  • Эмиттерно-связанная логика (ЭСЛ)
  • КМОП-логика
  • Интегральная инжекционная логика (И2Л)

Наиболее распространенной на сегодня является КМОП-технология, обеспечивающая низкое энергопотребление и высокую степень интеграции.

Проектирование с использованием логических элементов

При разработке цифровых устройств на основе логических элементов применяются следующие подходы:

  1. Составление функциональной схемы устройства
  2. Описание логики работы с помощью таблиц истинности
  3. Получение логических выражений
  4. Минимизация логических выражений
  5. Построение принципиальной схемы на логических элементах
  6. Моделирование работы схемы

Современные САПР позволяют автоматизировать многие этапы проектирования цифровых устройств на логических элементах.

Перспективы развития логических элементов

Основные направления совершенствования логических элементов включают:


  • Уменьшение размеров транзисторов до единиц нанометров
  • Снижение энергопотребления
  • Повышение быстродействия
  • Использование новых материалов (графен, углеродные нанотрубки)
  • Разработка оптических и квантовых логических элементов

Развитие элементной базы позволяет создавать все более производительные и энергоэффективные цифровые устройства.

Заключение

Логические элементы являются фундаментальными «кирпичиками» цифровой техники. Понимание принципов их работы необходимо для проектирования любых цифровых устройств — от простых логических схем до сложных процессоров. Таблицы истинности позволяют полностью описать функционирование логических элементов и служат основой для синтеза более сложных цифровых схем.


Какому логическому элементу соответствует таблица истинности — MOREREMONTA

Электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными, называется логическим элементом. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня.

Операнды в данном случае подаются в двоичной системе счисления — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное. 1 — ИСТИНА, 0 — ЛОЖЬ.

Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.

Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.

В зависимости от устройства схемы элемента, от ее электрических параметров, логические уровни (высокие и низкие уровни напряжения) входа и выхода имеют одинаковые значения для высокого и низкого (истинного и ложного) состояний.

Традиционно логические элементы выпускаются в виде специальных радиодеталей — интегральных микросхем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов.

Далее рассмотрим каждый из этих типов логических элементов более внимательно.

Логический элемент «И» — конъюнкция, логическое умножение, AND

«И» — логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.

Условные обозначения логических элементов «И» с разным количеством входов приведены на рисунке. В тексте логический элемент «И» с тем или иным числом входов обозначается как «2И», «4И» и т. д. — элемент «И» с двумя входами, с четырьмя входами и т. д.

Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе И на втором входе. В остальных трех возможных случаях на выходе будет ноль.

На западных схемах значок элемента «И» имеет прямую черту на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «&».

Логический элемент «ИЛИ» — дизъюнкция, логическое сложение, OR

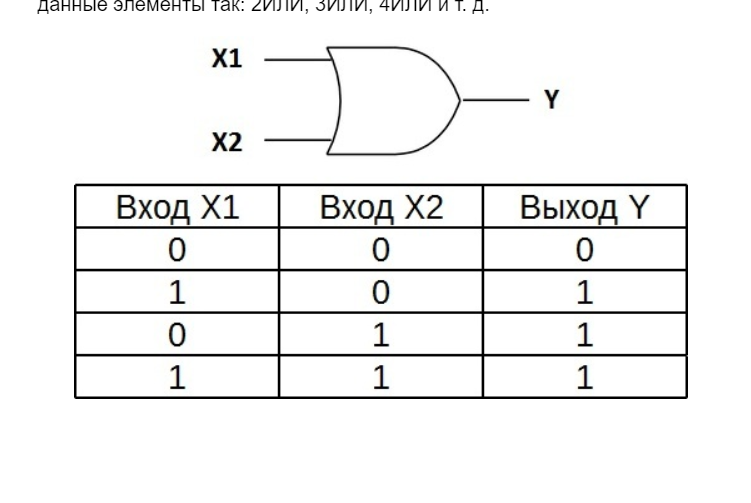
«ИЛИ» — логический элемент, выполняющий над входными данными операцию дизъюнкции или логического сложения. Он так же как и элемент «И» выпускается с двумя, тремя, четырьмя и т. д. входами и с одним выходом. Условные обозначения логических элементов «ИЛИ» с различным количеством входов показаны на рисунке. Обозначаются данные элементы так: 2ИЛИ, 3ИЛИ, 4ИЛИ и т. д.

Таблица истинности для элемента «2ИЛИ» показывает, что для появления на выходе логической единицы, достаточно чтобы логическая единица была на первом входе ИЛИ на втором входе. Если логические единицы будут сразу на двух входах, на выходе также будет единица.

На западных схемах значок элемента «ИЛИ» имеет закругление на входе и закругление с заострением на выходе. На отечественных схемах — прямоугольник с символом «1».

Логический элемент «НЕ» — отрицание, инвертор, NOT

«НЕ» — логический элемент, выполняющий над входными данными операцию логического отрицания.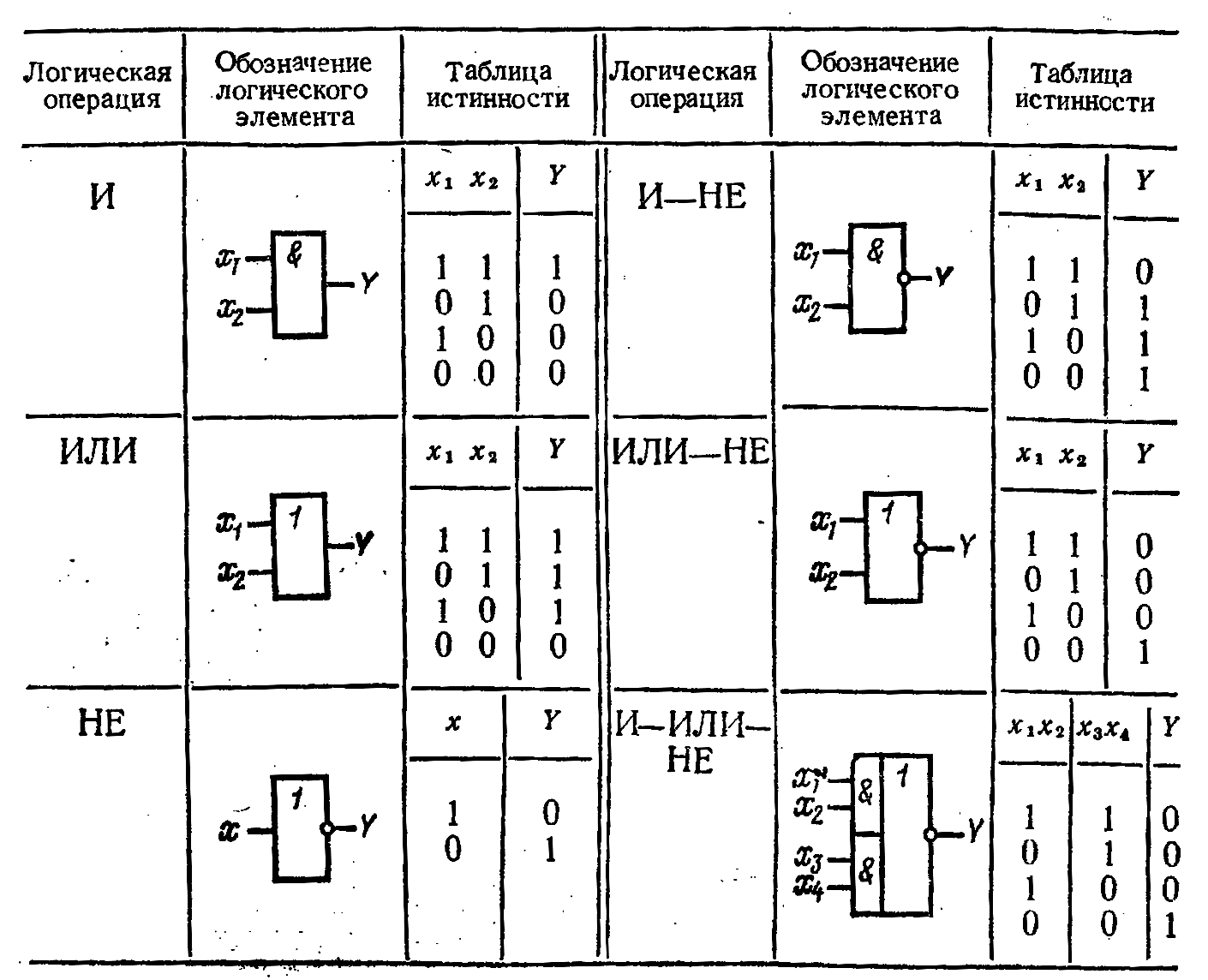 Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал. На рисунке приведено условное обозначение логического элемента «НЕ».

Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот.

На западных схемах значок элемента «НЕ» имеет форму треугольника с кружочком на выходе. На отечественных схемах — прямоугольник с символом «1», с кружком на выходе.

Логический элемент «И-НЕ» — конъюнкция (логическое умножение) с отрицанием, NAND

«И-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Другими словами, это в принципе элемент «И», дополненный элементом «НЕ». На рисунке приведено условное обозначение логического элемента «2И-НЕ».

Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И».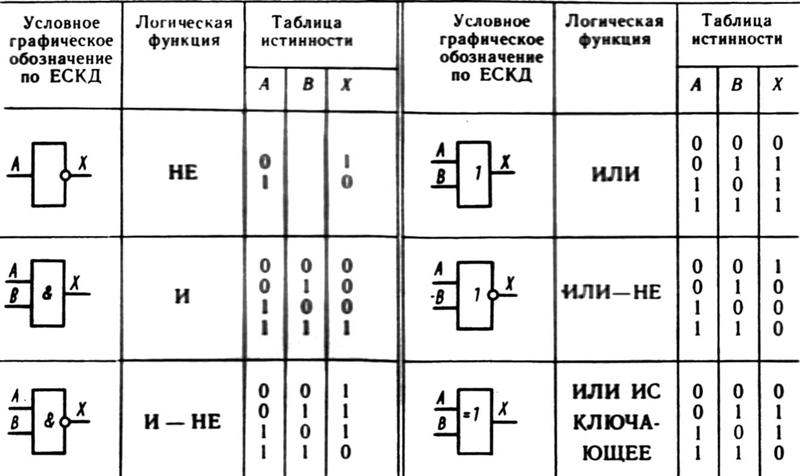 Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой логической операции в 1913 году. Обозначается как «И», только с кружочком на выходе.

Логический элемент «ИЛИ-НЕ» — дизъюнкция (логическое сложение) с отрицанием, NOR

«ИЛИ-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Иначе говоря, это элемент «ИЛИ», дополненный элементом «НЕ» — инвертором. На рисунке приведено условное обозначение логического элемента «2ИЛИ-НЕ».

Таблица истинности для элемента «ИЛИ-НЕ» противоположна таблице для элемента «ИЛИ». Высокий потенциал на выходе получается лишь в одном случае — на оба входа подаются одновременно низкие потенциалы. Обозначается как «ИЛИ», только с кружочком на выходе, обозначающим инверсию.

Логический элемент «исключающее ИЛИ» — сложение по модулю 2, XOR

«исключающее ИЛИ» — логический элемент, выполняющий над входными данными операцию логического сложения по модулю 2, имеет два входа и один выход. Часто данные элементы применяют в схемах контроля. На рисунке приведено условное обозначение данного элемента.

Изображение в западных схемах — как у «ИЛИ» с дополнительной изогнутой полоской на стороне входа, в отечественной — как «ИЛИ», только вместо «1» будет написано «=1».

Этот логический элемент еще называют «неравнозначность». Высокий уровень напряжения будет на выходе лишь тогда, когда сигналы на входе не равны (на одном единица, на другом ноль или на одном ноль, а на другом единица) если даже на входе будут одновременно две единицы, на выходе будет ноль — в этом отличие от «ИЛИ». Данные элементы логики широко применяются в сумматорах.

Так же, как и стандартные Булевы выражения, информация на входах и выходах различных логических элементов или логических схем может быть собрана в единую таблицу – таблицу истинности.

Таблица истинности дает наглядное представление о системе логических функций. В таблице истинности отображаются сигналы на выходах логических элементов при всех возможных комбинациях сигналов на их входах.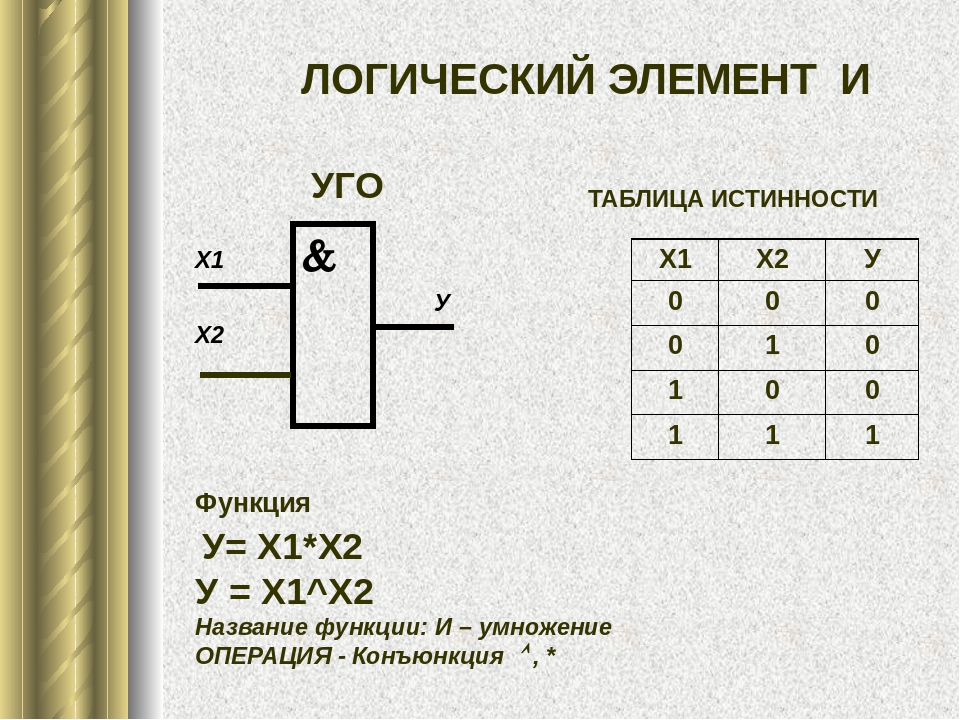

В качестве примера, рассмотрим логическую схему с двумя входами и одним выходом. Входные сигналы отметим как «А» и «В», а выход «Q». Есть четыре (2²) возможных комбинаций входных сигналов, которые можно подать на эти два входа («ON — наличие сигнала» и «OFF — отсутствие сигнала»).

Однако, когда речь идет о логических выражениях и, особенно о таблице истинности логических элементов, вместо общего понятия «наличие сигнала» и «отсутствие сигнала» используют битные значения, которые представляют собой логический уровень «1» и логический уровень «0» соответственно.

Тогда четыре возможные комбинации «А» и «В» для 2-входного логического элемента можно представить в следующем виде:

  1. «OFF» — «OFF» или (0, 0)
  2. «OFF» — «ON» или (0, 1)
  3. «ON» — «OFF» или (1, 0)
  4. «ON» — «ON» или (1, 1)

Следовательно, у логической схемы имеющей три входа будет восемь возможных комбинаций (2³) и так далее. Для обеспечения легкого понимания сути таблицы истинности, мы будем изучать ее только на простых логических элементах с числом входов не превышающим двух.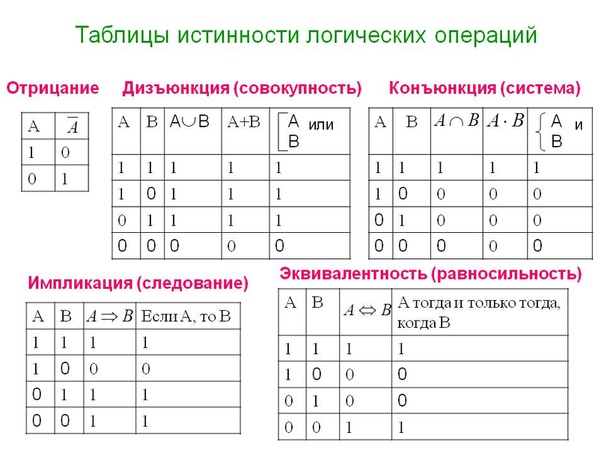 Но, несмотря на это, принцип получения логических результатов для многовходных элементов схемы остается таким же.

Практически, таблица истинности состоит из одного столбца для каждой из входных переменных (например, А и В), и один последний столбец для всех возможных результатов логической операции (Q). Следовательно, каждая строка таблицы истинности содержит один из возможных вариантов входных переменных (например, A = 1, B = 0), и результат операции с этими значениям.

Таблица истинности

Элемент «И»

Для логического элемента «И» выход Q будет содержать лог.1, только если на оба входа («А» и «В») будет подан сигнал лог.1

Микросхемы, содержащие логический элемент «И»:

  • К155ЛИ1, аналог SN7408N
  • К155ЛИ5 с открытым коллектором, аналог SN74451N
  • К555ЛИ1, аналог SN74LS08N
  • К555ЛИ2 с открытым коллектором, аналог SN74LS09N

Элемент «ИЛИ»

Выход Q, элемента «ИЛИ», будет иметь лог.1, если на любой из двух входов или же на оба входа сразу подать лог. 1


Микросхемы, содержащие логический элемент «ИЛИ»:

  • К155ЛЛ1, аналог SN7432N
  • К155ЛЛ2 с открытым коллектором, аналог SN75453N
  • К555ЛЛ1, аналог SN74LS32N

Элемент «НЕ»

В данном случае выход Q, логического элемента «НЕ», будет иметь сигнал противоположный входному сигналу.

Микросхемы, содержащие логический элемент «НЕ»:

  • К155ЛН1, аналог SN7404N
  • К155ЛН2 с открытым коллектором, аналог SN7405N
  • К155ЛН3, аналог SN7406N
  • К155ЛН5 с открытым коллектором, аналог SN7416N
  • К155ЛН6, аналог SN7466N

Элемент «И-НЕ»

На выходе Q элемента «И-НЕ» будет лог.1 если на обоих входах одновременно отсутствует сигнал лог.1

Микросхемы, содержащие логический элемент «И-НЕ»:

  • К155ЛА3, аналог SN7400N
  • К155ЛА8, аналог SN7401N
  • К155ЛА9 с открытым коллектором, аналог SN7403N
  • К155ЛА11 с открытым коллектором, аналог SN7426N
  • К155ЛА12 с открытым коллектором, аналог SN7437N
  • К155ЛА13 с открытым коллектором, аналог SN7438N
  • К155ЛА18 с открытым коллектором, аналог SN75452N

Элемент «ИЛИ-НЕ»

Только если на оба входа логического элемента «ИЛИ-НЕ» подать лог.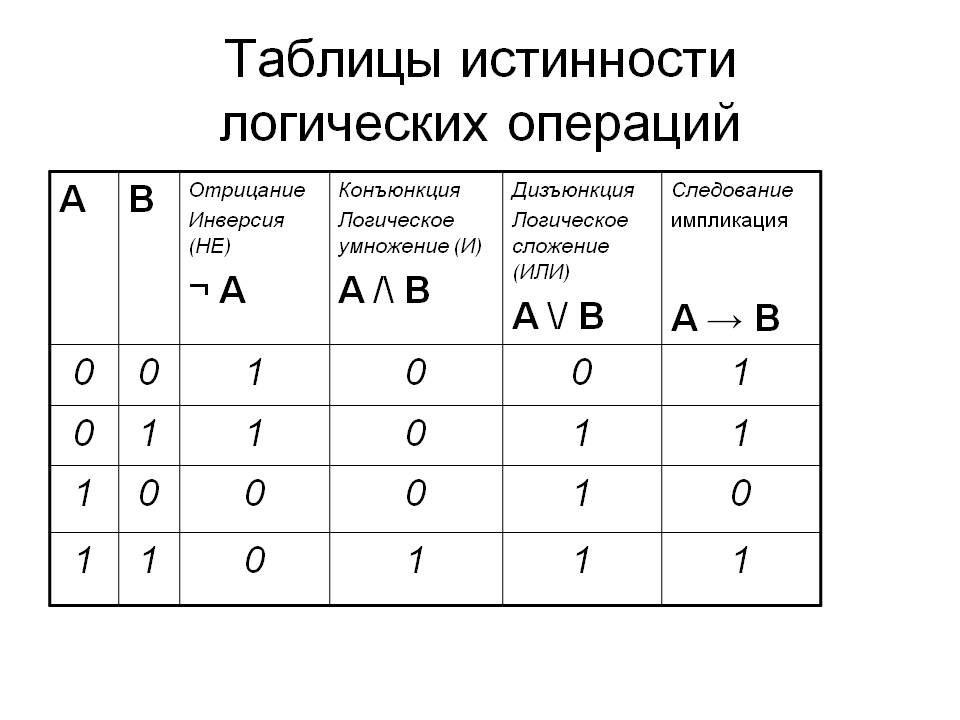 0 мы получим на его выходе Q сигнал соответствующий лог.1

Микросхемы, содержащие логический элемент «ИЛИ-НЕ»:

  • К155ЛЕ1, аналог SN7402N
  • К155ЛЕ5, аналог SN7428N
  • К155ЛЕ6, аналог SN74128N

Элемент «Исключающее ИЛИ»

В данном случае выход Q будет содержать лог.1, если на вход элемента «Исключающее ИЛИ» поданы два противоположных друг другу сигнала.

Микросхемы, содержащие логический элемент «Исключающее ИЛИ»:

Подведем итог, собрав все полученные ранее результаты работы логических элементов в единую таблицу истинности:

Абсолютно все цифровые микросхемы состоят из одних и тех же логических элементов – «кирпичиков» любого цифрового узла. Вот о них мы и поговорим сейчас.

Логический элемент – это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.

Итак, какие бывают элементы?

Элемент «И» (AND)

Иначе его называют «конъюнктор».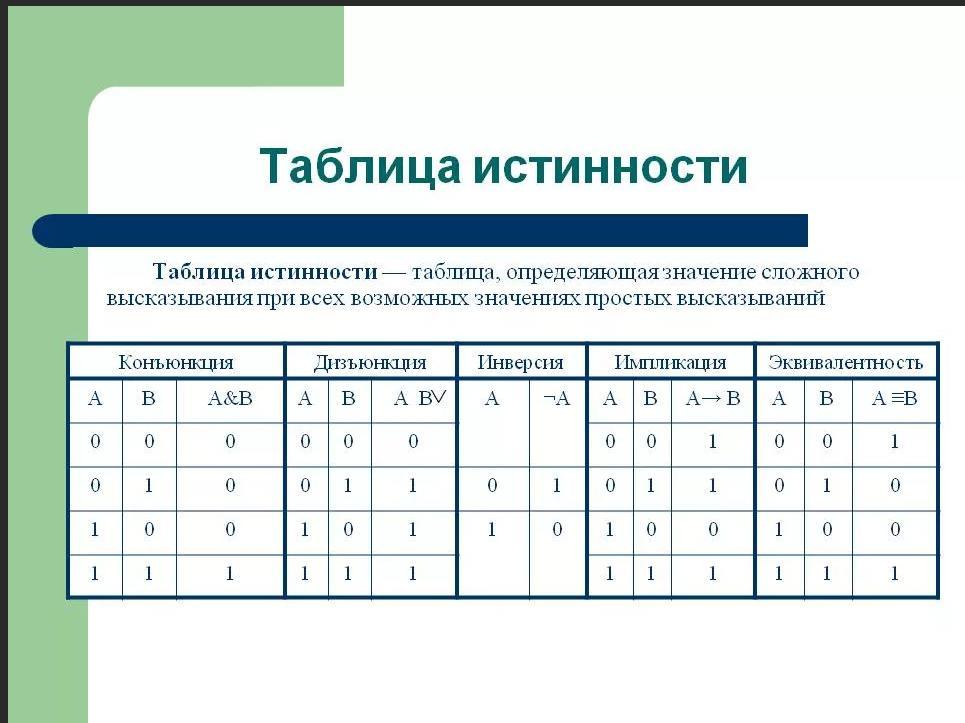

Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Такая таблица называется «таблица истинности». Таблицы истинности широко применяются в цифровой технике для описания работы логических схем.

Вот так выглядит элемент «И» и его таблица истинности:

Поскольку вам придется общаться как с русской, так и с буржуйской тех. документацией, я буду приводить условные графические обозначения (УГО) элементов и по нашим и по не нашим стандартам.

Смотрим таблицу истинности, и проясняем в мозгу принцип. Понять его не сложно: единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.

Если посмотреть чуток иначе, то можно сказать так: на выходе элемента «И» будет ноль в том случае, если хотя бы на один из его входов подан ноль. Запоминаем.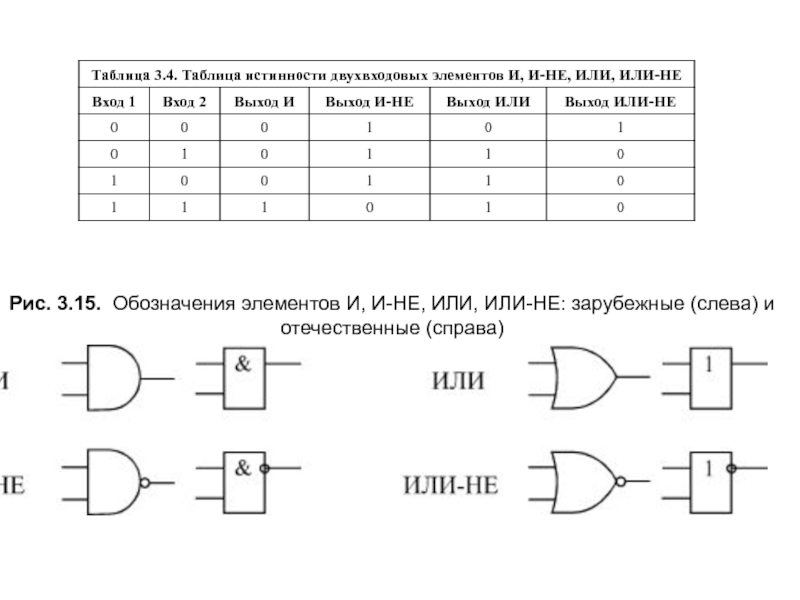 Идем дальше.

Элемент «ИЛИ» (OR)

По другому, его зовут «дизъюнктор».

Опять же, название говорит само за себя.

На выходе возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица. Этот элемент можно назвать также элементом «И» для негативной логики: ноль на его выходе бывает только в том случае, если и на один и на второй вход поданы нули.

Едем дальше. Дальше у нас очень простенький, но очень необходимый элемент.

Элемент «НЕ» (NOT)

Чаще, его называют «инвертор».

Надо чего-нибудь говорить по поводу его работы?

Ну тогда поехали дальше. Следующие два элемента получаются путем установки инвертора на выход элементов «И» и «ИЛИ».

Элемент «И-НЕ» (NAND)

Элемент И-НЕ работает точно так же как «И», только выходной сигнал полностью противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» — единица.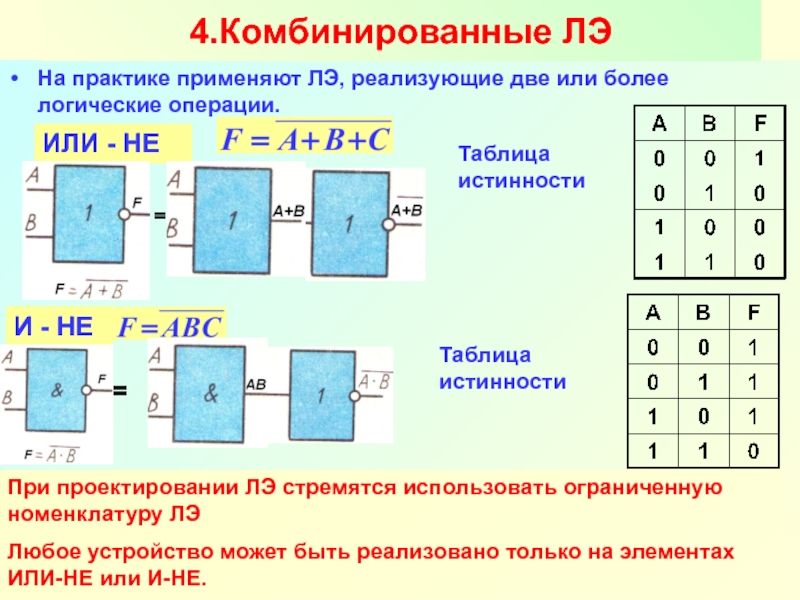 И наоборот. Э то легко понять по эквивалентной схеме элемента:

Элемент «ИЛИ-НЕ» (NOR)

Та же история – элемент «ИЛИ» с инвертором на выходе.

Следующий товарищ устроен несколько хитрее:
Элемент «Исключающее ИЛИ» (XOR)

Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры.

Смотрим таблицу истинности. Когда на выходе единицы? Правильно: когда на входах разные сигналы. На одном – 1, на другом – 0. Вот такой он хитрый.

Эквивалентная схема примерно такая:

Ее запоминать не обязательно.

Собственно, это и есть основные логические элементы. На их основе строятся абсолютно любые цифровые микросхемы. Даже ваш любимый Пентиум 4.

Далее мы позанудствуем о том, как синтезировать цифровую схему, имея ее таблицу истинности. Это совсем несложно, а знать надо, ибо пригодится (еще как пригодится) нам в дальнейшем.

Ну и напоследок – несколько микросхем, внутри которых содержатся цифровые элементы. Около выводов элементов обозначены номера соответствующих ног микросхемы. Все микросхемы, перечисленные здесь, имеют 14 ног. Питание подается на ножки 7 (-) и 14 (+). Напряжение питания – смотри в таблице в предыдущем параграфе.

Примерные ответы на профильные билеты

Профильная школа. Экзамены

Е.А. Еремин, А.П. Шестаков

Продолжение. Начало см. в № 19 – 23/2006

1. Основные понятия и операции формальной логики. Законы логики. Логические переменные. Логические выражения и их преобразования. Построение таблиц истинности логических выражений

Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности) и логических операций над ними.

Под логическим высказыванием понимается любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно. Например, логическим высказыванием будет “Земля — третья планета от Солнца”, но не является таковым “Довольно морозная в этом году зима”.

Чаще на практике приходится иметь дело с высказывательными формами — повествовательными предложениями, прямо или косвенно содержащими переменные; высказывательная форма становится логическим высказыванием, если значения всех переменных, входящих в нее, заданы. Например, высказывательная форма “x кратно 5” при x = 34 ложна, а при x = 105 — истинна. В языках программирования высказывательные формы записываются в виде логических выражений.

Буквы, обозначающие переменные высказывания, называются высказывательными переменными (логическими переменными).

Простые логические высказывания могут быть объединены в более сложные — составные — с использованием логических операций. Основными логическими операциями являются НЕ (отрицание, или инверсия), И (конъюнкция, или логическое умножение), ИЛИ (дизъюнкция, или логическое сложение).

Рассмотрим более подробно логические операции.

Если для арифметических операций используются таблицы сложения и умножения, задающие правила выполнения этих операций для цифр системы счисления и которые в дальнейшем используются при выполнении сложения и вычитания, умножения и деления соответственно, так и для логических операций строят аналогичные таблицы, называя их таблицами истинности.

Операция инверсии (отрицания) выполняется над одним операндом (так в математике называются величины, над которыми выполняют ту или иную операцию).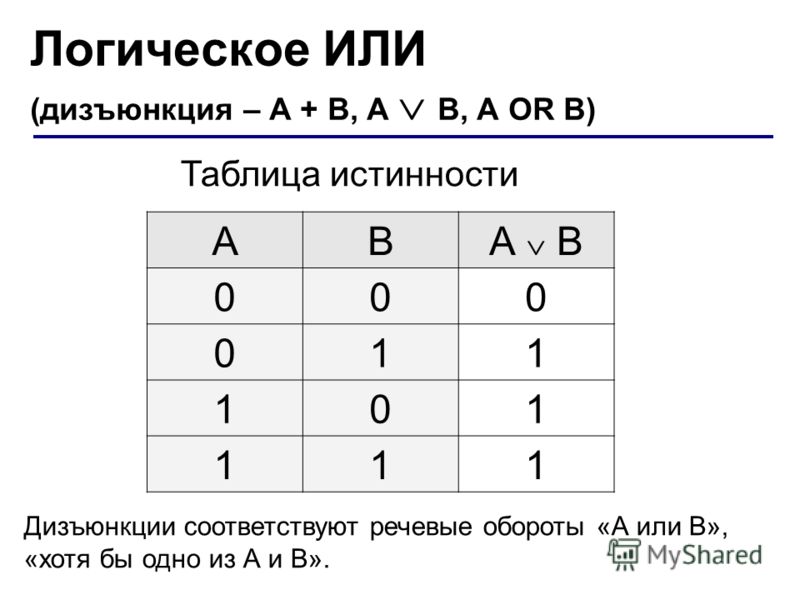 Общее правило, заложенное в построение таблицы истинности для этой операции, звучит так: отрицание изменяет значение операнда на противоположное.

Обозначение операции: A, .

Операция дизъюнкции выполняется над двумя операндами. Общее правило, заложенное в построение таблицы истинности для этой операции, звучит так: дизъюнкция ложна тогда и только тогда, когда ложны оба операнда. В таблице истинности перечисляются все возможные сочетания значений операндов и соответствующие значения операции.

В литературе операцию дизъюнкции обозначают по-разному: ИЛИ, . В языках программирования также имеется эта операция. В Pascal и Вasic она обозначается OR, в С/C++, JavaScript — ||, и т.д.

Логическим сложением эту операцию называют по той причине, что если заменить значение истина на 1, а ложь — на 0, то таблица истинности в определенной мере будет соответствовать таблице сложения в двоичной системе счисления. В действительности роль дизъюнкции в алгебре логики аналогична роли операции сложения в арифметике.

Операция конъюнкции выполняется над двумя операндами. Общее правило, заложенное в построение таблицы истинности для этой операции, звучит так: конъюнкция истинна тогда и только тогда, когда истинны оба операнда. В таблице истинности перечисляются все возможные сочетания значений операндов и соответствующие значения операции.

В литературе операцию конъюнкции обозначают по-разному: И, , & (достаточно часто в записи выражений знак конъюнкции пропускают по аналогии со знаком умножения в записи алгебраических выражений). В языках программирования также присутствует эта операция. В Pascal и Basic она обозначается AND, в С/C++, JavaScript — &&, и т.д.

Логическим же умножением эту операцию называют по той причине, что если заменить значение истина на 1, а ложь — на 0, то таблица истинности будет соответствовать таблице умножения в двоичной системе счисления.

Операция следования (импликации) выполняется над двумя операндами. Общее правило, заложенное в построение таблицы истинности для этой операции, звучит так: импликация ложна, если из истины следует ложь, и истинна во всех остальных случаях. В таблице истинности перечисляются все возможные сочетания значений операндов и соответствующие значения операции (обозначается импликация обычно ).

Операция эквивалентности (эквиваленции) выполняется над двумя операндами. Общее правило, заложенное в построение таблицы истинности для этой операции, звучит так: эквиваленция истинна тогда и только тогда, когда оба операнда принимают одинаковые значения. В таблице истинности перечисляются все возможные сочетания значений операндов и соответствующие значения операции (обозначается эквиваленция обычно ).

Свойства логических операций (или законы логики; знак “” обозначает “эквивалентно”, “тождественно истинно”):

Логические выражения определяют порядок вычисления логического значения. Путем преобразования исходных логических выражений с использованием законов логики можно получать равносильные им более простые выражения. В общем случае равносильность логических выражений определяется совпадением таблиц истинности для этих выражений.

Пример 1. Упростить выражение и убедиться, что результат равносилен исходному выражению.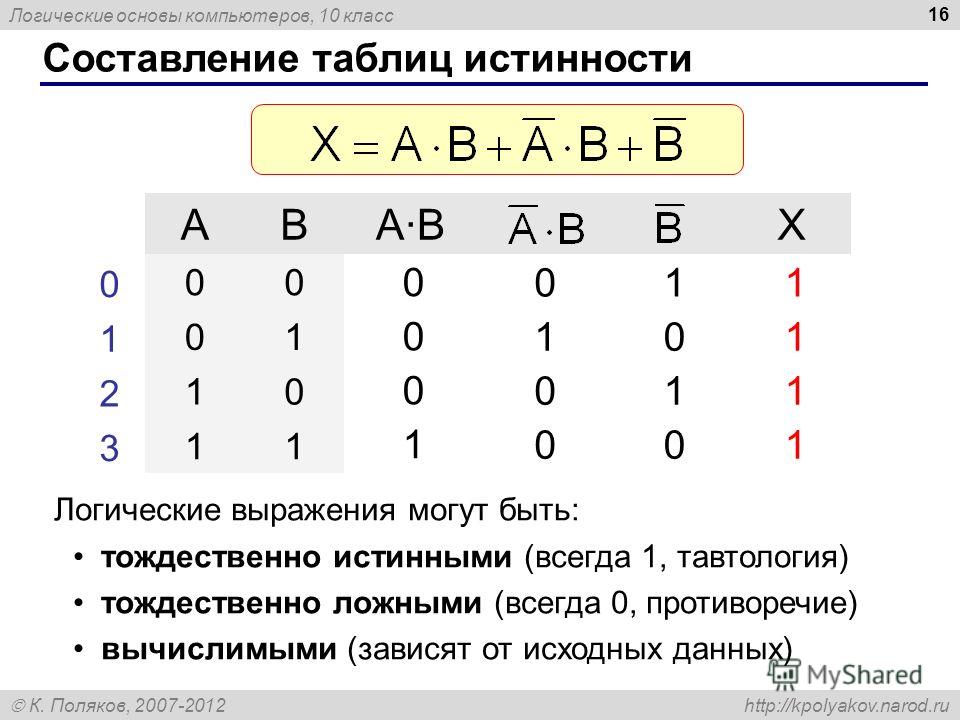

(в записи выражения знак конъюнкции пропущен).

Преобразование выполним последовательно.

Рассмотрим вторую скобку: . По закону поглощения получаем Y.

В третьей скобке используем закон де Моргана: .

Таким образом, получили . Используя законы коммутативный, противоречия, а также правило , приходим к выводу, что выражение .

Таким образом, .

Предлагаем читателю самостоятельно, с помощью составления таблиц истинности для исходного и конечного выражений, убедиться в их равносильности.

Пример 2. Доказать, что выражение является тавтологией1.

Проведем доказательство путем упрощения исходного выражения.

Проведем доказательство путем составления таблицы истинности для данного выражения:

Таким образом, вновь получаем тот же результат: выражение является тавтологией.

Литература

1. Шауцукова Л.З. Информатика: Учебное пособие для 10–11-х классов общеобразовательных учреждений. 2-е изд., дораб. М.: Просвещение, 2002, 416 с.

2. Андреева Е.В. Математические основы информатики. Элективный курс: Учебное пособие / Е.В. Андреева, Л.Л. Босова, И.Н. Фалина. М.: БИНОМ. Лаборатория Знаний, 2005, 328 с.

3. Семакин И., Залогова Л., Русаков С., Шестакова Л. Информатика: учебник по базовому курсу. М.: Лаборатория Базовых Знаний, 1998.

4. Угринович Н. Информатика и информационные технологии. Учебное пособие для общеобразовательных учреждений. М.: БИНОМ, 2001, 464 с. (Введение в информатику, с. 13–16.)

5. http://comp-science.narod.ru.

1Тавтология — тождественно истинное выражение.

2. С помощью электронной таблицы вычислить значение функции, заданной рекуррентным соотношением

Пример. Получить в электронной таблице первые 15 значений функции n!

Решение. Зададим факториал рекуррентным соотношением: an = an-1•n, a1 = 1

Пусть столбец A хранит значения n, а столбец
B — n!. Тогда в ячейки A2:A16 занесем значения n от 1 до 15. В ячейку B2 поместим значение 1, а в ячейке B3 запишем формулу =B2 * A3, выражающую записанное рекуррентное соотношение; далее скопируем эту формулу во все последующие ячейки столбца и получим требуемый результат.

 

Варианты заданий

Получить в электронной таблице первые k значений последовательности (k задается учителем).

.

.
3. Представить на языке программирования вычислительный алгоритм, записанный в виде блок-схемы. (Получить результат в виде значения переменной.)

Пример. Написать программу, исполняющую алгоритм, записанный в виде нижеприведенной блок-схемы. Распечатать значение переменной с.

Решение.

QBasic

B = 0 : C = 1

While B <> 11

C = C + B * C

B = B + 1

Wend;

PRINT C

Pascal

Var b, c: longint;

Begin

B := 0; C := 1;

While B <> 11 do

Begin

C := C + B * C;

B := B + 1

End;

Writeln(C)

End.

C++

#include <iostream.h>

void main()

{ long B, C;

B = 0; C = 1;

while (B != 11)

{ C = C + B * C;

B++; }

cout << C;

}

Результат вычислений: 39 916 800.

Варианты заданий

Написать программу, исполняющую алгоритм, записанный в виде одной из нижеприведенных блок-схем. Выполнить указанное задание.

1. Вывести значение переменной K для n = 12 981.

2. Вывести значение переменной P при k = 5.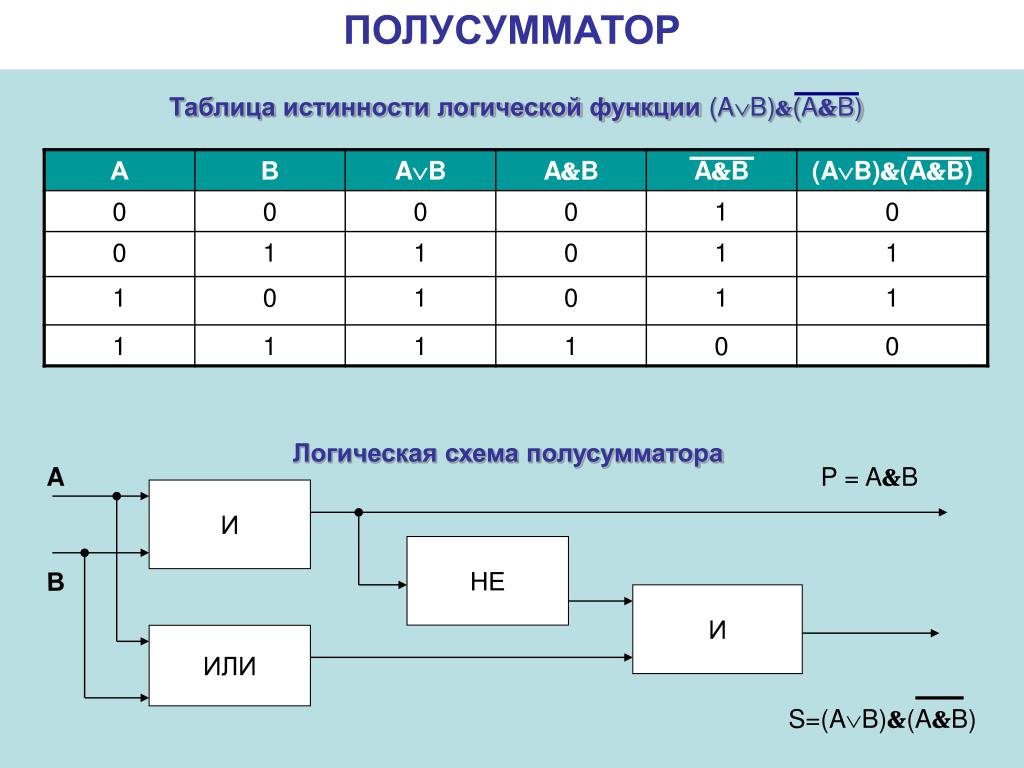

3. Вывести значение переменной K для n = 12 981.

4. Какое количество членов ряда будет просуммировано при e = 10–2?

.

1. Логические элементы и схемы. Типовые логические устройства компьютера: полусумматор, сумматор, триггеры, регистры. Описание архитектуры компьютера с опорой на составляющие ее логические устройства

Обсудив в билете № 8 теоретические аспекты логических функций, сегодня мы поговорим об их практической реализации в виде логических элементов. Следует особо подчеркнуть, что в настоящее время основу всех компьютерных устройств (включая даже встроенные в бытовую технику!) составляют двоичные электронные логические элементы1.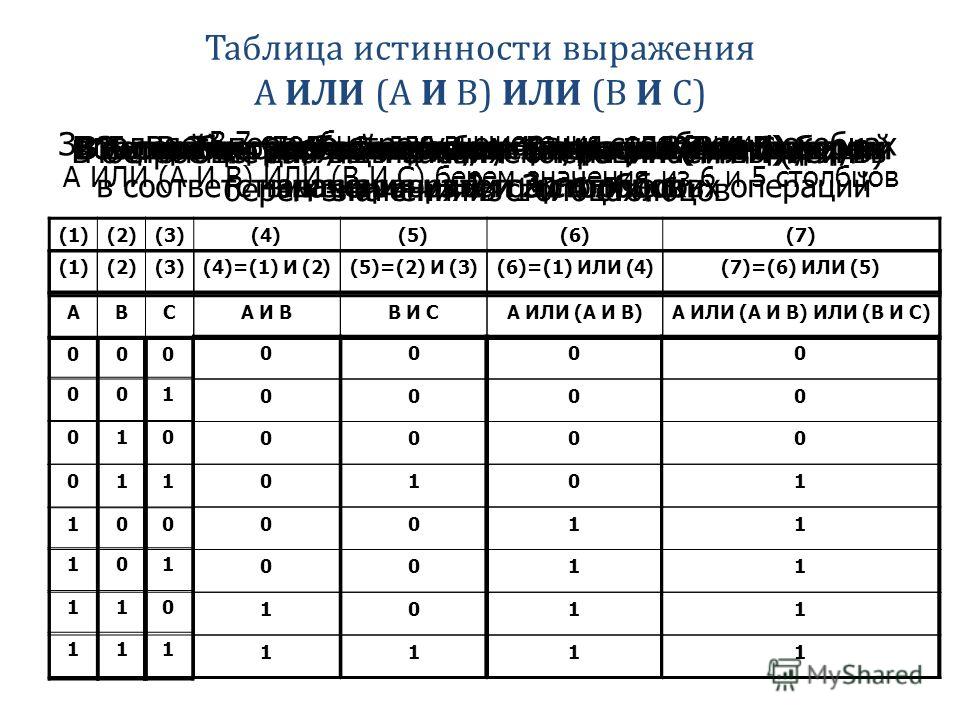 Поэтому понимание базовых идей их функционирования для представления об общей логике работы компьютера весьма полезно.

Может показаться, что для реализации всевозможных логических функций требуется большое разнообразие логических элементов. Как ни удивительно, но это не так. Из теории логических функций следует, что достаточно их очень небольшого базового набора, чтобы с помощью различных комбинаций, его составляющих, можно было получить абсолютно произвольную функцию, сколь бы сложной она не была. Следовательно, и количество базовых логических элементов, которые соответствуют данным функциям, к счастью, невелико. Базисный набор может быть сформирован различными способами, но, как правило, используется классическая “тройка” логических операций И, ИЛИ, НЕ. Именно эта “тройка” применяется в книгах по логике, а также во всех языках программирования — от машинных кодов до языков высокого уровня.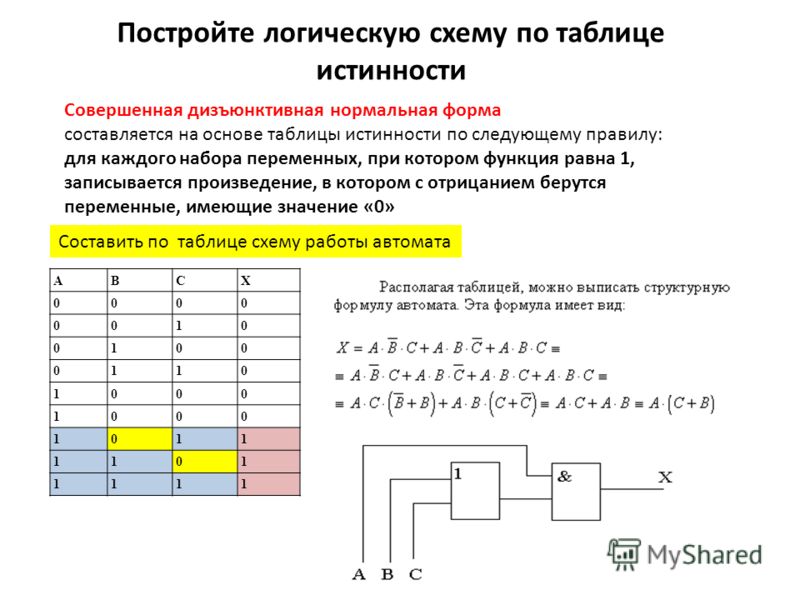 Обозначения логических элементов2, реализующих соответствующие операции, приведены на рис. 1a–b.

Рис. 1. Обозначения основных логических элементов

Внутренняя схема логического элемента может быть различной, более того, она может существенно совершенствоваться по мере развития технологий производства, но логические функции всегда остаются неизменными.

Часто для удобства синтеза логических схем к перечисленному списку добавляют еще элемент “исключающее ИЛИ” (рис. 1г), который позволяет сравнивать двоичные коды на совпадение. Данная операция имеет и другие практически полезные свойства, в частности, восстанавливает исходные данные в случае повторного применения, что удобно использовать для временного наложения видеоизображений.

Тем не менее классический базис не является единственным. Более того, для практической реализации логических схем инженеры предпочитают альтернативный вариант — на базе единственного комбинированного логического элемента И-НЕ (рис. 1д). Читатели, которые заинтересовались данным вопросом, могут обратиться к книге Р.Токхейма [2] или аналогичной, где показано, как из элементов И-НЕ можно построить все остальные примитивы классического базиса.

Отметим, что на практике логические элементы могут иметь не только два, но и значительно большее количество входов (для примера см. рис. 4 на с. 24).

Первоначально тезис о построении любых логических устройств на основе некоторого простого базиса был технически реализован “один к одному”: были разработаны и выпускались интегральные микросхемы (ИМС), соответствующие основным логическим действиям. Потребитель, комбинируя имеющиеся в его распоряжении элементы, мог получить схему с реализацией любой необходимой логики. Довольно быстро стало ясно, что подобное “строительство здания из отдельных кирпичиков” слишком трудоемко и не может удовлетворить постоянно растущие практические потребности. Промышленность увеличила степень интеграции микросхем и начала выпускать более сложные типовые узлы: триггеры, регистры, счетчики, дешифраторы, сумматоры и т.д. (продолжая аналогию со строительством, этот шаг, видимо, следует уподобить панельному способу домостроения). Новые микросхемы давали возможность реализовывать еще более сложные электронные логические устройства, но зато ассортимент выпускаемых микросхем расширился. Поскольку человечеству свойственно не останавливаться на достигнутом, рост возможностей породил новые потребности. Необходимым образом последовал переход к большим интегральным схемам (БИС), представлявшим собой функционально законченные узлы, а не отдельные компоненты для их создания (как тут не вспомнить блочный метод постройки здания из готовых комнат). Наконец, дальнейшая эволюция технологий производства ИМС привела к настолько высокой степени интеграции, что в одной БИС содержалось функционально законченное изделие: часы, калькулятор, небольшая специализированная ЭВМ.

Примечание. Немногие, вероятно, знают, что появление первых микропроцессоров было связано вовсе не с попытками воспроизвести ЭВМ в одном кристалле: действительной причиной явилось стремление существенно ограничить ассортимент логических микросхем, повышая их универсальность и, как следствие, понижая стоимость за счет резкого роста объемов производства. Весьма поучительная история о замене дюжины специализированных микросхем одной программируемой, что, собственно, и привело к созданию инженером М.Хоффом первого микропроцессора Intel 4004, рассказывается в книге
А.П. Частикова [3].

Если мы посмотрим на внутреннее устройство типичного современного компьютера, то увидим там ИМС очень высокого уровня интеграции: микропроцессор, модули ОЗУ, контроллеры внешних устройств и др. Фактически каждая микросхема или небольшая группа микросхем3 образует функционально законченный блок. Уровень сложности блока таков, что разобраться в его внутреннем устройстве для неспециалиста не то чтобы нецелесообразно, а просто невозможно. К тому же выпускаемые промышленностью ИМС постоянно совершенствуются и усложняются. В результате оказывается, что для понимания наиболее общих принципов работы современной ЭВМ удобнее и правильнее рассмотреть несколько типовых узлов, а изучение поведения отдельных БИС заменить изучением функциональной схемы компьютера.

В качестве характерных цифровых устройств мы выберем два наиболее важных и интересных — сумматор и триггер. Первое из них замечательно тем, что составляет основу арифметико-логического устройства процессора, а второе, будучи универсальным устройством для хранения одного бита информации, имеет еще более широкое применение — от регистров процессора до элементов памяти. Дополнительно подчеркнем, что выбранные логические схемы принадлежат к разным типам. Выходные сигналы сумматора определяются исключительно установившимися на входе напряжениями и никак не зависят от поступавших ранее сигналов (в литературе такие схемы часто называют комбинационными). Состояние триггера, напротив, зависит от предыстории, т.е. схема имеет память.

Перейдем к описанию логической схемы сумматора.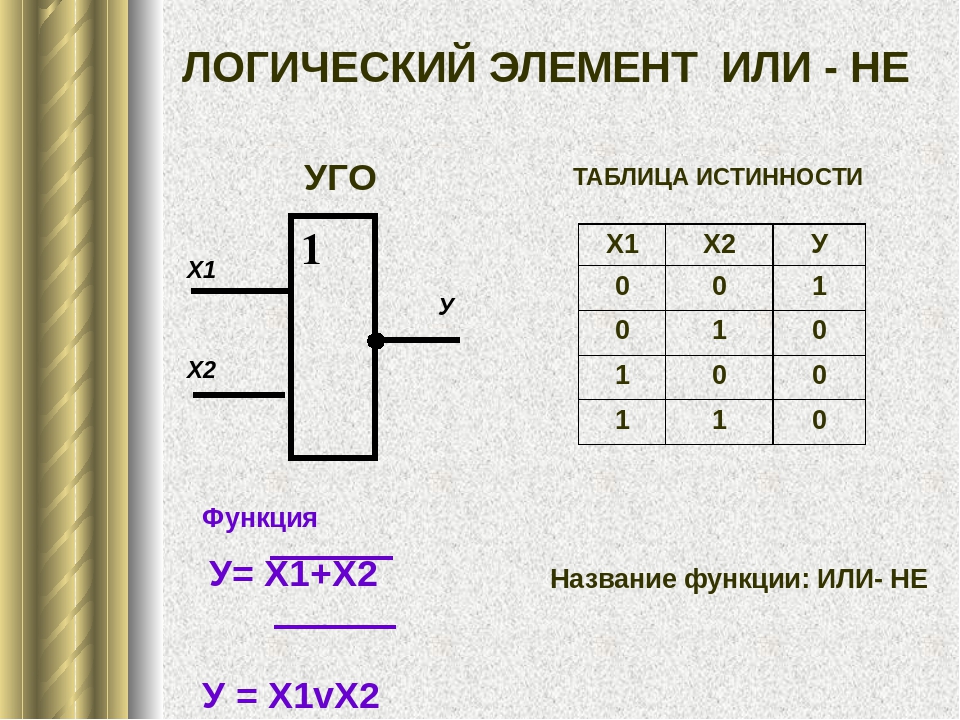 Для простоты ограничимся изучением работы отдельного двоичного разряда. В этом случае сумматор будет содержать три входа — бит первого слагаемого А, второго — В и перенос из предыдущего разряда Ci (обозначение происходит от английских слов Carry in — входной перенос). Тем, для кого термин перенос звучит незнакомо, уместно вспомнить, что означает словосочетание “ноль пишем один в уме”, которое они часто повторяли про себя, суммируя в младших классах числа на листке бумаги.

Таблица истинности для полного одноразрядного сумматора имеет вид:

Особых комментариев к этой таблице не требуется. Может быть, только стоит напомнить тот факт, что 1 + 1 = 0 и 1 “в уме” (т.е. на выходе Co, что расшифровывается как Carry out, т. е. выходной перенос), поскольку все действия выполняются в двоичной системе.

Построить сразу полный сумматор — задача для начинающего непростая. Она еще более усложняется, если при этом требуется использовать логические элементы из реально существующего ассортимента интегральных микросхем. Вариант схемы сумматора, приведенный, например, в книгах [4] и [5], состоит из 9 логических элементов. Минимизированная схема, полученная в [6], построена на базе 6 классических элементов. К счастью, для понимания принципов работы суммирующих схем ЭВМ существует еще более простое решение, если воспользоваться логическими элементами “исключающее ИЛИ” [7].

При построении схемы удобно сумматор представить в виде двух полусумматоров, из которых первый складывает разряды А и В, а второй к полученному результату прибавляет бит переноса из предыдущего разряда Ci.

Таблица истинности для полусумматора значительно упрощается:

Теперь мысленно объединим в приведенной таблице столбцы A, B и Co. Что напоминает вам полученная таблица? Конечно же базовый логический элемент И! Аналогично, сравнив первые три столбца A, B и S с таблицей истинности для элемента “исключающее ИЛИ”, можно убедиться, что они совпадут (рекомендуем читателям самостоятельно убедиться в этом, а также проверить тот факт, что сумма S равна 1 только в случае несовпадения исходных битов). Таким образом, для реализации полусумматора достаточно соединить параллельно входы двух логических элементов (см. рис. 2a)!

Рис. 2. Простейшая реализация сумматора

Заметим, что для суммирования младшего разряда одного полусумматора уже достаточно, т.к. в этом случае сигнал входного переноса отсутствует. А если соединить два полусумматора, как показано на рис. 2б, то получится полный сумматор, способный осуществить сложение одного бита чисел с учетом возможности переноса.

Перейти к многоразрядным числам можно, например, путем последовательного соединения соответствующего количества сумматоров. Мы не будем обсуждать возникающие при этом детали, связанные с необходимостью ускорения процесса переноса в такой схеме; думается, мы уже изучили вполне достаточно, чтобы иметь некоторое представление о том, как компьютер производит свои вычисления.

Стоит особо подчеркнуть, что сумматор играет важную роль в реализации не только сложения, но и других арифметических действий. Например, вычитание обычно заменяется сложением с дополнительным кодом вычитаемого, а алгоритм умножения “столбиком” легко сводится к комбинации сложений и сдвигов. Таким образом, сумматор необходимой разрядности фактически является основой арифметического устройства современного компьютера.

Рис. 3. Схема RS-триггера

Перейдем теперь к описанию работы триггера. Его схема приведена на рис. 3, а таблица истинности имеет следующий вид:

 

Как видно из рис. 3, триггер собран из четырех логических элементов И-НЕ, причем два из них играют вспомогательную роль инверторов входных сигналов. Триггер имеет два входа, обозначенные на схеме R и S, а также два выхода, помеченные буквой Q, — прямой и инверсный (черта над Q у инверсного выхода означает отрицание). Триггер устроен таким образом, что на прямом и инверсном выходах сигналы всегда противоположны.

Как работает триггер? Пусть на входе R установлена 1, а на S — 0. Логические элементы D1 и D2 инвертируют эти сигналы, т.е. меняют их значения на противоположные; в результате на вход элемента D3 поступает 1, а на D4 — 0. Поскольку на одном из входов D4 имеется 0, независимо от состояния другого входа на его выходе (он же является инверсным выходом триггера!) обязательно установится 1. Эта единица передается на вход элемента D3 и в сочетании с 1 на другом входе порождает на выходе D3 логический 0. Итак, при R = 1 и S = 0 на прямом выходе триггера устанавливается 0, а на инверсном — 1.

Обозначение состояния триггера по договоренности связывается с прямым выходом. Тогда при описанной выше комбинации входных сигналов результирующее состояние можно условно назвать нулевым: говорят, что триггер устанавливается в 0 или сбрасывается. Сброс по-английски называется Reset, отсюда вход, появление сигнала на котором приводит к сбросу триггера, принято обозначать буквой R.

Проведите аналогичные рассуждения для “симметричного” случая R = 0 и S = 1. Вы увидите, что теперь, наоборот, на прямом выходе получится логическая 1, а на инверсном — 0. Триггер перейдет в единичное состояние — установится (установка по-английски Set).

Далее рассмотрим наиболее распространенную и интересную ситуацию R = 0 и S = 0, когда входных сигналов нет. Тогда на входы элементов D3 и D4, связанные с R и S, будет подана 1, и их выходной сигнал будет зависеть от напряжения на других входах. Нетрудно убедиться, что такое состояние будет устойчивым. Пусть, например, на прямом выходе была 1. Тогда наличие единиц на обоих входах элемента D4 “подтверждает” нулевой сигнал на его выходе. В свою очередь, наличие 0 на инверсном выходе передается на D3 и поддерживает его выходное единичное состояние. Аналогично доказывается устойчивость картины и для противоположного состояния триггера, когда Q = 0.

Таким образом, при отсутствии входных сигналов триггер сохраняет свое “предыдущее” состояние. Иными словами, если на вход R подать 1, а затем убрать, триггер установится в нулевое состояние и будет его сохранять, пока не поступит сигнал на другой вход S. В последнем случае он перебросится в единичное состояние и после прекращения действия входного сигнала будет сохранять на прямом выходе 1.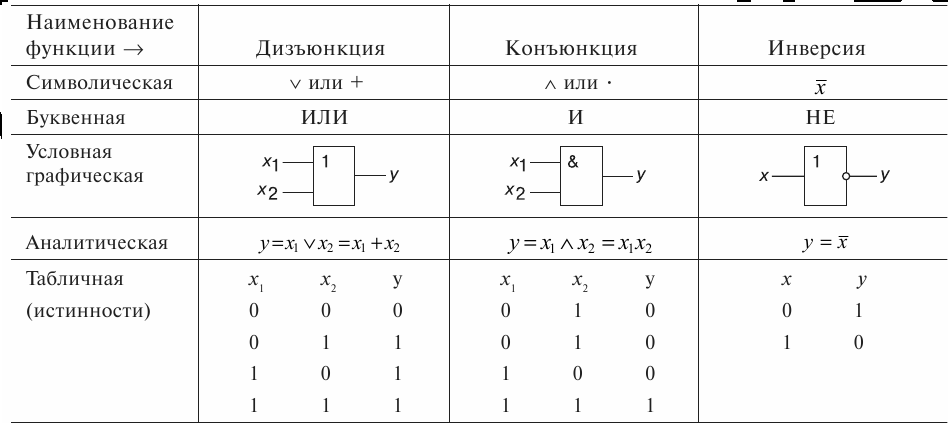 Мы видим, что триггер обладает замечательным свойством: после снятия входных сигналов он сохраняет свое состояние, а значит, может служить устройством для хранения одного бита информации.

В заключение проанализируем последнюю комбинацию входных сигналов R = 1 и S = 1. Нетрудно убедиться (проделайте необходимые рассуждения самостоятельно), что в этом случае на обоих выходах триггера установится 1! Такое состояние, помимо своей логической абсурдности, еще и является неустойчивым: после снятия входных сигналов триггер случайным образом перейдет в одно из своих устойчивых состояний. Вследствие этого комбинация R = 1 и S = 1 на практике не используется и является запрещенной.

Мы рассмотрели простейший RS-триггер. Существуют и другие разновидности этого интересного и полезного устройства. Все они различаются не столько принципом работы, сколько входной логикой, усложняющей “поведение” триггера.

Подобно тому, как объединяются для обработки двоичных чисел однобитовые схемы сумматоров, для хранения многоразрядных данных триггеры объединяются в единый блок, называемый регистром. Над регистром, как над единым целым, можно производить ряд стандартных операций: сбрасывать (обнулять), заносить в него код и некоторые другие. Причем часто регистры способны не просто хранить информацию, но и обрабатывать ее. Типичными примерами такого типа могут служить регистр, который способен сдвигать находящийся в нем двоичный код, или регистр, подсчитывающий количество поступающих импульсов, — счетчик.

С выходов триггеров регистра сигналы могут поступать на другие цифровые устройства. Особый интерес с точки зрения принципов функционирования компьютера представляет схема анализа равенства (или неравенства) регистра нулю, которая позволяет организовать по этому признаку условный переход. Для n-разрядного двоичного регистра потребуется n-входовый элемент И4 (см. рис. 4), сигналы для которого удобнее снимать с инверсных выходов триггеров. Фактически такая схема анализа выполняет комбинированную логическую операцию НЕ-И.

Рис. 4. Схема анализа состояния регистра

В самом деле, пусть содержимое всех битов регистра равно 0. Тогда на вход элемента И с инверсных выходов триггеров поступают все 1 и результат z = 1. Если же хотя бы один из разрядов отличен от 0, то с его инверсного выхода снимается 0 и этого, как известно, уже достаточно, чтобы получить выходной сигнал z = 0 независимо от состояния всех остальных входов элемента И.

Таким образом, изображенная на рис. 4 логическая схема вырабатывает управляющий сигнал равенства результата 0, что может использоваться, например, для организации ветвления по соответствующему условию. Кстати, переход по знаку числа реализовать еще проще — достаточно проанализировать состояние знакового (обычно старшего) разряда: если он установлен в 1, то регистр содержит отрицательное число [5].

Наличие управляющих признаков, устанавливаемых в зависимости от полученного результата операции, является неотъемлемым свойством процессоров. Оно необходимо для организации выполнения инструкций ветвления и цикла5.

Триггеры очень широко применяются в компьютерной технике. Помимо уже описанного применения в составе разнообразных регистров, на их основе могут еще изготовляться быстродействующие ИМС статического ОЗУ (в том числе кэш-память). Так что в состав любого микропроцессора входит множество триггеров, выполняющих самые разнообразные функции.

Мы с вами изучили только два из многочисленных устройств вычислительной техники — сумматор и регистры. Казалось бы, много ли можно понять, зная всего два этих устройства? Оказывается, не так уж и мало. Можно, например, весьма успешно попытаться представить себе, как строится арифметическое устройство процессора. В самом деле, подумаем, каким образом можно спроектировать схему для реализации сложения двух чисел. Очевидно, что для хранения исходных чисел потребуется два триггерных регистра. Их выходы подадим на входы сумматора, так что на выходах последнего сформируются сигналы, соответствующие двоичному коду суммы. Для фиксации (запоминания) результирующего числа потребуется еще один регистр, который можно снабдить описанными выше схемами формирования управляющих признаков. Наша картина получается настолько естественной и реалистичной, что мы можем найти ее в наиболее подробной учебной литературе в качестве основы устройства простых учебных моделей компьютера. В частности, очень похоже выглядит описание внутреннего устройства процессора учебного компьютера “Нейман”, которое дано в книгах [8, 9]6.

Подводя итоги, подчеркнем, что в процессе рассмотрения материала билета мы прошли путь от изучения простейшего единичного логического элемента до понимания наиболее общих идей построения весьма крупных узлов ЭВМ, таких, как арифметическое устройство. Следующий уровень знакомства с логикой работы компьютера — на уровне функциональных устройств (процессор, память и устройства ввода/вывода), будет подробно изложен в билете № 12.

Примечание. Очевидно, что материал, который включается в экзаменационные билеты, имеет существенную значимость для изучаемого учебного предмета. В связи с этим автору данных строк особо хотелось бы подчеркнуть важность темы с точки зрения формирования у учеников некоторого единого представления об устройстве компьютера. Мировоззрение складывается не только (а может, даже и не столько) в ходе рассуждений “о высоких материях”, но и в результате создания некоторой единой связной картины изучаемого материала. Очень важно, чтобы темы отдельных уроков не казались независимыми, выбранными по странной прихоти какого-то неведомого теоретика. В этом смысле значение вопроса, соединяющего отдельные логические элементы с узлами реального вычислительного устройства, трудно переоценить. Иными словами, ценность материала заключается в том, что он “перекидывает мостик” между разрозненными абстрактными знаниями о логических элементах и архитектурой реального компьютера.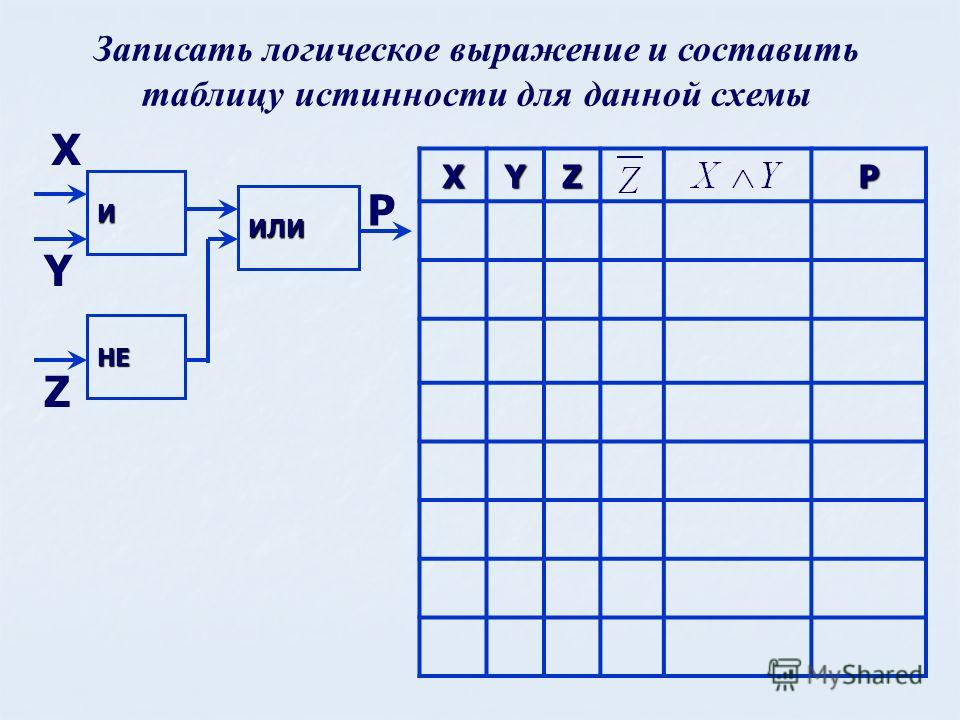 В школьной практике это служит надежным средством борьбы с традиционным “Зачем все это нужно?”.

Литература

1. Ямпольский В.С. Основы автоматики и электронно-вычислительной техники: Учебное пособие для студентов физико-математического факультета педагогических институтов. М.: Просвещение, 1991, 223 с.

2. Токхейм Р. Основы цифровой электроники. М.: Мир, 1988, 392.

3. Частиков А.П. История компьютера. М.: Информатика и образование, 1996, 128 с.

4. Касаткин В.Н. Информация, алгоритмы, ЭВМ: Пособие для учителя. М.: Просвещение, 1991, 192 с.

5. Андреева Е.В., Босова Л.Л., Фалина И.Н. Математические основы информатики. Элективный курс. М.: БИНОМ. Лаборатория Знаний, 2005, 328 с.

6. Акулов О.А., Медведев Н.В. Информатика: базовый курс: Учебное пособие для студентов вузов. М.: Омега-Л, 2005, 552 с.

7. Кушниренко А.Г., Лебедев Г.В., Зайдельман Я.Н. Информатика, 7–9-е классы: Учебник для общеобразовательных учебных заведений. М.: Дрофа, 2000, 336 с.

8. Основы информатики и вычислительной техники в базовой школе / Л.А. Залогова, С.В. Русаков, И.Г. Семакин, Е.К. Хеннер, Л.В. Шестакова; под ред. И.Г. Семакина. Пермь, 1995.

9. Семакин И.Г. Информатика. Беседы об информации, компьютерах и программах: Книга для учащихся 8–9-х классов. Часть 2. Пермь: Изд-во Пермского университета, 1997, 168 с.

10. Информатика в понятиях и терминах: Книга для учащихся старших классов средней школы /
Г. А. Бордовский, В.А. Извозчиков, Ю.В. Исаев,
В.В. Морозов. Под ред. В.А. Извозчикова. М.: Просвещение, 1991, 208 с.

11. Шауцукова Л.З. Информатика: Учебное пособие для 10–11-х классов общеобразовательных учреждений. М.: Просвещение, 2003, 416 с.

2. С помощью электронной таблицы построить график функции

Пример. С помощью электронной таблицы построить график функции

Решение.

1) Необходимо протабулировать функцию (вычислить ее значения) на заданном отрезке. Табулирование будем осуществлять с шагом 0,1.

2) С помощью мастера диаграмм выполнить построение графика.

Результат представлен на рисунке.

Варианты заданий

С помощью электронной таблицы построить график функции y = F(x) на заданном отрезке [a, b].

3. Записать на языке программирования алгоритм для вычисления значения функции при заданных значениях аргументов. Произвести вычисления

Пример. Написать алгоритм, вычисляющий значение функции y = |x2 + 3x + 1| для любого х.

Решение. Алгоритм решения этой задачи является линейным. Необходимо ввести x, вычислить значение y и вывести результат.

Варианты заданий

1 Достаточно давно в некоторых промышленных автоматических устройствах использовались пневматические логические элементы, в которых электрический ток заменяло движение воздуха.

2 Обозначения логических элементов не являются строго стандартизированными, в частности, в иностранных книгах они существенно иные; в статье используются обозначения согласно учебнику [1].

3 Часто используется термин чипсет — набор чипов, т.е. микросхем.

4 Если n велико, то стандартных ИМС с таким количеством входов может не быть и схема, выполняемая на базе отдельных ИМС, усложнится; в то же время при проектировании БИС количество разрядов принципиального значения не имеет.

5 Важно понимать, что наличие в системе команд процессора специальных инструкций цикла вовсе не обязательно.

6 К сожалению, в учебник по базовому курсу авторы этот материал не включили.

2.4. Тест — Таблицы истинности


        1) Какое логическое действие называется дизъюнкцией?

  1. логическое умножение
  2. отрицание
  3. вычитание
  4. логическое сложение

2) С помощью таблицы истинности получите результат логической функции А \/ B:

  1. 0010
  2. 1101
  3. 0100
  4. 1000

3) Что такое логика?

  1. наука о суждениях и рассуждениях
  2. наука, изучающая законы и методы накопления, обработки и сохранения информации с помощью ЭВМ
  3. наука о формах и законах человеческого мышления и, в частности, о законах доказательных рассуждений

4) Определите, является ли данное выражение логическим тождеством? (A \/ B)=(A) /\ (B)

  1. Да
  2. Нет

5) Какому логическому элементу соответствует логическая схема?

A

B

C

0

0

0

1

0

1

0

1

1

1

1

1

  1. дизъюнкция
  2. конъюнкция
  3. отрицание
  4. импликация

6) С помощью таблицы истинности получите результат логической функции А \/ B:

  1. 1011
  2. 0011
  3. 0001

  4. 0010

7) В чем смысл закона двойного отрицания?

  1. если истинно А или В, но В не выполнено, то должно выполняться А
  2. двойное отрицание исключает отрицание
  3. истинно либо суждение, либо его отрицание

8) Как формулируется закон тождества?

  1. не могут быть одновременно истинны утверждение и его отрицание
  2. любое утверждение должно предполагать наличие аргументов и фактов, достаточных для его обоснования
  3. предмет обсуждения должен быть строго определен и не должен меняться до конца обсуждения

Логика – наука о формах и способах мышления.

⭐ Бесплатные PDF на Cdnpdf.com ✔️

Презентация по слайдам:

Слайд #1

Основы логики Логика – наука о формах и способах мышления.

Слайд #2

Понятие –это форма мышления, фиксирующая основные, существенные признаки объекта. Содержание Объем

Слайд #3

Высказывание — это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно.

Слайд #4

Умозаключение — -это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).

Слайд #5

Алгебра высказываний Логическое умножение (конъюнкция) Логическое сложение (дизъюнкция) Логическое отрицание (инверсия)

Слайд #6

Логическое умножение (конъюнкция) Составное высказывание, образованное в результате операции логического умножения истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.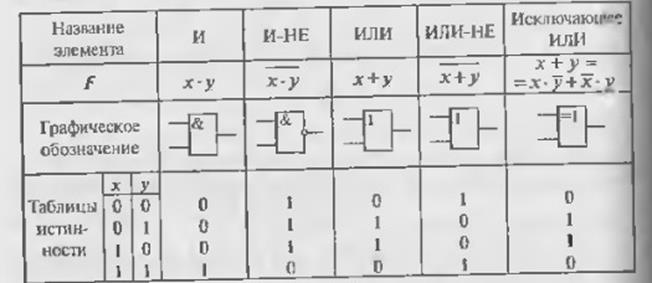 «и», &,

Слайд #7

Таблица истинности логического умножения

Слайд #8

Логическое сложение (дизъюнкция) Составное высказывание, образованное в результате логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний. «Или», v

Слайд #9

Таблица истинности логического сложения

Слайд #10

Логическое отрицание (инверсия) Делает истинное высказывание ложным и наоборот, ложное — истинным. «не», а,

Слайд #11

Таблица истинности функции логического отрицания

Слайд #12

Логическое равенство (эквивалентность) Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны. «…тогда и только тогда, когда …»

Слайд #13

Таблица истинности логической функции эквивалентности

Слайд #14

Логическое следование (импликация) Составное высказывание, образованное с помощью операции логического следования (импликации) ложно тогда и только тогда, когда из истиной предпосылки следует ложный вывод.

Слайд #15

Таблица истинности

Слайд #16

Логические выражения (формулы) Логические переменные Знаки логических операций

Слайд #17

Таблицы истинности AVB

Слайд #18

Таблица истинности A&B

Слайд #19

Логические законы 1. Закон тождества А=А 2. Закон непротиворечия А&А=0 3.Закон исключенного третьего AVА=1 4.Закон двойного отрицания А=А

Слайд #20

5. Законы де Моргана АVВ=A&B A&B=AVB

Слайд #21

6. Закон коммутативности A&B=B&A AVB=BVA

Слайд #22

7. Закон ассоциативности (A&B)&C=A&(B&C) (AVB)VC=AV(BVC)

Слайд #23

8. Закон дистрибутивности (A&B)V(A&C)=A&(BVC) (AVB)&(AVC)=AV(B&C)

Слайд #24

Диктант 1. Напишите таблицу истинности для операции конъюнкция. 2. Напишите таблицу истинности для операции дизъюнкция. 3. Напишите таблицу истинности для операции импликация. 4. Напишите таблицу истинности для операции эквивалентность.

Слайд #25

Тест 1. С помощью таблицы истинности получите результат логической функции A& B 2. Какому логическому элементу соответствует логическая схема:

Слайд #26

3.Дана логическая схема. Напишите по ней логическую функцию и составьте таблицу истинности. V & V Х У А

Слайд #27

4.Упростите выражение: A&BV(C&B)

Слайд #28

5. Для составления цепочек используются бусины A, B,C, D,E. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором – любая гласная, если первая буква согласная и любая согласная, если первая гласная. На третьем месте одна из бусин C,D,E, не стоящая в цепочке на 1-ом месте. Какая из цепочек создана по этому правилу? 1)СВE 2)ADD 3)ECE 4)EAD

Логика – наука о формах и способах мышления


Чтобы посмотреть презентацию с картинками, оформлением и слайдами, скачайте ее файл и откройте в PowerPoint на своем компьютере.
Текстовое содержимое слайдов презентации:
Основы логики Логика – наука о формах и способах мышления. Понятие –это форма мышления,фиксирующая основные, существенные признаки объекта. СодержаниеОбъем Высказывание — это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно. Умозаключение — -это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение). Алгебра высказываний Логическое умножение (конъюнкция)Логическое сложение (дизъюнкция)Логическое отрицание (инверсия) Логическое умножение (конъюнкция) Составное высказывание, образованное в результате операции логического умножения истинно тогда и только тогда, когда истинны все входящие в него простые высказывания. «и», &, 1 1 1 0 0 1 0 1 0 0 0 0 F=A&B B А Таблица истинностилогического умножения Логическое сложение (дизъюнкция) Составное высказывание, образованное в результате логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.«Или», v 1 1 1 1 0 1 1 1 0 0 0 0 F=AVB B A Таблица истинности логического сложения Логическое отрицание (инверсия) Делает истинное высказывание ложным и наоборот, ложное — истинным.«не», а, 0 1 1 0 F=A A Таблица истинности функции логического отрицания Логическое равенство (эквивалентность) Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.«…тогда и только тогда, когда …» 1 1 1 0 0 1 0 1 0 1 0 0 F B A Таблица истинности логической функции эквивалентности Логическое следование (импликация) Составное высказывание, образованное с помощью операции логического следования (импликации) ложно тогда и только тогда, когда из истиной предпосылки следует ложный вывод. 1 1 0 1 1 1 0 0 1 1 0 0 F=A B B А Таблица истинности Логические выражения (формулы) Логические переменныеЗнаки логических операций 0 1 1 0 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 0 0 AVB AVB В А В А Таблицы истинности AVB 1 1 1 0 0 1 0 1 0 0 0 0 A&B B A Таблица истинности A&B Логические законы 1. Закон тождестваА=А2. Закон непротиворечия А&А=03.Закон исключенного третьегоAVА=14.Закон двойного отрицания А=А 5. Законы де Моргана АVВ=A&B A&B=AVB 6. Закон коммутативности A&B=B&A AVB=BVA 7. Закон ассоциативности (A&B)&C=A&(B&C) (AVB)VC=AV(BVC) 8. Закон дистрибутивности (A&B)V(A&C)=A&(BVC) (AVB)&(AVC)=AV(B&C) Диктант 1. Напишите таблицу истинности для операции конъюнкция.2. Напишите таблицу истинности для операции дизъюнкция.3. Напишите таблицу истинности для операции импликация.4. Напишите таблицу истинности для операции эквивалентность. 1 1 1 0 1 0 0 0 1 0 0 0 С В А Тест 1. С помощью таблицы истинности получите результат логической функции A& B2. Какому логическому элементу соответствует логическая схема: V & V Х У А 3.Дана логическая схема. Напишите по ней логическую функцию и составьте таблицу истинности. 4.Упростите выражение: A&BV(C&B) 5. Для составления цепочек используются бусины A, B,C, D,E. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором – любая гласная, если первая буква согласная и любая согласная, если первая гласная. На третьем месте одна из бусин C,D,E, не стоящая в цепочке на 1-ом месте. Какая из цепочек создана по этому правилу?1)СВE 2)ADD 3)ECE 4)EAD

Приложенные файлы

Построение сумматоров на логических элементах.

⇐ ПредыдущаяСтр 19 из 46Следующая ⇒

Наличие логических элементов, реализующих логические операции, позволяет реализовать простейшие операции двоичной арифметики, а именно операции сложения и вычитания (через сложение с использованием дополнительных кодов). Рассмотрим, как из логических элементов можно сконструировать устройство для сложения двух двоичных чисел — так называемый одноразрядный сумматор. Это устройство должно формировать на выходе следующие сигналы:

0 + 0 = 0 (перенос в старший разряд) 0 (в данном разряде)

0 + 1 = 0 1

1 + 0 = 0 1

1 + 1 = 1 0

Составим таблицу истинности для этого сумматора, обозначив слагаемые X и Y, а результаты P (перенос в старший разряд) и Z (в данном разряде).

Логические выражения для формирования выходных сигналов данного разряда Z и переноса в старший разрядP имеют следующий вид:

P = X и Y

Z=(Х или Y) и [не (X и Y)]

Тогда схема одноразрядного сумматора будет иметь вид, представленный на рис.3.10. Такая схема зачастую называется одноразрядным полусумматором. Если необходимо построить многоразрядный (двух- и более) сумматор двоичных чисел, то в этом случае одноразрядный сумматор должен быть несколько усложнен; он должен быть видоизменен таким образом, чтобы учитывать перенос из предыдущего разряда.

Рис.3.10.Схема одноразрядного сумматора (полусумматора) на логических элементах.

3.10.Тренировочные тестовые задания по разделу 3.

(правильные ответы см. в конце пособия).

 

I. Система счисления — это?

1. Произвольная последовательность цифр 0,1,2,3,…,8,9

2. Бесконечная последовательность цифр 0,1,0,1,0,1,…

3. Множество натуральных чисел

4. Знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита (например, цифр)

5. Совокупность символов некоторого алфавита, например, I, V, X, D, C, M, R, A,…

 

II. В позиционной системе счисления весовые значения цифр каждого разряда записи числа зависят?

1. От значения числа

2. От значения соседних знаков

3. От позиции, которую занимает знак в записи числа

4. От значения знака в старшем разряде записи числа

5. От значения суммы соседних знаков

 

III. Какая из указанных систем счисления не используется в компьютерах?

1. Двадцатеричная

2. Двоичная

3. Шестнадцатеричная

4. Восьмеричная

5. Двоично-десятичная

 

IV. Сколько чисел можно записать при использовании шести первых разрядов двоичной системы счисления?

1. 32

2. 64

3. 128

4. 1024

5. 16

 

V. Укажите максимальное число в десятичном представлении, которое можно записать девятью начальными двоичными разрядами?

1. 1024

2. 255

3. 511

4. 1023

5. 512

VI. Числу 1310 в десятичной системе при переводе его в двоичную систему соответствует запись

1. 10012

2. 01102

3. 10102

4. 11112

5. 11012

 

VII. Двоичному числу 1110,12 в десятичной системе соответствует число?

1. 13,2510

2. 14,510

3. 1510

4. 1410

5. 12,510

 

VIII. Числу 13214, заданному в системе счисления с основанием 4, в десятичной системе соответствует число?

1. 12110

2. 11210

3. 11310

4. 5310

5. 12210

 

IX. Шестнадцатеричному числу 1816 в десятичной системе соответствует число?

1. 1610

2. 2410

3. 910

4. 1010

5. 1210

 

X. Шестнадцатеричному числу D3F,416 в десятичной системе соответствует число?

1. 3328,5,10

2. 339110

3. 3391,2510

4. 3931,510

5. 11310

 

XI. Какая из приведенных двоичных записей соответствует десятичному числу 5210?

1. 1110112

2. 1011102

3. 1110102

4. 1101002

5. 1111102

 

XII. Десятичному числу 13210 в пятеричной системе счисления соответствует запись?

1. 11125

2. 10105

3. 10125

4. 1125

5. 6605

 

XIII. Десятичному числу 55510 в восьмеричной системе счисления соответствует запись?

1. 11538

2. 10518

3. 15538

4. 10058

5. 10538

 

XIV. Десятичному числу 58506 в шестнадцатеричной системе счисления соответствует запись?

1. 99FA16

2. A38A16

3. E48A16

4. 9D8A16

5. F58B16

 

XV. Какая из приведенных восьмеричных записей соответствует двоичному числу 11011001,10112?

1. 661,548

2. 331,548

3. 331,138

4. 664,138

5. 662,548

 

XVI. Какая из приведенных шестнадцатеричных записей соответствует двоичному числу 110 1110 0101, 1010 112?

1. DC5,AC16

2. 6E5,2B16

3. DC6,2B16

4. 6E5,AC16

5. 6D5,AC16

 

XVII. Какая из приведенных двоичному записей соответствует восьмеричному числу 57,28?

1. 101111,012

2. 111001,00010112

3. 101111,0001012

4. 111001,012

5. 111111,012

XVIII. Укажите самое большое число?

1. 1613

2. 1610

3. 168

4. 1612

5. 1616

 

XIX. Какая из приведенных записей десятичного вещественного числа соответствует нормализованной записи с плавающей запятой, принятой в компьютерах?

1. 15,25·102

2. 152,5·101

3. 1525,0

4. 0,1525·104

5. 1525

 

XX. Какая из приведенных запись вещественного двоичного числа 101101 является нормализованной?

1. 1011,01·210

2. 1011,01·22

3. 0,101101·26

4. 1,01101·2101

5. 0,101101·2110

 

XXI. Чему равна сумма двоичных чисел 1011,101 и 1110,001?

1. 10101,100

2. 11001,110

3. 11111,101

4. 11001,1001

5. 00101,110

 

XXII. Чему равна сумма шестнадцатеричных чисел 9C52,616 и 3BF6,D16?

1. D844,316

2. D894,516

3. D849.316

4. E849,316

5. D869,116

 

 

XXIII. Чему равна разность двоичных чисел 1010,012 и 101,112?

1. 11,102

2. 10,012

3. 10,102

4. 10,112

5. 100,102

 

XXIV. Чему равна разность восьмеричных чисел 7530,62 и 4271,718?

1. 3257,718

2. 3336,718

3. 3236,718

4. 3266,018

5. 3239,918

 

 

XXV. Чему равен дополнительный двоичный код десятичного числа 4110?

1. 0101102

2. 1010102

3. 0110002

4. 0101112

5. 1001102

 

XXVI. Какой вид примет логическое выражение (X & Y) Ú (Х Ú Y) & (Х Ú Z)после упрощения с использованием теорем Х1 & (Х2 Ú Х3) = (Х1 & Х2) Ú (Х1 & Х3), Х1 Ú (Х1 & Х2) = Х1, Х1 & (Х1 Ú Х2) = Х1?

1. (Y Ú Z)

2. Y

3. Х & Y

4. Х + Y & Z

5. (Х & Z)

 

XXVII. Какому логическому элементу соответствует приведенная таблица истинности?

 

.

1. ИЛИ-НЕ
2. И
3. Исключающее ИЛИ
4. И-НЕ
5. ИЛИ

 

.

 

_________ .

XXVIII. Чему равно логическое выражениеA. & (C Ú D) & B после упрощения?

1. `A &`C &`D Ú`B

2. `A Ú`C &`D Ú`B

3. `A Ú`C &`D &`B

4. `A Ú`C Ú`D Ú`B

5. `A &`C Ú`D &`B

. .

XXIX. Чему равно логическое выражение(A & B Ú C ) & (A & B Ú C )после упрощения?

1. A

2. A & B

3. 0

4. 1

5. `A

 

 

XXX. Какое выражение из представленных описывает работу следующей переключательной схемы ?

1. A & B

2. A Ú`B

3. `A & B

4. `A Ú B

5. A &`B

 

XXXI. Какое будет состояние в точках A, B, C ниже представленной логической схемы при следующем состоянии входных сигналов: X1 = 0, X2 = 1,X3 = 0?

1. A= 1,B= 0,C= 0

2. A= 0,B= 1,C= 0

3. A= 1,B= 1,C= 0

4. A= 1,B= 0,C= 1

5. A= 0,B= 0,C= 1

XXXII. Какую логическую функцию реализует логический элемент И-НЕ?

.

1. Х1 & X2

. .

2. Х1 Ú X2

. ______ .

3. Х1 & X2

. . .

4. Х1 Å X2

. .

5. Х1 Å X2


4. Компьютер

p Архитектура компьютера.

p Базовая аппаратная конфигурация персонального компьютера (ПК).

p Системный блок.

p Микропроцессоры ПК.

p Классификация памяти ПК.

p Периферийные (внешние) устройства ПК.

p Классификация программного обеспечения ПК.

p Файловая система и файловая структура.

p Правовая охрана программ и данных.

Поиск по сайту:

Логика высказываний

Логика высказываний

Логические выражения

Мы можем определять логические выражения, используя рекурсивное определение:

  1. Пропозициональные переменные (значение которых ИСТИНА или ЛОЖЬ) а пропозициональные константы ИСТИНА и ЛОЖЬ являются логическими выражениями.
  2. Если LE1 и LE2 — логические выражения, то LE1 AND LE2 — логическое выражение, значение которого ИСТИНА, если оба LE1 и LE2 имеют значение ИСТИНА, и ЛОЖЬ в противном случае.
  3. Если LE1 и LE2 — логические выражения, то LE1 OR LE2 — логическое выражение, значение которого ИСТИНА, если либо LE1, либо LE2 имеют значение TRUE, и ЛОЖЬ в противном случае.
  4. Если LE1 является логическим выражением, тогда НЕ LE1 является логическим выражением, значение которого ИСТИНА, если LE1 имеет значение ЛОЖЬ, и ЛОЖЬ в противном случае.

Уровни приоритета логических операторов:

  1. НЕ
  2. И
  3. ИЛИ

Присваивая значения переменным в логическом выражении, мы также присваиваем значение самому выражению.

Пример: задано выражение «(p AND q) OR r», если p = TRUE, q = TRUE и r = FALSE, то значение выражения — TRUE.

Логические функции и таблицы истинности

Смысл (или значение) логического выражения является логическим. функция из множества возможных присвоений истинностных значений для переменных в выражении к значениям {ИСТИНА, ЛОЖЬ}.

Пример: используя выражение «(p AND q) OR r», мы можем описать логическая функция, определяющая значение выражения путем рассмотрения всех комбинаций присвоений значений для p, q и r.

      p q r (p AND q) ИЛИ r
      ------------------------------
      Т Т Т Т
      Т Т Ф Т
      Т Ф Т Т
      T F F F
      F T T T
      F T F F
      F F T T
      F F F F

Приведенная выше таблица с описанием логической функции «(p AND q) OR r» называется таблицей истинности . В таблице истинности есть столбец для каждой переменной в выражение, и каждая строка в таблице соответствует присвоение значений переменным.В последнем столбце указано значение выражения для конкретный набор присвоений переменных, указанный в строке.

Мы можем определить основные операторы в терминах таблицы истинности следующим образом (где мы используем 1 и 0 вместо ИСТИНА и ЛОЖЬ):

     p q p И q p ИЛИ q НЕ p
     ------------------------------------
     0 0 0 0 1
     0 1 0 1 1
     1 0 0 1 0
     1 1 1 1 0

Обратите внимание, что таблица истинности для функции N переменных имеет 2 ^ N строк.N различных булевых функций от N переменных.

Вот некоторые дополнительные функции двух переменных, которые часто используются:

     p q p-> q p == q p NAND q p NOR q
     -------------------------------------------
     0 0 1 1 1 1
     0 1 1 0 1 0
     1 0 0 0 1 0
     1 1 1 1 0 0

Комментарии к этим функциям:

  • Следствие: «p -> q» или «p подразумевает q» означает, что всякий раз, когда p истинно, q тоже.Единственный способ «p -> q» может быть ЛОЖЬ, если p ИСТИНА, а q ЛОЖЬ.
  • Эквивалентность: «p == q» означает что p и q имеют одинаковое значение.
  • NAND: «p NAND q» то же самое, что «NOT (p AND q)».
  • NOR: «p NOR q» совпадает с «NOT (p OR q)».
  • Приоритет (от высшего к низшему): НЕ, И-НЕ, ИЛИ, И, ИЛИ, ->, ==.

Вычисление выражений с таблицами истинности

Мы можем вычислить значение выражения, используя таблицы истинности.Создаем таблицу для всех возможных значений переменных, и все подвыражения в выражении.

Вычислите значение следующего выражения E для всех возможные присвоения истинности: (p -> q) -> (q -> r)

      p q r p-> q q-> r E
      ---------------------------
      0 0 0 1 1 1
      0 0 1 1 1 1
      0 1 0 1 0 0
      0 1 1 1 1 1
      1 0 0 0 1 1
      1 0 1 0 1 1
      1 1 0 1 0 0
      1 1 1 1 1 1

Обратите внимание, что столбец для значения q-> r такой же как столбец для значения всего выражения E.Мы установили эквивалентность этих двух столбцов, что значит:

       (p -> q) -> (q -> r) == q-> r.

Генерация выражений из функций

Нам часто дают булеву функцию в виде таблицы истинности. и должен получить соответствующее логическое выражение.

Например, цифровые схемы построены из цифровых элементы, которые вычисляют основные логические операции (например, НЕ и И-НЕ).

Для конкретной функции, выраженной в виде результатов присвоения переменных (например, схема, которая добавляет два битов вместе и производит сумму и бит переноса, все что выражается в форме таблицы истинности), мы бы как соответствующее логическое выражение, так что мы может построить схему для функции.

Мы можем построить такое логическое выражение непосредственно из таблица истинности для функции.

Результирующее выражение использует в качестве операторов только AND, OR и NOT.

Исключительное Или: выражение из таблицы истинности

Исключающее ИЛИ (XOR) — еще одна хорошо известная функция двух переменных. Таблица истинности для XOR:

      p q XOR
      ---------------
      0 0 0
      0 1 1
      1 0 1
      1 1 0

Мы можем построить выражение для XOR в терминах AND, OR и НЕ, используя следующие рассуждения:

  • Вторая строка говорит нам, что p XOR q истинно. когда p — ЛОЖЬ, а q — ИСТИНА.Другими словами, p XOR q ИСТИНА, если НЕ p И q ИСТИНА.
  • Третья строка сообщает нам, что p XOR q истинно. когда p — ИСТИНА, а q — ЛОЖЬ. Другими словами, p XOR q истинно, если p AND NOT q истинно.
  • Остальные строки говорят нам, что p XOR q имеет значение FALSE в все остальные случаи.
  • Итак, p XOR q ИСТИНА, если НЕ p И q ИСТИНА, или если истинно p AND NOT q.

Из вышеизложенного мы определяем, что следующее логическое выражение для функции p XOR q:

      (НЕ p И q) ИЛИ (p И НЕ q)

Конъюнктивная и дизъюнктивная нормальные формы

Логическое выражение находится в дизъюнктивной нормальной форме если оно выражено как сумма (ИЛИ) произведений (И).То есть логическое выражение B находится в дизъюнктивной нормальной форме если это написано как:

      A1 ИЛИ A2 ИЛИ A3 ИЛИ ... An
где каждый Ai выражается как
      Т1 И Т2 И ... И Тм
где каждый Ti — простая переменная, или отрицание (НЕ) простой переменной. Каждый из терминов Ai называется minterm .

Логическое выражение находится в конъюнктивной нормальной форме если оно выражено как произведение (И) сумм (ИЛИ).То есть логическое выражение B находится в конъюнктивной нормальной форме если это написано как:

      O1, O2, O3, и ...
где каждый Oi выражается как
      Т1 ИЛИ Т2 ИЛИ ... ИЛИ Tm
где каждый Ti — простая переменная, или отрицание (НЕ) простой переменной. Каждый из терминов Oi называется maxterm .

Нормальные формы в таблицах истинности

Конъюнктивные и дизъюнктивные нормальные формы двойственны друг другу; любой из них может использоваться для генерации логического выражения из таблицы истинности.

С помощью этих нормальных форм мы можем быть более точными о том, как сгенерировать логическое выражение из таблицы истинности.

Чтобы построить логическое выражение в дизъюнктивной нормальной форме из таблица истинности:

  • Создайте minterm для каждой строки таблицы, в которой функция истинна.
  • Для каждой переменной, значение которой равно 1 в этой строке, мы включаем переменная в minterm; если переменная в этой строке равна 0, мы включаем отрицание переменной в minterm.
  • Выражение состоит из ИЛИ всех минтермов.

Конечно, мы могли бы построить выражение в дизъюнктивном нормальном форма с использованием maxterms и И.

Логическое выражение для сумматора

Двоичный сумматор целых чисел может быть построен из ряда однобитовых сумматоров. Однобитовый сумматор принимает два однобитовых операнда (x и y) и бит переноса из предыдущего однобитового сумматора (ci), и производит сумму этих битов, и выносной бит (со).

Мы можем определить логическую функцию, соответствующую сумматору в виде таблицы истинности. Затем мы можем построить логические выражения для s и co, из которого мы могли построить схему.

  x y ci co s
  ---------------------
  0 0 0 0 0
  0 0 1 0 1 с: НЕ x И НЕ y И ci
  0 1 0 0 1 с: НЕ x И y И НЕ ci
  0 1 1 1 0 co: НЕ x, y и ci
  1 0 0 0 1 с: x И НЕ y И НЕ ci
  1 0 1 1 0 co: x И НЕ y И ci
  1 1 0 1 0 co: x И y И НЕ ci
  1 1 1 1 1 co, s: x, y и ci

Логическое выражение для s:

  (НЕ x И y И ci) ИЛИ (x И НЕ y И ci) ИЛИ
  (x AND y И НЕ ci) ИЛИ (x AND y AND ci)

Логическое выражение для co:

  (НЕ x И НЕ y И ci) ИЛИ (НЕ x И Y И НЕ ci)
  ИЛИ (x И НЕ y И НЕ ci) ИЛИ (x И y И ci)

Полнота логических операторов

Предыдущее построение логического выражения из таблица истинности показала, как представить любую логическую функцию как сумма произведений или произведение сумм.

Поскольку мы можем представить любую логическую функцию с помощью И, ИЛИ, и НЕ, эти операторы образуют полный набор для Логические функции.

Мы можем показать, что одного оператора И-НЕ достаточно для генерации каждой логической функции, показывая, как реализовать И, ИЛИ, и НЕ с точки зрения NAND.

      p q p NAND 1 q NAND 1 p NAND q E1 E2
      --------------------------------------------
      0 0 1 1 1 0 0
      0 1 1 0 1 0 1
      1 0 0 1 1 0 1
      1 1 0 0 0 1 1
  
    E1: p AND q == ((p NAND q) НЕ ИСТИНА)
    E2: p ИЛИ q == ((p НЕ И ИСТИНА) ИЛИ (q НЕ И ИСТИНА))
    E3: (НЕ p) == (p НЕ ИСТИНА)

Подобная конструкция может использоваться, чтобы показать, что NOR — это также достаточно для генерации каждой логической функции.

Таким образом, мы можем сгенерировать цифровые схемы для любой булевой функции используя только операторы NAND или NOR (или компоненты).

Тавтологии

Тавтология — это логическое выражение, которое всегда ИСТИНА, независимо от присвоения значений истинности переменным в выражениях.

Примеры тавтологий:

  • ИСТИНА
  • ИСТИНА ИЛИ p
  • p ИЛИ НЕ p
  • НЕ (p И НЕ p)
  • p == p
  • (p OR q) == p OR (НЕ p AND q)
  • (p == q) -> (p -> q)

Если мы сможем установить, что «LE1 == LE2» является тавтологией, тогда независимо от того, какие значения мы присваиваем переменным в LE1 и LE2, мы знаем, что «LE1 == LE2» имеет значение ИСТИНА.

Если «LE1 == LE2» — тавтология, тогда мы можем заменить LE2 на LE1. (или наоборот) в любом выражении, без изменения значения выражения.

Задача тавтологии

Интересный вопрос — задать ли данное логическое выражение — тавтология. Этот вопрос известен как «проблема тавтологии».

Для решения проблемы тавтологии нам достаточно построить таблица истинности логического выражения.кн) время, т.е. экспоненциальное время.

Не существует известного алгоритма решения задачи тавтологии, который занимает меньше экспоненциального времени. Такие проблемы называются «трудноразрешимыми», потому что в больших случаях эти проблемы не могут быть решены в разумные сроки.

Еще одна такая трудноразрешимая проблема — это «проблема выполнимости». который спрашивает, есть ли присвоение истинностных значений переменные в логическом выражении, которое делает выражение ИСТИННЫМ.Не существует известного алгоритма решения этой проблемы, более того эффективнее, чем перебор всех возможных комбинаций присвоения истинности для переменных.

Таблицы истинности, тавтологии и логические эквивалентности

Таблицы истинности, тавтологии и логические эквивалентности

Математики обычно используют двузначное число . логика : Каждый оператор либо Истина , либо Неверно . Это называется . Закон Исключенного Среднего .

Утверждение в логике предложений строится из простых утверждений с использованием логические связки,,, и. Правда или ложь утверждения, построенного с помощью этих связок, зависит от истины или ложность его составляющих.

Например, составной оператор строится с использованием логических связок, и. Правда или ложь зависит от правды или ложность P, Q и R.

Таблица истинности показывает, как правда или ложь составного утверждения зависит от истинности или ложности простого утверждения, из которых он построен.Итак, мы начнем с рассмотрения таблицы истинности для пяти логических связок.

Вот таблица для отрицания:

Эта таблица проста для понимания. Если P равно истинно , его отрицание это ложный . Если P ложно , то истинно .

должно быть истинно , когда и P, и Q истинно и ложно иначе:

равно истинно , если либо P равно истинно , либо Q равно правда (или оба — помните, что мы используем «или» в инклюзивном смысле).Это только ложь , если и P, и Q равны ложь .

Вот таблица для логического вывода:

Чтобы понять, почему эта таблица такая, как она есть, рассмотрим следующие пример:

«Если вы получите пятерку, я дам вам доллар».

Утверждение будет истинным , если я сдержу свое обещание и ложь , если я этого не сделаю.

Предположим, что истинно, вы получили оценку A, а истинно . что я даю вам доллар.Поскольку я сдержал свое обещание, подразумевается правда . Это соответствует первой строке в таблице.

Предположим, что истинно , что вы получили A, но это ложно что я даю вам доллар. Поскольку я не сдержал своего обещания , подразумевается ложный . Это соответствует второму строка в таблице.

Что, если вы получите пятерку неверно? Независимо от того, даю ли я вам доллар, я не нарушил свое обещание.Таким образом, подтекст не может быть false, поэтому (поскольку это двузначная логика) оно должно быть истинным. Этот объясняет последние две строки таблицы.

означает, что P и Q равны эквивалент . Таким образом, двойное значение истинно , если P и Q оба истинны или если P и Q оба ложны ; в противном случае двойная импликация ложна.

Вы должны помнить — или уметь составлять — таблицы истинности для логических связок.Вы будете использовать эти таблицы для построения таблицы для более сложных предложений. Проще продемонстрировать что делать, чем описывать словами, чтобы вы увидели порядок действий отработано в примерах.

Замечание. (а) Когда вы конструируете истину таблице, вы должны рассмотреть все возможные присвоения True (T) и Ложь (F) для операторов компонентов. Например, предположим, что операторы компонентов — это P, Q и R. Каждый из этих операторов может быть либо истинно, либо ложно, значит, есть возможности.

Когда вы перечисляете возможности, вы должны присваивать значения истинности к операторам компонентов систематическим образом, чтобы избежать дублирования или упущение. Самый простой подход — использовать лексикографический порядок . Таким образом, для составного оператора с три компонента P, Q и R, я бы перечислил возможности этого способ:

(б) Существуют разные способы составления таблиц истинности. Вы можете для например, запишите значения истинности «под» логическим связки составного высказывания, постепенно наращивая столбец для «первичной» связки.

Я напишу подробности, построив столбцы для каждого «кусок» составного высказывания и постепенно наращивая к составному оператору. Любой стиль хорош, пока ты показываешь достаточно работы, чтобы оправдать ваши результаты.

Пример. Постройте таблицу истинности для формула.

Сначала я перечисляю все альтернативы для P и Q.

Затем в третьем столбце я перечисляю значения, основанные на значениях P.Я использую таблицу истинности для отрицание: когда P истинно, ложно, а когда P ложно, правда.

В четвертом столбце я перечисляю значения для. Убедитесь сами, что это только ложь («F»), если P истинно («T») и Q ложно («F»).

Пятый столбец дает значения для моего составного выражения. Это «и» (третий столбец) и (четвертый столбец). «И» верно, только если обе части «и» верны; в противном случае это ложь. Итак, я смотрю на третья и четвертая колонки; если оба верны («T»), я ставлю T в пятом столбце, иначе я поставил F.

Тавтология — это формула, которая «всегда истина «— то есть верно для каждого присвоения истины ценности к его простым компонентам. Вы можете думать о тавтологии как о правило логики .

Противоположность тавтологии — противоречие , формула, которая «всегда ложна». В другими словами, противоречие ложно для каждого присвоения истины ценности к его простым компонентам.

Пример. Показать, что это тавтология.

Я составляю таблицу истинности и показываю, что формула всегда верна.

Последний столбец содержит только буквы T. Следовательно, формула представляет собой тавтология.

Пример. Постройте таблицу истинности для.

Вы можете видеть, что построение таблиц истинности для утверждений с множеством связок или множества простых утверждений довольно утомительно и подвержен ошибкам.Хотя могут быть некоторые применения этого (например, для цифровых схем), в какой-то момент лучше всего было бы написать программа для построения таблиц истинности (и это, безусловно, было сделано).

Дело здесь в том, чтобы понять, как истинное значение сложного утверждение зависит от истинности его простых утверждений и его логические связки. В большинстве работ математики обычно не используйте операторы, которые очень сложны с логической точки зрения Посмотреть.

Пример. (a) Предположим, что P ложно и истинно. Скажите, является ли Q истинным, ложным или его истинным значение не может быть определено.

(b) Предположим, что это неверно. Расскажи является ли Q истинным, ложным или его истинное значение не может быть определено.

(a) Поскольку истинно, либо P истинно, либо истинно. Поскольку P ложно, должно быть верно. Следовательно, Q должно быть ложным.

(b) Утверждение «если-то» неверно, когда часть «если» истина, а часть «тогда» — ложь.Поскольку ложно, верно. Утверждение «и» верно только когда обе части верны. В частности, должно быть истинным, поэтому Q ложно.

Пример. Предположим

» » правда.

«» ложно.

«У Кэлвина Баттерболла фиолетовые носки» — правда.

Определите истинность утверждения

Для простоты пусть

P = «».

Q = «».

R = «У Кэлвина Баттерболла фиолетовые носки».

Я хочу определить истинное значение. Поскольку мне были даны конкретные значения истинности для P, Q, и R, я установил таблицу истинности с единственной строкой, используя данный значения для P, Q и R:

Следовательно, утверждение истинно .

Пример. Определите истинное значение утверждение

Утверждение «» ложно. Ты не можешь сказать есть ли в заявлении «Икабод Ксеркс шоколад» кексы «верно или неверно, но это не имеет значения.Если «если» часть утверждения «если-то» ложна, тогда утверждение «если-то» верно. (Проверить правду таблица, если вы не уверены в этом!) данное утверждение должно быть верным.

Два оператора X и Y логически равны эквивалент , если это тавтология. Другой способ сказать это: Для каждого присвоения значений истинности простому элементу операторы , которые составляют X и Y, операторы X и Y имеют идентичные значения истинности.

С практической точки зрения вы можете заменить выражение в доказательство любым логически эквивалентным утверждением.

Чтобы проверить, являются ли X и Y логически эквивалентными, вы можете настроить таблица истинности, чтобы проверить, является ли тавтология — это есть ли «все ли Т в его столбце». Однако проще создать таблицу, содержащую X и Y, а затем проверьте, совпадают ли столбцы для X и Y.

Пример. Покажите, что и логически эквивалентны.

Поскольку столбцы для и идентичны, два оператора логически эквивалент.Эта тавтология называется условной . Дизъюнкция . Вы можете использовать эту эквивалентность для замены условно дизъюнкцией.

Существует бесконечное количество тавтологий и логических эквивалентностей; Я перечислил несколько ниже; более обширный список приведен в конце эта секция.

Когда тавтология имеет форму двоякого условия, два утверждения которые составляют двусмысленные, логически эквивалентны. Следовательно, вы может заменить одну сторону на другую без изменения логического имея в виду.

Вам часто нужно будет отрицать математическое утверждение . К посмотрим, как это сделать, мы начнем с того, что покажем, как отрицать символическое заявления.

Пример. Запишите отрицание следующие утверждения, упрощающие так, чтобы только простые утверждения отрицается.

(а)

(б)

(а) Я отвергаю данное утверждение, а затем упрощаю, используя логические эквивалентности. Я дал названия логических эквивалентов на правильно, чтобы вы могли видеть, какие из них я использовал.

(б)

Я показал это и логически эквивалентен в предыдущем примере.

В следующих примерах мы будем отрицать утверждения, написанные словами. Это более типично для того, что вам нужно делать по математике. В идея состоит в том, чтобы преобразовать слово-оператор в символическое утверждение, тогда используйте логические эквивалентности, как в предыдущем примере.

Пример. Используйте закон ДеМоргана, чтобы написать отрицание следующего утверждения, упрощая так, чтобы отрицаются только простые утверждения:

«Кальвина нет дома, или Бонзо в кино.»

Пусть C будет утверждением «Кальвин дома» и пусть B будет заявление «Бонзо в движении». Данное заявление . Я должен опровергнуть это утверждение, затем упростите:

Результат: «Кальвин дома, а Бонзо нет в доме». фильмы ».

Пример. Используйте закон ДеМоргана, чтобы написать отрицание следующего утверждения, упрощая так, чтобы отрицаются только простые утверждения:

«Если Фиби покупает пиццу, то Кэлвин покупает попкорн.»

Пусть P будет утверждением «Фиби покупает пиццу» и пусть C будет заявление «Кэлвин покупает попкорн». Данное заявление . Чтобы упростить отрицание, я буду использовать тавтологию условного дизъюнкции , которая говорит

То есть я могу заменить на (или наоборот).

Итак, вот отрицание и упрощение:

Результат: «Фиби покупает пиццу, а Кэлвин не покупает. Попкорн».

Далее мы применим нашу работу с таблицами истинности и отрицательными утверждениями к задачи, связанные с построением обратного, обратного и противоположность утверждению «если-то».

Пример. Заменить следующую инструкцию на его противоположность:

«Если x и y рациональны, то рационально».

В силу контрапозитивной эквивалентности это утверждение совпадает с утверждением «Если нерационально, значит, это не так. что и x, и y рациональны «.

Этот ответ верен в его нынешнем виде, но мы можем выразить его в немного лучший способ, который удаляет некоторые явные отрицания. Большинству людей легче понять положительное утверждение, чем отрицательное заявление.

По определению действительное число — это иррациональное , если это не рационально. Так что я мог бы заменить часть «если» в противоположно выражению «иррационально».

«Тогда» часть контрапозитива — это отрицание «и» заявление.Вы могли бы повторить это так: «Это не случай, когда и x рационально, и y рационально «. (Слово «оба» гарантирует, что отрицание применимо ко всему «И», а не только «х рационально».)

По закону ДеМоргана это эквивалентно: «x нерационально или y не рационально «. В качестве альтернативы я мог бы сказать:» x есть иррационально или y иррационально ».

Объединив все вместе, я мог бы выразить контрапозитив так: «Если иррационально, то либо x иррационально или y иррационально «.

(Как обычно, я добавил слово «либо», чтобы было ясно, что часть «затем» — это целое выражение «или».)

Пример. Покажите, что обратное и обратное обратное условному выражению логически эквивалентны.

Позвольте быть условным. Обратное. Обратное.

Я мог бы показать, что обратное и обратное эквивалентны построение таблицы истинности для. Вместо этого я воспользуюсь некоторыми известными тавтологиями.

Начнем с:

Помните, что я могу заменить выражение логическим эквивалент.Например, на последнем шаге я заменил Q, потому что два оператора эквивалентны Двойное отрицание.

Пример. Предположим, что x — действительное число. Рассмотреть возможность заявление

«Если, то.»

Постройте обратное, обратное и противоположное. Определите истинность или ложность четырех утверждений — исходное утверждение, обратное, обратное и противоположное — используя свои знания алгебры.

Обратное — «Если, то».

Обратное — «Если, то».

Контрапозитив — «Если, то».

Исходное утверждение неверно:, но. Поскольку исходное утверждение эквивалентно контрапозитивный, контрапозитивный тоже должен быть ложным.

Верно и обратное. Обратное логически эквивалентно обратное, значит, верно и обратное.

\новая страница

\ centerline {\ bigssbold Список тавтологий}

Контактная информация

Домашняя страница Брюса Икенаги

Авторские права 2019 Брюс Икенага

Основные логические ворота с таблицами истинности

В наши дни компьютеры стали неотъемлемой частью жизни, поскольку они выполняют множество задач и операций за довольно короткий промежуток времени.Одной из наиболее важных функций ЦП в компьютере является выполнение логических операций с использованием аппаратного обеспечения, такого как программные технологии и электронные схемы интегральных схем. Но как это оборудование и программное обеспечение выполняют такие операции — загадочная загадка. Чтобы лучше понять такую ​​сложную проблему, мы должны познакомиться с термином «логическая логика», разработанным Джорджем Булем. Для простой операции компьютеры используют двоичные цифры, а не цифровые.Все операции выполняются воротами базовой логики. В этой статье обсуждается обзор того, что такое базовые логические вентили в цифровой электронике и их работа.

Что такое базовые логические вентили?

Логический вентиль — это базовый строительный блок цифровой схемы, имеющей два входа и один выход. Отношения между i / p и o / p основаны на определенной логике. Эти затворы реализованы с помощью электронных ключей типа транзисторов, диодов. Но на практике базовые логические вентили строятся с использованием технологии CMOS, полевых транзисторов и полевых транзисторов MOSFET (Metal Oxide Semiconductor FET).Логические вентили используются в микропроцессорах, микроконтроллерах, встроенных системных приложениях, а также в электронных и электрических схемах проектов. Основные логические элементы делятся на семь категорий: AND, OR, XOR, NAND, NOR, XNOR и NOT. Эти логические вентили с их символами логических вентилей и таблицами истинности объясняются ниже.


Работа основных логических вентилей

Что такое 7 основных логических вентилей?

Основные логические вентили подразделяются на семь типов: вентиль И, вентиль ИЛИ, вентиль ИЛИ, вентиль И-НЕ, вентиль ИЛИ, вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ и вентиль НЕ.Таблица истинности используется для демонстрации функции логического элемента. Все логические элементы имеют два входа, кроме элемента НЕ, который имеет только один вход.

При построении таблицы истинности используются двоичные значения 0 и 1. Каждая возможная комбинация зависит от количества входов. Если вы не знаете о логических вентилях и их таблицах истинности и нуждаетесь в руководстве по ним, просмотрите следующую инфографику, которая дает обзор логических вентилей с их символами и таблицами истинности.

Почему мы используем базовые логические вентили?

Основные логические элементы используются для выполнения основных логических функций.Это основные строительные блоки цифровых ИС (интегральных схем). Большинство логических вентилей используют два двоичных входа и генерируют один выход, например 1 или 0. В некоторых электронных схемах используется несколько логических вентилей, тогда как в некоторых других схемах микропроцессоры включают миллионы логических вентилей.

Реализация логических вентилей может осуществляться с помощью диодов, транзисторов, реле, молекул и оптики, иначе говоря, различных механических элементов. По этой причине основные логические вентили используются как электронные схемы.


Двоичные и десятичные числа

Прежде чем говорить о таблицах истинности логических вентилей, важно знать предысторию двоичных и десятичных чисел. Все мы знаем десятичные числа, которые мы используем в повседневных вычислениях, например от 0 до 9. Такая система счисления включает в себя десятичную систему счисления. Таким же образом двоичные числа, такие как 0 и 1, могут использоваться для обозначения десятичных чисел, если основание двоичных чисел равно 2.

Значение использования двоичных чисел здесь состоит в том, чтобы обозначать положение переключения, в противном случае положение напряжения цифрового компонента .Здесь 1 представляет высокий сигнал или высокое напряжение, тогда как «0» указывает низкое напряжение или низкий сигнал. Таким образом, была начата булева алгебра. После этого каждый логический вентиль обсуждается отдельно, он содержит логику логического элемента, таблицу истинности и ее типичный символ.

Типы логических вентилей

Различные типы логических вентилей и символов с таблицами истинности обсуждаются ниже.

Базовые логические вентили
И вентиль

Логический вентиль И представляет собой цифровой логический вентиль с «n» i / ps и одним o / p, который выполняет логическое соединение на основе комбинаций своих входов.Выход этого вентиля истинен только тогда, когда все входы истинны. Когда один или несколько входов i / ps логического элемента И являются ложными, тогда только выход логического элемента И является ложным. Таблица символов и истинности логического элемента И с двумя входами показана ниже.

Логический элемент И и его таблица истинности
Логический элемент ИЛИ

Логический элемент ИЛИ — это цифровой логический вентиль с n i / ps и одним o / p, который выполняет логическое соединение на основе комбинаций своих входов. Выход логического элемента ИЛИ истинен только тогда, когда один или несколько входов истинны.Если все i / ps логического элемента ложны, то ложным является только выход логического элемента ИЛИ. Таблица символов и истинности логического элемента ИЛИ с двумя входами показана ниже.

Логический элемент ИЛИ и его таблица истинности
Элемент НЕ

Элемент НЕ — это цифровой логический вентиль с одним входом и одним выходом, который управляет инверторной операцией входа. Выход логического элемента НЕ является обратным входу. Когда вход логического элемента НЕ истинен, тогда выход будет ложным, и наоборот. Таблица символов и истинности логического элемента НЕ с одним входом показана ниже.Используя этот вентиль, мы можем реализовать вентили ИЛИ и И-НЕ.

Шлюз НЕ и его таблица истинности
Шлюз И-НЕ

Логический вентиль И-НЕ — это цифровой логический вентиль с ‘n’ i / ps и одним o / p, который выполняет вентиль И, за которым следует вентиль НЕ. вентиль НЕ разработан путем объединения вентилей И и НЕ. Если вход логического элемента И-НЕ высокий, то выход элемента будет низким. Ниже показаны символы и таблица истинности логического элемента И-НЕ с двумя входами.

Шлюз И-НЕ и его таблица истинности
Шлюз ИЛИ

Элемент ИЛИ — это цифровой логический вентиль с n входами и одним выходом, который выполняет операцию логического элемента ИЛИ, за которым следует вентиль НЕ.Ворота NOR спроектированы путем объединения ворот OR и NOT. Когда любой из i / ps логического элемента ИЛИ-НЕ истинен, тогда выход логического элемента ИЛИ-НЕ будет ложным. Таблица символов и истинности ворот ИЛИ-НЕ с таблицей истинности показана ниже. Логический элемент

ИЛИ и его таблица истинности
Элемент исключающего ИЛИ

Элемент исключающего ИЛИ — это цифровой логический вентиль с двумя входами и одним выходом. Краткая форма этих ворот — Ex-OR. Он работает на основе операции логического элемента ИЛИ. . Если на каком-либо из входов этого логического элемента высокий уровень, то выход элемента EX-OR будет высоким.Символы и таблица истинности EX-OR показаны ниже. Элемент

EX-OR и его таблица истинности
Элемент Exclusive-NOR

Элемент Exclusive-NOR — это цифровой логический элемент с двумя входами и одним выходом. Краткая форма этих ворот — Ex-NOR. Он работает на основе работы логического элемента ИЛИ-НЕ. Когда оба входа этого логического элемента имеют высокий уровень, тогда выход элемента ИСКЛЮЧАЮЩЕЕ НЕ будет высоким. Но если один из входов высокий (но не оба), то выход будет низким. Символы и таблица истинности EX-NOR показаны ниже.

Шлюз EX-NOR и его таблица истинности

Применение логических вентилей в основном определяется на основе их таблицы истинности, то есть режима их работы. Базовые логические вентили используются во многих схемах, таких как кнопочный замок, охранная сигнализация с включением света, предохранительный термостат, автоматическая система полива и т.д. общий метод известен как таблица истинности. Эта таблица включает все комбинации входных логических состояний: высокий (1) или низкий (0) для каждой входной клеммы логического элемента через эквивалентный выходной логический уровень, такой как высокий или низкий.Схема логического элемента НЕ показана выше, и ее таблица истинности действительно чрезвычайно проста.

Таблицы истинности логических элементов очень сложны, но больше, чем вентиль НЕ. Таблица истинности каждого гейта должна включать много строк, как будто есть возможности для эксклюзивных комбинаций для входных данных. Например, для логического элемента НЕ есть две возможности ввода: 0 или 1, тогда как для логического элемента с двумя входами есть четыре возможности, такие как 00, 01, 10 и 11. Таким образом, он включает четыре строки для эквивалентная таблица истинности.

Для логического элемента с 3 входами существует 8 возможных входов, таких как 000, 001, 010, 011, 100, 101, 110 и 111. Следовательно, требуется таблица истинности, включающая 8 строк. Математически необходимое количество строк в таблице истинности эквивалентно двум, увеличенным в степени «нет». i / p терминалов.

Анализ

Сигналы напряжения в цифровых схемах представлены двоичными значениями, такими как 0 и 1, вычисленными относительно земли. Недостаток напряжения в основном означает «0», тогда как наличие полного напряжения питания постоянного тока означает «1».

Логический вентиль — это особый тип схемы усилителя, который в основном предназначен для входных и выходных логических напряжений. Схемы логического затвора чаще всего обозначаются схематической диаграммой через их собственные эксклюзивные символы вместо их основных резисторов и транзисторов.

Как и в случае с операционными усилителями, соединения источника питания с логическими вентилями часто неуместны на схематических диаграммах в целях упрощения. Он включает возможные комбинации входных логических уровней через их конкретные выходные логические уровни.

Какой самый простой способ выучить логические ворота?

Ниже объясняется самый простой способ изучить функции основных логических вентилей.

  • Для логического элемента И — Если оба входа имеют высокий уровень, то и выход также высокий
  • Для ворот ИЛИ — Если минимум одного входа высокий, то выход высокий
  • Для элемента ИСКЛЮЧАЮЩЕЕ ИЛИ — Если минимальный вход высокий, тогда высокий только выход
  • NAND Gate — Если минимальный один вход низкий, то выход высокий
  • NOR Gate — Если оба входа низкие, то выход высокий.

Теорема Де Моргана

Первая теорема ДеМоргана утверждает, что логический вентиль, такой как И-НЕ, равен вентилю ИЛИ с пузырьком. Логическая функция логического элемента И-НЕ:

A’B = A ’+ B’

Вторая теорема ДеМоргана утверждает, что логический элемент ИЛИ-НЕ равен логическому элементу И с пузырьком. Логическая функция логического элемента ИЛИ-НЕ:

(A + B) ’= A’. B ’

Преобразование логического элемента И-НЕ

Логический элемент И-НЕ может быть сформирован с использованием логического элемента И и НЕ.Булево выражение и таблица истинности показаны ниже.

Формирование логических ворот NAND

Y = (A⋅B) ‘

A

B Y ′ = A ⋅B

0

0 0 1

0

1 0 0

1

1 1 907 907
Преобразование логического элемента ИЛИ

Элемент ИЛИ-НЕ может быть сформирован с использованием логического элемента ИЛИ и НЕ.Булево выражение и таблица истинности показаны ниже.

Формирование логических ворот NOR

Y = (A + B) ‘

-ИЛИ Преобразование ворот

Элемент Ex-OR может быть сформирован с помощью элемента НЕ, И и ИЛИ.Булево выражение и таблица истинности показаны ниже. Этот логический вентиль может быть определен как вентиль, который дает высокий выход, когда на любом его входе высокий уровень. Если оба входа этого затвора имеют высокий уровень, выход будет низким.

Формирование логических вентилей Ex-OR

Y = A⊕B или A’B + AB ‘

A

B Y ′ = A + B

0

0 0 1
0 1 907 907 1 0 1

0

1 1 1
9454
A B

Y

0 0

0

 1

1

1 0

1

1

1

1

1
Преобразование ворот Ex-NOR

Вентиль Ex-NOR может быть сформирован с использованием ворот EX-OR & NOT.Булево выражение и таблица истинности показаны ниже. В этом логическом элементе, когда на выходе высокий уровень «1», оба входа будут либо «0», либо «1».

Формирование ворот Ex-NOR

Y = (A’B + AB ‘)’

Базовые логические вентили с использованием универсальных вентилей

Универсальные вентили, такие как вентиль И-НЕ и вентиль ИЛИ-НЕ, могут быть реализованы с помощью любого логического выражения без использования какого-либо другого типа логического элемента. И их также можно использовать для проектирования любых базовых логических вентилей. Кроме того, они широко используются в интегральных схемах, поскольку они просты и экономичны в изготовлении.Базовая конструкция логических вентилей с использованием универсальных вентилей обсуждается ниже.

Базовые логические вентили могут быть спроектированы с помощью универсальных вентилей. Он использует ошибку, небольшой тест, иначе вы можете использовать логическую логику для их достижения через уравнения логических вентилей для логического элемента И-НЕ, а также для элемента ИЛИ-НЕ. Здесь логическая логика используется для решения требуемых выходных данных. Это займет некоторое время, но необходимо выполнить это, чтобы получить представление о логической логике, а также основных логических вентилях.

Базовые логические вентили, использующие вентиль И-НЕ

Проектирование базовых логических вентилей, использующих вентиль И-НЕ, обсуждается ниже.

Проектирование логического элемента НЕ с использованием NAND

Проектирование логического элемента НЕ выполняется очень просто, просто соединяя оба входа как один.

Проектирование логического элемента И с использованием NAND

Проектирование логического элемента И с использованием логического элемента И-НЕ может быть выполнено на выходе логического элемента И-НЕ, чтобы изменить его и получить логику И.

Проектирование логического элемента ИЛИ с использованием NAND

Проектирование логического элемента ИЛИ с использованием логического элемента И-НЕ может быть выполнено путем соединения двух вентилей НЕ с использованием вентилей И-НЕ на входах И-НЕ для получения логики ИЛИ.

Проектирование логического элемента ИЛИ с использованием NAND

Проектирование логического элемента ИЛИ с использованием логического элемента И НЕ может быть выполнено простым подключением другого логического элемента НЕ через логический элемент ИЛИ к выходу логического элемента ИЛИ через NAND.

Проектирование ворот EXOR с использованием NAND

Это немного сложно. Вы разделяете два входа с тремя воротами. Выход первого И-НЕ является вторым входом для двух других. Наконец, другая И-НЕ принимает выходные данные этих двух вентилей И-НЕ, чтобы дать окончательный результат.

Базовые логические вентили, использующие вентиль ИЛИ-НЕ

Проектирование основных логических вентилей, использующих вентиль ИЛИ-НЕ, обсуждается ниже.

Шлюз НЕ с использованием NOR

Проектирование логического элемента НЕ с вентилем НЕ выполняется просто путем соединения обоих входов как одного.

Логический элемент ИЛИ с использованием NOR

Проектирование логического элемента ИЛИ с логическим элементом ИЛИ-НЕ выполняется просто путем подключения к выходу логического элемента ИЛИ-НЕ для его реверсирования и получения логики ИЛИ.

Логический элемент И с использованием NOR

Проектирование логического элемента И с использованием логического элемента ИЛИ-НЕ может быть выполнено путем соединения двух вентилей НЕ с ИЛИ-НЕ на входах ИЛИ-НЕ для получения логики И.

Шлюз И-НЕ с использованием NOR

Проектирование шлюза И-НЕ с использованием логического элемента ИЛИ-НЕ может быть выполнено простым подключением другого шлюза НЕ через вентиль ИЛИ к выходу логического элемента И с помощью ИЛИ.

EX-NOR Gate с использованием NOR

Этот тип подключения немного сложен, потому что два входа могут использоваться совместно с тремя логическими вентилями. Первый выход логического элемента ИЛИ-НЕ является следующим входом для оставшихся двух вентилей. Наконец, другой вентиль ИЛИ-НЕ использует два выхода логического элемента ИЛИ-НЕ для обеспечения последнего выхода.

Приложения

приложений базовых логических вентилей очень много, однако они в основном зависят от своих таблиц истинности, иначе формы операций. Базовые логические элементы часто используются в схемах, таких как замок с кнопкой, автоматическая система полива, сигнализация о взломе, активируемая светом, предохранительный термостат и другие типы электронных устройств.

Основное преимущество базовых логических вентилей состоит в том, что они могут использоваться в другой комбинированной схеме.Кроме того, количество логических вентилей, которые можно использовать в одном электронном устройстве, не ограничено. Но его можно ограничить из-за указанного физического зазора внутри устройства. В цифровых ИС (интегральных схемах) мы обнаружим коллекцию блока области логического элемента.

При использовании комбинации основных логических вентилей часто выполняются расширенные операции. Теоретически не существует ограничений на количество ворот, которые могут быть одеты во время одного устройства. Однако в приложении есть ограничение на количество ворот, которые могут быть упакованы в определенную физическую область.Массивы блока логических вентилей находятся в цифровых интегральных схемах (ИС). По мере развития технологии ИС желаемый физический объем для каждого отдельного затвора уменьшается, и цифровые устройства эквивалентного или меньшего размера становятся способными выполнять более сложные операции с постоянно увеличивающейся скоростью.

Инфографика логических вентилей

Это все об обзоре того, что такое базовый логический вентиль, такие типы, как вентиль И, вентиль ИЛИ, вентиль И-НЕ, вентиль ИЛИ, вентиль ИЛИ ИЛИ и вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ.В этом случае вентили И, НЕ и ИЛИ являются основными логическими вентилями. Используя эти вентили, мы можем создать любой логический вентиль, комбинируя их. Где ворота NAND и NOR называются универсальными воротами. У этих ворот есть особое свойство, с помощью которого они могут создавать любое логическое логическое выражение, если они спроектированы надлежащим образом. Кроме того, по любым вопросам, касающимся этой статьи или проектов в области электроники, просьба оставлять отзывы, комментируя их в разделе комментариев ниже.

2. Схемы и таблицы истинности — Sireum Logika

В этой главе мы рассматриваем основные понятия о воротах и ​​изучаем взаимосвязь между схемами и компьютерными программами на основе назначений.Это готовит почву для анализа современных программ.

2.1. Гейтс и таблицы истинности

Вот четыре основных входа:

P AND Q

P OR Q

НЕ P

P IMPLY Q

На приведенных выше чертежах входные провода обозначены именами P и К .Вычисляемый выходной сигнал исходит от крайнего правого провода, выходящего из ворота. Для этих простых вентилей можно полностью проверить каждую перестановку потенциальных входов и суммируйте результаты в таблице, называемой таблицей истинности.

Давайте исследуем логический элемент AND. Логический элемент И излучает высокое напряжение ( 1 ) точно при обнаружении высокого напряжения на входных проводах P и Q ; иначе излучается низкое напряжение ( 0 ). Физическое поведение ворот можно описать следующим образом: в следующей таблице.:

 И: P Q |
------------
     1 1 | 1
     1 0 | 0
     0 1 | 0
     0 0 | 0

В оставшейся части этого курса мы будем использовать T (читать «верно») для 1 и F (читать «ложно») для 0 . Это потому, что мы будем изучать приложения, которые выходят далеко за рамки теории схем. и арифметика с основанием два. Вот таблицы истинности для вентилей AND, OR, NOT и IMPLY:

Примечание

Заглавные буквы P и Q предназначены для заполнения, а не переменные строго названы P и Q.Их использование позволяет избежать многословного: «Правая рука. Боковой операнд »и« Левый операнд ».

OR иногда называют «включающим или», поскольку пока одно из его входы — истина, тогда его выход — истина. Это отличается от обычного United Утверждает использование английского языка. Как правило, в устном и письменном английском слово «или» несет в себе эксклюзивный оттенок. Если предлагается выбор «кофе или чай», это понимается что вы можете выбрать одно, но не оба. Логическое «или» допускает возможность обоих. Это более точно переводится на английский язык как «и / или».

Значение ворот IMPLY будет рассмотрено позже в этой главе. это включены сюда, чтобы объединить всю информацию о воротах.

Стандартно записывать каждый вентиль в линейной записи, то есть вместо рисунок, пишем P ∧ Q . (Традиция писать линейные обозначения для представления двумерных Структуры уходят в прошлое на века в физике и математике.) Обозначения следующие (традиционные математические обозначения предусмотрены для Ваш справочник.)

.

Выход

ASCII

Математика

UNICODE

И

∧

∧

∧

ИЛИ

v

∨

∨

НЕ

~

¬

¬

ПОДРАЗУМЕВАЕТСЯ

->

⇒

→

В этих примечаниях обычно используются нотации UNICODE.

Мы также можем составить ворота для определения новых операций.

Например, эта схема, записанная ¬ (P ∧ Q) , определяет это расчет выходов:

 P Q | ¬ (P ∧ Q)
--------------
Т Т | F
T F | Т
F T | Т
F F | Т

, который мы можем проработать поэтапно, например:

Мы начинаем с записи значения каждого набора входов слева под их соответствующий символ справа. Затем мы применяем оператор (гейт) с наивысший приоритет (рассматривается в разделе «Приоритет логических операторов» ниже).В нашем случае «()» делает символ И ( ∧ ) наивысшим.

Назначение истинности — это уникальная перестановка возможных входов для системы. Для-гейта это последовательность с двумя переменными. Рассматривая первую строку, мы видим у нас есть «T ∧ T» — глядя на это в таблице истинности ∧-ворот, мы видим, что результат также «T», и мы записываем это под символом «∧». Мы делаем одно и то же все другие задания правды.

После первоначальной расшифровки значений истинности под их соответствующие переменные, мы ищем истинностные значения в таблицах ворот, а не переменные.Также обратите внимание, что хотя ∧ является симметричным, то есть «T F» == «F T» == «F» ПОДРАЗУМЕВАЕМЫЙ ворот нет.

Теперь мы ищем значение под символом «» в таблице ¬ gate. Во-первых строке мы видим, что присвоение истинности для первой строки, «T», равно «F», и запись его под символом «¬». Сделайте это для каждого ряда, и все готово.

2.1.1. Описание таблиц истинности

В нашем исследовании логики будет удобно характеризовать логические формулы с помощью описание их таблиц истинности.Если все присвоения истинности для логической формулы Верно, формула называется тавтологией. Формула p ∨ ¬ p является тавтология. В следующем примере * обозначает верхний уровень или последний оценивается оператор.

 *
------------
p | п ∨ ¬ п
------------
Т | Т Т Ф Т
F | F T T F
------------
Тавтология

Формула, для которой каждое присвоение истинности ложно, называется противоречивой. В Формула p ∧ ¬ p противоречива (или противоречит).

 *
------------
p | п ∧ ¬ п
------------
Т | T F F T
F | F F T F
------------
Противоречивый

Формула, для которой одни присвоения истинности ложны, а другие истинны, называется контингент. Уравнение p q | ¬ (q ∧ q) , сверху условно.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12 
 *
---------------
p q | ¬ (p ∧ q)
---------------
Т Т | F T T T
T F | Т Т F F
F T | T F F T
F F | T F F F
---------------
Условный
- T: [T F] [F T] [F F]
- F: [T T]

В этом разделе мы использовали таблицы истинности Logika.Они объясняются более подробно подробности ниже. В этом классе, если вы создадите таблицу истинности как часть ответа, он должен соответствовать синтаксису Logika.

2.1.2. Таблицы истинности как доказательства

Это урок логики. 2 истинности заданий), конечно, возможно (хотя и раздражает) вычислить эти столы своими руками.32 записи. Это займет немного (предназначено каламбур) более 1100 лет, чтобы написать вручную, если вы можете в среднем одно задание истины в секунду.

Учитывая, что вас, вероятно, никогда не попросят написать реальное приложение так же просто, как сложение целых чисел, легко сделать вывод, что это невозможно доказать правильность программ по таблицам истинности. Неспособность протестировать программу исчерпывающая проверка каждого входа или состояния известна как комбинаторный взрыв проблема.

Хорошо … тогда почему мы заставляем вас учить таблицы истинности? Ну даже когда более продвинутый методы применяются для доказательства логических утверждений, подчеркивая их надежность это примитивные правила, которые легко выразить и усвоить с помощью таблиц истинности.

2.2. Таблицы истинности Logika

С этого момента в курсе предполагается, что вы будете использовать форматирование Logika. таблицы истинности. Таблица истинности Logika для формулы ¬ (P ∧ Q) :

 *
------------
p | п ∨ ¬ п
------------
Т | Т Т Ф Т
F | F T T F
------------
Тавтология

Таблицы истинности Logika имеют стандартный формат (синтаксис) и семантическое значение. Все элементы таблицы истинности должны быть включены, чтобы считаться правильными.

Первая строка всегда будет содержать одну звездочку ( * ) над последним вычисленным оператором. в формуле. Это также может называться «высший уровень» или «низший прецедент». оператор. Почему он называется оператором «верхнего уровня», будет рассмотрено конец этой главы.

Далее идет строка из - (знак минус) символов, длина этих строк должна быть не менее в качестве третьей строки, чтобы избежать ошибок.

Третья строка содержит «переменные | формула ».Поскольку Logika использует заглавные буквы в качестве зарезервированные слова, в качестве имен переменных используются строчные буквы. Кроме того, переменные должны быть перечислены в алфавитном порядке.

Четвертая строка — это еще один ряд - .

Далее идут задания истины. Соглашение должно начинаться со всего Истины и прогресса линейно ко всем False. Необходимо использовать Capital T и F . В задании правды каждой переменной сопоставляется истина или ложь.

После назначений Правды идет еще один ряд - .

Наконец идет стол. Когда все присвоение истины заставляет формулу быть истинной, слово Тавтология используется без сопроводительной таблицы. Аналогично, когда все присвоения истины ложны, используется Противоречивое . Все остальные результаты Contingent , см. пример на рисунке выше.

Порядок приоритета логических операторов от высшего к низшему:

Круглые скобки изменяют порядок операций, как в нормальной алгебре.Выражения в круглых скобках оцениваются от наиболее глубоко вложенных к наименее глубоко вложенные (внутри наружу).

2.3. Странная история Импли-ворот

Проницательный читатель заметит, что таблицы истинности → очень отличаются от ∧ и ∨ . Начнем с того, что присвоения истинности ∧ и ∨ симметричны; если [T F] == F, то [F T] == F. Это неверно в отношении импликации, потому что p → q является составным утверждение, которое утверждает, что p обладает знаниями, достаточными для вывода q.

Давайте использовать конкретный пример из K-State. Если я знаю, что ты по специальности в информатике (факт p), тогда я знаю, что вы специализируетесь на инженерии (факт q).

 специальность информатика → специальность инженер
           p → q

Однако, наоборот, по специальности "Инженерное дело" → по специальности "Информатика" не обязательно верно.

Некоторые студенты склонны объединять «p обладает знаниями, достаточными для вывода q», чтобы означать «P == q», и удивлены и возмущены тем, что назначение истины [F T] в ПОДРАЗУМЕВАЕМЫЕ ворота ИСТИНА. p → q не означает p == q или q == p

В таблице истинности для p → q результат отражает существование серийного номера. связь между p и q . Сначала p должно быть истинным, затем q также должно быть быть правдой, чтобы утверждение было правдой.

Если оба верны, ссылка верно, и импликация (связь) между p и q верна.

Если p верно, а q ложно, очевидно, что p не обладает достаточными знаниями чтобы вывести q, поэтому связь не верна (ложь).

Наконец, если p не истинно, нет никакого способа узнать, сохраняются ли отношения. В этом случае подразумевается истина или пустая истина. Конечно нет доказательства того, что это ложь.

Последствия в логике были формализованы Уильямом Оккамом в его книге Summa Logicae в 14 веке. Эти несколько запутанные правила добавляют огромную выразительную силу логике и вычислениям. Без них в программах не было бы ветвлений (без IF, без FOR, без WHILE).

2.4. Общая логическая формула (схема) Эквивалентность

2.4.1. Равенство

Два (или более) логических оператора считаются равными IFF (тогда и только тогда, когда ↔ ), они имеют одинаковое значение истинности для каждого присвоения истинности; т.е. их таблицы истинности оценивать точно так же. Примером равных являются q ∧ p и p ∧ (q ∧ p)

.
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12 
 *
--------------
p q | (p ∧ q)
--------------
Т Т | Т Т Т
T F | T F F
F T | F F T
F F | F F F
---------------
Условный
- T: [T T]
- F: [F F] [F T] [T F]
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12 
 *
-------------------
p q | p ∧ (q ∧ p)
-------------------
Т Т | Т Т Т Т Т
T F | Т F F F T
F T | F F T F F
F F | F F F F F
--------------------
Условный
- T: [T T]
- F: [F F] [F T] [T F]

Поиск эквивалентных логических выражений меньшего числа вентилей (состояний) важен для несколько полей.В компьютере наука, меньшее количество состояний может привести к меньшему количеству памяти, меньшему количеству операций и меньшему количеству программ. В компьютерная инженерия, меньшее количество ворот означает меньшее количество цепей, меньшее количество энергии и меньше тепла.

С технической точки зрения, двусмысленность — это еще один способ выразить качество. Однако мы еще не ввели оператор «равно».

p = q ↔ (p → q) ∧ (q → p)

2.4.2. Двойное отрицание

В Logika и во многих других логических приложениях двойное отрицание эффективно компенсируют друг друга.Это не единственно возможная интерпретация из ¬п , но именно он реализован в Logika. Мы можем обсудить другие интерпретации в разделе логики высказываний.

2.4.3. Исключающее ИЛИ (XOR)

Как обсуждалось ранее, «или» широко используется в английском языке в исключительном смысле. (p XOR q) можно выразить несколькими способами:

 (п ∧ ¬ q) ∨ (¬p ∧ q)
(p ∨ q) ∧ ¬ (p ∧ q)

В классе мы не принимаем использование оператора XOR, вы должны выразить все формулы в терминах AND, OR, NOT и IMPLY.

2.4.4. Закон Де Моргана

Закон Де Моргана — это утверждение о взаимосвязи между AND и НЕ-ИЛИ (ИЛИ) ( ¬ (p ∨ q) ). В частности:

p ∧ q ↔ ¬ (¬ p ∨ ¬ q)

p ∨ q ↔ ¬ (¬ p ∧ ¬ q)

Это имеет важное значение для компьютерной инженерии, позволяя все логические конструкции должны быть выражены только двумя типами основных ворота, И-НЕ и НЕ; значительная экономия интегрированного производства микросхем.

Огастес Де Морган также ввел термин «математическая индукция» и предоставил подход для его доказательства.Математическая индукция — основа многих доказательства информатики в области алгоритмов, языков и вычислительная сложность.

2.4.5. Эквивалентность следствия

Наконец, импликация может быть выражена как отрицание и ИЛИ; или как его контрположительное заявление.

(p → q) ↔ ¬ p ∨ q

(p → q) ↔ (¬ q → ¬ p) контрпозитивное утверждение

Обратное предположение может быть правдой, а может и не быть

(p → q) ??? (q → p) обратное (НЕ ОБЯЗАТЕЛЬНО ЭКВИВАЛЕНТНОСТЬ)

Примечание

Хотя большинство формул, представленных в этом разделе, верны эквивалентности, ЕСЛИ вас попросят доказать, что они равны по таблице истинности, ожидается, что вы составите таблицу истинности для каждой стороны ↔ и показать, что их ценности совпадают для каждого задания истинности.

2,5. Почему его называют оператором «верхнего уровня»

Вернемся к 2-битному сумматору и рассмотрим только схему Q1. В цепи, можно сказать, что знания текут по проводам, где они трансформируются воротами, и новое знание переходит к следующей точке.

В аннотированной выше схеме видно, какие знания (факты и выведенные факты) в каждом сегменте провода. Обычная математика, отсюда и информатика методика заключается в представлении этого типа потока знаний в специализированном виде Граф называется деревом.Дерево представлено набором узлов и ребер, один узел выбирается в качестве «корня», и все узлы имеют уникальный путь (набор ребер), ведущие к корневому узлу. Условно дерево рисуют перевернутым, с корнем наверху и листьями, свисающими снизу.

В информатике в качестве корня выбирается узел, обеспечивающий «Окончательный ответ» на проблему. Как видите, ребра несут факты и узлы. операторы, которые выводят новые факты.

Древовидное представление компьютерной программы является фундаментальной абстракцией для специалист в области информатики.Современные компиляторы и интерпретаторы берут написанную программу на языке программирования высокого уровня и преобразовать его в абстрактное синтаксическое дерево (AST), который тогда преобразован в машинный код. Для языков в функциональной парадигме (C # и Java находятся в императивной и / или объектной парадигмах), существует сильная корреляция между структурой программы высокого уровня и структурой AST.

Когда мы сравниваем дерево с логическим оператором, мы видим самый низкий приоритет оператор — корень дерева; отсюда и термин «оператор верхнего уровня».

 *
(¬ (A1 ∧ B1)) ∧ (A1 ∧ B1)

2.6. Знания путешествуют по проводам цепи

До сих пор мы делали вид, что уровни низкого и высокого напряжения проходят по проводке. схемы. Но на самом деле по кругу движутся знания. Это можно понять по некоторым картинкам. Вот схема:

, а вот его кодировка в уравнениях:

 R = P ∧ Q
S = R ∨ Q
Т = ¬ S

Перерисуем схему по вертикали и положим рядом с заданием. уравнения:

Каждому проводу в цепи присвоено имя.Это всего лишь имен переменных . Действительно, первых (электронных) компьютерных программ в 1940-х годах были Описание электрических схем как это. Современный компьютер с хранимой программой, разработанный Джоном фон Нейманом в 1950-х годах, использовали регистры хранения для хранения значений имен переменных и использовали процессор для вычисления значений уравнений. Таким образом, процессор плюс регистры может моделировать схему, и все компьютерные программы — это просто описания схем, в которых протекает по проводам (переменным) .

Это источник компьютерного программирования на основе переменных и присваиваний. Теперь в каждой из программных точек , отмеченных звездочками на приведенной выше диаграмме, что информация путешествует по проводам? Мы могли бы использовать схему с некоторыми входами, чтобы увидеть, «что происходит». Скажем, мы поставляем true для P и false для Q :

На схеме показаны значения на проводах с маркировкой P , Q , R и S когда они путешествуют по цепи.Но это просто отслеживание значений переменных в программе присваивания. мы написали! «Выходная переменная» / запись с именем T имеет значение true .

Не менее интересно то, что мы можем анализировать программу / схему до , это полностью протестирован. Например, предположим, что схема будет вставлена ​​в плату, на которой находится ее P wire всегда будет получать на входе t, но мы не знаем, что получит Q . Что мы можем предсказать о поведении схемы, когда она встроена в плату? Это:

На диаграмме мы видим, что R = Q указано после логического элемента И.Откуда нам это знать? Во-первых, мы знаем, что R = P ∧ Q . Но P = истинное . Мы заменяем true на P и получаем R = true ∧ Q . Затем мы проводим анализ случаев и рассматриваем варианты возможной стоимости Q : Если Q — это истинное , то истинное ∧ Q истинное истинное , что упрощает до истинно , то есть к стоимости Q . Точно так же, когда Q является ложным , тогда t ∧ Q также является ложным .Следовательно, в обоих случаях истинных ∧ Q равен Q .

Приведенное выше рассуждение является вычетом — мы вывели из фактов P = истинное и R = P ∧ Q , что R = Q . Весь смысл этого курса — научиться делать такие выводы.

Другие вычеты в примере рассчитываются с аналогичным использованием подстановка, упрощение и анализ случаев.

Смысл предыдущего примера в том, что мы можем вывести (предсказать) свойства схему перед ее использованием.Эти вычеты дополняют тестирование.

Затем предположим, что мы ничего не знаем о P и Q в качестве входных данных. Что можно сказать о выходе схемы? Ну а вот это:

констатирует очевидное! Но, внимательно изучив таблицы истинности, мы можем также заявить, что Т = ¬Q . Позже в ходе курса мы узнаем правил вычета , которые вычисляют этот результат, а не полагаясь на таблицы истинности.

Наконец, мы можем создавать схемы с тремя или более входами, например.грамм., (¬ (P ∧ Q)) ∨ рэнд вычисляет:

Здесь столбец под OR определяет вывод. Мы видим, что эта схема излучает ложь только тогда, когда P и Q оба истинны и R ложно. Это намек на то, что схема ¬ (P ∧ Q ∧ ~ R) ведет себя точно так же. (имеет ту же таблицу истинности), что и приведенная выше. Еще одна эквивалентная схема — (¬P) ∨ (¬Q) ∨ R . (Почему?)

В схемотехнике поиск эквивалентных схем с меньшим числом вентилей и переменных экономит электроэнергию, время и материал.

Эта заметка была адаптирована из CIS 301 Дэвида Шмидта, 2008 г., Глава 0 примечание курса.

Он был обновлен в 2018 году доктором Джоном Хэтклиффом и Джорджем Лавецци
, чтобы он соответствовал синтаксису Logika и более точно соответствовал курсу
KSU CIS 301, который преподавался весной 2018 года.

Логические ворота

В реальном мире цифровые устройства не являются абстрактными логическими выражениями булевой алгебры, а являются аппаратными реализациями этих выражений.Логические выражения транслируются в структуры устройства, называемые логическими вентилями . Логический вентиль является как символическим представлением логической операции, так и при использовании в цифровой электронике может быть реальной схемой в оборудовании. Один логический вентиль обычно состоит из нескольких транзисторов, разделенных пространством со многими другими в интегральной схеме.

Каждый из основных операторов, о которых мы узнали в разделе выражений, имеет символ ворот. Символ заменяет оператор, а переменные являются входными данными для логического элемента.Результирующее значение из уравнения выражения является выходом ворот. Выход элемента может быть конечным результатом или может быть подключен как вход к еще одному элементу.

Символы ворот

Логические элементы — это символы, которые могут напрямую заменять выражение в логической арифметике. Каждый из них имеет разную форму, чтобы показать свою особую функцию. Входные данные (логические переменные) вводятся слева от символа, а выходные данные — справа. При объединении несколько ворот могут образовать сложную логическую систему оценки, имеющую множество входов и выходов.Цифровые компьютеры созданы путем соединения тысяч или миллионов этих ворот вместе.

Элемент НЕ

Элемент НЕ представляет собой стрелку вперед с маленьким кружком на выходе. Круглая часть символа означает, что выход отрицает вход.

Вентиль ИЛИ

Вентиль ИЛИ имеет изогнутую входную сторону и заостренный выход.

Логический элемент И

Логический элемент И имеет плоскую входную сторону и круглую выходную сторону.

Элемент исключающего ИЛИ (XOR)

Символ логического элемента исключающее ИЛИ аналогичен вентилю ИЛИ, но имеет дополнительную изогнутую линию, пересекающую входы.

Комбинированная логика

Когда вы соединяете несколько вентилей вместе, вы получаете комбинированную логическую систему или комбинаторную логику . Чтобы разработать комбинированную логическую систему, мы можем использовать таблицы истинности для сопоставления логических выходов для различных входных условий. Логические выражения записываются из условий в таблице.Затем мы можем напрямую преобразовать выражение в схему логических вентилей.

Возможно, вы помните, что еще в логических элементах мы видели, что в коде для XOR нет оператора. Он был составлен с помощью комбинации операторов AND, OR и NOT:

  пусть A = false
пусть B = false
пусть Q = (A || B) &&! (A && B)

Давайте сопоставим входные и выходные условия в таблице истинности для комбинированной логической системы для XOR. Мы найдем все условия, которые вызывают истинный результат , и создадим для них логическое выражение.

А Б A ⊕ B
Ф. F F
Ф. Т Т
Т F Т
Т Т F

Есть два условия, при которых столбец результатов имеет истинных значений. Первое условие: A — это ложный , а B — истинный , что выражается как ~ A · B .Второе условие: A — это истинное , а B — ложное , которое выражается как A · ~ B . Наше выражение XOR — true , когда одно из этих условий — true , которое записывается как:

A ⊕ B = (~ A · B) + (A · ~ B)

В коде это выражение формируется с помощью следующих логических блоков:

  пусть A = false
пусть B = false
пусть Q = (! A && B) || (A &&! B)

Покрытие уравнения до логических вентилей дает следующую диаграмму.Обратите внимание, как каждый вентиль «связывает» переменные вместе, как и логические блоки в приведенном выше коде.

Однако, если мы возьмем два других неиспользуемых условия из таблицы истинности, которые делают операцию XOR ложной , мы можем составить отрицательное уравнение для XOR, называемое NXOR:

~ (A ⊕ B) = (~ A · ~ B) + (A · B)

Чтобы вернуться к A ⊕ B , мы должны отрицать это отрицательное уравнение. Затем, с помощью Thereom Де Моргана, мы получаем другое уравнение для XOR, но оно все еще логически эквивалентно исходному.

A ⊕ B = (A + B) · ~ (A · B)

Когда это уравнение преобразуется в логические вентили, их на один вентиль меньше, чем на первой диаграмме.

Эта диаграмма менее сложна, чем первая. Уменьшение количества вентилей для достижения одного и того же логического результата — одна из основных целей проектирования цифровой логики. Для электронных устройств это позволяет большему количеству вентилей использовать ограниченное пространство на интегральной схеме.

Ошибка разрыва связи

    Приборная панель

    ECE 1240-001 Весна 2019

    Перейти к содержанию Приборная панель

    • Авторизоваться

    • Приборная панель

    • Календарь

    • Входящие

    • История

    • Помощь

    Закрывать