Калькулятор катушки индуктивности без сердечника. Расчет катушки индуктивности без сердечника: формулы, методы и онлайн-калькулятор

Как рассчитать индуктивность катушки без сердечника. Какие формулы используются для расчета числа витков и длины провода. Где найти онлайн-калькулятор для быстрого расчета параметров катушки индуктивности. Какие факторы влияют на индуктивность воздушной катушки.

Что такое катушка индуктивности и для чего она нужна

Катушка индуктивности — это элемент электрической цепи, обладающий значительной индуктивностью при малой емкости и низком активном сопротивлении. Она представляет собой провод, намотанный в виде спирали на каркас.

Основные области применения катушек индуктивности:

• Фильтрация высокочастотных сигналов
• Создание колебательных контуров
• Накопление энергии магнитного поля
• Сглаживание пульсаций тока
• Разделение сигналов по частоте

Катушки без сердечника (воздушные) отличаются простотой конструкции, но имеют меньшую индуктивность по сравнению с катушками на магнитных сердечниках. При этом они не подвержены насыщению и имеют стабильные параметры.

Факторы, влияющие на индуктивность воздушной катушки

На величину индуктивности катушки без сердечника влияют следующие основные факторы:

• Число витков — чем больше витков, тем выше индуктивность
• Диаметр катушки — с увеличением диаметра индуктивность растет
• Длина намотки — при увеличении длины индуктивность уменьшается
• Плотность намотки — чем плотнее намотка, тем выше индуктивность
• Форма сечения катушки — круглое сечение обеспечивает максимальную индуктивность

При проектировании важно учитывать взаимное влияние этих параметров для получения требуемой индуктивности.

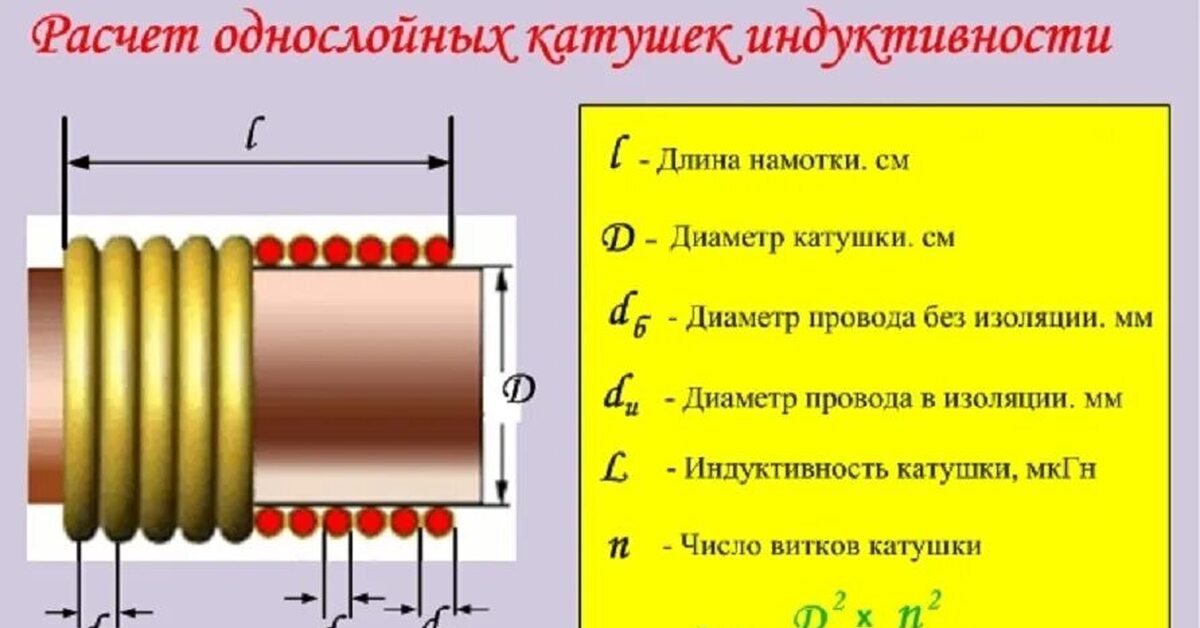
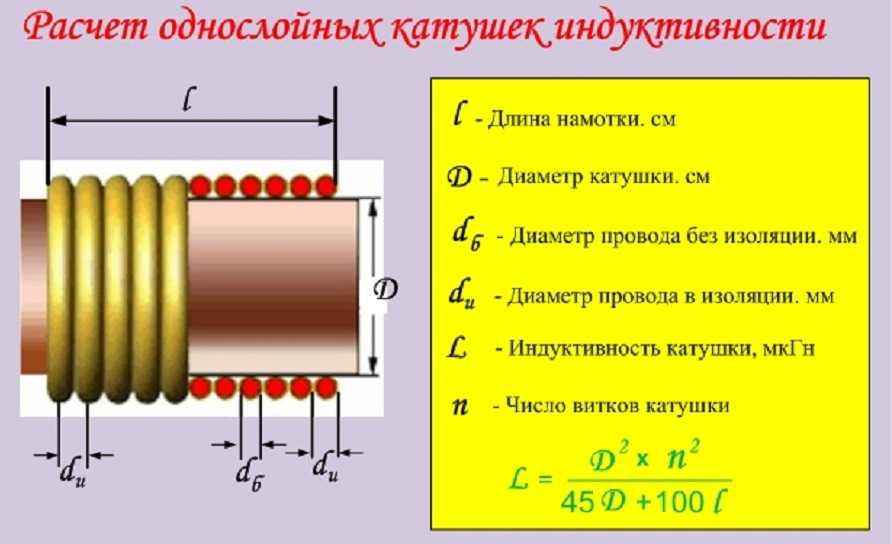
Формулы для расчета индуктивности однослойной цилиндрической катушки

Для расчета индуктивности однослойной цилиндрической катушки без сердечника чаще всего используется формула:

L = (μ0 * N^2 * S) / l

где:

• L — индуктивность катушки (Гн)
• μ0 — магнитная проницаемость вакуума (4π * 10^-7 Гн/м)
• N — число витков
• S — площадь поперечного сечения катушки (м^2)
• l — длина намотки (м)

Эта формула дает приближенное значение, не учитывающее ряд факторов. Для более точного расчета применяются усложненные формулы, например формула Уилера:

L = (N^2 * R^2) / (9R + 10H)

где R — радиус катушки, H — длина намотки.

Расчет числа витков и длины провода

Для определения необходимого числа витков катушки при заданной индуктивности можно использовать следующую формулу:

N = sqrt((L * l) / (μ0 * S))

Длина провода для намотки катушки рассчитывается по формуле:

Lпр = π * D * N

где D — диаметр каркаса катушки.

При расчетах важно учитывать, что реальная длина провода будет немного больше из-за выводов катушки.

Онлайн-калькуляторы для расчета параметров катушки

Для быстрого расчета параметров катушки индуктивности удобно использовать онлайн-калькуляторы. Они позволяют быстро рассчитать индуктивность по заданным размерам или определить необходимое число витков.

Примеры популярных калькуляторов:

• Калькулятор катушек indukcia.ru
• Расчет однослойных катушек на сайте cxem.net
• Универсальный калькулятор radiohlam.ru

При использовании онлайн-инструментов важно внимательно вводить исходные данные и учитывать единицы измерения.

Практические советы по намотке катушек

При самостоятельном изготовлении катушек индуктивности следует учитывать ряд практических моментов:

• Используйте каркас из диэлектрического материала
• Обеспечьте плотную и равномерную намотку витков
• Закрепите концы обмотки для предотвращения разматывания
• Покройте катушку лаком для защиты от влаги
• Оставьте запас по длине выводов

Для повышения добротности катушки рекомендуется использовать провод большего диаметра и обеспечивать зазоры между витками.

Проверка расчетной индуктивности

После изготовления катушки важно проверить ее реальную индуктивность. Для этого можно использовать следующие методы:

• Измерение с помощью RLC-метра
• Расчет по резонансной частоте колебательного контура
• Косвенное измерение по импедансу на заданной частоте

При значительном расхождении расчетной и измеренной индуктивности необходимо скорректировать число витков катушки.

Заключение

Расчет катушки индуктивности без сердечника — важный этап при разработке радиоэлектронных устройств. Современные методы расчета и онлайн-инструменты значительно упрощают этот процесс. При этом важно учитывать особенности конкретной конструкции и проводить экспериментальную проверку полученных результатов.

Расчёт катушки индуктивности без сердечника онлайн

Катушки индуктивности предназначены для фильтрации токов высокой частоты. Они устанавливаются в колебательных контурах и используются для других целей в электрических и электронных схемах. Готовое устройство заводского изготовления надёжнее в работе, но дороже, чем изготовленное своими руками. Кроме того, не всегда удаётся приобрести элемент с необходимыми характеристиками.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Онлайн-расчет катушки индуктивности
• Расчет катушки индуктивности
• Расчет многослойной катушки
• Расчет катушек индуктивности без сердечника
• Проектирование однослойной воздушной катушки
• Расчет катушки индуктивности
• Онлайн калькулятор расчета индуктивности катушки с воздушным сердечником

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Дроссель, зачем нужен и что такое индуктивность

Онлайн-расчет катушки индуктивности

Катушкой индуктивности — это элемент электрической цепи с высоким значением индуктивности, при этом низкими емкостью и активным сопротивлением. Их используют:. Катушка представляет собой намотанную на каркасе проволоку в виде спирали, а намотка может быть однослойной или многослойной, виток к витку или с расстоянием. Они бывают различных типов и форм, например, без сердечника обладают небольшой индуктивностью, а с сердечником она значительно увеличивается.

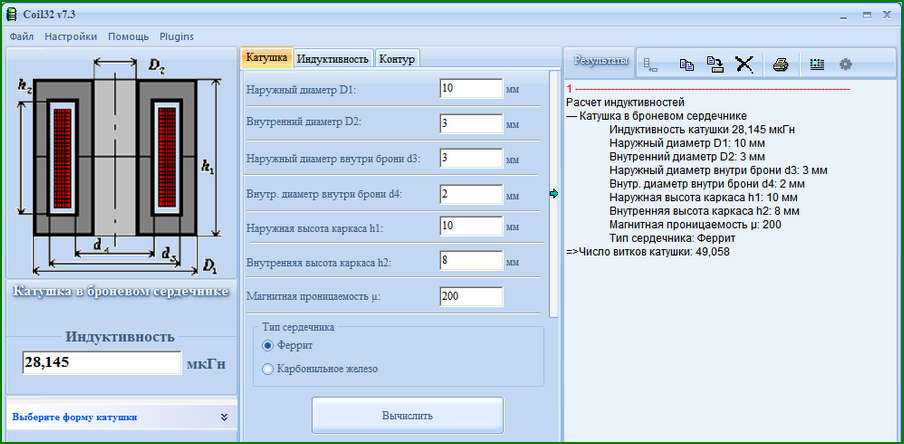
Это обусловлено магнитной проницаемостью материала. Форма сердечника может быть разной, выделяют броневые, стержневые и тороидальные. Для улучшения массогабаритных параметров катушки наматывают на ферритовом кольце — такой вариант называется тороидальным способом намотки. Как рассчитать катушку в онлайн калькуляторе и вручную? На её параметры влияет количество витков длина провода , наличие и материал сердечника.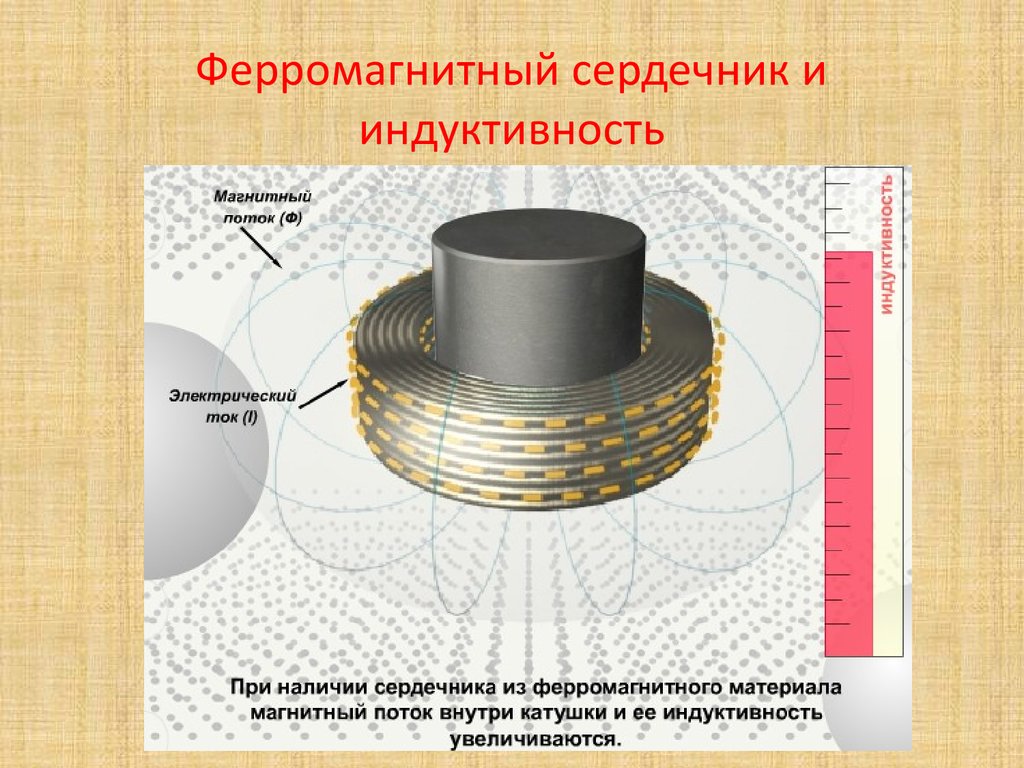

Форма последнего выбирается исходя из других требований, таких как размеры — они влияют на возможность расположения элемента в корпусе.

Но вы можете сделать это и своими руками. Воспользовавшись формулой для расчёта, зная индуктивность катушки:. Преимущества онлайн калькулятора перед этой формулой — быстрый и простой расчет. Нужно внести необходимую индуктивность, диаметр каркаса и длину намотки. После этого вы должны определится с тем, какой у вас есть провод, измерить диаметр его жилы и, если он изолирован, внешний диаметр по изоляции.

Ваш e-mail не будет опубликован. Вы здесь: Главная Калькуляторы. Автор: Александр Мясоедов. Калькулятор для расчета катушки индуктивности. Опубликовано: Их используют: В фильтрах частот, например, в акустических системах для разделения сигнала по частотам для воспроизведения на соответствующих динамиках, или фильтрации электромагнитных помех.

В источниках питания, например, для включения светодиодов от одного элемента питания, где она используется в качестве накопителя энергии и повышения понижения напряжения. В таком случае этот источник называется импульсным бестрансформаторным преобразователем напряжения.

В радиопередающих устройствах, в качестве элемента колебательного контура, настроенного на нужную частоту и в других устройствах. При этом вы можете подобрать соответствующий частоте конденсатор. Требуемая индуктивность L. Добавить комментарий Отменить ответ Ваш e-mail не будет опубликован. Другие статьи по теме Калькулятор для расчета плавкой вставки предохранителя.

Расчет катушки индуктивности

При заданной индуктивности, диаметре каркаса катушки и толщины намотки можно рассчитать число витков катушки, а так же определить диаметр провода и число слоев намотки. Следующая форма расчета позволит рассчитать кол-во витков катушки в зависимости от диаметра провода имеющегося у Вас в наличии. Для отправки комментария вам необходимо авторизоваться. Ваш IP: Расчет числа витков многослойной катушки без сердечника.

Форма для онлайн расчета дросселя, катушки индуктивности.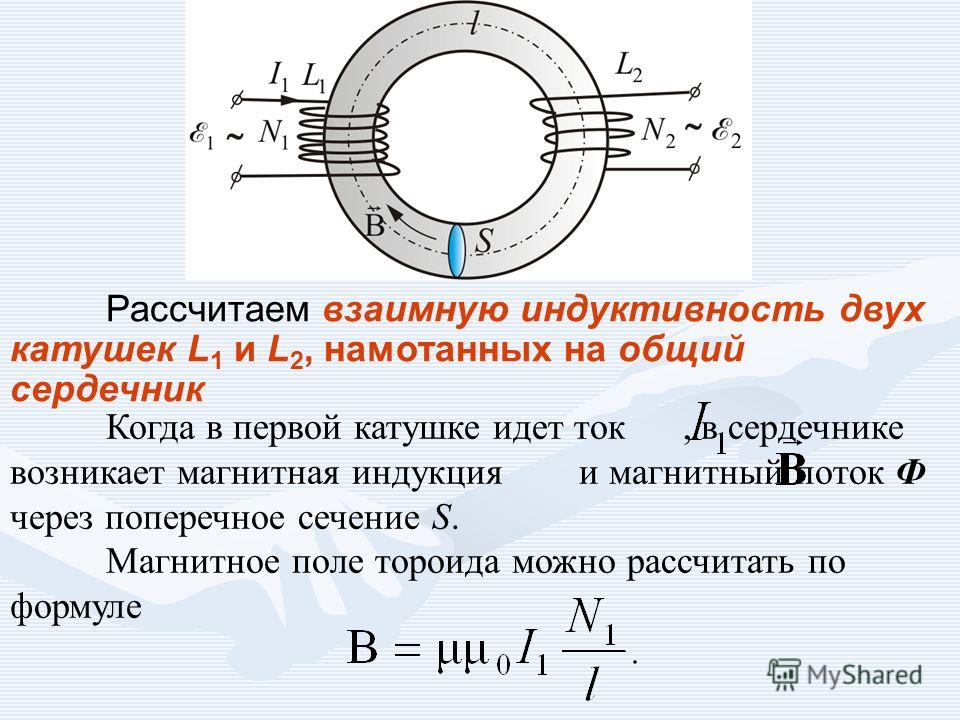 Для изготовления Предлагаемый скрипт рассчитан на Ш и П — образные сердечники.

Расчет многослойной катушки

Всем доброго времени суток. В прошлых статьях часть 1, часть 2, часть 3 я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами. В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость. Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения.

Расчет катушек индуктивности без сердечника

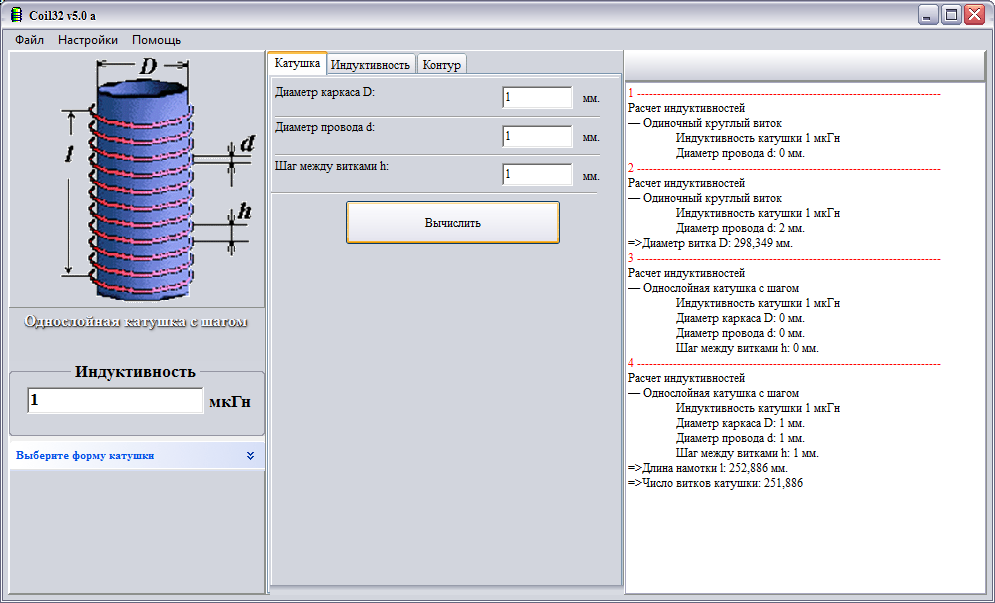
Катушки индуктивности являются неотъемлемым элементом различных радиоэлектронных схем. Основным её свойством является наличие большой индуктивности при малой емкости и низком активном сопротивлении. Для автоматического расчета наиболее часто используется программа Coil Её можно бесплатно скопировать с одноименного сайта либо воспользоваться онлайн калькулятором.

Сначала цифрами указывается величина начальной магнитной проницаемости, затем марка используемого материала, и потом размер кольца в миллиметрах:. Где — величина начальной магнитной проницаемости, НН — марка материала, D — внешний диаметр, d — внутренний диаметр, h — толщина кольца, все размеры в миллиметрах.

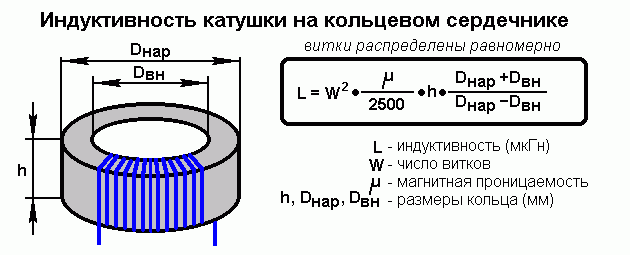
Проектирование однослойной воздушной катушки

Индуктивность катушки зависит от её геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше её индуктивность. Если катушка наматывается плотно виток к витку, то индуктивность её будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется намотать катушку по заданным размерам и нет провода нужного диаметра, то при намотке её более толстым проводом надо несколько увеличить, а тонким — уменьшить число витков катушки, чтобы получить необходимую индуктивность. При расчёте катушки могут встретиться два случая:. В первом случае все исходные данные, входящие в формулу, известны, и расчёт не представляет затруднений.

Расчет катушки индуктивности

Для работы калькулятора необходимо включить JavaScript в вашем браузере! Об особенностях расчета однослойных катушек можно узнать здесь. Программа Coil32 ведет расчет по другой методике и результат, полученный в ней, может незначительно отличаться от результата этого калькулятора. Кроме того Coil32 также позволяет рассчитать конструктивную добротность катушки и ее собственную емкость. Имя обязательное. E-Mail обязательное. Подписаться на уведомления о новых комментариях. Главное меню.

Катушка индуктивности катушки без сердечника можно.

Онлайн калькулятор расчета индуктивности катушки с воздушным сердечником

На практике нередко случаются ситуации, когда при выходе со строя катушки индуктивности, ее необходимо восстановить — намотать новую проволоку взамен старой. При этом вам уже известны геометрические параметры катушки, но требуется узнать, сколько сделать витков, слоев, их толщину и длину необходимого для этого провода. Стоит отметить, что при намотке витки должны ложиться вплотную без зазора.

Катушка индуктивности является неотъемлемым элементом большинства современных приборов. При этом она используется для различных целей в работе электрических цепей. В случае необходимости замены можно использовать как заводскую, так и изготовленную самостоятельно катушку. Но при этом необходимо учитывать ее основной параметр — индуктивность. Для того чтобы рассчитать индуктивность катушки без сердечника можно воспользоваться универсальной формулой:.

Довольно часто перед радиолюбителем встает вопрос: Как рассчитать индуктивность катушки?

При заданной индуктивности, диаметре каркаса катушки и толщины намотки можно рассчитать число витков катушки, а так же определить диаметр провода и число слоев намотки. Следующая форма расчета позволит рассчитать кол-во витков катушки в зависимости от диаметра провода имеющегося у Вас в наличии. Для расчета достаточно задать нужную Вам индуктивность катушки, диаметр каркаса, длину намотки и указать диаметр провода в изоляции. Используя формулу расчета индуктивности многослойной катушки, можно рассчитать индуктивность при заданных значениях среднего диаметра катушки, толщины намотки, числе витков и длины намотки. К мультиметру собирают приставку описанную в этой статье.

На практике нередко случаются ситуации, когда при выходе со строя катушки индуктивности, ее необходимо восстановить — намотать новую проволоку взамен старой. При этом вам уже известны геометрические параметры катушки, но требуется узнать, сколько сделать витков, слоев, их толщину и длину необходимого для этого провода. Стоит отметить, что при намотке витки должны ложиться вплотную без зазора.

Схема замещения катушки индуктивности малого номинала на

Онлайн калькулятор расчёта эквивалентной LC-цепи.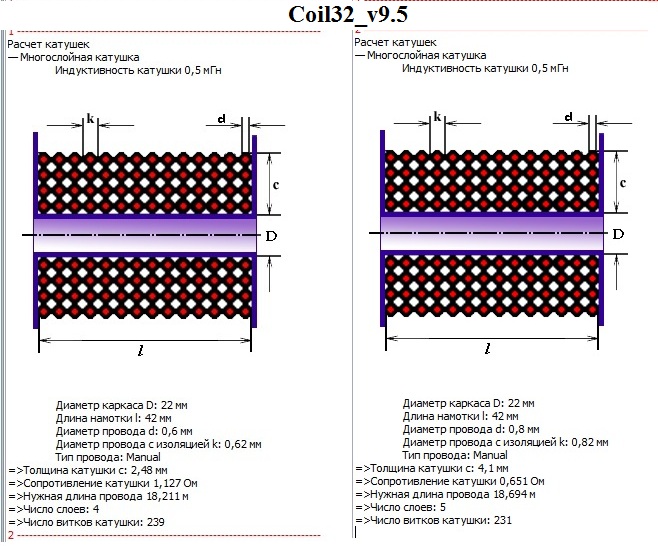

Казалось бы, какие проблемы могут быть связаны с малыми значениями индуктивностей катушек?
Наоборот — витков поменьше, провод потолще… Сиди и радуйся, не умеешь радоваться — просто сиди. А радоваться, действительно, есть чему: это и приемлемые массогабаритные характеристики, и низкие потери, и высокая добротность подобных моточных изделий.
Так ведь нет, что-то душеньке радиолюбительской неймётся при встрече с изображениями катушек наногенриевых номиналов.
Причём, если с величинами индуктивностей 25 — 35нГн особых проблем не возникает (это 2-3 витка миллиметрового провода, намотанного на 5мм оправке), то номиналы менее 10нГн порой вызывают замешательство и чувство недоумения на лице молодого разработчика.
Опытные СВЧисты, конечно, посмеются подобной постановке проблемы, они-то прекрасно знают, что подобные катушки легко и непринуждённо реализуются на полосковых линиях. Однако для нас, простых пацанов, а также недоступных для понимания и логического анализа загадочных девушек, окажется весьма кстати эквивалентная схема замещения катушки малого номинала на изделие, доступное для внятной намотки.
Тут ничего изобретать не надо, схема эта известна и приведена на Рис.1.

Рис.1

Поскольку в последовательном контуре суммарный сдвиг фаз между напряжениями на катушке и на конденсаторе составляет 180°, то равенство характеристических сопротивлений обеих цепей будет выглядеть следующим образом:
X_L = X_L1 — X_{C1 ;}

Произведя необходимые преобразования, получим формулу для расчёта ёмкости конденсатора С1 для требуемого значения индуктивности L1:
C₁ = 1/[(2πF)²×(L₁ — L)] ;

Сдобрим полученную формулу калькулятором.

РАСЧЁТ ЭЛЕМЕНТОВ ЦЕПИ ЗАМЕЩЕНИЯ КАТУШКИ ИНДУКТИВНОСТИ.

Рабочая частота F (МГц)
Первоначальная индуктивность L (нГн)
Требуемая индуктивность L1 (L1>L) (нГн)
Ёмкость конденсатора С1 (пФ)

Будда призывал своих учеников не верить никому на слово (даже ему), и, прежде чем принять чьи-то советы, тщательно выяснять, а соответствуют ли они действительности. Поступим так же и мы.

Рис.2

Для начала рассмотрим схему цепи согласования выходного каскада передатчика с антенной (Рис.2). Расчёт элементов был произведён для частоты 145МГц на странице  ссылка на страницу.
А теперь давайте посмотрим, как поведёт себя коэффициент передачи и АЧХ цепи при замене катушки индуктивности L1 номиналом 7нГн на цепочку, представленную на Рис.1.

Рис.3

На верхней диаграмме Рис.3 приведена АЧХ цепи при изначальной L1=7нГн, ниже — при замене L1 на цепочку, состоящую из: 20нГн и 91пФ, ещё ниже — при замене на цепочку: 40нГн и 36пФ.
Ну, что тут скажешь? Налицо незначительное уменьшение коэффициента передачи и значительное сужение полосы пропускания. Причём, чем большее значение принимает новая катушка по отношению к первоначальной, тем сильнее проявляются данные эффекты.

А теперь давайте то же самое проделаем с межкаскадной согласующей цепью, рассчитанной на странице  ссылка на страницу.

Рис.4

Рис.5

Катушки индуктивности в данном случае были использованы номиналами 6.5, 20 и 40нГн.
Тенденция наблюдается такая же, как и в предыдущем случае, но менее ярко выраженная. Да это и понятно — при столь низком сопротивлении нагрузки добротность нагруженного контура получается значительно ниже.

Какие можно сделать выводы, наблюдая за описанными выше потоками движения электронов в модифицированных катушках?
В принципе, подобная схема замещения малых индуктивностей на катушки бОльших номиналов имеет право на жизнь. Несмотря на некоторое ухудшение передаточных характеристик и сужение полосы пропускания согласующих устройств, возможность изготовления моточного изделия с предсказуемыми параметрами может для кого-то явиться решающим фактором при выборе данного схемотехнического решения.
Тут важно не сильно усердствовать и не гнаться за значительными величинами, а ограничиться коэффициентом повышения индуктивности — в 3-4 раза.

 

Учебное пособие по двигателю постоянного тока

. Расчеты двигателей постоянного тока без сердечника

Ниже приведен метод определения параметров двигателя на примере двигателя постоянного тока без сердечника 2668W024CR. Сначала мы объясним более эмпирический подход, затем проведем теоретический расчет.

Одним из широко используемых методов графического отображения характеристик двигателя является использование кривых крутящий момент-скорость. Хотя использование кривых крутящий момент-скорость гораздо более распространено в технической литературе для более крупных машин постоянного тока, чем для небольших устройств без сердечника, этот метод применим в любом случае.

Обычно кривые крутящий момент-скорость строятся путем построения графика скорости двигателя, тока двигателя, механической выходной мощности и КПД в зависимости от крутящего момента двигателя. В следующем обсуждении будет описано построение набора кривых крутящий момент-скорость для типичного двигателя постоянного тока на основе серии измерений необработанных данных.

Номинальное напряжение 2668W024CR составляет 24 В. Если у вас есть несколько основных элементов лабораторного оборудования, вы можете измерить кривые крутящий момент-скорость для двигателя постоянного тока без сердечника серии 2668 CR в заданной рабочей точке.

Шаг 1: Измерьте основные параметры

Многие параметры можно получить непосредственно с помощью контроллера движения, например, одного из контроллеров движения FAULHABER MC3. Большинство производителей контроллеров предлагают программное обеспечение, такое как FAULHABER Motion Manager, которое включает в себя функцию записи кривой, отображающую напряжение, ток, положение, скорость и т. д. Они также могут предоставить точный моментальный снимок работы двигателя в мельчайших деталях. Например, контроллеры движения семейства MC3 (MC 5004, MC 5005 и MC 5010) могут измерять множество параметров движения. Это, вероятно, самый быстрый метод получения данных для построения кривой крутящий момент-скорость, но это не единственный метод.

Если контроллер с возможностью записи трассировки недоступен, мы также можем использовать базовое лабораторное оборудование для определения характеристик двигателя в условиях останова, номинального состояния и без нагрузки. Используя источник питания, настроенный на 24 В, запустите 2668W024CR без нагрузки и измерьте скорость вращения с помощью бесконтактного тахометра (например, стробоскопа). Кроме того, измерьте ток двигателя в этом состоянии без нагрузки. Токовый пробник идеально подходит для этого измерения, так как он не добавляет сопротивления последовательно с работающим двигателем. Используя нагрузку с регулируемым крутящим моментом, такую ​​как тормоз мелких частиц или динамометр с регулируемым гистерезисом, к валу двигателя может быть присоединена нагрузка.

Теперь увеличьте крутящий момент двигателя до точки, при которой происходит остановка. В остановленном состоянии измерьте крутящий момент от тормоза и ток двигателя. Для этого обсуждения предположим, что муфта не добавляет нагрузки к двигателю и что нагрузка от тормоза не включает неизвестные фрикционные компоненты. В этот момент также полезно измерить терминальное сопротивление двигателя. Измерьте сопротивление, прикоснувшись к клеммам двигателя омметром. Затем прокрутите вал двигателя и выполните еще одно измерение. Измерения должны быть очень близки по значению. Продолжайте вращать вал и сделайте не менее трех измерений. Это гарантирует, что измерения не проводились в точке минимального контакта с коммутатором.

Теперь мы измерили:

N ₀ = Скорость без нагрузки
I ₀ = ток без нагрузки
M _H = ROOR CORQU

Шаг 2. Постройте график зависимости тока от крутящего момента и скорости от крутящего момента

Вы можете построить график с крутящим моментом двигателя по оси абсцисс (горизонтальная ось), скоростью по левой оси ординаты (вертикальная ось) и током по правой стороне ординаты. Масштабируйте оси на основе измерений, сделанных на первом шаге. Проведите прямую линию от левого начала графика (нулевой крутящий момент и нулевой ток) к току останова на правой стороне ординаты (момент останова и ток останова). Эта линия представляет собой график зависимости тока двигателя от крутящего момента двигателя. Наклон этой линии представляет собой текущую константу k _I  которое представляет собой константу пропорциональности отношения между током двигателя и крутящим моментом двигателя (в единицах тока на единицу крутящего момента или А/мНм). Обратная величина этого наклона представляет собой постоянную крутящего момента k _M (в единицах крутящего момента на единицу тока или мНм/А).

Где:
k _I  = постоянная тока
k _M = постоянная крутящего момента

Для целей данного обсуждения предполагается, что двигатель не имеет внутреннего трения.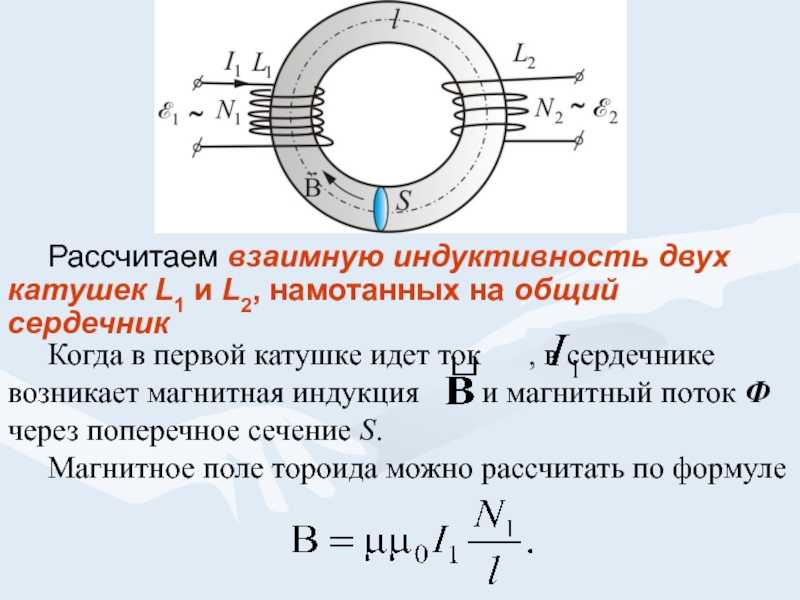 На практике момент трения двигателя M _R  определяется путем умножения постоянной крутящего момента k _M  двигателя на измеренный ток холостого хода I ₀ . Линия крутящего момента в зависимости от скорости и линия крутящего момента в зависимости от тока затем начинаются не от левой вертикальной оси, а со смещением по горизонтальной оси, равным расчетному моменту трения.

Где:
M _R  = Момент трения

Шаг 3: График зависимости мощности от крутящего момента и эффективности от крутящего момента

В большинстве случаев можно добавить две дополнительные вертикальные оси для построения зависимости мощности и эффективности от крутящего момента. Вторая вертикальная ось обычно используется для эффективности, а третья вертикальная ось может использоваться для мощности. Для упрощения этого обсуждения КПД в зависимости от крутящего момента и мощность в зависимости от крутящего момента будут нанесены на тот же график, что и графики зависимости скорости от крутящего момента и тока от крутящего момента (пример показан ниже).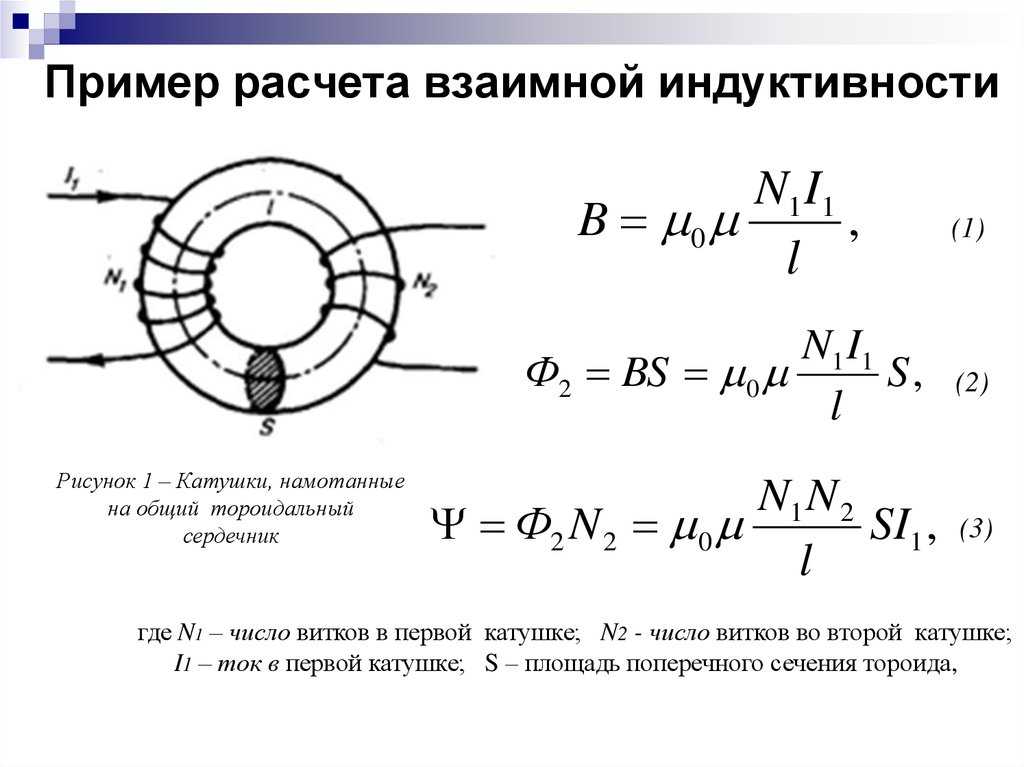

Составьте таблицу механической мощности двигателя в различных точках от холостого хода до момента остановки. Поскольку выходная механическая мощность — это просто произведение крутящего момента и скорости с поправочным коэффициентом для единиц измерения (см. раздел о расчете начальной требуемой мощности), мощность можно рассчитать, используя ранее построенную линию зависимости скорости от крутящего момента.

Пример таблицы расчетов для двигателя 2668W024CR показан в Таблице 1. Затем каждая расчетная точка для мощности наносится на график. Результирующая функция представляет собой параболическую кривую, как показано ниже на графике 1. Максимальная механическая мощность возникает примерно при половине крутящего момента срыва. Скорость в этот момент составляет примерно половину скорости холостого хода.

Составьте таблицу КПД двигателя в различных точках от скорости холостого хода до крутящего момента. Задано напряжение, приложенное к двигателю, и нанесен ток при различных уровнях крутящего момента. Произведение тока двигателя и приложенного напряжения представляет собой потребляемую двигателем мощность. В каждой точке, выбранной для расчета, КПД η двигателя представляет собой выходную механическую мощность, деленную на потребляемую электрическую мощность. Опять же, примерная таблица для двигателя 2668W024CR показана в таблице 1, а примерная кривая — на графике 1. Максимальный КПД достигается примерно при 10% крутящего момента двигателя.

Определения участка

• Синий = скорость против крутящего момента ( N против M )
• Красный = ток против крутящего момента ( I против M )
• Green = Effqueptialty Vs. Courte (Torque. η по сравнению с M )
• Коричневый = мощность по отношению к крутящему моменту ( P по сравнению с M )

Характеристики двигателя

Примечание. Обратите внимание на изменение всех четырех сплошных графиков в результате увеличения сопротивления в медных обмотках и ослабления выходного крутящего момента из-за повышения температуры. Таким образом, ваши результаты могут немного отличаться в зависимости от того, холодный или теплый двигатель, когда вы строите графики.

Load current	2,79 A
Load voltage	24,11 V
Motor winding temperature	140,23 °C
Motor housing temperature	105, 03 °C
Motor speed	7370 min -1
Required load torque	68 mNm
Output power	52,48 W
Эффективность (общая)	77,97 %

Примечание. Из-за нехватки места показан пример расчета для одной точки.

Теоретический расчет параметров двигателя

Другим полезным параметром при выборе двигателя является постоянная двигателя. Правильное использование этого показателя качества существенно сократит итерационный процесс выбора двигателя постоянного тока. Он просто измеряет внутреннюю способность преобразователя преобразовывать электрическую энергию в механическую.

Максимальный КПД достигается примерно при 10% крутящего момента двигателя. Знаменатель известен как резистивная потеря мощности. С помощью некоторых алгебраических преобразований уравнение можно упростить до:

Пожалуйста, имейте в виду, что k _m (постоянная двигателя) не следует путать с k _M (постоянная крутящего момента). Обратите внимание, что нижний индекс константы двигателя записывается строчными буквами « м », в то время как нижний индекс константы крутящего момента использует заглавные буквы « M 9».0022».

Для щеточного или бесщеточного двигателя постоянного тока относительно небольшого размера зависимости, управляющие поведением двигателя в различных обстоятельствах, могут быть получены из законов физики и характеристик самих двигателей. Правило напряжения Кирхгофа гласит: «Сумма повышений потенциала в контуре цепи должна равняться сумме падений потенциалов». Применительно к двигателю постоянного тока, соединенному последовательно с источником питания постоянного тока, правило напряжения Кирхгофа может быть выражено как «Номинальное напряжение питания от источника питания должно быть равно по величине сумме падения напряжения на сопротивлении обмоток и противо-ЭДС, создаваемой двигателем».

Где:

U = источник питания в V
I = ток в
R = Сопротивление терминала в ω
U _E = Back-Emf-Emf-Emf в V 9003

генерируемая двигателем, прямо пропорциональна угловой скорости двигателя. Константа пропорциональности – это константа противо-ЭДС двигателя.

Где:

ω  = угловая скорость двигателя
k _E  = постоянная противо-ЭДС двигателя

Таким образом, путем замены:

Константа противо-ЭДС двигателя обычно указывается производителем двигателя в В/об/мин или мВ/об/мин. Чтобы получить осмысленное значение противо-ЭДС, необходимо указать скорость двигателя в единицах, совместимых с заданной константой противо-ЭДС.

«Сумма повышений потенциала в контуре цепи должна равняться сумме падений потенциалов». (правило напряжения Кирхгофа)

Постоянная двигателя зависит от конструкции катушки, силы и направления силовых линий в воздушном зазоре. Хотя можно показать, что обычно указанные три константы двигателя (константа противо-ЭДС, константа крутящего момента и константа скорости) равны, если используются соответствующие единицы измерения, расчет облегчается заданием трех констант в общепринятых единицах измерения.

Крутящий момент, создаваемый ротором, прямо пропорционален току в обмотках якоря. Константа пропорциональности – это константа крутящего момента двигателя.

Где:

M _m = крутящий момент, развиваемый двигателем
k _M  = постоянный крутящий момент двигателя крутящий момент двигателя плюс крутящий момент нагрузки (из-за внешней механической нагрузки):

Где:

M _R = момент трения двигателя
M _L  = крутящий момент нагрузки сумма момента трения и момента нагрузки.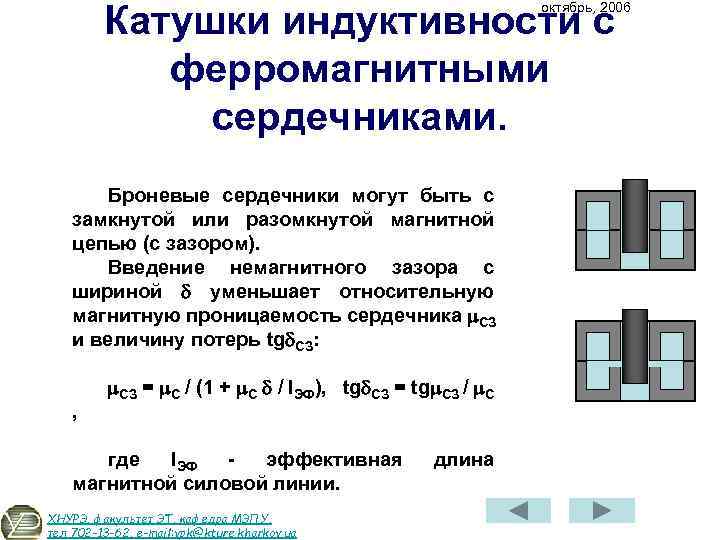 Константа пропорциональности представляет собой наклон кривой крутящий момент-скорость. Производительность двигателя лучше, когда этот наклон имеет меньшее значение. Чем круче падение наклона, тем хуже производительность, которую можно ожидать от данного двигателя без сердечника. Это соотношение можно рассчитать по формуле:

Где:

ΔN = изменение скорости
ΔM = изменение крутящего момента
M _H = Крутящий момент NOT-BOURD
N ₀ = NO-BOAD SPEEP

N ₀ = NO-BEAD SPEED

N ₀ = NO-BOAD SPEED

N ₀ = NO-BEAD SPEED

AN ₀ = NO-BEAD SPEED

. это значение для определения скорости, n :

С помощью исчисления мы дифференцируем обе части по отношению к M , что дает:

или

Хотя мы не показываем здесь отрицательный знак, подразумевается, что результат даст уменьшающийся (отрицательный) наклон.

Пример теоретического расчета двигателя

Давайте немного углубимся в теоретические расчеты. Двигатель постоянного тока без сердечника 2668W024CR должен работать с напряжением 24 В, подаваемым на клеммы двигателя, и с крутящим моментом 68 мН·м. Найдите результирующую постоянную двигателя, скорость двигателя, ток двигателя, КПД двигателя и выходную мощность. Из паспорта двигателя видно, что скорость холостого хода двигателя при 24 В составляет 7 800 мин ^-1 . Если крутящий момент не соединен с валом двигателя, двигатель будет работать на этой скорости.

Во-первых, давайте получим общее представление о работе двигателя, рассчитав константу двигателя k _m . В этом случае мы получаем константу 28,48 мНм/А. «Согласно техпаспорту двигателя, электрическое сопротивление составляет 1,03 Ом в холодном состоянии для варианта 24 В».

Скорость двигателя под нагрузкой — это просто скорость холостого хода за вычетом снижения скорости из-за нагрузки. Константа пропорциональности для соотношения между скоростью двигателя и крутящим моментом двигателя представляет собой наклон кривой зависимости крутящего момента от скорости, определяемый отношением скорости холостого хода двигателя к крутящему моменту двигателя. В этом примере мы рассчитаем снижение скорости (без учета влияния температуры), вызванное крутящим моментом 68 мНм, путем исключения единиц мНм:

Теперь путем замены:

Скорость двигателя под нагрузкой должна быть приблизительно равна:

Ток двигателя под нагрузкой представляет собой сумму тока холостого хода и тока, возникающего под нагрузкой.

Константа пропорциональности, относящая ток к нагрузке крутящего момента, представляет собой константу крутящего момента ( k _{M )} . Это значение составляет 28,9 мНм/А. Взяв обратную величину, мы получим постоянную тока k _I , которая может помочь нам рассчитать ток при нагрузке. В этом случае нагрузка составляет 68 мН·м, а ток, вытекающий из этой нагрузки (без учета тепловыделения), примерно равен:

Общий ток двигателя можно приблизительно определить путем суммирования этого значения с током двигателя без нагрузки. В техническом описании ток холостого хода двигателя указан как 78 мА. После округления общий ток примерно равен:

Выходная механическая мощность двигателя представляет собой просто произведение скорости двигателя и крутящего момента с поправочным коэффициентом для единиц (при необходимости). Таким образом, выходная мощность двигателя будет приблизительно равна:

Механическая мощность, потребляемая двигателем, является произведением приложенного напряжения и полного тока двигателя в амперах. В этом приложении:

Так как эффективность η  это просто выходная мощность, деленная на входную мощность, давайте рассчитаем ее в нашей рабочей точке:

Оценка температуры обмотки двигателя во время работы:

Ток I , протекающий через сопротивление R , приводит к потере мощности в виде тепла I ² · R . В случае двигателя постоянного тока произведение квадрата полного тока двигателя на сопротивление якоря представляет собой потери мощности в виде тепла в обмотках якоря. Например, если общий ток двигателя 0,203 А, а сопротивление якоря 14,5 Ом, потери мощности на тепло в обмотках составляют:

Тепло, возникающее в результате I ²  · R потерь в катушке, рассеивается за счет теплопроводности через компоненты двигателя и поток воздуха в воздушном зазоре. Легкость, с которой это тепло может быть рассеяно в двигателе (или любой системе), определяется тепловым сопротивлением.

Термическое сопротивление (которое является обратной величиной теплопроводности) показывает, насколько хорошо материал сопротивляется передаче тепла по определенному пути. Производители двигателей обычно указывают способность двигателя рассеивать тепло, обеспечивая тепловое сопротивление R _й значений. Например, алюминиевая пластина большого сечения будет иметь очень низкое тепловое сопротивление, в то время как значения для воздуха или вакуума будут значительно выше. В случае двигателей постоянного тока существует тепловой путь от обмоток двигателя к корпусу двигателя и второй тепловой путь между корпусом двигателя и окружающей средой двигателя (окружающий воздух и т. д.). Некоторые производители двигателей указывают тепловое сопротивление для каждого из двух тепловых путей, в то время как другие указывают только их сумму как общее тепловое сопротивление двигателя. Значения термического сопротивления указаны в приросте температуры на единицу потерь мощности. Всего I ²  · R  потери в катушке (источнике тепла) умножаются на тепловые сопротивления для определения установившейся температуры якоря. Повышение температуры двигателя в установившемся режиме ( T ) определяется по формуле:

Где:

ΔT = изменение температуры в К
I = ток через обмотки двигателя в А обмотки двигателя в Ом
R _th2  = Тепловое сопротивление от обмоток к корпусу в К/Вт
R _th3  = Термическое сопротивление корпуса к окружающей среде в К/Вт

Продолжим наш пример, используя двигатель 2668W024CR, работающий с током 2,458 А в обмотках двигателя, с сопротивлением якоря 1,03 Ом, а тепловое сопротивление между обмоткой и корпусом 3 К/Вт и тепловое сопротивление между корпусом и окружающей средой 8 К/Вт. Повышение температуры обмоток определяется по приведенной ниже формуле; мы можем заменить Ploss на I ²  · R :

Поскольку шкала Кельвина использует тот же приращение единицы, что и шкала Цельсия, мы можем просто заменить значение Кельвина, как если бы оно было значением Цельсия. Если предположить, что температура окружающего воздуха составляет 22°C, то конечную температуру обмоток двигателя можно приблизительно представить как:

Где:

T _теплый = температура обмотки

Важно убедиться, что конечная температура обмоток не превышает номинальное значение двигателя, указанное в паспорте. В приведенном выше примере максимально допустимая температура обмотки составляет 125°C. Поскольку расчетная температура обмотки составляет всего 90,4°C, тепловое повреждение обмоток двигателя не должно быть проблемой в этом приложении.

Подобные расчеты можно было бы использовать для ответа на вопрос другого типа. Например, приложение может потребовать, чтобы двигатель работал с максимальным крутящим моментом, в надежде, что он не будет поврежден в результате перегрева. Предположим, требуется запустить двигатель с максимально возможным крутящим моментом при температуре окружающего воздуха 22°C. Разработчик хочет знать, какой крутящий момент двигатель может обеспечить без перегрева. Опять же, в техническом описании двигателя постоянного тока без сердечника 2668W024CR указана максимальная температура обмотки 125°C. Таким образом, поскольку температура окружающей среды составляет 22°C, максимально допустимое повышение температуры ротора составляет: 125°C – 22°C = 103°C

Теперь мы можем рассчитать увеличение сопротивления катушки из-за рассеяния тепловой мощности:

Где:

α _Cu  = Температурный коэффициент меди в единицах К нагрева катушки и магнита за счет рассеивания мощности от потерь I ² · R сопротивление катушки увеличилось с 1,03 Ом до 1,44 Ом. Теперь мы можем пересчитать новую константу крутящего момента  k _M  для наблюдения за влиянием повышения температуры на производительность двигателя:

Где:

α _M = Температурный коэффициент магнита в единицах К Постоянная ЭДС k _E и наблюдайте за результатами. Из формулы, которую мы вывели выше:

Как мы видим, константа крутящего момента ослабевает в результате повышения температуры, как и константа противо-ЭДС! Таким образом, сопротивление обмотки двигателя, постоянная крутящего момента и постоянная противо-ЭДС оказывают негативное влияние по той простой причине, что они являются функциями температуры.

Мы могли бы продолжить расчет дополнительных параметров из-за более горячих катушки и магнита, но наилучшие результаты дает выполнение нескольких итераций, что лучше всего делать с помощью количественного программного обеспечения. Поскольку температура двигателя продолжает расти, каждый из трех параметров будет изменяться таким образом, что ухудшаются характеристики двигателя и увеличиваются потери мощности. При непрерывной работе двигатель может даже достичь точки «теплового разгона», что потенциально может привести к повреждению двигателя, не подлежащему ремонту. Это может произойти, даже если первоначальные расчеты показали приемлемое повышение температуры (используя значения  R и k _M при температуре окружающей среды).

Обратите внимание, что максимально допустимый ток через обмотки двигателя можно увеличить, уменьшив тепловое сопротивление двигателя. Термическое сопротивление между ротором и корпусом R _th2 в основном определяется конструкцией двигателя. Тепловое сопротивление корпуса к окружающей среде R _th3  можно значительно снизить за счет добавления радиаторов. Термическое сопротивление двигателя для небольших двигателей постоянного тока обычно указывается для двигателя, подвешенного на открытом воздухе. Поэтому обычно имеет место некоторый отвод тепла в результате простой установки двигателя в теплопроводящую раму или шасси. Некоторые производители более крупных двигателей постоянного тока указывают тепловое сопротивление двигателя, установленного на металлической пластине известных размеров и материала.

Для получения дополнительной информации о расчетах бессердечных щеточных двигателей постоянного тока и о том, как рассеивание тепловой мощности может повлиять на характеристики электродвигателя, обратитесь к квалифицированному инженеру FAULHABER. Мы всегда готовы помочь.

Процедура проектирования магнитного трансформатора без сердечника

• title={Процедура проектирования магнитного трансформатора без сердечника}, автор = {Кристина Фернндес и Роберто Прието и {\’O} шрам Гарсиа и Хосе {\’e} Антонио Кобос}, journal={36-я конференция специалистов по силовой электронике IEEE, 2005 г.}, год = {2005}, страницы={1548-1554} }
  • C. Fernández, R. Prieto, J. Cobos
  • Опубликовано 16 июня 2005 г.
  • Физика
  • 2005 36-я конференция специалистов по силовой электронике IEEE

  Расчет сопротивления и индуктивности компонентов не является простая задача. Поскольку распределение магнитного поля является двумерным/трехмерным, модели, которые необходимо применять, должны учитывать такое распределение поля. Использование аналитических выражений может помочь получить грубую аппроксимацию значения индуктивности. Однако точный расчет связи и сопротивления требует более точного подхода, такого как решатели FEA. В этом документе описана полная процедура проектирования без сердечника… 

  View on IEEE

  doi.org

  Modeling Coreless Transformers With a Relatively Large Wire Gauge Using an Optimization Method

  • Renan Bergonsi Muller, Daniela Wolter Ferreira, L. Lebensztajn

  • Engineering, Physics

    IEEE Transactions on Magnetics

  • 2014

  В данной статье предлагается метод, который позволяет моделировать сосредоточенные параметры трансформаторов без сердечника, включая вихревые токи, используя поиск алгоритма оптимизации через решатель генетического алгоритма.

  Реализация формулы Неймана для расчета взаимной индуктивности между плоскими катушками индуктивности на печатной плате

  В этой статье представлен метод оценки взаимной индуктивности между двумя планарными катушками индуктивности на печатной плате с прямыми дорожками. Сначала тонкие медные дорожки моделируются как кратные…

  Проектирование и анализ обратноходового преобразователя без сердечника с плоским трансформатором на печатной плате

  В этой статье представлена ​​разработка преобразователя постоянного тока в постоянный мощностью 1 Вт. Он основан на обратноходовом преобразователе для простых приложений. Трансформатор выполнен в виде спиральной катушки на печатной плате. В…

  Реализация различных компоновок планарного трансформатора без сердечника для обратноходового преобразователя

  Реализация различных компоновок планарного трансформатора без сердечника для обратноходового преобразователя для преобразователя постоянного тока мощностью 0,5 Вт была разработана, и некоторые результаты по различной геометрии и частоте представлены показано.

  Проектирование и анализ различной конструкции планарного трансформатора без сердечника для обратноходового преобразователя

  • А. Буабана, К. Суркунис, М. Маллах

  • Машиностроение, бизнес

    Международный симпозиум по силовой электронике Силовая электроника, электрические приводы, автоматизация и движение

  • 2012

  В этой статье представлена ​​разработка преобразователя постоянного тока в постоянный мощностью 0,5 Вт. Особенностью преобразователя является то, что обратноходовой преобразователь выполнен без сердечника на печатной плате. В документе показан способ…

  Моделирование и экспериментальная проверка универсальной платформы для бесконтактной зарядки аккумуляторов с локализованными функциями зарядки

  В этой статье представлено имитационное исследование методом конечных элементов плоской бесконтактной зарядной платформы для портативного электронного оборудования. Графики магнитного поля зарядной платформы…

  Проект резонансного преобразователя LLC для гибкого силового преобразователя

  В этой статье представлен подход к проектированию резонансного преобразователя LLC с гибким трансформатором. Сначала рассчитываются электрические параметры резонансного преобразователя LLC на основе…

  Многофазный преобразователь без сердечника с трансформаторной связью

  • М.К. Gonzalez, N. Ferreros, H. Visairo

  • Engineering, Physics

    2010 IEEE Energy Conversion Congress and Exposition

  • 2010

  Связанный многофазный преобразователь, в котором связь между фазами осуществляется с помощью планарных трансформаторов без сердечника приложениями могут быть «трансформаторы постоянного тока» для двухступенчатых систем электропитания и источников питания с масштабированием напряжения.

  Расчет саморезонансных спиральных катушек для беспроводных систем передачи энергии с использованием линии передачи

  Представлена ​​математическая модель для расчета саморезонансных плоских катушек с произвольной функцией намотки. Он состоит из модели линии передачи и позволяет проводить быстрые вычисления. It…

  Сравнение структур массива катушек для платформы для бесконтактной зарядки аккумуляторов

  Предлагаются две новые топологии катушек для платформы для бесконтактной зарядки аккумуляторов, которые состоят из катушек квадратной печатной платы (PCB), сгруппированных в два слоя на печатной плате.

  ПОКАЗАНЫ 1-10 ИЗ 12 ССЫЛОК

  СОРТИРОВАТЬ ПОРелевантностьНаиболее влиятельные статьиНедавность

  Модель емкостных эффектов в магнитных компонентах

  Разработана модель емкостных эффектов в магнитных компонентах импульсных источников питания (ИИП). Может применяться для многообмоточных трансформаторов. Анализ конечных элементов (FEA)…

  Моделирование магнитных компонентов на основе методов конечных элементов

  • J. Pleite, R. Prieto, R. Asensi, J. Cobos, E. Olías

  • Engineering

    V IEEE International Power Electronics Congress Technical Proceedings, CIEP 96

  • 1996

  В этом документе описывается полная процедура моделирования магнитных компонентов на основе методов анализа методом конечных элементов (МКЭ), а также практические аспекты инструмента МКЭ. обдуманный. Используемая модель…

  Моделирование высокочастотных трансформаторов без сердечника с использованием анализа методом конечных элементов

  • C. Fernández, R. Prieto, Ó. Гарсия, П. Эрранц, Х. Кобос, Х. Уседа

  • Инженерное дело

    2002 33-я ежегодная конференция IEEE Power Electronics Specialists Conference. Proceedings (Cat. No.02Ch47289)

  • 2002

  Предложена модель магнитных компонентов без сердечника, основанная на методе конечных элементов (МКЭ). Отсутствие нелинейного магнитопровода является преимуществом с точки зрения моделирования. Характеристика…

  Вопросы проектирования трансформатора без сердечника для бесконтактного применения

  • C. Fernández, Ó. Гарсия, Р. Прието, Дж. Кобос, С. Габриэльс, Г. Ван Дер Борхт

  • Инженерия, Физика

    АТЭС. Семнадцатая ежегодная конференция и выставка IEEE по прикладной силовой электронике (кат. № 02Ch47335)

  • 2002

  В этой статье представлен набор правил проектирования трансформаторов без сердечника для бесконтактных приложений. При бесконтактной передаче энергии существует относительно большое расстояние между…

  Преодоление разрыва между решением поля FEA и моделью магнитного компонента

  • R. Prieto, R. Asensi, C. Fernández, J. Cobos

  • Business

    Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, 2005. APEC 2005.

  • 2005 02 для изучения распределения поля является обычной практикой проектирования магнитных компонентов, изготовленных по индивидуальному заказу. Однако использование информации о распределении поля для…

    Расчет собственных и взаимных импедансов в планарных магнитных конструкциях

    • W. G. Hurley, M. Duffy

    • Физика

    • 1995

    Высокочастотная работа магнитных компонентов в таких приложениях, как фильтры, делает их идеальными кандидатами для толстопленочной технологии наряду с резисторами и конденсаторами. Это, в свою очередь, приводит к…

    Высокочастотные эффекты в планарном магнетизме: включая скин-эффект

    Планарные магнитные компоненты играют все более важную роль в повышении мощности источников питания и в производстве магнитных компонентов используя…

    Расчет индуктивности: рабочие формулы и таблицы

    • F.