Катушка индуктивностью l 0 08. Катушка индуктивности в цепи переменного тока: расчет резонанса и характеристик цепи

Как рассчитать емкость конденсатора для достижения резонанса в цепи переменного тока с катушкой индуктивности. Какие параметры цепи влияют на резонансную частоту. Как определить амплитуду тока в резонансном контуре.

Расчет емкости конденсатора для резонанса в цепи переменного тока

В цепь переменного тока с частотой 400 Гц включена катушка индуктивностью 0,1 Гн. Определим, какой емкости конденсатор нужно включить в эту цепь, чтобы осуществился резонанс.

Для расчета воспользуемся формулой Томсона для резонансной частоты колебательного контура:

f = 1 / (2π√LC)

где f — частота переменного тока, L — индуктивность катушки, C — емкость конденсатора.

Выразим из этой формулы емкость C:

C = 1 / (4π²f²L)

Подставим известные значения:

C = 1 / (4 * 3,14² * 400² * 0,1) = 1,58 * 10⁻⁶ Ф = 1,58 мкФ

Таким образом, для достижения резонанса в данной цепи необходимо включить конденсатор емкостью 1,58 мкФ.

Влияние параметров цепи на резонансную частоту

Резонансная частота колебательного контура зависит от индуктивности катушки и емкости конденсатора. Как изменится резонансная частота при изменении этих параметров?

• При увеличении индуктивности катушки резонансная частота уменьшится
• При уменьшении индуктивности катушки резонансная частота увеличится
• При увеличении емкости конденсатора резонансная частота уменьшится
• При уменьшении емкости конденсатора резонансная частота увеличится

Эти зависимости следуют из формулы Томсона: f = 1 / (2π√LC).

Расчет амплитуды тока в резонансном контуре

Как рассчитать амплитуду силы тока в резонансном контуре? Для этого необходимо знать следующие параметры:

• Амплитуда напряжения в цепи Um
• Активное сопротивление цепи R

Амплитуда тока при резонансе определяется по формуле:

Im = Um / R

Например, если амплитуда напряжения Um = 100 В, а активное сопротивление цепи R = 10 Ом, то амплитуда тока составит:

Im = 100 В / 10 Ом = 10 А

Добротность колебательного контура

Важной характеристикой колебательного контура является его добротность Q. Она показывает, во сколько раз запасенная в контуре энергия больше потерь энергии за один период колебаний.

Добротность определяется по формуле:

Q = ωL / R

где ω — циклическая частота, L — индуктивность, R — активное сопротивление.

Чем выше добротность контура, тем меньше потери энергии и тем острее выражен резонанс.

Применение явления резонанса в электрических цепях

Где на практике используется явление резонанса в электрических цепях?

• В радиоприемниках для настройки на нужную частоту
• В генераторах электромагнитных колебаний
• В фильтрах для выделения сигналов определенной частоты
• В беспроводных зарядных устройствах
• В системах беспроводной передачи энергии

Резонанс позволяет эффективно передавать энергию на определенной частоте и отфильтровывать нежелательные частоты.

Расчет мощности в цепи переменного тока

Как рассчитать мощность, выделяемую в цепи переменного тока? Для этого используется формула:

P = I * U * cos φ

где I — действующее значение силы тока, U — действующее значение напряжения, cos φ — коэффициент мощности.

Коэффициент мощности cos φ показывает сдвиг фаз между током и напряжением:

• При чисто активной нагрузке cos φ = 1
• При чисто индуктивной нагрузке cos φ = 0
• При чисто емкостной нагрузке cos φ = 0

При резонансе cos φ = 1, поэтому вся подводимая мощность выделяется на активном сопротивлении.

Векторные диаграммы для цепей переменного тока

Для анализа цепей переменного тока удобно использовать метод векторных диаграмм. Как строить векторные диаграммы?

1. Выбираем масштаб и начало координат
2. Откладываем вектор напряжения U вдоль горизонтальной оси
3. Откладываем вектор тока I под углом φ к вектору U:
• Для активной нагрузки φ = 0°
• Для индуктивной нагрузки φ = 90°
• Для емкостной нагрузки φ = -90°
4. Строим векторы напряжений на отдельных элементах цепи
5. Проверяем замкнутость векторного многоугольника напряжений

Векторные диаграммы наглядно показывают соотношения между токами и напряжениями в цепи переменного тока.

Расчет импеданса цепи переменного тока

Как рассчитать полное сопротивление (импеданс) цепи переменного тока? Для этого используется формула:

Z = √(R² + (XL — XC)²)

где R — активное сопротивление, XL = ωL — индуктивное сопротивление, XC = 1/(ωC) — емкостное сопротивление.

При резонансе XL = XC, поэтому импеданс минимален и равен активному сопротивлению: Z = R.

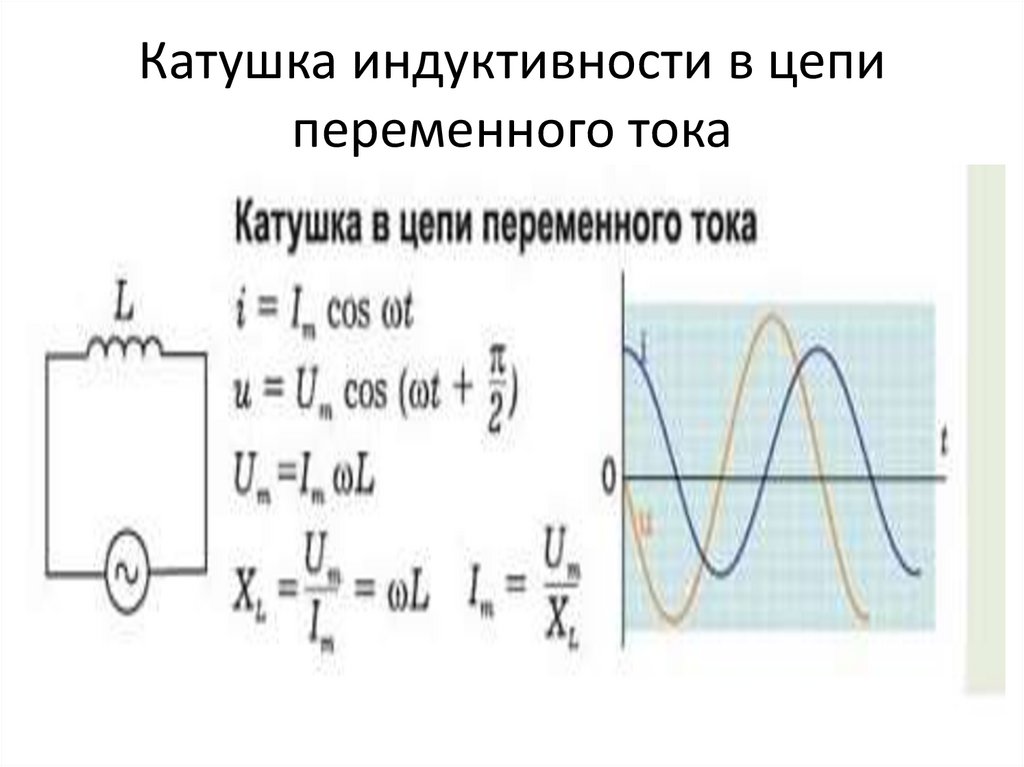
Зная импеданс, можно рассчитать ток в цепи по закону Ома:

I = U / Z

Влияние частоты на параметры цепи переменного тока

Как влияет изменение частоты на параметры цепи переменного тока?

• При увеличении частоты:
  • Индуктивное сопротивление XL увеличивается
  • Емкостное сопротивление XC уменьшается
• При уменьшении частоты:
  • Индуктивное сопротивление XL уменьшается
  • Емкостное сопротивление XC увеличивается

Активное сопротивление R не зависит от частоты.

Заключение

Мы рассмотрели основные параметры и расчеты для цепей переменного тока с катушкой индуктивности и конденсатором. Ключевые моменты:

• Резонанс наступает при равенстве индуктивного и емкостного сопротивлений
• Резонансная частота зависит от индуктивности и емкости
• При резонансе ток максимален, а импеданс минимален
• Векторные диаграммы помогают анализировать цепи переменного тока
• Частота влияет на индуктивное и емкостное сопротивления

Понимание этих принципов позволяет эффективно проектировать и анализировать цепи переменного тока для различных применений.

StudyPort.Ru — Механические и электромагнитные колебания

Страница 1 из 6

4. Колебания и волны

1. Гармонические колебания величины s описываются уравнением s = 0,02 cos (6πt + π/3), м. Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.

2. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой A = 8 см, если за t = 1 мин совершается n = 120 колебаний и начальная фаза колебаний равна 45°.

3. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения x

0 = 2 см.

4. Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.

5. Напишите уравнение гармонического колебания точки, если его амплитуда A = 15 см, максимальная скорость колеблющейся точки v_max = 30 см/с, начальная фаза φ = 10°.

6. Точка совершает гармонические колебания по закону x = 3 cos (πt/2 + π/8), м. Определите: 1) период T колебаний: 2) максимальную скорость V_max точки; 3) максимальное ускорение a_max точки.

7. Точка совершает гармонические колебания с амплитудой A = 10 см и периодом T = 5 с. Определите для точки: 1) максимальную скорость; 2) максимальное ускорение.

8. Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6 sin 2 πt, м/с. Запишите зависимость смещения этой точки от времени.

9. Материальная точка совершает колебания согласно уравнению x = A sin ωt. В какой-то момент времени смещение точки x₁ = 15 см. При возрастании фазы колебания в два раза смещение x₂ оказалось равным 24 см. Определите амплитуду A колебания.

10. Материальная точка совершает гармонические колебания согласно уравнению x = 0,02 cos (πt + π/2), м. Определите: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия.

11. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой A = 3 см и периодом T = 4 с.

12. Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой х

0 = 5 см, со скоростью v₀ = -15 см/с. Определите амплитуду колебаний.

13. Тело массой m = 10 г совершает гармонические колебания по закону х = 0,1 cos(4πt + π/4), м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.

14. Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению x = 0,1 cos 3πt/2, м. Определите: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е точки.

15. Материальная точка массой m = 20 г совершает гармонические колебания по закону x = 0,1 cos(4πt + π/4), м. Определите полную энергию Е этой точки.

16. Полная энергия E гармонически колеблющейся точки равна 10 мкДж, а максимальная сила F_max, действующая на точку, равна -0,5 мН. Напишите уравнение движения этой точки, если период T колебаний равен 4 с, а начальная фаза φ = π/6.

17. Определите отношение кинетической энергии T точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.

18. Определите полную энергию материальной точки массой m, колеблющейся по закону x = A cos(ω₀t + φ).

19. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A = 8 см. Определите жесткость k пружины, если известно, что максимальная кинетическая энергия T_max груза составляет 0,8 Дж.

20. Материальная точка колеблется согласно уравнению х = A cos ωt, где A = 5 см и ω = π/12 с^-1. Когда возвращающая сила F в первый раз достигает значения -12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу ωt.

В цепь переменного тока у которого частота колебаний равна 400 гц включена катушка индуктивностью



Примеры решения задач. Упражнение 4. Краткие итоги главы 4

Примеры решения задач

1. Максимальный заряд на обкладках конденсатора колебательного контура q_m = 10 -6 Кл. Амплитудное значение силы тока в контуре I_m = 10 -3 А. Определите период колебаний. (Потерями на нагревание проводников можно пренебречь.)

Р е ш е н и е. Амплитудные значения силы тока и заряда связаны соотношением:

2. Рамка площадью S = 3000 см 2 имеет N = 200 витков и вращается в однородном магнитном поле с индукцией В = 1,5 • 10 -2 Тл. Максимальная ЭДС в рамке

Определите время одного оборота.

Р е ш е н и е. Магнитный поток, пронизывающий рамку, равен:

Согласно закону электромагнитной индукции:

е = -Ф’ = BSNω sin ωt.

Амплитуда ЭДС индукции

Время одного оборота рамки равно:

3. В цепь переменного тока с частотой v = 500 Гц включена катушка индуктивностью L = 10 мГн. Определите емкость конденсатора, который надо включить в эту цепь, чтобы наступил резонанс.

Р е ш е н и е. Электрическая цепь согласно условию задачи представляет собой колебательный контур. Резонанс в этой цепи наступит, когда частота переменного тока будет равна собственной частоте колебательного контура (v = v_).

Упражнение 4

1. После того как конденсатору колебательного контура был сообщен заряд q = 10 -5 Кл, в контуре возникли затухающие колебания. Какое количество теплоты выделится в контуре к тому времени, когда колебания в нем полностью затухнут? Емкость конденсатора С = 0,01 мкФ.

2. Колебательный контур состоит из катушки индуктивностью L = 0,003 Гн и плоского конденсатора емкостью С = 13,4 пФ. Определите период свободных колебаний в контуре.

3. В каких пределах должна изменяться индуктивность катушки колебательного контура, чтобы частота колебаний изменялась от 400 до 500 Гц? Емкость конденсатора 10 мкФ.

4. Определите амплитуду ЭДС, наводимой в рамке, вращающейся в однородном магнитном поле, если частота вращения составляет 50 об/с, площадь рамки 100 см 2 и магнитная индукция 0,2 Тл.

5. Катушка индуктивностью L = 0,08 Гн присоединена к источнику переменного напряжения с частотой v = 1000 Гц. Действующее значение напряжения U = 100 В. Определите амплитуду силы тока I_m в цепи.

Краткие итоги главы 4

1. При электромагнитных колебаниях происходят периодические изменения электрического заряда, силы тока и напряжения. Электромагнитные колебания подразделяются на свободные, затухающие, вынужденные и автоколебания.

2. Простейшей системой, в которой наблюдаются свободные электромагнитные колебания, является колебательный контур. Он состоит из проволочной катушки и конденсатора. Уравнение, описывающее электромагнитные колебания в контуре, имеет вид

где q — заряд конденсатора; q» — вторая производная заряда по времени;

— квадрат циклической частоты колебаний, зависящей от индуктивности L и емкости С.

3. Решение уравнения, описывающего свободные электромагнитные колебания, выражается либо через косинус, либо через синус:

q = qm cos ω_{t или q — qm sin ωt.}

4. Колебания, происходящие по закону косинуса или синуса, называются гармоническими. Максимальное значение заряда qm на обкладках конденсатора называется амплитудой колебаний заряда. Величина со0 называется циклической частотой колебаний и выражается через число v колебаний в секунду: ω _{= 2πv.}

Период колебаний выражается через циклическую частоту следующим образом:

Величину, стоящую под знаком косинуса или синуса в решении для уравнения свободных колебаний, называют фазой колебаний. Фаза определяет состояние колебательной системы в данный момент времени при заданной амплитуде колебаний.

5. Из-за наличия у контура сопротивления колебания в нем с течением времени затухают.

6. Вынужденные колебания, т. е. переменный электрический ток, возникают в цепи под действием внешнего периодического напряжения. Между колебаниями напряжения и силы тока в общем случае наблюдается сдвиг фаз φ.

7. Мощность в цепи переменного тока определяется действующими значениями силы тока и напряжения: Р = IU cos φ.

8. При совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура наступает резонанс — резкое возрастание амплитуды силы тока при вынужденных колебаниях. Резонанс выражен отчетливо лишь при достаточно малом активном сопротивлении контура.

Одновременно с возрастанием силы тока при резонансе происходит резкое увеличение напряжения на конденсаторе и катушке. Явление электрического резонанса используется при радиосвязи.

9. Автоколебания возбуждаются в колебательном контуре генератора на транзисторе за счет энергии источника постоянного напряжения. В генераторе используется транзистор, т. е. полупроводниковое устройство, состоящее из эмиттера, базы и коллектора и имеющее два р—n-перехода. Колебания тока в контуре вызывают колебания напряжения между эмиттером и базой, которые управляют силой тока в цепи колебательного контура (обратная связь). От источника напряжения в контур поступает энергия, компенсирующая потери энергии в контуре на резисторе.

Источник

Цепь переменного тока у которого частота колебаний равна 400 герц включена катушка индуктивностью 0, 1 г Определите конденсатор Какой емкости надо включить в эту цепь чтобы осуществился резонанс?

Физика | 10 — 11 классы

Цепь переменного тока у которого частота колебаний равна 400 герц включена катушка индуктивностью 0, 1 г Определите конденсатор Какой емкости надо включить в эту цепь чтобы осуществился резонанс.

В этом задачи ты должен решить эту задачу с формулой n = 1 / (2h)

Здесь h равно на 3. 2L) = 1.

В цепь переменного тока с частотой 400 Гц включена катушка индуктивностью 0, 1 Гн?

В цепь переменного тока с частотой 400 Гц включена катушка индуктивностью 0, 1 Гн.

Определите, какой емкости конденсатор надо включить в эту цепь, чтобы осуществился резонанс.

Катушка с активным сопротивлением 2 Ом и индуктивностью 75 мГн включена последовательно с конденсатором в сеть переменного тока с напряжением 50 В и частотой 50 Гц?

Катушка с активным сопротивлением 2 Ом и индуктивностью 75 мГн включена последовательно с конденсатором в сеть переменного тока с напряжением 50 В и частотой 50 Гц.

Чему равна емкость конденсатора при резонансе напряжений в данной цепи?

В цепь переменного тока частотой 50 Гц включены последовательно конденсатор емкостью 20 мкФ, катушка сопротивлением 150 Ом и индуктивностью 5мГн?

В цепь переменного тока частотой 50 Гц включены последовательно конденсатор емкостью 20 мкФ, катушка сопротивлением 150 Ом и индуктивностью 5мГн.

Определить мощность данной цепи, если по ней идет ток силой 0, 5Ф.

В цепь переменного тока с частотой 500гц включена катушка индуктивностью L = 3, 33мгн?

В цепь переменного тока с частотой 500гц включена катушка индуктивностью L = 3, 33мгн.

Определить ёмкость конденсатора, который надо включить в эту цепь, чтобы наступил резонанс.

Катушка с активным сопротивлением 2 Ом и индуктивностью 75 мГн включена последовательно с конденсатором в сеть переменного тока с напряжением 50В и частотой 50 Гц?

Катушка с активным сопротивлением 2 Ом и индуктивностью 75 мГн включена последовательно с конденсатором в сеть переменного тока с напряжением 50В и частотой 50 Гц.

Чему равна емкость конденсатора при резонансе напряжений в данной цепи?

В цепь включены последовательно катушка и конденсатор?

В цепь включены последовательно катушка и конденсатор.

Определите индуктивность катушки, если при частоте 500 Гц наступает резонанс колебаний.

Емкость конденсатора 2 мФ.

1)Индуктивность 20Гн, емкость 2000мкФ?

1)Индуктивность 20Гн, емкость 2000мкФ.

Найдите период, частоту, циклическую частоту?

2)В цепи переменного тока с частотой 500Гц включена катушка индуктивностью 10мГн.

Какой емкости надо включить конденсатор чтобы наступил резонанс?

Пожалуйста помогите?

В цепь переменного тока с частотой 600Гц включена катушка с индуктивностью 20мГн.

Какой емкости конденсатор надо включить в эту цепь, чтобы наступил резонанс?

Определить частоту переменного тока в цепи с конденсатором емкостью 40 мкФ и катушкой индуктивности 400 мГн?

Определить частоту переменного тока в цепи с конденсатором емкостью 40 мкФ и катушкой индуктивности 400 мГн.

В цепь включены последовательно резистор сопротивлением 5 Ом, катушка индуктивностью 0, 5мГн и конденсатор емкостью 0, 15 мкФ?

В цепь включены последовательно резистор сопротивлением 5 Ом, катушка индуктивностью 0, 5мГн и конденсатор емкостью 0, 15 мкФ.

При какой частоте произойдет резонанс?

На этой странице сайта, в категории Физика размещен ответ на вопрос Цепь переменного тока у которого частота колебаний равна 400 герц включена катушка индуктивностью 0, 1 г Определите конденсатор Какой емкости надо включить в эту цепь чтобы осуществился резонанс?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Источник

§ 2.14. Примеры решения задач

При решении задач на электрические колебания рекомендуется учесть следующее. В задачах на свободные колебания в контуре, кроме формулы для периода свободных электрических колебаний (2.3.2), можно применять закон сохранения энергии.

При решении задач на расчет цепей переменного тока следует иметь в виду, что амперметры и вольтметры в этих цепях показывают действующие значения силы тока (2.5.4) и действующие значения напряжения (2.5.5).

В отличие от цепей постоянного тока, обладающих только активным сопротивлением, цепи переменного тока могут иметь еще емкостное сопротивление (2.7.4) и индуктивное сопротивление (2.8.5). Полное сопротивление цепи с последовательно соединенными резистором, конденсатором и катушкой индуктивности определяется по формуле (2.9.4). Закон Ома для цепи переменного тока имеет вид (2.9.5).

При последовательном соединении потребителей в цепях переменного тока действующие или амплитудные значения напряжений складываются методом векторной диаграммы. При параллельном соединении потребителей в цепях переменного тока векторно складываются амплитуды сил токов или их действующие значения. В этом случае тоже следует строить векторные диаграммы. При построении векторных диаграмм надо хорошо знать фазовые соотношения между колебаниями силы тока и напряжения в цепях переменного тока.

Мощность вычисляется по формуле (2.10.4). Явление резонанса в электрической цепи имеет место при условии (2.11.1).

Задача 1

Колебательный контур состоит из катушки индуктивностью L = 6 • 10 -3 Гн и конденсатора емкостью С = 15 мкФ. Максимальная разность потенциалов на конденсаторе U_m = 200 В. Чему равна сила тока i в контуре, когда разность потенциалов на конденсаторе уменьпгилась в n = 2 раза? Потерями энергии пренебречь.

Решение. Когда напряжение на обкладках конденсатора максимально, вся энергия контура сосредоточена в электрическом поле конденсатора (см. § 2.2.). Она равна

. При уменьшении напряжения на обкладках конденсатора до значения энергия контура распределяется между конденсатором и катушкой. Энергия электрического поля конденсатора становится равной , а энергия магнитного поля катушки будет равна .

Согласно закону сохранения энергии имеем:

Задача 2

Напряжение на концах участка цепи, по которому течет переменный ток, изменяется с течением времени по закону

В момент времени

мгновенное значение напряжения u = 10 В. Определите амплитуду напряжения U_m и циклическую частоту ω, если период колебаний силы тока Т = 0,01 с. Начертите график зависимости изменения напряжения от времени.

Решение. Сначала найдем значение циклической частоты:

Далее записываем выражение для мгновенного значения напряжения в момент времени

:

График изменения напряжения в зависимости от времени представлен на рисунке 2.33.

Задача 3

В цепь переменного тока стандартной частоты (v = 50 Гц) последовательно включены резистор сопротивлением R = 21 Ом, катушка индуктивностью L = 0,07 Гн и конденсатор емкостью С = 82 мкФ (см. рис. 2.20). Определите индуктивное, емкостное и полное сопротивления цепи, а также сдвиг фаз между силой тока и напряжением.

Решение. Индуктивное сопротивление находим по формуле (2.8.5):

Емкостное сопротивление вычисляется по формуле (2.7.4):

Полное сопротивление согласно формуле (2.9.4) равно:

Задача 4

К магистрали переменного тока с напряжением U = 120 В (U — действующее значение напряжения) через катушку (дроссель) с индуктивностью L = 0,05 Гн и активным сопротивлением R = 1 Ом подключена осветительная сеть квартиры (рис. 2.34, а). Каково напрялсение U₁ на входе в квартиру, если сила потребляемого тока I = 2 А? Частота тока стандартная (V = 50 Гц). Индуктивностью и емкостью электрической цепи квартиры пренебречь.

Решение. Дроссель и осветительная сеть квартиры подключены к магистрали последовательно, поэтому сила тока одинакова на всех участках цепи. Напряжение U₁ и напряжение U_R на активном сопротивлении дросселя совпадают по фазе с силой тока I. Напряжение U₁ на индуктивном сопротивлении дросселя опережает силу тока по фазе на π/2. Следовательно, векторная диаграмма для действующих значений напряжений и силы тока имеет вид, изображенный на рисунке 2.34, б.

По теореме Пифагора

где ω = 2πv. Так как действующее значение напряжения всегда пололсительно, то

Задача 5

В цепи (рис. 2.35) параметры R, L и С известны. Напряжение между точками А и В равно U. Постройте векторную диаграмму сил токов в данной цепи и определите силу тока в неразветвленном участке цепи. Найдите сдвиг фаз между колебаниями силы тока и напряжения. При каком условии сила тока в неразветвленном участке цепи окажется минимальной? Чему равен сдвиг фаз между силой тока и напряжением в этом случае?

Решение. В этой задаче рассматривается электрическая цепь, состоящая из двух ветвей, соединенных параллельно. Одна ветвь содержит резистор и катушку индуктивности, другая — конденсатор.

Построение векторной диаграммы начнем с вектора действующего значения напряжения , поскольку напряжение одинаково для обеих ветвей цепи. Направим вектор горизонтально вправо (рис. 2.36).

Сила тока i является суммой сил токов i₁ и i₂ (см. рис. 2.35). Колебания силы тока i₁ отстают по фазе от колебаний напряжения на угол φ₁

, так как верхний участок цепи содержит катушку индуктивности.

Поэтому вектор

₁ повернут относительно вектора на угол φ₁ в отрицательную сторону (по часовой стрелке). Сила тока i₂. текущего через конденсатор, опережает по фазе напряжение на π/2. Соответствующий вектор ₂ повернут относительно вектора на угол π/2 в положительную сторону (против часовой стрелки). Его модуль I₂ = ωCU. Действующее значение силы тока в неразветвленной части цепи находится с помощью векторной диаграммы (см. рис. 2.36):

Пользуясь теоремой косинусов, из векторной диаграммы определяем

Так как α =

— φ₁, то cos α = sin φ₁ и

Как видно из векторной диаграммы (см. рис. 2.36), вектор силы тока

образует с вектором напряжения угол φ_c. Из рисунка находим

Учитывая, что

получим

Из выражения (2.14.1) вытекает, что сила тока в неразветвленном участке цепи минимальна, если LCω 2 — 1 = 0, т. е. если ω = . Но = ω _{— это циклическая частота собственных колебаний контура, входящего в состав данной цепи. В этом случае говорят, что в цепи наступил резонанс токов.}

При резонансе токов, как следует из формулы (2.14.2),

При малом активном сопротивлении (R ⇒ 0)

Это значит, что при резонансе токов при малом активном сопротивлении сдвиг фаз между силой тока и напряжением равен нулю (рис. 2.37). Важно обратить внимание на то, что при резонансе сила тока I в неразветвленной части цепи меньше силы тока I₁ в ветви, содержащей последовательно соединенные резистор сопротивлением R и катушку индуктивностью L, а также меньше силы тока I₂ в ветви с конденсатором емкостью С.

Задача 6

В колебательный контур (см. рис. 2.20) включен источник переменной ЭДС е = E_m cos ωt, причем амплитуда E_m = 2 В. Определите амплитуду напряжения на конденсаторе при резонансе. Резонансная частота контура V _{= 10 5 Гц, индуктивность катушки L = 1 мГн и ее активное сопротивление R = 3 Ом.}

Решение. При резонансе амплитуда напряжения на конденсаторе, равная амплитуде напряжения на катушке U_mL (U_mC = U_mL), больше амплитуды напряжения на зажимах цепи U_m в отношении

. Если пренебречь внутренним сопротивлением источника переменной ЭДС, то U_m = E_m. Тогда

Упражнение 2

1. После зарядки конденсатора емкостью С от источника постоянного напряжения U переключатель замыкают на катушку индуктивностью L₁ (см. рис. 2.5, б). В контуре возникают гармонические колебания с амплитудой силы тока I_m1. Опыт повторяют по прежней схеме, заменив катушку на другую индуктивностью L₂ = 2L₁. Найдите амплитуду силы тока I_m2 во втором случае.

2. Колебательный контур состоит из дросселя индуктивностью L = 0,2 Гн и конденсатора емкостью С = 10 -5 Ф. Конденсатор зарядили до напряжения U = 20 В. Чему равна сила тока при разрядке конденсатора в момент, когда энергия контура оказывается распределенной поровну между электрическим и магнитным полями?

3. Определите частоту собственных колебаний в контуре, состоящем из соленоида длиной l — 15 см, площадью поперечного сечения S₁ = 1 см 2 и плоского конденсатора с площадью пластин S₂ = 6 см 2 и расстоянием между ними d = 0,1 см. Число витков соленоида N = 1000.

4. Электрический контур состоит из конденсатора постоянной емкости и катушки, в которую может вдвигаться сердечник. Один сердечник спрессован из порошка магнитного соединения железа (феррита) и является изолятором. Другой сердечник изготовлен из меди. Как изменится частота собственных колебаний контура, если в катушку вдвинуть: а) медный сердечник; б) сердечник из феррита?

5. Для чего в телефонной трубке нужен постоянный магнит (рис. 2.38)? Почему магнитная индукция этого магнита должна быть больше максимальной индукции, создаваемой током, проходящим по обмотке катушки телефона?

6. На вертикально отклоняющие пластины осциллографа подано напряжение u₁ = U_m1 cos ωt, а на горизонтально отклоняющие — напряжение u₂ = U_m2 cos (ωt — φ). Какую траекторию опишет электронный луч на экране осциллографа, если разность фаз между напряжениями на пластинах равна: а) φ₁ =

; б) φ₂ = π?

7. Кипятильник работает от сети переменного тока с напряжением U = 120 В*. При температуре t₁ = 20 °С спираль имеет сопротивление R₁ = 25 Ом. Температурный коэффициент сопротивления материала спирали α = 2 • 10 -2 К -1 . Определите массу воды, после закипания превратившейся в пар за время τ = 1 мин. Удельная теплота парообразования воды r = 2,26 • 10 6 Дж/кг.

8. При включении катушки в сеть переменного тока с напряжением 120 В и частотой 50 Гц сила тока в ней равна 4 А. При включении той же катупхки в сеть постоянного тока с напряжением 50 В сила тока в катупхке оказывается равной 5 А. Определите индуктивность катушки.

9. Определите сдвиг фаз между силой тока и напряжением в электрической цепи, если генератор отдает в цепь мощность Р = 8 кВт, амплитуда силы тока в цепи I_m = 100 А и амплитуда напряжения на зажимах генератора U_m = 200 В.

10. В сеть стандартной частоты с напряжением 100 В последовательно включены резистор сопротивлением 150 Ом и конденсатор емкостью 16 мкФ. Найдите полное сопротивление цепи, силу тока в ней, напряжения на зажимах резистора и конденсатора и сдвиг фаз между силой тока и напряжением.

11. Каковы показания приборов в цепях, представленных схемами на рисунке 2.39, а, 61 Напряжение сети U = 250 В, R = 120 Ом, С = 20 мкФ. Постройте для обеих схем векторные диаграммы.

12. В сеть переменного тока стандартной частоты с напряжением 210 В включены последовательно резистор сопротивлением 40 Ом и катушка индуктивностью 0,2 Гн. Определите силу тока в цепи и сдвиг фаз между силой тока и напряжением. Конденсатор какой емкости надо включить последовательно в цепь, чтобы сдвиг фаз оказался равным нулю? Какой будет сила тока в цепи в этом случае?

13. Каковы показания приборов в цепях, схемы которых изображены на рисунке 2.40, а, б? Напряжение сети U = 119 В, активное сопротивление R = 8 Ом, индуктивность L = 0,048 Гн. Постройте для схемы, изображенной на рисунке 2.40, б, векторную диаграмму.

14. Найдите показания приборов в цепи, схема которой представлена на рисунке 2.41. Напряжение на зажимах цепи U = 216 В, R = 21 Ом, L = 70 мГн, С = 82 мкФ. Частота стандартная. Постройте векторную диаграмму сил токов.

15. Электродвигатель мощностью Р = 10 кВт присоединен к сети с напряжением U = 240 В, cos φ₁ = 0,6, частота v = 50 Гц. Вычислите емкость конденсатора, который нужно подключить параллельно двигателю для того, чтобы коэффициент мощности установки повысить до значения cos φ₂ = 0,9.

16. В цепи, схема которой изображена на рисунке 2.42, R = 56 Ом, С = 106 мкФ и L = 159 мГн. Активное сопротивление катушки мало. Частота тока в сети v = 50 Гц. Определите напряжение в сети U, если амперметр показывает 2,4 А. Постройте векторную диаграмму.

17. В катушке индуктивности сила тока линейно увеличивается со скоростью

= 10 А/с. Найдите ЭДС индукции, возникающую при этом в катушке, если резонансная частота колебательного контура с этой катушкой и конденсатором емкостью С = 100 пФ равна v = 100 кГц.

18. Резонанс в колебательном контуре с конденсатором емкостью С₁ = 1 мкФ наступает при частоте v₁ = 400 Гц. Когда параллельно конденсатору С1 подключают другой конденсатор емкостью C₂, то резонансная частота становится равной V₂ = 100 Гц. Определите емкость C₂. Активным сопротивлением контура пренебречь.

19. На рисунке 2.43 изображены два соленоида, каждый из которых может быть использован в ламповом генераторе в качестве катушки обратной связи. В один и тот же момент в обеих катушках ток течет сверху вниз. Однако при включении одной катушки генератор работает, а при включении другой — нет. Почему?

20. Конец пружины опущ;ен в ванночку со ртутью (рис. 2.44). Что произойдет, если замкнуть ключ и пропустить через пружину достаточно сильный ток?

* В этой и последующих задачах даются действующие значения напряжения и силы тока.

Источник

Механические и электромагнитные колебания

81. Определите закон убывания заряда конденсатора со временем при его разряде в апериодическом режиме, т.е. когда δ = ω_.

82. Определите минимальное активное сопротивление при разрядке лейденской банки, при котором разряд будет апериодическим. Емкость С лейденской банки равна 1,2 нФ, а индуктивность проводов составляет 3 мкГн.

84. Определите резонансную частоту колебательной системы, если собственная частота колебаний ν _{= 300 Гц, а логарифмический декремент Θ = 0,2 .}

85. Собственная частота ν _{колебаний некоторой системы составляет 500 Гц. Определите частоту ν затухающих колебаний этой системы, если резонансная частота νрез = 499 Гц.}

86. Период затухающих колебаний системы составляет 0,2 с, а отношение амплитуд первого и шестого колебаний равно 13. Определите резонансную частоту данной колебательной системы.

87. Гиря массой m = 0,5 кг, подвешенная на спиральной пружине жесткостью k = 50 Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления r = 0,5 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F = 0,1 cos ωt, Н. Определите для данной колебательной системы: 1) коэффициент затухания δ; 2) резонансную амплитуду A_рез.

88. Гиря массой m = 400 г, подвешенная на спиральной пружине жесткостью k = 40 Н/м, опущена в масло. Коэффициент сопротивления r для этой системы составляет 0,5 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F = cos ωt, Н. Определите: 1) амплитуду вынужденных колебаний, если частота вынуждающей силы вдвое меньше собственной частоты колебаний; 2) частоту вынуждающей силы, при которой амплитуда вынужденных колебаний максимальна; 3) резонансную амплитуду.

89. Гиря массой m = 200 г, подвешенная на спиральной пружине жесткостью k = 50 Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления r = 0,2 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F = 0,2 cos ωt, Н. Определите: 1) частоту ν _{собственных колебаний; 2) резонансную частоту νрез; 3) резонансную амплитуду Aрез; 4) статическое отклонение.}

90. Амплитуды двух вынужденных колебаний системы с одинаковыми собственными частотами при всех значениях частоты вынуждающей силы различаются вдвое. Определите, какой одной (и только одной) из величин (массой, коэффициентом сопротивления среды, коэффициентом упругости, амплитудой вынуждающей силы) отличаются эти системы.

91. В цепь колебательного контура, содержащего последовательно соединенные резистор сопротивлением R = 40 Ом, катушку индуктивностью L = 0,36 Гн и конденсатор емкостью C = 28 мкФ, подключено внешнее переменное напряжение с амплитудным значением U_m = 180 В и частотой ω = 314 рад/с. Определите: 1) амплитудное значение силы тока I_m в цепи; 2) сдвиг φ по фазе между током и внешним напряжением.

92. В цепь колебательного контура, содержащего катушку индуктивностью L = 0,2 Гн и активным сопротивлением R = 9,7 Ом, а также конденсатор емкостью C = 40 мкФ, подключено внешнее переменное напряжение с амплитудным значением U_m = 180 В и частотой ω = 314 рад/с. Определите: 1) амплитудное значение силы тока I_m в цепи; 2) разность фаз φ между током и внешним напряжением; 3) амплитудное значение напряжения U_Lm на катушке; 4) амплитудное значение U_Cm на конденсаторе.

93. Последовательно соединенные резистор с сопротивлением R = 110 Ом и конденсатор подключены к внешнему переменному напряжению с амплитудным значением U_m = 110 В. Оказалось, что амплитудное значение установившегося тока в цепи I_m = 0,5 А. Определите разность фаз между током и внешним напряжением.

94. В колебательный контур, содержащий последовательно соединенные конденсатор и катушку с активным сопротивлением, подключено внешнее переменное напряжение, частоту которого можно менять, не меняя его амплитуды. При частотах внешнего напряжения ω₁ = 400 рад/с и ω₂ = 600 рад/с амплитуды силы тока в цепи оказались одинаковыми. Определите резонансную частоту тока.

95. Колебательный контур содержит катушку индуктивностью L = 0,1 мГн, резистор сопротивлением R = 3 Ом, а также конденсатор емкостью C = 10 нФ. Определите среднюю мощность, потребляемую контуром, необходимую для поддержания в нем незатухающих колебаний с амплитудным значением напряжения на конденсаторе U_m = 2 В.

96. В цепь переменного тока напряжением 220 В и частотой 50 Гц последовательно включены резистор сопротивлением R = 100 Ом, катушка индуктивностью L = 0,5 Гн и конденсатор емкостью C = 10 мкФ. Определите амплитудное значение: 1) силы тока в цепи; 2) падения напряжения на активном сопротивлении; 3) падения напряжения на конденсаторе; 4) падения напряжения на катушке.

97. В цепь переменного тока частотой ν = 50 Гц включена катушка длиной l = 20 см и диаметром d = 5 см, содержащая N = 500 витков медного провода площадью поперечного сечения S = 0,6 мм 2 . Определите, какая доля полного сопротивления катушки приходится на реактивное сопротивление. Удельное сопротивление меди ρ = 17 нОм*м.

98. В цепь переменного тока частотой ν = 50 Гц включена катушка длиной l = 30 см и площадью поперечного сечения S = 10 см 2 , содержащая N = 1000 витков. Определите активное сопротивление катушки, если известно, что сдвиг фаз φ между напряжением и током составляет 30°.

99. К зажимам генератора присоединен конденсатор емкостью C = 0,15 мкФ. Определите амплитудное значение напряжения на зажимах, если амплитудное значение силы тока равно 3,3 А, а частота тока составляет 5 кГц.

100. Определите в случае переменного тока (ν = 50 Гц) полное сопротивление участка цепи, состоящего из параллельно включенного конденсатора емкостью C = 10 мкФ и резистора сопротивлением R = 50 Ом.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Источник

Источник — переменный ток — Большая Энциклопедия Нефти и Газа, статья, страница 3

Источник — переменный ток

Cтраница 3

Мощность источника переменного тока, применяемого для испытания изоляции между выводами конденсатора, должна соответствовать его реактивной мощности при испытательном напряжении. Эта мощность может достигать больших величин.  [32]

К источнику переменного тока присоединены параллельно активное сопротивление г и индуктивное L2 16 ом.  [34]

К источнику переменного тока с частотой 50 гц присоединены две ветви: первая содержит активное сопротивление г2 ом и индуктивность L, вторая — только емкость С.  [35]

К источнику переменного тока, изменяющегося по закону / 2sin200TA, подключили последовательно катушку индуктивностью 86 мГн, конденсатор емкостью 160 мкФ и сопротивление 100 Ом.  [36]

К источнику переменного тока присоединены параллельно активное сопротивление R и индуктивное Хь 2 16 Ом.  [37]

К источнику переменного тока с частотой / 1500 Гц и действующим значением напряжения i / 10 В подключена катушка, обладающая индуктивностью L0 08 Гн и активным сопротивлением R 400 Ом. Параллельно ей включен конденсатор переменной емкости.  [38]

К источнику переменного тока с частотой / 25 Гц подключена индуктивная катушка.  [39]

К источнику переменного тока поочередно подключают две катушки индуктивности. Для одной катушки полная и активная мощности 51000 В-А и Р320 Вт, действующее значение тока / 4 А.  [40]

К источнику переменного тока с действующим значением напряжения t / 50 В подключены параллельно соединенные катушка с индуктивным сопротивлением XL — 8 Ом и резистор сопротивлением 40 Ом.  [41]

К источнику переменного тока с частотой / и напряжением U подключена нагрузка, состоящая из последовательно включенных R, L и С.  [42]

К источнику переменного тока подключен резистор R с последовательно включенным конденсатором С. Как изменится ток в цепи, если: а) последовательно подключается катушка индуктивностью L; б) закорачивается конденсатор С. Как при этом изменяется фазовый сдвиг между током и напряжением.  [43]

К источнику переменного тока с частотой / 25 Гц подключена индуктивная катушка.  [44]

К источнику переменного тока поочередно подключают две катушки индуктивности. Для одной катушки полная и активная мощности 5 1000 В-А и / 320 Вт, действующее значение тока 14 А.  [45]

Страницы:      1    2    3    4

Индуктивные элементы Радиоэлементы и их электрические и эксплуатационные свойства Любительская Радиоэлектроника

 

Индуктивные элементы

 

Индуктивные элементы делятся на катушки индуктивности и трансформаторы.

По назначению катушки индуктивности можно разделить на четыре группы:

а) катушки контуров,

б) катушки связи,

в) дроссели высокой частоты и

г) дроссели низкой частоты.

По конструктивному признаку катушки могут быть разделены на однослойные и многослойные; цилиндрические, спиральные и тороидальные; экранированные и неэкранированные; катушки без сердечников и катушки с сердечниками и др.

Катушки индуктивности характеризуются следующими основными параметрами: индуктивностью и точностью, добротностью, собственной емкостью и стабильностью.

Однослойные катушки применяются на частотах выше 1500 кГц. Намотка может быть сплошная и с принудительным шагом. Однослойные катушки с принудительным шагом отличаются высокой добротностью (Q=150…400) и стабильностью;

применяются в основном в контурах коротких (KB) и ультракоротких (УКВ) волн [47]. Высокостабильные катушки, применяемые в контурах гетеродинов на KB и УКВ, наматываются при незначительном натяжении проводом, нагретым до 80…120 С.

Для катушек с индуктивностью выше 15…20 мкГн применяется сплошная однослойная намотка. Целесообразность перехода на сплошную намотку определяется диаметром катушки. Ориентировочные значения индуктивности, при которых целесообразен переход на сплошную намотку:

Диаметр каркаса (в мм) 6 10 15 20 25
Индуктивность (в мкГн) 1,8 4 10 20 30

Катушки со сплошной намоткой также отличаются высокой добротностью и широко используются в контурах на коротких, промежуточных и средних волнах, ее ли требуется индуктивность не выше 200…500 мкГн. Целесообразное гь перехода на многослойную намотку определяется диаметром катушки. Ориентировочные значения индуктивности, при которых целесообразен переход на многослойную намотку:

Диаметр каркаса (в мм) 10 15 20 25 30
Индуктивность (в мкГн) 30 50 100 200 500

Индуктивность однослойной катушки рассчитывается по формуле:

L=0,01DN²/(l/D+0.44), где L — индуктивность (в мкГн), D — диаметр катушки (в см), 1 — длина намотки (в см), N — число витков.

Добротность однослойных катушек определяется в основном диаметром провода и шагом намотки (расстоянием между витками) х. Установлено , что на высоких частотах оптимальное значение диаметра намоточного провода определяется из выражения: d=0,707x.

Многослойные катушки разделяются на простые и сложные. Примерами простых намоток являются рядовая многослойная намотка и намотка «кучей» (или в навал). Не  секционированные многослойные катушки с простыми намотками отличаются пониженной добротностью и стабильностью, большой собственной емкостью, требуют применения каркасов. Индуктивность многослойной катушки рассчитывается по формуле: L=0,08(DN)²/(3D+9l+10t), где L — индуктивность катушки, мкГн; D — средний диаметр намотки, см; l— длина намотки, см; t — толщина катушки, см; N — число витков.

Если задана индуктивность и нужно рассчитать число витков, то следует задать величины D, l и t и подсчитать необходимое число витков. После этого следует произвести проверку толщины катушки по формуле: t=zNd²/l, где d — диаметр провода с изоляцией (в мм), z=1,05…1,3 — коэффициент не плотности намотки при d=1…0,08 соответственно.

Секционированные катушки индуктивности характеризуются достаточно высокой добротностью, пониженной собственной емкостью, меньшим наружным диаметром и допускают в небольших пределах регулировку индуктивности путем смещения секций. Они применяются как в качестве контурных в контурах длинных и средних волн, так и в качестве дросселей высокой частоты. Каждая секция представляет собой обычную многослойную катушку с небольшим числом витков. Число секций может быть от двух до восьми, иногда даже больше. Расчет секционированных катушек сводится к расчету индуктивности одной секции. Индуктивность секционированной катушки, состоящей из п секций: L= Lc[n+2k(n-1)], где Lc — индуктивность секции, k — коэффициент связи между смежными секциями (k=0.3 при расстоянии между секциями, равном половине ширины секции, которая равна среднему радиусу катушки).

Собственная емкость катушки понижает добротность и стабильность настройки контуров. В диапазонных контурах эта емкость уменьшает коэффициент перекрытия диапазона. Величина собственной емкости определяется типом намотки и размерами катушки. Наименьшая собственная емкость (несколько пФ) у однослойных катушек, намотанных с принудительным шагом. Многослойные катушки обладают большей емкостью, величина которой зависит от способа намотки. Так, емкость катушек с универсальной намоткой составляет 5…25 пФ, а с рядовой многослойной намоткой может быть выше 50 пф.

Дросселем высокой частоты называют катушки индуктивности, используемые в цепях питания в качестве фильтрующих элементов. Индуктивность дросселя должна быть достаточно большой, а собственная емкость — малой. Конструктивно дроссели высокой частоты выполняются в виде однослойных или многослойных катушек. Для дросселей длинных и средних волн применяется секционированная многослойная намотка. Дроссели для коротких волн и для метровых волн обычно имеют однослойную намотку — сплошную или с принудительным шагом. В качестве каркаса часто используются керамические стержни от резисторов. Расчет числа витков дросселя производится так же, как и расчет числа витков катушек индуктивности.

В катушках с большой индуктивностью применяются сердечники из ферромагнитных материалов. Индуктивность катушки с замкнутым стальным сердечником L=0,0126mSN²/lc, [мкГн], где m — магнитная проницаемость материала (для электротехнических сталей находится в диапазоне 200… 500), S — сечение сердечника (в см²), N — число витков катушки, 1„ — средняя длина магнитного пути, см (например, для круглого сердечника — длина его средней окружности).

 

 

Системы беспроводной передачи энергии на основе NFC

Введение

Рынок устройств с технологией NFC (Near field communication, NFC — «коммуникация ближнего поля», «ближняя бесконтактная связь») экспоненциально растет, и ожидается, что к 2024 году он достигнет $47 млрд [4]. В настоящее время уже имеется более 2 млрд мобильных устройств с технологией NFC и около 2,1 млрд человек во всем мире пользуются услугами мобильных платежей на основе этой удобной бесконтактной технологии связи.

NFC — это технология радиочастотной беспроводной связи с малым радиусом действия с невысокой пропускной способностью, которая обеспечивает стандартизованную связь между двумя устройствами, такими как смартфоны, смарт-карты, наклейки или бирки. В технологии NFC используется та же несущая частота, что и в метках радиочастотной идентификации (radio frequency identification, RFID), а именно 13,56 МГц. Хотя RFID может принимать и передавать данные на расстояние до нескольких метров, технология NFC для безопасности передачи данных ограничивается очень близкой дистанцией до 10 см. Скорость передачи данных NFC составляет 106–848 кбит/с. Кроме того, технология NFC всегда включает «инициатор», такой как устройство для чтения банковских карт, и «цель», например, кредитную карту. При этом инициатор активно генерирует ВЧ-поле, которое питает цель [2].

В устройствах, использующих технологию NFC, имеется три различных режима связи. Первые два — это режим чтения/записи и режим эмуляции карты, в которых предусмотрены схемы пассивной связи, где пассивная цель использует ВЧ-поле, генерируемое инициатором. Режим чтения/записи позволяет читать информацию, хранящуюся на NFC-метках или смарт-картах. Режим эмуляции карты предоставляет возможность мобильному устройству с поддержкой NFC функционировать как бесконтактная смарт-карта (например, кредитная карта, карта доступа или электронный транспортный билет). В статье описывается пассивный режим чтения/записи и режим эмуляции карты [3].

Третий режим, одноранговый, может применяться как с активной, так и с пассивной схемой связи. При активном взаимодействии инициатор и цель генерируют собственное поле. Одноранговый режим используется для обмена информацией, такой как данные «визитной» карточки, между двумя мобильными NFC-устройствами, например в смартфонах.

В современных системах с NFC максимальная скорость передачи данных составляет 848 кбит/с. Поскольку мощность радиочастотного поля ограничена 1 Вт, то NFC в основном используется для целей связи. И наоборот, системы беспроводной передачи мощности (wireless power transfer, WPT) могут обеспечивать мощность в диапазоне сотен ватт или более, но при низких скоростях внутриполосной передачи данных — до нескольких сотен байт/с.

Теперь мы, команда инженеров-разработчиков компании Würth Elektronik, объединили преимущества высокой скорости передачи данных NFC-связи и высокой мощности передачи до 100 Вт в одном небольшом и экономичном комбинированном устройстве WPT/NFC, что позволило создать эффективное решение для коммерческих и финансовых транзакций и управления операционными процессами промышленных предприятий.

 

Система на основе комбинации WPT/NFC

Организация системы WPT/NFC

В ходе проекта была создана следующая концепция построения система WPT/NFC. Для части WPT для беспроводной передачи энергии использовался отладочный комплект Power Transfer Development Kit 760308EMP мощностью 200 Вт собственной разработки компании Würth Elektronik, он подробно описан в [5]. Коммуникационная часть системы была выполнена с помощью комплекта разработки NFC OM27462CDK компании NXP, который описан в [6].

На рис. 1 представлена упрощенная блок-схема системы WPT/NFC. В качестве пассивных целей применялись образцы NFC-карт, которые входят в комплект разработчика NFC. Карты, используемые на этом этапе разработки, изначально представляют собой теги NFC типа 2. В режиме чтения/записи они обеспечивают скорость передачи данных 106 кбит/с. Также имелась карта MifareDESFire EV1, которая обеспечивает максимальную скорость передачи данных 848 кбит/с и работает в режиме эмуляции карты [8].

Рис. 1. Упрощенная блок-схема WPT/NFC-системы

В настоящее время компания Würth Elektronik предлагает четыре различные катушки WPT/NFC, одну в качестве передатчика и три в качестве приемника, как это показано в таблице 1.

Таблица 1. Комбинированные WPT/NFC-катушки компании Würth Elektronik

Катушка	Номер заказа	Индуктивность L1, мкГн	Индуктивность L2, мкГн	Добротность Q1	Добротность Q2	Тип
A	760308103305	8,8	1,4	30	47	Rx
B	760308102306	8	1,4	19	47	Rx
C	760308103307	7,8	1,6	19	47	Rx
D	760308101312	24	0,7	125	30	Tx

В таблице 1 L₁ и Q₁ — это индуктивность и добротность части катушек с WPT, измеренная на частоте 125 кГц, а L₂ и Q₂ — индуктивность и добротность части катушек с NFC, измеренная на частоте 13,56 МГц. Катушка D использовалась в комбинированной системе WPT/NFC и показана на рис. 2.

Рис. 2. Катушка типа D системы WPT/NFC, предлагаемая компанией Würth Elektronik

Часть NFC-катушки D используется на стороне инициатора, а часть WPT — на сторонах передатчика и приемника. Характеристики фильтра и согласующей схемы инициатора, резонансные контуры приемника и передатчика были определены путем расчета, моделирования и уточнены по результатам измерения прототипа.

Согласование импеданса катушки NFC с ИС NFC

Согласование импеданса — это очень важная процедура при проектировании радиочастотных схем, обеспечивающая максимально возможную передачу энергии от источника к его нагрузке и минимизирующая отражения сигнала обратно к источнику.

В комбинированной WPT/NFC-системе согласование импеданса необходимо для согласования дифференциального выходного импеданса NFC ИС, равного 50 Ом, с импедансом NFC-катушки. С этой целью на выходе NFC ИС используется фильтр. Он решает две задачи: фильтрация гармоник сигнала NFC и решение проблемы электромагнитной совместимости (ЭМС), а также используется для преобразования импеданса. В качестве фильтра электромагнитных помех (ЭМП) рекомендуется фильтр нижних частот (ФНЧ) второго порядка, состоящий из катушки индуктивности и конденсатора. Частота среза такого фильтра должна быть выше, чем частота верхней боковой полосы, определяемая самой высокой скоростью передачи данных в системе, а это, как уже было сказано, 848 кбит/с. Фильтр ЭМП и согласующая схема должны преобразовать импеданс катушки NFC до уровня 50 Ом.

На рис. 3 показана электрическая принципиальная схема фильтра ЭМП и согласующая цепь для режима чтения/записи, включая эквивалентную схему катушки NFC. Контакты Tx1 и Tx2 являются выходными контактами дифференциальной передачи NFC ИМ, а TVSS — контактом заземления.

Рис. 3. Стандартный фильтр ЭМП и согласующая схема для режима чтения/записи [7]

На схеме рис. 3 L₀ и C₀ — это индуктивность и емкость фильтра ЭМП; C_S и C_P — это согласующие конденсаторы, которые размещены в виде Г-звена, а R_q — демпфирующий резистор, уменьшающий добротность катушки, что необходимо для подавления переходных процессов. Элементы R_a, L_a и C_a на схеме — эквивалентные сопротивление катушки, индуктивность и ее собственная емкость.

Для решения проблемы согласования импеданса во время проектирования были выполнены следующие шаги:

1. Измерение последовательного сопротивления R_S, параллельного сопротивления R_P, индуктивности L_a, собственной резонансной частоты f_S катушки NFC и определение значений эквивалентной цепи катушки.
2. Расчет индуктивности и емкости конденсатора фильтра ЭМП.
3. Определение компонентов согласующей схемы путем моделирования для режима чтения/записи.
4. Адаптация согласования итоговой схемы для режима эмуляции карты.

На правой части рис. 4 показана последовательная эквивалентная схема катушки.

Рис. 4. Последовательная эквивалентная схема катушки [1]

На рис. 4 R_P — это эквивалентный параллельный резистор катушки; R_S — внутреннее собственное последовательное сопротивление катушки; L_a — индуктивность катушки; C_a — параллельная эквивалентная емкость на собственной резонансной частоте f_S; R_a — эквивалентный последовательный резистор. Значения R_P, R_S и L_a должны быть измерены на рабочей частоте f_op = 13,56 МГц. Необходимо вычислить C_a и R_a.

С помощью измерений с использованием векторного анализатора цепей были получены следующие значения элементов эквивалентной схемы:

• f_S = 63 МГц;
• L_a (13,56 МГц) = 0,7 мкГн;
• R_S (13,56 МГц) = 1,7 Ом;
• R_P (13,56 МГц) = 1,9 кОм.

Значение емкости конденсатора C_a можно рассчитать по следующей формуле (1) из [1]:

Подставляя в формулу 1 измеренные и начальные значения, получаем C_a = 9,12 пФ.

Значение R_a, также можно рассчитать с помощью формулы (2) из [1]:

Подставляя в формулу 2 измеренные и начальные значения, получаем R_a = 3,57 Ом.

Далее частоту среза f_C фильтра ЭМП можно рассчитать с помощью общеизвестной формулы (3):

Принимая во внимание верхнюю боковую полосу для максимальной передачи данных (13,56 МГц + 848 кГц), частота среза определяется равной 14,8 МГц, что, согласно определенному ранее условию, находится выше частоты верхней боковой полосы 14,4 МГц.

Для рассматриваемого случая была выбрана индуктивность фильтра L₀ = 470 нГн, что из уравнения (3) приводит к емкости конденсатора фильтра C₀ = 247 пФ. В свою очередь емкости конденсаторов C_S и C_P и значение сопротивления демпфирующего резистора R_q были определены путем моделирования с помощью программы Advanced Design System (ADS) от компании Keysight Technologies.

Схема, показанная на рис. 3, была промоделирована. Схема, использованная для моделирования, показана на рис. 5.

Рис. 5. Схема стандартного фильтра ЭМП и согласующей цепи, использованная для моделирования с помощью программы Advanced Design System от компании Keysight Technologies

Инструмент оптимизации ADS применялся для определения значений C_S, C_P и R_q. Моделирование приводит нас к следующим значениям этих элементов схемы:

• C_S = 12 нФ;
• C_P = 284 пФ;
• R_q = 11 Ом.

Эти компоненты, идентифицированные путем измерения, расчета и моделирования, были собраны в схему, показанную на рис. 5. Поскольку в моделировании используются идеальные сосредоточенные элементы, а реальные компоненты имеют допуски и потери, значения C_S, C_P и R_q корректируются для улучшения согласования. В результате для режима эмуляции карты, который необходим для скорости передачи данных 848 кбит/с, схема, представленная на рис. 3, была расширена до схемы, показанной на рис. 6.

Рис. 6. Расширенная схема фильтра ЭМП и соответствующая согласующая схема для режима эмуляции карты для режима чтения/записи в системе WPT/NFC

Номиналы элементов C_ant и R_X были выбраны равными 82 пФ и 4,7 кОм, как это рекомендовано в руководстве к комплекту моделирования и проверки решения NFC от компании NXP — UM10883 PN7462AU Quick Start Guide [6].

Определение характеристик резонансных контуров на стороне передатчика и приемника

Для того чтобы оптимизировать эффективность передачи системы беспроводной передачи энергии WPT, конденсаторы резонансных контуров, имеющихся в составе передатчика и приемника, должны быть правильно рассчитаны. Резонансный контур состоит из индуктивности катушки и последовательного конденсатора, то есть мы имеем дело с резонансом токов. Значения резонансных конденсаторов были определены путем измерения и расчета. Чтобы учесть влияние катушки передатчика, измеряется индуктивность катушки приемника L′_s, когда катушка приемника отделена от катушки передатчика. Измерения проводились на расстоянии 4 мм. Для этого расстояния значение L′_s, измеренное с помощью LCR, составило 31,2 мкГн на частоте 100 кГц.

Резонансный конденсатор C_R, который должен быть интегрирован на стороне приемника, может быть рассчитан по формуле (4) следующим образом:

где f₀ — рабочая частота передачи энергии, равная 100 кГц.

С учетом измеренного значения L′_s емкость C_R составила 81 нФ.

Индуктивность катушки L_P передатчика измеряется на том же расстоянии между приемником и передатчиком, как указано выше. Измеренное на частоте 100 кГц значение индуктивности L_P для этого расстояния составляет 29,8 мкГн.

Значение емкости конденсатора C_T, который является резонансным конденсатором на стороне передатчика, рассчитывается аналогично по формуле (5):

С учетом измеренного значения L_p емкость C_T составила 85 нФ.

 

Полученные результаты

Согласование импедансов

Как уже было сказано, для проверки решения использована расширенная согласующая схема (рис. 6), а также смоделированные и измеренные значения элементов. Для улучшения согласования применялось более высокое значение R_q, равное 20 Ом.

Коэффициент отражения на входном порте (между выводами Tx1 и Tx2) был измерен с помощью векторного анализатора цепей VNA. На рис. 7 показан измеренный коэффициент отражения в диапазоне частот 12–15 МГц, представленный в дБ.

Рис. 7. Изменение коэффициента отражения расширенного фильтра ЭМП и согласующей схемы в зависимости от частоты

Видно, что коэффициент отражения на рабочей частоте 13,56 МГц имеет значение около –27 дБ. Это означает, что всего лишь около 0,2% падающей мощности отражается обратно на вход.

Связь и передача энергии

Со стандартным фильтром и согласующим звеном, показанным на рис. 3, и с использованием смоделированных значений согласования и катушки D может быть достигнута связь с NFC-меткой типа 2 со скоростью передачи данных 106 кбит/с на расстоянии до 3 см.

Используя расширенный фильтр и схему согласования, представленные на рис. 6, с измененным значением демпфирующего резистора на 20 Ом, можно увеличить скорость передачи данных до 848 кбит/с, хотя разделение обмена данными между инициатором и целью (в ее роли выступала смарт-карта Mifare DESFire EV1) уменьшилось до 4 мм.

Для передачи энергии на стороне передатчика и приемника использовалась часть WPT катушки D. При использовании резонансного емкостного конденсатора CR = 81 нФ на стороне приемника и CT = 85 нФ на стороне передатчика, при расстоянии между катушками 4 мм была достигнута эффективность DC/DC-преобразования около 85%. При этом беспроводная передача мощности до 60 Вт была достигнута при стандартных температурных условиях.

Максимальный КПД системы h_max WPT можно рассчитать с помощью формулы (6) из [9]:

Добротность Q — это совокупный коэффициент добротности системы двух отдельных катушек, который можно рассчитать с помощью формулы (7) из [9]:

Для расчета коэффициента связи k катушек использовалось следующее уравнение:

L_P в формуле (8) — измеренная индуктивность катушки передатчика при заданном расстоянии между катушками 4 мм; L_leakp — паразитная индуктивность катушки передатчика, которая измеряется путем закорачивания катушки приемника на этом расстоянии и измерения индуктивности катушки передатчика. Используя формулы (6)–(8), можно вычислить максимальную эффективность комбинированных катушек передатчика и приемника, которая приводит к значениям, сведенным в таблицу 2.

Таблица 2. Комбинации WPT/NFC-катушек компании Würth Elektronik и максимальные значения эффективности (КПД)

Tx катушка (табл. 1)	Rx катушка (табл. 1)	Коэффициент связи k	Добротность Q	ηmax, %
D	A	0,56	61	94
D	B	0,52	48	92
D	C	0,33	48	87

Таблица 2 показывает, что максимальная эффективность системы беспроводной передачи энергии WPT составляет 94%, что достигается с катушкой A на стороне приемника и катушкой D на стороне передатчика. Причины потерь WPT-катушек — это омические потери, взаимное влияние из-за близости и скин-эффекты. Кроме того, для оценки общей эффективности системы во внимание должны быть приняты потери в инверторе на стороне передатчика и потери синхронного выпрямителя на стороне приемника.

 

Выводы

В статье описана основа WPT/NFC-системы на катушках компании Würth Elektronik. В частности, рассмотрены параметры согласования и схема фильтров для части NFC. При этом показано, что может быть реализована скорость передачи данных 106 кбит/с на расстоянии между инициатором и целью до 3 см и 848 кбит/с на расстоянии до 4 мм. Для части WPT был выполнен расчет резонансных контуров и протестирована сама система беспроводной передачи данных. При этом был достигнут КПД 85% при расстоянии между передатчиком и приемником 4 мм с использованием части WPT катушки D в качестве передатчика и приемника. Для комбинации катушки D в качестве передатчика и катушки A в качестве приемника может быть достигнута максимальная эффективность системы 94%.

Следующим шагом в процессе разработки станет изготовление системы приемника, способной демодулировать поток битов NFC и визуализировать переданное сообщение. NFC-часть катушек A и C будет использоваться в качестве меток. Другая цель — продемонстрировать, что связь и передача энергии могут работать одновременно.

Примером применения такой WPT/NFC-системы может служить система беспроводной зарядки для мобильных устройств, обеспечивающая платежные услуги. Преимущество подобной WPT/NFC-системы заключается в том, что высокая скорость передачи данных системы NFC может быть достигнута при одновременной беспроводной передаче высокой мощности в одном небольшом и эффективном устройстве.

Дополнительная информация по тематике статьи доступна в [10, 11].

Литература

1. AN11564 PN7120 Antenna Design and Matching Guide, Rev. 1.1. 18 April 2016, 299411. Application note.
2. Coskun V., Ok K., Ozdenizci B. Near Field Communication from theory to practice. Wiley, 2012.
3. Desai E., Shajan M. G. A Review on the Operating Modes of Near Field Communication, International Journal of Engineering and Advanced Technology (IJEAT). 2012.
4. The exponential growth of mobile internet application and advancement of 3G and 4G networks is anticipated to drive the market.
5. Würth Elektronik eiSos, ANP70c, Proprietary wireless power transfer solution for high performance including data transmission. Application Note, 2018. 
6. UM10883 PN7462 family Quick Start Guide – Development Kit. User manual. Rev. 1.6. 14 May 2018, 319816.
7. Baier T. Automated Impedance Adjustment of 13.56 MHz NFC Reader Antennas. Master Thesis, 2014.
8. NFC Tags & Tag Types. 
9. Bosshard R., Muhlethaler J., Kolar J. W., Stevanovic I. Optimized magnetic design for inductive power transfer coils. Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC). Long Beach, CA, USA, 2013.
10. Унтеррайтмайер А. Решение компании Würth Elektronik для высокоэффективной беспроводной передачи энергии и данных по одному каналу // Компоненты и технологии. 2019. № 3.
11. Надлер А., Сом К. Беспроводная передача энергии большой мощности для устройств, работающих в условиях индустриальной среды // Компоненты и технологии. 2017. № 7, 8.

Физическая природа индуктивности

Источник — Свободный взгляд Физическая природа индуктивности. Катушки индуктивности обладают свойством оказывать реактивное сопротивление переменному току при незначительном сопротивлении постоянному току. Совместно с конденсаторами они используются для создания фильтров, осуществляющих частотную селекцию электрических сигналов, а так же для создания элементов задержки сигналов и запоминающих элементов, осуществления связи между цепями через магнитный поток и т.д. В отличие от резисторов и конденсаторов они не являются стандартизованными изделиями, а изготавливаются для конкретных целей и имеют такие параметры, которые необходимы для осуществления тех или иных преобразований электрических сигналов, токов и напряжений. Функционирование катушек индуктивности основано на взаимодействии тока и магнитного потока. Известно, что при изменении магнитного потока Ф в проводнике, находящемся в магнитном поле, возникает ЭДС, определяемая скоростью изменения магнитного потока (2.25) Поэтому при подключении к проводнику источника постоянного напряжения ток в нем устанавливается не сразу, так как в момент включения изменяется магнитный поток и в проводе индуцируется ЭДС, препятствующая нарастанию тока, а спустя некоторое время, когда магнитный поток перестает изменяться. Если же к проводнику подключен источник переменного напряжения, то ток и магнитный поток будут изменяться непрерывно и наводимая в проводнике ЭДС будет препятствовать протеканию переменного тока, что эквивалентно увеличению сопротивления проводника. Чем выше частота изменения напряжения, приложенного к проводнику,, тем больше величина ЭДС, наводимая в нем, следовательно, тем больше сопротивление, оказываемое проводником протекающему току. Это сопротивление XL не связано с потерями энергии, поэтому является реактивным. При изменении тока по синусоидальному закону наводимая ЭДС будет равна (2.26) Она пропорциональна частоте w, а коэффициентом пропорциональности является индуктивность L. Следовательно, индуктивность характеризует способность проводника оказывать сопротивление переменному току. Величина этого сопротивления ХL=wL Индуктивность короткого проводника (мкГн) определяется его размерами: (2.26) где l -длина провода в см, d — диаметр провода в см. Если провод намотан на каркас, то образуется катушка индуктивности. В этом случае магнитный поток концентрируется и величина индуктивности возрастает. 2.3.2.Конструкции катушек индуктивности. Конструкционной основой катушки индуктивности является диэлектрический каркас, на который наматывается провод в виде спирали. Обмотка может быть как однослойной (рис.2.21,а), так и многослойной (рис.2.21,6). В некоторых случаях многослойная обмотка делается секционированной (рис.2.21,в). В интегральных схемах применяются плоские спиральные катушки индуктивности (рис.2.21,г). Для увеличения индуктивности применяют магнитные сердечники. Помещенный внутрь катушки сердечник концентрирует магнитное поле и тем самым увеличивает ее индуктивность. Перемещением сердечника внутри каркаса можно изменяп, индуктивность. На рис.2.22 представлены три  разнидности цилиндрических сердечников: С — стержневой, Т — трубчатый и ПР — подстроечный резьбовой и две разновидности броневых. Броневые сердечники состоят из двух чашек 2, изготовленных из карбонильного железа или ферритаов. Они могут иметь либо замкнутый магнитопровод (тип СБ — а), либо разомкнутый (тип С Б — б). Для изменения индуктивности служит подстроечный цилиндрический сердечник 1. Помимо цилиндрических и броневых сердечников применяют торроидальные (кольцевые) сердечники. На высоких частотах (десятки-сотни МГц) применяют подстроечные цилиндрические сердечники из диамагнетиков (латунь, медь). При введении этих сердечников внутрь катушки индуктивность уменьшается. В катушках индуктивности, работающих на низких в качестве сердечников используют пермаллои. При этом рается из тонких пластин толщиной 0,002-0,1мм. Для уменьшения влияния электромагнитного поля катушки на другие элементы схемы, а также для уменьшения влияния внешних полей на катушку индуктивности, ее располагают внутри металлического экрана, как это показано на рис.2.23 (1 — заглушка, 2 — экран, 3 — корпус, 4 — обмотка, 5 — каркас, 6 -подстроечный стержень, 7 — чашка сердечника, 8 — основание, 9 — заливка). 2.3.3. Индуктивность и собственная емкость катушек индуктивности. Индуктивность является основным параметром катушки индуктивности. Ее величина (мкТн) определяется соотношением где W — число витков, D — диаметр катушки в см, L0 — коэффициент, зависящий от отношения длины катушки / к ее диаметру О. Для однослойных катушек величина L0 определяется соотношением (2.29) Оптимальными в этом случае являются отношение   а диаметр катушки в пределах от 1 до 2 см. При расчете диаметр катушки D принимается равным диаметру каркаса D0 Для многослойных катушек величина L0зависит не только от величины   1/D , но и от отношения толщины намотки t к диаметру катушки D. Она определяется по графикам (рис.2.24). В этом случае внешний диаметр катушки D=D0 + 2t При расчете катушки индуктивности предварительно задаются геометрическими размерами катушки и определяют коэффициент L0, а затем по заданной величине индуктивности L находят число витков: (2.30) где I, — в мкГн , D — в см. Для намотки катушки обычно применяют провод оптимального диаметра, который рассчитывается с помощью эмпирических формул и графиков. Для этого по графику S=f(t/D;l/D) (рис.2.25) находят вспомогательный коэффициент S. Затем рассчитывают коэффициент (2.31) где f -в мкГц , D — в см. Затем рассчитывают коэффициент a1 где f — частота в Гц. После чего по графику b1=f(a1)  (рис. 2.26) находят  вспомогательный коэффициент b1S и расчитывают оптимальный диаметр провода (мм) (2.32)   Полученное значение  округляется до ближайшего стандартного значения (табл.2.6) и выбирается марка провода с диаметром  dиз Таблица 2.6 Основные параметры обмоточных проводов d, мм Sn, мм~ Максимальный диаметр в изоляции , мм     ПЭВТЛК ПЭМ-1 ПЭВ-1 ПЭВ-2,ПЭТВ ПЭМ-2 0,063 0,0028 0.11 0,09 0,085 0,09 0,071 0,0038 0,12 0,09 0,095 0,1 0,08 0,005 0,13 0,1 0,105 0,11 0,09 0,0064 0,14 0,11 0,115 0,12 0,1 0,0079 0,15 0,12 0,125 0,13 0,112 0,0095 0,16 0,14 0,135 0,14 0,125 0,0113 0,17 0,15 0,15 0,155 0,14 0,0154 0,185 0,16 0,165 0,17 0,16 0,02 0,2 0,19 0,19 0,2 0,18 0,0254 0,23 0,21 0,21 0,22 0,2 0,0314 0,25 0,23 0,23 0,24 0,224 0,0415 0,27 0,25 0,26 0,27 0,25 0,0491 0,3 0,29 0,29 0,3 0,28 0,0615 0,34 0,32 0,32 0,33 0,315 0,0755 0,37 0,35 0,355 0,365 0,355 0,0962 0,405 0,39 0,395 0,415 0,4 0,126 0,47 0,44 0,44 0,46 0,45 0,158 — 0,49 0,49 0,51 0,5 0,193 — 0,55 0,55 0,57 0,56 0,246 — 0,61 0,61 0,63 0,63 0,311 — 0,68 0,68 0,7 0,71 0,39 — 0,76 0,76 0,79 0,75 0.435 — 0,81 0,81 0,84 0,8 0,503 — 0,86 0,86 0,89 0,85 0,567 — 0,91 0,91 0,94 0,9 0,636 — 0,96 0,96 0,99 0,95 0,71 — 1,01 1,01 1,04 1 0,785 — 1,08 1,07 1, 11 После выбора оптимального диаметра провода проверяют возможность размещения обмотки в заданных размерах  l и t. Для однослойных катушек рассчитывают шаг намотки (2.33) Если  t>dиз;   то обмотка размещается. В противном случае задаются большей  величиной l и повторяют расчет. Для многослойных катушек рассчитывают толщину обмотки (2.34) где а — коэффициент неплотности обмотки ( a = 1,05…1,3), и находят фактическое значение наружного диаметра катушки D=D0+2t. Если эта величина отличается от выбранной в начале расчета более чем на 10%, то задаю тся новыми значениями l и t и расчет повторяют. При помещении катушки в экран индуктивность катушки уменьшается (2.35) где h — коэффициент, зависящий от отношения l/D (рис.2.27), D — диаметр катушки, Dэк-диаметр экрана. Индуктивность уменьшается тем больше, чем меньше диаметр экрана. В большинстве случаев Dэк/D >1,6ё1,8.При этом индуктивность уменьшается не более чем на 20%. Многослойные катушки обычно выполняют с сердечниками броневого типа, при использовании которых большая часть силовых линий магнитного поля катушки замыкается через сердечник, а меньшая-через воздух, вследствие чего влияние экрана на индуктивность катушки значительно ослабляется. Применение сердечников из магнитных материалов позволяет уменьшить число витков катушки индуктивности и соответственно ее габариты. Основным параметром сердечника является магнитная проницаемость  mс При его наличии индуктивность катушки становится равной Поскольку в расчетные формулы входят эмпирические коэффициенты, то индуктивность изготовленной катушки отличается от расчетной. Применение подстроечных магнитных сердечников позволяет получить требуемое значение индуктивности. Собственная емкость является паразитным параметром катушки индуктивности, ограничивающим возможности ее применения. Ее возникновение обусловлено конструкцией катушки индуктивности: емкость существует между отдельными витками катушки, между витками и сердечником, витками и экраном, витками и другими элементами конструкции. Все эти распределенные емкости можно объединить в одну, называемую собственной емкостью катушки CL Наименьшей собственной емкостью обладают однослойные катушки индуктивности Приближенно она рассчитывается по формуле (пФ) СL  >(0,5ё1.0)D, (2.37) где D — диаметр катушки в см. Обычно она не превышает 1-2пФ. Собственная емкость многослойных катушек значительно больше. При многослойной рядовой намотке она достигает ЗОпФ; при намотке «внавал» она несколько меньше. Существенное уменьшение емкости многослойных катушек достигается при использовании универсальной обмотки, при выполнении которой провод укладывается под некоторым углом к образующей цилиндрического каркаса. Схема такой намотки показана на рис.2.28. Как только провод доходит до края катушки, направление укладки меняется. Цикл универсальной обмотки выбирается таким, что, совершив один оборот вокруг каркаса, провод возвращается к положение, отличающееся от исходного на угол b. Этот угол выбирается таким, чтобы каждый последующий виток находился рядом с предыдущим. Очевидно, что (2.38) Угол   j  , под которым осуществляется укладка провода, находится из соотношения (2.39) где l-осевая длина катушки, D — диаметр витка. Наименьшее значение угла j получается для витков, имеющих наименьший диаметр, равный диаметру каркаса D0. Обычно при использовании универсальной обмотки длину катушки принимают в пределах от 2 до 10мм. Количество циклов намотки связано с рачетнным числом витков W соотношением (2.40) Величина собственной емкости катушек с универсальной обмоткой составляет от 3 до 8пФ. Дополнительное снижение емкости достигается серкцонированием обмотки, как показано на рис.2.21,в. Совместное действие индуктивности и емкости можно учесть введением понятия об эквивалентной индуктивности катушки, определяемой из уравнения откуда (2.41) где  -собственная резонансная частота катушки индуктивности. Если рабочая частота много ниже собственной резонансной частоты wL, то приближенно можно считать Lэ=L. В процессе работы на катушку действуют различные внешние факторы:температура, влага и другие, влияющие на ее индуктивность.Наиболее существенным является влияние температуры, которое оценивают температурным коэффициентом . Температурная нестабильность индуктивности обусловлена целым рядом факторов: при нагреве увеличивается длина и диаметр провода обмотки, увеличивается длина и диаметр каркаса, в результате чего изменяются шаг и диаметр витков; кроме того при изменении температуры изменяются диэлектрическая проницаемость материала каркаса, что ведет к изменению собственной емкости катушки. Для повышения температурной стабильности применяют каркасы из материала с малым значением коэффициента линейного расширения. Этим требованиям в наибольшей степени удовлетворяет керамика. Повышению температурной стабильности катушек способствует прочное сцепление обмотки с каркасом. С этой целью обмотку выполняют методом вжигания серебра в керамический каркас. В этом случае изменение размеров токопроводящего слоя определяется только линейным расширением каркаса. Такие катушки индуктивности имеют TKL >(5-100).10-6Стабильность многослойных катушек существенно хуже, так как в них невозможно избежать изменения линейных размеров провода обмотки. Многослойные катушки имеют TKL> (50-100).10-6 2.3.4. Потери в катушках индуктивности. В катушках индуктивности помимо основного эффекта взаимодействия тока и магнитного поля наблюдаются паразитные эффекты, вследствие которых сопротивление катушки не является чисто реактивным и равным ХL. Наличие паразитных эффектов ведет к появлению потерь в катушке, оцениваемых сопротивлением потерь RП , которое определяет добротность катушки индуктивности (2.42) Потери складываются из потерь в проводах, диэлектрике, сердечнике и экране. Потери в проводах вызваны тремя причинами. Во-первых, провода обмотки обладают омическим сопротивлением (2.43) где l -длина провода обмотки, d- диаметр провода, р- удельное сопротивление. Это сопротивление (Ом) можно выразить через число витков W и средний диаметр катушки DСР (2.44) где -диаметр провода в см. Во-вторых, сопротивление провода обмотки переменному току возрастает с ростом частоты, что обусловлено поверхностным эффектом, суть которого состоит в том, что ток протекает не по всему сечению проводника, а по кольцевой части поперечного сечения (рис.2.29), ширина (мм) которой равна (2.45) где f— частота в МГц, r— удельное сопротивление в мкOм· м. Вследствие этого провод длиной l имеет сопротивление переменному току равное (2.46) где SЭФ — площадь кольца, которая равна (2.47) где После преобразования получаем (2.48) В третьих, в проводах обмотки, свитой в спираль, проявляется эффект близости (рис.2.30), суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля к периферии провода, прилегающей к каркасу, в результате чего сечение, по которому протекает ток, принимает серповидный характер, что ведет к дополнительному возрастанию сопротивления провода. Сопротивление rБ, обусловленное эффектом близости, прямо пропорционально диаметру провода, а сопротивление rП, обусловленное эфектом, обратно пропорционально диаметру провода ( рис.2.31). Существует оптимальный диаметр провода dопт , при котором сопротивление провода току высокой частоты rf = rБ + rП оказывается минимальным. Для однослойных катушек dопт= 0,2-0,6мм, для многослойных dопт =0,08-0,2мм. Существенно уменьшить потери в проводах можно применяя провод «литцендрат», состоящий из большего числа жилок, скрученных в жгут. При небольшом диаметре тонких жилок ослабляется поверхностный эффект, а скручивание жилок в жгут ослабляет эффект близости. Существует методика расчета сопротивления rf , по которой предварительно рассчитывается вспомогательный коэффициент (2.49) где f — частота в Гц, d- диаметр провода в см. Затем по таблице находятся коэффициенты F(z) и G(z). Z F(z) G(z) 0,5 1 0,001 0,6 1 0,002 0,7 1 0,004 0,8 1 0,006 0,9 1 0,01 1 1,01 0,015 1,5 1,03 0,07 2 1,08 0,17 2,5 1,18 0,3 3 1,3 0,4 4 1,7 0,6 5 2 0,8 7-.5 2,9 1,2 10 3,8 1,6 20 7,3 3,4 25 9,1 4,3 50 18 8,2 100 36 18 После этого по графику (рис.2.32) определяется вспомогательный коэффициент Кз , зависящий от геометрии катушки. По (2.50) рассчитывается сопротивление провода катушки току высокой частоты (2.50) где D— наружный диаметр катушки в см, d -диаметр провода в см. Если однослойная катушка намотана проводом оптимального диаметра и параметр z >5, то сопротивление rf можно определить по формуле (2.51) где D — в см,  d — в см,   f‘- в МГц. Потери в диэлектрике обусловлены тем, что между соседними витками катушки существует емкость, имеющая две составляющих-емкость через воздух Сов и емкость через диэлектрик Сод (рис.2.33). Потери в диэлектрике учитываются величиной tgd, зная которую можно рассчитать сопротивление потерь rД   = 0,25Содtg dL2f 3 . 10-3 (2.52) где  Сод — в пф, L — в мкГн,  f — в МГц. Потери в сердечнике складываются из потерь на вихревые токи  dв, потерь на гистерезис dг и начальных потерь dп и учитываются как тангенс угла потерь в сердечнике tg dс = dв f + dгН + dп (2.53) В справочниках приводятся значения. tg dс  для различных типов сердечников. Сопротивление потерь определяется по формуле Потери в экране обусловлены тем, что ток, протекающий по катушке, индуцирует ток в экране. Потери, вносимые экраном, определяются по формуле (2.55) где Dэ — диаметр экрана в см, lэ — длина экрана в см, f — частота в МГц. Величина  h = f(l/D)  определяется по графику (рис.2.27). Таким образом суммарное сопротивление потерь в катушке индуктивности, определяющее ее добротность, равно Rп = rf + rд +rc + rэ (2.56) Практически величина добротности лежит в пределах от 30 до 200. Повышение добротности достигается оптимальным выбором диаметра провода, увеличением размеров катушки индуктивности и применением сердечников с высокой магнитной проницаемостью и малыми потерями. С учетом потерь и паразитной емкости катушку индуктивности можно представить в виде эквивалент- ной схемы (рис.2.34,а), где  Rп = rf + rд +rc + rэ.  эта схема может быть приведена к более удобному виду (рис.2.34,б), где Lэ -эквивалентная индуктивность, учитывающая собственную емкость. Величины. Lэ и Rп, а следовательно, добротность Q = wL/Rп  зависят от температуры. Зависимость Q от температуры определяется температурным коэффициентом добротности ТКД=DQ/QDТ 2.3.5.Разновидности катушек индуктивности. Контурные катушки индуктивности. Эти катушки используются совместно с конденсаторами для получения резонансных контуров. Они должны иметь высокую стабильность, точность и добротность. В диапазоне длинных и средних волн эти катушки многослойные, как правило, с намоткой типа «универсаль». Для повышения добротности применяют многожильные провода типа «литцендрат». Для изменения индуктивности применяют цилиндрические сердечники из альсифера или карбонильного железа. В диапазоне коротких и ультракоротких волн используются однослойные катушки с индуктивностью порядка единиц микрогенри и добротностью порядка 50 — 100. Число витков таких катушек не превышает одного-двух десятков, диаметр каркаса 10 — 20 мм. В качестве каркасов используют керамику, полиэтилен и полистирол. Для уменьшения собственной емкости применяют ребристые каркасы. Обмотка выполняется одножильным медным проводом диаметром около 1 мм. На УКВ применяют бескаркасные катушки из неизолированного провода. Катушки связи. Эти катушки применяются для обеспечения индуктивной связи между отдельными цепями и каскадами. Такая связь позволяет разделить по постоянному току цепи базы и коллектора и т.д. К таким катушкам не предъявляются жесткие требования на добротность и точность, поэтому они выполняются из тонкого провода в виде двух обмоток небольших габаритов. Основными параметрами этих катушек являются индуктивность и  коэффициент связи где L1 и L2 — индуктивность связанных катушек, М — взаимная индуктивность между ними. Величина коэффициента связи зависит от расстояния между катушками, чем оно меньше, тем больше k. Вариометры. Это такие катушки, в которых предусмотрена возможность изменения индуктивности в процессе эксплуатации для перестройки колебательных контуров. Они состоят из двух катушек, соединенных последовательно. Одна из катушек неподвижная (статор), другая располагается внутри первой и вращается (ротор). При изменении положения ротора относительно статора изменяется величина взаимоиндукции, а следовательно, индуктивность вариометра Такая система позволяет изменять индуктивность в 4 — 5 раз. Дроссели. Это катушки индуктивности, обладающие высоким сопротивлением переменному току и малым сопротивлением постоянному . Обычно включаются в цепях питания усилительных устройств. Предназначены для защиты источников питания от попадания в них высокочастотных сигналов. На низких частотах они используются в фильтрах цепей питания и обычно имеют металлические сердечники. Катушки индуктивности для ГИС. На частотах порядка 10 — 100 МГц находят применение тонкопленочные спиральные катушки. На площади в 1 кв.см, располагается не более 10 витков. Добротность таких катушек не превышает 20-30. Поэтому они находят ограниченное применение. В ГИС предпочтительны миниатюрные торроидальные катушки на ферритовых сердечниках, индуктивность которых достигает десятков тысяч микрогенри. В последнее время наметилась тенденция замены катушек специальными схемами на транзисторах (гираторы) и электромеханическими, пьезоэлектрическими и акустоэлектронными фильтрами, основанными на принципе механических упругих колебаний и механического резонанса. Скорость распространения упругих колебаний в твердом теле примерно в 100 тысяч раз меньше скорости распространения электромагнитных волн, что позволяет создавать очень компактные механические резонаторы с распределенными параметрами, обладающие добротностью порядка 103. Развитие микроэлектроники привело к появлению фильтров на приборах с зарядовой связью и фильтров на поверхностных акустических волнах. Кроме того, в ИМС широкое применение находят активные RC — фильтры, в которых используются операционные усилители с глубокой частотно-зависимой обратной связью. Источник — Свободный взгляд

Катушки индуктивности Onelec.ru

SMD индуктивности
	AIML	1 нГн — 330 мкГн	±10%(K) ±20%(M)	45 мОм — 4 Ом	1 мА — 600 мА	-25..85 °С	Многослойные	0402, 0402C, 0603, 0603C, 0805, 0805C, 1206, 1210
	AISC	1 нГн — 1 мГн	±5%(J) ±10%(K)	30 мОм — 21 Ом	40 мА — 1.36 А	-55..125 °С (кер.) -55..85 °С (фер.)	Проволочные, high current, керамические, ферритовые	0402, 0603, 0805, 1008, 1210, 1812
	AISM	10 нГн — 10 мГн	±5%(J) ±10%(K) ±20%(M)	30 мОм — 150 Ом	25 мА — 1.8 А	-25..85 °С	Литой корпус	1008, 1210, 1812, 2220
	LQH	0.1 мкГн — 10 мГн	±10%(K) ±20%(M)	7 мОм — 140 Ом	20 мА — 6 А	-25..85 °С	Проволочные, high current, керамические (1206C, 1210C, 1812C), экранированные (1210S, 2220S)	1008, 1206, 1210, 1812, 2220, 1206C, 1210S, 2220S, 1210C, 1812C
	SDR	1 мкГн — 560 мкГн	±10%(K) ±15%(L) ±20%(M)	28 мОм — 20 Ом	50 мА — 4.5 А	-40..85 °С	Проволочные, high current	0302, 0403, 0504, 0703, 0705, 1004, 1005
	SDRS	10 мкГн — 820 мГн	±10%(K) ±20%(M)	50 мОм — 2 Ом	330 мА — 2.65 А	-40..85 °С	Экранированные	0603, 0704, 1005, 1205
	SDRH	1.2 мкГн — 1 мГн	±10%(K) ±20%(M)	7 мОм — 9.44 Ом	80 мА — 9.8 А	-25..85 °С	Экранированные, низкопрофильные	0603, 0605, 0703, 0704, 1204, 1205, 1207
	SDRH-D	1 мкГн — 680 мкГн	±10%(K) ±20%(M)	14 мОм — 8.9 Ом	110 мА — 6.4 А	-40..105 °С	Магнитный экран, низкопрофильные	2D11, 2D18, 3D16, 4D18, 4D28, 5D18, 5D28, 6D28, 6D38, 8D28, 8D43
	SDRHxxxx	1 мкГн — 1.5 мГн	±10%(K) ±20%(M) ±30%(N)	14 мОм — 7.8 Ом	120 мА — 6.2 А	-40..105 °С	Магнитный экран, низкопрофильные	3818, 5018, 5020, 5028, 6025, 6028, 7028, 7030, 7032, 7045, 10145, 12555, 12565, 12575
	SDRh20x	10 мкГн — 1 мГн	±10%(K) ±20%(M) ±30%(N)	26 мОм — 1.94 Ом	350 мА — 3.5 А	-40..105 °С -25..85 °C	Магнитный экран, низкопрофильные	103, 104, 105
	SDR-T	1 мкГн — 1.2 мГн	±10%(K) ±20%(M)	10 мОм — 6.2 Ом	150 мА — 7.2 А	-40..105 °С	Магнитный экран, низкопрофильные проволочные	0703T, 0704T, 7030T, 7045T, 1030T, 1045T, 1305T, 1308T
	SDR-LCB	0.82 мкГн — 150 мкГн	±10%(K) ±20%(M)	13 мОм — 917 мОм	310 мА — 3.6 А	-25..85 °C	Магнитный экран, низкопрофильные силовые	62LCB, 62CB, 63LCB, 63CB
	SMD-D	2.2 мкГн — 100 мкГн	±20%(M)	60 мОм — 3.3 Ом	170 мА — 950 мА	-25..85 °C	Силовые, низкопрофильные, ферритовые сердечники (4D11, 4D13)	4D06, 4D08, 4D11, 4D13
	CEP-HT	0.36 мкГн — 10.5 мкГн	±10%(K) ±20%(M)	1.2 мОм — 17.2 мОм	Ток насыщ. 4.7 А — 30 А	-40..105 °С	Высокочастотные, экранированные, низкопрофильные	104HT, 105HT, 124HT, 125HT, 126HT, 135HT, 159HT,
	SDRH Dual Chip	10 мкГн — 1 мГн	±20%(M)	25 мОм — 15.4 Ом	72 мА — 4 А	-55..125 °С	Проволочные, 2 чипа	0602D, 1205D
	SPI	1 мкГн — 4,7 мГн	±10%(K) ±20%(M)	72 мОм — 13 Ом	4 мА — 1.34 А	-40..105 °С	Силовые, проволочные	0603S, 0603T
	SPI-T	1 мкГн — 1.2 мГн	±20%(M)	9 мОм — 12 Ом	100 мА — 20 А	-40..85 °С	Силовые, проволочные	0402T, 0802T, 804T, 0810T, 1109T, 1306T
	SPI-S	1 мкГн — 10 мГн	±10%(K) ±20%(M)	20 мОм — 32 Ом	20 мА — 5 А	-40..85 °С	Силовые, экранированные	0402S, 0802S, 0804S, 1306S
	SPI-C	1 мкГн — 1 мГн	±20%(M)	40 мОм — 22.6 Ом	45 мА — 2.5 А	-55..85 °С	Силовые, низкопрофильные, керамический корпус	0401C, 0402C, 0602C,
	SB-T	1.2 мкГн — 5.6 мГн	±10%(K) ±20%(M)	20 мОм — 72 Ом	48 мА — 3.4 А	-40..105 °С	Ферритовый сердечник, низкопрофильные	0602T, 0603T
	SB	1.5 мкГн — 15 мГн	±15%(Y) ±20%(M)	14 мОм — 40 Ом	70 мА — 5.6 А	-40..105 °С	Магнитный экран, силовые	0906, 0908
Аксиальные катушки индуктивности
	LGA	0.22 мкГн — 33 мГн	±10%(K) ±20%(M)	22 мОм — 250 Ом	8 мА — 3.8 А	-25..85 °С -25..105 °С	Магнитный сердечник, ферритовый сердеченик	0204, 0305, 0307, 0410, 0510, 0512, 0612
	LTM	0.22 мкГн — 1 мГн	±10%(K) ±20%(M)	30 мОм — 33 Ом	40 мА — 3.05 А	-25..85 °С	Ферритовый сердечник	0307, 0410, 0511
	LCHA	18 мкГн — 150 мГн	±10%(K) ±20%(M)	7 мОм — 89.7 Ом	30 мА — 6 А	-55..125 °С	Термоусадочная трубка	1425, 1122, 0617, 0410
Радиальные катушки индуктивности
	LGB	0.22 мкГн — 56 мГн	±5%(J) ±10%(K) ±20%(M)	6 мОм — 295 Ом	18 мА — 5.9 А	-25..105 °С	Ферритовый сердечник, пластиковые	0606, 0810, 0909, 0709, 0809, 1112, 1315
	AIRD	1 мкГн — 100 мГн	±10%(K) ±20%(M)	1.2 мОм — 6.6 Ом	800 мА — 55 А	-25..85 °С	Термоусадочная трубка	01, 02, 03, 04, 05, 06, 06A, 07, 07A
	LCHB	10 мкГн — 47 мГн	±10%(K)	15 мОм — 110 Ом	15 мА — 5.3 А	-55..125 °С	Термоусадочная трубка	04, 06
	LCh5W	6.3 мкГн — 39 мГн	±10%(K) ±20%(M)	22 мОм — 58 Ом	90 мА — 5.3 А	-55..125 °С	Проволочные	1006, 1008, 1010, 1014
	LCH	10 мкГн — 47 мГн	±10%(K) ±20%(M)	40 мОм — 96 Ом	38 мА — 2.9 А	-40..105 °С	Проволочные	0605, 0606, 0805, 0807, 0809
	LGS	22 мкГн — 1.2 Гн	±5%(J) ±10%(K) ±20%(M)	80 мОм — 845 Ом	8.4 мА — 1.6 А	-40..105 °С	Магнитный экран, силовые	0606, 0708, 1009, 1014, 1216, 1519
	AIFC	1 мкГн — 10 мГн	±10%(K)	12 мОм — 70 Ом	70 мА — 7 А	-40..105 °С	Ферритовый сердечник, силовые	1010
Тококомпенсирующие дроссели для сквозного монтажа
	TRF	1 мГн — 102 мГн	-10..100%(Y)	22 мОм — 1.75 Ом	300 мА — 8 А	-40..105 °С	Тококомпенсирующие	102, 112, 114, 122, 142, 152, 202, 212, 214, 222, 242, 252
Тороидальные катушки индуктивности
	TR	10 мкГн — 8.2 мГн	±20%(M)	—	0.5 А — 10 А	-55..85 °С	Силовые, high current	30, 44, 50, 60, 67, 68, 72, 77, 80, 94, 106, 130, 141
	AIMT	5 мкГн — 960 мкГн	±20%(M)	7 мОм — 13 Ом	500 мА — 10 А	-55..85 °С	Силовые, high current	01
	AIGT	5 мкГн — 500 мкГн	±20%(M)	13 мОм — 940 мОм	1 А — 10 А	-55..85 °С	Силовые, high current	10, 20
	TRF	200 мкГн — 120 мГн	-10..100%(Y)	5 мОм — 1.15 Ом	1 А — 18 А	-40..105 °С	Синфазные	1814, 2317, 2620, 3525, 3523, 3518, 3622, 4525, 5230

индуктивность | Физика II

Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы. Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется , индуктивность . Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. См. Рис. 1, где простые катушки индуцируют ЭДС друг в друге.

Рис. 1. Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2.(Обратите внимание, что « E ₂ индуцированная» представляет наведенную ЭДС в катушке 2.)

Во многих случаях, когда геометрия устройств является фиксированной, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока, Δ I / Δ t , как причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как

[латекс] {\ text {emf}} _ {2} = — M \ frac {\ Delta {I} _ {1}} {\ Delta t} \\ [/ latex],

, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на Рисунке 1 имеют небольшой размер M по сравнению с катушками трансформатора на Рисунке 3 от Transformers. Единицами измерения для M являются (В с) / A = Ом ⋅ с, который назван генри (H) в честь Джозефа Генри. То есть 1 H = 1 Ω⋅s. Природа здесь симметрична. Если мы изменим ток I ₂ в катушке 2, мы индуцируем ЭДС ₁ в катушке 1, что равно

[латекс] {\ text {emf}} _ {1} = — M \ frac {\ Delta {I} _ {2}} {\ Delta t} \\ [/ latex],

, где M то же самое, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M . Большая взаимная индуктивность M может быть, а может и не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки против ветра, чтобы нейтрализовать создаваемое магнитное поле.(См. Рисунок 2.)

Рис. 2. Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.

Самоиндукция , действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока Δ I через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается

[латекс] \ text {emf} = — L \ frac {\ Delta I} {\ Delta t} [/ latex],

, где L — собственная индуктивность устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется катушкой индуктивности и обозначено символом на рисунке 3.

Рисунок 3.

Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера L , например, за счет встречной намотки катушек, как показано на рисунке 2.Катушка индуктивности 1 H — это большая катушка индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1,0 Гн, через которое протекает ток 10 А. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная как ЭДС = — L (Δ I / Δ t ), будет препятствовать изменению. Таким образом, ЭДС будет индуцирована ЭДС = — L (Δ I / Δ t ) = (1,0 H) [(10 A) / (1,0 мс)] = 10 000 В. Знак плюс означает, что это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению.Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока. Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт.(Вы можете услышать пронзительный вой от трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки. (См. Рисунок 4.)

Рис. 4. Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.

Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле.В большинстве случаев это сложно из-за сложности создаваемого поля. Таким образом, в этом тексте индуктивность L обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как ЭДС = — Н (Δ Φ / Δ t ) и, по определению самоиндукции, как ЭДС = — L . (Δ I / Δ т ).Приравнивая эти доходности к

[латекс] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} = — L \ frac {\ Delta I} {\ Delta t} \\ [/ latex]

Решение для л дает

[латекс] L = N \ frac {\ Delta \ Phi} {\ Delta I} \\ [/ latex]

Это уравнение для самоиндукции L устройства всегда верно. Это означает, что самоиндукция L зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше Δ Φ / Δ I .Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь A соленоида является фиксированной, изменение магнитного потока составляет Δ Φ = Δ ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется выражением [латекс] B = {\ mu} _ {0} {nI} = {\ mu} _ {0} \ frac {NI} { \ ell} \\ [/ латекс]. {2} \ влево (1.{2} \ right)} {0.100 \ text {m}} \\ & = & 0.632 \ text {mH} \ end {array} \\ [/ latex].

Обсуждение

Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.”) См. Рисунок 5.

Рис. 5. Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)

Катушка индуктивности L разделена на два класса 12 по физике CBSE

Совет: Определите индуктивность катушек индуктивности, разделенных на две равные части. Используйте формулу эквивалентной индуктивности двух параллельно соединенных катушек индуктивности.

Используемая формула:
Эквивалентная индуктивность \ [{L_ {eq}} \] двух катушек индуктивности, соединенных параллельно, составляет
\ [\ dfrac {1} {{{L_ {eq}}}} = \ dfrac {1 } {{{L_1}}} + \ dfrac {1} {{{L_2}}} \] …… (1)
Здесь \ [{L_1} \] — индуктивность первой катушки индуктивности, а \ [{L_2 } \] — индуктивность второй катушки индуктивности.

Полный пошаговый ответ:
Катушка индуктивности \ [L \] разделена на две равные части, и эти две части соединены параллельно. 2}}} {4}}} \]
\ [\ Rightarrow \ dfrac {1} {{{L_ {экв. }}}} = \ dfrac {4} {L} \]
\ [\ Rightarrow \ dfrac {1} {{{L_ {eq}}}} = \ dfrac {4} {L} \]
\ [\ поэтому {L_ {eq}} = \ dfrac {L} {4} \]

Следовательно, чистая индуктивность двух равных частей индукторов, соединенных параллельно, равна \ [\ dfrac {L} {4} \].

Итак, правильный ответ — «Вариант D».

Дополнительная информация:
Для катушек индуктивности, соединенных параллельно, полезная индуктивность всегда меньше наименьшей индуктивности индуктора.

Для последовательно соединенных индукторов напряжения на всех индукторах одинаковы.

Чистая индуктивность \ [{L_ {eq}} \] для двух последовательно соединенных катушек индуктивности является суммой двух индуктивностей последовательно соединенных катушек индуктивности.
\ [{L_ {eq}} = {L_1} + {L_2} \]

Здесь \ [{L_1} \] — индуктивность первой катушки индуктивности, а \ [{L_2} \] — индуктивность второй индуктор.

Примечание:
можно забыть взять обратную величину от ответа, полученного путем решения эквивалентной индуктивности. Если обратный ответ не получен, он будет обратным чистой или эквивалентной индуктивности, а не чистой или эквивалентной индуктивности.

Глава 2, Справочник по детекторам трафика: Третье издание — Том I

Этот отчет является заархивированной публикацией и может содержать техническую, контактную и ссылочную информацию с датой

Номер публикации: FHWA-HRT-06-108 Дата: май 2006 г.

ГЛАВА 2.СЕНСОРНАЯ ТЕХНОЛОГИЯ

В этой главе описывается работа датчиков проезжей части и проезжей части. Представленные технологии включают в себя индуктивные петлевые детекторы, магнитометры, процессоры видеоизображений, микроволновые радарные датчики (обнаружение присутствия и доплеровские), лазерные радарные датчики, пассивные инфракрасные датчики, ультразвуковые датчики, пассивные акустические датчики и устройства, в которых используется комбинация технологий. Информация предназначена для того, чтобы дать практикующему инженеру по дорожному движению и инженеру-электрику знания, необходимые для выбора подходящей сенсорной технологии для конкретных приложений.

ДЕТЕКТОРЫ ИНДУКТИВНОЙ ПЕТЛИ

С момента своего появления в начале 1960-х годов датчик с индукционной петлей стал наиболее часто используемым датчиком в системе управления дорожным движением. Основные компоненты системы детекторов с индуктивным контуром включают:

• Один или несколько витков изолированного контурного провода, намотанного в неглубокую прорезь, пропиленную в мостовой.
• Подводящий кабель от тягового ящика к бордюру к шкафу управления перекрестками.
• Блок электроники, расположенный в соседнем шкафу контроллера.

На рис. 2-1 показана условная схема системы обнаружения с индукционной петлей, а также транспортных средств и элементов стальной арматуры на проезжей части, с которыми она реагирует.

Рисунок 2-1. Индуктивно-петлевой детектор (условный).

Электронный блок передает энергию в проволочные петли на частотах от 10 кГц до 200 кГц, в зависимости от модели. Система индуктивного контура ведет себя как настроенная электрическая цепь, в которой провод контура и подводящий кабель являются индуктивными элементами.Когда транспортное средство проезжает по петле или останавливается внутри петли, транспортное средство наводит вихревые токи в проводных петлях, которые уменьшают их индуктивность. Пониженная индуктивность приводит в действие выходное реле электронного блока или твердотельный оптически изолированный выход, который посылает на контроллер импульс, указывающий на проезд или присутствие транспортного средства.

Транспортные средства, проезжающие или останавливающиеся в зоне обнаружения индуктивного детектора, уменьшают индуктивность контура.Блок электроники воспринимает это событие как уменьшение частоты и отправляет на контроллер импульс, указывающий на проезжание или присутствие транспортного средства.

В следующих разделах описывается теория индуктивной системы, характеристики контура и электронный блок.

ТЕОРИЯ РАБОТЫ

Принципы работы детекторной системы с индуктивным контуром, обсуждаемые ниже, являются общими для всех конструкций систем с индуктивным контуром, описанных в главе 4.Контурный провод и подводящий кабель содержат комбинацию сопротивления, индуктивности и емкости (как межпроводную, так и межпроводную связь с землей).

СОПРОТИВЛЕНИЕ ПЕТЛИ И КАБЕЛЯ

Для проводов с индуктивным контуром, подводящих проводов и вводных кабелей обычно используется провод № 12, № 14 или № 16 американского калибра проводов (AWG) с сопротивлением низкой частоте или постоянному току, измеряемым в единицах Ом (). Сопротивление проволоки обратно пропорционально квадрату диаметра проволоки и увеличивается с уменьшением диаметра проволоки.Вольт-омметр (ВОМ) измеряет сопротивление постоянному току. Сопротивление провода протеканию переменного тока увеличивается с увеличением частоты, потому что проводящая площадь провода уменьшается из-за неоднородного потока внутри провода. Сопротивление на высоких частотах не может быть измерено с помощью VOM, но может быть получено путем измерения добротности, как определено далее в этой главе.

Петля в проезжей части также содержит наведенное сопротивление (называемое сопротивлением заземления), вызванное трансформаторной связью между петлей и индуцированными токами, протекающими в дорожном полотне и материалах земляного полотна.В Приложении А приводится подробный вывод сопротивления заземления. Таблица 2-1 содержит значения сопротивления постоянному току или низкочастотного сопротивления для имеющихся в продаже контурных проводов и вводных кабелей.

Таблица 2-1. Сопротивление кабелей, которые обычно встречаются в детекторных системах с индуктивным контуром.

Тип провода или кабеля производителя	Функция	Калибр провода (AWG)	Сопротивление постоянному току (/ фут)
9438	Контурный провод	14	0.0025
8718	Вводной кабель	12	0,0019
8720	Вводной кабель	14	0,0029
8719	Вводной кабель	16	0,0045

ИНДУКТИВНОСТЬ КОНТУРА

Все проводники, по которым проходит электрический ток, образуют линии магнитного потока, которые окружают формирующий их ток.Магнитный поток вызывает электрическое свойство, называемое индуктивностью, которое измеряется в генри (Гн). Индуктивность провода называется самоиндукцией. Если поток от тока, протекающего по одному проводу, переходит в другие провода, результирующая индуктивность называется взаимной индуктивностью.

На рис. 2-2 показан поток вокруг однооборотной проволочной петли. Плоскость, содержащая поток, перпендикулярна току в проводе, где направление потока определяется правилом правой руки. Это правило применяется следующим образом: поместите правую руку под провод с пальцами, загнутыми в направлении силовых линий.Большой палец указывает в направлении тока. Внутри контура все силовые линии имеют одинаковое направление.

На рис. 2-3 показаны линии магнитного потока для соленоида или катушки, длина которых больше диаметра. Магнитный поток внутри катушки однороден, за исключением концов. Магнитное поле для этой геометрии катушки равно

.

(2-1)

, где

H = Магнитное поле, ампер-витков на метр, не путать с единицами индуктивности в генри
N = количество витков
I = ток катушки, амперы
л = Длина катушки, метры.

Рисунок 2-2. Магнитный поток вокруг петли. Черные стрелки представляют ток, протекающий в проводе, а белые стрелки — индуцированный поток, определяемый правилом правой руки.

Рисунок 2-3. Магнитный поток для соленоида (катушки). Черные стрелки представляют поток тока, в то время как круги с черным центром и центром «X» представляют индуцированный поток потока из и в плоскость рисунка, соответственно.

Поскольку магнитный поток внутри катушки однороден, он равен

.

(2-1)
, где

= Магнитный поток, сетка
B = Плотность магнитного потока, сетка на м ²
A = Площадь поперечного сечения катушки, м ² .

Плотность магнитного потока выражается как

(2-3)
, где

_r = относительная проницаемость материала (1 для воздуха)

₀ = 4 x 10 ^-7 генри на метр.

Индуктивность катушки определяется как

(2-4)
, где

L = индуктивность, генри
Н = количество витков
I = ток катушки, амперы.

Индуктивность катушки, длина которой намного превышает площадь катушки для обеспечения равномерного магнитного потока внутри катушки, определяется как

(2-5)

Индуктивный контур проезжей части имеет неоднородное магнитное поле, которое дает значение индуктивности, заданное уравнением 2-6.

Это уравнение показывает, что индуктивность катушки прямо пропорциональна квадрату витков и площади катушки и обратно пропорциональна длине катушки.Хотя формула индуктивности в том виде, в каком она написана, не применима напрямую к индуктивной петле дороги, формула может быть изменена с коэффициентом F ‘для учета неоднородного потока в индуктивной петле дороги. Таким образом

(2-6)

Уравнение 2-6 применяется к расчету индуктивности контура в Приложении B. В этом случае l упоминается как «длина токового листа». Уравнение 2-6 показывает, что железо с относительной проницаемостью больше единицы увеличивает индуктивность контура.Хотя наибольшее увеличение индуктивности происходит, когда железный сердечник проходит непосредственно через контур, железная масса двигателя транспортного средства, трансмиссии или дифференциала немного увеличивает индуктивность контура. Это состояние называется «ферромагнитным эффектом».

ФЕРРОМАГНИТНЫЙ ЭФФЕКТ И ОБНАРУЖЕНИЕ АВТОМОБИЛЯ

Однако ферромагнитный эффект, создаваемый железной массой двигателя, трансмиссии или дифференциала, не создает индикацию присутствия или прохождения контроллером.Когда тяжелый двигатель из черных металлов входит в зону обнаружения индуктивного контура, он увеличивает индуктивность проволочного контура. Этот эффект возникает из-за того, что введение любого железного сердечника в поле любого индуктора снижает сопротивление (то есть член, который соответствует сопротивлению магнитной цепи) пути потока и, следовательно, увеличивает полезную индуктивность. Однако периферийный металл транспортного средства оказывает противоположное влияние на индуктивность из-за возникающих вихревых токов. Уменьшение индуктивности из-за вихревых токов более чем компенсирует увеличение массы железа в двигателе, и в итоге получается общее снижение индуктивности проволочного контура.

Ферромагнитный эффект увеличивает индуктивность контура. Однако вихревые токи, вызванные транспортным средством, еще больше уменьшают индуктивность контура. Следовательно, результирующий эффект заключается в уменьшении индуктивности контура, когда транспортное средство проходит через зону обнаружения индуктивного контура.

ХАРАКТЕРИСТИКИ ПЕТЛИ

Детектор с индуктивной петлей предоставляет инженерам дорожного движения широкий спектр геометрических форм для удовлетворения разнообразных приложений управления дорожными сигналами, как описано в главе 4.Размер и количество витков петли или комбинации петель вместе с длиной подводящего кабеля должны давать значение индуктивности, совместимое с диапазоном настройки электронного блока и другими требованиями, установленными транспортным потоком. инженер. Стандарты NEMA для индуктивных детекторов (см. Приложение J) определяют, что блок электроники должен обеспечивать удовлетворительную работу в диапазоне индуктивности от 50 до 700 микрогенри (мкГн). Некоторые блоки допускают гораздо большие значения индуктивности, например, от нескольких последовательно соединенных контуров.Хотя более высокие значения индуктивности технически возможны, NEMA установило консервативный верхний предел, чтобы продвигать методы, совместимые со всеми существующими блоки электроники.

ЕМКОСТЬ ПЕТЛИ

На рис. 2-4 показаны основные явления емкостной связи, которые существуют между (1) самими проводами контура и (2) проводами контура и боковыми стенками паза для распиловки. Емкость, относящаяся к пазу пилы, прямо пропорциональна диэлектрической проницаемости материала уплотнения паза.Рисунок 2-5 представляет собой эквивалентную электрическую схему, представляющую сопротивление провода индуктивной петли R s , индуктивность L s и емкость C p , которые образуются при установке петли на дорожное покрытие.

Рисунок 2-4. Емкостная связь между самими проводами контура и боковыми стенками паза.

Рисунок 2-5. Эквивалентная электрическая схема для индуктивного контура с емкостной связью с боковыми стенками паза пропила.

Данные измерений на Рисунке 2-6 показывают влияние емкости C p на увеличение индуктивности на выводах контура при увеличении рабочей частоты. (1) Если материал уплотнения паза гигроскопичен (т.е. легко впитывает и удерживает воду) или неполный (т. е. не заполняет прорезь или не герметизирует провода, позволяя воде проникать в прорезь и проникать между витками контурного провода), изменение емкости и, следовательно, индуктивности будет большим из-за большой диэлектрической проницаемости воды .

Рисунок 2-6. Средние значения индуктивности контура в зависимости от частоты измерения для последовательного, параллельного и последовательно-параллельного соединения индуктивных контуров 6 x 6 футов (1,8 x 1,8 м). Графики представляют кривые, соответствующие измеренным данным.

Емкость системы контура должна быть минимизирована для правильной работы на частотах 10 килогерц (кГц) и выше.

Таким образом, изменение емкости из-за воды может привести к нестабильной работе детектора индуктивного контура.На частотах 1 килогерц (кГц) влияние емкости незначительно. На частотах 10 кГц и выше важен емкостной эффект. Когда индуктивность контура измеряется на частоте 20 кГц или выше, необходимо указать частоту измерения, поскольку измеренная индуктивность зависит от частоты. Большое количество витков на контурах большой площади дополнительно увеличивает емкость контура и снижает частоту собственного резонанса контура (т. Е. Индуктивность контура не измеряется на выводах контура, когда контур саморезонансный).

На рис. 2-6 также показано, как различные последовательные, параллельные и последовательно-параллельные конфигурации проводных контуров влияют на результирующую индуктивность контура и скорость ее изменения с частотой. Влияние метода подключения на индуктивность системы обсуждается далее в разделе «Расчет индуктивности системы контура» далее в этой главе.

КОЭФФИЦИЕНТ КАЧЕСТВА ПЕТЛИ Q

Резонансный КПД контура выражается через безразмерную добротность Q .Если потери в катушке индуктивности велики, Q будет низким. Идеальный индуктор не имеет потерь; следовательно, в катушке индуктивности нет рассеивания энергии, и Q бесконечен.

Коэффициент качества контура Q — это мера потерь в системе детектора с индуктивным контуром.

Суммарные потери энергии в катушке индуктивности с потерями рассчитываются путем моделирования катушки индуктивности как эквивалентной катушки индуктивности без потерь, соединенной последовательно с резистором.Добротность равна отношению индуктивного реактивного сопротивления к резистивным потерям катушки индуктивности. Поскольку индуктивное реактивное сопротивление является величиной, зависящей от частоты, частота должна быть указана при измерении добротности. Формула для Q записывается как
(2-7)

где

Q = добротность
= 3,14159 (постоянная)
f = частота возбуждения системы индуктивного контура, Гц
L _S = индуктивность последовательного контура, генри
R _S = Сопротивление шлейфа, Ом
= Радианная частота = 2 f .

Резонансная частота 0 эквивалентной индуктивной петле электрической цепи, представленной на рисунке 2-5, задается как
(2-8)

Из уравнения 2-7,

(2-9)

Следовательно, уравнение для коэффициента качества контура Q ₀ резонансного контура становится

(2-10)

Электронный блок добавляет сопротивление нагрузки R _L параллельно конденсатору C _P , показанному в эквивалентной электрической цепи индуктивного контура на Рисунке 2-5.Эффект R _L заключается в снижении добротности. Результирующий коэффициент качества равен
(2-11)

или

(2-12)

, где R ‘ _P — преобразованное последовательное сопротивление параллельно с R _L .

Нагруженная добротность Q _L схемы на рисунке 2-5 с сопротивлением нагрузки R _L параллельно конденсатору C _P составляет

(2-13)

Коэффициенты качества 5 и выше рекомендуются при установке индуктивных детекторов, поскольку генераторы в большинстве электронных блоков не будут работать с низким значением Q .Влага в дорожном покрытии и земляном полотне может увеличить сопротивление заземления контура, так что Q системы индуктивного контура упадет ниже 5, тем самым снизив чувствительность большинства электронных блоков индуктивного контура. Емкость контура также уменьшит Q .

Нагруженный коэффициент качества Q _L , определяемый уравнением 2-13, применяется к приложениям с низкими потерями, где коэффициент качества большой и f , L _S и R _S могут быть легко измерить.С другой стороны, индуктивные петлевые детекторы, используемые на дорогах, не так хорошо адаптируются к приведенному выше анализу, поскольку индуктивность распределена по петле и подводящему кабелю и ее трудно измерить. Расчет добротности для дорожных петель еще больше усложняется из-за большего фактического сопротивления петлевого провода и подводящего кабеля по сравнению с последовательным значением, измеренным с помощью омметра. Дополнительные потери возникают из-за высокочастотного возбуждения и токов заземления в дорожном покрытии, связанных с конфигурацией петли и дорожной обстановкой вблизи провода.В результате, Q с идентичной конфигурацией проводов будет варьироваться от места к месту.

Потери, вызванные возбуждением высокочастотной петли и токами заземления в мостовой около провода, дополнительно снижают добротность. В результате, Q с идентичной конфигурацией проводов будет варьироваться от места к месту.

На рисунке 2-7 показано вычисление коэффициента качества индуктивной системы с использованием Q ₀ и Q _P .В таблицах с 2-2 по 2-4 перечислены рассчитанные коэффициенты качества для прямоугольных, квадрупольных и круглых индуктивных контуров, соответственно, на 1, 2, 3, 4 и 5 витков. В этих таблицах петли возбуждаются на частоте 20 кГц с поперечным расстоянием между проводниками и / или квадруполями 200 мил. Все индуктивность и добротность являются кажущимися значениями (т. Е. Включаются емкость и сопротивление контура).

Рисунок 2-7. Расчет выборки добротности замкнутой системы.

Таблица 2-2. Индуктивность прямоугольного контура и параметры добротности при f = 20 кГц.*

* Петля 6 x 6 футов (1,8 x 1,8 м). ** С вводным кабелем.

Петля диаметром 7 футов (2,1 м).

ВХОДНОЙ ПРОВОД ПЕТЛЕЙ

Таблица 2-5 содержит значения индуктивности, емкости и сопротивления подводящего провода коробки «петля-тяга» для двух распространенных типов проводов. Два подводящих провода от начала и конца витков петли должны быть скручены вместе, чтобы сформировать симметрично скрученную пару от петли к вытяжной коробке. Скручивание снижает перекрестные помехи и шум в подводящем проводе.Большинство производителей рекомендуют не менее пяти витков на фут (16,5 витков на метр). Скрутки проволоки образуют небольшие петли вдоль проволоки, чередующиеся по направлению намотки. Внешнее магнитное поле из-за шума или перекрестных помех индуцирует напряжения в небольших контурах, которые почти устраняются, тем самым уменьшая помехи. Важность скручивания подводящего провода обсуждается далее в главе 5.

Таблица 2-5. Характеристики подводящего провода витой петли.

Изготовитель и тип провода	Тип изоляции провода	Номер AWG	Диаметр оболочки (мил)	Число витков на фут	Индуктивность (H / фут)	Емкость (пФ / фут)	Сопротивление (/ футов)
XHHW	Сшитый полимер	14-ниточный	130	от 3 до 4	0.24	10	0,006
Belden 9438	Полиэтилен высокой плотности	14-ниточный	139	5,5	0,22	10	0,00252

ВВОДНЫЙ КАБЕЛЬ

Экранированные скрученные пары проводов используются для подводящего кабеля (кабеля домашней прокладки), который проходит от вытяжной коробки к клеммам электронного блока в шкафу контроллера. Проводящий экран снижает помехи от внешних электрических полей.Значения индуктивности, емкости и сопротивления подводящего кабеля для нескольких типов кабеля приведены в таблице 2-6.

Таблица 2-6. Технические характеристики вводного кабеля для коммерческого использования.

Производитель и тип кабеля		Тип изоляции провода	Номер AWG	Диаметр изоляции (мил)	Тип изоляции кабеля	Индуктивность (H / фут)	Емкость (пФ / фут)	Сопротивление (/ фут)
Belden	8718	Полиэтилен	12	37	Винил	0.2	25	0,0019
	8720	Полиэтилен	14	32	Винил	0,2	24	0,0029
	8719	Полиэтилен	16	32	Винил	0,2	23	0,0045
Клиффорд	IMSA	Полиэтилен	12	30	Полиэтилен	0.2	25	0,0016
	Спецификация	Полиэтилен	14	30	Полиэтилен	0,2	24	0,0025
	50-2-1984	Полиэтилен	16	30	Полиэтилен	0,2	23	0.0040

Измерения коэффициента качества петлевой системы (при 100 футах (30 м) экранированного подводящего кабеля, подключенного к петле) в Приложении D показывают, что от использования проводов большего диаметра в экранированных выводах мало пользы. в кабеле. Например, коэффициент качества, связанный с экранированным вводным кабелем № 14 AWG, существенно не снижается при замене кабеля № 12. Основные потери связаны с типом экранирования, а не с диаметром проводника. В таблице 2-7 показано, как тип и длина подводящего кабеля влияют на коэффициент качества.

РАСЧЕТ ИНДУКТИВНОСТИ

Существует несколько упрощенных формул для расчета приблизительной индуктивности детектора с индукционной петлей. Более точные значения индуктивности получаются с помощью метода взаимной связи, описанного в Приложении A.

Упрощенные формулы обеспечивают приемлемую точность самоиндукции многооборотных, прямоугольных, квадрупольных и круглых контуров, имеющих большую площадь относительно расстояния между проводниками. Приближения выгодно отличаются от диапазона измеренных значений индуктивности индуктивного контура.

Приложение C содержит расчетные значения индуктивности контура для контуров различных размеров и форм (прямоугольных, квадрупольных и круглых). Индуктивность и добротность для нескольких витков провода были рассчитаны с использованием формулы взаимной связи, обсуждаемой далее в этой главе.

Размер контура 6 x 6 футов (1,8 x 1,8 м). Частота возбуждения 20 кГц.
* Измеренное последовательное сопротивление петли на высоте 3 фута (0,9 м) над полом лаборатории.
** Расчетное значение сопротивления 8719.
† Длина подводящего кабеля составляет 100 футов.

РАСЧЕТ ИНДУКТИВНОСТИ КОНТУРНОЙ СИСТЕМЫ

Индуктивность вводного кабеля добавляется к индуктивности контура провода из расчета 21 Гн на 100 футов (30 м) вводного кабеля # 14 AWG. Например, прямоугольная петля размером 6 x 6 футов (1,8 x 1,8 м) должна иметь три витка в соответствии с Приложением C и индуктивность 74 Н. Если длина подводящего кабеля составляет 200 футов (61 м). по длине общая индуктивность

(2-14)

Индуктивность L двух или более контуров, соединенных последовательно, является аддитивной, так что L = L ₁ + L ₂ ± 2M , где L ₁ и L ₂ представляют собой индуктивность каждого из отдельных последовательно соединенных контуров, M — взаимную индуктивность между двумя контурами, а знак M является положительным, если поток увеличивается током, текущим в том же направлении в ближайший к нему шлейф.

Взаимная индуктивность пренебрежимо мала, когда контуры разнесены на большое расстояние. В этом случае L = L ₁ + L ₂ , т. Е. Контуры соединены последовательно, обеспечивая максимальную индуктивность контура.

Если контуры соединены параллельно, то общая индуктивность рассчитывается как 1/ L = 1/ L ₁ + 1/ L ₂ . Например, объединенная индуктивность двух 6х6 футов (1.8- x 1,8-м) петли из трех витков, каждый из которых соединен параллельно, определяется как

(2-15)

Таким образом, 2L = 74 H и L = 37 H.

Таким образом, параллельное соединение шлейфов снижает индуктивность. Хорошая практика проектирования требует, чтобы индуктивность комбинированного контура была больше нижнего предела в 50 Н. Следовательно, описанное выше параллельное соединение не подходит в качестве датчика транспортного средства.

В некоторых случаях желательно как последовательное, так и параллельное соединение индуктивных контуров.Рассмотрим, например, четыре трехвитковых контура 6 x 6 футов (1,8 x 1,8 м), установленных на расстоянии 9 футов (2,7 м) друг от друга, чтобы обеспечить обнаружение на полосе левого поворота. На Рисунке 2-8 показаны три возможных типа подключений. Последовательное соединение дает индуктивность 4 x 74 = 296 Гн. Параллельное соединение дает только 18,5 Гн ( 4L = 74 Гн, L = 18,5 мкГн). Последовательно-параллельная конфигурация, при которой две верхние петли соединены последовательно, а две нижние петли соединены последовательно, образует две пары петель, которые затем соединяются параллельно, чтобы получить общую индуктивность 74 Гн.

Рисунок 2-8. Четыре трехвитковых контура размером 6 x 6 футов (1,8 x 1,8 м), соединенные последовательно, параллельно и последовательно-параллельно.

КОЛИЧЕСТВО НЕОБХОДИМЫХ ХОДОВ

Проволочные петли должны иметь достаточное количество витков, чтобы обеспечить номинальную минимальную индуктивность 100 Гн на петлю для обеспечения стабильной работы системы индуктивной петли. Эмпирическое правило для количества витков, необходимых для получения значения индуктивности в требуемом диапазоне:

• Если периметр петли меньше 9 м (30 футов), используйте три витка провода.
• Если периметр петли превышает 9 м (30 футов), используйте два витка провода.

ЧУВСТВИТЕЛЬНОСТЬ КОНТУРА К ЭЛЕКТРОПРОВОДЯЩЕМУ ОБЪЕКТУ

Ток, протекающий через контурный провод, создает магнитное поле вокруг провода, как это задается уравнениями 2-1, 2.1 и 2-3. Если транспортное средство (или любой другой электропроводящий объект) входит в это магнитное поле, и магнитное поле или составляющая магнитного поля перпендикулярны области объекта, в проводящем объекте индуцируются вихревые токи.Вихревые токи создают другое магнитное поле, которое противодействует магнитному полю петли, вызывая уменьшение общего магнитного поля вокруг петли. Поскольку индуктивность контура пропорциональна магнитному потоку, индуктивность контура уменьшается.

Вихревые токи индуцируются в электропроводящем объекте, таком как металлическое транспортное средство, магнитным полем, создаваемым током, протекающим через проволочную петлю. Затем вихревые токи создают магнитное поле, которое противодействует исходному магнитному полю, создаваемому индуктивной петлей.В результате уменьшается индуктивность контура.

Чувствительность контура к проводящему объекту может быть проверена с помощью провода длиной 12 дюймов (30 см), сформированного в круг диаметром примерно 4 дюйма (10 см). Круговая петля образует разомкнутую электрическую цепь, когда концы проводов удерживаются так, чтобы они не касались друг друга. Не должно происходить срабатывания, когда разомкнутый круговой контур быстро перемещается горизонтально по индуктивному контуру проезжей части. Когда концы круговой петли соприкасаются, образуя замкнутую цепь, прежде чем они будут проталкиваться через дорожную петлю, произойдет срабатывание из-за протекания вихревых токов.Это демонстрирует, что для срабатывания важен именно закороченный виток, а не масса провода или транспортного средства.

МОДЕЛИ ОБНАРУЖЕНИЯ ВЕЛОСИПЕДОВ И МОТОРИЗОВАННЫХ АВТОМОБИЛЕЙ

На рис. 2-9 показано обнаружение велосипеда или мотоцикла с помощью индуктивной петли. Эти средства передвижения можно смоделировать как вертикальный проводящий объект относительно плоскости петли. Когда цикл проходит по контурному проводу, в проводящих ободах колес и раме индуцируются вихревые токи. Когда цикл проходит непосредственно над проводом контура, связь между индуктивным контуром и циклом максимальна.

Рисунок 2-9. Обнаружение велосипеда, показывающее индуцированные вихревые токи. Черные стрелки представляют ток в проводе контура, а белые стрелки — индуцированный поток.

Ходовая часть, напротив, является горизонтальной мишенью. Как показано на рис. 2-10, ходовая часть моделируется как проводящая прямоугольная пластина, ширина которой равна ширине транспортного средства, а длина равна длине транспортного средства при некоторой средней высоте шасси.

Проводящая сетка может использоваться для аппроксимации электрических характеристик сплошной пластины. Когда сетка симметрично расположена над индуктивной петлей для обеспечения максимальной чувствительности, все индуцированные внутренние токи сетки нейтрализуются. Это приводит к протеканию одиночного индуцированного тока по периметру сетки, что эквивалентно однооборотной прямоугольной проволочной петле или закороченному витку. Трансформатор с воздушным сердечником справа на рис. 2-10 моделирует соединение между ходовой частью транспортного средства, представленное закороченным витком провода, и проводом индуктивного контура.

Максимальная чувствительность обнаружения транспортного средства достигается за счет короткого замыкания на минимальном расстоянии от проводов контура. Следовательно, идеальный детектор с индукционной петлей имеет форму, которая приближается к периферии транспортного средства. То есть квадратная петля размером 6 x 6 футов (1,8 x 1,8 м) будет предпочтительнее петли размером с двигатель транспортного средства.

Из-за высоты ходовой части грузовики с высокой платформой трудно обнаружить. Обнаружение этих транспортных средств максимально, когда ширина петли равна ширине грузовика, если позволяет ширина полосы движения.Длина петли не должна быть меньше ее ширины, чтобы избежать потери чувствительности.

Рисунок 2-10. Модель ходовой части автомобиля. В верхней части рисунка изображены электрические модели ходовой части автомобиля, а в нижней — провод индукционной петли.

ВЗАИМНАЯ ИНДУКТИВНОСТЬ

Самоиндукция индуктивного контура определяется с помощью магнитного потока контура. Когда магнитный поток петли соединяется с транспортным средством, связанный поток используется для определения взаимной индуктивности.

На рис. 2-10 показана магнитная связь между контуром и закороченным витком, которая ведет себя как трансформатор с воздушным сердечником. Взаимная индуктивность между первичной цепью (т. Е. Индуктивной петлей) и вторичной цепью (т. Е. Закороченным витком) равна

.

(2–16)

, где

M ₂₁ = взаимная индуктивность между контуром 1 (контур) и контуром 2 (закороченный виток), henrys
N ₂ = количество витков (равно 1 для закороченного витка)
₂₁ = Магнитный поток, нормальный к закороченной области витка, перемычки
I ₁ = Ток, протекающий в контуре, амперы.

ЧУВСТВИТЕЛЬНОСТЬ ПЕТЛИ

Чувствительность контура SL индуктивного детектора определяется как

(2-17)

Чувствительность контура равна изменению индуктивности системы контура, вызванному проводящим металлическим предметом, деленному на исходную индуктивность системы контура.

, где

L _NV = индуктивность в отсутствие транспортного средства, генри
L _В = индуктивность при наличии транспортного средства, генри.
Чувствительность S _L для трансформатора с воздушным сердечником, показанного на рисунке 2-10, при условии, что коэффициент качества Q больше 10, определяется как

.

процентов (2-18)

где

K = коэффициент связи
M ₂₁ = взаимная связь между петлей и закороченным витком, генри
L ₁₁ = собственная индуктивность петли
L ₂₂ = Самоиндукция закороченного витка, Генрис.
Упрощенные выражения для самоиндукции и взаимной связи могут быть получены, если предположить, что влияние железа транспортного средства незначительно. Тогда r = 1 и собственная индуктивность дорожной петли длиной l ₁ находится из уравнения 2-6 как

(2-19)

Индуктивность замкнутого витка длиной l ₂ определяется как

(2-20)

Взаимная индуктивность между закороченной витой петлей и дорожной петлей определяется по формуле

(2-21)

, где

A _V = Площадь ходовой части автомобиля, (метры) 2
d ₂₁ = Расстояние между петлей и коротким поворотом, метры.
Чувствительность тогда выражается как

(2-22)
, где A _V A .

Уравнение 2-22 показывает, что чувствительность уменьшается для участков петли, превышающих площадь ходовой части транспортного средства. Чувствительность уменьшается по мере удаления шасси от петли в квадрате. Чувствительность не зависит от количества витков контура; однако разведение поворотов немного увеличивает чувствительность за счет увеличения l ₁ за счет более глубокой прорези в проезжей части.

Приложение E содержит более сложные формулы для расчета S _L для двухвитковых и других многооборотных индуктивных контуров. В этом приложении также доступны сравнения измеренной и рассчитанной чувствительности.

Рисунок 2-11 иллюстрирует изменение чувствительности контура в зависимости от высоты ходовой части автомобиля для 6 x 2 футов (1,8 x 0,6 м), 6 x 4 футов (1,8 x 1,2 м) и 6 x Трехвитковые индукционные петли длиной 6 футов (1,8 x 1,8 м). Чувствительность 6 x 2 фута (1,8 x 0.6-м) петля небольшая из-за малой длины л ₁ .

Рисунок 2-11. Расчетная чувствительность трехвитковых индуктивных контуров в зависимости от высоты шасси автомобиля.

На рисунке 2-12 показано уменьшение чувствительности контура, которое происходит при добавлении вводного кабеля длиной 200 футов (60 м) к контурам, указанным на рисунке 2-11. Петля 6 x 2 фута (1,8 x 0,6 м), вероятно, будет вдвое больше для грузовика с высокой платформой в этих условиях.

На рис. 2-13 показано уменьшение чувствительности контура для транспортного средства, центрированного в длинных индуктивных контурах с двумя витками, по сравнению с чувствительностью трехвитковых контуров.Чувствительность контура еще больше уменьшается при добавлении вводного кабеля.

ВЛИЯНИЕ АРМАТИВНОЙ СТАЛИ

На рис. 2-14 показано снижение чувствительности контура, которое происходит при установке индуктивного детектора на стальную арматурную сетку. Эффект от армирующей стали моделируется как закороченный виток на двойном расстоянии между ячейками от петли. Армирующая сталь уменьшает магнитное поле вокруг проводников проводов контура, что вызывает уменьшение индуктивности контура и чувствительности контура.В таблице 2-8 показано влияние на индуктивность контура при добавлении арматурной стали в основание дорожного покрытия. Значения консервативны, поскольку предполагается, что сетка является идеальным проводником. Современные электронные блоки индуктивного детектора способны обнаруживать транспортные средства, даже если контурный провод проложен на арматуре перед заливкой бетона.

Рисунок 2-12. Расчетная чувствительность трехвитковых индуктивных контуров с подводящим кабелем 200 футов (60 м) в зависимости от высоты шасси автомобиля.

1 фут = 0,3 м

Рисунок 2-13. Расчетная чувствительность двухвитковых длинных индуктивных контуров в зависимости от высоты шасси автомобиля.

1 фут = 0,3 м

Рисунок 2-14. Расчетная чувствительность индукционной петли размером 6 x 6 футов (1,8 x 1,8 м) к арматурной стали.

Индуктивные контуры не функционируют как автомобильные датчики при установке над стальной арматурой, части которой соединены таким образом, что ток течет через арматуру.Этот индуцированный ток полностью или частично нейтрализует индуцированный транспортным средством ток в индуктивном контуре. Если расстояние между арматурными стержнями достаточно велико, токи могут не подавляться. И наоборот, если арматурный стержень не закорочен при установке, он не будет поддерживать поток противотоков, которые ухудшают работу индуктивного контура.

89308

Таблица 2-8. Влияние арматурной стали на индуктивность контура (H).

Число витков	Без армирующей стали	Сталь диаметром 1 дюйм	Сталь диаметром 2 дюйма	Сталь диаметром 4 дюйма
1	11	9	10	10
2	35	28	31	33
3	73	56	63	68
	4	112
5	179	127	151	166
6	248	167	206	228				298
1 дюйм = 2.5 см

Эпоксидные покрытия, обычно наносимые на арматуру, по своей природе являются изоляционными. Однако характер процесса нанесения покрытия обычно оставляет в покрытии пустоты, через которые проходят токи. Количество допустимых пустот может быть указано в строительной документации. Противоток может увеличиваться в зимние месяцы в холодном климате, когда соли попадают на проезжую часть или настил моста.

ЧУВСТВИТЕЛЬНОСТЬ КОНТУРНОЙ СИСТЕМЫ

Чувствительность системы контура определяется как наименьшее изменение индуктивности на клеммах электронного блока, которое вызывает срабатывание контроллера.Эта чувствительность должна быть равна или превышать порог для электронного блока. Во многих штатах указывается, что блок электроники должен реагировать на изменение индуктивности на 0,02 процента. Стандарты NEMA (см. Раздел 15.3.2 Приложения J), признавая различия в конструкции блока электроники ( L / L или L ), определяют порог чувствительности для трех классификаций тестовых автомобилей, когда они сосредоточены в одном 6 — x 6 футов (1,8 x 1,8 м) трехвитковая петля с длиной 100 футов (30.5 м) подводящего кабеля. Классы автомобилей:

Индуктивность, включенная последовательно или параллельно с индуктивно-петлевым детектором, снизит чувствительность петлевой системы на входных клеммах электронного блока.

Исследование, проведенное для проекта SCANDI в Детройте, показало, что на продолжительность вызова влияет высота магнитного поля, которое, в свою очередь, зависит от наличия и глубины арматурной стали и других факторов, специфичных для местоположения. ⁽²⁾ Исследование показало, что регулируемые ромбовидные петли компенсируют такие факторы в каждом месте, обеспечивая одинаковую продолжительность от петли к петле для данного транспортного средства на заданной скорости.

ЧУВСТВИТЕЛЬНОСТЬ ИНДУКТОРОВ ДВУХ СЕРИЙ

На рис. 2-15 показан расчет полной индуктивности для комбинации двух отдельных индуктивных контуров, соединенных последовательно, как один эквивалентный контур. (Рисунок 2-19 иллюстрирует соединение двух контуров таким образом.) Эквивалентная общая последовательная индуктивность L _TS составляет

(2-23)
, где L _A и L _B — индивидуальные значения индуктивности контуров.

Рисунок 2-15. Эквивалентная общая индуктивность от двух последовательно включенных индуктивных контуров.

Эквивалентная общая последовательная чувствительность STS составляет

(2-24)

где Чувствительность контура при вхождении транспортного средства в контур A.

ЧУВСТВИТЕЛЬНОСТЬ ДВУХ ПАРАЛЛЕЛЬНЫХ ИНДУКТОРОВ

Рисунок 2-16 иллюстрирует расчет чувствительности для двух отдельных индуктивных контуров, соединенных параллельно как эквивалентный одиночный контур. (Рисунок 2-21 иллюстрирует соединение двух контуров таким образом.) Эквивалентная общая параллельная индуктивность L _TP составляет

(2-25)

Эквивалентная общая параллельная чувствительность S _TP составляет

(2-26)

Рисунок 2-16. Эквивалентная общая индуктивность от двух параллельных индуктивных контуров.

ПРИМЕР ОДНОГО КОНТУРА

1. Какова чувствительность контура на тяговом ящике для транспортного средства с высокой платформой (4 фута (1.2-м) ходовая) переходит петлю? Рисунок 2-17 иллюстрирует этот случай и показывает длину подводящих проводов. Эквивалентная электрическая схема показана на Рисунке 2-18.

Рисунок 2-17. Одиночный индуктивный контур, подключенный к вытяжной коробке и электронному блоку.

Рисунок 2-18. Эквивалентная одноконтурная электрическая схема.

Чувствительность S _L для ходовой части высотой 4 фута (1,2 м) и трехвитковой ходовой части 6 x 6 футов (1.Петля 8 x 1,8 м) провода # 14 AWG составляет 0,1 процента от рисунка 2-11. Скрученные петли образуют подводящий провод длиной примерно 24 фута (7,3 м) к вытяжной коробке. Индуктивность на фут для контурного провода № 14 AWG с 5 витками на фут составляет 0,22 Гн / фут (0,7 Гн / м). Подводящая индуктивность L _S составляет

(2-27)

Собственная индуктивность L _L трехвитковой петли длиной 1,8-1,8 м (6 x 6 футов) из провода № 14 AWG на частоте 20 кГц из Приложения C составляет 74 Гн.Следовательно, чувствительность S _P (в процентах) на вытяжной коробке составляет

(2-28)

2. Какова чувствительность системы индуктивного контура на входных клеммах электронного блока с экранированным подводящим кабелем типа 8720 длиной 200 футов (61 м) между вытяжной коробкой и электронным блоком?

Из таблицы 2-6 индуктивность кабеля типа 8720 составляет 0,22 Гн / фут. Общая последовательная индуктивность между контуром и входными клеммами электронного блока составляет

(2-29a)

(2-29b)

Тогда чувствительность S _D на входных клеммах блока электроники будет

(2-30)

3.Какова чувствительность системы индуктивного контура на входных клеммах блока электроники с экранированным вводным кабелем типа 8720 длиной 200 футов (61 м) между вытяжной коробкой и блоком электроники, если четырехвитковый, 6 — x Используется петля длиной 6 футов (1,8 x 1,8 м) # 14 AWG?

Чувствительность S _L для ходовой части 4 фута (1,2 м) и четырехвитковой петли 6 x 6 футов (1,8 x 1,8 м) составляет 0,1 процента. Согласно Приложению C, собственная индуктивность контура составляет 125 Гн при 20 кГц. Последовательная индуктивность такая же, как в предыдущем примере.

Следовательно

(2-31)

ДВЕ ПЕТЛИ ПОСЛЕДОВАТЕЛЬНО ПРИМЕР

1. Какова чувствительность системы индуктивного контура на входных клеммах электронного блока, когда второй идентичный контур включен последовательно с контуром, определяющим транспортное средство? На Рис. 2-19 показана конфигурация контура и показаны длины подводящих проводов. Последовательное соединение осуществляется в вытяжной коробке.

Рисунок 2-19. Две индуктивные петли, подключенные последовательно к вытяжной коробке и электронному блоку.

На рисунке 2-20 показана эквивалентная электрическая схема. Чувствительная петля представляет собой трехвитковую петлю размером 6 x 6 футов (1,8 x 1,8 м) из провода # 14 AWG. Собственная индуктивность второго контура (т. Е. Последовательного контура B) составляет 74 Н. Индуктивность подводящего провода контура B составляет

(2-32)

Общая последовательная индуктивность контура B и подводящего провода к вытяжной коробке составляет

(2-33)

, а общая последовательная индуктивность между двумя контурами и входными клеммами электронного блока составляет

(2-34a)

(2-34b)

Рисунок 2-20.Эквивалентная электрическая схема для двух контуров, последовательно подключенных к вытяжной коробке и электронному блоку.

Затем

(2-35)

ДВА ПЕТЛИ В ПАРАЛЛЕЛЬНОМ ПРИМЕРЕ

1. Какова чувствительность системы шлейфов на клеммах блока электроники при двух идентичных шлейфах, соединенных параллельно? На Рис. 2-21 показана конфигурация контура и показаны длины подводящих проводов. Эквивалентная электрическая схема показана на Рисунке 2-22. Все параметры такие же, как в предыдущем примере цикла серии.Общая индуктивность и чувствительность на входе в блок электроники рассчитываются как

(2-36)
и

(2-37)

.

Рисунок 2-21. Две индуктивные петли, подключенные параллельно к вытяжной коробке и электронному блоку.

Рисунок 2-22. Эквивалентная электрическая схема для двух контуров, подключенных параллельно к вытяжной коробке и блоку электроники.

Пусть

(2-38)

и (2-39)

Тогда

(2-40)

(2-41)

и

(2-42)
(2-43)

Следовательно

(2-44 )

РЕЗОНАНСНАЯ ЦЕПЬ

Многие самонастраивающиеся электронные блоки с индуктивным контуром используют сдвиг частоты или изменение периода генератора, чтобы указать прохождение или присутствие транспортного средства.Частота генератора регулируется параллельным резонансным контуром, иногда называемым резервуарным контуром, состоящим из эквивалентной индуктивности системы контура и настроечной емкости электронного блока. Эквивалентная емкость системы контура также включает емкостные эффекты из-за размещения проводов контура в пропиле. Соответствующий эквивалентный коэффициент качества учитывает влияние потерь сопротивления системы. Если эквивалентная индуктивность системы контура слишком мала, генератор не будет колебаться.Изготовитель блока электроники указывает допустимый диапазон индуктивности системы контура и минимальный коэффициент качества системы контура.

Частота генератора рассчитывается как

(2-45)

, где L _D , C _D , Q _D — это индуктивность, емкость и добротность соответственно. , контура резервуара.

Уравнение 2-45 показывает, что уменьшение индуктивности увеличивает резонансную частоту.Кроме того, коэффициент качества выше пяти будет иметь незначительное влияние на характеристики резонансного контура.

ВРЕМЕННЫЕ ПЕТЛИ

Несколько производителей и государственных агентств стремились разработать долговечную и экономичную временную петлю, которая удовлетворяет потребности в программах контроля скорости, подсчета транспортных средств, классификации транспортных средств и портативных программ взвешивания в движении (WIM). Ниже описаны два типа временных и переносных петлевых систем.

МАТОВЫЕ ПЕТЛИ

Временная петля типа мата состоит из прочного резинового мата, в который заделано несколько витков проволоки.Маты обычно меньше по ширине, чем типичная индукционная петля длиной 1,8 м. Стандартные размеры варьируются от 4 x 6 футов (1,2 x 1,8 м) до 3 x 6 футов (0,9 x 1,8 м). Коврики располагаются в центре полосы движения, причем более длинный размер параллелен потоку движения, так что большинство транспортных средств преодолевают коврик, тем самым продлевая срок службы коврика. Типичная установка показана на Рисунке 2-23. Гвозди и шайбы обычно используются для крепления мата к поверхности дороги. Широкий 3-дюймовый (7.6 см) наклеивается прочная клейкая лента, чтобы края мата не поднимались. Подводящие провода от коврика к оборудованию для сбора данных на обочине дороги заключены между двумя слоями ленты.

Рисунок 2-23. Типовая установка временного индуктивного петлевого детектора матового типа.

Некоторые агентства изготовили этот тип датчика в собственном магазине. Однако изготовление этих матов вручную было слишком трудоемким, чтобы быть рентабельным. Коврики были надежными, но в условиях интенсивного движения грузовиков некоторые из них прослужили не более нескольких часов.

КОНФИГУРАЦИЯ ОТКРЫТОГО КОНТУРА

Один производитель производит предварительно отформованную временную переносную петлю размером 4 x 6 футов (1,2 x 1,8 м). Петля состоит из пяти слоев, как показано на рис. 2-24. Нижний слой представляет собой антиадгезионный бумажный лист шириной 4 дюйма (101,6 мм), который защищает полосу клейкой битумно-резиновой смеси шириной 2 дюйма (50,8 мм). Его верхняя поверхность отделана полиэтиленовой пленкой высокой плотности. Эта прокладочная полоса является основой для трех витков контурного провода №22 AWG.Аналогичная 2-дюймовая (50,8 мм) прокладка закрывает провода контура. Верхний слой представляет собой полосу клеевого битумного компаунда шириной 4 дюйма (101,6 мм), армированную тканой полипропиленовой сеткой.

Предварительно сформированная конфигурация с разомкнутым контуром может быть доставлена ​​в выбранное место и установлена ​​одним человеком за несколько минут. Установка состоит из снятия нижней подкладки, размещения петли на проезжей части и приложения давления, достаточного для обеспечения сцепления. Стандартно — пять футов защищенного подводящего провода.Доступны другие размеры петли и длины защищенных подводящих проводов.

Другой подход к конфигурации разомкнутого контура был разработан Отделом специальных исследований Министерства транспорта штата Невада (DOT). ⁽³⁾ В Nevada DOT ранее использовалась переносная петля размером 6 x 6 футов (1,8 x 1,8 м), состоящая из трех витков многожильного медного провода № 14 AWG, обмотанного черной изолентой. По мере увеличения использования переносных петель возрастали трудоемкие проблемы, связанные с долговечностью и обслуживанием.Это привело к тестированию различных лент, резиновых трубок и материала резинового мата в качестве замены клейкой ленты, покрывающей оригинальные петли.

Рисунок 2-24. Пятиуровневая временная конфигурация детектора разомкнутого контура.

Битумная лента производства Polyguard Products была в конечном итоге выбрана для ограждения проволочных петель. Это армированный тканью резиноподобный материал с одной клейкой стороной. Окончательная конфигурация состоит из четырех витков медного провода # 14 AWG, намотанных в цеху и скрепленных вместе для удобства использования.Петли заключены в две обертки из материала Polyguard и установлены, как показано на Рисунке 2-25.

1 фут = 0,3 м
1 дюйм = 2,5 см

Рисунок 2-25. Портативная установка с открытым контуром в Неваде.

Был проведен ряд испытаний для измерения прочности и точности петель по сравнению с обычными петлями, установленными в пазах для пиления. В других тестах сравнивали конфигурацию 4 x 6 футов (1,2 x 1,8 м) с конфигурацией 6 x 6 футов (1,8 x 1,8 м).Испытательные контуры были установлены на сельской двухполосной проезжей части ФАП с высоким процентом грузовиков, состоящих из нескольких единиц. В обеих сериях испытаний использовался один и тот же самописец счетчика / классификатора.

После почти 5000 срабатываний разница между количеством транспортных средств, подсчитываемых с помощью переносной петли этого типа и петли, установленной пропилом, составила менее 1 процента. Также было обнаружено, что размер петли 4 x 6 футов (1,2 x 1,8 м) практически такой же, как размер петли 6 x 6 футов (1,8 x 1,8 м), независимо от того, была ли петля в пиле. в разрезе или в переносном виде.

Переносные петли все еще работали после более чем годичного испытания продукта на долговечность, состоящего из более миллиона активаций. Эта оценка, проведенная на шоссе US 395 между Рино и Карсон-Сити, штат Невада, показала, что петли являются чрезвычайно прочными и способны выдерживать широкий диапазон погодных условий. Дорога была покрыта асфальтом, и через несколько месяцев петли вросли в тротуар, что, возможно, способствовало их долговечности. Ожидается, что на бетонной поверхности эти петли прослужат более полумиллиона срабатываний.Петли также использовались с накладками и были способны выдерживать высокую температуру, связанную с этим процессом.

Испытания в полупостоянном месте увеличили срок службы петли, поскольку петли не подвергались повторному удалению и повторной установке. Однако другие петли того же типа неоднократно устанавливались без признаков чрезмерного износа. В результате этих тестов и опыта работы с этими петлями, Nevada DOT теперь использует петлю Polyguard во всех своих переносных установках петли.

БЛОКИ ЭЛЕКТРОНИКИ

Блок электроники, который генерирует частоту возбуждения индуктивного контура и контролирует работу системы индуктивного контура, значительно изменился с 1970-х годов. Ранние версии электронных блоков с индуктивным контуром работали на фиксированной резонансной частоте, используя кристалл для стабилизации частоты. Было много проблем с блоками кристаллической электроники, особенно при использовании с длинными подводящими кабелями.

Одним из них был дрейф резонансной частоты из-за изменений температуры и влажности окружающей среды.Эти устройства были выведены из эксплуатации в 1970-х годах и первоначально были заменены конструкциями, в которых использовались аналоговые фазовращатели, которые были способны компенсировать (или отслеживать) дрейф, вызванный изменениями окружающей среды. Современные электронные блоки стабилизируют частоту колебаний и обнаруживают транспортные средства с конфигурациями, которые включают цифровой сдвиг частоты, цифровой пропорциональный сдвиг частоты, цифровой сдвиг периода и цифровой пропорциональный сдвиг периода. Теория работы этих устройств описана ниже.Аналоговые блоки электроники с фазовым сдвигом все еще используются ограниченно для классификации транспортных средств.

АНАЛОГОВЫЙ БЛОК ЭЛЕКТРОНИКИ С ПЕРЕМЕЩЕНИЕМ ФАЗЫ

Это устройство было разработано для удовлетворения требований европейского рынка, где необходимо обнаруживать велосипеды. Как и модель с кварцевым резонатором, он работает как датчик фазового сдвига, но использует два генератора переменной частоты, а не один генератор, управляемый кристаллом. Генератор контура работает на частоте от 25 до 170 кГц, что определяется контуром и подводящим проводом.Генератор контура соединен со вторым внутренним генератором, так что процедура начальной ручной настройки приводит два генератора в синхронизацию по частоте и фазе.

Ручка настройки перемещает ферритовый сердечник взад и вперед внутри индуктора, заставляя подключенный к нему генератор изменять свою частоту (и фазу) в соответствии с частотой генератора контура. Прибытие транспортного средства в контур уменьшает индуктивность контура, и генератор контура пытается выйти из синхронизации со своим сопутствующим генератором.Он не может изменять частоту из-за резистора перекрестной связи, но развивается фазовый сдвиг, который является основой для обнаружения транспортного средства.

Благодаря этой концепции конструкции электронный блок способен компенсировать (или отслеживать) дрейф окружающей среды. Когда температура внутри шкафа контроллера изменяется, два осциллятора смещаются одинаково. Выход двух генераторов подается на схему сравнения фаз, которая вырабатывает постоянное напряжение, пропорциональное величине сдвига; Таким образом, термин аналоговый, потому что он использует переменные напряжения, а не цифровые подсчеты для обозначения проезда или присутствия транспортного средства.

Когда в зоне обнаружения нет транспортных средств, постоянное напряжение сохраняется и запоминается конденсатором памяти. Когда автомобиль вызывает изменение выходного сигнала фазового компаратора, разница между ним и конденсатором памяти заставляет реле изменять состояние. За очень медленными изменениями постоянного напряжения следует конденсатор памяти, который позволяет схеме компенсировать дрейф из-за изменений окружающей среды. Схема памяти в конечном итоге забудет о транспортном средстве, припаркованном над петлей, и сбросит этот вызов.Подробная информация о компенсации дрейфа окружающей среды будет включена позже в разделе «Электронный блок цифрового сдвига частоты».

ОБЗОР ЦИФРОВОЙ ЭЛЕКТРОНИКИ

Стабильность и дополнительные функции, обеспечиваемые электронной цифровой обработкой, привели к тому, что большинство производителей электронных устройств с индуктивными детекторами стали производить цифровые устройства. Цифровые методы позволяют более надежные, точные и точные измерения, чем аналоговые методы.

При использовании блоков цифровой электроники необходимо учитывать взаимосвязь между повышенной чувствительностью и, как следствие, увеличением времени отклика.Большое время отклика может привести к значительной ошибке в измерениях скорости транспортного средства, когда в конфигурации устройства ограничения скорости используются два контура (т. Е. Разделенные известным и измеренным расстоянием). Время отклика зависит от производителя электронного блока.

Цифровые электронные блоки обнаруживают изменение частоты или периода формы сигнала. Частота генератора или сдвиг периода вызваны уменьшением индуктивности контура, создаваемым, когда транспортное средство находится в зоне обнаружения контура.Частота генератора для коэффициента качества Q , равного 5 или выше, определяется как

(2-46)

.

, где

f _D = частота генератора, Гц
L _D = общая индуктивность (т. Е. Контур плюс подводящий кабель) на входных клеммах электронного блока, henrys
C _D = Общая емкость на входных клеммах электронного блока, Генри.

Нормализованное изменение частоты генератора из-за нормализованного изменения индуктивности на входных клеммах электронного блока, когда Q равно 5 или больше, определяется как

(2-47)

, где

f _D = Изменение частоты генератора электронного блока, Гц
L _D = Изменение индуктивности на входных клеммах электронного блока, henrys
S _D = Чувствительность блока электроники к изменению индуктивности.

Обнаружение транспортного средства системой детектора индуктивной петли в первую очередь индуцируется приближением транспортного средства к скрытой индуктивной проволочной петле, что вызывает изменение индуктивности петли в цепи генератора индуктивности-емкости ( LC ), образованной петлей, вывод в кабеле, а входной конденсатор находится в блоке электроники. Некоторые производители обнаруживают автомобили по процентному изменению индуктивности контура L _L / L _L , в то время как другие просто используют изменение индуктивности контура L _L .Ни одна из этих величин не может быть измерена непосредственно на входных клеммах электронного блока. Однако для определения чувствительности некоторые производители предоставляют частотомеры для измерения резонансной частоты и величины изменения частоты.

Опыт показывает, что процентное изменение индуктивности ( L _L / L _L ) от незанятого контура до занятого контура чрезвычайно воспроизводимо для данного размера и геометрии контура, данного размера и геометрии транспортного средства, а также заданное расположение автомобиля относительно петли.Поскольку такие параметры, как фактическая индуктивность контура и рабочая частота контура, не влияют на L _L / L _L , но влияют на L _L , следующие обсуждения и вычисления относятся к L _L / L _L концепт. Термин «чувствительность электронного блока» в контексте этого обсуждения определяется как значение L _L / L _L , которое приводит в действие электронный блок с меньшими значениями, которые интерпретируются как обозначающие большую чувствительность.

Для коротких вводных кабелей с незначительной индуктивностью последовательного кабеля

(2-48)

, где

L _L = Изменение индуктивности контура при обнаружении транспортного средства, Генри
L _L = Индуктивность контура, Генри
S _L = Чувствительность контура к транспортному средству в зоне обнаружения.

Период генератора T _D определяется как инверсия частоты f _D .Для Q из 5 или более T _D задается по

(2-49)

Нормализованное изменение периода генератора, вызванное нормализованным изменением индуктивности на входной клемме электронного блока, когда Q равно 5 или больше, примерно равно

(2-50)

Отрицательный знак указывает, что изменение периода противоположно изменению индуктивности.

С появлением сложных цифровых микропроцессоров и доступностью информации о резонансной частоте контурной сети на входных клеммах электронного блока, можно относительно легко получить точные измерения следующих параметров:

• Сдвиг частоты ( f _D ).
• Относительный сдвиг частоты ( f _D / f _D ).
• Сдвиг периода ( T _D ).
• Относительный сдвиг периода ( T _D / T _D ).

Четыре типа блоков цифровой электроники, каждый из которых использует один из этих методов измерения, представлены ниже. Подробный анализ и блок-схемы каждого устройства представлены в Приложениях с F по I.

БЛОК ЦИФРОВОГО ПЕРЕМЕНА ЧАСТОТЫ

Агрегаты данного типа не производятся. Тем не менее, теория и рабочие характеристики, связанные с этой концепцией, включены, чтобы можно было лучше понять работу электронного блока цифрового пропорционального сдвига частоты.

Цифровой процессор в электронном блоке цифрового переключения передач будет сравнивать отсчеты, пропорциональные частоте генератора, когда транспортное средство присутствует, с контрольным отсчетом, проводимым периодически, когда транспортных средств нет.Счетчик ссылок хранится в памяти. Во время обнаружения транспортного средства, когда счетчик превышает контрольный счетчик на предварительно установленный счетчик порога чувствительности, инициируется вызов автомобиля.

Чувствительность электронного блока сдвига частоты рассчитывается по уравнению 2-47 как

(2-51)

Приложение F показывает, что

(2-52)

, где

N _ft = Количество пороговых значений фиксированной частоты, выбираемое переключателем чувствительности
N _fc = Количество циклов генератора, подсчитываемых переменной частотомер
K _f = постоянная частотной чувствительности.

В методе цифрового частотного сдвига S _D пропорционально квадратному корню из произведения L _D C _D . Поскольку большие значения S _D представляют собой пониженную чувствительность, отсюда следует, что чувствительность уменьшается пропорционально квадратному корню из произведения L _D C _D с измерением f _D . Следовательно, каждый раз, когда переключатель частоты изменяется в новое положение (например,g., чтобы избежать перекрестных помех), чувствительность изменится и, в случае критичности, потребует новой настройки переключателя чувствительности.

Увеличенная длина подводящего кабеля увеличивает индуктивность подводящего кабеля и, следовательно, вызывает некоторую потерю чувствительности. Увеличенный продукт L _D C _D приведет к еще большей потере чувствительности. Следовательно, этот тип измерения нецелесообразен.

БЛОК ЦИФРОВОГО ПЕРЕКЛЮЧЕНИЯ ЧАСТОТЫ

Цифровой процессор в электронном блоке цифрового пропорционального сдвига частоты сравнивает отсчеты, пропорциональные частоте генератора, когда транспортное средство присутствует, с контрольным отсчетом, производимым периодически, когда транспортное средство отсутствует.Счетчик ссылок хранится в памяти. Когда счет во время обнаружения транспортного средства превышает счетчик ссылок на предварительно установленный счетчик порога чувствительности, инициируется вызов транспортного средства.

Электронный блок пропорционального сдвига частоты отличается от блока сдвига частоты тем, что счетчик частоты поддерживается приблизительно постоянным (как поясняется далее в Приложении G).

Чувствительность не зависит от индуктивности L _D и емкости C _D на клеммах электронного блока.Чувствительность рассчитывается как

(2-53)

, где

N _футов = счетчик порога фиксированной частоты
N _fc = счетчик фиксированной частоты.
Согласно Приложению G, время отклика измерения t ^f составляет
(2-54)
где м — множитель частоты.

Преимущество независимости чувствительности от индуктивности и емкости на входных клеммах электронного блока показано на следующем примере.Этот пример также применим к электронному блоку цифрового пропорционального сдвига периода, обсуждаемому позже.

Предположим, что четыре петли одинакового размера, скажем, 6 x 6 футов (1,8 x 1,8 м), с равным числом витков, скажем, тремя. Соедините петли, как показано на рисунке 2-8, а именно

.

• Все серии (296 H).
• Последовательно-параллельный (74 H).
• Все параллельные (18,5 Н).

Для простоты длина подводящего кабеля не учитывается. Чувствительность электронного блока пропорционального частотного или пропорционального сдвига периода идентична для трех вышеупомянутых конфигураций подключения контура.Соответственно, порог чувствительности, достаточный для обнаружения небольшого мотоцикла по одному из четырех контуров при последовательном подключении, не должен изменяться при повторном подключении последовательно-параллельно или полностью параллельно.

Хотя длина подводящего кабеля выше не рассматривалась, слишком длинный подводящий кабель будет вызывать различную величину изменения индуктивности из-за разделения индуктивности. Величина изменения зависит от длины подводящего кабеля и схемы подключения, используемой для нескольких шлейфов. На рис. 2-26 представлена ​​оценка изменения индуктивности на входных клеммах электронного блока, создаваемого небольшим мотоциклом, движущимся по одному из четырех контуров. ⁽¹⁾

1 фут = 0,3 м

Рисунок 2-26. Изменение индуктивности небольшого мотоцикла в зависимости от длины подводящего кабеля для последовательного, параллельного и последовательно-параллельного соединения четырех петель размером 6 x 6 футов.

БЛОК ЦИФРОВОГО ПЕРИОДА ПЕРЕКЛЮЧЕНИЯ ЭЛЕКТРОНИКИ

Концепция цифрового сдвига периода использует период частоты генератора контура, где период определяется как время, необходимое для одного полного цикла частоты генератора.Период рассчитывается путем деления единицы на частоту в Гц или эквивалентного деления единицы на частоту в циклах в секунду.

Цифровые электронные блоки

со сдвигом периода используют опорные тактовые импульсы, работающие на частотах в мегагерцах (МГц), то есть от 20 до 100 раз быстрее, чем частота колебаний индуктивного контура, для измерения периода колебаний контура, как показано на рисунке 2-27. Точность измерения повышается без потери большого количества времени между измерениями за счет определения времени для 32 циклов колебаний для чувствительности 1, 64 циклов для чувствительности 2 и т. Д.Период колебаний контура рассчитывается исходя из числа n опорных тактовых циклов, содержащихся в этом периоде. Поскольку частота колебаний увеличивается, когда транспортное средство проезжает по петле, период колебаний уменьшается, поскольку он равен обратной частоте. Уменьшение периода колебаний приводит к меньшему количеству циклов опорных часов в течение периода колебаний. Когда количество эталонных циклов уменьшается больше, чем предварительно выбранный порог, инициируется вызов, чтобы указать присутствие транспортного средства.

Рисунок 2-27. Измерение периода колебаний индуктивного контура эталонными часами
(Источник: L.A. Klein, Sensor Technologies and Data Requirements for ITS (Artech House, Norwood, MA, 2001)).

Разумный выбор опорной тактовой частоты и порогового значения (4 счета ± 2 счета) делает конструкцию цифрового сдвига периода практичной на любой частоте, встречающейся на практике. Время обнаружения достаточно короткое, чтобы электроника могла последовательно сканировать или управлять четырьмя небольшими контурами, по одному, несколько раз в секунду.(Многоканальность обсуждается позже.)

Блок электроники смещения периода полностью самонастраивается при установке и, как и большинство других конструкций, может отслеживать дрейф окружающей среды. Подобно блоку цифрового сдвига частоты, большинство моделей прекращают отслеживание на некоторое время после того, как транспортное средство входит в петлю, чтобы гарантировать, что вызов, сделанный небольшим транспортным средством, удерживается достаточно долго, чтобы вызвать зеленый цвет к этому подходу.

Чувствительность электронного блока со сдвигом периода определяется из уравнения 2-50 как

(2-55)

Приложение H показывает, что

(2-56)

, где

N _pt = Счетчик порога фиксированной частоты, выбранный переключателем чувствительности
N _pc = Счетчик, произведенный счетчиком переменной частоты
K _p = Константа частотной чувствительности.

Чувствительность обратно пропорциональна квадратному корню из продукта L _C с измерением T. Когда принимает малые значения, чувствительность увеличивается. Следовательно, при увеличении длины подводящего кабеля часть потери чувствительности из-за добавленной индуктивности подводящего кабеля автоматически компенсируется увеличением продукта L _C . К сожалению, компенсация не идеальна из-за отношения квадратного корня.

Время отклика t ^p электронного блока, как показано в Приложении H, составляет

(2-57)

В большинстве электронных блоков используется трансформатор для подключения клемм внешнего индуктивного контура к внутреннему генератору. Слабосвязанный трансформатор создает последовательную индуктивность рассеяния или затухания. Эта индуктивность снижает влияние вводного кабеля на чувствительность за счет общей чувствительности.

Если в электронном блоке используется индуктивность L _T , то

(2-58)

Например, пусть

N _pt = 4
L _T = 150 H
L _D = 75 H
f _D = 2.22 МГц
= 0,005%.

Затем

(2-59)

Процентная погрешность в скорости транспортного средства, полученная из датчика скорости с использованием двух индуктивных контуров на известном расстоянии друг от друга, определяется как

(2-60)

, где

S / S = Ошибка скорости автомобиля, проценты
T = Ошибка измеренного времени, секунды
X = Расстояние между передними кромками контура, единицы расстояния
S = Скорость автомобиля, единицы расстояния в секунду.

Максимальная измеренная временная ошибка в измерениях скорости автомобиля или присутствия людей связана с временем отклика электронного блока. Ошибка измерения скорости, вызванная конечным временем отклика, проиллюстрирована следующим примером.

Пусть

S / S = Неизвестная ошибка скорости автомобиля, проценты
T = 2 x 216 миллисекунд (мс) = 432 мс (ошибка 0,432 секунды в измеренном времени)
X = 100 футов ( 30,5 м) расстояние между передними кромками контура
S = 60 миль в час (миль / ч) = 88 фут / с (96.6 километров в час (км / час) = 2,68 м / с) скорость автомобиля.

Затем

(2-61)

Этот пример показывает, что контурная система должна быть спроектирована так, чтобы ее чувствительность была как можно большей. Устанавливая электронный блок в менее чувствительный диапазон, время отклика уменьшается, обеспечивая более точное измерение скорости автомобиля.

Увеличение тактовой частоты электронного блока с 2,22 МГц до 22,2 МГц снижает процентную ошибку скорости с 38 процентов до 3.8 процентов. Многие из новых электронных блоков используют тактовые частоты от 20 до 25 МГц и, таким образом, способны уменьшить процентную ошибку скорости.

БЛОК ЦИФРОВОГО ПЕРИОДА ПЕРЕКЛЮЧЕНИЯ ПЕРИОДА

Цифровой процессор в этой конструкции сравнивает отсчеты, пропорциональные периоду генератора, когда транспортное средство присутствует, с контрольным отсчетом, производимым периодически, когда транспортное средство отсутствует. Счетчик ссылок хранится в памяти. Когда счет во время обнаружения меньше, чем контрольный счет на предварительно установленный счетчик порога чувствительности, инициируется вызов транспортного средства.Электронный блок пропорционального сдвига периода отличается от электронного блока сдвига периода тем, что пороговое значение N _pt не является фиксированным.

Пороговое значение (см. Приложение I) определяется по номеру

(2-62)

Поскольку чувствительность электронного блока не зависит от счетчика периода, чувствительность также не зависит от частоты. Время отклика такое же, как у электронного блока цифрового сдвига периода.

СРАВНЕНИЕ БЛОКОВ ЦИФРОВОЙ ЭЛЕКТРОНИКИ

В таблице 2-9 сравниваются различные концепции блоков цифровой электроники с индуктивным контуром с точки зрения чувствительности и времени отклика.

МНОГОКАНАЛЬНЫЕ ЦИФРОВЫЕ МОДЕЛИ

Пространство в шкафу контроллера можно сэкономить, если электронный блок может работать более чем с одним шлейфом. Большинство производителей блоков цифровой электроники предлагают изделия, которые могут работать с четырьмя и более контурами. Некоторые модели решают проблему перекрестных помех, предоставляя переключатель разделения частот, в то время как другие разделяют контуры с помощью процесса сканирования с временным разделением.

Блок сканирующей электроники одного производителя активирует и анализирует каждый из четырех или более каналов последовательно до 100 раз в секунду. Электронный блок цифрового сдвига периода по своей природе достаточно быстр, чтобы разрешить сканирование. Время для анализа канала зависит от желаемой чувствительности, поскольку высокая точность определения пороговых значений требует больше времени для подсчета опорных импульсов.

Например, если три контура по 150 Н были подключены и использовались с чувствительностью 1, 4 и 6, а четвертый канал был выключен, то для четырех каналов потребовалось бы 2.3, 9, 63 и 0,9 мс соответственно, всего 75 мс. Каждый канал будет включен и проанализирован 1000 ÷ 75 = 13 раз в секунду. Использование контуров с более высокими значениями индуктивности снижает скорость сканирования, как и выбор самых высоких настроек чувствительности на устройстве. Если задействовано более четырех одинаковых и близлежащих контуров, переключатель частоты или размер и / или количество витков в контурах могут быть изменены для обеспечения защиты от перекрестных помех. Уравнение 2-40 и таблицы 2-2, 2-3 и 2-4 могут использоваться для расчета частотного разноса 7 процентов или более.

Производители используют более высокие тактовые частоты, чтобы обеспечить более высокую скорость сканирования. Например, при более низких настройках чувствительности время выборки составляет 0,5 мс на канал. Таким образом, общее время сканирования всех четырех каналов составляет 2 мс. Когда канал выключен, время сканирования для этого канала равно нулю.

ДОБАВЛЕННЫЕ ФУНКЦИИ ДЛЯ ЦИФРОВОЙ ЭЛЕКТРОНИКИ

В 1980-х годах в блоки цифровой электроники индуктивного детектора было внесено несколько усовершенствований. Признавая высокую потребность в расходах на техническое обслуживание, некоторые производители добавили схемы, снижающие частоту вызовов неисправностей, для сброса блоков, подключенных к неисправным шлейфам.Эти функции, предназначенные для снижения затрат на обслуживание и увеличения производительности трафика, включают в себя тестирование разомкнутого контура, автоматический сброс и удаленный сброс, как описано ниже.

Тест с разомкнутым контуром

Эта функция позволяет электронному блоку продолжать работу в системе с периодически разомкнутым контуром. Кратковременное размыкание, вызванное обрывом провода, плохим соединением или ненадежным соединением, будет сохранено в памяти. Если соединение восстановится, устройство сразу же перенастроится и продолжит работать должным образом.Если открытие продолжается, это приведет к постоянному вызову.

При обращении в сервисный центр на перекрестке техник может заметить световой индикатор, который будет мигать определенным образом, если произошло обрыв. В случае блоков электроники других марок технический специалист нажимает кнопку «Проверка разомкнутого контура», чтобы определить, произошло ли размыкание с момента последнего обращения в сервисный центр. Память разомкнутого контура можно запрашивать повторно, поскольку ее можно сбросить только при отключении питания (например, при извлечении модуля из каркаса для карт и повторной установке) или путем нажатия общей кнопки сброса на электронном блоке.Это представляет собой сброс системы, который очищает память разомкнутого контура.

Автоматический сброс

Некоторые электронные блоки могут быть запрограммированы на генерацию внутреннего сброса, если вызов (т. Е. Выход электронного блока) превышает запрограммированное время. Сброс управляется завершением соответствующей фазы зеленого цвета. Одно агентство утверждает, что эта функция снизила затраты на техническое обслуживание электронного блока на 42 процента.

Удаленный сброс

Удаленный сброс позволяет автоматически расследовать подозрительные вызовы, генерируемые компьютерными или программно-программными системами управления.Удаленный мастер, контролирующий срабатывание каждого датчика системы, может заподозрить неисправность электронного блока. Подтверждая команду сброса, устройство часто можно вернуть в нормальный режим работы. Сброс вызывает очистку вызовов присутствия, но не очищает память разомкнутого цикла и не предотвращает вызовы разомкнутого цикла.

Если после сброса не удается восстановить нормальную работу, неисправность можно распознать и распечатать для обслуживания. Разомкнутый контур, который постоянно вызывается, может быть отключен от сети, чтобы он не влиял ложным образом на рабочие параметры системы.

НЕЗАВИСИМЫЙ ВЫХОД ОТКАЗА КОНТУРА

В дополнение к обычному выходу блока электроники на некоторых моделях предусмотрен второй выход для состояния контура. Каждый раз, когда индуктивность контура подвергается ступенчатому изменению на ± 25 процентов или более, включается выход неисправности контура. Если индуктивность возвращается к значению менее ± 25 процентов от задания, выход неисправности контура отключается. Это позволяет удаленно запрашивать статус петли.

Другие алгоритмы обнаружения неисправностей встроены в микропроцессоры современных контроллеров.Эти алгоритмы выводят цифровые коды, которые идентифицируют тип неисправности, в контроллер, который передает информацию в центральный пункт.

КЛАССИФИКАЦИЯ АВТОМОБИЛЯ

Более новые электронные блоки индуктивного детектора и конфигурации контуров позволяют классифицировать транспортные средства. Модуль электроники, показанный на рисунке 2-28, использует программное обеспечение искусственной нейронной сети для классификации потока трафика по 23 категориям, показанным на рисунке 2-29. Первые 13 — это стандартные классы FHWA, а остальные — автомобили с уникальными характеристиками. ⁽⁴⁾

Рисунок 2-28. Индуктивный классификатор транспортных средств и датчик скорости модели S-1500 (фотография любезно предоставлена ​​Reno A&E, Рино, Невада).

Рисунок 2-29. Классы, доступные с помощью классифицирующего датчика с индуктивным контуром
(Источник: Руководство по установке и эксплуатации модели IVS-2000 , ред. 1.53 (Intersection Development Corp, Дауни, Калифорния, сентябрь 1997 г.)).

Были разработаны специальные конфигурации индуктивных контуров для определения осей и их относительного положения в транспортном средстве.Такие системы используются на пунктах взимания платы за проезд для получения правильной оплаты в зависимости от класса транспортного средства. В приложении, показанном на рис. 2-30, массив контуров оси расположен между двумя основными контурами. Наличие оси определяется массивом петель оси. Взаимное положение осей в транспортном средстве определяется по сигнатурам основных контуров. Полученные данные включают длину транспортного средства, скорость, ускорение, тип транспортного средства, количество осей и расстояние между осями. Информация о профиле также может быть получена для уточнения и подтверждения классификации в неоднозначных случаях.Этот блок электроники, а также блок, показанный на рис. 2-28, можно использовать для идентификации транзитных автобусов и обеспечения приоритетной обработки сигналов светофора.

Рисунок 2-30. Расположение осей и классификация транспортных средств с использованием набора индуктивных контуров
(Рисунок любезно предоставлен компанией Peek Traffic, Inc. — Сарасота, Сарасота, Флорида).

Предыдущая | Содержание | Следующие

FHWA-HRT-06-108

(5 точек) Самоиндукция (L) наклона определяется как постоянная пропорциональности между током катушки (i)…

вопрос 6, пожалуйста 5. ucta Используя результаты предыдущей задачи (7.4), выведите следующий параметр самоиндукции …

вопрос 6 пожалуйста 5. ucta Используя результаты предыдущей задачи (7.4), выведите следующие параметры самоиндукции; a) Плотность магнитного потока B внутри соленоида длиной h и магнитный материал u внутри. b) Полный поток Φ tot-J B-dS на внутреннем контуре соленоида c) Потоковая связь, соединяющая все контуры структура d) Собственная индуктивность L соленоида e) Теперь перейдем к тонкой проволоке магнита (медь…

Часть 2 Пожалуйста, сделайте оба примера, я поставлю оценку Упражнение 12 Магнитная цепь имеет А-12 …

Часть 2 Пожалуйста, сделайте оба примера, я поставлю оценку Упражнение 12 Магнитопровод имеет площадь A-12 см2; -50м, 20000; N, — 500 витков, N-1000 tums Первая часть Реактивное сопротивление магнитной цепи составляет: R- Магнитный поток, обусловленный в настоящее время, равен 4- NA R Потоковые связи двух катушек следующие: NA A NA Самоиндуктивность of collis 42,14 Взаимная индуктивность — вторая часть. Аналогично первой части. Рис. 25: Схема для задачи 12 (a)…

источник постоянного напряжения R W 2000 Катушка представлена ​​чистой индуктивностью и внутренним сопротивлением L c * …

источник постоянного напряжения R W 2000 Катушка, представленная чистой индуктивностью и внутренним сопротивлением L c * переменный конденсатор + Рисунок 10.1: Схема последовательного резонанса LRC. Индуктор в цепи представляет собой катушку из 1500 витков медной проволоки. 1. Предположим, у вас есть катушка, сделанная из одиночной петли из проволоки радиуса r, по которой проходит ток I. Найдите выражение для магнитного поля B в центре петли.2. Если вы сейчас …

Вопрос 2 A5: Объясните самоиндукцию и взаимную индукцию Магнеде Две катушки, coil1 и coil2 размещены …

Вопрос 2 A5: Объясните самоиндукцию и взаимную индукцию Магнеде Две катушки, coil1 и coil2, расположены рядом друг с другом. Катушка 1 подключена к переменному напряжению V, которое обеспечивает изменяющийся ток в катушке 1 (i) Нарисуйте диаграмму (i) Объясните наведенную ЭДС собственной индуктивностью и обозначьте диаграмму и (iii) Объясните наведенную ЭДС взаимной индуктивностью и обозначьте ту же диаграмму (1,2,2 балла) Вопрос 3 B3: Объясните ММЖ и перечислите уравнения, которые связывают его с другими факторами (i)…

Катушка, обеспечивающая самоиндукцию 3,0 Генри (3 В / (А / с)), подключена между клеммами A и B, чьи …

Катушка с самоиндукцией 3,0 Генри (3 В / (А / с)) подключена между клеммами A и B, соединения которых поддерживают постоянный потенциал на A на 7,5 В ниже, чем на B При t = 5,2 с, ток I_AB = 3,5 A течет от A к B. Каков ток I_AB при t = 5,8 с?

Периодическая таблица констант, часть A Цель обучения: Предположим, что ток в соленоиде равен I (t)….

Периодическая таблица констант, часть A Цель обучения: Предположим, что ток в соленоиде равен I (t). Какое магнитное поле внутри соленоида, но далеко от его концов, возникает из-за этого тока? Выразите свой ответ в терминах I (t), величин, указанных во введении, и соответствующих констант (например, MI). Узнать о самоиндукции на примере длинного соленоида. Чтобы объяснить самоиндукцию, полезно рассмотреть конкретный пример длинного соленоида, как показано на рисунке..

mework # 2 Срок сдачи: 26 сентября 2019 г. ПРОБЛЕМЫ 2.1 Длина соленоида 24 дюйма, и я …

mework # 2 Срок сдачи: 26 сентября 2019 г. ПРОБЛЕМЫ 2.1 Длина соленоида составляет 24 дюйма, а диаметр — 1 дюйм. он плотно намотан одним слоем проволоки диаметром 0,025 дюйма, который имеет сопротивление 16 Ом на 1000 футов. Для тока в 2 тока найдите (а) поле в центре. (b) необходимое напряжение и (c) потребляемая мощность (22 Для соленоида из предыдущей задачи нанесите поле на оси от…

Я уже решил другие задачи, кроме (d). Хотя я не могу понять (d). Решите (d) и …

Я уже решил другие задачи, кроме (d). хотя я не могу понять (г). Решите (d) и подробно опишите объяснение. ——————————————— Это настоящая проблема. Я разместил не ту проблему. пожалуйста решите эту проблему. извиняюсь. Каков мгновенный и усредненный по времени крутящий момент при этом условии? 4.30 Рисунок 4.42 показано схематическое поперечное сечение явнополюсной синхронной машины, имеющей две идентичные обмотки статора а и b на многослойном стальном сердечнике. Явнополюсный ротор выполнен из стали и …

Примечание. Этот тест содержит десять вопросов с глав 19 по 27. Для полного признания вы …

Примечание. Этот тест содержит десять вопросов с глав 19 по 27. Для получения полной оценки вы должны показать все этапы ваших числовых ответов. Просто круг за правильные ответы не заработает.Глава 19 — Электрический потенциал и электрическая потенциальная энергия 1. Два точечных заряда + 7 мкКл и -4 ° С удерживаются в углах прямоугольника, как показано. Длины сторон прямоугольника 0,15 м, а 0,05 …

PM600,610,620 Series Datasheet от Bourns Inc.

Серия PM500 / PM / PM520 I.WMilla ‘

Muilt — 6 шт., Индукторы и трансформаторы

PM600 / PM610 / PM620 Series

Part

Number L (uH)

@ 100KHz DCR (Ω)

Макс.

Isat

(A) Irms

(A)

PM600-01 201,6 ± 30% 0,324 0,02 0,46

PM600-02 89,6 ± 30% 0,137 0,03 0,71

PM600-03 27,4 ± 10% 0,324 0,31 0,46

PM600-04 12,2 ± 10% 0,137 0,47 0,71

PM600-05 14,7 ± 10% 0,324 0,58 0,46

PM600-06 6,5 ± 10% 0,137 0,87 0,71

PM600-07 10,9 ± 10% 0,324 0,88 0,46

PM600-08 4,9 ± 10% 0,137 1,32 0,71

PM600-09 8,5 ± 10% 0,324 1,23 0,46

PM600-10 3.8 ± 10% 0,137 1,85 0,71

PM610-01 160,0 ± 30% 0,202 0,04 0,68

PM610-02 78,4 ± 30% 0,094 0,06 1,00

PM610-03 21,6 ± 10% 0,202 0,67 0,68

PM610-04 10,6 ± 10% 0,094 0,96 1,00

PM610-05 11,6 ± 10% 0,202 1,30 0,68

PM610-06 5,7 ± 10% 0,094 1,86 1,00

PM610-07 8,3 ± 10% 0,202 2,00 0,68

PM610-08 4,1 ± 10% 0,094 2,86 1,00

PM610-09 6,6 ± 10% 0,202 2,30 0,68

PM610-10 3,2 ± 10% 0,094 3,29 1,00

PM620-01 160.6 ± 30% 0,094 0,03 1,28

PM620-02 77,0 ± 30% 0,065 0,04 1,54

PM620-03 131,8 ± 20% 0,094 0,08 1,28

PM620-04 63,2 ± 20% 0,065 0,12 1,54

PM620-05 23,3 ± 10% 0,094 0,36 1,28

PM620-06 11,2 ± 10% 0,065 0,52 1,54

PM620-07 14,2 ± 10% 0,094 0,76 1,28

PM620-08 6,8 ± 10% 0,065 1,10 1,54

PM620-09 9,3 ± 10% 0,094 1,11 1,28

PM620-10 4,5 ± 10% 0,065 1,60 1,54

PM620-11 7,9 ± 10% 0,094 1,40 1,28

PM620-12 3.8 ± 10% 0,065 2,02 1,54

Особенности:

• Шесть обмоток позволяют использовать множество катушек индуктивности или трансформаторов

конфигурация

• Высокая магнитная связь

• Конструкция сердечника без зазора и зазора

• Низкие потери в сердечнике на высокой частоте области применения

• Низкий уровень шума излучения

• Компактный размер и низкий профиль

• Диэлектрическая прочность: 500 В среднекв. между обмотками

• Рабочая температура: от -40 до +105 ºC

• Лента и катушка:

PM600, 600 / катушка

PM610, 300 / катушка

PM620, 200 / катушка

Типичные применения:

• Индукторы: понижающие, повышающие, понижательно-повышающие, связанные, вход,

выход, дроссель, фильтр, резонансный, высокий- Q, EMI / RFI

фильтрация, дифференциальный, прямой, общий режим

• Трансформаторы: обратный, прямой, двухтактный, мост,

, несколько выходов, инвертор, повышающий, понижающий, вентиль

привод, базовый привод, сигнал, широкополосный, импульсный,

импеданс, изоляция, преобразователь

Примечания:

1.Ток насыщения рассчитан на каждую обмотку, при этом

вызывает снижение индуктивности на 30% от исходного значения.

2. Каждой обмотке соответствует действующий ток, который вызывает повышение температуры

на 40 ° C.

3. PM600-01, -02, PM610-01, -02

PM620-01, -02 — сердечник без зазора.

.W.Mille

M A G N E T I C S

306 E. Alondra Blvd., Gardena, CA
-1059 • (310) 515-1720 • Факс (310) 515-1962

w w w. j w m i l l e r.c o m

электрических цепей — Почему отключение электрической катушки вызвало сотрясение моей руки?

Механический аналог гидроудара. Или пытаюсь остановить крутящийся маховик. Или как инерция за ускоряющимся поездом не оказывает на вас силы, пока вы не попытаетесь замедлить или остановить его.

Ток — это импульс (масса со скоростью позади нее) поезда или воды. Напряжение — это сила (или импульс), создаваемая этим движением поезда или воды, когда вы ставите что-то на его пути, чтобы замедлить его.

Название называется индуктивный удар или индуктивный обратный ход .

Когда вы пропускаете ток через катушку индуктивности, она будет использовать энергию этого тока для поддержания магнитного поля. Когда источник питания, который подавал ток через катушку индуктивности, исчезает, катушка индуктивности пытается сохранить ток, протекающий через нее, и делает это, используя энергию, запасенную в магнитном поле.

Катушка индуктивности использует энергию магнитного поля (которое соответствует схлопыванию магнитного поля по мере потребления его энергии) для поддержания тока как можно ближе к тем же уровням, что и при исчезновении источника тока.

Катушка индуктивности делает это, становясь источником энергии, использующим энергию, запасенную в магнитном поле, для создания напряжения настолько высокого, насколько необходимо, чтобы протолкнуть этот уровень тока через любые препятствия, чтобы ток, протекающий через катушку индуктивности, был одинаковым. Если самый простой путь лежит через воздушный зазор открытых контактов механического переключателя или реле, напряжение, необходимое для искры через этот воздушный зазор, будет очень высоким, так что это напряжение, которое будет создаваться. Для этого требуется много энергии, а энергия, запасенная в магнитном поле, конечна, поэтому ток схлопнется до нуля быстрее, чем в противном случае.

Для индуктивностей $ V = L \ frac {di} {dt} $. Таким образом, чтобы изменить ток очень быстро, вы должны использовать высокое напряжение. Но наоборот, если вы измените ток очень быстро, вы получите высокое напряжение. Поэтому, если вы очень быстро уменьшите ток (то есть прервете его), будет генерироваться очень большое прямое напряжение, поскольку катушка индуктивности будет пытаться протолкнуть и удержать тот же ток, проходящий через только что созданный вами высокий импеданс.

Напряжение, которое возникает на катушке, когда вы пытаетесь увеличить через нее ток, называется обратной ЭДС , потому что она сопротивляется потоку тока от источника напряжения.

Напряжение, которое возникает на катушке, когда вы пытаетесь уменьшить ток через нее, называется прямой ЭДС , потому что оно управляет потоком тока через себя.

Заклинивающее действие, которое вы почувствовали, могло быть связано с сваркой контактов дугой (ток, протекающий через воздух, когда индуктор расходует энергию в своем магнитном поле, чтобы протолкнуть ток, чтобы он протекал через себя).

5. Применение ODE: Серия RL Circuit

Схема RL

Цепь RL на показанном выше резисторе и катушке индуктивности соединены последовательно.Постоянное напряжение В применяется, когда переключатель находится в закрыто.

(переменное) напряжение на резисторе определяется по формуле:

`V_R = iR`

(переменное) напряжение на катушке индуктивности определяется по формуле:

`V_L = L (di) / (dt)`

Закон Кирхгофа по напряжению гласит, что направленная сумма напряжений в цепи должна быть равна нулю. Это приводит к следующему дифференциальное уравнение:

`Ri + L (di) / (dt) = V`

Когда переключатель замкнут, ток в цепи непостоянен.(- (R «/» L) t)) `

Проба

Начнем с:

`Ri + L (di) / (dt) = V`

Вычитая Ri с обеих сторон:

`L (di) / (dt) = V-Ri`

Разделите обе стороны на L :

`(di) / (dt) = (V-Ri) / L`

Умножьте обе стороны на dt и разделите обе на ( V — Ri ):

`(ди) / (V-Ri) = (dt) / L`

Интегрировать (см. (- (R» / «L) t))`

[Мы сделали ту же проблему, но с определенными значениями в разделе 2.(-t «/» \ tau)) `

Давайте теперь рассмотрим несколько примеров схем RL.

Пример 1

Цепь RL имеет ЭДС 5 В, сопротивление 50 Ом, индуктивность 1 Гн, начальный ток отсутствует.

Найти ток в цепи в любой момент t . Различают переходный и установившийся ток.

Ответ

Метод 1 — Решение DE

Формула: `Ri + L (di) / (dt) = V`

После замены: `50i + (di) / (dt) = 5`

Мы перестраиваем для получения:

`(di) / (dt) + 50i = 5`

Это линейное дифференциальное уравнение первого порядка.(-50т)) `.

В этом примере постоянная времени TC равна

.

`тау = L / R = 1/50 = 0,02`

Итак, мы видим, что ток достиг установившегося состояния на t = 0,02 \ times 5 = 0,1 \ «с».

Метод 3: Использование решения ODE

от Scientific Notebook

Если у вас есть Scientific Notebook, действуйте следующим образом:

Этот DE имеет начальное условие i (0) = 0. (- 5t)) `.(-5t) `(серым цветом).

Постоянная времени TC для этого примера:

`тау = L / R = 10/50 = 0,2`

ПРИМЕЧАНИЕ (только для интереса и сравнения): Если бы мы не могли использовать формулу в (a) и не использовали разделение переменных, мы могли бы признать, что DE является линейным 1-го порядка, и поэтому мы могли бы решить его, используя интегрирующий фактор.

Используем формулу:

`Ri + L (di) / (dt) = V`

Требуемый DE:

`10 (di) / (dt) + 50i = 100`

`(di) / (dt) + 5i = 10`

«» И.(-5т)) `

Работает 🙂

Цепи с двумя ячейками

Следующие два примера относятся к типам с двумя сетками, в которых дифференциальные уравнения становятся более сложными. Мы будем использовать Scientific Notebook для выполнения основной работы после того, как составим правильные уравнения.

Пример 3

В сети с двумя ячейками, показанной ниже, коммутатор замкнут в t = 0, а источник напряжения равен В = 150 sin 1000 t V. Найдите сеточные токи i ₁ и i ₂ , как показано на диаграмме.

Ответ

Раньше мы не видели, как решать «2-ячеистые» сети. Мы рассматриваем полное напряжение внутреннего контура и полное напряжение внешнего контура. Затем мы решаем полученные два уравнения одновременно.

Используем основную формулу: `Ri + L (di) / (dt) = V`

С учетом внутреннего цикла:

`10 (i_1 + i_2) + 5i_1 + 0,01 (di_1) / (dt) =` 150 sin 1000t`

`15 \ i_1 + 10 \ i_2 + 0,01 (di_1) / (dt) =` 150 sin 1000t`

`3i_1 + 2i_2 + 0.002 (di_1) / (dt) = « 30 sin 1000t \ \ \ … (1) `

Теперь, учитывая внешний цикл:

`10 (i_1 + i_2) + 5i_2 = 150 sin 1000t`

`10i_1 + 15i_2 = 150 sin 1000t`

`2i_1 + 3i_2 = 30 sin 1000t \ \ \ … (2)`

Теперь мы решаем (1) и (2) одновременно:

(1) × 3 — (2) × 2 дает:

`5i_1 + 0,006 (di_1) / (dt) = 30 sin 1000t`

Решение этой проблемы с использованием SNB с граничным условием i ₁ (0) = 0 дает:

`i_1 (t) = — 2.(-833т) `

График i ₂ :

График текущего `i_2` в момент` t`. Он также находится в устойчивом состоянии примерно на «t = 0,007».

Пример 4

Коммутатор замкнут при t = 0 в двухъячеистой сети показано ниже. Источник напряжения: В = 30 sin 100 t В. Найдите сеточные токи i ₁ и i ₂ , как показано на диаграмме.

Ответ

Решаем 2 способами:

1.Составление уравнений и получение помощи SNB для их решения.

2. Непосредственное использование SNB для одновременного решения 2 уравнений.

Решение 1

Используем основную формулу: `Ri + L (di) / (dt) = V`

Рассматривая левую петлю, ток через резистор 8 Ом противоположен для «i_1» и «i_2». Мы рассматриваем i_1 как имеющее положительное направление:

`0,2 (di_1) / (dt) +8 (i_1-i_2) =` `30 sin 100t \ \ \ … (1)`

Теперь мы рассматриваем правую петлю и считаем направление i_2 положительным:

`8 (i_2-i_1) + 4i_2 = 0`

`12i_2-8i_1 = 0`

`i_2 = 2 / 3i_1 \ \ \.(-13,3 т) `

Это, конечно, тот же график, только это «2/3» амплитуды:

График текущего `i_2` в момент` t`. Он также находится в устойчивом состоянии примерно на t = 0,25.

Решение 2. Прямое использование SNB

Если мы попытаемся решить его с помощью Scientific Notebook следующим образом, он потерпит неудачу , потому что он может решить только 2 дифференциальных уравнения одновременно (вторая строка не является дифференциальным уравнением):

`0,2 (di_1) / (dt) +8 (i_1-i_2) = 30 sin 100t`

`i_2 = 2 / 3i_1`

`i_1 (0) = 0`

`i_2 (0) = 0`

Но если мы дифференцируем вторую строку следующим образом (превращая ее в дифференциальное уравнение, чтобы у нас было 2 DE с 2 неизвестными), SNB с радостью решит его с помощью команды Compute → Solve ODE.