Что такое двоично-десятичные коды. Какие виды двоично-десятичных кодов существуют. Как используются двоично-десятичные коды в цифровой электронике. Чем отличаются взвешенные и невзвешенные двоично-десятичные коды. Каковы преимущества и недостатки различных двоично-десятичных кодов.
Что такое двоично-десятичные коды и зачем они нужны
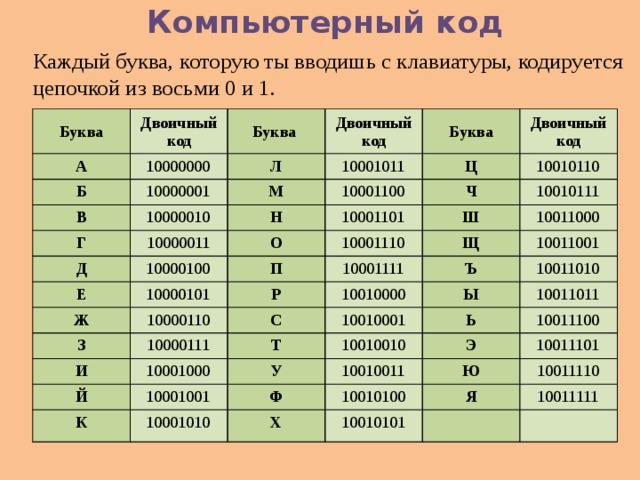
Двоично-десятичные коды (BCD — Binary-Coded Decimal) — это способ представления десятичных чисел в двоичной системе счисления. В отличие от обычного двоичного представления, каждая десятичная цифра кодируется отдельно, обычно 4 битами.
Основные причины использования двоично-десятичных кодов:
- Упрощение преобразования между двоичной и десятичной системами
- Более точное представление десятичных дробей
- Удобство при выполнении арифметических операций над десятичными числами
- Совместимость с устройствами ввода-вывода, работающими с десятичными числами
Основные виды двоично-десятичных кодов
Существует несколько основных видов двоично-десятичных кодов:
1. Код 8421 (стандартный BCD)
Это наиболее распространенный BCD-код, в котором веса разрядов соответствуют степеням двойки: 8, 4, 2, 1. Например:
- 0 = 0000
- 5 = 0101
- 9 = 1001
2. Код 2421
В этом коде используются веса 2, 4, 2, 1. Особенность — для цифр от 5 до 9 старший разряд всегда равен 1:
- 0 = 0000
- 5 = 1011
- 9 = 1111
3. Код 5421
Использует веса 5, 4, 2, 1. Преимущество — легко определить, больше ли число 4 или нет:
- 0 = 0000
- 5 = 1000
- 9 = 1111
Взвешенные и невзвешенные BCD-коды
BCD-коды можно разделить на две основные категории:
Взвешенные коды
В этих кодах каждому биту присваивается определенный вес. Сумма весов активных битов дает значение цифры. Примеры:
- 8421 (стандартный BCD)
- 2421
- 5421
Невзвешенные коды
В этих кодах нет прямой связи между весом бита и его позицией. Значение определяется по таблице соответствия. Примеры:
- Код с избытком 3
- Код Грея
Особенности кода с избытком 3
Код с избытком 3 (Excess-3) — это невзвешенный BCD-код, в котором к каждой десятичной цифре добавляется 3 перед кодированием. Особенности:
- Нет комбинаций 0000-0010
- Упрощает выполнение некоторых арифметических операций
- Код цифры 9 (1100) является обратным коду цифры 0 (0011)
Пример кодирования в Excess-3:
- 0 = 0011
- 5 = 1000
- 9 = 1100
Применение кода Грея в цифровой электронике
Код Грея — это невзвешенный BCD-код, в котором соседние числа отличаются только одним битом. Основные применения:
- Датчики положения и углового перемещения
- Аналого-цифровые преобразователи
- Минимизация ошибок при передаче данных
- Решение задач оптимизации в программировании
Пример последовательности в коде Грея:
- 0 = 000
- 1 = 001
- 2 = 011
- 3 = 010
- 4 = 110
- 5 = 111
- 6 = 101
- 7 = 100
Сравнение различных BCD-кодов
Каждый BCD-код имеет свои преимущества и недостатки:
Код 8421 (стандартный BCD)
Преимущества:
- Простота преобразования в десятичную систему
- Широкая распространенность
Недостатки:
- Неэффективное использование битов (6 комбинаций не используются)
Код 2421
Преимущества:
- Самодополняющийся код (9 — обратный код 0)
- Упрощает некоторые арифметические операции
Недостатки:

- Сложнее в реализации, чем 8421
Код с избытком 3
Преимущества:
- Упрощает выполнение вычитания
- Самодополняющийся код
Недостатки:
- Требует дополнительных преобразований при вводе-выводе
Практическое применение BCD-кодов в электронике
BCD-коды широко используются в различных областях цифровой электроники:
1. Цифровые измерительные приборы
Многие цифровые вольтметры, амперметры и другие измерительные приборы используют BCD-коды для внутреннего представления измеренных значений. Это упрощает отображение результатов на семисегментных индикаторах.
2. Калькуляторы
В большинстве электронных калькуляторов используется BCD-арифметика для выполнения операций. Это обеспечивает точное представление десятичных дробей и упрощает работу с дисплеем.
3. Системы управления
BCD-коды часто применяются в промышленных системах управления, особенно когда требуется взаимодействие с устройствами, использующими десятичное представление (например, датчики, исполнительные механизмы).
4. Телекоммуникации
В некоторых телекоммуникационных протоколах, например, в системах сигнализации SS7, используются BCD-коды для передачи номеров телефонов и другой числовой информации.

Преобразование между различными BCD-кодами
Иногда возникает необходимость преобразования чисел из одного BCD-кода в другой. Рассмотрим некоторые примеры:
Из 8421 в код с избытком 3
Чтобы преобразовать число из стандартного BCD (8421) в код с избытком 3, нужно добавить 0011 к каждой тетраде:
- 5 (0101) → 0101 + 0011 = 1000
- 9 (1001) → 1001 + 0011 = 1100
Из 8421 в код Грея
Преобразование в код Грея выполняется по следующему алгоритму:
- Старший бит остается без изменений
- Каждый следующий бит — это XOR текущего и предыдущего бита в исходном коде
Пример: 5 (0101) → 0111
Ошибки при использовании BCD-кодов
При работе с BCD-кодами могут возникать различные ошибки:
1. Недопустимые комбинации
В стандартном BCD (8421) комбинации от 1010 до 1111 не используются. Если такая комбинация появляется, это указывает на ошибку в вычислениях или передаче данных.2. Переполнение
При сложении BCD-чисел может возникнуть переполнение, если сумма превышает 9. В этом случае необходима коррекция результата.
3. Ошибки округления
При выполнении операций с плавающей точкой в BCD-формате могут возникать ошибки округления, особенно при делении.
4. Несовместимость кодов
Использование разных BCD-кодов в одной системе без соответствующего преобразования может привести к неправильной интерпретации данных.
Будущее BCD-кодов в цифровой электронике
Несмотря на широкое распространение двоичной арифметики, BCD-коды продолжают играть важную роль в некоторых областях:
1. Финансовые вычисления
В финансовой сфере точность представления десятичных дробей критически важна. BCD-арифметика позволяет избежать ошибок округления, характерных для двоичной системы.
2. Интернет вещей (IoT)
В устройствах IoT, особенно связанных с измерениями и отображением данных, BCD-коды могут оказаться более эффективными, чем чисто двоичное представление.
3. Квантовые вычисления
В некоторых подходах к квантовым вычислениям рассматривается использование BCD-подобных кодов для представления информации в кубитах.
4. Обратная совместимость
BCD-коды останутся важными для обеспечения совместимости с существующими системами и устройствами, особенно в промышленных приложениях.
Таким образом, хотя BCD-коды могут казаться устаревшими, они продолжают играть важную роль в современной цифровой электронике и, вероятно, найдут новые применения в будущем.
Двоично-десятичный код 8421 с избытком 3
|
10 код |
2/10 код |
10 код |
2/10 код |
Остальные комбинации — запрещенные |
|
0 |
0011 |
5 |
1000 | |
|
1 |
0100 |
6 |
1001 | |
|
2 |
0101 |
7 |
1010 | |
|
3 |
0110 |
8 |
1011 | |
|
4 |
0111 |
9 |
1100 |
Преобразование числа в обратный код
Запись отрицательного числа в прямом коде
Инверсия полученного в п.

Преобразование числа в дополнительный код
Выполнить операции 1-2 из преобразования в обратный код
В младшую тетраду добавить + 0001 — Результат сложения – число в дополнительном коде.
Например: -4619; — 2843; – в обр.код
-5648; — 1237 – в доп.код
Правила выполнения арифметических операций
Если при сложении не было переноса из анализируемой тетрады, то в нее надо добавить + 1101.
Если был перенос в старшую тетраду, то в нее надо добавить + 0011.
Если получена неправильная тетрада, то в нее надо добавить + 0110.
Поправки вводятся при блокировке межтетрадного переноса.
Например: 283 + 749=1032
Примеры:
926 – 1097 выполнить алгебр. сложение в обратном коде
-756 – 359 выполнить алгебр. сложение в обратном коде
— 254-1 выполнить алгебр. сложение в дополнительном коде
—
1000 0011 0101 + 1001 0100 0110 выполнить алгебр. сложение в дополнительном коде
сложение в дополнительном коде
Решение:
Домашнее задание.
Выполнить алгебраическое сложение в двоичной системе счисления. Результат представить в 10 с/с. Разрядная сетка 8 бит. Указать на переполнение разрядной сетки, если есть.
|
9-2 |
Обратный код |
-20-19 |
Обратный код |
-120-15 |
Обратный код |
|
2-9 |
Дополнительный код |
50-25 |
Дополнительный код |
-126-1 |
Дополнительный код |
|
-5-7 |
Обратный код |
127-1 |
Обратный код |
-101+43 |
Обратный код |
|
-4-10 |
Дополнительный код |
-75-12 |
Дополнительный код |
-73+45 |
Дополнительный код |
Выполнить арифметическое и алгебраическое сложение в коде прямого замещения (8421) и коде 8421 с избытком 3
операнды представлять в дополнительном коде
операнды представлять в обратном коде
-60-678 операнды представлять в дополнительном коде
6754+1234 операнды представлять в дополнительном коде
9876+4656 операнды представлять в обратном коде
-28-27 операнды представлять в обратном коде
16
Помогите решить / разобраться (М)
| valery99 |
|
||
|
26/12/17 |
|
||
|
|||
| Евгений Машеров |
|
|||
11/03/08 |
|
|||
|
||||
| ewert |
|
|||
11/05/08 |
|
|||
|
||||
| grizzly |
|
|||
09/09/14 |
|
|||
|
||||
| wrest |
|
||
|
05/09/16 |
|
||
|
|||
| valery99 |
|
||
|
26/12/17 |
|
||
|
|||
| wrest |
|
||
|
05/09/16 |
|
||
|
|||
| wrest |
|
||
|
05/09/16 |
|
||
|
|||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 |
[ Сообщений: 8 ] |
Модераторы: Модераторы Математики, Супермодераторы
Двоичные коды в двоичной системе счисления
В этом уроке мы узнаем об одном из основных требований цифровой электроники, а именно о двоичных кодах в двоичной системе счисления. Некоторые из популярных двоичных кодов: BCD (8421), 2421, 5211, Excess-3, Grey.
Некоторые из популярных двоичных кодов: BCD (8421), 2421, 5211, Excess-3, Grey.
Схема
Введение
Первой успешной системой электрической связи был телеграф, который был изобретен Сэмюэлем Ф.Б. Морзе в 1832 году. Телеграфисты использовали код щелчков для отправки сообщений. Если клавиша нажата в течение короткого времени, это азбука Морзе называется «точка», а если клавиша нажата в течение длительного времени, это «тире». Пример азбуки Морзе показан ниже:
Если следовать логике, с помощью приведенного выше кода можно записать различные бесчисленные комбинации точек и тире любых слов (даже предложений). Таким же образом можно использовать и двоичные числа для создания таких различных бесчисленных комбинаций. Их можно рассматривать как двоичные коды.
Помимо обычно используемого кода 8421 или кода BCD, также популярны другие двоичные коды, такие как код 2421, код 5211, отражающий код, последовательный код, невзвешенный код, код избытка-3 и код Грея.
Обычно используемые двоичные коды
Прежде чем углубляться в детали отдельных двоичных кодов, давайте кратко рассмотрим некоторые из часто используемых двоичных кодов. Ниже приведен список:
- 8421 Коды
- 2421 Коды
- 5211 Коды
- Превышение-3 Коды
- Коды серого
В приведенном выше списке первые три, т. е. 8421, 2421 и 5211, являются взвешенными двоичными кодами, а два других — невзвешенными двоичными кодами.
Взвешенные двоичные системы
Значения, присвоенные последовательным разрядам в десятичной системе, которая является разрядной системой, составляют 10⁴, 10³, 10², 10¹, 10⁰, 10⁻¹, 10⁻², 10⁻³… и т. д. от слева направо. Легко понять, что вес цифры десятичной системы равен «10».
Например:
(3546,25) 10 = 3 x 10³ + 5 x 10² + 4 x 10¹ + 6 x 10⁰ + 2 x 10⁻¹ + 5 x 10⁻²
Таким же образом значения, присвоенные последовательным разрядам в двоичной системе, которая также является разрядной системой, называются взвешенной двоичной системой.
Вес в двоичной системе равен 2⁴, 2³, 2², 2¹, 2⁰, 2⁻¹, 2⁻², 2⁻³… слева направо. Легко понять, что вес цифры двоичной системы равен «2».
Например:
(1110110) 2 = 1 x 2⁶+ 1 x 2⁵ + 1 x 2⁴ + 0 x 2³ + 1 x 2² + 1 x 2¹ + 0 x 2⁰
= 64 + 32 + 16 + 0 + 4 + 2 + 0 = (118) 10
Двоичные веса
Всякий раз, когда появляется какое-либо двоичное число, его десятичный эквивалент можно легко найти следующим образом.
- Если в позиции цифры стоит 1, следует добавить вес этой позиции.
- Если в позиции цифры стоит 0, вес этой позиции следует игнорировать.
Например, двоичное число 1100 имеет десятичный эквивалент 8 + 4 + 0 + 0 = 12.
8421 Код или двоично-десятичный код
Десятичные числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 могут быть выражены в двоичных числах, как показано в следующей таблице. Все эти двоичные числа снова выражены в последнем столбце путем расширения до 4 бит. Что касается взвешенных двоичных цифр, 4-битные двоичные числа могут быть выражены в соответствии с их разрядностью слева направо как 8421 (2³ 2² 2¹ 2⁰ = 8421).
| | | |
|---|---|---|
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
В соответствии с приведенным выше выражением все десятичные числа записываются в 4-битном двоичном коде в форме 8421, и это называется кодом 8421, а также двоично-десятичным двоично-десятичным кодом.
Поскольку это прямой код, любое десятичное число может быть легко выражено, потому что веса позиций являются прямыми для легкого преобразования в этот код 8421.
Существуют и другие формы кодов, не столь популярные, но довольно запутанные. Это код 2421, код 5211, отражающий код, последовательный код, невзвешенный код, код избытка-3 и код Грея. Они имеют собственное значение для некоторых эксклюзивных приложений и могут быть полезны для некоторых специальных приложений.
2421 Код
Этот код также является 4-битным прикладным кодом, в котором двоичные веса передаются 2, 4, 2, 1 слева направо.
| | | |
|---|---|---|
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
5211 Код
Этот код также является 4-битным прикладным кодом, в котором двоичные веса передаются 5, 2, 1, 1 слева направо.
| | | |
|---|---|---|
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
Отражающий код
Можно заметить, что в кодах 2421 и 5211 код десятичной цифры 9 является дополнением кода десятичной цифры 0, код десятичной цифры 8 является дополнением кода десятичной цифры 1, код десятичной цифры 7 является дополнением кода десятичной цифры 2, код десятичной цифры 6 является дополнением кода десятичной цифры 3, код десятичной цифры 5 является дополнением кода десятичной цифры 4. Эти коды называются Рефлексивные коды. То же самое можно наблюдать в следующей таблице:
Эти коды называются Рефлексивные коды. То же самое можно наблюдать в следующей таблице:
| | | | |
|---|---|---|---|
| | |
|
|
| | |
|
|
| | |
| 100902 8 000 |
| | |
| 100902 01078 01 |
| | |
|
|
| | |
| |
| | |
| 100 30902 1001079 8 8 |
| | |
|
|
| | |
|
|
| | |
|
|
ПРИМЕЧАНИЕ.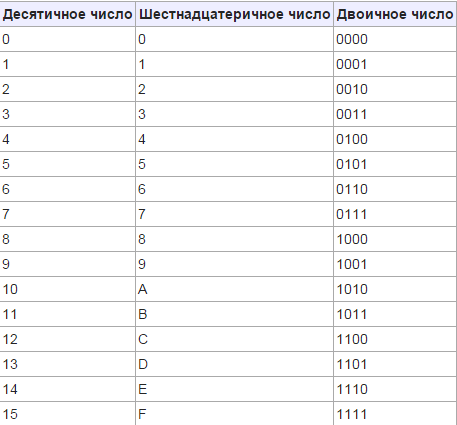 Код 8421 не является отражающим кодом.
Код 8421 не является отражающим кодом.
Последовательные коды
Последовательные коды — это коды, в которых 2 последовательных числа в двоичном представлении отличаются только одной цифрой. Коды 8421 и Excess-3 являются примерами последовательных кодов. Коды 2421 и 5211 не относятся к последовательным кодам.
| | | | |
|---|---|---|---|
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
Невзвешенные коды
Некоторые коды не соответствуют весам двоичных чисел последовательности, они называются невзвешенными кодами. Код ASCII и код Грея являются одними из примеров, когда они закодированы для некоторых приложений специального назначения и не следуют вычислениям взвешенных двоичных чисел.
Код ASCII и код Грея являются одними из примеров, когда они закодированы для некоторых приложений специального назначения и не следуют вычислениям взвешенных двоичных чисел.
Код Excess-3
Как упоминалось выше, некоторые коды не будут следовать двоичным весам, например код Excess-3 является важным 4-битным кодом. Превышение – 3 кода десятичного числа достигается добавлением числа 3 к коду 8421.
Например, чтобы преобразовать 15 в код избытка 3, сначала нужно добавить 3 к каждой цифре, как показано ниже.
Избыток – 3 примера кода
- Найдите код избытка-3 для (237.75) 10
- Найдите десятичное число избытка-3 числа 110010100011.01110101.
Сол:
1) Код избытка-3 для (237) 10 получается путем добавления 3 ко всем цифрам по отдельности, то есть 2, 3 и 7 станут 5, 6 и 10 соответственно. Эти 5, 6 и 10 десятичных знаков необходимо преобразовать в двоичную форму, и в результате получится 010101101010.
Код избытка-3 для (.75) 10 получается путем замены 7 и 5 на 10 и 8 соответственно путем добавления 3 к каждой цифре. То есть код избытка-3 для (.75) 10 — это .10101000.
Комбинируя результаты целой и дробной частей, код избытка-3 для (237,75) 10 равен 010101101010.10101000.
2) Код избытка-3 равен 110010100011.01110101
Разделив 4 бита на группу, эквивалентный код избытка-3 задается как 1100 1010 0011.0111 0101. : 1001 0111 0000,0100 0010.
Следовательно, десятичный эквивалент равен (970.42) 10 .
Код Грея
Код Грея — это код, в котором один бит отличается от предыдущего числа. Например, десятичные числа 13 и 14 представлены кодовыми числами Грея 1011 и 1001, эти числа отличаются только одной позицией, то есть второй позицией справа. Точно так же первая позиция слева меняется на 7 и 8, которые равны 0100 и 1100, и это также называется кодом единичного расстояния. Код Грея занимает особое место в цифровой электронике.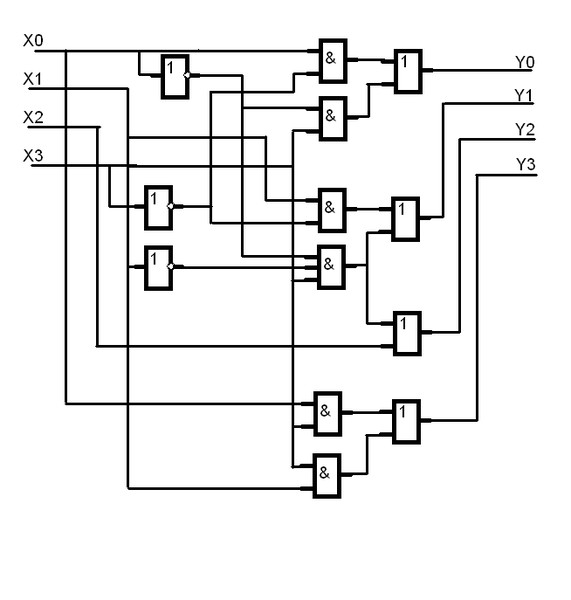
| | | |
|---|---|---|
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
Заключение
Вводный курс по двоичным кодам.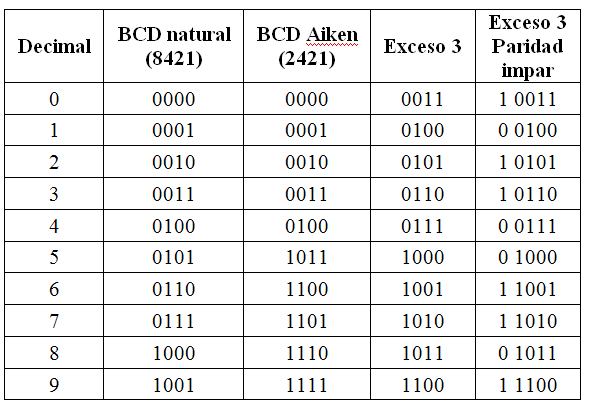 Вы изучили различные двоичные коды, такие как BCD (8421), 2421, 5211, Excess-3 и коды Грея.
Вы изучили различные двоичные коды, такие как BCD (8421), 2421, 5211, Excess-3 и коды Грея.
Код HS 8421- Классификация тарифов
Заголовок/
Статья Описание
Блок количества
Общий
Специальный
Heading/ Subheading
8421
Статья. оборудование и аппараты для фильтрования или очистки жидкостей или газов; их части
Единица количества
Общие
Специальные
Заголовок/Подзаголовок
Article Description
Centrifuges, including centrifugal dryers
Unit of Quantity
General
Special
Heading/Subheading
8421.11.00.00
Article Description
Cream separators
Unit of Quantity
No.General
Бесплатно
Специальная
Заголовок/Подзаголовок
8421.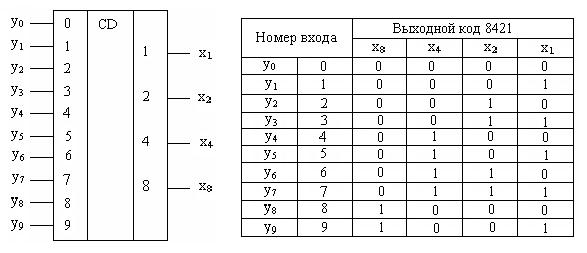 12.00.00
12.00.00
Артикул Описание
Сушилки для белья
Unit of Quantity
No.General
Free
Special
Heading/Subheading
8421.19.00.00
Article Description
Other
Unit of Quantity
No.General
1.3%
Special
Бесплатно (A,AU,BH,C,CL,CO,D,E,IL,JO,KR,MA,OM,P,PA,PE,S,SG)
Заголовок/подзаголовок
Описание статьи
Машины и устройства для фильтрования или очистки жидкостей
Unit of Quantity
General
Special
Heading/Subheading
8421.21.00.00
Article Description
For filtering or purifying water
Unit of Quantity
No.General
Free
Special
Heading /Подсубпозиция
8421. 22.00.00
22.00.00
Описание изделия
Для фильтрации или очистки напитков, кроме воды
Единица количества
№Общие положения
Free
Special
Heading/Subheading
8421.23.00.00
Article Description
Oil or fuel filters for internal combustion engines
Unit of Quantity
No.General
2.5%
Special
Free (A, AU, B, BH, C, CL, CO, D, E, IL, JO, KR, MA, OM, P, PA, PE, S, SG)
Заголовок/подзаголовок
8421.29.00
Артикул Описание
Другое
Единица количества
Общий
БЕСПЛАТНЫЙ
Специальный
Заголовок/подзаголовок
8421.29.00.05
Описание статьи
ОБЩЕСТВЕННЫЕ ИСПРАВЛЕНИЯ И РЕКОЗКА. Описание
Прочие
Единица количества
Общие
Специальные
Заголовок/Подзаголовок
8421. 29.00.15
29.00.15
Описание изделия
Oil-separation equipment
Unit of Quantity
No.General
Special
Heading/Subheading
Article Description
Other
Unit of Quantity
General
Special
Heading/Subheading
8421.29 .00.40
Артикул Описание
Фильтры гидравлической жидкости, рассчитанные на
Единица количества
№Общее
Специальный
Заголовок/подзаголовок
8421.29.00.65
Статья Описание
Другие
Блок количества
№Общие
Специальные
Заголовок/подло для газов
Единица количества
Общий
Специальный
Заголовок/подзаголовок
8421.31.00.00
Артикул Описание
Впускные воздушные фильтры для двигателей внутреннего сгорания
Единица количества
№Общие
2,5%
Специальные
Бесплатно (A, AU, B, BH, C, CL, CO, D, E, IL, JO,KR,MA,OM,P,PA,PE,S,SG)
Заголовок/подзаголовок
8421. 32.00.00
32.00.00
Изделие Описание
Каталитические нейтрализаторы или сажевые фильтры, комбинированные или некомбинированные, для очистки или фильтрации выхлопных газов газы двигателей внутреннего сгорания
Единица количества
№Общий
БЕСПЛАТНЫЙ
Специальный
Заголовок/подзаголовка
8421.39.01
Описание статьи
ДРУГИЕ
СПЕЦИАЛЬНЫЙ СПЕЦИАЛЬНЫЙ
. Описание
Оборудование для сбора пыли и очистки воздуха
Единица количества
Общие
Специальные
Заголовок/Подзаголовок
8421.39.01.05
Статья Описание
Для станках заголовков с 8456 по 8465, включительно
Блок количества
кгОбщие
Специальная
Заголовок/подразделение
8421. 39.01.15
39.01.15
Общий
Специальный
Заголовок/Подзаголовок
Описание товара
Прочее
Единица количества
Общий
Специальный
Заголовок/подзаголовка
Описание
Оборудование для очистки промышленного газа
Блок количества
Общие
Специальное
Заголовок/подголовок
8421.39.01.20
. Количество
№Общий
Специальный
Заголовок/Подзаголовок
8421.39.01.30
Артикул Описание
Другое
Единица количества
№Общий
Специальный
Заголовок/подзаголовок
8421.39.01.40
Описание
СПАСИЖДЕНИЕ
ЕДИНИЦА ИСПОЛЬЗОВАНИЯ
№Общее
. Заголовок/подзаголовок
Заголовок/подзаголовок
Описание товара
Другое
Единица количества
Общий
Специальный
Заголовок/подзаголовок
8421.39.01.60
Article Description
Pneumatic fluid power filters, rated at
Unit of Quantity
No.General
Special
Heading/Subheading
8421.39.01.90
Описание изделия
Прочее
Единица количества
кгОбщее
Специальное
Заголовок/подзаголовок
Описание изделия
Части
Единица количества0003General
Special
Heading/Subheading
8421.91
Article Description
Of centrifuges, including centrifugal dryers
Unit of Quantity
General
Special
Heading/Subheading
8421. 91.20.00
91.20.00
Article Описание
Сушильные камеры для сушилок для белья субпозиции 8421.12 и другие части сушилок для белья, включающие сушильные камеры
Единица количества
No.General
Free
Special
Heading/Subheading
8421.91.40.00
Article Description
Furniture designed to receive the clothes-dryers of subheading 8421.12
Unit of Quantity
No.General
Бесплатно
Специальный
Заголовок/Подзаголовок
8421.91.60.00
Описание товара
Прочее
Единица количества
кгОбщий
Free
Special
Heading/Subheading
8421.99.01
Article Description
Other
Unit of Quantity
General
Free
Special
Heading/Subheading
8421.


 02.2018, 23:22
02.2018, 23:22 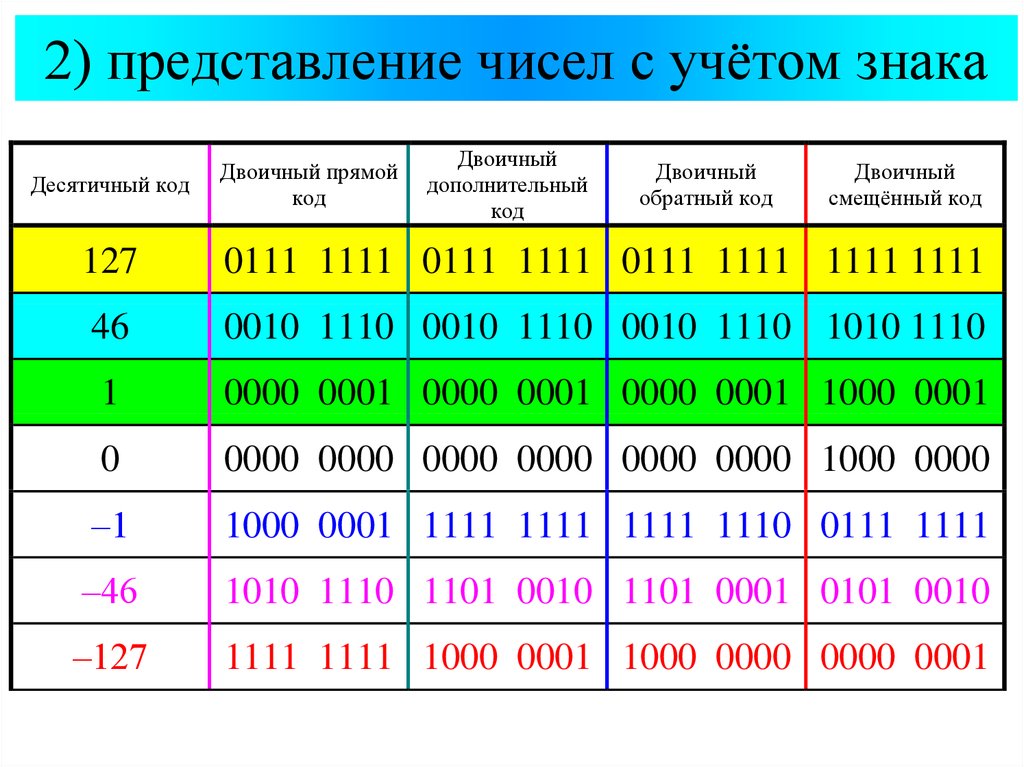 02.2018, 23:32
02.2018, 23:32  02.2018, 23:33
02.2018, 23:33  02.2018, 23:53
02.2018, 23:53  02.2018, 08:57
02.2018, 08:57 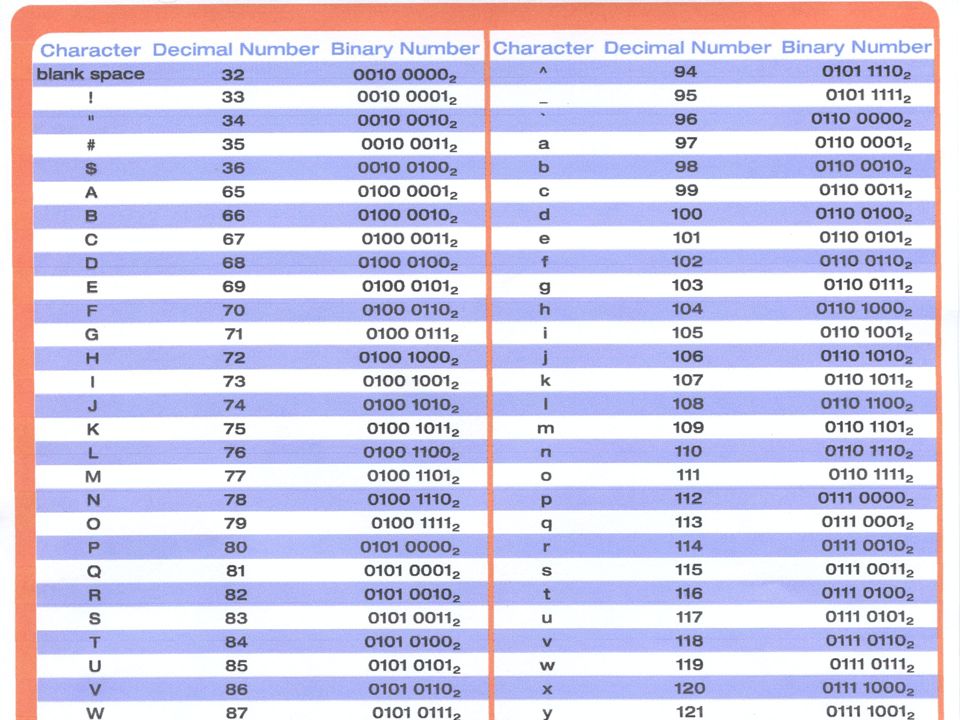
 Как получить цифры от 5 до 9
Как получить цифры от 5 до 9 02.2018, 11:29
02.2018, 11:29  В коде 5421 соответственно к цифрам 5-9 прибавляем не 6-ку, а 3-ку. А в коде 7421 прибавляем 1-цу, но не к 5-9, а к 7-9.
В коде 5421 соответственно к цифрам 5-9 прибавляем не 6-ку, а 3-ку. А в коде 7421 прибавляем 1-цу, но не к 5-9, а к 7-9.