Как ведут себя конденсатор и катушка в цепи переменного тока. Что такое емкостное и индуктивное сопротивление. Как возникает резонанс в электрической цепи. Какие факторы влияют на резонансную частоту.
Особенности поведения конденсатора в цепи переменного тока
В цепи постоянного тока конденсатор представляет собой разрыв. Однако в цепи переменного тока через конденсатор может протекать ток. Это объясняется тем, что при изменении напряжения на обкладках конденсатора происходит его периодическая зарядка и разрядка.
Основные особенности поведения конденсатора в цепи переменного тока:
- Ток через конденсатор опережает по фазе напряжение на π/2
- Амплитуда тока обратно пропорциональна емкости конденсатора
- Вводится понятие емкостного сопротивления XC = 1/(ωC)
Чем это обусловлено? Когда напряжение на конденсаторе достигает максимума, ток через него равен нулю, так как заряд перестает изменяться. И наоборот, максимальный ток течет в моменты, когда напряжение проходит через ноль, меняя знак.
Катушка индуктивности в цепи переменного тока
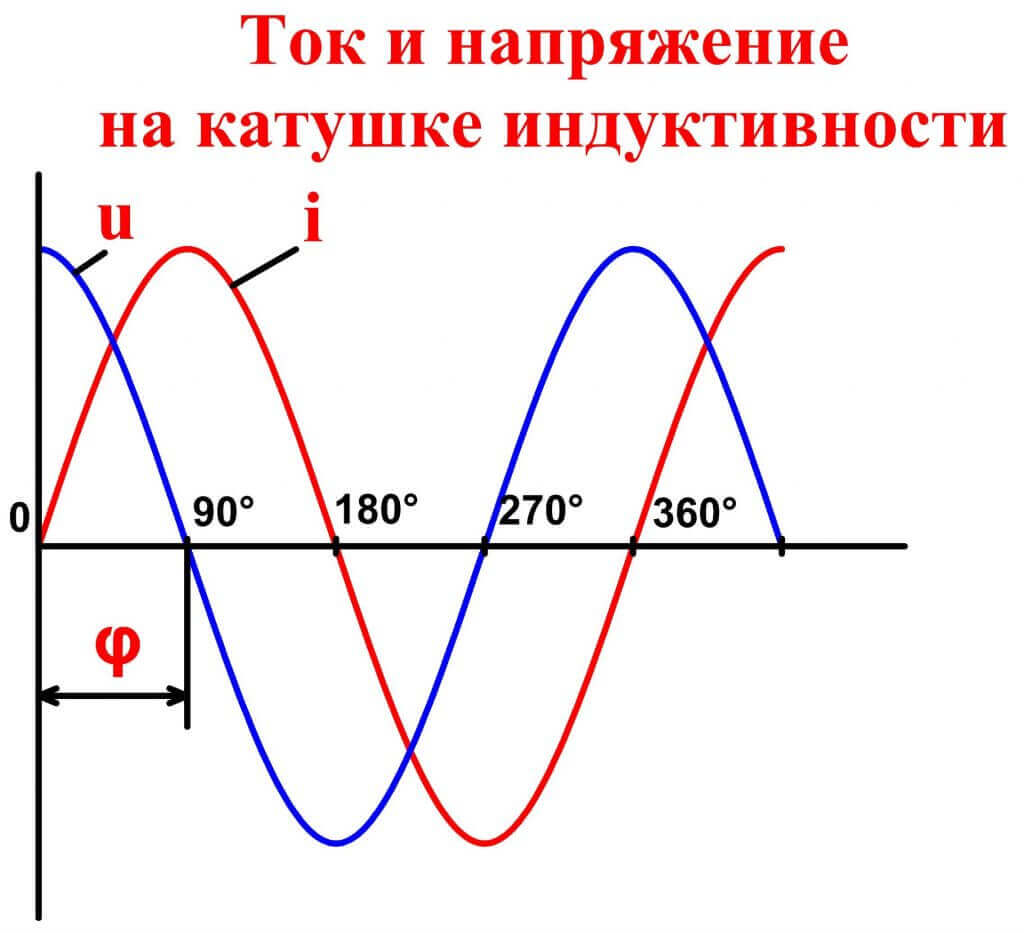
Катушка индуктивности в цепи переменного тока также обладает рядом особенностей:
- Ток через катушку отстает по фазе от напряжения на π/2
- Амплитуда тока обратно пропорциональна индуктивности катушки
- Вводится понятие индуктивного сопротивления XL = ωL
Это связано с возникновением ЭДС самоиндукции в катушке при изменении тока. Когда ток достигает максимума, его изменение равно нулю, поэтому напряжение на катушке в этот момент равно нулю. И наоборот, максимальное напряжение возникает при максимальной скорости изменения тока, то есть когда ток проходит через ноль.
Резонанс в электрической цепи переменного тока
При последовательном соединении конденсатора и катушки индуктивности в цепи переменного тока может возникнуть явление резонанса. Это происходит, когда емкостное и индуктивное сопротивления равны друг другу:
XL = XC
Или:
ωL = 1/(ωC)
Отсюда можно выразить резонансную частоту:
ω0 = 1/√(LC)
При резонансе наблюдается резкое увеличение амплитуды тока в цепи. Это связано с тем, что емкостное и индуктивное сопротивления взаимно компенсируют друг друга.

Факторы, влияющие на резонансную частоту
На резонансную частоту колебательного контура влияют следующие факторы:
- Индуктивность катушки L — при ее увеличении резонансная частота уменьшается
- Емкость конденсатора C — при ее увеличении резонансная частота уменьшается
- Активное сопротивление цепи R — влияет на добротность контура, но не на саму резонансную частоту
Зная эти зависимости, можно настраивать колебательный контур на нужную частоту, изменяя параметры его элементов.
Применение явления резонанса в технике
Резонанс в электрических цепях нашел широкое применение в различных областях техники:
- Радиоприемники — для выделения сигнала нужной частоты
- Генераторы электрических колебаний
- Фильтры частот в электронике
- Устройства для беспроводной передачи энергии
В то же время, в некоторых случаях резонанс может быть вредным явлением, например, в энергетических системах. Поэтому важно уметь как использовать резонанс, так и предотвращать его возникновение в нежелательных ситуациях.
Практические примеры расчетов
Рассмотрим несколько типовых задач на расчет цепей переменного тока с конденсаторами и катушками индуктивности:
Пример 1. Расчет емкостного сопротивления
Конденсатор емкостью 100 мкФ включен в цепь переменного тока частотой 50 Гц. Определить емкостное сопротивление.
Решение: XC = 1/(2πfC) = 1/(2π · 50 · 100·10^-6) = 31.8 Ом
Пример 2. Расчет индуктивного сопротивления
Катушка индуктивностью 0.1 Гн включена в цепь переменного тока частотой 1 кГц. Определить индуктивное сопротивление.
Решение: XL = 2πfL = 2π · 1000 · 0.1 = 628 Ом
Пример 3. Определение резонансной частоты
Колебательный контур состоит из катушки индуктивностью 5 мГн и конденсатора емкостью 400 пФ. Найти резонансную частоту контура.
Решение: f0 = 1/(2π√(LC)) = 1/(2π√(5·10^-3 · 400·10^-12)) ≈ 112.5 кГц
Заключение
Понимание поведения конденсаторов и катушек индуктивности в цепях переменного тока, а также явления резонанса, крайне важно для анализа и проектирования электрических цепей. Эти знания находят широкое применение в радиотехнике, электронике, энергетике и других областях. Умение рассчитывать параметры цепей переменного тока позволяет создавать эффективные устройства и системы, используя особенности поведения реактивных элементов.
Конденсатор и катушка индуктивности в цепи переменного тока
Как мы с вами говорили, в цепи переменного тока, содержащей активное сопротивление, происходят постоянные потери энергии, сопровождающиеся выделением тепла. При этом, количество теплоты, выделяющееся на активном сопротивление при прохождении по нему переменного тока, можно рассчитать, как и в случае с постоянным током, по закону Джоуля — Ленца:
Однако быстрое изменение величины и направления переменного тока
обусловливает ряд особенностей, отличающих его действия от действий тока постоянного.
Так, например, переменный ток не годится для технических применений
электролиза. Дело в том, что величина переменного тока зависит не только от
напряжения и сопротивления цепи, но и от индуктивности проводников, включённых
в цепь. В этом можно убедиться на следующем опыте. Включим в цепь
постоянного тока катушку, содержащую большое количество витков медной проволоки
и амперметр.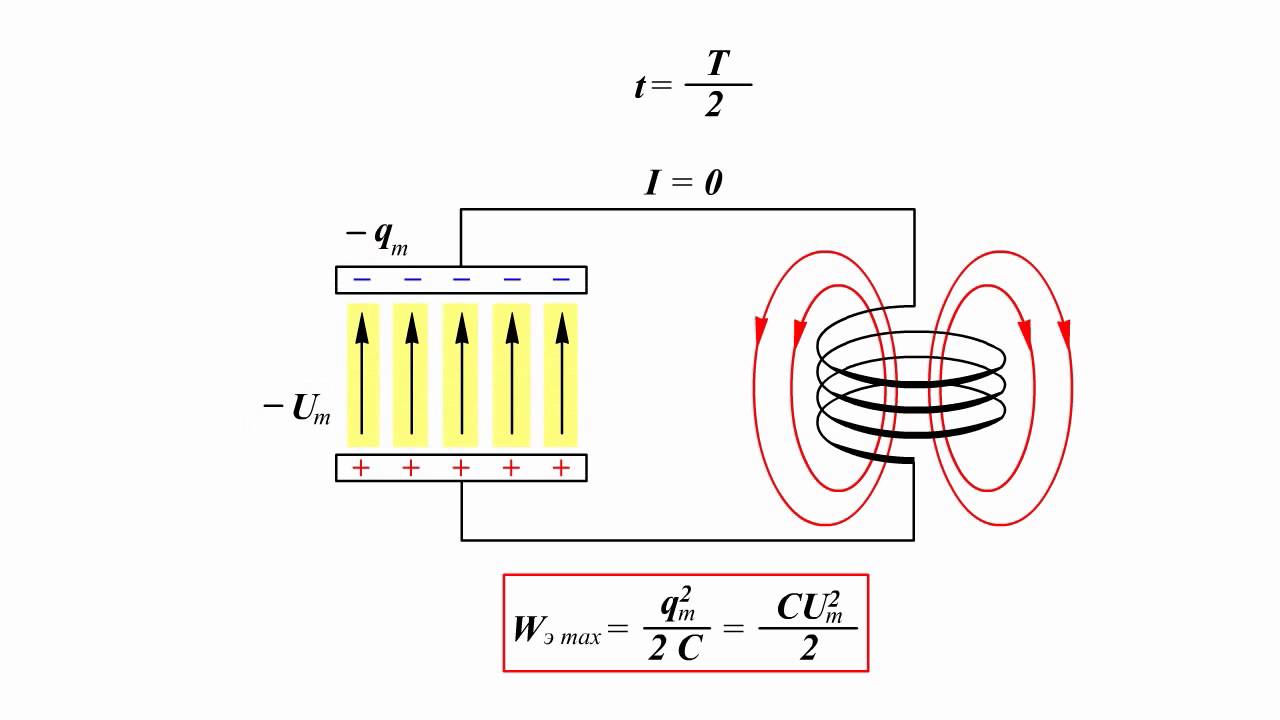
Снимем показания амперметра. А теперь вдвинем в катушку железный сердечник — ток при этом не изменился.
Посмотрим, что будет происходить в этой же цепи, но при включении в неё источника переменного тока с действующим напряжением, равным напряжению постоянного тока.
Нетрудно заметить, что ток в катушке уменьшился. Введение же в катушку железного сердечника приведёт к ещё большему ослаблению тока. Следовательно, индуктивность цепи переменного тока уменьшает величину тока.
Причиной этого является возникающая в цепях переменного тока ЭДС самоиндукции, которая препятствует нарастанию тока. Вследствие ЭДС самоиндукции в момент, когда напряжение в цепи достигает максимума, ток не успевает достигнуть той величины, которую он достиг бы в отсутствие самоиндукции.
Например, представим, что у нас есть катушка, на которую
намотано 600 витков медной проволоки, диаметром 1 мм. Предположим, что на эту
катушку пошло 150 метров этой проволоки. Тогда, исходя из определения, её
сопротивление примерно равно 3,2 Ом. Но если измерить сопротивление этой
катушки в цепи переменного тока частотой 50 Гц, то оно окажется равным примерно
20 Ом.
Но если измерить сопротивление этой
катушки в цепи переменного тока частотой 50 Гц, то оно окажется равным примерно
20 Ом.
Это говорит нам о том, что индуктивность в цепи переменного тока действует в отношении величины тока так же, как и активное сопротивление.
Сопротивление, которым обладает цепь вследствие наличия в ней индуктивности, называется индуктивным сопротивлением. Узнаем от чего оно зависит. Итак, пусть в цепи, содержащей катушку индуктивности, протекает переменный ток, сила которого изменяется по гармоническому закону:
Тогда, ЭДС самоиндукции будет равна произведению индуктивности катушки и первой производной силы тока по времени, взятому с обратным знаком:
Если активное сопротивление катушки равно нулю, то и
напряжённость электрического поля внутри проводника в любой момент времени
должна быть равна нулю. В противном случае сила тока была бы бесконечно большой
(это следует из закона Ома). Равенство нулю напряжённости поля оказывается
возможным потому, что напряжённость, вихревого электрического поля,
порождаемого переменным магнитным полем, в каждой точке равна по модулю и
противоположна по направлению напряжённости кулоновского поля, создаваемого в
проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Следовательно, удельная работа вихревого поля (то есть ЭДС самоиндукции) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, то напряжение в цепи переменного тока, будет обратно по знаку ЭДС самоиндукции:
Произведение величин, стоящих перед функцией косинуса, является амплитудой напряжения:
Давайте перепишем уравнение для мгновенного напряжения, воспользовавшись введённым обозначением, а также заменим косинус на синус, воспользовавшись формулой приведения:
Отсюда следует, что колебания напряжения на катушке опережают колебания силы тока на
Давайте выразим из формулы для амплитуды напряжения амплитуду силы тока в катушке:
Величина, равная произведению циклической частоты и индуктивности катушки и есть индуктивное сопротивление:
Тогда можно записать, что амплитудное значение силы тока в
цепи переменного тока, содержащую только катушку индуктивности, прямо
пропорционально амплитудному напряжению и обратно пропорционально индуктивному
сопротивлению.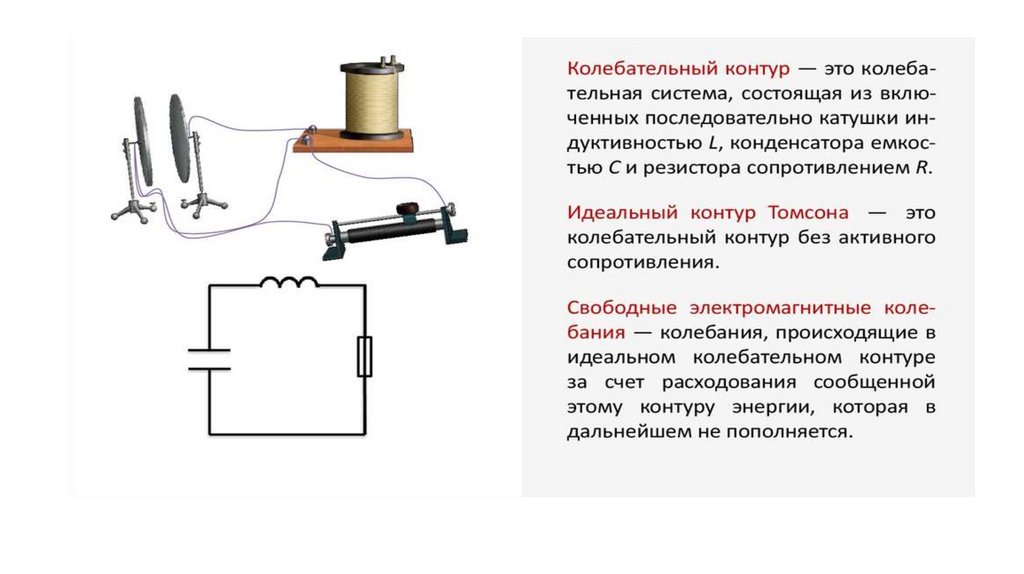
А теперь давайте определим мгновенную мощность в данной цепи:
Как видим, потребляемая идеальной катушкой, периодически изменяется с двойной частотой, а её среднее значение за период равно нулю, так как равно нулю среднее значение синуса двойного аргумента. Следовательно, так же как активное сопротивление, индуктивное сопротивление ограничивает силу тока в цепи, но в отличие от активного сопротивления на нём электрическая энергия не превращается необратимо в другие виды энергии.
Теперь давайте с вами соберём цепь постоянного тока, содержащую последовательно соединённые конденсатор и лампочку. Замкнув цепь, мы обнаружим, что никакого тока в цепи нет. Это вполне понятно, так как пластины конденсатора отделены друг от друга изолятором. Поэтому через конденсатор постоянный ток течь не может.
А теперь заменим источник постоянного тока на источник
переменного напряжения. Лампочка горит. Объясняется это достаточно просто. В
цепи переменного тока электроны совершают колебательное движение.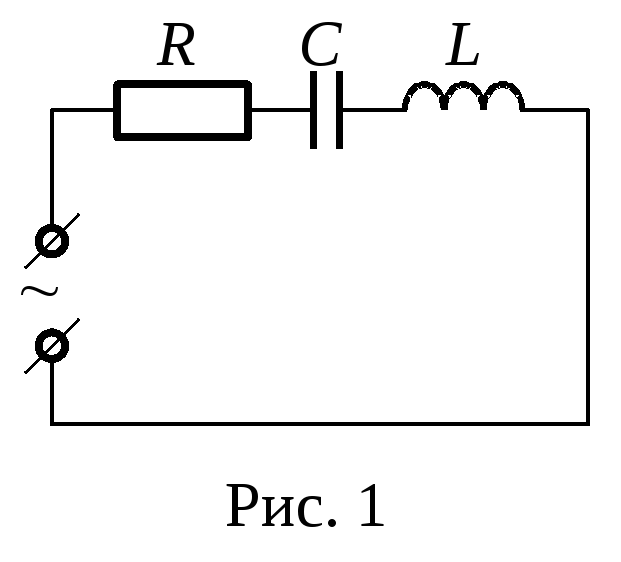 Это приводит
к тому, что обкладки конденсаторов попеременно заряжаются то положительно, то
отрицательно. Электроны же в проводах цепи движутся то в одном, то в другом
направлении, нагревая спираль лампы. Если выключить конденсатор из цепи, то
лампочка будет гореть ярче. Следовательно, наличие конденсатора в цепи
переменного тока увеличивает сопротивление цепи.
Это приводит
к тому, что обкладки конденсаторов попеременно заряжаются то положительно, то
отрицательно. Электроны же в проводах цепи движутся то в одном, то в другом
направлении, нагревая спираль лампы. Если выключить конденсатор из цепи, то
лампочка будет гореть ярче. Следовательно, наличие конденсатора в цепи
переменного тока увеличивает сопротивление цепи.
Сопротивление, которым обладает цепь вследствие наличия в ней ёмкости, называется ёмкостным сопротивлением.
Выясним, от чего оно зависит. Для этого рассмотрим цепь, состоящую из генератора переменного напряжения, конденсатора и проводов, сопротивление которых пренебрежимо мало.
Пусть напряжение на конденсаторе изменяется синусоидально:
Следовательно, и заряд конденсатора будет изменяться со временем по закону синуса:
Найдём силу тока в цепи, как первую производную заряда по времени:
Произведение величин, стоящих перед функцией синуса, является амплитудой силы тока:
Перепишем предыдущее уравнение с учётом введённых обозначений, и воспользуемся формулой приведения для перехода от функции косинуса к функции синус:
Отсюда следует, что колебания силы тока опережают по фазе колебания напряжения на конденсаторе на π/2:
Теперь давайте перепишем уравнение для амплитуды силы тока так, как это показано на экране:
Величина, обратная произведению ёмкости конденсатора и циклической частоты является ёмкостным сопротивлением:
Подставив данное уравнение в предыдущее равенство, найдём, что амплитудное значение силы тока в цепи переменного тока, содержащую только конденсатор, прямо пропорционально амплитудному напряжению и обратно пропорционально ёмкостному сопротивлению:
Теперь определим мгновенную мощность в данной цепи:
Как и в предыдущем случае, при наличии в цепи только ёмкостного
сопротивления частота изменения мощности вдвойне больше частоты изменения силы
тока, а её среднее значение за период равно нулю.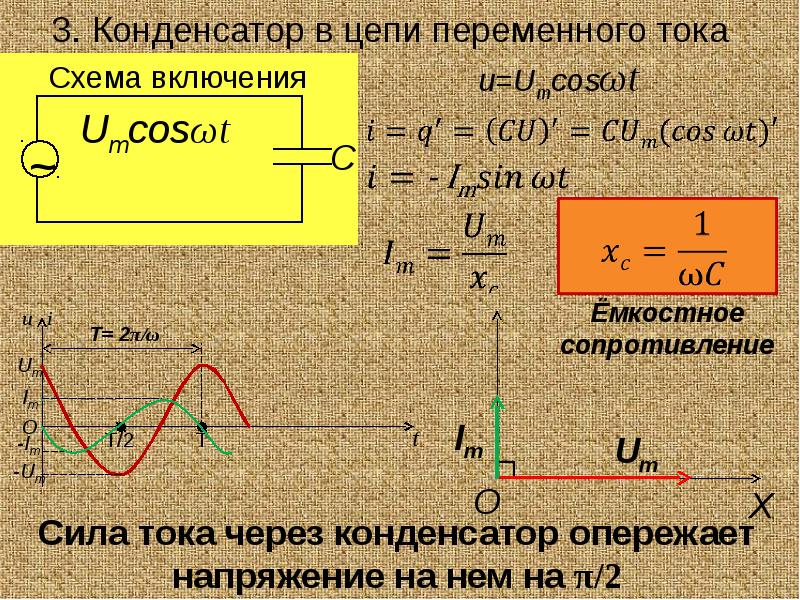
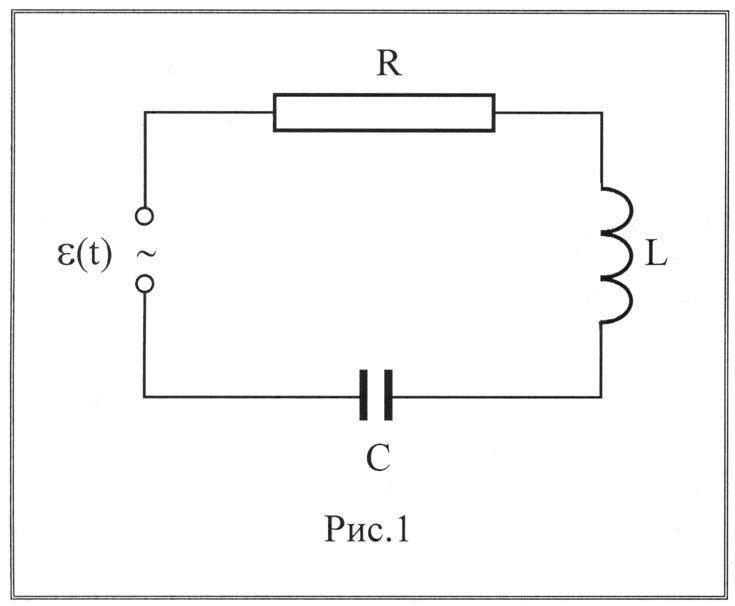
Теперь рассмотрим цепь, содержащую все элементы: резистор, катушку индуктивности, конденсатор и источник переменного напряжения.
Так как электромагнитные взаимодействия распространяются со скоростью света, то во всех последовательно включённых элементах цепи изменения силы тока происходят практически одновременно. Однако колебания мгновенных значений напряжения на каждом из элементов не совпадают по фазе с колебаниями силы тока. Но в любой момент времени сумма мгновенных значений напряжений на последовательно включённых элементах цепи равна ЭДС источника:
Учитывая, что на активном сопротивлении колебания силы тока совпадают, на ёмкостном опережают, а на индуктивном отстают от колебаний напряжения, то последнее равенство можно записать так:
Амплитуду колебаний напряжения в цепи можно выразить через
амплитудные значения напряжения на отдельных её элементах, воспользовавшись
методом векторных диаграмм.
Амплитудное значение силы тока в цепи совпадает по фазе с амплитудным значением напряжения на резисторе. Из этой диаграммы можно найти амплитуду приложенного напряжения, которая равна геометрической сумме этих амплитуд.
Используя теорему Пифагора, выразим квадрат амплитуды колебаний напряжения в цепи:
Далее, используя закон Ома для участка цепи, выразим амплитудные значения напряжений, стоящих в правой части равенства, через амплитудное значение силы тока и реактивные сопротивления:
Выражая из полученного уравнение амплитудное значение силы тока, получим закон Ома для участка цепи переменного тока
Величина, стоящая в знаменателе формулы, называется полным сопротивлением цепи:
Величина же, стоящая в скобках под знаком корня, называется реактивным сопротивлением.
Конденсатор, катушка и резонанс в цепи переменного тока 🐲 СПАДИЛО.
 РУ
РУОпишем колебания, которые происходят в цепи переменного тока при включении в нее конденсатора и катушки индуктивности. А также рассмотрим условия, при выполнении которых в цепи переменного тока наступает резонанс. Получим формулы для вычисления амплитуд напряжений, введем понятия емкостного и индуктивного сопротивления и выясним, какую роль играют эти величины.
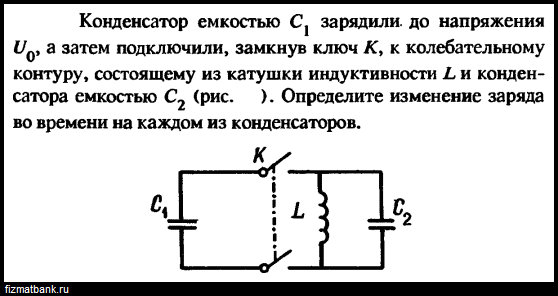
Конденсатор в цепи переменного тока
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
рис. выше). Напряжение на конденсаторе будет равно:
u=φ1−φ2=qC..
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
qC..=Umaxcos.ωt
Следовательно, заряд конденсатора меняется по гармоническому закону:
q=CUmaxcos.ωt
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i=q´=−CUmaxsin.ωt=CUmaxcos.(ωt+π2..)
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π2.. (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
Амплитуда силы тока равна:
Imax=UmaxCω
Примем, что:
1Cω..=XC
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
ОпределениеI=UXC..
Величина XC, равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура qmax=10−6 Кл. Амплитудное значение силы тока в контуре Imax=10−3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q2max2C..=LI2max2..
Отсюда:
LC=q2maxI2max..
√LC=qmaxImax..
T=2π√LC=2πqmaxImax..=2·3,1410−610−3..≈6,3·10−3 (с)
Катушка индуктивности в цепи переменного тока
Соберем две электрических цепи, состоящих из лампы накаливания, катушки индуктивности и источника питания: в первом случае постоянного, во втором — переменного (см. рисунки «а» и «б» ниже).
рисунки «а» и «б» ниже).
Опыт покажет, что в цепи постоянного тока лампа светится ярче по сравнению с той, что включена в цепь переменного тока. Это говорит о том, что сила тока в цепи постоянного тока выше действующего значения силы тока в цепи переменного тока.
Результат опыта легко объясняется явлением самоиндукции. При подключении катушки к постоянному источнику тока сила тока нарастает постепенно. Возрастающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь спустя какое-то время сила тока достигает наибольшего значения, соответствующему данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не успевает достигнуть максимального значения. Поэтому максимальное значение силы тока в цепи переменного тока с катушкой индуктивности ограничивается индуктивность. Чем больше индуктивность и чем больше частота приложенного напряжения, тем меньше амплитуда силы переменного тока.
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (см. рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.
рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна равняться нулю. Иначе, согласно закону Ома, сила тока была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля →Ei, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля →Eк, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства →Ei=−→Eк следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции ei) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Учитывая, что удельная работа кулоновского поля равна напряжения на концах катушки, можно записать:
ei=−u
Напомним, что сила переменного тока изменяется по гармоническому закону:
i=Imaxsin.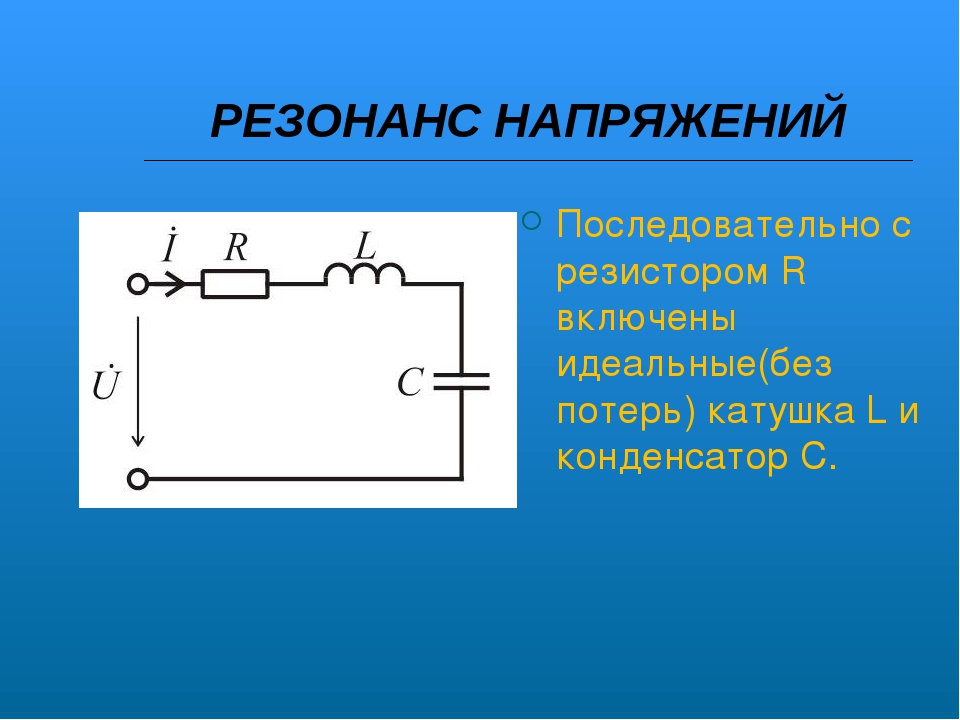 ωt
ωt
Тогда ЭДС самоиндукции равна:
ei=−Li´=−LωImaxcos.ωt
Так как u=−ei, то напряжение на концах катушки оказывается равным:
u= LωImaxcos.ωt=LωImaxsin.(ωt+π2..)=Umax(ωt+π2..)
Амплитуда напряжения равна:
Umax=LωImax
Следовательно, колебания напряжения на катушке опережают колебания силы тока на π2.., или колебания силы тока отстают от колебаний напряжения на π2.., что одно и то же.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (см. график ниже).
Но в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Амплитуда силы тока в катушке равна:
Imax=UmaxLω..
Введем обозначение:
Lω=XL
Также будем использовать вместо амплитуд действующие значения силы тока и напряжения. Тогда получим:
ОпределениеI=UXL..
Величина XL, равная произведению циклической частоты на индуктивность, называется индуктивным сопротивлением. Индуктивное сопротивление зависит от частоты. Поэтому в цепи постоянного тока, в котором отсутствует частота, индуктивное сопротивление катушки равно нулю.
Индуктивное сопротивление зависит от частоты. Поэтому в цепи постоянного тока, в котором отсутствует частота, индуктивное сопротивление катушки равно нулю.
Пример №2. Катушка с индуктивным сопротивлениемXL=500 Ом присоединена к источнику переменного напряжения, частота которого ν = 1000 Гц. Действующее значение напряжения U = 100 В. Определите амплитуду силы тока Imax в цепи и индуктивность катушки L. Активным сопротивлением пренебречь.
Индуктивное сопротивление катушки выражается формулой:
XL=Lω=2πνL
Отсюда:
Так как амплитуда напряжения связана с его действующим значением соотношением Umax=U√2, то для амплитуды силы тока получаем:
Резонанс в электрической цепи
Механические и электромагнитные колебания имеют разную природу, но процессы, происходящие при этом, идентичны. Поэтому можно предположить, что резонанс в электрической цепи так же реален, как резонанс в колебательной системе, на которую действует периодическая сила.
Напомним, что в механической системе резонанс тем более заметен, чем меньше в колебательной системе трение между ее элементами. Роль трения в электрической цепи играет активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника, который при этом нагревается. Следовательно, резонанс в электрической цепи будет отчетливо наблюдаться при малом активном сопротивлении R.
Если активное сопротивление мало, то собственная частота колебаний в колебательном контуре определяется формулой:
ω0=1√LC..
Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру равна собственной частоте колебательного контура:
ω=ω0=1√LC..
ОпределениеРезонанс в электрическом колебательном контуре — явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
После включения внешнего переменного напряжения резонансное значение силы тока в цепи устанавливается не моментально, а постепенно. Амплитуда колебаний силы тока возрастает до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
I2maxR2..=UmaxImax2..
Упростив это уравнение, получим:
ImaxR=Umax
Следовательно, амплитуда установившихся колебаний силы тока при резонансе определяется уравнением:
Imax=UmaxR..
При сопротивлении, стремящемся к нулю, сила тока возрастает до бесконечно больших значений. При большом сопротивлении сила тока возрастает незначительно. Это хорошо видно на графике ниже.
Пример №3. В цепь переменного тока с частотой ν = 500 Гц включена катушка индуктивностью L = 10 мГн. Какой емкости конденсатор надо включить в эту цепь, чтобы наступил резонанс?
Электрическая цепь, описываемая в условии, представляет собой колебательный контур.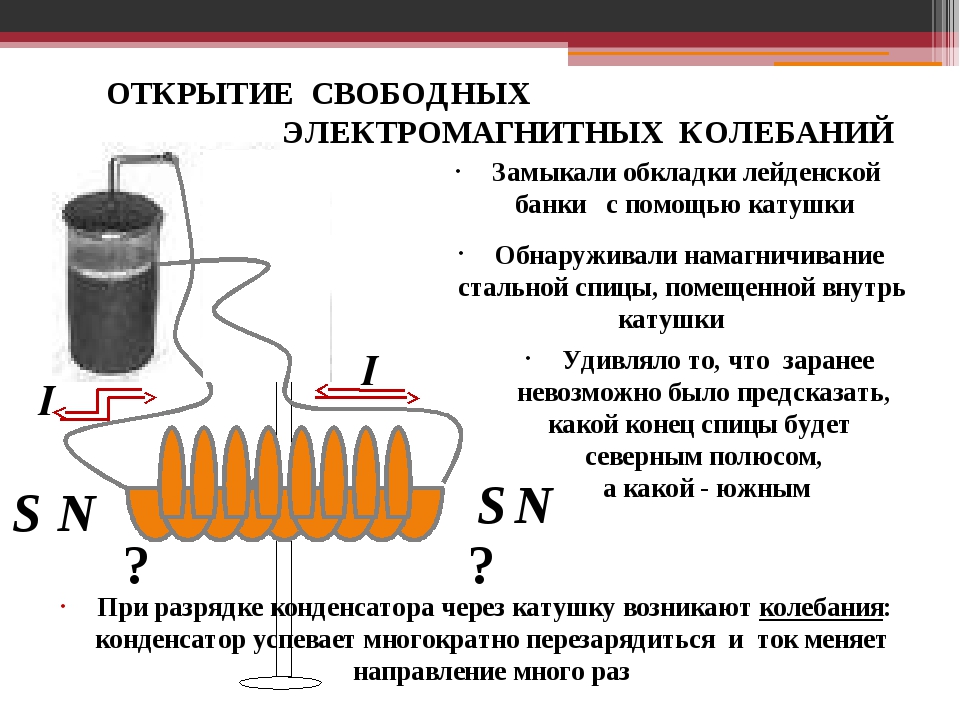 Резонанс в этой цепи наступит, когда частота переменного тока будет равна собственной частоте колебательного контура (ν = ν0).
Резонанс в этой цепи наступит, когда частота переменного тока будет равна собственной частоте колебательного контура (ν = ν0).
Но:
ν0=12π√LC..
Тогда:
ν=12π√LC..
Отсюда:
Задание EF22579К колебательному контуру подсоединили источник тока, на клеммах которого напряжение гармонически меняется с частотой ν.
Индуктивность L катушки колебательного контура можно плавно менять от максимального значения Lmax до минимального Lmin, а ёмкость его конденсатора постоянна.
Ученик постепенно уменьшал индуктивность катушки от максимального значения до минимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.
Алгоритм решения
1.Установить, что вызывает увеличение амплитуды силы тока.
2.Объяснить, какие изменения вызвало уменьшение индуктивности.
3.Объяснить, при каком условии в течение всего эксперимента амплитуда силы тока может только расти.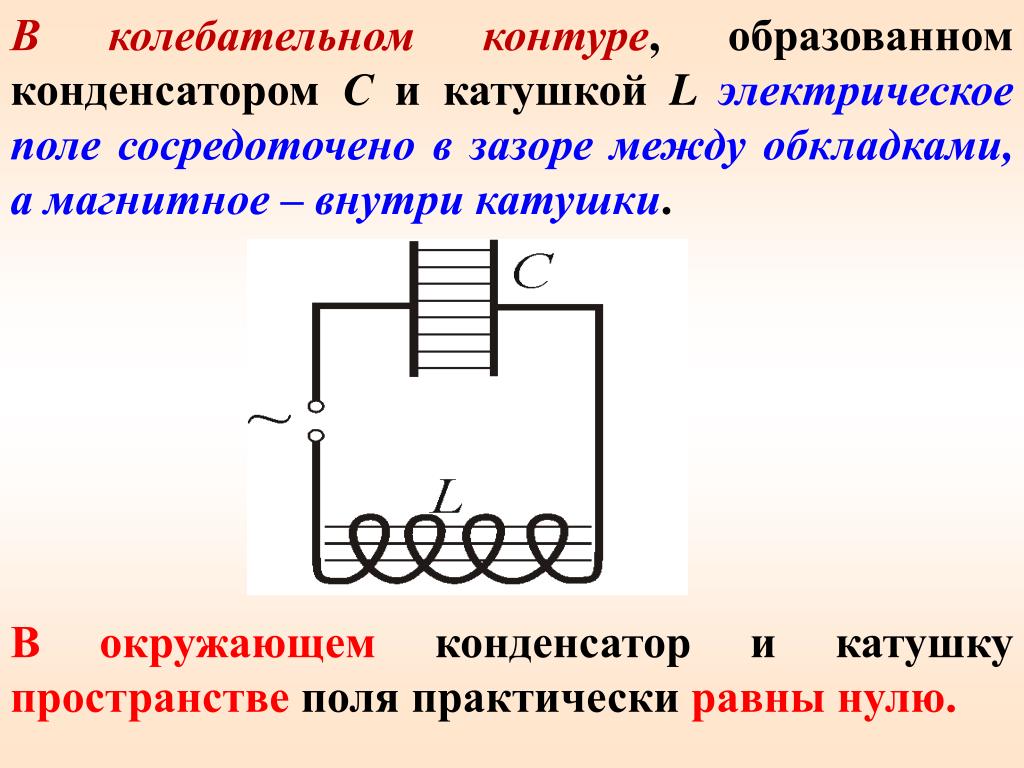
Решение
В колебательном контуре источником тока возбуждаются вынужденные колебания. Частота этих колебаний равна частоте источника — ν. Амплитуда колебаний зависит от того, как соотносятся между собой внешняя частота и частота собственных электромагнитных колебаний, которая определяется формулой:
ν0=12π√LC..
По мере увеличения внешней частоты от нуля до ν0 амплитуда растет. Она достигает максимума тогда, когда происходит резонанс. При этом внешняя частота равна частоте собственных электромагнитных колебаний: ν = ν0. Затем амплитуда начинает убывать.
В данном случае, ученик меняет не внешнюю частоту, а частоту собственных электромагнитных колебаний. При плавном уменьшении индуктивности контура от максимального значения Lmax до минимального Lmin частота возрастает от ν0min до ν0max. Причем:
ν0min=12π√LminC..
ν0max=12π√LmaxC..
Из того факта, что амплитуда всё время увеличивалась, можем сделать вывод, что частота ν0 всё время приближалась к частоте источника тока, при этом ν > ν0max. В противном случае наблюдалось бы уменьшений амплитуды силы тока.
В противном случае наблюдалось бы уменьшений амплитуды силы тока.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22785В колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания.
Из приведённого ниже списка выберите две величины, которые остаются постоянными при этих колебаниях.
Ответ:
а) период колебаний силы тока в контуре
б) фаза колебаний напряжения на конденсаторе
в) заряд конденсатора
г) энергия магнитного поля катушки
д) амплитуда колебаний напряжения на катушке
Алгоритм решения
- Определить, от чего зависит каждая из перечисленных величин.
- Установить, какие величины меняются, а какие нет.
Решение
В колебательном контуре происходят гармонические колебания. Поэтому период колебаний силы тока в контуре — величина постоянная.
Фаза — это величина, которая определяет положение колебательной системы в любой момент времени. Поскольку в системе происходят колебания, фаза меняется.
Заряд конденсатора — колебания происходят за счет постоянной перезарядки конденсатора. Следовательно, эта величина тоже меняется.
Энергия магнитного поля катушки — в колебательном контуре происходят взаимные превращения энергии магнитного поля катушки в энергию электрического поля конденсатора, и обратно. Поэтому энергия магнитного поля катушки постоянно меняется.
В условии задачи сказано, что колебания незатухающие. Это значит, что полная механическая энергия колебательной системы сохраняется. Поскольку именно от нее зависит амплитуда колебаний напряжения на катушке, то эта величина также остается постоянной.
Ответ: адpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18656 На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.
Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.Алгоритм решения
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2..=4π√LC2π√LC. .=2
.=2
Отсюда:
T2=T12..=4·10−62..=2·10−6 (с)=2 (мкс)
Ответ: 2pазбирался: Алиса Никитина | обсудить разбор | оценить
Конденсатор и катушка в цепи переменного тока
Мультимедийное приложение к уроку изучения новой темы «Индуктивное и ёмкостное сопротивление» для 11 класса по учебнику Г.Я. Мякишева, Б.Б. Буховцева, В.М. Сотского. На уроке организуется исследовательская деятельность через фронтальный эксперимент, урок сопровождается презентацией, применение которой облекчает работу учителя при объяснении нового материала и помогает ученику повысить уровень усвоения информации, изучаемой на уроке.
Просмотр содержимого документа
«Конденсатор и катушка в цепи переменного тока »
§ 33-34
— ёмкостное сопротивление – сопротивление конденсатора ~ току.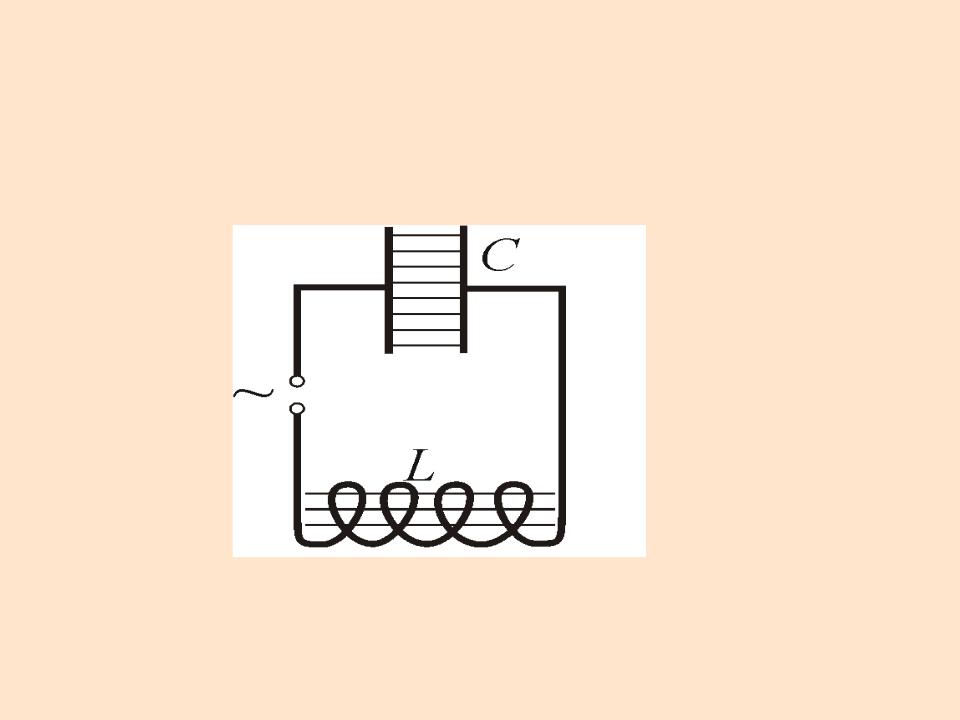
Величину , обратную произведению циклической частоты на электроёмкость конденсатора называют ёмкостным сопротивлением
1
2
+
~
~
—
~
С
1). С = const — изменяется
Закон Ома для участка цепи с конденсатором
С — изменяется
2).
~
Найдём как меняется сила тока со временем в цепи, содержащей только конденсатор.
— на конденсаторе
~
— на концах цепи
Найдём силу тока:
Колебания силы тока опережают колебания напряжения на конденсаторе на
Амплитуда силы тока
— Индуктивное сопротивление – дополнительное сопротивление катушкой индуктивности ~ току.
2
1
Величину , равную произведению на называют индуктивным сопротивлением.
+
—
~
L
1) . L=const — изменяется
Закон Ома для участка цепи с катушкой
~
2). — const L — изменяется
~
Найдём как меняется со временем сила тока в цепи, содержащая только катушку.
— В катушке возникает ЭДС самоиндукции
~
По закону э/м индукции:
Из математики:
— Амплитуда напряжения
Колебания силы тока отстают от колебаний напряжения на
Резистор, индуктивная катушка и конденсатор в цепи синусоидального тока
Лекция № 4 Резистор, индуктивная катушка и конденсатор в цепи синусоидального тока.
Термин «сопротивление» для цепей переменного тока, оказывается недостаточно полным, поскольку сопротивление переменному току оказывают не только те элементы цепи, в которых выделяется энергия в виде теплоты (их называют активными сопротивлениями), но и те элементы цепи, в которых энергия периодически запасается в электрическом или магнитном полях. Такие элементы цепи называют реактивными сопротивлениями. Реактивными сопротивлениями обладают индуктивности и емкости.
Активное сопротивление в цепи синусоидального тока.
Если по активному сопротивлению течет ток тогда
по закону Ома
или
где
Т. е. в активном сопротивлении элемента цепи комплекс тока совпадает с комплексом напряжения
е. в активном сопротивлении элемента цепи комплекс тока совпадает с комплексом напряжения
Рис. 4.1 – Графики мгновенных значений
Мгновенная мощность
=
или
т. е. мгновенная мощность имеет постоянную составляющую и переменную составляющую меняющуюся с частотой равной (на рис. 4.1)
Индуктивность в цепи переменного синусоидального тока.
Практически любая обмотка (катушка) обладает некоторой индуктивностью и активным сопротивлением .
Схема замещения катушки может быть представлена в виде последовательного соединения индуктивности и активного сопротивления .
Выделим из схемы одну индуктивность
Рис. 4.2
Если через индуктивность течет ток , то в катушке наводится ЭДС самоиндукции — .
Для прохождения переменного тока через индуктивность необходимо, чтобы на ее зажимах было напряжение , равное и противоположно направленное .
,
где — индуктивное сопротивление
где — частота, Гц,
— индуктивность, Гн.
Движению переменного тока через индуктивность оказывается сопротивление за счет накопления энергии , это сопротивление называется индуктивным.
Размерность индуктивного сопротивления
.
Значение тока в цепи с индуктивностью опережает ЭДС самоиндукции на 90°, но т. к. вектор напряжения на катушке индуктивности направлен в противоположную сторону ЭДС.
т. е.
т. о. в цепи с индуктивностью вектор тока отстает от вектора напряжения на угол 90°.
Действующее значение тока в цепи с индуктивностью равно действующему значению напряжения, деленному на индуктивное сопротивление.
т. е.
Приведенная формула похожа на закон Ома. Это внешнее сходство позволяет определить ток в цепи с индуктивностью, подобно тому, как в цепи с активным сопротивлением. Но нужно помнить, что индуктивное сопротивление с физической точки зрения с обычным сопротивлением ничего общего не имеет.
Понятие об индуктивном сопротивлении формально введено для облегчения расчета.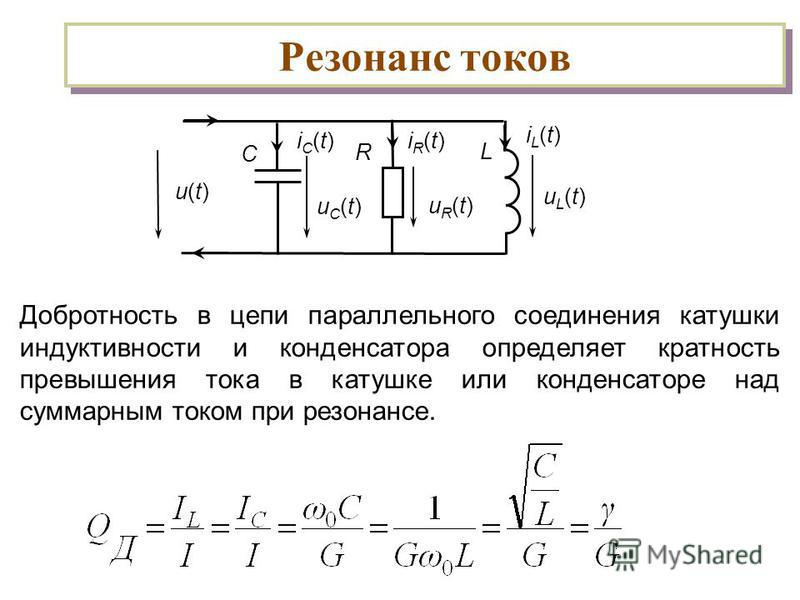
Оно заменяет фактическое влияние ЭДС самоиндукции на ток в цепи.
Мгновенная и реактивная мощность
Мгновенное значение мощности или
График изменения мощности представляет собой синусоиду двойной частоты с амплитудой
.
Наибольшее значение мощности в цепи с индуктивностью равно произведению действующих значений напряжения и тока.
В первую четверть периода, когда ток в цепи увеличивается, энергия накапливается в магнитном поле катушки за счет энергии источника. Катушка в это время является приемником энергии: ток направлен против ЭДС самоиндукции.
Во вторую четверть периода, когда ток уменьшается, энергия возвращается в сеть (источнику). Направление ЭДС самоиндукции и тока совпадают. Катушка является источником энергии.
В следующую половину периода процесс повторяется.
Средняя активная мощность за период равна нулю , т. к. в цепи с индуктивностью преобразования электрической энергии в другие виды энергии не происходит.
Цепь с емкостью –
К конденсатору с идеальным диэлектриком, т. е. в нем нет потерь энергии, подведено напряжение
Определим ток и мощность
Ток в цепи.
Заряд конденсатора пропорционален напряжению между его обкладками, поэтому изменение напряжения сопровождается изменением заряда.
Скорость изменения заряда пропорциональна скорости изменения напряжения.
но скорость изменения заряда равна электрическому току
т. к.
то
Сопоставляя:
получаем, что ток через конденсатор по фазе опережает напряжение на конденсаторе на угол 90°. На векторной диаграмме вектор тока опережает вектор напряжения на угол 90°.
Амплитуда тока
Действующее значение тока
или
где — реактивное сопротивление конденсатора
Построение графика мгновенной мощности конденсатора выполняют также как и для индуктивной катушки.
т. к.
В первую четверть периода, когда напряжение на конденсаторе возрастает, энергия накапливается в электрическом поле конденсатора за счет работы источника, конденсатор в это время заряжается, т. е. является приемником энергии. Направления тока и напряжения совпадают.
е. является приемником энергии. Направления тока и напряжения совпадают.
Во вторую четверть периода, когда напряжение уменьшается, энергия в том же количестве возвращается в сеть к источнику. Ток направлен против напряжения сети – конденсатор является источником энергии ( разряжается ) и так в 3й и 4й части периода.
Активная мощность равна нулю, а реактивная
Установившийся режим в простейшей неразветвленной цепи с сосредоточенными параметрами.
Электрические цепи характеризуются двумя режимами: переходным и установившимся.
Переходные режимы возникают в результате перераспределения энергии электрических и магнитных полей в и при резком изменении параметров электрической цепи.
Простейшая электрическая цепь переменного тока с
Общее сопротивление такой цепи
где — реактивное сопротивление
или
где
Если по цепи протекает ток, то:
или
в комплексной форме
Отсюда или
— закон Ома в комплексной форме
где — комплексное сопротивление
— модуль комплексного сопротивления
Величина обратная комплексному сопротивлению называется комплексной проводимостью.
(сименс)
Умножая на сопряженный комплекс получаем
где — активная проводимость,
— реактивная проводимость.
,
по модулю
Умножив сопротивление на ток получим треугольник U.
Напряжение можно представить в виде двух составляющих
Цепь
Пусть
По второму закону Кирхгофа
где и — синусоидальные напряжения
В комплексной форме
тогда
или
где — комплекс полного сопротивления индуктивной катушки (цепи )
Показательная форма записи
где — модуль комплекса полного сопротивления цепи
— аргумент.
Если , а ,
тогда
где , а
Если ток , то .
— Комплекс тока в цепи с равен комплексу напряжения деленному на комплекс полного сопротивления катушки.
Умножив треугольники на получим:
– полная мощность (ВА)
— реактивная мощность (ВАp)
— активная мощность (Вт)
или
— коэффициент мощности, зависит от соотношения и по его величине судят о том, какую часть полной мощности цепи составляет активная мощность.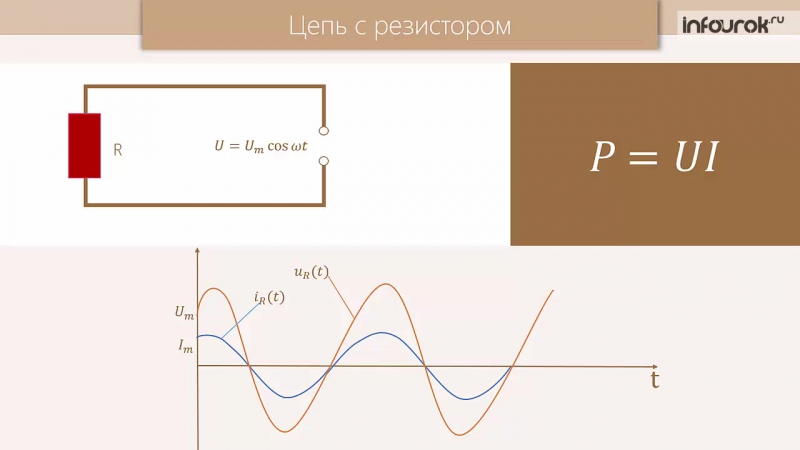
Активную мощность измеряют ваттметром.
Цепь
Пусть .
По второму закону Кирхгофа
, т. к. напряжение отстает от тока
или
– комплекс полного сопротивления
— модуль комплекса
— аргумент
Напряжение на входе цепи отстает от тока на угол сдвига фаз
т. о. , т. к.
Аналогично цепи
или
Сложные цепи, состоящие из последовательных и параллельных участков
Расчет
1. При расчете цепи определяют активные и реактивные проводимости параллельных ветвей
; ; ; .
2. Далее определяют активную и реактивную проводимость разветвления аb
3.Преобразуют схему в эквивалентную
4.Определяют активное и реактивное сопротивление всей цепи
тогда ; ; ; ,
где , а .
Построение векторной диаграммы (по активным и реактивным составляющим).
Лучше построение векторной диаграммы начать с последней ветви и идти к началу цепи, т. е.к общему току и напряжению.
В нашем случае построение начнем с напряжения — откладываем его произвольно в масштабе.
Топографическая диаграмма:
при последовательном соединении напряжений и параллельных токов.
Топографическая диаграмма – такая векторная диаграмма, каждая точка которой соответствует определенной точке электрической цепи.
Резонанс при последовательном и параллельном соединении элементов
Резонанс – такой режим цепи содержащей , индуктивность и емкость, при котором ее входное сопротивление (или проводимость) имеет активный характер.
В зависимости от вида цепи (последовательное или параллельное соединение) существует резонанс напряжений и токов.
1. Последов. соединение R, L,C.
Условие резонанса:
или
т. к. , а , т. о.
, т. е. или
где — резонансная угловая частота.
при резонансе
При последовательном соединении и в резонансном режиме , т. е. имеется резонанс напряжений.
При резонансе значения и могут значительно превышать напряжения на зажимах.
Ток при резонансе
или , т. к. , а
т. о. , делим на , сокращаем
,
где — характеристическое (волновое) сопротивление контура имеет размерность сопротивления.
т. к. ; ; .
Отношение напряжения на индуктивности (или емкости) к напряжению на зажимах цепи при резонансе называется добротностью контура.
.
Величина обратная называется затуханием ()
Параллельное соединение
Условие резонанса: , т. е .
При равенстве реактивных проводимостей ветвей противоположные по фазе реактивные составляющие токов и равны по величине.
Такой режим работы цепи называют резонансом токов.
,
,
тогда
или ,
т. к. , то .
т. е. общий ток носит чисто активный характер (совпадает с ) и может быть меньше и .
е. общий ток носит чисто активный характер (совпадает с ) и может быть меньше и .
Символический метод анализа электрических цепей синусоидального тока.
В режиме синусоидального тока можно перейти от уравнений составленных для мгновенных значений (дифференциальных уравнений) к алгебраическим уравнениям, составленным относительно комплексов тока и ЭДС.
Например ,
Для схемы:
или
,
т. к. амплитуда действующего напряжения на , то знак говорит о том, что опережает на 90°.
Для емкости — напряжение отстает от тока на 90°.
Если – комплексная амплитуда действующей ЭДС, то
и ,
т. о.умножение на равносильно повороту вектора на 90°, а на — на “-90°”.
Три формы записи комплексных чисел:
— алгебраическая форма,
— показательная форма,
— тригонометрическая.
Операции с комплексными числами
Сложение и вычитание комплексных чисел производится в алгебраической форме.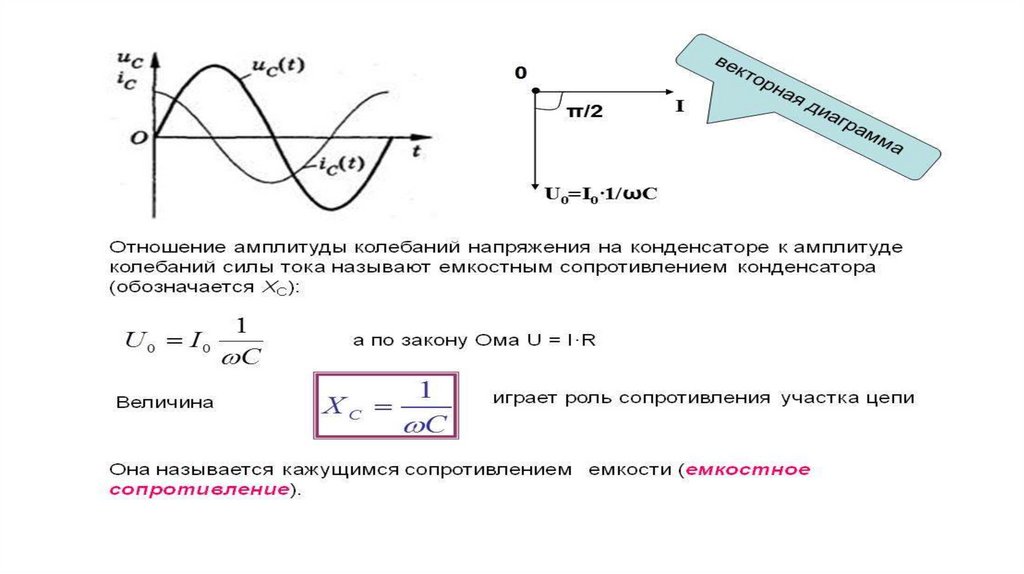
.
Деление и умножение производится в показательной форме:
;.
,
где , а .
Катушка индуктивности
Катушка индуктивности, как показано на рис. 4.11, представляет собой простомоток провода. Условное обозначение катушки индуктивности показано на рис. 4.12. В отличие от конденсатора, который препятствует изменению приложенного к нему напряжения, катушка индуктивности препятствует изменению протекающего через нее тока. Иными словами,Рис. 4.12. Условное обозначение катушки индуктивности. Рис. 4.13
если ток, подаваемый в схему, которая содержит катушку, резко увеличить, то ток в схеме будет нарастать плавно до достижения своего максимального значения.
Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L, единицей ее измерения является генри (Гн).
Постоянная времени RС-цепи
На рис. 4.13 последовательная цепочка из конденсатора и резистора соединяется через ключ с источником питания. Когда ключ находится в положении 1, конденсатор постепенно заряжается через сопротивление, пока напряжение на нем не достигнет уровня Е т. е. ЭДС или напряжения источника питания.
Процесс заряда конденсатора показан на рис. 4.14(а) экспоненциальной кривой. Время, за которое напряжение на конденсаторе достигает значения 0,63 от максимума, т. е. в данном случае 0,63Е, называется постоянной времени контура или цепи.
Вернемся к рис. 4.13. Если ключ установить в положение 2, конденсатор будет сохранять запасенную энергию. При переведении ключа в положение3 конденсатор начинает разряжаться на землю через резистор R, и напряжение на нем постепенно падает до нуля. Процесс разряда конденсаторапоказан на рис. 4.14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения.
Рис. 4.14. Кривые заряда (а) и разряда (б) конденсатора, где t — постоянная времени.
Как для случая заряда, так и для случая разряда конденсатора через резистор R постоянная времени цепи выражается формулой
где t — постоянная времени в секундах, С — емкость в фарадах, R — сопротивление, выраженное в омах.
Например, для случая С = 10мкФ и R= 10 кОм постоянная времени цепи равна
На рис. 4.15 изображены графики процессов заряда для цепей с малой и с большой постоянной времени.
Рис. 4.15. Процессы заряда для цепей с малой и с большой постоянной времени.
Постоянная времени RL-цепи
Рассмотрим схему, изображенную на рис. 4.16. Катушка индуктивности L соединена последовательно с резистором R, имеющим сопротивление 1 кОм. В момент замыкания ключа S ток в цепи равен нулю, хотя под действиемЭДС источника он, казалось бы, должен резко увеличиться. Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе R станет равным приложенному напряжению Е. Установившееся значение тока равно
Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе R станет равным приложенному напряжению Е. Установившееся значение тока равно
E/R = 20 В/1 кОм = 20 мА.
Скорость изменения тока в цепи зависит от конкретных значений R и L. Время, необходимое для того, чтобы сила тока достигла значения, равного 0,63 от его максимальной величины, носит название постоянной времени цепи. Постоянная времени вычисляется по формуле L/R где L выражается в генри, а R — в омах. В этом случае постоянная времени получается в секундах. Используя значения L и R, указанные на рисунке, получаем
Следует заметить, что, чем больше R, тем меньше L/R и тем быстрее изменяется ток в цепи.
Рис. 4.16.
Рис. 4.17. Экспоненциальное увеличение тока, протекающего через катушку индуктивности.
Сопротивление по постоянному току
Катушка индуктивности, включенная в цепь, не препятствует протеканию постоянного тока, если, конечно, но принимать во внимание очень малое сопротивление провода, из которого она сделана. Следовательно, катушка индуктивности имеет нулевое или очень малое сопротивление и может рассматриваться в цепи постоянного тока как цепь короткого замыкания. Конденсатор же в связи с наличием в нем изолирующего диэлектрика имеет бесконечное или очень большое сопротивление и может рассматриваться в цепи постоянного тока как разрыв.
Векторное представление
Сигнал синусоидальной формы может быть представлен в виде вектора ОА, вращающегося против часовой стрелки с угловой скоростью ω= 2πf, где f – частота сигнала (рис.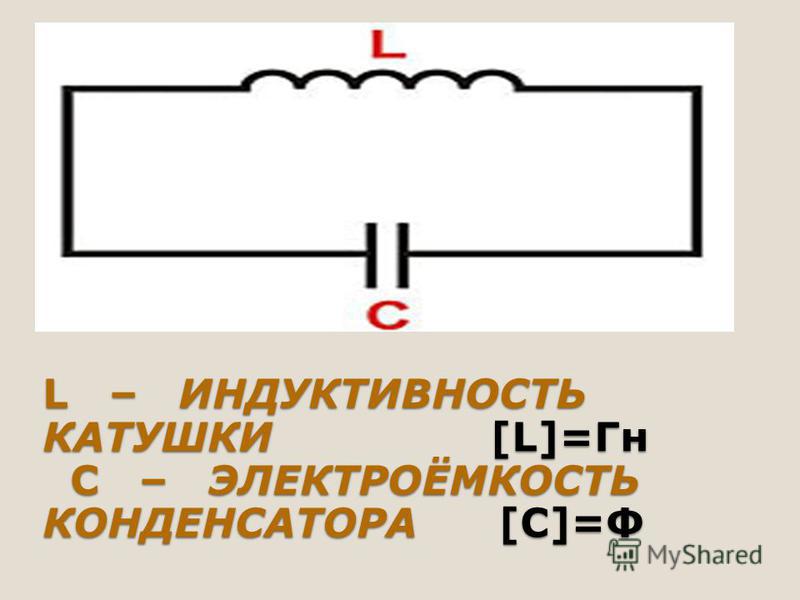 4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) соответствует одному полному периоду. Половина оборота (180°, или π) соответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).
4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) соответствует одному полному периоду. Половина оборота (180°, или π) соответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).
Теперь рассмотрим два синусоидальных сигнала, представленных на рис. 4.19(а) векторами ОА и ОВ соответственно. Если оба сигнала имеют одинаковые частоты, то векторы ОА и ОВ будут вращаться с одинаковой угловой скоростью ω= 2πf. Это означает, что угол между этими векторами
Рис. 4.18. Векторное представление синусоидального сигнала.
Рис. 4.19. Разность фаз. Вектор ОА опережает вектор ОВ
Разность фаз. Вектор ОА опережает вектор ОВ
(или вектор ОВ отстает от вектора ОА) на угол θ.
изменяться не будет. Говорят, что вектор ОА опережает вектор ОВ на угол θ, а вектор ОВ отстает от вектора ОА на угол в. На рис. 4.19(б) эти сигналы развернуты во времени.
Если оба этих синусоидальных сигнала сложить, то в результате получим другой синусоидальный сигнал, имеющий ту же частоту f, но другую амплитуду. Результирующий сигнал может быть представлен вектором ОТ, который, как показано на рис. 4.19(в), является векторной суммой векторов ОА и ОВ. Вектор ОТ опережает вектор ОВ на угол α и отстает от вектора ОА на угол γ. Дальше вы увидите, что векторное представление является весьма удобным приемом при анализе и расчете цепей переменного тока.
В этом видео рассказывается о катушке индуктивности:
Добавить комментарий
Немного теорииКак вы таки уже догадались
– 1-катушка, 2-пуля. Основная мысль работы гауссгана: На катушку подается короткий импульс тока. За этот импульс катушка успевает «всасать» с помощью ЭМ-поля в себя пулю, дав ей некоторую скорость. Когда пуля находится внутри катушки – импульс тока кончается, катушка перестает взаимодействовать на снаряд и он преспокой но летит дальше с некоторой скоростью. Вот мы и ускорили пулю)) Для создания мощного электрического импульса в катушке используются электролитические конденсаторы, которые разряжаются на катушку. Получаем вот такую электрическую схему: Рассмотрим работу схемы:
Рассмотрим разряд конденсатора на катушку подробнее: Схема:
Графики: Соединение конденсатора с
катушкой наз-ют колебательным контуром. Как таки ви уже догадались
– при разряде конденсатора на катушку в нем возникают
колебания. Энергия, первоначально запасенная в конденсаторе, переходит
в катушку, потом из катушки в конденсатор, из конденсатора в катушку и
т д. И колебались бы они так веки вечные, если бы не активное
сопротивление
(активное сопротивление – сопротивление, которое встречает
электричество при прохождении через проводник в связи с торможением
электронов об атомы проводника)
контура, которое на каждом переходе энергии пожирает ее, и колебания
через некоторое время затухают. Разберемся, в каком виде хранят энергию конденсатор и катушка. Конденсатор.Энергия конденсатора равна Ec=U2*С\2, Где:
Для простоты я использую формулу Ec=U2*C\2.000.000 Где:
Т. Е. энергия в конденсаторе хранится в виде напряжения. То бишь, зарядил мы конденсатор – он лежит себе спокойно, и хранит в себе некоторую энергию. (Если быть точнее, энергия в конденсаторе хранится в виде электрического поля (отличайте его от магнитного поля), которое зависит от напряжения) Часто энергию конденсатора
сравнивают с потенциальной энергией в механике. Обычные значения энергии конденсаторов в гауссе на одну ступень – 30..150Дж (естественно, это я чисто условно – может быть и побольше и поменьше) Обыденные значения напряжения на конденсаторе в гауссе – 200-450В Катушка.Энергия катушки равна El=I2*L\2 Где:
Энергия в катушке запасается в
виде магнитного поля
вокруг нее, которое (магнитное поле) зависит и прямопропорционально от тока,
через катушку протекающего. Аналогия энергии магнитного
поля в механике – кинетическая энергия, равная mv2/2
(m — масса v – скорость тела), эта формула очень похожа на
формулу энергии катушки – скорость это как бы ток, а масса
– индуктивность. А напряжение — это сила взаимодействия
движущегося тела на другие предметы. Например, летит кирпич со
скоростью 10м\с. Если этот кирпич мы столкнем с монолитной стальной
стеной, то сила взаимодействия кирпича и стены будет большой, зато
время действия этой силы будет очень мало. Переходя в электричество это
равносильно очень большому выбросу напряжения (который нахрен пробьет
изоляцию) за очень короткое время, когда мы «остановим
ток», т е отключим катушку в момент прохода по ней большого
тока. А теперь столкнем кирпич с чем-нибудь мягким, например с песком.
Тогда сила взаимодействия будет намного меньше, но и длиться
взаимодействие будет дольше. Ну-с, начнем таки наконец-то разбирать сам разряд. Посмотрите на графеги. Они показывают напряжение на конденсаторе и ток через катушку – от этих величин соответственно и зависит энергия на конденсаторе\катушке в данный момент
|
Индуктор против конденсатора
В некоторых ситуациях катушки индуктивности и конденсаторы могут заменять друг друга. В других они не могут. Конечно, они никогда не заменяют напрямую . Это означает, что некоторые схемы могут быть слегка изменены, так что вместо конденсатора используется индуктор, или наоборот, для достижения той же цели. Некоторые схемы не могут.
Индуктор хранит не заряд в своем магнитном поле, а энергию. Когда магнитное поле может разрушаться, индуктор самопроизвольно генерирует напряжение. Напряжение обычно намного выше, чем любое напряжение, которое ранее подавалось на индуктор. Конденсатор никогда не будет показывать напряжение, которое больше, чем то, что было приложено к нему. Так, например, конденсатор нельзя использовать для создания катушки зажигания для бензинового двигателя.
Напряжение обычно намного выше, чем любое напряжение, которое ранее подавалось на индуктор. Конденсатор никогда не будет показывать напряжение, которое больше, чем то, что было приложено к нему. Так, например, конденсатор нельзя использовать для создания катушки зажигания для бензинового двигателя.
Последовательный конденсатор в некотором смысле похож на параллельный индуктор. Оба подхода могут создать фильтр с одинаковой частотной характеристикой. Однако эффекты загрузки этих цепей не одинаковы. Конденсатор последовательно блокирует постоянный ток, и поэтому для источника постоянного тока он выглядит как бесконечный импеданс: максимально возможная нагрузка. Параллельный индуктор — это полная противоположность: короткое замыкание. Эти два устройства выглядят одинаково только с точки зрения нагрузочного устройства: оно видит сигнал, прошедший фильтрацию верхних частот и не имеющий постоянного тока. Но DC не удаляется таким же образом. Блокировка сигнала с открытой нагрузкой — это не то же самое, что замыкание сигнала на землю.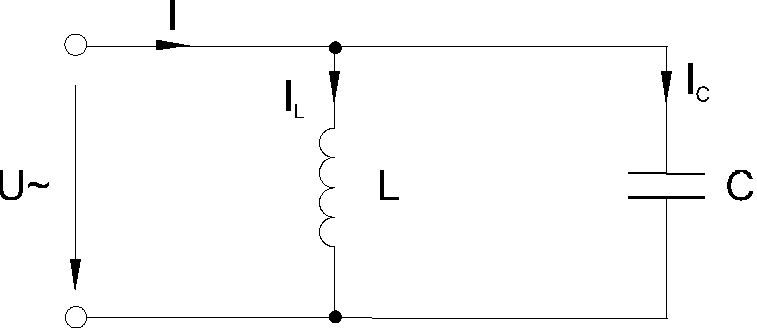
Аналогично, последовательно соединенные катушки индуктивности аналогичны параллельно подключенным конденсаторам, но, опять же, эффект нагрузки не одинаков. Мы можем использовать конденсатор, чтобы предотвратить попадание переменного тока или переменного тока выше определенных частот в цепь путем шунтирования этих сигналов на возврат. Иногда это приемлемо, например, при блокировке РЧ-шума от входа в устройство. В некоторых других случаях шунтирование переменного тока на землю может создать неприемлемую нагрузку на источник этого сигнала. Индуктор может блокировать переменный ток, создавая высокий импеданс против него.
Таким образом, даже в цепях, где мы можем потенциально заменить параллельные индукторы последовательными конденсаторами и наоборот, учет различий в нагрузке может потребовать от нас выбора одного или другого.
Основное различие между конденсатором и индуктором
Конденсатор и индуктор являются электрическими компонентами, используемыми для противодействия изменениям тока в электрических и электронных цепях.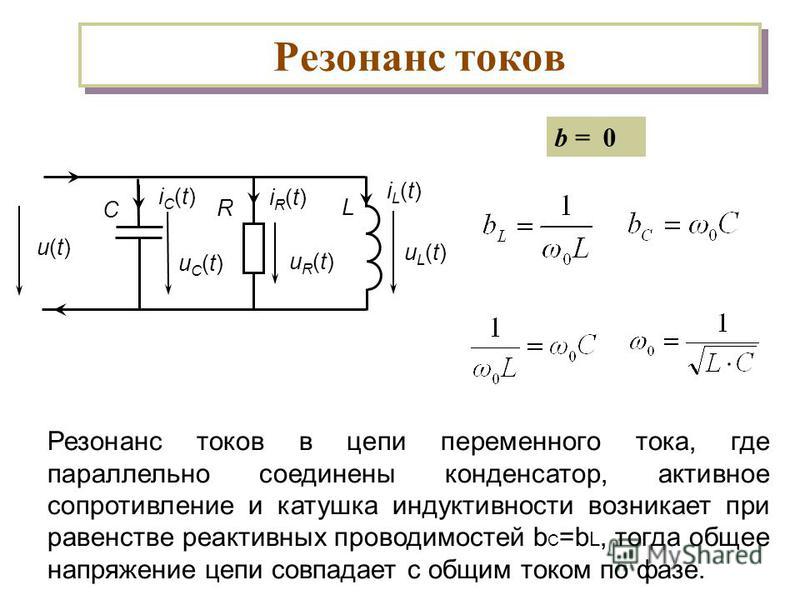 Эти компоненты представляют собой пассивные элементы, которые получают питание от накопителя, цепи и затем разряжаются. Оба компонента широко используются в системах переменного тока (AC), а также в приложениях для фильтрации сигналов. Основное различие между конденсатором и индуктором заключается в том, что индуктор используется для хранения энергии в форме магнитного поля, тогда как конденсатор хранит энергию в форме электрического поля.В этой статье дается обзор того, что такое конденсатор, катушка индуктивности, различия, типы, использование и его характеристики.
Эти компоненты представляют собой пассивные элементы, которые получают питание от накопителя, цепи и затем разряжаются. Оба компонента широко используются в системах переменного тока (AC), а также в приложениях для фильтрации сигналов. Основное различие между конденсатором и индуктором заключается в том, что индуктор используется для хранения энергии в форме магнитного поля, тогда как конденсатор хранит энергию в форме электрического поля.В этой статье дается обзор того, что такое конденсатор, катушка индуктивности, различия, типы, использование и его характеристики.
Что такое конденсатор и индуктор?
Конденсатор — это электрический компонент, состоящий из двух проводников, разделенных изолятором. Когда на оба вывода подается разность потенциалов, формируется электрическое поле и накапливаются электрические заряды. Судя по характеристикам, конденсатор широко применяется для построения электронных схем.В качестве электрического вещества можно использовать любое непроводящее вещество. Но некоторые из предпочтительных диэлектрических материалов — тефлон, майлар, фарфор, слюда и целлюлоза. Конденсатор определяется на основе выбранного материала, например электрода или диэлектрика. Диэлектрический материал в основном используется для хранения электрической энергии. Емкость конденсатора может определяться размером клемм, расстоянием между двумя клеммами и типом используемого материала. Пожалуйста, перейдите по ссылке ниже, чтобы узнать больше о: Типах конденсаторов и их применении.
Но некоторые из предпочтительных диэлектрических материалов — тефлон, майлар, фарфор, слюда и целлюлоза. Конденсатор определяется на основе выбранного материала, например электрода или диэлектрика. Диэлектрический материал в основном используется для хранения электрической энергии. Емкость конденсатора может определяться размером клемм, расстоянием между двумя клеммами и типом используемого материала. Пожалуйста, перейдите по ссылке ниже, чтобы узнать больше о: Типах конденсаторов и их применении.
Конденсатор
Катушка индуктивности или дроссель — это устройство с двумя выводами, которое используется для построения различных цепей. Основная функция индуктора — накопление энергии в магнитном поле. Он состоит из проволоки, обычно скрученной в катушку. Когда через эту катушку протекает ток, он временно сохраняет его в катушке. Абсолютный индуктор эквивалентен короткому замыканию для постоянного тока и предоставляет силу, противоположную переменному току, которая зависит от частоты тока.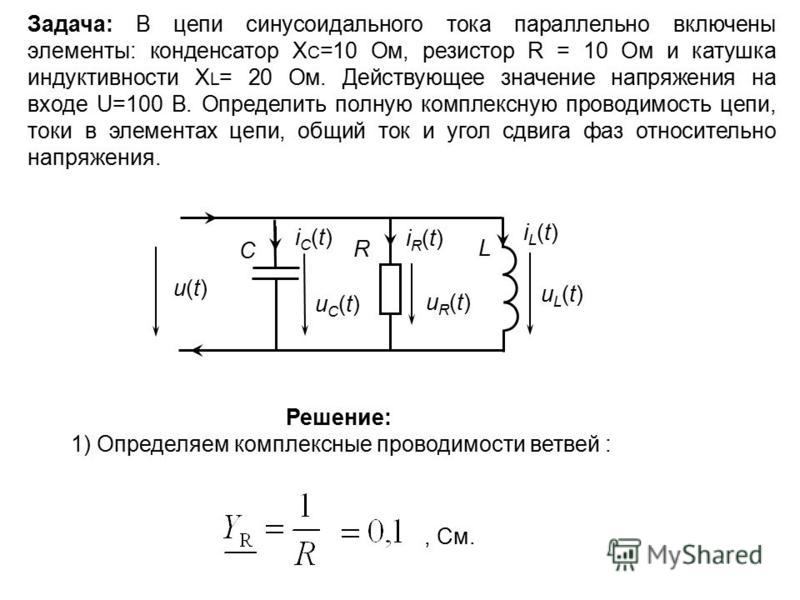 Противодействие протеканию тока в катушке индуктивности связано с частотой протекающего через нее тока. Иногда эти устройства обозначаются как «катушки», потому что большая часть физической конструкции индуктора спроектирована с использованием намотанных секций провода. Пожалуйста, перейдите по ссылке ниже, чтобы узнать больше о: Знайте все о индукторах и расчетах индуктивности.
Противодействие протеканию тока в катушке индуктивности связано с частотой протекающего через нее тока. Иногда эти устройства обозначаются как «катушки», потому что большая часть физической конструкции индуктора спроектирована с использованием намотанных секций провода. Пожалуйста, перейдите по ссылке ниже, чтобы узнать больше о: Знайте все о индукторах и расчетах индуктивности.
Разница между конденсатором и индуктором
Конденсатор использует
- Высоковольтный электролитический конденсатор используется в источниках питания.
- Осевой электролитический конденсатор используется с меньшим напряжением и меньшим размером для общего назначения, где необходимы принципы большой емкости.
- Высоковольтный дисковый керамический конденсатор отличается небольшими размерами, величиной емкости и отличными характеристиками допусков.
- Конденсатор из металлизированного полипропилена имеет небольшой размер, рассчитанный на значения до 2 мкФ и хорошую надежность.

- Конденсатор для поверхностного монтажа имеет относительно высокую емкость для размера, достигаемого несколькими слоями.Фактически, множество конденсаторов параллельно.
Использует индуктор
- Катушки индуктивности широко используются в приложениях переменного тока, таких как телевидение, радио и т. Д.
- Дроссели — Основное свойство индуктора используется в цепях питания, где источник питания переменного тока желательно заменить на источник постоянного тока. .
- Накопитель энергии — используется для создания искры, которая зажигает бензин в автомобильных двигателях.
- Трансформаторы — индукторы с распределительной магнитной полосой могут быть объединены в трансформатор.
Единица измерения
- Емкость измеряется в фарадах, обозначенных буквой F. Она равна и идентична [Ампер-секунда вольт]. Поскольку ампер — это [кулоновская секунда], мы также можем сказать, что F = CV
- Индуктивность — это величина индуктивности, и она измеряется в Генри.
 Фактически, это единица измерения индуктивности в системе СИ, равная вольт-секундному амперу.
Фактически, это единица измерения индуктивности в системе СИ, равная вольт-секундному амперу.
Типы конденсаторов и индукторов
Основные типы конденсаторов делятся на три типа: керамические, танталовые и электролитические.
Типы конденсаторовОсновные типы индукторов подразделяются на три типа, а именно: многослойные индукторы, связанные индукторы, формованные индукторы и индукторы с керамическим сердечником.
Типы индукторов
Взаимосвязь между напряжением и напряжением в линейной цепи
- In конденсатор, напряжение изолирует за током π2
- В катушке индуктивности напряжение изолирует за напряжением π2
Короткое замыкание
- Для переменного тока конденсатор выполняет функцию короткого замыкания.
- Индуктор аналогичен короткому замыканию на постоянный ток.
Характеристики конденсатора и индуктора
- Конденсаторы, соединенные параллельно, объединяются как резисторы последовательно
- Конденсаторы, соединенные последовательно, объединяются, как резисторы параллельно последовательно
Таким образом, все дело в разнице между конденсатором и катушкой индуктивности.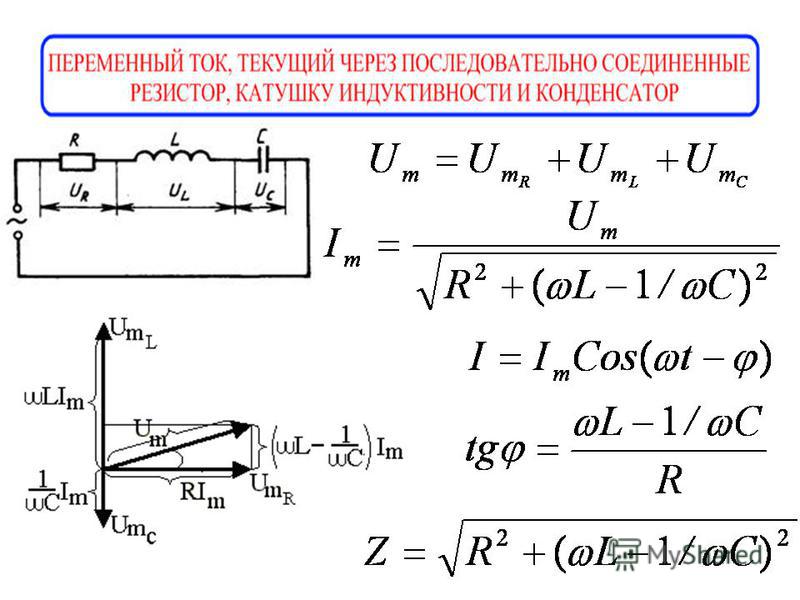 Мы надеемся, что вы лучше поняли эту статью. Кроме того, любые вопросы относительно этой концепции или проектов в области электрики и электроники, пожалуйста, дайте свои ценные предложения, комментируя в разделе комментариев ниже. Вот вам вопрос, , каковы основные функции конденсатора и катушки индуктивности ?
Мы надеемся, что вы лучше поняли эту статью. Кроме того, любые вопросы относительно этой концепции или проектов в области электрики и электроники, пожалуйста, дайте свои ценные предложения, комментируя в разделе комментариев ниже. Вот вам вопрос, , каковы основные функции конденсатора и катушки индуктивности ?
Идите вперед, подключите катушку индуктивности и конденсатор и посмотрите, что произойдет
Что происходит, когда вы подключаете катушку индуктивности и конденсатор в цепь? Что-то классное — и действительно важное.
Что такое индуктор?
Вы можете изготавливать всевозможные типы индукторов, но наиболее распространенным типом является цилиндрическая катушка с проволокой — соленоид.
Когда ток проходит через первый контур, он создает магнитное поле, которое проходит через другие контуры. Магнитные поля на самом деле ничего не делают, если их величина не меняется. Изменяющееся магнитное поле создаст электрическое поле в других контурах. Направление этого электрического поля вызывает изменение электрического потенциала, действующего как батарея.
Направление этого электрического поля вызывает изменение электрического потенциала, действующего как батарея.
В конце концов, у нас есть устройство, разность потенциалов которого пропорциональна скорости изменения тока во времени (поскольку ток создает магнитное поле). Это можно записать как:
В этом уравнении следует указать на два момента. Во-первых, L — это индуктивность. Это зависит только от геометрии соленоида (или любой другой формы), и его значение измеряется в единицах Генри. Во-вторых, есть отрицательный знак. Это означает, что изменение потенциала на катушке индуктивности препятствует изменению тока.
Как индуктор ведет себя в цепи? Если у вас постоянный ток, то нет никаких изменений (постоянный ток) и, следовательно, нет разницы потенциалов на катушке индуктивности — он действует так, как будто ее даже нет. Если есть ток высокой частоты (цепь переменного тока), то на индукторе будет большая разность потенциалов.
Что такое конденсатор?
Опять же, существует множество различных конфигураций конденсатора.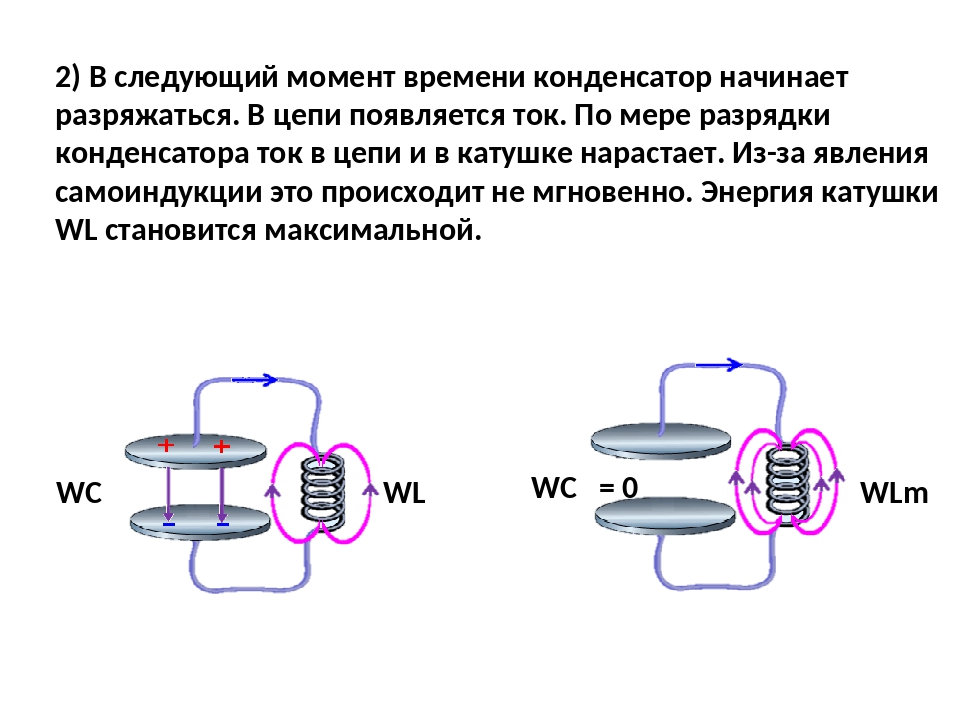 В простейшей форме используются две параллельные проводящие пластины с электрическим зарядом на каждой пластине (но с нулевым чистым зарядом).
В простейшей форме используются две параллельные проводящие пластины с электрическим зарядом на каждой пластине (но с нулевым чистым зарядом).
Электрический заряд на этих пластинах создает электрическое поле внутри конденсатора. Поскольку существует электрическое поле, также должно происходить изменение электрического потенциала на пластинах. Величина этой разности потенциалов зависит от количества заряда. Разность потенциалов на конденсаторе может быть записана как:
Здесь C — значение емкости в единицах Фарад — это также зависит только от физической конфигурации устройства.
Если в конденсатор идет ток, величина заряда на пластинах изменится. Если есть постоянный (или низкочастотный) ток, этот ток будет продолжать добавлять заряд к пластинам для увеличения электрического потенциала, так что со временем этот потенциал в конечном итоге будет действовать как разомкнутая цепь с напряжением конденсатора, равным напряжению батареи ( или блок питания). Если у вас высокочастотный ток, заряд будет как добавляться, так и сниматься с пластин конденсатора без накопления заряда, и конденсатор будет действовать так, как будто его даже нет.
Если у вас высокочастотный ток, заряд будет как добавляться, так и сниматься с пластин конденсатора без накопления заряда, и конденсатор будет действовать так, как будто его даже нет.
Что происходит, когда вы соединяете конденсатор и катушку индуктивности?
Предположим, мы начинаем с заряженного конденсатора и подключаем его к катушке индуктивности (в цепи нет сопротивления, потому что я использую идеальные физические провода). Подумайте о том моменте, когда эти двое связаны. Предположим, есть переключатель, тогда я могу нарисовать следующие схемы.
Вот что происходит. Во-первых, нет тока (поскольку переключатель разомкнут). Когда переключатель замкнут, может возникнуть ток, и без сопротивления этот ток будет подскакивать до бесконечности.Однако такое большое увеличение тока означает, что на индукторе произойдет изменение электрического потенциала. В какой-то момент изменение потенциала на катушке индуктивности будет больше, чем на конденсаторе (поскольку конденсатор теряет заряд с течением тока), а затем ток изменит направление и зарядит конденсатор обратно. Процесс повторяется — бесконечно, поскольку нет сопротивления.
Процесс повторяется — бесконечно, поскольку нет сопротивления.
Моделирование LC-цепи.
Это называется LC-цепью, потому что в ней есть катушка индуктивности (L) и конденсатор (C) — я думаю, это очевидно.Изменение электрического потенциала вокруг всей цепи должно быть нулевым (потому что это петля), чтобы я мог написать:
Индуктор против конденсатора — Электротехника
В некоторых ситуациях катушки индуктивности и конденсаторы могут заменять друг друга. В других случаях они не могут. Конечно, они никогда не заменяют напрямую . Это означает, что некоторые схемы можно немного изменить, чтобы вместо конденсатора использовалась катушка индуктивности или наоборот для достижения той же цели.Некоторые схемы не могут.
Катушка индуктивности накапливает в своем магнитном поле не заряд , а скорее энергию. Когда магнитному полю позволяют схлопнуться, индуктор самопроизвольно генерирует напряжение. Напряжение обычно намного выше, чем любое напряжение, которое ранее было приложено к катушке индуктивности. Конденсатор никогда не будет показывать напряжение, превышающее приложенное к нему. Так, например, конденсатор нельзя использовать для сборки катушки зажигания бензинового двигателя.
Конденсатор никогда не будет показывать напряжение, превышающее приложенное к нему. Так, например, конденсатор нельзя использовать для сборки катушки зажигания бензинового двигателя.
Конденсатор, включенный последовательно, в некотором смысле похож на индуктивность, включенную параллельно. Оба подхода позволяют создать фильтр с одинаковой частотной характеристикой. Однако эффекты нагрузки этих схем не одинаковы. Последовательный конденсатор блокирует постоянный ток, и поэтому для источника постоянного тока это выглядит как бесконечное сопротивление: самая легкая из возможных нагрузок. Параллельное включение индуктора — это полная противоположность: короткое замыкание. Они выглядят одинаково только с точки зрения устройства нагрузки: оно видит сигнал, прошедший высокочастотную фильтрацию и не содержащий постоянного тока.Но DC не снимается таким же образом. Блокировка сигнала при разомкнутой нагрузке — это не то же самое, что замыкание сигнала на землю.
Аналогичным образом, последовательно включенный индуктор аналогичен параллельному конденсатору, но, опять же, эффект нагрузки не такой же. Мы можем использовать конденсатор, чтобы предотвратить попадание переменного тока или переменного тока выше определенных частот в цепь, путем шунтирования этих сигналов на возврат. Иногда это приемлемо, например, при блокировке проникновения радиочастотного шума в устройство. В некоторых других случаях шунтирование переменного тока на землю может создать недопустимую нагрузку на источник этого сигнала.Катушка индуктивности может блокировать переменный ток, создавая против нее высокое сопротивление.
Мы можем использовать конденсатор, чтобы предотвратить попадание переменного тока или переменного тока выше определенных частот в цепь, путем шунтирования этих сигналов на возврат. Иногда это приемлемо, например, при блокировке проникновения радиочастотного шума в устройство. В некоторых других случаях шунтирование переменного тока на землю может создать недопустимую нагрузку на источник этого сигнала.Катушка индуктивности может блокировать переменный ток, создавая против нее высокое сопротивление.
Таким образом, даже в схемах, где мы потенциально можем заменить параллельные катушки индуктивности последовательными конденсаторами и наоборот, учет различий в нагрузке может потребовать от нас выбора того или другого.
Какой конденсатор приобрести для катушки реле?
Какой конденсатор приобрести для катушки реле? — Обмен электротехнического стекаСеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Electrical Engineering Stack Exchange — это сайт вопросов и ответов для профессионалов в области электроники и электротехники, студентов и энтузиастов.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 4к раз
\ $ \ begingroup \ $Я ссылаюсь на схему из этой ветки: Какая польза от конденсатора в этой схеме реле?, Которая также показана ниже.Если бы я использовал конденсатор для своей катушки реле (12 В с фиксацией), в которой уже установлен обратный диод, на какое номинальное напряжение , емкость и типа (например, электролитический, керамический) мне следует обратить внимание? Кроме того, если бы я использовал несколько конденсаторов для своей установки, можно ли было бы комбинировать разные типы конденсаторов (например, электролитические, керамические) или не рекомендовать?
Создан 24 фев.
Craver2000Craver20005311 серебряный знак66 бронзовых знаков
\ $ \ endgroup \ $ 0 \ $ \ begingroup \ $Параллельное соединение катушки с конденсатором может немного усложнить работу драйвера (что может привести к его выходу из строя) и может вызвать кратковременный провал в питании 24 В, что может вызвать сбои.Если драйвер относительно медленный или ток ограничен, может быть полезно уменьшить электромагнитные помехи от катушки, однако контакты обычно преобладают над шумом, и в любом случае схема драйвера, вероятно, определит, насколько большой вы можете безопасно сделать конденсатор.
Скорее всего, разумным значением будет несколько нФ, и лучше всего будет использовать керамический конденсатор с соответствующим номинальным напряжением.
Создан 24 фев.
Спехро Пефани291k1212 золотых знаков240240 серебряных знаков607607 бронзовых знаков
\ $ \ endgroup \ $ 2 \ $ \ begingroup \ $Я настоятельно рекомендую вам не использовать конденсатор в этой системе, это не переменный ток, и вам не нужно компенсировать реактивный ток катушки.
Напротив, он создает проблемы, он создает пик тока, который может вызвать нежелательные всплески в линии питания, он нагружает драйвер пиковым током, он замедляет рост напряжения, отражаясь в более слабом соединении во время приближения контактов. Никто не использует эти конденсаторы в системах постоянного тока
Рассел МакМахон ♦13k1515 золотых знаков187187 серебряных знаков347347 бронзовых знаков
Создан 02 июля ’20 в 22: 002020-07-02 22:00
\ $ \ endgroup \ $ 1 \ $ \ begingroup \ $Большинство людей им не пользуются.
Диод будет улавливать большую часть энергии при выключении реле, поэтому конденсатор нужен только на короткое время, прежде чем диод начнет проводить ток. Если это проблема, используйте более медленный переключатель.
Создан 24 фев.
Ясен22.7k11 золотых знаков2424 серебряных знака4444 бронзовых знака
\ $ \ endgroup \ $ 1 \ $ \ begingroup \ $Конденсатор не нужен.Диод тоже может не понадобиться, даже если в реле его не было. Драйверы, которые я использовал в прошлом, имели встроенный диод. См. ULN5801 и т. Д.
Создан 24 фев.
Роберт ЭндлРоберт Эндл2,1139 серебряных знаков1111 бронзовых знаков
\ $ \ endgroup \ $ 4 Электротехнический стек Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Может ли комбинация индуктивности / конденсатора / резистора излучать ту же частоту, что и данный кварцевый генератор?
Генератор — это усилитель с положительной обратной связью и «элемент определения частоты».Это может быть кристалл или резонансный «резервуар» ЖК. Генератор LC обычно недостаточно стабилен для большинства приложений. Вот что обычно происходит, когда вы создаете свой первый LC-генератор.
Во-первых, механические свойства настраивающего элемента (обычно переменного конденсатора) таковы, что после его настройки он слегка «расслабляется», вызывая изменение частоты. Таким образом, вы в конечном итоге настраиваете его выше желаемой частоты и позволяете ему «стабилизироваться» обратно на целевую частоту.
Затем вы обнаружите, что, когда вы убираете руку от цепи, частота снова изменяется.Паразитная емкость, добавляемая вашим телом, влияет на частоту. В конечном итоге вы перемещаете руку в сторону схемы или от нее, чтобы поддерживать частоту. Затем вы обнаруживаете, что даже если вы держите руку неподвижно, частота дрейфует, и вам придется снова двигать рукой, чтобы исправить это. Этот дрейф может быть вызван изменением температуры, напряжения или другими механическими изменениями.
Итак, ответ — «да», но со временем вы понимаете, что жизнь могла бы быть намного проще, если бы вы использовали кристалл.Кристаллы не идеальны, но они на порядок лучше. Им также требуется меньше энергии для поддержания колебаний. Можно построить хорошие генераторы LC; они будут иметь хорошо отрегулированный источник напряжения, жестко смонтированные компоненты и металлический экран, закрывающий цепь. Также будет температурная компенсация (или температурный контроль).
Были замечания по поводу умножения частоты. Этого можно добиться, внося искажения в генератор, который производит гармоники.Затем еще один контур LC-резервуара настраивается на гармонику исходной частоты. Другой усилитель может быть использован для усиления результирующего сигнала. Так это делалось во времена чисто аналоговой схемотехники.
Разница между конденсатором и индуктором
Основные различия между конденсаторами и индукторами обсуждаются с учетом нескольких характеристик, таких как протекание тока, расчет сохраненной энергии, основное определение, их поведение на диаграммах постоянного и переменного тока, их единицы, различие в формах конденсаторов и катушек индуктивности, их устойчивость к различным модификациям в приложениях и соотношение между током и напряжением.
Независимо от различий между конденсатором и индуктором, два наиболее широко используемых электронных прибора — это индукторы и конденсаторы. Оба предназначены для экономии энергии и служат в качестве основных энергетических ресурсов. Однако, если вы хотите узнать, что отличает их друг от друга, этот пост представляет вам четкое сравнение между ними, чтобы полностью объяснить конденсатор и индуктор.
Введение в конденсатор и индуктор
Конденсатор и катушка индуктивности — это особые виды пассивных компонентов, которые сохраняют и отправляют энергию в цепь, но не используют ее.Оба прибора в основном используются в определенных приложениях, связанных с установками переменного тока, в частности, при фильтрации сигналов. Существенная разница между конденсатором и катушкой индуктивности заключается в том, что конденсатор связан с dV / dt (резкое изменение напряжения), а индуктор связан с dI / dt (резкое изменение тока).
Кроме того, конденсаторы экономят энергию на основе электрического поля (1 / 2CV 2 ), а катушки индуктивности накапливают энергию на основе магнитного поля (1 / 2LI 2 ).Этот пост представлен, чтобы показать фундаментальные различия между катушками индуктивности и конденсаторами в зависимости от единиц, типов, приложений и т. Д.
Конденсатор против индуктора (Ссылка: electronicsb2b.com )
Конденсатор и индуктор — это электрические приборы, используемые для обнаружения изменений тока в электрических цепях. Эти устройства представляют собой пассивные элементы, которые используют энергию системы, а затем разряжают ее. Оба прибора обычно используются для обработки переменного тока и сигналов.
Основное отличие конденсатора от индуктора заключается в том, что индуктор используется для подачи энергии в зависимости от магнитного поля, в то время как конденсатор работает на основе электрического поля. Эта ссылка представляет важные особенности двух физических эффектов, которые используются в электрических цепях, чтобы наглядно продемонстрировать зависимость конденсатора от индуктора.
Что такое конденсатор и индуктор?
Конденсатор — это электрический прибор, состоящий из двух проводников, покрытых изоляторами.Электрическое поле создается, и электрические заряды сохраняются, когда на оба терминала подается разность потенциалов. Конденсаторы обычно используются для проектирования электронных систем в соответствии с их свойствами.
Что такое конденсатор? (Ссылка: elprocus.com )
Некоторые из обычных диэлектрических материалов, используемых в их конструкции, — это майлар, тефлон, слюда, фарфор и целлюлоза. Конденсатор вводится в соответствии с выбранным материалом, например, диэлектрик или электрод.Диэлектрическое вещество обычно применяется для хранения электроэнергии. Количество конденсатора можно оценить по положению двух выводов, их размеру и типу используемых материалов.
Конденсаторы и емкость
Емкость проявляется везде, где проводящее вещество разделяется изолирующей крышкой. Емкостные форматы позволяют экономить энергию в виде электрического поля; когда емкостная структура моделируется как электрическая секция с определенным значением емкости, она вводится как конденсатор.
Цепь емкости(Ссылка: allaboutcircuits.com )
Мы используем зарядку и разрядку конденсаторов, чтобы определять, соответственно, состояние, в котором прибор получает питание, и состояние, в котором устройство обеспечивает питание. Как показано на рисунке, мы можем заряжать прибор от аккумулятора. Напряжение заставляет ток двигаться, и этот ток обеспечивает электрический заряд конденсатора.
Значение заряда формирует напряжение внутри конденсатора, которое немедленно увеличивается, когда ток в цепи уменьшается.Если конденсатор отключен от источника и подключен к инструменту, например, резистору, он работает как альтернативный источник из-за сохраненной энергии в электрическом поле. Он может преобразовывать накопленное хранилище в полезный заряд или электрический ток.
Напряжение и ток связаны друг с другом, и их поведение можно оценить по кривым на следующем рисунке. Следует учитывать, что ось времени основана на методе «RC»; здесь используется временной коэффициент RC: значение времени, которое связано со значением емкости конденсатора, улучшенным сопротивлением в последовательном соединении.
Диаграмма емкости(Ссылка: allaboutcircuits.com )
Емкость устройства является заметным параметром при проектировании схемы, поскольку она может влиять на скорость изменения напряжения или тока во время процесса зарядки или разрядки. Большая емкость означает, что напряжение в конденсаторе увеличивается слишком медленно, когда он находится в процессе зарядки, и медленно снижается, если он находится на этапе разрядки.
Катушки индуктивности и индуктивность
Если у вас есть некоторая информация об основных понятиях емкости, это в целом может помочь вам понять индуктивность, потому что эти два эффекта очень похожи, даже их можно представить как «равные, но противоположные» явления.Например, конденсатор экономит энергию за счет электрического поля, а индуктор работает в соответствии с магнитным полем.
Катушка индуктивности — это особый дроссель или катушка, имеющая двухконтактную структуру и используемую для построения различных цепей. Основное назначение индуктора — накопление энергии в магнитных полях. Он включает в себя провод, обычно собранный в виде катушки. Если ток движется внутри этой катушки, он может сохраняться в этой катушке.
Идеальный индуктор работает как короткое замыкание, направляя ток и создавая альтернативную силу, зависящую от частоты тока.Состояние протекания тока в катушке индуктивности пропорционально частоте этого тока через нее. Эти инструменты представлены как «Катушки», потому что большая часть их конструкции моделируется на основе сечения провода и катушки. На следующем рисунке четко показана структура силовых линий магнитного поля.
Структура индуктора(Ссылка: allaboutcircuits.com )
Когда конденсатор соединен с источником напряжения, его напряжение может увеличиваться, поэтому его ток постепенно уменьшается; когда индуктор подключен к источнику напряжения, его ток увеличивается, а его напряжение постепенно падает.
Скорость зарядки и разрядки определяется временным коэффициентом RC с конденсатором, но мы используем постоянную времени RL с катушкой индуктивности, а индуктивность (L) может быть улучшена за счет размещения сопротивления в последовательном формате.
Когда индуктивная цепь отключена от источника питания, индуктор обычно может экономить ток. Можно сказать, что конденсаторы устойчивы к изменениям напряжения, а катушки индуктивности — к изменениям тока.
Все проводники, включая контакты и провода компонентов, состоят из индуктивности.Чтобы сформировать индуктор, мы используем специальные методы, которые улучшают магнитное поле и немедленно увеличивают индуктивность. Полный индуктор — это просто скрученный провод.
Разница между конденсатором и индуктором
Чтобы противопоставить конденсатор и индуктивность, мы должны рассмотреть различные аспекты, как указано ниже:
Используется конденсатор
- Конденсаторы с высоковольтным электролитом могут быть использованы в электроэнергетике.
- Осевые электролитические конденсаторы используются в приложениях с низким напряжением и меньшими размерами, где требуются большие значения емкости.
- Дисковые керамические конденсаторы с высоким напряжением, небольшими размерами и особой емкостью подходят для приложений с особыми допусками.
- Конденсаторы из металлизированного полипропилена обладают хорошей надежностью, небольшими размерами и желательны для номиналов до 1 мкФ.
- Конденсаторы для поверхностного монтажа имеют относительно высокие значения, подходящие для различных применений, покрытые несколькими слоями. Они работают как параллельное соединение множества конденсаторов.
Использует индуктор Катушки индуктивности
широко используются в приложениях переменного тока, таких как радио, телевидение и т. Д.
Использование индуктора(Ссылка: elprocus.com )
- Дроссели: Основная особенность индуктора — использование в цепях источника питания, где переменный ток обеспечивает управление питанием, которое может быть изменено на источник постоянного тока.
- Накопитель энергии: используется для создания искры, обеспечивающей возгорание бензина в автоматических двигателях.
- Трансформаторы: Катушки индуктивности с определенным значением магнитного поля могут использоваться для создания трансформатора.
Единица измерения
Стоимость конденсаторов определяется в фарадах, введенных Ф.Его можно оценить на основе ампер в секунду вольт. Поскольку ампер равен кулоновской секунде, можно сказать, что F = CV.
В противном случае индуктивность является значением индуктивности и рассчитывается в Генри (H). Как правило, это единица измерения этого значения в системе СИ, основанная на вольтах в секунду в амперах.
Типы конденсаторов и индукторов
Основные типы конденсаторов делятся на три вида; включая тантал, керамику и электролит.
Типы конденсаторов (Ссылка: elprocus.com )
Основные типы индукторов делятся на четыре типа; включая связанные индукторы, многослойные индукторы, индукторы с керамическим сердечником и формованные индукторы.
Типы индукторов (Ссылка: elprocus.com )
Взаимосвязь между напряжением и напряжением в линейной цепи
- Напряжение отстает от силы тока в конденсаторе на π / 2
- Напряжение сдвигается вперед Ток в катушке индуктивности на π / 2
Короткое замыкание
Конденсатор работает как короткое замыкание для переменного тока, а катушка индуктивности выполняет ту же операцию для приложений постоянного тока.
Характеристики конденсатора и индуктора
- Конденсаторы, расположенные параллельно, работают как резисторы при последовательном расположении.
- Последовательное соединение конденсаторов аналогично параллельному соединению резисторов. Катушки индуктивности
- , включенные последовательно, работают как последовательная конфигурация резисторов.
- Катушки индуктивности в параллельном соединении работают как резисторы в параллельной форме.
В результате, это все важные советы о том, как противопоставить конденсатор и конденсатор.индуктор полностью. Мы надеемся, что вы лучше поняли информацию из этого поста. Следующая диаграмма даст вам краткое сравнение конденсатора и катушки индуктивности в компактной форме.
Сравнительная таблица между конденсатором и индуктором(Ссылка: byjus.com )
Ключевое различие между конденсатором и индуктором
Ключевые отличия для обеспечения полного сравнения проблемы конденсатора и индуктивности заключаются в следующем:
Конденсатор работает аналогично короткому замыканию в системах переменного тока.Индуктор работает в цепях постоянного тока как при коротком замыкании. С другой стороны, конденсаторы работают как разомкнутая цепь в системах постоянного тока в установившемся состоянии, в то время как катушки индуктивности показывают состояние короткого замыкания в установившейся ситуации в цепях постоянного тока.
Энергия, сэкономленная в конденсаторах, оценивается на основе напряжения и формулы 1 / 2CV 2 в соответствии с электрическим полем. В то время как мощность, запасенная в индукторах, может быть рассчитана в соответствии с током, магнитным полем и уравнением 1 / 2LI 2 .Емкость определяется единицей Фарада (F), а индуктивность — единицей Генри (H).
Ток больше напряжения на 90 градусов в системе переменного тока для конденсаторов и отстает от напряжения на 90 o в индукторах. По своей внутренней структуре конденсаторы противостоят изменениям напряжения, а катушки индуктивности — изменениям тока.
Внутри пластин конденсаторов ток не течет, но ток может проходить через катушку в катушках индуктивности. Конденсаторы действуют как специальный изолятор для устройств постоянного тока, в то время как индукторы работают как проводники в цепи постоянного тока.
В системе с катушкой индуктивности, когда она сочетается с последовательным расположением резисторов, величина тока в пусковой части мала, но со временем она будет постепенно увеличиваться. Однако, когда конденсатор объединяется в последовательную конфигурацию с резисторами на схеме постоянного тока, ток сразу становится большим, но позже падает до 0.
цепей переменного тока | Безграничная физика
Индуктивность
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока, например изменением тока в проводнике.
Цели обучения
Опишите свойства индуктора
Основные выводы
Ключевые моменты
- В случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике, называемое самоиндукцией, так и в любых соседних проводниках, называемое взаимной индуктивностью.
- Согласно закону Ленца, изменяющийся электрический ток в цепи с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока.
- Взаимная индуктивность обозначена. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, индуцирует эдс 2 в другом. Мы выражаем это в форме уравнения как [латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]. M то же самое для обратного процесса.
- Самоиндукция — это действие закона индукции Фарадея устройства на самого себя. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока, задаваемой [latex] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ латекс].
- Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.
Ключевые термины
- взаимная индуктивность : Отношение напряжения в цепи к изменению тока в соседней цепи.
- самоиндукция : Отношение напряжения к изменению тока в той же цепи.
- индуктор : Пассивное устройство, которое вводит индуктивность в электрическую цепь.
Индуктивность
ОБЗОР
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. В частности, в случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике (самоиндукция), так и в любых соседних проводниках (взаимная индуктивность). Этот эффект основан на двух фундаментальных физических наблюдениях: во-первых, постоянный ток создает постоянное магнитное поле, а во-вторых, изменяющееся во времени магнитное поле индуцирует напряжение в соседнем проводнике (закон индукции Фарадея).Согласно закону Ленца, изменяющийся электрический ток через цепь с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока (если бы это было не так, можно легко увидеть, что энергия не может быть сохранена, при этом изменяющийся ток усиливает изменение тока. петля положительной обратной связи).
ВЗАИМНАЯ ИНДУКТИВНОСТЬ
Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе.Посмотрите, где простые катушки наводят друг на друга ЭДС.
Взаимная индуктивность в катушках : Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2. (Обратите внимание, что «E2 индуцированная» представляет наведенную ЭДС в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока.Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, индуцирует эдс 2 в другом. Мы выражаем это в форме уравнения как
[латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]
, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Единицы измерения для M : (В · с) / A = Ω · с, который назван генри (H) в честь Джозефа Генри (обнаружил самоиндукцию). То есть 1 H = 1 Ом.
Природа здесь симметрична. Если мы изменим ток I 2 в катушке 2, мы индуцируем ЭДС 1 в катушке 1, что равно
[латекс] \ text {emf} _1 = — \ text {M} \ frac {\ Delta \ text {I} _2} {\ Delta \ text {t}} [/ latex]
, где M то же, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью М.
Большая взаимная индуктивность M может быть или нежелательна. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки против ветра, чтобы нейтрализовать создаваемое магнитное поле.(Видеть ).
Противоточная намотка : Нагревательные катушки электрической сушилки для белья могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.
САМОПРОВОДКА
Самоиндукция, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, и поэтому изменение магнитного потока полностью связано с изменением тока ΔI через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
[латекс] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ latex]
, где L — собственная индуктивность устройства.Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.
.Обозначение индуктора
Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться.Чтобы избежать этого эффекта, необходимо добиться небольшого L, например, за счет встречной намотки катушек, как в.
СОЛЕНОИДЫ
Можно рассчитать L для катушки индуктивности, учитывая ее геометрию (размер и форму) и зная создаваемое ею магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Индуктивность L обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму.{2} \ text {A}} {\ mathscr {\ text {l}}} [/ latex] (соленоид).
Поучительно вывести это уравнение, но мы оставляем его в качестве упражнения для читателя. (Подсказка: начните с того, что отметьте, что индуцированная ЭДС определяется законом индукции Фарадея как ЭДС = −N (Δ / Δt), а по определению самоиндукции задается как ЭДС = −L (ΔI // Δt) и приравняем эти два выражения). Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением. {\ frac {- \ text {t }} {\ tau}} [/ латекс].В первом временном интервале τ ток падает в раз [латекс] \ frac {1} {\ text {e}} [/ latex] до [latex] 0,368 \ cdot \ text {I} _0 [/ latex].
Ключевые термины
- характеристическая постоянная времени : Обозначается $ \ tau $, в цепях RL она задается $ \ tau = \ frac {L} {R} $, где R — сопротивление, а L — индуктивность. Когда переключатель замкнут, это время, за которое ток затухает с коэффициентом 1 / e.
- индуктор : Устройство или компонент схемы, который демонстрирует значительную самоиндукцию; устройство, которое хранит энергию в магнитном поле.
RL Схемы
Цепь резистор-индуктор (цепь RL) состоит из резистора и катушки индуктивности (последовательно или параллельно), приводимых в действие источником напряжения.
Обзор
Напомним, что индукция — это процесс, в котором ЭДС индуцируется изменением магнитного потока. Взаимная индуктивность — это действие закона индукции Фарадея одного устройства на другое, в то время как самоиндукция — это действие закона индукции Фарадея устройства на самого себя.Катушка индуктивности — это устройство или компонент схемы, который демонстрирует самоиндукцию.
Энергия индуктора
Мы знаем из закона Ленца, что индукторы противодействуют изменениям тока. Мы можем думать об этой ситуации с точки зрения энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, а также время, чтобы истощить ее; следовательно, есть противодействие быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства.{2} [/ латекс].
Катушки индуктивности в цепях
Мы знаем, что ток через катушку индуктивности L нельзя включить или выключить мгновенно. Изменение тока изменяет магнитный поток, вызывая противодействие изменению ЭДС (закон Ленца). Как долго длится противостояние? Текущий будет течь, а можно выключить , но сколько времени это займет? На следующем рисунке показана схема переключения, которую можно использовать для измерения тока через катушку индуктивности как функции времени.
Ток в цепи RL : (a) Цепь RL с переключателем для включения и выключения тока. В положении 1 батарея, резистор и катушка индуктивности включены последовательно, и устанавливается ток. В положении 2 аккумулятор извлекается, и ток в конечном итоге прекращается из-за потери энергии в резисторе. (b) График роста тока в зависимости от времени, когда переключатель перемещен в положение 1. (c) График уменьшения тока, когда переключатель перемещен в положение 2.
Когда переключатель сначала перемещается в положение 1 (при t = 0 ), ток равен нулю и в конечном итоге возрастает до I 0 = В / R , где R — полное сопротивление цепи, а V — напряжение батареи.{\ frac {- \ text {t}} {\ tau}}) [/ latex]
— это ток в цепи RL при включении. (Обратите внимание на сходство с экспоненциальным поведением напряжения на зарядном конденсаторе.) Начальный ток равен нулю и приближается к I 0 = В / R с характеристической постоянной времени для цепи RL , задаваемой формулой :
[латекс] \ tau = \ frac {\ text {L}} {\ text {R}} [/ latex],
, где [latex] \ tau [/ latex] имеет единицы измерения в секундах, поскольку [latex] 1 \ text {H} = 1 \ Omega \ cdot \ text {s} [/ latex].В первый период времени [латекс] \ тау [/ латекс] ток возрастает от нуля до 0,632I 0 , так как I = I 0 (1 − e −1 ) = I 0 ( 1−0,368) = 0,632I 0 . В следующий раз ток составит 0,632 от остатка. Хорошо известным свойством экспоненциальной функции является то, что конечное значение никогда не достигается точно, но 0,632 остатка от этого значения достигается за каждое характерное время [латекс] \ тау [/ латекс]. Всего за несколько кратных промежутков времени [latex] \ tau [/ latex] конечное значение почти достигнуто (см. Часть (b) на рисунке выше).
Характерное время [латекс] \ тау [/ латекс] зависит только от двух факторов: индуктивности L и сопротивления R . Чем больше индуктивность L , тем она больше, что имеет смысл, поскольку большая индуктивность очень эффективна в противодействии изменению. Чем меньше сопротивление R, тем больше [латекс] \ тау [/ латекс]. Опять же, это имеет смысл, поскольку небольшое сопротивление означает большой конечный ток и большее изменение, чтобы добраться до него. В обоих случаях (большой L и маленький R) больше энергии хранится в катушке индуктивности, и требуется больше времени для ее ввода и вывода.
Когда переключатель на (a) перемещается в положение 2 и отключает батарею из цепи, ток падает из-за рассеивания энергии резистором. Однако это также не происходит мгновенно, поскольку катушка индуктивности противодействует уменьшению тока, вызывая ЭДС в том же направлении, что и батарея, управляющая током. Кроме того, в катушке индуктивности накапливается определенное количество энергии, (1/2) LI 0 2 , и она рассеивается с конечной скоростью. Когда ток приближается к нулю, скорость убывания замедляется, поскольку скорость рассеяния энергии составляет I 2 R.{\ frac {- \ text {t}} {\ tau}} [/ latex]
В (c), в первый период времени [latex] \ tau = \ text {L} / \ text {R} [/ latex] после того, как переключатель замкнут, ток падает до 0,368 от своего начального значения, поскольку I = I 0 e −1 = 0,368I 0 . В каждый последующий раз [латекс] \ тау [/ латекс] ток падает до 0,368 от предыдущего значения, а через несколько кратных [латекс] \ тау [/ латекс] ток становится очень близким к нулю.
Цепь серииRLC: на больших и малых частотах; Фазорная диаграмма
Отклик цепи RLC зависит от частоты возбуждения — на достаточно больших частотах преобладает индуктивный (емкостной) член.
Цели обучения
Различать поведение цепей серии RLC на больших и малых частотах
Основные выводы
Ключевые моменты
- RLC-схемы можно описать (обобщенным) законом Ома. Что касается фазы, то при приложении синусоидального напряжения ток отстает от напряжения на 90 ° по фазе в цепи с индуктором, в то время как ток опережает напряжение на 90 ° в цепи с конденсатором.
- На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока только с индуктор.Следовательно, среднеквадратичный ток будет Vrms / XL, а ток отстает от напряжения почти на 90 °.
- На достаточно малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока с конденсатор. Следовательно, среднеквадратичное значение тока будет равно В / X C, , а ток опережает напряжение почти на 90 ∘ .
Ключевые термины
- Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
- резонанс : Увеличение амплитуды колебаний системы под действием периодической силы, частота которой близка к собственной частоте системы.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
В предыдущих версиях Atoms мы узнали, как последовательная цепь RLC, показанная на рисунке, реагирует на источник переменного напряжения. Объединив закон Ома (I среднеквадратичное значение = V среднеквадратичное значение / Z; I среднеквадратичное значение и V среднеквадратичное значение представляют собой среднеквадратичное значение тока и напряжения) и выражения для импеданса Z из:
Цепь RLC серии : Цепь последовательного RLC: резистор, катушка индуктивности и конденсатор (слева).2}} [/ латекс].
Из уравнения мы исследовали условия резонанса для контура. Мы также изучили фазовые соотношения между напряжениями на резисторе, конденсаторе и катушке индуктивности: при подаче синусоидального напряжения ток отстает от напряжения на 90º по фазе в цепи с катушкой индуктивности, в то время как ток опережает напряжение на 90 ∘ . в цепи с конденсатором. Теперь мы исследуем отклик системы в пределах больших и малых частот.
На больших частотах
На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] X L намного больше, чем X C .Если частота достаточно высока, так что X L также намного больше, чем R, то в импедансе Z преобладает индуктивный член. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {L} [/ latex], схема почти эквивалентна цепи переменного тока с одним индуктором. Следовательно, среднеквадратичный ток будет составлять В / X L , а ток отстает от напряжения почти на 90, ∘ . Этот отклик имеет смысл, потому что на высоких частотах закон Ленца предполагает, что полное сопротивление катушки индуктивности будет большим.
на малых частотах
В импедансе Z на малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] преобладает емкостный член, предполагая, что частота достаточно высока, так что X C намного больше R. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {C} [/ latex], схема почти эквивалентна AC схема только с конденсатором. Следовательно, среднеквадратичное значение тока будет равно В / X C, , а ток опережает напряжение почти на 90 ∘ .
Резисторы в цепях переменного тока
В цепи с резистором и источником питания переменного тока по-прежнему действует закон Ома ( В = IR ).
Цели обучения
Применение закона Ома для определения силы тока и напряжения в цепи переменного тока
Основные выводы
Ключевые моменты
- При напряжении переменного тока, определяемом следующим образом: [latex] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex], ток в цепи определяется как : [latex] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex] Это выражение происходит от Ohm закон: [латекс] \ text {V} = \ text {IR} [/ latex].2} {2 \ text {R}} [/ латекс].
Ключевые термины
- Закон Ома : Согласно наблюдениям Ома, постоянный ток, протекающий в электрической цепи, состоящей только из сопротивлений, прямо пропорционален приложенному напряжению.
Постоянный ток (DC) — это поток электрического заряда только в одном направлении. Это установившееся состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник переменного напряжения. Переменный ток (AC) — это поток электрического заряда, который периодически меняет направление.Если источник периодически меняется, особенно синусоидально, цепь называется цепью переменного тока. Примеры включают коммерческую и бытовую энергетику, которая обслуживает так много наших потребностей. показывает графики зависимости напряжения и тока от времени для типичных источников постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.
Синусоидальное напряжение и ток : (a) Постоянное напряжение и ток постоянны во времени после установления тока.(б) График зависимости напряжения и тока от времени для сети переменного тока 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления. Частоты и пиковое напряжение источников переменного тока сильно различаются.
Мы изучили закон Ома:
[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R}} [/ latex]
, где I — ток, В, — напряжение, а R — сопротивление цепи. Закон Ома применяется как к цепям переменного тока, так и к цепям постоянного тока.Следовательно, при напряжении переменного тока, определяемом по формуле:
[латекс] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex]
, где В 0 — пиковое напряжение, а [латекс] \ nu [/ latex] — частота в герцах, ток в цепи задается как:
[латекс] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex]
В этом примере, в котором у нас есть резистор и источник напряжения в цепи, напряжение и ток считаются синфазными, как показано на (b).Ток в резисторе чередуется взад и вперед без разницы фаз, как и напряжение возбуждения.
Рассмотрим идеальный резистор, который увеличивает и уменьшает яркость 120 раз в секунду, когда ток постоянно проходит через ноль. 2} {\ text {R}} \ cdot \ sin (2 \ pi \ nu \ text {t}) [/ latex]
Чтобы найти среднюю мощность, потребляемую этой схемой, нам нужно взять среднее значение функции по времени.2} {2 \ text {R}} [/ латекс]
Конденсаторыв цепях переменного тока: емкостное сопротивление и фазовые диаграммы
Напряжение на конденсаторе отстает от тока. Из-за разности фаз для описания этих схем полезно вводить векторы.
Цели обучения
Объясните преимущества использования векторного представления
Основные выводы
Ключевые моменты
- Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.
- Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно.
- Действующее значение тока в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}}} {\ text {X} _ \ text {C}} [/ latex], где [latex] \ text {X} _ \ text {c} [/ latex] — емкостное реактивное сопротивление.
Ключевые термины
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
В предыдущем Atom «Резисторы в цепях переменного тока» мы представили источник питания переменного тока и изучили, как резисторы ведут себя в цепях переменного тока. Там мы использовали закон Ома (V = IR), чтобы получить соотношение между напряжением и током в цепях переменного тока. В этом и последующих разделах «Атомы» мы обобщим закон Ома, чтобы мы могли использовать его, даже если в цепи присутствуют конденсаторы и катушки индуктивности. Чтобы добраться туда, мы сначала представим очень общий графический способ представления синусоидальной волны с помощью фазора.
Конденсаторы в цепях переменного тока с фазорами
Phasor
Ключевая идея представления вектора состоит в том, что сложный, изменяющийся во времени сигнал может быть представлен как произведение комплексного числа (которое не зависит от времени) и сложного сигнала (которое зависит от времени). Фазоры разделяют зависимости от A (амплитуда), [latex] \ nu [/ latex] (частота) и θ (фаза) на три независимых фактора. Это может быть особенно полезно, потому что частотный коэффициент (который включает временную зависимость синусоиды) часто является общим для всех компонентов линейной комбинации синусоид.{\ text {i} \ theta} [/ латекс]. Поскольку векторы представлены величиной (или модулем) и углом, они графически представлены вращающейся стрелкой (или вектором) в плоскости x-y.
Рис. 3 : Вектор можно рассматривать как вектор, вращающийся вокруг начала координат в комплексной плоскости. Функция косинуса — это проекция вектора на действительную ось. Его амплитуда — это модуль вектора, а его аргумент — полная фаза \ omega t + \ theta. Фазовая постоянная \ theta представляет собой угол, который вектор образует с действительной осью при t = 0.
Конденсаторы в цепях переменного тока
Ранее в предыдущем Atom мы изучали, как напряжение и ток меняются со временем. Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно. Мы говорим, что ток и напряжение совпадают по фазе.
Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.Ток имеет максимум (пик) за четверть цикла до пиков напряжения. Инженеры говорят, что «ток опережает напряжение на 90 ∘ ». Это показано на.
.Рис. 2 : Пик тока (имеет максимум) за четверть волны до напряжения, когда конденсатор подключен к переменному напряжению.
Для цепи с конденсатором мгновенное значение V / I непостоянно. Однако значение V max / I max полезно и называется емкостным реактивным сопротивлением (X C ) компонента.Поскольку это по-прежнему напряжение, деленное на ток (например, сопротивление), единицей измерения является ом. Значение X C (C означает конденсатор) зависит от его емкости (C) и частоты (f) переменного тока. [латекс] \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ latex].
Конденсатор влияет на ток, имея возможность полностью его остановить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором.Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичный ток I среднеквадратичное значение в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}}} {\ text {X} _ \ text {C}} [/ latex], где V rms — это действующее значение напряжения. Обратите внимание, что X C заменяет R в версии закона Ома для постоянного тока.
Фазовое представление
Поскольку напряжение на конденсаторе отстает от тока, вектор, представляющий ток и напряжение, будет иметь вид.На схеме стрелки вращаются против часовой стрелки с частотой [латекс] \ ню [/ латекс]. (Следовательно, ток ведет к напряжению.) В следующих атомах мы увидим, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.
Рис. 4 : Фазорная диаграмма для цепи переменного тока с конденсатором
Индукторы в цепях переменного тока: индуктивно-реактивные и фазовые диаграммы
В цепи переменного тока с катушкой индуктивности напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца.
Цели обучения
Объясните, почему напряжение на катушке индуктивности «опережает» ток в цепи переменного тока с катушкой индуктивности
Основные выводы
Ключевые моменты
- С индуктором в цепи переменного тока напряжение опережает ток на одну четверть цикла или на фазовый угол 90º.
- Среднеквадратичный ток I среднеквадратичное значение через катушку индуктивности L определяется версией закона Ома: [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ { \ text {rms}}} {\ text {X} _ \ text {L}} [/ latex].X L называется индуктивным реактивным сопротивлением, которое задается как [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex].
- Фазоры — это векторы, вращающиеся против часовой стрелки. Вектор для катушки индуктивности показывает, что напряжение опережает ток по фазе 90º.
Ключевые термины
- Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
- phasor : представление комплексного числа в виде комплексной экспоненты.
Предположим, что индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке. Разумно предположить, что сопротивление пренебрежимо мало, потому что на практике мы можем сделать сопротивление индуктора настолько малым, что оно окажет незначительное влияние на схему. График показывает напряжение и ток как функции времени.(б) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля, затем повышается до своего пика после управляющего им напряжения (как показано в предыдущем разделе, когда было включено напряжение постоянного тока).
Источник переменного напряжения, подключенный последовательно с индуктором : (a) Источник переменного напряжения, подключенный последовательно с индуктором, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.
Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным.Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c, где оно начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Следовательно, когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.
Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока вызывает ЭДС.Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I RMS через катушку индуктивности L определяется версией закона Ома: [latex] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text { rms}}} {\ text {X} _ \ text {L}} [/ latex] где V rms — среднеквадратичное напряжение на катушке индуктивности, а [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex] с [latex] \ nu [/ latex] частота источника переменного напряжения в герцах. X L называется индуктивным реактивным сопротивлением. Поскольку катушка индуктивности препятствует прохождению тока, X L имеет единицы измерения Ом (1 Гн = 1 Ом · с, так что частота, умноженная на индуктивность, составляет (циклов / с) (Ом · с) = Ом), что соответствует его роли эффективное сопротивление.
Представление фазора
Напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца. Следовательно, вектор, представляющий ток и напряжение, будет иметь вид. Опять же, вектора — это векторы, вращающиеся против часовой стрелки с частотой [latex] \ nu [/ latex] (вы можете видеть, что напряжение опережает ток) . В последующих выпусках Atoms будет обсуждаться, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.
Векторная диаграмма : Векторная диаграмма для цепи переменного тока с индуктором.
Фазоры для индукторов в цепях переменного тока
Резонанс в цепях RLC
Резонанс — это тенденция системы к колебаниям с большей амплитудой на некоторых частотах — в последовательной цепи RLC он возникает на [latex] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}} }[/латекс].
Цели обучения
Сравнить резонансные характеристики цепей с высоким и низким сопротивлением
Основные выводы
Ключевые моменты
- Условие резонанса последовательной цепи RLC может быть получено приравниванием X L и X C , так что два противоположных вектора компенсируют друг друга.
- В резонансе влияние катушки индуктивности и конденсатора компенсируется, так что Z = R, а I среднеквадратичное значение является максимальным.
- Цепи с более высоким сопротивлением не так сильно резонируют по сравнению с цепями с более низким сопротивлением, и при этом они не будут такими избирательными, например, в радиоприемнике.
Ключевые термины
- реактивное сопротивление : Противодействие изменению протекания тока в цепи переменного тока из-за индуктивности и емкости; мнимая часть импеданса.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
- импеданс : Мера сопротивления течению переменного тока в цепи; совокупность его сопротивления, индуктивного и емкостного сопротивления. Обозначается символом Z.
Резонанс — это тенденция системы к колебаниям с большей амплитудой на одних частотах, чем на других. Частоты, при которых амплитуда отклика является относительным максимумом, известны как резонансные частоты системы.2}} [/ latex],
, где I rms и V rms — среднеквадратичные значения тока и напряжения соответственно. Реактивные сопротивления изменяются в зависимости от частоты [латекс] \ nu [/ latex], при этом X L большое на высоких частотах и X C большое на низких частотах, представленных как:
[латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L}, \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ латекс].
На некоторой промежуточной частоте [latex] \ nu_0 [/ latex] реактивные сопротивления будут равны и отменены, давая Z = R — это минимальное значение для импеданса, а максимальное значение для I rms .Мы можем получить выражение для [latex] \ nu_0 [/ latex], взяв X L = X C . Подстановка определений X L и X C дает:
[латекс] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} [/ латекс].
[латекс] \ nu_0 [/ latex] — это резонансная частота последовательной цепи RLC. Это также собственная частота, на которой цепь будет колебаться, если не будет управляться источником напряжения. В [latex] \ nu_0 [/ latex] эффекты катушки индуктивности и конденсатора нейтрализуются, так что Z = R, а I среднеквадратичное значение является максимальным.Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы.
Приемник в радиостанции — это RLC-цепь, которая лучше всего колеблется на своем [latex] \ nu_0 [/ latex]. Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в I rms в [латексе] \ nu_0 = \ text {f} _0 [/ latex].Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них. Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепи с более высоким сопротивлением не резонируют так сильно, и, например, в радиоприемнике они не будут такими избирательными.
Зависимость тока от частоты : График зависимости тока от частоты для двух цепей серии RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире.Источник управляющего переменного напряжения имеет фиксированную амплитуду V0.
Мощность
Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается сопротивлением в цепи и задается как [латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms }} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ latex]. Здесь [latex] \ phi [/ latex] называется фазовым углом.
Цели обучения
Рассчитать мощность, подаваемую в цепь переменного тока серии RLC с учетом тока и напряжения.
Основные выводы
Ключевые моменты
- Фазовый угол ϕ — это разность фаз между напряжением источника V и током I.См. Векторную диаграмму в.
- На резонансной частоте или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны.
- Среднюю мощность, рассеиваемую в цепи RLC, можно рассчитать, взяв среднее значение мощности по времени, P (t) = I (t) V (t), за период.
Ключевые термины
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
Если ток изменяется в зависимости от частоты в цепи RLC, то мощность, подаваемая на него, также зависит от частоты.Однако средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных схемах. Как было замечено в предыдущих атомах, напряжение и ток в цепи RLC не совпадают по фазе. Между напряжением источника V и током I существует фазовый угол ϕ, равный
.[латекс] \ cos {\ phi} = \ frac {\ text {R}} {\ text {Z}} [/ latex], как показано на рисунке
Векторная диаграмма для последовательной цепи RLC : Векторная диаграмма для последовательной цепи RLC. \ phi — фазовый угол, равный разности фаз между напряжением и током.
Например, на резонансной частоте [латекс] (\ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}}) [/ latex] или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем в резонансе, потому что напряжение и ток не совпадают по фазе, а I среднеквадратичное значение ниже.
Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь.Можно показать, что средняя мощность
[латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms}} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ латекс]
(уравнение, полученное путем взятия среднего значения мощности по времени, P (t) = I (t) V (t), за период. I (t) и V (t) — ток и напряжение в момент времени t). Таким образом, cosϕ называется коэффициентом мощности, который может находиться в диапазоне от 0 до 1. Коэффициенты мощности, близкие к 1, желательны, например, при разработке эффективного двигателя. На резонансной частоте cosϕ = 1.
Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается только за счет сопротивления.Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают энергию из цепи. Скорее, они передают энергию вперед и назад друг другу, а резистор рассеивает именно то количество, которое источник напряжения дает цепи. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора (например, радиоволн).
Схема аналогична колесу автомобиля, движущемуся по гофрированной дороге, как показано на рисунке. Неровности на дороге с равномерным интервалом аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз.Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний. Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.
Принудительное демпфированное движение колеса на автомобильной пружине : Принудительное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC.Амортизатор гасит движение и рассеивает энергию аналогично сопротивлению в цепи RLC. Масса и пружина определяют резонансную частоту.




 Например, на краю стола
лежит кирпич. Относительно пола он имеет потенциальную энергию Eпот=hmg
(Eпот
– потенциальная энергия кирпича; h – высота стола;
m – масса кирпича; g – ускорение свободного
падения, равная 9,8м/с2),
и пока мы не столкнем кирпич, он будет хранить в себе энергию(точнее, в
своем положении).
Например, на краю стола
лежит кирпич. Относительно пола он имеет потенциальную энергию Eпот=hmg
(Eпот
– потенциальная энергия кирпича; h – высота стола;
m – масса кирпича; g – ускорение свободного
падения, равная 9,8м/с2),
и пока мы не столкнем кирпич, он будет хранить в себе энергию(точнее, в
своем положении).
 Однако, катушка не конденсатор – запасти в ней энергию и
просто так хранить нельзя.
Однако, катушка не конденсатор – запасти в ней энергию и
просто так хранить нельзя.
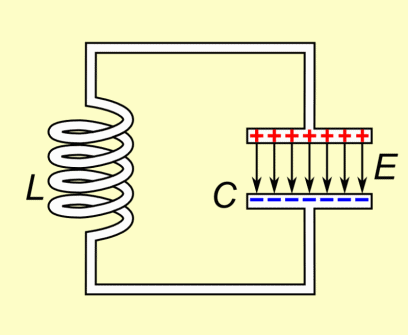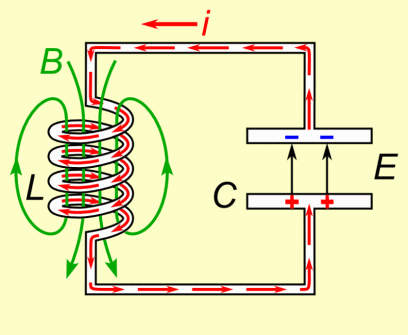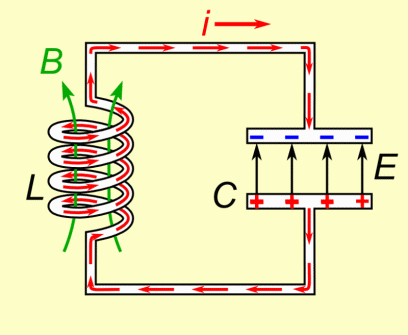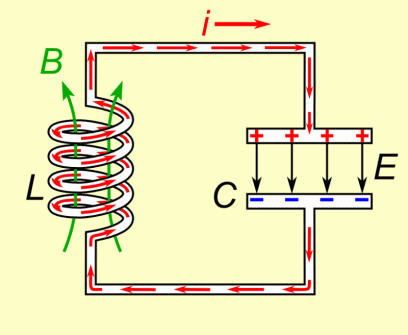 В переходе в электричество, мы как бы в
момент прохода большого тока по катушке быстро подключили ее к
резистору не очень большого сопротивления. Выброс напряжения будет не
сильным, зато его длительность будет больше.
В переходе в электричество, мы как бы в
момент прохода большого тока по катушке быстро подключили ее к
резистору не очень большого сопротивления. Выброс напряжения будет не
сильным, зато его длительность будет больше.
 С этого момента начинается зарядка конденсатора обратным
напряжением за счет запасенной в катушке энергии. Однако хочу обратить
внимание на то, что хоть конденсатор и начинает заряжаться в обратной
полярности, направление тока в цепи не изменилось – он (ток)
все также течет по стрелке, показанной на схеме.
С этого момента начинается зарядка конденсатора обратным
напряжением за счет запасенной в катушке энергии. Однако хочу обратить
внимание на то, что хоть конденсатор и начинает заряжаться в обратной
полярности, направление тока в цепи не изменилось – он (ток)
все также течет по стрелке, показанной на схеме.
