Как рассчитать емкостное сопротивление конденсатора в цепи переменного тока. Какова зависимость емкостного сопротивления от частоты. Как определить ток и напряжение на конденсаторе в цепи переменного тока. Какие факторы влияют на характеристики конденсатора в цепи переменного тока.
Емкостное сопротивление конденсатора в цепи переменного тока
Емкостное сопротивление конденсатора в цепи переменного тока зависит от его емкости и частоты тока. Чем больше емкость конденсатора и чем выше частота, тем меньше его емкостное сопротивление.
Формула для расчета емкостного сопротивления:
XC = 1 / (2πfC)
где:
- XC — емкостное сопротивление (Ом)
- f — частота переменного тока (Гц)
- C — емкость конденсатора (Ф)
Расчет тока через конденсатор в цепи переменного тока
Ток через конденсатор в цепи переменного тока можно рассчитать по закону Ома:
I = U / XC
где:
- I — действующее значение тока (А)
- U — действующее значение напряжения (В)
- XC — емкостное сопротивление конденсатора (Ом)
Напряжение на конденсаторе в цепи переменного тока
Напряжение на конденсаторе в цепи переменного тока отстает по фазе от тока на 90°. Амплитудное значение напряжения можно рассчитать по формуле:
Um = Im * XC
где:
- Um — амплитудное значение напряжения (В)
- Im — амплитудное значение тока (А)
- XC — емкостное сопротивление (Ом)
Факторы, влияющие на характеристики конденсатора в цепи переменного тока
На характеристики конденсатора в цепи переменного тока влияют следующие факторы:
- Емкость конденсатора
- Частота переменного тока
- Приложенное напряжение
- Температура окружающей среды
- Тип диэлектрика конденсатора
При увеличении емкости конденсатора или частоты тока емкостное сопротивление уменьшается, а ток через конденсатор возрастает.
Применение конденсаторов в цепях переменного тока
Конденсаторы в цепях переменного тока используются для следующих целей:
- Сглаживание пульсаций напряжения
- Разделение цепей по постоянному току
- Фазовый сдвиг напряжения
- Фильтрация высокочастотных помех
- Компенсация реактивной мощности
Правильный выбор параметров конденсатора позволяет эффективно решать эти задачи в электрических цепях переменного тока.
Расчет мощности, выделяемой на конденсаторе
В идеальном конденсаторе активная мощность не выделяется, так как ток и напряжение сдвинуты по фазе на 90°. Однако реальные конденсаторы имеют некоторые потери, которые можно оценить с помощью тангенса угла диэлектрических потерь:

P = U2 * 2πfC * tgδ
где:
- P — активная мощность потерь (Вт)
- U — действующее напряжение (В)
- f — частота (Гц)
- C — емкость (Ф)
- tgδ — тангенс угла диэлектрических потерь
Последовательное и параллельное соединение конденсаторов в цепи переменного тока
При последовательном соединении конденсаторов в цепи переменного тока:
- Общая емкость уменьшается
- Общее емкостное сопротивление увеличивается
- Напряжение распределяется обратно пропорционально емкостям
При параллельном соединении конденсаторов:
- Общая емкость увеличивается
- Общее емкостное сопротивление уменьшается
- Токи распределяются прямо пропорционально емкостям
Правильный выбор схемы соединения позволяет получить требуемые параметры емкости в цепи.
Резонанс в цепи с конденсатором
В цепи переменного тока, содержащей конденсатор и катушку индуктивности, при определенной частоте может возникнуть резонанс напряжений. Условие резонанса:
XL = XC
где XL — индуктивное сопротивление, XC — емкостное сопротивление.
При резонансе:
- Полное сопротивление цепи минимально
- Ток в цепи максимален
- Напряжения на конденсаторе и катушке могут многократно превышать напряжение источника
Резонанс напряжений используется в колебательных контурах радиотехники.
Выбор конденсатора для работы в цепи переменного тока
При выборе конденсатора для работы в цепи переменного тока необходимо учитывать следующие параметры:
- Номинальное напряжение (должно быть выше амплитудного значения переменного напряжения)
- Допустимый ток пульсаций
- Диапазон рабочих частот
- Температурный коэффициент емкости
- Тангенс угла диэлектрических потерь
- Срок службы при заданных условиях эксплуатации
Правильный выбор типа и параметров конденсатора обеспечивает его надежную и долговременную работу в цепи переменного тока.
Измерение параметров конденсаторов в цепи переменного тока
Для измерения параметров конденсаторов в цепи переменного тока используются следующие методы и приборы:
- Измерение емкости с помощью RLC-метра
- Определение тангенса угла потерь мостовым методом
- Измерение импеданса векторным анализатором цепей
- Контроль напряжения и тока осциллографом
Измерения позволяют оценить реальные параметры конденсатора и их соответствие расчетным значениям.

Влияние температуры на характеристики конденсатора
Температура оказывает существенное влияние на параметры конденсатора в цепи переменного тока:
- С ростом температуры емкость большинства типов конденсаторов увеличивается
- Повышается тангенс угла диэлектрических потерь
- Снижается электрическая прочность диэлектрика
- Уменьшается срок службы конденсатора
При расчете и выборе конденсаторов необходимо учитывать температурные зависимости их параметров.
Заключение
Конденсаторы являются важными элементами цепей переменного тока. Правильный расчет и выбор их параметров позволяет эффективно решать различные задачи в электротехнике и электронике. Понимание особенностей работы конденсаторов на переменном токе необходимо для грамотного проектирования электрических схем.
Однофазные цепи переменного тока (страница 2)
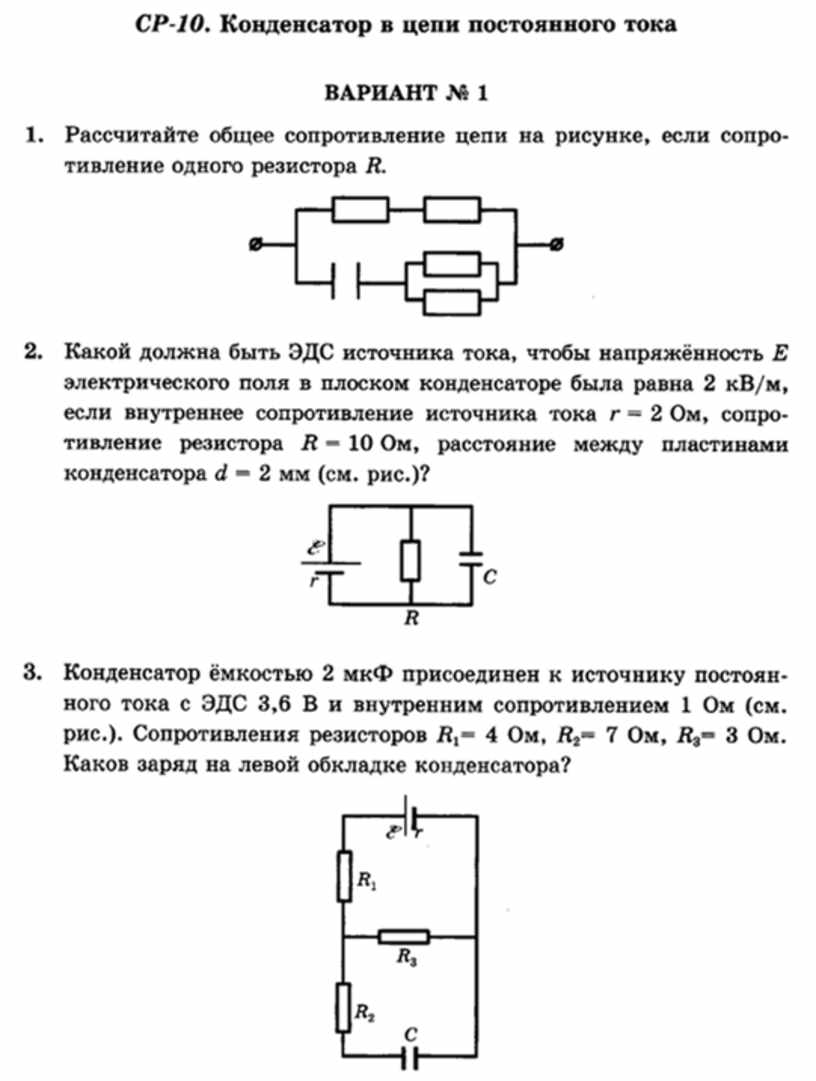
12. Конденсатор емкостью С = 8,36 мкФ включен на синусоидальное напряжение U=380 В частотой f=50 Гц.
Определить ток в цепи конденсатора.
Решение:
Емкостное сопротивление
Ток в цепи конденсатора при синусоидальном напряжении 380 В
Для получения больших токов требуются при данной частоте большие значения емкости.
13. При включении конденсатора на синусоидальное напряжение U=220 В частотой f=50 Гц в цепи установился ток I=0,5 А.
Какую емкость имеет конденсатор?
Решение:
На основании закона Ома емкостное сопротивление
Из формулы емкостного сопротивления
емкость
Метод определения емкости конденсатора, рассмотренный в данной задаче, является наименее точным, но он прост и не требует больших затрат для применения на практике.
14. При включении разомкнутого на конце кабеля на напряжение U=6600 В частотой f=50 Гц в цепи установился ток I=2 А.
Пренебрегая электрическим сопротивлением кабеля, определить приближенно емкость кабеля на 1 км его длины, если длина кабеля 10 км.
Решение:
Изолированные друг от друга жилы кабеля представляют собой конденсатор. Если пренебречь сопротивлением жил кабеля, то ток холостой работы кабеля, т. е. ток в кабеле, разомкнутом на конце, можно считать чисто емкостным. В этом случае действительно соотношение
где
— емкостная проводимость.
Отсюда
При частоте f=50 Гц угловая частота
, следовательно,
Емкость кабеля на 1 км его длины
Описанный способ определения емкости кабеля на 1 км его длины является очень приближенным (в нем пренебрегают активным сопротивлением жил кабеля и активной проводимостью утечки от жилы к жиле вследствие несовершенства изоляции; допускается равномерное распределение емкости по длине кабеля).
15. Какая емкость батареи конденсаторов требуется для получения реактивной (емкостной) мощности 152 ВАР при напряжении U=127 В и частоте f=50 Гц.
Решение:
При частоте f=50 Гц угловая частота
. Так как ток батареи считается чисто
реактивным (опережающим по фазе напряжение на 1/4 периода), то реактивная мощность равна произведению напряжения и тока:
откуда
Емкостный ток равен произведению напряжения на емкостную проводимость, поэтому
Емкость батареи конденсаторов
Реактивную (емкостную) мощность можно представить в виде
, выразив ток через напряжение и емкостную проводимость; отсюда следует, что при данном напряжении и частоте реактивная (емкостная) мощность пропорциональна емкости. Если изоляция пластин батареи конденсаторов допускает повышение напряжения (например, в раз), то реактивная (емкостная) мощность увеличится пропорционально квадрату напряжения (т. е. в 3 раза). Таким образом, в рассматриваемом случае важное значение имеет отношение напряжения от номинального.
16. В катушке (см. задачу 10), включенной на переменное напряжение U=12 В частотой f=50 Гц установился ток 1,2 А.
В катушке (см. задачу 10), включенной на переменное напряжение U=12 В частотой f=50 Гц установился ток 1,2 А.
Определить индуктивность катушки.
Решение:
Отношение переменного напряжения, приложенного к катушке, к току, устанавливающемуся в ней, называется полным сопротивлением z катушки;
В задаче 10 было определено, что активное сопротивление катушки r=2,8 Ом. Сопротивление катушки при перееденном токе больше сопротивления г при постоянном токе вследствие наличия э. д. с. самоиндукции, препятствующей изменению переменного тока. Это равносильно появлению в катушке сопротивления, называемого индуктивным:
где L — индуктивность, Гн
f — частота, Гц.
Связь между полным сопротивлением z, индуктивным сопротивлением
и активным сопротивлением r такая же, как между гипотенузой и катетами в прямоугольном треугольнике:
откуда индуктивное сопротивление
Индуктивность катушки
В рассматриваемой катушке ток отстает по фазе от напряжения, причем тангенс угла сдвига фаз
. Из таблиц тригонометрических величин .
Из таблиц тригонометрических величин .
17. В схеме (рис. 23) вольтметр показывает 123 В, амперметр 3 А и ваттметр 81 Вт, частота сети 50 Гц.
Oпределить параметры катушки.
Решение:
Отношение напряжения к току равно полному сопротивлению катушки:
Ваттметр измеряет активную мощность цепи, которая в данной задаче является потерей мощности в сопротивлении r, поэтому сопротивление катушки
Полное сопротивление z, активное сопротивление r и индуктивное сопротивление
катушки связаны между собой таким же соотношением, как гипотенуза и катеты в прямоугольном треугольнике.
Следовательно,
При частоте f=50 Гц угловая частота
Индуктивное сопротивление
равно произведению угловой частоты ω и индуктивности L; следовательно,
Коэффициент мощности катушки
. Из таблиц тригонометрических величин .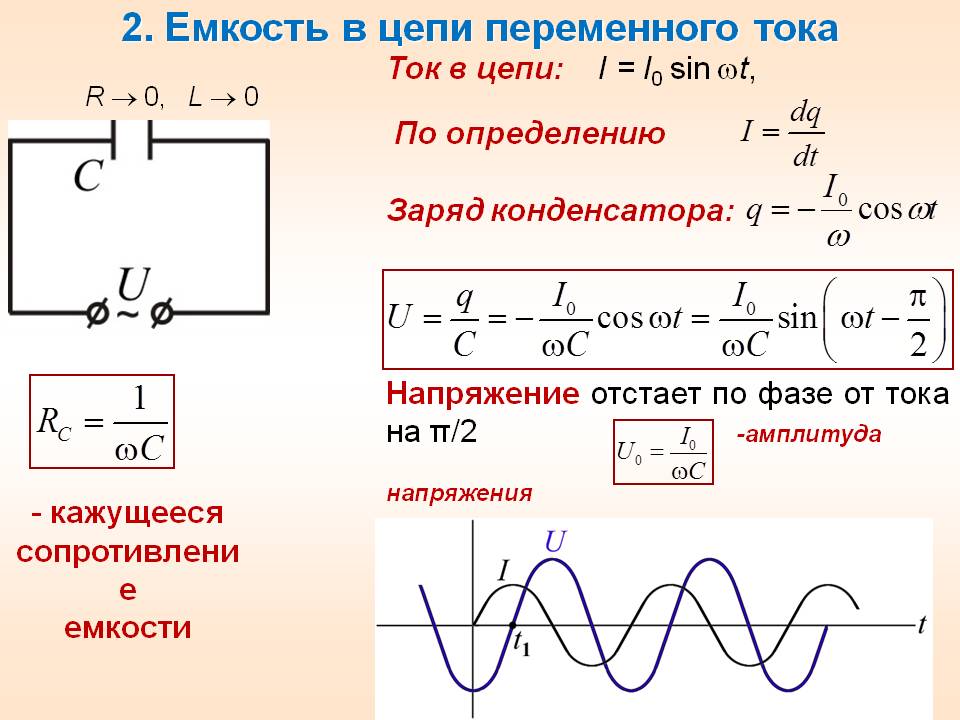
18. Катушка без стального сердечника включена на постоянное напряжение 2,1 В, ток которой равен 0,3 А. При включении этой же катушки на синусоидальное напряжение частотой 50 Гц с действующим значением 50 В ток имеет действующее значение 2 А.
Определить параметры катушки, активную и полную мощности.
Решение:
Отношение постоянного напряжения к постоянному току в катушке практически равно (если пренебречь увеличением сопротивления из-за вытеснения переменного тока на поверхность провода) активному сопротивлению:
Это один из параметров катушки. Отношение этих же величин при переменном токе в катушке равно полному сопротивлению:
Индуктивное сопротивление:
Индуктивность катушки — второй ее параметр:
Коэффициент мощности катушки:
Из таблиц тригонометрических величин
.
Активная мощность
Полная мощность
Коэффициент мощности
В задачах 17 и 18 рассмотрены два различных способа определения параметров катушки.
19. Батарея конденсаторов емкостью С=50 мкФ соединена последовательно с реостатом сопротивлением r=29,1 Ом.
Определить напряжения на батарее конденсаторов и реостате, а также ток в цепи и мощность, если приложенное напряжение U=210 В и частота сети f=50 Гц.
Решение:
Частоте 50 Гц и емкости 50 мкФ соответствует емкостное сопротивление, в 50 раз меньшее, чем емкости в 1 мкФ. Следовательно,
Здесь 3185 Ом — сопротивление конденсатора емкостью 1 мкФ.
По условию, сопротивление реостата r=29,1 Ом. Полное сопротивление цепи связано с активным и емкостным сопротивлениями таким же соотношением, как гипотенуза и катет прямоугольного треугольника:
На основании закона Ома ток в цепи
Напряжение на реостате
Напряжение на батарее конденсаторов
В силу последовательного соединения большее напряжение оказалось на элементе цепи, имеющем большее сопротивление.
Коэффициент мощности
Из таблиц тригонометрических величин угол сдвига фаз
.
Активная мощность цепи
Полная мощность цепи равна произведению действующих значений напряжения и тока:
Полная мощность намного больше активной мощности, так как коэффициент мощности мал, т. е. полное сопротивление цепи во много раз превышает активное сопротивление.
20. Электрическую лампу мощностью Р=60 Вт при напряжении
необходимо подсоединить к сети с переменным напряжением U=220 В и частотой 50 Гц. Для компенсации части этого напряжения последовательно с лампой включается конденсатор.
Какой емкости необходимо взять конденсатор?
Решение:
Напряжение на лампе будет активной составляющей приложенного напряжения сети, а напряжение на конденсаторе — его реактивной (емкостной) составляющей. Эти напряжения связаны соотношением
Напряжение на конденсаторе
Ток в конденсаторе тот же, что и в лампе, т. е.
На основании закона Ома емкостное сопротивление
Так как при частоте f=50 Гц емкости С=1 мкФ соответствует емкостное сопротивление
, то емкость рассматриваемого конденсатора приблизительно равна 8,7 мкФ.
Избыточное напряжение можно было бы скомпенсировать и путем последовательного включения реостата с лампой. Так как реостат, как и электрическая лампа, представляет чисто активное сопротивление, то напряжения на этих элементах цепи совпадают по фазе с общим током, а следовательно, и между собой. В этом случае будет действительно соотношение
где
— напряжение на реостате, равное
При токе лампы 0,5 А сопротивление реостата должно составлять
В реостате будет расходоваться энергия, переходящая в тепло, причем потери мощности в реостате
В случае включения емкости «погашение» напряжения происходит без потерь энергии.
21. В случае электрической сварки дугой тонких листов при переменном токе в ней развивается мощность
при токе I=20 A. Напряжение источника U=120 В, частота сети f=50 Гц (рис. 24). Чтобы иметь необходимое напряжение на дуге, последовательно с ней включили индуктивную катушку, сопротивление которой r=1 Ом.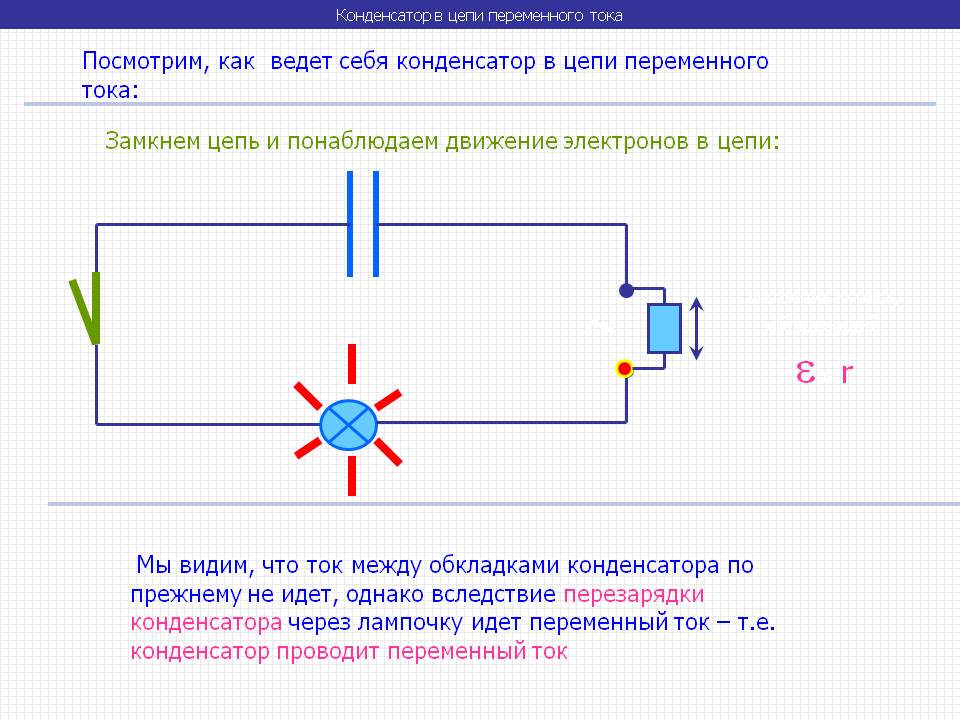
Определить индуктивность катушки; сопротивление реостата, который можно было бы включить вместо катушки; к.п.д. схемы при наличии в ней катушки и реостата.
Решение:
Полное сопротивление схемы
Полная мощность на входе схемы
Потери мощности в обмотке катушки
Активная мощность схемы
Коэффициент мощности схемы
Из таблиц тригонометрических величин
.
Активное сопротивление схемы
сопротивление дуги
Индуктивное сопротивление цепи представлено индуктивным сопротивлением катушки:
Эту же величину можно определить из треугольника сопротивлении (рис. 25, масштаб )
Искомая индуктивность катушки
Если бы вместо катушки был включен реостат, то сопротивление схемы имело бы ту же величину 6 Ом, но было бы чисто активным:
откуда
Потери мощности в катушке
Потери мощности в реостате
Отсюда ясно, что к. п. д. схемы выше при «погашении» избытка напряжения индуктивной катушкой. Действительно, к. п. д. при наличии катушки
п. д. схемы выше при «погашении» избытка напряжения индуктивной катушкой. Действительно, к. п. д. при наличии катушки
к. п. д. при наличии реостата
Не следует забывать, что «погашение» избытка напряжения катушкой (или конденсатором) ухудшает коэффициент мощности (в данном примере
при наличии катушки и при наличии реостата).
22. Последовательно с катушкой, параметры которой
и L=15,92 мГн, включен реостат сопротивлением, . Цепь включена на напряжение U=130 В при частоте f=50 Гц.
Определить ток в цепи; напряжение на катушке и реостате; коэффициент мощности цепи и катушки.
Решение:
Индуктивное сопротивление катушки
Полное сопротивление катушки
Активное сопротивление цепи, состоящей из последовательно соединенных катушки и реостата,
Полное сопротивление цепи
На основании закона Ома ток в цепи
Напряжение на катушке
Напряжение на реостате
Арифметическая сумма
много больше приложенного напряжения U=130 В. Коэффициент мощности цепи
Коэффициент мощности цепи
Коэффициент мощности катушки
Следовательно, реостат увеличивает коэффициент мощности и сопротивление цепи, но уменьшает ток, увеличивает потребление энергии схемой.
Действительно, активная мощность катушки
активная мощность реостата
Так как цепь неразветвленная и ток один, то с него целесообразно начать построение векторной диаграммы (рис. 26).
Напряжение на реостате, представляющем собой чисто активное сопротивление, совпадает по фазе с током; на диаграмме вектор этого напряжения совпадает по направлению с вектором тока. Из конца вектора в сторону опережения вектора тока I, под углом в сторону, противоположную вращению стрелки часов, откладываем вектор напряжения на катушке . Векторы построены так с целью сложения по правилу многоугольника.
23. Неразветвленная цепь составлена из двух катушек: у первой катушки индуктивность
и сопротивление , у второй катушки индуктивность и сопротивление .
Определить ток в цепи и напряжения на каждой катушке, а также построить в масштабе векторную диаграмму, если частота f=50 Гц и приложенное напряжение U=12,6 В.
Решение:
Индуктивное сопротивление первой катушки
т. е. оно численно равно активному сопротивлению
, что обусловливает отставание тока по фазе от напряжения на 1/8 периода (на 45°).
Действительно, тангенс угла сдвига фаз
Индуктивное сопротивление второй катушки
Так как ее активное сопротивление
то тангенс угла сдвига фаз
Построим в масштабе треугольник сопротивлений для рассматриваемой цепи. Для этого зададимся масштабом сопротивлений
. Тогда на диаграмме сопротивление 1,57 Ом будет изображено отрезком 15,7 мм, сопротивление 2,7 Ом — отрезком 27 мм и т. д. На рис. 27 отрезок, изображающий активное сопротивление , отложен в горизонтальном направлении, а отрезок, изображающий индуктивное сопротивление , — в вертикальном направлении под прямым углом к .
Полное сопротивление
первой катушки является гипотенузой прямоугольного треугольника. Из вершины с этого треугольника в горизонтальном направлении отложен отрезок, изображающий сопротивление , и под прямым углом к нему вверх — отрезок, изображающий сопротивление . Гипотенуза се прямоугольного треугольника означает полное сопротивление второй катушки.
Из рис. 27 видно, что отрезок ае, изображающий полное сопротивление z неразветвленной цепи из двух катушек, не равен сумме отрезков ас и се, т. е. . Чтобы определить полное сопротивление z рассматриваемой цепи, следует сложить отдельно активные (, отрезок аf) и индуктивные (, отрезок ef) сопротивления катушек.
Гипотенуза ае, означающая полное сопротивление z цепи, определяется по теореме Пифагора:
Ток в цепи определяется по закону Ома:
Напряжение на первой катушке
Напряжение на второй катушке
Строим векторную диаграмму (рис. 28), приняв масштабы:
а) для тока
; тогда вектор тока изобразится отрезком длиной 25 мм;
б) для напряжения ; при этом вектор напряжения будет иметь длину 55,2 мм, вектор напряжения — длину 71 мм, а вектор приложенного напряжения — длину 126 мм.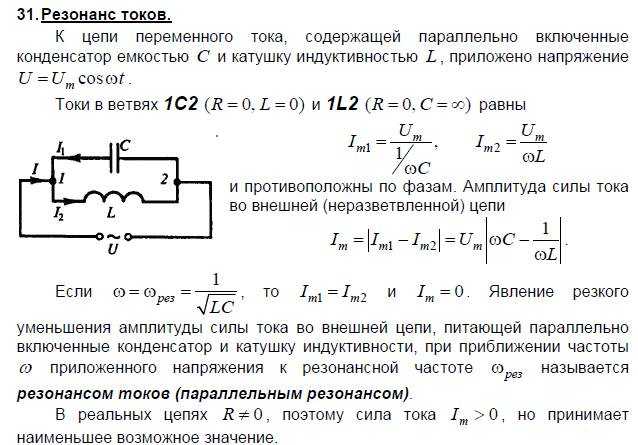
Начало вектора совмещено с концом вектора для возможности сложения векторов напряжений но правилу многоугольника (напряжение, приложенное к неразветвленной цепи катушек, равно геометрической сумме напряжений отдельных катушек).
| ПЕРЕМЕННЫЙ ТОК ВАРИАНТ 1
ПЕРЕМЕННЫЙ ТОК ВАРИАНТ 2
ПЕРЕМЕННЫЙ ТОК ВАРИАНТ 3
ПЕРЕМЕННЫЙ ТОК ВАРИАНТ 4
|
Показать на рисунке Сеть из пяти конденсаторов, подключенных к источнику питания 100 В.
 Рассчитайте общий заряд и энергию, запасенную в сети.
Рассчитайте общий заряд и энергию, запасенную в сети. СОВРЕМЕННАЯ ПУБЛИКАЦИЯ-КОНДЕНСАТОР-ПРИМЕР
20 видеоРЕКЛАМА
Ab Padhai каро бина адс ке
Khareedo DN Про и дехо сари видео бина киси ад ки рукаават ке!
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Похожие видео
На рис. показана сеть из пяти конденсаторов, подключенных к источнику питания 100 В. Рассчитайте общий заряд и энергию, запасенную в сети.
12297368
Найдите общую энергию, хранящуюся в конденсаторах в сети, показанной на рис.
12297371
चित्रिता प नेटव नेटव000 300 V संभरण (सप्लाई) के साथ प्रत्येक संधारित्र का आवेश व उसकी वोल्टा प्राप्त कीजिए।।।।।। कीजिए
52810910
Сеть из четырех конденсаторов емкостью 15 мкФ каждый по четыре конденсатора емкостью мкФ подключена к источнику питания 500 В, как показано на рисунке. Определить (а) эквивалентную емкость сети и (б) заряд каждого конденсатора.
Определить (а) эквивалентную емкость сети и (б) заряд каждого конденсатора.
56434931
Сеть из четырех конденсаторов по 6 мкФ подключена к сети 240 В. Определить заряд каждого конденсатора.
102371910
Сеть из четырех конденсаторов емкостью 20 мкФ подключена к источнику питания 600 В, как показано на рисунке.
Эквивалентная емкость сети составляет
112441342
Сеть из 4 конденсаторов, каждый по 6 мкФ, подключена к источнику питания 240 В, как показано на рисунке. Чему равен заряд конденсаторов С2 и С4?
127329927
Найдите полную энергию, запасенную в конденсаторах данной сети.
236919688
Сеть из четырех конденсаторов емкостью 10 мкФ подключена к источнику питания 500 В, как показано на рисунке. Определите (а) эквивалентную емкость сети и (б) заряд каждого конденсатора.
467054908
Найдите общий заряд, хранящийся в сети конденсаторов, подключенных между A и B, как показано на рисунке.
529319317
Text Solution
Сеть из четырех конденсаторов емкостью 10 мкФ подключена к источнику питания 500 В, как показано на рисунке. Определить (а) эквивалентную емкость сети и (б) заряд каждого конденсатора.
562113867
चार, 20 мкф का संधारित्रों नेटवर्क चितшить नेटवर्क की तुल्य धारिता क्या होगी?
575620836
चार, 20 мкф संधारित्en
संधारित्रों C1 एवं C2 पर आवेश होगा-
575620837
На рисунке показана сеть из пяти конденсаторов, подключенных к источнику питания 100 В. Рассчитайте общую энергию, накопленную в сети.
606266490
Текст Решение
Найдите полную энергию, запасенную в конденсаторах данной схемы на рис.


 Напряжение на зажимах цепи U = 216 В, R = 21 Ом, L = 70 мГн, С = 82 мкФ. Частота стандартная. Постройте векторную диаграмму сил токов.
Напряжение на зажимах цепи U = 216 В, R = 21 Ом, L = 70 мГн, С = 82 мкФ. Частота стандартная. Постройте векторную диаграмму сил токов.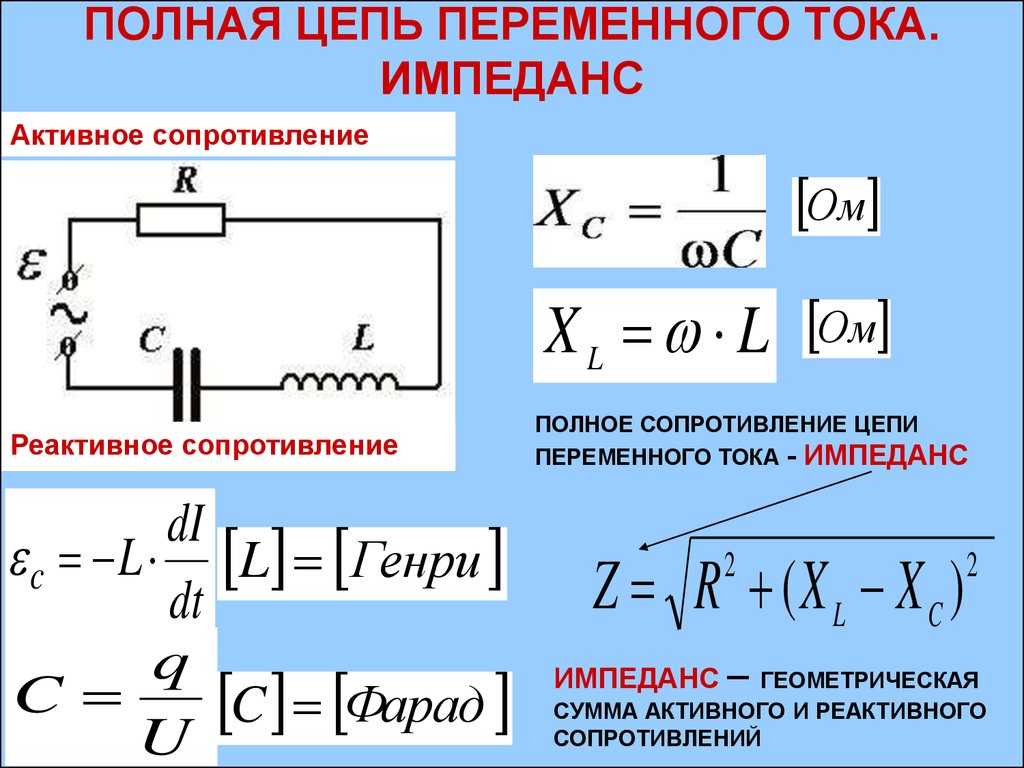 Какова сила тока в конденсаторе, если напряжение в сети 120 В?
Какова сила тока в конденсаторе, если напряжение в сети 120 В? Активное сопротивление катушки мало. Частота тока в сети ν = 50 Гц. Определите напряжение в сети U, если амперметр показывает 2,4 А. Постройте векторную диаграмму.
Активное сопротивление катушки мало. Частота тока в сети ν = 50 Гц. Определите напряжение в сети U, если амперметр показывает 2,4 А. Постройте векторную диаграмму.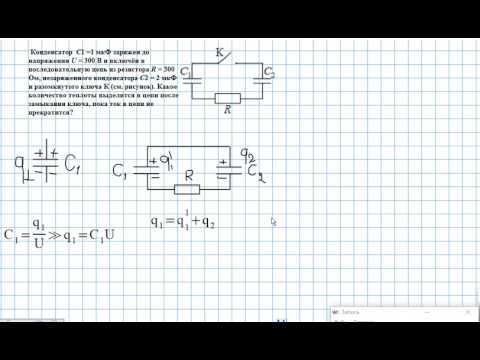 Найдите амплитуду ЭДС индукции в рамке.
Найдите амплитуду ЭДС индукции в рамке.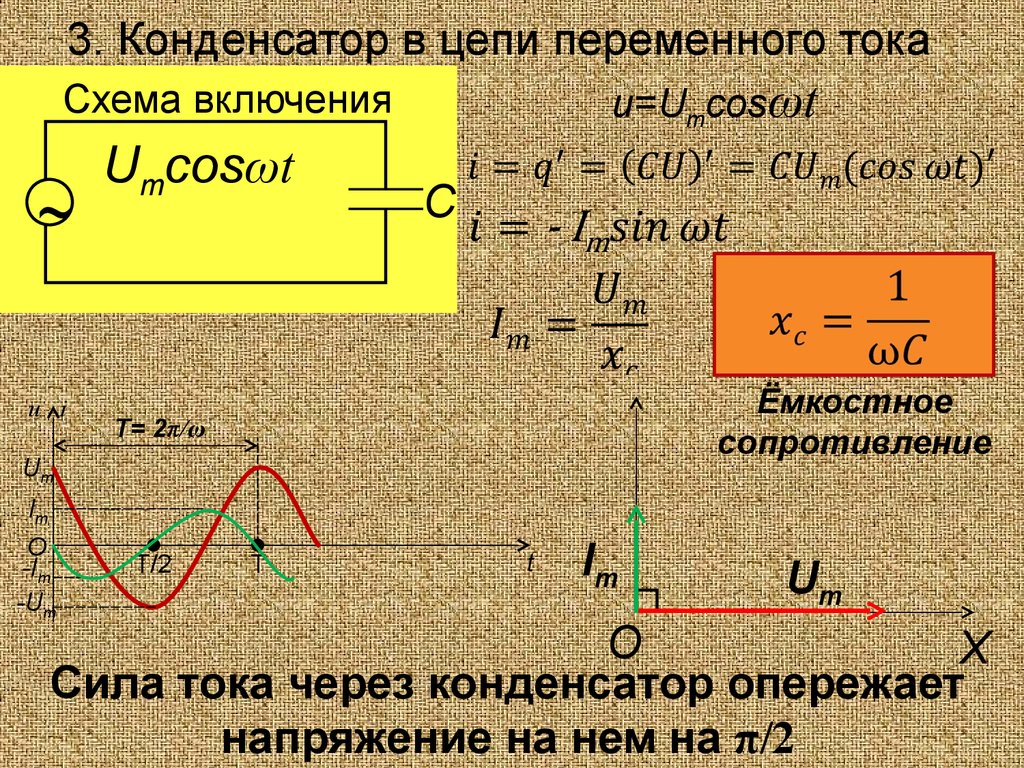 Постройте векторную диаграмму сил токов.
Постройте векторную диаграмму сил токов. Емкостное сопротивление конденсатора 5 кОм. Какой должна быть индуктивность катушки, чтобы резонанс наступил в цепи при частоте колебаний силы тока 20 кГц?
Емкостное сопротивление конденсатора 5 кОм. Какой должна быть индуктивность катушки, чтобы резонанс наступил в цепи при частоте колебаний силы тока 20 кГц?