Что такое логические элементы в информатике. Как работают конъюнкторы, дизъюнкторы и инверторы. Для чего используются логические вентили в компьютерах. Какие основные логические операции существуют.
Основные логические элементы и их функции
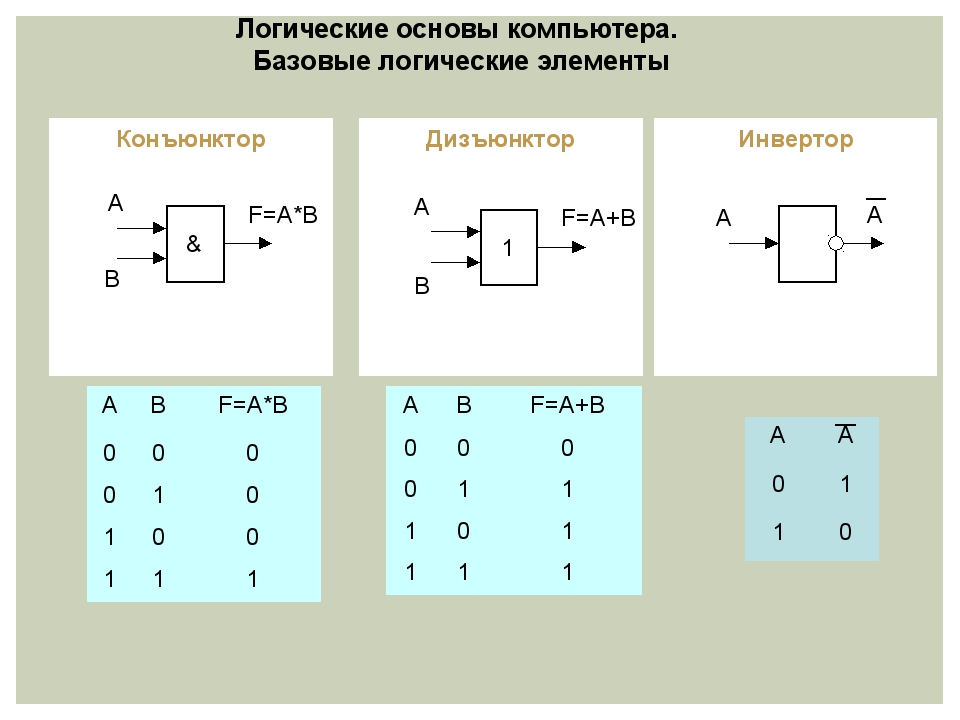
Логические элементы являются фундаментальными компонентами цифровых схем и компьютеров. Они реализуют базовые логические операции, на основе которых строятся более сложные вычислительные устройства.
Основными логическими элементами являются:
- Конъюнктор (элемент И)
- Дизъюнктор (элемент ИЛИ)
- Инвертор (элемент НЕ)
Рассмотрим подробнее принцип работы каждого из этих элементов.
Конъюнктор (элемент И)
Конъюнктор реализует логическую операцию «И». Его выход равен 1 только в том случае, если все входы равны 1. Во всех остальных случаях выход равен 0.
Таблица истинности для двухвходового конъюнктора:
| Вход A | Вход B | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Дизъюнктор (элемент ИЛИ)
Дизъюнктор реализует логическую операцию «ИЛИ». Его выход равен 1, если хотя бы один из входов равен 1. Выход равен 0 только если все входы равны 0.
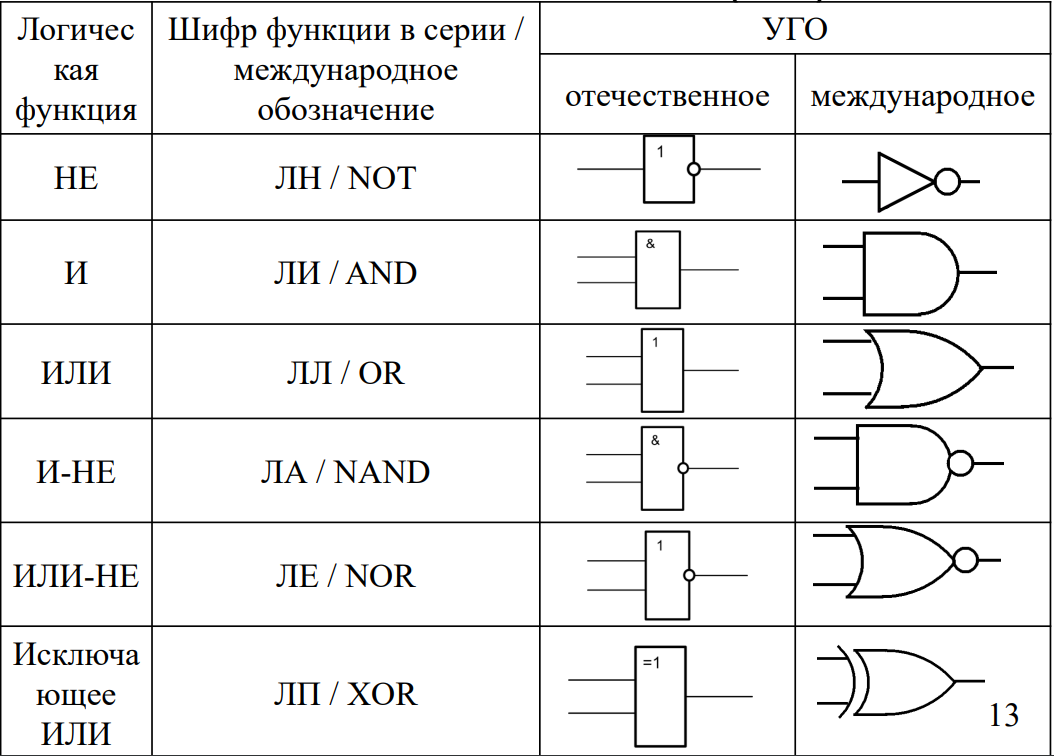
Таблица истинности для двухвходового дизъюнктора:
| Вход A | Вход B | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Инвертор (элемент НЕ)
Инвертор реализует логическую операцию отрицания. Он инвертирует входной сигнал — если на входе 0, то на выходе 1, и наоборот.
Таблица истинности для инвертора:
| Вход | Выход |
|---|---|
| 0 | 1 |
| 1 | 0 |
Применение логических элементов в цифровых схемах
Логические элементы являются базовыми строительными блоками для создания более сложных цифровых устройств. Они широко применяются в следующих областях:
- Проектирование процессоров и микроконтроллеров
- Создание арифметико-логических устройств
- Разработка устройств памяти
- Построение систем управления
- Реализация алгоритмов шифрования
Комбинируя простые логические элементы, можно создавать сложные функциональные блоки, такие как сумматоры, триггеры, регистры и др.
Реализация логических элементов на транзисторах
Логические элементы физически реализуются с помощью электронных компонентов, чаще всего транзисторов. Рассмотрим простейшие схемы на транзисторах для основных логических элементов:

Инвертор на транзисторе
Простейший инвертор можно реализовать на одном транзисторе:
- Если на вход подан низкий уровень (логический 0), транзистор закрыт и на выходе высокий уровень (логическая 1)
- Если на вход подан высокий уровень (логическая 1), транзистор открыт и на выходе низкий уровень (логический 0)
Конъюнктор на транзисторах
Схема конъюнктора содержит два последовательно соединенных транзистора:
- Выход будет иметь высокий уровень только если оба транзистора открыты (на обоих входах высокий уровень)
- В остальных случаях хотя бы один транзистор закрыт и на выходе низкий уровень
Дизъюнктор на транзисторах
Схема дизъюнктора содержит два параллельно соединенных транзистора:
- Выход будет иметь низкий уровень только если оба транзистора закрыты (на обоих входах низкий уровень)
- В остальных случаях хотя бы один транзистор открыт и на выходе высокий уровень
Логические вентили и их условные обозначения
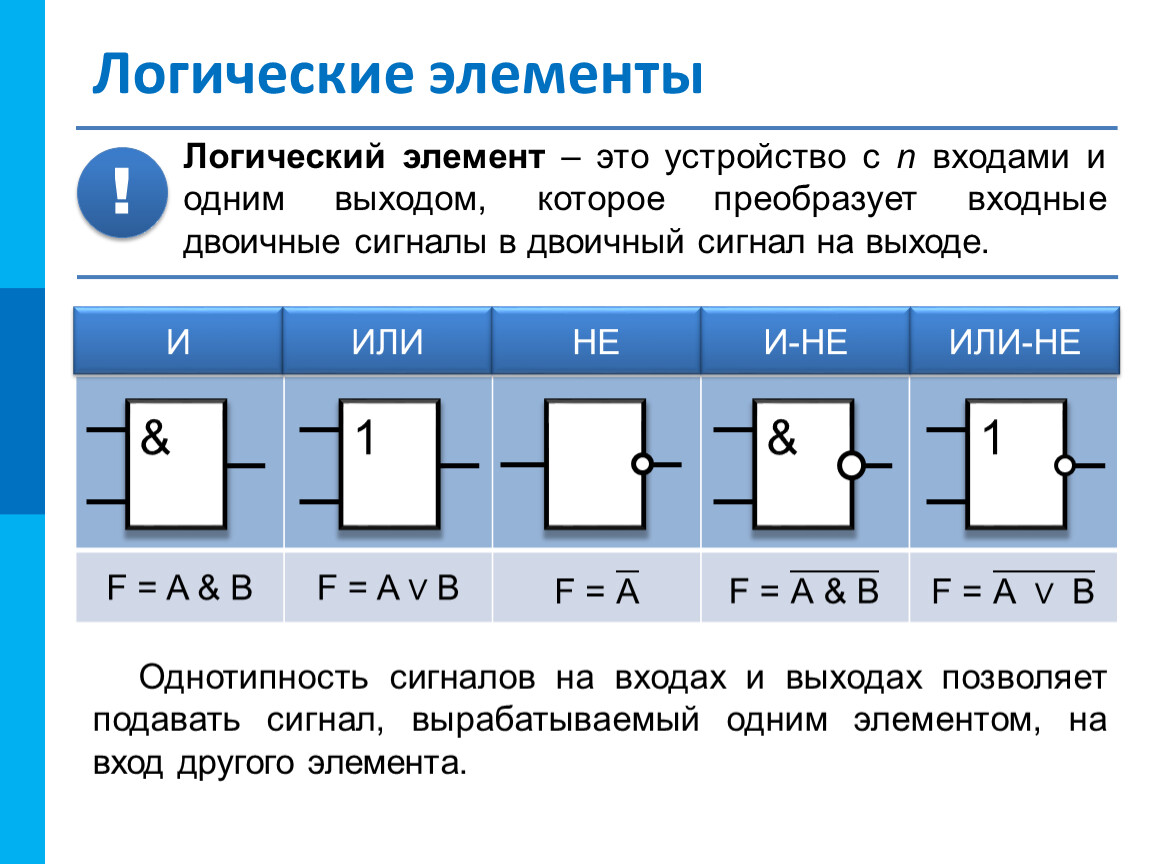
Логические элементы на схемах обозначаются специальными символами, которые называются логическими вентилями. Основные условные обозначения:
- Конъюнктор (И) — &
- Дизъюнктор (ИЛИ) — ≥1
- Инвертор (НЕ) — 1
Эти обозначения стандартизированы и широко используются при проектировании цифровых схем. Они позволяют наглядно представить логику работы устройства.
Базовые логические операции и их свойства
Рассмотрим основные логические операции и их ключевые свойства:
Конъюнкция (операция И)
Обозначается символом ∧. Основные свойства:
- Коммутативность: A ∧ B = B ∧ A
- Ассоциативность: (A ∧ B) ∧ C = A ∧ (B ∧ C)
- Идемпотентность: A ∧ A = A
- Дистрибутивность относительно дизъюнкции: A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C)
Дизъюнкция (операция ИЛИ)
Обозначается символом ∨. Основные свойства:
- Коммутативность: A ∨ B = B ∨ A
- Ассоциативность: (A ∨ B) ∨ C = A ∨ (B ∨ C)
- Идемпотентность: A ∨ A = A
- Дистрибутивность относительно конъюнкции: A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C)
Отрицание (операция НЕ)
Обозначается символом ¬. Основные свойства:
- Двойное отрицание: ¬(¬A) = A
- Законы де Моргана: ¬(A ∧ B) = ¬A ∨ ¬B, ¬(A ∨ B) = ¬A ∧ ¬B
Функциональная полнота логических операций
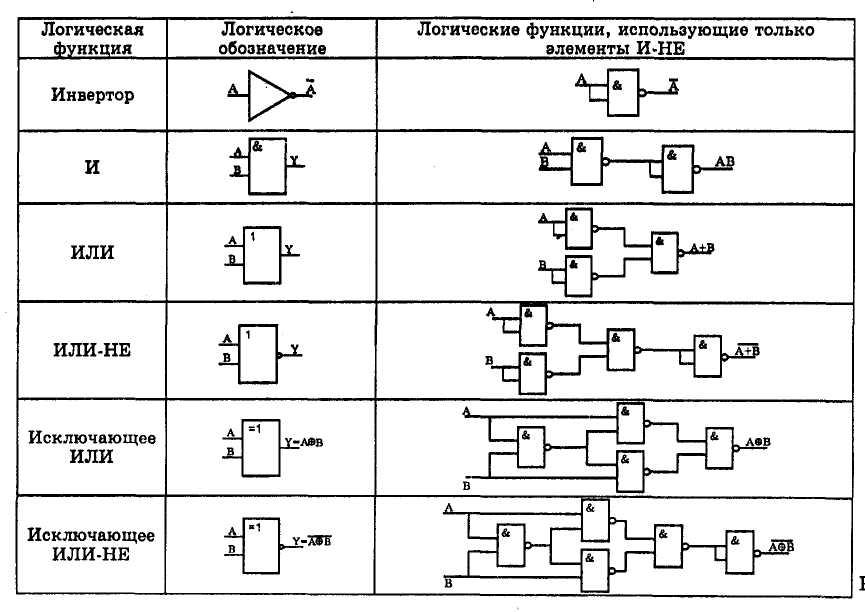
Важным понятием в алгебре логики является функциональная полнота. Набор логических операций называется функционально полным, если с его помощью можно выразить любую логическую функцию.
Функционально полными являются следующие наборы операций:
- {И, ИЛИ, НЕ}
- {И, НЕ}
- {ИЛИ, НЕ}
- {И-НЕ}
- {ИЛИ-НЕ}
Это означает, что используя только элементы И-НЕ или только элементы ИЛИ-НЕ, можно построить любую логическую схему. Поэтому эти элементы часто используются как базовые при проектировании цифровых устройств.
Применение логических элементов в современных компьютерах
В современных компьютерах логические элементы используются повсеместно. Вот некоторые примеры их применения:
Процессоры
Центральный процессор компьютера состоит из миллионов транзисторов, образующих сложные логические схемы. Эти схемы выполняют арифметические и логические операции, управляют потоками данных и командами программ.
Оперативная память
Ячейки памяти реализуются на основе логических элементов. Триггеры, построенные из логических вентилей, способны хранить один бит информации.
Кэш-память
Быстрая кэш-память процессора также построена на основе логических элементов. Схемы сравнения адресов, реализованные на логических вентилях, позволяют быстро определять наличие данных в кэше.
Шины данных
Логические элементы используются для управления потоками данных по шинам компьютера. Они обеспечивают правильную маршрутизацию сигналов между компонентами системы.
Графические процессоры
Современные GPU содержат огромное количество параллельно работающих вычислительных блоков, построенных на основе логических элементов. Это позволяет им эффективно обрабатывать графику и выполнять параллельные вычисления.
Таким образом, логические элементы лежат в основе работы всех цифровых устройств, от простейших микроконтроллеров до сложнейших суперкомпьютеров.
(в теоретических работах по алгебре логики). В формулах, как и в обычной алгебре, знак чаще всего опускается.
Запись в языках программирования: х1 AND х2.
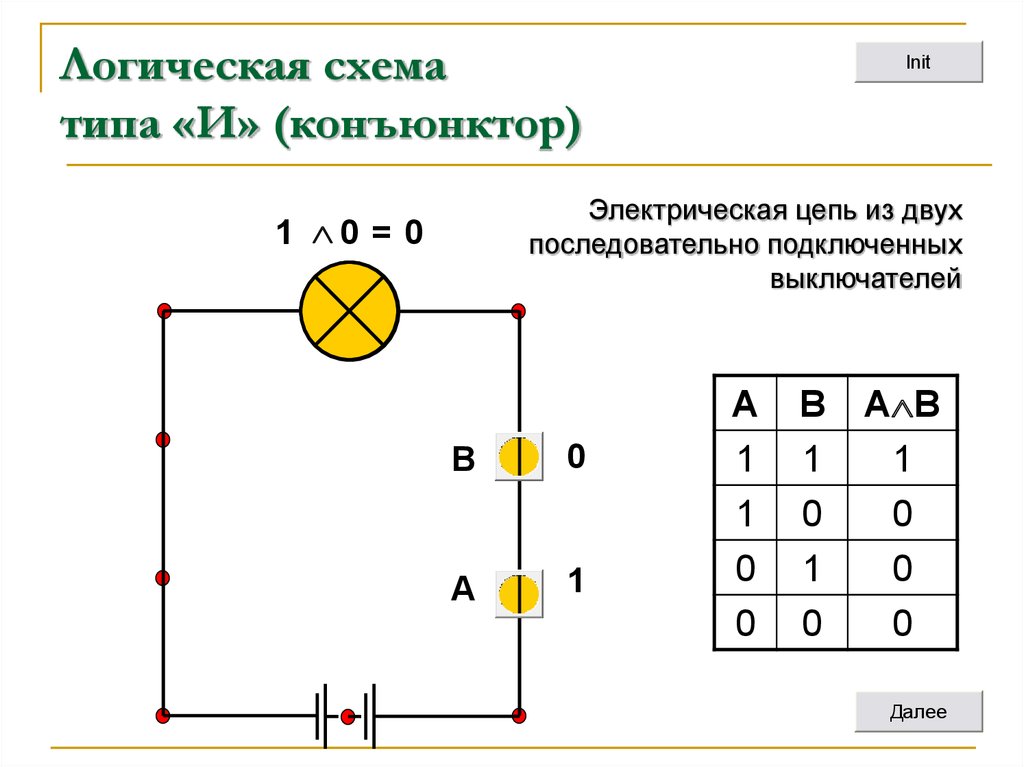
Функцию И реализуют, например, соединенные последовательно замыкающие контакты нескольких реле. Цепь в этом случае будет замкнута только тогда, когда сработают все реле (реализация схемы «вопрос решён положительно, только тогда, когда «за» проголосуют все. Конъюнкцию реализует логическая схема (вентиль), называемая конъюнктором, логика работы которой представлена на рис. 4.5(a,b,c):
Рис. 4.5a.
Рис. 4.5b.
Рис. 4.5c. Принцип работы конъюнктора
Конъюнктор можно условно изобразить схематически электрической цепью вида (рис. 4.6)
Рис. 4.6. Электрический аналог схемы конъюнктора
Схематически
инвертор, дизьюнктор и конъюнктор на
логических схемах различных устройств
можно изображать условно следующим
образом (рис. 4.7 а, б, в). Есть и другие
общепринятые формы условных обозначений.
4.7 а, б, в). Есть и другие
общепринятые формы условных обозначений.
Рис. 4.7. а, б, в. Условные обозначения вентилей (вариант)
Пример. Транзисторные схемы, соответствующие логическим схемам (инвертор), (дизъюнктор), (конъюнктор) имеют, например, следующий вид (рис. 4.8 а, б, в):
Рис. 4.8a. Инвертор
Рис. 4.8b. Дизъюнктор
Рис. 4.8c. Конъюнктор
Из указанных
простейших базовых логических элементов
собирают, конструируют сложные логические
схемы ЭВМ, например, сумматоры, шифраторы,
дешифраторы и др. Большие (БИС) и
сверхбольшие (СБИС) интегральные схемы
содержат в своем составе (на кристалле
кремния площадью в несколько квадратных
сантиметров) десятки тысяч вентилей.
Это возможно еще и потому, что базовый
набор логических схем (инвертор,
конъюнктор, дизъюнктор) является
функционально полным (любую логическую
функцию можно представить через эти
базовые вентили), представление логических
констант в них одинаково (одинаковы
электрические сигналы, представляющие
1 и 0) и различные схемы можно «соединять»
и «вкладывать» друг в друга
(осуществлять композицию и суперпозицию
схем).
Таким способом конструируются более сложные узлы ЭВМ – ячейки памяти, регистры, шифраторы, дешифраторы, а также сложнейшие интегральные схемы.
Задача
Пусть в некотором конкурсе решается вопрос о допуске того или иного участника к следующему туру тремя членами жюри: Р,Q, R. Решение положительно тогда и только тогда, когда хотя бы двое членов жюри высказываются за допуск, причем среди них обязательно должен быть председатель жюри . Необходимо разработать устройство для голосования, в котором каждый член жюри нажимает на одну из двух кнопок — «За» или «Против», а результат голосования всех трех членов жюри определяется по тому, загорится (решение принято) или нет (решение не принято) сигнальная лампочка.
Формально это
можно выразить так: требуется составить
функциональную схему устройства, которое
на выходе выдавало бы 1, если участник
допускается к следующему туру, и 0, если
не допускается.
Рис. 4.9. Сводная таблица описания логических элементов, моделирующих работу элементарных логических операций
20. Логический вентиль, инвертор, дизъюнктор, конъюнктор, принципы работы.
В основе построения компьютеров, а точнее аппаратного обеспечения, лежат так называемые вентили. Они представляют собой достаточно простые элементы, которые можно комбинировать между собой, создавая тем самым различные схемы. Одни схемы подходят для осуществления арифметических операций, а на основе других строят различную память ЭВМ.
Простейший вентиль представляет собой транзисторный инвертор, который преобразует низкое напряжение в высокое или наоборот (высокое в низкое). Это можно представить как преобразование логического нуля в логическую единицу или наоборот. Т.е. получаем вентиль НЕ.
Соединив пару транзисторов различным
способом, получают вентили ИЛИ-НЕ и
И-НЕ. Эти вентили принимают уже не один,
а два и более входных сигнала. Выходной
сигнал всегда один и зависит (выдает
высокое или низкое напряжение) от входных
сигналов. В случае вентиля ИЛИ-НЕ получить
высокое напряжение (логическую единицу)
можно только при условии низкого
напряжении на всех входах. В случае
вентиля И-НЕ все наоборот: логическая
единица получается, если все входные
сигналы будут нулевыми. Как видно, это
обратно таким привычным логическим
операциям как И и ИЛИ. Однако обычно
используются вентили И-НЕ и ИЛИ-НЕ, т.к.
их реализация проще: И-НЕ и ИЛИ-НЕ
реализуются двумя транзисторами, тогда
как логические И и ИЛИ тремя.
Выходной
сигнал всегда один и зависит (выдает
высокое или низкое напряжение) от входных
сигналов. В случае вентиля ИЛИ-НЕ получить
высокое напряжение (логическую единицу)
можно только при условии низкого
напряжении на всех входах. В случае
вентиля И-НЕ все наоборот: логическая
единица получается, если все входные
сигналы будут нулевыми. Как видно, это
обратно таким привычным логическим
операциям как И и ИЛИ. Однако обычно
используются вентили И-НЕ и ИЛИ-НЕ, т.к.
их реализация проще: И-НЕ и ИЛИ-НЕ
реализуются двумя транзисторами, тогда
как логические И и ИЛИ тремя.
Выходной сигнал вентиля можно выражать как функцию от входных.
Транзистору требуется очень мало времени для переключения из одного состояния в другое (время переключения оценивается в наносекундах). И в этом одно из существенных преимуществ схем, построенных на их основе.
________________________________________________________________________________________________________
Так как же связываются между собой
простые логические высказывания, образуя
сложные? В естественном языке мы
используем различные союзы и другие
части речи. Например, «и», «или», «либо»,
«не», «если», «то», «тогда». Пример
сложных высказываний: «у него есть
знания и навыки», «она приедет во вторник,
либо в среду», «я буду играть тогда,
когда сделаю уроки», «5 не равно 6». Как
мы решаем, что нам сказали правду или
нет? Как-то логически, даже где-то
неосознанно, исходя из предыдущего
жизненного опыта, мы понимает, что правда
при союзе «и» наступает в случае
правдивости обоих простых высказываний.
Стоит одному стать ложью и все сложное
высказывание будет лживо. А вот, при
связке «либо» должно быть правдой только
одно простое высказывание, и тогда все
выражение станет истинным.
Например, «и», «или», «либо»,
«не», «если», «то», «тогда». Пример
сложных высказываний: «у него есть
знания и навыки», «она приедет во вторник,
либо в среду», «я буду играть тогда,
когда сделаю уроки», «5 не равно 6». Как
мы решаем, что нам сказали правду или
нет? Как-то логически, даже где-то
неосознанно, исходя из предыдущего
жизненного опыта, мы понимает, что правда
при союзе «и» наступает в случае
правдивости обоих простых высказываний.
Стоит одному стать ложью и все сложное
высказывание будет лживо. А вот, при
связке «либо» должно быть правдой только
одно простое высказывание, и тогда все
выражение станет истинным.
Булева алгебра переложила этот жизненный опыт на аппарат математики, формализовала его, ввела жесткие правила получения однозначного результата. Союзы стали называться здесь логическими операторами.
Алгебра логики предусматривает множество
логических операций. Однако три из них
заслуживают особого внимания, т.к. с их
помощью можно описать все остальные,
и, следовательно, использовать меньше
разнообразных устройств при конструировании
схем. Такими операциями являются
конъюнкция (И), дизъюнкция (ИЛИ) и отрицание
(НЕ). Часто конъюнкцию обозначают &,
дизъюнкцию — ||, а отрицание — чертой над
переменной, обозначающей высказывание.
Такими операциями являются
конъюнкция (И), дизъюнкция (ИЛИ) и отрицание
(НЕ). Часто конъюнкцию обозначают &,
дизъюнкцию — ||, а отрицание — чертой над
переменной, обозначающей высказывание.
При конъюнкции истина сложного выражения возникает лишь в случае истинности всех простых выражений, из которых состоит сложное. Во всех остальных случаях сложное выражение будет ложно.
При дизъюнкции истина сложного выражения наступает при истинности хотя бы одного входящего в него простого выражения или двух сразу. Бывает, что сложное выражение состоит более, чем из двух простых. В этом случае достаточно, чтобы одно простое было истинным и тогда все высказывание будет истинным.
Отрицание – это унарная операция, т.к выполняется по отношению к одному простому выражению или по отношению к результату сложного. В результате отрицания получается новое высказывание, противоположное исходному.
конъюнктор | Dental-Dictionary.com
Алмазные инструменты
Алмазные инструменты обычно ротационные и осесимметричные, иногда колеблющиеся, стоматологические инструменты почти всегда используются в приводных устройствах (наконечниках, угловых наконечниках, турбинах…
Алмазные инструменты Алмазные инструменты, как правило, вращающиеся и вращательно-симметричные, иногда колеблющиеся, стоматологические инструменты, почти всегда используемые в приводных узлах (наконечники, угловые наконечники, турбины) во всех областях стоматологической медицины и техники для самых разных целей, начиная от препарирования и обрезки консервативных или протезных реставрации для уменьшения проксимальной части эмали во время ортодонтического лечения или хирургического вмешательства. Алмазные инструменты изготавливаются путем встраивания одного или нескольких слоев многогранных частиц природного или технического алмаза в слой связующего (часто гальванически связанного или спеченного с металлической заготовкой). Края частиц стирают ткани и многие типы материалов (в основном твердые ткани зуба, такие как эмаль и дентин). Изношенные края и частицы, вырывающиеся из бондера, приводят к затуплению инструментов. Спеченные алмазы и силиконовые («резиновые») полиры не только «покрываются» на поверхности, весь инструмент пропитывается алмазными частицами, что делает их самозатачивающимися (но их первоначальный размер и форма изнашиваются). Кольца с цветовой маркировкой используются для классификации алмазных инструментов в зависимости от их абразивности (в зависимости от размера частиц) от сверхгрубых (около 150 мкм для быстрого уменьшения структуры) до сверхмелких (около 15 мкм для окончательной обработки). Алмазный бор При тщательном изготовлении (точные размеры геометрии инструмента, качество, острота/однородность частиц, качество стали) алмазные инструменты работают плавно, эффективно и долговечны. Различные формы и размеры алмазных инструментов могут быть обозначены цифрами и единообразно в соотв. DIN EN ISO 6360-1 (например, длина хвостовика/материал, размер зерна, диаметр рабочей части). Алмазный бор в форме бугорка В зависимости от приложенного давления, скорости, диаметра, зернистости и силы тяги приводного устройства создается сила трения разной степени. Чтобы предотвратить нежелательные эффекты теплоты трения в тканях (например, коагуляция белков) или материалах (например, треснувший диоксид циркония или расплавленный акрил), алмазные инструменты часто («обязательно» при внутриротовом использовании) постоянно охлаждают водой. Это гарантирует, что частицы пыли могут быть смыты одновременно, что предотвращает засорение инструмента. Интеграция лезвий из карбида вольфрама, направляющих выступов, областей без покрытия и т. д. позволяет защитить определенные конструкции от обжатия или еще больше обжать. Большинство алмазных инструментов можно автоклавировать и использовать многократно. Стерильные одноразовые алмазные инструменты все чаще используются в клинических целях. Том 13, Выпуск 1, 2020, Страницы 201 — 211 Авторов Ana Pradera 1 , * , Sebastia Massanet 2 , 3 , Daniel Ruiz 2 , 3 , Joan Torrens 2 , 3 , Joan Torrens 2 , 3 . la Computación, Arquitectura de Computadores, Lenguajes y Sistemas Informáticos y Estadística e Investigacion Operativa, Universidad Rey Juan Carlos, 28933 Móstoles, Madrid, Spain 2 Мягкие вычисления, обработка изображений и агрегация (SCOPIA) Research Groups and Department of Mathematic Информатика, Университет Балеарских островов, 07122 Пальма, Испания 3 Институт медицинских исследований Балеарских островов (IdISBa), 07010 Пальма, Испания * Автор, ответственный за переписку. Автор, ответственный за переписку Ана Прадера Получено 14 мая 2019 г., принято 4 февраля 2020 г., доступно в Интернете 14 февраля 2020 г. /ijcis.d.200205.002Как использовать DOI? Правило вывода Modus Ponens широко исследовалось в рамках приближенных рассуждений, особенно для случая t-норм. В последнее время также рассматривались более общие виды конъюнкторов, такие как полусвязки, связки и конъюнктивные унинормы. Общим признаком всех этих видов конъюнкторов является то, что они имеют нейтральный элемент e∈]0,1]. Настоящая статья посвящена изучению Modus Ponens для конъюнкторов с нейтральным элементом без дополнительных условий. Доказано, что многие свойства необходимы для того, чтобы функция нечеткой импликации I удовлетворяла Modus Ponens относительно конъюнктора с нейтральным элементом e∈]0,1]. Скачать статью (PDF) 4 5
4 5
4
 Некоторые алмазные инструменты предназначены только для ручного использования, например, для придания шероховатости участкам, подготовленным для штифтов перед приклеиванием.
Некоторые алмазные инструменты предназначены только для ручного использования, например, для придания шероховатости участкам, подготовленным для штифтов перед приклеиванием.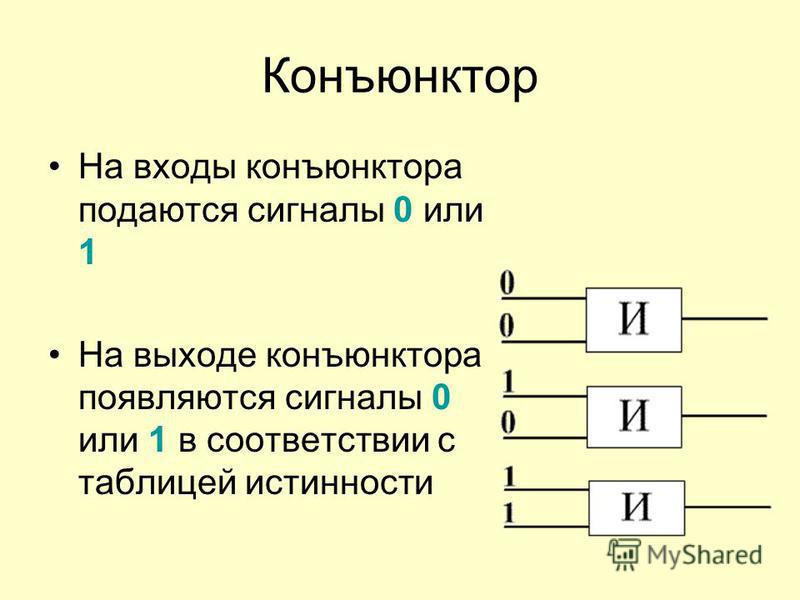
 Канавки без покрытия, осевые или спиральные вокруг инструмента, имеют тот же эффект.
Канавки без покрытия, осевые или спиральные вокруг инструмента, имеют тот же эффект. Об использовании конъюнкторов с нейтральным элементом в неравенстве Modus Ponens
 Электронная почта: [email protected]
Электронная почта: [email protected] 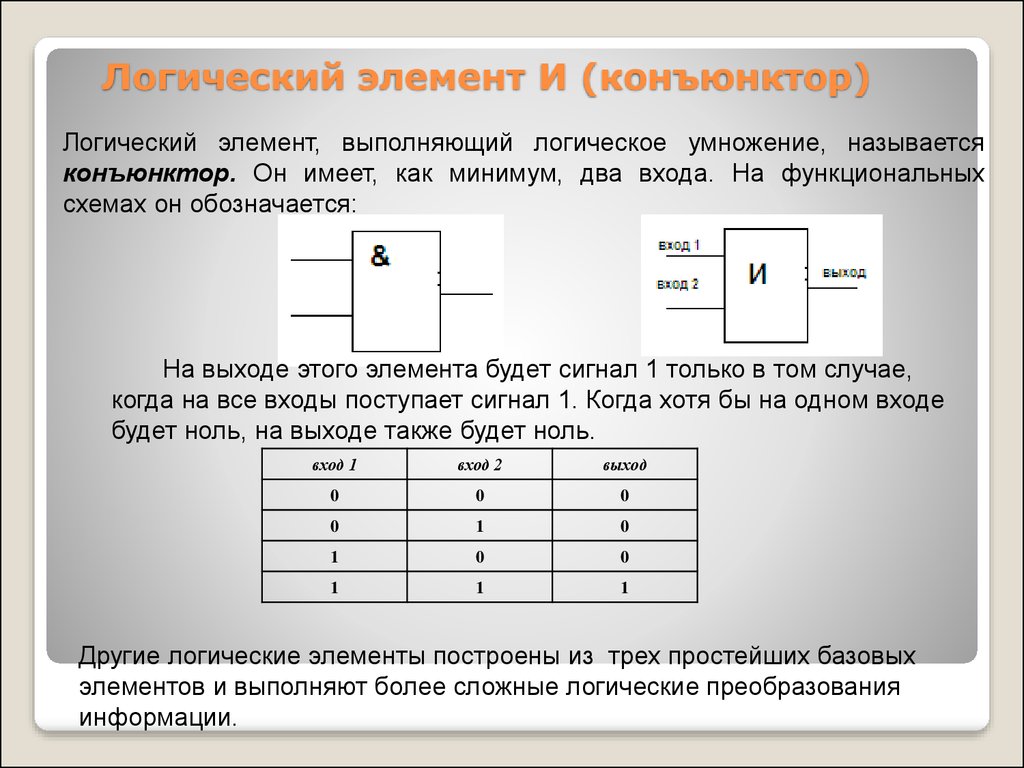 Хотя самые обычные семейства функций нечеткой импликации не удовлетворяют всем этим свойствам, приводятся другие возможности для I, показывающие множество новых примеров и обобщающие некоторые уже известные результаты по этой теме. При этом все функции нечеткой импликации, удовлетворяющие Modus Ponens относительно наименьшего (и относительно наибольшего) конъюнктора с нейтральным элементом e∈]0,1[ охарактеризованы. Частный случай e=1, обеспечивающий полусвязки, изучается отдельно, что позволяет получить многие известные результаты, которые можно легко вывести из текущего исследования.
Хотя самые обычные семейства функций нечеткой импликации не удовлетворяют всем этим свойствам, приводятся другие возможности для I, показывающие множество новых примеров и обобщающие некоторые уже известные результаты по этой теме. При этом все функции нечеткой импликации, удовлетворяющие Modus Ponens относительно наименьшего (и относительно наибольшего) конъюнктора с нейтральным элементом e∈]0,1[ охарактеризованы. Частный случай e=1, обеспечивающий полусвязки, изучается отдельно, что позволяет получить многие известные результаты, которые можно легко вывести из текущего исследования.
Просмотреть полный текст (HTML)
3 Страницы 

