Что такое логические элементы и как они работают. Какие бывают типы логических элементов. Как используются таблицы истинности. Где применяются логические элементы в электронике.
Основы логических элементов в цифровой электронике
Логические элементы являются фундаментальными строительными блоками всех цифровых систем и схем. Это простейшие электронные устройства, которые выполняют базовые логические операции над двоичными сигналами.
Ключевые особенности логических элементов:
- Имеют один или несколько входов и один выход
- Работают только с двоичными сигналами (0 и 1)
- Выполняют элементарные логические функции (И, ИЛИ, НЕ и др.)
- Поведение описывается таблицей истинности
- Являются основой для построения более сложных цифровых схем
Работа логических элементов базируется на булевой алгебре, разработанной математиком Джорджем Булем. Это позволяет описывать работу элементов с помощью логических выражений и таблиц истинности.
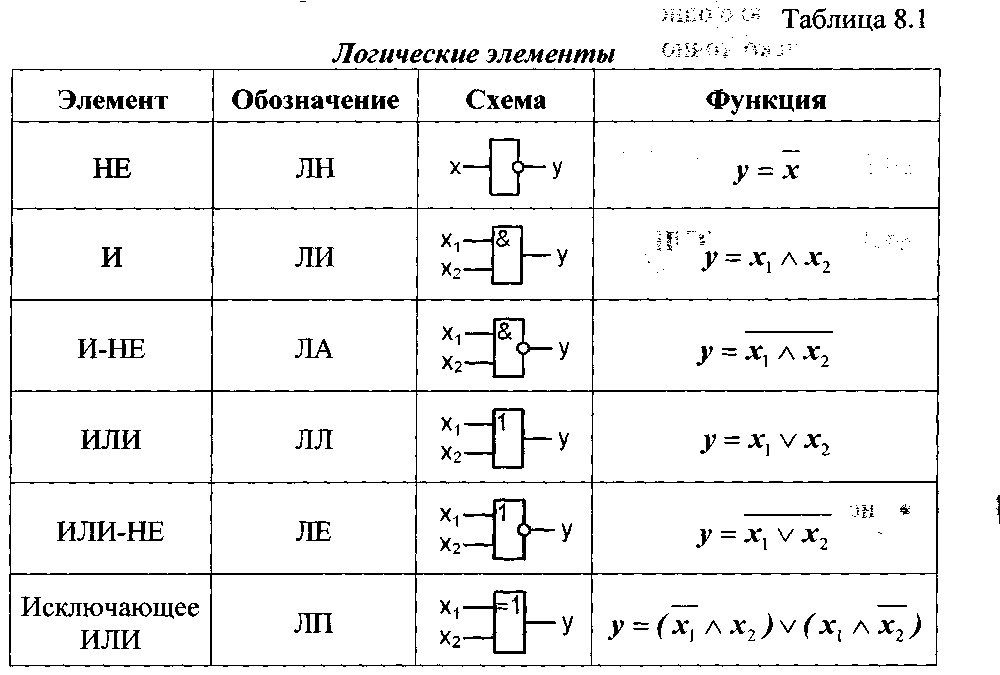
Основные типы логических элементов
Существует несколько базовых типов логических элементов, из которых строятся все остальные цифровые схемы:
1. Элемент И (AND)
Выдает 1 на выходе только если все входы равны 1. Таблица истинности для двухвходового элемента И:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2. Элемент ИЛИ (OR)
Выдает 1 на выходе, если хотя бы один вход равен 1. Таблица истинности:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
3. Элемент НЕ (NOT)
Инвертирует входной сигнал. Таблица истинности:
| A | Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
Универсальные логические элементы
Существуют два типа универсальных логических элементов, с помощью которых можно реализовать любую логическую функцию:
1. Элемент И-НЕ (NAND)
Является комбинацией элементов И и НЕ. Таблица истинности:
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
2. Элемент ИЛИ-НЕ (NOR)
Объединяет функции элементов ИЛИ и НЕ. Таблица истинности:
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Применение логических элементов в электронике
Логические элементы находят широкое применение во многих областях электроники и вычислительной техники:
- Микропроцессоры и микроконтроллеры
- Оперативная и постоянная память
- Цифровые сигнальные процессоры
- Программируемые логические интегральные схемы
- Системы автоматического управления
- Цифровая обработка сигналов
- Устройства кодирования и шифрования данных
На основе логических элементов строятся более сложные функциональные блоки, такие как:
- Сумматоры и вычитатели
- Мультиплексоры и демультиплексоры
- Шифраторы и дешифраторы
- Триггеры и регистры
- Счетчики
Как работают логические элементы на физическом уровне
Физическая реализация логических элементов может быть различной, но чаще всего используются следующие технологии:
Транзисторно-транзисторная логика (TTL)
Основана на биполярных транзисторах. Преимущества: высокое быстродействие, низкая стоимость. Недостатки: высокое энергопотребление.
КМОП-логика
Использует комплементарные пары полевых МОП-транзисторов. Преимущества: сверхнизкое энергопотребление в статическом режиме, высокая помехоустойчивость. Недостатки: чувствительность к статическому электричеству.
ЭСЛ-логика
Эмиттерно-связанная логика на биполярных транзисторах. Преимущества: сверхвысокое быстродействие. Недостатки: большое энергопотребление, сложность реализации.
Проектирование цифровых схем на основе логических элементов
При разработке цифровых устройств на основе логических элементов используются следующие этапы:
- Определение функциональных требований к устройству
- Составление таблицы истинности
- Минимизация логической функции (например, с помощью карт Карно)
- Построение логической схемы на основе минимизированной функции
- Моделирование работы схемы
- Физическая реализация схемы
- Тестирование и отладка готового устройства
Современные САПР значительно упрощают процесс проектирования сложных цифровых схем, позволяя автоматизировать многие этапы разработки.
Перспективы развития логических элементов
Основные направления совершенствования логических элементов включают:
- Уменьшение размеров транзисторов для повышения плотности интеграции
- Снижение энергопотребления
- Увеличение быстродействия
- Разработка новых архитектур (например, обратимые логические элементы)
- Использование новых материалов (графен, углеродные нанотрубки и др.)
- Развитие квантовых вычислений на основе кубитов
Развитие технологий производства логических элементов напрямую влияет на прогресс всей вычислительной техники и электроники в целом.
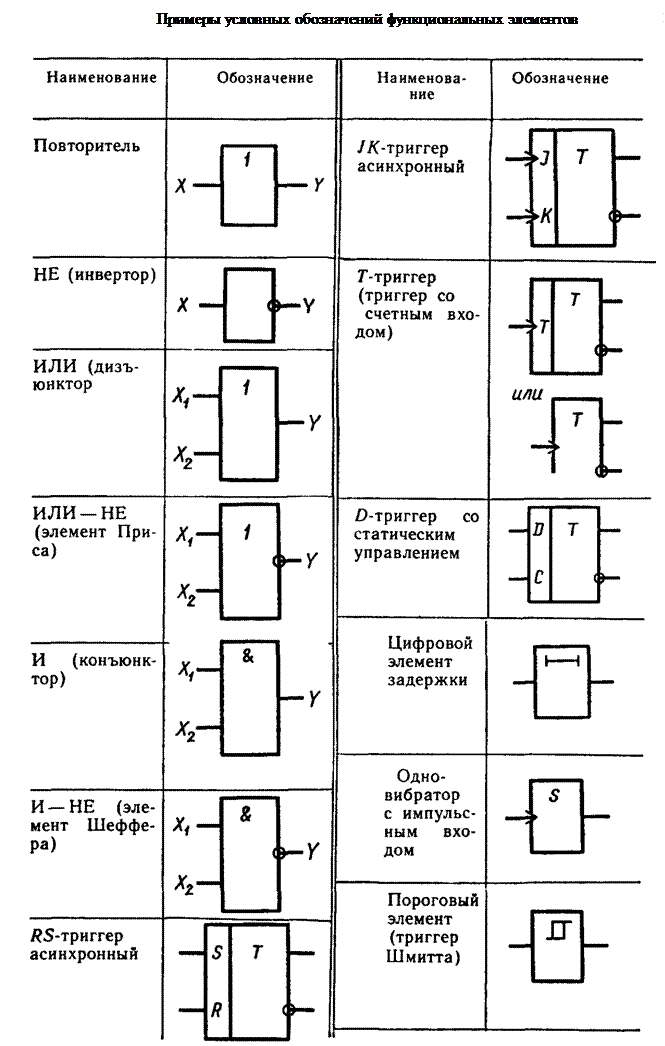
Логические элементы
Любые цифровые микросхемы строятся на основе простейших логических элементов «НЕ», «ИЛИ», «И». В настоящее время используется несколько технологий построения логических элементов:
- транзисторно-транзисторная логика (ТТЛ, TTL)
- логика на основе комплементарных МОП транзисторов (КМОП, CMOS)
- логика на основе сочетания комплементарных МОП и биполярных транзисторов (BiCMOS)
Простейшим логическим элементом является инвертор, который работает в соответствии со следующей таблицей:
| Рис 1 Таблица истинности логического инвертора | |
| Рис 2 Изображение логического инвертора на принципиальных схемах. |
Чаще всего существуют не отдельные схемы логического «И», а более сложные схемы, выполняющие одновременно логическую функцию «И» и логическую функцию «НЕ» Таблица истинности и изображение схемы, выполняющей логическую функцию «И-НЕ» изображены на рис 3 и 4 соответственно:
Рис 3 Таблица истинности схемы,
выполняющей логическую функцию «И-НЕ». | |
| Рис 4 Изображение схемы, выполняющей логическую функцию «И-НЕ». |
Точно также как не существует отдельных схем логического «И», выполненных по технологии ТТЛ, не существует отдельных схем логического «ИЛИ». Таблица истинности и изображение схемы, выполняющей логическую функцию «ИЛИ-НЕ» изображены на рис 5 и 6 соответственно:
| Рис 5 Таблица истинности схемы, выполняющей логическую функцию «ИЛИ-НЕ». | |
| Рис 6 Изображение схемы, выполняющей логическую функцию «ИЛИ-НЕ». |
Построение произвольной таблицы истинности.
Любая логическая схема без памяти полностью описывается таблицей истинности. При построении сложных логических схем с произвольной таблицей истинности используется сочетание простейших схем «И» «ИЛИ» «НЕ».
При построении схемы, реализующей произвольную
таблицу истинности, каждый выход анализируется
(и строится схема) отдельно.
Для реализации
таблицы истинности при помощи логических
элементов «И» достаточно рассмотреть только
те строки таблицы истинности, которые содержат
логические «1» в выходном сигнале. Строки,
содержащие в выходном сигнале логический 0 в
построении схемы не участвуют. Каждая строка,
содержащая в выходном сигнале логическую
«1», реализуется схемой логического «И»
с количеством входов, совпадающим с количеством
входных сигналов в таблице истинности. Входные
сигналы, описанные в таблице истинности
логической «1» подаются на вход этой схемы
непосредственно, а входные сигналы, описанные в
таблице истинности логическим «0» подаются
на вход через иверторы. Объединение сигналов с
выходов схем, реализующих отдельные строки
таблицы истинности, производится при помощи
схемы логического ИЛИ. Количество входов в этой
схеме определяется количеством строк в таблице
истинности, в которых в выходном сигнале
присутствует логическая «1».
Рассмотрим конкретный пример. Пусть необходимо реализовать таблицу истинности, приведенную на рисунке 7:
Рисунок 7 Произвольная таблица истинности.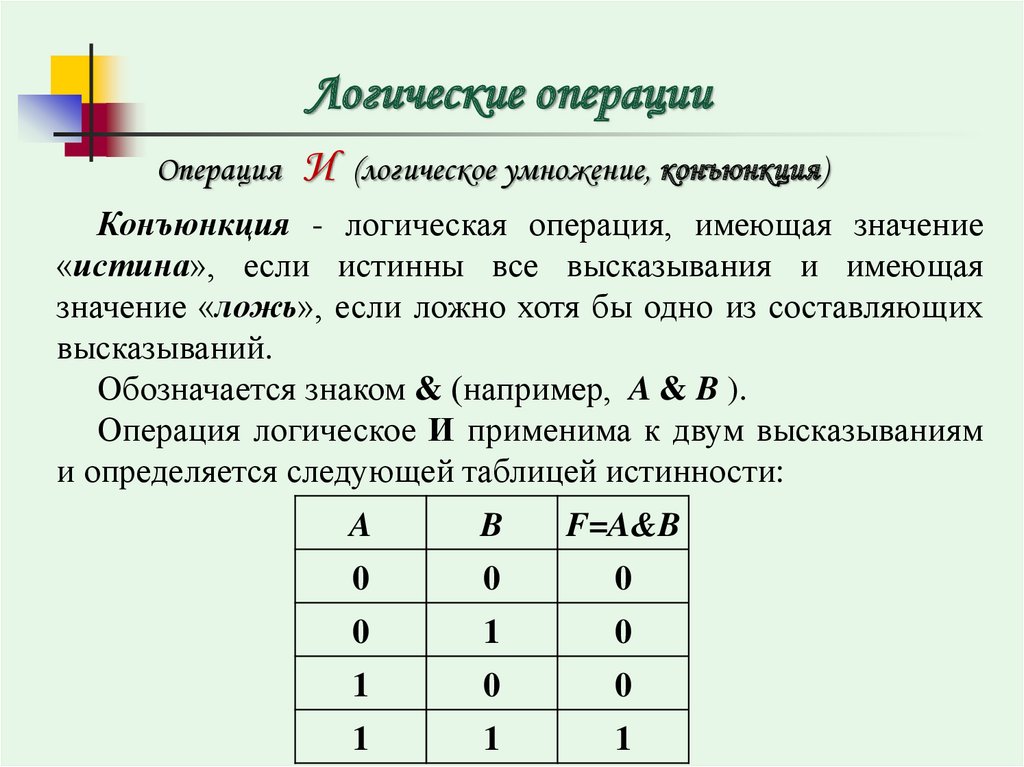
Для построения схемы, реализующей сигнал Out1, достаточно рассмотреть строки, выделенные красным цветом. Эти строки реализуются микросхемой D2 на рисунке 8. Каждая строка реализуется своей схемой «И», затем выходы этих схем объединяются Для построения схемы, реализующей сигнал Out2, достаточно рассмотреть строки, выделенные зеленым цветом. Эти строки реализуются микросхемой D3.
Рисунок 8. Принципиальная схема, реализующая таблицу истинности, приведенную на рисунке 7.
[Содержание] [Вперёд]
Урок N 16. Логические элементы и логические функции.
Элементы математической логики.
Логическая функция — это функция логических переменных, которая
может принимать только два значения : 0 или 1. В свою очередь,
сама логическая переменная (аргумент логической функции) тоже может
принимать только два значения : 0 или 1.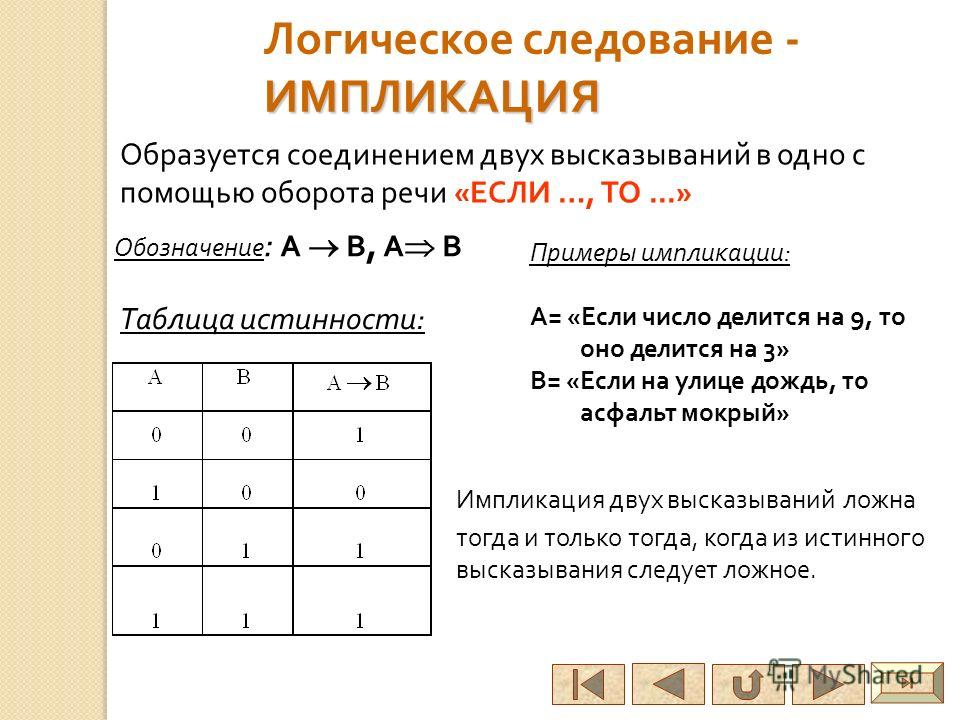
n.
Логические функции одной переменной
Таблица истинности функции одной переменной Y=f(X) содержит всего
2 строки, а число функций одной переменной равно 4.
1. Функция константа 0, Y=0. Техническая реализация этой функции —
соединение вывода Y с общей шиной с нулевым потенциалом.
Таблица истинности функции константа 0 имеет вид:
2. Функция Y=f(X)=X — функция повторения. Техническая реализация
этой функции — соединение между собой выводов X и Y.
Таблица истинности функции повторения имеет вид:
3. Функция Y=f(X)=NOT(X) — отрицание НЕ или инверсия (NOT(X) — это НЕ X).
Техническая реализация этой функции — инвертор на любом транзисторе
или логическом элементе, или транзисторный ключ.
Таблица истинности функции отрицания имеет вид:
Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)
4.
Функция константа 1, Y=1. Техническая реализация этой функции —
соединение вывода Y с источником питания.
Таблица истинности функции константа 1 имеет вид:
Важнейшей функцией одной переменной является отрицание НЕ,
остальные функции являются тривиальными.
Логические функции двух переменных
Таблица истинности функции двух переменных Y=f(X1,Х2) содержит 4
строки, а число функций двух переменных равно 16.
Мы рассмотрим только несколько основных функций двух переменных.
1. Логическое ИЛИ (логическое сложение, дизъюнкция):
Y= X1 + X2 = X1VX2
Техническая реализация этой функции — два параллельно соединенных
ключа:
Таблица истинности логического ИЛИ имеет вид:
Логический элемент ИЛИ обозначается на схемах следующим образом:
2.
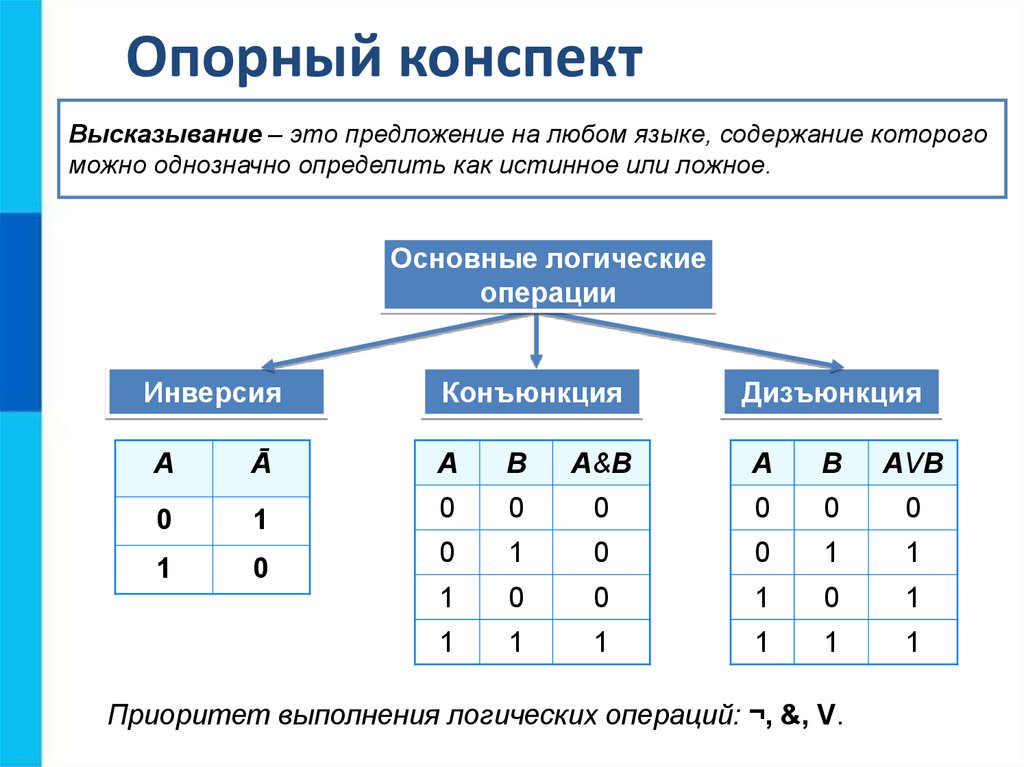Логическое И (логическое умножение, конъюнкция, схема совпаде-
ний): Y = X1X2 = X1&X2
Техническая реализация этой функции — два последовательно сое-
диненных ключа:
Таблица истинности логического И имеет вид:
Логический элемент И обозначается на схемах следующим образом:
3. Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2)
Таблица истинности функции ИЛИ-НЕ имеет вид:
Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом
:
4. Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2)
Таблица истинности функции И-НЕ имеет вид:
Логический элемент И-НЕ обозначается на схемах следующим образом:
Есть ещё три логические функции двух переменных, имеющие специ-
альные названия: импликация, эквивалентность, неравнозначность
(исключающее ИЛИ, сложение по модулю 2).
Последние две функции
являются взаимно обратными, также как, например, функция И и
функция штрих Шеффера.
Элемент памяти — RS-триггер
Триггер — это логическое устройство, способное хранить 1 бит ин-
формации. К триггерам относятся устойства, имеющие два устойчивых
состояния. Простейший триггер — RS-триггер, образован из двух
элементов И-НЕ (или ИЛИ-НЕ). Он позволяет запоминать 1 бит инфор-
мации, поскольку информация в компьютере представляется в двоич-
ном виде. Его схема приведена ниже.
Действие RS-триггера поясняется в приведенной ниже таблице ис-
тинности. S-вход установки (Set), R-вход сброса (Reset).
В обычном (исходном) состоянии на входы триггера поданы 1. Для
записи информации на вход R подан 0. Для сброса информации и под-
готовки к приёму новой информации на вход S подается 0 и триггер
вернётся в исходное состояние.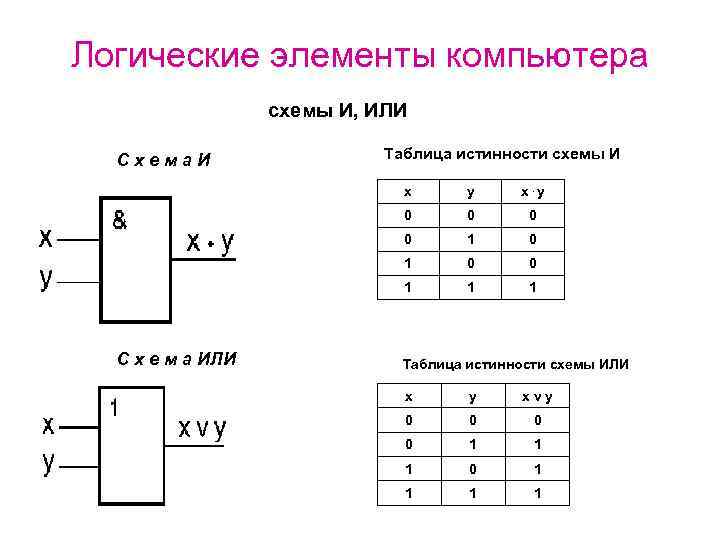
Поскольку один триггер запоминает 1 бит информации, то для запо-
минания 1 байта (8 бит) нужно 8 триггеров, для запоминания 1 Кб
(1024 байт) надо 8192 триггеров. Современные микросхемы ОЗУ спо-
собны запоминать десятки мегабайт информации.
Элементы математической логики
Существуют такие наборы логических функций, с помощью которых
можно выразить любые другие логические функции. Они называются
функционально полными или базисами. Наиболее известный базис —
это набор функций И, ИЛИ, НЕ. Функция штрих Шеффера является ба-
зисной, также как и функция стрелка Пирса. Поэтому, с помощью ло-
гических элементов ИЛИ-НЕ или И-НЕ можно собрать любую логическую
схему. На таких элементах собран микропроцессор компьютера и дру-
гие логические устройства. Логические схемы состоят из логических
элементов, осуществляющих логические операции.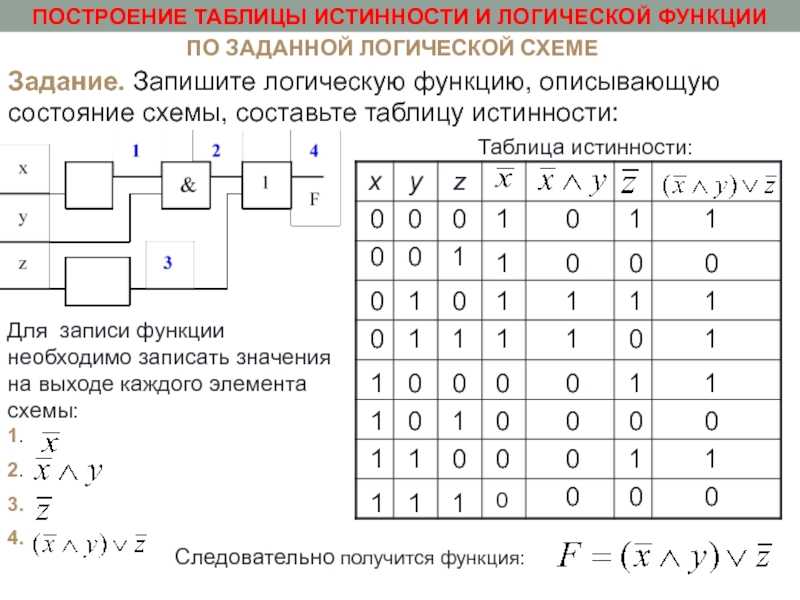
Логика — наука, изучающая методы установления истинности или лож-
ности одних высказываний на основе истинности или ложности других
высказываний (утверждений). Логика изучает методы доказательств и
опровержений. Логика составляет основу всякого управления, в том
числе технологическими процессами.
Математическая логика — современная форма логики, опирающаяся на
формальные математические методы.
Основные объекты логики — высказывания, то есть предложения, ко-
торые могут быть либо истинными, либо ложными. Существуют два
подхода установления истинности высказываний: эмпирический (опыт-
ный) и логический. При эмпирическом подходе истинность высказыва-
ний устанавливается на основе наблюдений, экспериментов, докумен-
тов и других фактов. При логическом подходе истинность высказыва-
ний доказывается на основе истинности других высказываний, то
есть чисто формально, на основе рассуждений без обращения к фак-
там.
В языках программирования QBasic и Turbo Pascal логические функ-
ции И, ИЛИ, НЕ реализуются в виде логических операций OR (ИЛИ),
AND (И), NOT (НЕ).
Множество всех логических функций, на котором определены три ло-
гические операции И, ИЛИ, НЕ называется булевой алгеброй (по име-
ни основоположника математической логики английского математика
Джорджа Буля). Упрощение формул в булевой алгебре производится на
основе эквивалентных преобразований, опирающихся на следующие ос-
новные законы (эквивалентные соотношения):
Кроме того, применяются ещё три соотношения:
Законы 1,2,3,7 показывают, что свойства конъюнкции очень похожи
на свойства умножения, поэтому её часто называют логическим умно-
жением. Из законов 6 и 8 следует, что используя отрицание, дизъ-
юнкцию можно выразить через конъюнкцию, и наоборот:
Это означает, что наборы И-НЕ и ИЛИ-НЕ также являются функцио-
нально полными или базисными.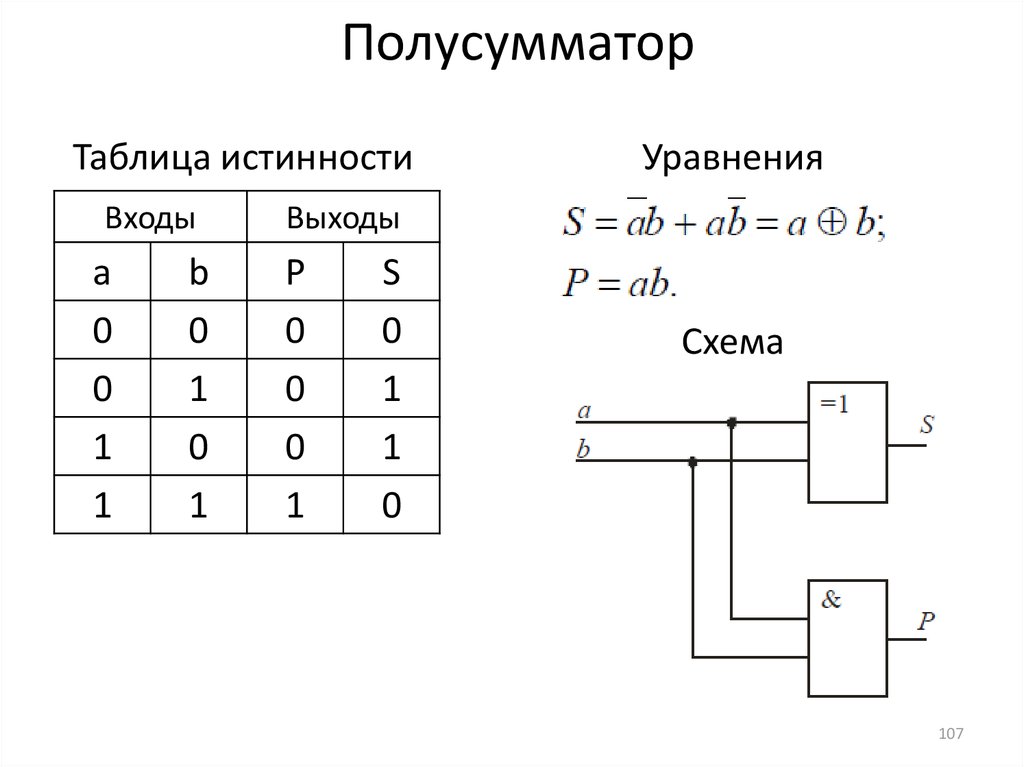
Вопросы
1. Что такое логическая функция и логический элемент?
2. Что такое таблица истинности и сколько в ней строк?
3. Какие функции одной переменной Вы знаете? Какая из них являет-
ся важнейшей?
4. Как зависит число функций от числа переменных?
5. Что такое конъюнкция и дизъюнкция? Как они реализуются?
6. Что такое функция стрелка Пирса? Какова её таблица истинности?
7. Что такое функция штрих Шеффера? Какова её таблица истинности?
8. Что такое базисная функция и какие базисы Вы знаете?
9. Что такое логика? Какие два подхода существуют в логике?
10. Как доказывается истинность или ложность высказываний? Приве-
дите примеры из практики.
11. Что такое булева алгебра?
12. Какие законы булевой алгебры Вы знаете? Где они применяются?
13. Что такое триггер? Как работает RS-триггер?
14.
Сколько надо триггеров, чтобы запомнить 1 Мб информации?
Логические ворота в электронике | Типы, таблица истинности, схема и работа
— Реклама —
Логика Элементы являются основой всех цифровых систем, как комбинационных, так и последовательных, схема следует определенной логике.
Проще говоря, логический элемент представляет собой цифровую схему с несколькими входами и одним выходом. Связь между входами и выходами логического элемента следует определенной логике. Эта логика придерживается правил булевой алгебры.
Чтобы развить глубокое понимание логических вентилей, мы должны понимать основы цифровых сигналов, двоичных систем счисления и булевой алгебры.
Рис.1 Логические вентили Базовый ввод-вывод— Реклама —
ПРИМЕЧАНИЕ: В логических схемах отсутствует петля обратной связи или блок памяти.
Цифровой сигнал Аналоговый сигнал представляет собой непрерывный изменяющийся во времени сигнал тока или напряжения, тогда как цифровой сигнал представляет собой пульсирующую форму волны с двумя дискретными значениями — высоким и низким.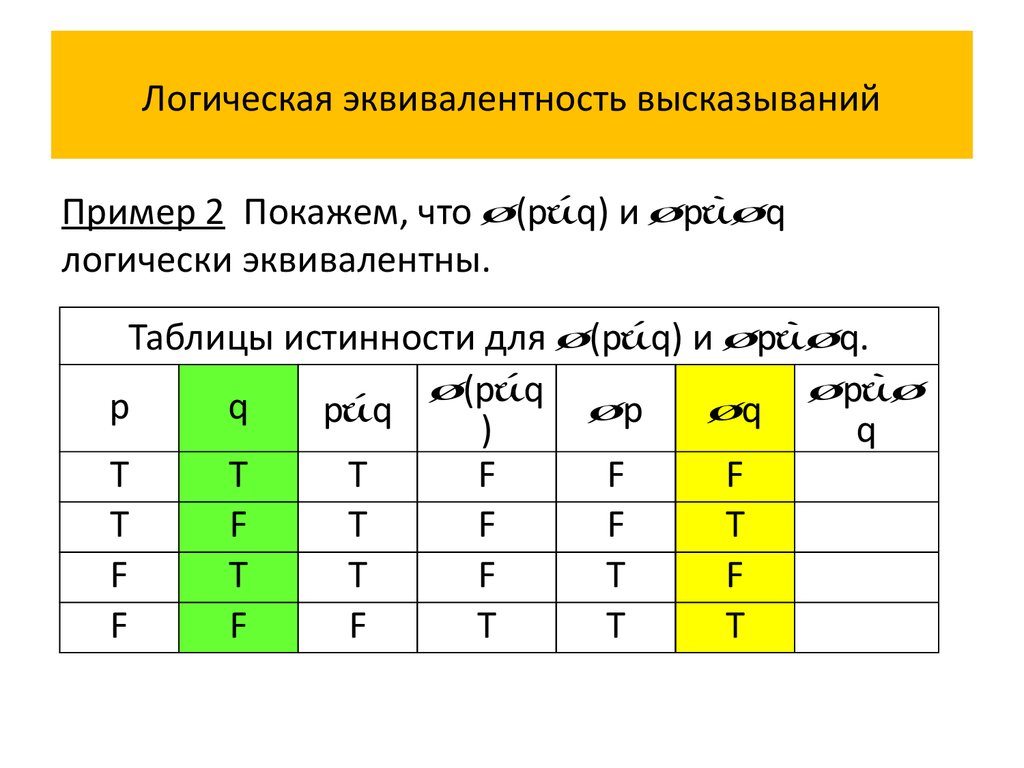
Эти два дискретных значения представлены двоичными числами 0 и 1. Цифровая схема — это электронная схема, которая обрабатывает цифровые сигналы.
Просто это либо ДА , либо НЕТ , ничего между ними.
В цифровых схемах
0 = Нет, Ложь, Выключение, Разомкнутая цепь и Низкий уровень.
1 = Да, Истина, Включение, Замкнутая цепь и Высокий уровень.
Двоичные числаДесятичная система имеет основание или основание 10, что означает, что число представлено десятью цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Аналогично , двоичная система имеет основание или основание 2 только с двумя цифрами: 0 и 1.
Двоичная система счисления представляет число как 0 или 1. Любое число, представленное в двоичной форме, подвергается двоичному преобразованию.
Пример: 1 — 001, 2 — 010, 3 — 011, 4 — 0100, 5 — 0101,… 15 — 1111 и так далее.
Булева алгебра Ирландский математик Джордж Буль разработал математическую систему с использованием символов.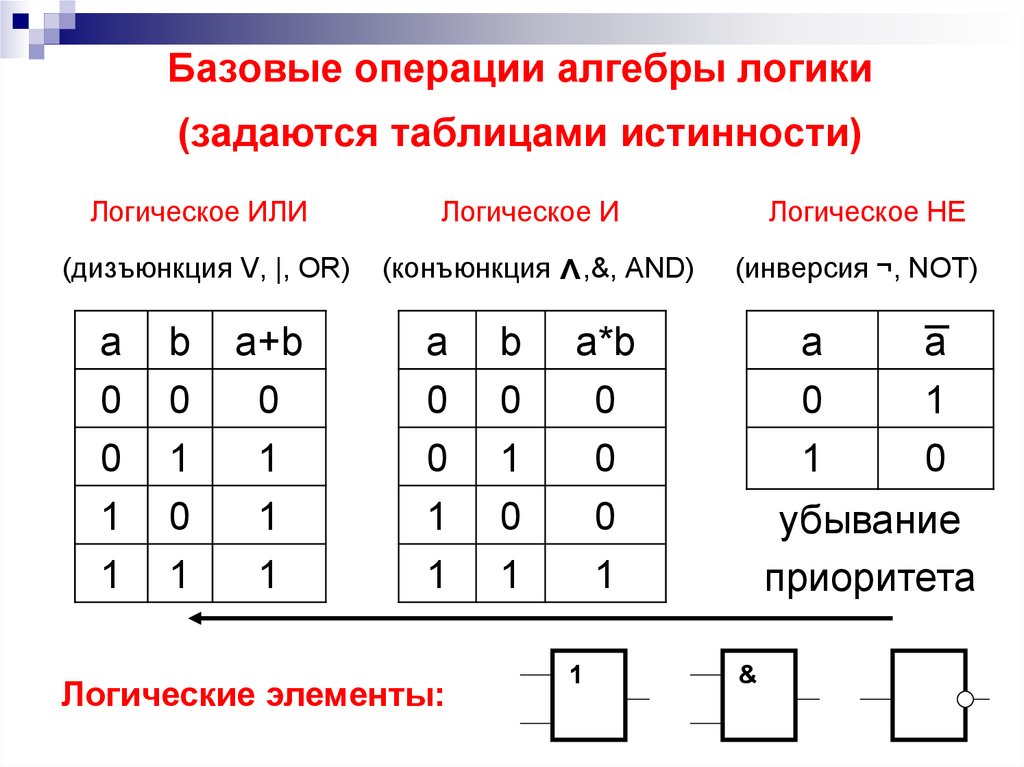
Система ведет себя аналогично алгебре для решения бинарных или логических задач.
Уравнение, представленное символами, но подчиняющееся законам булевой алгебры, известно как логическое выражение.
Три операции, используемые в булевой алгебре, составляют
1) или операция
2) и операция
3) не работают
Логические операции 1) или операция:или операция. логического сложения, представленного знаком (+) с двумя или несколькими входами, дающими один выход. Операция ИЛИ выдает ВЫСОКИЙ уровень на выходе (1), только если один или все входы цифровой схемы имеют ВЫСОКИЙ уровень (1). Если оба входа имеют НИЗКИЙ уровень (0), выход цифровой схемы также будет НИЗКИМ (0).
Давайте разберем это на примере:
Рассмотрим схему с двумя переключателями, подключенными параллельно к светодиоду. Светодиод будет гореть, если через цепь протекает ток. Чтобы ток протекал, один из переключателей должен быть замкнут.
ПРИМЕЧАНИЕ: МЫ ТАКЖЕ МОЖЕМ ИСПОЛЬЗОВАТЬ ЛАМПОЧКУ.
Случай 1:
Переключатель A=РАЗОМКНУТ, переключатель B=РАЗОМКНУТ
Если оба переключателя разомкнуты, ток в цепи не течет и светодиод не светится.
Случай 2:
Переключатель A=РАЗОМКНУТ, Переключатель B=ЗАМКНУТ
Благодаря параллельному соединению, даже если один из переключателей замкнут, а другой разомкнут, по цепи протекает ток. Это заставляет светодиод светиться.
Случай 3:
Переключатель A = ЗАКРЫТ, переключатель B = ОТКРЫТ
В цепи протекает ток, и светодиод горит ЗАКРЫТО
Если оба переключателя замкнуты, через цепь протекает сильный ток, и светодиод светится.
| СНО | ВЫКЛЮЧАТЕЛЬ А | ВЫКЛЮЧАТЕЛЬ B | Светодиод |
| КОРПУС 1 | ОТКРЫТЬ | ОТКРЫТЬ | ВЫКЛ |
| КОРПУС 2 | ОТКРЫТЬ | ЗАКРЫТО | НА |
| КОРПУС 3 | ЗАКРЫТО | ОТКРЫТЬ | НА |
| КОРПУС 4 | ЗАКРЫТО | ЗАКРЫТО | НА |
Логическое выражение для операции ИЛИ:
Y= A + B
Где Y= Выход; А= Вход 1; B= Вход 2
2) Операция И: Операция И — это форма логического умножения, представленная знаком (.
) с двумя или несколькими входами, дающими один выход. Операция И выдает ВЫСОКИЙ уровень на выходе (1) только в том случае, если все входы цифровой схемы имеют ВЫСОКИЙ уровень (1). Если один или оба входа имеют НИЗКИЙ уровень (0), выход цифровой схемы также будет НИЗКИМ (0).
Давайте разберем это на примере:
Рассмотрим схему с двумя переключателями, последовательно соединенными со светодиодом. Светодиод будет гореть, если через цепь протекает ток. Чтобы ток протекал, оба переключателя должны быть замкнуты. Если один из переключателей разомкнут, ток не будет течь.
Рис.3 Логический вентиль И ОперацияСлучай 1:
Переключатель A=ОТКРЫТ, переключатель B= ОТКРЫТ
Поскольку оба переключателя разомкнуты, ток не протекает по цепи и светодиод не светится. .
Случай 2:
Переключатель A=РАЗОМКНУТ, Переключатель B=ЗАМКНУТ
Если один из переключателей разомкнут в цепи последовательного соединения, протекание тока невозможно.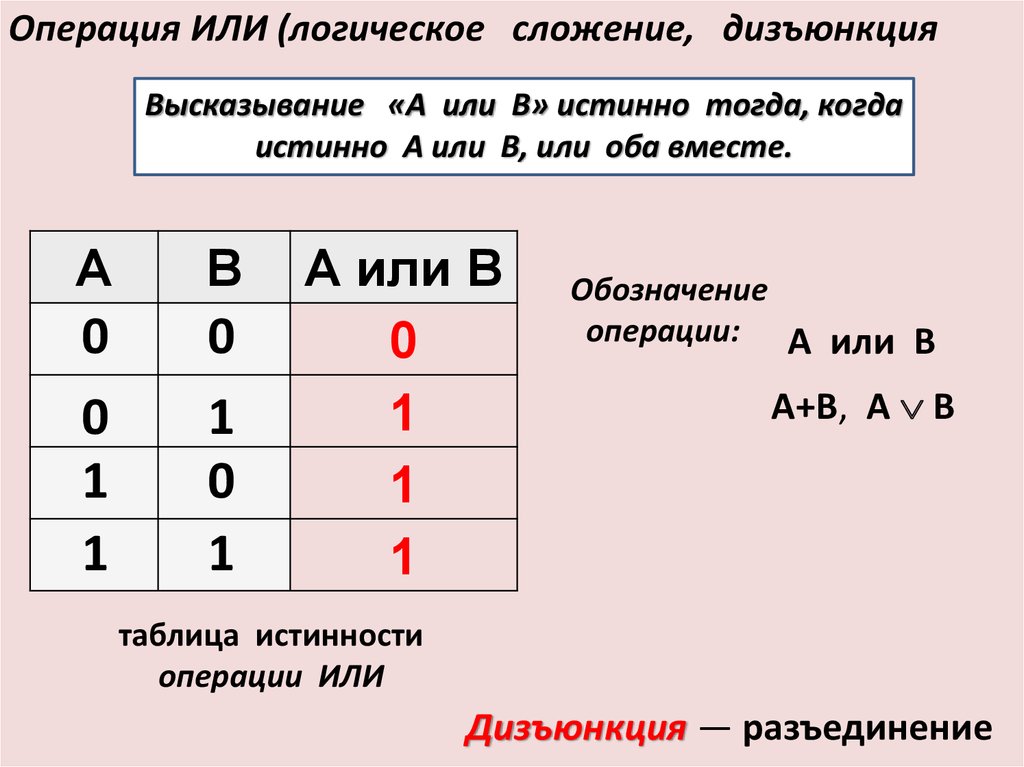
Следовательно, светодиод не светится.
Случай 3:
Переключатель A = ЗАКРЫТ, переключатель B = РАЗОМКНУТ
Если один из переключателей разомкнут, ток в цепи не протекает и светодиод не светится.
Случай 4:
Переключатель A=ЗАКРЫТО, Переключатель B=ЗАКРЫТО
Если оба переключателя замкнуты, через цепь протекает сильный ток, и светодиод светится.
| СНО | ВЫКЛЮЧАТЕЛЬ А | ВЫКЛЮЧАТЕЛЬ B | Светодиод |
| КОРПУС 1 | ОТКРЫТЬ | ОТКРЫТЬ | ВЫКЛ |
| КОРПУС 2 | ОТКРЫТЬ | ЗАКРЫТО | ВЫКЛ |
| ДЕЛО 3 | ЗАКРЫТО | ОТКРЫТЬ | ВЫКЛ |
| КОРПУС 4 | ЗАКРЫТО | ЗАКРЫТО | НА |
Логическое выражение для операции И:
Y= A .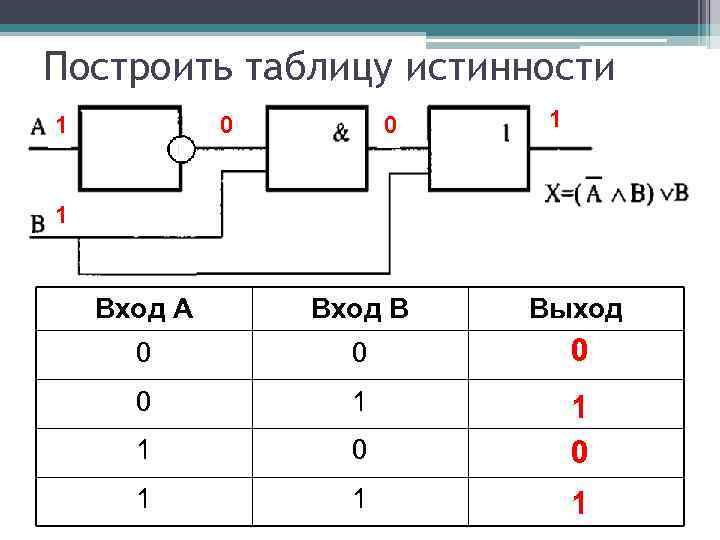
B
В большинстве случаев точка (.) удаляется
Y= AB
Где Y= Выход; А= Вход 1; B= Вход 2
3) Операция НЕ:НЕ является операцией в форме логической инверсии, известной как дополнение. Существует единственный вход, производящий единственный выход. Операция НЕ создает ВЫСОКИЙ (1) выход для НИЗКОГО (0) входа и НИЗКИЙ (0) выход для ВЫСОКОГО (1) входа.
Представляется полосой ( ˉ ) над переменной.
Давайте разберем это на примере:
Рассмотрим групповой переключатель. Если один из переключателей разомкнут, другой автоматически закроется, и наоборот.
Рис.4 Логический вентиль НЕ работает| ПЕРЕКЛЮЧАТЕЛЬ A | ВЫКЛЮЧАТЕЛЬ B |
| ОТКРЫТЫЙ | ЗАКРЫТО |
| ЗАКРЫТО | ОТКРЫТЬ |
Логическое выражение для операции НЕ:
Y= A ˉ
Где Y= выход; A= Вход
Логические элементы Логический элемент представляет собой цифровую схему с одним выходом, значение которого зависит от логической связи между входом(ами) и выходом.
Проще говоря, связь между входными и выходными значениями основана на определенной «логике», поэтому эти схемы рассматриваются как логические вентили.
Логические элементы имеют только один выход для одного входа или нескольких входов. Чтобы понять работу логического вентиля, составляется таблица истинности, в которой указываются все комбинации входных данных вместе с выходными данными.
Существует 3 типа логических вентилей:
1) Базовые вентили: вентили ИЛИ, И и НЕ.
2) Универсальные вентили: NAND и NOR Gates.
3) Производные вентили: вентилей XOR и вентилей XNOR.
Давайте разберемся со всеми тремя логическими вентилями поглубже.
1) Базовые вентилиСуществует три типа базовых логических вентилей — вентили ИЛИ, И и НЕ. Логический вентиль Basic ведет себя так же, как и соответствующий логический оператор.
A) Логический элемент ИЛИ: Для двух или более входов вентиль ИЛИ выдает ВЫСОКИЙ (1) выходной сигнал, только если один или все входы имеют ВЫСОКИЙ (1) уровень.
Это работает аналогично операции ИЛИ Логика.
Логическое выражение для вентиля ИЛИ:
Y= A OR B
Рис.5 Символ вентиля ИЛИСлучай 1: А= 0, В= 0; Y= 0
В этом случае оба входа имеют НИЗКИЙ уровень (0), поэтому логический элемент ИЛИ выдает НИЗКИЙ (0) выходной сигнал.
Случай 2: А= 0, В= 1; Y= 1
В этом случае один из входов ВЫСОКИЙ (1), поэтому логический элемент ИЛИ выдает ВЫСОКИЙ (1) выход.
Случай 3: А= 1, В= 0; Y= 1
В этом случае один из входов ВЫСОКИЙ (1), поэтому логический элемент ИЛИ выдает ВЫСОКИЙ (1) выход.
Случай 4: А= 1, В= 1; Y= 1
В этом случае оба входа имеют ВЫСОКИЙ уровень (1), поэтому логический элемент ИЛИ выдает ВЫСОКИЙ уровень (1) на выходе.
Таблица истинности шлюза OR:
| A | Б | Y=A ИЛИ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
B) Логический элемент И:
Для двух или более входов логический элемент И выдает ВЫСОКИЙ (1) выходной сигнал, только если оба входа имеют ВЫСОКИЙ (1).
Он выдает НИЗКИЙ (0) выход, даже если один из входов НИЗКИЙ (0). Это работает аналогично логической операции И
Логическое выражение для вентиля И:
Y= A AND B
Рис. 6 Символ вентиля ИСлучай 1: A= 0, B= 0; Y= 0
В этом случае оба входа имеют НИЗКИЙ уровень (0), поэтому логический элемент И выдает НИЗКИЙ (0) выходной сигнал.
Случай 2: А= 0, В= 1; Y= 0
В этом случае один из входов имеет НИЗКИЙ уровень (0), поэтому логический элемент И выдает НИЗКИЙ (0) выходной сигнал.
Случай 3: А= 1, В= 0; Y= 0
В этом случае один из входов НИЗКИЙ (0), поэтому логический элемент И выдает НИЗКИЙ (0) выход.
Случай 4: А= 1, В= 1; Y= 1
В этом случае оба входа имеют ВЫСОКИЙ уровень (1), логический элемент И выдает ВЫСОКИЙ уровень (1) на выходе.
И Таблица истинности шлюза:
| А | Б | Y=A И B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
C) Логический элемент НЕ:
Для одного входа логический элемент НЕ создает выходной сигнал как дополнение к входному.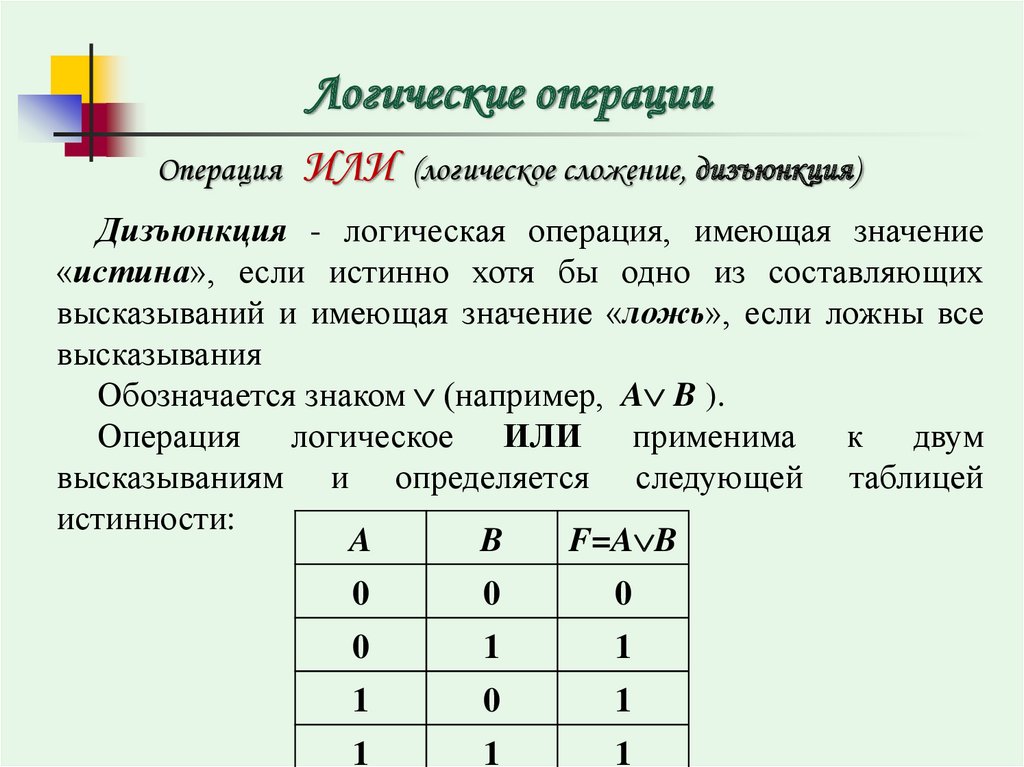
Вентиль НЕ выдает ВЫСОКИЙ (1) выход, только если вход НИЗКИЙ (0), и НИЗКИЙ (0) выход, если вход ВЫСОКИЙ (1). Это работает аналогично логической операции НЕ.
Логическое выражение для шлюза НЕ:
Y=A ˉ
Рис.7 Символ шлюза НЕСлучай 1: A=0; Y= 1
Вход вентиля НЕ НИЗКИЙ (0), выход становится ВЫСОКИМ (1).
Случай 2: А=1; Y= 0
Вход вентиля НЕ ВЫСОКИЙ (1), поэтому выход становится НИЗКИМ (0).
Таблица истинности шлюза NOT:
| A | Y=А ˉ |
| 0 | 1 |
| 1 | 0 |
2) Универсальные логические элементы
Универсальные логические элементы могут реализовать любое логическое выражение самостоятельно, это означает, что они не требуют каких-либо других элементов для реализации. Один универсальный логический вентиль способен построить логическую схему.
Существует два типа универсальных логических вентилей
Логический элемент И-НЕ является дополнением вентильного элемента И или просто комбинацией вентильного элемента НЕ и вентиля И. Он называется И-НЕ, так как N означает НЕ, что означает НЕ-И-гейт. Для двух или более входов логический элемент И-НЕ выдает ВЫСОКИЙ (1) выходной сигнал, только если один из входов НИЗКИЙ (0).
Логическое выражение вентиля И-НЕ обозначается дополнением И.
Y= (AB) ˉ
Рис. 8 Символ вентиля И-НЕСлучай 1: A= 0, B= 0; Y= 1
В этом случае оба входа имеют НИЗКИЙ уровень (O), логический элемент И-НЕ выдает ВЫСОКИЙ (1) выходной сигнал.
Случай 2: А= 0, В= 1; Y= 1
В этом случае один из входов НИЗКИЙ (0), вентиль И-НЕ выдает ВЫСОКИЙ (1) выход.
Случай 3: А= 1, В= 0; Y= 1
В этом случае один из входов НИЗКИЙ (0), вентиль И-НЕ выдает ВЫСОКИЙ (1) выход.
Случай 4: А= 1, В= 1; Y= 0
В этом случае оба входа имеют ВЫСОКИЙ (1), логический элемент И-НЕ выдает НИЗКИЙ (0) выходной сигнал.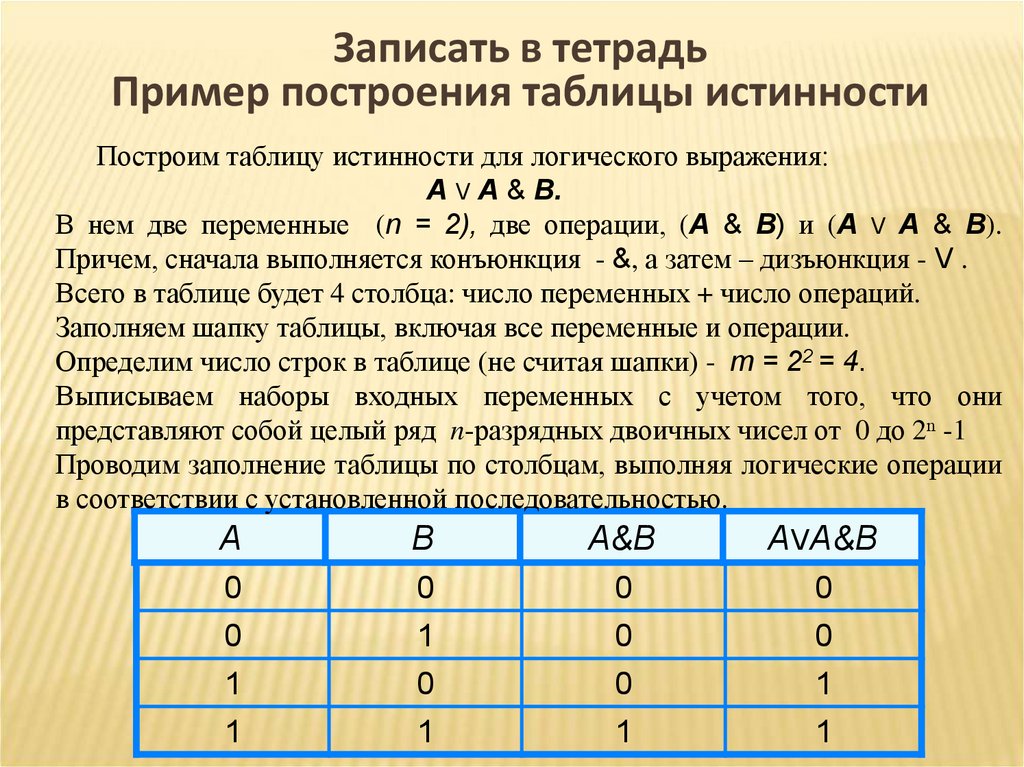
Таблица истинности шлюза NAND:
| А | Б | Y=A НЕ-И B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
B) Схема НЕ-ИЛИ:
Схема НЕ-ИЛИ является дополнением схемы ИЛИ или комбинацией схемы НЕ и схемы ИЛИ. Это называется ИЛИ, поскольку N означает НЕ, что означает ворота НЕ ИЛИ. Для двух или более входов логический элемент ИЛИ-НЕ выдает на выходе ВЫСОКИЙ (1); только оба входа имеют НИЗКИЙ уровень (0).
Логическое выражение NOR Gate обозначается дополнением OR.
Y= (A+B) ˉ
Рис.9 Символ вентиля NORСлучай 1: A= 0, B= 0; Y= 1
В этом случае оба входа имеют НИЗКИЙ уровень (O), логический элемент ИЛИ-НЕ выдает ВЫСОКИЙ (1) выходной сигнал.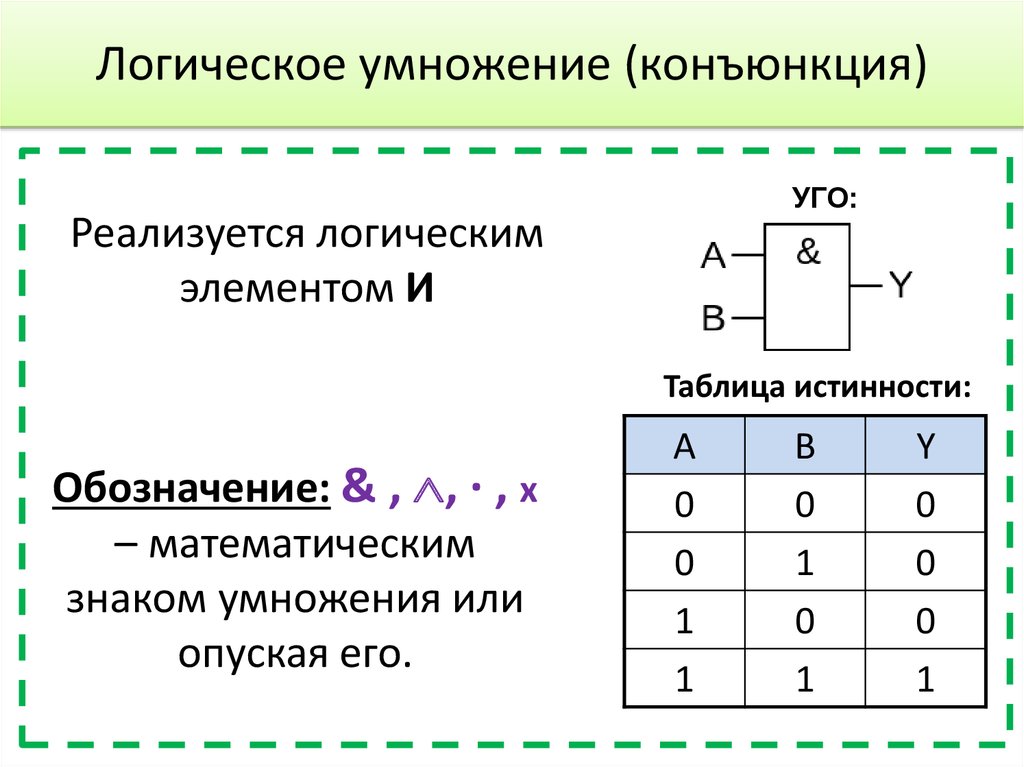
Случай 2: А= 0, В= 1; Y= 0
В этом случае, один из входов ВЫСОКИЙ (1), логический элемент ИЛИ-НЕ выдает НИЗКИЙ (0) выход.
Случай 3: А= 1, В= 0; Y= 0
В этом случае, один из входов ВЫСОКИЙ (1), логический элемент ИЛИ-НЕ выдает НИЗКИЙ (0) выход.
Случай 4: А= 1, В= 1; Y= 0
В этом случае оба входа имеют ВЫСОКИЙ уровень (1), логический элемент ИЛИ-НЕ формирует на выходе НИЗКИЙ уровень (0).
Таблица истинности шлюза NOR:
| A | Б | Y=A ИЛИ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
3) Производные логические элементы:
Производные или специальные элементы предназначены для конкретных приложений, таких как половинные сумматоры, полные сумматоры и вычитатели.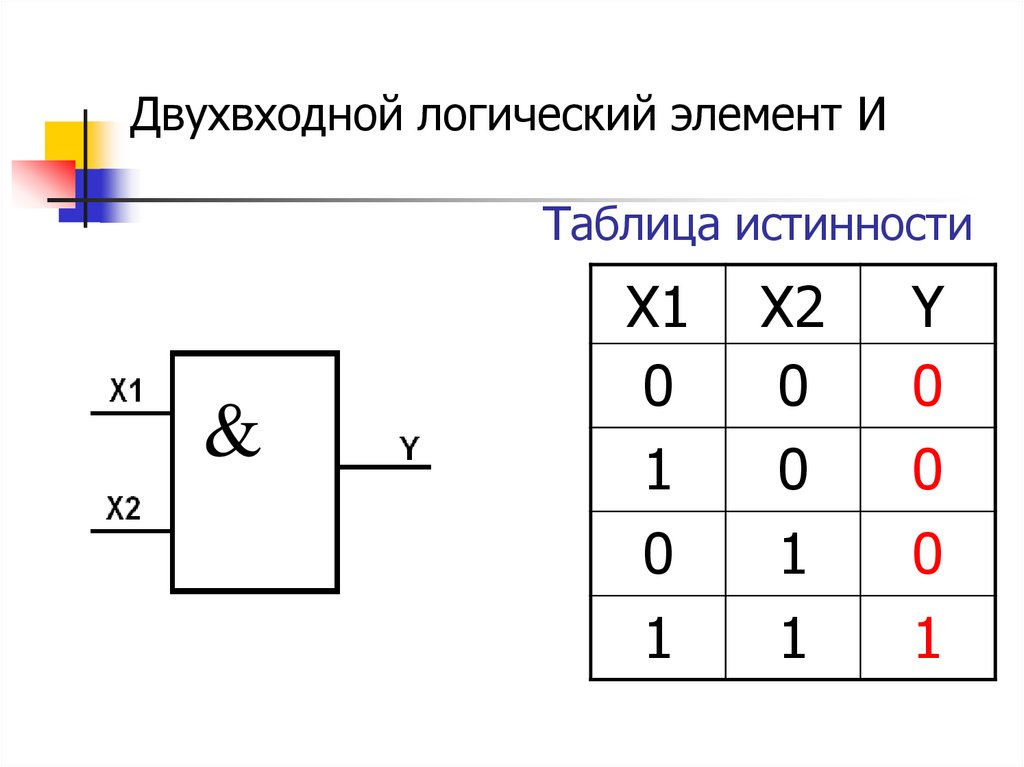
Есть два производных логических элемента, сделанных из вентилей ИЛИ и НЕ.
Вентиль Ex-OR имеет два или более входа, но один выход. Логический элемент Ex-OR генерирует ВЫСОКИЙ (1) выход, если оба входа не находятся на одном и том же логическом уровне A≠B.
Рис. 10 Символ вентиля XORСлучай 1: A= 0, B= 0; Y= 0
В этом случае оба входа имеют НИЗКИЙ уровень (O) с одинаковым логическим уровнем. В результате вентиль Ex-OR выдает НИЗКИЙ (0) выходной сигнал.
Случай 2: А= 0, В= 1; Y= 1
В этом случае один из входов НИЗКИЙ (0), а другой ВЫСОКИЙ (1). Следовательно, они не находятся на одном и том же логическом уровне. В результате вентиль Ex-OR выдает ВЫСОКИЙ (1) выходной сигнал.
Случай 3: A= 1, B= 0; Y= 1
В этом случае один из входов ВЫСОКИЙ (1), а другой НИЗКИЙ (0). Следовательно, они не находятся на одном и том же логическом уровне.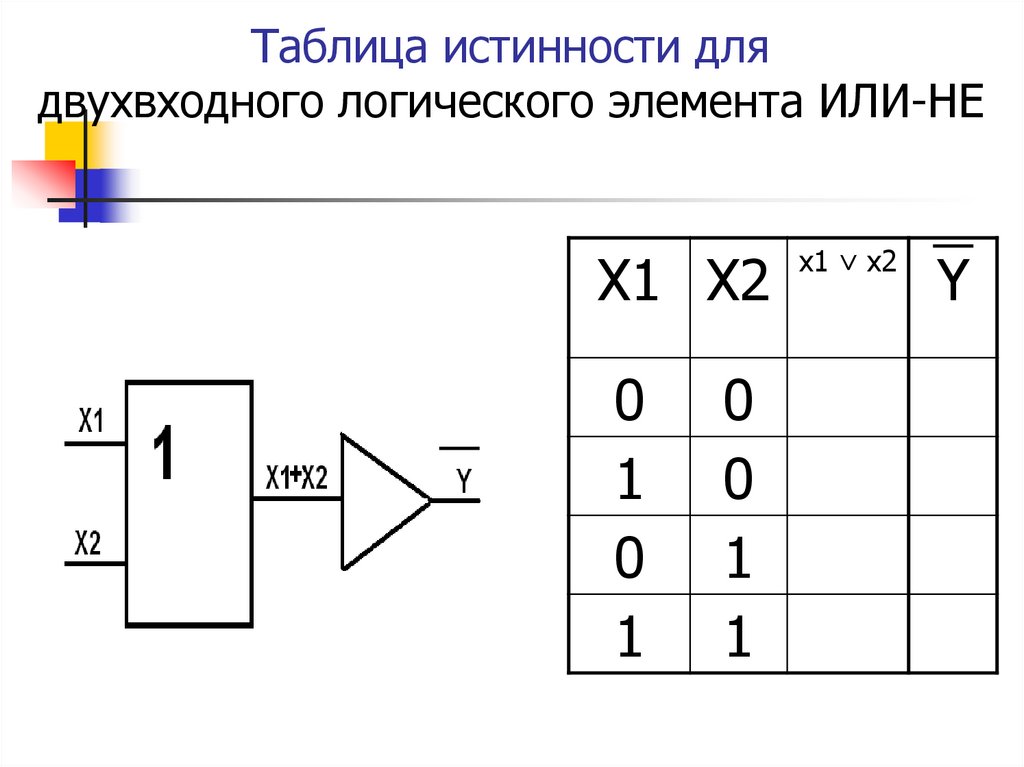
В результате вентиль Ex-OR выдает ВЫСОКИЙ (1) выходной сигнал.
Случай 4: А= 1, В= 1; Y= 0
В этом случае оба входа имеют ВЫСОКИЙ уровень (1) с одинаковым логическим уровнем. В результате вентиль Ex-OR выдает НИЗКИЙ (0) выходной сигнал.
XOR Gate Truth Table:
| А | Б | Y=A Исключающее ИЛИ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
B) Исключительное ИЛИ, EX-NOR или XNOR Gate
EX-NOR Gate имеет два или более входов, но один выход. Логический элемент EX-NOR генерирует ВЫСОКИЙ (1) выход, если оба входа имеют одинаковый логический уровень A=B.
Рис. 11 Символ вентиля XNORСлучай 1: A= 0, B= 0; Y= 1
В этом случае оба входа имеют НИЗКИЙ уровень (O) с одинаковым логическим уровнем.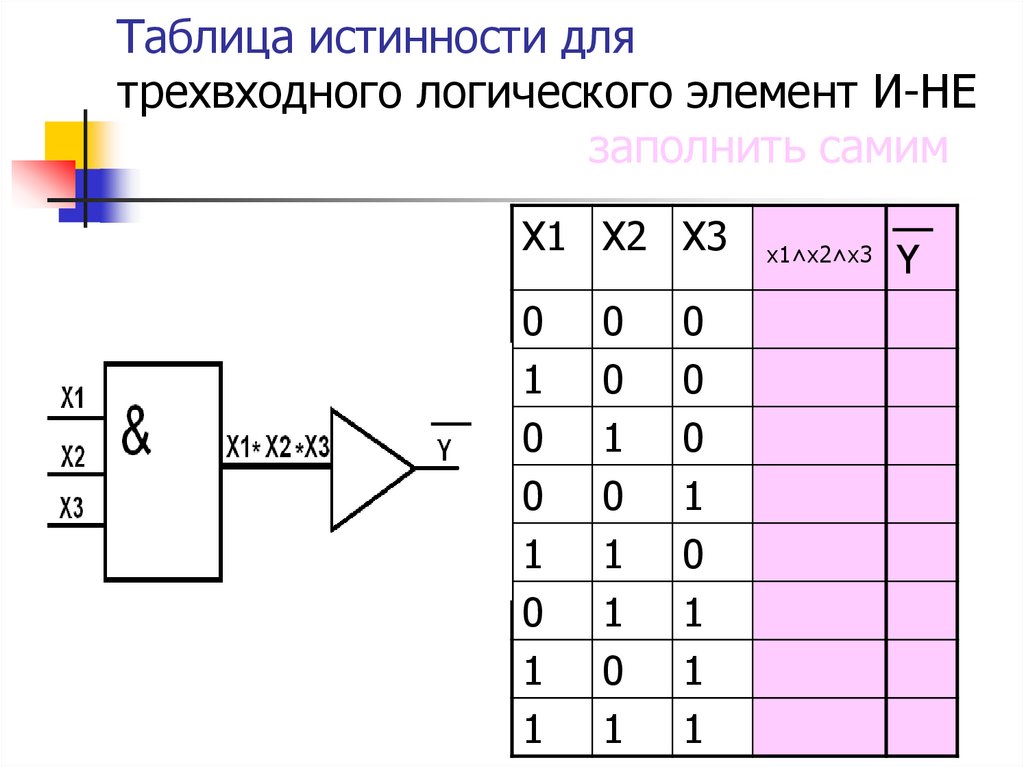
В результате шлюз EX-NOR выдает ВЫСОКИЙ (1) выходной сигнал.
Случай 2: А= 0, В= 1; Y= 0
В этом случае один из входов НИЗКИЙ (0), а другой ВЫСОКИЙ (1). Следовательно, они не находятся на одном и том же логическом уровне. В результате вентиль EX-NOR выдает НИЗКИЙ (0) выходной сигнал.
Случай 3: А= 1, В= 0; Y= 0
В этом случае один из входов ВЫСОКИЙ (1), а другой НИЗКИЙ (0). Следовательно, они не находятся на одном и том же логическом уровне. В результате шлюз EX-NOR выдает НИЗКИЙ (0) выходной сигнал.
Случай 4: А= 1, В= 1; Y= 1
В этом случае оба входа имеют ВЫСОКИЙ уровень (1) с одинаковым логическим уровнем. В результате шлюз EX-NOR выдает ВЫСОКИЙ (1) выходной сигнал.
Таблица истинности шлюза XNOR:
| A | Б | Y=A Исключающее ИЛИ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Надеемся, теперь у вас есть четкое представление обо всех логических элементах.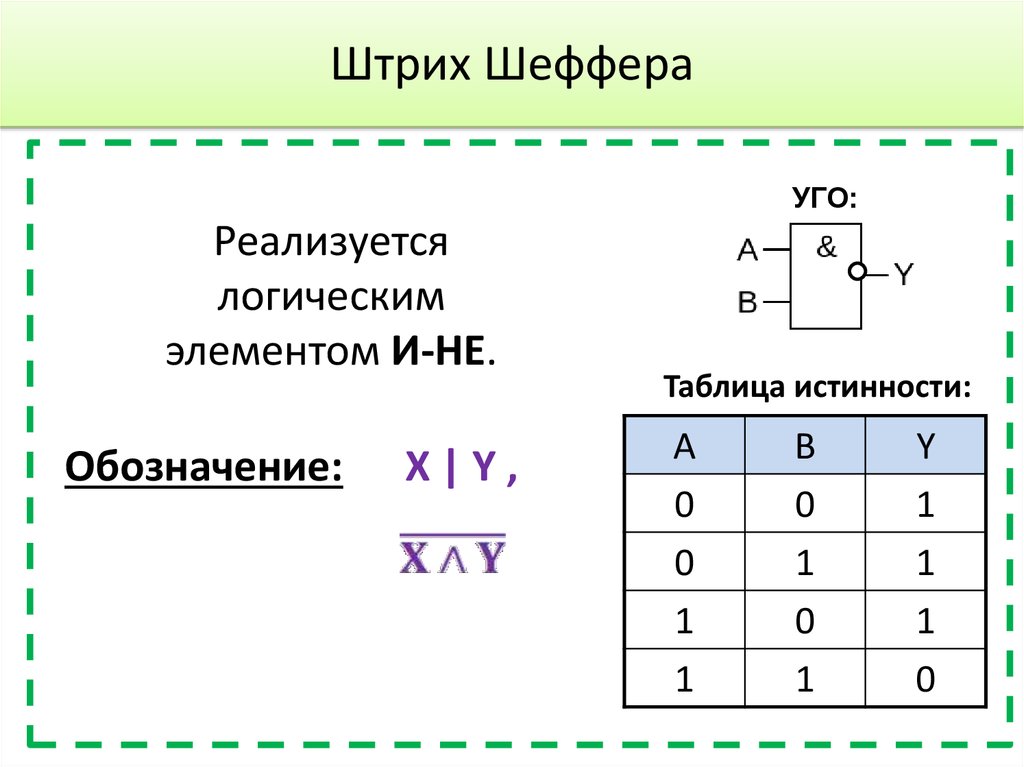
Но если у вас есть какие-либо сомнения, не стесняйтесь спрашивать в комментариях ниже. Или вы можете использовать наш форум, чтобы связаться с сообществом энтузиастов и экспертов в области электроники.
Логические элементы и таблицы истинности – Mathigon
Обзор и цель
На этом уроке учащиеся изучают использование логических элементов в разделе «Логика и вычисления» в Polypad. Если вы новичок в логических вентилях, этот учебник может быть полезен для чтения в первую очередь. Таблицы истинности часто используются для организации и передачи различных комбинаций входов и выходов через логические элементы.
Разминка
Предложите учащимся открыть холст Polypad и добавить два входа и один выход на холст. Предложите им посмотреть, могут ли они вызвать действие на выходе каждого из входов. Ниже приведен пример кнопки и выключателя, включающих свет:
После того, как учащиеся выполнили это задание, предложите им добавить вентиль ИЛИ между входами и выходами.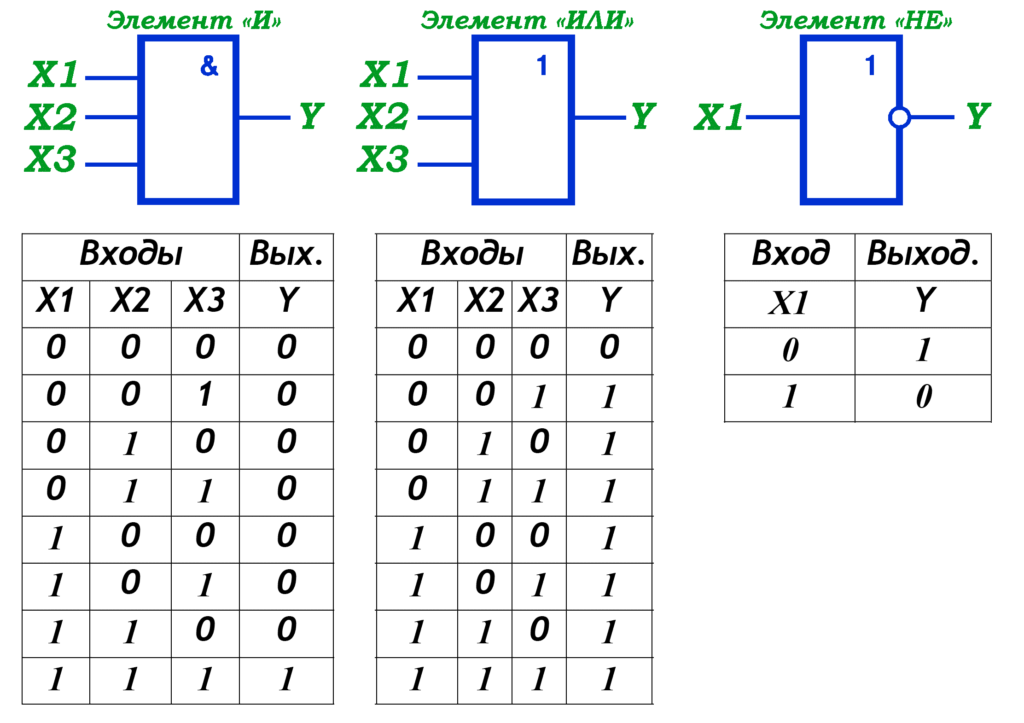
Посмотрите, смогут ли они определить логику, когда включается свет.
Студенты, скорее всего, увидят, что свет включается, когда один или оба входа включены. Используйте эту информацию для создания таблицы истинности в качестве класса для вентиля ИЛИ . Расскажите учащимся, что верхний вход ворот — A, нижний вход — B, а выход — Q.
В таблице истинности 0 означает ВЫКЛ, а 1 — ВКЛ. So the truth table for the OR gate is as follows:
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
В этой таблице численно показано, что только выход (Q) включен (1), а один или оба входа (A и B) включены (1).
Основное задание
Теперь учащиеся готовы приступить к созданию таблиц истинности для других логических элементов в Polypad.
В зависимости от ваших предпочтений вы можете предложить учащимся составить таблицу истинности для всех ворот, позволить им выбрать некоторые ворота, поработать в группах, чтобы разделить задание и т. д.
Учащиеся могут создавать свои таблицы непосредственно в Polypad, используя таблицы в разделе «Диаграммы и статистика» раздела «Вероятность и данные». Щелкните здесь, чтобы узнать о создании классов в Mathigon и о том, как учащиеся сохраняют свою работу.
Дайте учащимся достаточно времени для создания таблиц истинности. Ответы перечислены ниже.
Поддержка и расширение
Учащимся, нуждающимся в поддержке, может быть полезно выполнить еще один пример вместе. Наличие таблицы на холсте для записи результатов каждого испытания может помочь учащимся организовать свою работу.
Ниже ссылка на холст шаблона с таблицами, уже созданными для каждого логического элемента:
Шаблон логических элементов — Polypad
polypad.
org/rDyyCfTiDg5KoA
Когда учащиеся закончат, предложите им изучить комбинирование входов, выходов, и логические вентили, чтобы увидеть, что они могут создать. Некоторые примеры холстов находятся в разделе «Примеры и шаблоны» в меню «Файл» в Polypad. Предлагает учащимся изучить эти полотна. Кроме того, вы можете предложить учащимся объединить два логических вентиля и составить таблицу истинности для их комбинации.
Answers
AND
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
XOR
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
BUFFER
NAND
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
NOR
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
XNOR
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
NOT
Создать бесплатный аккаунт!
Бесплатные учетные записи Mathigon позволяют вам сохранять свою работу, настраивать классы и давать задания ученикам.
