Логический элемент и выполняет: Логические элементы

Логические элементы

 

Глава 1. КОМБИНАЦИОННЫЕ СХЕМЫ И ЦИФРОВЫЕ АВТОМАТЫ

 

1.1.  Логические элементы

Различают комбинационные схемы и цифровые автоматы. В комбинационных схемах состояние на выходе в данный момент времени однозначно определяется состояниями на входах в тот же момент времени. Комбинационными схемами, например, являются логические элементы И, ИЛИ, НЕ и их комбинации. В цифровом автомате состояние на выходе определяется не только состояниями на входах в данный момент времени, но и предыдущим состоянием системы. К цифровым автоматам относятся триггеры.

Логическими элементами называются элементы, выполняющие логические операции И, ИЛИ, НЕ и комбинации этих операций. Указанные логические операции можно реализовать с помощью контактно-релейных схем  и с помощью электронных схем. В настоящее время  в подавляющем большинстве применяется  электронные логические элементы, причем электронные логические элементы входят в состав микросхем. Имея в распоряжении логические элементы И, ИЛИ, НЕ, можно сконструировать цифровое электронное устройство любой сложности. Электронная часть любого компьютера состоит из логических элементов.

Система простых логических функций, на основе которой можно получить любую логическую функцию, называется функционально полной.

 Отсюда следует, что для построения логического устройства любой сложности достаточно иметь однотипные логические элементы, например, И-НЕ  или ИЛИ-НЕ.

Логические элементы могут работать в режимах положительной и отрицательной логики. Для электронных логических элементов в режиме положительной логики логической единице соответствует высокий уровень напряжения, а логическому нулю — низкий уровень напряжения. В режиме отрицательной логики логической единице соответствует низкий уровень напряжения, а логическому нулю — высокий.

Для контактно-релейных схем в режиме положительной логики логической единице соответствует замкнутый контакт ключа или реле, а логическому нулю — разомкнутый. Светящийся индикатор (лампочка, светодиод) соответствует логической единице, а несветящийся — логическому нулю.

Логические элементы, реализующие для режима положительной логики операцию И, для режима отрицательной логики выполняют операцию ИЛИ, и наоборот. Так, например, микросхема, реализующая для положительной логики функции элемента 2И-НЕ, будет выполнять для отрицательной логики функции элемента 2ИЛИ-НЕ.

Как правило, паспортное обозначение логического элемента соответствует функции, реализуемой «положительной логикой». Логические элементы И, ИЛИ, НЕ  имеют один выход, число входов логических элементов  И, ИЛИ  может быть любым начиная с двух. Логические элементы И и ИЛИ, выпускаемые в составе микросхем, обычно имеют  2, 3, 4, 8 входов. В названии элемента первая цифра указывает число входов.

Прежде всего, рассмотрим реализацию логических элементов с помощью контактно-релейных схем. Рассмотрим логический элемент  2И. Он выполняет операцию логического умножения. На рисунке 1.1,а приведена контактно-релейная схема логического элемента 2И для режима положительной логики.

Обозначение логического элемента 2И на принципиальных схемах  показано на рисунке 1.1,б. Знак  & (амперсант) в левом верхнем углу прямоугольника  указывает, что это логический элемент И. Первые две буквы обозначения  DD1.2  указывают на то, что это цифровая микросхема, цифра слева от  точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы.

Функционирование логического элемента обычно задают  таблицей  истинности. Контактно-релейная схема логического элемента 2И (режим положительной логики) позволяет легко составить таблицу истинности этого элемента. Так как микросхема имеет для подачи входных сигналов два входа, то возможны  2²=4 различных комбинации входных сигналов. Необходимо проанализировать состояние лампочки при различных положениях тумблеров Sa1, Sa2, т.е. рассмотреть 4 различных комбинации состояний тумблеров (рис. 1.1,в).   

Введение понятия активного логического уровня существенно облегчает анализ функционирования сложных цифровых устройств. Активным логическим уровнем на входе элемента (логический нуль, логическая единица) называется такой уровень, который однозначно задает состояние на выходе элемента независимо от логических уровней на остальных входах элемента. Активный логический уровень на одном из входов элемента определяет уровень на его выходе. Уровни, обратные активным, называются пассивными логическими уровнями.

Активным логическим уровнем для элементов И является логический нуль. Пусть, например, имеем логический элемент 8И.  Необходимо проанализировать 2⁸=256 различных состояний для составления таблицы истинности этого элемента. Воспользуемся понятием активного логического уровня. Если хотя бы на одном из входов этого элемента будет активный логический уровень, то состояние на выходе элемента определено однозначно и нет необходимости анализировать состояния на остальных входах элемента.

 Таким образом, таблицу истинности логического элемента 8И можно свести к двум строчкам: на выходе этого элемента будет логическая единица, если на всех входах будут сигналы логической единицы и на выходе будет логический нуль, если хотя бы на одном из входов элемента будет сигнал логического нуля.

Логический элемент 2ИЛИ выполняет логическую операцию логического сложения  у=х1+х2. Контактно-релейная схема элемента приведена на рисунке 1.2,а, а его условное обозначение – на рисунке 1.2,б. Знание контактно-релейной схемы элемента позволяет составить таблицу истинности (рис.1.2,в). Лампочка будет гореть, если замкнуты контакты хотя бы одного тумблера, т.е. активным логическим уровнем для элементов ИЛИ является уровень логической единицы.

Логический элемент НЕ выполняет операцию отрицания, и для этого элемента проще составить сразу таблицу истинности, а не вычерчивать сначала контактно-релейную схему, а затем по ней составлять таблицу истинности. Для логических элементов И и ИЛИ проще сначала вычертить контактно-релейную схему, а уже потом составлять таблицу истинности.

Напомним алгоритм работы электромагнитного реле с нормально замкнутыми контактами: при отсутствии электрического тока через обмотку реле контакты реле замкнуты, а при протекании достаточного тока через обмотку реле контакты реле разомкнуты. Контактно релейная схема элемента НЕ приведена на рисунке 1.3а, а его условное обозначение – на рисунке 1.3б.

Проанализируем работу контактно-релейной схемы логического элемента НЕ (рис. 1.3а). Если контакты ключа Sa1 разомкнуты, то через обмотку К электромагнитного реле ток протекать не будет. Контакты К1.1 (цифра слева от точки указывает номер реле на принципиальной схеме, а цифра справа  – номер контактной группы данного реле) будут замкнуты (электромагнитное реле с нормально замкнутыми контактами). Электрическая лампочка HL1 в этом случае будет гореть, что для режима положительной логики будет означать логическую единицу. При замкнутых контактах ключа Sa1 (на входе элемента логическая единица) через обмотку реле протекает ток, достаточный для размыкания контактов К1.1,  поэтому лампочка перестает гореть (логический нуль). В результате анализа мы получили, что сигнал на выходе элемента противоположен сигналу на входе, т.е. если на входе элемента сигнал логической единицы, то на выходе элемента сигнал логического нуля и наоборот (рис. 1.3,в).

При анализе работы логических элементов следует помнить о режиме их работы (режим положительной или отрицательной логики). Логические элементы, реализующие для режима положительной логики операцию И, для

режима отрицательной логики выполняют операцию ИЛИ и наоборот.  Решим следующую задачу.

Задача. Какую логическую операцию выполняет контактно-релейная схема, приведенная на рисунке 1.4.

Правильным ответом в этой задаче будет следующий. Указанная контактно-релейная схема выполняет операцию 3И для режима положительной логики и 3ИЛИ для режима отрицательной логики (решение обосновать самостоятельно).

В практической работе широко используются комбинации логических элементов и особенно элементы И-НЕ и ИЛИ-НЕ. Рассмотрим подробнее контактно-релейную схему элемента 2ИЛИ-НЕ, приведенную на рисунке 1.5,а. Условное обозначение элемента на принципиальных схемах показано на рисунке 1.5,б. Заполним таблицу истинности, приведенную на рисунке 1.5в. Если оба ключа разомкнуты (Х1=0, Х2=0), то лампочка HL1 горит, что соответствует логической единице на выходе элемента (Y=1). Замкнем контакты ключа Sa1 (Х1=1), оставляя ключ Sa2 разомкнутым (Х2=0). Лампочка HL1 в этом случае не горит (Y=0). Если замкнут хотя бы один ключ, то лампочка не горит. Следовательно, активным логическим уровнем на входе элемента ИЛИ-НЕ является уровень логической единицы.

Для двух аргументов логического элемента возможны 16 логических функций. В данном пособии рассматриваются логические функции: логическое И, логическое ИЛИ, логическое НЕ, логическое И-НЕ, логическое ИЛИ-НЕ, сумма по модулю 2.

В таблице 1.1 приведены условные обозначения элементов 2И, 2ИЛИ, НЕ, 2И-НЕ, 2ИЛИ-НЕ, исключающее ИЛИ (сумма по модулю 2), условные обозначения выполняемых этими элементами логических операций, таблицы их истинности и контактно-релейные схемы. При анализе контактно-релейной схемы элемента исключающее ИЛИ необходимо учитывать, что положения переключателей SA1 и SA2 в таблице 1.1 соответствуют логическим единицам (верхнее положение подвижного контакта переключателя соответствует логической единице), т.е. Х1=1 и Х2=1. Лампочка HL1 горит лишь в том случае, когда подвижный контакт одного из переключателей находится в верхнем положении, а подвижный контакт второго переключателя в нижнем положении. Из анализа работы данной контактно-релейной схемы получаем таблицу истинности элемента исключающее ИЛИ.

Рассмотрим решение следующей задачи: имея в распоряжении логические  элементы 2И-НЕ, сконструировать устройство,  реализующее операцию  3ИЛИ-НЕ для режима положительной логики. Эту  задачу решим в  два этапа. Сначала сконструируем устройство, выполняющее операцию 3И-НЕ для режима положительной логики (рис. 1.6,а), а потом на входах и выходе элемента 3И-НЕ установим логические элементы НЕ (рис. 1.6,б).

По мере развития вычислительной техники электронные логические элементы совершенствовались. Рассмотрим принципиальную схему логического элемента 2И (рис. 1.7,а), построенного на диодах и резисторах. Для простоты рассмотрения будем считать, что напряжение  логического «0» на входе элемента равно 0 В, а напряжение логической  «1» — 5 В. Внутреннее сопротивление вольтметра значительно больше сопротивления резистора R1.

Вспомним особенности вольтамперной характеристики полупроводникового кремниевого диода небольшой мощности. При обратном напряжении ток, протекающий через диод, составляет десятые доли микроампера. Напряжение на диоде при протекании через него в прямом направлении тока в десятки миллиампер, равно приблизительно 0,7-0,8 В. Определим примерно параметры логических уровней на выходах данного элемента, если на входе действуют логические уровни с указанными ранее параметрами. Если на оба входа поданы напряжения логических «1», то токи через диоды VD1 и VD2 не протекают, и напряжение на выходе элемента при условии, что сопротивление  нагрузки значительно больше сопротивления резистора R1,  будет примерно равно напряжению питания. Если хотя бы один из входов элемента соединить с минусовым проводом источника питания, то на выходе элемента в случае кремниевых диодов будет напряжение 0,7 — 0,8 В (зависит от сопротивления резистора  R1 и напряжения источника питания).

Примечание: для рассмотренного логического элемента логическая «1» на входе будет, если вход никуда не подключен или подключен к плюсовому выводу источника питания.

На рисунке 1.7,б приведена схема простого и удобного в работе стенда для исследования диодно-резистивного логического элемента 2И. Светодиоды VD3 — VD5 являются индикаторами логических сигналов на входах и выходе логического элемента. Вольтметр V  позволяет определить напряжения логической единицы и логического нуля. Для диодно-резистивного логического элемента 2И напряжение логического нуля на выходе примерно 0,7-0,8 В, а напряжение логической единицы чуть меньше напряжения на зажимах источника питания (определяется соотношением сопротивлений резистора R1 и нагрузки).

На рисунках 1.8,а и 1.8,б приведены схемы для исследования диодно-резистивного логического элемента 2ИЛИ. Для этого элемента напряжение логического нуля на выходе равно 0 В, а напряжение логической единицы равно напряжению питания минус 0,7-0,8 В.

Следующим этапом совершенствования элементной базы цифровой техники  было создание логических  элементов  диодно-транзисторной  логики.

Рассмотрим принципиальную схему логического элемента 2И-НЕ диодно-транзисторной логики (рис. 1.9,а).

Для понимания принципа работы логического элемента  2И-НЕ диодно-транзисторной логики необходимо знать, какой вид имеет зависимость тока коллектора транзистора от напряжения база-эмиттер при постоянном напряжении эмиттер- коллектор. Эта характеристика имеет примерно такой же вид, как и прямая ветвь вольтамперной характеристики полупроводникового диода. Для кремниевых транзисторов при напряжении база-эмиттер (в прямом направлении) менее 0,5 В ток в цепи коллектор-эмиттер практически равен нулю при любых допустимых напряжениях коллектор-эмиттер (транзистор закрыт, сопротивление между коллектором и эмиттером закрытого транзистора VТ1 может достигать единиц МОм). При незначительном увеличении напряжения база-эмиттер (в прямом направлении) более 0,5 В ток коллектора значительно увеличивается, говорят, что транзистор  открывается.

Диоды VD1, VD2 и резистор R1 (рис. 1.9,а) образуют логический элемент 2И. Роль инвертора выполняет транзистор VT1. Если транзистор закрыт, то ток в цепи: плюс источника питания, резистор R2, коллектор-эмиттер транзистора VT1, минус источника питания не протекает и напряжение между эмиттером и коллектором транзистора будет равно напряжению на зажимах источника питания. Диоды VД3, VД4 необходимы для надежного закрытия транзистора VТ1, когда хотя бы на одном из входов элемента было напряжение логического нуля.

Если на обоих входах Х1, Х2 присутствуют сигналы логических единиц, транзистор VT1 открывается током базы, протекающим по цепи: плюс источника питания, резистор R1, диоды VD3, VD4, переход база-эмиттер транзистора VT1, минус источника. На выходе элемента будет напряжение 0,1-0,2 В, что соответствует логическому нулю.

На рисунке 1.9,б приведен вариант логического элемента 2И-НЕ на транзисторах. Инвертор на транзисторе VT1 не обеспечивает большую нагрузочную способность, поэтому в качестве инверторов применяют более сложные схемы. Сложный инвертор в микросхемах транзисторно-транзисторной логики будет рассмотрен чуть позже. Сейчас остановимся на принципе работы инверторов, схемы которых приведены на рисунке 1.10.

Рассмотрим делитель напряжения (делитель напряжения источника питания) образованного резистором R3 и цепью коллектор-эмиттер транзистора VТ1 (рис.1.10,а). Если на входе элемента логическая единица (подвижный контакт переключателя SA1 в верхнем положении), то транзистор VT1 открыт и в его коллекторной цепи  протекает ток. Напряжение между коллектором и эмиттером транзистора составляет десятые доли вольта (не более 0,4 В). При логическом нуле на входе элемента транзистор закрыт и напряжение на выходе элемента равно напряжению питания, что соответствует логической единице.

На рисунках 1.10,б и 1.10,в приведены схемы инверторов с использованием полевых транзисторов. Напомним устройство и принцип действия полевых транзисторов.  Существуют следующие виды полевых транзисторов: полевые транзисторы с управляющим p-n переходом, полевые транзисторы с изолированным затвором со встроенным каналом, полевые транзисторы с изолированным затвором с индуцированным каналом.   

Полевые транзисторы называются также униполярными, одноканальными. Полевой транзистор в отличие от биполярного имеет большое входное сопротивление по цепи управления. Ток в выходной цепи полевого транзистора управляется напряжением,  в то время как в биполярном транзисторе ток в выходной цепи транзистора управляется током  во входной цепи транзистора. Таким образом, мощность управления в полевом транзисторе значительно меньше, чем в биполярном.

Полевой транзистор имеет 3 вывода: исток, сток, затвор. Исток – это вывод полевого транзистора, от которого основные носители заряда идут в канал. Сток – это вывод полевого транзистора, к которому идут основные носители заряда из канала. Затвор — это вывод полевого транзистора, на который подается управляющее напряжение относительно истока или относительно стока.

Наибольшее распространение имеют схемы включения транзистора с общим истоком, когда управляющее напряжение подается на затвор  относительно истока.

В вычислительной технике в качестве электронных ключей широко используются полевые транзисторы с изолированным затвором с индуцированным каналом. Рассмотрим устройство и принцип действия  полевого транзистора с изолированным затвором с индуцированным каналом n-типа (рис. 1.11). В полупроводнике p-типа сделаны два кармана с проводимостью n-типа. Знак n⁺ указывает на большую концентрацию электронов, что делается для уменьшения сопротивлений выводов стока и истока. Металлический затвор изолирован от кристалла полупроводника.

При напряжении затвор-исток, равном  нулю, в цепи сток-исток ток не протекает  при любых допустимых напряжениях сток-исток, так как образуются два p-n  перехода, причем верхний подключен в обратном направлении.

Подадим на затвор относительно истока положительный потенциал.  В полупроводниках p-типа имеются неосновные носители заряда (электроны). Рассмотрим  движение электронов и дырок  в слое полупроводника p-типа, прилежащем к затвору. Для упрощения рассмотрения соединим область p-типа с выводом истока. Под действием электрического поля, обусловленного наличием напряжения затвор – исток, дырки будут  двигаться вправо, а электроны влево, т.е. в  полупроводнике в приграничной к затвору области концентрация дырок  уменьшается, а концентрация электронов увеличивается. При определенном напряжении затвор-исток в указанной области концентрация электронов станет больше концентрации дырок, наступит инверсия  проводимости, т.е. в приграничной к затвору области появится слой полупроводника n-типа. В этом случае в цепи сток-исток протекает ток, т.к. между выводами стока и истока появился канал n-типа. Этот канал называется индуцированным (наведенным).

Для понимания принципа работы логических элементов на полевых транзисторах необходимо знать, что собой представляет стоко-затворная характеристика полевого транзистора. Стоко-затворная характеристика полевого транзистора в схеме включения с общим истоком (исток является общим для входной и  выходной цепи) — это зависимость тока  стока от напряжения затвор-исток при постоянном напряжении сток-исток. Эта характеристика полевого транзистора с изолированным затвором с индуцированным каналом n-типа приведена на рисунке 1.12. Особенности стоко-затворных характеристик полевых транзисторов с изолированным затвором с индуцированным каналом позволяют использовать эти транзисторы в качестве электронных ключей. Сравним основные характеристики электронного ключа на полевом транзисторе с характеристиками механического ключа. Сопротивление разомкнутого механического ключа можно считать бесконечно большим (пока не наступит электрический пробой), сопротивление ключа на полевом транзисторе порядка 10 МОм. Когда контакты механического ключа замкнуты  сопротивление между контактами составляет сотые доли ома, для такого же состояния  полевого транзистора сопротивление между стоком и истоком сотни Ом.

Если на входе инвертора, схема которого приведена на рисунке 1.10,б, напряжение логической единицы, то сопротивление между выводами сток и исток транзистора мало. Сопротивление резистора R1 выбирают значительно больше сопротивления между стоком и истоком открытого полевого транзистора и, следовательно, напряжение на выходе элемента будет близко к нулю вольт. При логическом нуле на входе логического элемента НЕ полевой транзистор будет закрыт, и на выходе элемента будет напряжение, примерно равное напряжению источника питания. Это обусловлено тем, что сопротивление резистора R1 выбирают во много раз меньше сопротивления между стоком и истоком закрытого транзистора.

Рассмотрим принцип работы инвертора (логического элемента НЕ) КМОП (комплиментарный, металл, окисел, полупроводник) структуры (рис. 1.10,в). Комплиментарный означает дополняющий друг друга по типу проводимости. Микросхемы КМОП имеют транзисторы как с каналом p-типа, так и с каналом n-типа. Учтем, что сопротивление между выводами сток-исток открытого транзистора — 200-300 Ом, а сопротивление между выводами сток-исток закрытого транзистора более 10 МОм.

Выберем напряжение питания 9 В. Пусть на вход Х подано напряжение логического «0», тогда транзистор VТ2 будет закрыт, а транзистор VТ1 открыт, так как потенциал затвора транзистора VТ1 относительно истока этого же транзистора равен минус 9В. На выходе элемента логическая единица.

Подадим на вход Х напряжение, соответствующее логической единице. Для рассмотренного случая это + 9 В относительно общего провода. В этом случае транзистор VТ2 будет открыт, а транзистор VТ1 – закрыт и на выходе элемента будет напряжение логического нуля.

Рассмотрим основные параметры, которыми характеризуются цифровые микросхемы.

Помехоустойчивость U_{п, макс} – наибольшее значение напряжения помехи на входе микросхемы, при котором еще не происходит изменения уровней ее выходного напряжения.

Напряжение логической единицы U¹ – значение высокого уровня напряжения для «положительной» логики и значение низкого уровня напряжения для «отрицательной» логики.

Напряжение логического нуля U⁰ – значение низкого уровня напряжения для «положительной» логики и значение высокого уровня напряжения для «отрицательной» логики.

Пороговое напряжение логической единицы U¹_пор – наименьшее значение высокого уровня напряжения для «положительной» логики или наибольшее значение низкого уровня напряжения для «отрицательной» логики на входе микросхемы, при котором она переходит из одного устойчивого состояния в другое.

Пороговое напряжение логического нуля U⁰_пор – наибольшее значение низкого уровня напряжения для «положительной» логики или наименьшее значение высокого уровня напряжения для «отрицательной» логики на входе микросхемы, при котором она переходит из одного устойчивого состояния в другое.

Входной ток логической единицы I¹_вх – измеряется при заданном значении напряжения логической единицы.

Входной ток логического нуля I⁰_вх – измеряется при заданном значении напряжения логического нуля.

Выходной ток логической единицы I¹_вых – измеряется при заданном значении напряжения логической единицы.

Выходной ток логического нуля I⁰_вых– измеряется при заданном значении напряжения логического нуля.

Ток потребления в состоянии логической единицы I¹_пот – значение тока, потребляемого микросхемой от источников питания при логических единицах на выходах всех элементов.

Ток потребления в состоянии логического нуля I⁰_пот – значение тока, потребляемого микросхемой от источников питания при логических нулях на выходах всех элементов.

Средний ток потребления I_{пот. ср.} – значение тока, равное полусумме токов, потребляемых цифровой микросхемой от источников питания в двух устойчивых различных состояниях.

Потребляемая мощность в состоянии логической единицы Р¹_пот – значение мощности, потребляемой микросхемой от источника питания при логических единицах на выходах всех элементов.

Потребляемая мощность в состоянии логического нуля Р⁰_пот – значение мощности, потребляемой микросхемой от источника питания при логических нулях на выходах всех элементов.

Средняя потребляемая мощность Р_{пот. ср.– полусумма мощностей, потребляемых микросхемой от источников питания в двух устойчивых различных состояниях.}

Время перехода интегральной микросхемы из состояния логической единицы в состояние логического нуля t^1,0 – интервал времени, в течение которого напряжение на выходе микросхемы переходит от напряжения логической единицы к напряжению логического нуля, измеренный на уровнях напряжения 0,1 и 0,9 от амплитуды импульса.

Время перехода интегральной микросхемы из состояния логического нуля в состояние логической единицы t^0,1 – интервал времени, в течение которого напряжение на выходе микросхемы переходит от напряжения логического нуля к напряжению логической единицы, измеренный на уровнях напряжения 0,1 и 0,9 от амплитуды импульса.

Время задержки распространения сигнала при включении t^1,0_{зд, р} – интервал времени между входным и выходным импульсами при переходе напряжения на выходе микросхемы от напряжения логической единицы к напряжению логического нуля, измеренный на уровне 0,5 амплитуды.

Время задержки распространения сигнала при выключении t^0,1_{зд, р} – интервал времени между входным и выходным импульсами при переходе напряжения на выходе микросхемы от логического нуля к логической единицы, измеренный на уровне 0,5 амплитуды.

Среднее время задержки распространения сигнала t_{зд, р.с.– интервал времени, равный полусумме времени задержки распространения сигнала при включении и выключении цифровой микросхемы.}

Коэффициент объединения по входу К_об – число входов микросхемы, по которым реализуется логическая функция.

Коэффициент разветвления по выходу К_раз – число единичных нагрузок, которые можно одновременно подключить к выходу микросхемы (единичной нагрузкой является один вход основного логического элемента данной серии интегральных микросхем).

Коэффициент объединения по выходу К_об.вых – число соединяемых между собой выходов интегральной микросхемы, при котором обеспечивается реализация соответствующей логической операции.

Сопротивление нагрузки R_н – значение активного сопротивления нагрузки, подключаемой к выходу интегральной микросхемы, при котором обеспечивается заданное значение выходного напряжения (выходного тока) или заданное усиление.

Емкость нагрузки С_н – максимальное значение емкости, подключенной к выходу интегральной микросхемы, при котором обеспечиваются заданные частотные и иные параметры.

Синхронизация работы отдельных узлов ЭВМ и других устройств цифровой техники осуществляется периодическими последовательностями прямоугольных импульсов напряжения. Импульсом напряжения называют отклонение напряжения от первоначального значения в течение короткого промежутка времени. Последовательность импульсов, мгновенные значения которых повторяются через равные промежутки времени, называют периодической последовательностью импульсов. Участок импульса, на котором происходит изменение напряжения от начального уровня до конечного, называют фронтом импульса, а участок, на котором напряжение возвращается к исходному уровню, называется срезом импульса. Длительностью фронта импульса считают время нарастания напряжения от 0,1 U_м  до 0,9 U_м, а длительностью среза – время изменения напряжения   от 0,9 U_м до 0,1 U_м, где U_м –  амплитуда импульса. Когда говорят о длительности импульса, то необходимо указывать, на каком уровне от амплитуды импульса проводились измерения: на уровне 0,1 U_м  или 0,5 U_м. Частота следования импульсов – это число импульсов в одну секунду. Период следования импульсов – это минимальное время, через которое повторяются мгновенные значения напряжения. Интервал времени между окончанием одного импульса и началом следующего называется паузой. Величину, равную отношению периода следования импульсов к длительности импульса, называют скважностью импульсов. Периодическая последовательность прямоугольных импульсов при скважности 2 называется меандром. Прямоугольный импульс напряжения иногда рассматривают как совокупность двух перепадов напряжения. Перепады напряжения – это быстрые изменения напряжения между двумя уровнями. Перепад называют положительным, если напряжение изменяется от низкого уровня к высокому, и отрицательным, если напряжение изменяется от высокого уровня к низкому. Перепад напряжения, у которого длительность равна нулю,  называется скачком напряжения. 

На рисунке 1.13 показано, как определяется длительность фронта входного импульса t_ф, время перехода интегральной микросхемы из состояния логической единицы в состояние логического нуля t^1,0, время перехода интегральной микросхемы из состояния логического нуля в состояние логической единицы t^0,1, время задержки распространения при включении t^1,0_{зд, р}, время задержки распространения при выключении t^0,1_{зд, р} .

 

 

4.4. Логические элементы и синтез логических схем. Информатика: аппаратные средства персонального компьютера

4.4. Логические элементы и синтез логических схем

Сложные цифровые логические устройства, входящие в состав компьютера, состоят из ряда элементарных логических элементов, построенных на базе средств электронной техники. При производстве этих электронных логических элементов используют различные технологии и схемотехнические решения, такие как: ДТЛ (диодно-транзисторная логика), ТТЛ (транзисторно-транзисторная логика), ЭСЛ (эмиттерно-связанная логика), технологии, основанные на использовании полевых транзисторов, и т. д. Логические элементы позволяют реализовать любую логическую функцию. Входные и выходные сигналы логических элементов, соответствующие двум логическим состояниям 1 и 0, могут иметь один из двух установленных уровней электрического напряжения, который зависит от схемотехнического решения логического элемента. Например, для логических элементов, основанных на технологии ТТЛ, высокий уровень электрического напряжения (2,4 ? 5 В) соответствует значению логической единицы (истина), а низкий уровень (0 ? 0,4 В)   – логическому нулю (ложь).

Три приведенных ниже логических элемента составляют функционально полную систему для проектирования цифровых логических устройств, в том числе и соответствующих логических блоков и устройств компьютера, поскольку реализуют функционально полный набор логических функций, состоящий из логических функций: И (конъюнкции), ИЛИ (дизъюнкции), НЕ (отрицания).

1. Логический элемент НЕ, который называется также инвертором, выполняет логическую операцию отрицания (инверсии).

2. Логический элемент И, называемый также конъюнктором, выполняет операцию логического умножения (конъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.

3. Логический элемент ИЛИ, называемый также дизъюнктором, выполняет операцию логического сложения (дизъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.

При проектировании цифровых логических устройств часто возникает задача по заданной таблице истинности записать выражение для логической функции и реализовать ее в виде логической схемы, состоящей из функционально полного набора логических элементов. Данную задачу называют также задачей синтеза логических схем или логических устройств.

Синтез логических схем на основе функционально полного набора логических элементов состоит из представления логических функций, описывающих данные логические схемы в нормальных формах. Нормальной формой представления считается форма, полученная посредством суперпозиций вспомогательных логических функций – минтермов и макстернов.

Минтермом называют логическую функцию, которая принимает значение логической единицы только при одном значении логических переменных и значение логического нуля при других значениях логических переменных. Например, минтермами являются логические функции F₂, F₃, F₅и F₉(см. рис. 4.3).

Макстерном называют логическую функцию, которая принимает значение логического нуля только при одном значении логических переменных и значение логической единицы при других значениях логических переменных. Например, макстернами являются логические функции F₈, F₁₂, F₁₄и F₁₅(см. рис. 4.3).

Из минтермов и макстернов методом суперпозиции можно составить логические функции, которые называются соответственно логической функцией, представленной посредством совершенных дизъюнктивных нормальных форм (СДНФ), и логической функцией, представленной посредством совершенных конъюнктивных нормальных форм (СКНФ). Полученные таким образом функции СДНФ и СКНФ будут представлять искомую логическую функцию по заданной таблице истинности. После получения функций СДНФ и СКНФ их необходимо преобразовать (минимизировать). Преобразование данных функций с целью их минимизации осуществляется с помощью законов алгебры логики и специальных разработанных методов: метод Квайна, карты Карно, диаграммы Вейча и т. д.

Рассмотрим задачу синтеза на примере модифицированной таблицы истинности, приведенной на рис. 4.6. Для данной таблицы истинности необходимо записать выражение для выходной функции F, провести ее преобразование (минимизацию) на основе законов алгебры логики и, используя основные логические элементы – НЕ, И и ИЛИ, разработать логическую схему реализации выходной функции F.

Рис. 4.6. Таблица истинности логических переменных A, В и С

Значения логических переменных А, В и С и соответствующие значения функции F приведены в таблице истинности (см. рис. 4.6), где в столбце № – указан номер комбинации логических переменных A, В и С.

Для решения указанной задачи представим логическую функцию F в виде СДНФ, а затем и в СКНФ. Найдем вспомогательные функции минтермы и макстермы. В заданной таблице истинности выходная функция F принимает логическое значение, равное логической единице, при комбинациях логических переменных A, В и С, указанных под номерами 3, 6, 8, а значение, равное логическому нулю – при комбинациях, указанных под номерами 1, 2, 4, 5,7.

Минтермы запишем в следующем виде:

Минтермы представляют собой логические произведения (конъюнкции) логических переменных А, В, и С при значениях логической функции F, равных логической единице (комбинации 3, 6, 8). Сомножители (логические переменные A, В и С) входят в минтерм в прямом виде (без отрицания), если их значения равны логической единице, и в инверсном (с отрицанием), если их значения равны логическому нулю. Логическая функция F в СДНФ будет равна логической сумме минтермов:

После минимизации логической функции Fc использованием законов алгебры логики получим ее искомое выражение:

Макстермы запишем в следующем виде:

Макстермы представляют собой логические суммы (дизъюнкции) логических переменных А, В, и С при значениях логической функции F, равных логическому нулю (комбинации 1, 2, 4, 5, 7). Слагаемые (логические переменные A, В, и С) входят в макстерм в прямом виде (без отрицания), если их значения равны логическому нулю, и в инверсном (с отрицанием), если их значения равны логической единице. Логическая функция F в СКНФ будет равна логическому произведению макстермов:

Поскольку полученное выражение для F в виде СКНФ является более громоздким по сравнению с представлением F в виде СДНФ, то в качестве окончательного выражения для F примем ее выражение в виде СДНФ, т. е.

Аналогичным образом можно получить выражение для любой логической функции, которая представлена с помощью заданной таблицы истинности с Означениями логических переменных.

Используем полученное выражение логической функции F для разработки (построения) логической схемы на основе функционально полного набора логических элементов НЕ, И и ИЛИ. При построении логической схемы необходимо учитывать установленные в алгебре логики правила (приоритеты) для выполнения логических операций, которые в данном случае реализуются с помощью логических элементов НЕ, И и ИЛИ. Порядок производимых логических операций будет следующий: операция инверсии (отрицания), операция логического умножения (конъюнкции) и затем операция логического сложения (дизъюнкции). Реализация функции F в виде логической схемы, приведена на рис. 4.7.

Рис. 4.7. Реализация функции F в виде логической схемы

Для графического отображения логических схем существуют различные компьютерные программы, называемые графическими редакторами. Данные программы могут быть включены в другие компьютерные программы, например в программах Microsoft Word и Microsoft Excel такие редакторы реализованы с помощью панелей инструментов «Рисование», или быть самостоятельными программами, например Paint, Microsoft Visio и т. д. Воспользуемся встроенным графическим редактором (панель «Рисование») программы MS Excel для графического отображения логической схемы функции F. Данная логическая схема показана на рис. 4.8.

Рис. 4.8. Графическое отображение логической функции F с помощью программы MS Excel

На основе функционально полного набора логических элементов построены различные электронные устройства, входящие в состав компьютера. К таким устройствам относятся сумматоры (выполняющие операции сложения двоичных чисел), триггеры (устройства, имеющие два устойчивых состояния: логического нуля и логической единицы и используемые в качестве двоичных элементов памяти), регистры памяти (состоящие из набора триггеров), двоичные счетчики, селекторы (переключатели сигналов), шифраторы, дешифраторы и т. д.

Рассмотренные выше таблицы истинности логических элементов показывают установившиеся значения логических переменных. Однако когда логические переменные представлены в виде электрических сигналов, то необходимо некоторое время для того, чтобы значение логической функции достигло уровня установившегося состояния из-за внутренних задержек по времени в электронных логических элементах. В среднем задержка электрического сигнала такого элемента составляет 10^-9 с. В компьютере двоичные сигналы проходят через множество электронных схем, и задержка по времени может стать значительной. В этом случае выделяется отрезок времени (такт) на каждый шаг логической операции. Если операция заканчивается раньше, чем заканчивается тактовое время, то устройство, входящее в состав компьютера, ожидает ее окончания. В результате скорость выполнения операций несколько снижается, но достигается высокая надежность, так как обеспечивается синхронизация между многими параллельно выполняющимися операциями в компьютере. Синхронизация устройств в компьютере обеспечивается с помощью специального генератора – генератора тактовой частоты, который вырабатывает электрические импульсы стабильной частоты.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Понятие о логических элементах и их применение в автоматизированном электроприводе

Страница 24 из 39

Релейно-контакторная аппаратура уже во многом не удовлетворяет требованиям автоматизации сложных технологических процессов в отношении надежности и быстроты действия, а также сроков службы. Поэтому на смену ей приходят так называемые логические элементы, которые в отличие от реле и контакторов не имеют движущихся частей, что повышает надежность их работы и практически приводит к неограниченному сроку службы. Логическим элементом называется устройство, имеющее один или несколько входов и один выход.
Логические элементы не имеют контактов, разрывающих ток, и поэтому взрывобезопасны. Они малочувствительны к влияниям внешней среды, не требуют регулирования и наладки в процессе эксплуатации. Все эти свойства открывают широкие перспективы к решению их применения. Логические элементы выполняют с использованием электронных ламп, полупроводниковых диодов, транзисторов и магнитных сердечников.

Рис. 12.21. К принципу работы логических элементов
Принцип работы логических элементов можно пояснить соответствующими действиями обычных контактных реле в схеме, приведенной на рис. 12.21, а, предусматривающей появление сигнала на выходе лишь в том случае, если поданы все сигналы на входе.
Логический элемент И с тремя входами действует подобно схеме с тремя реле (рис. 12.21,б). Катушка контактора К в релейной схеме получит питание лишь в случае одновременного замыкания контакторов реле РП1, РП2, и РП3, катушки которых могут получить питание при замыкании контактов а, b, с.

Рис. 12.22. Таблица основных логических элементов

Рис. 12.23. Схема включения логического элемента, выполненная с применением электронной лампы

 В схеме с логическим элементом катушки контактора получат питание также в случае замыкания контактов а, b, с, подающих сигнал на вход, при этом логический элемент И выполняет функции трех электромагнитных реле (рис. 12.21, в). Комбинации из основных логических элементов дают возможность получить более сложные схемы. Логические элементы различаются в зависимости от того, какое действие на выходе вызывает подача сигнала на входе.
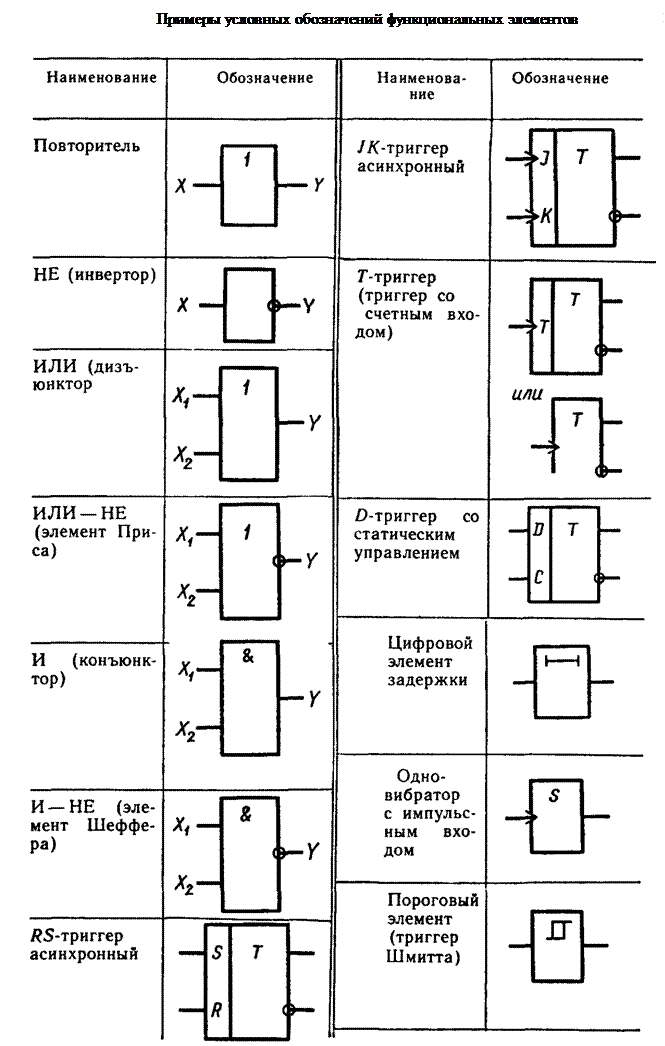
Логический элемент, у которого при подаче сигнала на вход появляется сигнал на выходе, называется повторителем. Логический элемент называется инвертором или элементом «нет», если при подаче сигнала на вход сигнал на выходе исчезает.
Логическим элементом ИЛИ называется такой элемент, сигнал на выходе которого появляется при подаче сигнала на один из входов. А логический элемент И — тот, у которого сигнал на выходе появляется в случае, если поданы сигналы на все входы.  На рис. 12.22 приведены условные обозначения, релейный эквивалент и функциональная формула основных логических элементов. Различные схемы автоматического управления, выполнявшиеся ранее на контактных реле, можно осуществить, применяя основные логические элементы или комбинации из них.
Дальше приводятся примеры применения логических элементов с бесконтактной аппаратурой взамен схем управления, которые ранее выполнялись на контактных реле. На рис. 12.23 показана принципиальная схема включения логического элемента НЕ на электронном триоде. Она состоит в следующем.
При отсутствии сигнала на входе сетка лампы имеет отрицательный потенциал Е с, лампа заперта, анодный ток I а отсутствует. Напряжение на выходе U вых, равное Еа — Iara≈Ео, будет иметь высокий потенциал, так как отсутствует падение напряжения на сопротивлении га. При подаче положительного сигнала на вход лампа открывается, появляется анодный ток и в результате падения напряжения на rа напряжение на выходе резко уменьшается, т. е. сигнал высокого уровня на выходе появляется при отсутствии сигнала на входе.

Логические элементы компьютера

Основные логические элементы реализуют 3 основные логические операции:

• логическое умножение;
• логическое сложение;
• инверсию (отрицание).

Устройства компьютера, которые выполняют обработку и хранение информации, могут быть собраны из базовых логических элементов, у которых $2$ входа и $1$ выход. К логическим устройствам компьютера относятся группы переключателей, триггеры, сумматоры.

Связь между алгеброй логики и компьютерной техникой также лежит в двоичной системе счисления, которая используется в ЭВМ. Поэтому в устройствах ПК можно хранить и обрабатывать как числа, так и значения логических переменных.

Определение 1

Логический элемент компьютера – это часть электронной схемы, которая выполняет элементарную логическую функцию.

Переключательные схемы

В ЭВМ используются электрические схемы, которые состоят из большого количества переключателей. Переключатель, находясь в замкнутом состоянии ток пропускает, в разомкнутом – не пропускает. Работа таких схем удобно описывается при помощи алгебры логики. В зависимости от состояния переключателя можно регулировать получение или неполучение сигналов на выходах.

Вентили

Среди логических элементов компьютеров выделяют электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и другие (их называют вентили).

Эти схемы позволяют реализовать любую логическую функцию, которая описывает работу устройств ПК. Обычно вентили имеют $2–8$ входов и $1$ или $2$ выхода.

Для представления двух логических состояний ($1$ и $0$) в вентилях, входные и выходные сигналы имеют разные уровни напряжения. Например, $+3 \ B$ (вольт) для состояния $«1»$ и $0 \ B$ для состояния $«0»$.

У каждого логического элемента есть условное обозначение, выражающее его логическую функцию, но не указывающее на электронную схему, которая в нем реализована. Такой подход реализован для упрощения записи и понимания сложных логических схем.

Готовые работы на аналогичную тему

Работа логических элементов описывается таблицами истинности.

Рисунок 1.

Триггер

Триггеры и сумматоры состоят из вентилей.

Триггер – важнейшая структурная единица оперативной памяти ПК и внутренних регистров процессора.

Определение 2

Триггер – логическая схема, которая способна хранить $1$ бит информации ($1$ или $0$). Строится на $2$-х элементах ИЛИ–НЕ или на $2$-х элементах И–НЕ.

Рисунок 2.

Самый распространённый тип триггера – $RS$-триггер (Reset/Set), который имеет $2$ входа $S$ и $R$ и два выхода $Q$ и $\bar{Q}$. На каждый из входов $S$ и $R$ могут подаваться входные сигналы в виде кратковременных импульсов (рис.3): есть импульс – $1$, нет импульса – $0$.

Рисунок 3. Кратковременный импульс

Сумматор

Сумматоры широко применяются в арифметико-логических устройствах процессора и отвечают за суммирование двоичных разрядов.

Определение 3

Сумматор – логическая схема, которая способна суммировать 2 одноразрядных двоичных числа с переносом из предыдущего разряда.

Рисунок 4.

Сумматор может находить применение и в других устройствах машины.

Для суммирования двоичных слов длиной от двух бит можно использовать последовательное соединение многоразрядных сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.

Пример реализации логической схемы

Рисунок 5.

Алгоритм реализации:

1. Определим количество переменных данного выражения, значит столько входов будет иметь схема. В данном случае это входы $A, B, C$.

2. С помощью базовых логических элементов реализуются основные операции в порядке их следования:

   I – инверсия переменных $A, B, C$ реализуется логическим элементом «НЕ»;

   II – логическое умножение реализуется логическим элементом «И»;

   III – логическое сложение реализуется логическим элементом «ИЛИ».

На выходе каждого элемента прописывается логическое выражение, которое реализуется данным элементом, что позволяет осуществить обратную задачу, т.е. по готовой схеме составить логическое выражение, которое реализует данная схема.

Логические элементы ТТЛ–технологии — КиберПедия

 

Логические элементы (узлы) предназначены для выполнения различных логических (функциональных) операций над дискретными сигналами при двоичном способе их представления.

Преимущественное распространение получили логические элементы потенциального типа. В них используются дискретные сигналы, нулевому значению которых соответствует уровень низкого потенциала, а единичному значению – уровень высокого потенциала (отрицательного или положительного). Связь потенциального логического элемента с предыдущим и последующими узлами в системе осуществляется непосредственно, без применения реактивных компонентов. Благодаря этому преимуществу именно потенциальные логические элементы нашли почти исключительное применение в интегральном исполнении в виде микросхем. С позиций использования логических микросхем потенциального типа и проводится далее рассмотрение логических элементов.

Логические биполярные микросхемы чаще выполняют на транзисторах типа п-р-п снапряжением питания Е_к> 0. Этим объясняется, что используемые здесь сигналы имеют положительную полярность. Уровню высокого положительного потенциала («1») на выходе соответствует закрытое состояние транзистора, а уровню низкого потенциала («0») – его открытое состояние. С этой точки зрения, в частности, и следует понимать действие сигнала на входе логического элемента, имеющего непосредственную связь с другими элементами в конкретной схеме. Для упрощения уровень низкого потенциала сигнала полагаем равным нулю, а процесс перехода транзистора из одного состояния в другое – достаточно быстрым.

Логические интегральные микросхемы являются элементами, на основе которых выполняются схемы цифровой техники.

 

Логический элемент ИЛИ. Логический элемент ИЛИ имеет несколько входов и один общий выход. Его условное обозначение показано на рис. 6.1, а.

Логический элемент ИЛИ выполняет операцию логического сложения (дизъюнкции):

F = х₁+ х₂+ х₃+ … + х_n,

 

где F – функция;

х₁ х₂, х₃,…, х_n – аргументы (переменные, двоичные сигналы на входах).

Здесь функция F = 0, когда все ее аргументы равны нулю, и F = 1 при одном, нескольких или всех аргументах, равных единице.

Работу схемы двухвходового логического элемента ИЛИ иллюстрирует таблица истинности.

 

Рис. 6.1. УГО элемента ИЛИ (а), его таблица истинности

 

На практике возможны случаи, когда число входов используемого логического элемента ИЛИ превышает количество входных сигналов. Неиспользуемые входы заземляют. Тем самым исключается возможность прохождения помех через элемент ИЛИ от наводок по неиспользованным входам.

 

Логический элемент И. Логический элемент И также имеет несколько входов и один выход. Его условное обозначение показано на рис. 6.2, а.

Логический элемент И выполняет операцию логического умножения (конъюнкции):

F = х₁• х₂• х₃• … • х_n.

 

Здесь функция F = 0, когда хотя бы один из ее аргументов равен нулю, и F = 1 при всех аргументах, равных единице.

Рис. 6.2. Условное обозначение логического элемента И (а),

его таблица истинности

 

Работу схемы двухвходового логического элемента И иллюстрирует таблица истинности. Элемент И является схемой совпадения: сигнал «1» на выходе появляется при совпадении сигналов «1» на всех входах.

В случае применения логического элемента И, имеющего число входов, большее количества входных сигналов, неиспользуемые входы элемента соединяют с шиной «+» источника питания (подают сигнал логической «1»). Это уменьшает вероятность прохождения помех на выход элемента И от наводок по неиспользованным входам. Поведение логического элемента будет зависеть от комбинации входных сигналов.

 

Логический элемент НЕ. Логический элемент НЕ имеет один вход и один выход. Его условное обозначение показано на рис. 6.3, а.

Рис. 6.3. Условное обозначение логического элемента НЕ (а),

его таблица истинности

Элемент НЕ выполняет операцию инверсии (отрицания), в связи, с чем его часто называют логическим инвертором. Им реализуется функция

F = х.

 

Сигналу х = 0 на входе соответствует F = 1 и, наоборот, при х = 1 F = 0.

Работу схемы логического элемента НЕ иллюстрируют таблица истинности.

Логический элемент НЕ представляет собой ключевую схему на транзисторе (рис. 6.4.). Открытое состояние транзистора обеспечивается заданием тока базы, вводящего транзистор в режим насыщения.

Рис. 6.4. Схема логического элемента НЕ. Условное обозначение логического элемента ИЛИ – НЕ (а), его функциональный эквивалент (б)

и таблица истинности (в)

Логический элемент ИЛИ – НЕ. Условное обозначение логического элемента ИЛИ – НЕ показано на рис. 6.5, а. Он объединяет элементы ИЛИ и НЕ с очередностью проведения операций, показанной на рис. 6.5 , б. В связи с этим входным сигналам, равным единице, соответствует логический «0» на выходе, а при нулевых сигналах на всех входах F = 1. Для двухвходового элемента ИЛИ – НЕ соотношение иллюстрирует таблица истинности, приведенная на рис. 6.5, в.

Функциональная операция, выполняемая элементом ИЛИ – НЕ при n входах, определяется выражением

 

F = x_l + x₂+ x₃ + … + х_n.

 

На рис. 6.6 приведена схема логического элемента ИЛИ – НЕ, представляющая собой последовательное соединение элемента ИЛИ на диодах и элемента НЕ. Логические схемы подобного сочетания определяют, в частности, класс элементов так называемой д и о д н о-транзисторной логики (ДТЛ).

 

Рис. 6.6

 

Логический элемент И – НЕ. Условное обозначение логического элемента И – НЕ показано на рис. 6.7, а. Ему эквивалентна структурная схема, показанная на рис 6.7, б. Логической «1» на всех информационных входах соответствует логический «0» на выходе элемента. При логическом «0» на одном из входов создается логическая «1» на выходе. Для двухвходового элемента И – НЕ сказанное отражено в таблице истинности на рис. 6.7, в. Логическая функция элемента И – НЕ при п входах отвечает выражению

 

F = x_l • x₂• x₃ • … • х_n.

 

 

Рис. 6.7.

 

На рис. 6.8 приведена другая схема элемента И–НЕ, реализованная на транзисторах Схемы такого типа образуют класс элементов так называемой транзисторно-транзисторной логики (ТТЛ).

Рис. 6.8.

Основой этого класса элементов является использование многоэмиттерного транзистора Т_м. Функция многоэмиттерного транзистора сводится к замене диодной части схемы элемента И–НЕ. Подобная замена технологически выгодна, поскольку изготовление многоэмиттерного транзистора в микросхемах не намного сложнее, чем изготовление обычного транзистора, а площадь, занимаемая многоэмиттерным транзистором в кристалле полупроводника, меньше диодной части элемента И–НЕ ДТЛ. От обычного транзистора многоэмиттерный транзистор отличается наличием нескольких (например, трех) эмиттерных областей с общими для всего транзистора базовым и коллекторным слоями,

Наличие усилительного элемента – транзистора – в логических микросхемах ИЛИ–НЕ и И–НЕ классов ДТЛ и ТТЛ определяет такое их важное преимущество, как сохранение неизменного уровня напряжения, соответствующего логической «1», в процессе передачи сигнала при их последовательном соединении. В связи о этим указанные элементы, а также элемент НЕ являются базовыми в микросхемотехнике. В общем корпусе выпускаемых микросхем обычно содержится несколько элементов одного типа.

Комбинированные логические элементы. Существуют логические элементы в микросхемном исполнении, представляющие комбинацию ранее рассмотренных элементов и позволяющие осуществлять более сложные логические операции. На рис. 6.9.приведен элемент 2И–ИЛИ–НЕ.

Рис. 6.9.

Параметры логических элементов. К основным параметрам логических элементов (логических микросхем) относятся функциональные возможности элемента, быстродействие, потребляемая мощность и помехоустойчивость.

Функциональные возможности логического элемента определяются коэффициентом разветвления n по выходу и коэффициентом объединения m no входу. Под коэффициентом разветвления п логического элемента понимают количество входов аналогичных элементов, которое может быть подключено к его выходу, а под коэффициентом объединения т – число входов, которое может иметь элемент. Иными словами, коэффициент п характеризует нагрузочную способность микросхем.

Чем выше коэффициенты п и т, тем меньшее количество микросхем потребуется для создания конкретного устройства. Препятствием к увеличению коэффициента п является ухудшение других показателей элемента (помехоустойчивости, быстродействия) или нарушение нормального режима его работы.

Нагрузочная способность активного логического элемента существенно зависит от типа используемого в нем выходного транзисторного каскада (инвертора). Как правило, для большинства типов интегральных микросхем коэффициент п не превышает 4–10. Для увеличения нагрузочной способности к выходу элемента в случае необходимости подключают так называемый буферный усилитель с мощным многотранзисторным инвертором.

Быстродействие характеризует время реакции логического элемента на изменение сигналов на входах.

Показателем быстродействия логических микросхем является среднее время задержки прохождения сигнала через элемент: t_з = (t_з1 + t_з2)/2.

Логические микросхемы подразделяются на сверхбыстродействующие (4.с <. 0,01 мкс), быстродействующие (4.с *в 0,01ч- 0,03 мкс), среднего быстродействия (t₃._c< 0,03ч- 0,3 мкс), низкого быстродействия (4.с > 0,3 мкс).

Существенным параметром логических элементов является также потребляемая мощность от источника питания +£„• В зависимости от типа (серии) мощность, потребляемая логической микросхемой, составляет 250 мВт — 1 мкВт. Ее обычно определяют по средней мощности, потребляемой элементом в состояниях «0» и «1». Потребляемая мощность связана с быстродействием микросхем. В частности, микросхемы, потребляющие большую мощность, отличаются, как правило, и высоким быстродействием.

Снижение потребляемой мощности при сохранении высокого быстродействия является одной из важнейших задач микроэлектроники. Имеются два пути ее решения. Первый путь предполагает снижение мощности за счет уменьшения токов и напряжений питания. По такому пути идет развитие микросхем на биполярных транзисторах. Второй путь связан с созданием логических элементов, потребляющих мощность только в режиме переключения и не потребляющих ее в статических состояниях («0», «1»). Такие элементы основываются на применении дополняющих МДП-транзисторов.

Помехоустойчивость характеризует меру невосприимчивости логических элементов к изменению своих состояний под воздействием напряжения помех. Помехи, действующие на входе логической микросхемы, подразделяются на статические и импульсные (статическая и импульсная помехоустойчивость). Статическими называют помехи, напряжение которых остается постоянным в течение времени, значительно превышающего длительность переходных процессов в схеме Причиной их появления являются падения напряжения в проводниках, соединяющих микросхемы в устройстве. Статическая помехоустойчивость характеризуется максимальным напряжением помехи и_п._стат, которое может быть подано на вход логического элемента, не вызывая при этом его ложного срабатывания.

Импульсные помехи обусловливаются различными наводками от окружающих работающих установок. По аналогии со статической помехоустойчивостью импульсная помехоустойчивость характеризуется напряжением импульса U_п.и. величина которого зависит от формы и длительности импульса.

К действию помех наиболее чувствительны микросхемы, имеющие низкий перепад логических уровней. На помехоустойчивость оказывают влияние вид схемы, режим работы транзисторов, напряжение источников питания и т. д.

Для уменьшения влияния помех необходимо рационально компоновать корпусы микросхем на печатных платах, осуществлять соответствующие развязки по целям напряжений питания, а в некоторых случаях экранировать цепи связи между элементами или отдельные блоки.

Элементной базой, используемой при построении ЦУ являются интегральные, логические элементы (ИЛЭ). В настоящее время выпускается широкая номенклатура ИЛЭ в составе различных серий интегральных микросхем на основе биполярных и полевых транзисторов. При построении ЦУ с заданными характеристиками выбор необходимых ИЛЭ производится в соответствии с определенным набором их параметров. Рассмотрим важнейшие из них.

Коэффициент разветвления по выходу Краз. Определяет число входов однотипных ИЛЭ, которые одновременно могут быть подключены к выходу данного логического элемента при сохранении его работоспособности в заданных условиях эксплуатации. Для различных элементов составляет от нескольких единиц до нескольких десятков.

Коэффициент объединения по входу Коб. Определяет число входных сигналов логического элемента, которые участвуют в формировании заданной логической функции.

Вид реализуемой логической функции. Используется широкий набор ИЛЭ: И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ. Перед обозначением логического элемента обычно указывается число его входов, по которым реализуется соответствующая логическая функция (т.е. коэффициент объединения по входу). В одной ИМС может быть несколько логических элементов, поэтому для сокращения обозначения состава микросхемы перед помещенным в круглые скобки наименованием элемента иногда указывают число этих элементов в одном корпусе микросхемы. Например, обозначению 4 (2И-НЕ) соответствует ИМС в составе четырех логических элементов И-НЕ с двумя входами каждый.

Статические характеристики: входная, определяющая зависимость входного тока от входного напряжения; выходная, задающая связь между выходными напряжениями и током; передаточная, которая определяет зависимость выходного напряжения от входного.

На рис. 6.10. приведена типовая передаточная характеристика ИЛЭ ТТЛ-типа. С ее помощью, например, можно оценить возможные уровни напряжения на всех входах и выходах логического элемента в том числе уровни напряжений, соответствующие состоянию логического нуля (U⁰) и логической единицы (U¹), допустимые уровни статической помехи относительно этих уровней U^о_пом и U¹_пом, при которых еще не происходит ложного переключения логических элементов.

Временные (динамические) параметры

От них зависит быстродействие логического элемента. Чаще всего оценивается время перехода элемента из состояния единицы в состояние нуля t^1,0 и перехода в обратное состояние t^0,1 (рис. 6.11.).

Рис. 6.10.

Указанные временные интервалы измеряются на уровнях 0,1-0,9 от установившихся значений в цепочке из однотипных элементов. Другим важнейшим параметром, определяющим быстродействие, является время задержки распространения сигнала при включении t^1,0_здр. и выключении t^0,1_здр. логического элемента.

Рис. 6.11.

Измеряется на выходе по отношению к входу на уровнях 0,5 от установившихся значений. Во многих случаях удобно пользоваться средним временем задержки распространения сигнала t_здр.ср., оцениваемым полусуммой t^0,1_здр. и t^1,0_здр.

Для построения ЦУ наиболее широкое применение находят ИДЭ на базе ТТЛ, ТТЛШ, ЭСЛ и КМОП-технологий.

 

Технология ИЛЭ	Выполняемые функции	Краз	Коб	U, U, В	Tздр.ср. ИС
ТТЛ   ТТЛШ     ЭСЛ     КМОП	И-НЕ, И-ИЛИ-НЕ, И, НЕ,ИЛИ   И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ, И, НЕ   ИЛИ-НЕ, ИЛИ,И   ИЛИ-НЕ, И-НЕ, И-ИЛИ	8-30           8-20	2-8   2-8     2-5     2-4	£0,4 ³2,4     £0,5 ³2,7   -1,6 -1,0   0 Uп	18-32       3-5     60-1200

 

Логический элемент не выполняет

Автор На чтение 14 мин. Опубликовано 12.12.2019

И, ИЛИ, НЕ и их комбинации

В Булевой алгебре, на которой базируется вся цифровая техника, электронные элементы должны выполнять ряд определённых действий. Это так называемый логический базис. Вот три основных действия:

ИЛИ – логическое сложение (дизъюнкция) – OR;

И – логическое умножение (конъюнкция) – AND;

НЕ – логическое отрицание (инверсия) – NOT.

Примем за основу позитивную логику, где высокий уровень будет «1», а низкий уровень примем за «0». Чтобы можно было более наглядно рассмотреть выполнение логических операций, существуют таблицы истинности для каждой логической функции. Сразу нетрудно понять, что выполнение логических функций «и» и «или» подразумевают количество входных сигналов не менее двух, но их может быть и больше.

Логический элемент И.

На рисунке представлена таблица истинности элемента «И» с двумя входами. Хорошо видно, что логическая единица появляется на выходе элемента только при наличии единицы на первом входе и на втором. В трёх остальных случаях на выходе будут нули.

Вход X1	Вход X2	Выход Y
1
	1
1	1	1

На принципиальных схемах логический элемент «И» обозначают так.

На зарубежных схемах обозначение элемента «И» имеет другое начертание. Его кратко называют AND.

Логический элемент ИЛИ.

Элемент «ИЛИ» с двумя входами работает несколько по-другому. Достаточно логической единицы на первом входе или на втором как на выходе будет логическая единица. Две единицы так же дадут единицу на выходе.

Вход X1	Вход X2	Выход Y
1		1
	1	1
1	1	1

На схемах элемент «ИЛИ» изображают так.

На зарубежных схемах его изображают чуть по-другому и называют элементом OR.

Логический элемент НЕ.

Элемент, выполняющий функцию инверсии «НЕ» имеет один вход и один выход. Он меняет уровень сигнала на противоположный. Низкий потенциал на входе даёт высокий потенциал на выходе и наоборот.

Вход X	Выход Y
	1
1

Вот таким образом его показывают на схемах.

В зарубежной документации элемент «НЕ» изображают следующим образом. Сокращённо называют его NOT.

Все эти элементы в интегральных микросхемах могут объединяться в различных сочетаниях. Это элементы: И–НЕ, ИЛИ–НЕ, и более сложные конфигурации. Пришло время поговорить и о них.

Логический элемент 2И-НЕ.

Рассмотрим несколько реальных логических элементов на примере серии транзисторно-транзисторной логики (ТТЛ) К155 с малой степенью интеграции. На рисунке когда-то очень популярная микросхема К155ЛА3, которая содержит четыре независимых элемента 2И – НЕ. Кстати, с помощью её можно собрать простейший маячок на микросхеме.

Цифра всегда обозначает число входов логического элемента. В данном случае это двухвходовой элемент «И» выходной сигнал которого инвертируется. Инвертируется, это значит «0» превращается в «1», а «1» превращается в «0». Обратим внимание на кружочек на выходах – это символ инверсии. В той же серии существуют элементы 3И–НЕ, 4И–НЕ, что означает элементы «И» с различным числом входов (3, 4 и т.д.).

Как вы уже поняли, один элемент 2И-НЕ изображается вот так.

По сути это упрощённое изображение двух объёдинённых элементов: элемента 2И и элемента НЕ на выходе.

Зарубежное обозначение элемента И-НЕ (в данном случае 2И-НЕ). Называется NAND.

Таблица истинности для элемента 2И-НЕ.

Вход X1	Вход X2	Выход Y
		1
1		1
	1	1
1	1

В таблице истинности элемента 2И – НЕ мы видим, что благодаря инвертору получается картина противоположная элементу «И». В отличие от трёх нулей и одной единицы мы имеем три единицы и ноль. Элемент «И – НЕ» часто называют элементом Шеффера.

Логический элемент 2ИЛИ-НЕ.

Логический элемент 2ИЛИ – НЕ представлен в серии К155 микросхемой 155ЛЕ1. Она содержит в одном корпусе четыре независимых элемента. Таблица истинности так же отличается от схемы «ИЛИ» применением инвертирования выходного сигнала.

Таблица истинности для логического элемента 2ИЛИ-НЕ.

Вход X1	Вход X2	Выход Y
		1
1
	1
1	1

Изображение на схеме.

На зарубежный лад изображается так. Называют как NOR.

Мы имеем только один высокий потенциал на выходе, обусловленный подачей на оба входа одновременно низкого потенциала. Здесь, как и на любых других принципиальных схемах, кружочек на выходе подразумевает инвертирование сигнала. Так как схемы И – НЕ и ИЛИ – НЕ встречаются очень часто, то для каждой функции имеется своё условное обозначение. Функция И – НЕ обозначается значком «&«, а функция ИЛИ – НЕ значком «1«.

Для отдельного инвертора таблица истинности уже приведена выше. Можно добавить, что количество инверторов в одном корпусе может достигать шести.

Логический элемент «исключающее ИЛИ».

К числу базовых логических элементов принято относить элемент реализующий функцию «исключающее ИЛИ». Иначе эта функция называется «неравнозначность».

Высокий потенциал на выходе возникает только в том случае, если входные сигналы не равны. То есть на одном из входов должна быть единица, а на другом ноль. Если на выходе логического элемента имеется инвертор, то функция выполняется противоположная – «равнозначность». Высокий потенциал на выходе будет появляться при одинаковых сигналах на обоих входах.

Вход X1	Вход X2	Выход Y
1		1
	1	1
1	1

Эти логические элементы находят своё применение в сумматорах. «Исключающее ИЛИ» изображается на схемах знаком равенства перед единицей «=1«.

На зарубежный манер «исключающее ИЛИ» называют XOR и на схемах рисуют вот так.

Кроме вышеперечисленных логических элементов, которые выполняют базовые логические функции очень часто, используются элементы, объединённые в различных сочетаниях. Вот, например, К555ЛР4. Она называется очень серьёзно 2-4И-2ИЛИ-НЕ.

Её таблица истинности не приводится, так как микросхема не является базовым логическим элементом. Такие микросхемы выполняют специальные функции и бывают намного сложнее, чем приведённый пример. Так же в логический базис входят и простые элементы «И» и «ИЛИ». Но они используются гораздо реже. Может возникнуть вопрос, почему эта логика называется транзисторно-транзисторной.

Если посмотреть в справочной литературе схему, допустим, элемента 2И – НЕ из микросхемы К155ЛА3, то там можно увидеть несколько транзисторов и резисторов. На самом деле ни резисторов, ни диодов в этих микросхемах нет. На кристалл кремния через трафарет напыляются только транзисторы, а функции резисторов и диодов выполняют эмиттерные переходы транзисторов. Кроме того в ТТЛ логике широко используются многоэмиттерные транзисторы. Например, на входе элемента 4И стоит четырёхэмиттерный транзистор.

Электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными, называется логическим элементом. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня.

Операнды в данном случае подаются в двоичной системе счисления — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное. 1 — ИСТИНА, 0 — ЛОЖЬ.

Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.

Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.

В зависимости от устройства схемы элемента, от ее электрических параметров, логические уровни (высокие и низкие уровни напряжения) входа и выхода имеют одинаковые значения для высокого и низкого (истинного и ложного) состояний.

Традиционно логические элементы выпускаются в виде специальных радиодеталей — интегральных микросхем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов. Далее рассмотрим каждый из этих типов логических элементов более внимательно.

Логический элемент «И» – конъюнкция, логическое умножение, AND

«И» – логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.

Условные обозначения логических элементов «И» с разным количеством входов приведены на рисунке. В тексте логический элемент «И» с тем или иным числом входов обозначается как «2И», «4И» и т. д. – элемент «И» с двумя входами, с четырьмя входами и т. д.

Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе И на втором входе. В остальных трех возможных случаях на выходе будет ноль.

На западных схемах значок элемента «И» имеет прямую черту на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «&».

Логический элемент «ИЛИ» – дизъюнкция, логическое сложение, OR

«ИЛИ» – логический элемент, выполняющий над входными данными операцию дизъюнкции или логического сложения. Он так же как и элемент «И» выпускается с двумя, тремя, четырьмя и т. д. входами и с одним выходом. Условные обозначения логических элементов «ИЛИ» с различным количеством входов показаны на рисунке. Обозначаются данные элементы так: 2ИЛИ, 3ИЛИ, 4ИЛИ и т. д.

Таблица истинности для элемента «2ИЛИ» показывает, что для появления на выходе логической единицы, достаточно чтобы логическая единица была на первом входе ИЛИ на втором входе. Если логические единицы будут сразу на двух входах, на выходе также будет единица.

На западных схемах значок элемента «ИЛИ» имеет закругление на входе и закругление с заострением на выходе. На отечественных схемах — прямоугольник с символом «1».

Логический элемент «НЕ» – отрицание, инвертор, NOT

«НЕ» – логический элемент, выполняющий над входными данными операцию логического отрицания. Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал. На рисунке приведено условное обозначение логического элемента «НЕ».

Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот.

На западных схемах значок элемента «НЕ» имеет форму треугольника с кружочком на выходе. На отечественных схемах — прямоугольник с символом «1», с кружком на выходе.

Логический элемент «И-НЕ» – конъюнкция (логическое умножение) с отрицанием, NAND

«И-НЕ» – логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Другими словами, это в принципе элемент «И», дополненный элементом «НЕ». На рисунке приведено условное обозначение логического элемента «2И-НЕ».

Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И». Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой логической операции в 1913 году. Обозначается как «И», только с кружочком на выходе.

Логический элемент «ИЛИ-НЕ» – дизъюнкция (логическое сложение) с отрицанием, NOR

«ИЛИ-НЕ» – логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Иначе говоря, это элемент «ИЛИ», дополненный элементом «НЕ» – инвертором. На рисунке приведено условное обозначение логического элемента «2ИЛИ-НЕ».

Таблица истинности для элемента «ИЛИ-НЕ» противоположна таблице для элемента «ИЛИ». Высокий потенциал на выходе получается лишь в одном случае – на оба входа подаются одновременно низкие потенциалы. Обозначается как «ИЛИ», только с кружочком на выходе, обозначающим инверсию.

Логический элемент «исключающее ИЛИ» – сложение по модулю 2, XOR

«исключающее ИЛИ» – логический элемент, выполняющий над входными данными операцию логического сложения по модулю 2, имеет два входа и один выход. Часто данные элементы применяют в схемах контроля. На рисунке приведено условное обозначение данного элемента.

Изображение в западных схемах — как у «ИЛИ» с дополнительной изогнутой полоской на стороне входа, в отечественной — как «ИЛИ», только вместо «1» будет написано «=1».

Этот логический элемент еще называют «неравнозначность». Высокий уровень напряжения будет на выходе лишь тогда, когда сигналы на входе не равны (на одном единица, на другом ноль или на одном ноль, а на другом единица) если даже на входе будут одновременно две единицы, на выходе будет ноль — в этом отличие от «ИЛИ». Данные элементы логики широко применяются в сумматорах.

Для выполнения логических операций и решать логические задачи с помощью средств электроники были изобретены логические элементы. Их создают с помощью диодов, транзисторов и комбинированных элементов (диодно-транзисторные). Такая логика получила название диодной логики (ДЛ), транзисторной (ТЛ) и диодно–транзисторной (ДТЛ). Используют как полевые, так и биполярные транзисторы. В последнем случае предпочтение отдается устройствам типа n-p-n, так как они обладают большим быстродействием.

Логический элемент «ИЛИ»

Схема логического элемента «ИЛИ» представлена на рисунке 1 а. На каждый из входов может подаваться сигнал в виде какого-то напряжения (единица) или его отсутствия (ноль). На резисторе R появиться напряжение даже при его появлении на каком – либо из диодов.

Рис. 1

Элементы или могут иметь несколько логических входов. Если используются не все входы, то те входы которые не используются следует соединять с землей (заземлять), чтобы избежать появления посторонних сигналов.

На рисунке 1б показано обозначение на электрической схеме элемента, а на 1в таблица истинности.

Логический элемент «И»

Схема элемента приведена на рис. 2. Если хотя – бы к одному из входов будет сигнал равный нулю, то через диод будет протекать ток. Падение напряжения на диоде стремится к нулю, соответственно на выходе тоже будет ноль. На выходе сможет появится сигнал только при условии, что все диоды будут закрыты, то есть на всех входах будет сигнал. Рассчитаем уровень сигнала на выходе устройства:

на рис. 2 б – обозначение на схеме, в – таблица истинности.

Логический элемент «НЕ»

В логическом элементе «НЕ» используют транзистор (рис.3 а). при наличии положительного напряжения на входе х=1 транзистор открывается и напряжение его коллектора стремится к нулю. Если х=0 то положительного сигнала на базе нет, транзистор закрыт, ток не проходит через коллектор и на резисторе R нет падения напряжения, соответственно на коллекторе появится сигнал Е. условное обозначение и таблица истинности приведены на рис. 3 б,в.

Логический элемент «ИЛИ-НЕ»

При создании различных схем на логических элементах часто применяют элементы комбинированные. В таких элементах совмещены несколько функций. Принципиальная схема показана на рис. 4 а.

Здесь диоды Д1 и Д2 выполняют роль элемента «ИЛИ», а транзистор играет роль инвертора. Обозначение элемента на схеме и его таблица истинности рис. 4б и в соответственно.

Логический элемент «И-НЕ»

Показана схема на рис. 5 а. Здесь диод Д3 выполняет роль так сказать фильтра во избежание искажения сигнала. Если на вход х1 или х2 не подан сигнал (х1=0 или х2=0), то через диод Д1 или Д2 будет протекать ток. Падение на нем не равно нулю и может оказаться достаточным для открытия транзистора. Последствием чего может стать ложное срабатывание и на выходе вместо единицы мы получим ноль. А если в цепь включить Д3, то на нем упадет значительная часть напряжения открытого на входе диода, и на базу транзистора практически ничего не приходит. Поэтому он будет закрыт, а на выходе будет единица, что и требуется при наличии нуля на каком либо из входов. На рис. 5б и в показаны таблица истинности и схемное обозначение данного устройства.

Логические элементы получили широчайшее применение в электронике и микропроцессорной технике. Многие системы управления строятся с использованием именно этих устройств.

Логические элементы — презентация онлайн

Логические элементы Логическим элементом называется электрическая схема, выполняющая какую-либо логическую операцию (операции) над входными данными, заданными в виде уровней напряжения, и возвращающая результат операции в виде выходного уровня напряжения.

Так как операнды логических операций задаются в двоичной системе счисления, то логический элемент воспринимает входные данные в виде высокого и низкого уровней напряжения на своих входах.

Соответственно, высокий уровень напряжения (напряжение логической 1) символизирует истинное значение операнда, а низкий (напряжение логического 0) — ложное.

Значения высокого и низкого уровней напряжения определяются электрическими параметрами схемы логического элемента и одинаковы как для входных, так и для выходных сигналов.

Обычно, логические элементы собираются как отдельная интегральная микросхема.

К числу логических операций, выполняемых логическими элементами относятся конъюнкция (логическое умножение, И), дизъюнкция (логическое сложение, ИЛИ), отрицание (НЕ) и сложение по модулю 2 (исключающее ИЛИ).

Рассмотрим основные типы логических элементов.

Элемент И Логический элемент И выполняет операцию логического умножения (конъюнкция) над своими входными данными и имеет от 2 до 8 входов и один выход (как правило, выпускаются элементы с двумя, тремя, четырьмя и восемью входами).

На рисунке изображены условные графические обозначения (УГО) логических элементов И с двумя, тремя и четырьмя входами соответственно.

Элементы И обозначаются как NИ, где N — количество входов логического элемента (например, 2И, 3И, 8И и т.д.).X1X2F000010100111 Таблица истинности для элемента И с двумя входами УГО элемента И Элемент И Соберите элементы как показано на схеме Элемент И Соедините элементы.

Запустите выполнение, нажав Ctrl+R, или иконку пуск.

Переключая входные значения следите за изменениями состояния светодиода.

Элемент ИЛИ Логический элемент ИЛИ выполняет операцию логического сложения (дизъюнкция) над своими входными данными и, также как и логический элемент И, имеет от 2 до 8 входов и один выход.

На рисунке изображены УГО логических элементов ИЛИ с двумя, тремя и четырьмя входами соответственно.

Элементы ИЛИ обозначаются также, как и элементы И (2ИЛИ, 4ИЛИ и т.д.).X1X2F000011101111 Таблица истинности для элемента ИЛИ с двумя входами УГО элемента ИЛИ Элемент ИЛИ Соберите схему как на рисунке.

Запустите выполнение, нажав Ctrl+R, или иконку пуск.

Переключая входные значения следите за изменениями состояния светодиода.

Элемент НЕ, ИЛИ-НЕ, И-НЕ Логический элемент НЕ выполняет операцию логического отрицания над своими входными данными и имеет один вход и один выход.

Иногда его называют инвертор, так как он инвертирует входной сигнал.

На рисунке изображено УГО элемента НЕ.

УГО элемента НЕ Логический элемент И-НЕ выполняет операцию логического умножения над своими входными данными, а затем инвертирует (отрицает) полученный результат и выдаёт его на выход.

Таким образом, можно сказать, что логический элемент И-НЕ — это элемент И с инвертором на выходе.

УГО элемента И- НЕ приведено на рисунке.

Логический элемент ИЛИ-НЕ выполняет операцию логического сложения над своими входными данными, а затем инвертирует (отрицает) полученный результат и выдаёт его на выход.

Таким образом, можно сказать, что логический элемент ИЛИ-НЕ — это элемент ИЛИ с инвертором на выходе.

УГО элемента ИЛИ-НЕ приведено на рисунке.

УГО элемента И-НЕУГО элемента ИЛИ-НЕ Пример выполнения заданияabca Не ab Не bc Не c Пример выполнения задания Далее, добавим шину и подключим к ней прямые и инверсные линии переменных a, b и c.

Подключаете каждый проводник последовательно, тогда нумерация будет так же последовательно соответствовать входам переменных.abca Не ab Не bc Не c Пример выполнения задания Добавим в схему элементы И и ИЛИ с тремя входами.

Если такой вкладки нет в программе, добавьте ее, загрузив соответствующую библиотеку (Меню Файл – Открыть библиотеку).

Пример выполнения задания Аналогичным образом подключим остальные проводники к оставшимся элементам И, согласно заданной функции.

Выходы элементов И подключим к входу элемента ИЛИ, выход которого подключен к светодиоды.

Проверим по таблице истинности правильность схемы.

Выполнить указанную логическую операцию на входе

Описание

Блок Logical Operator выполняет указанную логическую операцию на своем входы. Входное значение истинно ( 1 ), если оно не равно нулю и ложно. ( 0 ), если он равен нулю.

Вы выбираете логическую операцию, соединяющую входы с Оператор список параметров. Если вы выберете прямоугольный в форме значка свойство, имя выбранного оператора отображается на значке блока.Если вы выберете отличительный в форме значка свойство, имя выбранного оператора не отображается на значке блока. Этот В таблице показаны поддерживаемые операции:

Операция	Описание
И	ИСТИНА, если все входы ИСТИННЫ
ИЛИ	ИСТИНА, если хотя бы один вход ИСТИНА
NAND	ИСТИНА, если хотя бы один вход ЛОЖЬ
NOR	ИСТИНА, если нет входов ИСТИНА
XOR	ИСТИНА, если нечетное количество входов ИСТИНА
NXOR	ИСТИНА, если четное количество входов ИСТИНА
НЕ	ИСТИНА, если на входе ЛОЖЬ

Если вы выберете отличительный в качестве формы значка , внешний вид блока указывает на его функцию.Программное обеспечение Simulink ^® отображает отличительную форму для выбранного оператора, соответствуют стандартным графическим символам IEEE ^® для логических функций.

Чтобы указать количество входных портов, используйте Количество входных портов параметр. Тип вывода указывается с использованием типа выходных данных параметр. Выходное значение: 1 , если ИСТИНА, и 0 , если ЛОЖНЫЙ.

Примечание

Тип выходных данных должен точно представлять ноль.Типы данных, которые удовлетворяют этому условию, включают целые числа со знаком и без знака, а также любые типы данных с плавающей запятой.

Размер вывода зависит от размера входного вектора и выбранного оператора:

• Если блок имеет более одного входа, любые нескалярные входы должны иметь одинаковые размеры. Например, если какой-либо вход представляет собой массив 2 на 2, все другие нескалярные входы также должны быть массивами 2 на 2.

  Скалярные входные данные расширяются до тех же размеров, что и нескалярные входные данные.

  Если блок имеет более одного входа, выход имеет те же размеры, что и входы. (после скалярного расширения), и каждый выходной элемент является результатом применения указанная логическая операция с соответствующими элементами ввода. Например, если указанная операция — И, а входы — массивы 2 на 2, на выходе — Массив 2 на 2, верхний левый элемент которого является результатом применения И к верхнему левые элементы входов и так далее.

• Для ввода одного вектора блок применяет операцию (кроме оператора НЕ) ко всем элементам вектора.На выходе всегда получается скаляр.

• Оператор NOT принимает только один ввод, который может быть скаляром или вектором. Если вход является вектором, выход представляет собой вектор того же размера, содержащий логические дополнения к элементам входного вектора.

При настройке в качестве логического элемента XOR с несколькими входами, этот блок выполняет сложение по модулю два работа в соответствии со стандартом IEEE для логических элементов.

Программирование M-файлов (программирование и типы данных)

Программирование M-файлов (программирование и типы данных)

Программирование и типы данных

Логические операторы

MATLAB предлагает три типа логических операторов и функций.

• Поэлементно — оперировать соответствующими элементами логических массивов.
• Побитовый — оперировать соответствующими битами целочисленных значений или массивов.
• Короткое замыкание — работа со скалярными логическими выражениями.

Значения, возвращаемые логическими операторами и функциями MATLAB, за исключением побитовых функций, имеют тип logic и подходят для использования с логической индексацией.

Элементные операторы и функции

Следующие логические операторы и функции выполняют поэлементные логические операции со своими входами для создания выходного массива аналогичного размера.В примерах, приведенных в следующей таблице, используются векторные входы A и B , где

Оператор	Описание	Пример
и	Возвращает 1 для каждого местоположения элемента, которое равно истинному (ненулевому) в обоих массивах и 0 для всех остальных элементов.	A и B = 01001
|	Возвращает 1 для каждого местоположения элемента, которое равно истинному (ненулевому) в одном или другом или обоих массивах и 0 для всех остальных элементов.	A | В = 11101
~	Дополняет каждый элемент входного массива, A .	~ А = 10010
xor	Возвращает 1 для каждого местоположения элемента, которое равно истинному (ненулевому) только в одном массиве и 0 для всех остальных элементов.	xor (A, B) = 10100

Для операторов и функций, которые принимают два операнда массива ( и , | и xor ), оба массива должны иметь одинаковые размеры, причем каждое измерение должно быть одинакового размера.Единственным исключением является случай, когда один операнд является скаляром, а другой — нет. В этом случае MATLAB проверяет скаляр на каждый элемент другого операнда.

Примечание MATLAB преобразует любые конечные ненулевые числовые значения, используемые в качестве входных данных, в логические выражения в логические 1 или истинные .

Перегрузка оператора. Вы можете перегрузить и , | и ~ , чтобы их поведение зависело от типа данных, для которых они используются.У каждого из этих операторов есть репрезентативная функция, которая вызывается всякий раз, когда используется этот оператор. Они показаны в таблице ниже.

Логическая операция	Эквивалентная функция
А и В	и (A, B)
A | В	или (A, B)
~ А	не (A)

Другие функции для работы с массивами. Две другие функции MATLAB, которые работают с массивами логически, но не поэлементно: любые и все . Эти функции показывают, являются ли любыми или всеми элементами вектора или вектором в матрице или массиве ненулевыми.

При использовании в матрице любые и все работают со столбцами матрицы. При использовании в N-мерном массиве они работают с первым неоднородным измерением массива.Или вы можете указать дополнительное измерение Вход для работы с конкретным измерением массива.

Примеры, показанные в следующей таблице, используют ввод массива A , где

Функция	Описание	Пример
любой (A)	Возвращает 1 для вектора, где любой элемент вектора равен true (ненулевой), и 0 , если нет элементов true .	любой (A) ans = 0 1 1
все (A)	Возвращает 1 для вектора, где все элементы вектора имеют значение true (ненулевое значение) и 0 , если все элементы не равны true .	все (A) ans = 0 1 0

Примечание Все функции и any игнорируют любые значения NaN во входных массивах.

Логические выражения, использующие функцию поиска. Функция find определяет индексы элементов массива, которые удовлетворяют заданному логическому условию. Функция полезна для создания масок и индексных матриц. В самом общем виде find возвращает единственный вектор индексов. Этот вектор можно использовать для индексации в массивы любого размера и формы.

Например,

Примечание Альтернативой использованию find в этом контексте является индексирование в матрице с использованием самого логического выражения.См. Пример ниже.

Последние два оператора предыдущего примера могут быть заменены этим одним оператором:

Вы также можете использовать find для получения индексов строки и столбца прямоугольной матрицы для значений массива, которые соответствуют логическому условию:

Битовые функции

Следующие функции выполняют побитовые логические операции с неотрицательными целочисленными входами. Входные данные могут быть скалярными или массивами.В массивах эти функции производят выходной массив аналогичного размера.

Примеры, показанные в следующей таблице, используют скалярные входные данные A и B , где

Функция	Описание	Пример
бит и	Поразрядно возвращает И двух неотрицательных целочисленных аргументов.	бит и (A, B) = 20 (10100 двоичный)
битор	Поразрядно возвращает ИЛИ двух неотрицательных целочисленных аргументов.	битор (A, B) = 29 (двоичный 11101)
bitcmp	Возвращает поразрядное дополнение как n -битное число, где n — второй входной аргумент для bitcmp .	бит cmp (A, 5) = 3 (двоичный 00011)
bitxor	Возвращает поразрядное исключающее ИЛИ из двух неотрицательных целочисленных аргументов.	bitxor (A, B) = 9 (двоичный 01001)

Операторы короткого замыкания

Следующие операторы выполняют операции AND и OR над логическими выражениями, содержащими скалярные значения.Они сокращают операторов в том смысле, что они оценивают свой второй операнд только тогда, когда результат не полностью определяется первым операндом.

Оператор	Описание
&&	Возвращает true ( 1 ), если оба входа оцениваются как true , и false ( 0 ), если нет.
||	Возвращает true ( 1 ), если один из входных данных или оба , оцениваются как true и false ( 0 ), если нет.

Показанный здесь оператор выполняет И двух логических членов: A и B :

Если A равно нулю, тогда все выражение будет оцениваться как false , независимо от значения B . В этих обстоятельствах нет необходимости оценивать B , потому что результат уже известен. В этом случае MATLAB сокращает оператор, оценивая только первый член.

Похожий случай, когда вы OR два члена, и первый член равен true .Опять же, независимо от значения B , оператор будет оценивать как истинное . Нет необходимости оценивать второй член, и MATLAB этого не делает.

Преимущество короткого замыкания. Операторы короткого замыкания можно использовать для оценки выражения только при выполнении определенных условий. Например, вы хотите выполнить функцию M-файла, только если M-файл находится на текущем пути MATLAB.

Короткое замыкание не позволяет следующему коду генерировать ошибку, когда файл myfun.м , нет данных:

Точно так же этот оператор позволяет избежать ошибок деления на ноль, когда b равно нулю:

Вы также можете использовать && и || операторов в if и в то время как операторы , чтобы воспользоваться их поведением при коротком замыкании:

Операторы отношения

Приоритет операторов

Операторы и выражения — Visual Basic

• 20.07.2015
• 2 минуты на чтение

В этой статье

Оператор — это элемент кода, который выполняет операцию с одним или несколькими элементами кода, которые содержат значения.Элементы значений включают переменные, константы, литералы, свойства, возвращаемые значения из процедур Function и Operator и выражения.

Выражение представляет собой серию элементов значения, объединенных с операторами, что дает новое значение. Операторы воздействуют на элементы значения, выполняя вычисления, сравнения или другие операции.

Типы операторов

Visual Basic предоставляет следующие типы операторов:

Элементы значения, которые объединяются с оператором, называются операндами этого оператора.Операторы, объединенные с элементами значений, образуют выражения, за исключением оператора присваивания, который формирует оператор . Для получения дополнительной информации см. Заявления.

Оценка выражений

Конечный результат выражения представляет собой значение, которое обычно имеет знакомый тип данных, например Boolean , String или числовой тип.

Ниже приведены примеры выражений.

5 + 4

'Предыдущее выражение оценивается как 9.

15 * System.Math.Sqrt (9) + x

'Предыдущее выражение дает результат 45 плюс значение x.

"Конкат" и "эна" и "тион"

'Предыдущее выражение оценивается как «Конкатенация».

763 <23

'Предыдущее выражение оценивается как False.

Несколько операторов могут выполнять действия в одном выражении или инструкции, как показано в следующем примере.2

В предыдущем примере Visual Basic выполняет операции в выражении справа от оператора присваивания ( = ), а затем присваивает полученное значение переменной x слева. Практического ограничения на количество операторов, которые можно объединить в выражение, нет, но понимание приоритета операторов в Visual Basic необходимо для получения ожидаемых результатов.

См. Также

Операторы | Функции и операторы | Руководство пользователя | Поддержка | Epi Info ™

АРИФМЕТИЧЕСКИЙ

Описание
Эти основные арифметические операторы можно использовать в сочетании с другими командами.Результат — числовое значение.

Синтаксис
[Выражение] <Оператор> [Выражение]

• [Выражение] — числовое значение или переменная, содержащая данные в числовом формате.

Комментарии
Результаты выражаются в числовом формате. Основные математические операторы, которые можно использовать в Epi Info, следующие:

• Сложение + Основной арифметический оператор, используемый для сложения; Результатом арифметического оператора обычно является числовое значение (т.е., EX. 3 + 3).
• Вычитание — (Используется для вычитания или отрицания.) Основной арифметический оператор, используемый для вычитания или отрицания; Результатом арифметического оператора обычно является числовое значение (например, Пример 3 — 1).
• Умножение * (звездочка) Основной арифметический оператор, используемый для умножения; Результатом арифметического оператора обычно является числовое значение.
• Деление / Основной арифметический оператор, используемый для деления; Результатом арифметического оператора обычно является числовое значение.
• Модуль или остаток MOD

Арифметические операторы показаны в порядке убывания приоритета. Круглые скобки могут использоваться для управления порядком, в котором оцениваются операторы. Однако порядок по умолчанию часто дает правильный результат.

Хотя можно выполнять математические вычисления с датами, считающимися количеством дней (например, IncubationDays = SymptomDateTime — ExposureDateTime), поведение служб базы данных, лежащих в основе Epi Info, делает более эффективным использование функций временных интервалов (например, IncubationDays = SymptomDateTime — ExposureDateTime).2 СПИСОК var1 var2 var3 var4 var5 var6

8. Бизнес-уровень: Спецификация ArchiMate® 3.1

8. Бизнес-уровень: Спецификация ArchiMate® 3.1 Спецификация ArchiMate® 3.1
Авторские права © 2012-2019 The Open Group

---

элементов бизнес-уровня используются для моделирования операционная организация предприятия в технологически независимой образом, тогда как элементы стратегии (глава 7) используются для моделирования стратегического направления и выбор предприятия.

На рисунке 52 показано обзор элементов бизнес-уровня и их взаимосвязей. «Внутренний бизнес Активный структурный элемент »,« Деловой внутренний поведенческий элемент »и« Деловой пассивный Элемент структуры »- абстрактные элементы; только их специализации (как определено в следующих разделах) создаются в моделях.

Рисунок 52: Метамодель бизнес-уровня

Примечание. На этом рисунке показаны не все разрешенные отношения; каждый элемент языка может иметь композицию, отношения агрегации и специализации с элементами одного типа.Более того, существуют косвенные отношения, которые можно вывести, как описано в Разделе 5.7.

8,2 Активные элементы структуры

Активная структура бизнеса Слой относится к статической структуре организации с точки зрения сущности, составляющие организацию, и их отношения. Активный сущности — это субъекты (например, субъекты бизнеса или бизнес-роли), которые выполнять такое поведение, как бизнес-процессы или функции (возможности).Субъектами бизнеса могут быть отдельные лица (например, клиенты или сотрудники), но также группы людей (организационные единицы) и ресурсы, которые имеют постоянный (или хотя бы долгосрочный) статус в организациях. Типичные примеры последние — это отдел и бизнес-единица.

Архитектурные описания сосредоточены на структуре, что означает, что взаимоотношения сущностей внутри организации играть важную роль. Чтобы сделать это явным, элемент делового сотрудничества был введен.

Введен элемент бизнес-интерфейса. для явного моделирования (логических или физических) мест или каналов, где можно получить доступ к службам, которые роль предлагает среде. Одинаковый услуга может быть предложена на нескольких различных интерфейсах; например, по почте, по по телефону или через Интернет. В отличие от моделирования приложений, это необычный в современных подходах к моделированию бизнес-уровня для распознавания элемент бизнес-интерфейса.

На бизнес-уровне три типа внутренних активных Определены элементы структуры: бизнес-субъект , бизнес-роль и деловое сотрудничество .

Рисунок 53: Элементы внутренней активной структуры бизнеса

Примечание. На этом рисунке показаны не все разрешенные отношения; каждый элемент языка может иметь композицию, отношения агрегации и специализации с элементами одного типа.Более того, существуют косвенные отношения, которые можно вывести, как описано в Разделе 5.7. Полная спецификация разрешенных отношения можно найти в Приложении B.

8.2.1 Бизнес-актер

Бизнес-субъект представляет бизнес-объект, который способен выполнять действия.

Субъект хозяйственной деятельности — это субъект хозяйствования, в отличие от техническому субъекту; т.е. принадлежит к бизнес-уровню.Актеры могут, тем не менее, включите сущности за пределами фактической организации; например, клиенты и партнеры. Субъект бизнеса может представлять такие субъекты хозяйствования на разных уровни детализации и могут соответствовать как субъекту, так и организационной единице в рамках TOGAF [4]. Примеры субъектов бизнеса: люди, отделы и бизнес-единицы.

Субъект бизнеса может быть назначен одному или нескольким бизнес-роли. Затем он может выполнять поведение, которое эти бизнес-роли назначены.Бизнес-субъект может быть объединен в одном месте. Имя бизнес-субъект предпочтительно должен быть существительным. Бизнес-субъекты могут быть конкретными частные лица или организации; например, «Джон Смит» или «ABC Corporation», или они может быть общим; например, «заказчик» или «поставщик».

Рисунок 54: Обозначение бизнес-субъекта

8.2.2 Деловая роль

Бизнес-роль представляет собой ответственность за выполнение определенного поведения, чтобы который может быть назначен актеру, или роль, которую актер играет в конкретном действие или событие.

Бизнес-роли с определенными обязанностями или навыки закреплены за бизнес-процессами или бизнес-функциями. Бизнесс субъект, которому назначена бизнес-роль, несет ответственность за обеспечение того, чтобы соответствующее поведение осуществляется либо путем его выполнения, либо путем делегирования и управление его производительностью. Помимо отношения к бизнес-роли с поведением бизнес-роль также полезна в (структурной) организационной смысл; например, при разделении труда внутри организации.

Бизнес-роль может быть назначена одному или нескольким бизнес-процессы или бизнес-функции, в то время как бизнес-субъект может быть назначен одной или нескольким бизнес-ролям. Бизнес-интерфейс или приложение интерфейс может выполнять бизнес-роль, в то время как бизнес-интерфейс может быть частью деловая роль. Желательно, чтобы название бизнес-роли было существительным.

Рисунок 55: Обозначение бизнес-ролей

Разработчики моделей ArchiMate могут представляют собой общие организационные единицы, которые ведут себя как бизнес-субъекты или бизнес-роли.Например, субъект бизнеса «Поставщик» изображает организационную единицу, а бизнес-роль «Поставщик» — обязанность. Определенные или общие бизнес-субъекты могут быть назначены для выполнения обязанностей изображены как бизнес-роли. Например, конкретный субъект бизнеса «ABC Корпорация »или общий бизнес-субъект« Деловой партнер »может быть назначен бизнес-роль «Поставщик».

8.2.3 Деловое сотрудничество

Бизнес сотрудничество представляет собой совокупность двух или более элементы внутренней активной структуры бизнеса, которые работают вместе для выполнения коллективное поведение.

Бизнес-процесс или функция могут быть интерпретируется как внутреннее поведение отдельной бизнес-роли. В некоторых случаях, поведение — это коллективные усилия более чем одной бизнес-роли; на самом деле сотрудничество двух или более бизнес-ролей приводит к коллективному поведению что может быть чем-то большим, чем просто суммой поведения отдельных ролей. Деловое сотрудничество представляет собой эти коллективные усилия. Деловые взаимодействия может использоваться для описания внутреннего поведения, которое имеет место в бизнесе сотрудничество.Деловое сотрудничество — это (возможно, временное) собрание бизнес-роли, участники или другое сотрудничество внутри организации, которое выполнять совместное поведение (взаимодействия). В отличие от отдела, бизнес сотрудничество не обязательно должно иметь официальный (постоянный) статус в рамках организация; он специально нацелен на конкретное взаимодействие или набор взаимодействия между ролями. Это особенно полезно при моделировании Business-to-Business. (B2B) взаимодействие между различными организациями, такими как сети поставщиков, а также для описания социальных сетей.

Деловое сотрудничество может объединять несколько бизнес-ролей, актеров или других совместных работ и может быть назначен одному или другие деловые взаимодействия или другие элементы внутреннего поведения бизнеса. А бизнес-интерфейс или интерфейс приложения могут служить бизнесу сотрудничество, в то время как деловое сотрудничество может иметь бизнес-интерфейсы (через композицию, а также через агрегацию через производные отношения). Желательно, чтобы название делового сотрудничества было существительным.Это также довольно часто оставляют безымянное деловое сотрудничество.

Рисунок 56: Нотация делового сотрудничества

8.2.4 Бизнес-интерфейс

Бизнес-интерфейс представляет собой точку доступа, в которой предоставляются бизнес-услуги. доступны для окружающей среды.

Бизнес-интерфейс раскрывает функциональность бизнес-услуг другим бизнес-ролям или участникам.Часто упоминается как канал (телефон, Интернет, местный офис и т. д.). Тот же бизнес сервис может быть представлен через разные интерфейсы.

Бизнес-интерфейс может быть частью бизнеса роль или актер через композиционные отношения, а бизнес-интерфейс может служить деловая роль. Бизнес-интерфейс может быть назначен одному или нескольким бизнесам. services, что означает, что эти службы предоставляются интерфейсом. В Желательно, чтобы название бизнес-интерфейса было существительным.

Рисунок 57: Обозначение бизнес-интерфейса

8.2.5 Пример

«Контактный центр ArchiSurance», смоделированный как субъект бизнеса, состоит из три сотрудника, также изображенные как субъекты бизнеса: «Грег», «Джоан» и «Ларри». «Контакт-центр ArchiSurance» имеет три бизнес-интерфейса для обслуживания клиенты: «Телефон», «Электронная почта» и «Веб-чат». Грег выполняет бизнес-роль «Аналитика претензий по страхованию путешествий», Джоан выполняет бизнес-роль «Домашнего Специалист по страховым продуктам », а Ларри выполняет бизнес-роль« Заказчика. Сервисный представитель ».Первые две бизнес-роли являются специализацией бизнес-роль «Специалист». «Рассмотрение претензий с высокой степенью риска» — это деловое сотрудничество двух бизнес-ролей: «Специалист» и «Представитель отдела обслуживания клиентов».

Пример 23: Элементы активной структуры бизнеса

Ориентация на услуги, важная конструкция решение для поведенческой части метамодели ArchiMate — это различие между «внешним» и «внутренним» поведением организации.

Внешне видимое поведение моделируется элемент бизнес-сервис . Бизнес-сервис представляет собой согласованный часть функциональности, которая предлагает дополнительную ценность для окружающей среды, независимая того, как эта функциональность реализована внутри. Можно провести различие между «внешними» бизнес-услугами, предлагаемыми внешним клиентам, и «Внутренние» бизнес-услуги, предлагающие вспомогательные функции для процессов или функции внутри организации.

Несколько типов элементов внутреннего поведения, которые можно реализовать услугу различаются. Хотя различие между два не всегда резкое, часто бывает полезно различить вид процесса и функциональный вид , вид по поведению; два элемента, связанные с этими представления, бизнес-процесс и бизнес-функция , определены. Оба элемента может использоваться для группировки более подробных бизнес-процессов / функций, но на основе разные критерии группировки.Бизнес-процесс представляет собой рабочий процесс состоящий из более мелких процессов / функций, с одним или несколькими четкими стартовыми очков и приводит к какому-то результату. Иногда это описывается как «от клиента к клиент », где этот клиент также может быть внутренним клиентом, в случае подпроцессы в организации. Цель такого бизнес-процесса — «Удовлетворить или порадовать покупателя» [10]. бизнес функция предлагает функции, которые могут быть полезны для одного или нескольких предприятий. процессы.Он группирует поведение на основе, например, необходимых навыков, ресурсов, поддержки (приложений) и т. д. Как правило, бизнес-процессы организации определяются на основе продуктов и услуг , которые организация предлагает, в то время как бизнес-функции являются основой для Например, выделение ресурсов задачам и поддержка приложения.

A бизнес-взаимодействия — это единица поведение аналогично бизнес-процессу или функции, но выполняется в сотрудничество двух или более ролей внутри организации.в отличие от концепция взаимодействия в AMBER [9], которая представляет собой атомных единица совместного поведения, бизнес-взаимодействие ArchiMate может быть разложился на более мелкие взаимодействия. Хотя взаимодействия внешние поведение с точки зрения ролей, участвующих в сотрудничестве, поведение является внутренним для сотрудничества в целом. Подобно процессам или функций, результат делового взаимодействия может быть предоставлен окружающая среда через бизнес-услуги.

Деловое мероприятие — это то, что происходит (внешне) и может влиять на бизнес-процессы, функции или взаимодействия. Элемент бизнес-события аналогичен элементам события BPMN, чтобы элемент триггера в AMBER [9], а начальное состояние и элементы конечного состояния в диаграммах активности UML. Однако бизнес ArchiMate событие более широко применимо в том смысле, что его также можно использовать для моделируйте другие типы событий, помимо триггеров.

На бизнес-уровне три типа внутреннего поведения определены: бизнес-процесс , бизнес-функция и бизнес Взаимодействие .

Рисунок 58: Элементы внутреннего поведения бизнеса

Примечание. На этом рисунке показаны не все разрешенные отношения; каждый элемент языка может иметь композицию, отношения агрегации и специализации с элементами одного типа.Более того, существуют косвенные отношения, которые можно вывести, как описано в Разделе 5.7. Полная спецификация разрешенных отношения можно найти в Приложении B.

8.3.1 Бизнес-процесс

Бизнес-процесс представляет собой последовательность бизнес-действий, которая достигает определенного результат, такой как определенный набор продуктов или бизнес-услуг.

Бизнес-процесс описывает внутреннюю поведение, выполняемое бизнес-ролью, которая требуется для создания набора продукты и услуги.Для потребителя товары и услуги актуальны а требуемое поведение — это просто черный ящик, отсюда и обозначение «внутреннее».

Сложный бизнес-процесс может быть агрегированием других, более мелкозернистых процессов. Каждой из них могут быть присвоены более тонкие роли. назначенный.

Существует потенциальная связь «многие-ко-многим» между бизнес-процессами и бизнес-функциями. Неформально говоря, процессы описывают некий «поток» действий, а функции группируют деятельность в соответствии с необходимыми навыками, знаниями, ресурсами и т. д.

Бизнес-процесс может быть запущен, или триггер, любой другой элемент делового поведения (например, деловое мероприятие, деловой процесс, бизнес-функция или бизнес-взаимодействие). Бизнес-процесс может получить доступ бизнес-объекты. Бизнес-процесс может реализовывать одну или несколько бизнес-услуг. и может использовать (внутренние) бизнес-сервисы или сервисы приложений. Деловая роль может быть назначен бизнес-процессу для выполнения этого процесса вручную. An автоматизированный бизнес-процесс может быть реализован с помощью прикладного процесса.Имя бизнес-процесса должен четко указывать заранее определенную последовательность действий с использованием глагола или комбинации глагол-существительное и может включать слово «процесс». Примеры: «рассмотрение иска», «прием на работу сотрудника», «процесс утверждения» или «финансовый отчет».

В модели ArchiMate существование бизнеса изображены процессы. Бизнес высокого уровня, сквозные процессы, макропотоки, и рабочие процессы могут быть выражены одним и тем же элементом бизнес-процесса в Язык ArchiMate.Однако в нем не перечислены потоки действий в деталь. Обычно это делается во время моделирования бизнес-процессов, когда бизнес-процесс можно расширить с помощью языка проектирования бизнес-процессов; например, BPMN [12].

Рисунок 59: Нотация бизнес-процесса

8.3.2 Бизнес-функция

Бизнес функция представляет собой набор бизнес-поведения на основе выбранного набора критериев (обычно требуемые бизнес-ресурсы и / или компетенций), тесно связанных с организацией, но не обязательно прямо регулируется организацией.

Так же, как бизнес-процесс, бизнес функция также описывает внутреннее поведение, выполняемое бизнес-ролью. Однако, хотя бизнес-процесс группирует поведение на основе последовательности или потока действий, необходимых для реализации продукта или услуги, бизнеса функция обычно группирует поведение на основе требуемых бизнес-ресурсов, навыки, компетенции, знания и т. д.

Существует потенциальная связь «многие-ко-многим» между бизнес-процессами и бизнес-функциями.Сложные процессы в целом включают действия, которые предлагают различные функции. В этом смысле бизнес процесс формирует ряд бизнес-функций. В общем, бизнес-функция обеспечивает добавленную стоимость с точки зрения бизнеса. Организационные подразделения или приложения могут совпадать с бизнес-функциями из-за их специфики группировка видов деятельности.

Бизнес-функция может быть инициирована, или триггер, любой другой элемент делового поведения (бизнес-событие, бизнес-процесс, бизнес-функция или деловое взаимодействие).Бизнес-функция может получить доступ к бизнесу объекты. Бизнес-функция может реализовывать одну или несколько бизнес-услуг и может быть обслуживается бизнесом, приложениями или технологическими службами. Деловая роль может быть назначен на бизнес-функцию. Название бизнес-функции должно быть ясно указывают на четко определенное поведение. Примеры: управление клиентами, претензии администрирование, обслуживание участников, переработка или обработка платежей.

Рисунок 60: Обозначение бизнес-функции

8.3.3 Деловое взаимодействие

Деловое взаимодействие представляет собой единицу коллективного делового поведения, выполняемого ( сотрудничество) двух или более субъектов бизнеса, бизнес-ролей или бизнеса сотрудничество.

Деловое взаимодействие похоже на бизнес процесс / функция, но в то время как процесс / функция может выполняться одним роль, взаимодействие осуществляется путем сотрудничества нескольких ролей. В роли в сотрудничестве разделяют ответственность за выполнение взаимодействие.

Деловое взаимодействие может быть инициировано, или триггер, любой другой элемент делового поведения (бизнес-событие, бизнес-процесс, бизнес-функция или деловое взаимодействие). Деловое взаимодействие может получить доступ к бизнесу объекты. Деловое взаимодействие может реализовывать одну или несколько бизнес-услуг и может использовать (внутренние) бизнес-сервисы или сервисы приложений. Бизнесс сотрудничество или два или более бизнес-субъектов или ролей могут быть назначены деловое взаимодействие.Желательно, чтобы название делового взаимодействия было глагол в простом настоящем времени.

Рисунок 61: Нотация бизнес-взаимодействия

8.3.4 Деловое мероприятие

Бизнес-событие представляет собой изменение организационного состояния.

Бизнес-процессы и другое бизнес-поведение может быть вызвано или прервано деловым событием. Также бизнес-процессы могут вызывать события, которые запускают другие бизнес-процессы, функции или взаимодействия.В отличие от бизнес-процессов, функций и взаимодействий, деловое событие происходит мгновенно: у него нет продолжительности. События могут происходят из среды организации (например, от клиента), но также могут происходить внутренние события, вызванные, например, другими процессами внутри организации.

Деловое событие может иметь атрибут времени, который обозначает момент или моменты, когда происходит событие. Например, это может использоваться для моделирования расписаний; е.g., чтобы смоделировать событие, которое запускает повторяющийся бизнес-процесс, выполняемый каждый первый понедельник месяца.

Бизнес-событие может инициироваться или быть инициировано (поднятый) бизнес-процессом, бизнес-функцией или бизнес-взаимодействием. А бизнес-событие может иметь доступ к бизнес-объекту и может состоять из других деловые мероприятия. Желательно, чтобы название делового мероприятия состояло из глагола в идеальное время; например, «претензия получена».

Рисунок 62: Обозначение бизнес-событий

8.3.5 Бизнес-сервис

Бизнес-сервис представляет собой явно определенное поведение, которое бизнес-роль, субъект бизнеса или деловое сотрудничество подвергается воздействию своего окружения.

Бизнес-сервис раскрывает функциональность бизнес-роли или сотрудничество в их среде. Эта функциональность доступ через один или несколько бизнес-интерфейсов.

Бизнес-служба должна предоставлять единицу поведение, значимое с точки зрения окружающей среды.Оно имеет цель, в которой говорится об этой утилите. Окружающая среда включает (поведение) пользователи извне, а также внутри организации. Деловые услуги могут быть внешние, ориентированные на клиентов услуги (например, страхование путешествий) или внутренние службы поддержки (например, служба управления ресурсами).

Бизнес-услуга связана со значением. А бизнес-сервис может обслуживать бизнес-процесс, бизнес-функцию или бизнес взаимодействие.Бизнес-процесс, бизнес-функция или бизнес-взаимодействие могут реализовать бизнес-услуги. Бизнес-интерфейс может быть назначен бизнесу услуга. Бизнес-сервис может иметь доступ к бизнес-объектам. Название бизнеса услуга предпочтительно должна быть глаголом, оканчивающимся на «-ing»; например, транзакция обработка. Также может использоваться имя, явно содержащее слово «услуга».

Рисунок 63: Обозначение бизнес-сервисов

8.3,6 Пример

«Претензии Администрирование »- это бизнес-функция, состоящая из ряда процессы и деловое взаимодействие. Эта бизнес-функция реализует «Претензии Обработка »бизнес-услуги. Деловое мероприятие «Претензия подана» запускает первый бизнес-процесс «Принять претензию», который, в свою очередь, запускает бизнес-процесс «Назначить Требовать». В зависимости от типа претензии бизнес-процесс «Вынести решение» Стандартная претензия »или деловое взаимодействие« Рассмотрение претензии с высокой степенью риска » выполненный.Рассмотрение претензий с высокой степенью риска — это деловое взаимодействие, потому что: согласно политике компании, в этом всегда должны быть задействованы два человека. деятельность по минимизации риска мошенничества. После вынесения решения бизнес-процессы «Уведомление клиента» и «Требование о выплате» выполняются параллельно, и когда оба завершено, запускается бизнес-процесс «Закрыть заявку».

Пример 24: Элементы делового поведения

Пассивный структурный аспект бизнеса Слой содержит пассивные структурные элементы (бизнес-объекты), которые управляется поведением, например бизнес-процессами или функциями.Пассивный сущности представляют собой важные концепции, в которых компания думает о домен.

На бизнес-уровне существует два основных типа элементы пассивной структуры: бизнес-объект и представление . Кроме того, контракт, используемый в контексте продукта, является специализацией. бизнес-объекта.

Рисунок 64: Элементы пассивной структуры бизнеса

8.4.1 Бизнес-объект

Бизнес-объект представляет собой концепцию, используемую в определенной бизнес-области.

Как объяснено в Разделе 3.6, язык ArchiMate в целом фокусируется на моделировании типов, а не экземпляров, поскольку это наиболее актуально на уровне описания архитектуры предприятия. Отсюда бизнес объект обычно моделирует тип объекта ( см. класс UML), из которых в операциях может существовать несколько экземпляров.Лишь изредка бизнес-объекты представляют собой фактические экземпляры информации, производимой и потребляемой поведением такие элементы, как бизнес-процессы. Это особенно верно для одиночные типы; то есть типы, которые имеют только один экземпляр.

Разнообразные бизнес-объекты могут быть определенным. Бизнес-объекты пассивны в том смысле, что они не запускают или выполнять процессы. Бизнес-объект может использоваться для представления информации активы, которые актуальны с точки зрения бизнеса и могут быть реализованы путем объекты данных.

Доступны бизнес-объекты (например, в в случае информационных объектов, они могут быть созданы, прочитаны или записаны) бизнесом процесс, функция, бизнес-взаимодействие, бизнес-событие или бизнес-услуга. А бизнес-объект может иметь ассоциацию, специализацию, агрегацию или композиционные отношения с другими бизнес-объектами. Бизнес-объект может быть реализуется представлением или объектом данных (или обоими). Имя бизнес-объект предпочтительно должен быть существительным.

Рисунок 65: Нотация бизнес-объекта

8.4.2 Контракт

Контракт представляет собой формальное или неофициальное описание соглашения. между поставщиком и потребителем, который определяет права и обязанности связаны с продуктом и определяют функциональные и нефункциональные параметры для взаимодействия.

Элемент контракта может использоваться для моделирования договор в юридическом смысле, но также и более неформальное соглашение, связанное с продукт.Это также может быть или включать SLA, описывающее соглашение о функциональность и качество услуг, входящих в состав продукта. А контракт — это специализация бизнес-объекта.

Отношения, применимые к бизнесу объект также относится к договору. Кроме того, в контракте может быть связь агрегирования с продуктом. Название контракта предпочтительно имя существительное.

Рисунок 66: Обозначение контракта

8.4.3 Представительство

Представление представляет собой воспринимаемую форму информации, которую несет бизнес-объект.

Представления (например, сообщения или документы) являются ощутимыми носителями информации, относящейся к бизнес-объекты. Если необходимо, представления можно классифицировать по разным способы; например, с точки зрения носителя (электронный, бумажный, звуковой и т. д.) или формат (HTML, ASCII, PDF, RTF и т. д.). Один бизнес-объект может иметь количество разных представлений. Кроме того, одно представление может реализовать один или несколько конкретных бизнес-объектов.

Значение может быть связано с представление, несущее это значение. Название представительства желательно существительное.

Рисунок 67: Обозначение представления

8.4.4 Пример

бизнес-объект «Претензия» может быть реализован одним из следующих трех физические представления (на разных этапах рассмотрения претензий процесса): «Форма подачи», «Резюме файла претензии» или «Письмо с претензией».Все эти представления относятся к представлению «Краткое изложение политики», которое реализует договор «Страховой полис».

Пример 25: Элементы пассивной структуры бизнеса

8,5 Композитные элементы

Бизнес-уровень содержит один составной элемент: продукт . Это объединяет или составляет услуги и пассивные структурные элементы на всех уровнях основного языка ArchiMate.

На рисунке 68 показан применимая часть метамодели. Это пересекает слои, как также описано в Глава 12.

Рисунок 68: Метамодель продукта

8.5.1 Товар

Продукт представляет собой согласованный набор услуг и / или пассивных элементы структуры, сопровождаемые контрактом / пакетом соглашений, который предлагается в целом (внутренним или внешним) клиентам.

Это определение охватывает как нематериальные, так и основанные на услугах или информационные продукты, которые распространены в информационноемкие организации и материальные, физические продукты. А финансовый или информационный продукт состоит из набора услуг и контракт, определяющий характеристики, права и требования связанный с продуктом. «Покупка» продукта дает покупателю право использовать сопутствующие услуги.

Обычно элемент product используется для укажите товар тип .Количество типов продуктов в организации обычно относительно стабильна по сравнению, например, с процессами, которые реализовывать или поддерживать продукты. «Покупка» обычно является одной из услуг. связан с продуктом, что приводит к созданию нового экземпляра этого продукта (принадлежащего конкретному заказчику). Точно так же могут быть службы для изменения или уничтожения продукт.

Продукт может объединять или составлять бизнес сервисы, сервисы приложений и технологические сервисы, бизнес-объекты, данные объекты, технологические объекты, а также договор.Следовательно, продукт может агрегировать или составлять элементы из других слоев, кроме бизнес-уровня.

С продуктом может быть связано значение. В название продукта — это обычно имя, которое используется при общении с клиенты или, возможно, более общее существительное (например, «туристическая страховка»).

Рисунок 69: Обозначение продукта

8.5.2 Пример

Продукт «Страхование» состоит из договора «Страховой полис» и бизнес-услуги «Клиент. Сервис », который объединяет четыре других бизнес-сервиса:« Приложение »,« Продление », «Обработка претензий» и «Апелляция».Продукт «Автострахование» — это специализация универсального продукта «Страхование» с дополнительной бизнес-услугой «Правильно води и экономь» и сопутствующий контракт «Право на ведение и экономия».

Пример 26: Бизнес-составной элемент: Продукт

Таблица 6 дает обзор элементов бизнес-уровня с их определениями.

Таблица 6: Элементы бизнес-уровня

Элемент	Описание	Обозначение
Деловой субъект	Представляет бизнес-объект, который способен к поведению.
Бизнес-роль	Представляет ответственность за выполнение определенного поведения, которому может быть назначен актер, или роль актер играет в определенном действии или событии.
Деловое сотрудничество	представляет собой совокупность двух или более предприятий. внутренние активные элементы структуры, которые работают вместе для выполнения коллективных поведение.
Бизнес-интерфейс	Представляет точку доступа, в которой бизнес-услуги становятся доступными для окружающей среды.
Бизнес-процесс	представляет последовательность бизнеса поведение, которое приводит к определенному результату, например, к определенному набору продуктов или бизнес-услуги.
Бизнес-функция	Представляет набор бизнес-поведения на основе выбранного набора критериев (обычно требуемые бизнес-ресурсы и / или компетенции), тесно связанных с организацией, но не обязательно прямо регулируется организацией.
Деловое взаимодействие	Представляет единицу коллективного делового поведения выполняется (в сотрудничестве) двумя или более субъектами бизнеса, бизнес-ролями, или деловое сотрудничество.
Деловое мероприятие	Представляет изменение состояния организации.
Деловые услуги	представляет явно определенное поведение что бизнес-роль, бизнес-субъект или деловое сотрудничество раскрывает его окружение.
Бизнес-объект	представляет концепцию, используемую в конкретная сфера деятельности.
Контракт	Представляет формальный или неформальный спецификация соглашения между поставщиком и потребителем, которое определяет права и обязанности, связанные с продуктом, и устанавливает функциональные и нефункциональные параметры взаимодействия.
Представительство	представляет собой ощутимую форму информация, переносимая бизнес-объектом.
Товар	представляет собой связную коллекцию услуги и / или пассивные элементы структуры, сопровождаемые контрактом / набором соглашения, которые предлагается в целом (внутренним или внешним) клиентам.

вернуться к началу страницы

---

Загрузки

Загрузки документации ArchiMate доступны по лицензии по ссылке «Загрузить» на информационном веб-сайте ArchiMate. Лицензия бесплатна для любого организация, желающая использовать документацию ArchiMate исключительно для внутренних целей. Книга также доступна в библиотеке Open Group как документ C197.

---

Copyright © 2012-2019 The Open Group, Все права защищены.
ArchiMate является зарегистрированным товарным знаком Open Group.

---

ArrayFire: или

Логический или из двух входов.

AFAPI af_err	af_or (af_array * out, const af_array lhs, const af_array rhs, const bool batch)
	Интерфейс C для выполнения логических или двух массивов. Подробнее …
AFAPI array	оператор || (const array & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const bool & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const int & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const unsigned & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const char & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const unsigned char & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const long & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const unsigned long & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const long long & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const unsigned long long & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const double & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const float & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const cfloat & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const cdouble & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const array & lhs, const bool & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const array & lhs, const int & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const array & lhs, const unsigned & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const array & lhs, const char & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const array & lhs, const unsigned char & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const array & lhs, const long & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const array & lhs, const unsigned long & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const array & lhs, const long long & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const array & lhs, const unsigned long long & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const array & lhs, const double & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const array & lhs, const float & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const array & lhs, const cfloat & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const array & lhs, const cdouble & rhs)
AFAPI array	operator || (const short & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const unsigned short & lhs, const array & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением. Подробнее …
AFAPI array	оператор || (const array & lhs, const short & rhs)
	Выполняет операцию логического ИЛИ над двумя массивами или массивом и значением.Подробнее …
AFAPI array	оператор || (const array & lhs, const unsigned short & rhs)

1.1 Логические операции

Математика обычно включает сочетание истинных (или гипотетически истинных) утверждения различными способами для создания (или доказательства) новых истинных утверждений. Начнем с разъяснения некоторых из этих фундаментальных идей.

Под предложением мы подразумеваем утверждение, которое имеет определенное значение истинности , истина (T) или ложь (F) — например,

«В 1492 году Колумб плавал по синему океану.» (T)

«Наполеон выиграл битву при Ватерлоо». (F)

В более общем смысле, формула означает утверждение, возможно, с участием некоторых переменных, которое либо истинно, либо false всякий раз, когда мы присваиваем определенные значения каждой из переменных. 2 + y = 12 $», то $ P (2,8) $ и $ P (3,3) $ равны истина, а $ P (1,4) $ и $ P (0,6) $ — ложь.Если $ Q (x, y, z) $ равно «$ x + y

Верно ли предложение или ложно, обычно зависит от того, что мы говорят — одно и то же предложение может быть верным или ложным в зависимости от по контексту; например, формула $ x | y $ означает `$ x $ делит $ y $ ‘. То есть $ x | y $, если есть некоторый $ z $, так что $ y = x \ cdot z $. Теперь, правда ли, что $ 3 | 2 $? Это зависит: если мы говорим о целых числах, ответ — нет; если мы говорим о рациональных числах, ответ да, потому что $ 2 = 3 \ cdot (2/3) $. (Конечно, если $ x \ not = 0 $ и $ y $ любых рациональных чисел, затем $ x | y $, так что это не очень полезное понятие.При нормальном использовании вид формулы «$ x | y $» означает , что $ x $ и $ y $ являются целыми числами.)

Вселенная дискурса для определенной области математики — это набор, который содержит все интересное по этой теме. Когда мы изучение математических формул типа `$ x $ делит $ y $ ‘на переменные Предполагается, что принимают значения в любой вселенной дискурса подходит для конкретной темы. Вселенная дискурса обычно это ясно из обсуждения, но иногда нам нужно определите это явно для ясности.Универсум дискурса обычно обозначается $ U $.

Сложные предложения и формулы складываются из более простых, используя небольшое количество логических операций . Просто горстка этих операций позволят нам сказать все, что нам нужно сказать в математика.

Если $ P $ — формула, то «not $ P $» — другое формула, которую мы символически записываем как $ \ lnot P $. Конечно, $ \ lnot P $ ложно, если $ P $ истинно, и наоборот — например,

«6 — не простое число» или «Неверно, что 6 — это простое число». премьер » или «$ \ lnot (\ hbox {6 простое число}) $ » (T)

«Рональд Рейган не был президентом.» (F)

Предположим, что $ P $ и $ Q $ — формулы. потом «$ P $ и $ Q $» — это формула, записанная символически. как $ P \ land Q $, называемое конъюнкцией $ P $ и $ Q $. Для $ P \ land Q $ верны и $ P $, и $ Q $ должно быть истинным, в противном случае — ложным, например,

«5 долларов = 6 долларов и 7 долларов = 8 долларов». (F)

«Сиэтл находится в Вашингтоне, а Бойсе — в Айдахо». (T)

«Толстой был русским, а Диккенс — Французский ». (F)

Если $ P $ и $ Q $ являются формулами, то формула «$ P $ или $ Q $» символически записывается как $ P \ lor Q $, называемая дизъюнкция $ P $ и $ Q $.это важно отметить, что это , включая , или, то есть «либо или оба». Итак, если $ P $, $ Q $ или и $ P $, и $ Q $ верны, так и $ P \ lor Q $. Единственный способ, которым $ P \ lor Q $ может быть ложным, — это если оба $ P $ и $ Q $ ложны — например,

«Вашингтон находится в Канаде, а Лондон — в Англии». (T)

«$ 5

«Ленин был испанцем или Ганди был итальянцем». (F)

Если $ P $ и $ Q $ — формулы, то «если $ P $, то $ Q $» или написано «$ P $ подразумевает $ Q $» $ P \ подразумевает Q $, используя условный символ , $ \ подразумевает $.Не очевидно (по крайней мере, для большинства людей), при каких условиях обстоятельства $ P \ подразумевают, что Q $ должно быть истинным. Отчасти это потому, что «if… then» используется более чем одним способом в обычном английском языке, однако нам нужно исправить правило, которое позволит нам точно знать, когда $ P \ подразумевает Q $ верно. Конечно, если $ P $ истинно, а $ Q $ ложно, $ P $ не может следует $ Q $, поэтому $ P \ означает, что Q $ в этом случае неверно. Чтобы помочь нам с в остальных случаях рассмотрим следующее утверждение:

«Если $ x $ меньше 2, тогда $ x $ меньше 4.»

Это утверждение должно быть верным независимо от значения $ x $. (при условии, что вселенная дискурса является чем-то знакомым, например целые числа). Если $ x $ равен 1, он оценивается как $ \ rm T \ implies T $, если $ x $ равно 3, оно становится $ \ rm F \ Impies T $, а если $ x $ равно 5, оно становится $ \ rm F \ влечет F $. Таким образом, кажется, что $ P \ подразумевает, что Q $ истинно, если $ P $ истинно, а $ Q $ ложно. Это правило, которое мы принимаем.

Наконец, биконсульт , записанный $ \ Leftrightarrow $, соответствует фраза «тогда и только тогда» или «если и только если» для краткости.Итак, $ P \ Leftrightarrow Q $ истинно, когда и $ P $, и $ Q $ имеют то же значение истинности, в противном случае — ложь.

Пример 1.1.2. Предположим, что $ P (x, y) $ — это «$ x + y = 2 $», а $ Q (x, y) $ равно «$ xy> 1 $». Тогда, когда $ x = 1 $ и $ y = 1 $, $ \ lnot P (x, y) $, $ P (x, y) \ land Q (x, y) $, $ P (x, y) \ lor Q (x, y) $, $ P (x, y) \ влечет Q (x, y) $ и $ P (x, y) \ Leftrightarrow Q (x, y) $ имеют значения истинности F, F, T, F, F, соответственно, и когда $ x = 2 $ и $ y = 3 $ имеют значения истинности T, F, T, T, F соответственно. $ \ квадрат $

Используя операции $ \ lnot $, $ \ land $, $ \ lor $, $ \ implies $, $ \ Leftrightarrow $, мы можем построить составные выражения, такие как $$ (P \ land (\ lnot Q)) \ подразумевает ((\ lnot R) \ lor ((\ lnot P) \ land Q)).$$ Как показывает этот пример, иногда необходимо включать много круглых скобок, чтобы сгруппировать термины в формуле ясно. Как и в алгебре, где умножение имеет приоритет перед сложением, мы можем убрать скобки согласование определенного порядка, в котором логические операции выполняются. Мы будет применять операции в этом порядке, начиная с от начала до конца: $ \ lnot $, $ \ land $, $ \ lor $, $ \ подразумевает $ и $ \ Leftrightarrow $. Так $$ A \ подразумевает B \ lor C \ land \ lnot D $$ это сокращение от $$ A \ подразумевает (B \ lor (C \ land (\ lnot D))).$$ Как и в алгебре, часто имеет смысл включить несколько дополнительных скобок, чтобы убедиться, что предполагаемое значение ясно. Большая часть информации, которую мы обсудили, может быть сведена в таблицы истинности . Например, таблица истинности для $ \ lnot P $ — это:

В этой таблице две строки, потому что есть только две возможности для истинное значение $ P $. В других логических операциях используются две переменные, поэтому им требуется 4 строки в их таблицах истинности.

$ P $	$ Q $	$ P \ land Q $	$ P \ lor Q $	$ P \ Rightarrow Q $	$ P \ Leftrightarrow Q $
T	T	T	T	T	T
F	T	F	T	T	F
T	F	F	T	F	F
F	F	F	F	T	T

У любого составного выражения есть таблица истинности.n $ строк в таблице, потому что есть много разных способов назначить Команды T и F для простых формул $ n $ в составном выражении. Таблица истинности для $ (P \ land Q) \ lor \ lnot R $:

R $

$ P $	$ Q $	$	$ P \ land Q $	$ \ lnot R $	$ (P \ land Q) \ lor \ lnot R $
T	T	T	T	F	T
F	T	T	F	F	F
T	F	T	F	F	F
F	F	T	F	F	F
T	T	F	T	T	T
F	T	F	F	T	T
T	F	F	F	T	T
F	F	F	F	T	T

Посмотрите, как включение промежуточных шагов упрощает рассчитывать и читать.

Тавтология — это логическое выражение, которое всегда оценивается как T, то есть последний столбец его таблицы истинности состоит только из Т. Иногда говорят, что тавтология действительна ; хотя «действительный» используется в других контекстах как что ж, это не должно вызывать путаницы. Например, $ (P \ land Q) \ lor P \ Leftrightarrow P $ — тавтология, поскольку ее таблица истинности:

$ P $	$ Q $	$ P \ land Q $	$ (P \ land Q) \ lor P $	$ (P \ land Q) \ lor P \ Leftrightarrow P $
T	T	T	T	T
F	T	F	F	T
T	F	F	T	T
F	F	F	F	T

Мы перечислим несколько важных тавтологий в следующей теореме.

Теорема 1.1.3 Справедливы следующие утверждения.

а) $ P \ Leftrightarrow \ lnot \ lnot P $

б) $ P \ lor Q \ Leftrightarrow Q \ lor P $

c) $ P \ land Q \ Leftrightarrow Q \ land P $

d) $ (P \ land Q) \ land R \ Leftrightarrow P \ land (Q \ land R) $

e) $ (P \ lor Q) \ lor R \ Leftrightarrow P \ lor (Q \ lor R) $

f) $ P \ land (Q \ lor R) \ Leftrightarrow (P \ земля Q) \ lor (P \ land R) $

г) $ P \ lor (Q \ land R) \ Leftrightarrow (P \ lor Q) \ land (P \ lor R) $

ч) $ (P \ подразумевает Q) \ Leftrightarrow (\ lnot P \ lor Q) $

i) $ P \ влечет (P \ lor Q) $

j) $ P \ land Q \ подразумевает Q $

k) $ (P \ Leftrightarrow Q) \ Leftrightarrow ((P \ подразумевает Q) \ land (Q \ влечет P)) $

l) $ (P \ подразумевает Q) \ Leftrightarrow (\ lnot Q \ подразумевает \ lnot P) $

Доказательство. Доказательства оставлены как упражнения. $ \ qed $

Заметим, что (b) и (c) — коммутативные законы, (d) и (e) — ассоциативные законы и (f) и (g) говорят, что $ \ land $ и $ \ lor $ распределяются друг над другом. Это говорит о том, что существует форма алгебры для логических выражений, аналогичных алгебре для числовых выражений. Этот предмет называется Булева алгебра и имеет множество применений, особенно в информатике.

Если две формулы всегда принимают одно и то же значение истинности, несмотря ни на что элементы из вселенной дискурса, которые мы заменяем различными переменных, тогда мы говорим, что они эквивалентны .Стоимость эквивалента формулы в том, что они говорят одно и то же. Это всегда правильный шаг в доказательстве заменить некоторую формулу на эквивалентную. Кроме того, многие тавтологии содержат важные идеи для построения доказательств. Для Например, (k) говорит, что если вы хотите показать, что $ P \ Leftrightarrow Q $, это возможно (и часто желательно) разбить доказательство на два частей, одна из которых доказывает, что из $ P \ следует Q $, а вторая Доказывая обратное , из $ Q \ следует P $.

Читая теорему 1.1.3 у вас может быть заметил, что $ \ land $ и $ \ lor $ удовлетворяют многим аналогичным свойствам. Они называются «двойственными» понятиями — для любого свойства один, есть почти идентичное свойство, которому удовлетворяет другой, при этом экземпляры двух операций поменялись местами. Это часто означает, что когда мы доказываем результат, включающий одно понятие, мы получаем соответствующий результат для его дуала без дополнительной работы.

Джордж Буль. логический (1815–1864) имел только общее школьное образование, хотя учился Греческий и латинский сами по себе.Он начал свою карьеру элементарным школьный учитель, но решил, что ему нужно больше узнать о математике, поэтому он начал изучать математику, а также языки, необходимые для чтения современной литературы на математика. В 1847 году он опубликовал небольшую книгу The Mathematical Анализ логики , который справедливо можно сказать, положил начало исследованию математической логики. Ключевой вклад работы был в новое определение «математики», чтобы не означать просто «изучение чисел и величина », но изучение символов и манипуляции с ними в соответствии с к определенным правилам.Важность этого уровня абстракции для будущее математики трудно переоценить. Наверное, на Благодаря этой работе он перешел на работу в Куинс-колледж в Корке.

В Исследование законов мысли , опубликованном в 1854 году, Буль установил настоящую формальную логику, развивая то, что сегодня называется Булева алгебра, или иногда алгебра множеств . Он использовал символы для сложение и умножение как операторы, но полностью абстрактно смысл.Сегодня эти символы все еще иногда используются в логических алгебры, хотя символы `$ \ land $ ‘и` $ \ lor $’, `$ \ cap $ ‘и Также используются `$ \ cup $ ‘. Бул применил алгебраические манипуляции к процесс рассуждения. Вот простой пример такого манипуляции, которые он совершил: уравнение $ xy = x $ (которое сегодня можно было бы записать $ x \ land y = x $ или $ x \ cap y = x $) означает, что `все, что удовлетворяет $ x $ удовлетворяет $ y $ ‘или, в наших терминах, $ x \ влечет y $. Если также $ yz = y $ (что есть, $ y \ подразумевает z $), то замена $ y = yz $ на $ xy = x $ дает $ x (yz) = x $ или $ (xy) z = x $.2 + bD + c = 0 $, лечение $ D $ под номером предоставляет информацию о решениях для дифференциальное уравнение.

Информация здесь взята из A History of Mathematics, by Карл Б. Бойер, Нью-Йорк: Джон Вили и сыновья, 1968. Подробнее информацию см. в Лекциях по десяти британским математикам , автор: Александр Макфарлейн, Нью-Йорк: John Wiley & Sons, 1916.

Упражнения 1.1

Пример 1.1.1 Постройте таблицы истинности для следующих логических выражений:

а) $ (P \ land Q) \ lor \ lnot P $

б) $ P \ подразумевает (Q \ land P) $

c) $ (P \ land Q) \ Leftrightarrow (P \ lor \ lnot R) $

г) $ \ lnot P \ подразумевает \ lnot (Q \ lor R) $

Пр. 1.1,2 Проверьте тавтологии теоремы 1.1.3.

Пример 1.1.3 Предположим, что $ P (x, y) $ — это формула «$ x + y = 4 $», а $ Q (x, y) $ — это формула «$ x

$ P (x, y) \ land Q (x, y) $, $ \ lnot P (x, y) \ lor Q (x, y) $,

$ P (x, y) \ влечет \ lnot Q (x, y) $, $ \ lnot (P (x, y) \ Leftrightarrow Q (x, y)) $,

используя значения:

a) $ x = 1, y = 3 $

c) $ x = 1, y = 2 $

b) $ x = 3, y = 1 $

d) $ x = 2, y = 1 $

Пр. 1.1,4

а) Найдите таблицы истинности для $$ P \ land (\ lnot Q) \ land R, \ quad \ quad (\ lnot P) \ land Q \ land (\ lnot R) $$

б) Используйте их, чтобы найти таблицу истинности для $$ (P \ земля (\ lnot Q) \ земля R) \ lor ((\ lnot P) \ land Q \ land (\ lnot R)) $$

c) Используйте метод, предложенный в частях (a) и (b) найти формулу со следующей таблицей истинности.

$

$ P $	$ Q $	$	???
T	T	T	T
F	T	T	F
T	F	T	F
F	F	T	F
T	T	F	T
F	T	F	T
T	F	F	F
F	F	F	F

г) Используйте метод, предложенный частями (a) — (c), чтобы объясните, почему любой список из $ 2 ^ n $ T и F является последний столбец таблицы истинности для некоторой формулы с $ n $ буквами.