Логичный и логический. Логичный или логический: в чем разница и как правильно использовать эти слова

Чем отличаются прилагательные «логичный» и «логический». Как правильно употреблять эти слова в речи. В каких контекстах уместно использовать каждое из них. Какие ошибки допускают при выборе между «логичный» и «логический».

Значение и происхождение слов «логичный» и «логический»

Прилагательные «логичный» и «логический» образованы от существительного «логика», но имеют разные значения и употребляются в разных контекстах. Разберемся подробнее в их значениях и особенностях использования.

Происхождение и значение слова «логичный»

«Логичный» происходит от слова «логика» и означает «последовательный, закономерный, разумный». Это прилагательное характеризует что-либо как соответствующее законам логики, правильное с точки зрения рассуждения.

Происхождение и значение слова «логический»

«Логический» также образовано от слова «логика», но имеет значение «относящийся к логике, связанный с ней». Это прилагательное используется для обозначения понятий и явлений, имеющих отношение к науке логике.

Основные различия в употреблении слов «логичный» и «логический»

Хотя эти прилагательные образованы от одного корня, их использование в речи различается. Рассмотрим ключевые отличия:

• «Логичный» характеризует качество рассуждения или действия, а «логический» указывает на принадлежность к логике как науке.
• «Логичный» может относиться к человеку, его мыслям и поступкам. «Логический» обычно характеризует научные термины и понятия.
• «Логичный» имеет степени сравнения (логичнее, самый логичный), а «логический» — нет.
• «Логичный» можно заменить синонимами «последовательный», «закономерный». «Логический» синонимов практически не имеет.

Правильное употребление слова «логичный»

«Логичный» уместно использовать, когда речь идет о разумности, последовательности, закономерности чего-либо. Это прилагательное часто характеризует:

• Мысли и рассуждения: логичный вывод, логичное объяснение
• Действия и поступки: логичный шаг, логичное решение
• Явления и процессы: логичное развитие событий
• Людей: логичный человек

Примеры правильного употребления:

• Его аргументы были вполне логичными.
• Логичным продолжением карьеры стала должность директора.
• Это самое логичное объяснение случившегося.

Правильное употребление слова «логический»

«Логический» применяется в контексте науки логики и для обозначения понятий, связанных с ней. Это прилагательное используется в сочетаниях:

• Научные термины: логический вывод, логическое умозаключение
• Разделы логики: математическая логическая система
• Методы мышления: логический анализ, логическое мышление

Примеры корректного использования:

• Изучение логических законов помогает развивать критическое мышление.
• В статье был проведен детальный логический анализ аргументов.
• Философ разработал новую логическую систему.

Типичные ошибки в употреблении слов «логичный» и «логический»

При использовании этих прилагательных часто допускают ошибки, путая их значения. Рассмотрим наиболее распространенные из них:

Неправильное использование слова «логичный» вместо «логический»

Ошибка: «Мы изучали логичные законы на уроке философии»

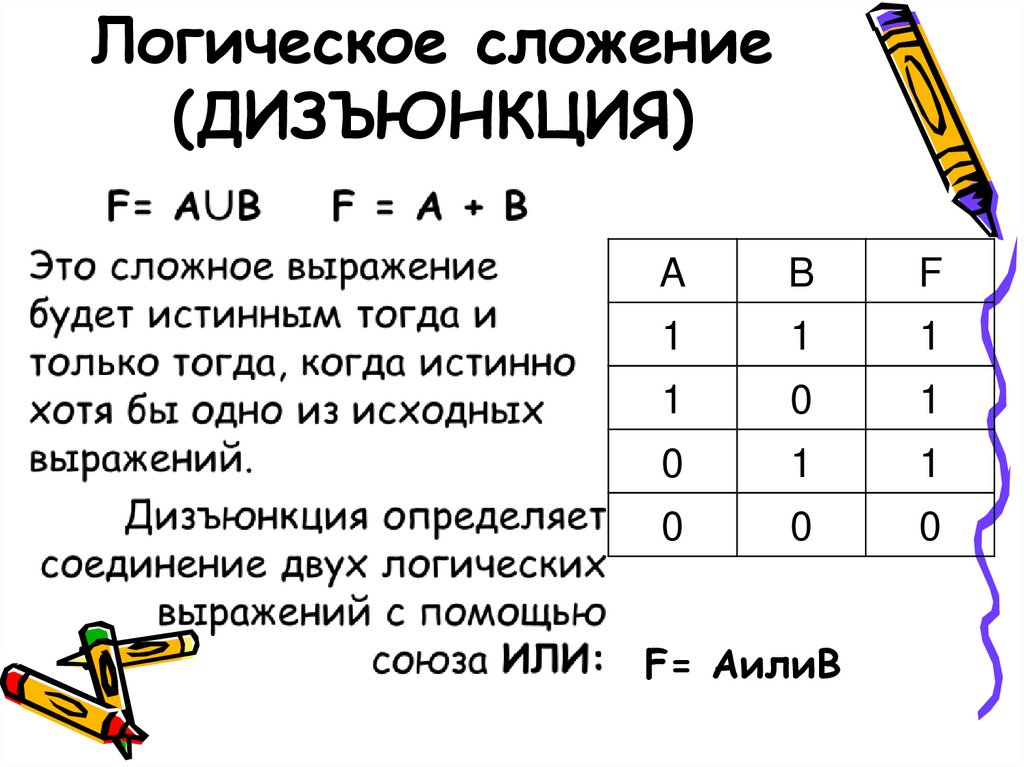
Правильно: «Мы изучали логические законы на уроке философии»

В данном случае речь идет о законах науки логики, поэтому корректно использовать прилагательное «логический».

Неуместное употребление слова «логический» вместо «логичный»

Ошибка: «Его поступок был вполне логическим в той ситуации»

Правильно: «Его поступок был вполне логичным в той ситуации»

Здесь характеризуется разумность поступка, а не его отношение к науке логике, поэтому верно использовать слово «логичный».

Контекстуальные особенности использования слов «логичный» и «логический»

Выбор между «логичный» и «логический» зависит от контекста и сферы употребления. Рассмотрим некоторые специфические случаи:

Использование в научной и академической среде

В научных текстах чаще встречается прилагательное «логический»: логический метод, логическая структура, логическое доказательство. Однако «логичный» также может использоваться, особенно когда речь идет об оценке научных теорий или гипотез.

Употребление в повседневной речи

В бытовом общении преимущественно используется слово «логичный»: логичный ответ, логичное решение, логичный вывод. «Логический» в разговорной речи встречается реже и обычно в устойчивых выражениях, например, «логическое мышление».

Синонимы и антонимы к словам «логичный» и «логический»

Для лучшего понимания различий между этими прилагательными полезно рассмотреть их синонимы и антонимы.

Синонимы к слову «логичный»

• Последовательный
• Закономерный
• Разумный
• Обоснованный
• Рациональный

Антонимы к слову «логичный»

• Нелогичный
• Абсурдный
• Противоречивый
• Непоследовательный
• Иррациональный

Синонимы к слову «логический»

У прилагательного «логический» практически нет точных синонимов, так как оно имеет узкое специальное значение. В некоторых контекстах могут использоваться слова:

• Рассудочный
• Умозрительный

Антонимы к слову «логический»

• Нелогический
• Алогичный (в значении «противоречащий логике»)

Исторические изменения в употреблении слов «логичный» и «логический»

Интересно проследить, как менялось использование этих прилагательных с течением времени:

• В XIX веке слово «логический» использовалось шире и могло применяться в значениях, которые сейчас передаются словом «логичный».
• К середине XX века произошло четкое разграничение значений этих слов.
• В современном русском языке наблюдается тенденция к более частому использованию слова «логичный» в разговорной речи.

Употребление слов «логичный» и «логический» в различных стилях речи

Выбор между «логичный» и «логический» также зависит от стиля речи:

Научный стиль

В научных текстах преобладает использование прилагательного «логический»: логическая операция, логическая формула, логический вывод. «Логичный» используется реже, обычно при оценке научных концепций.

Публицистический стиль

В публицистике встречаются оба прилагательных. «Логический» чаще используется в контексте анализа или рассуждения, а «логичный» — при оценке событий или действий.

Художественный стиль

В художественной литературе чаще используется «логичный» для характеристики действий персонажей или развития сюжета. «Логический» может встречаться в научно-фантастических произведениях или при описании мыслительных процессов героев.

Практические рекомендации по правильному использованию слов «логичный» и «логический»

Чтобы избежать ошибок при выборе между «логичный» и «логический», следуйте этим рекомендациям:

1. Определите контекст: если речь идет о науке логике, используйте «логический».
2. Подумайте о значении: если нужно охарактеризовать разумность или последовательность, выбирайте «логичный».
3. Проверьте возможность замены синонимом: если можно заменить на «последовательный» или «закономерный», то верно использовать «логичный».
4. Обратите внимание на сочетаемость: «логическое мышление», но «логичный поступок».
5. В сомнительных случаях обращайтесь к словарям и справочникам по культуре речи.

Заключение: важность правильного употребления слов «логичный» и «логический»

Правильное использование слов «логичный» и «логический» важно для точного выражения мысли и избежания двусмысленности в речи. Понимание различий между этими прилагательными помогает:

• Точнее выражать свои мысли
• Избегать ошибок в научных и официальных текстах
• Улучшить качество письменной и устной речи
• Повысить уровень языковой культуры

Внимательное отношение к выбору слов «логичный» и «логический» свидетельствует о высоком уровне владения языком и способствует более эффективной коммуникации.

Логическое мышление — развитие логики

Каждый день мы сталкиваемся с множеством задач, решение которых требует от нас способности к логическому мышлению. Логика как умение думать и рассуждать последовательно и непротиворечиво, требуется нам во многих жизненных ситуациях, начиная с решения сложных технических и бизнес- задач, заканчивая убеждением собеседников и совершением покупок в магазине.

Но несмотря на высокую потребность в этом умении мы часто совершаем логические ошибки, сами того не подозревая. Ведь среди многих людей бытует мнение, что правильно мыслить можно на основе жизненного опыта и так называемого здравого смысла, не пользуясь законами и специальными приемами «формальной логики». Для совершения простых логических операций, высказывания элементарных суждений и несложных выводов может подойти и здравый смысл, а если нужно познать или объяснить что-то более сложное, то здравый смысл нередко приводит нас к заблуждениям.

 

Кроме того достаточно примитивно объясняют нам принципы поиска решения заданий. Что касается развития словесно-логического мышления (или вербально-логического), умения правильно совершать мыслительные операции, последовательно приходить к умозаключениям, то этому нас почему-то не учат. Именно поэтому уровень развития логического мышления людей недостаточно высок.

Мы считаем, что логическое мышление человека и его способность к познанию должны развиваться системно и на основании специального терминологического аппарата и логического инструментария. На занятиях данного онлайн-тренинга вы узнаете о методиках самообразования для развития логического мышления, познакомитесь с основными категориями, принципами, особенностями и законами логики, а также найдете примеры и упражнения для применения полученных знаний и навыков.

Оглавление:

• Что такое логическое мышление?
• Применение логики
• Составляющие логического мышления
• Как этому научиться?
• Уроки логики
• Как проходить занятия?
• Вспомогательные материалы: тесты, игры, книги
• Цитаты известных людей о логике

Что такое логическое мышление?

Чтобы объяснить, что такое «логическое мышление», разделим это понятие на две части: мышление и логику. Теперь дадим определение каждой из этих составляющих.

Мышление человека — это психический процесс обработки информации и установления связей между предметами, их свойствами или явлениями окружающего мира. Мышление позволяет человеку находить связи между феноменами действительности, но чтобы найденные связи, действительно, отражали истинное положение дел, мышление должно быть объективным, правильным или, другими словами, логичным, то есть подчиненным законам логики.

Логика в переводе с греческого имеет несколько значений: «наука о правильном мышлении», «искусство рассуждения», «речь», «рассуждение» и даже «мысль». В нашем случае мы будем исходить из самого популярного определения логики как нормативной науки о формах, методах и законах интеллектуальной мыслительной деятельности человека. Логика изучает способы достижения истины в процессе познания опосредованным путём, не из чувственного опыта, а из знаний, полученных ранее, поэтому её также можно определить как науку о способах получения выводного знания.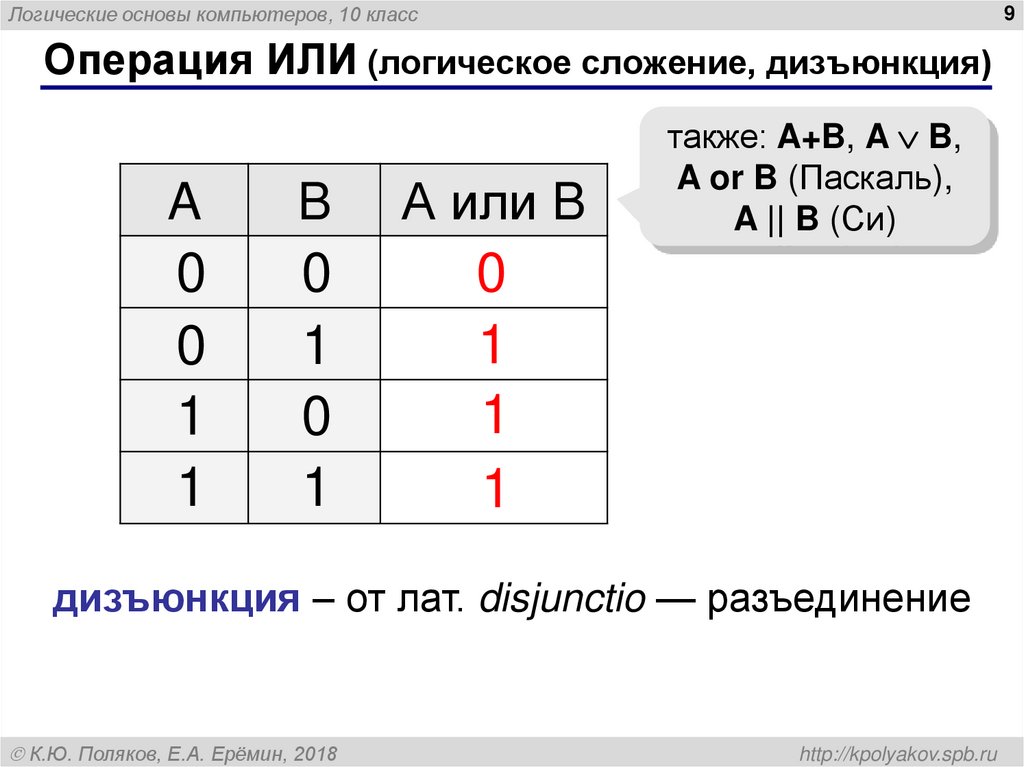 Одна из главных задач логики — определить, как прийти к выводу из имеющихся предпосылок и получить истинное знание о предмете размышления, чтобы глубже разобраться в нюансах изучаемого предмета мысли и его соотношениях с другими аспектами рассматриваемого явления.

Теперь мы можем дать определение самому логическому мышлению.

Логическое мышление – это мыслительный процесс, при котором человек использует логические понятия и конструкции, которому свойственна доказательность, рассудительность, и целью которого является получение обоснованного вывода из имеющихся предпосылок.

Также выделяют несколько видов логического мышления, перечислим их, начиная с самого простого:

1

Образно-логическое мышление

Образно-логическое мышление (наглядно-образное мышление) – различные мыслительные процессы так называемого «образного» решения задач, которое предполагает визуальное представление ситуации и оперирование образами составляющих её предметов. Наглядно-образное мышление, по сути, является синонимом слова «воображение», которое позволяет нам наиболее ярко и четко воссоздавать все многообразие различных фактических характеристик предмета или явления. Данный вид мыслительной деятельности человека формируется в детском возрасте, начиная, примерно, с 1,5 лет.

Чтобы понять, насколько у вас развит этот вид мышления, предлагаем вам пройти Тест на IQ «Прогрессивные матрицы Равена»

Тест Равена — это шкала прогрессивных матриц для оценки коэффициента интеллекта и уровня умственных способностей, а также логичности мышления, разработанная в 1936 году Джоном Равеном в соавторстве с Роджером Пенроузом. Данный тест может дать максимально объективную оценку IQ тестируемых людей, независимо от их уровня образования, социального сословия, рода деятельности, языковых и культурных особенностей. То есть можно с большой вероятностью утверждать, что данные, полученные в результате данного теста у двух людей из разных точек мира будут одинаково оценивать их IQ. Объективность оценки обеспечивается тем фактом, что основу этого теста составляют исключительно изображения фигур, а поскольку матрицы Равена относятся к числу невербальных тестов интеллекта, его задания не содержат текста.

Тест состоит из 60 таблиц. Вам будут предложены рисунки с фигурами, связанными между собой определенной зависимостью. Одной фигуры не хватает, она дается внизу картинки среди 6-8 других фигур. Ваша задача — установить закономерность, связывающую между собой фигуры на рисунке, и указать номер правильной фигуры, выбрав из предлагаемых вариантов. В каждой серии таблиц содержатся задания нарастающей трудности, в то же время усложнение типа заданий наблюдается и от серии к серии.

Cтатистика На весь экран

2

Абстрактно-логическое мышление

Абстрактно-логическое мышление – это совершение мыслительного процесса при помощи категорий, которых нет в природе (абстракций). Абстрактное мышление помогает человеку моделировать отношения не только между реальными объектами, но также и между абстрактными и образными представлениями, которые создало само мышление.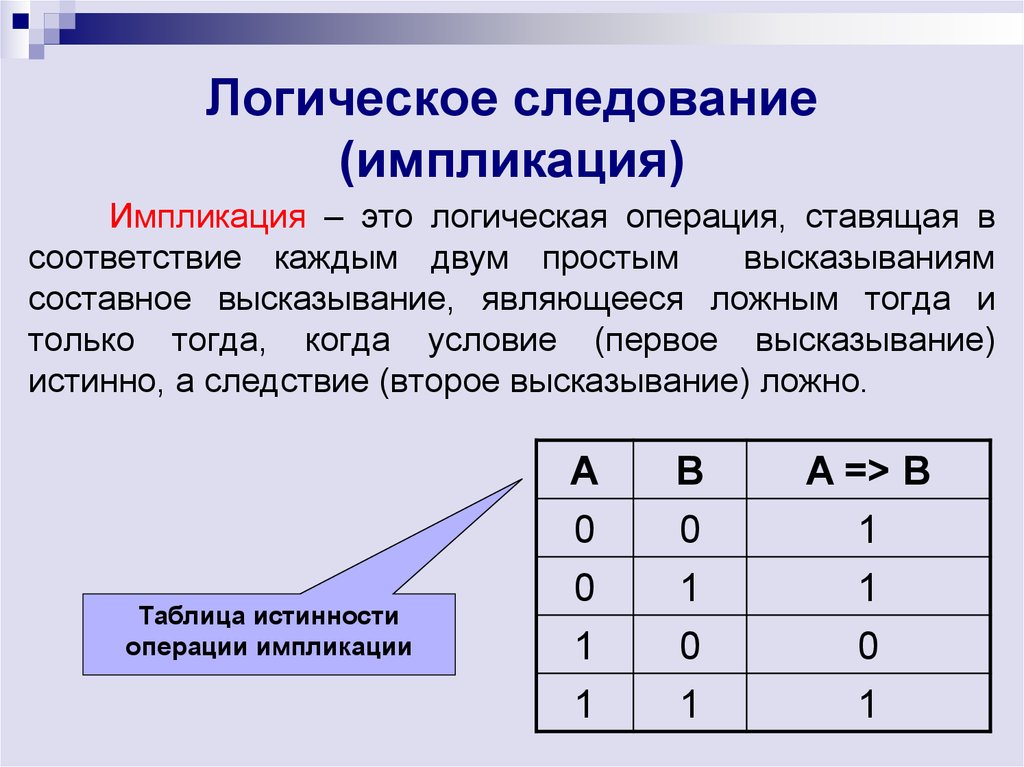 Абстрактно-логическое мышление имеет несколько форм: понятие, суждение и умозаключение, о которых вы сможете подробнее узнать в уроках нашего тренинга.

3

Словесно-логическое мышление

Словесно-логическое мышление (вербально-логическое мышление)— один из видов логического мышления, характеризующийся использованием языковых средств и речевых конструкций. Данный вид мышления предполагает не только умелое использование мыслительных процессов, но и грамотное владение своей речью. Словесно-логическое мышление необходимо нам для публичных выступлений, написания текстов, ведения споров и в других ситуациях, где нам приходится излагать свои мысли при помощи языка.

На этом моменте предлагаем немного потренироваться:

 

А теперь продолжим.

Применение логики

Мышление с использованием инструментария логики необходимо практически в любой области человеческой деятельности, в том числе в точных и гуманитарных науках, в экономике и бизнесе, риторике и ораторском мастерстве, в творческом процессе и изобретательстве. В одних случаях применяется строгая и формализованная логика, например, в математике, философии, технике. В других случаях логика лишь снабжает человека полезными приемами для получения обоснованного вывода, например, в экономике, истории или просто в обычных «жизненных» ситуациях.

Как уже было сказано, часто мы пытаемся мыслить логически на интуитивном уровне. Кому-то это удается хорошо, кому-то хуже. Но подключая логический аппарат, лучше все-таки знать, какие именно мыслительные приемы мы используем, так как в этом случае мы можем:

• Точнее подобрать нужный способ, который позволит прийти к правильному выводу.
• Мыслить быстрее и качественнее – как следствие из предыдущего пункта.
• Лучше излагать свои мысли.
• Избежать самообмана и логических заблуждений.
• Выявлять и устранять ошибки в умозаключениях других людей, справиться с софистикой и демагогией.
• Применять нужную аргументацию для убеждения собеседников.

Составляющие логического мышления

Часто применение логического мышления связывают с быстрым решением заданий на логику и прохождением тестов на определение уровня интеллектуального развития (IQ). Но это направление связано в большей степени с доведением мыслительных операций до автоматизма, что является весьма незначительной частью того, чем логика может быть полезна человеку.

Умение логически мыслить объединяет в себе множество навыков по использованию различных мыслительных действий и включает в себя:

1. Знание теоретических основ логики.
2. Умение правильно совершать такие мыслительные операции, как: классификация, конкретизация, обобщение, сравнение, аналогия и другие.
3. Уверенное использование ключевых форм мышления: понятие, суждение, умозаключение.
4. Способность аргументировать свои мысли в соответствии с законами логики.
5. Навык быстро и эффективно решать сложные логические задачи (как учебные, так и прикладные).

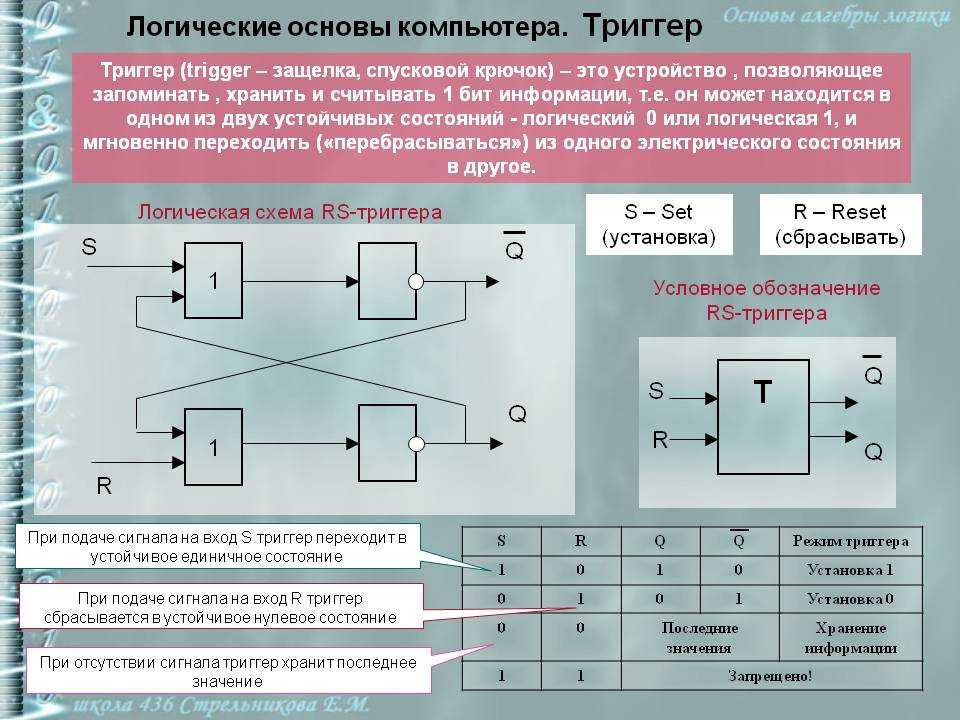
Конечно, такие операции мышления с применением логики как определение, классификация и категоризация, доказательство, опровержение, умозаключение, вывод и многие другие применяются каждым человеком в его мыслительной деятельности. Но используем мы их неосознанно и часто с погрешностями без отчетливого представления о глубине и сложности тех мыслительных действий, из которых состоит даже самый элементарный акт мышления. А если вы хотите, чтобы ваше логическое мышление было действительно правильным и строгим, этому нужно специально и целенаправленно учиться.

Как этому научиться?

Логическое мышление не дается нам с рождения, ему можно только научиться. Существует два основных аспекта обучения логике: теоретический и практический.

Теоретическая логика, которая преподается в университетах, знакомит студентов с основными категориями, законами и правилами логики.

Практическое обучение направлено на применение полученных знаний в жизни.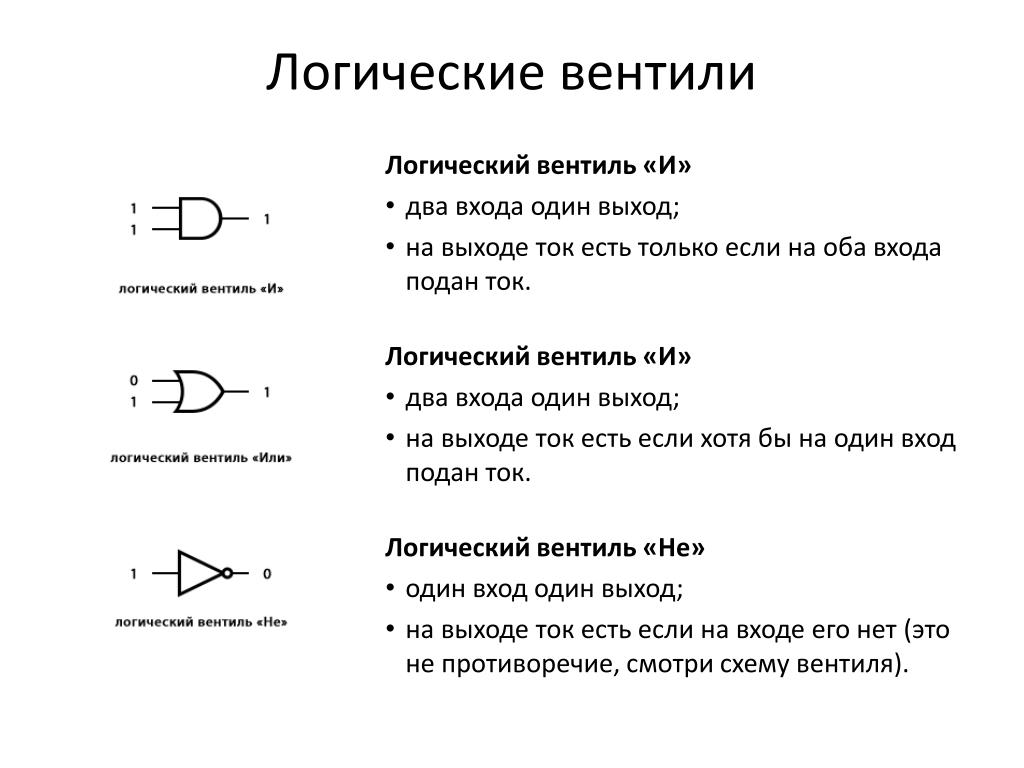 Однако в действительности современное обучение практической логике обычно связано прохождением разных тестов и решением задач на проверку уровня развития интеллекта (IQ) и почему-то не затрагивает применение логики в реальных жизненных ситуациях.

Чтобы на самом деле освоить логику, следует совместить теоретические и прикладные аспекты. Уроки и упражнения должны быть направлены на формирование интуитивно понятного, доведенного до автоматизма логического инструментария и закрепление полученных знаний с целью их применения в реальных ситуациях.

По этому принципу и был составлен онлайн-тренинг, который вы сейчас читаете. Цель данного курса – научить вас логически мыслить и применять методы логического мышления. Занятия направлены на ознакомление с основами логического мышления (тезаурус, теории, методы, модели), мыслительными операциями и формами мышления, правилами аргументации и законами логики. Кроме того, каждый урок содержит в себе задания и упражнения для тренировки использования полученных знаний на практике.

Уроки логики

Собрав широкий спектр теоретических материалов, а также изучив и адаптировав опыт обучения прикладным формам логического мышления, мы приготовили ряд уроков для полноценного овладения данным навыком.

Урок 1. Логический анализ языка

Первый урок нашего курса мы посвятим сложной, но очень важной теме – логическому анализу языка. Сразу стоит оговориться, что эта тема многим может показаться абстрактной, нагруженной терминологией, неприменимой на практике. Не пугайтесь! Логический анализ языка – это основа любой логической системы и правильного рассуждения. Те термины, которые мы здесь узнаем, станут нашим логическим алфавитом, без знания которого просто нельзя пойти дальше, но постепенно мы научимся пользоваться им с лёгкостью.

Урок 2. Понятие в логике

Логическое понятие — это форма мышления, отражающая предметы и явления в их существенных признаках. Понятия бывают разных видов: конкретные и абстрактные, единичные и общие, собирательные и несобирательные, безотносительные и соотносительные, положительные и отрицательные, и другие. В рамках логического мышления важно уметь отличать эти виды понятий, а также производить новые понятия и определения, находить отношения между понятиями и совершать специальные действия над ними: обобщение, ограничение и деление. Всему этому вы научитесь в данном уроке.

Урок 3. Определение в логике

В первых двух уроках мы говорили о том, что задача логики – помочь нам перейти от интуитивного употребления языка, сопровождаемого ошибками и разногласиями, к более упорядоченному его использованию, лишённому двусмысленности. Умение правильно обращаться с понятиями представляет собой один из необходимых для этого навыков. Другой не менее важный навык – умение правильно давать определения. В этом уроке мы расскажем, как этому научиться и как избежать самых распространённых ошибок.

Урок 4. Логическое суждение

Логическое суждение — это форма мышления, в которой утверждается или отрицается что-либо об окружающем мире, предметах, явлениях, а также отношениях и связях между ними. Суждения в логике состоят из субъекта (о чем идет речь в суждении), предиката (что говорится о субъекте), связки (что соединяет субъект и предикат) и квантора (объема субъекта). Суждения могут быть различных видов: простые и сложные, категорические, общие, частные, единичные. Также отличаются и формы связок между субъектом и предикатом: равнозначность, пересечение, подчинение и совместимость. Кроме того, в рамках составных (сложных) суждений могут быть свои связки, которые определяют ещё шесть видов сложных суждений. Умение логически мыслить предполагает способность правильно строить различные виды суждений, понимать их структурные элементы, признаки, отношения между суждениями, а также проверять является суждение истинным или ложным.

Урок 5. Законы логики

Перед тем как перейти к последней третьей форме мышления (умозаключению), важно понять, какие существуют логические законы, или, другими словами, объективно существующие правила построения логического мышления. Их предназначение, с одной стороны, в помощи построения умозаключений и аргументации, а с другой – в предупреждении ошибок и нарушений логичности, связанных с рассуждениями. данном уроке будут рассмотрены следующие законы формальной логики: закон тождества, закон исключённого третьего, закон противоречия, закон достаточного основания, а также законы де Моргана, законы дедуктивных умозаключений, закон Клавия и законы деления. Изучив примеры и выполнив специальные упражнения, вы научитесь целенаправленно использовать каждый из этих законов.

Урок 6. Умозаключение

Умозаключение — это третья форма мышления, в которой из одного, двух или нескольких суждений, называемых посылками, вытекает новое суждение, называемое заключением или выводом. Умозаключения делятся на три вида: дедуктивные, индуктивные и умозаключения по аналогии. При дедуктивном умозаключении (дедукции) из общего правила делается вывод для частного случая. Индукция — это умозаключения, в которых из нескольких частных случаев выводится общее правило. В умозаключениях по аналогии на основе сходства предметов в одних признаках делается вывод об их сходстве и в других признаках. На этом занятии вы познакомитесь со всеми видами и подвидами умозаключений, научитесь строить разнообразные причинно-следственные связи.

Урок 7. Силлогизмы

Этот урок будет посвящён многопосылочным умозаключениям. Так же как и в случае однопосылочных умозаключений, вся необходимая информация в скрытом виде будет присутствовать уже в посылках. Однако, поскольку посылок теперь будет много, то способы её извлечения становятся более сложными, а потому и добытая в заключении информация не будет казаться тривиальной. Кроме того, нужно отметить, что существует много разных видов многопосылочных умозаключений. Мы с вами сосредоточимся только на силлогизмах. Они отличаются тем, что и в посылках и в заключении имеют категорические атрибутивные высказывания и на основании наличия или отсутствия каких-то свойств у объектов позволяют сделать вывод о наличии или отсутствии у них других свойств.

Урок 8. Типы рассуждений

В предыдущих уроках мы поговорили о разных логических операциях, которые составляют важную часть любого рассуждения. Среди них были операции над понятиями, определения, суждения и умозаключения. Значит, на данный момент должно быть ясно, из каких компонентов рассуждения состоят. Однако мы ещё нигде не касались вопросов о том, каким образом может быть организовано рассуждение в целом и какими в принципе бывают типы рассуждений. Это и станет темой последнего урока. Начнём с того, что рассуждения делятся на дедуктивные и правдоподобные. Все виды умозаключений, рассмотренные в предыдущих уроках: умозаключения по логическому квадрату, обращения, силлогизмы, энтимемы, сориты, – представляют собой именно дедуктивные рассуждения. Их отличительный признак состоит в том, что посылки и заключения в них связаны отношением строгого логического следования, в то время как в случае правдоподобных рассуждений подобная связь отсутствует. Сначала поговорим подробнее о дедуктивных рассуждениях.

Как проходить занятия?

Сами уроки со всеми упражнениями можно пройти за 1-3 недели, усвоив теоретический материал и немного попрактиковавшись. Но для развития логического мышления важно заниматься системно, много читать и постоянно тренироваться.

Для максимального эффекта рекомендуем вам сначала просто прочитать весь материал, потратив на это 1-2 вечера. Затем проходите по 1 уроку ежедневно, выполняя необходимые упражнения и следуя предложенным рекомендациям. После того как вы освоите все уроки, займитесь эффективным повторением по данной методике, чтобы запомнить материал надолго. Далее старайтесь чаще применять приёмы логического мышления в жизни, при написании статей, писем, при общении, в спорах, в делах и даже на досуге. Подкрепляйте свои знания чтением книг и учебников, а также с помощью дополнительного материала, о котором речь пойдет ниже.

Дополнительные материалы

Помимо уроков в данном разделе мы постарались подобрать много полезного материала по рассматриваемой тематике:

• Логические задачи;
• Тесты на логическое мышление;
• Логические игры;
• Самые умные люди России и мира;
• Видеоуроки и мастерклассы.

А также книги и учебники, статьи, цитаты, вспомогательные тренинги.

На данной странице мы подобрали полезные книги и учебники, которые помогут вам углубить свои знания в логике и логическом мышлении:

• «Прикладная логика». Николай Николаевич Непейвода;
• «Учебник логики». Георгий Иванович Челпанов;
• «Логика: конспект лекций». Дмитрий Шадрин;
• «Логика. Учебный курс» (учебно-методический комплекс). Дмитрий Алексеевич Гусев;
• «Логика для юристов» (сборник задач). А.Д. Гетманова;
• «Логика. Учебник для юридических вузов». В.И. Кириллов, А.А.Старченко
• «Логика. Учебник для средней школы». Виноградов С.Н., Кузьмин А.Ф.
• «Логика. Учебник для гуманитарных факультетов». А.А.Ивин
• «Логика». Иванов Е.А.
• И другие.

Статьи о логическом мышлении

Также обратите внимание на раздел «Логика и интеллект» нашего блога, в котором мы собираем интересные материалы по данной тематике, среди которых:

• 4 закона логики
• Эвристика
• Кот Шрёдингера – суть простыми словами
• Что нужно знать о тестах на IQ
• Пафос, логос, этос
• И другие статьи наших авторов

Тренинги

Тренировка и развитие логического мышления могут быть дополнены следующими тренингами, которые вы сможете бесплатно пройти на нашем сайте:

1. Память и внимание являются важными способностями для логического мышления, которые позволят концентрироваться на большом количестве мыслительных объектов, над которыми осуществляются логические операции.

2. Творческое мышление вместе с логикой даст вам возможность не только строить правильные выводы, но искать нестандартные решения там, где логика «зашла в тупик».

3. Ораторское искусство и писательское мастерство формируют словесно-логическое мышление, а также позволяют на практике применить полученные знания в данном курсе.

4. Устный счет и скорочтение подходят для развития и тренировки интеллектуальных способностей.

5. Психология человека является полезной в понимании логического мышления, ведь именно психология как наука изучает мыслительные операции, мотивы, стимулы человека.

Цитаты известных людей о логике

О логическом мышлении высказывались многие великие люди, и вот некоторые цитаты, которые мы посчитали уместными в данном тренинге:

Мыслю, следовательно, существую (или на латинском Cogito, ergo sum, или в оригинале на французском Je pense, donc je suis).

Рене Декарт

Лишь немногие люди мыслят логично. В большинстве своем мы необъективны, предубеждены, заражены предвзятыми мнениями, ревностью, подозрительностью, страхом, гордыней и завистью.

Дейл Карнеги

Логика, которая одна может дать достоверность, есть орудие доказательства.

Анри Пуанкаре

Логика – это анатомия мышления.

Джон Локк

Логика не тождественна знанию, хотя область ее и совпадает с областью знания. Логика есть общий ценитель и судья всех частных исследований.

Джон Стюарт Милль

Мудрость – это самая точная из наук. Ошибаться можно различно, верно поступать можно лишь одним путём, поэтому-то первое легко, а второе трудно; легко промахнуться, трудно попасть в цель.

Аристотель

А теперь предлагаем приступить к занятиям.

Желаем вам успеха в освоении навыка логического мышления!

Ксения ГаланинаЕвгений Буянов

1 Логический анализ →

Значение слов — сборник словарей на Glosum.ru

Значение слов — сборник словарей на Glosum.ru

• Главная
• Контакты
• Добавить слово

Возможно, запрашиваемая Вами страница была перенесена или удалена. Также возможно, Вы допустили небольшую опечатку при вводе адреса – такое случается, поэтому еще раз внимательно проверьте.

Вы можете продолжить перейдя на главную страницу

• Популярное за все время
• Любовь
• Родина
• Обожать
• Вертеп
• Дружба
• Мужик
• Красота
• Надежда
• Искусство
• Панталык
• Стерва
• Паскуда
• Мир
• Тварь
• Дурак

• за месяц
• Член
• Краля
• Богатый
• Урод
• Бобыль
• Халда
• При
• Справедливость
• Привет
• Жрать
• Лукавый
• Рдеть
• Определение
• Человек
• Язык

• за неделю
• Пелена
• Безалаберный
• Жупел
• Мазурик
• Коллега
• Нравственность
• Ратовать
• Волонтер
• Информация
• Богатырь
• Неистовый
• Друг
• Организация
• Кумир
• Легенда

• за день
• Ублюдок
• Оный
• Юродивый
• Яр
• Дебелый
• История
• Гордость
• Показать
• Басурман
• Тать
• Романтик
• Вовсе
• Царь
• Честь
• Оказия

Важное

• Политика конфиденциальности
• Пользовательское Соглашение

Наши соц. сети

• Телеграм канал
• Телеграм бот

© 2012–2023

Сравнение и логические операторы | Codecademy

Перейти к содержимомуМини-значок со стрелкой внизFavicon Icon

Codecademy Team

Мини-значок с круглым кружком

Используйте эту статью в качестве справочного листа для сравнения JavaScript и логических операторов.

Используйте эту статью в качестве справочного материала для сравнения JavaScript и логических операторов.

• Операторы сравнения — операторы, сравнивающие значения и возвращающие true или false . Среди операторов: > , < , >= , <= , === и !== .
• Логические операторы — операторы, которые объединяют несколько логических выражений или значений и обеспечивают один логический вывод. К операторам относятся: && , || и ! .

Операторы сравнения

Возможно, вы знакомы с операторами сравнения по математике. Убедитесь, что в ваших знаниях нет пробелов.

• Меньше чем ( < ) — возвращает true , если значение слева меньше значения справа, иначе возвращает false .
• Больше чем ( > ) — возвращает true , если значение слева больше значения справа, в противном случае возвращает false .
• Меньше или равно ( <= ) — возвращает true , если значение слева меньше или равно значению справа, в противном случае возвращает ложь .
• Больше или равно ( >= ) — возвращает true , если значение слева больше или равно значению справа, в противном случае возвращает false .
• Equal to ( === ) — возвращает true , если значение слева равно значению справа, иначе возвращает false .
• Не равно ( !== ) — возвращает true , если значение слева не равно значению справа, иначе возвращает ложь .

Логические операторы

Операторы сравнения позволяют нам утверждать равенство оператора с JavaScript. Например, мы можем утверждать, равны ли два значения или выражения с === или одно значение больше другого с > .

Однако существуют сценарии, в которых мы должны установить, верны ли несколько значений или выражений. В JavaScript мы можем использовать логических операторов для выполнения этих утверждений.

Оператор && требует, чтобы оба выражения были истинными, чтобы выражение было истинным. Поскольку одно выражение ложно, а другое истинно, выражение ложно и оценивается как false .

Путь квалификации

Кодовые фонды

Freadner Florning,

15 Уроки

Карьера

Инженер с полным стеклом

Подходит для новичков,

169 Massons 9000

. 0003

Руководство по логическим операторам в R (ИЛИ, НЕ и И в R)

Предположим, мы хотим изменить или сравнить результаты сравнений, сделанных с помощью операторов отношения. Как бы мы это сделали?

 R делает это с помощью операторов AND, OR и NOT .

Логические операторы в R

• Оператор И: Представленный с помощью амперсанда, этот оператор принимает два логических значения и возвращает ИСТИНА , только если оба значения равны ИСТИНА себя.
• Оператор ИЛИ:  Обозначенный символом пики, этот оператор принимает два логических значения и возвращает ИСТИНА , если только одно значение равно ИСТИНА .
• Оператор NOT: Представленный восклицательным знаком, этот оператор инвертирует логическое значение, для которого он используется.

 

Оператор И «&»

Оператор И принимает два логических значения и возвращает ИСТИНА , только если оба значения равны ИСТИНА себя. Это означает, что ИСТИНА и ИСТИНА оценивается как ИСТИНА , но ЛОЖЬ и ИСТИНА , ИСТИНА и ЛОЖЬ и ЛОЖЬ и ЛОЖЬ оцениваются как ЛОЖЬ .

Только ИСТИНА и ИСТИНА дадут нам ИСТИНА. | Скриншот: Линда Нго

Вместо использования логических значений мы можем использовать результаты сравнений. Предположим, у нас есть переменная x , равная 12. Чтобы проверить, больше ли эта переменная пяти, но меньше 15, мы можем использовать x больше пяти и x меньше 15.

 x <- 12
x > 5 & x < 15 

Первая часть, x > 5 , будет оцениваться как TRUE , поскольку 12 больше пяти. Вторая часть, x < 15 , также будет оцениваться как ИСТИНА , потому что 12 также меньше 15. Таким образом, результатом этого выражения будет ИСТИНА , поскольку ИСТИНА и ИСТИНА равно ИСТИНА . Это имеет смысл, потому что 12 лежит между пятью и 15.

Однако, если бы x было 17, выражение x > 5 & x < 15 упростилось бы до ИСТИНА и ЛОЖЬ , что привело бы к выражению ЛОЖЬ .

Подробнее о R: группировка данных с помощью R: Руководство

 

И Пример задачи оператора

Рассмотрим следующий вектор и переменную:

 linkedin <- c(16, 9, 13, 5, 2, 17, 14 )
last <- tail(linkedin, 1) 

The linkedin 9Вектор 0013 представляет собой количество просмотров вашего профиля в LinkedIn за последние семь дней. Последняя переменная представляет последнее значение вектора linkedin .

Определите, находится ли переменная last в диапазоне от 15 до 20, исключая 15, но включая 20. last > 15 & last <= 20 Последняя переменная LinkedIn — 14, которая не находится между 15 и 20. | Скриншот: Линда Нго

 

Оператор И Пример задачи 2

Рассмотрим следующие векторы:

 linkedin <- c(16, 9, 13, 5, 2, 17, 14)
facebook <- c(17, 7, 5, 16, 8, 13, 14) 

Вектор linkedin представляет просмотры вашего профиля LinkedIn за последние семь дней, а вектор facebook представляет просмотры вашего Профиль Facebook за последние семь дней.

Определите, когда количество просмотров LinkedIn превысило 10, а количество просмотров Facebook не достигло 10 за определенный день. Используйте linkedin и facebook векторов.

 

Пример 2 Решение

 # linkedin больше 10, но facebook меньше 10
linkedin > 10 и facebook < 10 

Только на третий день число просмотров LinkedIn превысило 10, а число просмотров Facebook — меньше 10. | Снимок экрана: Линда Нго

 

И Пример задачи оператора 3

Рассмотрим следующую матрицу:

 просмотров <- matrix(c(linkedin, facebook), nrow = 2, byrow = TRUE) 

Переменная linkedin и facebook соответствует тем же векторам в предыдущем примере.

Первая и вторая строки в матрице представлений соответствуют векторам linkedin и facebook соответственно.

Определите, когда матрица просмотров равна числу от 11 до 14, исключая 11 и включая 14.

 

Пример 3 Решение

 # Когда количество просмотров находится между 11 (исключительно) и 14 (включительно)?
просмотров > 11 и просмотров <= 14 

На третий и последний день количество просмотров LinkedIn составляло от 11 (без учета) до 14 (включительно). На шестой и последний день количество просмотров в Facebook составляло от 11 (исключительно) до 14 (включительно). | Скриншот: Линда Нго

 

ИЛИ Оператор «|»

Оператор ИЛИ | работает аналогично оператору И и , но разница в том, что только одно из логических значений должно быть равно ИСТИНА для того, чтобы вся операция ИЛИ оценивалась как ИСТИНА .

Это означает, что ИСТИНА | ИСТИНА равно ИСТИНА , а также ИСТИНА | ЛОЖЬ и ЛОЖЬ | ИСТИНА оценивается как ИСТИНА . Когда обе логические ЛОЖЬ в операции ИЛИ, ЛОЖЬ | ЛОЖЬ , результат ЛОЖЬ . Помните, что операция ИЛИ не является операцией исключающего ИЛИ, поэтому TRUE | ИСТИНА также равна ИСТИНА .

Только ЛОЖЬ и ЛОЖЬ дадут нам ЛОЖЬ. | Скриншот: Линда Нго

С оператором И только ИСТИНА и ИСТИНА дает ИСТИНА , все остальное равно ЛОЖЬ . С оператором ИЛИ только FALSE | ЛОЖЬ дает ЛОЖЬ , все остальное ИСТИНА .

Как и в операциях И, мы можем использовать сравнения вместе с оператором ИЛИ. Предположим, у нас есть переменная y , равная четырем. Чтобы увидеть, меньше ли эта переменная пяти или больше 15, мы можем использовать следующее выражение:

 г <- 4
у < 5 | y > 15 

R сначала выполнит сравнение, в результате чего TRUE | FALSE , что, в свою очередь, приводит к TRUE .

Теперь предположим, что y равно 14. Выражение y < 5 | y > 15 теперь оценивается как FALSE | ЛОЖЬ . Ни одно из сравнений не является ИСТИНА , поэтому результат ЛОЖЬ .

Подробнее о науке о данных: 8 способов фильтрации кадров данных Pandas

 

Пример задачи оператора ИЛИ 1

Используя те же переменные из «Пример задачи оператора И 3», определите, является ли last меньше пяти или больше 10.

 linkedin <- c(16, 9, 13, 5, 2, 17, 14)
last <- tail(linkedin, 1) 

 

Пример 1 Решение

 # Last меньше 5 или больше 10?
последний < 5 | last > 10 

Последний элемент LinkedIn имеет номер 14, и хотя он меньше пяти, он больше 10, поэтому выражение оценивается как истинное. | Скриншот: Линда Нго

 

Пример оператора ИЛИ Задача 2

Рассмотрим те же векторы linkedin и facebook из предыдущего примера.

 линкин <- c(16, 9, 13, 5, 2, 17, 14)
facebook <- c(17, 7, 5, 16, 8, 13, 14) 

Определите, когда один или оба социальных профиля были посещены не менее 12 раз.

 

Пример 2 Решение

 # Когда одно или оба посещения были по крайней мере 12 раз?
связанный >= 12 | фейсбук >= 12 

В дни 1, 3, 4, 6 и 7 один или оба социальных профиля были посещены не менее 12 раз. | Скриншот: Линда Нго

 

НЕ Оператор «!»

Оператор НЕ, представленный восклицательным знаком ! просто инвертирует логическое значение, для которого оно используется. То есть !TRUE оценивается как FALSE , а !FALSE оценивается как TRUE .

!TRUE оценивается как FALSE, а !FALSE оценивается как TRUE. | Скриншот: Линда Нго

Как и операторы ИЛИ и И, мы можем использовать оператор НЕ в сочетании с логическими операторами. Это не всегда необходимо. Например, !(x < 5) совпадает с x >= 5 .

Однако в R есть случаи, когда оператор NOT особенно удобен. Например, встроенная функция R is.numeric() проверяет, является ли объект R числовым. Нет соответствующей встроенной функции, которая проверяет, не является ли это числом. Для проверки нам пришлось бы инвертировать результат ( !is.numeric() ). Таким образом, is.numeric(5) оценивается как TRUE , так как пять является числом. Если мы отрицаем этот результат, используя оператор НЕ ( !is.numeric(5) ), мы получаем FALSE . Однако если мы используем is.numeric("hello") , мы получаем FALSE . Отрицание этого результата ( !is.numeric("hello") ) дает нам TRUE .

 

Логические операторы и векторы

Итак, как логические операторы работают с векторами и матрицами? Как и реляционные операторы, они выполняют операции поэлементно. Рассмотрим эти два вектора:

 c(ИСТИНА, ИСТИНА, ЛОЖЬ) и c(ИСТИНА, ЛОЖЬ, ЛОЖЬ) 

Операция И над этими двумя векторами приводит к вектору с элементами ИСТИНА , ЛОЖЬ и ЛОЖЬ .

 ИСТИНА ЛОЖЬ ЛОЖЬ 

Первые элементы обоих векторов равны ИСТИНА , поэтому первый элемент результирующего вектора содержит ИСТИНА . То же самое относится ко вторым элементам, где ИСТИНА и ЛОЖЬ приводят к ЛОЖЬ , и к третьим элементам, где ЛОЖЬ и ЛОЖЬ дать ЛОЖЬ .

То же самое происходит с оператором ИЛИ:

 c(ИСТИНА, ИСТИНА, ЛОЖЬ) | c(ИСТИНА, ЛОЖЬ, ЛОЖЬ) 

ИСТИНА | ИСТИНА дает ИСТИНА, ИСТИНА | ЛОЖЬ также дает ИСТИНА и ЛОЖЬ | ЛОЖЬ дает ЛОЖЬ . Итак, мы получили бы результат:

 ИСТИНА ИСТИНА ЛОЖЬ 

Оператор НЕ работает также с каждым элементом вектора:

 !c(ИСТИНА, ИСТИНА, ЛОЖЬ) 

ИСТИНА преобразуются в ЛОЖЬ , а ЛОЖЬ преобразуются в ИСТИНА . Таким образом, мы получили бы результат:

 FALSE FALSE TRUE 

Использование логических операторов для утверждений true-false. | Снимок экрана: Линда Нго

 

Логические операторы и примеры Пример задачи

Что вернет следующий набор выражений R:

 x <- 5
у <- 7
!(!(x < 4) & !!!(y > 12)) 

 

Решение

 FALSE 

Чтобы найти ответ, полезно разбить запрос на более мелкие выражения.

Сначала у нас есть левое выражение !(x < 4) внутреннего выражения (!(x < 4) & !!!(y > 12)) .

1. x < 4 : Поскольку x равно пяти, а 5 < 4 неверно, это утверждение оценивается как FALSE .
2. !(x < 4) : Из предыдущего шага мы определили, что x < 4 оценивается как FALSE . Отрицание этого результата дает нам !FALSE , что равно TRUE .

Далее у нас есть правильное выражение !!!(y > 12) внутреннего выражения (!(x < 4) & !!!(y > 12)) .

1. y > 12 : Поскольку y равно семи, а 7 > 12 неверно, это выражение дает FALSE .
2. !(y > 12) : Отрицая результат первого шага, получаем !ЛОЖЬ или ИСТИНА .
3. !!(y > 12) : отрицая результат второго шага, мы получаем !TRUE или FALSE .
4. !!!(y > 12) : Отрицая результат третьего шага, мы получаем !FALSE или TRUE .

Итак, для внутреннего выражения (!(x < 4) & !!!(y > 12)) , оно оценивается как TRUE & TRUE , что равно TRUE .

Внешний оператор НЕ ! отрицает это ИСТИНА , что дает !(!(x < 4) & !!!(y > 12)) равно !ИСТИНА или ЛОЖЬ .

Учебник по логическим операторам в R. | Видео: DataCamp

Подробнее о науке о данных: как отобразить все столбцы и строки в Pandas DataFrame

 

Одиночные и двойные операторы «&» против «&&», «|» против «||»

В чем разница между одинарным и двойным амперсандом или вертикальной чертой? В R вы можете использовать как версию с одним знаком, так и версию с двумя знаками, но результат выполняемой вами логической операции может быть другим. Самая большая разница возникает, когда вы используете два типа операций над векторами.

 c(TRUE, TRUE, FALSE) & c(TRUE, FALSE, FALSE) 

Как мы видели ранее, приведенное выше выражение оценивается как вектор:

 TRUE FALSE FALSE 

Однако, если мы используем && , мы просто получаем TRUE .

 c(TRUE, TRUE, FALSE) && c(TRUE, FALSE, FALSE) 

Это связано с тем, что операция двойного И проверяет только первый элемент каждого вектора.