Что такое соленоид и как он создает магнитное поле. Как рассчитать индукцию магнитного поля внутри соленоида. Какие факторы влияют на силу магнитного поля соленоида. Где применяются соленоиды на практике.
Что такое соленоид и как он создает магнитное поле
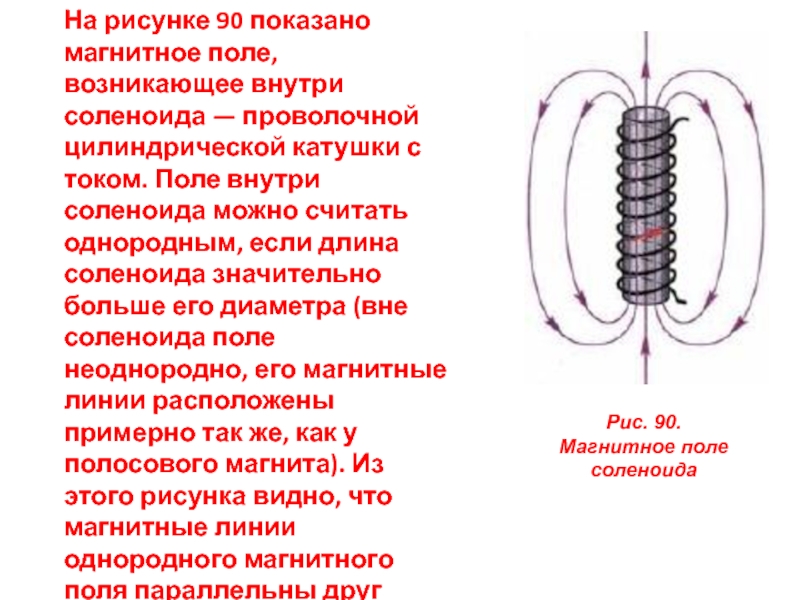
Соленоид представляет собой катушку из изолированного провода, намотанного в виде спирали. При пропускании электрического тока через витки соленоида внутри него возникает магнитное поле. Это поле обладает рядом важных особенностей:
- Внутри длинного соленоида магнитное поле однородно и направлено вдоль его оси
- Снаружи соленоида магнитное поле практически отсутствует
- Напряженность поля прямо пропорциональна силе тока и числу витков на единицу длины
Таким образом, соленоид позволяет создавать сильное и однородное магнитное поле в ограниченном объеме. Это делает его очень удобным инструментом для многих практических применений.
Расчет индукции магнитного поля внутри соленоида
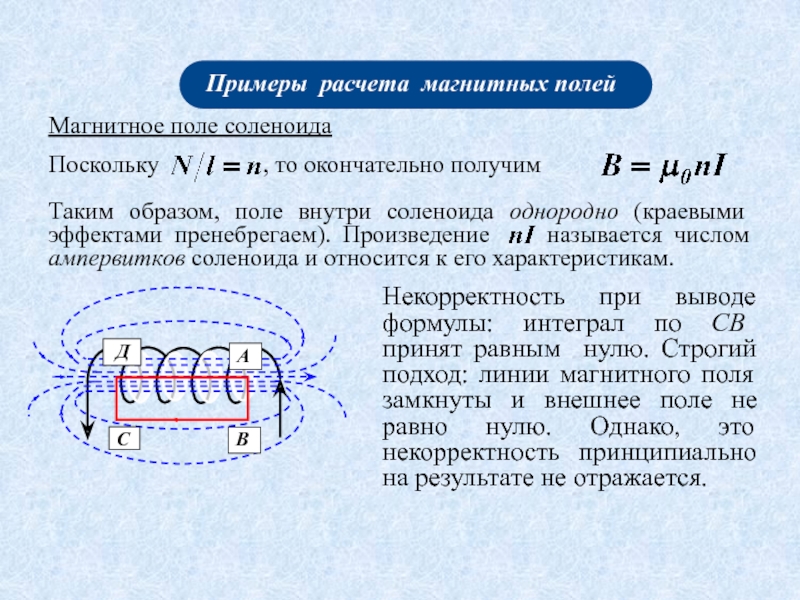
Индукция магнитного поля B внутри бесконечно длинного соленоида рассчитывается по формуле:

B = μ0nI
Где:
- μ0 — магнитная постоянная (4π × 10^-7 Гн/м)
- n — число витков на единицу длины соленоида
- I — сила тока в обмотке
Для соленоида конечной длины L формула принимает вид:
B = μ0nI × L/√(L^2 + 4R^2)
Где R — радиус соленоида.
Как видно из формул, индукция магнитного поля соленоида прямо пропорциональна силе тока и плотности намотки. Чем больше витков и сильнее ток, тем сильнее магнитное поле внутри соленоида.
Факторы, влияющие на силу магнитного поля соленоида
На интенсивность магнитного поля, создаваемого соленоидом, влияют следующие основные факторы:
- Сила тока в обмотке — чем больше ток, тем сильнее поле
- Число витков на единицу длины — более плотная намотка усиливает поле
- Длина соленоида — у длинных соленоидов поле более однородно
- Диаметр соленоида — у тонких соленоидов поле сильнее
- Материал сердечника — ферромагнитный сердечник многократно усиливает поле
Изменяя эти параметры, можно регулировать характеристики магнитного поля соленоида в широких пределах. Это позволяет создавать соленоиды с оптимальными свойствами для различных применений.
Практическое применение соленоидов
Благодаря способности создавать сильное и управляемое магнитное поле, соленоиды широко используются в технике и науке:
- Электромагниты и реле
- Электродвигатели и генераторы
- Электромагнитные клапаны
- Магнитно-резонансные томографы
- Ускорители заряженных частиц
- Электромагнитные пушки
- Системы магнитной левитации
Во всех этих устройствах соленоиды позволяют преобразовывать электрическую энергию в механическую работу или управлять движением заряженных частиц с помощью магнитного поля.
Энергия магнитного поля соленоида
Магнитное поле соленоида обладает энергией, которая может быть рассчитана по формуле:
W = (1/2)LI^2
Где:
- W — энергия магнитного поля
- L — индуктивность соленоида
- I — сила тока
Эта энергия накапливается в магнитном поле при протекании тока через соленоид. При выключении тока энергия поля преобразуется обратно в электрическую, вызывая ЭДС самоиндукции.
Понимание энергетических процессов в соленоиде важно для расчета и проектирования различных электромагнитных устройств.
Влияние материала сердечника на магнитное поле соленоида
Размещение внутри соленоида сердечника из ферромагнитного материала (например, железа) значительно усиливает создаваемое магнитное поле. Это происходит за счет явления магнитной индукции в ферромагнетике. Усиление поля может достигать сотен и тысяч раз по сравнению с соленоидом без сердечника.
При этом индукция магнитного поля в соленоиде с сердечником рассчитывается по формуле:
B = μ0μrn I
Где μr — относительная магнитная проницаемость материала сердечника.
Использование ферромагнитных сердечников позволяет создавать очень сильные электромагниты при относительно небольших токах. Однако при этом возникают эффекты магнитного гистерезиса и насыщения, которые необходимо учитывать при проектировании устройств.
Сравнение магнитного поля соленоида и постоянного магнита
Магнитное поле соленоида во многом аналогично полю постоянного магнита-соленоида. Их основные различия:
- Поле соленоида существует только при протекании тока, поле магнита — постоянно
- Напряженность поля соленоида легко регулируется изменением тока
- Поле соленоида может быть быстро включено, выключено или изменено
- Соленоид позволяет получить более сильное и однородное поле
Эти особенности делают электромагниты на основе соленоидов более универсальными и управляемыми по сравнению с постоянными магнитами. В то же время постоянные магниты не требуют источника питания, что удобно в ряде применений.

Понимание сходств и различий между этими типами магнитных полей важно для правильного выбора решения в конкретных технических задачах.
Магнитное поле соленоида
Применим теорему о циркуляции вектора для вычисления простейшего магнитного поля – бесконечно длинного соленоида, представляющего собой тонкий провод, намотанный плотно виток к витку на цилиндрический каркас (рис. 2.11).
Рис. 2.11
Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью.
Бесконечно длинный соленоид симметричен любой, перпендикулярной к его оси плоскости. Взятые попарно (рис. 2.12), симметричные относительно такой плоскости витки создают поле, в котором вектор перпендикулярен плоскости витка, т.е. линии магнитной индукции имеют направление параллельное оси соленоида
Рис. 2.12
Из параллельности вектора оси соленоида вытекает, что поле как внутри, так и вне соленоида должно быть однородным.
Возьмём воображаемый прямоугольный контур 1–2–3–4–1 и разместим его в соленоиде, как показано на рисунке 2.13.
Рис. 2.13
Второй и четвёртый интегралы равны нулю, т.к. вектор перпендикулярен направлению обхода, т.е .
Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда
где – магнитная индукция на участке 1–2 – внутри соленоида, – магнитная проницаемость вещества.
Если отрезок 1–2 внутри соленоида, контур охватывает ток:
где n – число витков на единицу длины, I – ток в соленоиде (в проводнике).
Тогда магнитная индукция внутри соленоида:
| , | (2.7.1) |
Вне соленоида:
и , т.е. .
Бесконечно длинный соленоид аналогичен плоскому конденсатору – и тут, и там поле однородно и сосредоточено внутри.
Произведение nI – называется число ампер витков на метр.
У конца полубесконечного соленоида, на его оси магнитная индукция равна:
| , | (2.7.2) |
Практически, если длина соленоида много больше, чем его диаметр, формула (2.7.1) справедлива для точек вблизи середины, формула (2.7.2) для точек около конца.
Если же катушка короткая, что обычно и бывает на практике, то магнитная индукция в любой точке А, лежащей на оси соленоида, направлена вдоль оси (по правилу буравчика) и численно равна алгебраической сумме индукций магнитных полей создаваемых в точке А всеми витками. В этом случае имеем:
· В точке, лежащей на середине оси соленоида магнитное поле будет максимальным:
| , | (2.7.3) |
где L – длина соленоида, R – радиус витков.
· В произвольной точке конечного соленоида (рис. 2.14) магнитную индукцию можно найти по формуле
| , | (2.7.4) |
Рис. 2.14
На рисунке 2.15 изображены силовые линии магнитного поля : а) металлического стержня; б) соленоида; в) железные опилки, рассыпанные на листе бумаги, помещенной над магнитом, стремятся вытянуться вдоль силовых линий; г) магнитные полюсы соленоида.
Рис. 2.15
Магнитное поле соленоида — Студопедия
Соленоидом называют катушку цилиндрической формы из проволоки, витки которой намотаны вплотную в одном направлении, а длина катушки значительно больше радиуса витка.
Магнитное поле соленоида можно представить как результат сложения полей, создаваемых несколькими круговыми токами, имеющими общую ось. На рисунке 3 видно, что внутри соленоида линии магнитной индукции каждого отдельного витка имеют одинаковое направление, тогда как между соседними витками они имеют противоположное направление.
Рис. 3
Поэтому при достаточно плотной намотке соленоида противоположно направленные участки линий магнитной индукции соседних витков взаимно уничтожаются, а одинаково направленные участки сольются в общую линию магнитной индукции, проходящую внутри соленоида и охватывающую его снаружи. Изучение этого поля с помощью опилок показало, что внутри соленоида поле является однородным, магнитные линии представляют собой прямые линии, параллельные оси соленоида, которые расходятся на его концах и замыкаются вне соленоида (рис. 4).
Рис. 4
Нетрудно заметить сходство между магнитным полем соленоида (вне его) и магнитным полем постоянного стержневого магнита (рис. 5). Конец соленоида, из которого магнитные линии выходят, аналогичен северному полюсу магнита N, другой же конец соленоида, в который магнитные линии входят, аналогичен южному полюсу магнита S.
Рис. 5
Полюсы соленоида с током на опыте легко определить с помощью магнитной стрелки. Зная же направление тока в витке, эти полюсы можно определить с помощью правила правого винта: вращаем головку правого винта по току в витке, тогда поступательное движение острия винта укажет направление магнитного поля соленоида, а следовательно, и его северного полюса. Модуль магнитной индукции внутри однослойного соленоида вычисляется по формуле
B = μμ 0 NI l = μμ 0 nl,
где Ν — число витков в соленоиде, I — длина соленоида, n — число витков, приходящееся на единицу длины соленоида.
| Намагничивание магнетика. Вектор намагниченности. | |||||||||
Если по проводнику течет ток, то вокруг проводника создаётся МП. Мы пока рассматривали провода, по которым текли токи, находящиеся в вакууме. Если провода, несущие ток, находятся в некоторой среде, то м.п. изменяется. Это объясняется тем, что под действием м.п. всякое вещество способно приобретать магнитный момент, или намагничиваться (вещество становится магнетиком). Вещества, намагничивающиеся во внешнем м.п. против направления поля называются
Истинное (микроскопическое) поле в магнетике сильно изменяется в пределах межмолекулярных расстояний. – усреднённое макроскопическое поле. Для объяснения намагничения тел Ампер предположил, что в молекулах вещества циркулируют круговые микроскопические токи, обусловленные движением электронов в атомах и молекулах. Каждый такой ток обладает магнитным моментом и создаёт в окружающем пространстве м.п. Если внешнее поле отсутствует, то молекулярные токи ориентированы беспорядочным образом, и обусловленное ими результирующее поле равно 0. Намагниченностью называют векторную величину, равную магнитному моменту единицы объёма магнетика:
где — физически бесконечно малый объём, взятый в окрестности рассматриваемой точки; — магнитный момент отдельной молекулы. Суммирование производится по всем молекулам, заключённым в объёме (вспомним где, — поляризованность диэлектрика , — дипольный элемент ). Намагниченность можно представить так: Токи намагничивания I’ . Намагничивание вещества связано с преимущественной ориентацией магнитных моментов отдельных молекул в одном направлении. Элементарные круговые токи, связанные с каждой молекулой, называются молекулярными. Молекулярные токи оказываются ориентированными, т.е. возникают токи намагничивания — . Токи, текущие по проводам, вследствие движения в веществе носителей тока называют токами проводимости — . Для электрона движущегося по круговой орбите по часовой стрелке; ток направлен против часовой стрелки и по правилу правого винта направлен вертикально вверх. Циркуляция вектора намагниченности по произвольному замкнутому контуру равна алгебраической сумме токов намагничивания, охватываемых контуром Г. Дифференциальная форма записи теоремы о циркуляции вектора .
Дифференциальная форма записи теоремы о циркуляции — формула (54.7) – ротор вектора намагниченности равен плотности тока намагничивания в той же точке пространства вещества |
Напряжённость магнитного поля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M.
В СИ: где — магнитная постоянная.
В СГС:
В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот изменения поля B и H просто пропорциональны друг другу, отличаясь просто числовым множителем (зависящим от среды) B = μ H в системе СГС или B = μ0μ H в системе СИ (см. Магнитная проницаемость, также см. Магнитная восприимчивость).
В системе СГС напряжённость магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике эрстед постепенно вытесняется единицей СИ — ампером на метр.
1 Э = 1000/(4π) А/м ≈ 79,5775 А/м.
1 А/м = 4π/1000 Э ≈ 0,01256637 Э.
Физический смысл
В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряжённость магнитного поля совпадает с вектором магнитной индукции с точностью до коэффициента, равного 1 в СГС и μ0 в СИ.
В магнетиках (магнитных средах) напряжённость магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».
Например, если поле создаётся катушкой с током, в которую вставлен железный сердечник, то напряжённость магнитного поля H внутри сердечника совпадает (в СГС точно, а в СИ — с точностью до постоянного размерного коэффициента) с вектором B0, который был бы создан этой катушкой при отсутствии сердечника и который в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, без всякой дополнительной информации о материале сердечника и его магнитных свойствах.
При этом надо иметь в виду, что более фундаментальной характеристикой магнитного поля является вектор магнитной индукции B. Именно он определяет силу действия магнитного поля на движущиеся заряженные частицы и токи, а также может быть непосредственно измерен, в то время как напряжённость магнитного поля H можно рассматривать скорее как вспомогательную величину (хотя рассчитать её, по крайней мере, в статическом случае, проще, в чём и состоит её ценность: ведь H создают так называемые свободные токи, которые сравнительно легко непосредственно измерить, а трудно измеримые связанные токи — то есть токи молекулярные и т. п. — учитывать не надо).
Правда, в обычно используемое выражение для энергии магнитного поля (в среде) B и H входят почти равноправно, но надо иметь в виду, что в эту энергию включена и энергия, затраченная на поляризацию среды, а не только энергия собственно поля. Энергия магнитного поля как такового выражается только через фундаментальное B. Тем не менее видно, что величина H феноменологически и тут весьма удобна.
Виды магнетиков Диамагнетики имеют магнитную проницаемость чуть меньше 1. Отличаются тем, что выталкиваются из области магнитного поля.
Парамагнетики имеют магнитную проницаемость чуть более 1. Подавляющее количество материалов являются диа- и пара- магнетиками.
Ферромагнетики обладают исключительно большой магнитной проницаемостью, доходящей до миллиона.
По мере усиления поля проявляется явление гистерезиса, когда при увеличении напряженности и при последующем уменьшении напряженности значения В(Н) не совпадают друг с другом. В литературе различают несколько определений магнитной проницаемости.
Начальная магнитная проницаемость mн — значение магнитной проницаемости при малой напряженности поля.
Максимальная магнитная проницаемость mmax — максимальное значение магнитной проницаемости, которое достигается обычно в средних магнитных полях.
Из других основных терминов, характеризующих магнитные материалы, отметим следующие.
Намагниченность насыщения — максимальная намагниченность, которая достигается в сильных полях, когда все магнитные моменты доменов ориентированы вдоль магнитного поля.
Петля гистерезиса — зависимость индукции от напряженности магнитного поля при изменении поля по циклу: подъем до определенного значения — уменьшение, переход через нуль, после достижения того же значения с обратным знаком — рост и т.п.
Максимальная петля гистерезиса — достигающая максимальной намагниченности насыщения.
Остаточная индукция Bост — индукция магнитного поля на обратном ходе петли гистерезиса при нулевой напряженности магнитного поля.
Коэрцитивная сила Нс — напряженность поля на обратном ходе петли гистерезиса при которой достигается нулевая индукция.
| Магнитные моменты атомов |
|
Магнитный момент Элементарные частицы обладают внутренним квантовомеханическим свойством известным как спин. Оно аналогично угловому моменту объекта вращающегося вокруг собственного центра масс, хотя строго говоря, эти частицы являются точечными и нельзя говорить об их вращении. Спин измеряют в единицах приведённой планковской постоянной ( ), тогда электроны, протоны и нейтроны имеют спин равный ½ . В атоме электроны обращаются вокруг ядра и обладают орбитальным угловым моментом помимо спина, в то время как ядро само по себе имеет угловой момент благодаря ядерному спину. Магнитное поле, создаваемое магнитным моментом атома, определяется этими различными формами углового момента, как и в классической физике вращающиеся заряженные объекты создают магнитное поле. Однако, наиболее значительный вклад происходит от спина. Благодаря свойству электрона, как и всех фермионов, подчиняться правилу запрета Паули, по которому два электрона не могут находиться в одном и том же квантовом состоянии, связанные электроны спариваются друг с другом, и один из электронов находится в состоянии со спином вверх, а другой — с противоположной проекцией спина — состояние со спином вниз. Таким образом магнитные моменты электронов сокращаются, уменьшая полный магнитный дипольный момент системы до нуля в некоторых атомах с чётным числом электронов. В ферромагнитных элементах, таких как железо, нечётное число электронов приводит к появлению неспаренного электрона и к ненулевому полному магнитному моменту. Орбитали соседних атомов перекрываются, и наименьшее энергетическое состояние достигается, когда все спины неспаренных электронов принимают одну ориентацию, процесс известный как обменное взаимодействие. Когда магнитные моменты ферромагнитных атомов выравниваются, материал может создавать измеримое макроскопическое магнитное поле. Парамагнитные материалы состоят из атомов , магнитные моменты которых разориентированы в отсутствии магнитного поля, но магнитные моменты отдельных атомов выравниваются при приложении магнитного поля. Ядро атома тоже может обладать ненулевым полным спином. Обычно при термодинамическом равновесии спины ядер ориентированы случайным образом. Однако, для некоторых элементов (таких как ксенон-129) возможно поляризовать значительную часть ядерных спинов для создания состояния с сонаправленными спинами —состояния называемого гиперполяризацией. Это состояние имеет важное прикладное значение в магнитно-резонансной томографии. |
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.
Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна
Wм = LI2/ 2
Электричество и магнетизм
Если длина соленоида много больше его диаметра (l >> 2R), мы возвращаемся к формуле для поля в бесконечно длинном соленоиде (6.20). Относительная разница этих двух значений равна
По условию эта разница мала: , то есть мало отношение диаметра соленоида к его длине: 2R/l << 1. Поэтому можно воспользоваться формулой разложения квадратного корня
Отсюда
или
Подставляя численное значение d, находим, что разница будет менее половины процента при выполнении соотношения
Иными словами, соленоид может рассматриваться как бесконечно длинный, если его длина в двадцать или более раз превышает радиус.
Пример 2. Найти магнитное поле Ве в крайней торцевой точке оси соленоида конечной длины l. Сравнить с результатом предыдущего примера.
Решение. Магнитное поле в торцевой точке оси соленоида конечной длины l дается тем же интегралом (6.19), но теперь пределы интегрирования будут выглядеть иначе
|
(6.22) |
Отношение полей в средней и крайней точках оси соленоида равно
Это отношение всегда меньше единицы (то есть поле на торце меньше поля в середине соленоида). При l >> R имеем
Этот результат легко понять. Представим себе бесконечный соленоид, который мысленно рассекаем пополам в точке наблюдения. Можно считать, что поле в этой точке создается двумя одинаковыми «полубесконечными» соленоидами, расположенными по разные стороны от нее. Ясно, что при удалении одного из них точка наблюдения становится торцом оставшегося «полубесконечного» соленоида, а магнитная индукция в ней уменьшиться именно в два раза.
Это — так называемый краевой эффект. Пример демонстрирует, что недостаточно выполнения соотношения l >> R, чтобы пользоваться формулами для бесконечно длинного соленоида; надо еще, чтобы точка наблюдения находилась далеко от его концов.
На рис. 6.25 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг соленоида. Поле соленоида, ось которого лежит в плоскости пластинки, сосредоточено в основном внутри соленоида. Силовые линии внутри имеют вид параллельных прямых вдоль оси катушки, а поле снаружи практически отсутствует.
Рис. 6.25. Визуализация силовых линий магнитного поля
Видео 6.1. Силовые линии магнитного поля проводников с током различной формы: прямой ток, соленоид, один виток.
Магнитное поле однослойного соленоида
Соленоид – это цилиндрическая обмотка из провода по которой протекает постоянный или переменный электрический ток.{N} I_i.\]
(1)
Если пренебречь краевыми эффектами, то первое и третье слагаемые в (1) будут равны нулю, так как магнитное поле перпендикулярно контуру и $B_l=0$. Если контур выбрать так, что $AD$ будет лежать на большом расстоянии от соленоида, где поле стремиться к нулю, то и четвёртое слагаемое в (1) также превратиться в нуль. Тогда, учитывая приближение однородности поля получим:
где $L$ – длина соленоида, $N$ – количество витков. Если ввести понятие плотности витков (число витков на единицу длины) $n=N/L$, то индукцию магнитного поля внутри соленоида (2) можно записать в виде:
Рис. 2: Соленоид с произвольными размерами $L$ и $R$.
Чтобы получить точное выражение для индукции магнитного поля в любой точке на оси конечного соленоида необходимо воспользоваться законом Био-Савара-Лапласа (Рис. 2), который приводит к следующему выражению:
\[B=\frac12\mu_0 nI (\cos\alpha_2-\cos\alpha_1).2}},\](5)
где $R$ – радиус соленоида. А на краю полубесконечного соленоида:
\[B=\frac12 \mu_0 nI.\]
(6)
Калькулятор
Индукция магнитного поля бесконечного соленоида (3)
Индукция магнитного поля конечного соленоида (5)
Распределение индукция магнитного внутри конечного соленоида (4)
Магнитное поле внутри соленоида. Напряженность магнитного поля
Особый интерес представляет магнитное поле внутри соленоида, длина которого значительно превосходит его диаметр. Внутри такого соленоида магнитная индукция имеет повсюду одно и то же направление, параллельное оси соленоида, и значит, линии поля параллельны между собой.
Измеряя каким-нибудь способом магнитную индукцию в разных точках внутри соленоида, мы можем убедиться в том, что если витки соленоида расположены равномерно, то индукция магнитного поля внутри соленоида имеет во всех точках не только одинаковое направление, но и одинаковое числовое значение. Итак, поле внутри длинного равномерно навитого соленоида однородно. В дальнейшем, говоря о поле внутри соленоида, мы всегда будем иметь в виду подобные «длинные» равномерные соленоиды и не будем обращать внимания на отступления от однородности поля в областях, близких к концам соленоида.
Подобные измерения, выполненные с разными соленоидами при различной силе тока в них, показали, что магнитная индукция поля внутри длинного соленоида пропорциональна силе тока и числу витков, приходящихся на единицу длины соленоида, т. е. величине , где – полное число витков соленоида, – его длина. Таким образом,
, (126.1)
где – коэффициент пропорциональности, называемый магнитной постоянной (ср. с электрической постоянной , § 11). Числовое значение магнитной постоянной
Тл×м/А.
Впоследствии (§ 157) выяснится, что единица, в которой выражена величина , может быть названа «генри на метр», где генри (Гн) – единица индуктивности. Следовательно, можно написать, что
Гн/м. (126.2)
В силу своей простоты поле соленоида используется в качестве эталонного поля.
Для характеристики магнитного поля, кроме магнитной индукции , используют также векторную величину , называемую напряженностью магнитного поля. В случае поля в вакууме величины и просто пропорциональны друг другу:
, (126.3)
так что введение величины не вносит ничего нового. Однако в случае поля в веществе связь с имеет вид
, (126.4)
где – безразмерная характеристика вещества, называемая относительной магнитной проницаемостью или просто магнитной проницаемостью вещества. При рассмотрении магнитных полей в веществе, например в железе, величина оказывается полезной. Подробнее об этом идет речь в § 144.
Из формул (126.1) и (126.3) следует, что в случае, когда соленоид находится в вакууме, напряженность магнитного поля
, (126.5)
т. е., как говорят, равна числу ампер-витков на метр.
С помощью измерений магнитной индукции поля, создаваемого током, текущим по очень длинному тонкому прямолинейному проводнику, было установлено, что
, (126.6)
где – сила тока в проводнике, – расстояние от проводника.
Согласно формуле (126.3) напряженность поля, создаваемого прямолинейным проводником, находящимся в вакууме, равна
. (126.7)
В соответствии с формулой (126.7) единица напряженности магнитного поля носит название ампер на метр (А/м). Один ампер на метр есть напряженность магнитного поля на расстоянии одного метра от тонкого прямолинейного бесконечно длинного проводника, по которому течет ток силой ампер.
126.1. Магнитная индукция поля внутри соленоида равна 0,03 Тл. Какой силы ток проходит в соленоиде, если длина его равна 30 см, а число витков равно 120?
126.2. Как изменится магнитная индукция поля внутри соленоида из предыдущей задачи, если соленоид растянуть до 40 см или сжать его до 10 см? Что произойдет, если сложить соленоид пополам так, чтобы витки одной его половины легли между витками второй половины?
126.3. По соленоиду длины 20 см, состоящему из 60 витков диаметра 15 см, идет ток. Что произойдет с магнитным полем внутри соленоида, если уменьшить диаметр его витков до 5 см, сохранив прежнюю длину соленоида и использовав тот же самый кусок провода? Каким способом можно получить прежнюю магнитную индукцию поля, сохранив неизменными длину и диаметр витков соленоида?
126.4. Внутри соленоида длины 8 см, состоящего из 40 витков, расположен другой соленоид с числом витков на 1 см длины соленоида, равным 10. Через оба соленоида проходит одинаковый ток 2 А. Какова магнитная индукция поля внутри обоих соленоидов, если северные концы их обращены: а) в одну сторону; б) в противоположные стороны?
126.5. Имеются три соленоида длины 30 см, 5 см и 24 см с числом витков 1500, 1000 и 600 соответственно. По первому соленоиду идет ток 1 А. Какие токи должны идти по второму и третьему соленоидам, чтобы магнитная индукция внутри всех трех соленоидов была одной и той же?
126.6. Вычислите магнитную индукцию поля в каждом из соленоидов задачи 126.5.
126.7. В соленоиде длины 10 см нужно получить магнитное поле с напряженностью, равной 5000 А/м. При этом ток в соленоиде должен быть равен 5 А. Из скольких витков должен состоять соленоид?
126.8. Какова магнитная индукция поля внутри соленоида, длина которого равна 20 см, а полное число витков равно 500, при токе 0,1 А? Как изменится магнитная индукция, если соленоид будет растянут до 50 см, а ток уменьшен до 10 мА?
Соленоид — Википедия
Соленоид с однослойной намоткой. Образование магнитного потока в соленоиде. В центре по длине на оси соленоида магнитное поле практически однородно.Солено́ид (от греч. solen — канал, труба и eidos — подобный) — разновидность катушки индуктивности. Обычно под термином «соленоид» подразумевается цилиндрическая обмотка из провода, причём длина такой обмотки многократно превышает её диаметр.
Конструктивно длинные соленоиды выполняются как в виде однослойной намотки (см. рис.), так и многослойной.
Если длина намотки значительно превышает диаметр намотки, то в полости соленоида при подаче в него электрического тока порождается магнитное поле, близкое к однородному.
Также часто соленоидами называют электромеханические исполнительные механизмы, обычно со втягиваемым ферромагнитным сердечником. В таком применении соленоид почти всегда снабжается внешним ферромагнитным магнитопроводом, обычно называемым ярмом.
Бесконечно длинный соленоид — это соленоид, длина которого стремится к бесконечности (то есть его длина много больше его поперечных размеров).
Соленоид на постоянном токе
Если длина соленоида намного больше его диаметра и не используется магнитный материал, то при протекании тока по обмотке внутри катушки создаётся магнитное поле, направленное вдоль оси, которое однородно и для постоянного тока по величине равно[1]:
B=μ0nI{\displaystyle B=\mu _{0}nI} (СИ) (1),{\displaystyle \qquad (1),}
B=4πcnI{\displaystyle B={\frac {4\pi }{c}}nI} (СГС) (2),{\displaystyle \qquad (2),}
где μ0{\displaystyle \mu _{0}} — магнитная проницаемость вакуума, n=N/l{\displaystyle n=N/l} — число витков на единицу длины соленоида, N{\displaystyle N} — число витков, l{\displaystyle l} — длина соленоида, I{\displaystyle I} — ток в обмотке.
Вследствие того, что две половины бесконечного соленоида в точке их соединения вносят одинаковый вклад в магнитное поле, магнитная индукция полубесконечного соленоида у его края вдвое меньше, чем в объёме. То же самое можно сказать о поле на краях конечного, но достаточно длинного соленоида[1]:
BKP=12μ0nI{\displaystyle B_{\mathrm {KP} }={\frac {1}{2}}\mu _{0}nI} (СИ) (3).{2}V\qquad (10),} эквивалентная предыдущим двум формулам.
Соленоид на переменном токе
При переменном токе соленоид создаёт переменное магнитное поле. Если соленоид используется как электромагнит, то на переменном токе величина силы притяжения изменяется. В случае якоря из магнитомягкого материала направление силы притяжения не изменяется. В случае магнитного якоря направление силы меняется. На переменном токе соленоид имеет комплексное сопротивление, активная составляющая которого определяется активным сопротивлением обмотки, а реактивная составляющая определяется индуктивностью обмотки.
Применение
Соленоиды постоянного тока чаще всего применяются как поступательный силовой электропривод. В отличие от обычных электромагнитов обеспечивает большой ход. Силовая характеристика зависит от строения магнитной системы (сердечника и корпуса) и может быть близка к линейной.
Соленоиды приводят в движение ножницы для отрезания билетов и чеков в кассовых аппаратах, язычки замков, клапаны в двигателях, гидравлических системах и пр. Один из самых известных примеров — «тяговое реле» автомобильного стартёра. Большое распространение соленоиды получили в энергетике, найдя широкое применение в приводах высоковольтных выключателей.
Соленоиды на переменном токе применяются в качестве индуктора для индукционного нагрева в индукционных тигельных печах.
Примечание
- ↑ 1 2 Савельев И. В. (1982), с. 148–152.
Источники
- Савельев И. В. Курс общей физики. — Т. 2. Электричество и магнетизм. Волны. Оптика.
См. также
Задачи физики: магнетизм: магнитная сила
Задача 18.
Магнитное поле 10 мТл создается соленоидом диаметром 10 см и длиной 20 см. Какой ток в соленоиде? Соленоид плотно намотан из проволоки диаметром 1,0 мм.
Решение
Задача 19.
Соленоид имеет диаметр 20 см и длину 10 см.Ток в соленоиде составляет 5 А, а общее количество витков — 10000. Какое магнитное поле внутри соленоида?
Решение
Задача 47.
Соленоид диаметром 4 см имеет 2000 витков на метр. На расстоянии 1 см от оси соленоида напряженность индуцированного электрического поля составляет. Какова скорость изменения тока через соленоид?
Решение
Задача 48.
ЭДС соленоида составляет 10 В, когда ток через него изменяется со скоростью 5 А / с. Найдите количество витков соленоида, если постоянный ток 0,5 А создает поток на оборот.
Решение
Задача 49.
Ток через катушку индуктивности 10 H изменяется со временем как, где ток выражается в А, а время — в секундах. Найдите разность потенциалов на катушке индуктивности.
Решение
Задача 50.
LC-цепь состоит из катушки индуктивности 10 мГн и конденсатора. Максимальное значение тока в цепи составляет 2 А при. Сколько времени осталось до полной зарядки конденсатора? Какой максимальный заряд на конденсаторе?
Решение
Задача 51.
LC-цепь состоит из катушки индуктивности 20 мГн и конденсатора. Максимальный ток в цепи составляет 5 А при. Какое максимальное напряжение на конденсаторе?
Решение
Задача 52.
В колеблющемся LC-контуре, когда 60% общей энергии хранится в магнитной энергии катушки индуктивности, сколько кратного максимального заряда находится на конденсаторе?
Решение
Задача 53.
В LC-цепи максимальная разность потенциалов на конденсаторе во время колебаний составляет 2,0 В, а максимальный ток через катушку индуктивности составляет 50 мА. Какая индуктивность если емкость.
Решение
Задача 57.
Две катушки находятся в фиксированных местах. Когда в катушке 2 отсутствует ток и ток в катушке 1 увеличивается со скоростью 5 А / с, ЭДС в катушке 1 равна 0.05 В. Найдите взаимную индуктивность двух катушек.
Решение
Задача 58.
Взаимная индуктивность двух катушек составляет 10 мГн. Ток в катушке 1 увеличивается со скоростью 10 А / с. Найдите ЭДС в катушке 2.
Решение
Задача 59.
Когда ток через катушку составляет 20 мА, поток через катушку составляет 40 мВт.Найдите индуктивность катушки.
Решение
Задача 60.
Индуктивность плотно упакованной катушки на 500 витков составляет 5 мГн. Ток в катушке составляет 2 А. Рассчитайте магнитный поток на один виток.
Решение
Задача 68.
Катушка индуктивности с индуктивностью и сопротивлением 25 мм подключена к батарее с ЭДС, зависящей от времени.Ток через катушку индуктивности зависит от времени как. Рассчитать ЭДС батареи как функцию времени?
Решение
Задача 69.
К аккумулятору подключена катушка индуктивности с индуктивностью 2 мм, эдс которой зависит от времени как. Рассчитайте ток через катушку индуктивности. Пренебрегайте сопротивлением цепи.
Решение
Задача 70.
Магнитный поток через 100-витковую катушку увеличивается со скоростью 0,1 Вт / с. Индуктивность катушки. Если сопротивление катушки 20 Ом и она подключена к внешней цепи с сопротивлением 40 Ом, найдите ток через катушку.
Решение
Задача 71.
Соленоид длиной 5 см имеет 2000 витков. Рассчитайте его индуктивность. Диаметр соленоида 5 мм.
Решение
Задача 72.
100-витковистый соленоид диаметром 10 см помещен в магнитное поле 0,01 Тл, параллельное оси соленоида. Соленоид вращается за 5 секунд. Рассчитайте среднюю ЭДС, генерируемую соленоидом.
Решение
Задача 73.
Катушка индуктивности 50 мГн подключается к батарее 20 В в нулевой момент времени.Найти ток в цепи при t = 0,1 с. Пренебрегайте сопротивлением цепи и внутренним сопротивлением аккумулятора.
Решение
Задача 74.
Катушка индуктивности 100 мГн подключена к идеальной батарее 10 В при t = 0. Найдите момент времени, когда ток в цепи равен 0,5 А. Сопротивлением цепи пренебречь.
Решение
| Найдите свою проблему в базе данных решенных физических задач (БЕСПЛАТНО) |
Соленоид, катушки магнитного поля, однородное магнитное поле
| Каталог продукции: |
| Описание продукта: |
Введение соленоида :
Soleniod — это своего рода важный инструмент для генерации магнитного поля, он обладает преимуществами простой конструкции, удобством использования, магнитным полем в осевом направлении после включения питания и постоянным линейным соотношением магнитного поля с электрическим током.Когда пропорция длины больше диаметра, она имеет хорошую однородность в центре магнитного поля, и чем больше соотношение, тем шире будет однородная площадь. Соленоид очень подходит для намагничивания прямых и длинных образцов. Многослойный соленоид может увеличить напряженность магнитного поля, более сильное магнитное поле требует большей мощности. Следует учитывать тепловыделение при длительном использовании, следует учитывать даже защитное действие электромагнитной силы.
Наша компания может изготовить различные соленоиды в соответствии с требованиями пользователя.Например, соленоид для длительного использования, максимальное магнитное поле может составлять до 0,7 Тл; соленоид с импульсным возбуждением магнитного поля может достигать 10T около
При оформлении заказа укажите необходимые показатели, чтобы мы выдвинули наиболее точный дизайн:
1. Используя внутренний диаметр
2. Макс. магнитное поле
3. Единая площадь
4. Однородность (ΔH / H)
5. Рабочее время и период
6. Нужен ли источник питания
Характеристики соленоидов серии DXSL
| Модель |
Длина (мм) |
Наружный диаметр (мм) |
Внутренний диаметр (мм) |
Макс.магнитное поле Hm |
Равномерная |
Однородность |
Масса |
Мощность |
| DXSL10-100 |
100 |
38 |
20 |
100 |
20 |
1% |
1.2 |
6 |
| DXSL10-500 |
100 |
85 |
20 |
500 |
15 |
1,5% |
5 |
50 |
| DXSL10-1000 |
100 |
190 |
20 |
1000 |
20 |
5% |
24 |
240 |
| DXSL20-100 |
200 |
73 |
50 |
100 |
20 |
0.5% |
3 |
25 |
| DXSL20-500 |
200 |
116 |
50 |
500 |
20 |
0,8% |
13 |
150 |
| DXSL20-1000 |
200 |
190 |
50 |
1000 |
20 |
0.8% |
42 |
450 |
| DXSL20-2000 |
200 |
350 |
50 |
2000 |
15 |
0,7% |
140 |
1800 |
| DXSL30-100 |
300 |
72 |
50 |
100 |
50 |
0.6% |
6 |
36 |
| DXSL30-500 |
300 |
115 |
50 |
500 |
50 |
0,7% |
20 |
200 |
| DXSL30-1000 |
300 |
180 |
50 |
1000 |
30 |
0.5% |
56 |
600 |
| DXSL30-2000 |
300 |
300 |
50 |
2000 |
30 |
0,6% |
180 |
1800 |
| DXSL50-100 |
500 |
115 |
80 |
100 |
50 |
0.1% |
12 |
110 |
| DXSL50-500 |
500 |
155 |
80 |
500 |
100 |
0,8% |
50 |
500 |
| DXSL50-1000 |
500 |
226 |
80 |
1000 |
50 |
0.5% |
130 |
1400 |
| DXSL50-2000 |
500 |
320 |
80 |
2000 |
50 |
0,5% |
300 |
3200 |
| DXSL70-100 |
700 |
135 |
100 |
100 |
70 |
0.1% |
20 |
200 |
| DXSL70-500 |
700 |
175 |
100 |
500 |
70 |
0,1% |
72 |
750 |
| DXSL70-1000 |
700 |
240 |
100 |
1000 |
70 |
0.2% |
195 |
2100 |
| DXSL70-2000 |
700 |
340 |
100 |
2000 |
70 |
0,5% |
455 |
5400 |
| DXSL100-100 |
1000 |
165 |
100 |
100 |
100 |
0.1% |
30 |
360 |
| DXSL100-500 |
1000 |
205 |
100 |
500 |
100 |
0,1% |
130 |
1480 |
| DXSL100-1000 |
1000 |
270 |
100 |
1000 |
100 |
0.1% |
320 |
3800 |
| DXSL100-2000 |
1000 |
360 |
100 |
2000 |
100 |
0,2% |
680 |
8200 |
Теплая подсказка
Максимум.магнитное поле: когда мощность достигает максимума, напряженность магнитного поля в центре магнитного поля;
Равномерная область: область относительного однородного магнитного поля вокруг центра магнитного поля или диапазон требуемой пользователем области магнитного поля;
Равномерность: степень отклонения магнитного поля в однородной области;
Стабильность: за один период рабочего времени степень изменения магнитного поля;
Время работы: самое продолжительное время работы;
Рабочий период: интервал между двумя непрерывными работами.
Магнитное поле соленоида конечной длины
Уважаемый господин / мисс,
Ниже вы найдете контекст, в котором я включил уравнение.
4. Инструменты 14
4.1 Био Савар и Лоренц 14
4.2 Конечный прямой провод 15
..1 Поле 15
..2 Сила 16
..3 Усилие между круглыми проволоками 17
4.3 Конечная плоскость 18
..1 Поле 18
..2 Сила 21
..3 Некубовидные магниты 23
4.4 Бесконечный бар 25
..1 Поле 25
..2 Сила 25
4,5 Конечный стержень 27
..1 Поле 27
..2 Сила 28
4,6 Кубоидальный магнит 33
..1 Поле 33
..2 Сила 34
4.7 Круглая катушка или магнит 38
..1 Поле 38
..2 Сила 42
..3 Взаимная индуктивность, коаксиальная 43
..4 Собственная индуктивность 44
..5 Взаимная индуктивность между некоаксиальными тонкостенными катушками 45
4.8 Собственная индукция, взаимная индуктивность и силы катушек прямоугольной формы и поперечного сечения 49
..1 Собственная индуктивность 49
..2 Взаимная индуктивность 55
..3 Сила 56
..4 Формула Неймана 58
4,9 Наличие железа 63
..5 Сила сопротивления 65
..6 Сила притяжения к железу 66
4,7 Круглая катушка или магнит
Поле
Для определения поля кругового магнита, такого как диск или цилиндр, сначала нужно поле круговой петли с
бесконечно тонкий проводник. Необходимо применить Био-Савара в координатах цилиндра, как это сделано в [19] и [20].
Полезно использовать полные эллиптические интегралы первого и второго рода, определяемые как:
(4.7.1)
Вывод через векторный потенциал описан в [21]. Векторный потенциал получается как:
(4.7.2)
с радиусом R и током I в точке (r, z) в качестве места наблюдения.
У тока есть только одна составляющая, направленная по касательной, то есть в направлении θ.
Следовательно, то же самое верно и для векторного потенциала.Компоненты поля получены через:
(4.7.3)
(4.7.4)
В качестве примера изображена одиночная петля из бесконечно тонкого проводника с током 1 А:
Рис. 4.7.1, силовые линии и плотность потока одиночной петли с центром в качестве эталона
Линии поля показаны на левом рисунке. Одинаковое количество магнитного потока может быть найдено между двумя силовыми линиями.
Чтобы получить силовые линии в аксиально-симметричном случае, нужно построить r.Aθ.
Доказательство: из следует с контуром C, охватывающей поверхность S,
как нормальный единичный вектор на S и единичный вектор вдоль C.
За флюс держит, итак.
Векторный потенциал имеет только тангенциальную составляющую, и эта составляющая не является функцией
тангенциального положения в этом случае осевой симметрии.
Выполнение интегрирования при фиксированном значении z по коаксиальной окружности r приводит к
Следовательно, для получения линий поля следует строить линии с постоянным значением.
Предыдущие выражения являются основой для поля катушки с бесконечно тонкой стенкой.
Интегрированием выражений для одиночного контура по высоте катушки получается поле.
Связь с круглым магнитом заключается в том, что магнит можно рассматривать как набор тонких катушек, например
круглый магнит с отверстием в центре.
Модель смоделирована в виде двух коаксиальных катушек с противоположным направлением тока.
Рис. 4.7.2, кольцевой магнит в виде набора катушек
Число ампер-витков равно HcJ, умноженному на высоту магнита.
Отображение магнита катушками, как указано, полностью разрешено, когда:
— относительная проницаемость μr близка к 1 (как и для NdFeB, SmCo и ферроксида)
— точка срабатывания находится в линейной части кривой BH
— намагниченность равномерная и однонаправленная.
Сначала следует определить функцию J как полный эллиптический интеграл третьего рода:
(4.7.5)
Полное упражнение для получения поля для катушки выполнено в [22]. Быстрая численная процедура для этого интеграла приведена в [23].
(4.7.6)
с катушкой радиуса R,
H половина высоты рулона,
r, координаты z,
N число витков,
I ток,
Z = Z (я)
к = к (я).
Эллиптический интеграл E, K и J не всегда доступен в качестве «внутренней» процедуры. В Приложении 10 представлена реализация системы Mathematica.
Рис. 4.7.3 Радиальное поле при N.I = -50 А
Рис. 4.7.4 Осевое поле при N.I = -50 А
Другой недавний источник поля постоянного магнита приведен в [24].
T.L. Тан опубликовал в [25] следующее уравнение для модифицированного векторного потенциала AÏ † (r, z) цилиндрической катушки с N витками, током I, радиусом R и высотой 2H:
(4.7,7)
с
Комбинация компонентов поля и векторного потенциала дает следующие цифры.
Рис. 4.7.5. Линии потенциала и направление поля цилиндрической катушки
Рис. 4.7.6 Линии потенциала и направление поля для двух цилиндрических катушек с противоположным направлением тока
Сфера тонкостенных цилиндрических катушек, дисковых и кольцевых магнитов может быть хорошо описана с помощью предыдущих выражений.
Выражения для поля толстостенных цилиндрических катушек все еще изучаются в публикациях,
, потому что компактной рецептуры еще не найдено.Конечно, конечно-элементный анализ даст правильные значения,
, но компактное аналитическое выражение было бы очень полезно для оптимизации.
Один из способов решить эту проблему — разрезать толстостенные катушки на слои и суммировать вклады, чтобы получить поле.
Это продемонстрировано на следующих рисунках, показывающих поле катушки с круглым и прямоугольным
сечения соответственно. Количество ампер-витков равно 1000, а количество слоев — 40.
Рис. 4.7.7. Линии потенциала, напряженность поля и направление поля круглой петли с круглым поперечным сечением и однородной плотностью тока
Рис. 4.7.8 линии потенциала, напряженность поля и направление поля круглой петли с прямоугольным поперечным сечением и однородной плотностью тока
Плоские катушки применяются на печатных платах и в системах беспроводной передачи энергии.
Аналитические описания магнитного поля дисковой катушки стали доступны за последние 10 лет,
, но предполагаемые преимущества теряются в значительной степени, потому что процесс решения становится более
сложнее и / или требует больше времени, чем добавление полей e.г. 10 концентрических колец, как показано на рис. 4.7.1.
В качестве примера 10 звонков по 100 ампер. с радиусом от 0,1 до 0,2 м. приводит к следующему рисунку.
Рис. 4.7.9. Линии потенциала, напряженность поля и направление поля дисковой катушки с 10 проводами, несущими 100 ампер. каждый.
Магнитные поля из-за соленоида
Соленоид состоит из токоведущего провода, намотанного на серию поворотов (желательно как можно ближе друг к другу).Магнитное поле из-за прямая длина провода показана на рисунке 1 — поле окружает провод и его величина (или сила) уменьшается с увеличением радиального расстояния от проволоки.
Рисунок 1: Магнитное поле от прямого провода
Рисунок 2: Магнитное поле в соленоиде
Это дает поле в центре соленоида.
Рисунок 3: Использование закона Ампера для расчета Bo
См. Рисунок 4. | B o | = & micro o i o N / L — амплитуда (максимальное значение) поля. Вы также можете сослаться на «среднее» значение | B o | называется среднеквадратичным (RMS) значением. B RMS = | B o | / sqrt (2).
Рисунок 4: Изменение магнитного поля в соленоиде во времени, также показывающее
B RMS .
Закон Био-Савара
где R = радиус петли. Третье уравнение показывает B как функцию от z, когда z >> R. Обратите внимание, что B быстро уменьшается с увеличением z.
Рисунок 5: изменение B по оси z
Электричество — подробное содержание
быстрая редакция: Линии магнитного поля следуют направлению свободно движущегося Северного полюса.
Магнитный поток φ (фи)
По определению, магнитный поток — это мера силы магнитного поля в данной области, перпендикулярной ему.
На приведенной ниже диаграмме показано, как магнитный поток φ на площади A изменяется вокруг полюса магнита.
к началу
Плотность потока B
Мы можем уточнить идею потока, сделав единицу площади (1 м 2 ).Это вводит новую концепцию — плотность магнитного потока B .
Для нормального участка (область под прямым углом),
общий магнитный поток = плотность потока x площадь
Шт.
Единицей измерения потока является Weber ( Wb ), а единицей плотности потока — Tesla ( T ).
Плотность потока 1 Тесла равна 1 Веберу на квадратный метр.
1 T = 1 Вт · м -2
Для области A под углом θ к магнитному полю нормальная магнитная индукция имеет величину Bcosθ .
Таким образом, полный нормальный поток на площади A под углом θ к полю определяется выражением:
к началу
Магнитные поля вокруг токоведущих проводов
Магнитное поле вокруг токоведущего провода представляет собой серию концентрических силовых линий.Поле не однородное. Строки расположены неравномерно. Поле неравномерное, линии плотно прилегают к проводу и далеко от него отстоят.
Направление силовых линий — по часовой стрелке в направлении текущего направления.
Поле вокруг плоской круглой катушки напоминает поле вокруг короткого стержневого магнита .
Поле вокруг соленоида напоминает поле вокруг стержневого магнита длиной шт.
к началу
Плотность потока для прямого провода
На приведенной ниже диаграмме показана плотность потока B в точке P на расстоянии a от провода.
Плотность магнитного потока B описывается уравнением:
, где μ o — проницаемость свободного пространства.
К сожалению, в настоящее время невозможно дать полный вывод этого уравнения.
к началу
Плотность потока для бесконечно длинного соленоида
На диаграмме показана плотность потока B в соленоиде с n витками и током катушки I .
Плотность магнитного потока B описывается уравнением:
, где μ o — проницаемость свободного пространства, а n — количество витков на единицу длины соленоида.
Значение B приближается к значению реального соленоида при условии, что длина соленоида не менее x10 его диаметра.
Количество нИ имеет значение. Он равен напряженности магнитного поля H в единицах ампер-виток / метр (Am -2 ).
примечание : витков n не имеет единиц
к началу
Однородные магнитные поля — Катушки Гельмгольца
Одноплоскостная катушка с радиусом r , витками N и током I создает плотность магнитного потока B в центре .
, где μ o — проницаемость свободного пространства.
Катушки Гельмгольца создают область однородного магнитного поля в дискретном объеме. Две одинаковые плоские катушки выровнены вдоль общей оси и расположены на расстоянии r друг от друга, где r — радиус катушки.
Ток I , проходящий через каждую катушку, одинаков и в одном направлении.
Плотность магнитного потока B в объеме однородного поля (заштриховано зеленым) определяется по формуле:
, где μ o — проницаемость свободного пространства.
КатушкиГельмгольца особенно полезны для отклонения электронных / ионных пучков. Все заряженные частицы движутся по круговой траектории при попадании в магнитное поле, перпендикулярное их движению. Измеряя радиус пути и независимо от того, идет ли путь по часовой стрелке или против часовой стрелки, можно получить важную информацию о заряде частицы и ее массе.
Этот метод особенно важен для различения α , β и γ частиц друг от друга.
к началу
| 217 | РОГ | Короткое замыкание на выходе звукового сигнала. |
| 218 | HYD PMP | Короткое замыкание гидравлического насоса.Поскольку это пропорциональный клапан, эту ошибку можно обнаружить только
при неработающем двигателе. |
| 219 | SLW LCK | Короткое замыкание соленоида блокировки поворота. |
| 220 | ВЕНТИЛЯТОР | Короткое замыкание соленоида вентилятора гидравлической системы. Неисправность может быть обнаружена только при неработающем двигателе. |
| 221 | SLW BRK | Короткое замыкание соленоида тормоза поворота. |
| 222 | SLW ST | Короткое замыкание соленоида отключения поворота. |
| 223 | LW WIPR | Короткое замыкание электродвигателя нижнего стеклоочистителя. |
| 224 | дворник | Короткое замыкание электродвигателя стеклоочистителя. |
| 225 | ЛЕВАЯ КАБИНА LT | Короткое замыкание рабочего освещения стрелы. |
| 226 | RH КАБИНА LT | Короткое замыкание рабочего освещения ящика для инструментов. |
| 227 | TL CHNG | Короткое замыкание в электромагнитном клапане изменения хода. |
| 228 | ШАЙБА | Короткое замыкание электродвигателя омывателя. |
| 229 | БУЛЬДОЗЕР | Короткое замыкание электромагнитного клапана бульдозера. |
| 230 | GRB CW | Короткое замыкание соленоида захвата / вращения по часовой стрелке. |
| 231 | GRB CCW | Короткое замыкание соленоида захвата / вращения против часовой стрелки. |
| 232 | LW ПОТОК | Короткое замыкание в соленоиде малого расхода. |
| 233 | ИЗОЛ | Короткое замыкание электромагнитного клапана выключателя. |
| 234 | ЭМГ СТП | Короткое замыкание в электромагнитном клапане аварийной остановки. |
| 235 | 2 ЭТАП | Короткое замыкание электромагнитного клапана сброса ступени 2 nd . |
| 236 | QK HTCH | Короткое замыкание в электромагнитном клапане быстрой сцепки. |
| 237 | TL ALRM | Короткое замыкание выхода аварийного сигнала движения. |
| 238 | МОЛОТОК | Короткое замыкание в соленоиде молотка. |
| 239 | ПОДУШКА | Короткое замыкание соленоида жесткой / мягкой подушки. |
| 240 | СТРЕЛА LT | Короткое замыкание рабочего освещения стрелы. |
| 241 | TLBX LT | Короткое замыкание рабочего освещения ящика для инструментов. |
| 242 | РУС SD | Короткое замыкание в соленоиде выключения двигателя. |
| 243 | GLW PLG | Короткое замыкание свечей накаливания. |
| 244 | CNT LT | Короткое замыкание рабочего фонаря противовеса. |
| 245 | LH IND | Короткое замыкание левого указателя поворота. |
| 246 | ЛЕВАЯ СТОРОНА | Короткое замыкание левого габаритного огня. |
| 247 | ЛЕВЫЙ ТУМАН | Короткое замыкание левой противотуманной фары. |
| 248 | LH ГЛАВНАЯ | Короткое замыкание в левом дальнем свете. |
| 249 | LH DIP | Короткое замыкание луча LH. |
| 250 | RH IND | Короткое замыкание правого указателя поворота. |
| 251 | ПРАВАЯ СТОРОНА | Короткое замыкание правого габаритного огня. |
| 252 | RH FOG | Короткое замыкание правой противотуманной фары |
| 253 | ПРАВЫЙ ГЛАВНЫЙ | Короткое замыкание в правом дальнем свете. |
| 254 | RH DIP | Короткое замыкание правого нижнего луча. |
| 255 | СветодиодHZD | Короткое замыкание светодиода опасности. |
| 256 | TL FLW3 | Короткое замыкание в соленоиде 3 рабочего потока. |
| 257 | TL FLW2 | Короткое замыкание в соленоиде 2 потока хода. |
| 258 | ГР ЧНГ | Короткое замыкание соленоида M2 или переключения передач. |
| 259 | BRKE LT | Короткое замыкание выхода стоп-сигнала. |
| 260 | МОСТ LK | Короткое замыкание в соленоиде блокировки оси. |
| 261 | СТАБИЛИЗАТОР | Короткое замыкание соленоида подъема стабилизатора. |
| 262 | STAB DN | Короткое замыкание соленоида опускания стабилизатора. |
| 263 | STAB LH | Короткое замыкание левого соленоида стабилизатора. |
| 264 | STAB RH | Короткое замыкание правого соленоида стабилизатора. |
| 265 | КРУИЗ | Короткое замыкание соленоида круиз-контроля. |
| 266 | DIG ISL | Короткое замыкание соленоида отключения конца копания. |
| 267 | ПРК БК | Короткое замыкание соленоида M1 или стояночного тормоза. |
| 268 | DRV ISL | Короткое замыкание изолирующего соленоида привода. |
| 300 | EC1 CAN | Модуль ECU1 больше не обменивается данными по шине CAN.
|

