Магнитное поле в соленоиде: расчет и анализ характеристик

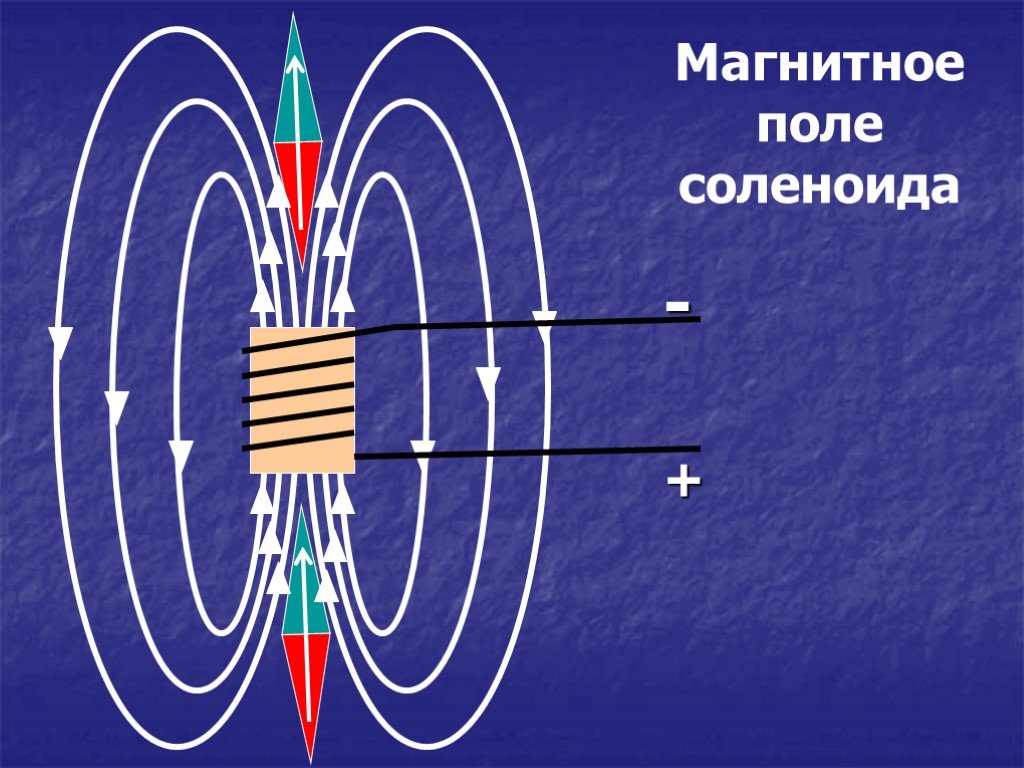
Как рассчитать магнитную индукцию в центре соленоида. Какие факторы влияют на силу магнитного поля соленоида. От чего зависит однородность магнитного поля внутри соленоида. Как изменяется магнитное поле соленоида при изменении его параметров.

Принцип работы и устройство соленоида

Соленоид представляет собой катушку из проводника, намотанную на цилиндрический каркас. При пропускании электрического тока через обмотку соленоида внутри него создается магнитное поле. Основные характеристики соленоида:

• Длина l
• Радиус r
• Число витков N
• Сила тока I

Магнитное поле внутри соленоида образуется как суперпозиция полей от отдельных витков. В идеальном бесконечно длинном соленоиде поле внутри однородно и направлено вдоль его оси.

Расчет индукции магнитного поля в центре соленоида

Для расчета индукции магнитного поля B в центре соленоида конечной длины используется формула:

B = μ0 * n * I

Где:

• μ0 — магнитная постоянная (4π * 10^-7 Гн/м)
• n — число витков на единицу длины соленоида
• I — сила тока

Число витков на единицу длины n определяется как:

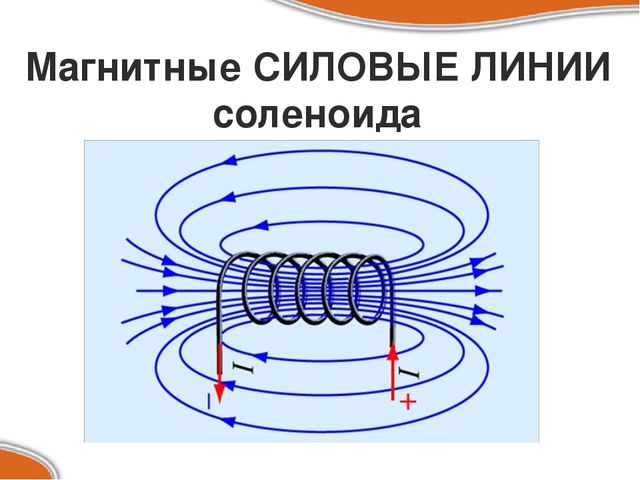
n = N / l

Где N — общее число витков, l — длина соленоида.

Факторы, влияющие на силу магнитного поля соленоида

Основные факторы, определяющие индукцию магнитного поля в соленоиде:

1. Сила тока I — прямо пропорциональная зависимость
2. Число витков на единицу длины n — прямо пропорциональная зависимость
3. Длина соленоида l — обратно пропорциональная зависимость
4. Наличие сердечника — ферромагнитный сердечник усиливает поле

При увеличении силы тока или числа витков магнитное поле усиливается. Увеличение длины соленоида при сохранении числа витков приводит к ослаблению поля.

Однородность магнитного поля внутри соленоида

Степень однородности магнитного поля внутри соленоида зависит от соотношения его длины и радиуса. Чем больше отношение длины к радиусу, тем более однородным будет поле вдали от краев соленоида.

Для получения однородного поля рекомендуется соблюдать условие:

l > 10r

Где l — длина соленоида, r — его радиус.

В центральной части длинного соленоида поле можно считать практически однородным. На краях соленоида наблюдаются краевые эффекты и неоднородность поля.

Изменение параметров соленоида и его влияние на магнитное поле

Рассмотрим, как изменение различных параметров соленоида влияет на создаваемое им магнитное поле:

1. Увеличение силы тока I:
   • Магнитное поле усиливается прямо пропорционально
   • Направление поля не меняется
2. Увеличение числа витков N при сохранении длины:
   • Магнитное поле усиливается
   • Увеличивается число витков на единицу длины n
3. Увеличение длины l при сохранении числа витков:
   • Магнитное поле ослабевает
   • Уменьшается число витков на единицу длины n
4. Добавление ферромагнитного сердечника:
   • Значительное усиление магнитного поля
   • Увеличение магнитной проницаемости среды

При изменении параметров соленоида важно учитывать их комплексное влияние на создаваемое магнитное поле.

Применение соленоидов в технике и науке

Благодаря способности создавать сильное магнитное поле, соленоиды широко применяются в различных областях:

• Электромагниты и реле
• Электродвигатели и генераторы
• Ускорители заряженных частиц
• Магнитно-резонансная томография
• Системы магнитной левитации

Понимание принципов работы соленоидов и расчета их характеристик позволяет эффективно применять их в инженерных и научных задачах.

Практический пример расчета магнитного поля соленоида

Рассмотрим пример расчета индукции магнитного поля в центре соленоида со следующими параметрами:

• Длина соленоида l = 20 см
• Число витков N = 1000
• Сила тока I = 2 А

Рассчитаем число витков на единицу длины:

n = N / l = 1000 / 0.2 м = 5000 витков/м

Теперь можем вычислить индукцию магнитного поля:

B = μ0 * n * I = 4π * 10^-7 * 5000 * 2 = 12.57 * 10^-3 Тл ≈ 12.6 мТл

Таким образом, в центре данного соленоида создается магнитное поле с индукцией около 12.6 миллитесла.

Ограничения и допущения при расчете магнитного поля соленоида

При использовании формулы B = μ0 * n * I для расчета магнитного поля соленоида следует учитывать некоторые ограничения и допущения:

1. Формула дает точный результат только для бесконечно длинного соленоида
2. Для соленоидов конечной длины результат приближенный, точность повышается с увеличением отношения длины к радиусу
3. Не учитываются краевые эффекты на концах соленоида
4. Предполагается идеальная намотка витков без промежутков
5. Не учитывается влияние внешних магнитных полей

Для более точных расчетов в сложных случаях может потребоваться использование численных методов или специализированного программного обеспечения.

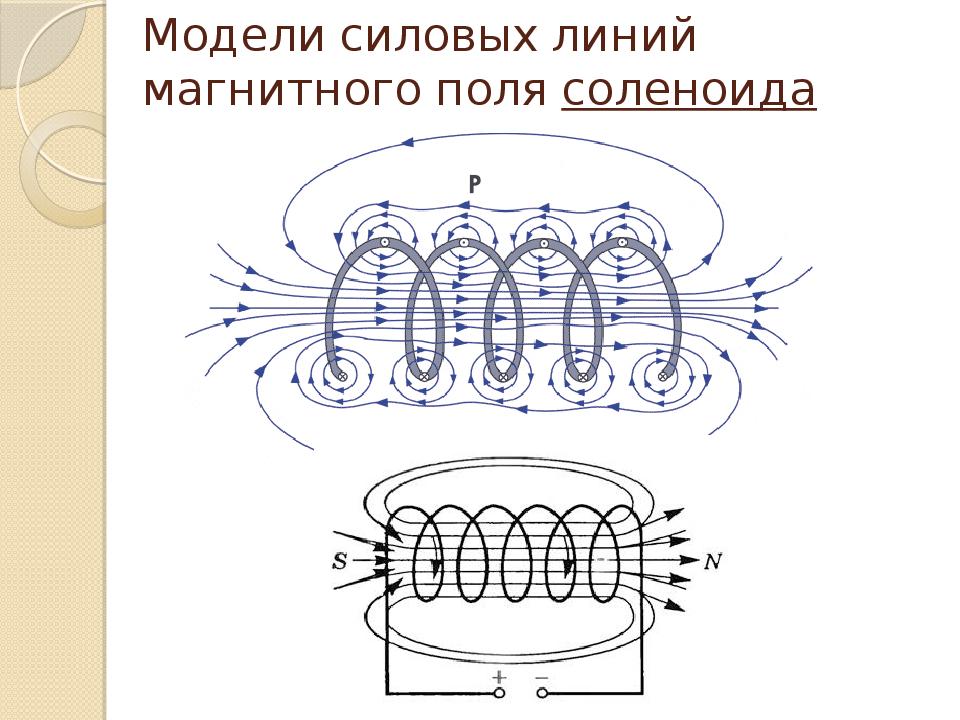
{N} I_i.\]

(1)

Если пренебречь краевыми эффектами, то первое и третье слагаемые в (1) будут равны нулю, так как магнитное поле перпендикулярно контуру и $B_l=0$. Если контур выбрать так, что $AD$ будет лежать на большом расстоянии от соленоида, где поле стремиться к нулю, то и четвёртое слагаемое в (1) также превратиться в нуль. Тогда, учитывая приближение однородности поля получим:

\[B_l L=\mu_0 NI,\]

(2)

где $L$ – длина соленоида, $N$ – количество витков. Если ввести понятие плотности витков (число витков на единицу длины) $n=N/L$, то индукцию магнитного поля внутри соленоида (2) можно записать в виде:

\[B=\mu_0 nI.\]

(3)

Рис. 2: Соленоид с произвольными размерами $L$ и $R$.

Чтобы получить точное выражение для индукции магнитного поля в любой точке на оси конечного соленоида необходимо воспользоваться законом Био-Савара-Лапласа (Рис. 2), который приводит к следующему выражению:

\[B=\frac12\mu_0 nI (\cos\alpha_2-\cos\alpha_1). 2}},\]

(5)

где $R$ – радиус соленоида. А на краю полубесконечного соленоида:

\[B=\frac12 \mu_0 nI.\]

(6)

Индукция магнитного поля бесконечного соленоида (3)

Плотность намотки n (м^-1)

Сила тока соленоида I (A)

B = Тл

---

Индукция магнитного поля конечного соленоида (5)

Плотность намотки n (м^-1)

Радиус намотки R (м)

Длина соленоида L (м)

Сила тока соленоида I (A)

B = Тл

---

Распределение индукция магнитного внутри конечного соленоида (4)

Плотность намотки n (м^-1)

Радиус намотки R (м)

Длина соленоида L (м)

Сила тока соленоида I (A)

---

Магнитное поле соленоида.

Формула, суть явления

• admin
• 13.08.2022
• 0 comments

Магнитное поле соленоида представляет собой суперпозицию отдельных полей, которые создаются каждым витком в отдельности. Через все витки протекает один и тот же ток. Оси всех витков лежат на одной лини. Соленоид представляет собой катушку индуктивности, имеющую цилиндрическую форму. Эта катушка намотана из проводящей проволоки. При этом витки уложены плотно друг к другу и имеют одном направление. При этом считается, что длинна катушки значительно превышает диаметр витков.

Давайте рассмотрим магнитную индукцию, создаваемую каждым витком. Видно, что индукция внутри каждого витка направлена в одну и ту же сторону. Если смотреть в центр витка, то индукция от его краев будет складываться. При этом индукция магнитного поля между двух соседних витков направлена встречно. Так как она создана одним и тем же током то она компенсируется.

Рисунок 1 — Поле создаваемое отдельными витками соленоида

 

Если витки соленоида намотаны достаточно плотно, то между всеми витками встречное поле будет компенсировано, а внутри витков произойдет сложение отдельных поле в одно общее.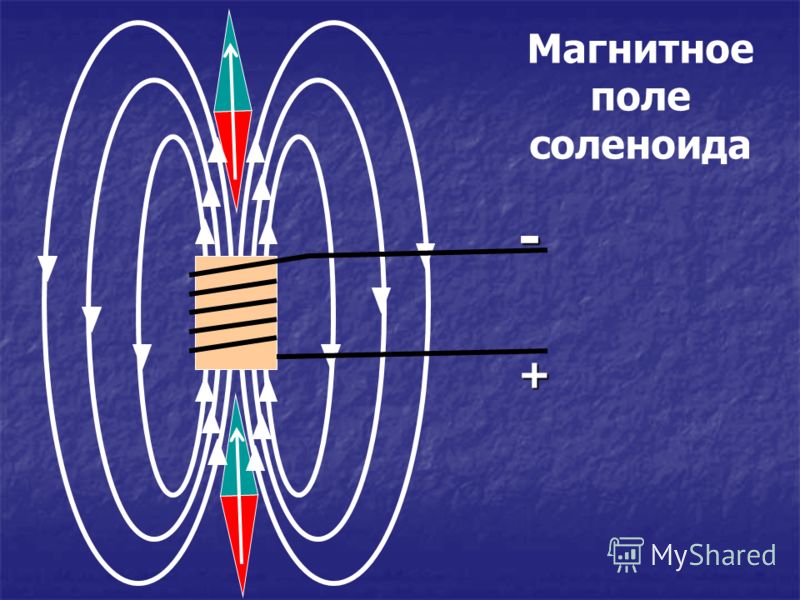 Линии этого поля будут проходить внутри соленоида, и охватывать его снаружи.

Если исследовать магнитное поле внутри соленоида любыми способами, например, с помощью железных опилок то можно сделать вывод, что оно однородно. Лини магнитного поля в этой области представляют собой параллельные прямые. Мало того что они параллельны сами себе но они еще параллельны оси соленоида. Выходя за приделы соленоида, они искривляются и замыкаются снаружи катушки.

Рисунок 2 — Поле создаваемое соленоидом

Из рисунка видно, что поле создаваемое соленоидом похоже на поле, которое создает постоянный стержневой магнит. На одном конце силовые линии выходят из соленоида и этот конец аналогичен северному полюсу постоянного магнита. А в другой они входят, и этот конец соответствует южному полюсу. Отличие же заключается в том, что поле присутствует и внутри соленоида. И если провести опыт с железными опилками, то они втянутся в пространство между витками.

Но если внутрь соленоида вставить деревянный сердечник либо сердечник из любого другого немагнитного материала, то при проведении опыта с железной стружкой картина поля постоянного магнита и соленоида будет идентична.

Так как деревянный сердечник не исказит силовые лини, но при этом не даст проникнуть опилкам внутрь катушки.

 Рисунок 3 — Картина поля постоянного стержневого магнита

Для определения полюсов соленоида можно использовать несколько методов. Например, самый простой, использовать магнитную стрелку. Она притянется к противоположному полюсу магнита. Если же известно направление тока в витке полюсы можно определить при помощи правила правого винта. Если вращать головку правого винта в направлении тока, то поступательное движение укажет направление поля в соленоиде. А зная, что поле направлено от северного полюса к южному и можно определить, где какой полюс находится.

Чтобы найти модуль магнитной индукции соленоида состоящего из одного слоя можно воспользоваться формулой.

Формула 1 — Модуль магнитной индукции соленоида

Где N число витков соленоида

 l длинна соленоида

  n число витков на единицу длинны

 I Ток в соленоиде

      Мю магнитная проницаемость среды находящейся внутри соленоида

      Мю0 магнитная постоянная

Магнитное поле соленоида

Магнитное поле соленоида
Next: Происхождение постоянного магнетизма Вверх: Магнетизм Предыдущий: Закон Ампера о круговых движениях Соленоид представляет собой плотно намотанную спиральную катушку проволоки, диаметр которой мал по сравнению с к его длине. Магнитное поле, создаваемое в центре или сердечнике , соленоида с током по существу равномерна и направлена ​​вдоль оси соленоида. Вне соленоида магнитное поле намного слабее. На рис. 27 показано (довольно схематично) магнитное поле, создаваемое типичным соленоидом. Соленоид намотан из одного спирального провода, по которому течет ток. Обмотка достаточно тугая, чтобы каждый виток соленоида хорошо приблизительно как круглая проволочная петля, лежащая в плоскости, перпендикулярной оси соленоид, по которому течет ток. Предположим, что там таких витков на единицу осевой длины соленоида. Что величина магнитного поля в сердечнике соленоида?

Рисунок 27: Соленоид.

Чтобы ответить на этот вопрос, применим схему Ампера. закон к прямоугольной петле. Сначала нужно найти линейный интеграл магнитного поля вокруг. Вдоль и магнитное поле практически перпендикулярна петле, поэтому вклада в линейный интеграл от этих участков контура. Вдоль магнитного поля примерно однородно, величины , скажем, и направлена ​​параллельно петле. Таким образом вклад в линейный интеграл от этого участка контура , где длина . Вдоль магнитного поля напряженность практически незначительна, поэтому этот участок цикла не влияет на линию интеграл. Отсюда следует, что линейный интеграл магнитное поле вокруг просто

(178)

По круговому закону Ампера этот линейный интеграл равен умножить на алгебраическую сумму токи, протекающие по контуру. Так как длина петля по оси соленоида , петля пересекает витков соленоида, через каждый из которых протекает ток. Таким образом, общая ток, протекающий по контуру, равен . Этот ток считается положительный ток, так как если мы посмотрим против направления токи текут в каждом витке ( т. е. на страницу на рисунке), цикл циркулирует эти токи против часовой стрелки.

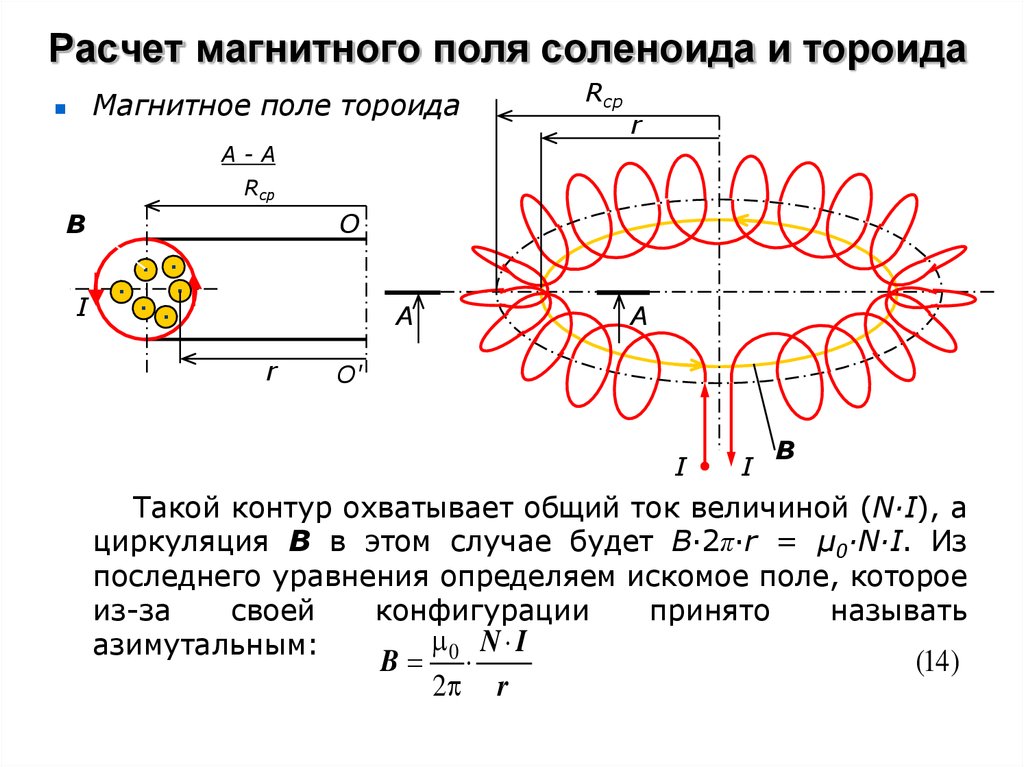Контурный закон Ампера дает

(179)

что сводится к

(180)

Таким образом, магнитное поле в сердечнике соленоида прямо пропорциональна произведению ток, протекающий вокруг соленоида, и число витков на единицу длины соленоида. Это, результат точно в предел, при котором длина соленоида намного превышает его диаметр.

---

Next: Происхождение постоянного магнетизма Вверх: Магнетизм Предыдущий: Закон Ампера о круговых движениях

Ричард Фицпатрик 2007-07-14

Объяснение урока: Магнитное поле, создаваемое током в соленоиде

В этом объяснении мы узнаем, как рассчитать магнитное поле, создаваемое ток в соленоиде.

Вспомните направление магнитного поля в петле провода с током. В центре петли магнитное поле имеет одно направление, как видно на схема ниже. Оранжевая линия — направление магнитного поля, черная линия — направление магнитного поля. петля.

Та же петля, вид спереди, с указанием направления магнитного поля вне экрана, будет выглядеть как на диаграмме ниже.

Напомним, что приведенные ниже символы используются для обозначения того, что направление выходит из или в экран.

Напряженность магнитного поля в центре петли можно увеличить, поместив больше петель в соответствии с ним. На диаграмме ниже показаны два набора петель с одинаковыми тока и того же радиуса выстроились таким образом.

Набор петель справа имеет более сильное магнитное поле, потому что у него больше петли.

Вместо набора петель усиление магнитного поля в центре может быть достигнуто с помощью одного провода с несколькими витками. На приведенной ниже диаграмме показано такой провод, с видом сбоку и спереди.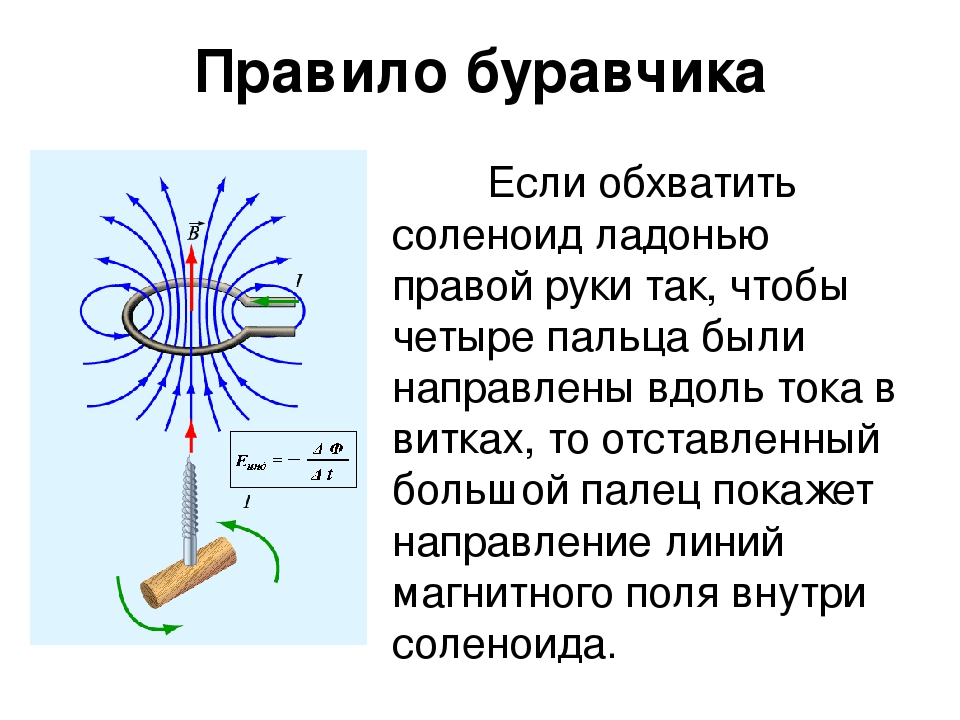

Провод с таким набором витков называется соленоидом. Каждый ход соленоид вносит свой вклад в силу магнитного поля в центре точно так же, как дополнительная петля будет.

Напряженность и направление магнитного поля в самом центре соленоида униформа. Он имеет одно направление и величину. Другие точки вокруг соленоида имеют различные направления и величины магнитного поля.

Прежде чем рассматривать силовые линии магнитного поля соленоида, давайте рассмотрим угол, с которого мы будем смотреть, используя один цикл. На приведенной ниже диаграмме показан одиночный виток провода с током и его результирующее магнитное поле от двух разные углы.

Вид сбоку этой петли показывает направление, в котором смотрит наблюдатель, обозначенное глазом, чтобы получить вид сверху вниз. Вид сверху вниз по-прежнему показывает направление тока, входящего и выходящего из экрана, но не показать нижнюю часть петли.

Теперь давайте посмотрим на вид сверху вниз на одну петлю с ее магнитным линии поля, выделенные серым цветом, на диаграмме ниже.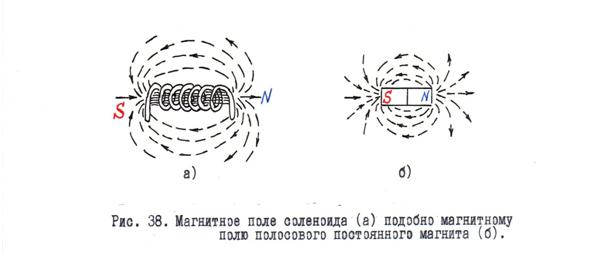

Когда силовые линии магнитного поля расположены близко друг к другу, это означает, что более сильное магнитное поле. Мы видим, что в самом центре петли силовые линии магнитного поля расположены очень близко друг к другу с одинаковым направлением, что означает в этой точке у него сильное магнитное поле.

Вне контура силовые линии магнитного поля напоминают стержневой магнит, как показано ниже.

Теперь посмотрим на соленоид с семью витками под этим углом. Диаграмма ниже показано это с соответствующим магнитным полем.

Обратите внимание, что силовые линии магнитного поля постоянны и прямые в самом центре эти провода поворачиваются, но становятся менее последовательными по направлению к концам соленоида. ближе к этим концам, тем менее однородны силовые линии.

Теперь давайте рассмотрим теоретически очень длинный соленоид. Это так долго, что мы можем относиться к нему так, как если бы у него не было концов. Это означало бы, что он имеет совершенно однородный магнитное поле внутри витков во всех точках.

Если бы мы измерили напряженность магнитного поля в разных точках в пределах витков этот теоретический соленоид, в каждом случае величина и направление магнитного напряженность поля была бы такой же. На приведенной ниже диаграмме показан теоретический соленоид. с тремя точками, обозначенными красными точками, которые имеют эквивалентное магнитное поле сильные стороны и направления.

Напряженность магнитного поля в витках этого теоретического соленоида может быть определяется с помощью уравнения.

Уравнение: напряженность магнитного поля в центре соленоида

Напряженность магнитного поля, 𝐵, внутри центра соленоида находится с помощью уравнения 𝐵=𝜇𝑁𝐼𝐿, где 𝐼 — ток соленоида, 𝑁 — количество витков соленоида, 𝐿 — длина соленоида, а 𝜇 — проницаемость свободного пространства, 4𝜋×10 Т⋅м/А.

Для реального соленоида ограниченной длины это уравнение все еще полезно для описывают напряженность магнитного поля точно в центре витков, так как это там, где она однородна. На диаграмме ниже показаны точки с одинаковыми магнитными напряженность и направление поля как на теоретическом, так и на реальном соленоиде.

Реальные соленоиды имеют достаточно постоянное направление магнитного поля внутри витков, но не напряженность магнитного поля. Только центр имеет постоянное магнитное поле. сила.

Глядя на уравнение, мы видим, что длина соленоида имеет значение, когда найти напряженность магнитного поля в центре. В частности, это магнитное напряженность поля обратно пропорциональна длине. На схеме ниже показаны два соленоиды с одинаковым током и числом витков, но с разным длины.

Так как нижний соленоид в два раза длиннее, он будет иметь половину напряженность магнитного поля в его центре.

Давайте рассмотрим пример с использованием этого уравнения.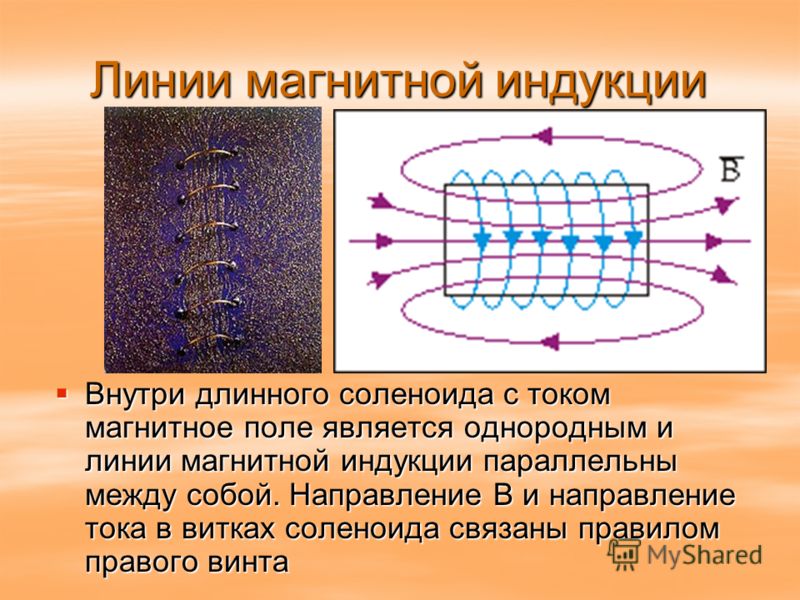

Пример 1: Напряженность магнитного поля в центре соленоида с витками и Длина

Соленоид имеет длину 3,2 см и состоит из 90 витков провода. По проводу течет постоянный ток 1,2 А. Рассчитайте напряженность магнитного поля в центре соленоида. Дайте свой ответ в тесла выражается в научной записи с точностью до одного десятичного знака. Используйте значение 4𝜋×10 Т⋅м/А для 𝜇.

Ответ

Мы будем использовать уравнение 𝐵=𝜇𝑁𝐼𝐿 найти напряженность магнитного поля в центре этого соленоида.

Прежде чем мы сможем подставить значения, которые нам даны, мы должны убедиться, что единицы все совпадают. Проницаемость свободного пространства использует метры, поэтому нам нужна длина 3,2 см в метров.

Есть 100 сантиметров в 1 метр: 1100 мкм

Итак, чтобы преобразовать 3,2 см в метры, умножаем на соотношение 1100×3,2=0,032 мкм см

Таким образом, 3,2 см составляет 0,032 м.

Теперь мы можем подставить значения в уравнение. Длина 0,032 м, ток 1,2 А, 90 витков, а проницаемость свободного пространства 4𝜋×10 Т⋅м/А. Это дает нам 𝐵=𝜇𝑁𝐼𝐿𝐵=4𝜋×10⋅/(90)(1,2)0,032.TmAAm

Умножим в числителе. Это отменяет единицы Ампер там, давать 𝐵=1,36×10⋅0,032.Tмм

Итак, теперь, когда мы разделим эти два числа, единицы метры отменить, оставив только тесла: 1,36×10⋅0,032=4,24×10,TmmT

Округлив до одного десятичного знака, напряженность магнитного поля в центре соленоид 4,2×10 T.

Напряженность магнитного поля в центре уравнения соленоида можно использовать для нахождения другие переменные в уравнении, если напряженность магнитного поля в центре соленоид известен. Чтобы показать это, давайте посмотрим на основное уравнение и положим все значения с точки зрения 𝐼. Начиная с уравнения 𝐵=𝜇𝑁𝐼𝐿, мы можем умножить обе части на 𝐿: 𝐵×𝐿=𝜇𝑁𝐼𝐿×𝐿.

Это отменяет 𝐿 справа, оставляя позади 𝐵𝐿=𝜇𝑁𝐼.

Из этой формы мы можем разделить обе части на 𝜇 и 𝑁: 𝐵𝐿𝜇𝑁=𝜇𝑁𝐼𝜇𝑁.

Отменяет 𝜇 и 𝑁 с правой стороны, оставив только 𝐼: 𝐵𝐿𝜇𝑁=𝐼.

Давайте рассмотрим пример, используя эту форму уравнения.

Пример 2: Определение тока в соленоиде с витками и длиной

Соленоид состоит из 35 витков провода на длине 42 мм. Магнитное поле в центре соленоида измеряется как 4.9×10 Тл. Рассчитайте силу тока в проводе. Дайте ответ в амперах на 2 десятичных разряда. Используйте значение 4𝜋×10 Т⋅м/А для 𝜇.

Ответ

Напомним, что уравнение 𝐵=𝜇𝑁𝐼𝐿 можно представить в виде, связывающем переменные с текущим: 𝐼=𝐵𝐿𝜇𝑁.

Перед тем, как мы непосредственно подставим полученные значения в эту форму уравнение, мы должны убедиться, что единицы совпадают. Проницаемость свободного пространства использует метры, поэтому нам нужна длина соленоида, 42 мм, чтобы также быть в с точки зрения метров.

1‎ ‎000 миллиметров в 1 метр: 11000.mmm

Таким образом, умножая это отношение на 42 мм даст нам значение в метров: 11000×42=0,042.мммммм

Длина соленоида в метрах составляет 0,042 м.

Теперь мы можем подставить значения в уравнение. Длина 0,042 м, магнитный напряженность поля 4,9×10 Т, витков 35, а проницаемость свободного пространства равна 4𝜋×10 Т⋅м/А. Это дает нам 𝐼=𝐵𝐿𝜇𝑁𝐼=4,9×10(0,042)(4𝜋×10⋅/)(35).TmTmA

Умножение на числитель дает единицы Т⋅м: 𝐼=2,06×10⋅(4𝜋×10⋅/)(35).TmTmA

Количество витков в соленоиде безразмерно, поэтому умножение на знаменатель не меняет единицы измерения: 𝐼=2,06×10⋅4,39×10⋅/. TmTmA

Разделение верхней части на нижнюю полностью аннулирует единицы Т⋅м и уходи за амперами на вершина. Глядя только на единицы, деление на дробь такое же, как умножение на обратное: (⋅)(⋅/)=(⋅)×(⋅)=.TmTmATmATmA

Итак, деление чисел дает 2,06×10⋅4,39×10⋅/=0,468.TmTmAA

Округлив до двух знаков после запятой, ответ будет таким 0,47 А.

Уравнение можно записать и в терминах других переменных. Допустим, у нас есть соленоид с неизвестной длиной, но с другими известными переменные. Начиная с основного уравнения 𝐵=𝜇𝑁𝐼𝐿, мы можем получить длину одной стороны уравнения, умножив обе части на 𝐿: 𝐵×𝐿=𝜇𝑁𝐼𝐿×𝐿.

Отменяет 𝐿 справа, давая 𝐵𝐿=𝜇𝑁𝐼.

Затем мы делим обе части на 𝐵, чтобы получить 𝐵𝐿𝐵=𝜇𝑁𝐼𝐵, который отменяет 𝐵 слева, оставляя только 𝐿: 𝐿=𝜇𝑁𝐼𝐵.

Давайте рассмотрим пример, в котором используется эта форма уравнения.

Пример 3: Длина соленоида

Соленоид, образованный из отрезка проволоки, имеет 80 витков. Соленоид несет постоянный ток 13 А и сила создаваемого магнитного поля измеряется как 7,3×10 Т в его центре. Вычислите длину соленоида, ответив на вопрос Ближайшая сантиметр. Используйте значение 4𝜋×10 Т⋅м/А для 𝜇.

Ответ

Напомним, что уравнение 𝐵=𝜇𝑁𝐼𝐿 можно представить в виде, связывающем переменные с длиной соленоида: 𝐿=𝜇𝑁𝐼𝐵.

Давайте подставим полученные значения в эту форму уравнение. Текущий 13 А, количество витков 80, напряженность магнитного поля в центре 7,3×10 Т, а проницаемость свободного пространства 4𝜋×10 Т⋅м/А. Это дает нам 𝐿=𝜇𝑁𝐼𝐵𝐿=4𝜋×10⋅/(80)(13)7,3×10.TmAAT

Умножая на числитель, единицы Ампер отменить, осталось только T⋅m: 𝐿=1,306×10⋅7,3×10. TmT

Деление этих чисел отменяет тесла, оставляя позади только метры: 1,306×10⋅7,3×10=0,179.TmTm

Итак, длина этого соленоида равна 0,179 метра. Мы еще не закончили, так как нам нужен окончательный ответ на проблему в сантиметры.

Чтобы выразить этот ответ в сантиметрах, напомнить, что есть 100 сантиметров в 1 метре: 1001.см

Умножив это на наш ответ в метров даст нам ответ в сантиметрах: 1001×0,179=17,9.смммсм

Итак, округляем до ближайшего сантиметр, этот соленоид имеет длину 18 сантиметров. Ответ 18 см.

Напомним, что длина соленоида обратно пропорциональна магнитному полю сила в его центре. Более длинной длине можно противодействовать, добавляя больше витков в провод, как показано на схеме ниже.

Оба соленоида имеют одинаковую напряженность магнитного поля, так как более длинный соленоид имеет пропорционально большее количество оборотов. Мы также можем видеть, что более длинный соленоид по сути то же самое, что и первое, но его просто больше.

Это означает, что добавление большего количества витков провода, увеличение длины соленоида в процессе, вообще не увеличивает напряженность магнитного поля в центре. Что увеличивает напряженность магнитного поля — это число витков на заданной длине. Это доказано, глядя на уравнение 𝐵=𝜇𝑁𝐼𝐿.

Если предположить, что ток одинаков для двух соленоидов, то единственный непостоянными переменными, влияющими на напряженность магнитного поля, являются число витков 𝑁 и длина 𝐿: 𝑁𝐿.

Мы видим, что удвоение витков до 2𝑁 и длины до 2𝐿 вообще не меняет эту пропорцию. Удвоенные значения исключают друг друга: 2𝑁2𝐿=𝑁𝐿.

Для упрощения уравнения эту пропорцию часто сокращают до простой строчной буквы. 𝑛, 𝑁𝐿=𝑛, единицами которых являются витки на единицу длины. Внутри полного уравнения это выглядит следующим образом.

Уравнение: магнитное поле в центре соленоида с числом оборотов на Длина блока

Напряженность магнитного поля, 𝐵, внутри центра соленоида находится с помощью уравнения 𝐵=𝜇𝑛𝐼, где 𝐼 — ток соленоида, 𝑛 — количество витков на единицу длины, а 𝜇 — проницаемость свободного пространства, 4𝜋×10 Т⋅м/А.

Единицы 𝑛 выражаются на единицу длины. Например, рассмотрите соленоид на диаграмме ниже.

Значение 𝑛 — это общее количество витков по всей длине: 𝑛=𝑁𝐿.

Итак, 6 витков и 3 см длины дает 63=2.turnscmturnspercentimetre

Если бы мы удвоили количество витков до 12 и удвоили длину до 6 см, мы бы увидели значение 𝑛 все тот же 126=2.turnscmturnspercentimetre

Только изменение пропорции оборотов к длине соленоида позволит изменение напряженности магнитного поля.

Давайте рассмотрим пример.

Пример 4: Изменения магнитного поля в соленоиде

Отрезок проволоки превращается в соленоид с 𝑛 витков провода на миллиметр. По проводу течет постоянный ток 𝐼. В результате магнитное поле напряженностью 𝐵 может быть измеряется в центре соленоида. Какое из следующих изменений в системе увеличит магнитное напряженность поля в центре соленоида, при условии, что все остальное остается постоянным?

1. Уменьшение длины соленоида путем удаления витков провода при сохраняя 𝑛 постоянным
2. Уменьшая 𝐼, ток в проводе
3. Уменьшая 𝑛, количество витков провода на миллиметр
4. Увеличение 𝐼, тока в проводе
5. Увеличение длины соленоида добавлением витков провода при сохраняя 𝑛 постоянным

Ответ

Вспомним форму уравнения с 𝑛 оборотов на единицу длины: 𝐵=𝜇𝑛𝐼.

Если 𝑛 не изменяется в этом уравнении, магнитное поле сила не меняется. Добавление или удаление частей соленоида, но сохранение постоянной 𝑛 означает напряженность магнитного поля остается такой же.

Уменьшение 𝑛, однако, уменьшит магнитное поле сила. Точно так же уменьшение тока также уменьшит магнитное поле. напряженность поля. Это связано с тем, что напряженность магнитного поля напрямую пропорциональна как 𝑛, так и 𝐼.

Единственный способ увеличить напряженность магнитного поля — увеличить 𝑛 или 𝐼. Единственный ответ с этим увеличение D, увеличение 𝐼.

Правильный ответ D, увеличение тока в проводе будет увеличиваться напряженность магнитного поля.

При использовании 𝑛 для выполнения вычислений обороты безразмерны, поэтому единицы 𝑛 указаны только на единицу длины. Это значит, что хотя мы бы сказали 5 оборотов в метр, внутри уравнения мы бы просто написали 5.м

Давайте рассмотрим пример.

Пример 5: Напряженность магнитного поля в центре соленоида

Провод, по которому течет постоянный ток 0,15 А представляет собой соленоид с 11 витками на сантиметр. Вычислите напряженность магнитного поля в центре соленоид. Дайте свой ответ в тесла выражается в научной записи с точностью до одного десятичного знака. Используйте значение 4𝜋×10 Т⋅м/А для 𝜇.

Ответ

Соленоид выглядит так, как показано на рисунке ниже.

Вспомните уравнение для напряженности магнитного поля в центре соленоид с использованием оборотов на единицу длины: 𝐵=𝜇𝑛𝐼.

Прежде чем подставлять значения в это уравнение, мы должны убедиться, что единицы совпадают. Проницаемость использования свободного пространства метры, поэтому нам нужно поставить 𝑛 с точки зрения метров также.

Значение 𝑛 составляет 11 витков на сантиметр, а там 100 сантиметров в 1 метре: 1001.см

Умножив это соотношение на 11 витков на сантиметр превратит его в число оборотов в метр: 1001×11=1100.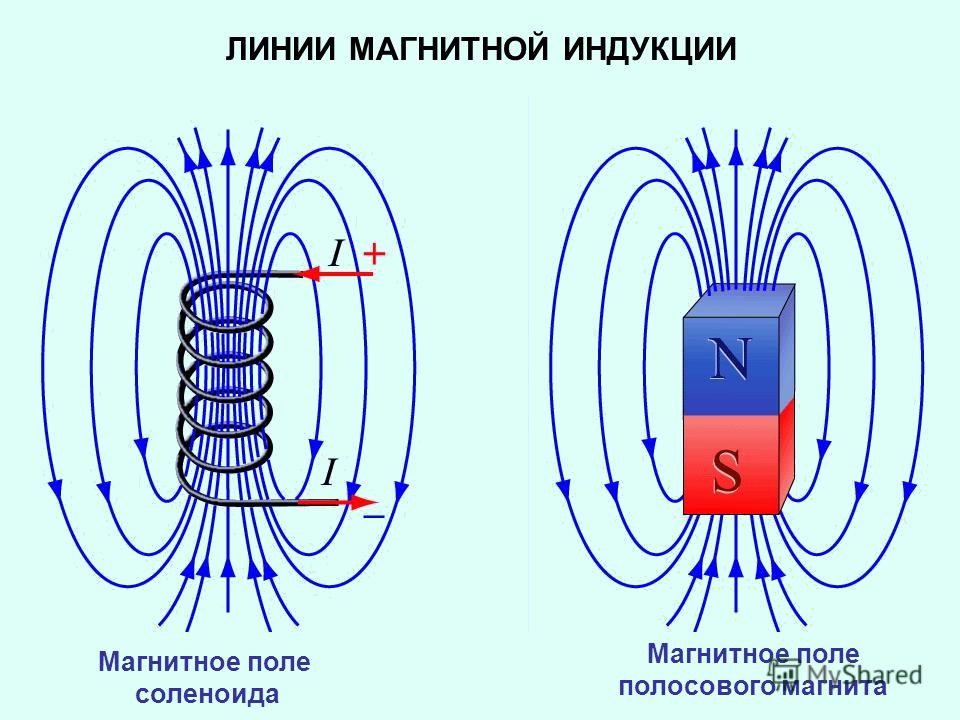 cmcmm

Теперь мы можем подставить значения в уравнение. Текущий 0,15 А, 𝑛 составляет 1‎ ‎100 оборотов в метр, и 𝜇 4𝜋×10 Т⋅м/А. Это дает нам 𝐵=𝜇𝑛𝐼𝐵=4𝜋×10⋅/1100(0,15).TmAmA

Умножение проницаемости свободного пространства на обороты на метр отменяет счетчики, оставлять позади 𝐵=1,38×10/(0,15).ТАА

Умножение двух последних чисел отменяет единицы измерения. ампер, оставив тесла, чтобы дать 1,38×10/(0,15)=2,07×10,TAAT

Таким образом, округляя до одного десятичного знака, напряженность магнитного поля в центр этого соленоида 2,1×10 T.

Как и в случае с другой версией уравнения напряженности магнитного поля, мы можем изолировать конкретные неизвестные переменные. Например, если нам дан соленоид с неизвестный ток, мы можем определить его, составив уравнение 𝐵=𝜇𝑛𝐼 с точки зрения 𝐼.

Для этого разделим обе части на 𝜇𝑛: 𝐵𝜇𝑛=𝜇𝑛𝐼𝜇𝑛.

Отменяет 𝜇𝑛 с правой стороны, оставляя позади только 𝐼: 𝐵𝜇𝑛=𝐼.

Давайте рассмотрим пример, использующий эту форму уравнения.

Пример 6: Определение тока в соленоиде с витками на длину

Соленоид состоит из отрезка провода, по которому течет постоянный ток 𝐼. Соленоид имеет 430 витков провода на метр. Магнитное поле в центре соленоида измеряется как 3,2×10 Т. Рассчитаем ток, 𝐼, в амперах. Дайте ответ с точностью до 1 знака после запятой. Использовать 𝜇=4𝜋×10⋅/TmA.

Ответ

Напомним, что уравнение 𝐵=𝜇𝑛𝐼 можно выразить в терминах 𝐼 следующим образом: 𝐼=𝐵𝜇𝑛.

Используя эту форму, подставим известные значения. Напряженность магнитного поля 3,2×10 Т, 𝑛 составляет 430 витков на метр, и 𝜇 4𝜋×10 Т⋅м/А. Это дает нам 𝐼=𝐵𝜇𝑛𝐼=3,2×10(4𝜋×10⋅/). TTmAm

Умножение на знаменатель удаляет единицы метров, дача 𝐼=3,2×105,4×10/.ТТА

Деление на дробь равносильно умножению на ее обратную величину. Это означает, что единственным юнитом после деления будет ампер: ТТАТАТА/=×=.

Итак, при делении чисел ответ становится 3,2×105,4×10/=5,92.TTAA

Округлив до ближайшего десятичного знака, ответ будет 5.9 A.

Давайте обобщим то, что мы узнали из этого объяснения.

Ключевые точки

• Соленоид представляет собой провод, состоящий из ряда витков или петель.
• Когда соленоид пропускает ток, он создает магнитное поле, которое сильнее всего в центре своих петель.
• В петлях соленоида напряженность магнитного поля 𝐵 дается уравнением 𝐵=𝜇𝑁𝐼𝐿, где 𝑁 — число витков в соленоиде, 𝐼 — ток в соленоиде, 𝐿 — длина соленоида, а 𝜇 — проницаемость свободной пространство, 4𝜋×10 Т⋅м/А.