Что такое магнитное поле. Как взаимодействуют магнитные поля и движущиеся заряды. Какие основные законы описывают магнитные явления. Как рассчитать силу Ампера и силу Лоренца. Чем отличаются различные типы магнетизма.
Природа и свойства магнитного поля
Магнитное поле — это особый вид материи, который возникает вокруг движущихся электрических зарядов и постоянных магнитов. В отличие от электрического поля, магнитное поле не оказывает воздействия на неподвижные заряды. Основные свойства магнитного поля:
- Характеризуется векторной величиной — магнитной индукцией B
- Силовые линии магнитного поля всегда замкнуты
- Магнитное поле не имеет источников и стоков
- Взаимодействует только с движущимися зарядами
Как возникает магнитное поле? Есть два основных источника:
- Движущиеся электрические заряды (электрический ток)
- Магнитные моменты электронов в атомах вещества
Взаимодействие магнитного поля с движущимися зарядами
Ключевой особенностью магнитного поля является его взаимодействие с движущимися электрическими зарядами. На заряд q, движущийся со скоростью v в магнитном поле с индукцией B, действует сила Лоренца:

F = qvB sin α
где α — угол между векторами скорости и магнитной индукции.
Направление силы Лоренца определяется по правилу левой руки: если расположить левую руку так, чтобы линии магнитной индукции входили в ладонь, а четыре пальца указывали направление движения положительного заряда, то отогнутый на 90° большой палец покажет направление силы.
Сила Ампера и ее применение
Сила Ампера — это сила, с которой магнитное поле действует на проводник с током. Она определяется формулой:
F = BIL sin α
где B — магнитная индукция, I — сила тока, L — длина проводника, α — угол между проводником и линиями магнитной индукции.
Как применяется сила Ампера на практике? Вот несколько примеров:
- Электродвигатели
- Электроизмерительные приборы
- Громкоговорители
- Электромагнитные реле
Закон Био-Савара-Лапласа и его применение
Закон Био-Савара-Лапласа позволяет рассчитать магнитное поле, создаваемое проводником с током произвольной формы. Для элемента проводника dl с током I магнитная индукция dB в точке, удаленной на расстояние r, определяется как:

dB = (μ0/4π) * (I dl × r) / r^3
где μ0 — магнитная постоянная.
Этот закон лежит в основе расчета магнитных полей различных систем:
- Прямолинейных проводников
- Круговых токов
- Соленоидов
- Тороидов
Магнитные свойства веществ
Различные вещества по-разному взаимодействуют с внешним магнитным полем. Выделяют следующие основные типы магнетизма:
- Диамагнетизм — слабое отталкивание от магнитного поля (медь, вода)
- Парамагнетизм — слабое притяжение к магнитному полю (алюминий, кислород)
- Ферромагнетизм — сильное притяжение к магнитному полю, способность намагничиваться (железо, никель)
- Антиферромагнетизм — магнитные моменты атомов ориентированы антипараллельно (хром, марганец)
- Ферримагнетизм — разновидность антиферромагнетизма с нескомпенсированным магнитным моментом (ферриты)
Применение магнитных явлений в технике
Магнитные явления нашли широкое применение в различных областях техники. Вот некоторые примеры:
- Электродвигатели и генераторы
- Трансформаторы
- Электромагниты
- Магнитная левитация
- Магнитно-резонансная томография
- Магнитная запись информации
Как работает магнитно-резонансный томограф? Он использует мощное магнитное поле и радиоволны для получения детальных изображений внутренних органов. Ядра водорода в тканях выстраиваются вдоль силовых линий магнитного поля. Затем их возбуждают радиоимпульсами, заставляя излучать слабые радиосигналы, которые регистрируются и преобразуются в изображение.

Магнитное поле Земли и его значение
Земля обладает собственным магнитным полем, которое играет важную роль в жизни планеты:
- Защищает от космической радиации и солнечного ветра
- Влияет на миграцию животных
- Используется для навигации
- Вызывает полярные сияния
Как образуется магнитное поле Земли? Согласно современным представлениям, оно генерируется движениями жидкого железа во внешнем ядре планеты. Этот механизм называется геодинамо.
Перспективные направления исследований в области магнетизма
Магнетизм остается активной областью научных исследований. Вот некоторые перспективные направления:
- Спинтроника — использование спина электронов для хранения и обработки информации
- Высокотемпературная сверхпроводимость
- Магнитные наноматериалы
- Квантовые магниты
- Магнитные методы лечения рака
Какие возможности открывает спинтроника? Она позволит создать более быстрые и энергоэффективные компьютеры, а также принципиально новые устройства, такие как квантовые компьютеры на основе спиновых кубитов.
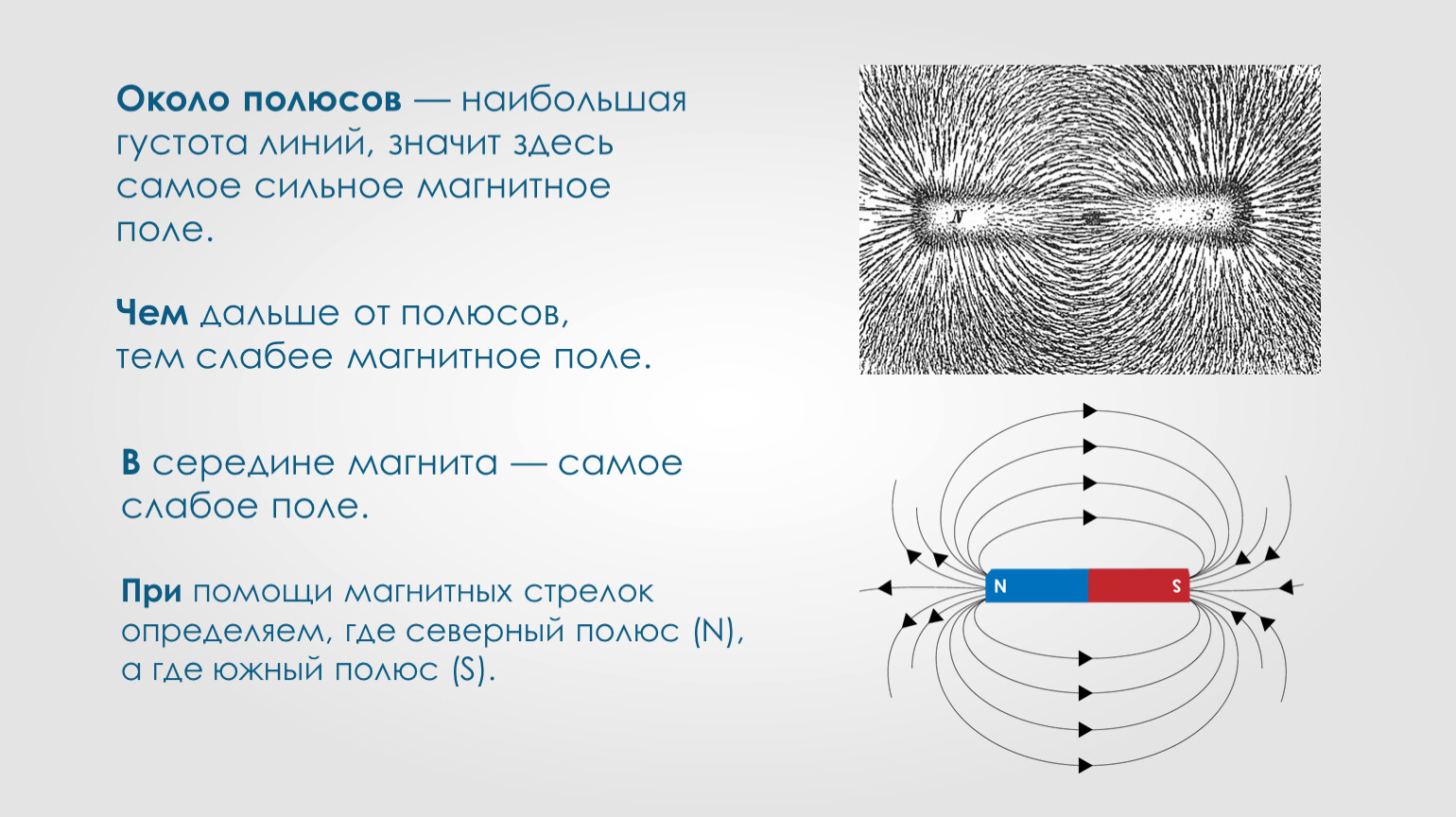
Магнитная сила Ампера
Возьмем прямой проводник, изготовленный из алюминия, и подвесим его на тонких и гибких проводах таким образом, чтобы он находился между полюсами подковообразного постоянного магнита как на рисунке (а). Если в проводнике пропустить ток, проводник отклонится от положения равновесия — рисунок (б). Причиной такого отклонения является сила, действующая на проводник с током со стороны магнитного поля. Доказал наличие этой силы и выяснил, от чего зависят ее значение и направление, французский физик, математик и химик Андре Мари Ампер. Именно поэтому это явление называют магнитной силой Ампера.

Сила Ампера — это сила, с которой магнитное поле действует на проводник с током.
Сила Ампера прямо пропорциональна силе тока в проводнике и длине активной части проводника (то есть части, которая расположена в магнитном поле). Сила Ампера увеличивается с увеличением индукции магнитного поля и зависит от того, под каким углом к линиям магнитной индукции расположен проводник.
Значение силы Ампера (FA) вычисляют по формуле:
где В — магнитная индукция магнитного поля; I — сила тока в проводнике; l — длина активной части проводника; α — угол между направлением вектора магнитной индукции и направлением тока в проводнике.
 Угол α — это угол между направлением вектора магнитной индукции и направлением тока в проводнике
Угол α — это угол между направлением вектора магнитной индукции и направлением тока в проводникеОбратите внимание! Магнитное поле не будет действовать на проводник с током (FA= 0), если проводник расположен параллельно магнитным линиям поля (sin α = 0).
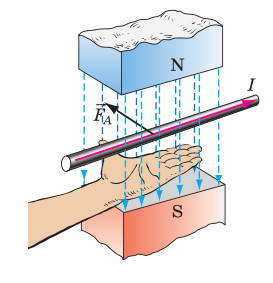 Определение
Определениенаправления силы Ампера
по правилу левой руки
Чтобы определить направление силы Ампера, используют правило левой руки:
Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутые пальцы указывали направление тока в проводнике, то отогнутый на 90 ° большой палец укажет направление силы Ампера.
Получаем формулу для определения модуля магнитной индукции
Если проводник расположен перпендикулярно к линиям магнитной индукции (α = 90 °, sin α = 1), то поле действует на проводник с максимальной силой:
Отсюда получаем формулу для определения модуля магнитной индукции:
Обратите внимание! Значение магнитной индукции не зависит ни от силы тока в проводнике, ни от длины проводника, а зависит только от свойств магнитного поля.
Например, если уменьшить силу тока в проводнике, то изменится и сила Ампера, с которой магнитное поле действует на проводник, а вот значение магнитной индукции останется неизменным.
В СИ единица магнитной индукции — тесла (Тл), единица силы — ньютон (Н), силы тока — ампер (А), длины — метр (м), поэтому:
1Тл — это индукция такого однородного магнитного поля, которое действует с максимальной силой 1 Н на проводник длиной 1 м, в котором течет ток силой 1 А.
Проверочные задачи по теме: магнитное взаимодействие токов и сила Ампера
Задача 1. Докажите, что два параллельных проводника, в которых текут токи одного направления, притягиваются.
Анализ задачи:
Вокруг любого проводника с током существует магнитное поле, следовательно, каждый из двух проводников находится в магнитном поле другого. На первый проводник действует сила Ампера со стороны магнитного поля, созданного током во втором проводнике, и наоборот. Определив по правилу левой руки направления этих сил, выясним, как вести себя проводники.
Решение:
В ходе решения выполним объяснительные рисунки: изобразим проводники А и В, покажем направление тока в них и др.
1) С помощью правила буравчика определим направление линий магнитной индукции магнитного поля, созданного проводником В (рисунок слева). Выясняется, что у проводника А магнитные линии направлены к нам (отметка «•»).
2) Воспользовавшись правилом левой руки, определим направление силы Ампера, действующая на проводник А со стороны магнитного поля проводника В.
3) Приходим к выводу: проводник А привлекается к проводнику В.
Теперь найдем направление силы Ампера, действующая на проводник В, находится в магнитном поле проводника А.
1) Определим направление линий магнитной индукции магнитного поля, созданного проводником А (рисунок справа). Выясняется, что у проводника В магнитные линии направлены от нас (отметка «х»).
2) Определим направление силы Ампера, действующая на проводник В.
3) Приходим к выводу: проводник В привлекается к проводнику А.
Ответ: два параллельных проводника, в которых текут токи одного направления, действительно притягиваются.
Задача 2. Прямой проводник (стержень) длиной 0,1 м массой 40 г находится в горизонтальном однородном магнитном поле индукцией 0,5 Тл. Стержень расположен перпендикулярно магнитных линий поля). Ток какой силы и в каком направлении следует пропустить в стержне, чтобы он не давил на опору (завис в магнитном поле)?
Анализ задачи:
Стержень не будет давить на опору, если сила Ампера уравновесит силу тяжести. Это произойдет при следующих условиях:
- сила Ампера будет направлена противоположно силе тяжести (то есть вертикально вверх)
- значение силы Ампера равна значению силы тяжести FA = Fтяж
Направление тока определим, воспользовавшись правилом левой руки.
Решение:
Определим направление тока. Для этого расположим левую руку так, чтобы линии магнитного поля входили в ладонь, а отогнутый на 90 ° большой палец был направлен вертикально вверх. Четыре вытянутые пальцы укажут направление от нас. Итак, ток в проводнике следует направить от нас.
Учитываем, что FA = Fтяж. FA= BIlsinα, где sin α = 1; Fтяж = mg
Из последнего выражения найдем силу тока: I = mg/Bl
Проверим единицу, найдем значение искомой величины.
Ответ: I = 8 А; Ток в направлении от нас.
Подводим итоги
Силу, с которой магнитное поле действует на проводник с током, называют силой Ампера. Значение силы Ампера вычисляют по формуле: FA= BIlsinα, где B — индукция магнитного поля; I — сила тока в проводнике; l — длина активной части проводника; α — угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Для определения направления магнитной силы Ампера используют правило левой руки: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь, а четыре вытянутые пальцы указывали направление тока в проводнике, то отогнутый на 90 ° большой палец укажет направление силы Ампера.
www.polnaja-jenciklopedija.ru
Kvant. Магнитная сила — PhysBook
Ромишевский Е. Эта загадочная магнитная сила //Квант. — 1999. — № 3. — С. 39-40.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Опытно установлено, что сила, действующая на точечный электрический заряд q, помещенный в электрическое и магнитное поля, зависит в общем случае от положения этого заряда и от его скорости движения. Обычно эту силу разделяют на две составляю- щие — электрическую \(~\vec F_e = q \vec E\), которая не зависит от движения заряда, а определяется его положением в электрическом поле с напряженностью \(~\vec E\), и магнитную \(~\vec F_m\), зависящую от скорости заряда \(~\vec \upsilon\) . Именно о магнитной силе и пойдет речь в дальнейшем.
В любой точке пространства магнитная сила перпендикулярна вектору скорости заряда. Перпендикулярна она также и определенному выбранному в пространстве направлению. Величина же магнитной силы (ее модуль) пропорциональна той составляющей скорости заряда, которая перпендикулярна этому выделенному направлению. Эти свойства магнитной силы можно описать, пользуясь понятием магнитного поля. Магнитное поле характеризуется вектором магнитной индукции \(~\vec B\), который и определяет выбранное направление в пространстве.
Для определения магнитной силы можно записать следующее выражение:
\(~\vec F_m = q \upsilon B \sin \alpha \vec \zeta\) ,где υ и B — модули векторов скорости заряда и индукции магнитного поля, α — угол между этими векторами, а единичный вектор \(~\vec \zeta\) — правый винт (или буравчик) — указывает только направление магнитной силы. Это направление соответствует направлению движения правого винта, головка которого лежит в плоскости векторов \(~\vec \upsilon\) и \(~\vec B\) и который мы закручиваем, поворачивая его на наименьший угол от вектора \(~\vec \upsilon\) к вектору \(~\vec B\) (рис.1). Магнитная сила \(~\vec F_m\) перпендикулярна и вектору \(~\vec \upsilon\) , и вектору \(~\vec B\) .
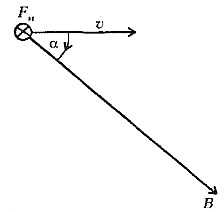
Рис. 1
Полную электромагнитную силу \(~\vec F = \vec F_e + \vec F_m\), действующую на электрический заряд q, называют силой Лоренца (заметим, что иногда силой Лоренца называют лишь магнитную силу). По действию силы Лоренца на электрический заряд известного знака можно, в принципе, определить модули и направления векторов \(~\vec E\) и \(~\vec B\).
Следует особо отметить, что на покоящийся электрический заряд магнитное поле не действует. Важной особенностью магнитной силы является также то, что она всегда перпендикулярна вектору скорости заряда, поэтому работы над зарядом не совершает. Это означает, что в постоянном магнитном поле кинетическая энергия заряженной частицы всегда остается неизменной, как бы частица ни двигалась.
Рис. 2
Рассмотрим, например, как будут двигаться две разноименно заряженные частицы с зарядами +q и —q, имеющие разные массы M1 = 2m и M2 = m, если в начальный момент скорости этих частиц равны \(~\vec \upsilon_0\) и направлены перпендикулярно границе области существования однородного магнитного поля с индукцией \(~\vec B\) (рис.2; вектор \(~\vec B\)-перпендикулярен плоскости листа и направлен от нас). На оказавшуюся в области однородного магнитного поля положительную частицу действует магнитная сила, равная \(~F_m = q \upsilon_0 B\) и направленная вначале вверх. На отрицательную частицу действует такая же по величине сила, но направленная вначале вниз. Каждая из частиц опишет полуокружность, после чего покинет область магнитного поля. Радиус окружности можно найти из второго закона Ньютона:
\(~q \upsilon_0 B = \frac{M \upsilon^2_0}{R}\) ,откуда
\(~R = \frac{M \upsilon_0}{qB}\) .Угловая скорость движения частицы по окружности и период ее полного обращения будут равны
\(~\omega = \frac{\upsilon_0}{R} = \frac{qB}{M}\) и \(~T = \frac{2\pi}{\omega} = \frac{2 \pi M}{qB}\) .Видно, что положительная частица (M1 = 2m) опишет полуокружность в два раза большего радиуса, чем отрицательная (M2 = m), которая будет двигаться в противоположную сторону. Возвратится же обратно тяжелая частица (зеркально отразившись) через промежуток времени, в два раза больший, чем отрицательная. Таким образом, однородное магнитное поле как бы разделяет в пространстве и во времени влетевшие вместе, но разные по заряду и по массе частицы.
Если магнитное поле воздействует только на движущиеся заряды, то, как показывает опыт, движущиеся заряды (электрические токи), в свою очередь, всегда возбуждают в пространстве магнитное поле. В результате обобщения экспериментальных данных был получен элементарный закон, определяющий индукцию \(~\vec B\) магнитного поля точечного заряда q, движущегося с постоянной скоростью \(~\vec \upsilon\) , много меньшей по величине скорости света с. Этот закон можно записать в виде
\(~\vec B = \frac{1}{4 \pi \varepsilon_0 c^2} \frac{q \upsilon \sin \alpha}{r^2} \vec \zeta\) ,где α — угол между вектором скорости заряда \(~\vec \upsilon\) и радиусом-вектором \(~\vec r\) , проведенным от заряда в точку наблюдения, \(~\vec \zeta\) — единичный «вектор буравчика», получаемый вращением вектора \(~\vec \upsilon\) к вектору \(~\vec r\) (рис.3) и отвечающий за направление вектора \(~\vec B\). Константу \(~\frac{1}{\varepsilon_0 c^2}\) обычно обозначают μ0 и называют магнитной постоянной.
Рис. 3
Заметим, что если умножить обе части приведенной формулы на число электронов \(~\Delta N = n \Delta l S\), находящихся в элементе провода длиной Δl, по которому течет ток \(~I = qn \upsilon S\), то получим известный закон Био — Савара для индукции \(~\Delta \vec B\) магнитного поля, созданного элементом тока \(~I \Delta \vec l\):
\(~\Delta \vec B = \frac{\mu_0}{4 \pi} \frac{I \Delta l \sin \alpha}{r^2} \vec \zeta\) .Рис. 4
Линии магнитной индукции в данном случае представляют собой концентрические окружности, окружающие линию движения заряда (рис.4), а величина магнитной индукции убывает с расстоянием пропорционально \(~\frac{1}{r^2}\) , как и величина напряженности электрического поля точечного заряда. Но магнитное поле не имеет источников и стоков, магнитные линии всегда замкнуты. Это физическое векторное поле уже иного свойства, его называют соленоидальным или вихревым.
Рассмотрим теперь такой пример.
Рис. 5
Пусть две достаточно массивные точечные частицы 1 и 2, заряженные одним и тем же зарядом q, движутся параллельно друг другу с одинаковыми нерелятивистскими скоростями \(~\vec \upsilon\) (рис.5). На каждую частицу действуют электрическая сила отталкивания, равкал \(~F_e = qE\), и магнитная сила притяжения, равная \(~F_m = q \upsilon B\) (скорость одной частицы перпендикулярна магнитному полю, создаваемому другой частицей). Сравним количественно эти две составляющие общей электромагнитной силы Лоренца, действующей, к примеру, на частицу 2:
\(~\frac{F_{m2}}{F_{e2}} = \frac{q \upsilon B_{21}}{q E_{21}}\) ,где B21 и E21 — индукция магнитного поля и напряженность электрического поля, создаваемых зарядом / в месте нахождения заряда 2. Подставив соответствующие значения индукции и напряженности, получим
\(~\frac{F_{m2}}{F_{e2}} = \frac{q \upsilon \frac{q \upsilon}{4 \pi \varepsilon_0 c^2 r^2}}{q \frac{q}{4 \pi \varepsilon_0 r^2}} = \frac{\upsilon^2}{c^2}\) .Это означает, что при нерелятивистских скоростях движения зарядов магнитная сила существенно меньше электрической и является очень малой поправкой к их общей силе электромагнитного взаимодействия — силе Лоренца.
А что если выбрать другую инерциальную систему отсчета, движущуюся равномерно и прямолинейно со скоростью \(~\vec \upsilon\) наших заряженных частиц? В этой системе заряды будут покоиться, пропадут их магнитные поля, пропадет и магнитная сила их взаимодействия. Иными словами, поскольку магнитная составляющая силы Лоренца зависит от скорости частицы, она изменяется при переходе от одной инерциальной системы отсчета к другой. Вместе с тем, сама сила Лоренца в нерелятивистском случае, как любая другая сила, не зависит от выбора инерциальной системы отсчета. Это означает, что в системе отсчета, в которой пропадает магнитная составляющая силы, должна изменяться и электрическая ее составляющая. Получается, что разделение полной силы Лоренца на электрическую и магнитную составляющие без указания конкретной системы отсчета не имеет смысла.
После рассмотренного нами примера движения двух заряженных частиц может возникнуть естественный вопрос — стоит ли вообще изучать и учитывать такие относительно малые магнитные силы? Оказывается, стоит, и вот почему.
Во-первых, полученное соотношение сил справедливо и при релятивистских скоростях υ ~ с, а тогда магнитные силы оказываются уже сравнимыми с электрическими. Так происходит, например, когда мы имеем дело с пучками быстрых заряженных частиц.
Во-вторых, бывают ситуации, когда ничтожная по величине магнитная сила является единственной действующей силой. Например — при движении электронов вдоль проводов (электрические токи), ибо в этом случае электрические силы отсутствуют в результате почти идеального баланса отрицательных и положительных зарядов в проводниках. Кроме того, участие в создании электрического тока громадного числа носителей зарядов (их примерно 1023 в одном кубическом сантиметре проводника) делает магнитную силу весьма значительной.
В-третьих, приходится встречаться с движением заряженных частиц в самых разных по величине внешних электрических и магнитных полях, создаваемых различным образом. В этих случаях соотношения между электрическими и магнитными силами могут быть самыми разнообразными.
www.physbook.ru
Магнит — Википедия
 Подковообразный магнит из альнико — сплава железа, алюминия, никеля и кобальта. Магниты изготовляются в виде подковы для того, чтобы приблизить полюса друг к другу с целью создать сильное магнитное поле, с помощью которого можно поднимать большие куски железа.
Рисунок линий силового поля магнита, полученный с помощью железных опилок
Подковообразный магнит из альнико — сплава железа, алюминия, никеля и кобальта. Магниты изготовляются в виде подковы для того, чтобы приблизить полюса друг к другу с целью создать сильное магнитное поле, с помощью которого можно поднимать большие куски железа.
Рисунок линий силового поля магнита, полученный с помощью железных опилок
Магни́т — тело, обладающее собственным магнитным полем. Возможно, слово происходит от др.-греч. Μαγνῆτις λίθος (Magnētis líthos), «камень из Магнесии» — от названия региона Магнисия и древнего города Магнесия в Малой Азии[1], где в древности были открыты залежи магнетита.[2]
Простейшим и самым маленьким магнитом можно считать электрон. Магнитные свойства всех остальных магнитов обусловлены магнитными моментами электронов внутри них. С точки зрения квантовой теории поля электромагнитное взаимодействие переносится безмассовым бозоном — фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля).
Постоянный магнит — изделие, изготовленное из ферромагнетика, способного сохранять остаточную намагниченность после выключения внешнего магнитного поля. В качестве материалов для постоянных магнитов обычно служат железо, никель, кобальт, некоторые сплавы редкоземельных металлов (как, например, в неодимовых магнитах), а также некоторые естественные минералы, такие как магнетиты. Постоянные магниты применяются в качестве автономных (не потребляющих энергии) источников магнитного поля. Свойства магнита определяются характеристиками размагничивающего участка петли магнитного гистерезиса материала магнита: чем выше остаточная индукция Br и коэрцитивная сила Hc, тем выше намагниченность и стабильность магнита. Характерные поля постоянных магнитов — до 1 Тл (10 кГс).
Электромагнит — устройство, магнитное поле которого создаётся только при протекании электрического тока. Как правило, это катушка-соленоид, со вставленным внутрь ферромагнитным (обычно железным) сердечником с большой магнитной проницаемостью μ≃10000{\displaystyle \mu \simeq 10000}. Характерные поля электромагнитов 1,5—2 Тл определяются так называемым насыщением железа, то есть резким спадом дифференциальной магнитной проницаемости при больших значениях магнитного поля.
Старинная легенда рассказывает о пастухе по имени Магнус (у Льва Толстого в рассказе для детей «Магнит» этого пастуха зовут Магнис). Он обнаружил однажды, что железный наконечник его палки и гвозди сапог притягиваются к чёрному камню. Этот камень стали называть «камнем Магнуса» или просто «магнитом», по названию местности, где добывали железную руду (холмы Магнезии в Малой Азии). Таким образом, за много веков до нашей эры было известно, что некоторые каменные породы обладают свойством притягивать куски железа. Об этом упоминал в 6 веке до нашей эры греческий физик и философ Фалес. Первое научное изучение свойств магнита было предпринято в 13 веке ученым Петром Перегрином. В 1269 году вышло его сочинение «Книга о магните», где он писал о многих фактах магнетизма: у магнита есть два полюса, которые ученый назвал северным и южным; невозможно отделить полюса друг от друга разламыванием. Перегрин писал и о двух видах взаимодействия полюсов — притяжении и отталкивании. К 12—13 векам нашей эры магнитные компасы уже использовались в навигации в Европе, в Китае и других странах мира[3].
В 1600 году вышло сочинение английского врача Уильяма Гильберта «О магните». К известным уже фактам Гильберт прибавил важные наблюдения: усиление действия магнитных полюсов железной арматурой, потерю магнетизма при нагревании и другие. В 1820 году датский физик Ганс Христиан Эрстед на лекции попытался продемонстрировать своим студентам отсутствие связи между электричеством и магнетизмом, включив электрический ток вблизи магнитной стрелки. По словам одного из его слушателей, он был буквально «ошарашен», увидев, что магнитная стрелка после включения тока начала совершать колебания. Большой заслугой Эрстеда является то, что он оценил значения своего наблюдения и повторил опыт. Соединив длинным проводом полюса гальванической батареи, Эрстед протянул провод горизонтально и параллельно свободно подвешенной магнитной стрелке. Как только был включён ток, стрелка немедленно отклонилась, стремясь встать перпендикулярно к направлению провода. При изменении направления тока стрелка отклонилась в другую сторону. Вскоре Эрстед доказал, что магнит действует с некоторой силой на провод, по которому идёт ток.
Открытие взаимодействия между электрическим током и магнитом имело огромное значение. Оно стало началом новой эпохи в учении об электричестве и магнетизме. Это взаимодействие сыграло важную роль в развитии техники физического эксперимента.
Узнав об открытии Эрстеда, французский физик Доминик Франсуа Араго начал серию опытов. Он обмотал медной проволокой стеклянную трубку, в которую вставил железный стержень. Как только замкнули электрическую цепь, стержень сильно намагнитился и к его концу крепко прилипли железные ключи; когда выключили ток, ключи отпали. Араго рассматривал проводник, по которому идёт ток, как магнит. Правильное объяснение этого явления было дано после исследования французского физика Андре Ампера, который установил внутреннюю связь между электричеством и магнетизмом. В сентябре 1820 года он сообщил Французской Академии наук о полученных им результатах.
Затем Ампер в своем «станке» заменил раму свободно подвешенным спиральным проводником. Этот провод при пропускании по нему тока приобретал свойство магнита. Ампер назвал его соленоидом. Исходя из магнитных свойств соленоида, Ампер предложил рассматривать магнетизм как явление, обязанное круговым токам. Он считал, что магнит состоит из молекул, в которых имеются круговые токи. Каждая молекула представляет собой маленький магнитик, располагаясь одноимёнными полюсами в одну и ту же сторону, эти маленькие магнитики и образуют магнит. Проводя вдоль стальной полосы магнитом (несколько раз в одну и ту же сторону), мы заставляем молекулы с круговыми токами ориентироваться в пространстве одинаково. Таким образом, стальная пластинка превратится в магнит. Теперь стал понятен и опыт Араго со стеклянной трубкой, обмотанной медным проводом. Вдвинутый в неё железный стержень стал магнитом потому, что вокруг него шёл ток. Это был электромагнит.
В 1825 году английский инженер Уильям Стёрджен изготовил первый электромагнит, представляющий собой согнутый стержень из мягкого железа с обмоткой из толстой медной проволоки. Для изолирования от обмотки стержень был покрыт лаком. При пропускании тока железный стержень приобретал свойства сильного магнита, но при прерывании тока он мгновенно их терял. Именно эта особенность электромагнитов позволила широко применять их в технике.
Термин «магнит», как правило, используется в отношении объектов, которые имеют собственное магнитное поле даже в отсутствие приложенного магнитного поля. Такое возможно лишь в некоторых классах материалов. В большинстве же материалов магнитное поле появляется в связи с приложенным внешним магнитным полем; это явление известно как магнетизм. Существует несколько типов магнетизма, и каждый материал имеет, по крайней мере, один из них.
В целом поведение магнитного материала может значительно варьироваться в зависимости от структуры материала и, не в последнюю очередь, его электронной конфигурации. Существует несколько типов взаимодействия материалов с магнитным полем, в том числе:
- Ферромагнетики и ферримагнетики — материалы, которые обычно и считаются магнитными. Они притягиваются к магниту достаточно сильно — так, что притяжение ощущается. Только эти материалы могут сохранять намагниченность и стать постоянными магнитами. Ферримагнетики сходны с ферромагнетиками, но слабее них. Различия между ферро- и ферримагнитными материалами связаны с их микроскопической структурой.
- Парамагнетики — такие вещества, как платина, алюминий и кислород, которые слабо притягиваются к магниту. Этот эффект в сотни тысяч раз слабее, чем притяжение ферромагнитных материалов, поэтому он может быть обнаружен только с помощью чувствительных инструментов или очень сильных магнитов.
- Диамагнетики — вещества, намагничивающиеся против направления внешнего магнитного поля. Диамагнитные, по сравнению с пара- и ферромагнитными, вещества, такие как углерод, медь, вода и пластики, отталкиваются от магнита. Все вещества, не обладающие одним из других типов магнетизма, являются диамагнитными; к ним относится большинство веществ. Силы, действующие на диамагнитные объекты от обычного магнита, слишком слабы, однако в сильных магнитных полях сверхпроводящих магнитов диамагнитные материалы, например кусочки свинца, могут пари́ть, а поскольку углерод и вода являются веществами диамагнитными, в мощном магнитном поле могут пари́ть даже органические объекты, например живые лягушки и мыши[4].
Также существуют и другие виды магнетизма, например спиновые стёкла, суперпарамагнетизм, супердиамагнетизм и метамагнетизм.
В системе СИ единицей магнитного потока является вебер (Вб), магнитной проницаемости — генри на метр (Гн/м), напряжённости магнитного поля — ампер на метр (А/м), индукции магнитного поля — тесла.
Вебер — магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивлением 1 ом проходит количество электричества 1 кулон.
Генри — международная единица индуктивности и взаимной индукции. Если проводник обладает индуктивностью в 1 Гн и ток в нём равномерно изменяется на 1 А в секунду, то на его концах индуктируется ЭДС в 1 вольт. 1 генри = 1,00052 · 109 абсолютных электромагнитных единиц индуктивности.
Тесла — единица измерения индукции магнитного поля в СИ, численно равная индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон.
- Магнитные носители информации: VHS кассеты содержат катушки из магнитной ленты. Видео и звуковая информация кодируется на магнитном покрытии на ленте. Также в компьютерных дискетах и жёстких дисках запись данных происходит на тонком магнитном покрытии. Однако носители информации не являются магнитами в строгом смысле, так как они не притягивают предметы. Магниты в жёстких дисках используются в ходовом и позиционирующем электродвигателях.
- Кредитные, дебетовые и ATM карты — ранние модели всех этих карт имеют магнитную полосу на одной стороне (магнитные полосы постепенно вытесняются микросхемами cмарт-карт). Эта полоса кодирует информацию, необходимую для соединения с финансовым учреждением и связи с их счетами.
- Обычные телевизоры и компьютерные мониторы: телевизоры и компьютерные мониторы, содержащие электронно-лучевую трубку используют электромагнит для управления пучком электронов и формирования изображения на экране. Плазменные панели и ЖК-дисплеи используют другие технологии.
- Громкоговорители и микрофоны: большинство громкоговорителей используют постоянный магнит и токовую катушку для преобразования электрической энергии (сигнала) в механическую энергию (движение, которое создает звук). Обмотка намотана на катушку, прикрепляется к диффузору и по ней протекает переменный ток, который взаимодействует с полем постоянного магнита.
- Другой пример использования постоянных магнитов в звукотехнике — в головке звукоснимателя электрофона и в простейших магнитофонах в качестве экономичной стирающей головки.
- Электродвигатели и генераторы: некоторые электрические двигатели (так же, как громкоговорители) основываются на комбинации электромагнита и постоянного магнита. Они преобразовывают электрическую энергию в механическую энергию. Генератор, наоборот, преобразует механическую энергию в электрическую энергию путём перемещения проводника через магнитное поле.
- Трансформаторы: устройства передачи электрической энергии между двумя обмотками провода, которые электрически изолированы, но связаны магнитно.
- Магниты используются в поляризованных реле. Такие устройства запоминают своё состояние на время выключения питания.
- Компасы: компас (или морской компас) является намагниченным указателем, который может свободно вращаться и ориентируется на направление магнитного поля, чаще всего магнитного поля Земли.
- Искусство: виниловые магнитные листы могут быть присоединены к живописи, фотографии и другим декоративным изделиям, что позволяет присоединять их к холодильникам и другим металлическим поверхностям.
 Магниты часто используются в игрушках. M-TIC использует магнитные стержни, связанные с металлическими сферами
Магниты часто используются в игрушках. M-TIC использует магнитные стержни, связанные с металлическими сферами
 Магниты редкоземельных элементов в форме эллипсоида, которые притягиваются друг к другу
Магниты редкоземельных элементов в форме эллипсоида, которые притягиваются друг к другу
- Игрушки: учитывая их способность противостоять силе тяжести на близком расстоянии, магниты часто используются в детских игрушках с забавными эффектами.
- Магниты могут использоваться для производства ювелирных изделий. Ожерелья и браслеты могут иметь магнитную застёжку, или могут быть изготовлены полностью из серии связанных магнитов и чёрных бусин.
- Магниты встречаются в сумках в виде вставленной внутрь закрывающей сумку кнопки намагниченной железной пластины; магниты также вшивают внутрь верхней одежды для закрывания клапана одежды элегантной, невидимой глазу застёжкой.
- Магниты могут поднимать магнитные предметы (железные гвозди, скобы, кнопки, скрепки), которые либо являются слишком мелкими, либо их трудно достать или они слишком тонкие чтобы держать их пальцами. Некоторые отвёртки специально намагничиваются для этой цели.
- Магниты могут использоваться при обработке металлолома для отделения магнитных металлов (железа, стали и никеля) от немагнитных (алюминия, цветных сплавов и т. д.). Та же идея может быть использована в рамках так называемого «Магнитного испытания», в которой кузов автомобиля обследуется с магнитом для выявления областей, отремонтированных с использованием стекловолокна или пластиковой шпатлевки.
- Маглев: поезд на магнитном подвесе, движимый и управляемый магнитными силами. Такой состав, в отличие от традиционных поездов, в процессе движения не касается поверхности рельса. Так как между поездом и поверхностью движения существует зазор, трение исключается, и единственной тормозящей силой является лишь сила аэродинамического сопротивления.
- Магниты используются в фиксаторах мебельных дверей.
- Если магниты поместить в губки, то эти губки можно использовать для мытья тонких листовых немагнитных материалов сразу с обеих сторон, причём одна сторона может быть труднодоступной. Это могут быть, например, стёкла аквариума или балкона.
- Магниты используются для передачи вращающего момента «сквозь» стенку, которой может являться, например, герметичный контейнер электродвигателя. Так была устроена игрушка ГДР «Подводная лодка». Таким же образом в бытовых счётчиках расхода воды передаётся вращение от лопаток датчика на счётный узел.
- Магниты совместно с герконом применяются в специальных датчиках положения. Например, в датчиках дверей холодильников и охранных сигнализаций.
- Магниты совместно с датчиком Холла используют для определения углового положения или угловой скорости вала.
- Магниты используются в искровых разрядниках для ускорения гашения дуги.
- Магниты используются при неразрушающем контроле магнитопорошковым методом (МПК)
- Магниты используются для отклонения пучков радиоактивных и ионизирующих излучений, например при наблюдении в камерах.
- Магниты используются в показывающих приборах с отклоняющейся стрелкой, например, амперметр. Такие приборы весьма чувствительны и линейны.
- Магниты применяются в СВЧ вентилях и циркуляторах.
- Магниты применяются в составе отклоняющей системы электронно-лучевых трубок для подстройки траектории электронного пучка.
- До открытия закона сохранения энергии, было много попыток использовать магниты для построения «вечного двигателя». Людей привлекала, казалось бы, неисчерпаемая энергия магнитного поля постоянного магнита, которые были известны очень давно. Но рабочий макет так и не был построен.
- Магниты применяются в конструкциях бесконтактных тормозов, состоящих из двух пластин, одна — магнит, а другая из алюминия. Одна из них жёстко закреплена на раме, другая вращается с валом. Торможение регулируется зазором между ними.
Из-за того, что человеческие ткани имеют очень низкий уровень восприимчивости к статическому магнитному полю, не существует научных доказательств его эффективности для использования в лечении любых заболеваний[5]. По той же причине отсутствуют научные свидетельства опасности для здоровья человека, связанной с воздействием этого поля. Однако если ферромагнитное инородное тело находится в человеческих тканях, магнитное поле будет взаимодействовать с ним, что может представлять собой серьёзную опасность[6].
В частности, если кардиостимулятор был встроен в грудную клетку пациента, следует держать его подальше от магнитных полей. Именно по этой причине больные с установленным кардиостимулятором не могут быть протестированы с использованием МРТ, которое представляет собой магнитное устройство визуализации внутренних органов и тканей.
Дети иногда могут глотать небольшие магниты из игрушек. Это может быть опасно, если ребёнок проглотил два или более магнита, так как магниты могут повредить внутренние ткани; был зафиксирован как минимум один смертельный случай[7].
Иногда намагниченность материалов становится нежелательной и возникает необходимость в их размагничивании. Размагничивание материалов может быть осуществлено тремя способами:
- нагревание магнита выше температуры Кюри всегда ведёт к размагничиванию;
- сильный удар молотком по магниту, или просто сильный удар ведет к размагничиванию.
- поместить магнит в переменное магнитное поле, превышающее коэрцитивную силу материала, а затем постепенно уменьшать воздействие магнитного поля или вывести магнит из него.
Последний способ применяется в промышленности для размагничивания инструментов, жёстких дисков, стирания информации на магнитных карточках и так далее.
Частичное размагничивание материалов происходит в результате ударов, так как резкое механическое воздействие ведёт к разупорядочению доменов.
ru.wikipedia.org
Магнитное поле Земли — Википедия
Обтекание магнитосферы Земли солнечным ветромМагни́тное по́ле Земли́ или геомагни́тное по́ле — магнитное поле, генерируемое внутриземными источниками. Предмет изучения геомагнетизма. Появилось 4,2 млрд лет назад[1].
Строение и характеристики магнитного поля Земли[править | править код]
Собственное магнитное поле Земли (геомагнитное поле) можно разделить на cледующие основные части[2]:
- главное поле,
- поля мировых аномалий,
- внешнее магнитное поле.
Главное поле[править | править код]
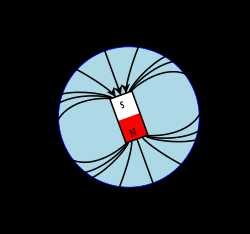 Земля как магнитный диполь.
Земля как магнитный диполь.
Более чем на 90 % оно состоит из поля, источник которого находится внутри Земли, в жидком внешнем ядре, — эта часть называется главным, основным или нормальным полем[3][4][5]. Оно аппроксимируется в виде ряда по гармоникам — ряда Гаусса, а в первом приближении вблизи поверхности Земли (до трёх её радиусов) близко к полю магнитного диполя, то есть имеет такой вид, как будто земной шар представляет собой полосовой магнит с осью, направленной приблизительно с севера на юг[2][6][3][7][8]. Центр этого диполя смещен относительно центра Земли, а ось наклонена к оси вращения Земли на угол около 10°. На такой же угол отстоят от соответствующих географических полюсов геомагнитные полюса — точки пересечения оси диполя с поверхностью Земли[4]. Их положение в различные моменты времени вычисляется в рамках той или иной модели магнитного поля, определяющей тем или иным образом первые три коэффициента в ряду Гаусса[3]. Эти глобальные модели — такие как Международное геомагнитное аналитическое поле (International Geomagnetic Reference Field, IGRF)[9] и Всемирная магнитная модель (World Magnetic Model, WMM)[en][10] — создаются различными международными геофизическими организациями, и каждые 5 лет утверждаются и публикуются обновлённые наборы коэффициентов Гаусса, определяющих все данные о состоянии геомагнитного поля и его параметрах[4]. Так, согласно модели WMM2015, северный геомагнитный полюс (по сути это южный полюс магнита) имеет координаты 80,37° с. ш. и 72,62° з. д., южный геомагнитный полюс — 80,37° ю. ш., 107,38° в. д., наклон оси диполя относительно оси вращения Земли — 9,63°[3][11].
Поля мировых аномалий[править | править код]
Реальные силовые линии магнитного поля Земли, хотя в среднем и близки к силовым линиям диполя, отличаются от них местными нерегулярностями, связанными с наличием намагниченных пород в коре, расположенных близко к поверхности. Из-за этого в некоторых местах на земной поверхности параметры поля сильно отличаются от значений в близлежащих районах, образуя так называемые магнитные аномалии[2][4][7][8]. Они могут накладываться одна на другую, если вызывающие их намагниченные тела залегают на разных глубинах[5].
Существование магнитных полей протяжённых локальных областей внешних оболочек приводит к тому, что истинные магнитные полюса — точки (вернее, небольшие области), в которых силовые линии магнитного поля абсолютно вертикальны, — не совпадают с геомагнитными, при этом они лежат не на самой поверхности Земли, а под ней[4][3][6]. Координаты магнитных полюсов на тот или иной момент времени также вычисляются в рамках различных моделей геомагнитного поля путём нахождения итеративным методом всех коэффициентов в ряду Гаусса. Так, согласно актуальной модели WMM, в 2015 г. северный магнитный полюс находился в точке 86° с. ш., 159° з. д., а южный — 64° ю. ш., 137° в.д[3]. Значения актуальной модели IGRF12 немного отличаются: 86,3° с. ш., 160° з. д., для северного полюса, 64,3° ю. ш., 136,6° в.д для южного[11].
Соответственно, магнитная ось — прямая, проходящая через магнитные полюса, — не проходит через центр Земли и не является её диаметром[6][7].
Положения всех полюсов постоянно смещаются — геомагнитный полюс прецессирует относительно географического с периодом около 1200 лет[2].
Внешнее магнитное поле[править | править код]
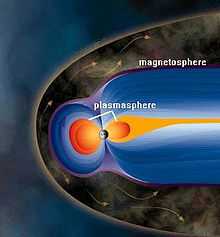
Оно определяется источниками в виде токовых систем, находящимися за пределами земной поверхности, в её атмосфере[2][4]. В верхней части атмосферы (100 км и выше) — ионосфере — её молекулы ионизируются, формируя плотную холодную плазму, поднимающуюся выше, поэтому часть магнитосферы Земли выше ионосферы, простирающаяся на расстояние до трёх её радиусов, называется плазмосферой. Плазма удерживается магнитным полем Земли, но её состояние определяется его взаимодействием с солнечным ветром — потоком плазмы солнечной короны[12].
Таким образом, на большем удалении от поверхности Земли магнитное поле несимметрично, так как искажается под действием солнечного ветра: со стороны Солнца оно сжимается, а в направлении от Солнца приобретает «шлейф», который простирается на сотни тысяч километров, выходя за орбиту Луны[2]. Эта своеобразная «хвостатая» форма возникает, когда плазма солнечного ветра и солнечных корпускулярных потоков как бы обтекают земную магнитосферу — область околоземного космического пространства, ещё контролируемая магнитным полем Земли, а не Солнца и других межпланетных источников[2][4][7][8]; она отделяется от межпланетного пространства магнитопаузой, где динамическое давление солнечного ветра уравновешивается давлением собственного магнитного поля. Подсолнечная точка магнитосферы в среднем находится на расстоянии 10 земных радиусов R⊕; при слабом солнечном ветре это расстояние достигает 15—20 R⊕, а в период магнитных возмущений на Земле магнитопауза может заходить за геостационарную орбиту (6,6 R⊕)[2]. Вытянутый хвост на ночной стороне имеет диаметр около 40 R⊕ и длину более 900 R⊕; начиная с расстояния примерно 8 R⊕, он разделен на части плоским нейтральным слоем, в котором индукция поля близка к нулю[2][4][7][8].
Искажение магнитного поля Земли под действием солнечного ветраГеомагнитное поле вследствие специфической конфигурации линий индукции создает для заряженных частиц — протонов и электронов — магнитную ловушку. Оно захватывает и удерживает огромное их количество, так что магнитосфера является своеобразным резервуаром заряженных частиц. Общая их масса, по различным оценкам, составляет от 1 кг до 10 кг. Они формируют так называемый радиационный пояс, охватывающий Землю со всех сторон, кроме приполярных областей. Его условно разделяют на два — внутренний и внешний. Нижняя граница внутреннего пояса находится на высоте около 500 км, его толщина — несколько тысяч километров. Внешний пояс находится на высоте 10—15 тыс. км. Частицы радиационного пояса под действием силы Лоренца совершают сложные периодические движения из Северного полушария в Южное и обратно, одновременно медленно перемещаясь вокруг Земли по азимуту. В зависимости от энергии они совершают полный оборот вокруг Земли за время от нескольких минут до суток[7].
Магнитосфера не подпускает к земле потоки космических частиц[8]. Однако в её хвосте, на больших расстояниях от Земли напряженность геомагнитного поля, а следовательно, и его защитные свойства, ослабляются, и некоторые частицы солнечной плазмы получают возможность попасть вовнутрь магнитосферы и магнитных ловушек радиационных поясов. Хвост таким образом служит местом формирования потоков высыпающихся частиц, вызывающих полярные сияния и авроральные токи[2]. В полярных областях часть потока солнечной плазмы вторгается в верхние слои атмосферы из радиационного пояса Земли и, сталкиваясь с молекулами кислорода и азота, возбуждает их или ионизирует, а при обратном переходе в невозбужденное состояние атомы кислорода излучают фотоны с λ = 0,56 мкм и λ = 0,63 мкм, ионизированные же молекулы азота при рекомбинации высвечивают синие и фиолетовые полосы спектра. При этом наблюдаются полярные сияния, особенно динамичные и яркие во время магнитных бурь. Они происходят при возмущениях в магнитосфере, вызванных увеличением плотности и скорости солнечного ветра при усилении солнечной активности[8][7].
Параметры поля[править | править код]
Наглядное представление о положении линий магнитной индукции поля Земли даёт магнитная стрелка, закреплённая таким образом, что может свободно вращаться и вокруг вертикальной, и вокруг горизонтальной оси (например, в кардановом подвесе), — в каждой точке вблизи поверхности Земли она устанавливается определённым образом вдоль этих линий.
Поскольку магнитные и географические полюса не совпадают, магнитная стрелка указывает направление с севера на юг только приблизительно. Вертикальную плоскость, в которой устанавливается магнитная стрелка, называют плоскостью магнитного меридиана данного места, а линию, по которой эта плоскость пересекается с поверхностью Земли, — магнитным меридианом[6][8]. Таким образом, магнитные меридианы — это проекции силовых линий магнитного поля Земли на её поверхность, сходящиеся в северном и южном магнитных полюсах[13]. Угол между направлениями магнитного и географического меридианов называют магнитным склонением. Оно может быть западным (часто обозначается знаком «−») или восточным (знак «+») в зависимости от того, к западу или востоку отклоняется северный полюс магнитной стрелки от вертикальной плоскости географического меридиана[6][7][8].
Далее, линии магнитного поля Земли, вообще говоря, не параллельны её поверхности. Это означает, что магнитная индукция поля Земли не лежит в плоскости горизонта данного места, а образует с этой плоскостью некий угол — он называется магнитным наклонением[6][8]. Оно близко к нулю лишь в точках магнитного экватора — окружности большого круга в плоскости, которая перпендикулярна к магнитной оси[3].
Магнитное склонение и магнитное наклонение определяют направление магнитной индукции поля Земли в каждом конкретном месте. А численное значение этой величины можно найти, зная наклонение и одну из проекций вектора магнитной индукции B{\displaystyle \mathbf {B} } — на вертикальную или горизонтальную ось (последнее оказывается более удобным на практике). Таким образом, три этих параметра — магнитное склонение, наклонение и модуль вектора магнитной индукции B (либо вектора напряжённости магнитного поля H{\displaystyle \mathbf {H} }) — полностью характеризуют геомагнитное поле в данном месте. Их точное знание для максимально большого числа пунктов на Земле имеет чрезвычайно важное значение[6][8]. Составляются специальные магнитные карты, на которых нанесены изогоны (линии одинакового склонения) и изоклины (линии одинакового наклонения), необходимые для ориентации с помощью компаса[8].
В среднем интенсивность магнитного поля Земли колеблется от 25 до 65 мкТл (0,25—0,65 Гс) и сильно зависит от географического положения[3]. Это соответствует средней напряжённости поля около 0,5 Э (40 А/м)[2]. На магнитном экваторе её величина около 0,34 Э, у магнитных полюсов — около 0,66 Э. В некоторых районах (магнитных аномалий) напряжённость резко возрастает: в районе Курской магнитной аномалии она достигает 2 Э[7].
Магнитный дипольный момент Земли на 2015 год составлял 7,72⋅1025Гс·см³ (или 7,72⋅1022 А·м²), уменьшаясь в среднем за последние десятилетия на 0,007⋅1025 Гс·см³ в год[11].
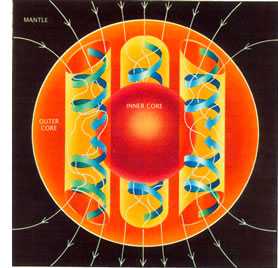 Схема динамо-механизма: конвекционные потоки расплавленного металла во внешнем ядре формируют циркулирующие по замкнутому контуру токи, которые генерируют магнитное поле[14]. Из-за вращения твёрдого ядра согласно теореме Тейлора-Праудмена[en] скорость потоков постоянна вдоль вертикальной оси образующихся таким образом столбов Тейлора[en], заключённых внутри цилиндра, ограничивающего внутреннее ядро, и подобных циклонам и антициклонам в атмосфере Земли[15][16]. Первичные (по/против часовой стрелки) и вторичные (вертикальные сходящиеся/расходящиеся на экваторе) потоки вытягивают и поворачивают линии магнитного поля, превращая азимутальную компоненту в меридиональную и затем обратно[17].
Схема динамо-механизма: конвекционные потоки расплавленного металла во внешнем ядре формируют циркулирующие по замкнутому контуру токи, которые генерируют магнитное поле[14]. Из-за вращения твёрдого ядра согласно теореме Тейлора-Праудмена[en] скорость потоков постоянна вдоль вертикальной оси образующихся таким образом столбов Тейлора[en], заключённых внутри цилиндра, ограничивающего внутреннее ядро, и подобных циклонам и антициклонам в атмосфере Земли[15][16]. Первичные (по/против часовой стрелки) и вторичные (вертикальные сходящиеся/расходящиеся на экваторе) потоки вытягивают и поворачивают линии магнитного поля, превращая азимутальную компоненту в меридиональную и затем обратно[17].
Впервые объяснить существование магнитных полей Земли и Солнца попытался Дж. Лармор в 1919 году[18], предложив концепцию динамо, согласно которой поддержание магнитного поля небесного тела происходит под действием гидродинамического движения электропроводящей среды. Однако в 1934 году Т. Каулинг[en][19] доказал теорему о невозможности поддержания осесимметричного магнитного поля посредством гидродинамического динамо-механизма. А поскольку большинство изучаемых небесных тел (и тем более Земля) считались аксиально-симметричными, на основании этого можно было сделать предположение, что их поле тоже будет аксиально-симметричным, и тогда его генерация по такому принципу будет невозможна согласно этой теореме[20]. Даже Альберт Эйнштейн скептически относился к осуществимости такого динамо при условии невозможности существования простых (симметричных) решений. Лишь гораздо позже было показано, что не у всех уравнений с аксиальной симметрией, описывающих процесс генерации магнитного поля, решение будет аксиально-симметричным, и в 1950-х гг. несимметричные решения были найдены[20][15].
С тех пор теория динамо успешно развивается, и на сегодняшний день общепринятым наиболее вероятным объяснением происхождения магнитного поля Земли и других планет является самовозбуждающийся динамо-механизм, основанный на генерации электрического тока в проводнике при его движении в магнитном поле, порождаемом и усиливаемом самими этими токами. Необходимые условия создаются в ядре Земли: в жидком внешнем ядре, состоящем в основном из железа при температуре порядка 4—6 тысяч кельвин, которое отлично проводит ток, создаются конвективные потоки, отводящие от твёрдого внутреннего ядра тепло (генерируемое благодаря распаду радиоактивных элементов либо освобождению скрытой теплоты при затвердевании вещества на границе между внутренним и внешним ядром по мере постепенного остывания планеты). Силы Кориолиса закручивают эти потоки в характерные спирали, образующие так называемые столбы Тейлора[en]. Благодаря трению слоёв они приобретают электрический заряд, формируя контурные токи. Таким образом, создаётся система токов, циркулирующих по проводящему контуру в движущихся в (изначально присутствующем, пусть и очень слабом) магнитном поле проводниках, как в диске Фарадея. Она создает магнитное поле, которое при благоприятной геометрии течений усиливает начальное поле, а это, в свою очередь, усиливает ток, и процесс усиления продолжается до тех пор, пока растущие с увеличением тока потери на джоулево тепло не уравновесят притоки энергии, поступающей за счет гидродинамических движений[14][21][16][22]. Высказывались предположения, что динамо может возбуждаться за счёт прецессии или приливных сил, то есть что источником энергии является вращение Земли, однако наиболее распространена и разработана гипотеза о том, что это всё же именно термохимическая конвекция[17].
Математически этот процесс описывается магнитогидродинамическим уравнением индукции[en][16][17][23]
- ∂B∂t=∇×(u×B)+η∇2B{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}=\mathbf {\nabla } \times (\mathbf {u} \times \mathbf {B} )+\eta \mathbf {\nabla } ^{2}\mathbf {B} },
где u — скорость потока жидкости, B — магнитная индукция, η = 1/μσ — магнитная вязкость[en] (коэффициент магнитной диффузии), σ — электропроводность жидкости, а μ — магнитная проницаемость, практически не отличающаяся при такой высокой температуре ядра от μ0 — проницаемости вакуума. Первое слагаемое в правой части соответствует формированию магнитного поля, а второе — его подавлению. При u=0 (без динамо) решение этого уравнения — поле, полностью угасающее через 6⋅104 лет[23].
Однако для полного описания необходимо записать систему магнитогидродинамических уравнений. В приближении Буссинеска (в рамках которого пренебрегается т. н. вековым охлаждением и все физические характеристики жидкости полагаются постоянными, кроме силы Архимеда, при расчёте которой учитываются изменения плотности вследствие разности температур и — в общем случае — концентрации лёгких элементов) это[16][17][23]:
- ρ0(∂u∂t+u⋅∇u)=−∇P+ρ0ν∇2u+ρg¯−2ρ0Ω×u+J×B{\displaystyle \rho _{0}\left({\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } \mathbf {u} \right)=-\nabla P+\rho _{0}\nu \mathbf {\nabla } ^{2}\mathbf {u} +\rho {\bar {\mathbf {g} }}-2\rho _{0}\mathbf {\Omega } \times \mathbf {u} +\mathbf {J} \times \mathbf {B} }.
Здесь ρ — плотность, ν — кинематическая вязкость, P=p−ρ02|Ω×r|2{\displaystyle P=p-{\frac {\rho _{0}}{2}}|\mathbf {\Omega } \times \mathbf {r} |^{2}} — «эффективное» давление с учётом центробежной силы (хотя в некоторых моделях она полагается пренебрежимо малой), g¯=g0rR0{\displaystyle {\bar {\mathbf {g} }}=g_{0}{\frac {\mathbf {r} }{R_{0}}}} — сила тяготения (R0 — радиус внешнего ядра), Ω — угловая скорость вращения мантии, полагаемая равной скорости вращения внутреннего ядра, J=1μ∇×B{\displaystyle \mathbf {J} ={\frac {1}{\mu }}\nabla \times \mathbf {B} } — плотность тока согласно закону Ампера, индекс «0» всюду обозначает значения на границе внешнего ядра. Левая часть уравнения — производная от импульса на единицу объёма, то есть производная по времени от величины ρ0V, увлекаемой движением жидкости; правая часть — сумма сил, вызывающих это изменение импульса: градиент давления[en], вязкость, гравитация (сила Архимеда), вращение (сила Кориолиса) и магнитное поле (сила Лоренца)[16].
Вращение Земли — один из важнейших факторов формирования геомагнитного поля, и его механизм схож с процессами в атмосфере Земли, приводящим к завихрению воздушных масс против часовой стрелки в северном полушарии и в обратном направлении в южном — циклонам и антициклонам. Аналогичные завихрения конвекционных потоков в ядре приводят к тому, что отдельные турбулентные конвекционные движения приобретают крупномасштабную (при усреднении по пульсациям скорости) зеркальную асимметрию и в совокупности приводят к генерации динамо в макроскопических масштабах благодаря электродвижущей силе, направленной уже вдоль, а не перпендикулярно среднему (которое определяется усреднением реального поля по его возможным статистическим реализациям) магнитному полю ⟨ε⟩=α⟨B⟩{\displaystyle \langle \mathbf {\varepsilon } \rangle =\alpha \langle \mathbf {B} \rangle }, где ε — ЭДС, а α — коэффициент пропорциональности, из-за которого этот механизм и получил название альфа-эффект[22][24]. В общем случае α — тензор, однако зеркальная антисимметрия даёт псевдоскаляр, которого и требует по построению эта формула, так как ε — истинный вектор, а B — псевдовектор[25]. Динамо, основанное исключительно на α-эффекте, называют α2-динамо, поскольку его действие выражается произведением двух членов, содержащих этот коэффициент[23], — оно характеризуется практически стационарным полем, испытывающим небольшие кратковременные вариации (порядка сотен лет для Земли) и долговременные полные инверсии (порядка миллиона лет для Земли). Возможен также механизм с действием омега-эффекта (более существенного для Солнца, чем для Земли, однако необходимого для объяснения природы наблюдаемого дрейфа геомагнитных неоднородностей) — это измеряемое градиентом скорости дифференциальное вращение, которое из направленного к наблюдателю полоидального (вытянутого вдоль меридианов, BS) магнитного поля создаёт скрытое в проводящем ядре планеты тороидальное (вытянутое вдоль параллелей, BT) поле. Альфа-эффект замыкает цикл генерации — превращая тороидальное поле в полоидальное за счёт вихрей, характеризуемых отрицательной спиральностью (эта характеристика выражается соотношением u⋅∇×u{\displaystyle \mathbf {u} \cdot \mathbf {\nabla } \times \mathbf {u} } и непосредственно связана с величиной α) в Северном полушарии и положительной в Южном: восходящие и нисходящие потоки в конвекционных цилиндрах вытягивают и поворачивают BT-линии в S-направлении[26][20][15][17]. Такая схема обычно называется αω-эффектом, она даёт переменные поля, и при этом BT>>BS, тогда как для α2-механизма эти компоненты сравнимы (экспериментально на сегодняшний день удалось получить только грубую оценку |BS|<|BT|<100|BS|). И если источником полоидального поля может быть только альфа-эффект, то тороидального — оба, причём если оба вносят существенный вклад, соответствующий механизм иногда обозначают α2ω. Большинство теоретических моделей магнитного динамо — типа α2. В обоих случаях, как альфа, так и омега-эффектов, таким образом снимаются ограничения теоремы Каулинга[16][23]. Однако существует ряд геометрий течений, для которых динамо также невозможно (например, чисто тороидальное поле скоростей[23][27]), в то же время при определённых условиях оно возможно и при нулевой суммарной завихрённости ∇×u{\displaystyle \mathbf {\nabla } \times \mathbf {u} } и нулевой спиральности; возможны и другие эффекты, приводящие к возникновению ЭДС, параллельной магнитному полю[25].
- ∂T∂t+u⋅∇T=κ∇2T+ϵ{\displaystyle {\frac {\partial T}{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } T=\kappa \mathbf {\nabla } ^{2}T+\epsilon },
где T — температура, κ = k/(ρcp) — температуропроводность (коэффициент тепловой диффузии), k — теплопроводность, cp — удельная теплоёмкость среды при постоянном давлении. Последнее слагаемое, ε, пропорционально выделению тепла, генерируемого теми или иными растворёнными в жидкости источниками (такими как радиоактивный распад), на единицу массы. В моделях, учитывающих перенос не только тепла, но и вещества, записывается соответствующее аналогичное уравнение относительно переменной ξ — массовой доли лёгких элементов (считается, что это сера и кислород) в составе ядра:
- ∂ξ∂t+u⋅∇ξ=κξ∇2ξ+ϵξ{\displaystyle {\frac {\partial \xi }{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } \xi =\kappa _{\xi }\mathbf {\nabla } ^{2}\xi +\epsilon _{\xi }},
где κξ — коэффициент (молекулярной) диффузии. В большинстве моделей динамо, однако для простоты разность температур и концентраций лёгких элементов объединяются в одну отвечающую за плавучесть переменную.
- ∇⋅u=0{\displaystyle \mathbf {\nabla } \cdot \mathbf {u} =0}.
- ∇⋅B=0{\displaystyle \mathbf {\nabla } \cdot \mathbf {B} =0}.
- ρ=ρ0[1−α(T−T0)]{\displaystyle \rho =\rho _{0}\left[1-\alpha (T-T_{0})\right]},
где α — коэффициент линейного теплового расширения (обозначение совпадает с коэффициентом пропорциональности в уравнении для альфа-эффекта). В общем случае, при учёте массопереноса, в квадратных скобках присутствует также слагаемое αξ(ξ−ξ0){\displaystyle \alpha _{\xi }(\xi -\xi _{0})}. Здесь α=−1ρ(∂ρ∂T)P,ξ{\displaystyle \alpha =-{\frac {1}{\rho }}\left({\frac {\partial \rho }{\partial T}}\right)_{P,\xi }}, αξ=−1ρ(∂ρ∂ξ)P,T{\displaystyle \alpha _{\xi }=-{\frac {1}{\rho }}\left({\frac {\partial \rho }{\partial \xi }}\right)_{P,T}}.
Естественно, необходимы также граничные условия для скорости потока, магнитного поля и разности температур, и многое зависит от того, как они ставятся в той или иной модели. Наибольший разброс имеет место в отношении потока тепла и вещества на границах между внутренним и внешним ядром, а также между внешним ядром и мантией, причём существенную роль играет неоднородность мантии и процессов в ней из-за тектоники плит[16][17][28], которые, что немаловажно, протекают на порядки медленнее, нежели в ядре, что значительно осложняет комплексный анализ задачи.
Удобнее решать эту систему уравнений в безразмерном виде, вводя характерные величины длины, времени, скорости, магнитного поля и т. д.; тогда в них будут входить следующие безразмерные параметры[16][17][29]:
ru.wikipedia.org
МАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
Содержание статьиМАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА. Простейшие проявления магнетизма известны очень давно и знакомы большинству из нас. Однако объяснить эти, казалось бы, простые явления на основе фундаментальных принципов физики удалось лишь сравнительно недавно.
Существуют магниты двух разных видов. Одни – так называемые постоянные магниты, изготовляемые из «магнитно-твердых» материалов. Их магнитные свойства не связаны с использованием внешних источников или токов. К другому виду относятся так называемые электромагниты с сердечником из «магнитно-мягкого» железа. Создаваемые ими магнитные поля обусловлены в основном тем, что по проводу обмотки, охватывающей сердечник, проходит электрический ток.
Магнитные полюса и магнитное поле.
Магнитные свойства стержневого магнита наиболее заметны вблизи его концов. Если такой магнит подвесить за среднюю часть так, чтобы он мог свободно поворачиваться в горизонтальной плоскости, то он займет положение, примерно соответствующее направлению с севера на юг. Конец стержня, указывающий на север, называют северным полюсом, а противоположный конец – южным полюсом. Разноименные полюса двух магнитов притягиваются друг к другу, а одноименные взаимно отталкиваются.
Если к одному из полюсов магнита приблизить брусок ненамагниченного железа, то последний временно намагнитится. При этом ближний к полюсу магнита полюс намагниченного бруска будет противоположным по наименованию, а дальний – одноименным. Притяжением между полюсом магнита и индуцированным им в бруске противоположным полюсом и объясняется действие магнита. Некоторые материалы (например, сталь) сами становятся слабыми постоянными магнитами после того, как побывают около постоянного магнита или электромагнита. Стальной стержень можно намагнитить, просто проведя по его торцу концом стержневого постоянного магнита.
Итак, магнит притягивает другие магниты и предметы из магнитных материалов, не находясь в соприкосновении с ними. Такое действие на расстоянии объясняется существованием в пространстве вокруг магнита магнитного поля. Некоторое представление об интенсивности и направлении этого магнитного поля можно получить, насыпав на лист картона или стекла, положенный на магнит, железные опилки. Опилки выстроятся цепочками в направлении поля, а густота линий из опилок будет соответствовать интенсивности этого поля. (Гуще всего они у концов магнита, где интенсивность магнитного поля наибольшая.)
М.Фарадей (1791–1867) ввел для магнитов понятие замкнутых линий индукции. Линии индукции выходят в окружающее пространство из магнита у его северного полюса, входят в магнит у южного полюса и проходят внутри материала магнита от южного полюса обратно к северному, образуя замкнутую петлю. Полное число линий индукции, выходящих из магнита, называется магнитным потоком. Плотность магнитного потока, или магнитная индукция (В), равна числу линий индукции, проходящих по нормали через элементарную площадку единичной величины.
Магнитной индукцией определяется сила, с которой магнитное поле действует на находящийся в нем проводник с током. Если проводник, по которому проходит ток I, расположен перпендикулярно линиям индукции, то по закону Ампера сила F, действующая на проводник, перпендикулярна и полю, и проводнику и пропорциональна магнитной индукции, силе тока и длине проводника. Таким образом, для магнитной индукции B можно написать выражение
где F – сила в ньютонах, I – ток в амперах, l – длина в метрах. Единицей измерения магнитной индукции является тесла (Тл) (см. также ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ).
Гальванометр.
Гальванометр – чувствительный прибор для измерения слабых токов. В гальванометре используется вращающий момент, возникающий при взаимодействии подковообразного постоянного магнита с небольшой токонесущей катушкой (слабым электромагнитом), подвешенной в зазоре между полюсами магнита. Вращающий момент, а следовательно, и отклонение катушки пропорциональны току и полной магнитной индукции в воздушном зазоре, так что шкала прибора при небольших отклонениях катушки почти линейна.
Намагничивающая сила и напряженность магнитного поля.
Далее следует ввести еще одну величину, характеризующую магнитное действие электрического тока. Предположим, что ток проходит по проводу длинной катушки, внутри которой расположен намагничиваемый материал. Намагничивающей силой называется произведение электрического тока в катушке на число ее витков (эта сила измеряется в амперах, так как число витков – величина безразмерная). Напряженность магнитного поля Н равна намагничивающей силе, приходящейся на единицу длины катушки. Таким образом, величина Н измеряется в амперах на метр; ею определяется намагниченность, приобретаемая материалом внутри катушки.
В вакууме магнитная индукция B пропорциональна напряженности магнитного поля Н:
где m0 – т.н. магнитная постоянная, имеющая универсальное значение 4pЧ10–7 Гн/м. Во многих материалах величина B приблизительно пропорциональна Н. Однако в ферромагнитных материалах соотношение между B и Н несколько сложнее (о чем будет сказано ниже).
На рис. 1 изображен простой электромагнит, предназначенный для захвата грузов. Источником энергии служит аккумуляторная батарея постоянного тока. На рисунке показаны также силовые линии поля электромагнита, которые можно выявить обычным методом железных опилок.
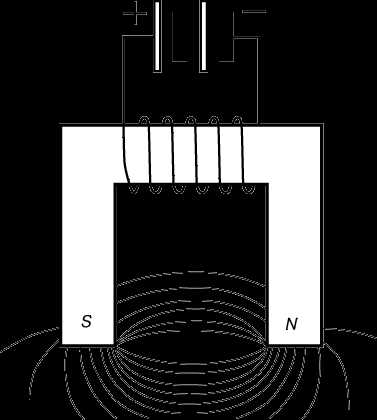
Крупные электромагниты с железными сердечниками и очень большим числом ампер-витков, работающие в непрерывном режиме, обладают большой намагничивающей силой. Они создают магнитную индукцию до 6 Тл в промежутке между полюсами; эта индукция ограничивается лишь механическими напряжениями, нагреванием катушек и магнитным насыщением сердечника. Ряд гигантских электромагнитов (без сердечника) с водяным охлаждением, а также установок для создания импульсных магнитных полей был сконструирован П.Л.Капицей (1894–1984) в Кембридже и в Институте физических проблем АН СССР и Ф.Биттером (1902–1967) в Массачусетском технологическом институте. На таких магнитах удавалось достичь индукции до 50 Тл. Сравнительно небольшой электромагнит, создающий поля до 6,2 Тл, потребляющий электрическую мощность 15 кВт и охлаждаемый жидким водородом, был разработан в Лосаламосской национальной лаборатории. Подобные поля получают при криогенных температурах.
Магнитная проницаемость и ее роль в магнетизме.
Магнитная проницаемость m – это величина, характеризующая магнитные свойства материала. Ферромагнитные металлы Fe, Ni, Co и их сплавы обладают очень высокими максимальными проницаемостями – от 5000 (для Fe) до 800 000 (для супермаллоя). В таких материалах при сравнительно малых напряженностях поля H возникают большие индукции B, но связь между этими величинами, вообще говоря, нелинейна из-за явлений насыщения и гистерезиса, о которых говорится ниже. Ферромагнитные материалы сильно притягиваются магнитами. Они теряют свои магнитные свойства при температурах выше точки Кюри (770° С для Fe, 358° С для Ni, 1120° С для Co) и ведут себя как парамагнетики, для которых индукция B вплоть до очень высоких значений напряженности H пропорциональна ей – в точности так же, как это имеет место в вакууме. Многие элементы и соединения являются парамагнитными при всех температурах. Парамагнитные вещества характеризуются тем, что намагничиваются во внешнем магнитном поле; если же это поле выключить, парамагнетики возвращаются в ненамагниченное состояние. Намагниченность в ферромагнетиках сохраняется и после выключения внешнего поля.
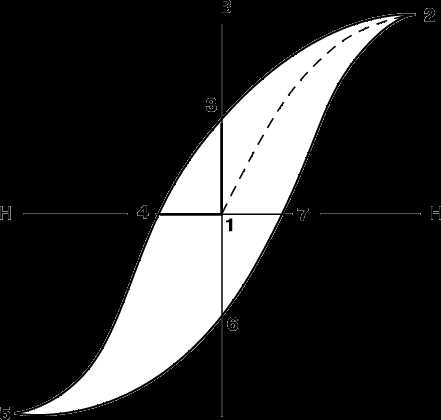
На рис. 2 представлена типичная петля гистерезиса для магнитно-твердого (с большими потерями) ферромагнитного материала. Она характеризует неоднозначную зависимость намагниченности магнитоупорядоченного материала от напряженности намагничивающего поля. С увеличением напряженности магнитного поля от исходной (нулевой) точки (1) намагничивание идет по штриховой линии 1–2, причем величина m существенно изменяется по мере того, как возрастает намагниченность образца. В точке 2 достигается насыщение, т.е. при дальнейшем увеличении напряженности намагниченность больше не увеличивается. Если теперь постепенно уменьшать величину H до нуля, то кривая B(H) уже не следует по прежнему пути, а проходит через точку 3, обнаруживая как бы «память» материала о «прошлой истории», откуда и название «гистерезис». Очевидно, что при этом сохраняется некоторая остаточная намагниченность (отрезок 1–3). После изменения направления намагничивающего поля на обратное кривая В (Н) проходит точку 4, причем отрезок (1)–(4) соответствует коэрцитивной силе, препятствующей размагничиванию. Дальнейший рост значений (-H) приводит кривую гистерезиса в третий квадрант – участок 4–5. Следующее за этим уменьшение величины (-H) до нуля и затем возрастание положительных значений H приведет к замыканию петли гистерезиса через точки 6, 7 и 2.
Магнитно-твердые материалы характеризуются широкой петлей гистерезиса, охватывающей значительную площадь на диаграмме и потому соответствующей большим значениям остаточной намагниченности (магнитной индукции) и коэрцитивной силы. Узкая петля гистерезиса (рис. 3) характерна для магнитно-мягких материалов – таких, как мягкая сталь и специальные сплавы с большой магнитной проницаемостью. Такие сплавы и были созданы с целью снижения обусловленных гистерезисом энергетических потерь. Большинство подобных специальных сплавов, как и ферриты, обладают высоким электрическим сопротивлением, благодаря чему уменьшаются не только магнитные потери, но и электрические, обусловленные вихревыми токами.

Магнитные материалы с высокой проницаемостью изготовляются путем отжига, осуществляемого выдерживанием при температуре около 1000° С, с последующим отпуском (постепенным охлаждением) до комнатной температуры. При этом очень существенны предварительная механическая и термическая обработка, а также отсутствие в образце примесей. Для сердечников трансформаторов в начале 20 в. были разработаны кремнистые стали, величина m которых возрастала с увеличением содержания кремния. Между 1915 и 1920 появились пермаллои (сплавы Ni с Fe) с характерной для них узкой и почти прямоугольной петлей гистерезиса. Особенно высокими значениями магнитной проницаемости m при малых значениях H отличаются сплавы гиперник (50% Ni, 50% Fe) и му-металл (75% Ni, 18% Fe, 5% Cu, 2% Cr), тогда как в перминваре (45% Ni, 30% Fe, 25% Co) величина m практически постоянна в широких пределах изменения напряженности поля. Среди современных магнитных материалов следует упомянуть супермаллой – сплав с наивысшей магнитной проницаемостью (в его состав входит 79% Ni, 15% Fe и 5% Mo).
Теории магнетизма.
Впервые догадка о том, что магнитные явления в конечном счете сводятся к электрическим, возникла у Ампера в 1825, когда он высказал идею замкнутых внутренних микротоков, циркулирующих в каждом атоме магнита. Однако без какого-либо опытного подтверждения наличия в веществе таких токов (электрон был открыт Дж.Томсоном лишь в 1897, а описание структуры атома было дано Резерфордом и Бором в 1913) эта теория «увяла». В 1852 В.Вебер высказал предположение, что каждый атом магнитного вещества представляет собой крошечный магнит, или магнитный диполь, так что полная намагниченность вещества достигается, когда все отдельные атомные магниты оказываются выстроенными в определенном порядке (рис. 4,б). Вебер полагал, что сохранять свое упорядочение вопреки возмущающему влиянию тепловых колебаний этим элементарным магнитам помогает молекулярное или атомное «трение». Его теория смогла объяснить намагничивание тел при соприкосновении с магнитом, а также их размагничивание при ударе или нагреве; наконец, объяснялось и «размножение» магнитов при разрезании намагниченной иглы или магнитного стержня на части. И все же эта теория не объясняла ни происхождения самих элементарных магнитов, ни явлений насыщения и гистерезиса. Теория Вебера была усовершенствована в 1890 Дж.Эвингом, заменившим его гипотезу атомного трения идеей межатомных ограничивающих сил, помогающих поддерживать упорядочение элементарных диполей, которые составляют постоянный магнит.
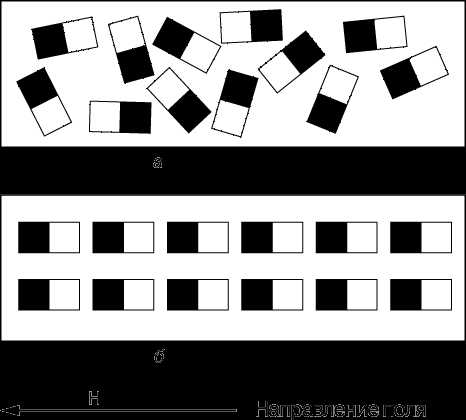
Подход к проблеме, предложенный когда-то Ампером, получил вторую жизнь в 1905, когда П.Ланжевен объяснил поведение парамагнитных материалов, приписав каждому атому внутренний нескомпенсированный электронный ток. Согласно Ланжевену, именно эти токи образуют крошечные магниты, хаотически ориентированные, когда внешнее поле отсутствует, но приобретающие упорядоченную ориентацию после его приложения. При этом приближение к полной упорядоченности соответствует насыщению намагниченности. Кроме того, Ланжевен ввел понятие магнитного момента, равного для отдельного атомного магнита произведению «магнитного заряда» полюса на расстояние между полюсами. Таким образом, слабый магнетизм парамагнитных материалов обусловлен суммарным магнитным моментом, создаваемым нескомпенсированными электронными токами.
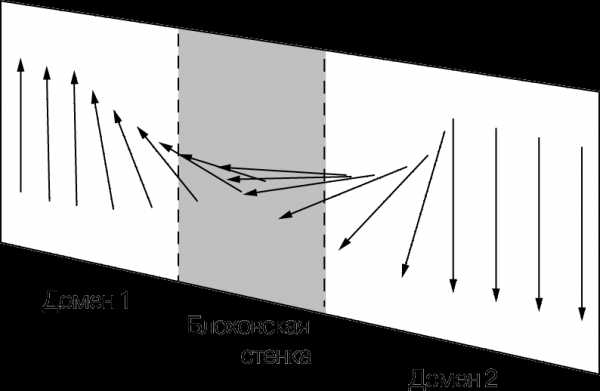
В 1907 П.Вейс ввел понятие «домена», ставшее важным вкладом в современную теорию магнетизма. Вейс представлял домены в виде небольших «колоний» атомов, в пределах которых магнитные моменты всех атомов в силу каких-то причин вынуждены сохранять одинаковую ориентацию, так что каждый домен намагничен до насыщения. Отдельный домен может иметь линейные размеры порядка 0,01 мм и соответственно объем порядка 10–6 мм3. Домены разделены так называемыми блоховскими стенками, толщина которых не превышает 1000 атомных размеров. «Стенка» и два противоположно ориентированных домена схематически изображены на рис. 5. Такие стенки представляют собой «переходные слои», в которых происходит изменение направления намагниченности доменов.
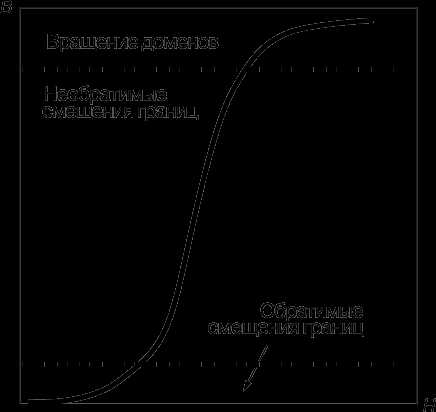
В общем случае на кривой первоначального намагничивания можно выделить три участка (рис. 6). На начальном участке стенка под действием внешнего поля движется сквозь толщу вещества, пока не встретит дефект кристаллической решетки, который ее останавливает. Увеличив напряженность поля, можно заставить стенку двигаться дальше, через средний участок между штриховыми линиями. Если после этого напряженность поля вновь уменьшить до нуля, то стенки уже не вернутся в исходное положение, так что образец останется частично намагниченным. Этим объясняется гистерезис магнита. На конечном участке кривой процесс завершается насыщением намагниченности образца за счет упорядочения намагниченности внутри последних неупорядоченных доменов. Такой процесс почти полностью обратим. Магнитную твердость проявляют те материалы, у которых атомная решетка содержит много дефектов, препятствующих движению междоменных стенок. Этого можно достичь механической и термической обработкой, например путем сжатия и последующего спекания порошкообразного материала. В сплавах алнико и их аналогах тот же результат достигается путем сплавления металлов в сложную структуру.
Кроме парамагнитных и ферромагнитных материалов, существуют материалы с так называемыми антиферромагнитными и ферримагнитными свойствами. Различие между этими видами магнетизма поясняется на рис. 7. Исходя из представления о доменах, парамагнетизм можно рассматривать как явление, обусловленное наличием в материале небольших групп магнитных диполей, в которых отдельные диполи очень слабо взаимодействуют друг с другом (или вообще не взаимодействуют) и потому в отсутствие внешнего поля принимают лишь случайные ориентации (рис. 7,а). В ферромагнитных же материалах в пределах каждого домена существует сильное взаимодействие между отдельными диполями, приводящее к их упорядоченному параллельному выстраиванию (рис. 7,б). В антиферромагнитных материалах, напротив, взаимодействие между отдельными диполями приводит к их антипараллельному упорядоченному выстраиванию, так что полный магнитный момент каждого домена равен нулю (рис. 7,в). Наконец, в ферримагнитных материалах (например, ферритах) имеется как параллельное, так и антипараллельное упорядочение (рис. 7,г), итогом чего оказывается слабый магнетизм.
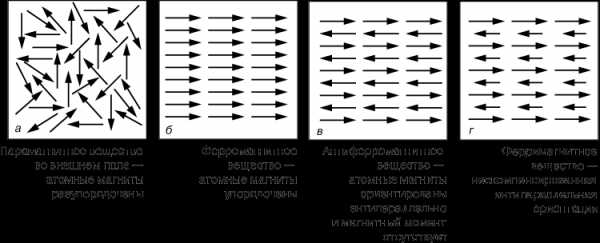
Имеются два убедительных экспериментальных подтверждения существования доменов. Первое из них – так называемый эффект Баркгаузена, второе – метод порошковых фигур. В 1919 Г.Баркгаузен установил, что при наложении внешнего поля на образец из ферромагнитного материала его намагниченность изменяется небольшими дискретными порциями. С точки зрения доменной теории это не что иное, как скачкообразное продвижение междоменной стенки, встречающей на своем пути отдельные задерживающие ее дефекты. Данный эффект обычно обнаруживается с помощью катушки, в которую помещается ферромагнитный стерженек или проволока. Если поочередно подносить к образцу и удалять от него сильный магнит, образец будет намагничиваться и перемагничиваться. Скачкообразные изменения намагниченности образца изменяют магнитный поток через катушку, и в ней возбуждается индукционный ток. Напряжение, возникающее при этом в катушке, усиливается и подается на вход пары акустических наушников. Щелчки, воспринимаемые через наушники, свидетельствует о скачкообразном изменении намагниченности.
Для выявления доменной структуры магнита методом порошковых фигур на хорошо отполированную поверхность намагниченного материала наносят каплю коллоидной суспензии ферромагнитного порошка (обычно Fe3O4). Частицы порошка оседают в основном в местах максимальной неоднородности магнитного поля – на границах доменов. Такую структуру можно изучать под микроскопом. Был предложен также метод, основанный на прохождении поляризованного света сквозь прозрачный ферромагнитный материал.
Первоначальная теория магнетизма Вейса в своих основных чертах сохранила свое значение до настоящего времени, получив, однако, обновленную интерпретацию на основе представления о нескомпенсированных электронных спинах как факторе, определяющем атомный магнетизм. Гипотеза о существовании собственного момента у электрона была выдвинута в 1926 С.Гаудсмитом и Дж.Уленбеком, и в настоящее время в качестве «элементарных магнитов» рассматриваются именно электроны как носители спина.
Для пояснения этой концепции рассмотрим (рис. 8) свободный атом железа – типичного ферромагнитного материала. Две его оболочки (K и L), ближайшие к ядру, заполнены электронами, причем на первой из них размещены два, а на второй – восемь электронов. В K-оболочке спин одного из электронов положителен, а другого – отрицателен. В L-оболочке (точнее, в двух ее подоболочках) у четырех из восьми электронов положительные, а у других четырех – отрицательные спины. В обоих случаях спины электронов в пределах одной оболочки полностью компенсируются, так что полный магнитный момент равен нулю. В M-оболочке ситуация иная, поскольку из шести электронов, находящихся в третьей подоболочке, пять электронов имеют спины, направленные в одну сторону, и лишь шестой – в другую. В результате остаются четыре нескомпенсированных спина, чем и обусловлены магнитные свойства атома железа. (Во внешней N-оболочке всего два валентных электрона, которые не дают вклада в магнетизм атома железа.) Сходным образом объясняется магнетизм и других ферромагнетиков, например никеля и кобальта. Поскольку соседние атомы в образце железа сильно взаимодействуют друг с другом, причем их электроны частично коллективизируются, такое объяснение следует рассматривать лишь как наглядную, но весьма упрощенную схему реальной ситуации.
Теорию атомного магнетизма, основанную на учете спина электрона, подкрепляют два интересных гиромагнитных эксперимента, один из которых был проведен А.Эйнштейном и В.де Гаазом, а другой – С.Барнеттом. В первом из этих экспериментов цилиндрик из ферромагнитного материала подвешивался так, как показано на рис. 9. Если по проводу обмотки пропустить ток, то цилиндрик поворачивается вокруг своей оси. При изменении направления тока (а следовательно, и магнитного поля) он поворачивается в обратном направлении. В обоих случаях вращение цилиндрика обусловлено упорядочением электронных спинов. В эксперименте Барнетта, наоборот, так же подвешенный цилиндрик, резко приведенный в состояние вращения, в отсутствие магнитного поля намагничивается. Этот эффект объясняется тем, что при вращении магнетика создается гироскопический момент, стремящийся повернуть спиновые моменты по направлению собственной оси вращения.
За более полным объяснением природы и происхождения короткодействующих сил, упорядочивающих соседние атомные магнитики и противодействующих разупорядочивающему влиянию теплового движения, следует обратиться к квантовой механике. Квантово-механическое объяснение природы этих сил было предложено в 1928 В.Гейзенбергом, который постулировал существование обменных взаимодействий между соседними атомами. Позднее Г.Бете и Дж.Слэтер показали, что обменные силы существенно возрастают с уменьшением расстояния между атомами, но по достижении некоторого минимального межатомного расстояния падают до нуля.
МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
Одно из первых обширных и систематических исследований магнитных свойств вещества было предпринято П.Кюри. Он установил, что по своим магнитным свойствам все вещества можно разделить на три класса. К первому относятся вещества с резко выраженными магнитными свойствами, подобными свойствам железа. Такие вещества называются ферромагнитными; их магнитное поле заметно на значительных расстояниях (см. выше). Во второй класс попадают вещества, называемые парамагнитными; магнитные свойства их в общем аналогичны свойствам ферромагнитных материалов, но гораздо слабее. Например, сила притяжения к полюсам мощного электромагнита может вырвать из ваших рук железный молоток, а чтобы обнаружить притяжение парамагнитного вещества к тому же магниту, нужны, как правило, очень чувствительные аналитические весы. К последнему, третьему классу относятся так называемые диамагнитные вещества. Они отталкиваются электромагнитом, т.е. сила, действующая на диамагнетики, направлена противоположно той, что действует на ферро- и парамагнетики.
Измерение магнитных свойств.
При изучении магнитных свойств наиболее важное значение имеют измерения двух типов. Первый из них –измерения силы, действующей на образец вблизи магнита; так определяется намагниченность образца. Ко второму относятся измерения «резонансных» частот, связанных с намагничением вещества. Атомы представляют собой крошечные «гироскопы» и в магнитном поле прецессируют (как обычный волчок под влиянием вращающего момента, создаваемого силой тяжести) с частотой, которая может быть измерена. Кроме того, на свободные заряженные частицы, движущиеся под прямым углом к линиям магнитной индукции, действует сила, как и на электронный ток в проводнике. Она заставляет частицу двигаться по круговой орбите, радиус которой дается выражением
R = mv/eB,
где m – масса частицы, v – ее скорость, e – ее заряд, а B – магнитная индукция поля. Частота такого кругового движения равна
где f измеряется в герцах, e – в кулонах, m – в килограммах, B – в теслах. Эта частота характеризует движение заряженных частиц в веществе, находящемся в магнитном поле. Оба типа движений (прецессию и движение по круговым орбитам) можно возбудить переменными полями с резонансными частотами, равными «естественным» частотам, характерным для данного материала. В первом случае резонанс называется магнитным, а во втором – циклотронным (ввиду сходства с циклическим движением субатомной частицы в циклотроне).
Говоря о магнитных свойствах атомов, необходимо особо остановиться на их моменте импульса. Магнитное поле действует на вращающийся атомный диполь, стремясь повернуть его и установить параллельно полю. Вместо этого атом начинает прецессировать вокруг направления поля (рис. 10) с частотой, зависящей от дипольного момента и напряженности приложенного поля.

Прецессия атомов не поддается непосредственному наблюдению, поскольку все атомы образца прецессируют в разной фазе. Если же приложить небольшое переменное поле, направленное перпендикулярно постоянному упорядочивающему полю, то между прецессирующими атомами устанавливается определенное фазовое соотношение и их суммарный магнитный момент начинает прецессировать с частотой, равной частоте прецессии отдельных магнитных моментов. Важное значение имеет угловая скорость прецессии. Как правило, это величина порядка 1010 Гц/Тл для намагниченности, связанной с электронами, и порядка 107 Гц/Тл для намагниченности, связанной с положительными зарядами в ядрах атомов.
Принципиальная схема установки для наблюдения ядерного магнитного резонанса (ЯМР) представлена на рис. 11. В однородное постоянное поле между полюсами вводится изучаемое вещество. Если затем с помощью небольшой катушки, охватывающей пробирку, возбудить радиочастотное поле, то можно добиться резонанса на определенной частоте, равной частоте прецессии всех ядерных «гироскопов» образца. Измерения сходны с настройкой радиоприемника на частоту определенной станции.
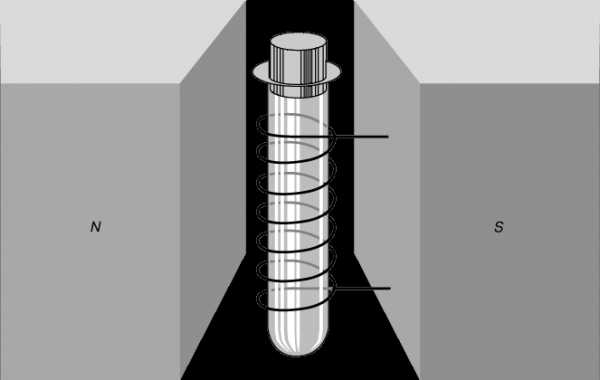
Методы магнитного резонанса позволяют исследовать не только магнитные свойства конкретных атомов и ядер, но и свойства их окружения. Дело в том, что магнитные поля в твердых телах и молекулах неоднородны, поскольку искажены атомными зарядами, и детали хода экспериментальной резонансной кривой определяются локальным полем в области расположения прецессирующего ядра. Это и дает возможность изучать особенности структуры конкретного образца резонансными методами.
Расчет магнитных свойств.
Магнитная индукция поля Земли составляет 0,5Ч10–4 Тл, тогда как поле между полюсами сильного электромагнита – порядка 2 Тл и более.
Магнитное поле, создаваемое какой-либо конфигурацией токов, можно вычислить, пользуясь формулой Био – Савара – Лапласа для магнитной индукции поля, создаваемого элементом тока. Расчет поля, создаваемого контурами разной формы и цилиндрическими катушками, во многих случаях весьма сложен. Ниже приводятся формулы для ряда простых случаев. Магнитная индукция (в теслах) поля, создаваемого длинным прямым проводом с током I (ампер), на расстоянии r (метров) от провода равна
Индукция в центре кругового витка радиуса R с током I равна (в тех же единицах):
Плотно намотанная катушка провода без железного сердечника называется соленоидом. Магнитная индукция, создаваемая длинным соленоидом c числом витков N в точке, достаточно удаленной от его концов, равна
Здесь величина NI/L есть число ампер (ампер-витков) на единицу длины соленоида. Во всех случаях магнитное поле тока направлено перпендикулярно этому току, а сила, действующая на ток в магнитном поле, перпендикулярна и току, и магнитному полю.
Поле намагниченного железного стержня сходно с внешним полем длинного соленоида с числом ампер-витков на единицу длины, соответствующим току в атомах на поверхности намагниченного стержня, поскольку токи внутри стержня взаимно компенсируются (рис. 12). По имени Ампера такой поверхностный ток называется амперовским. Напряженность магнитного поля Ha, создаваемая амперовским током, равна магнитному моменту единицы объема стержня M.
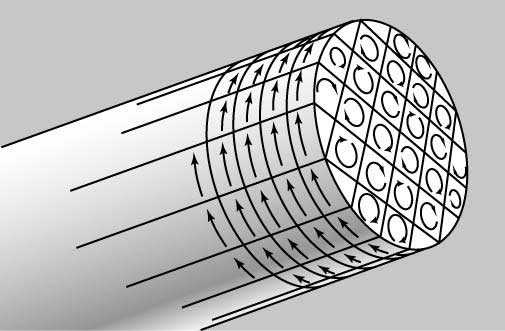
Если в соленоид вставлен железный стержень, то кроме того, что ток соленоида создает магнитное поле H, упорядочение атомных диполей в намагниченном материале стержня создает намагниченность M. В этом случае полный магнитный поток определяется суммой реального и амперовского токов, так что B = m0(H + Ha), или B = m0(H + M). Отношение M/H называется магнитной восприимчивостью и обозначается греческой буквой c ; c – безразмерная величина, характеризующая способность материала намагничиваться в магнитном поле.
Величина B/H, характеризующая магнитные свойства материала, называется магнитной проницаемостью и обозначается через ma, причем ma = m0m, где ma – абсолютная, а m – относительная проницаемости,
В ферромагнитных веществах величина c может иметь очень большие значения –до 104ё106. Величина c у парамагнитных материалов немного больше нуля, а у диамагнитных – немного меньше. Лишь в вакууме и в очень слабых полях величины c и m постоянны и не зависят от внешнего поля. Зависимость индукции B от H обычно нелинейна, а ее графики, т.н. кривые намагничивания, для разных материалов и даже при разных температурах могут существенно различаться (примеры таких кривых приведены на рис. 2 и 3).
Магнитные свойства вещества весьма сложны, и для их глубокого понимания необходим тщательный анализ строения атомов, их взаимодействий в молекулах, их столкновений в газах и их взаимного влияния в твердых телах и жидкостях; магнитные свойства жидкостей пока наименее изучены.
www.krugosvet.ru
Магнитодвижущая сила — Википедия
Материал из Википедии — свободной энциклопедии
Магнѝтодви́жущая си́ла (МДС) — физическая величина, характеризующая способность электрических токов создавать магнитные потоки. Используется при расчётах магнитных цепей; является аналогом ЭДС в электрических цепях.
Величина измеряется в амперах (СИ) или же в гилбертах (СГС), причём 1 А = 4π10{\displaystyle {\frac {4\pi }{10}}} Гб ≈ 1,257 Гб. На практике для обозначения единицы МДС часто используется термин «ампер-виток», численно равный единице в СИ.
Магнитодвижущая сила F{\displaystyle {\mathcal {F}}} в катушке или электромагните вычисляется по формуле
- F=wI,{\displaystyle {\mathcal {F}}=wI,}
где w{\displaystyle w} — количество витков в обмотке, I{\displaystyle I} — ток в проводнике.
Выражение для магнитного потока в магнитной цепи, называемое иногда законом Гопкинсона, имеет следующий вид:
- F=ΦRm{\displaystyle {\mathcal {F}}=\Phi R_{m}}
где Φ{\displaystyle \Phi } — величина магнитного потока, Rm{\displaystyle R_{m}} — магнитное сопротивление проводника. Данная запись является аналогом закона Ома в магнитных цепях.
ru.wikipedia.org
Магнитные силы — Энциклопедия по машиностроению XXL
Нагрузки могут быть распределены не только по поверхности, но и по объему (силы веса, силы инерции, магнитные силы и др.). Они также характеризуются интенсивностью, но имеющей размерность, например, даН/м [c.123]Магнитные опоры применяют в некоторых измерительных приборах, имеющих малый вес и вертикальную ось вращения. Для удержания оси в вертикальном положении в них используются магнитные силы. На рис. 27.27 показана схема магнитной опоры диска электрического счетчика, состоящая из двух магнитов / и 2. Магнит 2 втягивается внутрь магнита / и поддерживает на весу подвижную систему счетчика. Центрирование вращающейся части осуществляется тонкими щтифтами 4 из нержавеющей стали, помещенными в графитовые втулки 3. Опоры этого типа имеют очень малый момент трения и не требуют ухода. [c.336]
Рассмотрим составляющие главного вектора внешних сил. Выделим главный вектор объемных сил Гм, т.е. сил, действующих на материальные точки, находящиеся внутри объема V, и обусловленных воздействием объектов, расположенных вне объема (гравитационные, электрические, магнитные силы, силы инерции и т.п.). Обозначим Коб — главный вектор сил, обусловленных действием ограничивающей объем V оболочки на материальные точки, находящиеся внутри объема и непосредственно примыкающие к этой оболочке, в тех случаях, когда оболочка не будет абсолютно проницаемой. Примем, что другие силы отсутствуют. Тогда, очевидно, [c.406]
Заметим, что закон Кулона (2.9) перестает выполняться точно, если заряды движутся. Электрическое взаимодействие движущихся зарядов оказывается сложным образом зависящим от их движения. Одну из частей этого взаимодействия, обусловленную движением, называют магнитной силой (отсюда и другое название данного взаимодействия —электромагнитное). При малых (нерелятивистских) скоростях магнитная сила составляет пренебрежимо малую часть электрического взаимодействия и оно с высокой степенью точности описывается законом [c.44]
Для сравнения действия электрических и магнитных сил с действием силы тяжести надо вспомнить, что на материальную точку массой М, находящуюся у поверхности Земли, действует сила тяжести, равная F = —Mgz, где z — единичный вектор, направленный от центра Земли. Вспомните также, что одноименные точечные электрические заряды, согласно закону Кулона, отталкиваются друг от друга с силой, обратно пропорциональной квадрату расстояния между ними и направленной вдоль линии, соединяющей заряды. Величина этой силы равна [c.113]
Результирующая сила, действующая на равномерно движущуюся частицу с зарядом q, представляет собой сумму электростатической и магнитной сил (8) и (9). Эта результирующая сила или только одна сила (9) называется силон Лоренца [c.117]
Можно вывести уравнение для циклотронной частоты также элементарным способом. Направленная внутрь траектории частицы магнитная сила qBv j создает центростремительное (направленное внутрь) ускорение, необходимое для кругового движения этой частицы. Величина центростремительного ускорения равна oi/л или ШцГ, потому что (ОцГ = ui. Следовательно, [c.125]
Оценки потенциалов взаимодействия между частицами в кристалле показывают, что магнитные силы здесь весьма малы, а гравитационными силами вообще можно пренебречь. Таким образом, характер сил межатомного взаимодействия в первую очередь определяется строением электронных оболочек взаимодействующих атомов. [c.55]
В преобразованиях изменяется время. Принцип относительности электродинамики вводит понятие времени, связанного с системой отсчета. Понятие абсолютного времени теряется. Затем электрические и магнитные силы ие существуют независимо от состояния движения координатной системы. [c.325]
С появлением дополнительного члена в уравнении движения электропроводной жидкости в магнитном поле (82) возникает необходимость ввести новый критерий подобия, учитывающий отношение магнитной силы к силе инерции. Следуя методу, изложенному в 7 гл. II, приведем последний член правой части уравнения (82) к безразмерному виду путем деления его на величину В результате получим [c.204]
Отклоняющиеся кверху носители тока заряжают верхнюю грань образца до определенного предела, который будет достигнут тогда, когда возникающее поперечное холловское поле Ёх уравновесит магнитную силу еУ[c.135]
В том случае, когда кроме работы расширения или сжатия телом производится работа, не связанная с изменением объема и обозначаемая в дальнейшем через Р(1 ) (без изменения объема совершается, например, работа против электрических и магнитных сил), полезная внешняя работа [c.22]
Уравнение Гиббса в форме (10.1) справедливо для изотропных систем, в которых отсутствуют электрические и магнитные силы. Можно обобщить это уравнение на случай любой системы в результате в правый член уравнений войдет дополнительно сумма 2] 1/ где — /-я обобщенная сила, [c.332]
Во всех типах приборов, которые мы здесь будем рассматривать, имеется определенная закономерная связь между измеряемой величиной и силой (часто моментом силы). Например, в магнитоэлектрических приборах момент магнитных сил поворачивает катушку с закрепленной на ней стрелкой до тех пор, пока он не станет равным моменту силы, действующей на катушку со стороны восстанавливающей пружины. [c.89]
Пусть на прямолинейный стержень, закрепленный в пространстве, действует внешняя нагрузка, непрерывно распределенная по его длине или даже по части его длины. В качестве примеров такой нагрузки уже упоминались силы собственного веса, магнитные силы, электродинамические силы, силы инерции в условиях неравномерного движ (ния стержня и т. д. Любая подобная нагрузка обычно задается с помощью функции ее интенсивности по длине. Эта физическая величина имеет размерность [сила/длина], например, [Н/м] или [кН/м . Будем обозначать интенсивность распределенной по длине стержня внешней нагрузки через q. Величина д может быть постоянна по длине стержня, а может быть и переменна. В последнем случае имеем [c.34]
Приведенные формулировки второго закона термодинамики подчеркивают специфичность теплоты при ее превращениях в механическую работу. Если механическая работа (а также электрическая работа, работа магнитных сил и т. п.) может быть целиком превращена в теплоту, то обратный полный переход теплоты в механическую работу невозможен аже в идеальной машине-двигателе. Часть этой теплоты [c.46]
Поверхности трения в магнитных опорах разделяются магнитными силами, создаваемыми при взаимодействии магнитных полей постоянных магнитов или электромагнитов, установленных в подшипнике или на валу. В зависимости от характера взаимодействия полюсов магнитов магнитные опоры бывают с одноименными полюсами (рис. 4.70, а), создающими силы отталкивания, и с разноименными полюсами (рис. 4.70, б), создающими силы притяжения. Чтобы не было смещения или опрокидывания осей валов, наряду с магнитными опорами предусматриваются вспомогательные опоры. [c.471]
В самом деле, на электрон, движущийся в магнитном поле Н со скоростью V, действует магнитная сила [c.39]
Действие осциллографа основано на свойстве движущихся электронов изменять направление движения под действием электрических или магнитных сил, например при прохождении в пространстве между двумя заряженными параллельными пластинами. Существует полная аналогия между пучком электронов, проходящим через электрические поля, и световым лучом, проходящим через преломляющие среды. Поэтому системы, предназначенные для отклонения электронного пучка, называются электронными линзами или призмами, а законы изменения направления движения электронов составляют предмет электронной оптики. [c.182]
Тяжесть у Гильберта — сила взаимного притяжения тел одной планеты, а не тяготение их к какой-то точке пространства, как учили перипатетики. Между планетами же действует магнитная сила, которая заставляет их вращаться одну около другой, не сближаясь. [c.52]
После выхода в свет сочинения Гильберта интерес к магнитным и электрическим явлениям сильно возрос. На эту тему публикуются статьи и трактаты, но ничего существенно нового в них не содержится, хотя даже делаются попытки измерения величины магнитной силы с помощью весов. [c.52]
Установив движение планет по эллипсам, он вынужден был отказаться от кинематики равномерных движений, заимствованных Коперником у Птолемея, и искать причины убыстрения (замедления) движений — ускорения . По Аристотелю же, во власти учения которого все еще находился Кеплер, неравномерные движения без поддержки сил должны прекратиться. В поисках их источника в реальном мире Кеплер поднимает божественный промысел выше Солнца, делая носителем движущих сил, гармонии и света животную силу Солнца (то есть на современном языке запас энергии, заключенной в нем), которое располагается у него в центре Вселенной, представляющей собой ограниченную сферу. Животная сила обеспечивает вращение Солнца вокруг собственной оси, в результате чего оно увлекает за собой планеты, распространяя вокруг себя силовые нити (почти силовые линии, которые введет через 200 лет Фарадей). Движущая сила Солнца, по Кеплеру, тождественна магнитным силам, распространяющимся в плоскости, а потому, как и последние, обратно пропорциональна расстоянию. Так объяснялось самодвижение планет вокруг Солнца по эллиптическим орбитам со скоростями, обратно пропорциональными расстоянию от него. [c.54]
По Ньютону, действие силы может быть непосредственным, контактным и — на расстоянии от какого-то силового центра. Силу, действующую на расстоянии, он называет центральной или центростремительной силой , с которой тела к некоторой точке как к центру отовсюду притягиваются, гонятся или как бы то ни было стремятся к этой категории он относит, например, силу тяжести, магнитную силу. Центральные силы имеют три величины . Абсолютная величина определяется действующей причиной , исходящей от силового центра (гравитационной массой, магнитной массой и т. д.) движущая величина выражает изменение количества движения, вызванное данной силой в единицу времени ускорительная величина пропорциональна ускорению, полученному телом под действием силы, при этом сила F, Лм [c.87]
Член Парижской академии наук, ученый н инженер Шарль Кулон, как и некоторые другие ученые, предполагал существование двух различных электрических флюидов, действующих противоположно. В нейтральном состоянии оба флюида находятся в теле в равном количестве. Электризация наступает при избытке одного из них. При этом электрические и магнитные силы уподоблялись силам тяготения Ньютона, а потому и действовали на расстоянии. Отсюда же делался вывод о том, что величина этих сил, как и сил тяготения, обратно пропорциональна квадрату расстояния между зарядами — пока предположительно. [c.104]
Таким образом, электрические и магнитные силы перестали быть вещью в себе . Понятия силы, работы и в неявной форме энергии и здесь становятся необходимы- [c.105]
В 1823 г. Фарадей записывает в свой дневник медной проволоки, помещенными одна в другую без контакта между ними. Когда ток включался и выключался в одной катушке, стрелка гальванометра, присоединенного к другой, отклонялась. Фарадей записал Ток от батареи при пропускании его через один проводник действительно индуцирует подобный же ток в другом проводнике, но… этот ток длится всего один момент . [c.112]
Движение частицы (твердой и жидкой) в потоке при наложении электромагнитных сил при Кет>1 исследовано Ивановым. В частности, измерениями показано, что скорость падения ртутной капли существенно отличается от режима обтекан-ия аналогичного закрепленного тела при Кет>40. Увеличение проводимости раствора приводит к растормаживапию поверхности капли и как следствие — к увеличению скорости осаждения в 1,5 раза. При уменьшении проводимости раствора эффект противоположен. Выявлено нарушение принципа аддитивности при воздействии электрических и магнитных сил. Так, например, поперечное магнитное поле вызывает горизонтальное перемещение частицы, изменяет ее скорость осаждения, подавляет пульсации в кормовой области капли. При Rei500 увеличивают скорость осаждения. [c.70]
Источником магнитного поля может быть петля с током, со леноид или постоянный магнит. Магнитная сила Рмаг направлена по нормали к плоскости, образованной векторами v и В. Ниже в этой главе мы покажем, что заряженная частица, движущаяся только в магнитном поле, будет описывать окружность (или, в более общем случае, спираль) вокруг оси, образуемой направлением магнитного поля. Проделав лабораторный опыт, легко можно убедиться, что магнитное поле, направленное перпендикулярно к движению электронного пучка в трубке осциллографа, отклонит этот пучок в направлении, перпендикулярном как к V, так и к В. Магнитная сила, соленоиды и магниты подробно разбираются в т. II. [c.117]
Применяя термодинамическое рассмотрение, мы будем предполагать, что магнитного поля равна g T,p) в сверхпроводящем состоянии и gn T,p)—в нормальном р— давление, Т — абсолютная температура). Не рассматривая незначительного влияния давления, можно сказать, что при температуре ниже точки перехода величина g. должна быт]> меньше так как в этой области сверхпроводящая фаза стабильна. При внесении образца в магнитное поле его ио.лная свободная энергия будет равна сумме g n работы магнитных сил, т. е. [c.634]
Обсуждение этого выражения для работы магнитных сил см. в статье Стонера [206]. [c.634]
Пленки п коллоиды. Намаз ниченность пленок в продольном магнитном ноле значительно меньше /Уд/4-it , что объясняется проникновением в них поля. В результате, когда приложенное иоле достигает критической величины Нуф,, отнесенная к единице объема работа магнитных сил оказывается меньшей так что для возникновении фазового перехода в пленке необходимо дальнейшее увеличение поля. Нужно также иметь в виду, что величина —поверхностная свободная энергия границы раздела между сверхпроводящей фазой п вакуумом — может отличаться от поверхностной энергии а границы раздела между нормальной фазой и вакуумом. Учитывая эту разницу поверхностных анергий, можно показать, что критическое ноле h для пленок толщиной 2а > X может быть представлено следующим образом [c.661]
Это поле, составляющее 10″ гаусс для частот порядка 10 сек , достаточно велико, чтобы его можно было обнаружить в сиециальных опытах. В системе координат, вращающейся вместе с телом, сила Кориолиса в первом порядке по со как раз уравновешивает действие магнитных сил. Это и составляет основу теоремы Лармора. [c.698]
Существует два вида внешних сил, которые могут воздействовать на тело. Силы, распределенные по поверхности тела, такие, как давление одного тела на другое или гидростатическое давление, называются поверхностными силами. Силы, распределенные по массе тела, такие, как силы тя-жести, магнитные силы или (в случае движения тела) силы инерции, называются массовыми силслш. Поверхностную силу, отнесенную к единице [c.23]
Благодаря равенству f = — f , во вращающейся координатной системе магнитная сила f,, будет уравновешена силой и. следовательно, орбита электрона относительно вращающейся координатной системы будет прежним кеплеро-вым эллипсом, а относительно неподвижной — эллипсом, прецессируюшим с угловой скоростью о. даваемой формулой (1). Введем вместо обычных сферических координат г, ft, у (см. рис. 15) координатную систему г, ft, х. вращающуюся вокруг направления магнитного поля Н с постоянной угловой скоростью о. Полагая, что Н совпадает по направлению с ON, получим [c.39]
В предыдущих параграфах мы уже указывали на существование ряда явлений, из которых следует, что представление об электронах, как механических частицах, не может быть сохранено. Понятие об электронах, как частицах, движущихся подобно материальным точкам классической механики по определенным траекториям, возникло на основании тех опытов, которые в начале этого столетия были произведены над электронными пучками и над отдельными быстрыми электронами. В вакуумной трубке можно с помощью диафрагм получить достаточно резко ограниченный пучок электронов. При воздействии на этот пучок, например, магнитного поля он искривляется так, как должны искривляться траектории отдельных заряженных частиц, на которые действует магнитная сила. Метод сцинтиляций позволяет регистрировать отдельные электроны, попадающие в определенное место флуоресцирующего экрана. В камере Вильсона можно заснять следы быстрых электронов. Но наряду с этими явлениями в двадцатых годах нынешнего столетия были открыты другие явления, обнаружившие волновые свойства электронов. Было установлено, что электроны при прохождении через кристаллы и при отражении от них обнаруживают свойства дифракции, вполне аналогичные тем, которые присущи рентгеновым лучам. Как показал де-Бройль, можно получить согласие с опытом, если допустить, что пучок однородных по скоростям электронов характеризуется частотой v и длиной волны X, связанными с кинетической энергией электронов и их количеством движения М соотношениями [c.87]
Так великие географические открытия сделали силы тяготения и магнитные силы загадкой века и разрушили фундамент важнейших церковносхоластических построений. И сразу же стали появляться теории, объясняющие и приводящие в систему новые опытные данные, — начиналась первая научная революция в естествознании. [c.49]
Однако в теории открытых явлений Гильберт не продвинулся дальше своих предшественников, в лучшем случае механицистов. Так, ои не считает совершенно абсурдным мнение Фалеса, приписывавшего магниту душу. Магнитная сила, по Гильберту, — это свойство материала, и действует она только на некоторые тела, электрическая же сила, возникающая от трения, — на многие. [c.52]
mash-xxl.info

